Расчет индуктивности катушки с сердечником: методы, формулы и практические советы

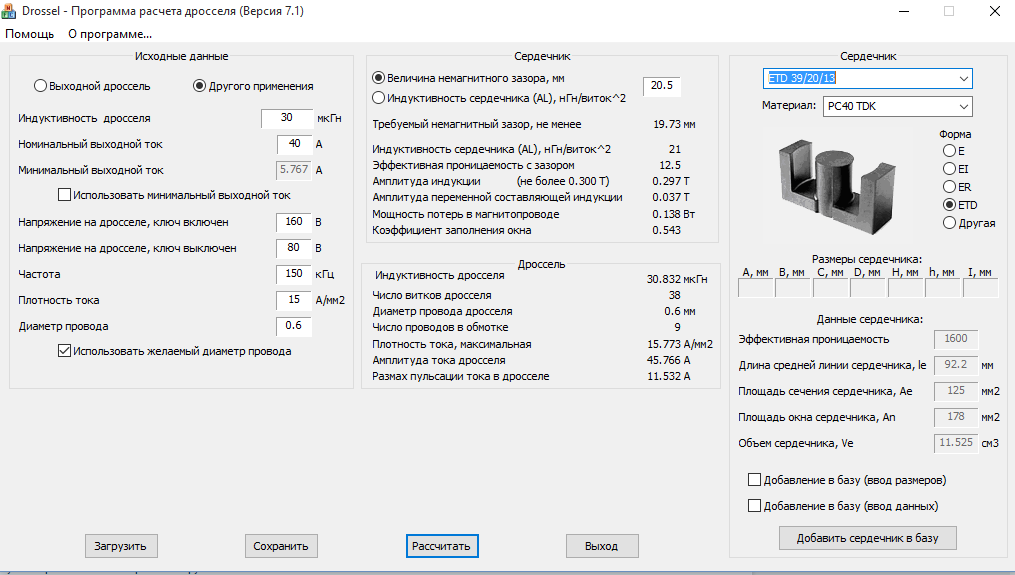
Как рассчитать индуктивность катушки с сердечником. Какие формулы использовать для расчета индуктивности. Как подобрать параметры сердечника и обмотки катушки. На что обратить внимание при самостоятельном изготовлении катушек индуктивности.

Основные принципы расчета индуктивности катушки

Индуктивность катушки зависит от нескольких ключевых параметров:

• Количества витков обмотки
• Геометрических размеров катушки
• Магнитных свойств сердечника
• Формы сердечника

Общая формула для расчета индуктивности катушки с сердечником:

L = μ0 * μr * N^2 * S / l

где:

• L — индуктивность в генри
• μ0 — магнитная проницаемость вакуума (4π * 10^-7 Гн/м)
• μr — относительная магнитная проницаемость сердечника
• N — число витков обмотки
• S — площадь поперечного сечения сердечника
• l — длина средней линии магнитного потока в сердечнике

Методы расчета индуктивности катушки с сердечником

Существует несколько основных методов расчета индуктивности катушки с сердечником:

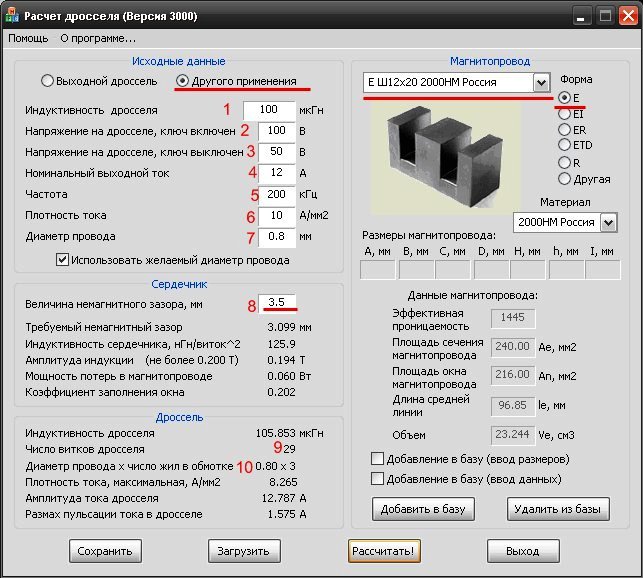
1. Аналитический расчет по формулам
2. Использование специализированных калькуляторов
3. Моделирование методом конечных элементов
4. Экспериментальное измерение

Рассмотрим особенности каждого метода подробнее.

Аналитический расчет индуктивности

Аналитический расчет основан на использовании математических формул. Основные преимущества:

• Универсальность — подходит для различных конструкций катушек
• Не требует специального ПО
• Позволяет понять физические принципы

Недостатки метода:

• Низкая точность для сложных геометрий сердечника
• Не учитывает краевые эффекты
• Трудоемкость расчетов вручную

Расчет с помощью калькуляторов

Онлайн-калькуляторы позволяют быстро рассчитать индуктивность по заданным параметрам. Их плюсы:

• Простота и скорость расчета
• Учет особенностей различных конструкций
• Возможность оптимизации параметров

Минусы использования калькуляторов:

• Ограниченность набора поддерживаемых конструкций
• Невозможность учета нестандартных особенностей
• Зависимость от точности встроенных формул

Выбор параметров сердечника катушки индуктивности

При выборе сердечника для катушки индуктивности необходимо учитывать следующие параметры:

Материал сердечника

Наиболее распространенные материалы для сердечников катушек:

• Феррит — высокая магнитная проницаемость, низкие потери на высоких частотах
• Альсифер — высокая индукция насыщения, подходит для силовых применений
• Пермаллой — высокая начальная проницаемость, малые потери
• Карбонильное железо — высокая температурная стабильность

Выбор материала зависит от требуемой индуктивности, рабочей частоты и мощности.

Форма сердечника

Основные формы магнитопроводов для катушек индуктивности:

• Кольцевые (тороидальные) — минимальные потери рассеяния
• Стержневые — простота намотки, возможность регулировки
• Ш-образные — высокая индуктивность при малых размерах
• Чашечные — хорошее экранирование

Форма сердечника влияет на распределение магнитного потока и эффективность катушки.

Геометрические размеры

Основные геометрические параметры сердечника:

• Площадь поперечного сечения
• Длина средней линии магнитного потока
• Внешний и внутренний диаметр (для кольцевых)
• Высота

От размеров зависят максимальная индуктивность, добротность и габариты катушки.

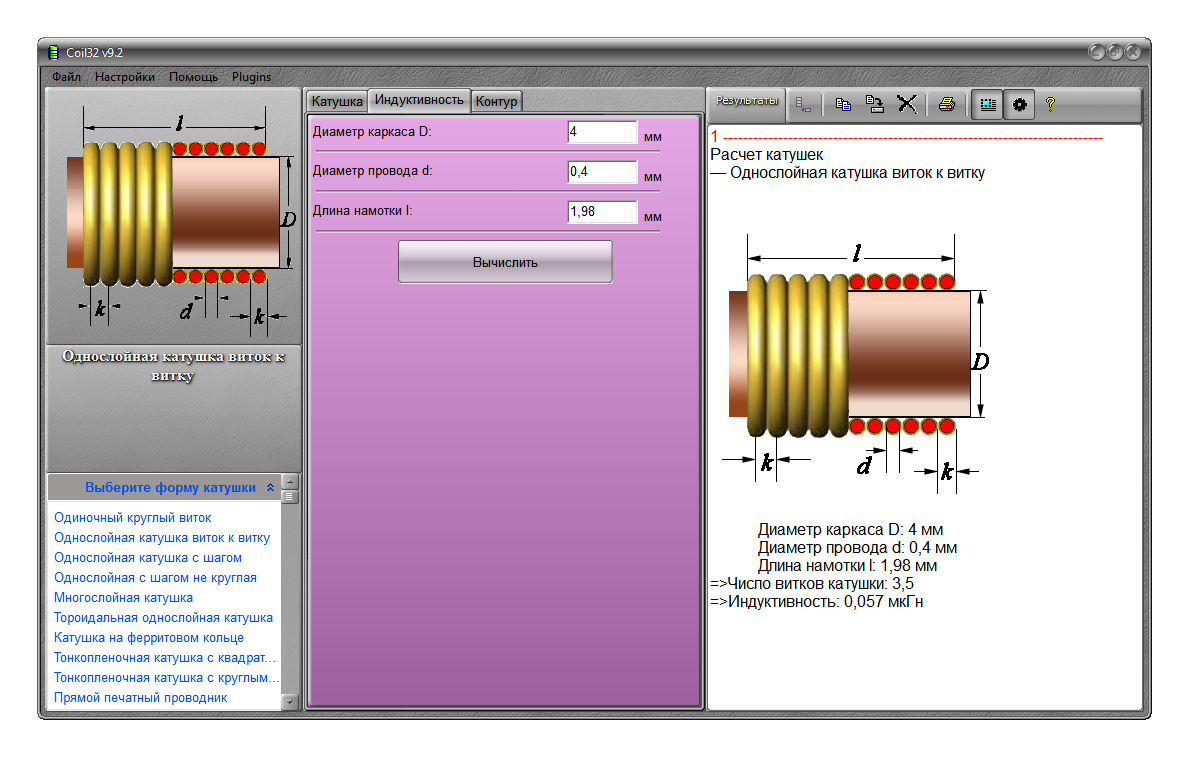
Подбор параметров обмотки катушки индуктивности

При расчете обмотки катушки индуктивности нужно определить:

Число витков

Количество витков N можно рассчитать по формуле:

N = √(L * l / (μ0 * μr * S))

где L — требуемая индуктивность. Число витков влияет на индуктивность квадратично.

Диаметр провода

Диаметр провода обмотки выбирается исходя из:

• Максимального тока через катушку
• Допустимой плотности тока (2-3 А/мм² для силовых катушек)
• Требуемого активного сопротивления
• Заполнения окна намотки

Для высокочастотных катушек учитывается скин-эффект.

Способ намотки

Основные способы намотки катушек:

• Однослойная — простая технология, хорошее охлаждение
• Многослойная — компактность, высокая индуктивность
• Секционная — снижение паразитной емкости
• Бифилярная — компенсация магнитного поля

Выбор способа намотки зависит от требований к параметрам катушки.

Особенности самостоятельного изготовления катушек индуктивности

При самостоятельном изготовлении катушек индуктивности следует обратить внимание на следующие моменты:

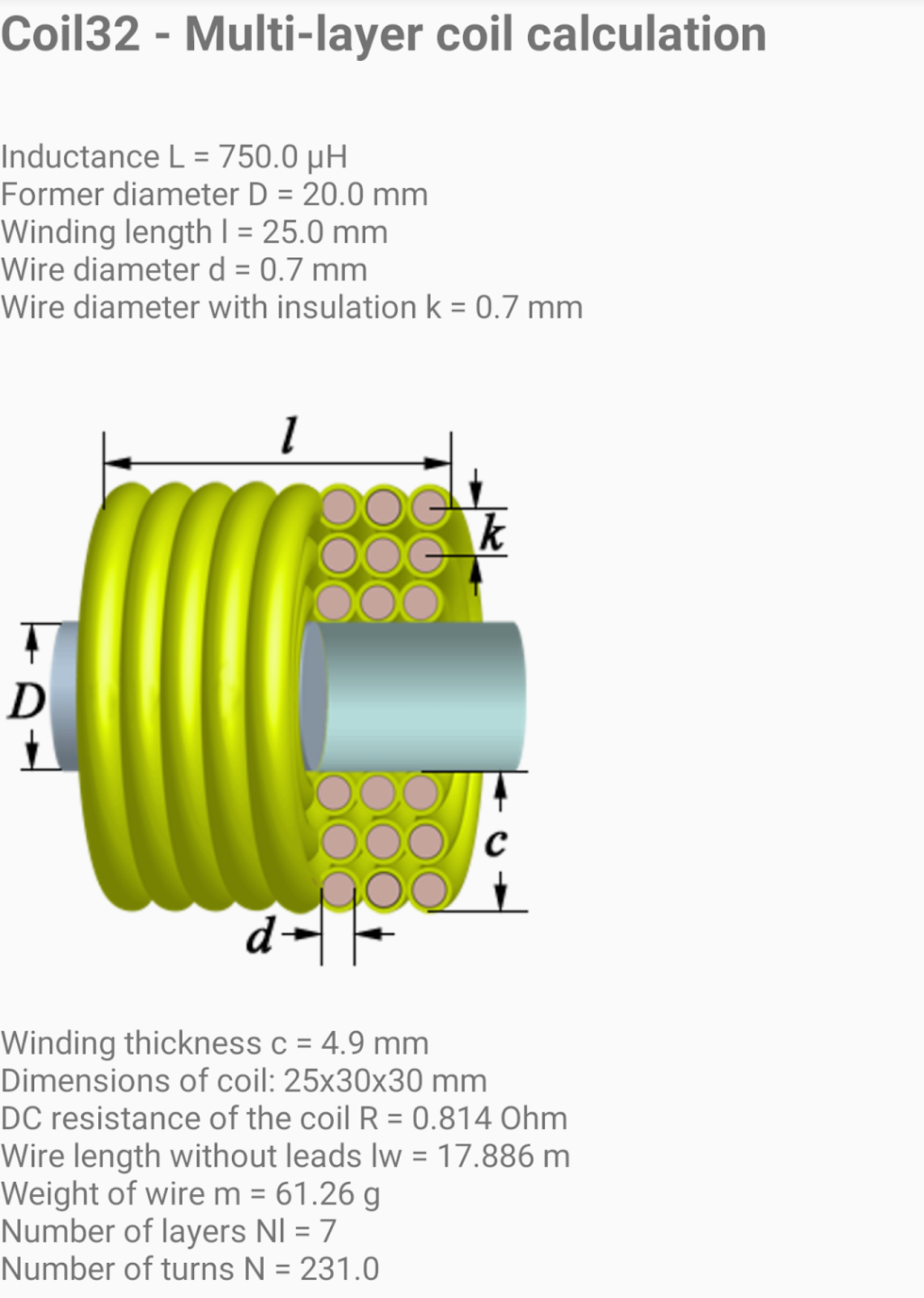
Выбор каркаса

Каркас катушки должен:

• Обеспечивать надежное крепление сердечника
• Иметь низкие диэлектрические потери
• Выдерживать температурные нагрузки
• Обеспечивать возможность намотки нужного числа витков

Распространенные материалы каркасов — полистирол, полиамид, фторопласт.

Технология намотки

Основные правила качественной намотки:

• Равномерное распределение витков
• Плотная укладка провода
• Отсутствие перехлестов между слоями
• Надежная фиксация концов обмотки
• Пропитка обмотки лаком для защиты от влаги

Качество намотки влияет на стабильность параметров катушки.

Измерение параметров

После изготовления катушки необходимо измерить:

• Индуктивность на рабочей частоте
• Активное сопротивление обмотки
• Добротность
• Собственную резонансную частоту

Измерения позволяют оценить соответствие параметров расчетным значениям.

Проверка и оптимизация конструкции катушки

После изготовления опытного образца катушки рекомендуется выполнить следующие шаги:

Сравнение с расчетными параметрами

Необходимо сравнить измеренные параметры с расчетными значениями:

• Индуктивность
• Активное сопротивление
• Добротность
• Собственная резонансная частота

При значительных отклонениях нужно выявить их причины.

Температурные испытания

Температурные испытания позволяют оценить:

• Стабильность параметров при нагреве
• Максимально допустимую температуру
• Эффективность теплоотвода

По результатам испытаний может потребоваться корректировка конструкции.

Оптимизация параметров

Возможные способы оптимизации катушки:

• Подстройка числа витков
• Изменение способа намотки
• Корректировка зазора сердечника
• Применение экранирования

Оптимизация позволяет улучшить характеристики катушки.

Заключение

Расчет и изготовление катушек индуктивности — сложная инженерная задача, требующая учета множества факторов. Применение современных методов расчета и моделирования позволяет создавать оптимальные конструкции катушек для различных применений. При самостоятельном изготовлении важно уделять внимание технологии намотки и контролю параметров готового изделия.

Расчет катушки на ферритовом стержне

Информация о материале

Опубликовано: 08 марта 2017

Обновлено: 22 декабря 2022

Просмотров: 14273

---

Для работы калькулятора необходимо включить JavaScript в вашем браузере!

Калькулятор имеет следующие ограничения в расчетах:

• шаг намотки не может превышать удвоенного диаметра провода;
• диаметр катушки не может быть больше удвоенного диаметра стержня;
• длина намотки должна быть меньше 3/4 длины стержня;
• при смещении катушки она не должна доходить до края стержня на 1/8 его длины;
• начальная магнитная проницаемость стержня должна быть больше 100;

 

ВВЕДИТЕ ИСХОДНЫЕ ДАННЫЕ:

---

L

= мГнμГннГн

– Требуемая индуктивность

Параметры ферритового стержня:

---

lf =	ммсм	– Длина стержня
df =	ммсм	– Диаметр стержня
µ =		– Начальная магнитная проницаемость

Coil parameters:

---

dc =	ммсм	– Диаметр каркаса
s =	ммсм	– Смещение от центра стержня
dw =	ммсм	– Диаметр провода
p =	ммсм	– Шаг намотки

---

Рассчитать

RESULT:

---

N =		– Число витков
µeff =		– Эффективная магнитная проницаемость стержня
lc =	ммсм	– Длина намотки

Первые 12 комментариев относятся к старой версии калькулятора, основанной на другой методике расчета.

С формулами и методом расчета можно ознакомиться здесь.

---

Другие калькуляторы:

1. Расчет катушки на Ш-образном ферритовом сердечнике

 

Катушка индуктивности. Описание, характеристики, формула расчета

Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.

Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.

Накопленная энергия в индуктивности

Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.

Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:

где L — индуктивность, I — ток, протекающий через катушку индуктивности.

Множители и приставки СИ для образования десятичных кратных и дольных единиц и их наименований

Кратные приставки СИ	Дольные приставки СИ
Дека-(101).	Деци- (10−1).
Гекто- (102).	Санти- (10−2).
Кило- (103).	Милли- (10−3).
Мега- (106).	Микро- (10−6).
Гига- (109).	Нано- (10−9).
Тера- (1012).	Пико- (10−12).
Пета- (1015).	Фемто- (10−15).
Экса- (1018).	Атто- (10−18).
Зетта- (1021).	Зепто- (10−21).
Иотта- (1024).	Иокто- (10−24).

Гидравлическая модель

Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.

Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.

Паяльный фен YIHUA 8858

Обновленная версия, мощность: 600 Вт, расход воздуха: 240 л/час…

Подробнее

Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.

Индуктивность в электрических цепях

В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.

В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:

Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:

где ω является угловой частотой резонансной частоты F:

Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.

Индуктивное сопротивление ХL определяется по формуле:

где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.

Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:

Схемы соединения катушек индуктивностей

Параллельное соединение индуктивностей

Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:

Последовательное соединение индуктивностей

Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:

Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.

Взаимоиндуктивность двух параллельных двухпроводных линий

Пусть две параллельные двухпроводные линии расположены симметрично так, как это было показано на рис. 1.4. При условии d> г0 внутренним потоком в проводах по сравнению с внешним можно пренебречь. Магнитный поток, пронизывающий первую линию и созданный током I2 второй, может быть найден как сумма потоков, создаваемых каждым из проводов второй линии в отдельности. Тогда магнитный поток, пронизывающий первую линию,

расстояния от провода линии 1 до проводов линии 2 .

Магнитный поток Ф одновременно является потокосцеплением первой линии, так как сцепляется с ней один раз; поэтому

а взаимоиндуктивность

Для уменьшения коэффициента связи между линиями связи l и передачи 2 применяют транспозицию линии связи, заключающуюся в перекрещивании проводов линии связи через равные расстояния; тогда суммарное потокосцепление будет равно нулю.

Добротность катушки индуктивности

На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.

Добротность катушки индуктивности может быть найдена через следующую формулу:

где R является собственным сопротивлением обмотки.

Катушка индуктивности. Формула индуктивности

Базовая формула индуктивности катушки:

• L = индуктивность в генри
• μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
• μ г = относительная проницаемость материала сердечника
• N = число витков
• A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
• l = длина катушки в метрах (м)

Индуктивность прямого проводника:

• L = индуктивность в нГн
• l = длина проводника
• d = диаметр проводника в тех же единицах, что и l

Индуктивность катушки с воздушным сердечником:

• L = индуктивность в мкГн
• r = внешний радиус катушки
• l = длина катушки
• N = число витков

Индуктивность многослойной катушки с воздушным сердечником:

• L = индуктивность в мкГн
• r = средний радиус катушки
• l = длина катушки
• N = число витков
• d = глубина катушки

Индуктивность плоской катушки:

• L = индуктивность в мкГн
• r = средний радиус катушки
• N = число витков
• d = глубина катушки

ОБЩАЯ ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА.

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Накопленная энергия в индуктивности Гидравлическая модель Индуктивность в электрических цепях Схемы соединения катушек индуктивностей Параллельное соединение индуктивностей Последовательное соединение индуктивностей Добротность катушки индуктивности Катушка индуктивности. Формула индуктивности Базовая формула индуктивности катушки Индуктивность прямого проводника Индуктивность катушки с воздушным сердечником Индуктивность многослойной катушки с воздушным сердечником Индуктивность плоской катушки Конструкция катушки индуктивности Применение катушек индуктивности Расчет катушек индуктивности Метод определения собственной ем­кости катушек Расчет и изготовление плоских катушек индуктивности Расчет однослойной катушки

Катушка индуктивности

— является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.

Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.

Конструкция катушки индуктивности

Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.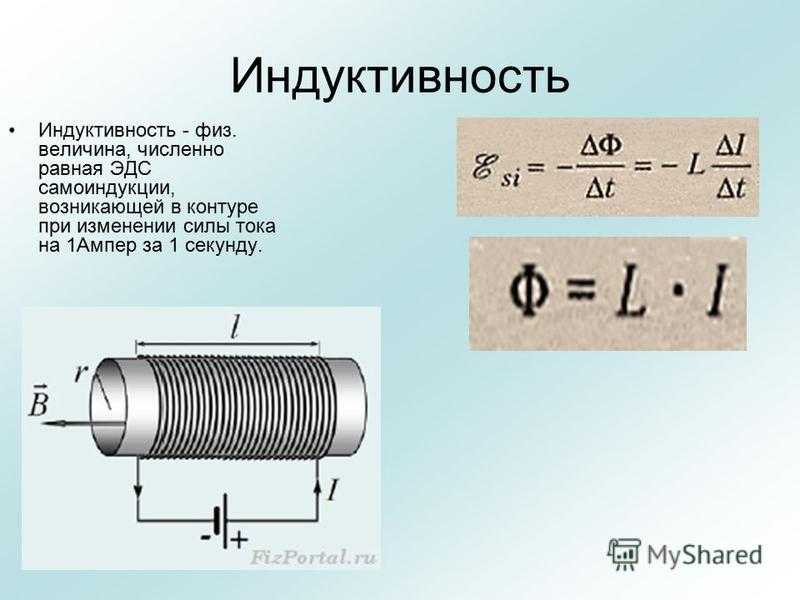

Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.

Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.

Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.

Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.

Применение катушек индуктивности

Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.

Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.

Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.

Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

Историческая справка

Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz), который известен своим вкладом в изучение электромагнетизма, и который вывел правило Ленца о свойствах индукционного тока. Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry), который открыл самоиндукцию. Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.

В числе учёных, принявших участие в исследованиях свойств индуктивности и разработке различных её применений, необходимо упомянуть сэра Генри Кавендиша, который проводил эксперименты с электричеством; Майкла Фарадея, который открыл электромагнитную индукцию; Николу Тесла, который известен своей работой над системами передачи электричества; Андре-Мари Ампера, которого считают первооткрывателем теории об электромагнетизме; Густава Роберта Кирхгофа, который исследовал электрические цепи; Джеймса Кларка Максвелла, который исследовал электромагнитные поля и частные их примеры: электричество, магнетизм и оптику; Генри Рудольфа Герца, который доказал, что электромагнитные волны действительно существуют; Альберта Абрахама Майкельсона и Роберта Эндрюса Милликена. Конечно, все эти ученые исследовали и другие проблемы, о которых здесь не упоминается.

Индуктивность

К Стивен Макфадьен on 3 июня 2012 г.

Когда в проводе течет ток, создается магнитное поле. Сила этого магнитного поля, перпендикулярного проводнику, называется магнитным потоком (измеряется в веберах, Вт). Индуктивность – это отношение магнитного потока к току в цепи. Единицей индуктивности является генри, Гн (Вб/А), и обычно она обозначается символом L.

Собственная индуктивность

Всякий раз, когда ток в катушке с проводом изменяется, создаваемое им магнитное поле будет изменяться. Это изменит магнитный поток через катушку и, следовательно, создаст напряжение на катушке. Это называется самоиндукцией, а катушка называется индуктором.

Пример – собственная индуктивность соленоида

Рассмотрим катушку проволоки вокруг магнитного сердечника, длина которой намного больше диаметра.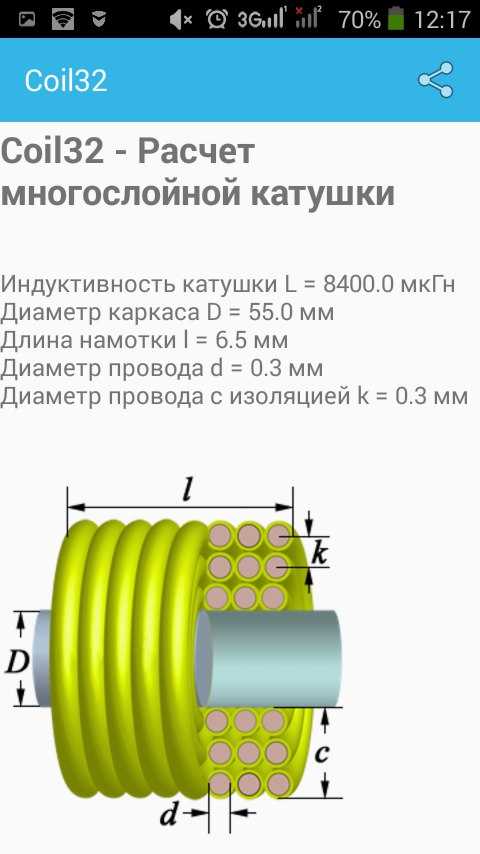

Учитывая проницаемость свободного пространства μ _o , относительная магнитная проницаемость магнитопровода μ _r , число витков N и длина соленоида l , при протекании тока i 9002 4 , плотность магнитного потока 902 3 B внутри катушки определяется как:

Магнитный поток Φ получается путем умножения плотности потока на площадь поперечного сечения А :

Учитывая, что индуктивность есть отношение магнитного потока к току, имеем:

Примечание: если соленоид намотан на немагнитный сердечник, то мк _r = 1.

Взаимная индуктивность

Когда магнитное поле одной катушки связано с магнитным полем другой катушки, изменение тока в первой катушке создаст связывающее магнитное поле со второй катушкой. Магнитное поле, связанное со второй катушкой, создаст напряжение внутри этой катушки. Это называется взаимной индуктивностью.

Для двух индукторов (катушек) имеем:

• L ₁₁ – собственная индуктивность индуктора 1
• L ₂₂ – собственная индуктивность катушки индуктивности 2
• L ₁₂ = L ₂₁ – взаимная индуктивность между двумя

Формулы индуктивности

В приведенной ниже таблице перечислены некоторые общие формулы для расчета теоретической индуктивности нескольких конструкций индукторов.

• L = индуктивность (Гн)
• μ ₀ = проницаемость свободного пространства = 4 π× 10 ^-7 (Гн/м)
• μ _r = относительная проницаемость материала сердечника

Цилиндрическая катушка:

Н = количество витков A = площадь поперечного сечения рулона в квадратных метрах (м 2 ) l = длина рулона в метрах (м)

 

Прямой провод:

l = длина провода (м) d = диаметр проводника (м)

 

Плоская спираль с воздушным сердечником:

r = средний радиус витка (м) N = количество витков d = глубина витка (внешний радиус минус внутренний радиус) (м)

Тороидальный сердечник, круглое сечение:

Н = количество витков r = радиус намотки катушки (м) D = общий диаметр тороида (м)

Применение в цепях

Количественная мера применения индуктивности L , в цепь, определяемую:

Катушка индуктивности может накапливать энергию. Мощность (= энергия/время), хранящаяся в катушке индуктивности, составляет:

Отсюда следует (небольшими вычислениями), что энергия, хранящаяся в катушке индуктивности, равна:

Пример расчета индуктивности

Индуктивность Пример расчета

 

Дэвид Микер

[email protected]

 

Сопутствующий файл: induct1a.fem

 

Введение

 

Распространенной задачей, к которой можно применить FEMM, является Расчет индуктивности катушки индуктивности с зазором. Хотя индуктивность можно оценить с помощью простого магнитного теории схем схемный подход обычно игнорирует утечку потока и окантовочные эффекты. Чтобы решить эти неидеальные эффекты более подробно анализ конечных элементов может быть занят. Цель настоящего Например, чтобы показать, как рассчитывается индуктивность в моделировании FEMM, и чтобы сравните этот результат с приближением, полученным с помощью магнитной цепи подход.

 

 

Пример геометрии

 

Пример геометрии состоит из слоистого EI с зазорами сердечник с поперечным сечением, как показано на рисунке 1. Сердечник E с центральным полюсом шириной 0,5 дюйма и внешними полюсами Ширина 0,25 дюйма отделена от I-образного обратного пути воздушным зазором.

 

 

Рис. 1. Пример геометрии

 

витки провода 18 AWG с толстой изоляцией, для примерно 66% меди заполнить фракцию в окне катушки. Это предполагается, что сердцевина простирается на 1 дюйм в направлении страницы. Для целей этой модели материал предполагается, что это линейный ферромагнитный материал с относительной магнитной проницаемостью из 2500.

 

 

Теория цепей Индуктивность

 

Для грубой аппроксимации индуктивности можно предположить, что нет утечки и окантовки, и что вклад железа сечения на сопротивление магнитной цепи тривиально по сравнению с взносы из воздуха. Затем, поток, текущий в магнитопроводе, получается путем решения уравнения цепи:

 

 

для ф , итого поток, соединенный катушкой. Р представляет сопротивление магнитной цепи, которое при наших предположениях можно записать как:

 

 

где g = 0,025″ , a _полюс = 0,5 в ² и м _o = 4 p (10 ^-7 ) ч/м. Так как общий поток, связывающий катушку, равен:

 

 

и полная собственная индуктивность равна произведению потока на общее количество поворотов:

, чтобы самостоятельно составила:

С. получается:

 

L = 1,39 мГн

 

Мы ожидаем, что индуктивность получена из конечного элемента вычислений, чтобы быть в окрестности 1,39мГн.

 

 

Индуктивность конечного элемента (I)

 

Для целей создания конечно-элементного решения Катушка индуктивности помещается в центр коробки размером 2 на 2,5 дюйма. На границах домена есть граница условие A=0 определено. Для Для выполнения конечно-элементного анализа ток 1 А несколько произвольно применяется к катушкам. Довольно грубая плотность сетки с ограничением размера сетки больше 0,05 дюйма определяется везде. Сетчатая проблемная область изображена на рисунке 2.9.0008

 

 

Рис. 2. Проблемная область, нарисованная в FEMM.

 

После выполнения анализа и запуска постпроцессора индуктивность можно получить, нажав кнопку Свойства цепи в окне post-processor:
Появится диалоговое окно с рядом свойств обмотки, если смотреть с клемм обмотки. Диалоговое окно «Свойства цепи» для этого примера показано ниже на рис. 3.

 

 

Рисунок 3: Цепь Диалог результатов свойств.

 

При отсутствии постоянных магнитов или других катушек, Результат потока/тока можно интерпретировать непосредственно как собственную индуктивность:

 

L = 1,73 мГн

 

Этот результат выше, чем 1,39 мГн, предсказанный простой подход теории цепей, потому что эффекты утечки и интерференции которыми пренебрегают в схемном подходе, имеют тенденцию немного повышать индуктивность.

 

Индуктивность методом конечных элементов (II)

 

Альтернативным подходом является получение энергии через Интеграл «Энергия магнитного поля». Для этого подхода энергия получается через:

 

 

где этот интеграл берется по всей задаче домен, а не только над катушками. Чтобы выполнить эту интеграцию в постпроцессор, переключитесь в блочный интегральный режим, нажав кнопку на панели задач. Затем выберите каждый регион в проблеме с помощью щелчки левой кнопки мыши. Когда выбрана вся проблемная область, нажмите кнопку Integral и выберите Интеграл энергии магнитного поля из выпадающего списка объемных интегралов. Если Вт представляет интегральный результат, результирующая индуктивность:

 

интеграция:

 

Вт = 0,000865042 Дж

 

Что при подстановке в формулу дает то же самое результат метода (I):

 

L = 1,73 мГн

 

Выводы

 

Был представлен простой пример, демонстрирующий, как FEMM можно использовать для получения индуктивности. Была рассмотрена двумерная плоская задача, и индуктивность получается из двух методы сравнивались друг с другом и с «проверкой работоспособности» оценка индуктивности из теории магнитной цепи.

 

Хотя результаты двух подходов конечных элементов чтобы получить индуктивность в этом случае идентичны, обычно лучше использовать метод (I). Причина в том, что некоторые граничные условия ( т. е. асимптотическое граничное условие, используемое для аппроксимация задачи с «открытой границей») предполагают, что некоторая энергия хранится вне смоделированной проблемной области. Внутри FEMM рассчитывает поток связь с использованием метода, учитывающего эту дополнительную энергию, тогда как интегрирование B*H по всем элементам — нет.

 

Строго говоря, один коэффициент индуктивности подразумевает линейная зависимость между приложенным током и результирующим потоком. По этой причине пример проблемы с рассматривались только линейные материалы.

 

Если в задаче есть нелинейные материалы и есть значительное насыщение, больше нет линейной зависимости между ток и поток. Однако есть много ситуаций, в которых применяется синусоидальный ток, и хотелось бы знать амплитуду основной гармоники потока, соответствующую приложенному текущий. В этом случае гармоника анализ можно запустить в FEMM ( , т.