Расчет катушек индуктивности. Расчет индуктивности катушек: формулы, методы и особенности

Как рассчитать индуктивность катушки. Какие факторы влияют на индуктивность. Какие формулы используются для расчета. Как учитывать конструктивные особенности катушек при расчете. Какие методы позволяют повысить точность расчета индуктивности.

Основные принципы расчета индуктивности катушек

Расчет индуктивности катушек является важной задачей при проектировании различных электронных устройств. Индуктивность зависит от множества факторов:

• Геометрических размеров катушки (диаметр, длина намотки)
• Количества витков
• Способа намотки (однослойная, многослойная)
• Материала сердечника
• Шага намотки

Существует несколько основных подходов к расчету индуктивности:

1. Использование упрощенных эмпирических формул
2. Применение точных аналитических выражений
3. Численное моделирование

Выбор метода зависит от требуемой точности и особенностей конструкции катушки. Рассмотрим основные формулы и методы расчета более подробно.

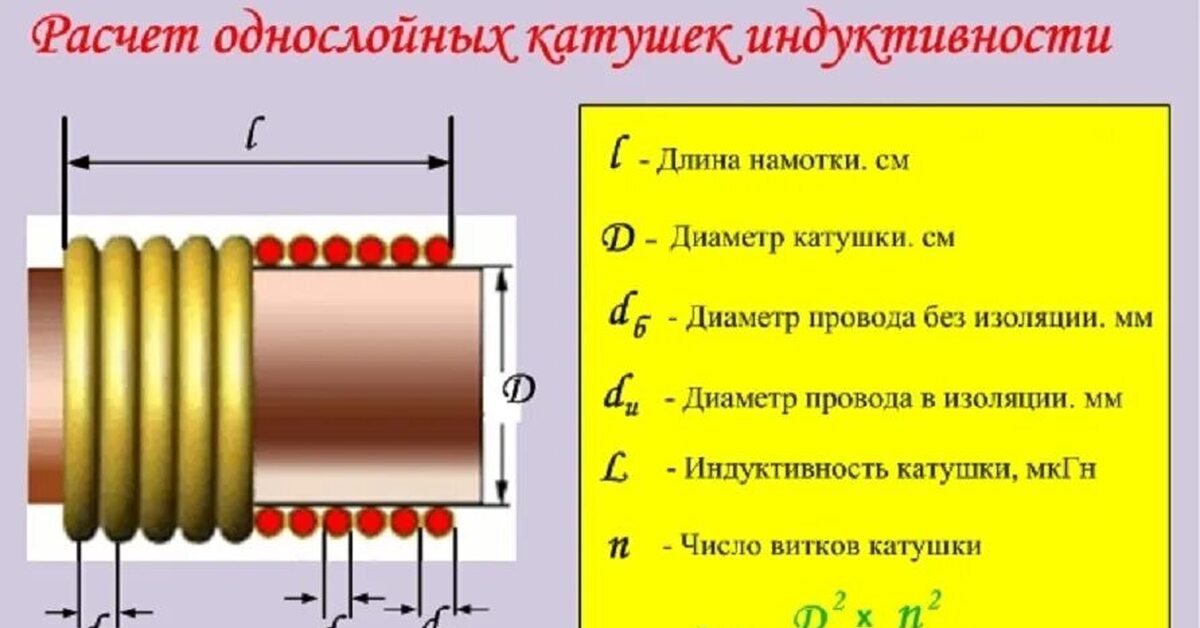
Формулы для расчета индуктивности однослойных катушек

Для однослойных цилиндрических катушек без сердечника чаще всего используется формула:

L = (μ0 * N^2 * S) / l

где:

• L — индуктивность в Генри
• μ0 — магнитная постоянная (4π * 10^-7 Гн/м)
• N — число витков
• S — площадь поперечного сечения катушки
• l — длина намотки

Однако эта формула дает завышенные результаты для коротких катушек. Более точной является формула Нагаока:

L = (μ0 * N^2 * D^2) / (4l) * K

где D — диаметр катушки, K — поправочный коэффициент Нагаока, зависящий от отношения длины к диаметру.

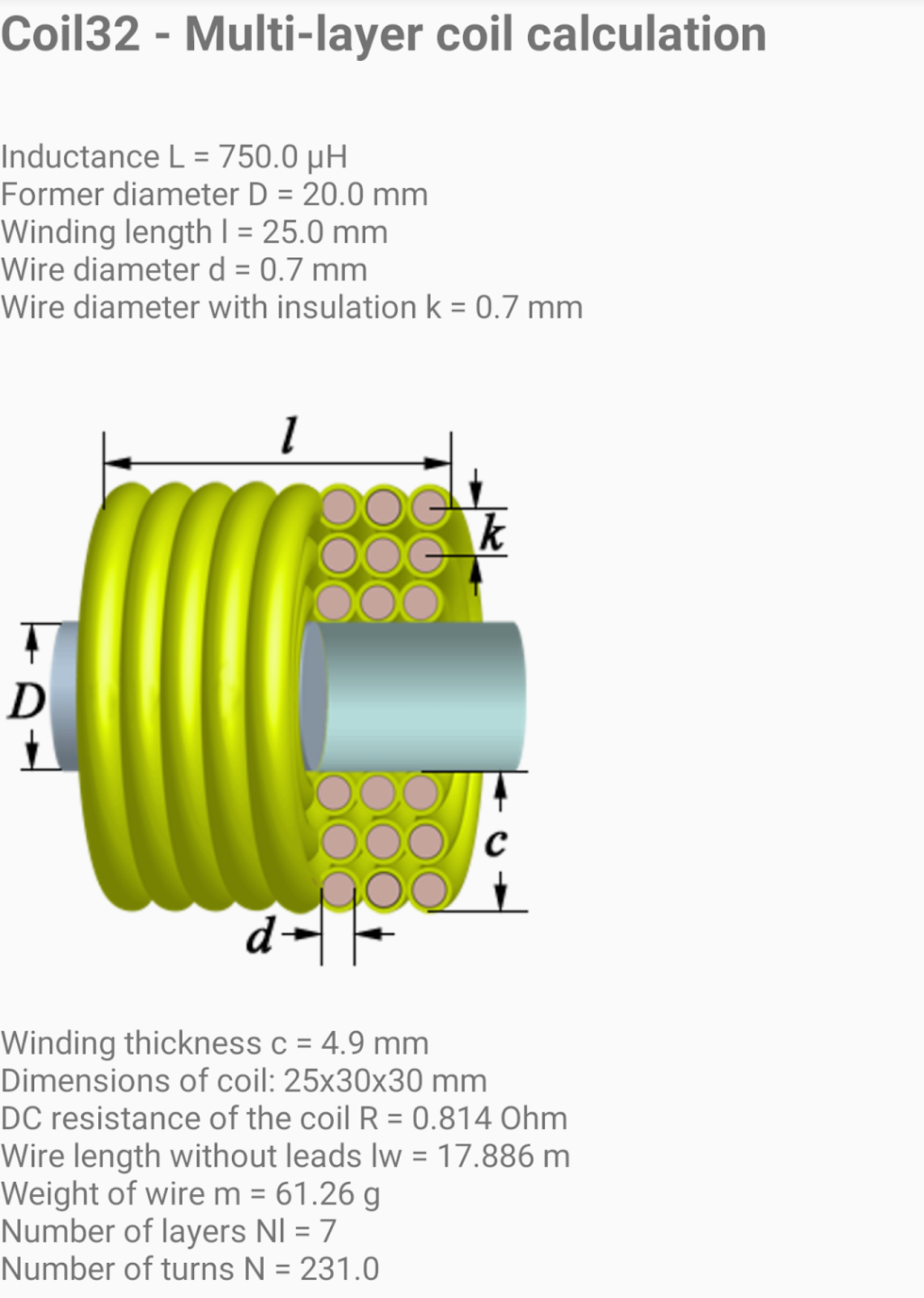
Расчет индуктивности многослойных катушек

Для многослойных катушек расчет усложняется. Одной из наиболее точных является формула Уиллера:

L = (0.8 * a^2 * N^2) / (6a + 9h + 10c)

где:

• a — средний радиус катушки
• h — высота намотки
• c — толщина намотки

Эта формула позволяет учесть геометрию многослойной катушки и дает достаточно точные результаты.

Учет влияния сердечника на индуктивность

При наличии магнитного сердечника индуктивность катушки существенно возрастает. Это учитывается с помощью коэффициента AL:

L = AL * N^2

где AL — индуктивность на виток квадратичный.

Значение AL зависит от материала и геометрии сердечника и приводится в справочных данных производителей.

Влияние шага намотки на индуктивность

При намотке катушки с зазором между витками индуктивность уменьшается. Это учитывается с помощью поправочного коэффициента:

L = L0 * (1 — k * (d/D)^2)

где:

• L0 — индуктивность при плотной намотке
• k — эмпирический коэффициент (0.2-0.3)
• d — диаметр провода
• D — диаметр катушки

Учет шага намотки позволяет повысить точность расчета для катушек с разреженной намоткой.

Численные методы расчета индуктивности

Для сложных конструкций катушек аналитические формулы могут давать большую погрешность. В таких случаях применяют численное моделирование методом конечных элементов. Это позволяет учесть:

• Сложную геометрию катушки
• Неоднородность магнитного поля
• Влияние экранов и близлежащих проводников
• Частотные свойства

Численные методы обеспечивают высокую точность, но требуют специализированного программного обеспечения и значительных вычислительных ресурсов.

Экспериментальное определение индуктивности

Наиболее точным методом определения индуктивности является экспериментальное измерение с помощью специальных приборов — измерителей RLC. Современные измерители позволяют определять индуктивность с погрешностью менее 1%.

При этом важно учитывать, что реальная индуктивность катушки может отличаться от расчетной из-за:

• Разброса параметров материалов
• Неидеальности геометрии
• Паразитных емкостей

Поэтому экспериментальная проверка расчетов всегда желательна для ответственных применений.

Факторы, влияющие на точность расчета индуктивности

При расчете индуктивности катушек следует учитывать следующие факторы, влияющие на точность:

• Неравномерность намотки и отклонения геометрии
• Влияние проводимости каркаса катушки
• Зависимость магнитной проницаемости сердечника от частоты и напряженности поля
• Скин-эффект в проводах на высоких частотах
• Паразитные емкости между витками

Учет этих факторов позволяет повысить точность расчета и приблизить ее к реальным значениям индуктивности.

Методы оптимизации конструкции катушек индуктивности

При проектировании катушек индуктивности часто требуется оптимизировать их параметры. Основные методы оптимизации включают:

• Подбор оптимального соотношения длины и диаметра
• Выбор оптимального шага намотки
• Применение секционирования обмотки
• Оптимизацию формы сердечника
• Использование литцендрата для снижения потерь на высоких частотах

Применение этих методов позволяет создавать катушки с высокой добротностью и стабильностью параметров.

Программное обеспечение для расчета катушек индуктивности

Для автоматизации расчетов катушек индуктивности применяется специализированное программное обеспечение. Наиболее популярные программы:

• Coil32 — бесплатная программа для расчета различных типов катушек
• Coil Designer — профессиональный пакет для проектирования катушек
• FEMM — свободное ПО для расчета магнитных полей методом конечных элементов
• COMSOL Multiphysics — универсальный пакет для численного моделирования

Использование специализированного ПО значительно упрощает процесс расчета и оптимизации катушек индуктивности.

Заключение

Расчет индуктивности катушек является важной инженерной задачей. Существует множество методов расчета — от простых эмпирических формул до сложного численного моделирования. Выбор метода зависит от требуемой точности и особенностей конструкции катушки.

Для получения наилучших результатов рекомендуется:

• Использовать наиболее подходящие формулы с учетом типа катушки
• Учитывать все значимые факторы, влияющие на индуктивность
• Применять численное моделирование для сложных конструкций
• Проводить экспериментальную проверку расчетов

Такой комплексный подход позволяет обеспечить высокую точность расчета индуктивности и оптимизировать конструкцию катушек для конкретных применений.

Расчет катушек индуктивности в 3D с помощью COMSOL Multiphysics

При проектировании индукционных устройств важно учитывать различные электродинамические эффекты. Модуль AC/DC пакета COMSOL Multiphysics предоставляет все необходимые инструменты для эффективного и простого моделирования и проектирования катушек индуктивности, а также для расчёта их сосредоточенных характеристик в соответствии с заданными требованиями.

Базовые принципы работы катушки индуктивности

Простейшая катушка индуктивности — это электрический провод (обмотка или катушка), намотанный вокруг магнитного материала (магнитопровода). Принцип действия катушки основывается на принципе индуктивности, вокруг устройства наводится магнитное поле, которое препятствует изменению тока, текущего по проводнику.

Простейшая катушка индуктивности, состоящая из медной обмотки и железного сердечника. Красными стрелками показано направление тока, а синими — магнитное поле вокруг сердечника. Изменение тока приводит к изменению магнитного потока через обмотку, что создаёт разность потенциалов в обмотке, которая препятствует изменению тока.

Индуктивность — это параметр, который обозначается буквой L и показывает, в какой степени происходит сопротивление протеканию тока, он является ключевой характеристикой идеального индуктора. К сожалению, в нашем мире нет идеальных вещей и в реальных катушках индуктивности наблюдаются резистивные эффекты, которые больше проявляются на низких частотах и характеризуются активным сопротивлением (R), и ёмкостные эффекты, которые наблюдаются на высоких частотах и характеризуются ёмкостью (C), приводащие в т.ч. авторезонансным процессам. На самом деле, принцип действия катушки индуктивности можно понять, рассмотрев простейшую RLC-цепь.

Эквивалентная схема катушки индуктивности.

С помощью набора пассивных элементов, можно собрать схему замещения, которая будет полностью соответствовать и описывать свойства индуктивности в различных приложениях. К примеру, если через катушку индуктивности протекает переменный ток, то она является низкочастотным фильтром, а последовательно соединённая с конденсатором – резонансным или полосовым фильтром. Катушки индуктивности играют очень важную роль в современном мире и повседневной жизни. Они используются в различных импульсных источниках питания и согласующих схемах, подключаемых к радиочастотным антеннам. Умный светофор, который загорается зелёным при вашем приближении, может быть индуктивным датчиком, который упрощает вашу жизнь в пути.

Оптимизация катушки индуктивности

Если в вашем устройстве присутствует катушка индуктивности, то важно знать некоторые её характеристики, чтобы полностью понимать, как работает устройство в целом. Ключевыми параметрами являются – индуктивность, активное сопротивление, электрическая ёмкость, резонансная частота и добротность (Q-factor), то есть ширина области резонанса. Эти параметры определяют частоту среза или полосу пропускания фильтра, либо просто реактивное сопротивление согласующей схемы.

Другой потенциально важной задачей при использовании катушек индуктивности является учет электромагнитных помех (ЭМП) или электромагнитной совместимости (ЭМС). Вокруг катушек индуктивности создаётся магнитное поле. При проектировании необходимо точно знать, насколько оно будет влиять на другие компоненты и близлежащие устройства. Это особенно актуально при нынешней миниатюризации всех устройств.

На данный момент существуют только грубые аналитические и эмпирические формулы, описывающие эти RLC параметры. С их помощью нельзя точно спроектировать современное устройство. Аналитические формулы в основном пригодны только для расчёта элементарных трёхмерных форм, например, куба, цилиндра, спирали и тора. Однако с помощью них невозможно рассчитать форму и поведение магнитного поля вокруг индуктивного устройства для ЭМП/ЭМС (EMI/EMC) исследований.

Дополнительно, часто требуется изготовление магнитопровода из нелинейного материала для увеличения индуктивности и ограничения окружающего магнитного поля. Это очевидно еще больше усложняет расчёты и приводит к очередной аналитической или эмпирической аппроксимации, что негативно сказывается на результате. Для получения точных рабочих характеристик трёхмерного индукционного устройства, численное моделирование является более надёжным и корректным решением.

3D-моделирование катушки индуктивности в COMSOL Multiphysics

COMSOL Multiphysics предлагает пользователю все необходимые инструменты для получения полных рабочих характеристик катушки индуктивности. Давайте рассмотрим данный функционал программы на учебном примере Modeling of a 3D Inductor (Моделирование катушки индуктивности в 3D). Он доступен в Application Gallery (Галерее моделей и приложений) для модуля AC/DC. Он как раз служит для наглядной иллюстрации процесса проектирования катушки индуктивности и расчета ее рабочих характеристик.

Геометрия катушки индуктивности для конечно-элементной модели.

В реальных устройствах протекающий через катушку ток можно задавать разными способами. Например, приложением напряжения, тока или мощности. Это может быть либо постоянная, либо периодическая величина, или какая-нибудь сложная функция, зависящая от времени. В нашем примере для задания тока используются условия Coil с опцией Single Turn (Одиночный проводник) и Lumped Port (Сосредоточенный порт) для низких и высоких частот соответственно. Таким образом, вы можете управлять катушками.

На видео продемонстрирована последовательность шагов по моделированию трёхмерной катушки индуктивности в COMSOL Multiphysics.

COMSOL Multiphysics позволяет легко добавлять в модель электрические сосредоточенные компоненты и цепи, которые можно как создать в самой программе, так и импортировать, как список SPICE. Благодаря мультифизическим связкам можно подключать данные цепи к распределенным устройствам, котороме моделируются методом конечных элементов. Всё это можно делать с помощью встроенных функций взаимосвязи. К примеру, вы можете подключить вашу катушки индуктивности к цепи управления, приложив минимум усилий. Программа сама находит те части, которые вы можете связать, и предлагает вам выбрать нужные из выпадающего списка.

При выборе нужной опции из выпадающего списка терминал катушки индуктивности (показан синим цветом) автоматически связывается с электрической цепью.

На высоких частотах (на которых может работать ваша катушка индуктивности) в проводниках с током в следствие скин-эффекта ток вытесняется к поверхности. В данном примере мы можем учесть данный эффект с помощью использования граничного условия Impedance boundary condition (Импедансное граничное условие). Решение задачи растекания тока в тонких слоях — это очень ресурсоёмкая задача. Но переходя к упрощенному описанию проводника с помощью граничного условия мы упрощаем данную задачу и значительно экономим время расчёта.

На рисунке изображён график распределения плотности тока (Am^-2) в катушке на высокой частоте. Обратите внимание, что учитывается неравномерное протекание тока.

Добротность катушки индуктивности во многом зависит от свойств материала магнитопровода, в частности от потерь. Возможности COMSOL Multiphysics позволяют отредактировать любой материал из библиотеки, чтобы добавить или заменить необходимые свойства. Любые потери на вихревые токи автоматически учитываются в расчёте. В данном примере диэлектрические потери в магнитопроводе задаются пользователем с помощью добавления мнимой части к диэлектрической постоянной, ε_r. Таким же образом вы можете добавить магнитные потери в вашу модель, задав комплексное значение магнитной проницаемости μ_r.

Постобработка и анализ результатов расчёта модели индуктора

Если вам необходимо произвести впечатление на клиентов или завоевать их доверие, буквально в несколько кликов вы можете создать красивейшие графики, благодаря встроенным возможностям постобработки результатов в COMSOL Multiphysics. Программное обеспечение автоматически вычисляет и предоставляет вам доступ к переменным, которые в полной мере характеризуют работу вашей спроектированной катушки индуктивности — магнитное поле, токи и величина потерь. В учебном примере трёхмерной катушки индуктивности продемонстрировано, как настроить детализированной изоражение ниже.

Чем тоньше магнитопровод, тем больше в нём магнитная индукция на поверхности (Тл). В катушке также показано распределение потенциала (В).

Для лучшей наглядности вы можете добавить другие типы трёхмерных графиков, например, Streamline (Силовые линии) или Arrow (Векторная диаграмма).

Магнитная индукция на поверхности магнитопровода (Тл). Силовые линии плотности тока (Aмм^-2) в катушке показывают более высокую плотность в закруглённых частях. Красными стрелками показано магнитное поле.

Наконец, для получения полных характеристик катушки индуктивности вам необходимо определиеть значения импеданса и резонансных частот. Одна из переменных в COMSOL Multiphysics автоматически рассчитывает точный импеданс для каждой частоты. Таким образом, графики данных величин можно построить очень легко. Используя встроенные операторы real (действительная часть) и imag (мнимая часть), можно строить графики активного (резистивного) и реактивного (индуктивного/ёмкостного) импеданса, на которых легко увидеть резонанс.

Действительная (слева) и мнимая (справа) части импеданса (Z) показывают резонанс и переключение между индуктивным и ёмкостным поведением.

На графике мнимой части можно также заметить, что после прохождения через резонансную частоту знак изменяется с положительного на отрицательный. Это значит, что на высоких частотах устройство больше проявляет ёмкостный характер, чем индуктивный, что вполне ожидаемо.

Учёт термических эффекто в модели катушки индуктивности

COMSOL Multiphysics специально проектировался, чтобы пользователям было легко связывать различные физические интерфейсы в одной модели. Как раз поэтому второе слово в названии — «multiphysics». Дальнейшим расширением модели может являться добавление и учет электромагнитного нагрева. Протекающие в катушке токи, вихревые токи и диэлектрические/магнитные потери в магнитопроводе, все они приводят к выделению тепла, которое распространяется по проводящим металлическим компонентам с высокой теплопроводностью и, отчасти, нагревает окружающие устройства и платы. Используя физический интерфейс Induction Heating (Индукционный нагрев), вы запросто сможете рассчитать интенсивность теплопередачи и распределение температур в индукционных устройствах.

Узнайте больше о моделировании индукционных устройств в COMSOL Multiphysics

• Ознакомьтесь с другими учебными моделями катушек индуктивности в галерее моделей и приложений:
  • Моделирование спиральной катушки индуктивности
  • Интегрированный индуктор квадратной формы в виде спирали
• Посмотрите, как используют COMSOL Multiphysics для проектирования индукционных устройств:
  • Упрощая переключение с помощью индукционной передачи энергии
  • Трансформатор тока, разработанный на основе конечно-элементного анализа и моделирования электрических цепей

Расчет параметров катушек индуктивности — КиберПедия

Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из по­вторяющихся рабочих циклов, каждый из которых соответствует… Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров… История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации… Интересное: Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются… Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все… Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция

⇐ ПредыдущаяСтр 11 из 14Следующая ⇒ При расчете основных параметров КИ используются геометрические размеры их обмоток: диаметр D, длина l и толщина t (последнее только для многослойных обмоток) (рисунок 3). В однослойной катушке диаметр D представляет собой диаметр окружности, образуемой центром тяжести активного сечения провода. На высоких частотах диаметр D можно принять равным внутреннему диаметру витков. Длина катушки  представляет собой расстояние между осевыми линиями крайних витков. Расстояние между осевыми линиями смежных витков называется шагом намотки . Величины  и  связаны между собой простым соотношением (1) где N −число витков; При сплошной намотке расстояние между смежными витками определяется диаметром провода в изоляции  и неплотностью прилегания витков друг к другу. Последнее может быть учтено коэффициентом неплотности , который зависит в основном от диаметра провода (таблица 3).   Таблица 3 − Значения коэффициента неплотности Диаметр провода, мм 0,08 — 0,11 0,15 — 0,25 0,35 — 0,41 0,51 — 0,93 >1,0 Коэффициент 1,3 1,25 1,2 1,1 1,05   Размеры многослойной катушки определяются наружным D и внутренним D 0 диаметрами и длиной намотки. Часто в расчетах используются толщина намотки  и средний диаметр Расчет индуктивности. Из теоретической электротехники известно следующее выражение для расчета индуктивности длинного соленоида круглого сечения (без сердечника): (2) Здесь индуктивность L получается выраженной в мкГн, если длину намотки  выразить в см, а площадь сечения S — в см2. В реальных катушках длина обычно соизмерима с диаметром, вследствие чего сильнее сказывается уменьшение магнитного сцепления крайних витков и фактическая индуктивность оказывается меньше расчетной. Точный учет этого явления приводит к громоздким и неудобным формулам. На практике используют простые полуэмпирические формулы с поправочными коэффициентами, зависящими от относительных размеров катушки. Для расчета индуктивности сплошной однослойной обмотки применяется следующая формула, обеспечивающая погрешность расчета не более 2-3 %: (3) где  − индуктивность, мкГн;  − диаметр катушки (каркаса), см;  − поправочный коэффициент, величина которого зависит от отношения          , а значения приведены в таблице 4. Таблица 4 − Значения коэффициента 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 20,2 15,8 13,4 11,6 10,4 9,4 8,6 7,9 7,3 6,8 1,0 2, 0 3, 0 4,0 5,0 6,0 7,0 8,0 9,0 10,0 6,8 4,0 2,9 2,2 1,8 1,53 1,33 1,17 1,05 0,95   При намотке с шагом происходит дополнительное уменьшение потокосцепления и индуктивности. Поэтому для более точного расчета индуктивности КИ, намотанной с шагом проводом круглого сечения, при числе витков не менее 4…5 следует использовать формулу: (4) где  − фактическая индуктивность, мкГн;    − индуктивность, рассчитанная для сплошной обмотки по формуле (3),         мкГн;  − диаметр катушки, см;   А и В − поправочные коэффициенты, зависящие соответственно от отноше-                 ния диаметра провода без изоляции к шагу намотки  и числа                витков (рисунок 4). Формула (4) может использоваться и для расчета индуктивности многослойных катушек. В этом случае в формулу в качестве  подставляется средний диаметр  а для более точного расчета необходимо учитывать зависимость коэффициента   не только от отношения  но и от отношения . Рисунок 4− Значения коэффициентов А и В для расчета индуктивности катушек, намотанных с шагом   Расчет числа витков. При проектировании КИ величина индуктивности, как правило, является исходной величиной. Может быть задан также один из размеров катушки, чаще всего− диаметр обмотки. Необходимо найти число витков и остальные размеры катушки, предварительно выбрав, если не заданы, конструкцию и тип намотки. Формулу для расчета числа витков можно получить из уравнения (3), решив его относительно : (5) Вследствие того, что коэффициент сложным образом зависит от размеров катушки, формула дает возможность определения требуемого числа витков, если известны все размеры катушки. Обычно хотя бы один из размеров является неизвестным. Поэтому расчет числа виттов должен производиться методом последовательного приближения. Расчет собственной емкости. Величина собственной емкости С0 зависит от размеров катушки, конструкции обмотки, диэлектрической проницаемости изоляции провода и каркаса, близости экрана или деталей корпуса прибора и ряда других факторов. Чем больше диаметр катушки, ближе друг к другу расположены витки, выше диэлектрическая проницаемость изоляции провода и материала каркаса, тем больше собственная емкость катушки индуктивности. Для однослойной неэкранированной КИ расчет С0 производится по выражению (6) где ,  −диаметр провода без изоляции. Наименьшей собственной емкостью (1…2 пф) обладают однослойные катушки, намотанные с шагом. Собственная емкость многослойных катушек зависит от способа и плотности намотки, толщины и диэлектрической проницаемости изоляции провода. Для простых многослойных обмоток собственную емкость приближенно можно определить по формуле (7) где  −средний диаметр обмотки, см;    −относительнаядиэлектрическая проницаемость изоляции провода. Собственная емкость катушек с универсальной намоткой обычно составляет 5-10 пф. Для значительного уменьшения собственной емкости многослойных катушек применяют секционирование.   ⇐ Предыдущая567891011121314Следующая ⇒ Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой… 

Катушки индуктивности — Библиотека уравнений электротехники

Библиотека уравнений

Уравнения, связанные с электроникой, и многое другое.

Прозрачный

Справочник по электронике

Индуктивность катушки

Способность электрического проводника, такого как катушка, создавать наведенное напряжение при изменении тока, протекающего через него, называется индуктивностью. Чтобы рассчитать индуктивность катушки на основе ее физической конструкции, вы можете использовать это уравнение, где:

L — Индуктивность катушки в Генри (Гн)
N — Количество витков
μ _r — Проницаемость сердечника
μ _o — Проницаемость воздуха или вакуума (1,26X10 ^–6 )
A — Закрытая площадь
l — Длина катушки

Катушки из проволоки, изготовленные с определенной величиной индуктивности, называются индукторами.

 

Зависимость напряжения от тока индуктора

Это уравнение показывает зависимость напряжения от тока в индукторе, где:

v — индуцируемое напряжение
L — индуктивность катушки индуктивности
di/dt — мгновенная скорость изменения тока через катушку индуктивности

3 прямо пропорциональна его индуктивности и мгновенной скорости изменения тока через индуктор. Таким образом, чем больше скорость изменения тока через катушку, тем выше индуцированное напряжение. Однако, если ток через индуктор не изменяется в конкретный момент времени, индуцированное напряжение равно нулю.

 

Индуктивное реактивное сопротивление

Индуктивное реактивное сопротивление (X _L ) является мерой сопротивления катушки индуктивности протеканию синусоидального переменного тока. Это зависит от величины индуктивности и частоты приложенного напряжения. Чтобы определить реактивное сопротивление катушки индуктивности, вы можете использовать это уравнение.

 

Сохраненная энергия катушки индуктивности

Как и конденсатор, катушка индуктивности в идеале не рассеивает электрическую энергию, подаваемую на нее источником напряжения. Однако энергия хранится в магнитном поле. Чтобы рассчитать энергию, запасенную в катушке индуктивности, вы можете использовать это уравнение.

 

Взаимная индуктивность



k — Коэффициент связи

Две катушки имеют взаимную индуктивность, когда ток в одной катушке может индуцировать напряжение в другой катушке. Как видно на схеме, если L ₁ подключен к источнику напряжения, но не физически, то L ₁ и L ₂ связаны магнитным полем. Изменение тока в L ₁ может индуцировать напряжение как на L ₁ , так и на L 9.0019 2 . Если к L ₂ подключена нагрузка, индуцированное напряжение через L ₂ может подавать ток на эту нагрузку. Вы можете использовать это уравнение для расчета взаимной индуктивности между двумя катушками.

Общая индуктивность двух серийных катушек с взаимной индуктивностью

—

СЕРИЯ-ОПИСАНИЯ

Общее индуктивное индуктивное индуктивное индуктивное индуст.0019 T ) зависит от степени взаимной связи и от того, соединены ли они последовательно-вспомогательно или последовательно-противоположно. Катушки соединены последовательно, когда общий ток создает одинаковое направление магнитного поля для двух катушек. Они соединены последовательно-встречно, когда их магнитное поле имеет противоположное направление.

Взаимная индуктивность (L _M ) является положительной и увеличивает общую индуктивность, когда две катушки соединены последовательно. В последовательно-противоположных взаимная индуктивность равна минусу и уменьшает общую индуктивность двух последовательных катушек.

 

Эквивалентная индуктивность последовательных катушек индуктивности

Общая или эквивалентная индуктивность (L _eq ) последовательных катушек индуктивности может быть просто определена путем сложения отдельных индуктивностей. В этом расчете предполагается, что между катушками индуктивности нет взаимной индукции.

 

Эквивалентная индуктивность параллельных индукторов

При параллельном соединении индукторов общая или эквивалентная индуктивность (L _eq ) рассчитывается таким же образом с параллельными резисторами.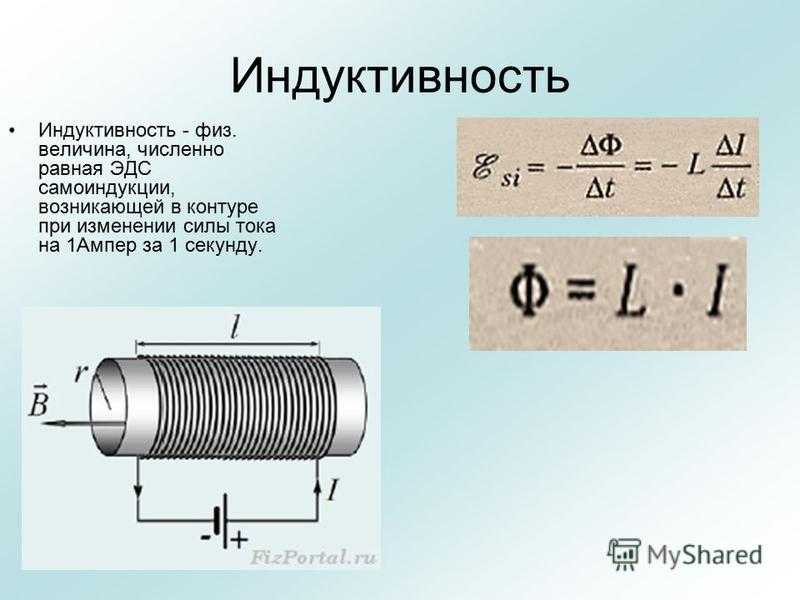 Эквивалентная индуктивность (L _eq ) может быть определена путем инвертирования суммы обратных значений всех индуктивностей. Опять же, в этом расчете предполагается, что между катушками индуктивности нет взаимной индукции.

 

Получите новейшие инструменты и руководства, только что из тостера.

Метод расчета значения индуктивности подвесных катушек индуктивности МЭМС с кремниевой подложкой

. 2018 17 ноября; 9(11):604.

дои: 10.3390/ми9110604.

Юань Ли ¹ , Цзяньхуа Ли ² , Лисинь Сюй ³

Принадлежности

• ¹ Школа мехатроники, Пекинский технологический институт, Пекин 100081, Китай. [email protected].
• ² Школа мехатроники, Пекинский технологический институт, Пекин 100081, Китай. [email protected].
• ³ Школа мехатроники, Пекинский технологический институт, Пекин 100081, Китай. [email protected].

• PMID: 30453626
• PMCID: PMC6265712
• DOI: 10.3390/ми9110604

Бесплатная статья ЧВК

Юань Ли и др. Микромашины (Базель). 2018 .

Бесплатная статья ЧВК

. 2018 17 ноября; 9 (11): 604.

дои: 10.3390/ми9110604.

Авторы

Юань Ли ¹ , Цзяньхуа Ли ² , Лисинь Сюй ³

Принадлежности

• ¹ Школа мехатроники, Пекинский технологический институт, Пекин 100081, Китай. [email protected].
• ² Школа мехатроники, Пекинский технологический институт, Пекин 100081, Китай. [email protected].
• ³ Школа мехатроники, Пекинский технологический институт, Пекин 100081, Китай. [email protected].

• PMID: 30453626
• PMCID: PMC6265712
• DOI: 10.3390/ми9110604

Абстрактный

Подвесные индукторы микроэлектромеханической системы (МЭМС) обладают превосходными радиочастотными (РЧ) характеристиками. Величина индуктивности является одной из основных характеристик, характеризующих рабочие характеристики катушек индуктивности. При точном расчете значения индуктивности важно учитывать влияние подложки и высоты подвеса. В данной работе предлагается метод расчета значения индуктивности провода подвесного индуктора МЭМС с кремниевой подложкой, так как провод является основным компонентом катушки индуктора. Затем метод распространяется на подвесные катушки индуктивности, состоящие из одной витковой катушки. Результаты расчетов, полученные этим предложенным методом, были проверены с помощью анализа конечных элементов (HFSS), и было обнаружено, что они хорошо согласуются с результатами моделирования HFSS.

Ключевые слова: подвесной индуктор МЭМС; значение индуктивности; микроэлектромеханическая система (МЭМС).

Заявление о конфликте интересов

Авторы заявляют об отсутствии конфликта интересов.

Цифры

Рисунок 1

Схема микроэлектромеханического…

Рисунок 1

Схема микроэлектромеханической системы (МЭМС) с подвесным индуктором, состоящая из одного…

фигура 1

Схема микроэлектромеханической системы (МЭМС) с подвешенным индуктором, состоящим из одного провода.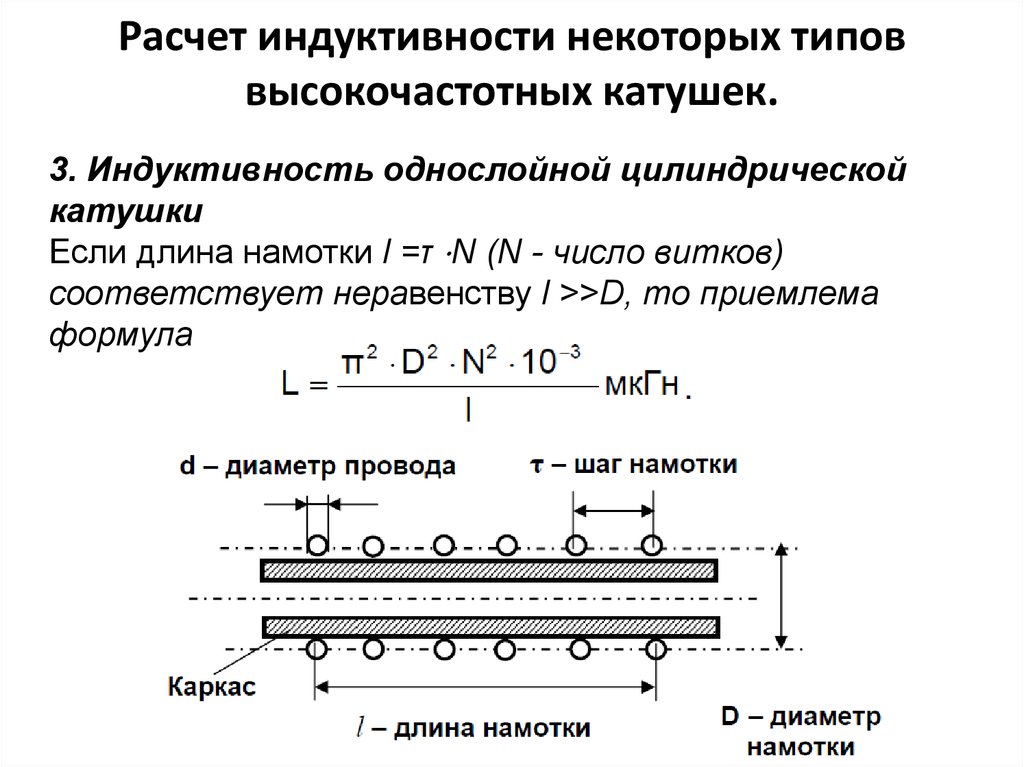

Рисунок 2

Геометрия провода при…

Рисунок 2

Геометрия провода на высоте d над подложкой.

фигура 2

Геометрия провода на высоте d над подложкой.

Рисунок 3

Вертикальный вид геометрии…

Рисунок 3

Вертикальный вид рассматриваемой геометрии.

Рисунок 3

Вертикальный вид рассматриваемой геометрии.

Рисунок 4

Схема МЭМС…

Рисунок 4

Схема подвесного индуктора МЭМС, состоящего из одной прямоугольной катушки.

Рисунок 4

Схема подвесного индуктора МЭМС, состоящего из одной прямоугольной катушки.

Рисунок 5

Симулятор высокочастотной структуры…

Рисунок 5

Модель провода с помощью высокочастотного симулятора структуры (HFSS).

Рисунок 5

Модель провода с помощью высокочастотного симулятора структуры (HFSS).

Рисунок 6

Расчетные значения индуктивности…

Рисунок 6

Значения индуктивности, рассчитанные по предложенному методу и HFSS, по сравнению с проволокой…

Рисунок 6

Значения индуктивности, рассчитанные предлагаемым методом и HFSS, в зависимости от длины провода.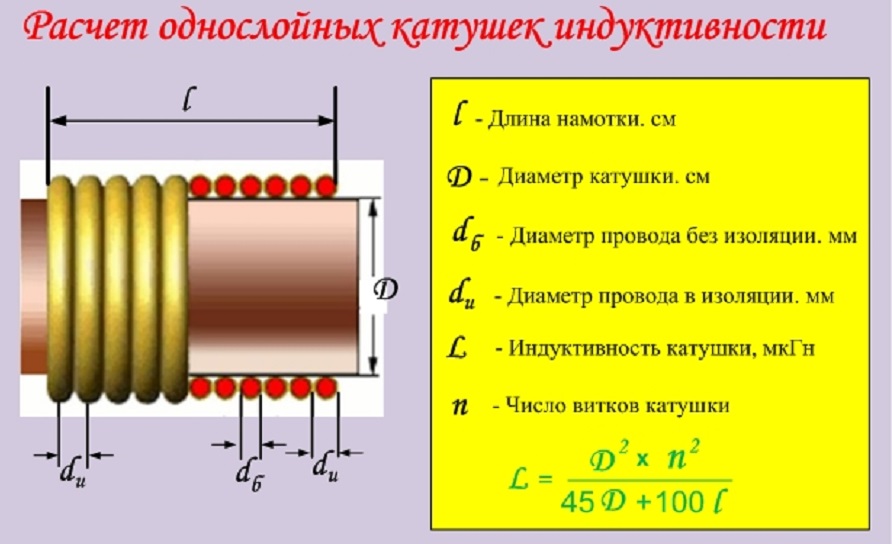

Рисунок 7

Значения индуктивности 200 мкм…

Рисунок 7

Значения индуктивности провода диаметром 200 мкм, рассчитанные по предлагаемому методу, HFSS,…

Рисунок 7

Значения индуктивности провода диаметром 200 мкм, рассчитанные предложенным методом, HFSS и методом Теплицы, в зависимости от частоты.

Рисунок 8

Значения индуктивности 400 мкм…

Рисунок 8

Значения индуктивности провода диаметром 400 мкм, рассчитанные по предлагаемому методу, HFSS,…

Рисунок 8

Значения индуктивности провода диаметром 400 мкм, рассчитанные предложенным методом, HFSS и методом Теплицы, в зависимости от частоты.

Рисунок 9

Модель HFSS…

Рисунок 9

HFSS модель одновиткового подвесного индуктора.

Рисунок 9

Модель HFSS одновиткового подвесного индуктора.

Рисунок 10

Значения индуктивности одного…

Рисунок 10

Значения индуктивности одновитковой катушки индуктивности (длина стороны 400 мкм)…

Рисунок 10

Значения индуктивности одновитковой катушки индуктивности (длина стороны 400 мкм), рассчитанные по предлагаемому методу, HFSS и методу Теплицы, в зависимости от частоты.

Рисунок 11

Значения индуктивности одного…

Рисунок 11

Значения индуктивности одновитковой катушки индуктивности (длина стороны 500 мкм)…

Рисунок 11

Значения индуктивности одновитковой катушки индуктивности (длина стороны 500 мкм), рассчитанные по предлагаемому методу, HFSS и методу Теплицы, в зависимости от частоты.

Рисунок 12

Значения индуктивности одного…

Рисунок 12

Значения индуктивности одновитковой катушки индуктивности (длина стороны 400 мкм)…

Рисунок 12

Значения индуктивности одновитковой катушки индуктивности (длина стороны 400 мкм), рассчитанные по предлагаемому методу и HFSS, в зависимости от высоты подвеса.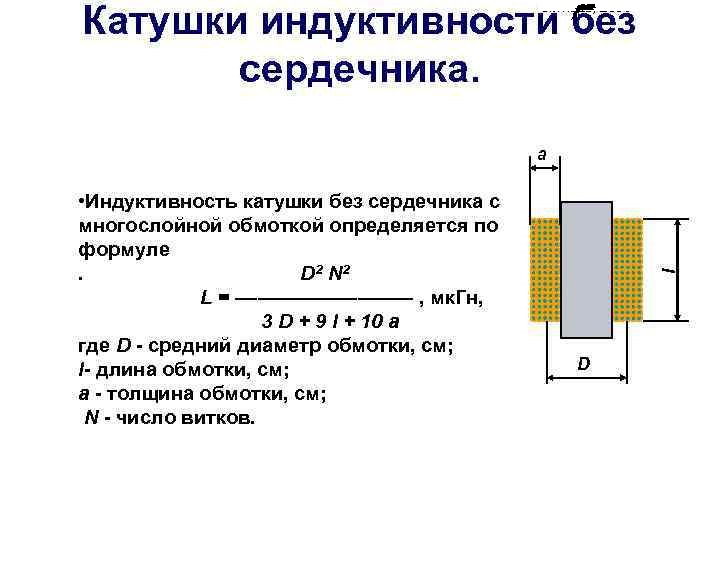

Рисунок 13

Значения индуктивности одного…

Рисунок 13

Значения индуктивности одновитковой катушки индуктивности (длина стороны 500 мкм)…

Рисунок 13

Значения индуктивности одновитковой катушки индуктивности (длина стороны 500 мкм), рассчитанные по предлагаемому методу и HFSS, в зависимости от высоты подвеса.

См. это изображение и информацию об авторских правах в PMC

Похожие статьи

• Анализ механизма изменения характеристик подвесных индукторов MEMS при механическом ударе.

  Ли Ю, Сюй Л, Ли Дж. Ли Ю и др. Микромашины (Базель). 2019 11 октября; 10 (10): 686. дои: 10.3390/ми10100686. Микромашины (Базель). 2019. PMID: 31614649 Бесплатная статья ЧВК.

• Механическая реакция индуктора MEMS со вспомогательной стойкой при ударе с высокой перегрузкой.

  Сюй Л., Ли Ю., Ли Дж., Лу С. Сюй Л. и др. Микромашины (Базель). 2018 11 апреля; 9 (4): 176. дои: 10.3390/ми

  76. Микромашины (Базель). 2018. PMID: 30424109 Бесплатная статья ЧВК.

• Анализ отказа и механизма изменения производительности подвесных индукторов MEMS со вспомогательными опорами при ударе с высокой перегрузкой.

  Сюй Л, Ли Ю, Ли Дж. Сюй Л. и др. Микромашины (Базель). 2020 25 октября; 11 (11): 957. дои: 10.3390/ми11110957. Микромашины (Базель). 2020. PMID: 33113862 Бесплатная статья ЧВК.

• Производство индукторов МЭМС и новые приложения в силовой электронике и нейротехнологиях.

  Ле Х.Т., Хак Р.И., Оуян З., Ли С.В., Фрид С.И., Чжао Д., Цю М., Хань А. Ле ХТ и др. Микросист Наноенг. 2021 авг 11;7:59. doi: 10.1038/s41378-021-00275-w. Электронная коллекция 2021. Микросист Наноенг. 2021. PMID: 34567771 Бесплатная статья ЧВК. Обзор.

• Последние достижения в области гибких радиочастотных МЭМС.

  Ши Ю, Шен З. Ши Ю и др. Микромашины (Базель). 2022 8 июля; 13 (7): 1088. дои: 10.3390/ми13071088. Микромашины (Базель). 2022. PMID: 35888905 Бесплатная статья ЧВК. Обзор.

Посмотреть все похожие статьи

Цитируется

• Влияние условий нанесения контактной пробки на утечку и контактное сопротивление в многоуровневом КМОП-устройстве логической связи.

  Цуй И, Чжон Джи, Гао И, Пё С.Г. Цуй Ю и др. Микромашины (Базель). 2020 6 февраля; 11 (2): 170. дои: 10.3390/ми11020170. Микромашины (Базель). 2020. PMID: 32041270 Бесплатная статья ЧВК.

использованная литература

1. 1. Се М.К., Фанг Ю.К., Чен Ч.Х. Разработка и изготовление подвешенных высокодобротных катушек индуктивности, совместимых с глубокой субмикронной КМОП-технологией. IEEE транс. Электронные устройства. 2004; 51: 324–331. doi: 10.1109/TED.2003.822864. — DOI
2. 1. Тай С.М., Ляо С.Н. Многоуровневые подвесные тонкопленочные индукторы на кремниевых пластинах. IEEE транс. Электронные устройства. 2007;54:1510–1514. doi: 10.1109/TED.2007.896347. — DOI
3. 1. Ишай Р.Б., Столярова С., Шапира С., Мусия М., Крыгер Д., Шило Ю., Немировский Ю. Малошумящий КМОП-усилитель со встроенным микромеханическим индуктором на передней панели. Микроэлектр. Дж. 2011; 42: 754–757. doi: 10.1016/j.mejo.2011.01.011. — DOI
4. 1. Хикмат О.Ф., Али М.С.М. Катушки индуктивности RF MEMS и их применение — обзор. Дж. Микроэлектромех. Сист. 2017;26:17–44.