Расчет магнитного поля соленоида. Магнитное поле соленоида: формулы, расчеты и применение

Как рассчитать магнитное поле внутри соленоида. Какие факторы влияют на его величину. Формулы для расчета индукции магнитного поля соленоида. Применение соленоидов в технике и электронике.

Что такое соленоид и как он создает магнитное поле

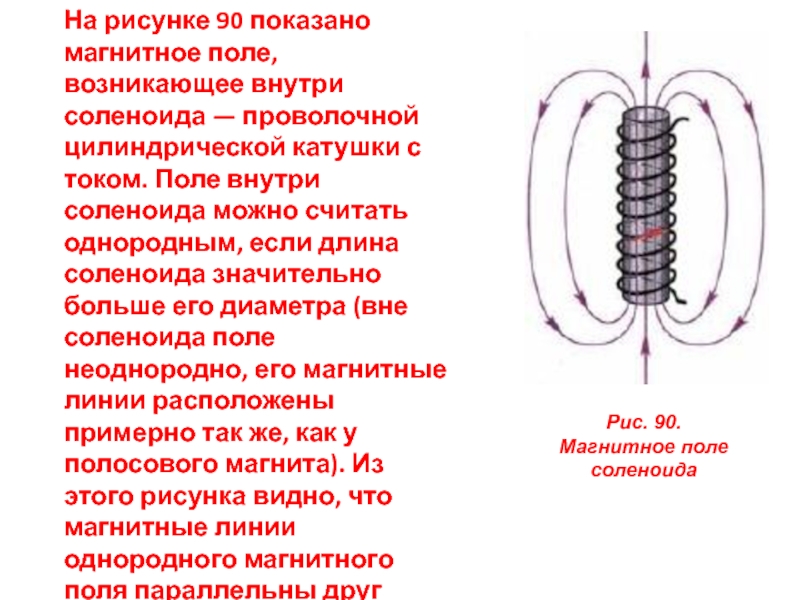
Соленоид представляет собой катушку из провода, намотанную в виде спирали на цилиндрический каркас. При пропускании электрического тока через витки соленоида внутри него возникает однородное магнитное поле. Основные характеристики магнитного поля соленоида:

• Индукция поля внутри соленоида постоянна по величине и направлению
• Линии магнитной индукции параллельны оси соленоида
• Поле внутри соленоида во много раз сильнее, чем снаружи
• Направление поля определяется правилом правого винта

Формула для расчета магнитного поля соленоида

Индукция магнитного поля B внутри бесконечно длинного соленоида рассчитывается по формуле:

B = μ0nI

где:

• μ0 — магнитная постоянная (4π × 10^-7 Гн/м)
• n — число витков на единицу длины соленоида
• I — сила тока в обмотке

Для соленоида конечной длины l формула принимает вид:

B = μ0NI / l

где N — общее число витков соленоида.

Факторы, влияющие на величину магнитного поля соленоида

Основные факторы, определяющие индукцию магнитного поля внутри соленоида:

1. Сила тока в обмотке — чем больше ток, тем сильнее поле
2. Число витков на единицу длины — чем плотнее намотка, тем сильнее поле
3. Длина соленоида — чем он длиннее, тем однороднее поле внутри
4. Материал сердечника — ферромагнетики многократно усиливают поле

Как рассчитать магнитное поле соленоида

Пошаговый алгоритм расчета индукции магнитного поля внутри соленоида:

1. Измерить длину соленоида l и его общее число витков N
2. Вычислить число витков на единицу длины: n = N / l
3. Определить силу тока I в обмотке соленоида
4. Подставить значения в формулу: B = μ0nI
5. Провести вычисления и получить значение индукции B

Пример расчета магнитного поля соленоида

Задача. Рассчитать индукцию магнитного поля внутри соленоида длиной 25 см с числом витков 500, при силе тока 2 А.

Решение:

1. Длина l = 0.25 м, число витков N = 500
2. Число витков на метр: n = 500 / 0.25 = 2000 витков/м
3. Сила тока I = 2 А
4. Подставляем в формулу: B = 4π × 10^-7 × 2000 × 2
5. B = 5.03 × 10^-3 Тл = 5.03 мТл

Таким образом, индукция магнитного поля внутри данного соленоида составляет 5.03 мТл.

Применение соленоидов на практике

Благодаря способности создавать сильное магнитное поле соленоиды широко применяются в технике и электронике:

• Электромагниты в подъемных кранах и системах сортировки
• Электромагнитные реле и контакторы
• Катушки индуктивности в электрических цепях
• Электромагнитные клапаны в гидро- и пневмосистемах
• Электромагнитные пушки и ускорители частиц
• Магнитно-резонансные томографы в медицине

Особенности магнитного поля реального соленоида

В отличие от идеального бесконечного соленоида, поле реального соленоида конечной длины имеет некоторые особенности:

• Поле неоднородно вблизи торцов соленоида
• Существует слабое магнитное поле снаружи соленоида
• Максимальная индукция наблюдается в центре соленоида
• На краях соленоида индукция примерно в 2 раза меньше, чем в центре

Как усилить магнитное поле соленоида

Основные способы увеличения индукции магнитного поля внутри соленоида:

1. Увеличить силу тока в обмотке
2. Использовать более плотную намотку провода
3. Увеличить число витков при той же длине соленоида
4. Применить ферромагнитный сердечник внутри соленоида
5. Использовать сверхпроводящую обмотку для создания очень сильных полей

Вопросы и ответы о магнитном поле соленоида

Вопрос: Как направлено магнитное поле внутри соленоида?

Ответ: Линии магнитной индукции внутри соленоида направлены параллельно его оси. Направление поля определяется по правилу правого винта — если ток течет по виткам в направлении вращения винта, то поле направлено вдоль оси в сторону поступательного движения винта.

Вопрос: Чему равно магнитное поле снаружи идеального соленоида?

Ответ: В случае бесконечно длинного идеального соленоида магнитное поле снаружи равно нулю. Для реального соленоида конечной длины снаружи существует слабое магнитное поле, быстро убывающее при удалении от соленоида.

Вопрос: Как зависит индукция поля от длины соленоида?

Ответ: При постоянном числе витков индукция магнитного поля обратно пропорциональна длине соленоида. То есть чем короче соленоид, тем сильнее поле внутри него при том же токе и числе витков.

Элементарный учебник физики Т2

Элементарный учебник физики Т2

Ландсберг Г.С. Элементарный учебник физики. Т.2. Электричество и магнетизм. — М.: Наука, 1985. — 479 c. Один из лучших курсов элементарной физики, завоевавший огромную популярность. Достоинством курса является глубина изложения физической стороны рассматриваемых процессов и явлений в природе и технике. В новом издании структура курса осталась прежней, однако в изложении проведена система единиц СИ, терминология и обозначения единиц физических величин приведены в соответствие с действующим ГОСТ. Для слушателей и преподавателей подготовительных отделений и курсов вузов, старшеклассников общеобразовательных и профессиональных школ, а также лиц, занимающихся самообразованием и готовящихся к поступлению в вуз. Оглавление ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ Глава I. Электрические заряды § 1. Электрическое взаимодействие. § 2. Проводники и диэлектрики. § 3. Разделение тел на проводники и диэлектрики § 4. Положительные и отрицательные заряды § 5. Что происходит при электризации? § 6. Электронная теория. § 7. Электризация трением. § 8. Электризация через влияние. § 9. Электризация под действием света. § 10. Закон Кулона. § 11. Единица заряда. Глава II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ § 12. Действие электрического заряда на окружающие тела. § 13. Понятие об электрическом поле. § 14. Напряженность электрического поля. § 15. Сложение полей. § 16. Электрическое поле в диэлектриках и в проводниках. § 17. Графическое изображение полей. § 18. Основные особенности электрических карт. § 19. Применение метода линий поля к задачам электростатики. § 20. Работа при перемещении заряда в электрическом поле. § 21. Разность потенциалов (электрическое напряжение). § 22. Эквипотенциальные поверхности. § 23. В чем смысл введения разности потенциалов? § 24. Условия равновесия зарядов в проводниках. § 25. Электрометр. § 26. В чем различие между электрометром и электроскопом? § 27. Соединение с Землей. § 28. Измерение разности потенциалов в воздухе. Электрический зонд. § 29. Электрическое поле Земли. § 30. Простейшие электрические поля. § 31. Распределение зарядов в проводнике. Клетка Фарадея. § 32. Поверхностная плотность заряда. § 33. Конденсаторы. § 34. Различные типы конденсаторов. § 35. Параллельное и последовательное соединение конденсаторов. § 36. Диэлектрическая проницаемость. § 37. Почему электрическое поле ослабляется внутри диэлектрика? § 38. Энергия заряженных тел. Энергия электрического поля. Глава III. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 39. Электрический ток и электродвижущая сила. § 40. Признаки электрического тока. 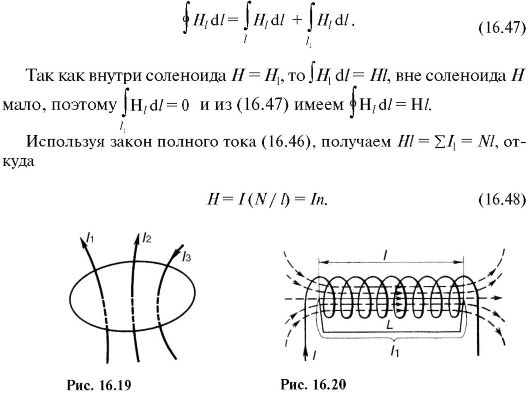§ 41. Направление тока. § 42. Сила тока. § 43. «Скорость электрического тока» и скорость движения носителей заряда. § 44. Гальванометр. § 45. Распределение напряжения в проводнике с током. § 46. Закон Ома. § 47. Сопротивление проводов. § 48. Зависимость сопротивления от температуры. § 49. Сверхпроводимость. § 50. Последовательное и параллельное соединение проводников. § 51. Реостаты. § 52. Распределение напряжения в цепи. § 53. Вольтметр. § 54. Каким должно быть сопротивление вольтметра и амперметра? § 55. Шунтирование измерительных приборов. Глава IV. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА § 56. Нагревание током. Закон Джоуля-Ленца. § 57. Работа, совершаемая электрическим током. § 58. Мощность электрического тока. § 59. Контактная сварка. § 60. Электрические нагревательные приборы. Электрические печи. § 61. Понятие о расчете нагревательных приборов. § 62. Лампы накаливания. § 63. Короткое замыкание. § 64. Электрическая проводка. Глава V. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ЭЛЕКТРОЛИТЫ § 65. Первый закон Фарадея. § 66. Второй закон Фарадея. § 67. Ионная проводимость электролитов. § 68. Движение ионов в электролитах. § 69. Элементарный электрический заряд. § 70. Первичные и вторичные процессы при электролизе. § 71. Электролитическая диссоциация. § 72. Градуировка амперметров при помощи электролиза. § 73. Технические применения электролиза. Глава VI. ХИМИЧЕСКИЕ И ТЕПЛОВЫЕ ГЕНЕРАТОРЫ ТОКА § 74. Введение. Открытие Вольты. § 75. Правило Вольты. Гальванический элемент. § 76. Как возникают э. д. с. и ток в гальваническом элементе? § 77. Поляризация электродов. § 78. Деполяризация в гальванических элементах. § 79. Аккумуляторы. § 80. Закон Ома для замкнутой цепи. § 81. Напряжение на зажимах источника тока и э. д. с. § 82. Соединение источников тока. § 83. Термоэлементы. § 84. Термоэлементы в качестве генераторов. § 85. Измерение температуры с помощью термоэлементов. Глава VII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ МЕТАЛЛЫ § 86. Электронная проводимость металлов. § 87. Строение металлов. § 88. Причина электрического сопротивления. § 89. Работа выхода. § 90. Испускание электронов накаленными телами. Глава VIII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ГАЗЫ § 91. Самостоятельная и несамостоятельная проводимость газов. § 92. Несамостоятельная проводимость газа. § 93. Искровой разряд. § 94. Молния. § 95. Коронный разряд. § 96. Применения коронного разряда. § 97. Громоотвод. § 98. Электрическая дуга. § 99. Применения дугового разряда. § 100. Тлеющий разряд. § 101. Что происходит при тлеющем разряде? § 102. Катодные лучи. § 103. Природа катодных лучей. § 104. Каналовые лучи. § 105. Электронная проводимость в высоком вакууме. § 106. Электронные лампы. § 107. Электроннолучевая трубка. Глава IX. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ПОЛУПРОВОДНИКИ § 108. Природа электрического тока в полупроводниках. § 109. Движение электронов в полупроводниках. § 110. Полупроводниковые выпрямители. § 111. Полупроводниковые фотоэлементы. Глава X. ОСНОВНЫЕ МАГНИТНЫЕ ЯВЛЕНИЯ § 112. Естественные и искусственные магниты. § 113. Полюсы магнита и его нейтральная зона. § 114. Магнитное действие электрического тока. § 115. Магнитные действия токов и постоянных магнитов. § 116. Происхождение магнитного поля постоянных магнитов. § 117. Гипотеза Ампера об элементарных электрических токах. Глава XI. МАГНИТНОЕ ПОЛЕ § 118. Магнитное поле и его проявления. Магнитная индукция. § 119. Магнитный момент. Единица магнитной индукции. § 120. Измерение магнитной индукции поля с помощью магнитной стрелки. § 121. Сложение магнитных полей. § 122. Линии магнитного поля. § 123. Приборы для измерения магнитной индукции. Глава XII. МАГНИТНЫЕ ПОЛЯ ЭЛЕКТРИЧЕСКИХ ТОКОВ § 124. Магнитное поле прямолинейного проводника и кругового витка с током. 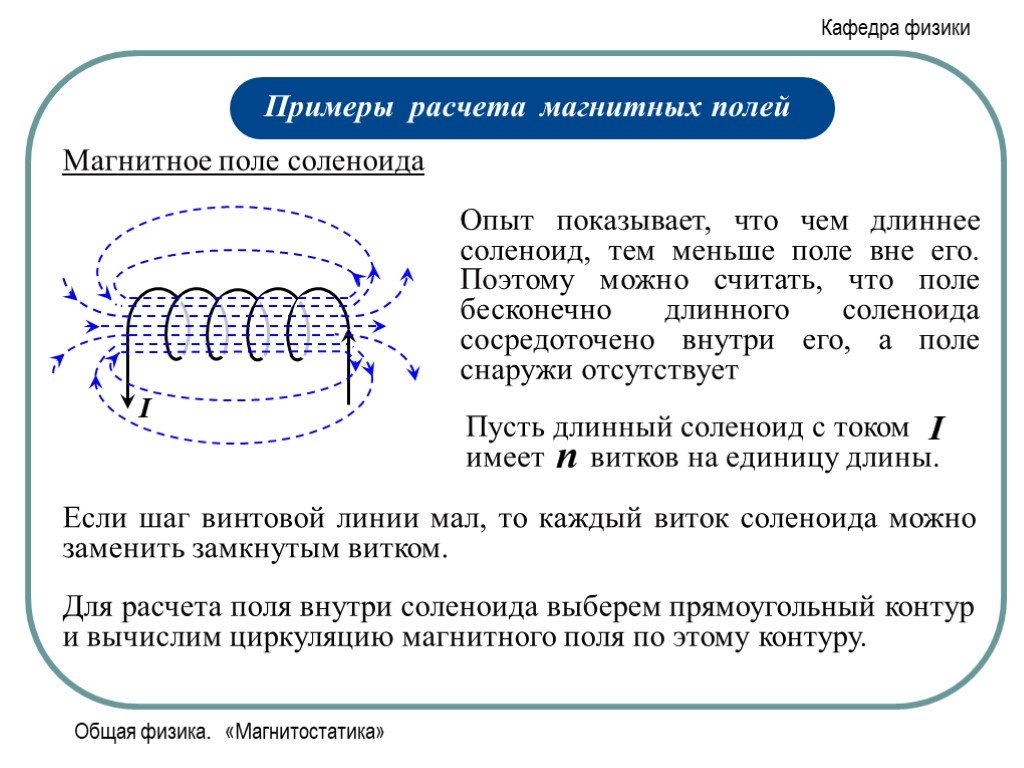§ 125. Магнитное поле соленоида. Эквивалентность соленоида и полосового магнита. § 126. Магнитное поле внутри соленоида. Напряженность магнитного поля. § 127. Магнитное поле движущихся зарядов. Глава XIII. МАГНИТНОЕ ПОЛЕ ЗЕМЛИ § 128. Магнитное поле Земли. § 129. Элементы земного магнетизма. § 130. Магнитные аномалии и магнитная разведка полезных ископаемых. § 131. Изменение элементов земного магнетизма с течением времени. Магнитные бури. Глава XIV. СИЛЫ, ДЕЙСТВУЮЩИЕ В МАГНИТНОМ ПОЛЕ НА ПРОВОДНИКИ С ТОКОМ § 132. Введение. § 133. Действие магнитного поля на прямолинейный проводник с током. Правило левой руки. § 134. Действие магнитного поля на виток или соленоид с током. § 135. Гальванометр, основанный на взаимодействии магнитного поля и тока. § 136. Сила Лоренца. § 137. Сила Лоренца и полярные сияния. Глава XV. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 138. Условия возникновения индукционного тока. § 139. Направление индукционного тока. 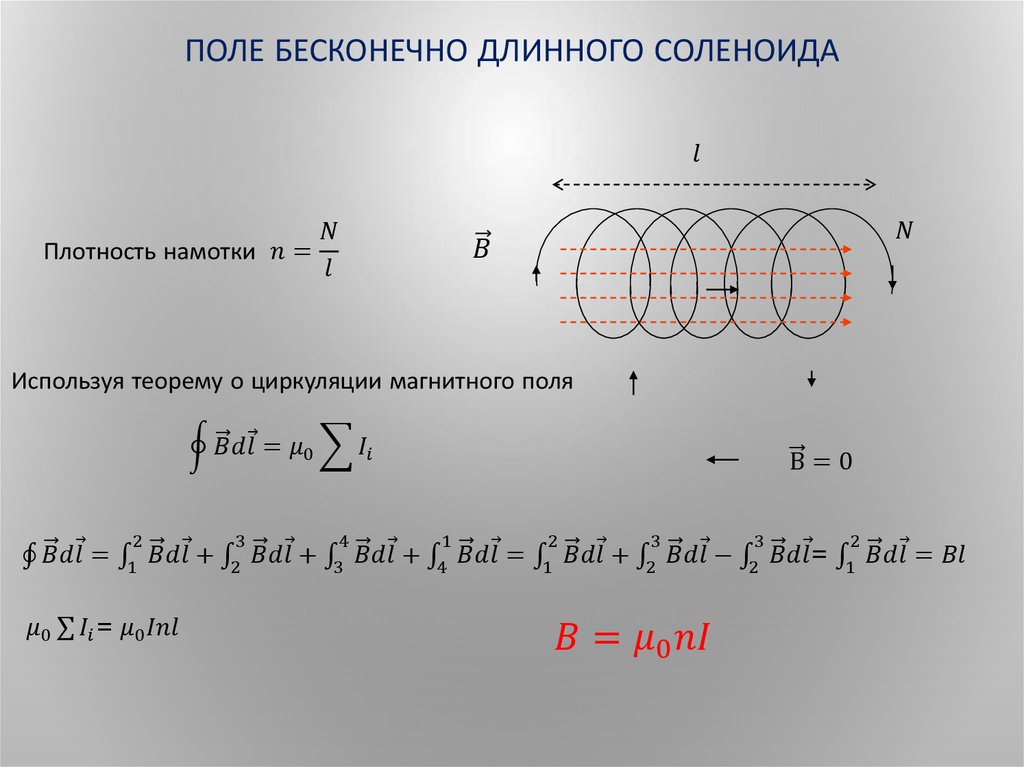Правило Ленца. § 140. Основной закон электромагнитной индукции. § 141. Электродвижущая сила индукции. § 142. Электромагнитная индукция и сила Лоренца. § 143. Индукционные токи в массивных проводниках. Токи Фуко. Глава XVI. МАГНИТНЫЕ СВОЙСТВА ТЕЛ § 144. Магнитная проницаемость железа. § 145. Магнитная проницаемость различных веществ. Вещества парамагнитные и диамагнитные. § 146. Движение парамагнитных и диамагнитных тел в магнитном поле. Опыты Фарадея. § 147. Молекулярная теория магнетизма. § 148. Магнитная защита. § 149. Особенности ферромагнитных тел. § 150. Основы теории ферромагнетизма. Глава XVII. ПЕРЕМЕННЫЙ ТОК § 151. Постоянная и переменная электродвижущая сила. § 152. Опытное исследование формы переменного тока. Осциллограф. § 153. Амплитуда, частота и фаза синусоидального переменного тока и напряжения. § 154. Сила переменного тока. § 155. Амперметры и вольтметры переменного тока. § 156. Самоиндукция. § 157. Индуктивность катушки. § 158. Прохождение переменного тока через конденсатор и катушку с большой индуктивностью. § 159. Закон Ома для переменного тока. Емкостное и индуктивное сопротивления. § 160. Сложение токов при параллельном включении сопротивлений в цепь переменного тока. § 161. Сложение напряжений при последовательном соединении сопротивлений в цепи переменного тока. § 162. Сдвиг фаз между током и напряжением. § 163. Мощность переменного тока. § 164. Трансформаторы. § 165. Централизованное производство и распределение электрической энергии. § 166. Выпрямление переменного тока. Глава XVIII. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ: ГЕНЕРАТОРЫ, ДВИГАТЕЛИ, ЭЛЕКТРОМАГНИТЫ § 167. Генераторы переменного тока. § 168. Генераторы постоянного тока. § 169. Генераторы с независимым возбуждением и с самовозбуждением. § 170. Трехфазный ток. § 171. Трехфазный электродвигатель. § 172. Электродвигатели постоянного тока. § 173. Основные рабочие характеристики и особенности двигателей постоянного тока с параллельным и последовательным возбуждением. § 174. Коэффициент полезного действия генератора и двигателя. § 175. Обратимость электрических генераторов постоянного тока. § 176. Электромагниты. § 177. Применение электромагнитов. § 178. Реле и их применения в технике и автоматике. Ответы и решения к упражнениям Приложения Предметный указатель Таблицы

12.7. Магнитное поле соленоида

Соленоид представляет собой провод, навитый равномерно в виде спирали на общий цилиндрический каркас (см. рис. 12.14). Произведение (IN) числа витков однослойной намотки соленоида на силу тока, обтекающего витки, называется числом ампер-витков.

Рис. 12.14

Соленоиды предназначены для создания в небольшом объеме пространства достаточно сильного магнитного поля. При плотной намотке витков поле соленоида эквивалентно полю системы круговых параллельных токов с общей осью. Если диаметр d витков соленоида во много раз меньше его длины (d  l), то соленоид считается бесконечно длинным (или тонким). Магнитное поле такого соленоида практически целиком сосредоточено внутри, причем вектор магнитной индукции _внутри направлен вдоль оси соленоида и связан с направлением тока правилом правого винта.

Рис. 12.15

Рассмотрим воображаемый замкнутый контур внутри соленоида (рис. 12.15). Этот контур не охватывает токов, поэтому по теореме о циркуляции

Разобьем этот круговой интеграл на четыре интеграла (по сторонам контура) и учтем, что на отрезках (1-2) и (3-4) вектор перпендикулярен, поэтому скалярное произведение (,) здесь обращается в ноль. Индукция поля во всех точках отрезка (2-3) одинакова и равна₂₃, а на отрезке (4-1) ₄₁, причем l₂₃ = l₄₁ = l.

Таким образом, обойдя контур по часовой стрелке, получим

Так как l 0, то В₂₃ = В₄₁ = В _{внутри.}

Поскольку контур внутри соленоида был выбран произвольно, то полученный результат справедлив для любых внутренних точек соленоида, то есть поле внутри соленоида однородное:

_внутри = const.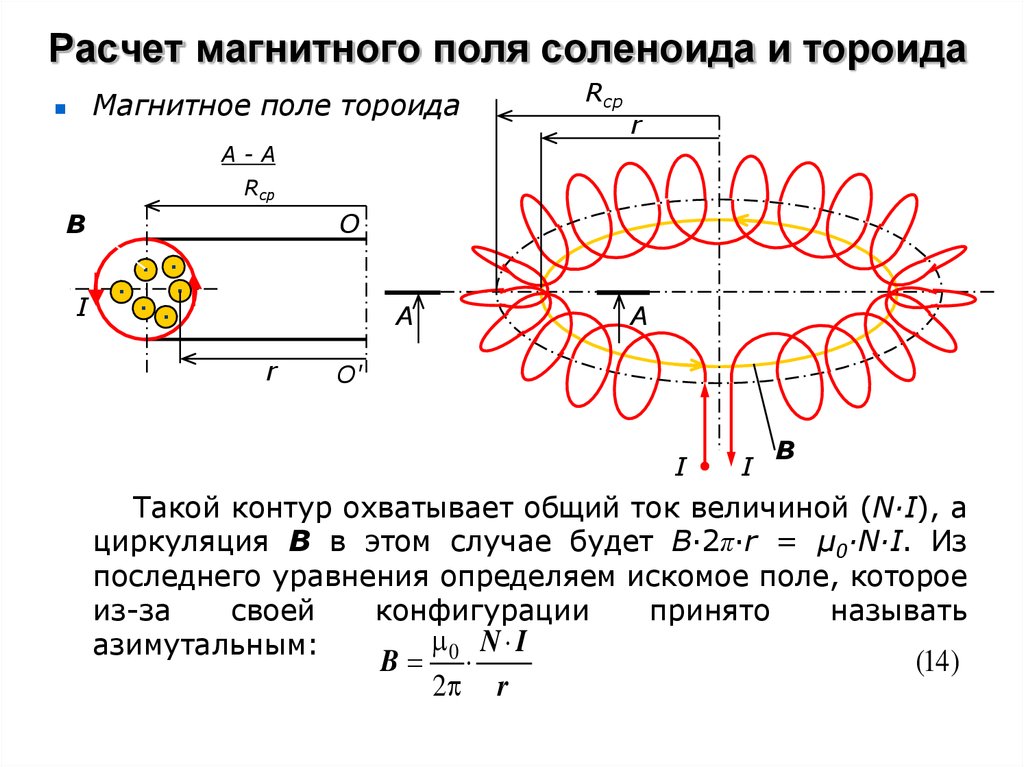

Чтобы найти величину индукции этого поля, рассмотрим контур L₂ (а –b –c –d –а ), охватывающий N витков с током (рис. 12.15). Согласно теореме о циркуляции (и на основании предыдущих рассуждений), получим соотношение

Поле снаружи бесконечно длинного соленоида очень слабое (_{снаружи} =0), им можно пренебречь, следовательно,

(12.35)

где n=N/l — число витков, приходящихся на единицу

длины соленоида.

Таким образом, индукция магнитного поля внутри бесконечно длинного соленоида одинакова по величине и направлению и пропорциональна числу ампер-витков, приходящихся на единицу длины соленоида.

Симметрично расположенные витки вносят одинаковый вклад в магнитную индукцию на оси соленоида, поэтому у конца полубесконечного соленоида на его оси магнитная индукция равна половине того значения, которое дает формула (12. 35), т.е.

(12.36)

Практически, если (l  d), то формула (12.35) справедлива для точек в средней части соленоида, а формула (12.36) – для точек на оси вблизи его концов.

Применяя закон Био-Савара-Лапласа, можно найти магнитную индукцию поля соленоида конечной длины (рис. 12.16) в произвольной точке А на его оси:

(12.37)

где- углы между осью соленоида и радиус- вектором, проведенным из рассматриваемой точки к концам соленоида.

Рис. 12.16

Поле такого соленоида неоднородное, величина индукции зависит от положения точки А и длины соленоида. Для бесконечно длинного соленоида ,, и формула (12.37) переходит в формулу (12.35).

Магнитное поле в соленоиде: Узнайте больше здесь

• Автор Саурав_C
• Последнее изменение 25-01-2023

При пропускании тока через проводник создается магнитное поле.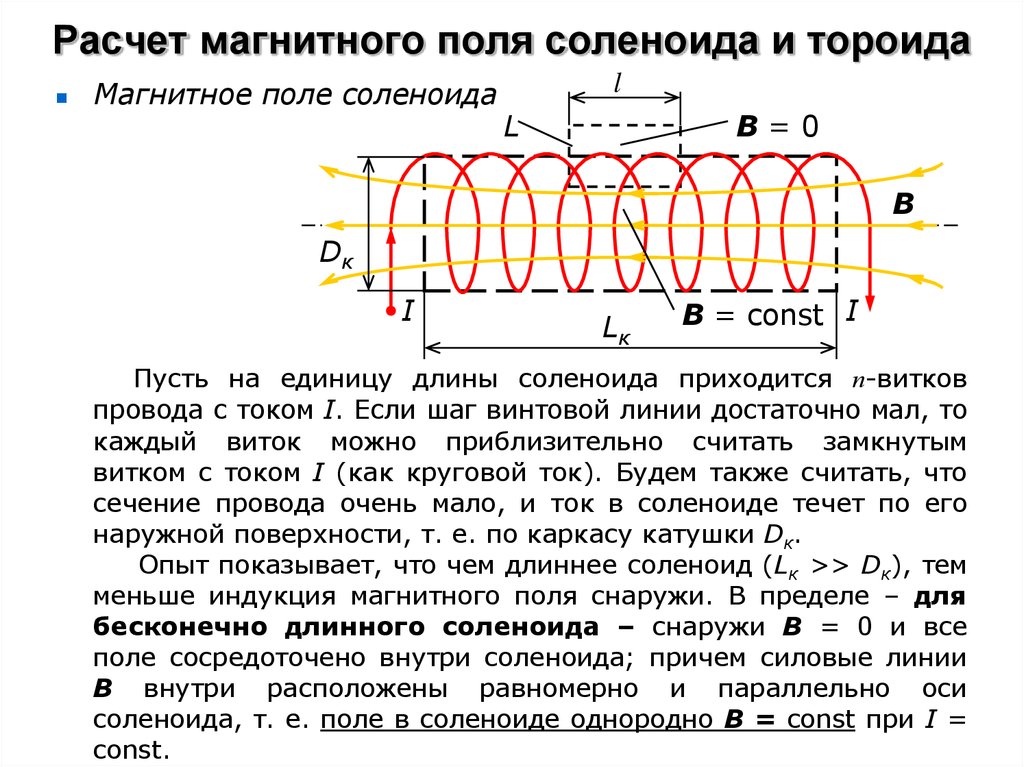 То же самое происходит с соленоидом, когда через него проходит электрический ток. Когда ток проходит через соленоид, он становится электромагнитом. Формула для магнитного поля в соленоиде : \(B = {\mu _0}nI.\)

.0009 однородное магнитное поле ? Знаете ли вы, как петля соленоида с током создает магнитное поле? В магнетике для расчета магнитного поля высокосимметричной конфигурации, несущей постоянный ток, мы используем закон Ампера. В этой статье мы обсудим магнитное поле внутри соленоида, формулу соленоида, магнитное поле, обусловленное током в соленоиде, и магнитное поле формулы соленоида.

Соленоид представляет собой длинный провод, намотанный в виде спирали, и с помощью этой конфигурации мы можем создать достаточно однородное магнитное поле. Мы можем рассматривать каждый виток соленоида как круговую петлю, когда витки расположены близко друг к другу, а чистое магнитное поле представляет собой векторную сумму полей, возникающих в результате всех витков.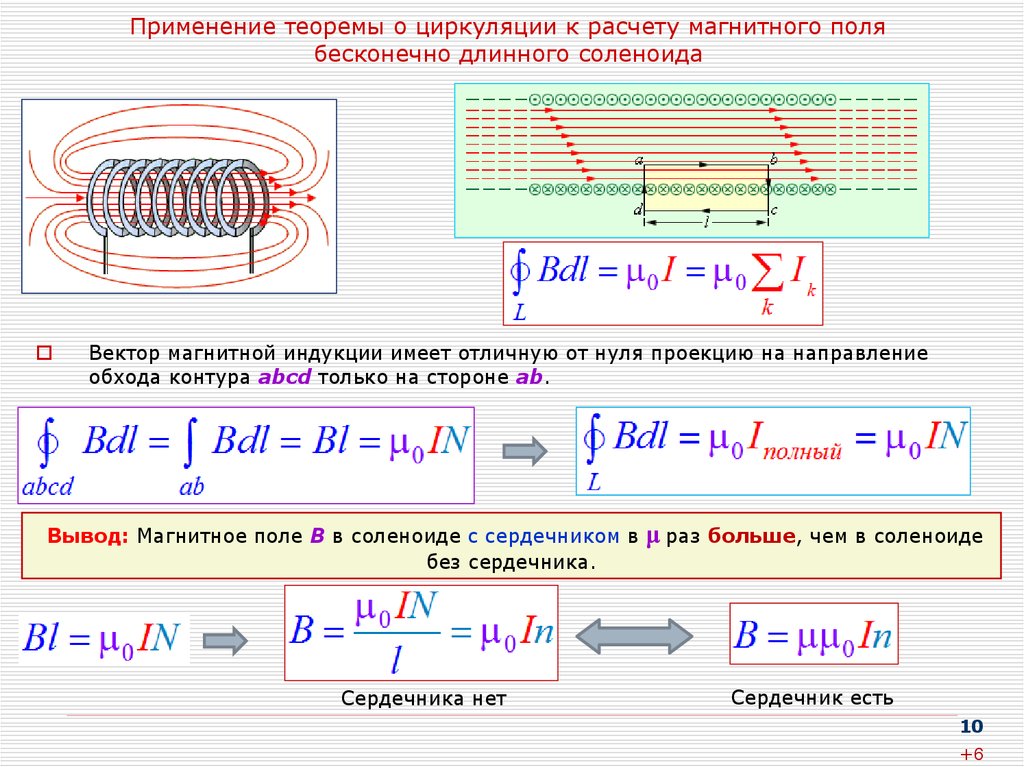 Внутреннее поле становится более однородным и по мере увеличения длины соленоида.

Когда витки расположены близко друг к другу, а длина намного больше радиуса витков, то мы можем аппроксимировать это как идеальный соленоид . Внешнее поле равно нулю, а внутреннее поле в этом случае однородно в большом объеме. Закон Ампера используется для получения выражения для магнитного поля в идеальном соленоиде.

Круговой закон Ампера

Рассмотрим границу, состоящую из множества мелких линейных элементов. Рассмотрим один такой элемент длины \((d\vec l).\) Возьмите тангенциальную составляющую магнитного поля, создаваемого этим элементом, и умножьте ее на длину этого элемента \((d\vec l).\) Все такие произведения складываются и считаются пределом по мере уменьшения длины элементов и увеличения их числа. Тогда сумма стремится к интегралу. Закон Ампера гласит, что линейный интеграл магнитного поля вокруг замкнутого контура пропорционален величине тока, протекающего по контуру.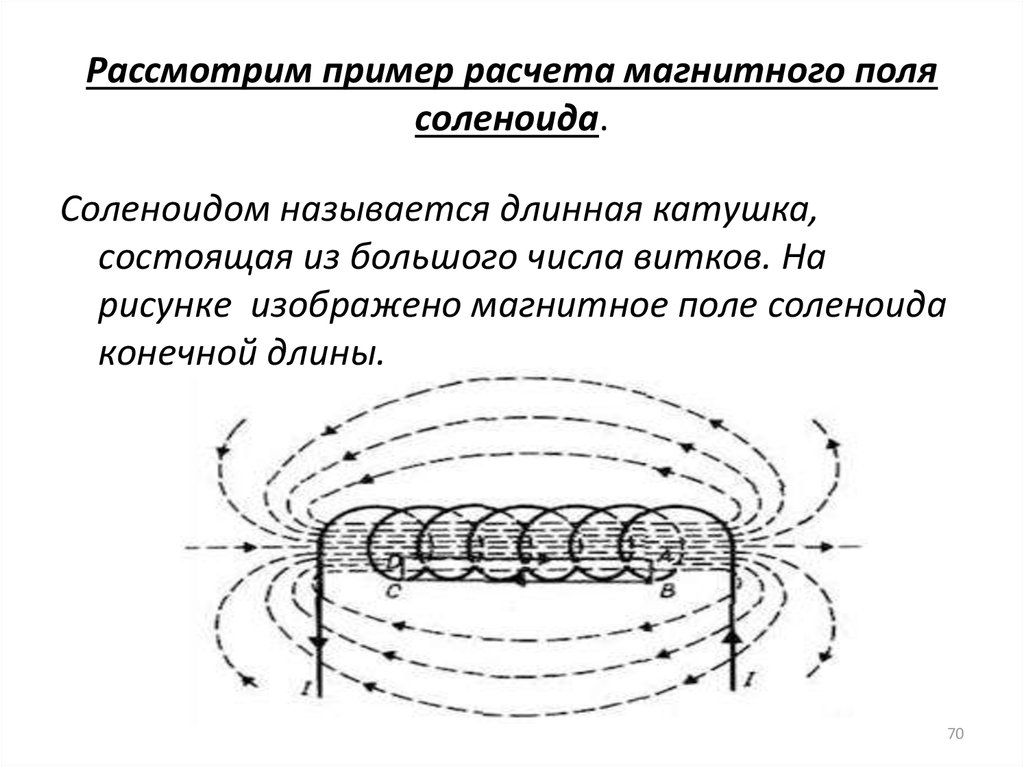 9{ – 7}}\;\rm{T – м/А}\)

Единица: Магнитное поле является векторной величиной и имеет единицу измерения СИ тесла \(\left( \rm{T} \right) .\)

Направление: Мы можем определить направление магнитного поля с помощью правила большого пальца правой руки.

Линии магнитного поля в соленоиде

Чтобы понять природу силовых линий магнитного поля внутри соленоида, давайте возьмем два одинаковых тока, несущих круговые петли, расположенные коаксиально рядом друг с другом. Магнитное поле, создаваемое каждой катушкой, показано на рисунке ниже. В любой точке \(P\) на некотором расстоянии (более радиуса катушки) от оси мы можем наблюдать, что магнитное поле каждой катушки имеет противоположное направление.

Если расстояние между обеими катушками будет очень маленьким, они почти нейтрализуют друг друга, и результирующее магнитное поле будет очень слабым. Возьмем другую точку \(Q\) на оси или вблизи оси. В этот момент магнитное поле из-за обеих катушек имеет одинаковое направление, поэтому результирующее поле будет более сильным по своей природе.

Когда стержень круглой катушки расположен близко друг к другу, он образует соленоид. В любой внешней точке поле любой катушки будет противодействовать другим соседним катушкам. Это вызовет тенденцию к нулевому магнитному полю вне катушки. С другой стороны, в любой внутренней точке поле каждой катушки будет аддитивным по своей природе. Это вызывает стремление иметь более сильное и однородное магнитное поле внутри катушки. Тенденция иметь нулевые поля снаружи и однородное поле внутри становится все более и более эффективной, когда соленоид плотно намотан и имеет большое количество катушек.

Для идеального соленоида магнитное поле в любой внешней точке будет равно нулю, а внутри будет однородным.

Формула магнитного поля в Соленое d

Чтобы применить закон Ампера, рассмотрим воображаемую петлю ампера в форме прямоугольника \(abcd,\), как показано на рисунке ниже. Вдоль \(cd,\) \(\vec B \cdot d\vec l\) равно нулю, потому что магнитное поле равно нулю, поскольку оно находится вне идеального соленоида. Вдоль поперечных сечений \(bc\) и \(ad,\) поле будет перпендикулярно пути, поэтому \(\vec B \cdot d\vec l\) будет равно нулю. Таким образом, эти два раздела не вносят вклада. Теперь на пути \(ab,\) поле имеет то же направление, что и \(d\vec l.\). Пусть поле вдоль \(ab\) равно \(\vec B.\) Таким образом, рассматриваемая длина амперова петля равна \(h(ab).\) И общее количество витков в петле будет \(nh,\), где \(n\) — количество витков на единицу длины.

Интеграл по замкнутому амперному прямоугольному пути будет равен
\(\oint {\vec B} \cdot d\vec l = Bh…..\left( 1 \right)\)
область, ограниченная путем интегрирования, равна присутствует в правой части уравнения закона Ампера. В этом случае
\({I_{{\text{enc}}}} = \left( {{\text{число}}\,{\text{из}}\,{\text{поворотов}}\ , {\ text {внутри}} \, {\ text {}} \, {\ text {область}}} \ right) \ times \ left ( {\ text {current}} \, {\ text {через }}\,{\text{каждый}}\,{\text{поворот}}} \вправо)\)
\({I_{{\text{enc }}}} = \left({nh}\right)\left( I \right)\quad \ldots …\left( 2 \right)\)
Используя закон Ампера мы имеем,
\(\oint {\vec B} \cdot d\vec l = {\mu _0}{I_{{\text{enc}}}}\)
Или,
Используя уравнения \(\left( 1 \right)\) и \(\left( 2 \right),\) имеем
\(Bh = {\mu _0}{I_{{\text{enc}}}},\)
\( \ Стрелка вправо Bh = {\mu _0}I\left({nh} \right),\)
\( \Стрелка вправо B = {\mu _0}nI\quad \ldots \left(3\right)\)
Формула магнитного поля дает хороший результат, когда длина соленоида много больше радиуса петли. Это уравнение используется для получения величины магнитного поля внутри длинного соленоида.
Итак, можно сказать, что магнитное поле внутри длинного идеального соленоида зависит от трех основных факторов.
(i) Число витков на единицу длины в соленоиде \(\left( n \right)\)
(ii) Сила тока в катушке соленоида \(\left( I \right)\)
(iii) Проницаемость материала внутри соленоида \(\left( \mu \right)\)

Решенные примеры

Магнитного поля в соленоиде

Q.1. Какова величина магнитного поля внутри длинного соленоида, если через него протекает ток \(5\;\rm{A}\)? Дано, что длина соленоида \(0,5\,\rm{м}\) и имеет \(500\) витков. 9{ – 7}}}} = 0,3\;\rm{A}\)

Резюме

Соленоид представляет собой длинный провод, намотанный в виде спирали, который может создавать достаточно однородное магнитное поле. Магнитное поле почти однородно внутри соленоида и близко к нулю вне соленоида. Мы используем закон Ампера, чтобы получить выражение для внутреннего магнитного поля в идеальном соленоиде, которое утверждает, что линейный интеграл магнитного поля вокруг замкнутого контура пропорционален величине тока, протекающего по контуру. 9{ – 7}}\;\rm{T – m/A}).\) Величина магнитного поля будет постоянной внутри длинного соленоида.

Часто задаваемые вопросы о магнитном поле в соленоиде

Q.1. Какова формула магнитного поля соленоида?
Ответ: Магнитное поле внутри идеального соленоида имеет величину \(B = {\mu _0}nI.\) Здесь количество витков на единицу длины равно \(n,\) длина равна \(L,\ ), а ток равен \(I.\). Его можно вычислить из выражения, полученного из закона Ампера.

Q.2. Какова природа магнитного поля внутри идеального соленоида?
Ans: Внутри идеального соленоида магнитное поле однородно, а силовые линии представляют собой прямые параллельные линии.

Q.3. Чему равно магнитное поле вне соленоида?
Ответ : Линии магнитного поля существуют вне соленоида, но количество силовых линий на единицу площади вне соленоида намного меньше по сравнению с количеством линий на единицу площади внутри соленоида.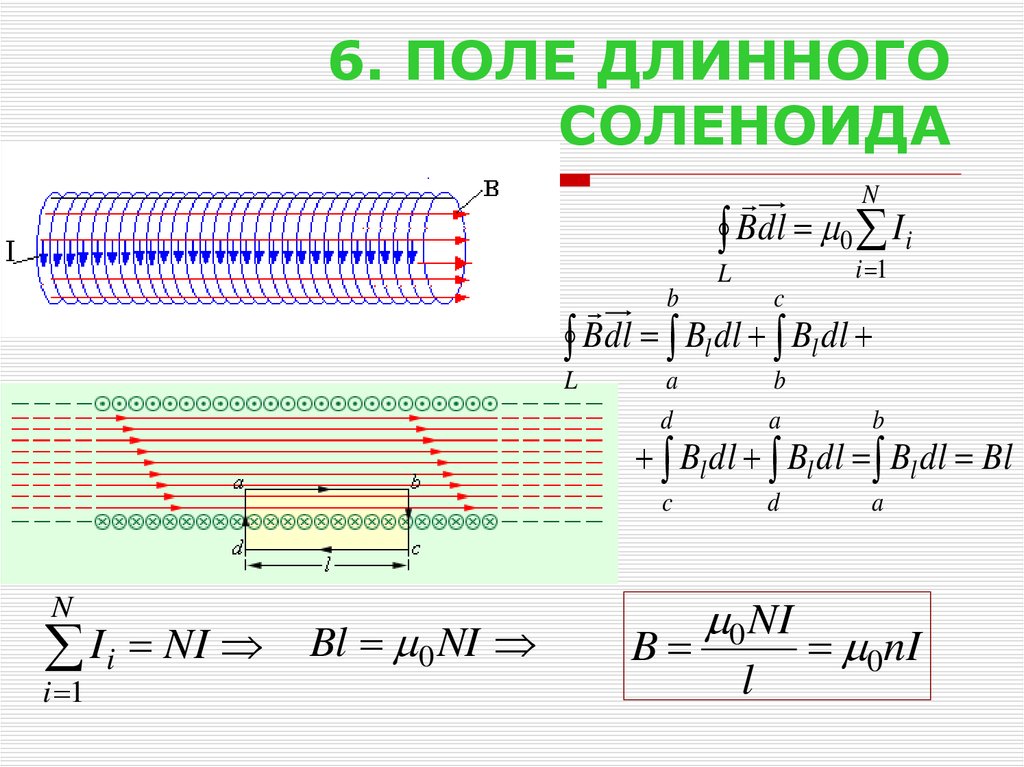 Следовательно, магнитное поле считается практически нулевым, потому что магнитное поле вне соленоида очень слабое. Для идеального соленоида его значение будет равно нулю.

Q.4. Каково использование соленоида?
Ответ : Когда ток проходит через соленоид, он становится электромагнитом. Электромагниты используются в магнитных дверных замках, клапанах давления воды в системах кондиционирования воздуха, аппаратах МРТ, жестких дисках, динамиках, микрофонах и т. д.

Q.5. Какие факторы влияют на соленоиды?
Ответ : Некоторые важные факторы, влияющие на соленоид, приведены ниже:
(i) Количество витков на единицу длины в соленоиде
(ii) Сила тока в катушке соленоида
(iii) Материал внутри соленоида

Калькулятор магнитного поля соленоида | Магнитное поле соленоида Формула

Воспользуйтесь помощью инструмента Калькулятор магнитного поля соленоида, чтобы получить магнитное поле внутри соленоида. Просто вы должны обеспечить ток, длина и количество витков в полях ввода калькулятора и нажмите кнопку расчета, чтобы получить магнитное поле, как только возможный.

Калькулятор магнитного поля соленоида: Расчет магнитное поле внутри катушки соленоида не просто. Получить магнитный значение поля быстро, предоставляя необходимые детали в этом легком для работать с калькулятором. Кроме того, проверьте пошаговый процесс, чтобы найти магнитное поле внутри катушки соленоида. Узнайте больше о концепции в следующие разделы.

Ознакомьтесь с подробными инструкциями по расчету магнитного поля. внутри соленоида легко. Ознакомьтесь с принципами, правилами и внимательно следи за ними.

• Получите количество тока, протекающего через соленоид, количество витков и длина соленоида.
• Умножьте количество витков на постоянную вакуумной проницаемости и текущий.
• Разделите произведение на длину соленоида, чтобы проверить магнитное поле.

Соленоид представляет собой провод, который туго намотан на длинную тонкую катушку. Если по проводу течет ток, вокруг него возникает магнитное поле.

Магнитное поле вне соленоида бесконечной длины равно нулю и константа для внутреннего соленоида. Формула для расчета магнитного поля внутри силеноида вдоль линий.

B = μoIN / L

Где

B — магнитное поле соленоида

I — ток, протекающий через соленоид

μo – вакуумная проницаемость, ее значение равно 1,26×10 ^-7 Тм/А.

N — количество витков

L — длина соленоида

Пример

Вопрос: Соленоид с 25 витками пропускает ток 15 А и длина 32см. Чему равно магнитное поле внутри катушки?

Решение:

Учитывая, что

Число витков N = 25

Ток I = 15 А

Длина L = 32 см = 0,32 м

Магнитное поле соленоида0011

В = (1,26×10 ^-7 х 15 х 25)/0,32

= (472,5 х 10 ^-7 )/0,32

= 1476,5 х 0 0 9 0 9 1 8 1 8 -6 7 Следовательно, магнитное поле внутри соленоида составляет 1476,5 х 10 ^-7 . А.

У Physicscalc.Com есть концепции как классическая механика, термодинамика, давление воды, гравитация и многие другие вместе с соответствующими калькуляторами все под одной крышей.

1. Чему равно магнитное поле внутри соленоида?

Соленоид представляет собой катушку провода, предназначенную для создания сильного магнитное поле внутри катушки. Это разновидность электромагнита, целью является создание управляемого магнитного поля.

---

2. Что такое магнитное поле в формуле соленоида?

Магнитное поле внутри соленоида прямо пропорционально приложенный ток и число витков на единицу длины. Его формула В = мкОИН/л.

---

3. Влияет ли длина соленоида на магнитное поле?

Да, длина соленоида влияет на магнитное поле. Как магнитный поле обратно пропорционально длине катушки, чем больше соленоид длина означает меньшее магнитное поле.