Расчет п контура онлайн. Расчет П-контура и согласование антенн: полное руководство

Как правильно рассчитать П-контур для согласования антенны. Какие параметры антенны нужно измерить перед настройкой. Как добиться максимальной эффективности работы антенны на разных диапазонах. Какие типы согласующих устройств лучше использовать для разных антенн.

Основы расчета П-контура для согласования антенн

П-контур является одним из наиболее распространенных типов согласующих устройств, используемых для подключения антенн к передатчикам. Правильный расчет параметров П-контура позволяет добиться максимальной эффективности работы антенны на заданной частоте.

Для расчета П-контура необходимо знать следующие параметры:

• Выходное сопротивление передатчика
• Входное сопротивление антенны
• Рабочая частота

Основные формулы для расчета элементов П-контура:

1. X_C1 = √(R₁ * R₂) — R₁
2. X_C2 = R₂ * X_C1 / R₁
3. X_L = X_C1 + X _C2

где R₁ — выходное сопротивление передатчика, R₂ — входное сопротивление антенны.

Измерение параметров антенны перед настройкой

Для эффективного согласования антенны необходимо измерить ее входное сопротивление и реактивную составляющую на рабочей частоте. Это можно сделать с помощью специальных приборов или самодельных устройств.

Основные параметры, которые нужно определить:

• Активное сопротивление излучения
• Реактивное сопротивление (емкостное или индуктивное)
• Резонансная частота антенны

Зная эти параметры, можно правильно рассчитать элементы согласующего устройства для конкретной антенны.

Типы согласующих устройств для разных антенн

Выбор оптимального типа согласующего устройства зависит от параметров антенны и передатчика:

• П-контур — универсальное решение для большинства случаев
• Г-контур — для антенн с высоким входным сопротивлением
• Т-контур — для антенн с низким входным сопротивлением
• Последовательный LC-контур — для компенсации реактивности

Для многодиапазонных антенн часто используют комбинированные схемы согласования с переключаемыми элементами.

Настройка антенны на разных диапазонах

При работе на нескольких диапазонах важно обеспечить эффективное согласование антенны на всех используемых частотах. Для этого применяют следующие методы:

1. Использование отдельных согласующих устройств для каждого диапазона
2. Применение широкополосных согласующих трансформаторов
3. Использование переключаемых элементов в согласующем устройстве
4. Установка дополнительных компенсирующих элементов в антенне

Важно учитывать, что параметры антенны могут сильно меняться при переходе с одного диапазона на другой. Поэтому необходимо проводить измерения и настройку отдельно для каждой рабочей частоты.

Практические рекомендации по настройке согласующих устройств

При настройке согласующих устройств следует придерживаться следующих рекомендаций:

• Начинать настройку с низкой мощности передатчика
• Использовать КСВ-метр для контроля согласования
• Добиваться минимального КСВ на рабочей частоте
• Проверять полосу пропускания антенны после настройки
• Контролировать нагрев элементов согласующего устройства

Правильно настроенное согласующее устройство обеспечивает максимальную передачу мощности в антенну и минимальные потери.

Расчет П-контура с помощью онлайн-калькуляторов

Для упрощения расчетов параметров П-контура можно использовать специализированные онлайн-калькуляторы. Они позволяют быстро подобрать оптимальные значения элементов схемы по заданным параметрам антенны и передатчика.

Основные преимущества использования калькуляторов:

• Экономия времени на расчеты
• Возможность быстрого перебора вариантов
• Учет реальных параметров компонентов
• Визуализация результатов расчета

При использовании калькуляторов важно правильно задать исходные данные и критически оценивать полученные результаты.

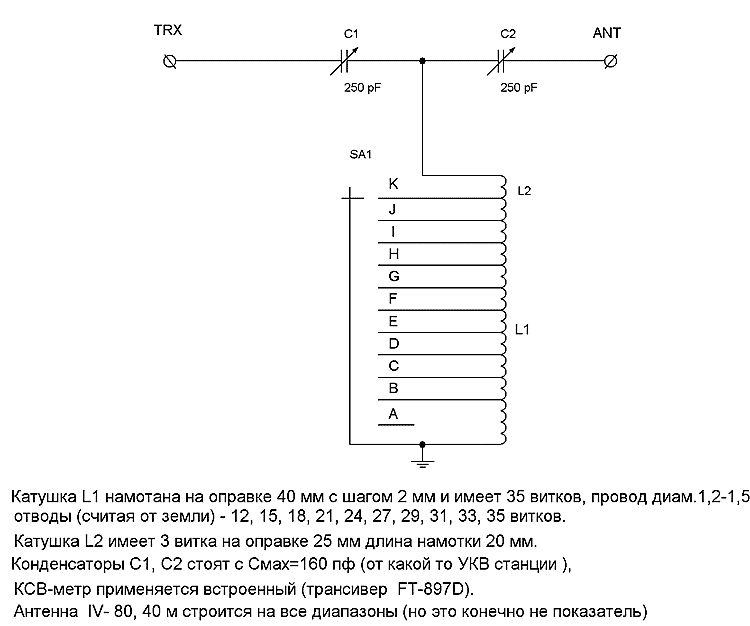
Особенности согласования коротких антенн

Короткие антенны, длина которых меньше четверти длины волны, имеют низкое входное сопротивление и высокую реактивность. Это создает определенные трудности при их согласовании.

Основные методы согласования коротких антенн:

1. Использование удлиняющих катушек индуктивности
2. Применение емкостных удлинителей
3. Использование трансформаторов сопротивления
4. Применение специальных схем согласования (L-контур, гамма-согласование)

При настройке коротких антенн особое внимание следует уделять обеспечению широкой полосы пропускания и снижению потерь в согласующих элементах.

Измерение эффективности работы антенны после настройки

После настройки согласующего устройства важно оценить эффективность работы антенны. Для этого проводят следующие измерения:

• Измерение КСВ в рабочей полосе частот
• Определение полосы пропускания антенны
• Измерение входного сопротивления антенны
• Оценка диаграммы направленности
• Измерение коэффициента усиления

Сравнение полученных результатов с теоретическими характеристиками антенны позволяет оценить качество настройки и выявить возможные проблемы.

Настройка и согласование антенн

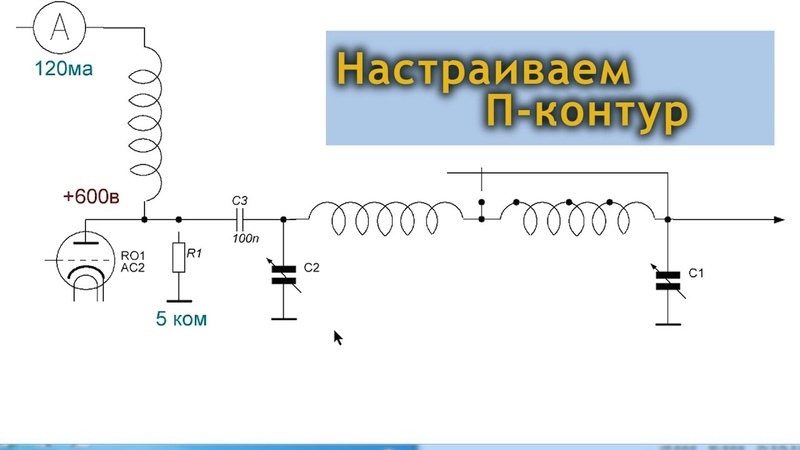
Варианты двухзвенных согласующих устройств. 1) Устройство согласующее активную нагрузку и активное эквивалентное совпротивление выходного контура. Если необходимо повысить фильтрующие способности этого устройства, то между конденсатором и индуктивностью включается последовательный контур настроенный на эту же частоту.. Тогда получается автотрансформаторный вход передатчика. Реактивное сопротивление конденсатора здесь равно сумме сопротивлений согласующего устройства и кондесатора дополнительного последовательного контура. Если пна подключаемых концах антенны имеется какое-то реактивное сопротивление, то оно может быть нейтрализовано изменением емкости С согласующего устройства. Таким образом это устройство может согласовывать нагрузки, если она меньше эквивалентного сопротивления выходного каскада. Для варианта Для этого устройства целесообразно провести новый расчет Представим это выражение в виде Далее, при последовательном подключении реактивного сопротивление от катушки L1 получим Наконец, введя обозначения и подсоединяя паралелльно катушку XL2 получим Условие резонанаса сводится к равенству нулю мнимого второго члена, что возможно при Отсюда Отсюда следуют два предельных случая , при котором XL2=0 и XL1=0 . После подстановки сюда a и b получим Это очень примечательное выражение, ибо оно дает возможность вычислить сопротивление индуктивности по известному сопротивлению нагрузки и емкостному реактивному соппротивлению параллельного контура. Отсюда видно, что подключение нагрузки к параллельному контуру изменяет частоту резонанса. Расчет по новому выражению для П-контура, для приведенных выше условий, дает значения: с1=60,11 пкф, с2=232пкф, L=9,31мкгн. Как видно, различие в значениях, особенно с2, с ранее приведенным, весьма большое. Именно по этим данным такая настройка и проводится практически. То есть этот расчет показывает, что правильно рассчитанный П-контур действительно хорошо фильтрует сигнал и согласует входное сопротивление антенны в случае отсутствия в нем реактивной составляющей. Но он удобен только в случае лампового выходного каскада с высоким эквивалентным сопротивлением. Для выходного каскада на транзисторах, с низким выходным сопротивлением, расчетные значения конденсаторов оказываются очень большими и трудно выполнимыми практически. Поэтому здесь целесообразно использовать второй вариант комбинации двух Г- образных звеньев, когда они меняются местами и соединяются своими точками с высоким напряжением, а точки с низким напряжением соединяются с антенной и выходным каскадом с низким эквивалентным сопротивлением,. Впрочем, можно несколько изменить Т- контур заменив индуктивности на емкости и наоборот. Тогда будет новый вариант. Можно ли работать на нескольких диапазонах с одной антенной? Судя по рассмотренным выше особенностям П-контура, его применение как согласующего устройства для работы с одной антенной на разных диапазонах, возможно, для ламповых выходных каскадов, если дополнительно компенсировать реактивные сопротивления в самой антенне. Оно ограничено только возможным диапазоном изменения переменных конденсаторов и переменных индуктивностей с переключателями на различное число витков. Допустим очень трудно регулировать очень малые емкости или создавать большие индуктивности. Если антенна питается через коаксиальный кабель, то в принципе это ничего не меняет, ибо надо только рассчитать какой ток он может выдержать в узлах. Для транзисторных выходных каскадов более подходит, описанный выше Т- контур. Однако все зависит еще и от фактических входных параметров антенны на разных диапазонах. Вообще желание иметь одну антенну на все диапазоны вполне осуществимое дело. Надо только хорошо разбираться как это сделать. Трудно ли определить сопротивление излучения и реактивную составляющую антенны на разных диапазонах? Эти параметры также являются весьма завуалированными в различных описаниях, ибо отсутствуют простые способы их определения. Автор практически опробовал несколько вариантов таких устройств и подобрал наиболее удачную схему. Для ее реализации нет необходимости строить специальное сооружение в корпусе ибо в таком виде оно даже может исказить результаты. На первых порах достаточно иметь ГИР (Например, промышленный ГИР1) , микроамперметр на 50 мка с выпрямляющим мостом, два переменных конденсатора 15-500 пкф, две катушки индуктивности в 30 мкгн., с напаянными выводами для захвата крокодильчиками через 2-3 витка, размещенных на корпусах диаметром 60 мм с шагом укладки намотки в 3-1,5мм -для удобства напайки жестких отводов. Можно также использовать катушки со скользящими контактами. Кроме этого надо иметь набор проводов длиной по 10-15 см с крокодильчиками на концах для проведения временных соединений. Затраты на изготовление и приобретение всего названного с лихвой окупятся эмоциональностью лицезрения действия многих полезных функций создаваемого прибора. Полная схема его показана на рис 3: Рис 3. Схема прибора. . Микроамперметр присоединяется параллельно к клеммам 1 совместно с клеммами ВЧ напряжения от ГИРа. Если используется источник ВЧ напряжения с низким выходным сопротивлением, то подключение проводится через резистор. Падение напряжения на нем как раз и фиксируется в резонансе. Установив нужную частоту источника, постепенно увеличивается напряжение ВЧ и проверяется наличие отклонения стрелки прибора.. Теперь можно приступить к первому этапу работы- тарировке емкости конденсаторов по углу поворота и индуктивности по числу витков. Сначала надо добиться резонанса вращением конденсатора С1 в сторону максимума показания прибора. После этого следует увеличить ВЧ напряжение до максимальной точки шкалы. Подключая параллельно контуру различные постоянные конденсаторы и восстанавливая резонанс находится несколько контрольных точек, по которым определяется зависимость емкости конденсатора от угла поворота. Затем по показаниям емкости тарируется катушка индуктивности. Эти данные заносятся в таблицу и интерполируются на целые деления угла поворота через 10 градусов. Аналогичная процедура проводится и с парой С2 , После этого можно приступить к измерениям. Для несведущих напомним, что любая антенна ведет себя двояко. С одной стороны ее можно представить как последовательный контур, соединяющий индуктивность и емкость, и некоторое активное сопротивление называемое сопротивлением излучения. Если к концам 2 на рис 3 подключить активное сопротивление то вместе с L2 и C2 как раз и будет образован последовательный контур. С другой стороны та же самая антенна может работать как параллельный контур по типу L1, C1 с концами 1 замкнутыми сопротивлением излучения. Эти сопротивления, для одной и той же антенны, отличается на порядок. Почему именно так работает антенна никому неизвестно, хотя и есть обоснованные предположения. Но что это именно так, можно убедиться из последующих измерений. Чтобы определить сопротивление излучения при параллельном подключении антенны используется только L1 и C1. Включив ГИР необходимо подать переменное напряжение на одном из рабочих диапазонов добившись резонанса по максимуму отклонения стрелки микроамперметра. Затем необходимо определить емкость конденсатора по углу поворота. После этого к концам катушки L1 подключаются выводы антенны (Для антенны типа длинный провод одним концом является заземление.). После подключения показания прибора снизятся. Это произойдет ввиду наличия в антенне реактивного и активного сопротивления. Вращая ручку конденсатора следует вновь добиться резонанса по максимуму показаний и определить емкость конденсатора. Необходимо также записать новое показание прибора. Если емкость конденсатора увеличилась, то это значит, что антенна обладает дополнительным индуктивным сопротивлением Xa, которое подключаясь параллельно к индуктивному сопротивлению L1 уменьшая его значение. Для определения индуктивного сопротивления антенны, именно в этом случае, необходимо вычислить емкостное сопротивление конденсатора, которое было до подключения антенны и после подключения Xc, Xca, и провести вычисления по формулам X=Xc-Xca Xa=X*Xc/(Xc-X) . Далее по Xa следует вычислить величину индуктивности за зажимах антенны. Подключая затем вместо антенны переменное сопротивление и устанавливая резонанс необходимо добиться того же показания прибора, которое было при подключенной антенне. Это как раз и будет сопротивлением излучения. Если емкость при подключении антенны, в резонансе, уменьшится, то это значит, что антенна обладает дополнительным емкостным сопротивление. Величина изменения емкости конденсатора как раз и будет равна входной емкости антенны. . Работа по определению сопротивления излучению при последовательном резонансе проводится после подключения антенны к разъему 2. При этом устанавливается максимум показаний при вращении конденсатора 1 и минимум показаний при вращении конденсатора 2. Это достигается последовательно несколькими настройками. После этого записываются показания двух конденсаторов и прибора. Далее вместо антенны подключается переменное сопротивление и, повторяя всю процедуру устанавливая резонанс двумя конденсаторами и величину сопротивления так, чтобы добиться прежнего показания прибора. После этого вновь записывают показания двух конденсаторов и тестером измеряют величину переменного сопротивления. Она и будет равна сопротивлению излучения. Величина емкости С1 должна автоматически быть той же, что и при подключении антенны. По значению отклонения С2 с антенной и с активным сопротивлением можно найти величину реактивного сопротивления антенны. Если емкость с антенной была меньше, чем с активным сопротивлением, то это значит, что антенна имеет дополнительное индуктивное входное сопротивление, которое в приборе компенсируется уменьшением емкости. Это уменьшение и будет численно равно индуктивному сопротивлению. Если, наоборот, емкость с антенной больше, что означает уменьшение емкостного сопротивления, то следовательно антенна имеет дополнительное емкостное сопротивление- как раз то, на которое уменьшилось сопротивление конденсатора. Точка подключения к контуру L1, C1 определяется удобством измерений. В качестве примера ниже приведены результаты таких измерение для антенны типа LW длинный провод с заземлением имеющей собственную резонансную частоту в 5,94 мгц. Сопротивление в омах Частота в мгц. Параллельное соединение Последовательное соединение 28 Активное 75 Реактивное -210 Активное 61 Реактивное -210 21 Активное 1600 Реактивное -25 Активное 100 Реактивное -25 14 Активное 3800 Реактивное 0 Активное 43 Реактивное -500 7 Активное 2300 Реактивное 170 Активное 44 Реактивное 700 3,5 Активное 25 Реактивное -130 Активное 22 Реактивное -510 1,84 Активное 1900 Реактивное -690 Активное 25 Реактивное -750 Как видно, результаты, что называется не предсказуемы. Точность измерений здесь находится в пределах 10-20 процентов. Менее точно измеряются параметры на более высоких диапазонах. Что же дальше? После определения сопротивления излучения и реактивного сопротивления на всех диапазонах антенна была подключена к П- контуру передатчика с возможностью регулировки мощности в пределах 1-20 ватт и минимальным эквивалентным сопротивлением выходного каскада на лампе ГУ-50 равным 7500 ом. В результате оказалось, что на 28 мгц антенна работала в последовательном резонансе с добротностью порядка 11, что можно подсчитать разделив 7500 на сопротивление излучения в 75 ом и извлекая квадратный корень из по полученного значения. На 21 мгц антенна работала в параллельном резонансе. На 14 мгц удалось добиться согласования регулировкой конденсаторов контура, но антенна работала в параллельном резонансе- то есть конденсатор связи пришлось уменьшить почти до предела. Естественно большое сопротивление нагрузки привело к уменьшению добротности до 1,4. При этом естественно фильтрация гармоник практически отсутствовала ( для нормальной работы добротность должна быть не ниже 8). На 7 мгц антенна также работала в параллельном подключении с плохими фильтрующими свойствами. На частотах 3,5 и 1,84 мгц добиться хотя бы удовлетворительной работы не удалось. Далее были предприняты попытки применить дополнительные согласующие устройства. На частоте 28 мгц оказалось удобным подключить в разрыв антенны последовательный контур настроенный на эту же частоту переменным конденсатором из того же набора, что и в измерениях. Установка последовательного контура здесь играет двойную роль. Он, с одной стороны, компенсирует излишнее реактивное сопротивление антенны, и действует как фильтр-пробка для гармоник. Путем последующей подстройки контура на 28 мгц удалось несколько улучшить согласование, то есть анодный ток увеличился. На 21 мгц таким добавлением также несколько улучшилось согласование. На частоте 14 мгц добиться перехода в последовательный резонанс не удалось. Но за счет установки последовательного контура значительно увеличилась добротность и емкость конденсатора связи стала больше. То есть произошло смещение в сторону последовательного резонанса и добротность стала равной примерно 8. Отдаваемая мощность увеличилась примерно на 20 процентов.. Это же самое произошло и на частоте 7 мгц., где мощность увеличилась на 25-30 процентов. На частоте 3,5 мгц., с помощью последовательного контура удалось полностью компенсировать реактивное сопротивление и антенна хорошо работала в последовательном резонансе отдавая полную мощность при высокой добротности- около 20-ти. На частоте 1,84 мгц оказалось целесообразным подключить антенну к параллельному контуру и того же набора, что и при измерениях. Затем на 1/5 витков катушки был подключен выход передатчика, что снизило сопротивление нагрузки до 760 ом Далее настройкой П-контура и конденсатора параллельного контура весьма своеобразным способом удалось добиться полного согласования и отдачи мощности так, что этот диапазон стал доступным несмотря на 13-метровую антенну. Из параметров антенны должно быть ясным почему именно на этом диапазоне пришлось применить параллельный контур- ведь сопротивление излучения в параллельном резонансе, для этого диапазона, очень велико. Таким образом в данном конкретном случае удалось согласовать имеющуюся антенну для работы на всех диапазонах без каких-либо действий над самой антенной, а лишь только путем установки дополнительного последовательного контура.. Только в диапазоне 1,84 мгц был установлен дополнительный параллельный контур. Думаю, что таким же образом можно исследовать любую антенну и добиться удовлетворительной или даже хорошей ее работы не загрязняя эфир побочными излучениями. Характерной особенностью работы настроенной антенны является полное совпадения максимума мощности с максимумом тока и напряжением в антенне и максимумом анодного тока, а также максимума напряженности поля. Таким образом однозначно решается вопрос о способе определении точки полной настройки антенны- ее можно определять только по максимальному анодному току. КСВ-метр оказался лишним. Кстати он определяет только отношение мощности отраженной или возвращаемой мощности, ввиду несогласованности, к подводимой, но не раскрывает причину почему это происходит. При полном согласовании полностью пропадают признаки какого-либо самовозбуждения или наличия ВЧ на ключе, педали управления и наушниках. Более того практически исчезают помехи телевидению там, где ранее, как казалось, они были неизбежны. Приведенный пример послужит помощью тем, кто уже имеет передатчик с П- контуром. Для тех же, кто имеет импортную аппаратуру с фиксированным выходным эквивалентным сопротивлением, например в 50 ом, то здесь несколько сложней добиться именно такого входного сопротивления от антенны. Очевидно придется сделать специальное согласующее устройство использующее свойства Г- образного звена последовательного контура… Беспокоиться о фильтрации гармоник здесь не придется ибо на выходе, как правило, сигнал уже хорошо отфильтрован. Надо только избавиться от реактивной составляющей за счет дополнительного значения последовательного включения емкости или индуктивности. Для тех, кто занимается конструированием передающей аппаратуры на транзисторах придется решать задачу согласования при очень маленьком эквивалентным сопротивлении выходного каскада. Как отмечено выше это удобней сделать Т-контуром. Например, антенна, с приведенными выше параметрами, согласовывалась с транзисторным выходом трансивера мощностью 2 ватта, с эквивалентным выходным сопротивлением в 35 ом, на трех диапазонах 14, 7 и 3,5 мгц. В первом случае, ввиду отсутствия реактивной составляющей антенны, использовался Т-контур, в котором катушка индуктивности подключалась одним концом к массе, а ко второму концу подключался корпус двухсекционного переменного конденсатора, неподвижные и изолированные секции которого образовывали две ветви. К одной из них подключалась антенна, а ко второй -выход передатчика. Затем подбором витков и настройкой в резонанс по максимуму коллекторного тока устанавливалось полное согласование. Впрочем на этом же диапазоне хорошо работал просто последовательный контур, у которого катушка индуктивности подключалась к массе, а конденсатор- к выходу трансивера. Антенна присоединялась к части витков катушки индуктивности так, чтобы при резонансе ток был максимально допустимым. Кстати, этот вариант очень простой и удобный. Надо только соблюдать условия достаточности фильтрации сигнала устанавливая значения емкости и индуктивности соответствующие большой добротности . Добротность рассчитывается как корень квадратный из частного от деления сопротивления в точке соединения этих элементов на эквивалентное сопротивление выходного каскада. На диапазоне 7 мгц использовался только последовательный контур подключенный как описано выше. Поскольку на этом диапазоне антенна имеет дополнительное индуктивное сопротивление, то, при подключении ее к части витков индуктивности контура, уменьшает индуктивность той части катушки, к которой она присоединяется. Это уменьшение компенсируется подстройкой конденсатора. На диапазоне 3,5 мгц также использовался последовательный контур. При этом катушка индуктивности подключалась к массе, а антенна- к конденсатору. Выход от передатчика подключался к части витков катушки индуктивности. Поскольку на этом диапазоне антенна имеет емкостное сопротивление, то оно компенсируется увеличенной индуктивностью контура. Таким образом и в этом случае удается добиться хорошего согласования. Заключение За долгую и славную эпоху существования радиолюбительского движения энтузиасты эфира внесли большой вклад в теорию и практику проведения связей и конструирования аппаратуры. Думаю, что появление этой статьи побудит новую волну многочисленных исследователей по раскрытию еще неизвестных закономерностей в области антенн. Мы просто должны преодолеть то, что нам еще неизвестно или в чем мы сомневаемся . Несмотря на появление специальных импортных Матч-боксов, в том числе и встроенных в трансивер, с автоматической подстройкой под любую антенну, которые как бы уже все решают, в основе их, все еще, просто механическая копировка известных решений без осмысленного применения. Основываясь на изложенных здесь принципах и при использовании компьютерных программ, можно быстро рассчитать любое устройство и, затем, с меньшими затратами провести опытную проверку с минимальной доработкой. Это дает также возможность внести изменения в существующие конструкции, где по разным причинам оказались скрытыми неучтенные возможности или погрешности в расчетах.

Расчёт растягивающих конденсаторов LC контура настройки

Как загнать пределы перестройки конденсатора переменной ёмкости (КПЕ) в колеба-
тельном LC контуре в нужный диапазон изменения частоты.
Онлайн калькулятор ёмкостей конденсаторов растяжки.

«В процессе конструирования генераторов сигналов и задающих генераторов передатчиков радиолюбители часто сталкиваются с трудностями приобретения конденсатора переменной ёмкости с нужными пределами изменения ёмкости. Я предлагаю читателям простой способ расчёта ёмкостей дополнительных конденсаторов С1 и С2 (см. рисунок), включение которых в колебательный контур генератора позволяет получить нужный диапазон перестройки».

Рис.1 Общая схема колебательного контура с растягивающими конденсаторами

Так начинается очень полезная статья, опубликованная в журнале Радио, 1992, №11, с.23, под авторством С. Бирюкова. Далее там приведены уравнения и довольно громоздкие итоговые формулы для расчёта величин растягивающих конденсаторов С1 и С2, а также практический пример расчёта контура с КПЕ.
Для желающих освоить теоретическую часть процесса порекомендую обратиться к статье в журнале, а для практиков приведу простую таблицу, позволяющую без излишнего напряга, калькулятора и деревянных счёт в режиме онлайн рассчитать значения искомых конденсаторов.
К тому же формулы уважаемого автора не учитывают ёмкости, обозначенной на Рис.1 — С_конт.
Тем не менее, эта ёмкость в реальном устройстве всегда присутствует и численно равна сумме: собственной ёмкости катушки индуктивности, общей ёмкости подключённых к ней радиоэлементов, а также ёмкости проводников печатного или какого-либо иного монтажа. И надо сильно постараться, чтобы величина этой суммарной ёмкости уложилась в десяток пикофарад. Даже при довольно продуманном монтаже значение С_конт, как правило, составляет 15…20 пФ.
Короче, для максимальной достоверности итогового результата — величину этой ёмкости учитывать необходимо!

КАЛЬКУЛЯТОР РАСЧЁТА РАСТЯГИВАЮЩИХ КОНДЕНСАТОРОВ LC-КОНТУРА.

Необходимо иметь в виду, что выбираемые значения исходных величин должны быть корректными. Например, это относится к частотам диапазона, который не должен быть чрезмерно широк для выбранного КПЕ. Важно следить за тем, чтобы посчитанный номинал ёмкости С1 был больше величины «максимальная ёмкость КПЕ с учётом С1, С2». Если это не так, то надо либо уменьшить индуктивность катушки, либо снизить ширину диапазона перестройки. Возможны иные варианты ограничений, в которых пользователь может разобраться самостоятельно, действуя методом проб и ошибок.

Ну а воспользовавшись простыми, как ситцевые трусы формулами для расчёта последовательно — параллельного соединения конденсаторов, можно решить обратную задачу и посмотреть, какой будет полоса перестройки контура при впаивании в схему конденсаторов из имеющегося у радиолюбителя ряда.

КАЛЬКУЛЯТОР ЧАСТОТ ПЕРЕСТРОЙКИ LC-КОНТУРА С РАСТЯГИВАЮЩИМИ КОНДЕНСАТОРАМИ.

Данный калькулятор не подвержен влиянию вводимых данных и покажет корректный результат при любых значениях исходных величин.

 

Расчет контура тока

Расчет начинается с внутреннего контура — контура тока. В этом контуре в качестве компенсируемой части объекта принимается входящая в него передаточная функция двигателя W_Д1(s). Некомпенсируемым звеном является усилитель, постоянную времени которого принимаем за малую постоянную времени контура тока, т. е. T_μт= T_У , где Т_μт – малая некомпенсируемая постоянная времени контура тока. Тогда, в соответствии с изложенным, ставиться задача определения передаточной функции регулятора тока W_PT(s) из условия получения передаточной функции разомкнутого контура тока W_KT(s) в виде однократно интегрирующей системы, т. е.

,

где Т₀ – параметр, определяемый настройкой регулятора.

Известно, что динамические качества контура определяются видом передаточной функции замкнутого контура. Для замкнутого контура тока имеем

. (2.1)

Выражение (2.1) может быть представлено как передаточная функция стандартного колебательного звена, т. е.

,

,,

где Т — постоянная времени колебательного звена; ζ — коэффициент затухания (или демпфирования) колебательного звена.

При ζ = 1, т. е. при имеем предельный случай апериодического звена. Однако при выборе соотношения, обеспечивается большее быстродействие, поскольку в технических системах длительность процесса определяется временем вхождения в зону установившегося значения с точностью%. В случаеи ζ=0.707 имеем колебательный процесс, но с максимальным перерегулированием всего 4.3 %, вот почему в этом случае быстродействие будет выше, чем при. Настройка контура на соотношениеи ζ = 0.707 является настройкой на модульный оптимум (МО). Итак, для контура тока имеем:

,

а так как ,то

. (2.2)

С другой стороны, из структурной схемы (рис. 2.2) имеем:

,

откуда

. (2.3)

Подставив в (2.3) выражения передаточных функций всех звеньев, а W_KT(s)из (2.2), получим передаточную функцию регулятора, при этом принятоW_Д1(s)без учета влияния ЭДС, так как в нашем случаеТ_ЭМ>>Т_Я:

,

или

,

где ;;.

Расчет контура скорости

Контур скорости включает в себя замкнутый контур тока. Структурная схема представлена на рис. 2.3. При настройке контура на модульный оптимум передаточная функция контура имеет вид:

,

где — некомпенсируемая малая постоянная времени контура скорости.

Из структурной схемы рис. 2.3 имеем

. (2.4)

Из (2.4) выражаем передаточную функцию регулятора скорости:

, (2.5)

где .

Тогда, приняв за малую некомпенсируемую постоянную времени контура скорости Т_μсвеличину, равную сумме малой постоянной времени контура тока 2Т_Уи постоянной времени фильтраТ_Ф, т. е., получим из (2.5) передаточную функцию регулятора скорости

. (2.6)

Таким образом, при настройке контура скорости на модульный оптимум получаем П-регулятор с коэффициентом передачи k_РС, определяемым выражением (2.6).

Важнейшим показателем, характеризующим качество системы стабилизации скорости, является статическая точность ее работы, т. е. значение установившейся ошибки при возмущающем воздействии. Рассчитать установившиеся ошибки по управляющему и возмущающему воздействиям можно, используя передаточные функции системы по сигналу ошибки. Однако проще и нагляднее их можно выразить из уравнения равновесия прохождения сигналов в исследуемой структуре. Для нее можно записать (см. рис. 2.3):

. (2.7)

Уравнение (2.7) записано в приращениях по управляющему U_З(s) и возмущающемуI_с(s) воздействиям. Выразить передаточные функции по соответствующему воздействию можно, полагаяI_с(s)= 0 илиU_з(s)= 0. Далее, устремивs0, получить значения установившихся ошибок. ПоложивU_з(s) = 0, выразим из (2.7) отношениеω(s)I_с(s) и после подстановки в него выражений для всех входящих передаточных функций и упрощений получим

, ,

и учитывая, что , получим

. (2.8)

В установившемся режиме (s0) относительный перепад скоростиω/Δω_сопределяется из (2.8) приs0 и выражается

,

где Δω_с— естественный статический перепад скорости от приложенной нагрузки.

Если полученное таким образом значение ошибки не соответствует техническим требованиям, необходимо повысить порядок астатизма в той части системы, которая существует слева от места приложения возмущающего воздействия (см. рис. 2.3). Чаще всего в этом случае переходят к настройке контура скорости на симметричный оптимум (СО), т. е. используют в качестве регулятора скорости ПИ-регулятор. В нашем случае

.

При настройке контура скорости на симметричный оптимум в системе наблюдается значительное увеличение динамической ошибки (перерегулирования) по управляющему воздействию, обусловленное наличием в регуляторе скорости форсирующего звена с передаточной функцией W(s) = 1+4(2T_У+T_Ф)s. Для того чтобы переходный процесс соответствовал прежней настройке контура на модульный оптимум, необходимо на входе системы перед задающим воздействием включить звено с передаточной функцией обратной передаточной функции форсирующего звена, то есть .

Данное входное звено W_вх(s) играет роль задатчика интенсивности. Структурная схема с входным звеном представлена на рис. 2.4.

Контурный плоттер

| Academo.org — Бесплатное интерактивное обучение.

---

Контурные линии Обозначение:

Если вы когда-либо смотрели на карту, особенно в холмистой или горной местности, вы могли заметить группы таких линий:

Они известны как контурные линии, и все точки на линии находятся на одной высоте. Контурные линии не ограничиваются только информацией о горах, они могут помочь нам визуализировать поверхность, описываемую математической функцией.2. Итак, если x = 2 и y = 2, z будет равно 4 — 4 = 0. Попробуйте навести указатель мыши на точку (2,2) выше. Вы должны увидеть на боковой панели, что индикатор (x, y, z) отображает (2,2,0).

Итак, это объясняет, почему мы видим контурную линию вдоль линии x = y. Потому что вдоль этой линии z всегда равно нулю. Попробуйте выбрать другую контурную линию и проследите по ней с помощью мыши. Посмотрите, как значение z всегда остается неизменным.

Вы также можете заметить, что, когда у вас есть много горизонтальных линий, расположенных близко друг к другу, если вы немного отклонитесь от линии, значение z быстро отклонится от значения z линии.Это потому, что вы смотрите на очень крутую часть графика, и небольшое изменение x или y будет иметь большое влияние на значение z.

Нет ничего особенного в том, какие контурные линии отображаются, это просто вопрос выбора. Вы можете изменить, какие значения должны отображать контурные линии, настроив ползунки «Диапазон уровней контура» и «Количество уровней контура». По умолчанию они установлены на (-100,100) и 21 соответственно, поэтому это означает, что отображаемые уровни контура будут начинаться с -100 и увеличиваться до +100 включительно с интервалами 20.Вы можете увидеть, как контурные линии соответствуют цветам в ключе чуть ниже графика.

Чтобы обновить функцию, отображаемую на графике, введите новую функцию в поле ввода и нажмите «обновить».

В таблице ниже перечислены функции, которые можно вводить в поле выражения.

Выражение	Описание
sin (x)	Синус x в радианах
cos (x)	Косинус x в радианах
желто-коричневый (x)	Тангенс x в радианах
asin (x), acos (x), atan (x)	Обратная из трех тригонометрических функций, перечисленных выше
sqrt (x)	Квадратный корень из x (только для положительного значения x)
журнал (x)	Натуральный логарифм x
pow (x, y)	Степень от x к y

Контурные линии могут быть немного трудными для понимания, поэтому, если у вас возникли проблемы, вы можете найти 3D-плоттер, который поможет визуализировать фактическую форму 3D-поверхности.

Пожалуйста, включите JavaScript, чтобы просматривать комментарии от Disqus.

Новые координаты вращением осей Калькулятор

[1] 2020/12/19 01:21 Женский / До 20 лет / Высшая школа / ВУЗ / Аспирант / Очень /

Цель использования

Геометрия — это не весело kids

Комментарий / запрос

действительно помогает, спасибо

[2] 2020/11/26 05:53 Мужчина / До 20 лет / Старшая школа / Университет / аспирант / Очень /

Цель использования

Мой мозг перегорел, поэтому я пытаюсь объяснить, как работают вращения

[3] 25.11.2020 08:39 Женщина / Моложе 20 лет / Начальная школа / Ученица неполной средней школы / Очень /

Цель использования

домашнее задание
хорошие оценки

Комментарий / запрос

добавить вариант для вращения против часовой стрелки и по часовой стрелке

[4] 2020/10/20 23:51 Мужчина / Моложе 20 лет / Высокий- школа / вуз / аспирант / Very /

Цель использования

оборотов заметок с координатами

[5] 2020/10/15 05:06 Женский / Моложе 20 лет / Начальная школа / Младший школьник / Очень /

Цель использования

Домашнее задание

[6] 2020/10/02 06:24 Мужской / До 20 лет / Начальная школа / Неполный ученик средней школы / Очень /

Цель использования

Школьные тесты

[7] 2020/10/02 02:30 Женский / До 20 лет / Начальная школа / Младший школьник / Совсем нет /

Цель использования

Школа Homeowrk

Комментарий / Запрос

Я хочу понять, что я поддерживаю наклоняться.

[8] 2020/09/28 02:14 Мужчина / До 20 лет / Средняя школа / Университет / аспирант / Немного /

Цель использования

Работа в школе

Комментарий / запрос

добавьте вариант по часовой / против часовой стрелки

[9] 2020/08/18 17:44 Мужчина / 50-летний уровень / Средняя школа / Университет / аспирант / Немного /

Цель использования

Требуется формула для этого, чтобы я мог рассчитать новую ограничивающую рамку

[10] 2020/05/28 23:17 Женщина / Моложе 20 лет / Начальная школа / Ученица неполной средней школы / Очень /

Цель использования

Та же девушка из прошлого, но я бы хотел, чтобы она делала только одно — против часовой стрелки.4) и
как 3/5.

Что означает построение кривых?

Построение кривой — это расчет для поиска всех характерных точек функции, например корни, пересечение оси Y, максимальные и минимальные точки поворота, точки перегиба.

Как получить эти очки?

Расчет производных. Затем вы устанавливаете функцию, а также производную равными нулю: корни являются решениями уравнения.Точки поворота могут лежать в основе деривации, т.е. вам нужно решить уравнение для нахождения максимальных / минимальных точек поворота. (если, если нет, то есть точка поворота в корне вывода, это можно проверить с помощью критерия изменения знака.) В точке перегиба должна быть вторая производная, поэтому для поиска точек перегиба решите уравнение.

Почему в наши дни рисование кривых выполняется меньше?

Это немного глупо: вам просто нужно научиться каждый раз выполнять одни и те же вычисления точек, не задумываясь об их значении.Поэтому упражнения, в которых вы должны думать о значении этих моментов, в наши дни становятся более важными.

Могу я взглянуть на пример?

Конечно. Нарисуем кривую.

Mathepower работает с этой функцией: Это график вашей функции. Dein Browser не использует HTML-Canvas-Tag nicht. Hol dir einen neuen.: P Корни в -1; 0; 1 Пересечение оси Y в (0 | 0) Максимальные и минимальные точки поворота в (-0,577 | 0,385); (0,577 | -0,385) Точки перегиба в (0 | 0) Это то, что рассчитала Mathepower: Корни: Ищем корни | Фактор. | Произведение равно 0.Так что либо коэффициент должен быть равен нулю. | + | Извлеките квадратный корень с обеих сторон. | Извлечь корень | Извлечь корень | или коэффициент должен быть равен нулю Итак, корни: {;;} Симметрия: — точка, симметричная относительно начала координат. Вычислите точку пересечения оси Y, вставив 0. Вставьте 0 в функцию: Итак, точка пересечения оси Y находится в точке (0 | 0) Диффенцируйте функцию Дифференцировать функцию: (Производная от) + (Производная от) + Таким образом, производная от равна . Итак, первая производная — это Вторая производная, т.е. производная от : Дифференцируйте функцию: Производная от) + (Производная от) + Итак, производная от is. Упростите дифференциацию: | Умножьте на = Итак, вторая производная — это Третья производная, то есть производная от : Производная от — Итак, третья производная — это Ищем точки поворота. Мы должны найти корни первой производной. Ищем корни | + | : | Извлеките квадратный корень с обеих сторон. | Извлечь корень | Извлеките корень Точки поворота могут быть в {;} Вставить корни первой производной во вторую производную: Вставить -0.577 в функцию: -3,464 меньше 0. Таким образом, есть максимум на. Вставьте -0,577 в функцию: Максимальная точка поворота (-0,577 | 0,385) Вставьте 0,577 в функцию: 3,464 больше 0. Таким образом, минимальное значение равно. Вставьте 0,577 в функцию: Минимальная точка поворота (0,577 | -0,385) Ищем точки перегиба. Нам нужно найти корни второй производной. Ищем корни | : Точки перегиба могут быть в {} Вставьте корни второй производной в третью производную: Третья производная не содержит x, поэтому вставка дает 6 6 больше 0, поэтому есть точка перегиба в. Вставьте 0 в функцию: Точка перегиба (0 | 0)

Калькулятор дробей

Использование калькулятора

Используйте этот калькулятор дробей для сложения, вычитания, умножения и деления дробей.Ответы представляют собой дроби в наименьшем значении или смешанные числа в сокращенном виде.

Введите правильные или неправильные дроби, выберите математический знак и нажмите Рассчитать. Это калькулятор дробей с шагами, указанными в решении.

Если у вас отрицательные дроби, поставьте перед числителем знак минус. Поэтому, если одна из ваших дробей равна -6/7, вставьте -6 в числитель и 7 в знаменатель.

Иногда в математических задачах используется слово «из», например Что такое 1/3 от 3/8? Of означает, что вам нужно умножить, поэтому вам нужно решить 1/3 × 3/8.

Для вычисления смешанных чисел (целых и дробных) используйте Калькулятор смешанных чисел.

Математика в дробях с разными знаменателями

Есть 2 случая, когда вам нужно знать, имеют ли ваши дроби разные знаменатели:

• , если вы складываете дроби
• , если вы вычитаете дроби

Как сложить или вычесть дроби

1. Найдите наименьший общий знаменатель
2. Вы можете использовать ЖК-калькулятор, чтобы найти наименьший общий знаменатель для набора дробей
3. Для первой дроби найдите, на какое число нужно умножить знаменатель, чтобы получить наименьший общий знаменатель.
4. Умножьте числитель и знаменатель вашей первой дроби на это число
5. Повторите шаги 3 и 4 для каждой дроби
6. Для сложения уравнений сложите числители дробей
7. Для уравнений вычитания вычтите числители дробей
8. Преобразование неправильных дробей в смешанные числа
9. Уменьшить дробь до наименьшего значения

Как умножать дроби

1. Умножить все числители вместе
2. Умножить все знаменатели вместе
3. Сократите результат до минимума

Как разделить дроби

1. Перепишите уравнение, как в «Сохранить, изменить, перевернуть»
2. Оставить первую дробь
3. Заменить знак деления на умножение
4. Переверните вторую дробь, переключив верхнее и нижнее числа
5. Умножить все числители вместе
6. Умножить все знаменатели вместе
7. Сократите результат до минимума

Формулы фракций

Есть способ складывать или вычитать дроби, не находя

Вычисление низкоуровневого контурного графика — MATLAB contourc

Синтаксис

C = contourc (Z)
C = contourc (Z, n)
C = contourc (Z, v)
C = contourc (x, y, Z)
С = contourc (x, y, Z, n)
C = contourc (x, y, Z, v)


Описание

contourc вычисляет матрицу контура C используется по контуру , контуру и контуру .Значения в Z определяют высоту контура. прямые относительно плоскости. При расчетах контура регулярно используется сетка с интервалом определяется размерами Z .

C = contourc (Z) вычисляет матрица контура из данных в матрице Z , где Z должно быть по крайней мере матрицей 2 на 2. Контуры представляют собой изолинии в единицах из Z . Количество контурных линий и соответствующие значения контурных линий выбираются автоматически.

C = contourc (Z, n) вычисляет контуры матрицы Z с контуром n уровни.

C = contourc (Z, v) вычисляет контуры матрицы Z с контурными линиями на значения, указанные в векторе v . Длина v определяет количество уровней контура. Чтобы вычислить одиночный контур уровня к , используйте contourc (Z, [k k]) .

C = contourc (x, y, Z) , C = contourc (x, y, Z, n) и C = contourc (x, y, Z, v) вычислить контуры Z с использованием векторов x и y до определить значения x и y . x и y должны быть монотонно возрастающим.

Советы

Дополнительные сведения о матрице контуров см. В свойстве ContourMatrix . для контурных объектов.

Задание нерегулярных векторов x и y — это не то же самое, что рисовать контуры нерегулярно расположенных данных. Если x или y равно неравномерно разнесенный, contourc рассчитывает контуры используя регулярную контурную сетку, затем преобразует данные в x или y .

Аппроксимация кривой с использованием неограниченного и ограниченного линейных методов наименьших квадратов

Калькулятор ниже использует линейный метод наименьших квадратов для аппроксимации кривой, другими словами, для аппроксимации одной функции переменной с помощью регрессионного анализа, как и калькулятор Аппроксимация функции с регрессионным анализом. Но, в отличие от предыдущего калькулятора, в этом можно найти аппроксимирующую функцию, если она дополнительно ограничена определенными точками, а это означает, что вычисленная аппроксимация кривой должна проходить через эти конкретные точки.

Множители Лагранжа используются для поиска аппроксимации кривой в случае ограничений. Это накладывает некоторые ограничения на используемую регрессионную модель, а именно: можно использовать только модели линейной регрессии. Поэтому, в отличие от вышеупомянутого калькулятора, в этом калькуляторе нет степенной и экспоненциальной регрессий. Однако он включает полиномиальные регрессии 4-го и 5-го порядка. Формулы и краткое изложение теории, как обычно, можно найти под калькулятором.

Обратите внимание: если поле значений x оставлено пустым, калькулятор предполагает, что x изменяется, начиная с нуля с шагом +1.

Аппроксимация кривой с использованием неограниченного и ограниченного методов линейных наименьших квадратов

83 71 64 69 69 64 68 59 81 91 57 65 58 62

Значения X, разделенные пробелом

183 168 171 178 176 172 165 158 183 182 163 175 164 175

Y значения, разделенные пробелом

добавить import_export mode_edit удалить

Функция должна проходить через определенные точки

Элементов на странице: chevron_left chevron_right

Функция должна проходить через определенные точки

Сохранить отменить

Импорт данных Ошибка импорта

«Один из следующих символов используется для разделения полей данных: табуляция, точка с запятой (;) или запятая (,)» Пример: -50.5; -50,5

Загрузить данные из файла .csv.

Импорт Назад отменить Типы аппроксимации Полиномиальная регрессия 4-го порядка Полиномиальная регрессия 5-го порядка Полиномиальная регрессия 6-го порядка Полиномиальная регрессия 7-го порядка Полиномиальная регрессия 8-го порядка Точность вычисления

Цифры после десятичной точки: 4

Коэффициент корреляции

Коэффициент детерминации

Средняя относительная погрешность,%

Коэффициент корреляции

Коэффициент

Относительная погрешность

,%

Полиномиальная регрессия 4-го порядка

Коэффициент корреляции

Коэффициент детерминации

Средняя относительная ошибка,%

Полиномиальная регрессия 5-го порядка

Коэффициент детерминации

Средняя относительная ошибка,%

Коэффициент линейной корреляции

Коэффициент детерминации

Средняя относительная ошибка,%

9000 3

Коэффициент корреляции

Коэффициент детерминации

Средняя относительная ошибка,%

Коэффициент корреляции

Коэффициент детерминации

.