Как рассчитать общее сопротивление при параллельном соединении резисторов. Какие формулы используются для расчета. В каких случаях применяется параллельное соединение резисторов. Какие преимущества дает параллельное подключение.
Что такое параллельное соединение резисторов
Параллельное соединение резисторов — это способ подключения, при котором все резисторы подсоединяются своими выводами к одним и тем же двум точкам электрической цепи. При таком соединении напряжение на всех резисторах одинаково, а общий ток делится между ними.
Основные особенности параллельного соединения резисторов:
- Напряжение на всех резисторах одинаково и равно напряжению на входе цепи
- Общий ток делится между резисторами обратно пропорционально их сопротивлениям
- Общее сопротивление цепи всегда меньше сопротивления любого из параллельно соединенных резисторов
Формулы для расчета параллельного соединения
Для расчета общего сопротивления при параллельном соединении резисторов используются следующие формулы:

Для двух резисторов:
R = (R1 * R2) / (R1 + R2)
Где R — общее сопротивление, R1 и R2 — сопротивления резисторов.
Для трех и более резисторов:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Где R — общее сопротивление, R1, R2, R3, …, Rn — сопротивления отдельных резисторов.
Применение параллельного соединения резисторов
Параллельное соединение резисторов применяется в следующих случаях:
- Для получения нужного номинала сопротивления из имеющихся резисторов
- Для увеличения максимальной мощности рассеивания
- В делителях напряжения
- В схемах с несколькими нагрузками, подключенными параллельно
- Для создания прецизионных резисторов из обычных
Преимущества параллельного соединения резисторов
Параллельное соединение резисторов дает следующие преимущества:
- Позволяет получить сопротивление меньше, чем у любого из используемых резисторов
- Увеличивает максимальную рассеиваемую мощность
- Улучшает надежность — при выходе из строя одного резистора цепь продолжает работать
- Дает возможность точной подстройки сопротивления
- Снижает влияние температурного коэффициента сопротивления
Расчет токов при параллельном соединении
При параллельном соединении резисторов ток в каждой ветви можно рассчитать по закону Ома:

I1 = U / R1 I2 = U / R2 …
Где I1, I2 — токи через резисторы, U — напряжение на резисторах, R1, R2 — сопротивления резисторов.
Общий ток равен сумме токов через все резисторы:
I = I1 + I2 + … + In
Пример расчета параллельного соединения
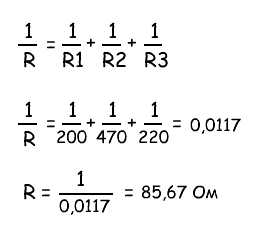
Рассмотрим пример расчета параллельного соединения трех резисторов:
- R1 = 10 Ом
- R2 = 20 Ом
- R3 = 30 Ом
Используем формулу:
1/R = 1/R1 + 1/R2 + 1/R3
Подставляем значения:
1/R = 1/10 + 1/20 + 1/30 = 0.1 + 0.05 + 0.0333 = 0.1833
Находим общее сопротивление:
R = 1 / 0.1833 = 5.45 Ом
Таким образом, общее сопротивление трех параллельно соединенных резисторов составляет 5.45 Ом.
Особенности параллельного соединения одинаковых резисторов
При параллельном соединении n одинаковых резисторов с сопротивлением R общее сопротивление рассчитывается по упрощенной формуле:
Rобщ = R / n
То есть общее сопротивление уменьшается в n раз по сравнению с сопротивлением одного резистора.
Например, при параллельном соединении трех резисторов по 30 Ом общее сопротивление составит:

Rобщ = 30 / 3 = 10 Ом
Сравнение параллельного и последовательного соединения
Основные отличия параллельного соединения резисторов от последовательного:
| Параметр | Параллельное соединение | Последовательное соединение |
|---|---|---|
| Общее сопротивление | Меньше любого из резисторов | Больше любого из резисторов |
| Напряжение | Одинаковое на всех резисторах | Сумма падений напряжения на резисторах |
| Ток | Делится между резисторами | Одинаковый через все резисторы |
Применение параллельного соединения в электронике
Параллельное соединение резисторов широко применяется в различных электронных схемах:
- В блоках питания для создания нагрузочных резисторов большой мощности
- В измерительных приборах для расширения пределов измерения
- В усилителях для создания обратных связей
- В фильтрах для формирования частотных характеристик
- В цепях защиты от перенапряжений
Ограничения при параллельном соединении резисторов
При использовании параллельного соединения резисторов следует учитывать некоторые ограничения:
- Увеличение общего тока через цепь
- Необходимость в резисторах с достаточной мощностью рассеивания
- Сложность точного расчета при большом количестве резисторов
- Влияние паразитных емкостей и индуктивностей на высоких частотах
Заключение
Параллельное соединение резисторов — важный инструмент в арсенале разработчика электронных устройств. Оно позволяет гибко управлять параметрами электрических цепей, получать нужные номиналы сопротивлений и решать различные схемотехнические задачи. Правильное применение параллельного соединения требует понимания его особенностей и умения выполнять необходимые расчеты.
Онлайн калькулятор расчета параллельного соединения резисторов
Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться. Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:
 Параллельное соединение резисторов
Параллельное соединение резисторовДанный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.
Для этого вам необходимо:
- Указать в графе «количество резисторов» их число, в нашем примере их три;
- После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;
- Далее нажмите кнопку «рассчитать» и в окошке «параллельное сопротивление в цепи» вы получите значение сопротивления в 10 Ом.
Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку «сбросить», чтобы обнулить значение параллельно включенных элементов калькулятора.
Для расчета суммарного сопротивления калькулятором используется такое соотношение:
Где,
- Rсум — суммарное сопротивление параллельно соединенных элементов
- R1 — сопротивление первого резистора;
- R2 — сопротивление второго резистора;
- R3 — сопротивление третьего резистора;
- Rn — сопротивление n-ого элемента.
Таким образом, в рассматриваемом примере параллельно включены три резистора, поэтому формула для определения суммарного сопротивления будет иметь такой вид:
Чтобы выразить величину суммарного сопротивления необходимо умножить обе половины уравнения на произведение сопротивлений всех трех резисторов. После этого перенести составляющие элементы по правилу пропорции и получить значение сопротивления:
Как видите, расчет параллельного сопротивления резисторов вручную требует немалых усилий, поэтому куда проще его сделать на нашем онлайн калькуляторе.
Обратите внимание, при наличии элементов с сопротивлением в разной размерности Ом, кОм, МОм, их необходимо привести к одной величине, прежде чем производить расчет. К примеру, в Ом и указывать в поле калькулятора для расчета параллельного соединения резисторов значение непосредственно в Омах.
www.asutpp.ru
Параллельное соединение резисторов калькулятор для расчета
Уникальнvй софт / Калькулятор соединения резисторов
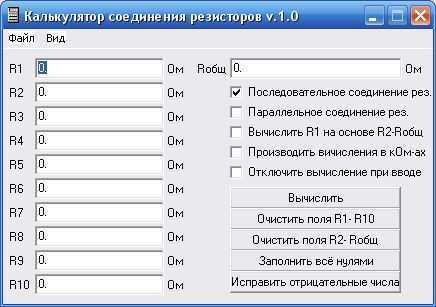
Калькулятор соединения резисторов v.1.0 — предоставляет возможность быстро вычислить и подобрать номиналы резисторов (до 10-ти резисторов в соединении) для параллельного и последовательного соединения. Вычисляет Rобщ на основе R1-R10 или подбирает нужный R1 для указанного Rобщ (с учетом резисторов R2-R10 при необходимости) для любого типа соединения резисторов (как последовательного так и параллельного). Вычисления делаются автоматически при вводе номиналов резисторов с возможностью отключения автоматического расчета при вводе. Возможен переход в диапазон кОм. Имеется возможность сохранения всех значений в текстовый файл. При необходимости, возможно включить параметр «Поверх всех окон».
Скачать программу Объём 167 кБ Всего загрузок: 1181
Из закона Ома и первого и второго правил Кирхгофа следует:
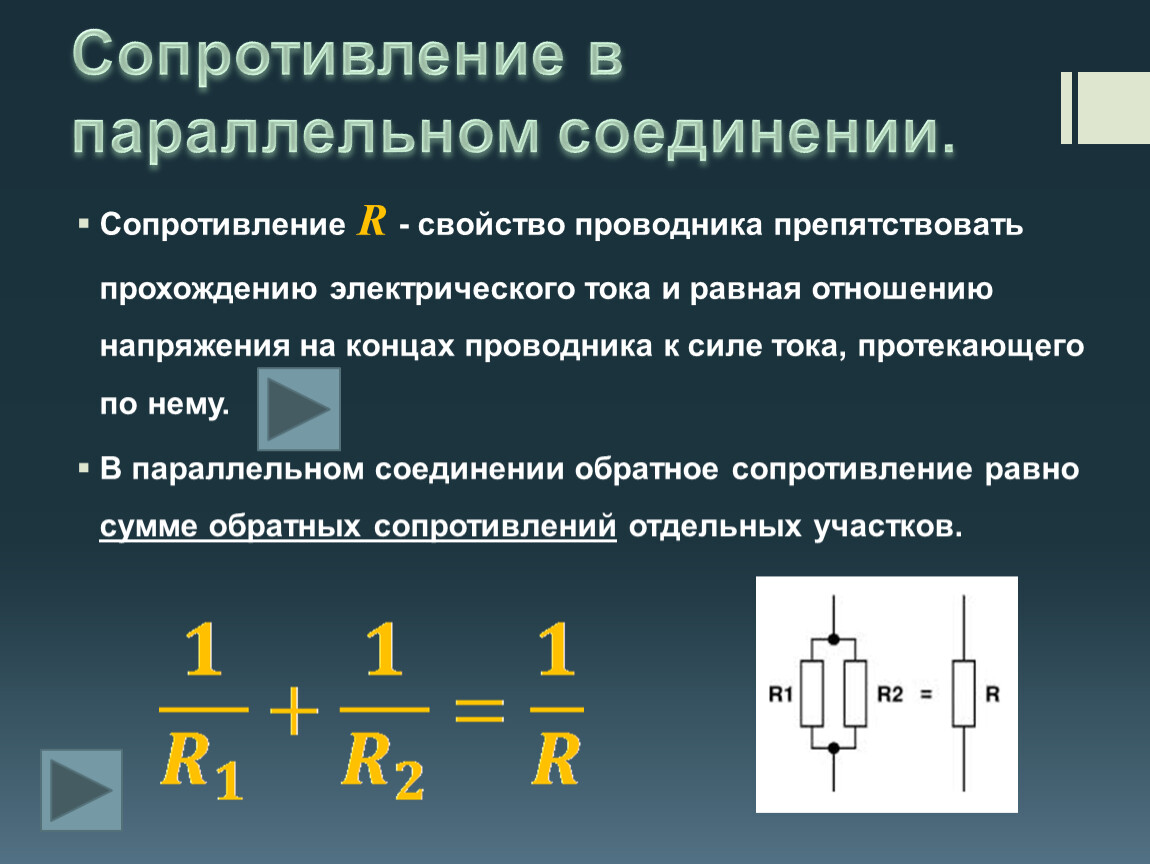
При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей.
При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.
Поскольку 1/R = G, т.е. проводимость, то
при параллельном соединении электрические проводимости отдельных ветвей складываются
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
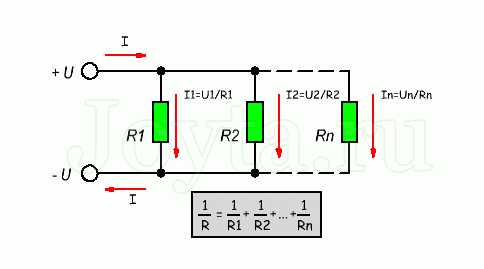
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
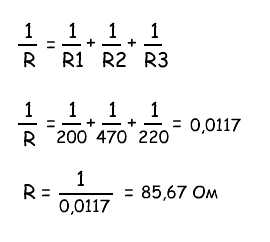
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
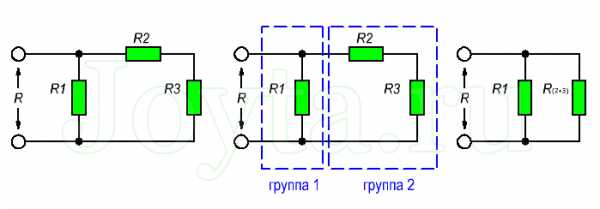
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
morflot.su
Формула расчета параллельного соединения резисторов
Из закона Ома и первого и второго правил Кирхгофа следует:
При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей.
При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.

Поскольку 1/R = G, т.е. проводимость, то
при параллельном соединении электрические проводимости отдельных ветвей складываются
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.
Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!
Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.
Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.
Последовательное соединение резисторов.
В жизни последовательное соединение резисторов имеет вид:
Последовательно соединённые резисторы серии МЛТ
Принципиальная схема последовательного соединения выглядит так:
На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.
Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.
Общее номинальное сопротивление составного резистора обозначено как Rобщ.
Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
Применяя последовательное соединение, стоит помнить одно простое правило:
Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.
Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.
Параллельное соединение резисторов.
Можно соединять резисторы и параллельно:
Два резистора МЛТ-2, соединённых параллельно
Принципиальная схема параллельного соединения выглядит следующим образом:
Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:
Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:
Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:
Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.
Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте тут.
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.
Типы проводников
 Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины
 Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
 Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
 Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов
Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.
Параллельное соединение
 При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.
При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.
Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).
При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:
- Номинал резистора в 16 Ом подойдет.
- Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).
В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:
- Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
- Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.
Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
Последовательное подключение
Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:
- Ток не изменяется на участке цепи.
- Общее напряжение равно сумме падений напряжений на каждом резисторе.
- Rобщ = R1 + R2 + … + Rn.
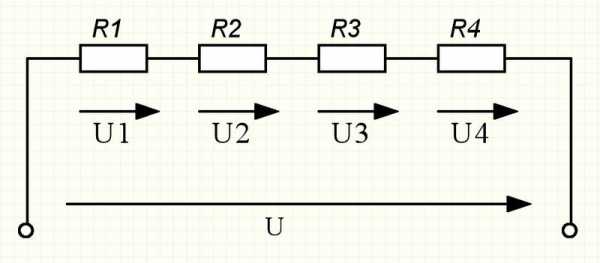
Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:
- I = I1 = I2 = 0,5 (А).
- Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
- Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).
Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.
Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.
mytooling.ru
Параллельное соединение резисторов
Господа, в прошлый раз мы с вами говорили про последовательное сопротивление резисторов. Сегодня я бы хотел вам рассказать про другой возможный вид соединения – параллельное.
Чем различается последовательное и параллельное соединение я уже писал в предыдущей статье. Но все-таки вытащу сюда картинку из той прошлой статьи, я ж знаю, что вам будет лень ходить по ссылкам .
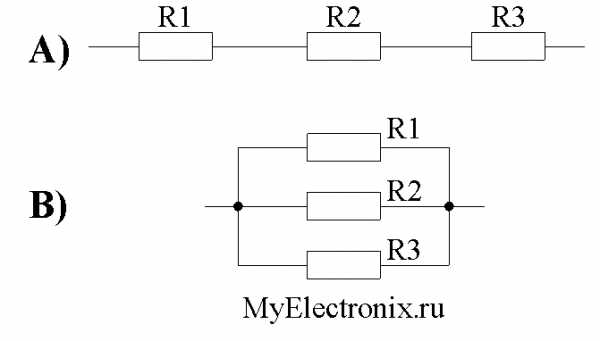
А) – Последовательное соединение
В) – Параллельное соединение
Рисунок 1 – Последовательное и параллельное соединение
Как мы видим из рисунка 1, параллельное соединение – это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы – в другой узел.
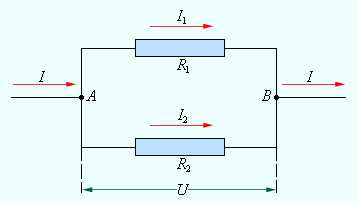
Сейчас наша задача будет разобраться, как ведут себя токи, напряжения, сопротивления и мощности при таком подключении. Для этого прошу вас взглянуть на рисунок 2, где подробно разрисован расклад дел для параллельного соединения. Будем полагать, что мы знаем величины R1, R2 и R3, а также величину приложенного к схеме напряжения U. Про токи же мы ничего не знаем.
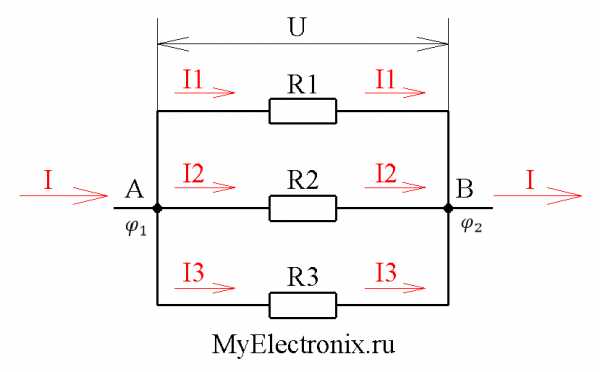
Рисунок 2 – Параллельное соединения
Что мы видим на рисунке 2? Ну, в первую очередь – два узла А и B. В узел А сходятся одни концы всех резисторов, а в узел В – другие концы. Пусть узел А имеет потенциал φ1, а узел В – потенциал φ2. Из рисунка 2 видно, что для всех резисторов R1, R2 и R3 у нас одна и та же разность потенциалов U.
Как следует из статьи про потенциалы, это означает, что напряжение на всех резисторах у нас одинаково и равно приложенному напряжению U. Это важный вывод, его следует хорошо запомнить.
С токами дело обстоит по-другому. Проанализируем рисунок 2 слева направо. Пусть у нас в цепи течет ток I. Течет он себе, течет, никого не трогает и тут вдруг натыкается на узел А. Что в этом случае говорит полюбившаяся вам статья про первый закон Кирхгофа? А то, что ток I в узле А разделится на три тока I1, I2, I3. При этом будет выполняться равенство
То есть через резистор R1 будет протекать ток I1, через резистор R2 – ток I2, а через резистор R3 – ток I3.
Итак, у нас в системе уже тихо-мирно текут себе три тока. И все хорошо, пока они не наткнуться на узел В. Тут снова вступает в силу первый закон Кирхгофа. Эти три тока I1, I2, I3 вновь соединятся в один ток I. Причем после узла В ток будет иметь такую же величину I, какой он был до узла А.
То есть если все вышесказанное воплотить в лаконичный язык наскальной живописи, положение дел можно представить себе вот так
Как же найти эти самые токи I1, I2, I3? Господа, полагаю, вы уже догадались, что на помощь нам придет горячо нами всеми любимый закон Ома. Действительно, мы знаем сопротивления резисторов и, кроме того, нам известно, что на всех них падает одно и тоже напряжение U. Поэтому легко находим токи
Отлично, мы разобрались с напряжениями и с токами в такой схеме. А помните в статье про последовательное сопротивление мы ловко преобразовали три резистора в один с эквивалентным им сопротивлением? Нельзя ли и здесь сделать что-то подобное? Оказывается, вполне себе можно. Как мы помним, токи в схеме распределены таким вот образом
Обзовем эквивалентное сопротивление буковкой R. И подставим в это выражение только что найденные нами токи I1, I2, I3
Видим, что здесь без проблем можно сократить левую и правую части на U. Получаем
Господа, важный вывод: при параллельном соединении резисторов обратное эквивалентное сопротивление равно сумме обратных сопротивлений отдельных резисторов.
То есть для упрощения различных расчетов электрических схем такую вот цепочку параллельно соединенных резисторов можно заменить одним резистором с соответствующим сопротивлением, как показано на рисунке 3.
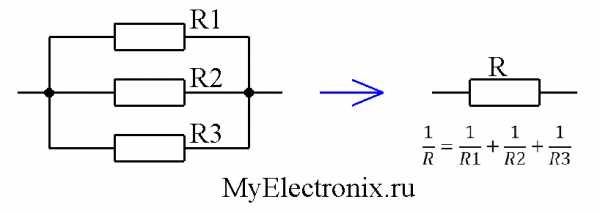
Рисунок 3 – Преобразование параллельного соединение
Весьма частый случай на практике, когда соединены параллельно не много резисторов, а всего два. Поэтому полезно знать наизусть итоговое сопротивление такой схемы. Давайте посмотрим, чему оно равно:
То есть, если у вас два сопротивления соединены параллельно, то по этой формуле вы легко высчитаете общее сопротивление. Рассмотрим пример. Пусть у нас параллельно соединены два резистора 10 кОм и 15 кОм. Чему равно их общее сопротивление?
Заметьте, господа, итоговое сопротивление у нас получилось 6 кОм, что меньше 10 кОм и 15 кОм. То есть при параллельном соединении общее сопротивление меньше любого из составляющих. Это всегда верно для любого количества резисторов, а не только для двух. Итоговое сопротивление всегда уменьшается (в отличии от последовательного сопротивления, где итоговое сопротивление всегда растет). Этот факт полезно запомнить.
Еще один часто встречающийся на практике случай – когда параллельно соединены несколько резисторов с одинаковым сопротивлением. Допустим, каждый из них обладает сопротивлением R1 и всего их N штук. Тогда по нашей общей формуле для эквивалентного сопротивления
То есть при параллельном соединении N одинаковых резисторов с сопротивлением R1 итоговое сопротивление будет в N раз меньше этого самого сопротивления R1.
Так-с, с током разобрались, с напряжением разобрались, с эквивалентным сопротивлением вроде тоже…осталась мощность. Для этого воспользуемся вот этим выражением, которое мы писали чуть выше в статье
Умножим левую и правую части на напряжение U.
Как мы помним из статьи про мощность произведение тока на напряжение есть мощность. То есть мы можем записать
где Р – мощность, выдаваемая источником;
P1 – мощность, рассеиваемая на резисторе R1;
P2 – мощность, рассеиваемая на резисторе R2;
P3 – мощность, рассеиваемая на резисторе R3.
Заметьте, господа, формула в точности такая же, как и для случая последовательного соединения резисторов. И там и там мощность, выдаваемая источником, равна сумме мощностей, рассеиваемых на резисторах цепи.
Итак, господа, мы рассмотрели основные соотношения при параллельном соединении резисторов. Теперь осталось поговорить, где это параллельное соединение можно использовать и для чего.
1) Ну, во-первых, параллельное соединение применяют во всех случаях, когда хотят запитать несколько нагрузок от одного источника напряжения. При этом пользуются тем свойством, что при параллельном соединении напряжения на всех нагрузках одинаково. То есть, допустим, вы берете источник напряжения, выставляете на нем напряжение 5 В и цепляете к этому источнику сразу несколько своих устройств. Узлами А и В в этом случае будут клеммы источника. На каждое из устройств в этом случае придет напряжение 5 В. Да и все устройства в вашей квартире (лампочки, компьютеры, телевизоры и все прочее) соединены между собой параллельно.
2) Второе возможное применение встречается не так часто, но, думаю, о нем тоже следует рассказать. Допустим, вы делаете какую-то схему, где необходим очень точный подгон сопротивления. Скажем, надо получить сопротивление 6 кОм. Такое сопротивление найти нелегко, их просто не продают. Зато у вас есть два сопротивления 10 кОм и 15 кОм. Вы их соединяете параллельно и получаете требуемые 6 кОм. Как показывает практика, 3 параллельных резисторов достаточно для получения итогового результирующего сопротивления требуемого номинала с весьма хорошей точностью. Конечно, таких вещей лучше избегать и, если есть возможность, всегда стараться применять стандартные сопротивления. Но бывают случаи, когда это невозможно, и тогда приходит на помощь этот метод.
3) Третий пункт будет немного похож на первый. Его суть заключается в следующим. Допустим, нам надо снять с источника питания 10 Вт мощности. А у нас в наличии только резисторы, которые позволяют рассеивать на себе 1 Вт. Что делать? Можно соединить 10 резисторов параллельно и с каждого снимать по 1 Вт. Мы же помним нашу формулу
Конечно, лучше брать не 10 резисторов, а хотя бы 15 и рассеивать на них меньше, чем 1 Вт. Работать на пределе никогда не следует.
Кстати, тут очень вовремя к моменту написания статьи пришли платы с производства! Господа, прошу вас взглянуть на рисунок 4.

Рисунок 4 – Плата нагревателя
На нем изображена плата нагревателя (флешка для масштаба). В чем суть? Имеется весьма сложное устройство, предназначенное для работы в арктических условиях. Найти же компоненты, которые надежно функционировать при температурах минус 55 градусов и при этом стоят адекватных денег и обладают адекватными размерами бывает непросто. Обычно элементная база в лучшем случае рассчитана на минус 40 градусов. И было принято решение разработать вот такой вот нагреватель для прогрева чувствительных к холоду аналоговых узлов устройства. Он управляется с микроконтроллера и автоматически включается при температурах меньше минус 40 градусов. Как вы можете видеть из рисунка 4, этот нагреватель представляет собой 30 параллельно соединенных резисторов с сопротивлениями 150 Ом. Каждый резистор, согласно документации, способен рассеивать до 1 Вт мощности. Используя изученные формулки, мы можем посчитать, что в сумме такая система обладает сопротивлением
и теоретически может рассеивать мощность
Ну, с сопротивлением вопросов нет, оно действительно равно 5 Ом. Ну, плюс-минус 5 % на допуск резисторов, что в данном случае вообще не критично. А вот с мощностью тут не так все однозначно. Помните про закон Джоуля-Ленца, который мы рассматривали? Резисторы будут греться, причем не слабо. Как показывает практика, если нагружать резисторы по полной, то есть рассеивать на каждом по 1 Вт, то в течении нескольких секунд их температура улетит за 150 градусов. Такая высокая температура критична для резистора и может привести к его разрушению. Я был готов к такому развитию событий, поэтому заложил для платы нагревателя максимальное напряжение 9 вольт. Это значит, что на каждом резисторе будет выделяться
что почти в два раза меньше максимально допустимой мощности в 1 Вт. В сумме на всей плате выделялось, соответственно
Эксперимент показал, что резисторы достигли температуры с комнатных 25 градусов до критичных 120 градусов приблизительно за 10 секунд работы и температура продолжала уверенно расти. Очевидно, если оставить на длительное время включенным такой нагреватель при комнатной температуре, он неминуемо выйдет из строя. Возможно, при работе на минус 55 градусах перегрев бы не был столь критичным, однако хотелось исключить вариант спалить плату на столе, поэтому я понизил напряжение, подаваемое на плату на 3 вольта: стал подавать 6 вольт. Теперь на каждом резисторе рассеивалось
а на всей плате
Теперь температура поднималась до 100-110 градусов примерно за 30-40 секунд работы и оставалась на этом уровне (выходила в точку термодинамического равновесия). Эта температура вполне подходит для нагревателя. Однако пока это были лишь эксперименты на столе при комнатной температуре, главный эксперимент – в термокамере на минус 55 градусах – впереди. Возможно, по его результатам потребуется чуть увеличить рассеиваемую мощность. А может все останется как есть и этой мощности будет достаточно для вывода девайса на режим за адекватное время, время покажет .
На сегодня все, господа. Удачи вам и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
myelectronix.ru
Онлайн калькулятор расчета последовательного соединения резисторов
При последовательном соединении резисторов конец одного из них соединяется с началом следующего. В такой схеме через все резистивные элементы протекает одинаковый ток I, но падение напряжения на каждом из них пропорционально величине сопротивления. Для расчета электрических величин в схемах используется сложение сопротивлений всех элементов в последовательной цепи для получения суммарной величины, как показано на рисунке:
 Последовательное соединение резисторов
Последовательное соединение резисторовДанный онлайн калькулятор позволяет выполнять расчет суммарного сопротивления для последовательно соединенных элементов цепи.
Чтобы воспользоваться калькулятором расчета вам необходимо:
- В окошке «количество резисторов» укажите число последовательно соединенных элементов, в данном случае, в схеме представлено три резистора, но может быть и другое количество;
- После этого в поле ниже появится несколько окошек, в которые вам необходимо внести значение сопротивления каждого резистора, к примеру, 10, 20 и 45 Ом;
- Нажмите кнопку «рассчитать» и в окошке «сопротивление» вы получите значение сопротивления в 75 Ом.
Для перехода к расчету следующей цепи или при необходимости подобрать другие элементы, нажмите кнопку «сбросить», чтобы обнулить значение последовательно включенных элементов калькулятора.
В работе калькулятора для определения сопротивления цепи последовательно соединенных резисторов используется принцип арифметического сложения. Поэтому формулу для определения суммарного значения можно представить следующим образом:
Rсум = R1 + R2 + R3 +…+ Rn
Где,
- Rсум — суммарное сопротивление последовательно соединенных элементов
- R1 — сопротивление первого резистора;
- R2 — сопротивление второго резистора;
- R3 — сопротивление третьего резистора;
- Rn — сопротивление n-ого элемента.
Так как в рассматриваемом примере включено только три элемента, то формула примет такой вид:
Rсум = R1 + R2 + R3
Подставив значение омического сопротивления каждого из элементов, получим:
Rсум = 10 + 20 + 45 = 75 Ом
Использование калькулятора для вычисления суммарного сопротивления в цепи последовательно соединенных резисторов наиболее актуально для схем с большим количеством элементов и дробными величинами.
Следует отметить, если вам известно омическое сопротивление каждого элемента в разных единицах измерения (Ом, кОм, МОм), то их следует привести к одной, к примеру, к Омам, так как калькулятор выполняет расчет для всех резисторов в одинаковой единице.
www.asutpp.ru
Расчет импеданса в параллельном соединении элементов цепи
Любая электрическая цепь включает в себя ряд элементов, среди которых встречаются активные и реактивные составляющие. При параллельном соединении активного, емкостного и индуктивного элемента схема выглядит таким образом:
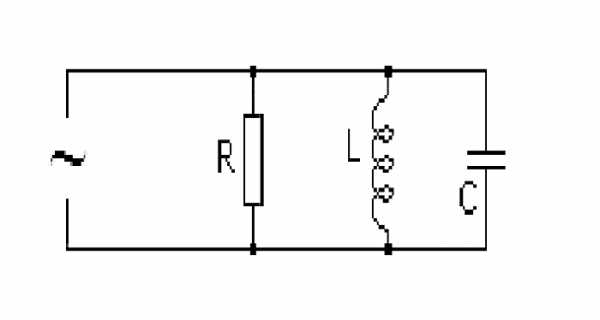 Рис. 1. Параллельное соединение элементов электрической цепи
Рис. 1. Параллельное соединение элементов электрической цепиВ зависимости от конкретной ситуации тот или иной элемент может исключаться из цепи, меняя тем самым характер нагрузки. Для геометрического определения суммарного значения всех сопротивлений производится сложение векторов. В зависимости от типа реактивной нагрузки результирующий вектор импеданса будет смещаться в положительный или отрицательный квадрант.
 Рис. 2. Векторное сложение сопротивления
Рис. 2. Векторное сложение сопротивленияДля вычисления полного сопротивления Z составляется уравнение согласно теоремы пифагора. Только сложению подлежит не сопротивление, а проводимость цепи. Из-за чего уравнение для определения сопротивления можно будет выразить по следующей формуле:
Где Z – комплексное сопротивление участка, R – активное сопротивление участка, X – реактивное сопротивление участка.
При этом реактивное сопротивление выражается как геометрическая сумма проводимости катушки и конденсатора.
А отдельно расчет XL и XC при известных параметрах сети, емкости и индуктивности самих элементов выполняется по таким формулам:
XL = w * L = 2 * π * f * L,
Для определения углов δ и φ необходимо применить тригонометрические функции к отношению соответствующих проводимостей или сопротивлений.
В связи с большим количеством расчетов, применяемых формул и необходимостью использования тригонометрических функций определение импеданса в параллельной цепи является достаточно сложной задачей, особенно, если делать это вручную. Но, при использовании онлайн калькулятора для расчета комплексного сопротивления достаточно ввести частоту, емкость конденсатора, индуктивность катушки и омическое сопротивление резистора. А все расчеты система произведет самостоятельно.
www.asutpp.ru
Формула сопротивления тока при параллельном соединении
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
Последовательное соединение проводников
По закону Ома, напряжения U1 и U2 на проводниках равны
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
Параллельное соединение проводников
Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом)
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при и некоторые другие технические вопросы.
Сопротивление проводника
Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.
Для ведения электротехнических расчётов применяется удельное сопротивление — ρ Ом·м/мм 2 . Все металлы — хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник — серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.
При расчёте сопротивления используется известная из школьного курса физики формула:
R = ρ · l/S, S — площадь сечения; l — длина.
Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.
и нагрев проводника
Для практических расчётов режимов работы проводников применяется понятие плотности тока — δ А/мм 2 , она вычисляется по формуле:
δ = I/S, I — ток, S — сечение.
Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.
Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.
Правилами регламентируется производить расчёт проводников на нагрев.
Способы соединения проводников
Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой — последовательное соединение.
На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .
Второй способ более сложный — параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.
Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.
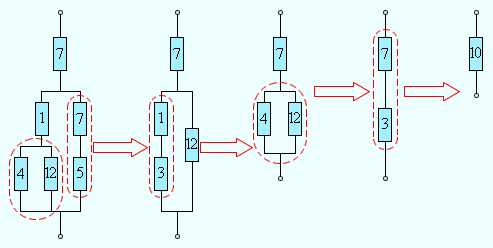
Третий способ соединения наиболее сложный — смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.
Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.
R2,3,4 = R2,3 · R4/(R2,3 + R4).
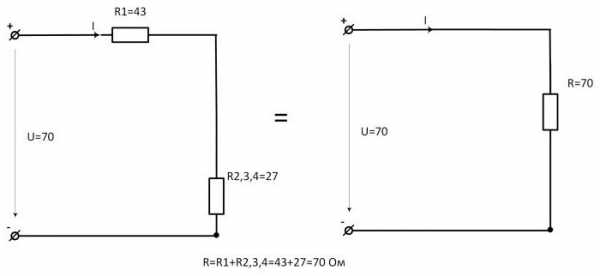
Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.
Виды проводников
В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.
Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.

Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.
Расчёт проводов на нагрев
Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника или кабеля).
На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.
Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.
Расчёт проводников на потерю напряжения
При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.

Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.
Здесь S — сечение провода линии, мм 2 .
Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.
С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Виды соединений
Резистор — пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:
Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:
Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.
Последовательное соединение проводников
В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.
Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.
Примером последовательного соединения проводников в быту является ёлочная гирлянда.
Параллельное соединение резисторов
При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.
Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.
В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.
Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.
Примеры параллельного соединения проводников:
- Освещение.
- Розетки в квартире.
- Производственное оборудование.
Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.
Смешанное соединение проводников
Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.
Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.
Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.
В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения резисторов, в частности о последовательном соединении и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
Тогда для вычисления общего напряжения можно будет использовать следующее выражение:
Но для общего напряжение также справедлив закон Ома:
Здесь – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например для следующей цепи:
Общее сопротивление будет равно:
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном соединении все сопротивления равны (), то общее сопротивление цепи составит:
в данной формуле равно количеству элементов цепи.
С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
Параллельное соединение резисторов.
При параллельном соединении напряжения на проводниках равны:
А для токов справедливо следующее выражение:
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
Подставим эти выражения в формулу общего тока:
А по закону Ома ток:
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
Данную формулу можно записать и несколько иначе:
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
Смешанное соединение резисторов.
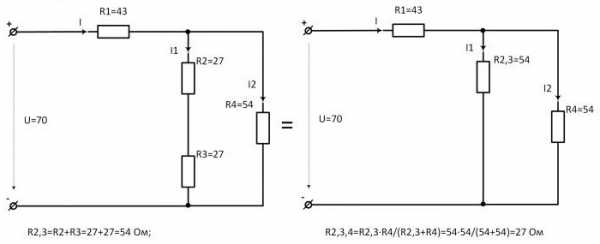
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов и – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором :
Теперь у нас образовались две группы последовательно соединенных резисторов:
Заменим эти две группы двумя резисторами, сопротивление которых равно:
Как видите, схема стала уже совсем простой ) Заменим группу параллельно соединенных резисторов и одним резистором :
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
Общее сопротивление цепи получилось равным:
Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов 😉
Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!
morflot.su

