Как рассчитать общее сопротивление параллельно соединенных резисторов. Какие формулы используются для вычисления эквивалентного сопротивления. Как работает онлайн-калькулятор параллельных резисторов. Какие преимущества дает параллельное соединение резисторов в электрических цепях.
Что такое параллельное соединение резисторов
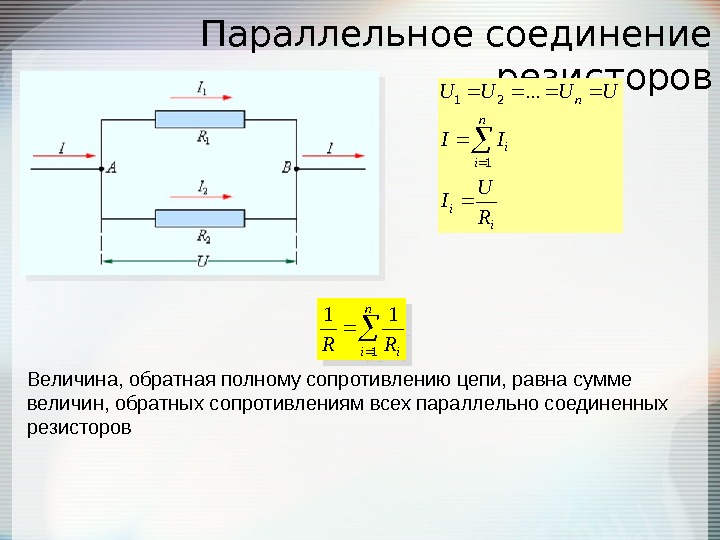
Параллельное соединение резисторов — это способ подключения двух или более резисторов, при котором их выводы соединяются в двух общих точках. При таком соединении напряжение на всех резисторах одинаково, а общий ток делится между ними.
Основные особенности параллельного соединения резисторов:
- Напряжение на всех резисторах одинаково и равно напряжению источника
- Общий ток равен сумме токов, протекающих через каждый резистор
- Общее сопротивление всегда меньше сопротивления самого малого резистора в цепи
- Чем больше параллельно соединенных резисторов, тем меньше общее сопротивление
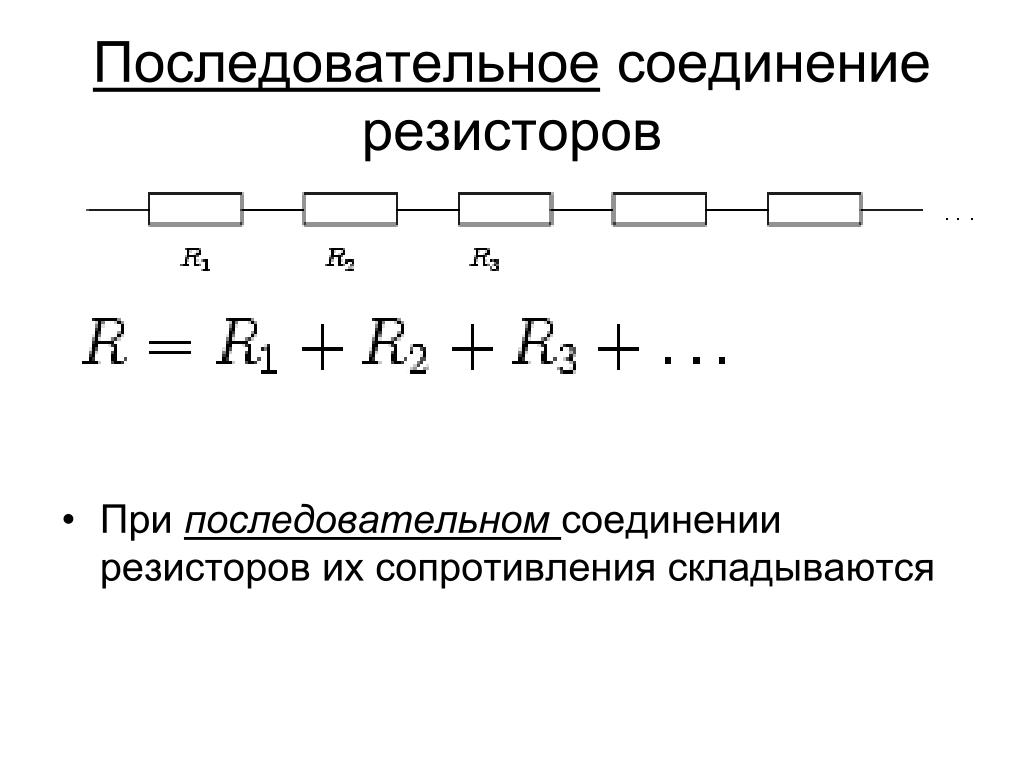
Формула расчета параллельного соединения резисторов
Для расчета общего сопротивления при параллельном соединении резисторов используется следующая формула:
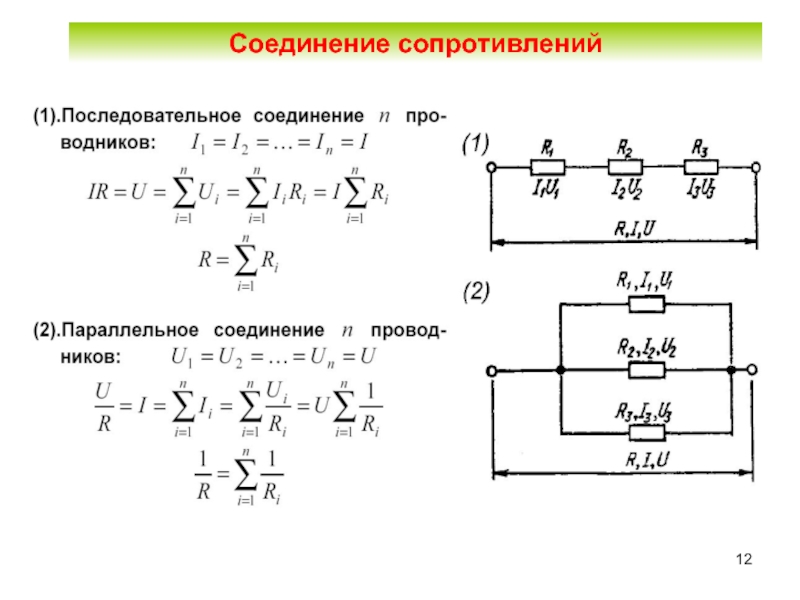
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Где R — общее сопротивление, а R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
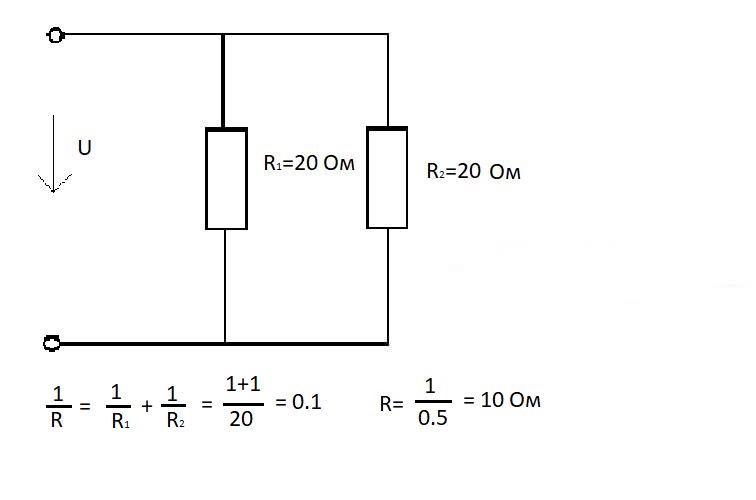
Для двух параллельно соединенных резисторов формула упрощается:
R = (R1 * R2) / (R1 + R2)
Как применять формулу на практике
Рассмотрим пример расчета общего сопротивления для трех параллельно соединенных резисторов 10 Ом, 20 Ом и 30 Ом:
- Записываем формулу: 1/R = 1/10 + 1/20 + 1/30
- Приводим дроби к общему знаменателю: 1/R = 6/60 + 3/60 + 2/60 = 11/60
- Переворачиваем дробь: R = 60/11 ≈ 5.45 Ом
Таким образом, общее сопротивление трех параллельно соединенных резисторов составляет примерно 5.45 Ом.
Преимущества параллельного соединения резисторов
Параллельное соединение резисторов имеет ряд важных преимуществ:
- Позволяет уменьшить общее сопротивление цепи
- Обеспечивает распределение тока между несколькими резисторами
- Дает возможность получить нестандартные номиналы сопротивлений
- Повышает надежность цепи за счет резервирования
- Позволяет регулировать общее сопротивление добавлением или удалением резисторов
Где применяется параллельное соединение резисторов
Параллельное соединение резисторов широко используется в различных электронных устройствах и схемах:
- В делителях напряжения и тока
- Для создания эквивалентных сопротивлений
- В схемах защиты от перегрузки
- В измерительных приборах
- Для расширения пределов измерения амперметров
Онлайн-калькулятор параллельных резисторов
Для быстрого расчета общего сопротивления параллельно соединенных резисторов удобно использовать онлайн-калькуляторы. Рассмотрим принцип работы такого калькулятора:
- Калькулятор автоматически применяет формулу расчета параллельного соединения
- Результат мгновенно отображается на экране
Онлайн-калькуляторы значительно упрощают и ускоряют расчеты, особенно при большом количестве резисторов или сложных значениях сопротивлений.
Расчет токов в параллельных ветвях
При параллельном соединении резисторов важно уметь рассчитывать токи, протекающие через каждый резистор. Для этого используется закон Ома:
I = U / R
Где I — ток через резистор, U — напряжение на резисторе (одинаковое для всех параллельных ветвей), R — сопротивление резистора.
Пример расчета токов
Рассмотрим пример с тремя параллельно соединенными резисторами 10 Ом, 20 Ом и 30 Ом при напряжении 12 В:
- I1 = 12 В / 10 Ом = 1.2 А
- I2 = 12 В / 20 Ом = 0.6 А
- I3 = 12 В / 30 Ом = 0.4 А
Общий ток в цепи равен сумме токов во всех ветвях: I = 1.2 А + 0.6 А + 0.4 А = 2.2 А
Правила выбора резисторов для параллельного соединения
При выборе резисторов для параллельного соединения следует учитывать несколько важных факторов:
- Номинальная мощность каждого резистора должна соответствовать расчетной рассеиваемой мощности
- Допуск (точность) резисторов влияет на точность общего сопротивления
- Температурный коэффициент сопротивления (ТКС) резисторов должен быть согласован
- Следует учитывать паразитные параметры резисторов, особенно на высоких частотах
Как правильно подобрать резисторы
Для оптимального выбора резисторов рекомендуется следовать таким правилам:
- Рассчитать требуемую мощность для каждого резистора
- Выбрать резисторы с запасом по мощности (обычно в 1.5-2 раза)
- Использовать резисторы одного типа и производителя
- Для прецизионных схем выбирать резисторы с малым допуском и ТКС
- При работе на высоких частотах учитывать паразитные параметры
Сравнение параллельного и последовательного соединения резисторов
Параллельное и последовательное соединения резисторов имеют свои особенности и области применения. Рассмотрим основные различия:
| Параметр | Параллельное соединение | Последовательное соединение |
|---|---|---|
| Общее сопротивление | Меньше наименьшего резистора | Сумма всех резисторов |
| Напряжение | Одинаковое на всех резисторах | Сумма напряжений на резисторах |
| Ток | Сумма токов через резисторы | Одинаковый через все резисторы |
| Применение | Уменьшение сопротивления, распределение тока | Увеличение сопротивления, деление напряжения |
Практические примеры использования параллельного соединения резисторов
Рассмотрим несколько практических примеров использования параллельного соединения резисторов в электронных схемах:
Расширение пределов измерения амперметра
Для расширения пределов измерения амперметра используется параллельное подключение шунтирующего резистора. Расчет шунта производится по формуле:Rш = Rа / (n — 1)
Где Rш — сопротивление шунта, Rа — сопротивление амперметра, n — коэффициент расширения предела измерения.
Создание эквивалентного сопротивления
Параллельное соединение позволяет получить нестандартные номиналы сопротивлений. Например, для получения сопротивления 220 Ом можно параллельно соединить резисторы 330 Ом и 660 Ом:
R = (330 * 660) / (330 + 660) = 220 Ом
Делитель тока
Параллельное соединение резисторов используется для создания делителей тока. Ток в каждой ветви обратно пропорционален сопротивлению этой ветви:
I1 / I2 = R2 / R1
Это свойство применяется в различных схемах распределения тока между несколькими нагрузками.
Заключение
Параллельное соединение резисторов — важный элемент многих электрических схем, позволяющий управлять распределением токов и создавать нужные эквивалентные сопротивления. Правильное применение параллельного соединения требует понимания основных формул и принципов расчета. Использование онлайн-калькуляторов значительно упрощает процесс вычислений и помогает быстро подобрать нужные номиналы резисторов для решения конкретных задач.
Параллельное соединение резисторов калькулятор для расчета
Содержание
- Уникальнvй софт / Калькулятор соединения резисторов
- Параллельное соединение двух сопротивлений
- Параллельное соединение двух сопротивлений
- Формула параллельного соединения резисторов
- Параллельное соединение резисторов — расчет
- Пример №1
- Пример расчета №2
- Как рассчитать сложные схемы соединения резисторов
- Ток, протекающий в цепи параллельно соединенных резисторах
- Параллельное соединение резисторов — онлайн калькулятор
- Подведем итог
Уникальнvй софт / Калькулятор соединения резисторов
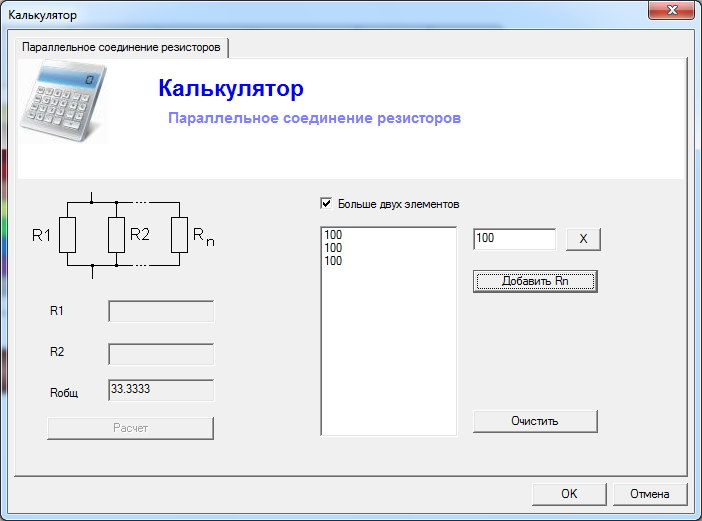
Калькулятор соединения резисторов v.1.0 – предоставляет возможность быстро вычислить и подобрать номиналы резисторов (до 10-ти резисторов в соединении) для параллельного и последовательного соединения. Вычисляет Rобщ на основе R1-R10 или подбирает нужный R1 для указанного Rобщ (с учетом резисторов R2-R10 при необходимости) для любого типа соединения резисторов (как последовательного так и параллельного).
Вычисления делаются автоматически при вводе номиналов резисторов с возможностью отключения автоматического расчета при вводе. Возможен переход в диапазон кОм. Имеется возможность сохранения всех значений в текстовый файл. При необходимости, возможно включить параметр «Поверх всех окон».
Скачать программу Объём 167 кБ Всего загрузок: 1181
Из закона Ома и первого и второго правил Кирхгофа следует:
При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей.
При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.
Поскольку 1/R = G, т.е. проводимость, то
при параллельном соединении электрические проводимости отдельных ветвей складываются
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.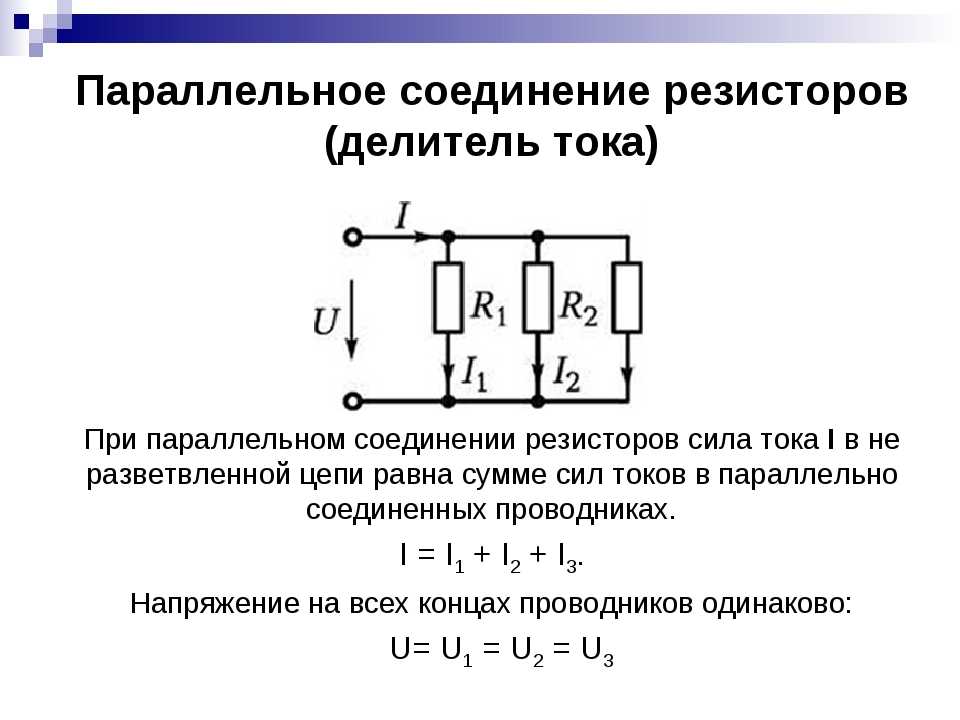
Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов.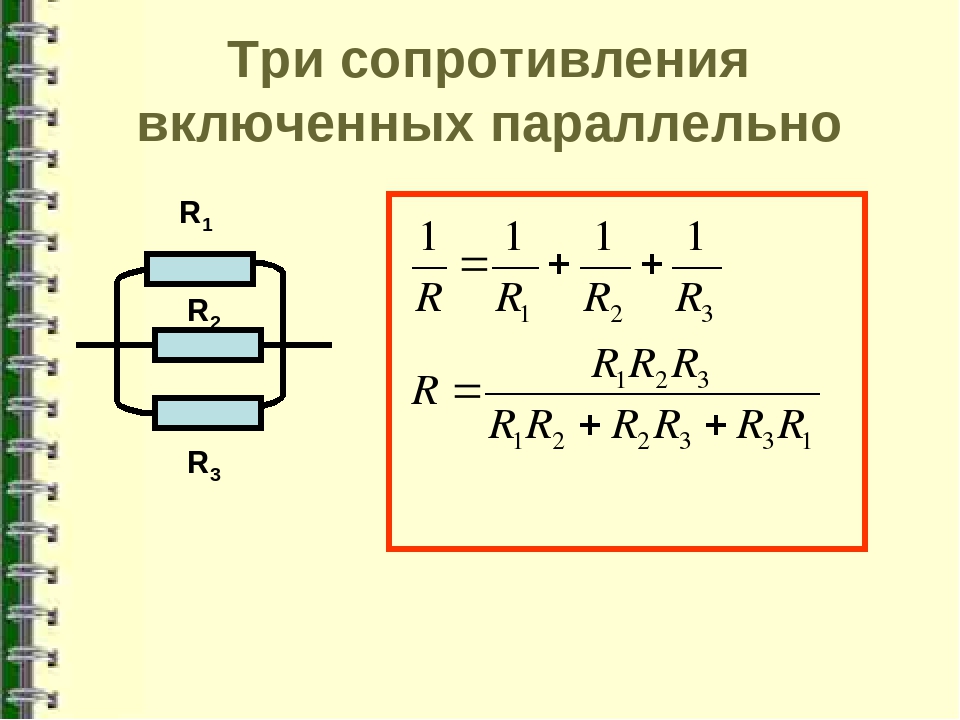
Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.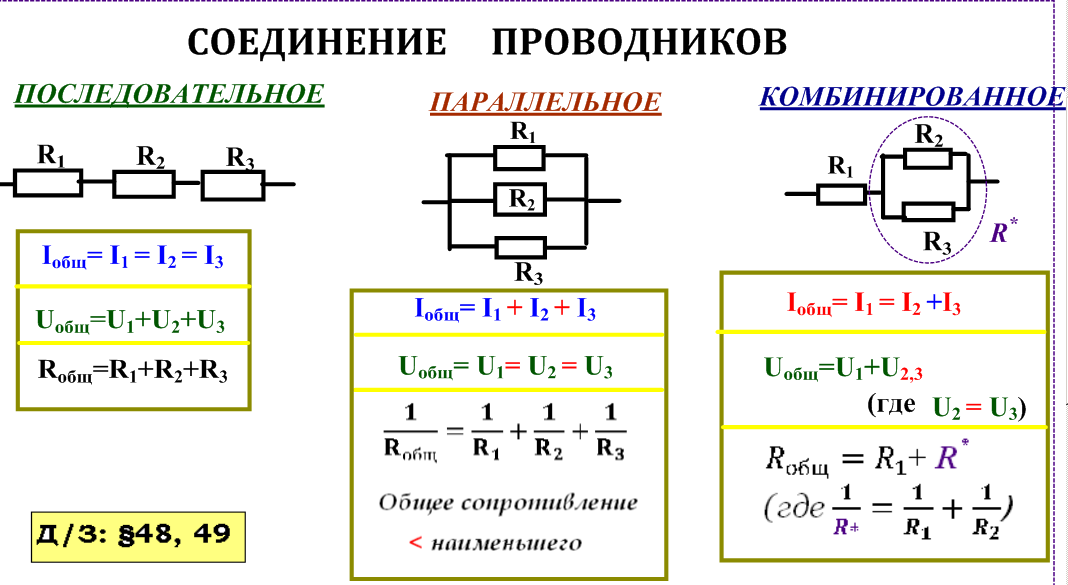
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Расчет сопротивления и интервала его абсолютной погрешности при параллельном включении резисторов и при последовательном включении этих же резисторов
Министерство образования и науки Российской Федерации
Новосибирский Государственный Технический Университет
Кафедра ТОР
Расчётно-графическая работа №1
По метрологии
Вариант №22
Факультет: РЭФ
Группа: РТС9-41
Студент: Подрезов Р.
В.Преподаватель: Абрамович В.И.
Новосибирск — 2007 г.
Задача 1.1Б:
При измерении частоты сигнала получены следующие результаты наблюдений :
18,305; 18,308; 18,312; 18,309; 18,304; 18,306; 18,309; 18,310; 18,303; 18,308.
Считать, что генеральная совокупность отклонений результатов наблюдений распределена по нормальному закону.
Определить: результат измерения частоты ; значения среднего квадратического отклонения результатов наблюдений (исключить, если имеются промахи), значения среднеквадратичной погрешности результата измерения , указать его доверительную вероятность ; интервал случайных погрешностей с доверительной вероятностью .
Решение:
Результат измерения вычисляется как среднее арифметическое значений полученных при наблюдениях.
Случайное отклонение определяется как разность полученного значения при наблюдении и результата измерения.
Таблица 1.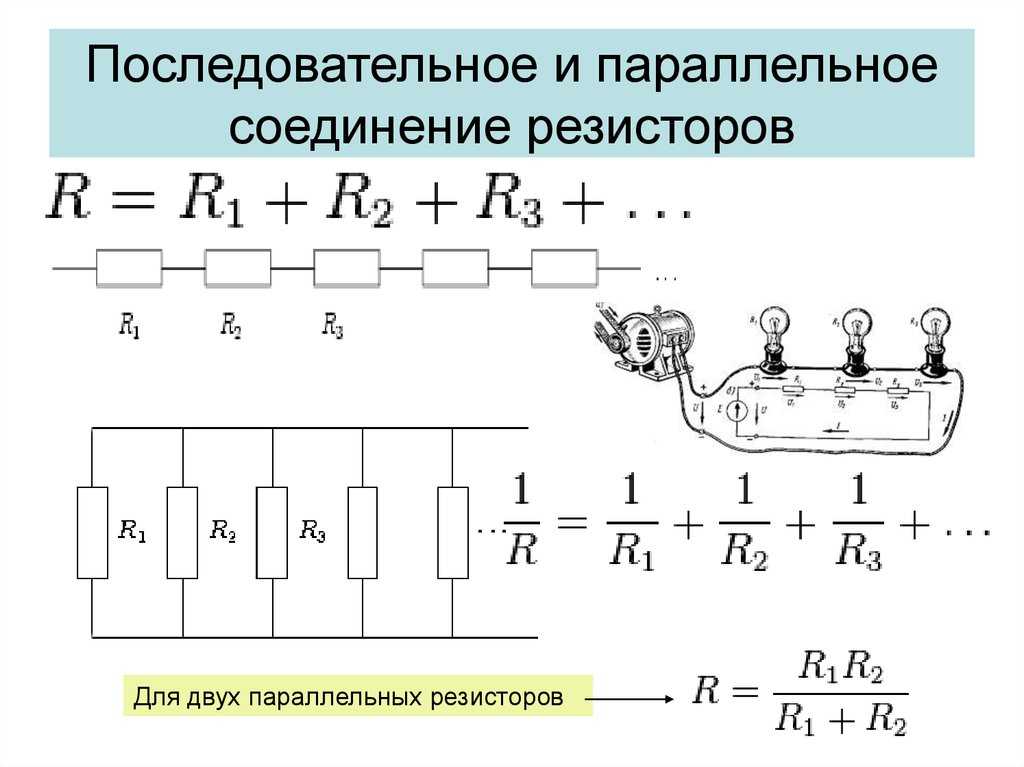
По данным таблицы 1 можно провести оценку среднего квадратического отклонения результатов наблюдений:
Зададимся уровнем значимости .Из таблицы наибольшего приведённого отклонения для соответствующих и находится величина допустимых значений . Наиболее сомнительный результат — , для которого . Проверим, выполняется ли неравенство:
:
Отсюда делаем вывод об отсутствии промахов.
Значение среднеквадратичной погрешности результата измерений рассчитывается из соотношения:
Интервал погрешности измерения с заданной доверительной вероятностью определяется по формуле:
где — коэффициент Стьюдента (обратное распределение Стьюдента)
Результат измерения: , ,
Задача 1.15
Сопротивление составлено из двух резисторов с и .
1. Чему равно
и интервал его абсолютной погрешности при параллельном включении резисторов.
2. Чему равно и интервал его абсолютной погрешности при последовательном включении этих же резисторов.
Решение:
; — абсолютная погрешность сопротивления первого резистора;
; — абсолютная погрешность сопротивления второго резистора;
При параллельном включении:
Ответ: ,
При последовательном включении:
Ответ: ,
Задача 2.2
Электрическая схема устройства сведена к эквивалентной, состоящей из последовательно включённых: источника постоянного напряжения, сопротивлений и . На измеряется падение напряжения вольтметром В2-27 с входным сопротивлением .
Определите, в какой цепи из трёх указанных ниже относительная погрешность измерения напряжения будет наибольшей, рассчитайте её величину, сформулируйте условия на соотношения ; при которых она будет мала.
1 цепь :
2 цепь
3 цепь
Решение:
Рисунок 2. Эквивалентная схема для расчёта истинного значения напряжения
Рисунок 2.
Эквивалентная
схема для расчёта измеренного значения напряжения
Выразим погрешность через сопротивления совершив некоторые математические выкладки:
1 цепь
2 цепь
3 цепь
Задача 3.6а
Какой минимальной верхней частотой полосы пропускания канала должен обладать осциллограф для измерения длительности фронта импульса порядка с погрешностью ?
Решение:
Измеренное значение длительности фронта импульса:
Отсюда время нарастания будет равным:
Согласно определению относительная погрешность:
Следовательно, измеренное значение длительности фронта можно выразить как:
Время нарастания при подстановке примет вид:
К тому же:
В итоге выражение для минимальной верхней частоты будет выглядеть так:
Калькулятор параллельного сопротивления серииРезистор R1:
ΩkΩMΩ
Резистор R2:
ΩkΩMΩ
Эквивалентное сопротивление (Req):
90:0003 ΩkΩ0MΩ ReqR1R2
Серийный/параллельный: SeriesParallel
Использование инструмента расчета последовательного сопротивления
Чтобы использовать инструмент последовательного сопротивления, установите для параметра Series/Parallel значение «Series».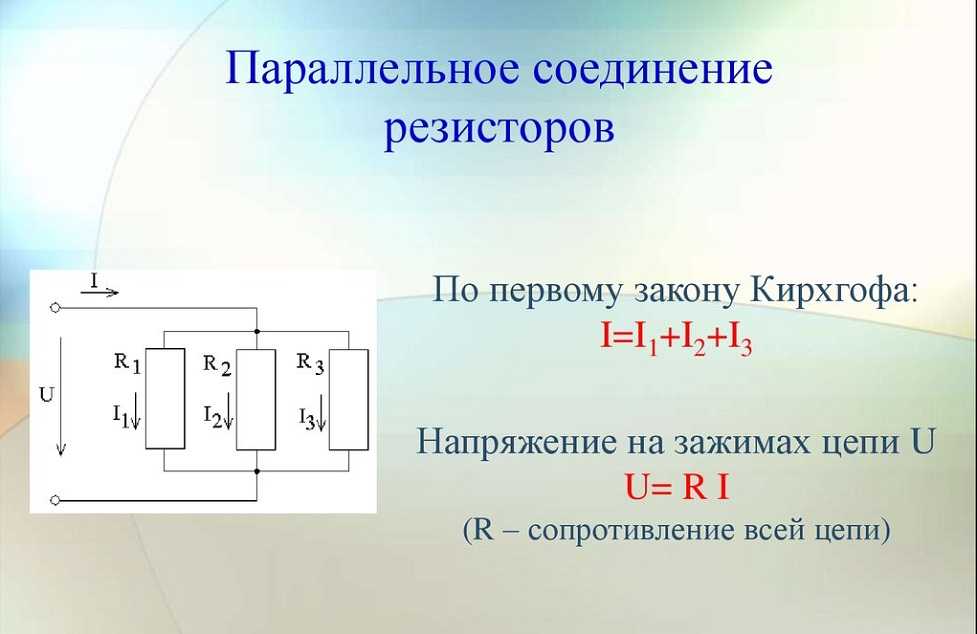
Затем в разделе «Значение для расчета» выберите значение, которое вы хотите рассчитать. Затем введите значения компонентов в поля R1, R2 или Req. Чтобы начать расчет, нажмите «Рассчитать».
Например, я установил R1 на 10 кОм и R2 на 1,2 кОм. Когда я нажму «Рассчитать», в поле «Требуется» появится эквивалентное сопротивление комбинации последовательностей.
Расчет последовательного эквивалентного сопротивления
Для расчета эквивалентного последовательного сопротивления резисторов n используйте стандартное уравнение последовательного сопротивления: на «Параллельно». Затем в разделе «Значение для расчета» выберите значение, которое вы хотите рассчитать. Чтобы начать расчет, нажмите «Рассчитать».
Например, я могу ввести 11 кОм в поле Req и 22 кОм в поле R1. Я устанавливаю инструмент для расчета R2, затем нажимаю «Рассчитать». Это приведет к 22 кОм для R2, давая мне понять, что для того, чтобы получить 11 кОм, мне понадобятся два резистора по 22 кОм, включенные параллельно.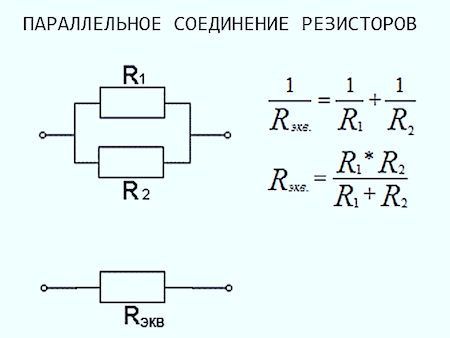
Расчет эквивалентного параллельного сопротивления
Для расчета эквивалентного параллельного сопротивления резисторов n используйте стандартное уравнение параллельного сопротивления:
Для расчета эквивалентного параллельного сопротивления резисторов два резистора , уравнение упрощается до:
Для расчета R1 или R2 используется следующее уравнение. Предположим, что вы хотите рассчитать R1 (уравнение такое же для R2):
Правила для номиналов резисторов
Калькулятор последовательного и параллельного сопротивления понимает следующие буквы и преобразует их в соответствующее значение резистора:
- k = килограмм = x1000
- М = Мега = x1000000
Например, 1k переводится как 1000, а 2.2M — как 2 200 000.
Любые другие буквы приводят к ошибке. Кроме того, не вводите в поля символ Ом, инструмент не распознает его, поскольку единицы измерения Ом уже приняты.
Познакомьтесь с автором:
Привет, я Доминик.
