Расчет синхронного двигателя на постоянных магнитах. Расчет и проектирование синхронного двигателя с постоянными магнитами: особенности, методика, преимущества

Как рассчитать синхронный двигатель с постоянными магнитами. Какие особенности нужно учитывать при проектировании. В чем преимущества данного типа двигателей. Какие этапы включает методика расчета.

Особенности конструкции синхронных двигателей с постоянными магнитами

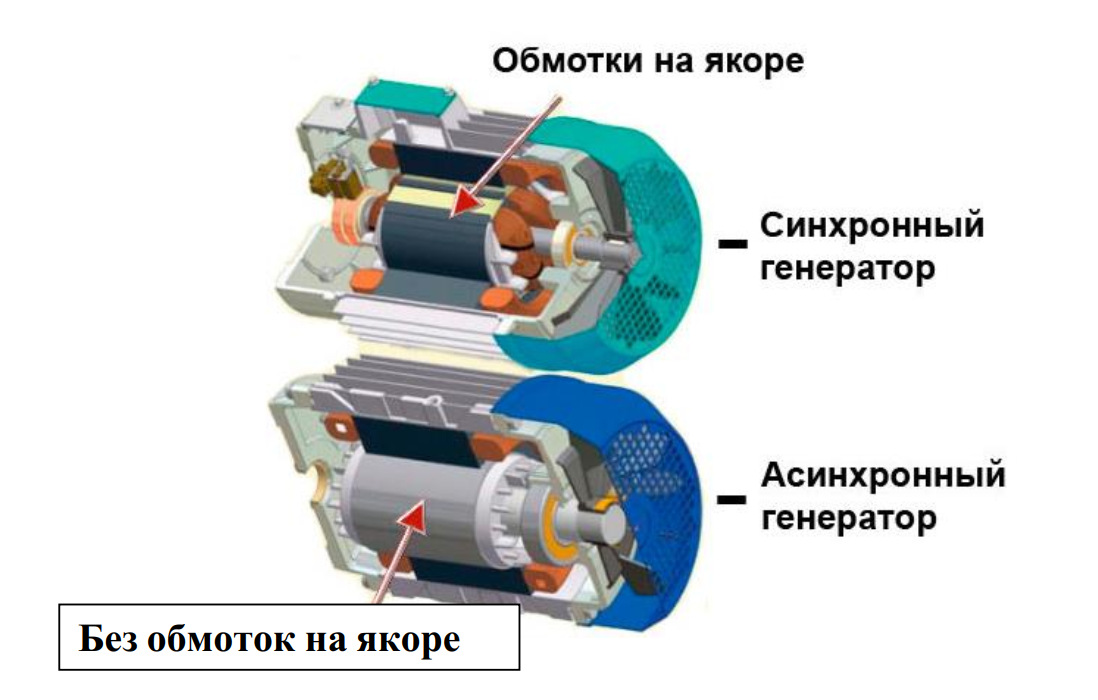
Синхронные двигатели с постоянными магнитами (СДПМ) имеют ряд конструктивных особенностей, отличающих их от других типов электрических машин:

• Отсутствие обмотки возбуждения на роторе — ее роль выполняют постоянные магниты
• Ротор может быть как внутренним, так и внешним
• Статор аналогичен статору асинхронного двигателя
• Применяются высококоэрцитивные редкоземельные магниты (например, NdFeB)
• Возможны различные конфигурации расположения магнитов на роторе

Какие преимущества дает такая конструкция СДПМ? Отсутствие обмотки возбуждения позволяет повысить КПД за счет исключения потерь на возбуждение. Применение мощных постоянных магнитов обеспечивает высокую удельную мощность и малые габариты двигателя.

Методика расчета синхронного двигателя с постоянными магнитами

Расчет СДПМ включает следующие основные этапы:

1. Выбор главных размеров двигателя
2. Проектирование магнитной системы ротора
3. Расчет обмотки статора
4. Определение параметров двигателя
5. Расчет рабочих характеристик

На каждом этапе необходимо учитывать специфику СДПМ. Например, при проектировании магнитной системы важно правильно выбрать тип и размеры постоянных магнитов, чтобы обеспечить требуемый магнитный поток в воздушном зазоре.

Выбор главных размеров СДПМ

Выбор главных размеров является ключевым этапом проектирования СДПМ. От него зависят все дальнейшие расчеты и характеристики двигателя. При выборе размеров учитываются следующие факторы:

• Требуемая мощность и частота вращения
• Число пар полюсов
• Электромагнитные нагрузки
• Коэффициент формы поля

Как определить оптимальные размеры СДПМ? Обычно используют эмпирические формулы и рекомендации по удельным показателям. Важно найти компромисс между габаритами, массой и энергетическими показателями двигателя.

Проектирование магнитной системы ротора СДПМ

Магнитная система ротора — ключевой элемент СДПМ. При ее проектировании решаются следующие задачи:

• Выбор типа и марки постоянных магнитов
• Определение размеров и формы магнитов
• Расчет магнитного потока в воздушном зазоре
• Оптимизация магнитной цепи ротора

Какие факторы влияют на выбор постоянных магнитов? Основными критериями являются остаточная индукция, коэрцитивная сила, максимальное энергетическое произведение. Для СДПМ обычно применяют редкоземельные магниты NdFeB или SmCo.

Расчет обмотки статора СДПМ

Обмотка статора СДПМ во многом аналогична обмотке асинхронного двигателя. Однако есть и особенности, которые необходимо учитывать при расчете:

• Согласование числа пазов статора с числом полюсов ротора
• Выбор типа обмотки (сосредоточенная или распределенная)
• Расчет числа витков и сечения проводников
• Определение электрических параметров обмотки

Как правильно выбрать тип обмотки СДПМ? Сосредоточенные обмотки позволяют уменьшить длину лобовых частей, но имеют больший коэффициент гармоник. Распределенные обмотки обеспечивают лучшую форму поля, но увеличивают расход меди.

Определение параметров и характеристик СДПМ

На завершающем этапе проектирования определяются основные параметры и рассчитываются рабочие характеристики СДПМ:

• Индуктивные сопротивления по осям d и q
• ЭДС холостого хода
• Электромагнитный момент
• КПД и коэффициент мощности
• Перегрузочная способность

Какие методы используются для расчета характеристик? Применяются как аналитические методы на основе схем замещения, так и численные методы конечных элементов. Последние позволяют учесть нелинейность магнитной цепи и получить более точные результаты.

Преимущества синхронных двигателей с постоянными магнитами

СДПМ обладают рядом существенных преимуществ по сравнению с другими типами электродвигателей:

• Высокий КПД (до 95-97%)
• Большая удельная мощность
• Малые габариты и масса
• Хорошие динамические характеристики
• Возможность прямого привода без редуктора

За счет чего достигаются эти преимущества? Отсутствие потерь на возбуждение и применение мощных постоянных магнитов позволяют получить высокие энергетические показатели при малых размерах двигателя. Это делает СДПМ привлекательными для многих применений.

Области применения синхронных двигателей с постоянными магнитами

Благодаря своим преимуществам СДПМ находят широкое применение в различных отраслях:

• Электротранспорт (электромобили, электробусы)
• Бытовая техника (стиральные машины, кондиционеры)
• Станкостроение (приводы подач и главного движения)
• Робототехника и сервоприводы
• Ветрогенераторы малой и средней мощности

Почему СДПМ так востребованы в этих областях? Высокая эффективность, компактность и хорошая управляемость делают их оптимальным выбором для многих современных применений, где важны энергосбережение и точность регулирования.

РАСЧЕТ ИНДУКТИВНОСТЕЙ СИНХРОННОГО ДВИГАТЕЛЯ С ИНКОРПОРИРОВАННЫМИ ПОСТОЯННЫМИ МАГНИТАМИ | Нго

1. Silvester, P. P. F Finite Elements for Electrical Engineers / P. P. Silvester, R. L. Ferrari. 3rd ed. New York: Cambridge University Press, 1996. 514 p.

2. Буль, О. Б. Методы расчета магнитных систем электрических аппаратов: магнитные цепи, поле и программа FEMM / О. Б. Буль. М.: Издательский центр «Академия», 2005. 336 c.

3. Иванов-Смоленский, А. В. Электрические машины: учеб. для вузов / А. В. Иванов-Смоленский. М.: Энергия, 1980. 928 c.

4. Вольдек, А. И. Электрические машины: учеб. для студентов высш. техн. учебн. заведений / А. И. Вольдек. 3-е изд. перераб. Л. : Энергия, 1978. 832 с.

5. Paul, C. Krause. Analysis of Electric Machinary and Drive System / C. Krause Paul, Oleg Wasunczuk, D. Sunhoff Scott. 2nd. New York: IEEE Press, 2002. 613 p.

6. Miller, T. J. E. Brushless Permanent Magnet and Reluctance Motor Drive / T. J. E. Miller. New York; Oxford: Clarendon Press, 1989. 207 p.

7. Gieras, Jacek F. Permanent Magnet Motor Technology Design / Jacek F. Gieras, Mitchell Wing. New York: Marcel Dekker, 2002. 590 p.

8. Ледовский, А. Н. Электрические машины с высококоэрцитивными постоянными магнитами / А. Н. Ледовский. М.: Энергоатомиздат, 1985. 168 c.

9. Нго, Фыонг Ле. Эквивалентная схема магнитной цепи синхронного двигателя с инкорпорированными магнитами / Фыонг Ле Нго, Г. И. Гульков // Энергетика. Изв. высш. учеб. заведений и энерг. объединений СНГ. 2015. № 4. С. 13–24.

10. Фираго, Б. И. Теория электропривода: учеб. пособие для вузов / Б. И. Фираго, Л. Б Павлячик. 2-е изд. Минск: Техноперспектива, 2007. 585 с.

Синхронные электродвигатели Toshiba на постоянных магнитах. Официальный сайт.

Описание

Синхронные (вентильные) электродвигатели на постоянных магнитах Toshiba поставляются по цене значительно меньшей, чем такие мировые бренды как ABB, Siemens и SEW, при превосходном качестве для ответственных применений. Компания СПИК СЗМА является эксклюзивным партнером Toshiba на рынке России и СНГ.

 

Стандартные функции

• полностью закрытый вентилятор
• повышение средней эффективности на 5-8% по сравнению с асинхронными двигателями
• высокая механическая прочность и коррозионная стойкость
• высокий КПД, соответствующий стандарту энергоэффективности IE4 по ГОСТ IEC 60034-30-1-2016
• номинальная частота сети 50 Гц
• номинальное напряжение сети (50 Гц): 400 В
• номинальные скорости (50 Гц): 1800, 3600 и 4500 об. /мин.
• трехфазные электродвигатели мощностью 0,37 … 315 кВт
• сервисный фактор (коэффициент перегрузки) 1.0
• конструкция формфакторов 71 — 315 по МЭК 60072-1
• изоляция класса F; Работа с частотными преобразователями, Превосходит требования МЭК 60034-25
• соответствует глобальным стандартным спецификациям, таким как IEC60034, МЭК 60072-1 , ГОСТ Р МЭК 60204-1— 2007
• степень защиты IP55
• отсутствие скольжения, синхронная частота вращения ротора и сети питания, точный контроль скорости и положения ротора
• отсутствие потерь I²R в роторе
• вращающаяся на 90˚ клеммная коробка в верхнем положении (F-3) с двумя точками заземления дополнена пластиковым кабельным вводом и заглушкой
• подходит для высокоскоростной работы до 20%. Допускается скорость выше номинальной при постоянной мощности (за пределами максимальной скорости NEMA)
• алюминиевый корпус для типоразмеров 71 … 132
• чугунный корпус для типоразмеров 160 … 315
• возможности монтажа в любом положении до типоразмеров меньше 160. Для всех типоразмеров — горизонтальное положение монтажа
• без NAFTA квалификации

 

 

Области применения электродвигателей с постоянными магнитами Tosh-ECO™

• насосы
• вентиляторы
• компрессоры
• конвейеры

Синхронные машины с постоянными магнитами

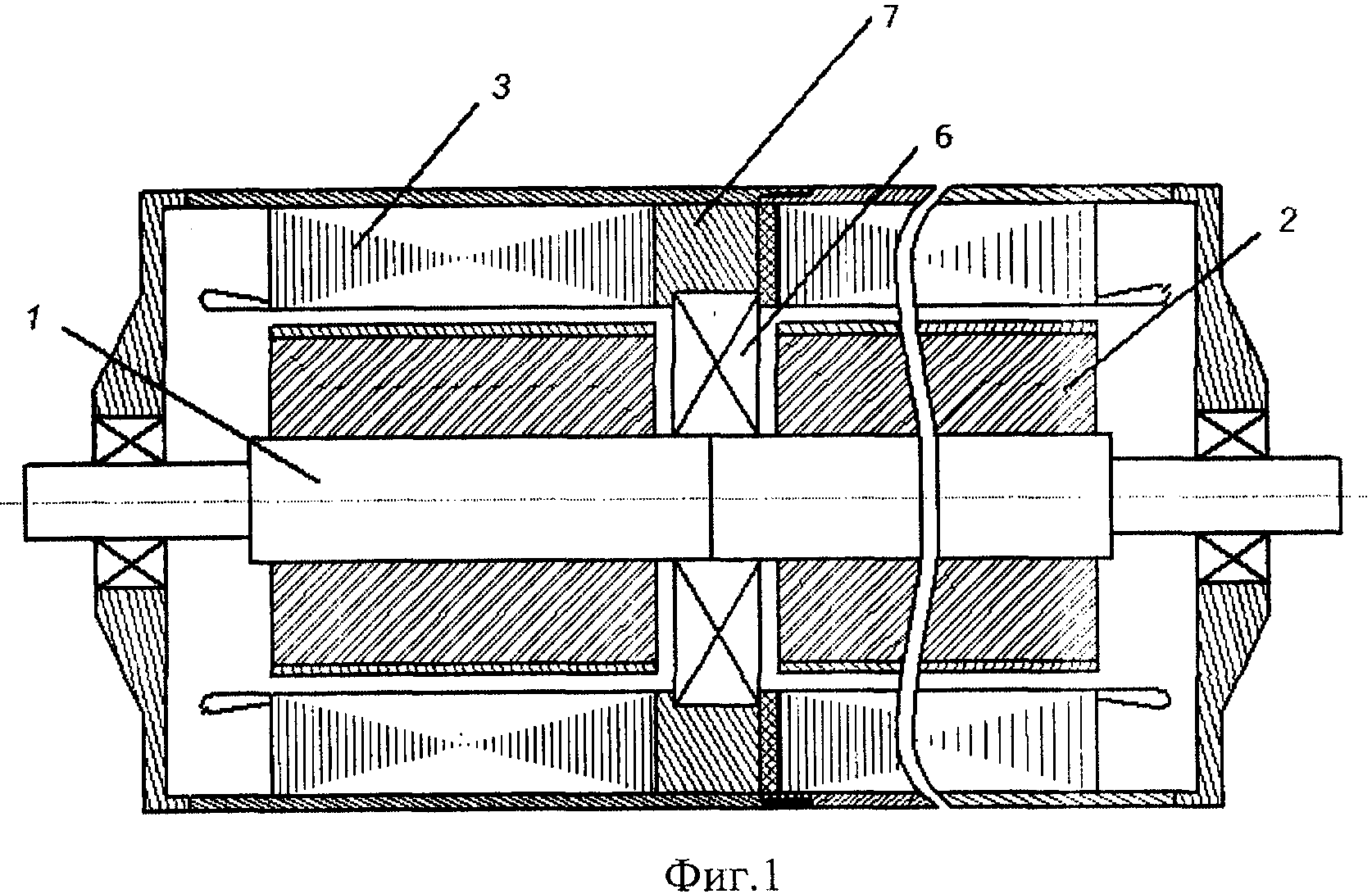
В синхронных машинах этого типа постоянно направленное поле возбуждения образуется с помощью постоянных магнитов. Синхронные машины с постоянными магнитами не нуждаются в возбудителе и благодаря отсутствию потерь на возбуждение и в скользящем контакте обладают высоким КПД, их надежность существенно выше, чем у обычных синхронных машин, в которых вращающаяся обмотка возбуждения и щеточное устройство достаточно часто повреждаются; кроме того, они практически не нуждаются в обслуживании в течение всего срока службы.
Постоянные магниты могут заменять обмотку возбуждения как в многофазных синхронных машинах обычного исполнения, так и во всех специальных исполнениях, которые были описаны выше (однофазных синхронных машинах, синхронных машинах с клюво- образными полюсами и в индукторных машинах).

Синхронные машины с постоянными магнитами отличаются от своих аналогов с электромагнитным возбуждением конструкцией индукторных магнитных систем. Аналогом ротора обычной неявнопо- люсной синхронной машины является цилиндрический кольцеобразный магнит, намагничиваемый в радиальном направлении (рис., 6).

Индукторные магнитные системы с цилиндрическим и звездообразным магнитами;
а — звездообразный магнит без полюсных башмаков; б — четырехполюсный цилиндрический магнит

Рис. 2. Ротор с когтеобразными полюсами, возбуждаемый постоянным магнитом:
1 — кольцевой постоянный магнит; 2 — диск с системой южных полюсов; 3 — диск с системой северных полюсов

Явнополюсному ротору обычной машины с электромагнитным возбуждением аналогичен ротор со звездообразным магнитом по рис.  1, а, в котором магнит 1 крепится на валу 3 заливкой из алюминиевого сплава 2.

В роторе с когтеобразиыми полюсами (рис. 2) кольцевой магнит, намагниченный в осевом направлении, заменяет кольцевую обмотку возбуждения. В разноименнополюсной индукторной машине по рис.   электромагнитное возбуждение может быть заменено магнитным, как показано на рис. 3 (вместо трех малых зубцов в каждой из зон I—IV  здесь имеется по одному зубцу в каждой из зон). Соответствующий аналог с магнитным возбуждением имеется и у одноименнополюсной машины. Постоянный магнит может быть в этом случае выполнен в виде намагниченного в осевом направлении кольца, которое вставлено между станиной и подшипниковым щитом.

Рис. 3. Индукторный разноименнополюсной генератор с магнитоэлектрическим возбуждением:
ОЯ — обмотка якоря; ПМ — постоянный магнит
Для описания электромагнитных процессов в синхронных машинах с постоянными магнитами вполне пригодна теория синхронных машин с электромагнитным возбуждением, основы которой изложены в предыдущих главах раздела. Однако для того, чтобы воспользоваться этой теорией и применить ее для расчета характеристик синхронной машины с постоянными магнитами в генераторном или двигательном режиме, нужно предварительно определить по кривой размагничивания постоянного магнита ЭДС холостого хода Е, или коэффициент возбужденности г = Ef / U и рассчитать индуктивные сопротивления Xad и X с учетом влияния магнитного сопротивления магнита, которое может быть настолько существенным, что Ха(1 < Xaq.
Машины с постоянными магнитами были изобретены еще на заре развития электромеханики. Однако широкое применение они получили в течение последних десятилетий в связи с разработкой новых материалов для постоянных магнитов с большой удельной магнитном энергией (например, типа магнико или сплавов на основе самария и кобальта). Синхронные машины с такими магнитами по своим массо- габаритным показателям и эксплуатационным характеристикам в определенном диапазоне мощностей и частот вращения вполне могут конкурировать с синхронными машинами, имеющими электромагнитное возбуждение.

Мощность быстроходных синхронных генераторов с постоянными магнитами для питания бортовой сети самолетов достигает десятков киловатт. Генераторы и двигатели с постоянными магнитами небольшой мощности применяются в самолетах, автомобилях, тракторах, где их высокая надежность имеет первостепенное значение. В качестве двигателей малой мощности они широко применяются и во многих других областях техники. По сравнению с реактивными двигателями они обладают более высокой стабильностью частоты вращения, лучшими энергетическими показателями, уступая им по стоимости и пусковым свойствам.
По способам пуска в ход синхронные двигатели малой мощности с постоянными магнитами делятся на самозапускающиеся двигатели и двигатели с асинхронным пуском.
Самозапускающиеся двигатели малой мощности с постоянными магнитами применяются для приведения в движение механизмов часов и различных реле, разнообразных программных устройств и т.п. Номинальная мощность этих двигателей не превышает нескольких ватт (обычно составляет доли ватта). Для облегчения пуска двигатели выполняют многополюсными (р > 8) и получают питание от однофазной сети промышленной частоты.
В нашей стране такие двигатели выпускаются в серии ДСМ, в которой для создания многополюсного поля применены клювообразное исполнение магнитопровода статора и однофазная якорная обмотка.
Запуск этих двигателей в ход осуществляется за счет синхронного момента от взаимодействия пульсирующего поля с постоянными магнитами ротора. Для того чтобы пуск произошел успешно и в нужную сторону, применяют специальные механические устройства, которые позволяют ротору вращаться только в одном направлении и отсоединяют его от вала во время синхронизации
Синхронные двигатели малой мощности с постоянными магнитами с асинхронным пуском выпускаются с радиальным расположением постоянного магнита и пусковой короткозамкнутой обмотки и с аксиальным расположением постоянного магнита и пусковой короткозамкнутой обмотки. По устройству статора эти двигатели ничем не отличаются от машин с электромагнитным возбуждением. Обмотка статора в обоих случаях выполняется двух- или трехфазной. Различаются они лишь по конструкции ротора.
В двигателе с радиальным расположением магнита и коротко- замкнутой обмоткой последняя размещается в пазах шихтованных полюсных наконечников постоянных магнитов Для получения приемлемых потоков рассеяния между наконечниками соседних полюсов имеются немагнитные промежутки. Иногда в целях увеличения механической прочности ротора наконечники объединяются с помощью насыщающихся перемычек в целый кольцевой сердечник.
В двигателе с аксиальным расположением магнита и коротко- замкнутой обмоткой часть активной длины занята постоянным магнитом, а на другой ее части рядом с магнитом размешается шихтованный магнитопровод с короткозамкнутой обмоткой, причем и постоянный магнит, и шихтованный магнитопровод укреплены на общем валу. В связи с тем что во время пуска двигатели с постоянными магнитами остаются возбужденными, их пуск протекает менее благоприятно, чем в обычных синхронных двигателях, возбуждение которых отключается. Объясняется это тем, что при пуске наряду с положительным асинхронным моментом от взаимодействия вращающегося поля с токами, индуктированными в короткозамкнутой обмотке, на ротор действует отрицательный асинхронный момент от взаимодействия постоянных магнитов с токами, индуктированными полем постоянных магнитов в обмотке статора.

Выбор электродвигателя и расчет его рабочих параметров

Правильность подбора электродвигателя, учитывающая специфику приводного механизма, условия работы и окружающей среды, определяет длительность безаварийной работы и надежность системы «двигатель – нагрузка».

Далее приведены рекомендации по выбору электродвигателя (последовательность, в которой они представлены, не является обязательной).

На первом этапе необходимо определиться с типом электрического двигателя. Ниже даны краткое описание, преимущества и недостатки, сферы предпочтительного применения основных типов двигателей.

Типы электрических двигателей

1. Двигатели постоянного тока

Основным преимуществом данных двигателей, которое определяло повсеместное их использование на этапе развития электрических приводов, является легкость плавного регулирования скорости в широких пределах. Поэтому с развитием полупроводниковой промышленности и появлением относительно недорогих преобразователей частоты процент их использования постоянно уменьшается. Там, где это возможно двигатели постоянного тока заменяются приводами на основе асинхронных двигателей с короткозамкнутым ротором.

Основные недостатки двигателя постоянного тока (невысокая надежность, сложность обслуживания и эксплуатации) обусловлены наличием коллекторного узла. Кроме того, для питания двигателя необходим источник постоянного тока или тиристорный преобразователь переменного напряжения в постоянное. При всех своих недостатках двигатели постоянного тока обладают высоким пусковым моментом и большой перегрузочной способностью. Что определило их использование в металлургической промышленности, станкостроении и на электротранспорте.

2. Синхронные двигатели

Основным преимуществом данных двигателей является то, что они могут работать с коэффициентом мощности cosφ=1, а в режиме перевозбуждения даже отдавать реактивную мощность в сеть, что благоприятно сказывается на характеристиках сети: увеличивается ее коэффициент мощности, уменьшаются потери и падение напряжения. Кроме того, синхронные двигатели устойчивы к колебаниям сети. Максимальный момент синхронного двигателя пропорционален напряжению, при этом момент асинхронного двигателя пропорционален квадрату напряжения. Следовательно, при снижении напряжения синхронный двигатель сохраняет большую перегрузочную способность, а возможность форсировки возбуждения увеличивает надежность их работы при аварийных понижениях напряжения.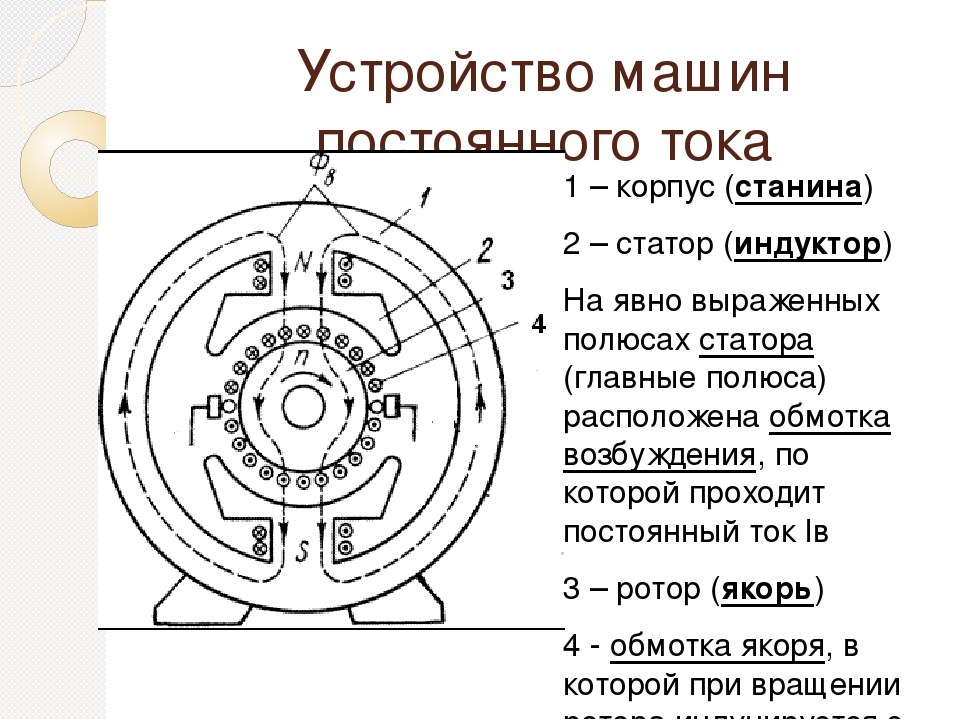 Больший воздушный зазор по сравнению с асинхронным двигателем и применение постоянных магнитов делает КПД синхронных двигателей выше. Их особенностью также является постоянство скорости вращения при изменении момента нагрузки на валу.

При всех достоинствах синхронного двигателя основными недостатками, ограничивающими их применение являются сложность конструкции, наличие возбудителя, высокая цена, сложность пуска. Поэтому синхронные двигатели преимущественно используются при мощностях свыше 100 кВт.

Основное применение – насосы, компрессоры, вентиляторы, двигатель-генераторные установки.

3. Асинхронные двигатели

По конструктивному принципу асинхронные двигатели подразделяются на двигатели с короткозамкнутым и фазным ротором. При этом большинство используемых электродвигателей являются асинхронными с короткозамкнутым ротором. Столь широкое применение обусловлено простотой их конструкции, обслуживания и эксплуатации, высокой надежностью, относительно низкой стоимостью. Недостатками таких двигателей являются большой пусковой ток, относительно малый пусковой момент, чувствительность к изменениям параметров сети, а для плавного регулирования скорости необходим преобразователь частоты. Кроме того, асинхронные двигатели потребляют реактивную мощность из сети. Предел применения асинхронных электродвигателей с короткозамкнутым ротором определяется мощностью системы электроснабжения конкретного предприятия, так как большие пусковые токи при малой мощности системы создают большие понижения напряжения.

Использование асинхронных двигателей с фазным ротором помогает снизить пусковой ток и существенно увеличить пусковой момент, благодаря введению в цепь ротора пусковых реостатов. Однако, ввиду усложнения их конструкции, и как следствие, увеличения стоимости их применение ограничено. Основное применение – приводы механизмов с особо тяжелыми условиями пуска. Для уменьшения пусковых токов асинхронного двигателя с короткозамкнутым ротором может быть использовано устройство плавного пуска или преобразователь частоты.

В системах, где необходимо ступенчатое изменение скорости (например, лифты) используют многоскоростные асинхронные двигатели. В механизмах, требующих остановки за определенное время и фиксации вала при исчезновении напряжения питания, применяются асинхронные двигатели с электромагнитным тормозом (металлообрабатывающие станки, лебедки). Существуют также асинхронные двигатели с повышенным скольжением, которые предназначены для работы в повторно-кратковременных режимах, а также режимах с пульсирующей нагрузкой.

После того, как определен тип электродвигателя, полностью учитывающий специфику рабочего механизма и условия работы, необходимо определиться с рабочими параметрами двигателя: мощностью, номинальным и пусковым моментами, номинальными напряжением и током, режимом работы, коэффициентом мощности, классом энергоэффективности.

Мощность и моменты

В общем случае для квалифицированного подбора электродвигателя должна быть известна нагрузочная диаграмма механизма. Однако, в случае постоянной или слабо меняющейся нагрузки без регулирования скорости достаточно рассчитать требуемую мощность по теоретическим или эмпирическим формулам, зная рабочие параметры нагрузки. Ниже приведены формулы для расчета мощности двигателя P₂ [кВт] некоторых механизмов.

1. Вентилятор

где Q [м³/с] – производительность вентилятора,

Н [Па] – давление на выходе вентилятора,

η_вент, η_пер – КПД вентилятора и передаточного механизма соответственно,

k_з – коэффициент запаса.

2. Насос

где Q [м³/с] – производительность насоса,

g=9,8 м/с² – ускорение свободного падения,

H [м] – расчетная высота подъема,

ρ [кг/м³] – плотность перекачиваемой жидкости,

η_нас, η_пер – КПД насоса и передаточного механизма соответственно,

k_з – коэффициент запаса.

3. Поршневой компрессор

где Q [м³/с] – производительность компрессора,

А [Дж/м³] – работа изотермического и адиабатического сжатия атмосферного воздуха объемом 1 м³ давлением 1,1·10⁵ Па до требуемого давления,

η_компр, η_пер – КПД компрессора и передаточного механизма соответственно,

k_з – коэффициент запаса.

Кроме того, необходимо сопоставить пусковой момент двигателя (особенно в случае асинхронного с короткозамкнутым ротором) и рабочего механизма, так как некоторые механизмы имеют повышенное сопротивление в момент трогания. Следует иметь в виду и то обстоятельство, что при замене трехфазного асинхронного двигателя на однофазный пусковой момент последнего почти в три раза меньше и механизм, успешно функционировавший ранее, может не тронуться с места.

Развиваемый электродвигателем момент M [Нм] и полезная мощность на валу Р₂ [кВт] связаны следующим соотношением

Полная мощность, потребляемая из сети:

для двигателей постоянного тока (она же активная)

для двигателей переменного тока

 

 

при этом потребляемые активная и реактивная мощности соответственно

В случае синхронного двигателя значение Q₁ может получиться отрицательным, это означает, что двигатель отдает реактивную мощность в сеть.

Важно отметить следующее. Не следует выбирать двигатель с большим запасом по мощности, так как это приведет к снижению его КПД, а в случае двигателя переменного тока также к снижению коэффициента мощности.

Напряжение и ток

При выборе напряжения электродвигателя необходимо учитывать возможности системы энергоснабжения предприятия. При этом нецелесообразно при больших мощностях выбирать двигатель с низким напряжением, так как это приведет к неоправданному удорожанию не только двигателя, но и питающих проводов и коммутационной аппаратуры вследствие увеличения расхода меди.

Если при трогании момент сопротивления нагрузки невелик и для уменьшения пусковых токов асинхронного двигателя с короткозамкнутым ротором может быть применен способ пуска с переключением со «звезды» на «треугольник», необходимо предусмотреть вывод в клеммную коробку всех шести зажимов обмотки статора. В общем случае применение схемы соединения «звезда» является предпочтительным, так как в схеме «треугольник» имеется контур для протекания токов нулевой последовательности, которые приводят к нагреву обмотки и снижению КПД двигателя, в соединении «звезда» такой контур отсутствует.

Режим работы

Нагрузка электродвигателя в процессе работы может изменяться различным образом. ГОСТом предусмотрены восемь режимов работы.

1. Продолжительный S1 – режим работы при постоянной нагрузке в течение времени, за которое температура двигателя достигает установившегося значения. Мощность двигателя, работающего в данном режиме, рассчитывается исходя из потребляемой механизмом мощности. Формулы расчета мощности некоторых механизмов (насос, вентилятор, компрессор) приведены выше.
2. Кратковременный S2 – режим, при котором за время включения на постоянную нагрузку температура двигателя не успевает достичь установившегося значения, а за время отключения двигатель охлаждается до температуры окружающей среды. В случае использования двигателя S1 для работы в режиме S2 необходимо проверить его только по перегрузочной способности, так как температура не успевает достичь допустимого значения.
3. Повторно-кратковременный S3 – режим с периодическим отключением двигателя, при котором за время включения температура не успевает достичь установившегося значения, а за время отключения – температуры окружающей среды. Расчет мощности электродвигателя обычного исполнения для работы в режиме S3 производится по методам эквивалентных величин с учетом пауз и потерь в переходных режимах. Кроме того, двигатель необходимо проверить на допустимое число включений в час. В случае большого числа включений в час рекомендуется использовать двигатели с повышенным скольжением. Данные электродвигатели обладают повышенным сопротивлением обмотки ротора, а, следовательно, меньшими пусковыми и тормозными потерями.
4. Повторно-кратковременный с частыми пусками S4 и повторно-кратковременный с частыми пусками и электрическим торможением S5. Данные режимы рассматриваются аналогично режиму S3.
5. Перемежающийся S6 – режим, при котором работа двигателя под нагрузкой, периодически заменяется работой на холостом ходу. Большинство двигателей, работающих в продолжительном режиме, имеют меняющийся график нагрузки.

При этом для обоснованного выбора двигателя с целью оптимального его использования рекомендуется применять методы эквивалентных величин.

Класс энергоэффективности

В настоящее время вопросам энергоэффективности уделяется огромное внимание. При этом под энергоэффективностью понимается рациональное использование энергетических ресурсов, с помощью которого достигается уменьшение потребления энергии при том же уровне мощности нагрузки. Основным показателем энергоэффективности двигателя является его коэффициент полезного действия

где Р₂ – полезная мощность на валу, Р₁ – потребляемая активная мощность из сети.

Стандартом IEC 60034-30 для асинхронных электродвигателей с короткозамкнутым ротором были установлены три класса энергоэффективности: IE1, IE2, IE3.

 

Рис. 1. Классы энергоэффективности

Так, например, использование двигателя мощностью 55 кВт повышенного класса энергоэффективности позволяет сэкономить около 8000 кВт в год от одного двигателя.

Степень защиты IP, виды климатических условий и категорий размещения

ГОСТ Р МЭК 60034-5 – 2007 устанавливает классификацию степеней защиты, обеспечиваемых оболочками машин.

Обозначение степени защиты состоит из букв латинского алфавита IP и последующих двух цифр (например, IP55).

Большинство электродвигателей, выпускаемых в настоящее время, имеют степени защиты IP54 и IP55.

Категория размещения обозначается цифрой:

1 – на открытом воздухе;

2 – под навесом при отсутствии прямого солнечного воздействия и атмосферных осадков;

3 – в закрытых помещениях без искусственного регулирования климатических условий;

4 – в закрытых помещениях с искусственно регулируемыми климатическими условиями.

Климатические условия:

У – умеренный климат;

УХЛ – умеренно холодный климат;

ХЛ – холодный климат;

Т – тропический климат.

Таким образом, при выборе электродвигателя необходимо учитывать условия окружающей среды (температура, влажность), а также необходимость защиты двигателя от воздействия инородных предметов и воды.

Например, использование электродвигателя с типом климатического исполнения и категорией размещения У3 на открытом воздухе является недопустимым.

Усилия, действующие на вал двигателя со стороны нагрузки

Наиболее нагруженными в двигателе являются подшипниковые узлы. Поэтому при выборе двигателя должны быть учтены радиальные и осевые усилия, действующие на рабочий конец вала двигателя со стороны нагрузки. Превышения допустимых значений сил приводит к ускоренному выходу из строя не только подшипников, но и всего двигателя (например, задевание ротора о статор).

Обычно допустимые значения сил для каждого подшипника приведены в каталогах. Рекомендуется в случае повышенных радиальных усилий (ременная передача) на рабочий конец вала установить роликовый подшипник, при этом предпочтительным является двигатель с чугунными подшипниковыми щитами.

Особенности конструкции двигателя при работе от преобразователя частоты

В настоящее время все большее распространение приобретает использование частотно-регулируемого привода (ЧРП), выполненного на основе асинхронного электродвигателя с короткозамкнутым ротором.

При использовании частотно-регулируемого привода достигается:

1. экономия электроэнергии;

2. плавность пуска и снижение пусковых токов;

3. увеличение срока службы двигателя.

В общем случае стандартный электродвигатель нельзя использовать в составе частотно-регулируемого привода, так как при уменьшении скорости вращения снижается эффективность охлаждения. При регулировании скорости вверх от номинальной резко увеличивается нагрузка от собственного вентилятора. В обоих случаях уменьшается нагрузочная способность двигателя. Кроме того, в случае использования двигателя в системах точного регулирования необходим датчик положения ротора двигателя.

При работе электродвигателя от преобразователя частоты в контуре вал – фундаментная плита могут протекать токи. При этом возникает точечная эрозия на шариках и роликах, на беговых кольцах подшипников качения, а также на баббитовой поверхности подшипников скольжения. От электролиза смазка чернеет, подшипники греются. Для разрыва контура прохождения подшипниковых токов на неприводной конец вала устанавливается изолированный подшипник. При этом по условиям безопасности установка изолированных подшипников с двух сторон двигателя не допустима.

Величина подшипниковых токов становится опасной для безаварийной работы двигателя при напряжении между противоположными концами вала более 0,5 В. Поэтому установка изолированного подшипника обычно требуется для электродвигателей с высотой оси вращения более 280 мм.

 Примечание

Необходимо отметить, что в случае отклонения условий эксплуатации двигателя (например, температуры окружающей среды или высоты над уровнем моря), мощность нагрузки должна быть изменена. Кроме того, при снижении мощности нагрузки в определенные моменты времени для рационального использования двигателя может быть изменена схема соединения обмотки, а, следовательно, и фазное напряжение.

 

Популярные товары

Шины медные плетеные

Шины изолированные гибкие и твердые

Шинодержатели

Изоляторы

Индикаторы наличия напряжения

Синхронные двигатели с постоянными магнитами на роторе: управление (синус и/или трапеция)

Например, термин PMSM (СДПМ) может применяться для обозначения двигателя с постоянными магнитами на роторе, независимо от формы его ЭДС, но так же часто его применяют, подразумевая исключительно синусоидальную форму ЭДС двигателя.

Термин BLDC (БДПТ) может применяться для обозначения двигателя с постоянными магнитами на роторе и трапецеидальной ЭДС, а может вообще обозначать не двигатель, а некий мехатронный узел, включающий в себя:

• двигатель с постоянными магнитами и трапецеидальной ЭДС
• датчик положения ротора
• управляемый по сигналам этого датчика полупроводниковый коммутатор.

Собственно этот мехатронный узел, который может, как и двигатель постоянного тока, управляться постоянным напряжением, и породил сам термин BLDC (БДПТ).

Ещё по отношению к синхронным двигателям с постоянными магнитами на роторе в отечественной литературе, можно встретить название «вентильный двигатель».

Попытки автора разобраться с этим термином быстро зашли в тупик, так как в различных источниках обнаружились явные противоречия.

Например, в книге Г.Б. Онищенко «Электрические двигатели» на стр. 47 «вентильным» называется двигатель соответствующий термину BLDC (БДПТ), что предполагает трапецеидальную ЭДС, и это понимаемо.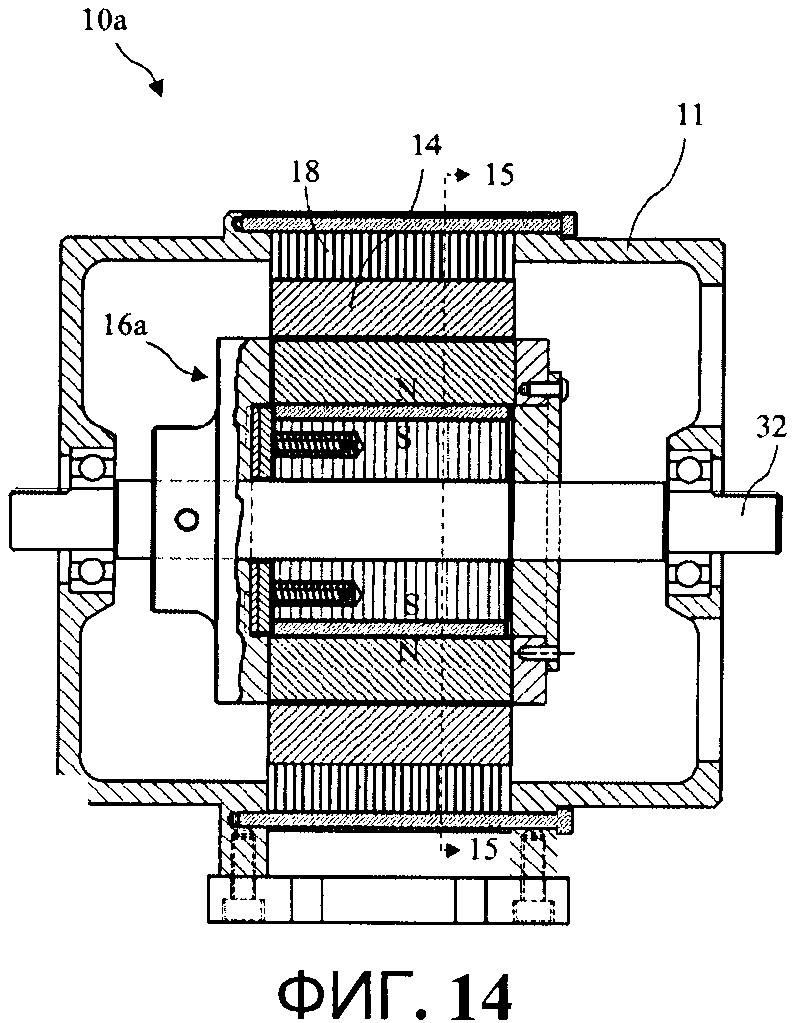

Но двигатели типа 5ДВМ сам производитель (ЧЭАЗ) называет «вентильными», хотя при этом утверждает, что они имеют синусоидальную ЭДС.

А вот «Википедия»: «Вентильный двигатель следует отличать от бесколлекторного двигателя постоянного тока (БДПТ), который имеет трапецеидальное распределение магнитного поля в зазоре…».

Ну…приехали…

Какой термин, какой форме ЭДС соответствует – непонятно.

А между тем, именно эта форма определяет выбор структуры системы управления двигателем.

Как человек, занимающийся этим управлением, хочу предложить:

• во избежание путаницы забыть термин «вентильный двигатель»
• термином БДПТ обозначать не двигатель, а исключительно описанный выше мехатронный узел (аналог двигателя постоянного тока)
• делить синхронные двигатели с постоянными магнитами на роторе (СДПМ) по типу ЭДС на две группы:
  с синусоидальной ЭДС (далее, для краткости, — СДПМс)
  с трапецеидальной ЭДС (далее, для краткости, — СДПМт)

Управление

При управлении двигателями с синусоидальной ЭДС используется векторное регулирование (подробно описано в книжке по ссылке http://3v-services. com/books/978-5-97060-766-4/978-5-97060-766-4_SimInTech-01.pdf). С точки зрения возможностей и качества управления это наилучший вариант.

Однако и двигатели с трапецеидальной ЭДС в силу более простой конструкции статорных обмоток и возможности более простого управления применяются довольно часто.

Конструкция двигателей

Форма ЭДС определяется конструкцией двигателя.

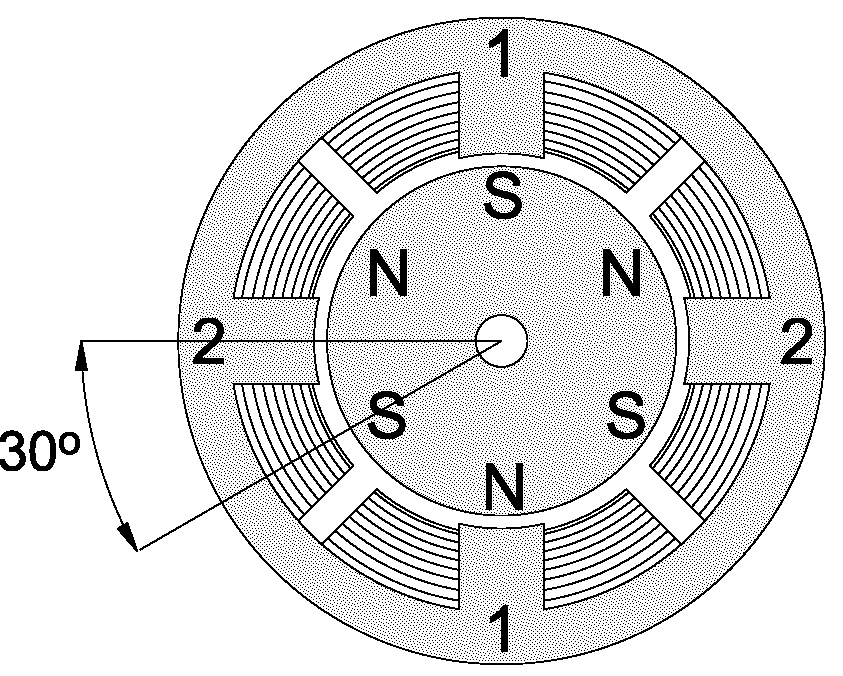
Ротор синхронных двигателей представляет собой магнит с различным количеством пар полюсов.

На Рис 1. показаны возможные конструкции статорных обмоток. Обычно синусоидальной ЭДС соответствует «распределенная» намотка, а трапецеидальной «сосредоточенная».

Рис.1

Статорная обмотка двигателя с трапецеидальной ЭДС проще и технологичнее, за счёт этого цена такого двигателя несколько ниже.

Далее остановимся более подробно на двигателе с трапецеидальной ЭДС (СДПМт)

Двигатель с одной парой полюсов будет выглядеть в разрезе так, как показано на Рис. 2.

Рис.2

На статоре СДПМт намотаны три обмотки (А, В, С), сдвинутые в пространстве на 120º. Каждая обмотка состоит из двух секций, включённых встречно. Таким образом, при протекании тока в обмотке она создаёт внутри двигателя два полюса (положительный и отрицательный), к которым и притягивается магнитный ротор. Поочередное изменение токов в обмотках переключает полюса обмоток и заставляет ротор двигаться вслед за полем. На этом и основан принцип работы двигателя.

Уравнения равновесия статорных обмоток двигателя
Уравнения равновесия статорных обмоток двигателя при его включении в «звезду» в неподвижных фазных координатах АВС имеют вид (1).

(1)

Здесь:

— фазные напряжения

— потокосцепления фазных обмоток

— токи фаз

— активное сопротивление фазной обмотки.

Поток в обмотке каждой фазы формируется из следующих составляющих:

• поток, наводимый собственным током фазы
• поток, наводимый магнитными полями других фазных обмоток
• поток, наводимый в обмотке магнитами ротора.

Проиллюстрируем это системой (2):

(2)

Где:

— индуктивность фазных обмоток

— взаимные индуктивности обмоток

— потокосцепления, наводимые в обмотках магнитом ротора.

В общем случае все индуктивности системы (2) могут являться переменными функциями угла поворота поля .

В частном случае для неявнополюсного двигателя (при цилиндрическом роторе) индуктивности и взаимные индуктивности обмоток не зависят от угла.

Обозначив

— индуктивность фазной обмотки,

— взаимная индуктивность двух фазных обмоток,

и подставив выражения (2) в систему (1), получим выражение (3):

 (3)

Заметив, что производные по времени от потокосцеплений магнитов ротора

есть не что иное, как наводимая магнитами ротора в этих обмотках ЭДС, систему (3) можно переписать в виде (4).

 (4)

Теперь введем понятие единичной функции формы ЭДС.

Единичная функция формы ЭДС — это функция от угла поля (), имеющая единичную амплитуду и повторяющая по форме ЭДС. Для фаз А, В, С обозначим эти функции: 

Используя единичные функции формы, мгновенные ЭДС в фазах можно
представить выражением (5):
 (5)

Где:
 — амплитуда потокосцепления ротора и фазной обмотки
 — скорость вращения поля
 — скорость вращения ротора
 — число пар полюсов двигателя.

Зависимости единичных функций формы ЭДС обмоток СДПМт от угла
поворота поля представлены На Рис.3.

Рис. 3

Вывод формулы для расчёта электромагнитного момента СДПМт

Момент, создаваемый двигателем, является суммой моментов, создаваемых его обмотками.

Посмотрим на уравнение равновесия обмотки фазы А из системы (4).

Умножив обе его части на ток обмотки, получим уравнение для мгновенной электрической мощности обмотки:

Рассмотрим составляющие этой мощности:

 — реактивная мощность обмотки
 — активная мощность, рассеивающаяся в обмотке
 — мощность, создающая электромагнитный момент.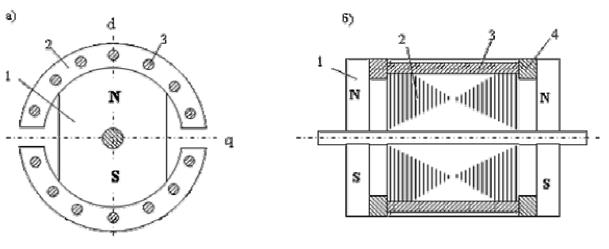

Если пренебречь потерями при переходе электрической мощности в механическую, то можно записать:

,

или:

 (6)

Где:

 — электромагнитный момент двигателя

 — угловая скорость вращения ротора.

Подставив в формулу (6) значения ЭДС из соотношений (5), получим формулу вычисления электромагнитного момента ротора (7).

 (7)

Коммутация обмоток СДПМт

В соответствии с формулой (7) момент СДПМт пропорционален сумме произведений фазных токов на функции формы соответствующих ЭДС.

Максимальное значение ЭДС обмотки соответствует плоским участкам трапеции ЭДС. Если бы нам удалось на этих участках угловой траектории сформировать в обмотках токи некоторой постоянной амплитуды, например, совпадающие по знаку со знаком ЭДС, то это позволило бы сформировать при этих токах максимальный постоянный положительный момент.

Для примера рассмотрим на Рис.3 участок угловой траектории от /6 до /2. На этом участке ЭДС в фазе А имеет максимально отрицательное значение, а в фазе В максимально положительное. Следовательно, для получения положительного момента на этом участке угловой траектории надо обеспечить в фазе А отрицательное, а в фазе В положительное значение тока. Для этого фазу А можно подключить на отрицательный, а фазу В на положительный полюса внешнего источника постоянного напряжения (U_dc). При этом фаза С не используется (отключена от источника U_dc).

Величина тока, протекающего через обмотки, будет в свою очередь определяться прикладываемым к обмоткам напряжением, величиной ЭДС и параметрами обмоток.

Если рассуждать таким образом, то можно составить таблицу коммутаций обмоток, обеспечивающих в зависимости от положения ротора момент нужного знака (Табл. 1).

Табл.1 Алгоритм коммутации

Обмотки трёхфазного двигателя можно коммутировать на внешний источник напряжения с помощью трехфазного мостового инвертора. Для этого состояние инвертора надо поставить в зависимость от положения ротора. Обычно это делается с помощью датчика положения ротора (ДПР). Этот датчик имеет три канала. Каждый канал выдает за один оборот двигателя импульс, соответствующий половине периода вращения, при этом импульсы в каналах сдвинуты на 120º.

Логическая обработка сигналов ДПР позволяет определить в каком из шести секторов в данный момент находится ротор.

Работа ДПР поясняется Табл. 2.

Возможная структура системы управления моментом СДПМт

Алгоритм, описанный в Табл.1, предполагает протекание одного и того же тока в двух фазах двигателя при единичном значении функции формы ЭДС в обмотках фаз. Поэтому выражение (7) можно переписать в виде (8).

(8)

Где:

— значение тока в фазах

 

То есть значение момента пропорционально величине тока в обмотках двигателя.

Вытекающая из формулы (8) структура системы управления моментом в приводе с СДПМт изображена на Рис. 4.

 

 

Рис. 4

 

Данная структура позволяет получить нужный момент, формируя в обмотках двигателя ток необходимой амплитуды, при сохранении алгоритма коммутации (Табл.1).

Эта задача решается с помощью создания на базе трёхфазного мостового инвертора контура тока с ШИМ.

Регулятор тока (ПИ-рег.) формирует сигнал задания напряжения обмоток (U), которое затем реализуется инвертором с ШИМ в соответствии с алгоритмом коммутации (Табл.1).

В качестве сигнала обратной связи в контуре можно использовать  трёхфазно-выпрямленные сигналы датчиков тока фаз или сигнал датчика тока в звене постоянного тока инвертора ().

На основе рассмотренного канала управления моментом можно строить внешние контуры управления скоростью и положением.

Однако
Если бы токи в обмотках спадали до нуля и нарастали до нужного уровня  мгновенно, то  момент двигателя, определяемый их величиной, в установившемся режиме был бы постоянным. В действительности же реальные переходные процессы при коммутации обмоток приводят  к пульсациям момента. В зависимости от параметров обмоток, а также соотношения величин текущей ЭДС и напряжения звена постоянного тока эти пульсации могут быть различны по длительности, амплитуде и знаку.

Кроме этих коммутационных пульсаций в рассматриваемой системе также будут иметь место пульсации момента на частоте ШИМ.

Ниже приведен пример работы модели системы регулирования скорости. Данная модель построена в среде SimInTehc на элементах специализированного тулбокса «Электропривод». Среда позволяет получить максимальное приближение моделируемых процессов к реальности с учетом эффектов временной и уровневой дискретизации.

Часть модели, а именно — модель цифровой системы управления скоростью приведена ниже, на Рис.5. Регулятор скорости системы (Рег.W) выдаёт сигнал момента, который отрабатывается структурой построенной в соответствии с Рис.4.

Рис. 5

 

Для управления был выбран двигатель со следующими параметрами:

Rs=2.875 Ом — сопротивление обмотки фазы

Ls=8.5e-3 Гн – индуктивность фазы

F=0.175 Вб – потокосцепление ротора

Zp=4 —  число пар полюсов

Jr=0. 06 кг∙м² — момент инерции ротора

Напряжение в звене постоянного тока привода было принято равным 100В.

В контуре тока электропривода использовалась ШИМ с частотой 5кГц.

В процессе регулирования  происходило ступенчатое увеличение частоты при постоянном моменте сопротивления на валу двигателя (10 Нм).

Графики, полученные в процессе работы модели, приведены на Рис.6.

Рис.6

На графике момента видны существенные пульсации.

Отметим, что в основном они связаны именно с переходными процессами при коммутации обмоток и имеют соответственно частоту ушестерённую по отношению к заданной.

Пульсации, связанные с ШИМ, в данном случае, невелики.

Заметим, что коммутационные пульсации существенно возрастают при увеличении момента, что связано с увеличением тока.

Несколько спасает то, что их влияние  на скорость снижает инерция.

А можно ли векторно управлять СДПМт?
Если очень хочется — то можно. Однако и здесь не без особенностей.

Математика и структура стандартной векторной системы управления исходит из синусоидальности поля в зазоре. При трапецеидальной ЭДС это условие нарушается, правда не очень сильно (трапеция это же почти синус).

 А результатом  этого «почти» будут опять же пульсации момента.

Вид модели цифровой системы векторного управления скоростью в среде SimInTech показан на Рис.7.

 

Рис.7

 

Ниже на Рис.8 показан график работы модели уже рассмотренного ранее СДПМт работающего в рассмотренном ранее  режиме, но под управлением векторной системы.

В графике момента мы опять наблюдаем пульсации (хотя по сравнению с предыдущим вариантом они несколько уменьшились).

Причины пульсации при векторном управлении и управлении по ДПР различны, но их частота та же – ушестерённая по отношению к заданной.

Заметим, что вследствие несинусоидальности ЭДС токи в обмотках двигателя также будут принципиально несинусоидальными (это действительно так, хотя в масштабе графика на Рис.8 и не слишком заметно).

 

Рис.8

А можно ли с помощью коммутации обмоток по ДПР управлять двигателем с синусоидальной ЭДС?

С точки зрения автора можно – но не нужно.

 

Наряду с коммутационными пульсациями момента синусоидальность ЭДС (отсутствие плоской вершины трапеции) в данном случае неминуемо вызовет ещё и дополнительные пульсации, снижающие качество регулирования даже по сравнению с управляемым по ДПР двигателем СДПМт.

А при векторном управлении двигателем с синусоидальной ЭДС пульсаций момента не будет.

Для подтверждения этого тезиса ниже (Рис.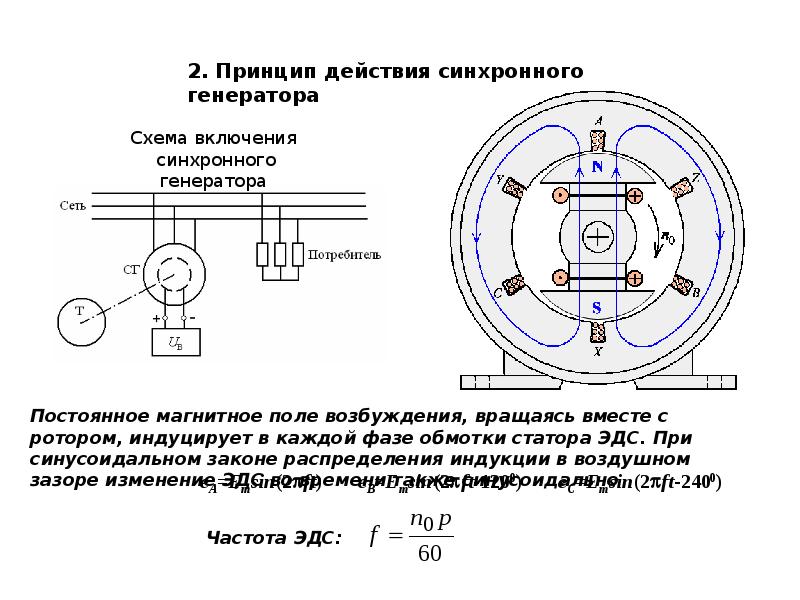 9) приведены графики работы модели двигателя с рассмотренными ранее параметрами, но с синусоидальной ЭДС и векторной системой управления скоростью.

Видно, что пульсации момента в этом случае практически отсутствуют. При правильной настройке регуляторов системы они связаны только с ШИМ-преобразованием и для данного случая почти не видны.

 

Рис.9

Итоги

Для синхронников с страпецеидальной ЭДС — коммутация по ДПР.

Так же возможно использование и более сложного векторного алгоритма регулирования, что может дать снижение уровня пульсации момента.

Для синхронников с синусоидальной ЭДС лучший вариант это векторное регулирование.

Это сочетание идеально для построения точного электропривода (что собственно и так было понятно).

 

 

Ю.Н. Калачёв

 

 

Список литературы

 

[1]   А. С. Пушкин «Полтава».

Управление током статора синхронного электродвигателя с возбуждением постоянными магнитами при частотном пуске

В статье рассмотрен контур регулирования тока статора синхронного двигателя с постоянными магнитами, получено условие устойчивости этого контура и исследована точность поддержания заданного тока с учетом ЭДС вращения, наводимой в обмотке статора.

Введение

В предыдущей статье автора [1] был рассмотрен частотный пуск синхронного двигателя (СД) с возбуждением постоянными магнитами при синусоидальных токах статора с неизменной амплитудой. Как известно, на ток статора оказывают существенное влияние многие факторы, например, увеличение ЭДС вращения и сопротивления обмоток вследствие повышения частоты при пуске СД, изменение величины прикладываемого напряжения. Следовательно, для поддержания тока статора неизменным необходимы специальные меры.

В электроприводе постоянного тока, построенном по принципу подчиненного управления, задачу ограничения тока и поддержания его на этом уровне в переходных режимах успешно решает контур регулирования тока.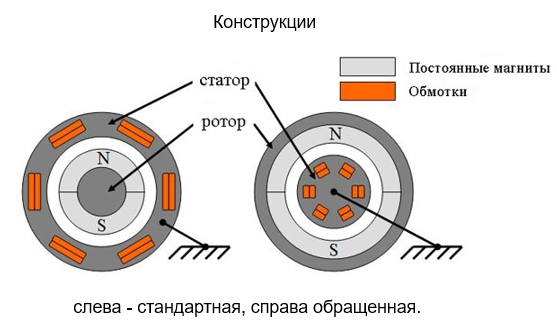 Поэтому логично использовать его и в электроприводе переменного тока. Поскольку при частотном управлении двигателями переменного тока используют обычно трехфазный автономный инвертор (АИН), построенный на транзисторах типа MOSFET или IGBT, весьма чувствительных к перегрузке по току, требования к динамическим свойствам регулятора тока статора достаточно высоки. С другой стороны, весьма жесткими оказываются и требования к ослаблению влияния возмущающих воздействий на величину тока. Как известно, при жестких требованиях к качеству управления возможно нежелательное проявление свойств широтно-импульсного управления инвертором, например, недопустимых субгармонических автоколебаний. Таким образом, необходим учет и этого фактора.

1. Математическое описание силовой части трехфазного контура регулирования тока

Рассмотрим АИН, нагруженный на обмотку статора СД, соединенную звездой (рис. 1) при следующих допущениях:

• в силу симметрии трехфазной обмотки статора r_a = r_b = r_c = r, L_a = L_b = L_c = L, M_ab = M_ba = M_ac = M_ca = M_bc = M_cb = –M;
• транзисторы инвертора считаем идеальными ключами;
• в любой момент времени включены три ключа — по одному из каждого плеча;
• ЭДС вращения e_a, e_b, e_c, наводимые в обмотке статора вращающимся ротором, образуют трехфазную симметричную систему.

Принятые допущения позволяют записать систему уравнений электрического равновесия:

Упрощения в двух последних уравнениях дают

Подставляя в уравнение (5) ток i_c, выраженный из уравнения (1), и складывая с удвоенным уравнением (4), получаем

С учетом равенств

первое из которых вытекает из трехфазной симметрии ЭДС вращения, а второе записано по второму закону Кирхгофа для внешнего контура статорных обмоток СД, уравнение (6) приводится к виду

По симметрии можно записать следующие два уравнения

Разумеется, любое из уравнений (8, 9, 10) является следствием двух других, поскольку из трех внутренних контуров статора СД независимые только два.

2. Построение регулятора фазных токов статора

Состояние ключей в каждом плече инвертора (рис. 1) будем изменять только один раз в течение периода коммутации Т. Длительность проводимости верхнего ключа обозначим τ_1i, а нижнего — τ_2i, где i = a, b, c. Очевидно,

Применение разрабатываемых в последнее время алгоритмов векторной широтно-импульсной модуляции (ШИМ) в трехфазном АИН [2, 3], обладающих определенными преимуществами для инверторов напряжения, в рассматриваемом случае нерационально. Причина этого — сложность реализации и применение законов коммутации ключей АИН, использующих более трех (4 или 6) переключений за период коммутации. При регулировании тока гораздо проще и рациональнее изменять длительности включения транзисторных ключей АИН не программным способом, как при векторной ШИМ, а в зависимости от ошибок управления регуляторов фазных токов. Вместо рекомендуемого числа переключений за период коммутации, равного 4 или 6, лучше увеличить частоту коммутации в 4/3 или в 2 раза.

При τ₁ = τ₂ = Т/2 в каждом плече АИН линейные напряжения статорной обмотки u_ab, u_bc, uca равны нулю, поскольку все три конца статорной обмотки (а, b и с) подключены к одной точке. В течение первой половины периода они соединены с «+» источника питания, а в оставшийся полупериод — с его «–».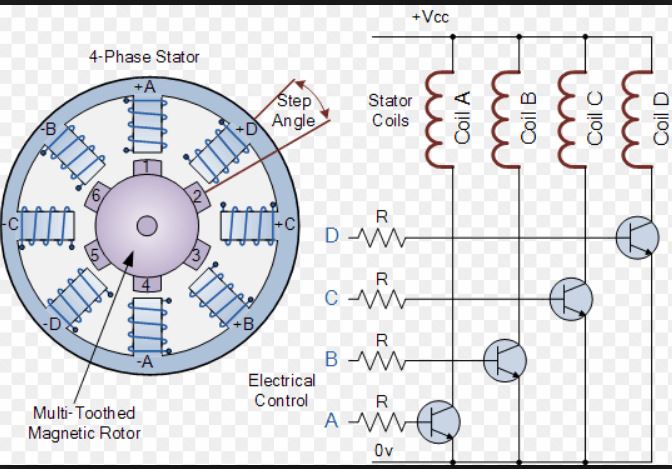

Изменение τ₁ и τ₂ только в одном плече моста, например, связанном с фазой а, вызывает изменение сразу двух линейных напряжений статорной обмотки: u_ab и u_ca. При этом очевидно, что

где 1(t) = 0 при t < 0 и 1(t) = 1 при t > 0 — единичная функция.

В случае τ_1а > T/2 u_ab представляет собой положительный прямоугольный импульс, а при τ_1а < T/2 — отрицательный. С учетом (11) в правых частях дифференциальных уравнений (8–10) получаем соответственно

Из выражений (12) очевидно, что увеличение времени подключения одной из фаз обмотки статора к «+» источника питания 1(τ_1j > T/2) приводит не только к появлению положительного импульса в правой части дифференциального уравнения для тока этой фазы, но и к отрицательным импульсам вдвое меньшей амплитуды в правых частях дифференциальных уравнений для токов двух других фаз. При (τ_1j < T/2) полярности всех трех упомянутых выше импульсов изменяются на противоположную. Меняется и положение импульсов на временной оси. В первом случае (τ_1j > T/2) они начинаются в середине периода, а во втором (τ_1j < T/2) в середине периода заканчиваются.

Таким образом, для увеличения тока в j-й фазе обмотки статора следует увеличивать τ_1j (уменьшать τ_2j) в j-м плече инвертора, а для уменьшения тока (с учетом его знака) следует уменьшать τ_1j (увеличивать τ_2j).

Следовательно, регулятор тока должен в случае положительной ошибки управления, увеличивать τ_1j, а при отрицательной ошибке — уменьшать τ_1j.

где I_зj и i_j – заданное и действительное значение тока.

Очевидно, что для надежного ограничения токов транзисторных ключей АИН в переходных режимах регулятор тока не должен быть слишком инерционным. В простейшем случае регулятор может быть пропорциональным.

Из изложенного выше ясно, что регуляторы не будут независимы, поскольку увеличение тока в одной фазе вызывает уменьшение токов в двух других фазах. Это взаимное влияние в общем случае нежелательно. Действительно, полагая равными ошибки управления всех трех контуров регулирования

и учитывая вытекающее из этого равенство

получаем из схемы силовой части рис. 1

Таким, образом, равные ошибки управления в контурах регулирования тока нарушают процесс регулирования токов статора СД.

Однако в рассматриваемом случае заданные токи: I_за (t), I_зb (t), I_зс (t) образуют симметричную трехфазную систему. Вследствие этого с учетом тождества (1) получаем

Следовательно, в рассматриваемом случае ошибки управления в контурах регулирования тока могут быть равными между собой только в случае равенства каждой из них нулю.

3. Разностные уравнения трехфазного регулятора тока при пропорциональных регуляторах и их анализ

Разностное уравнение необходимо для анализа устойчивости контура с учетом нелинейного дискретного характера управления и для определения ошибок управления.

А. Вначале для простоты положим r = 0, и будем считать постоянными ЭДС вращения

a также и заданные значения токов

Допущения (17) и (18) тем более верны, чем ниже частота заданных токов и чем быстрее протекают электромагнитные переходные процессы по сравнению с механическими.

Пренебрегая дискретностью значений ошибок управления, вычисляемых в микропроцессоре, определяемой ограниченной разрядной сеткой, будем полагать

где τ_1jn – значение τ_1j в n-ом периоде коммутации,

δ_m – граница линейной зоны широтно-импульсного модулятора, К_р – коэффициент усиления пропорционального регулятора.

В линейной зоне ШИМ, то есть при

выполняется условие

Для определенности положим

Это позволяет построить временные диаграммы линейных напряжений: u_ab (t), u_bc (t) и u_ca (t) (рис. 2) и определить импульсы напряжения в правых частях уравнений (8–10) в n-ом периоде коммутации:

Структура полученных выражений позволяет предположить, что и при других соотношениях между τ_1an, τ_1bn, τ_1cn, отличных от принятых (22), выражения импульсов (23) останутся неизменными. Это утверждение несложно проверить.

Интегрирование уравнений (8–10) с учетом принятых допущений дает выражения (24).

В полученных разностных уравнениях значения τ_1jn, j = a, b, c определяются уравнением модуляции (19).

Очевидно, разностные уравнения (24) сохраняют силу и вне линейной зоны ШИМ, когда хотя бы при одном значении j

При выполнении же условия (20) контур регулирования тока можно описать системой линейных разностных уравнений

где β = EК_рT/[6(L + M)δ_m], ? = T/(L + M).

С учетом тождества (16) система разностных уравнений (26) распадается на три независимых разностных уравнения

где α = 1 – 3β = 1 – EК_рT/[2δ_m (L + M)].

Установившееся решение уравнений (27) имеет вид

где

Решения (28) разностных уравнений (27) устанавливаются только при их асимптотической устойчивости. Для асимптотической устойчивости необходимо и достаточно выполнения неравенства

Несложно проверить, что неравенство (30) ограничивает коэффициент усиления регулятора тока условием

Заметим, что 0 < α α 1 соответствует монотонному затуханию переходного процесса установления δ_j∞, а–1 < α < 0 – колебательному с частотой вдвое меньшей частоты коммутации. Особое место занимает значение α = 0, при котором переходный процесс в пределах линейной зоны ШИМ заканчивается за 1 период коммутации. Поэтому рационально с точки зрения быстродействия выбирать соответствующее значение К_р

Последнее значение К_р обеспечивает двукратный запас устойчивости контура регулирования тока, что следует из (31) и (32).

Величина установившейся ошибки при выборе К_р из условия максимального быстродействия в линейной зоне ШИМ (32) имеет значение

Из последнего выражения видно, что уменьшение периода коммутации при сохранении двукратного запаса устойчивости позволяет пропорционально уменьшать ошибки управления контура регулирования тока, вызываемые ЭДС вращения, наводимыми в статорной обмотке.

Разумеется, формула (33) справедлива в случае значения установившихся ошибок управления, удовлетворяющих условию линейности ШИМ (20)

Из последнего выражения с учетом (32) получаем минимально необходимую величину напряжения питания инвертора

где e_m — амплитуда ЭДС, наводимой полюсами вращающегося ротора в фазовых обмотках статора.

Согласно (33) при постоянном задающем воздействии (18) установившаяся ошибка вызвана только возмущающим воздействием (17). Причина этого в допущении о равенстве нулю активного сопротивления статорной обмотки и нулевом падении напряжения, создаваемом постоянным током на индуктивности.

При изменяющемся задающем воздействии неизбежна составляющая ошибки управления, создающая на чисто индуктивной нагрузке напряжение, необходимое для изменения тока в ней. Кроме того, в действительности и возмущающее воздействие не удовлетворяет условию (17).

Б. Учтем гармоническое изменение задающего воздействия

где φ_a = 0, φ_b = 2π/3,φ_c = 4π/3, и возмущающего воздействия

Поскольку при пуске СД скорость повышения частоты напряжения на его статорных обмотках ограничена механической инерционностью СД и его нагрузки, при анализе значительно более быстрых электромагнитных переходных процессов в контуре регулирования тока можно считать Ω = const.

Интегрирование уравнений (8–10) дает при r = 0 выражения (37):

Полагая работу контура регулирования тока в линейной зоне ШИМ (20), с учетом очевидных выражений

систему разностных уравнений (37) несложно привести к виду

Линейные разностные уравнения (39) имеют две составляющие установившихся решений, то есть

Первая составляющая δ_ej∞(nT) вызвана изменением задающих воздействий (35), а вторая — δ_зj∞(nT) — возмущающими воздействиями (36).

При выборе К_р согласно (32), что обеспечивает окончание переходных процессов при работе в линейной зоне ШИМ в первом периоде коммутации, из (39) легко получить

Из формул (41–44) очевидно, что при ΩT, стремящемся к нулю, (ΩT?0) ошибки, вызванные изменением задающего воздействия, обращаются в 0, а ошибки, вызванные возмущающими воздействиями, стремятся к значениям, определяемым формулой (33), в которой e_j = –E_msin(φ_j + ?), j = a, b, c. Таким образом, предыдущий результат представляет собой частный случай последнего.

Напряжение питания инвертора, необходимое для работы контура регулирования тока в линейной зоне ШИМ, определим для наиболее тяжелого режима, в котором ошибки δ_зj∞ и δ_ej∞(nT) совпадают по фазе. Для этого случая необходимо выполнить неравенство

Учитывая рост ЭДС вращения при разгоне СД, требуемое напряжение питания АИН оказывается наибольшим в конце разгона. Его минимальное допустимое значение согласно (45) равно удвоенной сумме амплитуд ЭДС вращения и падения напряжения на индуктивном сопротивлении фазы статорной обмотки СД.

4. Учет влияния активного сопротивления статорных обмоток

Интегрирование дифференциальных уравнений (8–10) при r ≠ 0 и гармонических ЭДС вращения e_j (t) (36) для известных значений τ_1j, j = a, b, c дает

где j = a, b, c, T_c = (L+M)/r — постоянная времени статорных обмоток, φ = arctgΩT_c,

C учетом (38) разностное уравнение (46) приводится к виду

Систему разностных уравнений удобно записать в векторно-матричной форме

Зависимость матрицы D(X_n) и скаляра σ(X_n) от вектора X_n нелинейна даже в линейной зоне ШИМ (20), поскольку τ_1jn, зависящие от элементов вектора X_n, входят в показатель степени экспонент, являющихся нелинейными функциями.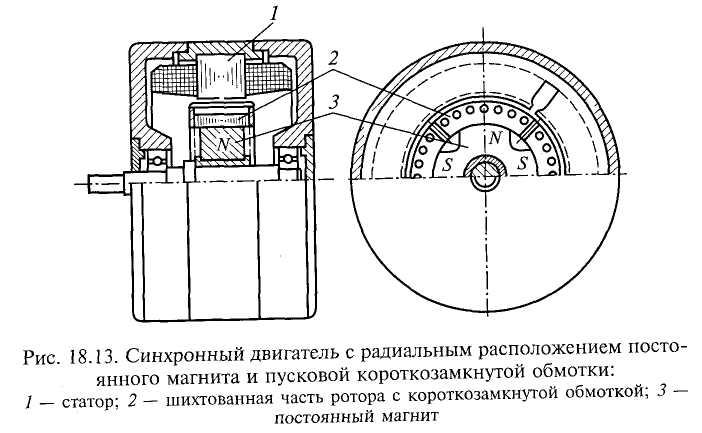 Таким образом, при учете активного сопротивления статорных обмоток контур регулирования тока представляет собой нелинейную импульсную систему.

Декомпозиции системы нелинейных разностных уравнений (48) на три независимых разностных уравнения препятствует наличие в каждом из системы трех уравнений (48) члена σ(nT), нелинейно зависящего от δ_a (nT), δ_b (nT) и δ_с (nT). Нелинейность разностных уравнений и невозможность их декомпозиции существенно усложняет анализ и синтез контура регулирования тока. Поэтому желательно аппроксимировать нелинейные разностные уравнения контура линейными уравнениями. Один из вариантов заключается в пренебрежении активным сопротивлением обмоток статора, что и было сделано выше. Другой подход основан на линеаризации экспоненциальной функции

Полагая работу контура регулирования тока в линейной зоне ШИМ (20), в результате подстановки (50) с учетом (16) получаем

Выражения (51, 52) свидетельствуют о декомпозиции и линеаризации системы разностных уравнений (48). Подстановка (52) в (48) дает

Из выражения (54) находим критическое значение коэффициента усиления регуляторов фазных токов, соответствующее границе устойчивости контура (α1 = –1):

Сравнивая (55) с (31), видим, что с учетом активного сопротивления обмоток статора критический коэффициент усиления регулятора оказывается в (1 + е^T/Tc)/2 ≈ 1 + rT/[2(L + M)] раз больше.

Соответствующее α₁ = 0 значение К_р, полученное из формулы (54), совпадает со значением, определяемым формулой (32) и найденным из условия α = 0 в уравнении (27). Выбрав указанное значение К_р, соответствующее максимальному быстродействию контура в линейной зоне ШИМ, получаем установившийся режим изменения ошибок управления фазных регуляторов

В наиболее неблагоприятном случае θ ≈ φ и согласно выражению (56) составляющие ошибки управления, вызванные задающим и возмущающим воздействиями, складываются. Поскольку в реальных случаях выполняются неравенства

из выражения (56) можно найти максимальную ошибку управления для фазовых контуров регулирования тока. Приравняв ее значению δ_m/К_р, соответствующему границе линейности ШИМ, несложно получить неравенство, определяющее выбор напряжения питания инвертора

Принимая во внимание малость r по сравнению с Ω(L+M) при максимальной частоте Ω и векторное суммирование падений напряжения на активном и индуктивном сопротивлениях статорной обмотки, величина Е, определенная с учетом активного сопротивления (57), незначительно отличается от значения (45), определяемого без учета активного сопротивления.

Из выражения (56) очевидно, что при уменьшении периода коммутации Т и сохранении неизменного запаса устойчивости ошибка управления контура регулирования тока уменьшается практически пропорционально, поскольку

5. Повышение точности контура регулирования тока

Если по энергетическим соображениям выбран период коммутации, недостаточный для получения допустимых ошибок управления, для повышения точности контура регулирования тока можно использовать принцип комбинированного управления, сочетающий управление по отклонению с управлением по задающему и возмущающему воздействию.

Для полного устранения составляющей ошибки, вызванной задающим воздействием, необходимо подавать на входы однофазных контуров регулирования тока задающие воздействия I_зj (t) (35), увеличенные на значение соответствующей ошибки. Очевидно, что, пренебрегая для простоты активным сопротивлением обмоток статора (r = 0), можно определять амплитуду добавки к задающему воздействию по формуле (42), а ее фазовый сдвиг по отношению к задающему воздействию принять равным ?/2 в сторону опережения. Физическая причина опережающего фазового сдвига на ?/2 состоит в том, что ток в индуктивности отстает по фазе от напряжения на ней на ?/2.

Для компенсации ошибки, вызываемой возмущающим воздействием, необходима полная информация о нем, то есть необходимо измерять ЭДС, наводимые в обмотках статора полюсами вращающегося ротора. Добавка к задающему воздействию при r = 0 должна иметь амплитуду, определяемую выражением (43), а по фазе должна практически совпадать с ЭДС вращения. Совпадение фаз объясняется тем, что для компенсации действия ЭДС вращения напряжение на обмотке необходимо повысить на величину этой ЭДС. Однако компенсация ошибки, вызванной возмущающим воздействием, может привести к образованию положительной обратной связи с коэффициентом больше критического и к самовозбуждению привода, поскольку ток статора влияет на скорость ротора и, следовательно, на величину ЭДС вращения. Указанная опасность в условиях нестабильных параметров и нелинейности системы допускает только частичную компенсацию ошибок управления, вызываемых ЭДС вращения.

6. Проверка полученных результатов

Проверка проводилась на математической модели контура регулирования тока, построенной в среде Matlab 6.5, Simulink 5, SimPower Systems, представленной на рис. 3.

С целью количественной проверки результатов в модели инвертора использованы идеальные ключи (Ideal Switch), а не модели MOSFET или IGBT. Индуктивную нагрузку инвертора моделирует блок 3-Phase RLC Branch2. Генератор заданных значений трехфазного тока (I_зj (t), j = a, b, c) построен на программируемом трехфазном генераторе напряжения (3-Phase Programmable Voltage Source 1), трехфазной активной нагрузке (3-Phase Series Branch) и трехфазном измерителе (3 – Phase V1 Measurement), моделирующем датчик трехфазного тока. Демультиплексоры Demux 1 и Demux 2 вместе с тремя сумматорами представляют трехфазный измеритель ошибок управления в контуре регулирования тока. Пропорциональные регуляторы тока моделируются тремя усилителями Gain 1, 2, и 3. Широтно-импульсные преобразователи, описываемые уравнением (19), представлены в модели фиксаторами нулевого порядка (Zero-Order Hold 1, 2 и 3) и блоками Subsystem 1, 2 и 3. Последние представляют собой широтноимпульсные модуляторы с синхронными генераторами линейно возрастающего опорного сигнала.

В модели установлены следующие гипотетические значения параметров:

Результаты моделирования при практически постоянных, полученных при очень низкой частоте Ω генератора 3-Phase Programmable Voltage, рассмотрены ниже. На рис. 4 представлен переходный процесс установления постоянных токов при значении

обеспечивающем наибольшее быстродействие контура, то есть окончание переходного процесса в первом периоде коммутации. Для протекания переходного процесса в линейной зоне ШИМ задано значение I_m√3/2 = 0,56 А. Увеличение К_р вдвое соответствует границе устойчивости контура регулирования тока. При тех же значениях I_зj переходный процесс начинается в зоне насыщения ШИМ. Со второго периода коммутации наблюдаются незатухающие колебания половинной частоты в линейной зоне ШИМ (рис. 5), соответствующие значению α = –1. Однако при критическом значении К_р контур регулирования тока является «негрубой» системой. Это означает, что достаточно ничтожного изменения любого из параметров, влияющих на его значение (31), чтобы контур регулирования тока сместился с колебательной границы устойчивости в область устойчивости или в область неустойчивости. В первом случае колебания со временем затухнут. Во втором же случае амплитуда колебаний возрастает. При вхождении колебаний в зону насыщения ШИМ рост амплитуды колебаний прекращается и устанавливаются автоколебания определенной амплитуды.

На рис. 6 представлен переходный процесс установления субгармонических автоколебаний при К_р = 3,4 (на 0,2 больше критического). Из рис. 6 видно, что частоты наблюдаемых автоколебаний оказываются разными в разных фазах. В фазах «b» и «c» наблюдаются автоколебания половинной частоты, а в фазе «a» автоколебания имеют частоту коммутации. Интересно, что в режиме автоколебаний постоянные составляющие токов i_a (t), i_b (t), i_c (t) отличаются от заданных значений I_за, I_зb, I_зc. При учете сопротивления статорных обмоток r = 6 Ом при том же значении К_р = 3,4 устанавливаются автоколебания половинной частоты во всех фазах (рис. 7). Происходят они в линейной зоне ШИМ. Объясняется это уже отмеченной выше нелинейностью контура регулирования тока при отличном от нуля активном сопротивлении обмоток статора.

Результаты моделирования процесса отработки гармонических токов (35) при нулевых начальных условиях, r = 0, К_р = 1,6, частоте Ω = 2? Ѕ 108 рад/с (108 Гц) и той же величине I_m, при которой исследовали отработку постоянных заданных токов (I_m√3/2 = 0,56 А) в линейной зоне, представлены на рис. 8. Контур регулирования тока выходит на установившийся режим уже в конце первого периода коммутации. Величины Ω и (L + M) взяты не из реальных условий, а из соображений наглядности временных диаграмм. Из рис. 8 видно, что отрабатываемые токи i_j (t) отличаются от заданных токов I_зj (t), j = a, b, c практически только по фазе. Это вызывает ошибки управления, показанные на рис. 9.

Для компенсации ошибок управления, вызываемых изменяющимися задающими воздействиями (35), достаточно прибавить к задающим воздействиям их производные с соответствующими коэффициентами. Дифференцируя (35), получаем

и сравнивая с выражением (41), записанным для реальных условий (Ωt << 1),

находим, что выходной сигнал дифференциатора надо умножить на коэффициент, равный периоду коммутации Т.

Математическая модель контура регулирования тока с компенсацией ошибки, вызываемой изменяющимся задающим воздействием, представлена на рис. 10. Дифференцирование задающего воздействия осуществляют блоки Transfer Function 1, 2, 3 c передаточной функцией 0,00025S/(0,000001S + 1), выходные сигналы которых складываются с задающими воздействиями.

На рис. 11 представлен переходный процесс отработки тех же, что и выше, гармонических задающих воздействий при компенсации ошибки их отработки. Из рис. 12, на котором показаны кривые изменения ошибок управления (13), видно, что после окончания переходного процесса ошибки управления содержат только пульсационную составляющую, как и ожидалось.

Выводы

1. Трехфазный контур регулирования тока при чисто индуктивном сопротивлении обмоток статора синхронного двигателя с постоянными магнитами на роторе в линейной зоне широтно-импульсного модулятора описывается тремя независимыми линейными разностными уравнениями первого порядка.
2. Учет активного сопротивления обмоток делает разностные уравнения нелинейными и зависимыми.
3. Превышение критического коэффициента усиления регуляторов тока вызывает неустойчивость контура регулирования тока, что приводит к субгармоническим автоколебаниям.
4. При чисто индуктивном сопротивлении статорных обмоток субгармонические автоколебания происходят в зоне насыщения ШИМ, а при активно-индуктивном сопротивлении могут существовать и в линейной зоне ШИМ.
5. При заданном запасе устойчивости в контуре регулирования тока его ошибки управления пропорциональны периоду коммутации автономного инвертора.
6. Точность контура регулирования тока можно существенно повысить за счет использования принципа комбинированного управления.
7. Напряжение питания автономного инвертора, обеспечивающее отработку заданных синусоидальных токов должно в 2 раза и более превышать сумму амплитуд ЭДС вращения и падения напряжения, создаваемого заданным током на сопротивлении обмотки статора синхронного двигателя.

Литература

1. Коршунов А. Равноускоренный частотный пуск синхронного двигателя с постоянными магнитами на роторе // Силовая электроника. 2007. № 1.
2. Изосимов Д. Б., Байда С. В. Алгоритмы векторной широтно-импульсной модуляции трехфазного автономного инвертора // Электротехника. 2004. № 4.
3. Крутиков К. К., Рожков В. В., Петрухин Ю. В. Анализ и моделирование симплексных алгоритмов управления трехфазным автономным инвертором для частотного асинхронного электропривода // Электротехника. 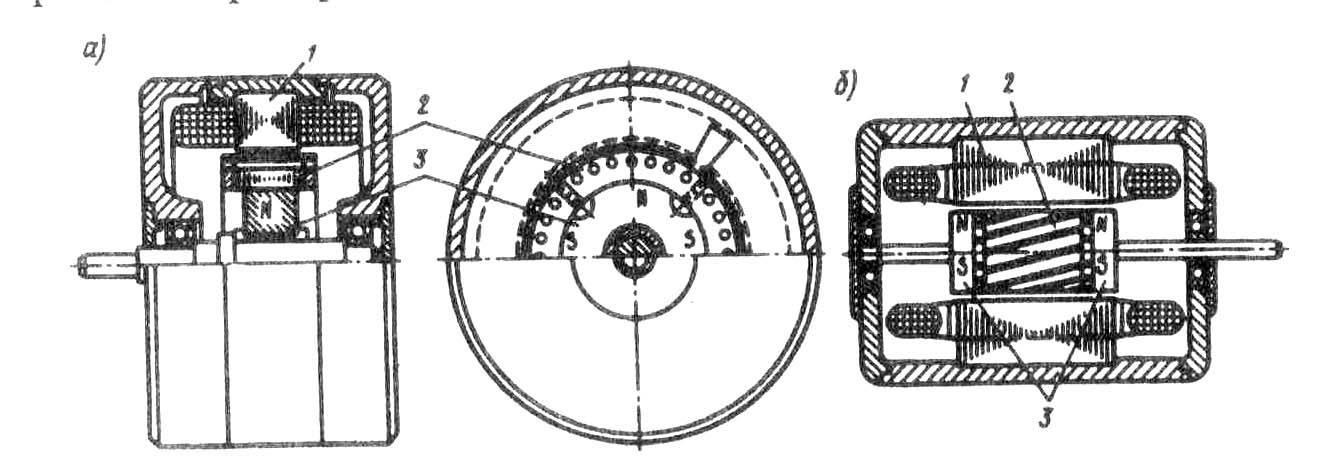2006. № 5.

Магнитные двигатели на постоянных магнитах (схема, видео)

Согласно закону сохранения энергии, любой современный эл. привод не может иметь КПД выше 100%, потому как часть энергии нужно потратить на собственные нужды. Решить этот вечный вопрос призван двигатель на постоянных магнитах (униполярный, линейный, роторный, гравитационный и т. п), в котором механическое перемещение компонентов происходит за счет их взаимодействия на уровне магнитных свойств.

Принцип действия вечного магнитного движителя

Большинство современных эл. двигателей используют принцип трансформации эл. тока в механическое вращение ротора, а вместе с ним и приводного вала. Это значит, что любой расчет покажет КПД меньше 100%, а сам агрегат является зависимым, а не автономным. Та же ситуация наблюдается в случае генерирующего устройства. Здесь уже момент вращения вала, которое происходит за счет тепловой, ядерной, кинетической или потенциальной энергии движения среды, приводит к выработке электрического тока на коллекторных пластинах.

Двигатель на постоянных магнитах использует совершенно иной подход к работе, который нивелирует или сводит к минимуму необходимость в сторонних источниках энергии. Описать принцип работы такого двигателя можно на примере «беличьего колеса». Для изготовления демонстративной модели не требуются особые чертежи или расчет надежности. Необходимо взять один постоянный магнит тарельчатого (дискового) типа, полюса которого располагаются на верхней и нижней плоскостях пластин. Он будет служить основой конструкции, к которой нужно добавить два кольцевых барьера (внутренний, внешний) из немагнитных, экранирующих материалов. В промежуток (дорожку) между ними помещается стальной шарик, который будет играть роль ротора. В силу свойств магнитного поля, он сразу же прилипнет к диску разноименным полюсом, положение которого не будет меняться при движении.

Статор представляет собой условно пластину из экранируемого материала, на которую по кольцевой траектории крепят постоянные магниты, например, неодимовые.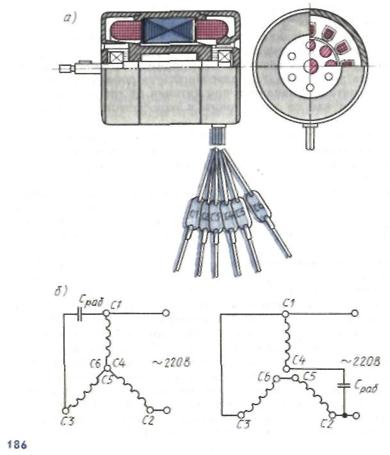 Их полюса расположены перпендикулярно по отношению к полюсам дискового магнита и ротора. В результате, когда статор приближается к ротору на определенное расстояние, возникает поочередное притяжение, отталкивание в магнитном поле, которое формирует момент затем перерастает во вращение шарика по кольцевой траектории (дорожке). Пуск и остановка происходят за счет приближения или отдаления статора с магнитами. Этот вечный двигатель на постоянных магнитах будет работать до тех пор, пока они не размагнитятся. Расчет ведется относительно размера коридора, диаметров шарика, пластины статора, а также цепи управления на реле или катушках индуктивности.

На подобном принципе действия было разработано немало моделей действующих образцов, например, синхронных двигателей, генераторов. Наиболее известными среди них являются двигатели на магнитной тяге Тесла, Минато, Перендев, Говарда Джонсона, Лазарева, а также линейные, униполярные, роторные, цилиндровые и т. д.

Рассмотрим каждый из примеров подробнее.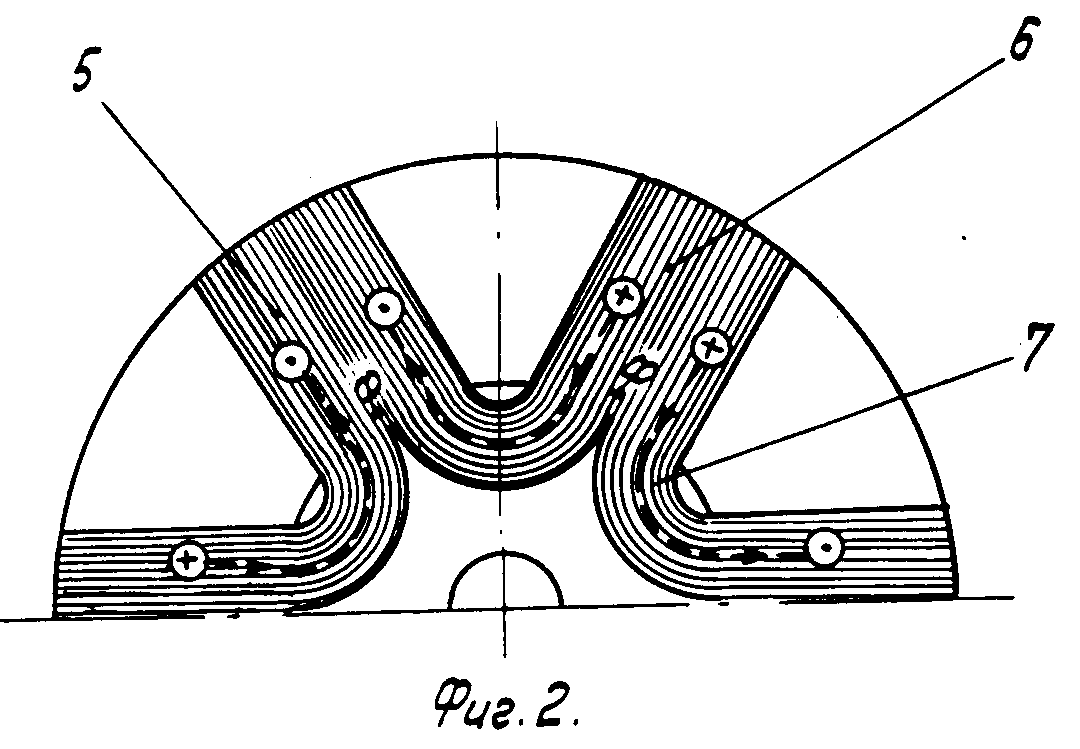

Магнитный униполярный двигатель Тесла

Выдающийся ученый, ставший в свое время пионером в области снабжения эл. током, асинхронных электродвигателей на переменном токе, не обделил своим вниманием и расчетом вопрос вечного источника энергии. В научной среде это изобретение именуется иначе, как униполярный генератор Тесла.

Первоначально расчет данного типа устройства вел Фарадей, но его прототип при сходном принципе действия не обладал должной эффективностью, стабильностью работы, то есть не достиг цели. Термин «униполярный» означает, что в схеме агрегата кольцевой, дисковый (пластина) или цилиндровый проводник расположен в цепи между полюсами постоянного магнита.

Магнитный двигатель Тесла и его схема

На схеме, которая была представлена в оригинальном патенте, есть конструкция с двумя валами, на которых размещаются две пары магнитов: В, В создают условно положительное поле, а С, С – отрицательное. Между ними располагаются униполярные диски с отбортовкой, используемые в качестве генерирующих проводников. Оба униполярных диска связаны между собой тонкой металлической лентой, которая может быть в принципе использована, как проводник (в оригинале) или для вращения диска.

Двигатель Минато

Еще одним ярким примером использования энергии магнетизма для самовозбуждения и автономной работы является сегодня уже серийный образец, разработанный более тридцати лет назад японцем Кохеи Минато. Его отличают бесшумность и высокая эффективность. По собственным заявлениям Минато, самовращающийся магнитный двигатель подобной конструкции имеет КПД выше 300%.

Двигатель Минато

Ротор имеет форму диска или колеса, на котором под определенным углом располагаются магниты. Когда к ним подводится статор с большим магнитом, возникает момент и колесо Минато начинает вращаться, используя попеременное сближение и отталкивание полюсов. Чем ближе статор к ротору, тем выше момент и скорость вращения. Питание осуществляется через цепь реле прерывателя.

Для предотвращения импульсов и биения при вращении колеса Минато, используют реле стабилизаторы и сводят к минимуму потребление тока управляющего эл. магнита. Недостатком можно считать отсутствие данных по нагрузочным характеристикам, тяге, используемых реле цепи управления, а также необходимость периодического намагничивания, о которой, кстати, тоже от Минато информации нет.

Может быть собран, как и остальные прототипы, экспериментально, из подручных средств, например, деталей конструктора, реле, эл. магнитов и т. п.

Двигатель Лазарева

Устройство двигателя Лазарева

Отечественный разработчик Николай Лазарев создал работающий и довольно простой вариант агрегата, использующего магнитную тягу. Его двигатель или роторный кольцар, состоит из емкости, разделенной пористой перегородкой потока на верхнюю и нижнюю части. Они сообщаются между собой за счет трубки, по которой из нижней камеры в верхнюю идет поток воды/жидкости. В свою очередь поры обеспечивают гравитационное перетекание вниз. Если под потоком жидкости поместить колесико, на лопастях которого будут закреплены магниты, то получиться добиться цели потока – вращения и создания постоянного магнитного поля. Схема роторного двигателя Николая Лазарева используется для расчета и сборки простейших самовращающихся устройств.

Магнитный мотор Говарда Джонсона

Магнитный мотор Говарда Джонсона

В своей работе и следующем за ней патенте на изобретение, Говард Джонсон использовал энергию, генерируемую потоком непарных электронов, присутствующих в магнитах для организации цепи питания мотора. Статор Джонсона представляет собой совокупность множества магнитов, дорожка расположения и движения которых будет зависеть от конструктивной компоновки агрегата Говарда Джонсона (линейной или роторной). Они закрепляются на специальной пластине с высокой степенью магнитной проницаемости. Одноименные полюса статорных магнитов направляются в сторону ротора. Это обеспечивает поочередное притяжение и отталкивание полюсов, а вместе с ними, момент и физическое смещение элементов статора и ротора относительно друг друга.

Организованный Говардом Джонсоном расчет воздушного зазора между ними позволяет корректировать магнитную концентрацию и силу взаимодействия в большую или меньшую сторону.

Генератор Перендева

Генератор Перендева

Еще одним неоднозначным примером действия магнитных сил является самовращающийся магнитный двигатель Перендев. Его создатель Майк Брэди, до того, как в его отношении начали уголовное производство, даже успел обзавестись патентом, создать одноименную фирму (Перендев) и поставить дело на поток. Если анализировать представленную в патенте схему и принцип, или чертежи самодельных эл. двигателей, то ротор и статор имеют форму диска и внешнего кольца. На них по кольцевой траектории размещают отдельные магниты, соблюдая определенный угол относительно центральной оси. За счет взаимодействия поля отдельных магнитов статора и ротора Перендев, возникает момент и происходит их взаимное перемещение (вращение). Расчет цепи магнитов сводится к определению угла расхождения.

Синхронный двигатель на постоянных магнитах

Устройство синхронного двигателя на магнитах

Одним из основных видов электродвигателей является синхронный, частота вращения магнитных полей статора и ротора которого равны. У обычного электромагнитного мотора обе эти части состоят из обмоток на пластинах. Но если конструкцию якоря поменять и вместо катушки поставить постоянные магниты, то можно получить интересную, эффективную, действующую модель синхронного двигателя. Статор имеет привычную компоновку магнитопровода из пластин и обмоток, в которых способно генерироваться вращающееся магнитное поле от электрического тока. Ротор создает постоянное поле, которое взаимодействует с предыдущим, и создает крутящий момент.

Также следует отметить, что в зависимости от схемы, относительное расположение статора и якоря могут меняться, например, последний будет выполнен в форме внешней оболочки. Для пуска мотора от тока из сети используется цепь из магнитного пускателя (реле, контактора) и теплового защитного реле.

(PDF) Расчет индуктивностей синхронной машины с постоянным магнитом

 Аннотация. Точное определение индуктивности постоянного магнита

синхронной машины (PMSM) было предметом

многочисленных исследований в течение длительного времени. По этой причине в данной статье

представлен расчет прямой и квадратурной индуктивностей

синхронной машины с постоянными магнитами методом конечных элементов

(FEM), где расчет этих параметров составляет

на основе магнитного зазора. распределение поля, которое составляет

основу анализа производительности электрических машин.Численные результаты

представлены в виде диаграмм, они обсуждались, а результаты

сравнивались с экспериментальным один раз, они показывают очень хорошее совпадение

. Это подтверждает обоснованность и эффективность метода конечных элементов

для решения этих задач.

Ключевые слова — конечный элемент, прямая индуктивность и квадратурная

, плотность магнитного потока, постоянный магнит

синхронная машина.

I. ВВЕДЕНИЕ

Синхронные двигатели с постоянными магнитами (PMSM)

широко используются в высокопроизводительных приводах, таких как промышленные роботы

и станки из-за их преимуществ в отношении высокой мощности

плотности, высокого крутящего момента, бесплатного обслуживания и скоро.За последние

лет магнитные и тепловые возможности ПМ

были значительно увеличены за счет использования высококоэрцитивных материалов

ПМ [1]. В последние несколько лет синхронный двигатель с постоянным магнитом

(PMSM), следовательно, приобретается в

все более и более широкомасштабном применении из-за его свойств

, таких как небольшой объем, легкий вес, высокая эффективность,

малая инерция ротор без проблем с нагревом и т. д.[2]. Очень важно рассчитать как можно точнее

значений параметров PMSM. Из наиболее важных значений

являются индуктивности

по прямой и квадратурной оси, поскольку они определяют соответствующие

синхронных реактивных сопротивлений [3]; Хорошо известно, что они являются наиболее важными параметрами

при работе с

в установившемся режиме и / или анализом динамических характеристик PMSM.. В настоящее время синхронный двигатель с постоянными магнитами

разработан не только для того, чтобы иметь более мощный двигатель

, но также с меньшей массой и меньшим моментом инерции

. Мы должны учитывать требуемую точность результатов

, а также надежность процедур тестирования для определения параметров машины

, когда мы разрабатываем модель синхронного двигателя с постоянными магнитами

. Традиционные методы испытаний

для определения параметров синхронной машины

не могут быть применены в случае

машины с постоянными магнитами.Единственная альтернатива

для решения этой проблемы — использование численных методов [4] — [6].

Рукопись получена 10 ноября 2013 г .; отредактировано 13 марта 2014 г.

Авторы работают с кафедрой электротехники, Баджи

Университет Мохтара, PO Box12, 23000 Аннаба, Алжир (электронная почта:

bellal.zaghdoud @ gmail.com, a_saadoun@yahoo.fr ).

В течение последних двух десятилетий метод конечных элементов

доказал, что он является наиболее подходящим численным методом с точки зрения

моделирования, гибкости и точности для решения нелинейного

уравнения Пуассона, определяющего магнитное поле, которое касается главного элемента. при расчете параметров станка

[5], [6].В настоящее время доступно несколько программ моделирования электрических машин

. Пакет конечных элементов

FEMM 4.2 (Finite Element Method Magnetic), разработанный

D. Meeker, доступный бесплатно на его веб-сайте, использовался для моделирования

PMSM.

II. РЕШЕНИЕ ЗАДАЧИ МАГНИТНОГО ПОЛЯ С ПОМОЩЬЮ

FEM

Метод конечных элементов — это численная процедура

, предназначенная для получения приближенного решения множества полевых задач

, управляемых дифференциальными уравнениями.Область решения

заменяется задачей подобластей

простых геометрических форм, называемых элементами, чтобы

реконструировал исходную область путем их сборки.

неизвестных переменных рассматриваемого поля затем выражаются

приближенной функцией, называемой функцией интерполяции [7],

[8]. Эти функции определены для каждого элемента с использованием

значений, которые переменная берет из поля на каждом узле.

Следовательно, знание узловых значений и функций интерполяции

позволяет полностью определить поведение поля переменной

для каждого элемента. После того, как узловые переменные

, которые фактически являются неизвестными факторами проблемы, вычислены

, значения переменных поля в любой точке

поля также могут быть определены с использованием функции интерполяции

. Точность метода зависит не только от размеров элементов

и их количества, но и от типа функции интерполяции

.Что касается численного метода, метод конечных элементов

сходится к точному решению

, предоставленному для увеличения количества подразделений области решения

и обеспечения непрерывности интерполяционной функции

ее первых производных по границам смежные

элементов [5], [7].

Основные этапы реализации метода конечных элементов

[9] описаны ниже.

А.Предварительная обработка

После того, как геометрия задачи определена, мы должны завершить

всей области электрической машины, задав свойства материала

и граничные условия. Путем наложения нуля векторного потенциала

на внешний диаметр машины

магнитное поле будет ограничено областью решения,

, в то время как условия периодичности 𝐴 (0) = 𝐴 (𝜋) могут ограничить область решения

на двухполюсный шаг.Основная идея приложения

FEM состоит в том, чтобы разделить эту сложную область на

Расчет индуктивности постоянного магнита

Синхронная машина

Беллал Загдуд и Абдалла Саадун

Journal of Computer and Electrical Engineering, Vol. 6, No. 3, июнь 2014 г.

267

DOI: 10.7763 / IJCEE.2014.V6.836

Страница не найдена | MIT

Перейти к содержанию ↓

• Образование
• Исследовать
• Инновации
• Прием + помощь
• Студенческая жизнь
• Новости
• Выпускников
• О MIT
• Подробнее ↓
  • Прием + помощь
  • Студенческая жизнь
  • Новости
  • Выпускников
  • О MIT

Меню ↓ Поиск Меню Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов

Предложения или отзывы?

Синхронный двигатель с постоянными магнитами: конструкция и принцип работы

В электрической системе синхронные двигатели являются наиболее широко используемыми стационарными трехфазными двигателями переменного тока, которые преобразуют электрическую энергию в механическую.Этот тип двигателя работает с синхронной скоростью, которая является постоянной и синхронной с частотой питающей сети, а период вращения равен интегральному номеру. циклов переменного тока. Это означает, что скорость двигателя равна вращающемуся магнитному полю. Этот тип двигателя в основном используется в энергосистемах для улучшения коэффициента мощности. Существуют синхронные двигатели без возбуждения и синхронные двигатели с возбуждением постоянным током, которые работают в соответствии с магнитной мощностью двигателя. Реактивные двигатели, двигатели с гистерезисом и двигатели с постоянными магнитами являются синхронными двигателями без возбуждения.Эта статья посвящена работе синхронного двигателя с постоянными магнитами.

Что такое синхронный двигатель с постоянными магнитами?

Синхронные двигатели с постоянными магнитами являются одним из типов синхронных двигателей переменного тока, в которых поле возбуждается постоянными магнитами, которые генерируют синусоидальную обратную ЭДС. Он содержит ротор и статор, такие же, как у асинхронного двигателя, но постоянный магнит используется в качестве ротора для создания магнитного поля. Следовательно, нет необходимости наматывать обмотку возбуждения на ротор.Он также известен как трехфазный бесщеточный двигатель с постоянной синусоидой. Схема синхронного двигателя с постоянным магнитом показана ниже.

Синхронный двигатель с постоянным магнитом

Теория синхронного двигателя с постоянным магнитом

Синхронный двигатель с постоянным магнитом очень эффективен, бесщеточный, очень быстр, безопасен и обеспечивает высокие динамические характеристики по сравнению с обычными двигателями. Он обеспечивает плавный крутящий момент, низкий уровень шума и в основном используется для высокоскоростных приложений, таких как робототехника.Это трехфазный синхронный двигатель переменного тока, который работает с синхронной скоростью с подключенным источником переменного тока.

Вместо использования обмотки для ротора установлены постоянные магниты для создания вращающегося магнитного поля. Поскольку нет источника постоянного тока, эти типы двигателей очень просты и дешевле. Он содержит статор с 3 установленными на нем обмотками и ротор с постоянным магнитом, установленным для создания полюсов поля. 3-фазный входной источник переменного тока подается на статор для начала работы.

Принцип работы

Принцип работы синхронного двигателя с постоянными магнитами аналогичен принципу работы синхронного двигателя.Это зависит от вращающегося магнитного поля, которое генерирует электродвижущую силу с синхронной скоростью. Когда на обмотку статора подается трехфазное питание, между воздушными зазорами создается вращающееся магнитное поле.

Это создает крутящий момент, когда полюса поля ротора удерживают вращающееся магнитное поле с синхронной скоростью, а ротор вращается непрерывно. Поскольку эти двигатели не являются самозапускающимися двигателями, необходимо обеспечить источник питания с регулируемой частотой.

ЭДС и уравнение крутящего момента

В синхронной машине средняя ЭДС, индуцированная на фазу, называется динамической индуктивной ЭДС в синхронном двигателе, поток, отсекаемый каждым проводником за оборот, равен Pϕ Weber
Тогда время, необходимое для завершения одного оборота составляет 60 / Н с

Среднее значение ЭДС, наведенной на проводник, можно рассчитать, используя

(PϕN / 60) x Zph = (PϕN / 60) x 2Tph

Где Tph = Zph / 2

Следовательно , средняя ЭДС на фазу составляет,

= 4 x ϕ x Tph x PN / 120 = 4ϕfTph

Где Tph = no.Число витков, соединенных последовательно на фазу

ϕ = поток / полюс в weber

P = нет. Количество полюсов

F = частота в Гц

Zph = нет. Проводов, соединенных последовательно по фазе. = Zph / 3

Уравнение ЭДС зависит от катушек и проводников на статоре. Для этого двигателя также учитываются коэффициент распределения Kd и коэффициент шага Kp.

Следовательно, E = 4 x ϕ xfx Tph xKd x Kp

Уравнение крутящего момента синхронного двигателя с постоянными магнитами задается как,

T = (3 x Eph x Iph x sinβ) / ωm

Прямое управление крутящим моментом синхронного двигателя с постоянными магнитами

Для управления синхронным двигателем с постоянными магнитами мы используем различные типы систем управления.В зависимости от поставленной задачи используется необходимая техника управления. Различные методы управления синхронным двигателем с постоянными магнитами:

Синусоидальная категория

• Скалярная
• Векторное: управление с ориентацией на поле (FOC) (с датчиком положения и без него)
• Прямое управление крутящим моментом

Трапецеидальная категория

• Разомкнутый контур
• Замкнутый контур (с датчиком положения и без него)

Технология прямого управления крутящим моментом этого двигателя представляет собой очень простую схему управления с эффективными динамическими характеристиками и хорошим диапазоном регулирования.Датчик положения ротора не требуется. Основным недостатком использования этого метода управления является то, что он создает высокий крутящий момент и колебания тока.

Конструкция

Синхронный двигатель с постоянными магнитами по конструкции аналогичен базовому синхронному двигателю, но отличается только ротором. Ротор не имеет обмотки возбуждения, но постоянные магниты используются для создания полюсов возбуждения. Постоянные магниты, используемые в PMSM, состоят из самария-кобальта и среды, железа и бора из-за их более высокой проницаемости.

Наиболее широко используемым постоянным магнитом является неодим-бор-железо из-за его эффективной стоимости и простоты доступности. В этом типе постоянные магниты установлены на роторе. По конструкции постоянного магнита на роторе синхронный двигатель с постоянным магнитом делится на два типа. Они есть,

PMSM для установки на поверхность

В этой конструкции магнит установлен на поверхности ротора. Он подходит для высокоскоростных приложений, поскольку не является надежным.Он обеспечивает равномерный воздушный зазор, поскольку проницаемость постоянного магнита и воздушного зазора одинаковы. Отсутствие реактивного момента, высокие динамические характеристики, подходит для высокоскоростных устройств, таких как робототехника и приводы инструментов.

Поверхностный монтаж

Скрытый PMSM или внутренний PMSM

В конструкции этого типа постоянный магнит встроен в ротор, как показано на рисунке ниже. Он подходит для высокоскоростных приложений и отличается повышенной надежностью. Возврат крутящего момента происходит из-за резкости мотора.

Скрытый PMSM

Работа синхронного двигателя с постоянными магнитами

Работа синхронного двигателя с постоянными магнитами очень проста, быстра и эффективна по сравнению с обычными двигателями. Работа PMSM зависит от вращающегося магнитного поля статора и постоянного магнитного поля ротора. Постоянные магниты используются в качестве ротора для создания постоянного магнитного потока, работают и блокируются с синхронной скоростью. Эти типы двигателей аналогичны бесщеточным двигателям постоянного тока.

Векторные группы образуются путем соединения обмоток статора друг с другом. Эти векторные группы соединяются вместе, образуя различные соединения, такие как звезда, треугольник, двойные и одиночные фазы. Для уменьшения гармонических напряжений обмотки следует коротко намотать друг на друга.

Когда на статор подается трехфазный переменный ток, он создает вращающееся магнитное поле, а постоянное магнитное поле индуцируется постоянным магнитом ротора. Этот ротор работает синхронно с синхронной скоростью.Вся работа PMSM зависит от воздушного зазора между статором и ротором без нагрузки.

Если воздушный зазор большой, потери двигателя уменьшаются. Полюса поля, создаваемые постоянным магнитом, очень заметны. Синхронные двигатели с постоянными магнитами не являются самозапускающимися двигателями. Итак, необходимо управлять переменной частотой статора электронным способом.

Синхронный двигатель с постоянным магнитом и BLDC

Различия между синхронным двигателем с постоянным магнитом (PMSM) и BLDC (бесщеточные двигатели постоянного тока) заключаются в следующем.

Синхронный двигатель с постоянным магнитом	BLDC
Это бесщеточные синхронные двигатели переменного тока	Это бесщеточные двигатели постоянного тока
Отсутствуют пульсации крутящего момента
Крутящий момент отсутствует
Высокий КПД	Низкий КПД
Более эффективный	Менее эффективный
Используется в промышленных приложениях, автомобилях, серводвигателях, робототехнике, приводах поездов и т.д. системы, системы отопления, вентиляции и кондиционирования воздуха, приводы гибридных поездов (электрические) и т. д.
Низкий уровень шума	Высокий уровень шума.

Преимущества

К преимуществам синхронного двигателя с постоянными магнитами относятся:

• обеспечивает более высокую эффективность при высоких скоростях
• доступны в небольших размерах в различных корпусах
• обслуживание и установка намного проще, чем асинхронный двигатель
• способен поддерживать полный крутящий момент на низких скоростях.
• высокая эффективность и надежность
• обеспечивает плавный крутящий момент и динамические характеристики

Недостатки

Недостатки синхронных двигателей с постоянными магнитами:

• Эти типы двигателей очень дороги по сравнению с асинхронными двигателями
• Как-то сложно запустить -вверх, потому что это не самозапускающиеся двигатели.

Применения

Применения синхронных двигателей с постоянными магнитами:

• Кондиционеры
• Холодильники
• Компрессоры переменного тока
• Стиральные машины с прямым приводом
• Автомобильный электрический усилитель рулевого управления
• Станки
• Большой мощности системы повышения опережающего и запаздывающего коэффициента мощности
• Контроль тяги
• Блоки хранения данных.
• Сервоприводы
• Промышленные приложения, такие как робототехника, аэрокосмическая промышленность и многие другие.

Таким образом, это все об обзоре синхронного двигателя с постоянными магнитами — определение, работа, принцип работы, диаграмма, конструкция, преимущества, недостатки, применения, ЭДС и уравнение крутящего момента. Вот вам вопрос: «Какова цель использования постоянного магнита в синхронных двигателях?»

Асинхронные двигатели

переменного тока и синхронные двигатели с постоянными магнитами

* Изображение предоставлено New Energy и Fuel.com

Авторы : Стив Бистак, региональный менеджер по продажам — NE, отдел приводов переменного тока / HMI, Fuji Electric Corp.of America, и Sun Y. Kim (Sean), старший региональный менеджер, ACDR / HMI, Fuji Electric Corp of America

Большинство насосов и вентиляторов, работающих в промышленных и коммерческих целях, в настоящее время приводится в действие асинхронными двигателями переменного тока. «ACIM», что означает «асинхронный двигатель переменного тока», представляет собой асинхронный тип двигателя, который использует электрический ток для вращения ротора. Крутящий момент создается электрическим током в роторе. Электрический ток создается за счет электромагнитной индукции магнитного поля обмоток статора.В ACIM ротор всегда вращается с меньшей скоростью, чем магнитное поле. «PMSM», что означает «синхронный двигатель с постоянными магнитами», полагается на магниты для вращения ротора, который вращается с той же скоростью, что и внутреннее вращающееся магнитное поле PMSM.

Есть несколько ключевых различий между асинхронными двигателями переменного тока и синхронными двигателями с постоянными магнитами.

Двигатели с постоянными магнитами ДОЛЖНЫ работать с приводом.

Асинхронные двигатели

переменного тока могут использоваться без частотно-регулируемого привода для привода насоса или вентилятора, но часто устанавливаются с частотно-регулируемыми приводами (VFD) в насосных или вентиляционных системах, чтобы повысить эффективность системы.Синхронным двигателям с постоянными магнитами для работы требуется привод. PMSM не могут работать без привода. Частотно-регулируемый привод необходим для точного управления скоростью PMSM в соответствии с требованиями приложения к давлению, расходу, объему и т. Д. Некоторые новые частотно-регулируемые приводы уже поставляются с опциями управления двигателем с постоянными магнитами в качестве стандартной функции, что позволяет операторам управлять двигателем с постоянными магнитами. для более эффективного управления вентилятором и / или насосом.

Двигатели с постоянными магнитами обеспечивают значительное повышение эффективности по сравнению с асинхронными двигателями переменного тока.

Эффективность полной нагрузки двигателя с постоянными магнитами выше, чем у асинхронного двигателя переменного тока. На рисунке 1 ниже показаны диапазоны эффективности между двумя стандартами асинхронных двигателей переменного тока и известными опубликованными двигателями с постоянными магнитами.

Рисунок 1 . Эффективность двигателя с постоянными магнитами на мощности частотно-регулируемого привода. ACIM на синусоиде. Двигатели ACIM теряют 0,5–1,5 балла кпд при работе с частотно-регулируемым приводом.

Важно отметить, что частотно-регулируемые приводы не улучшают КПД двигателя; ЧРП помогают повысить эффективность системы в диапазонах рабочих скоростей, поскольку большинство систем не всегда работают на максимальных скоростях.Добавление частотно-регулируемого привода помогает повысить эффективность вашей системы, поскольку он может замедлять двигатель и вентилятор или насос, а не поворачивать клапан для дросселирования насоса или закрывать заслонку, чтобы блокировать поток воздуха.

Взгляните на рисунок 2, на котором сравнивается 10-сильный синхронный двигатель с постоянным магнитом 1800 об / мин и двигатель NEMA Premium, работающий с переменной нагрузкой по крутящему моменту в диапазоне скоростей от 3 до 1. Вы можете видеть, что в обоих случаях эффективность обоих типов двигателей падает. КПД двигателя NEMA Premium Motor падает с примерно 90% до примерно 72% при 600 об / мин, а ECPM падает примерно с 94% до 83%.Хотя работа системы влияет на эффективность оборудования, было доказано, что двигатели с постоянными магнитами демонстрируют более высокий КПД по сравнению с асинхронными двигателями переменного тока.

Рисунок 2 . Сравнение относительной эффективности двигателя PMSM и ACIM с диапазоном изменения 3: 1.

Преимущества и недостатки двигателей с постоянными магнитами

Хотя асинхронные двигатели переменного тока чаще встречаются в системах с моторным приводом, они часто больше по размеру и менее эффективны, чем двигатели с постоянными магнитами.Хотя решения с двигателями с постоянными магнитами обычно имеют более высокую начальную стоимость, они могут предлагать меньший размер для более компактных механических блоков и, что более важно, более высокую эффективность.

Двигатели с постоянными магнитами обычно дороже, чем асинхронные двигатели переменного тока, и, как известно, их труднее запускать, чем асинхронные двигатели переменного тока. Однако преимущества двигателей с постоянными магнитами включают в себя более высокий КПД (как обсуждалось выше), меньшие размеры (двигатели с постоянными магнитами могут составлять до одной трети от большинства размеров двигателей переменного тока, что значительно упрощает установку и обслуживание) и способность PMSM поддерживать полный крутящий момент на низких оборотах.

Тенденция меняется

Использование PMSM в сочетании с VFD не новость; однако инженеры-конструкторы и владельцы оборудования начинают устанавливать больше двигателей с постоянными магнитами для вентиляторов и насосов из-за их меньшего размера и более высокой эффективности. До этого момента частотно-регулируемые приводы требовали специальной формулы для управления двигателем с постоянными магнитами; Сейчас на рынке доступно несколько новых частотно-регулируемых приводов, которые имеют встроенную стандартную функцию для управления двигателями с постоянными магнитами без дополнительных затрат.

По мере того, как все больше производителей частотно-регулируемых приводов начинают добавлять функции для более эффективного управления модулями управления двигателем, владельцы и операторы будут устанавливать более эффективные двигательные системы в меньших корпусах и с меньшими затратами.

Синхронный двигатель с постоянными магнитами на основе магнитного потока

Описание

Блок PMSM на основе магнитного потока реализует трехфазный постоянный двигатель на основе магнитного потока. магнитный синхронный двигатель (PMSM) с табличной электродвижущей силой.Блок использует трехфазные входные напряжения для регулирования отдельных фазных токов, что позволяет контроль крутящего момента или скорости двигателя.

Модели двигателей на основе магнитного потока учитывают магнитное насыщение и потери в стали. К рассчитать магнитное насыщение и потери в железе, PMSM на основе потока блок использует обратные потокосцепления. Чтобы получить параметры блока, вы можете использовать конечно-элементный анализ (FEA) или измерение фазных напряжений с помощью динамометра.

По умолчанию блок устанавливает Simulation Введите параметр на Непрерывный , чтобы использовать непрерывный время выборки во время моделирования. Если вы хотите сгенерировать код для двойного и фиксированного шага цели одинарной точности, учитывая установку параметра на Дискретный . Затем укажите время выборки , Ts параметр.

Для выполнения расчетов потерь мощности, подходящих для целей генерации кода, которые ограничивают memory, выберите Включить 2D LUT с оптимизацией памяти .

Трехфазная синусоидальная модель электрической системы

Блок реализует уравнения, которые выражаются в опорном состоянии неподвижного ротора. (dq) кадр. Ось d совмещена с a — ось. Все величины в системе отсчета ротора равны относится к статору.

Блок использует эти уравнения.

Расчет	Уравнение
q — и d — ось напряжение	vd = dψddt + Rsid − ωeψqvq = dψqdt + Rsiq + ωeψd
q — и d -ось ток	id = f (ψd, ψq) iq = g (ψd, ψq)
Электромеханический момент	Te = 1.5P [ψdiq − ψqid]

Эти переменные используются в уравнениях.

ω м	Механическая скорость ротора
ω e	Электрическая скорость ротора
Θ da	dq электрический угол статора относительно ротора ось а
R s , R R	Сопротивление обмоток статора и ротора, соответственно
i q , i d	q — и d — ось ток соответственно
v q , v d	q — и d — ось напряжение соответственно
Ψ q , Ψ д	q — и d — ось магнитный поток соответственно
п.	Количество пар полюсов
T e	Электромагнитный момент

Преобразователи

Для расчета напряжений и токов в сбалансированных трехфазных ( a , b ) количества, квадратурные двухфазные ( α , β ) величин, а вращение ( d , q ) опорных кадров, блок использует Преобразования Кларка и Парка.

В уравнениях преобразования.

Преобразование	Описание	Уравнения
Кларк	Преобразует сбалансированные трехфазные величины ( a , b ) в балансный двухфазные квадратурные величины ( α , β ).	xα = 23xa− 13xb −13xcxβ = 32xb− 32xc
Парк	Преобразует сбалансированные двухфазные ортогональные стационарные величины. ( α , β ) в ортогональный вращающийся опорный кадр ( d , q ).	xd = xαcosθe + xβsinθexq = −xαsinθe + xβcosθe
Обратный Кларк	Преобразует сбалансированные двухфазные квадратурные величины. ( α , β ) в сбалансированное трехфазные величины ( a , б ).	xa = xaxb = −12xα + 32xβxc = −12xα− 32xβ
Инверсный парк	Преобразует вращающийся ортогональный опорный кадр. ( d , q ) в сбалансированное двухфазные ортогональные стационарные величины ( α , β ).	xα = xdcosθe− xqsinθexβ = xdsinθe + xqcosθe

Преобразования используют эти переменные.

ω м	Механическая скорость ротора
п.	Пары полюсов двигателя
ω e	Электрическая скорость ротора
Θ e	Ротор электрический угловой
x	Фазный ток или напряжение

Механическая система

Угловая скорость ротора определяется как:

ddtωm = 1J (Te − Tf − Fωm − Tm) dθmdt = ωm

Эти переменные используются в уравнениях.

Крутящий момент вала ротора

J	Комбинированная инерция ротора и нагрузки
F	Комбинированное трение ротора нагрузка
θ м	Механическое угловое положение ротора
T м
Электромагнитный крутящий момент
T f	Комбинированный момент трения ротора и нагрузки

Учет мощности

Для учета мощности блок реализует эти уравнения.

68

3

PwmTe Psisd2 + Rsisq2) P _мех

Сигнал шины			Описание	Переменная	Уравнения
Pwr163fo	Pwr163fo	PwrTrnsfrd - Мощность, передаваемая между блоками	PwrMtr	Механическая мощность	P mot	Pmot = −ωmTe
			Мощность		Pbus = vania + vbnib + vcnic
			PwrNotTrnsfrd - Мощность, пересекающая блок пограничная, но не переданная	PwrElecLoss	Потеря резистивной мощности	P elec	Pelec = −32 (Rsisd2 + Rsisq2000
Когда Port Configuration установлен на Крутящий момент : Pmech = - (ωm2F + | ωm | Tf) Когда порт Конфигурация настроена на Скорость : Pmech = 0
PwrStored - Скорость изменения накопленной энергии	PwrMtrStored	Сохраненная мощность двигателя	P str	Pstr = Pbus + Pmot + Pelec + Pelec + Pmech 3. комбинированный двигатель R s Сопротивление статора i a , i b , i c Ток фаз a, b и c статора i sq , i sd Токи статора по осям q и d v an , v млрд , v cn Напряжение фаз a, b и c статора ω м Угловая механическая скорость ротора Комбинированный двигатель и вязкостное демпфирование нагрузки T e Электромагнитный момент Оптимизация памяти в интерполяционной таблице Данные для Соответствующий ток оси d, id и Соответствующий ток по оси q, таблицы поиска iq функции оси d и q поток. Для включения текущих вычислений, подходящих для целей генерации кода, которые ограничивают memory, выберите Включить 2D LUT с оптимизацией памяти . Блок использует линейная интерполяция для оптимизации значений текущей таблицы поиска для кода поколение. В этой таблице приводится сводная информация о реализации оптимизации. Вариант использования Реализация d - и q - ось потока выравнивается с поиском таблица значений точки останова. Оптимизированный для памяти ток - это текущее значение таблицы поиска на пересечении значений магнитного потока. d - и q - ось потока не совпадает с значения точки останова в таблице поиска, но находятся в пределах диапазон. Ток, оптимизированный для памяти, представляет собой линейную интерполяцию между соответствующими значениями потока. d - и q - ось потока не совпадает с значения точки останова в таблице поиска и вне диапазон. Невозможно вычислить ток, оптимизированный для памяти. Блок использует экстраполированные данные. Экстраполяция Таблицы поиска, оптимизированные для генерации кода, не поддерживают экстраполяцию для данных, выходящих за пределы допустимого диапазона.Однако вы можете включить предварительно рассчитанные значения экстраполяции в справочной таблице потерь мощности, выбрав Задайте экстраполяцию . Блок использует параметры конечной точки для изменения размера данных таблицы. Пользовательский ввод Экстраполяция Ссылки «Высокоточное нелинейное моделирование IPM на основе измеряется потокосцепление обмотки статора ». IEEE ® Транзакции в отраслевых приложениях , Vol. 51, №4, г. Июль / август 2015 г. [2] Чен, Сяо, Цзябинь Ван, Бхаскар Сен, Панайотис Ласари, Тианфу Сунь. «Высокая точность и вычислительно эффективная модель для машин с внутренним постоянным магнитом, учитывающая Магнитное насыщение, пространственные гармоники и эффект потери железа ». IEEE Transactions on Industrial Electronics , Vol.62, No. 7, июль 2015. [3] Оттоссон, Дж., М. Алакула. «А компактная реализация контроллера ослабления поля ». Международный симпозиум по Силовая электроника, электрические приводы, автоматизация и движение , июль, 2006. IRJET-Запрошенная вами страница не была найдена на нашем сайте IRJET приглашает статьи из различных инженерных и технологических дисциплин для Тома 8, выпуск 4 (апрель-2021) Отправить сейчас IRJET Vol-8 Выпуск 4, апрель 2021 г. Публикация продолжается... Обзор статей IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год. Проверить здесь IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством. IRJET приглашает специалистов по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 4 (апрель-2021 г.) Отправить сейчас IRJET Vol-8, выпуск 4, апрель 2021 г. Публикация продолжается... Обзор статей IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год. Проверить здесь IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством. IRJET приглашает специалистов по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 4 (апрель-2021 г.) Отправить сейчас IRJET Vol-8, выпуск 4, апрель 2021 г. Публикация продолжается... Обзор статей IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год. Проверить здесь IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством. IRJET приглашает специалистов по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 4 (апрель-2021 г.) Отправить сейчас IRJET Vol-8, выпуск 4, апрель 2021 г. Публикация продолжается... Обзор статей IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год. Проверить здесь IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством. IRJET приглашает специалистов по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 4 (апрель-2021 г.) Отправить сейчас IRJET Vol-8, выпуск 4, апрель 2021 г. Публикация продолжается... Обзор статей IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год. Проверить здесь IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством. IRJET приглашает специалистов по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 4 (апрель-2021 г.) Отправить сейчас IRJET Vol-8, выпуск 4, апрель 2021 г. Публикация продолжается... Обзор статей IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год. Проверить здесь IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством. IRJET приглашает специалистов по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 4 (апрель-2021 г.) Отправить сейчас IRJET Vol-8, выпуск 4, апрель 2021 г. Публикация продолжается... Обзор статей IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год. Проверить здесь IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством. IRJET приглашает специалистов по различным инженерным и технологическим дисциплинам, научным дисциплинам для Тома 8, выпуск 4 (апрель-2021 г.) Отправить сейчас IRJET Vol-8, выпуск 4, апрель 2021 г. Публикация продолжается... Обзор статей IRJET получил «Импакт-фактор научного журнала: 7,529» за 2020 год. Проверить здесь IRJET получил сертификат регистрации ISO 9001: 2008 для своей системы управления качеством. Динамика и анализ крутящего момента синхронного генератора с постоянными магнитами из магнитомягкого композитного материала Ключевые слова: синхронный генератор с постоянными магнитами, вибрация, радиальная сила, ветряная турбина, MEC, FEA, SMC. 1. Введение По мере того, как ветряные турбины становятся все более рентабельными, их использование в национальной энергосистеме растет. Различные концепции ветряных турбин были разработаны и построены для максимального использования энергии, минимизации затрат и улучшения качества электроэнергии в течение последних двух десятилетий. Если рассматривать тип генератора, систему генератора можно разделить на машины с электрическим возбуждением и машины с постоянными магнитами (PM). Эволюция ветряных турбин в промышленность от заводов началась в дни пика добычи нефти в 1970-х годах.В связи с этим кризисом стало важным технологическое развитие, а также спрос на сырье. В начале 80-х годов популярность энергии ветра резко возросла, и начали создаваться ветряные электростанции. Возобновляемые источники энергии стали более важными не только из-за нехватки обычного сырья, но и из-за двух важных вопросов энергетической политики: надежности и устойчивости, которые делают использование этих ресурсов обязательным. В возобновляемых источниках энергии, несомненно, используется в первую очередь энергия ветра. Синхронные машины с постоянными магнитами обладают высокой удельной мощностью и производительностью. Синхронную машину с постоянными магнитами можно рассматривать как машину, возбуждающую стабильным током возбуждения, которая содержит магниты вместо обмоток ротора традиционной синхронной машины. Следовательно, он действует как традиционная синхронная машина в состоянии синусоидального питания фиксированной частоты на PMSM. Поскольку PMSM не содержит обмоток на роторе, потеря возбуждения в традиционных синхронных машинах превалирует, и, таким образом, охлаждение машины становится более легким.В синхронных двигателях с постоянными магнитами есть три основных компонента крутящего момента. К ним относятся: момент возникает из-за взаимодействия поля ротора и токов статора, момент сопротивления, связанный со структурой ротора, и крутящий момент возникает из-за постоянных магнитов и пазов. В пределах этих моментов зубчатый момент не влияет на центрирующий момент, хотя, особенно на низких скоростях, скорость способствует колебаниям и вибрации. Синхронная машина с постоянным магнитом для поверхностного монтажа не имеет реактивного момента.Однако его зубчатый момент довольно высок. Эта составляющая крутящего момента приводит к пульсации крутящего момента и увеличивает вибрацию. При использовании обмоток с дробным пазом возможны различные комбинации количества полюсов и зубцов. Однако магнитное поле этих обмоток имеет больше пространственных гармоник, включая субгармоники. Эти нежелательные гармоники приводят к нежелательным эффектам, таким как локальное насыщение сердечника, шум и вибрация, а также потери на вихревые токи в магнитах, которые являются основными недостатками этих типов обмоток.Распределение радиальной плотности силы на поверхности статора, которое возникает из-за магнитного поля в воздушном зазоре в условиях холостого хода (разомкнутой цепи) и под нагрузкой, является основной причиной электромагнитно-индуцированного шума и вибрации. Важно правильно определить плотность магнитного потока в воздушном зазоре синхронной машины с постоянными магнитами, чтобы оценить характеристики машины, такие как аналитически полученный момент и обратная ЭДС. Есть много параметров, которые влияют на производительность машины.Характеристики материалов и геометрическая структура станка являются исходными. Каждая деталь должна быть разработана по эскизному проекту. Конструкция этих машин связана с правильным расчетом характеристик эскизных проектов. Геометрия машины и возбуждение обмоток статора влияют на распределение магнитного поля, тем самым влияя на крутящий момент. Другой компонент силы в PMSM - это радиальная сила, которая потенциально может вызвать радиальные колебания в статоре.Как уже упоминалось, компоненты крутящего момента зависят от распределения магнитного поля в воздушном зазоре [1]. Недавно материалы SMC использовались во многих приложениях переменного тока, таких как двигатели, трансформаторы и датчики [2]. Новые мягкие магнитные композитные материалы (SMC) имеют множество преимуществ по сравнению с обычной ламинированной сталью в приложениях электромагнитных систем [3]. Наиболее важные из этих преимуществ: • изотопные магнитные и термические материалы, • с низкими вихревыми потерями, • с низкими полными потерями на средних и высоких частотах. В этом исследовании радиальные силы, обратная ЭДС и крутящий момент синхронной машины с постоянным магнитом SMC анализируются с помощью теоремы о двумерной магнитной эквивалентной схеме. Анализируемая машина имеет 9 слотов и 10 полюсов. В этом исследовании сравнивается материал SMC и обычная сталь. 2. Свойства материала SMC Основная структура SMC - это стальные частицы высокой чистоты. Эти частицы покрыты покрытием из органического материала. Покрытые частицы вдавливаются в жесткий материал с помощью обжима.Материалы такого типа обычно являются магнитно-изотопными из-за того, что они являются естественными частицами, что упрощает их проектирование [2-3]. SMC включают частицы железа, покрытые диэлектрической пленкой. Эти частицы железа защищали друг друга электрической изоляцией. Из-за этого такие материалы обладают высоким электрическим сопротивлением. Эти материалы структурированы прессованными частицами. Удельное сопротивление SMC зависит от механических и ферромагнитных характеристик SMC, размеров и плотности частиц железа, изоляционного материала, процесса прессования и тепловых характеристик.Магнитные и механические характеристики материала SMC зависят не только от частиц железа, но и от количества масла и смолы, а также от процесса холодного или горячего прессования. Если материал SMC не спеченный, износостойкость будет ниже по сравнению с ламинированным или спеченным SMC. Характеристики материала SMC могут быть сделаны пригодными для специальных применений [4-5]. Принципиальная схема составных частей порошкового сердечника представлена ​​на рисунке 1. Изотопные магнитные характеристики обеспечивают плотность потока в магнитной цепи ротора в осевом направлении, таким образом, общая осевая длина двигателя может быть уменьшена без потери характеристик двигателя [7].Магнитные цепи создают трехмерные магнитные линии, и используются различные радиальные топологии для получения высоких характеристик двигателя [2]. Благодаря трехмерному распределению магнитного потока в материалах SMC зубья могут быть увеличены в осевом направлении, таким образом, магнитный поток на зубьях и ярме ротора увеличивается. При такой конструкции активная длина воздушного зазора стала максимальной [7]. Материал SMC особенно удобен для изготовления 3D-флюсовых машин [8]. Кроме того, он снимает ограничения магнитного поля ламинирования. Из-за изоляции частиц железа поверхностным покрытием и когерентами он имеет более низкие потери на завихрение, чем многослойная сталь, особенно на высоких частотах.При полной потере гистерезисные потери выше. За счет увеличения частоты возбуждения рост потерь в сердечнике SMC ниже, чем в электротехнической стали. Материалы SMC очень полезны для двигателей, работающих на высоких частотах, но на низких и средних частотах они не так хороши, как электротехническая сталь с высокой степенью ламинирования. SMC подходит для крупногабаритных двигателей по низким ценам. Рис. 1. Принципиальная схема составных элементов порошкового сердечника [6] Рис.2. Сравнение кривых B-H для электротехнической стали и материала SMC. В литературе есть много исследований, посвященных развитию двух важных характеристик материала SMC. Эти две характеристики: • Повышение чистоты и уменьшение деформации между частицами за счет уменьшения коэрцитивной силы и увеличения магнитной проницаемости магнитных частиц, • повышение плотности, электрического сопротивления и термического сопротивления под давлением [3]. Для машин с сердечником из многослойной кремнистой стали хорошие магнитные характеристики могут быть получены с помощью плоской магнитной линии. Это обеспечивает двухмерную магнитную цепь. Покрытие изолятора SMC имеет изотропные магнитные характеристики. Таким образом, трехмерные магнитопроводы могут быть получены из электрических машин, сконструированных из этого материала. Насыщенность материала SMC зависит от композита, чистоты и плотности. Плотность потока насыщения, относительная проницаемость и индукция материала SMC ниже, чем у кремнистой стали.Индукция связана с проницаемостью в слабых магнитных полях. Насыщенность важна в сильных магнитных полях. Благодаря низкой индукции MMF может быть увеличен за счет увеличения магнитного потока в сердечнике, таким образом, можно увеличить площадь зубьев. Увеличение площади зубьев невозможно без увеличения ширины паза, поэтому увеличение площади зубьев увеличивает габариты двигателя. Лучший способ увеличить МДС - использовать постоянный магнит с более высокой коэрцитивной силой [8, 9]. Другой метод - изменение структуры материала SMC.При подготовке материала SMC, если может быть обеспечено внешнее магнитное взаимодействие, проницаемость будет увеличена, а магнитное сопротивление уменьшено. Этот метод называется внешним потоком взаимодействия. С помощью этого метода потери стали SMC могут быть уменьшены до 6,25% [10]. Кривые намагничивания SMC и кремнистой стали показаны на рисунке 2. 3. 10-полюсный 9-слотовый SMC malzemeli синхронный генератор с постоянными магнитами MEC анализ Двумерный разрез машины показан на рисунке 3.Обмотки статора сосредоточены вокруг каждого полюса статора. Количество витков обмотки каждой фазы - 216. Редкоземельный магнит «Nd-Fe-B» утоплен в железе ротора. Остаточная плотность магнитного потока Br и коэрцитивная сила Hc постоянного магнита составляют примерно 1,3 Тл и 1000 кА / м соответственно. Для представленного анализа были сделаны следующие допущения: • используемые материалы имеют однородные свойства, • Ns = Нм, • сначала без нагрузки, • зубья статора и постоянные магниты жесткие; эти компоненты не испытывают деформации из-за радиальной и тангенциальной силы, • гистерезис и вихревые токи не учитываются, • ток принимается синусоидальным, • В сердечнике статора используется материал SMC. Рис. 3. Двумерный разрез синхронной машины с постоянными магнитами Для метода MEC сначала изучается состояние холостого хода. Перед расчетом обратной ЭДС, плотность потока в воздушном зазоре (Bg) определяется решением MEC на рисунке 4 как: (1) X1 = G1-Gt, 200… -Gt, 1G2-Gt, 30… 0-Gt, 2G3-Gt, 4 ……………… 00… -Gt, Ns-1GNsNs × Ns, (2) Y1 = -Gl, 10000… 0-Gl, 2000… 00-Gl, 300… 000-Gl, 40 ………………… 0000… -Gl, NsNs × Ns, (3) Z1 = Ggap1,1-Gmut1,100… -Gmut1,1Ggap2,2-Gmut3,30… 0-Gmut2,2Ggap3,3-Gmut4,4 ……………… 00… -GmutNs-1, Ns-1GgapNs, NsNs × Ns, (9) Rs = wsbμ0μrec, stellAs, , где Rm - сопротивление магнита, Rg - сопротивление воздушного зазора, Rr - сопротивление ротора, Rs - сопротивление статора, Rl - сопротивление утечки, а Kl - коэффициент утечки, и его значение меньше единицы. Рис. 4. MEC для щелевой конструкции при отсутствии нагрузки Вот: GNs = 1Rsy, Ns + Rt, Ns + Rt, Ns-1 + Rl, Ns, GgapNs, Ns = 1Rg, Ns + Rl, Ns + Rg, Ns-1 + Rm, Ns + Rm, Ns-1, Gmut1, Ns = 1Rg, Ns-1 + Rm, Ns-1. Секунда изучается по состоянию нагрузки. Следующее уравнение используется для получения количества столбцов MEC в условиях нагрузки: (11) GCD (10, 9) = 1, Номер столбца = NsGCD (Ns, 2p) = 9. Магнитное сопротивление магнита Rm [A / Wb] и сопротивление зазора Rg [A / Wb] рассчитываются отдельно от магнитного сопротивления модели без нагрузки, потому что поток реакции якоря пересекает воздушный зазор и магниты на расстоянии одного шага паза τs [м] (см. рис. 5): (12) X2 = Gload1-Gloadt, 200… -Gloadt, 1Gload2-Gloadt, 30… 0-Gloadt, 2Gload3-Gloadt, 4 ……………… 00… -Gloadt, Ns-1GloadNsNs × Ns, (13) Y2 = -Gm, δ, 10000… 0-Gm, δ, 2000… 00-Gm, δ, 300… 000-Gm, δ, 40 ………………… 00000-Gm, δ, NsNs × Ns, (14) Z2 = Gload, gap1,1-Gload, mut1,100… -Gload, mut1,1Gload, gap2,2-Gload, mut3,30… 0-Gload, mut2,2Gload, gap3,3-Gload, mut4,4 …… ………… 00….-Gload, mutNs-1, Ns-1Gload, gapNs, NsNs × Ns, (19) Rs = wsbμ0μrec, stellAs. Общий поток: Вот: Gload, зазор = 12 × Rg + 2 × Rm + Rm, δ, Gload, mut = 1Rg + Rm. Рис. 5. MEC в условиях нагрузки 4. 10-полюсный 9-слотовый SMC malzemeli синхронный генератор с постоянными магнитами Анализ МКЭ Эта машина анализируется программой Flux 3D. Рассчитываются плотность потока в воздушном зазоре ротора и значение крутящего момента двигателя.Чтобы сравнить характеристики двигателей из разных материалов, PMSM с материалом SMC и PMSM со сталью M19 имеют одинаковую структуру статора и ротора с одинаковыми размерами, номинальная мощность обоих двигателей составляет 1,5 кВт. Размеры ротора и статора показаны в Таблице 1 и Таблице 2. На Рис. 6 показан паз статора. Таблица 1. Параметры статора PMSM Внутренний радиус статора 20.6 мм Внешний радиус статора 38 мм Длина воздушного зазора 0,6 мм Ширина зазора 7,5 мм Таблица 2. Параметры ротора ПМСМ Внутренний радиус ротора 8 мм Внешний радиус ротора 20 мм Длина магнита 2.5 мм Рис. 6. Размеры паза статора На рис. 7 плотность магнитного потока показана как для станка из материала SMC, так и для стального станка. Как видно из рисунков, машина SMC имеет меньшую плотность магнитного потока. Таким образом, значения крутящего момента и обратной ЭДС будут ниже, но уменьшение крутящего момента и обратной ЭДС очень мало. См. Также данные в таблицах 3 и 4. Рис.7. а) Плотность потока синхронной машины с постоянными магнитами со стальным статором, б) Плотность потока синхронной машины с постоянными магнитами со статором SMC а) б) Таблица 3. Сравнение FEA и MEC для машины SMC Для стали ФЭМ MEC Bgmax 1.15 1,1 Btmax 1,8 1,77 Bsymax 1,5 1.45 Таблица 4. Сравнение FEA и MEC для стальной машины для SMC ФЭМ MEC Bgmax 1.05 1,0 Btmax 1,4 1,35 Bsymax 0,8 0.75 5. Структура обмотки Набор обмоток влияет на характеристики электрических машин, в частности противоэлектродвижущую силу. Тип обмотки электрической машины определяется количеством q пазов на полюс на фазу машины в соответствии со следующими правилами: • интегральная q> 1, распределенная обмотка со встроенными пазами, • q = 1, сосредоточенная обмотка со встроенным пазом, • дробное q> 1, дробно-щелевая распределенная обмотка, • дробная q <1, дробно-щелевая концентрированная обмотка. Распределенная обмотка - наиболее распространенная конфигурация для больших электрических машин. При наличии одного паза на полюс на фазу коэффициент намотки равен 1. Недостатком концентрированных обмоток является низкий коэффициент намотки и высокая пульсация крутящего момента. Преимуществами этой конфигурации являются более короткие концевые обмотки и простой монтаж [13]. Работы по генерированию концентрированной обмотки немало. Дж. Кросс и П. Вигур представили специализированные концентрированные двухслойные обмотки [14].Векторы конфигурации обмотки выводятся за семь шагов: 1. Для значений меньше 1; q, паз на полюс на фазу, уменьшается до двух целых неделимых чисел q = bc. 2. Повторяющиеся серии из 0 и 1 последовательности находятся по равенству выше. Начальная повторяемая последовательность получается по следующему уравнению: 000 ... 0⏟b-c111 ... 1⏟b⏞c. 3. Начальная последовательность должна быть переставлена ​​таким образом, чтобы единицы регулярно распределялись между 0. 4. Перестановочная последовательность записывается рядом 3 раза. 5. Классическая последовательность имеет вид A + C - B + A - C + B - . 6. Первый слой обмотки выстраивается с соответствием 1 с. 7. Второй слой намотки достигается смещением первой линии до шага винта. Структура обмотки в данном исследовании рассчитана на конфигурацию с 9 пазами и 10 полюсами: q = 93 * 10 = 310. В этой ситуации в последовательности будет 3 единицы и 7 нулей. (1) Начальная последовательность: 0000000111. (2) Оптимальная последовательность: 1001001000. (3) Перестановочная последовательность записывается рядом 3 раза: 1001001000 | 1001001000 | 1001001000. (4) Классическая последовательность: A + C - B + A - C + B -: 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 1 0 0 0, A + C - B + A - C + B - A + C - B + A - C + B - + C - B + A - C + B - A + C - B + A - C + B - A - A - A C - B + A - C + B -. (5) Первый слой обмотки будет заказан под номером 1: . A + A - A + C + C - C + B + B - B + . (6) Второй слой намотки получается смещением первой линии на зуб: A + A - A + C + C - C + B + B - B + , A - A + A - C - C + C - B - B + B - . (7) Последнюю структуру обмотки можно нарисовать, как показано ниже (см. Рис. 8). Рис. 8. Структура обмотки для конфигурации с 9 и 10 полюсами 6. Анализ радиальной силы синхронного генератора с постоянными магнитами Наиболее частый источник вибрации в синхронной машине с постоянными магнитами вызван радиальной силой, возникающей из-за электромагнитной силы. Проблемы вибрации и шума являются чрезвычайно серьезными, когда частоты радиального воздействия совпадают с одной или несколькими механическими или структурными резонансными частотами в машине.Поэтому важно точно знать распределение плотности потока в воздушном зазоре для прогнозирования формы сигнала обратной ЭДС, крутящего момента и радиальной силы [15]. Альтернативой получению электромагнитного момента с использованием подхода баланса энергии является получение компонентов силы из магнитного поля с использованием метода тензора напряжений Максвелла. В частности, в воздушном зазоре машины местные радиальные составляющие плотности силы могут быть выражены [16]: , где Bgpm, Btpm, Bgs и Bts обозначают тангенциальную и радиальную плотности потока, создаваемые PM и обмотками статора соответственно.Если для конструкции, которая обсуждается в этой работе, создается структура обмотки для конфигурации с 9 пазами и 10 полюсами, уравнение (23) может быть сформулировано, как показано ниже, поскольку тангенциальная сила имеет незначительный уровень по сравнению с радиальной силой: Равенство радиальных сил создается после того, как плотность магнитного потока генерируется посредством равенства выше. После того, как плотность магнитного потока получена из приведенных выше уравнений, радиальная сила получена из уравнения (26) (см. Рис.9). Рис. 9. Радиальная сила от FEA и MEC 7. Анализ крутящего момента синхронного генератора с постоянными магнитами Крутящий момент зубчатого зацепления и электромагнитный момент машины с постоянными магнитами рассчитываются в соответствии с методом тензора напряжений Максвелла как: Согласно методу Арккио, лучше вычислить среднее значение электромагнитного момента по всей поверхности воздушного зазора. Таким образом, крутящий момент можно рассчитать как: где S - поверхность воздушного зазора, образованная слоями между статором и ротором, g - длина воздушного зазора.Согласно методу виртуальной работы, электромагнитный момент равен производной магнитной со-энергии Wm по углу ротора при постоянном токе [17]: По уравнению (29) получаем: (30) T = ∂W'∂t∂t∂θ = ∂W'∂t∂θ∂t = Pω = eaia + ebib + ecicω. Согласно результатам крутящего момента, приведенным на рисунке 10, разница между результатами MEC и FEA составляет менее 1%, когда в статоре используется сталь, и согласно результатам крутящего момента, приведенным на рисунке 11, разница между результатами MEC и FEA составляет 2%, когда в статоре используется сталь. Рис. 10. Форма кривой крутящего момента SMC-PMSM Рис.11. Форма волны крутящего момента Steel-PMSM 8. Выводы После определения распределения магнитного потока методом эквивалентной магнитной схемы были рассчитаны плотность радиальной силы и крутящий момент. Как видно на рисунках 10 и 11, наблюдается снижение крутящего момента на 12,5% при использовании материала SMC в статоре PMSM.Поскольку материал SMC является рентабельным и не требует затрат на пресс-форму на этапе производства, материал SMC намного более рентабелен по сравнению со сталью. Кроме того, затраты на рабочую силу ниже, потому что он более формуемый. Когда сравниваются результаты по крутящему моменту, полученные методом эквивалентной магнитной схемы и методом конечных элементов, видно, что разница не превышает 2%. Радиальные силы исследуемой машины очень низкие. Благодаря этому колебания и вибрации очень низкие.Радиальные силы прямо пропорциональны квадрату плотности магнитного потока в воздушном зазоре. Когда плотность потока в воздушном зазоре увеличивается, радиальные силы увеличиваются. В то же время мощность, получаемая от машины, также увеличивается. При оптимизации машины необходимо учитывать номинальные радиальные силы. Таким образом, вибрация и резонанс крутящего момента машины уменьшаются. При анализе радиальных сил используется комбинация аналитических методов и методов МКЭ. . Похожие записи 21.11.2024 0 Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании 19.11.2024 0 Новорожденный какает слизью: причины появления слизи в кале грудничка 19.11.2024 0 Гемангиома у новорожденных: причины, виды, лечение и профилактика Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт