Расчет соединения катушек индуктивности смешанное. Смешанное соединение катушек индуктивности, резисторов и конденсаторов: расчет и применение

Как рассчитать смешанное соединение катушек индуктивности, резисторов и конденсаторов. Какие формулы применяются для расчета общего сопротивления и импеданса цепи. В каких устройствах используются такие соединения элементов. Как правильно подобрать номиналы компонентов.

Основные принципы смешанного соединения RLC-цепей

Смешанное соединение катушек индуктивности, резисторов и конденсаторов представляет собой комбинацию последовательного и параллельного подключения этих элементов в одной электрической цепи. Такие схемы широко применяются в различных электронных устройствах для фильтрации сигналов, согласования импедансов, частотной коррекции и других целей.

При расчете смешанных RLC-цепей необходимо учитывать следующие ключевые моменты:

• Для последовательно соединенных элементов складываются их импедансы
• Для параллельно соединенных элементов складываются их проводимости
• Необходимо учитывать фазовые сдвиги между токами и напряжениями на реактивных элементах
• Расчет удобно вести в комплексной форме, используя метод комплексных амплитуд

Расчет эквивалентного сопротивления смешанной RLC-цепи

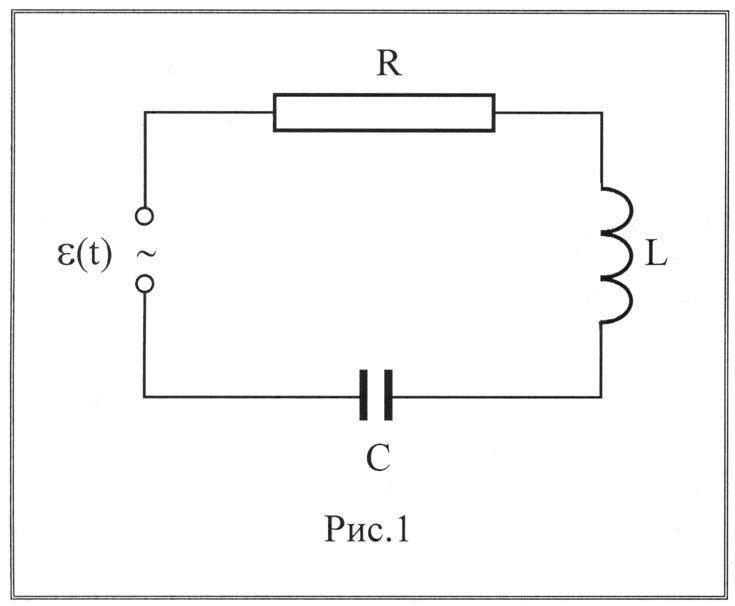
Рассмотрим пример расчета эквивалентного сопротивления смешанной RLC-цепи, состоящей из последовательно соединенных резистора R, катушки индуктивности L и параллельного им конденсатора C:

1. Импеданс последовательной RL-цепи: Z_RL = R + jωL
2. Импеданс конденсатора: Z_C = 1 / jωC
3. Общий импеданс цепи: 1/Z = 1/Z_RL + 1/Z_C
4. После преобразований получаем:

Z = (R + jωL) / (1 — ω²LC + jωRC)

Здесь ω — угловая частота сигнала, j — мнимая единица.

Применение смешанных RLC-цепей в электронике

Смешанные соединения катушек индуктивности, резисторов и конденсаторов находят широкое применение в различных областях электроники и радиотехники:

• Фильтры высоких и низких частот
• Полосовые и режекторные фильтры
• Цепи частотной коррекции усилителей
• Согласующие цепи в радиопередатчиках
• Частотно-зависимые делители напряжения
• Колебательные контуры генераторов

Особенности расчета смешанных RLC-цепей

При расчете сложных смешанных RLC-цепей следует учитывать ряд важных аспектов:

• Необходимо правильно выбирать метод расчета в зависимости от конфигурации цепи
• Для сложных цепей удобно использовать методы контурных токов или узловых потенциалов
• При высоких частотах нужно учитывать паразитные параметры компонентов
• Для точных расчетов следует использовать специализированные программы моделирования

Выбор номиналов компонентов для смешанных RLC-цепей

Правильный выбор номиналов резисторов, конденсаторов и катушек индуктивности критически важен для работы смешанных RLC-цепей. При этом необходимо учитывать:

• Требуемую частотную характеристику цепи
• Входное и выходное сопротивление
• Допустимые потери и добротность
• Нагрузочную способность компонентов
• Температурные коэффициенты и стабильность параметров

Моделирование смешанных RLC-цепей

Для анализа работы сложных смешанных RLC-цепей удобно использовать компьютерное моделирование. Популярные программы для этого:

• LTspice — бесплатный SPICE-симулятор с широкими возможностями
• Multisim — профессиональный пакет для моделирования электронных схем
• QucsStudio — свободная программа для моделирования аналоговых и цифровых схем
• TINA — мощный инструмент для анализа и проектирования электронных схем

Практические рекомендации по расчету смешанных RLC-цепей

При проектировании и расчете смешанных RLC-цепей рекомендуется придерживаться следующего алгоритма:

1. Определить требуемые характеристики цепи (АЧХ, ФЧХ, входное/выходное сопротивление)
2. Выбрать подходящую топологию схемы
3. Рассчитать предварительные номиналы компонентов
4. Провести компьютерное моделирование схемы
5. Оптимизировать номиналы для достижения нужных параметров
6. Проверить работу схемы с учетом допусков и паразитных параметров
7. Изготовить макет и провести экспериментальную проверку

Заключение

Смешанные RLC-цепи являются мощным инструментом для создания различных электронных устройств. Правильный расчет и выбор компонентов позволяет реализовать требуемые частотные и импедансные характеристики. Использование современных методов компьютерного моделирования существенно упрощает процесс проектирования сложных смешанных RLC-цепей.

16. Смешанное соединение резистора, катушки индуктивности и конденсатора.

Рис. 16.1.

Рассмотрим двухполюсник, состоящий из смешанного соединения резистора, катушки индуктивности и конденсатора (рис. 16.1). Он подключен к источнику синусоидального напряжения, амплитуда которого постоянна.

Будем понимать эту цепь как модель энергетической системы, состоящей из источника напряжения е, соединенного линией электропередач с нагрузкой в виде последовательно соединенных резистораRи катушки индуктивностиL. Такая модель выбрана, потому что в энергетике большую долю нагрузки составляют электродвигатели и трансформаторы, которые необратимо отбирают электрическую энергию из сети (так, как это делает резистор), а также периодически запасают энергию в магнитном поле своих индуктивностей и отдают ее обратно в цепь (так, как это делает катушка индуктивности).

Емкость С рассчитаем так, чтобы токIв линии электропередач был минимальным. Это позволит свести к минимуму потери энергии в проводах линии электропередач, соединяющей источник энергии и нагрузку (см. п.14, а также лабораторную работу №3 по общей электротехнике). Такой режим часто называют компенсацией реактивной мощности нагрузки.

Согласно определению полной проводимости двухполюсника (см. п.13),

,

то есть, при заданном напряжении Uминимум токаIдостигается при минимуме полной проводимостиy. Найдем эту проводимость, используя эквивалентные преобразования сопротивлений.

Комплексное сопротивление последовательно включенных резистора и катушки будет равно сумме комплексных сопротивлений этих элементов (см. п. 13):

.

Комплексная проводимость ветви с резистором и катушкой будет обратна к комплексному сопротивлению этой ветви:

.

При параллельном соединении проводимости складываются, поэтому

.

Чтобы найти у, удобно выделить действительную и мнимую частьY. Сделаем это, умножив числитель и знаменатель дроби на выражение, комплексно сопряженное знаменателю:

.

Используем принятые в электротехнике обозначения: – активная проводимость двухполюсника,– реактивная проводимость двухполюсника (см. п.13).

Согласно определению полной проводимости (см. п.13).

Так как gне зависит от емкости конденсатораС, тоукак функция отСдостигает минимума при. Отсюда получаем формулу для емкости конденсатора:

.

Обратим внимание на то, что – это условие фазового резонанса (см. п.15). Так как при этом сопротивление двухполюсника максимально, то это в данном случае фазовый резонанс совпадает с резонансом токов.

Построим векторную диаграмму напряжений и токов. Вначале нарисуем комплекс напряжения (рис. 16.2). Его фазу будем считать нулевой, поэтому векторнаправим вдоль действительной оси. Затем найдем сдвиг фаз между напряжением и током ветви

RL(см. пример п. 13):- это угол между действительной осью и вектором, изображающим комплекс тока ветвиRL.

Найдем значение тока ветви RL:- это длина вектора, изображающего комплекс тока ветвиRL(в некотором графическом масштабе).

Нарисуем на диаграмме комплекс тока ветви RL (рис. 16.2).

Ток всего двухполюсника равен сумме тока ветвиRLи тока конденсатора:. Ток конденсатора сдвинут по фазе относительно напряжения на. Нарисуем комплекс тока конденсатора и сложим его с комплексом тока ветвиRL, получим ток (рис. 16.3).

Рис. 16.2. Напряжение и ток ветви RL.

Рис. 16.3. Векторная диаграмма напряжения и тока смешанного соединения RLC (частичная компенсация реактивного тока).

Рис. 16.4. Полная компенсация реактивного тока (резонанс токов).

На рис. 16.3 видно, что наличие в цепи тока конденсатора приводит к уменьшению тока в линии электропередачпо сравнению с током нагрузки. На рис. 16.4 показан случай, когда токподобран так, что он обеспечивает минимум тока.

Расчет индуктивности для двунаправленного преобразователя постоянного напряжения в автономных подводных аппаратах | Публикации

Введение

Подводный аппарат — небольшое судно или техническое устройство, используемое для выполнения разнообразных задач в толще воды и на морском дне. В отличие от подводной лодки, как правило, имеет ограниченные возможности по автономности и поэтому работает во взаимодействии с обеспечивающим судном-носителем. Подводные аппараты могут работать на глубине, недоступной для подводных лодок и водолазов. Данные аппараты предназначены для выполнения различных операций: визуального исследования линий подводных коммуникаций, патрулирования, исследования морского дна, контроля биоресурсной базы, разработки подводных месторождений полезных ископаемых, сейсморазведки, использования в качестве средств оповещения в чрезвычайных ситуациях и т. д.

Состояние проблемы и постановка задачи

В ведущих странах мира наблюдается тенденция к разработке автономных подводных аппаратов. Автономные подводные аппараты могут нести на борту акустические, оптические и электромагнитные сенсоры, которые необходимы для выполнения их работы. Теоретически использование подобных аппаратов позволяет существенно расширить радиус действия, снизить затраты на техническое обеспечение надводными судами, несущими специальное оборудование. В связи с этим возникает проблема питания данных аппаратов. Основным источником питания выступают аккумуляторные батареи.

С качественным изменением силовых электронных преобразователей и устройств хранения электроэнергии в последнее время в электроэнергетическом комплексе наблюдается повышенное внимание к использованию сетей постоянного тока [1] благодаря определённым преимуществам, по сравнению с классическими двигателями внутреннего сгорания или турбинными двигателями. Опыт электромобилей показывает, что интерес к данной теме не является беспочвенным [2]. Питание автономных устройств осуществляется с помощью аккумуляторов, имеющих относительно низкое напряжение, в то время как большинство потребителей должны питаться более высоким уровнем напряжения, что связано с обеспечением силовых узлов высокой энергоэффективностью [3].

Одним из основных вопросов, связанных с проектированием преобразователей постоянного напряжения, является расчёт и выбор катушки индуктивности. Значение индуктивности сильно влияет на характер работы преобразователя. Главной проблемой являются весогабаритные характеристики мощной катушки — самого тяжёлого и массивного компонента во всём преобразователе постоянного напряжения. Наиболее предпочтительным вариантом, с точки зрения проектировщика, является катушка малой индуктивности, обладающая небольшим весом и габаритами, которые позволяют создать более компактное устройство. С другой стороны, низкое значение индуктивности может не обеспечить непрерывность тока на нагрузки. Выбор значения индуктивности состоит в том, чтобы ток, сглаживаемый катушкой индуктивности, был бы непрерывным и при этом катушка имела минимальные массогабаритные показатели [4].

Теоретические исследования

На рис. 1 показан двунаправленный преобразователь постоянного напряжения со смешанным переключением, состоящий из двух коммутационных ячеек (ключей) S1 и S2 и индуктивности L. Ключи состоят из IGBT-транзистора и включённого антипараллельно ему диода. На стороне первичного напряжения размещается аккумуляторная батарея, а с другой стороны — нагрузка R, напряжение на которой можно регулировать путём открытия/закрытия IGBT-транзисторов. Преобразователь также содержит высокочастотный конденсатор в качестве энергетического буфера со стороны нагрузки C2 и сглаживающий конденсатор со стороны аккумуляторной батареи C1.

Рис. 1 Двунаправленный преобразователь постоянного напряжения

Для преобразователя постоянного напряжения в повышающем режиме минимальное значение индуктивности, необходимое для обеспечения работы преобразователя в режиме непрерывного тока, зависит от рабочего цикла установившегося режима, периода переключения и сопротивления нагрузки [5].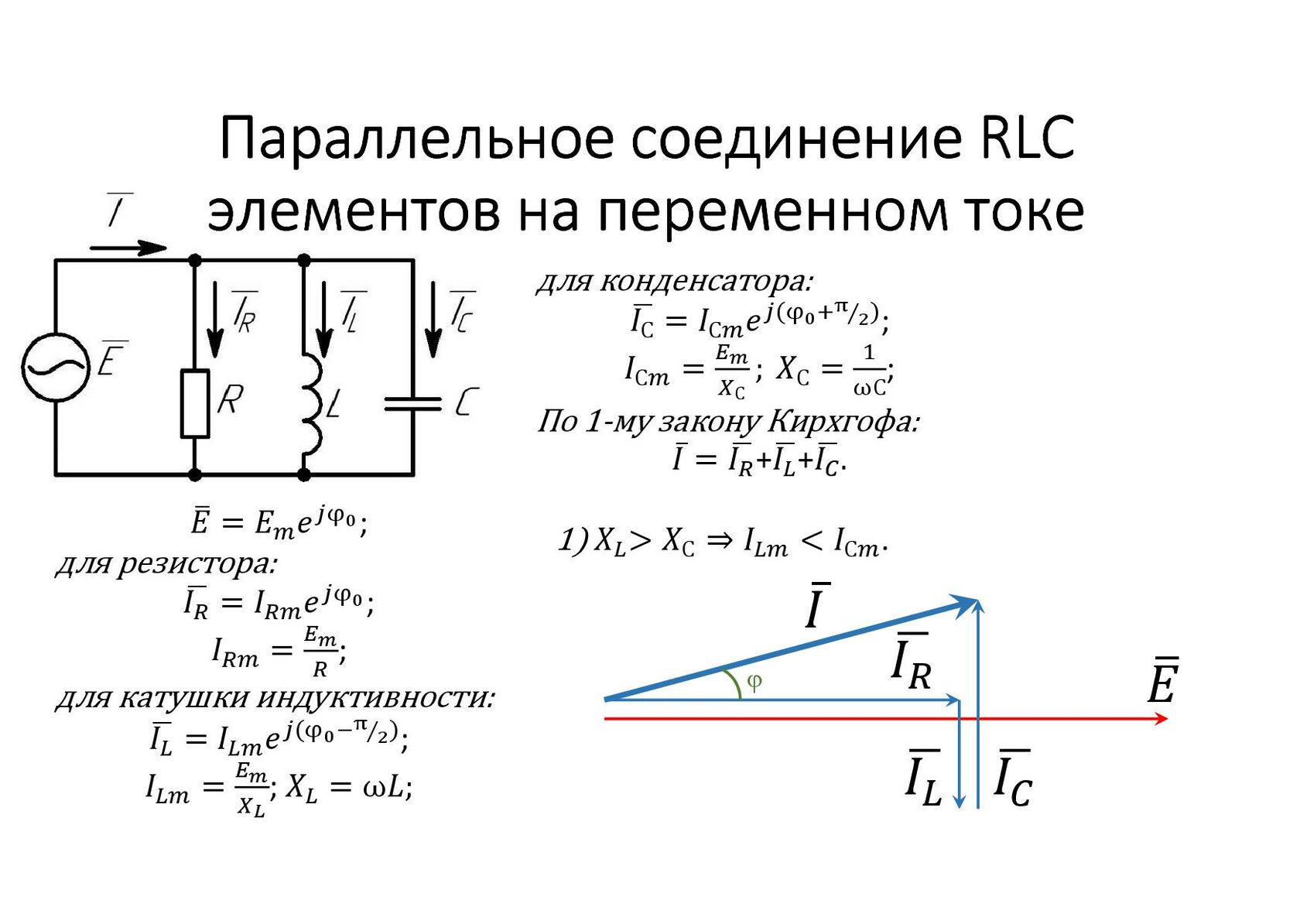

Длительность включенного состояния рассчитывается как T_O=DT,

где D — это рабочий цикл, заданный схемой управления, выраженный как отношение времени включения коммутатора к времени одного полного цикла переключения T.

Продолжительность выключения:
T_З = (1 − D) T.

Во время включенного состояния S2, которое имеет низкое сопротивление, наблюдается небольшое падение напряжения U_VT в IGBT-транзисторе. Существует также небольшое падение напряжения на индуктивности, равное I_RL. Таким образом, на катушку индуктивности подаётся напряжение, равное U_L = U_вх − (U_VT = I_RL).

Диод коммутационной ячейки S1 в это время не пропускает через себя ток. Напряжение, прикладываемое к правой стороне L, представляет собой напряжение на U_VT коммутационной ячейки S2. Ток катушки индуктивности протекает из положительной клеммы аккумуляторной батареи U_вх через S2 и далее идёт на отрицательную клемму. Во время включенного состояния напряжение на индукторе постоянно и равно входному. Ток в катушке индуктивности увеличивается в результате приложенного напряжения, и поскольку приложенное напряжение является постоянным, ток через катушку индуктивности будет увеличивается линейно [6].

Увеличение тока индуктора может быть рассчитано с использованием известного соотношения:

Так как частота коммутации велика (порядка нескольких десятков кГц), то выражение можно переписать в виде:

Увеличение тока в катушке индуктивности во включенном состоянии определяется выражением:

где ∆I⁺ — пульсационный ток индуктора. В течение этого периода весь ток выходной нагрузки подаётся выходным конденсатором С2 [7].

Когда S2 выключен, он представляет собой разрыв цепи. Поэтому, поскольку ток, текущий в катушке индуктивности, не может мгновенно меняться, ток перенаправляется от S2 к S1. Из-за уменьшения тока в катушке индуктивности напряжение на ней поменяет полярность, пока диод ключа S1 не откроется.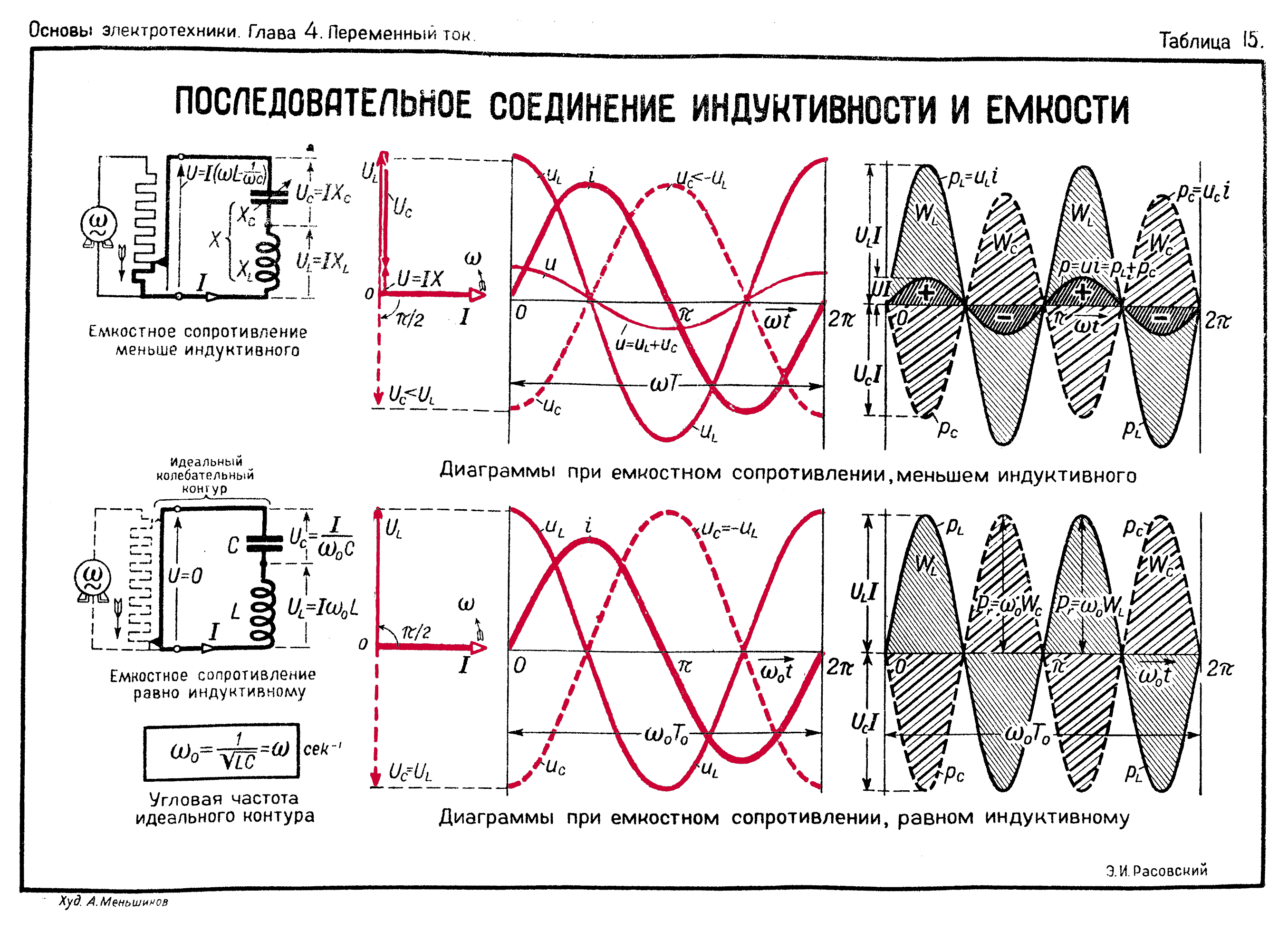 Напряжение, приложенное к левой стороне катушки, остаётся таким же, как и раньше (U_вх − U_VT − I_LR_L). Напряжение, приложенное к правой стороне катушки индуктивности, теперь является выходным напряжением Uвых. Ток катушки индуктивности теперь течёт от аккумуляторной батареи через диод ключа S1 до выходного конденсатора C2 и нагрузки. В выключенном состоянии напряжение на индукторе постоянное и равно U_L=(U_вых + U_VD + IR_L) − U_вх.

Следовательно, ток в катушке индуктивности уменьшается в выключенном состоянии S2:

Величина ∆I^— также является пульсационным током катушки индуктивности.

В стационарных условиях увеличение тока ∆I⁺ во время включения и уменьшение тока ∆I^— во время выключения равны. В противном случае ток катушки индуктивности будет иметь или увеличение, или уменьшение от цикла к циклу, которое не будет являться уравновешенной системой. Установка двух значений ∆I, равных друг другу, эквивалентна балансировке вольт-секунд на индуктивности. Вольт-секунда, подаваемая на индуктор, является произведением прилагаемого напряжения и временем его применения. Поэтому эти два уравнения могут быть приравнены:

Выразив U_вых через U_вх , можно записать:

С учётом того, что мощность на катушке может быть найдена:

а ток I может быть найден путём сложения тока при открытом и закрытом ключе S2, ток пульсации катушки индуктивности также можно выразить следующим уравнением:

Среднеквадратичный ток в катушке индуктивности превосходит ток нагрузки на 1/3 от выходного тока. Поэтому в двунаправленном преобразователе в повышающем режиме катушка индуктивности, силовые переключатели и конденсатор работают под более высокими токами по сравнению с каскадным преобразователем, что приводит к большей потери мощности, а также вызывает насыщение активной катушки [8]. Ток через катушку индуктивности можно представить в следующем виде:

Если номинальная мощность нагрузки определяется P_H= U_выхI_H , то

С учётом того, что

I_min=I − ∆I^—; I_max= I + ∆I⁺,

можно записать максимальные и минимальные значения тока в катушке индуктивности. В силовых цепях потерями напряжения на полупроводниковой технике можно пренебречь, т. к.

U_вх >> U_VT + U_VD(1 − D),

поэтому можно записать:

Значение индуктивности, для которого ток индуктивности будет находиться только на краю режима прерывистого тока, будет определяться уравнением

Приняв U_VT, U_VT и R_L равными нулю, можно записать:

Результаты моделирования

Графики зависимостей I_min = f (L) и I_max = f (L), полученные при U_вх = 10 В; U₂ = 20 В; f = 10 кГц;

I_Н = 10 А, представлены на рис. 2.

Рис. 2. Графики зависимостей Imin = f (L) и Imax = f (L) для преобразователя постоянного напряжения

Из графика видно, что при значении индуктивности L = 2,2·10^—5 Гн ток катушки достигает отрицательного значения, поэтому следует выбрать значение индуктивности преобразователя равным L = 22 мкГн. Однако из-за небольшого падения напряжения на катушке индуктивности и полупроводниковых ключей полученные значения будут немного отличаться от реальных.

На рис. 3 представлена симуляция преобразователя постоянного тока, выполненная в пакете Simulink.

Рис. 3. Модель преобразователя постоянного токаРис. 4. Осциллограммы тока и напряжения на выходе преобразователя постоянного напряжения

Как можно заметить из графиков тока и напряжения на нагрузке, значение индуктивности полностью удовлетворяет минимальному уровню индуктивности для обеспечения режима непрерывного тока. В то же время симуляция показала, что D должно составлять не 0,5, а 0,35 из-за падения сопротивления в катушке индуктивности (0,1 Ом), IGBT-транзисторе и диоде (Uпр = 0,6 В; R = 0,001 Ом).

Для защиты IGBT-транзисторов можно использовать демпфирующие конденсаторы, ёмкость которых определяется по формуле [9]

Таким образом, рассмотренным выше методом можно найти значение индуктивности для преобразователя постоянного напряжения, необходимое для обеспечения режима непрерывного тока.

Заключение

Рассмотрено применение преобразователей постоянного тока для питания приёмников в автономных подводных аппаратах. Выведено выражение, описывающее колебания тока в режиме непрерывного тока с определёнными допущениями. Показано, что для обеспечения работы преобразователя постоянного тока в режиме непрерывного тока индуктивность должна быть больше определённого значения, при этом массогабаритные показатели катушки должны быть минимальными. Проведённая симуляция преобразователя постоянного тока, выполненная в пакете Simulink, подтверждает правильность методики определения минимального значения индуктивности для обеспечения работы преобразователя постоянного тока в режиме непрерывного тока.

Список литературы

1. Chernyi S., Zhilenkov A. Modeling of complex structures for the ship’s power complex using xilinx system // Transport and telecommunication. 2015. V. 16 (1). P. 73–82. DOI: 10.1515/ttj-2015-0008.
2. Avdeyev B. A., Vyngra A. V. Increase of operating efficiency of ship electrical generating plant with shaft generator // Интеллектуальные энергосистемы: тр. V Междунар. молодёж. форума (Томск, 9–13 октября 2017 г.): в 3 т. Томск: Изд-во ТПУ, 2017. Т. 1. C. 255–258.
3. Nyrkov A., Sokolov S., Zhilenkov A., Chernyi S. Complex modeling of power fluctuations stabilization digital control system for parallel operation of gas-diesel generators // Proceedings of the 2016 IEEE north west Russia section young researchers in electrical and electronic engineering conference (Санкт-Петербург, 2–3 февраля 2016 г.): Eiconrusnw, 2016. P. 636–640. DOI: 10.1109/EIConRusNW.2016.7448264.
4. Иванов А. В., Немировский А. Е. Силовая электроника. Выпрямители: учеб. пособие. Вологда: Изд-во ВоГУ, 2015. 119 с.
5. Лукутин Б. В., Обухов С. Г. Силовые преобразователи в электроснабжении: учеб. пособие. Томск: Изд-во ТПУ, 2007. 144 с.
6. Lai J. S., Nelson D. J. Energy management power converters in hybrid electric and fuel cell vehicles // Proceedings of the IEEE. 2007. V. 95. P. 766–777.
7. Токарев Л. Н. Судовая электротехника и электромеханика. СПб.: Береста, 2006. 320 с.
8. Chung Y., Liu W., Schoder K., Cartes D. A. Integration of a bi-directional DC-DC converter model into a real-time system simulation of a shipboard medium voltage DC system // Electric Power Systems Research. 2011. V. 81. P. 1051–1059.
9. Dijk E. PWM-Switch Modeling of DC–DC Converters // IEEE Transactions on Power Electronics. 1995. V. 10. N. 6. P. 659–665.

Информация об авторе

Борис Александрович Авдеев — доцент кафедры электрооборудования судов и автоматизации производства, Керченский государственный морской технологический университет.

Источник: ©Б. А. Авдеев, «Вестник АГТУ». Серия «Морская техника и технология», №4 2018

Катушки индуктивности

в последовательном и параллельном соединении — Wira Electrical

Катушки индуктивности в последовательном и параллельном соединении мало чем отличаются от последовательно соединенных или параллельных резисторов. Просто открытие, эквивалентная индуктивность для последовательных катушек индуктивности представляет собой сумму всех индуктивностей.

Научная причина этого может быть доказана из объяснений и примеров ниже. Но поскольку он находится в той же группе, что и резисторы, мы можем проанализировать его, используя напряжение и ток.

Как рассчитать эквивалентную индуктивность

Помните, что катушка индуктивности также является пассивным элементом, мы можем использовать инструмент последовательно-параллельной комбинации. То, как мы рассчитываем эквивалентную индуктивность, можно определить, проанализировав напряжение и ток в реальной электрической цепи.

Мы по-прежнему будем использовать наши предыдущие формулы, где мы узнали о формуле индуктивности.

Наведенное напряжение в катушке индуктивности, когда через нее протекает ток:

Мы будем рассматривать это наведенное напряжение как падение напряжения на резисторе, чтобы нам было легче его запомнить.

Без лишних слов перейдем к следующим формулам.

Формула последовательной индуктивности

Обратите внимание, что приведенная ниже схема состоит из n катушек индуктивности,

. через них.

Ток в цепи равен

По закону напряжения Кирхгофа общее напряжение равно

Подстановка

Результат в

Мы можем перерисовать приведенную выше схему в

Следовательно, эквивалентная индуктивность при последовательном соединении равна

900 02

В заключение

Эквивалентная индуктивность n катушек индуктивности в ряд представляет собой сумму всех отдельных индуктивностей.

Суммарная индуктивность последовательных катушек индуктивности всегда больше, чем наибольшая индивидуальная индуктивность в расчете.

В качестве примера предположим, что у нас есть три катушки индуктивности, как показано ниже:

Используя формулу последовательного соединения катушек индуктивности, мы получаем

Таким образом, мы можем вспомнить, что и катушки индуктивности, и резисторы имеют одинаковую характеристику при последовательном соединении. связь. Но верно ли это и для параллельных катушек индуктивности? Читаем следующую часть.

Формула параллельной индуктивности

Обратите внимание, что приведенная ниже схема состоит из n катушек индуктивности,

Поскольку это параллельная цепь, напряжение на всех катушках индуктивности будет одинаковым, а ток через каждую из них может быть разным.

Напряжение на катушках индуктивности

Суммарный ток в цепи

Замена

Результат в

Мы можем перерисовать схему в

Следовательно, эквивалентная индуктивность при параллельном соединении

Согласно закону тока Кирхгофа начальный ток i(t ₀ ) через L _eq (при t=t ₀ ) представляет собой сумму всех токов через каждую катушку индуктивности, in при t ₀ .

Если у нас есть только две параллельные катушки индуктивности, мы можем просто использовать приведенное ниже уравнение.

В качестве примера предположим, что у нас есть три параллельные катушки индуктивности, как показано ниже:0002

В заключение,

Эквивалентная индуктивность n катушек индуктивности, включенных параллельно, является обратной величиной суммы всех отдельных индуктивностей.

Суммарная индуктивность параллельных индукторов всегда меньше наименьшей индивидуальной индуктивности при расчете.

Из приведенной выше формулы для последовательного и параллельного индуктивности мы можем сделать вывод, что способ нахождения эквивалентной индуктивности такой же, как и при нахождении эквивалентного сопротивления.

Резюме – Катушки индуктивности в последовательной и параллельной формуле

После прочтения и изучения приведенных выше простых и полных объяснений мы можем резюмировать их в нескольких строках:

• Способ, которым мы вычисляем эквивалентные последовательные катушки индуктивности, будет таким же, как мы вычисляем эквивалентные серии. резисторы.
• Способ расчета эквивалентных параллельных катушек индуктивности будет таким же, как расчет эквивалентных параллельных резисторов.
• Эквивалентная индуктивность n катушек индуктивности, соединенных последовательно, представляет собой сумму всех индивидуальных индуктивностей.
• Эквивалентная индуктивность n катушек индуктивности, включенных параллельно, является обратной величиной суммы всех отдельных индуктивностей.

Катушки индуктивности — Библиотека электрических уравнений

Библиотека уравнений

Уравнения, связанные с электроникой, и многое другое.

Прозрачный

Справочник по электронике

Индуктивность катушки

Способность электрического проводника, такого как катушка, создавать наведенное напряжение при изменении тока, протекающего через него, называется индуктивностью. Чтобы рассчитать индуктивность катушки на основе ее физической конструкции, вы можете использовать это уравнение, где:

L — Индуктивность катушки в Генри (Гн)
N — Количество витков
μ _r — Проницаемость сердцевины
μ _o — Проницаемость воздуха или вакуума (1,26X10 ^–6 )
A — Закрытая площадь
l — Длина катушки

Катушки из проволоки, изготовленные с определенным значением индуктивности, называются индукторами.

 

Зависимость напряжения от тока индуктора

Это уравнение показывает зависимость напряжения от тока в индукторе, где:

v — индуцированное напряжение
L — индуктивность катушки индуктивности
di/dt — мгновенная скорость изменения тока через катушку индуктивности 9 0003

Наведенное напряжение на катушке индуктивности равно прямо пропорциональна его индуктивности и мгновенной скорости изменения тока через индуктор. Таким образом, чем больше скорость изменения тока через катушку, тем выше индуцированное напряжение. Однако, если ток через индуктор не изменяется в конкретный момент времени, индуцированное напряжение равно нулю.

 

Индуктивное реактивное сопротивление

Индуктивное реактивное сопротивление (X _L ) является мерой сопротивления катушки индуктивности протеканию синусоидального переменного тока. Это зависит от величины индуктивности и частоты приложенного напряжения.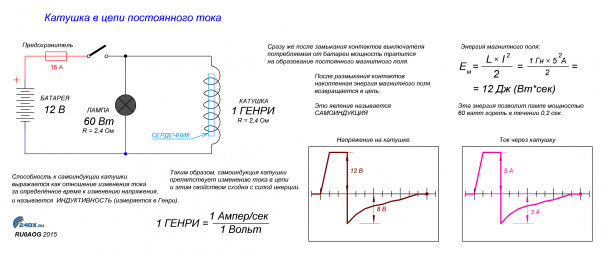 Чтобы определить реактивное сопротивление катушки индуктивности, вы можете использовать это уравнение.

 

Сохраненная энергия катушки индуктивности

Как и конденсатор, катушка индуктивности в идеале не рассеивает электрическую энергию, подаваемую на нее источником напряжения. Однако энергия хранится в магнитном поле. Чтобы рассчитать энергию, запасенную в катушке индуктивности, вы можете использовать это уравнение.

 

Взаимная индуктивность



k — Коэффициент связи

Две катушки имеют взаимную индуктивность, когда ток в одной катушке может индуцировать напряжение в другой катушке. Как видно на схеме, если L ₁ подключен к источнику напряжения, но не физически, то L ₁ и L ₂ связаны магнитным полем. Изменение тока в L ₁ может индуцировать напряжение как на L ₁ , так и на L ₂ . Если к L ₂ подключена нагрузка, индуцированное напряжение через L ₂ может подавать ток на эту нагрузку. Вы можете использовать это уравнение для расчета взаимной индуктивности между двумя катушками.

 

Суммарная индуктивность двух последовательных катушек с взаимной индуктивностью ING

Суммарная индуктивность двух последовательных катушек с взаимной индуктивностью (L _T ) зависит от степени взаимной связи и от того, соединены ли они последовательно-вспомогательно или последовательно-противоположно. Катушки соединены последовательно, когда общий ток создает одинаковое направление магнитного поля для двух катушек. Они соединены последовательно-встречно, когда их магнитное поле имеет противоположное направление.

Взаимная индуктивность (L _M ) положительная и увеличивает общую индуктивность, когда две катушки соединены последовательно. В последовательно-противоположных взаимная индуктивность равна минусу и уменьшает общую индуктивность двух последовательных катушек.

 

Эквивалентная индуктивность последовательных катушек индуктивности

Общая или эквивалентная индуктивность (L _eq ) последовательных катушек индуктивности может быть просто определена путем сложения отдельных индуктивностей.