Расчет сопротивления при последовательном соединении. Последовательное и параллельное соединение проводников: расчет сопротивления, тока и напряжения

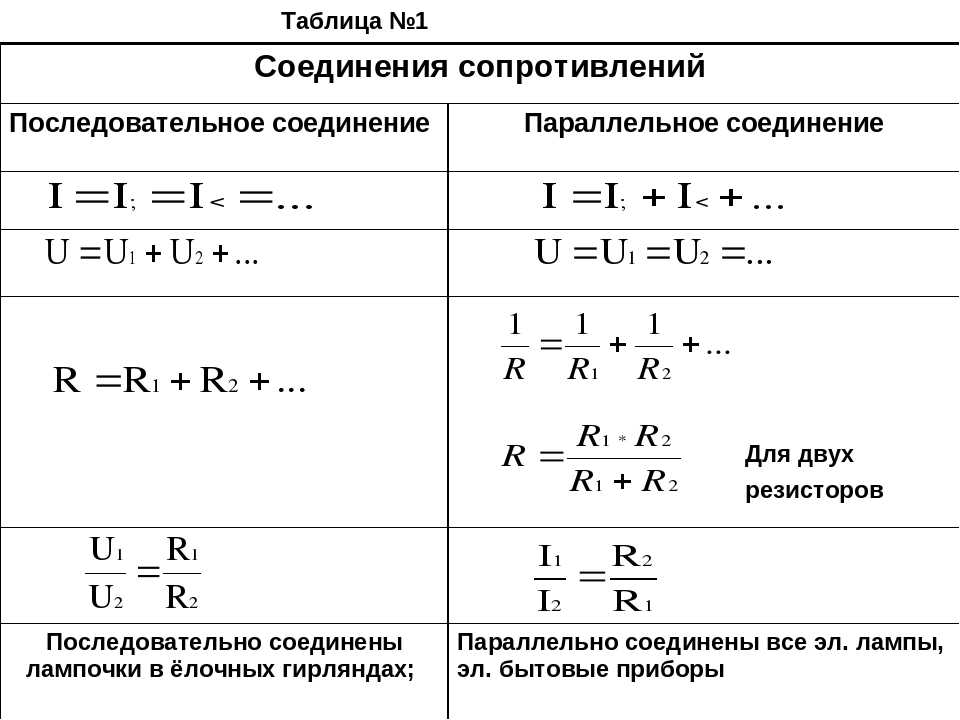
Как рассчитать общее сопротивление при последовательном и параллельном соединении проводников. Как распределяются ток и напряжение в цепи с последовательным и параллельным соединением. Какие формулы используются для расчета параметров электрической цепи при различных видах соединения проводников.

Последовательное соединение проводников: основные характеристики

При последовательном соединении проводники соединяются друг за другом в одну цепочку. Основные характеристики такого соединения:

• Сила тока одинакова во всех проводниках цепи
• Общее напряжение равно сумме напряжений на отдельных проводниках
• Общее сопротивление цепи равно сумме сопротивлений отдельных проводников

Расчет общего сопротивления при последовательном соединении

Формула для расчета общего сопротивления при последовательном соединении проводников:

R = R1 + R2 + R3 + … + Rn

где R — общее сопротивление цепи, R1, R2, R3 и т.д. — сопротивления отдельных проводников.

Распределение тока и напряжения при последовательном соединении

При последовательном соединении:

• Сила тока одинакова во всех участках цепи: I = I1 = I2 = I3 = … = In
• Общее напряжение равно сумме напряжений на отдельных проводниках: U = U1 + U2 + U3 + … + Un

Параллельное соединение проводников: ключевые особенности

При параллельном соединении все проводники подключаются к одним и тем же точкам цепи. Основные характеристики:

• Напряжение одинаково на всех параллельно соединенных проводниках
• Общий ток равен сумме токов через отдельные проводники
• Величина, обратная общему сопротивлению, равна сумме величин, обратных сопротивлениям отдельных проводников

Формула расчета общего сопротивления при параллельном соединении

Для расчета общего сопротивления при параллельном соединении используется формула:

1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

где R — общее сопротивление цепи, R1, R2, R3 и т.д. — сопротивления отдельных проводников.

Как распределяются ток и напряжение при параллельном соединении?

При параллельном соединении:

• Напряжение одинаково на всех проводниках: U = U1 = U2 = U3 = … = Un
• Общий ток равен сумме токов через отдельные проводники: I = I1 + I2 + I3 + … + In

Сравнение последовательного и параллельного соединения проводников

Давайте сравним основные характеристики последовательного и параллельного соединения проводников:

Характеристика	Последовательное соединение	Параллельное соединение
Сила тока	Одинакова во всех проводниках	Разная в каждом проводнике
Напряжение	Сумма напряжений на проводниках	Одинаково на всех проводниках
Общее сопротивление	Больше сопротивления любого проводника	Меньше сопротивления любого проводника

Практическое применение последовательного и параллельного соединения

Знание особенностей последовательного и параллельного соединения проводников широко применяется в электротехнике и электронике. Вот несколько примеров:

• Елочные гирлянды часто используют последовательное соединение лампочек
• В бытовой электропроводке розетки обычно соединяются параллельно
• Аккумуляторы в устройствах могут соединяться последовательно для увеличения напряжения
• Солнечные панели часто соединяют параллельно для увеличения силы тока

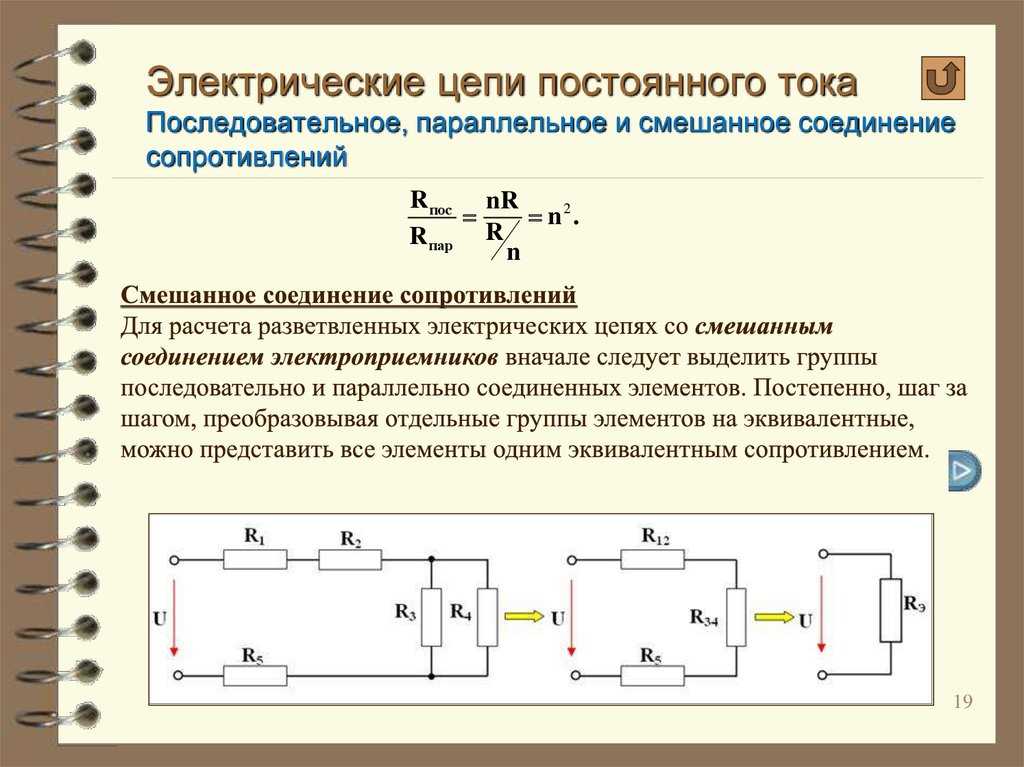
Расчет параметров электрической цепи при смешанном соединении

На практике часто встречаются цепи со смешанным соединением, где присутствуют как последовательные, так и параллельные участки. Как рассчитать параметры такой цепи?

1. Разбейте цепь на участки с однотипным соединением
2. Рассчитайте эквивалентное сопротивление для каждого участка
3. Замените участки их эквивалентными сопротивлениями
4. Повторяйте процесс, пока не получите простую цепь
5. Рассчитайте общий ток и напряжение
6. Используя полученные данные, рассчитайте параметры для исходных элементов цепи

Закон Ома для участка цепи с последовательным и параллельным соединением

Закон Ома остается справедливым как для последовательного, так и для параллельного соединения проводников. Однако его применение имеет некоторые особенности:

Последовательное соединение:

I = U / (R1 + R2 + … + Rn)

где I — общий ток, U — общее напряжение, R1, R2, … Rn — сопротивления отдельных проводников.

Параллельное соединение:

I = U * (1/R1 + 1/R2 + … + 1/Rn)

где I — общий ток, U — общее напряжение (одинаковое для всех проводников), R1, R2, … Rn — сопротивления отдельных проводников.

Мощность в цепях с последовательным и параллельным соединением

Расчет мощности в цепях с различными типами соединения проводников имеет свои особенности:

Мощность при последовательном соединении:

Общая мощность равна сумме мощностей на отдельных проводниках:

P = P1 + P2 + … + Pn = I^2 * R1 + I^2 * R2 + … + I^2 * Rn

Мощность при параллельном соединении:

Общая мощность также равна сумме мощностей на отдельных проводниках, но рассчитывается иначе:

P = P1 + P2 + … + Pn = U^2 / R1 + U^2 / R2 + … + U^2 / Rn

Практические задачи на расчет параметров цепи

Для лучшего понимания темы рассмотрим несколько практических задач:

Задача 1: Последовательное соединение

Три резистора с сопротивлениями 10 Ом, 20 Ом и 30 Ом соединены последовательно. Напряжение на концах цепи 120 В. Определите:

1. Общее сопротивление цепи
2. Силу тока в цепи
3. Напряжение на каждом резисторе

Решение:

1. Общее сопротивление: R = 10 + 20 + 30 = 60 Ом
2. Сила тока: I = U / R = 120 / 60 = 2 А
3. Напряжение на резисторах:
   • U1 = I * R1 = 2 * 10 = 20 В
   • U2 = I * R2 = 2 * 20 = 40 В
   • U3 = I * R3 = 2 * 30 = 60 В

Задача 2: Параллельное соединение

Два резистора сопротивлением 6 Ом и 3 Ом соединены параллельно. Напряжение на концах цепи 12 В. Определите:

1. Общее сопротивление цепи
2. Общий ток в цепи
3. Ток через каждый резистор

Решение:

1. Общее сопротивление: 1/R = 1/6 + 1/3 = 1/2, R = 2 Ом
2. Общий ток: I = U / R = 12 / 2 = 6 А
3. Ток через резисторы:
   • I1 = U / R1 = 12 / 6 = 2 А
   • I2 = U / R2 = 12 / 3 = 4 А

Выводы и рекомендации по применению знаний о соединениях проводников

Понимание принципов последовательного и параллельного соединения проводников крайне важно для работы с электрическими цепями. Вот несколько ключевых выводов и рекомендаций:

• При последовательном соединении увеличивается общее сопротивление цепи, что может быть полезно для ограничения тока
• Параллельное соединение уменьшает общее сопротивление, что позволяет увеличить ток в цепи
• Выбор типа соединения зависит от конкретной задачи и требуемых параметров цепи
• При работе со сложными цепями всегда разбивайте их на простые участки для облегчения расчетов
• Помните о законе сохранения энергии: общая мощность в цепи всегда равна сумме мощностей на отдельных элементах

Применение этих знаний позволит вам эффективно проектировать и анализировать электрические цепи в различных областях — от бытовой электроники до промышленных электроустановок.

Расчет мощности при последовательном соединении – Tokzamer

Мощность при параллельном и последовательном соединении резисторов

Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при параллельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.

1. Свойства и технические характеристики резисторов
2. Мощность при последовательном соединение
3. Мощность при параллельном соединение

Свойства и технические характеристики резисторов

Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется параллельное соединение резисторов, а для делителей напряжения – последовательное.

На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.

Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.

Для соединения резисторов в схемах используются три разных способа подключения – параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.

Мощность при последовательном соединение

При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.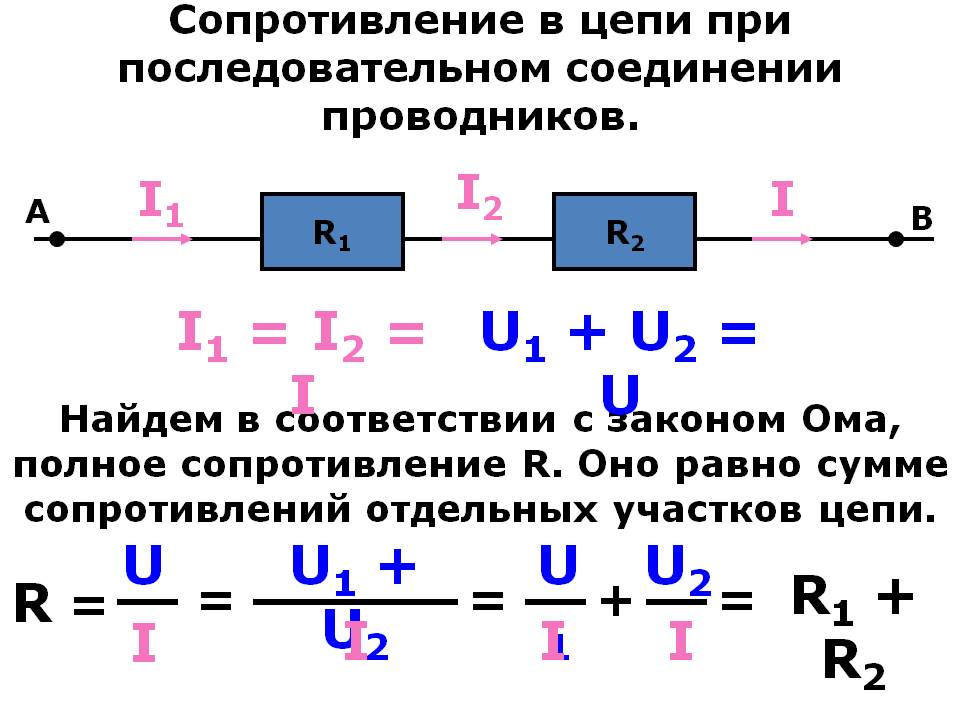

Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:

• P₁ = I 2 x R₁ = 0,256 2 x 200 = 13,11 Вт;
• P₂ = I 2 x R₂ = 0,256 2 x 100 = 6,55 Вт;
• P₃ = I 2 x R₃ = 0,256 2 x 51 = 3,34 Вт;
• P₄ = I 2 x R₄ = 0,256 2 x 39 = 2,55 Вт.

Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.

Мощность при параллельном соединение

При параллельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.

Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:

• 1/R = 1/R₁+1/R₂+1/R₃+1/R₄ = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
• Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
• Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
• Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
• Расчет силы тока для каждого резистора выполняется по формулам: I₁ = U/R₁ = 100/200 = 0,5A; I₂ = U/R₂ = 100/100 = 1A; I₃ = U/R₃ = 100/51 = 1,96A; I₄ = U/R₄ = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.

Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов: P₁ = U 2 /R₁ = 100 2 /200 = 50 Вт; P₂ = U 2 /R₂ = 100 2 /100 = 100 Вт; P₃ = U 2 /R₃ = 100 2 /51 = 195,9 Вт; P

4 = U 2 /R₄ = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р₁+Р₂+Р₃+Р₄ = 50+100+195,9+256,4 = 602,3 Вт.

Таким образом, мощность при последовательном и параллельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.

Последовательное и параллельное соединение резисторов

Напряжение при последовательном и параллельном соединении резисторов

Сопротивление при последовательном и параллельном соединении резисторов

Параллельное соединение резисторов

Последовательное и параллельное соединение проводников

Как определяется мощность цепи при последовательном соединении?

Как распределяется мощность при последовательном соединении?

Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…

Как распределяются напряжения на резисторах при последовательном соединении?

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома: Т.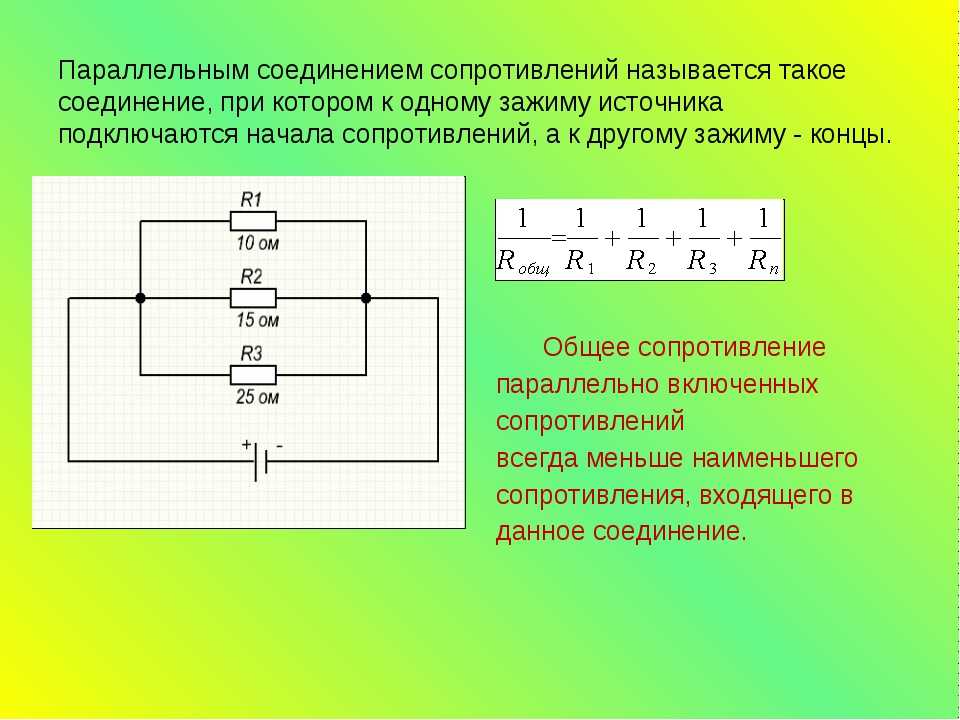 е чем большее сопротивление резистора, тем большее напряжение на него падает.

Какие физические величины сохраняются при последовательном соединении конденсаторов?

Последовательное соединение конденсаторов

заряды одинаковы, складываются величины, обратные емкости.

Какой формулой для мощности удобнее пользоваться при расчете цепи с последовательно соединенными резисторами?

Что происходит с мощностью при последовательном соединении?

Мощность при последовательном соединение

Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. … Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A.

Что такое мощность тока определение?

Мощность электрического тока — это отношение произведенной им работы ко времени в течение которого совершена работа.

Как складываются сопротивления при параллельном соединении?

Из закона Ома и первого и второго правил Кирхгофа следует: При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей. При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.

Как найти R при параллельном соединении?

Как распределяется ток в цепи?

Ток через цепь равен сумме токов через каждый из проводников, образующих цепь; Напряжение на выводах цепи равно напряжению на любом из проводников, образующих цепь.

Какая физическая величина одинакова при последовательном соединении?

При последовательном соединении проводников сила тока во всех проводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников. При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов.

Какие физические величины бывают одинаковыми при параллельном соединении проводников?

Какие физические величины сохраняются при последовательном соединении проводников? … При последовательном соединении сила тока во всех резисторах одинакова, а общее напряжение равно сумме напряжений на каждом из проводников.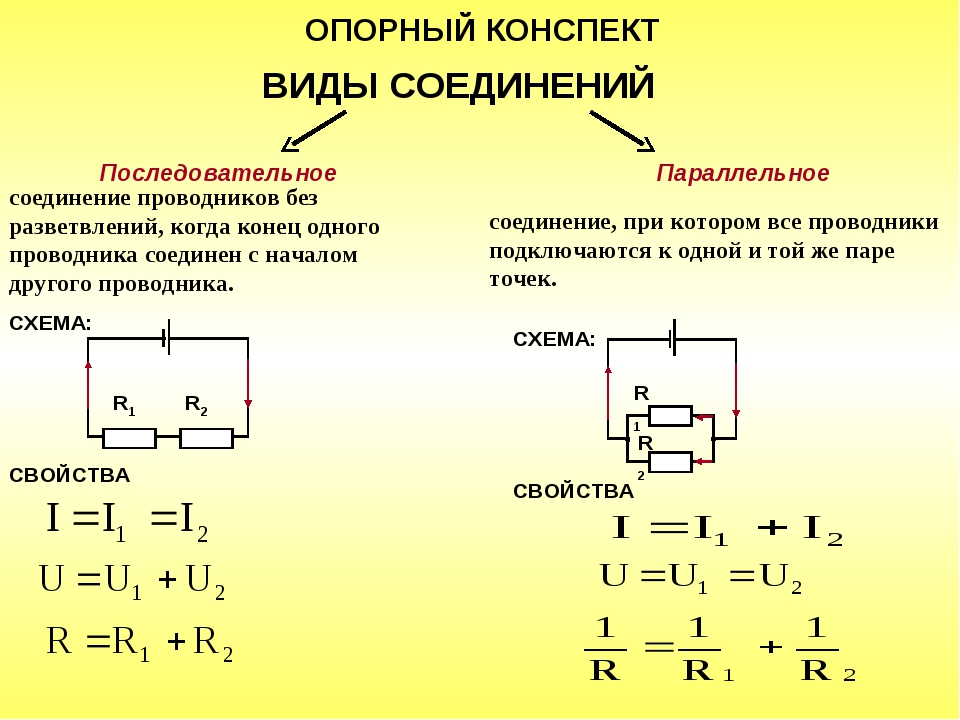 Общее сопротивление цепи равно сумме сопротивлений всех резисторов.

Какое сопротивление проводников называется последовательным?

Как определить суммарную мощность?

Определите мощность источника питания.

1. Мощность равна произведению силы тока на напряжение, то есть 1 Вт = 1 А х 1 В. Формула: Р = I х V. …
2. Например, если сила тока равна 3 А, а напряжение равно 110 В, то мощность равна: 3 х 110 = 330 Вт. …
3. Вот почему внесистемной единицей измерения мощности является вольт-ампер.

Как рассчитать мощность зная ток и напряжение?

Формула расчета мощности электрического тока

Согласно закону Ома, сила тока(I) пропорциональна напряжению(U) и обратно пропорциональна сопротивлению(R), а мощность(P) рассчитывается как произведение напряжения и силы тока. Исходя из этого, ток в участке сети рассчитывается: I = P/U.

Закон Ома для участка цепи. Закон Джоуля — Ленца.

Работа и мощность электрического тока. Виды соединения проводников.

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивлению этого участка.

Выполняется для металлов и электролитов.

Закон Джоуля — Ленца.

Дж. Джоуль (1841—1843) Э. X. Ленц (1842—1843) независимо друг от друга экспери­ментально установили

В электрической цепи происходит преобразование энергии упорядоченного движения заряженных частиц в тепловую. Согласно з-ну сохранения энергии работа тока равна количеству выделившегося тепла.

Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток:

Работа и мощность электрического тока.

Работа электрического тока:

Мощность электрического тока (работа в единицу времени):

В электричестве иногда применяется внесистемная единица работы — кВт . ч (киловатт-час).

1 кВт . ч = 3,6 . 10 6 Дж.

Виды соединения проводников.

Последовательное соединение.

1. Сила тока во всех последовательно соединенных участках цепи одинакова:

I₁=I₂=I₃=. =I_n=.

2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке:

U=U₁+U₂+. +U_n+.

3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка:

R=R₁+R₂+.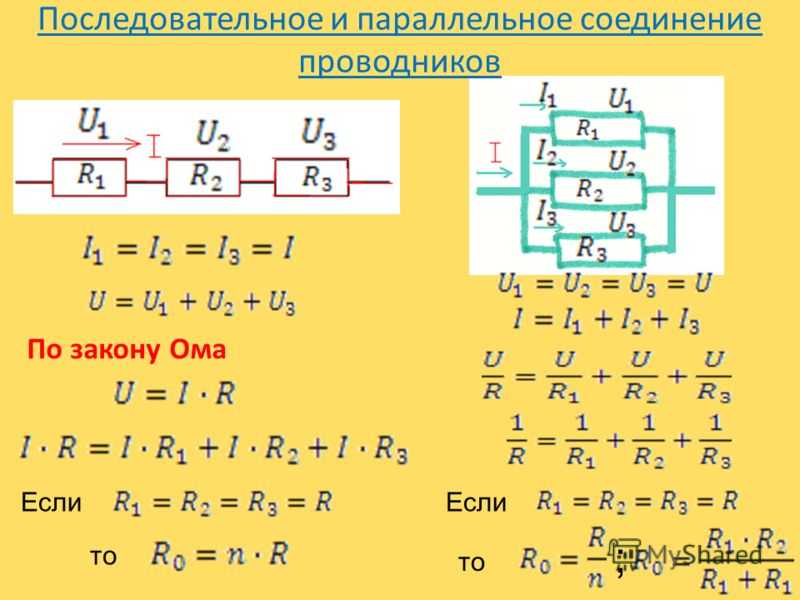 +R_n+.

Если все сопротивления в цепи одинаковы, то:

R=R₁ . N

При последовательном соединении общее сопротивление увеличивается (больше большего).

Параллельное соединение.

1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках.

2. Напряжение на всех параллельно соединенных участках цепи одинаково:

U₁=U₂=U₃=. =U_n=.

3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению):

Если все сопротивления в цепи одинаковы, то:

При параллельном соединении общее сопротивление уменьшается (меньше меньшего).

4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках:

5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках:

P=P₁+P₂+. +P_n+.

6. Т.к. силы тока во всех участках одинаковы, то: U₁:U₂. U_n. = R₁:R₂. R_n.

Для двух резисторов: — чем больше сопротивление, тем больше напряжение.

4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках:

A=A₁+A₂+. +A_n+.

т.к. .

5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках:

P=P₁+P₂+. +P_n+.

6. Т.к. напряжения на всех участках одинаковы, то:

Для двух резисторов: — чем больше сопротивление, тем меньше сила тока.

Резистор и сопротивление

Каталог

Показать каталог

• Arduino и совм. платы
• Raspberry
• Наборы Arduino
• Платы расширения
• Модули
  • Радиомодули
  • Bluetooth
  • RFID
  • Wi-Fi, Ethernet, GPS, GSM
  • Звук и видео
  • Свет
  • Память и RTC
  • Генераторы сигналов
  • Расширения
  • Термоэлектрические
• Датчики
  • Газа
  • Климатические
  • Механического воздействия
  • Пространства
  • Света и цвета
  • Тактильные
  • Холла и тока
• Реле
• Двигатели
  • Коллекторные
  • Бесколлекторные
  • Сервоприводы
  • Шаговые
  • Драйверы
• Механика
  • Платформы
  • Колеса
  • Замки
• Радиоконструкторы
• Радиокомпоненты
  • Резисторы
    • Постоянные
    • Потенциометры
    • Варисторы
    • Термисторы
    • Фоторезисторы
  • Конденсаторы
  • Диоды
  • Светодиоды
  • Стабилитроны
  • Диодные мосты
  • Транзисторы
    • Биполярные
    • IGBT
    • Полевые | MOSFET
  • Стабилизаторы
  • Предохранители
  • Индуктивность
  • Резонаторы
  • Тиристоры
• Дисплеи и индикаторы
• Макетные платы
  • Паечные
  • Беспаечные
• Провода и шлейфы
• Кабели и переходники
• Адаптеры, разъемы и штекеры
• Микроконтроллеры и микросхемы (IC)
• Программаторы и преобразователи
• Управление и ввод
• Элементы питания
  • Аккумуляторы и батареи
  • Зарядные устройства
  • Отсеки и коннекторы
  • Преобразователи и блоки питания
  • BMS платы
  • Сетевые фильтры
• Измерительные приборы
  • Мультиметры и щупы
  • Тестеры
  • Вольтметры / Амперметры
  • USB-нагрузка
• Всё для пайки
  • Паяльники и паяльные наборы
  • Оборудование для пайки
  • Расходные материалы
  • Изоляторы
• Светодиодная продукция
  • Светодиодные ленты
  • Светодиодные модули
  • Контроллеры
  • Кабели и клипсы
  • Гирлянды
• Инструменты и материалы
  • Инструменты
  • Корпуса и крепления
  • Магниты
  • Расходные материалы
  • Органайзеры и пакеты
  • Кулеры
• Карты памяти и ридеры

Резистор и сопротивление

Теория

КОМПОНЕНТЫ

• Адресуемая светодиодная лента
• Геркон
• Диод
• Зуммер
• Кнопка
• Кварцевый резонатор
• Конденсатор
• Макетная плата
• Резистор
• Реле
• Светодиод
• Светодиодные индикаторы
• Сервопривод
• Транзистор

ARDUINO

• Что такое Arduino?
• Среда разработки Arduino IDE
• Онлайн-сервис TinkerCAD – эмулятор Arduino
• Сравнение плат Arduino. Какую выбрать?
• Как прошить плату Arduino с помощью другой Arduino (ArduinoISP)

RASPBERRY

ИНТЕРФЕЙСЫ ПЕРЕДАЧИ ДАННЫХ

1 кОм = 1000 Ом,
1 МОм = 1000 кОм,
1 ГОм = 1000 МОм

Последовательное соединение резисторов

Это справедливо и для большего количества соединённых последовательно резисторов:

Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее, чем у любого резистора из этой цепи.

При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.

Мощность при последовательном соединении

R = 200 + 100 + 51 + 39 = 390 Ом

Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять

I = U/R = 100 В/390 Ом = 0,256 A

На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле:

P = I 2 x R = 0,256 2 x 390 = 25,55 Вт

Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:

P₁ = I 2 x R₁ = 0,256 2 x 200 = 13,11 Вт;
P₂ = I 2 x R₂ = 0,256 2 x 100 = 6,55 Вт;
P₃ = I 2 x R₃ = 0,256 2 x 51 = 3,34 Вт;
P₄ = I 2 x R₄ = 0,256 2 x 39 = 2,55 Вт.

Если сложить полученные мощности, то общая Р составит:

Р_общ = 13,11 + 6,55 + 3,34 + 2,55 = 25,55 Вт

Параллельное соединение резисторов

Расчет параллельного сопротивления двух параллельно соединённых резисторов R₁ и R₂ производится по следующей формуле:

Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:

Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.

Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.

Мощность при параллельном соединении

1/R = 1/200 + 1/100 + 1/51 + 1/39 ≈ 0,06024 Ом
R = 1 / 0,06024 ≈ 16,6 Ом

Используя значение напряжения 100 В, по закону Ома рассчитывается сила тока

I = U/R = 100 В x 0,06024 Ом = 6,024 A

Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом

P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт

Расчет силы тока для каждого резистора выполняется по формулам:

На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.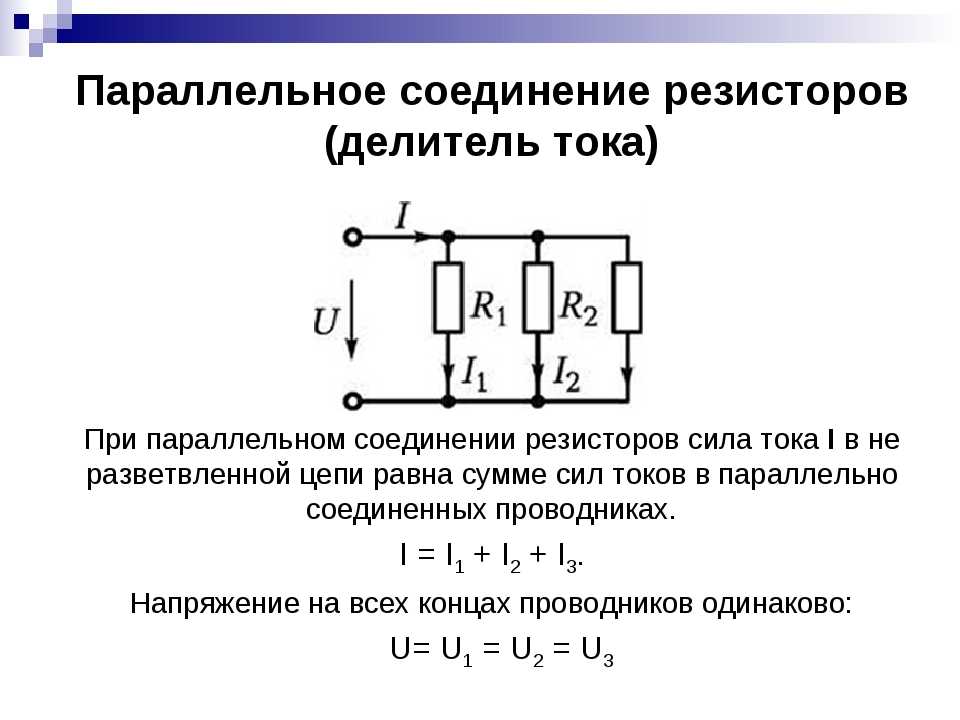

Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов:

P₁ = U 2 /R₁ = 100 2 /200 = 50 Вт;
P₂ = U 2 /R₂ = 100 2 /100 = 100 Вт;
P₃ = U 2 2/R₃ = 100 2 /51 = 195,9 Вт;
P₄ = U 2 2/R₄ = 100 2 /39 = 256,4 Вт

Если сложить полученные мощности, то общая Р составит:

Р_общ = 50 + 100 + 195,9 + 256,4 = 602,3 Вт

Последовательное и параллельное соединение

Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей – проводников.

Для начала давайте вспомним, что такое проводник? Проводник – это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:

ρ – это удельное сопротивление, Ом × м

R – сопротивление проводника, Ом

S – площадь поперечного сечения, м 2

l – длина проводника, м

Более подробно об этом я писал здесь.

Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.

Последовательное соединение проводников

Сопротивление при последовательном соединении проводников

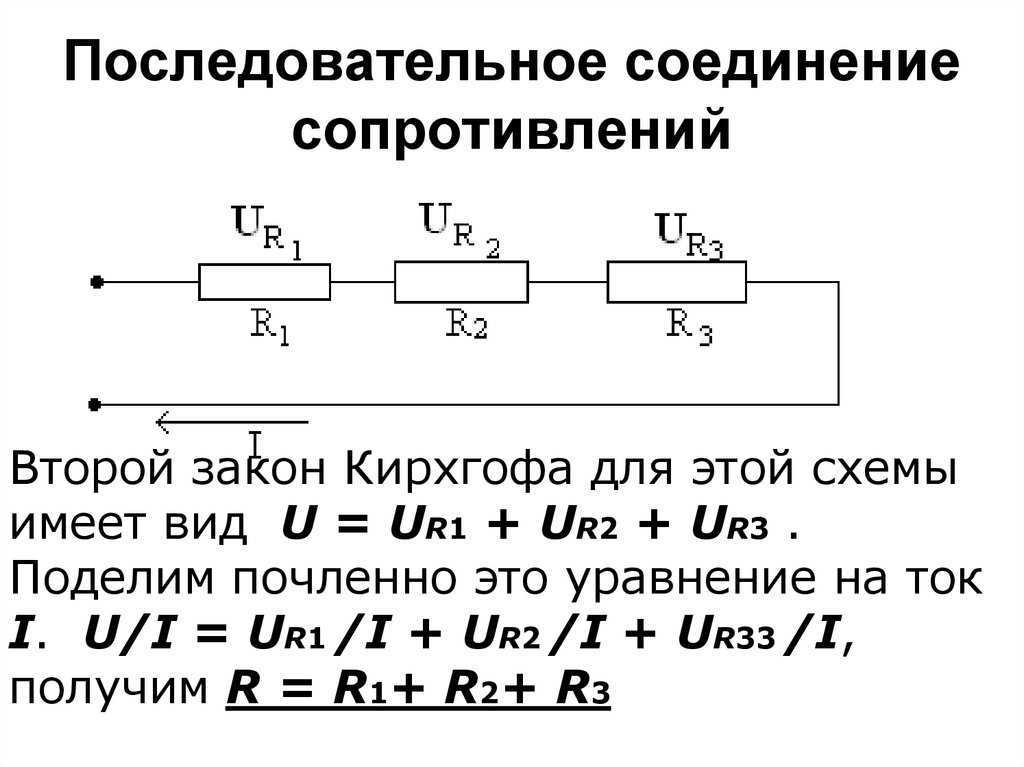
Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

последовательное соединение резисторов

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

формула при последовательном соединении резисторов

Пример

У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.

Решение

То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор R_AB .

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:

Сила тока через последовательное соединение проводников

Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор R_AB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R₁ , R₂ , R₃ , то получится, что через них течет та же самая сила тока, которая текла через резистор R_AB .

сила тока через последовательное соединение проводников

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R₁ течет такая же сила тока, как и через резистор R₂ и такая же сила тока течет через резистор R₃ .

Напряжение при последовательном соединении проводников

Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?

Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.

Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае R_AB =R₁ + R₂ + R₃ = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.

Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения U_R1 , U_R2 , U_R3 . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.

Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.

Мы получили самый простой делитель напряжения.

Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.

Параллельное соединение проводников

Параллельное соединение проводников выглядит вот так.

параллельное соединение резисторов

Ну что, думаю, начнем с сопротивления.

Сопротивление при параллельном соединении проводников

Давайте пометим клеммы как А и В

В этом случае общее сопротивление R_AB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников

Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.

Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников

Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.

Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что

Если бы у нас еще были резисторы, соединенные параллельно, то для них

В этом случае, сила тока в цепи будет равна:

Задача

Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Решение

Воспользуемся формулами, которые приводили выше.

Если бы у нас еще были резисторы, соединенные параллельно, то для них

Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи

2-ой способ найти I

Чтобы найти R_общее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть R_общее = 1,25 Ом.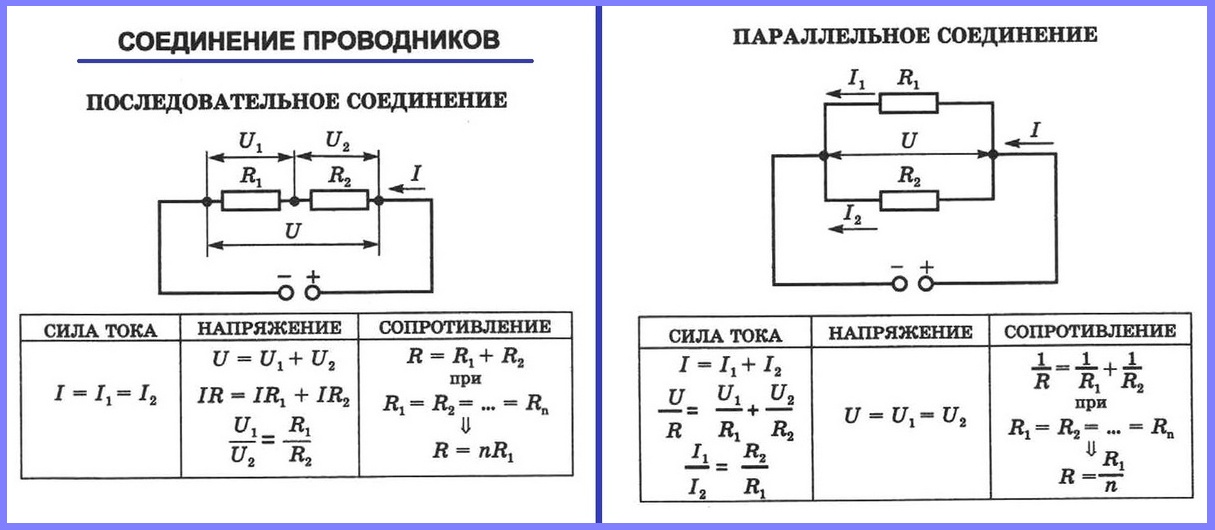

I=U/R_общее = 10/1,25=8 Ампер.

Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.

Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.

Последовательное и параллельное соединение проводников

Проводники в электрических цепях могут соединяться последовательно и параллельно.

При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:

I1 = I2 = I.

Рисунок 1.9.1. Последовательное соединение проводников

По закону Ома, напряжения U₁ и U₂ на проводниках равны

U1 = IR1,   U2 = IR2.

Общее напряжение U на обоих проводниках равно сумме напряжений U₁ и U₂:

U = U1 + U2 = I(R1 + R2) = IR,

где R – электрическое сопротивление всей цепи. Отсюда следует:

R = R1 + R2.

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

При параллельном соединении (рис. 1.9.2) напряжения U₁ и U₂ на обоих проводниках одинаковы:

U1 = U2 = U.

Сумма токов I₁ + I₂, протекающих по обоим проводникам, равна току в неразветвленной цепи:

I = I1 + I2.

Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I₁Δt + I₂Δt. Следовательно, I = I₁ + I₂.

Рисунок 1.9.2. Параллельное соединение проводников

Записывая на основании закона Ома

где R – электрическое сопротивление всей цепи, получим

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Этот результат справедлив для любого числа параллельно включенных проводников.

Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.

Рисунок 1.9.3. Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны в омах (Ом)

Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.

Рисунок 1. 9.4. Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников

Цепи, подобные изображенной на рис. 1.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.

Опубликовано в разделах: Электродинамика, Постоянный электрический ток

Как рассчитать эквивалентное сопротивление (примеры последовательной и параллельной цепи)

В электрических и электронных цепях сопротивление или электрическое сопротивление определяется как величина трения в потоке электрического тока (или электрического заряда), создаваемая материал проводника. Элемент электрической цепи, который используется для введения электрического сопротивления в цепь, называется резистором. Резистор — это пассивный элемент цепи, который управляет протеканием тока через цепь и преобразует дополнительное количество электрической энергии в тепло.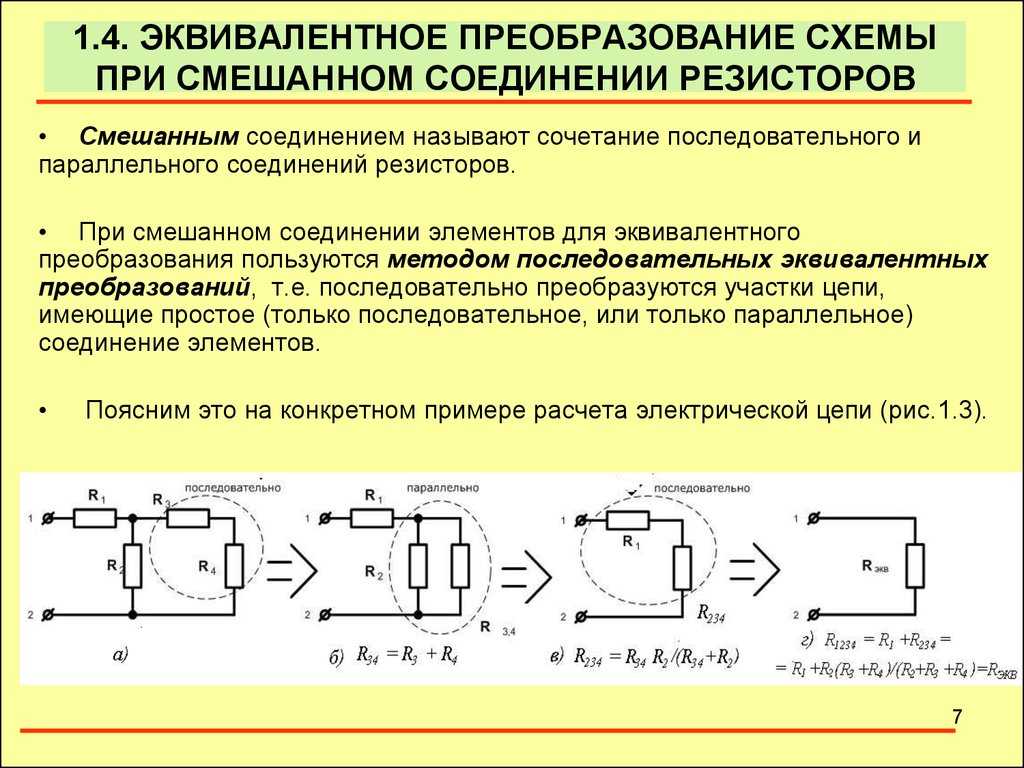

Иногда у нас нет резистора нужного сопротивления, которое требуется в схеме. По этой причине мы соединяем два или более резистора определенным образом, чтобы получить желаемое сопротивление в цепи.

В этом уроке мы поймем, что такое эквивалентное сопротивление , как определить эквивалентное сопротивление резисторов при их последовательном или параллельном или последовательном соединении и параллель . Мы также обсудим численные примеры для каждой из трех комбинаций для лучшее понимание концепции.

Как рассчитать эквивалентное сопротивление последовательно?

Комбинация резисторов, в которой они соединены встык цепным образом, и обеспечивает только один путь для протекания электрического тока, он называется 9соединение серии 0003 резисторы или просто резисторы в серии .

Чтобы понять расчет последовательного эквивалентного сопротивления, рассмотрим N-резистор а именно R ₁ , R ₂ , R ₃ ,… R _N соединены последовательно, как показано на рисунке 1. Пусть полное напряжение на комбинация равна V вольт, а I — общий ток через комбинацию. Следует отметить что ток I общий для всех резисторов.

По закону Ома имеем

$$\mathrm{V_{1}=IR_{1};\: V_{2}=IR_{2};\: \cdot \cdot \cdot V_{N} =IR_{N}}$$

Также

$$\mathrm{V=V_{1}+V_{2}+V_{3}+\cdot \cdot \cdot + V_{N}}$$

$$\mathrm{\Rightarrow V=IR_{1}+IR_{2}+IR_{3}+\cdot \cdot \cdot + IR_{N}}$$

$$\mathrm{\Rightarrow V =I\left ( R_{1}+R_{2}+R_{3}+\cdot \cdot \cdot + R_{N} \right )}$$

Но,

$$\mathrm{\frac {V}{I}=R_{eq}}$$

Следовательно,

$$\mathrm{R_{eq}=R_{1}+R_{2}+R_{3}+\cdot \cdot \cdot +R_{N}}$$

Следовательно, , когда количество резисторов соединенных последовательно, то эквивалентное сопротивление последовательное сочетание сопротивлений может быть просто рассчитано путем сложения всех сопротивлений.

Особый случай — Когда N-резисторы с одинаковым значением сопротивления, например R, соединены последовательно, тогда их эквивалентное сопротивление рассчитывается по формуле,

$$\mathrm{R_{eq}=N\times R}$$

Где N — общее количество резисторов, соединенных последовательно.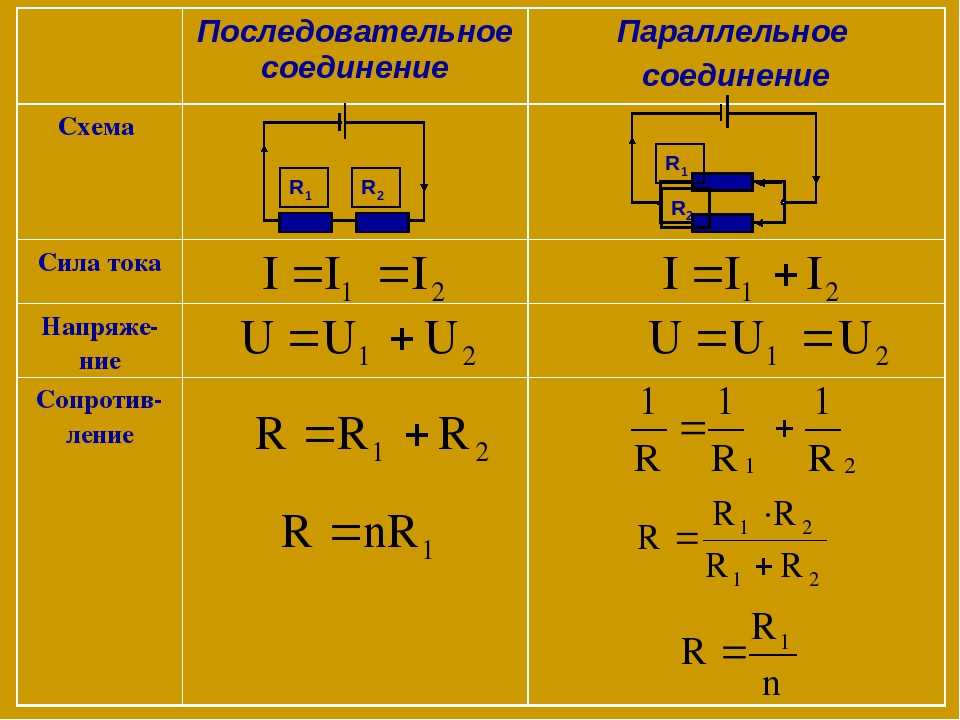

Вот список всех важных моментов, на которые следует обратить внимание при выборе серийной комбинации резисторы −

• Эквивалентное сопротивление последовательного соединения представляет собой просто сумму всех сопротивлений.

• Эквивалентное сопротивление последовательной комбинации резисторов всегда больше, чем наибольшее сопротивление, присутствующее в комбинации.

• Ток через все последовательно соединенные сопротивления одинаков.

• Падение напряжения на каждом сопротивлении различно и зависит от значения сопротивления.

• Резисторы соединены последовательно, чтобы разделить напряжение на несколько меньших значений напряжения.

Как рассчитать эквивалентное сопротивление параллельно?

Комбинация резисторов, в которой один конец всех резисторов соединен с общей точкой а другой конец всех резисторов соединяется с другой общей точкой так, чтобы количество резисторов и число токовых путей равны, это называется параллельная комбинация резисторов .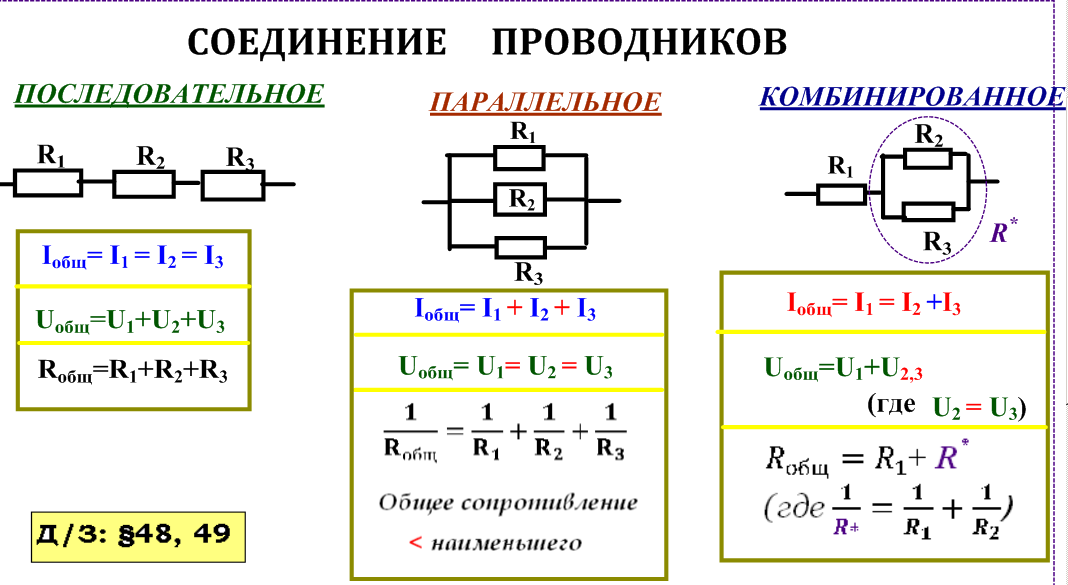

Теперь, чтобы понять процесс расчета эквивалентного сопротивления параллельного комбинация резисторов, рассмотрим N-резисторы, соединенные параллельно, как показано на рисунке 2. Из рисунка-2 видно, что напряжение на всех резисторах одинаковое и равно V вольт, но ток через каждый резистор разный в зависимости от значения сопротивления.

Согласно закону Ома,

$$\mathrm{I_{1}=\frac{V}{R_{1}};\:I_{2}=\frac{V}{R_{2}}; \: I_{3}=\frac{V}{R_{3}};\: \cdot \cdot \cdot I_{N}=\frac{V}{R_{N}} }$$

Кроме того,

$$\mathrm{I=I_{1}+I_{2}+I_{3}+ \cdot \cdot \cdot +I_{N}}$$

$$\mathrm{\ Стрелка вправо I=\frac{V}{R_{1}}+\frac{V}{R_{2}}+\frac{V}{R_{3}}+ \cdot \cdot \cdot +\frac{V }{R_{N}}}$$

$$\mathrm{\Rightarrow I=V\left ( \frac{1}{R_{1}}+\frac{1}{R_{2}}+\ frac {1} {R_ {3}} + \ cdot \ cdot \ cdot + \ frac {1} {R_ {N}} \ right )} $ $

Но,

$ $ \ mathrm {\ frac {I }{V}=\frac{1}{R_{eq}}}$$

Следовательно,

$$\mathrm{\frac{1}{R_{eq}}=\frac{1}{R_{ 1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+ \cdot \cdot \cdot +\frac{1}{R_{N}}}$$

Следовательно, при параллельном соединении нескольких сопротивлений обратная величина эквивалентное сопротивление комбинации равно сумме обратных величин отдельных сопротивления.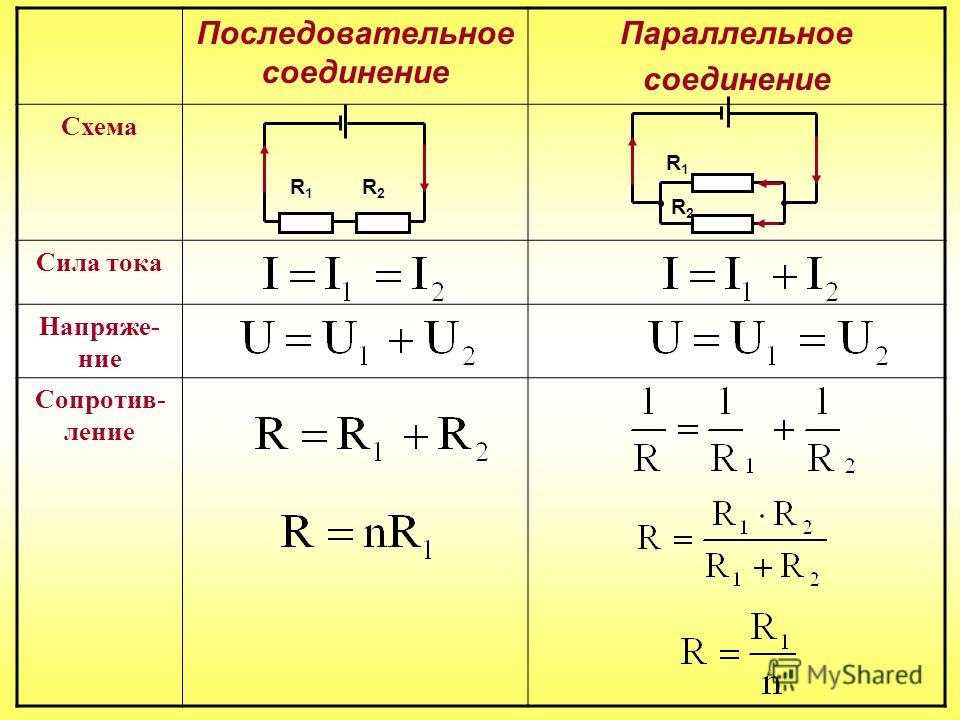

При параллельном соединении только двух резисторов эквивалентное сопротивление равно определяется как,

$ $ \ mathrm {\ frac {1} {R_ {eq}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} = \ frac {R_ {1}+R_{2}}{R_{1}R_{2}}}$$

$$\mathrm{\следовательно, R_{eq}=\frac{R_{1}R_{2}}{R_ {1}+R_{2}}}$$

Следовательно, при параллельном соединении двух резисторов эквивалентное сопротивление комбинация равна произведению, деленному на сумму двух сопротивлений.

Особый случай − Когда все N-резисторы, соединенные параллельно, имеют одинаковое значение сопротивления (скажем, R), тогда эквивалентное сопротивление комбинации определяется как

$$\mathrm{ R_{eq}=\frac{R}{N}}$$

Ниже приведены важные моменты, касающиеся параллели. комбинация резисторов −

• Эквивалентное сопротивление параллельной комбинации резисторов меньше наименьшего сопротивления в комбинации.

• Ток через каждое сопротивление разный.

• Напряжение на всех сопротивлениях одинаковое.

• Параллельная комбинация резисторов действует как делитель тока, поскольку она делит один электрический ток на несколько токов.

Эквивалентное сопротивление последовательно-параллельной комбинации резисторов

Иногда мы имеем дело с такими электрическими цепями, в которых несколько резисторов соединены последовательно. и некоторые другие параллельно. Такая комбинация резисторов обычно называется последовательно-параллельная комбинация резисторов . На рис. 3 показана сеть резисторов, которая с резисторами, соединенными последовательно-параллельно.

Эквивалентное сопротивление последовательно-параллельной комбинации резисторов рассчитывается в следующие два шага —

Шаг 1

Рассчитайте эквивалентное сопротивление всех параллельно соединенных резисторов. Для приведенного примера у нас есть,

$$\mathrm{ R_{cd}=\frac{R_{2}R_{3}}{R_{2}+R_{3}}}$$

Шаг 2

Вычислить эквивалент сопротивления последовательно соединенных резисторов. Таким образом, для данного Например, у нас есть

$$\mathrm{ R_{eq}=R_{1}+R_{cd}+R_{4}}$$

Или

$$\mathrm{ R_{eq}=R_ {1}+\влево ( \frac{R_{2}R_{3}}{R_{2}+R_{3}} \right )+R_{4}}$$

Числовой пример (1)

Рассчитайте эквивалентное сопротивление следующей резистивной цепи −

Решение

Как видно, в данной цепи резисторы соединены последовательно. Таким образом, их эквивалентное сопротивление будет равно

$$\mathrm{ R_{eq}=10 + 20 + 10 + 20 + 10}$$

$$\mathrm{ R_{eq}=70\: \Omega }$$

Числовой пример (2)

Рассчитайте эквивалентное сопротивление следующей резистивной цепи −

Решение

При осмотре видно, что резисторы сети расположены параллельно. Таким образом эквивалентное сопротивление комбинации будет,

$$\mathrm{\frac{1}{R_{eq}} =\frac{1}{10}+\frac{1}{20}+\frac{1} {20} }$$

$$\mathrm{\frac{1}{R_{eq}} =\frac{2 + 1 + 1}{20}+=\frac{4}{20}}$$

$$\mathrm{\следовательно, R_{eq} =5 \: \Omega } $$

Численный пример (3)

Рассчитайте эквивалентное сопротивление следующей резистивной сети.

Решение

Как мы видим, в сети есть несколько резисторов, соединенных последовательно, и несколько резисторов, соединенных параллельно.

Эквивалентное сопротивление параллельных сопротивлений 10 Ом и 20 Ом составляет {\Rightarrow R_{cd} =\frac{ 200}{30}=6,67\, \Omega }$$

Теперь все резисторы соединены последовательно. Таким образом, эквивалентное сопротивление сети есть,

$$\mathrm{ R_{eq} =5 + 6,67 + 5=16,67\, \Omega } $$

Заключение

В этом уроке мы обсудили, что набор резисторов можно комбинировать тремя способами — последовательно, параллельные и последовательно-параллельные. При последовательном соединении эквивалентное сопротивление комбинация равна сумме всех сопротивлений. При параллельном соединении взаимное эквивалентного сопротивления комбинации равно обратному значению отдельных сопротивления.

Сопротивления объединяются последовательно и параллельно в соответствии с требованиями схемы или для ввести нужное значение сопротивления в цепи, когда нет одиночного сопротивления доступным для этого конкретного значения сопротивления.

Как найти последовательное сопротивление: подробная информация —

Каушики Банерджи

В этой статье мы изучим методы, как найти последовательное сопротивление. Расчет эквивалентного сопротивления в последовательной цепи относительно прост и не требует сложной математики.

Предположим, у нас есть два резистора, R ₁ и R ₂ , как показано на рисунке 1. Мы знаем, что ток остается одним и тем же в каждой точке последовательной цепи, а потенциал падает на каждом резисторе.

Следовательно, V ₁ = iR ₁ и V ₂ = iR ₂ .

Суммарное напряжение в цепи V= V ₁ + V ₂ = iR ₁ + iR ₂ .

If R is the equivalent resistance, then V= iR

So,iR= iR ₁ + iR ₂ and R= R ₁ + R ₂ .

Как найти последовательное сопротивление – часто задаваемые вопросы

Каковы характеристики последовательного сопротивления?

Последовательные сопротивления имеют довольно много особенностей в цепи, из которых наиболее важным является то, что эквивалентное сопротивление представляет собой простое сложение всех резисторов, соединенных посредством последовательного соединения.

Прочие характеристики последовательного сопротивления:

1. Ток, проходящий через каждый последовательно соединенный резистор, одинаков.
2. Падение напряжения на последовательном резисторе зависит от номинала этого резистора и равно значению тока × сопротивления.
3. Эквивалентное последовательное сопротивление всегда больше, чем сопротивление отдельных элементов.

«Два последовательно соединенных резистора» компании Puregin лицензируется в соответствии с CC BY-SA 3. 0

Как последовательное сопротивление влияет на ток?

В отличие от параллельных сопротивлений ток остается неизменным, когда он проходит через последовательные резисторы. Это отношение напряжения источника и эквивалентного сопротивления, т. е. сумма сопротивлений.

Для протекания тока в цепи требуется некоторое сопротивление в цепи. Ток на каждом резисторе, соединенном последовательно, одинаков. Так как при последовательном соединении ответвление отсутствует, то и ток не разделяется. Следовательно, мы получаем везде одинаковый ток в цепи, который является полным током.

Подробнее….Как рассчитать напряжение в последовательной цепи: подробные факты

Как найти последовательное сопротивление – часто задаваемые вопросы

Каково падение напряжения в последовательной цепи?

Из закона Ома мы понимаем падение напряжения в последовательной цепи. Это падение напряжения при прохождении тока через проводник, измеряемое между двумя конечными точками, лежащими вдоль проводника.

Для любого резистора, подключенного последовательно, падение напряжения линейно зависит от значения сопротивления. Падение напряжения между двумя сторонами резистора = сопротивление резистора × ток, протекающий через последовательную цепь. Чем больше сопротивление, тем больше величина падения напряжения.

Подробнее… Как рассчитать падение напряжения в последовательной цепи: подробные факты

В любой цепи сопротивление контролирует и ограничивает ток. Дисбаланс сопротивления может вызвать обрыв цепи (если сопротивление очень мало) или короткое замыкание (если сопротивление очень велико), что приведет к повреждению.

Резисторы в последовательной цепи часто называют «ограничителями тока», поскольку они ограничивают протекание тока. Например, в светоизлучающем диоде (LED) мы ограничиваем ток, проходящий через светодиод, чтобы защитить его от перегрева. Последовательный резистор ограничивает ток, чтобы светодиод мог взорваться без повреждений.

Читайте также… Постоянно ли напряжение в последовательном соединении: полная информация и ответы на часто задаваемые вопросы

Как найти последовательное сопротивление – числовые задачи

A. Вычислите следующие значения для схемы, показанной на рисунке

1.Equivalent 1.Equivalent последовательное сопротивление

2. Ток через каждый резистор

3. Падение напряжения на каждом резисторе

В схеме мы видим три последовательно соединенных резистора. Поэтому эквивалентное последовательное сопротивление = R ₁ + R ₂ + R ₃ = 2+3+5 = 10 Ом.

Мы знаем, что общий ток i = напряжение источника/эквивалентное сопротивление = 25/10 = 2,5 А

Теперь падение напряжения на любом последовательном резисторе = общий ток в последовательной цепи * сопротивление этого резистора.

Следовательно, падение напряжения на резисторе 2 Ом = 2,5 * 2 = 5 В

Падение напряжения на резисторе 3 Ом = 2,5 * 3 = 7,5 В

Падение напряжения на резисторе 5 Ом = 2,5 * 5 = 12,5 В.