Расчет сопротивления резисторов при параллельном соединении. Параллельное и смешанное соединение резисторов: расчет сопротивления в электрических цепях

Как рассчитать общее сопротивление при параллельном соединении резисторов. Какие формулы используются для смешанного соединения резисторов. Чем отличается параллельное соединение от последовательного. Какие основные правила нужно знать при расчете параллельных цепей.

Основные виды соединения резисторов в электрических цепях

В электротехнике выделяют три основных способа соединения резисторов в цепях:

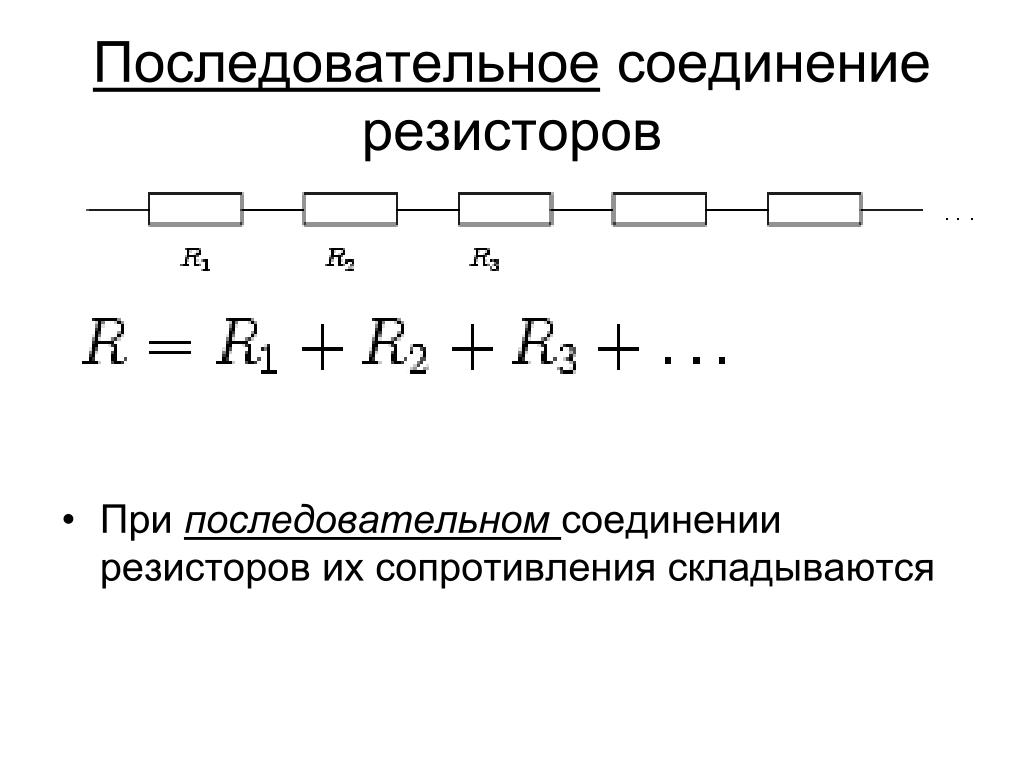
• Последовательное соединение
• Параллельное соединение
• Смешанное (комбинированное) соединение

Каждый из этих типов соединений имеет свои особенности и формулы для расчета общего сопротивления цепи. Рассмотрим их подробнее.

Параллельное соединение резисторов: принцип и формулы расчета

При параллельном соединении начала всех резисторов подключены к одной точке цепи, а концы — к другой. Ток в такой цепи распределяется по нескольким путям. Каковы основные характеристики параллельного соединения?

• Напряжение на всех резисторах одинаково и равно напряжению источника
• Общий ток цепи равен сумме токов через каждый резистор
• Общее сопротивление всегда меньше сопротивления любого из параллельно включенных резисторов

Для расчета общего сопротивления при параллельном соединении используется следующая формула:

1/R общее = 1/R1 + 1/R2 + … + 1/Rn

Где R общее — общее сопротивление цепи, R1, R2, Rn — сопротивления отдельных резисторов.

Для двух параллельно соединенных резисторов можно использовать упрощенную формулу:

R общее = (R1 * R2) / (R1 + R2)

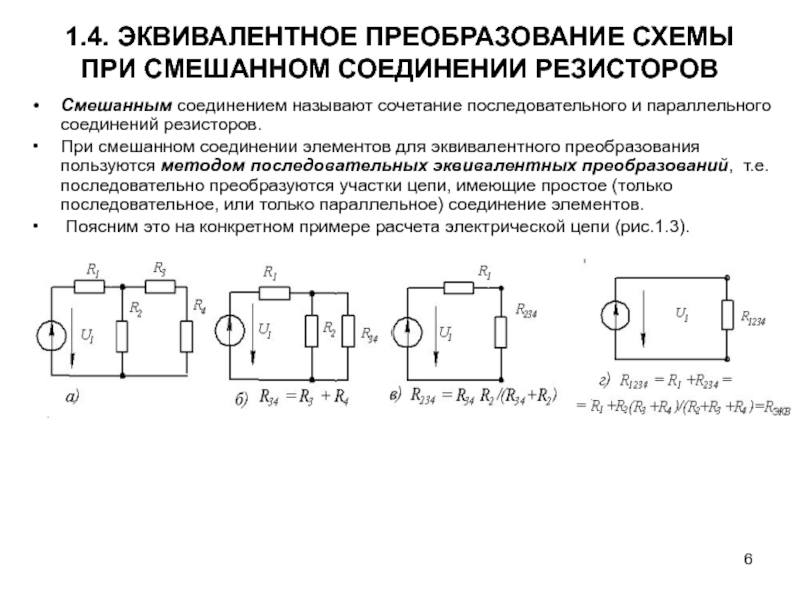
Смешанное соединение резисторов: особенности расчета

В реальных электрических схемах часто встречается смешанное (комбинированное) соединение, сочетающее последовательные и параллельные участки. Как рассчитать общее сопротивление в таком случае?

1. Разбить схему на участки с одинаковым типом соединения
2. Рассчитать эквивалентное сопротивление для каждого участка
3. Объединить полученные значения, используя формулы для последовательного или параллельного соединения

Пример: есть схема с тремя последовательно соединенными резисторами, к которым параллельно подключен четвертый резистор. Алгоритм расчета:

1. Найти сумму сопротивлений трех последовательных резисторов
2. Рассчитать общее сопротивление параллельного участка
3. Получить итоговое значение

Сравнение параллельного и последовательного соединения резисторов

Чем отличается параллельное соединение от последовательного? Основные различия:

Параметр	Последовательное соединение	Параллельное соединение
Общее сопротивление	Сумма сопротивлений всех резисторов	Меньше сопротивления любого из резисторов
Ток	Одинаковый во всех резисторах	Разный, зависит от сопротивления каждого резистора
Напряжение	Сумма напряжений на резисторах равна общему напряжению	Одинаковое на всех резисторах

Правила расчета параллельных цепей

При работе с параллельными цепями следует помнить несколько важных правил:

1. Напряжение на всех параллельных ветвях одинаково
2. Общий ток равен сумме токов в отдельных ветвях
3. Общее сопротивление всегда меньше наименьшего из параллельных сопротивлений
4. Если одно из параллельных сопротивлений в 10 и более раз больше другого, им можно пренебречь

Применение параллельного соединения резисторов на практике

Где используется параллельное соединение резисторов? Основные области применения:

• Регулировка яркости светодиодов
• Создание делителей тока
• Увеличение мощности нагрузки
• Получение дробных номиналов сопротивлений
• Схемы защиты от перенапряжения

Понимание принципов параллельного соединения позволяет грамотно проектировать и анализировать электрические цепи в различных устройствах.

Методы расчета сопротивления при параллельном соединении

Существует несколько способов вычисления общего сопротивления параллельно соединенных резисторов:

1. Метод обратных величин

Это основной метод, использующий формулу 1/R общее = 1/R1 + 1/R2 + … + 1/Rn. Удобен при любом количестве резисторов, но требует вычисления обратных значений.

2. Метод произведения и суммы

Для двух резисторов: R общее = (R1 * R2) / (R1 + R2). Простой способ, не требующий вычисления обратных величин.

3. Метод равных сопротивлений

Если все параллельные резисторы имеют одинаковое сопротивление R, то общее сопротивление R общее = R / n, где n — количество резисторов.

4. Метод проводимостей

Основан на понятии проводимости G = 1/R. Общая проводимость равна сумме проводимостей отдельных резисторов.

Решение задач на параллельное соединение резисторов

Рассмотрим несколько типовых задач для закрепления материала:

Задача 1

Три резистора с сопротивлениями 10 Ом, 20 Ом и 30 Ом соединены параллельно. Найти общее сопротивление цепи.

Решение:

1. Используем формулу 1/R общее = 1/R1 + 1/R2 + 1/R3
2. Подставляем значения: 1/R общее = 1/10 + 1/20 + 1/30
3. Приводим к общему знаменателю: 1/R общее = 6/60 + 3/60 + 2/60 = 11/60
4. Находим R общее: R общее = 60/11 ≈ 5.45 Ом

Задача 2

К источнику напряжения 12 В параллельно подключены два резистора 100 Ом и 200 Ом. Определить токи в ветвях и общий ток цепи.

Решение:

1. Находим токи в ветвях по закону Ома: I1 = U/R1 = 12/100 = 0.12 А I2 = U/R2 = 12/200 = 0.06 А
2. Общий ток равен сумме токов в ветвях: I общий = I1 + I2 = 0.12 + 0.06 = 0.18 А

Ошибки при расчете параллельных цепей

При работе с параллельными соединениями резисторов часто допускаются следующие ошибки:

• Суммирование сопротивлений как при последовательном соединении
• Забывание о том, что общее сопротивление всегда меньше наименьшего из параллельных
• Неправильное применение закона Ома для расчета токов в ветвях
• Игнорирование правила о пренебрежении большими сопротивлениями

Чтобы избежать этих ошибок, важно четко понимать принципы параллельного соединения и внимательно применять соответствующие формулы.

Последовательное и параллельное соединение резисторов

Последовательное и параллельное соединение резисторов в схемах являются самыми распространенными, также – это база для расчета более сложных схем.

Последовательное подключение

Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше.

Рис. Последовательное подключение.

Обозначение:

Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим. Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях – складываем, в параллельных – это обратно пропорциональная величина.

Параллельное соединение

Рис. Параллельное подключение.

Данный вид подключения характерен тем, что все элементы цепи соединяется выводами в одной точке друг другу, т.е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах – //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток. Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле.
Более наглядно это можно представить в виде формул:
1. Каждый вид соединения находится под одинаковым напряжением:
U = U1 = U2;
2. Суммарная сила тока равняется суммарному значению тока каждого участка
I = I1 + I2;
3. Сопротивление цепи равно сумме величина обратных сопротивлению участка:
1/R = 1/R1 + 17R2 + . . . + 1/Rn;
4. Сила тока пропорциональна сопротивлению каждого участка
I1/I2=R2/R1.
Далее рассмотрим схему как работает не только последовательное параллельное, но и смешанное соединение резисторов.

Смешанное подключение

Рис. Смешанное подключение резисторов

В электрических схемах используются не только типовые схемы, но и смешанное, созданное из критерий определенных требований. Чаще всего в схемах встречается третий вариант, представляющий набор из элементарных типов схем. В смешанных участках учитываются не только элементы, но и направления движения тока.
При вычислении мощности резисторов смешанного подключения используются формулы для параллельного и последовательного соединения резисторов, формула также является составной.

Основные законы электротехники, наиболее часто используемые для расчетов

Рассмотрим основные законы электротехники и свойства последовательного и параллельного соединения резисторов для участка цепи

Закон Ома

Напряжение находится по закону Ома по формуле I=U/R – чем больше сопротивление, тем меньше ток. Напряжение можно найти из этой же формулы. U=R*I, ток умножается на сопротивление. Запишем эту формулу для каждого участка U1=R1· I1, Un=Rn · In.

Законы Кирхгофа

Первый закон

Ещё один очень важный закон — это закон Кирхгофа. Для участка цепи постоянного тока их два.

Рис. иллюстрация к пояснению действия первого закона Кирхгофа.

Первый закон имеет формулировку: Сумма всех токов, входящих в узел и выходящих из него равна нулю.
Если посмотреть на схему, I1 – это ток, который заходит в узел, I2 и I3 – это электроны, которые вытекают из него.
Применяя формулировку первого закона можно записать формулу по-другому:
I1-I2+I3=0. В этой формуле знаки плюс имеют значения, которые прибывают в узел, минус, который отходит от него.

Второй закон Кирхгофа.

Рис. иллюстрация к пояснению действия второго закона Кирхгофа.

Если к цепи с включенными сопротивлениями подключен один источник ЭДС (батарея питания) тогда всё понятно, можно обойтись законом Ома. А, если, источников несколько и схема с различным схемным расположением элементов, тогда вступает в силу второй закон, который гласит: сумма токов всех источников питания для замкнутого контура, равна сумме падений напряжения на всех сопротивлениях участка в этом контуре.
E1- Е2 = – UR1 – UR2 или E1 = Е2 – UR1 – UR2.

Параллельное и последовательное соединение резисторов,  решение задач

Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно.

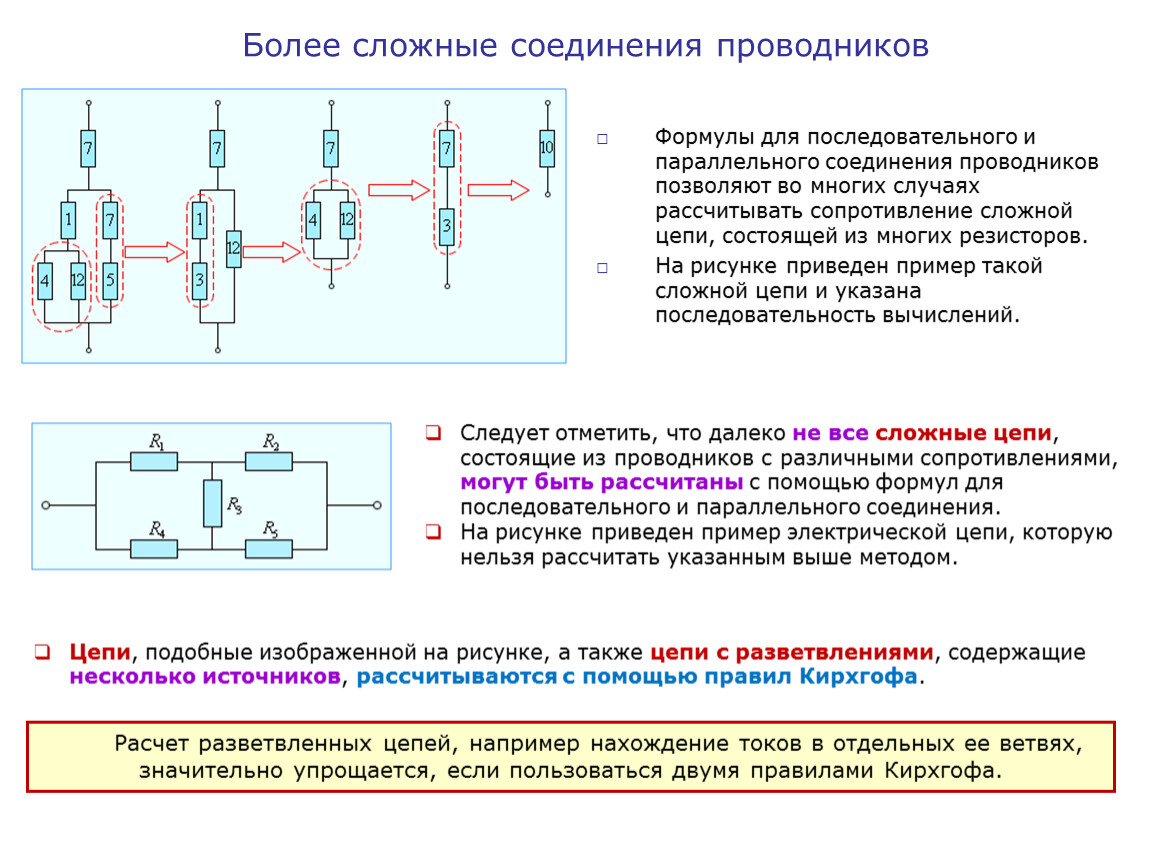
Рис. Порядок замещения при расчете сложных позиций более простыми.

Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. Рассмотрим схему №1 на рис.
На схеме присутствует параллельная и последовательная часть соединения элементов. Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1). Как же правильно определить параллельное и последовательное соединение резисторов?

Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.

Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом.
Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше (рис 3).

Теперь образовалась ситуация – включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом. Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех.

Заменяем эти сопротивление одним эквивалентным R23465. В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом.
Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.

Схема с подключением сопротивлений «треугольником»

Рис. Расчетная схема соединения резисторов в треугольник.

Иногда некоторые затруднения возникают при разборе схемы соединения в треугольник.

Рассмотрим на примере рисунка расчет резисторов по этому подключению.
Из схемы видно, что R1 и R2 соединены последовательно Rэ12 будет соединяться R3 последовательно.

Затем Rэ123 соединяется с сопротивлением R4, R5 в последовательную цепь. Затем все это объединяется с Rэ в //.

Проведем несложные вычисления учитывая, что
R1, R2, R4, R5 равняется 1 Ом. R3, R7 – 2 Ом.
RЭ1,2 = R1+R2 = 1+1=2 Ом.

Вычисляем параллельное подключение: Rэ 12 с R3. Rэ1,3 = (Rэ12*R3) /(Rэ12+R3) = (2*2) /(2+2) = 1Ом.

Далее мы видим последовательное: RЭ123 + R4 + R5 = 1+1+1 = 3 Ом.
И последнее – Rэ123 4 5 с R6 – параллельное.

Общее сопротивление цепи Rц = Rоб = (RЭ1,2,3,4,5 *R6) /(RЭ1,2,3,4,5+R6) = (3 * 2) / (3+2) = 1,2 Ом. Как видно, что расчет подобного варианта также не сложный.

Расчет последовательного и параллельного подключения резисторов онлайн

Подсчитать значение мощность и сопротивлений подставляя их в формулы можно только в учебных целях, или, когда объемы не очень большие. Наиболее практичный вариант расчета является онлайн калькуляторы, которые расположены на многочисленных интернет ресурсах. Для расчёта любой сложности нужно правильно определить тип соединения резисторов последовательное или параллельное и внести данные для расчета в поля калькулятора.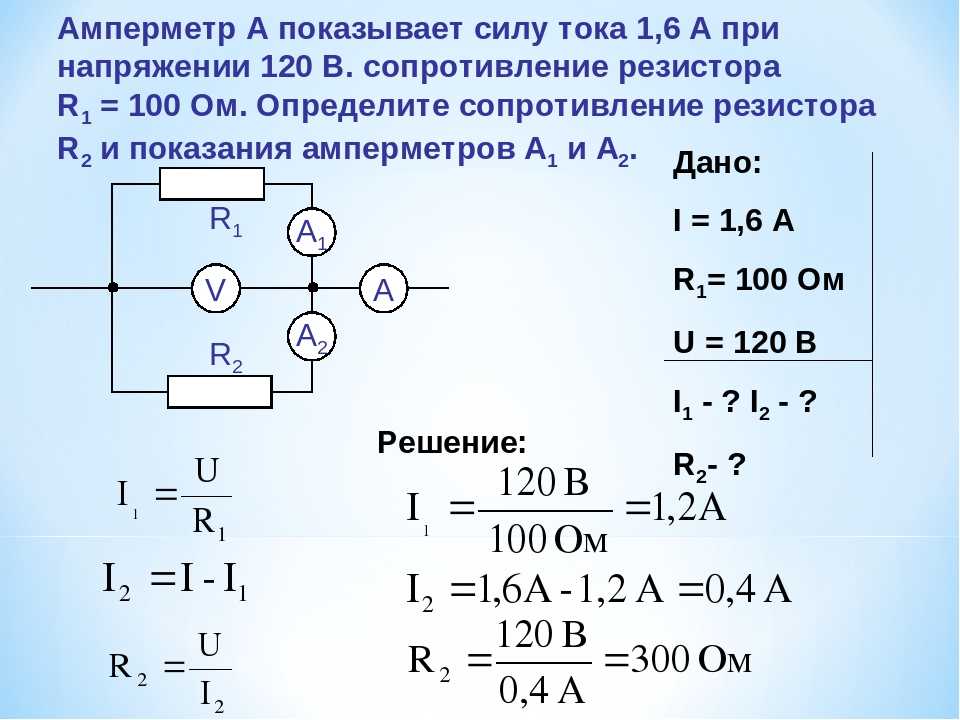

Также такая форма расчета подойдет и для проверки результатов решения учебных задач.

Последовательное и параллельное соединение резисторов и конденсаторов

Электрические цепи состоят не только из резисторов, в них применяется большое количество различных деталей, например, конденсатор, которые подключаются в последовательное, // и смешанное соединение.

Рис. Замещения последовательно включенных элементов.

Определение этому элементу можно дать следующее: Конденсатор – это совокупность проводящих тел служащий для накопления электрического заряда.
Элементарный конденсатор имеет две пластины, форма этих пластин может быть различной: сферической, круглой, цилиндрической, прямоугольной – по форме пластин разделяется и тип конденсатора.

Важное свойство. Одно из важных свойств конденсатора: если заряжается одна пластина конденсатора, то благодаря явлению электростатической индукции заряжается и вторая половина, но с противоположным знаком.

Устройство конденсатора

Плоский конденсатор состоит из двух плоских пластин отстоящих друг от друга на маленькое расстояние. У конденсатора к двум пластинам припаивается вывод всего их получается два.

Типовые схемы подключения конденсаторов

Рассмотрим различные виды подключения конденсатора.

Последовательное

Первый вид — это последовательное соединение.
Предположим, что емкость этих конденсаторов будут равны. Тогда заряды также будут равны: q1=q2=q3, как и в примере с резисторами,  сложный тип позиций с конденсатором можно упростить, заменив несколько элементов одним. У элементов соединенных друг за другом, общая емкость будет обратно пропорциональная всем имеющимся элементам. То есть: Rэк будет равняться 1/С1 + 1/С2 +…. 1/Сn/
Напряжение складывается,  U эк = U1 + U2+ … Un.

Параллельное

Второй тип подключения конденсаторов – это соединение в паралель

Рис. Схема замещения элементов, включенных в параллель.

Соответственно эти конденсаторов обозначены C1, C2, … Cn заряды: Q1, Q2, … Qn и напряжение: U1, U2, … Un.

У элементов в // емкость складывается Сэ = C1 + C2 + … C n.
Напряжение Un на каждом конденсаторе будет равно напряжению на эквивалентном
Uэ = U1 = U2 =… = Un – это особенность параллельного подсоединения всех элементов цепи.

Емкость будет складываться из суммы отдельных элементов Сэ =С1 + С2 + … Сп.

Рис. Расчетные позиции элементов при различном включении.

Простая позиция, которая не требует преобразования №1 – последовательное подключение. По известной формуле для этих поз. запишем 1/Сэ = 1/С1 +1/С2 +1/С3,  подставив формулу значения, которые даны в условии задачи, получим 1/Сэ = 1/С1 +1/С2 +1/С3 = 59 мФ.

Не требует преобразования и 2 схема: емкость общего конденсатора будет равняться сумме конденсаторов которые включены в параллельной цепи: Сэ =С1 +С2 +С3
Сэ = 100 + 200 + 500 = 800 мФ.

Рассмотрев рис. №3 видно, что пара конденсаторов включена параллельно и один последовательно. Алгоритм преобразования таких цепей мы уже рассматривали, поэтому: сразу же находим емкость конденсатора Сэ соединения: Сэ = С1+С2 = 200+500 = 700 мФ.

Теперь находим общие эквивалентную емкость элементов с последовательным подключением 1/Сэ = 1/С2,3 +1/ С1 = 89 мф.
Практическая задача решена.

Внимание покупателей подшипников Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению  подшипников и комплектующих на почту или звоните сейчас:      +7(499)403 39 91          [email protected]       Доставка подшипников  по РФ  и зарубежью.   Каталог подшипников на сайте themechanic.ru

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
+74951086120
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте

themechanic.ru

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
+74951086120
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте

themechanic.ru

Параллельное и смешанное соединение резисторов: разные способы подключения сопротивления

Ни одна операция в электронике или электротехнике не обходится без вычисления сопротивления.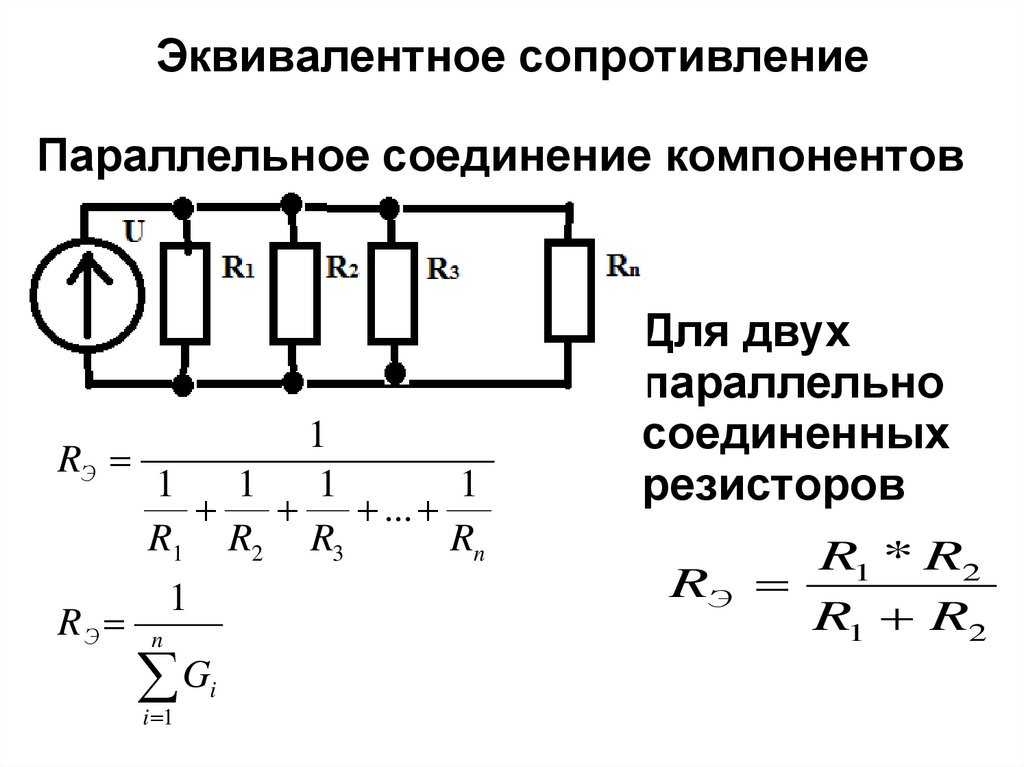 В этом случае рассматривают только тот участок цепи, в котором находится смешанное соединение резисторов. Инженерам и физикам необходимо понимать то, как именно происходят расчёты в таких схемах. Всего разделяют несколько видов подключения, которые используются в цепях различной сложности.

• Последовательное соединение
• Параллельное подключение
• Смешанный вариант

Последовательное соединение

Выделяют такие способы соединения резисторов: последовательное, параллельное и комбинированное. При последовательном подключении конец первого резистора подключают к началу второго, его часть к третьему. Так действуют со всеми составляющими. То есть все компоненты цепи следуют друг за другом. Через них в таком подключении будет проходить один общий электрический ток. Для таких схем физики применяют формулу, в которой между точками А и В есть только один путь протекания заряженных электронов.

От количества подключённых резисторов зависит сопротивление протекающему электричеству. Чем больше составляющих, тем оно выше. Его рассчитывают по формуле: R общее = R1+R2+…+Rn, где:

• R общее — это сумма всех сопротивлений;
• R1 — первый резистор;
• R2 — второй компонент;
• Rn — последняя составляющая в цепи.

Параллельное подключение

Параллельное соединение подразумевает подключение начал резисторов к одной точке, а концов к другой. Сами компоненты при этом расположены на одинаковом расстоянии друг от друга, а их количество не ограничено. По каждой составляющей электричество протекает отдельно, выбирая один из нескольких путей.

Из-за того, что в цепи находится несколько компонентов и путей прохода тока, сопротивление значительно меньше, чем при последовательном соединении. То есть общая сумма противодействия уменьшается пропорционально увеличению количества составляющих. Формула для определения общей суммы противостояния электричеству: 1/R общее = 1/R1+1/R2+…+1/Rn.

В расчётах общее сопротивление всегда должно быть меньше любого из составляющих цепи. Способ вычисления суммы противостояния для схемы из двух резисторов немного отличается: 1/R общее = (R1 х R2)/(R1+R2). Если в системе у компонентов одинаковые показатели сопротивления, то общее число будет равно половине одного из составляющих.

Смешанный вариант

В смешанном соединении сопротивлений комбинируют последовательную и параллельную схему подключений. В этом случае несколько компонентов соединяют одним способом, а другие — вторым, но все они включены в одну цепь. В физике такой метод соединения называют последовательно-параллельным.

Для вычисления суммы противостояния электричеству схему нужно разбить на мелкие участки, в которых резисторы подключены одинаковым способом. Затем расчёты проводят по алгоритму:

• в цепи с параллельно соединёнными компонентами высчитывают эквивалентное сопротивление;
• после этого высчитывают противостояние на последовательно подключённых участках схемы;
• наглядную иллюстрацию нужно перерисовать, обычно получается цепь с последовательным соединением резисторов;
• рассчитывают сопротивление в новой схеме по одной из двух формул.

Лучше понять методы вычислений поможет пример. Если в схеме всего пять компонентов, они могут располагаться по-разному. Начало первого резистора подключено к точке А, конец — к В. От неё идёт отдельная схема с комбинированным соединением. Вторая и третья составляющие находятся на последовательной линии, четвёртый компонент параллелен им. От конечной точки этой цепи — Г — исходит последний резистор.

Сначала высчитывают сумму сопротивления последовательного участка внутренней схемы: R2+R3. После этого цепь перерисовывают так, чтобы второй и третий компоненты были соединены в один. В результате внутренняя цепь имеет параллельное подключение. Теперь высчитывают её противостояние: (R2,3xR4)/(R2,3+R4). Можно второй раз изобразить полученную цепь.

В схеме будет три резистора, соединённые последовательным методов. Причём средний включает параметры второго, третьего и четвёртого компонента.

Теперь можно узнать общую сумму сопротивлений. Для этого складывают показатели противостояний электричеству первого, пятого и остальных составляющих. Формула будет иметь вид: R1+(R2,3xR4)/(R2,3+R4)+R5. Можно сразу подставить в неё все параметры компонентов.

На практике последовательный и параллельный метод соединения используются редко, ведь в приборах схемы обычно сложные. Поэтому в цепях резисторы часто соединены комбинированным способом. Сопротивление в таких случаях высчитывают пошагово.

Если сразу выводить числа в общую формулу, то можно ошибиться и получить неверные результаты. А это может отрицательно сказаться на работе электрического прибора.

Resistors in Parallel Formula — GeeksforGeeks

Параллельное подключение резисторов определяется как цепь, в которой два или более резистора соединены параллельно друг с другом так, что обе клеммы одного резистора соединены с каждой клеммой другого резистора или резисторов. Параллельная цепь также известна как делитель тока, поскольку ток цепи в параллельной сети резисторов может проходить более чем по одному каналу, поскольку для него существует несколько путей. В результате ток не одинаков во всех ветвях параллельной сети. С другой стороны, падение напряжения на всех резисторах в параллельной резистивной сети является постоянным.

 

Формула

Общее сопротивление параллельной цепи оценивается путем расчета эквивалентного сопротивления цепи. Его формула гласит, что обратная величина эквивалентного сопротивления равна сумме обратных величин отдельных сопротивлений, соединенных параллельно. Эквивалентное сопротивление обозначается символом R _eq . Его единицей измерения СИ является ом (Ом), а размерная формула определяется как [M ¹ L ² А ^-2 Т ^-3 ].

1/ _Треб. = 1/R ₁ + 1/R ₂ + 1/R ₃ + …. . + 1/R _n

где,

Р _eq — эквивалентное сопротивление,

R ₁ — сопротивление первого резистора,

R ₂ — сопротивление второго резистора,

R ₃ — сопротивление третьего резистора, и так на.

Вывод

Предположим, у нас есть цепь напряжения V и тока I. Резисторы R ₁ , R ₂ и R ₃ подключены параллельно цепи.

Известно, что в параллельной цепи ток делится на количество частей, равное количеству резисторов.

Пусть I ₁ , I ₂ и I ₃ будут значениями, на которые делится ток I. Мы знаем,

I = I ₁ + I ₂ + I ₃

Разделив обе части на V, получим,

I/V = I ₁ /V + I _{2 90 012 /В + Я 3 /V}

1/(V/I) = 1/(V/I ₁ ) + 1/(V/I ₂ ) + 1/(V/I ₃ )

По Ому закон, V = IR. Итак, приведенное выше уравнение принимает вид:

1/R _eq = 1/R ₁ + 1/R ₂ + 1/R ₃

Отсюда выводится формула для эквивалентного сопротивления в параллельной цепи.

Примеры задач

Задача 1. Вычислить эквивалентное сопротивление, если три сопротивления 5 Ом, 2 Ом и 7 Ом соединены параллельно.

Решение:

Имеем,

R ₁ = 5 Ом

R ₂ = 2 Ом 9000 3

R ₃ = 7 Ом

Используя формулу получаем,

1/R _экв. = 1/R ₁ + 1/R ₂ + 1/R ₃

1/R _экв. = 1/5 + 1/2 + 1/7

1/R _экв. = 1/1,2

R _экв. = 1,2 Ом

Задача 2. Вычислить эквивалентное сопротивление, если три сопротивления 2 Ом, 1 Ом и 3 Ом соединены параллельно.

Решение:

Имеем,

R ₁ = 2 Ом

R ₂ = 1 Ом 9000 3

R ₃ = 3 Ом

Используя формулу получаем,

1/р _экв. = 1/R ₁ + 1/R ₂ + 1/R ₃

1/R _экв. = 1/2 + 1/1 + 1/3

1/Р _eq = 1/0,55

R _eq = 0,55 Ом

Задача 3. Вычислить эквивалентное сопротивление, если три сопротивления 4 Ом, 6 Ом и 10 Ом соединены параллельно.

Решение:

Имеем,

R ₁ = 4 Ом

R ₂ = 6 Ом 9000 3

R ₃ = 10 Ом

Используя формулу, получаем, 1 3

1/Р _экв. = 1/4 + 1/6 + 1/10

1/R _экв. = 1/1,9

R _экв. = 1,9 Ом

90 007 Задача 4. Вычислить эквивалентное сопротивление, если три сопротивления 5 Ом, 3 Ом и 8 Ом соединены параллельно.

Решение:

У нас есть,

R ₁ = 5 Ом

R ₂ = 3 Ом

R ₃ = 8 Ом

По формуле получаем,

90 002 1/R _eq = 1/R ₁ + 1/R ₂ + 1/R ₃

1/R _экв. = 1/5 + 1/3 + 1/8

1/R _экв. = 1/1,5 9 0003

Р _eq = 1,5 Ом

Задача 5. Найдите неизвестное сопротивление, если три сопротивления 3 Ом, 8 Ом и x Ом соединены параллельно, чтобы получить эквивалентное сопротивление 1,8 Ом.

Решение:

У нас есть,

R ₁ = 3 Ом

R ₂ = 8 Ом

R _eq = 1,8 Ом

Используя формулу получаем,

1/R _eq = 1/R ₁ + 1/R ₂ + 1/R ₃

=> 1/1,8 = 1/3 + 1/8 + 1/R _{3 900 12}

=> 1/R ₃ = 1/1,8 – 1/3 – 1/8

=> 1/R ₃ = 1/11

=> R ₃ = 11 Ом

Задача 6. Найдите неизвестное сопротивление, если три сопротивления 2,5 Ом, 1,5 Ом и x Ом соединены параллельно, что дает эквивалентное сопротивление 0,76 Ом.

Решение:

Имеем,

R ₁ = 2,5 Ом

R ₂ = 1,5 Ом

R _экв = 0,76 Ом

Используя формулу получаем,

1/R _экв. = 1/R ₁ + 1/R ₂ + 1/R ₃

=> 1/0,76 = 1/2,5 + 1/1,5 + 1/R ₃

=> 1/R ₃ = 1/0,76 – 1/2,5 – 1/1,5

= > 1/R ₃ = 1/4

=> R ₃ = 4 Ом

Задача 7. Найти неизвестное сопротивление, если три сопротивления 3 Ом, 6 Ом и x Ом соединены параллельно дают эквивалентное сопротивление 1,6 Ом.

Решение:

Имеем,

R ₁ = 3 Ом

R ₂ = 6 Ом

R _экв = 1,6 Ом

Используя формулу получаем,

1/R _экв = 1/R 900 11 1 + 1/R ₂ + 1 /R ₃

=> 1/1,6 = 1/3 + 1/6 + 1/R ₃

=> 1/R ₃ = 1/1,6 – 1/3 – 1/6

=> 1/R ₃ = 1/8

=> R ₃ = 8 Ом

Параллельные цепи

Ваш браузер не поддерживает Java-апплеты

Цепь с более чем одним путь прохождения тока представляет собой параллельную цепь.

НАПРЯЖЕНИЕ В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ

Полное напряжение равно напряжение любого параллельного сопротивления.

ТОК В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ

Полный ток равен сумма токов каждой параллельной составляющей.

СОПРОТИВЛЕНИЕ ПАРАЛЛЕЛЬНО ЦЕПИ

Общее сопротивление может быть рассчитывается по закону Ома, если известны напряжение и полный ток.

Общее сопротивление всегда меньше минимального значения сопротивления.

Метод равенства значений

Для параллельных сопротивлений в что все резисторы имеют одинаковое значение, сопротивление можно рассчитать по формуле деление номинала одного из резисторов на количество резисторов.

Обратный метод

Для параллельных сопротивлений в что все резисторы имеют одинаковое значение, сопротивление можно рассчитать по формуле деление номинала одного из резисторов на количество резисторов.

1/R _T = 1/R ₁ + 1/R ₂ + 1/R _N

R _EQ = 1 / ( 1/R ₁ + 1/R ₂ + . .. + 1/Р _Н )

Метод произведения на сумму

Для расчета сопротивления двух резисторов, включенных параллельно, можно использовать эту формулу:

R _EQ = (R ₁ * R ₂ ) / (R ₁ + R ₂ )

Правило приближения 10 к 1

Если два резистора соединены параллельно и один резистор в 10 и более раз больше по номиналу, чем другой резистор, резистор большего номинала можно не учитывать.

ПРОВОДИМОСТЬ

Суммарная проводимость равна к сумме проводимостей каждого компонента.

ПИТАНИЕ В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ

Суммарная мощность равна сумма мощностей каждого компонента. (Это то же самое, что и с рядом схемы).

Правила для параллельных цепей постоянного тока

1. такое же напряжение есть на каждой ветви параллельной цепи и равно напряжению источника.
2. Ток через параллельная ветвь обратно пропорциональна величине сопротивления ветвь.