Расчетов нет. Искусство понимания: почему важно искать решение до использования калькулятора

Почему профессор Санджой Махаджан советует «никогда не вычислять, не зная ответа». Как развитие интуиции и понимания помогает решать задачи эффективнее, чем слепое использование формул и калькулятора. Какие преимущества дает подход, основанный на поиске решения до вычислений.

Проблема чрезмерной зависимости от калькуляторов

В современном образовании наблюдается тенденция чрезмерного использования калькуляторов даже для простейших вычислений. Студенты часто прибегают к калькулятору, не пытаясь осмыслить задачу. Это приводит к нескольким проблемам:

• Отсутствие понимания сути задачи
• Неспособность оценить правдоподобность полученного результата
• Слабое развитие математической интуиции
• Сложности при решении нестандартных задач

Чтобы бороться с этой проблемой, профессор Санджой Махаджан предлагает радикальный подход: «Никогда не вычисляйте, не зная ответа!»

Кто такой Санджой Махаджан и почему его мнение важно

Санджой Махаджан — адъюнкт-профессор прикладных наук и инженерии в колледже Олин. Он также сотрудничает с Массачусетским технологическим институтом, помогая улучшать учебные программы. Махаджан является автором книги «Математика уличных боев», изданной MIT Press. Его подход к обучению математике и решению задач основан на развитии интуиции и понимания, а не на механическом применении формул.

Преимущества поиска решения до вычислений

Профессор Махаджан приводит несколько примеров, иллюстрирующих преимущества поиска решения до использования калькулятора:

1. Более глубокое понимание сути задачи
2. Способность оценить правдоподобность результата
3. Развитие математической интуиции
4. Возможность находить нестандартные решения
5. Снижение когнитивной нагрузки при работе со сложными формулами

Пример 1: Распространение аромата в комнате

В этом примере профессор Махаджан демонстрирует, как формальная модель диффузии дает неправдоподобный результат (97 секунд), в то время как простое рассуждение с учетом движения воздуха позволяет получить более реалистичную оценку (около 30 секунд).

Ключевые выводы из примера:

• Сложные модели не всегда дают точные результаты
• Учет дополнительных факторов (в данном случае — движения воздуха) может значительно улучшить оценку
• Простое рассуждение часто приводит к более правдоподобным результатам, чем слепое использование формул

Пример 2: Расчет среднего потока солнечной энергии

В этом примере Махаджан подчеркивает важность визуального мышления при решении задач. Он отмечает, что зрительная кора мозга развилась намного раньше, чем языковые центры, поэтому нам легче мыслить образами, чем словами или формулами.

Преимущества визуального подхода:

• Более эффективное использование мозговых ресурсов
• Улучшение понимания сложных концепций
• Возможность быстрее находить нестандартные решения
• Снижение когнитивной нагрузки при работе со сложными задачами

Пример 3: Определение глубины колодца

В этом примере профессор Махаджан вводит понятие «энтропии выражений» и объясняет, почему сложные формулы с высокой энтропией создают большую когнитивную нагрузку. Он предлагает альтернативный подход, основанный на простых рассуждениях и оценках.

Концепция энтропии выражений:

Энтропия выражения определяется как log(количество правдоподобных версий выражения). Выражения с высокой энтропией сложнее для понимания и обработки человеческим мозгом.

Преимущества подхода с низкой энтропией:

• Снижение когнитивной нагрузки
• Возможность решать задачи без калькулятора
• Более глубокое понимание сути проблемы
• Способность быстро оценивать правдоподобность результатов

Общие преимущества «Искусства Проницательности»

Подводя итоги рассмотренных примеров, можно выделить следующие ключевые преимущества подхода, предложенного профессором Махаджаном:

1. Развитие математической интуиции
2. Улучшение способности оценивать правдоподобность результатов
3. Возможность находить нестандартные решения
4. Снижение зависимости от калькуляторов и формул
5. Более глубокое понимание сути решаемых задач
6. Эффективное использование визуального мышления
7. Уменьшение когнитивной нагрузки при работе со сложными проблемами

Как развивать «Искусство Проницательности»

Чтобы научиться применять подход, предложенный профессором Махаджаном, можно следовать следующим рекомендациям:

• Перед использованием калькулятора попытайтесь оценить примерный результат
• Используйте визуализацию для лучшего понимания задачи
• Ищите простые аналогии и модели для сложных проблем
• Практикуйте оценочные вычисления в уме
• Анализируйте полученные результаты на предмет их правдоподобности
• Старайтесь понять физический смысл используемых формул и выражений
• Регулярно решайте задачи, требующие нестандартного подхода

Применение «Искусства Проницательности» в реальной жизни

Подход, предложенный профессором Махаджаном, может быть полезен не только в академической среде, но и в повседневной жизни. Вот несколько примеров его применения:

• Оценка времени в пути с учетом пробок
• Планирование бюджета и оценка расходов
• Анализ рисков при принятии важных решений
• Оценка энергоэффективности бытовых приборов
• Прогнозирование результатов спортивных соревнований

Заключение: почему важно развивать «Искусство Проницательности»

Подход, предложенный профессором Санджоем Махаджаном, предлагает альтернативу слепому использованию калькуляторов и формул. Развивая интуицию и понимание, мы можем более эффективно решать задачи, лучше понимать суть проблем и находить нестандартные решения. Этот навык полезен не только в академической среде, но и в повседневной жизни, помогая принимать более обоснованные решения и лучше понимать окружающий мир.

В договоре с контрагентом нет возможности выбрать валюту расчетов, как исправить ситуацию в программе 1С: Бухгалтерия 8 ред. 3.0?

+7 (495) 784-71-73

Написать нам

Имя*

Фамилия*

Телефон *

E-mail*

Сообщение

Я даю согласие на обработку персональных данных

Ваша заявка принята. Мы решим ваш вопрос в течение 2-х рабочих часов!

Стать клиентом 1С

Имя: *

Фамилия: *

Телефон: *

E-mail*

Сообщение

Я даю согласие на обработку персональных данных

Спасибо! Ваша заявка принята.
Мы свяжемся с вами в ближайшее время!

Заказать обратный звонок 1С

Имя: *

Фамилия: *

Телефон: *

Я даю согласие на обработку персональных данных

Спасибо! Мы свяжемся с вами через несколько минут

1С:Бухгалтерия 8 | Pro 1C

Вопрос:

В договоре с контрагентом нет возможности выбрать валюту расчетов, как исправить ситуацию в программе 1С: Бухгалтерия 8 ред. 3.0?

Ответ:

Нужно открыть «Главное меню» — команда «Все функции», перейти в «Константы», установить галочку «Использовать валютный учет», затем перейти к выбору валюты расчетов.

Свидетельство о регистрации СМИ: Эл № ФС77-67462 от 18 октября 2016 г. Контакты редакции: +7 (495) 784-73-75, smi@4dk. ru

По этой теме

Pro 1C Как сформировать Универсальный отчет в программе 1С:Комплексная автоматизация, ред.2.5? Pro 1C Как начисляется аванс и удерживается НДФЛ с аванса с 01.01.2023 в программе 1С:Бухгалтерия предприятия, ред.3.0? Pro 1C В каком отчете посмотреть все используемые графики сотрудников в программе 1С:Зарплата и управление персоналом, ред.3.1?

Подробнее

Обучение 1С

1С:ФРЕШ

Маркировка в 1С

Бухгалтерский аутсорсинг

14.11.2022 — 24.11.2022

Курс повышения квалификации

Практический курс. Бухгалтерская отчетность бюджетных и автономных учреждений. Порядок составления, правила проверки, устранение рисков допущения ошибок

15. 11.2022 — 16.11.2022

Вебинар

ОНЛАЙН. Новые ФСБУ и их влияние на показатели отчетности — готовимся к формированию бухгалтерской отчетности за 2022 год

Email:

Поздравляем! Вы успешно подписались на рассылку

Нет

Получите полный доступ к КонсультантПлюс бесплатно!

Попробовать

Да

Вы переходите в систему КонсультантПлюс

Перейти

Акт сверки не является доказательством наличия задолженности \ Акты, образцы, формы, договоры \ КонсультантПлюс

• Главная
• Правовые ресурсы
• Подборки материалов
• Акт сверки не является доказательством наличия задолженности

Подборка наиболее важных документов по запросу Акт сверки не является доказательством наличия задолженности (нормативно–правовые акты, формы, статьи, консультации экспертов и многое другое).

• Обязательства:
• Административные правоотношения
• Акт сверки взаимных расчетов
• Акт сверки взаимных расчетов кто подписывает
• Акт сверки взаимных расчетов это
• Акт сверки как признание долга
• Ещё…

Судебная практика: Акт сверки не является доказательством наличия задолженности

Зарегистрируйтесь и получите пробный доступ к системе КонсультантПлюс бесплатно на 2 дня

Открыть документ в вашей системе КонсультантПлюс:
Постановление Восемнадцатого арбитражного апелляционного суда от 01.11.2022 N 18АП-12676/2022 по делу N А07-11136/2022
Требование: О взыскании долга по договору субподряда.
Решение: Требование удовлетворено.Довод подателя жалобы о том, что акт сверки взаимных расчетов сам по себе не подтверждает наличие задолженности, судом не принимается, поскольку этот акт сверки не является единственным доказательством наличия задолженности. В силу статьи 68 АПК РФ доказательством выполнения работ являются акты о приемке выполненных работ, представленные истцом в материалы дела, которые не оспорены ответчиком. Подписанный сторонами акт сверки взаимных расчетов отражает только мнения сторон о состоянии расчетов между ними.

Зарегистрируйтесь и получите пробный доступ к системе КонсультантПлюс бесплатно на 2 дня

Открыть документ в вашей системе КонсультантПлюс:
Постановление Двадцатого арбитражного апелляционного суда от 05.07.2022 N 20АП-3965/2022 по делу N А09-10791/2021
Требование: О взыскании задолженности по договору поставки, неустойки.
Решение: Требование удовлетворено.Вместе с тем, ссылки ответчика на то, что требования истца не подлежат удовлетворению ввиду отсутствия акта сверки взаимных расчетов, основаны на неверном толковании норм действующего законодательства, поскольку акт сверки не является единственным доказательством наличия задолженности. Акт сверки взаимных расчетов только подтверждает наличие или отсутствие задолженности одной из сторон, возникшей на основании первичных учетных документов, и не носит правоустанавливающего характера, поскольку не приводит к возникновению, изменению или прекращению правоотношений лиц, его подписавших, а только констатирует итоги их расчетов по договору.

Статьи, комментарии, ответы на вопросы: Акт сверки не является доказательством наличия задолженности

Путеводитель по судебной практике. Подряд. Общие положенияКроме того, акты о приемке выполненных работ подписаны с замечаниями относительно правильности определения подрядчиком стоимости этих работ, изложенными в претензиях N 3727/ЗабДИ от 09.11.2016, N 43 от 25.12.2016, N 129/ЗабДИ от 19.01.2017, N 4363/ЗабДИ от 29.12.2016. Необходимо также отметить, что акт сверки взаимных расчетов без подтверждения первичными бухгалтерскими документами безусловным доказательством наличия задолженности не является…»

Зарегистрируйтесь и получите пробный доступ к системе КонсультантПлюс бесплатно на 2 дня

Открыть документ в вашей системе КонсультантПлюс:
Вопрос: Можно ли взыскать задолженность на основании акта сверки с контрагентом?
(Консультация эксперта, 2022)Сам по себе без первичных учетных документов акт сверки не является бесспорным доказательством наличия или отсутствия задолженности одного участника гражданского оборота перед другим. Вместе с тем акт сверки взаиморасчетов может иметь дополнительное (факультативное) доказательственное значение в случае возникновения спора относительно размера задолженности одной стороны договора перед другой при условии, что он был подписан обеими сторонами. Акт сверки можно учитывать только в совокупности с иными доказательствами, в числе которых он может усиливать доказательственную базу, однако сам по себе он достаточным доказательством не является (см., например, Постановления Арбитражного суда Западно-Сибирского округа от 09.07.2020 N Ф04-5669/2019 по делу N А70-9106/2018, Арбитражного суда Северо-Западного округа от 05.03.2020 N Ф07-1130/2020 по делу N А26-13452/2018, Арбитражного суда Московского округа от 17.07.2018 N Ф05-4128/2018 по делу N А40-8569/17).

Нормативные акты: Акт сверки не является доказательством наличия задолженности

Зарегистрируйтесь и получите пробный доступ к системе КонсультантПлюс бесплатно на 2 дня

Открыть документ в вашей системе КонсультантПлюс:
Решение Новосибирского УФАС России от 04. 02.2022 N 054/01/18.1-151/2022
Обстоятельства: По мнению Заявителя, Заказчиком допущены нарушения порядка оценки заявок на участие в процедуре, выразившиеся в неверном определении баллов, подлежащих присвоению Заявителю.
Решение: Признать жалобу необоснованной.Акт сверки расчетов не является первичным учетным документом, подтверждающим совершение хозяйственной операции, так как при его оформлении не изменяется финансовое состояние сторон хозяйствующих субъектов. Как отметил Арбитражный суд Волго-Вятского округа в Постановлении от 18.07.2016 N Ф01-2768/2016, составленный в одностороннем порядке акт сверки взаимных расчетов без первичных документов, подтверждающих поставку товара, не доказывает получение этого товара, следовательно, не подтверждает наличие задолженности в учете.

расчетов без формул! | Прайор Обучение

Лори Коффи Категории: Excel®

Некоторые люди используют Excel, потому что им НРАВИТСЯ числа и математика. Некоторые используют Excel, потому что НЕТ! Ник рассчитывает, что Excel сделает всю тяжелую математическую работу. Ему нужно вычислить ряды данных, но мысль о создании формул и последующей проверке ответов кажется обескураживающей. Если вы чувствуете то же самое, вам могут понравиться автоматические вычисления, которые Excel может выполнять без необходимости создавать одну формулу!

Представьте, что вы просто нажимаете на ячейки с числами, и сразу же появляется сумма! Это быстрее, чем искать свой калькулятор! После включения он всегда доступен для просмотра в строке состояния каждый раз, когда вы выбираете несколько ячеек, содержащих данные. Это отлично подходит для быстрого просмотра, чтобы увидеть, как работают разные продавцы, офисы или продукты.

Итак, как его включить? Щелкните правой кнопкой мыши строку состояния (это небольшая панель инструментов под вкладками рабочего листа с надписью 9).0013 Готов ). Затем нажмите, чтобы проверить расчеты, которые вы хотите отобразить. Он остается включенным, пока вы не выключите его в том же месте.

Это упростит ваши итоги с начала года! Допустим, вы отслеживаете количество просмотров страниц вашего сайта. Обычно вы создаете формулу для добавления итогов нового месяца к итогам прошлого месяца, чтобы создать текущий год. Вы должны создать новую формулу для каждого нового месяца в течение года.

Вместо того, чтобы создавать все эти формулы, просто скопируйте новую сумму за месяц, а затем вставьте ее поверх данных за текущий год. ЗА ИСКЛЮЧЕНИЕМ вместо использования Ctrl + V для вставки используйте Ctrl + Alt + V. Это открывает Специальную вставку. В разделе «Операция» выберите Добавьте , затем ОК и появятся итоги! Затем каждый месяц копируйте свои текущие номера и используйте «Специальная вставка», . Добавьте к текущему году. Никаких формул и никаких проблем!

Объединение более сложно, но оно может сэкономить вам массу времени, когда вам нужно собрать числа из нескольких разных источников на нескольких листах, а затем суммировать их все на одном листе. Например, каждый из ваших рабочих листов содержит данные о продажах для каждого из регионов вашей компании. Каждая позиция представляет собой отдельный продукт, который продается не во всех регионах. Какой громоздкий процесс вам придется следовать! Во-первых, чтобы отсортировать все продукты на каждом листе, а затем создать формулу для сбора всех итогов, обеспечивающую соответствие данных продуктам.

Консолидация — это ОГРОМНАЯ простая кнопка! Он будет искать все те же продукты (даже если они НЕ в порядке сортировки) и суммировать их на новом листе (даже если на некоторых листах продукт не указан).

В чем подвох? Там — это . Требуется небольшая настройка: убедитесь, что на всех рабочих листах одинаковые столбцы отображаются в одном и том же порядке с одинаковыми именами столбцов. (Совет: если вы регулярно получаете рабочие листы и они не настроены одинаково, используйте макрос для их реструктуризации.)

Затем создайте новый рабочий лист для итогов и поместите курсор в ячейку A1. На вкладке Данные нажмите Консолидировать .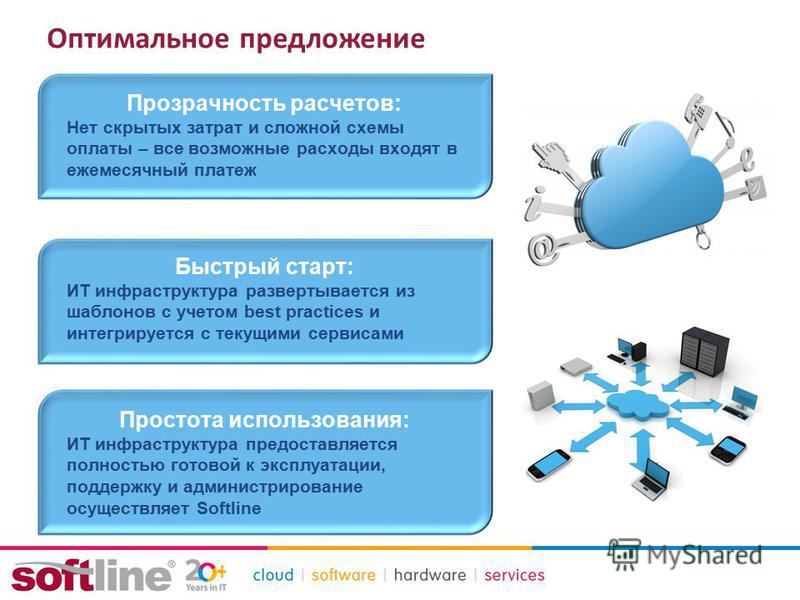 В разделе «Справочник» нажмите кнопку свернуть (она выглядит как крошечный рабочий лист). Перейдите на первый рабочий лист и выберите данные. Вернувшись в диалоговое окно «Консолидация», нажмите «Добавить ». Установите флажок «Использовать метки» в параметрах Top Row и Left Column . Повторите для каждого из рабочих листов. Затем нажмите ОК . После того, как вы выбрали, где находятся данные, Excel сделает всю математику за вас. Какая экономия времени!

Было бы разумно позволить Excel выполнять ваши рутинные вычисления, чтобы вы могли тратить свое время и умственные способности на более важные вещи, такие как поиск калькулятора!

PRYOR+ 7 ДНЕЙ БЕСПЛАТНОГО ОБУЧЕНИЯ

---

Курсы по обслуживанию клиентов, Excel, управлению персоналом, лидерству, ОСАГО и многое другое. Нет кредитной карты. Без комментариев. Индивиды и команды.

НАЧАТЬ ПРОБНЫЙ ПЕРИОД

«Никогда не считайте, не зная ответа!»

Если вы недавно были на уроке математики в старшей школе, вы, вероятно, помните, что видели огромное количество калькуляторов. Вы могли также наблюдать, как студенты вводили в машины что-нибудь от 999*999 до sin(π/6) до 7-1 . Привычка к калькулятору настолько сильна, что даже 5+7 (=12) требует машинной помощи. А привычки умирают с трудом.

Чтобы бороться с нашей одержимостью калькулятором, Санджой Махаджан предлагает радикально отказаться от зависимости от калькулятора: что, если бы мы знали решение раньше, чем вычисление? По словам профессора Махаджана, «никогда не вычисляйте, не зная ответа!» Звучит странно, но позвольте ему объяснить, и вы будете заинтригованы.

Во-первых, краткое введение. Санджой Махаджан — адъюнкт-профессор прикладных наук и инженерии в колледже Олин. В Массачусетском технологическом институте профессор Махаджан также является знакомой и желанной фигурой. Он сотрудничал с профессорами Массачусетского технологического института, чтобы улучшить их учебные планы, и опубликовал книгу «9».0013 Математика уличных боев , издательство MIT Press (читать книгу можно здесь).

Санджой Махаджан видит общую тенденцию к прагматизму в Соединенных Штатах, когда студенты хотят просто решить проблему, не спрашивая основных «как» или «почему». Тогда научные задачи становятся не чем иным, как повторным применением одной формулы с помощью калькулятора. К сожалению, даже самые сложные формулы могут быть ошибочными. Калькуляторы не могут этого показать, но лучшее понимание, или понимание , из материала может. В своем выступлении 19 мая xTalk «Искусство понимания», организованном Управлением цифрового обучения Массачусетского технологического института, профессор Махаджан привел несколько примеров, чтобы проиллюстрировать преимущества поиска решения до того, как он потянется за калькулятором.

---

ПРИМЕР #1 : представьте себе, что вы находитесь в комнате с бумажным полотенцем, на которое недавно набрызгали духи (как во время выступления профессора Махаджана). Вопрос: через какое время все зрители почувствуют аромат? 97 секунд, или примерно ⅓ в год, тогда как в реальной жизни задние ряды ощутили запах примерно через 30 секунд! Официальная модель проблемы с калькулятором далека от идеала. Несмотря на сложность, он не может дать разумного ответа.

Проницательность:
Добавьте к соображению «четырехбуквенное слово»: ветер. При ветре или дрейфе вы можете начать делать гораздо большие, хотя и медленные шаги к решению, вместо маленьких и быстрых шагов диффузионной модели. Преимущество этой модели, основанной на здравом смысле, заключается в контроле поиска: пространство поиска становится намного более удобным за счет его расширения.

---

ПРИМЕР #2 : рассчитайте средний поток солнечной энергии над поверхностью Земли. 3 раз дольше, чем можем говорить о нем! Зрительная кора развилась задолго до языка, поэтому нам легче думать визуальными образами. Даже самое важное слово профессора Махаджана во время выступления, «прозрение», имеет встроенное слово «видение». Фактически, во многих языках слово «видение» содержится в словах, означающих «понимание». Урок здесь: используйте свою большую зрительную кору всякий раз, когда можете. 92. Вопрос: примерно, насколько глубока скважина? Варианты ответа: а) 20 м, б) 100 м, в) 500 м.

Формальная модель:
Давайте сначала рассмотрим правильный математический способ решения задачи. Для этого мы должны включить время, необходимое звуку для прохождения вверх по скважине (фактор, который мы обычно не учитываем, поскольку в нашем сценарии им можно пренебречь). Получаем квадратное уравнение, которое выводится по следующей формуле для высоты скважины: .

Немного подавляюще, не так ли? И, конечно же, бесполезен в ситуации погони на высокой скорости. По словам профессора Махаджана, ответ проблематичен по одной конкретной причине: у него высокая энтропия.

В химии энтропия химических веществ определяется как log(# состояний) энтропии , своего рода квантификатор того, насколько «грязным» или «хаотичным» является вещество. Хотя обычно мы не думаем, что энтропия применима к математическим выражениям, профессор Махаджан предполагает, что мы можем фактически измерить энтропию выражений, переопределив формулу из химии как энтропии log(количество правдоподобных версий выражения ) .

Теперь подумайте, сколько способов мы можем изменить в формуле, перемещая константы вокруг столбцов дробей и квадратных корней (например, одним из простых изменений будет перемещение  в верхнюю часть столбца дробей). Это математическое выражение имеет высокую энтропию структуры.

Проблема с выражениями с высокой энтропией заключается в том, что они несут высокую когнитивную нагрузку, а именно то, сколько оперативной памяти вам нужно использовать для их обработки. Как люди, у нас есть приблизительно бесконечная долговременная память. Однако, чтобы хранить информацию в долгосрочной перспективе, нам нужно получить ее через ограниченную рабочую/кратковременную память. Там у нас есть серьезные когнитивные ограничения, и высокоэнтропийные выражения, подобные приведенному выше, значительно увеличивают нагрузку на рабочую память. Таким образом, энтропия также измеряет, сколько информации вы можете обрабатывать за раз. 92 ~ 80 м. Когда у вас есть понимание проблемы и предварительная оценка, вы можете улучшить результат, рассматривая t(sound) отдельно. Преимущество понимания здесь — низкая энтропия/низкая когнитивная нагрузка. Кроме того, нет необходимости в калькуляторе, инструменте, который не всегда доступен во время дерзкого побега.

---

Здесь вы можете сказать, что мы просто рассмотрели три непересекающихся примера, а не общую идею: какую пользу мы извлекаем из Искусства Проницательности. Давайте подведем итоги, чтобы рассмотреть все преимущества рассуждения, а не вычисления решения.