Рассчитать индуктивность. Расчет индуктивности катушек: формулы, калькуляторы и практические рекомендации — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как рассчитать индуктивность катушки. Какие факторы влияют на индуктивность. Как использовать онлайн-калькуляторы для расчета индуктивности. Какие формулы применяются для вычисления индуктивности разных типов катушек.

Содержание

Что такое индуктивность и от чего она зависит

Индуктивность — это физическая величина, характеризующая способность проводника создавать магнитное поле при протекании через него электрического тока. Индуктивность измеряется в генри (Гн).

Основные факторы, влияющие на индуктивность катушки:

Количество витков — чем больше витков, тем выше индуктивность
Диаметр катушки — при увеличении диаметра индуктивность растет
Длина намотки — чем короче катушка при том же числе витков, тем выше индуктивность
Наличие сердечника — магнитный сердечник значительно увеличивает индуктивность
Форма сечения провода — плоская лента дает большую индуктивность, чем круглый провод

Для точного расчета индуктивности используются специальные формулы, учитывающие геометрические параметры катушки и свойства материала сердечника.

Формулы для расчета индуктивности различных типов катушек

Однослойная цилиндрическая катушка без сердечника

Для расчета индуктивности однослойной цилиндрической катушки без сердечника применяется формула:

L = (μ0 * N^2 * S) / l

где:

L — индуктивность (Гн)
μ0 — магнитная постоянная (4π * 10^-7 Гн/м)
N — число витков
S — площадь поперечного сечения катушки (м^2)
l — длина катушки (м)

Многослойная цилиндрическая катушка

Для многослойных катушек используется более сложная формула:

L = (0.0002 * π * N^2 * D^2 * K) / (l + 0.45 * D)

где:

L — индуктивность (мкГн)
N — число витков
D — диаметр катушки (см)
l — длина намотки (см)
K — коэффициент, зависящий от отношения длины к диаметру

Онлайн-калькуляторы для расчета индуктивности

Для упрощения расчетов можно воспользоваться онлайн-калькуляторами индуктивности. Рассмотрим несколько популярных вариантов:

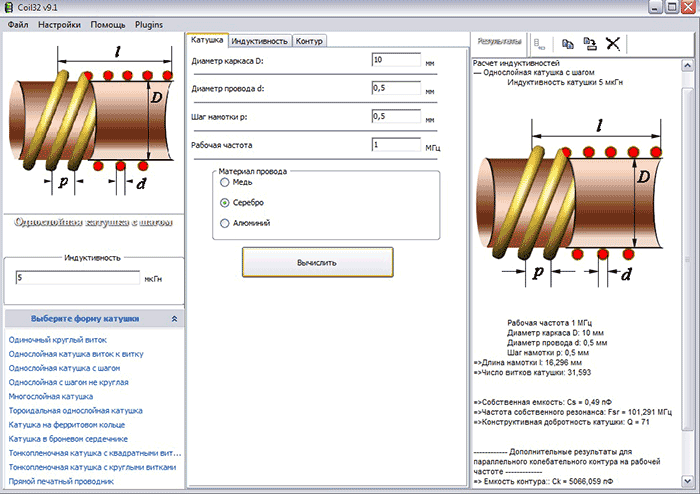
1. Калькулятор индуктивности однослойной катушки

Этот калькулятор позволяет рассчитать индуктивность однослойной цилиндрической катушки без сердечника. Для расчета необходимо ввести следующие параметры:

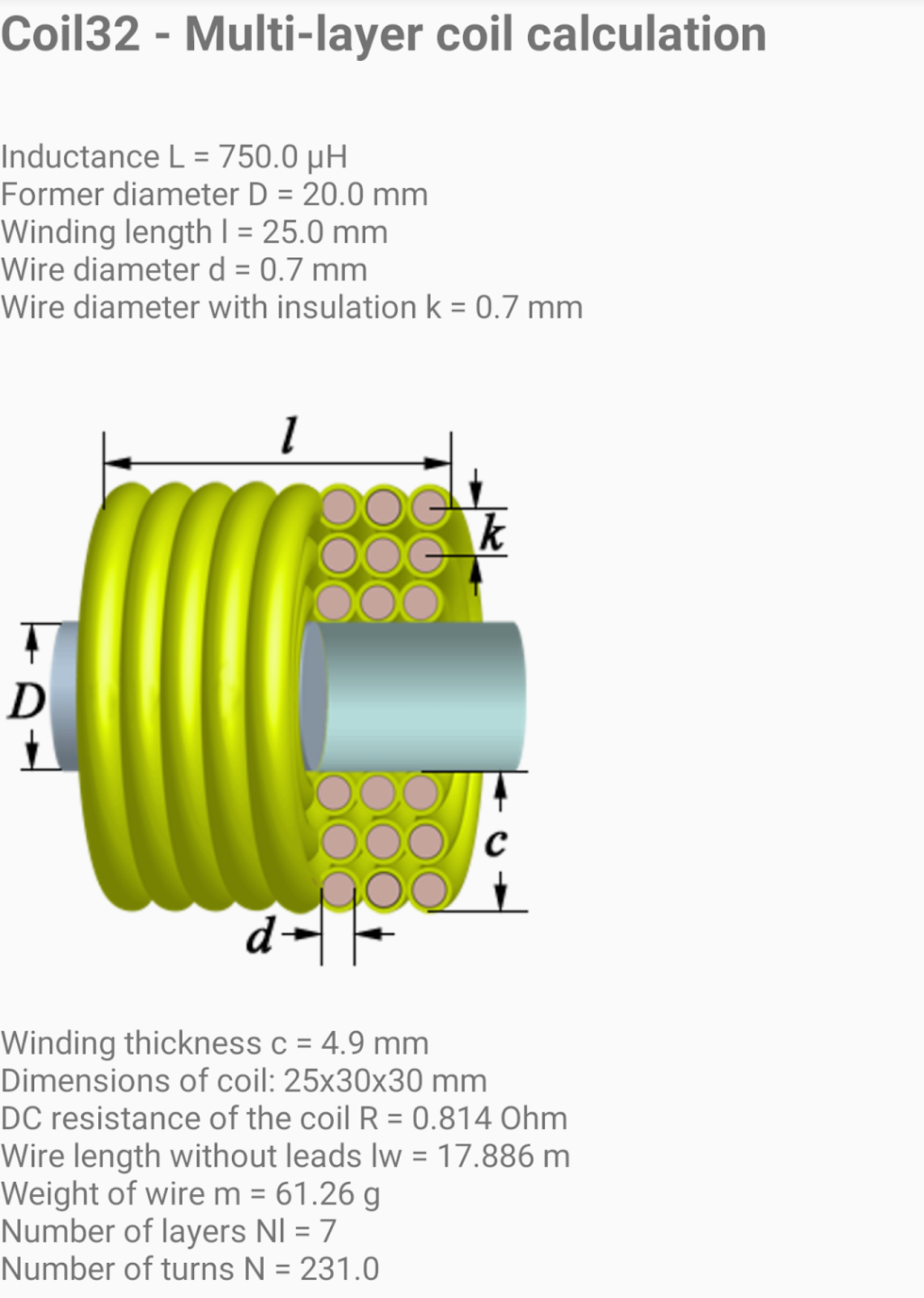
Диаметр каркаса катушки
Количество витков
Длина намотки

После ввода данных калькулятор выдаст значение индуктивности в мкГн.

2. Калькулятор для расчета многослойных катушек

Более сложный калькулятор для многослойных катушек учитывает дополнительные параметры:

Внутренний диаметр каркаса
Внешний диаметр обмотки
Высота намотки
Диаметр провода
Количество слоев

Такой калькулятор позволяет получить более точные результаты для сложных многослойных конструкций.

Практические рекомендации по расчету и изготовлению катушек индуктивности

При расчете и изготовлении катушек индуктивности следует учитывать ряд практических моментов:

Выбирайте оптимальное соотношение длины к диаметру катушки — обычно от 0.5 до 2.
Используйте провод подходящего сечения, чтобы избежать перегрева катушки.
Для увеличения добротности применяйте литцендрат на высоких частотах.
Учитывайте паразитную емкость между витками при работе на высоких частотах.
Для точной настройки индуктивности предусмотрите возможность подстройки числа витков.

Соблюдение этих рекомендаций позволит создать катушку с требуемыми параметрами и хорошими характеристиками.

Применение катушек индуктивности в электронных схемах

Катушки индуктивности широко применяются в различных электронных устройствах:

Фильтры высоких и низких частот
Колебательные контуры
Трансформаторы и дроссели
Антенны и согласующие устройства
Электромагниты и реле

В каждом применении к катушкам предъявляются свои требования по индуктивности, добротности, рабочему току и другим параметрам. Правильный расчет индуктивности позволяет создать оптимальную катушку для конкретной задачи.

Измерение индуктивности готовых катушек

После изготовления катушки рекомендуется измерить ее реальную индуктивность. Для этого используются специальные приборы — измерители индуктивности (LCR-метры). Процесс измерения включает следующие шаги:

Подключите катушку к измерительным клеммам прибора
Выберите подходящий диапазон измерения
Установите рабочую частоту, на которой будет измеряться индуктивность
Считайте показания с дисплея прибора

Измеренное значение может отличаться от расчетного из-за неидеальности намотки, наличия паразитных параметров и погрешностей измерения. Для ответственных применений рекомендуется проводить калибровку катушек по эталонным индуктивностям.

Заключение

Расчет индуктивности катушек — важный этап при проектировании электронных устройств. Правильный подбор параметров катушки позволяет добиться оптимальных характеристик схемы. Использование онлайн-калькуляторов и специализированных программ значительно упрощает процесс расчета. При изготовлении катушек важно учитывать практические аспекты и проводить контрольные измерения готовых изделий.

Калькулятор индуктивности однослойной катушки • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения

Однослойная катушка индуктивности: D — диаметр оправки или каркаса катушки, D_c — диаметр катушки, p — шаг намотки катушки, d — диаметр провода без изоляции и d_i — диаметр провода с изоляцией.

Калькулятор определяет индуктивность однослойной катушки.

Пример: рассчитать индуктивность однослойной катушки без сердечника, состоящей из 10 витков на цилиндрическом каркасе диаметром 2 см; длина катушки 1 см.

Входные данные

Диаметр каркаса или оправки катушки

Dмиллиметр (мм)сантиметр (см)дюйм

Количество витков

Длина катушки

lмиллиметр (мм)сантиметр (см)дюйм

Выходные данные

Индуктивность катушки

L мГн

Введите диаметр каркаса катушки, число витков и длину катушки, выберите единицы и нажмите кнопку Рассчитать.

Пример: рассчитать число витков и длину намотки катушки 10 мкГн, намотанной эмалированным проводом 0,65 мм (диаметр с изоляцией 0,7 мм) на оправке 2 см.

Входные данные

Требуемая индуктивность

Lгенри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)

Диаметр каркаса или оправки катушки

Dмиллиметр (мм)сантиметр (см)метр (м)дюйм

Диаметр провода без изоляции

dмиллиметр (мм)сантиметр (см)метр (м)дюймАмериканский калибр проводов

Диаметр изолированного провода

d_iмиллиметр (мм)сантиметр (см)метр (м)дюйм

Выходные данные

Длина намотки

l мм

Количество витков

На рисунке выше показана однослойная катушка индуктивности: D_c — диаметр катушки, D — диаметр оправки или каркаса катушки, p — шаг намотки катушки, d — диаметр провода без изоляции и d_i — диаметр провода с изоляцией

Для расчета индуктивности L_S применяется приведенная ниже формула из статьи Р. Уивера (R. Weaver) Численные методы расчета индуктивности:

Здесь

D — диаметр оправки или каркаса катушки в см,

l — длина катушки в см,

N — число витков и

L — индуктивность в мкГн.

Эта формула справедлива только для соленоида, намотанного плоским проводом. Это означает, что катушка намотана очень тонкой лентой без зазора между соседними витками. Она является хорошим приближением для катушек с большим количеством витков, намотанных проводом круглого сечения с минимальным зазором между витками. Американский физик Эдвард Беннетт Роса (Edward Bennett Rosa, 1873–1921) работавший в Национального бюро стандартов США (NBS, сейчас называется Национальное бюро стандартов и технологий (NIST) разработал так называемые корректирующие коэффициенты для приведенной выше формулы в форме (см. формула 10.1 в статье Дэвида Найта, David W. Knight):

Здесь L_S — индуктивность плоской спирали, описанная выше, и

где k_s — безразмерный корректирующий коэффициент, учитывающий разницу между самоиндукцией витка из круглого провода и витка из плоской ленты; k_m — безразмерный корректирующий коэффициент, учитывающий разницу в полной взаимоиндукции витков из круглого провода по сравнению с витками из плоской ленты; D_c — диаметр катушки в см, измеренный между центрами проводов и N — число витков.

Величина коэффициента Роса k_m определяется по формуле 10.18 в упомянутой выше статье Дэвида Найта:

Коэффициент Роса k_s, учитывающий различие в самоиндукции, определяется по формуле 10.4 в статье Д. Найта:

Здесь p — шаг намотки (расстояние между витками, измеренное по центрам проводов) и d — диаметр провода. Отметим, что отношение p/d всегда больше единицы, так как толщина изоляции провода конечна, а минимально возможное расстояние между двумя соседними витками с очень тонкой изоляцией, расположенными без зазора, равна диаметру провода d.

Факторы, влияющие на индуктивность катушки

На индуктивность катушки влияют несколько факторов.

Количество витков. Катушка с большим количеством витков имеет бóльшую индуктивность по сравнению с катушкой с меньшим количеством витков.
Длина намотки. Две катушки с одинаковым количеством витков, но разной длиной намотки имеют разную индуктивность. Более длинная катушка имеет меньшую индуктивность. Это связано с тем, что магнитное поле менее компактной катушки более слабое и оно не может хорошо концентрироваться в растянутой катушке.
Диаметр катушки. Две плотно намотанные катушки с одинаковым количеством витков и разными диаметрами имеют разную индуктивность. Катушка с бóльшим диаметром имеет бóльшую индуктивность.
Сердечник. Для увеличения индуктивности в катушку часто вставляется сердечник из материала с высокой магнитной проницаемостью. Сердечники с более высокой магнитной проницаемостью позволяют получить более высокую индуктивность. Сердечники, изготовленные из магнитной керамики — феррита, часто используются в катушках и трансформаторах различных электронных устройств, так как у них очень низкие потери на вихревые токи.

Упрощенная эквивалентная схема реальной катушки индуктивности: R_w — сопротивление обмотки и ее выводов; L — индуктивность идеальной катушки; R_l — сопротивление вследствие потерь в сердечнике; и C_w — паразитная емкость катушки и ее выводов.

Эквивалентная схема реальной катушки индуктивности

В этом калькуляторе мы рассматривали идеальную катушку индуктивности. В то же время, в реальной жизни таких катушке не бывает. Катушки обычно конструируются с минимальными размерами таким образом, чтобы они помещались в миниатюрное устройство. Любую реальную катушку индуктивности можно представить в виде идеальной индуктивности, к которой параллельно подключены емкость и сопротивление, а еще одно сопротивление подключено последовательно. Параллельное сопротивление учитывает потери на гистерезис и вихревые токи в магнитном сердечнике. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и магнитного потока в сердечнике.

Паразитная емкость появляется в связи с тем, что витки катушки находятся близко друг к другу. Любые два витка провода можно рассмотреть как две обкладки маленького конденсатора. Витки разделяются изолятором, таким как воздух, изоляционный лак, лента или иной изоляционный материал. Относительная диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта проницаемость, тем выше емкость. В некоторых случаях дополнительная емкость может появиться также между катушкой и противовесом, если катушка расположена над ним. На высоких частотах реактивное сопротивление паразитной емкости может быть весьма высоким и игнорировать его нельзя. Для уменьшения паразитной емкости используются различные методы намотки катушек.

Для уменьшения паразитной емкости катушки с высокой добротностью для радиопередатчиков наматывают так, чтобы было достаточно большое расстояние между витками

Если индуктивность большая, то сопротивление обмотки (R_w на схеме) игнорировать уже нельзя. Тем не менее, оно мало по сравнению с реактивным сопротивлением больших катушке на высоких частотах. Однако, на низких частотах и на постоянном токе это сопротивление необходимо учитывать, так как в этих условиях через катушку могут протекать значительные токи.

Катушки индуктивности и обмотки в различных устройствах

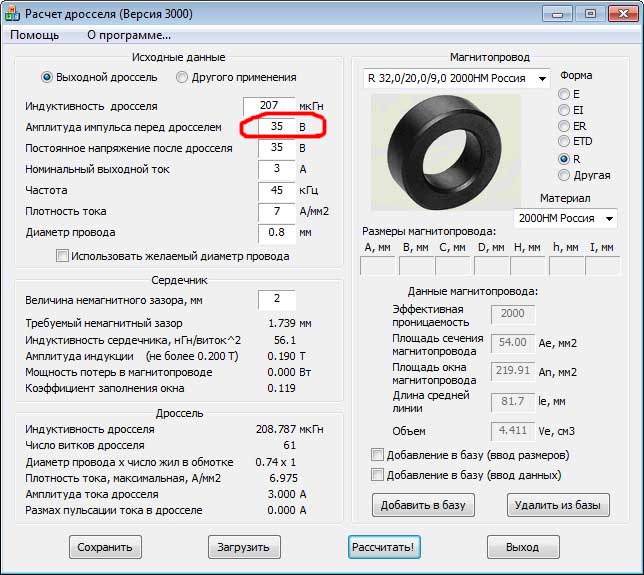
Расчет дросселей и катушек индуктивности на ферритовых кольцах, формула и калькулятор

Радиоэлектроника, схемы, статьи и программы для радиолюбителей.

Схемы
- Аудио аппаратура
  - Схемы транзисторных УНЧ
  - Схемы интегральных УНЧ
  - Схемы ламповых УНЧ
  - Предусилители
  - Регуляторы тембра и эквалайзеры
  - Коммутация и индикация
  - Эффекты и приставки
  - Акустические системы
- Спецтехника
  - Радиомикрофоны и жучки
  - Обработка голоса
  - Защита информации
- Связь и телефония
  - Радиоприёмники
  - Радиопередатчики
  - Радиостанции и трансиверы
  - Аппаратура радиоуправления
  - Антенны
  - Телефония
- Источники питания
  - Блоки питания и ЗУ
  - Стабилизаторы и преобразователи
  - Защита и бесперебойное питание
- Автоматика и микроконтроллеры
  - На микроконтроллерах
  - Управление и контроль
  - Схемы роботов
- Для начинающих
  - Эксперименты
  - Простые схемки
- Фабричная техника
  - Усилители мощности
  - Предварительные усилители
  - Музыкальные центры
  - Акустические системы
  - Пусковые и зарядные устройства
  - Измерительные приборы
  - Компьютеры и периферия
  - Аппаратура для связи
- Измерение и индикация
- Бытовая электроника
- Автомобилисту
- Охранные устройства
- Компьютерная техника
- Медицинская техника
- Металлоискатели

Мастер Винтик. Всё своими руками!Бесплатный калькулятор для расчёта катушек индуктивности — Md Coil Mate

Добавил: Chip,Дата: 25 Май 2017

«Md Coil Mate» — бесплатный калькулятор для расчета катушек индуктивности, поисковых катушек металлодетекторов.

Для изготовления поисковых катушек для металлоискателей необходимо рассчитать точные её параметры.

Для этого предлагаем воспользоваться специализированной простой бесплатной программой —

Md Coil Mate.

Программа написана под «.NET v2.0» в «VS 2008 Express Edition» а посему для работы программы возможно придётся скачать и установить «.NET v2.0».

В соответствующие окна вводим необходимые значения параметров катушки.

Формулы расчетов собирались из разных мест сети интернет.

При наведении курсора на окна, выводятся подсказки.

Платформа: Windows

Размер программы: 133kB

Язык: русский (английский)

Сайт разработчика:bypetrucho.narod.ru

>>> СКАЧАТЬ

КАЛЬКУЛЯТОР ДЛЯ РАСЧЁТА КАТУШЕК ИНДУКТИВНОСТИ

БЕСПЛАТНО <<<

ПОДЕЛИТЕСЬ С ДРУЗЬЯМИ

П О П У Л Я Р Н О Е:

Бесплатный конвертер в формат PDF

ВИРТУАЛЬНЫЙ ПРИНТЕР

Если у Вас нет принтера, а распечатать что нибудь необходимо, то можно воспользоваться бесплатной программой —

PDFCreator.

А иногда нужно файл не распечатать, а просто преобразовать в формат PDF. Это формат не только удобный для чтения, но безопасный в плане копирования и последующего редактирования. Давайте подробнее рассмотрим бесплатный конвертер документов — PDFCreator.

Осцилограф, анализатор спектра, звуковой измеритель и генератор в одной программе Wavetools

Wavetools

Осцилограф.

Эта программа имитирует двухканальный запоминающий осциллограф.

Следующие элементы управления доступны:

Позволяет регулировать усиление Оси Y в шагах на 10 дБ. В 0 дБ, на экране, показывает полномасштабный звуковой вход.
Подробнее…

Бесплатная программа для проверки скорости Интернет

У Вас медленно работает компьютер, планшет или телефон? «Подвисает» и «тормозит»? Одна из возможных причин — это низкая скорость Интернет соединения.

Как проверить скорость Интернета? Для этого есть разные способы. Одна из них — это бесплатная программа SPEEDTEST, о которой пойдет речь в этой статье.

Подробнее…

Популярность: 2 740 просм.

Калькулятор взаимной индуктивности

— Последовательные индуктивности • Электрические, радиочастотные и электронные калькуляторы • Онлайн-конвертеры единиц

Этот калькулятор определяет взаимную индуктивность и эквивалентную индуктивность двух соединенных последовательно индукторов.

Пример: Рассчитайте эквивалентную индуктивность двух последовательно соединенных индукторов 10 мкГн и 5 мкГн с коэффициентом связи 0,5 и вспомогательной связью.

Вход

Индуктивность первой катушки, л ₁

генри (Гн) миллигенри (мГн) микрогенри (мкГн) наногенри (нГн) пикогенри (pH)

Индуктивность второй катушки, L

(мГн)

Коэффициент связи, к

0 ≤ к ≤ 1

Тип муфты

Противоположный

Вспомогательный

Выход

Взаимная индуктивность

0005 мри

Mry Индуктивность

л _т миллигенри (мГн)

Введите индуктивность, тип связи и значения коэффициента связи, выберите единицы индуктивности в генри (Гн), миллигенри (мГн), микрогенри (мкГн), наногенри (nH) или пикогенри (pH) и нажмите или коснитесь кнопки Calculate .

В калькуляторе сопротивлений мы показали, что полное сопротивление резисторов, соединенных последовательно, равно сумме их сопротивлений. То же можно сказать и об индукторах. Они подчиняются одному и тому же закону, и если несколько последовательно соединенных катушек индуктивности не связаны, их общая индуктивность равна сумме их индивидуальных индуктивностей. Если мы посмотрим на изображение нескольких последовательно соединенных индуктивностей (ниже), мы увидим, что их витки катушек суммируются, и их индуктивности также суммируются:

Это уравнение работает только при отсутствии взаимных индуктивностей между индукторами. .Обратите внимание, что это идеальная ситуация. В реальной жизни магнитные поля катушек взаимодействуют с обмотками соседних катушек, даже если расстояния между ними довольно большие. Если две индуктивности соединены последовательно и влияют друг на друга, возможны два случая в зависимости от того, как их магнитные поля влияют друг на друга. Если магнитный поток, создаваемый током, протекающим через обе катушки, имеет одинаковое направление для обеих катушек, говорят, что они кумулятивно связаны или помогают .Если, однако, магнитный поток, создаваемый током в обеих катушках, имеет противоположное направление, они называются дифференциально связанными или противоположными .

Вспомогательные индукторы, соединенные последовательно

Вспомогательные индукторы серии

Давайте рассмотрим два взаимно связанных индуктора L₁ и L₂, соединенных последовательно. Катушка индуктивности L₁ взаимно связана с индуктором L₂, и их взаимная индуктивность равна M₁₂. Катушка индуктивности L₂ взаимно связана с индуктором L₁, и их взаимная индуктивность равна M₂₁.Поскольку их магнитные поля помогают друг другу, их общая индуктивность составляет

. По взаимности M = M₁₂, поэтому мы имеем

, где M — взаимная индуктивность двух катушек, а L₁ и L₂ — самоиндукции две катушки. В нашем калькуляторе взаимной индуктивности мы показали, что взаимная индуктивность определяется как

Таким образом, в этом калькуляторе используется следующая формула для расчета полной индуктивности двух вспомогательных катушек L₁ и L₂ с коэффициентом связи k:

Противоположные индукторы

, соединенные последовательно Противоположные индукторы серии

Если два индуктора L₁ и L₂ подключены, как показано на этом рисунке, одинаковый ток течет через каждую катушку в противоположном направлении.Электродвижущая сила, которая появляется в индукторе L₁ за счет эффекта взаимной индуктивности индуктора L₂, противоположна ЭДС, вызванной самоиндукцией индуктора L₁. То же самое можно сказать и об ЭДС в индукторе L₂, вызванной магнитным полем, создаваемым индуктором L₁. Как мы видим, взаимные индуктивности нейтрализуют самоиндукции. Из-за этой отмены знак минус используется вместо знака плюс в уравнении для противоположных катушек индуктивности:

Это уравнение используется в этом калькуляторе для расчета общей индуктивности двух противоположных катушек L₁ и L₂ с учетом связи коэффициент k.

Катушки индуктивности на плате источника питания: трансформаторы обозначены красными стрелками, а дроссели — синими стрелками

Конструкция трансформатора и индуктора — Switchcraft

Максимальный магнитный поток в сердечнике затем рассчитывается как:

\ [\ Phi = B \ cdot A = 1,3 \ cdot 0,00135 = 0,00176 Вт \]

Максимальное изменение магнитного потока в сердечнике, однако, удваивается, так как сердечник может намагничиваться в обоих направлениях, то есть: \ (0,00352 Вт \).

Число витков, необходимых для получения этого потока, определяется как:

\ begin {уравнение *}
N = \ frac {V \ cdot t} {\ Phi}
\ end {уравнение *}

Где \ ( V \) — среднее напряжение, приложенное к обмотке.{\ pi} \]

\ (\ cos (0) = 1 \) и \ (\ cos (\ pi) = -1 \), следовательно:

\ [V_ {avg} = \ frac {2 V_p } {\ pi} \]

Для нашего примера среднее напряжение вычисляется как:

\ [V_ {avg} = \ frac {2 \ cdot 230 \ cdot \ sqrt {2}} {\ pi} = 207 V \]

Требуемое количество витков рассчитывается как:

\ [N = \ frac {207 \ cdot 0,01} {0,00352} = 588 \]

Следовательно, выраженное в единицах среднеквадратичного значения, мы имеем 0,39 вольт на оборот, или 2,56 витка на вольт. Для вторичной обмотки необходимое количество витков затем просто вычисляется путем умножения на 2.56 на желаемое напряжение.

Например, если требуемое вторичное напряжение равно \ (18 \; В \) (что может быть подходящим для линейного регулируемого источника питания 12 В), необходимое количество витков будет:

\ begin {уравнение *}
2,56 \ cdot 18 = 46
\ end {формула *}

Допустимая мощность

Вычислить мощность не так просто, как вычислить необходимое количество витков. Однако для небольших трансформаторов обычно безопасно делать некоторые предположения, основанные на опыте. Одно из таких предположений — эффективность 90%, т.е.2} {R} = \ frac {230 \ cdot 0.05} {8.59} = 15.4 Вт \]

Номинальная входная мощность трансформатора затем вычисляется как:

\ [P = \ frac {15.4} {0.1} = 154 Вт \]

Замечание о постоянном токе

Постоянный ток в трансформаторе обычно не очень хорошо. Он будет вносить вклад , а не в мощность, передаваемую трансформатором, но он будет способствовать магнитному потоку в сердечнике. Это означает, что ядро будет ближе к насыщению. Если трансформатор предназначен для работы на границе насыщения без постоянного тока, он будет насыщаться.

Если вы намереваетесь иметь постоянный ток в трансформаторе, вы должны применить те же конструктивные ограничения, что и при проектировании индуктора, предназначенного для постоянного тока. Обычно это означает добавление к сердцевине воздушного зазора для уменьшения эффективной проницаемости.

Индуктивность — это параметр любой электрической сети, описывающий ее способность сопротивляться изменению тока.

\ begin {Equation}
\ text {EMF} = -L \ frac {\ mathrm {d} i} {\ mathrm {d} t} \ Rightarrow L = — \ text {EMF} \ frac {\ mathrm { d} t} {\ mathrm {d} i}
\ end {формула}

Накопление энергии

Накопление энергии обычно нежелательно в трансформаторах, однако часто это основная цель индуктора.2
\ end {формула}

Где \ (I \) — ток намагничивания. Т.е. при вычислении накопителя энергии в трансформаторе он будет меньше полного тока.

Добротность

Добротность индуктора описывает устройство по отношению к идеальному компоненту. Это особенно важно в приложениях RF.

Добротность катушки индуктивности определяется по формуле:

\ begin {уравнение}
Q_L = \ frac {X_L} {R_L} = \ frac {2 \ pi f L} {R_L}
\ end {уравнение}

Следовательно, коэффициент качества зависит от частоты, при которой используется индуктор.2 \) площадь поперечного сечения. Лучший способ увеличить мощность — уменьшить индуктивность и, следовательно, увеличить ток в сердечнике. Помните, что мощность зависит от тока в квадрате.

При введении воздушного зазора в магнитопроводе эффективная проницаемость будет уменьшаться, и, следовательно, значение \ (A_L \) также уменьшится.

Энергия, запасенная в сердечнике, может быть извлечена второй обмоткой на том же сердечнике, как в топологии обратного хода. В качестве альтернативы его можно использовать, подключив катушку индуктивности к другой цепи после ее зарядки, как в топологиях понижающего / повышающего напряжения.

Тороиды

Тороидальные сердечники можно разделить на две основные категории в зависимости от материала, из которого они изготовлены. Сердечники из феррита и железного порошка.

Феррит имеет самую высокую проницаемость, но он не подходит для высоких частот. Кроме того, как мы видели, высокая проницаемость не всегда является преимуществом.

Полезный веб-сайт со спецификациями для различных тороидальных сердечников находится по адресу: http://toroids.info/

Как упоминалось ранее, во избежание насыщения сердечника необходимо ограничить плотность потока.Для ферритовых тороидальных сердечников это накладывает ограничение:

\ begin {уравнение}
\ frac {V} {2 f NA} \ le 0.3
\ end {уравнение}

Где \ (N \) — количество витков обмотки , \ (A \) — площадь поперечного сечения сердечника.

PPT — INDUCTANCE PowerPoint Presentation, скачать бесплатно

INDUCTANCE • План: • Индуктивность • Расчет индуктивности • Индукторы с магнитными материалами

Индуктор • Конденсатор накапливает энергию в электрическом поле • Индуктор накапливает энергию в электрическом поле • магнитное поле

Взаимная индуктивность Поток в контуре 2 пропорционален току в контуре 1.

Самоиндуктивность Изменяющийся ток не только индуцирует ЭДС в близлежащих контурах, но и вызывает ЭДС в самом контуре источника.

Ток i создает B внутри катушки • При изменении тока в той же катушке возникает ЭДС.

Единицы: вольт-секунда / ампер (Генри)

Расчет индуктивности NB называется потокосцеплением

Геометрическое свойство соломенного тока

903 n — количество витков на единицу длины.

Упражнение • Индуктивность замкнутой упакованной катушки на 400 витков составляет 8,0 мГн. Рассчитайте магнитный поток через катушку при токе 5 мА.  = 1 x 10-7 Вт

Упражнение • Круглая катушка имеет радиус 10,3 см и состоит из 34 тесно намотанных витков проволоки. Создаваемое извне магнитное поле 2,62 мТл перпендикулярно катушке. • (a) Если в катушке нет тока, каково количество магнитопроводов?

(б) Когда ток в катушке равен 3.77 A чистый поток в катушке исчезает. Найдите индуктивность катушки. L = 7,88 x 10-4H

Индуктивность тороида

Ток увеличивается или уменьшается? • Ответ: уменьшение

Каково значение индуктивности, если скорость изменения тока составляет 25 кА / с, а эдс 17 В. • Ответ: L = 6,8 x 10-4 H

Магнитные материалы в индукторах • Диэлектрическое вещество увеличивает емкость • Таким же образом, заполнение магнитным материалом может увеличить индуктивность.

m — проницаемость материала

Индуктивность увеличивается в m

Последовательные индукторы  = 1 + 2

параллельно • Ток через каждую катушку индуктивности добавляется к общему току.

Тороид с квадратным поперечным сечением 5,20 см и внутренним радиусом 15,3 см имеет 536 витков провода и пропускает ток 810 мА.Рассчитайте магнитный поток через сечение h = 5,20 см, a = 15,3 см, N = 536 b = (5,2 + 15,3) см,

Ответ: B = 1,32 x 10-6 Wb

Ток через катушку индуктивности 4,6 H изменяется со временем, как показано. Вычислить наведенную ЭДС во временных интервалах

(a) T = от 0 до t = 2 мс • Ans: 1,6 x 104 В

(a) T = 5 до t = 6 мс Ответ: 2,3 x 104 В

Коаксиальный кабель имеет внутренний провод радиуса a и внешнюю металлическую оболочку с внутренним радиусом b.Ток I течет по внутреннему проводу и обратно через оболочку. Какова собственная индуктивность единицы длины кабеля?

Найдите магнитный дипольный момент сферической оболочки Rd

Магнитное поле внутри соленоида имеет значение 6,5 x 10-4 Тл, когда соленоид пуст.