Реактивная составляющая тока. Активная и реактивная мощность в цепях переменного тока: особенности и способы повышения коэффициента мощности

Что такое активная и реактивная мощность в цепях переменного тока. Как они влияют на работу электрических систем. Какими способами можно повысить коэффициент мощности. Почему важно компенсировать реактивную мощность.

Понятие активной и реактивной мощности в цепях переменного тока

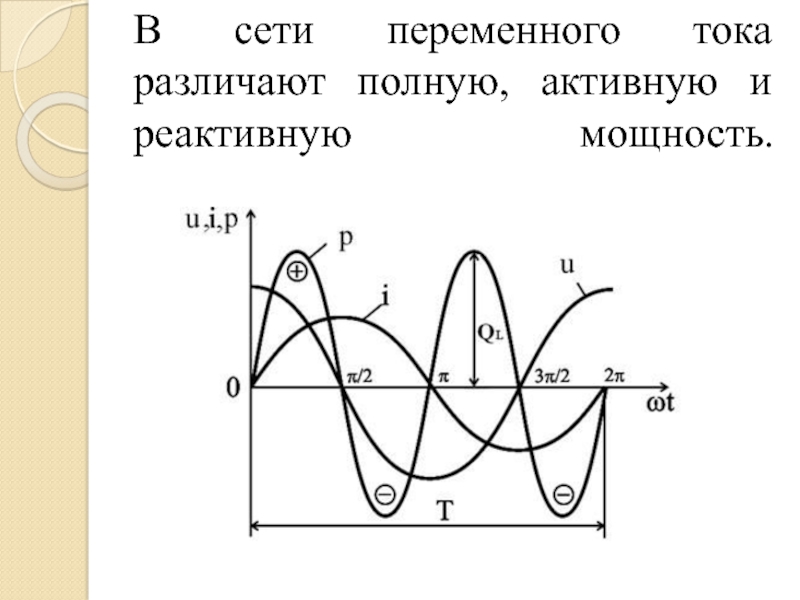
В цепях переменного тока различают два вида мощности — активную и реактивную. Активная мощность характеризует скорость преобразования электрической энергии в другие виды энергии (механическую, тепловую и т.д.). Реактивная мощность связана с обменом энергией между источником и магнитными и электрическими полями в цепи.

Активная мощность P измеряется в ваттах (Вт) и определяется по формуле:

P = U * I * cos φ

где U — действующее значение напряжения, I — действующее значение тока, cos φ — коэффициент мощности.

Реактивная мощность Q измеряется в вольт-амперах реактивных (ВАр) и определяется как:

Q = U * I * sin φ

Влияние реактивной мощности на работу электрических систем

Реактивная мощность, хоть и не совершает полезной работы, оказывает существенное влияние на работу электрических систем:

• Увеличивает потери в линиях электропередачи и трансформаторах
• Снижает пропускную способность сетей
• Вызывает дополнительные падения напряжения
• Ухудшает коэффициент мощности установок

Поэтому важной задачей является компенсация реактивной мощности для повышения энергоэффективности систем.

Коэффициент мощности и его значение

Коэффициент мощности cos φ показывает, какую долю полной мощности S составляет активная мощность P:

cos φ = P / S

Чем ближе cos φ к единице, тем эффективнее используется электроэнергия. Низкий коэффициент мощности приводит к перегрузке сетей и увеличению потерь.

Способы повышения коэффициента мощности

Основные методы повышения коэффициента мощности включают:

1. Установку компенсирующих устройств (конденсаторных батарей)
2. Замену недогруженных двигателей
3. Применение синхронных двигателей вместо асинхронных
4. Использование специальных компенсаторов реактивной мощности

Компенсация реактивной мощности с помощью конденсаторных батарей

Наиболее распространенным способом компенсации является установка конденсаторных батарей параллельно нагрузке. Конденсаторы генерируют реактивную мощность, противоположную по знаку индуктивной мощности нагрузки.

Мощность конденсаторной батареи выбирают из условия:

Qc = P * (tg φ1 — tg φ2)

где φ1 — начальный угол сдвига фаз, φ2 — требуемый угол после компенсации.

Экономический эффект от компенсации реактивной мощности

Компенсация реактивной мощности позволяет получить следующие преимущества:

• Снижение потерь электроэнергии в сетях на 10-20%
• Увеличение пропускной способности линий и трансформаторов
• Улучшение качества напряжения у потребителей
• Уменьшение платы за потребляемую реактивную энергию

Срок окупаемости установок компенсации реактивной мощности обычно составляет 1-2 года.

Выбор мощности компенсирующих устройств

Мощность компенсирующих устройств выбирают исходя из следующих соображений:

1. Достижение заданного коэффициента мощности (обычно 0,92-0,95)
2. Снижение потерь электроэнергии до экономически обоснованного уровня
3. Обеспечение требуемых уровней напряжения у потребителей
4. Повышение пропускной способности элементов сети

Требуемую мощность конденсаторов можно определить по формуле:

Qc = P * (tg φ1 — tg φ2)

где P — активная мощность нагрузки, φ1 и φ2 — углы сдвига фаз до и после компенсации.

Автоматическое регулирование мощности компенсирующих устройств

Для обеспечения оптимальной компенсации при переменных нагрузках применяют автоматические регуляторы. Они включают/отключают секции конденсаторных батарей в зависимости от текущего коэффициента мощности.

Основные типы регуляторов:

• По току компенсации
• По напряжению
• По коэффициенту мощности
• По времени суток

Автоматическое регулирование позволяет поддерживать заданный коэффициент мощности и избежать перекомпенсации.

Компенсация реактивной мощности в распределительных сетях

В распределительных сетях 0,4-10 кВ компенсацию осуществляют следующими способами:

1. Индивидуальная компенсация у отдельных электроприемников
2. Групповая компенсация для группы потребителей
3. Централизованная компенсация на шинах подстанций

Выбор способа компенсации определяется технико-экономическим расчетом. Индивидуальная компенсация наиболее эффективна, но и наиболее затратна.

Различные формы записи комплексных величин. Активная и реактивная составляющие напряжения и тока. Соединение сопротивлений. Мощности. Векторные диаграммы

1. Приборы, подключенные к цепи (рис. 2.20), дали следующие показания: U=65 В, I=5 А, Р=300 Вт.
Вычислить комплексные сопротивления и проводимости цепи для случаев: .

Решение:
Модуль сопротивления и его аргумент определяют по формулам:

Искомые комплексные сопротивления и проводимости цепи:

2. Комплексное напряжение и ток пассивного двухполюсника равны:

Вычислить комплексные сопротивление , проводимость и указать, каковы эквивалентные параметры двухполюсника. Чему равен сдвиг фаз между напряжением и током? Определить активную и реактивную составляющие напряжения и тока, активную, реактивную и полную мощности. Построить векторную диаграмму напряжений и токов.

Решение:
Запишем комплексные напряжение и ток в показательной форме и изобразим их на векторной диаграмме (рис. 2.21):

Определим комплексное сопротивление:

Следовательно, эквивалентными параметрами цепи являются резистивное R=2,4 0м и индуктивное сопротивления, соединенные последовательно.
Комплексную проводимость цепи определяют по формуле:

Эквивалентные параметры цепи: резистивная G=0,15 См и реактивная (индуктивная) В=0,2 См проводимости, соединенные параллельно.
Угол сдвига фаз между напряжением и током (он же аргумент )
Резистивные и реактивные составляющие напряжения и тока:

Необходимо обратить внимание на то, что вещественные и мнимые составляющие комплексных напряжения и тока в общем случае отличаются от их активных и реактивных составляющих.
Активная, реактивная и полная мощности:

Те же мощности можно определить по формуле:

3. Последовательно с катушкой, параметры которой R=3 Ом, L=25 мГн, включен реостат сопротивлением (рис. 2.23, а). Определить напряжение на катушке , его сдвиг фазы по отношению к приложенному напряжению, а также мощность, расходуемую в катушке. К цепи подведено напряжение U=120 В, f=50 Гц. Построить векторную диаграмму напряжений и тока.

Решение:
Комплексное сопротивление всей цепи

Направим вектор U по оси вещественных чисел, т. е.
Комплексный ток

Напряжение на катушке

Оно сдвинуто по фазе по отношению к приложенному напряжению на угол . Векторная диаграмма приведена на рис. 2.23, б.
Мощность, расходуемая в катушке

Та же мощность может быть подсчитана и другим путем:

 

4. В цепи (рис. 2.31, в) дано:

Определить токи активные и реактивные мощности всей цепи и отдельных ветвей. Построить векторную диаграмму.

Решение:
Полное сопротивление цепи:

В неразветвленной части цепи проходит ток

Токи в параллельных ветвях могут быть выражены через ток в неразветвленной части цепи:

Токи можно найти и другим путем:

Найдем мощности (активные) всей цепи и отдельных ее ветвей:

Проверка показывает, что .
Определим реактивные мощности всей цепи и отдельных ее ветвей:

Учитывая, что реактивные мощности катушек положительны, а реактивная мощность конденсатора отрицательна, получим .
На рис. 2.31. б приведена векторная диаграмма. Порядок ее построения следующий: по результатам расчетов отложены векторы токов , затем по направлению отложен вектор и перпендикулярно ему в сторону опережения — вектор . Их сумма дает вектор . Далее в фазе с построен вектор и перпендикулярно ему в сторону отставания (так как отрицательно) вектор , а их сумма дает вектор напряжения на параллельном участке . Тот же вектор можно получить, если в фазе с отложить и к нему прибавить вектор опережающий на . Сумма векторов дает вектор приложенного напряжения.

5. Параметры цепи (рис. 2.35): . Определить значение и характер сопротивления , если известно, что оно чисто реактивно и через него проходит ток , а напряжение, приложенное к цепи, .

Решение:
Сопротивление разветвленной части цепи

Общее сопротивление цепи . Оно может быть выражено и так: . Отсюда .
Возможны два решения задачи: искомое сопротивление имеет индуктивный характер и равно либо , либо .

 

6. Каким резистивным сопротивлением следует зашунтировать сопротивление , чтобы ток, проходящий через , отставал от приложенного напряжения U на 90° (рис. 2.36, а)? Сопротивления: . Построить векторную диаграмму.

Решение:
Обозначим: тогда

Ток в неразветвленной части цепи

Через сопротивление проходит ток

Для того чтобы ток отставал по фазе от напряжения U на 90°, знаменатель последнего выражения должен быть чисто мнимым (по знаку положительным) значением.
Выпишем этот знаменатель и выделим в нем вещественную и мнимую составляющие

Вещественную часть полученного выражения приравняем нулю

отсюда

Векторная диаграмма представлена на рис. 2.36, б.

7. Вычислить резистивное сопротивление , которое надо подключить к зажимам 2—2′ цепи (рис. 2.41), чтобы отношение напряжения на этом сопротивлении к напряжению на входе цепи равнялось Н. Числовой расчет проделать при .

Решение:
Входное сопротивление всей цепи

где

Вычислим напряжение , для чего сначала найдем токи

Отсюда определим отношение комплексных напряжений

и отношение модулей напряжений

Подставляя числовые значения, после простых преобразований получим квадратное уравнение относительно .
Решение этого уравнения дает значение искомого сопротивления

 

Активные и реактивные составляющие токов и напряжений

 

При расчете электрических цепей переменного тока реальные элементы цепи (при­емники, источники) заменяются эквивалентными схемами замещения, состоящими из ком­бинации идеальных схемных элементов

R, L и С.

Пусть некоторый приемник энергии носит в целом активно-индуктив­ный характер (например, электродвигатель). Такой приемник может быть пред­ставлен двумя простей­шими схемами замещения, состоящими из 2-х схемных элементов R и L: а) последовательной (рис. 51а) и б) параллельной (рис. 51б):

 

Обе схемы будут эквивалентны друг другу при условии равенства пара­метров ре­жима на входе: , .

Для последовательной схемы (рис. 51а) справедливы соотношения:

,

.

Для параллельной схемы (рис. 51б) справедливы соотношения:

,

.

Сравнивая правые части уравнений для U и I, получим соотношения между пара­метрами эквивалентных схем:

, , , .

Из анализа полученных уравнений следует сделать вывод, что в общем случае и и соответственно и , как это имеет место для цепей постоян­ного тока.

Математически любой вектор можно представить состоящим из суммы нескольких векторов или составляющих.

Последовательной схеме замещения соответствует представление век­тора напряже­ния в виде суммы двух составляющих: активной составляющей U_а, совпадающей с векто­ром тока I, и реактивной составляющей U_р, перпенди­кулярной к вектору тока (рис. 52а):

 

 

 

Из геометрии рис. 52а следуют соотношения: , , . Треугольник, составленный из векто­ров , , получил назва­ние треугольника напряжений.

Если стороны треугольника напряжений разделить на ток I, то полу­чится новый треугольник, подобный исходному, но сторонами которого явля­ются полное сопротивление

Z, активное сопротивление R и реактивное сопро­тивление X. Треугольник со сторонами Z, R, X называется треугольником со­противлений (рис. 52б). Из треугольника сопротивлений следуют соотношения: R=Z×cosφ, X=Z×sinφ, , .

Параллельной схеме замещения соответствует представление вектора тока в виде суммы двух составляющих: активной составляющей I_а, совпадаю­щей с вектором напряже­ния U, и реактивной составляющей I_р, перпендикуляр­ной к вектору U (рис. 53а):

 

Из геометрии рисунка следуют соотношения:

, , .

Треугольник, составленный из векторов получил название треугольника токов.

Если стороны треугольника токов разделить на напряжение U, то полу­чится новый треугольник, подобный исходному, но сторонами которого явля­ются проводимости: пол­ная –

Y, активная — G, реактивная – B (рис. 53б). Тре­угольник со сторонами Y, G, B называется треугольником проводимостей. Из треугольника проводимостей следуют соотношения:

, , , .

Разложение напряжений и токов на активные и реактивные составляющие является математическим приемом и применяется на практике для расчета не­сложных цепей пере­менного тока.

 

10. Передача энергии от активного двухполюсника (источника) к пас­сивному двухполюснику (приемнику)

 

Двухполюсником называется устройство или часть схемы (цепи) с двумя выводами (полюсами). Если внутри двухполюсника содержатся источники энергии, то он называется активным (A), в противном случае – пассивным (П).

Энергетические характеристики передачи энергии от активного двухпо­люсника (источника) к пассивному двухполюснику (приемнику) на переменном токе зависят от со­отношения параметров приемника и источника между собой (рис. 54)

 

 

По закону Ома ток в схеме равен:

.

Активная мощность приемника:

.

Активная мощность источника: P_E=E×I.

При постоянных параметрах источника энергии активная мощность приемника за­висит от его параметров: . Исследуем эту функцию на максимум при измене­нии отдельных параметров.

Условие первое: X₂ = var, R₂=const:

или .

Максимум мощности приемника имеет место при условии равен­ства реактив­ных сопротивлений приемника и источника по модулю и противо­положности их по знаку, например, если реактивное сопротивление источника носит индуктивный характер, то реак­тивное сопротивление приемника должно быть емкостным, и наоборот.

Условие второе: R₂ = var, X₂ = const.

или .

Максимум мощности приемника имеет место при равенстве активных сопротивле­ний приемника и источника.

Абсолютный максимум мощности приемника наблюдается при выпол­нении обоих условий и равен:

.

В режиме максимума потребляемой мощности работают приемники в ли­ниях связи.

Коэффициент полезного действия передачи энергии от источника к при­емнику равен отношению активных мощностей и не зависит от величины их реактивных сопротивлений.

В режиме абсолютного максимума мощности приемника КПД составляет только 0,5. Линии электропередачи (ЛЭП) работают с КПД h = 0,90÷0,95, что соот­ветствует соотношению активных сопротивлений приемника и источника (ге­нератора + ЛЭП) R₂/R₁=10÷20.

На графической диаграмме рис. 2 показаны энергетические характери­стики передачи энергии при R₂= var, Х₂=const в функции тока:

P₂, h = f(I).

 

 

Узнать еще:

ПОВЫШЕНИЕ КОЭФФИЦИЕНТА МОЩНОСТИ

⇐ ПредыдущаяСтр 8 из 14Следующая ⇒

Итак, только активная составляющая тока определяет преобразование электроэнергии в другие виды энергии, т. е. позволяет количественно оценить совершаемую работу. Реактивная же составляющая тока никакой работы не производит. Однако при ее наличии увеличивается полный ток.

Рис. 8.5. Электрическая цепь с параллельным включением конденсатора
для повышения коэффициента мощности:
а ¾ схема; б ¾ векторная диаграмма токов

Представим электроприемник, потребляющий активную и индуктивную составляющие тока, схемой последовательного соединения элементов R_пр и L_пр (рис. 8.5, а). На векторной диаграмме (рис. 8.5, б) вектор тока приемника составляет с вектором напряжения угол j_пр, причем

В отсутствие емкости С, включенной параллельно с приемником , ток в линии передачи равен току приемника. Если в проводах линии передачи (сопротивление которых R) протекает ток , то теряемая в них мощность Р_п.л =RI².

Так как в данном случае

I_л = I_пр = P_пр / (Uсos j_пр),

то при постоянной мощности приемника и постоянном питающем напряжении (Р_пр = const и U = const) с уменьшением коэффициента мощности Сos j_пр увеличиваются ток, в линии, а следовательно, и потеря мощности

P_п.л = (P²_пр R/U²) (1/cosj_пр).

Таким образом, для уменьшения потерь мощности в передающих устройствах необходимо увеличивать коэффициент мощности приемников электроэнергии.

Каждому промышленному предприятию задают то средневзвешенное значение коэффициента мощности (реактивной мощности), которое должно быть обеспечено. Получению заданного коэффициента мощности способствует правильный выбор электрооборудования. Однако при этом всегда необходимо принимать дополнительные меры, например, использовать батареи конденсаторов и т. д.

Конденсаторы емкостью С включают параллельно электроприемнику (рис. 8.5, а). Ток конденсатора является практически чисто реактивным, опережающим напряжение на угол p/2 (рис. 8.5, б). Этот ток компенсирует реактивную индуктивную составляющую тока приемника, в результате чего общая реактивная составляющая тока уменьшается.

При емкости конденсатора, равной С, и токе ток в линии , или I_л <I_пр.

Угол сдвига фаз jмежду напряжением и током уменьшился, а коэффициент мощности увеличился (cоs j₂ >cоs j_пр).

С увеличением емкости конденсатора ток I_С = В_СU = w CU увеличивается так, что при некотором значении емкости С_рез можно получить равенство I_С = I_L (режим резонанса токов). В этом случае реактивная составляющая тока приемника I_L полностью компенсируется и ток в линии достигает минимального значения, равного активной составляющей тока приемника I_а.пр (рис. 8.5, б). При дальнейшем увеличении емкости конденсаторов I_С > I_L и реактивная составляющая тока в линии, а, следовательно, и полный ток в ней увеличиваются. Наступает режим перекомпенсации, когда реактивная составляющая тока в линии носит емкостной характер.

На рис. 8.6 показано, как изменяется ток I_л при изменении емкости С конденсатора при Р_пр = const и U = const. Сначала с ростом С ток I_л уменьшается, достигая минимума в режиме резонанса токов, а затем снова начинает увеличиваться. Коэффициент мощности изменяется в обратном порядке, достигая максимума при полной компенсации (cos = 1 при I_С = I_L). Следует помнить, что при подключении конденсаторов потребляемая реактивная индуктивная мощность электроприемника остается неизменной, но ее источником становится батарея конденсаторов, установленная вблизи приемника. В результате в линии передачи реактивные токи уменьшаются.

Рис. 8.6. Зависимость тока в линии и коэффициента мощности от емкости конденсаторов:
I ¾ область недокомпенсации, II ¾ область перекомпенсации

Для обеспечения заданного значения коэффициента мощности необходимо устанавливать конденсаторы определенной мощности или емкости. Если электроприемники имеют мощность Р = const и cоsj_пр, то они потребляют из сети реактивную индуктивную мощность Q_пр = P tgj_пр. При заданном значении cоsj₂, которое должно обеспечить предприятие (cоsj₂ > cоsj_пр), потребляемая реактивная мощность Q₂ = P tgj₂.

Разность реактивных мощностей Q_пр — Q₂ компенсируется емкостной реактивной мощностью конденсаторов

Q_c = Q_пр — Q₂ = Р(tgj_пр — tgj₂). (8.8)

Реактивную мощность конденсаторов можно также определить не формуле:

Q_c = B_CU² = w CU². (8.9)

Приравнивая правые части уравнений (8.8) и (8.9), получим

C = P (tgj_пр — tgj₂) / (2pfU²).

При этом емкость выражается в фарадах, если мощность выражена в ваттах, а напряжение ¾ в вольтах.

Для полной компенсации (j₂ = 0) необходимо, чтобы С = Ptgj_пр / (2pfU²).

Таким образом, на лекции рассмотрены вопросы, характеризующие мощность в однофазной цепи синусоидального тока, ее вариации, коэффициент мощности и способы его повышения.

 

Рекомендация:

Для самоконтроля полученных знаний выполните тренировочные задания
из набора объектов к текущему параграфу

 

Рекомендуемые страницы:

Определение тока холостого хода трансформатора

Электротехника Определение тока холостого хода трансформатора

просмотров — 853

Ток первичной обмотки трансформатора, возникающий при холостом ходе при номинальном синусоидальном напряжении и номинальной частоте, принято называть током холостого хода.

При расчет тока холостого хода трансформатора отдельно определяют его активную и реактивную составляющие.

Активная составляющая тока холостого хода вызывается наличием потерь холостого хода. Активная составляющая тока, А,

I_х.а = Р_х / (mU_ф),

где Р_х – потери холостого хода, Вт; U_ф – фазное напряжение первичной обмотки, В.

Обычно определяют не абсолютное значение тока холостого хода и его составляющих, а их относительное значение по отношению к номинальному току трансформатора i_оа, i_0р, i_о, выражая их в процентах номинального тока.

Тогда активная составляющая, %,

,

или

i_оа = Р_х /(10S),

где S – мощность трансформатора, кВ· А; Р_х – потери холостого хода, Вт.

Расчет реактивной составляющей тока холостого хода усложняется наличием в магнитной цепи трансформатора немагнитных зазоров. При этом расчете магнитная система трансформатора разбивается на четыре участка – стержни, ярма, за исключением углов магнитной системы, углы и зазоры. Для каждого из этих участков подсчитывается требуемая намагничивающая мощность, суммируемая затем по всœей магнитной системе. Также как и потери, реактивная составляющая тока холостого хода зависит от базовых магнитных свойств стали магнитной системы и ряда конструктивных и технологических факторов, оказывающих на эту составляющую существенно большое влияние, чем на потери.

Немагнитные зазоры в шихтованной магнитной системе имеют особую форму – в месте зазора стыки пластин чередуются со сквозными пластинами. Магнитный поток вместе стыка проходит частично через зазор между пластинами и частично – через сосœеднюю сквозную пластину. Индукция в сквозных пластинах в зоне, лежащей против стыков, увеличивается. Вместе с этим происходит местное увеличение потерь и реактивной составляющей тока холостого хода, однако общая намагничивающая мощность для зазора оказывается существенно меньшей, чем при стыке частей стыковой магнитной системы.

В практике расчета намагничивающая мощность для зазоров шихтованных магнитных систем, собираемых из пластин горячекатаной или холоднокатаной стали, определяется для условного немагнитного зазора, по площади сечения стали в данном стыке, ᴛ.ᴇ. по активному сечению стержня или ярма, и по удельной намагничивающей мощности, отнесенной к единице площади активного сечения, q_з, В∙А/м², и определяемой экспериментально для каждой марки стали.

Удельные намагничивающие мощности для стали марок 3404 и 3405 приведены в табл.26.

Таблица 26. Полная удельная намагничивающая мощность в стали q и в зоне шихтованного стыка q₃ для холоднокатаной стали марок 3404 и 3405 толщиной 0,35 и 0,30 мм при различных индукциях и f = 50 Гц

В, Тл	Марка стали и ее толщина	qз, В∙А/м2
3404, 0,35 мм	3404, 0,30 мм	3405, 0,35 мм	3405, 0,30 мм
1,30 1,32 1,34 1,36 1,38   1,40 1,42 1,44 1,46 1,48   1,50 1,52 1,54 1,56 1,58   1,60 1,62 1,64 1,66 1,68   1,70 1,72 1,74 1,76 1,78   1,80 1,82 1,84 1,86 1,88	0,900 0,932 0,964 0,996 1,028   1,060 1,114 1,168 1,222 1,276   1,330 1,408 1,486 1,575 1,675   1,775 1,958 2,131 2,556 3,028   3,400 4,480 5,560 7,180 9,340   11,500 20,240 28,980 37,720 46,460	0,870 0,904 0,938 0,972 1,006   1,040 1,089 1,139 1,188 1,238   1,289 1,360 1,431 1,511 1,600   1,688 1,850 2,012 2,289 2,681   3,073 4,013 4,953 6,364 8,247   10,130 17,670 25,210 32,750 40,290	0,860 0,892 0,924 0,956 0,988   1,020 1,065 1,110 1,156 1,210   1,246 1,311 1,376 1,447 1,524   1,602 1,748 1,894 2,123 2,435   2,747 3,547 4,347 5,551 7,161   8,770 15,110 21,450 27,790 34,130	0,850 0,880 0,910 0,940 0,970   1,000 1,041 1,082 1,123 1,161   1,205 1,263 1,321 1,383 1,449   1,526 1,645 1,775 1,956 2,188   2,420 3,080 3,740 4,736 6,068   7,400 12,540 17,680 22,820 27,960

При экспериментальных исследованиях стали удельная намагничивающая мощность, отнесенная к 1 кг стали или к 1 м² площади зазора q, может определяться как полная мощность или как ее реактивная составляющая. В табл. 26 приведены значения полной удельной намагничивающей мощности.

Полная намагничивающая мощность трансформатора, В∙А, для магнитной системы может быть определœена из следующего выражения:

Q_x = Q_x.c + Q_x.я + Q_x.з = q_cG_c + q_яG_я + ∑n_зq_зП_з,

Где q_c и q_я – удельные намагничивающие мощности для стержня и ярма, определяемые по табл.26 для холоднокатаной стали в зависимости от соответствующих индукций, В∙А/кг; G_c и G_я – масса стали в стержнях и ярмах, кг; n_з – число немагнитных зазоров (стыков) в магнитной системе; q_з – удельная намагничивающая мощность, В∙А/м², для немагнитных зазоров, определяемая для индукции в стержне по табл.26; П_з площадь зазора, ᴛ.ᴇ. активное сечение стержня или ярма, м².

При расчете тока холостого хода для плоской стержневой шихтованной магнитной системы, собранной из пластин холоднокатаной анизотропной стали, также как и при расчете потерь холостого хода, приходиться считаться с факторами конструктивными – форма стыков стержней и ярм, форма сечения ярма, способ прессовки стержней и ярм – и технологическими – резка рулонов стали на пластины, удаление заусенцев, отжиг пластин, покрытие их лаком, прессовка магнитной системы при сборке и перешихтовка верхнего ярма при установке обмоток.

От воздействия этих факторов реактивная составляющая тока холостого хода увеличивается при несовпадении линий магнитной индукции и прокатки стали, а также в результате механических воздействий при заготовке пластин и сборке остова. Отжиг пластин ведет к уменьшению реактивной составляющей тока холостого хода. На токе холостого хода влияние этих факторов сказывается более резко, чем на потерях.

Полный фазный ток холостого хода, А,

I_x = Q_x/(mU_ф).

Относительное значение тока холостого в процентах номинального тока

i₀ = Q_x/10S.

Активная составляющая тока холостого хода, фазное значение, А,

I_x.а = Р_х/(mU_ф)

и в процентах номинального тока

i_оа = Р_х/(10S).

Реактивная составляющая тока холостого хода, А,

I_x.р =

и в процентах номинального тока

i_op =

Полученное значение тока холостого хода должно быть сверено с предельно допустимым значением по ГОСТ, техническим условиям или заданию на расчет трансформатора. Отклонение расчетного значения тока холостого хода от заданного гарантийного не следует допускать более чем на половину допуска разрешенного ГОСТ (по ГОСТ 11677-85 разрешенный допуск +30%).

При расчете тока холостого хода по намагничивающей мощности определяется среднее значение, тока холостого хода для всœех стержней трансформатора. В симметричных магнитных системах, к примеру однофазных, или пространственных, это среднее значение будет совпадать с действительным значением тока холостого хода для каждого стержня.

В несимметричной магнитной системе ток холостого хода в обмотке среднего стержня меньше, чем в обмотках крайних стержней. Током холостого хода трансформатора в этом случае считается среднее значение токов трех фаз.

Читайте также

— Определение тока холостого хода трансформатора

Ток первичной обмотки трансформатора, возникающий при холостом ходе при номинальном синусоидальном напряжении и номинальной частоте, называется током холостого хода. При расчет тока холостого хода трансформатора отдельно определяют его активную и реактивную… [читать подробенее]

Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока. (Лекция №7)

Передача энергии w по электрической цепи (например, по линии электропередачи), рассеяние энергии, то есть переход электромагнитной энергии в тепловую, а также и другие виды преобразования энергии характеризуются интенсивностью, с которой протекает процесс, то есть тем, сколько энергии передается по линии в единицу времени, сколько энергии рассеивается в единицу времени. Интенсивность передачи или преобразования энергии называется мощностью р. Сказанному соответствует математическое определение:

.

(1)

Выражение для мгновенного значения мощности в электрических цепях имеет вид:

.

(2)

Приняв начальную фазу напряжения за нуль, а сдвиг фаз между напряжением и током за , получим:

.

(3)

Итак, мгновенная мощность имеет постоянную составляющую и гармоническую составляющую, угловая частота которой в 2 раза больше угловой частоты напряжения и тока.

Когда мгновенная мощность отрицательна, а это имеет место (см. рис. 1), когда u и i разных знаков, т.е. когда направления напряжения и тока в двухполюснике противоположны, энергия возвращается из двухполюсника источнику питания.

Такой возврат энергии источнику происходит за счет того, что энергия периодически запасается в магнитных и электрических полях соответственно индуктивных и емкостных элементов, входящих в состав двухполюсника. Энергия, отдаваемая источником двухполюснику в течение времени t равна .

Среднее за период значение мгновенной мощности называется активной мощностью .

Принимая во внимание, что , из (3) получим:

.

(4)

Активная мощность, потребляемая пассивным двухполюсником, не может быть отрицательной (иначе двухполюсник будет генерировать энергию), поэтому , т.е. на входе пассивного двухполюсника . Случай Р=0, теоретически возможен для двухполюсника, не имеющего активных сопротивлений, а содержащего только идеальные индуктивные и емкостные элементы.

1. Резистор (идеальное активное сопротивление).

Здесь напряжение и ток (см. рис. 2) совпадают по фазе , поэтому мощность всегда положительна, т.е. резистор потребляет активную мощность

2. Катушка индуктивности (идеальная индуктивность)

При идеальной индуктивности ток отстает от напряжения по фазе на . Поэтому в соответствии с (3) можно записать
.

Участок 1-2: энергия , запасаемая в магнитном поле катушки, нарастает.

Участок 2-3: энергия магнитного поля убывает, возвращаясь в источник.

3. Конденсатор (идеальная емкость)

Аналогичный характер имеют процессы и для идеальной емкости. Здесь . Поэтому из (3) вытекает, что . Таким образом, в катушке индуктивности и конденсаторе активная мощность не потребляется (Р=0), так как в них не происходит необратимого преобразования энергии в другие виды энергии. Здесь происходит только циркуляция энергии: электрическая энергия запасается в магнитном поле катушки или электрическом поле конденсатора на протяжении четверти периода, а на протяжении следующей четверти периода энергия вновь возвращается в сеть. В силу этого катушку индуктивности и конденсатор называют реактивными элементами, а их сопротивления Х_L и Х_С , в отличие от активного сопротивления R резистора, – реактивными.

Интенсивность обмена энергии принято характеризовать наибольшим значением скорости поступления энергии в магнитное поле катушки или электрическое поле конденсатора, которое называется реактивной мощностью.

В общем случае выражение для реактивной мощности имеет вид:

(5)

Она положительна при отстающем токе (индуктивная нагрузка- ) и отрицательна при опережающем токе (емкостная нагрузка- ). Единицу мощности в применении к измерению реактивной мощности называют вольт-ампер реактивный (ВАр).

В частности для катушки индуктивности имеем:

, так как .

.

Из последнего видно, что реактивная мощность для идеальной катушки индуктивности пропорциональна частоте и максимальному запасу энергии в катушке. Аналогично можно получить для идеального конденсатора:

.

Полная мощность

Помимо понятий активной и реактивной мощностей в электротехнике широко используется понятие полной мощности:

.

(6)

Активная, реактивная и полная мощности связаны следующим соотношением:

.

(7)

Отношение активной мощности к полной называют коэффициентом мощности. Из приведенных выше соотношений видно, что коэффициент мощности равен косинусу угла сдвига между током и напряжением. Итак,

.

(8)

Комплексная мощность

Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:

,

(9)

где — комплекс, сопряженный с комплексом .

.

Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует (активно-индуктивная нагрузка), для которого имеем:

Применение статических конденсаторов для повышения cos

Как уже указывалось, реактивная мощность циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению в силовых электрических цепях.

Следует указать, что подавляющее большинство потребителей (электродвигатели, электрические печи, другие различные устройства и приборы) как нагрузка носит активно-индуктивный характер.

Если параллельно такой нагрузке (см. рис. 5), включить конденсатор С, то общий ток , как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е. увеличивается, а общая величина тока (а следовательно, потери) уменьшается при постоянстве активной мощности . На этом основано применение конденсаторов для повышения .

Какую емкость С нужно взять, чтобы повысить коэффициент мощности от значения до значения ?

Разложим на активную и реактивную составляющие. Ток через конденсатор компенсирует часть реактивной составляющей тока нагрузки :

;

(10)

;

(11)

.

(12)

Из (11) и (12) с учетом (10) имеем

,

но , откуда необходимая для повышения емкость:

.

(13)

Баланс мощностей

Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.

а) Постоянный ток

Для любой цепи постоянного тока выполняется соотношение:

(14)

Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.

Следует указать, что в левой части (14) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).

б) Переменный ток.

Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.

(15)

В ТОЭ доказывается (вследствие достаточной громоздкости вывода это доказательство опустим), что баланс соблюдается и для реактивных мощностей:

,

(16)

где знак “+” относится к индуктивным элементам , “-” – к емкостным .

Умножив (16) на “j” и сложив полученный результат с (15), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности):

или

.

Литература

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. Что такое активная мощность?
2. Что такое реактивная мощность, с какими элементами она связана?
3. Что такое полная мощность?
4. Почему необходимо стремиться к повышению коэффициента мощности ?
5. Критерием чего служит баланс мощностей?
6. К источнику с напряжением подключена активно-индуктивная нагрузка, ток в которой . Определить активную, реактивную и полную мощности.

Ответ: Р=250 Вт; Q=433 ВАр; S=500 ВА.

7. В ветви, содержащей последовательно соединенные резистор R и катушку индуктивности L, ток I=2 A. Напряжение на зажимах ветви U=100 B, а потребляемая мощность Р=120 Вт. Определить сопротивления R и XL элементов ветви.

Ответ: R=30 Ом; XL=40 Ом.

8. Мощность, потребляемая цепью, состоящей из параллельно соединенных конденсатора и резистора, Р=90 Вт. Ток в неразветвленной части цепи I1=5 A, а в ветви с резистором I2=4 A. Определить сопротивления R и XC элементов цепи.

Ответ: R=10 Ом; XС=7,5 Ом.

Барданов А.И. Вектор мгновенной реактивной мощности в трехфазных несимметричных сетях

Барданов Алексей Игоревич
Национальный Минерально-Сырьевой Университет «Горный», г.Санкт-Петербург
кафедра электротехники, электромеханики, электроэнергетики

Bardanov Alexey Igorevich
St.Petersburg National Mining-Resorses University
department of electrical engineering, electro mechanic, electrical energy

Библиографическая ссылка на статью:
Барданов А.И. Вектор мгновенной реактивной мощности в трехфазных несимметричных сетях // Современные научные исследования и инновации. 2015. № 9. Ч. 1 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2015/09/57392 (дата обращения: 08.06.2021).

Известно, что реактивная мощность трехфазной системы сложная величина, которая зависит от характера нагрузки, симметрии, наличия или отсутствия нулевого провода, уровня искажений в токе и питающем напряжении. Понятие реактивной мощности однозначно определено для симметричных систем в синусоидальном режиме. Однако такой режим, практически не встречается.

Для построения эффективных систем управления потоками мощности требуется точно определить причины возникновения неактивных токов для выбора средств компенсации. В качестве основы для анализа токов реальных систем можно использовать теорию мгновенных мощностей [1,2,3].

Основы были заложены Фризе в 1936 г.[4]. Было предложено рассматривать ток в цепи как сумму активного и неактивного токов в функции от времени, но на момент разработки теория Фризе не нашла применения и в течение 60 лет оставалась неизвестной, пока в конце прошлого столетия ее не начали использовать для управления активными фильтрами.

,	(1)
где: – активная составляющая тока,  – неактивная составляющая тока.

Активная составляющая тока , согласно теории, пропорциональна активной мощности и в фазе с напряжением, что значит, что неактивная составляющая тока  полезной работы не выполняет и является причиной дополнительных потерь в линии.

Для трехфазной цепи можно представить напряжение и ток трехкомпонентными векторами, координаты которых пропорциональны токам и напряжениям в фазах, а скалярное произведение равно сумме мгновенных мощностей трех фаз:

,	(2)
где:  – фазные токи,  – орты системы координат.
,	(3)
где:  – фазные напряжения.
,	(4)
где: p – мгновенная мощность системы.

Как и в теории Фризе ток системы делится на две составляющие: векторы активного и неактивного тока. Активная составляющая является проекцией вектора тока на вектор напряжения, неактивная составляющая находится к вектору напряжения под прямым углом, образуя с активной составляющей и вектором тока прямоугольный треугольник:

,	(5)
где:  – вектор активного тока системы,  – вектор неактивного тока системы.

Неактивная составляющая в любой момент времени определяется помощью вектора мгновенной реактивной мощности (МРМ), который в свою очередь определяется как векторное произведение векторов тока и напряжения системы:

,	(6)
где: q – вектор МРМ системы.

 

Рассмотрим два случая активной трехфазной несимметричной нагрузки с нулевым проводом и без него.

Рисунок 1 – Годографы векторов напряжения и тока трехфазной системы с нулевым проводом и координаты вектора мгновенной реактивной мощности при активной несимметричной нагрузке

Рисунок 1 отражает изменение координат векторов напряжения и тока системы во времени, представлены годографы векторов за три четверти периода, чтобы лучше показать положение векторов в пространстве друг относительно друга. Изменение вектора мгновенной реактивной мощности можно проследить по изменению его координат во времени (на рисунке справа). Видно, что координаты изменяются по синусоидальному закону, и каждая имеет постоянную составляющую, отличную от нуля. Уравнение координаты вектора МРМ по оси а:

,	(7)

где:  – постоянная составляющая координаты вектора мгновенной реактивной мощности по оси а,– амплитуда переменной составляющей координаты вектора по оси а,  – круговая частота вектора напряжения,  – начальная фаза переменной составляющей координаты вектора.

В векторе МРМ можно выделить постоянную несимметричную составляющую:

,	(8)

где:  – постоянная несимметричная составляющая вектора мгновенной реактивной мощности,  – постоянная составляющая координаты вектора по оси b,  – постоянная составляющая координаты вектора по оси c.

В системе без нулевого провода вектор МРМ меняет свое поведение (рис.2).

Рисунок 2 – Годографы векторов мгновенных напряжений и токов трехфазной системы без нулевого провода и координаты вектора мгновенной реактивной мощности при активной несимметричной нагрузке

Вектор симметрично изменяется по синусоидальному закону и не имеет постоянной составляющей. В этом случае векторы тока и напряжения вращаются постоянно в одной плоскости.

Интересна для анализа система с чисто индуктивной нагрузкой (рис.3).

 

Рисунок 3 – Годографы векторов мгновенных напряжений и токов трехфазной системы с нулевым проводом и координаты вектора мгновенной реактивной мощности при индуктивной несимметричной нагрузке

Вектор тока за период описывает эллипс в плоскости отличной от плоскости вектора напряжения. При этом координаты вектора МРМ имеют постоянную и переменную составляющие. Постоянная составляющая в отличие от предыдущего случая значительно смещена в седьмой октант.

Рисунок 4 демонстрирует поведение вектора МРМ при отсутствии нулевого провода. Вектор имеет симметричную постоянную составляющую и переменную, изменяющуюся по синусоидальному закону.

 

Рисунок 4 – Годографы векторов мгновенных напряжений и токов трехфазной системы без нулевого провода и координаты вектора мгновенной реактивной мощности при индуктивной несимметричной нагрузке

Исходя из полученных результатов вектор МРМ, можно разделить, на три составляющие: симметричную постоянную ,  несимметричную постоянную , появляющуюся в случае наличия нулевого провода и переменную составляющую .

,

(9)

Сравнивая поведение вектора в симметричных[5] и несимметричных системах, можно сделать вывод о том, что симметричная постоянная составляющая вектора пропорциональна реактивной мощности системы. При наличии нулевого провода в несимметричной системе появляется постоянная несимметричная составляющая вектора МРМ.

Подводя итог вышесказанному, нужно отметить, что анализ вектора МРМ в несимметричных системах возможен. Вектор, а значит и неактивный ток трехфазной систем имеет составляющие: симметричные и несимметричные, постоянные и изменяющиеся во времени, появляющиеся в зависимости от нагрузки. Несимметричная постоянная составляющая вектора появляется только в несимметричных системах с нулевым проводом, в то время как симметричная постоянная составляющая появляется всегда при наличии реактивной нагрузки.

Библиографический список

1. H. Akagi, Y. Kanazawa, A. Nabae, “Instantaneous reactive power compensator’s comprising switching device without energy storage components,” IEEE Trans. Ind. Applications,vol. .IA-20, May/June 1984, pp. 625-630.
2. H. Akagi, H. Kim “” IEEE International Conference on Power Electronics and Drive Systems, PEDS’99, July 1999, Hong Kong.
3. Жеменов Г.Г. Ильина О.В. «Теория мощности Фризе и современные теории мощности» Электротехника и электромеханика №6, 2007 с.63-65
4. S. Frize, “Active and Apparent power in non-sinusoidal systems”. Przeglad Electrot (In Poland), no 7, 1931, p.p. 193-203.
5. Шклярский А.Я., Барданов А.И. «Анализ вектора мгновенной Реактивной мощности трехфазной сети при различной симметричной нагрузке», Естественные и технические науки №3, М.:Спутник, 2015. с.127-131

---

Количество просмотров публикации: Please wait

Все статьи автора «Алексей Барданов»

Активная и реактивная составляющие тока в асинхронном двигателе

Рис.11.1 Механическая (зависимость от M) и электромеханическая (зависимость от I) характеристики асинхронного двигателя

Уменьшение момента после достижения критического скольжения (Рис.11.1 точка В, соответствует максимальному, критическому моменту при критическом скольжении) объясняется тем, что в создании момента асинхронного двигателя участвует только активная составляющая тока.Активная составляющая тока при уменьшении скорости уменьшается и доходит до минимального значения при остановке ротора .

А реактивная составляющая тока ротора при неподвижном роторе имеет максимальное значение, за счёт того, что индуктивное сопротивление ротора имеетмаксимальное значение

при ,, то есть,когда ротор неподвижен (зачение частоты тока ротораравно частоте тока статора: ).

В однородном магнитном поле на проводник с током действует электромагнитная сила

.

Эта формула справедлива, когда магнитное поле и проводник длинойс токомдвижутся в пространстве с одинаковой скоростью и взаимно неподвижны.

Рассмотрим появление активной и реактивной составляющей тока в асинхронном двигателе[гер 343] .

Если прямолинейный проводник с синусоидальным током

находится в пульсирующем с той же частотоймагнитном поле статора с индукцией

и углом сдвига фаз вектора магнитной индукции и вектора тока равным углу _, тогда электромагнитная сила, действующая на проводник с токомдлиной, находящемся в магнитном поле с индукциейпериодически изменяется с двойной частотой:

Постоянная (средняя) составляющая электромагнитной силы :

Постоянная (средняя) составляющая электромагнитной силызависитот временного сдвига по фазе (от угол) синусоидальных токаи магнитной индукции, а также зависит отдействующих значений и.

У электрических переменного тока машин, имеющих большую массу ротора на частоте тока 50 Гц за один полупериод изменения силыприращение импульса ротора имеет очень малое значение по сравнению с импульсом при установившейся номинальной скорости. Поэтому при рассмотрении установившихся режимов работы электропривода составляющейможно пренебречь и учитывать только постоянную составляющую силыпрямопропорциональную.

В случае асинхронного двигателя, в обмотке ротора вращающееся магнитное поле статора наводит электродвижущюю силу Э.Д.С. и под действием Э.Д.С.по проводникам ротора протекает синусоидальный ток.

Мгновенное значение Э.Д.С. обмотки ротора асинхронного двигателя пропорционально магнитной индукции, длине проводника и скорости относительного перемещения проводника и магнитного поля .

В электрических машинах переменного тока Э.Д.С. обмотки ротора совпадает по фазе с магнитной индукцией поля статора. Поэтому угол сдвига фаз между Э.Д.С.и током обмотки ротораравен углу, углу сдвига фаз магнитной индукции и тока.

Следовательно, в формуле произведение определяет значение проекции векторана вектор, другими словами является активной составляющей тока ротора.

Из вышеизложенного следует, что постоянная (средняя) составляющая электромагнитной силы , действующая на проводник с синусоидальным током, находящимся в пульсирующем с той же частотоймагнитном поле статора асинхронного двигателя,пропорциональна активной составляющей тока ротора =

= .

Моментасинхронного двигателя, как и любой электрической машины,пропорционален магнитному потоку Ф и активной составляющей тока. Активная составляющая тока ротора пропорциональна косинусу угла, углу между вектором Э.Д.С. ротора и вектором тока ротора [чил 80].

где : конструктивная постояннаяасинхронного двигателя;

угол сдвига фаз между Э.Д.С. () и током обмотки ротора.

Непропорциональность между моментом асинхронного двигателя и током при пуске (пусковой момент меньше максимального момента несмотря на то, что пусковой токе достигает максимального значения рис.11.1) объясняется значительным снижением магнитного потока двигателя, а также уменьшением коэффициента мощности цепи ротора при пуске, за счёт максимального значения индуктивного сопротивления ротора[чил 80].

При изменении нагрузки на валу двигателя [гер392] от нуля до номинальной значения скольжения постепенно увеличиваются до значения . При этом сохраняется неравенство

<< и= ,

т.е. активная составляющая тока ротора пропорциональна скольжению при значениях скольжения меньших0.05 (при ) [гер393].

При увеличении нагрузки скольжение так же возрастает и растёт ЭДС ротора =, а также растёт ток роторав соответствии с , асимптотически стремясь к некоторому предельному значению. А с ростомуменьшается (причём на рабочем участке механической характеристикиуменьшается очень мало, рис.11.1 участокDB), асимптотически стремясь к нулю при скольжении, стремящемся к бесконечности .

Магнитный поток двигателя также уменьшается при возрастании тока из-за падения напряжения на сопротивлениях обмотки статора [чил81]. Все эти процессы и обуславливают отсутствие пропорциональности между током и моментом двигателя.

А реактивная составляющая тока ротора

с двойной частотой и ротор, имея большую инерцию не успевает проворачиваться два раза при частоте 50Гц. Двойная частота 100Гц. Если бы ротор был тонким проводником он бы успевал проворачиваться [гер344]. Поэтому при анализе установившихся режимов нужно учитывать толькопостоянную (средную) составляющую электромагнитной силы .

Реактивные электронные компоненты и фазовый угол

Если вы брезгливо относитесь к электричеству или не заботитесь об электричестве, вы можете пропустить это. Но мы собираемся поговорить о некоторых вещах, которые являются довольно интересными, важными для мира электроники и совершенно классными, если вы хотите остаться.

В недавних блогах говорилось о резисторах, конденсаторах и индукторах, которые, наряду с диодами различного назначения, являются строительными блоками электронных схем. В этих блогах описывалось поведение устройств, когда они использовались вместе с источником постоянного напряжения.В этом блоге мы исследуем, что происходит, когда источником напряжения является переменный ток вместо постоянного.

Примечание. На рисунках ниже показаны примеры «устойчивого состояния». Уникальные условия, которые возникают при первом включении или отключении переменного тока или напряжения, не рассматриваются, поскольку они, хотя и интересны, в настоящее время не имеют отношения к теме.

Резистор —

Резисторы — это «пассивные» устройства.Это приятные и простые вещи — вы пропускаете через них ток, и возникает падение напряжения из-за их сопротивления потоку электричества. Они полностью соответствуют закону Ома: напряжение = сила тока, умноженная на сопротивление (E = IR). Ток в точности соответствует напряжению. Резисторы не накапливают энергию. Пока вы используете среднеквадратичные значения для измерений напряжения и силы тока, они работают точно так же с постоянным током, как и с переменным током. Энергия, которую они потребляют, рассеивается в виде тепла. Резисторы используются в основном как делители напряжения и ограничители тока в электронных схемах.Тостер — это просто большой резистор.

Реактивные компоненты —

Конденсаторы и катушки индуктивности — это «реактивные» компоненты, которые реагируют на изменения. В отличие от резисторов, конденсаторы и катушки индуктивности накапливают и выделяют энергию в зависимости от изменений приложенного напряжения или тока и не подчиняются закону Ома.

Конденсатор —

В случае конденсаторов электроны накапливаются на проводящих пластинах при увеличении напряжения. Они высвобождаются при уменьшении или снятии приложенного напряжения и приложении нагрузки («нагрузка» — это токопроводящий путь для электричества).Идеальный конденсатор с бесконечным внутренним сопротивлением, поскольку пластины изолированы друг от друга, поэтому в этом процессе не выделяется тепло. Фактически, конденсаторы имеют некоторое внутреннее сопротивление, поэтому неизбежно выделяется некоторое количество тепла, но, как правило, его очень мало.

Конденсаторы хранят электроны так же, как батарейки. В то время как батарея накапливает электроны, вызывая химические изменения внутри батареи, конденсатор накапливает электроны непосредственно на проводящих пластинах и может делать это очень быстро по сравнению с батареей.Сохраненные электроны высвобождаются, когда приложенное напряжение уменьшается или снимается, а нагрузка подключается к заряженному конденсатору. Обратите внимание на приведенную выше иллюстрацию с подключенным источником переменного напряжения, что, когда напряжение равно нулю, ток является самым высоким (или самым низким). Электрики сказали бы, что ток ведет к напряжению. Среднее общее потребление энергии равно нулю в течение цикла зарядки и разрядки. Конденсаторы в основном используются для поддержания постоянного напряжения в цепях, питаемых от переменного напряжения, как в случае переменного тока.Конденсаторы также могут использоваться для умножения напряжений, если они правильно настроены для хранения напряжения, а затем высвобождают его в последовательной конфигурации (например, несколько батарей, соединенных последовательно в фонарике, производят больше напряжения, чем одна батарея).

Индуктор —

В случае катушек индуктивности энергия накапливается в виде магнитного поля, создаваемого протеканием тока через индуктор. В отличие от идеального конденсатора с бесконечным сопротивлением, идеальный индуктор НЕ имеет внутреннего сопротивления, поэтому не выделяется тепло.На самом деле, у индукторов есть некоторое сопротивление, поэтому они рассеивают небольшое количество тепла.

Катушки индуктивности накапливают энергию в магнитном поле. Когда сохраненное магнитное поле схлопывается из-за изменения приложенного тока, энергия высвобождается в форме тока в попытке противостоять изменению. В этом случае ток отстает от напряжения. Катушка индуктивности фактически возвращает энергию источнику, чтобы обеспечить нулевое среднее потребление энергии (по крайней мере, в случае синусоидального возбуждения).Это немного сложно представить (по крайней мере, для меня), но если вы думаете о трансформаторе, на самом деле это индуктор со второй катушкой провода, отводящей магнитное поле, создаваемое первичной катушкой устройства. При отсутствии нагрузки на вторичную катушку трансформатор представляет собой просто индуктор и (теоретически) не потребляет энергию из линии электропередачи до тех пор, пока нагрузка не будет подключена ко второй катушке для отвода магнитного поля.

Значение вышесказанного заключается в том, что фазовый угол (выравнивание между напряжением и током во времени) электрического потока изменяется этими реактивными устройствами.Изменение фазового угла делает недействительным использование закона Ома в условиях переменного тока, переводя анализ цепей в совершенно новую область математики, включающую «мнимые числа», чтобы приспособиться к обратному потоку энергии к источнику. Некоторые из вас, возможно, слышали о терминах «прямая мощность» и «отраженная мощность». Здесь все начинается и может быть важным фактором при оценке производительности высокочастотного электронного оборудования, включая ультразвуковые устройства.

— JF —

Активная, реактивная и полная мощность

Активная мощность:

Активная мощность — это реальная мощность, потребляемая в электрической цепи.Это полезная мощность, которая может быть преобразована в другую форму энергии, такую ​​как тепловая энергия в нагревателе, энергия света в лампочке и т. Д. Она также известна как истинная или реальная мощность и измеряется в ваттах, кВт (киловаттах) или МВт (1 Мега Вт = 10 ⁶ Вт).

Значение:

Требуется для выполнения разного рода полезной работы. Для работы любого устройства или нагрузки требуется активная мощность, например, телевизор, двигатель, холодильник и т. Д.

Реактивная мощность:

Реактивная мощность не выполняет никакой реальной работы.Здесь настоящая работа означает, что эту мощность нельзя использовать для обогрева, освещения или других полезных целей. Он только пульсирует взад и вперед по контуру. Он измеряется в кВАр (реактивное напряжение в киловольтах) или в мВАр (реактивное мегавольтное напряжение).

Значение:

Хотя реактивная мощность не выполняет никакой полезной работы, она все же необходима для удовлетворительной работы электрической машины. В воздушном зазоре машины необходимо создать магнитное поле, без которого активная мощность не может генерироваться генератором и потребляться двигателем.

Полная мощность:

Полная мощность — это вольт-ампер электрического прибора или машины. Если на машину подается напряжение V (среднеквадратичное значение), а через машину протекает ток I (среднеквадратичное значение), то это умножение среднеквадратического значения напряжения и тока, т. Е. VI. Измеряется в кВА или МВА.

Полная мощность, S = VI

Значение:

Потери в электрической машине зависят только от напряжения и тока. Это не зависит от коэффициента мощности.Таким образом, полная мощность дает представление о потерях в машине.

Расчет активной и реактивной мощности:

Электрическая нагрузка может быть резистивной, индуктивной, емкостной или их комбинациями. Природа тока, протекающего через эти нагрузки при подключении к источнику напряжения, следующая:

• Чисто резистивная нагрузка принимает ток в фазе с приложенным напряжением.
• Чисто индуктивная нагрузка воспринимает ток, отстающий от приложенного напряжения на 90 градусов.
• Чисто емкостная нагрузка принимает ток, опережающий приложенное напряжение на 90 градусов.

Таким образом, угол между напряжением и током для чисто резистивных, индуктивных и емкостных нагрузок составляет 0º, 90º и 90º градусов соответственно. Но когда нагрузка состоит из индуктивности и сопротивления, ток I через нагрузку будет отставать от напряжения V на некоторый угол Ø, как показано ниже.

Этот ток I теперь можно разделить на две составляющие:

• По напряжению i.е. Icos Ø
• Перпендикулярно напряжению, т.е. Isin Ø

Активный ток:

Составляющая тока нагрузки вдоль напряжения называется активным током. Нагрузка потребляет активную мощность из-за этой составляющей тока. Следовательно, истинная или реальная мощность задается как

.

Реальная мощность = напряжение x (активный ток)

= VIcos Ø

Реактивный ток:

Составляющая тока нагрузки, перпендикулярная напряжению, называется реактивным током.Реактивная мощность в цепи возникает из-за этой составляющей тока. Следовательно,

Реактивная мощность, Q = напряжение x (реактивный ток)

= Висин Ø

Активная / активная мощность	Реактивная мощность	Полная мощность
VIcos Ø	Висин Ø	VI

Почему сопротивление потребляет только реальную мощность?

Как обсуждалось ранее в этом посте, угол Ø для чистого сопротивления составляет 0º, а для индуктора и конденсатора — 90º.Это означает, что чистое сопротивление будет потреблять только активную мощность, поскольку VIcos0 = VI, и не будет реактивной мощности, поскольку VIsin0 = 0.

Почему индуктор и конденсатор не потребляют реальной энергии?

Чистая катушка индуктивности и конденсатор потребляет только реактивную мощность, как VIsin90 = VI, и не активную мощность, как VIcos90 = 0. Это также можно понять по-другому. Какая бы мощность ни была получена от источника в одном полупериоде этими элементами схемы, такое же количество энергии возвращается к источнику в следующем полупериоде.Следовательно, средняя потребляемая мощность за полный цикл равна нулю. Следовательно, истинная мощность не потребляется.

Реактивный компонент

— обзор

Интеграторный операционный усилитель (фильтр «полюс-ноль»)

Прежде чем мы перейдем к пассивным сетям, включающим и два реактивных компонента , давайте рассмотрим интересный активный RC- фильтр на основе (первого порядка). Для обсуждения здесь выбран , «интегратор», потому что он является фундаментальным строительным блоком любой «компенсационной сети».”

Инвертирующий операционный усилитель, представленный на рис. 12.5, имеет только конденсатор в цепи обратной связи. Мы знаем, что в условиях постоянного постоянного тока все конденсаторы по существу «выходят из поля зрения». Таким образом, в нашем случае мы остаемся с без отрицательной обратной связи на всех при постоянном токе — и, следовательно, с бесконечным усилением постоянного тока (хотя на практике реальные операционные усилители будут ограничивать это очень высоким, но конечным значением). Но, что еще более удивительно, это не мешает нам знать точное усиление на более высоких частотах .Если мы вычислим передаточную функцию этой схемы, мы увидим, что что-то «особенное» снова происходит в точке f = 1 / (2 π × RC). Однако, в отличие от пассивного RC-фильтра, эта точка не является ни точкой излома, ни полюсом, ни положением нуля. Это точка, где коэффициент усиления равен y (0 дБ). Обозначим эту частоту как «fp0».

Рисунок 12.5. Интегратор (полюс в нуле) операционного усилителя и некоторые связанные математики.

Обратите внимание, что пока, как показано на Рисунок 12.5, интегратор присутствует только на этапе . Таким образом, в данном конкретном случае «fp0» совпадает с наблюдаемой частотой кроссовера «fcross». Но в целом этого не будет. В общем, в этой главе «fp0» будет относиться к частоте кроссовера, которую каскад интегратора произвел бы , если бы он присутствовал только .

Обратите внимание, что интегратор имеет однополюсный датчик на «нулевой частоте», хотя 0 не может отображаться в логарифмической шкале. Мы всегда стремимся ввести этот полюс в нуле, потому что без него система имела бы довольно плохое усиление по постоянному току (низкочастотное). Интегратор — это самый простой способ получить как можно большее усиление по постоянному току. Наличие высокого коэффициента усиления по постоянному току — это способ добиться хорошего установившегося регулирования в любом преобразователе мощности. Это также показано на рисунке 12.3 (помечено как «DC shift»). Высокое усиление постоянного тока уменьшит сдвиг постоянного тока.

На правой стороне рисунка 12.4 мы намеренно сделали граф геометрически квадратным . С этой целью мы назначили равное количество делений сетки на двух осях, то есть оси масштабируются и пропорциональны одинаково.Кроме того, мы нанесли 20 × log ( f ) на ось y (вместо просто log ( f )). Сделав таким образом оси x и y идентичными во всех отношениях, мы понимаем, почему наклон называется «-1» — он действительно падает ровно на 45 ° (теперь мы видим это и визуально).

Мы пользуемся этой возможностью, чтобы показать, как выполнить простую математику в логической плоскости. Это показано в нижней части рисунка 12.5. Мы вывели одно конкретное полезное соотношение между произвольной точкой «A» и частотой кроссовера «fcross.Также включен числовой пример.

fcross = GainA × fA

Обратите внимание, что, как правило, передаточная функция любой функции «полюс в нуле» всегда будет иметь следующий вид ( X — общее действительное число)

1s × (X ) (функция передачи полюса в нуле)

Тогда частота кроссовера будет

fcross = 12π (X) (частота кроссовера)

В нашем случае ( X ) — это постоянная времени RC.

реактивный ток + компонент — перевод на китайский

▷ Уменьшение одного и того же компонента кальциевого тока киназами a и c: дифференциальная чувствительность к коклюшному токсину… ▷ Аппаратура и метод полевых испытаний полимерных изоляторов … ▷ Электронные ловушки и избыточный ток, индуцированный инжекцией горячих отверстий в тонкие SiO-пленки … ▷ Схема экспериментальной установки …. ▷ Функциональные и молекулярные различия между напряжением и закрытые k — каналы интернейронов с быстрым выбросом импульсов и пирамидных нейронов гиппокампа крысы … ▷ Прогностическое управление скоростью двигателя постоянного тока с помощью модели с конечным контролем … ▷ Комплексный коэффициент редукции для цилиндрического электронного пучка с переменной амплитудой переменной составляющей тока в twt… ▷ Динамика взвешенных отложений над затопленными сложными песчаными волнами, наблюдаемая во время приливного цикла … ▷ Очень быстрое управление, ориентированное на поле для синхронного двигателя с гистерезисом постоянного магнита … ▷ 146 несколько стратегий системы реактивный программируют несколько стратегий реактивный системный программный синтез … системы, такие как операционные системы или системы управления лифтами, — это системы, которые в идеале никогда не завершаются и предназначены для поддержания некоторого взаимодействия со своей средой … Клини алгебра… Мы представляем стратегию проверки для реактивных программ с большим или бесконечным пространством состояний с использованием алгебраических законов для реактивных отношений … ▷ Обнаружение трехфазной гармоники и реактивного тока на основе мгновенного реактивной теории мощности Аннотация — Чтобы точно и в реальном времени обнаруживать сетевые гармоники и реактивный ток, в этой статье был предложен метод определения гармоник и реактивного тока в реальном времени, применяемый к фильтру активной мощности на основе трехфазной цепи мгновенного действия реактивного теория власти… ▷ Реактивное функциональное программирование … Программирование реактивных систем является сложной задачей без языковой поддержки для действий, запускаемых событиями … ▷ Реактивные конструкции в isabelle / utp Реактивные конструкции объединяют теории UTP реактивных процессы и конструкции для характеристики реактивных программ … ▷ Мультистратегическое обучение адаптивных реактивных контроллеров … Однако конфигурация реактивного контроллера сильно зависит от условий эксплуатации робота и окружающей среды; таким образом, реактивный контроллер , сконфигурированный для одного класса сред, может не работать должным образом в другом… ▷ Reactive spin and promela Reactive Promela — это расширение языка Promela, которое позволяет пользователю определять конфигурации реактивных автоматов … ▷ Оптимизация реактивной мощности с использованием алгоритма дифференциальной эволюции Оптимизация мощности — это нелинейная задача программирования с несколькими переменными и множественными ограничениями, которая делает процесс оптимизации многогранным … ▷ Практический функционал реактивное программирование … Мы представляем наш опыт интеграции функционального программирования Reactive (FRP) в новый основной язык, Python, и различные вычислительные контексты: игровой движок, систему графического интерфейса пользователя и встроенный контроллер … … Reactive c: расширение c для программирования реактивных систем … В этой статье описывается расширение языка программирования C под названием RC (для ‘ Reactive C’) для программирования реактивных систем … ▷ Мгновенно активные и реактивный метод составляющих тока для активных фильтров в условиях симметричного и несимметричного сетевого напряжения для 3-фазной 3-проводной системы… Чтобы преодолеть эту проблему, APF (фильтр активной мощности) привлек больше внимания из-за его превосходных характеристик подавления гармоник и компенсации реактивной мощности … ▷ Моделирование и анализ шунтирующего фильтра активной мощности с использованием теории irp, подаваемой на индукционный привод. .. Технология активного фильтра мощности представляет собой наиболее эффективный способ компенсации реактивной мощности и нейтрализации низших гармоник, генерируемых нелинейными нагрузками … ▷ Сравнение аналогово-цифровых вычислителей тока по сравнению с DSP для систем с автономным питанием от сети переменного тока… Обе схемы работают с мгновенным активным и реактивным методом id-iq компонента тока … ▷ Сравнение методов оценки опорного компенсирующего тока для шунтирующего активного фильтра … Сравниваемые методы — метод мгновенного активного и реактивного power pq. , Метод мгновенного баланса мощности, Мгновенная активная и Реактивная , метод id-iq компонента тока, метод ряда Фурье и метод регулирования напряжения промежуточного контура … ▷ Обобщенная мгновенная теория реактивной мощности в многофазной мощности Фильтры, APF, для компенсации нелинейных нагрузок, расширили использование теории мгновенной реактивной мощности … ▷ Модульный многоуровневый инвертор в виде трехфазного шунтирующего фильтра активной мощности с унифицированным управлением интегрированием постоянной частоты … Эти нелинейные нагрузки генерируют гармоники и реактивных токов , что приводит к низкому коэффициенту мощности, низкой энергоэффективности и малой мощности и вредные помехи для других устройств … ▷ Шунтирующий фильтр активной мощности на основе понижающего преобразователя с устранением сквозных пробоев для повышения качества электроэнергии … Схема мгновенной активной и реактивной мощности (pq) и мгновенной активной и реактивной Схема управления компонентом тока (id-iq) была реализована для уменьшения гармоник тока источника… ▷ Повышение производительности шунтирующих АТЭ с использованием различных топологий, схем управления и методов оптимизации Вслед за появлением технологии твердотельной силовой электроники широкое использование нелинейных нагрузок привело к серьезным помехам, таким как гармоники, несимметричные токи, чрезмерный ток нейтрали и реактивный Энергетическая нагрузка в трехфазных энергосистемах …

1 миллиард переводов с разбивкой по видам деятельности на 28 языках

Наиболее частые запросы Английский: 1-200, -1k, -2k, -3k, -4k, -5k, — 7k, -10k, -20k, -40k, -100k, -200k, -500k, -1000k, -2000k,

Наиболее частые запросы Китайский: 1-200, -1k, -2k, -3k, -4k, — 5k, -7k, -10k, -20k, -40k, -100k, -200k, -500k, -1000k, -2000k,

Traduction Translation Traducción Übersetzung Tradução Traduzione Traducere Vertaling Tłumaczenie MετάφρασäjäjtalingTłumaczenie MετάφρασäjäjtalingTłumaczenie MετάφρασäjäjtalingTłumaczenie Mετάφρασäjäjjt » Fordítás Tulkojumi Перевод Překlad Prijevod 翻 訳 번역 翻译 Перевод

Разработано для TechDico

Publisher

Положения и условия

Политика конфиденциальности

© techdico

Что такое активная, реактивная и полная мощность?

Мощность, потребляемая нагрузкой для выполнения работы, называется истинной мощностью, или активной мощностью, или реальной мощностью.Когда электрическая энергия подается на нагрузку, электрическая энергия преобразуется в другие формы энергии, такие как тепловая, механическая или химическая. Таким образом, мощность, фактически потребляемая электрической нагрузкой, называется активной мощностью. Нагреватель на 220 вольт, 400 ватт потребляет 400 ватт, когда на его резистивный элемент подается 220 вольт. Мощность в 400 ватт, потребляемая нагревателем, является реальной мощностью или активной мощностью. Активная мощность измеряется в киловаттах (кВт) или МВт.

Для расчета активной мощности рассчитывается ток, протекающий синфазно с приложенным напряжением.

Произведение напряжения и тока по фазе с напряжением дает реальную мощность или активную мощность.

Реактивная мощность

Мощность, которая течет от источника к нагрузке и от нагрузки к источнику, называется реактивной энергией. Реактивная энергия течет в обоих направлениях. Реактивная мощность измеряется в киловольтах-амперах, реактивная (кВАр) или мВАр.

Индуктивная нагрузка вызывает реактивное сопротивление по отношению к току и, следовательно, ток отстает от приложенного напряжения.Емкостная нагрузка вызывает реактивное сопротивление приложенному напряжению, и, таким образом, ток опережает приложенное напряжение. Сдвиг фаз между напряжением и током всегда существует, если нагрузка емкостного или реактивного типа.

Импеданс, обеспечиваемый емкостной и индуктивной нагрузкой, вызывает перетекание мощности назад и вперед от источника к нагрузке и от нагрузки к источнику. В чистой индуктивной цепи ток отстает от напряжения на 90 электрических градусов. В чисто емкостной цепи ток опережает напряжение на 90 электрических градусов.

Активная мощность в случае чисто индуктивной и емкостной цепи VICosΦ = VI Cos90 = 0. Реактивная мощность в случае чисто индуктивной и емкостной цепи VISinΦ = VI Sin90 = VI.

Полная мощность

Если нагрузка не является ни резистивной, ни чисто реактивной, ток, потребляемый нагрузкой, имеет две составляющие тока.

Активная составляющая тока:

Ток, который находится в фазе с приложенным напряжением, называется активной составляющей тока.Активная или реальная потребляемая мощность нагрузки зависит от активной составляющей тока цепи.

Реактивная составляющая тока:

Ток, который на 90 градусов не совпадает по фазе с приложенным напряжением, называется реактивной составляющей тока или током без мощности. Реактивная составляющая тока вносит вклад в реактивную мощность.

Нагрузка, потребляющая активный или реактивный ток, общий ток системы будет увеличиваться.Следовательно, мощность электрической системы выражается в полной мощности, кВА или МВА. Система должна обрабатывать как активный, так и реактивный ток, поэтому система разработана с учетом полной мощности.

Пусть электрическая индуктивная нагрузка потребляет ток I и сдвиг фаз между напряжением и током равен Φ.

Активную, реактивную и полную мощность, потребляемую индуктивной нагрузкой, можно рассчитать следующим образом.

Активная составляющая тока в фазе с напряжением — это ICosΦ, а реактивная составляющая тока, не совпадающая по фазе с напряжением, — ISinΦ.

Активная мощность однофазной нагрузки

Активная мощность (P)

= Напряжение x Ток в фазе с напряжением

= V x ICos Φ

= V I Cos Φ

Активная мощность трехфазной нагрузки

Активная мощность (P)

= Напряжение x Ток в фазе с напряжением

= √3 Vx ICos Φ

= √3 В I CosΦ

Реактивная мощность однофазной нагрузки

Реактивная мощность (Q)

Q = Напряжение x Ток не в фазе с напряжением

= V x ISin Φ

= V I Sin Φ

Реактивная мощность трехфазной нагрузки

Реактивная мощность (Q)

Q = Напряжение x Ток не в фазе с напряжением

= √3V x ISinΦ

= √3 В I Sin Φ

Полная мощность — это векторная сумма активной и реактивной мощности.

Для однофазной системы питания полная потребляемая мощность кулачка может быть выражена следующим математическим выражением.

Для трехфазной нагрузки полная мощность составляет;

Определение реактивной мощности — Руководство по электрическому монтажу

Для большинства электрических нагрузок, таких как двигатели, ток I отстает от напряжения V на угол φ.

Если токи и напряжения являются идеально синусоидальными сигналами , для представления может использоваться векторная диаграмма.

На этой векторной диаграмме вектор тока можно разделить на две составляющие: одна в фазе с вектором напряжения (составляющая I _a ), вторая в квадратуре (отставание на 90 градусов) с вектором напряжения (составляющая I _r). ). См. Рис. L1.

I называется активной составляющей тока.

I _r называется реактивной составляющей тока.

Рис. L1 — Векторная диаграмма токов

Предыдущая диаграмма, составленная для токов, также применима к мощности путем умножения каждого тока на общее напряжение V.См. Рис. L2.

Таким образом, мы определяем:

• Полная мощность : S = V x I (кВА)
• Активная мощность : P = V x Ia (кВт)
• Реактивная мощность : Q = V x Ir (квар)

Рис. L2 — Векторная диаграмма мощности

На этой диаграмме мы видим, что:

• Коэффициент мощности : P / S = cos φ

Эта формула применима для синусоидального напряжения и тока. Вот почему коэффициент мощности обозначается как «Коэффициент мощности смещения» .{2}}

Коэффициент мощности, близкий к единице, означает, что полная мощность S минимальна. Это означает, что номинальные параметры электрического оборудования минимальны для передачи данной активной мощности P на нагрузку. Тогда реактивная мощность мала по сравнению с активной. мощность.

Низкое значение коэффициента мощности указывает на противоположное состояние.

Полезные формулы (для сбалансированных и почти сбалансированных нагрузок в 4-проводных системах):

• Активная мощность P (в кВт)
  • Однофазный (1 фаза и нейтраль): P = V.I.cos φ
  • Однофазный (между фазами): P = U.I.cos φ
  • Трехфазный (3 провода или 3 провода + нейтраль): P = √3.U.I.cos φ
• Реактивная мощность Q (в квар)
  • Однофазный (1 фаза и нейтраль): Q = V.I.sin φ
  • Однофазный (между фазами): Q = U.I.sin φ
  • Трехфазный (3 провода или 3 провода + нейтраль): Q = √3.U.I.sin φ
• Полная мощность S (в кВА)
  • Однофазный (1 фаза и нейтраль): S = V.Я
  • Однофазный (между фазами): S = U.I
  • Трехфазный (3 провода или 3 провода + нейтраль): S = √3.U.I

где:

В = Напряжение между фазой и нейтралью
U = Напряжение между фазами
I = Линейный ток
φ = Фазовый угол между векторами V и I.

Пример расчета мощности (см.

Рис. L3)

Рис. L3 — Пример расчета активной и реактивной мощности

Тип цепи		Полная мощность S (кВА)	Активная мощность P (кВт)	Реактивная мощность Q (квар)
Однофазный (фаза и нейтраль)		S = VI	P = VI cos φ	Q = VI sin φ
Однофазный (между фазами)		S = UI	P = UI cos φ	Q = UI sin φ
Пример: нагрузка 5 кВт, cos φ = 0.5		10 кВА	5 кВт	8,7 квар
Трехфазное 3-проводное или 3-проводное + нейтраль		S = 3 {\ displaystyle {\ sqrt {3}}} пользовательского интерфейса	P = 3 {\ displaystyle {\ sqrt {3}}} UI cos φ	Q = 3 {\ displaystyle {\ sqrt {3}}} грех пользовательского интерфейса φ
Пример	Двигатель Pn = 51 кВт	65 кВА	56 кВт	33 квар
	cos φ = 0,86
	ρ = 0.91 (КПД двигателя)

Расчеты для трехфазного примера, приведенного выше, следующие:

Pn = поставленная мощность на валу = 51 кВт

P = потребляемая активная мощность

P = Pnρ = 510,91 = 56 кВт {\ displaystyle P = {\ frac {Pn} {\ rho}} = {\ frac {51} {0.91}} = 56 \, кВт}

S = полная мощность

S = Pcosφ = 560,86 = 65 кВА {\ displaystyle S = {\ frac {P} {cos \ varphi}} = {\ frac {56} {0.86}} = 65 \, кВА}

Таким образом, при обращении к рис. L16 или использовании карманного калькулятора значение tan φ, соответствующее cos φ, равному 0.{2}}} = 33 \, квар}

Рис. L4 — Расчетная диаграмма мощности

Активная, реактивная и полная мощность

Многие практические схемы содержат комбинацию резистивных, индуктивных и емкостных элементов. Эти элементы вызывают фазовый сдвиг между параметрами электропитания, такими как напряжение и ток.

Из-за поведения напряжения и токов, особенно при воздействии на эти компоненты, количество мощности может иметь разные формы.

В цепях переменного тока амплитуды напряжения и тока будут непрерывно изменяться с течением времени.Поскольку мощность равна напряжению, умноженному на ток, она будет максимальна, когда токи и напряжения выровнены друг с другом.

Это означает, что нулевая и максимальная точки на осциллограммах тока и напряжения возникают одновременно. Это можно назвать полезной мощностью.

В случае элементов индуктивности или конденсатора существует 90 ⁰ фазовый сдвиг между напряжением и током. Таким образом, мощность будет иметь нулевое значение каждый раз, когда напряжение или ток будут иметь нулевое значение.

Это нежелательное состояние, потому что с нагрузкой не выполняется никаких работ, даже если источник вырабатывает энергию. Эта мощность называется реактивной мощностью. Давайте кратко обсудим эти формы мощности в электрических цепях переменного тока.

Мощность в цепях переменного тока

Мощность в любой электрической цепи может быть получена путем умножения значений напряжения и тока в этой цепи. Это применимо как для цепей постоянного, так и для переменного тока.

т.е. мощность = (текущее значение) x (значение напряжения)

P = V x I

Мощность измеряется в ваттах.В цепях постоянного тока и цепях чистого переменного тока без каких-либо нелинейных компонентов формы сигналов тока и напряжения «синфазны».

Таким образом, мощность в любой момент времени в этой цепи получается путем умножения напряжения и тока. Однако в случае цепей переменного тока этого не будет (как уже упоминалось выше о существовании фазового сдвига).

Рассмотрим приведенную выше схему, в которой переменный ток подается на нагрузку. Напряжения и токи в цепи заданы как

v = Vm sin ωt ⇒ v = √2 V sin ωt

i = Im sin ωt ⇒ i = √2 I sin (ωt ± ϕ)

Где V (= Vm / √2) и I (= Im / √2) — среднеквадратичные значения приложенного напряжения и тока, протекающего по цепи, соответственно.Φ — это разность фаз между напряжением и током, для которой знак + указывает начальный фазовый угол, а отрицательный — отстающий фазовый угол.

Тогда мгновенная мощность, передаваемая на нагрузку источником, определяется выражением

p = vi = 2 VI sin wt sin (ωt ± ϕ)

= VI (cos ϕ — cos (2ωt ± ϕ)

p = VI cos ϕ (1 — cos 2wt) ± VI sin ϕ sin2wt

Приведенное выше уравнение мощности состоит из двух членов, а именно:

1. Член, пропорциональный VI cos ϕ, который пульсирует вокруг среднего значения VI cos ϕ
2. Член пропорциональный VI sin ϕ, пульсирующий с удвоенной частотой питания, производя в среднем ноль за цикл.

Итак, в цепях переменного тока есть 3 формы мощности. Это

1. Активная мощность или Истинная мощность или Реальная мощность
2. Реактивная мощность
3. Полная мощность

Активная мощность

Фактическое количество мощности, рассеиваемой или выполняющей полезную работу в цепи, называется активной или истинной или реальный сила. Он измеряется в ваттах, а в энергосистемах практически измеряется в кВт (киловаттах) и МВт (мегаваттах).

Обозначается буквой P (заглавная) и соответствует среднему значению p = VI cos ϕ.Это желаемый результат электрической системы, которая управляет цепью или нагрузкой.

P = VI cos ϕ

Реактивная мощность

Среднее значение второго члена в приведенном выше производном выражении равно нулю, поэтому мощность, вносимая этим членом, равна нулю. Компонент, который пропорционален VI sin ϕ, называется реактивной мощностью и обозначается буквой Q.

Хотя это мощность, но не измеряется в ваттах, так как это неактивная мощность и, следовательно, она измеряется в Вольт-ампер-реактивный (ВАР).Значение этой реактивной мощности может быть отрицательным или положительным в зависимости от коэффициента мощности нагрузки.

Это связано с тем, что индуктивная нагрузка потребляет реактивную мощность, а емкостная нагрузка генерирует реактивную мощность.

Q = VI sin ϕ

Значение реактивной мощности

Реактивная мощность — это одна из составляющих полной мощности, которые перемещаются вперед и назад в цепи или линии. Это можно назвать скоростью изменения энергии по отношению ко времени, которая продолжает течь от источника к реактивным компонентам в течение положительного полупериода и обратно к компонентам от источника во время отрицательного цикла.Следовательно, нагрузка никогда не расходуется.

В обычном смысле эта фиктивная мощность — это вовсе не мощность, а всего лишь подобная мощности мера реактивной составляющей тока. Если имеется избыточное количество реактивной мощности, коэффициент мощности значительно снижается. Такой низкий коэффициент мощности нежелателен с точки зрения эффективности работы и эксплуатационных затрат.

А также эта мощность заставляет потреблять дополнительный ток от источника питания, что приводит к дополнительным потерям и большей мощности оборудования.Вот почему эту мощность в шутливой форме называют холестерином линий электропередач.

Чтобы минимизировать потери и увеличить мощность имеющегося оборудования, коммунальные предприятия используют методы компенсации VAR или оборудование коррекции коэффициента мощности. Как правило, эти методы компенсации реактивной мощности реализуются на стороне нагрузки.

Однако эта реактивная мощность полезна для создания необходимых магнитных полей для работы индуктивных устройств, таких как трансформаторы, двигатели переменного тока и т. Д.Это также помогает регулировать напряжение в тяжелых механизмах электропитания.

Полная мощность

Сложная комбинация истинной или активной мощности и реактивной мощности называется полной мощностью. Без учета фазового угла произведение напряжения и тока дает полную мощность. Полная мощность полезна для оценки силового оборудования.

Его также можно выразить как квадрат тока, умноженный на полное сопротивление цепи. Он обозначается буквой S и измеряется в вольт-амперах (ВА), практические единицы включают в себя кВА (киловольт-вольт-амперы) и МВА (мегавольт-амперы).

Полная мощность = действующее значение напряжения × действующее значение тока

Полная мощность, S = V × I

В сложной форме S = VI *

S = V ∠0 ⁰ I ∠ ϕ (для запаздывающего тока нагрузки)

S = VI ∠ ϕ

S = VI cos ϕ + jV I sin ϕ

S = P + jQ

или S = ​​I ² Z

Треугольник мощности

Соотношение между активной, реактивной и полной мощностью может быть выражено представлением величин в виде векторов, что также называется методом степенного треугольника, как показано ниже.На этой векторной диаграмме напряжение рассматривается как опорный вектор. Векторная диаграмма напряжения и тока является основой для формирования треугольника мощности.

На рисунке (а) ток отстает от приложенного напряжения на угол ϕ. Горизонтальная составляющая тока равна I cos ϕ, а вертикальная составляющая тока — I sin ϕ. Если каждый вектор тока умножить на напряжение V, получится треугольник мощности, как показано на рисунке (b).

Активная мощность обеспечивается составляющей I cos ϕ по фазе с напряжением, в то время как реактивная мощность создается квадратурной составляющей.

Следовательно, полная мощность или гипотенуза треугольника получается путем векторного комбинирования активной и реактивной мощности.

Используя теорему Пифагора, сумма квадратов двух смежных сторон (активная мощность и реактивная мощность) равна квадрату диагонали (полная мощность). т.е.

(Полная мощность) ² = (Фактическая мощность) ²

S ² = P ² + Q ²

S = √ ((Q ² + P ² ))

Где

S = полная мощность, измеренная в киловольт-амперах, кВА

Q = реактивная мощность, измеренная в киловольт-амперах, реактивная, кВАр

P = активная мощность, измеренная в киловаттах, кВт

В единицах резистивной, индуктивной и элементы полного сопротивления, формы мощности могут быть выражены как

Активная мощность = P = I ² R

Реактивная мощность = Q = I ² X

Полная мощность = S = I ² Z

Где

X — индуктивность

Z — полное сопротивление.

Коэффициент мощности

Коэффициент мощности — это косинусоидальный угол между напряжением и током. Коэффициент мощности может быть выражен в терминах рассмотренных выше форм мощности. Рассмотрим треугольник мощности на рисунке выше, в котором коэффициент мощности представляет собой отношение активной мощности к полной мощности. Коэффициент мощности определяет эффективность схемы.

Коэффициент мощности (PF) = (Активная мощность в ваттах) / (Полная мощность в ваттах)

PF = VI cos ϕ / VI

PF = cos ϕ

Пример проблемы

Если источник питания переменного тока 100 В , 50 Гц подключен к нагрузке с сопротивлением 20 + j15 Ом.Затем рассчитайте ток, протекающий по цепи, активную мощность, полную мощность, реактивную мощность и коэффициент мощности.

Учитывая, что Z = R + jXL = 20 + j 15 Ом

Преобразуя импеданс в полярную форму, мы получаем

Z = 25 ∠36,87 Ом

Ток, протекающий по цепи,

I = V / Z = 100∠0 ⁰ /25 ∠36,87

I = 4 ∠ – 36,87

Активная мощность, P = I ² R = 42 × 20 = 320 Вт

Или P = VI cos ϕ = 100 × 4 × cos (36.