Реактивное сопротивление цепи. Реактивное сопротивление в цепях переменного тока: основные понятия и расчеты

Что такое реактивное сопротивление. Как рассчитать индуктивное и емкостное сопротивление. Какая разница между активным и реактивным сопротивлением. Как определить полное сопротивление цепи переменного тока.

Что такое реактивное сопротивление

Реактивное сопротивление — это сопротивление, которое оказывают переменному току в электрической цепи катушки индуктивности и конденсаторы. В отличие от активного сопротивления, реактивное сопротивление не приводит к потерям энергии в виде тепла.

Различают два вида реактивного сопротивления:

• Индуктивное сопротивление (XL) — создается катушками индуктивности
• Емкостное сопротивление (XC) — создается конденсаторами

Реактивное сопротивление измеряется в омах (Ом), как и активное сопротивление. Однако его величина зависит от частоты переменного тока.

Как рассчитать индуктивное сопротивление

Индуктивное сопротивление катушки индуктивности рассчитывается по формуле:

XL = 2πfL

где:

• XL — индуктивное сопротивление (Ом)
• π ≈ 3,14
• f — частота переменного тока (Гц)
• L — индуктивность катушки (Гн)

Из формулы видно, что индуктивное сопротивление прямо пропорционально частоте тока и индуктивности катушки. Чем выше частота и индуктивность, тем больше индуктивное сопротивление.

Расчет емкостного сопротивления

Емкостное сопротивление конденсатора определяется по формуле:

XC = 1 / (2πfC)

где:

• XC — емкостное сопротивление (Ом)
• π ≈ 3,14
• f — частота переменного тока (Гц)
• C — емкость конденсатора (Ф)

Емкостное сопротивление обратно пропорционально частоте и емкости. При увеличении частоты или емкости емкостное сопротивление уменьшается.

Отличие реактивного сопротивления от активного

Основные отличия реактивного сопротивления от активного:

1. Реактивное сопротивление не приводит к потерям энергии в виде тепла
2. Величина реактивного сопротивления зависит от частоты переменного тока
3. Реактивное сопротивление вызывает сдвиг фаз между током и напряжением

При наличии в цепи только активного сопротивления ток и напряжение совпадают по фазе. Реактивное сопротивление приводит к сдвигу фаз:

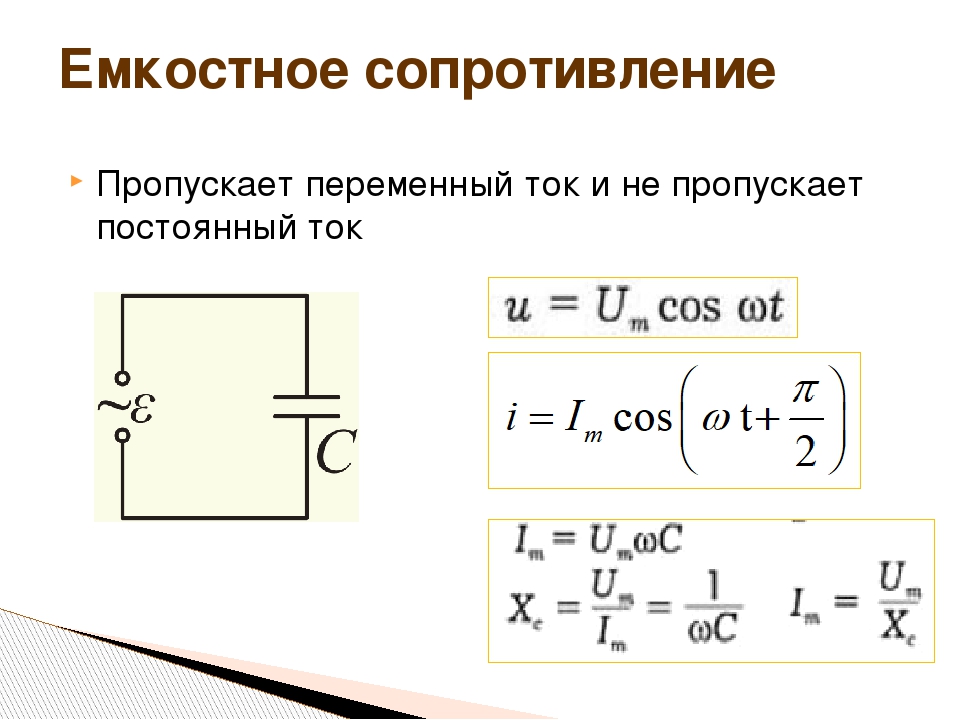
• Индуктивное сопротивление вызывает отставание тока от напряжения на 90°
• Емкостное сопротивление вызывает опережение тока относительно напряжения на 90°

Как определить полное сопротивление цепи переменного тока

Полное сопротивление цепи переменного тока (импеданс) складывается из активного и реактивного сопротивлений. Его можно рассчитать по формуле:

Z = √(R² + X²)

где:

• Z — полное сопротивление (импеданс)
• R — активное сопротивление
• X — реактивное сопротивление

Реактивное сопротивление X определяется как разность индуктивного и емкостного сопротивлений:

X = XL — XC

Таким образом, для расчета полного сопротивления цепи переменного тока необходимо:

1. Определить активное сопротивление R
2. Рассчитать индуктивное XL и емкостное XC сопротивления
3. Найти результирующее реактивное сопротивление X
4. Вычислить импеданс Z по формуле

Векторная диаграмма сопротивлений

Соотношение между активным, реактивным и полным сопротивлением можно наглядно представить в виде векторной диаграммы:

• Активное сопротивление R откладывается по горизонтальной оси
• Реактивное сопротивление X — по вертикальной оси
• Полное сопротивление Z — гипотенуза прямоугольного треугольника

Это позволяет легко определить угол сдвига фаз φ между током и напряжением:

tg φ = X / R

Векторная диаграмма наглядно показывает, что полное сопротивление всегда больше активного и реактивного по отдельности.

Примеры расчета реактивного сопротивления

Рассмотрим несколько примеров расчета реактивного сопротивления для типичных элементов электрических цепей.

Пример 1. Индуктивное сопротивление катушки

Дано: катушка с индуктивностью L = 0,1 Гн, частота тока f = 50 Гц.

Расчет:

XL = 2πfL = 2 × 3,14 × 50 × 0,1 = 31,4 Ом

Пример 2. Емкостное сопротивление конденсатора

Дано: конденсатор емкостью C = 100 мкФ, частота тока f = 1 кГц.

Расчет:

XC = 1 / (2πfC) = 1 / (2 × 3,14 × 1000 × 100 × 10⁻⁶) = 1,59 Ом

Пример 3. Полное сопротивление RLC-цепи

Дано: R = 100 Ом, XL = 50 Ом, XC = 30 Ом

Расчет:

1. X = XL — XC = 50 — 30 = 20 Ом
2. Z = √(R² + X²) = √(100² + 20²) = 102 Ом

Практическое применение реактивного сопротивления

Понимание реактивного сопротивления важно для многих практических задач электротехники:

• Расчет и проектирование электрических цепей переменного тока
• Компенсация реактивной мощности в электрических сетях
• Создание резонансных контуров в радиотехнике
• Разработка фильтров и частотно-избирательных цепей
• Анализ работы электрических машин и трансформаторов

Учет реактивного сопротивления позволяет корректно рассчитывать токи, напряжения и мощности в цепях переменного тока, а также оптимизировать их работу.

Активное и реактивное сопротивления в цепи перемен тока

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

R,C,L в цепи переменного тока
Вопросы для изучения:
1. Действующие значения тока и напряжения. Активное
сопротивление в цепи ~ тока
2. Конденсатор в цепи ~ тока
3. Индуктивность в цепи ~ тока
4. Использование частотных свойств конденсатора и
катушки индуктивности
RCL
в цепи переменного тока -1
1.Действующие значения
тока и напряжения. Активное
сопротивление в цепи
переменного тока
Действующие значения тока и напряжения, виды сопротивлений
Рассмотрим активное сопротивление в цепи переменного тока:
U U m cos t
R
Мгновенное значение силы
тока через активное
сопротивление
пропорционально
мгновенному значению
напряжения
U U m cos t
i
I m cos t
R
R
Колебания напряжения и силы тока на активном сопротивлении
совпадают по фазе
u = Um cos ω t – мгновенное значение напряжения
i = Im cos ω t – мгновенное значение силы тока

I=
Im
– действующее значение
силы тока
2
U
I=
R
Um
Im =
R
U=
Um
2
– действующее значение
напряжения
– закон Ома для цепи переменного тока с
резистором, R – активное сопротивление
P = IU = I2R – действующее значение
мощности
i, u
u
i
t
В цепи переменного тока, содержащей активное
сопротивление, колебания силы тока i и
напряжения и совпадают по фазе
2. Конденсатор в цепи
переменного тока
C
Конденсатор в цепи переменного тока
Давайте вспомним, что такое конденсатор
Конденсатор – это система из двух
проводников, разделенных слоем
диэлектрика (воздуха, слюды,
керамики …)
Ясно, что конденсатор
– это разрыв в цепи
(подобно
разомкнутому
выключателю),
поэтому постоянный
ток конденсатор не
проводит
Конденсатор в цепи переменного тока
Итак, конденсатор проводит переменный ток, однако он
оказывает току сопротивление, которое называется ёмкостным
сопротивлением
1
1
XС
C 2 C
XС
— ёмкостное
сопротивление
— циклическая частота протекающего тока
С – электроемкость конденсатора
— частота тока
q = C Um cos ω t — мгновенное значение заряда
u = Um cos ω t — мгновенное значение напряжения
i = q΄= – С Um ω sin ω t
Im = Um C ω — максимальное значение силы тока
i = Im cos (ω t + π) — мгновенное значение силы тока
U
I=
XC
– закон
Ома для цепи переменного тока с
конденсатором
1
XC
C
– емкостное сопротивление
i, u
i
u
t
В цепи переменного тока, содержащей
конденсатор, колебания силы тока i опережают
колебания напряжения u на
3. Индуктивность в цепи
переменного тока
L
Индуктивность в цепи переменного тока
Давайте вспомним, что такое индуктивность
Индуктивность L– это физическая величина,
подобная массе в механике. Как в механике для
изменения скорости тела нужно время, и масса
является мерой этого времени (инерция), так и
электродинамике для изменения тока через
проводник нужно время и индуктивность является
мерой этого времени (самоиндукция)
L
Катушка индуктивности –
это обычный проводник с
необычной формой,
обладающий активным
сопротивлением.
Поэтому катушка хорошо
проводит постоянный ток,
значение которого
ограничено только его
активным сопротивлением
Явление самоиндукции возникает только в моменты включения и
выключения (препятствует любому изменению тока)
Индуктивность в цепи переменного тока
Посмотрим, как ведет себя индуктивность в цепи переменного
тока:
Замкнем цепь и сравним яркость горения лампочек 1 и 2
Л1
Л2
R
L
~
Источник ~ тока,
обладающий
и
r
В цепи сопротивление R поберем равным активному сопротивлению L
Лампочка Л1 горит гораздо ярче, чем Л2
Почему ?
Индуктивность в цепи переменного тока
Все дело в явлении самоиндукции, возникающей в катушке при
любом изменении тока, которое мешает этому изменению –
поэтому у катушки индуктивности кроме активного
сопротивления провода, из которого она сделана, появляется
еще одно сопротивление, обусловленное явлением
самоиндукции и называемое индуктивным сопротивлением
X L L 2 L
—
циклическая частота протекающего тока
L – индуктивность катушки
— частота тока
XL
i = Im sin ωt — мгновенное значение силы тока
еi = – L i΄= – L Im ω cos ωt
и = – еi = Um sin (ωt + ) – мгновенное значение напряжения
U
I=
XL
Um = L Im ω
– закон Ома для цепи переменного тока с
катушкой индуктивности
XL = ω L – индуктивное сопротивление
i, u
u
i
t
В цепи переменного тока, содержащей катушку
индуктивности, колебания напряжения и опережают
колебания силы тока i на
5. Использование частотных свойств конденсатора и катушки
Таким образом, в цепи переменного тока можно выделить 3 вида
сопротивлений (или три вида элементов, оказывающих сопротивление
току)
СОПРОТИВЛЕНИЕ
R
активное
реактивное
XL индуктивное
ёмкостное XC
Реальные электрические цепи содержат все виды сопротивлений
(активное, индуктивное и ёмкостное), поэтому ток в реальной цепи зависит
от ее полного (эквивалентного) сопротивления, а сдвиг фаз определяется
величиной L и C цепи
стр.100(2)
Р-976
Р-971
ДОМАШНЕЕ ЗАДАНИЕ
СПАСИБО
ЗА УРОК!
§§ 21, 22.
Письменно ответить
на вопросы § 21(в.3,4)
Решить задачи Р-975, 978

English     Русский Правила

Формулы. Электрическое сопротивление проводника при постоянном токе, зависимость сопротивления проводника от температуры, индуктивное и ёмкостное (реактивное) сопротивление, полное реактивное сопротивление, полное сопротивление цепи при переменном токе

		Раздел недели: Обезжиривающие водные растворы и органические растворители. Составы для очистки и обезжиривания поверхности.
Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница / / Техническая информация/ / Физический справочник / / Электрические и магнитные величины / / Понятия и формулы для электричества и магнетизма. / / Формулы. Электрическое сопротивление проводника при постоянном токе, зависимость сопротивления проводника от температуры, индуктивное и ёмкостное (реактивное) сопротивление, полное реактивное сопротивление, полное сопротивление цепи при переменном токе Поделиться:    Электротехнические расчетные формулы. Электрическое сопротивление проводника при постоянном токе, зависимость сопротивления проводника от температуры, индуктивное (реактивное) сопротивление, ёмкостное (реактивное) сопротивление, полное реактивное сопротивление, полное сопротивление цепи при переменном токе (последовательное соединение). Величина Формула Обозначение и единица измерения Cопротивление проводника при постоянном токе, Ом  r = ρ  l   S  ρ — удельное сопротивление, Ом·м; l — длина, м; S — поперечное сечение проводника, м2. Зависимость сопротивления проводника от температуры  r2 = r1[1 + α(t2 − t1)] r2, r1 — сопротивление проводника соответственно при температурах t2 и t1, Ом; α — температурный коэффициент сопротивления, 1/град. Индуктивное (реактивное) сопротивление, Ом xL = ωL = 2πfL ω — угловая частота, рад/с; π≈3,14; f — частота, Гц; L — коэффициент самоиндукции (индуктивность), Гн; C — емкость, Ф. Емкостное (реактивное) сопротивление, Ом xC =   1   =   1   ωC 2πfC Полное реактивное сопротивление, Ом x = xL − xC xL, xC — индуктивное и емкостное сопротивления, Ом. Полное сопротивление цепи при переменном токе (последовательное соединение), Ом z = √  r2 + x2  = √ r2+(xL−xC)2 z — полное сопротивление цепи, Ом; r — активное сопротивление, Ом; x — реактивное сопротивление, Ом. Поиск в инженерном справочнике DPVA. Введите свой запрос: Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Основы определения реактивного сопротивления проводника и падения напряжения. Часть 1

Переменный ток создает индуктивность, емкость и связанные с ними свойства индуктивного и емкостного сопротивления. Хотя эти свойства не приводят к потерям энергии, которые напрямую связаны с этими свойствами, необходимо подавать напряжение и ток, сдвинутые по фазе на 90 градусов, чтобы можно было поддерживать созданные магнитные и электрические поля. В результате произойдет небольшое увеличение потерь в проводнике I ² R.

Конечно, есть и другие реактивные сопротивления, не связанные с проводниками, из которых состоит общее реактивное сопротивление системы , такое как реактивное сопротивление утечки аппаратуры и степень контроля коэффициента мощности. Мы ограничим наше обсуждение здесь реактивным сопротивлением проводника.

Индуктивное, емкостное реактивное сопротивление

Это мера способности катушки индуктивности подобно резистору сопротивляться току . Оно выражается следующим уравнением:

X _L = 2ϖfL (уравнение 1)

Где X _L — индуктивное сопротивление (в омах), f — частота (в герцах), а L — индуктивность (в генри). .

Обратите внимание, что индуктивное сопротивление прямо пропорционально частоте. С увеличением частоты увеличивается и индуктивное сопротивление. Вы должны знать тот факт, что индуктивное сопротивление заставляет ток отставать от напряжения на 90 градусов.

Емкостное реактивное сопротивление является мерой способности конденсатора, подобно резистору или катушке индуктивности, противостоять току. Это выражается следующим уравнением:

X _C = 1 ÷ (2ϖfC) (Уравнение 2)

Где X _C — емкостное реактивное сопротивление (в омах), а C — емкость (в фарадах).

Обратите внимание, что емкостное сопротивление обратно пропорционально частоте. Следовательно, с увеличением частоты емкостное сопротивление уменьшается. Вы также должны отметить, что емкостное реактивное сопротивление заставит ток опережать напряжение на 90 градусов.

Геометрия проводника

Индуктивность и, как следствие, индуктивное реактивное сопротивление кабеля зависят от его геометрии и физического отношения к другим кабелям. Большинство инженеров и производителей кабелей используют очень сложные серии уравнений для расчета индуктивного сопротивления кабелей. Однако вы можете использовать следующее упрощенное уравнение:

X _L = 2ϖf × [(0,1404 × log ₁₀ (S ÷ r)) + 0,0153 ] × 10 ^-3 (Уравнение 3)

Где X _L 100 футов до нейтрали), f — частота (в герцах), S — расстояние между центрами одножильных кабелей (в дюймах) и r — радиус одножильного кабеля (в дюймах).

Вы также можете использовать следующее уравнение:

X _L = 0,023 × [(log _e 2 × (S ÷ d)) + K ] (Уравнение 4)

Где d — диаметр одиночной жилы (в дюймах), а K равен 0,25 для кабеля со скруткой класса B.

Уравнение 3 или 4 можно применять к кабелям с разомкнутой оболочкой и к одножильным кабелям, уложенным случайным образом в кабелепроводах.

Чтобы упростить вам задачу, производители предоставляют номограммы расчета реактивного сопротивления, которые позволяют определить реактивное сопротивление в зависимости от толщины изоляции и размера проводника для проводников с различным расстоянием между ними, образец которого показан на Рисунок (щелкните здесь, чтобы увидеть Рисунок ).

(Номограмма — это графическое вычислительное устройство и двумерная диаграмма, предназначенная для приблизительного графического вычисления функции. Обычно она имеет три шкалы: две шкалы представляют известные значения, а одна — шкала, по которой считывается результат. Известные шкалы располагаются снаружи (т. е. шкала результата находится в центре).На внешних шкалах отмечается каждое известное значение расчета, а между каждой отметкой проводится линия.Там, где линия пересекается с внутренней шкалой Эти значения реактивного сопротивления получены из уравнения 3. В зависимости от конструкции проводника и/или кабеля необходимо применить поправочные коэффициенты, показанные на Таблица для любых значений реактивного сопротивления, которые вы получите.

Поскольку результирующие значения реактивного сопротивления находятся в омах от до нейтрали, вам необходимо выполнить дополнительный шаг, чтобы найти реактивное сопротивление между фазами . Для 3-фазной системы реактивное сопротивление фаза-фаза в 1,732 раза превышает значение реактивности фаза-нейтраль.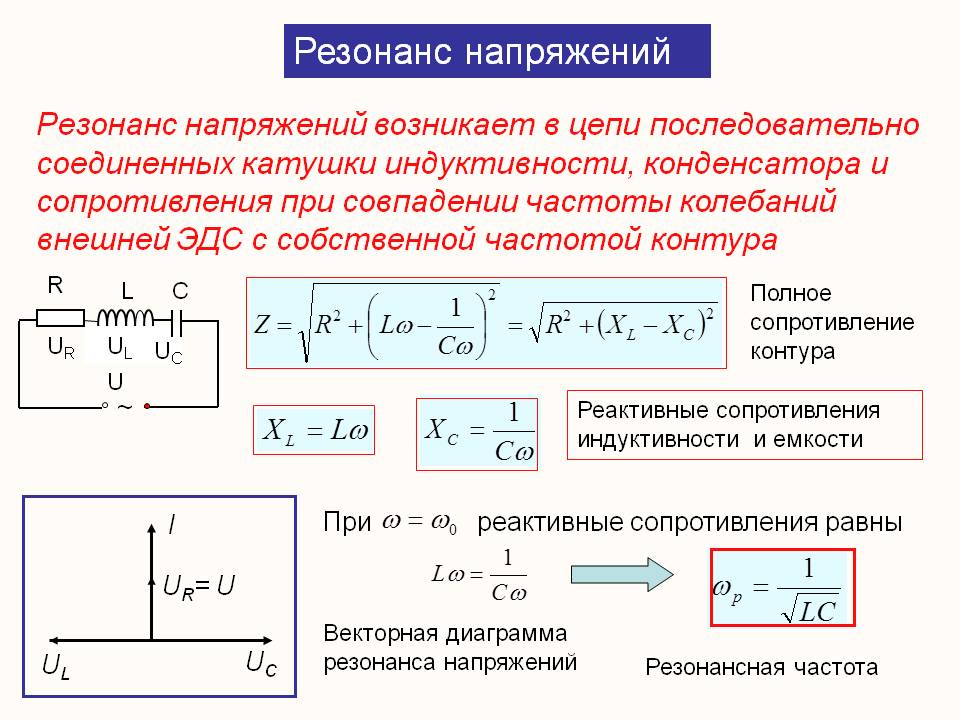 Для однофазной системы полное реактивное сопротивление в два раза превышает реактивное сопротивление между фазой и нейтралью.

Примеры задач на индуктивное сопротивление

Задача 1 . Предположим, у вас есть 3-жильный кабель 500 ксм, 600 В с оцинкованной блокированной броней в 3-фазной, 3-проводной, 60 Гц фидерной цепи. Каждый проводник имеет изоляцию толщиной 65 мил. Каково межфазное реактивное сопротивление кабеля?

Поскольку в трехжильном кабеле есть одиночные провода на 600 В, каждый отдельный одиночный проводник нет имеет разделительные ленты, полупроводниковые ленты, экраны или другие покрытия. Таким образом, вы можете обратиться к таблицам реактивного сопротивления и напрямую использовать значение реактивного сопротивления, указанное в столбце «65 мил» для 500 тыс.см мил, что составляет 0,0251 Ом на 1000 футов до нейтрали.

Поскольку стальная блокированная броня многожильного кабеля аналогична магнитному связующему, вам необходимо умножить это значение на соответствующий поправочный коэффициент, указанный в таблице, который в данном случае равен 1,122. Таким образом, X _L равно 0,0251, умноженному на 1,122, или 0,0282 Ом на 1000 футов до нейтрали.

Междуфазное реактивное сопротивление для этой цепи равно 0,0282 умножить на 1,732 или 0,0488 Ом на 1000 футов.

Задача 2 . Предположим, у вас есть фидер на 15 кВ, состоящий из трех одиночных проводников произвольной свивки, 350 тыс. см3, 100% уровня изоляции, каждый с экранами из концентрических проволочных прядей, в кабелепроводе из оцинкованной стали. Каждый проводник имеет наружный диаметр. 1,34 дюйма

Поскольку конструкция 15 кВ включает в себя разделительную ленту, полупроводниковую ленту, концентрическую скрутку провода и оболочку, вы не можете просто использовать толщину изоляции, обычно указанную для 100% уровня изоляции, которая обычно составляет 175 мил. Чтобы быть более точным, вам необходимо рассчитать толщину изоляции, используя следующее уравнение:

Толщина = [(наружный диаметр одножильного провода 2 наружных диаметра неизолированного провода) ÷ 2]

Теперь вы знаете наружный диаметр проводника. составляет 1,34 дюйма. Из литературы по проводам и кабелям вы можете узнать, что 37-жильный неизолированный проводник класса B с номинальным наружным диаметром 350 000 000 см. 0,681 дюйма. Таким образом, толщина изоляции равна количеству 1,34 дюйма минус 0,681 дюйма, деленному на 2, или 0,33 дюйма (330 мил). Согласно таблицам реактивного сопротивления значение реактивного сопротивления составляет 0,0373.

Поскольку проводники находятся в магнитопроводе, вы должны умножить это значение на 1,50 (увеличение на 50%). Следовательно, индуктивное сопротивление нейтрали при частоте 6 Гц в омах на 100 футов (X _L ) равно 0,0373, умноженному на 1,50, или 0,0560. Межфазное реактивное сопротивление составляет 0,0560 умножить на 1,732, или 0,097 Ом на 1000 футов.

В следующем месяце мы поговорим о том, как рассчитать индуктивное сопротивление в случаях, когда кабели не соприкасаются, но имеют определенную геометрическую конфигурацию.

Зависимости реактивного сопротивления, импеданса и мощности в цепях переменного тока Физика

До этого момента индуктивность и емкость объяснялись отдельно в цепях переменного тока. Остальная часть этой части будет посвящена комбинации индуктивности, емкости и сопротивления в цепях переменного тока.

Для объяснения различных свойств цепей переменного тока будет использоваться последовательная цепь RLC. Рисунок (4) представляет собой принципиальную схему последовательной цепи RLC. Символ E, показанный на рис. 4-4, является общим символом, используемым для обозначения источника переменного напряжения.

Серия RLC-цепей

РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ

Эффект индуктивного реактивного сопротивления заключается в том, что ток отстает от напряжения, в то время как емкостное реактивное сопротивление заставляет ток опережать напряжение. Следовательно, поскольку индуктивное сопротивление и емкостное сопротивление прямо противоположны по своим эффектам, каков будет результат их объединения? Нетрудно заметить, что чистый эффект представляет собой тенденцию компенсировать друг друга, при этом совокупный эффект равен разнице между их значениями. Эта результирующая называется РЕАКТИВНОСТЬ; обозначается символом X; и выражается уравнением X = X _L  – X _C  или X = X _C  – X _L . Таким образом, если цепь содержит 50 Ом индуктивного сопротивления и 25 Ом емкостного сопротивления последовательно, чистое реактивное сопротивление, или X, составляет 50 Ом — 25 Ом или 25 Ом индуктивного сопротивления.

В качестве практического примера предположим, что у вас есть цепь, содержащая катушку индуктивности 100 мкГн последовательно с конденсатором 0,001 мкФ и работающая на частоте 4 МГц. Каково значение чистого реактивного сопротивления, или X?

Дано f = 4 МГц, L = 100 мкГн, C = 0,001 мкФ

Решение: x _L = 2πfl

= 6,28 x 4 МГц x 100 мкН = 2512 ω

x _C = 1/2πFC

= 1/6,28 x 4 МГц x 0,001 мкф

= 1/6,28 x 4 МГц x 0,001 мкф

= 1/6,28 x 4 МГц.

= 39,8 Ом

X = X _L – X _C

X = 24722 Ом (индуктивная) цепь переменного тока. Однако есть еще один фактор, сопротивление, которое также препятствует протеканию тока. Поскольку на практике цепи переменного тока, содержащие реактивное сопротивление, также содержат сопротивление, они объединяются, чтобы противостоять протеканию тока. Это комбинированное сопротивление сопротивления и реактивного сопротивления называется ИМПЕДАНСОМ и обозначается символом Z.

Поскольку значения сопротивления и реактивного сопротивления даны в омах, на первый взгляд может показаться возможным определить значение импеданса, просто сложив их вместе. Однако сделать это так просто не получится. Вы знаете, что в цепи переменного тока, содержащей только сопротивление, ток и напряжение будут ступенчатыми (то есть синфазными) и достигнут своих максимальных значений в один и тот же момент. Вы также знаете, что в цепи переменного тока, содержащей только реактивное сопротивление, ток либо опережает, либо отстает от напряжения на четверть периода или на 90 градусов. Следовательно, напряжение в чисто реактивной цепи будет отличаться по фазе на 90 градусов от напряжения в чисто резистивной цепи, и по этой причине реактивное сопротивление и сопротивление объединяются простым их сложением.

При объединении реактивного сопротивления и сопротивления значение импеданса будет больше любого из них. Верно также и то, что ток не будет идти в ногу с напряжением и не будет отличаться по фазе точно на 90 градусов от напряжения, а будет где-то между совпадающим и 90 градусов.0-градусные условия отклонения от шага. Чем больше реактивное сопротивление по сравнению с сопротивлением, тем ближе разность фаз будет приближаться к 90°. Чем больше сопротивление по сравнению с реактивным сопротивлением, тем ближе разность фаз будет приближаться к нулю градусов.

Если значение сопротивления и реактивного сопротивления нельзя просто сложить вместе, чтобы найти импеданс или Z, как его определить? Поскольку ток через резистор находится в шаге от напряжения на нем, а ток в реактивном сопротивлении отличается на 90 градусов от напряжения на нем, они находятся под прямым углом друг к другу. Следовательно, их можно комбинировать тем же методом, что и при построении прямоугольного треугольника.

Предположим, вы хотите найти полное сопротивление последовательной комбинации сопротивления 8 Ом и индуктивного сопротивления 5 Ом. Начните с рисования горизонтальной линии R, представляющей сопротивление 8 Ом, в качестве основания треугольника.

Тогда, поскольку действие реактивного сопротивления всегда происходит под прямым углом, или 90 градусов к сопротивлению, нарисуйте линию X _L , представляющую индуктивное сопротивление 5 Ом, как высоту треугольника. Это показано на рисунке (5). Теперь достройте гипотенузу (самую длинную сторону) треугольника. Тогда гипотенуза представляет импеданс цепи.

Векторная диаграмма, показывающая соотношение сопротивления, индуктивного сопротивления и полного сопротивления в последовательной цепи.

Одно из свойств прямоугольного треугольника:

(гипотенуза) ² = (база) ² + (высота) ²

Гипотеновая = (сопротивление) ² + (реактивность) ²

Импеданс = √ (сопротивление) ² + (реактивность) ²

Импеданс = √ (сопротивление) ^{2 +} (Rectrance) ^{2 2}

Z = √R ²  + X ²

Теперь предположим, что вы применяете это уравнение для проверки результатов в приведенном выше примере.

Дано: R = 8 Ом, x _L = 5 Ом

Решение: z = √r ² + x _L ²

= √ (8 Ом) ² + (5 Ом) ²

= √64 + 25

= √89 Ом = 9,4 Ом

. направление. Это показано на рисунке (6). Линия проведена вниз для емкостного реактивного сопротивления, чтобы указать, что оно действует в направлении, противоположном индуктивному реактивному сопротивлению, которое направлено вверх. В последовательной цепи, содержащей емкостное реактивное сопротивление, уравнение для нахождения импеданса принимает вид:

Z = √R ²  + X _C ²

Во многих последовательных цепях сопротивление сочетается как с индуктивным, так и с емкостным сопротивлением. Поскольку вы знаете, что значение реактивного сопротивления X равно разнице между значениями индуктивного сопротивления X _L и емкостного сопротивления X _C , уравнение для импеданса в последовательной цепи, содержащее R,X _L и X _C тогда становятся:

z = √r ² + (x _L — x _C ) ² или z = √r ² + x ²

Примечание: Formulas z = √r ² + X _C ² , Z = √R ² + X ² и Z = √R ² + X _L ²  соединены последовательно.

В приведенных выше выражениях вы увидите метод, который можно использовать для определения импеданса в последовательной цепи, состоящей из сопротивления, индуктивности и емкости.

Предположим, что индуктивное сопротивление 10 Ом и емкостное сопротивление 20 Ом соединены последовательно с сопротивлением 40 Ом. Пусть горизонтальная линия представляет собой сопротивление R. Линия, проведенная вверх от конца R, представляет собой индуктивное реактивное сопротивление, X _L . Представьте емкостное сопротивление линией, проведенной вниз под прямым углом от одного и того же конца R. Результирующая X _L  и X _C  находят путем вычитания X _L из X _C . Этот результат представляет собой значение X.

Таким образом: X = X _C  – X _L  = 20 Ом – 10 Ом

= 10 Ом

Примечание. Если индуктивное сопротивление меньше емкостного, то оно вычитается из емкостного.

Эти два примера иллюстрируют важный момент: при последовательном соединении емкостного и индуктивного сопротивлений меньшее всегда вычитается из большего, и результирующее реактивное сопротивление всегда принимает характеристики большего.

Вопрос

1. Дано X _L = 10 Ом, X _C = 20 Ом, R = 40 Ом, рассчитайте импеданс.
2. 40 Ом B. 41,2 Ом C. 56 ОД D. 45,3 Ом

.

Расчет емкостного реактивного сопротивления

801 Ом B. 235 Ом C. 769 Ом D. 745 Ом

Теперь предположим, что имеется цепь, содержащая катушку индуктивности 100 мкГн, включенную последовательно с конденсатором 0,0002 мкФ, и работающая на частоте 1 МГц. Какова величина результирующего реактивного сопротивления в этом случае?

168 Ом B. 200 Ом C. 265 Ом D. 158 Ом

Как и в случае с емкостным сопротивлением, напряжение на катушке индуктивности определяется выражением

Присоединяйтесь к дискуссионному форуму и выполняйте задание : Найдите вопросы в конце каждого урока. Нажмите здесь, чтобы обсудить свои ответы на форуме

Вы хотите учиться в Великобритании или КАНАДЕ? : Воспользуйтесь нашим БЕСПЛАТНЫМ калькулятором, чтобы узнать, сколько вам нужно будет показать посольству! Это БЕСПЛАТНО Нажмите здесь, чтобы начать путешествие за границу.