Реактивное сопротивление катушки формула. Реактивное сопротивление катушки: формулы, расчеты и особенности

Что такое реактивное сопротивление катушки индуктивности. Как рассчитать реактивное сопротивление катушки. От чего зависит реактивное сопротивление катушки индуктивности. Какая формула используется для расчета реактивного сопротивления катушки.

Что такое реактивное сопротивление катушки индуктивности

Реактивное сопротивление катушки индуктивности — это сопротивление, которое катушка оказывает протеканию переменного тока. В отличие от активного сопротивления, реактивное сопротивление не приводит к потере энергии, а лишь создает сдвиг фаз между током и напряжением.

Основные особенности реактивного сопротивления катушки:

• Измеряется в Омах, как и обычное сопротивление
• Обозначается символом XL
• Зависит от частоты переменного тока
• Увеличивается с ростом частоты
• При постоянном токе равно нулю

Формула для расчета реактивного сопротивления катушки

Реактивное сопротивление катушки индуктивности рассчитывается по формуле:

XL = 2πfL

Где:

• XL — реактивное сопротивление в Омах
• π — число пи (≈3,14)
• f — частота переменного тока в Герцах
• L — индуктивность катушки в Генри

От чего зависит реактивное сопротивление катушки

Из формулы видно, что реактивное сопротивление катушки индуктивности зависит от двух параметров:

1. Частоты переменного тока (f). С увеличением частоты реактивное сопротивление возрастает.
2. Индуктивности катушки (L). Чем больше индуктивность, тем выше реактивное сопротивление.

При этом зависимость от частоты является линейной — при удвоении частоты реактивное сопротивление также удваивается.

Как частота влияет на реактивное сопротивление катушки

Влияние частоты на реактивное сопротивление катушки можно описать следующим образом:

• При f = 0 (постоянный ток) XL = 0
• При увеличении f значение XL линейно возрастает
• При f → ∞ значение XL также стремится к бесконечности

Это означает, что на высоких частотах катушка индуктивности представляет собой большое сопротивление для переменного тока. А на низких частотах и постоянном токе катушка ведет себя как проводник с малым сопротивлением.

Почему возникает реактивное сопротивление катушки

Физическая причина возникновения реактивного сопротивления катушки связана с явлением самоиндукции. При протекании переменного тока через катушку возникает переменное магнитное поле. Это поле индуцирует ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока.

Чем быстрее изменяется ток (выше частота), тем сильнее ЭДС самоиндукции и, соответственно, выше реактивное сопротивление катушки. Поэтому на высоких частотах катушка сильнее препятствует протеканию переменного тока.

Векторная диаграмма напряжений и токов для катушки индуктивности

Для наглядного представления процессов в цепи с катушкой индуктивности используется векторная диаграмма. На ней изображаются векторы напряжения и тока:

• Вектор тока I
• Вектор напряжения на активном сопротивлении UR
• Вектор напряжения на индуктивности UL
• Вектор полного напряжения U

Особенности векторной диаграммы для идеальной катушки:

• Вектор тока I отстает от вектора напряжения U на 90°
• Вектор UL опережает вектор тока I на 90°
• Вектор U совпадает с вектором UL

Для реальной катушки с активным сопротивлением угол сдвига фаз между током и напряжением меньше 90°.

Треугольник сопротивлений для цепи с катушкой индуктивности

Для анализа цепей переменного тока с катушкой индуктивности используется треугольник сопротивлений. Он позволяет наглядно представить соотношение между активным, реактивным и полным сопротивлением цепи.

В треугольнике сопротивлений:

• Катет R — активное сопротивление
• Катет XL — реактивное сопротивление катушки
• Гипотенуза Z — полное сопротивление цепи

Соотношение между сопротивлениями:

Z = √(R² + XL²)

Угол φ между Z и R равен углу сдвига фаз между током и напряжением в цепи.

Как рассчитать реактивное сопротивление катушки

Для расчета реактивного сопротивления катушки индуктивности необходимо:

1. Определить индуктивность катушки L (в Генри)
2. Узнать частоту переменного тока f (в Герцах)
3. Подставить значения в формулу: XL = 2πfL
4. Выполнить вычисления

Пример расчета:

Дано: L = 0,1 Гн, f = 50 Гц

XL = 2 * 3,14 * 50 * 0,1 = 31,4 Ом

Таким образом, реактивное сопротивление данной катушки на частоте 50 Гц составляет 31,4 Ом.

Применение реактивного сопротивления катушек

Знание реактивного сопротивления катушек индуктивности важно во многих областях электротехники и электроники:

• Расчет и проектирование фильтров
• Согласование импедансов в радиотехнике
• Компенсация реактивной мощности
• Настройка колебательных контуров
• Расчет трансформаторов

Например, в LC-фильтрах реактивное сопротивление катушки растет с частотой, а конденсатора — падает. Это позволяет создавать частотно-избирательные цепи.

Отличие реактивного сопротивления от активного

Реактивное сопротивление катушки индуктивности имеет ряд важных отличий от активного сопротивления:

1. Не приводит к потере энергии (нагреву)
2. Создает сдвиг фаз между током и напряжением
3. Зависит от частоты
4. Равно нулю на постоянном токе
5. Препятствует изменению тока, а не его величине

При этом реактивное сопротивление, как и активное, измеряется в Омах и подчиняется закону Ома для переменного тока.

Зависимость реактивного сопротивления от конструкции катушки

На реактивное сопротивление катушки влияют следующие конструктивные параметры:

• Количество витков — чем больше витков, тем выше индуктивность и XL
• Диаметр катушки — увеличение диаметра повышает индуктивность
• Длина намотки — удлинение катушки снижает индуктивность
• Материал сердечника — ферромагнитный сердечник увеличивает индуктивность
• Форма сечения — круглое сечение обеспечивает максимальную индуктивность

Изменяя эти параметры, можно регулировать реактивное сопротивление катушки в широких пределах для конкретных применений.

Реактивное сопротивление трансформатора: формулы расчета

Мы привыкли считать, что все магнитные потоки в трансформаторе пронизывают обе обмотки и магнитопровод. Если бы существовал идеальный трансформатор, то это действительно так бы и происходило. К сожалению, в реальности часть магнитного потока преодолевает изоляционное пространство, выходит за пределы обмоток и замыкается в них (см. рис. 1). В результате возникает реактивное сопротивление трансформатора. Такое явление ещё называют рассеиванием магнитных потоков.

Рис. 1. Схема, иллюстрирующая рассеивание магнитных потоков

В катушках существуют и другие сопротивления, являющиеся причинами потерь мощности. Таковыми являются: внутреннее сопротивление материалов обмоток, и рассеивания, вызванные индуктивными сопротивлениями. Совокупность рассеиваний магнитных потоков называют внутренним сопротивлением или импедансом трансформатора.

Потери реактивных мощностей

Вспомним, как работает идеальный двухобмоточный трансформатор (см. рис. 2). Когда первичная обмотка окажется под переменным напряжением (например, от электрической сети), возникнет магнитный поток, который пронизывает вторичную катушку индуктивности. Под действием магнитных полей происходит возбуждение вторичных обмоток, в витках которых возникает ЭДС. При подключении активной мощности к прибору во вторичной цепи начинает протекать переменный ток с частотой входного тока.

Рис. 2. Устройство трансформатора

В идеальном трансформаторе образуется прямо пропорциональная связь между напряжениями в обмотках. Их соотношение определяется соотношением числа витков каждой из катушек. Если U₁ и U₂ – напряжения в первой и второй обмотке соответственно, а w₁ и w₂ – количество витков обмоток, то справедлива формула: U₁ / U₂ = w₁ / w₂.

Другими словами: напряжение в рабочей обмотке во столько раз больше (меньше), во сколько раз количество мотков второй катушки увеличено (уменьшено) по отношению к числу витков, образующих первичную обмотку.

Величину w₁ / w₂ = k принято называть коэффициентом трансформации. Заметим, что формула, приведённая выше, применима также для автотрансформаторов.

В реальном трансформаторе часть энергии теряется из-за рассеяния магнитных потоков (см. рис. 1). Зоны, где происходит концентрация потоков рассеяния обозначены пунктирными линиями. На рисунке видно, что индуктивность рассеяния охватывает  магнитопровод и выходит за пределы обмоток.

Наличие реактивных сопротивлений в совокупности с активным сопротивлением обмоток приводят к нагреванию конструкции. То есть, при расчётах КПД необходимо учитывать импеданс трансформатора.

Обозначим активное сопротивление обмоток символами R₁ и R₂ соответственно, а реактивное – буквами X₁ и X₂. Тогда импеданс первичной обмотки можно записать в виде: Z₁= R₁+jX₁. Для рабочей катушки соответственно будем иметь: Z₂= R₂+jX₂, где j – коэффициент, зависящий от типа сердечника.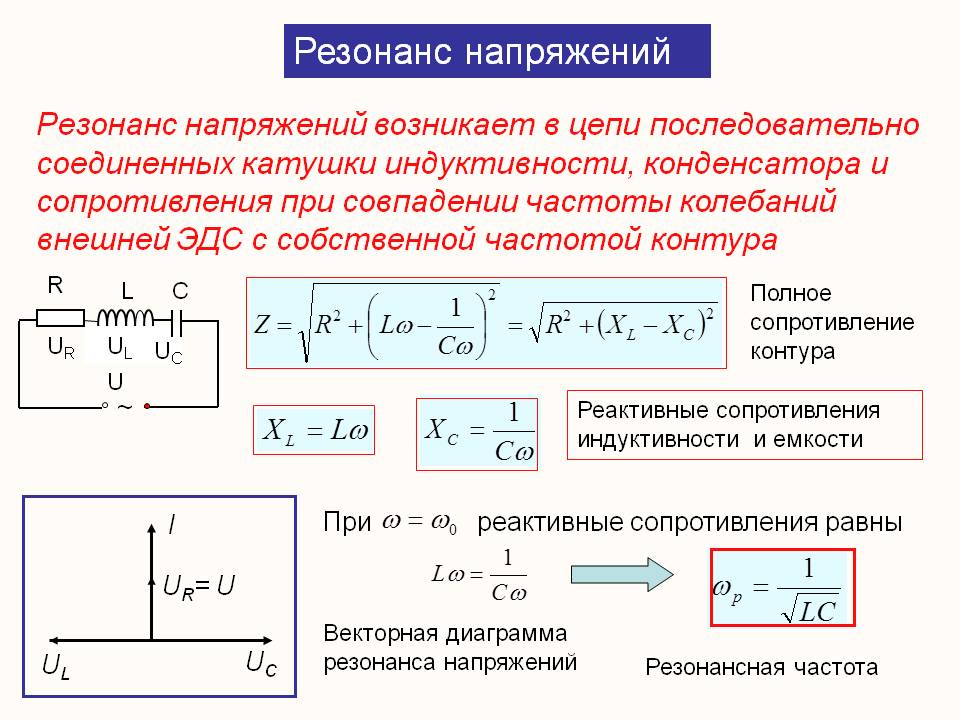

Реактивное сопротивление можно представить в виде разницы индукционного и ёмкостного показателя: X = R_L – R_C. Учитывая, что R_L =  ωL, а R_C = 1/ωC, где ω – частота тока, получаем формулу для вычисления реактивного сопротивления: X = ωL – 1/ωC.

Не прибегая к цепочке преобразований, приведём готовую формулу для расчёта полного сопротивления, то есть, для определения импеданса трансформатора:

Суммарное сопротивление трансформатора необходимо знать для определения его КПД. Величины потерь в основном зависят от материала обмоток и конструктивных особенностей трансформаторного железа. Вихревые потоки в монолитных стальных сердечниках значительно больше, чем многосекционных конструкциях магнитопроводов. Поэтому на практике сердечники изготавливаются из тонких пластин трансформаторной стали. С целью повышения удельного сопротивления материала, в железо добавляют кремний, а сами пластины покрывают изоляционным лаком.

Для определения параметров трансформаторов важно найти активное и реактивное сопротивление, провести расчёты потерь холостого хода. Приведённая выше формула не практична для вычисления импеданса по причине сложности измерений величин индукционного и ёмкостного сопротивлений. Поэтому на практике пользуются другими методами для расчёта, основанными на особенностях режимов работы силовых трансформаторов.

Режимы работы

Двухобмоточный трансформатор способен работать в одном из трёх режимов:

• вхолостую;
• в режиме нагрузки;
• в состоянии короткого замыкания.

Для проведения расчётов режимов электрических цепей проводимости заменяют нагрузкой, величина которой равна потерям при работе в режиме холостого хода. Вычисления параметров схемы замещения проводят опытным путём, переводя трансформатор в один из возможных режимов: холостого хода, либо в состояние короткого замыкания. Таким способом можно определить:

• уровень потерь активной мощности при работе на холостом ходу;
• величины потерь активной мощности в короткозамкнутом приборе;
• напряжение короткого замыкания;
• силу тока холостого хода;
• активное и реактивное сопротивление в короткозамкнутом трансформаторе.

Параметры режима холостого хода

Для перехода в работу на холостом ходу необходимо убрать отсутствует нагрузку на вторичной обмотке, то есть – разомкнуть электрическую цепь. В разомкнутой катушке напряжение отсутствует. Главной составляющей тока в первичной цепи является ток, возникающий на реактивных сопротивлениях. С помощью измерительных приборов довольно просто найти основные параметры переменного тока намагничивания, используя которые можно вычислить потери мощности, умножив силу тока на подаваемое напряжение.

Схема измерений на холостом ходу показана на рисунке 3. На схеме показаны точки для подключения измерительных приборов.

Рис. 3. Схема режима холостого хода

Формула, применяемая для  расчётов параметров реактивной проводимости, выглядит так: В_т = I_х%*S_ном  / 100* U_{в ном}²  Умножитель 100 в знаменателе применён потому, что величина тока холостого хода I_х обычно выражается в процентах.

Режим короткого замыкания

Для перевода трансформатора на работу в режиме короткого замыкания закорачивают обмотку низшего напряжения. На вторую катушку подают такое напряжение, при котором в каждой обмотке циркулирует номинальный ток. Поскольку подаваемое напряжение существенно ниже номинальных напряжений, то потери активной мощности в проводимости настолько малы, что ими можно пренебречь.

Таким образом, у нас остаются активные мощности в трансформаторе, которые расходуются на нагрев обмоток: ΔP_k = 3* I_1ном * R_т. Выразив ток I_{1 ном} через напряжение U_ка и сопротивление R_т, умножив выражение на 100, получим формулу для вычисления падения напряжения в зонах активного сопротивления (в процентах):

Активное сопротивление двухобмоточного силового трансформатора вычисляем по формуле:

Подставив значение R_т в предыдущую формулу, получим:

Вывод: в короткозамкнутом трансформаторе падение напряжения в зоне активного сопротивления (выраженная в %) прямо пропорционально размеру потерь активной мощности.

Формула для вычисления падения напряжения в зонах реактивных сопротивлений имеет вид:

Отсюда находим:

Величины реактивных сопротивлений в современных трансформаторах гораздо меньше активного. Поэтому можно считать что падение напряжения в зоне реактивного сопротивления U_{к р} ≈ U_к, поэтому для практических расчётов можно пользоваться формулой: X_T = U_k*U_{в ном}² / 100*S_ном

Рассуждения, приведённые выше, справедливы также для многообмоточных, в том числе и для трёхфазных трансформаторов. Однако вычисления проводятся по каждой обмотке в отдельности, а задача сводится к решению систем уравнений.

Знание коэффициентов мощности, сопротивления рассеивания и других параметров магнитных цепей позволяет делать расчёты для определения величин номинальных нагрузок. Это, в свою очередь, обеспечивает работу трансформатора в промежутке номинальных мощностей.

Список использованной литературы

• Сивухин Д. В. «Общий курс физики» 1975
• Н.А. Костин, О.Г.Шейкина «Теоретические основы электротехники» 2007
• Нейман Л.Р., Демирчян К.С. «Теоретические основы электротехники» 1981
• Бартош А.И. «Электрика для любознательных» 2019

Активное и реактивное сопротивление

ТОЭ › Расчет цепей синусоидального тока

Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R. Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону

u = Umsinωt

Найдём ток и мощность в цепи.

Активное сопротивление

И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента — резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, «активный — это деятельный, энергичный, проявляющий инициативу». Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.

То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.

Как смотреть силу тока в цепи через осциллограф

Чем же резистор отличается от катушки индуктивности и конденсатора? Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:

На схеме мы видим генератор частоты и резистор.

Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты

А также цифровой осциллограф:

С помощью него мы будем смотреть напряжение и силу тока .

Что?

Силу тока?

Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто). Для этого достаточно вспомнить правило шунта.

Кто не помнит — напомню. Имеем обыкновенный резистор:

Что будет, если через него прогнать электрический ток?

На концах резистора у нас будет падение напряжения. То есть, если замерить с помощью мультиметра напряжение на его концах, мультиметр покажет какое-то значение в Вольтах

И теперь главный вопрос: от чего зависит падение напряжения на резисторе? В дело опять же вступает закон Ома для участка цепи: I=U/R. Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока

Мощность

При наличии активного сопротивления, значительно снижается мощность этой цепи. Это значение зависит от скорости снижения напряжения и преобразования электрической энергии. В электрической схеме мощность обозначается буквой «P».

Для того чтобы добиться минимального снижения средней и мгновенной мощностей, которые образуются в момент появления активного сопротивления, снижения напряжения и преобразования энергий, необходимо чтобы простейшие цепи состояли из идеальных элементов с высокой электрической проводимостью.

Осциллограмма силы тока на активном сопротивлении

В данном опыте нам не обязательно знать номинал силы тока в цепи. Мы будем просто смотреть, от чего зависит сила тока и изменяется ли вообще?

Поэтому, наша схема примет вот такой вид:

В этом случае шунтом будет являться резистор сопротивлением в 0,5 Ом. Почему именно 0,5 Ом? Да потому что он не будет сильно греться, так как обладает маленьким сопротивлением, а также его номинал вполне достаточен, чтобы снять с него напряжение.

Осталось снять напряжение с генератора, а также со шунта с помощью осциллографа. Если вы не забыли, со шунта мы снимаем осциллограмму силы тока в цепи. Красная осциллограмма — это напряжение с генератора Uген , а желтая осциллограмма — это напряжение с шунта Uш , в нашем случае — сила тока. Смотрим, что у нас получилось:

Частота 28 Герц:

Частота 285 Герц:

Частота 30 Килогерц:

Как вы видите, с ростом частоты сила тока у нас осталась такой же.

Давайте побалуемся формой сигнала:

Как мы видим, сила тока полностью повторяет форму сигнала напряжения.

Итак, какие можно сделать выводы?

1) Сила тока через активное (омическое) сопротивление имеет такую же форму, как и форма напряжения.

2) Сила тока и напряжение на активном сопротивлении совпадают по фазе, то есть куда напряжение, туда и ток. Они двигаются синфазно, то есть одновременно.

3) С ростом частоты ничего не меняется (если только на очень высоких частотах).

Сопротивления цепи

Уравнение (5-30) можно переписать в следующем виде

U

= √(
Ir
)2 + (
IxL
)2 =
I
√
r
2 +
x
2L =
Iᴢ
откуда ток в цепи

I

=
U
/
z
=
U
/ √(
r
2 +
x
2L)

Величина

z

= √(
r
2 +
x
2L) = √(
r
2 + ω
L
)2

называется полным сопротивлением цепи.

Сопротивления r

,
x
L и
z
графически можно изобразить сторонами прямоугольного треугольника — треугольника сопротивлении (рис. 5-20),который можно получить из треугольника напряжений, уменьшив каждую из его сторон в
I
раз.

Так как треугольники сопротивлений и напряжений подобны, то угол сдвига φ между напряжением и током, равный углу между сторонами треугольника z

и
r
, можно определить через

cos φ = U

a /
U
Рис 5-20. Треугольник сопротивлений цепи с активным сопротивлением и индуктивностью

Конденсатор в цепи переменного тока

Ну а теперь давайте вместо резистора поставим конденсатор.

Смотрим осциллограммы:

Как вы видите, конденсатор обладает сопротивлением, так как сила тока в цепи значительно уменьшилась. Но обратите внимание, что произошел сдвиг желтой осциллограммы, то бишь осциллограммы силы тока.

Вспоминаем алгебру старшие классы. Итак, полный период T — это 2П

Теперь давайте прикинем, какой сдвиг фаз у нас получился на графике:

Где-то примерно П/2 или 90 градусов.

Почему так произошло? Во всем виновато физическое свойство конденсатора. В самые первые доли секунд, конденсатор ведет себя как проводник с очень малым сопротивлением, поэтому сила тока в этот момент будет максимальна. В этом можно легко убедиться, если резко подать на конденсатор напряжение и в начальный момент времени посмотреть, что происходит с силой тока

Красная осциллограмма — это напряжение, которое мы подаем на конденсатор, а желтая — это сила тока в цепи конденсатора. По мере заряда конденсатора сила тока падает и достигает нуля при полном заряде конденсатора.

К чему приведет дальнейшее увеличение частоты? Давайте посмотрим:

50 Герц.

100 Герц

200 Герц

Как вы видите, с увеличением частоты, у нас сила тока в цепи с конденсатором возрастает.

Зависимость

Величина активного сопротивления во многом зависит от диаметра проводников. При подаче высокочастотных токов, сопротивление проводника может быть снижено, только если его поверхностный слой намного тоньше основного. Для того чтобы добиться идеального сечения, этот слой должен состоять из материала с очень высокой проводимостью, например, золота или серебра. Данный эффект возникает по причине взаимодействия напряжения и магнитного поля, образованного им. Поле сильно влияет на ток, протекающий по проводнику и выталкивает его на поверхностный слой. Таким образом ближе к поверхности проводника проводимость снижается и становится критично малой в его верхнем слое.

Так же присутствуют следующие эффекты: потери утечки и диэлектрические потери. Оба эффекта связаны с наличием конденсатора в цепи. Диэлектрические потери возникают за счет увеличения температуры диэлектрика внутри конденсатора. Потеря утечки возникает в следствии доли пробоя изолятор конденсатора.

Гистерезис. Это тоже тип потери энергии переменного тока. Такая потеря возникает при формировании магнитного поля вокруг предметов из металла. Электромагнитное воздействие приводит к нагреванию металла, а значит преобразованию энергии.

Последним фактором утечки является радиоизлучение. Радиоволны появляются по причине сильного магнитного поля и его взаимодействия с металлами цепи. Для подавления, особенно в радиоаппаратуре, используются экраны, которые впитывают часть поля и отталкивают остальную долю.

Реактивное сопротивление конденсатора

Как мы увидели с прошлого опыта, с увеличением частоты растет сила тока! Кстати, у резистора не росла. То есть получается в данном случае из закона Ома, что сопротивление конденсатора зависит от частоты! Да, все так оно и есть. Но называется оно не просто сопротивлением, а реактивным сопротивлением и вычисляется по формуле:

где

Хс — реактивное сопротивление конденсатора, Ом

П — постоянная и приблизительно равна 3,14

F — частота, Гц

С — емкость конденсатора, Фарад

Треугольник сопротивлений

Схема цепи, подключенной к переменному току, имеет полное сопротивление, которое можно определить в виде суммы квадратов реактивного и активного сопротивлений.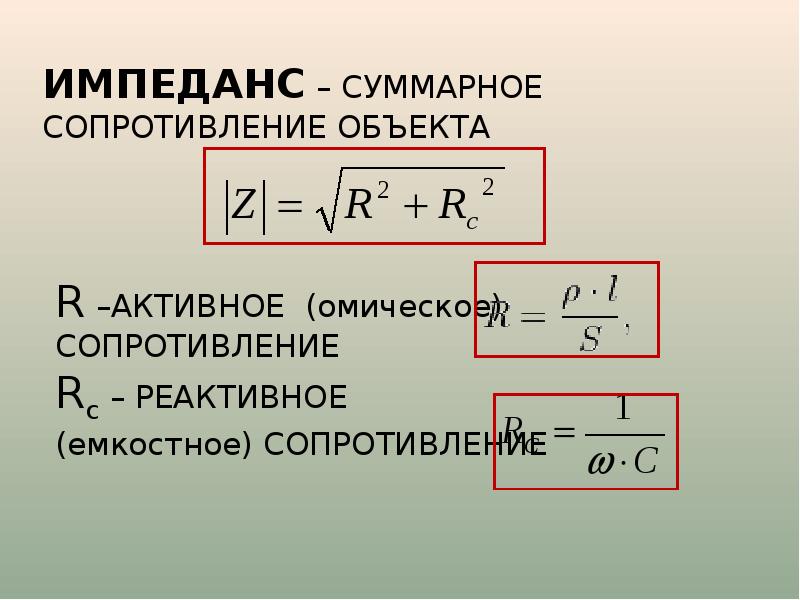

Если изобразить это выражение в виде графика, то получится треугольник сопротивлений. Он образуется, если рассчитать последовательную цепь всех трех видов сопротивлений.

По этому треугольному графику можно увидеть, что катеты представляют собой активное и реактивное сопротивление, а гипотенуза является полным сопротивлением.

Реактивное сопротивление катушки индуктивности

Из опыта выше мы можем сделать вывод, что сопротивление катушки зависит от частоты и вычисляется по формуле

где

ХL — сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

F — частота, Гц

L — индуктивность

Подробнее здесь: https://www.ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/

где

ХL — сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

F — частота, Гц

L — индуктивность

Подробнее здесь: https://www.ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/

где

ХL — сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

F — частота, Гц

L — индуктивность

Подробнее здесь: https://www. ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/

где

ХL — реактивное сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

Подробнее здесь: https://www.ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/

П — постоянная и приблизительно равна 3,14

F — частота, Гц

L — индуктивность, Генри

Решая это уравнение относительно f , находим

(3.40)
При резонансе напряжений частота источника равна собственной частоте колебаний контура.

Выражение (3.40) является формулой Томсона, определяющей за­висимость собственной частоты колебаний контура

, от параметровL

и
С
. Следует вспомнить, что если конденсатор контура зарядить от ис­точника постоянного тока, а затем замкнуть его на индуктивную ка­тушку, то в контуре возникнет переменный ток частоты

. Вследствие потерь колебания в контуре будут затухать, причем время затухания зависит от величины потерь.

Рис. 55

Резонансу напряжений соответствует векторная диаграмма, при­веденная на рис.55. На основании этой диаграммы и закона Ома для цепи с r,
L
и
С
сформулируем признаки резонанса напряжений:

а) сопротивление всей цепи

мини­мальное и чисто активное;

б) ток цепи совпадает по фазе с напряже­нием источника и достигает максимального значения;

Рис. 56 Рис. 57

в) напряжение на индуктивной катушке равно напряжению на емкости и каждое в отдельности может во много раз превышать напряжение на зажимах цепи.

Физически это объясняется тем, что напряжение источника при резонансе идет только на покрытие потерь в контуре. Напряже­ние на индуктивности и емкости обусловлено накопленной в них энергией, величина которой тем больше, чем меньше потери в цепи.

Количествен­но указанное явление характеризуется добротностью кон­тура
Q
, которая представляет собой отношение напряжения на ка­тушке или емкости к напряжению на зажимах цепи при резонансе;

. (3.41)
При резонансе

Величина

называется волновым сопротивлением контура. Таким образом,

(3.42)

Способность колебательного контура выделять токи резонансных частот и ослаблять токи других частот характеризуется резонансной кривой (рис. 56).

Резонансная кривая показывает зависимость действующего значе­ния тока в контуре от частоты источника при неизменной собственной частоте контура.

Эта зависимость определяется законом Ома для цепи с r,L

и
С
. Действительно,
I =Uz
, где

(3.43)

На рис. 57 показана зависимость реактивного сопротивления

от частоты источника. Анализ этого графика и выражения (3.43) показывает, что при низких и высоких частотах реактивное со­противление велико и ток в контуре мал. При частотах, близких

реактивное сопротивление мало и ток контура велик. При этом, чем больше добротность контураQ

, тем острее резонансная кривая кон­тура.

Вывод формулы и векторная диаграмма

Катушка индуктивности обычно представляет собой катушку проволоки. Когда ток проходит через эту катушку, создается электрическое поле. Таким образом, поле будет индуцироваться. Индуктивное поле зависит от количества витков и это индуктивность. Катушка индуктивности благодаря своей индуктивности сопротивляется протеканию переменного тока. По закону Ленца индуктор будет сопротивляться изменению тока. Реактивное сопротивление определяется как сопротивление, оказываемое переменному току только конденсаторами и катушками индуктивности. Обычно реактивное сопротивление обозначается X, частота — f, индуктивность — L, а емкость — C. Индуктивное реактивное сопротивление зависит от частоты. Расчет этого можно сделать с помощью простых формул.

Индуктивное реактивное сопротивление определяется как эффект, посредством которого уменьшается протекание переменного тока в катушке индуктивности. Любой переменный ток или переменный ток будут затруднены из-за связанной с ним индуктивности.

Дроссели и катушки индуктивности в основном представляют собой петли из проволоки или катушек, намотанных на какой-либо ферромагнитный материал или на полую трубчатую форму для увеличения их индуктивного значения, называемого индуктивностью. Когда напряжение подается на клеммы индуктора, индукторы накапливают энергию в виде магнитного поля. Для катушки индуктивности напряжение обратной ЭДС пропорционально скорости изменения тока, протекающего через нее.

Индуктивное реактивное сопротивление

Если мы начали изучать или наблюдать самоиндукцию и эффекты, возникающие в цепи, то мы можем легко узнать причину этого индуктивного реактивного сопротивления. Чтобы определить это в простой форме, это как противодействие текущему течению.

Когда на катушку индуктивности подается переменное напряжение, протекание тока будет отличаться от того, когда на нее подается постоянное напряжение. Разность фаз между сигналами напряжения и тока будет создаваться синусоидальным питанием. Как частота сигнала, так и индуктивность катушки определяют противодействие протеканию тока в обмотках катушки в цепи переменного тока.

Сопротивление переменному току определяет сопротивление тока, протекающего через катушку в цепи переменного тока, и обычно известно как импеданс (Z) цепи. Чтобы отличить сопротивление постоянному току от сопротивления переменному току, сопротивление всегда связано с цепями постоянного тока, и для этого используется общий термин — реактивное сопротивление. Значение реактивного сопротивления измеряется в омах, как и сопротивление. Чтобы узнать разницу между реактивным значением и резистивным значением, значение реактивного сопротивления обозначается «X».

Поскольку мы сосредоточились на компоненте индуктора, реактивное сопротивление индуктора называется индуктивным реактивным сопротивлением. Чтобы упростить его в другой форме, его можно определить как электрическое сопротивление индуктора при использовании в цепи переменного тока. Символ индуктивного сопротивления — XL.

Формула индуктивного реактивного сопротивления

Индуктивное реактивное сопротивление можно рассчитать по следующей формуле. Индуктивное сопротивление равно произведению умноженного на 2 пи на индуктивность катушки и частоту переменного тока. Таким образом, формула может быть обозначена как

XL= 2πfL

Где «XL» — индуктивное сопротивление, измеряемое в омах

f — частота переменного тока источника питания в герцах

«L» — индуктивность стоимость катушки в генри.

Из этой формулы для индуктивного сопротивления мы можем ясно знать, что индуктивное сопротивление будет увеличиваться при увеличении частоты или индуктивности. Индуктивное сопротивление будет достигать бесконечности, когда частота приближается к бесконечности, и это действует как разомкнутая цепь. Точно так же он будет приближаться к нулю, когда частота уменьшится до нуля, и это действует как короткое замыкание. он четко определяет, что частота и индуктивное сопротивление прямо пропорциональны.

Идеальная катушка индуктивности имеет только индуктивность, но не имеет сопротивления и емкости. Хотя идеальных катушек индуктивности не существует. Чтобы определить формулы и расчеты, представим себе размещение идеального индуктора. Если к идеальному индуктору приложена синусоидальная волна, реактивное сопротивление препятствует протеканию тока и подчиняется закону Ома 9.0003

XL =V/I

‘XL’ — индуктивное сопротивление в омах

‘I’ — ток в амперах

‘V’ — напряжение в вольтах эта частота прямо пропорциональна частоте. Следовательно, мы видим, что индуктор имеет нулевое реактивное сопротивление на постоянном токе, а индуктор имеет бесконечное реактивное сопротивление на высоких частотах.

Вывод формулы индуктивного реактивного сопротивления

Синусоидальный переменный

Напряжение В = Vmsinwt

Противоэдс индукции, e =Ldi/dt

e=v

Ldi/dt=Vmsinwt

Di=Vm/l sinwtdt

Интегрирование с обеих сторон

/∫m dim L sinwtdt

I= Vm/wL sin (wt-π/2)

At wt=π sin (wt-π/2) =1

Im =Vm/wL

Vm/Im =wL

Вт =2πf

Индуктивное сопротивление XL =Vm/Im =2πfL

Питание переменным током через цепь серии LR

В основном мы рассматриваем чисто индуктивную катушку, но каждый раз рассматривать чисто индуктивную катушку будет невозможно, но соленоиды будут иметь определенное сопротивление, не имеет значения, насколько малы были связанные с катушками витки провода, который используется.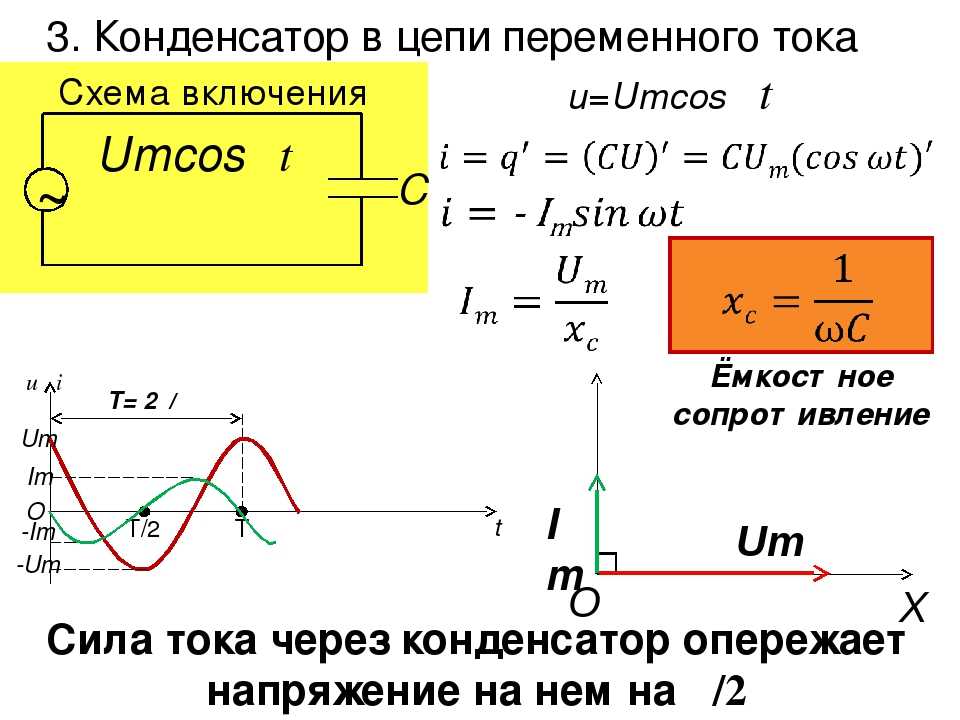 Так что мы можем рассматривать эту простую катушку как последовательное сопротивление с индуктивностью.

Сопротивление «R» и индуктивность «L» присутствуют в цепи переменного тока, и напряжение V будет суммой векторов VL и VR. Фазовый угол цепи определяется новым фазовым углом между током и напряжением и обозначается греческим символом фи.

Векторная диаграмма результирующего напряжения

Здесь линия OB — эталон горизонтального тока, OA — напряжение на резистивном компоненте, синфазное с током, OC — индуктивное напряжение, равное 90 градусов перед током, OD даст результирующее напряжение питания.

Векторная диаграмма результирующего напряжения

В = среднеквадратичное значение приложенного напряжения

I = среднеквадратичное значение последовательного тока

VR = IR падение напряжения на сопротивлении, которое находится в фазе с током

VL = падение напряжения на индуктивности что опережает ток на 90 градусов

Фазовый угол

Когда две или более индуктивных катушек соединены последовательно или одна катушка при последовательном соединении с большим количеством неиндуктивных сопротивлений, общее сопротивление резистивных элементов будет равно R1+R2+R3 и т. д. это даст общее значение сопротивления цепи.

Фазовый угол

Если говорить о реактивном сопротивлении, общее реактивное сопротивление индуктивных элементов равно X1+X2+X3 и т. д. и дает значение полного реактивного сопротивления цепи.

Разница между индуктивностью и реактивным сопротивлением включает

• Реактивное сопротивление – это влияние индуктивности на заданной частоте.
• Индуктивность определяется как физическое свойство проводника или катушки. Единицы — генри, и это не зависит от частоты сигнала в компоненте
• Что касается реактивного сопротивления, оно зависит от частоты сигнала.

Перейдите по этой ссылке, чтобы узнать больше о MCQ по закону Ома.

Это полное описание индуктивного сопротивления, его формулы, единиц измерения и размеров. Вот вопрос, в чем разница между реактивным сопротивлением и емкостью.

Формула индуктивного реактивного сопротивления — HardwareBee Semipedia

17/12/2021, hardwarebee

В этой статье рассматривается формула индуктивного реактивного сопротивления , но перед этим давайте начнем со знакомства с катушкой индуктивности.

 

Катушка индуктивности представляет собой катушку из проволоки, намотанной на центральный сердечник. Магнитный поток (N), создаваемый током (I), протекающим через индуктор, пропорционален потоку тока (I). На рис. 1 изображено условное обозначение индуктора. Как видно ниже, наличие сплошных или пунктирных параллельных линий рядом с проволочной катушкой разделяет различные типы сердечников. Индукторы классифицируются как полые сердечники (свободный воздух), твердые железные сердечники или мягкие ферритовые сердечники в зависимости от типа внутреннего сердечника, вокруг которого они обернуты.

 

Рис. 1. Символы индуктора и подключенный индуктор

 

Катушки индуктивности препятствуют колебаниям прохождения переменного тока (AC) или препятствуют им, но они могут легко пропускать постоянный постоянный ток (DC). Индуктивность — это сопротивление скорости изменения тока, протекающего через индуктор, из-за генерации самоиндуцируемой энергии внутри его магнитного поля. Эффективное сопротивление, оказываемое катушкой индуктивности проходящему через нее электрическому току, известно как индуктивное реактивное сопротивление или индуктивное сопротивление.

 

Индуктивное реактивное сопротивление

 

Уменьшение протекающего тока определяется как влияние индуктивного реактивного сопротивления на протекание переменного тока в катушке индуктивности. Из-за индуктивности любой переменный ток или переменный ток будут затруднены.

 

Дроссели и катушки индуктивности состоят из проволочных петель или катушек, намотанных вокруг ферромагнитного материала или формы полой трубы для повышения индуктивности. Когда на их клеммы подается напряжение, катушки индуктивности накапливают энергию в виде магнитного поля. Напряжение противо-ЭДС катушки индуктора определяется скоростью изменения тока, протекающего через нее.

 

Протекание тока катушки индуктивности с переменным напряжением отличается от протекания тока катушки индуктивности с постоянным напряжением. Несовпадение фаз между сигналами напряжения и тока вызвано синусоидальным питанием. В цепи переменного тока противодействие протеканию тока в обмотках катушки определяется как частотой формы волны, так и индуктивностью катушки.

 

Сопротивление переменному току, также известное как импеданс цепи, определяет сопротивление тока, протекающего через катушку в цепи переменного тока (Z). При отделении сопротивления постоянному току от сопротивления переменному току сопротивление обычно связывают с цепями постоянного тока, и стандартным термином для этого является реактивное сопротивление. Сопротивление и реактивное сопротивление измеряются в омах. Значение реактивного сопротивления обозначается «X», чтобы отличить его от значения сопротивления.

 

Реактивное сопротивление индуктора называется индуктивным реактивным сопротивлением, поскольку мы концентрируемся на компоненте индуктора. Другими словами, его можно описать как электрическое сопротивление катушки индуктивности, когда она используется в цепи переменного тока. Индуктивное сопротивление обозначается буквой XL.

 

Формула индуктивного реактивного сопротивления

Аналогична сопротивлению резистора в том смысле, что оба сопротивления препятствуют прохождению электрического заряда. С другой стороны, электроны, сталкивающиеся с ним при прохождении через резисторы, вызывают противодействие. В индукторе самоиндуцируемое электрическое магнитное поле (ЭДС) сопротивляется нарастанию и спаду тока.

 

Рассмотрим приведенную ниже схему, в которой есть катушка индуктивности и источник переменного напряжения (рис. 2). Поскольку количество и направление переменного тока постоянно изменяются, катушка индуктивности будет генерировать ЭДС, чтобы противостоять любому изменению тока, проходящего через нее.

Рисунок 2: Индикатор с источником переменного тока прохождение через петлю).

где:

L — Самоиндукция;

di/dt — Скорость изменения тока в катушке индуктивности.

Мы можем применить модифицированную версию закона Ома, чтобы получить средний ток (I) через индуктор.

где индуктивное сопротивление (X _L .) пропорционально частоте сигнала переменного тока (f): схема, как показано ниже:

Блок индуктивного реактивного сопротивления

Для расчета единицы индуктивного реактивного реакции, провести анализ размеров формулы для индуктивного реактивного реактивного вещества:

одинаковы, согласно размерному анализу предыдущей формулы. В результате индуктивное сопротивление выражается в омах (Ом).

 

Мы используем ту же единицу измерения проводимости, что и проводимость, а именно сименс (S).

 

 

Напряжение и ток не совпадают по фазе на девяносто градусов, потому что напряжение максимально при наибольшем изменении тока. Это часто упускаемый момент.