Резистивный делитель тока: Делитель тока

Делитель тока

Делитель тока – устройство позволяющее поделить ток в цепи на две составные части, с целью использования одной из них. Другими словами, делитель тока необходим в том случае, если устройство не рассчитано на большой ток, и нам необходима лишь некоторая часть этого тока.

Принцип действия делителя тока основан на первом законе Кирхгофа – сумма токов сходящихся в узле равна нулю. Если провести аналогию с водой, то его  можно представить как русло реки, которое разветвляется на два более маленьких оттока.

 

Для нахождения токов I₁ и I₂ воспользуемся законом Ома, но для начала найдем эквивалентное сопротивление для параллельного соединения. 

Делители тока применяются в измерительных устройствах, например при измерении больших токов. С помощью добавочного сопротивления – “шунта” расширяют предел измерения амперметра. Для этого, шунт подключается параллельно амперметру.

В результате, через амперметр протекает ток, зная который, можно найти общий ток, протекающий в цепи. Обычно шунт имеет сопротивление меньше, чем амперметр, для того чтобы значительная часть тока ушла через него.

Выведем коэффициент деления (шунтирования) n. Будем считать, что параметры с индексом 1 принадлежат амперметру (прибору), а параметры с индексом 2 – шунту. Параметры без индексов общие.

Рассмотрим пример.

Амперметром с пределом измерения 1 А и внутренним сопротивлением 12 Ом, необходимо измерить ток в 3 А. Каким должно быть сопротивление шунта?

Из формулы для коэффициента шунтирования, выразим R_ш 

Еще один пример

Каким станет новый предел измерения амперметра, после его шунтирования сопротивлением в 10 Ом, если старый предел был равен 0,5 А? Сопротивление измерительного механизма амперметра – 25 Ом.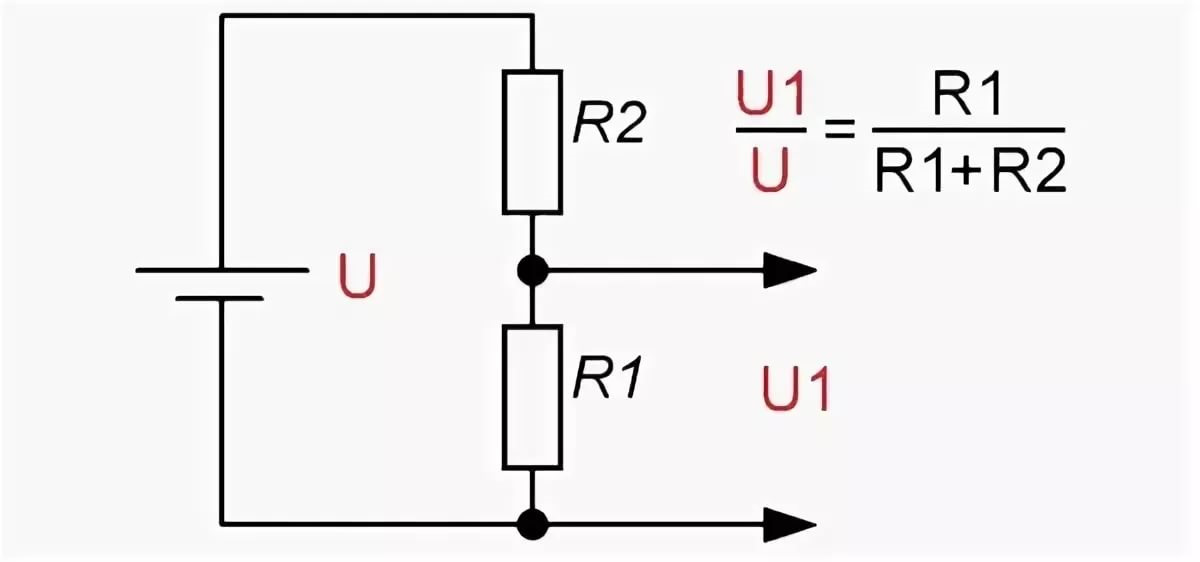

Посчитаем коэффициент шунтирования 

Тогда новый предел измерения амперметра

 

Спасибо за внимание!

Рекомендуем — делитель напряжения

Просмотров: 12456

3. Делители тока | 5. Схемы делителей и законы Кирхгофа | Часть1

3. Делители тока

Делители тока

Давайте проанализируем простую параллельную цепь и определим силу тока на каждом из ее резисторов:

 

 

Как вы уже знаете, напряжение на всех компонентах параллельной цепи одинаково. Исходя из этого можно заполнить верхнюю строчку рассмотренной ранее таблицы:

 

Теперь, используя закон Ома (I = U/R), мы можем рассчитать силу тока на каждом резисторе (в каждой ветви):

 

 

Один из принципов параллельных цепей гласит, что общая сила тока в таких цепях равна сумме отдельных токов. Поэтому, суммируя 6 мА, 2мА и 3мА, мы можем заполнить ячейку общей силы тока в нашей таблице:

 

 

И наконец, вычислим общее сопротивление нашей цепи. Сделать это можно при помощи закона Ома (R = U/I), или при помощи формулы параллельного соединения резисторов. В обоих случаях мы получим одинаковый ответ:

 

 

Из данной таблицы видно, что сила тока через каждый резистор связана с его сопротивлением (учитывая равенство напряжений на всех резисторах). Причем взаимосвязь эта обратнопропорциональна. К примеру, сила тока через резистор R

1 вдвое больше, чем через резистор R₃, хотя сопротивление последнего в два раза превышает сопротивление первого.

Если мы изменим напряжение питания этой схемы, то обнаружим, что пропорциональность соотношений не изменится:

 

 

Несмотря на то, что напряжение источника питания изменилось, ток через резистор R₁ по-прежнему в два раза превышает ток через резистор R₃.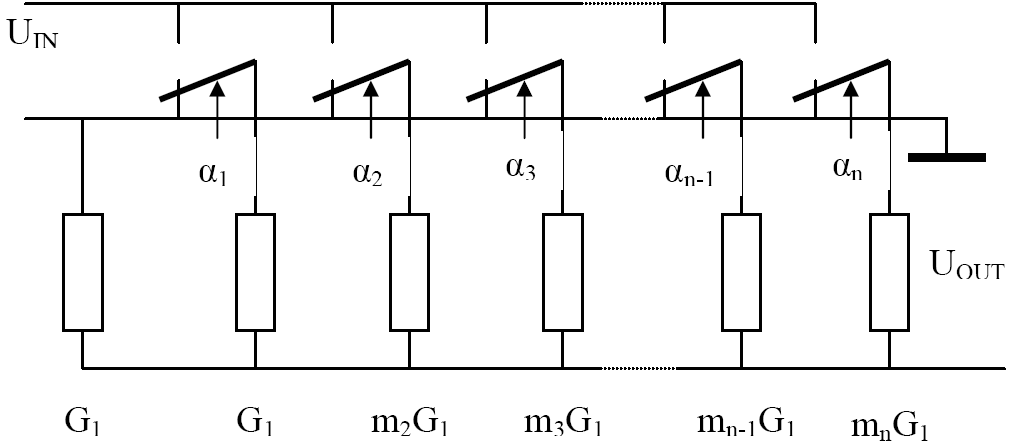 Таким образом, пропорциональность между токами различных ветвей цепи является исключительно функцией сопротивления.

Кроме того, токи отдельных ветвей цепи составляют фиксированные пропорции от ее общей силы тока. Несмотря на четырехкратное увеличение напряжения источника питания, соотношение между током любой ветви и общим током осталось неизменным:

 

 

Благодаря способности делить общий ток на пропорциональные части, параллельные цепи часто называют делителями тока. Поэкспериментировав немного с математикой, мы можем вывести формулу для расчета отдельных токов цепи, имея данные о сопротивлениях резисторов, общем сопротивлении цепи и общей силе тока:

 

 

Отношение общего сопротивления к отдельным сопротивлениям имеет ту же пропорцию, что и отношение отдельных токов к общей силе тока цепи.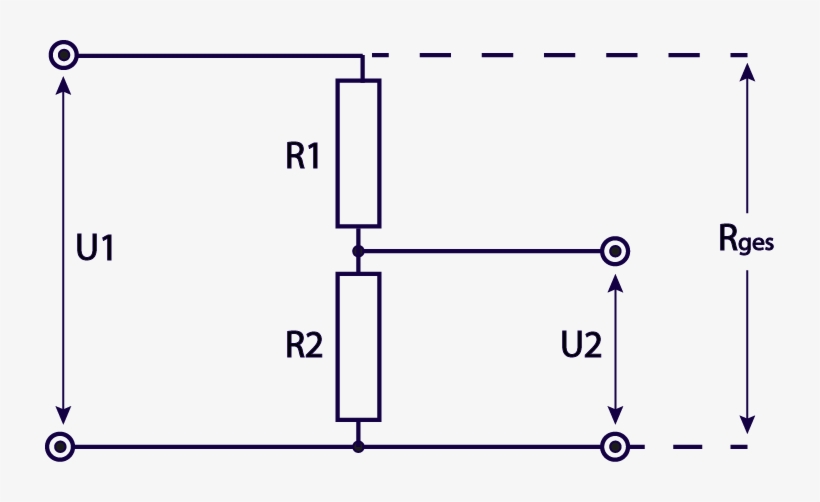 Полученная выше формула называется

формулой делителя тока, с ее помощью легче определять токи отдельных ветвей параллельной цепи, если известна общая сила тока.

Давайте повторно рассчитаем токи каждой из ветвей нашей параллельной цепи, используя только что полученную формулу делителя тока (будем считать, что общая сила тока и общее сопротивление нам известны):

 

 

Если сравнить формулы делителя напряжения и делителя тока, то можно увидеть, что они удивительно похожи друг на друга. Однако, в формуле делителя напряжения R_n (отдельное сопротивление)  делится на  R_общ., а в формуле делителя тока — наоборот, R_общ. делится на R_n:

 

Именно из-за отношения сопротивлений очень легко перепутать эти формулы. В целях избежания путаницы вы должны знать, что отношение сопротивлений в обоих уравнениях должно быть меньше единицы (в конце концов это уравнения делителей, а не умножителей!).

Если отношение будет больше единицы, значит вы перепутали уравнения. Зная, что общее сопротивление последовательной цепи (делитель напряжения) всегда больше любого из ее отдельных сопротивлений, R_общ. мы должны поставить в знаменатель отношения, а R_n — в числитель (только в этом случае отношение будет меньше единицы). И наоборот, зная что общее сопротивление параллельной цепи (делитель тока) всегда меньше любого из ее отдельных сопротивлений, R_общ. мы должны поставить в числитель отношения, а R_n — в знаменатель.

Схемы делителей токов, как и делителей напряжений,  нашли применение в электрических цепях измерительных приборов, где часть измеряемого тока необходимо пропустить через чувствительный прибор:

 

Делитель напряжения: теория и принцип действия

Делитель напряжения позволяет получить меньшее напряжение из большего, напряжение может быть как постоянным, так и переменным.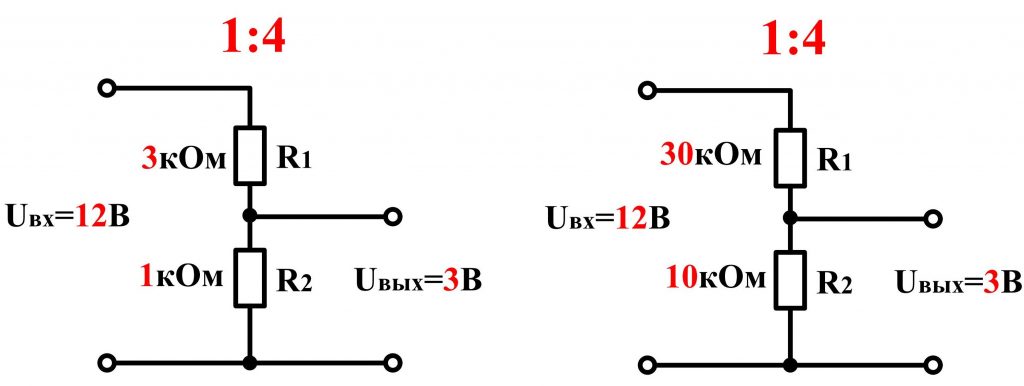

Рис. 1. Схема простейшего делителя напряжения

Простейшая схема делителя напряжения содержит минимум два сопротивления. Если величины сопротивлений одинаковы, то согласно закону Ома, на выходе делителя будет получено напряжение, в два раза меньшее, чем на входе, так как падение напряжений на резисторах будет одинаковым. Для других случаев величина падения напряжений на резисторах делителя определяется по формулам

U_R1 = I*R1; U_R2 = I*R2       (1)

где U_R1, U_R2 — падения напряжения на резисторах R1 и R2 соответственно, I — ток в цепи. В схемах делителей выходное напряжение обычно снимают с нижнего по схеме резистора.

Сумма падений напряжений U_R1, U_R2 на резисторах равна напряжению источника питания. Ток в цепи будет равен напряжению источника питания, делённому на сумму сопротивлений резисторов R1 и R2:

I = U_пит / (R1 + R2)       (2)

Рассмотрим практическую схему делителя постоянного напряжения (рис. 2)

Рис. 2. Делитель постоянного напряжения.

Ток, протекающий в этой схеме, согласно формуле (2) будет равен

I = 10 / (10000+40000) = 0,0002 А = 0,2 мА.

Тогда согласно формуле (1) падение напряжения на резисторах делителя напряжения будет равно:

U_R1 = 0,0002*10000 = 2 В;
U_R2 = 0,0002*40000 = 8 В.

Если из формулы (1) вывести ток:

I = U_R1 / R1       (3)

И подставить его значение в формулу (2), то получится универсальная формула для расчёта делителя напряжения:

U_R1 / R1 = U_пит / (R1 + R2)

Откуда

U_R1 = U_пит * R1 / (R1 + R2)       (4)

Подставляя значения напряжения и сопротивлений в формулу (4), получим величину напряжения на резисторе R1:

U_R1 = 10 * 10000 / (10000+40000) = 2 В,

и на резисторе R2:

U_R2 = 10 * 40000 / (10000+40000) = 8 В.

Делитель напряжения с реактивными элементами в цепи переменного тока

В вышеприведённой схеме делителя напряжения (рис. 2) были использованы активные элементы — резисторы, и питание схемы осуществлялось постоянным напряжением (хотя схему можно питать и переменным током). Делитель напряжения может содержать так же и реактивные компоненты (конденсаторы, катушки индуктивности), но в этом случае для нормальной работы потребуется питание синусоидальным током (рис. 3).

Рис. 3. Ёмкостный делитель напряжения в цепи переменного тока.

Изображённый на рисунке 3 ёмкостный делитель напряжения работает аналогично резистивному делителю, но рассчитывается несколько иначе, поскольку реактивное сопротивление конденсаторов обратно пропорционально их ёмкости:

R_c = 1/(2 * π * f * C)

Здесь R_c — реактивное сопротивление конденсатора;
π — число Пи = 3,14159…;
f — частота синусоидального напряжения, Гц;
C — ёмкость конденсатора, Фарад.

То есть чем больше ёмкость конденсатора, тем меньше его сопротивление, и следовательно в схеме делителя напряжения на конденсаторе с большей ёмкостью падение напряжения будет меньше, чем на конденсаторе с меньшей ёмкостью.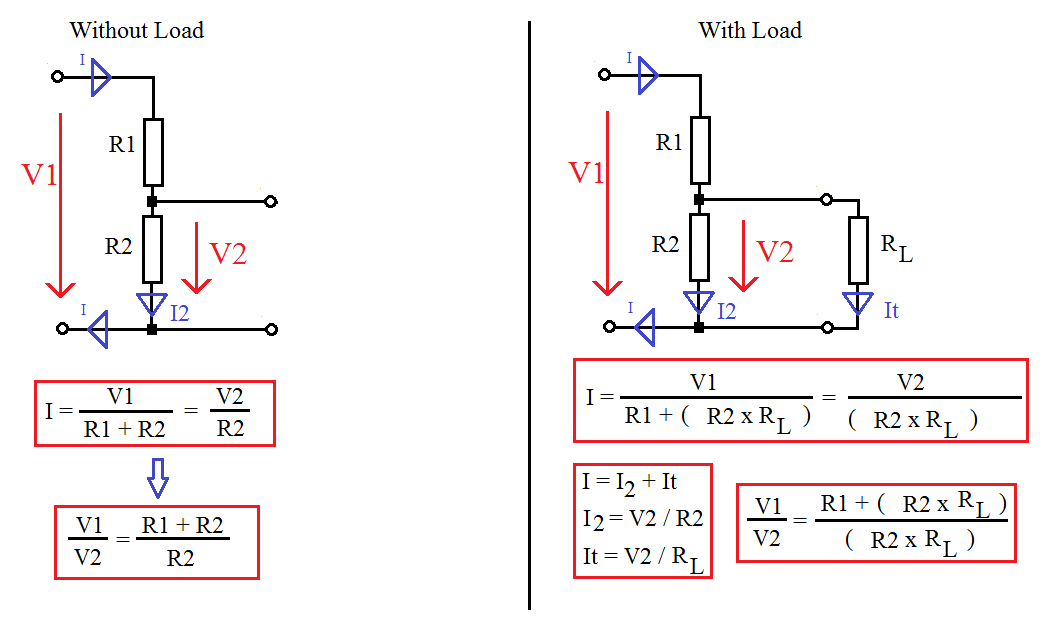 Следовательно, формула (4) для ёмкостного делителя напряжения примет следующий вид:

U_С1 = U_пит * С2 / (С1 + С2)       (5)

U_С1 = 10 * 40*10^-9 / (10*10^-9+40*10^-9) = 8 В,
U_С2 = 10 * 10*10^-9 / (10*10^-9+40*10^-9) = 2 В.

Индуктивный делитель напряжения (рис. 4.) так же как и ёмкостный требует для своей работы синусоидальное питающее напряжение.

Рис. 4. Индуктивный делитель напряжения в цепи переменного тока.

Поскольку реактивное сопротивление катушки индуктивности в цепи переменного тока пропорционально номиналу катушки:

R_L = 2 * π * f * L

Здесь R_c — реактивное сопротивление катушки индуктивности;
π — число Пи = 3,14159…;
f — частота синусоидального напряжения, Гц;
L — индуктивность катушки, Генри.

То следовательно и формула для расчёта индуктивного делителя напряжения будет точно такой же, как и формула для расчёта резистивного делителя напряжения (4), где вместо сопротивлений будут использоваться индуктивности:

U_L1 = U_пит * L1 / (L1 + L2)       (6)

Подставив в эту формулу параметры элементов из рисунка 4, получим:

U_L1 = 10 * 10*10^-6 / (10*10^-6+40*10^-6) = 2 В,
U_L2 = 10 * 40*10^-6 / (10*10^-6+40*10^-6) = 8 В.

В заключении следует отметить, что во всех расчётах величина нагрузки была принята равной бесконечности, поэтому полученные значения верны при работе рассмотренных делителей на сопротивление нагрузки, во много раз большее, чем величина собственных сопротивлений.

BACK

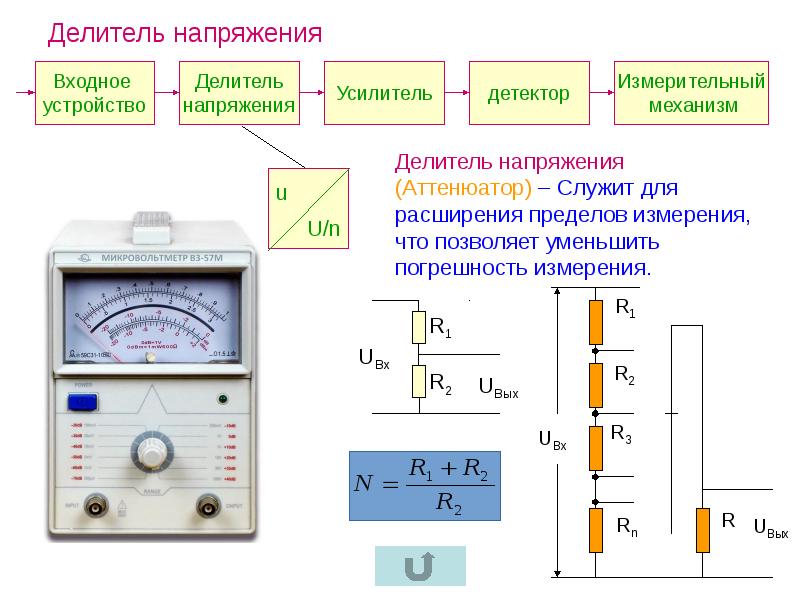
Резистивные делители тока и напряжения

Резистивные делители широко применяются в электрических цепях приборов. Схемы простейших делителей тока и напряжения приве­дены на рис. 2-5, а, б. Коэффициенты передачи, или коэффициенты деления, делителей равны ; и определяются отношением сопротивлений входящих в них резисторов, поэтому точность коэффициента деления определя­ется не точностью самих сопротивлений резисторов, а лишь точностью поддержания их отношения. Приведенные выражения справедливы для случая, когда можно пренебречь внутренними сопротивлениями источников и нагрузок, полагая, что для делителя напряжения R_H = ¥, а для делителя тока R_Н® 0.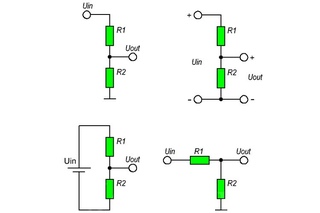

 

 

 

 

 

 

Рис. 2-5

 

 

С учетом сопротивлений источников и нагрузок выходной ток и выходное напряжение определяются формулами:

; .

Коэффициент деления тока не зависит от сопротивления цепи, вклю­ченной последовательно с делителем, т.е. от сопротивления источника. При постоянных сопротивлениях делителя и нагрузки изменение коэф­фициента деления учитывается формулами:

; .

Или, учитывая, что выходные сопротивления делителей составляют

, ,

коэффициенты деления можно представить в виде:

; .

Из приведенных формул легко определить погрешность делителей при изменении сопротивления нагрузки или выходных сопротивлений делителей. Однако, даже если нагрузки остаются неизменными, вклю­чение нагрузок, имеющих сопротивления, сравнимые с выходными сопротивлениями делителей, крайне нежелательно, так как это при­водит к существенному возрастанию погрешностей делителей под влиянием внешних факторов.

Для ненагруженных делителей погрешности от влияния внешних факторов пренебрежимо малы, так как используемые в них резисторы идентичны и отношение их сопротивлений является инвариантной величиной. По-разному влияют внешние воздействия на сопротивле­ния делителя и нагрузки, так как последние выполняются из различ­ных материалов, и поэтому возрастают соответствующие погрешности. Полагая, что под действием температуры относительная погрешность резисторов делителя составляет g_R, а относительная погрешность сопротивления нагрузки g_Rн можно написать следующие выражения для погрешностей коэффициентов деления:

; .

Если на вход резистивного делителя подается переменное напря­жение достаточно высокой частоты или напряжение, содержащее высо­кочастотные гармоники, то необходимо учитывать реактивные состав­ляющие сопротивлений, входящих в делитель резисторов.

Для того чтобы избежать частотной погрешности, должно выпол­няться следующее условие:

R₁/R₂ = L₁ /L₂ =C₂/C₁,

где L₁, L₂, C₁и C₂– параметры эквивалентной схемы резисторов.

Влияние индуктивной составляющей комплексного сопротивления обычно невелико, что объясняется соответствующей конструкцией не­проволочных резисторов и бифилярной намоткой высокочастотных проволочных резисторов. Емкостная же составляющая сопротивления может вносить заметную погрешность. Эту погрешность можно исключить, выравнивая постоянные времени резисторов делителя, для чего подбирают небольшие конденсаторы, включаемые параллельно ре­зисторам. Использование подобной емкостной коррекции позволяет снизить частотную погрешность делителей до десятых долей процента для частот звукового диапазона при применении микропроволочных резисторов типа МВСГ и для частот вплоть до нескольких десятков мегагерц при использовании непроволочных резисторов.

Дальнейшее снижение частотной погрешности возможно при при­менении более сложных схем частотной коррекции.

Существенно увеличиваются частотные погрешности делителей при включении сопротивления нагрузки. В рабочем диапазоне частот, где резисторы делителя имеют чисто активные сопротивления, частот­ные погрешности, вызванные реактивными составляющими сопротивле­ний нагрузок, определяются формулами:

; ,

если считать, как это и бывает в большинстве случаев, что нагрузка делителя тока имеет индуктивную составляющую, а нагрузка делителя напряжения – емкостную.

Многоступенчатые резистивные делители напряжения и тока приведены на рис. 2-5, г и д, где в качестве примеров указаны значения сопротивлений.

Подобные схемы используются для переключения пределов амперметров и аналоговых электронных вольтметров. Особую роль играют многоступенчатые делители с многозначными регу­лируемыми коэффициентами деления, используемые в современных цифровых приборах и компенсаторах ручного уравновешивания. В ка­честве примера на рис. 2-6 показан трехзначный делитель, который может выполняться как с ручным, так и с автоматическим изменением коэффициента деления. Принцип действия делителя поясняется рис. 2-6, а. Делитель состоит из идентичных резисторов, по которым перемещаются два механически соединенных, но электрически изоли­рованных движка. Часть резистора, к которой приложено напряже­ние, показана штриховкой; та часть резистора, с которой снимается напряжение, показана более густой штриховкой.На рис. 2-6, б, в представлены построенные на этом принципе делитель с ручным управлением (при указанном положении движков U_ВЫХ = 0,120·U_ВХ) и с автоматическим управлением путем замыкания и размыкания соответствующих контактов реле (при указанном положе­нии контактов U_ВЫХ = 0,538 U_ВХ).

 

 

 

Рис. 2-6

 

Число знаков коэффициента деления определяется возможным диа­пазоном сопротивлений резисторов, поскольку, как видно из рис. 2-6, в,для того чтобы не сказывались остаточные параметры ключей, то сопротивление из них, которое меньше, должно быть на 1–2 порядка больше сопротивления r_к замкнутого ключа, а то, которое больше на 2–3 порядка меньше сопротивления R_к разомкнутого ключа.

Если предположить, что r_к = 0,01 Ом, а R_к = 10⁸ Ом, то можно реализовать пятизначный делитель, в котором коэффициент деления будет иметь погрешность, не превышающую последнего знака. Анали­зируя различные схемы делителей, нужно обратить внимание на следующие характеристики: постоянство входного сопротивления, постоянство выходного сопротивления, наличие общей шины между цепями входного и выходного напряжения, влияние остаточных пара­метров ключей, число используемых в делителе номиналов резисторов.

В современных цифровых приборах применяются лестничные делители тока и напряжения на выполненных по интегральной технологии мат­рицах резисторов, содержащих всего два номинала резисторов R и 2R. Схемы таких делителей показаны на рис. 2-7.

В делителе напряжения (рис. 2-7, a) используется один источник напряжения и усилитель с бесконечно большим входным сопротивле­нием, с выхода которого снимается нужная часть входного сигнала. В делителе тока (рис. 2-7, б) используется несколько идентичных источ­ников тока и суммирующий усилитель с бесконечно малым входным сопротивлением. На рис. 2-7, в и г показаны эквивалентные схемы того и другого делителя при замыкании (n–2)-го ключа в положе­ние 1.

а) б)

Рис. 2-7

 

Резистивная матрица имеет постоянное выходное сопротивление R_вых=R. Коэффициенты деления делителя тока и делителя напря­жения составляют:

,

где a_i принимают значения 0 и 1 в зависимости от положения ключей.

Лучшие делители имеют до 16 разрядов, погрешность линейности ±0,002%, температурную погрешность ±0,0007% на 1 К.

 

Коэффициент деления по напряжению. Резистивный делитель напряжения. Расчет делителя напряжения на резисторах

Делители напряжения получили широкое распространение в электронике, потому что именно они позволяют оптимальным образом решать задачи регулировки напряжения. Существуют различные схематичные решения: от простейших, например, в некоторых настенных светильниках, до достаточно сложных, как в платах управления переключением обмоток нормализаторов сетевого напряжения.

Что такое делитель напряжения? Формулировка проста — это устройство, которое в зависимости от коэффициента передачи (настраивается отдельно) регулирует значение выходного напряжения относительно входного.

Раньше на прилавках магазинов часто можно было встретить светильник-бра, рассчитанный на две лампы. Его особенностью являлось то, что сами лампы были рассчитаны на работу с напряжением 127 Вольт. При этом вся система подключалась к бытовой электросети с 220 В и вполне успешно работала. Никаких чудес! Все дело в том, что способ соединения проводников формировал не что иное, как делитель напряжения. Вспомним основы электротехники, а именно потребителей. Как известно, при последовательном способе включения равна, а напряжение изменяется (вспоминаем закон Ома). Поэтому в примере со светильником однотипные лампы включены последовательно, что дает уменьшение питающего их напряжения в два раза (110 В). Также делитель напряжения можно встретить в устройстве, распределяющем сигнал с одной антенны на несколько телевизоров. На самом деле примеров много.

Давайте рассмотрим простейший делитель напряжения на основе двух резисторов R1 и R2. Сопротивления включены последовательно, на свободные выводы подается входное напряжение U. Из средней точки проводника, соединяющего резисторы, есть дополнительный вывод. То есть получается три конца: два — это внешние выводы (между ними полное значение напряжения U), а также средний, формирующий U1 и U2.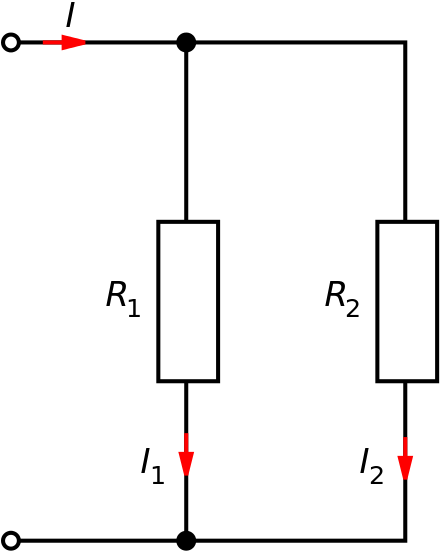

Выполним расчет делителя напряжения, воспользовавшись законом Ома. Так как I = U / R, то U является произведением тока на сопротивление. Соответственно, на участке с R1 напряжение составит U1, а для R2 составит U2. Ток при этом равен Учитывая закон для полной цепи, получаем, что питающее U является суммой U1+U2.

Чему же равен ток при данных условиях? Обобщая уравнения, получаем:

I = U / (R1+R2).

Отсюда можно определить значение напряжения (U exit) на выходе делителя (это может быть как U1, так и U2):

U exit = U * R2 / (R1+R2).

Для делителей на регулируемых сопротивлениях существует ряд важных особенностей, которые необходимо учитывать как на этапе расчетов, так и при эксплуатации.

Прежде всего, такие решения нельзя использовать для регулировки напряжения мощных потребителей. Например, таким способом невозможно запитать электродвигатель. Одна из причин — это номиналы самих резисторов. Сопротивления на киловатты если и существуют, то представляют собой массивные устройства, рассеивающие внушительную часть энергии в виде тепла.

Значение сопротивления подключенной нагрузки не должно быть меньше, чем схемы самого делителя, в противном случае всю систему потребуется пересчитывать. В идеальном варианте различие R делителя и R нагрузки должно быть максимально большим. Важно точно подобрать значения R1 и R2, так как завышенные номиналы повлекут за собой излишнее а заниженные будут перегреваться, затрачивая энергию на нагрев.

Рассчитывая делитель, обычно подбирают значение его тока в несколько раз (например, в 10) больше, чем ампераж подключаемой нагрузки. Далее, зная ток и напряжение, вычисляют суммарное сопротивление (R1+R2). Далее по таблицам подбирают ближайшие стандартные значения R1 и R2 (учитывая их допустимую мощность, чтобы избежать чрезмерного нагрева).

В составе делителя напряжения для получения фиксированного значения напряжения используют резисторы. В этом случае выходное напряжение U вых связано с входным U вх (без учета возможного сопротивления нагрузки) следующим соотношением:

U вых = U вх х (R2 / R1 + R2)

Рис. 1. Делитель напряжения

Пример. С помощью резисторного делителя нужно получить на нагрузке сопротивлением 100 кОм напряжение 1 В от источника постоянного напряжения 5 В. Требуемый коэффициент деления напряжения 1/5 = 0,2. Используем делитель, схема которого приведена на рис. 1.

Сопротивление резисторов R1 и R2 должно быть значительно меньше 100 кОм. В этом случае при расчете делителя сопротивление нагрузки можно не учитывать.

Следовательно, R2 / (R1 +R2) R2 = 0,2

R2 = 0 ,2R1 + 0,2R2 .

R1 = 4R2

Поэтому можно выбрать R2 = 1 кОм, R1 — 4 кОм. Сопротивление R1 получим путем последовательного соединения стандартных резисторов 1,8 и 2,2 кОм, выполненных на основе металлической пленки с точностью ±1% (мощностью 0,25 Вт).

Следует помнить, что сам делитель потребляет ток от первичного источника (в данном случае 1 мА) и этот ток будет возрастать с уменьшением сопротивлений резисторов делителя.

Для получения заданного значения напряжения следует применять высокоточные резисторы.

Недостатком простого резисторного делителя напряжения является то, что с изменением сопротивления нагрузки выходное напряжение (U вых) делителя изменяется. Ддя уменьшения влияния нагрузки на U выхнеобходимо выбирать соротивление R2 по крайней мере в 10 раз меньше минимального сопротивления нагрузки.

Важно помнить о том, что с уменьшением сопротивлений резисторов R1 и R2 растет ток, потребляемый от источника входного напряжения. Обычно этот ток не должен превышать 1-10 мА.

Резисторы используются также для того, чтобы заданную долю общего тока направить в соответствующее плечо делителя. Например, в схеме на рис. 2 ток I составляет часть общего тока I вх, определяемую сопротивлениями резисторов Rl и R2, т.е. можно записать, что I вых = I вх х (R1 / R2 + R1)

Пример. Стрелка измерительного прибора отклоняется на всю шкалу в том случае, если постоянный ток в подвижной катушке равен 1 мА. Активное сопротивление обмотки катушки составляет 100 Ом. Рассчитайте сопротивление так, чтобы стрелка прибора максимально отклонялась при входном токе 10 мА (см. рис. 3) .

Рис. 2 Делитель тока

Рис. 3.

Коэффициент деления тока определяется соотношением:

I вых / I вх = 1/10 = 0,1 = R1 / R2 + R1 , R2 = 100 Ом.

Отсюда,

0,1R1 + 0,1R2 = R1

0,1R1 + 10 = R1

R1 = 10/0 ,9 = 11,1 Ом

Требуемое сопротивление резистора R1 можно получить путем последовательного соединения двух стандартных резисторов сопротивлением 9,1 и 2 Ом, выполненных на основе толстопленочной технологии с точностью ±2% (0,25 Вт). Заметим еще раз, что на рис. 3 сопротивление R2 — это .

Для обеспечения хорошей точности деления токов следует использовать высокоточные (± 1 %) резисторы.

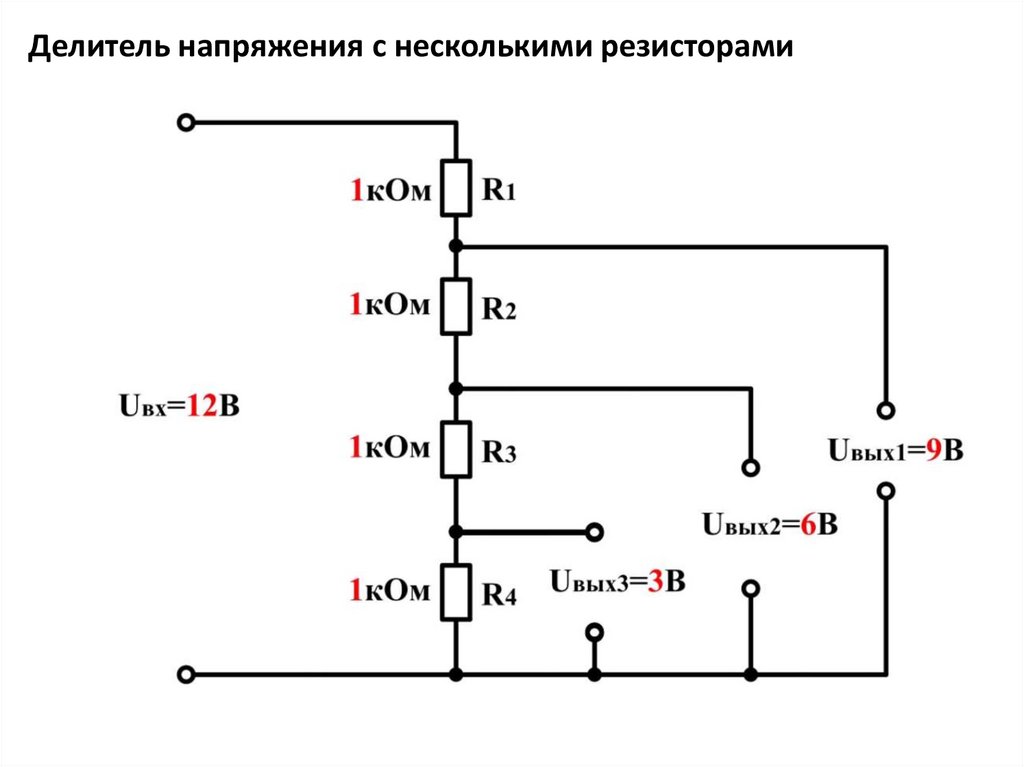
При проектировании электрических цепей возникают случаи, когда необходимо уменьшить величину напряжения (разделить его на несколько частей) и только часть подавать на нагрузку. Для этих целей используют делители напряжения . Они основаны на втором законе Кирхгофа .

Самая простая схема — резистивный делитель напряжения. Последовательно с подключаются два сопротивления R1 и R2.

При последовательном подключении сопротивлений через них протекает одинаковый ток I.

В результате, согласно закону Ома , напряжения на резисторах делится пропорционально их номиналу.

Подключаем нагрузку параллельно к R1 или к R2. В результате на нагрузке будет напряжение равное U R2 .

Примеры применения делителя напряжения

1. Как делитель напряжения. Представьте, что у Вас есть лампочка, которая может работать только от 6 вольт и есть батарейка на 9 вольт. В этом случае при подключении лампочки к батарейке, лампочка сгорит. Для того, чтобы лампочка работала в номинальном режиме, напряжение 9 В необходимо разделить на 6 и 3 вольта. Данную задачу выполняют простейшие делители напряжения на резисторах.
2. Датчик параметр — напряжение. Сопротивление резистивных элементов зависит от многих параметров, например температура. Помещаем одно из сопротивлений в среду с изменяющейся температурой. В результате при изменении температуры будет изменяться сопротивление одного из делителей напряжения. Изменяется ток через делитель. Согласно закону Ома входное напряжение перераспределяется между двумя сопротивлениями.
3. Усилитель напряжения. Делитель напряжения может использоваться для усиления входного напряжения. Это возможно, если динамическое сопротивление одного из элементов делителя отрицательное, например на участке вольт-амперной характеристики туннельного диода.

Ограничения при использовании резистивных делителей напряжения

• Номинал сопротивлений делителя напряжения на резисторах должен быть в 100 — 1000 раз меньше, чем номинальное сопротивление нагрузки, подключаемой к делителю. В противном случае сопротивление нагрузки уменьшит величину разделенного делителем напряжения.
• Малые значения сопротивлений, являющихся делителем напряжения, приводят к большим потерям активной мощности . Через делитель протекают большие токи. Необходимо подбирать сопротивления, чтобы они не перегорали и могли рассеять такую величину отдаваемой энергии в окружающую среду.
• Резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины , нагревательные элементы, индукционные печи.
• Снижение КПД схемы за счет потерь на активных элементах делителя напряжения.
• Для получения точных результатов в делителе напряжения необходимо использовать прецизионные (высокоточные) сопротивления.

). Можно представить как два участка цепи, называемые плечами , сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним , а другое — верхним . Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного. Такие делители используются для задания потенциалов и рабочих напряжений в различных точках электронных схем.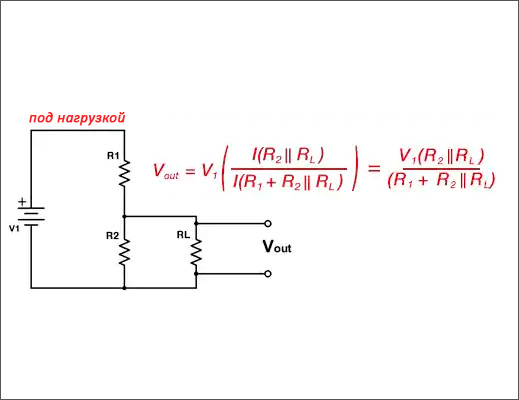 В нелинейных делителях выходное напряжение зависит от коэффициента нелинейно. Нелинейные делители напряжения применяются в функциональных потенциометрах . Сопротивление может быть как активным , так и реактивным .

Резистивный делитель напряжения

Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения . Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с Первым правилом Кирхгофа . Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):

Для каждого резистора:

Разделив выражение для на выражение для в итоге получаем:
Таким образом, отношение напряжений и в точности равно отношению сопротивлений и .
Используя равенство
, в котором , а
И, выражая из него соотношение для тока:

Получим формулу, связывающую выходное () и входное () напряжение делителя:

Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму . Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения . Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления . Остается только взять конкретные значения сопротивлений из стандартного ряда , отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления , допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность , где — ток источника при отключенной нагрузке (в этом случае через резисторы течет максимально возможный ток) .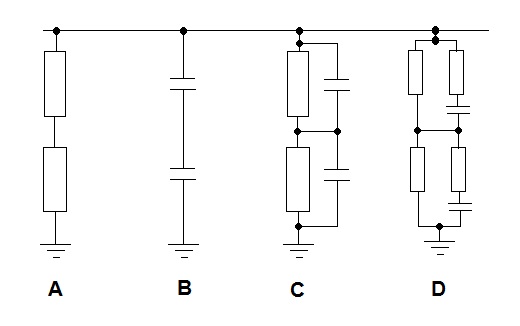

Применение

Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр , а в качестве нелинейного — параметрический стабилизатор напряжения .

Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ . В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.

Усилитель напряжения

Делитель напряжения может использоваться для усиления входного напряжения — это возможно, если , а — отрицательно, например как на участке вольт-амперной характеристики туннельного диода

Ограничения в применении резистивных делителей напряжения

• Номинал сопротивлений делителя должен быть в 100 — 1000 раз меньше, чем номинальное сопротивление нагрузки.

• Малые значения сопротивлений, являющихся делителем напряжения, приводят к возникновению больших токов в делителе. Снижается КПД схемы из-за нагрева сопротивлений.

• Резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы.

Нормативно-техническая документация

• ГОСТ 11282-93 (МЭК 524-75) — Резистивные делители напряжения постоянного тока

Примечания

Ссылки

Wikimedia Foundation . 2010 .

Смотреть что такое «Делитель напряжения» в других словарях:

делитель напряжения — делитель напряжения Преобразующее устройство, состоящее из плеч высокого и низкого напряжения, таких, что напряжение входа прикладывается ко всему устройству, а напряжение выхода снимается с плеча низкого напряжения. [МЭС… … Справочник технического переводчика

Большой Энциклопедический словарь

Устройство, позволяющее снимать (использовать) только часть имеющегося постоянного или переменного напряжения посредством элементов электрической цепи, состоящей из резисторов, конденсаторов или катушек индуктивности. Используется в радио и… … Энциклопедический словарь

делитель напряжения — įtampos dalytuvas statusas T sritis automatika atitikmenys: angl. potential divider; voltage divider vok. Spannungsteiler, m rus. делитель напряжения, m pranc. diviseur de tension, m … Automatikos terminų žodynas

делитель напряжения — įtampos dalytuvas statusas T sritis Standartizacija ir metrologija apibrėžtis Įtaisas nuolatinei ar kintamajai įtampai dalyti į dvi ar daugiau dalių. atitikmenys: angl. potential divider; voltage divider vok. Spannungsteiler, m rus. делитель… …

делитель напряжения — įtampos dalytuvas statusas T sritis Standartizacija ir metrologija apibrėžtis Įtaisas, sudarytas iš rezistorių, induktyvumo ričių, kondensatorių, transformatorių arba iš šių elementų derinio taip, kad tarp dviejų šio įtaiso taškų susidarytų… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

делитель напряжения — įtampos dalytuvas statusas T sritis chemija apibrėžtis Įtaisas nuolatinei ar kintamajai įtampai dalyti į dvi ar daugiau dalių. atitikmenys: angl. potential divider; voltage divider rus. делитель напряжения … Chemijos terminų aiškinamasis žodynas

делитель напряжения — įtampos dalytuvas statusas T sritis fizika atitikmenys: angl. voltage divider vok. Spannungsteiler, m rus. делитель напряжения, m pranc. diviseur de tension, m … Fizikos terminų žodynas

Электротехническое устройство для деления напряжения постоянного или переменное тока на части. Любой Д. н. состоит из активных или реактивных электрических сопротивлений. Обычно Д. н. применяют для измерения напряжения. При низких… … Большая советская энциклопедия

Электротехническое устройство, позволяющее снимать (использовать) только часть имеющегося постоянного или переменного напряжения посредством элементов электрической цепи, состоящей из резисторов, конденсаторов или катушек индуктивности. При… … Энциклопедия техники

Устройство, в котором входное и выходное напряжение связаны коэффициентом передачи. Делитель можно представить, как два участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Чаще всего делитель напряжения строится из двух резисторов. Такой делитель называют резисторным. Каждый резистор в таком делителе называют плечом. Плечо соединённое с землёй называют нижним, то что соединено с плюсом — верхним. Точка соединения двух резисторов называется средним плечом или средней точкой. Если говорить совсем упрощённо, то можно представить среднее плечо, как бассейн. Делитель напряжения позволяет нам управлять двумя «шлюзами», «сливая» напряжение в землю (уменьшая сопротивление нижнего плеча) или «подливая» напряжения в бассейн (уменьшая сопротивление верхнего плеча). Таким образом, делитель может использоваться для того, чтобы получить из исходного напряжения лишь его часть.

Принципиальная схема делителя напряжения

В рассматриваемом примере на вход (Uвх) подаётся напряжение 9В. Предположим, нам нужно получить на выходе (Uвых) 5В. Каким образом расчитать резисторы для делителя напряжения?

Расчёт делителя напряжения

Многие сталкиваются с тем, что не существует формул для расчёта сопротивлений в делителе. На самом деле, такие формулы легко вывести. Но обо всё по порядку. Для наглядности, начнём расчёт с конца, т.е. расчитаем напряжение на выходе, зная номиналы резисторов.

Ток, протекающий через R1 и R2 одинаков, пока к среднему плечу (Uвых) ничего не подключено. Общее сопротивление резисторов при последовательном соединении равняется сумме их сопротивлений:

Rобщ = R1 + R2 = 400 + 500 = 900 Ом

По закону Ома находим силу тока, протекающего через резисторы:

I = Uвх / Rобщ = 9В / 900 Ом = 0.01 А = 10 мА

Теперь, когда нам известен ток в нижнем плече (ток, проходящий через R2), раcчитаем напряжение в нижнем плече (Опять закон Ома):

Uвых = I * R2 = 0.01А * 500 Ом = 5В

Или упрощая цепочку вычислений:

Uвых = Uвх * (R2 / (R1+R2))

Применив немного математики и прочих знаний, сдобрив всё законом Ома, можно получить следующие формулы:

R1 = (Uвх-Uвых)/Iд+Iн

R2 = Uвых / Iд

Здесь Iд и Iн — ток делителя и ток нагрузки соответственно.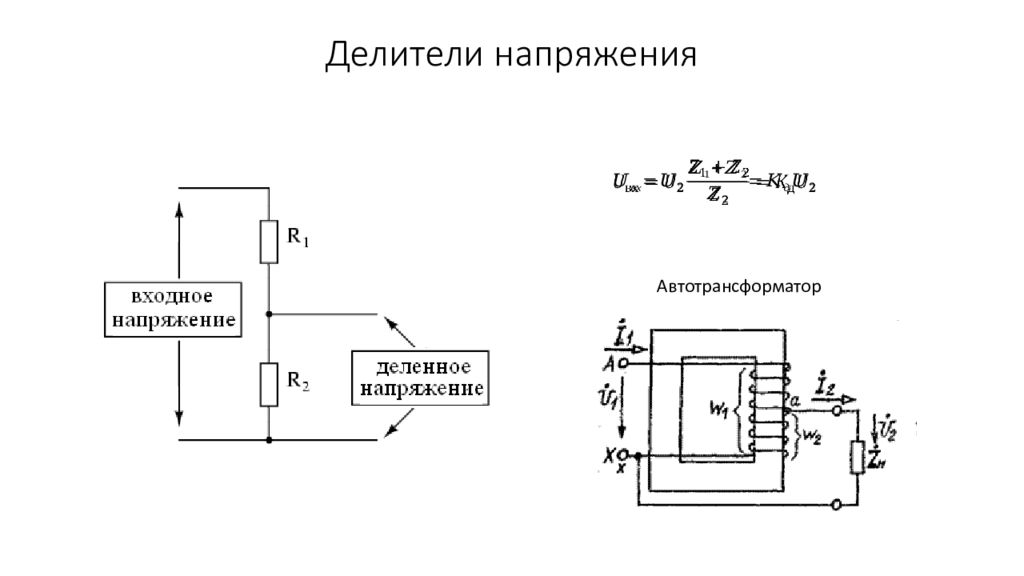 В общем случае, не нужно даже знать, что это за токи такие. Можно просто принять их равными Iд = 0.01 А (10 мА), а Iн = 0. То есть рассматривать делитель без нагрузки. Это приемлемо до тех пор, пока мы используем делитель только для измерений напряжения (а во всех примерах в нашей базе знаний он именно так и используется). Тогда формулы упростятся:

R1 = (Uвх-Uвых) * 100

R2 = Uвых * 100

P.S. Это совсем не важно, но обратите внимание: 100 — это не физическая величина. После принятия условия, что Iд у нас всегда равен 0.01 А, это просто коэффициент, получившийся при переносе 0.01 в числитель.

Проверяем:

Входящее напряжение у нас 9 вольт, хотим получить 5 вольт на выходе. Подставляем значения в формулу, получаем:

R1 = (9-5) * 100 = 400 Ом

R2 = 5 * 100 = 500 Ом

Всё сходится!

Применение делителя напряжений

В основном делитель напряжения используется там, где нужно измерить изменяющееся сопротивление.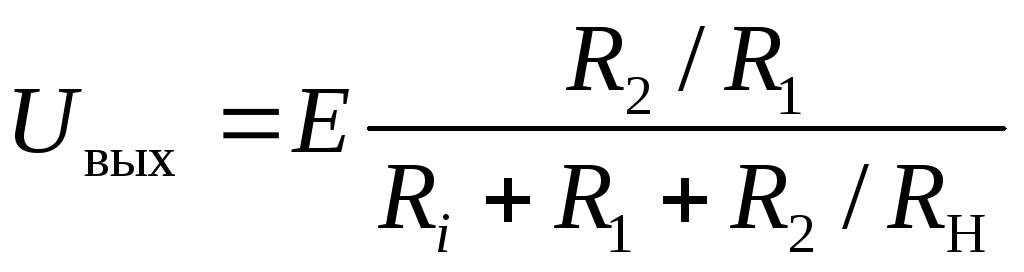 На этом принципе основано считывание значений с фоторезистора: фоторезистор включается в делитель в качестве одного плеча. Второе плечо представляет собой постоянный резистор. Аналогичным образом можно считывать показания терморезистора.

Высоковольтные малогабаритные резистивные делители переменного тока из микропровода Текст научной статьи по специальности «Электротехника, электронная техника, информационные технологии»

ВЫСОКОВОЛЬТНЫЕ МАЛОГАБАРИТНЫЕ РЕЗИСТИВНЫЕ ДЕЛИТЕЛИ ПЕРЕМЕННОГО ТОКА ИЗ МИКРОПРОВОДА

В.П.Берзан, M-Л.Шит (Институт Энергетики АН Молдовы), Ю.И.Колпакович, Д.И.Кожокару, В.Г.Клейменов, Центр «CRDEIMT», Институт «ELIRI» S.A., Республика Молдова, г.Кишинев

Аннотация. В работе рассмотрены конструктивные параметры и характеристик нового изделия, резистивного делителя напряжения переменного тока из микропровода для измерения высоковольтного напряжения переменного тока. Резистивные делители предназначены для применения в сетях переменного тока промышленной частоты и в тяговых сетях электрического транспорта. Делители имеют меньшие массогабаритные размеры по сравнению с измерительными трансформаторами напряжения и более высокий класс точности 0,2 при фиксированной частоте.

Ключевые слова: резистивный делитель, микропровод, высокое напряжение.

DIVIZOARE REZISTIVE DE TENSIUNE tNALTA DE CURENT ALTERNATIV DIN MICROCONDUCTOARE CU GABARIT REDUS

Berzan V.P., §it M. L.(IE A§M), Colpacovici Iu.,I., Cojocaru D.I., KleimenovV.G., «ELIRI» S.A.

Rezumat. Se examineaza realizarea constructive, parametrii §i caracteristicile unui nou produs, divizoare resistive din microconductoare petru masurarea tensiunii de current alternative de tensiune inalta pentru energetica §i transportul electrificat. Divizoarele se caractetrizeaza de o masa redusa §i precizie ridicata de masurare a tensiunii §i corespund clasei de precizie 0,2.

Cuvinte-cheie: divizor rezistiv, tensiune inalta, microconductoare.

HIGH VOLTAGE SMALL — SIZED ALTERNATIVE CURRENT RESISTIVE DIVIDERS FROM MICROWIRE

Berzan V.P., Sit M. L. (IE A§M), Kolpacovich Iu.,I., Kojokaru D.I., Kleimenov V.G., «ELIRI» S.A.

Republic of Moldova

Abstract. The paper discusses the design parameters and characteristics of the new product, the resistive voltage divider produced from microwire for measuring high-voltage alternating current. Resistive dividers are designed for use in AC circuits and power-frequency electric traction network traffic. Dividers have smaller mass-dimensional size compared with the measuring voltage transformers and higher accuracy class 0.2 at a fixed frequency.

Keywords: resistive high voltage dividers, microwire.

1. Введение

Современные системы учета и распределения электрической энергии нуждаются в достоверной информации о величине питающего напряжения и его отклонениях в процессе эксплуатации. Электроснабжающие предприятия и организации электрифицированного транспорта нуждаются в высокоточных, надежных и малогабаритных масштабных преобразователях высокого напряжения от 3 до 36 кВ, обеспечивающих получение указанной информации.

Одним из видов масштабных преобразователей высокого напряжения являются резистивные делители напряжения, обладающие рядом преимуществ по сравнению с трансформаторами и емкостными делителями. Из этих преимуществ следует отметить

высокую точность и стабильность, малые габариты, чрезвычайно низкое электропотребление, отсутствие резонансных эффектов, наличие экрана. Реализации этих преимуществ в области точности коэффициента деления делителя напряжения на переменном токе требует тщательного учета и компенсации паразитных параметров — емкости и индуктивности резистивных элементов делителей напряжения.

2. Конструктивные особенности малогабаритных высоковольтных резистивных делителей напряжения

Известные конструкции таких делителей представляют собой множество резистивных элементов собранных в длинные гирлянды для уменьшения паразитной емкости. Такие конструкции очень громоздки и нетранспортабельны. Уменьшение габаритных размеров, удовлетворение требованиям стабильности и транспортабельности может быть достигнуто за счет делителей напряжения на основе микропровода в стеклянной изоляции. Для этого имеются следующие предпосылки [1]:

— высокое погонное сопротивление провода — до 300 кОм/м, что при уменьшении размеров позволяет уменьшить паразитную распределенную емкость и индуктивность резистивных секций,

— высокое значение пробивного напряжения стеклянной изоляции микропровода — до 500 В;

— возможность точной настройки любого значения коэффициента деления на постоянном токе,

— возможность настройки и поверки при рабочем высоком напряжении на постоянном токе [2];

— возможность проверки амплитудной и фазовой погрешности на переменном токе при низком напряжении (до 1 кВ).

Ответственной частью высоковольтного делителя напряжения является высоковольтная резистивная секция (рис.1), габариты которой зависит от величины рабочего напряжения делителя ( для одного и того же номинала могут быть несколько типоразмеров).

Рис.1. Резистивная секция высоковольтного делителя напряжения

В качестве таких секций используются высоковольтные резисторы, сопротивление которого образовано обмоткой высокоомного микропровода с погонным сопротивлением 40- 150 кОм/м при диаметре провода 5-15 мкм. Индуктивность и емкость обмотки такого резистора, а также емкость токоподводов составляет паразитные параметры секции и существенно влияет на частотную погрешность делителя напряжения.

3. Схемы замещения и параметры резистивной секции из микропровода

Эти схемы представляют интерес при оценке параметров влияющих на показатели точности резистивных делителей напряжения. Простейшая схема замещения с сосредоточенными параметрами включает RLC элементы, значение которых необходимо определить. Для нашей задачи наиболее приемлемы расчетные методы. Поскольку резистивные элементы делителей являются по своей геометрии и по процессам близкими аналогами катушек индуктивности. Для катушек индуктивности, особенно однослойных, получены достаточно точные расчетные формулы, которые мы и используем при расчете параметров резистивных элементов делителей из микропровода [3]. На рис. 2 приведена простейшая схема замещения резистивного элемента с сосредоточенными параметрами.

L1 R1

______ R1- сопротивление секции (или плеча делителя)

С1- собственная паразитная емкость

О

L1 — собственная паразитная индуктивность

Рис. —1———1—1——1—1 (2)

я1

где о — круговая частота.

Для оценки влияния паразитных емкости и индуктивности приведем их оценочный расчет.

Индуктивность резистивной секции. Индуктивность секции определим как индуктивность однослойной катушки [1], так как микропроволочные сопротивления по конструкции представляют собой катушки из высокоомного провода:

= 2-Ю • Вп (3)

1 9В + 20Н

где В — диаметр намотки (диаметр каркаса резистивной секции),

Н — длина намотки (длина каркаса резистивной секции), п — число витков намотки (число витков резистивной секции):

Собственная емкость секций и плеч делителя напряжения. п (4)

1=1 Н

из которой видно, что для уменьшения собственной емкости необходимо уменьшать как диаметр провода, так и число витков, а для этого необходимо применение более высокоомного микропровода.

Обозначим погрешность модуля сопротивления резистивной секции как 5К :

6, = (|21| — ,)/Л. (5)

и тогда

21 = Л1(1 + 6Л ) (6)

В табл.1 приведены расчетные данные высоковольтной секции делителя напряжения общим сопротивлением , = 109От при различных значениях погонного сопротивления, индуктивности и емкости секции.

Таблица.1. Составляющие погрешности высоковольтного плеча делителя напряжения в зависимости от частоты переменного тока £=50 Н

Ло, Ц, Погрешность модуля, 5К, % Фаза, рк , мин

От Гн С1=0,5пФ С1=1пФ С1=1,5пФ С1=2пФ С1=0,5пФ С1=1пФ С1=1,5пФ С1=2пФ

50103 24,9

100 103 6,24 -0,012 -0,046 -0,095 -0,153 -8,9 -17,4 -25,2 -32,1

150 103 2,77

200 103 1,56

£=400 Гц

50 103 24,9

100 103 6,24 -0,038 -0,630 -0,744 -0,804 -51,5 -68,3 -75,1 -78,7

150103 2,77

200 103 1,56

Из расчетов получается, что практически для всех значений индуктивности секции, погрешность модуля и фазы сопротивления принимает одинаковые значения на частотах до 400 Гц.4р ЛЯ0

С1е =——————п (7)

1е 1п( Ве / В)

где Ве — диаметр экрана.

В табл.2 приведены расчетные данные высоковольтной секции делителя напряжения общим сопротивлением Д = 109От при различных значениях погонного сопротивления для резистивного элемента, помещенного в экранах с различным значением диаметра.

Конечно, приведенные расчеты являются приближенными, так как не учитывается ряд факторов, таких как емкость между токоподводами и экраном и др., формула для емкости витка приблизительная и т.д. Однако полученные результаты позволяют судить о поведении делителя на переменном токе, показывают возможность компенсации реактивности обмотки резистивных секций, поскольку погрешность модуля и фазы сопротивления от собственной емкости и от емкости на экран имеют противоположные знаки.

Таблица.2. Составляющие погрешности экранированного высоковольтного плеча делителя напряжения £=50 Гц

До, От Погрешность модуля, дсе, % Фаза, (рсе, мин

Бе= 50мм Бе= 100 мм Бе= 150мм Бе= 200мм Бе= 50мм Бе= 100мм Бе= 150мм Бе= 200мм

50103 0,00959 0,00240 0,00143 0,00107 366 183 141 122

100103 0,00240 0,00060 0,00036 0,00027 129 64,6 50,0 43,1

150103 0,00107 0,00027 0,00016 0,00012 70,4 35,2 27,2 23,5

200 103 0,00060 0,00015 0,00009 0,00007 45,7 22,9 17,7 15,2

£=400 Гц

До, От Погрешность модуля, 8се, % Фаза (Рсе , мин

Бе= 50мм Бе= 100 мм Бе= 150мм Бе= 200мм Бе= 50мм Бе= 100мм Бе= 150мм Бе= 200мм

50103 0,614 0,153 0,092 0,068 2930 1460 1130 975

100103 0,153 0,038 0,023 0,017 1030 517 400 345

150103 0,068 0,017 0,010 0,008 563 281 218 188

200 103 0,038 0,009 0,006 0,004 366 183 141 122

В результате моделирования и экспериментальных исследований найдено оптимальное соотношение конструктивного отношения диаметров экрана и резистивной секции, в зависимости от ее сопротивления. При этом достигается минимальное значение фазовой погрешности делителя — до 10 мин, при погрешности коэффициента деления не превышающей 0,1-0,2% на частоте 50 Гц.

Входное сопротивление делителя, в зависимости от рабочего напряжения составляет от 10 до 100 МОм. Делители напряжения из микропровода имеют малое значение температурного коэффициента деления, не превышающего 5-10-бК-1, а также имеют малое значение коэффициента зависимости от напряжения (нелинейности).

Резистивные делители из микропровода имеют низкое значение входной и выходной емкости, не превышающей единиц пикофарад, что обусловлено способом компенсации его частотной погрешности. Наличие экранирующей оболочки существенно

устраняет влияние внешних предметов на коэффициент деления и значительно уменьшает воздействие внешних электромагнитных воздействий и помех.

На рис.5-8 показаны малогабаритные делители напряжения 6-35 кВ, а на рис.9 частотные погрешности образца делителя типа БИТ 24 кВ определенные эксперимен-

тально.

Рис. 5. Резистивные делители напряжения переменного тока БИТ 24 кВ

Рис. 4. Резистивные делители напряжения переменного тока БЯТ 6-10 кВ

Рис. 6. Резистивные делители напряжения переменного тока БИТ 35 кВ

Частота, Гц

Рис.7. Зависимость погрешностей делителей DRT частоты

Выводы

1. Резистивные делители из микропровода имеют низкое значение входной и выходной емкости, не превышающей единиц пикофарад, что обусловлено способом компенсации его частотной погрешности.

2. Наличие экранирующей оболочки существенно устраняет влияние внешних предметов на коэффициент деления и значительно уменьшает воздействие внешних электромагнитных воздействий и помех.

3. Указанные делители напряжения могут найти применение в приборах учета электроэнергии в энергетике, а также на электрическом транспорте. По своим массогабаритным параметрам делители напряжения из микропровода значительно эффективнее традиционно применяемых измерительных трансформаторов напряжения.

Работа выполнена в рамках проекта » 09.808.05.01A . Structuri rezistive coaxiale în straturi de generale nouä de convertoare pentru mäsurarea tensiunii înalte (35 -110 kV) de curent alternativ”, Государственная Программа “Ingineria si tehnologiile electronice in relansarea economiei ”.

Литература.ii in metrologie, certificare, informatizare §i inovare. Chi§inau, 2003, p. 50-55.

3. Журавлев А.А., Шит М.Л., Колпакович Ю.И., Кожокару Д.И., Клейменов В.Г. Высоковольтный резистивный делитель на базе литого микропровода в стеклянной изоляции на рабочие напряжения 6 — 24 кВ переменного тока промышленной частоты. Problemele energeticii regionale. №3, 2008.

Берзан Владимир Петрович — др.хаб. техн. наук, директор Института энергетики АН Молдовы. Область научных интересов: неразрушающие методы диагностики электроэнергетического оборудования, нестационарные процессы в цепях с распределенными параметрами, математическое моделирование, передача электрической энергии на большие расстояния, возобновляемые источники энергии. Автор более 160 научных работ, включая 10 монографий. E-mail: [email protected]

Шит Михаил Львович — к.т.н., зав. Лабораторией «Энергетической эффективности и систем управления» Института энергетики АНМ. Область научных интересов: тепловые насосы на диоксиде углерода, автоматическое управление технологическими процессами в энергетике, промышленности, сельском хозяйстве. e-mail: mihail [email protected]

Колпакович Ю.И. — зав. Лабораторией S.A. ELIRI, к.т.н. Область научных интересов — метрология, технология производства микропровода и измерительного оборудования на базе микропровода, системы автоматизации процессов обработки данных и поверки измерительного оборудования.

Кожокару Д.В. — инженер S.A. ELIRI. Область научных интересов — метрология, технология производства микропровода и измерительного оборудования на базе микропровода.

Клейменов В. — инженер S.A. ELIRI. Область научных интересов — метрология, технология производства микропровода и измерительного оборудования на базе микропровода.

ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ • Большая российская энциклопедия

Схемы низковольтных делителей напряжения: а – резистивного; б – ёмкостного; в – индуктивного; u и U – напряжения; r и R – резисторы; C1 и C2 – конденсаторы; L1 и L2…

ДЕЛИ́ТЕЛЬ НАПРЯЖЕ́НИЯ, элек­тро­тех­нич. уст­рой­ст­во, по­зво­ляю­щее сни­мать (ис­поль­зо­вать) толь­ко часть имею­ще­го­ся по­сто­ян­но­го или пе­ре­мен­но­го на­пря­же­ния по­сред­ст­вом эле­мен­тов элек­трич. це­пи, со­стоя­щей из ре­зи­сто­ров, кон­ден­са­то­ров или ка­ту­шек ин­дук­тив­но­сти. Обыч­но при­ме­ня­ет­ся для из­ме­ре­ния на­пря­же­ния. Осн. ха­рак­те­ри­сти­ка Д. н. – ко­эф. де­ле­ния, оп­ре­де­ляе­мый от­но­ше­ни­ем вход­но­го (из­ме­ряе­мо­го) на­пря­же­ния к вы­ход­но­му (сни­мае­мо­му). Про­стей­ший Д. н. пред­став­ля­ет со­бой два по­сле­до­ва­тель­но со­еди­нён­ных ре­зи­сто­ра (два пле­ча де­ли­те­ля), на ко­то­рые по­да­ёт­ся вход­ное на­пря­же­ние $U$ (рис., а). Ко­эф. де­ле­ния при от­сут­ст­вии на­груз­ки оп­ре­де­ля­ет­ся фор­му­лой $$K=U/u=R/(R+r),$$ где $R$ и $r$ – со­про­тив­ле­ния ре­зи­сто­ров, $u$ – сни­мае­мое нап­ря­же­ние. От­кло­не­ния $R$ и $r$ (а сле­до­ва­тель­но, и $K$) от но­ми­наль­ных зна­че­ний обу­слов­ли­ва­ют по­греш­ность де­ли­те­ля. В Д. н. вы­со­кой точ­но­сти при­ме­ня­ют ре­зи­сто­ры с ма­лым тем­пе­ра­тур­ным ко­эф. со­про­тив­ле­ния и вы­со­кой вре­мен­нóй ста­биль­но­стью (напр., из ман­га­ни­но­вой про­во­ло­ки). В це­пях пе­ре­мен­но­го то­ка по­ми­мо ре­зи­стив­ных Д. н. ис­поль­зу­ют­ся так­же ём­ко­ст­ные с кон­ден­са­то­ра­ми по­сто­ян­ной или пе­ре­мен­ной ём­ко­сти (рис., б) и ин­дук­тив­ные (рис., в).

Д. н. мо­гут быть од­но­пре­дель­ны­ми (с од­ним но­ми­наль­ным $K$) и мно­го­пре­дель­ны­ми; с по­сто­ян­ным и ре­гу­ли­руе­мым (плав­но, дис­крет­но или ком­би­нир. спо­со­бом) от­но­ше­ни­ем плеч. Д. н. вхо­дят в со­став мн. средств из­ме­ре­ния в ка­че­ст­ве зве­на из­ме­рит. це­пи. Напр., ре­зи­стив­ные де­ли­те­ли с но­ми­наль­ны­ми зна­че­ния­ми $K$, рав­ны­ми 10, 100 и 1000, при­ме­ня­ют­ся во вход­ных це­пях мно­го­пре­дель­ных ана­ло­го­вых и циф­ро­вых вольт­мет­ров. Ём­ко­ст­ные Д. н., со­стоя­щие из не­сколь­ких по­сле­до­ва­тель­но со­еди­нён­ных кон­ден­са­то­ров вы­со­кой точ­но­сти, слу­жат для от­бо­ра мощ­но­стей от ЛЭП вы­со­ко­го на­пря­же­ния (до 500 кВ). При­ме­ром Д. н. на ин­дук­тив­ных со­про­тив­ле­ни­ях яв­ля­ет­ся ав­то­транс­фор­ма­тор.

Урок 20 — Цепи делителя тока

«Покупка DVD с репетитором по алгебре, математике и физике была лучшим вложением в образование».

«В прошлом семестре я перешел с« C »на
и получил« пятерку »!»

Les J.
Matawan, NJ

---

«DVD Math Tutor просто фантастические!
Джейсон представляет материал в ясной и хорошо организованной форме.

Я был полностью
в ужасе от физики,
, но сразу после первой лекции я почувствовал себя непринужденно.«

С. Дидс-Рубин
Лос-Анджелес, Калифорния

---

«Ваши методы настолько ясны, что мой семилетний
-летний сын усваивал уроки тригонометрии. Я тоже подбираю около
новых вещей».

Гэри Г.

---

«Смотреть справочные видео по математике — это замечательно, потому что, работая над задачами, вы показываете и объясняете каждый шаг».

M. Dalrymple
Lancaster, CA

«Все инструкции
и примеры на DVD с репетитором математики очень четко объяснены, и стиль преподавания Джейсона определенно делает зрителя очень комфортным с представленным материалом.«

Д. Форбс
Мидлтаун, штат Нью-Джерси

---

«Я нашел лекции
очень четкими, прямо по делу, и темп был как раз для меня, который не видел никаких расчетов или триггеров за последние 10 лет и должен быстро набрать скорость».

София

---

«Просто хотел сообщить вам, что благодаря
фундаменту, который я получил от вашего DVD с математической справкой (особенно DVD с предварительным расчетом), я смог пройти свой курс предварительного расчета в этом семестре на пятерку!»

Дж.Ректон

«У вас серьезный педагогический дар.
Доказательство того, что я смотрю ваши DVD, когда обычно я
бывал вне дома. Никогда не думал, что смогу выучить математику. Я сразу перехожу к исчислению, а затем к физике. Я действительно наслаждайтесь этим, и я подумываю о смене карьеры. Отличная работа! »

Д. Смит

Делитель напряжения (делитель потенциала) и делитель тока

Делитель напряжения и Делитель тока — наиболее распространенные правила, применяемые в практической электронике.Как вы знаете, в схеме есть два типа комбинаций: последовательное и параллельное соединение. Параллельные схемы также известны как схемы делителей тока, потому что в этих схемах ток делится через каждый резистор. В то время как последовательные цепи известны как схемы делителей напряжения, потому что здесь напряжение делится на все резисторы. Правило деления напряжения и правило деления тока необходимы для понимания напряжения и тока, протекающих через каждый резистор.Эти правила разделения используются в большинстве распространенных электронных устройств.

Схема делителя напряжения

Чтобы пропустить ток через электрический проводник, необходимо приложить электродвижущую силу. Когда мы говорим, что ток I проходит через резистор R, из этого логически следует, что сила, действующая на резистор R. Эта сила известна как разность потенциалов или падение напряжения на резисторе R. любая часть электрической цепи трех величин i.е. напряжение, ток и сопротивление сочетаются.

Как мы узнали, последовательная схема называется схемой делителя напряжения. Это схема, которая делит напряжение на мелкие части. Итак, с источником питания и двумя резисторами мы можем сделать простую схему делителя напряжения. Здесь нам нужно соединить два резистора последовательно, а затем подать источник напряжения на последовательную цепь.

Схема делителя напряжения

В этом случае подключаются резистор R1 на 5 Ом и резистор R2 с сопротивлением 10 Ом.Напряжения V _out1 и V _out2 делятся между резисторами R1 и R2. Их можно рассчитать с помощью простого уравнения деления напряжения.

Где R _x — это резистор, на котором нам нужно найти напряжение, а R _total — полное сопротивление (R1 + R2) в цепи. Его можно просто рассчитать, сложив их все, поскольку они соединены последовательно. Таким образом, в данной схеме значения напряжения на каждом резисторе равны

Следовательно, напряжение на R1 составляет 4 В, а напряжение на R2 — 8 В.Таким образом, здесь напряжение делится в цепи между резисторами. Следовательно, это называется схемой делителя напряжения.

Делители напряжения

используются во многих приложениях, но они широко используются во всех типах переменных резисторов. Возьмем пример потенциометра. Потенциометр — это переменный резистор, который можно использовать для создания регулируемого делителя напряжения. Потенциометр имеет три клеммы, две клеммы подключены к концам резистора, а средняя клемма подключена к дворнику.У него одно сопротивление. Два внешних контакта подключены к источнику напряжения, а средний вывод действует как делитель напряжения.

Цепь делителя тока

Делитель тока — это цепь, которая делит ток на мелкие части. Как мы узнали, параллельные цепи представляют собой схему делителя тока. Таким образом, с источником питания и двумя параллельными резисторами мы можем сделать простую схему делителя тока. Как и в схеме делителя тока, здесь нам нужно соединить два резистора параллельно, а затем подать источник тока через параллельную цепь.

Цепь делителя тока

«I ₁ » и «I ₂ » — это ток, разделенный между резисторами R1 и R2. Их можно рассчитать с помощью простого уравнения деления тока.

«I _n » — это требуемый ток, протекающий через резистор R _n . R _eq — эквивалентное сопротивление параллельных резисторов.

Эквивалентное сопротивление (R _экв ) равно

Таким образом, ток, протекающий через резисторы R1 и R2, будет равен

.

Здесь резисторы одинакового номинала, поэтому ток через каждый резистор будет делиться ровно пополам.Таким образом, это известно как схема делителя тока.

Практически каждая цепь, с которой мы сталкиваемся, представляет собой схему делителя напряжения или тока, либо они могут быть обеими сразу. Делители напряжения используются во множестве приложений, таких как переменные резисторы (потенциометры), LDR, термисторы и современные устройства, такие как акселерометр. Цепи делителя тока в основном используются для упрощения схем, которые упрощают прогнозирование выбора резистора.

Делителей тока — Electronics-Lab.com

Введение

Мы видели в предыдущем руководстве о делителях напряжения и что процесс деления напряжения стал возможным благодаря объединению одних и тех же компонентов в последовательную конфигурацию. В этой статье мы сосредоточимся на процессе текущего деления , выполняемом Current Divider , которые представляют собой параллельные объединения компонентов.

Наиболее распространенный тип делителя тока обсуждается в первом разделе, в его простейшей форме он состоит из двух параллельно включенных резисторов.

Еще несколько конфигураций и подробностей о резистивных делителях тока рассматриваются во втором разделе.

Наконец, в следующих разделах представлены альтернативные формы делителей тока, частично сделанных из реактивных компонентов.

Презентация

Самая простая конфигурация резистивного делителя тока представлена ​​на рис. 1 ниже:

рис 1: Изображение резистивного делителя тока

Теперь мы продемонстрируем формулы делителя тока, то есть выражения I ₁ и I ₂ как функцию источника I _S и сопротивлений R ₁ и R ₂ .

Прежде всего, мы выражаем оба тока как функцию напряжения V согласно закону Ома: I ₁ = V / R ₁ и I ₂ = V / R ₂ .

Согласно закону тока Кирхгофа, источник тока можно записать как сумму независимых токов в каждой ветви: I _S = I ₁ + I ₂ = V × (1 / R ₁ +1 / R ₂ ).

При том же знаменателе это выражение принимает вид V = (R ₁ × R ₂ / (R ₁ + R ₂ )) × I _S .Наконец, мы заменим V в выражениях I ₁ и I ₂ , чтобы получить формулы резистивного делителя тока:

уравнение 1: Соотношение резистивного делителя тока

Безразмерные коэффициенты в этих выражениях находятся в диапазоне от 0 (R ₂ = 0 в выражении I ₁ или R ₁ = 0 для I ₂ ) до 1 (R ₁ = 0 для I ₁ и R ₂ = 0 для I ₂ ), что интересно получить любое возможное значение выходного тока от 0 до I _S , установив правильные значения для резисторов.

На практике значения сопротивления никогда не равны 0 по той простой причине, что сопротивление проводов невелико, но не равно нулю. Однако мы все же можем сказать, что для R ₁ >> R ₂ , I ₁ = 0 и I ₂ = I _S , а для R ₂ >> R ₁ , I ₁ = I _S и I ₂ = 0.

Выражения Уравнение 1 можно обобщить для любого компонента, который составляет делители тока, для этого мы используем формализацию импеданса:

уравнение 2: Общие соотношения между делителями тока

Так как делители тока состоят из соединений компонентов, включенных параллельно, часто рекомендуется использовать проводимость вместо импеданса, чтобы упростить вычисления.Действительно, полная проводимость резистора R записывается как Y = 1 / R, и в параллельной конфигурации проводимости просто складываются: Y _до = Y ₁ + Y ₂ +…

Чтобы проиллюстрировать усовершенствования упрощения этого метода, мы пересмотрим схему на Рисунок 1 с допусками:

Рис. 2: Резистивный делитель тока с обозначением полной проводимости

Здесь эквивалентная параллельная проводимость дается просто как Y _tot = Y ₁ + Y ₂ .Следовательно, мы имеем отношение V × Y _к = I _S . При замене V в выражении I ₁ = V / R ₁ = V × Y ₁ и I ₂ = V / R ₂ = V × Y ₂ , получаем следующие соотношения:

уравнение 3: Форма полной проводимости резистивного делителя тока

Очень полезным применением делителей тока является безопасное измерение токов с одновременной защитой измерительного прибора и пользователя. Пример измерения тока приведен на следующем рисунке Рисунок 3 :

рис. 3: Процесс безопасного измерения высокого постоянного тока

Форма компонентов учитывает пропорции, которые должны принимать резисторы.Действительно, чтобы защитить амперметр от высоких токов, резистор R ₂ должен быть больше, чем R ₁ , чтобы ограничить ток через измерительное устройство.

В качестве примера, если источник обеспечивает ток I _S = 1 А, но амперметр принимает максимум 0,05 А, мы можем выбрать значения для R ₁ и R ₂ так, чтобы соотношение R ₁ / (R ₁ + R ₂ ) равно или меньше 1/20. Значения R ₁ = 1 кОм и R ₂ = 19 кОм, например, удовлетворяют этому условию.

Наконец, чтобы отобразить правильное значение для пользователя, амперметр просто умножает измеренное значение на обратную дробь (R ₁ + R ₂ ) / R ₁ .

Общие / конфигурация сети

Общая конфигурация делителя тока или делителя тока сети выполняется с более чем двумя параллельными резисторами. На следующем рисунке , рис. 4 , мы проиллюстрировали резистивный сетевой делитель тока с 4 компонентами:

рис. 4: Схема резистивного делителя тока.

Для такой схемы или для любого делителя тока сети, состоящего из N резисторов, общая формула для любого тока задается формулой Уравнение 4 , где R _eq является значением параллельного эквивалентного сопротивления.

уравнение 4: Выражения токов в сети делителя тока

Сеть делителя тока может использоваться для ограничения тока на выходе, как показано с амперметром на рис. 3 , но, более того, для ограничения тока в каждом отдельном резисторе.

В качестве примера, если мы пересмотрим конфигурацию, приведенную в рис. 3 , мы можем вычислить мощность, рассеиваемую на каждом резисторе:

• P ₁ = R ₁ × I ₁ ² = 1000 × (0.95) ² = 903 Вт
• P ₂ = R ₂ × I ₂ ² = 19 × 10 ³ × (0,05) ² = 47 Вт

Значение 900 Вт в резисторе R ₁ явно слишком велико для обработки и может расплавить структуру резистора даже со специально разработанными мощными прикладными резисторами.

С помощью схемы делителя тока мы можем разделить общую мощность (1000 Вт) более равномерно и с меньшими значениями в каждом резисторе.Мы могли бы выбрать, например, соединить 20 резисторов параллельно с одинаковыми номиналами (1 кОм). В этом случае каждый резистор будет поглощать только 0,05 A и рассеивать низкое значение 1000 × (0,05) ² = 2,5 Вт , что соответствует как условиям резисторов, так и защитам измерительного устройства.

Делители реактивного тока

При рассмотрении , рис. 2 , мы можем заменить одну из проводников (скажем, Y ₂ ) на реактивный компонент, такой как конденсатор или катушка индуктивности .Эти возможные ассоциации придают делителю тока интересные свойства в режиме переменного тока.

Резисторно-конденсаторный делитель тока

В этой конфигурации резистор подключается параллельно конденсатору, как показано на рис. 5 . Мы называем этот текущий делитель ассоциацией R // C.

Рис. 5: Связь цепи R // C

Можно показать, что ток через резистор и конденсатор зависит от частоты и может быть выражен следующими соотношениями, показанными в Уравнение 5 .Текущее выражение I _R получается с помощью обобщенной формулы делителя тока и выражения I _C путем простого применения закона Кирхгофа.

уравнение 5: Выражения тока в ассоциации R // C

Мы выбираем R = 1 кОм, C = 5 мкФ и I _S = 1 A, чтобы показать пример графика этих токов:

Рис. 6: Графики токов IR (ω) и IC (ω) в ассоциации R // C

Как мы видим, из-за реактивного сопротивления конденсатора ток I _C равен нулю для низких частот и увеличивается до короткое замыкание на высокие частоты.С другой стороны, ток резистора уменьшается при увеличении частоты источника. Обратите внимание, что I _R + I _C является константой и равен I _S = 1 A.

На практике схемы R / C используются в качестве фильтров нижних частот , чтобы срезать высокие частоты на выходе. Более того, параллельный конденсатор часто используется в биполярных усилителях в качестве компонента связи и развязки, чтобы сократить до земли нежелательные высокочастотные сигналы.

Делитель тока резистор-дроссель

Дополнительную цепь к ассоциации R // C можно создать благодаря параллельному соединению резистора и индуктивности, что мы называем ассоциацией R // L.

рис. 7: Связь цепи R // L

Токи снова зависят от частоты источника переменного тока, и их выражения даются в виде Уравнение 6 :

уравнение 6: Текущие выражения в ассоциации R // L

Мы выбираем R = 1 кОм, L = 5 мФ и I _S = 1 A, чтобы показать пример графика этих токов:

Рис. 8: Графики токов I _R (ω) и I _C (ω) в ассоциации R // L

Импеданс катушки индуктивности увеличивается с увеличением частоты, в результате ток I _L уменьшается.Когда частота увеличивается, через резистор проходит больший ток. Обратите внимание, что I _R + I _L — это константа, равная I _S = 1 A.

На практике делители тока R // L используются в качестве фильтров верхних частот , поскольку высокие частоты могут собираться в ветви резистора. Эта схема является двойной схемой R // C, представленной ранее.

Заключение

Делители тока представляют собой параллельные соединения по крайней мере двух электронных компонентов, которые разделяют ток, исходящий от источника, на несколько меньших токов.

Такие конфигурации могут обеспечить хорошее значение тока, соответствующее динамике любого каскада в цепи.

В первом разделе мы подробно описываем наиболее распространенный и простой делитель тока, который состоит из двух параллельно включенных резисторов . Мы демонстрируем отношения резистивного делителя тока и объясняем, как работает схема. Кроме того, представлен еще один формализм с допусками вместе с простым примером приложения.

Конфигурации с более чем двумя резисторами представлены во втором разделе, такая конфигурация полезна для разделения мощности на большее количество компонентов и предотвращения несчастных случаев.

Наконец, в последнем разделе показаны простые делители тока с реактивными компонентами . Из-за их частотно-зависимых импедансов конденсаторы и катушки индуктивности могут использоваться параллельно с резисторами, чтобы разделить ток на определенный диапазон частот.

Правило разделения тока и напряжения

Правило текущего дивизиона

Параллельная цепь действует как делитель тока, поскольку ток делится во всех ветвях параллельной цепи, а напряжение на них остается неизменным.Правило деления тока определяет ток через полное сопротивление цепи. Текущее деление объясняется с помощью схемы, показанной ниже:

Ток I разделен на I ₁ и I ₂ на две параллельные ветви с сопротивлением R ₁ и R ₂ , а V — падение напряжения на сопротивлении R ₁ и R ₂ .

Как известно,

В = ИК …… .. (1)

Тогда уравнение тока запишется как:

Пусть полное сопротивление цепи равно R и определяется уравнением, показанным ниже:

Уравнение (1) также можно записать как:

I = V / R ……….(3)

Теперь, подставив значение R из уравнения (2) в уравнение (3), мы получим

Но

Подставляя значение V = I ₁ R ₁ из уравнения (5) в уравнение (4), мы, наконец, получаем уравнение:

А теперь, учитывая V = I ₂ R ₂ , уравнение будет:

Таким образом, из уравнений (6) и (7) значение тока I ₁ и I ₂ соответственно определяется уравнением ниже:

Таким образом, в правиле деления тока сказано, что ток в любой из параллельных ветвей равен отношению сопротивления противоположной ветви к общему сопротивлению, умноженному на общий ток.

Правило разделения напряжения

Правило деления напряжения можно понять, рассмотрев последовательную схему, показанную ниже. В последовательной цепи напряжение делится, а ток остается прежним.

Рассмотрим последовательно подключенный к нему источник напряжения E с сопротивлением r ₁ и r ₂ .

Как известно,

I = V / R или можно сказать I = E / R

Следовательно, ток (i) в контуре ABCD будет:

Помещая значение I из уравнения (8) в уравнение (9), напряжение на сопротивлении r ₁ и r ₂ соответственно определяется уравнением, показанным ниже, как:

Таким образом, напряжение на резисторе в последовательной цепи равно значению этого резистора, умноженному на общее приложенное напряжение на последовательных элементах, деленное на общее сопротивление последовательных элементов.

M1K Basics и делители напряжения / тока [Analog Devices Wiki]

После освоения основных операций прикладного программного обеспечения M1K и PixelPulse полезно показать, как построить простые схемы на беспаечной макетной плате, подключить их к M1K, генерировать напряжения и токи и измерять напряжения на дисплее PixelPulse. В этой лабораторной работе мы сначала покажем, как беспаечная макетная плата используется для построения схем. Затем мы строим делитель напряжения и делитель тока, каждый из которых состоит из резисторов, на беспаечной макетной плате и показываем детали, касающиеся подключения схемы к M1K.Наконец, мы используем источник напряжения и источник тока в M1K, управляемый программным обеспечением PixelPulse, для управления этими цепями и измеряем напряжения на резисторах на дисплее компьютера с помощью программного обеспечения M1K и PixelPulse.

Получить базовое представление о том, как использовать программное обеспечение M1K, PixelPulse и компоненты из набора аналоговых деталей ADALP2000 для создания схем и проведения экспериментов с этими схемами. Чтобы понять, как основные схематические символы, такие как те, которые используются для обозначения заземления схемы и напряжения источника питания, интерпретируются при построении и анализе реальной схемы.Чтобы понять, как работают схемы делителей напряжения и тока и как рассчитывать отдельные напряжения в делителях напряжения и отдельные токи в делителях тока. По завершении этой лабораторной работы вы сможете объяснить основные операции программного обеспечения M1K и PixelPulse, как построить схемы на беспаечной макетной плате для оценки и рассчитать все напряжения и токи в схемах делителей напряжения и тока.

Эта лабораторная работа преследует две основные цели. Первый — это познакомиться с основными схематическими символами с акцентом на «землю» и с тем, как преобразовать их в реальные схемы, которые подключаются к генераторам и анализаторам реальных сигналов.Вторая цель — построить и проанализировать две простые схемы: делитель напряжения, состоящий из последовательно соединенных резисторов, и делитель тока, состоящий из резисторов, соединенных параллельно. Делитель напряжения питается от источника напряжения, а делитель тока питается от источника тока. В делителе напряжения мы вычисляем и измеряем напряжение на резисторах, а в делителе тока мы рассчитываем напряжение на резисторах и ток через каждый резистор. Мы выводим «правило делителя напряжения» и «правило делителя тока» ниже.

Понятие «земля» в цепях иногда может привести к путанице. Такие термины, как «сигнальное заземление», «заземление», «заземление шасси», «защитное заземление», «несимметричный», «дифференциальный», «сбалансированный», «синфазный», «контуры заземления» и многие другие. бросаются в разные стороны, часто без полного понимания их смысла. Здесь представлена ​​основная концепция идеального заземления, которая может быть распространена на любую систему, а недостатки в системах заземления можно понять и устранить путем моделирования системы заземления с сосредоточенными и распределенными элементами схемы.

Прежде всего необходимо подчеркнуть, что все напряжения составляют разностей и электрических потенциалов между двумя отдельными точками. Поэтому нет смысла говорить о напряжении в одной точке без привязки этой точки к другой точке. Это что-то вроде относительных скоростей. Два автомобиля, движущиеся в одном направлении с одинаковой скоростью, движутся с нулевой скоростью по отношению друг к другу, но могут двигаться со скоростью 60 миль в час по отношению к дороге. Они движутся с разными скоростями относительно Солнца и так далее.Напряжение между двумя выводами аккумулятора может быть номинально 9 вольт, но напряжение между одним из выводов аккумулятора и выводом аккумулятора, подключенного к другой системе, — это совсем другое. В системах, которые используют опорную землю, иногда упускается из виду тот факт, что напряжения измеряются относительно этой земли.

Идеальное заземление в системе имеет точно такое же напряжение, что и идеальный эталон, независимо от того, где в земле измеряется это напряжение (это означает, что земля является частью системы с эквипотенциальным потенциалом ).Все напряжения в этой системе измеряются относительно этого идеального потенциала земли. Явным требованием к этому идеальному заземлению является то, что оно должно иметь нулевой импеданс, чтобы любые токи, протекающие внутри него, не вызывали падения напряжения, которое нарушило бы требование эквипотенциальности. Такой тип идеального заземления невозможно реализовать, но его можно приблизить с помощью высококачественных проводов. На низких частотах преобладает резистивная составляющая импеданса заземления, а на более высоких частотах скин-эффект увеличивает сопротивление, и начинает проявляться индуктивная составляющая импеданса.Все это вызывает нежелательные падения напряжения в земле. Есть много способов реализовать заземления, оптимизированные для конкретных приложений и частот сигналов, которые выходят далеко за рамки этой лаборатории и любых экспериментов, которые могут быть проведены для M1K. Для наших целей мы можем использовать приближение идеального заземления, потому что индуктивность в земле пренебрежимо мала из-за встречающихся низких частот сигналов, а межсоединения заземления имеют незначительное сопротивление по сравнению с уровнями сопротивления, встречающимися в лабораториях.

На схематических диаграммах используется ряд различных символов для обозначения различных типов заземления. Некоторые распространенные типы показаны ниже. {Вставьте рисунок, когда компьютер вернется из ИТ-отдела}

Когда мы видим определенный символ заземления на схематическом чертеже, мы знаем, что он представляет собой один из опорных потенциалов, используемых нашей системой. На схеме может быть много таких символов заземления, и мы можем представить, что все они соединены вместе.

Макетная плата без пайки, используемая с M1K, состоит из пластикового блока с двусторонним набором отверстий с внутренними металлическими контактами, которые расположены в виде сетки.Каждая сторона массива состоит из ряда рядов с пятью отверстиями, в которых все металлические контакты соединены вместе. Это позволяет нам подключать схемы, помещая выводы элементов, которые мы хотим соединить, в один ряд. См. Пример на иллюстрации ниже {Поместите сюда иллюстрацию, когда компьютер вернется из ИТ-отдела}

При создании лабораторий на беспаечной макетной плате все заземляющие соединения, указанные на схеме, должны быть соединены вместе и с одним или обоими портами GND на M1K.Мы можем рассматривать землю как опорный нулевой потенциал для всех напряжений, генерируемых и измеряемых в лабораториях.

Последовательные цепи определяются как цепи, в которых одинаковый ток течет через все элементы. Все элементы проводят одинаковый ток, но напряжение в последовательной цепи делится между ее последовательными элементами. По этой причине последовательную схему иногда называют делителем напряжения . Нам часто требуется знать напряжение на конкретном элементе схемы, и это можно легко вычислить с помощью правила делителя напряжения , которое требует только знания значений элементов схемы и напряжения на последовательной цепи.Мы будем использовать резистивную схему, чтобы вывести правило делителя напряжения.

Если мы подадим напряжение В _T (T для Всего ) через последовательную цепь, состоящую из резисторов, как показано ниже, в цепи протекает ток I, который рассчитывается с использованием закона Ома как

Напряжение В _м на конкретном резисторе R _м рассчитывается как

Если мы подставим ток из первого уравнения во второе и решим для В _м , мы получим правило делителя напряжения:

Таким образом, правило делителя напряжения для резисторов показывает, что напряжение на любом резисторе в последовательном соединении равно напряжению в последовательной цепи, умноженному на отношение значения интересующего резистора к сумме всех сопротивлений в цепи. .Это соотношение представляет собой процент от общего напряжения в последовательной цепи, которое появляется на интересующем резисторе. Мы можем применить правило делителя напряжения к последовательной цепи, проанализированной в лаборатории, следующим образом:

Обратите внимание, что напряжение на резисторе 1,5 кОм измеряется между соединением двух резисторов и нулевым потенциалом земли.

Параллельные цепи определяются как цепи, в которых одинаковое напряжение присутствует на всех элементах.Хотя все элементы имеют одинаковое напряжение на них, ток, протекающий в параллельном контуре, делится между его параллельными элементами. По этой причине параллельную схему иногда называют делителем тока . Нам часто нужно знать ток, протекающий через конкретный элемент схемы, и это можно легко вычислить с помощью правила делителя тока , которое требует только знания значений элементов схемы и тока, протекающего в последовательной цепи.Существует по крайней мере две формы правила делителя тока, которые широко используются, и мы будем использовать ту, которая имеет ту же общую форму, что и правило делителя напряжения, так как эту форму легко запомнить после того, как вы изучите правило делителя напряжения. Мы будем использовать резистивную схему, чтобы вывести правило делителя тока.

Если мы подадим ток I _T (T для Всего ) через параллельную цепь, состоящую из резисторов, как показано ниже, в цепи появится напряжение В, .Ток I _T представляет собой сумму токов, протекающих в каждом резисторе, и рассчитывается с использованием закона Кирхгофа по току как:

Теперь самое время ввести проводимость , G, которая определяется как величина, обратная сопротивлению, или G = 1 / R. Мы можем заменить G на 1 / R в приведенном выше уравнении и переписать его как:

Ток I _м , протекающий через резистор R _м в параллельной цепи, можно рассчитать по закону Ома как:

Если мы подставим V из первого уравнения в приведенное выше уравнение, мы можем решить для I _m как:

Из этого результата мы можем видеть, что правило делителя тока имеет ту же форму, что и правило делителя напряжения, с заменой I _T на В _T и проводимостью вместо сопротивлений.Правило делителя тока для резисторов показывает, что ток, протекающий через любой резистор при параллельном соединении, равен полному току, протекающему в параллельном контуре, умноженному на отношение значения интересующей проводимости к сумме всех проводимости в схема. Это соотношение представляет собой процент от общего тока, протекающего в параллельной цепи, который протекает через интересующий резистор. Мы можем применить правило делителя тока к параллельной цепи, анализируемой в лаборатории, следующим образом:

Правила делителя напряжения и делителя тока могут быть распространены на другие элементы схемы, если эти элементы находятся в последовательной и параллельной цепях, соответственно.

6.1: Цепи делителя напряжения — Workforce LibreTexts

Давайте проанализируем простую последовательную схему, определив падение напряжения на отдельных резисторах:

Определите полное сопротивление цепи

Из приведенных значений отдельных сопротивлений мы можем определить общее сопротивление цепи, зная, что сопротивления складываются последовательно:

Использование закона Ома для расчета потока электронов

Отсюда мы можем использовать закон Ома (I = E / R) для определения общего тока, который, как мы знаем, будет таким же, как ток каждого резистора, при этом токи одинаковы во всех частях последовательной цепи:

Теперь, зная, что ток в цепи равен 2 мА, мы можем использовать закон Ома (E = IR) для расчета напряжения на каждом резисторе:

Должно быть очевидно, что падение напряжения на каждом резисторе пропорционально его сопротивлению, учитывая, что ток одинаков на всех резисторах.Обратите внимание, что напряжение на R ₂ вдвое больше, чем напряжение на R ₁ , так же как сопротивление R ₂ вдвое больше, чем у R ₁ .

Если бы мы изменили общее напряжение, мы бы обнаружили, что эта пропорциональность падений напряжения остается постоянной:

Напряжение на R ₂ все еще ровно вдвое больше, чем падение R ₁ , несмотря на то, что напряжение источника изменилось. Пропорциональность падений напряжения (соотношение между ними) строго зависит от значений сопротивления.

При более внимательном рассмотрении становится очевидным, что падение напряжения на каждом резисторе также является фиксированной пропорцией напряжения питания. Напряжение на R ₁ , например, составляло 10 вольт при питании от батареи 45 вольт. Когда напряжение батареи было увеличено до 180 вольт (в 4 раза больше), падение напряжения на R ₁ также увеличилось в 4 раза (с 10 до 40 вольт). Однако соотношение между падением напряжения R ₁ и общим напряжением не изменилось:

Аналогичным образом, ни один из других коэффициентов падения напряжения не изменился с увеличением напряжения питания:

Формула делителя напряжения

По этой причине последовательную схему часто называют делителем напряжения из-за ее способности пропорционально или делить общее напряжение на дробные части постоянного отношения.Приложив немного алгебры, мы можем вывести формулу для определения падения напряжения на последовательном резисторе, учитывая не что иное, как общее напряжение, отдельное сопротивление и общее сопротивление:

Отношение отдельного сопротивления к общему сопротивлению такое же, как отношение отдельного падения напряжения к общему напряжению питания в цепи делителя напряжения. Это известно как формула для делителя напряжения , и это сокращенный метод определения падения напряжения в последовательной цепи без выполнения расчетов тока по закону Ома.

Используя эту формулу, мы можем повторно проанализировать падение напряжения на примере схемы за меньшее количество шагов:

Делители напряжения

находят широкое применение в схемах электросчетчиков, где определенные комбинации последовательных резисторов используются для «деления» напряжения на точные пропорции как часть устройства измерения напряжения.

Одним устройством, часто используемым в качестве компонента деления напряжения, является потенциометр , который представляет собой резистор с подвижным элементом, перемещаемым ручкой или рычагом.Подвижный элемент, обычно называемый скребком , контактирует с резистивной полосой материала (обычно называемой скользящей проволокой , если она сделана из резистивной металлической проволоки) в любой точке, выбранной ручным управлением:

Контакт стеклоочистителя — это обращенная влево стрелка, нарисованная посередине вертикального резистивного элемента. По мере продвижения вверх он контактирует с резистивной полосой ближе к клемме 1 и дальше от клеммы 2, уменьшая сопротивление на клемме 1 и повышая сопротивление на клемме 2.При движении вниз возникает противоположный эффект. Сопротивление, измеренное между клеммами 1 и 2, постоянно для любого положения стеклоочистителя.

Поворотные и линейные потенциометры

Здесь показаны внутренние иллюстрации двух типов потенциометров, поворотного и линейного:

Некоторые линейные потенциометры приводятся в действие прямолинейным движением рычага или ползунковой кнопки. Другие, подобные изображенному на предыдущем рисунке, приводятся в действие поворотным винтом для возможности точной регулировки.Последние единицы иногда называют подстроечными элементами , потому что они хорошо работают в приложениях, требующих «подгонки» переменного сопротивления до некоторого точного значения. Следует отметить, что не все линейные потенциометры имеют такое же назначение клемм, как показано на этом рисунке. У некоторых клемма стеклоочистителя находится посередине между двумя концевыми клеммами.

На следующей фотографии показан реальный поворотный потенциометр с открытым стеклоочистителем и проводом для удобного просмотра.Вал, приводящий в движение грязесъемник, повернут почти полностью по часовой стрелке, так что грязесъемник почти касается левого конечного конца скользящего провода:

Вот тот же потенциометр с валом стеклоочистителя, перемещенным почти в крайнее положение против часовой стрелки, так что стеклоочиститель находится около другого крайнего конца хода:

Если постоянное напряжение приложено между внешними клеммами (по длине скользящей проволоки), положение стеклоочистителя будет отводить часть приложенного напряжения, измеряемого между контактом стеклоочистителя и любой из двух других клемм.Дробное значение полностью зависит от физического положения дворника:

Важность применения потенциометров

Так же, как и фиксированный делитель напряжения, коэффициент деления напряжения потенциометра строго зависит от сопротивления, а не от величины приложенного напряжения. Другими словами, если ручка или рычаг потенциометра перемещается в положение 50 процентов (точное центральное положение), падение напряжения между стеклоочистителем и любой внешней клеммой будет ровно 1/2 от приложенного напряжения, независимо от того, каким это напряжение окажется. , или каково полное сопротивление потенциометра.Другими словами, потенциометр функционирует как регулируемый делитель напряжения, где коэффициент деления напряжения устанавливается положением стеклоочистителя.

Это применение потенциометра является очень полезным средством получения переменного напряжения от источника постоянного напряжения, такого как аккумулятор. Если для схемы, которую вы строите, требуется определенное количество напряжения, которое меньше значения доступного напряжения батареи, вы можете подключить внешние клеммы потенциометра к этой батарее и «набрать» любое необходимое вам напряжение между потенциометром. стеклоочиститель и один из внешних выводов для использования в вашей цепи:

При использовании таким образом название потенциометра имеет смысл: они измеряют (контролируют) приложенный к ним потенциал (напряжение), создавая переменное отношение делителя напряжения.Такое использование трехполюсного потенциометра в качестве переменного делителя напряжения очень популярно в схемотехнике.

Здесь показаны несколько небольших потенциометров, которые обычно используются в бытовом электронном оборудовании, а также любителями и студентами при конструировании схем:

Меньшие блоки слева и справа предназначены для подключения к макетной плате без пайки или для пайки в печатную плату. Средние блоки предназначены для установки на плоской панели с проводами, припаянными к каждой из трех клемм.

Вот еще три потенциометра, более специализированных, чем только что показанный набор:

Большой блок «Helipot» представляет собой лабораторный потенциометр, предназначенный для быстрого и легкого подключения к цепи. Блок в нижнем левом углу фотографии представляет собой потенциометр того же типа, только без корпуса и счетного диска на 10 оборотов. Оба этих потенциометра представляют собой прецизионные устройства, в которых используются многооборотные спиралевидные резистивные полоски и стеклоочистители для выполнения небольших регулировок.Блок в правом нижнем углу представляет собой потенциометр для монтажа на панели, предназначенный для работы в тяжелых промышленных условиях.

Обзор

• Пропорция последовательных цепей, или делят , общее напряжение питания между отдельными падениями напряжения, пропорции строго зависят от сопротивлений: E _Rn = E _Всего (R _n / R _Total )
• Потенциометр — это компонент переменного сопротивления с тремя точками подключения, часто используемый в качестве регулируемого делителя напряжения.

Цепь параллельных резисторов

и простая схема делителя тока

Формула для параллельного резистора будет нашим основным фокусом здесь. После обсуждения последовательного резистора и делителя напряжения давайте узнаем о параллельных резисторах и делении тока. Параллельный резистор относится к одному из пассивных элементов.

Вы узнаете, включены ли резисторы параллельно или последовательно, просто по их клеммному соединению. Мы называем резисторы подключенными параллельно, если их выводы соединены вместе, соответственно, от резистора к резистору.

Определение параллельной цепи

Этот параллельный резистор отличается от последовательного резистора, где есть только один прямой путь, проходящий через резисторы. В параллельном резисторе будет много путей от головы к голове и от хвоста к хвосту. Исходя из этого термина, параллельный резистор используется как делитель тока, а последовательный резистор — как делитель напряжения.

Поскольку ток разделен на несколько путей или ответвлений, ток для каждой ветви может отличаться друг от друга.Но падение напряжения на каждом резисторе будет одинаковым для каждого другого. Отсюда следует вывод, что для резисторов, включенных параллельно, они могут иметь разный ток через каждый из них, но всегда иметь одинаковое падение напряжения на каждом из них.

Зачем нам нужно изучать формулу для параллельного резистора? Вы должны знать, прочитав этот пост, пока не закончите.

Определение параллельных резисторов — это резистивная схема, в которой резисторы подключены вместе к одним и тем же узлам и образуют более одного пути тока, подключенного к одному источнику напряжения.Если вы все еще не понимаете, как мы делаем параллельную резистивную схему, мы можем найти ее ниже.

Схема параллельной цепи

Пример ниже представляет собой простой параллельный резистор в цепи. Мы используем три резистора R ₁ , R ₂ и R ₃ . Из объяснения выше, падение напряжения на резисторах при параллельном подключении будет одинаковым для друг друга и равным источнику напряжения.

Следовательно,

Все три резистора соединены между собой между A и B.

В отличие от последовательных резистивных цепей, где эквивалентное сопротивление является суммой всех резисторов, параллельный резистор рассчитывается по-другому. Мы используем величину, обратную сопротивлению (1 / R) для каждого сложенного резистора.

Формула для параллельного резистора

Как мы уже упоминали выше, эквивалентное сопротивление параллельных резисторов является суммой, обратной величине каждого резистора. Если резисторы, соединенные параллельно, имеют одинаковое значение, это будет очень просто.

Как мы уже упоминали выше, мы можем посмотреть на пример ниже:

Если два резистора, подключенных параллельно, имеют одинаковое сопротивление, то эквивалентное сопротивление, R _T — это половина сопротивления одного резистора. резистор. Следовательно, эквивалентное сопротивление двух резисторов, соединенных параллельно, если они имеют одинаковое сопротивление, равно R / 2. Если параллельно подключено три резистора, эквивалентное сопротивление равно R / 3 и так далее.

Помимо последовательных резисторов, этот тип цепи является наиболее распространенным типом электрических цепей.Для анализа схемы параллельного резистора мы можем использовать тот же метод для последовательного резистора, используя законы Кирхгофа и закон Ома.

Рассмотрим схему на рисунке. (1),

Рисунок 1. Параллельное подключение резистора

, где два резистора подключены параллельно и, следовательно, имеют одинаковое напряжение на них.

По закону Ома

(1)

Применение KCL в узле a дает полный ток i как

(2)

Подстановка уравнения.(1) в (2) имеем

(3)

, где R _eq — эквивалентное сопротивление резисторов, включенных параллельно:

(4)

или

(5)

Следовательно ,

Эквивалентное сопротивление двух параллельных резисторов равно произведению их сопротивлений на их сумму.

Выше приведено простейшее уравнение параллельного резистора, которое мы можем использовать каждый раз, когда нам это нужно.

Следует отметить, что уравнение.(5) работает только для двух параллельно подключенных резисторов.

Мы можем расширить уравнение параллельного резистора в уравнении (4) до общего случая схемы с N резисторами, включенными параллельно. Эквивалентное сопротивление составляет

(6)

. Обратите внимание, что R _eq всегда меньше, чем сопротивление наименьшего резистора в параллельном соединении. Если R ₁ = R ₂ =… = R _N = R , то

(7)

Например, если 4 резистора с сопротивлением 100 Ом подключены параллельно, их эквивалентное сопротивление составляет 25 Ом.

Имейте в виду, что,

Эквивалентное сопротивление параллельных резисторов всегда меньше, чем сопротивление наименьшего резистора, подключенного к этой сети. Следовательно, эквивалентное сопротивление RT будет уменьшаться каждый раз, когда у нас есть дополнительные параллельные резисторы.

Формула проводимости для параллельной цепи

Из-за этого простого, но сложного уравнения параллельного резистора для эквивалентного сопротивления мы узнаем о новом значении, известном как проводимость (G), измеренном в Сименсах (S).Проводимость обратно пропорциональна сопротивлению, где G = 1 / R. После того, как мы получим проводимость, мы преобразуем ее обратно обратно, чтобы получить эквивалентное сопротивление R _T параллельных резисторов.

При параллельном подключении резисторов легче использовать проводимость, чем сопротивление.

Из уравнения (6) эквивалентная проводимость для резисторов N составляет

(8)

, где:

Уравнение.(8) указывает:

Эквивалентная проводимость резисторов, соединенных параллельно, является суммой их индивидуальных проводимостей.

Это означает, что мы можем перерисовать рисунок (1) на (2), где мы заменим сопротивления на проводимости.

Эквивалентные сопротивления параллельных резисторов получаются таким же образом, как эквивалентные сопротивления последовательных резисторов.

Напротив, эквивалентные проводимости последовательных резисторов получаются таким же образом, как эквивалентные сопротивления параллельных резисторов.

Рисунок 2. Эквивалентное сопротивление или проводимость

Следовательно, эквивалентная проводимость G _eq последовательно соединенных резисторов N составляет

(9)

Учитывая общий ток i, входящий в узел a на рисунке. (1) с одинаковые значения напряжения, получаем

(10)

Мы определяем параллельные резисторы как резисторы, соединенные между собой между одними и теми же двумя точками. Сам параллельный резистор имеет различные формы схемы.

Как найти ток в параллельной цепи

Поскольку ток в параллельной цепи зависит от ее сопротивления, теперь мы узнаем, как найти ток в параллельной цепи.Токи I ₁ , I ₂ ,…, I _n , входящие в параллельный путь резисторов, зависят от сопротивления этой ветви. Полный ток I _T представляет собой сумму токов в параллельных ветвях. Если сопротивление между ветвями равно, то токи также будут разделены поровну.

Если R ₁ = R ₂ , то I ₁ = I ₂ = 0.5 Я _Т . Это означает, что общий ток I _T делится поровну на две ветви. Если сопротивление R ₁ отличается от сопротивления R ₂ , тогда нам нужно рассчитать I ₁ и I ₂ по-разному. Даже если напряжения на ветвях равны, ток может отличаться по закону Ома.

Для примера параллельной схемы давайте посмотрим на схему ниже и попытаемся найти все токи,

Поскольку R ₁ и R ₂ имеют разные значения, тогда токи I ₁ и I ₂ гарантированно имеют разные значения.Помните один из законов Кирхгофа?

Текущие законы Кирхгофа гласят:

Общий ток, выходящий из узла, равен току, входящему в тот же самый узел.

Следовательно,
Полный ток в цепи может быть выражен как:

После этого мы будем использовать закон Ома для расчета тока, поступающего в каждую ветвь через резисторы. I ₁ — это входящий ток R ₁ , а I ₂ — это входящий ток R ₂ .Источник напряжения В _с имеет 12 В, и мы получаем:

И мы получаем полный ток,

Чтобы прояснить это, мы используем закон Ома для вычисления I _T из В. _s и R _T .
Общее сопротивление R _T равно

Тогда общий ток I _T равен

Следовательно, это проясняет наши расчеты.

Мы заключаем, что

Уравнение делителя тока

Комбинируя уравнения. (1) и (10) мы получаем уравнение текущего делителя.

(11)

, который показывает, что полный ток i распределяется между резисторами обратно пропорционально их сопротивлениям.

Это известно как принцип деления тока , а схема на рисунке (1) известна как делитель тока .

Обратите внимание, что больший ток проходит через меньшее сопротивление.

Рисунок 3. Короткое замыкание и разрыв в параллельном соединении

Предположим, что один из резисторов на рисунке (1) равен нулю, скажем, R ₂ = 0; поэтому R ₂ — это короткое замыкание, как видно на рисунке. (3a).

Из уравнения (11), R ₂ = 0 означает, что i ₁ = 0, i ₂ = i . Это означает, что весь ток i обходит R ₁ и протекает через короткое замыкание R ₂ = 0, путь с наименьшим сопротивлением.
При коротком замыкании цепи, как показано на рисунке (3a), обратите внимание, что:

1. Эквивалентное сопротивление R _eq = 0
2. Весь ток протекает через короткое замыкание.

В качестве другого крайнего примера, где R ₂ = ∞, то есть R ₂ является разомкнутой цепью, как показано на рисунке (3b).
Ток по-прежнему течет по пути с наименьшим сопротивлением, R ₁ .
Уравнение (11) преобразуется в

(12)

В общем, если делитель тока имеет N проводников, параллельных току источника i , N -й проводник будет иметь ток

(13)

Очень удобно комбинировать резисторы последовательно и параллельно в одно эквивалентное сопротивление R _eq .

Такое эквивалентное сопротивление должно иметь те же значения тока и напряжения, что и исходная сеть на выводе.

Примеры параллельного резистора

Давайте рассмотрим приведенный ниже пример для лучшего понимания
Найдите R _eq для схемы на рисунке. (4)

Рисунок 4. Пример параллельного резистора

6 Ом и 3 Ом в параллельно

1 Ом и 5 Ом последовательно

2 Ом и 2 Ом последовательно

6 Ом и 4 Ом параллельно

Три резистора последовательно

.