Что такое резистивный делитель тока. Как работает делитель тока на резисторах. Какие существуют формулы для расчета делителя тока. Где применяются делители тока в электронике и электротехнике. Какие есть ограничения при использовании резистивных делителей тока.
Что такое резистивный делитель тока
Резистивный делитель тока — это простая электрическая схема, позволяющая разделить входной ток на две или более частей. Принцип работы делителя тока основан на параллельном соединении резисторов.
Простейший делитель тока состоит из двух параллельно включенных резисторов R1 и R2, подключенных к источнику тока. Входной ток I делится между резисторами на токи I1 и I2 обратно пропорционально их сопротивлениям.
Как работает делитель тока на резисторах
Принцип работы делителя тока можно объяснить следующим образом:
- Входной ток I поступает в узел схемы
- Согласно первому закону Кирхгофа, сумма токов, входящих в узел, равна сумме выходящих токов
- Ток распределяется между параллельными ветвями R1 и R2 обратно пропорционально их сопротивлениям
- Чем меньше сопротивление ветви, тем больший ток через нее протекает
- На выходе мы получаем два тока I1 и I2, сумма которых равна входному току I
Формулы для расчета делителя тока
Основные формулы для расчета делителя тока на двух резисторах:
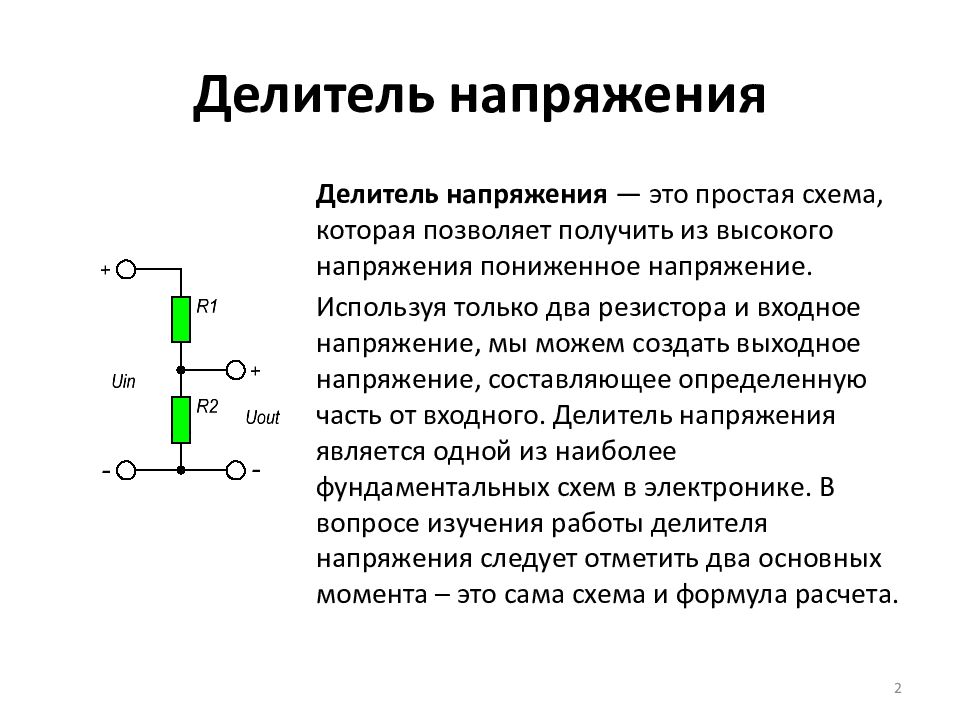
- I = I1 + I2 — общий ток равен сумме токов в ветвях
- I1 = I * R2 / (R1 + R2) — ток через первый резистор
- I2 = I * R1 / (R1 + R2) — ток через второй резистор
Для расчета делителя тока с n параллельными резисторами используется обобщенная формула:
Ii = I * (R1*R2*…*Rn / Ri) / (R1 + R2 + … + Rn)
Где Ii — ток через i-й резистор, I — входной ток, Ri — сопротивление i-го резистора.
Применение делителей тока в электронике
Делители тока находят широкое применение в электронике и электротехнике:
- Измерение больших токов с помощью амперметров с малым током полного отклонения (шунтирование амперметров)
- Создание источников тока с регулируемым выходным током
- Распределение тока между параллельно работающими устройствами
- Преобразование тока в напряжение в измерительных схемах
- Токовые датчики на основе изменения сопротивления под воздействием внешних факторов
Шунтирование амперметров с помощью делителя тока
Одно из важных применений делителя тока — это шунтирование амперметров для измерения больших токов. Принцип работы такой схемы:

- Параллельно амперметру подключается шунт — резистор с малым сопротивлением
- Большая часть измеряемого тока протекает через шунт
- Через амперметр протекает небольшой ток, пропорциональный измеряемому
- По показаниям амперметра и коэффициенту шунтирования определяется полный ток
Это позволяет расширить пределы измерения амперметров в десятки и сотни раз.
Ограничения резистивных делителей тока
При использовании резистивных делителей тока следует учитывать некоторые ограничения:
- Сопротивление нагрузки должно быть намного больше сопротивлений делителя
- Делитель потребляет дополнительную мощность, снижая КПД схемы
- Требуются высокоточные и стабильные резисторы для обеспечения точности деления
- На высоких частотах возникают паразитные емкости и индуктивности
Поэтому в ряде случаев вместо резистивных делителей тока применяются более сложные схемы, например, на основе операционных усилителей.
Расчет делителя тока онлайн
Для удобства расчета параметров делителей тока существуют онлайн-калькуляторы. С их помощью можно быстро рассчитать токи в ветвях по заданным сопротивлениям и входному току.

Такие калькуляторы позволяют:
- Рассчитать токи в ветвях делителя
- Подобрать номиналы резисторов для требуемого распределения токов
- Определить входной ток по токам в ветвях
- Рассчитать мощность, рассеиваемую на резисторах
Это значительно упрощает проектирование схем с делителями тока.
Сравнение делителей тока и напряжения
Делители тока и напряжения имеют схожий принцип работы, но отличаются схемой включения резисторов:
- Делитель напряжения — последовательное включение резисторов
- Делитель тока — параллельное включение резисторов
Основные отличия:
- Делитель напряжения уменьшает напряжение, делитель тока — ток
- В делителе напряжения ток одинаков во всех резисторах
- В делителе тока напряжение одинаково на всех резисторах
При этом формулы для расчета делителей тока и напряжения очень похожи, что упрощает их применение.
Делитель тока на резисторах — электротехническое устройство, позволяющее разделять ток и использовать только часть от подаваемого в цепь тока посредством элементов электрической цепи, состоящей из резисторов.
При проектировании электрических цепей возникают случаи, когда в цепи протекает ток одного номинала, а номинально-допустимый ток нагрузки должен быть меньше. Для этих целей используют делители тока. Делители тока основаны на первом законе Кирхгофа.
Самая простая схема резистивного делителя тока — это два параллельно подключенных сопротивления и источник напряжения или тока.
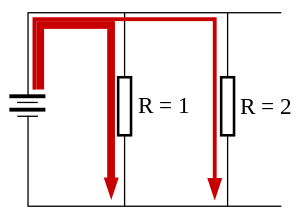
На приведенной ниже схеме ток I при достижении узла разделяется на два тока I2 и I3. Согласно первому закону Кирхгофа ток I равен сумме токов I2 и I3.

Напряжение на сопротивлениях UR2 и UR3 одинаковое, т.к. они соединены параллельно.
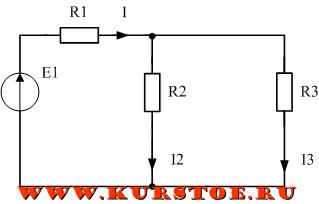
Если к сопротивлениям R2 и R3 приложено напряжение U, то ток через сопротивления, согласно закону Ома:

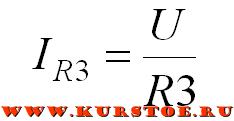
Подключаем нагрузку последовательно к R1 или к R2. Выбираем то сопротивление, через которое протекает нужный ток. В результате через нагрузку будет протекать ток IR3=I3.
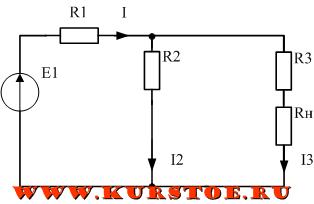
Примеры применения делителя тока
- Как делитель тока. Представьте, что у Вас есть светодиод, номинальный ток через который 17 мА (миллиампер) и есть схема, через которую протекает ток 30 мА. При маленьком токе светодиод будет гореть тускло, при большем — выйдет из строя. Для того, чтобы светодиод работала в номинальном режиме (ток 17 мА) необходимо ток 30 мА разделить на 17 и 13 миллиампер. Данную задачу выполняют простейшие делители тока на резисторах.
- Датчик параметр — ток. Сопротивление резистивных элементов зависит от многих параметров, например растяжение и сжатие. Начинаем выполнять механические воздействия над одним из сопротивлений. В результате изменяется его сопротивление. Согласно закону Ома ток через это сопротивление будет изменяться. Согласно первому закону Кирхгофа общий ток так же будет изменяться.
- Измерение больших токов. Через первое сопротивление пропускается почти весь ток, через второй малая часть (миллиамперы или микроамперы). Измерение производится миллиамперов.
Ограничения при использовании резистивных делителей тока
Номинал сопротивления нагрузки должен быть на несколько порядков меньше, чем величина сопротивлений делителя тока. В противном случае нагрузка будет влиять на протекающий через цепь ток. В результате делитель напряжения будет работать неверно.
Резистивный делитель тока уменьшает КПД электрической цепи за счет потребления активной мощности сопротивлениями.
Необходимо использовать высокоточные прецизионные сопротивления.
Делитель тока | Практическая электроника
Что такое делитель тока
Какие ассоциации у вас возникают при словосочетании “делитель тока”? У меня сразу возникает ассоциация с делителем потока. Давайте представим себе реку, у которой очень большой поток.

Это поток воды бежит с очень большой скоростью! Он смывает на своем пути камни, землю, деревья. Представьте, что эта река находится рядом с вашим домом. Через год-два ваш дом смоет под чистую! Чтобы этого не произошло, надо ослабить течение реки, чтобы ее поток был слабый. Например как здесь:

Но как это сделать? А почему бы нам не прорыть большой канал, чтобы бОльшая часть воды текла через него. А это хорошая идея не так ли?

Весь смак заключается в том, что в каждой отдельной речке скорость воды будет меньше. В электротехнике и электронике все тоже самое! Река – это провод, сила потока – это сила тока, ширина реки – сопротивление, напряжение – угол наклона реки. Все элементарно и просто!
Делитель тока на резисторах
Для того, чтобы разделить силу тока, нам потребуются два резистора. В статье про сопротивление мы знаем, что резисторы можно соединять последовательно и параллельно. При последовательном соединении резисторов у нас на каждом резисторе падало напряжение, тем самым мы получили делитель напряжения. При параллельном соединении резисторов мы получим делитель тока.
Давайте рассмотрим вот такую схемку, состоящую из двух резисторов, соединенных параллельно:
Вот эти два резистора можно заменить одним резистором. Общее сопротивление будет равно:

Напряжение U между точками A и В считается общим для каждого резистора, так как у нас эти два резистора соединены параллельно. Значит, через них должен также протекать общий ток. Запомните правило, при параллельном соединении напряжение на резисторах одно и то же, а ток будет равен:

Как же нам определить, какой ток у нас проходит через каждый резистор? Согласно Закону Ома

Следовательно получаем:

Отсюда
 и
и 
Проще говоря, если вместо какого-то резистора подсоединить какую-нибудь нагрузку, например, вентилятор от компьютера, то мы можем регулировать в ней силу тока, а следовательно и мощность, параллельно выводам подключив какой-нибудь резистор. А какой именно, можно посмотреть на формулы. Этот процесс называется шунтирование.
Делитель тока на практике
Вот два наших резистора
Замеряем значение сопротивления первого толстого резистора. Кто не помнит, как это делается, прошу сюда.
Замеряем значение второго маленького резистора
Берем наш лабораторный блок питания и выставляем на нем 12 Вольт
Спаиваем два конца резисторов и замеряем силу тока сначала на толстом резисторе
Потом замеряем силу тока на тонком резисторе
Спаиваем их параллельно и замеряем силу тока на параллельно соединенных резисторах
У нас получилось, что общая сила тока через оба резистора будет равняться сумме токов, протекающих через каждый отдельный резистор. 0,06 + 0,14 = 20. У нас же амперметр на блоке питания показал 0,21 Ампер. 0,01 – погрешность прибора.
Отсюда делаем вывод: сила тока, протекающая через параллельно соединенные резисторы будет равняться сумме токов, протекающих через каждый отдельный резистор.
Также про делитель тока можно прочитать в Википедии по этой ссылке.
Дели́тель то́ка — простейшая линейная электрическая цепь, выходной ток которой представляет собой часть входного тока. Это обеспечивается распределением тока между ветвями делителя.
В качестве делителя тока обычно применяют элементы с регулируемым сопротивлением (потенциометры), подключаемые параллельно.[источник не указан 775 дней] Можно представить как русло реки, разделяющееся на несколько рек. Согласно первому закону Кирхгофа, сумма токов, входящих в узел и выходящих из узла, равна нулю. Применяемые сопротивления для деления токов могут быть как активными, так и реактивными. Реактивные сопротивления возможно использовать только на переменном токе.
Резистивный делитель тока
Простейший резистивный делитель тока — это два параллельно включённых резистора R 1 {\displaystyle R_{1}} и R 2 {\displaystyle R_{2}} , подключённых к источнику напряжения U {\displaystyle U} . Поскольку резисторы соединены параллельно, то к ним приложено одинаковое напряжение.
Ток через них можно определить согласно закону Ома:
I 1 = U / R 1 {\displaystyle \ I_{1}=U/R_{1}} .
I 2 = U / R 2 {\displaystyle \ I_{2}=U/R_{2}} .
Общий ток в цепи согласно первому закону Кирхгофа
I = I 1 + I 2 {\displaystyle \ I=I_{1}+I_{2}} .
Применение
- Делитель тока имеет важное значение в схемотехнике в качестве элемента цепи для подключения устройства с номинальным током меньшим, чем протекающий в цепи.
- Датчик параметр-ток. На величину сопротивления влияют внешние факторы, например температура. Изменение температуры приводит к изменению сопротивления делителя тока. В результате изменяется ток через ветвь цепи.
- Измерение больших величин токов. Подключается два сопротивления. Через одно протекает малый ток (миллиамперы), через второе (называемое шунтом) — весь оставшийся ток. Измеряется ток через первое сопротивление. Далее выполняется расчет общего тока.
Ограничения в применении резистивных делителей тока
Для поддержания приемлемой точности работы делителя, необходимо, чтобы величина тока, протекающего через сопротивления делителя, была не менее чем в 10 раз больше, чем ток, протекающий в нагрузке (см. аналогичное требование у делителя напряжения). Увеличение этого показателя (до ×100,×1000 или больше) пропорционально увеличивает точность работы делителя, однако это также увеличивает поперечное сечение проводников, что увеличивает размеры, стоимость и снижает КПД схемы. Это одна из причин, по которой делители тока малопригодны в качестве источников постоянного тока для питания нагрузок. Для этой цели применяют иные схемотехнические решения, например стабилизаторы тока.
См. также
Ссылки
Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.
Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.
Схема делителя напряжения на резисторах
Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.
Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.
Расчет делителя напряжения на резисторах
Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.
Формула делителя напряжения
Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома.
Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:
Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:
Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:
Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:
И, на какое-то время, мы можем упростить схему:
Закон Ома в его наиболее простом вид: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:
А так как I1 равно I2, то:
Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.
Делитель напряжения — калькулятор онлайн
Применение делителя напряжения на резисторах
В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.
Потенциометры
Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.
Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.
Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.
Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.
Резистивные датчики
Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.
Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).
Пример работы делителя напряжения на фоторезисторе.
Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.
Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.
Делитель тока

 В этой статье расскажем о делители тока, где он применяется и примеры решения задач.
В этой статье расскажем о делители тока, где он применяется и примеры решения задач.
Представьте, что течёт река, и вдруг ширина её русла резко уменьшается, через некоторое расстояние ширина русла снова увеличивается. Что же происходит в том месте, где русло узкое? Скорость потока воды резко возрастает, вода пытается расширить русло реки, происходит разрушение берегов и углубление русла. Для того, чтобы скорость потока упала, достаточно прорыть дополнительный параллельный канал, по которому пустить часть потока. При этом, этот искусственный канал можно использовать в своих целях, например крутить водяное колесо (по современному — гидроэлектростанцию). Как правило, сначала делают «колесо», а потом перекрывают основное русло реки. Другими словами — поток воды делят на два потока, которые потом всё равно объединяются, но при этом один из потоков используют в своих определённых целях. В частности, на гидроэлектростанциях всегда имеется два потока — один используется для вращения турбин электростанции, а другой в зависимости от полноводности реки — «сброс», или дополнительный канал отвода воды — водосливную плотину, предназначенную для регулирования уровня воды перед плотиной ГЭС.
Делитель тока на резисторах предназначен для того, чтобы, не изменяя общего тока протекающего через электрическую цепь, часть его направить в другое плечо делителя, а после выполнения определённой функции вернуть эту часть обратно.

 Где применяется делитель тока? Делитель тока применяется в измерительных приборах, когда необходимо измерить большой ток (единицы, или сотни Ампер) прибором, рассчитанным на маленький ток (миллиамперы или даже микроамперы). В этом случае, внутреннее сопротивление измерительного прибора выступает в качестве одного из резисторов, а второй резистор в таком случае называют «шунтом», так как он шунтирует проходящий ток (основная часть тока бежит через него). Шунт в схеме измерения имеет сопротивление, которое намного меньше внутреннего сопротивления измерительного прибора. Кроме того, делитель тока применяется в различных схемах автоматического регулирования, использующих в качестве контролируемого параметра — ток, проходящий через электрическую цепь. Делитель тока может применяться в различных каскадах передачи, или усиления тока, когда один пассивный, или усилительный элемент по своим электрическим параметрам не способен обеспечить прохождение через него большого тока. В этом случае их подключают параллельно, разделяя ток на равные доли (пополам). Наглядным примером использования делителя тока является его применение в цепи автоматического регулирования и измерения в Универсальном зарядном устройстве, или в цепи контроля схемы защиты от перегрузки по току и удвоения мощности выходных транзисторов в Универсальном блоке стабилизированного питания.
Где применяется делитель тока? Делитель тока применяется в измерительных приборах, когда необходимо измерить большой ток (единицы, или сотни Ампер) прибором, рассчитанным на маленький ток (миллиамперы или даже микроамперы). В этом случае, внутреннее сопротивление измерительного прибора выступает в качестве одного из резисторов, а второй резистор в таком случае называют «шунтом», так как он шунтирует проходящий ток (основная часть тока бежит через него). Шунт в схеме измерения имеет сопротивление, которое намного меньше внутреннего сопротивления измерительного прибора. Кроме того, делитель тока применяется в различных схемах автоматического регулирования, использующих в качестве контролируемого параметра — ток, проходящий через электрическую цепь. Делитель тока может применяться в различных каскадах передачи, или усиления тока, когда один пассивный, или усилительный элемент по своим электрическим параметрам не способен обеспечить прохождение через него большого тока. В этом случае их подключают параллельно, разделяя ток на равные доли (пополам). Наглядным примером использования делителя тока является его применение в цепи автоматического регулирования и измерения в Универсальном зарядном устройстве, или в цепи контроля схемы защиты от перегрузки по току и удвоения мощности выходных транзисторов в Универсальном блоке стабилизированного питания.
Изобразим цепь делителя тока:


На рисунке видно, что общий входящий ток делится на два, и проходя цепь, снова объединяется в один.
Расчёт делителя тока на резисторах основывается на законе Ома, правиле сложения токов (законе Кирхгофа) и формуле параллельного соединения резисторов:
(14)


(15)


(16)


Выведем закон Ома для этой цепи. Его можно записать в следующем виде:
(17)


Преобразовывая указанные формулы так, как нам удобно, мы можем определить:
1. Определить ток I1 и I2 в плечах резисторов R1, R2 по известным значениям общего тока Iобщ и сопротивлений резисторов R1, R2 :
(18)


(19)


Пример: Определить значения I1 и I1 делителя тока, если значение общего тока Iобщ = 0,6А, сопротивление R1 =100 Ом, а R2 = 20 Ом.
Решение: По формуле (18) вычисляем : I1 = 0,6 * 20 / (100 + 20) = 0,1 А; По формуле (19) вычисляем : I2 = 0,6 * 100 / (100 + 20) = 0,5 А; Не забывайте, что резисторы поглощают мощность, поэтому её необходимо рассчитать, (формула3):
P = I * I * R
Определим рассеиваемую мощность резисторов по формуле (3):
Для резистора R1 : P = 0,1 * 0,1 * 100 = 1 Вт; по правилу (1) выбираем резистор мощностью P = 2 Вт;
Для резистора R2 : P = 0,5 * 0,5 * 20 = 5 Вт; по правилу (1) выбираем резистор мощностью P = 10 Вт.
2. Рассчитать шунт R2 в цепи измерительного прибора, при известных: внутреннем сопротивлении R1, максимальном токе обмотки катушки прибора I1 и максимальном значении общего тока Iобщ цепи делителя тока, представленного на схеме:


(19)


Пример: Полное отклонение стрелки миллиамперметра при значении I1 = 1 мА, внутреннее сопротивление катушки прибора R1 = 200 Ом. Рассчитайте шунт R2, чтобы стрелка прибора отклонялась на максимальное значение при общем токе Iобщ = 1 А.
Решение: По формуле (19) вычисляем : R2 = 0,001 * 200 / (1 – 0,001) = 0,2 Ом; Рассчитаем поглощаемую (рассеиваемую) мощность R2 (формула 3): P = I2 * I2 * R2 , где I2 = Iобщ — I1 = 999 мА, P = 0,999 * 0,999 * 0,2 = 0,199 Вт; по правилу (1) выбираем резистор мощностью P = 0,25 Вт
Для достижения точности в измерительных цепях, выбирают высокоточные резисторы, кроме того, используют их последовательное и параллельное соединение.
Как и в случае с делителем напряжения, Вы спросите: Если это делитель, должен быть коэффициент деления? Да он есть, но в определении необходимых величин, пользоваться им крайне неудобно, поэтому не буду ломать голову ни себе, ни Вам.
Далее будем рассматривать Конденсатор.
Делитель тока — Википедия
Материал из Википедии — свободной энциклопедии
Дели́тель то́ка — простейшая линейная электрическая цепь, выходной ток которой представляет собой часть входного тока. Это обеспечивается распределением тока между ветвями делителя.
В качестве делителя тока обычно применяют элементы с регулируемым сопротивлением (потенциометры), подключаемые параллельно.[источник не указан 749 дней] Можно представить как русло реки, разделяющееся на несколько рек. Согласно первому закону Кирхгофа, сумма токов, входящих в узел и выходящих из узла, равна нулю. Применяемые сопротивления для деления токов могут быть как активными, так и реактивными. Реактивные сопротивления возможно использовать только на переменном токе.
Резистивный делитель тока

Простейший резистивный делитель тока — это два параллельно включённых резистора R 1 {\displaystyle R_{1}} и R 2 {\displaystyle R_{2}} , подключённых к источнику напряжения U {\displaystyle U} . Поскольку резисторы соединены параллельно, то к ним приложено одинаковое напряжение.
Ток через них можно определить согласно закону Ома:
I 1 = U / R 1 {\displaystyle \ I_{1}=U/R_{1}} .
I 2 = U / R 2 {\displaystyle \ I_{2}=U/R_{2}} .
Общий ток в цепи согласно первому закону Кирхгофа
I = I 1 + I 2 {\displaystyle \ I=I_{1}+I_{2}} .
Применение
- Делитель тока имеет важное значение в схемотехнике в качестве элемента цепи для подключения устройства с номинальным током меньшим, чем протекающий в цепи.
- Датчик параметр-ток. На величину сопротивления влияют внешние факторы, например температура. Изменение температуры приводит к изменению сопротивления делителя тока. В результате изменяется ток через ветвь цепи.
- Измерение больших величин токов. Подключается два сопротивления. Через одно протекает малый ток (миллиамперы), через второе (называемое шунтом) — весь оставшийся ток. Измеряется ток через первое сопротивление. Далее выполняется расчет общего тока.
Ограничения в применении резистивных делителей тока
Для поддержания приемлемой точности работы делителя, необходимо, чтобы величина тока, протекающего через сопротивления делителя, была не менее чем в 10 раз больше, чем ток, протекающий в нагрузке (см. аналогичное требование у делителя напряжения). Увеличение этого показателя (до ×100,×1000 или больше) пропорционально увеличивает точность работы делителя, однако это также увеличивает поперечное сечение проводников, что увеличивает размеры, стоимость и снижает КПД схемы. Это одна из причин, по которой делители тока малопригодны в качестве источников постоянного тока для питания нагрузок. Для этой цели применяют иные схемотехнические решения, например стабилизаторы тока.
См. также
Ссылки
Делитель тока — Википедия
Материал из Википедии — свободной энциклопедии
Дели́тель то́ка — простейшая линейная электрическая цепь, выходной ток которой представляет собой часть входного тока. Это обеспечивается распределением тока между ветвями делителя.
В качестве делителя тока обычно применяют элементы с регулируемым сопротивлением (потенциометры), подключаемые параллельно.[источник не указан 749 дней] Можно представить как русло реки, разделяющееся на несколько рек. Согласно первому закону Кирхгофа, сумма токов, входящих в узел и выходящих из узла, равна нулю. Применяемые сопротивления для деления токов могут быть как активными, так и реактивными. Реактивные сопротивления возможно использовать только на переменном токе.
Резистивный делитель тока

Простейший резистивный делитель тока — это два параллельно включённых резистора R 1 {\displaystyle R_{1}} и R 2 {\displaystyle R_{2}} , подключённых к источнику напряжения U {\displaystyle U} . Поскольку резисторы соединены параллельно, то к ним приложено одинаковое напряжение.
Ток через них можно определить согласно закону Ома:
I 1 = U / R 1 {\displaystyle \ I_{1}=U/R_{1}} .
I 2 = U / R 2 {\displaystyle \ I_{2}=U/R_{2}} .
Общий ток в цепи согласно первому закону Кирхгофа
I = I 1 + I 2 {\displaystyle \ I=I_{1}+I_{2}} .
Применение
- Делитель тока имеет важное значение в схемотехнике в качестве элемента цепи для подключения устройства с номинальным током меньшим, чем протекающий в цепи.
- Датчик параметр-ток. На величину сопротивления влияют внешние факторы, например температура. Изменение температуры приводит к изменению сопротивления делителя тока. В результате изменяется ток через ветвь цепи.
- Измерение больших величин токов. Подключается два сопротивления. Через одно протекает малый ток (миллиамперы), через второе (называемое шунтом) — весь оставшийся ток. Измеряется ток через первое сопротивление. Далее выполняется расчет общего тока.
Ограничения в применении резистивных делителей тока
Для поддержания приемлемой точности работы делителя, необходимо, чтобы величина тока, протекающего через сопротивления делителя, была не менее чем в 10 раз больше, чем ток, протекающий в нагрузке (см. аналогичное требование у делителя напряжения). Увеличение этого показателя (до ×100,×1000 или больше) пропорционально увеличивает точность работы делителя, однако это также увеличивает поперечное сечение проводников, что увеличивает размеры, стоимость и снижает КПД схемы. Это одна из причин, по которой делители тока малопригодны в качестве источников постоянного тока для питания нагрузок. Для этой цели применяют иные схемотехнические решения, например стабилизаторы тока.
См. также
Ссылки
90000 Current Divider Rule | Current Division Principle 90001 90002 Let’s consider an electrical circuit which contains a single current source and two parallel resistors. The current I 90003 90002 enters the node. A parallel circuit has the same voltage across all components, but current always divide into parallel components. We are interested to find the current flowing through resistor R 90003 90002. The formula for current divider law is now: 90003 90002 90009 90010 I 90011 x 90012 = (R 90011 t 90012 / R 90011 x 90012) * I 90011 t 90012.90019 90020 90003 90002 Where R 90011 t 90012 is the equivalent resistance of parallel resistors. 90003 90026 Current Divider Rule Examples 90027 An electric circuit has two parallel resistors of 2 and 10 ohms. Apply the current divider equation to find the current flowing through both resistors when the input is 5 A. 90028 90002 Let’s consider another example where three parallel resistors of 1 Ω, 2 Ω, and 3 Ω are connected in parallel to 14 A source. 90003 90026 Basic Useful concepts you should know 90027 90033 What is node, How it is formed in electric circuits 90034 90002 A node is a common point or a junction where two or more than two components are joined.The electrical node is a common point where two or more than two electronic components are joined. 90003 90033 What are parallel components and how to solve them 90034 90002 The components which are connected in the parallel configuration. Simply saying if heads of components share one common node and tails of components share other nodes then such components are referred as parallel components. Such components can be solved by using the formula: 90003 90002 (1/90009 90010 R 90011 t 90012 90019 90020) = (1/90009 90010 R 90011 1 90012 90019 90020) + (1/90009 90010 R 90011 2 90012 90019 90020) +… (1/90009 90010 R 90011 n 90012 90019 90020) 90003 90002 For example, previously we solved 2-ohm resistor in parallel to 10-ohm resistor. Let’s see how to do it: 90003 90002 (1/90009 90010 R 90011 t 90012 90019 90020) = (1/90009 90010 R 90011 1 90012 90019 90020) + (1/90009 90010 R 90011 2 90012 90019 90020) 90003 90002 (1/90009 90010 R 90011 t 90012 90019 90020) = (1/90010 90009 2 ohm 90020 90019) + (1/90010 90009 10 ohm 90020 90019) 90003 90002 (1/90009 90010 R 90011 t 90012 90019 90020) = 0.5 ohm + 0.1 ohm 90003 90002 and 90009 90010 R 90011 t 90012 90019 90020 = 1 / 0.6 ohms = 1.667 ohms 90003 90002 For our second example we used the formula: 90003 90002 (1/90010 R 90011 t 90012 90019) = (1/90010 R 90011 1 90012 90019) + (1/90010 R 90011 2 90012 90019) + (1/90010 R 90011 3 90012 90019) 90028 Continue learning: 90003 .90000 Current Divider Rule [Statement, Formula, Examples, and Derivation] 90001 In parallel electrical circuits, the current does not remain same. The current divide rule is used to find the divided current in parallel circuits. What you’ll learn: 90002 90003 90004 The statement of current divider 90005 90004 General formula 90005 90004 Formula for two resistors with Examples 90005 90004 Formula for three resistors with Examples 90005 90004 Its derivation 90005 90014 90015 90016 Statement and formula of Current Divider 90017 90018 90019 90016 Statement: 90021 The electrical current entering the node of a parallel circuit is divided into the branches.Current divider formula is employed to calculate the magnitude of divided current in the circuits. 90022 90017 90024 Let’s understand the basic definitions: 90002 Node: A point where two or more than two components are joined. 90002 Parallel circuit: The circuit in which one end of all components share a common node, and the other end of all components share the other common node. You can learn more about parallel circuit configuration here. 90002 90015 General formula 90018 A parallel circuit with ‘n’ number of resistors and an input voltage source is illustrated below.We are interested to find the current which is flowing through R 90030 x 90031. 90002 90002 In the above formula: 90002 I 90030 x 90031: The current through R 90030 x 90031. 90002 I 90030 t 90031: The total current which enters the circuit. 90002 R 90030 x 90031: The resistance of the component whose current value is to be determined 90002 R 90030 t 90031: The equivalent resistance of the parallel circuit 90002 90049 For two resistors 90050 Let’s consider a parallel circuit having two resistors R 90030 1 90031 and R 90030 2 90031.The current I 90030 t 90031 enters the node. We are interested to calculate the current that is flowing through. The general formula and circuit now take the form: 90019 90002 We can modify the previous equation to obtain an alternative formula: 90024 90002 Let’s solve an example to better understand the formulas. 90019 Example # 1: A 5 kΩ resistor connects in parallel to a 20 kΩ resistor. 5 A current enters the node. Find the current across both resistors. 90002 Solution: 90002 90002 90024 90049 Current divider rule for three resistors 90050 90019 Let’s consider the third case where we have three parallel resistors.The easy method which should be followed here is to find the equivalent resistance first, and then to apply the original formula: 90024 90049 Derivation of Current Divider formula 90050 90019 The derivation of CDR formula is very simple. Let’s reconsider the general circuit: 90024 90019 Apply the Ohm’s law on R 90030 x 90031. 90024 90019 I 90030 x 90031 = E / R 90030 x 90031 90024 90019 where E = I 90030 t 90031 R 90030 t 90031. 90024 90019 I 90030 x 90031 = I 90030 t 90031 R 90030 t 90031 / R 90030 x 90031.90024 90019 or 90024 90019 I 90030 x 90031 = [R 90030 t 90031 / R 90030 x 90031] * I 90030 t 90031 90024 .90000 Resistive voltage dividers — Electronic Products 90001 90002 Which type you choose can have a big influence on performance 90003 BY JERRY SEAMS 90004 TT electronics, IRC Advanced Film Div. 90004 Corpus Christi, TX 90004 http://www.irctt.com 90004 90002 Whether your application is a precision voltage reference or an instrumentation amplifier, voltage dividers account for a large percentage of precision resistor applications. Resistive voltage dividers are simple circuits, yet questions and misconceptions still pop up when discussing their design: 90003 90002 • If my system is specified to operate from -55 ° to 125 ° C, how much will my output voltage vary from the ideal? 90003 90002 • What happens to the divider output over a range of temperatures? 90003 90002 • My output voltage will be within ± 0.1% of ideal if I use ± 0.1% resistors, right? 90003 90002 Choosing a method 90003 90002 There are basically two ways to achieve a resistive voltage divider: by connecting two discrete chip resistors at a common point or by using a resistor network with the connection made inside the divider package. Which type you choose can have a big influence on the performance of your divider. 90003 90002 A simple resistive voltage divider consists of two resistors connected in series (see Fig. 1). The input voltage is connected to the top of the divider, the output voltage is found at the node between the two resistors, and the reference voltage (usually circuit ground) is connected to the bottom of the divider.90003 Fig. 1. A simple two-resistor voltage divider. 90002 The divider works according to Ohm’s law: V = IR. If a voltage (VIN) is applied to the divider input, a current (I) flows through both resistors. Ohm’s law then says there will be a voltage developed across each of the resistors that will be a portion of the input voltage. V1 = I (R1), VOUT = I (R2) and VIN = V1 + VOUT. The input voltage is «Divided» into two voltages. 90003 90002 The transfer function of the divider is found by dividing the output voltage by the input voltage: 90003 90002 The transfer function shows that the output voltage depends on the input voltage and the values of R1 and R2.In this ideal example, VOUT depends on VIN by exactly the ratio of 90003 90002 and at all temperatures the resistor elements see in operation. But resistors are not ideal. Real resistors have initial tolerance and temperature coefficients that can introduce significant errors into electronic systems. 90003 Fig. 2. Voltage divider constructed using discrete chip resistors. 90002 How do these effects contribute to the error of a nonideal voltage divider? Let’s take a look at the effect of initial tolerance on a divider’s output voltage.If the voltage divider consists of two separate resistors (See Fig. 2), the output error depends not only on the initial tolerances of the discrete resistors, but also on the ratio of the divider. If R1 = R2, then the maximum error at the output voltage due to the tolerance of the resistors is equal to the initial tolerance of the resistors. But what about when R1 ≠ R2? 90003 Fig. 3. Divider output error increases as the ratio increases. 90002 When R1 and R2 are different values, the voltage output error approaches two times the initial resistor tolerance as shown in Fig.3. The worst case for voltage divider design occurs when the tolerance of one resistor is opposite the other. If the divider is designed with ± 0.1% tolerance resistors, the output error may be as bad as ± 0.2% at high divider ratios. 90003 90002 Balancing tolerance 90003 90002 Figure 4 illustrates a way to reduce this twofold tolerance error. By depositing and patterning precision thin-film resistors on a single monolithic substrate, the resistor elements have very similar electrical characteristics.Because we are concerned about the «Divided» output voltage that depends on the ratio of R1 to R2, the absolute tolerance of each resistor element is irrelevant. By purchasing a thin-film resistor divider with a ratio tolerance of ± 0.1%, we are assured of a maximum output error of ± 0.1% due to initial tolerance regardless of the tolerance of each individual resistor — twice as good as the discrete solution. 90003 Fig. 4. Voltage divider constructed using thin film on a monolithic substrate. 90002 Not only does the idea of using a monolithic thin-film voltage divider make sense for reducing output error due to tolerance effects, it has similar benefits for reducing error over temperature as well.Typical precision chips have ± 25 ppm / ° C temperature coefficients (TCRs). This means that each resistor can change by as much as ± 0.25% if the resistor temperature reaches 125 ° C (100 ° above room temperature). The output voltage can have an error as high as two times this (or ± 0.5%) if the temperature coefficients of R1 and R2 move in opposite directions. 90003 90002 Conventional thin-film voltage dividers have TCR tracking between the two resistor elements of ± 5 ppm / ° C. Again, because the thin-film resistor elements are deposited and processed identically on a monolithic substrate, they move together over temperature.And again, because the ratio of the two resistor elements is important to the output voltage, the absolute temperature coefficient of each resistor element is irrelevant to the accuracy of the divider. By purchasing a thin-film divider with a ± 5 ppm / ° C TCR tracking spec, the output voltage error due to temperature effects is reduced over the 100 ° C span from ± 0.5% to ± 0.05%; a tenfold improvement. 90003 90002 The table summarizes the two approaches. When designing a voltage divider using 0.1% discrete resistors, the maximum output error due to tolerance and TCR is 0.7%. The maximum output error when using precision thin-film resistors is ± 0.15% — more than a fourfold improvement in performance. 90003 90002 It is tempting to assume that a divider output voltage will be within the tolerances of the resistors chosen to construct the divider. Further investigation reveals that the expected output voltage is affected by the ratio of the resistors in the divider as well as their initial tolerances and temperature coefficients. 90003 90002 By selecting a precision thin-film voltage divider on a monolithic substrate the designer ensures that the resistor elements in the divider have very similar electrical properties and will track well over temperature and time.The similarity of materials and processing on a common substrate promises a more stable and better-performing voltage divider over all ratios and environments. ■ 90003 90048 90049 90050 Comparing voltage dividers 90051 90052 90049 90054 90051 90054 Tolerance 90051 90054 ToleranceOutput Error 90051 90054 TCR 90051 90054 TCR Output Error (100C span) 90051 90054 TotalOutput Error 90051 90052 90049 90054 Discrete Chips 90051 90054 ± 0.1% absolute 90051 90054 ± 0.2% 90051 90054 ± 25 ppm / C absolute 90051 90054 ± 0.5% 90051 90054 ± 0.7% 90051 90052 90049 90054 Monolithic Divider 90051 90054 ± 0.1% ratio 90051 90054 ± 0.1% 90051 90054 ± 5 ppm / C tracking 90051 90054 ± 0.05% 90051 90054 ± 0.15% 90051 90052 90095 90004.90000 Solve Using Current Division Rule 90001 90002 Find current of resistors, use the current division rule. 90003 90004 90003 Suppose that 90006, 90007, 90008, 90009 and 90010 90003 90003 Solution: 90003 90014 and 90015 are parallel. The current of 90016 is passing through them and it is actually divided between them. The branch with lower resistance has higher current because electrons can pass through that easier than the other branch. Using the current division rule, we get 90003 90003 90019 90003 90021.90003 Note that 90023 because 90024. 90003 90003 What is the direction for 90027 and 90028? It is with the same direction as 90016: 90003 90031 90003 We have found 90027 and 90028, now we need to find 90035. 90003 90003 If you look at the circuit carefully, 90038, 90039 and 90016 are all in series. The bottom node of 90016 is connected to the bottom node of 90039 and there is no other component connected there. And the other node of 90039 is connected to 90038, again no other component here.This means that all current of 90016 should pass through 90039 and the same current must go through 90038. So, the current of 90038 can be easily found: 90003 90050. 90003 90003 The direction is the same current as the current source direction: 90003 90054 90003 Now, tell me what is the voltage drop across the current source? 90003 90057 .

