Резистор формула. Расчет мощности резистора: формулы, примеры и рекомендации — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как рассчитать мощность резистора в электрической цепи. Какие формулы использовать для вычисления мощности. Как правильно подобрать резистор по мощности. На что обратить внимание при выборе резистора.

Содержание

Что такое мощность резистора и почему она важна

Мощность резистора — это максимальное количество тепловой энергии, которое резистор может рассеять без повреждения. Этот параметр измеряется в ваттах (Вт) и является одной из ключевых характеристик при выборе резистора для электрической схемы.

Почему мощность резистора так важна.

При прохождении тока резистор нагревается. Чем выше ток, тем сильнее нагрев.
Если мощность рассеивания слишком мала, резистор может перегреться и выйти из строя.
Перегрев резистора может привести к изменению его сопротивления и нарушению работы всей схемы.
В худшем случае перегретый резистор может загореться и повредить другие компоненты.

Поэтому при проектировании электрических схем крайне важно правильно рассчитать и подобрать мощность резисторов.

Формулы для расчета мощности резистора

Существует несколько формул для расчета мощности резистора в зависимости от известных параметров цепи:

1. По току и сопротивлению:

P = I² * R

Где: P — мощность (Вт) I — ток через резистор (А) R — сопротивление резистора (Ом)

2. По напряжению и сопротивлению:

P = U² / R

Где: U — напряжение на резисторе (В) R — сопротивление резистора (Ом)

3. По току и напряжению:

P = U * I

Где: U — напряжение на резисторе (В) I — ток через резистор (А)

Важно помнить, что эти формулы дают расчетную мощность. На практике рекомендуется выбирать резистор с запасом по мощности.

Пример расчета мощности резистора

Рассмотрим конкретный пример расчета мощности резистора в простой цепи.

Дано: — Напряжение источника питания: 12 В — Сопротивление резистора: 100 Ом

Решение:

Рассчитаем ток в цепи по закону Ома: I = U / R = 12 В / 100 Ом = 0.12 А

Теперь рассчитаем мощность по формуле P = I² * R: P = 0.12² * 100 = 1.44 Вт

Таким образом, расчетная мощность резистора составляет 1.44 Вт. Для надежной работы следует выбрать резистор с номинальной мощностью 2 Вт или выше.

Как правильно подобрать резистор по мощности

При выборе резистора по мощности следует руководствоваться следующими рекомендациями:

Выбирайте резистор с номинальной мощностью в 1.5-2 раза выше расчетной. Это обеспечит запас надежности.
Учитывайте условия работы схемы — при высокой температуре окружающей среды запас должен быть еще больше.
Для ответственных участков схемы рекомендуется брать резистор с 3-4 кратным запасом по мощности.
При использовании SMD-резисторов запас по мощности должен быть выше из-за худших условий охлаждения.
Если есть сомнения — выбирайте резистор большей мощности. Это не повлияет на работу схемы.

Стандартный ряд мощностей резисторов

Резисторы выпускаются в стандартных номиналах мощности. Наиболее распространенные значения:

0.062 Вт (1/16 Вт)
0.125 Вт (1/8 Вт)
0.25 Вт (1/4 Вт)
0.5 Вт (1/2 Вт)
1 Вт
2 Вт
5 Вт
10 Вт

При выборе резистора следует ориентироваться на ближайшее большее стандартное значение мощности.

Влияние температуры на мощность резистора

Температура окружающей среды оказывает существенное влияние на способность резистора рассеивать тепло. При повышении температуры максимальная мощность рассеивания снижается.

Как учитывать температурный фактор при выборе резистора:

Номинальная мощность резисторов обычно указывается для температуры 25°C.
При повышении температуры на каждые 10°C мощность рассеивания снижается примерно на 10%.

Если схема будет работать при высоких температурах, следует выбирать резистор с большим запасом по мощности.
Для работы при температурах выше 70-80°C рекомендуется использовать специальные высокотемпературные резисторы.

Особенности расчета мощности для SMD-резисторов

SMD-резисторы (Surface Mounted Device) имеют ряд особенностей при расчете и выборе мощности:

Из-за малых размеров SMD-резисторы хуже отводят тепло.
Их номинальная мощность обычно ниже, чем у выводных резисторов аналогичного номинала.
При расчетах для SMD-резисторов рекомендуется брать 2-3 кратный запас по мощности.
Важно учитывать плотность монтажа — при плотном расположении компонентов теплоотвод ухудшается.

Мощность SMD-резисторов часто кодируется в их типоразмере. Например:

0603 — обычно 0.1 Вт
0805 — обычно 0.125 Вт
1206 — обычно 0.25 Вт

Как определить мощность резистора по внешнему виду

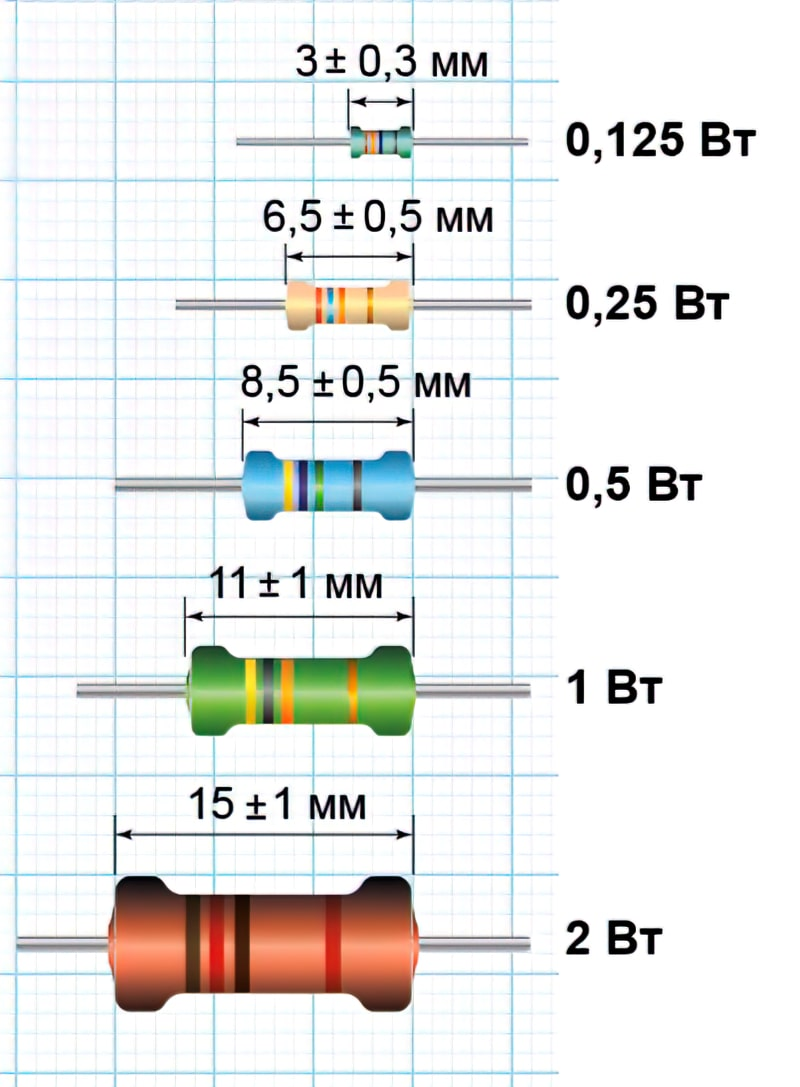
Определить мощность резистора по его внешнему виду можно приблизительно, основываясь на размерах корпуса:

Маленькие резисторы (длина до 6-7 мм) обычно имеют мощность 0.125 — 0.25 Вт.
Средние резисторы (длина 10-12 мм) — 0.5 — 1 Вт.
Крупные резисторы (длина более 15 мм) — 2 Вт и выше.
Резисторы с радиатором или керамическим корпусом обычно рассчитаны на большие мощности — от 5 Вт и выше.

Однако точно определить мощность можно только по маркировке или документации. Размер дает лишь приблизительное представление.

Типичные ошибки при расчете мощности резисторов

При расчете и выборе мощности резисторов часто допускаются следующие ошибки:

Неправильное применение формул — например, использование напряжения всей схемы вместо падения напряжения на резисторе.
Игнорирование температурного фактора — выбор резистора без учета реальных условий работы.
Отсутствие запаса по мощности — выбор резистора с мощностью точно равной расчетной.

Неучет пульсаций тока — в схемах с импульсными токами пиковая мощность может быть значительно выше средней.
Ошибки в единицах измерения — например, путаница между миллиамперами и амперами при расчетах.

Чтобы избежать этих ошибок, всегда перепроверяйте расчеты и внимательно изучайте условия работы схемы.

Резистор и сопротивление [База знаний]

Резистор и сопротивление

Теория

КОМПОНЕНТЫ

ARDUINO

RASPBERRY

ИНТЕРФЕЙСЫ ПЕРЕДАЧИ ДАННЫХ

Резистор — искусственное «препятствие» для тока. Сопротивление в чистом виде. Резистор ограничивает силу тока, переводя часть электроэнергии в тепло. Сегодня невозможно изготовить ни одно, сколько-нибудь функциональное, электронное устройство без резисторов. Они используются везде: от компьютеров до систем охраны.

Сопротивление резистора — его основная характеристика. Основной единицей электрического сопротивления является Ом. На практике используются также производные единицы — килоом (кОм), мегаом (МОм), гигаом (ГОм), которые связаны с основной единицей следующими соотношениями:

1 кОм = 1000 Ом,
1 МОм = 1000 кОм,
1 ГОм = 1000 МОм

Ниже на рисунке видна маркировка резисторов на схемах:

Наклонные линии обозначают мощность резистора до 1 Вт. Вертикальные линии и знаки V и X (римские цифры), указывают на мощность резистора в несколько Ватт, в соответствии со значением римской цифры.

Для соединения резисторов в схемах используются три разных способа подключения: параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.

Последовательное соединение резисторов

Последовательное соединение резисторов применяется для увеличения сопротивления. Т.е. когда резисторы соединены последовательно, общее сопротивление равняется сумме сопротивлений каждого резистора. Например, если резисторы R1 и R2 соединены последовательно, их общее сопротивление высчитывается по формуле: R_общ = R₁ + R₂

Это справедливо и для большего количества соединённых последовательно резисторов:

R_общ = R₁ + R₂ + R₃ + … + R_n

Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее, чем у любого резистора из этой цепи.

При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.

Мощность при последовательном соединении

При соединении резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200 + 100 + 51 + 39 = 390 Ом

Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять

I = U/R = 100 В/390 Ом = 0,256 A

На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле:

P = I² x R = 0,256² x 390 = 25,55 Вт

Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:

P₁ = I² x R₁ = 0,256² x 200 = 13,11 Вт;
P₂
= I² x R₂ = 0,256² x 100 = 6,55 Вт;
P₃ = I² x R₃ = 0,256² x 51 = 3,34 Вт;
P₄ = I² x R₄ = 0,256² x 39 = 2,55 Вт.

Если сложить полученные мощности, то общая Р составит:

Р_общ = 13,11 + 6,55 + 3,34 + 2,55 = 25,55 Вт

Параллельное соединение резисторов

Параллельное соединение резисторов необходимо для уменьшения общего сопротивления и, как вариант, для увеличения мощности нескольких резисторов по сравнению с одним.

Расчет параллельного сопротивления двух параллельно соединённых резисторов R₁ и R₂ производится по следующей формуле:

R_общ = (R₁ × R₂) / (R₁ + R₂)

Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:

1 / R_общ = 1 / R₁ + 1 / R₂ + … + 1 / R_n

Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.

Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.

Мощность при параллельном соединении

При параллельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же. 1/R = 1/200 + 1/100 + 1/51 + 1/39 ≈ 0,06024 Ом
R = 1 / 0,06024 ≈ 16,6 Ом

Используя значение напряжения 100 В, по закону Ома рассчитывается сила тока

I = U/R = 100 В x 0,06024 Ом = 6,024 A

Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом

P = I² x R = 6,024² x 16,6 = 602,3 Вт

Расчет силы тока для каждого резистора выполняется по формулам:

I₁ = U/R₁ = 100/200 = 0,5 A;
I₂ = U/R₂ = 100/100 = 1 A;
I₃ = U/R₃ = 100/51 = 1,96 A;
I₄ = U/R₄ = 100/39 = 2,56 A

На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.

Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов:

P₁ = U²/R₁ = 100²/200 = 50 Вт;
P₂ = U²/R₂ = 100²/100 = 100 Вт;
P₃ = U²2/R₃ = 100²/51 = 195,9 Вт;
P₄ = U²2/R₄ = 100²/39 = 256,4 Вт

Если сложить полученные мощности, то общая Р составит:

Р_общ = 50 + 100 + 195,9 + 256,4 = 602,3 Вт

Калькулятор

Цветовая маркировка резисторов

Наносить номинал резистора на корпус числами — дорого и непрактично: они получаются очень мелкими. Поэтому номинал и допуск кодируют цветными полосками. Разные серии резисторов содержат разное количество полос, но принцип расшифровки одинаков. Цвет корпуса резистора может быть бежевым, голубым, белым. Это не играет роли. Если не уверены в том, что правильно прочитали полосы, можете проверить себя с помощью мультиметра или калькулятора цветовой маркировки.

Калькулятор цветовой маркировки резисторов

Основные характеристики

Сопротивление (номинал)	R	Ом
Точность (допуск)	±	%
Мощность	P	Ватт

Переменный резистор

Переменный резистор — это резистор, у которого электрическое сопротивление между подвижным контактом и выводами резистивного элемента можно изменять механическим способом. Переменные резисторы (их также называют реостатами или потенциометрами) предназначены для постепенного регулирования силы тока и напряжения. Разница в том, что реостат регулирует силу тока в электрической цепи, а потенциометр — напряжение. Выглядят переменные резисторы так:

На радиосхемах переменные резисторы обозначаются прямоугольником с пририсованной к их корпусу стрелочкой.

Регулировать величину сопротивления переменных резисторов можно с помощью вращения специальной ручки. Те из резисторов, у которых регулировка сопротивления резистора может осуществляться только с помощью отвертки или специального ключа-шестигранника, называются подстроечными переменными резисторами.

Термисторы, варисторы и фоторезисторы

Кроме реостатов и потенциометров есть и другие виды резисторов: термисторы, варисторы и фоторезисторы. Термисторы, в свою очередь, делятся на термисторы и позисторы. Позистор – это термистор, у которого сопротивление возрастает вместе с ростом температуры окружающей среды. У термисторов, наоборот, чем выше температура вокруг, тем меньше сопротивление. Это свойство обозначают как ТКС – тепловой коэффициент сопротивления.

В зависимости от ТКС (отрицательный он или положительный) обозначают на схеме термисторы следующим образом:

Следующий особый класс резисторов – это варисторы. Они изменяют силу сопротивления в зависимости от подаваемого на них напряжения. Зная свойства варистора, можно догадаться, что такой резистор защищает электрическую цепь от перенапряжения.

На схемах варисторы обозначаются так:

В зависимости от интенсивности освещения изменяет свое сопротивление еще один вид резисторов – фоторезисторы. Причем не важно, каков источник освещения: искусственный или естественный. Их особенность еще и в том, что ток в них протекает как в одном, так и в другом направлении, то есть еще говорят, что фоторезисторы не имеют p-n перехода.

А на схемах изображаются так:

Мощность резистора, что это, как подобрать, как узнать

Резисторы есть в любой электрической схеме. Но в разных схемах протекают различной величины ток. Не могут же одни и те же элементы работать при 0,1 А и при 100 А. Ведь при прохождении тока сопротивление греется. Чем выше ток, тем более интенсивный нагрев. Значит, и резисторы должны быть на разную величину тока. Так и есть. Отображает их способность работать при различных токах такой параметр, как мощность резистора. На деталях покрупнее она указывается прямо на корпусе. Для мелких корпусов есть другой метод определения (см. ниже).

Содержание статьи

Что такое мощность резистора

Мощность определяется как произведение силы тока на сопротивление: P = I * R и измеряется в ваттах (закон Ома). Рассеиваемая мощность резистора — это максимальный ток, который сопротивление может выдерживать длительное время без ущерба для работоспособности. То есть, этот параметр надо выбирать для каждой схемы отдельно — по максимальному рабочему току.

Как определить мощность резистора по внешнему виду: надо знать соответствие размеров и мощностей

Физически рассеиваемая мощность резистора — это то количество тепла, которое его корпус может «отдать» в окружающую среду и не перегреться при этом до фатальных последствий. При этом, нагрев не должен слишком сильно влиять на сопротивление резистора.

Стандартный ряд мощностей резисторов и их обозначение на схемах

Обратите внимание, что резисторы одного номинала могут быть с разной мощностью рассеивания. Этот параметр зависит от технологии изготовления, материала корпуса. Есть определенный ряд мощностей и их графическое обозначение по ГОСТу.

Вт	Условное обозначение не схемах
мощность резистора 0,05 Вт	Как обозначается на схеме мощность рассеивания резистора 0,05 Вт
мощность резистора 0,125 Вт	Мощность резистора 0,125 Вт на схеме
мощность резистора 0,025 Вт	Как на схеме выглядит резистор мощностью 0,25 Вт
мощность резистора 0,5 Вт	Так на схеме обозначается резистор мощностью 0,5 Вт
мощность резистора 1 Вт	Мощность резистора 1 Вт схематически обозначается так
мощность резистора 2 Вт	Рассеиваемая на резисторе мощность 2 Вт
мощность резистора 5 Вт	Обозначение на схеме мощности резистора 5 Вт

Графическое обозначение мощности резисторов на схеме — черточки и римские цифры, нанесенные на поверхность сопротивления. Самое малое стандартное значение 0,05 Вт, самое большое — 25 Вт, но есть и более мощные. Но это уже специальная элементная база и в бытовой аппаратуре не встречается.

Как обозначаются мощность маломощных резисторов надо просто запомнить. Это косые линии на прямоугольниках, которыми обозначают сопротивления на схемах. Количество косых черточек обозначает количество четвертей дюйма. При номиналах сопротивлений от 1 Вт на изображении ставятся римские цифры: I, II, III, V, VI и т.д. Цифра эта и обозначает мощность резистора в ваттах. Тут немного проще, так как соответствие прямое.

Как определить по внешнему виду

На принципиальной схеме указана нужная мощность резистора — тут все понятно. Но как определить мощность сопротивления по внешнему виду на печатной плате? Вообще, чем больше размер корпуса, тем больше тепла он рассеивает. На достаточно крупных по размеру сопротивлениях указывается номинальное сопротивление и его мощность в ваттах.

Тут есть некоторая путаница, но не все так страшно. На отечественных сопротивлениях рядом с цифрой ставят букву В. В зарубежных ставят W. Но эти буквы есть не всегда. В импортных может стоять V или SW перед цифрой. Еще в импортных может тоже стоять буква B, а в отечественных МЛТ может не стоять ничего или буква W. Запутанная история, конечно. Но с опытом появляется хоть какая-то ясность.

Как определить мощность резистора: стоит в маркировке

А ведь есть маленькие резисторы, на которых и номинал-то с трудом помещается. В импортных он нанесен цветными полосками. Как у них узнать мощность рассеивания?

В старом ГОСТе была таблица соответствий размеров и мощностей. Резисторы отечественного производства по прежнему делают в соответствии с этой таблицей. Импортные, кстати, тоже, но они по размерам чуть меньше отечественных. Тем не менее их также можно идентифицировать. Если сомневаетесь, к какой группе отнести конкретный экземпляр, лучше считать что он имеет более низкую способность рассеивать тепло. Меньше шансов, что деталь скоро перегорит.

Тип резистора	Диаметр, мм	Длинна, мм	Рассеиваемая мощность, Вт
ВС	2,5	7,0	0,125
УЛМ, ВС	5,5	16,5	0,25
ВС	5,5	26,5	0,5
	7,6	30,5	1
	9,8	48,5	2
	25	75	5
	30	120	10
КИМ	1,8	3,8	0,05
	2,5	8	0,125
МЛТ	2	6	0,125
	3	7	0,125
	4,2	10,8	0,5
	6,6	13	1
	8,6	18,5	2

С размерами сопротивлений и их мощностью вроде понятно. Не все так однозначно. Есть резисторы большого размера с малой рассеивающей способностью и наоборот. Но в таких случаях, проставляют этот параметр в маркировке.

Мощность SMD-резисторов

SMD-компоненты предназначены для поверхностного монтажа и имеют миниатюрные размеры. Мощность резисторов SMD определяется по размерам. Также она есть в характеристиках, но необходимо знать серию и производителя. Таблица мощности СМД резисторов содержит наиболее часто встречающиеся номиналы.

Размеры SMD-резисторов — вот по какому признаку можно определить мощность этих элементов

Код imperial	Код metrik	Длинна inch/mm	Ширина inch/mm	Высота inch/mm	Мощность, Вт
0201	0603	0,024/0,6	0,012/0,3	0,01/0,25	1/20 (0,05)
0402	1005	0,04/1,0	0,02/0,5	0,014/0,35	1/16 (0,062)
0603	1608	0,06/1,55	0,03/0,85	0,018/0,45	1/10 (0,10)
0805	2112	0,08/2,0	0,05/1,2	0,018/0,45	1/8 (0,125)
1206	3216	0,12/3,2	0,06/1,6	0,022/0,55	1/4 (0,25)
1210	3225	0,12/3,2	0,10/2,5	0,022/0,55	1/2 (0,50)
1218	3246	0,12/3,2	0,18/4,6	0,022/0,55	1,0
2010	5025	0,20/2,0	0,10/2,5	0,024/0,6	3/4 (0,75)
2512	6332	0,25/6,3	0,12/3,2	0,024/0,6	1,0

В общем-то, у этого типа радиоэлементов нет другого оперативного способа определения тока, при котором они могут работать, кроме как по размерам. Можно узнать по характеристикам, но их найти не всегда просто.

Как рассчитать мощность резистора в схеме

Чтобы рассчитать мощность резисторов в схеме, кроме сопротивления (R) необходимо знать силу тока (I). На основании этих данных можно рассчитать мощность. Формула обычная: P = I² * R. Квадрат силы тока умножить на сопротивление. Силу тока подставляем в Амперах, сопротивление — в Омах.

Если номинал написан в килоомах (кОм) или мегаомах (мОм), его переводим в Омы. Это важно, иначе будет неправильная цифра.

Схема последовательного соединения резисторов

Для примера рассмотрим схему на рисунке выше. Последовательное соединение сопротивлений характерно тем, что через каждый отдельный резистор цепи протекает одинаковый ток. Значит мощность сопротивлений будет одинаковой. Последовательно соединенные сопротивления просто суммируется: 200 Ом + 100 Ом + 51 Ом + 39 Ом = 390 Ом. Ток рассчитаем по формуле: I = U/R. Подставляем данные: I = 100 В / 390 Ом = 0,256 А.

По расчетным данным определяем суммарную мощность сопротивлений: P = 0,256² * 390 Ом = 25,549 Вт. Аналогично рассчитывается мощность каждого из резисторов. Например, рассчитаем мощность резистора R2 на схеме. Ток мы знаем, его номинал тоже. Получаем: 0,256А² * 100 Ом = 6,55 Вт. То есть, мощность этого резистора должна быть не ниже 7 Вт. Брать с более низкой мощностью точно не стоит — быстро перегорит. Если позволяет конструктив прибора, то можно поставить резистор большей мощности, например, на 10 Вт.

Есть резисторы серии МЛТ, в которых мощность рассеивания тепла указана сразу после названия серии без каких-либо букв. В данном случае — МЛТ-2 означает, что мощность этого экземпляра 2 Вт, а номинал 6,8 кОм.

При параллельном подключении расчет аналогичен. Нужно только правильно рассчитать ток, но это тема другой статьи. А формула расчета мощности резистора от типа соединения не зависит.

Как подобрать резистор на замену

Если вам необходимо поменять резистор, брать надо либо той же мощности, либо выше. Ни в коем случае не ниже — ведь резистор и без того вышел из строя. Происходит это обычно из-за перегрева. Так что установка резистора меньшей мощности исключена. Вернее, вы его поставить можете. Но будьте готовы к тому, что скоро его снова придется менять.

Примерно определить мощность резистора можно по размерам

Если место на плате позволяет, лучше поставить деталь с большей мощностью рассеивания, чем была у заменяемой детали. Или поднять резистор той же мощности повыше (можно вообще не подрезать выводы) — чтобы охлаждение было лучше. В общем, при замене резистора, мощность берем либо ту же, либо выше на шаг.

Как рассчитать сопротивление резистора для светодиода: формула, онлайн калькулятор

Светодиоды пришли на смену традиционным системам освещения – лампам накаливания и энергосберегающим лампам. Чтобы диод работал правильно и не перегорел, его нельзя подключать напрямую в питающую сеть. Дело в том, что он имеет низкое внутреннее сопротивление, потому если подключить его напрямую, то сила тока окажется высокой, и он перегорит. Ограничить силу тока можно резисторами. Но нужно подобрать правильный резистор для светодиода. Для этого проводятся специальные расчеты.

Расчет резистора для светодиода

Чтобы компенсировать сопротивление светодиода, нужно прежде всего подобрать резистор с более высоким сопротивлением. Такой расчет не составит труда для тех, кто знает, что такое закон Ома.

Математический расчет

Исходя из закона Ома, рассчитываем по такой формуле:

где Un – напряжение сети; Uvd – напряжение, на которое рассчитана работа светодиода; Ivd – ток.

Допустим, у нас светодиод с характеристиками:

2,1 -3, 4 вольт – рабочее напряжение (Uvd). Возьмем среднее значение 2, 8 вольт.

20 ампер – рабочий ток (Ivd)

220 вольт – напряжение сети (Un)

В таком случае мы получаем величину сопротивления R = 10, 86. Однако этих расчетов недостаточно. Резистор может перегреваться. Для предотвращения перегрева нужно учитывать при выборе его мощность, которая рассчитывается по следующей формуле:

Обратите внимание, что резистор подведен на плюсовой контакт диода.

Для наглядности рекомендуем посмотреть видео:

Графический расчет

Графический способ – менее популярный для расчета резистора на светодиод, но может быть даже более удобный. Зная напряжение и ток диода (их называют еще вольтамперными характеристиками – ВАХ), вы можете узнать сопротивление нужного резистора по графику, представленному ниже:

Тут изображен расчет для диода с номинальным током 20мА и напряжением источника питания 5 вольт. Проводя пунктирную линию от 20 мА до пересечения с «кривой led» (синий цвет), чертим пересекающую линию от прямой Uled до прямой и получаем максимальное значение тока около 50 мА. Далее рассчитываем сопротивление по формуле:

Получаем значение 100 Ом для резистора. Находим для него мощность рассеивания (Силу тока берем из Imax):

Теория

Математический расчет

Ниже представлена принципиальная электрическая схема в самом простом варианте.

В ней светодиод и резистор образуют последовательный контур, по которому протекает одинаковый ток (I). Питается схема от источника ЭДС напряжением (U). В рабочем режиме на элементах цепи происходит падение напряжения: на резисторе (UR) и на светодиоде (ULED). Используя второе правило Кирхгофа, получается следующее равенство: или его интерпретация

В приведенных формулах R – это сопротивление рассчитываемого резистора (Ом), RLED – дифференциальное сопротивление светодиода (Ом), U – напряжения (В).

Значение RLED меняется при изменении условий работы полупроводникового прибора. В данном случае переменными величинами являются ток и напряжение, от соотношения которых зависит величина сопротивления. Наглядным объяснением сказанного служит ВАХ светодиода.

На начальном участке характеристики (примерно до 2 вольт) происходит плавное нарастание тока, в результате чего RLED имеет большое значение. Затем p-n-переход открывается, что сопровождается резким увеличением тока при незначительном росте прикладываемого напряжения.

Путём несложного преобразования первых двух формул можно определить сопротивление токоограничивающего резистора:

ULED является паспортной величиной для каждого отдельного типа светодиодов.

Графический расчет

Имея на руках ВАХ исследуемого светодиода, можно рассчитать резистор графическим способом. Конечно, такой способ не имеет широкого практического применения. Ведь зная ток нагрузки, из графика можно легко вычислить величину прямого напряжения. Для этого достаточно с оси ординат (I) провести прямую линию до пересечения с кривой, а затем опустить линию на ось абсцисс (ULED). В итоге все данные для расчета сопротивления получены.

Тем не менее, вариант с использованием графика уникален и заслуживает определенного внимания.

Рассчитаем резистор для светодиода АЛ307 с номинальным током 20 мА, который необходимо подключить к источнику питания 5 В. Для этого из точки 20 мА проводим прямую линию до пересечения с кривой LED. Далее через точку 5 В и точку на графике проводим линию до пересечения с осью ординат и получаем максимальное значение тока (Imax), примерно равное 50 мА. Используя закон Ома, рассчитываем сопротивление:

Чтобы схема была безопасной и надёжной нужно исключить перегрев резистора. Для этого следует найти его мощность рассеивания по формуле:

Онлайн-калькулятор расчета сопротивления

Задача усложняется, если вы хотите подключить не один, а несколько диодов.

Для облегчения самостоятельных расчетов мы подготовили онлайн-калькулятор расчета сопротивления резисторов. Если подключать несколько светодиодов, то нужно будет выбрать между параллельным и последовательным соединениями между ними. И для этих схем нужны дополнительные расчеты для источника питания. Можно их легко найти в интернете, но мы советуем воспользоваться нашим калькулятором.

Вам понадобится знать:

Напряжение источника питания.
Характеристику напряжения диода.
Характеристику тока диода.
Количество диодов.

А также нужно выбрать параллельную или последовательную схему подключения. Рекомендуем ознакомиться с разницей между соединениями в главах, которые мы подготовили ниже.

Последовательное соединение светодиодов

Часто несколько светодиодов подключают последовательно к одному источнику напряжения. При последовательном соединении одинаковых светодиодов их общий ток потребления равняется рабочему току одного светодиода, а общее напряжение равно сумме напряжений падения всех светодиодов в цепи.

Поэтому, в данном случае, нам достаточно использовать один резистор для всей последовательной цепочки светодиодов.

Пример расчета сопротивления резистора при последовательном подключении.

В этом примере два светодиода соединены последовательно. Один красный светодиод с напряжением 2В и один ультрафиолетовый светодиод с напряжением 4,5В. Допустим, оба имеют номинальную силу тока 30 мА.

Из правила Кирхгофа следует, что сумма падений напряжения во всей цепи равна напряжению источника питания. Поэтому на резисторе напряжение должно быть равно напряжению источника питания минус сумма падения напряжений на светодиодах.

Используя закон Ома, вычисляем значение сопротивления ограничительного резистора:

Резистор должен иметь значение не менее 183,3 Ом.

Обратите внимание, что после вычитания падения напряжений у нас осталось еще 5,5 вольт. Это дает возможность подключить еще один светодиод (конечно же, предварительно пересчитав сопротивление резистора)

Параллельное соединение

Для тех, кто уже сталкивался на практике со схемами подключения светодиодного освещения, вопрос о выборе между параллельным и последовательным соединением обычно не стоит. Чаще всего выбирают схему последовательного соединения. У параллельного соединения для светодиодов есть один важный недостаток – это удорожание и усложнение конструкции, потому что для каждого диода нужен отдельный резистор. Но такая схема имеет и большой плюс – если сгорела одна линия, то перестанет светить только один диод, остальные продолжат работу.

Расчет резисторов при параллельно – последовательном соединении светодиодов

Часто на практике нам нужно подключить к источнику питания большое количество светодиодов, несколько десятков. Если все светодиоды подключить последовательно через один резистор, то в таком случае напряжения на источнике питания нам не хватит. Решением данной проблемы является параллельно-последовательное соединение светодиодов, как это показано на рис.3.

Исходя из напряжения источника питания, определяется максимальное количество светодиодов, которые можно соединить последовательно.

Рис.3 – Схема подключения светодиодов при параллельно — последовательном соединении

Например у нас имеется источник питания 12 В, исходя из напряжения источника питания максимальное количество светодиодов для одной цепи будет равно: 10В/2В = 5 шт, учитывая что на светодиоде (красного цвета) падение напряжения — 2 В.

Почему 10 В, а не 12 В мы взяли, связано это с тем, что на резисторе также будет падение напряжения и мы должны оставить, где то 2 В.

Сопротивление резистора для одной цепи, исходя из рабочего тока светодиодов определяется по формуле:

R = (Uн.п – Uд1 + Uд2 + Uд3+ Uд4+ Uд5)/Iд = (12В — 2В + 2В + 2В + 2В + 2В)/0,02А = 100 Ом.

Выбираем ближайшее сопротивление из номинального ряда Е24 в сторону увеличения — 110 Ом.

Количество таких цепочек из пяти светодиодов параллельно соединенных практически не ограничено!

Можно ли обойтись без резисторов

В бюджетных или просто старых приборах используются резисторы. Также они используются для подключения всего только нескольких светодиодов.

Но есть более современный способ – это понижение тока через светодиодный драйвер. Так, в светильниках в 90% встречаются именно драйверы. Это специальные блоки, которые через схему преобразуют характеристики тока и напряжения питающей сети. Главное их достоинство – они обеспечивают стабильную силу тока при изменении/колебании входного напряжения.

Ограничение тока протекающего через светодиод

Таким образом, мы должны ограничить ток светодиода. У нас есть два варианта:

использовать питание стабильным током (не более 30мА в соответствии с технической спецификацией светодиода)
ограничить ток по-другому.

В данной статье мы займемся вторым способом, а именно, мы подключим резистор последовательно со светодиодом. На этом резисторе будет происходить падение части напряжения источника питания, который обозначим как VR:

В соответствии с приведенным выше вторым законом Кирхгофа, распределение напряжений будет определяться по формуле:

VCC = VR + VF

В нашем случае мы знаем типовое значение напряжения нашего светодиода, которое составляет 2 вольт, а также напряжение питания 5 вольт:

Таким образом, мы можем вычислить необходимое падение напряжения на резисторе R, для того чтобы на диоде было только необходимые 2 вольта:

VR = VCC — VF

VR = 5В — 2В = 3В

то есть, мы стремимся к получению следующих напряжений в нашей схеме:

Теперь мы используем первый закон Кирхгофа:

сумма значений силы токов, входящих в узел равна сумме значений силы токов, вытекающей из этого узла

Нашим узлом является место соединения резистора и светодиода, и это означает, что через резистор будет проходить тот же ток, что и через светодиод. Поскольку мы предположили, что через светодиод может течь ток IF= 20мА, то:

Сопротивление резистора вычислим с помощью Закона Ома:

то есть в нашем случае:

и наконец, мы можем вывести общую формулу:

После расчета сопротивления, выбирается резистор из номинального ряда. В нашем случае это резистор точно такой же, как рассчитали, то есть, 150 Ом, который имеется в номинальных рядах E24, E12 и E6.

А что делать, когда сопротивление резистора не соответствует ни одному значению из номинального ряда? В этом случае следует выбрать одно из двух ближайших к расчетному сопротивлению, при этом необходимо учитывать следующее:

Если сопротивление будет меньше, чем рассчитывали, то это увеличит значение тока, протекающего через светодиод.

Если сопротивление будет больше, чем рассчитывали, то это уменьшит световой поток, испускаемый светодиодом.

Как подобрать резистор для одиночного светодиода

Для ограничения тока светоизлучающего диода можно использовать резистор, включенный таким образом:

Теперь определяем, какой резистор нужен. Для расчета сопротивления используется формула:

где U пит — напряжение питания,

U пад- падение напряжения на светодиоде,

I — требуемый ток светодиода.

При этом мощность, рассеиваемая на резисторе, будет пропорциональна квадрату тока:

Например, для красного светодиода Cree C503B-RAS типовое падение напряжения составляет 2.1 В при токе 20 мА. При напряжении питания 12 В сопротивление резистора будет составлять

Из стандартного ряда сопротивлений Е24 подбираем наиболее близкое значение номинала – 510 Ом. Тогда мощность, рассеиваемая на резисторе, составит

Таким образом, потребуется гасящий резистор номиналом 510 Ом и мощностью рассеивания 0.25 Вт.

Может сложиться впечатление, что при низких напряжениях питания можно подключать led без резистора. На этом видео наглядно показано, что произойдет со светоизлучающим диодом, включенного таким образом, при напряжении всего 5 В:

Светодиод сначала будет работать, но через несколько минут просто перегорит. Это вызвано нелинейным характером его ВАХ, о чем говорилось в начале статьи.

Никогда не подключайте светодиод без гасящего резистора даже при низком напряжении питания. Это ведет к его выгоранию и, в лучшем случае, к обрыву цепи, а в худшем – к короткому замыканию.

Количество теплоты на резисторе формула — MOREREMONTA

В электрической схеме, показанной на рисунке, ключ К замкнут.

Заряд конденсатора ЭДС батарейки её внутреннее сопротивление сопротивление резистора Найдите количество теплоты, которое выделяется на резисторе после размыкания ключа К в результате разряда конденсатора. Потерями на излучение пренебречь.

Количество теплоты, выделяющееся на резисторе после размыкания ключа:

Напряжение на конденсаторе равно падению напряжения на резисторе. С учетом закона Ома для полной цепи:

Комбинируя эти формулы, находим:

Ответ:

полностью одобряю ваш метод, но нельзя ли решить более «простым» способом? Не сочтите меня за глупца.

Смеяться не буду 🙂 Все в порядке.

А теперь о Вашем решении. Что тут могу сказать. Так решать, конечно, нельзя, и получившийся у Вас ответ, отличный от приведенного в решении, — одно из тому подтверждений. Не буду комментировать все, скажу только, что формулу здесь использовать «в лоб» нельзя, так как через конденсатор будет течь не постоянный ток, а уменьшающийся по величине: чем больше заряд на конденсаторе, тем быстрее он стремится разрядиться. Так что закон сохранения энергии — наиболее простой и верный способ решения.

Ежели Вы настаиваете на на применении своей формулы, то тут потребуется большие знания из математического анализа: производные, интегралы, дифференциальные уравнения. Если интересно, приведу такое решение (но особого смысла в нем разбираться — нет, так как такие знания за рамками того, что проверяется на ЕГЭ). Кроме того, все равно получится, что нужно просто посчитать начальную энергию конденсатора.

Сложное решение этой задачи 🙂

Определим зависимость тока, текущего через резистор от времени. Так как конденсатор подключен к резистору параллельно, напряжения на них совпадают в любой момент времени: . По закону Ома, напряжение на резисторе пропорционально величине текущего через него тока: . Напряжение на конденсаторе связано с зарядом на нем соотношением: . Пусть за небольшой интервал времени заряд на конденсаторе изменился на (так как конденсатор разряжается ). Тогда через резистор за это время протек заряд . Следовательно сила тока равна . Скомбинировав все равенства и переходя к бесконечно малому интервалу времени, получаем дифференциальное уравнение на величину заряда конденсатора:

Решая это уравнение и используя, что в начальный момент времени заряд на конденсаторе равен , имеем: . То есть, математически конденсатор разряжается бесконечно долго.

Значит ток через конденсатор равен

Определим теперь тепловую мощность, выделяющуюся на резисторе:

Мощность уменьшается со временем. Для того, чтобы найти полное тепло необходимо просуммировать по всему времени разрядки, то есть взять интеграл:

Вот и она, начальная энергия конденсатора 🙂

Главная
Обучение
Предварительный просмотр

Мероприятия / ВИШР
Обучение
Тренажер ЕГЭ
Учебные пособия
Игры
120 лет ТПУ. Викторина онлайн
Университетские субботы
Высшая инженерная школа России

Физика

3.2.9.1. Тепловая мощность, выделяемая на резисторе

Тепловая мощность, выделяемая на резисторе

Электрический ток, проходящий по проводнику, нагревает его. Это объясняется тем, что свободные электроны, перемещаясь под действием электрического поля, взаимодействуют с ионами или атомами вещества и передают им свою энергию. В результате работы электрического тока внутренняя энергия вещества увеличивается, повышается его температура. Нагретый проводник передает свою энергию окружающим телам. Если проводник не движется, то вся энергия электрического тока переходит во внутреннею энергию проводника. Работа тока определяется

Количество теплоты, выделяемое на резисторе, обозначим через Q Так как Q = A, то

или используя закон Ома (U = I*R) , получим

Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени.

Эта формулировка называется законом Джоуля — Ленца

Закон Джо́уля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока.<2>> является константой, то тепло выделяемое на проводе обратно пропорционально квадрату напряжения на потребителе. Повышая напряжение мы снижаем тепловые потери в проводах. Это, однако, снижает электробезопасность линий электропередачи.

Выбор проводов для цепей [ править | править код ]

Тепло, выделяемое проводником с током, в той или иной степени выделяется в окружающую среду. В случае, если сила тока в выбранном проводнике превысит некоторое предельно допустимое значение, возможен столь сильный нагрев, что проводник может спровоцировать возгорание находящихся рядом с ним объектов или расплавиться сам. Как правило, при выборе проводов, предназначенных для сборки электрических цепей, достаточно следовать принятым нормативным документам, которые регламентируют выбор сечения проводников.

Электронагревательные приборы [ править | править код ]

Если сила тока одна и та же на всём протяжении электрической цепи, то в любом выбранном участке будет выделять тепла тем больше, чем выше сопротивление данного участка.

За счёт сознательного увеличения сопротивления участка цепи можно добиться локализованного выделения тепла в этом участке. По этому принципу работают электронагревательные приборы. В них используется нагревательный элемент — проводник с высоким сопротивлением. Повышение сопротивления достигается (совместно или по отдельности) выбором сплава с высоким удельным сопротивлением (например, нихром, константан), увеличением длины проводника и уменьшением его поперечного сечения. Подводящие провода имеют обычное низкое сопротивление и поэтому их нагрев, как правило, незаметен.

Плавкие предохранители [ править | править код ]

Для защиты электрических цепей от протекания чрезмерно больших токов используется отрезок проводника со специальными характеристиками. Это проводник относительно малого сечения и из такого сплава, что при допустимых токах нагрев проводника не перегревает его, а при чрезмерно больших перегрев проводника столь значителен, что проводник расплавляется и размыкает цепь.

Резистор (теория)

Резистор – элемент электрической цепи, применяемый с целью сопротивления электрическому току на отдельном участке цепи.

Сопротивление является главной характеристикой резистора, Ω (Om, Ом) — его единица измерения. Определенная часть тока проходящего через резистор преобразовывается в тепло. Чем больше величина сопротивления, тем большее количество тока рассеивается в тепло.

Общее сопротивление резисторов при последовательном соединении рассчитывается по формуле: R_общ= R₁ + R₂. При параллельном соединении резисторов общее сопротивление рассчитывается по данной формуле: R_общ= R₁ * R₂ / (R1 + R₂). Данным способом можно выходить из ситуации складывающейся при отсутствии резисторов необходимого сопротивления.

Не маловажной характеристикой является мощность резисторов, она показывает максимальную нагрузку, которую в состоянии пропустить через себя резистор. На данный момент выпускают резисторы мощностью 0,125 Watt; 0,25 Watt; 0,5 Watt; 1 Watt; 2 Watt; 5 Вт, но используются в радиолюбительской технике (исключая специализированную) — 0,25 Watt; 0,5 Watt; 1 Watt. На главном изображении поста приведен внешний вид резисторов разной мощности. Нагрузку, действующую на резистор можно посчитать по формуле: P = I² *R = I * U = U²/ R, где R – сопротивление, U – напряжение, а I – сила тока.

При превышении максимально допустимой нагрузки, резистор будет нагреваться, и вносить помехи в стоящие рядом радио детали (подверженные тепловым изменениям), а при большом превышении нагрузки резистор перегорает (в буквальном смысле этого слова).

Благодаря закону Ома, зная величину силы тока (I) и напряжения (U тоже, что и V) можно определить сопротивление (R) по следующей формуле: R = U / I.

На практике резисторы выполняют три назначения и служат:

— делителями напряжения;

— токоограничивающими резисторами;

— подтягивающими и стягивающими резисторами.

Делитель напряжения необходим для того, чтобы получать всего его часть, например из 12v получить 9v. Про делители напряжения будет отдельная большая статья с примерами, по окончанию ее написания ссылку размещу в комментариях к данному посту.

Токоограничивающий резистор применяют в случае, когда какая-либо деталь не рассчитана на работу при определенно высоком уровне тока, и его необходимо уменьшить. В данной ситуации резистор устанавливается последовательно между положительным контактом источника питания участка цепи (детали) и самим участком цепи (деталью) на котором уровень тока необходимо уменьшить.

Подтягивающий и стягивающий резистор необходим только для работы с логическими компонентами, для которых важно присутствие нуля и единицы на контакте (отсутствие или присутствие напряжения). Без подтягивающих и стягивающих резисторов возможны сбои в работе системы из-за неверного истолкования шумов, улавливаемых контактами логики, как присутствие нуля или единицы.

Рассмотрим примеры с использованием микроконтроллера и кнопки. Один контакт кнопки подключен к входу микроконтроллера, а другой к источнику сигнала.

Для гарантирования правильного считывания положительного сигнала используют стягивающий резистор, установленный одним концом в промежуток между кнопкой и контактом микроконтроллера, а другим соединенным с землей (GND). В этом случае все возможные шумы, способные дать неверный сигнал на микроконтроллер, будут уходить в землю. В роли стягивающего резистора применяют сопротивления более 10 kOm, чтобы при нажатии кнопки не происходило короткое замыкание. Когда кнопка нажата, цепь замыкается, ток из-за большого сопротивления резистора не уходит весь в землю и сигнал поступает на контакт микроконтроллера.

Подтягивающий резистор подобен токоограничивающему и аналогичен стягивающему. Он поддерживает на контакте микроконтроллера логическую единицу до тех пор, пока цепь разомкнута. Сопротивление для подтягивающего резистора необходимо брать также не менее 10 kOm, это предотвращает короткое замыкание и сводит к минимуму потери энергии при нажатии кнопки.

Разновидность резисторов, применяемая в радиоаппаратуре: варисторы – сопротивление меняется от приложенного напряжения; фоторезисторы – от освещения, терморезисторы – от температуры, магниторезисторы – от величины магнитного поля, тензорезисторы – от деформации корпуса резистора.

Калькулятор расчета величины сопротивления резистора по цветам (цветовой маркировке) можно найти ЗДЕСЬ.

основные параметры, мощность, сопротивление. Обозначение резисторов

электрика, сигнализация, видеонаблюдение, контроль доступа (СКУД), инженерно технические системы (ИТС)

Резистор — это электротехническое изделие, вносящее в электрическую цепь определенное сопротивление.

Основными параметрами резистора являются мощность и сопротивление. Кроме того, резистор обладает некоторой емкостью, индуктивностью, зависимостью сопротивления от температуры, собственными шумами и пр., но достаточно часто этим можно пренебречь.

На резисторе указывается его номинальное сопротивление. На практике резистор может иметь сопротивление, отличное от указанного на величину допустимого отклонения, которая измеряется в процентах: ±20%; ±10%; ±5%.

Сопротивление резистора измеряется в Омах (Ом), также применяются производные единицы: 1 кОм=10³Ом, 1 мОм=10⁶Ом. Конкретные номиналы резисторов определяются рядами номинальных сопротивлений.

Номинальная мощность рассеяния — мощность, которую резистор может рассеивать на протяжении длительного времени без недопустимо большого перегрева, приводящего к необратимым изменениям сопротивления.

Мощность резистора, вернее мощность, которая выделяется на резисторе (Р) определяется законом Ома и может быть рассчитана по формулам:

P=I²*R — (1) или P=U²/R — (2), где

R — сопротивление резистора
U — напряжение на нем
I — ток, протекающий через резистор

Обратите внимание, чтобы получить мощность в Ваттах (Вт) следует применять следующие единицы измерения:

сопротивление — Ом,
напряжение — Вольт (В),
ток — Ампер (А).

На практике это бывает не всегда удобно, поэтому для формулы (1) можно использовать следующие размерности: сопротивление — кОм (1кОм=10³Ом), ток — миллиампер (1 мА=10^-3А).

ОБОЗНАЧЕНИЯ РЕЗИСТОРОВ

Условные обозначения резисторов на схемах приведены на рисунке 1.

В верхнем ряду показаны:

общее обозначение;
резистор мощностью 0,125 Вт;
0,25 Вт;
0,5 Вт;
1 Вт.

Мощность резистора 1 Вт и более на схемах указывается размещением внутри его обозначения соответствующего римского числа.

Кроме того, на схеме рядом с обозначением могут указываться (второй ряд, слева направо):

буквенное обозначение резистора и его порядковый номер,
номинальное значение сопротивления,
буквенное обозначение и номинал,
мощность резистора в комбинации со всеми перечисленными вариантами.

РЯДЫ НОМИНАЛЬНЫХ СОПРОТИВЛЕНИЙ

Значения сопротивлений производимых резисторов подчиняются определенной закономерности, которая ниже приведена в таблице.

Там должно быть все ясно, поясню только, что:

номер ряда определяет количество базовых значений сопротивлений и их допустимое отклонение,
получив при расчете какое — либо значение, по приведенной таблице Вы можете выбрать максимально близкий номинал и его допуск.

Представленные на сайте материалы имеют информационный характер и не могут быть использованы в качестве руководящих и нормативных документов

Резисторы переменные, постоянные вся истина!

Друзья, всем привет! На дворе зима а календарь говорит мне, что будни перетекают в приятные праздничные выходные, так что самое время для новой статьи. Для тех кто меня не знает, скажу, что меня зовут Владимир Васильев и я веду вот этот самый радиолюбительский блог, так что добро пожаловать!

В прошлой статье мы разбирались с понятием электрического тока и напряжения. В ней буквально на пальцах я постарался объяснить что представляет собой электричество. В помощь применял некие «сантехнические аналогии».

Боле того, я наметил для себя написать ряд обучающих статей для совсем начинающих радиолюбителей- электронщиков, так что дальше будет больше — [urlspan]не пропустите.[/urlspan]

Содержание статьи

Сегодняшняя статья будет не исключением, сегодня я постараюсь как можно подробнее осветить тему резисторов. Резисторы хоть и являются, наверно самыми простыми радиокомпонентами, но у начинающих могут вызвать массу вопросов. А отсутствие ответов на них может привести к полному бардаку в голове и привести к отсутствию мотивации и желанию развиваться.

Что такое сопротивление?

Резистор — это пассивный элемент электрической цепи, обладающий фиксированным или переменным значением электрического сопротивления.

Резисторы обладают сопротивление, а что такое сопротивление? Постараемся с этим разобраться.

Чтобы ответить на этот вопрос, давайте вернемся снова к нашей сантехнической аналогии. Под действием силы тяжести или под действием давления насоса, вода устремляется от точки большего давления в точку с меньшим давлением. Так и электрический ток под действием напряжения течет из точки большего потенциала в точку с меньшим потенциалом.

Что может помешать движению воды по трубам? Движению воды может помешать состояние труб, по которым она бежит. Трубы могут быть широкими и чистыми, а могут быть загажены и вообще представлять собой печальное зрелище. В каком случае скорость водного потока будет больше? Естественно, что вода будет течь быстрее если ее движению не будет оказываться никакого сопротивления.

В случае с чистым трубопроводом так и будет, воде будет оказываться наименьшее сопротивление и ее скорость будет практически неизменной. В загаженной трубе сопротивление на водный поток будет значительным, и соответственно скорость движения воды будет не очень.

Хорошо, теперь переносимся из нашей водопроводной модели в реальный мир электричества. Теперь становится понятно, что скорость воды в наших реалиях представляет собой силу тока измеряемую в амперах. Сопротивление которое оказывали трубы на воду, в реальной токоведущей системе будет сопротивление проводов измеряемое в омах.

Как и трубы, провода могут оказывать сопротивление на ток. Сопротивление напрямую зависит от материала из которого сделаны провода. Поэтому совсем не случайно провода часто изготавливают из меди, так как медь имеет небольшое сопротивление.

Другие металлы могут оказывать очень большое сопротивление электрическому току. Так для примера, удельное сопротивление (Ом*мм²) нихрома составляет 1.1Ом*мм². Величину сопротивления нетрудно оценить сравнив с медью у которой удельное сопротивление 0,0175Ом*мм². Неплохо да?

При пропускании тока через материал с высоким сопротивлением, мы можем убедиться, что ток в цепи будет меньше, достаточно провести несложные замеры.

Как выглядит резистор?

В природе встречаются абсолютно различные резисторы. Есть резисторы с постоянным сопротивление, есть резисторы с переменным сопротивлением. И каждый вид резисторов находит свое применение. Так давайте остановимся и постараемся уделить вниманием некоторые из них.

Постоянные резисторы.

Само название говорит о том, что они обладают постоянным фиксированным сопротивлением. Каждый такой резистор изготавливается с определенным сопротивлением, определенной рассеиваемой мощностью.

Рассеиваемая мощность — это еще одна характеристика резисторов, так же как и сопротивление. Мощность рассеяний говорит о том, какую мощность может рассеять резистор в виде тепла (вы наверное замечали, что резистор во время работы может значительно нагреваться).

Естественно, что на заводе не могут изготавливать резисторы абсолютно любые. Поэтому постоянные резисторы имеют определенную точность указываемую в процентах. Эта величина показывает в каких пределах будет гулять результирующее сопротивление.И естественно, чем точнее резистор, тем дороже он будет. Так зачем переплачивать?

Также сама величина сопротивления не может быть любой. Обычно сопротивление постоянных резисторов соответствует определенному номинальному ряду сопротивлений. Эти сопротивления обычно выбираются из рядов типо Е3, Е6, Е12,Е24

Как видите резисторы из ряда Е24 имеют более богатый набор сопротивлений. Но это еще не предел так как существуют номинальные ряды E48, E96, E192.

На электрических схемах постоянные резисторы обозначаются эдаким прямоугольником с выводами. На самом условном графическом обозначении может надписываться мощность рассеяния.

Переменные резисторы

Вы когда-нибудь обращали внимание на различные «крутилки» в старой аналоговой технике. Например, задумывались ли о том что вы крутите, прибавляя громкость в старом, возможно даже ламповом телевизоре?

Многие регуляторы и различные «крутилки»представляют собой переменные резисторы. Так же как и постоянные резисторы, переменные также имеют различную рассеивающую мощность. Однако их сопротивление может меняться в широких пределах.

Переменные резисторы служат для регулирования напряжения или тока в уже готовом изделии. Как я уже упоминал этим резистором может регулироваться сопротивление в схеме формирования звука. Тогда громкость звука будет меняться пропорционально углу поворота ручки резистора. Так сам корпус находится внутри устройства, а та самая крутилка остается на поверхности.

Более того, бывают еще и сдвоенные , строенные , счетверенные и так далее переменные резисторы. Обычно их применяют, когда нужно параллельное изменение сопротивления сразу в нескольких участках схемы.

Условное графическое изображение резистора на электрических схемах.

Подстроечные резисторы.

Переменный резистор это очень хорошо, но что если нам нужно изменение или подстройка сопротивления лишь на этапе сборки изделия?

Переменный резистор нам в этом не очень подходит. Переменный резистор обладает меньшей точностью нежели постоянный. Это плата за возможность регулировки, в результате которой сопротивление может гулять в некоторых пределах.

Конечно на этапе налаживания изделия может применяться так называемый подборочный резистор. Это обычный постоянный резистор, только при монтаже он подбирается из кучки резисторов с близкими номиналами.

Подбор резисторов имеет место быть когда требуется регулировка параметров изделия и при этом требуется высокая точность работы (чтобы требуемый параметр как можно меньше плавал). Таким образом нужно чтобы резистор был как можно большей точностью 1% или даже 0,5%.

Так для подстройки параметров схемы чаще всего применяют подстроечные резисторы. Эти резисторы специально придуманы для этих целей. Подстройка осуществляется посредством тоненькой часовой отвертки, причем после достижения требуемой величины сопротивления ползунок резистора часто фиксируют краской или клеем.

Условное графическое изображение подстроечного резистора

Формулы и свойства

При выборе резистора, помимо его конструктивной особенности, следует обращать внимания на основные его характеристики. А основными его характеристиками, как я уже упоминал, являются сопротивление и мощность рассеяния.

Между этими двумя характеристиками есть взаимосвязь. Что это значит? Вот допустим в схеме у нас стоит резистор с определенной величиной сопротивления. Но по каким-либо причинам мы выясняем, что сопротивление резистора должно быть значительно меньше того, что есть сейчас.

И вот что получается, мы ставим резистор с значительно меньшим сопротивлением и в соответствии с законом Ома мы можем получить небольшое западло.

Так как сопротивление резистора было большим, а напряжение в цепи у нас фиксированное, то вот что получилось. При уменьшении номинала резистора общее сопротивление в цепи упало, следовательно ток в проводах возрос.

Но что если мы поставили резистор с прежней мощностью рассеяния? При возросшем токе , новый резистор может и не выдержать нагрузки и умереть, его душа улетит вместе с клубком дыма из бездыханного тельца резистора 🙂

Выходит, что при номинале резистора 10 Ом, в цепи будет течь ток равный 1 А. Мощность которая будет рассеиваться на резисторе будет равняться

Видите какие грабли могут подстерегать на пути. Поэтому при выборе резистора, обязательно нужно смотреть его допустимую мощность рассеяния.

Последовательное соединение резисторов

А давайте теперь посмотрим как будут меняться свойства цепи при последовательном расположении резисторов. Итак у нас есть источник питания и далее стоят последовательно три резистора с различным сопротивлением.

Попробуем определить какой ток протекает в цепи.

Здесь хочется упомянуть, для тех кто не в теме, что электрический ток в цепи только один. Есть правило Кирхгофа, которое гласит что сумма токов втекающих в узел равно сумме токов вытекающих из узла. А так как в данной схеме у нас последовательное расположение резисторов и никаких узлов и в помине нет , то ясно, что ток будет один.

Для определения тока, нам нужно определить полное сопротивление цепи. Находим сумму всех резисторов показанных на схеме.

Здесь я приведу формулу полного сопротивления при последовательном расположении резисторов.

Полное сопротивление получилось равным 1101 Ом. Теперь зная что полное напряжение (напряжение источника питания)равно 10 В, а полное сопротивление равно 1101 Ом, тогда ток в цепи равняется I=U/R=10В/1101 Ом=0,009 А =9 мА

Зная ток мы можем определить напряжение, высаживаемое на каждом резисторе. Для этого также воспользуемся законом Ома. И получается напряжение на резисторе R1 будет равно U1=I*R1=0.009А*1000Ом=9В. Ну и тогда для остальных резисторов U2=0.9В, U3=0.09В. Теперь можно и проверить сложив все эти напряжения, ну и получив в результате значенье близкое напряжению питания.

Ах да вот вам и делитель напряжения. Если сделать отвод после каждого резистора то можно убедиться в наличии еще некоторого набора напряжений. Если при этом использовать равные сопротивления то эффект делителя напряжения будет еще более очевиден.

Кликните для увеличения

На изображении видно как меняется напряжение между разными точками -потенциалами.

Так как резисторы сами по себе являются хорошими потребителями тока, то понятно, что при использовании делителя напряжения, стоит выбирать резисторы с минимальными сопротивлениями. Кстати мощность расходуемая на каждом резисторе будет одинаковой.

Для резистора R1 мощность будет равняться P=I*R1=3.33A*3.33В=11,0889Вт. Округляем и получаем 11Вт. И каждый резистор естественно должен быть на это рассчитан. Потребляемая мощность всей цепи будет P=I*U=3.33A*10В=33,3Вт.

Сейчас я вам покажу какая мощность будет для резисторов имеющих разное сопротивление.

Кликните для увеличения

Мощность потребляемая всей цепочкой, изображенной на рисунке, будет равняться P=I*U=0.09A*10В=0,9Вт.

Теперь рассчитаем мощность потребляемую каждым резистором:
Для резистора R1: P=I*U=0.09A*0.9В=0,081Вт;

Для резистора R2: P=I*U=0.09A*0.09В=0,0081Вт;

Для резистора R3: P=I*U=0.09A*9В=0,81Вт.

Из этих наших расчетов становится понятной закономерность:

Чем больше общее сопротивление цепочки резисторов, тем меньше будет ток в цепи
Чем больше сопротивление конкретного резистора в цепи, тем большая мощность будет на нем выделяться и тем больше он будет греться.

Поэтому становится понятной необходимость подбирать номиналы резисторов в соответствии с их потребляемой мощностью.

Параллельное соединение резисторов

С последовательным расположение резисторов думаю более менее понятно. Так давайте рассмотрим параллельное соединение резисторов.

Здесь на этом изображении схемы показано различное расположение резисторов. Хотя в заголовке я упомянул о параллельном соединении, думаю наличие последовательно соединенного резистора R1 позволит нам разобраться в некоторых тонкостях.

Итак суть заключается в том что последовательная схема соединения резисторов является делителем напряжения, а вот параллельное соединение представляет собой делитель тока.

Рассмотрим это подробнее.

Ток течет от точки с большим потенциалом к точке с меньшим потенциалом. Естественно, что ток из точки с потенциалом 10В стремится к точке нулевого потенциала — земле. Маршрут тока будет : Точка10В —>>точка А—>>точка В—>>Земля.

На участке пути Точка 10 —Точка А, ток будет максимальным, ну просто потому, что ток бежит по прямой и не разделяется на развилках.

Далее по правилу Кирхгофа, ток будет раздваиваться. Получается ток в цепи резисторов R2 и R4 будет одним а в цепи с резистором R3 другим. Сумма токов этих двух участков будет равняться току на самом первом отрезке (от источника питания до точки А).

Давайте рассчитаем эту схему и узнаем значение тока на каждом участке.

Для начала узнаем сопротивление участка цепи резисторов R2, R4

Значение резистора R3 нам известен и равен 100Ом.

Теперь находим сопротивления участка АВ. Сопротивление цепи резисторов, соединенных параллельно будет вычислено по формуле:

Ага, подставили в формулу наши значения для суммы резисторов R2 и R4 (Сумма равна 30 Ом и подставляется вместо формульной R1) и значение резистора R3 равное 100 Ом (Подставляется вместо формульной R2). Вычисленное значение сопротивления на участке АВ равняется 23 Ом.

Как видите выполнив несложные вычисления наша схема упростилась и свернулась и стала нам уже более знакомой.

Ну и полное сопротивление цепи будет равняться R=R1+R2=23Ом+1Ом=24Ом. Это мы нашли уже по формуле для последовательного соединения. Мы это рассматривали так что на этом останавливаться не будем.

Теперь ток на участке до разветвлений (участок Точка 10В —>>Точка А) мы сможем найти по формуле Ома.

I=U/R=10В/24Ом=0,42A . Получилось 0,42 ампера. Как мы уже обсуждали этот ток будет один на всем пути от точки максимального потенциала, до точки А. На участке А В, значение тока будет равно сумме токов с участков полученных после разделения.

Чтобы определить ток на каждом участке между точками А и В, нам нужно найти напряжение между точками А и В.

Оно как уже известно будет меньше напряжения питания 10В. Его мы найдем по формуле U=I*R=0.42A*23Ом=9,66В.

Как вы могли заметить полный ток в точе А (равный сумме токов параллельных участков) умножается на результирующее сопротивление запараллеленных (сопротивление резистора R1 мы не учитываем) участков цепи.

Теперь мы можем найти ток в цепи резисторов R2, R4. Для этого напряжение между точками А и В разделим на сумму этих двух резисторов. I=U/(R2+R4)=9.66В/ 30Ом=0,322А.

Ток в цепи резистора R3 тоже найти не сложно. I=U/R3=9.66В/100Ом=0,097А.

Как видите при параллельно соединении резисторов ток делится пропорционально значениям сопротивлений. Чем больше сопротивление резистора, тем меньше будет ток на этом участке цепи.
В тоже время напряжение между точками А и В, будет относиться к каждому из параллельных участков (напряжение U=9.66В мы использовали для расчетов и там и там ).
Здесь хочется сказать как напряжение и ток распределяются по схеме.
Как я уже говорил ток до разветвления равен сумме токов после развилки. Впрочем умный мужик Кирхгоф нам это уже рассказывал.
Получается следующее: Ток I на развилке разделится на три I1, I2, I3, а затем снова воссоединится в I как было и в самом начале, получаем I=I1+I2+I3.
Для напряжения или разности потенциалов, что есть одно и тоже будет следующее. Разность потенциалов между точками А и С (далее буду говорить напряжение AC), не равна напряжениям BE, CF,DG. В тоже время напряжения BE, CF,DG , будут равны между собой. Напряжение на участке FH вообще равно нулю, так как напряжению просто не на чем высаживаться (нет резисторов).

Думаю тему параллельного соединения резисторов я раскрыл, но если есть еще какие-то вопросы то пишите в комментариях, чем смогу помогу 🙂

Преобразование звезды в треугольник и обратно

Существуют схемы, в которых резисторы соединены так, что не совсем понятно где есть последовательное соединение а где параллельное. И как же с этим быть?

Для этих ситуаций есть способы упрощения схем и вот одни из них это преобразование треугольника в эквивалентную звезду или наоборот, если это необходимо.

Для преобразования треугольника в звезду считать будем по формулам:

Для того чтобы совершить обратное преобразование нужно воспользоваться несколько другими формулами:

С вашего позволения я не буду приводить конкретные примеры, все что требуется это только подставить в формулы конкретные значения и получить результат.

Этот метод эквивалентного преобразования будет служить хорошим подспорьем в мутных случаях, когда не совсем понятно с какой стороны подступиться к схеме. А тут порой поменяв звезду на треугольник ситуация проясняется и становится более знакомой.

Ну чтож дорогие друзья вот и все, что я хотел вам сегодня рассказать. Мне кажется эта информация будет полезной для вас и принесет свои плоды.

Хочу еще добавить, что многое из того что я здесь выложил очень хорошо расписано в книгах «Искусство схемотехники» и «Занимательная микроэлектроника», так что рекомендую прочитать обзорные статьи и скачать себе эти книжки. А будет еще лучше, если вы их раздобудете где-нибудь в бумажном варианте.

P.S. У меня на днях возникла одна идея о том как можно получить интересный способ заработка на знаниях электроники и вообще радиолюбительском хобби так что обязательно [urlspan]подпишитесь на обновления.[/urlspan]

Кроме того относительно недавно появился еще один прогрессивный способ подписки через форму сервиса Email рассылок, так что люди подписываются и получают некие приятные бонусы, так что добро пожаловать.

А на этом у меня действительно все, я желаю вам успехов во всем , прекрасного настроения и до новых встреч.

С н/п Владимир Васильев.

Конструктор ЗНАТОК 320-Znat «320 схем»

Конструктор ЗНАТОК 320-Znat «320 схем» — это инструмент, который позволит получить знания в области электроники и электротехники а также достичь понимания процессов происходящих в проводниках.

Конструктор представляет собой набор полноценных радиодеталей имеющих спец. конструктив, позволяющий их монтаж без помощи паяльника. Радиокомпоненты монтируются на специальную плату — основание, что позволяет в конечном итоге получить вполне функциональные радиоконструкции.

Используя этот конструктор можно собрать до 320 различных схем, для построения которых есть развернутое и красочное руководство. А если подключить фантазию в этот творческий процесс то можно получить бесчисленное количество различных радиоконструкций и научиться анализировать их работу. Этот опыт я считаю очень важен и для многих он может оказаться бесценным.

Вот несколько примеров того, что Вы можете сделать благодаря этому конструктору:

Летающий пропеллер;
Лампа,включаемая хлопком в ладоши или струей воздуха;
Управляемые звуки звездных войн, пожарной машины или скорой помощи;
Музыкальный вентилятор;
Электрическое световое ружье;
Изучение азбуки Морзе;
Детектор лжи;
Автоматический уличный фонарь;
Мегафон;
Радиостанция;
Электронный метроном;
Радиоприемники, в том числе FM диапазона;
Устройство, напоминающее о наступлении темноты или рассвета;
Сигнализация о том, что ребенок мокрый;
Защитная сигнализация;
Музыкальный дверной замок;
Лампы при параллельном и последовательном соединении;
Резистор как ограничитель тока;
Заряд и разряд конденсатора;
Тестер электропроводимости;
Усилительный эффект транзистора;
Схема Дарлингтона.

Сопротивление резистора

— стенограмма видео и урока

Расчет сопротивления

Поскольку сопротивление резистора зависит от материала, из которого он сделан, это учитывается в формуле для расчета сопротивления, которая математически может быть прочитана как:

В этом уравнении R обозначает сопротивление. Греческая буква ρ, похожая на букву p , обозначает удельное сопротивление материала, из которого изготовлен резистор. L обозначает длину резистора. А А обозначает площадь поперечного сечения резистора. Сопротивление измеряется в Ом.

Возможно использование двух резисторов одинакового размера из разных материалов с разным сопротивлением. Но не думайте, что сопротивление есть только у резисторов. Провода, которые сами проводят электричество, также имеют определенное сопротивление. Все, что проводит электричество, имеет определенное сопротивление.Провода обычно имеют гораздо меньшее сопротивление, чем резистор, предназначенный для защиты от электричества. Вы можете иметь сопротивление от нескольких Ом до миллионов Ом.

Вот пример расчета сопротивления углеродного резистора длиной 0,005 метра (5 миллиметров) и диаметром 0,001 метра (1 миллиметр). Этот конкретный углеродный резистор имеет удельное сопротивление 45 x 10-5 Ом-метр. По сути, мы умножаем это удельное сопротивление на 0.005 метров и разделите это на время π 0,0005 квадратных метров.

Как мы видим, этот угольный резистор имеет сопротивление примерно 2,86 Ом. Обратите внимание, что символ ома — большая греческая буква омега (Ω).

Закон Ома

Все цепи, проводящие электричество, подчиняются так называемому закону Ома. Этот закон говорит вам, как ваше напряжение и ток связаны с вашим сопротивлением.

R обозначает сопротивление, В обозначает напряжение, а I обозначает ток.Единицами измерения являются омы для сопротивления, вольт для напряжения и амперы для тока. Эта формула говорит вам, что ваше сопротивление всегда равно напряжению, деленному на ток. Вы также можете сказать, что ваше напряжение равно вашему току, умноженному на ваше сопротивление, или V = IR в форме уравнения, где R = V / I .

Итак, если ваш резистор в вашей цепи имеет сопротивление 100 Ом, а ток, протекающий по цепи, равен 0.5 ампер, тогда напряжение вашей цепи рассчитывается следующим образом:

Напряжение в вашей цепи составляет 50 В.

Расположение резисторов

Способ размещения резисторов также может по-разному изменить значение сопротивления.

Если ваши резисторы расположены последовательно, так что они соединены друг с другом, как в ожерелье, то полное или эквивалентное сопротивление является суммой значений ваших резисторов.Ток, проходящий через каждый резистор, будет одинаковым, но напряжение, протекающее через каждый резистор, разное.

Например, у вас есть резисторы на 200, 50 и 25 Ом, включенные последовательно. Общее сопротивление вашей цепи составляет 200 + 50 + 25 = 275 Ом.

Если ваши резисторы расположены параллельно, то есть каждый резистор подключен к одному источнику напряжения, то эквивалентное сопротивление находится по следующей формуле:

Напряжение для каждого резистора будет одинаковым, но ток, протекающий через каждый резистор, будет разным.

Например, у вас есть те же резисторы на 200, 50 и 25 Ом, подключенные параллельно. Общее сопротивление можно найти следующим образом:

1/200 + 1/50 + 1/25 = 1/200 + 4/200 + 8/200 = 13/200 = 1 / 15,38

Обратите внимание, как последний шаг делит числитель и знаменатель на числитель. Это дает вам единицу по общему сопротивлению. Как только вы это сделаете, ваше полное сопротивление окажется 15,38 Ом.

Итоги урока

Хорошо, давайте рассмотрим.Резистор — это кусок материала, препятствующий прохождению электрического тока. Сопротивление резистора рассчитывается по следующей формуле:

Как мы узнали, в этой формуле R означает сопротивление. Греческая буква ρ, похожая на букву p , обозначает удельное сопротивление материала, из которого изготовлен резистор. L обозначает длину резистора. И, наконец, A обозначает площадь поперечного сечения резистора.Сопротивление измеряется в омах, а ваша длина и площадь — в метрах.

Все цепи следуют закону Ома, который говорит вам, что напряжение в цепи равно току, умноженному на сопротивление, или В = IR в форме уравнения, где R = В / I . И в этом случае R обозначает сопротивление, V обозначает напряжение, а I обозначает ток. Единицами измерения являются омы для сопротивления, вольт для напряжения и амперы для тока.

Если ваши резисторы включены последовательно, то эквивалентное сопротивление, которое видит схема, является суммой значений ваших резисторов. С другой стороны, если ваши резисторы размещены параллельно, то эквивалентное сопротивление определяется путем сложения значений, обратных вашим значениям резисторов.

Резистор, конденсатор и индуктор в последовательно-параллельном соединении

Резистор, конденсатор и индуктор в последовательном и параллельном соединении — формулы и уравнения

Следующее основное и полезное уравнение и формулы можно использовать для проектирования, измерения, упрощения и анализа электрических цепей для различные компоненты и электрические элементы, такие как резисторы, конденсаторы и катушки индуктивности, соединенные последовательно и параллельно.

Сопротивление в последовательном и параллельном уравнениях

Сопротивление:

Общее эквивалентное сопротивление резисторов, подключенных последовательно или параллельно, определяется по следующей формуле:

Сопротивление последовательно:

Когда два или более двух резисторов подключены последовательно, как показано на рисунке, их эквивалентное сопротивление рассчитывается по формуле:

R _Eq = R ₁ + R ₂ + R ₃ +… R _n

Сопротивление параллельно:

, когда резисторы в параллельной конфигурации, эквивалентное сопротивление становится:

Где

R _Eq — эквивалентное сопротивление всех резисторов (R ₁, R ₂, R ₃… R _n)

Похожие сообщения:

Дельта Δ к звездам Y (Pi к Te e) Преобразование:

Межсоединение треугольник (Δ) также упоминается как межсоединение Pi , а межсоединение звезда (Y) также обозначается как межсоединение Тройник (Т) .

От треугольника (Δ) до звезды (Y) Межсоединение:

От звезды (Y) к треугольнику (Δ) Межсоединение

Для получения более подробной информации примеры, проверьте преобразование звезды в дельту и дельта в звезду.

Емкость в последовательном и параллельном уравнениях

Емкость:

Общая емкость конденсатора, подключенного параллельно и последовательно, приведена ниже:

Емкость последовательно:

Когда конденсаторы подключены последовательно В конфигурации эквивалентная емкость становится:

Параллельная емкость:

Емкость суммируется, когда они соединяются вместе в параллельной конфигурации

C _Eq = C ₁ + C ₂ + C ₃ +… C _n

Где

C _Eq — эквивалентная емкость всех конденсаторов (C ₁, C ₂, C ₃… C _n )

Похожие сообщения:

Индуктивность в последовательном и параллельном уравнениях

Индуктивность:

9 0004 Расчет полной индуктивности катушек индуктивности внутри цепи аналогичен расчету резисторов.

Последовательная индуктивность:

Когда индукторы включены последовательно, как показано на рисунке, их индуктивности складываются.

L _Eq = L ₁ + L ₂ + L ₃ +… L _n

Параллельная индуктивность:

Параллельная комбинация, эквивалентная катушки индуктивности задаются по формуле

, где

L _Eq — эквивалентная индуктивность всех катушек индуктивности (L ₁, L ₂, L ₃… L _n)

Связанные формулы и Equations Сообщений:

Тепло, рассеиваемое резисторами | Блестящая вики по математике и науке

Из микроскопической интерпретации закона Ома, сопротивление в классической формуле V = IRV = IRV = IR для тока, протекающего в цепи при заданном управляющем напряжении, может быть расширено как:

V = I (mne2τ) La, V = I (\ frac {m} {n {e} ^ {2} \ tau}) \ frac {L} {a}, V = I (ne2τm) aL,

, где mmm и eee — масса и заряд электрона соответственно, LLL и aaa — длина и площадь проводящего материала, составляющего резистор, nnn — плотность носителей заряда, а τ \ tau τ — интервал времени между два столкновения электронов в резисторе.Сопротивление также можно расширить до:

R = ρLA, R = \ frac {\ rho L} {A}, R = AρL,

, где ρ \ rhoρ — удельное сопротивление , — свойство материала резистора, а LLL и AAA — длина и площадь поперечного сечения резистора соответственно.

Неупругие столкновения электронов, движущихся по проводнику, являются причиной сопротивления. Кристаллическая структура атомов металла в проводнике препятствует прохождению через него электронов. В любой данный момент электроны имеют определенную вероятность неупругого рассеяния от металлической решетки, передавая часть своей энергии решетке в виде кинетической энергии, т.е.е. нагревать. Это рассеивание тепла в решетке, называемое нагревом Джоулей , является источником рассеивания мощности в резисторе. Обратите внимание, что хотя межэлектронные столкновения могут давать свою собственную связанную тепловую энергию движения, эта энергия остается внутренней по отношению к системе до тех пор, пока она не рассеивается в металлической решетке, которая не переносит ток.

Расчет среднего времени свободного пробега электронов, движущихся через проводник, показывает, что электроны проходят через большое количество узлов решетки, прежде чем существенно взаимодействуют с катионами металлов.Объяснение этому факту исходит из квантовой механики и дуализма волна-частица. Из-за волновой природы электрона электроны могут распространяться без неупругого рассеяния на большее расстояние через решетку, чем ожидалось, и вероятность рассеяния гораздо более чувствительна к дефектам решетки, чем плотность решетки.

Описание шума резистора

— Блог о пассивных компонентах

Источник: EDN, статья

Hugo Coolens в своей статье EDN подробно объясняет шум резистора.

Вводные курсы по шумам в электронных схемах часто начинаются с формулировки следующей формулы для шумового напряжения холостого хода резистора:

В формуле 1 k = 1,3806 x 10 ^-23 [Дж / К] — постоянная Больцмана, T — температура в Кельвинах и R — значение сопротивления в Ом.

Рисунок 1 Интерпретация формулы E _{N, RMS} = √4 kTR · BW

Давайте еще немного поясним формулу 1, посмотрев на Рисунок 1 . E _{N, RMS} — напряжение, которое показывал бы идеализированный вольтметр, измеряющий среднеквадратичное значение, если бы он имел следующие характеристики:

Входное сопротивление, равное бесконечности
Без внутреннего шума
Амплитудная характеристика, показанная на рисунке 1, с полосой пропускания в Гц, равной: BW = f _h — f _l

Вы, наверное, возразите, что это много условий; правда, но давайте сделаем вещи немного более реалистичными.Во-первых, напряжение, которое мы будем измерять, будет небольшим, поэтому нам обязательно придется ввести некоторое усиление, скажем, коэффициент усиления по напряжению A, вместо единицы. Тогда наш счетчик покажет:

Кроме того, невозможно реализовать характеристику кирпичной стены, поскольку можно доказать, что такой фильтр не является причинным. Так что давайте заменим его реализуемой характеристикой фильтра, как показано на рис. 2 .

Рисунок 2 Интерпретация формулы E _{N, RMS} для реализуемого фильтра

Если мы рассмотрим только бесконечно малую полосу пропускания d f , что аналогично применению фильтра кирпичной стены с полосой пропускания d f и усилением | H (jω) |, формула 3 преобразуется в:

Количество

называется шириной полосы, эквивалентной шуму ( NEB ) ¹.√4 kTR называется плотностью напряжения шума, представим его стильным ε , чтобы избежать путаницы с самим напряжением E . Таким образом, мы также могли написать:

Теперь давайте подробнее рассмотрим уравнение 6. Что бы произошло, если бы мы использовали характеристику фильтра с бесконечной полосой пропускания? Вы могли подумать, что можете ожидать бесконечного напряжения на выводах вашего резистора. На самом деле это, конечно, не может быть правдой. Что здесь не так? Объяснение уходит корнями в квантовые явления.Формула ε _{N, RMS} = √4 kTR — это , а не полная формула, это только приближение, точная формула:

В формуле 7 h = 6,6261 · 10 ^-34 [Джс] — постоянная Планка. Коэффициент p ( f ) стремится к нулю для f при переходе к + ∞, это сохранит значение ε _{N, RMS} конечным. Давайте проверим это для системы с бесконечной пропускной способностью:

К счастью, интеграл в предыдущей строке, называемый интегралом Бозе, имеет известное отличное решение.

Это показывает, что при сопротивлении 1 МОм и температуре 300 К напряжение никогда не может стать больше 0.41V. Вы также можете проверить, что процентная разница в E _{N, RMS} , рассчитанная по обеим формулам для ε _{N, RMS} , будет не более 1%, пока вы остаетесь ниже 500 ГГц. Конечно, вы можете возразить, что такие частоты нереальны в мире электроники, но не забывайте, что в наши дни уже созданы схемы, колеблющиеся на частотах выше 1 ТГц ². производить?

Из любопытства я проверил несколько симуляторов на основе Spice — я проверил четыре из них ³ — чтобы увидеть, насколько хорошо они моделируют шум на этих частотах.Несмотря на то, что они небрежно имитируют экстремальные частоты, такие как 10 ТГц, я заметил, что ни один из них не использует правильную модель шума резистора на этих частотах.

Несмотря на то, что это объяснение верно, более практичные люди могут с некоторым подозрением относиться к объяснениям, проистекающим из квантовых явлений. Кто мог их винить, если даже покойный великий Ричард Фейнман сказал: «Если вы думаете, что понимаете квантовую механику, то вы не понимаете квантовую механику». Таким образом, даже несмотря на то, что формула 7 объясняет, почему вы никогда не получите бесконечное напряжение на выводах резистора, в практических электронных схемах два других фактора будут определять вклад шума вашего резистора: резистор всегда будет иметь некоторую паразитную емкость и / или также будет ограничение пропускной способности.Вопрос о паразитной емкости чаще всего рассматривается при стандартном выводе среднеквадратичного значения напряжения на резисторе, подключенном параллельно конденсатору:

снова удивительный результат, когда вы видите его в первый раз, поскольку напряжение не зависит от номинала резистора. Этот результат также можно объяснить, обратившись к квантово-механическому миру, см. Шум Джонсона-Найквиста.

Однако есть также объяснение, которое больше нравится большинству электронщиков или, по крайней мере, убеждает их в результате: увеличение параллельного сопротивления добавит шум, но полоса пропускания системы уменьшится, так что общий результат останется прежним.Математически это доказать несложно. Однако означает ли это, что важна только паразитная емкость? Нет, поскольку ваш резистор обычно подключается к другим частям схемы, которые имеют ограниченную полосу пропускания, это также играет роль. Простейшим примером такой системы является резистор, включенный параллельно конденсатору, за которым следует система первого порядка, как показано на , рис. 3, .

Рисунок 3 Система с входной емкостью и усилителем первого порядка с усилением по постоянному току A ₀ с полосой пропускания BW

Если мы позвоним

, то мы можем получить выходное напряжение шума:

Формула 8 позволяет определить вклад входной емкости (или постоянной времени входа) и ширины полосы усилителя в шумовое напряжение на выходе.Обратите внимание, что когда

результат уменьшается до:

, что неудивительно. Когда

получаем в результате:

Для практических целей мы, наконец, можем вывести следующее эмпирическое правило: когда одна постоянная времени по крайней мере в 10 раз меньше другой, мы сделаем ошибку менее 5 процентов, пренебрегая меньшей постоянной времени.

Список литературы

Некоторые учебники нормализуют NEB, разделив «наш NEB» на A2 REF, где AREF — усиление на постоянном токе или на опорной частоте e.грамм. усиление в полосе пропускания.
Миниатюрный передатчик устанавливает рекорд частоты: разработан революционный передатчик терагерцового диапазона, Технический университет Дармштадта
Spice 2G6, ngspice rev 26, PSpice AD Lite из OrCAD17.2 и LTspice XVII

Номиналы стандартных резисторов

— RF Cafe

«Исследователи из Hewlett Packard Labs, где создан первый практический мемристор, изобретена новая вариация на устройство — а мемристорный лазер… «

резисторы являются одним из четырех основных типов пассивных электронных компонентов; другой три индуктора, конденсатор, а мемристор. Базовая единица сопротивления — ом (Ом).

Значения стандартного базового резистора приведены в следующих таблицах для большинства часто используемые допуски (1%, 2%, 5%, 10%), а также с типично доступными диапазонами сопротивления. Чтобы определить значения, отличные от базовых, умножьте базовое значение на 1, 10, 100, 1k или 10k.

Стандартные номиналы резисторов рассчитаны используя простую формулу, приведенную ниже. Округлите результаты до нужного числа значащие цифры (три для 1% и 2%, два для 5% и 10%). Как показано на диаграмме справа (создан в Excel), нанесение значений на логарифмический масштаб дает прямую линию из-за экспоненты в уравнении.

Пример: Расчеты показывают необходимость в резисторе 355 кОм. и допуск 1%.Посмотрите в таблице 1% и выберите значение 35,7 (ближайшее доступное стандартное значение). Умножить на 10000 для преобразования в 357 кОм.

10,0	10,2	10,5	10,7	11,0	11,3	11,5	11,8	12,1	12,4	12,7	13,0
13.3	13,7	14,0	14,3	14,7	15,0	15,4	15,8	16,2	16,5	16,9	17,4
17,8	18,2	18,7	19,1	19,6	20,0	20,5	21,0	21,5	22.1	22,6	23,2
23,7	24,3	24,9	25,5	26,1	26,7	27,4	28,0	28,7	29,4	30,1	30,9
31,6	32,4	33,2	34,0	34,8	35.7	36,5	37,4	38,3	39,2	40,2	41,2
42,2	43,2	44,2	45,3	46,4	47,5	48,7	49,9	51,1	52,3	53,6	54,9
56,2	57.6	59,0	60,4	61,9	63,4	64,9	66,5	68,1	69,8	71,5	73,2
75,0	76,8	78,7	80,6	82,5	84,5	86,6	88,7	90,9	93,1	95.3	97,6

10,0	10,5	11,0	11,5	12,1	12,7	13,3	14,0	14,7	15,4	16,2	16,9
17,8	18,7	19,6	20,5	21.5	22,6	23,7	24,9	26,1	27,4	28,7	30,1
31,6	33,2	34,8	36,5	38,3	40,2	42,2	44,2	46,4	48,7	51,1	53,6
56.2	59,0	61,9	64,9	68,1	71,5	75,0	78,7	82,5	86,6	90,9	95,3

10	11	12	13	15	16	18	20	22	24	27	30
33	36	39	43	47	51	56	62	68	75	82	91

Калькулятор цепи конденсатора резистора — Дюймовый калькулятор

Рассчитайте время заряда, энергию и характеристическую частоту или импеданс, реактивное сопротивление и угловую частоту цепи резистор-конденсатор.

Расчет энергии и времени зарядки

Расчет импеданса и реактивного сопротивления

Цепь резистор-конденсатор, или RC-цепь, представляет собой цепь с последовательно соединенными резистором и конденсатором. Конденсатор в цепи накапливает энергию, а резистор изменяет скорость заряда и разряда конденсатора. Эти схемы чаще всего используются для фильтрации формы волны и используются для создания фильтров нижних, верхних частот и полосовых фильтров.

Схема, показывающая цепь резисторного конденсатора.

Формулы RC цепей

RC-цепи имеют несколько характеристик, включая постоянную времени, накопление энергии, заряд, импеданс, емкостное реактивное сопротивление, характеристическую частоту и угловую частоту. Расчет каждой из этих характеристик схемы можно выполнить по следующим формулам.

Формула постоянной времени

Постоянная времени, выраженная как tau (τ), — это время в секундах, в течение которого конденсатор в RC-цепи достигает 63.2% заряда. Формула для расчета постоянной времени:

τ = RC

Постоянная времени τ равна сопротивлению R в омах, умноженному на емкость C в фарадах. Конденсатор достигнет заряда 63,2% за τ, 86,5% за 2τ и 99,3% за 5τ.

Энергетическая формула

Энергия, запасенная в полностью заряженном конденсаторе RC-цепи, может быть найдена по формуле:

E = CV ² 2

Энергия E в джоулях равна емкости C в фарадах, умноженной на квадрат напряжения V, деленной на два.

Формула заряда

Максимальный заряд в цепи конденсатора резистора можно найти по формуле:

Q = CV

Заряд Q в кулонах равен емкости C в фарадах, умноженной на напряжение V.

Текущая формула

Максимальный ток RC-цепи можно найти с помощью закона Ома. Формула:

I = VR

Ток I в амперах равен напряжению V, деленному на сопротивление R в омах.

Формула характеристической частоты

Характеристическая частота цепи, часто называемая обычной или циклической частотой, может быть найдена по следующей формуле:

f = 12πRC

Частота f в герцах равна 1, деленному на 2, умноженное на π, умноженное на сопротивление R в омах, умноженное на емкость C в фарадах.

Формула угловой частоты

Угловую частоту контура можно найти по формуле:

ω = 2πf

Угловая частота ω в радианах в секунду равна удвоенной π-кратной характеристической частоте f в герцах.

Формула импеданса

Импеданс RC-цепи можно найти с помощью нескольких формул:

Z = R + 1jωC
| Z | = √ (R ² + 1 (ωC) ²)

Где j — мнимая единица, Z — импеданс в омах, R — сопротивление в омах, C — емкость в фарадах, а ω — угловая частота в рад / с.

Формула емкостного реактивного сопротивления

Емкостное реактивное сопротивление RC-цепи можно найти по формуле:

X = 1ωC

Емкостное реактивное сопротивление X равно 1, деленному на угловую частоту ω, умноженную на емкость C.

Формула разности фаз

Эта формула выражает разность фаз между полным напряжением и полным током.

φ = загар ^-1 (-1ωCR)

φ — разность фаз, ω — угловая частота, C — емкость, R — сопротивление.

Цепь параллельных резисторов

и простая схема делителя тока

Формула для параллельного резистора будет нашим основным фокусом здесь. После обсуждения последовательного резистора и делителя напряжения давайте узнаем о параллельных резисторах и делении тока.Параллельный резистор относится к одному из пассивных элементов.

Вы узнаете, включены ли резисторы параллельно или последовательно, просто по их клеммному соединению. Мы называем резисторы подключенными параллельно, если их выводы соединены вместе, соответственно, от резистора к резистору.

Определение параллельной цепи

Этот параллельный резистор отличается от последовательного резистора, в котором через резисторы проходит только один прямой путь. В параллельном резисторе будет много путей от головы к голове и от хвоста к хвосту.Исходя из этого термина, параллельный резистор используется как делитель тока, а последовательный резистор — как делитель напряжения.

Поскольку ток разделяется на несколько путей или ответвлений, ток для каждой ветви может отличаться друг от друга. Но падение напряжения на каждом резисторе будет одинаковым для каждого другого. Отсюда следует, что для резисторов, включенных параллельно, они могут иметь разный ток через каждый из них, но всегда иметь одинаковое падение напряжения на каждом из них.

Зачем нам нужно изучать формулу для параллельного резистора? Вы должны знать, прочитав этот пост, пока не закончите.

Определение параллельных резисторов — это резистивная схема, в которой резисторы подключены вместе к одним и тем же узлам и образуют более одного пути тока, подключенного к одному источнику напряжения. Если вы все еще не понимаете, как мы делаем параллельную резистивную схему, мы можем найти ее ниже.

Схема параллельной цепи

Пример ниже представляет собой простой параллельный резистор в цепи. Мы используем три резистора R ₁, R ₂ и R ₃.Из объяснения выше, падение напряжения на резисторах при параллельном подключении будет одинаковым для друг друга и равным источнику напряжения.

Следовательно,

Все три резистора соединены между собой между A и B.

В отличие от последовательных резистивных цепей, где эквивалентное сопротивление является суммой всех резисторов, параллельный резистор рассчитывается по-другому. Мы используем величину, обратную сопротивлению (1 / R) для каждого сложенного резистора.

Формула для параллельного резистора

Как мы уже упоминали выше, эквивалентное сопротивление параллельных резисторов является суммой, обратной величине каждого резистора. Если резисторы, соединенные параллельно, имеют одинаковое значение, это будет очень просто.

Как мы уже упоминали выше, мы можем посмотреть на пример ниже:

Если два резистора, подключенных параллельно, имеют одинаковое сопротивление, то эквивалентное сопротивление, R _T — это половина сопротивления одного резистора. резистор.Следовательно, эквивалентное сопротивление двух резисторов, соединенных параллельно, если они имеют одинаковое сопротивление, равно R / 2. Если параллельно подключено три резистора, эквивалентное сопротивление равно R / 3 и так далее.

Помимо последовательных резисторов, этот тип цепи является наиболее распространенным типом электрических цепей. Для анализа схемы параллельного резистора мы можем использовать тот же метод для последовательного резистора, используя законы Кирхгофа и закон Ома.

Рассмотрим схему на рисунке (1),

на рисунке 1.Параллельное соединение резисторов

, при котором два резистора соединены параллельно и, следовательно, имеют одинаковое напряжение на них.

Из закона Ома

(1)

Применение KCL в узле a дает полный ток i как

(2)

Подставляя уравнение (1) в (2), мы получаем

(3)

, где R _eq — эквивалентное сопротивление резисторов, включенных параллельно:

(4)

или

(5)

Следовательно,

Эквивалентное сопротивление двух параллельных резисторов равно произведение их сопротивлений, деленное на их сумму.

Выше приведено простейшее уравнение параллельного резистора, которое мы можем использовать каждый раз, когда нам это нужно.

Следует отметить, что уравнение (5) работает только для двух параллельно подключенных резисторов.

Мы можем расширить уравнение параллельного резистора в уравнении (4) до общего случая схемы с N резисторами, включенными параллельно. Эквивалентное сопротивление составляет

(6)

Обратите внимание, что R _eq всегда меньше, чем сопротивление наименьшего резистора в параллельном соединении.Если R ₁ = R ₂ =… = R _N = R , то

(7)

Например, если 4 резистора с сопротивлением 100 Ом подключены параллельно, их эквивалентное сопротивление составляет 25 Ом.

Имейте в виду, что,

Эквивалентное сопротивление параллельных резисторов всегда меньше, чем сопротивление наименьшего резистора, подключенного к этой сети. Следовательно, эквивалентное сопротивление RT будет уменьшаться каждый раз, когда у нас есть дополнительные параллельные резисторы.

Формула проводимости для параллельной цепи

Из-за этого простого, но сложного уравнения параллельного резистора для эквивалентного сопротивления мы узнаем о новом значении, известном как проводимость (G), измеренном в Сименсах (S). Проводимость обратно пропорциональна сопротивлению, где G = 1 / R. После того, как мы получим проводимость, мы преобразуем ее обратно, чтобы получить эквивалентное сопротивление R _T параллельных резисторов.

При параллельном подключении резисторов легче использовать проводимость, чем сопротивление.

Из уравнения (6) эквивалентная проводимость для резисторов N составляет

(8)

где:

Уравнение. (8) утверждает:

Эквивалентная проводимость резисторов, подключенных параллельно, равна сумме их индивидуальная проводимость.

Это означает, что мы можем перерисовать рисунок (1) на (2), где мы заменим сопротивления на проводимости.

Эквивалентные сопротивления параллельных резисторов получаются таким же образом, как эквивалентные сопротивления последовательных резисторов.

Напротив, эквивалентные сопротивления последовательных резисторов получаются таким же образом, как эквивалентные сопротивления параллельных резисторов.

Рисунок 2. Эквивалентное сопротивление или проводимость

Следовательно, эквивалентная проводимость G _eq последовательно соединенных резисторов N составляет

(9)

Учитывая общий ток i, входящий в узел a на рисунке. (1) с одинаковые значения напряжения, получаем

(10)

Мы определяем параллельные резисторы как резисторы, соединенные между собой между двумя одинаковыми точками.Сам параллельный резистор имеет различные формы схемы.

Как найти ток в параллельной цепи

Поскольку ток в параллельной цепи зависит от ее сопротивления, теперь мы узнаем, как найти ток в параллельной цепи. Токи I ₁, I ₂,…, I _n , входящие в параллельный путь резисторов, зависят от сопротивления этой ветви. Полный ток I _T представляет собой сумму токов в параллельных ветвях.Если сопротивление между ветвями равно, то токи также будут разделены поровну.

Если R ₁ = R ₂, то I ₁ = I ₂ = 0,5 I _T . Это означает, что общий ток I _T делится поровну на две ветви. Если сопротивление R ₁ отличается от сопротивления R ₂, тогда нам нужно рассчитать I ₁ и I ₂ по-разному.Даже если напряжения на ветвях равны, ток может отличаться по закону Ома.

Для примера параллельной схемы давайте посмотрим на схему ниже и попытаемся найти все токи,

Поскольку R ₁ и R ₂ имеют разные значения, тогда токи I ₁ и I ₂ гарантированно имеют разные значения. Помните один из законов Кирхгофа?

Текущие законы Кирхгофа гласят:

Общий ток, выходящий из узла, равен току, входящему в тот же самый узел.

Следовательно,
Полный ток в цепи может быть выражен как:

После этого мы будем использовать закон Ома для расчета тока, поступающего в каждую ветвь через резисторы. I ₁ — это входящий ток R ₁, а I ₂ — входящий ток R ₂. Источник напряжения В _с имеет 12 В, и мы получаем:

И мы получаем полный ток,

Чтобы прояснить это, мы используем закон Ома для вычисления I _T из В. _s и R _T .
Общее сопротивление R _T равно

Тогда полный ток I _T равен

Следовательно, это проясняет наши расчеты.

Мы заключаем, что

Уравнение делителя тока

Комбинируя уравнения. (1) и (10) мы получаем уравнение текущего делителя.

(11)

, который показывает, что полный ток i распределяется между резисторами обратно пропорционально их сопротивлениям.

Это известно как принцип деления тока , а схема на рисунке (1) известна как делитель тока .

Обратите внимание, что больший ток проходит через меньшее сопротивление.

Рисунок 3. Короткое замыкание и разрыв в параллельном соединении

Предположим, что один из резисторов на рисунке (1) равен нулю, скажем, R ₂ = 0; поэтому R ₂ — это короткое замыкание, как видно на рисунке. (3a).

Из уравнения.(11), R ₂ = 0 означает, что i ₁ = 0, i ₂ = i . Это означает, что весь ток i обходит R ₁ и протекает через короткое замыкание R ₂ = 0, путь с наименьшим сопротивлением.
При коротком замыкании цепи, как показано на рисунке (3a), обратите внимание, что:

Эквивалентное сопротивление R _экв = 0
Весь ток протекает через короткое замыкание.

В качестве другого крайнего примера, где R ₂ = ∞, то есть R ₂ является разомкнутой цепью, как показано на рисунке (3b).
Ток по-прежнему течет по пути с наименьшим сопротивлением, R ₁.
Уравнение (11) преобразуется в

(12)

В общем, если в делителе тока есть N проводников, параллельных току источника i , N -й проводник будет иметь ток

(13)

Очень удобно комбинировать резисторы последовательно и параллельно в одно эквивалентное сопротивление R _eq .

Такое эквивалентное сопротивление должно иметь те же значения тока и напряжения, что и исходная сеть на выводе.

Примеры параллельного резистора

Давайте рассмотрим приведенный ниже пример для лучшего понимания
Найдите R _eq для схемы на рисунке.