Резонансная частота: физическое явление, формулы и применение в музыке

Что такое резонансная частота. Как рассчитать резонансную частоту. Какие условия необходимы для возникновения резонанса. Как используется резонанс в музыкальных инструментах. Почему резонанс важен для акустики.

Понятие резонансной частоты и условия возникновения резонанса

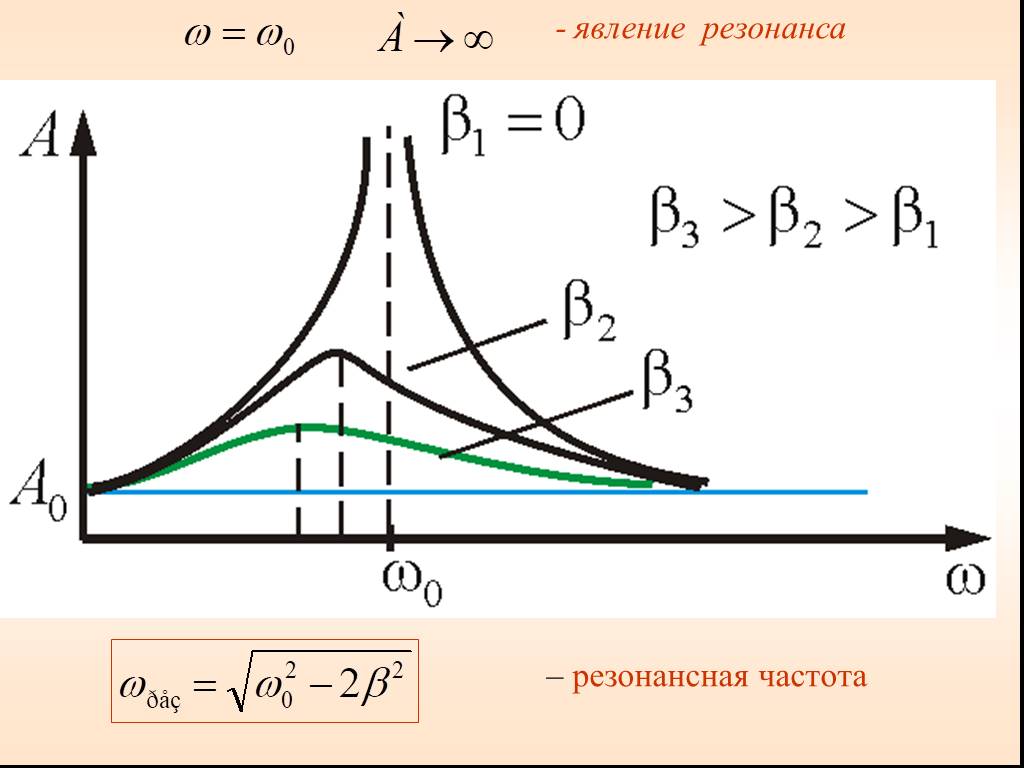
Резонансная частота — это частота, на которой колебательная система наиболее эффективно поглощает энергию внешних воздействий. При совпадении частоты внешней силы с собственной частотой системы возникает явление резонанса, характеризующееся резким увеличением амплитуды колебаний.

Основные условия возникновения резонанса:

• Наличие колебательной системы с собственной частотой колебаний
• Воздействие на систему периодической внешней силы
• Совпадение или близость частоты внешней силы к собственной частоте системы
• Малое затухание колебаний в системе

Резонанс может возникать в механических, электрических, акустических и других колебательных системах. Это явление широко используется в технике, но может быть и опасным, вызывая разрушения конструкций.

Формула резонансной частоты и ее применение

Для простейшей колебательной системы (гармонического осциллятора) резонансная частота рассчитывается по формуле:

f = 1 / (2π√(LC))

где:

• f — резонансная частота в герцах
• L — индуктивность в генри
• C — емкость в фарадах

Эта формула применяется для расчета резонансной частоты электрических колебательных контуров. Для механических систем используются аналогичные формулы с учетом параметров жесткости и массы.

Резонанс в акустических системах и музыкальных инструментах

В акустике резонанс играет ключевую роль в формировании звука музыкальных инструментов. Основные примеры использования резонанса:

• Струнные инструменты — резонанс корпуса усиливает колебания струн
• Духовые инструменты — резонанс воздушного столба в трубе
• Ударные инструменты — резонанс мембран и полостей

Настройка музыкальных инструментов основана на подборе резонансных частот элементов конструкции. Это позволяет усиливать нужные частоты и формировать характерный тембр звучания.

Расчет резонансной частоты струны

Для колеблющейся струны резонансная частота основного тона определяется формулой:

f = (1/2L) * √(T/μ)

где:

• f — частота колебаний в герцах
• L — длина струны в метрах
• T — сила натяжения струны в ньютонах
• μ — линейная плотность струны в кг/м

Эта формула показывает, как частота звука струнного инструмента зависит от его параметров. Укорачивание струны или увеличение ее натяжения повышает частоту звука.

Резонанс в воздушных столбах музыкальных инструментов

В духовых инструментах резонанс возникает в воздушном столбе внутри трубы. Для трубы, открытой с обоих концов, резонансные частоты определяются формулой:

f = nv / 2L

где:

• f — частота колебаний
• n — номер гармоники (1, 2, 3…)
• v — скорость звука в воздухе
• L — длина трубы

Для трубы, закрытой с одного конца:

f = (2n-1)v / 4L

Эти формулы позволяют рассчитать частоты звуков, издаваемых духовыми инструментами в зависимости от их размеров.

Применение резонанса в акустике помещений

В акустике помещений учет резонансных явлений необходим для создания качественного звучания. Основные аспекты применения:

• Расчет собственных частот помещения для предотвращения нежелательных резонансов
• Использование резонаторов для поглощения определенных частот
• Проектирование формы и размеров концертных залов с учетом резонансных характеристик
• Применение рассеивающих и поглощающих элементов для управления резонансами

Правильный учет резонансных явлений позволяет создавать помещения с отличной акустикой для музыки и речи.

Нежелательные эффекты резонанса и способы их предотвращения

Хотя резонанс широко используется в технике и музыке, он может вызывать и нежелательные последствия:

• Разрушение конструкций при совпадении частоты внешних воздействий с собственной частотой
• Возникновение вибраций в механизмах
• Появление акустических помех в электронных устройствах

Для предотвращения негативных эффектов резонанса применяются следующие методы:

• Изменение собственной частоты конструкции
• Использование демпферов для гашения колебаний
• Применение динамических гасителей колебаний
• Экранирование от внешних воздействий

Правильный учет резонансных явлений на этапе проектирования позволяет создавать надежные и эффективные технические системы.

Заключение: важность понимания резонанса

Резонанс — фундаментальное физическое явление, играющее важную роль во многих областях науки и техники. Понимание механизмов возникновения резонанса и умение рассчитывать резонансные частоты необходимо для:

• Проектирования музыкальных инструментов
• Создания акустических систем
• Расчета прочности конструкций
• Разработки электронных устройств
• Анализа колебательных процессов в природе

Изучение резонансных явлений остается актуальной задачей современной физики и техники, открывая новые возможности для создания совершенных акустических систем и музыкальных инструментов.

Резонансная частота | это… Что такое Резонансная частота?

Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.

Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений. Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам. При этом в математическом аспекте не очень существенно, являются ли собственные числа комплексными или действительными. В физическом аспекте явление резонанса обычно связывают только с колебательными динамическими системами. Наиболее ярко понятие явления резонанса развито в современной теории динамических систем. Примером является известная теория Колмогорова-Арнольда-Мозера. Центральная проблема этой теории — вопрос сохранения квазипериодического или условно-периодического движения на торе (теорема КАМ). Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям синхронизма.

Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы

Содержание 1 Механика 2 Электроника 3 Акустика 3. 1 Струна 4 Примечания 5 См. также 6 Ссылки

Механика

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:

,

где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.

В основе работы механических резонаторов лежит преобразование кинетической энергии в потенциальную и обратно. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах.

Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Электроника

В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален.

Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения ωL = 1/ωC, где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.

Акустика

Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, мембрана у барабанов.

Струна

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:

,

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.

Увеличение натяжения струны и уменьшение её длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

Примечания

См. также

• Диссипативная структура
• Солитон
• Интерференция
• Журавлёв, Виктор Филиппович (см. в кн. «Прикладные методы в теории колебаний» (1988, совместно с Д. М. Климовым))

Ссылки

Richardson LF (1922), Weather prediction by numerical process, Cambridge.

Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457-472.

Бломберген Н. (1965), Нелинейная оптика, М.: Мир — 424 с.

Захаров В.Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431-453.

Арнольд В.И. (1979), Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны, ред. А.В. Гапонов-Грехов, М.: Наука, 116-131.

Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275-309.

Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.

Филлипс O.М. (1984), Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. М.: Мир, 297-314.

Журавлёв В.Ф., Климов Д.М. (1988), Прикладные методы в теории колебаний, М.:Наука

Сухоруков А.П. (1988), Нелинейные волновые взаимодействия в оптике и радиофизике, М. : Наука — 232 с.

Брюно А.Д. (1990), Ограниченная задача трех тел, М.:Наука

Резонансная частота | это… Что такое Резонансная частота?

Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.

Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений. Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам. При этом в математическом аспекте не очень существенно, являются ли собственные числа комплексными или действительными. В физическом аспекте явление резонанса обычно связывают только с колебательными динамическими системами. Наиболее ярко понятие явления резонанса развито в современной теории динамических систем. Примером является известная теория Колмогорова-Арнольда-Мозера. Центральная проблема этой теории — вопрос сохранения квазипериодического или условно-периодического движения на торе (теорема КАМ). Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям синхронизма.

Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы

Содержание 1 Механика 2 Электроника 3 Акустика 3.1 Струна 4 Примечания 5 См. также 6 Ссылки

Механика

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:

,

где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.

В основе работы механических резонаторов лежит преобразование кинетической энергии в потенциальную и обратно. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Электроника

В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения ωL = 1/ωC, где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.

Акустика

Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, мембрана у барабанов.

Струна

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:

,

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.

Увеличение натяжения струны и уменьшение её длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

Примечания

См. также

• Диссипативная структура
• Солитон
• Интерференция
• Журавлёв, Виктор Филиппович (см. в кн. «Прикладные методы в теории колебаний» (1988, совместно с Д. М. Климовым))

Ссылки

Richardson LF (1922), Weather prediction by numerical process, Cambridge.

Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457-472.

Бломберген Н. (1965), Нелинейная оптика, М.: Мир — 424 с.

Захаров В.Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431-453.

Арнольд В.И. (1979), Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны, ред. А.В. Гапонов-Грехов, М.: Наука, 116-131.

Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275-309.

Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.

Филлипс O.М. (1984), Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. М.: Мир, 297-314.

Журавлёв В.Ф., Климов Д.М. (1988), Прикладные методы в теории колебаний, М.:Наука

Сухоруков А.П. (1988), Нелинейные волновые взаимодействия в оптике и радиофизике, М. : Наука — 232 с.

Брюно А.Д. (1990), Ограниченная задача трех тел, М.:Наука

Формула резонансной частоты — GeeksforGeeks

Резонансная частота определяется как частота контура, когда значения емкостного импеданса и индуктивного импеданса становятся равными. Она определяется как частота, при которой тело или система достигает наивысшей степени колебаний. Резонансный контур состоит из параллельно соединенных конденсатора и катушки индуктивности. Он в основном используется для создания заданной частоты или для учета определенной частоты в сложной цепи. Резонансная частота существует только тогда, когда цепь является чисто резистивной.

Формула

Формула резонансной частоты представляет собой обратную величину произведения удвоенного числа пи и квадратного корня из произведения индуктивности и емкости. Он представлен символом f _или . Его стандартной единицей измерения являются герцы или секунды (Гц или с ^-1 ), а его размерная формула определяется как [M ⁰ L ⁰ T ^-1 ].

f _или = 1/2π√(LC)

где,

f _o – резонансная частота,

L – индуктивность цепи,

C – емкость цепи.

Вывод

Предположим, у нас есть цепь, в которой резистор, катушка индуктивности и конденсатор соединены последовательно под источником переменного тока.

Значение сопротивления, индуктивности и емкости равно R, L и C. 

Теперь известно, что полное сопротивление цепи Z определяется выражением,

0002 Z = R + jωL – j/ωC

Z =R + j (ωL – 1/ωC)

Для выполнения условия резонанса цепь должна быть чисто резистивной. Следовательно, мнимая часть импеданса равна нулю.

ωl — 1/ωc = 0

ωl = 1/ωc

ω ² = 1/lc

Положение ω = 1/2πf _O , мы получаем

(1/2πf _O ), мы получаем

(1/2πf _{). ² = 1/LC}

f _o = 1/2π√(LC)

Отсюда выводится формула для резонансной частоты.

Проблемы с образцами

Задача 1. Рассчитайте резонансную частоту для цепи индуктивности 5 ч и емкость 3 F.

Решение:

. 3

Используя формулу, которую мы имеем,

f _о = 1/2π√(LC)

= 1/ (2 × 3,14 × √(5 × 3))

= 1/24,32

90,0042 = 1/24,32

1 Гц

Задача 2. Вычислить резонансную частоту для цепи с индуктивностью 3 Гн и емкостью 1 Ф.

Решение:

Мы имеем,

L = 3

C = 1

Используем формулу, которую мы имеем,

F _O = 1/2πлья (2 × 3,14 × √(3 × 1))

= 1/10,86

= 0,092 Гц

Задача 3. Вычислить резонансную частоту цепи с индуктивностью 4 Гн и емкостью 2,5 Ф. Решение:

Имеем,

L = 4

C = 2,5

Используя формулу, которую мы имеем,

f _o = 1/2π√(LC)

= 1/(2 × 3,14 × √(4 × 2,5))

= 1/60,38

= 0,159 Гц

Задача 4. Рассчитайте индуктивность цепи, если емкость равна 4 Ф, а резонансная частота равна 0,5 Гц.

Решение:

Имеем,

f _o = 0,5

C = 4

Используя формулу f

3 _o = 1/2π√(LC)

=> L = 1/4π ² Cf _o ²

= 1/ (4 × 3,14 × 3,14 × 900,3 0,5 0,5) = 1/39,43

= 0,025 Гн

Задача 5. Вычислить индуктивность цепи, если емкость равна 3 Ф, а резонансная частота равна 0,023 Гц.

Решение:

Имеем,

f _o = 0,023

C = 3

Используя формулу имеем,

F _O = 1/2π√ (LC)

=> L = 1/4π ² CF _O ²

= 1/(4 × 3,14 × 3.14 × 3 × 0,023 × 0,023 )

= 1/0,0199

= 50,25 Гн

Задача 6. Вычислить емкость цепи, если индуктивность равна 1 Гн, а резонансная частота равна 0,3 Гц.

Решение:

Имеем,

f _o = 0,3

L = 1

Используя формулу имеем,

f _o = 1/2π√(LC)

=> C = 1/4π ² Lf _o ²

х 3 х 3 х 3,0 х 3,14 )

= 1/3,54

= 0,282 Ф

Задача 7. Вычислить емкость цепи, если индуктивность равна 0,1 Гн, а резонансная частота равна 0,25 Гц.

Решение:

Имеем,

f _o = 0,25

L = 0,1

Используя формулу имеем,

F _O = 1/2π√ (LC)

=> C = 1/4π ² LF _O ²

= 1/(4 × 3,14 × 3,14 × 0,25 × 0,25 )

= 1/0,246

= 4,06 F

Учебное пособие по физике: резонанс

применить это понимание к анализу музыки и музыкальных инструментов. До сих пор в этом разделе применялись принципы звуковых волн для обсуждения битов, музыкальных интервалов, акустики концертного зала, различий между шумом и музыкой и производства звука музыкальными инструментами. В Уроке 5 основное внимание будет уделено применению математических соотношений и концепций стоячей волны к музыкальным инструментам. Будут исследованы три основные категории инструментов: инструменты с вибрирующими струнами (включая гитарные струны, струны скрипки и струны фортепиано), инструменты с открытым концом (включая духовые инструменты, такие как тромбон, и деревянные духовые инструменты, такие как флейта и блокфлейта), а также инструменты с закрытым концом (в том числе органная труба и бутылки из-под оркестр поп-бутылки ). Четвертая категория — вибрационные механические системы (к которым относятся все ударные инструменты) — обсуждаться не будет. Эти категории инструментов могут быть необычными для некоторых; они основаны на сходстве их моделей стоячих волн и математических соотношениях между частотами, создаваемыми инструментами.

 

Резонанс

Как упоминалось в Уроке 4, музыкальные инструменты приходят в вибрационное движение с их естественной частотой, когда человек ударяет, ударяет, наигрывает, щипает или каким-либо образом мешает объекту. Каждая собственная частота объекта связана с одним из множества паттернов стоячих волн, по которым этот объект может вибрировать. Собственные частоты музыкального инструмента иногда называют гармоники прибора. Инструмент может быть вынужден вибрировать на одной из своих гармоник (с одной из его моделей стоячей волны), если другой взаимосвязанный объект толкает его на одной из этих частот. Это известно как -резонанс , когда один объект, вибрирующий с той же собственной частотой, что и второй объект, заставляет этот второй объект колебаться.

Слово резонанс происходит от латыни и означает «звучать» — издаваться вместе с громким звуком. Резонанс является частой причиной возникновения звука в музыкальных инструментах. Одна из наших лучших моделей резонанса в музыкальном инструменте — это резонансная трубка (полая цилиндрическая трубка), частично заполненная водой и приводящаяся в вибрацию камертоном. Камертон — это объект, который заставил воздух внутри резонансной трубы войти в резонанс. Поскольку зубцы камертона вибрируют на своей собственной частоте, они создают звуковые волны, которые воздействуют на отверстие резонансной трубы. Эти сталкивающиеся звуковые волны, создаваемые камертоном, заставляют воздух внутри резонансной трубки вибрировать с той же частотой. Тем не менее, в отсутствие резонанса звук этих вибраций недостаточно громкий, чтобы его можно было различить. Резонанс возникает только тогда, когда первый объект вибрирует с собственной частотой второго объекта. Так что, если частота, с которой вибрирует камертон, не идентична одной из собственных частот столба воздуха внутри резонаторной трубы, резонанса не произойдет, и два объекта не будут звучать вместе с громким звуком. Но расположение уровня воды можно изменить, поднимая и опуская резервуар с водой, тем самым уменьшая или увеличивая длину столба воздуха. Как мы узнали ранее, увеличение длины колебательной системы (в данном случае воздуха в трубе) увеличивает длину волны и уменьшает собственную частоту этой системы. И наоборот, уменьшение длины колебательной системы уменьшает длину волны и увеличивает собственную частоту. Таким образом, поднимая и опуская уровень воды, собственная частота воздуха в трубке может быть согласована с частотой, с которой вибрирует камертон. Когда совпадение достигнуто, камертон заставляет столб воздуха внутри резонансной трубы вибрировать с собственной частотой, и достигается резонанс. Результатом резонанса всегда является большая вибрация, то есть громкий звук.

Другая распространенная физическая демонстрация, которая служит прекрасной моделью резонанса, — знаменитая демонстрация «поющего жезла». В его центре удерживается длинный полый алюминиевый стержень. Будучи обученным музыкантом, учитель лезет в канифольный мешок, чтобы подготовиться к мероприятию. Затем с большим энтузиазмом он медленно проводит рукой по всей длине алюминиевого стержня, заставляя его издавать громкий звук. Это пример резонанса. Когда рука скользит по поверхности алюминиевого стержня, трение скольжения между рукой и стержнем вызывает вибрации алюминия. Вибрации алюминия заставляют столб воздуха внутри стержня вибрировать с собственной частотой. Совпадение колебаний воздушного столба с одной из собственных частот поющего жезла вызывает резонанс. Результатом резонанса всегда является большая вибрация, то есть громкий звук.

 

Знакомый шум моря , который слышен, когда к уху подносят морскую ракушку, также объясняется резонансом. Даже в кажущейся тихой комнате существуют звуковые волны разного диапазона частот. Эти звуки в основном неслышны из-за их низкой интенсивности. Этот так называемый фоновый шум наполняет морскую раковину, вызывая вибрации внутри раковины. Но у морской раковины есть набор собственных частот, на которых она будет вибрировать. Если одна из частот в комнате заставляет воздух внутри морской раковины вибрировать на своей собственной частоте, создается резонансная ситуация. И всегда результатом резонанса является большая вибрация, то есть громкий звук. На самом деле, звук достаточно громкий, чтобы его можно было услышать. Итак, в следующий раз, когда вы услышите звук моря в ракушке, помните, что все, что вы слышите, это усиление одной из многочисленных фоновых частот в комнате.

 

Резонанс и музыкальные инструменты

Музыкальные инструменты воспроизводят выбранные звуки таким же образом. Духовые инструменты обычно состоят из мундштука, прикрепленного к длинной трубке, наполненной воздухом. Трубку часто скручивают, чтобы уменьшить размер инструмента. Металлическая трубка просто служит контейнером для столба воздуха. Именно колебания этой колонны производят звуки, которые мы слышим. Длину вибрирующего столба воздуха внутри трубки можно регулировать либо сдвигая трубку для увеличения и уменьшения ее длины, либо открывая и закрывая отверстия, расположенные вдоль трубки, чтобы контролировать, где воздух входит и выходит из трубки. Духовые инструменты предполагают вдувание воздуха в мундштук. Вибрации губ относительно мундштука производят диапазон частот. Одна из частот в диапазоне частот соответствует одной из собственных частот столба воздуха внутри духового инструмента. Это заставляет воздух внутри колонны совершать резонансные колебания. Результатом резонанса всегда является большая вибрация, то есть громкий звук.

Деревянные духовые инструменты работают аналогичным образом. Только источником вибраций являются не губы музыканта, прижатые к мундштуку, а вибрация трости или деревянной планки. Работа деревянного духового инструмента часто моделируется на уроках физики с помощью пластиковой соломинки. Концы соломинки обрезаются ножницами, образуя сужающийся язычок . Когда воздух продувается через тростник, тростник вибрирует, создавая турбулентность с диапазоном вибрационных частот. Когда частота вибрации трости совпадает с частотой вибрации столба воздуха в соломинке, возникает резонанс. И еще раз, результатом резонанса является большая вибрация — тростник и воздушный столб звучат вместе, производя громкий звук. Как будто это было недостаточно глупо, длину соломинки обычно укорачивают, отрезая небольшие кусочки от ее противоположного конца.