Шаговое напряжение что это такое как передвигаться. Шаговое напряжение: что это такое и как безопасно передвигаться в зоне его действия

Что такое шаговое напряжение. Как оно возникает. Какую опасность представляет для человека и животных. Как правильно передвигаться в зоне шагового напряжения. Какие меры безопасности необходимо соблюдать.

Что такое шаговое напряжение

Шаговое напряжение — это разность электрических потенциалов между двумя точками на поверхности земли, находящимися на расстоянии шага человека (около 0,8 м). Оно возникает при растекании электрического тока в земле от упавшего на нее провода, находящегося под напряжением.

Основные характеристики шагового напряжения:

• Возникает в радиусе до 20 м от места касания провода с землей
• Максимальное значение — у самого провода
• Уменьшается по мере удаления от провода
• Зависит от силы тока и удельного сопротивления грунта
• Особенно опасно во влажном грунте

Как возникает шаговое напряжение

Шаговое напряжение может возникнуть в следующих случаях:

1. При обрыве и падении на землю провода действующей линии электропередачи
2. При замыкании токоведущих частей электроустановок на землю
3. При ударе молнии в землю или наземный объект (дерево, опору ЛЭП и т.д.)

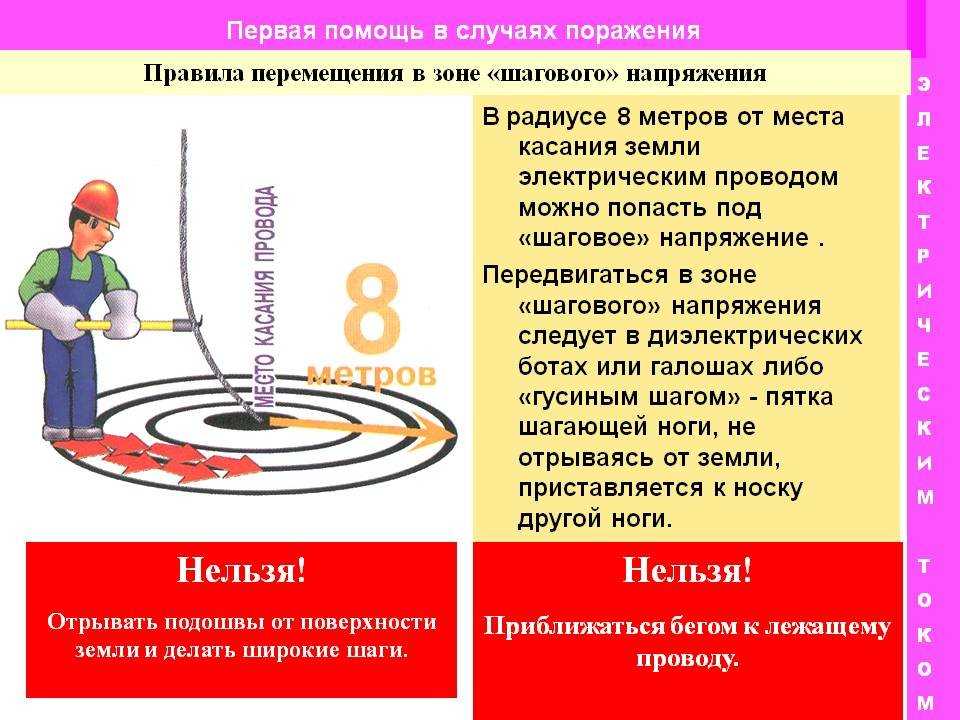
Схема возникновения шагового напряжения:

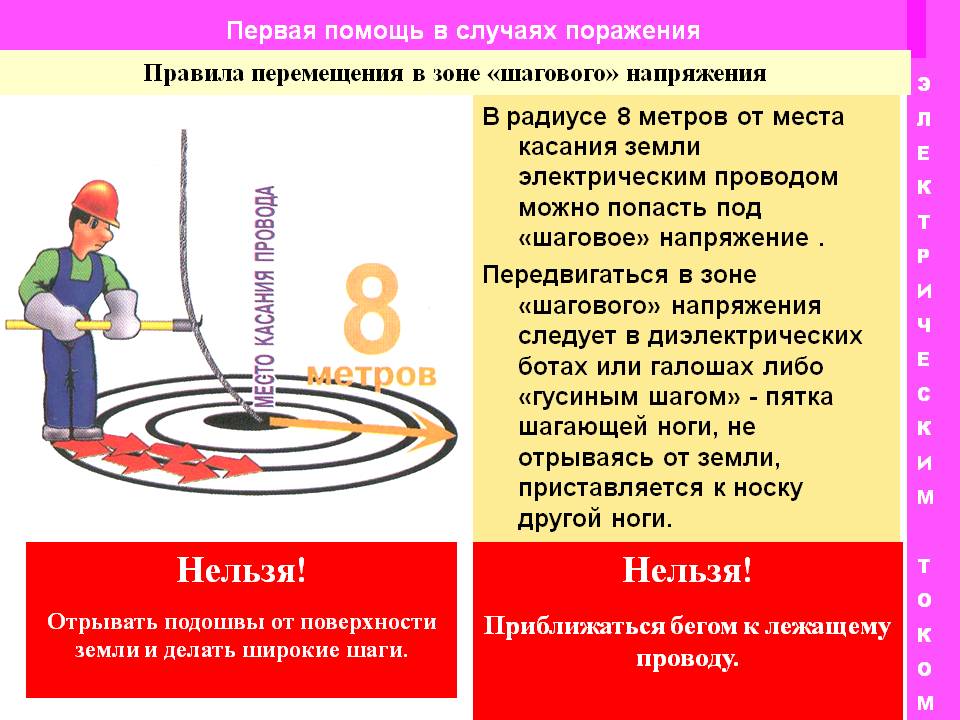
1. Электрический ток от провода растекается в земле во все стороны
2. Вокруг точки контакта образуется зона повышенного потенциала
3. Потенциал уменьшается по мере удаления от провода
4. Между двумя точками на поверхности возникает разность потенциалов

Опасность шагового напряжения для человека и животных

Шаговое напряжение представляет серьезную опасность для людей и животных, оказавшихся в зоне его действия. Основные факторы риска:

• Поражение электрическим током при попадании под напряжение шага
• Непроизвольное сокращение мышц ног, приводящее к падению
• Образование цепи тока через тело после падения
• Тяжелые электротравмы вплоть до летального исхода

Особенно опасно шаговое напряжение для крупных животных из-за большого расстояния между передними и задними ногами. Нередки случаи гибели скота от воздействия шагового напряжения вблизи упавших проводов.

Правила передвижения в зоне шагового напряжения

При попадании в зону действия шагового напряжения необходимо соблюдать следующие правила передвижения:

1. Передвигаться только мелкими шажками, не отрывая ног от земли
2. Держать ступни ног вместе
3. Выходить из опасной зоны «гусиным шагом»
4. Прыгать на одной ноге, если невозможно передвигаться «гусиным шагом»
5. Не делать широких шагов
6. Не бежать

«Гусиный шаг» выполняется так: пятка шагающей ноги, не отрываясь от земли, приставляется к носку другой ноги. Это позволяет свести к минимуму разность потенциалов между ногами.

Меры безопасности в зоне шагового напряжения

При обнаружении упавшего провода или попадании в зону шагового напряжения необходимо соблюдать следующие меры безопасности:

• Не приближаться к лежащему на земле проводу ближе 8-10 метров
• Не прикасаться к проводу или окружающим металлическим предметам
• Не пытаться самостоятельно убрать провод
• Предупредить окружающих об опасности
• Вызвать аварийную службу
• Покинуть опасную зону «гусиным шагом»

Категорически запрещается приближаться к пострадавшему, попавшему под шаговое напряжение, без средств защиты. Сначала необходимо обесточить электроустановку.

Первая помощь пострадавшему от шагового напряжения

Алгоритм оказания первой помощи при поражении шаговым напряжением:

1. Освободить пострадавшего от действия электрического тока
2. Вызвать скорую медицинскую помощь
3. Проверить наличие сознания, дыхания, пульса
4. При необходимости начать сердечно-легочную реанимацию
5. Обработать возможные электроожоги и травмы
6. Обеспечить покой до приезда врачей

Помощь пострадавшему должен оказывать человек, знающий правила освобождения от действия электрического тока и способы оказания первой помощи.

Профилактика поражения шаговым напряжением

Основные меры профилактики поражения шаговым напряжением:

• Соблюдение правил электробезопасности
• Установка защитного заземления и зануления электроустановок
• Применение устройств защитного отключения (УЗО)
• Своевременный ремонт и обслуживание электросетей
• Ограждение опасных зон вокруг электроустановок
• Вынос заземлителей молниеотводов за пределы территории
• Обучение персонала правилам электробезопасности

Знание правил поведения в зоне шагового напряжения и соблюдение мер электробезопасности позволяет существенно снизить риск поражения электрическим током.

Шаговое напряжение что это такое? Меры по защите, определение по ПУЭ

Человек и любое живое существо, попадая в зону воздействия электрического тока, рискуют получить электротравму и даже при определенных обстоятельствах лишиться жизни. Прохождение такого тока через тело вызывается во время прикосновения к таким предметам:

• неизолированному проводу, по которому протекает ток;
• проводу, у которого повреждена изоляция;
• корпусу электрооборудования с неисправной изоляцией или к оголенным контактам;
• металлическому предмету, который оказался под напряжением.

Поражение электротоком может произойти в случае обрыва провода на линии передачи электроэнергии напряжением 0,4 В и выше, если она не отключена от энергопоставляющей компании. Общеизвестный факт – земля это проводник электротока, особенно когда она влажная. Точка на грунте, находящаяся в зоне растекания тока, имеет потенциал (напряжение) определенной величины. Живое существо, попадая под действие электрического тока в момент, когда ноги на определенном расстоянии касаются 2 точек земли, может оказаться пораженным током.

Эту разницу потенциалов называют шаговым напряжением. И чем она больше, т.е. чем больше расстояние между ногами, тем опаснее действие тока. На шаговое напряжение оказывает влияние удельное сопротивление земли, ее состояние, сила протекающего тока и путь прохождения по организму живого существа.

Шаговое напряжение возникает при ударе молнии в металлическую опору, молниеотвод, высокое дерево или любой металлический предмет. Если ноги расставлены на определенную величину, то ток молнии, растекаясь в земле, проходит и под ногами живого существа. Заряд входит в одну ногу и уходит, проходя через тело и другую в землю. Это тот случай, когда возникает напряжение шаговое и живое существо находится под его влиянием. У человека обычно шаг э0,6 ÷ 0,8 м, у животного гораздо больше, что усиливает воздействие на организм живого существа.

Наибольшее значение шагового напряжения, которое может поразить живое существо, находится вблизи лежащего на земле оборванного кабеля или провода, наименьшее – на расстоянии 20 м и больше. Опасной зоной, проводящей смертельной величины электрический ток, считается в радиусе 8 ÷ 10 м от лежащего электропровода.

При попадании в зону действия шагового напряжения, необходимо придерживаться таких правил:

• не касаться лежащего на земле провода;
• не приближаться к человеку или живому существу;
• не касаться руками и телом лежащих металлических предметов;
• не трогать и не тормошить живое существо.

Во время грозы нельзя прятаться под деревьями, стоять под опорами электропередач, держать в руках металлические предметы. Именно они притягивают молнию.

Если человек оказался в зону действия шагового напряжение, то он должен знать как правильно из нее выходить.

Необходимо передвигаться гусиным шагом, т.е. не отрывать подошвы обуви от земли и носок одной ноги приставлять к пятке другой. Таким шагом, медленно покинуть зону, величина которой должна быть не менее 8 м.

При поражении живого существа в районе действия шагового напряжения в первую очередь необходимо попытаться обесточить объект, если это возможно. Для этого необходимо вырубить в щите рубильник, УЗО, автомат или вынуть вилку электрооборудования или прибора из розетки.

Необходимо помнить, что влажная земля увеличивает радиус действия тока и учитывать этот фактор при покидании зоны шагового напряжения.

Если в этой зоне упал человек, то его необходимо правильно вывести в безопасное место. Для этого необходимо убедиться, что на теле человека не лежит провод. Если он там есть, то в первую очередь необходимо его убрать. Для этого надо гусиными шагами приблизиться к лежащему проводу или кабелю и с помощью сухой длинной палки (обязательно смухой) отбросить провод. Затем, передвигаясь все тем же гусиным шагом, ухватившись за одежду лежащего, перетянуть его в безопасную зону.

Далее необходимо поступить таким образом:

• вызвать скорую помощь;
• сообщить об аварии в энергопоставляющую компанию;
• приступить к выполнению искусственного дыхания с закрытым массажем сердца. Эти действия необходимо выполнять до приезда скорой помощи.

Не пренебрегайте данными выше сведениями и советами и тогда, даже попав в зону действия шагового напряжения, вы сможете спасти себя или других в этой ситуации. При подозрение на неисправность электроустановки обращайтесь к специалистам нашей электротехнической лаборатории!

Шаговое напряжение, что это такое? Электробезопасность

Здравствуйте, дорогие читатели. В этой статье мы вам расскажем, про шаговое напряжение, а так же рассмотрим правила перемещения в зоне шагового напряжения. И так начнём. Электричество никаких признаков присутствия опасности не проявляет – нет ни запаха, ни видимых причин для беспокойства, ни каких-либо других проявлений, которые могли бы вызвать тревогу или беспокойство. Поэтому человек узнает о том, что попал в зону воздействия электрического тока только тогда, когда уже слишком поздно.

Электрический ток поражает внезапно, когда человек оказывается включенным в электрическую цепь прохождения тока. Возможностью прохождения электрического тока через тело человека могут послужить непреднамеренное прикосновение к неизолированному проводу (или с поврежденной изоляцией), корпуса устройства или прибора с неисправной изоляцией и любого металлического предмета, случайно оказавшегося под напряжением, а с другой стороны – прикосновении к заземленным предметам, земли и т. д.

Кроме того существует опасность поражения током при попадании под «шаговое напряжение» — это напряжение возникающее при обрыве и падении провода на землю действующей линии электропередач 0,4 кВ и выше. Путь протекания тока не прекращается, если линия электропередач не была отключена. Земля является проводником электрического тока и становится как бы продолжением провода электропередачи. Любая точка на поверхности земли, находящаяся в точке растекания получает определенный потенциал, который уменьшается по мере удаления от точки соприкосновения провода с землей.

   Шаговое напряжение

Попадание под действие электрического тока происходит в момент, когда ноги человека касаются двух точек земли, имеющих разные электрические потенциалы. Поэтому шаговое напряжение – это разница потенциалов между двумя точками соприкосновения с землей, чем шире шаг – тем больше разница потенциалов и тем вероятнее поражение электрическим током. Шаговое напряжение зависит от удельного сопротивления грунта и силы протекающего через него тока.

Опасность шагового напряжения

Напряжение между двумя точками поверхности земли, от стоящими друг от друга на расстоянии шага (0,7-0,8 м), в зоне растекания токов замыкания в радиусе до 20 м случайно оборванного электрического провода, называется шаговым напряжением. Наибольшую величину шаговое напряжение будет иметь при подходе человека к упавшему проводу, а наименьшее — при нахождении его на расстоянии 20 м и более от него. При попадании под шаговое напряжение возникают непроизвольные судорожные сокращения мышц ног и как следствие этого падение человека на землю. В этот момент прекращается действие на человека шагового напряжения и возникает иная, более тяжелая ситуация: вместо нижней петли в теле человека образуется новый, более опасный путь тока, обычно от рук к ногам и создается реальная угроза смертельного поражения током. При попадании в область действия шагового напряжения необходимо выходить из опасной зоны минимальными шажками или прыжками на одной ноге.

Особо опасно шаговое напряжение для крупного рогатого скота, т. к. расстояние шага у этих животных очень велико и соответственно велико напряжение, под которое они попадают. Нередки случаи гибели скота от шагового напряжения.

Рядом с проводом высокого напряжения на поверхности земли в радиусе 8 метров образуется опасная зона, проводящая электрический ток – зона «шагового» напряжения.

Правила перемещения в зоне «шагового» напряжения

НЕЛЬЗЯ

Приближаться бегом или обычным шагом к лежащему проводу или человеку на земле!

НЕЛЬЗЯ

Отрывать подошвы от поверхности земли и делать широкие шаги!

Передвигаться следует только «гусиным шагом» — пятка шагающей ноги, не отрываясь от земли, приставляется к носку другой ноги.

НЕДОПУСТИМО

Прикасаться к пострадавшему или к металическим предметам без предварительного обесточивания!

НЕОБХОДИМО

Как можно быстрее отключить электричество с помощью выключателя, рубильника, вынуть вилку из розетки и т. д.

Способы защиты, электробезопасность

Если вы увидите лежащий на земле провод – ни в коем случае нельзя к нему приближаться. Опасная зона может быть от 5-8 метров вокруг точки соприкосновения провода с землей и больше, в зависимости от класса напряжения линии и состояния земли (мокрая земля увеличивает пространство растекания электрического тока).

При ударе молнии в дерево, молниеотвод или опору электропередач электрический ток поступает в землю и растекается в грунте во все стороны до нескольких десятков метров. В таких местах и может быть шаговое напряжение. То же самое происходит и возле упавшего на землю электрического провода, находящегося под напряжением. Представим себе, что разряд молнии пришелся в дерево, вблизи которого в это время стоял человек. Электрический ток молнии, попадая в землю и растекаясь в ней, проходит и под ногами человека. Если ноги расставлены, то ток входит в одну ногу и, пройдя через тело, уходит в землю через другую. Это и есть шаговое напряжение, в этом случае человек находится под шаговым напряжением.

Чтобы человек не подвергался воздействию тока, там где шаговое напряжение, необходимо все устройства защитного заземления размещать там, где нет людей. В частности, молниеотводы в сельской местности следует заземлять не ближе 4 метров от стен домов и обязательно их ограждать.

Во время грозы надо держаться подальше от опор электропередач, нельзя стоять вблизи высоких деревьев, особенно на открытой местности. Это необходимо и потому, что возле любого выделяющегося на поверхности земли предмета (дерево, мачта, опора ЛЭП, молниеотвод) во время грозы создаются условия, при которых молния устремляется именно к этому предмету, где может случиться шаговое напряжение. Как правило, она поражает все, находящееся в радиусе десятков метров.

При поражении молнией человека, там где произошло шаговое напряжение, пострадавшему надо обязательно сделать искусственное дыхание и закрытый массаж сердца. И немедленно доставить в лечебное учреждение или вызвать «скорую помощь».

В энергетике существует такой термин как «Техника безопасности» – он появился не просто так. Каждая строчка этого свода правил безопасности на действующих и отключенных электроустановках имеет свою историю, которая закончилась плачевно. Поэтому не стоит пренебрегать этими простыми советами, чтобы не попасть под действие электрического тока совершенно неожиданно для себя.

 

Будем рады, если подпишетесь на наш Блог!

[wysija_form id=»1″]

RC переходная характеристика | Spinning Numbers

Пошаговый ответ $\text{RC}$ — самая популярная статья на Spinning Numbers. Презентация состоит из следующих четырех статей:

Переходная характеристика RC — интуиция

Переходная характеристика RC — вывод

Принудительная реакция

Теорема о дифференциальном уравнении — существенная часть вывода переходной характеристики

---

Это моя оригинальная статья RC Step Response, сочетающая в себе интуицию и деривацию. Теперь он обновлен и расширен в виде отдельных статей, перечисленных выше. Рекомендую обновленные статьи.

---

RC Step Response (оригинальная статья)

Когда что-то меняется в цепи, напряжения и токи приспосабливаются к новым условиям. Если изменение представляет собой резкий шаг, реакция называется пошаговой реакцией . Эта пошаговая реакция происходит в цифровых устройствах миллиарды раз каждую секунду. Это означает, что это самая важная аналоговая схема в цифровой электронике.

Мы применяем резкое изменение напряжения в цепи резистор-конденсатор $(\text{RC})$ и наблюдаем, что происходит с напряжением на конденсаторе, $\goldC{v(t)}$.

Мы вводим метод вынужденной плюс естественной реакции для решения сложного неоднородного дифференциального уравнения, моделирующего ступенчатую схему $\text R\text C$.

Прежде чем углубляться в реакцию на шаг, вы можете просмотреть естественную реакцию RC — интуиция и естественную реакцию RC — вывод.

Автор Вилли Макаллистер.

---

Содержимое

• Интуиция
  • Исходное состояние
  • Переходный период
  • Конечное состояние
  • Резюме интуиции
• Формальный вывод переходной характеристики $\text{RC}$
  • Почему так сложно решить?
  • Принудительная реакция плюс естественная реакция
  • Суперпозиция
  • Решение управляемой схемы
  • Принудительный ответ
  • Естественная реакция
  • Всего ответов
• Информированная интуиция 9{-t/\text{RC}}$

  Где $\text V_\text S$ — высота входного шага, а $\text V_0$ — пусковое напряжение на конденсаторе.

  По сути, это означает, что напряжение начинается с его начального значения, $\text V_0$, и заканчивается с его конечным значением, $\text V_\text S$. Между ними напряжение имеет экспоненциальную форму с постоянной времени $\text{RC}$.

  ---

  Пошаговый ввод — это распространенный способ немного «подтолкнуть» схему, чтобы посмотреть, что она делает. Это говорит нам довольно много о свойствах схемы.

  Вот схема, которую мы собираемся изучить,

  Вход представляет собой резкий скачок напряжения, начинающийся с $\text V_0$ и мгновенно увеличивающийся до $\text V_{\text S}$ при $t = 0$ . Мы хотим найти напряжение на конденсаторе $\goldC{v(t)}$ как функцию времени.

  шаг мгновенный

  Ступенчатая функция — идеальная математическая идея. Напряжение имеет два значения: $\text V_0$ и $\text V_{\text S}$. Промежуточных значений нет. Когда мы рисуем ступеньку вертикальной оранжевой линией в точке $t = 0$, это просто графическая связь между верхней и нижней горизонтальными линиями. Вертикальная линия не означает, что при $t = 0$ существуют промежуточные значения напряжения. Технически ступенчатая функция не соответствует определению математической функции, так как есть странность при $t=0$.

  В реальном мире ступенчатые функции всегда имеют некоторый конечный наклон. Мы по-прежнему называем это шагом, если наклон действительно крутой по сравнению с откликом схемы $\text{RC}$. Это достаточно близко к идеальному шагу, если он выглядит как шаг в интересующей нас шкале времени.

  Интуиция

  Исходное состояние

  Как всегда, прежде чем что-либо произойдет, мы начнем с просмотра состояния схемы.

  До $t = 0$ источник напряжения обеспечивает постоянное напряжение $\text V_0$. В далеком прошлом заряд стекал на пластины конденсатора, и напряжение на конденсаторе росло. В конце концов, напряжение на резисторе, $\text V_0 -v$, стало равным $0$ и ток прекратился.

  Начальное состояние схемы: $i(0) = 0$ и $v(0) = \text V_0$.

  Переходный период

  После шага схема выполняет свои настройки. Время между начальным состоянием и конечным состоянием называется переходным периодом . Регулировка, которую производит схема, называется переходной характеристикой . Поскольку наш вход представляет собой шаг, его также называют ответом на шаг .

  Мы уже изучали схему $\text{RC}$, когда вычисляли естественный отклик. Мы узнали, что естественный отклик $\text{RC}$ имеет характерную экспоненциальную форму. Когда мы запускаем схему с шагом, мы можем ожидать, что $i(t)$ и $v(t)$ будут иметь некоторое сходство с естественным откликом.

  переходный период , вероятно, будет какой-то плавной кривой.

  Конечное состояние

  Теперь прыгайте намного позже по времени, чтобы waaaay после шага. Входное напряжение было $\text V_\text S$ в течение долгого времени. Давайте разберемся, где заканчиваются напряжение и ток. По цепи протекал ток. На конденсаторе появляется все больше и больше заряда, что приводит к повышению его напряжения.

  В какой-то момент возрастающее напряжение на конденсаторе $v$ становится равным $\text V_\text S$. Когда это происходит, напряжение на резисторе $\text V_\text S -v$ становится $0$. Подумайте о законе Ома, когда напряжение равно нулю. Больше нет причин для протекания тока, поэтому он останавливается.

  конечное состояние схемы: $i(\infty) = 0$ и $v(\infty) = \text V_\text S$.

  Краткий обзор интуиции

  Напряжение начинается с начального значения и заканчивается при ступенчатом напряжении, заданном входом. Между начальным и конечным состояниями напряжение и ток совершают интересный переход (показаны три возможности). Цепь начинается без тока и заканчивается без тока. Между ними какой-то ток течет от источника к конденсатору.

  Далее мы приходим к точному пониманию переходной характеристики.

  Формальный вывод переходной характеристики $\text{RC}$

  Существует другой эквивалентный способ рисования этой схемы. Мы меняем источник напряжения на постоянный $\text V_{\text S}$ и вставляем переключатель, чтобы вызвать скачок. Начальное напряжение подается непосредственно на конденсатор,

  Эта версия схемы лучше соответствует математике, поскольку начальное условие $v(0) = \text V_0$ более очевидно.

  как туда попадает $\text V_0$?

  Я просто хочу, чтобы вы поверили, что я могу зарядить конденсатор, чтобы получить $\text V_0$. Если вам просто нужно знать, вот схема, которая может это сделать,

  Оба переключателя срабатывают одновременно. Тот, что справа открывается, а тот, что слева, закрывается при $t = 0$.

  Мы моделируем цепь, записывая уравнение для токов, протекающих из верхнего правого узла, используя закон тока Кирхгофа,

  $\begin{массив}{cccc} i_\text R && + && i_\text C &= 0 \\ \\ \dfrac{v — \text V_\text S}{\text R} && + && \text C\,\dfrac{dv}{dt}&= 0 \end{массив}$

  Давайте немного изменим условия, чтобы отформатировать его как дифференциальное уравнение,

  $\dfrac{v}{\text R} — \dfrac{\text V_\text S}{\text R} + \text C\ ,\dfrac{dv}{dt} = 0$

  $\text C\,\dfrac{dv}{dt} + \dfrac{v}{\text R} = \dfrac{\text V_\text S} {\ text R} $

  $ \ dfrac {dv} {dt} + \ dfrac {v} {\ text {RC}} = \ dfrac {\ text V_ \ text S} {\ text {RC}} \ qquad $ начальное условие: $v(0) = \text V_0$

  Это дифференциальное уравнение, которое мы должны решить.

  Почему так сложно решить?

  Между этим уравнением и уравнением, полученным нами для естественной реакции, есть важное отличие. Справа стоит $\text V_\text S/\text{RC}$ вместо $0$. $\text V_\text S/\text{RC}$ не связан с $v$ или производным от $v$. Из-за этого мы говорим, что это уравнение неоднородно . Решение неоднородного дифференциального уравнения — не самая простая вещь на свете. На самом деле это боль в шее.

  Причина, по которой это трудно решить, заключается в том, что есть два источника энергии. Входной сигнал и внутренняя энергия, хранящиеся в конденсаторе, проявляются в дифференциальном уравнении. Проблема в том, что они никак не связаны друг с другом. Входной сигнал может быть любым. Отсутствие взаимосвязи делает проблему слишком сложной, чтобы решить ее сразу.

  Наша стратегия, как обычно, состоит в том, чтобы разбить проблему на части. Мы собираемся разбить схему на две более простые схемы. Одна версия будет игнорировать накопленную энергию, а другая версию будет игнорировать входную энергию. Затем мы воспользуемся суперпозицией, чтобы собрать две схемы обратно в одну.

  Принудительный ответ плюс естественный ответ

  Теперь мы опишем стратегию, которую вы, возможно, не видели раньше. Мы разделяем сложную задачу на две более простые, разбивая вынужденную реакцию и естественную реакцию . Раздельное решение вынужденной реакции и естественной реакции приведет нас к ответу гораздо быстрее, чем прямое нападение на неоднородное уравнение.

  Что такое принудительный ответ ? Вход заставляет вывод куда-то идти. В нашем случае это то место, где в конечном итоге заканчивается напряжение конденсатора (после того, как вся внутренняя энергия рассеется). «Назначение» принудительной реакции зависит от входной принудительной функции. Когда мы думаем о вынужденной реакции, мы игнорируем внутреннюю накопленную энергию.

  Что такое естественная реакция ? Естественная реакция говорит нам, что схема делает «естественно», когда ее внутренняя энергия рассеивается. «Назначение» естественной реакции — исчезнуть. Нулевое напряжение и нулевой ток. Когда мы думаем о естественной реакции, мы игнорируем входной сигнал.

  Используя суперпозицию, мы комбинируем (складываем) вынужденную и естественную реакции, чтобы получить полную историю, называемую общей реакцией . Вынужденная реакция накладывает свою волю на схему, в то время как естественная реакция сообщает нам, что происходит, когда система переходит в конечное состояние. Принудительный ответ приводит к тому, что естественный ответ имеет место назначения, отличное от нуля.

  Суперпозиция

  Почему мы можем это сделать? Как мы можем оправдать эту стратегию? Это работает благодаря суперпозиции. Всякий раз, когда у вас есть схема с двумя источниками энергии, такими как две батареи, или входной источник плюс некоторая внутренняя энергия, возможность использования суперпозиции должна прийти вам в голову.

  Суперпозиция работает в любой цепи, состоящей из линейных компонентов (резисторы, конденсаторы, катушки индуктивности), питаемой от идеального источника. Эта принудительная стратегия плюс естественная стратегия — отличный пример суперпозиции в действии.

  $v_t = v_f + v_n$

  Индексы $t$, $f$, $n$ обозначают полную, вынужденную и естественную реакции.

  $\begin{массив}{с л с с} && \underline{\text{Начальные условия}}& \underline{\text{Входные данные}} \\ & v_f \,\text{принудительный ответ} & 0 & {in(t)} \\ + &v_n \,\text{естественный ответ} & \text{i.c.} & 0 \\ = &\overline{v_t \,\text{общий ответ}\phantom{xxx}} & \text{i.c.’s} & {in(t)} \end{массив}$

  Внутренне накопленная энергия называется начальные условия или i.c.’s.

  математический словарь

  Математики используют следующие термины. Вы можете увидеть их на уроке линейной алгебры.

  $\begin{массив}{с л с с} && \underline{\text{Начальные условия}}& \underline{\text{Входные данные}} \\ & \text{частное решение} & 0 & {in(t)} \\ + &\text{однородный раствор} & \text{i.c.} & 0 \\ = & \overline{\text{полное решение}\phantom{xxx}} & \text{i. c.’s} & {in(t)} \end{массив}$

  Однородный раствор также можно назвать дополнительным раствором .

  Еще математический жаргон,

  Наше дифференциальное уравнение представляет собой полное
  неоднородное обыкновенное дифференциальное уравнение первого порядка с постоянными коэффициентами .

  • Однородный* означает, что уравнение содержит $v$ и производные от $v$, и ничего больше. В частности, нет постоянного термина.
  • Неоднородный означает, что существует некоторый термин, который не является $v$ или одной из его производных. В нашем уравнении есть член $\text V_{\text S}$, не связанный с $v$.
  • Первый порядок означает, что старшей производной является первая производная $dv/dt$.
  • Постоянный коэффициент означает, что значения компонентов $(\text{R, C})$ постоянны и не меняются с течением времени. Это также называется временным инвариантом , и вы можете увидеть систему, описываемую аббревиатурой LTI для линейного временного инварианта . LTI означает, что если вы запустите схему сегодня и завтра с одинаковыми начальными условиями, она будет делать одно и то же оба дня. Это хорошая собственность.
  • Обычный означает, что существует только одна независимая переменная, $t$.

  Решение управляемой цепи

  Шаги для решения схемы, управляемой внешним входом,

  • Решите вынужденную реакцию с начальными условиями, установленными на $0$.
  • Решите естественный ответ, введя значение $0$.
  • Добавьте принудительную реакцию к естественной реакции, чтобы получить общую реакцию.
  • Используйте начальные условия для разрешения любых неизвестных констант.

  Вынужденная реакция

  Для вынужденной реакции $\goldC{v_f(t)}$ мы хотим найти любое решение дифференциального уравнения, и нам не нужно обращать внимание на начальное условие в начале Шаг. Это ключ к тому, чтобы найти вынужденную реакцию, не сойдя с ума. Это то же самое, что сказать, что мы ищем конечное состояние спустя долгое время после того, как исходная накопленная энергия рассеялась.

  Принудительная реакция часто выглядит как ввод плюс его производные. Обычно он имеет ту же форму, что и входные данные, масштабированные с некоторым коэффициентом.

  Угадайте решение и попробуйте его: Поскольку вход является константой после замыкания переключателя, давайте предположим, что принудительная реакция также является константой,

  $v_{f} = K_f$, где $K_f$ — некоторое число .

  Подставьте предложенное решение в дифференциальное уравнение и посмотрите, что получится,

  $\dfrac{dK_f}{dt} + \dfrac{K_f}{\text{RC}} = \dfrac{\text V_\text S} {\text{RC}}$

  Главный член является производной от константы, поэтому он становится равным $0$. Это оставляет нам

  $\dfrac{K_f}{\text{RC}} = \dfrac{\text V_\text S}{\text{RC}}$

  Таким образом, вынужденное дифференциальное уравнение верно, если

  $v_{ f} = K_f = \text V_\text S$

  Принудительный ответ на ступенчатый ввод выглядит следующим образом:

  Принудительный ответ выглядит точно так же, как ввод. (Это происходит не всегда.) Обратите внимание, как отклик силы решает уравнение, но полностью пропускает начальное условие, $v(0) = \text V_0$. Это нормально. Об этом позаботится естественная реакция. Принудительный ответ говорит нам, что через долгое время напряжение на конденсаторе будет $\text V_{\text S}$.

  На этом и других графиках я использую шаг напряжения с $V_0 = 2\,\text V$ и $\text V_{\text S} = 6\,\text V$.

  Что произойдет, если догадка окажется неверной?

  Как это выглядит, если вы угадываете решение, и оно не работает?

  Вы угадываете решение, например, $v(t) = K\text{(что-то)}$. Затем вы проверяете его, подставляя в дифференциальное уравнение. Ваша догадка работает, если вы можете найти константу $K$, и она на самом деле оказывается константой.

  В качестве примера предположим, что вы угадали решение $v(t) = K\cdot t$ (вместо $v(t) = K)$. Когда вы подставляете v(t) в дифференциальное уравнение,

  $\dfrac{dKt}{dt} + \dfrac{Kt}{\text{RC}} = \dfrac{\text V_\text S}{\text{RC}}$

  Вы получаете,

  $K + Kt = V/\text{RC}$

  Когда вы решаете это за $K$, вы не можете избавиться от этого срока. Это говорит о том, что $K$ зависит от времени, поэтому оно непостоянно. Это провал для предлагаемого решения.

  Естественная реакция

  Теперь решим естественную реакцию. (Мы проработали полный вывод в естественном отклике RC — вывод. Вывод ниже довольно быстрый.) Для естественного отклика мы используем начальные условия, но подавляем (выключаем, устанавливаем на ноль) ввод.

  Отключение ввода означает замену источника напряжения на короткое замыкание. Напряжение на коротком замыкании равно $0$. (Если вход поступает от источника тока, мы заменим его разомкнутой цепью. Дополнительные сведения о подавлении источников см. в разделе «Суперпозиция».) 9{st}$ никогда не становится $0$. Если любой из них станет $0$, ответ будет скучным. Однако мы получаем нетривиальное решение, если

  $s + \dfrac{1}{\text{RC}} = 0$

  система. В будущем мы увидим их гораздо больше. Решите характеристическое уравнение относительно $s$ (это также называется «найти корни характеристического уравнения»).

  $s=-\dfrac{1}{\text{RC}}$

  Это дает нам общую форму естественного отклика, 9{-t/\text{RC}}$

  Естественный отклик представляет собой экспоненциальную кривую, скорость спуска которой определяется произведением $\text{RC}$. Нам еще нужно выяснить конкретное значение $K_n$. Мы сделаем это через мгновение, как часть общего ответа.

  Общий ответ

  Принудительный ответ учитывал входной сигнал.
  Естественная реакция учитывала начальные условия.
  Теперь мы объединяем их, чтобы получить общий ответ с учетом обоих, 9{-t/\text{RC}}$

  Использование начальных условий для нахождения $K_n$

  Это точка, в которой мы используем начальные условия для нахождения $K_n$. Мы должны знать, каким должно быть напряжение в определенный момент времени. Мы знаем, что при $t = 0$ напряжение должно быть $v_t = \text V_0$. (Общее напряжение отклика , а не только естественный отклик.) Давайте сделаем $t = 0$ и заменим $v_t$ на $\text V_0$ в уравнении полного отклика,

  $\text V_0 = \text V_\ текст S + K_n\,e^{-0/\text{RC}}$ 9{-t/\text{RC}}\right )$

  Вам не нужно запоминать уравнение для переходного процесса. Вы знаете, что происходит,

  • Вывод начинается с некоторого значения перед шагом.
  • При достижении шага выходное напряжение направляется к месту назначения, возрастая (или падая) с гладкой экспоненциальной формой, управляемой постоянной времени $\text{RC}$.
  • Вывод заканчивается на каком-то новом значении.

  Это аналоговая схема, которую хорошо понимают все разработчики компьютерного оборудования. Он устанавливает ограничение скорости, с которой может работать цифровая система. Резистор идет от управляющего затвора плюс проводка. Емкость поступает от проводки плюс входной контакт ведомого затвора.

  Проверка концепции

  Предположим, что чуть позже входное напряжение сделает еще один шаг в сторону уменьшения, от $\text V_{\text S}$ обратно до $\text V_0$.

  Предположим, что $\text V_0 = 2\,\text V$ и $\text V_{\text S} = 6\,\text V$. Пусть $\text R = 3\,\text K\Omega$, $\text C = 0,4\,\mu\text F$.

  Как реагирует напряжение на конденсаторе?

  $v(t) = $ ________

  показать ответ

  Интересующим моментом является шаг вниз, поэтому переназначьте $t=0$ как время шага вниз. Перемещая $t=0$, мы можем использовать приведенное выше выражение ступенчатого отклика. Роли высокого и низкого напряжения меняются местами, так что вы можете думать об этом так, 9{-t/1.2\,\text{мс}}$

  Имитационная модель

  Для дальнейшего изучения запустите эту имитационную модель цепи.

  • Щелкните DC в верхней строке меню, чтобы выполнить статический анализ постоянного тока. Каково начальное напряжение на конденсаторе? Каков начальный ток?
  • Щелкните TRAN , чтобы запустить анализ переходных процессов (напряжение в зависимости от времени). См. переходную характеристику $\text{RC}$ для напряжения и тока.
  • Двойной щелчок по источнику напряжения. Измените начальное и конечное напряжения и посмотрите, что произойдет. Что произойдет, если начальное напряжение выше конечного?
  • Изменить источник напряжения со ступенчатого на прямоугольный с частотой $50\,\text{Гц}$. TRAN снова за 50$\,\text{мсек}$. Сравните и противопоставьте шаг вниз шагу вверх. Какая разница? Что такое же?
  • Измените частоту прямоугольного сигнала на $200\,\text{Гц}$ и смоделируйте за $25\,\text{мс}$. Что происходит? Доходит ли напряжение до $\text V_\text S$?
  • Уменьшите страницу со схемой и создайте копию схемы рядом с оригиналом. Попробуйте разные значения для $\text R$ и $\text C$ в новой схеме. Поставьте щупы на два напряжения (удалите щуп тока). Смоделируйте и сравните оба напряжения на одном графике.

  Резюме

  Мы решили схему резистор-конденсатор, управляемую ступенчатым напряжением. Мы использовали закон тока Кирхгофа, чтобы создать дифференциальное уравнение, представляющее цепь. Затем мы решили ее суперпозицией методом вынужденного плюс естественного отклика .

  • Принудительная реакция — это то, что схема делает в ответ на ввод с начальными условиями, установленными на ноль.

  • Естественная реакция 9{-t/\text{RC}}$

    $\text V_\text S$ — шаговое напряжение, а $\text V_0$ — напряжение, с которого начинается конденсатор.

    анализ цепи – переходная характеристика RC и определение напряжения на конденсаторе

    Задавать вопрос

    спросил 2 года 10 месяцев назад

    Изменено 2 года, 9несколько месяцев назад

    Просмотрено 123 раза

    \$\начало группы\$

    У меня есть эта задача с этой схемой:

    и вопрос:

    Сначала я посмотрел, что произойдет, когда t = 0:

    Для начала, Vc(0) = 0 В, причина потому что t = 0, а до этого переключатель был разомкнут очень долгое время, что приводит к тому, что конденсатор не успел зарядиться, и поэтому на конденсаторе 0 В. 9(-t/τ)

    И затем я посмотрел, что произойдет, когда t = ∞:

    Если я позволю цепи работать в течение длительного времени, это означает, что конденсатор будет действовать как разомкнутая цепь. Это приводит к тому, что напряжение на клеммах a и b будет напряжением на конденсаторе.

    Vc(∞) = Vab

    Что дало мне эту схему:

    Редактировать: я неправильно поставил 6 А на ВА, но, конечно, это должно быть 6 В. Я хочу рассчитать Vab, и мой главный вопрос заключается в том, могу ли я использовать правило делителя напряжения и рассчитать его как:

    10000(R2)/(10000(R2)+5000(R3)) * 6 В = 4 В

    или нужно учитывать и R1? Должен ли я думать по-другому?

    • анализ цепи
    • переходная характеристика

    \$\конечная группа\$

    1

    \$\начало группы\$

    Вы делаете это сложным образом, когда на самом деле вы можете преобразовать три резистора в один резистор, и источник напряжения становится 3 вольта. Таким образом, источник напряжения 6 вольт, R1 и R2 образуют делитель потенциала, который имеет напряжение холостого хода 3 вольта.