Что такое сила тока, мощность и напряжение. Как они связаны между собой. Какие формулы используются для их расчета. Как применять эти понятия на практике при работе с электрическими цепями.
Основные понятия электротехники: сила тока, напряжение и мощность
Сила тока, напряжение и мощность являются фундаментальными понятиями в электротехнике. Понимание их сути и взаимосвязи крайне важно для работы с электрическими цепями и устройствами.
Что такое сила тока?
Сила тока — это количество электрического заряда, проходящего через поперечное сечение проводника за единицу времени. Измеряется в амперах (А). Чем больше сила тока, тем интенсивнее поток электронов в проводнике.
Что такое напряжение?
Напряжение — это разность электрических потенциалов между двумя точками электрической цепи. Измеряется в вольтах (В). Напряжение можно представить как «давление», заставляющее электроны двигаться по проводнику.
Что такое мощность?
Мощность — это скорость совершения работы или преобразования энергии. В электротехнике мощность показывает, сколько электрической энергии потребляется или вырабатывается за единицу времени. Измеряется в ваттах (Вт).

Взаимосвязь силы тока, напряжения и мощности
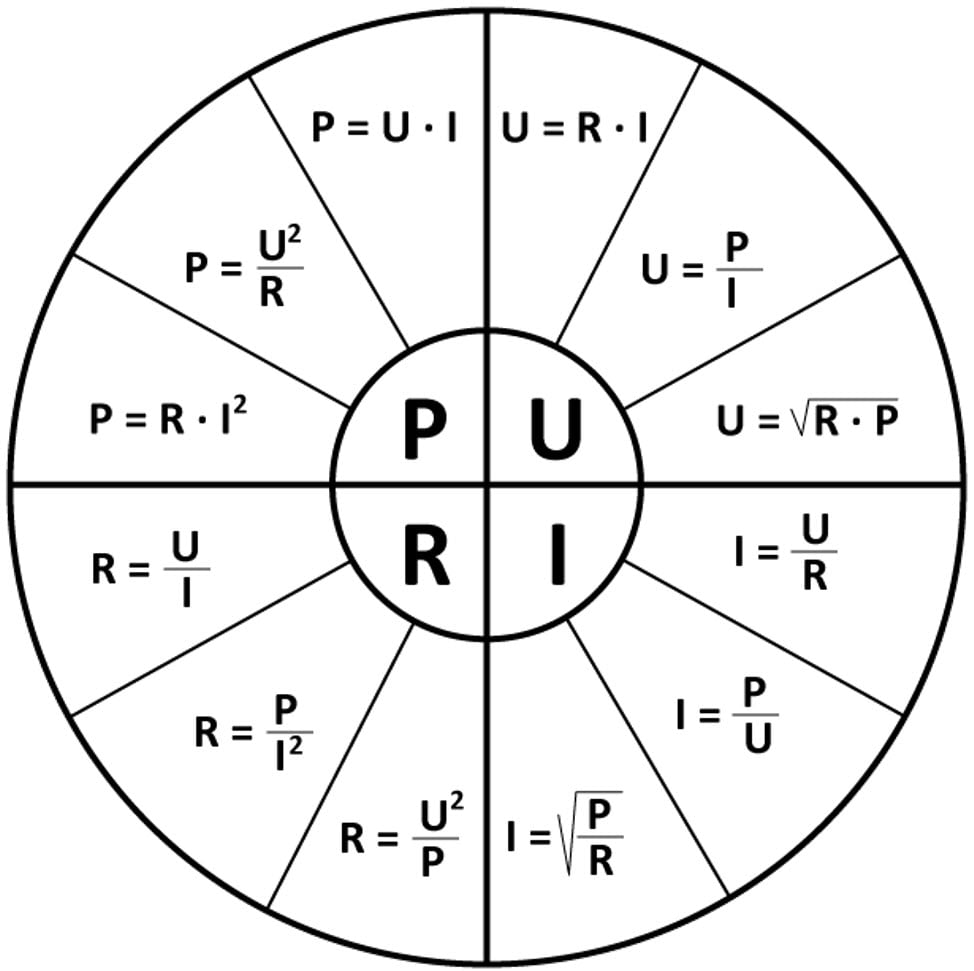
Сила тока, напряжение и мощность тесно связаны между собой. Их взаимосвязь описывается законом Ома и формулой электрической мощности.
Закон Ома
Закон Ома устанавливает связь между силой тока, напряжением и сопротивлением:
I = U / R
где I — сила тока (А), U — напряжение (В), R — сопротивление (Ом).
Формула электрической мощности
Мощность связана с силой тока и напряжением следующей формулой:
P = U * I
где P — мощность (Вт), U — напряжение (В), I — сила тока (А).
Практическое применение понятий силы тока, напряжения и мощности
Понимание взаимосвязи силы тока, напряжения и мощности крайне важно при работе с электрическими цепями и устройствами. Рассмотрим несколько практических примеров.
Расчет параметров электрической цепи
Зная два параметра из трех (сила тока, напряжение, мощность), можно легко рассчитать третий:
- I = P / U — сила тока через мощность и напряжение
- U = P / I — напряжение через мощность и силу тока
- P = U * I — мощность через напряжение и силу тока
Выбор электрических компонентов
При выборе электрических компонентов (резисторов, конденсаторов, транзисторов и т.д.) необходимо учитывать их номинальные параметры по току, напряжению и мощности. Превышение этих параметров может привести к выходу компонента из строя.
Измерение силы тока, напряжения и мощности
Для измерения электрических параметров цепи используются специальные приборы:
Амперметр
Амперметр используется для измерения силы тока. Он включается последовательно в цепь.
Вольтметр
Вольтметр применяется для измерения напряжения. Подключается параллельно участку цепи.
Ваттметр
Ваттметр позволяет измерить мощность в электрической цепи. Состоит из токовой обмотки (включается последовательно) и обмотки напряжения (подключается параллельно).
Сила тока, напряжение и мощность в различных типах электрических цепей
Рассмотрим, как проявляются сила тока, напряжение и мощность в цепях постоянного и переменного тока.
Цепи постоянного тока
В цепях постоянного тока значения силы тока, напряжения и мощности остаются неизменными во времени. Это упрощает расчеты и измерения.
Цепи переменного тока
В цепях переменного тока значения силы тока и напряжения периодически изменяются. Здесь используются понятия действующих значений тока и напряжения, а также активной и реактивной мощности.

Энергоэффективность и управление мощностью
Понимание взаимосвязи силы тока, напряжения и мощности важно для повышения энергоэффективности электрических устройств.
Снижение потерь мощности
Потери мощности в проводниках пропорциональны квадрату силы тока. Поэтому для снижения потерь при передаче электроэнергии используют высокое напряжение и низкий ток.
Управление энергопотреблением
В современных электронных устройствах применяются различные методы управления энергопотреблением, основанные на регулировании напряжения и тока для оптимизации мощности.
Безопасность при работе с электричеством
Знание основ электротехники критически важно для обеспечения безопасности при работе с электрическими устройствами и системами.
Опасность высокого напряжения
Высокое напряжение представляет серьезную опасность для человека. Даже относительно небольшой ток при высоком напряжении может быть смертельным.
Защита от перегрузки по току
Для защиты электрических цепей от чрезмерных токов используются предохранители и автоматические выключатели, срабатывающие при превышении допустимой силы тока.
Современные тенденции в электротехнике
Развитие технологий приводит к появлению новых подходов в работе с электрическими параметрами.
Цифровое управление питанием
Современные микроконтроллеры позволяют точно контролировать напряжение, ток и мощность в реальном времени, оптимизируя работу электронных устройств.
Интеллектуальные сети электроснабжения
Умные электросети способны адаптивно управлять распределением мощности, учитывая текущее потребление и доступные источники энергии.
Перевести ватты (Вт) в амперы (А): онлайн-калькулятор, формула
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
Инструкция по использованию: Чтобы перевести ватты (Вт) в амперы (А), введите мощность P в ваттах (Вт), напряжение U в вольтах (В), выберите коэффициент мощности PF от 0,1 до 1 (для переменного тока), затем нажмите кнопку “Рассчитать”. Таким образом будет получено значение силы тока I в амперах (А).
- Калькулятор Вт в А (постоянный ток)
- Калькулятор Вт в А (1 фаза, переменный ток)
- Калькулятор Вт в А (3 фазы, переменный ток, линейное напряжение)
- Калькулятор Вт в А (3 фазы, переменный ток, фазное напряжение)
Калькулятор Вт в А (постоянный ток)
Формула для перевода Вт в А
Сила тока I в амперах (А) сети с постоянным током равняется мощности P в ваттах (Вт), деленной на напряжение U в вольтах (В).
Калькулятор Вт в А (1 фаза, переменный ток)
Формула для перевода Вт в А
Сила тока I в амперах (А) однофазной сети с переменным током равняется мощности P в ваттах (Вт), деленной на произведение коэффициента мощности PF и напряжения U в вольтах (В).
Калькулятор Вт в А (3 фазы, переменный ток, линейное напряжение)
Формула для перевода Вт в А
Сила тока I в амперах (А) трехфазной сети с линейным напряжением равна мощности P в ваттах (Вт), деленной на произведение коэффициента мощности PF, напряжения U в вольтах (В) и квадратного корня из трех.
Калькулятор Вт в А (3 фазы, переменный ток, фазное напряжение)
Формула для перевода Вт в А
Сила тока I в амперах (А) трехфазной сети с фазным напряжением равна мощности P в ваттах (Вт), деленной на утроенное произведение коэффициента мощности PF и напряжения U в вольтах (В).
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Как рассчитать мощность стабилизатора
Ох, эти непонятные кВт и кВА.
 ..
..Многие до сих путаются в мощностях стабилизаторов: киловатты (кВт) и киловольт-амперы (кВА), как они связаны между собой, как понять сколько киловатт (кВт) выдаёт стабилизатор и прочие вопросы. Сейчас постараемся всё подробно объяснить. Но чтобы разобраться, придётся вспомнить некоторые основы электротехники.
Для начала следует разобраться с параметрами электрических цепей. Нас будут интересовать, в первую очередь, напряжение (обозначается U, измеряется в вольтах, В) и сила тока (обозначается I, измеряется в амперах, А). Чтобы наглядно представить себе эти параметры, можно сравнить электричество с водой, а электрическую цепь с трубопроводом. В таком сравнении напряжение будет давлением воды, а сила тока — скорость течения воды по трубам.
Важное замечание, трубопровод может находиться под давлением, но краны перекрыты, и вода по трубам не течёт. Таким образом, переходя к электричеству, есть напряжение, а тока нет — это случай, когда не включен ни один прибор. Как только мы включаем любой прибор (это аналогично открыванию вентилей в водопроводе), по цепи потечёт электрический ток.
Любой электроприбор обладает такой характеристикой, как сопротивление (обозначается R, измеряется в омах, Ом). Сопротивление прибора характеризует величину тока, который появится в сети после включения этого прибора. Если сопротивление прибора маленькое, то потечёт большой ток, если сопротивление большое — ток будет маленьким. В аналогии с водой прибор можно рассматривать как фильтр. Если это фильтр грубой очистки, то он практически не повлияет на скорость течения воды, его сопротивление низкое. А если это фильтр тонкой очистки, то он создаст серьёзное препятствие на пути воды, и скорость потока значительно снизится — его сопротивление большое.
Теперь потихоньку переходим к мощности. Как же всё-таки рассчитать мощность стабилизатора? Из курса физики ещё известно, что электрическая мощность определяется как произведение силы тока на напряжение: P = I×U. Поскольку U всегда должно быть 220 В, то именно ток фактически определяет мощность, а он, в свою очередь, определяется сопротивлением нагрузки.
И когда мы говорим о постоянном напряжении, всё достаточно банально. Например, напряжение в цепи 12 В; подключили какой-то прибор и измерили ситу тока в цепи — получилось 3, А, значит мощность равна 12 вольт×3 ампера = 36 Вт (ватт).
Но напряжение в наших розетках переменное, с частотой 50 Гц (50 раз в секунду) оно по синусоиде меняет свое значение с + на — и наоборот. И мощность, как произведение тока и напряжения, надо рассматривать уже более детально:
Здесь синяя линия — напряжение, ток — красная линия, меняется синхронно с напряжением. Их произведение, мощность, обозначена чёрной линией (как помним, минус на минус даёт плюс, и даже когда напряжение и ток имеют отрицательные значения, мощность остаётся положительной).
Это случай, когда подключена чисто активная нагрузка, которая не создаёт задержки тока, и ток меняется синхронно с изменением напряжения. В этом случае формула P = I × U остаётся верна, и произведение тока на напряжение будет давать ватты (Вт).
Но, как известно, существуют элементы, которые задерживают ток — это, в первую очередь, конденсаторы, катушки индуктивности, дроссели, трансформаторы.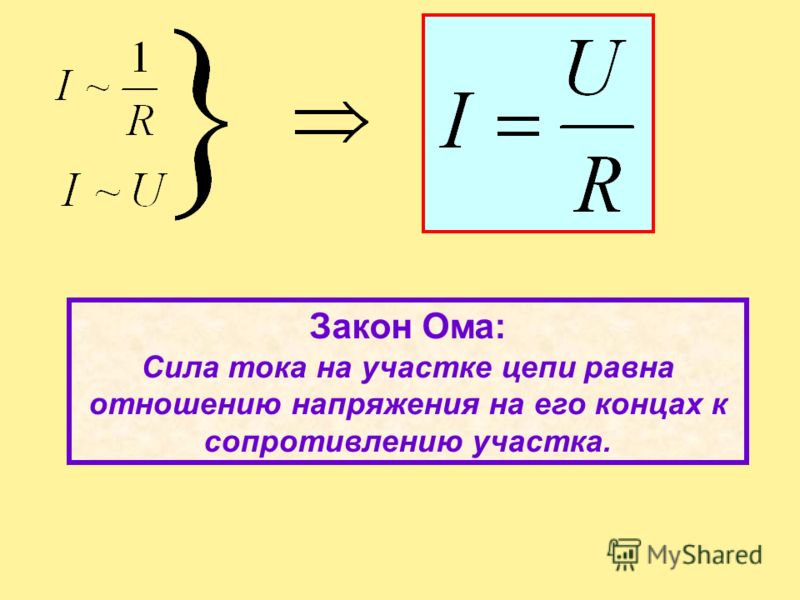 Эти элементы есть почти в любом приборе. И вот что происходит, если эти элементы задерживают ток:
Эти элементы есть почти в любом приборе. И вот что происходит, если эти элементы задерживают ток:
Как видим, ток (красная линия) смещён относительно напряжения (синяя линия), и в некоторые моменты мощность (чёрная линия) становится отрицательной.
Физически это означает, что в эти моменты времени мы не потребляем мощность, а наоборот, выбрасываем её назад в электросеть!
Получается, что ток остался таким же, что в предыдущем случае, а потребили мы меньше мощности, часть выбросив назад в электросеть. А коль ток остался таким же, то электросчетчик накрутил нам столько-же, провода так же нагрелись, а мощности потребили меньше.
Вот теперь формула P = I × U перестала нам давать ватты (Вт). Поскольку ватты — это именно та мощность, которую мы потребили, а, коль скоро, часть мощности мы выбросили назад, то потребили мы меньше, чем развили. Другими словами, развиваем мы полную мощность, а используем её не всю.
Выходит, что у любого прибора в цепи переменного напряжения есть не один параметр мощности, а два: полная (развиваемая) мощность, и потребляемая (активная) мощность.
Полная мощность вычисляется по старой формуле P = I × U, но она уже не даёт Ватты, а она даёт Вольт-Амперы (произведение вольт на амперы). А вот чтобы вычислить ватты (мощность со знаком +, потребляемую мощность), нужно вспомнить тригонометрию. Если ток смещён относительно напряжения на угол fi, то мощность со знаком + (активную, потребляемую мощность) можно вычислить по формуле Pа = I × U × Cos(fi) — именно она измеряется в Ваттах (Вт). Выбрасываемая назад мощность вычисляется по формуле Pр = I × U / Cos(fi) — измеряется в ВАРах (вольт-ампер-реактивных) и называется реактивной мощностью.
Параметр Cos(fi) принято называть коэффициентом реактивной мощности или просто коэффициентом мощности.
Вот типичные значения коэффициента мощности разных приборов:
Обогреватели, лампочки накаливания — 1,0;
Телевизор — 0,9…0,95;
Микроволновка — 0,8;
Электродвигатель (насос, циркулярка, компрессор холодильника) — 0,7.
Теперь небольшой пример. Для ограничения мощности подключения используются автоматы защиты, которые отключаются при достижении током порогового значения. Пусть какая-то вымышленная дача подключена автоматом на 40, А:
Пусть какая-то вымышленная дача подключена автоматом на 40, А:
Сколько обогревателей мощностью 1 кВт можно подключить к этой электросети? А сколько насосов аналогичной мощности?
Считаем. Цепь с напряжением 220 В. Полная мощность, которую можно развить в этой цепи до срабатывания автомата защиты 40×220 = 8800 ВА.
Полная мощность обогревателя P = 1 кВт × Cos(fi), как помним, у обогревателя Cos(fi) = 1, а значит его полная мощность P = 1×1 = 1 кВА = 1000 ВА. И сможем включить мы в сеть таких обогревателей 8800 / 1000 = 8 штук.
А вот коэффициент мощности насоса уже 0,7, а значит его полная мощность P = 1 кВт / 0,7 = 1,428 кВА = 1428 ВА. И включить насосов в эту сеть мы сможем лишь 8800 / 1428 = 6 шт.
Вот такой парадокс получается, что вроде и приборы все на 1 кВт, но одних можно включить в сеть 8 штук, а вторых лишь 6 штук.
Теперь перейдём к стабилизаторам. Их мощность задаётся по величине полной мощности (активная + реактивная, кВА), а значит однозначного ответа на вопрос: «какова мощность этого стабилизатора напряжения в киловаттах (кВт, ну или в ваттах, Вт)?», нет и быть не может!
Как и в предыдущем примере, киловатты стабилизатора определяются исходя из коэффициента мощности подключенной к нему нагрузки. Если подключаем чисто активную нагрузку (Cos(fi) = 1), то его мощность в ВА равна мощности в Вт. А вот если нагрузка имеет коэффициент мощности менее 1 (Cos(fi) < 1), то и мощность стабилизатора в ваттах (Вт) будет меньше.
Если подключаем чисто активную нагрузку (Cos(fi) = 1), то его мощность в ВА равна мощности в Вт. А вот если нагрузка имеет коэффициент мощности менее 1 (Cos(fi) < 1), то и мощность стабилизатора в ваттах (Вт) будет меньше.
Но и это ещё не все. Как мы все знаем, в любой системе должен выполняться закон сохранения энергии. Стабилизатор не исключение. Количество энергии на входе стабилизатора должно быть равно количеству энергии на выходе. Количество энергии это мощность (полная) в единицу времени, т. е. I × U. Отсюда можно записать следующее равенство:
Iвх × Uвх = Iвых × Uвых
Теперь представим ситуацию. Человек получил разрешение на подключение своей дачи к электросети с мощностью отбора 9 киловатт (кВт). Электрики должны ограничить потребление. Мощность — величина вычисляемая, но не измеряемая, её ограничить нельзя. А значит будут ограничивать величину измеряемую — амперы! Электрики прикинули, что при Cos(fi) = 1, 9000 Вт — это 9000 ВА. А при напряжении 220 В 9000 ВА — это ток в 9000 / 220 = 40,9, А, и повесили ограничительный автомат в 40 А.
Но человек жалуется, что напряжение у него не 220 В, а лишь 150 В — насосы не тянут, лампы горят в полнакала, обогреватели еле греют. И принимает решение купить стабилизатор напряжения. Поскольку разрешенная мощность у него 9 кВт, то он берёт стабилизатор на 10 кВт (с запасом).
Стабилизатор должен выдать человеку 10 кВА? Почему же у него не работает всего 3 обогревателя по 2 кВт каждый? Ведь он купил стабилизатор на 10 кВт!
А давайте прикинем с точки зрения сохранения энергии. Максимум, на что человек может рассчитывать — это взять из электросети всего 40, А (ограничительный автомат). А напряжение там всего 150 В. А на выходе стабилизатор выдаёт 220 В. Давайте подставим эти данные в закон сохранения энергии:
40 А × 150 В = Iвых × 220 В
Отсюда, Iвых = 40×150 / 220 = 27, А при напряжении на выходе в 220 В. Если теперь посчитать мощность выхода на стабилизаторе, получим 220×27 = 5940 ВА. Грубо говоря, стабилизатор мощностью 10 кВА, выдаст всего 5,9 кВА!!!
А уж если подключать к нему насосы с коэффициентом мощности 0,7, то подключить к нему можно всего 4 насоса по 1 кВт!
Стабилизатор тут, конечно же, ни причём. Вся «соль» в том, что при разрешённой мощности в 9 кВт, реально забрать с линии можно лишь 150 В × 40, А = 6000 ВА (6 кВА). А стабилизатор лишь поднимает напряжение за счёт тока (уменьшая максимальную силу тока выхода).
Вся «соль» в том, что при разрешённой мощности в 9 кВт, реально забрать с линии можно лишь 150 В × 40, А = 6000 ВА (6 кВА). А стабилизатор лишь поднимает напряжение за счёт тока (уменьшая максимальную силу тока выхода).
Теперь вы должны понимать, что выходная мощность стабилизатора напряжения определяется типом нагрузки, подключенной к стабилизатору, входным напряжением и ограничением входного тока (автоматы).
Калькулятор законаОм | DigiKey Electronics
Сопутствующие инструменты
Объяснение закона Ома
Закон Ома гласит, что разность напряжений между двумя точками, электрический ток, протекающий между ними, и сопротивление пути тока пропорциональны и связаны друг с другом.
Закон Ома объясняет взаимосвязь между напряжением, током и сопротивлением, утверждая, что ток в проводнике между двумя точками прямо пропорционален разности потенциалов между двумя точками.
Это может быть выражено математически в следующих уравнениях через V разность напряжений, I ток в амперах и R сопротивление в омах.
На практике это означает, что ток, проходящий через двухконтактное устройство, такое как резистор с фиксированным значением сопротивления, напрямую связан с разностью напряжений, приложенных к клеммам.
Закон гласит, что . Это означает, что для данного постоянного напряжения более высокое сопротивление влечет за собой более низкий ток. Верно и обратное: при том же заданном постоянном напряжении более низкое сопротивление будет означать более высокий ток.
Примеры
Напряжение V в вольтах (В) равно току I в амперах (А), умноженному на сопротивление R в омах (Ом):
Итак, для цепи с сопротивлением 5 Ом (Ом) которому для работы требуется ток 3 ампера (А), требуемое напряжение составит 15 В.
Мощность, рассеиваемую цепью, также можно определить, используя значения закона Ома. Например, мощность P в ваттах (Вт) равна напряжению V в вольтах (В), умноженному на ток I в амперах (А):
Для цепи с 20 вольтами (В) и током 2 ампера ( А) общая мощность 40 Вт (Вт).
Связанный контент
Как читать схему
В этом видео представлены основы чтения и понимания принципиальных схем. Умение читать схемы помогает в сборке или поиске и устранении неисправностей цепей.
Узнать Подробнее
Выберите резистор для светодиода
Светоизлучающие диоды (СИД) — неизбежная ступенька при погружении в электронику. Независимо от того, используете ли вы их для индикации, связи, освещения или просто для придания изюминки проекту, все светодиоды имеют один общее: они не в состоянии регулировать ток.
Узнать больше
Резисторы 101
В этом разделе Резисторы 101 представлен обзор типов резисторов и общей терминологии, прежде чем перейти к обзору резисторной продукции и различных технологий.
Узнать Подробнее
Связанные инструменты
Как рассчитать рассеиваемую мощность | Блоги
Понимание рассеиваемой мощности отдельного компонента, электрического блока или даже всей электронной системы очень важно для инженеров-электронщиков. Важно не только избежать превышения максимальных пределов компонентов, но и рассчитать неизвестные параметры на входе или выходе, поскольку рассеиваемая мощность связана с напряжением и током системы. В этой статье я описываю свои методы анализа рассеиваемой мощности в электронных устройствах.
Сначала я расскажу об основах рассеивания мощности, на которых основаны все мои методы анализа. Первое правило, относящееся к мощности, звучит так: Входная мощность системы всегда больше выходной мощности, и никогда не может быть наоборот, т.е. всегда есть некоторая потеря мощности (Ploss) в компонентах, и это ее мощность рассеяния. Тогда формула рассеивания мощности будет выглядеть так: Pin – Pout.
Основной поток рассеиваемой мощности представлен на Рисунке 1. Если мы вводим мощность в систему, часть этой мощности теряется внутри системы на нагрев, и выходная мощность уменьшается. Таким образом, выходная мощность должна быть меньше входной мощности.
Рисунок 1. Системный график рассеяния мощности Большая часть потерь мощности в конечном итоге превращается в тепло внутри компонента; обычно считается, что это рассеивание мощности. В случае активных компонентов часть всей мощности может передаваться в другие формы энергии, что обычно считается потребляемой мощностью. Например, в светодиодах мощность состоит из излучаемого света (потребляемая мощность) и тепла (рассеиваемая мощность). Таким образом, рассеиваемая мощность — это тепло, а потребляемая мощность — это мощность, которую мы хотели получить от системы. В формулах рассеивания мощности мы не анализируем передачу мощности, например, от электричества к свету, а только то, насколько система или компонент рассеивают мощность.
Второе правило — зависимость электрической мощности от напряжения и тока. Как известно, это добавленное напряжение, умноженное на потребляемый системой ток, т.е. P = UI. Связь между напряжением и током представляет собой сопротивление или импеданс, что соответствует известному закону Ома U = RI или U = ZI. С помощью этих двух уравнений и их комбинаций мы делаем все следующие расчеты рассеиваемой мощности. Полезно помнить, что эти законы действуют всегда. Мы имеем точно такую же электрическую мощность, если добавленное напряжение составляет 5 В, а ток составляет 1 А через резистор 5 Ом, или добавленное напряжение составляет 1 В, но потребляемый ток составляет 5 А через резистор 0,2 Ом. В обоих случаях рассеиваемая мощность составляет 5 Вт, независимо от того, рассчитываем ли мы ее по напряжению и току или по току и сопротивлению. В текущих расчетах мы получаем P = RI², где P = 5 Ом * 1 A² = 5 Вт или P = 0,2 Ом * 5 A² = 5 Вт.
Третьим важным параметром при анализе рассеиваемой мощности является КПД, ƞ. Эффективность показывает, насколько хорошо энергия передается от входа к выходу.
Эффективность показывает, насколько хорошо энергия передается от входа к выходу.
- ƞ = Pout/ Pin
Поскольку выходная мощность всегда меньше входной мощности, КПД всегда меньше 1. В спецификациях многих «силовых» компонентов указан КПД, и с помощью этого числа мы можем оценить количество мощности, передаваемой от входа к выходу, и, таким образом, рассчитать уровни напряжения и тока. Четвертый важный момент, который нужно знать, это то, что меняется в системе; это напряжение, ток или и то, и другое? Как правило, пассивные компоненты и светодиоды представляют собой «системы», в которых напряжение меняется от входа к выходу, а ток остается прежним. В активных системах могут изменяться либо ток, либо напряжение, либо и то, и другое. Например, импульсные преобразователи обычно имеют разные входные напряжения и токи по сравнению с выходными.
Часто рассеиваемая мощность непостоянна, а периодически меняется во времени. В этих ситуациях мы по-прежнему используем те же принципы для анализа рассеиваемой мощности, но мы должны понимать, что нужно рассчитывать. Если изобразить мощность рассеяния как функцию времени для средней и пиковой мощности рассеяния, то мы получим нечто похожее на то, что представлено на рисунке 2. Средняя мощность рассеяния постоянна во времени, но при переменной мощности рассеяния мы видим пики мощности на графике . Рассеиваемая мощность представляет собой временной интеграл периода [1], [2], а для случаев, показанных на рис. 2, рассеиваемая мощность равна T = t3.
Если изобразить мощность рассеяния как функцию времени для средней и пиковой мощности рассеяния, то мы получим нечто похожее на то, что представлено на рисунке 2. Средняя мощность рассеяния постоянна во времени, но при переменной мощности рассеяния мы видим пики мощности на графике . Рассеиваемая мощность представляет собой временной интеграл периода [1], [2], а для случаев, показанных на рис. 2, рассеиваемая мощность равна T = t3.
На практике интеграл вычисляет площадь, ограниченную кривыми мощности. На Рисунке 2 рассеиваемая переменная мощность обозначена как A2, а постоянная рассеиваемая мощность — как A1. Если обе мощности рассеяния измеряются одним и тем же устройством, интегральный расчет дает одинаковый результат для обоих случаев, так что площадь A2 равна площади A1.
Рисунок 2. Средняя и пиковая рассеиваемая мощность в зависимости от времени. При анализе формул рассеяния мощности нам необходимо понимать, как учитывать рассеивание мощности при переменном токе в наших расчетах. Усреднение суммирует всю мощность, рассеянную за период, и равномерно распределяет ее в течение этого периода. Пиковое рассеивание мощности – это максимальное рассеивание мощности в конкретный момент, т.е. максимум p(t) в уравнении (1) [1]. Средняя рассеиваемая мощность включает пиковую рассеиваемую мощность, а также моменты, когда рассеиваемая мощность меньше или равна нулю. Таким образом, средняя рассеиваемая мощность полезна, когда нас интересует мощность, которая нагревает компонент. Пиковое рассеивание мощности полезно, когда мы используем его для анализа пиков тока и напряжения. Согласно ссылке [3], некоторые мультиметры измеряют в режиме переменного тока среднеквадратичное значение (RMS) сигнала, и это значение имеет прямое отношение к средней рассеиваемой мощности. Ссылки [1] & [2] показывают, как средняя рассеиваемая мощность коррелирует с измеренными среднеквадратичными значениями сигналов переменного тока, и это соотношение:
Усреднение суммирует всю мощность, рассеянную за период, и равномерно распределяет ее в течение этого периода. Пиковое рассеивание мощности – это максимальное рассеивание мощности в конкретный момент, т.е. максимум p(t) в уравнении (1) [1]. Средняя рассеиваемая мощность включает пиковую рассеиваемую мощность, а также моменты, когда рассеиваемая мощность меньше или равна нулю. Таким образом, средняя рассеиваемая мощность полезна, когда нас интересует мощность, которая нагревает компонент. Пиковое рассеивание мощности полезно, когда мы используем его для анализа пиков тока и напряжения. Согласно ссылке [3], некоторые мультиметры измеряют в режиме переменного тока среднеквадратичное значение (RMS) сигнала, и это значение имеет прямое отношение к средней рассеиваемой мощности. Ссылки [1] & [2] показывают, как средняя рассеиваемая мощность коррелирует с измеренными среднеквадратичными значениями сигналов переменного тока, и это соотношение:
- Pᴬⱽᴱ = Iᴿᴹˢ * Uᴿᴹˢ
Если мы вычисляем среднюю рассеиваемую мощность, мы можем проверить расчеты, просто измерив переменные токи и напряжения, используя настройки переменного тока мультиметра. Конечно, если мы знаем, что в нашей системе есть условия постоянного тока, нам необходимо измерить ток и напряжение в режиме постоянного тока.
Конечно, если мы знаем, что в нашей системе есть условия постоянного тока, нам необходимо измерить ток и напряжение в режиме постоянного тока.
Первый пример прост, но подходит для всех электронщиков: регулятор LDO. Эти регуляторы могут быть смоделированы аналогично рисунку 3. Мы также можем быстро определить, что входной ток и выходной ток почти одинаковы, но напряжения на входе и выходе различаются. Для систем с очень малым потреблением тока ток покоя LDO становится важным, но если выходной ток намного больше, чем ток покоя, мы можем его игнорировать.
Рисунок 3. Пример схемы LDO.В этом примере у нас есть входное напряжение 5 В, регулируемое выходное напряжение 3,6 В и выходной постоянный ток 140 мА. Расчет рассеиваемой мощности для этого LDO следующий:
- Ploss = Pin – Pout
- = Вин * Вх — Вых * Iвых
- = 5 В * 0,14 А — 3,6 В * 0,14 А
- = 0,7 Вт – 0,504 Вт
- = 0,196 Вт
Эффективность равна
- ƞ = 0,504 Вт/0,7 Вт = 0,72
На рисунке 4 мы видим реальные результаты измерений для этого примера LDO. Мы видим, что входной и выходной ток одинаковы, а входное и выходное напряжение разные.
Мы видим, что входной и выходной ток одинаковы, а входное и выходное напряжение разные.
Мы видим, что критическим параметром с точки зрения рассеиваемой мощности в системах с постоянным током является разница напряжений между входом и выходом. Для них вы должны тщательно проанализировать падение напряжения по отношению к току и заметить, что оно заканчивается теплом. Вы должны убедиться, что выбранный компонент может выдержать расчетную рассеиваемую мощность, и спроектировать его на 80 % от максимума, указанного в спецификации. Точно так же мы можем анализировать рассеиваемую мощность пассивных компонентов, светодиодов, диодов, транзисторов и т. д.
Наш второй пример более сложен: импульсный регулятор. Понижающе-повышающий преобразователь, представленный на рисунке 5, представляет собой систему, в которой изменяются как напряжение, так и ток. В этом примере диапазон входного напряжения составляет от 10 до 20 В, входной ток неизвестен, так как он также зависит от входного напряжения, расчетное выходное напряжение зафиксировано на уровне 13,5 В, а требуемый выходной ток нагрузки составляет 80 мА.
Мы начнем анализ рассеиваемой мощности с оценки входного тока, который потребляет преобразователь. Для этого мы используем вычисление мощности по закону Ома и формулы КПД. Выходная мощность преобразователя
- Pвых = Vвых* Iвых
Для этого складываем уравнение КПД и получаем
- Vвых * Iвых = ƞ * Пин
Продолжая расчеты с вещественными числами (Vin 20В), представленными ранее, получаем:
- 13,5В*0,08А = ƞ * 20В* Iin
- 1,08 Вт = ƞ * 20 В* Iin
У нас есть два неизвестных параметра, и из таблицы данных импульсного преобразователя нам нужно проверить эффективность для используемых диапазонов напряжения и тока. В этом случае он примерно равен ƞ = 0,85. Теперь мы можем рассчитать входной ток нашего импульсного стабилизатора:
- Iin = 1,08 Вт/(0,85*20 В) = 64 мА
Теперь у нас есть все параметры для расчета рассеиваемой мощности импульсного преобразователя, и получаем формулу:
- Ploss = Pin – Pout = 0,064A*20V – 0,08A*13,5V = 1,28W – 1,08W = 0,2W
Реальное измерение подтверждает правильность расчетов, как показано на рисунке 6. Мы видим, что эффективность в этом реальном образце немного лучше, чем в наших расчетах, но в целом мы видим, что эта модель анализа полностью точна.
Мы видим, что эффективность в этом реальном образце немного лучше, чем в наших расчетах, но в целом мы видим, что эта модель анализа полностью точна.
Точно так же, как мы можем рассчитать рассеиваемую мощность в форсированном режиме, мы снова можем увидеть корреляцию между нашим расчетом и реальными измерениями, как показано на рисунке 7. Теперь анализируемый входной ток равен
- Iin = 13,5 В * 0,08 А. / 0,85 * 10 В = 0,129 А
Рассеиваемая мощность в форсированном режиме тогда:
- Ploss = Pin – Pout = 0,129A*10V – 0,08A*13,5V = 1,29Вт – 1,08 Вт = 0,21 Вт
Импульсный преобразователь является примером рассеивания мощности электрического блока. Он не учитывает рассеяние мощности отдельных компонентов, а только рассеивание мощности всей системы.
Рассеиваемая мощность тесно связана с нагревом компонента, и важно проводить расчеты для всех компонентов, которые мы считаем критическими. Этими компонентами могут быть стабилизаторы напряжения, транзисторы, диоды, светодиоды и пассивы. Для критических компонентов мы должны проверять минимально экстремальные максимальные условия, что обычно происходит при максимальном среднеквадратичном потреблении тока. Нам необходимо сравнить рассчитанное максимальное значение с максимальным значением компонента и убедиться, что оно ни в коем случае не превышается при нормальной работе продукта.
Во-вторых, нам необходимо проанализировать рассеиваемую мощность критически важных электронных блоков, таких как импульсные преобразователи, схемы драйверов и силовые каскады. Для этого мы можем использовать расчеты рассеиваемой мощности в качестве базовой проектной работы, как мы видели в примере с импульсным преобразователем. Кроме того, расчетную рассеиваемую мощность стоит сравнивать со значениями из таблицы данных, но выбор отдельных компонентов для блоков электроники должен основываться на дизайне и моделировании.

