Как магнитное поле действует на движущиеся заряды. Какая сила возникает при движении заряда в магнитном поле. Как определяется сила Лоренца. Как магнитное поле действует на проводник с током. Что такое сила Ампера и как она рассчитывается.
Действие магнитного поля на движущиеся заряды
Магнитное поле оказывает силовое воздействие только на движущиеся электрические заряды. На неподвижные заряды магнитное поле не действует. Как же проявляется это действие?
При движении заряженной частицы в магнитном поле на нее действует сила, получившая название силы Лоренца. Эта сила обладает рядом особенностей:
- Сила Лоренца всегда перпендикулярна вектору скорости частицы и вектору магнитной индукции поля
- Величина силы Лоренца зависит от значения заряда частицы, ее скорости и индукции магнитного поля
- Направление силы Лоренца определяется по правилу левой руки
Формула для расчета силы Лоренца
Математически сила Лоренца выражается следующей формулой:
F = qvBsinα
где:
- F — сила Лоренца
- q — заряд частицы
- v — скорость частицы
- B — индукция магнитного поля
- α — угол между векторами скорости и магнитной индукции
Как видно из формулы, сила Лоренца максимальна, когда частица движется перпендикулярно линиям магнитной индукции. Если же частица движется вдоль линий магнитного поля, то сила Лоренца равна нулю.
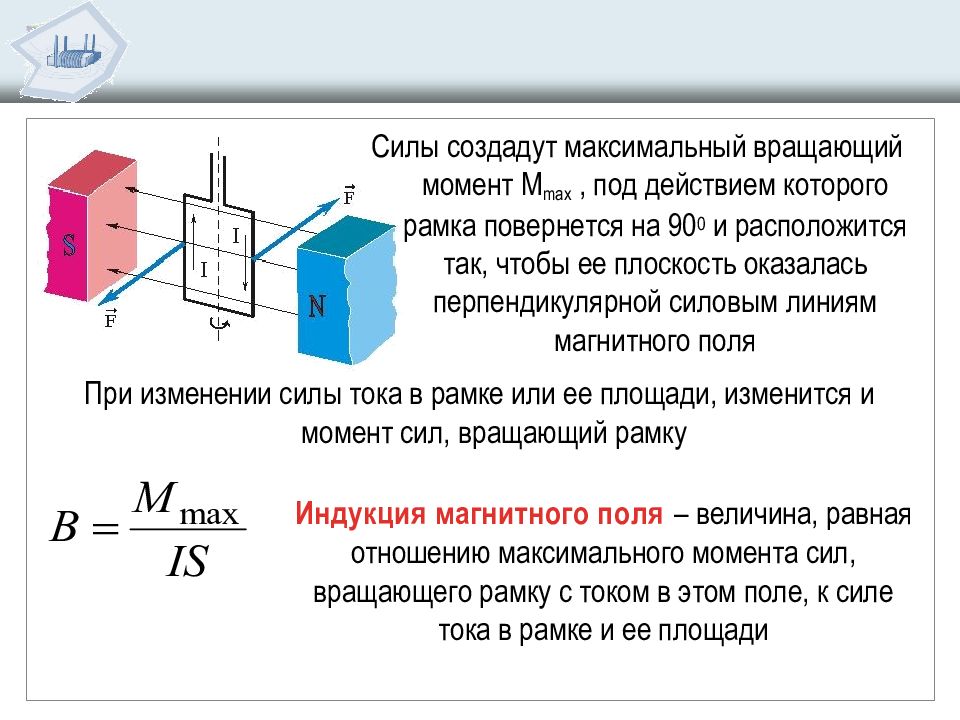
Определение направления силы Лоренца
Для определения направления силы Лоренца используется правило левой руки:
- Левую руку располагают так, чтобы линии магнитной индукции входили в ладонь
- Четыре пальца направляют по движению положительного заряда (или против движения отрицательного)
- Отогнутый на 90° большой палец покажет направление силы Лоренца
Это правило позволяет легко определить направление действия силы в любой ситуации.
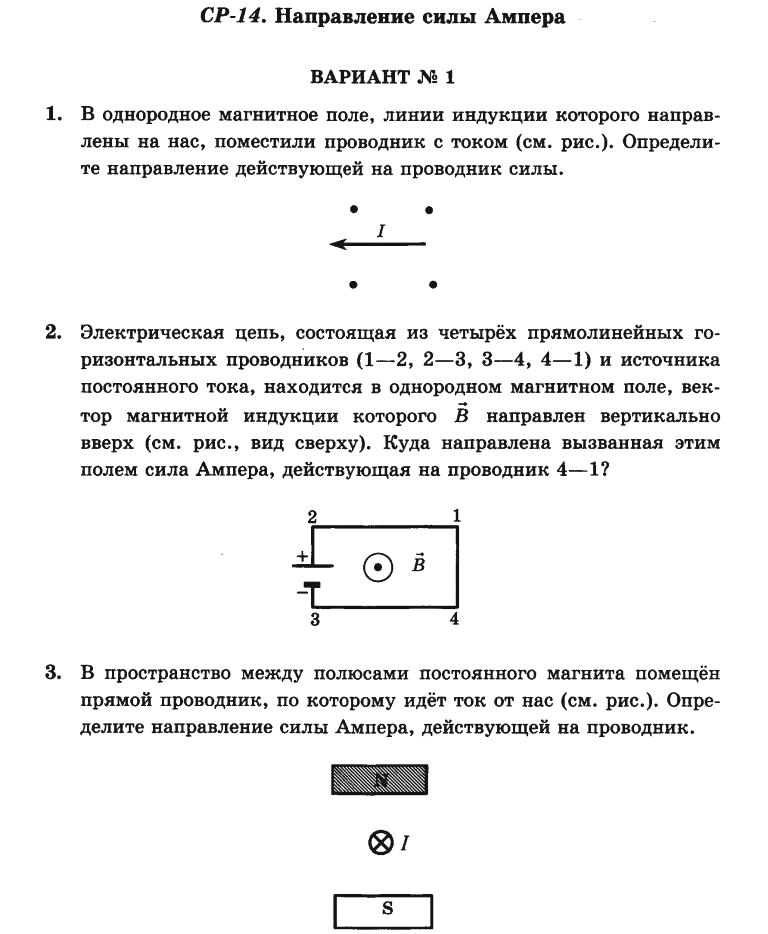
Движение заряженных частиц в магнитном поле
Как же ведут себя заряженные частицы под действием силы Лоренца? Рассмотрим основные случаи:- Если частица влетает в однородное магнитное поле перпендикулярно линиям индукции, она движется по окружности
- При движении частицы под углом к линиям индукции траектория представляет собой спираль
- Влетая в магнитное поле параллельно линиям индукции, частица продолжает двигаться прямолинейно
Таким образом, магнитное поле искривляет траекторию движения заряженных частиц, но не изменяет модуль их скорости.
Действие магнитного поля на проводник с током
Магнитное поле оказывает силовое воздействие не только на отдельные движущиеся заряды, но и на проводники с током. Ведь электрический ток — это направленное движение заряженных частиц.
На проводник с током в магнитном поле действует сила, называемая силой Ампера. Эта сила обладает следующими свойствами:
- Сила Ампера перпендикулярна и проводнику, и линиям магнитной индукции
- Величина силы Ампера зависит от силы тока, длины проводника и индукции магнитного поля
- Направление силы Ампера определяется по правилу левой руки
Формула для расчета силы Ампера
Математически сила Ампера выражается формулой:
F = IBLsinα
где:
- F — сила Ампера
- I — сила тока в проводнике
- B — индукция магнитного поля
- L — длина проводника
- α — угол между проводником и линиями магнитной индукции
Из формулы видно, что сила Ампера максимальна, когда проводник расположен перпендикулярно линиям магнитного поля. Если же проводник параллелен линиям индукции, то сила Ампера равна нулю.
Определение направления силы Ампера
Для определения направления силы Ампера также используется правило левой руки:
- Левую руку располагают так, чтобы линии магнитной индукции входили в ладонь
- Четыре пальца направляют по току
- Отогнутый на 90° большой палец покажет направление силы Ампера
Это универсальное правило позволяет легко определять направление действия магнитных сил.
Применение сил в магнитном поле
Силы, возникающие при взаимодействии токов и движущихся зарядов с магнитным полем, нашли широкое применение в технике. Вот некоторые примеры:
- Электродвигатели — преобразуют электрическую энергию в механическую за счет действия силы Ампера
- Электроизмерительные приборы — отклонение стрелки происходит под действием магнитных сил
- Ускорители заряженных частиц — разгоняют частицы с помощью магнитных полей
- Масс-спектрометры — разделяют ионы по массам, используя их движение в магнитном поле
Таким образом, понимание взаимодействия токов и зарядов с магнитным полем имеет большое практическое значение.
Сравнение силы Лоренца и силы Ампера
Сила Лоренца и сила Ампера тесно связаны между собой. Фактически, сила Ампера является макроскопическим проявлением силы Лоренца, действующей на отдельные носители тока в проводнике. Давайте сравним эти силы:
- Сила Лоренца действует на движущиеся заряженные частицы, а сила Ампера — на проводники с током
- Сила Лоренца зависит от заряда и скорости частицы, а сила Ампера — от силы тока и длины проводника
- Направление обеих сил определяется по правилу левой руки
- Обе силы перпендикулярны магнитному полю и направлению движения зарядов/тока
Понимание связи между этими силами помогает глубже осознать природу взаимодействия токов и магнитных полей.
Движение заряженных частиц в скрещенных электрическом и магнитном полях
Интересная ситуация возникает, когда на заряженную частицу одновременно действуют электрическое и магнитное поля, направленные перпендикулярно друг другу. В этом случае:
- Электрическое поле стремится ускорить частицу
- Магнитное поле отклоняет частицу от прямолинейного движения
- При определенном соотношении скорости частицы и напряженностей полей силы могут уравновесить друг друга
Такая конфигурация полей используется в некоторых приборах, например, в масс-спектрометрах для селекции частиц по скоростям.
Эффект Холла
Еще одно интересное явление, связанное с движением зарядов в магнитном поле — эффект Холла. Он заключается в возникновении поперечной разности потенциалов в проводнике с током, помещенном в магнитное поле. Этот эффект обусловлен действием силы Лоренца на носители тока.
Эффект Холла нашел применение в различных датчиках магнитного поля и тока. Он позволяет измерять магнитные поля, определять тип проводимости полупроводников и концентрацию носителей заряда в них.
Заключение
Силы, возникающие при взаимодействии движущихся зарядов и токов с магнитным полем, играют важную роль в современной физике и технике. Понимание природы этих сил и умение их рассчитывать необходимо для создания многих электротехнических и электронных устройств.
Ключевые моменты, которые следует запомнить:
- Магнитное поле действует только на движущиеся заряды
- Сила Лоренца определяет действие магнитного поля на отдельные заряженные частицы
- Сила Ампера характеризует действие магнитного поля на проводники с током
- Направление обеих сил определяется по правилу левой руки
- Эти силы лежат в основе работы многих технических устройств
Дальнейшее изучение электромагнитных явлений позволит вам глубже понять принципы работы окружающих нас технологий и откроет новые горизонты в мире современной физики.
Магнитное поле. Силы — материалы для подготовки к ЕГЭ по Физике
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: сила Ампера, сила Лоренца.В отличие от электрического поля, которое действует на любой заряд, магнитное поле действует только на движущиеся заряженные частицы. При этом оказывается, что сила зависит не только от величины, но и от направления скорости заряда.
Сила Лоренца
Сила, с которой магнитное поле действует на заряженную частицу, называется силой Лоренца. Опыт показывает, что вектор силы Лоренца находится следующим образом.
1. Абсолютная величина силы Лоренца равна:
(1)
Здесь — абсолютная величина заряда, — скорость заряда, — индукция магнитного поля, — угол между векторами и .
2. Сила Лоренца перпендикулярна обоим векторам и . Иными словами, вектор перпендикулярен плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля.
Остаётся выяснить, в какое полупространство относительно данной плоскости направлена сила Лоренца.
3. Взаимное расположение векторов , и для положительного заряда показано на рис. 1.
Рис. 1. Сила Лоренца
Направление силы Лоренца определяется в данном случае по одному из двух альтернативных правил.
Правило часовой стрелки. Сила Лоренца направлена туда, глядя откуда кратчайший поворот вектора скорости частицы v к вектору магнитной индукции B виден против часовой стрелки.
Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление скорости частицы, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Лоренца.
Для отрицательного заряда направление силы Лоренца меняется на противоположное.
Всё вышеперечисленное является обобщением опытных фактов. Формула (1) позволяет связать размерность индукции магнитного поля с размерностями других физических величин:
Сила Ампера
Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера.
Происхождение силы Ампера легко понять. Ведь ток в металле является направленным движением электронов, а на каждый электрон действует сила Лоренца. Все эти силы Лоренца, действующие на свободные электроны, имеют одинаковое направление и одинаковую величину; они складываются друг с другом и дают результирующую силу Ампера.
Направление силы Ампера определяется по тем же двум правилам, сформулированным выше.
Правило часовой стрелки . Сила Ампера направлена туда, глядя откуда кратчайший поворот тока к полю виден против часовой стрелки .
Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление тока, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Ампера
Взаимное расположение тока, поля и силы Ампера указано на рис. 2.
Рис. 2. Сила Ампера
На этом рисунке проводник имеет длину , а угол между направлениями тока и поля равен .
Мы сейчас выведем выражение для абсолютной величины силы Ампера.
На каждый свободный электрон действует сила Лоренца:
где — скорость направленного движения свободных электронов в проводнике.
Пусть — число свободных электронов в данном проводнике, — их концентрация (число в единице объёма). Тогда:
где — объём проводника, — площадь его поперечного сечения. Получаем:
Мы не случайно выделили скобками четыре сомножителя. Ведь это есть не что иное, как сила тока: (вспомните выражение силы тока через скорость направленного движения свободных зарядов!). В результате приходим к окончательной формуле для силы Ампера:
(2)
Хорошую возможность поупражняться в нахождении направлений магнитного поля и силы Ампера даёт взаимодействие параллельных токов. Оказывается, два параллельных провода отталкиваются, если направления токов в них противоположны, и притягиваются, если направления токов совпадают (рис.
3).
Рис. 3. Взаимодействие параллельных токов
Обязательно убедитесь в этом самостоятельно! Делаем так. Сначала берём произвольную точку на первом проводе и определяем направление магнитного поля, создаваемого в этой точке вторым проводом (правило вам известно — см. предыдущий листок>). Ну а затем находим направление силы Ампера, действующей на первый провод со стороны магнитного поля второго провода.
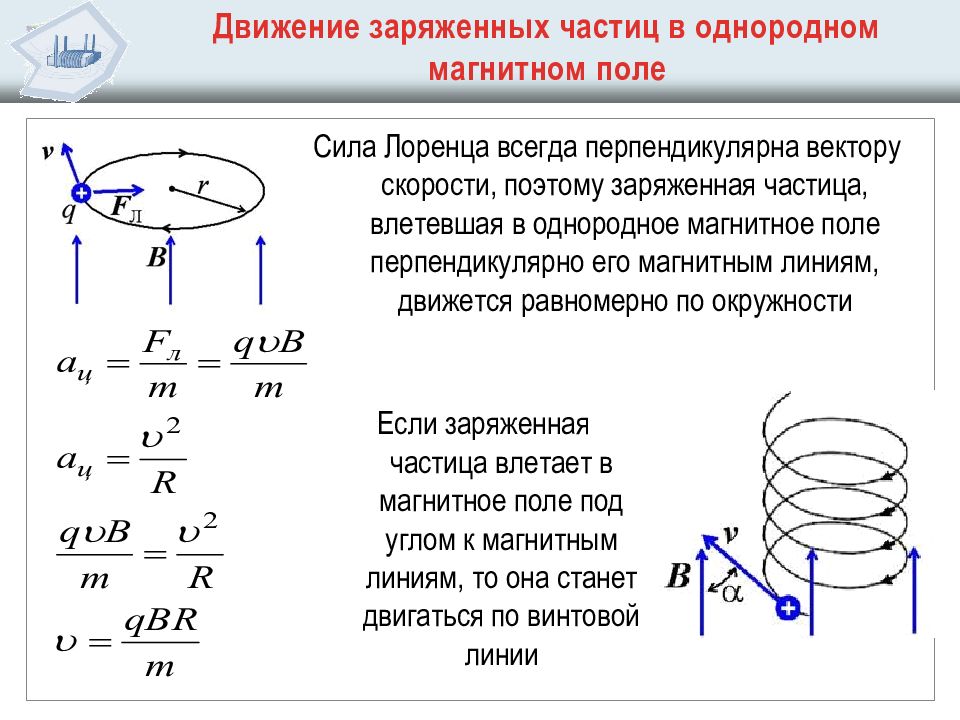
Рамка с током в магнитном поле
В листках по термодинамике мы говорили о важности циклически работающих машин: они снабжают нас энергией. Понимание законов термодинамики позволило сконструировать тепловые двигатели, которые исправно служат нам и по сей день.
Понимание же законов электромагнетизма дало возможность создать циклическую машину другого типа — электродвигатель.
Мы рассмотрим один из элементов электродвигателя — рамку с током в магнитном поле. Разобравшись в её поведении, мы сможем уловить основную идею функционирования электродвигателя.
Пусть прямоугольная рамка может вращаться вокруг горизонтальной оси (рис. 4, слева). Рамка находится в вертикальном однородном магнитном поле . Ток течёт по рамке в направлении ; это направление показано соответствующими стрелками.
Рис. 4. Рамка с током в магнитном поле
Вектор называется вектором нормали; он перпендикулярен плоскости рамки и направлен туда, глядя откуда ток кажется циркулирующим против часовой стрелки. (Иными словами, вектор сонаправлен с вектором индукции магнитного поля, которое создаётся током в рамке.) Поворот рамки измеряется углом между векторами и .
Теперь определим направления сил Ампера, которые действуют на рамку со стороны магнитного поля. Эти силы расставлены на рисунке; вот вам ещё одно упражнение на правило часовой стрелки (левой руки) — обязательно проверьте правильность указанных направлений!
Силы и , приложенные к сторонам и , действуют вдоль оси вращения. Они лишь растягивают рамку и не вызывают её вращение.
Куда более интересны силы и , приложеные соответственно к сторонам и . Они лежат в горизонтальной плоскости и перпендикулярны оси вращения. Эти силы вращают рамку в направлении по часовой стрелке, если смотреть справа (рис. 4, правая часть). Вычислим момент этой пары сил относительно оси вращения рамки.
Пусть длина стороны равна . Тогда
Пусть длина стороны равна . Плечо силы , как видно из рис. 4 (справа) равно:
Таким же будет плечо силы . Отсюда получаем момент сил, вращающий рамку:
Теперь заметим, что — площадь рамки. Окончательно имеем:
(3)
В этой формуле площадь служит единственной геометрической характеристикой рамки.Это наводит на мысль, что только площадь рамки и существенна в выражении для вращающего момента. И действительно, можно доказать (разбивая рамку на бесконечно узкие полоски, неотличимые от прямоугольников), что формула (3) справедлива для рамки любой формы с площадью .
Как видно из формулы (3), максимальный вращающий момент равен:
Эта максимальная величина момента достигается при , то есть когда плоскость рамки параллельна магнитному полю.
Вращающий момент становится равным нулю при и . Оба этих положения по-своему интересны.
При плоскость рамки перпендикулярна полю, а векторы и направлены в разные стороны. Данное положение является положением неустойчивого равновенсия: стоит хоть немного шевельнуть рамку, как силы Ампера начнут её вращать в том же направлении, поворачивая вектор к вектору (убедитесь!).
При плоскость рамки также перпендикулярна полю, а векторы и сонаправлены. Это — положение устойчивого равновенсия: при отклонении рамки возникает вращающий момент, стремящийся вернуть рамку назад (убедитесь!). Начнутся колебания рамки, постепенно затухающие из-за трения. В конце концов рамка остановится в положении ; в этом положении вектор индукции магнитного поля рамки сонаправлен с вектором индукции внешнего магнитного поля (вот почему при намагничивании вещества элементарные токи ориентируются так, что их поля направлены в сторону внешнего магнитного поля).
Полезное сопоставление: рамка занимает такое положение, что её положительная нормаль ориентируется в том же направлении, что и северный конец стрелки компаса, помещённой в это магнитное поле.
Таким образом, поведение рамки в магнитном поле становится ясным: если отклонить рамку от положения устойчивого равновесия и отпустить, то рамка будет совершать колебания. С точки зрения совершения механической работы это не очень хорошо: если намотать нить на ось вращения и подвесить к нити груз, то груз будет то подниматься, то опускаться.
Но вот если исхитриться и заставить ток менять направление в нужные моменты, то вместо колебаний рамки начнётся её непрерывное вращение и, соответственно, непрерывный подъём подвешенного груза. Тогда-то и получится полноценный электродвигатель; идея с переменой направления тока реализуется с помощью коллектора и щёток.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Магнитное поле. Силы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена: 08.03.2023
Силы Ампера и Лоренца 10 класс онлайн-подготовка на Ростелеком Лицей
Силы Ампера и Лоренца
Магнитное поле действует не только на магниты, но и на движущиеся заряды. Здесь может быть два случая:
- Действие на движение отдельных зарядов в свободном пространстве.
- Действие на движение зарядов в проводнике.
1. Действие магнитного поля на отдельный заряд
Магнитное поле не действует на неподвижные заряды – только на движущиеся. Магнитное поле действует действует на заряды не прямолинейно, а всегда вбок.
Рассмотрим заряд, движущийся с некоторой скоростью.
Если магнитное поле направленно вдоль этой скорости, то никакая сила со стороны магнитного поля не действует.
Сила появляется, если магнитное поле направленно перпендикулярно скорости частицы. Эта сила перпендикулярна и вектору индукции магнитного поля B ⃗, и скорости.
Сила, действующая на отдельный заряд со стороны магнитного поля:
Когда магнитное поле перпендикулярно скорости, сила тем больше, чем сильнее магнитное поле, больше заряд и больше его скорость:
F=qυB
Если магнитное поле направленно под углом, то разложим магнитное поле на перпендикулярную и продольную составляющие. И вспомним, что продольная составляющая не действует на частицу; действует только перпендикулярная составляющая. Т.е. в выражении для силы надо вместо B написать B⊥. Если угол между магнитным полем и скоростью alpha, то можно это выражение переписать в виде:
FL=qυBsinα
Эта сила называется силой Лоренца.
Направление этой силы можно определить с помощью правила левой руки: 1. Приложить левую руку так, чтобы скорость была направленна вдоль четырех пальцев.
2. Повернуть руку так, чтобы магнитное поле входило в ладонь.
3. Оттопыренный под прямым углом большой палец укажет направление силы.
Это работает для положительного заряда. Если заряд отрицательный, то направление силы будет противоположным.
2. Действие магнитного поля на проводник с током
Предположим, что магнитное поле перпендикулярно проводнику. Ток – это движение заряженных частиц, поэтому их скорости в среднем направленны вдоль проводника. И на каждую из них действует магнитное поле. Поэтому на проводник будет действовать некоторая суммарная сила, называемая силой Ампера.
В общем случае выражение для силы:
FA = IBlsinα
По сути, сила Ампера – это макроскопическое проявление силы Лоренца.
Поэтому полезно сравнить размерности выражений для этих сил. Если все записано правильно, они должны совпадать. Действительно, для обоих выражений мы получаем Кл⋅м/c⋅Тл.
Направление силы Ампера также определяется правилом левой руки. Четыре пальца направляются на этот раз по току, магнитное поле входит в ладонь, большой палец указывает направление силы.
В таблице с формулами описывающими создание поля зарядами и действие поля на заряды добавились две формулы.
Задача
Рейка с сопротивлением R, массы m и длины l может без трения скользить по двум направляющим, оставаясь при этом всегда перпендикулярным им. К направляющим подключен источник, создающий напряжение U. Система помещена в однородное магнитное поле с индукцией B, перпендикулярное плоскости рисунка. Рейку отпускают без начальной скорости. До какой скорости она разгонится, пройдя расстояние L? Сопротивлением направляющих пренебречь.
Решение
Перед нами система, которая может ускорять металлические объекты
Вспомним урок «закон сохранения энергии»
Такая система называется рельсотрон.
В мирных целях, она может двигать транспорт, разгонять объекты до огромных скоростей и даже имитировать падение космических микрометеоритов.
Электромагнитные силы и поля
Магнитное поле природного магнетита слишком слабое, чтобы его можно было использовать в таких устройствах, как современные двигатели и генераторы; эти магнитные поля должны исходить от электрических токов. Магнитные поля воздействуют на движущиеся заряды, а движущиеся заряды создают магнитные поля; поэтому понятия магнетизма и электричества тесно переплетены.Магнитные поля и силовые линии
Стержневой магнит притягивает к своим концам железные предметы, называемые полюсов . Один конец — это северный полюс , а другой — южный полюс . Если стержень подвешен так, что он может свободно двигаться, магнит выровняется так, что его северный полюс будет указывать на географический север Земли. Подвешенный стержневой магнит действует как компас в магнитном поле Земли.
Если два стержневых магнита сблизить, то одноименные полюса будут отталкиваться, а разноименные притягиваться. (Примечание: по этому определению магнитный полюс под северным географическим полюсом Земли является южным полюсом магнитного поля Земли.)
Это магнитное притяжение или отталкивание можно объяснить как воздействие одного магнита на другой, или можно сказать, что один магнит создает магнитное поле вокруг себя, которое воздействует на другой магнит. Магнитное поле в любой точке является вектором. Направление магнитного поля ( B ) в указанной точке — это направление, которое северный конец стрелки компаса указывает на это положение. Линии магнитного поля , аналогичные силовым линиям электрического поля, описывают силу, действующую на магнитные частицы, помещенные в поле. Железные опилки будут выровнены, чтобы показать образцы линий магнитного поля.
Сила на движущийся заряд
Если заряд движется через магнитное поле под углом, на него действует сила.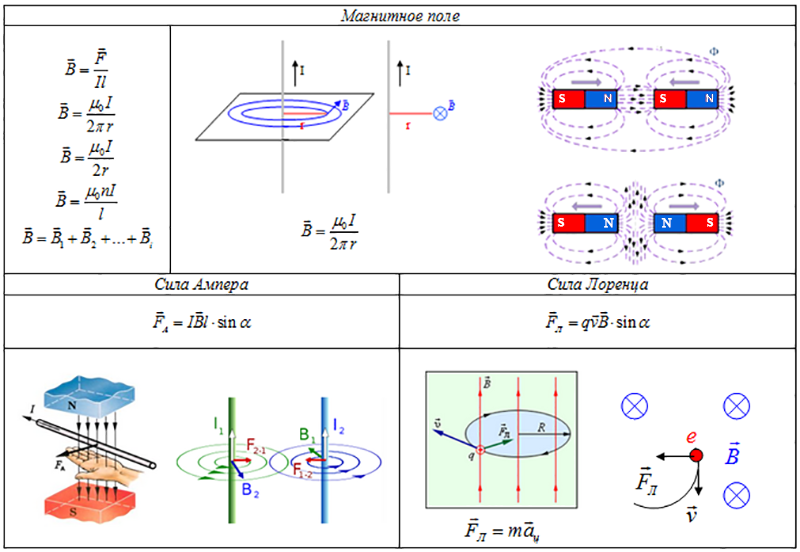
Уравнение имеет вид F = q v × B или F = qvB sin θ, где q — заряд, B — магнитное поле, v — скорость, а θ — угол между направлениями магнитного поля и скорости; таким образом, используя определение перекрестного произведения, определение магнитного поля равно
Магнитное поле выражается в единицах СИ как тесла (Тл), который также называется вебером на квадратный метр:
Направление F определяется по правилу правой руки, показанному на рисунке 1.
| ||
Чтобы найти направление силы, действующей на заряд, направьте большой палец ладони в направлении скорости положительного заряда, а пальцы — в направлении магнитного поля.
Направление силы выходит за пределы ладони. (Если движущийся заряд отрицателен, укажите большим пальцем направление, противоположное его движению.) Математически эта сила представляет собой перекрестное произведение вектора скорости и вектора магнитного поля.
Если скорость заряженной частицы перпендикулярна однородному магнитному полю, сила всегда будет направлена к центру окружности радиусом r , как показано на рисунке 2. x символизирует магнитное поле в плоскость бумаги — хвост стрелы. (Точка обозначает вектор вне плоскости бумаги — кончик стрелки.)
| ||
Магнитная сила обеспечивает центростремительное ускорение:
или
Радиус пути пропорционален массе заряда.
Это уравнение лежит в основе работы масс-спектрометр , который может разделять одинаково ионизированные атомы немного разных масс. Однократно ионизированным атомам даны равные скорости, и поскольку их заряды одинаковы и они проходят через одни и те же B , они будут двигаться немного разными путями и затем могут быть разделены.
Сила, действующая на проводник с током
Заряды, закрепленные в проводах, также могут испытывать силу в магнитном поле. Ток (I) в магнитном поле ( B ) испытывает силу ( F ), определяемую уравнением направление тока. Направление силы можно найти по правилу правой руки, аналогичному показанному на рис. В этом случае укажите большим пальцем направление тока — направление движения положительных зарядов. Ток не будет испытывать силы, если он параллелен магнитному полю.
Крутящий момент в токовой петле
Петля с током в магнитном поле может испытывать крутящий момент, если она может свободно вращаться. На рисунке (а) изображена квадратная петля из проволоки в магнитном поле, направленном вправо. Представьте на рисунке (b), что ось провода повернута под углом (θ) к магнитному полю, и что вид смотрит вниз на верхнюю часть петли. x в круге изображает ток, перемещающийся на страницу от зрителя, а точка в круге изображает поток, выходящий из страницы к зрителю.
Рисунок 3
(a) Квадратная токовая петля в магнитном поле B . (b) Вид с вершины текущей петли. (c) Если петля наклонена относительно B , возникает крутящий момент.
Правило правой руки определяет направление сил. Если петля поворачивается, эти силы создают крутящий момент, поворачивающий петлю. Величина этого крутящего момента равна t = Н I А × B , где Н — число витков петли, В — магнитное поле, I — ток, а А — площадь петли, представленная вектором, перпендикулярным петле.
Гальванометры, амперметры и вольтметры
Крутящий момент на токовой петле в магнитном поле обеспечивает основной принцип работы гальванометра , чувствительного устройства для измерения тока. К токовой катушке прикреплена игла — набор петель. Крутящий момент дает определенное отклонение стрелки, которое зависит от тока, и стрелка перемещается по шкале, чтобы можно было считывать показания в амперах.
Амперметр представляет собой прибор для измерения тока, состоящий из механизма гальванометра, соединенного параллельно с резистором. Амперметры изготавливаются для измерения различных диапазонов тока. Вольтметр состоит из механизма гальванометра, включенного последовательно с резистором. Вольтметр измеряет небольшую часть тока, а шкала показывает разность потенциалов — вольт — между двумя точками цепи.
Магнитное поле длинного прямого провода
Проводник с током создает магнитное поле магнитудой B по кругу вокруг провода.
Уравнение для магнитного поля на расстоянии r от провода имеет вид
, где I — ток в проводе, а μ (греческая буква мю) — константа пропорциональности. Константа, называемая константой проницаемости , имеет значение
.Направление поля задается вторым правилом правой руки, показанным на рис. 4.
| ||
Возьмитесь за провод так, чтобы большой палец указывал в направлении тока. Ваши пальцы будут скручиваться вокруг провода в направлении магнитного поля.
Закон Ампера
Закон Ампера позволяет рассчитывать магнитные поля.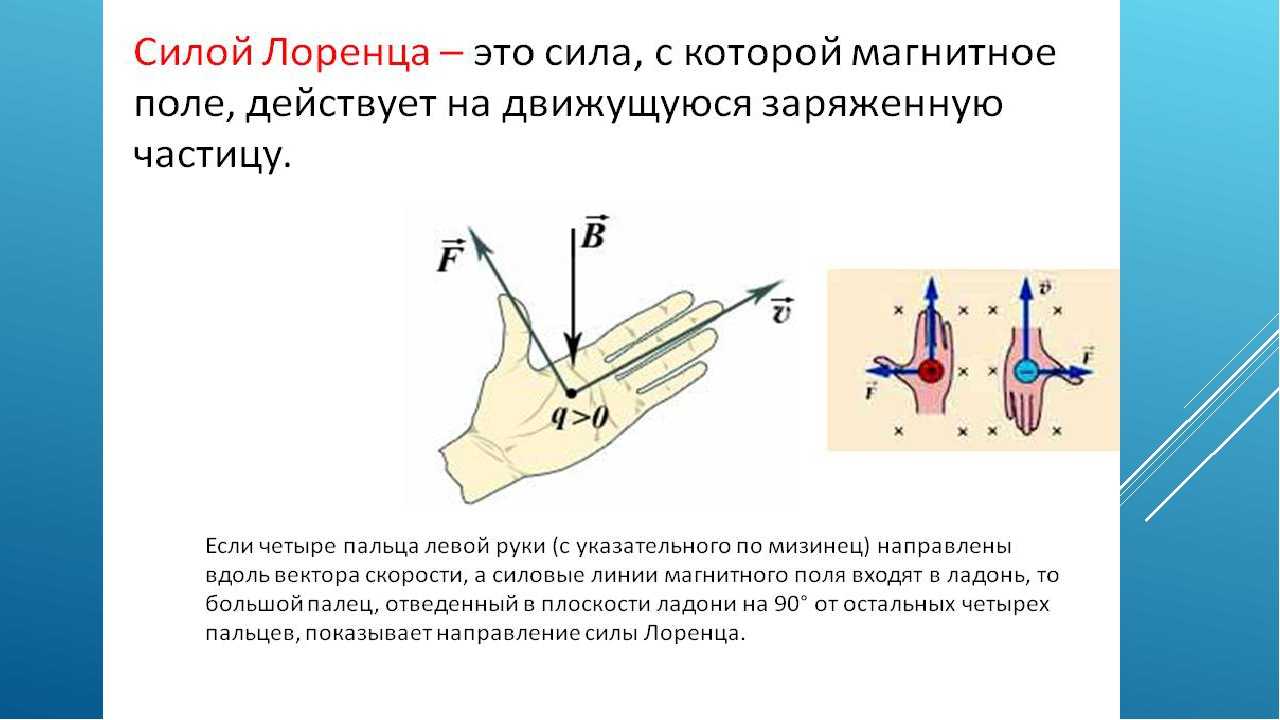
Рассмотрим круговой путь вокруг тока, показанный на рисунке. Путь разбивается на мелкие элементы длины (Δ l ). Обратите внимание на составляющую B , которая параллельна Δ l , и возьмите произведение этих двух величин как B ∥ Δ l . Закон Ампера гласит, что сумма этих произведений на замкнутом пути равна произведению тока и μ
Или в цельной форме
Несколько аналогично тому, как закон Гаусса можно использовать для нахождения электрического поля для высокосимметричных зарядовых конфигураций, закон Ампера можно использовать для нахождения магнитных полей для токовых конфигураций с высокой симметрией. Например, закон Ампера можно использовать для получения выражения для магнитного поля, создаваемого длинным прямым проводом:
Магнитные поля контура, соленоида и тороида
Ток создает магнитное поле, и поле различается по мере того, как ток имеет форму (а) петли, (б) соленоида (длинной катушки провода) или (в) тороида (бубликообразной катушки из проволоки).
проволока). Далее следуют уравнения для величин этих полей. Направление поля в каждом случае можно найти по второму правилу правой руки. На рис. 5 показаны поля для этих трех разных конфигураций.
| ||
а. Поле в центре одной петли равно
., где r — радиус петли.
б. Поле, создаваемое соленоидом, равно B = μ 0 NI , где N — количество витков на единицу длины.
в. Поле, создаваемое тороидом, равно
., где R — радиус до центра тороида.
Сила перпендикулярна как скорости v заряда q, так и
магнитное поле В.
