Сложение магнитных полей: Сложение магнитных полей — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Содержание

Сложение магнитных полей

Магнитная индукция поля характеризуется модулем и направлением. Поэтому ее можно изображать в виде отрезка, направление которого указывает направление магнитной индукции, а длина дает в выбранном масштабе — модуль магнитной индукции.

Пусть какие-то магниты или токи создают в точке поле с магнитной индукцией (рис. 212). Допустим теперь, что мы устранили магниты и токи, создававшие поле , и заменили их другими магнитами или токами, которые создают поле с магнитной индукцией . Поставим вопрос: какова будет магнитная индукция поля, если одновременно действуют и источники, обусловливавшие поле , и источники, создававшие поле ? Опыт показывает, что в этом случае получается поле, магнитная индукция которого изображается диагональю параллелограмма, построенного на отрезках и .

Рис. 212. Сложение магнитных индукций полей

Полученный результат показывает, что магнитные индукции полей складываются по правилу параллелограмма.

Это означает независимость действия магнитных полей. Так же как и в случае электрического поля (§ 15), эти опыты доказывают, что магнитная индукция поля есть векторная величина.

121.1. В некоторой точке складываются два магнитных поля: одно – вертикальное, направленное сверху вниз и равное 0,003 Тл, другое – горизонтальное, направленное с востока на запад и равное 0,004 Тл. Как направлено результирующее поле и чему будет равна его магнитная индукция?

121.2. Найдите магнитную индукцию в точке, в которой существуют одновременно два поля: первое с горизонтальной составляющей (с востока на запад), равной 0,005 Тл, и вертикальной составляющей (снизу вверх), равной 0,004 Тл, и второе с горизонтальной составляющей (с востока на запад), равной 0,006 Тл, и вертикальной составляющей (сверху вниз), равной 0,001 Тл. Решите задачу с помощью вычислений и графически.

121.3. Решите ту же задачу с тем отличием, что горизонтальная составляющая второго поля направлена не с востока на запад, а с севера на юг.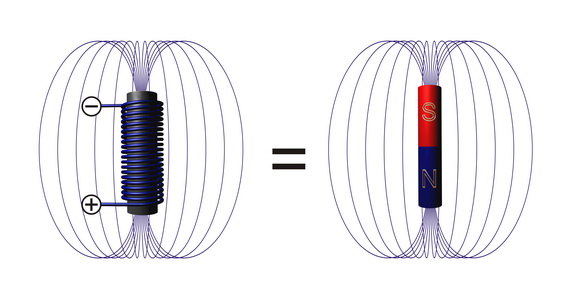

121.4. Магнитная индукция поля равна 0,01 Тл. Направление ее образует угол 30° с вертикалью. Разложите эту индукцию на две составляющие: вертикальную и горизонтальную, и вычислите значение каждой из них.

Магнитная защита

Само собой разумеется, что намагничивание ферромагнитных, парамагнитных и диамагнитных тел происходит не только тогда, когда мы помещаем их внутрь соленоида, но и вообще всегда, когда вещество помещается в магнитное иоле. Во всех этих случаях к магнитному полю, которое существовало до внесения в него вещества, добавляется магнитное поле, обусловленное намагничиванием этого вещества, в результате чего магнитное поле изменяется. Из сказанного в предыдущих параграфах ясно, что наиболее сильные изменения поля происходят при внесении в него ферромагнитных тел, в частности железа. Изменение магнитного поля вокруг ферромагнитных тел очень удобно наблюдать, пользуясь картиной линий поля, получаемой при помощи железных опилок. На рис. 281 изображены, например, изменения, наблюдающиеся при внесении куска железа прямоугольной формы в магнитное поле, которое раньше было однородным.

Как видим, поле перестает быть однородным и приобретает сложный характер; в одних местах оно усиливается, в других – ослабляется.

Рис. 281. Изменение магнитного поля при внесении в него куска железа

148.1. Когда на современных судах устанавливают и выверяют компасы, то вводят поправки к показаниям компаса, зависящие от формы и расположения частей судна и от положения компаса не нем. Объясните, почему это необходимо. Зависят ли поправки от сорта стали, примененной при постройке судна?

148.2. Почему суда, снаряжаемые экспедициями для исследования магнитного поля Земли, строят не стальные, а деревянные и для скрепления обшивки применяют медные винты?

Очень интересна и практически важна картина, которая наблюдается при внесении в магнитное поле замкнутого железного сосуда, например полого шара. Как видно из рис. 282, в результате сложения внешнего магнитного поля с полем намагнитившегося железа поле во внутренней области шара почти исчезает.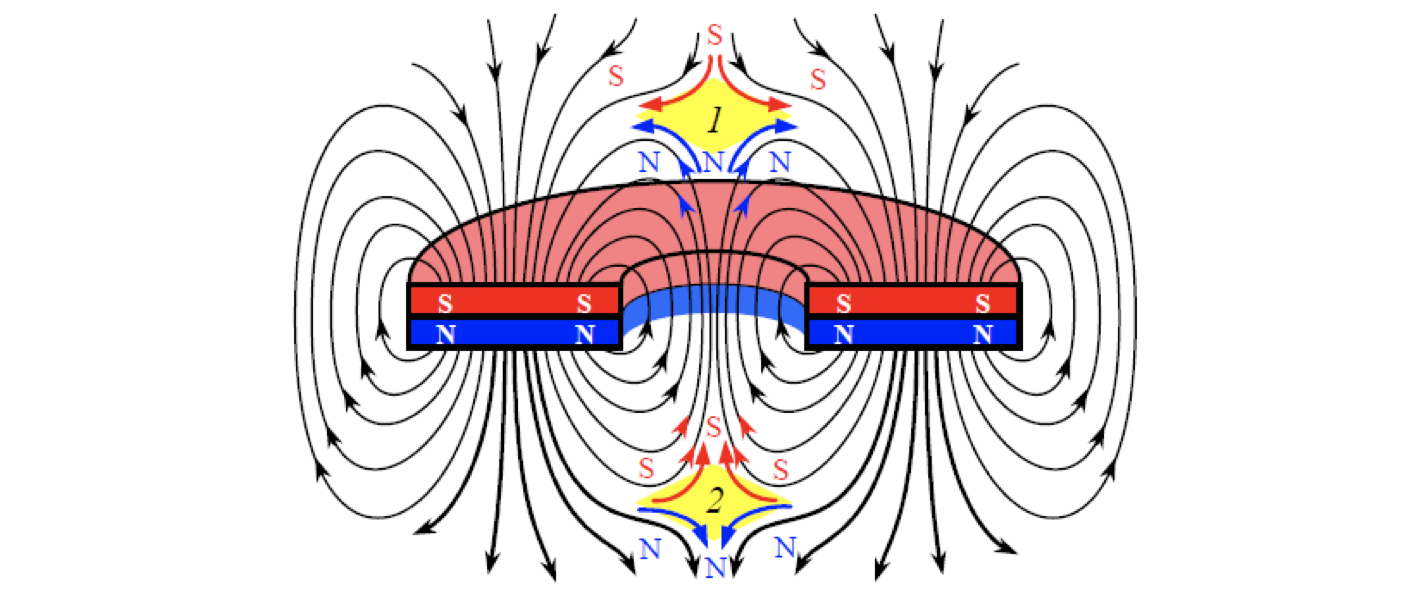 Этим пользуются для создания магнитной защиты или магнитной экранировки, т. е. для защиты тех или иных приборов от действия внешнего магнитного поля.

Рис. 282. Полый железный шар внесен в однородное магнитное поле

Картина, которую мы наблюдаем при создании магнитной защиты, внешне напоминает создание электростатической защиты при помощи проводящей оболочки. Однако между этими явлениями есть глубокое принципиальное различие. В случае электростатической защиты металлические стенки могут быть сколь угодно тонкими. Достаточно, например, посеребрить поверхность стеклянного сосуда, помещенного в электрическое поле, чтобы внутри сосуда не оказалось поля, которое обрывается на поверхности металла. В случае же магнитного поля тонкие железные стенки не являются защитой для внутреннего пространства: магнитные поля проходят сквозь железо, и внутри сосуда оказывается некоторое магнитное поле. Лишь при достаточно толстых железных стенках ослабление поля внутри полости может сделаться настолько сильным, что магнитная, защита приобретает практическое значение, хотя и в этом, случае поле внутри не уничтожается полностью.

И в этом случае ослабление поля не есть результат обрыва его на поверхности железа; линии магнитного поля отнюдь не обрываются, но по-прежнему остаются замкнутыми, проходя сквозь железо. Изображая графически распределение линий магнитного поля в толще железа и в полости, получим картину (рис. 283), которая и показывает, что ослабление поля внутри полости есть результат изменения направления линий поля, а не их обрыва.

Рис. 283. Линии магнитного поля сосредоточены в железном кольце, внесенном в магнитное поле

Слободянюк А.И. Физика 10/13.1 — PhysBook

Содержание книги

Предыдующая страница

§13. Взаимодействие магнитного поля с веществом

13.1 Намагниченность вещества.

Ранее мы ввели магнитную характеристику контура с электрическим током – его магнитный момент: вектор, модуль которого равен произведению силы тока на площадь контура \(p_m = IS\), и направленный по нормали к контуру. Укажем еще одно свойство этой характеристики – ее аддитивность:

если система состоит из нескольких контуров, то магнитный момент такой системы равен векторной сумме магнитных моментов отдельных контуров.

Это свойство очевидно, если наложить два геометрически одинаковых контура друг на друга. В этом случае сложение моментов обосновывается сложением сил токов, текущих в контурах (Рис. 67).

Легко также проиллюстрировать свойство аддитивности для двух плоских прямоугольных контуров с одинаковыми силами токов, если эти контуры приставить друг к другу, так, чтобы одна пара их сторон совпадала (Рис. 68).

В этом случае площадь образованного контура будет равна сумме площадей исходных, а результирующая сила тока в совпадающих сторонах будет равна нулю, так как эти токи текут в противоположных направлениях.

В конце концов, любая физическая характеристика придумана человеком для описания тех или иных свойств. Поэтому математические свойства этих характеристик обосновываются свойствами физических явлений, для описания которых придуманы эти характеристики.

В магнитостатике малый контур с током играет двоякую роль: во-первых, он служит для обнаружения магнитного поля; во-вторых он является источником поля.

Правило сложения магнитных моментов может быть обосновано правилом сложения механических моментов^[1]. Действительно, механический момент, действующий на контур в магнитном поле, пропорционален магнитному моменту контура. Поэтому для вычисления суммарного механического момента, действующего на систему, состоящую из нескольких контуров, можно сначала сложить магнитные моменты этих контуров.

Далее, контур с током создает магнитное поле, которое пропорционально магнитному моменту контура. Если поле создается системой из нескольких контуров, то для расчета суммарного поля по принципу суперпозиции необходимо просуммировать индукции полей, создаваемых каждым контуром, а можно сначала просуммировать магнитные моменты, а затем найти поле, создаваемое этим результирующим магнитным моментом.

Наконец, электрические дипольные моменты мы тоже складывали.

Если в магнитном поле каждая молекула вещества приобретает магнитный момент, то и все каждая часть объема вещества в целом приобретает некоторый магнитный момент, равный сумме магнитных моментов молекул, находящихся в этой выделенной части.

Таким образом, можно ввести характеристику воздействия магнитного поля на вещество – намагниченность. Намагниченностью (вектором намагниченности) вещества называется отношение суммарного магнитного момента выделенного части вещества к объему этой части

\(~\vec J = \frac{\sum_k \vec p_{mk}}{\Delta V}\) , (1)

где \(~\vec p_{mk}\) — магнитный момент k -той молекулы, находящейся внутри выделенной части объема ΔV, суммирование проводится по всем молекулам, внутри этого объема.

Как обычно, чтобы сделать намагниченность точечной характеристикой, мы должны выделенную часть сделать бесконечно малой, или математически устремить ее объем к нулю ΔV → 0 . С физической точки зрения такой переход, строго говоря, невозможен, так как бессмысленно говорить о магнитном моменте выделенной части, если ее объем меньше объема молекулы. Поэтому, говоря об определении (1), мы подразумеваем достаточно малый объем, но в котором содержится достаточно много молекул.

Фактически данное определение намагниченности подразумевает пространственное усреднение характеристик магнитного поля, созданного отдельными электронами, атомами, молекулами. Если мысленно заглянуть внутрь вещества, то рассматриваемое магнитное поле резко изменяется в зависимости от расстояния до той или иной молекулы, кроме того, оно также является переменным во времени. Мы же рассматриваем некоторое поле, усредненное по объему, значительно превышающему объем отдельной молекулы, и по промежуткам времени, значительно превышающим периоды обращения электронов в атомах.

Примечания

↑ Очередной раз мы сталкиваемся с «терминологической бедностью» — одно слово «момент» описывает различные характеристики.

Следующая страница

Изобретения. Физика. Мельниченко Андрей. Трансгенерация. Мнение 1.

Трансгенерация энергии электромагнитного поля

Сущность исследований:

Основным направлением исследований является изучение теоретической и технической возможности создания устройств генерирующих электроэнергию за счет открытого автором физического процесса трансгенерации энергии электромагнитного поля. Суть эффекта заключается в том, что при сложении электромагнитных полей (постоянных и переменных) складываются не энергии, а амплитуды поля. Энергия поля пропорциональна квадрату амплитуды суммарного электромагнитного поля. В результате, при простом сложении полей энергия суммарного поля может во много раз превышать энергия всех исходных полей по отдельности. Такое свойство электромагнитного поля называется неаддитивностью энергии поля. Например, при сложении в стопку трех плоских дисковых постоянных магнитов энергия суммарного магнитного поля возрастает в девять раз! Аналогичный процесс происходит при сложении электромагнитных волн в фидерных линиях и резонансных системах. Энергия суммарной стоячей электромагнитной волны может во много раз превосходить энергию волн и электромагнитного поля до сложения. В итоге суммарная энергия системы возрастает. Процесс описывается простой формулой энергии поля:

При сложении трех постоянных дисковых магнитов объем поля уменьшается в три раза, а объемная плотность энергии магнитного поля возрастает в девять раз. В итоге, энергия суммарного поля трех магнитов вместе оказывается в три раза больше энергии трех разъединенных магнитов.

При сложении в одном объеме электромагнитных волн (в фидерных линиях, резонаторах, катушках, также происходит увеличение энергии электромагнитного поля по сравнению с исходной).

Теория электромагнитного поля демонстрирует возможность генерации энергии за счет переноса (транс-) и сложения электромагнитных волн, полей. Разработанная автором теория трансгенерации энергии электромагнитных полей не противоречит классической электродинамике. Представление о физическом континууме, как о сверхплотной диэлектрической среде с огромной скрытой энергией массы приводит к тому, что физическое пространство обладает энергией и трансгенерация не нарушает полный закон сохранения энергии (с учетом энергии среды). Неаддитивность энергии электромагнитного поля демонстрирует, что для электромагнитного поля простое выполнение закона сохранения энергии не происходит. Например, в теории вектора Умова-Пойтинга сложение векторов Пойтинга приводит к тому, что складывается электрическое и магнитное поля одновременно. Поэтому, например, при сложении трех векторов Пойтинга, общий вектор Пойтинга возрастает в девять раз, а не в три, как кажется на первый взгляд.

Результаты исследований:

Возможность получения энергии за счет сложения электромагнитных волн исследований исследовались экспериментально в различных типах фидерных линий — волноводах, двухпроводных, полосковых, коаксиальных. Диапазон частот составляет от 300 МГц до 12,5 ГГц. Мощность измерялась как прямо — ваттметрами, так и косвенно — детекторными диодами и вольтметрами. В результате, при выполнении определенных настроек в фидерных линиях получены положительные результаты. При сложении амплитуд полей (в нагрузках) выделяемая мощность в нагрузке превосходит мощность подаваемую с разных каналов (использовались делители мощности). Самым простым опытом, иллюстрирующим принцип сложения амплитуд, является эксперимент, в котором три узконаправленные антенны синфазно работают на одну приемную, к которой подключен ваттметр. Результат этого опыта: мощность фиксируемая на приемной антенне в девять раз больше чем дает каждая передающая антенна в отдельности. На приемной антенне складываются амплитуды (три) от трех передающих антенн, а мощность приема пропорциональна квадрату амплитуды. То есть при сложении трех синфазных амплитуд мощность приема возрастает в девять раз!

Следует заметить, что интерференции в воздухе (вакууме) является многофазной, по ряду признаков отличается от интерференции в фидерных линиях, объемных резонаторах, стоячих волнах в катушках и пр. В так называемой, классической картине интерференции наблюдается как сложение, так и вычитание амплитуд электромагнитного поля. Поэтому, в целом, при многофазной интерференции нарушение закона сохранения энергии носит локальный характер. В резонаторе или при наличии стоячих волн в фидерных линиях, наложение электромагнитных волн не сопровождается перераспределением электромагнитного поля в пространстве. При этом в четверть и полуволновых резонаторах происходит только сложение амплитуд полей. Энергия сложенных в одном объеме волн происходит энергию прошедшую от генератора в резонатор.

Экспериментальные исследования полностью подтверждают теорию трансгенерации. Из практики СВЧ известно, что даже при обычном электрическом пробое в фидерных линиях мощность превосходит мощность подаваемую от генератора. Например волновод, рассчитанный на мощность СВЧ 100 МВт, пробивается сложением двух СВЧ мощности по 25 МВт каждая, — при сложении двух встречных волн СВЧ в волноводе. Это может произойти при отражении мощности СВЧ от конца линии.

Разработаны ряд оригинальных принципиальных схем для генерации энергии с использованием различных типов интерференции. Основной диапазон частот — это метровый и дециметровый (СВЧ), вплоть до сантиметрового. На основе трансгенерации можно создать компактные автономные источники электроэнергии.

Часть вторая >>

Синфазное сложение волн А. Мельниченко — EnergyScience.ru

Синфазная интерференция электромагнитных волн и трансгенерация энергий.

Согласно классической электродинамике Максвелла и теории электромагнитных полей и волн, при интерференции волн в пространстве происходит не простое суммирование энергии волн, а более сложный процесс. В интерференционных максимумах интенсивность результирующей волны больше интенсивности падающих волн, а в интерференционным минимумах меньше их суммы. Под интенсивностью здесь понимается энергия электромагнитного поля.

При интерференции складываются и вычитаются амплитуды электромагнитного поля. А энергия поля пропорциональна квадрату амплитуды результирующего электромагнитного поля. W~A2. При сложении двух амплитуд энергия колебаний возрастает в четыре раза, а не просто складывается. При вычитании двух равных амплитуд энергия результирующих колебаний становится равной нулю. Закон сохранения энергии при интерференции локально нарушается, но в целом по большому объему пространства сложение и вычитание электромагнитных волн взаимно компенсируют дуг друга, и общая энергия — это сумма энергий всех интерферирующих волн.

Локально нарушение закона сохранения энергии происходит из-за того, что при сложении электромагнитных волн складываются не сами энергии волн, а только амплитуды (напряженности) электромагнитного поля. Энергия же суммарной волны пропорциональна квадрата результирующей амплитуды (напряженности E, H). Наглядный опыт: если взять две или три узконаправленные (например, рупорные) антенны и синфазно направить их на приемную антенну, подключенную к ваттметру, то мощность на приемной антенне возрастет не в 2 — 3 раза по сравнению с одной передающей антенной, а в 4 — 9 раз соответственно. Одно из условий опыта — антенны не должны влиять друг на друга через эфир или фидерную линию. Такие опыты автором ставились неоднократно. Вопрос, почему мощность на приемной антенне возрастает в 9, а не в три раза при трех передающих антеннах? Дело в том, что на приемной антенне в три раза возрастает наведенная ЭДС, а мощность пропорциональна квадрату ЭДС. P=E2/ RН, где Е — ЭДС, RН — сопротивление нагрузки. Поэтому мощность на приемной антенне возрастает в девять раз, а не в три раза, как можно было бы подумать. Обычная классическая интерференция является многофазной, — в разных областях пространства электромагнитные волны складываются в разных фазах, где-то складываются, где-то вычитаются. Поэтому в целом эти два эффекта взаимно компенсируют друг друга и приращения энергии не происходит. Однако есть так называемая синфазная интерференция, при которой происходить только сложение (синфазное) амплитуд электромагнитных волн в нагрузке. При этом в нагрузке генерируется дополнительная энергия в виде тепла или электрического тока.

Синфазная интерференция электромагнитных полей и волн происходит например, в резонаторах, — объемных, диэлектрических коаксиальных, а также при образовании стоячих волн в катушках (т.н. трансформаторы Тесла). При этом радиомагнитные волны складываются строго в фазе (синфазно) в резонаторе. Если рассмотреть переходный процесс в идеальном (без потери затухания) резонаторе, то обнаружится весьма интересный энергетический эффект. Амплитуды радиоволн вошедших в резонатор суммируются арифметически (без потерь), но энергия внутри резонатора пропорциональна квадрату амплитуды (напряженности) электромагнитного поля. Энергия же потреблённая резонатором во время переходного процесса растёт линейно. Так как амплитуда в резонаторе растёт линейно то энергия растёт квадратично, т.е. энергия внутри идеального (без затухания) резонатора растёт из-за не линейности значительно быстрее чем энергия потреблённая от генератора, через фидерную линию. Так как фидерная линия больше длинны радиоволны то генератор и резонатор полностью развязаны.

Эту энергетическую особенность резонаторов можно использовать в специальных устройствах с высокочастотным сбросом энергии из резонатора в нагрузку.

Разработан ряд схем, на них имеются патентные заявки Р.С.Т. Принцип действия хорошо демонстрируется и доказывается математически.

Рассмотрим опыт. В прямоугольном волноводе находится диэлектрическая нагрузка. В качестве нагрузки может быть вода. На эту диэлектрическую нагрузку с двух сторон падают две СВЧ — волны. Параметры нагрузки подобраны так, что две электромагнитные волны почти полностью поглощаются в нагрузке. Такая нагрузка называется согласованной. Размеры нагрузки так же подобранны так, что амплитуды электромагнитных волн перекрывают друг друга и складываются в нагрузке. Так как амплитуды складываются, а мощность пропорциональна квадрату амплитуды W(P) = E2/R = T2 R RН, Pm ~ E2 то мощность в нагрузке будет больше, чем просто сумма двух падающих электромагнитных волн на нагрузку с двух сторон. Например, при подаче с двух каналов мощности по W1,2 = 100 Вт, всего 100+100 = 200 Вт. В нагрузке при частично перекрытых амплитудах измерялась мощность в интервале от 200 до 400 Вт » 300 Вт в среднем, при частотах от 2-104 Hz в разных волноводах fn= 2-104 Hz Мощность в нагрузке превышала мощность падающую на нагрузку с 2-х сторон в 1,5-2 раза. Этот результат является следствием синфазной интерференции СВЧ волн (SHF) в фидерной линии. В качестве фидерной линии может быть волновод: полосковая или коаксиальная линия и даже двухпроводная линия.

В любой из этих фидерных линий физические процессы происходят по одинаковым закономерностям. Например, две вечно бегущие электромагнитные волны образуют стоячую электромагнитную волну. В стоячей электромагнитной волне амплитуды прямой и встречной электромагнитной волны складываются, если они равны, то напряженность электрического и магнитного поля удваивается. E1,2=E1+E2 и Н1,2=Н1+Н2 Н0 электромагнитная мощность бегущей и стоячей электромагнитной волны пропорциональна квадрату напряжённости электрического поля: Р~Е2, в прямоугольном волноводе для волны СВЧ Н10 мощность электромагнитной волны определяется формулой: Рср= Е0*a*b/4*Zc*(1-[Л/2a]**2)**1/2, где a и b размеры волновода, Z — импеданс фидера, Л- длина волны СВЧ, где Е0 — амплитудное значение напряжённости электрического поля, ** — возведение в степень. Итак видно, что при сложении двух встречно-бегущих электромагнитных волн мощность результирующей электромагнитной волны увеличивается в четыре раза. Это приводит к тому, что электрический пробой в фидерных линиях происходит по неаддитивному энергетическому закону. Например, при длине волны l=30см в прямоугольном волноводе (воздушное заполнение) электрический пробой должен происходить при предельной мощности: Рпред=112МВт. Но пробой происходит и тогда, когда мощность Р=28МВт отражается от конца фидерной линии. В сумме мощность прямой волны Рпр=28МВт и отражённой Ротр=28МВт, что в сумме составляет всего Рпр+Ротр=56МВт, что явно недостаточно для электрического пробоя. Но из-за того, что энергия электромагнитных полей и волн неаддитивная, мощность прямой и обратной волны не складываются арифметически, а учетверяются, то происходит увеличение мощности результирующей электромагнитной волны до Р=112МВт. Это доказывает, что энергия электромагнитного поля и волн не складываются просто арифметически, по закону сохранения энергии.

Соответствует ли это теории электромагнитного поля? Рассмотрим возможность этого на простой физической модели. Есть три объема электромагнитного поля.

Условно будет считать энергию каждого объёма (кубика) W=1Дж. Всего три объёма по 1Дж. Всего имеет W=1+1+1=3Дж. Итак, начальная энергия W=3Дж. Теперь сложим все три объёма электромагнитного поля в один объём так, что вектора электромагнитного поля сложились в один объём синфазно. В таком случае напряжённость электромагнитного поля возрастёт в три раза, а объём поля уменьшится в 3 раза. Постоянное или переменное электромагнитное поле не имеет значение. Напряжённость электромагнитного поля возросла при сложении полей в три раза. Энергия поля определяется формулой: W=V0*w=(V0*Е**2)*e0/2=V0*(Н**2)*р/2, где W — энергия электромагнитного поля V0 — объём поля, w — объёмная плотность энергии электромагнитного поля. w0=(Е**2)*e0/2=(H**2)*m0/2.

Как уже говорилось, объем поля уменьшился в три раза, а объемная плотность энергии возросла в 9 раз. В результате получаем, что полная энергия получившегося электромагнитного поля возросла в три раза и составляет 9 Дж, а не 3 Дж. Это в три раза превышает первоначальный запас энергии. Как видно, сложение электромагнитных полей приводит к появлению дополнительной энергии поля. Это логически следует из того, что энергия электромагнитного поля — неаддитивная величина. Поэтому при сложении электромагнитных полей и волн складываются напряженности электромагнитного поля, а не энергии полей. Это справедливо как для волн, так и для постоянных полей. К примеру, если взять три плоских дисковых магнита, каждый — энергией магнитного поля в 1 Дж, и сложить их в плоскую стопку, то магнитные поля магнитов сложатся, и напряженность магнитного поля возрастет в три раза, а энергия магнитного поля — в девять раз. Если такую стопку размагнитить, то магнитная энергия может перейти в контур, охватывающий магнит, при этом энергии выделится в три раза больше, чем было затрачено на намагничивание трех магнитов по отдельности, до соединения. Такой результат не противоречит теории поля, так как энергии полей не складываются арифметически, и закон сохранения энергии в арифметической (аддитивной) форме к электромагнитному и волнам неприменим в принципе.

Получены экспериментальные доказательства возможности получения энергии за счет сложения электромагнитных полей и волн на нагрузке. Разработано более тридцати схем устройств. На изобретение имеются заявки на патенты, в том числе и заявки РСТ. Возможна разработка устройств для получения дополнительной энергии, например, нагрева воды и пр. теплоносителей, а также для преобразования энергии СВЧ-волн в постоянный ток и пр.

Принцип суперпозиции электрических и магнитных полей

Как экспериментальные, так и теоретические исследования электромагнитного поля убедили ученых в том, что на электрические и магнитные силы распространяется общий принцип сложения сил как векторов. Данный всеобъемлющий принцип получил название принципа суперпозиции. Для электрического поля он звучит следующим образом:

Напряженность электростатического поля в данной точке пространства – есть векторная сумма напряженностей, создаваемых всей системой зарядов в обозримой вселенной.

Разумеется, сколько-нибудь существенное влияние на заряд оказывает только часть зарядов, сила воздействия которых на данный по закону Кулона достаточно велика. Но, как бы там ни было, данные силы складываются именно как векторы. С математической точки зрения это означает линейность уравнений электромагнитного поля. Везде, где мы имеем линейные уравнения – мы получаем аналогичный закон суперпозиции. Объясняется это очень просто – такие уравнения можно складывать без образования дополнительных членов высших степеней. Существуют и другие формулировки принципа суперпозиции, но они ничего не добавляют к вышесказанному, а лишь затуманивают суть дела. Запомнить следует одно: электростатические силы складываются так же, как силы в классической «ньютоновской» механике.

От рассмотрения электростатических сил имеет смысл перейти к принципу суперпозиции для магнитного поля, а также связанным с ним положениям, вроде закона Био-Савара-Лапласа.

Принцип суперпозиции для магнитного поля

Как известно, магнитное поле являет собой результат движения электронов, т.е. электрического тока. Вокруг проводника с пропущенным через него электрическим током (или даже одиночного движущегося заряда) возникает магнитное поле. Законы, описывающие магнитное поле также носят линейный характер, поэтому на сложение магнитных сил также распространяется принцип суперпозиции. Иными словами, несколько токов оказывают на заряд такое же действие, как векторная сумма магнитных полей, порождаемых каждым из токов в отдельности. Изменения электрического и магнитного поля вокруг проводника с током взаимосвязаны и эта взаимосвязь выражается законом Био-Cавара:

Более общие закономерности, объединяющие в одно целое и электричество и магнетизм, были получены Максвеллом и окончательно сформулированы в его уравнениях единого электромагнитного поля.

геомагнитного поля | Определение, сила и факты

Представление поля

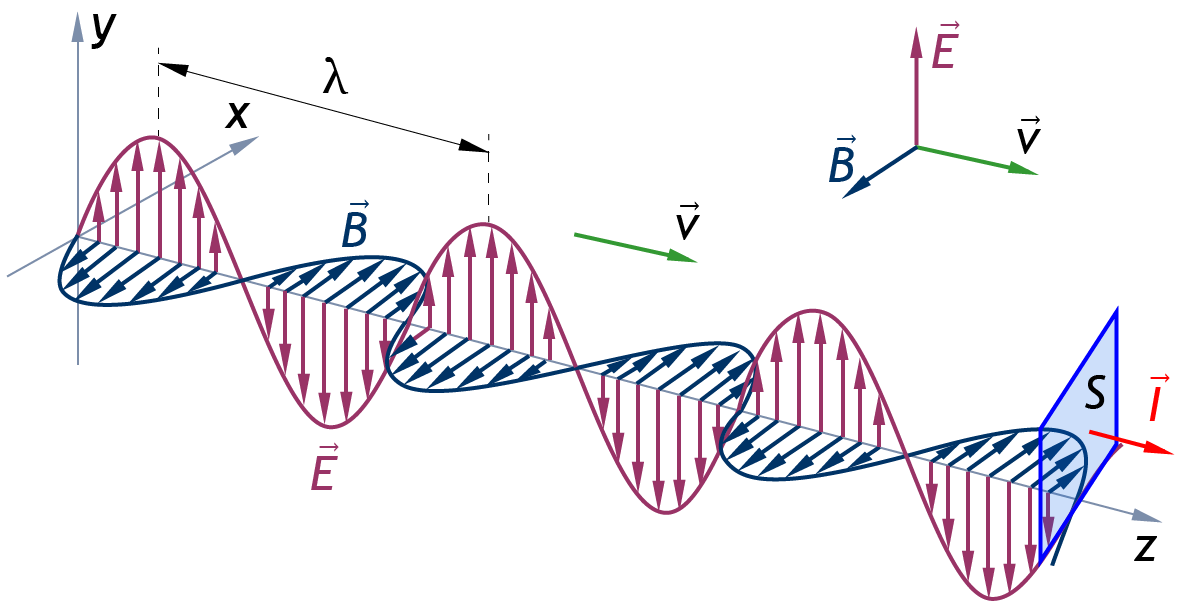
Электрические и магнитные поля создаются фундаментальным свойством материи — электрическим зарядом. Электрические поля создаются зарядами, находящимися в состоянии покоя относительно наблюдателя, тогда как магнитные поля создаются движущимися зарядами. Эти два поля представляют собой разные аспекты электромагнитного поля, которое является силой, заставляющей электрические заряды взаимодействовать. Электрическое поле E в любой точке вокруг распределения заряда определяется как сила на единицу заряда, когда в эту точку помещается положительный тестовый заряд.Для точечных зарядов электрическое поле направлено радиально от положительного заряда в сторону отрицательного заряда.

Магнитное поле создается движущимися зарядами, т. Е. Электрическим током. Магнитная индукция B может быть определена аналогично E как пропорциональная силе, приходящейся на единицу силы полюса, когда испытательный магнитный полюс приближается к источнику намагничивания. Однако чаще его определяют с помощью уравнения силы Лоренца. Это уравнение утверждает, что сила, воспринимаемая зарядом q , движущимся со скоростью v, определяется выражением F = q (vx B ).

В этом уравнении жирным шрифтом обозначены векторы (величины, которые имеют как величину, так и направление), а жирным шрифтом обозначены скалярные величины, такие как B , длина вектора B. Символ x указывает на перекрестное произведение (т. Е. Вектор справа углы как к v, так и к B, длиной v B sin θ). Тета — это угол между векторами v и B. (B обычно называют магнитным полем, несмотря на то, что это название зарезервировано для величины H, которая также используется в исследованиях магнитных полей.) Для простого линейного тока поле имеет цилиндрическую форму вокруг тока. Чувство поля зависит от направления тока, которое определяется как направление движения положительных зарядов. Правило правой руки определяет направление B, утверждая, что оно указывает в направлении пальцев правой руки, когда большой палец указывает в направлении тока.

В Международной системе единиц (СИ) электрическое поле измеряется скоростью изменения потенциала, вольт на метр (В / м).Магнитные поля измеряются в единицах тесла (Тл). Тесла — это большая единица для геофизических наблюдений, и обычно используется меньшая единица, нанотесла (нТл; одна нанотесла равна 10 ^-9 тесла). Нанотесла эквивалентна одной гамме, единице, первоначально определенной как 10 ⁻⁵ гаусс, которая является единицей магнитного поля в системе сантиметр-грамм-секунда. И гаусс, и гамма все еще часто используются в литературе по геомагнетизму, хотя они больше не являются стандартными единицами измерения.

И электрическое, и магнитное поля описываются векторами, которые могут быть представлены в различных системах координат, таких как декартова, полярная и сферическая. В декартовой системе вектор раскладывается на три компонента, соответствующих проекциям вектора на три взаимно ортогональных оси, которые обычно обозначаются x , y , z . В полярных координатах вектор обычно описывается длиной вектора в плоскости x — y , его азимутальным углом в этой плоскости относительно оси x и третьей декартовой компонентой z .В сферических координатах поле описывается длиной вектора полного поля, полярным углом этого вектора относительно оси z и азимутальным углом проекции вектора в плоскости x — y . В исследованиях магнитного поля Земли широко используются все три системы.

Номенклатура, используемая при изучении геомагнетизма для различных компонентов векторного поля, кратко представлена на рисунке. B — векторное магнитное поле, а F — величина или длина B. X , Y и Z — это три декартовых компонента поля, обычно измеряемых относительно географической системы координат. X — север, Y — восток, и, завершая правостороннюю систему, Z вертикально вниз к центру Земли. Величина поля, проецируемого в горизонтальной плоскости, называется H . Эта проекция составляет угол D (для склонения), измеренный положительным с севера на восток.Угол наклона, I (для наклона), представляет собой угол, который общий вектор поля составляет по отношению к горизонтальной плоскости, и является положительным для векторов ниже плоскости. Это дополнение к обычному полярному углу сферических координат. (Географический и магнитный север совпадают по «агонической линии».)

Компоненты вектора магнитной индукции B показаны в трех системах координат: декартовой, полярной и сферической.

Encyclopædia Britannica, Inc.

Магнетизм и Солнце: магнитные поля

Магнетизм и Солнце: магнитные поля Магнитные поля

<-Назад | Далее->

Один из способов описать магнетизм — это магнитных полей .Магнитный поле определяет магнитную силу, «толчок» или «притяжение», ощущаемый частицей независимо от его заряда и скорости (скорость и направление частица) из-за наличия других движущихся зарядов. Чем сильнее поле, тем сильнее магнитная сила, ощущаемая частицей. Точно так же чем слабее поле, тем слабее магнитная сила. Помимо описания сила магнитной силы в различных точках пространства, магнитная поле также описывает направление силы на частицу относительно к его скорости.

Магнитные поля можно визуализировать с помощью линий магнитного поля . Эти линии представляют собой кривые, где:

В каждой заданной точке касательная (линия, пересекающая кривую только в данной точке на бесконечно малом расстоянии) находится в том же направление как магнитное поле . Если бы кто-то поместил компас в магнитное поле, стрелка будет указывать по касательной к магнитному полю линия.
Величина магнитного поля пропорциональна плотности линий. г. чем ближе силовые линии друг к другу, тем сильнее магнитное поле. Чем больше чем они разложены, тем слабее магнитное поле.

Наблюдение за магнитными полями Эксперимент: Магнитные поля магнита косвенно можно наблюдать, используя железные опилки.

Оборудование:
стержневых магнитов
кусок картона, намного больше стержневого магнита
железных опилок
стол
Сборка:
Поместите стержневой магнит на стол
Положите картон поверх магнита.
Равномерно разложите железные опилки по картону.
Процедура:
Обратите внимание на железные опилки. Направлены ли они в каком-то определенном направлении? где Концентрируются ли опилки вблизи областей с более слабым или сильным магнитным поле?
Руководствуясь рисунком из железных опилок, нарисуйте магнитный диаграмма силовых линий для данного магнита.
На схеме силовых линий магнитного поля отметьте, где находятся силовые линии. разнесены или сосредоточены.Используя пару магнитов, определите, какой части магнита сильнее или слабее. Установите отношения между магнитные силы, которые вы почувствовали, используя пару магнитов, и концентрацию линий поля на диаграмме.
Что происходит?
Магнитное поле, создаваемое стержневым магнитом, индуцирует магнитное поле. поле в железных опилках. Железные опилки превращаются в маленькие магниты. Потому как железные опилки имеют форму стержней, они имеют тенденцию образовывать свои полюса в продольном направлении.В результате они указывают в одном направлении. приложенного магнитного поля стержневого магнита, как стрелка компаса делать когда подносят к магниту.

Магнитные поля на Земле: гигантский стержневой магнит

Та же картина, которую мы наблюдали в эксперименте с магнитным полем банка можно увидеть на Земле. Благодаря своему глобальному магнитному полю Земля действует как гигантский стержневой магнит. Поскольку мы не можем размещать железные опилки вокруг Земли Чтобы наблюдать магнитные поля, мы собираемся моделировать поля, используя апплет Java.

Магнитные поля на Солнце

В отличие от Земли, Солнце имеет очень слабую общую магнитную поле (среднее дипольное поле). Однако поверхность Солнца имеет очень сильную и чрезвычайно сложные магнитные поля. Поскольку поверхность магнитная поля настолько сложны, что ученые-солнечники используют компьютеры и моделируют Магнитные поля Солнца, как мы это делали для Земли с помощью Java-апплета в предыдущем упражнении. Изображение выше взято с компьютера. симуляция нагрева солнечной короны или внешней атмосферы своим «магнитным ковром».»Петли, входящие в корону, магнитны. силовые линии, соединяющие северный и южный полюсы в «магнитном ковре».

Магнитограммы

Магнитный поля также можно визуализировать в виде магнитограмм , которые используются для наблюдений за Солнцем. Магнитограммы визуальные представления полярности и силы магнитных полей, которые указывайте прямо в сторону или в сторону наблюдателя. В черных регионах самые сильные южное поле (поле направлено от наблюдателя к Солнцу), и белые области имеют самое сильное северное поле (поле указывает к наблюдателю и от Солнца).В серых областях мало или нет магнитного поля. Один такой инструмент, который генерирует магнитограммы из его наблюдения — это доплеровский тепловизор Майкельсона (MDI) на борту SOHO спутник. Ежедневно доступны магнитограммы с этого прибора.

<-Назад | Далее->

Возвращение К деятельности

Последний раз редактировал Евгений 26 августа 1999 г.

8.Статические магнитные поля, подобные тем, которые используются в медицинской визуализации

8. Статические магнитные поля, подобные тем, которые используются в медицинской визуализации

8.1 Каковы источники статических магнитных полей?
8.2 Какие возможные воздействия статических магнитных полей на здоровье были изучены?

8.1 Каковы источники статических магнитных полей?

Сканеры МРТ используют статические магнитные поля.
Кредит: Касуга Хуанг

Магнитное поле — это силовое поле, созданное магнитом или как следствие движение обвинений (поток электричества).Величина (интенсивность) магнитного поле обычно измеряется в Тесла (Т или мТл).

Статические магнитные поля делают не меняются со временем и поэтому не имеют частоты (0 Гц). Примерами являются поля, создаваемые постоянным магнитом или Магнитное поле Земли.

Искусственная статика магнитные поля генерируется везде, где используется электричество в виде постоянный ток (DC), например как в некоторых системах железной дороги и метро, в промышленных процессах, таких как производство алюминия, хлорно-щелочной процесс и газ сварка.

Количество искусственных источников таких полей ограничено, но есть быстрое развитие новых технологий, производящих статические поля. Количество людей с имплантированным металлом устройства, такие как кардиостимуляторы, на которые может воздействовать статический магнитные поля также растет.

Одно известное применение сильной статики магнитные поля Магнитно-резонансная томография (МРТ), который обеспечивает трехмерные изображения мягкого тела ткани, такие как мозг и спинной мозг.Этот метод медицинской визуализации использует очень мощные постоянные магниты, которые могут привести к сильной засветке уровни как для пациентов, так и для операторов.

Предыдущие оценки здоровья в основном смотрели на воздействие только статические поля, но многие приложения, особенно МРТ, может привести к облучению к сильным статическим полям в сочетании с радиочастотой и другие поля.Таким образом, недавние исследования начали рассматривать различные комбинации полей и их потенциальные эффекты. Подробнее …

8.2 Какие возможные воздействия статических магнитных полей на здоровье были изучены?

Имеется несколько исследований воздействия на человеческие популяции. статических полей и имеющихся свидетельств недостаточно для сделать какие-либо выводы о потенциальных последствиях воздействия на здоровье к статике магнитные поля.

Большое количество экспериментальных исследований по клеточные культуры были проводится с целью обнаружения биологических эффектов статического магнитные поля. Экспериментальными данными установлено, что статические магнитные поля может привести к изменению ориентации приложенных сил на биологические молекулы и клеточные компоненты с магнитными свойствами, такие как гемоглобин, родопсин (визуальный пигмент), свободные радикалы и оксид азота.Такие изменения могут влияют на эти биологические молекулы.

Исследования на добровольцах указывают на возможность мгновенного влияние на функционирование нейронов при движении через статический магнитное поле или поле градиент, используемый в клинической практике.Эти исследования требуют подтверждение.

Недавние исследования на животных подтверждают ранее сделанные выводы о том, что статический магнитные поля нескольких Milliteslas (mT) может оказывать прямое воздействие на нейроны. Исследования по клеточные культуры также показывают что воздействие статических магнитных полей в диапазоне миллитесла может изменить свойства мембраны.Эти изменения могут привести к изменения в функционировании нейронов, хотя эффекты кажутся обратимый.

Исследования по снижению боли у животных при воздействии статического электричества. магнитные поля в Миллитесла интересны. Вопрос в том, грызуны — адекватная модель для человека в этом отношении, поскольку не наблюдалось уменьшения боли у людей после воздействия статические магнитные поля в 10 раз сильнее.

Недавние эксперименты на животных показывают влияние статических полей на кровоток, рост сосудов, а также на рост и развитие, но некоторые результаты противоречивы и не проясняют смешанные результаты предыдущих исследований.

Статические поля, кажется, влияют на выражение специфические гены в клетки человека и другие млекопитающих, и эти эффекты могут зависеть от продолжительности воздействия и градиенты поля.Повреждение генетический материал был сообщили, хотя кажется, что эти эффекты можно исправить и не являются постоянными.

Хотя в 2007 г. было опубликовано изрядное количество исследований, 2008 г., до сих пор нет адекватных данных для надлежащего оценка риска статического магнитные поля.Больше необходимы исследования, особенно для выяснения многих смешанных и иногда противоречивые результаты.

Кратковременные эффекты наблюдались прежде всего на сенсорном уровне. функции для острого воздействия. Однако нет последовательного доказательства устойчивых неблагоприятное воздействие на здоровье от кратковременное воздействие до нескольких тесла.Подробнее …

Понимание разбавленных дисперсий суперпарамагнитных частиц в сильных магнитных полях: обзор концепций, теории и моделирования

DOI: 10.1039 / C3SM00132F (Обзорная статья) Soft Matter, 2013, 9 , 6654-6664

Получено 11 января 2013 г. , Принято 1 марта 2013 г.

Впервые опубликовано 22 марта 2013 г.

В последние годы был достигнут значительный прогресс в разработке суперпарамагнитных частиц, нацеленных на широкий спектр приложений, включая такие разные области, как биотехнология или удаление отходов.Однако физика, лежащая в основе их поведения в обычных условиях (разбавленные дисперсии и сильные магнитные поля), имеет много фундаментальных, открытых вопросов. В этом обзоре мы пересматриваем достижения в основных физических концепциях и средствах прогнозного анализа и моделирования. Мы сосредоточены на последних достижениях в понимании и предсказании явлений, индуцированных магнитными полями как в однородных полях (например, образование цепочек), так и в магнитных градиентах (кооперативный магнитофорез).

Хорди Фараудо

Хорди Фараудо получил докторскую степень по физике в Автономном университете Барселоны (UAB), Испания, в 1999 году.В 2007 году он поступил на работу в Барселонский институт материаловедения (ICMAB-CSIC) в качестве штатного ученого. Его исследовательские интересы лежат в области теории и моделирования мягкой материи, с особым упором на самосборку и на проблемы, связанные с коллоидными взаимодействиями, выходящими за рамки классической теории DLVO.

Хорди С. Андреу

Хорди Андреу получил степень по физике в Автономном университете Барселоны (UAB), Испания, в 2005 году.Он получил докторскую степень в области материаловедения в UAB в 2013 году под руководством докторов Фараудо и Камачо, защитив диссертацию, посвященную теории и моделированию суперпарамагнитных коллоидных дисперсий в магнитных полях.

Хуан Камачо

Хуан Камачо был доцентом кафедры физики Автономного университета Барселоны с 1995 года. В настоящее время его исследовательские интересы связаны с областями сложности и статистической физикой.В частности, его интересуют биологические системы и статистическая физика магнитных дисперсий, включая основы и приложения.

1 Введение

Суперпарамагнитные коллоиды — успешный пример развития нового поведения, возникающего в наномасштабе, который вышел на рынок (см., Например, ссылку 1 для обзора коммерчески доступных частиц, предназначенных для биотехнологических применений). Своеобразное магнитное поведение, известное как суперпарамагнетизм, проявляется только нанометровыми зернами магнитных материалов, таких как оксиды железа.² При нулевом приложенном поле намагниченность суперпарамагнитных частиц равна нулю. В присутствии внешнего поля частицы приобретают магнитный диполь. В сильных полях могут быть получены большие значения насыщения намагниченности, отсюда и термин суперпарамагнетизм. Магнитные коллоиды, используемые в типичных применениях, представляют собой композиционные материалы, изготовленные из суперпарамагнитных наночастиц, вставленных в матрицу из немагнитного материала, такого как полистирол или диоксид кремния (см., Например, исх.3 и 4). Таким образом, можно получить композитные частицы размером порядка 10 ² нм или больше, которые все еще являются суперпарамагнитными (обсуждение взаимосвязи между магнитным откликом композита и их отдельными компонентами см. В ссылке 5). . Высокий магнитный отклик этих композитов делает их подходящими для таких приложений, как T ₂ контрастные вещества в магнитном резонансе. ⁶ Также возможно множество других биомедицинских приложений (см. Исх.1 и 7 для обзоров).

Во многих применениях суперпарамагнитные коллоиды функционализированы соответствующими химическими группами для связывания или захвата определенных целей. ^8,9 После того, как частицы связались со своей целью или захватили желаемую молекулу, их можно удалить с помощью магнитных градиентов. Здесь следует отметить, что однородные магнитные поля не могут вызвать дрейфовую скорость в магнитных частицах, поэтому требуется магнитный градиент. Движение магнитных частиц в магнитном градиенте называется магнитофорезом.¹⁰ Есть много недавних примеров, которые включают использование функционализированных суперпарамагнитных частиц и их восстановление с помощью магнитофореза. Например, биотехнологические приложения включают выделение белка, разделение клеток, доставку лекарств и биокатализ. ¹¹ Другие интересные применения включают улавливание и извлечение загрязняющих веществ ^12,13 и обработку бактерий для биотоплива. ¹⁴ На рынке компании предлагают суперпарамагнитные микросферы для использования в сочетании с магнитофоретическими системами в качестве альтернативы обычным хроматографическим смолам в автоматизированных высокопроизводительных протоколах, заменяющих центрифугирование, органические растворители и фильтрацию.

Здесь удобно сравнивать интересующие нас магнитные дисперсии с более классическими и хорошо зарекомендовавшими себя применениями дисперсий магнитных частиц, таких как феррожидкости или магнитореологические (MR) жидкости. ¹⁵ Жидкости MR обычно представляют собой высококонцентрированные дисперсии магнитных частиц, цель которых — адаптировать механический отклик глобального объекта (жидкости MR) с использованием соответствующих ингредиентов в его составе. Чтобы ознакомиться с недавним обзором жидкостей для МРТ, читатель может обратиться к исх.16. Напротив, в рассматриваемых здесь системах основное внимание уделяется отдельной частице и ее функциональному поведению. Хотя они в основном используются в разбавленных дисперсиях (типичные концентрации порядка 1 г / л ^-1 ), они демонстрируют богатую и интересную физику из-за их сильного магнитного отклика. В качестве примера на рис. 1 представлены изображения магнитофореза разбавленной дисперсии (1 гл ⁻¹ ) коммерческих частиц Estapor® M1-30 / 40 (d = 410 нм) под стержневым магнитом ¹⁷ (видео этих экспериментов в свободном доступе в сети ^18,19).Подобные изображения можно найти в других экспериментах, см., Например, исх. 20 и 21. Большие индуцированные магнитные диполи заставляют частицы организовываться в анизотропные структуры, выровненные в направлении внешнего поля. Поскольку приложенное магнитное поле неоднородно, структуры движутся в направлении градиента напряженности магнитного поля, указанного на рисунке стрелками. Интересным наблюдением является то, что в этих экспериментах наблюдаемые структуры растворяются после подавления магнитного поля, восстанавливая начальное состояние дисперсии без цепочек частиц (см. Бесплатное видео ¹⁸, а также эксперименты в ссылке.20). Это, конечно, происходит из-за отсутствия магнитного момента частиц в отсутствие магнитного поля (а также из-за хорошей коллоидной стабилизации частиц). Тот факт, что структуры, возникающие в дисперсиях суперпарамагнитных коллоидов, могут полностью контролироваться внешним полем, представляет большой интерес для многих приложений. Это также существенное различие между дисперсиями суперпарамагнитных и ферромагнитных частиц: в случае частиц с постоянным магнитным диполем (ферромагнитные частицы) агрегаты все еще наблюдаются в отсутствие магнитного поля из-за остаточного диполь-дипольного взаимодействия.


	Рис.1 Оптическая микрофотография раствора с концентрацией 1 гл ⁻¹ частиц Estapor® M1-030 / 40 под стержневым магнитом временами (а) 0 с , (б) 120 с, (в) 240 с и (г) 360 с после размещения магнита. Масштабная линейка в (a) действительна от (a) до (d). Линейные агрегаты образуются в направлении локального поля (вертикальное) и движутся в направлении градиента магнитного поля (влево), как показано белыми стрелками.Со временем агрегаты сталкиваются сбоку, и образуются более толстые агрегаты (рисунок воспроизводится из ссылки 17). Смотрите также видео этих экспериментов на YouTube. ^18,19

Важно помнить, что формирование структур, показанных на рис. 1, играет важную роль во многих приложениях. Например, мы показали, ^17,22, что эта индуцированная полем обратимая агрегация значительно усиливает магнитофорез. Напротив, в терапевтических применениях агрегация часто является нежелательным эффектом, влияющим на биосовместимость.Другой интересный пример касается частиц, разработанных для приложений обработки изображений. Было показано, что T ₂ отклик молекул воды в экспериментах по магнитному резонансу сильно модифицируется, если суперпарамагнитные частицы, используемые в качестве контрастных агентов, образуют цепочки в сильных полях (> 1 Тл), используемых в этих приложениях. ²³ Некоторые суперпарамагнитные частицы, разработанные для этих применений (которые предназначены для большой намагниченности насыщения) ⁴, не наблюдаются для образования цепочек ²⁴, но другие имеют тенденцию образовывать цепочки в этих сильных полях.^23,25

Таким образом, очевидно, что возможность предсказания поведения коллоидных дисперсий суперпарамагнитных частиц в магнитном поле имеет огромное практическое значение, помимо фундаментального физико-химического интереса. Сюда входят прогнозы об условиях, необходимых для образования агрегатов или цепочек в сильных полях, их размере и форме, а также их кинетике, а также количественные прогнозы их влияния на различные интересующие процессы (например, магнитофоретическая скорость).Наша цель в этом обзоре — осветить последние достижения в этом направлении.

2 Суперпарамагнитные дисперсии в магнитных полях: взаимодействия между частицами

2.1 Диполь-дипольное взаимодействие

В практических приложениях коллоидные дисперсии суперпарамагнитных частиц находятся под действием внешнего магнитного поля, которое может быть интенсивным (типичные поля находятся в диапазоне 0,1–1 Тл). В этом случае суперпарамагнитные частицы приобретают большие наведенные магнитные диполи и возникают сильные диполь-дипольные взаимодействия.Энергия взаимодействия двух суперпарамагнитных частиц с диполем m (индуцированным внешним магнитным полем), разделенным расстоянием r, определяется как:


	(1)

где θ — угол между направлением внешнего магнитного поля и линии, соединяющей центры двух частиц, а μ ₀ = 4π10 ⁻⁷ NA ⁻² — магнитная проницаемость свободного пространства.Поскольку частицы находятся в дисперсии в жидкости, релевантность этого магнитного взаимодействия частица-частица зависит от того, насколько оно интенсивно по сравнению с тепловой энергией. Отношение диполь-дипольного взаимодействия (уравнение (1)) к тепловой энергии k _B T (k _B = 1,38 × 10 ⁻²³ JK ⁻¹ — Постоянная Больцмана, T — температура) можно записать как:


	(2)

где λ _B — длина магнитного Бьеррума, определяемая по формуле:


	)

Физически λ _B можно интерпретировать как характерный масштаб длины, на котором магнитные взаимодействия значительны по сравнению с тепловыми эффектами.Концепция длины Бьеррума — ключевой элемент классической теории (электростатического) образования пар между электролитами в растворе, и этот магнитный аналог был введен в [4]. 17 и 22. Энергия взаимодействия, определяемая уравнением (2), представлена на рис. 2 для типичного значения λ _B . Как видно на этом рисунке, диполь-дипольное взаимодействие сильно анизотропно с областями сильного притяжения или отталкивания из-за зависимости θ в уравнении (1). Следовательно, анизотропия взаимодействия частицы оправдывает тенденцию частиц формировать анизотропные структуры или сборки в растворе, как показано на рис.1. Диполь-дипольное взаимодействие (уравнение (1)) является притягивающим для углов θ, меньших, чем θ ₀ = 54,7 °, и отталкивающим при θ> θ ₀ . Минимальная энергетическая конфигурация соответствует θ = 0 и межчастичному расстоянию r = d (где d — диаметр частиц) и имеет энергию U ^max _dd / k _B T = −λ _B ³ / d ³ .Следовательно, разумно характеризовать силу магнитного взаимодействия параметром магнитной связи Γ, определяемым как ²⁶


	(4)


	Рис. 2 Энергия магнитного диполь-дипольного взаимодействия (уравнение (2)), испытываемая воображаемой пробной частицей из-за взаимодействия с (идентичной) суперпарамагнитной частицей, показанной черным цветом. Расчет соответствует случаю Γ = 15 (λ _B 2.47d). Желтая стрелка указывает диполь частицы, направленный в направлении поля. Энергия взаимодействия, показанная в виде цветовой шкалы, дана в единицах k _B T, а расстояние (в цилиндрических координатах) измеряется в единицах диаметров частицы d. Красный цвет соответствует областям притяжения, а зеленый цвет — областям отталкивания.

В уравнении (4) мы считаем, что частицы находятся в намагниченности насыщения с диполями m _s (т.е.е. они имеют максимальный диполь, который может быть получен в сильном поле). Следовательно, параметр Γ сравнивает максимально возможную силу притягивающего магнитного взаимодействия частица-частица (т.е. получаемого в сильных полях) с тепловой энергией. ²⁶ Физически Γ ≫ 1 соответствует ситуации, в которой преобладают магнитные взаимодействия, тогда как в противоположном пределе Γ ≪ 1 преобладает тепловое возбуждение.

Какие типичные значения Γ доступны в лаборатории? В случае суперпарамагнитных наночастиц типичные значения лежат в диапазоне 0.5–5. Например, для нанокристаллов маггемита размером 12 нм (γ-Fe ₂ O ₃ ), использованных в ссылке. 24, имеем Γ = 2,5. Это означает, что при намагниченности насыщения магнитное взаимодействие между этими наночастицами является значительным (по сравнению с тепловой энергией) на расстояниях, в ∼1,4 раза превышающих размер частицы (начиная с λ _B 1,4d). В этом случае экспериментально образования цепи не наблюдалось.

Для композитных коллоидов существует широкий диапазон значений Γ в зависимости от типа и количества наночастиц, внедренных в составную частицу.В качестве примера мы упоминаем здесь две разные частицы, разработанные как контрастные вещества для магнитно-резонансной томографии (МРТ). В одном случае были получены ⁴ композитных частиц диаметром 160 нм с примерно 40 наночастицами оксида железа. Эти композиты имеют ²⁴ Γ = 3,5 и не образуют цепочек в сильных полях. В исх. 23 авторы имели композитные частицы диаметром около 88 нм, Γ = 247, и в этом случае наблюдалось образование цепочек. Могут быть получены еще большие значения Γ.Коммерческие частицы Estapor® M1-30 / 40 (d = 410 нм), использованные в экспериментах, показанных на рис. 1, соответствуют экстремальной ситуации с Γ ∼ 10 ³ .

Во всех этих примерах Γ больше 1, поэтому ожидается, что диполь-дипольные взаимодействия будут доминировать. Однако в некоторых из этих примеров не наблюдается образования структур (цепочек), как упоминалось ранее. Это очень важный момент, на который следует обратить внимание, поскольку на основании предыдущих работ по феррожидкостям (см., Например, исх.15) исследователи обычно предполагают, что, когда магнитная энергия больше тепловой энергии (Γ> 1), будет происходить образование цепочки. Однако упомянутые выше экспериментальные данные показывают, что реальность более сложна. Критерий, который позволяет правильно предсказать наблюдаемое начало образования цепи, был недавно получен ²⁶, и он будет обсуждаться в следующем разделе. Перед этим нам нужно обсудить еще несколько результатов, касающихся взаимодействия частицы с частицами.

2.2 Коллоидная стабильность и вторичный минимум

В коллоидной науке хорошо известно, что частицы в дисперсиях имеют сильную тенденцию к агрегированию из-за сил Ван-дер-Ваальса. ^27,28 По этой причине дисперсии требуют стабилизации путем добавления подходящего отталкивающего взаимодействия между частицами, чтобы предотвратить необратимую флокуляцию дисперсии. Конечно, это также относится к суперпарамагнитным частицам в дисперсии, поэтому нам необходимо обсудить и этот вопрос здесь, прежде чем переходить к более конкретным темам.Существует две общие стратегии стабилизации коллоидной дисперсии и предотвращения ее флокуляции, а именно электростатическая стабилизация и стерическая стабилизация. Электростатическая стабилизация основана на силе отталкивания, возникающей между электрическими зарядами со знаком равенства. Как правило, стабильность частиц достигается за счет покрытия поверхности частицы заряженными группами (такими как сульфатные или карбоксильные группы), придавая частице чистый поверхностный заряд и создавая между ними силу отталкивания, способную преодолеть ван-дер-ваальсовую силу. силы.Другой вариант — стерическая стабилизация, которая заключается в покрытии частиц достаточно длинными цепными молекулами (обычно полимерами), предотвращающими сближение частиц в диапазоне сил притяжения.

Классическая теория, описывающая коллоидную стабильность, — это так называемая теория DLVO (названная в честь Дерягина, Ландау, Вервея и Овербека), которая предоставляет явные формулы для вычисления сил Ван-дер-Ваальса притяжения и электростатических сил отталкивания. ²⁸ В нашем случае эту теорию легко обобщить, добавив магнитное взаимодействие, задаваемое уравнением (2).Здесь мы опишем предсказания теории качественно, в то время как явные расчеты для интересующих частиц можно найти, например, в ссылке. 22 и 30. Типичная форма энергии взаимодействия между двумя электростатически стабилизированными суперпарамагнитными частицами в магнитном поле показана на рис. 3. При очень коротких расстояниях существует глубокий первичный минимум из-за притяжения Ван-дер-Ваальса. В этом примере частицы не могут приблизиться к этому первичному минимуму через энергетический барьер, создаваемый электростатическим отталкиванием (электростатическая стабилизация).Перед энергетическим барьером находится вторичный минимум (глубиной, зависящий от значения Γ), ответственный за обратимую агрегацию частиц в присутствии магнитного поля. Если энергетический барьер достаточно велик, частица, захваченная во вторичный минимум, останется там, не упав в первичный минимум. Как только магнитное поле удаляется, вторичный минимум исчезает, и частицы, захваченные во вторичном минимуме, снова диспергируются без необходимости обработки ультразвуком или добавления энергии в систему (редиспергирование частиц, находящихся в первичном минимуме, требует больших затрат энергии в виде обработки ультразвуком, например).


	Рис.3 Схема, показывающая профиль свободной энергии взаимодействия между двумя суперпарамагнитными частицами в сильном магнитном поле в соответствии с обобщенной теорией DLVO, включая магнитные взаимодействия (адаптировано из работ 22 и 29) . Предполагается, что частицы стабилизируются электростатически.

Обоснованность предсказаний теории и, в частности, обоснованность концепций, проиллюстрированных на рис.3 проверены экспериментально в разных работах. Например, в исх. 31 авторы измеряют кривые зависимости силы от расстояния для суперпарамагнитных частиц в магнитных полях с разрешением ∼0,2 нм по расстоянию и разрешающей способностью силы меньше pN. В случае электростатически стабилизированных коллоидов они нашли отличное согласие с предсказаниями теории DLVO. Возможность переходов между первичным и вторичным минимумом экспериментально исследовали Martinez-Pedrero et al.в исх. 29. Добавляя электролиты в различных концентрациях, они настраивали высоту электростатического барьера, разделяющего первичный и вторичный минимум (см. Рис. 3). Для концентраций одновалентного электролита ниже 0,50 мМ агрегированные частицы располагались во вторичном минимуме, и все агрегаты растворялись после подавления магнитного поля. По мере увеличения концентрации электролита высота барьера уменьшается (из-за экранирования электростатического отталкивания электролитом), и наблюдались переходы от вторичного к первичному минимуму.После подавления магнитного поля в растворе все еще оставались агрегаты, соответствующие частицам, захваченным в первичный минимум. Для концентраций моновалентного электролита 50 мМ или более энергетический барьер не мог предотвратить переход частиц из вторичного минимума в первичный, и агрегаты все еще оставались после подавления магнитного поля.

В случае стерической стабилизации частиц теория DLVO должна быть заменена теорией, описывающей стерические взаимодействия между частицами в дополнение к силе притяжения Ван-дер-Ваальса.В случае частиц, покрытых длинными цепочками полимеров, стерическое отталкивание хорошо описывается теорией среднего поля Милнера и др. ³² (на основе масштабных аргументов Александра и де Женнов ³³). В этом случае теория предсказывает подавление первичного минимума, поэтому в принципе флокуляция всегда подавляется. В отсутствие магнитного поля взаимодействие между частицами всегда является отталкивающим и сильно затухает при их разделении. Добавление магнитного взаимодействия вызывает появление небольшого минимума свободной энергии, очень похожего на вторичный минимум, показанный на рис.3. Теория была экспериментально проверена Ли и др. ³¹ для случая суперпарамагнитных частиц, покрытых олигомерами разной длины. В случае частиц, покрытых олигомерами из 75 и 50 оснований, согласие между теорией и экспериментом было превосходным. Однако в случае олигомеров на основе 15 и 35 оснований стерическое отталкивание между суперпарамагнитными частицами значительно слабее, чем предсказывает теория.

3 Прогнозирование образования цепей в однородных полях

Как мы уже говорили, возможность прогнозирования условий (намагниченность частиц, концентрация дисперсии,…), при которых возникает индуцированная полем агрегация, представляет большой интерес.Чтобы установить условия для образования цепочек и получить более полное представление о явлениях образования цепочек, мы изучили ²⁶ простейшую возможную модель дисперсии суперпарамагнитных коллоидных частиц. В этой простой модели у нас есть заданное количество магнитных сфер диаметром d внутри вязкой жидкости, и мы предполагаем, что намагниченность коллоидов достигла насыщения. Это означает, что каждая сфера имеет диполь m _s , соответствующий намагниченности насыщения, направленный в направлении магнитного поля (это разумная гипотеза для полей больше 0.1 Тл, типичный для многих экспериментальных ситуаций). Модель характеризуется двумя безразмерными параметрами: параметром магнитной связи Γ и объемной долей частиц ϕ ₀ . Здесь следует подчеркнуть, что в этой простой модели не учитываются механизм стабилизации частиц (электростатический или стерический) и их влияние на формирование цепочки. Эта упрощенная модель предполагает, что в отсутствие магнитного поля дисперсия коллоидно устойчива, а также что в присутствии магнитного поля получается вторичный минимум (обратимая агрегация).

Модель была исследована с помощью компьютерного моделирования (динамика Ланжевена) и аналитически с использованием приближения среднего поля. Чтобы проиллюстрировать типичные результаты моделирования, мы показываем здесь (рис. 4) результаты для четырех различных значений Γ и фиксированного значения ϕ ₀ = 5,23 × 10 ⁻⁴ объемной доли (что соответствует 0,5 гл ⁻¹ , если частицы имеют плотность 1 г см ⁻³ ).Результаты для других (разбавленных) концентраций также представлены в оригинальной работе. ²⁶ Во всех случаях Γ> 1, поэтому диполь-дипольное взаимодействие между двумя близко расположенными частицами сильнее теплового перемешивания. Мы обнаружили три различных возможности поведения системы: (а) отсутствие агрегации, (б) состояние равновесия с постоянным значением для среднего размера цепочек и (в) неравновесное состояние с непрерывным ростом цепочек. со временем. На рис. 4 показан пример случая (а) для Γ = 3.В этом случае мы не обнаружили образования цепочек, что противоречит классическому критерию образования цепочек (Γ> 1). Мы также напоминаем здесь, что этот результат согласуется с экспериментами в [5]. 24, упомянутый в предыдущем разделе. На рис. 4 также показаны два примера случая (b), соответствующих Γ = 10 и Γ = 11. В этом случае мы получаем состояние равновесия со средней длиной цепи, которая сильно зависит от Γ. Следует подчеркнуть, что это состояние равновесия является динамическим в том смысле, что во время моделирования мы наблюдаем как создание, так и разрушение цепочек, которые происходят с одинаковой скоростью.Для достаточно больших Γ мы получаем режим (c), в котором цепи очень устойчивы и разрушение цепей становится редким событием. В этом случае средняя длина цепочек увеличивается со временем, как показано на рис. 4 для Γ = 40.


	Рис.4 Временная эволюция среднего размера цепочки 〈N〉 (данные из ссылки 26), полученные в результате моделирования с различными значениями Γ и объемной долей ϕ ₀ = 5.23 × 10 ⁻⁴ (концентрация 0,5 г л ⁻¹ ). Вставка: снимок моделирования с Γ = 10, иллюстрирующий цепочки, сформированные в состоянии равновесия (показана только небольшая часть системы).

Термодинамический анализ среднего поля этой простой модели, также представленный в ссылке. 26, позволяет глубже понять результаты моделирования. Главный результат анализа состоит в том, что поведение системы контролируется параметром агрегации N *, определяемым как:


	(5)

В случае N * ≤ 1 система не образует цепочек.При N *> 1 состояние равновесия системы состоит из цепочек разного размера с распределением:


n _s ∝ ϕ _s / s ≃ (1 — 1 / N ) ^s ≈ e ^{−s / N } ,	(6)

где n _s — количество цепочек, содержащих s частиц в единице объема, а ϕ _s — объемная доля, занимаемая цепочками из s-частиц.Среднее количество частиц в цепочке определяется при условии, что N *> 1 (в противном случае цепочки не образуются).

Теперь мы можем понять, почему в определенных ситуациях с Γ> 1 не наблюдается образования цепочек. Например, в моделировании рис. 4 с Γ = 3 и ϕ ₀ = 5,23 · 10 ⁻⁴ , уравнение (5) дает N * = 0,06. Следовательно, наша теория правильно предсказывает, что цепочки не должны наблюдаться в этой системе. Можно также понять отсутствие образования цепей в экспериментах [5].24, упомянутые в разделе 2.1. В случае диспергирования 10 г l ⁻¹ наночастиц маггемита 12 нм с Γ = 2,5 получаем N * = 0,1. Для дисперсии 1 г л ⁻¹ частиц ядро – оболочка размером 160 нм с Γ = 3,5 получаем N * = 0,2.

На рис. 5 мы сравниваем предсказания нашей теории среднего поля (уравнения (5) и (7)) со средним числом частиц в цепочке 〈N〉 в состоянии равновесия, полученным в результате моделирования с различными значениями Γ. и разные концентрации.²⁶ Примечательно, что с помощью этих очень простых уравнений можно правильно предсказать результаты моделирования, которые требуют длительных вычислений (месяцы использования процессора). Здесь следует подчеркнуть, что ранняя модель феррожидкости Пинкуса и де Жена ^15,34 также предсказывала существование состояния равновесия с явным предсказанием равновесного значения 〈N〉, которое зависит от Γ и ϕ . Однако их модель не смогла уловить поведение, наблюдаемое в наших симуляциях, особенно поведение, наблюдаемое на рис.