Как влияет добавление резисторов на общее сопротивление при параллельном соединении. Почему общее сопротивление уменьшается, а не увеличивается. Какие физические процессы происходят при параллельном подключении резисторов.
Почему общее сопротивление уменьшается при параллельном соединении резисторов
При параллельном соединении резисторов общее сопротивление цепи уменьшается по сравнению с сопротивлением отдельных резисторов. Это может показаться парадоксальным на первый взгляд — ведь мы добавляем дополнительное сопротивление, но общее сопротивление при этом падает. Давайте разберемся, почему так происходит.
Физический смысл параллельного соединения
При параллельном соединении резисторов:
- Напряжение на всех резисторах одинаково и равно напряжению источника
- Общий ток разветвляется между параллельными ветвями
- Каждый резистор создает дополнительный путь для протекания тока
Таким образом, добавление параллельного резистора увеличивает количество путей для тока, что приводит к уменьшению общего сопротивления цепи.
Аналогия с водопроводом
Чтобы лучше понять этот процесс, можно провести аналогию с водопроводом:
- Резисторы — это трубы
- Ток — это поток воды
- Напряжение — это давление воды
Если добавить дополнительную параллельную трубу, это создаст новый путь для воды. Общий поток воды увеличится, а сопротивление потоку уменьшится.
Математическое объяснение уменьшения сопротивления
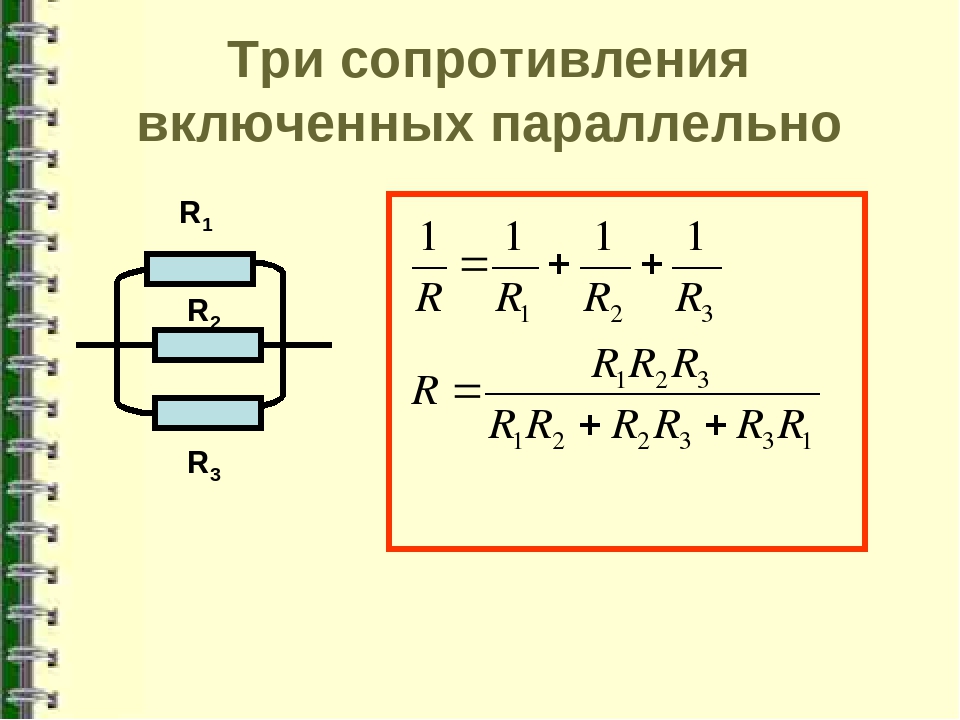
Рассмотрим формулу для расчета общего сопротивления при параллельном соединении резисторов:
1/R = 1/R1 + 1/R2 + 1/R3 + …
Где R — общее сопротивление, R1, R2, R3 — сопротивления отдельных резисторов.
Из этой формулы видно, что:
- При добавлении нового резистора в знаменателе появляется дополнительное слагаемое
- Знаменатель увеличивается
- Общая дробь уменьшается
- Следовательно, общее сопротивление R уменьшается
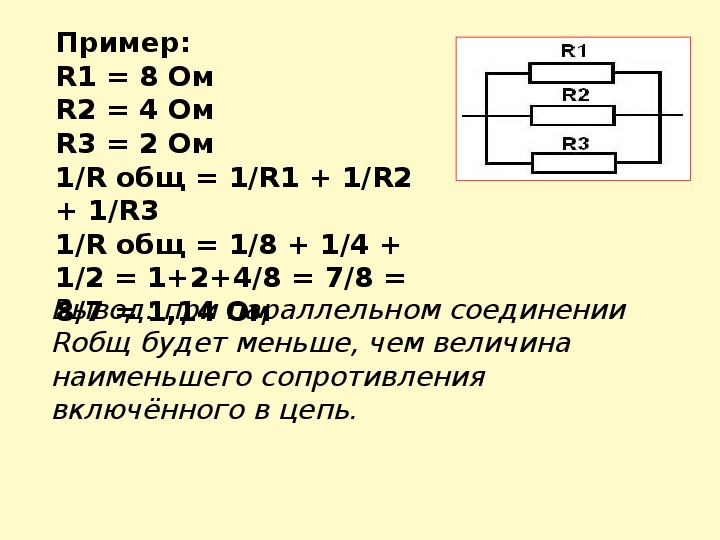
Численный пример уменьшения сопротивления
Рассмотрим конкретный пример с цифрами:
- Пусть у нас есть два резистора по 100 Ом
- При параллельном соединении общее сопротивление будет: 1/R = 1/100 + 1/100 = 2/100 R = 50 Ом
- Если добавить третий резистор 100 Ом параллельно, получим: 1/R = 1/100 + 1/100 + 1/100 = 3/100 R ≈ 33.3 Ом
Как видим, общее сопротивление уменьшилось с 50 Ом до 33.3 Ом при добавлении третьего резистора.
Влияние параллельного соединения на ток и напряжение
При параллельном подключении дополнительных резисторов:
- Общий ток через цепь увеличивается
- Напряжение на резисторах остается неизменным
- Ток через каждый отдельный резистор уменьшается
Это объясняется тем, что при постоянном напряжении источника и уменьшении общего сопротивления ток через всю цепь растет согласно закону Ома.
Практическое применение параллельного соединения резисторов
Уменьшение общего сопротивления при параллельном соединении резисторов используется на практике в различных целях:
- Увеличение тока в цепи без изменения напряжения
- Создание делителей тока
- Точная подстройка сопротивления в схемах
- Повышение мощности рассеивания в резистивных цепях
Понимание этого принципа помогает инженерам-электронщикам проектировать более эффективные электрические схемы.
Влияние количества параллельных резисторов на общее сопротивление
Чем больше одинаковых резисторов соединяется параллельно, тем сильнее уменьшается общее сопротивление. При этом:
- Общее сопротивление всегда меньше сопротивления одного резистора
- Общее сопротивление стремится к нулю при увеличении числа параллельных резисторов
- Наибольшее изменение происходит при добавлении первых нескольких резисторов
Для n одинаковых параллельных резисторов общее сопротивление равно R/n, где R — сопротивление одного резистора.
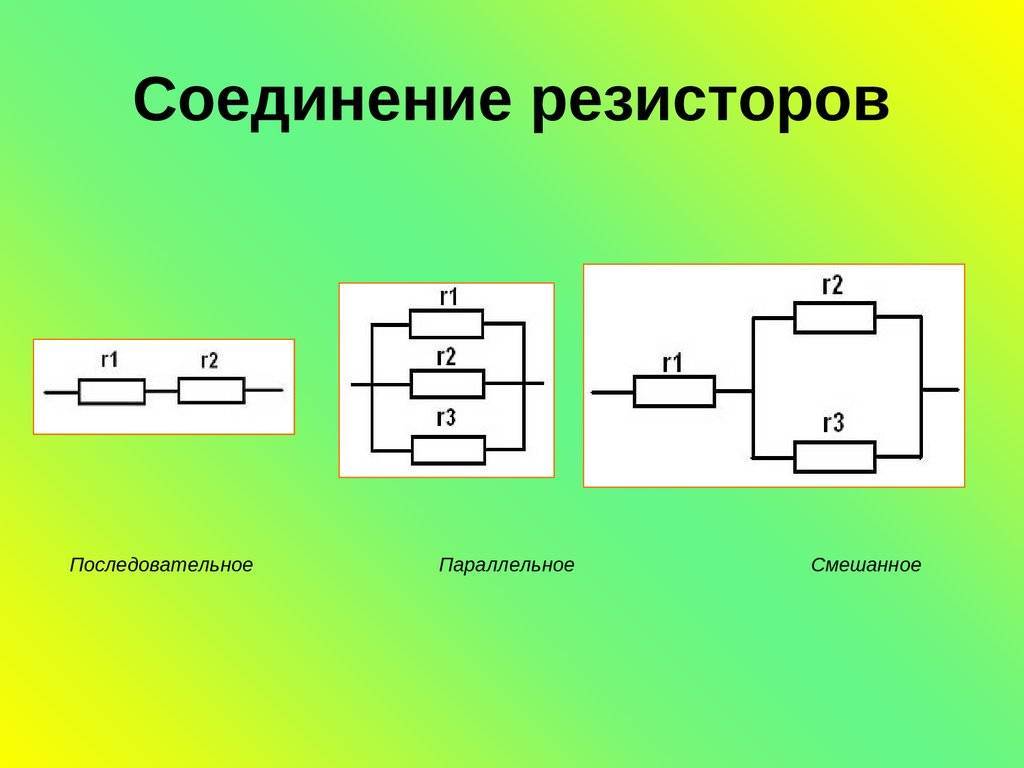
Сравнение параллельного и последовательного соединения резисторов
Параллельное и последовательное соединение резисторов имеют противоположный эффект на общее сопротивление цепи:
| Параллельное соединение | Последовательное соединение |
|---|---|
| Общее сопротивление уменьшается | Общее сопротивление увеличивается |
| Общий ток увеличивается | Общий ток уменьшается |
| Напряжение на резисторах одинаково | Ток через резисторы одинаков |
Эти различия позволяют использовать оба типа соединений для решения разных задач в электрических схемах.
Заключение: ключевые моменты о параллельном соединении резисторов
Подведем итоги основных аспектов параллельного соединения резисторов:
- Общее сопротивление уменьшается при добавлении параллельных резисторов
- Это происходит из-за увеличения путей для протекания тока
- Математически это объясняется формулой 1/R = 1/R1 + 1/R2 + …
- Параллельное соединение увеличивает общий ток через цепь
- Напряжение на всех параллельных резисторах одинаково
- Этот принцип широко применяется в электронике
Понимание этих принципов важно для анализа и проектирования электрических цепей.
Калькулятор параллельных индуктивностей • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
1 мГн = 0,001 Г. 1 мкГн = 0,000001 = 10⁻⁶ Гн. 1 нГн = 0,000000001 = 10⁻⁹ Гн. 1 пГн = 0,000000000001 = 10⁻¹² Г. Подробнее о единицах измерения индуктивности.
Индуктивность характеризует способность электрического проводника преобразовывать электрический ток в изменение электрического потенциала в данном проводнике (самоиндукция) и в расположенных рядом проводниках (взаимоиндукция). Индуктивность обычно обозначается символом L в честь русского физика немецкого происхождения Эмилия Христиановича Ленца (Heinrich Lenz).
По определению самоиндукции напряжение v(t) и ток i(t) в катушке индуктивности связаны выражением
На всех соединенных параллельно катушках индуктивности имеется одно и то же напряжение V. В соответствии с правилом Кирхгофа для тока общий ток I равен сумме токов, протекающих через отдельные катушки:
Общая индуктивность Leq соединенных параллельно трех катушек индуктивности, расположенных далеко друг от друга и не имеющих общего магнитного поля равна величине, обратной сумме величин, обратных их индуктивностям:
Или для n несвязанных катушек индуктивности:
Эта формула для Leq используется для расчетов в этом калькуляторе.
Например, общая индуктивность трех катушек индуктивности 10, 15 and 20 мкГн, соединенных параллельно, будет равна
мкГн.
Отметим, что если одна или несколько величин индуктивности равны нулю, то Leq стремится к нулю. Представьте себе очень короткий прямой проводник, шунтирующий катушку индуктивности — он и будет иметь почти нулевую индуктивность. Отметим также, что невозможно создать схему с нулевой индуктивностью.
Если параллельно соединены только две катушки индуктивности, имеем:
или
Эквивалентная индуктивность n одинаковых соединенных параллельно катушек индуктивности L равна
Отметим, что формула для расчета общей индуктивности нескольких катушек индуктивности, соединенных параллельно, используется и для расчета сопротивления группы резисторов, соединенных параллельно.
Отметим также, что для группы из любого количества соединенных параллельно катушек индуктивности эквивалентная индуктивность всегда будет меньше самой малой индуктивности в группе катушек индуктивности, а добавление еще одной катушки всегда будет уменьшать эквивалентную индуктивность группы.
Тороидальные катушки индуктивности в модуле питания принтера
Если индукторы расположены в магнитном поле друг друга, эти формулы работать не будут из-за явления взаимоиндукции (взаимной индукции), которое рассматривается в нашем калькуляторе взаимной индукции. Эффект взаимоиндукции может уменьшить или увеличить общую индуктивность катушек в зависимости от того как работает магнитная связь между катушками. Величина взаимной индукции зависит от расстояния между катушками и их ориентации. При этом взаимоиндукция может увеличивать или уменьшать общую индуктивность.
Если несколько катушек индуктивности соединены последовательно, их эквивалентная индуктивность определяется простым сложением индуктивностей отдельных катушек.
Для n соединенных последовательно катушек индуктивности имеем
Возможно, вы уже заметили, что катушки индуктивности ведут себя точно так же, как резисторы: если катушки соединены последовательно, их эквивалентные индуктивности всегда будет выше, чем индуктивности отдельных катушек, соединенных последовательно, а при параллельном соединении эквивалентная индуктивность всегда будет меньше индуктивностей отдельных катушек.
Многослойная пакетная спиральная катушка индуктивности в микросхеме и ее упрощенная эквивалентная схема
Зачем соединять катушки последовательно, если можно просто намотать большую катушку индуктивности? Вот один из примеров.
В микроэлектронике для реализации довольно больших индуктивностей на единицу площади интегральной микросхемы используется комбинирование спиральных катушек в нескольких слоях металлизации. Для этой цели используется многослойная пакетная конфигурация катушек индуктивности. Несколько слоев металлизации со спиральными катушками располагают точно один над другим. Катушки соединяют последовательно, чтобы индуктивности складывались для получения одной большой катушки индуктивности. Без такого пакетного расположения при использовании планарной технологии было бы невозможно создать большие индуктивности. Благодаря такому пакетному расположению коэффициент связи катушек k ≈ 1.
В этом калькуляторе мы рассматриваем только идеальные катушки индуктивности.
Однако мы живем в реальном мире, где реальные катушки обладают как активным сопротивлением, так и емкостью. В другом калькуляторе мы рассмотрим характеристики неидеальных катушек индуктивности, обладающих сопротивлением, которые описываются эквивалентной схемой из последовательно соединенных индуктивности и сопротивления, в частности их временные характеристики.
Бескаркасные катушки индуктивности без сердечников в радиочастотном модуле
Автор статьи: Анатолий Золотков
Параллельное соединение сопротивлений
На рис 30. представлена разветвленная цепь переменного тока, состоящая из трех параллельных ветвей.
Стрелками обозначены положительные направления токов. Все ветви цепи находятся под одним общим напряжением, мгновенное значение которого .
Д ля любого момента времени можно написать
первый закон Кирхгофа:
Ток в 1-й ветви i1 является отстающим, ток во 2-й ветви
i2 — опережающим и
ток в 3-й ветви i3 —
отстающим.
Сдвиги фаз между токами и напряжениями можно определить из соотношений:
.
А
Рис.30 Цепь с параллельным соединением сопротивлений
лгебраическое сложение синусоидальных величин одного периода можно заменить геометрическим сложением векторов, представляющих синусоидальные величины. Путем такого сложения
будет получен вектор, представляющий амплитуду результирующего
тока: . Равенство будет справедливо и для действующих значений токов: .
Результирующий ток можно определить и другим способом.
Раскладывают токи в ветвях на активные
(совпадающие по направлению с напряжением)
и реактивные (перпендикулярные к
напряжению) составляющие. Затем складывают
их алгебраически. Результирующий ток
определится как геометрическая сумма
составляющих (проекций) токов по осям:
совпадающей с направлением U и
перпендикулярной к нему.
Сумма активных составляющих токов в ветвях: .
Сумма реактивных составляющих токов в ветвях: .
Т
Рис.31 Векторная диаграмма цепи с параллельным сосоединением
огда результирующий ток: или .
Но
соединением.
.
Здесь — активная проводимость, — реактивная стоимость.
При параллельном соединении катушек индуктивности и конденсаторов их эквивалентная проводимость равна .
В обоих случаях положительное значение общего сопротивления цепи соответствует индуктивному, а отрицательное — емкостному характеру цепи.
Для последовательной и параллельной резонансных цепей можно записать:
, .
Частота переменного тока, при которой возникает резонанс напряжении в цепи: .
Для резонанса токов при параллельном соединении элементов справедлива формула:
.
Для характеристики резонансных контуров используется волновое сопротивление и добротность (при последовательном соединении) или (при параллельном соединении элементов), которая характеризует собой отношение энергии накопленной в контуре, к тепловой энергии, расходуемой в резисторе.
При переменном токе как ток, так и напряжение периодически изменяются во времени. Следовательно, в любой момент времени мощность, равная произведению мгновенных значений напряжения и тока (p = ui) является также переменной величиной.
При активной нагрузке, когда сдвиг фаз между током и напряжением отсутствует (φ = о или cosφ = 1), мощность представляет собой произведение действующих значений напряжения и тока и выражается в вaттax, т. е. P = IU.
В
Рис. 32 График мгновенных значений
цепи, содержащей активное сопротивление
и индуктивность, ток отстает по фазе от
напряжения и мгновенное значение
мощности оказывается как положительным,
так и отрицательным, т.
е. нагрузка
потребляет энергию в одну часть периода
и возвращает ее в сеть в другую часть.
Мощность переменного тока можно представить в виде активной и реактивной мощностей. Активная мощность потребляется активным сопротивлением, где происходит процесс преобразования энергии электрической в энергию другого вида. В двигателях переменного тока большая часть активной мощности превращается в механическую мощность, остальная часть преобразуется в тепло.
Активная мощность . Имея в виду, что , получим
,
где U и I — действующие значения напряжения и тока ;
Ua— падение напряжения на активном сопротивлении.
Реактивная мощность накапливается
индуктивностью при возрастании тока в
цепи в виде магнитного поля индуктивной
катушки. При уменьшении тока в цепи
энергия, накопленная в магнитном поле,
преобразуется в электрическую и
возвращается источнику энергии.
Реактивная мощность выражается в вольт-амперах реактивных (вар), Она не потребляется приемником энергии и не участвует в процессе преобразования электрической энергии в энергию иного вида. Реактивная мощность циркулирует между источником и приемником энергии, нагружая провода их обмоток и линий, соединяющих приемник энергии с источником, также увеличивая потери энергии в них.
Произведение действующих значений напряжения и тока называется полной мощностью
и выражается в вольт-амперах ( ).
Габариты электрических аппаратов и машин определяются полной мощностью, так как сечение обмоточных проводов зависит от тока, протекающего через них, а изоляция токоведущих частей — от напряжения, под которым они находятся.
Отношение активной мощности к полной показывает, какая доля полной энергии
потребляется цепью, и называется
коэффициентом мощности, равным косинусу
угла сдвига фаз между напряжением и
током.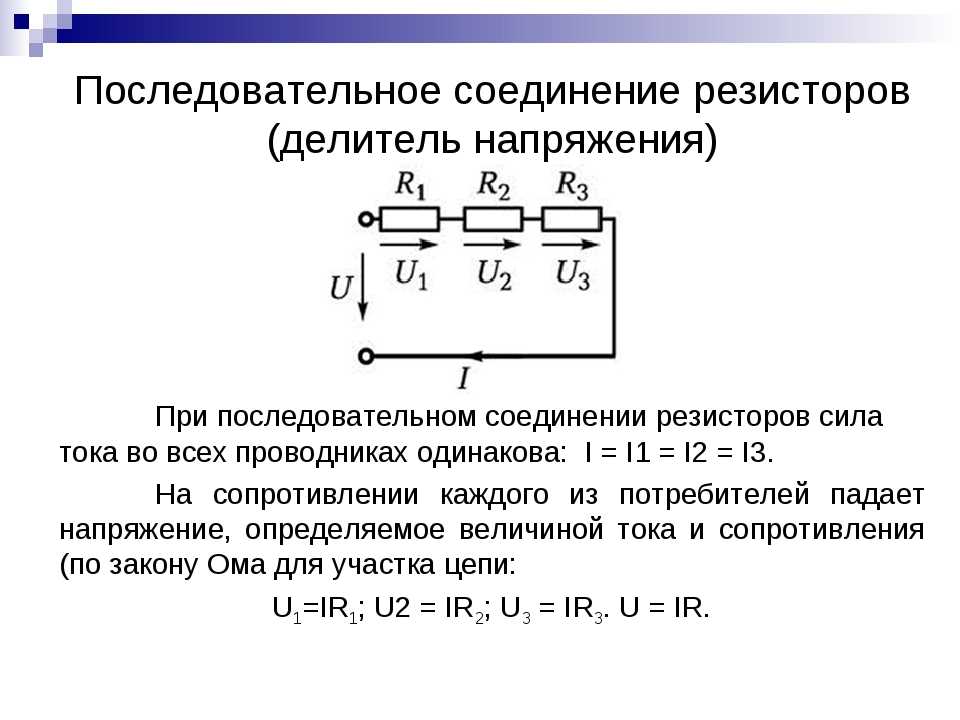
При активной нагрузке и ,
т. е. электрическая машина имеет наибольшую
активную мощность. Величину cosφ
можно косвенно определить по показаниям
ваттметра, вольтметра и амперметра: .
Коэффициент мощности можно также
измерить фазометром.
Получение треугольника мощностей:
В электрических сетях промышленных предприятий всегда имеются такие потребители энергии (асинхронные двигатели, сварочные и другие трансформаторы, индукционные печи и т. д.) которые нуждаются в реактивной мощности для создания переменных магнитных полей. Поэтому cosφ в таких сетях очень низкий. Генератор, не развивая полной активной мощности, может быть загружен током до номинальной величины. В этом случае он используется неэффективно, а потери в питающей линии получаются весьма большими.
Если к потребителю, нуждающемуся в получении реактивной энергии,
подключить конденсатор, то cosφ увеличится.
При увеличении емкости конденсатора опережающие реактивные
токи скомпенсируют отстающие токи в питающей линии, в результате
чего общий линейный ток при постоянной активной нагрузке будет
уменьшаться, a cosφ — увеличиваться.
Р
Рис.33 Подключение конденсатора для повышения cosφ
авенство опережающих и отстающих токов (резонанс токов)
обеспечит их полную компенсацию при cosφ = 1. В этом случае
общий ток будет наименьшим.
Дальнейшее увеличение емкости вызывает увеличение общего тока в линии и снижение при опережающем общем токе.
Подставим полученные значения активных и реактивных токов в ветвях: ; .
Результирующий ток
где у — эквивалентная полная проводимость разветвления.
Треугольник ОАВ, изображенный на векторной диаграмме называется треугольником токов.
Если каждую сторону треугольника токов разделить на величину напряжения U, то можно получить подобный треугольник проводимостей, из которого следует:
, ; ; .
домашнее задание и упражнения — Параллельные цепи — Общее сопротивление уменьшается с дополнительным резистором
Вопрос задан
Изменено 9 лет, 5 месяцев назад
Просмотрено 32k раз
$\begingroup$
Этот вопрос вряд ли поможет будущим посетителям; это относится только к небольшой географической области, определенному моменту времени или чрезвычайно узкой ситуации, которая обычно не применима к всемирной аудитории Интернета.
Чтобы получить более широкое применение этого вопроса, посетите справочный центр.
Закрыт 9 лет назад.
Допустим, имеется параллельная цепь с двумя одинаковыми резисторами, включенными параллельно друг другу. Если параллельно первым двум добавить третий резистор, идентичный двум другим, общее сопротивление уменьшится.
Почему это общее сопротивление уменьшается?
- домашние задания и упражнения
- электрические цепи
- домашний опыт
- электрический ток
- электрическое сопротивление
$\endgroup$
4
$\begingroup$
Почему это общее сопротивление уменьшается?
Более элегантный и изощренный способ понять , почему существует через понятие двойственности .
В теории электрических цепей проводимость (обратная величина сопротивления) равна двойному сопротивлению.
Другие двойные пары:
напряжение — ток
последовательно — параллельно
индуктивность — емкость
Тевенин — Нортон
и так далее …
Например, рассмотрим закон Ома: $v = iR$. Двойственное значение: $i = vG$
Вы, наверное, интуитивно понимаете, что добавление резистора в ряда увеличивает общее сопротивление.
Двойной добавляет проводимость к параллельной , увеличивает общую проводимость .
Но если проводимость увеличивается, то обратная величина, т. е. сопротивление, уменьшает .
Математически:
Параллельные проводимости добавить:
$G_{total}=G_1 + G_2 + G_3 = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3 } = \dfrac{1}{R_{total}}$
или
$R_{total} = \dfrac{1}{\dfrac{1}{R_1} + \dfrac{1}{R_2} + \ dfrac{1}{R_3}}$
Теперь ясно, что при параллельном добавлении еще одного резистора увеличивает знаменатель, таким образом, уменьшает общее сопротивление.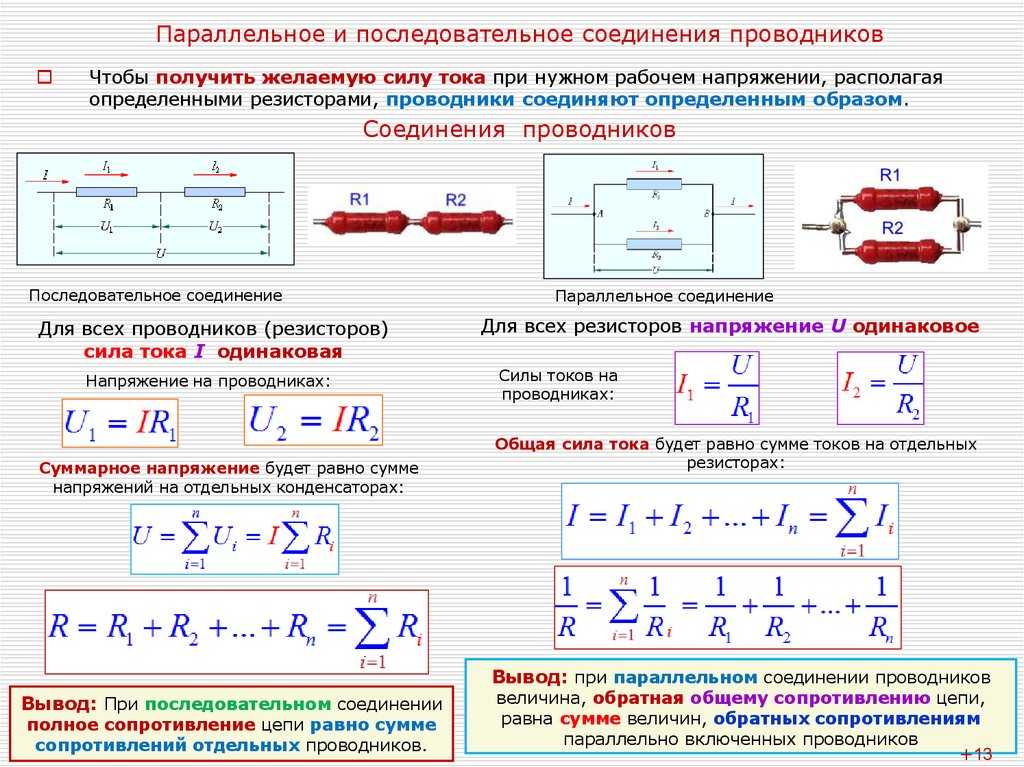
$\endgroup$ 9{(N)} = \frac{R}{N} $$ и поэтому сопротивление уменьшается при параллельном добавлении каждого последующего резистора.
$\endgroup$
8
$\begingroup$
Причина, по которой параллельное подключение резисторов снижает общее сопротивление, заключается в том, что параллельное подключение резисторов увеличивает эффективную площадь поперечного сечения цепи. Ток пропорционален площади поперечного сечения, поэтому общий ток, потребляемый от батареи (при условии, что цепь постоянного тока) увеличивается. Однако добавление резистора параллельно не меняет разность потенциалов на новом резисторе или других существующих параллельных резисторах (это следует из самого определения параллельности). Если цепь подчиняется макроскопическому закону Ома ($\Delta V = IR$), то сопротивление является отношением разности потенциалов и силы тока.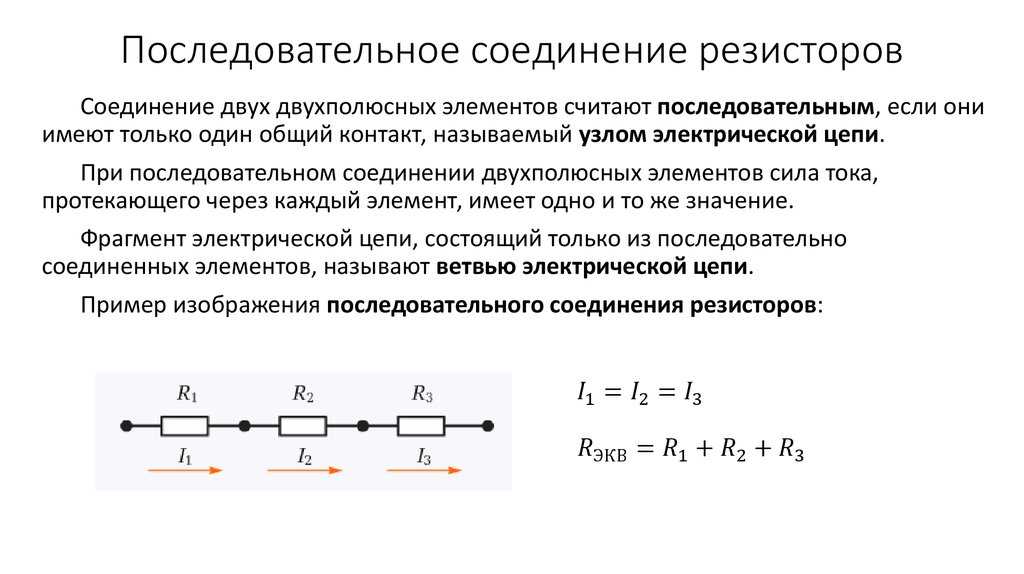
Разность потенциалов не меняется при добавлении нового параллельного резистора, но ток увеличивается, поэтому частное уменьшается. Принятый ответ математически верен, но на самом деле не отвечает на ваш вопрос.
$\endgroup$
$\begingroup$
Основная идея заключается в том, что все резисторы могут быть смоделированы как единый материал, сопротивление которого является функцией либо его площади поперечного сечения $A$ , либо только его длины $L$. Это связано с тем, что у всех резисторов $0 То же самое можно сделать и с длинами — зафиксируйте область и отрегулируйте длину, чтобы получить любое сопротивление, которое вам нравится. Во-первых, последовательная схема. Рассмотрим без ограничения общности два резистора $R_1$ и $R_2$ разной длины при прочих равных условиях. Теперь представьте себе базовый параллельный участок цепи с двумя параллельными резисторами, снова $R_1$ и $R_2$. Суммарная площадь резисторов равна $A=A_1+A_2.$ Поскольку сопротивление обратно пропорционально площади, $R_{eq}$ соответствует $1/A$, а $A_1$ соответствует $1/R_1$, и т. д. Из приведенного выше мы получаем правило, что $1/R_{eq}=1/R_1+1/R_2$. Короче говоря, два последовательных резистора подобны одному более длинному резистору, а два параллельных резистора подобны одному более толстому. Тогда легко понять, почему последовательные резисторы увеличивают общее сопротивление, а параллельные резисторы уменьшают его. Это также распространяется на любое количество резисторов, соединенных последовательно или параллельно. $\endgroup$ 3 $\begingroup$ Я почти не ответил, но, возможно, это поможет кому-то лучше понять принятый ответ. Некоторые люди съеживаются при мысли об этом, но я часто сравниваю электричество с водопроводом. Это работает достаточно хорошо в вашем вопросе и помогает мне визуализировать правильный ответ Джошфизики. Это то же самое, что и большая дырявая ванна. Добавление большего количества дренажных труб заставит ванну стекать быстрее. В этом случае на сливных патрубках больше резисторов. Добавление крошечного дренажного отверстия (представляющего собой дополнительный резистор большого номинала), несомненно, приведет к большему протеканию тока. $\endgroup$ $\begingroup$ Предположим, у нас есть простая схема только с одним резистором. Предположим, что напряжение в цепи составляет 10 В, а ток, скажем, 2 ампера. Теперь предположим, что мы добавили дополнительный компонент в цепь параллельно, как показано на следующей диаграмме: Напряжение на каждом компоненте не уменьшилось в результате этого действия, и теперь у нас есть 10-вольтовая нагрузка на оба компонента в цепи. Если мы рассмотрим первую составляющую, мы можем использовать формулу $V = I_1R_1$, чтобы найти ток равным $I_1 = \frac{V}{R_1}$ (это будет равно 2 Ампер, как и в исходной схеме ). Аналогично можно найти ток по второй составляющей по формуле $V=I_2R_2$ и, следовательно, $I_2 = \frac{V}{R_2}$. Напряжение здесь такое же, как и раньше, потому что параллельное добавление дополнительных резисторов не снижает тяговую силу аккумулятора. Общий ток в цепи затем получается путем сложения тока, протекающего в каждом из компонентов, чтобы получить $I_T = I_1 + I_2 = \frac{V}{R_1} + \frac{V}{R_2} = V (\frac{1}{R_1} + \frac{1}{R_2})$. Теперь мы можем рассматривать два резистора как один большой резистор с сопротивлением $R_T$ и использовать формулу $V = I_TR_T$. Следовательно, $R_T = \frac{V}{V(\frac{1}{R_1} + \frac{1}{R_2})} = \frac{1}{(\frac{1}{R_1} + \frac{1}{R_2})}$ — формула, используемая в одном из приведенных выше ответов. Теперь мы можем интуитивно понять, почему сопротивление уменьшилось. $\endgroup$ Очень активный вопрос . Заработайте 10 репутации (не считая бонуса ассоциации), чтобы ответить на этот вопрос. Требование к репутации помогает защитить этот вопрос от спама и отсутствия ответа. Как последовательно и параллельно добавлять компоненты? Добавление резисторов последовательно и параллельно: R = R1 + R2 + R3 = 1К + 2,2К + 3,9К = 7,1К Обратите внимание, что общее последовательное сопротивление всегда больше, чем наибольшее сопротивление. Однако, если три резистора соединены параллельно, они складываются в обратном порядке следующим образом: или, вычисление R для облегчения жизни путем явного отображения обратной величины вместо 90 196 определения уравнения в терминах 1/R уравнение будет выглядеть так: R = 1/(1/R1+1/R2+1/R3) = 1/(1/1K+ 1/2,2К+1/3,9К) = 1/0,0017 = 584,5 Ом Обратите внимание, что общее параллельное сопротивление всегда меньше наименьшего сопротивления. Существует особый параллельный случай, когда все резисторы имеют одинаковое значение. В этом случае общее сопротивление равно общему значению сопротивления, деленному на количество параллельно соединенных резисторов. Например, если параллельно подключить пять резисторов номиналом 10 кОм, общее сопротивление будет равно 10 кОм/5, или 2 кОм. Формула взаимности тоже сработает, но этот метод более быстрый. Другой метод определения номинала двух резисторов, включенных параллельно, заключается в использовании следующего уравнения: Все эти уравнения справедливы как для импедансов, так и для сопротивлений. Добавление конденсаторов последовательно и параллельно: C = C1 + C2 + C3 = 0,1 мкФ + 0,022 мкФ + 0,01 мкФ = 0,132 мкФ Обратите внимание, что общая параллельная емкость всегда больше наибольшей емкости. Также обратите внимание, что номинальное напряжение параллельных конденсаторов равно наименьшему из двух, если они не равны. Если они равны, номинальное напряжение такое же, как у одиночного конденсатора. Однако, если три конденсатора соединены последовательно, они складываются в обратном порядке следующим образом: 1/C = 1/C1 + 1/C2 + 1/C3 = 1/0,1 мкФ + 1/0,022 мкФ + 1/0,01 мкФ = 1/0,0064, поэтому C = 0,0064 мкФ Обратите внимание, что общая последовательная емкость всегда меньше наименьшей емкости. Существует специальный корпус серии, в котором все конденсаторы имеют одинаковую емкость. В этом случае общая емкость равна общему значению емкости, деленному на количество последовательно соединенных конденсаторов. Например, если три конденсатора по 1 мкФ соединены последовательно, общая емкость будет равна 1 мкФ/3 или 0,333 мкФ. Формула взаимности тоже сработает, но этот метод более быстрый. Другой метод определения емкости двух последовательно соединенных конденсаторов заключается в использовании следующего уравнения: Добавление катушек индуктивности последовательно и параллельно: L = L1 + L2 + L3 = 1 мГн + 10 мГн + 33 мГн = 44 мГн Обратите внимание, что общая последовательная индуктивность всегда больше наибольшей индуктивности. Однако, если три катушки индуктивности соединены параллельно, они взаимно складываются следующим образом: 1/L = 1/L1 + 1/L2 + 1/L3 = 1/1 мГн + 1/10 мГн + 1/33 мГн = 1/0,885 мГн, поэтому L = 0,885 мГн или 885 мкГн Обратите внимание, что общая параллельная индуктивность всегда меньше наименьшей индуктивности. Существует особый параллельный случай, когда все катушки индуктивности имеют одинаковое значение. В этом случае общая индуктивность равна общему значению индуктивности, деленному на количество катушек индуктивности, соединенных параллельно. Например, если четыре катушки индуктивности по 1 мГн соединены параллельно, общая индуктивность будет равна 1 мГн/4 или 250 мкГн. Формула взаимности тоже сработает, но этот метод более быстрый. Другой метод определения значения двух катушек индуктивности, включенных параллельно, заключается в использовании следующего уравнения: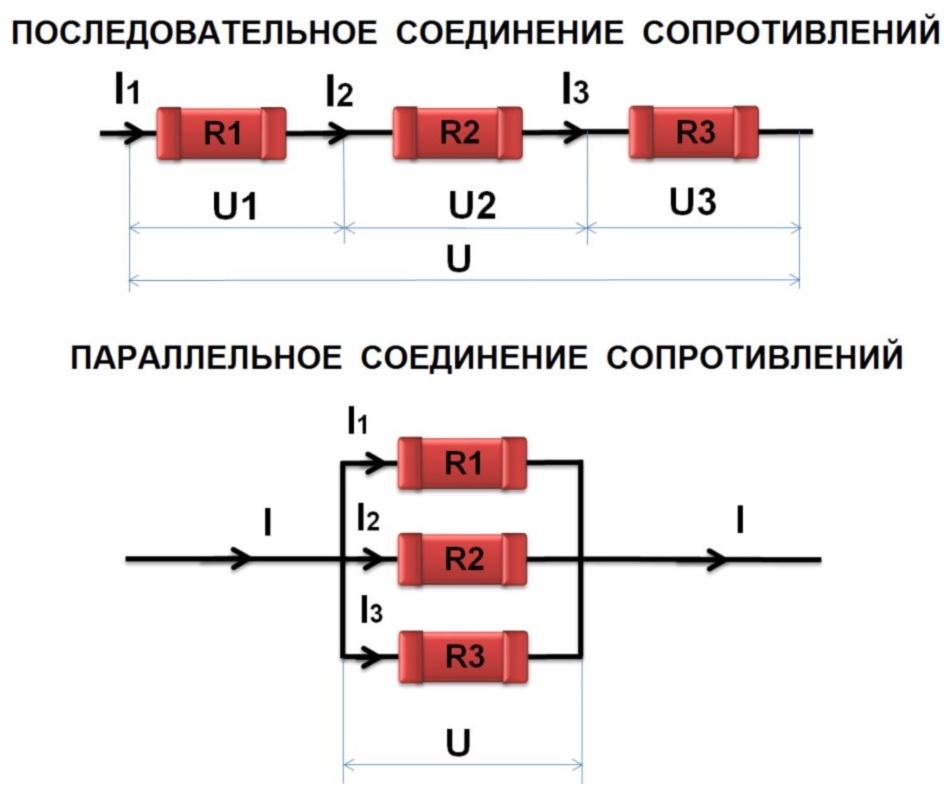
Когда мы складываем их вместе, длина увеличивается, так что общая длина $L=L_1+L_2$. $R_{eq}$ пропорционально $L$, что делает сопротивление «эквивалентного резистора» $R_{eq}=R_1+R_2.$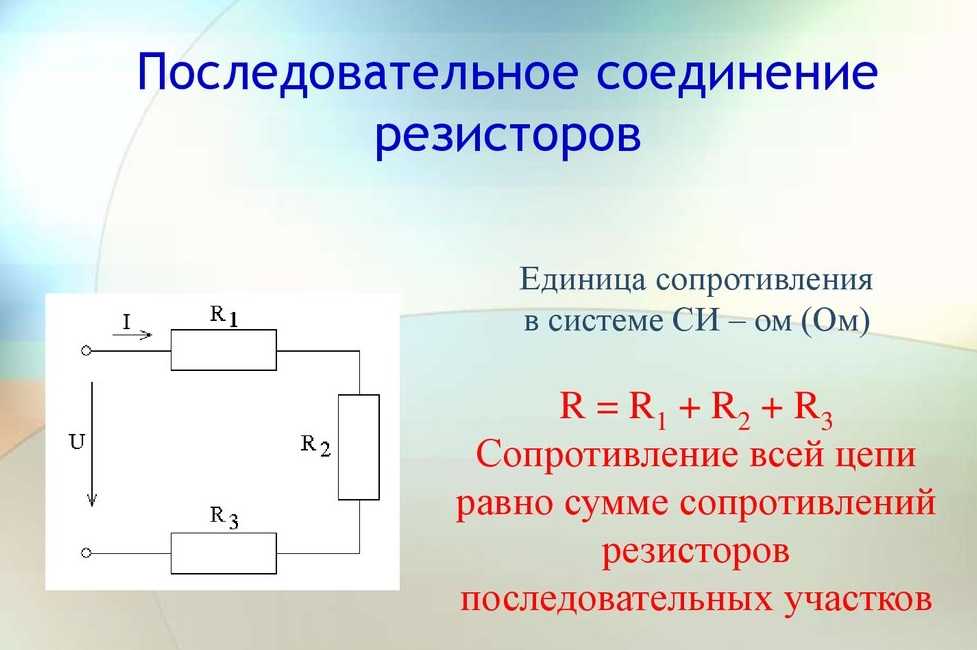
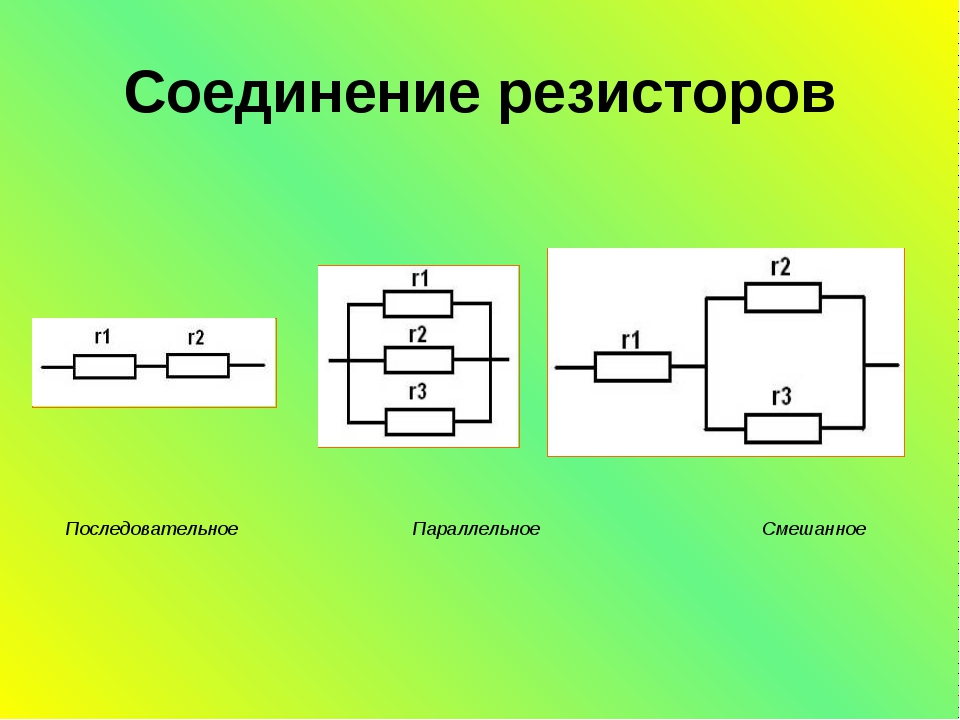Это связано с тем, что добавление второго резистора позволило получить дополнительный ток $I_2$, который в сочетании с первоначальным током $I_1$ образует больший ток, чем раньше. Когда ток увеличивается по сравнению с постоянным напряжением, мы можем сказать, что общее сопротивление цепи уменьшилось. Добавление компонентов последовательно и параллельно
Когда два или более пассивных компонента соединены последовательно или параллельно, их значения складываются по-разному, в зависимости от типа подключаемых компонентов.
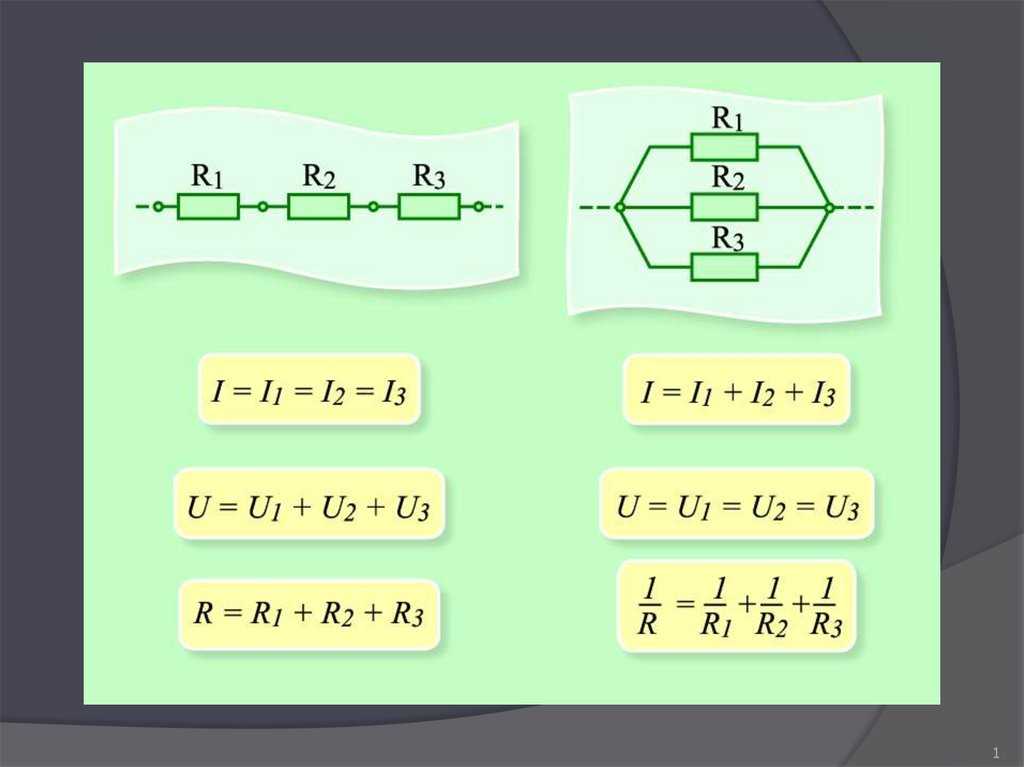
Значения резисторов обычно складываются при последовательном соединении, но складываются обратно при параллельном соединении. Например, если три резистора со значениями 1K, 2,2K и 3,9K соединены последовательно, общее сопротивление будет:
Р = (Р1*Р2)/(Р1+Р2)
Например, если резистор 470К подключен параллельно резистору 220К, общее сопротивление будет равно (470К*220К)/(470К+220К) = 149,9К. Этот результат можно было бы получить с помощью обратного уравнения: 1/R = 1/470К + 1/220К = 1/149,9К, следовательно, R = 149,9К. Можно использовать любое уравнение, но может быть желательно одно или другое, если решаются символьные уравнения или если результат является частью более крупного уравнения.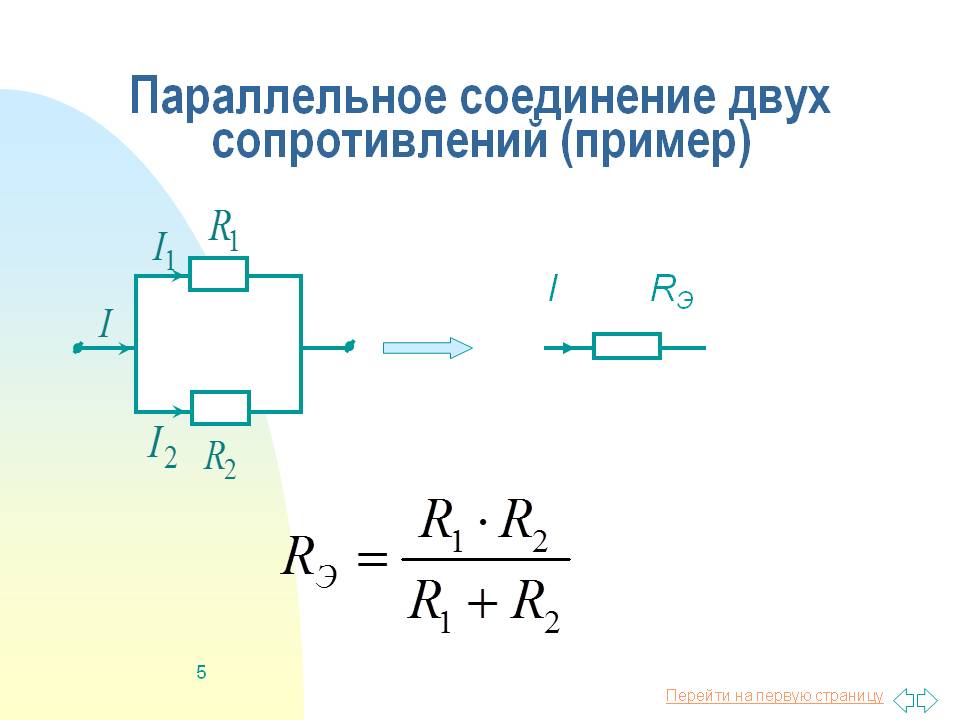
Значения конденсаторов обычно складываются при параллельном соединении, но складываются обратно при последовательном соединении, что в точности противоположно резисторам. Например, если три конденсатора номиналами 0,1 мкФ, 0,022 мкФ и 0,01 мкФ соединены параллельно, общая емкость будет:
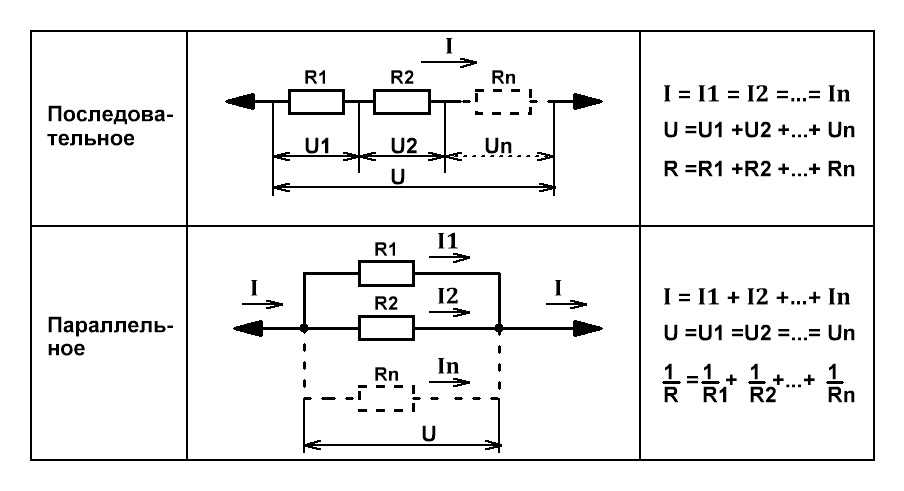Также обратите внимание, что номинальное напряжение последовательных конденсаторов равно сумме номинальных напряжений отдельных конденсаторов , если они имеют одинаковое значение. Если конденсаторы разной емкости и используются в цепи переменного тока, деление напряжения не будет одинаковым. Дополнительную информацию об этом см. в документе, озаглавленном «Правило делителя напряжения». С = (С1*С2)/(С1+С2)
Например, если конденсатор 470 пФ соединить последовательно с конденсатором 47 пФ, общая емкость будет равна (470 пФ * 47 пФ)/(470 пФ + 47 пФ) = 42,7 пФ.
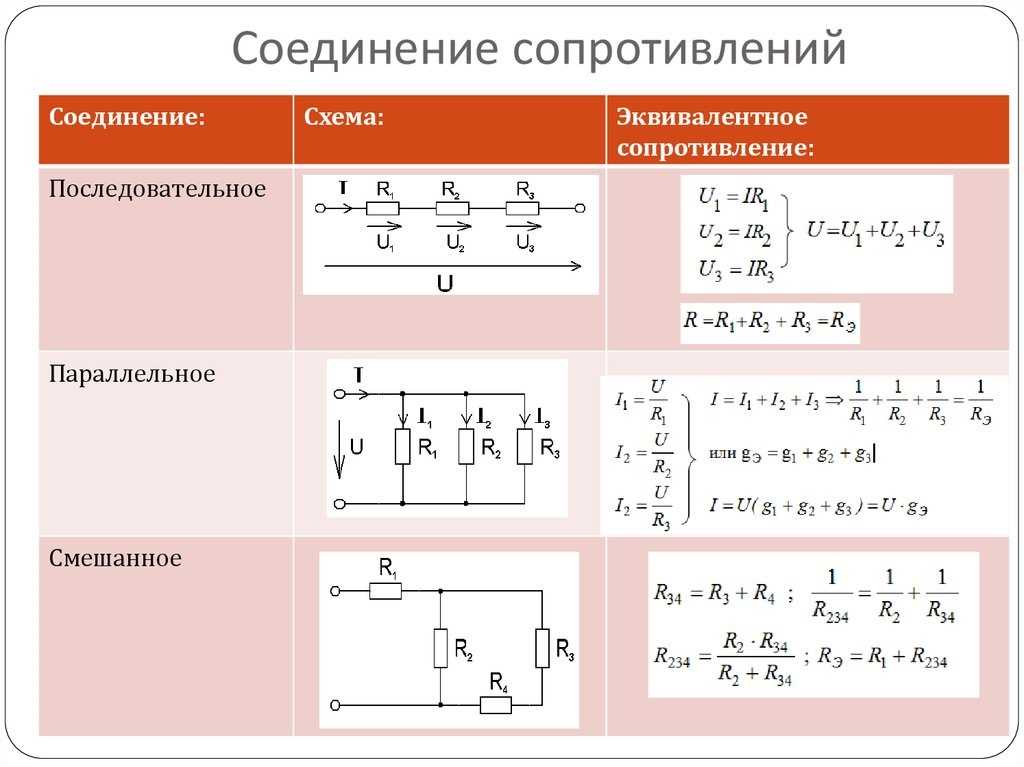Этот результат можно было бы получить с помощью обратного уравнения: 1/C = 1/470 пФ + 1/47 пФ = 1/42,7 пФ, поэтому C = 42,7 пФ. Опять же, можно использовать любое уравнение, в зависимости от того, какое из них более удобно. Значения индуктивности обычно складываются при последовательном соединении, но складываются обратно при параллельном соединении, как и резисторы. Например, если три катушки индуктивности со значениями 1 мГн, 10 мГн и 33 мГн соединены последовательно, общая индуктивность будет:
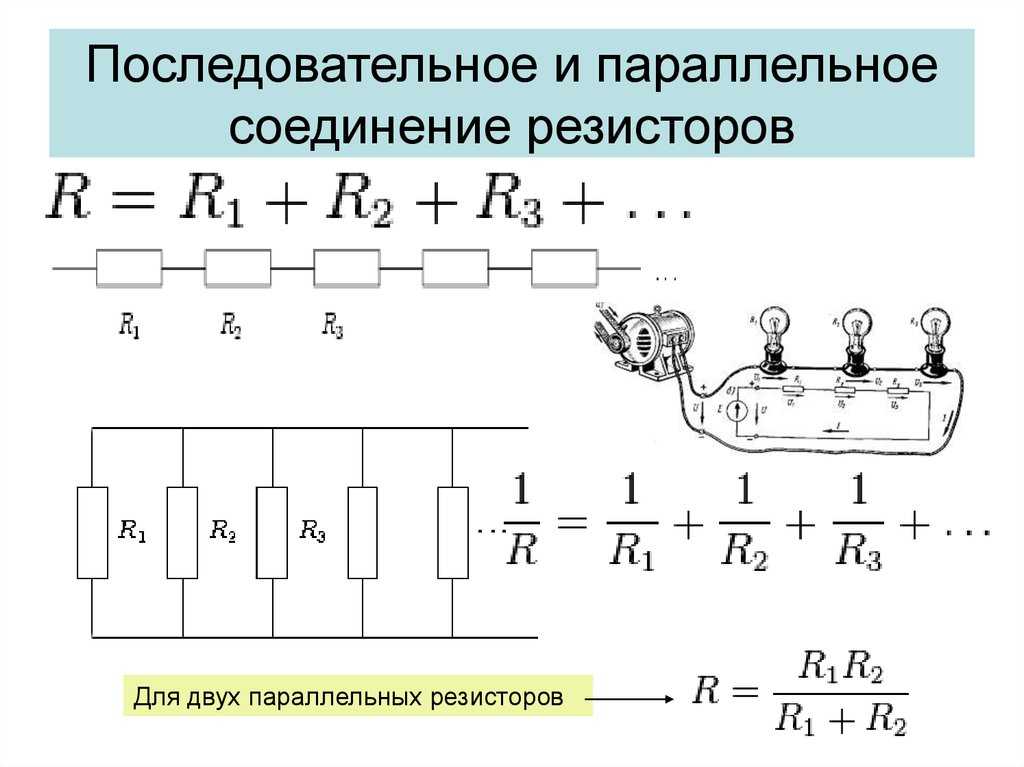
Д = (Д1*Д2)/(Д1+Д2)
Например, если катушка индуктивности 22 мГн соединена параллельно с катушкой индуктивности 33 мГн, общая индуктивность будет равна (22 мГн * 33 мГн) / (22 мГн + 33 мГн) = 13,2 мГн. Этот результат можно было бы получить с помощью обратного уравнения: 1/L = 1/22 мГн + 1/33 мГн = 1/13,2 мГн, следовательно, L = 13,2 мГн. Опять же, можно использовать любое уравнение, в зависимости от того, какое из них более удобно.
