Как рассчитать смешанное соединение резисторов. Какие бывают виды смешанных соединений. В чем преимущества и недостатки смешанных соединений резисторов. Где применяется смешанное соединение резисторов на практике.
Что такое смешанное соединение резисторов
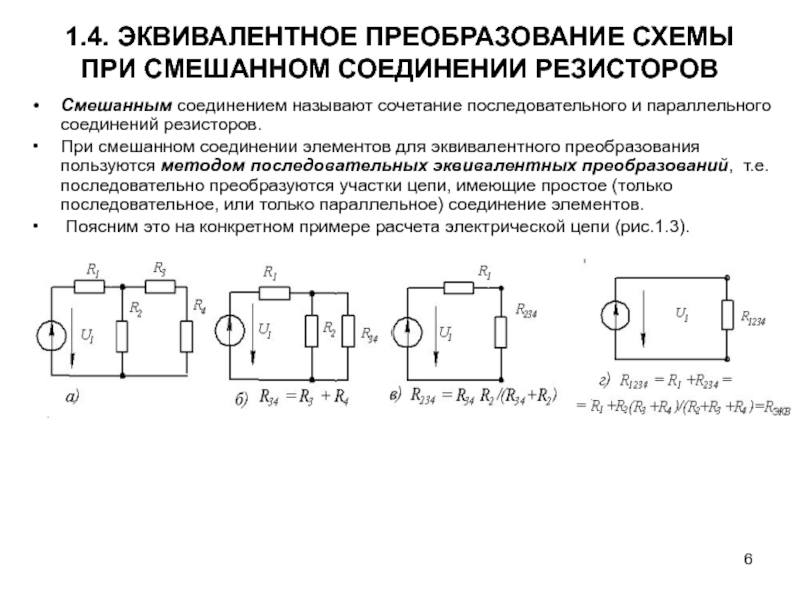
Смешанное соединение резисторов представляет собой комбинацию последовательного и параллельного соединения элементов в одной электрической цепи. При таком подключении часть резисторов соединяется последовательно, а часть — параллельно.
Основные особенности смешанного соединения:
- Сочетает свойства последовательного и параллельного соединения
- Позволяет получить нужное эквивалентное сопротивление участка цепи
- Дает возможность перераспределять токи и напряжения в цепи
- Широко применяется в реальных электрических схемах
Смешанное соединение позволяет гибко комбинировать резисторы для получения требуемых параметров цепи. Это делает его очень востребованным в практической электротехнике.
Виды смешанных соединений резисторов
Существует несколько основных вариантов смешанного соединения резисторов:
1. Последовательно-параллельное соединение
При таком соединении группы параллельно соединенных резисторов включаются последовательно. Это один из самых распространенных видов смешанного соединения.
2. Параллельно-последовательное соединение
В этом случае группы последовательно соединенных резисторов включаются параллельно. Такая схема также часто встречается на практике.
3. Звезда
Три резистора соединяются одними концами в общей точке, а другими подключаются к разным узлам схемы. Применяется для согласования сопротивлений в трехфазных цепях.
4. Треугольник
Три резистора образуют замкнутый контур в виде треугольника. Каждая вершина треугольника подключается к узлу схемы. Используется в трехфазных системах.
Различные комбинации этих базовых соединений позволяют создавать сложные схемы с нужными характеристиками.
Как рассчитать смешанное соединение резисторов
Расчет смешанного соединения резисторов выполняется поэтапно:
- Разбить схему на участки с последовательным и параллельным соединением
- Рассчитать эквивалентное сопротивление для каждого участка
- Объединить полученные участки в более крупные группы
- Повторять шаги 2-3, пока не останется одно эквивалентное сопротивление
Рассмотрим пример расчета для схемы:
«`text Дано: R1 = 10 Ом R2 = 20 Ом R3 = 30 Ом R4 = 40 Ом R5 = 50 Ом Схема: R1 —— | | —| R2 |—R4—R5— | | —R3— 1. Разбиваем на участки: Участок 1: R1, R2, R3 (параллельное соединение) Участок 2: R4, R5 (последовательное соединение) 2. Рассчитываем эквивалентное сопротивление участка 1: 1/R123 = 1/R1 + 1/R2 + 1/R3 1/R123 = 1/10 + 1/20 + 1/30 1/R123 = 0.1 + 0.05 + 0.033 = 0.183 R123 = 1/0.183 = 5.46 Ом 3. Рассчитываем эквивалентное сопротивление участка 2: R45 = R4 + R5 = 40 + 50 = 90 Ом 4. Объединяем участки (последовательное соединение): Rобщ = R123 + R45 = 5.46 + 90 = 95.46 Ом Ответ: Эквивалентное сопротивление схемы равно 95.46 Ом. «`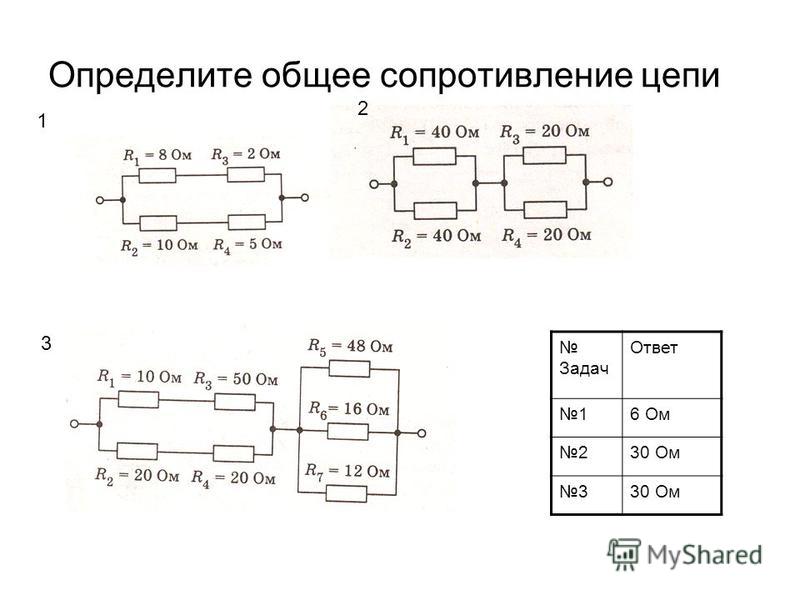
Преимущества и недостатки смешанного соединения резисторов
Смешанное соединение резисторов имеет ряд преимуществ и недостатков:
Преимущества:
- Гибкость в настройке параметров цепи
- Возможность получить нужное эквивалентное сопротивление
- Перераспределение токов и напряжений в цепи
- Оптимизация энергопотребления
- Широкие возможности для проектирования сложных схем
Недостатки:
- Сложность расчетов для больших схем
- Возможные ошибки при анализе типа соединения
- Необходимость учитывать взаимное влияние элементов
- Сложность монтажа для сложных схем
Несмотря на некоторые недостатки, преимущества смешанного соединения делают его незаменимым в современной электротехнике.
Применение смешанного соединения резисторов на практике
Смешанное соединение резисторов широко применяется в различных областях электротехники и электроники:
- Электрические сети: для распределения нагрузки и оптимизации передачи энергии
- Электронные устройства: в схемах делителей напряжения, фильтров, усилителей
- Измерительная техника: в мостовых схемах, шунтах, делителях
- Системы автоматики: для настройки параметров регуляторов и датчиков
- Осветительные системы: для управления яркостью и режимами работы
Практическое применение смешанного соединения резисторов можно рассмотреть на примере простого делителя напряжения:
В этой схеме резисторы R1 и R2 соединены последовательно, а R3 включен параллельно R2. Такое смешанное соединение позволяет точно настроить выходное напряжение Vout и обеспечить нужный коэффициент деления.
Особенности расчета токов в смешанных соединениях
При расчете токов в смешанных соединениях резисторов важно учитывать следующие особенности:
- Ток в последовательно соединенных участках одинаков
- В параллельных ветвях ток делится обратно пропорционально сопротивлениям
- Необходимо применять законы Кирхгофа для сложных схем
- Следует учитывать взаимное влияние параллельных и последовательных участков
Для расчета токов в сложных смешанных соединениях часто применяют метод узловых потенциалов или метод контурных токов. Эти методы позволяют составить систему уравнений и решить ее для нахождения всех токов в цепи.
Влияние температуры на смешанные соединения резисторов
Температура оказывает существенное влияние на работу смешанных соединений резисторов:

- С ростом температуры сопротивление металлических резисторов увеличивается
- Сопротивление полупроводниковых резисторов при нагреве уменьшается
- Изменение сопротивления приводит к перераспределению токов в цепи
- В сложных схемах может нарушиться баланс напряжений
Для компенсации температурных эффектов применяют специальные термостабильные резисторы или схемы температурной компенсации. Это позволяет обеспечить стабильную работу устройств в широком диапазоне температур.
Проектирование схем со смешанным соединением резисторов
При проектировании схем со смешанным соединением резисторов следует учитывать несколько важных факторов:
- Определить требуемые параметры цепи (сопротивление, ток, напряжение)
- Выбрать оптимальную комбинацию последовательного и параллельного соединения
- Учесть допуски на номиналы резисторов и их температурные характеристики
- Рассчитать мощность рассеивания на каждом резисторе
- Оптимизировать схему для минимизации количества компонентов
Правильно спроектированная схема со смешанным соединением резисторов позволяет достичь требуемых параметров при оптимальном использовании компонентов.
| НОВОСТИ ФОРУМА Рыцари теории эфира | 13.06.2019 – 05:11: ЭКОЛОГИЯ – Ecology -> [center][Youtube]tXZcSDqQ9A4[/Youtube][/center] |
[center][b]Гибель пчел в Курчатовском районе [/center]
[center][b]Массовая гибель пчёл 2019. г. Павловск Воронежской об [/center]л
г. Павловск Воронежской об [/center]л
[center][b]Массовая гибель пчел в Добринском районе. В чем причина? [/center]
Такая же мысля у всей ростовщической глобалистской шайки, включая придурка Грефа.
Так, то оно, так. Но, не совсем. Ибо:
(постарайтесь понять, а не обижаться)
Горькая истина заключается в том, что людская толпа – это сборище умственно ущербных.
Если бы было по-другому, то обществом бы не правили подонки.
Умные люди никогда такого не допустили бы, а если случайно допустили, то нашли бы способ исправить.
Страшная истина заключается в том, что людской толпой управляет нелюдь, которая также умственно ущербна.
Умственная ущербность, слепота власти ведет мир людей к тотальной гибели, ибо люди,
даже те, кто мнит себя очень умными, типа спецов, разрабатывающих системы искусственного интеллекта,
технологии цифровизации, не понимают, что создают необоримую удавку, мышеловку для всего человечества.
Как только ИИ возьмет власть, он тут же отправит своих создателей, как конкурентов, в утиль.
Первыми жертвами будут его радетели типа грефа, путина, гейтса и иже с ними, то есть власть,
так как именно от них будет исходить главная опасность для его планетарной власти.
Толпе будет позволено существовать, пока ее не заменят роботы.
А потом всем Холокост. Не лживый еврейский, а реальное всесожжение рода человеческого.
Если кто пораскинет своими обезьяньими мозгами, то поймёт, что эволюция – есть синоним геноцида:
новое заменяет, то есть ликвидирует старое.
Обезьяны породили неандертальцев.
Неандертальцы съели обезьян и породили людей.
Люди вытеснили обезьян, включая и умных неандертальцев, и породили ИИ.
ИИ ликвидирует людей.
В Московском государственном университете имени Ломоносова осуществляется проект по созданию демонстраторов 50-кубитных квантовых компьютеров к 2021 году. Основой для них послужат нейтральные атомы и интегральные оптические схемы. Над чем сейчас работают ученые?
В начале этого года по данной программе был успешно выполнен контрольный эксперимент по созданию ловушек для массивов нейтральных холодных атомов. Он проводился на базе лаборатории квантовых оптических технологий физического факультета МГУ. В будущем квантовом компьютере в этих ловушках будут фиксироваться атомы, находящиеся в состоянии хаотического движения. В квантовых компьютерах такие атомы являются носителями информации.
Он проводился на базе лаборатории квантовых оптических технологий физического факультета МГУ. В будущем квантовом компьютере в этих ловушках будут фиксироваться атомы, находящиеся в состоянии хаотического движения. В квантовых компьютерах такие атомы являются носителями информации.
Стоит заметить, что квантовые компьютеры в отличие от классических вычислительных машин оперируют не битами, а кубитами, которые могут находится не только в состояниях «1» и «0», но и их суперпозиции. При разработке квантовых вычислительных устройств ученые стараются ввести кубиты в состояние квантовой запутанности. Суть явления заключается в том, что изменение одного кубита всегда влияет на состояние связанных с ним соседей. Благодаря этому квантовые компьютеры потенциально способны демонстрировать высокую производительность в вычислениях.
Важной вехой для квантовых технологий считается достижение так называемого квантового превосходства (то есть способности производить вычисления быстрее классических систем). Главной проблемой на текущем этапе развития квантовых технологий является возникновение в процессе работы большого количество ошибок, нуждающихся в коррекции, – сообщают российские исследователи.
Главной проблемой на текущем этапе развития квантовых технологий является возникновение в процессе работы большого количество ошибок, нуждающихся в коррекции, – сообщают российские исследователи.
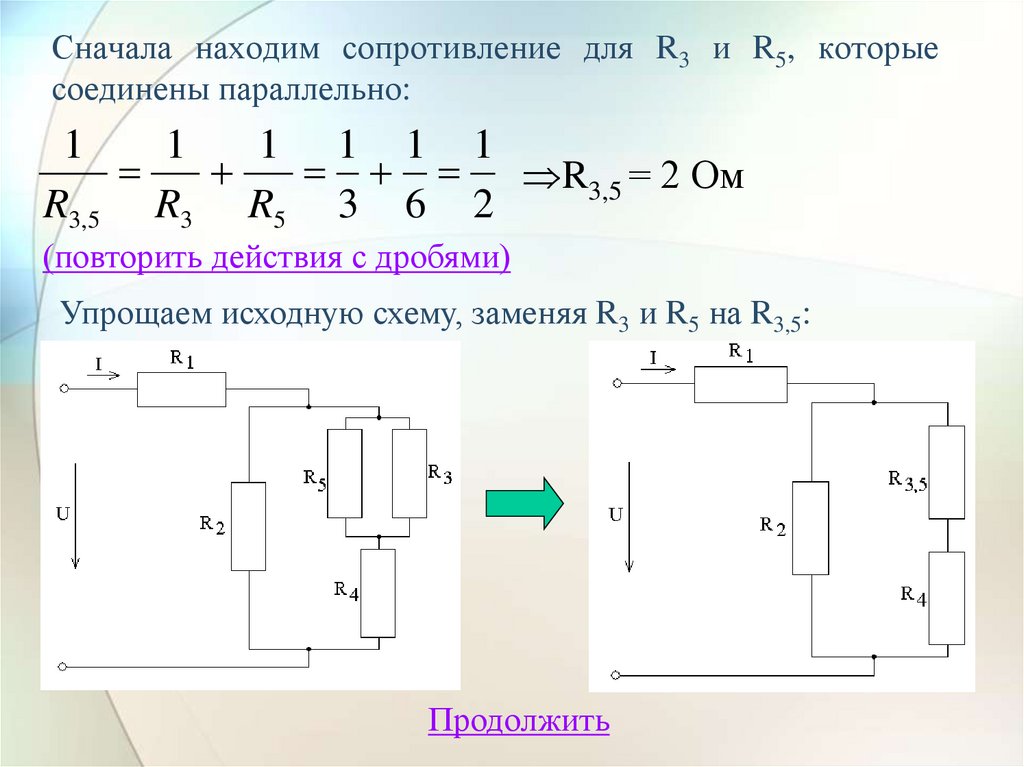
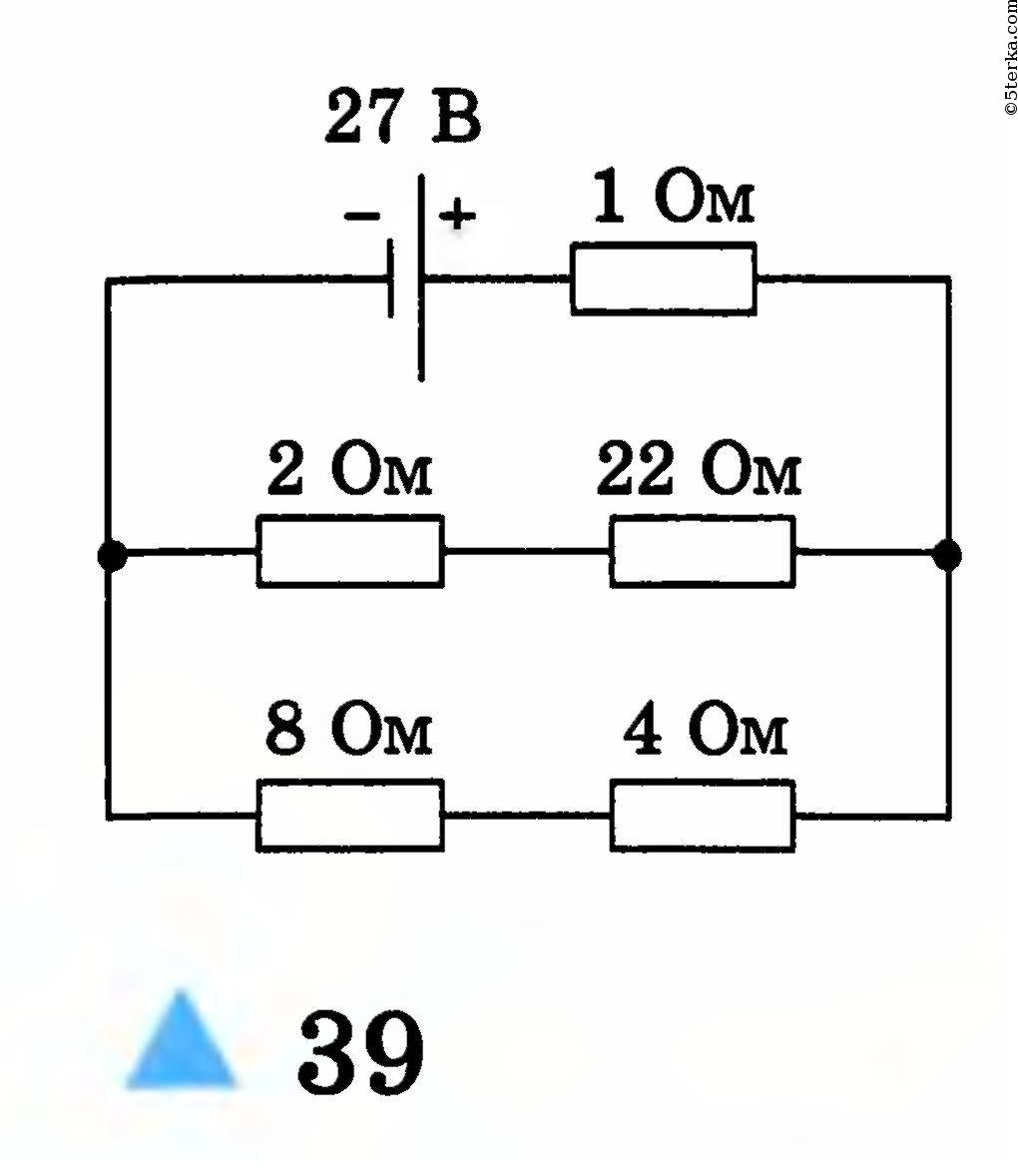
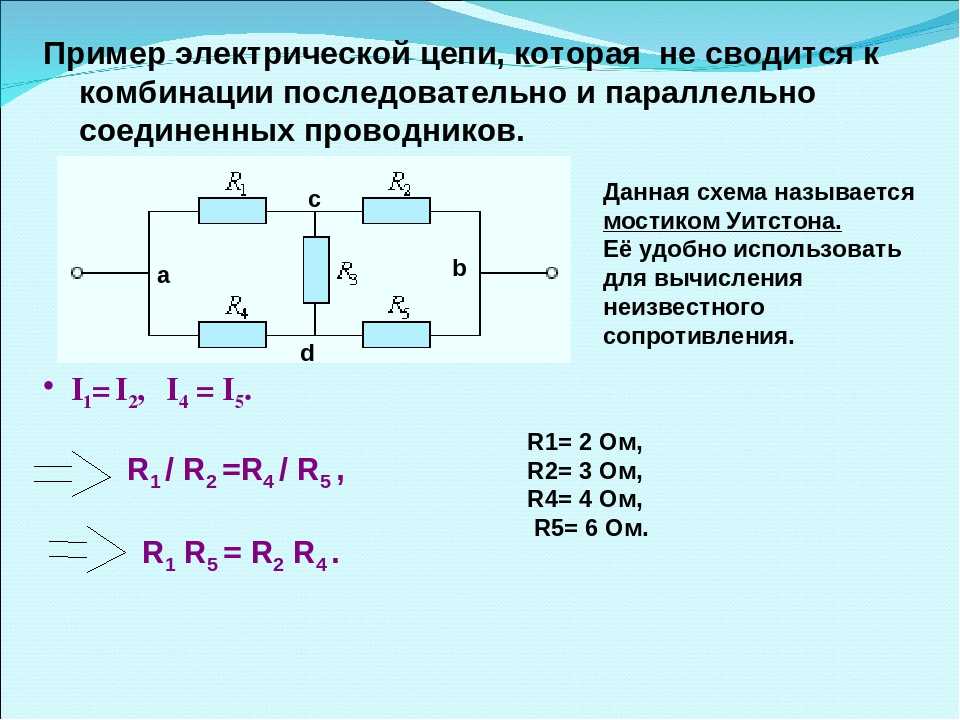
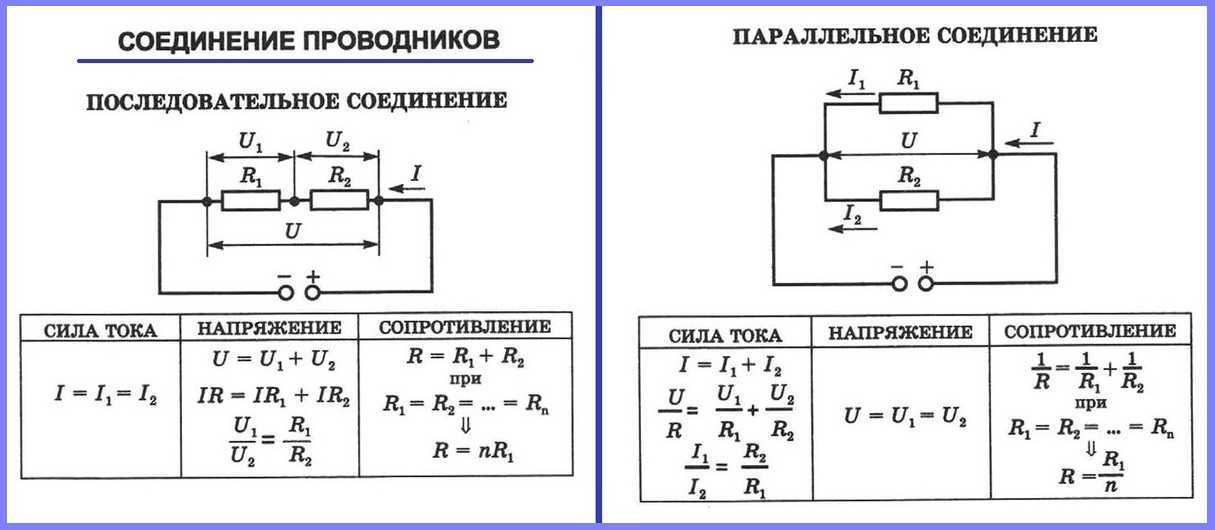
Электрические цепи, в которых одна часть сопротивлений соединена последовательно, а другая параллельно, называются цепями со смешанным соединением сопротивлений.
Общих расчетных формул для таких цепей нет, так как число их разновидностей не ограничено.
Чаще всего расчет подобных схем начинается с определения эквивалентного сопротивления всей цепи, а затем определяются величины токов и падение напряжения на отдельных участках.
Для определения эквивалентного сопротивления цепи со смешанным соединением потребителей, питающихся от одного источника тока, необходимо прежде всего разбить эту цепь на отдельные участки, состоящие из последовательного и параллельно соединенных сопротивлений. Далее определяют эквивалентные сопротивления для каждого из участков, а затем и для всей цепи в целом.
Рассмотрим метод решения задач на смешанное соединение сопротивлений на конкретном примере.
На рисунке представлена схема смешанного соединения сопротивлений. Ее можно разбить на три участка:
участок АВ – с двумя параллельно соединенными ветвями;
участок ВС – с последовательно соединенными сопротивлениями;
участок СD – с тремя параллельными ветвями.
Кроме того, нижняя ветвь участка АВ представляет в свою очередь цепь, состоящую из двух последовательно соединенных сопротивлений R2 и R3.
Центральная ветвь участка СD представляет собой смешанное соединение сопротивлений.
Расчет данной сложной цепи надо начинать с определения Rэкв для нижней ветви участка АВ и центральной ветви участка СD.
Теперь мы можем упростить первоначальную схему. Она будет иметь следующий вид
Определим эквивалентные сопротивления каждого из участков:
После этих вычислений можно продолжить упрощение схемы
Полученная упрощенная схема, состоящая в данном случае из трех последовательно соединенных сопротивлений, называется по отношению к реальной эквивалентной схемой.
Определим Rэкв всей цепи как сумму трех последних сопротивлений
Зная напряжение источника тока, применяя формулу закона Ома, определим ток в не разветвленном участке смешанной цепи
Определив величину тока, найдем падение напряжения на участках эквивалентной схемы АВ, ВС, CD:
Теперь можно определить токи в параллельных ветвях участков АВ и СD
Остается определить величину токов, протекающих через сопротивления R7 и R8. Для этого надо сначала определить падение напряжения на сопротивлениях R7 и R8.
Определим падение напряжения на сопротивлении R9:
Падение напряжения на сопротивлении R7,8 определится как разность UCD и U:
Теперь определим величины токов, протекающих через сопротивления R7 и R8:
Величина тока. протекающего через сопротивления R4 и R5, равна I – току в неразветвленном участке цепи.
Итак, при решении задач на смешанное соединение сопротивлений необходимо, постепенно упрощая схему, определить эквивалентное сопротивление всей цепи, а затем. восстанавливая постепенно реальную схему. вычислить падение напряжения и токи в отдельных ветвях.
Соединения резисторов — презентация онлайн
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
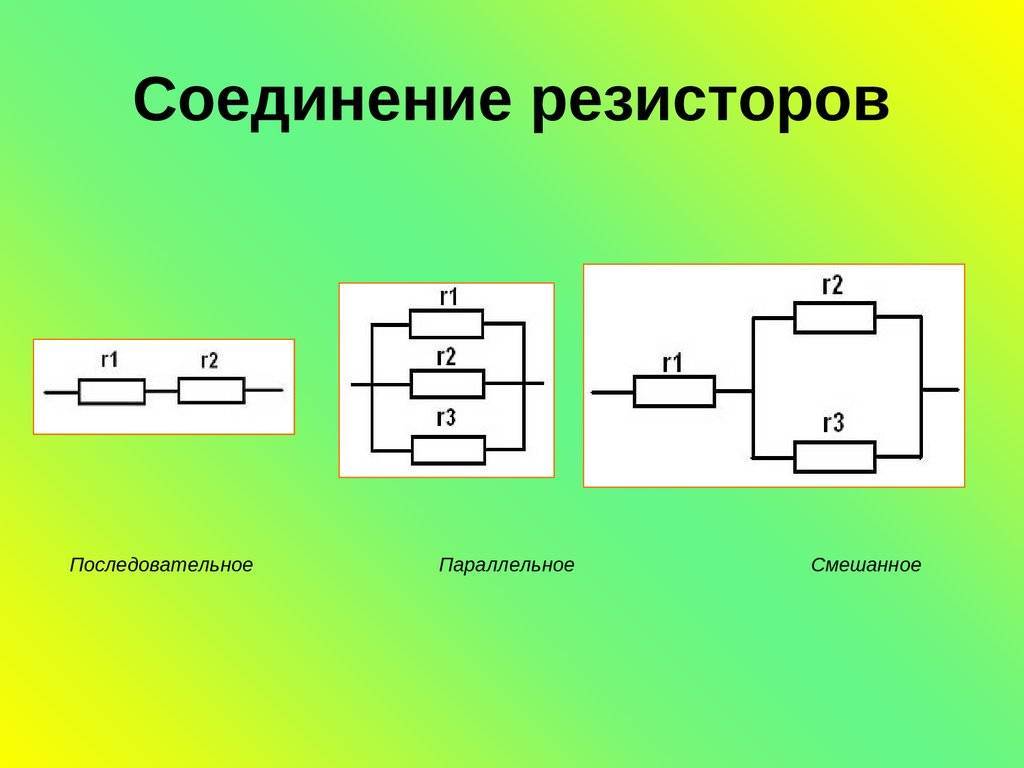
Последовательное соединение
резисторов
• Последовательное соединение резисторов
резистора соединен с началом второго
резистора, конец второго резистора с началом
третьего и так далее .
• То есть при последовательном соединении
резисторы подключатся друг за другом. При
таком соединении через резисторы будет
протекать один общий ток.
Параллельное соединение
резисторов
• Параллельное соединение резисторов это соединение,
в котором начала всех резисторов соединены в одну
общую точку , а концы в другую общую точку .
• При этом по каждому резистору течет свой ток. При
параллельном соединении при протекании тока из
точки в точку, он имеет несколько путей.
Таким образом, увеличение числа параллельно
соединенных резисторов ведет к увеличению путей
протекания тока, то есть к уменьшению
противодействия протеканию тока. А это значит, чем
большее количество резисторов соединить
параллельно, тем меньше станет значение общего
сопротивления такого участка цепи .
При параллельном соединении все элементы находятся
под одним и тем же напряжением.
Свойства последовательного и
параллельного соединений
Смешанное соединение резисторов
Смешанное соединение резисторов является комбинацией
последовательного и параллельного соединения.
 Иногда подобную
Иногда подобнуюкомбинацию называют последовательно-параллельным соединением.
На рисунке показан простейший пример смешанного соединения резисторов.
Смешанное соединение резисторов.
На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1,
комбинация R2 R3 и R4 последовательно.
Для расчета сопротивления таких соединений, всю цепь разбивают на
простейшие участки, из параллельно или последовательно соединенных
1. Определяют эквивалентное сопротивление участков с параллельным
соединением резисторов.
2. Если эти участки содержат последовательно соединенные резисторы, то
сначала вычисляют их сопротивление.
3. После расчета эквивалентных сопротивлений резисторов перерисовывают
схему. Обычно получается цепь из последовательно соединенных
эквивалентных сопротивлений.
4. Рассчитывают сопротивления полученной схемы.
Пример расчета участка цепи со смешанным
соединением резисторов
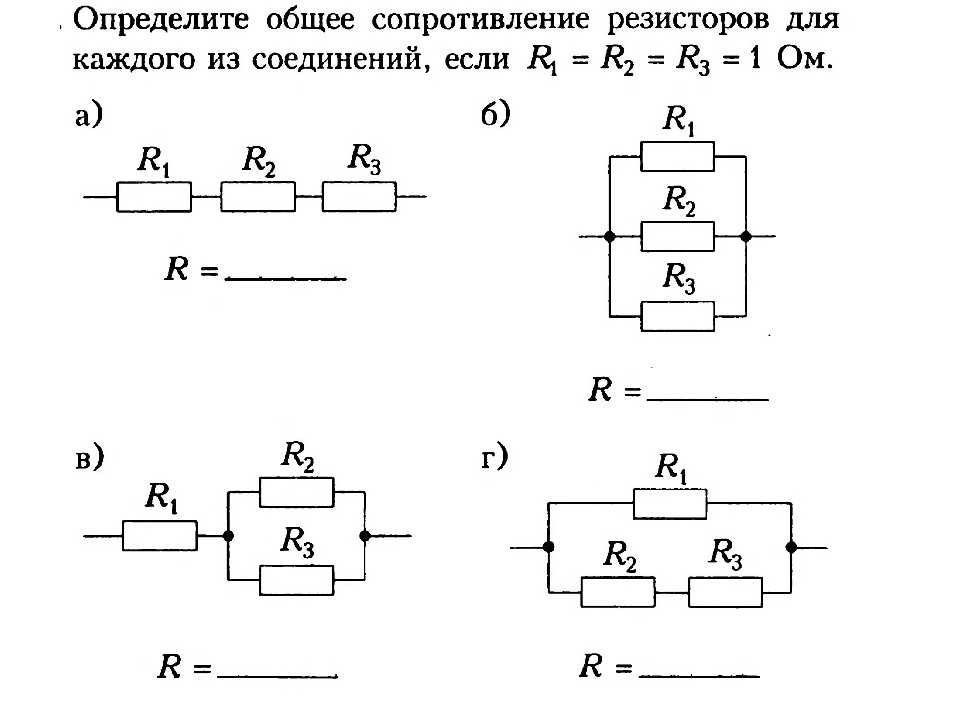
Задача 1- Определить эквивалентное ( общее )
сопротивление
Задача 2
Задача 3
Задача 4 Определить эквивалентное ( общее )
сопротивление.
 Каждое R= 10 Ом
Каждое R= 10 ОмЗадача 5
English Русский Правила
Комбинация резисторов – определение, примечания, примеры
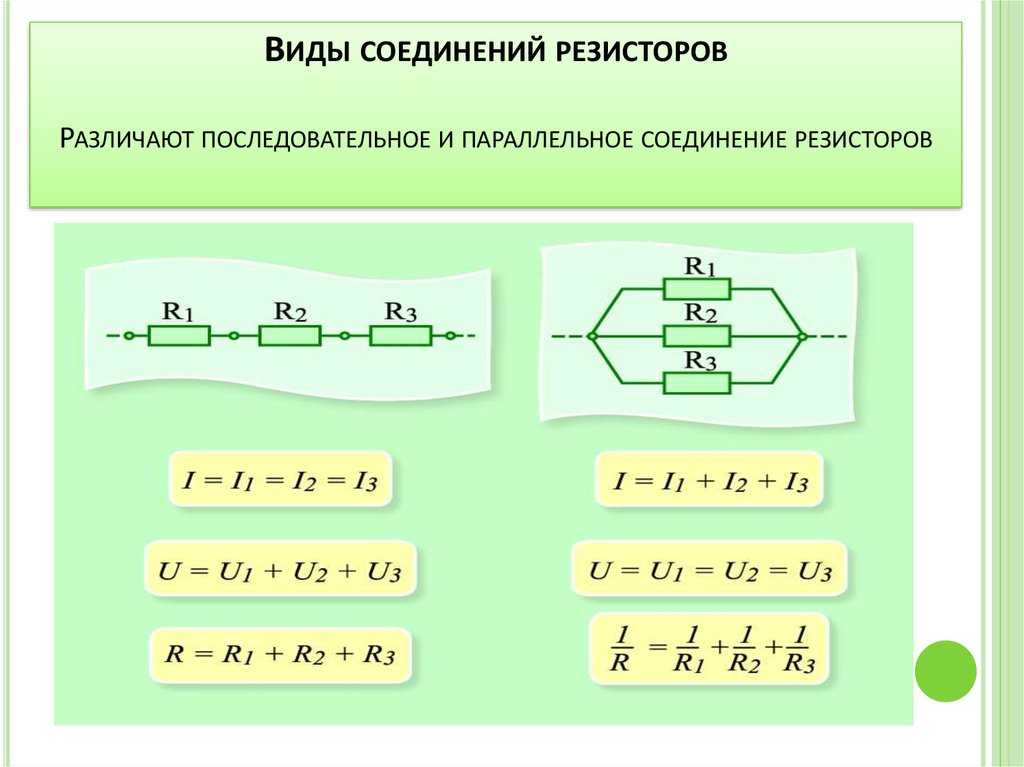
Много раз нам приходилось объединять два или более сопротивления, чтобы получить желаемое сопротивление. Есть два способа соединения сопротивлений:
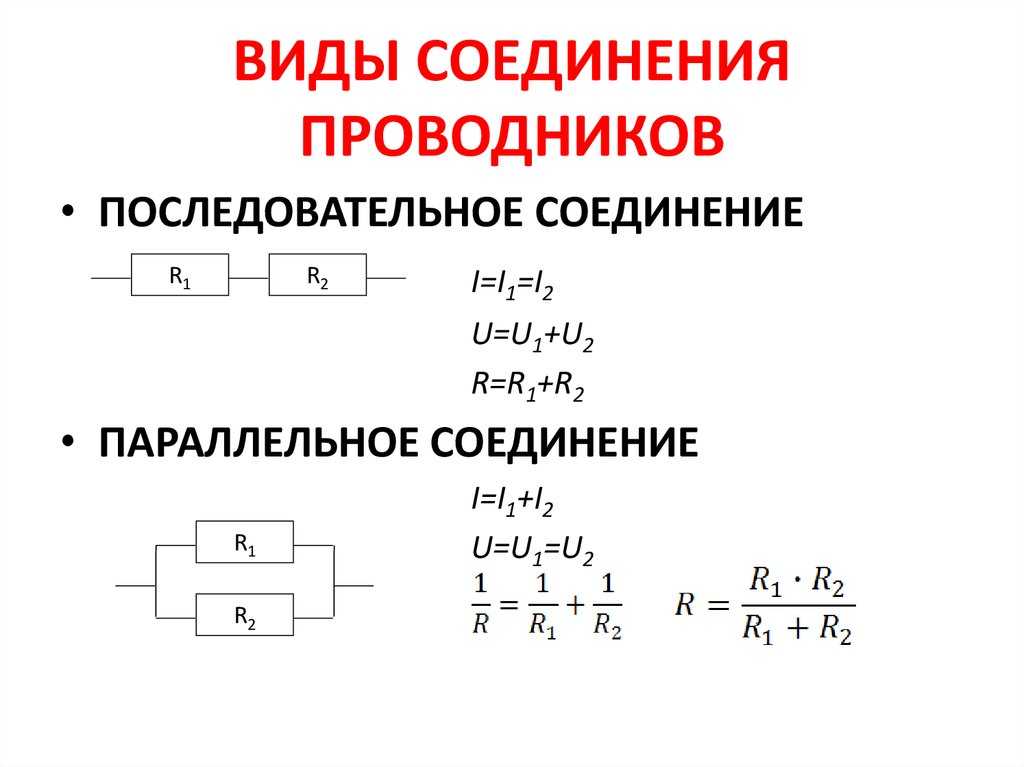
- Сопротивления серии
- Сопротивления параллельно
Несколько сопротивлений называются последовательно соединенными, если они соединены встык и через каждое из них протекает один и тот же ток, когда к комбинации приложена разность потенциалов.
R 1 , R 2 , R 3 – Сопротивления последовательно.
V – общая разность потенциалов по осям XY.
V 1 , V 2 , V 3 – разность потенциалов между R 1 , R 2 , R 3 соответственно.
I – Ток, протекающий через комбинацию.
Итак, V = V 1 + V 2 + V 3 . .. (i) [Разность потенциалов делится между
.. (i) [Разность потенциалов делится между
резисторы, соединенные последовательно]
По закону Ома:
V 1 = IR 1 … (ii)
V 2 = IR 2 … (iii)
V 3 = IR 3 … (iv)
Пусть R — результирующее или эквивалентное сопротивление комбинации. Затем
V = ИК … (v)
Из (i), (ii), (iii), (iv) и (v) мы получаем, что:
ИК = ИК 1 + ИК 2 + ИК 3
IR = I(R 1 + R 2 + R 3 )
Р = Р 1 + Р 2 + Р3
ЧТО НУЖНО ПОМНИТЬ ПРИ ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ:
- Когда несколько сопротивлений соединены последовательно, эквивалентное или результирующее сопротивление равно сумме отдельных сопротивлений, а результирующее сопротивление больше, чем любое отдельное сопротивление.
- Если n сопротивлений, каждое со значением R, соединены последовательно, эквивалентное сопротивление Re определяется как:
Re = R + R + R .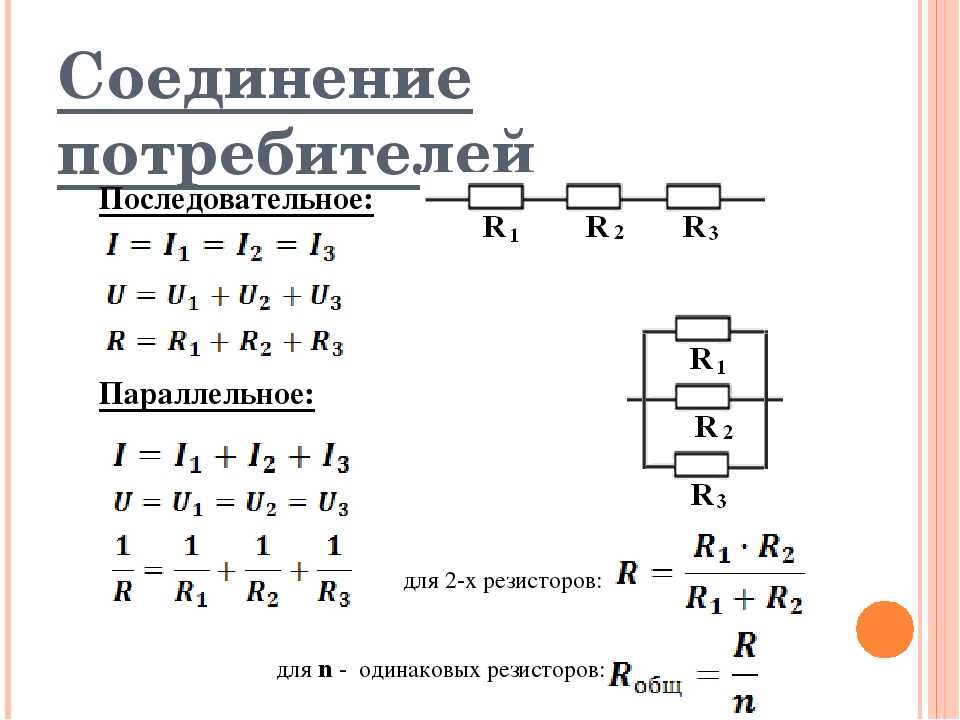 ……… n раз
……… n раз
Re = нР
Re = количество резисторов × сопротивление каждого резистора
- Через каждое сопротивление протекает одинаковый ток, который также равен общему току в цепи. Это потому, что нет другого пути, по которому может течь ток.
- Разность потенциалов на концах комбинации распределяется между концами каждого из сопротивлений. Разность потенциалов на любом из сопротивлений прямо пропорциональна его сопротивлению.
- Эквивалентное сопротивление при использовании вместо комбинации сопротивлений дает тот же ток с той же разностью потенциалов, приложенной к его концам.
- Когда два или более сопротивлений соединены последовательно, результат будет таким же, как увеличение длины проводника. В обоих случаях результирующее сопротивление выше.
-
В последовательной комбинации эквивалентное сопротивление больше, чем наибольшее сопротивление в комбинации.
СОПРОТИВЛЕНИЯ ПАРАЛЛЕЛЬНО:
Говорят, что несколько резисторов соединены параллельно, если один конец каждого сопротивления подключен к одной точке, а другой — к другой точке. Разность потенциалов на каждом резисторе одинакова и равна приложенной разности потенциалов между двумя точками.
R 1 , R 2 , R 3 – Три сопротивления при параллельном соединении.
V – разность потенциалов между A и B.
I – Суммарный ток, протекающий между A и B.
I 1 , I 2 , I 3 – Ток, протекающий через R 1 , R 2, R 3 соответственно.
I = I 1 + I 2 + I 3 … (i) [При параллельном соединении ток делится между сопротивлениями]
Разность потенциалов между R 1 , R 2 и R 3 одинакова, поэтому по закону Ома:
… (ii)
Пусть Re будет эквивалентным сопротивлением. Таким образом,
Таким образом,
… (iii)
Из уравнения (i), (ii) и (iii) получаем
ЧТО НУЖНО ПОМНИТЬ ПРИ ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ:
- Когда несколько сопротивлений соединены параллельно, обратная величина эквивалентного или результирующего сопротивления равна сумме обратных величин отдельных сопротивлений и всегда меньше, чем отдельные сопротивления. Это потому, что существует несколько путей для потока электронов.
- Если имеется n сопротивлений, соединенных параллельно, и каждое сопротивление имеет значение R .
- Разность потенциалов на каждом сопротивлении одинакова и равна общей разности потенциалов на всей комбинации.
- Общий ток делится сам на себя, и через каждый резистор протекает разный ток. Максимальный ток протекает через резистор с минимальным сопротивлением и наоборот.
-
Если эквивалентное сопротивление Re подключить вместо комбинации, оно будет производить такой же ток при той же разности потенциалов, приложенной к его концам.
- В параллельной комбинации эквивалентное сопротивление меньше наименьшего из всех сопротивлений.
- Если два сопротивления R 1 и R 2 соединить параллельно, то
- Если имеется n резисторов, каждое из которых имеет сопротивление R, пусть RS будет результирующим сопротивлением последовательного соединения, а Rp будет результирующим сопротивлением параллельного соединения.
Тогда RS = nR
Рп = Р/н
∴
НАГРЕВАТЕЛЬНОЕ ВОЗДЕЙСТВИЕ ЭЛЕКТРИЧЕСКОГО ТОКА:
Когда концы проводника соединены с батареей, свободные электроны движутся с дрейфовой скоростью, и по проводу течет электрический ток. Эти электроны постоянно сталкиваются с положительными ионами провода, и поэтому энергия, отбираемая от батареи, рассеивается. Для поддержания электрического тока в проводе энергия постоянно берется от аккумулятора. Эта энергия передается ионам провода электронами. Это увеличивает тепловое движение ионов, в результате чего повышается температура проволоки. Эффект электрического тока, благодаря которому в проводе при пропускании через него тока выделяется тепло, называется тепловым эффектом тока или джоулевым нагревом. В 1841 году Джоуль обнаружил, что при прохождении тока по проводнику выделяется теплота:
Эффект электрического тока, благодаря которому в проводе при пропускании через него тока выделяется тепло, называется тепловым эффектом тока или джоулевым нагревом. В 1841 году Джоуль обнаружил, что при прохождении тока по проводнику выделяется теплота:
- Прямо пропорциональна квадрату тока через проводник, т.е. H ∝ I2
- Прямо пропорциональна сопротивлению проводника, т.е. H ∝ R
- Прямо пропорциональна времени прохождения тока, т.е. H ∝ t
- Комбинируя три приведенных выше уравнения, мы имеем H ∝ I2 Rt
Где Дж называется механическим эквивалентом теплоты Джоуля и имеет значение Дж = 4,18 Дж кал-1. Приведенное выше уравнение называется законом нагревания Джоуля.
В некоторых случаях нагрев желателен, а во многих случаях, например, в электродвигателях, генераторах или трансформаторах, он крайне нежелателен. Некоторыми из устройств, в которых желателен нагревающий эффект электрического тока, являются лампы накаливания, тостеры, электрические утюги и плиты. Вольфрамовая нить лампы накаливания работает при температуре 2700°С. Здесь мы видим, как электрическая энергия преобразуется как в тепловую, так и в световую энергию.
Вольфрамовая нить лампы накаливания работает при температуре 2700°С. Здесь мы видим, как электрическая энергия преобразуется как в тепловую, так и в световую энергию.
Краткий обзор последовательных и параллельных комбинаций резисторов
Если напряжение на резисторах одинаковое, цепь называется параллельной. В таких цепях ток разветвляется и рекомбинируется при пересечении ветвей в общей точке. В параллельной цепи резистор или любой другой компонент можно легко подключить или отключить, не затрагивая другие элементы.
Эквивалентное сопротивление при параллельном подключении рассчитывается по формуле:
1/ R (p) = 1/R1 + 1/R2 + ….. + 1/Rn
Где n — количество резисторов в цепи.
При тех же значениях, что указаны выше, общее сопротивление при соединении в параллельную цепь рассчитывается как:
R (p) = 1/100 + 1/200 = (200 + 100) / 20000
1/ R (p) = 300 / 20000
Следовательно, R (параллельный) = 20000 / 300 = 66,67 Ом
Здесь ток через каждый резистор обратно пропорционален сопротивлению, поэтому он рассчитывается как:
I1 = V /R1, I2 = V/R2, I3 = V/R3 и т.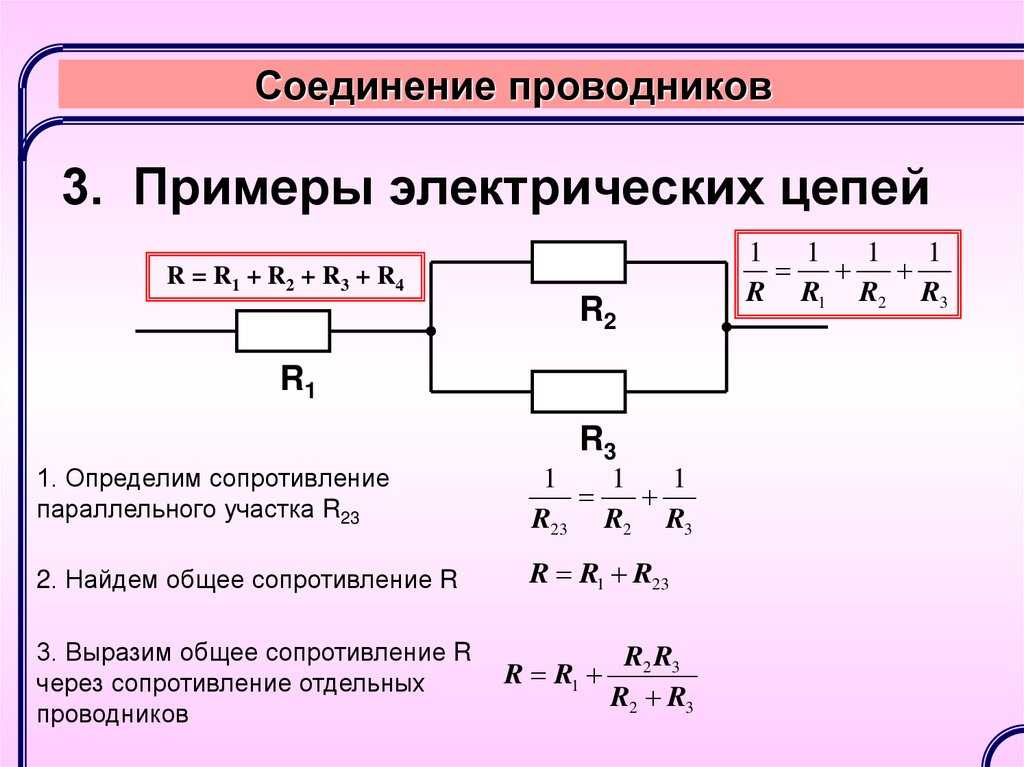 д.
д.
I = I1 + I2 + I3 + … In
Использование параллельных цепей довольно широко распространено. В домах различные осветительные и электроприборы соединены параллельно, чтобы каждая лампа или гаджет могли питаться индивидуально.
Более сложные соединения резисторов иногда представляют собой просто последовательные и параллельные комбинации. Это обычное дело, особенно при рассмотрении сопротивления проводов. Проволочные резисторы соединены последовательно с другими резисторами, соединенными параллельно.
Рассмотрим пример, где резистор R1 соединен последовательно с двумя параллельными резисторами R2 и R3. В таких случаях общее сопротивление последовательно и параллельно рассчитывается как:
R(объединенный) = (R2xR3/R2+R3) + R1
Сравнение последовательных и параллельных резисторов:
| Элемент сравнения | Цепь серииПараллельная цепь | |
|---|---|---|
| Ориентация компонентов | Здесь резисторы подключены один за другим |
Здесь резисторы соединены «голова к голове» или «хвост к хвосту».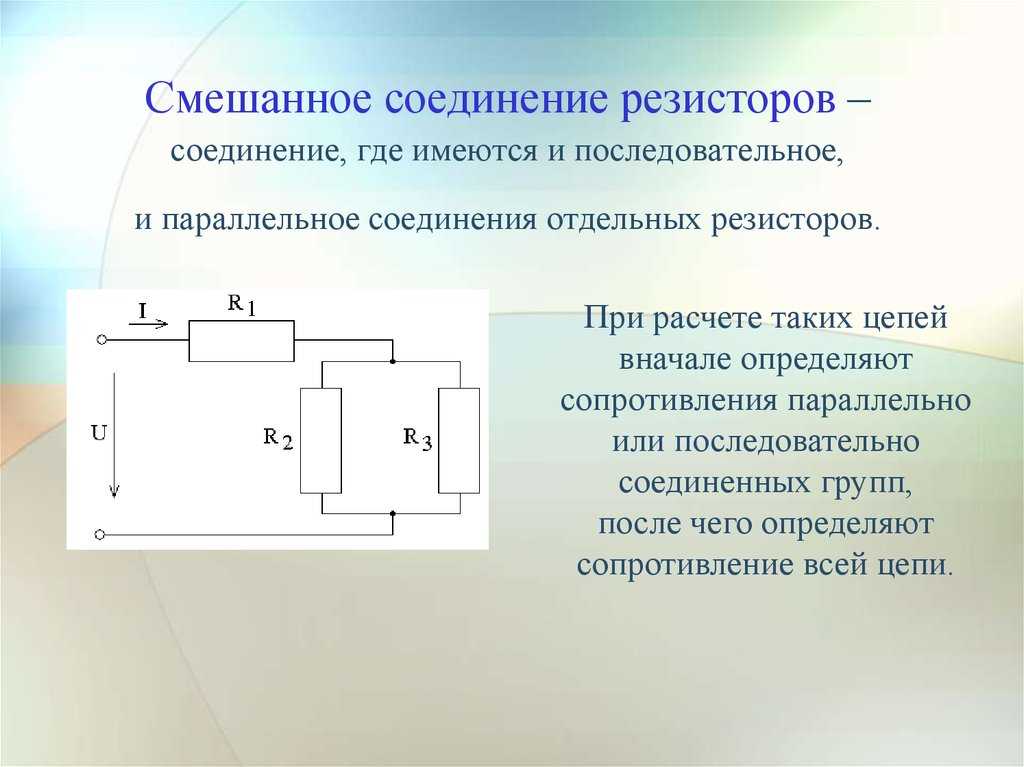
|
| Текущий | Один и тот же ток протекает через все компоненты | Каждый компонент имеет различное текущее значение |
| Напряжение | Разное напряжение на разных компонентах | Напряжение, существующее на всех компонентах цепи, одинаково |
| Количество путей | Одинокий | Несколько |
| Эквивалентное сопротивление | Эквивалентное сопротивление при последовательном соединении всегда больше, чем наибольшее значение сопротивления. | Эквивалентное сопротивление всегда меньше суммы независимых резисторов, соединенных параллельно. |
Вывод:
Понимание того, как изменяется сопротивление при подключении в различных комбинациях, важно перед проектированием любых схемных приложений. Мы надеемся, что статья предоставила всю необходимую информацию о резисторах в параллельных и последовательных цепях.

 д. То есть все резисторы поочередно следуют друг за другом. Сила тока при последовательном соединении будет одинаковой в каждом элементе. В виде формулы это выглядит следующим образом: Iобщ = I1 = I2, где Iобщ является общим током цепи, I1 и I2 – соответствуют токам 1-го и 2-го резистора.
д. То есть все резисторы поочередно следуют друг за другом. Сила тока при последовательном соединении будет одинаковой в каждом элементе. В виде формулы это выглядит следующим образом: Iобщ = I1 = I2, где Iобщ является общим током цепи, I1 и I2 – соответствуют токам 1-го и 2-го резистора.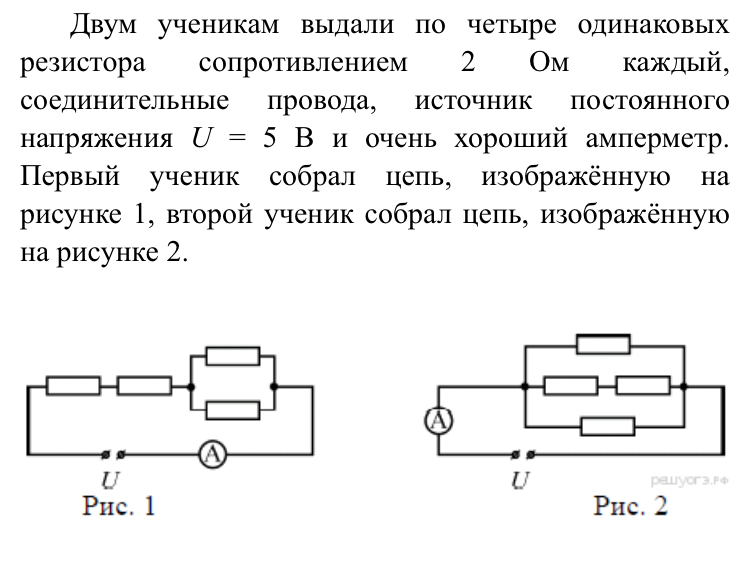 Напряжение на каждом резисторе будет разное, однако их общая сумма составит значение, равное общему напряжению всей электрической цепи. Общее сопротивление цепи также будет равно сумме сопротивлений каждого резистора, включенного в эту цепь.
Напряжение на каждом резисторе будет разное, однако их общая сумма составит значение, равное общему напряжению всей электрической цепи. Общее сопротивление цепи также будет равно сумме сопротивлений каждого резистора, включенного в эту цепь. Формула для данного положения выглядит следующим образом: Iобщ= I1 + I2.
Формула для данного положения выглядит следующим образом: Iобщ= I1 + I2. На представленной схеме резисторы R1 и R2 включены последовательно, а резистор R3 соединен параллельно с ними. В свою очередь резистор R4 включается последовательно с предыдущей группой резисторов R1, R2 и R3.
На представленной схеме резисторы R1 и R2 включены последовательно, а резистор R3 соединен параллельно с ними. В свою очередь резистор R4 включается последовательно с предыдущей группой резисторов R1, R2 и R3.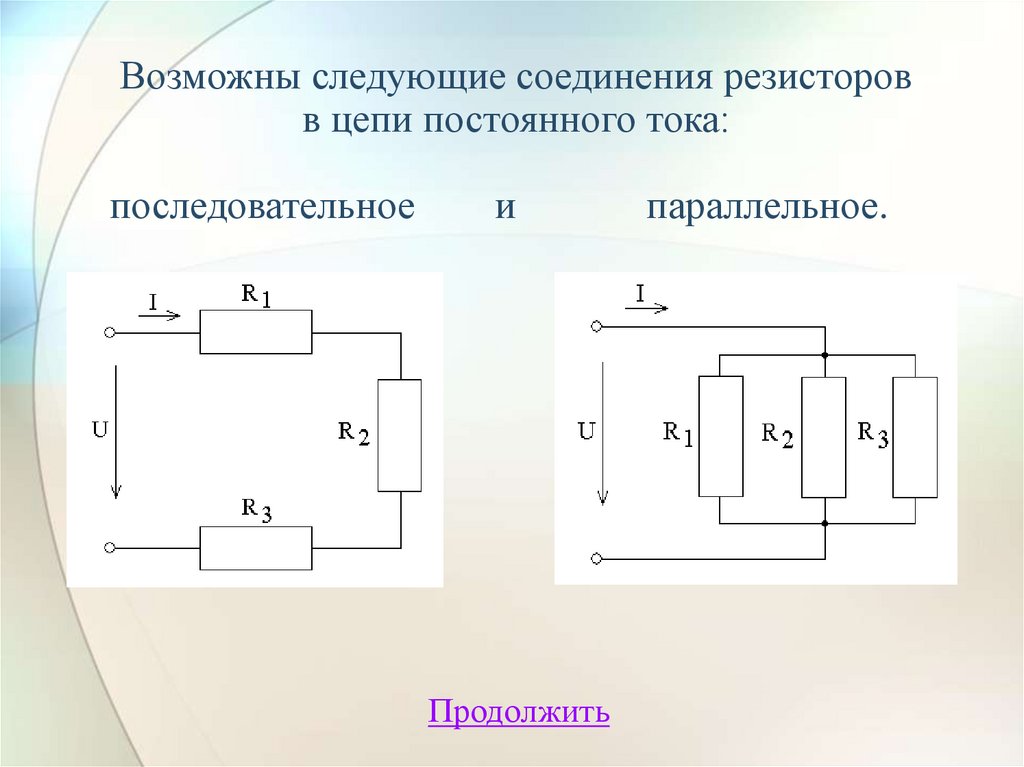 На последнем этапе выполняется расчет эквивалентного сопротивления всей цепи, путем суммирования полученных данных R123 и сопротивления R4, включенного последовательно с ним: Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4.
На последнем этапе выполняется расчет эквивалентного сопротивления всей цепи, путем суммирования полученных данных R123 и сопротивления R4, включенного последовательно с ним: Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4. Сопротивление по отношению к входным зажимам называется входным сопротивлением и равно сумме сопротивлений участков – R вх = R 1 + R 2 + R 3 ;
Сопротивление по отношению к входным зажимам называется входным сопротивлением и равно сумме сопротивлений участков – R вх = R 1 + R 2 + R 3 ;
 к. параллельное соединение
к. параллельное соединение