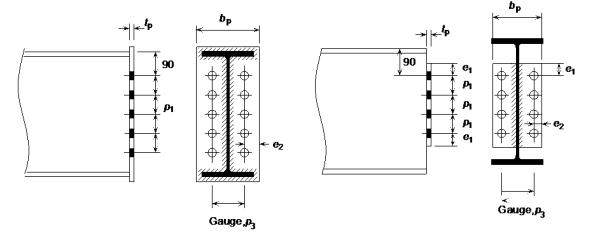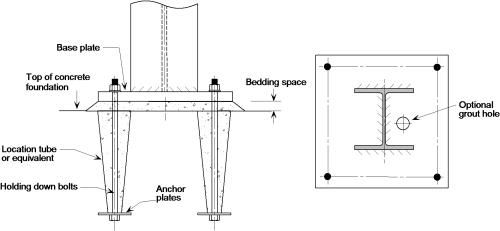Как рассчитать общее сопротивление при последовательном и параллельном соединении резисторов. Какие формулы применяются для смешанного подключения. Как изменяется ток и напряжение при различных способах соединения сопротивлений. Что нужно учитывать при подключении резисторов в электрическую цепь.
Что такое резистор и для чего он нужен в электрической цепи
Резистор — это пассивный элемент электрической цепи, который обладает электрическим сопротивлением и ограничивает силу тока в цепи. Основные функции резистора:
- Ограничение тока до заданного значения
- Снижение напряжения на участке цепи
- Преобразование электрической энергии в тепловую
- Создание падения напряжения для питания других элементов схемы
Резисторы бывают постоянные (с фиксированным номиналом сопротивления) и переменные (с регулируемым сопротивлением). Они широко применяются практически во всех электронных устройствах.
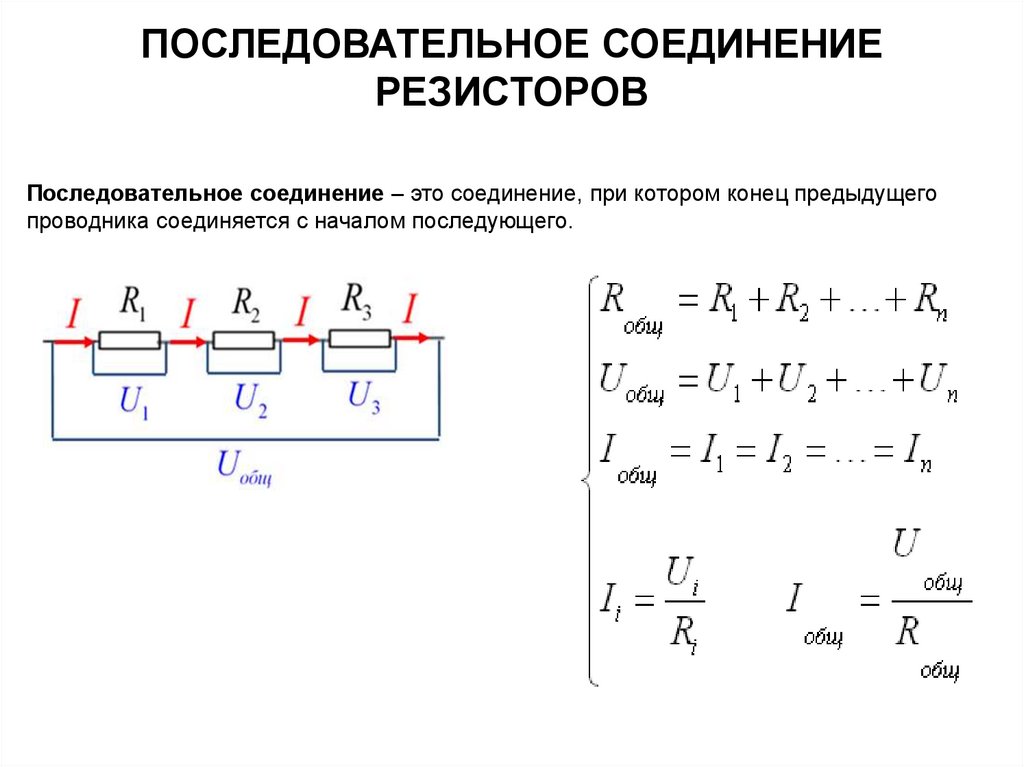
Последовательное соединение резисторов
При последовательном соединении резисторы включаются в цепь друг за другом — конец одного резистора соединяется с началом следующего. Основные свойства последовательного соединения:
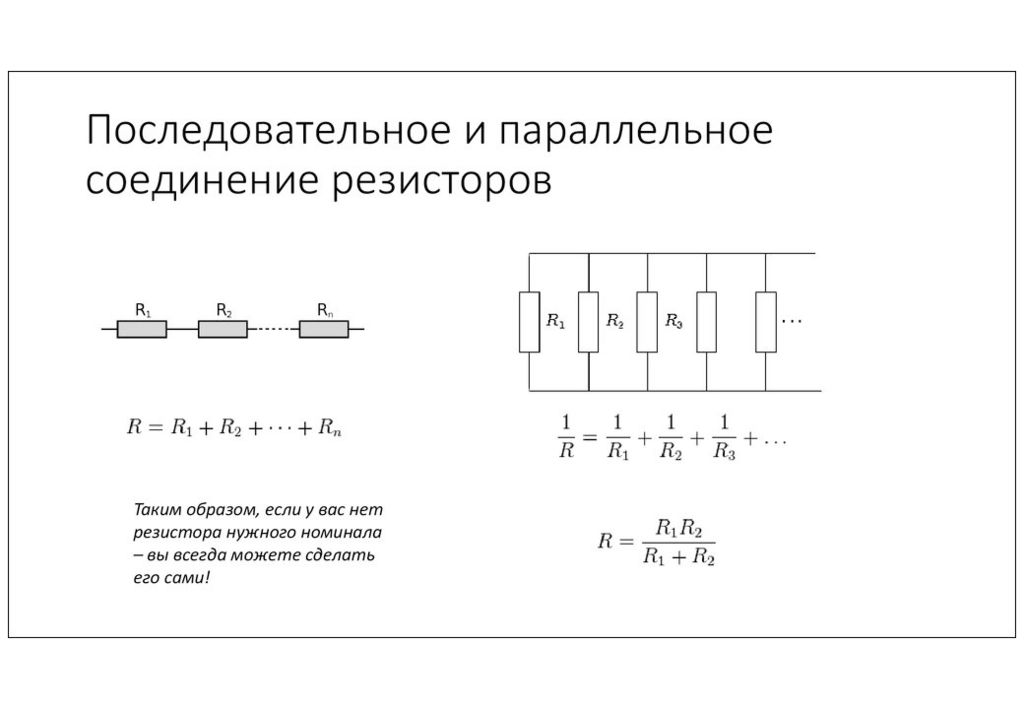
- Через все резисторы протекает одинаковый ток
- Напряжение на участке цепи равно сумме напряжений на отдельных резисторах
- Общее сопротивление цепи равно сумме сопротивлений всех резисторов
Формула для расчета общего сопротивления при последовательном соединении:
R = R1 + R2 + R3 + … + Rn
где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
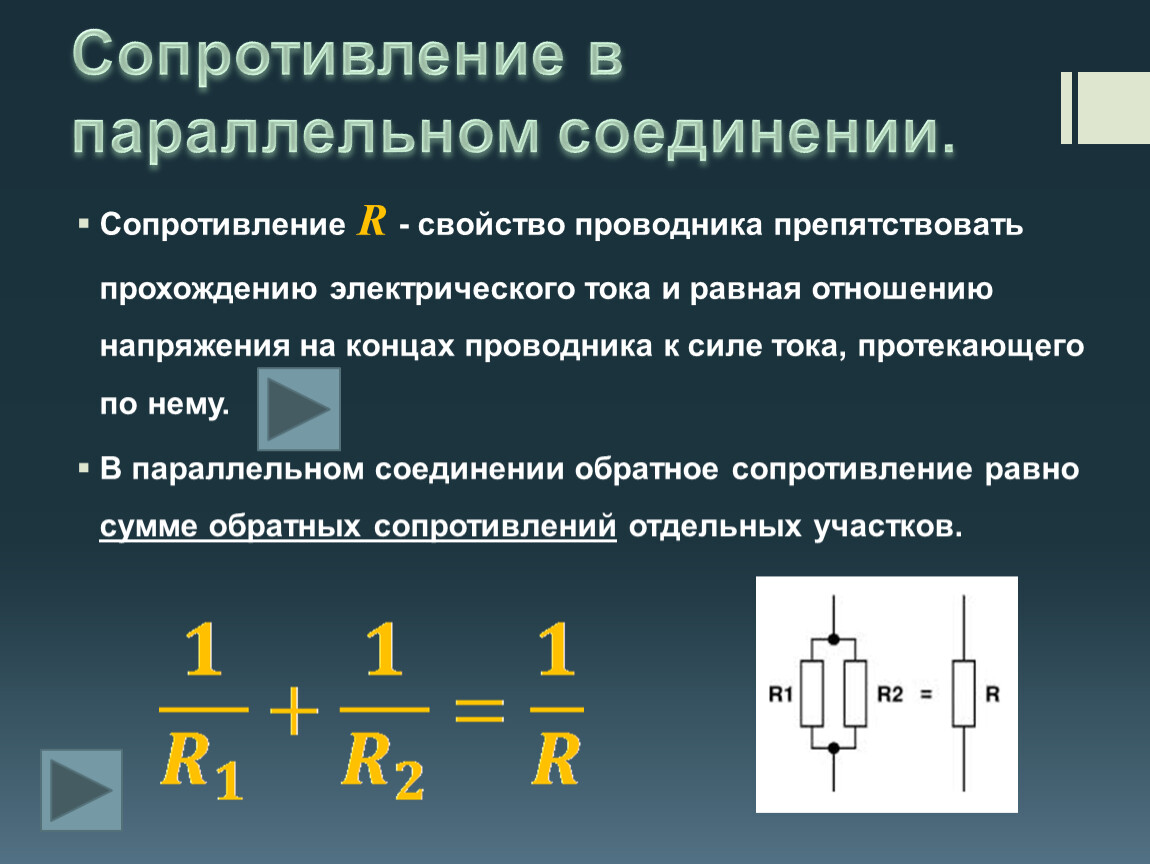
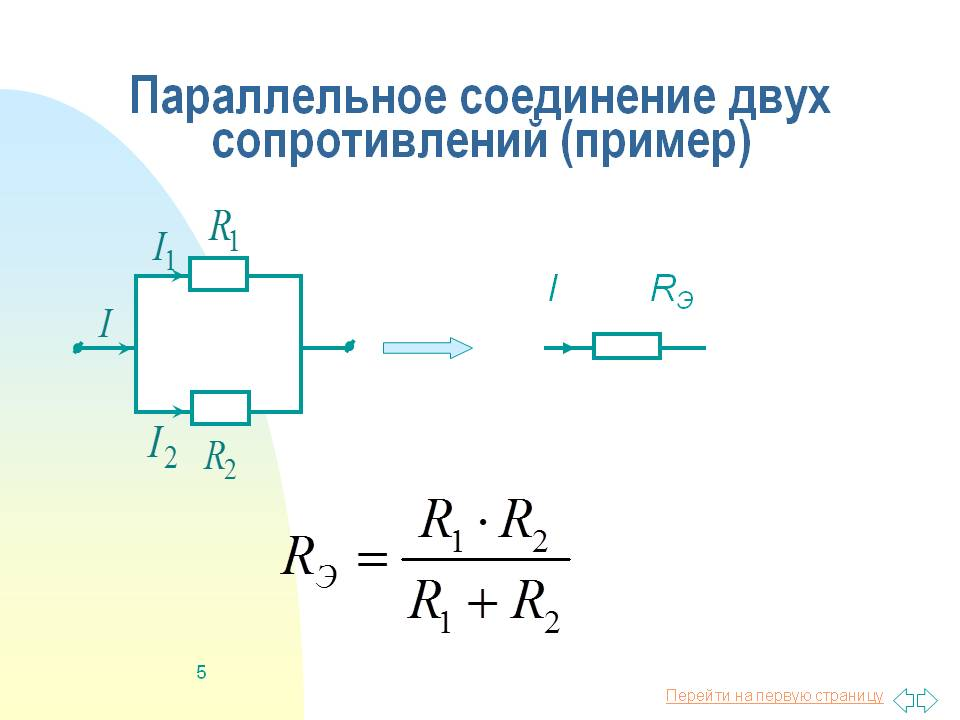
Параллельное соединение резисторов
При параллельном соединении все резисторы подключаются к одним и тем же точкам цепи. Особенности параллельного соединения:
- Напряжение на всех резисторах одинаково и равно напряжению источника
- Общий ток в цепи равен сумме токов через отдельные резисторы
- Общее сопротивление цепи меньше сопротивления любого из параллельно включенных резисторов
Формула для расчета общего сопротивления при параллельном соединении:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Для двух параллельно соединенных резисторов можно использовать упрощенную формулу:
R = (R1 * R2) / (R1 + R2)
Смешанное соединение резисторов
Смешанное соединение представляет собой комбинацию последовательного и параллельного подключения резисторов в одной схеме. Для расчета такой цепи необходимо:
- Разбить схему на участки с однотипным соединением (последовательным или параллельным)
- Рассчитать эквивалентное сопротивление для каждого участка
- Объединить полученные участки и рассчитать общее сопротивление
Пример расчета смешанного соединения:
«` «`1. R4 и R5 соединены параллельно. Рассчитаем их эквивалентное сопротивление R45:
1/R45 = 1/R4 + 1/R5
2. R1, R2, R3 и R45 соединены последовательно. Общее сопротивление цепи:
R = R1 + R2 + R3 + R45
Что нужно учитывать при подключении резисторов
При расчете и проектировании схем с резисторами важно учитывать следующие факторы:
- Мощность рассеивания — при превышении допустимой мощности резистор может перегреться и выйти из строя
- Температурный коэффициент сопротивления — изменение сопротивления при нагреве
- Точность номинала — реальное сопротивление может отличаться от номинального в пределах допуска
- Паразитные параметры — наличие собственной индуктивности и емкости у реальных резисторов
При последовательном соединении увеличивается общее падение напряжения и рассеиваемая мощность. При параллельном — возрастает общий ток через резисторы.
Как рассчитать силу тока при различных соединениях резисторов
Расчет силы тока производится по закону Ома:
I = U / R
где I — сила тока, U — напряжение, R — сопротивление.
При последовательном соединении ток одинаков во всех резисторах и равен:
I = U / (R1 + R2 + … + Rn)
При параллельном соединении общий ток равен сумме токов через отдельные резисторы:
I = I1 + I2 + … + In
где I1 = U/R1, I2 = U/R2 и т.д.
Преимущества и недостатки различных способов соединения резисторов
Последовательное соединение:
Преимущества:
- Простота расчета общего сопротивления
- Возможность получить большое общее сопротивление
Недостатки:
- При выходе из строя одного резистора размыкается вся цепь
- Неравномерное распределение напряжения между резисторами
Параллельное соединение:
Преимущества:
- Меньшее общее сопротивление
- Равномерное распределение напряжения
- Работоспособность схемы при выходе из строя одного резистора
Недостатки:
- Сложность расчета общего сопротивления
- Увеличение общего тока в цепи
Практическое применение различных способов соединения резисторов
Последовательное соединение применяется:
- Для получения большого общего сопротивления
- В делителях напряжения
- Для ограничения тока в цепи
Параллельное соединение используется:
- Для уменьшения общего сопротивления
- В схемах суммирования токов
- Для увеличения мощности рассеивания
Смешанное соединение позволяет комбинировать преимущества обоих способов и применяется в сложных электронных схемах для получения нужных характеристик цепи.
Все разнообразие схем построено на двух типах соединения — параллельном и последовательном. Для разных соединений действуют разные законы, что и дает возможность создания устройств с различными характеристиками. Рассмотрим последовательное и параллельное соединение резисторов.
Содержание статьи
Что такое резистор и для чего он нужен
Например, светодиоды требуют небольшого тока, иначе перегревается и быстро выходит из строя. Чтобы ограничить ток, перед светодиодом поставьте сопротивление. Ток в цепи станет меньше.

Для чего нужны резисторы: для подстройки параметров питания
Постоянные сопротивления — это те, которые не меняют своего номинала в процессе работы. Если это и происходит, то считается выходом из строя.

Так выглядят переменные и постоянные резисторы
Переменные резисторы, наоборот, отличаются тем, что их сопротивление можно изменять. Они имеют бегунок или поворотную ручку, при помощи которых и изменяется номинал. На основе таких устройств делают регуляторы. Например, регулятор громкости, накала греющего элемента и т.д.
Последовательное соединение сопротивлений
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.

Лампы накаливания соединенные последовательно, можно рассматривать как сопротивления
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2).

Последовательно соединенные сопротивления. I1 — ток протекающий через резистор R1, I2 — ток протекающий через резистор R2
Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают.
R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых.
Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В.

Так понятнее, что такое последовательное соединение
Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом. Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В.
Параллельное соединение резисторов
Параллельное соединение — это когда входы нескольких деталей соединяются в одной точке. Точно так же — в одну точку — соединяют их выходы.

Так выглядит параллельное соединение на схеме и в реальности
Теория и законы параллельного соединения
Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение. То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение.
U = U1 = U2 = U3.
Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.

Так выглядит параллельное соединение резисторов на схеме
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле:
1/R = 1/R1 + 1/R + 1/R3+…
Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.

Формулы расчета сопротивления при параллельном подключении двух и трех резисторов
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала.
Примеры расчета параллельного соединения сопротивлений
Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
- Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
- Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.
Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.

Как высчитывать сопротивление составных резисторов
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.

Еще один пример с лампочками
При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее. Но картина не отличается:
- Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом.
- Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом.
Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Смешанное соединение
Как быть, если в схеме есть и параллельное, и последовательное соединение резисторов? В таком случае считают общее сопротивление по участкам. Можно при этом перерисовывать схему, заменяя составные сопротивления на один «прямоугольник», но проставляя над ним высчитанный результат.

Пример расчета сопротивления при смешанном соединении резисторов. Рассматриваем исходную схему как совокупность параллельных и последовательных соединений
Шаг 1. Нашли общее сопротивление последовательно соединенных резисторов R3 и R4:
R3-4 = 3 кОм + 3 кОм = 6 кОм;
Шаг 2. Рассчитали сопротивление параллельно соединенных резисторов R2 и R3-4:
R2-4 = 3 кОм * 6 кОм / (3 кОм + 6 кОм) = 18 кОм/9 кОм = 2 кОм;
Шаг 3. Рассчитали общее сопротивление последовательно соединенных резисторов R1 и R2-4:
R1-4 = R1 + R2-4 = 1 кОм + 2 кОм = 3 кОм.
Практическое применение параллельного и последовательного соединения резисторов
Для чего практически можно использовать параллельное и последовательное соединение резисторов? Случается, что при ремонте электронной аппаратуры, не всегда в наличии сопротивление нужного номинала. Ехать в магазин за одним копеечным элементом — накладно. Вот тут и могут пригодиться составные резисторы. Просто надо последовательно или параллельно соединить их, подобрав требуемый номинал.

Последовательное и параллельное соединение резисторов применяют для подбора требуемого номинала. Контролировать точное значение получившегося сопротивления можно при помощи цифрового мультиметра
При соединении резисторов, их ножки первоначально скручивают. Какой стороной разворачивать сопротивление — неважно (в отличие от диодов, резисторы одинаково пропускают ток в обоих направлениях). На концах скрутку слегка обжимают плоскогубцами, затем пропаивают. Следите за тем, чтобы корпуса были друг от друга подальше — так они будут лучше охлаждаться при работе.
Соединение сопротивлений | ldsound.ru
Последовательное соединение (рис. 1, а). Величина тока в любой точке неразветвленной цепи одна и та же:
I – I1 = I2 = I3
Общее (эквивалентное) сопротивление равно сумме всех последовательно соединенных сопротивлений:
R = R1 + R2 + R3
Общее напряжение (падение напряжения) равно сумме напряжений (падений напряжений) на отдельных участках цепи:
U = U1 + U2 + U3
Рис. 1. Схемы соединений сопротивлений:
- последовательного;
- параллельного.
Напряжения на участках цепи прямо пропорционально сопротивлениям этих участков:
U1 = IR1; U2 = IR2; U3 = IR3,
следовательно,
I = U1/R1 = U2/R2 = U3/R3 = U/R
Параллельное соединение (рис. 1, б). Ток в неразветвленной части цепи равен сумме токов в ветвях:
I = I1 + I2 + I3
Общая проводимость разветвления равна сумме проводимостей отдельных ветвей:
g = g1 + g2 + g3
Общее сопротивление равно обратной величине общей проводимости R = 1/g и меньше наименьшего сопротивления. Общее сопротивление определяется из формулы:
1/R = 1/R1 + 1/R2 + 1/R3
Ток в каждой ветви определяется согласно закону Ома:
I1 = U/R1 = Ug1; I2 = U/R2 = Ug2; I3 = U/R3 = Ug3.
Токи в ветвях прямо пропорциональны проводимостям или обратно пропорциональны сопротивлениям ветвей:
I1 : I2 : I3 = g1 : g2 : g3
или
I1 : I2 : I3 = I/R1 : I/R2 : I/R3.
Формулы для расчета часто встречающегося параллельного соединения двух сопротивления приведены в таблице 1.
Таблица 1:
Для быстрого определения общего сопротивления двух параллельно соединенных сопротивлений можно пользоваться номограммой, приведенной на рис. 2. При пользовании этой номограммы все сопротивления необходимо брать в одинаковых единицах (Ом, кОм, МОм).
Рис. 2:
Соединение резисторов — Основы электроники
Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике.
Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов.
Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно), что показано на рисунке 1.
Рисунок 1. Соединение резисторов.
Последовательное соединение резисторов
Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее (рисунок 2).
Рисунок 2. Последовательное соединение резисторов.
То есть при последовательном соединении резисторы подключатся друг за другом. При таком соединении через резисторы будет протекать один общий ток.
Следовательно, для последовательного соединения резисторов будет справедливо сказать, что между точками А и Б есть только один единственный путь протекания тока.
Таким образом, чем больше число последовательно соединенных резисторов, тем большее сопротивление они оказывают протеканию тока, то есть общее сопротивление Rобщ возрастает.
Рассчитывается общее сопротивление последовательно соединенных резисторов по следующей формуле:
Rобщ = R1 + R2 + R3+…+ Rn.
Параллельное соединение резисторов
Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку (Б) (см. рисунок 3).
Рисунок 3. Параллельное соединение резисторов.
При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей.
Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи (сопротивления между точкой А и Б.)
Общее сопротивление параллельно соединенных резисторов определяется следующим отношением:
1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn
Следует отметить, что здесь действует правило «меньше — меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора.
Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле:
Rобщ= R1*R2/R1+R2
Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них.
Смешанное соединение резисторов
Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением.
На рисунке 4 показан простейший пример смешанного соединения резисторов.
Рисунок 4. Смешанное соединение резисторов.
На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно.
Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:
1. Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.
2. Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.
3. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.
4. Рассчитывают сопротивления полученной схемы.
Пример расчета участка цепи со смешанным соединением резисторов приведен на рисунке 5.
Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Способы соединений сопротивлений — Студопедия
При последовательном соединении конец предыдущего проводника соединяют с началом последующего проводника.
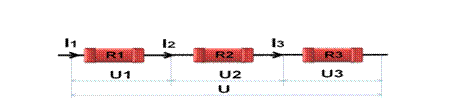
Рис.2.5. Последовательное соединение резисторов.
При последовательном соединении сила тока во всех проводниках одинакова:
I1 = I2 = I3 = ······ = I
Напряжение U на концах всей цепи равно сумме напряжений на проводниках. Например, для случая трёх проводников:
U = U1 + U2 + U3
По закону Ома для участка цепи:
U1 = I ·R1; U2 = I · R2; U3 = I · R3; U = I · R, где
R1, R2, R3 — сопротивления проводников.
R — общее сопротивление всего участка цепи.
Подставив в формулу закона Ома получим:
I · R = I · (R1 + R2 + R3), откуда R = R1 + R2 + R3
Для n последовательно включённых проводников:
R = R1 + R2 + R3 +······+ Rn
Если все они имеют одинаковое сопротивление R1, то R = n · R1
При последовательном соединении проводников общее сопротивление равно сумме сопротивлений всех проводников.
Из соотношения (2.10) следует, что
U1 / U2 = R1 / R2 (2/13)
Напряжения на последовательно соединённых проводниках прямо пропорционально их сопротивлениям.
При параллельном соединении начала всех проводников соединяют в одной точке, а их концы — в другой.
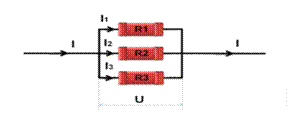
Рис.2.6. Параллельное соединение резисторов.
В этом случае сила тока I в неразветвлённой цепи равна сумме сил токов в параллельно соединённых проводниках:
I = I1 + I2 + I3
Напряжение на концах проводников одинаково:
U1 = U2 = U3 = U
По закону Ома: I1 = U / R1; I2 = U / R2; I3 = U / R3; I = U / R , где
R1, R2, R3 — сопротивления проводников,
R — общее сопротивление участка цепи.
После подстановки в уравнение токов получия:
U / R = U / R1 + U / R2 + U / R3, откуда:
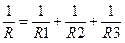
При параллельном соединении величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям всех проводников.
Если имеем n параллельно соединённых проводников, имеющих одинаковое сопротивление R1, то общее сопротивление цепи:
R = R1 / n.
Подставив в формулу закона Ома получим:
Из (2.16) следует: I1 / I2 = R2 / R1 (2.19)
Силы токов в параллельно соединённых проводниках обратно пропорциональны их сопротивлениям.
Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением.
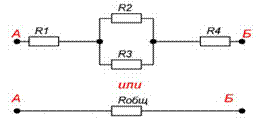
Рис.2.7. Смешанное соединение резисторов.
На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно.
Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:
Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.
Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.
После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.
Рассчитывают сопротивления полученной схемы.
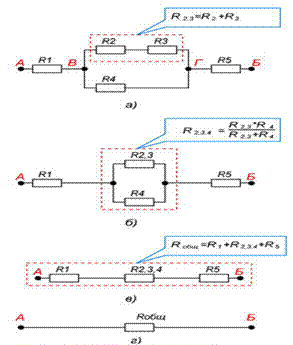
Рисунок 2.8. Расчет сопротивления участка цепи при смешанном соединении резисторов
Автор Aluarius На чтение 7 мин. Просмотров 527 Опубликовано
Ни одна электрическая схема не обходится без резисторов. Что это такое, для чего он нужен и какими способами их подключают в электрическую цепь рассмотрим подробно.
Что такое резистор и для чего он нужен
Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.
Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.
Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.
Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).
Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.
Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:
- С правого края – правый.
- С левого края – левый.
Понятие параллельного подключения резисторов
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.

При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.

Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.
Последовательное подключение
При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.

При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.

Смешанное подключение
При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.
 Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.
Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.
Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.
Что ещё нужно учитывать при подключении резисторов
Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.
При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.
Какая мощность тока при последовательном и параллельном соединении
Определение мощности отдельного резистивного элемента производится по формуле
P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.
Мощность при параллельном соединении
Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где
- R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
- I – сила тока в цепи.
При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.
Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.
Мощность при последовательном соединении
Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где
- R – рассчитанное нами сопротивление для определенной схемы;
- U – падение напряжения на данном резистивном элементе.
Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.
Как правильно рассчитать сопротивление
Применяется закон Ома для участка цепи – расчет сопротивления делается по формуле R = U/I, где
- U – падение напряжение на конкретном резистивном элементе;
- I – ток, протекающий через него.
При последовательном соединении
Для двух элементов считаем Rобщ = R1+R2.
Для нескольких сопротивлений разного номинала Rобщ = R1+R2+R3+…+Rn.
При параллельном соединении
Расчет для двух резисторов делаем по формуле Rобщ = (R1×R2)/(R1+R2).
Сопротивление параллельных резисторов с разным номиналом рассчитываем по формуле
Rобщ = 1/(1/R1+1/R2+1/R3+…+1/Rn).
Для элементов, соединенных в параллель, суммарное сопротивление всегда ниже наименьшего номинального.
Как рассчитать сложные схемы соединения резисторов
Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.
 Перед нами сложная схема – задача рассчитать общее сопротивление:
Перед нами сложная схема – задача рассчитать общее сопротивление:
- R2, R3, R4 объединим в последовательную группу – применим формулу R2,3,4 = R2+R3+R4.
- R5 и R2,3,4 – параллельно соединенные резисторы, рассчитаем R5,2,3,4 = 1/ (1/R5+1/R2,3,4).
- R5,2,3,4, R1, R6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R5,2,3,4+R1+R6.
Для больших схем существуют специальные методы, облегчающие расчет. Один из таких методов – эквивалентное преобразование «треугольника» в «звезду». Такая система расчета применяется в том случае, когда невозможно по схеме определить последовательное или параллельное подключение резисторов.
Преобразование «звезда-треугольник»
Для соединения резистивных элементов, кроме вышеописанных способов, существует несколько других видов соединения:
- «звезда» – соединение трех ветвей с одним общим узлом;
- «треугольник» – соединение ветвей схемы в виде треугольника, сторонами которого служат ветви, вершины представляют узлы.
Справка: Узел – точка, в которой соединяются три и более проводника электрической цепи.
Эквивалентность замены предполагает стабильность токов, входящих в каждый узел, при одинаковых напряжения между одноименными узлами «треугольника» и «звезды».

Сопротивление резистора луча «звезды» равно произведению сопротивлений резисторов прилегающих сторон «треугольника», деленному на сумму сопротивлений резисторов трех сторон «треугольника».
RA = RAB RAC/(RAB+RAC+RDC).
Сопротивление резисторов сторон «треугольника» равно сумме произведения сопротивлений резисторов двух прилегающих лучей «звезды», деленного на сопротивление третьего луча.
RAB=(RARB+RARC+RBRС)/RC

О разнице подключения звезда и треугольник читайте здесь.
Чему равна сила тока в цепи при параллельном соединении резисторов
Согласно правилу Кирхгофа ток, поступающий в узел, равен току, выходящему из узла, – величина тока до группы параллельных резисторов и после нее должна быть неизменной.
Ток в группе параллельных резисторов распределяется по цепи в зависимости от их номинала, после прохождения через сопротивления суммируется в узле и выходит из него неизменным I = I1+I2+I3+…+In.
Как определить величину эквивалентного сопротивления при последовательном соединении резисторов
Справка: Эквивалентом сопротивления называется замена части схемы, состоящей из нескольких резистивных элементов, одним элементом.
Для последовательного соединения эквивалентное сопротивление равно сумме сопротивлений резисторов, включенных в группу, для расчета применяется формула Rэкв = R1+R2+…+Rn.
Например: Нужно посчитать эквивалентное сопротивление данной схемы.
 Решение задачи производится путем разделения резистивных элементов на системные группы.
Решение задачи производится путем разделения резистивных элементов на системные группы.
Выделяем первую группу из последовательно соединенных элементов – R2, R3, R4.
Считаем сопротивление Rобщ1 = R2+R3+R4.

Выделяем вторую группу из последовательных элементов R1, R5, R6.

Считаем сопротивление Rобщ2 = R1+R5+R6.
Получаем величину двух эквивалентных сопротивлений Rобщ1 и Rобщ2, соединенных параллельно.
Делаем расчет всей схемы Rэкв= Rобщ1× Rобш2/ (Rобщ1+ Rобщ2).
Зная способы соединения и формулы расчета можно рассчитать любую сложную схему соединения резистивных элементов, однако существует множество онлайн калькуляторов, которые сделают это быстрей человека, достаточно только ввести нужные параметры компонентов схемы.
Резистор (сопротивление) — один из наиболее распространённых компонентов в электронике. Его назначение — простое: сопротивляться течению тока, преобразовывая его часть в тепло.
Основной характеристикой резистора является сопротивление. Единица измерения сопротивления — Ом (Ohm, Ω). Чем больше сопротивление, тем большая часть тока рассеивается в тепло. В схемах, питаемых небольшим напряжением (5 – 12 В), наиболее распространены резисторы номиналом от 100 Ом до 100 кОм.
Закон Ома
Закон Ома позволяет на заданном участке цепи определить одну из величин: силу тока I, напряжение U, сопротивление R, если известны две остальные:
Для обозначения напряжения наряду с символом U используется V.
Рассмотрим простую цепь
Расчитаем силу тока, проходящего через резистор R1 и, соответственно, затем через лампу L1. Для простоты будем предполагать, что сама лампа обладает нулевым собственным сопротивлением.
Аналогично, если бы у нас был источник питания на 5 В и лампа, которая по документации должна работать при токе 20 мА, нам нужно бы было выбрать резистор подходящего номинала.
В данном случае, разница в 10 Ом между идеальным номиналом и имеющимся не играет большого значения: можно смело брать стандартный номинал — 240 или 220 Ом.
Аналогично, мы могли бы расчитать требуемое напряжение, если бы оно было не известно, а на руках были значения сопротивления и желаемая сила тока.
Соединение резисторов
При последовательном соединении резисторов, их сопротивление суммируется:
При параллельном соединении, итоговое сопротивление расчитывается по формуле:
Если резистора всего два, то:
В частном случае двух одинаковых резисторов, итоговое сопротивление при параллельном соединении равно половине сопротивления каждого из них.
Таким образом можно получать новые номиналы из имеющихся в наличии.
Применеие на практике
Среди ролей, которые может выполнять резистор в схеме можно выделить следующие:
Токоограничивающий резистор (current-limiting resistor)
Стягивающий, подтягивающий резистор (pull-down / pull-up resistor)
Делитель напряжения (voltage divider)
Токоограничивающий резистор
Пример, на котором рассматривался Закон Ома представляет собой также пример токоограничевающего резистора: у нас есть компонент, который расчитан на работу при определённом токе — резистор снижает силу тока до нужного уровня.
В случае с Ардуино следует ограничивать ток, поступающий с выходных контактов (output pins). Напряжение, в состоянии, когда контакт включен (high) составляет 5 В. Исходя из документации, ток не должен превышать 40 мА. Таким образом, чтобы безопасно увести ток с контакта в землю понадобится резистор номиналом R = U / I = 5 В / 0.04 А = 125 Ом или более.
Стягивающие и подтягивающие резисторы
Стягивающие (pull-down) и подтягивающие (pull-up) резисторы используются в схемах рядом со входными контактами логических компонентов, которым важен только факт: подаётся ноль вольт (логический ноль) или не ноль (логическая единица). Примером являются цифровые входы Ардуино. Резисторы нужны, чтобы не оставить вход в «подвешенном» состоянии. Возьмём такую схему
Мы хотим, чтобы когда кнопка не нажата (цепь разомкнута), вход фиксировал отсутствие напряжения. Но в данном случае вход находится в «никаком» состоянии. Он может срабатывать и не срабатывать хаотично, непредсказуемым образом. Причина тому — шумы, образующиеся вокруг: провода действуют как маленькие антенны и производят электричество из электромагнитных волн среды. Чтобы гарантировать отсутствие напряжения при разомкнутой цепи, рядом с входом ставится стягивающий резистор:
Теперь нежелательный ток будет уходить через резистор в землю. Для стягивания используются резисторы больших сопротивлений (10 кОм и более). В моменты, когда цепь замкнута, большое сопротивление резистора не даёт большей части тока идти в землю: сигнал пойдёт к входному контакту. Если бы сопротивление резистора было мало (единицы Ом), при замкнутой цепи произошло бы короткое замыкание.
Аналогично, подтягивающий резистор удерживает вход в состоянии логической единицы, пока внешняя цепь разомкнута:
То же самое: используются резисторы больших номиналов (10 кОм и более), чтобы минимизировать потери энергии при замкнутой цепи и предотвратить короткое замыкание при разомкнутой.
Делитель напряжения
Делитель напряжения (voltage divider) используется для того, чтобы получить из исходного напряжения лишь его часть. Например, из 9 В получить 5. Он подробно описан в отдельной статье.
Мощность резисторов
Резисторы помимо сопротивления обладают ещё характеристикой мощности. Она определяет нагрузку, которую способен выдержать резистор. Среди обычных керамических резисторов наиболее распространены показатели 0.25 Вт, 0.5 Вт и 1 Вт. Для расчёта нагрузки, действующей на резистор, используйте формулу:
При превышении допустимой нагрузки, резистор будет греться и его срок службы может сильно сократиться. При сильном превышении — резистор может начать плавиться и вызвать воспламенение. Будьте осторожны!
Большое разнообразие схем основано на двух видах соединений – последовательное параллельное. Для каждого типа существуют свои собственные законы и принципы. Именно это и позволяет создавать устройства с самыми различными техническими параметрами, в том числе и резисторы. Что же такое резистор?
Резистор – радиодеталь, созданная для контроля напряжения и тока в цепи, увеличивая либо понижая его. Резисторы могут быть двух видов – постоянные и переменные. Так, например, светодиоды требуют для себя совсем небольшого тока. Для этого в электрическую цепочку перед светодиодом устанавливается резистор, который обеспечивает необходимое напряжение для работы последнего.
В статье подробны рассмотрены все аспекты последовательного и параллельного подключения резисторов. Бонусом к статье являются видеоролик и детальная информационная статья на рассматриваемую тему.
Последовательное подключение
 Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше. Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим.
Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше. Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим.
Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях — складываем, в параллельных — это обратно пропорциональная величина.
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2). Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают. R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых. Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.

Последовательное подключение.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
 Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.
Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В. Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Материал по теме: Как проверить варистор мультиметром.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Параллельное подключение резисторов.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.
То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.
Предлагаем также почитать интересный материал про малоизвестные факты о двигателях постоянного тока в другой нашей статье.
Схема параллельного соединения
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
 Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом. Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Как высчитывать сопротивление составных резисторов
 Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.
Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Параллельное соединение резисторов
Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку. При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей. Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи. Общее сопротивление параллельно соединенных резисторов определяется следующим отношением: 1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn.

Формулы расчета параллельного и последовательного подключения.
Следует отметить, что здесь действует правило «меньше – меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора. Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле: Rобщ= R1*R2/R1+R2.
Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них. Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви.
 Заменяя лампы резисторами с сопротивлениями R1, R2, R3, При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома: I1=U/R1; I2=U/R2; I3=U/R3.
Заменяя лампы резисторами с сопротивлениями R1, R2, R3, При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома: I1=U/R1; I2=U/R2; I3=U/R3. 
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3, или I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк . Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой 1/Rэк = 1/R1 + 1/R2 + 1/R3. Вводя в формулу (24) вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:
Gэк = G1+ G2 +G3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается. Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3 = G1 + G2 + G3.
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам. Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи – Rэк=R1R2/(R1+R2) при трех параллельно включенных резисторах Rэк=R1R2R3/(R1R2+R2R3+R1R3).
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
Rэк = R1 / n.
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока: I1 = I / n. При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Более подробную информацию можно узнать, прочитав файл по данной теме “Расчет мощности резисторов”. Всю новую информацию по этой и многим другим темам, вы сможете найти в группе. Подписывайтесь на нашу группу в социальной сети «Вконтакте».
Для этого вам необходимо будет перейти по следующей ссылке https://vk.com/electroinfonet. Также в группе можно задавать вопросы и получать на них подробные ответы от профи. В завершение объемной статьи хочу выразить благодарность источникам, откуда мы черпали информацию:
www.elektroznatok.ru
www.themechanic.ru
www.electrono.ru
www.hightolow.ru
www.sxemotehnika.ru
ПредыдущаяРезисторыКак рассчитать резистор для светодиода?
СледующаяРезисторыЧто такое фоторезистор?
физики для науки и техники II
из Управления академических технологий на Vimeo.
Пример — соединение последовательных и параллельных сопротивлений
Хорошо. Давайте сделаем пример, связанный со связями сопротивлений. Давайте предположим, что у нас есть несколько сопротивлений, которые связаны в этой форме. R 1, R 2 подключено здесь, и R 3 подключено здесь. R 4 здесь и тогда у нас есть сопротивление R 6 здесь, которое в конечном итоге связано с сопротивлением R 7 здесь.Затем, скажем, мы применяем разность потенциалов по всей комбинации, подключая концы этих соединений к клеммам электродвижущей силы, которая генерирует ε вольт.
Давайте посмотрим, вопрос в том, какая сила рассеивается через каждое сопротивление? Теперь, чтобы иметь возможность определить мощность, если вы помните, что она была равна рассеиваемой мощности — давайте использовать индекс рассеиваемой мощности — была равна и , что в 2 раза больше сопротивления R . Квадрат тока, проходящего через сопротивление, умноженный на значение сопротивления этого резистора, даст нам, сколько энергии превращается в тепло в секунду.
Ну, очевидно, давайте скажем, что числовые значения наших сопротивлений даны. Допустим, R 1 равно 2 Ом, R 2 равно 6 Ом и R 3 равно 12 Ом. R 4 равно 4 Ом, а R 6 равно 10 Ом и, наконец, R 7 равно 3 Ом. Итак, зная числовые значения этих сопротивлений, поэтому, если мы сможем определить величину тока, протекающего через каждый резистор, то мы сможем определить мощность, рассеиваемую через каждый резистор.
Хорошо. Чтобы сделать это, сначала мы попытаемся определить эквивалентное сопротивление цепи, а затем проследим его обратно, чтобы определить ток, протекающий через каждое сопротивление. Если вспомнить закон Ома, который был просто равен из определения сопротивления и который был равен отношению разности потенциалов между двумя точками к величине тока, проходящего через эти точки.
Когда мы смотрим на этот закон, мы видим, что для того, чтобы определить любую из этих величин: напряжение, ток, сопротивление, нам нужно знать две другие из этих величин.Итак, мы собираемся попытаться определить эти величины, поскольку даны сопротивления, мы попытаемся определить ток, и чтобы это сделать, нам нужно определить разность потенциалов на каждом резисторе. Таким образом, применяя свойства, связанные с параллельными и последовательными соединениями, мы определим эти величины, следовательно, в конечном итоге ток через каждое сопротивление, и как только мы определим это, мы сможем рассчитать рассеиваемую мощность.
Хорошо.Если мы посмотрим на нашу схему, то увидим, что сначала эти три сопротивления R 2, R 3 и R 4 соединены параллельно. Сначала отметим точки соединения. Это точки, в которых мы получаем разные ветви для тока. Когда мы смотрим здесь, на схему, мы видим, что у нас есть точка соединения здесь, еще одна здесь, другая там, и еще одна здесь. Таким образом, мы легко видим, что эти три сопротивления соединены параллельно.
Другими словами, я могу перерисовать эту схему в этой форме. Это R 1, и теперь из этой точки соединения я могу перерисовать его как R 2, R 3 и R 4, которые соединены через эти точки соединения, которые я также могу нарисовать таким образом , У нас есть R 6, а затем мы имеем этот сегмент провода, просто провод, и подключаем его параллельно, который в конечном итоге подключается к R 7 таким образом. Следовательно, ток можно перерисовать в этой форме, чтобы можно было ясно видеть соединения, и это эквивалентно нашей первоначальной схеме.
Таким образом, мы перерисовали схему, чтобы иметь возможность четко видеть соединения, и мы можем легко видеть, что эти три сопротивления теперь соединены параллельно. Поэтому сначала мы заменим их эквивалентами. По мере того, как мы это делаем, мы перерисовываем схему, и вот электродвижущая сила, сопротивление R 1. Мы собираемся заменить это на, давайте назовем это как R экв 1, и давайте просто сконцентрируемся на этом параллельном соединении здесь.Когда мы смотрим на этот сегмент схемы, следуя току, который выходит из источника питания, который будет разделен на три ветви по мере прохождения через R 2, R 3 и R 4, и это присоединится, а затем снова составит и .
Теперь, когда ток достигает этой точки, заряды будут видеть два доступных пути. Один из них — этот, а другой — этот. Поэтому, когда они попытаются пройти через эти две ветви, они увидят, что вдоль этой ветви есть сопротивление R 6, тогда как вдоль этой ветви нет сопротивления.Поэтому, естественно, заряды выберут путь, по которому нет сопротивления. Другими словами, они будут проходить напрямую по этому пути, и ни один из токов не пройдет через сопротивление R 6. Следовательно, в качестве эквивалента этого сегмента мы можем просто записать или заменить его простым проводом без сопротивления на все, и тогда мы получим следующее сопротивление, которое последовательно соединено с этим, которое равно R 7. Таким образом, цепь будет приведена в эту упрощенную форму.
Теперь давайте просто посчитаем R экв 1, поскольку это эквивалент параллельного соединения R 2, R 3, R 4. 1 более R экв 1 будет равно 1 более R 2 плюс 1 более R 3 плюс 1 более R 4, из свойств параллельных соединений сопротивлений. Двигаясь дальше, 1 больше R экв 1 будет равно, R 2 равно 6 Ом, 1 больше 6, плюс R 3 равно 12 Ом, 1 больше 12, плюс R 4 равно 4 Ом, так что у нас здесь будет 1 на 4.Теперь, если у вас есть общие знаменатели, то мы должны умножить это отношение, как числитель, так и знаменатель, на 2, это всего на 1, а это на 3, потому что у них будет общий знаменатель 12.
Двигаясь дальше, 1 более R экв 1 будет равно 2 плюс 1 плюс 3 более 12, что будет равно 6 более 12, и это равно 1 более R экв 1 Чтобы получить R eq 1, мы возьмем обратное значение, которое будет равно 12 на 6, и это даст нам 2 Ом.Следовательно, значение R экв 1 будет равно 2 Ом. Другими словами, если мы просто возьмем этот параллельный блок и поместим здесь сопротивление 2 Ом, он будет выполнять ту же работу, что и эти три в параллельном соединении.
Теперь мы сделаем еще один шаг и найдем эквивалент этих трех сопротивлений, соединенных последовательно. Прежде чем мы это сделаем, позвольте мне также показать вам, почему у нас не будет тока, протекающего через R 6. Опять же, если мы просто будем думать об этом как о параллельном соединении сопротивлений и попытаемся выяснить эквивалентное сопротивление этого блока — давайте назовите это единица как 1 на R экв 2 — эквивалентное сопротивление этой единицы здесь будет равно 1 на R 6 плюс 1 на сопротивление этого сегмента.Мы собираемся предположить, что сопротивление провода намного, намного меньше, чем сопротивление этого резистора, поэтому мы предположим, что оно почти равно 0. Другими словами, у нас будет 1 больше 0 или 1 больше очень маленькое число, поэтому, если мы разделим 1 на чрезвычайно малое число, которое будет уходить в бесконечность, то это будет 1 на 6 плюс бесконечность. Конечно, весь этот термин уйдет в бесконечность, потому что не имеет значения, добавим ли мы число к очень большому числу или вычтем его.
Оттуда, если мы решим для R экв 2, это будет наоборот. Другими словами, число, деленное на бесконечность, перейдет в 0, потому что если мы разделим 1 на очень большое число, то мы получим чрезвычайно малое число. Следовательно, эквивалентное сопротивление всего этого устройства будет равно 0. Это означает, что через это сопротивление ток не будет течь. Все нынешние предпочитают идти по этому гораздо менее резистивному пути, другими словами, почти до 0 резистивного пути.
Хорошо. Теперь, когда мы выяснили, что весь ток проходит через эту ветвь, мы можем легко рассчитать эквивалентное сопротивление всех этих трех сопротивлений в последовательном соединении. Это будет равно эквивалентному сопротивлению всей цепи. Давайте также приведем численное значение для этой электродвижущей силы. Предположим, что это количество также дано и равно 7 вольт. Здесь мы можем вычислить эквивалентное сопротивление всей цепи, которое будет равно эквиваленту всех этих трех сопротивлений: R 1 плюс R экв 1 плюс R 7.Подставляя числовые значения, эквивалентное сопротивление окажется равным: R 1 равно 2 Ом, плюс R eq 1 также равно 2 Ом, плюс R 7 равно 3 Ом, и это составит 7 Ом. Ом. Следовательно, эквивалентное сопротивление всей цепи составляет 7 Ом.
Теперь, как только мы определим эквивалентное сопротивление, мы можем определить, какой ток будет проходить через эту цепь, другими словами, какой ток будет потребляться от электродвигательной силы 7 Вольт.Для этого мы применим закон Ома, поскольку знаем, что R eq будет равно разности потенциалов на резисторе, которая будет равна любой разности потенциалов, подаваемой источником питания, и что равно ε вольт, разделенных на величину тока, протекающего через этот резистор, и это i . Решая для и , мы будем иметь ε над R экв . ε составляет 7 вольт, а R экв составляет 7 Ом, поэтому, следовательно, оно будет равно 1 амперу.Следовательно, через эту цепь будет течь 1 ампер тока.
Как только мы определили это, будем прослеживать наши цепи в обратном направлении, поэтому мы перейдем к этой схеме. Теперь, когда мы идем туда, мы знаем, что, поскольку R eq выполняет работу, которую выполняют эти три сопротивления в цепи, и источник питания одинаковый, следовательно, ток i будет проходить через эта схема. Поскольку все эти три сопротивления соединены последовательно, то ток, протекающий через каждое из них, будет одинаковым током, равным и , или, другими словами, 1 Ампер.
Теперь мы знаем, что 1 А тока протекает через R 1, через R экв 1 и через R 7. Поэтому мы можем легко рассчитать мощность, рассеиваемую через каждое из этих сопротивлений. Хорошо, давайте назовем первый как P1. Значение P1 будет равно i 12 раз R 1, но i 12 равно i , поэтому это будет i 2 R 1. i 2 равно 1 A умноженное на квадраты R 1 и R 1 составляло 2 Ом, поэтому это будет равно 2 Вт мощности, рассеиваемой через сопротивление R 1.
Аналогично, мы можем рассчитать мощность, рассеиваемую через R 7, так как мы знаем, что ток протекает через R 7. Это будет равно i, , 72 раза, R 7, но i 7 равно и . i 2 раза R 7, и это снова будет равно 1 A в квадрате раз R 7 и R 7 составляли 3 Ом, что даст нам 3 Вт рассеиваемой мощности по току протекает через сопротивление R 7.
Хорошо. Мы определили мощность, рассеиваемую через два сопротивления. Теперь мы пойдем дальше, проследим это до первого круга. Мы видим, что R экв 1 является эквивалентом этих трех сопротивлений, и они соединены параллельно. Мы знаем, что при параллельном соединении разность потенциалов по всей комбинации равна разностям потенциалов на каждом резисторе, которые подключены параллельно. Поэтому, если мы найдем разность потенциалов на R экв 1, назовем это В экв 1, то есть будет такая же разность потенциалов на каждом резисторе в параллельном соединении.Таким образом, все эти три сопротивления будут иметь одинаковую разность потенциалов В, , , экв. , 1.
.Мы можем легко рассчитать это. Так как мы знаем сопротивление, мы также знаем ток. Тогда мы знаем две из этих величин, сопротивление и ток, поэтому мы можем легко вычислить разность потенциалов. В этом случае В экв 1 будет равно i раз R экв 1, что будет равно 1 А умножению R экв 1, позвольте мне рассчитать его, +2 Ом.Следовательно, разность 1 от 2 до 2 вольт — это разность потенциалов на сопротивлении R экв 1. Теперь, как только мы проследим его до первоначальной схемы здесь, то для всех R 2, R 3 и R 4 разность потенциалов между их концами будет одинаковой, и они будут быть равным В экв 1.
В этом случае теперь мы знаем разность потенциалов и сопротивление. Поэтому мы можем выяснить, какой ток течет через каждое из этих сопротивлений, потому что, как вы можете видеть, как только ток i попадет в эту точку соединения, некоторая доля пройдет через R 2.Давайте назовем это, например, i 2. Некоторая доля пройдет через R 3 как i 3, а затем оставшаяся часть пройдет через R 4 как i 4. Таким образом, зная разницу потенциалов, а также значение сопротивления, мы можем вычислить i 2, i 3 и i 4.
Опять же, напомнив закон Ома, ток будет равен В через R , поэтому i 2 будет равен В 2 через R 2, но В 2 будет равный В экв 1, и подставляя числовые значения, В экв 1 равен 2 вольт, разделенному на R 2, и цифровое значение R 2 было 6 Ом, и это даст нас 1 более 3 ампер.
i 3 будет равно В 3 над R 3, что будет равно В экв 1 над R 3, поскольку разность потенциалов через R 3 равна до В экв 1. Опять же, В экв 1 составляет 2 В, а R 3 составляло 12 Ом. Это будет равно 1 на 6 ампер.
Наконец, i 4 будет равно V 4 по R 4, что будет равно V eq 1 по R 4.Это даст нам 2 вольта, деленные на R 4, а R 4 было равно 4 Ом. Это даст нам 1 более 2 ампер. Таким образом, это токи, протекающие через R 2, R 3 и R 4.
Зная эти значения тока, мы можем рассчитать мощность, рассеиваемую через эти резисторы, и поэтому P 2 будет равно i 22 раза R 2 более 32 раз R 2 и R 2 было 6 Ом , который будет равен 1 более 9 раз 6.Опять же, мы можем упростить это как 2 и 3 здесь, поэтому ответ будет 2 на 3 Вт. Это количество энергии, рассеиваемой через сопротивление R 2.
Аналогичным образом, P 3 будет равно i 3 в квадрате, умноженному на R 3 и i 3, равное 1 на 6, поэтому 1 на 6 больше, чем R 3, и это 12 Ом, что составляет чтобы быть равным 1 на 36 раз 12. Опять же, мы можем сделать упрощение здесь, что даст нам только 1 на 3 Вт.Наконец, мощность, рассеиваемая через R 4, будет равна i 42, умноженной на R 4 и i 4, равной 1 на 2 ампера, поэтому мы возьмем квадрат, умноженный на R 4. 4 Ом, что будет равно 1 на 4 в 4 раза, и это даст нам просто 1 Вт.
Итак, выполняя эти расчеты, мы определили, какая мощность рассеивается через каждое из этих сопротивлений. Давайте посчитаем общую рассеиваемую мощность.Она будет равна сумме мощности, рассеиваемой через каждое сопротивление, поэтому P 1 плюс P 2 плюс P 3 плюс P 4 плюс P 5 плюс P 6 плюс P 7. То есть, через P 1 мы нашли 2 Вт, плюс через P 2, 2 более 3 Вт, через P 3, 1 более 3 Вт и через P 4, мы нашел 1 ватт, и через P 5 я фактически пропустил P 5 и обозначил его как R 6, поэтому давайте удалим P 5 из наших уравнений.Оказывается, я пропустил один из них численно. Ладно.
Через P 6 мы обнаружили, что ток не проходит через R 6, следовательно, нет рассеиваемой мощности, поскольку i составляет от 0 до P 6, и это было 0. Через P 7 мы имеем Найдено 3 Вт, мощность рассеивается. Таким образом, общая рассеиваемая мощность будет равна, здесь у нас будет 2 на 3 плюс 1 на 3, мы получим 3 на 3, так что получится 1. 1 плюс 1 равно 2, плюс 3 равно 5, плюс 2 составляет 7 Вт.7 ватт мощности рассеивается. Другими словами, столько энергии превращается в тепло каждую секунду.
Давайте также посчитаем потребляемую мощность. Подаваемая мощность, по определению, равна величине тока, потребляемого от источника питания, и равна × , умноженная на разность потенциалов между клеммами источника питания, и она составляет 9009 вольт. Как вы помните, мы обнаружили, что ток, потребляемый от электродвижущей силы, составлял 1 А, а разность потенциалов между клеммами источника питания составляла 7 Вольт.Это будет равно, следовательно, 7 Вт.
Это подтверждает, что наши расчеты верны, и когда мы сравниваем мощность, рассеиваемую с поставляемой мощностью, мы видим, что эти две величины равны друг другу. Это хороший контрольный пункт, потому что из принципа сохранения энергии мы знаем, что эти две величины должны быть равны друг другу. Если они не были равны, то мы должны были вернуться и проверить наши численные расчеты и посмотреть, где была ошибка. Следовательно, это хорошая контрольная точка, когда вы сталкиваетесь с этими типами проблем схемы.
,Простые соединения — SteelConstruction.info
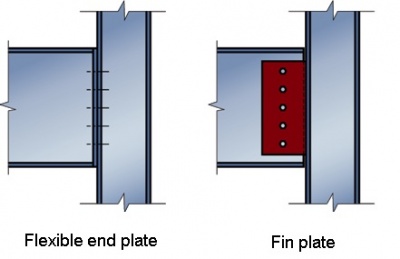
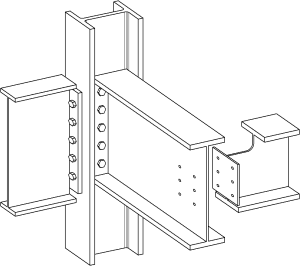
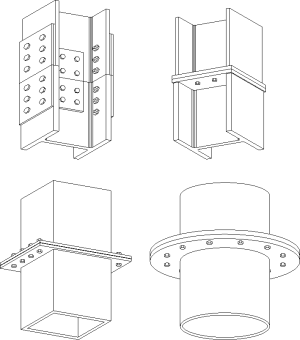
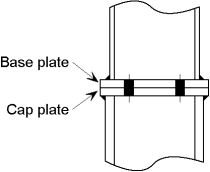
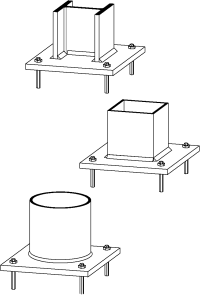
В этой статье рассматриваются номинально закрепленные соединения (простые соединения), которые используются в многоэтажных стальных каркасах в Великобритании. Эта форма жесткой конструкции с номинально закрепленными соединениями называется «простой конструкцией».
В статье перечислены типы простых соединений, которые чаще всего используются в Великобритании. В нем представлены процедуры их разработки для Eurocode 3 и обсуждаются относительные достоинства типов соединений на конце балки.Преимущества стандартизации соединений обсуждаются для соединений балка-балка и балка-колонна с использованием ребристой пластины и гибких соединений концевой пластины.
Соединения колонн, основания колонн и крепежные соединения также обсуждаются вместе с кратким упоминанием специальных соединений.
Детали соединения стандартной ребристой пластины
[top] Типы простых соединений
Простые соединения — это номинально закрепленные соединения, которые, как предполагается, передают только поперечный сдвиг и имеют незначительное сопротивление вращению.Поэтому не передавайте значимые моменты в предельном предельном состоянии. Это определение лежит в основе конструкции многоэтажных рамных конструкций в Великобритании, спроектированных как «простая конструкция», в которой балки имеют простую опору, а колонны рассчитаны на осевую нагрузку и небольшие моменты, вызванные конечными реакциями от балки. Устойчивость обеспечивается каркасом за счет крепежа или бетонного сердечника.
Простые соединения
В Великобритании используются две основные формы простого подключения (как показано справа):
Обычно встречающиеся простые соединения включают в себя:
Простые соединения могут также потребоваться для перекосов, балок, эксцентричных к колоннам, и для соединения с стенками колонн.Они классифицируются как специальные соединения и обрабатываются отдельно.
[вверху] Процедуры проектирования
Конструкция простых соединений основана на BS EN 1993-1-8 [1] и сопровождающем его Национальном приложении [2] . Возможности компонентов подключения основаны на правилах, приведенных в пункте 3.6. Расстояние между крепежными элементами соответствует пункту 3.5 и соответствует рекомендациям, изложенным в «Зеленой книге» (SCI P358).
ECCS публикация №126 [3] также содержит полезные рекомендации по проектированию простых соединений с Eurocode 3.
[вверх] Совместные соображения
[вверх] Объединенная классификация
В соответствии с BS EN 1993-1-8 [1] , номинально закрепленные соединения:
- Должен быть способен передавать внутренние силы, не создавая значительных моментов, которые могут неблагоприятно повлиять на элементы или конструкцию в целом, и
- Быть способным принимать результирующие повороты при расчетных нагрузках
Кроме того, сустав должен:
- обеспечивают направленное ограничение для членов, которое было принято в конструкции элемента
- имеют достаточную прочность, чтобы удовлетворить требования структурной целостности (сопротивление связыванию).
BS EN 1993-1-8 [1] требует, чтобы все соединения были классифицированы; жесткостью, которая подходит для упругого глобального анализа, или прочностью, которая подходит для жесткого пластического глобального анализа, или жесткостью и прочностью, которая подходит для упругопластического глобального анализа.
Классификация по жесткости:
Начальная вращательная жесткость соединения, рассчитанная в соответствии с BS EN 1993-1-8 [1] , 6.3.1 сравнивается с границами классификации, приведенными в BS EN 1993-1-8 [1] , 5.2.2.
В качестве альтернативы, суставы могут быть классифицированы на основе экспериментальных данных, опыта предыдущих удовлетворительных показателей в аналогичных случаях или на основе расчетов на основе результатов испытаний.
Классификация по прочности:
Следующие два требования должны быть выполнены, чтобы классифицировать соединение как номинально закрепленное на основе его прочности:
- Расчетное моментное сопротивление соединения не превышает 25% расчетного моментного сопротивления, необходимого для полнослойного соединения
- Шарнир должен выдерживать повороты, возникающие в результате проектных нагрузок.
В Национальном приложении Великобритании к BS EN 1993-1-8 [2] указано, что соединения, спроектированные в соответствии с «Зеленой книгой» (SCI P358), могут классифицироваться как соединения с номинальным закреплением.
Все стандартные соединения, указанные в «Зеленой книге» (SCI P358), могут быть классифицированы как номинально закрепленные на основании требований к прочности вместе с обширным опытом использования деталей на практике. Следует позаботиться о внесении поправок в стандартные детали, так как получающееся в результате соединение может выходить за пределы положений Национального Приложения Великобритании [2] .В частности:
- Вращательная способность деталей стандартной пластины оребрения была продемонстрирована тестом; измененные детали не могут быть пластичными
- Толщина концевых пластин полной глубины была ограничена, чтобы обеспечить моментное сопротивление менее 25% от полной прочности соединения и, таким образом, может быть классифицирована как номинально закрепленная.
[top] Структурная целостность
Строительные нормы и правила Великобритании требуют, чтобы все здания были спроектированы так, чтобы избежать непропорционального обрушения.Обычно это достигается путем проектирования соединений в стальной раме (соединения балки с колонной и сращивания колонны) для сил соединения. Руководство по расчетным значениям сил сцепления дано в BS EN 1991-1-7 [4] , Приложение A, и в его Национальном приложении Великобритании [5] . Требования относятся к классу здания с расчетным значением силы горизонтального связывания, как правило, не менее 75 кН и, как правило, значительно выше. Детали торцевой пластины полной глубины были разработаны для обеспечения более высокого сопротивления связыванию по сравнению с деталями торцевой пластины частичной глубины.Более подробная информация о структурной устойчивости представлена в SCI P391.
[top] Выбор типа подключения
Выбор соединений конца луча часто может быть довольно сложным. Относительные достоинства трех типов соединений (концевые пластины частичной глубины, концевые пластины полной глубины и ребристые пластины) приведены в таблице ниже. Выбор балок и соединений, как правило, является обязанностью подрядчика по изготовлению металлоконструкций, который выберет тип соединения в соответствии с производственной нагрузкой, экономичностью и временной устойчивостью во время монтажа.
| Концевая пластина с частичной глубиной | Концевая пластина полной глубины | Пластина ребра | |
|---|---|---|---|
| Дизайн | |||
| Сопротивление сдвигу — процент сопротивления луча | До 75% | 100% | До 50% До 75% с двумя вертикальными линиями болтов |
| Сопротивление связыванию | Ярмарка | Хорошо | хорошо |
| Особые соображения | |||
| перекос суставов | Ярмарка | Ярмарка | хорошо |
| Балки эксцентриковые к колоннам | Ярмарка | Ярмарка | хорошо |
| Соединение с полотнами колонн | Хорошо | Хорошо | Fair Для облегчения монтажа может потребоваться снятие фланцев.Для пластин с длинными ребрами может потребоваться жесткость |
| Изготовление и обработка | |||
| Изготовление | Хорошо | Хорошо | Хорошо Для пластин с длинными ребрами может потребоваться жесткость |
| Обработка поверхности | Хорошо | Хорошо | хорошо |
| Монтаж | |||
| Легкость монтажа | Ярмарка Необходима помощь при двустороннем подключении |
Ярмарка Необходима помощь при двустороннем подключении |
хорошо |
| Настройка сайта | Ярмарка | Ярмарка | Ярмарка |
| Временная стабильность | Ярмарка | Хорошо | Ярмарка |
[top] Композитные полы
Признано, что взаимодействие с композитным полом будет влиять на поведение простого соединения.Обычной практикой является проектирование таких соединений без использования преимуществ непрерывности армирования через бетонную плиту. Тем не менее, SCI P213 позволяет обеспечить непрерывность армирования, обеспечивая относительно простые соединения концевых пластин на всю глубину с существенным сопротивлением моменту. В рамке со скобами это сопротивление может использоваться для уменьшения момента среднего отклонения и отклонения, облегчая выбор луча меньшего размера.
[top] Расходы
Простые соединения всегда дешевле в изготовлении, чем соединения с сопротивлением моменту, потому что они требуют гораздо меньших производственных усилий, особенно при сварке.
Трудно дать конкретное руководство по затратам, так как уровень качества работы Подрядчика может значительно варьироваться и зависит от уровня инвестиций в оборудование и машины. Однако основная цель — минимизировать содержание работы. Стоимость материала для фитингов и болтов невелика по сравнению с затратами на изготовление, в которых преобладает содержание сварки. В типичной производственной мастерской стоимость изготовления соединений может составлять от 30% до 50% от общей стоимости изготовления.
Стандартизированные соединения эффективны при их производстве. Подрядчики по изготовлению металлоконструкций оборудуют свои мастерские специализированным оборудованием, которое увеличивает скорость изготовления, позволяя им производить фитинги и готовить детали гораздо быстрее, чем если бы каждый раз отличалась конфигурация соединения.
Стандартизированные детали означают, что стальные конструкции просты в монтаже, что обеспечивает более безопасную рабочую среду для стальных монтажников.
Из-за особенностей большинства болтовых соединений соединения могут быть разборными в конце срока службы конструкции.Металлоконструкции могут быть демонтированы, использованы повторно или переработаны, что снижает воздействие строительства на окружающую среду.
[top] Стандартизированные соединения
[вверх] Преимущества стандартизации
В типичной многоуровневой рамке в скобках соединения могут составлять менее 5% веса рамы и 30% или более от общей стоимости. Таким образом, эффективные соединения будут иметь наименьшую рабочую силу при детализации, изготовлении и монтаже.
| Компонент | Предпочтительный вариант | Примечания |
|---|---|---|
| Фитинги | Материал сорта S275 | Рекомендуемые размеры концевых и ребристых пластин — см. Таблицу ниже |
| болтов | М20 8.8 болтов, полностью резьбовые | Для некоторых сильно нагруженных соединений могут потребоваться болты большего диаметра. Фундаментные болты могут быть М20, М24, М30, 8.8 или 4.6. |
| Отверстий | Обычно диаметр 22 мм, перфорированный или сверлильный | диаметр 26 мм для болтов М24 размер больше 6 мм для фундаментных болтов |
| сварных швов | Угловые швы, как правило, 6 мм или 8 мм, длина ножки | Для некоторых основ колонн могут потребоваться более крупные сварные швы |
| Фитинги | Расположение | ||
|---|---|---|---|
| Размер (мм) | Толщина (мм) | Концевая пластина | Пластина ребра |
| 100 | 10 | • | |
| 120 | 10 | • | |
| 150 | 10 | • | • |
| 160 | 10 | • | |
| 180 | 10 | • | • |
| 200 | 12 | • | |
[вверху] Соединения между балками и балками
Процедуры проектирования, приведенные ниже, подходят либо для ручного расчета, либо для подготовки компьютерного программного обеспечения.
Проектирование соединений вручную может быть трудоемким процессом, поэтому полный набор таблиц сопротивления включен в «Зеленую книгу» (SCI P358).
Проверка прочности номинально закрепленного соединения включает три этапа:
- Обеспечение того, чтобы соединение было детализировано таким образом, чтобы оно развивало только номинальные моменты, которые не оказывают отрицательного воздействия на элементы или само соединение. Сустав должен быть детализирован так, чтобы он вел себя пластично.
- Идентификация пути нагрузки через соединение i.е. от луча к опорному элементу.
- Проверка сопротивления каждого компонента.
Для нормального проектирования существует десять проверок методики расчета для всех частей соединения балки или балки с колонной для вертикального сдвига.
Еще шесть проверок необходимо для проверки сопротивления соединения. Соединения балки с колонной должны быть способны противостоять боковым связующим усилиям, если только этим силам не противостоят другие элементы конструкции, такие как плиты перекрытия.
В таблице ниже приведены проверки процедуры проектирования, необходимые для концевых пластин частичной глубины, концевых пластин полной глубины и ребристых пластин. Процедуры проектирования полностью описаны в «Зеленой книге» (SCI P358).
| Процедура проектирования проверок | Концевая пластина с частичной глубиной | Концевая пластина полной глубины | Пластина ребра |
|---|---|---|---|
| 1 Рекомендуемая практика детализации | ✔ | ✔ | ✔ |
| 2 Опорная балка | сварных швов | сварных швов | Группа болтов |
| 3 Поддерживаемая балка | N / A | N / A | Пластина плавника |
| 4 Поддерживаемая балка | Паутина в сдвиге | ||
| 5 Поддерживаемая балка | Сопротивление на отметке | N / A | Сопротивление на ступеньке |
| 6 Поддерживаемая балка | Локальная стабильность зубчатой балки | N / A | Локальная стабильность зубчатой балки |
| 7 Несдерживаемая опорная балка | Общая стабильность зубчатой балки | N / A | Общая стабильность зубчатой балки |
| 8 Соединение | Группа болтов | Группа болтов | сварных швов |
| 9 Соединение | Концевая пластина в срезе | N / A | N / A |
| 10 Опорная балка / колонна | Сдвиг и подшипник | ||
| 11 Сопротивление связыванию | Пластина и болты | ||
| 12 Сопротивление связыванию | Поддерживаемая балка | ||
| 13 Сопротивление связыванию | сварных швов | ||
| 14 Сопротивление связыванию | Поддержка веб-колонки (UKC или UKB) | ||
| 15 Сопротивление связыванию | Опорная стенка колонны (RHS или SHS) | ||
| 16 Сопротивление связыванию | N / A | N / A | Опорная стенка колонны (CHS) |
Примечания: В эту таблицу включены проверки на сопротивление изгибу, сдвигу, локальное и боковое изгибание сечения балки с надрезом, поскольку обычно на стадии детализации устанавливается требование к надрезам, после чего необходимо провести проверку редуцированного сечения.
Соединения между лучами
Соединения балки с колонной
[верхняя часть] Соединения гибких концевых панелей
Концевая пластина балки к колонне и соединения балки с балкой
Типичные соединения гибких концевых панелей показаны на рисунке справа.Торцевая пластина, которая может быть частичной глубиной или полная глубина, приварена к балкам в мастерском. Балка затем прикрепляется болтами к несущей балке или колонне на месте.
Этот тип подключения является относительно недорогим, но имеет тот недостаток, что у него мало возможностей для настройки сайта. Общая длина балок должна быть изготовлена в жестких пределах, хотя пакеты можно использовать для компенсации допусков на изготовление и допусков на монтаж.
Торцевые пластины, вероятно, являются наиболее популярными из простых соединений балок, используемых в настоящее время в Великобритании.Они могут использоваться с наклонными балками и могут выдерживать умеренные смещения в соединениях балки с колонной.
Flowdrill, Hollo-Bolts, Blind-bolts или другие специальные узлы используются для соединений с полыми колоннами.
Требования к детализации и проверки конструкции для соединений концевых пластин частичной и полной глубины, которые применимы к соединениям между балками, а также соединениям между колоннами, подробно рассмотрены в «Зеленой книге» (SCI P358) , К ним относятся процедуры, рабочие примеры, подробные и проектные таблицы сопротивления.
Также доступен инструмент для конструирования концевых пластин.
Стандартные детали гибких концевых панелей (концевые пластины полной и частичной глубины) показаны на рисунке ниже вместе с рекомендуемыми размерами и фитингами.
Стандартные соединения гибких концевых панелей
| Опорная балка | Рекомендуемый размер концевой пластины b p × t p |
Болт-манометр p 3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| до 533 UB | 150 × 10 | 90 | ||||||||||
| 533 UB и выше | 200 × 12 | 140 | ||||||||||
| ||||||||||||
| Опорная балка | Рекомендуемый размер концевой пластины b p × t p |
Болт-манометр p 3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| до 533 UB | 180 × 10 | 90 | ||||||||
| 533 UB и выше | 200 × 12 | 110 | ||||||||
| ||||||||||
[верхняя] ребристые пластины
Ребристая пластина балка к колонне и балка к балке
Соединения с ребристыми пластинамиэкономичны в изготовлении и просты в монтаже.Эти соединения популярны, так как они могут быть самыми быстрыми соединениями для возведения и преодоления проблемы общих болтов в двусторонних соединениях.
соединительной пластины плавника состоит из длины пластины сваренной в мастерской к опорному элементу, к которому поддерживается веб луч болтового на месте, как показано на рисунке, приведенном ниже. Существует небольшой зазор между концом балки и опорной колонной.
Пластинчатые соединения
При проектировании соединения с ребристой пластиной важно определить подходящую линию действия ножниц.Есть две возможности: либо сдвиг действует на лицевой части колонны, либо он действует вдоль центра группы болтов, соединяющих ребристую пластину с полотном балки. По этой причине обе критические секции должны быть проверены на минимальный момент, взятый как произведение вертикального сдвига и расстояния между лицевой стороной колонны (или стенкой балки) и центром группы болтов. Затем обе критические секции проверяются на результирующий момент в сочетании с вертикальным сдвигом. Из-за неопределенности момента, приложенного к ребристой пластине, сварные швы ребристой пластины имеют размеры, соответствующие полной прочности.
Соединения пластины ребра получают свою вращательную способность в плоскости из-за деформации болта при сдвиге, из-за искажения отверстий под болты в подшипнике и из-за изгиба пластины ребра вне плоскости. Обратите внимание, что пластины ребер с длинными выступами имеют тенденцию скручиваться и разрушаться при боковом скручивании при кручении. Дополнительная проверка, чтобы рассмотреть это поведение, включена в процедуры проектирования для соединений пластин ребра.
«Зеленая книга» (SCI P358) содержит подробные требования, проверки конструкции и процедуры, применимые к конструкции пластины ребра.Отработанные примеры и расчетные таблицы сопротивления также приведены в этой публикации.
Также доступен инструмент для конструирования пластин ребер.
Детали соединения стандартной ребристой пластины
| Номинальная поддерживаемая балка (мм) |
Вертикальные линии болтов n 2 |
Рекомендуемый размер пластины ребра (мм) |
Горизонтальное расстояние между болтами, e 2 / e 2 или e 2 / p 2 / e 2 (мм) |
Разрыв, г ч (мм) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ≤610 | 1 | 100 × 10 | 50/50 | 10 | ||||||
| > 610 * | 1 | 120 × 10 | 60/60 | 20 | ||||||
| ≤610 | 2 | 160 × 10 | 50/60/50 | 10 | ||||||
| > 610 * | 2 | 180 × 10 | 60/60/60 | 20 | ||||||
| ||||||||||
|
* Для балок с номинальной глубиной более 610 мм отношение ширины пролета к глубине не должно превышать 20, а вертикальное расстояние между крайними болтами не должно превышать 530 мм. | ||||||||||
Растущий интерес к использованию S355 для пластин ребер вызвал вопросы о жесткости таких
связи — они все еще номинально закреплены? Чтобы ответить на этот вопрос, BCSA и Steel for Life поручили SCI провести исследование, сравнивающее поведение соединений пластин ребер с пластинами ребер S275 и S355.Исследование пришло к выводу, что при соблюдении стандартизированной геометрии соединений, представленной в Зеленой книге, пластины с ребрами 10 мм в S355 классифицируются как номинально закрепленные соединения и могут использоваться в качестве альтернативы пластинам S275. Дополнительная информация доступна в статье в майском номере журнала NSC за 2018 год.
[вверху] Колонка сращивания
Соединения для сращивания
Соединения колонн в многоэтажной конструкции необходимы для обеспечения прочности и непрерывности жесткости по обеим осям колонн.Типичные соединения колонн с болтовыми соединениями, используемые для проката I и полых элементов секции, показаны на рисунке справа.
Соединения, как правило, предоставляются каждые два или три этажа и обычно расположены примерно на 600 мм над уровнем пола. Это приводит к удобной длине для изготовления, транспортировки и монтажа, и обеспечивает легкий доступ со смежного пола для закрепления на месте. Предоставление сращиваний на каждом уровне яруса редко бывает экономичным, поскольку экономия на материале колонны, как правило, значительно перевешивается затратами на материалы, изготовление и монтаж при изготовлении сращивания.
[верхняя часть] Сращивания на болтовых накладках для I секций:
Для этого типа соединения есть две категории:
- тип подшипника
- ненесущего типа.
В соединении подшипника типа (см. Рисунок ниже) нагрузки передаются в прямом подшипнике с верхнего вала либо напрямую, либо через разделительную пластину. Соединение типа подшипника представляет собой более простое соединение, обычно имеющее меньше болтов, чем соединение без подшипника, и, следовательно, наиболее часто используемое на практике.
Если нет натяжения нетто, можно использовать стандартное соединение, однако BS EN 1993-1-8 [1] требует, чтобы соединительные пластины и болты передавали не менее 25% от максимального сжимающего усилия в колонка.
Для соединений типа подшипника сопротивление скручиванию может быть критической проверкой.
Соединения опорных колонн для катаных I секций
Соединители, классифицированные как не подшипникового типа (см. Рисунок ниже), передают нагрузки через болты и соединительные пластины.Любое прямое отношение между элементами игнорируется, иногда связь детализируется с физическим зазором между двумя валами. Конструкция не несущего соединения является более сложной, так как все силы и моменты должны передаваться через болты и соединительные пластины. Для сращиваний не несущего типа минимальные требования в BS EN 1993-1-8 [1] очень обременительны и основаны на пропускной способности элемента, а не на приложенном усилии.
Поскольку сращивания обычно выполняются чуть выше уровня пола, момент из-за действия распорки считается незначительным.Однако следует учитывать моменты, индуцированные в соединениях, размещенных в других положениях.
Соединения для несущих колонн для проката I сечений
Соединения колонн должны удерживать соединенные элементы на одной линии, и, где это практически целесообразно, элементы должны быть расположены таким образом, чтобы центральная ось материала сращивания совпадала с центральной осью осей колонки над и под соединением.Если секции колонн смещены (например, для поддержания постоянной внешней линии), момент из-за эксцентриситета должен учитываться в проекте соединения.
Проектные проверки, необходимые для сращивания болтовых колпачков, а также процедуры, рабочие примеры, подробные требования и таблицы проектного сопротивления доступны в главе 6 «Зеленой книги» (SCI P358).
[верхний] Болтовые соединения «колпачок и основание» или «концевая пластина» для трубчатых и катаных I сечений
«Крышка и основание» или «Концевая пластина» сращивания
Этот тип соединения, состоящий из пластин, которые приварены к концам нижней и верхней колонн и затем просто скреплены болтами на месте, обычно используется в трубчатой конструкции, но также может использоваться для открытых секций.
Самая простая форма соединения показана на рисунке справа и является удовлетворительной, если концы каждого вала подготовлены так же, как для соединения типа подшипника. Следует учитывать возможность изменения нагрузки, в дополнение к стабильности при монтаже и требованиях к обвязке.
Несмотря на то, что они широко используются, трудно доказать, что колпачок и базовые соединения соответствуют требованиям BS EN 1993-1-8 [1] , пункт 6.2.7.1 (14). Если используются эти типы соединений, общепринятая практика заключается в том, чтобы пластины были толстыми и чтобы болты располагались близко к фланцам для увеличения жесткости соединения.Могут использоваться удлиненные пластины с болтами за пределами профиля секции. Если стыки крышка и основание пластины расположены вдали от точки пресечения, особое внимание должно быть уделено обеспечению адекватной жесткости, так что дизайн элемент не признан недействительным.
Соединения колонок «колпачок и основание» или «концевая пластина» описаны в главе 6 «Зеленой книги» (SCI P358). Подробные требования, процедуры проектирования, рабочие примеры и таблицы сопротивления конструкции приведены.
[вверху] Основания колонн
Типичные основания колонн
Типичные основания колонн, как показано на рисунке справа, состоят из единого пластинчатого буртика, приваренного к концу колонны и прикрепленного к фундаменту четырьмя прижимными болтами.Болты вмонтированы в бетонное основание в опорных трубах или конусах и снабжены анкерными плитами для предотвращения вытягивания. Высокопрочный раствор заливается в пространство под плитой (см. Рисунок ниже).
Такие основания колонн часто подвергаются только осевому сжатию и сдвигу. Однако подъем и горизонтальный сдвиг могут быть расчетным случаем для оснований колонн в связных бухтах.
Болты крепления основания колонны
Соединение основания колонны
Пример заглушки среза
Простая прямоугольная или квадратная опорная плита почти повсеместно используется для колонн в простой конструкции.Опорная плита должна быть достаточного размера и прочности, чтобы передавать осевое сжимающее усилие от колонны к фундаменту через подкладочный материал, не превышая местного сопротивления подшипника фундамента.
базовой инструмент пластины дизайн доступен.
Колонка основы, как правило, предназначены для передачи усилия от колонны к опорной плите в прямом подшипника. Удерживающие системы предназначены для стабилизации колонны во время строительства и противостоят любому подъему в закрепленных отсеках.В некоторых случаях предполагается, что скромный горизонтальный сдвиг также осуществляется прижимными болтами.
[top] Горизонтальный сдвиг
Способ передачи горизонтальных сдвиговых усилий на фундамент недостаточно изучен. Некоторые разработчики проверяют сопротивление прижимных болтов и обеспечивают их достаточную заливку. Эта практика была успешно применена для основ портала, которые имеют значительный сдвиг.
Скрученные отсеки могут иметь относительно высокие усилия сдвига.Проектировщики могут выбрать, чтобы обеспечить сдвиг заглушки, приваренную к нижней плите основания, хотя выемка может осложнить отливки фундамента, и особое внимание должно быть уделено цементирующей операции. Методы проектирования, которые охватывают этот тип деталей, приведены в «Зеленой книге» (SCI P398).
сдвига между концом колонны и опорной пластиной будет передаваться между сварными швами колонной и опорной плитой. Сварные швы могут быть предусмотрены только для полотна или вокруг частей профиля — обычно оказывается, что сопротивление сварному шву более чем достаточно для умеренных сдвиговых усилий.
[вверху] Соединения крепления
Типичное крепежное соединение с косынкой
Крепежные элементы включают в себя плоскости, углы, каналы, I-секции и полые секции. Крепежные устройства могут включать в себя крепежные элементы, работающие только на растяжение или на растяжение и сжатие. В большинстве случаев крепежный элемент крепится болтами к пластине со вставкой, которая сама приварена к балке, к колонне или, более часто, приварена к балке и ее концевому соединению, как показано на рисунке справа.
Системы крепления обычно анализируются в предположении, что все силы пересекаются на осевых линиях элементов. Тем не менее, реализация этого предположения в деталях соединения может привести к соединению с очень большой пластиной, особенно если скобы пологие или крутые. Часто бывает удобнее расположить пересечения элементов, чтобы сделать более компактное соединение, и локально проверить наличие вводимых эксцентриситетов.
Соединения для крепления обычно выполняются с помощью предварительно не нагруженных болтов в зазорах.По крайней мере, в теории это допускает некоторое движение в соединении, но на практике это игнорируется в ортодоксальной конструкции. В некоторых случаях может случиться так, что движение по развороту недопустимо — в этих обстоятельствах следует использовать предварительно загруженные соединения.
Общий процесс проектирования:
- Определите путь загрузки через соединение
- Организовать соединение, чтобы убедиться, что проектные намерения участников реализованы, например, соединения луча остаются номинально закрепленными
- Включите эффекты любого значительного эксцентриситета
- Проверьте компоненты в соединении.
Штифтовое соединение для трубчатого элемента крепления
Правила проектирования для определения сопротивления косынки приведены в «Зеленой книге» (SCI P358).
Также имеется инструмент для конструирования пластин Gusset.
[вверху] Специальные соединения
Соединения стальных конструкций для простой конструкции, показанной выше, как правило, производят наиболее экономичную стальную раму. Отступление от этих соединений неизбежно приведет к увеличению общей стоимости.Увеличение затрат на детализацию, изготовление и монтаж может составить более 100%, если нестандартные соединения составляют большинство используемых соединений.
Необходимость в специальных соединениях часто можно избежать путем разумного выбора размеров элементов. Структура минимального веса вряд ли будет наиболее экономически эффективной. Поэтому эффективная экономическая практика заключается в том, чтобы стальные конструкции можно было размещать с осевыми линиями на установленных решетках. Верхние фланцы балок должны, по возможности, находиться на постоянном уровне, но это менее критично для стоимости, чем эксцентриковые соединения.
При проектировании специальных соединений может оказаться возможным использовать модифицированную версию одного из стандартизированных соединений, указанных в Зеленой книге, при условии дополнительных проверок проекта. Принципы проектирования и правила определения размеров компонентов, приведенные в Зеленой книге, должны быть максимально включены в проектирование соединений.
Типичные примеры ситуаций, когда требуются специальные соединения, представлены в «Зеленой книге» (SCI P358).
[вверх] Ссылки
- ↑ 1.0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 BS EN 1993-1-8: 2005. Еврокод 3: Проектирование металлоконструкций. Проектирование стыков, BSI
- ↑ 2.0 2.1 2.2 NA к BS EN 1993-1-8: 2005. Национальное приложение Великобритании к Еврокоду 3: Проектирование стальных конструкций. Проектирование стыков, BSI
- ↑ Публикация ECCS № 126 Европейские рекомендации по проектированию простых соединений в стальных конструкциях.J.P. Jaspart et al. 2009.
- ↑ BS EN 1991-1-7: 2006 + A1: 2014. Еврокод 1: Действия над структурами. Общие действия. Случайные действия. BSI
- ↑ NA + A1: 2014 — BS EN 1991-1-7: 2006 + A1: 2014. Национальное приложение Великобритании к Еврокоду 1: Действия на сооружениях. Общие действия. Случайные действия. BSI
[вверх] Дальнейшее чтение
- Руководство для дизайнеров по стали 7-е издание. Редакция B Davison & G W Оуэнс. Институт стальных конструкций 2012, глава 27
- Архитектурное проектирование в стали — Trebilcock P и Lawson R M, опубликованные Spon, 2004
[вверх] Ресурсы
Инструменты проектирования соединений:
[вверху] Смотри также
,Соединение сдвига в композитных мостовых балках
Соединения сдвига на верхних фланцах стальных балок обеспечивают средства для достижения композитного действия между плитой и балками, увеличивая, таким образом, жесткость и прочность. В этой статье рассматривается поведение разъемов и правила проектирования для соединения сдвига в BS EN 1994-2 [1] . Дополнительные указания приведены в разделе 6.5 SCI P356, а примеры расчета сопротивления сдвигу приведены в SCI P357.
Шпильки на стальных балках для соединения сдвига
A41 Aston Clinton Bypass
[top] Необходимость соединения среза
Сдвиг потока между стальной балкой и железобетонной палубной плитой является естественным следствием требования к составным действиям. Если бы не было никакого соединения, балка и плита согнулись бы, как показано схематически ниже.Наличие сдвигового соединения предотвращает проскальзывание между двумя компонентами и обеспечивает гораздо более жесткий и сильный луч.
Изгиб двух компонентов без сдвигового соединения
При наличии сдвигового соединения два компонента ведут себя как один.
[вверху] Продольный сдвиг, упругая конструкция
В соответствии с теорией упругости при изгибе, напряжения и деформации в балке при изгибе изменяются линейно от волокна с экстремальным натяжением до волокна с экстремальным сжатием, а сдвиговое течение на любом уровне (относительно нейтральной оси) в поперечном сечении определяется как :
Как для A, так и для I, площадь бетона должна быть взята за ее преобразованную площадь, т.е.е. его фактическая площадь делится на модульное соотношение. При оценке сдвига для областей с крутящимся моментом, плита должна рассматриваться как не растрескавшаяся. (Это является консервативным упрощением и применимо, за исключением случаев, когда жесткое растяжение и бетон с избыточной прочностью явно учтены, хотя в BS EN 1994-2 [1] нет рекомендаций по оценке в таких ситуациях.)
На практике величина сдвигового потока изменяется вдоль луча, и может быть обеспечено требуемое сопротивление, чтобы точно соответствовать этому изменению, но гораздо проще обеспечить равномерное сопротивление по всему лучу или, что более экономично, на нескольких длинах. единообразного положения.
Для последнего варианта в каждой длине однородного сопротивления сопротивление может быть сделано, чтобы соответствовать пиковому значению сдвигового потока по этой длине, но дальнейшее упрощение допускается BS EN 1994-2 [1] , пункт 6.6. .1.2, которая позволяет при любой длине постоянного сопротивления расчетному потоку сдвига превышать сопротивление на единицу длины при условии, что:
- пиковый сдвиг потока в пределах каждой длины не превышает расчетное продольное сопротивление сдвигу на единицу длины более чем на 10%
- и общий расчетный продольный сдвиг по длине не превышает общее расчетное сопротивление для этой длины.
Сдвиговое соединение обычно обеспечивается рядами соединителей среза. Вышеупомянутое правило позволяет конструктору определять ряды, как правило, с одинаковым расстоянием вдоль балки: больше рядов предусмотрено в рядах рядом с опорами, где сдвиг является наибольшим. В некоторых случаях расстояние между рядами может быть увеличено в средних областях. Во всех случаях расстояние рядов шпилек и расстояние поперечной арматуры должны быть согласованы, чтобы избежать столкновений.
[вверху] Продольный сдвиг, пластиковая конструкция
Если сопротивление балок основано на пластическом сопротивлении поперечных сечений, приведенные выше выражения для сдвигового потока недопустимы, поскольку поведение материала нелинейное, а сдвиговые потоки не могут быть рассчитаны на основе линейного упругого анализа.BS EN 1994-2 [1] пункт 6.6.2.2 (1) охватывает этот случай для членов классов 1 и 2.
BS EN 1994-2 [1] В пункте 6.6.2.2 (2) приведены конкретные случаи сжатия бетонной плиты. Продольный сдвиговый поток должен быть определен с учетом изменения силы в плите по длине, где изгибающий момент превышает упругое сопротивление. В пункте 6.6.2.2 (3) рассматриваются плиты с натяжением, а в пункте 6.6.2.2 (4) предлагается альтернативный подход, в котором используется анализ упругого сечения на основе свойств сечения без трещин.Немного неконсервативное пренебрежение неэластичностью в этом случае компенсируется консервативным предположением, что сечение не имеет трещин.
[top] Сопротивление сдвиговому соединению
[верхняя часть] Соединители со срезанными головками
Как упоминалось выше, наиболее распространенной формой соединения для сдвига является шпилька с головкой, приваренная к верхнему фланцу. Шпильки обычно располагаются в ряды, причем расстояние (и, следовательно, число на единицу длины) зависит от расчетного усилия сдвига между балкой и плитой.
-

Типичный соединитель шпилек, сразу после сварки
-

Группы соединителей сдвига
Для соединителей со сдвигом шипа расчетное сопротивление одиночного шипа является наименьшим из сопротивления самого шипа и бетона вокруг шипа. Это выражено в BS EN 1994-2 [1] , так как расчетное сопротивление ниже:
Ограничения даны на расстоянии между шипами — см. Дальнейшее обсуждение ниже.
Расчетное сопротивление сдвигу 19 мм штыревых разъемов
От того, зависит ли прочность стойки или прочность бетона, зависит относительная прочность стойки и бетона. Разброс значений, заданных двумя выражениями, может быть выражен графически — для 19-миллиметрового шпильки соотношения такие, как показано справа.
Обратите внимание, что BS EN 1994-2 [1] относится к прочности соединителей с шипами согласно BS EN ISO 13918 [2] .В этом стандарте есть два типа соединителей из углеродистой стали; прочность шпильки более высокого качества составляет 450 Н / мм 2 , и это обычно будет тип, который используется.
Таким образом, можно видеть, что для большинства композитных мостов, у которых класс бетона превышает C25 / 30, прочность соединения определяется самим шпилькой.
Плиты имеют тенденцию «подъезжать» к сварной манжете, поэтому согласно BS EN 1994-2 [1] требуется минимальное сопротивление растяжению в 10% от сопротивления сдвигу [1] — считается, что оно обеспечивается за счет шпилек с головкой.Расчетные силы растяжения меньше, чем это может быть проигнорировано.
Для большей расчетной силы растяжения не дано никакого отношения взаимодействия между натяжением и сопротивлением сдвигу, но в Hendy and Johnson [3] предполагается, что можно использовать следующий критерий:
Усталостное сопротивление соединителей сдвига также следует учитывать
[top] Другие формы соединителя сдвига
BS EN 1994-2 [1] не содержит правил для любого другого типа соединителя сдвига, хотя принципы даны для определения сопротивления других типов соединения.Целью было не исключение альтернативных форм, а стимулирование инноваций. Если рассматриваются альтернативные формы соединителя сдвига (например, когда требуется более высокое сопротивление сдвигу на соединитель, например, в некоторых соединениях на встроенных опорах), в BS EN 1994-2 [1] приводится следующее руководство:
- Все сдвиговые соединители должны иметь сопротивление натяжению 0,1P Rd для предотвращения разъединения
- Правила для прочности бетона и стальных компонентов в BS EN 1992 и BS EN 1993 могут быть использованы для определения сопротивления.
Hendy и Johnson [3] дают вывод сопротивления блочных и кольцевых соединителей, который является распространенной альтернативной формой соединителя. Конструкция этого типа разъема основана на следующей предпосылке:
- Сопротивление сдвигу определяется путем ограничения давления бетонного подшипника на лицевой стороне блока (давление подшипника см. В разделе 6.7 BS EN 1992-1-1 [4] ).
- Обруч рассчитан на сопротивление подъему не менее 0.1P Rd .
- Сварные швы спроектированы в соответствии с BS EN 1993-1-8 [5] для результирующего сдвига, растяжения и изгиба.
- Усталость сварного соединения проверяется в соответствии с BS EN 1993-1-9 [6] .
[top] Детализация
Правила приведены в BS EN 1994-2 [1] относительно расположения шпилек и их высоты относительно поперечной арматуры.
[вверху] Сопротивление отрыву
Во избежание создания плоскостей потенциального разрушения при сдвиге, которые проходят над соединителями сдвига и под поперечной арматурой, расстояние между соединителями и высота нижней арматуры ограничены в BS EN 1994-2-2000000 [1] , пункт 6.6.5. Испытания показали, что продольные поверхности разрушения не всегда плоские. Продольный разрез по поверхности возможного разрушения показан. Указанные размеры приведены до пределов в BS EN 1994-2 [1] . Пример показывает, что α составляет около 8 °. Hendy и Johnson [3] считают это слишком плоским, чтобы предотвратить сбой, и рекомендуют минимальное значение 17 °. Это дало бы максимальное расстояние 450 мм с нижней крышкой 50 мм и срезной шпилькой высотой 125 мм (длина после сварки обычно составляет 120 мм).

Плоскость сдвига над шпильками
[вверху] Максимальное расстояние между разъемами
Максимальное продольное расстояние между соединителями указано в BS EN 1994-2 [1] , пункт 6.6.5.5 (3) как 4h c (где h c — толщина плиты), но не более 800 мм.
BS EN 1994-2 [1] В пункте 6.6.5.5 (2) приводятся дополнительные ограничения на расстояние между разъемами на балках, где фланец считается классом 1 и 2, но без соединения с плитой класс. 3 или 4.
BS EN 1994-2 [1] В пункте 6.6.5.5 (4) приведены правила, позволяющие группировать соединители в карманы (полезно при использовании сборных блоков полной глубины), но затем говорится, что необходимо следующее быть проверенным:
- Предположение о плоскости сечения оставшейся плоскости
- Вертикальное разделение
- Пряжка стального фланца
- Усилие разрыва от группы соединителей (правила поперечной арматуры могут быть недостаточными).
Штыревые соединители
BS EN 1994-2 [1] пункт 6.6.5.7 дает минимальные размеры для головных срезных шпилек. Минимальное расстояние в направлении поперечной силы составляет 5d, а минимальное расстояние в направлении, поперечном к поперечной силе в «твердых плитах», составляет 2,5d. Обратите внимание, что ссылка на твердые плиты должна быть принята, чтобы исключить плиты с загибами (следует использовать минимальный интервал 4d).
BS EN 1994-2 [1] , пункт 6.6.5.6, дает расстояние от края до шпилек не менее 25 мм. Однако, если используется постоянная опалубка, необходимо предусмотреть возможность установки опалубки на балке в соответствии с требованиями производителя.Кроме того, защитное покрытие должно быть нанесено не менее чем на 25 мм от края фланца или, если используется постоянная опалубка, на расстоянии 25 мм от края опалубки (см. Soubry [7] ). Обычно расстояние до края 100 мм достаточно.
- Лакокрасочное покрытие накладывается на край балки, примыкающей к шпилькам
-

-
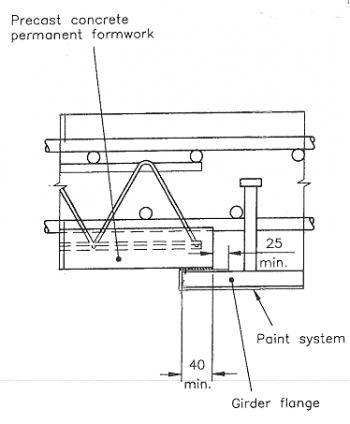
[top] Продольное сопротивление сдвигу плиты
Продольные поверхности сдвига
Чтобы проверить адекватность плиты силам, передаваемым соединителями сдвига, необходимо рассмотреть несколько возможных поверхностей разрушения.Две поверхности сдвига показаны справа.
BS EN 1994-2 [1] , пункт 6.6.6 требует, чтобы продольное сопротивление сдвигу плиты проверялось на поверхностях сдвига типа A-A и B-B; расчетная прочность на сдвиг бетонного фланца приведена в BS EN 1992-1-1 [4] .
BS EN 1994-2 [1] , пункт 6.6.2, определяет расчетный продольный сдвиг на единицу длины V L, Ed между сталью и бетоном как скорость изменения силы в стальном или бетонном элементе.В BS EN 1992-1-1 [4] модели фермы для сдвига между плитой и балкой приведены требования в отношении расчетного напряжения сдвига V Ed . Существует некоторое несоответствие между BS EN 1992-1-1 [4] и BS EN 1994-2 [1] при выражении напряжения сдвига, но для поверхностей сдвига типа AA это следует рассматривать как расчетный сдвиг на единицу длины на одна сторона разделена на h f , где h f — глубина плиты, а для поверхностей сдвига типа BB это общая расчетная величина сдвига, деленная на h f , где h f — длина сдвига самолет.
Площадь поперечной арматуры A sf на расстоянии s f , которая пересекает поверхность сдвига, требуется согласно BS EN 1992-1-1 [4] , выражение (6.21) для удовлетворения:
Для поверхностей A-A, A и — это сумма площадей верхней и нижней поперечной арматуры; для поверхностей типа B-B удваивается площадь нижней арматуры.

Усиление поперечного нижнего мата между стойками и постоянной опалубкой
Кроме того, продольное напряжение сдвига должно удовлетворять выражению BS EN 1992-1-1 [4] (6.22) во избежание сдавливания компрессионных стоек во фланце.
Для рассмотрения взаимодействия с поперечным изгибающим моментом:
- В плоскости A-A поперечное усиление должно быть больше, чем требуется только для продольного сдвига, и вдвое меньше, чем для продольного сдвига, плюс то, что требуется для поперечного изгиба.
- В плоскости B-B площадь усиления днища, необходимая для поперечного изгибающего момента, должна быть полностью добавлена к той, которая требуется для продольного сдвига (хотя это не указано в BS EN 1994-2 [1] )
Для рассмотрения взаимодействия с напряжением:
- Если плита находится в поперечном натяжении через A-A (например,грамм. если ферма является поперечной балкой в зоне захвата основного луча), требования к натяжению должны полностью сочетаться с продольным сдвигом.
[вверх] Ссылки
- 1. 1.00 1.01 1.09 000 1.16 1,17 1,18 1,19 1,20 1,21 BS EN 1994-2: 2005. Еврокод 4: Проектирование композитных стальных и бетонных конструкций. Общие правила и правила для мостов. BSI
- ↑ BS EN ISO 13918: 2018
Сварка. Шпильки и керамические наконечники для дуговой сварки. BSI
- ↑ 3.0 3.1 3.2 Руководство для дизайнеров по BS EN 1994-2 Еврокод 4: Проектирование композитных стальных и бетонных конструкций. Часть 2. Общие правила и правила для мостов.Hendy, C.R .; Джонсон Р.П. (2006). Томас Телфорд Лтд
- ↑ 4,0 4,1 4,2 4,3 4,4 4,5 BS EN 1992-1-1: 2004 + A1: 2014. Еврокод 2: Проектирование бетонных конструкций. Общие правила и правила для зданий. BSI
- ↑ BS EN 1993-1-8: 2005. Еврокод 3: Проектирование металлоконструкций. Дизайн суставов. BSI
- ↑ BS EN 1993-1-9: 2005. Еврокод 3: Проектирование металлоконструкций. Усталость. BSI
- guide Руководство по детализации моста.(C543). Субри, М. (2001). CIRIA
[вверх] Ресурсы
[вверху] См. Также
[top] Внешние ссылки
, Как работают 4-контактные резисторы — Лаборатория стандартов мощности
Как работают 4-контактные резисторы
В 4-контактном резисторе сверхточный резистор (зеленый) подключается к 4 контактам через небольшие, но неизвестные резисторы (красный).
Эти неизвестные резисторы представляют собой сочетание сопротивления выводов, сопротивления винтовых клемм, сопротивления соединительного провода и других источников ошибок.
Типичные значения для этих неизвестных резисторов варьируются от 0.От 01 Ом до 0,2 Ом, и значения часто нестабильны.
Значения могут изменяться, например, при ослаблении или затягивании винта или при замене более длинного измерительного провода.
Стандарты электропитания Предельный уровень сопротивления лаборатории
:
0,09999863 Ом
Чтобы использовать 4-контактный резистор, мы подаем ток с клеммы 1 на клемму 2. Это ток, поэтому неизвестные сопротивления, подключенные к клемме 1 и клемме 2, не влияют на величину тока. Одинаковое количество электронов в секунду протекает от T1 до T2 независимо от сопротивления.
Вольтметр измеряет результирующее падение напряжения на сверхточном резисторе, измеряя через неизвестные резисторы, подключенные к клемме 3 и клемме 4. Входное сопротивление вольтметра очень, очень высоко по сравнению с неизвестными резисторами, поэтому неизвестные резисторы имеют практически нулевой эффект (обычно менее 0,1 части на миллион).
Таким образом, ток течет через резистор 0,100 Ом, не подверженный влиянию неизвестных резисторов, и мы измеряем напряжение на 0.Резистор 100 Ом, не подвержен влиянию неизвестных резисторов.
И вот как работает 4-контактный резистор.
Итак, о каких ошибках мы беспокоимся, когда используем резисторы такого типа? Мы обычно измеряем эти ошибки в частях на миллион, или в расчете на миллион (одна промилле = 0,0001%).
Существует пять основных источников ошибок: погрешность калибровки, индуктивность, температура, старение и контакты металл-металл.
- Национальный институт стандартов и технологий США калибрует стандартный резистор PSL с погрешностью 0.5 PPM — устанавливает абсолютный предел неопределенности измерений в PSL
- Резистор обычно изготавливается из отрезка провода, намотанного на катушку; В большинстве прецизионных резисторов направление обмотки меняется на половину оборота, чтобы минимизировать индуктивность. Тем не менее, оптимальная точность достигается при 0 Гц или DC. Даже при типичных частотах мощности в несколько десятков герц индуктивность может вносить погрешности в несколько PPM
- Проволока изготовлена из материала с минимальным температурным коэффициентом.Тем не менее, изменение степени или двух может привести к ошибкам от десятков до сотен частей на миллион. Это не только температура окружающей среды масляной ванны, либо; мы должны беспокоиться о саморазогреве, когда пропускаем ток через резистор. Таким образом, контроль температуры играет важную роль
- Все резисторы меняют значения при старении. Большинство исследований показывают, что в течение первых нескольких лет жизни резистора происходит первоначальное старение (иногда это происходит с намеренным ускорением при нагревании), а затем резистор стабилизируется.По этой причине PSL предпочитает калибровочные резисторы, которым не менее 25 лет.
- Важно учитывать гальванические напряжения, возникающие при контакте разнородных металлов. Хотя значение неизвестных резисторов не влияет на функцию калибровочного резистора, даже микровольт гальванического напряжения на клемме 3 или клемме 4 будет влиять на показания 10 PPM при 1 ампере. Поэтому мы очень осторожно используем правильные типы разъемов для измерительных проводов на этих клеммах (и на клеммах вольтметра)
Вопросы? Пожалуйста, свяжитесь с нами для получения дополнительной информации
,

Типичный соединитель шпилек, сразу после сварки

Группы соединителей сдвига
Для соединителей со сдвигом шипа расчетное сопротивление одиночного шипа является наименьшим из сопротивления самого шипа и бетона вокруг шипа. Это выражено в BS EN 1994-2 [1] , так как расчетное сопротивление ниже:
Hendy и Johnson [3] дают вывод сопротивления блочных и кольцевых соединителей, который является распространенной альтернативной формой соединителя. Конструкция этого типа разъема основана на следующей предпосылке:

Штыревые соединители
BS EN 1994-2 [1] пункт 6.6.5.7 дает минимальные размеры для головных срезных шпилек. Минимальное расстояние в направлении поперечной силы составляет 5d, а минимальное расстояние в направлении, поперечном к поперечной силе в «твердых плитах», составляет 2,5d. Обратите внимание, что ссылка на твердые плиты должна быть принята, чтобы исключить плиты с загибами (следует использовать минимальный интервал 4d).




Кроме того, продольное напряжение сдвига должно удовлетворять выражению BS EN 1992-1-1 [4] (6.22) во избежание сдавливания компрессионных стоек во фланце.
Для рассмотрения взаимодействия с напряжением:
Как работают 4-контактные резисторы
В 4-контактном резисторе сверхточный резистор (зеленый) подключается к 4 контактам через небольшие, но неизвестные резисторы (красный).
Эти неизвестные резисторы представляют собой сочетание сопротивления выводов, сопротивления винтовых клемм, сопротивления соединительного провода и других источников ошибок.
Типичные значения для этих неизвестных резисторов варьируются от 0.От 01 Ом до 0,2 Ом, и значения часто нестабильны.
Значения могут изменяться, например, при ослаблении или затягивании винта или при замене более длинного измерительного провода.
:
0,09999863 Ом
Чтобы использовать 4-контактный резистор, мы подаем ток с клеммы 1 на клемму 2. Это ток, поэтому неизвестные сопротивления, подключенные к клемме 1 и клемме 2, не влияют на величину тока. Одинаковое количество электронов в секунду протекает от T1 до T2 независимо от сопротивления.
Вольтметр измеряет результирующее падение напряжения на сверхточном резисторе, измеряя через неизвестные резисторы, подключенные к клемме 3 и клемме 4. Входное сопротивление вольтметра очень, очень высоко по сравнению с неизвестными резисторами, поэтому неизвестные резисторы имеют практически нулевой эффект (обычно менее 0,1 части на миллион).
Таким образом, ток течет через резистор 0,100 Ом, не подверженный влиянию неизвестных резисторов, и мы измеряем напряжение на 0.Резистор 100 Ом, не подвержен влиянию неизвестных резисторов.
И вот как работает 4-контактный резистор.
Итак, о каких ошибках мы беспокоимся, когда используем резисторы такого типа? Мы обычно измеряем эти ошибки в частях на миллион, или в расчете на миллион (одна промилле = 0,0001%).
Существует пять основных источников ошибок: погрешность калибровки, индуктивность, температура, старение и контакты металл-металл.
- Национальный институт стандартов и технологий США калибрует стандартный резистор PSL с погрешностью 0.5 PPM — устанавливает абсолютный предел неопределенности измерений в PSL
- Резистор обычно изготавливается из отрезка провода, намотанного на катушку; В большинстве прецизионных резисторов направление обмотки меняется на половину оборота, чтобы минимизировать индуктивность. Тем не менее, оптимальная точность достигается при 0 Гц или DC. Даже при типичных частотах мощности в несколько десятков герц индуктивность может вносить погрешности в несколько PPM
- Проволока изготовлена из материала с минимальным температурным коэффициентом.Тем не менее, изменение степени или двух может привести к ошибкам от десятков до сотен частей на миллион. Это не только температура окружающей среды масляной ванны, либо; мы должны беспокоиться о саморазогреве, когда пропускаем ток через резистор. Таким образом, контроль температуры играет важную роль
- Все резисторы меняют значения при старении. Большинство исследований показывают, что в течение первых нескольких лет жизни резистора происходит первоначальное старение (иногда это происходит с намеренным ускорением при нагревании), а затем резистор стабилизируется.По этой причине PSL предпочитает калибровочные резисторы, которым не менее 25 лет.
- Важно учитывать гальванические напряжения, возникающие при контакте разнородных металлов. Хотя значение неизвестных резисторов не влияет на функцию калибровочного резистора, даже микровольт гальванического напряжения на клемме 3 или клемме 4 будет влиять на показания 10 PPM при 1 ампере. Поэтому мы очень осторожно используем правильные типы разъемов для измерительных проводов на этих клеммах (и на клеммах вольтметра)
Вопросы? Пожалуйста, свяжитесь с нами для получения дополнительной информации
,