Соединение звезда и треугольник формулы. Уравнение звезда-треугольник: расчет расстояния до звезд методом параллакса

Как рассчитать расстояние до звезд с помощью метода параллакса. Что такое триангуляция в астрономии. Как измерить угол параллакса звезды. Какие формулы используются для вычисления расстояния до звезд по параллаксу.

Метод триангуляции для измерения расстояний в астрономии

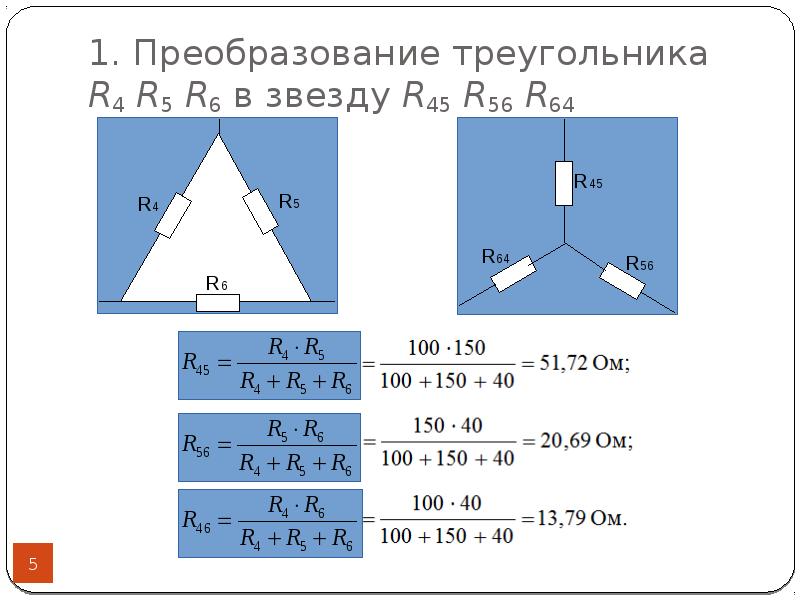
Метод триангуляции широко применяется в астрономии для измерения расстояний до небесных объектов. Его суть заключается в использовании геометрических свойств треугольника для определения недоступных для прямого измерения расстояний.

Основные этапы метода триангуляции включают:

1. Выбор базисной линии известной длины
2. Измерение углов между базисной линией и направлением на объект с двух концов базиса
3. Расчет расстояния до объекта по измеренным углам и длине базиса с помощью тригонометрических формул

В астрономии в качестве базисной линии обычно используется орбита Земли вокруг Солнца. Ее диаметр составляет около 300 миллионов километров, что позволяет измерять расстояния до ближайших звезд.

Параллакс звезд и его измерение

Параллакс звезды — это видимое смещение ее положения на небесной сфере при наблюдении с разных точек орбиты Земли. Чем ближе звезда, тем больше ее параллакс.

Для измерения параллакса выполняют следующие шаги:

1. Фотографируют участок неба со звездой с интервалом в 6 месяцев, когда Земля находится в противоположных точках своей орбиты
2. Измеряют видимое смещение положения звезды относительно далеких звезд фона
3. Рассчитывают угол параллакса, зная масштаб изображения

Угол параллакса p связан с расстоянием до звезды r формулой:

r = 1 / p

Где r выражено в парсеках, а p — в угловых секундах. 1 парсек равен 3,26 световых лет.

Расчет расстояния до звезды HT Cas по ее параллаксу

Рассмотрим пример определения расстояния до звезды HT Cas по ее годичному параллаксу:

1. На двух снимках, сделанных с интервалом 6 месяцев, измеряем смещение HT Cas относительно опорных звезд
2. Зная, что угол между двумя ближайшими к HT Cas звездами составляет 0.000002778°, находим масштаб изображения
3. Рассчитываем угол параллакса HT Cas в угловых секундах
4. Определяем расстояние до звезды в парсеках по формуле r = 1 / p
5. Переводим парсеки в световые годы

Таким образом, метод параллакса позволяет достаточно точно измерять расстояния до ближайших звезд, находящихся на расстоянии до нескольких сотен световых лет.

Преимущества и ограничения метода параллакса

Основные преимущества метода параллакса:

• Прямое измерение расстояний без дополнительных предположений
• Высокая точность для близких звезд
• Возможность калибровки других методов определения расстояний

Ограничения метода:

• Применим только для относительно близких звезд (до ~1000 световых лет)
• Требует очень точных угловых измерений (до 0.001 угловой секунды)
• Ограничен атмосферными искажениями при наземных наблюдениях

Для измерения больших межзвездных расстояний используются другие методы, основанные на физических свойствах звезд.

Исторические аспекты измерения звездных параллаксов

Попытки измерить параллаксы звезд предпринимались астрономами на протяжении веков:

• 1572 г. — Тихо Браге безуспешно пытался обнаружить параллакс сверхновой звезды
• 1838 г. — Ф.В. Бессель впервые успешно измерил параллакс звезды 61 Лебедя
• 1989 г. — запуск космического аппарата Hipparcos для массового измерения звездных параллаксов
• 2013 г. — начало работы космической обсерватории Gaia для сверхточных астрометрических измерений

Современные космические миссии позволяют измерять параллаксы с точностью до микросекунд дуги, что существенно расширило возможности этого метода.

Связь параллакса с другими астрометрическими величинами

Параллакс звезды тесно связан с другими важными астрометрическими характеристиками:

• Собственное движение — скорость перемещения звезды по небесной сфере
• Лучевая скорость — скорость движения звезды вдоль луча зрения
• Абсолютная звездная величина — истинная светимость звезды

Зная параллакс и видимую звездную величину, можно рассчитать абсолютную звездную величину и светимость звезды. Это позволяет определять фундаментальные физические характеристики звезд.

Практическое применение звездных параллаксов

Измерения звездных параллаксов имеют важное практическое значение в астрономии:

• Построение трехмерной карты окрестностей Солнца
• Изучение структуры и динамики Млечного Пути
• Калибровка шкалы расстояний во Вселенной
• Исследование звездных популяций и эволюции звезд
• Поиск экзопланет методом астрометрии

Таким образом, метод параллакса остается одним из фундаментальных инструментов современной астрометрии и астрофизики.

Расчет мощности двигателя при схеме соединения звезда-треугольник

В этой статье я хотел бы рассказать как изменяется мощность двигателя при схеме соединения обмоток звезда – треугольник и наоборот.

В связи со спецификой своей работы я сталкиваюсь с ремонтов различных асинхронных двигателей и в большинстве случаев выход из строя двигателя происходит при неправильном переключении обмоток двигателя, так как люди не понимают, как изменяется мощность двигателя при переключении с треугольника на звезду и обратно, и как это может отразится на работоспособности самого двигателя.

Определение мощности при схеме соединения звезда

Известно [Л1. с. 34], что при соединении в звезду линейные токи Iл и фазные токи Iф равны между собой, при этом между фазным Uф и линейным напряжением Uл существует соотношение, где Uл = √3*Uф , в результате Uф = Uл/√3.

Исходя из этого, полная мощность определяется через линейные величины:

Определение мощности при схеме соединения треугольник

При схеме соединения в треугольник, фазные и линейные напряжения равны между собой Uл = Uф, при этом между токами существует соотношение: Iл = √3*Iф, в результате Iф = Iл/√3.

Исходя из этого, полная мощность определяется, как:

Для определения активной и реактивной мощности используются формулы:

Из-за того что формулы для схемы соединения звезды и треугольника имеют одинаковый вид, у мало опытных инженеров происходят недоразумения, будто вид соединения безразличен и ни на что не влияет.

Рассмотрим на примере, на сколько ошибочные данные утверждения. В данном примере будем рассматривать электродвигатель типа АИР90L2, который имеет две схемы подключения ∆/Y, технические характеристики двигателя:

• коэффициент мощности cosφ = 0,84;
• коэффициент полезного действия, η = 78,5%;

Определяем ток двигателя при напряжении 380 В и схеме соединения треугольник, мощность при таком соединении составляет 3 кВт:

Теперь соединим обмотки двигателя в звезду. В результате на фазную обмотку пришлось на 1,73 раза более низкое напряжение Uф = Uл/√3, соответственно и ток уменьшился в 1,73 раза, но так как при соединении в треугольник Uл = Uф, а линейный ток был в 1,73 раза больше фазного Iл = √3*Iф, то получается, что при соединении в звезду, мощность уменьшится в √3*√3 = 3 раза, соответственно и ток уменьшиться в 3 раза.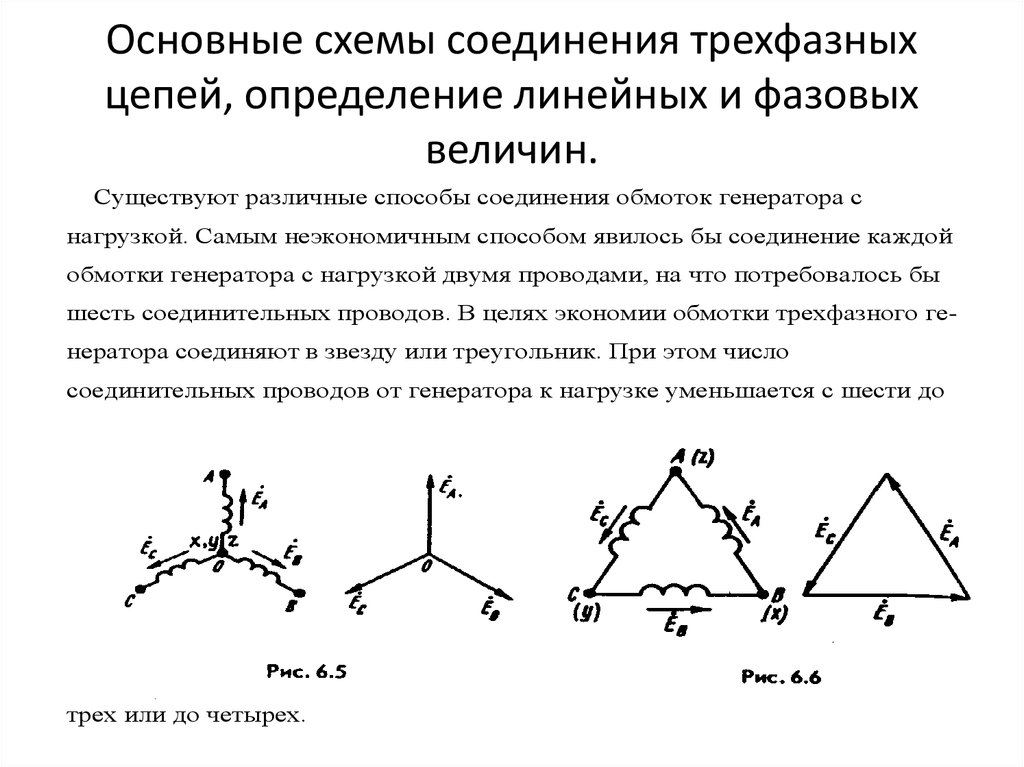

Из всего выше изложенного можно сделать, следующие выводы:

1. При переключении двигателя со звезды на треугольник, мощность двигателя увеличивается в 3 раза и наоборот. Использовать данные переключения, можно если схемы подключения двигателя позволяет выполнять переключения ∆/Y, в противном случае, двигатель может сгореть, когда Вы будете выполнять переключение со звезды на треугольник.

2. Как Вы уже поняли, используя схему переключения обмоток двигателя со звезды на треугольник, мы уменьшаем пусковые токи при пуске двигателя на пониженном напряжении, а затем его повышаем до номинального. Когда обмотки двигателя соединены в звезду, к каждой из них подводиться напряжение меньше номинального в 1,73 раза. В процессе пуска, двигатель увеличивает скорость вращения и ток снижается. В это время происходит переключение на треугольник.

Обращаю Ваше внимание, что двигатели, которые недогружены, работают с очень низким cosφ. Поэтому рекомендуется заменить недогруженный двигатель, на двигатель меньшей мощности.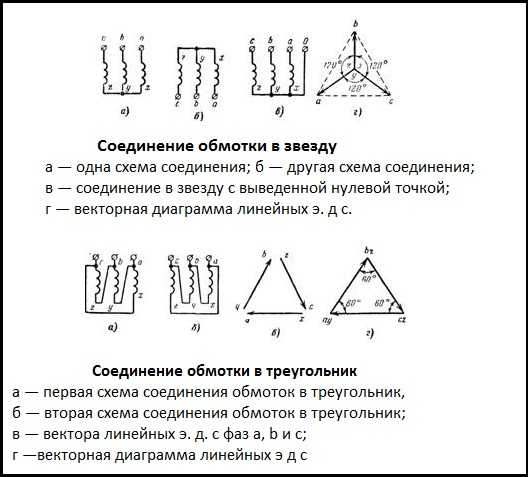 Если же у недогруженного двигателя, запас мощности велик, то cosφ можно поднять путем переключения

обмоток с треугольника на звезду без риска перегреть двигатель.

Как мы видим ничего сложного нету в определении мощности при схеме звезда и треугольник.

Литература:

1. Звезда и треугольник. Е.А. Каминский, 1961 г.

Всего наилучшего! До новых встреч на сайте Raschet.info.

звезда-треугольник, мощность двигателя при звезде, соединение обмоток двигателя, схема соединения обмоток звезда-треугольник, треугольник звезда

Поделиться в социальных сетях

Соединение фаз потребителей электроэнергии в звезду

Схема соединения фаз электроприемников «звезда» получила очень широкое распространение в электроэнергетике. Принципиальная схема соединения звездой показана ниже:

Из схемы видно, что фазные напряжения приемника U_a, U_b, U_c не равны линейным напряжениям U_ab, U_bc, U_ca.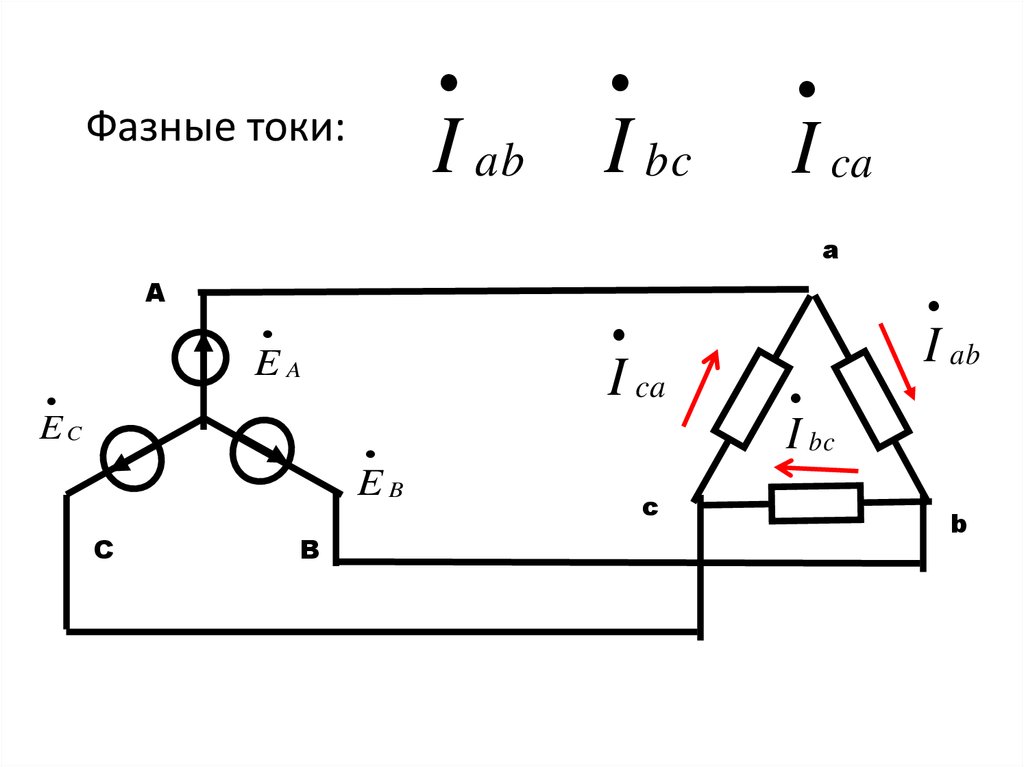 Если применить к контурам aNba, bNcb, cNac второй закон Кирхгофа получим соотношение для фазных и линейных напряжений:

Если сопротивления нейтрального провода и линейных проводов не учитывать, то можно предположить, что напряжение на клеммах генератора и электроприемника равны. Вследствие указанного равенства векторные диаграммы для источника и приемника электрической энергии будут одинаковы.

Фазные и линейные напряжения приемника, как и источника, будут образовывать две симметричные системы напряжений. Соответственно между фазными и линейными значениями напряжений будет существовать определенная зависимость:

Далее будет показано, что соотношение (2) будет справедливо лишь при определенных условиях, а также в случае отсутствия нулевого провода, то есть в трехпроводной сети.

Исходя из указанного выше соотношения (2) можно сделать вывод, что соединение звездой лучше применять в случае, когда каждая фаза трехфазного электроприемника или однофазные приемники рассчитаны на напряжение в раз меньше, чем номинальное линейное напряжение сети.

Также из схемы соединения звезда (смотри схему выше) видно, что при соединении приемников звездой фазные токи будут равны линейным:

Применив первый закон Кирхгофа можно получить соотношение между токами при соединении электроприемников звездой:

Зная фазные токи с помощью формулы (4) можно вычислить ток нейтрального провода I_N. В случае отсутствия нейтрального провода справедливо будет выражение:

Симметричная нагрузка при соединении приемников звездой

Нагрузка считается симметричной тогда, когда реактивные и активные сопротивления каждой фазы будут равны, то есть выполняется равенство:

Условие симметричности также может быть выражено через комплексные сопротивления Z_a = Z_b = Z_c.

Симметричная нагрузка в сети возникает при подключении трехфазных электроприемников. Будем считать, что данная система имеет нейтральный провод.

В отношении любой из фаз при симметричной нагрузке будут справедливы все формулы, полученные для однофазной сети, например для фазы А:

Так как в четырехпроводной цепи U_a = U_b = U_c = U_л /  , то при симметричной нагрузке:

Векторная диаграмма при симметричной активно-индуктивной нагрузке приведена выше.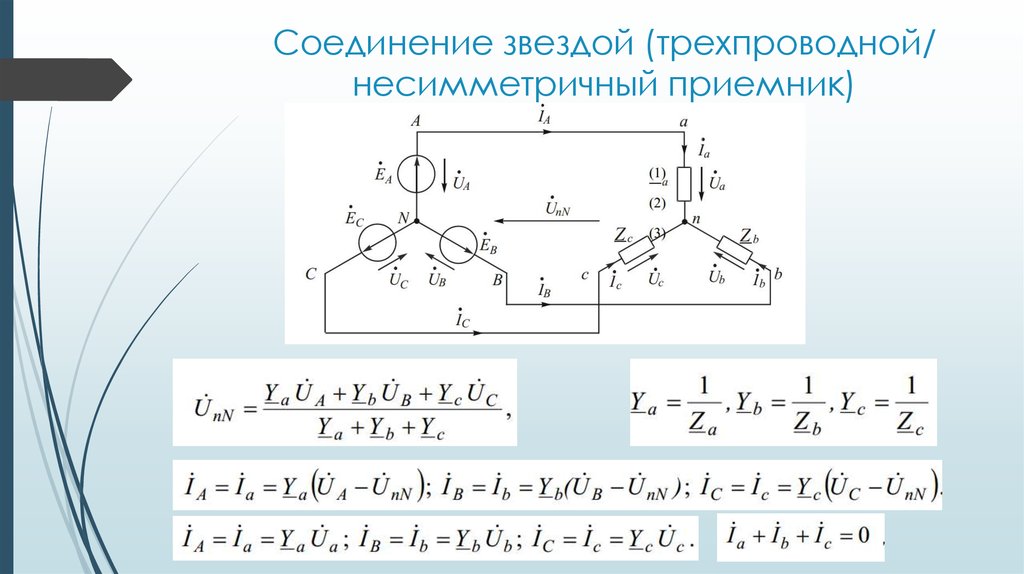 Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке образуется симметричная система токов, поэтому ток в нейтральном проводе будет равен I_N = I_a + I_b + I_c = 0.

Отсюда можно сделать вывод, что при симметричной нагрузке отключение нейтрального провода не приведет к серьезным нарушениям работы электроприемников, то есть не произойдет изменение фазных напряжений, углов сдвига, токов, мощностей.

Из сказанного выше следует, что при симметричной нагрузке в нейтральном проводе нет необходимости, и довольно часто в симметричных системах нейтральный провод не применяется.

Мощность трехфазного приемника электрической энергии при симметричной нагрузке можно выразить формулами:

Как правило, для трехфазных приемников электрической энергии в качестве номинальных параметров указываются линейные напряжения и токи. Исходя из этого, целесообразней выражать мощность трехфазной цепи тоже через линейные напряжения и тока, поэтому подставим в формулу (6) линейные значения и получим:

Пример

К трехфазной электрической цепи с линейным напряжением U_л = U_ab = U_bc = U_ca = 380 В необходимо подключить трехфазный электроприемник, каждая фаза которого рассчитывается на фазное напряжение в 220 В и имеет активное сопротивление r_ф = 10 Ом и индуктивное сопротивление х_ф = 10 Ом, которые соединены последовательно.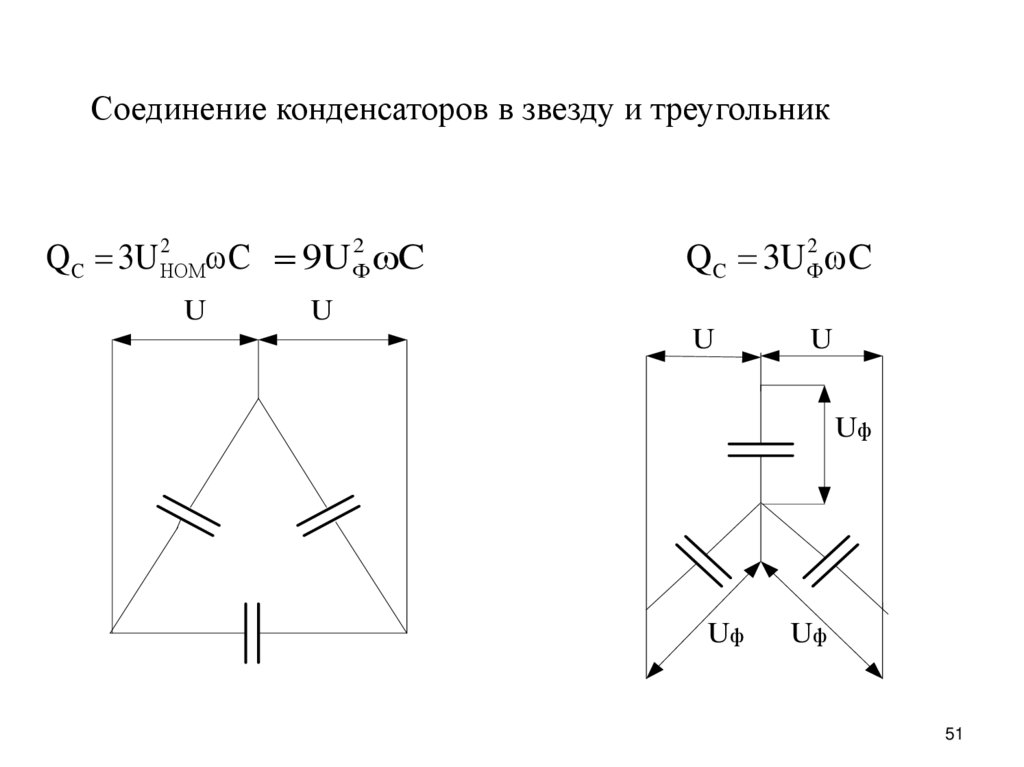 Необходимо определить мощности, углы сдвига между токами и напряжениями (cos φ) и фазные токи.

Решение

Каждая фаза потребителя электрической энергии рассчитана на напряжение в раз меньше номинального, то фазы потребителя нужно соединять в звезду. Поскольку нагрузка в данном случае симметричная, то нулевой провод (нейтраль) к потребителю можно не подводить.

Фазные тока, углы сдвига cos φ, а также полны сопротивления фаз будут иметь вид:

Активная, реактивная и полная мощности  приемника, а также любой фазы будут равны:

Векторная диаграмма для данной системы приводилась выше.

Несимметричная нагрузка при соединении приемников звездой

Нагрузка трехфазной электрической сети будет считаться несимметричной, если хотя бы одно из фазных сопротивлений не равно другим. Проще говоря, сопротивления фаз не равны, например: r_a = r_b = r_c, x_a = x_b ≠ x_c. В общем случае  считают, что несимметричная нагрузка возникает при отключении одной из фаз.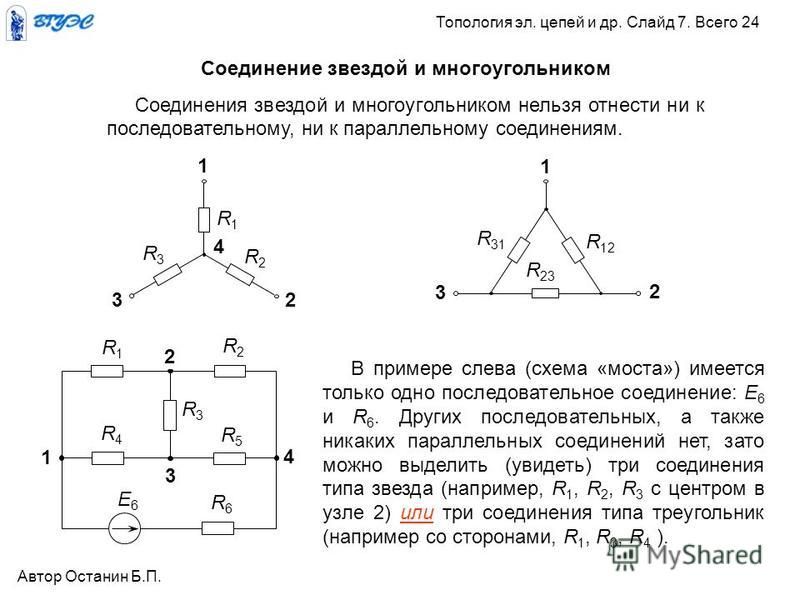

Возникает не симметрия чаще всего при подключении к трехфазной сети однофазных электроприемников. Они могут иметь различные мощности, режимы работы, различное территориальное расположение, что тоже влияет на величину фазной нагрузки.

В случае, когда необходимо подключить однофазные потребители электрической энергии, для более равномерной загрузки их делят на три примерно одинаковые по мощности группы.

Один вывод однофазных потребителей подключают к одной из трех фаз, а второй вывод подключают к нейтральному проводу. Так как все электроприемники рассчитываются на одно напряжение, то в пределах каждой фазы они соединяются параллельно.

Главной особенностью электрической сети несимметричной нагрузкой является то, что она должна в обязательном порядке иметь нейтральный провод. Это объяснимо тем, что при его отсутствии величины фазных напряжений будут в значительной степени зависеть от величины не симметрии сети, то есть от величин и характера сопротивления каждой из фаз.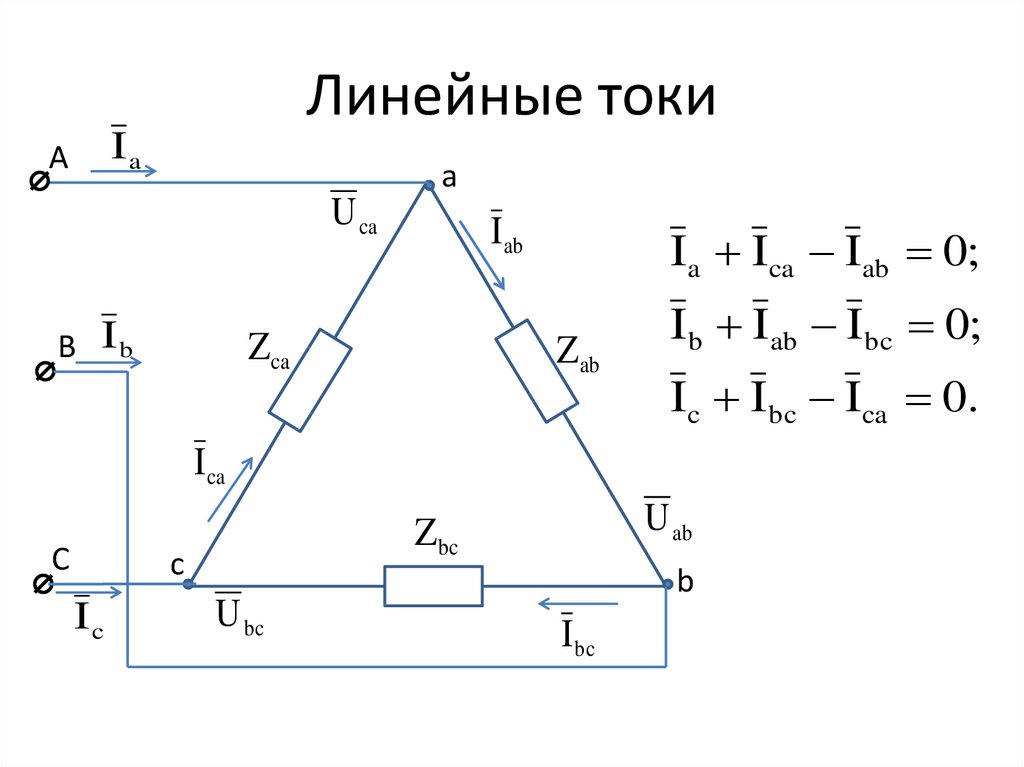 Поскольку сопротивления фаз могут варьироваться довольно в широких пределах в зависимости от количества подключенных электроприемников, также широко будет варьироваться и напряжения на потребителях электрической энергии, а это недопустимо.

Для иллюстрации выше сказанного ниже приведена векторная диаграмма для трехфазной несимметричной цепи при наличии нейтрального провода:

Ниже приведена приведена векторная диаграмма для этой же цепи, но при отсутствии нулевого рабочего (нейтрального) провода:

Также можно посмотреть видео, где объясняется, что может произойти в электрической цепи при обрыве нулевого провода:

Необходимость нулевого провода станет еще более очевидной, если представить, что вам необходимо подключить однофазного потребителя к одной из фаз, при этом остальные две подключать нельзя, так как приемник рассчитан на фазное напряжение 220 В, а не на линейное 380В, как в таком случае получить замкнутый контур для протекания электрического тока? Только использовать нулевой рабочий проводник.

Для повышения надежности соединения электроприемников в цепь нулевого рабочего проводника не устанавливают коммутационную аппаратуру (автоматические выключатели, предохранители или разъединители).

Фазные токи, углы сдвига, а также фазные мощности при несимметричной нагрузке будут различными. Для вычисления их фазных значений можно применить формулу (5), а вот для вычисления трехфазной мощности формула (6) уже не подходит. Для определения мощностей необходимо пользоваться выражением:

Если существует необходимость определения тока нейтрального провода, то необходимо решать задачу комплексным методом. Если существует векторная диаграмма, то определить ток можно по ней.

Пример

В осветительной электрической сети с напряжением в 220 В в фазе А включено 20 ламп, фазе В – 10 ламп, а в фазе С – 5 ламп. Параметры лампы U_ном = 127 В, Р_ном = 100 Вт. Необходимо определить ток нейтрального провода и каждой лампы.

Решение

Если учесть, что лампы накаливания имеют только активное сопротивление (реактивное слишком мало и им пренебрегают), то по формуле мощности определим ток лампы, а по закону Ома ее сопротивление:

Зная число и сопротивление ламп нетрудно определить сопротивления фаз, а также фазные токи:

Для определения тока в нейтральном проводе I_N решим задачу комплексным методом. Так как при сделанных ранее допущениях комплексные напряжения приемника равны комплексным ЭДС источника, получим:

Где комплексные значения фазных сопротивлений будут равны Z_a = 8,05 Ом, Z_b = 16,1 Ом, Z_с = 32,2 Ом.

Комплексные значения токов, а также действующее значение тока нейтрального провода будут иметь вид:

Уравнение звезда-треугольник (Янг-Бакстер) | Высшая статистическая механика

Фильтр поиска панели навигации Oxford AcademicAdvanced Statistical MechanicsМатематическая и статистическая физикаКнигиЖурналы Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Oxford AcademicAdvanced Statistical MechanicsМатематическая и статистическая физикаКнигиЖурналы Введите поисковый запрос

Расширенный поиск

• Иконка Цитировать Цитировать

• Разрешения

• Делиться
  • Твиттер
  • Подробнее

Укажите

Маккой, Барри М. , «Уравнение звезды-треугольника (Янга-Бакстера)», Advanced Statistical Mechanics , Международная серия монографий по физике (

Oxford

, 2009; онлайн-издание, Oxford Academic, 1 февраля 2010 г.), https://doi.org/10.1093/acprof:oso/9780199556632.003.0013, по состоянию на 15 февраля 2023 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Фильтр поиска панели навигации Oxford AcademicAdvanced Statistical MechanicsМатематическая и статистическая физикаКнигиЖурналы Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Oxford AcademicAdvanced Statistical MechanicsМатематическая и статистическая физикаКнигиЖурналы Введите поисковый запрос

Advanced Search

Abstract

В этой главе определяются передаточные матрицы, и существование однопараметрического семейства коммутирующих передаточных матриц определяется как условие интегрируемости.

Локальное уравнение звезды-треугольника (Янга-Бакстера) вводится для моделей вершин, спинов и граней и используется для демонстрации коммутации передаточных матриц. Уравнение звезды-треугольника решается для шестивершинной, восьмивершинной, SOS, RSOS, твердого шестиугольника и киральной модели Поттса. Получена коммутация матрицы переноса с соответствующей квантовой спиновой цепочкой.

Ключевые слова: уравнение звезда-треугольник, уравнение Янга–Бакстера, восьмивершинная модель, шестивершинная модель, модель RSOS, киральная модель Поттса, модель жесткого шестиугольника

Предмет

Математическая и статистическая физика

В настоящее время у вас нет доступа к этой главе.

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Щелкните Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
3. При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
• Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

Ведение счетов организаций

Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.

Покупка

Наши книги можно приобрести по подписке или купить в библиотеках и учреждениях.

Информация о покупке

Earth Science Today, Star lab

Earth Science Today, Star lab Земля Наука сегодня
Расс Колсон
Университет штата Миннесота Мурхед

Лаборатория наук о Земле сегодня, Расстояние до звезд (35-70 минут, в зависимости от знакомства с математикой)

Часть 1: Метод триангуляции
Расстояние до ближайших звезд определяется методом триангуляции. Концепция триангуляции довольно проста: вам нужно представить прямоугольный треугольник, где одна сторона треугольника расстояние, которое вы хотите измерить (вспомните упражнение по измерению дерева). Если вы можете измерить один угол треугольника, кроме прямого угла (любой из них работает) и длину одной другой стороны треугольника, то интересующая сторона может быть рассчитана геометрическим или тригонометрическим методами.
     Вот упражнение для практики «нахождение» треугольников, прежде чем мы попытаемся сделать звезды. Определить длину одного из лабораторных столов без фактического измерения его длины.
     Вы можете использовать транспортир и линейка (можно измерить ширину стола или расстояние до стола, но вы не можете использовать линейку для измерения длины стола).
     Вы можете положить какой-нибудь предмет на дальнем конце стола (камень, карандаш) для триангуляции (то есть измерения угол навстречу).
Вы можете сделать это, используя одинаковые треугольники или тригонометрия. Ты можете использовать подобные треугольники, нарисованные транспортиром, если хотите (измеряя длина сторон, которая будет пропорциональна сторонам на вашем «табличный» треугольник), или приведенное ниже тригонометрическое уравнение.
Танк = х/у или x = y· (tanq ).

Длина стола (в дюймах): ____________________
____________________________________________________________________________________________________________________________
Часть 2: Фактическое расстояние до звезды
Все мы знакомы с концепцией параллакса. Держите большой палец на расстоянии вытянутой руки и закройте сначала один глаз, а затем другой. Заметили сдвиг на более дальнем фоне? Это параллакс. Теперь поднесите большой палец к себе на полпути и сделайте тоже самое. Заметили, что сдвиг кажется большим? Разница в смещении дает возможность измерить расстояние до вашего большой палец (или к звездам). Но сначала нужно найти воображаемый треугольник который будет работать, измерьте угол и измерьте одну сторону треугольника.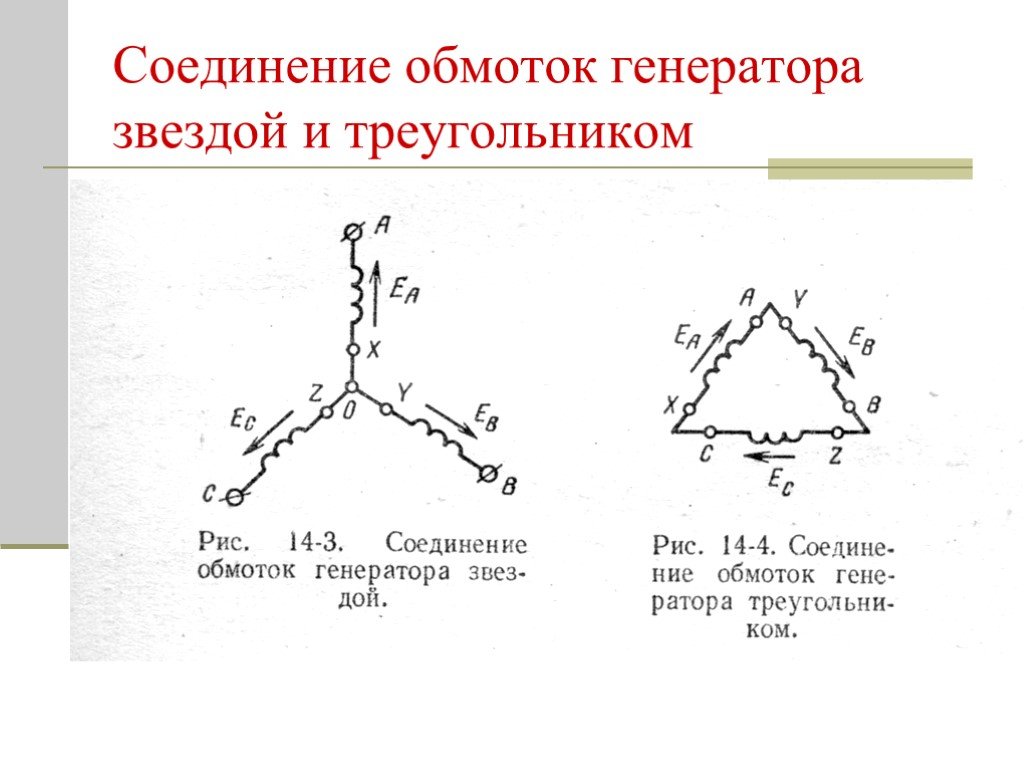 При измерении расстояния до звезд одна сторона треугольника принимается за расстояние от Земли до Солнца (величина, которую мы знаем). угол измеряется путем наблюдения за параллаксом, то есть насколько далеко звезда смещается на фоне звезд по мере того, как Земля вращается вокруг Солнце (аналогично закрытию одного глаза, затем другого). Иллюстрация параллакса (источник неизвестен).

Два изображения ниже сделаны с разницей в 6 месяцев (таким образом, Земля переместилась с одной стороны Солнца на другую сторону на расстояние около 2AU). Звезда HT Cas является ближайшей на Землю звезд на этом изображении. Угол между двумя звездами ближайший к HT Cas (кроме самого HT Cas) составляет 0,000002778 градусов. Этот value — это «шкала», по которой можно определить другие углы.
 
Шаг 1 ) выяснить, какая звезда является HT Cas (подсказка: какой из них, кажется, переместился?)

Шаг 2 ) определить угол, под которым HT Cas сместился из-за изменения положения Земли в течение 6 месяцев.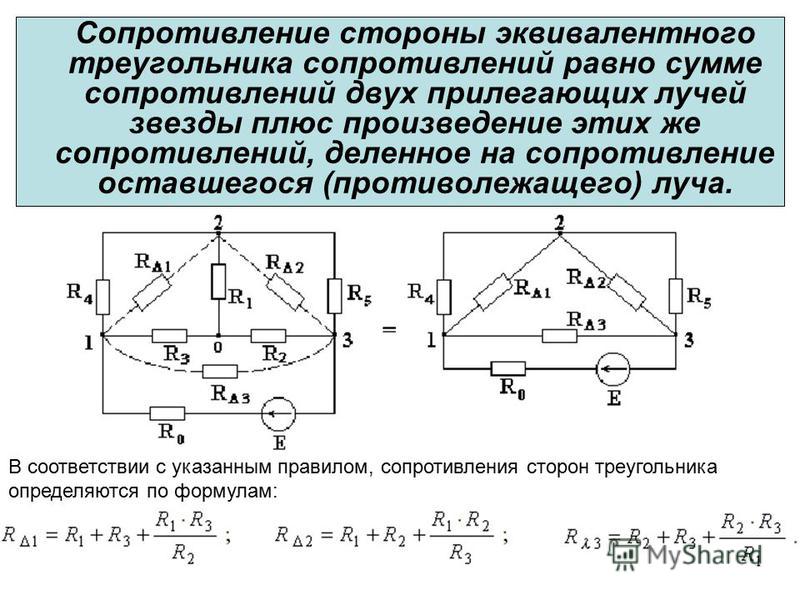
Подсказка: на этих рисунках важен угол угол между двумя воображаемыми линиями, проведенными между вами (на Земле) и каждое положение звезды. Таким образом, интересующий вас угол не в плоскости картины! Однако этот угол пропорционален к расстояниям между звездами, как видно на изображении звезд выше. Следовательно, вы можете вычислить углы, измерив расстояния между звездочки на изображении (с линейкой).

Измерение угла осуществляется путем наблюдения расстояние до видимого смещения звезды на фотографиях, сделанных 6 мес. отдельно. Это смещение пропорционально углу, с более дальним звезды, имеющие меньшие углы и меньшие расстояния смещения.

Расстояние можно преобразовать в угол с помощью известный угол между двумя другими звездами, которые не меняют положение. В этой головоломки известный угол находится между двумя ближайшими к HTCas звездами и составляет 0,000002778 градусов.

Наконец, мы можем рассчитать угол смещения HTCas путем сравнения с известным углом между ближайшими звездами.