Как рассчитать индукцию магнитного поля соленоида с переменным током. Какие факторы влияют на величину магнитной индукции соленоида. Как на практике определить индуктивность соленоида. Какие формулы используются для расчета характеристик соленоида с переменным током.
Теоретические основы индукции магнитного поля соленоида
Соленоид представляет собой катушку из проводника, намотанного на цилиндрический каркас. При протекании по обмотке соленоида электрического тока внутри него возникает магнитное поле. Индукция этого поля зависит от ряда параметров:
- Силы тока в обмотке
- Числа витков обмотки
- Длины соленоида
- Магнитной проницаемости сердечника
Для расчета индукции магнитного поля внутри бесконечно длинного соленоида используется формула:
B = μ0μnI
где:
- B — магнитная индукция
- μ0 — магнитная постоянная
- μ — относительная магнитная проницаемость сердечника
- n — число витков на единицу длины соленоида
- I — сила тока
Особенности соленоида с переменным током
При протекании по обмотке соленоида переменного тока возникают дополнительные эффекты:
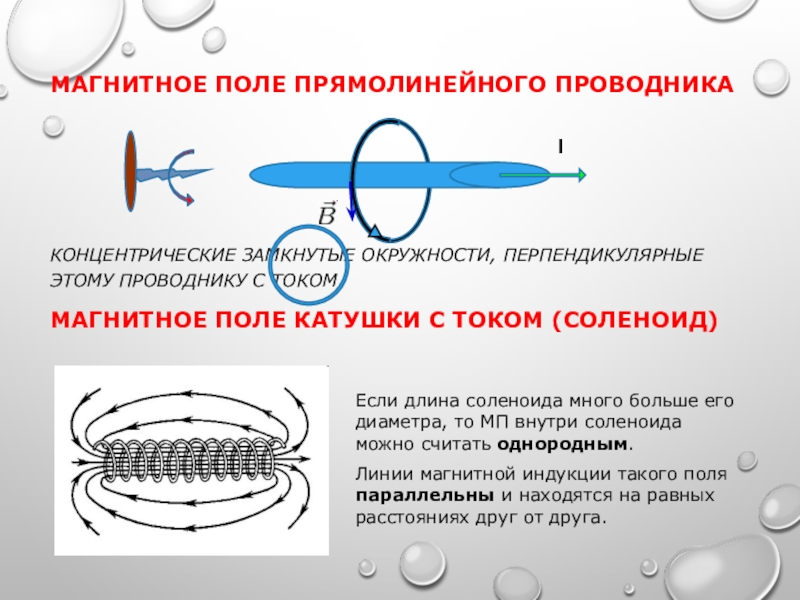
- Индуцированная ЭДС самоиндукции
- Индуктивное сопротивление
- Сдвиг фаз между током и напряжением
Для переменного тока формула индукции принимает вид:
B = μ0μnIm sin(ωt)
где Im — амплитудное значение силы тока, ω — циклическая частота.
Расчет индуктивности соленоида
Важной характеристикой соленоида является его индуктивность. Она может быть рассчитана теоретически по формуле:
L = μ0μn2πr2l
где r — радиус соленоида, l — его длина.
Как определить индуктивность соленоида на практике? Для этого можно использовать метод измерения импеданса при подключении соленоида к источнику переменного тока:
- Измеряют амплитуду напряжения Um и тока Im
- Измеряют частоту f переменного тока
- Рассчитывают индуктивность по формуле:
L = √((Um/Im)2 — R2) / (2πf)
где R — активное сопротивление обмотки соленоида.
Факторы, влияющие на индукцию магнитного поля соленоида
На величину магнитной индукции соленоида оказывают влияние следующие факторы:
- Сила тока — прямо пропорциональная зависимость
- Число витков — прямо пропорциональная зависимость
- Длина соленоида — обратно пропорциональная зависимость
- Магнитная проницаемость сердечника — прямо пропорциональная зависимость
- Частота переменного тока — не влияет на амплитуду индукции, но определяет скорость ее изменения
Применение соленоидов с переменным током
Соленоиды с переменным током находят широкое применение в различных областях техники:
- Электромагнитные реле и пускатели
- Трансформаторы и дроссели
- Электромагнитные клапаны
- Электродвигатели
- Генераторы электромагнитных колебаний
Благодаря способности создавать сильное магнитное поле, соленоиды используются для управления различными механизмами и преобразования электрической энергии.
Экспериментальное исследование характеристик соленоида
Для изучения свойств соленоида с переменным током можно провести следующий эксперимент:
- Собрать электрическую цепь, включающую исследуемый соленоид, амперметр, вольтметр и источник переменного напряжения регулируемой частоты.
- Измерить активное сопротивление обмотки соленоида.
- При фиксированной частоте изменять напряжение и измерять ток. Построить вольт-амперную характеристику.
- При фиксированном напряжении изменять частоту и измерять ток. Построить частотную характеристику.
- Рассчитать индуктивность соленоида по результатам измерений.
Такой эксперимент позволяет наглядно исследовать зависимость характеристик соленоида от параметров питающего тока.
Расчет мощности в цепи с соленоидом
При протекании переменного тока через соленоид в цепи выделяется активная и реактивная мощность. Активная мощность обусловлена активным сопротивлением обмотки и рассчитывается по формуле:
P = I2R
Реактивная мощность связана с периодическим накоплением энергии в магнитном поле соленоида:
Q = I2XL
где XL = ωL — индуктивное сопротивление.
Полная мощность определяется как:
S = √(P2 + Q2)
Коэффициент мощности равен:
cos φ = P / S
Этот коэффициент показывает, какая часть полной мощности преобразуется в активную.
Применение закона электромагнитной индукции к соленоиду
При изменении силы тока в соленоиде возникает ЭДС самоиндукции, которая определяется законом электромагнитной индукции Фарадея:
ε = -L(dI/dt)
где L — индуктивность соленоида.
Эта ЭДС препятствует изменению тока. При увеличении тока она направлена навстречу приложенному напряжению, а при уменьшении — совпадает с ним по направлению.
Явление самоиндукции приводит к тому, что ток в цепи с соленоидом не может мгновенно установиться при включении или прерваться при выключении. Это необходимо учитывать при проектировании электрических схем с индуктивными элементами.

Заключение
Соленоид с переменным током является важным элементом многих электротехнических устройств. Понимание процессов, происходящих в нем, необходимо для эффективного проектирования и эксплуатации электрооборудования. Основные характеристики соленоида — индуктивность и индукция магнитного поля — могут быть рассчитаны теоретически или определены экспериментально. При работе с переменным током необходимо учитывать такие явления, как индуктивное сопротивление и ЭДС самоиндукции.
Акопов Вачакан Ваграмович /AkopovVachakanVagramovich – учитель физики МОУ СОШ №6, Ставропольский край Курский район,село Полтавское Аннотация: в статье представлен вывод формул индукции поля соленоида, созданного переменным током. Эту формулу можно использовать для углубленного изучения учащимися темы «Магнитное поле» и при решении задач. Ключевые слова: индукция, соленоид, магнитный поток, частота, индуктивность, индуцированное напряжение, мощность переменного тока. При переменном токе соленоид создаёт переменное магнитное поле. При этом, как известно, индуктивность соленоида определяется формулой [1, с.101]: L =
|
||
Электричество и магнетизм
Если длина соленоида много больше его диаметра (l >> 2R), мы возвращаемся к формуле для поля в бесконечно длинном соленоиде (6.20). Относительная разница этих двух значений равна
По условию эта разница мала: , то есть мало отношение диаметра соленоида к его длине: 2R/l << 1. Поэтому можно воспользоваться формулой разложения квадратного корня
Отсюда
или
Подставляя численное значение d, находим, что разница будет менее половины процента при выполнении соотношения
Иными словами, соленоид может рассматриваться как бесконечно длинный, если его длина в двадцать или более раз превышает радиус.
Пример 2. Найти магнитное поле Ве в крайней торцевой точке оси соленоида конечной длины l. Сравнить с результатом предыдущего примера.
Решение. Магнитное поле в торцевой точке оси соленоида конечной длины l дается тем же интегралом (6.19), но теперь пределы интегрирования будут выглядеть иначе
|
(6.22) |
Отношение полей в средней и крайней точках оси соленоида равно
Это отношение всегда меньше единицы (то есть поле на торце меньше поля в середине соленоида). При l >> R имеем
Этот результат легко понять. Представим себе бесконечный соленоид, который мысленно рассекаем пополам в точке наблюдения. Можно считать, что поле в этой точке создается двумя одинаковыми «полубесконечными» соленоидами, расположенными по разные стороны от нее. Ясно, что при удалении одного из них точка наблюдения становится торцом оставшегося «полубесконечного» соленоида, а магнитная индукция в ней уменьшиться именно в два раза.
Это — так называемый краевой эффект. Пример демонстрирует, что недостаточно выполнения соотношения l >> R, чтобы пользоваться формулами для бесконечно длинного соленоида; надо еще, чтобы точка наблюдения находилась далеко от его концов.
На рис. 6.25 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг соленоида. Поле соленоида, ось которого лежит в плоскости пластинки, сосредоточено в основном внутри соленоида. Силовые линии внутри имеют вид параллельных прямых вдоль оси катушки, а поле снаружи практически отсутствует.
Рис. 6.25. Визуализация силовых линий магнитного поля
Видео 6.1. Силовые линии магнитного поля проводников с током различной формы: прямой ток, соленоид, один виток.
Вывод формул индукции поля соленоида, созданного переменным током Текст научной статьи по специальности «Электротехника, электронная техника, информационные технологии»
Вывод формул индукции поля соленоида, созданного переменным током
Акопов В.В.
Акопов Вачакан Ваграмович /Лкороу Уаекакап Vagramovich — учитель физики, МОУ СОШ№6, Ставропольский край, Курский район, село Полтавское
Аннотация: в статье представлен вывод формул индукции поля соленоида, созданного переменным током. Эту формулу можно использовать для углубленного изучения учащимися темы «Магнитное поле» и при решении задач.
Ключевые слова: индукция, соленоид, магнитный поток, частота, индуктивность, индуцированное напряжение, мощность переменного тока.
При переменном токе соленоид создает переменное магнитное поле. При этом, как известно, индуктивность соленоида определяется формулой [1, с.101]:
Ь = -Ц- , (1)
• I
где
и — индуцированное в соленоиде напряжение, V— частота переменного тока, I—сила переменного тока.
С другой стороны, индуктивность соленоида определяется формулой [2, с.253]:
Ь = Ф , (2)
I
где Ф — магнитный поток соленоида. Приравнивая выражения (1) и (2), получим:
Ф = и . (3) 2лv
При этом полный магнитный поток соленоида определяется и другой формулой [2, с.242]:
Ф =В-Б-М , (4)
где:
В — индукция магнитного поля, N — число витков соленоида,
£ — площадь поперечного сечения магнитного поля. Приравняв выражения (3) и (4), получим
В = -и—(5)
2^-£ • n
Таким образом, индукция поля соленоида, созданного переменным током, прямо пропорциональна индуцированному в соленоиде напряжению.
Как известно, магнитную индукцию поля, созданного постоянным током, текущим по виткам бесконечно длинного соленоида, внутри этого соленоида на его оси определяют по формуле [2, с.232]:
Мп •п
В = —-— (в вакууме), (6)
где:
п=Ш — число ампер-витков соленоида,
I — длина соленоида,
¡ло -магнитная постоянная.
Единица магнитной индукции (тесла) может быть установлена по формуле (6):
_ Гн А • виток Гн • А • виток
[В] =——2-, (7)
мм м
С другой стороны единица магнитной индукции (тесла) может быть установлена по формуле (5):
В • с
[В] = -— , (8)
м
Перемножив выражения (7) и (8), получим:
. _ Гн гн
9 Гн • А • виток В • с А •В •с—виток Вт • — • виток
[в]2 = Гн •А •виток • В_с =_м_= м , (9)
2 2 3
м м м 1
м3
с
Тогда, заменив единицы измерения в выражении (9) физическими величинами, получим формулу для индукции поля соленоида, созданного переменным током:
в2= М • Р • N
v•V ‘
отсюда
В = , ■Р ■к V у ■У
где V — объем соленоида, Р — мощность переменного тока.
Таким образом, индукция магнитного поля соленоида увеличивается при увеличении мощности переменного тока и уменьшается при увеличении объема соленоида.
Задача 1. Магнитная индукция поля внутри соленоида, состоящего из 2000 витков диаметра 2,8см, подключенного к источнику переменного тока с частотой 50Гц, равна 0,72мТл. Каково индуцированное в соленоиде напряжение?
Дано: СИ:
N = 2000 витков
ё = 2,8 см = 2,8 -10″2 м
В = 0,72 мТл =0,72 ■Ю»3 Тл
у = 50 Гц
и — ?
Решение:
Индукция поля соленоида определяется формулой:
и
в = —;—т, (1)
2лту ■ Б ■ N
Учитывая, что
72
£ =
4
(2)
и, используя выражения (1) и (2), найдем
и =17й2 уN■ В . 2
(3)
Подставляя исходные данные в выражение (3), получим: и = 1 ■ (3,14)2 ■ (2,8 ■ 102м)2 ■ 50с 1 ■ 2 ■ 103 ■ 0,72 ■ 10ъТл = 0,278 В.
Ответ: и = 0,278 В.
Задача 2. Индуцированное в соленоиде напряжение 0,2В. Магнитная индукция поля внутри соленоида, созданного переменным током с частотой 50 Гц, равна 0,52 мТл и диаметр магнитного поля равен 2,8см. Сколько витков содержит соленоид?
Дано: СИ:
и = 0,2 В
ё = 2,8 см = 2,8 -10″2 м
В = 0,52 мТл =0,52 ■Ю»3 Тл
у = 50 Гц
N — ?
Решение:
Индукция поля соленоида выражается формулой:
и
В = —— , (1)
27У ■ Б ■ N
Учитывая, что
7й2
£ =
4
(2)
и, используя выражения (1) и (2), получим
N = ^4^.0=1,256-10″6 Гн В = \Мо ■ р ■ n V у ■у ‘ отсюда
м v = 6,15 -10″5 м3 N = 400 витков В2 ■у■¥ Р =-. Но ■ N
Подставляя исходные данные, получим:
P — ? (0,72 • 10″37л)2 • 50с1 • 6,15 • 105м\ 3,2 мкВт. Р ~ Гн ~ 1,256 •10″6—400
м
Ответ: Р и 3,2 мкВт.
Литература
1. Мякишев Г.Я., Буховцев Б.Б. Физика. Учебник для общеобразовательных учреждений. М.: Просвещение, 2007. 336 с.
2. Мустафаев Р.А., Кривцов В.Г. Физика. М.: Высшая школа, 1989. 496 с.
лабораторная работа 49
Цель работы - определение индуктивности соленоида по его сопротивлению переменному току.
Приборы и принадлежности: исследуемый соленоид, звуковой генератор, электронный осциллограф, миллиамперметр переменного тока, соединительные провода.
Явление самоиндукции. Индуктивность
Явление электромагнитной индукции наблюдается во всех случаях, когда изменяется магнитный поток, пронизывающий проводящий контур. В частности, если электрический ток течет в проводящем контуре, то он создает пронизывающий этот контур магнитный поток Ф.
При изменении силы тока I в любом контуре изменяется и магнитный поток Ф, вследствие этого в контуре возникает электродвижущая сила (ЭДС) индукции, которая вызывает дополнительный ток (рис. 1, где 1 - проводящий замкнутый контур, 2 — силовые линии магнитного поля, создаваемого током контура). Это явление называется самоиндукцией, а дополнительный ток, вызываемый ЭДС самоиндукции, – экстратоком самоиндукции.
Явление самоиндукции наблюдается в любой замкнутой электрической цепи, в которой протекает элетрический ток, при замыкании или размыкании этой цепи.
Рассмотрим, от чего зависит величина ЭДС εs самоиндукции. Магнитный поток Ф, пронизывающий замкнутый проводящий контур, пропорционален магнитной индукции В магнитного поля, создаваемого током, протекающим в контуре, а индукция В пропорциональна силе тока.
Рис. 1
Тогда магнитный поток Ф пропорционален силе тока, т.е.
Ф = L · I, (1)
где L — индуктивность контура, Гн (Генри).
Из (1) получим
L = Ф/I . (2)
Индуктивностью контура L называется скалярная физическая величина, равная отношению магнитного потока Ф, пронизывающего данный контур, к величине силы тока, текущего в контуре.
Генри — это индуктивность такого контура, в котором при силе тока в 1А возникает магнитный поток 1Вб, т.е. 1 Гн = 1.
Согласно закону электромагнитной индукции
. (3)
Подставляя (1) в (3), получим ЭДС самоиндукции:
. (4)
Формула (4) справедлива при L=const.
Опыт показывает, что при увеличении индуктивности L в электрической цепи сила тока в цепи увеличивается постепенно (см. рис. 2), а при уменьшении L сила тока уменьшается так же медленно (рис. 3).
Сила тока в электрической цепи при замыкании изменяется по закону , а при размыкании – по закону .
Кривые изменения силы тока показаны на рис. 2 и 3.
Рис. 2 Рис.3
Индуктивность контура зависит от формы, размеров и деформации контура, от магнитного состояния среды, в которой находится контур, а также от других факторов.
Найдем индуктивность соленоида. Соленоид — это цилиндрическая трубка, изготовленная из немагнитного непроводящего материала, на которую плотно, виток к витку, намотана тонкая металлическая проводящая проволока. На рис. 4 показан разрез соленоида вдоль цилиндрической трубки по диаметру (1 — силовые линии магнитного поля).
Рис. 4
Длина l соленоида намного
больше, чем диаметр d,
т.е.
l>> d. Если l< d, то соленоид можно рассматривать как
короткую катушку.
Диаметр тонкой проволоки намного меньше, чем диаметр соленоида. Для увеличения индуктивности внутрь соленоида помещают ферромагнитный сердечник с магнитной проницаемостью μ. Если l>>d, то при протекании тока внутри соленоида возбуждается однородное магнитное поле, индукция которого определяется формулой
В=μо μnI, (5)
где μо = 4π·10-7 Гн/м – магнитная постоянная; n = N/l – число витков единицы длины соленоида; N – число витков соленоида.
Вне соленоида магнитное поле практически равно нулю. Поскольку соленоид имеет N витков, то полный магнитный поток ψ (потокосцепление), пронизывающий поперечное сечение S соленоида, равен
Ψ = NФ = NВS, (6)
где Ф = BS – поток, пронизывающий один виток соленоида.
Подставляя (5) в (6) и с учётом того, что N = nl, получим
Ψ = μо μn2 lSI . (7)
С другой стороны,
Ψ = LI . (8)
Сравнивая (7) и (8), получим
L = μо μn2lS = μо μS. (9)
Площадь сечения соленоида равна
. (10)
С учётом (10) формула (9) запишется в виде
L = μо μ. (11)
Определить индуктивность соленоида можно, подключив соленоид в электрическую цепь переменного тока с частотой ω. Тогда полное сопротивление (импеданс) определится формулой
, (12)
где R – активное сопротивление, Ом; = хL – индуктивное сопротивление; = хс – ёмкостное сопротивление конденсатора с
ёмкостью С.
Если в электрической цепи отсутствует конденсатор, т.е. электроёмкость цепи мала, то хс<< хL и формула (12) будет иметь вид
. (13)
Тогда закон Ома для переменного тока запишется в виде
, (14)
где Im , Um – амплитудные значения силы тока и напряжения.
Так как ω = 2πν, где ν – частота колебаний переменного тока, то (14) примет вид
. (15)
Из (15) получим рабочую формулу для определения индуктивности:
. (16)
Ход работы
Для выполнения работы собрать цепь по схеме рис. 5.
1. Установить на звуковом генераторе частоту колебаний, указанную преподавателем.
2. Измерить с помощью осциллографа амплитуду напряжения Um и частоту .
3. С помощью миллиамперметра определить действующее значение силы тока в цепи ; пользуясь соотношением и решая его относительно Ie, определить амплитуду тока в цепи.
Рис. 5
4. Данные занести в таблицу.
Таблица
|
ν, Гц |
Ie, мА |
Im, мА |
Um, В |
R, Ом |
N |
d, м |
l, м |
L, Гн |
Lпров, Гн |
ΔL=L-Lпров, Гн |
|
|
|
|
|
|
|
|
|
|
|
|
6. По формуле (16) рассчитать индуктивность соленоида.
7. По формуле (11) рассчитать проверочное значение индуктивности соленоида, исходя из его геометрии и числа витков.
Справочные данные: активное сопротивление соленоида
R = 56 Ом; длина
соленоида l = 40 см; диаметр соленоида
d = 2 см;
число витков соленоида N = 2000.
Рекомендуемая частота переменного тока .
Вопросы для допуска к работе
1. Сформулируйте цель работы.
2. Дайте определение индуктивности?
3. Какова единица измерения индуктивности?
4. Запишите рабочую формулу для определения индуктивности соленоида.
Вопросы для защиты работы
1. Получите формулу для определения индуктивности соленоида, исходя из его геометрических размеров и числа витков.
2. Что называется импедансом?
3. Как связаны между собой максимальное и действующее значения силы тока и напряжения в цепи переменного тока?
4. Выведите рабочую формулу индуктивности соленоида.
5. Опишите явление самоиндукции.
6. Каков физический смысл индуктивности?
Индуктивность соленоида
Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока внутри катушки является фактически постоянной и (приближенно) равна
где − магнитная постоянная, − число витков, − ток и − длина катушки. Пренебрегая краевыми эффектами на концах соленоида, получим[16], что потокосцепление через катушку равно плотности потока , умноженному на площадь поперечного сечения и число витков :
Отсюда следует формула для индуктивности соленоида (без сердечника):
Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель — относительную магнитную проницаемость[17]сердечника:
В случае, когда , можно (следует) под S понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.
Более точные формулы для соленоида конечного размера
Для однослойного (с очень тонкой намоткой) соленоида конечных размеров (не бесконечно длинного) существуют более точные, хотя и более сложные формулы[18]:
где
— количество витков,
— радиус цилиндра,
— длина его образующей,
,
,
— Эллиптические интегралы.
Это дает
для
для
Трансформатор. Энергия магнитного поля. Основы теории Максвелла. Уравнения Максвелла в интегральной форме.
Электрический колебательный контур. Затухающие электромагнитные колебания. Вынужденные электромагнитные колебания. Явление резонанса
Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания
Резонансная частота контура определяется так называемой формулой Томсона:
Принцип действия
Пусть конденсатор ёмкостью C заряжен до напряжения . Энергия, запасённая в конденсаторе составляет
При соединении конденсатора с катушкой индуктивности, в цепи потечёт ток , что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.
Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора . Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна
, где — индуктивность катушки, — максимальное значение тока.
После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения .
В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.
В общем, описанные выше процессы в параллельном колебательном контуре называются резонанс токов, что означает, что через индуктивность и ёмкость протекают токи, больше тока проходящего через весь контур, причем эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Стоит также заметить, что сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности (в отличие от последовательного колебательного контура, сопротивление которого на резонансной частоте стремится к нулю), а это делает его незаменимым фильтром.
Стоит заметить, что помимо простого колебательного контура, есть ещё колебательные контуры первого, второго и третьего рода, что учитывают потери и имеют другие особенности.
Вынужденными электромагнитными колебаниями называют периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника. Внешним источником ЭДС в электрических цепях являются генераторы переменного тока, работающие на электростанциях.
Принцип действия генератора переменного тока легко показать при рассмотрении вращающейся рамки провода в магнитном поле.
В однородное магнитное поле с индукцией В помещаем прямоугольную рамку, образованную проводниками (abсd).
Пусть плоскость рамки перпендикулярна индукции магнитного поля В и ее площадь равна S.
Магнитный поток в момент времени t0 = 0 будет равен Ф = В*8.
При равномерном вращении рамки вокруг оси OO1 с угловой скоростью w магнитный поток, пронизывающий рамку, будет изменяться с течением времени по закону:
Изменение магнитного потока возбуждает в рамке ЭДС индукцию, равную
где Е0= ВSw — амплитуда ЭДС.
Если с помощью контактных колец и скользящих по ним щеток соединить концы рамки с электрической цепью, то под действием ЭДС индукции, изменяющейся со временем по гармоническому закону, в электрической цепи возникнут вынужденные гармонические колебания силы тока — переменный ток.
На практике синусоидальная ЭДС возбуждается не путем вращения рамки в магнитном поле, а путем вращения магнита или электромагнита (ротора) внутри статора — неподвижных обмоток, навитых на сердечники из магнитомягкого материала. В этих обмотках находится переменная ЭДС, что позволяет избежать снятия напряжения с помощью контактных колец.
Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением.
Общее условие резонанса для любого двухполюсника можно сформулировать в виде Im[Z]=0 или Im[Y]=0, где Z и Y комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии.
ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ СОЛЕНОИДА — Студопедия
Приборы и принадлежности: лабораторная установка с соленоидом, источник питания, милливольтметр, амперметр.
Краткая теория
Соленоидом называется цилиндрическая катушка, содержащая большое, число витков провода, по которому идет ток. Если шаг винтовой линии проводника, образующего катушку, мал, то каждый виток с током можно рассматривать как отдельный круговой ток, а соленоид — как систему последовательно соединенных круговых токов одинакового радиуса, имеющих общую ось.
Магнитное поле внутри соленоида можно представить как сумму магнитных полей, создаваемых каждым витком. Вектор индукции магнитного поля внутри соленоида перпендикулярен плоскости витков, т.е. направлен по оси соленоида и образует с направлением кольцевых токов витков правовинтовую систему. Примерная картина силовых линий магнитного поля соленоида показана на рис. 1. Силовые линии магнитного поля замкнуты.
На рис, 2 показано сечение соленоида длиной L и с числом витков N и радиусом поперечного сечения R. Кружки с точками обозначают сечения витков катушки, по которым идет ток I , направленный от чертежа на нас, а кружки с крестиками — сечения витков, в которых ток направлен за чертеж. Число витков на единицу длины соленоида обозначим .
Индукция магнитного поля в точке А , расположенной на оси соленоида, определяется путем интегрирования магнитных полей, создаваемых каждым витком, и равна
, (1)
где и — углы, образуемые с осью соленоида радиус-векторами и , проведенными из точки А к крайним виткам соленоида, -магнитная проницаемость среды, магнитная постоянная.
Таким образом, магнитная индукция В прямо пропорциональна силе тока, магнитной проницаемости среды, заполняющей соленоид, и числу витков на единицу длины. Магнитная индукция также зависит от положения точки А относительно концов соленоида. Рассмотрим несколько частных случаев:
1. Пусть точка А находится в центре соленоида, тогда , и . Если соленоид достаточно длинный, то и (2)
2. Пусть точка A находится в центре крайнего витка, тогда , и . Если соленоид достаточно длинный, то , и (3)
Из формул (2) и (3) видно, что магнитная индукция соленоида на его краю вдвое меньше по сравнению с ее величиной в центре.
3. Если длина соленоида во много раз больше радиуса его витков
(«бесконечно» длинный соленоид), то для всех точек, лежащих внутри
соленоида на его оси, можно положить . Тогда
поле можно считать в центральной части соленоида однородным и рассчитывать его по формуле
(4)
Однородность магнитного поля нарушается вблизи краев соленоида. В этом случае индукцию можно определять по формуле
, (5)
где k — коэффициент, учитывающий неоднородность поля.
Экспериментальное изучение магнитного поля соленоида в данной работе осуществляется с помощью специального зонда — маленькой катушки, укрепленной внутри штока с масштабной линейкой. Ось катушки совпадает с осью соленоида, катушка подключается к милливольтметру переменного тока, входное сопротивление которого много больше сопротивления катушки-зонда. Если через соленоид идет переменный ток стандартной частоты ( =50 Гц), то внутри соленоида и на его краях индукция переменного магнитного поля изменяется по закону (см. (5)):
Амплитуда магнитной индукции в этой формуле зависит от положения точки внутри соленоида. Если поместить в соленоид катушку-зонд, то в соответствии с законом электромагнитной индукции, в ней возникает ЭДС индукции:
, (6)
где N1 — число витков в катушке, S — площадь поперечного сечения катушки, Ф — магнитный поток ( , т.к. ось катушки совпадает с осью соленоида и, следовательно, вектор магнитной индукции перпендикулярен плоскости поперечного сечения катушки.).
Так как величина индукции B изменяется по закону , , то из (6) получается формула для расчета ЭДС:
(7)
Из выражения (7) видно, что амплитуда ЭДС зависит от . Таким образом, измеряя амплитуду ЭДС, можно определить :
(8)
Коэффициент k учитывающий неоднородность магнитного поля соленоида на краях, можно о определить., по формуле. (5), зная и :
(9)
где — амплитуда переменного тока, идущего через соленоид.
Из формул (7) и (9) следует, что амплитуда ЭДС индукции прямо пропорциональна амплитуде переменного тока :
(10)
Включенные в цепь переменного тока амперметр и милливольтметр измеряют действующие значения тока и ЭДС , которые связаны с амплитудами и соотношениями:
;
Для действующих значений тока и ЭДС формула (10) имеет вид
(11)
Из формулы (11) следует, что отношение пропорционально коэффициенту K неоднородности индукции магнитного поля в точке соленоида, где проводятся измерения
(12)
где А — коэффициент пропорциональности.
В данной работе требуется выполнить два задания: 1) определить распределение индукции вдоль оси соленоида при некотором постоянном значении тока; 2) определить значение коэффициента к.
Техника безопасности:
1. Не подключают/ самостоятельно источник питания и милливольтметр к сети 220 В.
2. Не производить переключения цепей, находящихся под напряжением.
Не прикасаться к неизолированным частям цепей.
3. Не оставлять без присмотра включенную схему.
Порядок выполнения работы
Задание № 1. Исследование распределения индукции магнитного поля вдоль оси соленоида.
1. Собрать измерительную цепь по схеме, приведенной на рис. 3. Для этого в цепь соленоида включить источник питания и амперметр, а к выводам катушки — зонда — милливольтметр (для измерения ) В данной установке катушка-зонд имеет следующие параметры: =200 витков, S=2*10-4м2, частота переменного тока = 50 Гц, Число витков на единицу длины соленоида n = 2400 1/м
1- лабораторный стенд Z — шток «
2- катушка-зонд
3- соленоид
5- амперметр
6- источник питания с регулятором выходного напряжения (тока), 7- милливольтметр.
2. Установить шток с масштабной линейкой так, чтобы катушка-зонд оказалась примерно в середине соленоида.
3.Включить источник питания соленоида и установить ток соленоида (по амперметру), равный =25мА. Включить милливольтметр и после прогрева (5 мин) снять показания .
4.Перемещая шток с масштабной линейной, измерить при помощи
милливольтметра действующее значение ЭДС индукции через каждый
сантиметр положения линейки. По формуле (8) вычислить .
Результаты измерений и расчетов занести в таблицу 1 (учтите, что ).
Таблица I
| № п/п | Положение линейки-Х | |||
| … |
Погрешность в каждой точке, соленоида определяется как систематическая погрешность косвенных измерений:
где м2, виток; =1 Гц; — погрешность измерения ; по милливольтметру.
5.Построить график
6.Зная амплитуду тока и число витков на единицу
длины соленоида n, определить в центре соленоида по
формуле (4) и сравнить с измеренным в той же точке значением
Задание 2. Измерение коэффициента неоднородности’ магнитного
поля соленоида.
1. Снять зависимость для данного соленоида. Дня этого установить шток в положение, когда катушка-зонд находится у края соленоидами, изменяя действующее значение тока соленоида с помощью источника питания, снять значения и и занести в таблицу 2.
Таблица 2.
По формуле (12) рассчитать , где
Контрольные вопросы
1. Сформулируйте закон электромагнитной индукции.
2. Нарисуйте картину силовых линий соленоида.
3. Перечислите основные способы исследования магнитного поля.
4. В каких случаях для исследования магнитного поля можно использовать катушку-зонд?
5. Выведите формулу для вектора магнитной индукции бесконечно длинного соленоида.
Литература
3. Скорохватов Н.А. Курс лекций по электромагнетизму. М: МИИГАиК, 2006.
4. Савельев И.В., Курс общей физики, т. 2 (любое издание).
5. Трофимова Т.И., Курс физики (любое издание).
|
Монография ученых Сибстрина отмечена дипломом конкурса «Книга года: Сибирь-Евразия» в номинации «Лучшая научная книга» Монография «Об определении параметров гидродинамических процессов в отдельных конструкциях и сооружениях», выполненная авторским коллективом под редакцией доктора технических наук, профессора, заведующего кафедрой Гидротехнических сооружений, безопасности и экологии НГАСУ (Сибстрин) Владимира Дегтярева отмечена дипломом конкурса «Книга года: Сибирь-Евразия» в номинации «Лучшая научная книга». Конкурс «Книга года: Сибирь-Евразия» проводится Новосибирской государственной областной научной библиотекой совместно с ГПНТБ СО РАН при поддержке Министерства культуры Новосибирской области. В этом году на конкурс поступило более 160 книг от издательств Новосибирска, Санкт-Петербурга, Москвы, Владивостока… |
|
Студент института строительства НГАСУ (Сибстрин) завоевал золотую медаль чемпионата EuroSkills Graz 2021, став лучшим молодым укладчиком напольных покрытий в Европе Студент Новосибирского государственного архитектурно-строительного университета (Сибстрин) Виталий Подколзин получил золотую медаль на европейском чемпионате рабочих профессий EuroSkills Graz 2021, став лучшим в компетенции «Укладка напольных покрытий». Чемпионат EuroSkills Graz 2021 проходил в австрийском городе Граце с 22 по 26 сентября. Участники российской команды завоевали 13 золотых, 6 серебряных и 8 бронзовых медалей по основным соревновательным компетенциям. Такое число наград стало рекордным результатом для России на чемпионате Европы. Большой вклад в победу сборной России внес студент 1 курса института строительства направления подготовки «Строительство уникальных зданий и сооружений» Виталий Подколзин. Стоить отметить, что он поступил в НГАСУ (Сибстрин), успешно окончив Новосибирский строительно-монтажный колледж. |
|
Ради экологичного будущего: студенты НГАСУ (Сибстрин) учат школьников сортировать мусор С 9 по 28 сентября 2021 года студенты Новосибирского государственного архитектурно-строительного университета (Сибстрин) по приглашению Департамента энергетики, жилищного и коммунального хозяйства мэрии города Новосибирска присоединились к серии эколого-просветительских акций «Экодвор». Цель акций – объединить жителей дворов важной идеей комфорта и экологичности, и большая роль в этом была отведена студентам-волонтерам Сибстрина. Именно им предстояло рассказать самым главным участникам «Экодворов» – школьникам – об экологичном образе жизни и раздельном сборе мусора. Для этого при методической поддержке Всероссийской общественной организацией волонтеров-экологов «Делай!» студенты проводили эстафету экоГТО, которая позволяет узнать больше о пользе переработки и экологических тенденциях, а также закрепить новые знания на практике. С поставленной задачей волонтеры Сибстрина справились – дети разных возрастов с неподдельным интересом и азартом участвовали в мероприятиях акции. |
|
4 октября в НГАСУ (Сибстрин) начнется Фестиваль архитектуры и дизайна Приглашаем вас принять участие в Фестивале архитектуры и дизайна в Сибстрине, объединяющем молодых профессионалов, студентов и учащихся образовательных учреждений России. Торжественное открытие фестиваля состоится 4 октября 2021 года (понедельник) в актовом зале главного корпуса НГАСУ (Сибстрин) (ул. Ленинградская, 113). Начало в 13.30. Фестиваль архитектуры и дизайна в Сибстрине пройдет с 4 октября по 26 ноября в Новосибирске на базе Новосибирского государственного архитектурно-строительного университета (Сибстрин). Его цель – вовлечение студентов-архитекторов в профессиональные мероприятия, активизация, развитие и повышение творческого уровня … |
Калькулятор магнитного поля соленоида
Калькулятор магнитного поля соленоида помогает вычислить магнитное поле внутри длинного соленоида. Хотите узнать, что такое соленоид и как рассчитать магнитное поле соленоида? Просто продолжайте читать. Вы также узнаете об уравнении магнитного поля соленоида.
Что такое соленоид?
Если пропустить через провод ток, вокруг него возникнет магнитное поле. Соленоид — это провод, плотно намотанный в длинную тонкую катушку.Из-за его формы, если мы пропустим ток через соленоид, внутри него будет сильное магнитное поле, а снаружи — небольшое.
Соленоидыиспользуются во многих практических приложениях, когда необходимо создать магнитное поле. В отличие от магнитов, мы можем контролировать силу магнитного поля, просто регулируя электрический ток. Соленоиды и в целом катушки также являются основными индуктивными элементами в электрических цепях. Чтобы узнать больше, воспользуйтесь нашим калькулятором индуктивности соленоида, калькулятором цепи RLC и калькулятором индуктивного реактивного сопротивления.
Уравнение магнитного поля соленоида
Соленоид бесконечной длины описать проще всего. Магнитное поле бесконечного соленоида точно равно нулю снаружи и имеет постоянное значение внутри соленоида. Бесконечный соленоид часто является разумным приближением реального соленоида конечной длины, если мы можем принять, что вблизи концов магнитное поле будет немного отличаться от рассчитанного для бесконечного соленоида.
Магнитное поле внутри длинного соленоида правильно рассчитывается с помощью перекрестного произведения и, возможно, правила правой руки, но все это можно упростить до:
B = µ₀ * N * I / L
где
- В — магнитное поле,
-
µ₀ = 1.-6 Тл * м / А— вакуумная проницаемость, - N — количество витков в соленоиде,
- I — электрический ток,
- L — длина соленоида.
Как рассчитать магнитное поле соленоида?
Самый простой способ рассчитать магнитное поле соленоида — использовать наш калькулятор. Просто укажите
- количество витков,
- электрический ток,
- длина соленоида,
, чтобы внутри него было магнитное поле.Чтобы узнать о влиянии магнитного поля на заряженные частицы, воспользуйтесь нашим калькулятором силы Лоренца.
Как рассчитать соленоид
Обновлено 28 декабря 2020 г.
Дэвид Латчман
Соленоид — это катушка из проволоки, длина которой значительно превышает ее диаметр, которая создает магнитное поле, когда через него проходит ток. На практике эта катушка наматывается на металлический сердечник, и сила магнитного поля зависит от плотности катушки, тока, проходящего через катушку, и магнитных свойств сердечника.
Таким образом, соленоид представляет собой тип электромагнита, предназначенный для создания управляемого магнитного поля. Это поле может использоваться для различных целей в зависимости от устройства, от использования для создания магнитного поля в качестве электромагнита, для предотвращения изменений тока в качестве индуктора или для преобразования энергии, хранящейся в магнитном поле, в кинетическую энергию в качестве электродвигателя. .
Магнитное поле производного соленоида
Магнитное поле производного соленоида можно найти с помощью закона Ампера .Получаем
Bl = \ mu_0 NI
, где B — плотность магнитного потока, l — длина соленоида, μ 0 — магнитная постоянная или магнитная проницаемость в вакууме. , N — количество витков в катушке, а I — ток через катушку.
Разделив на l , мы получим
B = \ mu_0 (N / l) I
, где N / l — плотность витков или количество витков на единицу. длина.Это уравнение применимо к соленоидам без магнитопроводов или в свободном пространстве. Магнитная постоянная 1,257 × 10 -6 Гн / м.
Магнитная проницаемость материала — это его способность поддерживать формирование магнитного поля. Некоторые материалы лучше других, поэтому проницаемость — это степень намагничивания, которое материал испытывает в ответ на магнитное поле. Относительная проницаемость мкм r говорит нам, насколько она увеличивается по отношению к свободному пространству или вакууму.
\ mu = \ mu_r \ mu_0
где μ — магнитная проницаемость, а μ r — относительность. Это говорит нам, насколько увеличивается магнитное поле, если через соленоид проходит материальный сердечник. Если мы поместим магнитный материал, например, железный стержень, и соленоид обернут вокруг него, железный стержень будет концентрировать магнитное поле и увеличивать плотность магнитного потока B . Для соленоида с материальным сердечником мы получаем формулу соленоида
B = \ mu (N / l) I
Расчет индуктивности соленоида
Одно из основных предназначений соленоидов в электрических цепях — препятствовать изменениям в электрических цепях. электрические схемы.{-1}
Решение для v получается
v = -L \ frac {dI} {dt}
Определение индуктивности соленоида
Закон Фарадея говорит нам сила наведенной ЭДС в ответ на изменение магнитного поля
v = -nA \ frac {dB} {dt}
где n — количество витков в катушке, а A — площадь поперечного сечения катушка. 2 A} {l}
Мы видим, что индуктивность L зависит от геометрии катушки — плотности витков и площади поперечного сечения — и магнитной проницаемости материала катушки. .
Магнитное поле в формуле соленоида
Термин «соленоид» по-гречески означает «трубчатый». Это тип электромагнита, его цель — генерировать контролируемое магнитное поле через катушку, намотанную в плотно упакованную спираль. Катушка может быть устроена так, чтобы создавать однородное магнитное поле в объеме пространства, когда через нее пропускается электрический ток. Согласно исследованию электромагнетизма, соленоид — это катушка, длина которой больше ее диаметра; это означает, что он имеет форму стержня.{-1} \], N — количество витков, I — ток, протекающий через соленоид, а l — длина соленоида.
[Изображение будет загружено в ближайшее время]
Магнитное поле внутри соленоида, формула
Магнитное поле внутри бесконечно длинного соленоида однородно, и его сила не зависит ни от расстояния от оси, ни от площади поперечного сечения соленоида.
Определение плотности магнитного потока, окружающего соленоид, достаточно длительное, чтобы можно было пренебречь краевыми эффектами.Мы сразу знаем, что из рисунка плотность потока векторных точек находится в положительном z-направлении внутри соленоида, а вне соленоида — в отрицательном z-направлении. Мы можем подтвердить это, применив правило правого захвата или правило правого большого пальца для поля, которое присутствует вокруг провода. Если мы обернем правую руку вокруг провода, направив большой палец в направлении тока, изгиб пальцев будет отражать поведение поля. Поскольку мы имеем дело с длинным соленоидом, из-за симметрии все компоненты магнитного поля, которые не направлены вверх, могут уравновешиваться.
[Изображение будет загружено в ближайшее время]
Теперь рассмотрим воображаемую петлю «c» на рисунке, она расположена внутри соленоида. По закону Ампера мы можем сказать, что линейный интеграл B, который представляет собой вектор плотности магнитного потока вокруг этой петли, равен нулю. Это происходит потому, что в нем нет электрического тока. Выше мы показали, что поле направлено вверх внутри соленоида, поэтому горизонтальные участки петли c не вносят никакого вклада в интеграл. Таким образом, интеграл верхней стороны фигуры, представляющей единицу, равен составной части второй стороны, которая движется вниз.Поскольку изменение размеров контура может производиться произвольно, чтобы получить тот же результат, подынтегральные выражения фактически равны. Это означает, что магнитное поле внутри соленоида радиально однородно.
Соленоид — это катушка из проволоки, по которой течет ток, а магнитное поле внутри нее определяется с помощью вклада каждой петли в соленоиде. Следовательно, полное магнитное поле зависит от количества витков катушки и длины соленоида.
Магнитное поле внутри соленоида максимальное, а магнитное поле внутри соленоида по формуле:
B = \ [\ mu_ {0} \] nI, Здесь n представляет количество витков, а I — ток, протекающий через соленоид.
Формула магнитного поля вне соленоида
Аналогичный аргумент можно применить к контуру, чтобы сделать вывод, что поле вне соленоида радиально однородно или постоянно. Также можно использовать интуитивный аргумент, чтобы показать, что плотность потока вне соленоида на самом деле равна нулю.Линии магнитного поля существуют только в форме петель, они не могут расходиться или сходиться в точку, как у силовых линий электрического поля. Силовые линии магнитного поля в соленоиде проходят по продольной траектории, поэтому вне соленоида эти силовые линии должны двигаться в противоположном направлении. Это происходит из-за линий, образующих петлю. Однако объем, который присутствует за пределами соленоида, намного больше, чем объем, присутствующий внутри. Таким образом, плотность силовых линий магнитного поля вне соленоида значительно снижается.Таким образом, можно сказать, что поле вне соленоида постоянно. Чтобы общее количество силовых линий было сохранено, внешнее поле должно стремиться к нулю по мере того, как соленоид становится длиннее.
Уравнение магнитного поля соленоида вне соленоида равно
B = \ [\ mu_ {0} \] nI, поскольку поле вне соленоида сравнительно меньше, поскольку оно присутствует внутри, мы можем считать его равным нулю, поскольку длина соленоид увеличивается, и, таким образом, B = 0.
Соленоид
СоленоидСоленоид [nb 1] представляет собой катушку, намотанную в плотно упакованную спираль.В физике термин соленоид относится к длинной тонкой петле из проволоки, часто обернутой вокруг металлического сердечника, который создает магнитное поле, когда через него проходит электрический ток. Соленоиды важны, потому что они могут создавать контролируемые магнитные поля и могут использоваться в качестве электромагнитов. Термин соленоид относится конкретно к магниту, предназначенному для создания однородного магнитного поля в объеме пространства (где можно провести некоторый эксперимент).
В технике термин соленоид может также относиться к множеству преобразователей, которые преобразуют энергию в поступательное движение.Этот термин также часто используется для обозначения соленоидного клапана, который представляет собой интегрированное устройство, содержащее электромеханический соленоид, который приводит в действие пневматический или гидравлический клапан, или соленоидный переключатель, который представляет собой особый тип реле, внутри которого используется электромеханический соленоид для управлять электрическим выключателем; например, соленоид автомобильного стартера или линейный соленоид, который является электромеханическим соленоидом.
Магнитное поле соленоида
Внутри
Это производное магнитного поля вокруг соленоида, достаточно длинное, чтобы можно было игнорировать краевые эффекты.На диаграмме справа мы сразу знаем, что поле указывает в положительном направлении z внутри соленоида и в отрицательном направлении z вне соленоида.
Мы видим это, применяя правило захвата правой рукой для поля вокруг проволоки. Если мы обхватим правой рукой провод, указав большим пальцем в направлении тока, изгиб пальцев покажет, как ведет себя поле. Поскольку мы имеем дело с длинным соленоидом, все компоненты магнитного поля, не направленные вверх, компенсируются симметрией.Снаружи происходит аналогичная отмена, а поле только направлено вниз.
Теперь рассмотрим воображаемую петлю c , которая находится внутри соленоида. По закону Ампера мы знаем, что линейный интеграл B (вектор магнитного поля) вокруг этого контура равен нулю, поскольку он не включает в себя электрические токи (можно также предположить, что циркулирующее электрическое поле, проходящее через контур, является постоянным при такие условия: постоянный или постоянно меняющийся ток через соленоид).Выше мы показали, что поле направлено вверх внутри соленоида, поэтому горизонтальные участки контура c ничего не вносят в интеграл. Таким образом, интеграл от верхней части 1 равен интегралу нижней стороны 2. Поскольку мы можем произвольно изменять размеры контура и получить тот же результат, единственное физическое объяснение состоит в том, что подынтегральные выражения фактически равны, то есть магнитное поле внутри соленоида радиально однородно. Однако обратите внимание, что ничто не запрещает ему изменяться в продольном направлении, что на самом деле так и есть.
Снаружи
Аналогичный аргумент можно применить к контуру и , чтобы сделать вывод о том, что поле вне соленоида является радиально однородным или постоянным. Этот последний результат, который строго верен только около центра соленоида, где силовые линии параллельны его длине, важен, поскольку он показывает, что внешнее поле практически равно нулю, поскольку радиусы поля вне соленоида будут стремиться к бесконечность.
Можно также использовать интуитивный аргумент, чтобы показать, что поле вне соленоида фактически равно нулю.Линии магнитного поля существуют только как петли, они не могут расходиться или сходиться к точке, как силовые линии электрического поля (см. Закон Гаусса для магнетизма). Линии магнитного поля следуют продольной траектории соленоида внутри, поэтому они должны идти в противоположном направлении за пределами соленоида, чтобы линии могли образовывать петлю. Однако объем снаружи соленоида намного больше, чем объем внутри, поэтому плотность силовых линий снаружи значительно снижается. Напомним, что внешнее поле постоянно.Чтобы общее количество силовых линий было сохранено, внешнее поле должно стремиться к нулю по мере того, как соленоид становится длиннее.
Количественное описание
Теперь мы можем рассмотреть воображаемую петлю b . Возьмите линейный интеграл B вокруг петли с длиной петли l . Горизонтальные компоненты исчезают, а внешнее поле практически равно нулю, поэтому закон Ампера дает нам:
, где μ 0 — магнитная постоянная, N — количество витков, i электрический ток.Это уравнение предназначено для соленоида без сердечника. Включение ферромагнитного сердечника, такого как железо, увеличивает величину магнитного поля в соленоиде. Это выражается формулой
, где мкм r — относительная проницаемость материала, из которого изготовлен сердечник. Этимология 27 соленоида: 18 Французский solénoïde , греческий solen «труба, канал» + комбинация греческого eidos «форма, форма» [1]
Ссылки
Внешние ссылки
Магнитные поля и Maxwell Revisited
Энергия, запасенная в магнитном поле
В индукторе энергия хранится в магнитном поле.
Цели обучения
Опишите поведение индуктора при изменении тока и выразите энергию, запасенную в магнитном поле, в форме уравнения
Основные выводы
Ключевые моменты
- Формула для энергии, запасенной в магнитном поле, E = 1/2 LI 2 .
- Энергия, запасенная в магнитном поле, равна работе, необходимой для создания тока через катушку индуктивности.
- Энергия хранится в магнитном поле.2} {2 \ mu} [/ латекс].
Ключевые термины
- индуктор : Устройство или компонент схемы, который демонстрирует значительную самоиндукцию; устройство, которое хранит энергию в магнитном поле.
Когда по проводнику проходит ток, создается магнитное поле, окружающее проводник. Результирующий магнитный поток пропорционален току. Если ток изменяется, изменение магнитного потока пропорционально скорости изменения тока во времени с помощью коэффициента, называемого индуктивностью (L).Поскольку природа не терпит быстрых изменений, создаваемое в проводнике напряжение ( электродвижущая сила , ЭДС ) противодействует изменению тока, которое также пропорционально изменению магнитного потока. Таким образом, индукторы противодействуют изменению тока, создавая напряжение, которое, в свою очередь, создает ток, противодействующий изменению магнитного потока; напряжение пропорционально изменению тока.
Энергия, запасенная в индукторе
Из-за энергосбережения энергия, необходимая для управления исходным током, должна иметь выход.2 [/ латекс]
(уравнение 1), где L — индуктивность в единицах Генри, а I — ток в единицах Ампера.
Энергия, запасенная в магнитном поле
Рассмотрим Рис. 1, пример соленоида (ℓ: длина, N: количество витков, I: ток, A: площадь поперечного сечения), который работает как индуктор. Из уравнения. 1, энергия, запасенная в магнитном поле, создаваемом соленоидом, составляет:
Магнитное поле, создаваемое соленоидом : Магнитное поле, создаваемое соленоидом (вид в разрезе), описанное с помощью силовых линий.2} {2 \ mu} [/ латекс].
Предсказания Максвелла и подтверждение Герца
Предсказание Максвелла об электромагнитной силе было подтверждено Герцем, который генерировал и обнаруживал электромагнитные волны.
Цели обучения
Объясните, как Герц
подтвердил предсказание Максвелла об электромагнитной силе.Основные выводы
Ключевые моменты
- Максвелл предсказал, что электрические и магнитные силы связаны. Уравнения
- Максвелла предсказывают, что независимо от длины и частоты волны все световые волны имеют одинаковую структуру.
- Hertz смог экспериментально подтвердить уравнение Максвелла, генерируя и обнаруживая определенные типы электромагнитных волн в лаборатории.
Ключевые термины
- электрическое поле : область пространства вокруг заряженной частицы или между двумя напряжениями; он воздействует на заряженные объекты поблизости.
- магнитное поле : Состояние в пространстве вокруг магнита или электрического тока, в котором существует обнаруживаемая магнитная сила и где присутствуют два магнитных полюса.
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
Предсказания Максвелла и подтверждение Герца
Объединив работы физиков, включая Эрстеда, Кулона, Гаусса и Фарадея, и добавив свои собственные идеи, Джеймс Клерк Максвелл разработал полную и всеобъемлющую теорию, показывающую, что электрические и магнитные силы не разделены, а представляют собой разные формы одного и того же: электромагнитная сила.В 1865 году он сделал это в форме четырех уравнений, которые утверждали следующее:
- Линии электрического поля берут начало на положительных зарядах и оканчиваются на отрицательных зарядах, а электрическое поле определяется как сила, приходящаяся на единицу заряда испытательного заряда. Сила силы связана с электрической постоянной ε 0 , также известной как диэлектрическая проницаемость свободного пространства.
- Линии магнитного поля непрерывны, не имеют ни начала, ни конца. О существовании магнитных монополей не известно.
- Изменяющееся магнитное поле индуцирует электродвижущую силу (ЭДС) и, следовательно, электрическое поле. Направление ЭДС противодействует изменению.
- Магнитные поля создаются движущимися зарядами или изменяющимися электрическими полями.
Уравнения Максвелла предсказывают, что независимо от длины и частоты волны все световые волны имеют одинаковую структуру. Это означает, что уравнения Максвелла предсказывали существование радио- и рентгеновских волн, хотя на самом деле они еще не были обнаружены.
Доказательство уравнений Максвелла
Известные уравнения Максвелла, простые и гениальные по своей проницательности, по-прежнему трудно доказать. Поскольку изменяющиеся электрические поля создают относительно слабые магнитные поля, их было нелегко обнаружить во время гипотезы Максвелла.
Только в 1888 году предсказание Максвелла прошло серьезную проверку, когда Генрих Герц создал и обнаружил определенные типы электромагнитных волн в лаборатории. Он провел серию экспериментов, которые не только подтвердили существование электромагнитных волн, но и подтвердили, что они движутся со скоростью света.
Герц использовал цепь переменного тока RLC (резистор-индуктор-конденсатор), которая резонирует на известной частоте, и подключила ее к петле из проводов, как показано на рисунке. Высокое напряжение, индуцированное через зазор в петле, вызывало искры, которые были видимым свидетельством наличия тока. в цепи, и это помогло генерировать электромагнитные волны. Через всю лабораторию Герц подключил еще один контур к другому контуру RLC, который можно было настроить (как циферблат на радио) на ту же резонансную частоту, что и первый, и, таким образом, можно было заставить принимать электромагнитные волны.В этой петле также был зазор, в котором возникали искры, что давало твердое свидетельство приема электромагнитных волн.
Аппарат, используемый Герцем : Аппарат, использованный Герцем в 1887 году для генерации и обнаружения электромагнитных волн. Схема RLC, подключенная к первому контуру, вызвала искры через разрыв в проводном контуре и генерировала электромагнитные волны. Искры в щели во второй петле, расположенной напротив лаборатории, свидетельствовали о том, что волны были приняты.
EM Wave : Распространение электромагнитной волны, предсказанное Максвеллом и подтвержденное Герцем.
Inductance — The Physics Hypertextbook
Обсуждение
введение
Готовы? Вот так.
Пуск с соленоидом. Пропустите через него ток, и вы получите электромагнит. Поле внутри задается формулой…
| B = μ 0 nI = μ 0 | N | Я |
| ℓ |
В то же время соленоид — это еще и устройство для улавливания магнитного потока.
Φ B = NBA
Статическая ситуация, безусловно, достаточно интересна, но когда дело доходит до потока, то, что нас действительно волнует, — это скорость изменения во времени. Это то, что дает нам электромагнитную индукцию или индуцированную электродвижущую силу, или как вы хотите это называть. Эта ситуация описывается законом Фарадея.
Давайте еще раз рассмотрим эти уравнения, но с изменяющимся во времени поворотом. Соленоид с изменяющимся током, проходящим через него, будет генерировать изменяющееся магнитное поле.
| дБ | = мк 0 | N | dI | |
| дт | ℓ | дт |
Это изменяющееся магнитное поле затем улавливается тем самым соленоидом, который его создал. Захваченное поле называется потоком, а изменяющийся поток генерирует ЭДС — в данном случае самоиндуцированную или обратную ЭДС.
| ℰ = — | d Φ B | = — N | ⎛ ⎜ ⎝ |
мкм 0 | N | dI | ⎞ ⎟ ⎠ |
А | |
| дт | ℓ | дт |
Немного переставив вещи, мы получаем это уравнение…
| ℰ = — | мкм 0 AN 2 | dI | |
| ℓ | дт |
, который может показаться не таким уж большим, пока вы не поймете, что члены первой дроби в значительной степени определяются геометрией соленоида.Если бы мы выбрали другую конфигурацию проводов, произошло бы то же самое.
Самоиндуцированная ЭДС в цепи прямо пропорциональна скорости изменения тока во времени ( dI / dt ), умноженной на константу ( L ). Эта постоянная называется индуктивностью (или, точнее, самоиндуктивностью ) и определяется геометрией схемы (или, чаще, геометрией отдельных элементов схемы).Например, индуктивность соленоида (как определено выше) определяется формулой…
Символ L для обозначения индуктивности был выбран в честь Генриха Ленца (1804–1865), чья новаторская работа в области электромагнитной индукции сыграла важную роль в развитии окончательной теории. Если вы помните, Закон Ленца гласит, что индуцированный ток в цепи всегда действует таким образом, чтобы противодействовать изменению, которое в первую очередь его вызвало. Это наблюдение является причиной того, почему во всех версиях закона Фарадея стоит знак минус.Ленц поставил нам знак минус, и мы чествуем его знаком L .
Индуктивность лучше всего определяется по ее роли в уравнении, выведенном из закона индукции Фарадея. Некоторым это не нравится, и они предпочитают определения, написанные в форме простого предложения субъект-глагол-объект.
На английском языке мы бы прочитали это как «самоиндуктивность ( L ) — это отношение обратной ЭДС () к временной скорости изменения тока, производящего ее ( dI / dt ).«Как я уже сказал, мне не очень нравится такое определение, но оно помогает нам определить подходящие единицы измерения.
| ⎡ ⎢ ⎣ |
H = | В | = | Дж / К | = | (кг · м 2 / с 2 ) / (А · с) | = | кг м 2 | ⎤ ⎥ ⎦ |
| А / с | пк / с | пк / с | A 2 с 2 |
Единицей индуктивности является генри , названный в честь Джозефа Генри (1797–1878), американского ученого, открывшего электромагнитную индукцию независимо и примерно в то же время, что и Майкл Фарадей (1791–1867) в Англии.Первым свои открытия опубликовал Фарадей, поэтому ему заслуга в большей степени. Генри также открыл самоиндукцию и взаимную индуктивность (которые будут описаны позже в этом разделе) и изобрел электромеханическое реле (которое легло в основу телеграфа). Схема с собственной индуктивностью в один генри будет испытывать противоэдс в один вольт, когда ток изменяется со скоростью один ампер в секунду.
Индуктивность это что-то. Индуктивность — это сопротивление элемента схемы изменениям тока.Индуктивность в цепи — это аналог массы в механической системе.
| ⇕ | |||||
|
|||||
| ⇕ | |||||
детектор индуктивной петли
Движение на некоторых перекрестках контролируется с помощью индуктивных петлевых детекторов (ILD).ILD — это петля из проводящего провода, проложенная всего на несколько сантиметров ниже тротуара. Когда автомобиль проходит через поле, он действует как проводник, изменяя индуктивность контура. Изменение индуктивности контура указывает на наличие автомобиля наверху. Затем эту информацию можно использовать для активации сигналов светофора, отслеживания транспортного потока или автоматического цитирования.
примеры
индуктивность зависит от геометрии
Соленоид ( A площадь поперечного сечения, N количество витков, длина ℓ, n количество витков на длину)
| Φ B | = N | В | А | ||
| Φ B | = N | мкм 0 НИ | А | ||
| ℓ | |||||
| Φ B | = | мкм 0 AN 2 | Я | ||
| ℓ | |||||
| d Φ B | = | мкм 0 AN 2 | dI | ||
| дт | ℓ | дт | |||
| L | = | мкм 0 AN 2 | = | мкм 0 Aℓn 2 | |
| ℓ |
коаксиальных проводников ( a внутренний радиус, b внешний радиус, длина ℓ)
| Φ B | = | ⌠ ⌡ |
B | · | d A | ||||
| б | б | ||||||||
| Φ B | = | ⌠ ⌡ |
мкм 0 I | ℓ др | = | мкм 0 Iℓ | ⌠ ⌡ |
др | |
| 2π r | 2π | р | |||||||
| a | a | ||||||||
| Φ B | = | мкм 0 ℓ | пер. | ⎛ ⎜ ⎝ |
a | ⎞ ⎟ ⎠ |
Я | ||
| 2π | б | ||||||||
| d Φ B | = | мкм 0 ℓ | пер. | ⎛ ⎜ ⎝ |
a | ⎞ ⎟ ⎠ |
dI | ||
| дт | 2π | б | дт | ||||||
| L | = | мкм 0 ℓ | пер. | ⎛ ⎜ ⎝ |
a | ⎞ ⎟ ⎠ |
|||
| 2π | б | ||||||||
тороид ( A площадь поперечного сечения, R радиус вращения, N число витков)
| Φ B | = | N | В | А | |
| Φ B | ≈ | N | мкм 0 НИ | А | |
| 2π R | |||||
| Φ B | ≈ | N | мкм 0 NA | Я | |
| 2π R | |||||
| d Φ B | ≈ | мкм 0 AN 2 | dI | ||
| дт | 2π R | дт | |||
| L | ≈ | мкм 0 AN 2 | |||
| 2π R | |||||
прямоугольная петля ( w ширина, h высота, a радиус провода )
| Φ B | = | N | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Φ B | = | N |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Φ B | = | 2 | мкм 0 N 2 | ⎡ ⎢ ⎣ |
y ln | ⎛ ⎜ ⎝ |
x | ⎞ ⎟ ⎠ |
+ | x дюйм | ⎛ ⎜ ⎝ |
y | ⎞ ⎟ ⎠ |
⎤ ⎥ ⎦ |
Я | |||||||||||||||||||||||||||||||||||||||||||||||||
| 2π | a | a | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| d Φ B | = | мкм 0 N 2 | ⎡ ⎢ ⎣ |
y ln | ⎛ ⎜ ⎝ |
x | ⎞ ⎟ ⎠ |
+ | x дюйм | ⎛ ⎜ ⎝ |
y | ⎞ ⎟ ⎠ |
⎤ ⎥ ⎦ |
dI | ||||||||||||||||||||||||||||||||||||||||||||||||||
| дт | π | a | a | дт | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| L | = | мкм 0 N 2 | ⎡ ⎢ ⎣ |
y ln | ⎛ ⎜ ⎝ |
x | ⎞ ⎟ ⎠ |
+ | x дюйм | ⎛ ⎜ ⎝ |
y | ⎞ ⎟ ⎠ |
⎤ ⎥ ⎦ |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| π | a | a | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Эта формула не совсем работает, поскольку игнорирует краевые эффекты.2} {/ экв}. Предположим, что магнитное поле внутри соленоида однородно, и пренебрегаем торцевыми эффектами.
(a) Напишите уравнение для магнитного поля {eq} B {/ eq}, производимый соленоидом. Выразите свой ответ через ток через катушку {экв} I {/ eq}, количество витков {eq} N {/ eq}, длина катушки {eq} d {/ eq}, а проницаемость свободного пространства {eq} \ mu_0 {/ экв}.
(b) Используя уравнение для магнитного поля, определенное в части (a), вычислите магнитный поток через одиночный контур соленоида с током {eq} I = 1.2} {/ eq} и состоит из {eq} N = 110 \, \ mathrm {turn} {/ экв}.
Соленоид — магнитное поле, магнитный поток, собственная индуктивность
Соленоид — это катушка, образующая большое количество витков из токопроводящей проволоки. Он используется для создания магнитного поля. Внутри соленоида магнитное поле почти однородное.
Магнитное поле задается уравнением {eq} B = \ dfrac {\ mu_0 N I} {l} {/ экв}.
Магнитный поток через область — это магнитное поле, проходящее через нормальную к ней область.он задается уравнением: {eq} \ Phi = B A {/ eq}.
Собственную индуктивность катушки можно получить из уравнения: {eq} L = \ dfrac {\ Phi} {I} {/ eq}
Здесь,
- B — магнитное поле
- n — общее количество витков в соленоиде
- l — длина соленоида
- I — ток в соленоиде
- А — площадь поперечного сечения соленоида
- L — собственная индуктивность.
Ответ и пояснение: 1
Данные
- Количество витков в соленоиде: {eq} N = 110 {/ eq}
- Длина соленоида {eq} d = 0,04 \ m {/ eq}
- Площадь сечения соленоида: …
См. Полный ответ ниже.
.
