Радио для всех — Лаборатория
В разделе представлены on-line калькуляторы
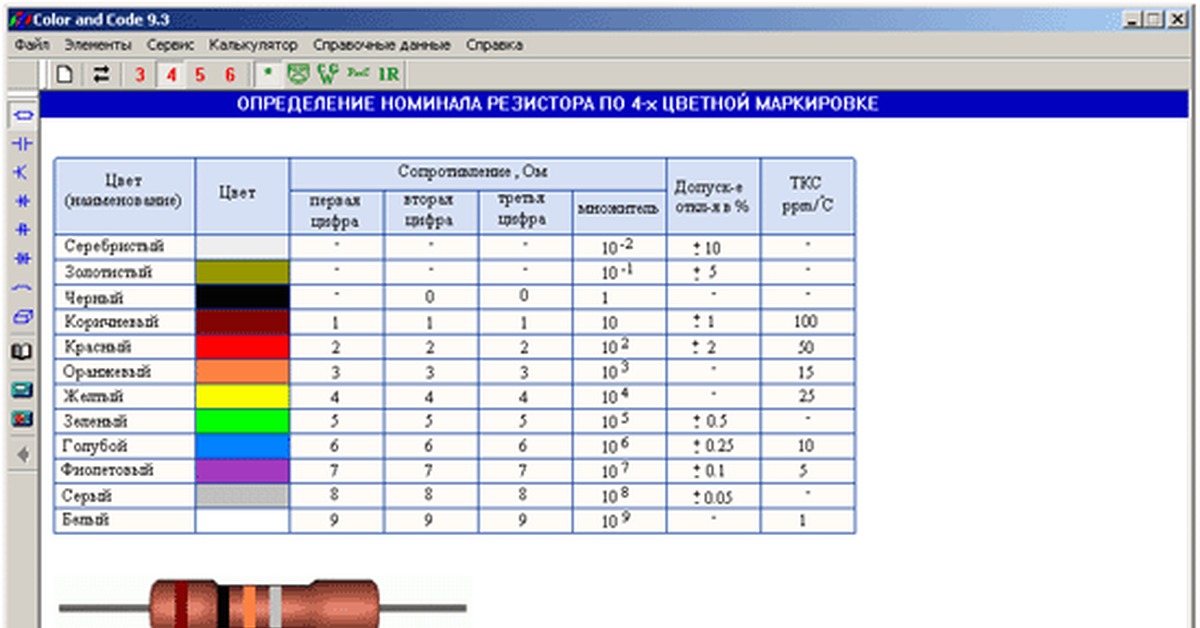
Цветовая маркировка резисторов
Расчет индуктивности
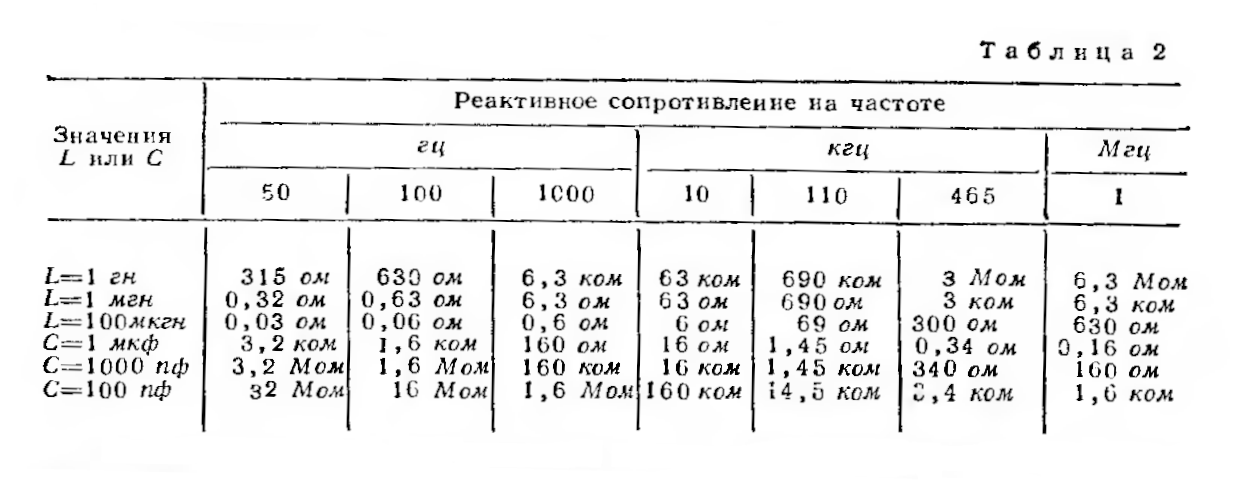
Расчёт реактивного сопротивления конденсатора C и реактивного сопротивления катушки L
Расчёт параллельного соединения резисторов и последовательного конденсаторов
Расчёт резистивного и ёмкостного делителей
Расчёт частоты колебательного контура и цепочки RC. Частота среза фильтра ФНЧ и ФВЧ
Компенсация реактивной мощности
Закон Ома. Расчёт напряжения, сопротивления, тока, мощности
Расчет элементов J антенны
Расчет резонансной частоты LC-контура
Расчет резистивного Пи аттенюатора
Делитель напряжения
Цветовой код конденсаторов
Стабилизация напряжения
Дроссели, намотанные на резисторах МЛТ
Реактивное сопротивление конденсатора
Реактивное сопротивление катушки индуктивности
Калькулятор определения номинала SMD-резистора
Расчет значения резистора для LM317
Онлайн калькулятор таймер 555
Расчет «Cantenna» (баночной антенны) для Wi Fi
Калькулятор расчета компактных монолитных усилителей
Расчет силового трансформатора
Расчет дискоконусной антенны
Сопротивления для согласующего трансформатора
Расчет для тороидальных (ферритовых) сердечников Amidon
Расчет петлевого вибратора
Калькулятор DC-DC преобразователя MC34063A
Расчет выпрямителя для блока питания
Расчет гасящего конденсатора в блоке питания
Расчет резистора для подключения светодиода
Цветовая маркировка резисторов
Расчет индуктивности
Расчёты электронных цепей.
Вписываем значения и кликаем мышкой в таблице
Расчёт реактивного сопротивления конденсатора C и реактивного сопротивления катушки L
|
Реактивное сопротивление ёмкости |
Реактивное сопротивление индуктивности |
Расчёт параллельного соединения резисторов и последовательного конденсаторов
|
Параллельное соединение двух сопротивлений |
Последовательное соединение двух ёмкостей |
Расчёт резистивного и ёмкостного делителей
|
Расчёт резистивного делителя напряжения |
Расчёт ёмкостного делителя напряжения |
Расчёт частоты колебательного контура и цепочки RC. Частота среза фильтра ФНЧ и ФВЧ
Частота среза фильтра ФНЧ и ФВЧ
|
Частота резонанса колебательного контура LC |
Пост. времени τ RC и частота среза RC-фильтра |
Компенсация реактивной мощности
|
Реактивная мощность Q = √((UI)²-P²) |
Закон Ома. Расчёт напряжения, сопротивления, тока, мощности
|
После сброса ввести два любых известных параметра I=U/R; U=IR; R=U/I; P=UI P=U²/R; P=I²R; R=U²/P; R=P/I² U=√(PR) I= √(P/R) |
Расчет элементов J антенны
Дополнение: Арифметические калькуляторы и конвертеры величин
Калькулятор | ColorAndCode
| LCD1602/2004 — HD44780 | |
|
Параллельное соединение резисторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. |
|
|
Последовательное соединение резисторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. |
|
|
Параллельное соединение конденсаторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. |
|
|
Последовательное соединение конденсаторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. |
|
| Реактивное сопротивление конденсатора | |
| Реактивное сопротивление конденсатора (+) | |
| Реактивное сопротивление катушки индуктивности | |
| Реактивное сопротивление катушки индуктивности (+) | |
| Обратное определение при параллельном соединении резисторов и последовательном конденсаторов | |
| Определение индуктивности из частоты и реактивного сопротивления | |
| Определение емкости из частоты и реактивного сопротивления | |
| Проводники | |
| Цилиндрические однослойные катушки | |
| Цилиндрические однослойные катушки (+) | |
|
Тороидальные катушки на ферритовых кольцах
Дополнительно: — Возможность использовать данные из справочника. |
|
| Программирование ДПКД (делитель с переменным коэффициентом деления) | |
|
Сопротивление резистора для светодиода Дополнительно: — Возможность использовать данные из справочника; — Вывод номинала в 4-х цветной маркировке для ряда E24 +/- 5 %. |
|
| Расчёт схемы на основе NE555 | |
| Расчёт схем на основе LM317, LM338, LM350 | |
| Расчёт схем на основе LM2596 | |
| Расчет катушек на ферритовых кольцах фирмы Amidon |
|
| Расчёт индуктивности квадратной плоской катушки |
|
| Индуктивность прямого провода над проводящей подложкой |
Дополнительный материал в статье:
— Полупроводниковая светотехника № 4 за 2019 год
— Радиолюбитель № 3 за 2010 год
— Компоненты и технологии № 6 за 2010 год
Расчёт блока питания с гасящим конденсатором + онлайн-калькулятор — radiohlam. ru
ru
Осторожно, текст под спойлером перегружен физикой!
Итак, процессы в этой схеме будут достаточно нелинейны, поэтому при рассчётах придётся делать различные упрощения и допущения.
Для начала давайте будем считать, что ёмкость конденсатора C2 достаточна для полного сглаживания пульсаций напряжения после моста, то есть напряжение на конденсаторе C2 = const. Далее попробуем нарисовать пару графиков, — напряжение на входе моста (UM) и ток через конденсатор C1 (IC1), опираясь на график сетевого напряжения UС(t). Будем считать, что сетевое напряжение у нас изменяется по синусоидальному закону и имеет амплитуду Uca (вообще-то рисовать мы будем косинусоиду, нам так будет удобнее, но это по сути одно и то же, только косинусоида сдвинута относительно синусоиды на π/2).
Рассуждаем следующим образом: в каждый момент времени полное напряжение и полный ток в этой цепи можно описать следующими уравнениями:
UC=UC1+UМ (1), iC=iC1+iМ (2)
В момент времени t0 уравнение напряжения примет вид: Uca=UC1+UМ.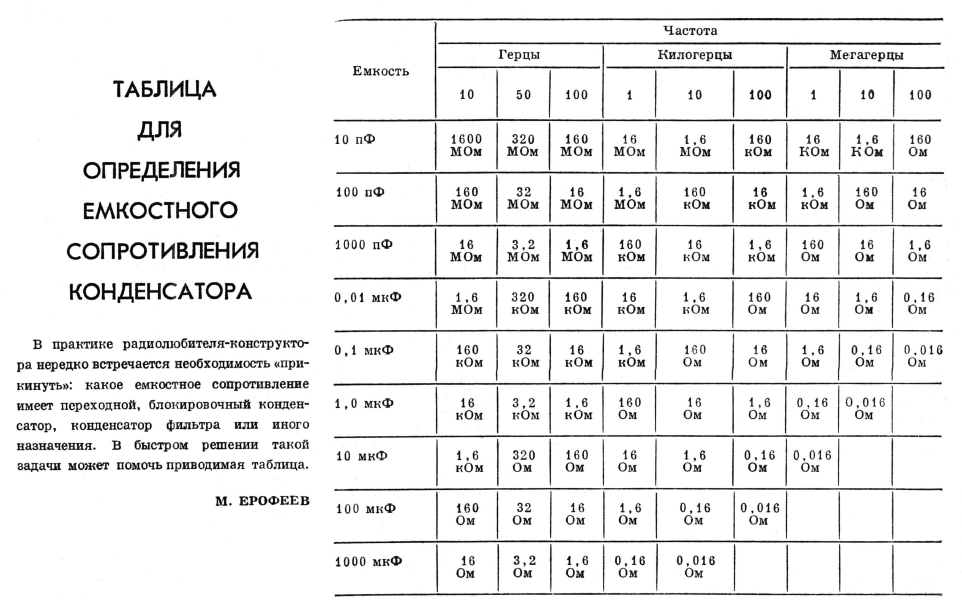 Поскольку Uca — это максимальное значение сетевого напряжения, то UC1 и UМ также в этот момент должны иметь максимальные значения (здесь в логике есть небольшой провал, максимум суммы — это не всегда сумма максимумов, функции могут быть сдвинуты по фазе, но… в общем, мы потом всё экспериментально проверим).
Поскольку Uca — это максимальное значение сетевого напряжения, то UC1 и UМ также в этот момент должны иметь максимальные значения (здесь в логике есть небольшой провал, максимум суммы — это не всегда сумма максимумов, функции могут быть сдвинуты по фазе, но… в общем, мы потом всё экспериментально проверим).
Максимальное значение UМ равно Uвых, поскольку если бы напряжение на мосту поднималось выше, то и конденсатор C2 заряжался бы до большего напряжения (мост бы открылся и к конденсатору C2 потёк бы зарядный ток, увеличивая напряжение на нём).
Токи через конденсатор и мост в момент

Далее сетевое напряжение (UC) начинает уменьшаться. При этом напряжение на C1 не меняется (тока-то через мост нет, заряд на C1 не меняется), следовательно вместе с падением UC уменьшается напряжение на входе моста.
В момент, когда сетевое напряжение упадёт до значения Uca-2Uвых (момент времени t1) — напряжение на входе моста достигнет значения -Uвых (находим с помощью формулы 1), диоды моста откроются и в первичной цепи (через мост и конденсатор C1) потечёт ток. При этом напряжение на входе моста перестанет меняться (помните, мы договорились, что ёмкость C2 достаточно большая для того, чтобы полностью сгладить пульсации).
Обратите внимание, что напряжение на входе моста в этот момент равно -Uм, так что ток потечёт в обратную сторону от того направления, в котором он тёк до момента времени t0. Этот ток, поскольку он течёт в обратную сторону, начнёт перезаряжать конденсатор C1.
К моменту времени t3 напряжение в сети достигнет максимума, только с противоположной относительно момента t0 полярностью. Соответственно, для этого момента экстремума сетевого напряжения будут справедливы все те же рассуждения касательно напряжений и токов, которые мы использовали для момента
Далее, по мере роста сетевого напряжения, напряжение на конденсаторе C1 будет оставаться неизменным, а напряжение на входе моста будет расти.
В момент времени t4, когда сетевое напряжение вырастет до значения -(Uca-2Uвых), напряжение на входе моста достигнет значения Uвых, диоды моста откроются и в первичной цепи (через мост и конденсатор C1) снова потечёт ток. Этот ток снова будет перезаряжать конденсатор C1, но уже напряжением положительной полярности.
Этот ток снова будет перезаряжать конденсатор C1, но уже напряжением положительной полярности.
В момент t6 напряжение на конденсаторе C1 достигнет максимального значения положительной полярности, а ток через C1 и мост упадёт до нуля.
Далее весь цикл повторится с самого начала.
Теперь давайте вспомним закон сохранения заряда. В соответствии с этим законом за один полный цикл через конденсатор C1, мост и нагрузку должно протекать одинаковое количество заряда. Поскольку ток нагрузки у нас постоянный, то количество заряда, протекающего через нагрузку за один цикл, можно найти по формуле Q=Iн*tцикла=Iн/fc, где fc — частота питающего сетевого напряжения. Количество заряда, протекающего через конденсатор C1, будет равно площади под графиком тока (заштрихованная площадь графика IC1(t)). Остаётся только найти эту площадь, приравнять её к заряду, протекающему за один цикл через нагрузку, и выразить из полученного выражения необходимую ёмкость конденсатора C1 в зависимости от тока нагрузки.
Подробные математические расчёты можно найти под вторым спойлером.
[свернуть]
Простой метод измерения ESR конденсаторов
Добавлено 13 декабря 2019 в 06:05
Сохранить или поделиться
Точное моделирование электронных схем, в том числе и силовых электронных преобразователей, должно учитывать последовательные сопротивления конденсаторов и катушек индуктивности. Рассмотрим, простой метод, который позволяет измерять эквивалентное последовательное сопротивление конденсатора (ESR).
Конденсаторы классифицируются по типу диэлектрика. Электролитические конденсаторы популярны в силовых электронных схемах благодаря их высокой эффективности относительно размеров и превосходному соотношению цены и качества [1]. К сожалению, с изменением рабочей частоты изменяются и их характеристики, тогда как сопротивление идеального конденсатора с ростом частоты должно уменьшаться. Но в реальном мире это не встречается. Увеличение частоты до определенной точки приводит к ожидаемому уменьшению полного сопротивления, но дальнейшее увеличение частоты вызывает увеличение импеданса, то есть конденсатор действует как резонансная схема. Для моделирования поведения реального конденсатора требуется к модели идеального конденсатора добавить дополнительные элементы. ESR – это фактически сопротивление, которое реальный конденсатор демонстрирует на границе между «поведением конденсатора» и «поведением индуктивности», то есть сопротивление на резонансной частоте.
Для моделирования поведения реального конденсатора требуется к модели идеального конденсатора добавить дополнительные элементы. ESR – это фактически сопротивление, которое реальный конденсатор демонстрирует на границе между «поведением конденсатора» и «поведением индуктивности», то есть сопротивление на резонансной частоте.
ESR является важным параметром при моделировании динамического поведения силовых преобразователей, поскольку он предсказывает пульсации выходного сигнала преобразователя, а также предсказывает срок службы конденсатора [2]. Мощность, рассеиваемая в ESR, вызывает повышение температуры конденсатора и уменьшение его емкости и срока службы.
Простой и прямой метод измерения ESR предложен в [3], в котором ESR определяется непосредственно отношением напряжения пульсаций на конденсаторе к току пульсаций. Но реализация довольно дорогая и хлопотная. Чтобы определить ESR, используя только измерения напряжения, Чен и другие [4] предположили, что в некоторых конкретных условиях ток пульсаций индуктивности можно считать постоянным, и, следовательно, выходное напряжение пульсации определяет ESR.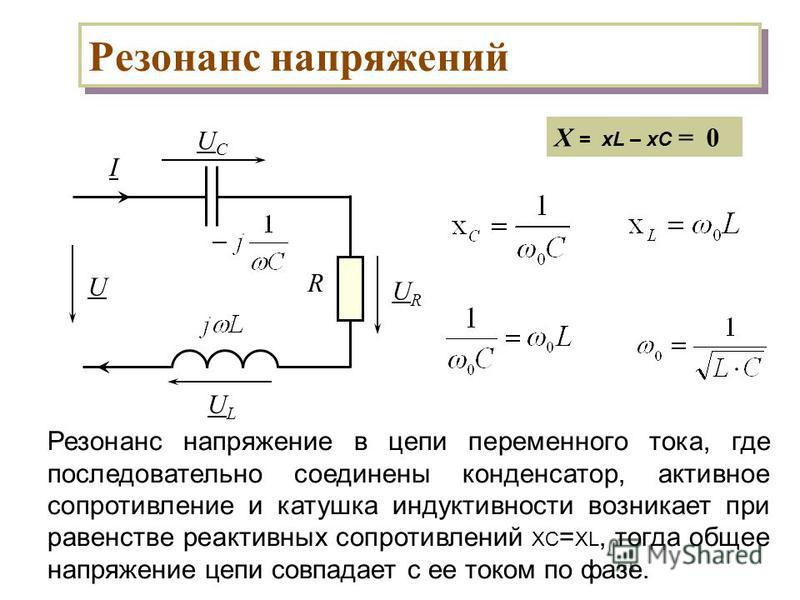 Однако предлагаемый способ имеет ограничения и его точность невелика.
Однако предлагаемый способ имеет ограничения и его точность невелика.
Лабораторный метод, который можно использовать для определения величины ESR электролитических конденсаторов, был предложен в [5]. Однако способ слишком дорогостоящий для реализации.
Здесь мы представляем простой метод измерения для определения ESR конденсатора.
Предлагаемый метод
Предположим, что модель, показанная на рисунке 1, представляет собой тестируемый конденсатор (CUT, Capacitor Under Test):
Рисунок 1 – Модель тестируемого конденсатораЭта модель игнорирует индуктивность выводов. Предположим, что, как показано на рисунке 2, тестируемый конденсатор подключен к генератору синусоидального сигнала с частотой Fг, внутреннее сопротивление генератора равно rг:
Рисунок 2 – Тестируемый конденсатор подключен к генератору синусоидального сигналаПередаточная функция этой схемы:
\[H(s) = {r_к \over r_к + r_г} \times { s + \frac{1}{r_к \times C} \over s + \frac{1}{(r_к + r_г) \times C} } \qquad (1)\]
Уравнение 1 показывает высокочастотный характер этой цепи. {\infty} {4 \times V_m \over n \times \pi} \sin(n \times \omega_0 \times t) \qquad (4)\]
{\infty} {4 \times V_m \over n \times \pi} \sin(n \times \omega_0 \times t) \qquad (4)\]
где:
\[\omega_0 = \frac{2\pi}{T} = \text{угловая частота прямоугольного сигнала}\]
Прямоугольный сигнал состоит из нечетных гармоник. Когда основная гармоника достаточно высока, конденсатор действует как короткое замыкание, а выходное напряжение примерно является ослабленной версией входного напряжения в устойчивом состоянии. Затухание цепи в установившемся режиме напрямую связано с эквивалентным последовательным сопротивлением конденсатора, rк, которое может быть получено путем измерения коэффициента затухания цепи и использования уравнения 3.
Результаты моделирования
Диаграмма Simulink показана на рисунке 3:
Рисунок 3 – Схема моделирования в SimulinkВ качестве возбуждения используется прямоугольный сигнал с амплитудой +1 и -1 вольт. Выходное сопротивление генератора сигналов принимается за 50 Ом, конденсатор составляет 30 мкФ с ESR 0,8 Ом. Установившаяся форма выходного сигнала показана на рисунке 4:
Рисунок 4 – Установившаяся форма выходного сигнала схемыРасчетный коэффициент затухания цепи составляет:
\[\alpha = { \text{выходное напряжение пик-пик} \over \text{входное напряжение пик-пик} } = \frac{0,315}{2} = 0,0158 \qquad (5)\]
и ESR тестируемого конденсатора рассчитывается как:
\[r_к = \alpha \times r_г = 0,0158 \times 50 = 0,7875\ Ом \qquad (5)\]
Лабораторные результаты
Возбуждение обеспечивает генератор сигналов с номинальным выходным сопротивлением 50 Ом. С помощью простого делителя напряжения намеряется выходное сопротивление 47,1 Ом. Выходное напряжение пик-пик в установившемся состоянии измеряется с помощью цифрового осциллографа. На рисунке 5 показан пример выходного напряжения.
С помощью простого делителя напряжения намеряется выходное сопротивление 47,1 Ом. Выходное напряжение пик-пик в установившемся состоянии измеряется с помощью цифрового осциллографа. На рисунке 5 показан пример выходного напряжения.
Расчетные значения ESR
| Размах входного напряжения, В | Размах выходного напряжения, мВ | Емкость, мкФ | Рассчитанное значение ESR, Ом |
|---|---|---|---|
| 1,68 | 58 | 4 | 1,68 |
| 1,68 | 80 | 6,8 | 2,35 |
| 1,68 | 66 | 47 | 1,88 |
| 1,72 | 44,8 | 220 | 1,26 |
| 1,72 | 48 | 470 | 1,35 |
| 1,68 | 42 | 660 | 1,18 |
| 1,72 | 45 | 2200 | 1,26 |
Этот простой метод измерения обеспечивает точные результаты и позволяет получить более точную модель силового преобразователя.
Ссылки
- Amaral A.M.R., Cardoso A.J.M.: An experimental technique for estimating the ESR and reactance intrinsic values of aluminium electrolytic capacitors. Proc. Instrumentation and Measurement Technology Conf., IMTC 2006, April 2006, pp. 1820–1825.
- Sankaran V.A., Rees F.L., Avant C.S.: Electrolytic capacitor life testing and prediction. Proc. 32nd Annual Meeting IEEE Industry Applications Society, October 1997, vol. 2, pp. 1058–1065
- Venet P., Perisse F., El-Husseini M.H., Rojat G.: Realization of a smart electrolytic capacitor circuit, IEEE Ind. Appl. Mag., 2002, 8, (1), pp. 16–20
- Chen Y.-M., Chou M.-W., Wu H.-C.: Electrolytic capacitor failure prediction of LC filter for switching-mode power converters. Proc. 40th Annual Meeting IEEE Industry Applications Society, October 2005, vol. 2, pp. 1464–1469.
- Amaral A.M.R., Cardoso A.J.M.: An ESR meter for high frequencies. Proc. Int. Conf. on Power Electronics and Drives Systems, PEDS, 2005, pp.
 1628–163
1628–163 - D.W. Hart, «Power electronics,» Mc Graw Hill, 2010.
- N. Mohan,T. M. Undeland , W. P. Robbins, «Power Electronics: Converters, Applications and Design,» John Wiley and Sons, 2002.
- R.W. Ericson, D. Maksimovic, «Fundamental of power electronics,» Springer, 2001.
- A.M.R. Amaral, A.J.M Cardoso: «An ESR meter for high frequencies». Proc. Int. Conf. on Power Electronics and Drives Systems, PEDS, 2005, pp. 1628–1633.
- R. Chen, J.D.V. Wyk, S. Wang, W.G. Odendaal: Improving the characteristics of integrated EMI filters by embedded conductive layers. IEEE Trans. Power Electron., 2005, pp. 611–619.
- A.M.R. Amaral, A.J.M Cardoso: An experimental technique for estimating the ESR and reactance intrinsic values of aluminium electrolytic capacitors. Proc. Instrumentation and Measurement Technology Conf., IMTC 2006, April 2006, pp. 1820–1825.
Оригинал статьи:
Теги
ESR (эквивалентное последовательное сопротивление)ГенераторИзмерениеКонденсаторМоделированиеОсциллографЭлектролитический конденсаторСохранить или поделиться
Микроволны101 | Калькуляторы
Если в микроволновой вселенной есть что-то, что вам нужен другой калькулятор
напишите нам, и мы увидим
что мы можем сделать, чтобы включить его сюда. Обязательно проверьте нашу загрузку
область для вещей, которые мы не могли уместить в простой калькулятор HTML. Прямо сейчас у нас есть
Таблицы Excel для:
Обязательно проверьте нашу загрузку
область для вещей, которые мы не могли уместить в простой калькулятор HTML. Прямо сейчас у нас есть
Таблицы Excel для:
Преобразователь задержки / длины / фазы
Калькулятор емкости параллельных пластин
Синтез фильтров Чебышева с сосредоточенными элементами (N = 3, N = 4 и N = 5),
Расчет ВЧ сопротивления листа до трех металлических слоев,
Расчет трансформаторов полного сопротивления N-образного сечения,
Расчет и нанесение на график K-фактора, максимально доступного усиления, групповой задержки и многого другого.
больше из S-параметров (наша знаменитая таблица S-Parameter Utilities!)
Удивительная таблица коаксиальных кабелей
Каскадный анализ усиления, P1dB и коэффициента шума,
…….. и больше!
Также есть ссылки на калькуляторы на нашем Cool Страница ссылок.
Калькулятор заряда и энергии конденсатора
Легко рассчитайте заряд и энергию любого конденсатора с учетом его емкости и напряжения. Поддерживает несколько единиц измерения (mv, V, kV, MV, GV, mf, F и т. Д.) Для входов и выходов (J, кДж, МДж, Cal, kCal, эВ, кэВ, C, kC, MC и т. Д.) .).
Д.) .).
Использование калькулятора заряда и энергии конденсатора
Этот инструмент работает как вычислитель заряда конденсатора и как вычислитель энергии конденсатора , при этом требуемые входные данные одинаковы в обоих случаях: емкость и напряжение, протекающие через конденсатор. Он поддерживает широкий диапазон входных и выходных единиц измерения. Просто введите два необходимых измерения и выберите единицы измерения для энергии и заряда (или используйте значения по умолчанию).
Калькулятор использует известные уравнения (как описано ниже) и операции преобразования.
Заряд конденсатора, энергия, емкость и напряжение объяснения
Конденсатор состоит из двух параллельных проводящих (металлических) пластин, разделенных специальным изоляционным материалом, который называется «диэлектрик». Когда на пластины подается напряжение, одна пластина заряжается положительно по отношению к напряжению питания, а другая имеет равный и противоположный отрицательный заряд. Это приводит к уникальному качеству конденсатора, заключающемуся в том, что он содержит электрический заряд, как и аккумулятор. Электрический заряд , который может удерживать конденсатор, обозначается как Q (измеряется в кулонах (C)).
Это приводит к уникальному качеству конденсатора, заключающемуся в том, что он содержит электрический заряд, как и аккумулятор. Электрический заряд , который может удерживать конденсатор, обозначается как Q (измеряется в кулонах (C)).
Напряжение (В) — это просто разница электрического потенциала между двумя точками, измеряемая в вольтах (В). Способность конденсатора накапливать электрический заряд между пластинами называется емкостью , , обозначается как C и измеряется в фарадах (F), что равно 1 кулон / вольт.Он пропорционален размеру пластин и обратно пропорционален расстоянию между пластинами. Энергия (E) — это количество работы, которую может выполнить накопленный заряд, и измеряется в Джоулях, электрон-вольтах, калориях и т. Д.
Уравнения заряда конденсаторов
Из соотношений между зарядом (Q), емкостью (C) и напряжением (V) мы можем выразить формулу заряда емкости в виде следующих трех уравнений:
Первый показывает, как найти емкость на основе заряда и напряжения, второй — уравнение заряда конденсатора, а третий — уравнение напряжения конденсатора.
Формула энергии конденсатора
Энергию (или работу) конденсатора также можно рассчитать, если известны его емкость (C) и напряжение (V), используя уравнение:
где E — энергия (иногда пишется как W для работы).
Примеры расчета заряда конденсатора и энергии
Пример 1: Известно, что конденсатор на материнской плате компьютера имеет емкость 5 Фарад, а напряжение — 50 мВ.Какой заряд конденсатора в фарадах? Поскольку 1 кулон = 1 фарад-вольт, мы сначала преобразуем 50 мВ в 0,050 В, а затем применим уравнение заряда конденсатора C = Q · V = 5 · 0,050 = 0,25 C.
Конечно, при использовании нашего калькулятора заряда конденсатора вам не нужно будет выполнять эти преобразования единиц измерения, поскольку они обрабатываются для вас «на лету».
Пример 2: Конденсатор имеет градуировку 0,1 Фарад, и известно, что напряжение составляет 10 Ватт. Какая энергия у конденсатора? Мы просто подставляем в приведенное выше уравнение энергии конденсатора: E = 0. 1 · 10 2 /2 = 10/2 = 5 Дж (Джоули).
1 · 10 2 /2 = 10/2 = 5 Дж (Джоули).
Список литературы
[1] Специальная публикация NIST 330 (2008 г.) — «Международная система единиц (СИ)», под редакцией Барри Н. Тейлора и Амблера Томпсона, с. 52
[2] «Международная система единиц» (СИ) (2006, 8-е изд.). Bureau International des poids et mesures pp. 142–143. ISBN 92-822-2213-6
| Тип конденсатора |
CP: конденсатор, бумажный диэлектрик, постоянный ток (Hermetica…CA: конденсатор, байпас, красный радиопомех … CZ, CZR: конденсатор, проходной, радиоинтерфейс … CQ, CQR: конденсатор, фиксированный пластик (или Paper-Pl … CH: Конденсатор, фиксированный, металлизированный (бумага, бумага … CHR: конденсатор, фиксированный, металлизированная бумага, бумага … CFR: конденсатор, фиксированный, пластик (или металлизированный P … CRH: конденсатор, фиксированный суперметаллизированный пластик . .. CM) : Конденсаторы, фиксированные, слюдяные диэлектрики … CMR: конденсаторные, фиксированные, слюдяные диэлектрики, устанавливаемые … CB: конденсаторные, фиксированные, слюдяные диэлектрики, кнопки … CY: конденсаторы, фиксированные, стеклянные диэлектрики…CYR: конденсатор, фиксированный, со стеклянным диэлектриком, Estab … CK: конденсатор, фиксированный, керамический диэлектрик (Gene … CKR: конденсатор, фиксированный, керамический диэлектрик (Gen … CC, CCR: конденсатор, фиксированный, керамический) Диэлектрический … CDR: конденсатор, микросхема, многослойный, фиксированный, C … CSR: конденсатор, фиксированный, электролитический (твердый элемент … CWR: конденсатор, фиксированный, электролитический (тантал) … CL: конденсатор, фиксированный , Электролитический (нетвердый E … CLR: конденсаторный, фиксированный, электролитический (нетвердый … CRL: конденсаторный, фиксированный, электролитический (нетвердый … CU, CUR: конденсаторный, фиксированный, электролитический (Alumu. .. CM) : Конденсаторы, фиксированные, слюдяные диэлектрики … CMR: конденсаторные, фиксированные, слюдяные диэлектрики, устанавливаемые … CB: конденсаторные, фиксированные, слюдяные диэлектрики, кнопки … CY: конденсаторы, фиксированные, стеклянные диэлектрики…CYR: конденсатор, фиксированный, со стеклянным диэлектриком, Estab … CK: конденсатор, фиксированный, керамический диэлектрик (Gene … CKR: конденсатор, фиксированный, керамический диэлектрик (Gen … CC, CCR: конденсатор, фиксированный, керамический) Диэлектрический … CDR: конденсатор, микросхема, многослойный, фиксированный, C … CSR: конденсатор, фиксированный, электролитический (твердый элемент … CWR: конденсатор, фиксированный, электролитический (тантал) … CL: конденсатор, фиксированный , Электролитический (нетвердый E … CLR: конденсаторный, фиксированный, электролитический (нетвердый … CRL: конденсаторный, фиксированный, электролитический (нетвердый … CU, CUR: конденсаторный, фиксированный, электролитический (Alumu. ..CE: Конденсатор, фиксированный, электролитический (постоянный ток, алюминий … CV: конденсатор, переменный, керамический диэлектрик (T … PC: конденсатор, переменный (поршневой, трубчатый …) CT: конденсаторный, переменный, воздушный диэлектрик (Trimm … CG: конденсаторный, фиксированный или регулируемый, вакуумный дизель … ..CE: Конденсатор, фиксированный, электролитический (постоянный ток, алюминий … CV: конденсатор, переменный, керамический диэлектрик (T … PC: конденсатор, переменный (поршневой, трубчатый …) CT: конденсаторный, переменный, воздушный диэлектрик (Trimm … CG: конденсаторный, фиксированный или регулируемый, вакуумный дизель … |
См. Таблицу типов конденсаторов | .Окружающая среда | G B (наземный, безопасный) G F (наземный, фиксированный) G M (наземный, мобильный) N S (военно-морской, защищенный) N U (военно-морской, без укрытия) A IC ( Воздушный, обитаемый, грузовой) A IF (воздушный, жилой, истребительный) A UC (воздушный, необитаемый, грузовой) A UF (воздушный, необитаемый, истребитель) A RW (воздушно-десантный, поворотнокрылый) S F (космос, полет) M F (ракета, полет) M L (ракета, запуск) C L (пушка, запуск) | Коды окружающей среды |