Сопротивление лампочки формула. Формула расчета сопротивления нити лампы накаливания: ключевые аспекты

Как рассчитать сопротивление нити лампы накаливания. Какие факторы влияют на сопротивление лампы. Почему сопротивление холодной и горячей нити различается. Какие формулы используются для расчета.

Основные принципы расчета сопротивления лампы накаливания

Расчет сопротивления нити лампы накаливания — важная задача для понимания работы этих осветительных приборов. При этом необходимо учитывать несколько ключевых факторов:

• Сопротивление нити зависит от температуры — при нагреве оно значительно увеличивается
• Для холодной и горячей нити используются разные формулы расчета
• На сопротивление влияют параметры самой лампы — мощность, номинальное напряжение
• Точный расчет возможен только для конкретного режима работы лампы

Формула расчета сопротивления горячей нити

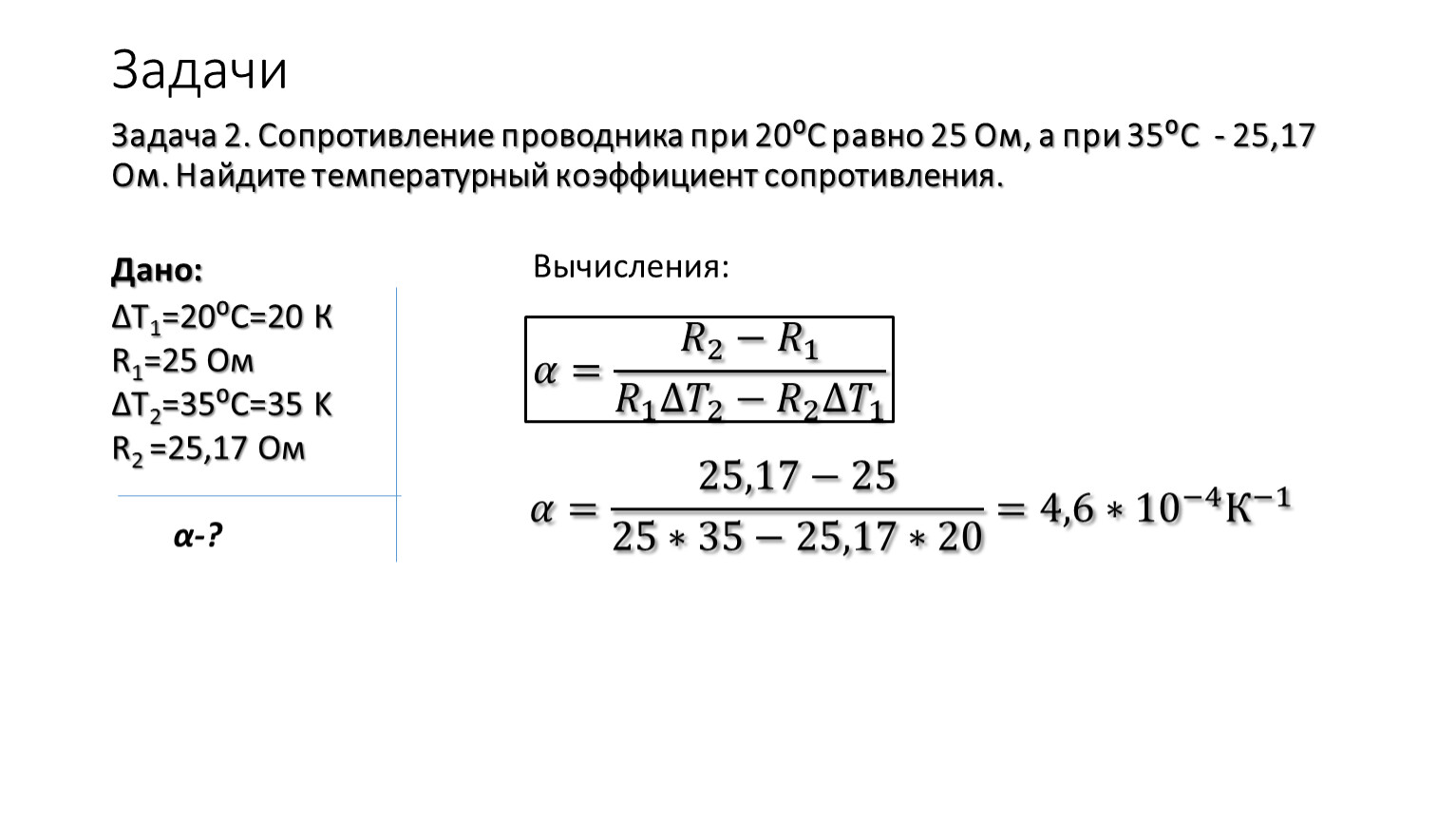
Для расчета сопротивления нагретой до рабочей температуры нити лампы накаливания используется следующая формула:

R = U^2 / P

Где:

• R — сопротивление нити (Ом)
• U — напряжение питания лампы (В)
• P — мощность лампы (Вт)

Особенности расчета сопротивления холодной нити

Сопротивление холодной (не нагретой) нити лампы накаливания значительно меньше, чем горячей. Для его приблизительной оценки можно использовать следующий подход:

1. Рассчитать сопротивление горячей нити по формуле выше
2. Разделить полученное значение на коэффициент 10-15

Таким образом, сопротивление холодной нити составляет примерно 1/10 — 1/15 от сопротивления нагретой нити. Точное значение зависит от конкретного типа лампы.

Факторы, влияющие на сопротивление нити лампы

На сопротивление нити лампы накаливания оказывают влияние следующие основные факторы:

• Температура нити — с ростом температуры сопротивление увеличивается
• Материал нити — обычно используется вольфрам
• Геометрические параметры нити — длина, диаметр
• Номинальные характеристики лампы — мощность, напряжение
• Наличие примесей в материале нити

Почему сопротивление горячей и холодной нити различается?

Существенное различие в сопротивлении нагретой и холодной нити лампы накаливания объясняется следующими причинами:

1. При нагреве происходит расширение металла нити, что увеличивает ее длину и уменьшает сечение
2. Повышение температуры приводит к увеличению амплитуды колебаний атомов кристаллической решетки металла
3. Возрастает рассеяние электронов на колеблющихся атомах, что повышает электрическое сопротивление

В результате сопротивление нагретой до рабочей температуры нити в 10-15 раз превышает сопротивление холодной нити.

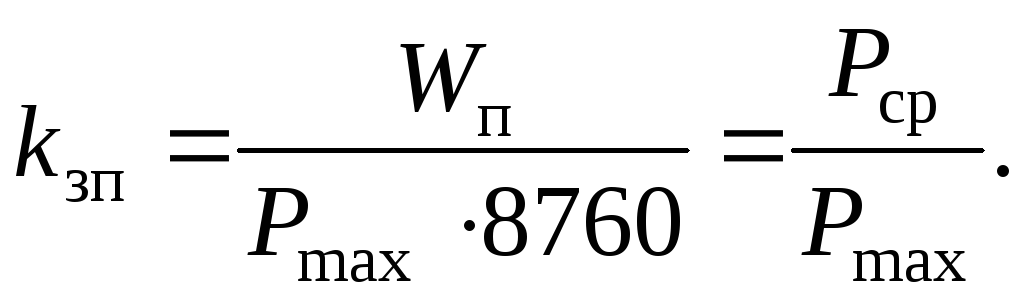
Пример расчета сопротивления лампы накаливания

Рассмотрим пример расчета сопротивления нити для лампы накаливания со следующими параметрами:

• Номинальное напряжение: 220 В
• Мощность: 100 Вт

Рассчитаем сопротивление горячей нити:

R = U^2 / P = 220^2 / 100 = 484 Ом

Оценим сопротивление холодной нити:

R холодной ≈ R горячей / 12 = 484 / 12 ≈ 40 Ом

Таким образом, сопротивление нагретой нити составляет 484 Ом, а холодной — около 40 Ом.

Ограничения формулы расчета сопротивления лампы

При использовании формулы для расчета сопротивления нити лампы накаливания необходимо учитывать следующие ограничения:

• Формула дает точные результаты только для номинального режима работы лампы
• При напряжениях, значительно отличающихся от номинального, возможны погрешности
• Не учитываются индивидуальные особенности конкретных экземпляров ламп
• Для очень малых напряжений формула может давать некорректные результаты

Практическое применение расчета сопротивления лампы

Расчет сопротивления нити лампы накаливания находит применение в следующих практических задачах:

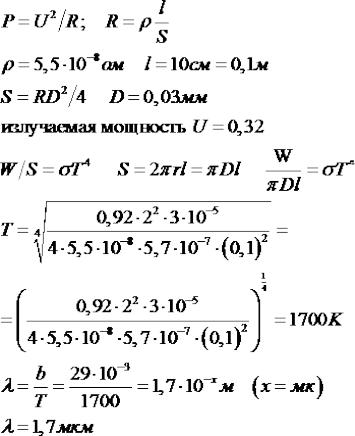
• Проектирование осветительных приборов и электрических цепей
• Расчет пусковых токов при включении ламп
• Оценка энергоэффективности и срока службы ламп
• Подбор защитных устройств в цепях с лампами накаливания
• Моделирование работы электрических схем с лампами

Альтернативные методы определения сопротивления лампы

Помимо расчетного метода, существуют и другие способы определения сопротивления нити лампы накаливания:

1. Прямое измерение омметром (для холодной нити)
2. Косвенное измерение по току и напряжению в рабочем режиме
3. Использование мостовых схем измерения
4. Применение специализированных приборов — измерителей сопротивления нити накала

Каждый из этих методов имеет свои преимущества и ограничения. Выбор конкретного способа зависит от требуемой точности и доступного оборудования.

Белые пятна лампы накаливания: Считаем сопротивление | СамЭлектрик.ру

Не смотря на обыденнность лампочки, не смотря на ее “повседневность”, особенности ее эксплуатации имеют то, что принято называть “белыми пятнами”.

В настоящий момент электрические параметры лампы накаливания невозможно рассчитать, если режим эксплуатации отличается от паспортного (от того режима на который лампочка спроектирована). Автор предлагает физическую модель, в рамках которой удается получить ряд формул, пригодных для решения широкого круга практических инженерных задач.

Статью не без оснований можно считать пусть маленьким, но вполне НОВЫМ словом в вопросах инженерно-практического применения таких “обычных но необычных” приборов, как лампочка накаливания.

Лампа накаливания

В указанной статье приведена формула, позволяющая обсчитывать параметры лампы накаливания в произвольных режимах, в том числе и в режимах, отличающихся от паспортных.

Формула зависимости напряжения и мощности лампочкиЭто основная формула статьи, вывод которой будет приведён ниже. Формула  выглядит так:

Это основная формула статьи, вывод которой будет приведён ниже. Формула  выглядит так:

Для любой лампы накаливания существует параметр, стабильный в широком диапазоне электрических режимов. Этим параметром является отношение куба напряжения к квадрату мощности.

Методика использования формулы проста.

Берем лампочку, читаем на колбе или на цоколе параметры,  на которые она расчитана  – напряжение и мощность, рассчитываем константу, потом вставляем в формулу любое произвольное напряжение и вычисляем мощность, которая выделится на лампочке.

Зная мощность, несложно вычислить ток.

Зная ток, несложно вычислить сопротивление нити накаливания.

Вот и рассмотрим вопросы, связанные с правильной эксплуатацией формулы, а так же с теми ограничениями, котрые неизбежны ввиду того что «абсолютных» формул просто не бывает.

Однако, сначала немножко «теории»…

Базовые «теоретические» предпосылки

Формула была получена в предположении того, что в металле (из которого состоит нить накаливания) ток и сопротивление имеют единую физическую сущность.

В упрощенном виде это можно рассуждать примерно так.

Сообразно современным воззрениям, ток представляет собой упорядоченное движение носителей заряда. Для металла это будут электроны.

Было сделано предположение, что электрическое сопротивление металла определяется  ХАОТИЧЕСКИМ движением тех же самых электронов.

С возрастанием температуры нити, хаотическое движение электронов возрастает, что, в конечном итоге, и приводит к возрастанию электрического сопротивления.

Еще раз. Ток и сопротивление в нити накаливания – суть одно и тоже. С той лишь разницей, что ток – это упорядоченное движение под действием электрического поля, а сопротивление – это хаотическое движение электронов.

Немножко «алгебраической схоластики»

Теперь,  когда с “теорией” покончено (улыбнулся), приведу алгебраические выкладки для вывода  «главной» формулы.

Каноническая запись закона Ома выглядит:

I  *  R  =  U

Для приведения в соответствие количественных значений, необходимо ввести соответствующие коэффициенты пропорциональности, для токовой компоненты – Кт и для резистивной компоненты – Кр:

Для приведения в соответствие количественных значений, необходимо ввести соответствующие коэффициенты пропорциональности, для токовой компоненты – Кт и для резистивной компоненты – Кр:

Самые общие соображения подвигают к мысли, что эти коэффициенты должны быть взаимно обратными величинами, а значит:

Самые общие соображения подвигают к мысли, что эти коэффициенты должны быть взаимно обратными величинами, а значит:

В этом случае, попарно перемножая правые и левые части (в системе уравнений),  мы возвращаемся к исходной записи закона Ома:

I * R = U

Окончательный вывод формулыРассмотрим подробнее систему уравнений:

Рассмотрим подробнее систему уравнений:

Возведем в квадрат первое уравнение и попарно перемножим их.

Возведем в квадрат первое уравнение и попарно перемножим их.

В левой части мы видим выражение для мощности, а так же памятуя о том, что произведение коэффициентов равно единице, окончательно перепишем:

В левой части мы видим выражение для мощности, а так же памятуя о том, что произведение коэффициентов равно единице, окончательно перепишем:

Отсюда получим выражение для токового коэффициента:

Отсюда получим выражение для токового коэффициента:

И для резистивного коэффициента (они взаимообратны):где Рном и Uном – это номинальные мощность и напряжение, маркированные на цоколе или на колбе лампы.

И для резистивного коэффициента (они взаимообратны):где Рном и Uном – это номинальные мощность и напряжение, маркированные на цоколе или на колбе лампы.

Осталось подставить эти значения коэффициентов в “РАСЩЕПЛЕННУЮ” формулу Закона Ома, и мы получим окончательные выражения для тока и сопротивления.

Осталось подставить эти значения коэффициентов в “РАСЩЕПЛЕННУЮ” формулу Закона Ома, и мы получим окончательные выражения для тока и сопротивления.

Домножая последнее соотношение на Ux, получим:

Домножая последнее соотношение на Ux, получим:

Чтобы не забивать себе голову этими квадратами, кубами и  корнями, достаточно запомнить простую зависимость, которая вытекает из последнего соотношения . Возводя  последнее соотношение  в квадрат, мы получаем ясную и понятную формулу:

Чтобы не забивать себе голову этими квадратами, кубами и  корнями, достаточно запомнить простую зависимость, которая вытекает из последнего соотношения . Возводя  последнее соотношение  в квадрат, мы получаем ясную и понятную формулу:

Для любой лампочки с вольфрамовой нитью накала отношение куба напряжения  к квадрату мощности является величиной ПОСТОЯННОЙ.

Полученные соотношения показали прекрасное соответствие практическим результатам (измерениям) в широком диапазоне изменения параметров напряжения и для весьма различных типов ламп накаливания, начиная от комнатных, автомобильных и заканчивая лампочками для карманных фонариков…

Некоторые общие рассуждения по сопротивлению лампочек накаливания

Безусловно,  для малых значений напряжения (когда приложенное напряжение ЗНАЧИТЕЛЬНО отличается  от паспортного), наши формулы будут “подвирать”.

Например, при расчете сопротивления комнатной лампочки накаливания 95W , 230V, подключенной  к источнику напряжения 1 вольт, формула

Например, при расчете сопротивления комнатной лампочки накаливания 95W , 230V, подключенной  к источнику напряжения 1 вольт, формула

дает значение сопротивления нити 36,7171 ом.

Если предположить, что мы подали на лампу напряжение 0,1 вольта, то расчетное сопротивление  нити составит 11,611 ом…

Интуиция подсказывает, что дело обстоит не совсем не так, а скорее совсем не так…

В области малых напряжений формула будет стабильно “низить” значение расчетного сопротивления по сравнению с фактическим, и дело тут вот в чем…

В рассматриваемой концепции неявно предполагается, что хаотическое движение электронов “ЗАМРЕТ” при отсутствии внешнего приложенного напряжения. Однако, очевидно, что движение электронов не  “замирает” даже в отсутствие приложенного внешнего напряжения (если лампа просто лежит на столе  и никуда не включена).

Хаотическое движение электронов имеет ТЕПЛОВУЮ природу и обусловлено ЕСТЕСТВЕННОЙ ТЕМПЕРАТУРОЙ нити накаливания.

Этот момент формулой не учитывается и прямое измерение сопротивления нити прибором неизбежно покажет отличие измеренного значения сопротивления против расчетного.

Излучение и КПД лампочки накаливания

Прежде чем разобраться с вопросом применимости формулы для обсчета режимов “малого напряжения”,  следует акцентировать внимание на один момент.

Лампочка представляет собой почти идеальный преобразователь электрической мощности в лучистую  энергию.

То обстоятельство, что разработчики лампочек упорно бьются за повышение КПД лампочки, никоим  образом не влияет на данное утверждение. Лампа накаливания – идеальный преобразователь электрической мощности в излучение.

Дело в том, что разработчики стремятся повысить выход СВЕТОВОЙ энергии, и именно в этом смысле  вычисляют КПД. Разработчик стремится повысить коэффициент преобразования электрической  мощности именно в СВЕТОВОЕ излучение, в излучение, находящееся в видимом диапазоне.

Этот КПД у лампочки действительно МАЛ. Однако лампочка прекрасно излучает ВО ВСЕМ спектре и очень много в инфракрасном диапазоне, там, где наш глаз не видит.

Для расчета сугубо электрических параметров нам совершенно не важно, В КАКОМ диапазоне излучает лампочка. Нам важно лишь помнить, что лампочка ИЗЛУЧАЕТ ВСЕГДА, если только на нее подано хоть какое-то (пусть даже самое малое) напряжение. И важно помнить, что подводимая мощность рассеивается именно в форме излучения.

Сколько электрической мощности подано на лампу, именно ТАКАЯ мощность и рассеется в форме излучения.

Закон сохранения энергии никто не отменял и второй закон термодинамики тоже никто не отменял. А значит, сколько прибыло – столько и убыть должно. И убудет именно в форме излучения, ибо больше энергии деваться просто НЕКУДА – только в излучение. Это очень важное обстоятельство.

Конструктивно нить накаливания представляет собой тонюсенькую вольфрамовую проволочку диаметром порядка 50 микрон и длиной порядка полуметра, свернутую в в спиральку замысловатой конфигурации.

Вакуум в колбе исключает возможность конвекционного теплообмена – ТОЛЬКО ЧЕРЕЗ ИЗЛУЧЕНИЕ.

Конечно, какая то доля тепла уходит через усики лампы, на которой крепится спиралька, но это мизер.

Чтобы наглядно представить себе эту малость, можно провести аналогию.

Повторю, сама вольфрамовая ниточка – аккурат размером с волосок из косички первоклассницы 50 см  в длину и 50 микрон в диаметре.

Если наглядно увеличить этот волосок.… это как если мы имеем проводочек диаметром 1 мм и длиной  10 метров! Здравый смысл подсказывает, что охлаждаться этот проводок вовсе НЕ путем теплообмена на краях. Да, что-то уйдет и в местах контакта, но основная мощность рассеется по всей длине проводка.

Для случая спирали, расположенной в вакууме, вся мощность уйдет В ИЗЛУЧЕНИЕ и не важно в каком  диапазоне спектра…

Важный эксперимент с измерением сопротивления Омметром

Любой, даже самый маленький ток БУДЕТ оказывать тепловое воздействие на проводок, НАГРЕВАЯ его…

Измеряя тестером сопротивление лампочки мы… пропускаем через нее ТОК. Ток от тестера маленький, но он ЕСТЬ. Следовательно, измеряя сопротивление нити, мы НАГРЕВАЕМ нить и, как следствие этого, меняем значение параметра самим фактом измерения.

Грубо говоря, тестер ТОЖЕ ВРЕТ. Тестер показывает НЕ ИСТИННОЕ значение сопротивления спирали.

Для того чтобы убедиться в этом обстоятельстве, можно проделать несложный эксперимент. Это доступно любому.

Можно ОДНИМ И ТЕМ ЖЕ тестером отобрать две лампочки с одинаковыми (близкими) значениями “холодного” сопротивления нити, и измерить сопротивление ДВУХ лампочек сначала каждую порознь, а потом соединенных последовательно.

Неоднократные измерения показывают, что сумма сопротивлений, измеренных порознь, НЕ СОВПАДАЕТ с суммарным сопротивлением последовательного включения…

Еще раз.

Мы измеряем сопротивления лампочек порознь.

Затем мы измеряем сопротивление последовательного включения.

И мы  УСТОЙЧИВО наблюдаем, что сумма сопротивлений измеренных “по одиночке” оказывается БОЛЬШЕ чем суммарное сопротивление лампочек, включенных последовательно.

Прибор один и тот же, диапазон измерения не переключался, так что методические погрешности измерения исключаются.

И все становится ПОНЯТНО.

Последовательное сопротивление двух спиралей УМЕНЬШАЕТ ток  от тестера, и нити нагреваются меньше.

А когда мы меряем лампочки порознь, то ток измерения больше и соответственно увеличиваются показания прибора за счет пусть даже небольшого, но УВЕЛИЧЕНИЯ температуры нитей вследствие нагрева в процессе измерения…

Раньше (четверть века назад, когда еще цифровые тестеры были экзотикой) было невозможно стрелочным индикатором уловить эту разницу. Сейчас в любом доме имеется  китайский цифровой тестер и любой человек, может проделать этот несложный эксперимент.

Разница в сопротивлениях невелика, но разница ОЧЕВИДНА, что исключает даже намек на возможную некорректность опыта.

Я подключил лампочки, подключил тестер и сфотографировал результаты таких экспериментов. На фотографиях прекрасно видно, что тестер показывает пониженное сопротивление лампочек, включенных последовательно.

Измерение сопротивления первой лампочки. 72 Ом.

Измерение сопротивления второй лампочки. 65,2 Ом.

На фотографиях для бытовых лампочек 60 Ватт 220 Вольт сумма сопротивлений, измеренных порознь:  72,0  +   65,2   =  137,2 ом.

Однако, измеряя сопротивление последовательно, прибор “низит” показание  до 136,8 ом!

Измерение сопротивления двух последовательно соединенных лампочек. 136,8 Ом

Аналогичная картина наблюдается для гирляндных лампочек:

Первая лампочка

Вторая лампочка

Две лампочки последовательно

Вывод. Расчетная формула показывает ЗАНИЖЕННОЕ значение сопротивления “холодной” спирали.

Измерение тестером показывает ЗАВЫШЕННОЕ сопротивление “холодной” спирали.

Возникает естественная мысль – Как страшно жить!!! Кому верить?

\смеюсь\

Попробуем разобраться в этом вопросе…

Мощность излучения по отношению к окружающему фону

Оценим мощность излучения лампы, соответствующую температуре окружающего фона.

Известно, что постоянная Стефана-Больцмана  σ = 5,670373·10-8 , тогда мощность излучения с квадратного метра

Р = σ SТ4

В качестве произвольного оценочного значения примем диаметр спирали 40 микрон, а длину 50 см. Температура нормальных условий 293К (20С). Подставив эти данные в формулу Стефана-Больцмана, получим мощность излучения при температуре 0,026258 Ватт.

Для интереса вычислим мощность при некоторых различных температурах окружающей среды:

Минус 40   (233К)                              0,0105 Ватт

Минус 20   (253К)                             0,0146 Ватт

Нуль           (273К)                              0,0198 Ватт

Плюс 20     (293К)                            0,026258 Ватт (норм.условия)

Плюс 40     (313К)                             0,0342 Ватт

Для курьеза можно привести расчет излучения лампы, когда температура окружающей среды равна 2300К:

Р =  99,7 Ватт.

Что вобщем неплохо согласуется с реальным положением вещей – лампа, расчитанная на 100 ватт нагревается до температуры 2300К.

Можно с высокой долей уверенности заявить, что данная геометрия спирали соответствует  «стоваттной» лампочке, рассчитанной на 220 вольт.

А теперь пересчитаем эти величины мощностей к «приведенному» напряжению. Как если бы температура окружающей среды соответствовала Абсолютному Нулю, а к лампе было приложено некоторое напряжение, нагревающее спираль.

Для пересчета используем полученное соотношение что напряжения и мощности соответствуют степеням «три» и «два».

Из таблицы видно, что “токовая” мощность лампочки при напряжении  на ней 0,902…Вольт нагревает спираль до температуры 293К. Аналогично, “токовая” мощность при напряжении 1,0758 Вольт нагреет спираль до температуры 313К (на 20 градусов выше).

Повторю еще раз, это при условии, что температура окружающей среды равна Абсолютному Нулю.

Вывод. Весьма малое изменение напряжения оказывает значительное влияние на температуру нити. Изменили напряжение на каких то семнадцать сотых Вольта (1,0758 – 0,902 = 0,1738) а температура возросла на 20 градусов.

Эти расчеты  весьма условны, но в качестве ОЦЕНОЧНЫХ величин их можно использовать.

Оценка естественно очень грубая, ибо закон Стефана-Больцмана описывает излучение «идеального» излучателя – абсолютно черного тела (АЧТ), а спираль весьма отличается от АЧТ, но, тем не менее, получили «цифирь» весьма правдоподобную…

Из экселовской таблички видно, что уже при напряжении на лампе 1 вольт, температура спирали будет 40 градусов по Цельсию. Приложим больше, будет больше.

Напрашивается естественный вывод, что при напржении 10-15 вольт нить будет достаточно горячая, хотя визуально это не будет видно.

На глаз нить будет казаться «ЧЕРНОЙ» (холодной) вплоть до температур 600 градусов (начало излучения в видимом диапазоне).

Желающие «погонять цифирь» могут это сделать самостоятельно, используя формулу Стефана- Больцмана.

Результаты будут условными, ввиду того что (как было сказано выше) спираль имеет некоторое альбедо и не соответствует излучателю АЧТ, НО(!)  оценка температур будет вполне достоверной…

Повторю – именно ОЦЕНКА. Нить начинает светиться примерно с 20 вольт.

Дополнительно хотел бы обратить внимание на разброс параметров лампочек.

На фотографии с тестером, маленькие лампочки (гирляндные) были мной отобраны и откалиброваны весьма тщательно. Для разных измерительных целей и опытов. Потому то они и показывают одинаковое сопротивление, что называется «пуля в пулю».

А вот большие лампочки, я их просто принес из магазина, не отбирая по параметрам и хорошо видно, что разброс магазинных лампочек наблюдается в весьма широком диапазоне. Вплоть до 10%.

Это обстоятельство дополнительно указывает, что погрешности расчета оказываются МЕНЬШЕ чем реальный разброс лампочек.

Некоторые дополнительные формулы

Выше я вывел формулу, что для любой лампочки отношение куба напряжения к квадрату мощности – есть величина постоянная .

Исключительно в целях удобства предлагаю представить эту константу в виде квадрата некоторой величины.  Назовем ее параметром S и перепишем главную формулу

Исключительно в целях удобства предлагаю представить эту константу в виде квадрата некоторой величины.  Назовем ее параметром S и перепишем главную формулу

Удобства предлагаемой методики просматриваются вот в каком аспекте. Поскольку параметр S оказывается неизменным в широком диапазоне напряжений, то открывается возможность обсчитывать схемы из лампочек, скомбинированных произвольным образом.

Для этого будет полезен ряд формул, которые легко выводятся самостоятельно.

Для этого будет полезен ряд формул, которые легко выводятся самостоятельно.

Для последовательного и параллельного сопротивления можно использовать формулы:

Для последовательного и параллельного сопротивления можно использовать формулы:

Схема  с балластным сопротивлением

Для случая, когда лампа включается последовательно с балластным резистором, для расчета напряжение на ней необходимо решить простенькое квадратное уравнение приведенного вида:

U  + ( Rрезист / Sлампы) * корень(U)  =  U питания.

Вывод формулы с балластным сопротивлением

На рисунке представлен порядок вывода формулы для случая, когда лампа последовательно соединена с балластным сопротивлением. Ток через лампу и через сопротивление одинаков.

Выражения для токов приравниваются. Небольшие алгебраические преобразования.  И получается окончательное квадратное уровнение относительно неизвестного Us.

Из рисунка понятно, что Us это напряжение на лампе.

#самэлектрик

Если интересно, оригинал статьи и обсуждение — ЗДЕСЬ.

Подписывайся, вступай в группу!

Закон Ома

— пожалуй самый наиболее используемый закон в электронике.

Многих начанаяющих отпугивает его строгая книжная формулировка, за которой кроется простота его применения.

Закон Ома гласит: величина тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению:

 

U=IxR; R=U/I; I=U/R;
где I — это ток в цепи, измеряется в Амперах
   U — это напряжение, измеряется в Вольтах
   R — это сопротивление, измеряется в Омах

Данная формула очень проста, чтобы было проще её запомнить, вы можете нарисовать себе на лююбом листке бумаги треугольник, котрый вы видите ниже. Это магический треугольник закона Ома — закрыв величину, которую вам необходимо найти, на оставшейся части треугольника вы увидите необходимую вам формулу.

 

 

например, мы знаем рабочий ток и напряжение лампы (на лампочках для фонариков они указываются прямо на цоколе). Как же найти сопротивление нити накаливания этой лампы? Все просто, закрываем сопротивление в треугольнике и видим, что остается напряжение деленное на ток:

Дано:

Источник тока 6.3 В (Вольта) (Аккамулятор)

Лампа на 6.3 Вольта, 100 мА (мили Ампер)

 

Согластно формуле получаем ответ: 6.3/100 = 0.63 Верблюда.

 

Лирическое отступление 1:

Почему верблюды? Да потому что Вольты нужно делить на амперы, а мили Волты делить на мили амперы, а микро Вольты делать на микро Амперы. При несоблюдении данного условия итог у нас будет выражен верюлюдами и кол-вом съеденных вашей бабушкой яблок, на её шестнадцатилетие.

 

Ну так вот, сделаем правильно – 6.3 В / 0.1 А,если кому понравится 6300 мВ делим на 100 мА – должен получится искомый результат. А ежли уж и совсем невтерпёж всё это можно перевести микро Вольты и микро Амперы.

Лирическое отступление 2:

Для пытливых умов будет нелишним знать, что полученный результат будет верен для работающей (включенной) лампочки. Сопротивление же холодной нити накала будет гораздо меньше.

 

Лирическое отступление 3:

Кстати лампы накаливания иногда используются как стабилизаторы тока.

 

Чтобы лучше понять слова напряжение, сопротивление приведу пример:

Представим насос, у которого есть вход и выход для воды – пусть это будет у нас источником тока с производительностью 12 литров воды… Извиняюсь – 12 Вольт. Далее трубой соединяем вход с выходом помпы и заливаем в систему воду. Итак, мы получаем самую простую гидравлическую систему. Когда насос включен, вода начинает циркулировать по кругу, чем больше мы даем мощности насосу, тем быстрее эта вода циркулирует. Так вот в данном случае скорость воды на определенном участке — это ток, а толщина трубы, от которой зависит сколько воды пройдет через её сечение это сопротивление цепи, а напряжение это количество этой воды во всей системе, являющееся по своей сути мощностью насоса, выраженной в литрах на отрезок времени.

 

Данный пример я привел в качестве показательного и все характеристики цепи нельзя представить в виде воды и помпы.

Теперь есть такое понятие как мощность, P — эта величина характеризует количественный показатель выполняемой работы так сказать. P = UxI; P = I²xR, тоесть ток в квадрате.

 

А теперь давайте разберемся, что же это все-таки значат все эти примудрости в простой форумуле, а именно, два сложноватых для понимания выражения: прямо пропорциональна и обратно пропорциональна.

Что же значит «величина тока прямо пропорциональна напряжению»? А это значит, что при увеличении напряжения цепи, увеличивается и сила тока. То есть, чем больше напряжение, тем больше ток. Всё это справедливо для участка цепи при неменяющимся напряжении.

Что касается «обратно пропорциональна его сопротивлению», то здесь все наоборот. Чем больше сопротивление цепи, тем меньше в ней ток. Это справедливо при неизменяющимся сопротивлении.

Рассматривая этот закон применительно к фонарику с лампой накаливания и тремя круглыми батарейками начертаем схему:

 

Электрическая схема фонарикус-вульгарус (фонарик обыкновенный):

GB1 — GB3 — источник тока (три батарейки)

S1 — выключатель

HL1 — лампочка

Согластно закону Ома: величина тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению. Рассмотрим участок цепи, состоящий их лампочки.

Теперь простой вопрос: от чего зависит яркость лампочки? Правильно — от силы тока, проходящего через нить накаливания этой лампочки. То есть яркость свечения лампочки мы можем использовать как наглядный показатель силы тока в цепи фонарика.

И действительно, какова будет яркость лампочки если заменить одну батарейку перемычкой?

«Естественно… она будет гореть тусклее!» — скажите Вы и будете правы. Вот собственно это и есть демонстрация фразы: «величина тока на участке цепи прямо пропорциональна напряжению». Чем больше батареек мы подключим (то есть чем большее напряжение приложим) к одной и той же лампочке, тем ярче она будет гореть ( и тем больший ток по ней протекает).

Решение задач на закон Ома для участка и полной цепи

Решение задач на закон Ома сводится к нахождению одной из трех неизвестных составляющих: тока, сопротивления или напряжения. Сам же закон описывает, как они соотносятся между собой.

Напомним, что согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

Формула закона Ома для участка цепи:

Формула закона Ома для полной цепи:

Задача 1

Утюг включенный в сеть напряжением 220 В, потребляет ток 1,2 А. Определите сопротивление утюга.

Дано  U = 220 В I = 1,2 А	Решение Согласно закону Ома для участка цепи:
Найти R — ?
Ответ: R = 183,3 Ом.

Задача 2

К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.

Дано  E = 12 В I = 0,5 А Rл = Rр/2 Rр = 10 Ом	Решение Найдем экв. сопротивление двух параллельно соединённых резисторов: Сопротивление лампочки: Согласно закону Ома для полной цепи:
Найти r — ?
Ответ: r = 14 Ом.

Задача 3

К участку цепи с напряжением 12 В через резистор сопротивлением 2 Ом подключены десять одинаковых лампочек сопротивлением 10 Ом. Найти напряжение на каждой лампочке.

Дано  Uобщ = 10 В Rр = 2 Ом Rл = 10 Ом	Решение Так как лампочки подключены параллельно, напряжение на них будет одинаковым, согласно закону Ома для участка цепи: При последовательном соединении ток в цепи общий: Выразим Uл через Uобщ: Найдем Rэкв: Окончательно получим:
Найти Uл — ?
Ответ: Uл = 4 В.

Задача 4

Как определить длину мотка медной проволоки, не разматывая его?

Решение:

Для решения данной задачи необходимо воспользоваться формулой:

отсюда длина проволоки

В этой формуле, l – длина проволоки, R – сопротивление, S – площадь поперечного сечения, ρ – удельное сопротивление металлов, в данном случае ρ для меди равно 0.0175 Ом/м.

Сопротивление R проволоки можно измерить с помощью омметра, а площадь S с помощью штангенциркуля, измерив  диаметр проволоки и по формуле Πr² вычислив ее значение. Значение удельного сопротивления ρ не только для меди, но и других металлов можно найти в справочнике, или тут. Подставив все известные величины в формулу, приведенную выше, получим длину проволоки.

Задача 5

Начертите схему электрической цепи, состоящей из источника тока, выключателя и двух ламп, включенных параллельно. Что произойдет в цепи при перегорании одной лампы?

Решение:

При перегорании одной из лампочек, вторая будет гореть, так как, при параллельном включении проводников токи I₁ и I₂ проходящие через них не зависят друг от друга и при разрыве параллельной цепочки ток продолжает протекать.

Просмотров: 49158

№10 Мощность лампы накаливания

ЛАБОРАТОРНАЯ РАБОТА № 10

Тема: «Исследование зависимости мощности, потребляемой лампой накаливания, от напряжения на её зажимах»

Цель: провести исследования зависимости между напряжением и мощностью на лампе накаливания, а так же выяснить, как зависит температура накала лампы от потребляемой мощности.

Оборудование: электрическая лампа, источник постоянного напряжения, реостат ползунковый, амперметр, вольтметр, ключ, соединительные провода.

Теоретическая часть

Мощность тока – величина, характеризующая, с какой скоростью совершается работа тока. Так как работа тока может быть определена по формуле

А= ∙U ∙ t ,

то мощность тока P можно вычислить, зная величину тока  и напряжение U:

( 1 ) P =U ∙ I [ P ] = Вт

Из формулы видно, что мощность тока зависит от напряжения.

Если в цепь подключено несколько потребителей, то мощность во всей внешней цепи при любом соединении равна сумме мощностей на отдельных участках цепи. При работе электрических приборов ток оказывает тепловое действие, которое влияет на их сопротивление, а значит и на потребляемую мощность.

Исследуем данные зависимости экспериментально.

Порядок проведения работы:

1. Составить цепь по схеме, изображенной на рисунке

2. При помощи реостата установить наименьшее значение напряжения и замкнуть цепь. Записать показания вольтметра и амперметра.

3. Постепенно выводя реостат, записывать значение напряжения и силы тока, сняв еще 2 показания.

4. Для каждого значения напряжения мощность, потребляемую лампой, подсчитать по формуле: P=U∙ I.

5. Для каждого опыта подсчитать:

а) сопротивление нити лампы в рабочем состоянии R_T= ;

б) изменение температуры нити лампы по формуле ,

где — температурный коэффициент сопротивления вольфрама;

R₀– сопротивление нити лампы при 0С (узнайте у преподавателя),

в) температуру накала лампы вычислить по формуле Т=Т₀+Т.

№ опыта	Напряжение на зажимах лампы U, В	Сила тока в лампе I, А	Мощность, потребляемая лампой P, Вт	Сопротивление нити накала RТ, Ом	Температура накала Т, К
1
2
3

7. По окончанию работы сделать вывод.

ОТЧЕТ ПО РАБОТЕ:

Контрольные вопросы

1. Сформулируйте физический смысл мощности.

2. Какие формулы для нахождения мощности электрической цепи вам известны? Какие из приведённых формул удобно использовать при последовательном и параллельном соединениях потребителей электрического тока? Почему?

3. Используя формулу , предложите дополнительную единицу измерения работы. Где вы встречали данную единицу измерения? Свяжите эту единицу с системной единицей работы.

4. а) Как называют прибор, используемый для измерения мощности тока?

б) Как называют прибор для измерения работы тока? Где вы с этим прибором встречались?

ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.Сформулируйте физический смысл мощности.

2. Какие формулы для нахождения мощности электрической цепи вам известны? Какие из приведённых формул удобно использовать при последовательном и параллельном соединениях потребителей электрического тока? Почему?

3.Используя формулу , предложите дополнительную единицу измерения работы. Где вы встречали данную единицу измерения? Свяжите эту единицу с системной единицей работы.

4. а) Как называют прибор, используемый для измерения мощности тока? б) Как называют прибор для измерения работы тока? Где вы с этим прибором встречались?

Сопротивление автомобильной лампочки 12 вольт – АвтоТоп

При замене штатной лампы накаливания на светодиодную автомобильную лампу Вы столкнулись с проблемой бортового компьютера? Он начал выдавать ошибку, «неисправность лампы»? Т.е. срабатывает система определения неисправностей. Она находится во многих современных автомобилях и сигнализирует о том, что какая-либо лампа вышла из строя. Происходит это по тому, что светодиодные лампы потребляют намного меньше энергии, чем галогеновые, на которые данная система и рассчитана.

Чтобы решить эту проблему надо установить специальный нагрузочный резистор. В народе его попросту называют «обманкой». Он создает нужную нагрузку в сети для исчезновения ошибки о замене ламп. Его мощность, в сумме с мощностью светодиодной лампы дает такое количество ватт, которое не выходит за рамки погрешностей систем контроля.

Вы установили светодиодные лампы в поворотники и при этом реле поворотов срабатывают чаще, как бывает при перегорании лампы. Происходит это из-за того, что реле поворотов рассчитаны на стандартные галогеновые лампы, которые потребляют гораздо больше мощности, чем светодиоды. Для того чтобы избавиться от нежелательного эффекта увеличения частоты мигания поворотов так же требуется установить резистор «обманку»

Установка довольно проста. Дополнительное оборудование не требуется. Благодаря этому монтаж можно произвести самостоятельно. В комплекте поставки имеются специальные коннекторы, с помощью которых и осуществляется подсоединение обманки к цепи лампы.

Нагрузочный резистор подойдёт к любой марке автомобиля!

Но стоит обратить внимание на то, что при работе резистор выделяет большое количество тепла. Поэтому рекомендуется устанавливать его к металлической поверхности на некотором расстоянии от легко плавящихся элементов.

У нас в наличии находятся два вида обманок. Первый вид является уже готовым к установке решением. Эти резисторы могут выполнять свои функции в поворотных огнях и стоп-сигналах.

Со вторым видом дела обстоят немного сложнее. Такие резисторы можно обозначить – «для профессионалов». Их монтаж необходимо проводить самостоятельно. Для этого в составе комплекта имеются специальные клеммы. Такие обманки применяют в противотуманных фарах и фарах ближнего или дальнего света.

Для тех кто думает что запись просто о замене ламп — вы ошибаетесь. Проблема оказалась куда глубже… Впрочем дальше вы все поймете 🙂

Сразу предупреждаю — букв будет очень много. Так что кому интересно — попытайтесь осилить 🙂 Для ленивых — совсем самое основное выделено жирным 🙂 Проблема, описанная тут думаю не у меня одного, да и вдруг кто то столкнется в дальнейшем.

Итак, одним прекрасным (ну или может быть не очень) днем, заметил я одну не очень приятную вещь — лампочки в стопах вместо красного света светили каким то непонятным бело-желто-розовым. Вытащив лампочку на свет присмотрелся и увидел что все красное напыление с нее просто выгорело. Ну точнее почти всё. Причина, по которой мне нужны именно красные лампы описана тут.
Кажется нужна то мелочь, либо купить такие же красные, либо поставить светодиодные. Первый вариант откинул сразу. С этими лампами я проездил полгода, но когда они выцвели — неизвестно — может день назад, а может через день после установки. Поэтому выбор мой пал на вариант номер 2 — установка светодиодных ламп. Тут опять же есть проблема — светодиоды имеют направленный пучок света, в отличии от обычной лампочки, у которой свет рассеянный, и могут смотреться просто как красные точки, что не есть безопасно при торможении. Но, на счастье, в магазине было замечено несколько видов красных ламп, у которых светодиоды стоят по кругу, то есть на отражатель будут попадать и светиться будет полностью весь стоп. После долгого перебора выбор мой пал вот на такие лампы:

Дел, кажется, буквально на 5 минут, вытащить лампы обычные и поставить светодиодные. Чем я сразу же и занялся. Вытащил левый патрон и плафона, вынул лампу, и попутно обнаружил что все таки китайские патроны дрянь, благо остались у меня еще от оригинальных осваров нормальные патроны, так что его под замену

Ну да это небольшое отступление. Поставил я обе светодиодных лампы, и вот тут то и началось все это веселое приключение, затянувшееся на 5 дней. Машина заглушена, стоит спокойно, а стопы светятся. Так, слегка, в полнакала, но горят. При нажатии на тормоз — загораются в полную силу. Вытаскиваю один светодиод, ставлю обычную лампу — все в порядке. Ясен пень, дело в сопротивлении, так как у диодов оно меньше, а у обычной лампы больше, то при одной лампе и одном светодиоде этого паразитного свечения нет.
Вот кстати для сравнения — диодный стоп и стоп с выгоревшей, бывшей когда то красной, лампой:

Но, все таки решил я погуглить что же это может быть, прав я или нет, и посправшивать людей на форумах. Поиски дали мало что, но все таки были такие же проблемы, сводилось все к сопротивлению. Хотя некоторые писали что может быть неисправен сам выключатель тормозных ламп, что лично мне показалось ерундой.
Итак, думал, думал я и вот что решил — если впаять в реле контроля исправности ламп (РКИЛ) вместо шунта резистор, то, наверное, это свечение светодиодов уйдет. Ну ладно, сказано — сделано. Везде пишут что паяется туда 1 Ом 1-3 Вт. Был куплен резистор 1Ом 2Вт и успешно внедрен вместо родного шунта. Процесс перепайки реле, и что и куда паять подробно описан тут.

Перепаял, пошел ставить (а надо сказать пошел уже третий день после покупки ламп). Поставил, радостный вставляю светодиоды в стопы, и… Нифига. Как светились, так и светятся. Хотя, конечно, ошибку БСК эта перепайка убрала, больше на светодиоды в стопах БСК не пищит.
Вернул обратно одну лампочку, чтоб ниче не светилось, пошел дальше искать решение проблемы.
Пришла мне в голову бешеная, идиотская идея — раз можно параллельно светодиоду поставить обычную лампу, чтоб он не светился, то вместо лампы можно поставить резистор, равный ей по номиналу. Где то даже откопал информацию что лампе 12V 21W соответствует резистор 6.8 Ом 20 Вт. Поехал в магазин. 6,8 не было, был 3,3. Купил. Увидев его размеры, что то как то желание ставить его отпало. Им убить можно, знаете ли…
По возвращении домой полез спрашивать народ на форумах. Господи, одному тебе известно сколько людей на форумах я задолбал своими глупыми вопросами. В итоге, все таки были даны мне дельные советы. Параллельно светодиоду подсоединить переменный резистор, крутить его от большего значения к меньшему, пока светодиоды не перестанут сами по себе светиться, замерить получившийся результат мультиметром и уже потом ставить постоянный резистор. Мощность резистора можно было рассчитать так — ток, потребляемый горящими стопами со светодиодами в амперах умноженный на напряжение (13-14 вольт).
Встал вопрос — а где же взять этот переменный резистор? ну понятно что они есть в магазинах… а вдруг дома тоже есть? Прицепился к маме, чтоб искала, благо подобной фигни дома много, правда ей уже лет по 30, но ведь главное чтоб работала, так? 🙂
Через час копаний на свет был извлечен переменный резистор, старше меня наверно раза в полтора, на 10 кОм

Вот и шикарно, не будет лишних трат)

Побежал замерять. Подцепил, кручу, верчу, светодиоды погасить хочу… Хоп, погасли! Меряем, что то около 5 кОм (решил на всякий случай взять поменьше, чтоб наверняка). Настало время мерять ток. Разъединил цепь на стоп в плюсе, щуп на клеммы, друг давит на педаль. 0.1 Ампер. То есть, постоянный резистор мне понадобится 4.5 кОм 1.4-1.5 Вт. Для перестраховки был куплен 4,7 кОм (не было 4,5) 2 Вт (оказывается — чем больше мощность резистора тем меньше он будет греться, запас важен).
Пошел ставить. Все говорят пайка, пайка… Я решил поступить по другому — резистор просто поджать в клеммы плюса и минуса стопов. Вытащил, переобжал, резистор на месте, все готово. Смотрю на стопы — паразитного свечения нет. Радости не было предела. Радовался как слон. Секунд 10, пока зажигание не включил. Стопы опять засветились. Да елки-бревна, че за напасть 🙁 как сразу не догадался что определять надо было на заведенной машине… И вот тут кстати выяснилась одна неприятная мелочь. Не знаю, видимо этот резистор как то повлиял, но БСК вообще никак не реагировал на отсутствие лампы. Ладно, главное не пищит, а у светодиодов срок службы должен быть большой, так что на первое время пойдет и так, дальше это все обязательно доработаю.
Так вот, увидев что стопы опять светятся, когда не надо, со злости выдернул резистор и подумал «а че я вообще сделал то? ну горели бы на заведенной машине, не страшно». Но, что не делается — все к лучшему. Не люблю, когда что то работает не так как должно, поэтому мне нужно было:
1) Срочная кото-терапия, для того чтоб успокоиться
2) Еще раз использовать переменный резиситор чтоб подобрать сопротивление правильно.

На российских дорогах часто можно встретить автомобили, владельцы которых заменили стандартные лампы на светодиодные. В отличие от традиционных ламп, светодиоды для автомобиля 12 вольт характеризуются более высокой светоотдачей и долговечностью. Эта инструкция призвана обучить автомобилистов правильно подключать светодиодные лампы, вся полезная информация, а также схема, представлены ниже.

Что нужно знать автолюбителю перед заменой?

Обычная светодиодная лампа

Перед тем, как вы решите подобрать и включить мощные и сверхъяркие светодиодные автомобильные лампы 12в вместо обычных, необходимо ознакомиться с основными данными. В первую очередь, поймите, что светодиод — это не лампа. Любые неправильные действия в процессе замены могут вызвать серьезные проблемы, и это касается не только диодных дамп, но и любых действий с проводкой в целом. В общем в этом процессе ничего сложного нет, но все-таки некоторые моменты следует учитывать.

Если вы решили подключить мощные и сверхъяркие автомобильные светодиодные лампочки, то учтите несколько нюансов:

1. Чтобы подключение было правильным, учитывайте напряжение бортовой сети. В авто этот показатель обычно составляет 12-13 вольт, если мотор заглушен и около 13-14.5 вольт, если мотор запущен.
2. Мощный и сверхъяркий мигающий светодиод обычно требует около 3.5 вольт напряжения, но здесь многое зависит от цвета. К примеру, желтые и красные диодные лампы потребляют около 2-2.5 вольт, в то время как белые, синие и зеленые — в районе 3-3.8 вольт. Если светодиодная лампочка для фары авто будет мощной, то типовой ток будет равен 350 мА, а если немощная — то около 20 мА.
3. Как показывает практика, не все автомобильные светодиоды, в отличие от традиционных ламп, позволяют должным образом осветить пространство вокруг. Данный момент необходимо учесть, если вы решили произвести замену диодных ламп в панели приборов. Кроме того, перед приобретением необходимо оценить тип линзы в лампе, возможно, есть смысл проконсультироваться с продавцом. К примеру, на узконаправленных диодных лампах расположена маленькая линза, это следует заранее проверить. Более оптимальным вариантом будет покупка нескольких видов, чтобы вы могли понять, какой из них вам более подойдет и какой нужен.
4. Любой диодный элемент 12 вольт имеет и плюс, и минус. Плюсом является анод, а минусом — катод (автор видео — TVTachki).

Помните о том, что вы не сможете просто извлечь автомобильную лампу из фары и включить мигающую диодную в бортовую сеть машины. Так вы его только сожжете, но результата не будет никакого. Также учитывайте, что автомобильные диодные элементы для фар и других целей разделяются по размерам, мощности, числу кристалликов, расположенных внутри. Кроме того, они обладают разной яркостью и цветом. В любом случае, в корпусе диодного компонента будет находиться полупроводниковый кристаллик, излучающий свет при прохождении напряжения через него.

Как делятся светодиоды для фар авто по мощности:

1. Маломощные диодные автомобильные элементы. Они не обладают охлаждением, поэтому являются менее долговечными. Кроме того, их использование в авто нецелесообразно, в основном они применяются в радиоаппаратуре.
2. Мощные диодные компоненты довольно долговечны, если вы будете правильно их использовать, то они могут прослужить около десяти лет. Также следует отметить, что такие мигающие диоды для фар авто почти не подвергаются нагрузкам.
3. Диодные автомобильные модули представляют собой алюминиевую пластинку, на которой расположен целый ряд светодиодов. Если пластина качественная, то ее стоимость будет довольно высокой. Что касается обычных китайских лент, то они сами по себе не мощные, соответственно, их использование актуально для подсветки вещевого ящика или приборной панели. Кроме того, они обладают пониженным ресурсом эксплуатации.

Учитывая все эти факторы, вы сможете определиться с тем, какой диод 12 вольт вам нужен. После этого можно приступать к подключению своими руками. Разумеется, если вы делаете это впервые, желательно использовать схему.

Схема подключения модуля для стоп-сигналов и габаритов

Подключаем светодиоды

Как правильно подключить лампочку на 12 вольт в авто своими руками? Неважно, мигающую или нет, в фару или панель приборов, об этом мы расскажем далее.

Рассмотрим пример подключения своими руками на модуле, учитывая несколько нюансов (схемы вы найдете ниже):

1. Панельки, то есть кластеры, рассчитываются на питание 12 вольт, такие устройства можно без проблем подключить к проводке авто и наслаждаться мигающими или просто яркими огоньками. Однако такие устройства обладают определенным недостатком — когда обороты мотора будут изменяться, яркость также будет то снижаться, то увеличиваться. Пусть это не критично, но глазу все же будет заметно. Но также нужно учесть, что такие кластеры хорошо светят тогда, когда напряжение в сети составляет 12.5 вольт, то есть если у вашем авто напряжение низкое, то светить лампочки будут слабо.
2. Сам по своей конструкции кластер состоит из самих диодов, а также резистора. Резисторы — это важный элемент любого кластера. На каждые три лампочки устанавливается один резистор, предназначенный для гашения лишнего напряжения. Если вы приобретаете ленту для фар, то, возможно, вам придется ее подрезать. При установке в фары нужно учитывать, что обрезать ленту необходимо в определенных местах.
3. Подключение светодиодов 12 вольт с резисторами в фары авто осуществляется последовательно. Вам необходимо сделать кластер, то есть подключить по очереди необходимое число лампочек друг к другу, а два вывода, которые будут находиться по краям — к сети авто. В этом случае речь идет о белых диодах, мощность которых составляет 3.5 W. То есть для сети с напряжением 12-14 вольт понадобится три лампочки, которые в общем будут потреблять не 12, а 10.5 вольт. Поскольку диоды обладают плюсом и минусом, последовательное соединение осуществляется таким образом, чтобы плюс одного элемента соединился с минусом другого (автор видео — Роман Щербань).

Пока еще кластер нельзя подключать напрямую своими руками, последовательно необходимо включить также резистор, то есть сопротивление. Показатель сопротивления должен быть равен 100-150 Ом, а мощность резистора должна составлять 0,5 Вт. Что касается резистора, то найти его — не проблема.

Подключение параллельно

При параллельном способе соединения своими руками вам потребуется подключить несколько цепей, каждая из которых будет состоять из трех лампочек и одного резистора сопротивления. В этом случае плюс подключается только к плюсу, соответственно, минус — только к минусу. Если подключается один автомобильный диод, то понадобится резистор с сопротивлением 550 Ом, для двух — сопротивление 300 Ом и т.д. Если информация вам непонятна, то изучите закон Ома.

Для сборки цепи своими руками вам потребуется только мультиметр.

Рассмотрим пример с диодом на 3.5 В и током 20 мА:

1. Сначала при помощи прибора следует произвести замеры показателя напряжения там, где вы планируете ставить лампу. Необходимо учитывать, что этот показатель может различаться в зависимости от места. К примеру, измерив напряжение, вы получаете 13 В.
2. Далее, от полученного показателя (в нашем случае 13 вольт), необходимо отнять 3.5 вольта светодиодной лампочки, в итоге вы получаете 9.5 В. Есть формула Ома, по которой делаются все соответствующие замеры. В ней указано, что ток измеряется в амперах, то есть показатель 20 мА равен 0.02 А.
3. Аналогичным образом по формуле следует понять, какое должно быть сопротивление. То есть полученный показатель 9.5В делится на 0.02 А. В итоге мы получаем 475 Ом.
4. Чтобы не допустить возможного перегревания резистора, необходимо заранее понять, какая должна быть мощность. Чтобы сделать это, следует напряжение умножить на ток, то есть 9.5*0.02. Показатель мощности составит 0.19 Вт. Но для того, чтобы все работало без перебоев, следует использовать небольшой запас, пусть мощность будет 0.5-1 Вт.
5. Затем мультиметр необходимо переключить на режим замера тока. Ваша задача заключается в том, чтобы измерить ток в разрыве сети между лампочкой и резистором. Заранее установите на приборе значение в 10А, далее, плюс АКБ подключается к плюсу мультиметра, а его минус подсоединяется к плюсу лампочки.
6. В итоге показатель на экране прибора должен составить около 20 мА. Поскольку на устройствах (диодах и резисторах) может быть разброс показаний, показатель будет различаться. Учтите, чем больше в лампочку будет попадать тока, тем мощнее она будет работать. Разумеется, слишком высокая яркость отражается на ресурсе эксплуатации лампы, соответственно, оптимальным вариантом будет выбрать ток 18 мА.

Схема подключения лампочки и резистора к прибору

Заключение

Несколько рекомендаций, которые позволят не допустить ошибок:

1. Желательно использовать стабилизатор, благодаря нему яркость диодов не будет изменяться. С помощью стабилизатора вы сможете ограничить количество тока, который поступает на лампу. В целом даже подключение киловатта не повлияет на мощность.
2. Разумный совет для владельцев автомобилей, которые любят подсветку и устанавливают ее буквально везде. В этом случае есть смысл подсоединить диодные лампы к проводам музыкальных колонок. Сами выводы подсоединяются параллельно к колонкам. Если кластер будет подключен параллельно, то нагрузка на мультимедиа систему будет снижена, что позволит избежать ее перегрева. Однако это же будет способствовать снижению эффективности работы и мощности музыкальных колонок.
3. Используйте только качественные резисторы, так как от них зависит многое. То же самое касается и лампочек, если вы не хотите регулярно заниматься их заменой.
4. Действия по подключению светодиодов требуют особых знаний, так что если вы ими не располагаете, то лучше доверьтесь квалифицированному электрику.

Видео «Как правильно установить светодиодную ленту на стоп-огни»

На примере автомобиля ВАЗ 2109 ознакомьтесь со всеми нюансами этого процесса (автор видео — Андрей Спас).

Извините, в настоящее время нет доступных опросов.

Закон Ома

На рисунке показана схема знакомой вам простейшей электрической цепи. Эта замкнутая цепь состоит из трех элементов:

• источника напряжения – батареи GB;
• потребителя тока – нагрузки R, которой может быть, например, нить накала электрической лампы или резистор;
• проводников, соединяющих источник напряжения с нагрузкой.

Схема простейшей электрической цепи.

Между прочим, если эту цепь дополнить выключателем, получится полная схема карманного электрического фонаря. Нагрузка R, обладающая определенным сопротивлением, является участком цепи.

Значение тока на этом участке цепи зависит от действующего на нем напряжения и его сопротивления: чем больше напряжение и меньше сопротивление, тем большим ток будет идти по участку цепи.

Эта зависимость тока от напряжения и сопротивления выражается следующей формулой:

I = U/R, где

• I – ток, выраженный в амперах, А;
• U – напряжение в вольтах, В;
• R – сопротивление в омах, Ом.

Зависимость силы тока от напряжения.

Читается это математическое выражение так: ток на участке цепи прямо пропорционален напряжению на нем и обратно пропорционален его сопротивлению. Это основной закон электротехники, именуемый законом Ома (по фамилии Г. Ома) для участка электрической цепи. Используя закон Ома, можно по двум известным электрическим величинам узнать неизвестную третью. Вот несколько примеров практического применения закона Ома:

1. Первый пример. На участке цепи, обладающем сопротивлением 5 Ом, действует напряжение 25 В. Надо узнать значение тока на этом участке цепи. Решение: I = U/R = 25 / 5 = 5 А.
2. Второй пример. На участке цепи действует напряжение 12 В, создавая в нем ток, равный 20 мА. Каково сопротивление этого участка цепи? Прежде всего ток 20 мА нужно выразить в амперах. Это будет 0,02 А. Тогда R = 12 / 0,02 = 600 Ом.
3. Третий пример. Через участок цепи сопротивлением 10 кОм течет ток 20 мА. Каково напряжение, действующее на этом участке цепи? Здесь, как и в предыдущем примере, ток должен быть выражен в амперах (20 мА = 0,02 А), сопротивление в омах (10 кОм = 10000 Ом). Следовательно, U = IR = 0,02×10000 = 200 В.

На цоколе лампы накаливания плоского карманного фонаря выштамповано: 0,28 А и 3,5 В. О чем говорят эти сведения? О том, что лампочка будет нормально светиться при токе 0,28 А, который обусловливается напряжением 3,5 В. Пользуясь законом Ома, нетрудно подсчитать, что накаленная нить лампочки имеет сопротивление R = 3,5 / 0,28 = 12,5 Ом.

Это сопротивление именно накаленной нити лампочки, сопротивление остывшей нити значительно меньше. Закон Ома справедлив не только для участка, но и для всей электрической цепи. В этом случае в значение R подставляется суммарное сопротивление всех элементов цепи, в том числе и внутреннее сопротивление источника тока. Однако при простейших расчетах цепей обычно пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.

В связи с этим нужно привести еще один пример: напряжение электроосветительной сети 220 В. Какой ток потечет в цепи, если сопротивление нагрузки равно 1000 Ом? Решение: I = U/R = 220 / 1000 = 0,22 А. Примерно такой ток потребляет электрический паяльник.

Закон Ома для участка цепи.

Всеми этими формулами, вытекающими из закона Ома, можно пользоваться и для расчета цепей переменного тока, но при условии, если в цепях нет катушек индуктивности и конденсаторов.

Закон Ома и производные от него расчетные формулы достаточно легко запомнить, если пользоваться вот этой графической схемой, это так называемый треугольник закона Ома.

Пользоваться этим треугольником легко, достаточно четко запомнить, что горизонтальная линия в нем означает знак деления (по аналогии дробной черты), а вертикальная линия означает знак умножения.

Теперь следует рассмотреть такой вопрос: как влияет на ток резистор, включаемый в цепь последовательно с нагрузкой или параллельно ей? Лучше разобрать это на примере. Имеется лампочка от круглого электрического, фонаря, рассчитанная на напряжение 2,5 В и ток 0,075 А. Можно ли питать эту лампочку от батареи 3336Л, начальное напряжение которой 4,5 В?

Нетрудно подсчитать, что накаленная нить этой лампочки имеет сопротивление немногим больше 30 Ом. Если же питать ее от свежей батареи 3336Л, то через нить накала лампочки, по закону Ома, пойдет ток, почти вдвое превышающий тот ток, на который она рассчитана. Такой перегрузки нить не выдержит, она перекалится и разрушится. Но эту лампочку все же можно питать от батареи 336Л, если последовательно в цепь включить добавочный резистор сопротивлением 25 Ом.

В этом случае общее сопротивление внешней цепи будет равно примерно 55 Ом, то есть 30 Ом – сопротивление нити лампочки Н плюс 25 Ом – сопротивление добавочного резистора R. В цепи, следовательно, потечет ток, равный примерно 0,08 А, то есть почти такой же, на который рассчитана нить накала лампочки.

Закон Ома для полной цепи.

Эту лампочку можно питать от батареи и с более высоким напряжением и даже от электроосветительной сети, если подобрать резистор соответствующего сопротивления. В этом примере добавочный резистор ограничивает ток в цепи до нужного нам значения. Чем больше будет его сопротивление, тем меньше будет и ток в цепи. В данном случае в цепь было включено последовательно два сопротивления: сопротивление нити лампочки и сопротивление резистора. А при последовательном соединении сопротивлений ток одинаков во всех точках цепи.

Можно включать амперметр в любую точку, и всюду он будет показывать одно значение. Это явление можно сравнить с потоком воды в реке. Русло реки на различных участках может быть широким или узким, глубоким или мелким. Однако за определенный промежуток времени через поперечное сечение любого участка русла реки всегда проходит одинаковое количество воды.

Добавочный резистор, включаемый в цепь последовательно с нагрузкой, можно рассматривать как резистор, «гасящий» часть напряжения, действующего в цепи. Напряжение, которое гасится добавочным резистором или, как говорят, падает на нем, будет тем большим, чем больше сопротивление этого резистора. Зная ток и сопротивление добавочного резистора, падение напряжения на нем легко подсчитать все по той же знакомой вам формуле U = IR, здесь:

• U – падение напряжения, В;
• I – ток в цепи, A;
• R – сопротивление добавочного резистора, Ом.

Применительно к примеру резистор R (см. рис.) погасил избыток напряжения: U = IR = 0,08×25 = 2 В. Остальное напряжение батареи, равное приблизительно 2,5 В, упало на нити лампочки. Необходимое сопротивление резистора можно найти по другой знакомой вам формуле R = U/I, где:

• R – искомое сопротивление добавочного резистора, Ом;
• U – напряжение, которое необходимо погасить, В;
• I – ток в цепи, А.

Для рассматриваемого примера сопротивление добавочного резистора равно: R = U/I = 2/0,075, 27 Ом. Изменяя сопротивление, можно уменьшать или увеличивать напряжение, которое падает на добавочном резисторе, таким образом регулируя ток в цепи. Но добавочный резистор R в такой цепи может быть переменным, то есть резистором, сопротивление которого можно изменять (см. рис. ниже).

Регулирование тока в цепи с помощью переменного резистора.

В этом случае с помощью движка резистора можно плавно изменять напряжение, подводимое к нагрузке Н, а значит, плавно регулировать ток, протекающий через эту нагрузку. Включенный таким образом переменный резистор называют реостатом. С помощью реостатов регулируют токи в цепях приемников, телевизоров и усилителей. Во многих кинотеатрах реостаты использовали для плавного гашения света в зрительном зале. Есть и другой способ подключения нагрузки к источнику тока с избыточным напряжением – тоже с помощью переменного резистора, но включенного потенциометром, то есть делителем напряжения, как показано на рисунке ниже.

Регулирование напряжения на нагрузке R2 с помощью переменного резистора включенного в электрическую цепь потенциометром.

Здесь R1 – резистор, включенный потенциометром, a R2 – нагрузка, которой может быть та же лампочка накаливания или какой-то другой прибор. На резисторе R1 происходит падение напряжения источника тока, которое частично или полностью может быть подано к нагрузке R2. Когда движок резистора находится в крайнем нижнем положении, к нагрузке напряжение вообще не подается (если это лампочка, она гореть не будет).

Закон Ома: схема и теория.

По мере перемещения движка резистора вверх мы будем подавать все большее напряжение к нагрузке R2 (если это лампочка, ее нить будет накаливаться). Когда же движок резистора R1 окажется в крайнем верхнем положении, к нагрузке R2 будет подано все напряжение источника тока (если R2 – лампочка карманного фонаря, а напряжение источника тока большое, нить лампочки перегорит). Можно опытным путем найти такое положение движка переменного резистора, при котором к нагрузке будет подано необходимое ей напряжение.

Переменные резисторы, включаемые потенциометрами, широко используют для регулирования громкости в приемниках и усилителях. Резистор может быть непосредственно подключен параллельно нагрузке. В таком случае ток на этом участке цепи разветвляется и идет двумя параллельными путями: через добавочный резистор и основную нагрузку. Наибольший ток будет в ветви с наименьшим сопротивлением.

Сумма же токов обеих ветвей будет равна току, расходуемому на питание внешней цепи. К параллельному соединению прибегают в тех cлучаях, когда надо ограничить ток не во всей цепи, как при последовательном включении добавочного резистора, а только на каком-то участке. Добавочные резисторы подключают, например, параллельно миллиамперметрам, чтобы ими можно было измерять большие токи. Такие резисторы называют шунтирующими или шунтами. Слово шунт означает ответвление.

Напряжение через закон ома. Закон Ома. Для цепей и тока. Формулы и применение

Один из самых применяемых законов в электротехнике. Данный закон раскрывает связь между тремя важнейшими величинами: силой тока, напряжением и сопротивлением. Выявил эту связь Георгом Омом в 1820-е годы именно поэтому этот закон и получил такое название.

Формулировка закона Ома следующая:
Величина силы тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению.

Эту зависимость можно выразить формулой:

Где I – сила тока, U — напряжение, приложенное к участку цепи, а R — электрическое сопротивление участка цепи.
Так, если известны две из этих величин можно легко вычислить третью.
Понять закон Ома можно на простом примере. Допустим, нам необходимо вычислить сопротивление нити накаливания лампочки фонарике и нам известны величины напряжения работы лампочки и сила тока, необходимая для ее работы (сама лампочка, чтобы вы знали имеет переменное сопротивление, но для примера примем его как постоянное). Для вычисления сопротивления необходимо величину напряжения разделить на величину силы тока. Как же запомнить формулу закона Ома, чтобы правильно провести вычисления? А сделать это очень просто! Вам нужно всего лишь сделать себе напоминалку как на указанном ниже рисунке.
Теперь закрыв рукой любую из величин вы сразу поймете, как ее найти. Если закрыть букву I, становится ясно, что чтобы найти силу тока нужно напряжение разделить на сопротивление.
Теперь давайте разберемся, что значат в формулировке закона слова « прямо пропорциональна и обратно пропорциональна. Выражение «величина силы тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку» означает, что если на участке цепи увеличится напряжение, то и сила тока на данном участке также увеличится. Простыми словами, чем больше напряжение, тем больше ток. И выражение «обратно пропорциональна его сопротивлению» значит, что чем больше сопротивление, тем меньше будет сила тока.
Рассмотрим пример с работой лампочки в фонарике. Допустим, что для работы фонарика нужны три батарейки, как показано на схеме ниже, где GB1 — GB3 — батарейки, S1 — выключатель, HL1 — лампочка.

Примем, что сопротивление лампочки условно постоянно, хотя нагреваясь её сопротивление увеличивается. Яркость лампочки будет зависеть от силы тока, чем она больше, тем ярче горит лампочка. А теперь, представьте, что вместо одной батарейки мы вставили перемычку, уменьшив тем самым напряжение.
Что случится с лампочкой?
Она будет светить более тускло (сила тока уменьшилась), что подтверждает закон Ома:
чем меньше напряжение, тем меньше сила тока.

Вот так просто работает этот физический закон, с которым мы сталкиваемся в повседневной жизни.
Бонус специально для вас шуточная картинка не менее красочно объясняющая закон Ома.

Это была обзорная статья. Более подробно об этом законе, мы говорим в следующей статье » «, рассматривая всё на других более сложных примерах.

Если не получается с физикой, английский для детей (http://www.anylang.ru/order-category/?slug=live_language) как вариент альтернативного развития.

Добавить сайт в закладки

На рисунке показана схема знакомой вам простейшей электрической цепи. Эта замкнутая цепь состоит из трех элементов:

• источника напряжения – батареи GB;
• потребителя тока – нагрузки R, которой может быть, например, нить накала электрической лампы или резистор;
• проводников, соединяющих источник напряжения с нагрузкой.

Между прочим, если эту цепь дополнить выключателем, получится полная схема карманного электрического фонаря. Нагрузка R, обладающая определенным сопротивлением, является участком цепи.

Значение тока на этом участке цепи зависит от действующего на нем напряжения и его сопротивления: чем больше напряжение и меньше сопротивление, тем большим ток будет идти по участку цепи.

Эта зависимость тока от напряжения и сопротивления выражается следующей формулой:

• I – ток, выраженный в амперах, А;
• U – напряжение в вольтах, В;
• R – сопротивление в омах, Ом.

Читается это математическое выражение так: ток на участке цепи прямо пропорционален напряжению на нем и обратно пропорционален его сопротивлению. Это основной закон электротехники, именуемый законом Ома (по фамилии Г. Ома) для участка электрической цепи. Используя закон Ома, можно по двум известным электрическим величинам узнать неизвестную третью. Вот несколько примеров практического применения закона Ома:

1. Первый пример. На участке цепи, обладающем сопротивлением 5 Ом, действует напряжение 25 В. Надо узнать значение тока на этом участке цепи. Решение: I = U/R = 25 / 5 = 5 А.
2. Второй пример. На участке цепи действует напряжение 12 В, создавая в нем ток, равный 20 мА. Каково сопротивление этого участка цепи? Прежде всего ток 20 мА нужно выразить в амперах. Это будет 0,02 А. Тогда R = 12 / 0,02 = 600 Ом.
3. Третий пример. Через участок цепи сопротивлением 10 кОм течет ток 20 мА. Каково напряжение, действующее на этом участке цепи? Здесь, как и в предыдущем примере, ток должен быть выражен в амперах (20 мА = 0,02 А), сопротивление в омах (10 кОм = 10000 Ом). Следовательно, U = IR = 0,02×10000 = 200 В.

На цоколе лампы накаливания плоского карманного фонаря выштамповано: 0,28 А и 3,5 В. О чем говорят эти сведения? О том, что лампочка будет нормально светиться при токе 0,28 А, который обусловливается напряжением 3,5 В. Пользуясь законом Ома, нетрудно подсчитать, что накаленная нить лампочки имеет сопротивление R = 3,5 / 0,28 = 12,5 Ом.

Это сопротивление именно накаленной нити лампочки, сопротивление остывшей нити значительно меньше. Закон Ома справедлив не только для участка, но и для всей электрической цепи. В этом случае в значение R подставляется суммарное сопротивление всех элементов цепи, в том числе и внутреннее сопротивление источника тока. Однако при простейших расчетах цепей обычно пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.

В связи с этим нужно привести еще один пример: напряжение электроосветительной сети 220 В. Какой ток потечет в цепи, если сопротивление нагрузки равно 1000 Ом? Решение: I = U/R = 220 / 1000 = 0,22 А. Примерно такой ток потребляет электрический паяльник.

Всеми этими формулами, вытекающими из закона Ома, можно пользоваться и для расчета цепей переменного тока, но при условии, если в цепях нет катушек индуктивности и конденсаторов.

Закон Ома и производные от него расчетные формулы достаточно легко запомнить, если пользоваться вот этой графической схемой, это так называемый треугольник закона Ома.

Пользоваться этим треугольником легко, достаточно четко запомнить, что горизонтальная линия в нем означает знак деления (по аналогии дробной черты), а вертикальная линия означает знак умножения.

Теперь следует рассмотреть такой вопрос: как влияет на ток резистор, включаемый в цепь последовательно с нагрузкой или параллельно ей? Лучше разобрать это на примере. Имеется лампочка от круглого электрического, фонаря, рассчитанная на напряжение 2,5 В и ток 0,075 А. Можно ли питать эту лампочку от батареи 3336Л, начальное напряжение которой 4,5 В?

Нетрудно подсчитать, что накаленная нить этой лампочки имеет сопротивление немногим больше 30 Ом. Если же питать ее от свежей батареи 3336Л, то через нить накала лампочки, по закону Ома, пойдет ток, почти вдвое превышающий тот ток, на который она рассчитана. Такой перегрузки нить не выдержит, она перекалится и разрушится. Но эту лампочку все же можно питать от батареи 336Л, если последовательно в цепь включить добавочный резистор сопротивлением 25 Ом.

В этом случае общее сопротивление внешней цепи будет равно примерно 55 Ом, то есть 30 Ом – сопротивление нити лампочки Н плюс 25 Ом – сопротивление добавочного резистора R. В цепи, следовательно, потечет ток, равный примерно 0,08 А, то есть почти такой же, на который рассчитана нить накала лампочки.

Эту лампочку можно питать от батареи и с более высоким напряжением и даже от электроосветительной сети, если подобрать резистор соответствующего сопротивления. В этом примере добавочный резистор ограничивает ток в цепи до нужного нам значения. Чем больше будет его сопротивление, тем меньше будет и ток в цепи. В данном случае в цепь было включено последовательно два сопротивления: сопротивление нити лампочки и сопротивление резистора. А при последовательном соединении сопротивлений ток одинаков во всех точках цепи.

Можно включать амперметр в любую точку, и всюду он будет показывать одно значение. Это явление можно сравнить с потоком воды в реке. Русло реки на различных участках может быть широким или узким, глубоким или мелким. Однако за определенный промежуток времени через поперечное сечение любого участка русла реки всегда проходит одинаковое количество воды.

Добавочный резистор, включаемый в цепь последовательно с нагрузкой, можно рассматривать как резистор, «гасящий» часть напряжения, действующего в цепи. Напряжение, которое гасится добавочным резистором или, как говорят, падает на нем, будет тем большим, чем больше сопротивление этого резистора. Зная ток и сопротивление добавочного резистора, падение напряжения на нем легко подсчитать все по той же знакомой вам формуле U = IR, здесь:

• U – падение напряжения, В;
• I – ток в цепи, A;
• R – сопротивление добавочного резистора, Ом.

Применительно к примеру резистор R (см. рис.) погасил избыток напряжения: U = IR = 0,08×25 = 2 В. Остальное напряжение батареи, равное приблизительно 2,5 В, упало на нити лампочки. Необходимое сопротивление резистора можно найти по другой знакомой вам формуле R = U/I, где:

• R – искомое сопротивление добавочного резистора, Ом;
• U – напряжение, которое необходимо погасить, В;
• I – ток в цепи, А.

Для рассматриваемого примера сопротивление добавочного резистора равно: R = U/I = 2/0,075, 27 Ом. Изменяя сопротивление, можно уменьшать или увеличивать напряжение, которое падает на добавочном резисторе, таким образом регулируя ток в цепи. Но добавочный резистор R в такой цепи может быть переменным, то есть резистором, сопротивление которого можно изменять (см. рис. ниже).

В этом случае с помощью движка резистора можно плавно изменять напряжение, подводимое к нагрузке Н, а значит, плавно регулировать ток, протекающий через эту нагрузку. Включенный таким образом переменный резистор называют реостатом. С помощью реостатов регулируют токи в цепях приемников, телевизоров и усилителей. Во многих кинотеатрах реостаты использовали для плавного гашения света в зрительном зале. Есть и другой способ подключения нагрузки к источнику тока с избыточным напряжением – тоже с помощью переменного резистора, но включенного потенциометром, то есть делителем напряжения, как показано на рисунке ниже.

Здесь R1 – резистор, включенный потенциометром, a R2 – нагрузка, которой может быть та же лампочка накаливания или какой-то другой прибор. На резисторе R1 происходит падение напряжения источника тока, которое частично или полностью может быть подано к нагрузке R2. Когда движок резистора находится в крайнем нижнем положении, к нагрузке напряжение вообще не подается (если это лампочка, она гореть не будет).

По мере перемещения движка резистора вверх мы будем подавать все большее напряжение к нагрузке R2 (если это лампочка, ее нить будет накаливаться). Когда же движок резистора R1 окажется в крайнем верхнем положении, к нагрузке R2 будет подано все напряжение источника тока (если R2 – лампочка карманного фонаря, а напряжение источника тока большое, нить лампочки перегорит). Можно опытным путем найти такое положение движка переменного резистора, при котором к нагрузке будет подано необходимое ей напряжение.

Переменные резисторы, включаемые потенциометрами, широко используют для регулирования громкости в приемниках и усилителях. Резистор может быть непосредственно подключен параллельно нагрузке. В таком случае ток на этом участке цепи разветвляется и идет двумя параллельными путями: через добавочный резистор и основную нагрузку. Наибольший ток будет в ветви с наименьшим сопротивлением.

Сумма же токов обеих ветвей будет равна току, расходуемому на питание внешней цепи. К параллельному соединению прибегают в тех cлучаях, когда надо ограничить ток не во всей цепи, как при последовательном включении добавочного резистора, а только на каком-то участке. Добавочные резисторы подключают, например, параллельно миллиамперметрам, чтобы ими можно было измерять большие токи. Такие резисторы называют шунтирующими или шунтами. Слово шунт означает ответвление.

Закон Ома был открыт немецким физиком Георгом Омом в 1826 году и с тех пор начал широко применяться в электротехнической области в теории и на практике. Он выражается известной формулой, с посредством которой можно выполнить расчеты практически любой электрической цепи. Тем не менее, закон Ома для переменного тока имеет свои особенности и отличия от подключений с постоянным током, определяемые наличием реактивных элементов. Чтобы понять суть его работы, нужно пройти по всей цепочке, от простого к сложному, начиная с отдельного участка электрической цепи.

Закон ома для участка цепи

Закон Ома считается рабочим для различных вариантов электрических цепей. Более всего он известен по формуле I = U/R, применяемой в отношении отдельного отрезка цепи постоянного или переменного тока.

В ней присутствуют такие определения, как сила тока (I), измеряемая в амперах, напряжение (U), измеряемое в вольтах и сопротивление (R), измеряемое в Омах.

Широко распространенное определение этой формулы выражается известным понятием: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению на конкретном отрезке цепи. Если увеличивается напряжение, то возрастает и сила тока, а рост сопротивления, наоборот, снижает ток. Сопротивление на этом отрезке может состоять не только из одного, но и из нескольких элементов, соединенных между собой .

Формулу закона Ома для постоянного тока можно легко запомнить с помощью специального треугольника, изображенного на общем рисунке. Он разделяется на три секции, в каждой из которых помещен отдельно взятый параметр. Такая подсказка дает возможность легко и быстро найти нужное значение. Искомый показатель закрывается пальцем, а действия с оставшимися выполняются в зависимости от их положения относительно друг друга.

Если они расположены на одном уровне, то их нужно перемножить, а если на разных — верхний параметр делится на нижний. Данный способ поможет избежать путаницы в расчетах начинающим электротехникам.

Закон ома для полной цепи

Между отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами.

Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока.

Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта. Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания. Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R.

Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока. По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами. Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет .

Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела. Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r). На размеры силы тока влияет такое понятие, как электродвижущая сила — ЭДС, прилагаемая к электродам, обозначенная символом Е.

Значение ЭДС возможно измерить на выводах батареи с использованием вольтметра при отключенном внешнем контуре. После подключения нагрузки на вольтметре появится наличие напряжения U. Таким образом, при отключенной нагрузке U = E, в при подключении внешнего контура U

ЭДС дает толчок движению зарядов в полной цепи и определяет силу тока I = E/(R+r). Данная формула отражает закон Ома для полной электрической цепи постоянного тока. В ней хорошо просматриваются признаки внутреннего и наружного контуров. В случае отключения нагрузки внутри батареи все равно будут двигаться заряженные частицы. Это явление называется током саморазряда, приводящее к ненужному расходу металлических частиц катода.

Под действием внутренней энергии источника питания сопротивление вызывает нагрев и его дальнейшее рассеивание снаружи элемента. Постепенно заряд батареи полностью исчезает без остатка.

Закон ома для цепи переменного тока

Для цепей переменного тока закон Ома будет выглядеть иначе. Если взять за основу формулу I = U/R, то кроме активного сопротивления R, в нее добавляются индуктивное XL и емкостное ХС сопротивления, относящиеся к реактивным. Подобные электрические схемы применяются значительно чаще, чем подключения с одним лишь активным сопротивлением и позволяют рассчитать любые варианты.

Сюда же включается параметр ω, представляющий собой циклическую частоту сети. Ее значение определяется формулой ω = 2πf, в которой f является частотой этой сети (Гц). При постоянном токе эта частота будет равной нулю, а емкость примет бесконечное значение. В данном случае электрическая цепь постоянного тока окажется разорванной, то есть реактивного сопротивления нет.

Цепь переменного тока ничем не отличается от постоянного, за исключением источника напряжения. Общая формула остается такой же, но при добавлении реактивных элементов ее содержание полностью изменится. Параметр f уже не будет нулевым, что указывает на присутствие реактивного сопротивления. Оно тоже оказывает влияние на ток, протекающий в контуре и вызывает резонанс. Для обозначения полного сопротивления контура используется символ Z.

Отмеченная величина не будет равной активному сопротивлению, то есть Z ≠ R. Закон Ома для переменного тока теперь будет выглядеть в виде формулы I = U/Z. Знание этих особенностей и правильное использование формул, помогут избежать неправильного решения электротехнических задач и предотвратить выход из строя отдельных элементов контура.

Закон Ома часто называют основным законом электричества. Открывший его в 1826 г. известный немецкий физик Георг Симон Ом установил зависимость между основными физическими величинами электрической цепи – сопротивлением, напряжением и силой тока.

Электрическая цепь

Чтобы лучше понять смысл закона Ома, нужно представлять, как устроена электрическая цепь.

Что же такое электрическая цепь? Это путь, который проходят электрически заряженные частицы (электроны) в электрической схеме.

Чтобы в электрической цепи существовал ток, необходимо наличие в ней устройства, которое создавало бы и поддерживало разность потенциалов на участках цепи за счёт сил неэлектрического происхождения. Такое устройство называется источником постоянного тока , а силы — сторонними силами .

Электрическую цепь, в которой находится источник тока, называют полной электрической цепью . Источник тока в такой цепи выполняет примерно такую же функцию, что и насос, перекачивающий жидкость в замкнутой гидравлической системе.

Простейшая замкнутая электрическая цепь состоит из одного источника и одного потребителя электрической энергии, соединённых между собой проводниками.

Параметры электрической цепи

Свой знаменитый закон Ом вывел экспериментальным путём.

Проведём несложный опыт.

Соберём электрическую цепь, в которой источником тока будет аккумулятор, а прибором для измерения тока – последовательно включенный в цепь амперметр. Нагрузкой служит спираль из проволоки. Напряжение будем измерять с помощью вольтметра, включенного параллельно спирали. Замкнём с помощью ключа электрическую цепь и запишем показания приборов.

Подключим к первому аккумулятору второй с точно таким же параметрами. Снова замкнём цепь. Приборы покажут, что и сила тока, и напряжение увеличились в 2 раза.

Если к 2 аккумуляторам добавить ещё один такой же, сила тока увеличится втрое, напряжение тоже утроится.

Вывод очевиден: сила тока в проводнике прямо пропорциональна напряжению, приложенному к концам проводника .

В нашем опыте величина сопротивления оставалась постоянной. Мы меняли лишь величину тока и напряжения на участке проводника. Оставим лишь один аккумулятор. Но в качестве нагрузки будем использовать спирали из разных материалов. Их сопротивления отличаются. Поочерёдно подключая их, также запишем показания приборов. Мы увидим, что здесь всё наоборот. Чем больше величина сопротивления, тем меньше сила тока. Сила тока в цепи обратно пропорциональна сопротивлению .

Итак, наш опыт позволил нам установить зависимость силы тока от величины напряжения и сопротивления.

Конечно, опыт Ома был другим. В те времена не существовало амперметров, и, чтобы измерить силу тока, Ом использовал крутильные весы Кулона. Источником тока служил элемент Вольта из цинка и меди, которые находились в растворе соляной кислоты. Медные проволоки помещались в чашки со ртутью. Туда же подводились концы проводов от источника тока. Проволоки были одинакового сечения, но разной длины. За счёт этого менялась величина сопротивления. Поочерёдно включая в цепь различные проволоки, наблюдали за углом поворота магнитной стрелки в крутильных весах. Собственно, измерялась не сама сила тока, а изменение магнитного действия тока за счёт включения в цепь проволок различного сопротивления. Ом называл это «потерей силы».

Но так или иначе эксперименты учёного позволили ему вывести свой знаменитый закон.

Георг Симон Ом

Закон Ома для полной цепи

Между тем, формула, выведенная самим Омом, выглядела так:

Это не что иное, как формула закона Ома для полной электрической цепи: « Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений внешней цепи и внутреннего сопротивления источника ».

В опытах Ома величина Х показывала изменение величины тока. В современной формуле ей соответствует сила тока I , протекающего в цепи. Величина а характеризовала свойства источника напряжения, что соответствует современному обозначению электродвижущей силы (ЭДС) ε . Значение величины l зависело от длины проводников, соединявших элементы электрической цепи. Эта величина являлась аналогией сопротивления внешней электрической цепи R . Параметр b характеризовал свойства всей установки, на которой проводился опыт. В современной обозначении это r – внутреннее сопротивление источника тока.

Как выводится современная формула закона Ома для полной цепи?

ЭДС источника равна сумме падений напряжений на внешней цепи (U ) и на самом источнике (U 1 ).

ε = U + U 1 .

Из закона Ома I = U / R следует, что U = I · R , а U 1 = I · r .

Подставив эти выражения в предыдущее, получим:

ε = I · R + I · r = I · (R + r) , откуда

По закону Ома напряжение во внешней цепи равно произведению силы тока на сопротивление. U = I · R . Оно всегда меньше, чем ЭДС источника. Разница равна величине U 1 = I · r .

Что происходит при работе батарейки или аккумулятора? По мере того, как разряжается батарейка, растёт её внутренне сопротивление. Следовательно, увеличивается U 1 и уменьшается U .

Полный закон Ома превращается в закон Ома для участка цепи, если убрать из него параметры источника.

Короткое замыкание

А что произойдёт, если сопротивление внешней цепи вдруг станет равно нулю? В повседневной жизни мы можем наблюдать это, если, например, повреждается электрическая изоляция проводов, и они замыкаются между собой. Возникает явление, которое называется коротким замыканием . Ток, называемый током короткого замыкания , будет чрезвычайно большим. При этом выделится большое количество теплоты, которое может привести к пожару. Чтобы этого не случилось, в цепи ставят устройства, называемые предохранителями. Они устроены так, что способны разорвать электрическую цепь в момент короткого замыкания.

Закон Ома для переменного тока

В цепи переменного напряжения кроме обычного активного сопротивления встречается реактивное сопротивление (ёмкости, индуктивности).

Для таких цепей U = I · Z , где Z — полное сопротивление, включающее в себя активную и реактивную составляющие.

Но большим реактивным сопротивлением обладают мощные электрические машины и силовые установки. В бытовых приборах, окружающих нас, реактивная составляющая настолько мала, что её можно не учитывать, а для расчётов использовать простую форму записи закона Ома:

I = U / R

Мощность и закон Ома

Ом не только установил зависимость между напряжением, током и сопротивлением электрической цепи, но и вывел уравнение для определения мощности:

P = U · I = I 2 · R

Как видим, чем больше ток или напряжение, тем больше мощность . Так как проводник или резистор не является полезной нагрузкой, то мощность, которая приходится на него, считается мощностью потерь. Она идёт на нагревание проводника. И чем больше сопротивление такого проводника, тем больше теряется на нём мощности. Чтобы уменьшить потери от нагревания, в цепи используют проводники с меньшим сопротивлением. Так делают, например, в мощных звуковых установках.

Вместо эпилога

Небольшая подсказка для тех, кто путается и не может запомнить формулу закона Ома.

Разделим треугольник на 3 части. Причём, каким образом мы это сделаем, совершенно неважно. Впишем в каждую из них величины, входящие в закон Ома — так, как показано на рисунке.

Закроем величину, которую нужно найти. Если оставшиеся величины находятся на одном уровне, то их нужно перемножить. Если же они располагаются на разных уровнях, то величину, расположенную выше, необходимо разделить на нижнюю.

Закон Ома широко применяется на практике при проектировании электрических сетей в производстве и в быту.

Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.

В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.

Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению

Так записывается основная формула:

Путем преобразования основной формулы можно найти и другие две величины:

Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

Формула мгновенной электрической мощности:

Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.

Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.

Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.

Вторая — метод треугольника. Его ещё называют магический треугольник закона Ома.

Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.

Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.

Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.

Этот круг также, как и треугольник можно назвать магическим.

Сопротивление лампочки

Лампа мощностью 100 Вт включается последовательно с лампой мощностью 40 Вт. Какая лампочка будет ярче при подключении к розетке на 120 вольт? Получается лампочка на 40 Вт.

Используйте уравнение мощности, чтобы рассчитать сопротивление двух лампочек. Лампы вырабатывают указанную на них мощность только при разности потенциалов 120 В.

Для лампы мощностью 100 Вт: R

=

DV 2 P

=

120 2 100

=

144 Вт

Для лампы мощностью 40 Вт: R

=

DV 2 P

=

120 2 40

=

360 Вт

Мы можем использовать закон Ома, чтобы найти ток, который обычно получает каждый резистор:

Для 100-ваттной лампы: I

=

ДВ R

=

120 144

=

0.83 А

Для лампы мощностью 40 Вт: I

=

ДВ R

=

120 360

=

0,33 А

Когда они соединены последовательно, общее сопротивление составляет около 500 Вт, поэтому каждая лампочка видит ток 120/500 = 0.24 А.

Используйте уравнение мощности, чтобы найти мощность для каждой лампочки, когда они включены последовательно друг с другом. Чем больше мощность, тем ярче лампочка.

Для 100-ваттной лампы: P = I ² R = 0,24 ² * 144 = 8 Вт

Для лампы мощностью 40 Вт: P = I ² R = 0,24 ² * 360 = 21 Вт

На самом деле это заниженная оценка, но она дает нам относительную яркость. Лампочки не такие горячие, как обычно, поэтому их сопротивление немного ниже, чем мы предполагали выше.

Напряжение, ток и сопротивление | HowStuffWorks

Как упоминалось ранее, количество электронов, движущихся в цепи, называется током и измеряется в амперах. «Давление», толкающее электроны, называется напряжением и измеряется в вольтах. Если вы живете в Соединенных Штатах, розетки в стене вашего дома или квартиры выдают 120 вольт каждая.

Если вам известны соответствующие амперы и вольт, вы можете определить количество потребляемой электроэнергии, которое мы обычно измеряем в ватт-часах или киловатт-часах .Представьте, что вы подключаете обогреватель к розетке. Вы измеряете силу тока, протекающего от розетки к обогревателю, и она составляет 10 ампер. Это означает, что это нагреватель мощностью 1200 ватт. Если вы умножите вольты на амперы, вы получите мощность. В этом случае 120 вольт, умноженное на 10 ампер, равняется 1200 ваттам. Это верно для любого электрического прибора. Если вы подключите свет, и он потребляет половину усилителя, это будет лампочка мощностью 60 Вт.

Допустим, вы включаете обогреватель, а затем смотрите на измеритель мощности снаружи.Счетчик предназначен для измерения количества электричества, поступающего в ваш дом, чтобы энергетическая компания могла выставить вам счет за него. Предположим — мы знаем, что это маловероятно, — что в доме больше ничего не включено, поэтому счетчик измеряет только электричество, используемое обогревателем.

Ваш обогреватель потребляет 1,2 кВт (1200 Вт). Если вы оставите обогреватель включенным на один час, вы будете использовать 1,2 киловатт-часа энергии. Если ваша энергетическая компания взимает с вас 10 центов за киловатт-час, то энергетическая компания будет взимать с вас 12 центов за каждый час, когда вы оставляете обогреватель.

Теперь добавим еще один коэффициент к току и напряжению: сопротивление , которое измеряется в Ом . Мы можем расширить аналогию с водой, чтобы понять сопротивление. Напряжение эквивалентно давлению воды, сила тока равна скорости потока, а сопротивление равно размеру трубы.

Основное уравнение электротехники, называемое законом Ома, объясняет, как соотносятся три члена. Ток равен напряжению, деленному на сопротивление. Он записывается так:

I = V / R

, где I — ток (измеренный в амперах), V, — напряжение (измеренный в вольтах), а R — сопротивление (измеренное в омах).

Допустим, у вас есть резервуар с водой под давлением, подключенный к шлангу, который вы используете для полива сада. Если вы увеличите давление в баке, из шланга будет выходить больше воды, верно? То же самое и с электрической системой: увеличение напряжения приведет к большему току.

Теперь предположим, что вы увеличили диаметр шланга и всех фитингов бака. Эта регулировка также приведет к тому, что из шланга будет выходить больше воды. Это похоже на уменьшение сопротивления в электрической системе, что увеличивает ток.

Если вы посмотрите на обычную лампочку накаливания, вы увидите аналогию с водой в действии. Нить накала лампочки — это очень тонкий провод. Этот тонкий провод сопротивляется потоку электронов. Вы можете рассчитать сопротивление провода с помощью уравнения сопротивления.

Допустим, у вас есть лампочка на 120 Вт, подключенная к розетке. Напряжение составляет 120 вольт, а через 120-ваттную лампочку протекает 1 ампер. Вы можете рассчитать сопротивление нити накала, переставив уравнение:

R = V / I

Таким образом, сопротивление составляет 120 Ом.

Помимо этих основных электрических концепций, существует практическое различие между двумя разновидностями тока. Часть тока является постоянным, а часть — переменным — и это очень важное различие.

19,4 Электроэнергия | Texas Gateway

Задачи обучения

К концу этого раздела вы сможете сделать следующее:

• Определить электрическую мощность и описать уравнение электрической мощности
• Расчет электрической мощности в цепях резисторов в последовательном, параллельном и сложном расположении

Основные термины раздела

электроэнергия

Энергия для многих ассоциируется с электричеством.Каждый день мы используем электроэнергию для работы наших современных приборов. Линии электропередачи — наглядные примеры электроэнергии, обеспечивающей мощность. Мы также используем электроэнергию для запуска автомобилей, работы компьютеров или освещения дома. Мощность — это скорость передачи энергии любого типа; электрическая мощность — это скорость, с которой электрическая энергия передается в цепи. В этом разделе мы узнаем не только, что это означает, но и какие факторы определяют электрическую мощность.

Для начала представим себе лампочки, которые часто характеризуются номинальной мощностью в ваттах.Давайте сравним лампочку мощностью 25 Вт с лампой мощностью 60 Вт (см. Рисунок 19.23). Хотя обе работают при одинаковом напряжении, лампа мощностью 60 Вт излучает больше света, чем лампа мощностью 25 Вт. Это говорит нам о том, что выходную мощность электрической цепи определяет нечто иное, чем напряжение.

Лампы накаливания, такие как две, показанные на рисунке 19.23, по сути являются резисторами, которые нагреваются, когда через них протекает ток, и становятся настолько горячими, что излучают видимый и невидимый свет. Таким образом, две лампочки на фото можно рассматривать как два разных резистора.В простой цепи, такой как электрическая лампочка с приложенным к ней напряжением, сопротивление определяет ток по закону Ома, поэтому мы можем видеть, что ток, а также напряжение должны определять мощность.

Рисунок 19.23 Слева лампочка мощностью 25 Вт, а справа лампочка мощностью 60 Вт. Почему их выходная мощность различается, несмотря на то, что они работают при одинаковом напряжении?

Формулу мощности можно найти путем анализа размеров. Рассмотрим единицы мощности. В системе СИ мощность указывается в ваттах (Вт), которые представляют собой энергию в единицу времени или Дж / с.

Напомним, что напряжение — это потенциальная энергия на единицу заряда, что означает, что напряжение имеет единицы Дж / Кл.

Мы можем переписать это уравнение как J = V × CJ = V × C и подставить его в уравнение для ватт, чтобы получить

W = Js = V × Cs = V × Cs.W = Js = V × Cs = V × Cs.

Но кулон в секунду (Кл / с) — это электрический ток, который мы можем видеть из определения электрического тока, I = ΔQΔtI = ΔQΔt, где ΔΔ Q — заряд в кулонах, а ΔΔ t — время в секундах. Таким образом, приведенное выше уравнение говорит нам, что электрическая мощность равна напряжению, умноженному на ток, или

Это уравнение дает электрическую мощность, потребляемую цепью с падением напряжения В и током I .

Например, рассмотрим схему на Рисунке 19.24. Согласно закону Ома, ток, протекающий по цепи, равен

19,49I = VR = 12 В 100 Ом = 0,12 AI = VR = 12 В 100 Ом = 0,12 А.

Таким образом, мощность, потребляемая цепью, составляет

19,50P = VI. = (12 В) (0,12 А) = 1,4 WP = VI = (12 В) (0,12 А) = 1,4 Вт.

Куда уходит эта мощность? В этой схеме мощность в основном идет на нагрев резистора в этой цепи.

Рисунок 19.24 Простая схема, потребляющая электроэнергию.

При вычислении мощности в цепи, показанной на рис. 19.24, мы использовали сопротивление и закон Ома, чтобы найти ток.Закон Ома дает ток: I = V / RI = V / R, который мы можем вставить в уравнение для электроэнергии, чтобы получить

P = IV = (VR) V = V2R.P = IV = (VR) V = V2R.

Это дает мощность с точки зрения только напряжения и сопротивления.

Мы также можем использовать закон Ома, чтобы исключить напряжение из уравнения для электроэнергии и получить выражение для мощности, выраженное только через ток и сопротивление. Если мы запишем закон Ома как V = IRV = IR и используем это, чтобы исключить V в уравнении P = IVP = IV, мы получим

P = IV = I (IR) = I2R.P = IV = I (IR) = I2R.

Это дает мощность с точки зрения только тока и сопротивления.

Таким образом, комбинируя закон Ома с уравнением P = IVP = IV для электроэнергии, мы получаем еще два выражения для мощности: одно через напряжение и сопротивление, а другое через ток и сопротивление. Обратите внимание, что в выражения для электрической мощности входят только сопротивление (не емкость или что-либо еще), ток и напряжение. Это означает, что физической характеристикой схемы, определяющей, сколько мощности она рассеивает, является ее сопротивление.Любые конденсаторы в цепи не рассеивают электроэнергию — напротив, конденсаторы либо накапливают электрическую энергию, либо отдают ее обратно в цепь.

Чтобы прояснить связь между напряжением, сопротивлением, током и мощностью, рассмотрим рисунок 19.25, на котором показано колесо формулы . Количества в центральной четверти круга равны количествам в соответствующей внешней четверти круга. Например, чтобы выразить потенциал V через мощность и ток, мы видим из колеса формул, что V = P / IV = P / I.

Рисунок 19.25 Колесо формул показывает, как связаны между собой вольт, сопротивление, ток и мощность. Количества во внутренней четверти окружности равны количеству в соответствующей внешней четверти окружности.

Рабочий пример

Найдите сопротивление лампочки

Типичная старая лампа накаливания имела мощность 60 Вт. Если предположить, что к лампочке приложено 120 В, каков ток через лампочку?

СТРАТЕГИЯ

Нам даны напряжение и выходная мощность простой схемы, содержащей лампочку, поэтому мы можем использовать уравнение P = IVP = IV, чтобы найти ток I , протекающий через лампочку.

Решение

Решение P = IVP = IV для тока и вставка данных значений для напряжения и мощности дает

19,51 P = IVI = PV = 60 Вт 120 V = 0,50 А. P = IVI = PV = 60 Вт 120 В = 0,50 А.

Таким образом, при подаче 120 В. через лампочку проходит половина ампера.

Обсуждение

Это значительное течение. Напомним, что в быту используется переменный, а не постоянный ток, поэтому 120 В, подаваемое от бытовых розеток, — это переменная, а не постоянная мощность. Фактически, 120 В — это усредненная по времени мощность, обеспечиваемая такими розетками.Таким образом, средний ток, протекающий через лампочку за период времени, превышающий несколько секунд, составляет 0,50 А.

Рабочий пример

Подогреватели сапог

Чтобы согреть ботинки в холодные дни, вы решили вшить цепь с некоторыми резисторами в стельку ботинок. Вам нужно 10 Вт тепла от резисторов в каждой стельке, и вы хотите, чтобы они работали от двух 9-вольтовых батарей (соединенных последовательно). Какое общее сопротивление вы должны приложить к каждой стельке?

СТРАТЕГИЯ

Нам известны требуемая мощность и напряжение (18 В, потому что у нас есть две батареи 9 В, соединенные последовательно), поэтому мы можем использовать уравнение P = V2 / RP = V2 / R, чтобы найти необходимое сопротивление.

Решение

Решая P = V2 / RP = V2 / R для сопротивления и вставляя данные напряжение и мощность, получаем

19,52P = V2RR = V2P = (18 В) 210 Вт = 32 Ом. P = V2RR = V2P = (18 В) 210 Вт = 32 Ом.

Таким образом, общее сопротивление в каждой стельке должно составлять 32 Ом · Ом.

Обсуждение

Давайте посмотрим, сколько тока пройдет через эту цепь. У нас есть 18 В, приложенное к сопротивлению 32 Ом, поэтому закон Ома дает

19,53 I = VR = 18 В 32 Ом = 0,56 А. I = VR = 18 В 32 Ом = 0,56 А.

На всех батареях есть этикетки, на которых указано, сколько заряда они могут обеспечить (в единицах силы тока, умноженного на время).Типичная щелочная батарея на 9 В может обеспечить заряд 565 мА · ч · мА · ч. (так две батареи 9 В обеспечивают 1130 мА · ч · мА · ч), поэтому эта система обогрева проработает в течение

часов. 19,54t = 1130 × 10−3 A⋅h0,56 A = 2,0 h.t = 1130 × 10−3 A⋅h0,56 A = 2,0 час.

Рабочий пример

Питание через ответвление цепи

Каждый резистор в приведенной ниже схеме имеет сопротивление 30 Ом. Какая мощность рассеивается средней ветвью схемы?

СТРАТЕГИЯ

Средняя ветвь схемы содержит последовательно включенные резисторы R3 и R5R3 и R5.Напряжение на этой ветви составляет 12 В. Сначала мы найдем эквивалентное сопротивление в этой ветви, а затем используем P = V2 / RP = V2 / R, чтобы найти мощность, рассеиваемую в ветви.

Решение

Эквивалентное сопротивление: R среднее = R3 + R5 = 30 Ом + 30 Ом = 60 Ом R среднее = R3 + R5 = 30 Ом + 30 Ом = 60 Ом. Мощность, рассеиваемая средней ветвью схемы, составляет

ед. 19,55P средний = V2R средний = (12 В) 260 Ом = 2,4 Вт. Средний = V2R средний = (12 В) 260 Ом = 2,4 Вт.

Обсуждение

Давайте посмотрим, сохраняется ли энергия в этой цепи, сравнив мощность, рассеиваемую в цепи, с мощностью, обеспечиваемой батареей.Во-первых, эквивалентное сопротивление левой ветви

19,56 Влево = 11 / R1 + 1 / R2 + R4 = 11/30 Ом + 1/30 Ом + 30 Ом = 45 Ом. Влево = 11 / R1 + 1 / R2 + R4 = 11/30 Ом + 1/30 Ом +30 Ом = 45 Ом.

Мощность через левую ветвь

19,57 Слева = V2R, слева = (12 В) 245 Ом = 3,2 Вт. Слева = V2R, слева = (12 В) 245 Ом = 3,2 Вт.

Правая ветвь содержит только R6R6, поэтому эквивалентное сопротивление Rright = R6 = 30 ΩRright = R6 = 30 Ω. Мощность через правую ветку

19,58 Правый = V2 Правый = (12 В) 230 Ом = 4,8 Вт. Правый = V2 Правый = (12 В) 230 Ом = 4,8 Вт.

Общая мощность, рассеиваемая схемой, представляет собой сумму мощностей, рассеиваемых в каждой ветви.

19,59P = складка + середина + прядь = 2,4 Вт + 3,2 Вт + 4,8 Вт = 10,4 WP = складка + середина + прядь = 2,4 Вт + 3,2 Вт + 4,8 Вт = 10,4 Вт

Мощность, обеспечиваемая аккумулятором, составляет

.

, где I — полный ток, протекающий через батарею. Поэтому мы должны сложить токи, проходящие через каждую ветвь, чтобы получить I . Ветви вносят токи

19,61 слева = VR слева = 12 В 45 Ом = 0.2667 AIсредний = VR средний = 12 В 60 Ом = 0.20 AIright = VRright = 12 В 30 Ом = 0,40 A. Левый = VR Левый = 12 В 45 Ом = 0,2667 AI Средний = VR средний = 12 В 60 Ом = 0,20 AIright = VRright = 12 В 30 Ом = 0,40 А.

Суммарный ток

19,62 I = слева + Imiddle + I right = 0,2667 A + 0,20 A + 0,40 A = 0,87 A. I = I слева + Imiddle + I right = 0,2667 A + 0,20 A + 0,40 A = 0,87 A.

, а мощность, обеспечиваемая аккумулятором, составляет

19,63P = IV = (0,87 A) (12 В) = 10,4 Вт. P = IV = (0,87 A) (12 В) = 10,4 Вт.

Это та же мощность, которая рассеивается на резисторах схемы, что показывает, что в этой цепи сохраняется энергия.

Электроэнергетика и энергия | Физика II

Цели обучения

К концу этого раздела вы сможете:

• Рассчитайте мощность, рассеиваемую резистором, и мощность, подаваемую источником питания.
• Рассчитайте стоимость электроэнергии при различных обстоятельствах.

Мощность в электрических цепях

У многих людей власть ассоциируется с электричеством. Зная, что мощность — это коэффициент использования или преобразования энергии, каково выражение для электроэнергии ? На ум могут прийти линии электропередач.Мы также думаем о лампочках с точки зрения их номинальной мощности в ваттах. Сравним лампочку на 25 Вт с лампой на 60 Вт. (См. Рис. 1 (а).) Поскольку оба работают от одного и того же напряжения, лампа мощностью 60 Вт должна потреблять больше тока, чтобы иметь большую номинальную мощность. Таким образом, сопротивление лампы на 60 Вт должно быть ниже, чем у лампы на 25 Вт. Если мы увеличиваем напряжение, мы также увеличиваем мощность. Например, когда лампочка мощностью 25 Вт, рассчитанная на работу от 120 В, подключена к 240 В, она на короткое время очень ярко светится, а затем перегорает.Как именно напряжение, ток и сопротивление связаны с электроэнергией?

Рис. 1. (a) Какая из этих лампочек, лампа мощностью 25 Вт (вверху слева) или лампа мощностью 60 Вт (вверху справа), имеет более высокое сопротивление? Что потребляет больше тока? Что потребляет больше всего энергии? Можно ли по цвету сказать, что нить накаливания мощностью 25 Вт круче? Является ли более яркая лампочка другого цвета, и если да, то почему? (кредиты: Дикбаух, Wikimedia Commons; Грег Вестфолл, Flickr) (б) Этот компактный люминесцентный светильник (КЛЛ) излучает такую ​​же интенсивность света, как и лампа мощностью 60 Вт, но при входной мощности от 1/4 до 1/10.(кредит: dbgg1979, Flickr)

Электрическая энергия зависит как от напряжения, так и от перемещаемого заряда. Проще всего это выражается как PE = qV , где q — это перемещенный заряд, а V — это напряжение (или, точнее, разность потенциалов, через которую проходит заряд). Мощность — это скорость перемещения энергии, поэтому электрическая мощность равна

.

[латекс] P = \ frac {PE} {t} = \ frac {qV} {t} \\ [/ latex].

Учитывая, что ток равен I = q / t (обратите внимание, что Δ t = t здесь), выражение для мощности принимает вид

P = IV

Электрическая мощность ( P ) — это просто произведение тока на напряжение.Мощность имеет знакомые единицы ватт. Поскольку единицей СИ для потенциальной энергии (PE) является джоуль, мощность выражается в джоулях в секунду или ваттах. Таким образом, 1 A ⋅V = 1 Вт. Например, в автомобилях часто есть одна или несколько дополнительных розеток, с помощью которых можно заряжать сотовый телефон или другие электронные устройства. {2} R \\ [/ latex].

Обратите внимание, что первое уравнение всегда верно, тогда как два других можно использовать только для резисторов. В простой схеме с одним источником напряжения и одним резистором мощность, подаваемая источником напряжения, и мощность, рассеиваемая резистором, идентичны. (В более сложных схемах P может быть мощностью, рассеиваемой одним устройством, а не полной мощностью в цепи.) Из трех различных выражений для электрической мощности можно получить различное понимание. Например, P = V ² / R подразумевает, что чем меньше сопротивление, подключенное к данному источнику напряжения, тем больше подаваемая мощность.Кроме того, поскольку напряжение возведено в квадрат в P = V ² / R , эффект от приложения более высокого напряжения, возможно, больше, чем ожидалось. Таким образом, когда напряжение увеличивается вдвое до лампочки мощностью 25 Вт, ее мощность увеличивается почти в четыре раза и составляет примерно 100 Вт, что приводит к ее перегоранию. Если бы сопротивление лампы оставалось постоянным, ее мощность была бы ровно 100 Вт, но при более высокой температуре ее сопротивление также будет выше.

Пример 1. Расчет рассеиваемой мощности и тока: горячая и холодная энергия

(a) Рассмотрим примеры, приведенные в Законе Ома: сопротивление и простые цепи и сопротивление и удельное сопротивление.Затем найдите мощность, рассеиваемую автомобильной фарой в этих примерах, как в горячую, так и в холодную погоду. б) Какой ток он потребляет в холодном состоянии?

Стратегия для (а)

Для горячей фары нам известны напряжение и ток, поэтому мы можем использовать P = IV , чтобы найти мощность. Для холодной фары нам известны напряжение и сопротивление, поэтому мы можем использовать P = V ² / R , чтобы найти мощность.

Решение для (a)

Вводя известные значения тока и напряжения для горячей фары, получаем

P = IV = (2.{2}} {0,350 \ text {} \ Omega} = 411 \ text {W} \\ [/ latex].

Обсуждение для (а)

30 Вт, рассеиваемые горячей фарой, являются типичными. Но 411 Вт в холодную погоду на удивление выше. Начальная мощность быстро уменьшается по мере увеличения температуры лампы и увеличения ее сопротивления.

Стратегия и решение для (b)

Ток при холодной лампочке можно найти несколькими способами. Переставляем одно из уравнений мощности, P = I ² R , и вводим известные значения, получая

[латекс] I = \ sqrt {\ frac {P} {R}} = \ sqrt {\ frac {411 \ text {W}} {{0.350} \ text {} \ Omega}} = 34,3 \ text {A} \\ [/ latex].

Обсуждение для (б)

Холодный ток значительно выше, чем установившееся значение 2,50 А, но ток быстро снизится до этого значения по мере увеличения температуры лампы. Большинство предохранителей и автоматических выключателей (используемых для ограничения тока в цепи) рассчитаны на кратковременную выдержку очень высоких токов при включении устройства. В некоторых случаях, например, с электродвигателями, ток остается высоким в течение нескольких секунд, что требует использования специальных плавких предохранителей с замедленным срабатыванием.

Чем больше электроприборов вы используете и чем дольше они остаются включенными, тем выше ваш счет за электроэнергию. Этот знакомый факт основан на соотношении энергии и мощности. Вы платите за использованную энергию. Поскольку P = E / t , мы видим, что

E = Pt

— это энергия, используемая устройством, использующим мощность P в течение интервала времени t . Например, чем больше горит лампочек, тем больше используется P ; чем дольше они работают, тем больше т .Единицей энергии в счетах за электричество является киловатт-час (кВт ч), что соответствует соотношению E = Pt . Стоимость эксплуатации электроприборов легко оценить, если у вас есть некоторое представление об их потребляемой мощности в ваттах или киловаттах, времени их работы в часах и стоимости киловатт-часа для вашей электросети. Киловатт-часы, как и все другие специализированные единицы энергии, такие как пищевые калории, можно преобразовать в джоули. Вы можете доказать себе, что 1 кВт ⋅ ч = 3.6 × 10 ⁶ Дж.

Потребляемую электрическую энергию ( E ) можно уменьшить либо за счет сокращения времени использования, либо за счет снижения энергопотребления этого прибора или приспособления. Это не только снизит стоимость, но и снизит воздействие на окружающую среду. Улучшение освещения — один из самых быстрых способов снизить потребление электроэнергии в доме или на работе. Около 20% энергии в доме расходуется на освещение, в то время как в коммерческих учреждениях эта цифра приближается к 40%.Флуоресцентные лампы примерно в четыре раза эффективнее ламп накаливания — это верно как для длинных ламп, так и для компактных люминесцентных ламп (КЛЛ). (См. Рис. 1 (b).) Таким образом, лампу накаливания мощностью 60 Вт можно заменить на КЛЛ мощностью 15 Вт, которая имеет такую ​​же яркость и цвет. КЛЛ имеют изогнутую трубку внутри шара или спиралевидную трубку, все они подключены к стандартному привинчиваемому основанию, которое подходит для стандартных розеток лампы накаливания. (В последние годы были решены исходные проблемы с цветом, мерцанием, формой и высокими начальными инвестициями для КЛЛ.) Теплопередача от этих КЛЛ меньше, и они служат до 10 раз дольше. В следующем примере рассматривается важность инвестиций в такие лампы. Новые белые светодиодные фонари (которые представляют собой группы небольших светодиодных лампочек) еще более эффективны (в два раза больше, чем у КЛЛ) и служат в 5 раз дольше, чем КЛЛ. Однако их стоимость по-прежнему высока.

Установление соединений: энергия, мощность и время

Отношение E = Pt может оказаться полезным во многих различных контекстах.Энергия, которую ваше тело использует во время упражнений, зависит, например, от уровня мощности и продолжительности вашей активности. Степень нагрева от источника питания зависит от уровня мощности и времени ее применения. Даже доза облучения рентгеновского изображения зависит от мощности и времени воздействия.

Пример 2. Расчет рентабельности компактных люминесцентных ламп (КЛЛ)

Если стоимость электроэнергии в вашем районе составляет 12 центов за кВтч, какова общая стоимость (капитальные плюс эксплуатация) использования лампы накаливания мощностью 60 Вт в течение 1000 часов (срок службы этой лампы), если стоимость лампы составляет 25 центов? (б) Если мы заменим эту лампочку компактной люминесцентной лампой, которая дает такой же световой поток, но составляет четверть мощности и стоит 1 доллар.50, но длится в 10 раз дольше (10 000 часов), какова будет общая стоимость?

Стратегия

Чтобы найти эксплуатационные расходы, мы сначала находим использованную энергию в киловатт-часах, а затем умножаем ее на стоимость киловатт-часа.

Решение для (a)

Энергия, используемая в киловатт-часах, определяется путем ввода мощности и времени в выражение для энергии:

E = Pt = (60 Вт) (1000 ч) = 60,000 Вт ч

В киловатт-часах это

E = 60.0 кВт ⋅ ч.

Сейчас стоимость электроэнергии

Стоимость

= (60,0 кВт ч) (0,12 долл. США / кВт час) = 7,20 долл. США.

Общая стоимость составит 7,20 доллара за 1000 часов (около полугода при 5 часах в день).

Решение для (b)

Поскольку CFL использует только 15 Вт, а не 60 Вт, стоимость электроэнергии составит 7,20 доллара США / 4 = 1,80 доллара США. КЛЛ прослужит в 10 раз дольше, чем лампа накаливания, так что инвестиционные затраты составят 1/10 стоимости лампы за этот период использования, или 0.1 (1,50 доллара США) = 0,15 доллара США. Таким образом, общая стоимость 1000 часов составит 1,95 доллара США.

Обсуждение

Следовательно, использование КЛЛ намного дешевле, даже если начальные вложения выше. Повышенная стоимость рабочей силы, которую бизнес должен включать в себя для более частой замены ламп накаливания, здесь не учитывается.

Подключение: Эксперимент на вынос — Инвентаризация использования электроэнергии

1) Составьте список номинальной мощности для ряда приборов в вашем доме или комнате.Объясните, почему что-то вроде тостера имеет более высокий рейтинг, чем цифровые часы. Оцените энергию, потребляемую этими приборами в среднем за день (оценивая время их использования). Некоторые приборы могут указывать только рабочий ток. Если бытовое напряжение составляет 120 В, используйте P = IV . 2) Проверьте общую мощность, используемую в туалетах на этаже или в здании вашей школы. (Возможно, вам придется предположить, что используемые длинные люминесцентные лампы рассчитаны на 32 Вт.) Предположим, что здание было закрыто все выходные, и что эти огни были оставлены включенными с 6 часов вечера.{2} R \\ [/ латекс].

• Энергия, используемая устройством с мощностью P за время t , составляет E = Pt .

Концептуальные вопросы

1. Почему лампы накаливания тускнеют в конце жизни, особенно незадолго до того, как их нити оборвутся?

Мощность, рассеиваемая на резисторе, равна P = V ² / R , что означает, что мощность уменьшается при увеличении сопротивления. Однако эта мощность также определяется соотношением P = I ² R , что означает, что мощность увеличивается при увеличении сопротивления.Объясните, почему здесь нет противоречия.

Задачи и упражнения

1. Какова мощность разряда молнии 1,00 × 10 ² МВ при токе 2,00 × 10 ⁴ A ?

2. Какая мощность подается на стартер большого грузовика, который потребляет 250 А тока от аккумуляторной батареи 24,0 В?

3. Заряд в 4,00 Кл проходит через солнечные элементы карманного калькулятора за 4,00 часа. Какова выходная мощность, если выходное напряжение вычислителя равно 3.00 В? (См. Рисунок 2.)

Рис. 2. Полоса солнечных элементов прямо над клавишами этого калькулятора преобразует свет в электричество для удовлетворения своих потребностей в энергии. (Источник: Эван-Амос, Wikimedia Commons)

4. Сколько ватт проходит через фонарик с 6,00 × 10 ² за 0,500 ч использования, если его напряжение составляет 3,00 В?

5. Найдите мощность, рассеиваемую в каждом из этих удлинителей: (a) удлинительный шнур с сопротивлением 0,0600 Ом, через который 5.00 А течет; (б) более дешевый шнур с более тонким проводом и сопротивлением 0,300 Ом.

6. Убедитесь, что единицами измерения вольт-ампер являются ватты, как следует из уравнения P = IV .

7. Покажите, что единицы 1V ² / Ω = 1W, как следует из уравнения P = V ² / R .

8. Покажите, что единицы 1 A ² Ω = 1 Вт, как следует из уравнения P = I ² R .

9. Проверьте эквивалент единиц энергии: 1 кВт ч = 3,60 × 10 ⁶ Дж.

10. Электроны в рентгеновской трубке ускоряются до 1,00 × 10 ² кВ и направляются к цели для получения рентгеновских лучей. Вычислите мощность электронного луча в этой трубке, если она имеет ток 15,0 мА.

11. Электрический водонагреватель потребляет 5,00 кВт на 2,00 часа в сутки. Какова стоимость его эксплуатации в течение одного года, если электроэнергия стоит 12,0 центов / кВт · ч? См. Рисунок 3.

Рисунок 3. Водонагреватель электрический по запросу. Тепло в воду подается только при необходимости. (кредит: aviddavid, Flickr)

12. Сколько электроэнергии необходимо для тостера с тостером мощностью 1200 Вт (время приготовления = 1 минута)? Сколько это стоит при 9,0 цента / кВт · ч?

13. Какова будет максимальная стоимость КЛЛ, если общая стоимость (капиталовложения плюс эксплуатация) будет одинаковой как для КЛЛ, так и для ламп накаливания мощностью 60 Вт? Предположим, что стоимость лампы накаливания составляет 25 центов, а электричество стоит 10 центов / кВтч.Рассчитайте стоимость 1000 часов, как в примере с КЛЛ по рентабельности.

14. Некоторые модели старых автомобилей имеют электрическую систему напряжением 6,00 В. а) Каково сопротивление горячему свету у фары мощностью 30,0 Вт в такой машине? б) Какой ток течет через него?

15. Щелочные батареи имеют то преимущество, что они выдают постоянное напряжение почти до конца своего срока службы. Как долго щелочная батарея с номиналом 1,00 А · ч и 1,58 В будет поддерживать горящую лампочку фонарика мощностью 1,00 Вт?

16.Прижигатель, используемый для остановки кровотечения в хирургии, выдает 2,00 мА при 15,0 кВ. а) Какова его выходная мощность? б) Какое сопротивление пути?

17. В среднем телевизор работает 6 часов в день. Оцените ежегодные затраты на электроэнергию для работы 100 миллионов телевизоров, предполагая, что их потребляемая мощность составляет в среднем 150 Вт, а стоимость электроэнергии составляет в среднем 12,0 центов / кВт · ч.

18. Старая лампочка потребляет всего 50,0 Вт, а не 60,0 Вт из-за истончения ее нити за счет испарения.Во сколько раз уменьшается его диаметр при условии равномерного утонения по длине? Не обращайте внимания на любые эффекты, вызванные перепадами температур.

Медная проволока калибра 19. 00 имеет диаметр 9,266 мм. Вычислите потери мощности в километре такого провода, когда он пропускает 1,00 × 10 ² A.

Холодные испарители пропускают ток через воду, испаряя ее при небольшом повышении температуры. Одно такое домашнее устройство рассчитано на 3,50 А и использует 120 В переменного тока с эффективностью 95,0%.а) Какова скорость испарения в граммах в минуту? (b) Сколько воды нужно налить в испаритель за 8 часов работы в ночное время? (См. Рисунок 4.)

Рис. 4. Этот холодный испаритель пропускает ток непосредственно через воду, испаряя ее напрямую с относительно небольшим повышением температуры.

21. Integrated Concepts (a) Какая энергия рассеивается разрядом молнии с током 20 000 А, напряжением 1,00 × 10 ² МВ и длиной 1.00 мс? (б) Какую массу древесного сока можно было бы поднять с 18ºC до точки кипения, а затем испарить за счет этой энергии, если предположить, что сок имеет те же тепловые характеристики, что и вода?

22. Integrated Concepts Какой ток должен вырабатывать подогреватель бутылочек на 12,0 В, чтобы нагреть 75,0 г стекла, 250 г детской смеси и 3,00 × 10 ² алюминия от 20 ° C до 90º за 5,00 мин?

23. Integrated Concepts Сколько времени требуется хирургическому прижигателю, чтобы поднять температуру на 1.00 г ткани от 37º до 100, а затем закипятите 0,500 г воды, если она выдает 2,00 мА при 15,0 кВ? Не обращайте внимания на передачу тепла в окружающую среду.

24. Integrated Concepts Гидроэлектрические генераторы (см. Рисунок 5) на плотине Гувера вырабатывают максимальный ток 8,00 × 10 ³ А при 250 кВ. а) Какая выходная мощность? (b) Вода, питающая генераторы, входит и покидает систему с небольшой скоростью (таким образом, ее кинетическая энергия не изменяется), но теряет 160 м в высоте.Сколько кубических метров в секунду необходимо при КПД 85,0%?

Рисунок 5. Гидроэлектрические генераторы на плотине Гувера. (кредит: Джон Салливан)

25. Integrated Concepts (a) Исходя из 95,0% эффективности преобразования электроэнергии двигателем, какой ток должны обеспечивать аккумуляторные батареи на 12,0 В 750-килограммового электромобиля: отдых до 25,0 м / с за 1,00 мин? (b) Подняться на холм высотой 2,00 × 10 ² м за 2,00 мин при постоянной 25.Скорость 0 м / с при приложении силы 5,00 × 10 ² Н для преодоления сопротивления воздуха и трения? (c) Двигаться с постоянной скоростью 25,0 м / с, прилагая силу 5,00 × 10 ² Н для преодоления сопротивления воздуха и трения? См. Рисунок 6.

Рис. 6. Электромобиль REVAi заряжается на одной из улиц Лондона. (кредит: Фрэнк Хебберт)

26. Integrated Concepts Пригородный легкорельсовый поезд потребляет 630 А постоянного тока напряжением 650 В при ускорении.а) Какова его мощность в киловаттах? (b) Сколько времени нужно, чтобы достичь скорости 20,0 м / с, начиная с состояния покоя, если его загруженная масса составляет 5,30 × 10 ⁴ кг, предполагая КПД 95,0% и постоянную мощность? (c) Найдите его среднее ускорение. (г) Обсудите, как ускорение, которое вы обнаружили для легкорельсового поезда, сравнивается с тем, что может быть типичным для автомобиля.

27. Integrated Concepts (a) Линия электропередачи из алюминия имеет сопротивление 0,0580 Ом / км. Какова его масса на километр? б) Какова масса на километр медной линии с таким же сопротивлением? Более низкое сопротивление сократит время нагрева.Обсудите практические ограничения ускорения нагрева за счет снижения сопротивления.

28. Integrated Concepts (a) Погружной нагреватель, работающий на 120 В, может повысить температуру 1,00 × 10 ² -граммовых алюминиевых стаканов, содержащих 350 г воды, с 20 ° C до 95 ° C за 2,00 мин. Найдите его сопротивление, предполагая, что оно постоянно в процессе. (b) Более низкое сопротивление сократит время нагрева. Обсудите практические ограничения ускорения нагрева за счет снижения сопротивления.

29. Integrated Concepts (a) Какова стоимость нагрева гидромассажной ванны, содержащей 1500 кг воды, от 10 ° C до 40 ° C, исходя из эффективности 75,0% с учетом передачи тепла в окружающую среду? Стоимость электроэнергии 9 центов / кВт⋅ч. (b) Какой ток потреблял электрический нагреватель переменного тока 220 В, если на это потребовалось 4 часа?

30 . Необоснованные результаты (a) Какой ток необходим для передачи 1,00 × 10 ² МВт мощности при 480 В? (b) Какая мощность рассеивается линиями передачи, если они имеют коэффициент 1.00 — сопротивление Ом? (c) Что неразумного в этом результате? (d) Какие предположения необоснованны или какие посылки несовместимы?

31. Необоснованные результаты (a) Какой ток необходим для передачи мощности 1,00 × 10 ² МВт при 10,0 кВ? (b) Найдите сопротивление 1,00 км провода, которое вызовет потерю мощности 0,0100%. (c) Каков диаметр медного провода длиной 1,00 км, имеющего такое сопротивление? (г) Что необоснованного в этих результатах? (e) Какие предположения необоснованны или какие посылки несовместимы?

32.Создайте свою проблему Представьте себе электрический погружной нагреватель, используемый для нагрева чашки воды для приготовления чая. Постройте задачу, в которой вы рассчитываете необходимое сопротивление нагревателя, чтобы он увеличивал температуру воды и чашки за разумный промежуток времени. Также рассчитайте стоимость электроэнергии, используемой в вашем технологическом процессе. Среди факторов, которые следует учитывать, — это используемое напряжение, задействованные массы и теплоемкость, тепловые потери и время, в течение которого происходит нагрев.Ваш инструктор может пожелать, чтобы вы рассмотрели тепловой предохранительный выключатель (возможно, биметаллический), который остановит процесс до того, как в погружном блоке будут достигнуты опасные температуры.

Глоссарий

электрическая мощность:

скорость, с которой электрическая энергия подается источником или рассеивается устройством; это произведение тока на напряжение

Избранные решения проблем и упражнения

1. 2,00 × 10 ¹² Вт

5.{6} \ text {J} \\ [/ latex]

11. 438 $ / год

13. $ 6.25

15. 1.58 ч

17. 3,94 миллиарда долларов в год

19. 25,5 Вт

21. (а) 2,00 × 10 ⁹ Дж (б) 769 кг

23. 45.0 с

25. (а) 343 A (б) 2,17 × 10 ³ A (в) 1,10 × 10 ³ A

27. (а) 1,23 × 10 ³ кг (б) 2,64 × 10 ³ кг

29. (a) 2,08 × 10 ⁵ A
(b) 4,33 × 10 ⁴ МВт
(c) Линии передачи рассеивают больше мощности, чем они должны передавать.
(d) Напряжение 480 В неоправданно низкое для напряжения передачи. В линиях передачи на большие расстояния поддерживается гораздо более высокое напряжение (часто сотни киловольт), чтобы уменьшить потери мощности.

Лампочка — это резистор?

Лампочка была одним из величайших изобретений в нашей истории.

Это помогло осветить наши дома, рабочие места, улицы и многие другие области и аспекты повседневной жизни.

Это означало, что мы могли выполнять задачи до поздней ночи, без необходимости носить с собой свечу, что было не очень эффективным способом освещения помещения.

А лампочка — это резистор? Лампочка не является традиционным резистором, но ведет себя как резистор. Резистор — это компонент, ограничивающий поток электронов. Когда эти электроны проходят через резистор, они сталкиваются с «сопротивлением», и большая часть их энергии преобразуется в другие формы энергии, такие как тепло.

Эта концепция верна и для лампочки. Когда электричество проходит через нить накала лампочки (которая по сути является резистором), энергия преобразуется в тепло и свет.

Почему лампочка не совсем резистор

Первое, что нам нужно понять, это резистор. Тогда мы сможем понять, почему лампочка не совсем резистор, а ведет себя как резистор.

Как упоминалось выше, резистор — это компонент, ограничивающий прохождение тока в электрических и электронных схемах.

Однако это еще не все. Омическое сопротивление — это сопротивление материала протеканию электрического тока, оно выражается в омах.

Существует формула, которая помогает нам найти омическое сопротивление резистора, которое показано ниже.

Омический резистор подчиняется закону Ома, что подтверждается приведенной выше формулой. Увеличение Voltage вызывает линейное увеличение Current . Омический резистор сохраняет свое значение независимо от того, какой ток через него протекает.

С другой стороны, неомический резистор не подчиняется закону Ома. Увеличение Напряжение создает нелинейное увеличение тока.

Сопротивление материала изменяется в зависимости от силы тока, проходящего через него.

Как электрическая лампочка ведет себя как резистор

Учитывая разницу между омическим и неомическим резистором, мы можем более подробно рассмотреть, как электрическая лампочка ведет себя как резистор, а не является традиционным омическим резистором.

Все лампочки содержат нить накала, обладающую некоторым сопротивлением. Когда электричество проходит через нить накала, оно встречает это сопротивление, и энергия преобразуется в свет и тепло.

Самый распространенный материал, используемый в нити накаливания — Вольфрам.

Вольфрам имеет сопротивление холоду 9,6 Ом при 100 Вт. Если приложить 120 вольт, по закону Ома мы получим ток 12,5 ампер.

Но температура вольфрама нагревается, как и его сопротивление. При том же напряжении 120 вольт сопротивление увеличивается до 144 Ом, а результирующий ток составляет 0,83 ампера.

Как видите, сопротивление нити накала изменяется и поэтому классифицируется как неомическое сопротивление.

Кроме того, если к лампочке приложить большее напряжение, температура нити накала повысится, а ее сопротивление уменьшится.

Другая причина, по которой он ведет себя как резистор, связана с тем, что нить накала представляет собой катушку. Прямой провод уже имеет сопротивление, при намотке в катушку это сопротивление увеличивается.

Можно ли использовать лампочку в цепи в качестве резистора?

Итак, теперь мы знаем, что лампочка — это не совсем обычный резистор (она не омическая), не могли бы вы использовать ее в цепи для замены резистора, чтобы выполнять ту же работу, которая заключается в обеспечении сопротивления.

Хотя он обеспечивает сопротивление, использование в цепи лампочки вместо обычного омического резистора было бы очень неэффективным. Как вы видели ранее, много энергии теряется из-за света и тепла.

Другая причина, по которой вы не захотите использовать лампочку в цепи для замены резистора, связана с тем, что лампочка не омическая. Его сопротивление не будет оставаться постоянным и подчиняться закону Ома.

Сопротивление лампочки будет меняться в зависимости от температуры и напряжения, что не идеально для электрической или электронной схемы, поскольку для этого требуется постоянное сопротивление.

Из какого материала в лампочке используется резистор?

Наиболее часто используемый сегодня в лампах материал, из-за которого они ведут себя как резистор, — это Вольфрам .

Однако на ранних этапах производства ламп вольфрам не использовался.

Первые нити накаливания для ламп накаливания были изготовлены из Карбонизированная бумага или Бамбук .

Опять же, эти материалы, используемые в лампочке, обладают сопротивлением, в результате чего лампочка ведет себя как резистор.

Углерод, используемый в лампочке, имеет отрицательный температурный коэффициент сопротивления. Это означает, что с повышением температуры его сопротивление уменьшается.

Это вызывает колебания мощности, поскольку ток в цепи изменяется при изменении сопротивления.

Уменьшается ли эффективность лампочки из-за того, что она ведет себя как резистор?

Создание лампочки было поворотным моментом в нашей истории, но это не самый эффективный способ осветить пространство.

Когда ток проходит через вольфрамовую нить накала, она нагревается до температур от 2000 до 3300 K (от 1730 до 3030 ° C; от 3140 до 5480 ° F). Однако эти температуры недостаточно высоки, чтобы расплавить вольфрамовую нить.

Мы знаем, что часть этой энергии преобразуется в свет, но большая часть энергии преобразуется в тепло из-за резистивной природы вольфрамовой нити.

Какие есть альтернативы лампочке, которая ведет себя не так, как резистор?

Светоизлучающий диод (LED) является альтернативой использованию лампочки.

Но у светодиода также есть какое-то сопротивление, которое заставляет его вести себя как резистор. Однако сопротивление светодиода намного ниже, чем у лампочки.

Кроме того, светодиод рассеивает такой же уровень тепла, что и лампочка, что делает его более эффективной альтернативой.

Изменилось ли сопротивление лампочки?

Да, поскольку большинство материалов, используемых в качестве нитей для ламп накаливания, имеют отрицательный температурный коэффициент сопротивления.

Итак, когда нить накала лампы нагревается, ее электрическое сопротивление уменьшается.

На температуру нити накала в значительной степени влияет сила тока, протекающего через нее.

Чем больше ток, тем горячее он становится и, следовательно, сопротивление уменьшается. По мере уменьшения тока температура и, следовательно, сопротивление возрастают.

9.6: Электроэнергия и мощность

ЦЕЛИ ОБУЧЕНИЯ

К концу этого раздела вы сможете:

• Выразить электрическую мощность через напряжение и ток
• Опишите мощность, рассеиваемую резистором в электрической цепи
• Расчет энергоэффективности и рентабельности приборов и оборудования

В электрической цепи электрическая энергия непрерывно преобразуется в другие формы энергии.Например, когда в проводнике течет ток, электрическая энергия преобразуется в тепловую энергию внутри проводника. Электрическое поле, создаваемое источником напряжения, ускоряет свободные электроны, увеличивая их кинетическую энергию на короткое время. Эта увеличенная кинетическая энергия преобразуется в тепловую энергию в результате столкновений с ионами решетчатой ​​структуры проводника. Ранее мы определяли мощность как скорость, с которой работа выполняется силой, измеряемой в ваттах. Мощность также можно определить как скорость передачи энергии.В этом разделе мы обсуждаем скорость передачи энергии или мощности в электрической цепи.

Мощность в электрических цепях

У многих людей власть ассоциируется с электричеством. На ум могут прийти линии электропередач. Мы также думаем о лампочках с точки зрения их номинальной мощности в ваттах. Каково выражение для электроэнергии ?

Давайте сравним лампу мощностью 25 Вт с лампой мощностью 60 Вт (рисунок \ (\ PageIndex {1a} \)). Лампа на 60 Вт светится ярче, чем лампа на 25 Вт.Хотя это не показано, лампа мощностью 60 Вт также теплее, чем лампа мощностью 25 Вт. Тепло и свет производятся путем преобразования электрической энергии. Кинетическая энергия, теряемая электронами при столкновениях, преобразуется во внутреннюю энергию проводника и излучения. Как напряжение, ток и сопротивление связаны с электроэнергией?

Рисунок \ (\ PageIndex {1} \): (a) На изображении выше показаны две лампы накаливания: лампа мощностью 25 Вт (слева) и лампа мощностью 60 Вт (справа). Лампа мощностью 60 Вт обеспечивает более интенсивный свет, чем лампа мощностью 25 Вт.Электрическая энергия, подаваемая в лампочки, преобразуется в тепло и свет. (b) Эта компактная люминесцентная лампа (КЛЛ) излучает такой же свет, что и лампа мощностью 60 Вт, но при входной мощности от 1/4 до 1/10. (кредит a: модификация работ «Dickbauch» / Wikimedia Commons и Грега Вестфолла; кредит b: модификация работ «dbgg1979» / Flickr)

Чтобы рассчитать электрическую мощность, рассмотрите разницу напряжений, существующую на материале (рисунок \ (\ PageIndex {2} \)). Электрический потенциал \ (V_1 \) выше, чем электрический потенциал в \ (V_2 \), а разность напряжений отрицательна \ (V = V_2 — V_1 \).Как обсуждалось в «Электрический потенциал», между двумя потенциалами существует электрическое поле, которое указывает от более высокого потенциала к более низкому. Напомним, что электрический потенциал определяется как потенциальная энергия заряда, \ (V = \ Delta U / q \), и заряд \ (\ Delta Q \) теряет потенциальную энергию, перемещаясь через разность потенциалов.

Рисунок \ (\ PageIndex {2} \): Когда есть разность потенциалов в проводнике, присутствует электрическое поле, которое указывает в направлении от более высокого потенциала к более низкому потенциалу.

Если заряд положительный, на него действует сила электрического поля \ (\ vec {F} = m \ vec {a} = \ Delta Q \ vec {E} \). Эта сила необходима, чтобы заряд двигался. Эта сила не ускоряет заряд на всем расстоянии \ (\ Delta L \) из-за взаимодействия заряда с атомами и свободными электронами в материале. Скорость и, следовательно, кинетическая энергия заряда не увеличиваются в течение всего пути через \ (\ Delta L \), а заряд, проходящий через область \ (A_2 \), имеет ту же скорость дрейфа \ (v_d \), что и заряд, который проходит через область \ (A_1 \).Однако с зарядом работает электрическое поле, которое изменяет потенциальную энергию. Поскольку изменение разности электрических потенциалов отрицательное, электрическое поле оказывается равным

.

\ [E = — \ dfrac {(V_2 — V_1)} {\ Delta L} = \ dfrac {V} {\ Delta L}. \]

Работа, совершаемая над зарядом, равна произведению электрической силы на длину приложения силы,

\ [W = F \ Delta L = (\ Delta Q E) \ Delta L = \ left (\ Delta Q \ dfrac {V} {\ Delta L} \ right) \ Delta L = \ Delta Q V = \ Delta U.\]

Заряд движется с дрейфовой скоростью \ (v_d \), поэтому работа, выполняемая над зарядом, приводит к потере потенциальной энергии, но средняя кинетическая энергия остается постоянной. Потерянная электрическая потенциальная энергия проявляется в материале как тепловая энергия. В микроскопическом масштабе передача энергии происходит из-за столкновений между зарядом и молекулами материала, что приводит к повышению температуры в материале. Потеря потенциальной энергии приводит к повышению температуры материала, которая рассеивается в виде излучения.2 / R \), эффект от приложения более высокого напряжения, возможно, больше, чем ожидалось. Таким образом, когда напряжение увеличивается вдвое до лампочки мощностью 25 Вт, ее мощность увеличивается почти в четыре раза и составляет примерно 100 Вт, что приводит к ее перегоранию. Если бы сопротивление лампы оставалось постоянным, ее мощность была бы ровно 100 Вт, но при более высокой температуре ее сопротивление также будет выше.

Пример \ (\ PageIndex {1} \): Расчет мощности в электрических устройствах

Двигатель лебедки постоянного тока рассчитан на 20,00 А при напряжении 115 В. Когда двигатель работает на максимальной мощности, он может поднимать объект весом 4900.00 N на расстояние 10,00 м, за 30,00 с, с постоянной скоростью.

1. Какая мощность потребляет двигатель?
2. Какая сила используется для подъема объекта? Не обращайте внимания на сопротивление воздуха. (c) Предполагая, что разница в мощности, потребляемой двигателем, и мощности, используемой для подъема объекта, рассеивается в виде тепла за счет сопротивления двигателя, оценить сопротивление двигателя?

Стратегия

1. Мощность, потребляемую двигателем, можно найти с помощью \ (P = IV \).2 R \).

Решение

1. Мощность, потребляемая двигателем, равна \ (P = IV \), а ток равен 20,00 A, а напряжение составляет 115,00 В: \ [P = IV = (20,00 \, A) 115,00 \, V = 2300.00 \, W. \]
2. Мощность, используемая для подъема объекта, равна \ (P = Fv \), где сила равна весу объекта (1960 Н), а величина скорости равна \ [v = \ dfrac {10.00 \, m } {30,00 \, s} = 0,33 \ dfrac {m} {s} \] \ [P = Fv = (4900 \, N) 0.2R) \).

   Упражнение \ (\ PageIndex {1} \)

   Электродвигатели обладают достаточно высоким КПД. Двигатель мощностью 100 л.с. может иметь КПД 90%, а двигатель мощностью 1 л.с. может иметь КПД 80%. Почему важно использовать высокопроизводительные двигатели?

   Ответ

   Несмотря на то, что электродвигатели имеют высокий КПД, 10–20% потребляемой мощности тратится впустую, а не используется для выполнения полезной работы. Большая часть 10–20% потерянной мощности передается в тепло, рассеиваемое медными проводами, используемыми для изготовления катушек двигателя.Это тепло увеличивает тепло окружающей среды и увеличивает потребность электростанций, обеспечивающих электроэнергию. Спрос на электростанцию ​​может привести к увеличению выбросов парниковых газов, особенно если электростанция использует уголь или газ в качестве топлива.

   Предохранитель

   А (рисунок \ (\ PageIndex {3} \)) — это устройство, которое защищает цепь от слишком высоких токов. Предохранитель — это, по сути, короткий отрезок провода между двумя контактами. Как мы видели, когда ток проходит по проводнику, кинетическая энергия носителей заряда преобразуется в тепловую энергию в проводнике.Кусок проволоки в предохранителе находится под напряжением и имеет низкую температуру плавления. Проволока рассчитана на нагрев и разрыв при номинальном токе. Предохранитель поврежден и подлежит замене, но он защищает остальную цепь. Предохранители срабатывают быстро, но есть небольшая задержка, пока провод нагревается и обрывается.

   Рисунок \ (\ PageIndex {3} \): Предохранитель состоит из отрезка провода между двумя контактами. Когда через провод проходит ток, превышающий номинальный, провод плавится, разрывая соединение.На фото — «перегоревший» предохранитель в месте обрыва провода, защищающего цепь (кредит: модификация работы «Шардайы» / Flickr). Автоматические выключатели

   также рассчитаны на максимальный ток и разомкнуты для защиты цепи, но могут быть сброшены. Автоматические выключатели реагируют намного быстрее. Работа автоматических выключателей выходит за рамки этой главы и будет обсуждаться в следующих главах. Еще один метод защиты оборудования и людей — прерыватель цепи замыкания на землю (GFCI), который широко используется в ванных комнатах и ​​кухнях.Торговые точки GFCI очень быстро реагируют на изменения тока. Эти выходы открываются при изменении магнитного поля, создаваемого токоведущими проводниками, что также выходит за рамки данной главы и рассматривается в следующей главе.

   Стоимость электроэнергии

   Чем больше электроприборов вы используете и чем дольше они остаются включенными, тем выше ваш счет за электроэнергию. Этот знакомый факт основан на соотношении энергии и мощности. Вы платите за использованную энергию.Поскольку \ (P = \ dfrac {dE} {dt} \), мы видим, что

   \ [E = \ int P dt \]

   — это энергия, используемая устройством, использующим мощность P в течение интервала времени t . Если мощность доставляется с постоянной скоростью, то энергия может быть найдена как \ (E = Pt \). Например, чем больше горело лампочек, тем больше использовалось P ; чем дольше они работают, тем больше т .

   Единица измерения энергии в счетах за электричество — киловатт-час \ ((кВт \ cdot h) \), что соответствует соотношению \ (E = Pt \).6 \, J \).

   Потребляемая электрическая энергия ( E ) может быть уменьшена либо за счет сокращения времени использования, либо за счет снижения энергопотребления этого прибора или приспособления. Это не только снижает стоимость, но и снижает воздействие на окружающую среду. Улучшение освещения — один из самых быстрых способов снизить потребление электроэнергии в доме или на работе. Около 20% энергии, потребляемой в доме, идет на освещение, а для коммерческих предприятий это число приближается к 40%.Флуоресцентные лампы примерно в четыре раза более эффективны, чем лампы накаливания — это верно как для длинных трубок, так и для компактных люминесцентных ламп (КЛЛ), например, рисунок \ (\ PageIndex {1b} \). Таким образом, лампу накаливания мощностью 60 Вт можно заменить КЛЛ мощностью 15 Вт, которая имеет такую ​​же яркость и цвет. КЛЛ имеют изогнутую трубку внутри шара или спиралевидную трубку, все они подключены к стандартному привинчиваемому основанию, которое подходит для стандартных розеток лампы накаливания. (В последние годы были решены исходные проблемы с цветом, мерцанием, формой и высокими начальными инвестициями для КЛЛ.)

   Теплопередача от этих КЛЛ меньше, и они служат до 10 раз дольше, чем лампы накаливания. В следующем примере рассматривается важность инвестиций в такие лампы. Новые белые светодиодные лампы (которые представляют собой группы небольших светодиодных лампочек) еще более эффективны (в два раза больше, чем у КЛЛ) и служат в пять раз дольше, чем КЛЛ.

   Пример \ (\ PageIndex {2 \): расчет рентабельности светодиодной лампы

   Типичная замена лампы накаливания мощностью 100 Вт — это светодиодная лампа мощностью 20 Вт.Светодиодная лампа мощностью 20 Вт может обеспечивать такое же количество света, как и лампа накаливания мощностью 100 Вт. Какова экономия затрат на использование светодиодной лампы вместо лампы накаливания в течение одного года, если предположить, что 0,10 доллара за киловатт-час — это средний тариф на электроэнергию, взимаемый энергетической компанией? Предположим, что лампочка включена на три часа в день.

   Стратегия

   1. Рассчитайте энергию, используемую в течение года для каждой лампочки, используя \ (E = Pt \).
   2. Умножьте энергию на стоимость.

   Решение

   1. Рассчитайте мощность для каждой лампы. \ [E_ {Incandescent} = Pt = 100 \, W \ left (\ dfrac {1 \, kW} {1000 \, W} \ right) \ left (\ dfrac {3 \, h} {day} \ right) (365 \, дней) = 109,5 \, кВт \ cdot ч \] \ [E_ {LED} = Pt = 20 \, W \ left (\ dfrac {1 \, kW} {1000 \, W} \ right) \ left (\ dfrac {3 \, h} {day} \ right) (365 \, days) = 21.9 \, кВт \ cdot h \]
   2. Рассчитайте стоимость для каждого. \ [cost_ {Incandescent} = 109,5 \, кВт \ cdot h \ left (\ dfrac {\ $ 0.10} {kW \ cdot h} \ right) = \ $ 10.95 \] \ [cost_ {LED} = 21.90 \, кВт \ cdot h \ left (\ dfrac {\ $ 0.10} {kW \ cdot h} \ right) = \ $ 2.19 \]

   Значение

   Светодиодная лампа потребляет на 80% меньше энергии, чем лампа накаливания, экономя 8,76 доллара по сравнению с лампой накаливания в течение одного года. Светодиодная лампа может стоить 20 долларов, а лампа накаливания мощностью 100 Вт может стоить 0,75 доллара, что следует учесть при расчетах. Типичный срок службы лампы накаливания составляет 1200 часов, а светодиодной лампы — 50 000 часов. Лампы накаливания хватило бы на 1.08 лет при 3 часах в день, а светодиодная лампа прослужит 45,66 года. Первоначальная стоимость светодиодной лампы высока, но стоимость для домовладельца составит 0,69 доллара за лампы накаливания по сравнению с 0,44 доллара за светодиодные лампы в год. (Обратите внимание, что светодиодные лампы дешевеют.) Экономия затрат в год составляет примерно 8,50 долларов США, и это только для одной лампы.

   Упражнение \ (\ PageIndex {2} \)

   Является ли эффективность различных лампочек единственным соображением при сравнении различных лампочек?

   Ответ

   Нет, эффективность — очень важный фактор для лампочек, но есть много других соображений.Как упоминалось выше, важными факторами являются стоимость лампочек и срок их службы. Например, лампы CFL содержат ртуть, нейротоксин, и их необходимо утилизировать как опасные отходы. При замене ламп накаливания, которые управляются диммером на светодиоды, может потребоваться замена диммера. Диммерные переключатели для светодиодных фонарей сопоставимы по цене с переключателями ламп накаливания, но это начальная стоимость, которую следует учитывать. Также следует учитывать спектр света, но существует широкий диапазон цветовых температур, поэтому вы сможете найти тот, который соответствует вашим потребностям.Ни одно из этих упомянутых соображений не предназначено для того, чтобы препятствовать использованию светодиодных или CFL лампочек, но они являются соображениями.

   Замена ламп накаливания на КЛЛ или светодиодные лампы — простой способ снизить потребление энергии в домах и коммерческих объектах. Лампы CFL работают с совершенно другим механизмом, чем лампы накаливания. Механизм сложен и выходит за рамки данной главы, но здесь приводится очень общее описание механизма.Лампы CFL содержат пары аргона и ртути, заключенные в трубку спиральной формы. В лампах CFL используется «балласт», который увеличивает напряжение, используемое лампой CFL. Балласт производит электрический ток, который проходит через газовую смесь и возбуждает молекулы газа. Возбужденные молекулы газа излучают ультрафиолетовый (УФ) свет, который, в свою очередь, стимулирует флуоресцентное покрытие внутри трубки. Это покрытие флуоресцирует в видимом спектре, излучая видимый свет. Традиционные люминесцентные лампы и лампы CFL имели короткую временную задержку до нескольких секунд, пока смесь «нагревалась» и молекулы переходили в возбужденное состояние.Следует отметить, что эти лампы содержат ртуть, которая ядовита, но если лампа сломана, ртуть никогда не выделяется. Даже если колба сломана, ртуть имеет тенденцию оставаться во флуоресцентном покрытии. Количество также довольно невелико, и преимущество экономии энергии может перевесить недостаток использования ртути.

   Лампы CFL заменяются на светодиодные, где LED означает «светоизлучающий диод». Диод был кратко обсужден как неомический прибор, сделанный из полупроводникового материала, который позволяет току течь в одном направлении.Светодиоды — это особый тип диодов, изготовленных из полупроводниковых материалов, наполненных примесями в комбинациях и концентрациях, которые позволяют преобразовывать дополнительную энергию движения электронов во время электрического возбуждения в видимый свет. Полупроводниковые устройства будут объяснены более подробно в Физике конденсированного состояния.

   Коммерческие светодиоды быстро становятся стандартом для коммерческого и жилого освещения, заменяя лампы накаливания и КЛЛ. Они предназначены для работы в видимой области спектра и изготовлены из галлия, легированного атомами мышьяка и фосфора.Цвет, излучаемый светодиодом, зависит от материалов, используемых в полупроводнике, и от силы тока. В первые годы развития светодиодов маленькие светодиоды на печатных платах были красного, зеленого и желтого цветов, но теперь светодиодные лампочки можно запрограммировать на получение миллионов цветов света, а также множества различных оттенков белого света.

   Сравнение ламп накаливания, КЛЛ и светодиодных ламп

   Экономия энергии может быть значительной при замене лампы накаливания или лампы CFL на светодиодную.Лампочки оцениваются по количеству энергии, потребляемой лампочкой, а количество светового потока измеряется в люменах. Люмен (лм) — это производная от системы СИ единица светового потока и мера общего количества видимого света, излучаемого источником. Лампу накаливания мощностью 60 Вт можно заменить лампой CFL мощностью 13–15 Вт или светодиодной лампой мощностью 6–8 Вт, все три из которых имеют световой поток примерно 800 лм. Таблица светоотдачи для некоторых часто используемых лампочек представлена ​​в Таблице \ (\ PageIndex {1} \).

   Срок службы лампочек трех типов значительно различается. Срок службы светодиодной лампы составляет 50 000 часов, у CFL — 8 000 часов, а лампы накаливания — всего 1200 часов. Светодиодная лампа является самой прочной, легко выдерживает грубое обращение, такое как сотрясение и удары. Лампа накаливания плохо переносит такое же обращение, поскольку нить накаливания и стекло могут легко сломаться. Лампа CFL также менее долговечна, чем светодиодная лампа, из-за своей стеклянной конструкции.Количество выделяемого тепла составляет 3,4 БТЕ / ч для светодиодной лампы мощностью 8 Вт, 85 БТЕ / ч для лампы накаливания мощностью 60 Вт и 30 БТЕ / ч для лампы КЛЛ. Как упоминалось ранее, основным недостатком лампы CFL является то, что она содержит ртуть, нейротоксин, и ее необходимо утилизировать как опасные отходы. Из этих данных легко понять, почему светодиодные лампы быстро становятся стандартом в освещении.

   Таблица \ (\ PageIndex {1} \): Световой поток светодиодных ламп, ламп накаливания и КЛЛ

   Световой поток (люмен)	Светодиодные лампы (Вт)	Лампа накаливания (Вт)	Лампа накаливания CFL (Вт)
   450	4-5	40	9−13
   800	6-8	60	13-15
   1100	9−13	75	18-25
   1600	16-20	100	23−30
   2600	25−28	150	30-55

   Сводка взаимоотношений

   В этой главе мы обсудили взаимосвязь между напряжением, током, сопротивлением и мощностью.2R \). Хотя все возможные комбинации могут показаться ошеломляющими, не забывайте, что все они являются комбинациями всего двух уравнений: закона Ома \ ((V = IR) \) и степени \ ((P = IV) \).

   Авторы и авторство

   • Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

   Electric Resistance — Practice — The Physics Hypertextbook

3. Используйте мощность и напряжение для определения сопротивления.

   R =	В 2	⇐	п =	В 2
   	R			п.

   Номера в. Отвечаю.

4. Нити накаливания лампочек, как и большинство проводов, представляют собой длинные тонкие цилиндры. Их поперечные сечения — кружки. Используйте уравнение для площади круга, чтобы получить площадь поперечного сечения нити накала.

   A = π r ²

   Это уравнение содержит r — r для радиуса. Проблема дает нам диаметр, потому что его намного легче измерить, чем радиус. Перед использованием этого уравнения разделите диаметр пополам и обратите внимание на единицы измерения. Единица мкм (микрометр) составляет одну миллионную метра.

   A = π (23 × 10 −6 м) 2 A = 1,66 × 10 −9 м 2

5. Есть уравнение, которое связывает некоторые свойства провода с его сопротивлением.

   Решите его для удельного сопротивления (ρ, «rho»).

   Понаблюдайте за отрядами еще раз. Длина указывается в сантиметрах, но выбранной единицей СИ является метр.

   ρ =	(240 Ом) (1,66 × 10 −9 м 2 )
   	(0,533 м)
   ρ = 7,48 × 10 −7 Ом · м

6. Вычисленное выше удельное сопротивление значительно превышает значение, указанное в стандартных справочных таблицах.

   7,48 × 10 −7 Ом · м	≈	в 13 раз больше , чем , по данным источника
   5.60 × 10 −8 Ом · м
   7,48 × 10 −7 Ом · м	≈	В 14 раз больше , чем , по данным источника
   5,28 × 10 −8 Ом · м

   Это потому, что в большинстве справочных таблиц указано удельное сопротивление для комнатной температуры (обычно 20 ° C или 300 K).Рабочая лампочка будет иметь температуру около 3500 К. Это примерно в 12 раз выше, чем комнатная температура.

   3500 К	≈ в 12 раз горячее
   300 К

   Сопротивление повышается при повышении температуры. Для многих материалов они в основном прямо пропорциональны, что и показывают эти числа.