Как рассчитать общее сопротивление при параллельном соединении резисторов. Какие формулы применяются для вычислений. Какие особенности нужно учитывать при расчетах параллельного соединения. Как решать задачи на параллельное соединение резисторов.
Что такое параллельное соединение резисторов
Параллельное соединение резисторов — это такой способ подключения, при котором все резисторы подсоединены к одним и тем же двум точкам электрической цепи. При этом напряжение на всех резисторах одинаковое, а общий ток делится между ними.
Основные особенности параллельного соединения:
- Напряжение на всех резисторах одинаковое
- Общий ток равен сумме токов через отдельные резисторы
- Общее сопротивление всегда меньше сопротивления любого из параллельно соединенных резисторов
Формулы для расчета параллельного соединения
Для расчета общего сопротивления при параллельном соединении резисторов используются следующие основные формулы:
1. Формула для произвольного количества резисторов:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
2. Формула для двух параллельных резисторов:
R = (R1 * R2) / (R1 + R2)
3. Формула для n одинаковых резисторов:
R = R1 / n
где R1 — сопротивление одного резистора, n — количество резисторов.
Как рассчитать общее сопротивление параллельного соединения
Чтобы рассчитать общее сопротивление при параллельном соединении резисторов, нужно выполнить следующие шаги:
- Определить количество и номиналы параллельно соединенных резисторов
- Выбрать подходящую формулу в зависимости от количества резисторов
- Подставить значения в формулу и произвести вычисления
- Округлить результат до нужной точности
Пример расчета параллельного соединения двух резисторов
Рассмотрим пример расчета общего сопротивления для двух параллельно соединенных резисторов:
Дано: R1 = 100 Ом, R2 = 200 Ом
Используем формулу для двух резисторов:

R = (R1 * R2) / (R1 + R2) = (100 * 200) / (100 + 200) = 20000 / 300 = 66,67 Ом
Таким образом, общее сопротивление параллельного соединения двух резисторов 100 Ом и 200 Ом составляет примерно 66,67 Ом.
Особенности расчета параллельного соединения
При расчете параллельного соединения резисторов следует учитывать некоторые важные особенности:
- Общее сопротивление всегда меньше сопротивления самого маленького из резисторов
- Чем больше параллельно соединенных резисторов, тем меньше общее сопротивление
- При большом количестве резисторов удобнее использовать калькулятор
- Важно правильно округлять результаты промежуточных вычислений
Применение параллельного соединения резисторов
Параллельное соединение резисторов широко применяется в электротехнике и электронике для решения следующих задач:
- Получение нужного значения сопротивления
- Увеличение мощности рассеивания
- Создание делителей тока
- Шунтирование измерительных приборов
- Регулировка параметров электрических цепей
Решение задач на параллельное соединение резисторов
При решении задач на параллельное соединение резисторов рекомендуется придерживаться следующего алгоритма:

- Внимательно прочитать условие задачи
- Начертить схему соединения резисторов
- Выписать известные данные
- Определить, что требуется найти
- Выбрать нужные формулы
- Произвести вычисления
- Проверить размерность результата
- Записать ответ
Часто задаваемые вопросы о параллельном соединении
Почему при параллельном соединении общее сопротивление уменьшается?
При параллельном соединении увеличивается количество путей для протекания тока, что приводит к уменьшению общего сопротивления цепи. Это можно сравнить с расширением русла реки — чем шире русло, тем меньше сопротивление течению воды.
Как изменится ток в цепи при добавлении параллельного резистора?
При добавлении параллельного резистора общее сопротивление цепи уменьшится, а значит общий ток увеличится согласно закону Ома. При этом напряжение на резисторах останется прежним.
Можно ли соединять параллельно резисторы разного номинала?
Да, можно соединять параллельно резисторы с разными номиналами. Общее сопротивление при этом рассчитывается по стандартным формулам для параллельного соединения.
Заключение
Расчет параллельного соединения резисторов — важный навык для понимания работы электрических цепей. Зная основные формулы и особенности, можно легко вычислить общее сопротивление при параллельном подключении нескольких резисторов. Это позволяет решать различные практические задачи в электротехнике и электронике.
Как считать сопротивление при параллельном соединении
Как правильно соединять резисторы?
О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.
Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!
Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.
Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.
Последовательное соединение резисторов.
В жизни последовательное соединение резисторов имеет вид:
Последовательно соединённые резисторы серии МЛТ
Принципиальная схема последовательного соединения выглядит так:
На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.
Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.
Общее номинальное сопротивление составного резистора обозначено как Rобщ.
Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
Применяя последовательное соединение, стоит помнить одно простое правило:
Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.
Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.
Параллельное соединение резисторов.
Можно соединять резисторы и параллельно:
Два резистора МЛТ-2, соединённых параллельно
Принципиальная схема параллельного соединения выглядит следующим образом:
Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:
Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:
Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:
Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.
Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте тут.
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов
Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.
Параллельное соединение
При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.
Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).
При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:
- Номинал резистора в 16 Ом подойдет.
- Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).
В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:
- Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
- Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.
Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
Последовательное подключение
Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:
- Ток не изменяется на участке цепи.
- Общее напряжение равно сумме падений напряжений на каждом резисторе.
- Rобщ = R1 + R2 + … + Rn.
Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:
- I = I1 = I2 = 0,5 (А).
- Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
- Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).
Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.
Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.
Параллельное соединение сопротивлений | Электрикам
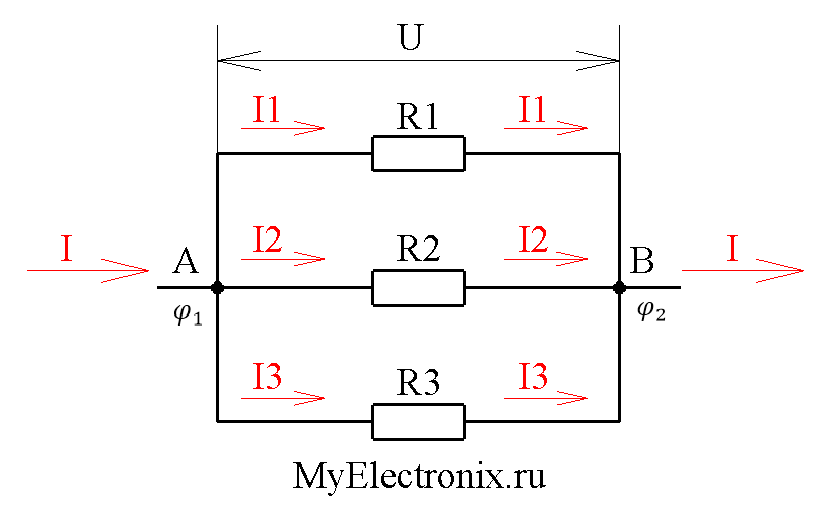
Параллельным соединением резисторов (или приемников энергии, ветвей, сопротивлений) называется такое, при котором к одним и тем же двум узлам электрической цепи (рисунок 1) присоединены несколько резисторов (ветвей).
Рис. 1 Изображение параллельного соединения трех резисторов
Проводимость при параллельном соединении
Сопротивление при параллельном соединении:
Для трёх параллельно соединенных сопротивлений
Для двух параллельно соединенных сопротивлений
Для ветвей с одинаковым сопротивлением где n количество ветвей
.
Ток при параллельном соединении
Мощность при параллельном соединении
Доказательство
Так как резисторы присоединены к одним и тем же узлам, то каждый из них находится под одинаковым напряжением U. Согласно закону Ома токи в сопртивлениях определяются по формулам
Из этих формул следует, что токи в параллельных ветвях с сопротивлениями распределяются прямо пропорционально проводимостям ветвей или обратно пропорционально их сопротивлениям. Ряд параллельно соединенных резисторов можно заменить эквивалентным с сопротивлением R, значение которого должно быть таким, чтобы при том же напряжении на выводах ток в эквивалентном резисторе был равен сумме токов в отдельных ветвях:
Эквивалентная проводимость
(1)
т. е. эквивалентная проводимость параллельного соединения резисторов равна сумме проводимостей всех параллельных ветвей. Следовательно, эквивалентное сопротивление будет меньше самого малого из параллельно соединенных резисторов.
Формула (1) дает возможность определить и эквивалентное сопротивление параллельного соединения резисторов. Например, при трех ветвях эквивалентная проводимость
и эквивалентное сопротивление
.
Для двух резисторов
Если сопротивление ветвей одинаково
в общем случае при соединении n резисторов с одинаковым сопротивлением R1 эквивалентное сопротивление равно
.
Мощности параллельно соединенных резисторов равна сумме мощностей всех резисторов
Параллельное соединение трех проводников. Теперь используем формулу расчета сопротивления. Последовательное соединение проводников
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение
Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:
Смешанное соединение
Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R 3 . Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 , соединены последовательно.
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема
Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
И находят сопротивления R 1 , R 2 и R 3 .
Содержание:Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.
Напряжение при последовательном соединении
При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.
Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: R общ = R 1 + R 2 .
Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.
Напряжение при параллельном соединении
При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.
Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.
На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.
В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.
Нужно вычислить сопротивление последовательной, параллельной или комбинированной цепей? Нужно, если вы не хотите сжечь плату! Эта статья расскажет вам, как это сделать. Перед чтением, пожалуйста, уясните, что у резисторов нет «начала» и нет «конца». Эти слова вводятся для облегчения понимания изложенного материала.
Шаги
Сопротивление последовательной цепи
Сопротивление параллельной цепи
Сопротивление комбинированной цепи
Некоторые факты
- Каждый электропроводный материал имеет некоторое сопротивление, являющееся сопротивляемостью материала электрическому току.
- Сопротивление измеряется в Омах. Символ единицы измерения Ом — Ω.
- Разные материалы имеют разные значения сопротивления.
- Например, сопротивление меди 0.0000017 Ом/см 3
- Сопротивление керамики около 10 14 Ом/см 3
- Чем больше значение сопротивления, тем выше сопротивляемость электрическому току. Медь, которая часто используется в электрических проводах, имеет очень малое сопротивление. С другой стороны, сопротивление керамики очень велико, что делает ее прекрасным изолятором.
- Работа всей цепи зависит от того, какой тип соединения вы выберете для подключения резисторов в этой цепи.
- U=IR. Это закон Ома, установленный Георгом Омом в начале 1800х. Если вам даны любые две из этих переменных, вы легко найдете третью.
- U=IR: Напряжение (U) есть результат умножения силы тока (I) * на сопротивление (R).
- I=U/R: Сила тока есть частное от напряжение (U) ÷ сопротивление (R).
- R=U/I: Сопротивление есть частное от напряжение (U) ÷ сила тока (I).
- Запомните: при параллельном соединении существует несколько путей прохождения тока по цепи, поэтому в такой цепи общее сопротивление будет меньше сопротивления каждого отдельного резистора. При последовательном соединении ток проходит через каждый резистор в цепи, поэтому сопротивление каждого отдельного резистора добавляется к общему сопротивлению.
- Общее сопротивление в параллельной цепи всегда меньше сопротивления одного резистора с самым низким сопротивлением в этой цепи. Общее сопротивление в последовательной цепи всегда больше сопротивления одного резистора с самым высоким сопротивлением в этой цепи.
Всем доброго времени суток. В прошлой статье я рассмотрел , применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса , называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье. Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и .
Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее. На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии
Пример последовательного подключения приемников энергии.
В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления
Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.
Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями
где R – эквивалентное последовательное сопротивление.
Применение последовательного соединения
Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр
Делитель напряжения (слева) и потенциометр (справа).
В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.
Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.
Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии. Пример такого соединения показан на рисунке ниже
Пример параллельного соединения приемников энергии.
Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви
Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений
Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.
Смешанное соединение приемников энергии
Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии
Пример смешанного соединения приемников энергии.
В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид
В результате получили цепь из двух последовательных приемников энергии R 12 R 345 эквивалентное сопротивление и ток, протекающий через них, составит
Тогда падение напряжения по участкам составит
Тогда токи, протекающие через каждый приемник энергии, составят
Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.
Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением
где ∑ — обозначает алгебраическую сумму.
Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа
Изображение первого закона Кирхгофа.
На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид
Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.
Как говорилось выше, второй закон Кирхгофа определяет соотношение между ЭДС и напряжениями в замкнутом контуре и звучит следующим образом: алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах этого контура. Второй закон Кирхгофа определяется следующим выражением
В качестве примера рассмотрим ниже следующую схему, содержащую некоторый контур
Схема, иллюстрирующая второй закон Кирхгофа.
Для начала необходимо определится с направлением обхода контура. В принципе можно выбрать как по ходу часовой стрелки, так и против хода часовой стрелки. Я выберу первый вариант, то есть элементы будут считаться в следующем порядке E1R1R2R3E2, таким образом, уравнение по второму закону Кирхгофа будет иметь следующий вид
Второй закон Кирхгофа применяется не только к цепям постоянного тока, но и к цепям переменного тока и к нелинейным цепям.
В следующей статье я рассмотрю основные способы расчёта сложных цепей с использованием закона Ома и законов Кирхгофа.
Теория это хорошо, но без практического применения это просто слова.
Параллельное и последовательное соединение проводников – способы коммутации электрической цепи. Электрические схемы любой сложности можно представить посредством указанных абстракций.
Определения
Существует два способа соединения проводников, становится возможным упростить расчет цепи произвольной сложности:
- Конец предыдущего проводника соединен непосредственно с началом следующего — подключение называют последовательным. Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
- Начала проводников соединены одной точкой, концы – другой, подключение называется параллельным. Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.
На практике чаще встречается смешанное включение проводников, часть соединена последовательно, часть – параллельно. Нужно разбить цепь простыми сегментами, решать задачу для каждого отдельно. Сколь угодно сложную электрическую схему можно описать параллельным, последовательным соединением проводников. Так делается на практике.
Использование параллельного и последовательного соединения проводников
Термины, применяемые к электрическим цепям
Теория выступает базисом формирования прочных знаний, немногие знают, чем напряжение (разность потенциалов) отличается от падения напряжения. В терминах физики внутренней цепью называют источник тока, находящееся вне – именуется внешней. Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию. Происходит нагрев сопротивлений.
Для обеспечения движения нужно на концах проводника поддерживать разность потенциалов. Это называется напряжением участка цепи. Если просто поместить проводник в поле вдоль силовых линий, ток потечет, будет очень кратковременным. Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.
Таким приводом движения электрической цепи выступает источник тока. Чтобы поддерживать потенциал, внутри совершается работа. Химическая реакция, как в гальваническом элементе, механические силы – генератор ГЭС. Заряды внутри источника движутся в противоположную полю сторону. Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:
- Внешняя часть цепи, где заряды движутся, увлекаемые полем.
- Внутренняя часть цепи, где заряды движутся против напряженности.
Генератор (источник тока) снабжен двумя полюсами. Обладающий меньшим потенциалом называется отрицательным, другой – положительным. В случае переменного тока полюсы непрерывно меняются местами. Непостоянно направление движения зарядов. Ток течет от положительного полюса к отрицательному. Движение положительных зарядов идет в направлении убывания потенциала. Согласно этому факту вводится понятие падения потенциала:
Падением потенциала участка цепи называется убыль потенциала в пределах отрезка. Формально это напряжение. Для ветвей параллельной цепи одинаково.
Под падением напряжения понимается и нечто иное. Величина, характеризующая тепловые потери, численно равна произведению тока на активное сопротивление участка. Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.
При решение физических задач для упрощения двигатель может включать в свой состав ЭДС, направление действия которой противоположно эффекту источника питания. Учитывается факт потери энергии через реактивную часть импеданса. Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.
Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников
Для решения реальных задач используются законы Ома и Кирхгофа. Первый выводил равенство чисто эмпирическим путем – экспериментально – второй начал математическим анализом задачи, потом проверил догадки практикой. Приведем некоторые сведения, помогающие решению задачи:
Посчитать сопротивления элементов при последовательном и параллельном соединении
Алгоритм расчета реальных цепей прост. Приведем некоторые тезисы касательно рассматриваемой тематики:
- При последовательном включении суммируются сопротивления, при параллельном — проводимости:
- Для резисторов закон переписывается в неизменной форме. При параллельном соединении итоговое сопротивление равняется произведению исходных, деленному на общую сумму. При последовательном – номиналы суммируются.
- Индуктивность выступает реактивным сопротивлением (j*ω*L), ведет себя, как обычный резистор. В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
- Мнимое сопротивление емкости записывается в виде: -j/ω*С. Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.
Тезисы легко распространяются на произвольные случаи. Падение напряжения на двух открытых кремниевых диодах равно сумме. На практике составляет 1 вольт, точное значение зависит от типа полупроводникового элемента, характеристик. Аналогичным образом рассматривают источники питания: при последовательном включении номиналы складываются. Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.
У некоторых вызывает затруднение случай: две батарейки разного номинала включены параллельно. Случай описывается вторым законом Кирхгофа, никакой сложности представить физику не может. При неравенстве номиналов двух источников берется среднее арифметическое, если пренебречь внутренним сопротивлением обоих. В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.
Пример решения уравнений Кирхгофа
Посмотрим изображение: по условию задачи, источник Е1 сильнее, нежели Е2. Направление токов в контуре берем из здравых соображений. Но если бы проставили неправильно, после решения задачи один получился бы с отрицательным знаком. Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:
- Работа первого (сильного) источника тратится на создание тока во внешней цепи, преодоление слабости соседа (ток I2).
- Второй источник не совершает полезной работы в нагрузке, борется с первым. Иначе не скажешь.
Включение батареек разного номинала параллельно является безусловно вредным. Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.
Напряжение и сопротивление при последовательном соединении
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
Последовательное соединение проводников
По закону Ома, напряжения U1 и U2 на проводниках равны
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
Параллельное соединение проводников
Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом)
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников
Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.
Напряжение при последовательном соединении
При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго – с началом третьего и т.д.
Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: Rобщ = R1 + R2.
Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: VRn = IRn x Rn. Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.
Напряжение при параллельном соединении
При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.
Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной зависимости с сопротивлением резистора. В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.
На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.
В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.
Последовательное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление R
общПри таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление R
общПри таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление R
общДля того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»:
Выведите формулы последовательного и параллельного соединений сопротивлений
Рисунок 1.9.4.Цепи, подобные изображенной на рис. 1.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.
Параллельное и последовательное соединение проводников
Элементы цепи могут быть подключены двумя способами:
Проиллюстрируем данные подключения на примере двух резисторов (рис. 1). Помним о том, что соединительные провода не имеют сопротивления (являются идеальными).
- последовательное соединение проводников
Рис. 1. Последовательное соединение проводников
Просмотрим движение электронов по ABC. Т.к. электроны «потеряться» или «задержаться» нигде внутри проводника не могут, при последовательном подключении элементов сила тока, проходящая через каждый из проводников, одинакова.
С точки зрения логики, отдельно взятый электрон нужно «протащить» между точками АB, а потом между точками BC. «Протащить» — это, фактически значит, совершить работу по переносу заряда (за нас это делает электрическое поле):
- где
- — работа по переносу заряда,
- — переносимый заряд,
- , — потенциалы конечной и начальной точки переноса заряда.
Нами ранее уже было введено понятие напряжения:
- где
- — напряжение (разность потенциалов) между точками 2 и 1,
- , — потенциалы соответствующих точек.
Тогда, используя (2) и рисунок 1, проанализируем напряжения. Пусть:
- — напряжение (разность потенциалов) между точками С и А,
- — напряжение (разность потенциалов) между точками В и А,
- — напряжение (разность потенциалов) между точками С и В.
Подставим (4) и (5) в (3):
Таким образом, напряжение в последовательной цепи равно сумме напряжений на каждом из элементов.
Рис. 2. Последовательное соединение проводников (общее сопротивление)
Часть задач школьной физики касается поиска общего сопротивления участка цепи, логика такого поиска: найти такое сопротивление, которым можно заменить цепь, чтобы параметры напряжения и силы тока остались неизменными (рис. 2). Пусть по цепи течёт ток , т.к. соединение последовательное, ток на каждом из элементов одинаков, тогда, используя закон Ома для участка цепи:
Подставим (7) — (9) в (6):
Или, сократив на :
Обобщив данное выражение на любое количество последовательно соединённых сопротивлений, получим:
- где
- — общее (полное) сопротивление цепи элементов, соединённых последовательно,
- — сумма последовательно соединённых сопротивлений.
- параллельное соединение проводников
Рис. 3. Параллельное соединение проводников
Ток, подходящий в точку А ( ), разделяется на два потока: , текущий через сопротивление и , текущий через сопротивление . В точке В оба этих тока складываются в изначальной ток (т.к. электроны не могут «потеряться»), тогда:
Напряжения на каждом из элементов одинаково, т.к. сопротивления и подключены к одним и тем же точкам А и В, а напряжение, по сути, есть разность потенциалов между точками.
Рис. 4. Параллельное соединение проводников (общее сопротивление)
Поищем общее сопротивление такого соединения. Пусть разность потенциалов (напряжение) между точками А и В — . Тогда, исходя из закона Ома для участка цепи:
Подставим (12)-(14) в (11):
Обобщив данное выражение на любое количество параллельно соединённых сопротивлений, получим:
- где
- — общее (полное) сопротивление цепи элементов, соединённых параллельно,
- — обратная сумма параллельно соединённых сопротивлений.
Для цепи из двух сопротивлений:
Вывод: в задачах, в которых присутствует цепь, необходимо рассмотреть, какое конкретно соединение рассматривается, а потом использовать соответствующую логику рассуждений:
- для последовательного соединения
- ток в каждом элементе постоянен ,
- напряжение во всей цепи есть сумма напряжений на каждом из элементов ,
- полное сопротивление цепи есть сумма сопротивлений каждого из элементов .
- для параллельного соединения
- ток во всей цепи есть сумма токов на каждом элементе ,
- напряжение на каждом элементе постоянно
- обратное значение полного сопротивление равно сумме обратных сопротивлений каждого из элементов .
Последовательное и параллельное соединение резисторов.
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения резисторов, в частности о последовательном соединении и о параллельном.
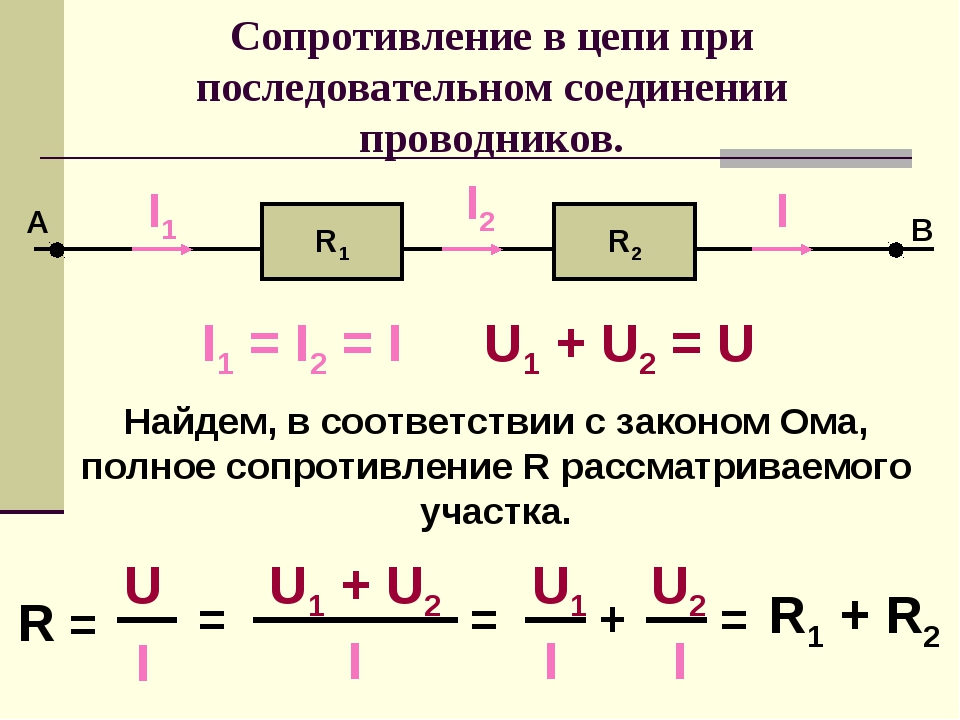
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
Тогда для вычисления общего напряжения можно будет использовать следующее выражение:
Но для общего напряжение также справедлив закон Ома:
Здесь
– это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например для следующей цепи:
Общее сопротивление будет равно:
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае А если при последовательном соединении все сопротивления равны (
), то общее сопротивление цепи составит:в данной формуле равно количеству элементов цепи.С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
Параллельное соединение резисторов.
При параллельном соединении напряжения на проводниках равны:
А для токов справедливо следующее выражение:
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
Подставим эти выражения в формулу общего тока:
А по закону Ома ток:
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
Данную формулу можно записать и несколько иначе:
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
Смешанное соединение резисторов.
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов
и – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором :Теперь у нас образовались две группы последовательно соединенных резисторов:
Заменим эти две группы двумя резисторами, сопротивление которых равно:
Как видите, схема стала уже совсем простой ) Заменим группу параллельно соединенных резисторов
и одним резистором :И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
Общее сопротивление цепи получилось равным:
Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов
Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!
Последовательное и параллельное соединение сопротивлений
Последовательное соединение сопротивлений
Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).
Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.
Рис 1 . Последовательное соединение сопротивлений
Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U1 = IR1 U2 = IR2 и U3 = IR3
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .
Поделив теперь обе части равенства на I , будем окончательно иметь R = R1 + R2 + R3
Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).
Рис. 2. Пример последовательного соединения трех сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи по закону Ома: 60 / 80 = 0 ,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75 х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.
Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.
Параллельное соединение сопротивлений
Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.
Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (—), заметим, что прибор покажет ту же величину силы тока.
Значит, сила тока в цепи до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1 , а во второй — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим
Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи .
Рассмотрим теперь, каково будет соотношение между токами в ветвях.
Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3 , непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R 1 и R2, так как он соединен с началом и концом каждого сопротивления.
Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2 ,
где U — напряжение на зажимах источника тока; U 1 — падение напряжения на сопротивлении R 1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .
Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2 , но так как U 1 = U2, то и I1R1 = I2R2 .
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.
Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей. Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.
Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:
I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА
I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1 + I2 = 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.
Действительно, R1 == 10 Ом вдвое меньше R 2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть ( I1 = 300 мА) пошла через меньшее сопротивление ( R1 = 10 Ом), а меньшая часть ( R2 = 150 мА) — через большее сопротивление ( R 2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.
Рис. 4 . Через тонкую трубу в один и тот же промежуток времени пройдет воды меньше, чем через толстую
Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления. Такое сопротивление называется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.
Точно так же для каждой ветви I1 = U1 / R1 , I2 = U2 / R2 , где I1 и I 2 — токи в ветвях; U 1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Так как при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )
Разделив теперь обе части равенства на U , будем окончательно иметь 1 / R = 1 / R1 + 1 / R2
Помня, что проводимостью называется величина, обратная сопротивлению , мы можем сказать, что в полученной формуле 1 / R — проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость второй ветви.
На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.
Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?
Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.
Чтобы убедиться в этом, рассмотрим следующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5 ).
Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями
Применяя для этой цепи формулу 1 / R = 1 / R1 + 1 / R2 , можем написать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R = 1 / 10 + 1 / 20 + 1 / 60
Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.
Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.
Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.
Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0, 2 А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 = 1,2 + 0,6 + 0,2 = 2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U / R = 12 / 6 = 2 А
Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.
На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.
Например, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / ( R1 + R2 ), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Оценка статьи:
Загрузка…Выведите формулы последовательного и параллельного соединений сопротивлений Ссылка на основную публикацию wpDiscuzAdblockdetector
Общее сопротивление при параллельном соединении проводников формула
Проводники в электрических цепях могут соединяться последовательно и параллельно.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
| Рисунок 1.9.1. |
По закону Ома, напряжения и на проводниках равны
Общее напряжение на обоих проводниках равно сумме напряжений 1 и 2:
где – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения 1 и 2 на обоих проводниках одинаковы:
Сумма токов 1 + 2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы и ) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу за время Δ подтекает заряд Δ, а утекает от узла за то же время заряд 1Δ + 2Δ. Следовательно, = 1 + 2.
| Рисунок 1.9.2. |
Записывая на основании закона Ома
где – электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
| Рисунок 1.9.3. |
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
| Рисунок 1.9.4. |
Цепи, подобные изображенной на рис. 1.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
Последовательное соединение проводников
По закону Ома, напряжения U1 и U2 на проводниках равны
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
Параллельное соединение проводников
Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом)
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников
Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.
- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R – общее сопротивление, R1 – сопротивление одного элемента, а n – количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является елочная гирлянда, когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный амперметр. Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 – силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 – сопротивления обеих лампочек, U = U1 = U2 – значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях – увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- Закон ома параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
При параллельном соединении ток. Соединение резисторов параллельно и последовательно
Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).
Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.
Рис 1
Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U = U1 + U2 + U3
где
U1 = IR1 U2 = IR2 и U3 = IR3
или
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .
Поделив теперь обе части равенства на I , будем окончательно иметь R = R1 + R2 + R3
Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В ( пренебрегаем).
Рис. 2. Пример последовательного соединения трех сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи : 60 / 80 = 0 ,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.
Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.
Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.
Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.
Значит, до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1 , а во второй — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим
Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи .
Рассмотрим теперь, каково будет соотношение между токами в ветвях.
Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3 , непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R1 и R2, так как он соединен с началом и концом каждого сопротивления.
Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2 ,
где U — напряжение на зажимах источника тока; U1 — падение напряжения на сопротивлении R1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .
Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2 , но так как U1 = U2, то и I1R1 = I2R2 .
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1
т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.
Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей.
Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.
Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:
I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА
I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1 +I2 = 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.
Действительно, R1 == 10 Ом вдвое меньше R 2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть (I1 = 300 мА) пошла через меньшее сопротивление (R1 = 10 Ом), а меньшая часть (R2 = 150 мА) -через большее сопротивление (R 2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.
Рис. 4
Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления. Такое сопротивление называется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.
Точно так же для каждой ветви I1 = U1 / R1
, I2 = U2 / R2
, где I1
и I
2 — токи в ветвях; U1
и U2 — напряжение на ветвях; R1
и R2
— сопротивления ветвей.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Так как при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )
Разделив теперь обе части равенства на U , будем окончательно иметь 1 / R = 1 / R1 + 1 / R2
Помня, что проводимостью называется величина, обратная сопротивлению , мы можем сказать, что в полученной формуле 1 / R — проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость второй ветви.
На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.
Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?
Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.
Чтобы убедиться в этом, рассмотрим следующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2
= 20 Ом и R3
= 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5
).
Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями
Применяя для этой цепи формулу 1 / R = 1 / R1 + 1 / R2 , можем написать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R = 1 / 10 + 1 / 20 + 1 / 60
Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.
Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.
Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.
Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0,2 А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 =1,2 + 0,6 + 0,2 = 2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U / R = 12 / 6 = 2 А
Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.
На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.
Например, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / (R1 + R2 ), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Знаете ли Вы,
что такое мысленный эксперимент, gedanken experiment?
Это несуществующая практика, потусторонний опыт, воображение того, чего нет на самом деле. Мысленные эксперименты подобны снам наяву. Они рождают чудовищ. В отличие от физического эксперимента, который является опытной проверкой гипотез, «мысленный эксперимент» фокуснически подменяет экспериментальную проверку желаемыми, не проверенными на практике выводами, манипулируя логикообразными построениями, реально нарушающими саму логику путем использования недоказанных посылок в качестве доказанных, то есть путем подмены. Таким образом, основной задачей заявителей «мысленных экспериментов» является обман слушателя или читателя путем замены настоящего физического эксперимента его «куклой» — фиктивными рассуждениями под честное слово без самой физической проверки.
Заполнение физики воображаемыми, «мысленными экспериментами» привело к возникновению абсурдной сюрреалистической, спутанно-запутанной картины мира. Настоящий исследователь должен отличать такие «фантики» от настоящих ценностей.
Релятивисты и позитивисты утверждают, что «мысленный эксперимент» весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: «Если факт не соответствует теории — измените факт» (В другом варианте » — Факт не соответствует теории? — Тем хуже для факта»).
Максимально, на что может претендовать «мысленный эксперимент» — это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
При одновременном включении нескольких приемников электроэнергии в одну и ту же сеть, эти приемники можно легко рассматривать просто как элементы единой цепи, каждый из которых обладает собственным сопротивлением.
В ряде случаев такой подход оказывается вполне приемлемым: лампы накаливания, электрические обогреватели и т. п. — можно воспринимать как резисторы. То есть приборы можно заменить на их сопротивления, и легко произвести расчет параметров цепи.
Способ соединения приемников электроэнергии может быть одним из следующих: последовательный, параллельный или смешанный тип соединения.
Последовательное соединение
Когда несколько приемников (резисторов) соединяются в последовательную цепь, то есть второй вывод первого присоединяется к первому выводу второго, второй вывод второго соединяется с первым выводом третьего, второй вывод третьего с первым выводом четвертого и т. д., то при подключении такой цепи к источнику питания, через все элементы цепи потечет ток I одной и той же величины. Данную мысль поясняет приведенный рисунок.
Заменив приборы на их сопротивления, рисунок преобразуем в схему, тогда сопротивления с R1 по R4, соединенные последовательно, примут каждый на себя определенные напряжения, которые в сумме дадут значение ЭДС на зажимах источника питания. Для простоты здесь и далее изобразим источник в виде гальванического элемента.
Выразив падения напряжений через ток и через сопротивления, получим выражение для эквивалентного сопротивления последовательной цепи приемников: общее сопротивление последовательного соединения резисторов всегда равно алгебраической сумме всех сопротивлений, составляющих эту цепь. А поскольку напряжения на каждом из участков цепи можно найти из закона Ома (U = I*R, U1 = I*R1, U2 = I*R2 и т. д.) и E = U, то для нашей схемы получаем:
Напряжение на клеммах источника питания равно сумме падений напряжений на каждом из соединенных последовательно приемников, составляющих цепь.
Так как ток через всю цепь течет одного и того же значения, то справедливым будет утверждение, что напряжения на последовательно соединенных приемниках (резисторах) соотносятся между собой пропорционально сопротивлениям. И чем выше будет сопротивление, тем выше окажется и напряжение, приложенное к приемнику.
Для последовательного соединения резисторов в количестве n штук, обладающих одинаковыми сопротивлениями Rk, эквивалентное общее сопротивление цепи целиком будет в n раз больше каждого из этих сопротивлений: R = n*Rk. Соответственно и напряжения, приложенные к каждому из резисторов цепи будут между собой равны, и окажутся в n раз меньше напряжения, приложенного ко всей цепи: Uk = U/n.
Для последовательного соединения приемников электроэнергии характерны следующие свойства: если изменить сопротивление одного из приемников цепи, то напряжения на остальных приемниках цепи при этом изменятся; при обрыве одного из приемников ток прекратится во всей цепи, во всех остальных приемниках.
В силу этих особенностей последовательное соединение встречается редко, и используют его лишь там, где напряжение сети выше номинального напряжения приемников, в отсутствие альтернатив.
К примеру напряжением 220 вольт можно запитать две последовательно соединенные лампы равной мощности, каждая из которых рассчитана на напряжение 110 вольт. Ежели данные лампы при одинаковом номинальном напряжении питания будут обладать различной номинальной мощностью, то одна из них будет перегружена и скорее всего мгновенно перегорит.
Параллельное соединение
Параллельное соединение приемников предполагает включение каждого из них между парой точек электрической цепи с тем, чтобы они образовывали параллельные ветви, каждая из которых питается напряжением источника. Для наглядности опять заменим приемники их электрическими сопротивлениями, чтобы получить схему, по которой удобно вести расчет параметров.
Как уже было сказано, в случае параллельного соединения каждый из резисторов испытывает действие одного и того же напряжения. И в соответствии с законом Ома имеем: I1=U/R1, I2=U/R2, I3=U/R3.
Здесь I — ток источника. Первый закон Кирхгофа для данной цепи позволяет записать выражение для тока в неразветвленной ее части: I = I1+I2+I3.
Отсюда общее сопротивление для параллельного соединения между собой элементов цепи можно найти из формулы:
Величина обратная сопротивлению называется проводимостью G, и формулу для проводимости цепи, состоящей из нескольких параллельно соединенных элементов, также можно записать: G = G1 + G2 + G3. Проводимость цепи в случае параллельного соединения образующих ее резисторов равна алгебраической сумме проводимостей этих резисторов. Следовательно, при добавлении в цепь параллельных приемников (резисторов) суммарное сопротивление цепи уменьшится, а суммарная проводимость соответственно возрастет.
Токи в цепи состоящей из параллельно соединенных приемников, распределяются между ними прямо пропорционально их проводимостям, то есть обратно пропорционально их сопротивлениям. Здесь можно привести аналогию из гидравлики, где поток воды распределяется по трубам в соответствии с их сечениями, тогда большее сечение аналогично меньшему сопротивлению, то есть большей проводимости.
Если цепь состоит из нескольких (n) одинаковых резисторов, соединенных параллельно, то общее сопротивление цепи будет ниже в n раз, чем сопротивление одного из резисторов, а ток через каждый из резисторов будет меньше в n раз, чем общий ток: R = R1/n; I1 = I/n.
Цепь, состоящая из параллельно соединенных приемников, подключенная к источнику питания, отличается тем, что каждый из приемников находится под напряжением источника питания.
Для идеального источника электроэнергии справедливо утверждение: при подключении или отключении параллельно источнику резисторов, токи в остальных подключенных резисторах не изменятся, то есть при выходе из строя одного или нескольких приемников параллельной цепи, остальные будут продолжать работать в прежнем режиме.
В силу данных особенностей параллельное соединение обладает значительным преимуществом перед последовательным, и по этой причине именно соединение параллельное наиболее распространено в электрических сетях. Например, все электроприборы в наших домах предназначены для параллельного подключения к бытовой сети, и если отключить один, то остальным это ничуть не навредит.
Сравнение последовательных и параллельных цепей
Под смешанным соединением приемников понимают такое их соединение, когда часть или несколько из них соединены между собой последовательно, а другая часть или несколько — параллельно. При этом вся цепь может быть образована из разных соединений таких частей между собой. Для примера рассмотрим схему:
Три последовательно соединенных резистора подключены к источнику питания, параллельно одному из них подключены еще два, а третий — параллельно всей цепи. Для нахождения полного сопротивления цепи идут путем последовательных преобразований: сложную цепь последовательно приводят к простому виду, последовательно вычисляя сопротивление каждого звена, и так находят общее эквивалентное сопротивление.
Для нашего примера. Сначала находят общее сопротивление двух резисторов R4 и R5, соединенных последовательно, затем сопротивление параллельного соединения их с R2, потом прибавляют к полученному значению R1 и R3, и после — вычисляют значение сопротивления всей цепи, включая параллельную ветвь R6.
Различные способы соединения приемников электроэнергии применяют на практике для различных целей, чтобы решать конкретные поставленные задачи. Например, смешанное соединение можно встретить в схемах плавного заряда в мощных блоках питания, где нагрузка (конденсаторы после диодного моста) сначала получает питание последовательно через резистор, затем резистор шунтируется контактами реле, и нагрузка оказывается подключенной к диодному мосту параллельно.
Андрей Повный
Параллельное и последовательное соединение проводников – способы коммутации электрической цепи. Электрические схемы любой сложности можно представить посредством указанных абстракций.
Определения
Существует два способа соединения проводников, становится возможным упростить расчет цепи произвольной сложности:
- Конец предыдущего проводника соединен непосредственно с началом следующего — подключение называют последовательным. Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
- Начала проводников соединены одной точкой, концы – другой, подключение называется параллельным. Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.
На практике чаще встречается смешанное включение проводников, часть соединена последовательно, часть – параллельно. Нужно разбить цепь простыми сегментами, решать задачу для каждого отдельно. Сколь угодно сложную электрическую схему можно описать параллельным, последовательным соединением проводников. Так делается на практике.
Использование параллельного и последовательного соединения проводников
Термины, применяемые к электрическим цепям
Теория выступает базисом формирования прочных знаний, немногие знают, чем напряжение (разность потенциалов) отличается от падения напряжения. В терминах физики внутренней цепью называют источник тока, находящееся вне – именуется внешней. Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию. Происходит нагрев сопротивлений.
Для обеспечения движения нужно на концах проводника поддерживать разность потенциалов. Это называется напряжением участка цепи. Если просто поместить проводник в поле вдоль силовых линий, ток потечет, будет очень кратковременным. Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.
Таким приводом движения электрической цепи выступает источник тока. Чтобы поддерживать потенциал, внутри совершается работа. Химическая реакция, как в гальваническом элементе, механические силы – генератор ГЭС. Заряды внутри источника движутся в противоположную полю сторону. Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:
- Внешняя часть цепи, где заряды движутся, увлекаемые полем.
- Внутренняя часть цепи, где заряды движутся против напряженности.
Генератор (источник тока) снабжен двумя полюсами. Обладающий меньшим потенциалом называется отрицательным, другой – положительным. В случае переменного тока полюсы непрерывно меняются местами. Непостоянно направление движения зарядов. Ток течет от положительного полюса к отрицательному. Движение положительных зарядов идет в направлении убывания потенциала. Согласно этому факту вводится понятие падения потенциала:
Падением потенциала участка цепи называется убыль потенциала в пределах отрезка. Формально это напряжение. Для ветвей параллельной цепи одинаково.
Под падением напряжения понимается и нечто иное. Величина, характеризующая тепловые потери, численно равна произведению тока на активное сопротивление участка. Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.
При решение физических задач для упрощения двигатель может включать в свой состав ЭДС, направление действия которой противоположно эффекту источника питания. Учитывается факт потери энергии через реактивную часть импеданса. Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.
Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников
Для решения реальных задач используются законы Ома и Кирхгофа. Первый выводил равенство чисто эмпирическим путем – экспериментально – второй начал математическим анализом задачи, потом проверил догадки практикой. Приведем некоторые сведения, помогающие решению задачи:
Посчитать сопротивления элементов при последовательном и параллельном соединении
Алгоритм расчета реальных цепей прост. Приведем некоторые тезисы касательно рассматриваемой тематики:
- При последовательном включении суммируются сопротивления, при параллельном — проводимости:
- Для резисторов закон переписывается в неизменной форме. При параллельном соединении итоговое сопротивление равняется произведению исходных, деленному на общую сумму. При последовательном – номиналы суммируются.
- Индуктивность выступает реактивным сопротивлением (j*ω*L), ведет себя, как обычный резистор. В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
- Мнимое сопротивление емкости записывается в виде: -j/ω*С. Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.
Тезисы легко распространяются на произвольные случаи. Падение напряжения на двух открытых кремниевых диодах равно сумме. На практике составляет 1 вольт, точное значение зависит от типа полупроводникового элемента, характеристик. Аналогичным образом рассматривают источники питания: при последовательном включении номиналы складываются. Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.
У некоторых вызывает затруднение случай: две батарейки разного номинала включены параллельно. Случай описывается вторым законом Кирхгофа, никакой сложности представить физику не может. При неравенстве номиналов двух источников берется среднее арифметическое, если пренебречь внутренним сопротивлением обоих. В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.
Пример решения уравнений Кирхгофа
Посмотрим изображение: по условию задачи, источник Е1 сильнее, нежели Е2. Направление токов в контуре берем из здравых соображений. Но если бы проставили неправильно, после решения задачи один получился бы с отрицательным знаком. Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:
- Работа первого (сильного) источника тратится на создание тока во внешней цепи, преодоление слабости соседа (ток I2).
- Второй источник не совершает полезной работы в нагрузке, борется с первым. Иначе не скажешь.
Включение батареек разного номинала параллельно является безусловно вредным. Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.
Если нам надо, чтобы электроприбор работал, мы должны подключить его к . При этом ток должен проходить через прибор и возвращаться вновь к источнику, то есть цепь должна быть замкнутой.
Но подключение каждого прибора к отдельному источнику осуществимо, в основном, в лабораторных условиях. В жизни же приходится иметь дело с ограниченным количеством источников и довольно большим количеством потребителей тока. Поэтому создают системы соединений, позволяющие нагрузить один источник большим количеством потребителей. Системы при этом могут быть сколь угодно сложными и разветвленными, но в их основе лежит всего два вида соединения: последовательное и параллельное соединение проводников. Каждый вид имеет свои особенности, плюсы и минусы. Рассмотрим их оба.
Последовательное соединение проводников
Последовательное соединение проводников – это включение в электрическую цепь нескольких приборов последовательно, друг за другом. Электроприборы в данном случае можно сравнить с людьми в хороводе, а их руки, держащие друг друга – это провода, соединяющие приборы. Источник тока в данном случае будет одним из участников хоровода.
Напряжение всей цепи при последовательном соединении будет равно сумме напряжений на каждом включенном в цепь элементе. Сила тока в цепи будет одинакова в любой точке. А сумма сопротивлений всех элементов составит общее сопротивление всей цепи. Поэтому последовательное сопротивление можно выразить на бумаге следующим образом:
I=I_1=I_2=⋯=I_n ; U=U_1+U_2+⋯+U_n ; R=R_1+R_2+⋯+R_n ,
Плюсом последовательного соединения является простота сборки, а минусом – то, что если один элемент выйдет из строя, то ток пропадет во всей цепи. В такой ситуации неработающий элемент будет подобен ключу в выключенном положении. Пример из жизни неудобства такого соединения наверняка припомнят все люди постарше, которые украшали елки гирляндами из лампочек.
Если в такой гирлянде выходила из строя хотя бы одна лампочка, приходилось перебирать их все, пока не найдешь ту самую, перегоревшую. В современных гирляндах эта проблема решена. В них используют специальные диодные лампочки, в которых при перегорании сплавляются вместе контакты, и ток продолжает беспрепятственно проходить дальше.
Параллельное соединение проводников
При параллельном соединении проводников все элементы цепи подключаются к одной и той же паре точек, можно назвать их А и В. К этой же паре точек подключают источник тока. То есть получается, что все элементы подключены к одинаковому напряжению между А и В. В то же время ток как бы разделяется на все нагрузки в зависимости от сопротивления каждой из них.
Параллельное соединение можно сравнить с течением реки, на пути которой возникла небольшая возвышенность. Вода в таком случае огибает возвышенность с двух сторон, а потом вновь сливается в один поток. Получается островок посреди реки. Так вот параллельное соединение – это два отдельных русла вокруг острова. А точки А и В – это места, где разъединяется и вновь соединяется общее русло реки.
Напряжение тока в каждой отдельной ветви будет равно общему напряжению в цепи. Общий ток цепи будет складываться из токов всех отдельных ветвей. А вот общее сопротивление цепи при параллельном соединении будет меньше сопротивления тока на каждой из ветвей. Это происходит потому, что общее сечение проводника между точками А и В как бы увеличивается за счет увеличения числа параллельно подключенных нагрузок. Поэтому общее сопротивление уменьшается. Параллельное соединение описывается следующими соотношениями:
U=U_1=U_2=⋯=U_n ; I=I_1+I_2+⋯+I_n ; 1/R=1/R_1 +1/R_2 +⋯+1/R_n ,
где I — сила тока, U- напряжение, R – сопротивление, 1,2,…,n – номера элементов, включенных в цепь.
Огромным плюсом параллельного соединения является то, что при выключении одного из элементов, цепь продолжает функционировать дальше. Все остальные элементы продолжают работать. Минусом является то, что все приборы должны быть рассчитаны на одно и то же напряжение. Именно параллельным образом устанавливают розетки сети 220 В в квартирах. Такое подключение позволяет включать различные приборы в сеть совершенно независимо друг от друга, и при выходе их строя одного из них, это не влияет на работу остальных.
Нужна помощь в учебе?
Предыдущая тема: Расчёт сопротивления проводников и реостаты: формулыСледующая тема:   Работа и мощность тока
Вконтакте
Одноклассники
Google+
Расчет параллельного сопротивления — Pi My Life Up
В этом руководстве мы покажем вам, как рассчитать параллельное сопротивление, а также предоставим вам простой в использовании калькулятор параллельного сопротивления.
Параллельное сопротивление — полезная часть электроники, но его может быть трудно рассчитать, когда вы начинаете иметь дело с более чем двумя резисторами.
Каждый резистор, который вы добавляете параллельно, уменьшает общее сопротивление. Такое поведение удобно, когда вам нужно определенное сопротивление, но нет резистора, который соответствует требуемому значению.
Уменьшение сопротивления вызвано тем, что у тока больше путей прохождения. Каждый новый резистор, включенный параллельно, пропускает больше тока через цепь и, следовательно, снижает общее сопротивление, с которым сталкивается ваша цепь.
Например, в цепи с двумя резисторами равного номинала, включенными параллельно, сопротивление будет уменьшено ровно наполовину. Математика немного отличается для разных сопротивлений и наличия большего количества резисторов. Мы углубимся в это позже в руководстве.
Если вы хотите увеличить сопротивление вашей цепи, а не уменьшать его, вы можете вместо этого использовать резисторы последовательно.
Чтобы помочь вычислить общее сопротивление в цепи с параллельными резисторами, у нас есть удобный калькулятор, который значительно упрощает процесс.
Если вас смущают цвета на резисторе, обязательно ознакомьтесь с руководством по цветовым кодам резистора, поскольку оно научит вас всему, что вам нужно знать.
Чтобы использовать наш калькулятор параллельного сопротивления, просто установите количество резисторов, для которых вы хотите рассчитать параллельное сопротивление.Затем введите значение для каждого резистора.
Общее сопротивление вашей параллельной цепи будет рассчитываться и обновляться по мере того, как вы устанавливаете значение каждого резистора.
Расчет общего сопротивления параллельно
Если вы предпочитаете учиться, вы можете вручную рассчитать сопротивление резисторов, подключенных параллельно. Этот процесс немного утомителен и может быстро усложниться, если вы имеете дело с несколькими резисторами параллельно.
Есть три различных уравнения, которые можно использовать для расчета общего сопротивления при параллельном подключении.
Суммарное сопротивление двух одинаковых резисторов
Первое уравнение может использоваться только в том случае, если у вас есть два параллельно включенных резистора с одинаковым сопротивлением.
Если у вас есть два резистора с одинаковым сопротивлением, подключенных параллельно, то общее сопротивление равно половине одного резистора.
Пример использования уравнения
Для этого примера предположим, что у нас есть два 200-омных резистора , подключенных параллельно, как показано на схеме ниже.
Зная, что параллельно подключено только два резистора и что они имеют одинаковое значение, мы можем использовать наше уравнение.
Отметив значение R1 как 200 , мы можем заполнить уравнение, как показано ниже. Теперь используйте уравнение для расчета общего сопротивления ( Rt ).
Чтобы получить полное сопротивление, все, что нам нужно сделать, это разделить наше значение 200 Ом на 2 .
Ответ очень легко найти: 100 .
После этого вы должны иметь представление о том, как поступить в простейшем случае, когда два резистора одинакового номинала включены параллельно.
Суммарное сопротивление двух разных резисторов
Второе уравнение — это упрощенная версия основного уравнения, которое мы будем использовать позже. Это уравнение используется, когда у вас есть два резистора с разным сопротивлением.
Есть еще несколько процессов, которые вам нужно выполнить для расчета сопротивления двух параллельно подключенных резисторов, но это не намного сложнее.
Пример использования уравнения
В этом примере мы будем предполагать, что у нас есть цепь с двумя параллельными резисторами разных значений.
В этой схеме у нас есть резистор 600 Ом и резистор 250 Ом , включенные параллельно. Теперь мы хотим вычислить полное сопротивление, обеспечиваемое этими резисторами.
Для начала нам нужно заполнить наше уравнение, где R1 является нашим резистором 600 Ом, а значение R2 является резистором 250 Ом.
Теперь, когда уравнение заполнено, мы должны выполнить верхнее умножение и нижнее сложение перед тем, как продолжить.
Умножение 600 (R1) на 250 (R2) даст результат 150 000 . Добавление 600 (R1) к 250 (R2) даст вам ответ 850 .
Когда оба значения определены, все, что нам нужно сделать, это разделить верхнее число на нижнее число. Таким образом, мы можем определить общее сопротивление двух параллельно включенных резисторов.
Вы должны выполнить математические вычисления в этом примере: 150 000 разделить на 850 .Отсюда вы должны получить результат 176,47 . Будут лишние десятичные точки, но мы округлим их до ближайших двух.
После этого вы должны иметь представление о том, как рассчитать полное сопротивление двух резисторов, включенных параллельно.
Далее мы покажем вам, как обращаться с тремя и более резисторами. Это уравнение — немного более сложный процесс, поскольку он включает в себя много делений, которые приводят к большим десятичным числам.
Общее сопротивление нескольких резисторов
Третье и последнее уравнение, с которым мы будем иметь дело, — это уравнение, которое вы будете использовать для трех или более резисторов, включенных параллельно.
Уравнение довольно простое по своей сути и может быть легко расширено для работы с большим количеством резисторов.
Единственным недостатком этого уравнения является то, что на него требуется больше времени, чем больше резисторов вы добавляете.
Простым решением является использование параллельного калькулятора резисторов, как мы включили выше.
Пример использования уравнения
В этом примере мы покажем, как использовать более сложное уравнение для параллельного резистора.
Для этого мы будем использовать несколько резисторов со значениями 100 Ом (R1) , 250 Ом (R2) , 200 Ом (R3) и 1 кОм (R4) .
Для начала нам нужно заполнить уравнение всеми нашими значениями.
Каждое из наших значений резистора будет делителем для 1 , и вы можете добавить столько резисторов, сколько вам нужно в это уравнение. В этом примере мы обрабатываем только четыре.
Наш следующий шаг — разделить 1 на каждое из значений резистора . Вы должны сохранить как можно больше десятичных знаков, поскольку точность влияет на окончательный расчет сопротивления.
Например, в наших расчетах мы делим 1 на 100 , что дает нам результат 0.01 .
После того, как вы закончили делить каждый набор значений, теперь нам нужно сложить каждое значение вместе.
Для схемы нашего примера это будет означать: 0,01 + 0,004 + 0,005 + 0,001 . К счастью для нас, это складывается довольно гладко и дает нам хорошее круглое число 0,02 .
Затем нам нужно переместить делитель из левой части уравнения вправо.
Этот ход будет означать, что наше вычисленное значение станет делителем 1 и должно выглядеть так, как показано ниже.
Наконец, разделите 1 на ваш делитель, и в нашем случае это 0,02 . Это уравнение рассчитает окончательное полное сопротивление ваших параллельных резисторов.
Резюме
Надеюсь, теперь вы накопили достаточно знаний о том, как рассчитать полное сопротивление резисторов, включенных параллельно. Вам будет удобно, если вы планируете делать какие-то проекты схем Raspberry Pi или любой другой проект электроники.
Если у вас есть отзывы или вопросы по этому руководству, пожалуйста, оставьте комментарий ниже.
параллельных резисторов
Электрические цепи используются в авиакосмической технике, от систем управления полетом до приборов в кабине и двигателей системы управления, чтобы аэродинамическая труба приборостроение и эксплуатация. Самая простая схема включает один резистор и источник электрического потенциала или напряжения . Электроны проходят через цепь вырабатывает ток электричества.Сопротивление, напряжение и ток связаны друг с другом соотношением Закон Ома. Обычно в практической схеме используется более одного резистора. При анализе сложной схемы мы часто можем группировать компоненты вместе и разработать эквивалентную схему . При анализе схем с несколько резисторов, мы должны определить, подвержены ли резисторы какое-то напряжение или такой же ток. Несколько резисторов в параллельной цепи подвергаются одинаковому напряжению.Несколько резисторов в последовательная цепь подвергаются одинаковому току. На этой странице мы обсуждаем эквивалентную схему для резисторов параллельно.
На рисунке изображена схема, состоящая из источника питания и трех резисторов. подключены параллельно. Если обозначить сопротивление R , ток и , а напряжение В , то закон Ома гласит, что для каждого резистора в цепи:
V = i Rя = V / R
Если рассматривать каждый резистор по отдельности, каждый резистор имеет свой ток. ( i1 , i2 и i3 ), сопротивление ( R1 , R2 и R3 ), и напряжение ( V1 , V2 и V3 ).Поскольку резисторы подключены параллельно друг другу, напряжение на каждый резистор одинаковый:
V = V1 = V2 = V3Ток через каждый резистор определяется законом Ома:
i1 = V / R1i2 = V / R2
i3 = V / R3
Если обозначить пересечение проводов, соединяющих резисторы, как узлов , В нашей схеме с тремя резисторами шесть узлов.На рисунке мы помечаем два узлы в правом верхнем углу схемы. В каждом узле ток, поступающий в узел должен равняться току, выходящему из узла, согласно закону Фарадея . Для узлов, расположенных выше и ниже резистора R2 , ток ib вход в узел определяется:
ib = i2 + i3Аналогично для узлов выше и ниже резистора R1 , ток ia вход в узел определяется:
ia = i1 + ib = i1 + i2 + i3Теперь мы знаем напряжение, сопротивление и ток в каждой части цепи.
Если бы мы построили эквивалентную схему, как показано в нижнем левом углу, мы бы имеют одинаковое напряжение В , такой же ток от источника питания ie = ia , и один эквивалентный резистор Re . Для нашей эквивалентной схемы закон Ома указывает, что:
ie = V / ReМы можем определить значение Re , используя небольшую алгебру:
V / Re = ie = i1 + i2 + i3V / Re = V / R1 + V / R2 + V / R3
1 / Re = 1 / R1 + 1 / R2 + 1 / R3
1 / Re = (R2 R3 + R1 R3 + R1 R2 / (R1 R2 R3)
Re = (R1 R2 R3) / (R2 R3 + R1 R3 + R1 R2).
Мы можем использовать эти знания о схеме параллельного резистора для анализа Мост Уитстона схема, которая используется для контроля температуры в аэродинамической трубе баланс сил используя электронные тензодатчики.
Навигация ..
- Руководство для начинающих Домашняя страница
| Детали с усилением
Используйте этот калькулятор для определения общего сопротивления сети. Этот калькулятор может давать результаты для последовательного, параллельного и любого их сочетания. Схема создается автоматически по мере добавления резисторов в сеть в качестве наглядного пособия.
Сложные резистивные схемы часто можно упростить до одного резистора эквивалентного номинала.В процессе упрощения используются два уравнения: резисторы в последовательном уравнении и резисторы в параллельном уравнении.
Резисторы серии
Резисторы включены последовательно при соединении в одну линию. Текущий ток является общим для всех резисторов в этой цепи. Это связано с тем, что ток, протекающий через первый резистор, проходит через каждый из следующих резисторов в цепи. Общее сопротивление должно равняться сумме номиналов каждого резистора, используемого в цепи.
$$ R _ {\ text {Equiv}} = R_1 + R_2 + R_3 + \ ldots R_n $$Мы можем рассматривать всю эту цепочку резисторов как один резистор со значением ~ R _ {\ text {Equiv}} ~.
Параллельные резисторы
Резисторы включены параллельно, если они используют одни и те же два узла. Падение напряжения на каждом резисторе в этой конфигурации обычное. Теперь ток имеет несколько путей и может не быть одинаковым для каждого резистора. Общее сопротивление резисторов, включенных параллельно, является суммой, обратной величине каждого используемого резистора.
$$ \ frac {1} {R _ {\ text {Equiv}}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} + \ ldots \ frac { 1} {R_n} $$Мы можем рассматривать эти параллельные резисторы как один резистор со значением ~ R _ {\ text {Equiv}} ~
Обратите внимание, что информация, представленная в этой статье, предназначена только для справочных целей. Amplified Parts не делает никаких заявлений, обещаний или гарантий относительно точности, полноты или адекватности содержания этой статьи и прямо отказывается от ответственности за ошибки или упущения со стороны автора.В отношении содержания данной статьи не дается никаких гарантий, подразумеваемых, выраженных или установленных законом, включая, помимо прочего, гарантии ненарушения прав третьих лиц, права собственности, товарной пригодности или пригодности для определенной цели. или его ссылки на другие ресурсы.
Сопротивление параллельной цепи— HVAC School
В цепи серии (нагрузки, соединенные в ряд, встык), легко вычислить общее сопротивление цепи, потому что вы просто складываете все сопротивления, чтобы получить общее.
В параллельной цепи p напряжение одинаково для всех нагрузок; сила тока просто складывается, но сопротивление немного сложнее.
Это сложно представить, потому что общее сопротивление цепи параллельных нагрузок уменьшается с увеличением количества добавленных нагрузок.
Например, если у вас есть одна лампочка, подключенная к источнику питания, полное сопротивление цепи равно сопротивлению лампы.
Добавьте еще одну лампочку в ПАРАЛЛЕЛЬНО , и сопротивление цепи станет на НИЖЕ .
Когда вы вычисляете полное сопротивление параллельной цепи, вы берете каждое отдельное сопротивление и делите его на (не на) одно. Затем вы складываете все сопротивления, которые были разделены на одно, и делите эту сумму на одно. Формула для диаграммы вверху статьи выглядит так:
1 ÷ Rt (полное сопротивление) = 1 ÷ R1 + 1 ÷ R2 + 1 ÷ R3
Для этого конкретного приложения, как показано выше, будет:
1 ÷ Rt (общее сопротивление) = 1 ÷ 120 + 1 ÷ 45 + 1 ÷ 360
Итак, 1 ÷ 120 = 0.0083 + 1 ÷ 45 = 0,022 + 1 ÷ 360 = 0,0028
Затем мы складываем их все:
0,0083 + 0,022 + 0,0028 = 0,0331
Затем, чтобы найти сумму, вы делите единицу на сумму:
1 ÷ 0,0331 = всего 30,21 Ом
Как вы заметите, 30,21 Ом меньше наименьшего сопротивления в цепи. Это имеет смысл, если подумать о законе Ома.
Чем ниже сопротивление, тем выше ток. Добавление дополнительных параллельных нагрузок УВЕЛИЧИВАЕТ силу тока в цепи.Мы видим это каждый день, когда замечаем, что усилители компрессора и усилители вентилятора конденсатора, сложенные вместе, равны общим усилителям конденсатора.
Итак, очевидно, что если более низкое сопротивление равняется более высокому току, и добавление большего количества параллельных нагрузок увеличивает ампер, то добавление большего количества параллельных нагрузок снижает сопротивление.
Еще один миф, который этот опровергает, — это идея о том, что электричество ТОЛЬКО идет по пути наименьшего сопротивления. Электричество фактически проходит все пути между положительными и отрицательными зарядами, и каждый дополнительный путь (параллельная цепь) просто уменьшает сопротивление между двумя точками разности потенциалов.Это явление увеличивает общую силу тока в цепи, поэтому выключатель срабатывает, когда вы пытаетесь включить два фена в одной цепи 15 А. Два фена, подключенных параллельно = меньшее общее сопротивление цепи = более высокий ток.
Не то чтобы я пользовалась двумя фенами… может, поэтому я почти лысая.
—Bryan
Сопутствующие
Параллельное сопротивление (шунт) для расширения диапазона измерения, онлайн-калькулятор и формулы
Калькуляторы и формулы для расчета параллельного сопротивления амперметра
Расширение диапазона измерения амперметра
Эта функция вычисляет параллельное сопротивление, чтобы расширить диапазон измерения амперметра.Однако в принципе эту функцию можно использовать и для любого другого компонента, чей текущий поток должен быть уменьшен.
Для расчета необходимо знать ток амперметра и полный ток. Также необходимо указать напряжение или сопротивление амперметра. Вход сопротивления амперметра предустановлен; его можно переключить на напряжение в раскрывающемся меню.
|
Расчет параллельного сопротивления с помощью амперметра напряжения
\ (\ Displaystyle R_p = \ гидроразрыва {U_ {tot}} {I_ {tot} -I_m} \)
Расчет параллельного сопротивления через сопротивление амперметра
\ (\ Displaystyle R_p = \ гидроразрыва {R_m} {п-1} \) \ (\ Displaystyle п = \ гидроразрыва {I_ {tot}} {I_m} \)
Легенда
\ (\ Displaystyle U_ {тот} \)
Общее напряжение / напряжение амперметра
\ (\ Displaystyle I_ {тот} \)
Общий ток
\ (\ Displaystyle I_ {м} \)
Ток в амперметре
\ (\ Displaystyle R_ {м} \)
Амперметр сопротивление
\ (\ Displaystyle R_ {p} \)
Значение параллельного сопротивления
\ (\ Displaystyle Р_ {р} \)
Мощность / нагрузочная способность параллельного резистора
|
Калькулятор параллельного сопротивления
— IX23
Префиксы SI
Вы должны это знать.Если вы этого не сделаете, вам нужно выучить их.
| Префикс | Символ | Значение | |
|---|---|---|---|
| пико– | п. | 10 −12 | = 0,000 000 000 001 |
| нано– | n | 10 −9 | = 0,000 000 001 |
| микро– | µ | 10 −6 | = 0,000 001 |
| милли– | м | 10 −3 | = 0.001 |
| кг– | к | 10 3 | = 1 000 |
| мега- | M | 10 6 | = 1 000 000 |
| гига– | G | 10 9 | = 1 000 000 000 |
| тера– | Т | 10 12 | = 1 000 000 000 000 |
Резисторы серии
Формула для расчета полного сопротивления последовательно соединенных резисторов довольно проста.
R всего = R 1 + R 2 + R 3 +… + R n
Например, если у вас есть три резистора номиналами 330 Ом, 47 кОм и 1 кОм, вы можете рассчитать R всего следующим образом:
R всего = 330 Ом + 47000 Ом + 1000 Ом = 48330 Ом или 48,33 кОм
Параллельные резисторы
Формула для расчета общего сопротивления резисторов, включенных параллельно, немного сложнее.
1 / R всего = 1 / R 1 + 1 / R 2 +… + 1 / R n
Шаг 1: Нам нужно очистить все дроби путем умножения на наименьший общий знаменатель, который равен ( рэндов всего × R 1 × R 2 ). Умножая обе части на наименьший общий знаменатель, получаем
( рэнд × R 1 х рэнд 2 ) × (1/ рэнд всего ) = (1 / R 1 + 1 / R 2 ) × ( рэнд всего × R 1 × R 2 )
Шаг 2: Используя свойство distributive (держу пари, вы хотели бы, чтобы вы обратили внимание на математический класс), мы получаем
( рэнд, всего рэндов × R 1 х рэнд 2 ) / рэндов всего = ( рэндов всего рэндов × R 1 х R 2 ) / R 1 + ( рэндов итого ) × R 1 × R 2 ) / R 2
Шаг 3: Упрощая уравнение, получаем
( R всего × R 1 × R 2 ) / R всего = (R всего × R 1 × R 2 ) / R 1 + (R всего × R 1 × R 2 ) / R 2
То же, что и
R 1 × R 2 = R всего × R 2 + R всего × R 1
Шаг 4: Собирая все члены R 1 слева от знака равенства, получаем
R 1 × R 2 — R всего × R 1 = R всего × R 2
То же, что и
R 1 × ( R 2 — R всего ) = R Всего × R 2
Шаг 5: Разделив обе стороны на ( 2 — всего ), получим
R 1 = ( рэндов 2 × рэндов всего ) / ( рэндов 2 — рэндов всего )
Таким же способом получаем
R 2 = ( R 1 × R всего ) / ( R 1 — R всего )
Шаг 6: Вернемся к шагу 3, у нас было
R 1 × R 2 = R всего × R 2 + R всего × R 1
Используя свойство распределения, получаем
R 1 × R 2 = R всего × ( 2 + R 1 )
Шаг 7: Разделите обе стороны на (R 2 + R 1 ), и мы получим
( 1 рэнд × 2 ) / ( 2 рэнд + 1 ) = рэнд всего
То же, что и
R всего = ( R 1 × R 2 ) / ( R 1 + R 2 )
Итак, когда у нас есть схема с двумя параллельными резисторами, наши три формулы для расчета значений R 1 , R 2 или R всего , когда у нас есть два из трех значений, равны
R всего = ( R 1 × R 2 ) / ( R 1 + R 2 )
R 1 = ( 2 R всего ) / ( 2 R всего )
R 2 = ( 1 R всего ) / ( 1 R всего )
Это большая работа, которую нужно делать вручную.К счастью, компьютер делает всю работу за нас. В следующем разделе у нас есть калькулятор параллельного сопротивления для цепей с двумя параллельными резисторами.
Калькулятор параллельного сопротивления для двух резисторов
Чтобы использовать калькулятор, введите значение резистора в два из трех полей. Будет вычислено третье значение параллельной цепи.
Например, вы можете ввести значения для 1 и 2 рандов и рассчитать рандов, всего рандов.Или вы можете ввести рандов всего и 1 и рассчитать 2 рандов. Или вы можете ввести рандов всего и 2 и рассчитать 1 рандов.
В раскрывающемся списке можно установить единицы измерения для R 1 , R 2 и R, всего . Вы можете выбрать µΩ (микроом), mΩ (миллиом), Ω (ом), kΩ (килоом) или MΩ (мегом).
Калькулятор параллельного сопротивления до 10 резисторов
Скоро в продаже…
Этот калькулятор может решать другие математические задачи. Этот калькулятор можно использовать для рабочих задач. Например, «А» может покрасить комнату за 5 часов, а «Б» покрасить комнату за 6 часов. Если они оба работают вместе, сколько времени займет работа? Введите 5 и 6 просто как если бы они были резисторами и получите свой ответ. Этот калькулятор можно использовать для задач «заполнения». Например, одна труба может наполнить воду. бак за 5 часов, в то время как другая труба может заполнить тот же бак за 6 часов. Если обе трубы работают одновременно …….. хммм кажется жутко знакомым к другой проблеме, не так ли? Удачи тебе с математическими задачами. Числа отображаются в экспоненциальном представлении с указанием количества значащие цифры, которые вы указываете. Для удобства чтения числа от 0,001 до 1000. будет ли не в экспоненциальной нотации, но все равно будет иметь ту же точность. Вы можете изменить количество значащих цифр, отображаемых изменив номер в поле выше. Большинство браузеров будут отображать ответы правильно, но если вы вообще не видите ответов, введите ноль в поле выше, что приведет к исключите все форматирование, но, по крайней мере, вы увидите ответы. | ||

