Как рассчитать сопротивление при последовательном и параллельном соединении резисторов. Какие формулы используются для вычислений. Какие особенности у каждого типа соединения. Где применяются различные схемы подключения резисторов.
Последовательное соединение резисторов: основные принципы
При последовательном соединении резисторы подключаются один за другим, образуя единую цепь. Основные особенности такого соединения:
- Через все резисторы протекает одинаковый ток
- Напряжение на участке цепи равно сумме напряжений на отдельных резисторах
- Общее сопротивление цепи равно сумме сопротивлений всех резисторов
Формула для расчета общего сопротивления при последовательном соединении:
R = R1 + R2 + R3 + … + Rn
где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Параллельное соединение резисторов: ключевые характеристики
При параллельном соединении все резисторы подключаются к одним и тем же точкам цепи. Особенности параллельного соединения:

- На всех резисторах одинаковое напряжение
- Общий ток равен сумме токов через отдельные резисторы
- Обратная величина общего сопротивления равна сумме обратных величин сопротивлений резисторов
Формула для расчета общего сопротивления при параллельном соединении:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Сравнение последовательного и параллельного соединения
Какое соединение выбрать — последовательное или параллельное? Рассмотрим основные отличия:
- При последовательном соединении общее сопротивление всегда больше сопротивления любого из резисторов
- При параллельном соединении общее сопротивление всегда меньше сопротивления любого из резисторов
- Последовательное соединение позволяет получить большое общее сопротивление
- Параллельное соединение используется для уменьшения общего сопротивления
Применение различных типов соединений резисторов
Где на практике применяются последовательное и параллельное соединение резисторов?
Последовательное соединение применяется:
- В делителях напряжения
- Для ограничения тока в цепи
- В измерительных приборах для расширения пределов измерения
Параллельное соединение используется:
- Для увеличения допустимой мощности рассеивания
- В шунтах измерительных приборов
- Для создания эквивалентных сопротивлений сложной формы
Расчет смешанного соединения резисторов
На практике часто встречаются схемы со смешанным соединением резисторов, когда присутствуют как последовательные, так и параллельные участки. Как рассчитать такую цепь?
- Разбить схему на участки с одинаковым типом соединения
- Рассчитать эквивалентное сопротивление для каждого участка
- Заменить участки эквивалентными резисторами
- Повторять шаги 1-3 до получения общего эквивалентного сопротивления
Такой метод позволяет рассчитать сопротивление даже в сложных схемах со смешанным соединением резисторов.
Практические примеры расчета сопротивлений
Рассмотрим несколько примеров расчета сопротивлений при различных соединениях резисторов:
Пример 1. Последовательное соединение
Дано: R1 = 100 Ом, R2 = 200 Ом, R3 = 300 Ом
R = R1 + R2 + R3 = 100 + 200 + 300 = 600 Ом
Пример 2. Параллельное соединение
Дано: R1 = 6 Ом, R2 = 3 Ом
1/R = 1/R1 + 1/R2 = 1/6 + 1/3 = 1/2
R = 2 Ом
Пример 3. Смешанное соединение
Рассмотрим схему из 4 резисторов:
- R1 и R2 соединены последовательно
- R3 и R4 соединены параллельно
- Группы (R1+R2) и (R3||R4) соединены последовательно
Дано: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 60 Ом
1. R12 = R1 + R2 = 10 + 20 = 30 Ом
2. 1/R34 = 1/R3 + 1/R4 = 1/30 + 1/60 = 3/60 = 1/20
R34 = 20 Ом
3. R = R12 + R34 = 30 + 20 = 50 Ом
Таким образом, общее сопротивление цепи составляет 50 Ом.
Особенности расчета токов и напряжений
При анализе электрических цепей важно не только рассчитать общее сопротивление, но и определить токи и напряжения на отдельных участках. Рассмотрим основные принципы:
Для последовательного соединения:
- Ток через все резисторы одинаковый: I = I1 = I2 = … = In
- Напряжение распределяется пропорционально сопротивлениям: U1 = I * R1, U2 = I * R2 и т.д.
- Общее напряжение равно сумме напряжений на резисторах: U = U1 + U2 + … + Un
Для параллельного соединения:
- Напряжение на всех резисторах одинаковое: U = U1 = U2 = … = Un
- Ток распределяется обратно пропорционально сопротивлениям: I1 = U / R1, I2 = U / R2 и т.д.
- Общий ток равен сумме токов через резисторы: I = I1 + I2 + … + In
Зависимость сопротивления от температуры
При расчетах электрических цепей важно учитывать, что сопротивление резисторов может меняться в зависимости от температуры. Для большинства металлов сопротивление увеличивается с ростом температуры по закону:
R = R0 * (1 + α * (T — T0))
где:
- R — сопротивление при температуре T
- R0 — сопротивление при начальной температуре T0
- α — температурный коэффициент сопротивления
Этот эффект особенно важен при работе с мощными резисторами или в условиях значительных колебаний температуры окружающей среды.
Заключение
Понимание принципов последовательного и параллельного соединения резисторов является фундаментальным для анализа и проектирования электрических цепей. Правильный выбор типа соединения позволяет достичь требуемых характеристик цепи, таких как общее сопротивление, распределение токов и напряжений. Умение рассчитывать сложные цепи со смешанным соединением резисторов — важный навык для инженеров-электриков и радиотехников.
При практическом применении важно учитывать не только теоретические расчеты, но и реальные характеristiki компонентов, включая допуски на номиналы резисторов и их зависимость от внешних факторов, таких как температура. Это позволит создавать надежные и эффективные электронные устройства.
Как рассчитать последовательное и параллельное соединение вместе. Как найти сопротивление последовательной и параллельной цепей
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение
Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:
Смешанное соединение
Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R 3 . Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 , соединены последовательно.
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема
Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
И находят сопротивления R 1 , R 2 и R 3 .
Отдельные проводники электрической цепи могут быть соединены между собой последовательно, параллельно и смешанно. При этом последовательное и параллельное соединение проводников являются основными видами соединений, а смешанное соединение это их совокупность.
Последовательным соединением проводников называется такое соединение, когда конец первого проводника соединен с началом второго, конец второго проводника соединен с началом третьего и так далее (рисунок 1).
Рисунок 1. Схема последовательного соединения проводников
Общее сопротивление цепи, состоящее из нескольких последовательно соединенных проводников, равно сумме сопротивлений отдельных проводников:
r = r 1 + r 2 + r 3 + … + r n .
Ток на отдельных участках последовательной цепи везде одинаков:
I 1 = I 2 = I 3 = I .
Видео 1. Последовательное соединение проводников
Пример 1. На рисунке 2 представлена электрическая цепь, состоящая из трех последовательно включенных сопротивлений r 1 = 2 Ом, r 2 = 3 Ом, r 3 = 5 Ом. Требуется определить показания вольтметров V 1 , V 2 , V 3 и V 4 , если ток в цепи равен 4 А.
Сопротивление всей цепи
r = r 1 + r 2 + r 3 = 2 + 3 + 5 =10 Ом.
Рисунок 2. Схема измерения напряжений на отдельных участках электрической цепи
В сопротивлении r 1 при протекании тока будет падение напряжения:
U 1 = I × r 1 = 4 × 2 = 8 В.
Вольтметр V 1 , включенный между точками а и б , покажет 8 В.
В сопротивлении r 2 также происходит падение напряжения:
U 2 = I × r 2 = 4 × 3 = 12 В.
Вольтметр V 2 , включенный между точками в и г , покажет 12 В.
Падение напряжения в сопротивлении r 3:
U 3 = I × r 3 = 4 × 5 = 20 В.
Вольтметр V 3 , включенный между точками д и е , покажет 20 В.
Если вольтметр присоединить одним концом к точке а , другим концом к точке г , то он покажет разность потенциалов между этими точками, равную сумме падений напряжения в сопротивлениях
Таким образом, вольтметр V , измеряющий напряжение на зажимах цепи и включенный между точками а и е , покажет разность потенциалов между этими точками или сумму падений напряжения в сопротивлениях r 1 , r 2 и r 3 .
Отсюда видно, что сумма падений напряжения на отдельных участках электрической цепи равна напряжению на зажимах цепи.
Так как при последовательном соединении ток цепи на всех участках одинаков, то падение напряжения пропорционально сопротивлению данного участка.
Пример 2. Три сопротивления 10, 15 и 20 Ом соединены последовательно, как показано на рисунке 3. Ток в цепи 5 А. Определить падение напряжения на каждом сопротивлении.
U
1 = I
× r
1 = 5 ×10 = 50 В,
U
2 = I
× r
2 = 5 ×15 = 75 В,
U
3 = I
× r
3 = 5 ×20 = 100 В.
Рисунок 3. К примеру 2
Общее напряжение цепи равно сумме падений напряжений на отдельных участках цепи:
U = U 1 + U 2 + U 3 = 50 + 75 + 100 = 225 В.
Параллельное соединение проводников
Параллельным соединением проводников называется такое соединение, когда начала всех проводников соединены в одну точку, а концы проводников – в другую точку (рисунок 4). Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.
Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А , растекается далее по трем сопротивлениям и равен сумме токов, уходящих от этой точки:
I = I 1 + I 2 + I 3 .
Если токи, приходящие к точке разветвления, считать положительными, а уходящие – отрицательными, то для точки разветвления можно написать:
то есть алгебраическая сумма токов для любой узловой точки цепи всегда равна нулю. Это соотношение, связывающее токи в любой точке разветвления цепи, называется первым законом Кирхгофа . Определение первого закона Кирхгофа может звучать и в другой формулировке, а именно: сумма токов втекающих в узел электрической цепи равна сумме токов вытекающих из этого узла.
Видео 2. Первый закон Кирхгофа
Обычно при расчете электрических цепей направление токов в ветвях, присоединенных к какой либо точке разветвления, неизвестны. Поэтому для возможности самой записи уравнения первого закона Кирхгофа нужно перед началом расчета цепи произвольно выбрать так называемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме.
Пользуясь законом Ома, можно вывести формулу для подсчета общего сопротивления при параллельном соединении потребителей.
Общий ток, приходящий к точке А , равен:
Токи в каждой из ветвей имеют значения:
По формуле первого закона Кирхгофа
I = I 1 + I 2 + I 3
Вынося U в правой части равенства за скобки, получим:
Сокращая обе части равенства на U , получим формулу подсчета общей проводимости:
g = g 1 + g 2 + g 3 .
Таким образом, при параллельном соединении увеличивается не сопротивление, а проводимость .
Пример 3. Определить общее сопротивление трех параллельно включенных сопротивлений, если r 1 = 2 Ом, r 2 = 3 Ом, r 3 = 4 Ом.
Пример 4. Пять сопротивлений 20, 30 ,15, 40 и 60 Ом включены параллельно в сеть. Определить общее сопротивление:
Следует заметить, что при подсчете общего сопротивления разветвления оно получается всегда меньше, чем самое меньшее сопротивление, входящее в разветвление.
Если сопротивления, включенные параллельно, равны между собой, то общее сопротивление r цепи равно сопротивлению одной ветви r 1 , деленному на число ветвей n :
Пример 5. Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 Ом каждое:
Для проверки попробуем найти сопротивление разветвления по формуле:
Как видим, ответ получается тот же.
Пример 6. Пусть требуется определить токи в каждой ветви при параллельном их соединении, изображенном на рисунке 5, а .
Найдем общее сопротивление цепи:
Теперь все разветвления мы можем изобразить упрощенно как одно сопротивление (рисунок 5, б ).
Падение напряжения на участке между точками А и Б будет:
U = I × r = 22 × 1,09 = 24 В.
Возвращаясь снова к рисунку 5, а видим, что все три сопротивления окажутся под напряжением 24 В, так как они включены между точками А и Б .
Рассматривая первую ветвь разветвления с сопротивлением r 1 , мы видим, что напряжение на этом участке 24 В, сопротивление участка 2 Ом. По закону Ома для участка цепи ток на этом участке будет:
Ток второй ветви
Ток третьей ветви
Проверим по первому закону Кирхгофа
Всем доброго времени суток. В прошлой статье я рассмотрел , применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса , называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье. Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и .
Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее. На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии
Пример последовательного подключения приемников энергии.
В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления
Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.
Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями
где R – эквивалентное последовательное сопротивление.
Применение последовательного соединения
Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр
Делитель напряжения (слева) и потенциометр (справа).
В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.
Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.
Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии. Пример такого соединения показан на рисунке ниже
Пример параллельного соединения приемников энергии.
Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви
Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений
Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.
Смешанное соединение приемников энергии
Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии
Пример смешанного соединения приемников энергии.
В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид
В результате получили цепь из двух последовательных приемников энергии R 12 R 345 эквивалентное сопротивление и ток, протекающий через них, составит
Тогда падение напряжения по участкам составит
Тогда токи, протекающие через каждый приемник энергии, составят
Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.
Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением
где ∑ — обозначает алгебраическую сумму.
Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа
Изображение первого закона Кирхгофа.
На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид
Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.
Как говорилось выше, второй закон Кирхгофа определяет соотношение между ЭДС и напряжениями в замкнутом контуре и звучит следующим образом: алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах этого контура. Второй закон Кирхгофа определяется следующим выражением
В качестве примера рассмотрим ниже следующую схему, содержащую некоторый контур
Схема, иллюстрирующая второй закон Кирхгофа.
Для начала необходимо определится с направлением обхода контура. В принципе можно выбрать как по ходу часовой стрелки, так и против хода часовой стрелки. Я выберу первый вариант, то есть элементы будут считаться в следующем порядке E1R1R2R3E2, таким образом, уравнение по второму закону Кирхгофа будет иметь следующий вид
Второй закон Кирхгофа применяется не только к цепям постоянного тока, но и к цепям переменного тока и к нелинейным цепям.
В следующей статье я рассмотрю основные способы расчёта сложных цепей с использованием закона Ома и законов Кирхгофа.
Теория это хорошо, но без практического применения это просто слова.
Подробности Категория: Статьи Создано: 06.09.2017 19:48Как подключить в кукольном домике несколько светильников
Когда вы задумываетесь о том как сделать освещение в кукольном домике или румбоксе, где не один, а несколько светильников, то встает вопрос о том, как их подключить, объединить в сеть. Существует два типа подключения: последовательное и параллельное, о которых мы слышали со школьной скамьи. Их и рассмотрим в этой статье.
Я постараюсь описать всё простым доступным языком, чтобы всё было понятно даже самым-самым гуманитариям, не знакомым с электрическими премудростями.
Примечание : в этой статье рассмотрим только цепь с лампочками накаливания. Освещение диодами более сложное и будет рассмотрено в другой статье.
Для понимания каждая схема будет сопровождена рисунком и рядом с чертежом электрической монтажной схемой.
Сначала рассмотрим условные обозначения на электрических схемах.
| Название элемента | Символ на схеме | Изображение |
| батарейка/ элемент питания | ||
| выключатель | ||
| провод | ||
| пересечение проводов (без соединения) | ||
| соединение проводов (пайкой, скруткой) | ||
| лампа накаливания | ||
| неисправная лампа | ||
| неработающая лампа | ||
| горящая лампа |
Как уже было сказано, существуют два основных типа подключения: последовательное и параллельное. Есть ещё третье, смешанное: последовательно-параллельное, объединяющее то и другое. Начнем с последовательного, как более простого.
Последовательное подключение
Выглядит оно вот так.
Лампочки располагаются одна за другой, как в хороводе держась за руки. По этому принципу были сделаны старые советские гирлянды.
Достоинства
— простота соединения.
Недостатки
— если перегорела хоть одна лампочка, то не будет работать вся цепь.
Надо будет перебирать, проверять каждую лампочку, чтобы найти неисправную. Это может быть утомительным при большом количестве лампочек. Так же лампочки должны быть одного типа: напряжение, мощность.
При этом типе подключения напряжения лампочек складываются. Напряжение обозначается буквой U , измеряется в вольтах V . Напряжение источника питания должно быть равно сумме напряжений всех лампочек в цепи.
Пример №1 : вы хотите подключить в последовательную цепь 3 лампочки напряжением 1,5V. Напряжение источника питания, необходимое для работы такой цепи 1,5+1,5+1,5=4,5V.
У обычных пальчиковых батареек напряжение 1,5V. Чтобы из них получить напряжение 4,5V их тоже нужно соединить в последовательную цепь, их напряжения сложатся.
Подробнее о том, как выбрать источник питания написано в этой статье
Пример №2: вы хотите подключить к источнику питания 12V лампочки по 6V. 6+6=12v. Можно подключить 2 таких лампочки.
Пример №3: вы хотите соединить в цепь 2 лампочки по 3V. 3+3=6V. Необходим источник питания на 6 V.
Подведем итог: последовательное подключение просто в изготовлении, нужны лампочки одного типа. Недостатки: при выходе из строя одной лампочки не горят все. Включить и выключить цепь можно только целиком.
Исходя из этого, для освещения кукольного домика целесообразно соединять последовательно не более 2-3 лампочек. Например, в бра. Чтобы соединить большее количество лампочек, необходимо использовать другой тип подключения — параллельное.
Читайте так же статьи по теме:
- Обзор миниатюрных ламп накаливания
- Диоды или лампы накаливания
Параллельное подключение лампочек
Вот так выглядит параллельное подключение лампочек.
В этом типе подключения у всех лампочек и источника питания одинаковые напряжения. То есть при источнике питания 12v каждая из лампочек должна иметь тоже напряжение 12V. А количество лампочек может быть различным. А если у вас, допустим, есть лампочки 6V, то и источник питания нужно брать 6V.
При выходе из строя одной лампочки другие продолжают гореть.
Лампочки можно включать независимо друг от друга. Для этого к каждой нужно поставить свой выключатель.
По этому принципу подключены электроприборы в наших городских квартирах. У всех приборов одно напряжение 220V, включать и выключать их можно независимо друг от друга, мощность электроприборов может быть разной.
Вывод : при множестве светильников в кукольном домике оптимально параллельное подключение, хотя оно чуть сложнее, чем последовательное.
Рассмотрим ещё один вид подключения, соединяющий в себе последовательное и параллельное.
Комбинированное подключение
Пример комбинированного подключения.
Три последовательные цепи, соединенные параллельно
А вот другой вариант:
Три параллельные цепи, соединенные последовательно.
Участки такой цепи, соединенные последовательно, ведут себя как последовательное соединение. А параллельные участки — как параллельное соединение.
Пример
При такой схеме перегорание одной лампочки выведет из строя весь участок, соединенный последовательно, а две другие последовательные цеписохранят работоспособность.
Соответственно, и включать-выключать участки можно независимо друг от друга. Для этого каждой последовательной цепи нужно поставить свой выключатель.
Но нельзя включить одну-единственную лампочку.
При параллельно-последовательном подключении при выходе из строя одной лампочки цепь будет вести себя так:
А при нарушении на последовательном участке вот так:
Пример:
Есть 6 лампочек по 3V, соединенные в 3 последовательные цепи по 2 лампочки. Цепи в свою очередь соединены параллельно. Разбиваем на 3 последовательных участка и просчитываем этот участок.
На последовательном участке напряжения лампочек складываются, 3v+3V=6V. У каждой последовательной цепи напряжение 6V. Поскольку цепи соединены параллельно, то их напряжение не складывается, а значит нам нужен источник питания на 6V.
Пример
У нас 6 лампочек по 6V. Лампочки соединены по 3 штуки в параллельную цепь, а цепи в свою очередь — последовательно. Разбиваем систему на три параллельных цепи.
В одной параллельной цепи напряжение у каждой лампочки 6V, поскольку напряжение не складывается, то и у всей цепи напряжение 6V. А сами цепи соединены уже последовательно и их напряжения уже складываются. Получается 6V+6V=12V. Значит, нужен источник питания 12V.
Пример
Для кукольных домиков можно использовать такое смешанное подключение.
Допустим, в каждой комнате по одному светильнику, все светильники подключены параллельно. Но в самих светильниках разное количество лампочек: в двух — по одной лампочке, есть двухрожковое бра из двух лампочек и трехрожковая люстра. В люстре и бра лампочки соединены последовательно.
У каждого светильника свой выключатель. Источник питания 12V напряжения. Одиночные лампочки, соединенные параллельно, должны иметь напряжение 12V. А у тех, что соединены последовательно напряжение складывается на участке цепи
. Соответственно, для участка бра из двух лампочек 12V (общее напряжение)делим на 2 (количество лампочек), получим 6V (напряжение одной лампочки).
Для участка люстры 12V:3=4V (напряжение одной лампочки люстры).
Больше трех лампочек в одном светильнике соединять последовательно не стоит.
Теперь вы изучили все хитрости подключения лампочек накаливания разными способами. И, думаю, что не составит труда сделать освещение в кукольном домике со многими лампочками, любой сложности. Если же что-то для вас ещё представляет сложности, прочитайте статью о простейшем способе сделать свет в кукольном домике, самые базовые принципы. Удачи!
В предыдущем конспекте был установлено, что сила тока в проводнике зависит от напряжения на его концах. Если в опыте менять проводники, оставляя напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению. Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = U/R . Этот закон, установленный экспериментально, называется закон Ома (для участка цепи).
Закон Ома для участка цепи : сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника. Прежде всего закон всегда верен для твёрдых и жидких металлических проводников. А также для некоторых других веществ (как правило, твёрдых или жидких).
Потребители электрической энергии (лампочки, резисторы и пр.) могут по-разному соединяться друг с другом в электрической цепи. Д ва основных типа соединения проводников : последовательное и параллельное. А также есть еще два соединения, которые являются редкими: смешанное и мостовое.
Последовательное соединение проводниковПри последовательном соединении проводников конец одного проводника соединится с началом другого проводника, а его конец — с началом третьего и т.д. Например, соединение электрических лампочек в ёлочной гирлянде. При последовательном соединении проводников ток проходит через все лампочки. При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.
Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: I 1 = I 2 = I .
Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений : R 1 + R 2 = R . Потому что при последовательном соединении проводников их общая длина увеличивается. Она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.
По закону Ома напряжение на каждом проводнике равно: U 1 = I* R 1 , U 2 = I*R 2 . В таком случае общее напряжение равно U = I ( R 1 + R 2) . Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике : U = U 1 + U 2 .
Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.
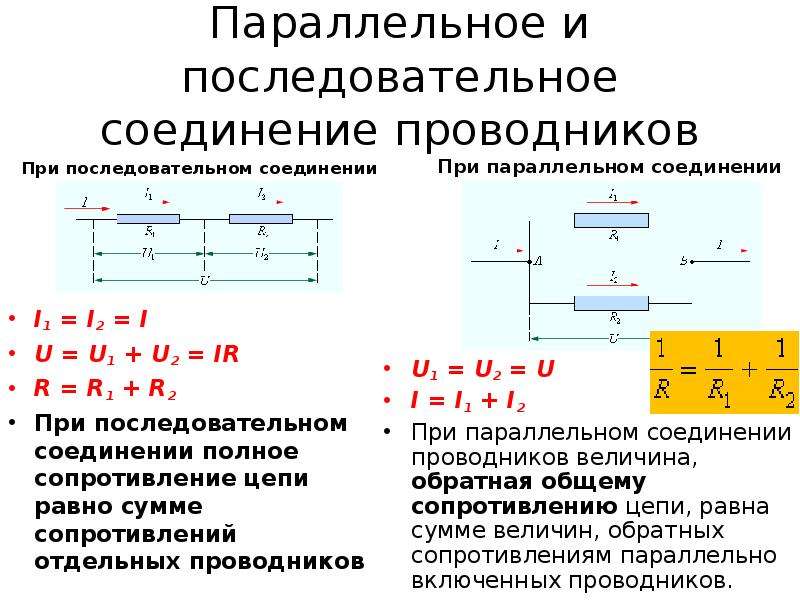
Для последовательного соединения проводников справедливы законы :1) сила тока во всех проводниках одинакова; 2) напряжение на всём соединении равно сумме напряжений на отдельных проводниках; 3) сопротивление всего соединения равно сумме сопротивлений отдельных проводников.
Параллельное соединение проводниковПримером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи. А вторым концом к другой точке цепи. Вольтметр, подключенный к этим точкам, покажет напряжение и на проводнике 1, и на проводнике 2. В таком случае напряжение на концах всех параллельно соединённых проводников одно и то же: U 1 = U 2 = U .
При параллельном соединении проводников электрическая цепь разветвляется. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: I = I 1 + I 2 .
В соответствии с законом Ома I = U/R, I 1 = U 1 /R 1 , I 2 = U 2 /R 2 . Отсюда следует: U/R = U 1 /R 1 + U 2 /R 2 , U = U 1 = U 2 , 1/R = 1/R 1 + 1/R 2 Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.
При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление г , то их общее сопротивление равно: R = г/2 . Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения. В результате уменьшается сопротивление.
Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно. Они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них. А также соответствие суммарной силы тока предельно допустимой силе тока.
Для параллельного соединения проводников справедливы законы:1) напряжение на всех проводниках одинаково; 2) сила тока в месте соединения проводников равна сумме токов в отдельных проводниках; 3) величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.
Физическая формула расчета эквивалентного сопротивления в цепи
Расчёт электрических схем, содержащих несколько сопротивлений (резисторов), при нахождении силы тока в цепи, напряжения или мощности, производится с использованием метода свёртывания. Метод заключается в том, чтобы найти эквивалентное сопротивление выделенных участков цепи. Основная задача – замена резисторов, имеющих различное подключение относительно друг друга, на эквивалент (Rэкв.).
Эквивалентное сопротивление резисторов
Определение эквивалентного сопротивления
При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.
Последовательное соединение элементов
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.
Последовательное включение резисторов
В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
I = U/R.
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
R = U/I.
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
I = I1= I2= … = In.
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
U = U1 + U2+ … + Un.
Следовательно, рассчитать можно общее:
Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Параллельное соединение
Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.
Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:
- общий ток: I = I1 + I2 + … + In;
- общее напряжение: U = U1 = U2 = … = Un;
- Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.
Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.
Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.
Параллельное включение резисторов
Расчёт при смешанном соединении устройств
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.
Способ расчёта при смешанном соединении
Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.
Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
U = 24 В.
Требуется рассчитать токи на всех резистивных элементах.
Исходная цепь
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
Последовательно соединённые резисторы R2 и R3
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
Смешанное включение на участке CD
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
Результат первого свёртывания
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.
Результат последующего свёртывания
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD:
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Стоит заметить! Ток, протекающий через R4 и R5, по своему значению равен току на отрезке, не имеющем разветвления.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Видео
fizika / Сопротивление проводников. Параллельное и последовательное соединение проводников
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему[1]. Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
где
R — сопротивление;
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
|
Рисунок 1.9.1. Последовательное соединение проводников |
По закону Ома, напряжения U1 и U2 на проводниках равны
|
U1 = IR1, U2 = IR2. |
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
|
U = U1 + U2 = I(R1 + R2) = IR, |
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
|
Рисунок 1.9.2. Параллельное соединение проводников |
Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получим
|
|
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
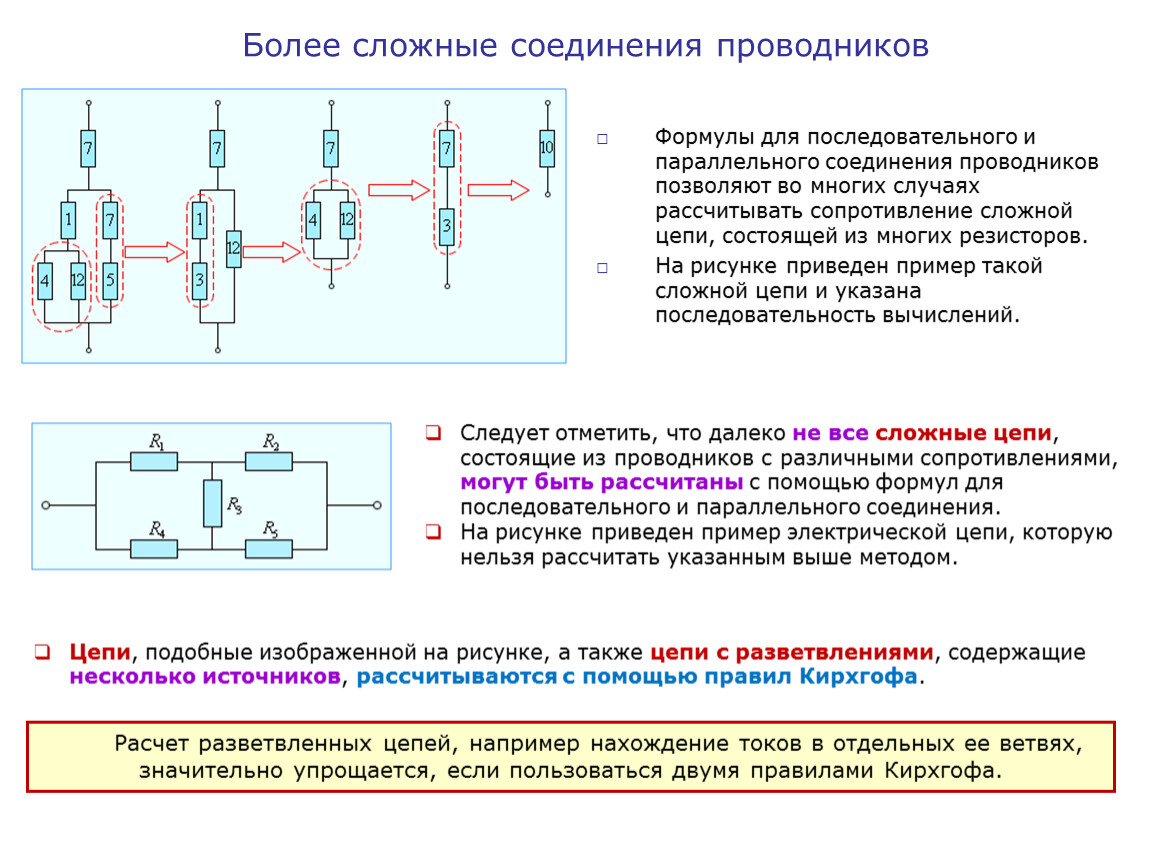
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
|
Рисунок 1.9.3. Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом) |
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
|
Рисунок 1.9.4. Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников |
Параллельное соединение — сопротивление — Большая Энциклопедия Нефти и Газа, статья, страница 4
Параллельное соединение — сопротивление
Cтраница 4
Смешанные делители применяются в основном двух типов: делители с параллельным соединением сопротивлений и емкостей и делители с последовательным соединением сопротивлений и емкостей. [46]
Лос — выходное сопротивление ОС, а знак / / — параллельное соединение сопротивлений. Следовательно, при параллельной ООС входное сопротивление усилителя уменьшается. [48]
Отметим, во-первых, что последовательному соединению пружины и поршня соответствует параллельное соединение сопротивления и емкости и наоборот. Во-вторых, рис. 9, б дает не единственный пример формальной аналогии между электрическими и механическими релаксационными процессами. [50]
Таким образом, для равнозначной емкости получается формула, аналогичная формуле параллельного соединения сопротивлений. [51]
В формулах ( 31) — ( 33) RBX образовано параллельным соединением сопротивления образца Яобр, входного сопротивления измерительного прибора и сопротивления утечки и обычно равно входному сопротивлению измерительной цепи. Емкость Свх равна сумме емкости образца С0бР, емкости подводящих проводов и входной емкости измерительного прибора. [52]
Из этого выражения следует, что комплексная проводимость электрической цепи при параллельном соединении сопротивлений оказывается равной сумме комплексных проводимостей соответствующих параллельных ветвей. Выражение для комплексной проводимости каждой из параллельных ветвей получается путем умножения числителя и знаменателя соответствующей проводимости на сопряженное значение комплексного сопротивления. [53]
Транзисторы TI и Т2 открыты, а прямое сопротивление замкнутого ключа Rnp равно параллельному соединению сопротивлений открытых транзисторов. Аналогично, при мвх — Е транзистор Tt заперт, а транзистор Т2 открыт под действием напряжения ишТ, 2Е и прямое сопротивление остается примерно прежним. [54]
В каком соотношении находятся токи в активном сопротивлении и ток всей цепи с параллельным соединением сопротивления, индуктивности и емкости. [55]
Эти электрические цепи могут быть разделены на участки с последовательным и участки с параллельным соединением сопротивлений. [56]
Отсюда в общем случае для произвольного числа параллельных ветвей активная проводимость электрической цепи при параллельном соединении сопротивлений оказывается равной сумме активных проводимостей всех параллельных ветвей, а реактивная проводимость цепи равной алгебраической сумме реактивных проводимостей всех параллельных ветвей, входящих в данную электрическую цепь. [57]
Если имеются центры рекомбинации более чем одного типа, то результирующее сопротивление рекомбинации R определяется параллельным соединением сопротивлений различных центров. Величина R, полученная для образцов А и D из экспериментальных значений С, составляет около г500 ом. Отсюда вытекает, что 8р0 8ерп и 8pb Stpp, или, другими словами, центры типа а находятся в равновесии с зоной проводимости, а центры типа Ъ — с валентной зоной. [58]
Страницы: 1 2 3 4
1 последовательное и параллельное соединение проводников. Последовательное и параллельное соединение
Последовательное соединение сопротивлений
Возьмем три неизменных сопротивления R1, R2 и R3 и включим их в цепь так, чтоб конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).
Такое соединение сопротивлений именуется поочередным. Разумеется, что ток в таковой цепи будет во всех ее точках один и тот же.
Рис 1 . Последовательное соединение сопротивлений
Как найти общее сопротивление цепи, если все включенные в нее поочередно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U = U1 + U2 + U3
где
U1 = IR1 U2 = IR2 и U3 = IR3
либо
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .
Поделив сейчас обе части равенства на I , будем совсем иметь R = R1 + R2 + R3
Таким макаром, мы сделали вывод, что при поочередном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на последующем примере. Возьмем три неизменных сопротивления, величины которых известны (к примеру, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их поочередно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).
Рис. 2. Пример поочередного соединения 3-х сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим наружное сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи по закону Ома: 60 / 80 = 0 ,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во наружной цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.
Мы получили таким макаром, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Разъясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув сейчас ключ выключатель К, можно убедиться по устройствам, что наши подсчеты приблизительно верны.
Возьмем два неизменных сопротивления R1 и R2 и соединим их так, чтоб начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив потом точки а и б с источником тока, получим замкнутую электронную цепь. Такое соединение сопротивлений именуется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, потому что тут сама цепь разветвляется на две отдельные ветки: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Любой из этих токов пойдет по собственной ветки до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким макаром, при параллельном соединении сопротивлений выходит разветвленная цепь. Поглядим, какое же будет соотношение меж токами в составленной нами цепи.
Включим амперметр меж положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив потом амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.
Означает, сила тока в цепи до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем сейчас включать амперметр попеременно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветки амперметр покажет силу тока I1 , а во 2-ой — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Как следует, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим
Это соотношение, имеющее огромное практическое значение, носит заглавие закона разветвленной цепи .
Разглядим сейчас, каково будет соотношение меж токами в ветвях.
Включим меж точками а и б вольтметр и поглядим, что он нам покажет. Во-1-х, вольтметр покажет напряжение источника тока, потому что он подключен, как это видно из рис. 3 , конкретно к зажимам источника тока. Во-2-х, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R1 и R2, потому что он соединен с началом и концом каждого сопротивления.
Как следует, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2 ,
где U — напряжение на зажимах источника тока; U1 — падение напряжения на сопротивлении R1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .
Потому для каждой ветки можно написать: U1 = I1R1 и U2 = I2R2 , но потому что U1 = U2, то и I1R1 = I2R2 .
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветки будет во столько раз больше (либо меньше) тока во 2-ой ветки, во сколько раз сопротивление первой ветки меньше (либо больше) сопротивления 2-ой ветки.
Итак, мы пришли к принципиальному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, назад пропорциональные величинам сопротивлении параллельных веток. По другому говоря, чем больше сопротивление ветки, тем наименьший ток потечет через нее, и, напротив, чем меньше сопротивление ветки, тем больший ток потечет через эту ветвь.
Убедимся в корректности этой зависимости на последующем примере. Соберем схему, состоящую из 2-ух параллельно соединенных сопротивлений R1 и R 2, присоединенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем поначалу, что покажет нам амперметр, включенный в каждую ветвь:
I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА
I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1 +I2 = 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется назад пропорционально сопротивлениям.
Вправду, R1 == 10 Ом в два раза меньше R 2 = 20 Ом, при всем этом I1 = 300 мА в два раза больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть (I1 = 300 мА) пошла через наименьшее сопротивление (R1 = 10 Ом), а наименьшая часть (R2 = 150 мА) -через большее сопротивление (R 2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением воды по трубам. Представьте для себя трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного поперечника (рис. 4). Потому что поперечник трубы Б больше поперечника трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает сгустку воды большее сопротивление.
Рис. 4
Разглядим сейчас, чему будет равно общее сопротивление наружной цепи, состоящей из 2-ух параллельно соединенных сопротивлений.
Под этим общим сопротивлением наружной цепи нужно осознавать такое сопротивление, которым можно было бы поменять при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при всем этом тока до разветвления. Такое сопротивление именуется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и поглядим, чему будет равно эквивалентное сопротивление 2-ух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во наружной цепи (до точки разветвления), U — напряжение наружной цепи, R — сопротивление наружной цепи, т. е. эквивалентное сопротивление.
Точно так же для каждой ветки I1 = U1 / R1 , I2 = U2 / R2 , где I1 и I 2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления веток.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Потому что при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )
Разделив сейчас обе части равенства на U , будем совсем иметь 1 / R = 1 / R1 + 1 / R2
Помня, что проводимостью именуется величина, оборотная сопротивлению , мы можем сказать, что в приобретенной формуле 1 / R — проводимость наружной цепи; 1 / R1 проводимость первой ветки; 1 / R2- проводимость 2-ой ветки.
На основании этой формулы делаем вывод: при параллельном соединении проводимость наружной цепи равна сумме проводимостей отдельных веток.
Как следует, чтоб найти эквивалентное сопротивление включенных параллельно сопротивлений, нужно найти проводимость цепи и взять величину, ей оборотную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветки, а это означает, что эквивалентное сопротивление наружной цепи меньше меньшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли более ординарную цепь, состоящую из 2-ух веток. Но на практике могут повстречаться случаи, когда цепь состоит из 3-х и поболее параллельных веток. Как поступать в этих случаях?
Оказывается, все приобретенные нами соотношения остаются справедливыми и для цепи, состоящей из хоть какого числа параллельно соединенных сопротивлений.
Чтоб убедиться в этом, разглядим последующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5 ). R = 1 / 6 Как следует, эквивалентное сопротивление R = 6 Ом.
Таким макаром, эквивалентное сопротивление меньше меньшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.
Поглядим сейчас, вправду ли это сопротивление является эквивалентным, т. е. таким, которое могло бы поменять включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при всем этом силы тока до разветвления цепи.
Допустим, что напряжение наружной цепи, а как следует, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0,2 А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 =1,2 + 0,6 + 0,2 = 2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если заместо 3-х параллельно включенных узнаваемых нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U / R = 12 / 6 = 2 А
Как лицезреем, отысканное нами сопротивление R = 6 Ом вправду является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных устройствах, если собрать схему с взятыми нами сопротивлениями, измерить ток во наружной цепи (до разветвления), потом поменять параллельно включенные сопротивления одним сопротивлением 6 Ом и опять измерить ток. Показания амперметра и в том и в другом случае будут приблизительно схожими.
На практике могут повстречаться также параллельные соединения, для которых высчитать эквивалентное сопротивление можно проще, т. е. не определяя за ранее проводимостей, сходу отыскать сопротивление.
К примеру, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно конвертировать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / (R1 + R2 ), т. е. при параллельном соединении 2-ух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
При одновременном включении нескольких приемников электроэнергии в одну и ту же сеть, эти приемники можно легко рассматривать просто как элементы единой цепи, каждый из которых обладает собственным сопротивлением.
В ряде случаев такой подход оказывается вполне приемлемым: лампы накаливания, электрические обогреватели и т. п. — можно воспринимать как резисторы. То есть приборы можно заменить на их сопротивления, и легко произвести расчет параметров цепи.
Способ соединения приемников электроэнергии может быть одним из следующих: последовательный, параллельный или смешанный тип соединения.
Последовательное соединение
Когда несколько приемников (резисторов) соединяются в последовательную цепь, то есть второй вывод первого присоединяется к первому выводу второго, второй вывод второго соединяется с первым выводом третьего, второй вывод третьего с первым выводом четвертого и т. д., то при подключении такой цепи к источнику питания, через все элементы цепи потечет ток I одной и той же величины. Данную мысль поясняет приведенный рисунок.
Заменив приборы на их сопротивления, рисунок преобразуем в схему, тогда сопротивления с R1 по R4, соединенные последовательно, примут каждый на себя определенные напряжения, которые в сумме дадут значение ЭДС на зажимах источника питания. Для простоты здесь и далее изобразим источник в виде гальванического элемента.
Выразив падения напряжений через ток и через сопротивления, получим выражение для эквивалентного сопротивления последовательной цепи приемников: общее сопротивление последовательного соединения резисторов всегда равно алгебраической сумме всех сопротивлений, составляющих эту цепь. А поскольку напряжения на каждом из участков цепи можно найти из закона Ома (U = I*R, U1 = I*R1, U2 = I*R2 и т. д.) и E = U, то для нашей схемы получаем:
Напряжение на клеммах источника питания равно сумме падений напряжений на каждом из соединенных последовательно приемников, составляющих цепь.
Так как ток через всю цепь течет одного и того же значения, то справедливым будет утверждение, что напряжения на последовательно соединенных приемниках (резисторах) соотносятся между собой пропорционально сопротивлениям. И чем выше будет сопротивление, тем выше окажется и напряжение, приложенное к приемнику.
Для последовательного соединения резисторов в количестве n штук, обладающих одинаковыми сопротивлениями Rk, эквивалентное общее сопротивление цепи целиком будет в n раз больше каждого из этих сопротивлений: R = n*Rk. Соответственно и напряжения, приложенные к каждому из резисторов цепи будут между собой равны, и окажутся в n раз меньше напряжения, приложенного ко всей цепи: Uk = U/n.
Для последовательного соединения приемников электроэнергии характерны следующие свойства: если изменить сопротивление одного из приемников цепи, то напряжения на остальных приемниках цепи при этом изменятся; при обрыве одного из приемников ток прекратится во всей цепи, во всех остальных приемниках.
В силу этих особенностей последовательное соединение встречается редко, и используют его лишь там, где напряжение сети выше номинального напряжения приемников, в отсутствие альтернатив.
К примеру напряжением 220 вольт можно запитать две последовательно соединенные лампы равной мощности, каждая из которых рассчитана на напряжение 110 вольт. Ежели данные лампы при одинаковом номинальном напряжении питания будут обладать различной номинальной мощностью, то одна из них будет перегружена и скорее всего мгновенно перегорит.
Параллельное соединение
Параллельное соединение приемников предполагает включение каждого из них между парой точек электрической цепи с тем, чтобы они образовывали параллельные ветви, каждая из которых питается напряжением источника. Для наглядности опять заменим приемники их электрическими сопротивлениями, чтобы получить схему, по которой удобно вести расчет параметров.
Как уже было сказано, в случае параллельного соединения каждый из резисторов испытывает действие одного и того же напряжения. И в соответствии с законом Ома имеем: I1=U/R1, I2=U/R2, I3=U/R3.
Здесь I — ток источника. Первый закон Кирхгофа для данной цепи позволяет записать выражение для тока в неразветвленной ее части: I = I1+I2+I3.
Отсюда общее сопротивление для параллельного соединения между собой элементов цепи можно найти из формулы:
Величина обратная сопротивлению называется проводимостью G, и формулу для проводимости цепи, состоящей из нескольких параллельно соединенных элементов, также можно записать: G = G1 + G2 + G3. Проводимость цепи в случае параллельного соединения образующих ее резисторов равна алгебраической сумме проводимостей этих резисторов. Следовательно, при добавлении в цепь параллельных приемников (резисторов) суммарное сопротивление цепи уменьшится, а суммарная проводимость соответственно возрастет.
Токи в цепи состоящей из параллельно соединенных приемников, распределяются между ними прямо пропорционально их проводимостям, то есть обратно пропорционально их сопротивлениям. Здесь можно привести аналогию из гидравлики, где поток воды распределяется по трубам в соответствии с их сечениями, тогда большее сечение аналогично меньшему сопротивлению, то есть большей проводимости.
Если цепь состоит из нескольких (n) одинаковых резисторов, соединенных параллельно, то общее сопротивление цепи будет ниже в n раз, чем сопротивление одного из резисторов, а ток через каждый из резисторов будет меньше в n раз, чем общий ток: R = R1/n; I1 = I/n.
Цепь, состоящая из параллельно соединенных приемников, подключенная к источнику питания, отличается тем, что каждый из приемников находится под напряжением источника питания.
Для идеального источника электроэнергии справедливо утверждение: при подключении или отключении параллельно источнику резисторов, токи в остальных подключенных резисторах не изменятся, то есть при выходе из строя одного или нескольких приемников параллельной цепи, остальные будут продолжать работать в прежнем режиме.
В силу данных особенностей параллельное соединение обладает значительным преимуществом перед последовательным, и по этой причине именно соединение параллельное наиболее распространено в электрических сетях. Например, все электроприборы в наших домах предназначены для параллельного подключения к бытовой сети, и если отключить один, то остальным это ничуть не навредит.
Сравнение последовательных и параллельных цепей
Под смешанным соединением приемников понимают такое их соединение, когда часть или несколько из них соединены между собой последовательно, а другая часть или несколько — параллельно. При этом вся цепь может быть образована из разных соединений таких частей между собой. Для примера рассмотрим схему:
Три последовательно соединенных резистора подключены к источнику питания, параллельно одному из них подключены еще два, а третий — параллельно всей цепи. Для нахождения полного сопротивления цепи идут путем последовательных преобразований: сложную цепь последовательно приводят к простому виду, последовательно вычисляя сопротивление каждого звена, и так находят общее эквивалентное сопротивление.
Для нашего примера. Сначала находят общее сопротивление двух резисторов R4 и R5, соединенных последовательно, затем сопротивление параллельного соединения их с R2, потом прибавляют к полученному значению R1 и R3, и после — вычисляют значение сопротивления всей цепи, включая параллельную ветвь R6.
Различные способы соединения приемников электроэнергии применяют на практике для различных целей, чтобы решать конкретные поставленные задачи. Например, смешанное соединение можно встретить в схемах плавного заряда в мощных блоках питания, где нагрузка (конденсаторы после диодного моста) сначала получает питание последовательно через резистор, затем резистор шунтируется контактами реле, и нагрузка оказывается подключенной к диодному мосту параллельно.
Андрей Повный
Содержание:Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для — последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав , нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: + 20, + 10, + 5, + 2, + 1% и так далее до величины + 0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Учитывая напряжение в цепи, равное 100 В, сила тока будет составлять I = U/R = 100/390 = 0,256 A.На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.
- P 1 = I 2 x R 1 = 0,256 2 x 200 = 13,11 Вт;
- P 2 = I 2 x R 2 = 0,256 2 x 100 = 6,55 Вт;
- P 3 = I 2 x R 3 = 0,256 2 x 51 = 3,34 Вт;
- P 4 = I 2 x R 4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при паралл ельном соединение
При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы — с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R 1 +1/R 2 +1/R 3 +1/R 4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I 1 = U/R 1 = 100/200 = 0,5A; I 2 = U/R 2 = 100/100 = 1A; I 3 = U/R 3 = 100/51 = 1,96A; I 4 = U/R 4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P 1 = U 2 /R 1 = 100 2 /200 = 50 Вт; P 2 = U 2 /R 2 = 100 2 /100 = 100 Вт; P 3 = U 2 /R 3 = 100 2 /51 = 195,9 Вт; P 4 = U 2 /R 4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р 1 +Р 2 +Р 3 +Р 4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
Темы кодификатора ЕГЭ : параллельное и последовательное соединение проводников, смешанное соединение проводников.Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.
Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.
Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис. 1 ):
Рис. 1. Резистор
Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.
Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.
Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2 ):
Рис. 2.
Стационарное поле совершает при этом положительную работу .
Так как alt=»q > 0″> и alt=»A > 0″> , то и alt=»\varphi_a — \varphi_b > 0″> , т. е. alt=»\varphi_a > \varphi_b»> .
Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .
Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3 ):
Рис. 3.
Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным . В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.
Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4 ). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.
Рис. 4. Последовательное соединение
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.
1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике .
Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:
Можно и более формально, без всяких словесных объяснений:
3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.
Пусть — сопротивление участка . По закону Ома имеем:
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .
Сопротивления проводников равны:
Эти два проводника образуют единый проводник длиной и сопротивлением
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Параллельное соединение
При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5 ).
Рис. 5. Параллельное соединение
Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями ; участок от к (по направлению тока) называется неразветвлённой частью цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.
1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .
Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:
что и требовалось.
3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:
Сокращая на , получим:
(1)
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1) можно найти :
(2)
К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением
(3)
Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:
Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.
Смешанное соединение
Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
Рассмотрим пример смешанного соединения проводников (рис. 6 ).
Рис. 6. Смешанное соединение
Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :
Ом.
Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:
Ом.
Сопротивление цепи:
Ом.
Теперь находим силу тока в цепи:
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)
Оба резистора и находятся под напряжением , поэтому:
(В сумме имеем А, как и должно быть при параллельном соединении.)
Сила тока в резисторах и одинакова, так как они соединены последовательно:
Стало быть, через резистор течёт ток A.
Во многих электрических схемах мы можем обнаружить последовательное и . Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление.
Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи.
Последовательное соединение резисторов
Пример № 1
Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:
Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:
Пример № 2
а) без подключенного резистора R3
б) с подключенным резистором R3
Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.
Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) — то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R).
Последовательное и параллельное сопротивление проводников. Закон Ома. Соединение проводников
Одним из китов, на котором держатся многие понятия в электронике, является понятие последовательного и параллельного подключения проводников. Знать основные отличия указанных типов подключения просто необходимо. Без этого нельзя понять и прочитать ни одной схемы.
Основные принципы
Электрический ток движется по проводнику от источника к потребителю (нагрузке). Чаще всего в качестве проводника выбирается медный кабель. Связано это с требованием, которое предъявляется к проводнику: он должен легко высвобождать электроны.
Независимо от способа подключения, электрический ток двигается от плюса к минусу. Именно в этом направлении убывает потенциал. При этом стоит помнить, что провод, по котору идет ток, также обладает сопротивлением. Но его значение очень мало. Именно поэтому им пренебрегают. Сопротивление проводника принимают равным нулю. В том случае, если проводник обладает сопротивлением, его принято называть резистором.
Параллельное подключение
В данном случае элементы, входящие в цепь, объединены между собой двумя узлами. С другими узлами у них связей нет. Участки цепи с таким подключением принято называть ветвями. Схема параллельного подключения представлена на рисунке ниже.
Если говорить более понятным языком, то в данном случае все проводники одним концом соединены в одном узле, а вторым — во втором. Это приводит к тому, что электрический ток разделяется на все элементы. Благодаря этому увеличивается проводимость всей цепи.
При подключении проводников в цепь данным способом напряжение каждого из них будет одинаково. А вот сила тока всей цепи будет определяться как сумма токов, протекающих по всем элементам. С учетом закона Ома путем нехитрых математических расчетов получается интересная закономерность: величина, обратная общему сопротивлению всей цепи, определяется как сумма величин, обратных сопротивлениям каждого отдельного элемента. При этом учитываются только элементы, подключенные параллельно.
Последовательное подключение
В данном случае все элементы цепи соединены таким образом, что они не образуют ни одного узла. При данном способе подключения имеется один существенный недостаток. Он заключается в том, что при выходе из строя одного из проводников все последующие элементы работать не смогут. Ярким примером такой ситуации является обычная гирлянда. Если в ней перегорает одна из лампочек, то вся гирлянда перестает работать.
Последовательное подключение элементов отличается тем, что сила тока во всех проводниках равна. Что касается напряжения цепи, то оно равно сумме напряжения отдельных элементов.
В данной схеме проводники включаются в цепь поочередно. А это значит, что сопротивление всей цепи будет складываться из отдельных сопротивлений, характерных для каждого элемента. То есть общее сопротивление цепи равно сумме сопротивлений всех проводников. Эту же зависимость можно вывести и математическим способом, используя закон Ома.
Смешанные схемы
Бывают ситуации, когда на одной схеме можно увидеть одновременно последовательное и параллельное подключение элементов. В таком случае говорят о смешанном соединении. Расчет подобных схем проводится отдельно для каждой из группы проводников.
Так, чтобы определить общее сопротивление, необходимо сложить сопротивление элементов, подключенных параллельно, и сопротивление элементов с последовательным подключением. При этом последовательное подключение является доминантным. То есть его рассчитывают в первую очередь. И только после этого определяют сопротивление элементов с параллельным подключением.
Подключение светодиодов
Зная основы двух типов подключения элементов в цепи, можно понять принцип создания схем различных электроприборов. Рассмотрим пример. во многом зависит от напряжения источника тока.
При небольшом напряжении сети (до 5 В) светодиоды подключают последовательно. Снизить уровень электромагнитных помех в данном случае поможет конденсатор проходного типа и линейные резисторы. Проводимость светодиодов увеличивают за счет использования системных модуляторов.
При напряжении сети 12 В может использоваться и последовательное, и параллельное подключение сети. В случае последовательного подключения используют импульсные блоки питания. Если собирается цепь из трех светодиодов, то можно обойтись без усилителя. Но если цепь будет включать большее количество элементов, то усилитель необходим.
Во втором случае, то есть при параллельном подключении, необходимо использование двух открытых резисторов и усилителя (с пропускной способностью выше 3 А). Причем первый резистор устанавливается перед усилителем, а второй — после.
При высоком напряжении сети (220 В) прибегают к последовательному подключению. При этом дополнительно используют операционные усилители и понижающие блоки питания.
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов
.
При последовательном соединении
нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк (19)
где R
эк
=
R 1 + R 2 + R 3
.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи
U = U 1 + U 2 +U 3 (20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U 1: U 2: U 3 = R 1: R 2: R 3 (21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов
. При параллельном соединении
нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов
. Смешанным соединением
называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Причем это могут быть не только проводники, но и конденсаторы. Здесь важно не запутаться в том, как выглядит каждое из них на схеме. А уже потом применять конкретные формулы. Их, кстати, нужно помнить наизусть.
Как различить эти два соединения?
Внимательно посмотрите на схему. Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.
Совсем другое дело, если рассматривается параллельное соединение. Тогда резисторы можно сравнить со спортсменами на старте. Они стоят каждый на своей дорожке, но направление движения у них одинаковое, и финиш в одном месте. Так же и резисторы — у каждого из них свой провод, но все они соединены в некоторой точке.
Формулы для силы тока
О ней всегда идет речь в теме «Электричество». Параллельное и последовательное соединение по-разному влияют на величину в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.
Так, ток при последовательном соединении проводников всегда одинаков. То есть в каждом из них значение силы тока не отличается. Провести аналогию можно, если сравнить провод с трубой. В ней вода течет всегда одинаково. И все препятствия на ее пути будут сметаться с одной и той же силой. Так же с силой тока. Поэтому формула общей силы тока в цепи с последовательным соединением резисторов выглядит так:
I общ = I 1 = I 2
Здесь буквой I обозначена сила тока. Это общепринятое обозначение, поэтому его нужно запомнить.
Ток при параллельном соединении уже не будет постоянной величиной. При той же аналогии с трубой получается, что вода разделится на два потока, если у основной трубы будет ответвление. То же явление наблюдается с током, когда на его пути появляется разветвление проводов. Формула общей силы тока при :
I общ = I 1 + I 2
Если разветвление составлено из проводов, которых больше двух, то в приведенной формуле на такое же количество станет больше слагаемых.
Формулы для напряжения
Когда рассматривается схема, в которой выполнено соединение проводников последовательно, то напряжение на всем участке определяется суммой этих величин на каждом конкретном резисторе. Сравнить эту ситуацию можно с тарелками. Удержать одну из них легко получится одному человеку, вторую рядом он тоже сможет взять, но уже с трудом. Держать в руках три тарелки рядом друг с другом одному человеку уже не удастся, потребуется помощь второго. И так далее. Усилия людей складываются.
Формула для общего напряжения участка цепи с последовательным соединением проводников выглядит так:
U общ = U 1 + U 2 , где U — обозначение, принятое для
Другая ситуация складывается, если рассматривается Когда тарелки ставятся друг на друга, их по-прежнему может удержать один человек. Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:
U общ = U 1 = U 2
Формулы для электрического сопротивления
Их уже можно не запоминать, а знать формулу закона Ома и из нее выводить нужную. Из указанного закона следует, что напряжение равно произведению силы тока и сопротивления. То есть U = I * R, где R — сопротивление.
Тогда формула, с которой нужно будет работать, зависит от того, как выполнено соединение проводников:
- последовательно, значит, нужно равенство для напряжения — I общ * R общ = I 1 * R 1 + I 2 * R 2;
- параллельно необходимо пользоваться формулой для силы тока — U общ / R общ = U 1 / R 1 + U 2 / R 2 .
Далее следуют простые преобразования, которые основываются на том, что в первом равенстве все силы тока имеют одинаковое значение, а во втором — напряжения равны. Значит, их можно сократить. То есть получаются такие выражения:
- R общ = R 1 + R 2 (для последовательного соединения проводников).
- 1 / R общ = 1 / R 1 + 1 / R 2 (при параллельном соединении).
При увеличении числа резисторов, которые включены в сеть, изменяется количество слагаемых в этих выражениях.
Стоит отметить, что параллельное и последовательное соединение проводников по-разному влияют на общее сопротивление. Первое из них уменьшает сопротивление участка цепи. Причем оно оказывается меньше самого маленького из использованных резисторов. При последовательном соединении все логично: значения складываются, поэтому общее число всегда будет самым большим.
Работа тока
Предыдущие три величины составляют законы параллельного соединения и последовательного расположения проводников в цепи. Поэтому их знать нужно обязательно. Про работу и мощность необходимо просто запомнить базовую формулу. Она записывается так: А = I * U * t , где А — работа тока, t — время его прохождения по проводнику.
Для того чтобы определить общую работу при последовательном соединении нужно заменить в исходном выражении напряжение. Получится равенство: А = I * (U 1 + U 2) * t, раскрыв скобки в котором получится, что работа на всем участке равна их сумме на каждом конкретном потребителе тока.
Аналогично идет рассуждение, если рассматривается схема параллельного соединения. Только заменять полагается силу тока. Но результат будет тот же: А = А 1 + А 2 .
Мощность тока
При выведении формулы для мощности (обозначение «Р») участка цепи опять нужно пользоваться одной формулой: Р = U * I. После подобных рассуждений получается, что параллельное и последовательное соединение описываются такой формулой для мощности: Р = Р 1 + Р 2 .
То есть, как бы ни были составлены схемы, общая мощность будет складываться из тех, которые задействованы в работе. Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.
Как влияет соединение проводников на ремонт новогодней гирлянды?
Сразу же после того, как перегорит одна из лампочек, станет ясно, как они были соединены. При последовательном соединении не будет светиться ни одна из них. Это объясняется тем, что пришедшая в негодность лампа создает разрыв в цепи. Поэтому нужно проверить все, чтобы определить, какая перегорела, заменить ее — и гирлянда станет работать.
Если в ней используется параллельное соединение, то она не перестает работать при неисправности одной из лампочек. Ведь цепь не будет полностью разорвана, а только одна параллельная часть. Чтобы отремонтировать такую гирлянду, не нужно проверять все элементы цепи, а только те, которые не светятся.
Что происходит с цепью, если в нее включены не резисторы, а конденсаторы?
При их последовательном соединении наблюдается такая ситуация: заряды от плюсов источника питания поступают только на внешние обкладки крайних конденсаторов. Те, что находятся между ними, просто передают этот заряд по цепочке. Этим объясняется то, что на всех обкладках появляются одинаковые заряды, но имеющие разные знаки. Поэтому электрический заряд каждого конденсатора, соединенного последовательно, можно записать такой формулой:
q общ = q 1 = q 2 .
Для того чтобы определить напряжение на каждом конденсаторе, потребуется знание формулы: U = q / С. В ней С — емкость конденсатора.
Общее напряжение подчиняется тому же закону, который справедлив для резисторов. Поэтому, заменив в формуле емкости напряжение на сумму, мы получим, что общую емкость приборов нужно вычислять по формуле:
С = q / (U 1 + U 2).
Упростить эту формулу можно, перевернув дроби и заменив отношение напряжения к заряду емкостью. Получается такое равенство: 1 / С = 1 / С 1 + 1 / С 2 .
Несколько по-другому выглядит ситуация, когда соединение конденсаторов — параллельное. Тогда общий заряд определяется суммой всех зарядов, которые накапливаются на обкладках всех приборов. А значение напряжения по-прежнему определяется по общим законам. Поэтому формула для общей емкости параллельно соединенных конденсаторов выглядит так:
С = (q 1 + q 2) / U.
То есть эта величина считается, как сумма каждого из использованных в соединении приборов:
С = С 1 + С 2.
Как определить общее сопротивление произвольного соединения проводников?
То есть такого, в котором последовательные участки сменяют параллельные, и наоборот. Для них по-прежнему справедливы все описанные законы. Только применять их нужно поэтапно.
Сперва полагается мысленно развернуть схему. Если представить ее сложно, то нужно нарисовать то, что получается. Объяснение станет понятнее, если рассмотреть его на конкретном примере (см. рисунок).
Ее удобно начать рисовать с точек Б и В. Их необходимо поставить на некотором удалении друг от друга и от краев листа. Слева к точке Б подходит один провод, а вправо направлены уже два. Точка В, напротив, слева имеет два ответвления, а после нее расположен один провод.
Теперь необходимо заполнить пространство между этими точками. По верхнему проводу нужно расположить три резистора с коэффициентами 2, 3 и 4, а снизу пойдет тот, у которого индекс равен 5. Первые три соединены последовательно. С пятым резистором они параллельны.
Оставшиеся два резистора (первый и шестой) включены последовательно с рассмотренным участком БВ. Поэтому рисунок можно просто дополнить двумя прямоугольниками по обе стороны от выбранных точек. Осталось применить формулы для расчета сопротивления:
- сначала ту, которая приведена для последовательного соединения;
- потом для параллельного;
- и снова для последовательного.
Подобным образом можно развернуть любую, даже очень сложную схему.
Задача на последовательное соединение проводников
Условие. В цепи друг за другом подсоединены две лампы и резистор. Общее напряжение равно 110 В, а сила тока 12 А. Чему равно сопротивление резистора, если каждая лампа рассчитана на напряжение в 40 В?
Решение. Поскольку рассматривается последовательное соединение, формулы его законов известны. Нужно только правильно их применить. Начать с того, чтобы выяснить значение напряжения, которое приходится на резистор. Для этого из общего нужно вычесть два раза напряжение одной лампы. Получается 30 В.
Теперь, когда известны две величины, U и I (вторая из них дана в условии, так как общий ток равен току в каждом последовательном потребителе), можно сосчитать сопротивление резистора по закону Ома. Оно оказывается равным 2,5 Ом.
Ответ. Сопротивление резистора равно 2,5 Ом.
Задача на параллельное и последовательное
Условие. Имеются три конденсатора с емкостями 20, 25 и 30 мкФ. Определите их общую емкость при последовательном и параллельном соединении.
Решение. Проще начать с В этой ситуации все три значения нужно просто сложить. Таким образом, общая емкость оказывается равной 75 мкФ.
Несколько сложнее расчеты будут при последовательном соединении этих конденсаторов. Ведь сначала нужно найти отношения единицы к каждой из этих емкостей, а потом сложить их друг с другом. Получается, что единица, деленная на общую емкость, равна 37/300. Тогда искомая величина получается приблизительно 8 мкФ.
Ответ. Общая емкость при последовательном соединении 8 мкФ, при параллельном — 75 мкФ.
Если нам надо, чтобы электроприбор работал, мы должны подключить его к . При этом ток должен проходить через прибор и возвращаться вновь к источнику, то есть цепь должна быть замкнутой.
Но подключение каждого прибора к отдельному источнику осуществимо, в основном, в лабораторных условиях. В жизни же приходится иметь дело с ограниченным количеством источников и довольно большим количеством потребителей тока. Поэтому создают системы соединений, позволяющие нагрузить один источник большим количеством потребителей. Системы при этом могут быть сколь угодно сложными и разветвленными, но в их основе лежит всего два вида соединения: последовательное и параллельное соединение проводников. Каждый вид имеет свои особенности, плюсы и минусы. Рассмотрим их оба.
Последовательное соединение проводников
Последовательное соединение проводников – это включение в электрическую цепь нескольких приборов последовательно, друг за другом. Электроприборы в данном случае можно сравнить с людьми в хороводе, а их руки, держащие друг друга – это провода, соединяющие приборы. Источник тока в данном случае будет одним из участников хоровода.
Напряжение всей цепи при последовательном соединении будет равно сумме напряжений на каждом включенном в цепь элементе. Сила тока в цепи будет одинакова в любой точке. А сумма сопротивлений всех элементов составит общее сопротивление всей цепи. Поэтому последовательное сопротивление можно выразить на бумаге следующим образом:
I=I_1=I_2=⋯=I_n ; U=U_1+U_2+⋯+U_n ; R=R_1+R_2+⋯+R_n ,
Плюсом последовательного соединения является простота сборки, а минусом – то, что если один элемент выйдет из строя, то ток пропадет во всей цепи. В такой ситуации неработающий элемент будет подобен ключу в выключенном положении. Пример из жизни неудобства такого соединения наверняка припомнят все люди постарше, которые украшали елки гирляндами из лампочек.
Если в такой гирлянде выходила из строя хотя бы одна лампочка, приходилось перебирать их все, пока не найдешь ту самую, перегоревшую. В современных гирляндах эта проблема решена. В них используют специальные диодные лампочки, в которых при перегорании сплавляются вместе контакты, и ток продолжает беспрепятственно проходить дальше.
Параллельное соединение проводников
При параллельном соединении проводников все элементы цепи подключаются к одной и той же паре точек, можно назвать их А и В. К этой же паре точек подключают источник тока. То есть получается, что все элементы подключены к одинаковому напряжению между А и В. В то же время ток как бы разделяется на все нагрузки в зависимости от сопротивления каждой из них.
Параллельное соединение можно сравнить с течением реки, на пути которой возникла небольшая возвышенность. Вода в таком случае огибает возвышенность с двух сторон, а потом вновь сливается в один поток. Получается островок посреди реки. Так вот параллельное соединение – это два отдельных русла вокруг острова. А точки А и В – это места, где разъединяется и вновь соединяется общее русло реки.
Напряжение тока в каждой отдельной ветви будет равно общему напряжению в цепи. Общий ток цепи будет складываться из токов всех отдельных ветвей. А вот общее сопротивление цепи при параллельном соединении будет меньше сопротивления тока на каждой из ветвей. Это происходит потому, что общее сечение проводника между точками А и В как бы увеличивается за счет увеличения числа параллельно подключенных нагрузок. Поэтому общее сопротивление уменьшается. Параллельное соединение описывается следующими соотношениями:
U=U_1=U_2=⋯=U_n ; I=I_1+I_2+⋯+I_n ; 1/R=1/R_1 +1/R_2 +⋯+1/R_n ,
где I — сила тока, U- напряжение, R – сопротивление, 1,2,…,n – номера элементов, включенных в цепь.
Огромным плюсом параллельного соединения является то, что при выключении одного из элементов, цепь продолжает функционировать дальше. Все остальные элементы продолжают работать. Минусом является то, что все приборы должны быть рассчитаны на одно и то же напряжение. Именно параллельным образом устанавливают розетки сети 220 В в квартирах. Такое подключение позволяет включать различные приборы в сеть совершенно независимо друг от друга, и при выходе их строя одного из них, это не влияет на работу остальных.
Нужна помощь в учебе?
Предыдущая тема: Расчёт сопротивления проводников и реостаты: формулыСледующая тема:   Работа и мощность тока
Параллельное соединение активного сопротивления, индуктивности и ёмкости в цепи переменного тока. Резонанс токов | Основы физики сжато и понятно
Для школьников.
На рисунке изображена электрическая цепь с параллельным соединением активного сопротивления, индуктивности и ёмкости. и обозначены токи, проходящие по ветвям, содержащим активное сопротивление, индуктивность и ёмкость.
Токи в ветвях назовём активным, индуктивным и емкостным, а ток в неразветвлённой части цепи — общим током.
Напряжение, приложенное к цепи одинаково для всех ветвей.
Нам предстоит рассмотреть, как находится общий ток и разность фаз между ним и приложенным к цепи напряжением.
Общий ток в каждый момент времени равен сумме мгновенных значений токов, проходящих по параллельным ветвям.
Для нахождения действующих значений токов воспользуемся векторной диаграммой токов, которую нам предстоит построить.
Посмотрим, что из себя представляет векторная диаграмма, затем построим её для нашего случая, то есть для параллельного соединения активного сопротивления, индуктивности и ёмкости..
Векторная диаграмма — это графическое изображение значений периодически изменяющихся величин и соотношений между ними при помощи направленных отрезков — векторов .
Например, мы знаем, что в цепи переменного тока напряжение на зажимах цепи меняется по синусоидальному закону, то есть колебания напряжения сети изображается синусоидой.
Мгновенные значения напряжения внешнего источника можно рассматривать как проекции вектора напряжения U (вектора ОВ) на вертикальную ось при равномерном вращении этого вектора против часовой стрелки.
Точно также векторами можно изобразить переменный ток в общей части цепи и в каждой ветви нашей цепи.
Колебания перечисленных величин имеют одну частоту, но сдвинуты по фазе относительно друг друга.
Их взаимное расположение со временем не меняется. Тогда их можно показать на одной диаграмме.
Действующее значение вектора общего тока цепи будет равно геометрической сумме векторов токов в каждой ветви.
На следующем рисунке показана векторная диаграмма токов для нашей цепи.
Строится она следующим образом.
Вектор напряжения откладываем в горизонтальном направлении вправо. Вектор тока, проходящего через активное сопротивление, совпадает по фазе с напряжением, поэтому его откладываем вдоль вектора U.
Вектор индуктивного тока отстаёт по фазе от напряжения на 90 градусов, поэтому откладываем его по вертикали вниз.
Вектор емкостного тока, проходящего через конденсатор, опережает напряжение по фазе на 90 градусов, поэтому откладываем его вверх от конца вектора индуктивного тока.
Складывая вектора токов в ветвях, получим вектор общего тока, направленный от О к С, и треугольник токов.
Из треугольника токов по теореме Пифагора получаем выражение для общего тока:
Зная токи, которые в каждой ветви находятся по закону Ома, через синус или косинус угла сможем найти угол «фи», то есть сдвиг фаз между общим током и приложенным к цепи напряжением.
Возможны следующие случаи:
Емкостной ток больше индуктивного. Тогда общий ток опережает по фазе приложенное к цепи напряжение (приведённый рисунок соответствует первому случаю).
Индуктивный ток больше емкостного. Тогда общий ток отстаёт по фазе от напряжения (вектор общего тока расположится ниже горизонтальной линии). Нарисуйте векторную диаграмму для этого случая или просто представьте её.
Емкостной ток равен индуктивному.
Тогда имеем:
В этом случае общий ток цепи совпадает по фазе с напряжением и равен активному току,
Такой режим называется резонансом токов.
При резонансе токов общий ток имеет наименьшее значение, что следует из диаграммы токов.
Токи же в ветвях с индуктивностью и ёмкостью могут быть значительно больше общего тока, поэтому режим и называется резонансом токов.
Пример.
Сопротивление R= 5 Ом включено параллельно индуктивности 0,003 Гн и конденсатору С в цепь переменного тока напряжением 120 В и частотой 50 Гц. При какой ёмкости конденсатора наступит резонанс токов в этой цепи, какой при этом будет общий ток?
Решение.
Индуктивное сопротивление
равно 0,942 Ом.
При резонансе токов емкостное сопротивление равно индуктивному,
значит тоже равно 0,942 Ом.
Через формулу емкостного сопротивления:
находим ёмкость конденсатора:
Ёмкость конденсатора равна 0,003 Ф.
Применив закон Ома к каждой ветви, найдём токи в ветвях::
Анодный ток равен 24 А.
Индуктивный ток:
равен 127 А.
Емкостной ток при резонансе токов равен индуктивному:
Из треугольника по теореме Пифагора находим общий ток:
Общий ток в нашем примере равен 24 А.
Видим, что при резонансе токов силы токов в ветвях с индуктивностью и ёмкостью значительно больше общего тока цепи.
В электрических цепях промышленных предприятий резонанса токов допускать нельзя из-за возможного пробоя изоляции катушки и конденсатора.
В то же время для получения большой активной (полезной) мощности надо добиваться, чтобы коэффициент мощности был близок к единице. В одной из последующих статей рассмотрим, как этого добиваются.
Ставьте лайки. Подписывайтесь на канал.
К.В. Рулёва
Предыдущая запись: Катушка в цепи переменного тока или последовательное соединение активного сопротивления и индуктивности.
Следующая запись: Краткий обзор темы: «Переменный электрический ток».
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 . .
Этот режим называется резонансом токов
Параллельные резисторы: уравнения, схемы, расчеты, сети
Когда оба вывода резистора соединены с каждым выводом другого резистора или резисторов, говорят, что они соединены параллельно. В отличие от цепей с последовательными резисторами, поскольку в сети с параллельными резисторами имеется несколько каналов для тока, ток в цепи может проходить по нескольким путям. Затем делители тока применяются к параллельным цепям.
В этой статье вы получите представление о параллельных резисторах, их схеме, уравнении, расчетах, диаграмме, сетях, токе и некоторых примерах.
Подробнее: Резисторы серии
Резисторы параллельно
Если выводы двух резисторов подключены к одним и тем же двум узлам, они параллельны. Общее эквивалентное сопротивление меньше, чем у наименьшего параллельного резистора. Поскольку ток питания может проходить во многих направлениях, ток может быть неодинаков во всех ветвях параллельной сети. Однако в параллельной резистивной сети падение напряжения на всех резисторах одинаково.Тогда все параллельно соединенные элементы имеют общее напряжение на них, и это справедливо для всех параллельно соединенных резисторов.
Таким образом, параллельная резистивная цепь определяется как цепь, в которой резисторы подключены к одним и тем же двум точкам (или узлам), и отличается наличием нескольких токовых путей, соединенных с одним и тем же источником напряжения. Напряжение на резисторе R1 равно напряжению на резисторе R2, которое равно напряжению на резисторе R3, равному напряжению питания в приведенном ниже примере с параллельным резистором.
Расчет эквивалентного сопротивления для резистора, включенного параллельно
На приведенной ниже схеме для формирования более сложных цепей резисторы часто соединяют последовательно или параллельно. На схеме выше вы можете увидеть пример параллельных резисторов. Каждый резистор в параллельной цепи имеет одинаковое напряжение. С другой стороны, ток обратно пропорционален сопротивлению каждого резистора. Эквивалентное сопротивление множества параллельных резисторов рассчитывается следующим образом:
1Req=n∑i=11Ri=1R1+1R2+⋯+1Rn1Req=∑i=1n1Ri=1R1+1R2+⋯+1Rn
Подробнее: Различные типы резисторов
Ток через каждый резистор определяется по формуле:
Ii=VRiIi=VRi
Краткий пример расчета параллельного сопротивления:
Разработчик схемы должен использовать резистор с сопротивлением 9 Ом и может выбрать предпочтительные значения из серии E-12 (…, 10, 12, 15, 18, 22, 27, 33, 39, 47, 56, 68). , 82, …).Значение 9 Ом, к сожалению, недоступно в этой серии. Он решает построить аналогичное сопротивление 9 Ом, соединив параллельно два стандартных значения. Эти процедуры используются для расчета эквивалентного значения сопротивления для двух параллельных резисторов:
1Req=1R1+1R21Req=1R1+1R2
1Req=R2R1⋅R2+R1R1⋅R21Req=R2R1·R2+R1R1·R2
1Req=R1+R2R1⋅R21Req=R1+R2R1·R2
Треб.=R1⋅R2R1+R2Необ.=R1·R2R1+R2
Подробнее: Знакомство с металлооксидными пленочными резисторами
Приведенное выше уравнение пытается объяснить, что если R1 равно R2, то Req равно половине значения одного из двух резисторов.Таким образом, для Req 9 Ом R1 и R2 должны иметь значение 2 x 9 = 18 Ом. Это стандартное значение для серии E.
Req=R1⋅R2R1+R2=18⋅1818+18=9ΩReq=R1·R2R1+R2=18·1818+18=9Ω
В качестве решения инженер соединяет два резистора по 18 Ом параллельно, чтобы обеспечить эквивалентное сопротивление 9 Ом, как показано на диаграмме ниже.
Решение сети с параллельными и последовательными резисторами
Методическое группирование резисторов обычно позволяет решать более сложные цепи резисторов.Три резистора соединены, как показано на левом изображении ниже. Резисторы R2 и R3 соединены последовательно. Они включены последовательно с резистором R1. Резисторы разделены на две группы для решения схемы, как показано на среднем изображении. R1 — единственный член группы 1. R2 и R3 составляют группу 2.
Сумму R2 и R3 можно легко использовать для расчета эквивалентного сопротивления группы 2:
Rгруппа2=R2+R3Rгруппа2=R2+R3
В результате получается упрощенная схема, изображенная справа, с двумя параллельными резисторами.Эквивалентное сопротивление этой цепи легко вычислить:
.1Req=1R1+1Rgroup21Req=1R1+1Rgroup2
Треб.=R1⋅Rгруппа2R1+Rгруппа2Req=R1·Rгруппа2R1+Rгруппа2
Требуется=R1⋅(R2+R3)R1+R2+R3Req=R1·(R2+R3)R1+R2+R3
Подробнее: Общие сведения о резисторах для поверхностного монтажа (резисторы для поверхностного монтажа)
Большие сети могут быть решены путем повторного использования этих принципов для расчета параллельных и последовательных резисторов. Законы Кирхгофа применимы и к более сложным сетям.Резисторы R1, R2 и R3 подключены параллельно между двумя точками A и B в следующих резисторах в параллельной цепи.
Цепь параллельного резистора
Общее сопротивление сети последовательных резисторов, RT, было равно сумме всех отдельных резисторов, сложенных вместе. Эквивалентное сопротивление цепи RT рассчитывается по-разному для параллельных резисторов.
Вместо непосредственного сложения сопротивлений обратные (1/R) значения отдельных сопротивлений складываются вместе, при этом обратная алгебраическая сумма дает эквивалентное сопротивление, как указано.
Уравнение параллельного резистора
Алгебраическая сумма обратных значений отдельных сопротивлений является обратной величиной эквивалентного сопротивления двух или более сопротивлений, соединенных параллельно.
Подробнее: Резисторы
Общее или эквивалентное сопротивление, RT, равно половине значения одного резистора, если два параллельных сопротивления или импеданса равны и имеют одно и то же значение. Р/2, Р/3, Р/4, Р/5, Р/6, Р/7, Р/8, Р/9, Р/10, Р/11, Р/12, Р/13, Р/ 14, р/15, р/16, р
Поскольку эквивалентное сопротивление всегда меньше наименьшего резистора в параллельной сети, при добавлении большего количества параллельных резисторов общее сопротивление RT всегда будет падать.
Параллельное сопротивление дает значение, известное как проводимость, символ G, с Сименсом, знак S, как единицу проводимости. (G = 1/R) Проводимость обратна или обратна сопротивлению. Чтобы преобразовать проводимость обратно в значение сопротивления, умножьте ее на обратную величину, что даст нам общее сопротивление RT параллельных резисторов.
Теперь мы знаем, что параллельные резисторы — это те, которые подключены между одними и теми же двумя точками. Однако параллельная резистивная цепь может иметь множество различных форм, кроме той, что показана выше, и ниже приведены некоторые примеры того, как резисторы могут быть соединены параллельно.
Различные цепи резисторов в параллельном соединении
Хотя пять резистивных цепей ниже кажутся разными, все они настроены как параллельные резисторы, поэтому применяются одни и те же требования и уравнения.
Резисторы в примерах параллельного расчета
Пример № 1
Взгляните на диаграмму ниже. Рассчитайте общее сопротивление RT резисторов в следующей параллельной сети.
Общее сопротивление RT между A и B рассчитывается следующим образом:
Подробнее: Понимание термистора
Любое количество отдельных сопротивлений, соединенных вместе в одной параллельной сети, может быть рассчитано с помощью этого обратного метода расчета.
Однако, если есть только два отдельных резистора, соединенных параллельно, мы можем определить общее или эквивалентное значение сопротивления, RT, используя гораздо более простую и быструю формулу, немного сократив обратные математические вычисления.
Ниже приведен значительно более быстрый способ вычисления двух резисторов параллельно, с равными или неравными значениями, методом произведения на сумму:
Резисторы в параллельном соединении Пример №2
Рассмотрим приведенную ниже схему, в которой просто используются два резистора в параллельной конфигурации.
Используя приведенную выше формулу для двух параллельно соединенных резисторов, общее сопротивление цепи R T можно рассчитать как:
При использовании параллельных резисторов следует помнить, что общее сопротивление цепи (RT) любых двух параллельно соединенных резисторов всегда МЕНЬШЕ, чем значение наименьшего резистора в комбинации.
Подробнее: Понимание варистора
Теперь давайте посмотрим на ток в цепи параллельного резистора, что приведет нас к последнему примеру.
Посмотрите видео ниже, чтобы узнать больше о параллельных резисторах:
Это видео расскажет вам о расчетах параллельных резисторов:
Подробнее: Конденсатор
Токи в цепи параллельного резистора
В параллельной резистивной цепи общий ток I T представляет собой сумму всех отдельных токов, протекающих во всех параллельных ветвях. Однако, поскольку значение сопротивления каждой ветви определяет величину тока, протекающего внутри этой ветви, величина тока, протекающего через каждую параллельную ветвь, может быть неодинаковой.
Несмотря на то, что параллельная комбинация имеет одинаковое напряжение на ней, сопротивления могут различаться, и, таким образом, ток, протекающий через каждый резистор, будет разным, как указано в Законе Ома.
Рассмотрим два резистора, соединенных последовательно выше. Ток, протекающий через каждый из параллельно включенных резисторов (IR1 и IR2), не всегда одинаков, поскольку определяется сопротивлением резистора. Мы знаем, однако, что ток, входящий в цепь в точке А, должен также выйти в точке В.
В соответствии с законами тока Кирхгофа, «общий ток, выходящий из цепи, равен общему току, входящему в цепь — никакой ток не теряется». В результате общий ток, протекающий в цепи, равен:
I T = I R1 + I R2
Используя закон Ома, ток, протекающий через каждый параллельный резистор в примере №2, можно рассчитать следующим образом:
Ток, протекающий через резистор R1, рассчитывается следующим образом:
I R1 = V S ÷ R 1 = 12V ÷ 22kΩ = 0.545 мА или 545 мкА
Ток, протекающий через резистор R2, рассчитывается как:
I R2 = V S ÷ R 2 = 12 В ÷ 47 кОм = 0,255 мА или 255 мкА
Итак, у нас есть полный ток I T , протекающий по цепи как:
I T = 0,545 мА + 0,255 мА = 0,8 мА или 800 мкА
Это также можно проверить напрямую, используя закон Ома, как:
I T = V S ÷ R T = 12 ÷ 15 кОм = 0.8 мА или 800 мкА (то же самое)
Подробнее: Понимание ультраконденсаторов
Ниже приводится уравнение для расчета полного тока, протекающего в параллельной цепи резисторов, который представляет собой сумму всех отдельных токов, объединенных вместе:
I всего = I 1 + I 2 + I 3 ….. + I n
Поскольку ток источника разделяется или разделяется между многочисленными параллельными ветвями, параллельные сети резисторов также можно рассматривать как «делители тока».В результате параллельная резисторная цепь с N резистивными цепями будет иметь N токовых путей при сохранении общего напряжения между собой. Параллельные резисторы также можно заменять, не влияя на общее сопротивление или ток в цепи.
Резисторы в параллельном соединении Пример №3
Рассчитайте токи отдельных ответвлений и общий ток, потребляемый от источника питания для следующего набора резисторов, соединенных параллельно, используя приведенную ниже диаграмму.
Мы можем использовать закон Ома для определения тока отдельной ветви в параллельной цепи, потому что напряжение питания распределяется между всеми резисторами.
Подробнее: Конденсаторы серии
Общий ток цепи, I T , протекающий через параллельную комбинацию резисторов, будет тогда:
Этот общий ток цепи, равный 5 амперам, также можно рассчитать и проверить, разделив напряжение питания VS на эквивалентное сопротивление цепи RT параллельной ветви.
Эквивалентное сопротивление цепи:
Тогда ток в цепи будет:
Подробнее: Знакомство с параллельными конденсаторами
Заключение
Говорят, что два или более резистора соединены параллельно, если оба их вывода подключены к каждому выводу другого резистора или резисторов.Напряжение на каждом резисторе в параллельной комбинации одинаково, но токи, протекающие через них, разные, как определяют их значения сопротивления и закон Ома. Тогда есть делители тока, которые представляют собой параллельные цепи. Это все для этой статьи, где обсуждаются схема, уравнение, расчеты, сети, ток и некоторые примеры параллельных резисторов.
Я надеюсь, что вы получили много полезного от чтения, если да, пожалуйста, поделитесь с другими учениками. Спасибо за чтение, увидимся!
резисторов в параллели — видео по физике от Brightstorm
Параллельные резисторы состоят из двух отдельных независимых цепей, поэтому, когда ток достигает резистора, ток может выбирать, через какой из них проходить.Большинство домов подключены параллельно, так что, в отличие от резисторов, соединенных последовательно, не все приборы в наших домах должны быть включены, чтобы работал один. Параллельное добавление резисторов снижает общее сопротивление. Наименьший ток будет проходить через самый большой резистор. Чтобы записать все резисторы как один резистор, используйте уравнение 1/(эффективное сопротивление) = 1/(резистор 1) + 1/(резистор 2). Эффективное сопротивление меньше, чем у любого из двух отдельных резисторов.
Итак, давайте поговорим о резисторных цепях, соединенных параллельно.Итак, во-первых, что означает параллель? Параллельность означает, что есть выбор, это означает, что в цепи есть ответвление, и может ли ток выбирать направление движения в том или ином направлении. Таким образом, параллельная сеть резисторов выглядит так. Поток приходит, и тогда у него есть выбор, он движется между теми же двумя точками, но есть 2 разных пути, по которым он может идти. Итак, в основном параллельные сети состоят из двух отдельных цепей, которые не зависят друг от друга. Итак, параллельная разность потенциалов одинакова, поэтому разность потенциалов между этими двумя точками одинакова, потому что это одни и те же две точки.Это были просто 2 разные ветки, которые прошли. Ток будет добавляться, поэтому здесь мы бы сказали, что i1 плюс i2 равно общему току i. i1 плюс i2 Хорошо, теперь, как всегда, мы хотели бы рассмотреть эту параллельную сеть как один эффективный резистор. Итак, я хочу, чтобы разность потенциалов была одинаковой, очевидно, что ток, протекающий здесь через мой эффективный резистор, будет равен i, и поэтому мы собираемся записать ток как дельта v над потенциалом r. разница деленная на сопротивление с нашим обязательным знаком минус.Таким образом, это будет минус разность потенциалов на r параллели, равна минус разность потенциалов на r1 минус разность потенциалов на r2.
Теперь разность потенциалов одинаковая, а это значит, что она уравновешивается со знаком минус, и это дает нам формулу для параллельного добавления резисторов. 1 над параллелью r равно 1 над r1 плюс 1 над r2. Таким образом, добавить резисторы параллельно сложнее, чем последовательно. Когда я добавляю их последовательно, я просто добавляю, когда я добавляю их параллельно, мы говорим, что обратные величины складываются.Таким образом, 1 на эффективное сопротивление равно 1 на r1 плюс 1 на r2. Теперь очень, очень заманчиво, но абсолютно неправильно пытаться перевернуть это с ног на голову и сказать, что просто означает, что r parallel равно r1 плюс r2, что неверно. Теперь мы можем думать о параллельных цепях как о попытке добраться из точки а в точку б. Если есть только одна дорога, то это будет раздражать, любой, кто хочет добраться из точки а в точку б, должен выбрать эту дорогу.
Если я добавлю параллельно, это будет похоже на строительство новой дороги, которая также ведет из точки а в точку б, и это на самом деле сократит трафик.Так что важно помнить о параллельном, и это сразу скажет нам, что вы не можете просто добавить. Когда я добавляю резисторы параллельно, я уменьшаю общее сопротивление, и теперь так, как будет работать эта параллельная сеть, у меня есть 5 ампер на входе, и у меня есть 2 резистора: 15 Ом и 10 Ом. Разность потенциалов одинакова, вы можете думать об этом как о точке b двух разных дорогах, представьте, что резисторы представляют собой светофоры. Чем больше сопротивление, тем больше светофоров на этом пути, а значит, и меньше машин будет туда ехать.Таким образом, наименьший ток будет проходить через самый большой резистор в параллельной комбинации. Итак, как мы собираемся определить, сколько тока проходит через 15 и сколько тока проходит через 10? На самом деле это очень просто, сначала мы добавим эти 2 резистора параллельно. Теперь помните, что сложение в параллельном немного сложнее, поэтому мы скажем, что 1 на r parallel равно 1 на 15 плюс 1 на 10.Так что это будет 10 плюс 15 на 150, хорошо. 10 плюс 15 — это 25 больше 150, и если мы сделаем это осторожно, мы можем отменить. Таким образом, это дает нам одну шестую часть. 1 над r parallel — это 1 над 6, так что это означает, что r parallel равно 6 в порядке. Обратите внимание, что наше эффективное сопротивление меньше, чем любое из двух сопротивлений, которые мы сложили вместе, меньше, чем любое из них в порядке. И в действии это число всегда будет лежать между этим, деленным на 2, и этим, деленным на 2, 5, 7 с половиной, 6, хорошо, это всегда будет работать так. Итак, теперь, когда у нас есть эффективное сопротивление, как мы собираемся определить ток через каждого из этих парней? Что ж, мы воспользуемся идеей, что разность потенциалов должна быть одинаковой при параллельном соединении всегда, всегда, всегда.Так какова разница потенциалов? Ну, разность потенциалов должна быть 5 умножить на 6, потому что эта сеть на самом деле всего лишь 6 Ом, 5 ампер. Итак, 5 умножить на 6 равно 30, значит, разность потенциалов должна быть равна 30.
Хорошо, чтобы получить разность потенциалов в 30 вольт на резисторе 15 Ом, 2 ампера, потому что 2 умножить на 15 равно 30, а как насчет здесь, я хочу 30 вольт через него, так сколько ампер мне нужно? 3 ампера и, конечно же, это следует из нашего предыдущего решения, что добавление тока 5 ампер идет на 2 и 1 ветвь, 3 на другую.Хорошо, еще один способ думать о параллельных цепях — это дома, так дома подключены, потому что я не хочу, чтобы мне было необходимо включать телевизор, чтобы заставить посудомоечную машину работать правильно, поэтому мы подключаем провода эти 2 цепи отдельно. Каждая розетка в вашем доме — это отдельная параллельная ветвь одной и той же цепи, и именно так мы заставляем жилье работать. Хорошо, это параллельные цепи резисторов.
17,5 Параллельные резисторы | Электрические цепи
17.5 параллельных резисторов (ESAFK)
Когда мы добавляем резисторы параллельно цепи:
-
Существует больше путей для протекания тока, что обеспечивает разделение тока по разным пути .
-
Напряжение такое же на резисторах. Напряжение на аккумуляторе в цепи равно напряжению на каждом из параллельных резисторов:
\[{V}_{\text{батарея}} = {V}_{1} = {V}_{2} = {V}_{3} \ldots\] -
Сопротивление протеканию тока уменьшается .Общее сопротивление, \({R}_{P}\), дано автор:
\[\frac{1}{{R}_{P}} = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots\ ]
При параллельном соединении резисторов начальная и конечная точки для всех резисторов одинаковы. Эти точки имеют одинаковую потенциальную энергию, поэтому разность потенциалов между ними одинакова независимо от того, что поставить между ними. Вы можете иметь один, два или несколько резисторов между двумя точками, разность потенциалов будет не изменить.Вы можете игнорировать любые компоненты, находящиеся между двумя точками в цепи, при вычислении разницы между двумя точками.
Посмотрите на следующие электрические схемы. Аккумулятор во всех случаях одинаков, меняется только количество резисторов. добавляются между точками, отмеченными черными точками. Если бы мы измерили разность потенциалов между две точки в этих схемах, мы получили бы один и тот же ответ для всех трех случаев.
Давайте посмотрим на два параллельных резистора более внимательно.Когда вы строите цепь, вы используете провода, и вы можете думаю, что измерение напряжения в разных местах проводов будет иметь значение. Это неправда. То разность потенциалов или измерение напряжения будут отличаться только в том случае, если вы измеряете другой набор компонентов. Все точки на проводах, между которыми нет компонентов цепи, дадут вам одинаковые измерения.
Все три измерения, показанные на рисунке ниже (т. е. A–B, C–D и E–F), дадут вам одинаковое напряжение.Между различными точками измерения слева нет компонентов, поэтому изменение потенциальной энергии. Точно то же самое относится к различным точкам справа. Когда вы измеряете разность потенциалов между точками слева и справа вы получите тот же ответ.
Рабочий пример 7: Напряжение I
Рассмотрим эту принципиальную схему:
Какое напряжение на резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батарейкой и одним резистором.Мы знаем напряжение на аккумуляторе. Мы хотим найти это напряжение на резисторе.
\[{V}_{\text{батарея}} = \text{2}\text{V}\]Применимые принципы
Мы знаем, что напряжение на аккумуляторе должно быть равно общему напряжению на всех остальных цепях. компоненты.
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]В цепи есть только один компонент — резистор.
\[{V}_{\text{всего}}={V}_{1}\]Это означает, что напряжение на батарее равно напряжению на резисторе.
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} = {V} _ {1} \\ {V}_{1} & = \text{2}\text{V} \конец{выравнивание*}Рабочий пример 8: Напряжение II
Рассмотрим эту схему:
Какое напряжение на неизвестном резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батарейкой и двумя резисторами.Мы знаем напряжение на аккумуляторе и одном из резисторы. Мы хотим найти это напряжение на резисторе.
\начать{выравнивать*} {V} _ {\ text {батарея}} & = \ text {2} \ text {V} \\ {V}_{B} & = \text{1}\text{V} \конец{выравнивание*}Применимые принципы
Мы знаем, что напряжение на аккумуляторе должно быть равно общему напряжению на всех остальных цепях. компоненты, которые находятся в последовательном соединении.
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]Общее напряжение в цепи равно сумме напряжений на отдельных резисторах
\[{V}_{\text{всего}} = {V}_{A} + {V}_{B}\]Использование соотношения между напряжением на батарее и полным напряжением на резисторах
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} \\\\ {V} _ {\ text {батарея}} & = {V} _ {1} + {V} _ {\ text {резистор}} \\ \text{2}\text{V} & = {V}_{1} + \text{1}\text{V} \\ {V}_{1} & = \text{1}\text{V} \конец{выравнивание*}Рабочий пример 9: Напряжение III
Рассмотрим принципиальную схему:
Какое напряжение на неизвестном резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батарейкой и тремя резисторами.Мы знаем напряжение на аккумуляторе и двух резисторы. Мы хотим найти это напряжение на неизвестном резисторе.
\начать{выравнивать*} {V} _ {\ text {батарея}} & = \ text {7} \ text {V} \\ {V} _ {\ text {известно}} & = {V} _ {A} + {V} _ {C} \\ & = \text{1}\text{V} + \text{4}\text{V} \конец{выравнивание*}Применимые принципы
Мы знаем, что напряжение на аккумуляторе должно быть равно общему напряжению на всех остальных цепях. компоненты, которые находятся в последовательном соединении.
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]Общее напряжение в цепи равно сумме напряжений на отдельных резисторах
\[{V} _ {\ text {всего}} = {V} _ {B} + {V} _ {\ text {известно}} \]Использование соотношения между напряжением на батарее и полным напряжением на резисторах
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} \\ {V} _ {\ text {батарея}} & = {V} _ {B} + {V} _ {\ text {известно}} \\ \text{7}\text{V} & = {V}_{B} + \text{5}\text{V} \\ {V}_{B} & = \text{2}\text{V} \конец{выравнивание*}Рабочий пример 10: Напряжение IV
Рассмотрим принципиальную схему:
Каково напряжение на параллельной комбинации резисторов в показанной цепи? Подсказка: остальное схема аналогична предыдущей задаче.
Быстрый ответ
Схема такая же, как и в предыдущем примере, и мы знаем, что разница напряжений между двумя точками в схема не зависит от того, что находится между ними, поэтому ответ такой же, как и выше \({V}_{\text{parallel}} = \text{2}\text{V}\).
Проверьте, что у вас есть и единицы измерения — подробный ответ
У нас есть схема с батареей и пятью резисторами (два последовательно и три параллельно).Мы знаем напряжение на аккумуляторе и двух резисторах. Мы хотим найти это напряжение на параллельном резисторы, \({V}_{\text{параллельные}}\).
\начать{выравнивать*} {V} _ {\ text {батарея}} = \ text {7} \ text {V} \\ {V}_{\text{известно}} = \text{1}\text{V} + \text{4}\text{V} \конец{выравнивание*}Применимые принципы
Мы знаем, что напряжение на аккумуляторе должно быть равно общему напряжению на всех остальных цепях. компоненты.
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]Напряжения складываются только алгебраически для компонентов, соединенных последовательно. Параллельные резисторы можно рассматривать как один компонент, который последовательно с другими компонентами, а затем напряжения могут быть добавлены.
\[{V} _ {\ text {всего}} = {V} _ {\ text {параллельно}} + {V} _ {\ text {известно}} \]Использование соотношения между напряжением на батарее и полным напряжением на резисторах
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} \\ {V} _ {\ text {батарея}} & = {V} _ {\ text {параллельно}} + {V} _ {\ text {известно}} \\ \text{7}\text{V} & = {V}_{\text{параллельно}} + \text{5}\text{V} \\ {V} _ {\ text {параллельно}} & = \ text {2} \ text {V} \конец{выравнивание*} temp textВ отличие от последовательного случая, когда мы добавляем резисторы параллельно, мы создаем еще путей вдоль какой ток может течь.Делая это, мы уменьшаем общее сопротивление цепи!
Взгляните на диаграмму ниже. Слева у нас такая же схема, как и в предыдущем разделе с аккумулятором и резистор. Амперметр показывает силу тока \(\text{1}\) \(\text{A}\). Справа мы добавили второй резистор параллельно первому резистору. Это увеличило количество путей (ответвлений), по которым может пройти заряд. по цепи — общее сопротивление уменьшилось.Вы видите, что ток в цепи вырос. Также обратите внимание, что ток в разных ветвях может быть разным.
Общее сопротивление ряда параллельно соединенных резисторов НЕ является суммой отдельных сопротивлений, поскольку общее сопротивление уменьшается с увеличением количества путей для тока. Общее сопротивление для параллельных резисторов дано автор:
\[\frac{1}{{R}_{P}}=\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}}+\ldots\ ]Давайте рассмотрим случай, когда у нас есть два резистора, включенных параллельно, и выясним, каким будет конечное сопротивление.Эта ситуация показана на диаграмме ниже:
Применяя формулу полного сопротивления имеем:
\начать{выравнивать*} \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots \\ & \text{Там всего два резистора} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} \\ & \text{Сложите дроби} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} \times \frac{{R}_{2}}{{R}_{2 }} + \frac{1}{{R}_{2}} \times \frac{{R}_{1}}{{R}_{1}} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2}}{{R}_{1}{R}_{2}} + \frac{{R} _{1}}{{R}_{1}{R}_{2}} \\ & \text{Переставить} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2} + {R}_{1}}{{R}_{1}{R}_{2} } \\ \frac{1}{{R}_{P}} & = \frac{{R}_{1} + {R}_{2}}{{R}_{1}{R}_{2} } \\ {R}_{P} & = \frac{{R}_{1}{R}_{2}}{{R}_{1} + {R}_{2}} \конец{выравнивание*}Теперь мы знаем, что для любых двух резисторов, включенных параллельно,
\[{R}_{P} = \frac{\text{произведение сопротивлений}}{\text{сумма сопротивлений}} = \frac{{R}_{1}{R}_{2}}{ {Р}_{1} + {Р}_{2}}\]Делители тока
Цель
Проверьте, что происходит с током и напряжением в последовательных цепях при добавлении дополнительных резисторов.
Аппарат
-
Аккумулятор
-
Вольтметр
-
Амперметр
-
Провода
-
Резисторы
Метод
-
Подключите каждую цепь, показанную ниже
-
Измерьте напряжение на каждом резисторе в цепи.
-
Измерьте ток до и после каждого резистора в цепи, а также до и после параллельного резистора. ветви.
Результаты и выводы
-
Сравните токи через отдельные резисторы друг с другом.
-
Сравните сумму токов через отдельные резисторы с током перед параллельным ветви.
-
Сравните различные измерения напряжения на параллельных резисторах.
Рабочий пример 11: Параллельные резисторы I
Цепь содержит два резистора, включенных параллельно. Резисторы имеют значения сопротивления \(\text{15}\) \(\text{Ω}\) и \(\text{7}\) \(\text{Ω}\).
Какое общее сопротивление в цепи?
Проанализируйте вопрос
Нам говорят, что резисторы в цепи находятся в параллельной цепи и что нам нужно рассчитать общую сопротивление.Значения двух резисторов указаны в правильных единицах, Ом.
Применять соответствующие принципы
Было показано, что общее сопротивление резисторов, включенных параллельно, представляет собой произведение сопротивлений, деленное на сумма. Мы можем использовать
\[{R}_{P} = \frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}\]У нас есть только два резистора и теперь мы сопротивления. {2}} {\ text {22} \ text { Ω}} \\ & = \text{4,77}\text{ Ом} \конец{выравнивание*}
Укажите окончательный результат
Суммарное сопротивление резисторов, включенных параллельно, равно \(\text{4,77}\) \(\text{Ом}\)
Рабочий пример 12: Параллельные резисторы II
Мы добавляем третий параллельный резистор к конфигурации (настройке) в предыдущем примере.Дополнительный резистор имеет сопротивление \(\text{3}\) \(\text{Ом}\).
Какое общее сопротивление в цепи?
Проанализируйте вопрос
Нам говорят, что резисторы в цепи находятся в параллельной цепи и что нам нужно рассчитать общую сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.
Применять соответствующие принципы
Общее сопротивление параллельно включенных резисторов составляет
. \[\frac{1}{{R}_{P}} = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots\ ]У нас есть три резистора и теперь мы сопротивления.В данном случае имеем:
\начать{выравнивать*} \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots \\ & \text{три резистора} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \frac{1 }{{R}_{3}} \\ & \text{сложить дроби} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} \times \frac{{R}_{2}{R}_{3}} {{R}_{2}{R}_{3}} + \frac{1}{{R}_{2}} \times \frac{{R}_{1}{R}_{3}}{{R}_{1}{R}_{3}} + \frac{1}{{R}_{3} } \times \frac{{R}_{1}{R}_{2}}{{R}_{1}{R}_{2}} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2}{R}_{3}}{{R}_{1}{R}_{2}{ Р}_{3}} + \frac{{R}_{1}{R}_{3}}{{R}_{1}{R}_{2}{R}_{3}} + \frac{{R}_{ 1}{R}_{2}}{{R}_{1}{R}_{2}{R}_{3}} \\ & \текст {переставить} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2}{R}_{3} + {R}_{1}{R}_{3} + { Р}_{2}{Р}_{3}}{{Р}_{1}{Р}_{2}{Р}_{3}} \\ {R}_{P} & = \frac{{R}_{1}{R}_{2}{R}_{3}}{{R}_{2}{R}_{3} + {R}_{1}{R}_{3} + {R}_{2}{R}_{3}} \\ {R}_{P} & = \frac{\left(\text{15}\text{Ω} \right)\left(\text{7}\text{Ω} \right)\left(\text{3}\text{ Ω} \right)}{\left(\text{7}\text{ Ω} \right)\left(\text{3}\text{ Ω} \right) + \left(\text{15}\text{ Ω} \right)\left(\text{3}\text{ Ω}\right) + \left(\text{7}\text{ Ω} \right)\left(\text{15}\text{ Ω}\right)} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {21 {\ Omega} ^ {2} + 45 {\ Omega} ^ {2} + 105 {\ Omega} ^ { 2}} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {171 {\ Omega} ^ {2}} \\ {R}_{P} & = \text{1,84}\text{ Ом} \конец{выравнивание*}Укажите окончательный результат
Суммарное сопротивление резисторов, включенных параллельно, равно \(\text{1,84}\) \(\text{Ом}\)
При расчете сопротивления для сложных конфигураций резисторов можно начать с любой комбинации двух резисторы (последовательно или параллельно) и рассчитайте их общее сопротивление.Затем вы можете заменить их одним резистор, который имеет общее сопротивление, которое вы рассчитали. Теперь используйте этот новый резистор в сочетании с любым другим резистор и повторяйте процесс, пока не останется только один резистор. В приведенном выше примере мы могли бы просто иметь использовали ответ из первого примера параллельно с новым резистором, и мы получили бы тот же ответ.
Рабочий пример 13: Параллельные резисторы III
Мы добавляем третий параллельный резистор к первой параллельной рабочей конфигурации (настройка).Дополнительный резистор имеет сопротивление \(\text{3}\) \(\text{Ом}\)
Какое общее сопротивление в цепи?
Проанализируйте вопрос
Нам говорят, что резисторы в цепи находятся в параллельной цепи и что нам нужно рассчитать общую сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.
Применять соответствующие принципы
Мы можем поменять местами резисторы без изменения схемы:
Мы уже подсчитали, что общее сопротивление двух резисторов в пунктирной рамке равно \(\text{4,77}\) \(\текст{Ω}\). {2}} {\ text {11,77} \ Omega} \\ & = \text{1,84}\text{ Ом} \конец{выравнивание*}
Укажите окончательный результат
Общее сопротивление резисторов, включенных параллельно, равно \(\text{1,84}\) \(\text{Ом}\).Это тоже самое результат, как если бы мы добавили все три резистора одновременно.
Сопротивление
Упражнение 17.1 из учебникаКак называется единица сопротивления и какое ее обозначение?
Решение пока недоступно
Объясните, что происходит с общим сопротивлением цепи при последовательном включении резисторов?
Решение пока недоступно
Объясните, что происходит с общим сопротивлением цепи при параллельном добавлении резисторов?
Решение пока недоступно
Почему разряжаются батареи?
Решение пока недоступно
Как рассчитать эквивалентное сопротивление в параллельной цепи | Физика
Как рассчитать эквивалентное сопротивление в параллельной цепи
Шаг 1 : Укажите номинал каждого резистора в цепи.
Шаг 2 : Рассчитайте эквивалентное сопротивление, используя уравнение {eq}\dfrac{1}{R_{eq}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + … + \dfrac{1}{R_N} {/экв}.
Что такое эквивалентное сопротивление в параллельной цепи?
Эквивалентное сопротивление : Эквивалентное сопротивление цепи — это общее электрическое сопротивление, вызванное всеми резисторами в цепи, действующими вместе на источник напряжения.
Эквивалентное сопротивление в параллельной цепи : Когда каждый резистор в цепи независимо подключен к источнику напряжения, говорят, что резисторы соединены параллельно.Поскольку более независимые пути для движения электронов в конечном итоге приводят к тому, что большее количество электронов проходит через цепь, параллельное подключение дополнительных резисторов приводит к уменьшению эквивалентного сопротивления цепи. Уравнение для расчета эквивалентного сопротивления набора из N резисторов, соединенных параллельно:
$$\dfrac{1}{R_{eq}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + … + \dfrac{1}{R_N} $$
Следующие две задачи демонстрируют, как рассчитать эквивалентное сопротивление в параллельной цепи.
Примеры расчета параллельного сопротивления в параллельной цепи.
Пример 1
Два резистора по 150 Ом соединены параллельно. Чему равно сопротивление этих двух резисторов?
Шаг 1 : Укажите номинал каждого резистора в цепи.
В этой цепи всего два резистора, каждый с одинаковым номиналом.
- {экв} R_1 = R_2 = 150\ \rm{\Omega} {/экв}
Шаг 2 : Рассчитайте эквивалентное сопротивление, используя уравнение {eq}\dfrac{1}{R_{eq}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + .{-1} = 75\ \rm{\Omega} $$
Эквивалентное сопротивление двух резисторов по 150 Ом составляет 75 Ом.
Пример 2
Каково эквивалентное сопротивление 4 резисторов номиналами 5 Ом, 12 Ом, 25 Ом и 50 Ом?
Шаг 1 : Укажите номинал каждого резистора в цепи.
Значения резисторов:
- {экв}R_1 = 5\\Омега {/экв}
- {экв}R_2 = 12\\Омега {/экв}
- {экв}R_3 = 25\\Омега {/экв}
- {экв}R_4 = 50\ \Омега {/экв}
Шаг 2 : Рассчитайте эквивалентное сопротивление, используя уравнение {eq}\dfrac{1}{R_{eq}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + .{-1} \примерно 2,9\\Омега $$
Четыре резистора имеют эквивалентное сопротивление 2,9 Ом.
Получите доступ к тысячам практических вопросов и пояснений!Пример: параллельные резисторы — Nexus Wiki
Понимание ситуации
В этом примере мы рассмотрим простейший пример параллельной цепи: одна батарея и два резистора, соединенные параллельно.
Два элемента цепи расположены параллельно означает, что они соединены таким образом, что любой потенциал на вершине одного из них является также потенциалом на вершине другого; точно так же основания двух элементов также имеют одинаковый потенциал. ( такое же изменение напряжения )
Посмотрим, как это работает, решив задачу на определение падений потенциала и токов в паре параллельно соединенных резисторов.
Демонстрация примера задачи
Два резистора сопротивлением $R_1$ и $R_2$ подключены друг к другу и к батарее, как показано на схеме(ах) справа.Если на клеммах батареи сохраняется разность напряжений $V_0$, найдите ток и падение напряжения на каждом резисторе. Предположим, что батарея и резисторы идеальны, а соединительные провода не имеют сопротивления.
Решение этой проблемы
Мы нарисовали диаграмму в двух формах: полуреалистичная слева и более стандартная символическая форма справа.
Чтобы ответить на вопросы задачи, у нас есть пять инструментов: принципы Кирхгофа, эвристика нулевого сопротивления и наше определение батареи.
- Общее количество тока, втекающего в любой объем электрической сети, равно количеству вытекающего. (К1)
- Падение потенциала на любом одиночном резисторе пропорционально току через резистор. Константой пропорциональности является сопротивление: $ΔV = IR$. (К2)
- При обходе любого контура в электрической сети потенциал должен вернуться к одному и тому же значению (сумма падений = сумма подъемов). (К3)
- Элемент (например,г., провод) с сопротивлением 0 находится под однородным потенциалом: падения потенциала нет, так как $R = 0$. (эвристика)
- Батарея представляет собой устройство, поддерживающее фиксированную разность потенциалов на своих клеммах. (Определение батареи)
Чтобы подойти к этой проблеме, давайте сначала поймем, что происходит («расскажем историю проблемы»). Батарея поддерживает разность потенциалов на своих клеммах в соответствии с принципом 5, поэтому она как бы пытается вытолкнуть ток из своего верхнего предела.Как только он соединен в петлю, он может создать поток — электрический ток. В устойчивом состоянии (что занимает около наносекунды для установления в такой схеме, которая поместилась бы на столе). Когда ток $I$ бежит по цепи, когда он проходит по проводам, с потенциалом ничего не происходит (он не меняется) по принципу 4. Когда ток достигает узла, соединяющего два резистора, он должен разделиться. Принцип 1 говорит нам, как это сделать. Часть будет проходить через один из резисторов, часть через другой.Мы еще не знаем, сколько, но можно ожидать, что через небольшое сопротивление пройдет больше («следуйте по пути наименьшего сопротивления»). Когда ток проходит через резисторы, он воссоединяется и проходит обратно через батарею. Для токов, протекающих через каждый резистор, существует падение, величина которого регулируется принципом 2.
Давайте разыграем это подробно с точки зрения символов. Назовите ток через батарею $I$. Достигнув перекрестка, он распадается. Мы не знаем как, но давайте дадим им имена.Пусть ток в $R_1$ равен $I_1$, а ток в $R_2$ равен $I_2$. Принцип 1 говорит нам, что
$$I= I_1 + I_2$$
, и, следовательно, когда они снова соединятся в нижней части резисторов, мы снова получим $I$ .
Полезным вторым шагом часто является «картирование потенциала». У нас есть только одна батарея, поэтому мы можем выбрать нижний предел батареи как 0 нашего потенциала.
Поскольку батарея поддерживает фиксированную разность потенциалов на своих клеммах, мы знаем верхний предел.Затем мы можем следовать за проводами в обоих направлениях, используя нашу эвристику для определения потенциала (поскольку в проводе без сопротивления нет никаких изменений). Когда мы доберемся до резистора, будет изменение, когда мы пересечем его.
В нашем примере с током было легко справиться, так как была только одна петля. Здесь это уже не так, поскольку текущий разделяется. Мы увидим, что в этом случае с напряжением действительно легче иметь дело. Если мы проследим за напряжениями вдоль проводов без сопротивления сверху и снизу батареи, мы увидим, что мы знаем напряжения везде.Нет необходимости вводить новое название для неизвестного напряжения.
Что еще мы знаем? Мы использовали принципы 1, 4 и 5 при построении наших диаграмм, и принцип 3 выполняется автоматически. (Вот что принцип 4 делает для нас в сети с одним контуром. Он не всегда будет делать это для нас.) Ясно, что мы должны удовлетворять принципу 2: закону Ома. Поскольку это верно ТОЛЬКО для одного резистора, мы должны применить его один раз для каждого резистора. Это дает следующие два уравнения:
$$V_0 = I_1R_1$$
$$V_0 = I_2R_2$$
В этом случае, поскольку мы знаем $V_0$ и $R_1$ и $R_2$, эти уравнения дают нам токи в резисторах.Поскольку они суммируются, чтобы дать нам $I$ в батарее, мы знаем все токи и все падения напряжения.
$$I = I_1 + I_2 = \frac{V_0}{R_1} + \frac{V_0}{R_2}$$
Осмысление результата
В общем случае решить проблему недостаточно; нам нужно посмотреть на наш ответ и убедиться, что он имеет смысл. Здесь это особенно важно, поскольку параллельное подключение резисторов будет компонентом более сложных проблем, которые мы будем анализировать. Давайте отступим и посмотрим, что произошло.{эффективный}_{параллельный}} = \frac{1}{R_1} + \frac{1}{R_2}.

