Сопротивление при параллельном подключении. Как рассчитать параллельное и последовательное соединение резисторов: формулы и примеры — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как рассчитать общее сопротивление при параллельном соединении резисторов. Какая формула используется для последовательного соединения. Чем отличается смешанное соединение проводников. Как правильно рассчитать параметры электрической цепи.

Содержание

Основные виды соединений резисторов в электрической цепи

В электротехнике выделяют три основных способа соединения резисторов и других элементов в электрической цепи:

Последовательное соединение
Параллельное соединение
Смешанное соединение

Каждый вид соединения имеет свои особенности и формулы для расчета общего сопротивления цепи. Рассмотрим их подробнее.

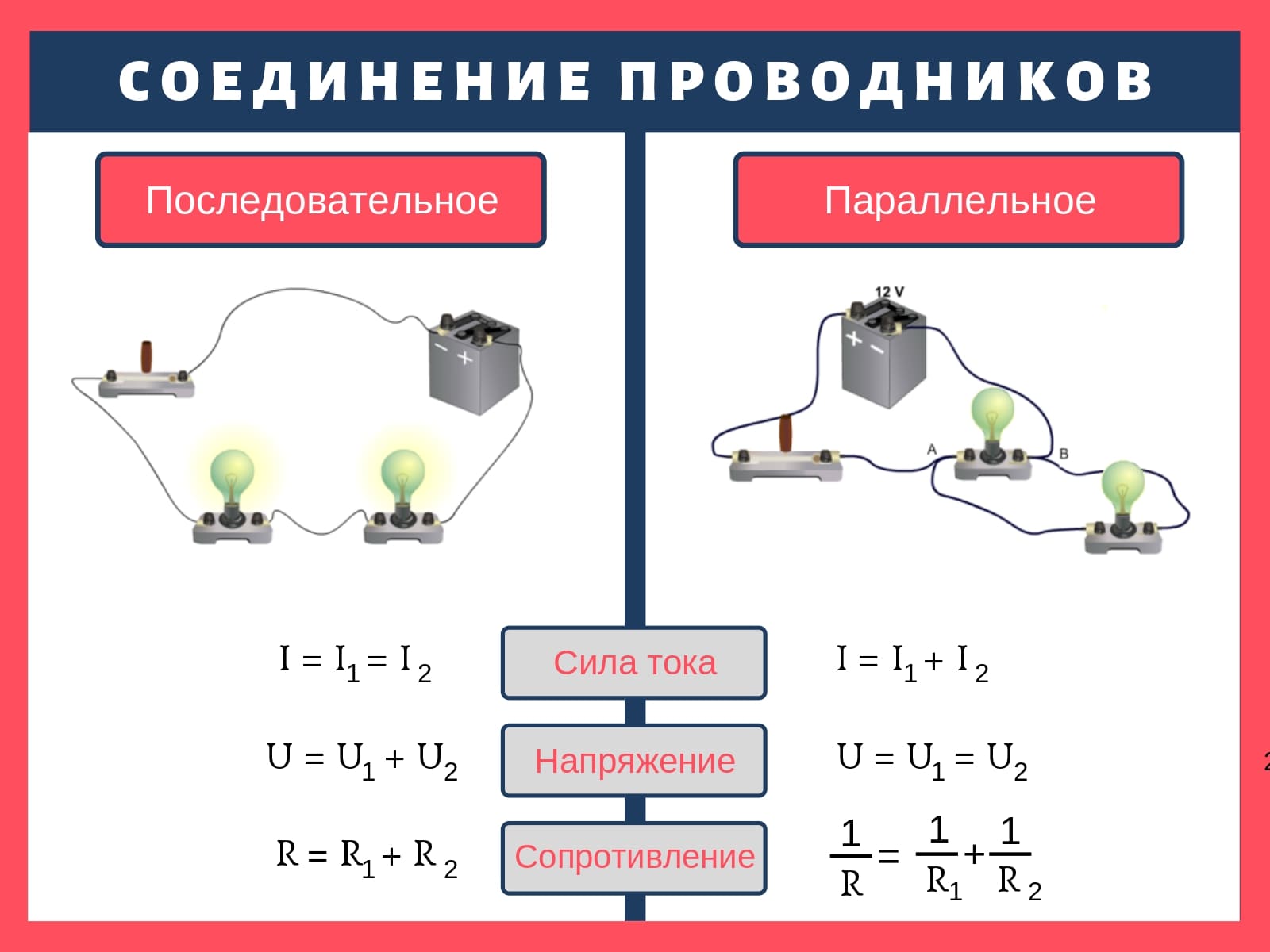
Последовательное соединение резисторов

При последовательном соединении резисторы включаются друг за другом, образуя единую цепочку. Схема такого соединения выглядит следующим образом:

[Схема последовательного соединения резисторов]

Основные свойства последовательного соединения:

Через все резисторы протекает одинаковый ток
Общее напряжение распределяется между резисторами

Общее сопротивление цепи увеличивается

Формула для расчета общего сопротивления при последовательном соединении:

R = R1 + R2 + R3 + … + Rn

Где R — общее сопротивление, R1, R2 и т.д. — сопротивления отдельных резисторов.

Параллельное соединение резисторов

При параллельном соединении все резисторы подключаются к одним и тем же двум точкам цепи. Схема выглядит так:

[Схема параллельного соединения резисторов]

Особенности параллельного соединения:

На всех резисторах одинаковое напряжение
Общий ток делится между параллельными ветвями
Общее сопротивление цепи уменьшается

Формула для расчета общего сопротивления при параллельном соединении:

1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

Где R — общее сопротивление, R1, R2 и т.д. — сопротивления отдельных резисторов.

Как рассчитать параллельное соединение двух резисторов?

Для частного случая параллельного соединения двух резисторов можно использовать упрощенную формулу:

R = (R1 * R2) / (R1 + R2)

Эта формула позволяет быстро рассчитать общее сопротивление для двух параллельно включенных резисторов.

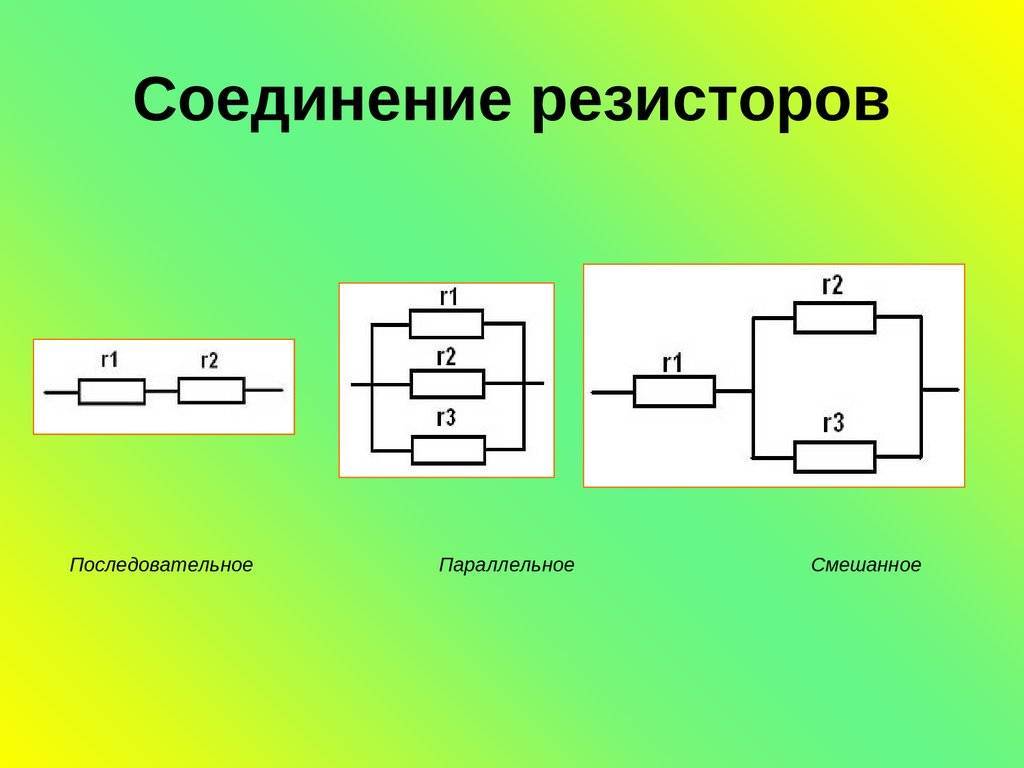
Смешанное соединение резисторов

На практике часто встречаются схемы, где присутствует как последовательное, так и параллельное соединение резисторов. Такое соединение называется смешанным или комбинированным.

Для расчета общего сопротивления при смешанном соединении необходимо:

Разбить схему на участки с однотипным соединением
Рассчитать сопротивление для каждого участка
Объединить полученные результаты

Пример схемы со смешанным соединением:

[Схема смешанного соединения резисторов]

Правила расчета электрических цепей

При анализе и расчете электрических цепей важно соблюдать следующие правила:

Определить тип соединения на каждом участке цепи
Применять соответствующие формулы для расчета сопротивлений
Учитывать распределение токов и напряжений
Проверять полученные результаты

Правильный расчет параметров цепи позволяет подобрать оптимальные номиналы компонентов и обеспечить корректную работу устройства.

Практические примеры расчетов

Рассмотрим несколько практических примеров расчета сопротивлений для разных видов соединений.

Пример 1. Последовательное соединение

Дано: три резистора с сопротивлениями 100 Ом, 220 Ом и 330 Ом соединены последовательно.

Решение:

R = R1 + R2 + R3 = 100 + 220 + 330 = 650 Ом

Ответ: общее сопротивление цепи равно 650 Ом.

Пример 2. Параллельное соединение

Дано: два резистора 100 Ом и 200 Ом соединены параллельно.

Решение:

Используем формулу для двух резисторов: R = (R1 * R2) / (R1 + R2) = (100 * 200) / (100 + 200) = 20000 / 300 ≈ 66,7 Ом

Ответ: общее сопротивление цепи приблизительно равно 66,7 Ом.

Применение формул на практике

Умение рассчитывать параметры электрических цепей с различными соединениями резисторов необходимо во многих областях:

Проектирование электронных устройств
Ремонт и обслуживание электрооборудования
Разработка систем электроснабжения
Создание измерительных приборов

Правильное применение формул позволяет грамотно подбирать компоненты, оптимизировать работу схем и предотвращать аварийные ситуации.

Заключение

Расчет параметров электрических цепей с разными видами соединений резисторов — важный навык для специалистов в области электротехники и электроники. Знание основных формул и умение их применять позволяет решать широкий спектр практических задач.

При работе со сложными схемами рекомендуется использовать специальные программы для моделирования и расчета электрических цепей. Это позволит быстро и точно определить все необходимые параметры.

5. Параллельное соединение проводников — ф8 т3.2 Закон Ома для участка цепи

Мысли бегут, скачут, прыгают, постоянно сменяя друг друга, а время параллельно утекает.

Параллельное соединение проводников

При параллельном соединении проводников все элементы цепи подключаются к одной и той же паре точек, можно назвать их А и В. К этой же паре точек подключают источник тока. То есть получается, что все элементы подключены к одинаковому напряжению между А и В. В то же время ток как бы разделяется на все нагрузки в зависимости от сопротивления каждой из них.Параллельное соединение можно сравнить с течением реки, на пути которой возникла небольшая возвышенность. Вода в таком случае огибает возвышенность с двух сторон, а потом вновь сливается в один поток. Получается островок посреди реки. Так вот параллельное соединение – это два отдельных русла вокруг острова. А точки А и В – это места, где разъединяется и вновь соединяется общее русло реки.

Напряжение тока в каждой отдельной ветви будет равно общему напряжению в цепи. Общий ток цепи будет складываться из токов всех отдельных ветвей. А вот общее сопротивление цепи при параллельном соединении будет меньше сопротивления тока на каждой из ветвей. Это происходит потому, что общее сечение проводника между точками А и В как бы увеличивается за счет увеличения числа параллельно подключенных нагрузок. Поэтому общее сопротивление уменьшается.

где I — сила тока, U- напряжение,

R – сопротивление, 1,2,…,n – номера элементов, включенных в цепь.

Огромным плюсом параллельного соединения является то, что при выключении одного из элементов, цепь продолжает функционировать дальше. Все остальные элементы продолжают работать.

Минусом является то, что все приборы должны быть рассчитаны на одно и то же напряжение. Именно параллельным образом устанавливают розетки сети 220 В в квартирах. Такое подключение позволяет включать

различные приборы в сеть совершенно независимо друг от друга, и при выходе их строя одного из них, это не влияет на работу остальных.

Интерактивный тест Параллельное соединение проводников…

Updating…

1 Параллельное соединение.ppt

(1368k)

Ольга Федотова,

5 янв. 2016 г., 08:39

1 формулы параллельного соединения.jpg

(32k)

Ольга Федотова,

5 янв. 2016 г., 08:39

1_1 параллельное соединение.swf

(115k)

Ольга Федотова,

5 янв. 2016 г., 08:39

1_2 конспект.gif

(29k)

Ольга Федотова,

5 янв. 2016 г., 08:39

2 практика.swf

(13k)

Ольга Федотова,

5 янв. 2016 г., 08:39

Ольга Федотова,

5 янв. 2016 г., 08:39

2 сила тока при параллельном соединении.swf

(241k)

Ольга Федотова,

5 янв. 2016 г., 08:39

2 формулы.jpg

(51k)

Ольга Федотова,

5 янв. 2016 г., 09:32

Ольга Федотова,

5 янв. 2016 г., 08:40

3 формула 2 8.png

(8k)

Ольга Федотова,

5 янв. 2016 г., 08:40

3 формула 2 сопротивления.png

(3k)

Ольга Федотова,

5 янв. 2016 г., 08:40

3 формула 3 сопротивления.jpg

(15k)

Ольга Федотова,

5 янв. 2016 г., 08:41

3 формула сопротивление.png

(1k)

Ольга Федотова,

5 янв. 2016 г., 08:41

5 Тест к уроку Параллельное соединение проводников.ppt

(101k)

Ольга Федотова,

5 янв. 2016 г., 08:41

Как считается параллельное сопротивление. Сопротивление при параллельном соединении: формула расчета

Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.

С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.

Виды соединений

Резистор — пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

Постоянные.
Переменные.

Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует

три вида соединения проводников:

Последовательное.
Параллельное.
Смешанное.

Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.

Последовательное соединение проводников

В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.

Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.

Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.

В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.

Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.

Примеры параллельного соединения проводников:

Освещение.
Розетки в квартире.
Производственное оборудование.

Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.

Смешанное соединение проводников

Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.

Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.

Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.

В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление R общ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление R общ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление R общ

Цепь разбивают на участки с только пареллельным или только последовательным соединением.
Вычисляют общее сопротивление для каждого отдельного участка.
Вычисляют общее сопротивление для всей цепи смешанного соединения.

Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:

Если резисторы соединяются последоватеьно — складывать.
Если резисторы соединяются параллельно — использовать условное обозначение «||».
Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

Определение параллельного соединения

Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.

Графическое обозначение схемы параллельного соеднинения

На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).

В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.

Формула для расчета параллельного соединения сопротивлений

При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:

Формулы для частного рассчета вытекают из основной формулы.

Формула для расчета параллельного соединения емкостей (конденсаторов)

При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:

Формула для расчета параллельного соединения индуктивностей

При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:

Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.

Пример свертывания параллельного сопротивления

Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.

Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.

Ток при параллельном соединении

При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.

Напряжение при параллельном соединении

При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.

Применение параллельного соединения

1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.

2. Делитель токов.

На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при и некоторые другие технические вопросы.

Сопротивление проводника

Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.

Для ведения электротехнических расчётов применяется удельное сопротивление — ρ Ом·м/мм 2 . Все металлы — хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник — серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.

При расчёте сопротивления используется известная из школьного курса физики формула:

R = ρ · l/S, S — площадь сечения; l — длина.

Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.

и нагрев проводника

Для практических расчётов режимов работы проводников применяется понятие плотности тока — δ А/мм 2 , она вычисляется по формуле:

δ = I/S, I — ток, S — сечение.

Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.

Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.

Правилами регламентируется производить расчёт проводников на нагрев.

Способы соединения проводников

Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой — последовательное соединение.

На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .

Второй способ более сложный — параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.

Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.

Третий способ соединения наиболее сложный — смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.

Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.

R2,3,4 = R2,3 · R4/(R2,3 + R4).

Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.

Виды проводников

В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.

Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.

Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.

Расчёт проводов на нагрев

Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника или кабеля).

На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.

Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.

Расчёт проводников на потерю напряжения

При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.

Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.

R л = ρ · 2L/S,

Здесь S — сечение провода линии, мм 2 .

Какие есть способы соединения приемников электрической энергии

Приемник электрической энергии — устройство, в котором происходит преобразование электрической энергии в другой вид энергии для ее использования.

При одновременном включении нескольких приемников электроэнергии в одну и ту же сеть, эти приемники можно легко рассматривать просто как элементы единой цепи, каждый из которых обладает собственным сопротивлением.

В ряде случаев такой подход оказывается вполне приемлемым: лампы накаливания, электрические обогреватели и т. п. — можно воспринимать как резисторы. То есть приборы можно заменить на их сопротивления, и легко произвести расчет параметров цепи.

Способ соединения приемников электроэнергии может быть одним из следующих: последовательный, параллельный или смешанный тип соединения.

Последовательное соединение

Когда несколько приемников (резисторов) соединяются в последовательную цепь, то есть второй вывод первого присоединяется к первому выводу второго, второй вывод второго соединяется с первым выводом третьего, второй вывод третьего с первым выводом четвертого и т. д., то при подключении такой цепи к источнику питания, через все элементы цепи потечет ток I одной и той же величины. Данную мысль поясняет приведенный рисунок.

Заменив приборы на их сопротивления, рисунок преобразуем в схему, тогда сопротивления с R1 по R4, соединенные последовательно, примут каждый на себя определенные напряжения, которые в сумме дадут значение ЭДС на зажимах источника питания. Для простоты здесь и далее изобразим источник в виде гальванического элемента.

Выразив падения напряжений через ток и через сопротивления, получим выражение для эквивалентного сопротивления последовательной цепи приемников: общее сопротивление последовательного соединения резисторов всегда равно алгебраической сумме всех сопротивлений, составляющих эту цепь. А поскольку напряжения на каждом из участков цепи можно найти из закона Ома (U = I*R, U1 = I*R1, U2 = I*R2 и т. д.) и E = U, то для нашей схемы получаем:

Напряжение на клеммах источника питания равно сумме падений напряжений на каждом из соединенных последовательно приемников, составляющих цепь.

Так как ток через всю цепь течет одного и того же значения, то справедливым будет утверждение, что напряжения на последовательно соединенных приемниках (резисторах) соотносятся между собой пропорционально сопротивлениям. И чем выше будет сопротивление, тем выше окажется и напряжение, приложенное к приемнику.

Для последовательного соединения резисторов в количестве n штук, обладающих одинаковыми сопротивлениями Rk, эквивалентное общее сопротивление цепи целиком будет в n раз больше каждого из этих сопротивлений: R = n*Rk. Соответственно и напряжения, приложенные к каждому из резисторов цепи будут между собой равны, и окажутся в n раз меньше напряжения, приложенного ко всей цепи: Uk = U/n.

Для последовательного соединения приемников электроэнергии характерны следующие свойства: если изменить сопротивление одного из приемников цепи, то напряжения на остальных приемниках цепи при этом изменятся; при обрыве одного из приемников ток прекратится во всей цепи, во всех остальных приемниках.

В силу этих особенностей последовательное соединение встречается редко, и используют его лишь там, где напряжение сети выше номинального напряжения приемников, в отсутствие альтернатив.

К примеру напряжением 220 вольт можно запитать две последовательно соединенные лампы равной мощности, каждая из которых рассчитана на напряжение 110 вольт. Ежели данные лампы при одинаковом номинальном напряжении питания будут обладать различной номинальной мощностью, то одна из них будет перегружена и скорее всего мгновенно перегорит.

Параллельное соединение

Параллельное соединение приемников предполагает включение каждого из них между парой точек электрической цепи с тем, чтобы они образовывали параллельные ветви, каждая из которых питается напряжением источника. Для наглядности опять заменим приемники их электрическими сопротивлениями, чтобы получить схему, по которой удобно вести расчет параметров.

Как уже было сказано, в случае параллельного соединения каждый из резисторов испытывает действие одного и того же напряжения. И в соответствии с законом Ома имеем: I1=U/R1, I2=U/R2, I3=U/R3.

Здесь I – ток источника. Первый закон Кирхгофа для данной цепи позволяет записать выражение для тока в неразветвленной ее части: I = I1+I2+I3.

Отсюда общее сопротивление для параллельного соединения между собой элементов цепи можно найти из формулы:

Величина обратная сопротивлению называется проводимостью G, и формулу для проводимости цепи, состоящей из нескольких параллельно соединенных элементов, также можно записать: G = G1 + G2 + G3. Проводимость цепи в случае параллельного соединения образующих ее резисторов равна алгебраической сумме проводимостей этих резисторов. Следовательно, при добавлении в цепь параллельных приемников (резисторов) суммарное сопротивление цепи уменьшится, а суммарная проводимость соответственно возрастет.

Токи в цепи состоящей из параллельно соединенных приемников, распределяются между ними прямо пропорционально их проводимостям, то есть обратно пропорционально их сопротивлениям. Здесь можно привести аналогию из гидравлики, где поток воды распределяется по трубам в соответствии с их сечениями, тогда большее сечение аналогично меньшему сопротивлению, то есть большей проводимости.

Если цепь состоит из нескольких (n) одинаковых резисторов, соединенных параллельно, то общее сопротивление цепи будет ниже в n раз, чем сопротивление одного из резисторов, а ток через каждый из резисторов будет меньше в n раз, чем общий ток: R = R1/n; I1 = I/n.

Цепь, состоящая из параллельно соединенных приемников, подключенная к источнику питания, отличается тем, что каждый из приемников находится под напряжением источника питания.

Для идеального источника электроэнергии справедливо утверждение: при подключении или отключении параллельно источнику резисторов, токи в остальных подключенных резисторах не изменятся, то есть при выходе из строя одного или нескольких приемников параллельной цепи, остальные будут продолжать работать в прежнем режиме.

В силу данных особенностей параллельное соединение обладает значительным преимуществом перед последовательным, и по этой причине именно соединение параллельное наиболее распространено в электрических сетях. Например, все электроприборы в наших домах предназначены для параллельного подключения к бытовой сети, и если отключить один, то остальным это ничуть не навредит.

Сравнение последовательных и параллельных цепей

Смешанное соединение

Под смешанным соединением приемников понимают такое их соединение, когда часть или несколько из них соединены между собой последовательно, а другая часть или несколько — параллельно. При этом вся цепь может быть образована из разных соединений таких частей между собой. Для примера рассмотрим схему:

Три последовательно соединенных резистора подключены к источнику питания, параллельно одному из них подключены еще два, а третий — параллельно всей цепи. Для нахождения полного сопротивления цепи идут путем последовательных преобразований: сложную цепь последовательно приводят к простому виду, последовательно вычисляя сопротивление каждого звена, и так находят общее эквивалентное сопротивление.

Для нашего примера. Сначала находят общее сопротивление двух резисторов R4 и R5, соединенных последовательно, затем сопротивление параллельного соединения их с R2, потом прибавляют к полученному значению R1 и R3, и после — вычисляют значение сопротивления всей цепи, включая параллельную ветвь R6.

Различные способы соединения приемников электроэнергии применяют на практике для различных целей, чтобы решать конкретные поставленные задачи. Например, смешанное соединение можно встретить в схемах плавного заряда электролитических конденсаторов в мощных блоках питания, где нагрузка (конденсаторы после диодного моста) сначала получает питание последовательно через резистор, затем резистор шунтируется контактами реле, и нагрузка оказывается подключенной к диодному мосту параллельно.

Ранее ЭлектроВести писали, что львовянка Оксана Денис подключила свою квартиру к солнечным панелям и ветроэнергетическим установкам.

По материалам: electrik.info.

Cила тока при параллельном соединении

Параллельное соединение элементов в электрической цепи

Прежде чем приступать к формированию электропроводки в любом типе помещения, разработке электрической цепи для других топов объектов, важно изучить основные способы соединений элементов, используемые на практике.

Наибольшее распространение получили следующие варианты:

параллельное;
последовательное;
смешанное соединение.

Если выбран вариант последовательного соединения, это означает, что все, используемые в цепи элементы, связываются друг с другом электрическими проводами последовательно. В результате, участок цепи, на котором устанавливается такой способ монтажа, не будет иметь в своей конструкции узлов.

Если соединение выполнено параллельно, то здесь объединение элементов в цепи будет выполнено при помощи двух узлов, при этом связь со всеми другими узлами будет отсутствовать. Важно разобраться, какая сила тока при параллельном соединении элементов будет в цепи.

Смешанный тип соединения может использоваться в сложных цепях, состоящих из множества различных элементов, многофункционального узла, выполняющего, как правило, широкий набор операций.

Сила тока в параллельном проводнике

Если в цепи использовано последовательное соединение отдельных ее элементов, то сила тока здесь на всех участках, во всех проводниках будет оставаться одинаковой. Рассчитать напряжение можно, используя простое правило – необходимо сложить все напряжения, получаемые на концах каждого из проводников и получим искомый результат.

Совсем по-другому проявляется сила тока в параллельном проводнике.

При любой нагрузке в электроцепи будет возникать определенное сопротивление. Оно, естественно, будет препятствовать прохождению электрического тока без каких-либо потерь. В целом, ток так и движется – постепенно, от источника по проложенным заранее проводникам к нагруженным элементам. Чтобы обеспечить легкое прохождение тока по проводникам, важно, чтобы этот проводник мог легко и просто отдавать электроны, т.е. – обладать хорошей проводимостью.

Большая часть современных цепей использует медные проводники, а обязательным элементом также являются приемники энергии. Каждый такой приемник создает определенную нагрузку и имеет то или иное электрическое сопротивление. От приведенных выше параметров, в конечном итоге, зависит сила тока при параллельном соединении проводников.

Особенности цепи, в которой используется параллельное соединение

Как уже отмечалось, в данном варианте монтажа электроцепи, все ее элементы, проводники, соединяются друг с другом параллельным методом. Соответственно, все начала проводников соединяются при помощи медных (преимущественно) проводников в один пучок. Аналогичным способом в одну точку также собираются и концы проводников. Как же рассчитывается сила тока в цепи при параллельном соединении? Лучше всего разобраться в данном вопросе поможет достаточно простой и понятный пример.

Нарисуем на листе бумаги такой вид соединения, который у специалистов называется «разветвленным» и обеспечим нахождение в каждой отдельной ветви по одному резистору (сопротивлению). Далее проследим, каким образом будет вести себя электрический ток, протекающий по цепи. Достигнув места разветвления, ток разделится на каждый резистор, установленный далее по определенной ветке линии. Следовательно, реальный ток в цепи будет равен величина, состоящей из суммы токов на всех сопротивлениях (с учетом количества разветвлений). Как считается сила тока разобрались, а вот напряжение при параллельном сопротивлении на всех элементах в сети будет оставаться одинаковым.

Примечательно, что все установленные на различных ветвях цепи резисторы можно заменить одним таким резистором, эквивалентным по сопротивлении сумме замещаемых элементов. Рассчитать, какова сила тока при параллельном соединении резисторов поможет важнейший закон Ома!

Область применения

А можно ли на практике использовать данные сведения? Есть ли от них реальная польза?

Люстра Arte Lamp Kenny A9514PL-5-1WG

Прежде всего, рассмотрим организацию соединения проводников и сопротивлений в домашних условиях. Как правило, такие схемы собираются доля обеспечения работы многорожковых люстр, светильников с некоторым количеством ламп освещения. Если использовать здесь последовательную схему, то все лампочки будут включаться одновременно. При использовании параллельного метода можно выводить необходимое количество светильников на один выключатель и включать одну, две и более лампочек в зависимости от ранее принятого решения, с учетом вопросов экономичности, целесообразности и, конечно же, дизайна.

Подведем итог

Наконец, все, используемые в квартире, загородном доме бытовые приборы и устройства подключены к сети напряжением 220В параллельно. Это подключение происходит с помощью распределительного щитка. Зная, чему равна сила тока при параллельном соединении, можно уверенно отметить, данный способ позволит эффективно управлять используемой электротехникой, приборами и предметами освещения в квартире.

Дайте определение параллельного сопротивления проводников

Сопротивление проводников. Параллельное и последовательное соединение проводников.

Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.

Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как

U — разность электрических потенциалов (напряжение) на концах проводника;

I — сила тока, протекающего между концами проводника под действием разности потенциалов.

При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:

Последовательное соединение проводников

По закону Ома, напряжения U₁ и U₂ на проводниках равны

Общее напряжение U на обоих проводниках равно сумме напряжений U₁ и U₂:

где R – электрическое сопротивление всей цепи. Отсюда следует:

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

При параллельном соединении (рис. 1.9.2) напряжения U₁ и U₂ на обоих проводниках одинаковы:

Сумма токов I₁ + I₂, протекающих по обоим проводникам, равна току в неразветвленной цепи:

Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I₁Δt + I₂Δt. Следовательно,I = I₁ + I₂.

Параллельное соединение проводников

Записывая на основании закона Ома

где R – электрическое сопротивление всей цепи, получим

Этот результат справедлив для любого числа параллельно включенных проводников.

Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.

Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом)

Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.

Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников

Определение параллельного соединения

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.

Графическое обозначение схемы параллельного соеднинения

Формула для расчета параллельного соединения сопротивлений

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

Формулы для частного рассчета вытекают из основной формулы.

Формула для расчета параллельного соединения емкостей (конденсаторов)

Формула для расчета параллельного соединения индуктивностей

Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.

Пример свертывания параллельного сопротивления

Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к источнику ЭДС E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.

Рассчитать эквивалентное сопротивлений R14 можно по формуле для двух сопротивлений.

Ток при параллельном соединении

Напряжение при параллельном соединении

Применение параллельного соединения

Проводники в электрических цепях могут соединяться последовательно и параллельно.

При последовательном соединении проводников (рис. 2.3) сила тока во всех проводниках одинакова:

; .

Общее напряжение U на обоих проводниках равно сумме напряжений U₁ и U₂:

где R – электрическое сопротивление всей цепи.

Отсюда следует:

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников. Этот результат справедлив для любого числа последовательно соединенных проводников.

Рис. 2.3. Последовательное соединение двух сопротивлений

При параллельном соединении (рис. 2.4) напряжения U₁ и U₂ на обоих проводниках одинаковы:

Сумма токов I₁ + I₂, протекающих по обоим проводникам, равна току в неразветвленной цепи:

Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, в узел A за время Δt втекает заряд IΔt, а вытекает их узла за то же время заряд I₁Δt + I₂Δt. Следовательно, .

Рис. 2.4. Параллельное соединение двух сопротивлений

Запишем на основании закона Ома

; ; ,

где R – электрическое сопротивление всей цепи, тогда получим

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников. Этот результат справедлив для любого числа параллельно включенных проводников.

Общее сопротивление n участков при их параллельном и последовательном соединении соответственно равны:

; .

Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 2.5 приведен пример такой сложной цепи и указана последовательность вычислений.

Рис. 2.5. Расчет сопротивления сложной цепи.

Сопротивления всех проводников указаны в Ом

Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 2.6 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.

Рис. 2.6. Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10096 — | 7530 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Расчет напряжения при параллельном соединении. Преимущества и недостатки параллельного и последовательного соединения лампочек

Последовательное и параллельное соединение проводников это основные виды соединения проводников, встречающиеся на практике. Так как электрические цепи, как правило, не состоят из однородных проводников одинакового сечения. Как же найти сопротивление цепи, если известны сопротивления ее отдельных частей.

Рассмотрим два типичных случая. Первый из них это когда два или боле проводников обладающих сопротивлением включены последовательно. Последовательно значит, что конец первого проводника подключен к началу второго и так далее. При таком включении проводников сила тока в каждом из них будет одинакова. А вот напряжение на каждом из них будет различным.

Рисунок 1 — последовательное соединение проводников

Падение напряжения на сопротивлениях можно определить исходя из закона Ома.

Формула 1 — Падение напряжения на сопротивлении

Сумма этих напряжений будет равна полному напряжению, приложенному к цепи. Напряжение на проводниках будет распределяться пропорционально их сопротивлению. То есть можно записать.

Формула 2 — соотношение между сопротивлением и напряжением

Суммарное же сопротивление цепи будет равно сумме всех сопротивлений включенных последовательно.

Формула 3 — вычисление суммарного сопротивления при параллельном включении

Второй случай, когда сопротивления в цепи включены параллельно друг другу. То есть в цепи есть два узла и все проводники обладающие сопротивлением подключаются к этим узлам. В такой цепи токи во всех ветвях в общем случае не равны друг другу. Но сумма всех токов в цепи после разветвления будет равна току до разветвления.

Рисунок 2 — Параллельное соединение проводников

Формула 4 — соотношение между токами в параллельных ветвях

Сила тока в каждой из разветвлённой цепи также подчиняется закону Ома. Напряжение на всех проводниках будет одинаково. Но сила тока будет разлучаться. В цепи, состоящей из параллельно соединенных проводников, токи распределяются пропорционально сопротивлениям.

Формула 5 — Распределение токов в параллельных ветвях

Чтобы найти полное сопротивление цепи в этом случае необходимо сложить величины обратные сопротивлениям то есть проводимости.

Формула 6 — Сопротивление параллельно включённых проводников

Также существует упрощённая формула для частного случая когда параллельно включены два одинаковых сопротивления.

1. Находят эквивалентное сопротивление участков цепи с параллельным соединением резисторов. Рисунок 2. Последовательное соединение резисторов. Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов.

Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Этот результат справедлив для любого числа параллельно включенных проводников.

На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений. Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения.

При последовательном соединении проводников сила тока во всех проводниках одинакова. При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов.

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов. При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно.

Цепь разбивают на участки с только пареллельным или только последовательным соединением. Вычисляют общее сопротивление для каждого отдельного участка. Вычисляют общее сопротивление для всей цепи смешанного соединения. Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Если резисторы соединяются последоватеьно — складывать.

То есть при последовательном соединении резисторы подключатся друг за другом. На рисунке 4 показан простейший пример смешанного соединения резисторов. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.4. Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.

В результате вы научитесь с нуля не тольно разрабатывать собственные устройства, но и сопрягать с ними различную переферию! Узел — точка разветвления цепи, в которой соединяются не менее трёх проводников. Последовательное соединение резисторов применяется для увеличения сопротивления.

Напряжение при параллельном соединении

Как видно, вычислить сопротивление двух параллельных резисторов значительно удобнее. Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением.

Общее сопротивление Rобщ

Такое соединение сопротивлений называется последовательным. Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.

Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.

Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Точно так же для каждой ветви I1 = U1 / R1, I2 = U2 / R2, где I1 и I2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.

Это значит, что общее сопротивление цепи всегда будет ниже любого параллельно включенного резистора. 2. Если эти участки включают последовательно соединенные резисторы, то сначала вычисляют их сопротивление. Применяя закон Ома для участка цепи, можно доказать, что полное сопротивление при последовательном соединении равно сумме сопротивлений отдельных проводников.

Содержание:

Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов — параллельное подключение и последовательное. Также возможно и смешанное, то есть последовательно параллельное соединение. Все зависит от назначения компонента и выполняемой им функции. А значит, и резисторы не избежали этих правил. Последовательное и параллельное сопротивление резисторов это по сути то же самое, что и параллельное и последовательное подключение источников света. В параллельной цепи схема подключения подразумевает вход на все резисторы из одной точки, а выход из другой. Попробуем разобраться, каким образом выполняется последовательное соединение, а каким — параллельное. И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение. Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения. Начать следует с определений и правил.

Способы подключения и их особенности

Виды соединения потребителей или элементов играют очень важную роль, ведь именно от этого зависят характеристики всей схемы, параметры отдельных цепей и тому подобное. Для начала попробуем разобраться с последовательным подключением элементов к схеме.

Последовательное соединение

Последовательное подключение — это такое соединение, где резисторы (равно, как и другие потребители или элементы схем) подключаются друг за другом, при этом выход предыдущего подключается на вход следующего. Подобный вид коммутации элементов дает показатель, равный сумме сопротивлений этих элементов схемы. То есть если r1 = 4 Ом, а r2 = 6 Ом, то при подключении их в последовательную цепь, общее сопротивление составит 10 Ом. Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом — это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений. При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.

Совершенно по другим формулам и правилам производится расчет общего сопротивления резисторов при параллельном подключении, вот на нем имеет смысл остановиться поподробнее.

Параллельное соединение

Параллельным называется соединение, при котором все входы резисторов объединены в одной точке, а все выходы — во второй. Здесь главное понять, что общее сопротивление при подобном подключении будет всегда ниже, чем тот же параметр резистора, имеющего наименьшее.

Имеет смысл разобрать подобную особенность на примере, тогда понять это будет намного проще. Существует два резистора по 16 Ом, но при этом для правильного монтажа схемы требуется лишь 8 Ом. В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления. Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.

Попробуем еще один пример. Параллельно соединены 2 резистора, с сопротивлением 4 и 10 Ом. Тогда общее будет равно 1/4 + 1/10, что будет равным 1:(0.25 + 0.1) = 1:0.35 = 2.85 Ом. Как видим, хотя резисторы и имели значительное сопротивление, при подключении их параллельнообщий показатель стал намного ниже.

Так же можно рассчитать общее сопротивление четырех параллельно подключенных резисторов, с номиналом 4, 5, 2 и 10 Ом. Вычисления, согласно формуле, будут такими: 1/Rобщ = 1/4+1/5+1/2+1/10, что будет равным 1:(0.25+0.2+0.5+0.1)=1/1.5 = 0.7 Ом.

Что же касается тока, протекающего через параллельно соединенные резисторы, то здесь необходимо обратиться к закону Кирхгофа, который гласит «сила тока при параллельном соединении, выходящего из цепи, равна току, входящему в цепь». А потому здесь законы физики решают все за нас. При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе. При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.

Последовательно-параллельное соединение

Последовательно-параллельное соединение — это когда схема последовательного соединения содержит в себе параллельные сопротивления. В таком случае общее последовательное сопротивление будет равно сумме отдельно взятых общих параллельных. Метод вычислений одинаковый в соответствующих случаях.

Подведем итог

Подводя итог всему вышеизложенному можно сделать следующие выводы:

При последовательном соединении резисторов не требуется особых формул для расчета общего сопротивления. Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.
При параллельном соединении резисторов, общее сопротивление высчитывается по формуле 1/Rобщ = 1/R1+1/R2…+Rn.
Эквивалентное сопротивление при параллельном соединении всегда меньше минимального подобного показателя одного из резисторов, входящих в схему.
Ток, равно как и напряжение в параллельном соединении остается неизменным, то есть напряжение при последовательном соединении равно как на входе, так и на выходе.
Последовательно-параллельное соединение при подсчетах подчиняется тем же законам.

В любом случае, каким бы ни было подключение, необходимо четко рассчитывать все показатели элементов, ведь параметры имеют очень важную роль при монтаже схем. И если ошибиться в них, то либо схема не будет работать, либо ее элементы просто сгорят от перегрузки. По сути, это правило применимо к любым схемам, даже в электромонтаже. Ведь провод по сечению подбирают также исходя из мощности и напряжения. А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники. А потому — внимательность и скрупулезность в расчетах — залог правильной работы схемы.

Содержание:

Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.

Свойства и технические характеристики резисторов

Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для — последовательное.

На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав , нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: + 20, + 10, + 5, + 2, + 1% и так далее до величины + 0,001%.

Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.

Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.

Мощность при последовательном соединение

При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, сила тока будет составлять I = U/R = 100/390 = 0,256 A.На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.

P 1 = I 2 x R 1 = 0,256 2 x 200 = 13,11 Вт;
P 2 = I 2 x R 2 = 0,256 2 x 100 = 6,55 Вт;
P 3 = I 2 x R 3 = 0,256 2 x 51 = 3,34 Вт;
P 4 = I 2 x R 4 = 0,256 2 x 39 = 2,55 Вт.

Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.

Мощность при паралл ельном соединение

При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы — с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.

Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:

1/R = 1/R 1 +1/R 2 +1/R 3 +1/R 4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
Расчет силы тока для каждого резистора выполняется по формулам: I 1 = U/R 1 = 100/200 = 0,5A; I 2 = U/R 2 = 100/100 = 1A; I 3 = U/R 3 = 100/51 = 1,96A; I 4 = U/R 4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.

Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P 1 = U 2 /R 1 = 100 2 /200 = 50 Вт; P 2 = U 2 /R 2 = 100 2 /100 = 100 Вт; P 3 = U 2 /R 3 = 100 2 /51 = 195,9 Вт; P 4 = U 2 /R 4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р 1 +Р 2 +Р 3 +Р 4 = 50+100+195,9+256,4 = 602,3 Вт.

Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.

Всем доброго времени суток. В прошлой статье я рассмотрел , применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса , называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье. Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и .

Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее. На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии

Пример последовательного подключения приемников энергии.

В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления

Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.

Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями

где R – эквивалентное последовательное сопротивление.

Применение последовательного соединения

Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр

Делитель напряжения (слева) и потенциометр (справа).

В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.

Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.

Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии. Пример такого соединения показан на рисунке ниже

Пример параллельного соединения приемников энергии.

Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви

Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений

Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.

Смешанное соединение приемников энергии

Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии

Пример смешанного соединения приемников энергии.

В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид

В результате получили цепь из двух последовательных приемников энергии R 12 R 345 эквивалентное сопротивление и ток, протекающий через них, составит

Тогда падение напряжения по участкам составит

Тогда токи, протекающие через каждый приемник энергии, составят

Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.

Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением

где ∑ — обозначает алгебраическую сумму.

Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа

Изображение первого закона Кирхгофа.

На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид

Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.

Как говорилось выше, второй закон Кирхгофа определяет соотношение между ЭДС и напряжениями в замкнутом контуре и звучит следующим образом: алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах этого контура. Второй закон Кирхгофа определяется следующим выражением

В качестве примера рассмотрим ниже следующую схему, содержащую некоторый контур

Схема, иллюстрирующая второй закон Кирхгофа.

Для начала необходимо определится с направлением обхода контура. В принципе можно выбрать как по ходу часовой стрелки, так и против хода часовой стрелки. Я выберу первый вариант, то есть элементы будут считаться в следующем порядке E1R1R2R3E2, таким образом, уравнение по второму закону Кирхгофа будет иметь следующий вид

Второй закон Кирхгофа применяется не только к цепям постоянного тока, но и к цепям переменного тока и к нелинейным цепям.
В следующей статье я рассмотрю основные способы расчёта сложных цепей с использованием закона Ома и законов Кирхгофа.

Теория это хорошо, но без практического применения это просто слова.

Последовательное и параллельное соединение проводников

Теория последовательного соединения

Если подсоединить электрическим проводом полюса источника тока, в проводнике начнется движение электронов по электрической цепи: плюс-минус источника по электрическому проводнику. Если разорвать провод в нескольких местах и подсоединить в разрыв нагрузку, например, две или три электрические лампочки, то подобное соединение будет называться последовательным. Последовательное соединение – это когда нагрузка включена в один провод, без ответвлений, выход от одной нагрузки является началом для другой. При такой комбинации напряжение источника будет равняться его сумме на нагрузке. Сила тока распределиться по источникам нагрузки одинаково.
Это отличительная черта данной комбинации.

Рис.1. последовательное соединение нагрузки

Практическое использование

Последовательно проводники соединяются если есть необходимость подключить несколько потребителей одним устройством включения. Классический пример включения гирлянды лампочек выключателем или кнопкой звонка и световой сигнализации. При замыкании контактов включением клавиши выключателя ток одновременно появляется на всех подключенных на этом проводе токоприемников.
Последовательное соединение является слишком прямолинейным и не может соответствовать всем необходимым потребностям. Включение освещения в жилых помещениях может иметь несколько ступеней, от подсветки до яркого верхнего света, раздельное включение в комнатах.
Включение различных нагрузок в производственных помещениях требует смешанного либо параллельной схемы соединения. Схема последовательного соединения на Рис. 1

Параллельное подключение

Этот вид соединения характерен тем, что вся нагрузка соединяется параллельно друг другу, т.е. начало и окончания проводников всех нагрузок соединены в одну точку. Электроны, двигающиеся по проводнику, доходя до общего соединение разделяются по количеству ветвей. Проводя параллель с водопроводными трубами, то можно сказать, что от одной общей трубы отходят несколько ответвлений. Количество воды, попадающие в них зависит от силы потока в основной трубе и диаметра отводов, в нашем случае, количество электронов в проводники от мощности, подключенной к ним нагрузки. Схема подключения на Рис. 2

Практическое применение параллельного соединения

В параллель нагрузка соединяется при необходимости раздельного подключения нескольких потребителей в одном помещении. При бытовой сети 220 В – это могут быть: люстра, телевизор, холодильник, электроплита и многие другие бытовые приборы.
При таком подключение напряжение 220В не делится на количество потребителей , а подключается к источнику напряжения каждый отдельно со своим выключателем.

Рис.2. Параллельное подключение нагрузки

Для понимания проходящих действий с током и напряжением в проводниках при подсоединении нагрузки все процессы обобщены в единые правила, которые получили статус закона и называются Законом последовательного и параллельного соединения проводников.
Одним из основных законов участка цепи является закон Ома. Закон ома для параллельного и последовательного соединения проводников выражает зависимость тока от сопротивления на участке и его напряжения: I=U/R – чем больше сопротивление, тем меньше ток. закон ома параллельное и последовательное подключения проводников.

При последовательном подключении общее значение тока распределяется по каждому участку: I = I1 = I2;

напряжение распределяться по количеству элементов нагрузки: U = U1 + U2 = I(R1 + R2) = IR;
Сопротивление элементов нагрузки в цепи будет просто складываться в общую сумму: R = R1 + R2.
Параллельное подключение проводников характеризует цепь, в которой напряжение равно на всех нагрузках: U = U1 = U2.
Количество тока равно сумме потребляемого тока в каждой нагрузки цепи с параллельного расположения I = I1 + I2.
Изучение последовательного и параллельного соединения проводников и понимание законов распределения токов дает необходимую основу для дальнейшего изучения электротехники и применения этих знаний на практике.

Для закрепления материала и лучшего понимания последующего рекомендуется посмотреть видеоурок последовательное и параллельное соединение проводников

Применение изученного материла на практике

Рис. 3 схемы последовательного и параллельного соединения проводников

Первое знакомство с практическим применением этих правил может состояться уже на лабораторной работе по изучению последовательного и параллельного соединения проводников.

Сбор схема состоит из нескольких этапов:
Первый этап – подготовка элементов к сборке схемы, (источник питания, соединительные провода, резьбовые зажимы клемм, источник нагрузки – лампочки).

Второй этап – изучения схемы. На этом этапе нужно чётко представить схему коммутации проводов.

Третий этап: сбор схемы, последовательность подключения для этого – сначала подсоединяются провода к клемме рубильника, затем от клеммы рубильника провод соединяется с минусом 1 нагрузки, затем подсоединяется клеммы плюс 2 нагрузки.
После окончания сборки нагрузки производится подключение источника питания: провод от рубильника подсоединяется к клемме + батареи и – к свободной клемме 2 нагрузки.

Правильность сборки проверяется преподавателем, после чего производится включение рубильника, при этом должны обе лампочки загореться равномерным свечением. Это говорит о том, что напряжение и ток на лампочках одинаковый, схема последовательного подключения собрана правильно.

Подключение источников нагрузки при параллельном подключении: для этого нагрузка соединяется двумя проводами плюс с плюсом минус с минусом, получается своеобразный квадрат. Далее все как в первом варианте. При этом если электрические параметры лампочек разные, то светиться они должны и разной яркостью.

Формулы последовательного и параллельного соединения в проводниках

При последовательном подключении:

1. Сила тока в них одинакова.

I = I1 = I2

2. Разность потенциалов каждого участка складывается в общую сумму

U = Uab + Ubc.

3. Сопротивление участка равно сумме сопротивлений каждого проводника.

R = R1 + R2.

4. Напряжение на участке пропорционально его сопротивлению.

U1/U2=R1/R2.

При параллельном подключении:

1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвленной части цепи.

U = U1 = U2;

2. Сила тока каждого участка цепи равна суммарного значения тока каждой ветке участка

I = I1 + I2;

3. Общее сопротивление участка равно сумме величин, обратных сопротивлениям ветвей

1/R = 1/R1 + /1R2 + . . . + 1/Rn.

Из этого вытекает другая формула: R = (R1 х R2) / (R1 + R2).

4. Сила тока на участке пропорциональна его сопротивлению

I1/I2=R2/R1.

Как это будет выглядеть в лабораторной работе?
Лабораторная работа :
Практическое подтверждение законов последовательного и параллельного подключения проводников.

Последовательная комбинация сопротивлений

Цель: экспериментально подтвердить теоретические выводы, закрепленные в законах.
Оборудование: батарея источника тока, переменный реостат, два резистора, рубильник включения, кабеля коммутации, которые подключены по схеме на рисунке.

Рис . 4

Результаты измерений и вычислений сводятся таблицы последовательного и параллельной комбинации подключения сопротивлений

Таблица вычислений для последовательной комбинации резисторов

Измерено						Вычислено
U1, В	U2, В	U, В	I1, A	I2, A	R1, Ом	R2, Ом	R, Ом	U1/U2, В	R1/R2, Ом
2	2,5	4,5	1	1	1	2	4,5	4,5/2,5 =1,8	4,5/2,5 =1,8

Параллельное включение

Рис. 5

Таблица вычислений для параллельного включения резисторов

Измерено						Вычислено
U1, В	U2, В	U, В	I1, A	I2, A	I, A	R1, Ом	R2, Ом	R, Ом	I1/I2, В	R1/R2, Ом
2	2	2	1	0,8	1,8	2	2,5	1,11	1,25	1,25

Смешанное включение резисторов

Рис.6. Смешанное комбинации проводников.

Кроме параллельного и последовательного существует смешанное соединение проводников.

Такое сочетание, понятно из названия – является совокупностью любых комбинаций в состав которой могут входить единичные резисторы, а также их отдельные составные части составляя сложную схему, чем больше деталей, тем сложнее схема.
Чтобы рассчитать смешанное сочетание необходимо хорошо знать и применять формулы расчета сопротивления при последовательном и параллельном соединении проводников научастке цепи, ничего особенного в расчетах нет, нужно только правильно увидеть и расчленить существующие схемы на элементарные участки.
Рассмотрим пример расчета смешанной комбинации проводников (рис. 6)

Пусть U = 14 В, R1 = 2 Ом, R2 = 3 Ом, R3 = 3 Ом, R4 = 5 Ом, R5 = 2 Ом.

Необходимо найти величину тока цепи и каждого резистора.
Показанная на рисунке цепь состоит из двух последовательно соединённых участков ab и bc. Сопротивление участка ab: Rab = (R1 х R2) / (R1 + R2) = (2 · 3) / (2 + 3) = 1,2 Ом.
На участке b.c. четко видно параллельное сочетание: два последовательно включённых резистора R3 и R4 подключены параллельно к резистору R5.
Тогда: Rbc = (R3 + R4) х R5 / (R3 + R4) + R5 = (3 + 5) х 2 / (3 + 5) + 2 = 1,6 Ом.
Сопротивление цепи: R = Rab + Rbc = 1,2 + 1,6 = 2,8 Ом.
Теперь находим силу тока в цепи: I = U R = 14 х 2,8 = 5 A.
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
Uab = I х Rab = 5 · 1,2 = 6 B; Ubc = I х Rbc = 5 · 1,6 = 8 B.

Теперь сложив полученное данные получим напряжение цепи 14 В, именно столько должно быть на последовательном участке.
Оба резистора R1 и R2 находятся под напряжением Uab, поэтому:

I1 = Uab / R1 = 6/ 2 = 3 A;

I2 = Uab R2 = 6 / 3 = 2 A.

(В сумме имеем 5 А, как и должно быть при параллельном сочетании.)
Сила тока в резисторах R3 и R4 одинакова, так как они расположены последовательно:
I3 = I4 = Ubc / (R3 + R4) = 8/ (3 + 5) = 1 A. Стало быть, через резистор R5 течёт ток

I5 = I − I3 = 5 − 1 = 4 A

В таком ключе на последовательное и параллельное соединение проводников происходит решение большинства задач.

Более четкое понимание материала и представление о физических процессах, происходящих в цепях постоянного тока при последовательном и параллельном соединении проводников дает презентация, выполненная в программе Power Point.
Выполнение слайдов в программе рекомендуется выполнять, разделив лист на 2 части. В левой части половины листа схемы электрических цепей, во второй – пояснительная часть с примерами расчёта.

Основным материалом для подготовки презентации должны стать учебники физики, в которых есть разделы для изучения последовательного и параллельного соединения проводников – это учебные пособия за 8 и 10 классы, в которых подробно расписана теория и примеры решения задач.

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:

+7(499)403 39 91

Доставка подшипников по РФ и зарубежью.

Каталог подшипников на сайте themechanic.ru

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
+7 (499) 113 36 18
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте

Внимание покупателей подшипников

Сопротивление параллельно — Ток, разность потенциалов, мощность и сопротивление — Higher Physics Revision

Ток

При параллельном подключении резисторов ток питания равен сумме токов, протекающих через каждый резистор. Другими словами, токи в ветвях параллельной цепи складываются с током питания.

\ [I_ {S} = I_ {1} + I_ {2} + I_ {3} \]

Это соотношение выражает закон сохранения заряда. Все электроны, вышедшие из источника, должны вернуться в источник, и каждый электрон может пройти только через одну параллельную ветвь.

Разность потенциалов

Когда резисторы подключены параллельно, они имеют одинаковую разность потенциалов. Другими словами, любые параллельные компоненты имеют одинаковую разность потенциалов.

Итак, в приведенной выше схеме \ (V_ {S} = V_ {1} = V_ {2} = V_ {3} \)

Сопротивление

Для схемы, приведенной выше, формула для определения общего сопротивления резисторов в параллель — это \ (\ frac {1} {{{R_P}}} = \ frac {1} {{{R_1}}} + \ frac {1} {{{R_2}}} + \ frac {1} {{ {R_3}}} \)

Вопрос

Устанавливается следующая сеть резисторов.

Рассчитайте полное сопротивление сети.

Показать ответ

\ [R_ {1} = 12 \ Omega \]

\ [R_ {2} = 18 \ Omega \]

\ [R_ {3} = 6 \ Omega \]

\ [\ frac {1} {{{R_T}}} = \ frac {1} {{{R_1}}} + \ frac {1} {{{R_2}}} + \ frac {1} {{{R_3]) }}} \]

\ [\ frac {1} {{{R_T}}} = \ frac {1} {{{12}}} + \ frac {1} {{{18}}} + \ frac {1} {{{6}}} \]

\ [\ frac {1} {{{R_T}}} = \ frac {3} {{{36}}} + \ frac {2} {{{ 36}}} + \ frac {6} {{{36}}} \]

\ [\ frac {1} {{{R_T}}} = \ frac {11} {{{36}}} \]

\ [11R_ {T} = 36 \]

\ [R_ {T} = \ frac {{36}} {{11}} \]

\ [R_ {T} = 3.27 \ Omega \]

Общее сопротивление составляет \ (3.27 \ Omega \)

Изучение основ последовательного и параллельного сопротивления [Краткое руководство]

Привет, надеюсь, у тебя хорошая жизнь. В этом посте я поделюсь с вами своими знаниями о последовательном и параллельном сопротивлении. Я поделюсь самыми основными моментами, которым я бы хотел, чтобы кто-нибудь научил меня, когда я изучал основы электроники.

При разработке электронной схемы резистор, вероятно, является наиболее важным и часто встречающимся компонентом.Почти все портативные схемы содержат очень сложные комбинации резисторов.

Следовательно, очень полезно иметь набор правил для определения эквивалентных сопротивлений для некоторых общих и общих схем резистивных элементов. И оказалось, что такие простые правила представляют собой параллельные последовательные комбинации.

Прежде всего, позвольте мне прояснить основную путаницу. Последовательно-параллельные комбинации аналогичны последовательным и параллельным цепям, но состоят только из резисторных элементов. Фактически, большинство пунктов, которые вы здесь изучите, также применимы к любой последовательной и параллельной схеме.

Таким образом, последовательные и параллельные цепи являются общими терминами, а последовательно-параллельное сопротивление — это конкретные цепи, в которых используются только резисторы.

Сопротивление серии

Резисторы, независимо от их размеров, подключены таким образом, чтобы через каждый из них протекал одинаковый ток. Эквивалентное сопротивление таких подключенных резисторов известно как последовательное сопротивление.

В последовательно соединенных сопротивлениях / резисторах есть только один путь для прохождения электрического тока. Все резисторы соединены в ряд как звенья цепи.При обрыве одного из звеньев цепи вся цепь становится бесполезной. То же самое и с последовательными резисторами, когда один резистор перегорает, вся цепь перестает работать.

Рис. 1 Блок-схема последовательного сопротивления (Программное обеспечение: NI Multisim Educational Edition)

Ток остается неизменным в любом узле в цепи последовательного сопротивления. Практически это можно доказать, используя мультиметр и схему, выполненную на макетной плате. Или просто смоделировав схему (рис. 1) в любом программном обеспечении для моделирования, как я сделал это в NI Multisim.

Как найти полное последовательное сопротивление?

Все резисторы, включенные последовательно, добавлены для получения эквивалентного последовательного сопротивления. Общая формула приведена ниже:

Чтобы найти эквивалентное последовательное сопротивление, удалите из цепи любой источник напряжения, а затем просуммируйте значения каждого резистора, присутствующего в цепи. Возьмем, к примеру, приведенную выше схему (рисунок: 1).

Сопротивление серии

может быть подключено к источнику тока.Те же шаги выполняются и для текущего источника. Удалите источник тока и просуммируйте значения резисторов. Пример приведен ниже:

Математический расчет:

Схема может иметь любую форму. Но резисторы нужно подключать точно так же, как звенья цепи. Следующая схема является последовательно соединенной.

Вы можете это доказать?

Можете ли вы найти эквивалентное последовательное сопротивление? (Ответ: 378КОм)

Следует помнить, что последовательно соединенные резисторы имеют только один общий узел друг с другом.Это очень важный момент, который нужно понять. Позже в этом посте я поделюсь примером схемы с комбинацией последовательной и параллельной комбинаций.

Тогда это будет немного запутать. Так что обратите особое внимание сейчас, потому что этот момент поможет нам идентифицировать последовательную комбинацию резисторов в сложной цепи.

Параллельное сопротивление

Резисторы, независимо от их размеров, подключены таким образом, чтобы на каждом резисторе было одинаковое напряжение.Эквивалентное сопротивление таких подключенных резисторов известно как параллельное сопротивление.

Или параллельное сопротивление можно определить как резисторы , подключенные параллельно, если узлы на обоих концах резисторов одинаковы. Параллельно подключенные резисторы (параллельное сопротивление) имеют разные пути прохождения электрического тока. Величина протекающего тока зависит от номиналов резисторов.

Параллельно подключенные резисторы

При параллельном подключении эквивалентное сопротивление всегда меньше, чем у наименьшего отдельного резистора.Например, эквивалентное сопротивление вышеупомянутой цепи всегда будет меньше 1 кОм. И напряжение на каждом резисторе составляет 12 В, поскольку все резисторы подключены к тем же узлам, что и резисторы 12 В.

Я говорил о резисторах параллельно, если узлы на обоих концах резисторов одинаковые. позвольте мне показать общие узлы в приведенной выше схеме.

Как найти полное параллельное сопротивление?

В параллельно соединенных резисторах эквивалентное сопротивление равно сумме обратных величин каждого резистора.Общая формула эквивалентного параллельного сопротивления приведена ниже:

Найдем значение полного сопротивления для указанной выше цепи.

Снимите источник напряжения и затем введите значения резисторов в приведенную выше общую формулу.

Ответ — меньше самого маленького отдельного резистора.

Приведем еще один пример:

Подскажите, как вообще эта схема параллельна?

Конечно, это параллельно включенная цепь.

Следуя критериям, резисторы включены параллельно, если узлы на обоих концах резисторов одинаковы.

Форма сбила нас с толку, правда? Но все же это резистивная цепь, включенная параллельно. Дело в том, что я говорю. Неважно, какую форму может иметь схема, вы должны знать базовую концепцию того, как идентифицировать параллельные резисторы в сложной схеме.

Мы можем перерисовать приведенную выше схему в чистом виде, как показано ниже:

Быстрый способ найти эквивалентное параллельное сопротивление

Когда все параллельно подключенные резисторы имеют одинаковые значения, эквивалентное параллельное сопротивление можно найти, просто разделив одно и то же значение на общее количество резисторов.Общая формула может быть записана так:

Давайте применим этот быстрый трюк на вышеупомянутой схеме.

Было бы хорошо, если бы вы потратили некоторое время, чтобы доказать это, используя общую формулу для параллельного сопротивления. Будет интересно увидеть, что оба метода дадут одинаковый ответ.

Различия между последовательным и параллельным сопротивлением

Я не знаю, сколько разницы между указанными сопротивлениями в целом. Ниже приведены различия, которые я узнал со временем.

1. При последовательном сопротивлении один и тот же ток протекает через каждый резистор, в то время как при параллельном сопротивлении каждый резистор имеет одинаковое напряжение на нем.

2. В последовательном сопротивлении полное напряжение равно падению напряжения на каждом резисторе. См. На следующей диаграмме:

Общее приложенное напряжение составляет 12 В (аккумуляторный источник), что означает, что общая сумма напряжений на каждом резисторе должна быть равна 12 В.

Попробуем вручную решить указанную выше схему.

Резисторы включены последовательно. Общее последовательное эквивалентное сопротивление можно найти, используя общую формулу для последовательного сопротивления.

По закону Ома полный ток можно определить следующим образом:

Мы рассчитали полный ток. Чтобы найти падение напряжения на каждом резисторе, умножьте общий ток на номинал резистора (закон Ома).

Мы получили те же значения, что и при моделировании Multisim. Суммирование всех рассчитанных напряжений закончится на 12 В.Вы можете доказать это, добавив их самостоятельно с помощью калькулятора.

3. При параллельном сопротивлении полный ток равен сумме токов, протекающих через каждый резистор.

Общий ток (22,0 мА) равен сумме токов, протекающих от каждого резистора. Вы можете доказать это, сложив их вместе с помощью калькулятора. Не путайте со знаком минус. Игнорируй это.

4. В последовательном сопротивлении, если один резистор не работает должным образом, остальная часть цепи также не работает.Параллельно выход из строя одного резистора не влияет на всю схему.

5. Падение напряжения в последовательном сопротивлении пропорционально размеру резистора. В то время как при параллельном подключении количество тока, протекающего в каждом резисторе, зависит от размера резистора. Увеличение размера резистора увеличивает падение напряжения, а также ток.

Зачем вообще нужны эти комбинации?

Есть очень важные применения последовательных и параллельных комбинаций.Прямо сейчас я делюсь тем, что знаю, и буду обновлять по мере того, как узнаю об этом больше.

Я работал над схемой, и мне понадобился резистор 2 кОм, которого у меня не было в то время. Я много искал в своей маленькой лаборатории, но все тщетно. Затем я собрал два резистора 1 кОм, чтобы получился резистор 2 кОм. Я сделал это, поставив последовательно два резистора 1кОм.

Я думаю, вы поняли. Последовательное и параллельное подключение могут быть очень полезны, если у вас нет резистора точного номинала. Это также может быть полезно, если вы разрабатываете схему и вам нужен резистор, которого нет на ближайшем рынке.Вы можете получить желаемое значение резистора, играя с последовательными и параллельными комбинациями резисторов.

Эти комбинации также находят применение в конструкции вольтметра и амперметра соответственно.

Последовательное сопротивление используется в качестве ограничителя тока в цепях. Его можно использовать как делитель напряжения для светодиодной схемы. Возможно, вы видели, что у каждого светодиода есть резистор, включенный последовательно. Задача резистора — ограничить ток, протекающий через светодиод.

Пример

Приведем пример, чтобы еще больше прояснить нашу концепцию последовательного параллельного соединения.Схема в примере имеет смешанные параллельные и последовательные комбинации. Поэтому, пожалуйста, обращайте пристальное внимание и старайтесь решать на каждом этапе.

Я рекомендую захватить с собой блокнот, калькулятор и хорошую ручку. И давай попробуем решить со мной.

Сводка

Резисторы подключены таким образом, что через каждый резистор протекает одинаковый ток, тогда эквивалентное сопротивление резисторов называется последовательным сопротивлением.
В серии ток остается неизменным независимо от размеров резисторов.А это возможно только тогда, когда резисторы соединены как звенья цепи.
В параллельно соединенных резисторах напряжение на каждом резисторе остается неизменным независимо от номинала каждого резистора.

Надеюсь, этот пост был для вас полезен. Вот что я знаю о последовательном и параллельном сопротивлении. И я буду продолжать обновлять этот пост по мере того, как узнаю что-то новое по упомянутой теме.

Большое спасибо за чтение и хорошей жизни.

Прочие полезные посты

резисторов последовательно и параллельно

Ultimate Electronics: практическое проектирование и анализ схем

Развитие интуиции для последовательных и параллельных цепей.Решение резисторных сетей. Читать 12 мин

Прежде чем вводить формальные правила протекания токов и напряжений в цепях в целом, давайте рассмотрим общий сценарий, чтобы попытаться развить интуицию на более высоком уровне.

Эти интуиции станут строительными блоками Закона Кирхгофа о напряжении и Закона Кирхгофа о текущем токе.

Во многих вводных текстах делается попытка использовать гидравлическую аналогию воды, протекающей по трубе, где скорость потока соответствует току, а давление — напряжению.

Внимание: эта аналогия работает на высоком уровне, но она быстро перестает работать, если вы присмотритесь слишком внимательно или зададите неправильное количество вопросов. (Является ли кран источником тока или источника напряжения? Что делать, если в трубе есть воздух?)

Гидравлическая аналогия работает, потому что сохранение заряда очень похоже на сохранение массы в проблеме потока жидкости (т.е. вода должна куда-то уходить!), И поскольку давление — это скалярная потенциальная энергия (на единицу объема), измерьте просто Подобное напряжение — это скалярная потенциальная энергия (на единицу заряда).

Одна из проблем заключается в том, что многие люди также не обладают хорошей механической интуицией в отношении потоков жидкости, и в этом случае аналогия не добавляет никакой ценности. Тем не менее, большинству людей легче визуализировать движение видимых частиц (например, воды), чем невидимых электронов, поэтому аналогия добавляет некоторую ценность. Инженеру-электрику часто бывает разумно взглянуть на схему и подумать о ней как о проблеме с водопроводом: где будет течь вода (заряд) и где упадет давление (напряжение)?

На самом деле возможно моделировать реальные жидкостные системы с помощью контуров, но это более тонкое искусство, чем вы можете подумать вначале, поэтому просто возьмите все, что вы можете, не слишком вдаваясь в детали.

Если гидравлическая аналогия не помогает вашей интуиции, не беспокойтесь об этом — возможно, вы просто нашли случай, когда аналогия не работает.

Два или более компонента в серии , если нет боковых путей для входа или выхода тока.

Есть пара узлов (или терминалов), которые являются началом и концом цепочки последовательных элементов.

Любой ток, который идет на первый терминал, должен выходить из второго терминала.

Для четырех компонентов, представленных выше, поскольку заряд сохраняется:

i1 = i2 = i3 = i4

Звучит не так круто, как уравнение, но это все, что означает «последовательно».

В мире схем модели с сосредоточенными элементами считается, что это происходит мгновенно. Почему? Потому что никакой чистый заряд никогда не может храниться внутри любых элементов схемы (или между ними). Любое накопление заряда отразит другие заряды и рассеется. (На самом деле такие детали, как скорость света, означают, что это не совсем мгновенно, но теперь мы говорим о проблемах, выходящих далеко за рамки этой главы!)

В гидравлической аналогии представьте садовый шланг, который уже полностью заполнен водой.если кран открывается шире, кран проталкивает больше воды в начало шланга, который немедленно выталкивает следующую порцию воды, и так далее, пока не достигнет конца. В результате, даже если длина шланга составляет 100 футов, вода по существу сразу же начинает выходить из конца, потому что шланг уже был предварительно заполнен.

Теперь, если мы подключим второй шланг к выходу из первого, через второй шланг должен протекать тот же ток, что и через первый. Предполагаем, что утечек нет! Но в том-то и дело — любые возможные пути утечки должны быть смоделированы как дополнительные пути на схеме, чтобы два шланга больше не были просто соединены последовательно.

«Последовательно» означает, что один и тот же поток (будь то заряд или вода), согласно компоновке системы, должен проходить через все компоненты серии.

Хотя количество потока воды одинаково, это не означает, что два последовательных шланга обязательно оказывают одинаковое влияние на поток воды.

Например, если у нас есть крошечный шланг (маленького диаметра), соединенный последовательно с огромным шлангом (большого диаметра), крошечный шланг будет иметь доминирующее влияние на ограничение потока воды, независимо от того, идет ли он первым или вторым. по направлению потока.Это может означать, что в качестве приближения мы можем игнорировать огромный шланг и рассматривать только крошечный шланг, когда пытаемся вычислить общую скорость потока; см. Алгебраические приближения.

Если у нас есть два или более последовательных компонента, и мы ограничиваем поток через , один из них (например, зажимая шланг), это ограничивает и снижает скорость потока через через обоих из них.

В электронике амперметр работает следующим образом: он подключается последовательно к измеряемому устройству, поэтому весь ток проходит через амперметр.(Хороший амперметр сам по себе вызывает очень небольшое падение напряжения.) Однако, если сопротивление амперметра слишком велико, это на самом деле окажет существенное влияние на цепь, которую вы пытаетесь измерить, — не очень хорошо!

В гидравлике расходомер работает так: он включен последовательно, так что вся вода проходит через расходомер. (Хороший расходомер вызывает очень небольшой перепад давления, если он сам по себе.) Однако, если сопротивление расходомера слишком велико, оно на самом деле окажет существенное влияние на расход, который вы пытаетесь измерить, — также нехорошо!

Два или более компонента соединены параллельно , если они подключены через одну и ту же пару входных и выходных узлов.(Слова «вход» и «выход» на самом деле ничего не значат в электронике, но предлагают правильную идею для гидравлической аналогии.) Это означает, что они имеют одинаковое входное и выходное напряжение и, следовательно, одинаковую разницу напряжений на их.

Мы рассмотрим эту схему более подробно в следующем разделе, а пока просто увидим, что V1 и R2 связаны через одни и те же два узла:

Оба элемента соединены между узлами A и B, поэтому:

v1 = v2VAB = VAB

Звучит очень просто как уравнение, но все это означает «параллельно».

В мире схем это означает, что существует два (или более) пути для прохождения тока из точки A в точку B. Свойства отдельных параллельных ветвей (ребер) будут определять, по какому маршруту будет проходить ток.

В гидравлической аналогии представьте себе сплиттер, подключенный к водопроводному крану, к которому подсоединены два садовых шланга. Давление на конце крана обоих одинаково, и давление на выходе (атмосферное давление) тоже такое же.

Следовательно, если мы откроем кран больше, дополнительный поток разделится между двумя шлангами.

В общем, если у нас есть два или более параллельных шланга, и мы ограничиваем поток через один из них (например, зажимая один из шлангов), это ограничит поток через эту ветвь, но другая ветвь не будет затронута — или он может даже получить больший поток, чем раньше (в зависимости от свойств источника).

В электронике вольтметр работает следующим образом: он включается параллельно с размываемыми компонентами, поэтому он измеряет ту же разницу напряжений, что и исследуемая ветвь.Однако, если сопротивление вольтметра слишком мало, это на самом деле окажет существенное влияние на цепь, которую вы пытаетесь измерить, создав нежелательный путь утечки — нехорошо!

В гидравлике манометр работает следующим образом: он подключается параллельно (обычно с одной стороны к интересующему давлению, с другой стороны к атмосфере, так называемое «манометрическое давление»), поэтому он измеряет то же давление, что и труба или любой другой компонент. интересный опыт.

Как обсуждалось в разделе «Сопротивление и закон Ома», отдельный резистор ведет себя как V = IR. .Итак, для двух последовательно включенных резисторов имеем:

VAB = i1R1VBC = i2R2

Как обсуждалось, для всех компонентов, включенных последовательно, ток должен быть одинаковым, поэтому:

i1 = i2 = I

Мы можем сложить полное напряжение на обоих резисторах:

В переменного тока = VAB + VBC = i1R1 + i2R2 = I (R1 + R2)

Общая последовательная ветвь с двумя резисторами ведет себя так, как будто есть единственный резистор со значением:

Rseries = R1 + R2

С внешней точки зрения двух клемм A и C этот единственный резистор Rseries ведет себя так же (на бумаге), что и два отдельных последовательно.

Обратите внимание, что в действительности один эквивалентный резистор может вести себя иначе: см. Практические резисторы: номинальная мощность (мощность) и Практические резисторы: температурный коэффициент. В частности, упрощая резисторы на схеме, мы часто скрываем тот факт, что тепло генерируется в двух разных компонентах; но на самом деле мы, инженеры, должны беспокоиться о каждом отдельно.

Для большего количества резисторов в серии просто добавляется:

Rseries = R1 + R2 + R3 +…

Мы рассмотрим это подробнее в разделе «Делители напряжения».

Два параллельно включенных резистора имеют одинаковое напряжение на обоих:

VAB = i1R1 = i2R2

В одиночку, эти два резистора ничем не управляют.

Но что, если мы подадим внешнее напряжение на эти два резистора или протолкнем через них ток? Общий ток делится между двумя путями:

итотал = i1 + i2 = VABR1 + VABR2 = VAB (1R1 + 1R2) = VAB (R1 + R2R1R2)

Так как I = VR , это то же самое, что и одиночный резистор:

итотал = VAB⋅1Rparallel1Rparallel = 1R1 + 1R2 = R1 + R2R1R2

Или можно перевернуть дробь:

R параллельный = 11R1 + 1R2 = R1R2R1 + R2

Эта дробь с дробями в обозначении знаменателя немного сложна, поэтому для экономии места иногда инженеры-электрики записывают эту дробь с двумя косыми чертами, как:

Rпараллельный = (R1 // R2) = 11R1 + 1R2

Обратите внимание, что в действительности один эквивалентный резистор может вести себя иначе, чем два отдельных резистора из-за проблем рассеивания тепла.

Для нескольких параллельно подключенных резисторов действует правило разделения тока:

Rparallel = R1 // R2 // R3 // ⋯ = 11R1 + 1R2 + 1R3 +…

Мы рассмотрим это подробнее в Current Dividers.

Единица сименса S = 1Ω , также называемый «mho» (ом, записанный наоборот!), является единицей проводимости. Электропроводность — это просто величина, обратная сопротивлению:

G = 1R

Хорошая особенность проводимости заключается в том, что для параллельных резистивных цепей проводимость просто добавляется:

1R параллельный = 1R1 + 1R2G параллельный = G1 + G2

Резисторы

, включенные последовательно и параллельно, предоставляют множество простых возможностей для упрощения предположений и приближений.

Если вы еще этого не сделали, просмотрите раздел «Алгебраические приближения», чтобы узнать об основных концепциях и инструментах, необходимых для приближения к этим упрощениям.

Для последовательных цепей, например, если R1 = 10k и R2 = 10 , то Rseries = R1 + R2 = 10010 = 10.01k . Это настолько близко к 10 кОм, что во многих ситуациях мы можем полностью игнорировать меньший резистор. Чтобы формализовать это правило:

Rseries = R1 + R2≈R1, если R1≫R2

Это соответствует нашей интуиции, потому что, поскольку мы должны «протолкнуть» одинаковое количество заряда через оба простых ограничения (низкое сопротивление R2 ) и более жесткое ограничение (более высокое сопротивление R1 ), потребуется гораздо больше энергии, чтобы преодолеть более жесткое ограничение, поэтому мы можем фактически игнорировать более легкое, чтобы вычислить общую необходимую энергию.

Для параллельных цепей, если R1 = 10k и R2 = 10 , то Rparallel = R1R2R1 + R2 = 10000010010 = 9,99 , что составляет примерно 10. Мы можем обобщить и это приближение:

Rпараллельно = 11R1 + 1R2 = R1R2R1 + R2≈R2, если R1≫R2

Это соответствует нашей интуиции, потому что, поскольку мы применяем одинаковое количество «толчка» к обоим путям, поток будет в основном следовать более легкому ограничению (низкое сопротивление R2 ) и в основном игнорируют более жесткое ограничение (более высокое сопротивление R1 ), поэтому более сложный путь лишь немного снижает общее ограничение, связанное с наличием только более простого пути.

Вы можете применить эти правила для упрощения комбинаций последовательных и параллельных цепей, но вы должны применять правила осторожно, по одному.

Для примера рассмотрим 1 резистор R1 последовательно с параллельной парой R2, R3 :

Общее эффективное сопротивление:

Rtotal = R1 + (R2 // R3) = R1 + ⎛⎜⎝11R2 + 1R3⎞⎟⎠ = R1 + ⎛⎜⎝1R2 + R3R2R3⎞⎟⎠ = R1 + (R2R3R2 + R3) = R1 (R2 + R3) + R2R3R2 + R3 = R1R2 + R1R3 + R2R3R2 + R3

Поскольку эти выражения могут быстро усложняться, удобно применять алгебраические приближения, обсуждаемые выше, где это возможно, или сохранять их в исходной, нерасширенной форме как можно дольше для лучшего понимания прочитанного.

В других случаях можно иметь резисторную сеть, в которой вы вообще не можете применять эти правила последовательного и параллельного подключения. Например, рассмотрим эту схему:

В этой схеме всего 5 резисторов, но некуда начинать применять правило последовательного или параллельного подключения.

Это не означает, что его нельзя свести к единственному эквивалентному сопротивлению. Этого просто невозможно сделать с помощью одних только этих последовательных и параллельных правил.

Хотя мы рассмотрели правила для резисторов в этом разделе, мы хотим разделить, какие части нашего анализа относятся к резисторам, а какие нет.

Единственный факт, который мы использовали о резисторах, это то, что они имеют определенную линейную зависимость напряжения от тока V = IR. , который не будет применяться к другим компонентам.

Однако есть два общих правила, которые применяются к любым компонентам , включенным последовательно или параллельно:

Любые два последовательно соединенных компонента имеют одинаковый ток.
Любые два параллельно включенных компонента имеют одинаковое напряжение.

Обычный вопрос от новичков: как упростить схему, подобную этой, с резистором, соединенным последовательно со светодиодом:

Exercise Щелкните, чтобы открыть и смоделировать схему выше.

Ответ: нельзя комбинировать резистор R1 с некоторым значением, подобным единственному резистору, для светодиода. Светодиод — это нелинейный компонент. Это не следует за V = IR . Таким образом, мы не можем получить единое эквивалентное сопротивление, которое охватило бы все ситуации.

Вы, , можете придумать одно уравнение для описания зависимости тока от напряжения для последовательной комбинации резистор + светодиод. Это просто не будет линейным уравнением!

Вот почему такие инструменты, как симуляторы схем, особенно удобны: хотя мы можем уменьшить линейные случаи (например, резисторы, включенные последовательно и параллельно) вручную, симулятор также способен решать нелинейные случаи.(См. Также: Линейные и нелинейные.)

В следующем разделе, Законе напряжения Кирхгофа и Законе тока Кирхгофа, мы будем использовать эту новую интуицию для разработки более широкого набора правил поведения напряжения и тока в цепи.

Роббинс, Майкл Ф. Ultimate Electronics: Практическое проектирование и анализ схем. CircuitLab, Inc., 2021, ultimateelectronicsbook.com. Доступно. (Авторское право © CircuitLab, Inc., 2021)

Series / Parallel Resistor Reduction (Resistors Networks)

Чтобы сделать последовательное или параллельное уменьшение резисторов, необходимо только сделать некоторые упрощения, используя формулы, которые мы уже знаем.Ситуация иная, когда вам нужно упростить схему, состоящую из комбинации резисторов, включенных последовательно, и резисторов, включенных параллельно. В этом случае необходимо последовательное / параллельное уменьшение резистора .

Последовательный / Параллельная процедура уменьшения резистора

Чтобы упростить сложную схему и получить эквивалентное сопротивление, мы следуем следующей процедуре:

1 — Вам необходимо перестроить схему, которую мы хотим упростить, чтобы четко видеть составные части и обнаружить части, которые уже соединены последовательно и параллельно.

2 — Каждой из этих частей мы присваиваем новое имя, например RA, RB, RC, RD и т. Д. (Посмотрите на первое изображение).

3 — Мы получаем эквивалентное сопротивление каждой детали по знакомым формулам. (резисторы последовательно и параллельно сопротивления).

4 — Заменяем детали в исходной цепи на значения эквивалентных сопротивлений (RA, RB и т. Д.), Полученные на предыдущем шаге.

5 — Мы анализируем полученную схему и ищем другие возможные комбинации групп (частей) сопротивления последовательно и параллельно, которые были созданы.

6 — Мы повторяем процесс снова, начиная с шага 2, с другими названиями эквивалентных сопротивлений, чтобы избежать путаницы (например, RX, RY, RZ и т. Д.), Пока мы не получим единственное окончательное эквивалентное сопротивление всей цепи.

Проанализируйте следующее изображение:

Уменьшение последовательного / параллельного резистора

Значения резисторов:

R1 = 120, R2 = 250, R3 = 68, R4 = 47, R5 = 68 (все в омах).
R6 = 5, R7 = 4, R8 = 2, R9 = 1,2. (все в килоомах).

Первое уменьшение

RA = R1 и R2 параллельно,
RA = R1 // R2 = R1 x R2 / (R1 + R2) = 120 x 250 / (120 + 250) = 81 Ом.
RB = R4 и R5 последовательно,
RB = R4 + R5 = 47 + 68 = 115 Ом.
RC = R6, R7 и R8 параллельно,
RC = R6 // R7 // R8 = 1 / (1 / R6 + 1 / R7 + 1 / R8) = 1 / (1 / 5K + 1 / 4K + 1 / 2K) = 1053 Ом.

Заменим эквивалентные значения, полученные на предыдущих шагах, в исходной схеме, и мы получим:

Процедура уменьшения последовательного / параллельного резистора

Мы снова упрощаем схему и получаем новые эквивалентные сопротивления. затем:

RD = RA и R3 последовательно,
RD = RA + R3 = 81 + 68 = 149 Ом.
RE = RC и R9 последовательно,
RE = RC + R9 = 1053 + 1200 = 2253 Ом.

И заменяя эти последние данные, получается следующая схема:

В последней схеме видно, что RB и RE параллельны, и мы получаем новое эквивалентное сопротивление RF, которое последовательно с RD:

RF = RB и RE параллельно,
RF = RB // RE = RB x RE / (RB + RE) = 115 x 2253 / (115 + 2253) = 109 Ом.

РФ идет последовательно с РД. Мы складываем их значения, чтобы получить окончательное значение резистора «Req».Это полное эквивалентное значение сопротивления всей цепи.

Тогда:

Req = RF и RD последовательно,
Req = RF + RD = 109 + 149 = 258 Ом.

Какова формула параллельного сопротивления?

Сумма токов, протекающих по каждому пути, равна общему току, протекающему от источника. Вы можете найти полное сопротивление в параллельной цепи по следующей формуле: 1 / Rt = 1 / R1 + 1 / R2 + 1 / R3 +… Если один из параллельных путей разорван, ток будет продолжать течь по всем другим путям. .

Что такое сопротивление и его формула?

Сопротивление выражается в единицах Ом (Ом), относящихся к вольтам и амперам на 1 Ом = 1 В / А. На резисторе возникает падение напряжения или IR, вызванное протекающим через него током, определяемое как V = IR.

Какова формула эффективного сопротивления?

Для цепи с сопротивлениями R1 и R2, включенными последовательно или параллельно, как показано на рисунке 2, эффективное сопротивление можно рассчитать, используя следующие правила. Раб = R1 + R2. Доказательство.Пусть Iab будет током от a до b.

Что такое эффективное сопротивление параллельно?

Параллельные резисторы Если каждый конец отдельных резисторов соединен друг с другом как один, говорят, что резисторы подключены параллельно. Эффективное сопротивление R трех резисторов сопротивлений R1, R2 и R3, соединенных параллельно, равно: 1R = 1R1 + 1R2 + 1R3.

Какое эффективное сопротивление между A и B?

, следовательно, эффективное сопротивление между A и B составляет 10 Ом

Что такое эффективное сопротивление?

Однако, если у вас была огромная и сложная схема с множеством резисторов, то эффективное сопротивление — это полное сопротивление цепи.Эффективное сопротивление обычно измеряется между 2 точками. На рисунке выше эффективное сопротивление обычно определяется как полное сопротивление батареи.

Какое эффективное сопротивление между?

Эффективное сопротивление — это мера общего сопротивления между двумя точками.

Какое сопротивление между A и B в следующей сети?

Ответ 2 Ом.

Какое сопротивление цепи?

Сопротивление — это мера сопротивления току в электрической цепи.Сопротивление измеряется в омах и обозначается греческой буквой омега (Ом). Ом назван в честь Георга Симона Ома (1784-1854), немецкого физика, изучавшего взаимосвязь между напряжением, током и сопротивлением.

Какое эквивалентное сопротивление цепи?

Эквивалентное сопротивление — это алгебраическая сумма сопротивлений (уравнение 10.3.2): RS = R1 + R2 + R3 + R4 + R5 = 20 Ом + 20 Ом + 20 Ом + 20 Ом + 10 Ом = 90 Ом. Ток в цепи одинаков для каждого резистора в последовательной цепи и равен приложенному напряжению, деленному на эквивалентное сопротивление: I = VRS = 9V90Ω = 0.1А.

Как добавить последовательное сопротивление?

Когда резисторы подключаются друг за другом, это называется последовательным соединением. Это показано ниже. Чтобы рассчитать общее общее сопротивление ряда резисторов, подключенных таким образом, вы складываете отдельные сопротивления. Это делается по следующей формуле: Rtotal = R1 + R2 + R3 и так далее.

Как узнать, является ли цепь параллельной или последовательной?

Как определить, какие из них параллельные или последовательные? Если весь ток, выходящий из одного резистора, попадает в другой резистор, два резистора включены последовательно.Если все напряжение на одном резисторе подается на другой резистор, два резистора включены параллельно. Два резистора на одном пути включены последовательно.

Как вы определяете устойчивость к тевенину?

Thevenin сопротивление рассчитывается путем «отключения» всех независимых источников тока и напряжения и вычисления сопротивления между двумя точками. При выключении источника напряжения напряжение на нем устанавливается равным 0, что приводит к короткому замыканию (0 Ом) параллельно резистору 275 Ом.

В чем разница между теоремой Тевенина и Нортона?

— Теорема Нортона использует источник тока, тогда как теорема Тевенина использует источник напряжения. — Теорема Тевенина использует резистор последовательно, в то время как теорема Нортона использует резистор, установленный параллельно источнику. — Теорема Нортона на самом деле является выводом теоремы Тевенина.

Как проверить теорему Тевенина?

RL = ВЛИЛ. 3) Снимите нагрузку, разомкнув переключатель S2 и считайте напряжение холостого хода (или эквивалентное напряжение Тевенина) Vth.
Rth = VI. 5) Теперь вычислите ток нагрузки.
IL = VthRth + RL. 6) Сравните вычисленный выше ток нагрузки с его значением, полученным на шаге (2), и проверьте теорему.

Как вы находите устойчивость к тевенину с зависимыми источниками?

Теорема Тевенина может применяться при анализе схемы с зависимыми источниками. В этом случае все независимые источники отключаются, и RTh рассчитывается путем подачи источника тока или напряжения на открытый вывод.При использовании источника напряжения для простых расчетов можно принять его равным 1 В.

Равно ли сопротивление Тевенина сопротивлению Нортона?

Сопротивления Тевенина и Нортона равны. Напряжение Thevenin равно току Нортона, умноженному на сопротивление Нортона. Ток Нортона равен напряжению Тевенина, деленному на сопротивление Тевенина.

Что такое эквивалентное сопротивление Тевенину?

«Эквивалентная схема Тевенина» — это электрический эквивалент B1, R1, R3 и B2, если смотреть из двух точек, где подключается наш нагрузочный резистор (R2).Другими словами, напряжение и ток нагрузочного резистора (R2) должны быть точно такими же при одинаковом значении сопротивления нагрузки в двух цепях.

Какой метод лучше всего подходит для источников напряжения?

Какой метод лучше всего подходит для источников напряжения? Объяснение: Каждый источник напряжения, подключенный к опорному узлу, сокращает решаемые уравнения. Таким образом, для источников напряжения лучше всего подходит метод узлового напряжения.

Что такое зависимый источник в цепи?

В теории электрических сетей зависимый источник — это источник напряжения или источник тока, значение которого зависит от напряжения или тока в другом месте сети.Операционный усилитель можно описать как источник напряжения, зависящий от дифференциального входного напряжения между его входными клеммами.

Суммируются ли напряжения параллельно?

Идеальные источники напряжения могут быть соединены между собой как параллельно, так и последовательно, как и любой элемент схемы. Последовательные напряжения складываются, а параллельные напряжения имеют одинаковое значение. Обратите внимание, что источники идеального напряжения с неравными характеристиками не могут быть соединены между собой напрямую параллельно.

Что произойдет, если два источника напряжения подключены параллельно?

Если два идеальных источника напряжения подключены параллельно, источник напряжения с немного более высоким напряжением будет передавать ток в источник напряжения с более низким напряжением.Будет течь сильный ток, так как идеальный источник имеет нулевое сопротивление. Могут протекать большие токи, которые могут повредить батареи.

Параллельное сопротивление

Этот калькулятор требует использования Javascript разрешенных и поддерживающих браузеров. Начните с ввода значений сопротивления в поле ввода сопротивления. Обязательно нажимайте кнопку «Ввести сопротивление» после каждого ввода, а затем щелкайте поле ввода сопротивления, чтобы подготовиться к вводу следующего значения резистора .Нет никаких разумных ограничений на количество записей, если вы следуете за каждой записью, нажимая кнопку «Enter Resistance» и снова в поле ввода, чтобы разрешить следующую запись. После ввода последнего значения сопротивления нажмите кнопку «Рассчитать сопротивление» для возвращенного значения сопротивления , параллельного и количества введенных значений резистора. Параллельное сопротивление НЕ то же самое, что и усреднение. Он использует формулу RT = 1 / ((1 / R1) + (1 / R2) + (1 / R3)).Существуют и другие формулы для определения сопротивления только 2 резисторов, но это работает с неограниченным количеством резисторов, включая 2. В приведенной формуле RT — полное (параллельное) сопротивление цепи, R1 — значение сопротивления первого. резистор, R2 — значение сопротивления второго резистора, R3 — значение сопротивления третьего резистора и включено до последнего резистора. Помните, что RT без исключения всегда меньше, чем резистор с наименьшим номиналом, подключенный параллельно.Предполагается, что входное значение составляет Ом, и возвращается с тем же входным значением. См. Информацию под калькулятором для объяснения формулы. Чтобы рассчитать последовательное сопротивление, используйте наш калькулятор сопротивления серии .

Пример (и проверка) формулы — использование трех резисторов, 100 Ом, 200 Ом и 300 Ом, все в цепи, включенной параллельно.Общее (параллельное) сопротивление составит 1 / (1/100 (0,01) + 1/200 (0,005) + 1/300 (0,00333)) или около 54,555 Ом. Точность соответствует возможностям вашего браузера, обычно 18 символов в окне дисплея. NaN указывает на ошибку при вводе данных или вычислении; повторите процесс еще раз, внимательно следя за вводом данных.

Обновлено 8.12.11

Вычислитель резисторов серии

/ параллельного подключения для HP-67/97

Последовательный / параллельный вычислитель резисторов для HP-67/97

Музей калькуляторов HP

Авторские права на эту программу принадлежат Джону Х.Мейера и используется здесь с разрешения.

Эта программа поставляется без каких-либо заверений и гарантий. Поэтому автор и Музей калькуляторов HP не несут никакой ответственности и не несут никакой ответственности, косвенной или иной, любого рода, возникающей в результате использования этого программного материала или любой его части.

Этикетки для карточек
Калькулятор последовательного / параллельного резистора
Сдвиг	R _Итого	% ошибка			Число / декада
Этикетка	R _мин.	R _макс	Серии	Параллельный
Ключ	А	B	C	D	E

Обзор и инструкции

Эта программа находит два стандартных резистора, которые при последовательном или параллельном подключении дают наиболее близкое приближение к желаемому нестандартному значению сопротивления.

Два стандартных резистора можно разместить последовательно или параллельно, чтобы приблизиться к желаемому сопротивлению. Стандартные значения сопротивления рассчитываются по следующей формуле:

[10 ^{(1 / n)}] ^x

, где n = количество стандартных значений сопротивления на декаду, а x = целое число. Каждое последующее целое число приводит к следующему стандартному значению. 5% резисторов составляют 12 к декаде, таким образом, n = 12. Номиналы прецизионных резисторов от 24 до декады, таким образом, n = 24.

Для расчета наиболее точного соответствия при последовательном соединении используется следующий алгоритм: (R ‘и R’ ‘- испытательные сопротивления; R = желаемое сопротивление)

R ‘= [10 ^{(1 / n)}] ^{INT [log (R) / log (10 ^{(1 / n)})]}
Установить флаг 2
R » = [10 ^{(1 / n)}] ^{INT [log (R — R ‘) / log (10 ^{(1 / n)})]}
Если R »> R ‘, программа завершена.
Ошибка вычисления = ABS [R- (R ‘+ R’ ‘)].Если это еще самая маленькая ошибка, сохраните R ‘и R’ ‘.
Если установлен флаг 2, умножьте R » на 10 ^{(1 / n)}, сбросьте флаг 2 и перейдите к шагу 5.
Разделить R ‘на 10 ^{(1 / n)}. Переходите к шагу 2.

Если R » падает ниже минимального сопротивления (Rmin), Rmin заменяется на R ». Программа аппроксимирует параллельное сопротивление путем замены 1 / R на R и обратной величиной максимально допустимого (R _max) для R _min.

Программа работает для конденсаторов и катушек индуктивности.Используйте параллельную программу, чтобы приблизительно определить последовательную емкость и наоборот.

Для использования программы:

Сторона нагрузки 1 и сторона 2.
Необязательно: введите количество стандартных компонентов на декаду (по умолчанию — 24). Нажмите [f] [E].
Установить отображение на единицу меньшее, чем количество значащих цифр, указанное в стандартных компонентах (например, для 9,09 кОм, установленного [DSP] [2]). Также установите для дисплея ENG.
Введите минимальное стандартное значение (R _мин).Нажмите A.
Введите максимальное стандартное значение (R _макс.). Пресс Б.
Введите желаемое сопротивление. Нажмите C, чтобы вычислить последовательные значения, или D, чтобы вычислить параллельные значения.
Необязательно: Вычислите полное сопротивление по общему значению (нажмите [f] [A]).
Дополнительно: вычислить% погрешности фактического сопротивления по сравнению с желаемым сопротивлением (нажмите [f] [B]).
Дополнительно:
Вызов R _мин. [RCL] [A]
Вызов R _макс. [RCL] [B]
Вызов R (желаемое сопротивление) [RCL] [C]
Вызов R ₁ (первый стандартный резистор ) [RCL] [D]
Вызов R ₂ (второй стандартный резистор) [RCL] [E]

Примечание. Шаги 2–5 выше можно выполнять в любом порядке и в любое время.Чтобы вычислить новое приближение, просто повторите шаг 6.

Программа

 КОД СТРОКИ КЛАВИШИ НАЖАТИЕ (67) КОММЕНТАРИИ
 001 31 25 00 Метка 0 [f] [LBL] [0] Вычислить R 'и R' '
 002 35 64 ABS [h] [ABS] согласно
 003 31 53 LOG [f] [LOG] формула на странице 1.
 004 34 08 RCL8 [RCL] [8]
 005 81 ÷ ÷
 006 31 83 ИНТ [f] [ИНТ]
 007 34 09 RCL9 [RCL] [9]
 008 35 52 X⇔Y [ч] [X⇔Y]
 009 35 63 Y ^x [h] [Y ^x]
 010 35 22 RTN [час] [RTN]
 011 32 25 15 Этикетка e [g] [LBL f] [e]
 012 35 51 00 SF0 [h] [SF] [0] Сохранить n
 013 33 03 STO3 [STO] [3]
 014 35 22 RTN [час] [RTN]
 015 31 25 11 Этикетка A [f] [LBL] [A]
 016 33 11 STOA [STO] [A] Хранить R _мин. 017 35 22 RTN [ч] [RTN]
 018 31 25 12 Этикетка B [f] [LBL] [B]
 019 33 12 STOB [STO] [B] Сохранить R _макс. 020 35 22 RTN [час] [RTN]
 021 32 25 11 Этикетка a [g] [LBL f] [a]
 022 35 23 ENG [ч] [ENG] Вычислить R _- 023 34 14 RCLD [RCL] [D]
 024 35 71 01 F1? [h] [F?] [1]
 025 35 62 1 / x [час] [1 / x]
 026 34 15 RCLE [RCL] [E]
 027 35 71 01 F1? [h] [F?] [1]
 028 35 62 1 / x [час] [1 / x]
 029 61 + +
 030 35 71 01 F1? [h] [F?] [1]
 031 35 62 1 / x [час] [1 / x]
 032 35 22 RTN [час] [RTN]
 033 32 25 12 Метка b [g] [LBL f] [b] Ошибка вычисления%
 034 34 13 RCLC [RCL] [C]
 035 32 22 11 GSBa [g] [GSB f] [a]
 036 32 82% Изменение [г] [% CH]
 037 31 23 FIX [f] [FIX]
 038 35 22 RTN [час] [RTN]
 039 31 25 14 Этикетка D [f] [LBL] [D] Параллельно прибл.040 35 62 1 / x [час] [1 / x]
 041 33 13 STOC [STO] [C]
 042 35 51 01 SF1 [h] [SF] [1]
 043 34 12 RCLB [RCL] [B]
 044 35 62 1 / x [час] [1 / x]
 045 22 04 GTO4 [GTO] [4]
 046 31 25 13 Этикетка C [f] [LBL] [C] Серия прибл.
 047 33 13 STOC [STO] [C]
 048 35 61 01 CF1 [h] [CF] [1]
 049 34 11 RCLA [RCL] [A]
 050 31 25 04 Метка 4 [f] [LBL] [4] Установите n = 24. Если флаг
 051 33 04 STO4 [STO] [4] 0 установлено, установить n
 052 35 23 ENG [h] [ENG] равно пользователю
 053 34 03 RCL3 [RCL] [3] поставленный номер
 054 02 2 2 значений
 055 04 4 4 за декаду
 056 35 71 00 F0? [h] [F?] [0]
 057 35 52 X⇔Y [ч] [X⇔Y]
 058 35 62 1 / x [час] [1 / x]
 059 32 53 10 ^x [g] [10 ^x] Вычислить 10 ^{(1 / n)} 060 33 09 STO9 [STO] [9]
 061 31 53 LOG [f] [LOG] журнал [10 ^{(1 / n)}]
 062 33 08 STO8 [STO] [8]
 063 34 13 RCLC [RCL] [C]
 064 33 07 STO7 [STO] [7] Ошибка инициализации = R
 065 31 22 00 GSB0 [f] [GSB] [0] Вычислить R '
 066 33 06 STO6 [STO] [6]
 067 31 25 01 Этикетка 1 [f] [LBL] [1]
 068 35 51 02 SF2 [ч] [SF] [2]
 069 34 13 RCLC [RCL] [C]
 070 51 - - Вычислить R '- R
 071 31 22 00 GSB0 [f] [GSB] [0] Вычислить R ''
 072 33 05 STO5 [STO] [5]
 073 34 04 RCL4 [RCL] [4]
 074 32 81 X> Y? [g] [X> Y?] Если R ''  мин.  075 33 05 STO5 [STO] [5] R _мин. → R ''
 076 31 25 02 Этикетка 2 [f] [LBL] [2]
 077 34 06 RCL6 [RCL] [6]
 078 34 05 RCL5 [RCL] [5]
 079 32 71 X≤Y? [g] [X≤Y?] Если R ''