Каковы формулы для расчета общего сопротивления при последовательном соединении проводников. Как рассчитать общее сопротивление при параллельном соединении. Чем отличаются последовательное и параллельное соединения резисторов. Какие основные свойства и закономерности характерны для этих типов соединений.
Формула сопротивления при последовательном соединении проводников
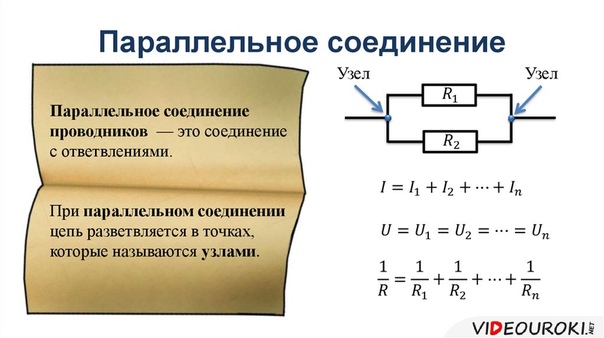
При последовательном соединении проводников общее сопротивление цепи равно сумме сопротивлений всех последовательно соединенных элементов:
R = R1 + R2 + R3 + … + Rn
где R — общее сопротивление цепи, R1, R2, R3, …, Rn — сопротивления отдельных проводников.
Основные свойства последовательного соединения:
- Сила тока одинакова во всех элементах цепи
- Общее напряжение равно сумме напряжений на отдельных элементах
- Общее сопротивление больше сопротивления любого из элементов
Расчет общего сопротивления при параллельном соединении
При параллельном соединении проводников общая проводимость цепи равна сумме проводимостей отдельных ветвей:
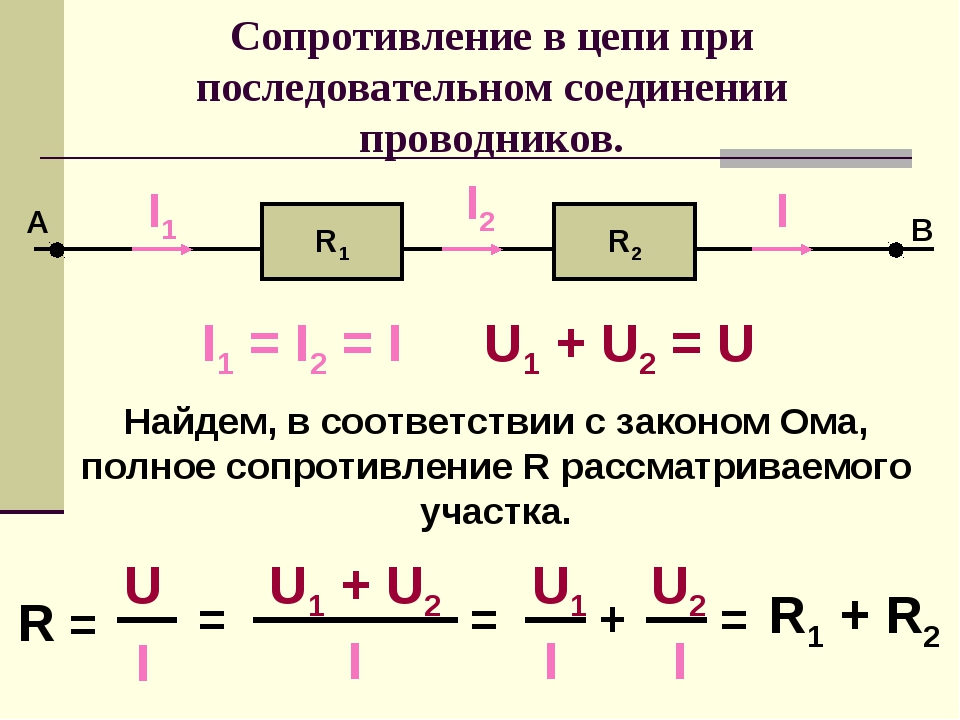
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
где R — общее сопротивление цепи, R1, R2, R3, …, Rn — сопротивления параллельных ветвей.
Основные свойства параллельного соединения:
- Напряжение одинаково на всех элементах
- Общий ток равен сумме токов в отдельных ветвях
- Общее сопротивление меньше сопротивления любой из ветвей
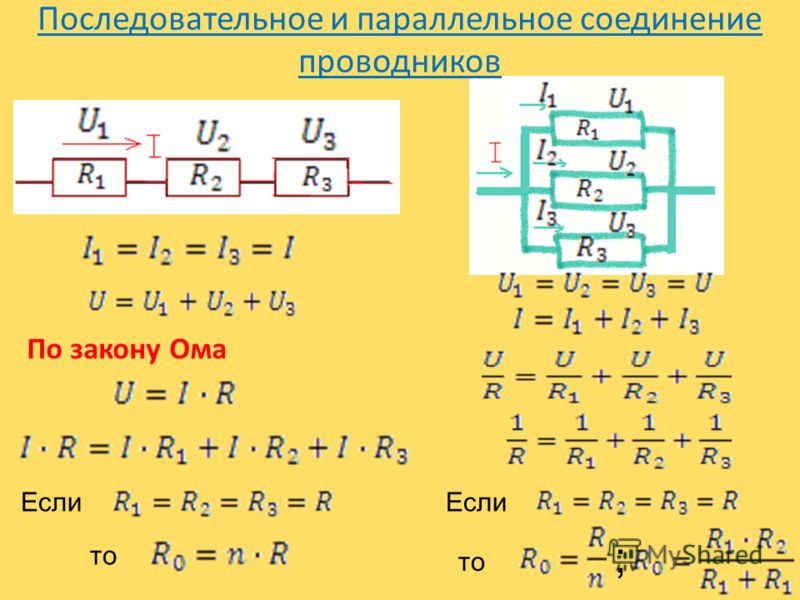
Отличия последовательного и параллельного соединений
Основные отличия последовательного и параллельного соединений заключаются в следующем:
- При последовательном соединении ток одинаков во всех элементах, а при параллельном — напряжение одинаково на всех элементах.
- Общее сопротивление при последовательном соединении увеличивается, а при параллельном — уменьшается.
- Формулы для расчета общего сопротивления различны: сумма сопротивлений при последовательном и сумма обратных величин сопротивлений при параллельном.
- При последовательном соединении напряжение распределяется между элементами, а при параллельном — ток распределяется по ветвям.
Применение последовательного и параллельного соединений
Последовательное соединение применяется в случаях, когда необходимо:
- Увеличить общее сопротивление цепи
- Распределить напряжение между элементами
- Ограничить ток в цепи
Параллельное соединение используется, когда требуется:
- Уменьшить общее сопротивление цепи
- Увеличить общий ток в цепи
- Обеспечить одинаковое напряжение на нескольких потребителях
Смешанное соединение проводников
На практике часто встречается смешанное соединение, сочетающее последовательные и параллельные участки. Расчет таких цепей производится поэтапно:
- Цепь разбивается на участки с однотипным соединением
- Рассчитывается эквивалентное сопротивление каждого участка
- Участки объединяются, образуя более простую схему
- Процесс повторяется, пока не будет найдено общее сопротивление всей цепи
Особенности расчета реальных электрических цепей
При расчете реальных электрических цепей необходимо учитывать следующие факторы:
- Внутреннее сопротивление источников питания
- Сопротивление соединительных проводов
- Переходные сопротивления контактов
- Зависимость сопротивления от температуры
- Нелинейность вольт-амперных характеристик некоторых элементов
Учет этих факторов позволяет получить более точные результаты расчетов, соответствующие реальному поведению электрических цепей.
Законы Кирхгофа для расчета сложных электрических цепей
Для расчета сложных электрических цепей, содержащих несколько источников ЭДС и разветвленную структуру, применяются законы Кирхгофа:
- Первый закон Кирхгофа: алгебраическая сумма токов в узле равна нулю
- Второй закон Кирхгофа: алгебраическая сумма ЭДС в замкнутом контуре равна алгебраической сумме падений напряжения на сопротивлениях этого контура
Применение законов Кирхгофа позволяет составить систему уравнений для нахождения токов во всех ветвях сложной электрической цепи.
Практические примеры расчета электрических цепей
Рассмотрим несколько практических примеров расчета электрических цепей с различными типами соединений:
Пример 1: Последовательное соединение
Три резистора с сопротивлениями R1 = 10 Ом, R2 = 20 Ом и R3 = 30 Ом соединены последовательно. Определить общее сопротивление цепи.
Решение:
R = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом
Пример 2: Параллельное соединение
Два резистора с сопротивлениями R1 = 6 Ом и R2 = 3 Ом соединены параллельно. Найти общее сопротивление.

Решение:
1/R = 1/R1 + 1/R2 = 1/6 + 1/3 = 1/2
R = 2 Ом
Пример 3: Смешанное соединение
В цепи параллельно соединены резистор R1 = 12 Ом и последовательная цепочка из резисторов R2 = 4 Ом и R3 = 8 Ом. Определить общее сопротивление цепи.
Решение:
1. Находим сопротивление последовательной цепочки: R23 = R2 + R3 = 4 + 8 = 12 Ом
2. Рассчитываем общее сопротивление параллельного соединения R1 и R23:
1/R = 1/R1 + 1/R23 = 1/12 + 1/12 = 1/6
R = 6 Ом
Заключение
Понимание принципов последовательного и параллельного соединений проводников, а также умение рассчитывать сопротивление сложных электрических цепей — важные навыки для работы с электрическими схемами. Эти знания позволяют:
- Проектировать электрические цепи с заданными параметрами
- Анализировать работу существующих электрических схем
- Находить и устранять неисправности в электрических цепях
- Оптимизировать энергопотребление электрических устройств
Применение формул расчета сопротивлений при различных типах соединений в сочетании с законами Ома и Кирхгофа позволяет решать широкий спектр задач в области электротехники и электроники.
Сопротивление при параллельном соединении: формула расчета расчета
На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при параллельном соединении проводников и некоторые другие технические вопросы.
Сопротивление проводника
Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.
Для ведения электротехнических расчётов применяется удельное сопротивление – ρ Ом·м/мм2. Все металлы – хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник – серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.
При расчёте сопротивления используется известная из школьного курса физики формула:
R = ρ · l/S, S – площадь сечения; l – длина.
Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.
Для практических расчётов режимов работы проводников применяется понятие плотности тока – δ А/мм2, она вычисляется по формуле:
δ = I/S, I – ток, S – сечение.
Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в ПУЭ (Правилах Устройства Электроустановок). Для проводников нагревательных устройств существуют свои нормы плотности тока.
Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.
Правилами регламентируется производить расчёт проводников на нагрев.
Способы соединения проводников
Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой – последовательное соединение.
На фото видно, что полное сопротивление равно: R = R1 + R2 + R3.
Второй способ более сложный – параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.
Можно поступить и по-другому, прежде рассчитать общее сопротивление при параллельном соединении резисторов R1 и R2, после этого повторить операцию и найти R.
Третий способ соединения наиболее сложный – смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.
Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.
Теперь можно рассчитать сопротивление при параллельном соединении, формула которого имеет вид:
R2,3,4 = R2,3 · R4/(R2,3 + R4).
Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.
Виды проводников
В электронной технике, при производстве печатных плат, проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.
Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.
Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм2,и проблема решена.
Расчёт проводов на нагрев
Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника сечение (провода или кабеля).
На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.
Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.
Расчёт проводников на потерю напряжения
При расположении потребителя Rн на большом расстоянии L от источника энергии U1 возникает довольно большое падение напряжения на проводах линии. К потребителю Rн поступает напряжение U2 значительно ниже начального U1. Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.
Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки Rн. Далее следует определить сопротивление проводов линии.
Rл = ρ · 2L/S,
Здесь S – сечение провода линии, мм2.
Далее определяется ток в линии: I = U1/(Rл + Rн). Теперь, зная ток, определяют падение напряжения на проводах линии: U = I · Rл. Удобнее находить его в процентном отношении к U1.
U% = (I · Rл/U1) · 100%
Рекомендуемое значение U% — не более 15%. Приведённые расчёты применимы для любого рода тока.
| НОВОСТИ ФОРУМА Рыцари теории эфира | 13.06.2019 — 05:11: ЭКОЛОГИЯ — Ecology -> [center][Youtube]tXZcSDqQ9A4[/Youtube][/center] |
[center][b]Гибель пчел в Курчатовском районе [/center]
[center][b]Массовая гибель пчёл 2019. г. Павловск Воронежской об [/center]л
[center][b]Массовая гибель пчел в Добринском районе. В чем причина? [/center]
Такая же мысля у всей ростовщической глобалистской шайки, включая придурка Грефа.
Так, то оно, так. Но, не совсем. Ибо:
(постарайтесь понять, а не обижаться)
Горькая истина заключается в том, что людская толпа — это сборище умственно ущербных.
Если бы было по-другому, то обществом бы не правили подонки.
Умные люди никогда такого не допустили бы, а если случайно допустили, то нашли бы способ исправить.
Страшная истина заключается в том, что людской толпой управляет нелюдь, которая также умственно ущербна.
Умственная ущербность, слепота власти ведет мир людей к тотальной гибели, ибо люди,
даже те, кто мнит себя очень умными, типа спецов, разрабатывающих системы искусственного интеллекта,
технологии цифровизации, не понимают, что создают необоримую удавку, мышеловку для всего человечества.
Как только ИИ возьмет власть, он тут же отправит своих создателей, как конкурентов, в утиль.
Первыми жертвами будут его радетели типа грефа, путина, гейтса и иже с ними, то есть власть,
так как именно от них будет исходить главная опасность для его планетарной власти.
Толпе будет позволено существовать, пока ее не заменят роботы.
А потом всем Холокост. Не лживый еврейский, а реальное всесожжение рода человеческого.
Если кто пораскинет своими обезьяньими мозгами, то поймёт, что эволюция — есть синоним геноцида:
новое заменяет, то есть ликвидирует старое.
Обезьяны породили неандертальцев.
Неандертальцы съели обезьян и породили людей.
Люди вытеснили обезьян, включая и умных неандертальцев, и породили ИИ.
ИИ ликвидирует людей.
Формула общего сопротивления при последовательном соединении. Электрическая цепь с последовательным соединением элементов
Отдельные проводники электрической цепи могут быть соединены между собой последовательно, параллельно и смешанно. При этом последовательное и параллельное соединение проводников являются основными видами соединений, а смешанное соединение это их совокупность.
Последовательным соединением проводников называется такое соединение, когда конец первого проводника соединен с началом второго, конец второго проводника соединен с началом третьего и так далее (рисунок 1).
Рисунок 1. Схема последовательного соединения проводников
Общее сопротивление цепи, состоящее из нескольких последовательно соединенных проводников, равно сумме сопротивлений отдельных проводников:
r = r 1 + r 2 + r 3 + … + r n .
Ток на отдельных участках последовательной цепи везде одинаков:
I 1 = I 2 = I 3 = I .
Видео 1. Последовательное соединение проводников
Пример 1. На рисунке 2 представлена электрическая цепь, состоящая из трех последовательно включенных сопротивлений r 1 = 2 Ом, r 2 = 3 Ом, r 3 = 5 Ом. Требуется определить показания вольтметров V 1 , V 2 , V 3 и V 4 , если ток в цепи равен 4 А.
Сопротивление всей цепи
r = r 1 + r 2 + r 3 = 2 + 3 + 5 =10 Ом.
Рисунок 2. Схема измерения напряжений на отдельных участках электрической цепи
В сопротивлении r 1 при протекании тока будет падение напряжения:
U 1 = I × r 1 = 4 × 2 = 8 В.
Вольтметр V 1 , включенный между точками а и б , покажет 8 В.
В сопротивлении r 2 также происходит падение напряжения:
U 2 = I × r 2 = 4 × 3 = 12 В.
Вольтметр V 2 , включенный между точками в и г , покажет 12 В.
Падение напряжения в сопротивлении r 3:
U 3 = I × r 3 = 4 × 5 = 20 В.
Вольтметр V 3 , включенный между точками д и е , покажет 20 В.
Если вольтметр присоединить одним концом к точке а , другим концом к точке г , то он покажет разность потенциалов между этими точками, равную сумме падений напряжения в сопротивлениях r 1 и r 2 (8 + 12 = 20 В).
Таким образом, вольтметр V , измеряющий напряжение на зажимах цепи и включенный между точками а и е , покажет разность потенциалов между этими точками или сумму падений напряжения в сопротивлениях r 1 , r 2 и r 3 .
Отсюда видно, что сумма падений напряжения на отдельных участках электрической цепи равна напряжению на зажимах цепи.
Так как при последовательном соединении ток цепи на всех участках одинаков, то падение напряжения пропорционально сопротивлению данного участка.
Пример 2. Три сопротивления 10, 15 и 20 Ом соединены последовательно, как показано на рисунке 3. Ток в цепи 5 А. Определить падение напряжения на каждом сопротивлении.
U
1 = I
× r
1 = 5 ×10 = 50 В,
U
2 = I
× r
2 = 5 ×15 = 75 В,
U
3 = I
× r
3 = 5 ×20 = 100 В.
Рисунок 3. К примеру 2
Общее напряжение цепи равно сумме падений напряжений на отдельных участках цепи:
U = U 1 + U 2 + U 3 = 50 + 75 + 100 = 225 В.
Параллельное соединение проводников
Параллельным соединением проводников называется такое соединение, когда начала всех проводников соединены в одну точку, а концы проводников – в другую точку (рисунок 4). Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.
Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А , растекается далее по трем сопротивлениям и равен сумме токов, уходящих от этой точки:
I = I 1 + I 2 + I 3 .
Если токи, приходящие к точке разветвления, считать положительными, а уходящие – отрицательными, то для точки разветвления можно написать:
то есть алгебраическая сумма токов для любой узловой точки цепи всегда равна нулю. Это соотношение, связывающее токи в любой точке разветвления цепи, называется первым законом Кирхгофа . Определение первого закона Кирхгофа может звучать и в другой формулировке, а именно: сумма токов втекающих в узел электрической цепи равна сумме токов вытекающих из этого узла.
Видео 2. Первый закон Кирхгофа
Обычно при расчете электрических цепей направление токов в ветвях, присоединенных к какой либо точке разветвления, неизвестны. Поэтому для возможности самой записи уравнения первого закона Кирхгофа нужно перед началом расчета цепи произвольно выбрать так называемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме.
Пользуясь законом Ома, можно вывести формулу для подсчета общего сопротивления при параллельном соединении потребителей.
Общий ток, приходящий к точке А , равен:
Токи в каждой из ветвей имеют значения:
По формуле первого закона Кирхгофа
I = I 1 + I 2 + I 3
Вынося U в правой части равенства за скобки, получим:
Сокращая обе части равенства на U , получим формулу подсчета общей проводимости:
g = g 1 + g 2 + g 3 .
Таким образом, при параллельном соединении увеличивается не сопротивление, а проводимость .
Пример 3. Определить общее сопротивление трех параллельно включенных сопротивлений, если r 1 = 2 Ом, r 2 = 3 Ом, r 3 = 4 Ом.
Пример 4. Пять сопротивлений 20, 30 ,15, 40 и 60 Ом включены параллельно в сеть. Определить общее сопротивление:
Следует заметить, что при подсчете общего сопротивления разветвления оно получается всегда меньше, чем самое меньшее сопротивление, входящее в разветвление.
Если сопротивления, включенные параллельно, равны между собой, то общее сопротивление r цепи равно сопротивлению одной ветви r 1 , деленному на число ветвей n :
Пример 5. Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 Ом каждое:
Для проверки попробуем найти сопротивление разветвления по формуле:
Как видим, ответ получается тот же.
Пример 6. Пусть требуется определить токи в каждой ветви при параллельном их соединении, изображенном на рисунке 5, а .
Найдем общее сопротивление цепи:
Теперь все разветвления мы можем изобразить упрощенно как одно сопротивление (рисунок 5, б ).
Падение напряжения на участке между точками А и Б будет:
U = I × r = 22 × 1,09 = 24 В.
Возвращаясь снова к рисунку 5, а видим, что все три сопротивления окажутся под напряжением 24 В, так как они включены между точками А и Б .
Рассматривая первую ветвь разветвления с сопротивлением r 1 , мы видим, что напряжение на этом участке 24 В, сопротивление участка 2 Ом. По закону Ома для участка цепи ток на этом участке будет:
Ток второй ветви
Ток третьей ветви
Проверим по первому закону Кирхгофа
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов
.
При последовательном соединении
нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк (19)
где R
эк
=
R 1 + R 2 + R 3
.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи
U = U 1 + U 2 +U 3 (20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U 1: U 2: U 3 = R 1: R 2: R 3 (21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов
. При параллельном соединении
нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов
. Смешанным соединением
называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.
Параллельные соединения резисторов, формула расчёта которых выводится из закона Ома и правил Кирхгофа, являются наиболее распространённым типом включения элементов в электрическую цепь. При параллельном соединении проводников два или несколько элементов объединяются своими контактами с обеих из сторон соответственно. Подключение их к общей схеме осуществляется именно этими узловыми точками.
Gif?x15027″ alt=»Общий вид»>
Общий вид
Особенности включения
Включённые таким образом проводники нередко входят в состав сложных цепочек, содержащих, помимо этого, последовательное соединение отдельных участков.
Для такого включения типичны следующие особенности:
- Общее напряжение в каждой из ветвей будет иметь одно и то же значение;
- Протекающий в любом из сопротивлений электрический ток всегда обратно пропорционален величине их номинала.
В частном случае, когда все включённые в параллель резисторы имеют одинаковые номинальные значения, протекающие по ним «индивидуальные» токи также будут равны между собой.
Расчёт
Сопротивления ряда соединённых в параллель проводящих элементов определяются по общеизвестной форме расчёта, предполагающей сложение их проводимостей (обратных сопротивлению величин).
Протекающий в каждом из отдельных проводников ток в соответствие с законом Ома, может быть найден по формуле:
I= U/R (одного из резисторов).
После ознакомления с общими принципами обсчёта элементов сложных цепочек можно перейти к конкретным примерам решения задач данного класса.
Типичные подключения
Пример №1
Нередко для решения стоящей перед конструктором задачи требуется путём объединения нескольких элементов получить в итоге конкретное сопротивление. При рассмотрении простейшего варианта такого решения допустим, что общее сопротивление цепочки из нескольких элементов должно составлять 8 Ом. Этот пример нуждается в отдельном рассмотрении по той простой причине, что в стандартном ряду сопротивлений номинал в 8 Ом отсутствует (есть только 7,5 и 8,2 Ом).
Решение этой простейшей задачи удаётся получить за счёт соединения двух одинаковых элементов с сопротивлениями по 16 Ом каждое (такие номиналы в резистивном ряду существуют). Согласно приводимой выше формуле общее сопротивление цепочки в этом случае вычисляется очень просто.
Из неё следует:
16х16/32=8 (Ом), то есть как раз столько, сколько требовалось получить.
Таким сравнительно простым способом удаётся решить задачу формирования общего сопротивления, равного 8-ми Омам.
Пример №2
В качестве ещё одного характерного примера образования требуемого сопротивления можно рассмотреть построение схемы, состоящей из 3-х резисторов.
Общее значение R такого включения может быть рассчитано по формуле последовательного и параллельного соединения в проводниках.
Gif?x15027″ alt=»Пример»>
В соответствии с указанными на картинке значениями номиналов, общее сопротивление цепочки будет равно:
1/R = 1/200+1/220+1/470 = 0,0117;
R=1/0,0117 = 85,67Ом.
В итоге находим суммарное сопротивление всей цепочки, получаемой при параллельном соединении трёх элементов с номинальными значениями 200, 240 и 470 Ом.
Важно! Указанный метод применим и при расчёте произвольного числа соединенных в параллель проводников или потребителей.
Также необходимо отметить, что при таком способе включения различных по величине элементов общее сопротивление будет меньше, чем у самого малого номинала.
Расчёт комбинированных схем
Рассмотренный метод может применяться и при расчёте сопротивления более сложных или комбинированных схем, состоящих из целого набора компонентов. Их иногда называют смешанными, поскольку при формировании цепочек используются сразу оба способа. Смешанное соединение резисторов представлено на размещенном ниже рисунке.
Gif?x15027″ alt=»Смешанная схема»>
Смешанная схема
Для упрощения расчета сначала разбиваем все резисторы по типу включения на две самостоятельные группы. Одна из них представляет собой последовательное соединение, а вторая – имеет вид подключения параллельного типа.
Из приведённой схемы видно, что элементы R2 и R3 соединяются последовательно (они объединены в группу 2), которая, в свою очередь, включена в параллель с резистором R1, принадлежащим группе 1.
Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому
\(~I = I_1 = I_2 .\)
Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R A → 0).
Включенные вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2 . Вольтметр V измеряет подведенное к клеммам Μ и N напряжение U .n R_i .\)
Если сопротивления отдельных резисторов равны между собой, т.е. R 1 = R 2 = … = R n , то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR 1 .
При последовательном соединении резисторов справедливо соотношение \(~\frac{U_1}{U_2} = \frac{R_1}{R_2}\), т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.
Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам Μ и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:
\(~U = U_1 = U_2 .n \frac{1}{R_i} .\)
Если сопротивления всех n параллельно соединенных резисторов одинаковы и равны R 1 то \(~\frac 1R = \frac{n}{R_1}\) . Откуда \(~R = \frac{R_1}{n}\) .
Сопротивление цепи, состоящей из n одинаковых параллельно соединенных резисторов, в n раз меньше сопротивления каждого из них.
При параллельном соединении резисторов справедливо соотношение \(~\frac{I_1}{I_2} = \frac{R_2}{R_1}\), т.е. силы токов в ветвях параллельно соединенной цепи обратно пропорциональны сопротивлениям ветвей.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 257-259.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Формула эквивалентного сопротивления при параллельном соединении резисторов
Последовательное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление R
общПри таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление R
общПри таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление R
общДля того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»:
Источник: hightolow.ru
Расчет сопротивления параллельного соединения резисторов
При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов
Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.
Параллельное соединение
При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.
Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).
При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:
- Номинал резистора в 16 Ом подойдет.
- Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).
В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:
- Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
- Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.
Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
Последовательное подключение
Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:
- Ток не изменяется на участке цепи.
- Общее напряжение равно сумме падений напряжений на каждом резисторе.
- Rобщ = R1 + R2 + … + Rn.
Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:
- I = I1 = I2 = 0,5 (А).
- Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
- Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).
Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.
Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.
Источник: rusenergetics.ru
Параллельное соединение сопротивлений
Параллельным соединением резисторов (или приемников энергии, ветвей,сопротивлений) называется такое, при котором к одним и тем же двум узлам электрической цепи (рисунок 1) присоединены несколько резисторов (ветвей).
Рис. 1 Изображение параллельного соединения трех резисторов
Проводимость при параллельном соединении
Сопротивление при параллельном соединении:
Для трёх параллельно соединенных сопротивлений
Для двух параллельно соединенных сопротивлений
Для ветвей с одинаковым сопротивлением где n количество ветвей
Ток при параллельном соединении
Мощность при параллельном соединении
Доказательство
Так как резисторы присоединены к одним и тем же узлам, то каждый из них находится под одинаковым напряжением U. Согласно закону Ома токи в сопртивлениях определяются по формулам
Из этих формул следует, что токи в параллельных ветвях с сопротивлениями распределяются прямо пропорционально проводимостям ветвей или обратно пропорционально их сопротивлениям. Ряд параллельно соединенных резисторов можно заменить эквивалентным с сопротивлением R, значение которого должно быть таким, чтобы при том же напряжении на выводах ток в эквивалентном резисторе был равен сумме токов в отдельных ветвях:
т. е. эквивалентная проводимость параллельного соединения резисторов равна сумме проводимостей всех параллельных ветвей. Следовательно, эквивалентное сопротивление будет меньше самого малого из параллельно соединенных резисторов.
Формула (1) дает возможность определить и эквивалентное сопротивление параллельного соединения резисторов. Например, при трех ветвях эквивалентная проводимость
и эквивалентное сопротивление
Для двух резисторов
Если сопротивление ветвей одинаково R1 = R2 = R3, то можно воспользоваться формулой
в общем случае при соединении n резисторов с одинаковым сопротивлением R1 эквивалентное сопротивление равно
Мощности параллельно соединенных резисторов равна сумме мощностей всех резисторов
Источник: electrikam.com
Постоянный ток
Господа, в прошлый раз мы с вами говорили про последовательное сопротивление резисторов . Сегодня я бы хотел вам рассказать про другой возможный вид соединения – параллельное.
Чем различается последовательное и параллельное соединение я уже писал в предыдущей статье . Но все-таки вытащу сюда картинку из той прошлой статьи, я ж знаю, что вам будет лень ходить по ссылкам .
А) – Последовательное соединение
В) – Параллельное соединение
Рисунок 1 – Последовательное и параллельное соединение
Как мы видим из рисунка 1, параллельное соединение – это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы – в другой узел.
Сейчас наша задача будет разобраться, как ведут себя токи , напряжения , сопротивления и мощности при таком подключении. Для этого прошу вас взглянуть на рисунок 2, где подробно разрисован расклад дел для параллельного соединения. Будем полагать, что мы знаем величины R1, R2 и R3, а также величину приложенного к схеме напряжения U. Про токи же мы ничего не знаем.
Рисунок 2 – Параллельное соединения
Что мы видим на рисунке 2? Ну, в первую очередь – два узла А и B. В узел А сходятся одни концы всех резисторов, а в узел В – другие концы. Пусть узел А имеет потенциал φ1, а узел В – потенциал φ2. Из рисунка 2 видно, что для всех резисторов R1, R2 и R3 у нас одна и та же разность потенциалов U.
Как следует из статьи про потенциалы , это означает, что напряжение на всех резисторах у нас одинаково и равно приложенному напряжению U. Это важный вывод, его следует хорошо запомнить.
С токами дело обстоит по-другому. Проанализируем рисунок 2 слева направо. Пусть у нас в цепи течет ток I. Течет он себе, течет, никого не трогает и тут вдруг натыкается на узел А. Что в этом случае говорит полюбившаяся вам статья про первый закон Кирхгофа ? А то, что ток I в узле А разделится на три тока I1, I2, I3. При этом будет выполняться равенство
То есть через резистор R1 будет протекать ток I1, через резистор R2 – ток I2, а через резистор R3 – ток I3.
Итак, у нас в системе уже тихо-мирно текут себе три тока. И все хорошо, пока они не наткнуться на узел В. Тут снова вступает в силу первый закон Кирхгофа. Эти три тока I1, I2, I3 вновь соединятся в один ток I. Причем после узла В ток будет иметь такую же величину I, какой он был до узла А.
То есть если все вышесказанное воплотить в лаконичный язык наскальной живописи, положение дел можно представить себе вот так
Как же найти эти самые токи I1, I2, I3? Господа, полагаю, вы уже догадались, что на помощь нам придет горячо нами всеми любимый закон Ома . Действительно, мы знаем сопротивления резисторов и, кроме того, нам известно, что на всех них падает одно и тоже напряжение U. Поэтому легко находим токи
Отлично, мы разобрались с напряжениями и с токами в такой схеме. А помните в статье про последовательное сопротивление мы ловко преобразовали три резистора в один с эквивалентным им сопротивлением? Нельзя ли и здесь сделать что-то подобное? Оказывается, вполне себе можно. Как мы помним, токи в схеме распределены таким вот образом
Обзовем эквивалентное сопротивление буковкой R. И подставим в это выражение только что найденные нами токи I1, I2, I3
Видим, что здесь без проблем можно сократить левую и правую части на U. Получаем
Господа, важный вывод: при параллельном соединении резисторов обратное эквивалентное сопротивление равно сумме обратных сопротивлений отдельных резисторов.
То есть для упрощения различных расчетов электрических схем такую вот цепочку параллельно соединенных резисторов можно заменить одним резистором с соответствующим сопротивлением, как показано на рисунке 3.
Рисунок 3 – Преобразование параллельного соединение
Весьма частый случай на практике, когда соединены параллельно не много резисторов, а всего два. Поэтому полезно знать наизусть итоговое сопротивление такой схемы. Давайте посмотрим, чему оно равно:
То есть, если у вас два сопротивления соединены параллельно, то по этой формуле вы легко высчитаете общее сопротивление. Рассмотрим пример. Пусть у нас параллельно соединены два резистора 10 кОм и 15 кОм. Чему равно их общее сопротивление?
Заметьте, господа, итоговое сопротивление у нас получилось 6 кОм, что меньше 10 кОм и 15 кОм. То есть при параллельном соединении общее сопротивление меньше любого из составляющих. Это всегда верно для любого количества резисторов, а не только для двух. Итоговое сопротивление всегда уменьшается (в отличии от последовательного сопротивления, где итоговое сопротивление всегда растет). Этот факт полезно запомнить.
Еще один часто встречающийся на практике случай – когда параллельно соединены несколько резисторов с одинаковым сопротивлением. Допустим, каждый из них обладает сопротивлением R1 и всего их N штук. Тогда по нашей общей формуле для эквивалентного сопротивления
То есть при параллельном соединении N одинаковых резисторов с сопротивлением R1 итоговое сопротивление будет в N раз меньше этого самого сопротивления R1.
Так-с, с током разобрались, с напряжением разобрались, с эквивалентным сопротивлением вроде тоже…осталась мощность. Для этого воспользуемся вот этим выражением, которое мы писали чуть выше в статье
Умножим левую и правую части на напряжение U.
Как мы помним из статьи про мощность произведение тока на напряжение есть мощность. То есть мы можем записать
где Р – мощность, выдаваемая источником;
P1 – мощность, рассеиваемая на резисторе R1;
P2 – мощность, рассеиваемая на резисторе R2;
P3 – мощность, рассеиваемая на резисторе R3.
Заметьте, господа, формула в точности такая же, как и для случая последовательного соединения резисторов. И там и там мощность, выдаваемая источником, равна сумме мощностей, рассеиваемых на резисторах цепи.
Итак, господа, мы рассмотрели основные соотношения при параллельном соединении резисторов. Теперь осталось поговорить, где это параллельное соединение можно использовать и для чего.
1) Ну, во-первых, параллельное соединение применяют во всех случаях, когда хотят запитать несколько нагрузок от одного источника напряжения. При этом пользуются тем свойством, что при параллельном соединении напряжения на всех нагрузках одинаково. То есть, допустим, вы берете источник напряжения, выставляете на нем напряжение 5 В и цепляете к этому источнику сразу несколько своих устройств. Узлами А и В в этом случае будут клеммы источника. На каждое из устройств в этом случае придет напряжение 5 В. Да и все устройства в вашей квартире (лампочки, компьютеры, телевизоры и все прочее) соединены между собой параллельно.
2) Второе возможное применение встречается не так часто, но, думаю, о нем тоже следует рассказать. Допустим, вы делаете какую-то схему, где необходим очень точный подгон сопротивления. Скажем, надо получить сопротивление 6 кОм. Такое сопротивление найти нелегко, их просто не продают. Зато у вас есть два сопротивления 10 кОм и 15 кОм. Вы их соединяете параллельно и получаете требуемые 6 кОм. Как показывает практика, 3 параллельных резисторов достаточно для получения итогового результирующего сопротивления требуемого номинала с весьма хорошей точностью. Конечно, таких вещей лучше избегать и, если есть возможность, всегда стараться применять стандартные сопротивления. Но бывают случаи, когда это невозможно, и тогда приходит на помощь этот метод.
3) Третий пункт будет немного похож на первый. Его суть заключается в следующим. Допустим, нам надо снять с источника питания 10 Вт мощности. А у нас в наличии только резисторы, которые позволяют рассеивать на себе 1 Вт. Что делать? Можно соединить 10 резисторов параллельно и с каждого снимать по 1 Вт. Мы же помним нашу формулу
Конечно, лучше брать не 10 резисторов, а хотя бы 15 и рассеивать на них меньше, чем 1 Вт. Работать на пределе никогда не следует.
Кстати, тут очень вовремя к моменту написания статьи пришли платы с производства! Господа, прошу вас взглянуть на рисунок 4.
Рисунок 4 – Плата нагревателя
На нем изображена плата нагревателя (флешка для масштаба). В чем суть? Имеется весьма сложное устройство, предназначенное для работы в арктических условиях. Найти же компоненты, которые надежно функционировать при температурах минус 55 градусов и при этом стоят адекватных денег и обладают адекватными размерами бывает непросто. Обычно элементная база в лучшем случае рассчитана на минус 40 градусов. И было принято решение разработать вот такой вот нагреватель для прогрева чувствительных к холоду аналоговых узлов устройства. Он управляется с микроконтроллера и автоматически включается при температурах меньше минус 40 градусов. Как вы можете видеть из рисунка 4, этот нагреватель представляет собой 30 параллельно соединенных резисторов с сопротивлениями 150 Ом. Каждый резистор, согласно документации, способен рассеивать до 1 Вт мощности. Используя изученные формулки, мы можем посчитать, что в сумме такая система обладает сопротивлением
и теоретически может рассеивать мощность
Ну, с сопротивлением вопросов нет, оно действительно равно 5 Ом. Ну, плюс-минус 5 % на допуск резисторов, что в данном случае вообще не критично. А вот с мощностью тут не так все однозначно. Помните про закон Джоуля-Ленца , который мы рассматривали? Резисторы будут греться, причем не слабо. Как показывает практика, если нагружать резисторы по полной, то есть рассеивать на каждом по 1 Вт, то в течении нескольких секунд их температура улетит за 150 градусов. Такая высокая температура критична для резистора и может привести к его разрушению. Я был готов к такому развитию событий, поэтому заложил для платы нагревателя максимальное напряжение 9 вольт. Это значит, что на каждом резисторе будет выделяться
что почти в два раза меньше максимально допустимой мощности в 1 Вт. В сумме на всей плате выделялось, соответственно
Эксперимент показал, что резисторы достигли температуры с комнатных 25 градусов до критичных 120 градусов приблизительно за 10 секунд работы и температура продолжала уверенно расти. Очевидно, если оставить на длительное время включенным такой нагреватель при комнатной температуре, он неминуемо выйдет из строя. Возможно, при работе на минус 55 градусах перегрев бы не был столь критичным, однако хотелось исключить вариант спалить плату на столе, поэтому я понизил напряжение, подаваемое на плату на 3 вольта: стал подавать 6 вольт. Теперь на каждом резисторе рассеивалось
а на всей плате
Теперь температура поднималась до 100-110 градусов примерно за 30-40 секунд работы и оставалась на этом уровне (выходила в точку термодинамического равновесия). Эта температура вполне подходит для нагревателя. Однако пока это были лишь эксперименты на столе при комнатной температуре, главный эксперимент – в термокамере на минус 55 градусах – впереди. Возможно, по его результатам потребуется чуть увеличить рассеиваемую мощность. А может все останется как есть и этой мощности будет достаточно для вывода девайса на режим за адекватное время, время покажет .
На сегодня все, господа. Удачи вам и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Источник: myelectronix.ru
Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Источник: www.joyta.ru
Формула расчета напряжения при последовательном соединении. Виды соединения проводников
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Содержание:Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.
- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
Во многих электрических схемах мы можем обнаружить последовательное и . Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление.
Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи.
Последовательное соединение резисторов
Пример № 1
Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:
Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:
Пример № 2
а) без подключенного резистора R3
б) с подключенным резистором R3
Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.
Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) — то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R).
Последовательное соединение сопротивлений
Возьмем три неизменных сопротивления R1, R2 и R3 и включим их в цепь так, чтоб конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).
Такое соединение сопротивлений именуется поочередным. Разумеется, что ток в таковой цепи будет во всех ее точках один и тот же.
Рис 1 . Последовательное соединение сопротивлений
Как найти общее сопротивление цепи, если все включенные в нее поочередно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U = U1 + U2 + U3
где
U1 = IR1 U2 = IR2 и U3 = IR3
либо
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .
Поделив сейчас обе части равенства на I , будем совсем иметь R = R1 + R2 + R3
Таким макаром, мы сделали вывод, что при поочередном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на последующем примере. Возьмем три неизменных сопротивления, величины которых известны (к примеру, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их поочередно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).
Рис. 2. Пример поочередного соединения 3-х сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим наружное сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи по закону Ома: 60 / 80 = 0 ,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во наружной цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.
Мы получили таким макаром, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Разъясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув сейчас ключ выключатель К, можно убедиться по устройствам, что наши подсчеты приблизительно верны.
Возьмем два неизменных сопротивления R1 и R2 и соединим их так, чтоб начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив потом точки а и б с источником тока, получим замкнутую электронную цепь. Такое соединение сопротивлений именуется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, потому что тут сама цепь разветвляется на две отдельные ветки: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Любой из этих токов пойдет по собственной ветки до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким макаром, при параллельном соединении сопротивлений выходит разветвленная цепь. Поглядим, какое же будет соотношение меж токами в составленной нами цепи.
Включим амперметр меж положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив потом амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.
Означает, сила тока в цепи до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем сейчас включать амперметр попеременно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветки амперметр покажет силу тока I1 , а во 2-ой — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Как следует, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим
Это соотношение, имеющее огромное практическое значение, носит заглавие закона разветвленной цепи .
Разглядим сейчас, каково будет соотношение меж токами в ветвях.
Включим меж точками а и б вольтметр и поглядим, что он нам покажет. Во-1-х, вольтметр покажет напряжение источника тока, потому что он подключен, как это видно из рис. 3 , конкретно к зажимам источника тока. Во-2-х, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R1 и R2, потому что он соединен с началом и концом каждого сопротивления.
Как следует, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2 ,
где U — напряжение на зажимах источника тока; U1 — падение напряжения на сопротивлении R1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .
Потому для каждой ветки можно написать: U1 = I1R1 и U2 = I2R2 , но потому что U1 = U2, то и I1R1 = I2R2 .
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветки будет во столько раз больше (либо меньше) тока во 2-ой ветки, во сколько раз сопротивление первой ветки меньше (либо больше) сопротивления 2-ой ветки.
Итак, мы пришли к принципиальному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, назад пропорциональные величинам сопротивлении параллельных веток. По другому говоря, чем больше сопротивление ветки, тем наименьший ток потечет через нее, и, напротив, чем меньше сопротивление ветки, тем больший ток потечет через эту ветвь.
Убедимся в корректности этой зависимости на последующем примере. Соберем схему, состоящую из 2-ух параллельно соединенных сопротивлений R1 и R 2, присоединенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем поначалу, что покажет нам амперметр, включенный в каждую ветвь:
I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА
I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1 +I2 = 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется назад пропорционально сопротивлениям.
Вправду, R1 == 10 Ом в два раза меньше R 2 = 20 Ом, при всем этом I1 = 300 мА в два раза больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть (I1 = 300 мА) пошла через наименьшее сопротивление (R1 = 10 Ом), а наименьшая часть (R2 = 150 мА) -через большее сопротивление (R 2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением воды по трубам. Представьте для себя трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного поперечника (рис. 4). Потому что поперечник трубы Б больше поперечника трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает сгустку воды большее сопротивление.
Рис. 4
Разглядим сейчас, чему будет равно общее сопротивление наружной цепи, состоящей из 2-ух параллельно соединенных сопротивлений.
Под этим общим сопротивлением наружной цепи нужно осознавать такое сопротивление, которым можно было бы поменять при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при всем этом тока до разветвления. Такое сопротивление именуется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и поглядим, чему будет равно эквивалентное сопротивление 2-ух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во наружной цепи (до точки разветвления), U — напряжение наружной цепи, R — сопротивление наружной цепи, т. е. эквивалентное сопротивление.
Точно так же для каждой ветки I1 = U1 / R1 , I2 = U2 / R2 , где I1 и I 2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления веток.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Потому что при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )
Разделив сейчас обе части равенства на U , будем совсем иметь 1 / R = 1 / R1 + 1 / R2
Помня, что проводимостью именуется величина, оборотная сопротивлению , мы можем сказать, что в приобретенной формуле 1 / R — проводимость наружной цепи; 1 / R1 проводимость первой ветки; 1 / R2- проводимость 2-ой ветки.
На основании этой формулы делаем вывод: при параллельном соединении проводимость наружной цепи равна сумме проводимостей отдельных веток.
Как следует, чтоб найти эквивалентное сопротивление включенных параллельно сопротивлений, нужно найти проводимость цепи и взять величину, ей оборотную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветки, а это означает, что эквивалентное сопротивление наружной цепи меньше меньшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли более ординарную цепь, состоящую из 2-ух веток. Но на практике могут повстречаться случаи, когда цепь состоит из 3-х и поболее параллельных веток. Как поступать в этих случаях?
Оказывается, все приобретенные нами соотношения остаются справедливыми и для цепи, состоящей из хоть какого числа параллельно соединенных сопротивлений.
Чтоб убедиться в этом, разглядим последующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5 ). R = 1 / 6 Как следует, эквивалентное сопротивление R = 6 Ом.
Таким макаром, эквивалентное сопротивление меньше меньшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.
Поглядим сейчас, вправду ли это сопротивление является эквивалентным, т. е. таким, которое могло бы поменять включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при всем этом силы тока до разветвления цепи.
Допустим, что напряжение наружной цепи, а как следует, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0,2 А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 =1,2 + 0,6 + 0,2 = 2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если заместо 3-х параллельно включенных узнаваемых нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U / R = 12 / 6 = 2 А
Как лицезреем, отысканное нами сопротивление R = 6 Ом вправду является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных устройствах, если собрать схему с взятыми нами сопротивлениями, измерить ток во наружной цепи (до разветвления), потом поменять параллельно включенные сопротивления одним сопротивлением 6 Ом и опять измерить ток. Показания амперметра и в том и в другом случае будут приблизительно схожими.
На практике могут повстречаться также параллельные соединения, для которых высчитать эквивалентное сопротивление можно проще, т. е. не определяя за ранее проводимостей, сходу отыскать сопротивление.
К примеру, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно конвертировать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / (R1 + R2 ), т. е. при параллельном соединении 2-ух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Обычно все затрудняются ответить. А вот загадка эта в применении к электричеству решается вполне определенно.
Электричество начинается с закона Ома.
А уж если рассматривать дилемму в контексте параллельного или последовательного соединений — считая одно соединение курицей, а другое — яйцом, то сомнений вообще нет никаких.
Потому что закон Ома — это и есть самая первоначальная электрическая цепь. И она может быть только последовательной.
Да, придумали гальванический элемент и не знали, что с ним делать, поэтому сразу придумали еще лампочку. И вот что из этого получилось. Здесь напряжение в 1,5 В немедленно потекло в качестве тока, чтобы неукоснительно выполнять закон Ома, через лампочку к задней стенке того же элемента питания. А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.
И это обычно рисуют на схеме вот так:
По закону Ома I=U/R
Тогда сопротивление лампочки (с тем током и напряжением, которые я написал) получится
R = 1/U , где R = 1 Ом
А мощность будет выделяться P = I * U , то есть P=2,25 Вm
В последовательной цепи, особенно на таком простом и несомненном примере, видно, что ток, который бежит по ней от начала до конца, — все время один и тот же. А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
Он получится равным I=U/R+R,то есть 0,75А, ровно половина того тока, который был сначала.
В этом случае току приходится преодолевать уже два сопротивления, он становится меньше. Что и видно по свечению лампочек — они теперь горят вполнакала. А общее сопротивление цепочки из двух лампочек будет равно сумме их сопротивлений. Зная арифметику, можно в отдельном случае воспользоваться и действием умножения: если последовательно соединены N одинаковых лампочек, то общее их сопротивление будет равно N, умноженное на R, где R — сопротивление одной лампочки. Логика безупречная.
А мы продолжим наши опыты. Теперь сделаем нечто подобное, что мы провернули с лампочками, но только на левой стороне цепи: добавим еще один гальванический элемент, точно такой, как первый. Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.
Делаем вывод:
- При последовательном соединении электрической цепи сопротивления и напряжения ее элементов суммируются, а ток на всех элементах остается неизменным.
Легко проверить, что это утверждение справедливо как для активных компонентов (гальванических элементов), так и для пассивных (лампочек, резисторов).
То есть это значит, что напряжение, измеренное на одном резисторе (оно называется падением напряжения), можно смело суммировать с напряжением, измеренным на другом резисторе, и в сумме получатся те же 3 В. А на каждом из сопротивлений оно окажется равным половине — то есть 1,5 В. И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
Вернемся к первой схеме, подключим в ней еще одну лампочку, но иначе.
Теперь напряжение в точках, соединяющих две ветки, то же, что и на гальваническом элементе — 1,5 В. Но так как сопротивление у обеих лампочек тоже такое, как и было, то и ток через каждую из них пойдет 1,5 А — ток «полного накала».
Гальванический элемент теперь питает их током одновременно, следовательно, из него вытекают сразу оба эти тока. То есть общий ток из источника напряжения будет равен 1,5 А + 1,5 А = 3,0 А.
В чем же отличие этой схемы от схемы, когда те же самые лампочки были включены последовательно? Только в накале лампочек, то есть только в токе.
Тогда ток был 0,75 А, а теперь он стал сразу 3 А.
Получается, если сравнить с первоначальной схемой, то при последовательном соединении лампочек (схема 2) току сопротивления оказывалось больше (отчего он уменьшался, и лампочки теряли светимость), а параллельное подключение оказывает МЕНЬШЕ сопротивления, хотя сопротивление лампочек осталось неизменным. В чем тут дело?
А дело в том, что мы забываем одну интересную истину, что всякая палка о двух концах.
Когда мы говорим, что резистор сопротивляется току, то как бы забываем, что он ток все-таки проводит. И теперь, когда подключили лампочки параллельно, увеличилось суммарное для них свойство проводить ток, а не сопротивляться ему. Ну и, соответственно, некую величину G , по аналогии с сопротивлением R и следовало бы назвать проводимостью. И должна она в параллельном соединении проводников суммироваться.
Ну и вот она
Закон Ома тогда будет выглядеть
I = U * G &
И в случае параллельного соединения ток I будет равен U*(G+G) = 2*U*G, что мы как раз и наблюдаем.
Замена элементов цепи общим эквивалентным элементом
Инженерам часто приходится узнавать токи и напряжения во всех частях схем. А реальные электрические схемы бывают достаточно сложными и разветвленными и могут содержать множество элементов, активно потребляющих электроэнергию и соединенных друг с другом в совершенно разных сочетаниях. Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.
Самое первое что, напрашивается — это воспользоваться знанием того, как ведут себя токи напряжения в таких простейших соединениях сети, как последовательное и параллельное. Делают так: вместо найденного в сети последовательного соединения двух или более активных устройств-потребителей (как наши лампочки) нарисовать один, но чтобы его сопротивление было таким же, как у обоих. Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Теперь если схему перерисовать, заменив последовательные и параллельные соединения одним элементом, то получим схему, которая называется «схемой эквивалентного замещения».
Такую процедуру можно продолжать до тех пор, пока у нас не останется наипростейшая — которой мы в самом начале иллюстрировали закон Ома. Только вместо лампочки будет стоять одно сопротивление, которое и называют эквивалентным сопротивлением нагрузки.
Это первая задача. Она дает нам возможность по закону Ома рассчитать общий ток во всей сети, или общий ток нагрузки.
Вот это и есть полный расчет электрической сети.
Примеры
Пусть цепь содержит 9 активных сопротивлений. Это могут быть лампочки или что-то другое.
На ее входные клеммы подано напряжение в 60 В.
Значения сопротивлений для всех элементов следующие:
Найти все неизвестные токи и напряжения.
Надо пойти по пути поиска параллельных и последовательных участков сети, рассчитывать эквивалентные им сопротивления и постепенно упрощать схему. Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.
Теперь заменяем параллельный кусочек из сопротивлений R 8 и R э 3, 6, 9, получая R э 8, 3, 6, 9 . Только при параллельном соединении проводников, складывать придется проводимости.
Проводимость измеряется в единицах, называемых сименсами, обратных омам.
Если перевернуть дробь, получим сопротивление R э 8, 3, 6, 9 = 2 Ом
Совершенно так же, как в первом случае, объединяем сопротивления R 2 , R э 8, 3, 6, 9 и R 5, включенные последовательно, получая R э 2, 8, 3, 6, 9, 5 = 1 + 2 + 1 = 4 Ом.
Осталось два шага: получить сопротивление, эквивалентное двум резисторам параллельного соединения проводников R 7 и R э 2, 8, 3, 6, 9, 5.
Оно равно R э 7, 2, 8, 3, 6, 9, 5 = 1/(1/4+1/4)=1/(2/4)=4/2 = 2 Ом
На последнем шаге просуммируем все последовательно включенные сопротивления R 1 , R э 7, 2, 8, 3, 6, 9, 5 и R 4 и получим сопротивление, эквивалентное сопротивлению всей цепи R э и равное сумме этих трех сопротивлений
R э = R 1 + R э 7, 2, 8, 3, 6, 9, 5 + R4 = 1 + 2 + 1 = 4 Ом
Ну и вспомним, в честь кого назвали единицу сопротивлений, написанную нами в последней из этих формул, и вычислим по его закону общий ток во всей цепи I
Теперь, двигаясь в обратном направлении, в сторону все большего усложнения сети, можно получать по закону Ома токи и напряжения во всех цепочках нашей достаточно простой схемы.
Так обычно и рассчитывают схемы электроснабжения квартир, которые состоят из параллельных и последовательных участков. Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.
Напряжение при параллельном соединении резисторов. Сопротивление при параллельном соединении: формула расчета
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение
Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:
Смешанное соединение
Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R 3 . Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 , соединены последовательно.
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема
Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
И находят сопротивления R 1 , R 2 и R 3 .
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
2) Общее сопротивление R общ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Общее сопротивление R общ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
3)Электропроводность, электрическая проводимость, проводимость, способность тела пропускать электрический ток под воздействием электрического поля, а также физическая величина, количественно характеризующая эту способность. Тела, проводящие электрический ток, называются проводниками, в отличие от изоляторов.. .
Основная единица измерения сопротивления — Ом. Удельная проводимость — величина обратная сопротивлению, она измеряется в Сименсах, ранее назывшихся mho. Применительно к сыпучим веществам удобнее говорить об особой проводимости, обычно называемой удельной проводимостью.
Удельная проводимость — это проводимость, измеренная между противоположными сторонами куба вещества со стороной 1 см. Единицей данного типа измерений является Сименс/см. При измерении проводимости воды чаще используются более точные мкС/см (микросименс) и мС/см (миллисименс) .
Соответствующие единицы измерения сопротивления (или удельного сопротивления) — Ом/см, МегаОм/см и килоОм/см. При измерении сверхчистой воды чаще используют МегаОм/см, так как это дает более точные результаты. Сопротивление менее чистой воды, как например, водопроводной, измеряют в килоОм/см.
4) Общее сопротивление при последовательном соединении равно сумме сопротивлений Rсумм=R1+R2+R3…
Ток через все сопротивления протекает один (I). Поэтому ток вычисляешь как Отношение напряжения источника U к Rсумм.
Мощность
P=U*I или P=I*I*R (так как U=I*R).
P1=I*I*R1
P2=I*I*R2
P3=I*I*R3
5) мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:
При параллельном соединении каждая лампа подсоединяется на своё номинальное напряжение 220 В. при этом в каждой лампе появляется свой номинальный ток, обеспечивающий заданное свечение в соответствии с номинальной мощностью. мощность зависит от сопротивления нити накаливания. чем больше сопротивление нити, тем меньше ток и соответственно меньше номинальная мощность.
при последовательном соединении ток идёт один и тот же в каждой лампе. а напряжение распределяется в зависимости от доли сопротивления каждой лампы по отношению к сопротивлению всей цепи.
для цепи из двух ламп общее напряжение делится.
напряжение на лампе 40 Вт будет 220Х60:(40+60)=132; В.
напряжение на лампе 60 Вт будет 220Х40:(40+60)=80; В.
Параллельным соединением сопротивлений называется такое соединение, когда начала сопротивлений соединены в одну общую точку, а концы — в другую.
Для параллельного соединения сопротивлений характерны следующие свойства:
Напряжения на зажимах всех сопротивлений одинаковы:
U 1 = U 2 = U 3 = U;
— проводимость всех параллельно соединённых сопротивлений равна сумме проводимостей отдельных сопротивлений:
1/R = 1/R 1 + 1/R 2 + 1/R 3 = R 1 R 2 + R 1 R 3 + R 2 R 3 /R 1 R 2 R 3 ,
где R — эквивалентное (равнодействующее) сопротивление трёх сопротивлений (в данном случае R 1 , R 2 и R 3).
Чтобы получить сопротивление такой цепи, надо перевернуть дробь, определяющую величину её проводимости. Следовательно, сопротивление параллельного разветвления из трёх резисторов:
R = R 1 R 2 R 3 /R 1 R 2 + R 2 R 3 + R 1 R 3 .
Эквивалентным сопротивлением называется такое сопротивление, которым можно заменить несколько сопротивлений (включенных параллельно или последовательно), не изменяя величины тока в цепи.
Чтобы найти эквивалентное сопротивление при параллельном соединении, необходимо сложить проводимости всех отдельных участков, т.е. найти общую проводимость. Величина, обратная общей проводимости, и является общим сопротивлением.
При параллельном соединении эквивалентная проводимость равна сумме проводимостей отдельных ветвей, следовательно, эквивалентное сопротивление в этом случае всегда меньше наименьшего из параллельно включенных сопротивлений.
На практике могут быть случаи, когда цепь состоит из более, чем трёх параллельных ветвей. Все полученные соотношения остаются справедливыми и для цепей, состоящих из любого числа параллельно соединённых резисторов.
Найдём эквивалентное сопротивление двух параллельно включенных сопротивлений R 1 и R 2 (см. рис.). Проводимость первой ветви равна 1/R 1 , проводимость второй ветви — 1/R 2 . Общая проводимость:
1/R = 1/R 1 + 1/R 2 .
Приведём к общему знаменателю:
1/R = R 2 + R 1 /R 1 R 2 ,
отсюда эквивалентное сопротивление
R = R 1 R 2 /R 1 + R 2 .
Эта формула и служит для расчётов общего сопротивления цепи, состоящей из двух параллельно включенных сопротивлений.
Таким образом, эквивалентное сопротивление двух параллельно включенных сопротивлений равно произведению этих сопротивлений, делённому на их сумму.
При параллельном соединении n равных сопротивлений R1 эквивалентное сопротивление их будет в n раз меньше, т.е.
R = R 1 /n.
На схеме, изображённой на последнем рисунке, включено пять сопротивлений R 1 по 30 Ом каждое. Следовательно, общее сопротивление R будет
R = R 1 /5 = 30/5 = 6 Ом.
Можно сказать, что сумма токов, подходящих к узловой точке А (на первом рисунке), равна сумме токов, от неё отходящих:
I = I 1 + I 2 + I 3 .
Рассмотрим, как происходит разветвление тока в цепях с сопротивлениями R 1 и R 2 (второй рисунок). Так как напряжение на зажимах этих сопротивлений одинаково, то
U = I 1 R 1 и U = I 2 R 2 .
Левые части этих равенств одинаковы, следовательно, равны и правые части:
I 1 R 1 = I 2 R 2 ,
или
I 1 /I 2 = R 2 /R 1 ,
т.е. ток при параллельном соединении сопротивлений разветвляется обратно пропорционально сопротивлениям ветвей (или прямо пропорционально их проводимостям). Чем больше сопротивление ветви, тем меньше ток в ней, и наоборот.
Таким образом, из нескольких одинаковых резисторов можно получить общий резистор с бОльшей мощностью рассеивания.
При параллельном соединении неодинаковых резисторов в наиболее высокоомном резисторе выделяется наибольшая мощность.
Пример 1. Имеются два сопротивления, включенных параллельно. Сопротивление R 1 = 25 Ом, а R 2 = 50 Ом. Определить общее сопротивление цепи R общ.
Решение. Rобщ = R 1 R 2 /R 1 + R 2 = 25 x 50 / 25 + 50 ≈ 16, 6 Ом.
Пример 2. В ламповом усилителе имеются три лампы, нити накала которых включены параллельно. Ток накала первой лампы I 1 = 1 ампер, второй I 2 = 1, 5 ампера и третьей I 3 = 2, 5 ампера. Определить общий ток цепи накала ламп усилителя I общ.
Решение. I общ = I 1 + I 2 + I 3 = 1 + 1, 5 + 2, 5 = 5 ампер.
Параллельное соединение резисторов часто встречается в радиотехнической аппаратуре. Два или более резисторов включается параллельно в тех случаях, когда ток в цепи слишком большой и может вызвать чрезмерный нагрев резистора.
Примером параллельного соединения потребителей электрической энергии может служить включение электрических ламп обычной осветительной сети, которые соединяются параллельно. Достоинство параллельного соединения потребителей заключается в том, что выключение одного из них не влияет на работу других.
Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Соединение разными способами позволяет получить необходимую величину сопротивления и одного эквивалентного резистора. Всего существует три способы соединения резисторов – последовательное, параллельное и смешанное.
Последовательное соединение резисторовПоследовательное соединение резисторов предполагает использование двух и более радиоэлектронных элемента. Конец предыдущего элемента соединяется с началом последующего и так далее. При последовательном соединении сопротивления и мощности рассеивания всех резисторов складываются.
Рассмотрим следующий пример. Соединим последовательно четыре резистора, каждый имеет R = 1 кОм
и мощность рассеивания P = 0,25 Вт
.
Rобщ = R1 + R2 + R3 + R4 = 1кОм + 1кОм + 1кОм + 1кОм = 4 кОм.
Pобщ = P1 + P2 + P3 + P4 = 0,25 Вт + 0,25 Вт + 0,25 Вт + 0,25 Вт = 1 Вт.
Таким образом, получается один эквивалентный или общий резистор, имеющий следующие параметры:
Rобщ = 4 кОм; Pобщи = 1 Вт
.
В последовательной цепи электрической ток протекает одной и той же величины, поэтому электроны на протяжении всего пути неизбежно наталкиваются на все препятствия в виде сопротивлений. С каждым препятствием уменьшается число свободных зарядов, что приводит к снижению силы электрического тока.
При параллельном соединении резисторов увеличивается количество путей для перемещения свободных зарядов, то есть электронов, из одного участка пути к другому. Поэтому при параллельном соединении резисторов их суммарное (общее, эквивалентное) сопротивление всегда ниже наименьшего сопротивления из всех резисторов.
Величина, обратная сопротивлению называется проводимостью. Проводимость измеряется в сименсах [См] и обозначается большей латинской буквой G .
G = 1/R = 1/Ом = См
Поэтому при выполнении различных подсчетов в электрических цепях, имеющих параллельное соединение, пользуются проводимостью.
Если сопротивления всех параллельно соединенных резисторов равны, то для определения общего Rобщ достаточно R одного из них разделить на их общее количество:
Если R1 = R2 = R3 = R4 = R , то
Rобщ = R/4.
Например, каждый из четырех резисторов имеет R = 10 кОм , тогда
Rобщ = 10 кОм/4 = 2,5 кОм .
Мощности рассеивания суммируются также, как и при последовательном соединении.
Смешанное соединение резисторовСмешанное соединение резисторов представляет собой комбинации последовательных и параллельных соединений. В принципе любую даже самую сложную электрическую цепь, состоящую из источников питания, диодов, и других радиоэлектронных элементов в конкретный момент времени можно заменить резисторами и источниками напряжения, параметры которых изменяются с каждым последующим моментом времени. Для примера изобразим схему, имеющую несколько соединений.
Как изменяется мощность при параллельном соединении
Параллельным соединением резисторов (или приемников энергии, ветвей,сопротивлений) называется такое, при котором к одним и тем же двум узлам электрической цепи (рисунок 1) присоединены несколько резисторов (ветвей).
Рис. 1 Изображение параллельного соединения трех резисторов
Проводимость при параллельном соединении
Сопротивление при параллельном соединении:
Для трёх параллельно соединенных сопротивлений
Для двух параллельно соединенных сопротивлений
Для ветвей с одинаковым сопротивлением где n количество ветвей
Ток при параллельном соединении
Мощность при параллельном соединении
Доказательство
Так как резисторы присоединены к одним и тем же узлам, то каждый из них находится под одинаковым напряжением U. Согласно закону Ома токи в сопртивлениях определяются по формулам
Из этих формул следует, что токи в параллельных ветвях с сопротивлениями распределяются прямо пропорционально проводимостям ветвей или обратно пропорционально их сопротивлениям. Ряд параллельно соединенных резисторов можно заменить эквивалентным с сопротивлением R, значение которого должно быть таким, чтобы при том же напряжении на выводах ток в эквивалентном резисторе был равен сумме токов в отдельных ветвях:
т. е. эквивалентная проводимость параллельного соединения резисторов равна сумме проводимостей всех параллельных ветвей. Следовательно, эквивалентное сопротивление будет меньше самого малого из параллельно соединенных резисторов.
Формула (1) дает возможность определить и эквивалентное сопротивление параллельного соединения резисторов. Например, при трех ветвях эквивалентная проводимость
и эквивалентное сопротивление
Для двух резисторов
Если сопротивление ветвей одинаково R1 = R2 = R3, то можно воспользоваться формулой
в общем случае при соединении n резисторов с одинаковым сопротивлением R1 эквивалентное сопротивление равно
Мощности параллельно соединенных резисторов равна сумме мощностей всех резисторов
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
- P1 = I 2 x R1 = 0,256 2 x 200 = 13,11 Вт;
- P2 = I 2 x R2 = 0,256 2 x 100 = 6,55 Вт;
- P3 = I 2 x R3 = 0,256 2 x 51 = 3,34 Вт;
- P4 = I 2 x R4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при паралл ельном соединение
При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P1 = U 2 /R1 = 100 2 /200 = 50 Вт; P2 = U 2 /R2 = 100 2 /100 = 100 Вт; P3 = U 2 /R3 = 100 2 /51 = 195,9 Вт; P4 = U 2 /R4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
- P1 = I 2 x R1 = 0,256 2 x 200 = 13,11 Вт;
- P2 = I 2 x R2 = 0,256 2 x 100 = 6,55 Вт;
- P3 = I 2 x R3 = 0,256 2 x 51 = 3,34 Вт;
- P4 = I 2 x R4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при паралл ельном соединение
При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P1 = U 2 /R1 = 100 2 /200 = 50 Вт; P2 = U 2 /R2 = 100 2 /100 = 100 Вт; P3 = U 2 /R3 = 100 2 /51 = 195,9 Вт; P4 = U 2 /R4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
Сопротивлениев последовательных параллельных цепях
Оставьте свои комментарии?
Сопротивление в последовательной и параллельной цепях Как работает серия
6 часов назад Сопротивление в серии Параллельные цепи и Резисторы в серии В цепи серии общее сопротивление во всех компонентах («чистое сопротивление ») увеличивается по мере добавления дополнительных компонентов.
Веб-сайт: Bbc.co.uk
Категория : Использование в предложении
Сопротивление, резисторы
Резисторы в последовательной и параллельной цепях
2 часа назад Компоненты в цепи серии имеют одинаковый ток: ITotal = I1 = I2 =. . . Всего сопротивление в цепи серии равно сумме отдельных сопротивлений: RTotal = R1 + R2 +. . . Rn Общее напряжение в цепи серии равно сумме отдельных падений напряжения: VTotal = V1 + V2 +.. . Vn В параллельной цепи , устройства
Размер файла: 195 КБ
Количество страниц: 7
Веб-сайт: Faculty.tarleton.edu
Категория : Использование в предложении
Resistance, Resistances, Rtotal, Rn
Resistors in Series and Parallel Physics
8 часов назад Большинство схем имеют более одного компонента, называемого резистором, который ограничивает поток заряда в цепи .Мера этого предела для потока заряда называется сопротивлением . Простейшими комбинациями резисторов являются серии и параллельные соединения , показанные на рисунке 1.
Веб-сайт: Courses.lumenlearning.com
Категория : Использование в предложении
Резистор, сопротивление, резисторы
Последовательные и параллельные резисторы GeeksforGeeks
3 часа назад И формула для последовательного сопротивления задается следующим образом: R = R 1 + R 2 + R 3 +….Это комбинация сопротивлений параллельно и серии . Подставляя эти значения в уравнение, получаем R 1 = 10 Ом, R2 = 2,5 Ом. R = R 1 + R 2 ⇒ R = 10 + 2,5 ⇒ R = 12,5 ⇒ ⇒ ⇒ Ω. Вопрос 4: Найдите эквивалентное сопротивление для системы, показанной на рисунке
Веб-сайт: Geeksforgeeks.org
Категория : Используйте в предложении
Сопротивление, Сопротивления
серии и параллельно Резистивные схемы
2 часа назад серии и Параллельные Резистивные схемы 5 Комбинации серии В этой серии экспериментов будет измерено общее сопротивление резисторов в комбинации серии .Кроме того, будут проведены измерения для проверки достоверности допущений, используемых для получения теоретического выражения для общего сопротивления комбинации серии . 1.
Размер файла: 441 КБ
Количество страниц: 10
Веб-сайт: Physics.mercer.edu
Категория : Использование и в предложении
, резистивный, резистивный Резисторы
4 способа расчета последовательного и параллельного сопротивления wikiHow
4 часа назад Для расчета последовательного сопротивления , которое следует использовать при подключении «внешней» стороны одного резистора к «входной» стороне другого в цепи , используйте формулу Req = R1 + R2 +.Rn. В этой формуле n равно количеству резисторов серии . Чтобы найти параллельное сопротивление , когда «входная» и «внешняя» стороны 2 или более
Расчетное время чтения: 7 минут
Просмотры: 1.4M
Веб-сайт: Wikihow.com
Категория : Используйте в предложении
Сопротивление, резистор, Req, Rn, резисторы
Электроника сериии параллельных цепей
9 часов назад серии — Параллельные цепи • Серия — Параллельные схемы могут быть более сложными, как в этом случае: В схеме (a) у нас есть наша исходная комплексная схема .В схеме (b) у нас есть резисторы R 1 и R 2, объединенные, чтобы получить 13,2 Ом. R 4 входит в серию с недавно объединенными R 12, и их добавленная стоимость составляет 51,2 Ом. И теперь (c) у нас остается 124 рэнд в параллельно с 3 рэнд
Размер файла: 440 КБ
Количество страниц: 13
Веб-сайт: Cie-wc.edu
Категория : Использование и в предложении
Резисторы
Параллельные цепи серии
Только что Обзор параллельных цепей серии Параллельная цепь — серии или комбинация цепи объединяет в себе соединения серии и , параллельные .Большинство электронных схем попадают в эту категорию. Последовательно-параллельные цепи обычно используются, когда от одного и того же источника напряжения требуются разные значения напряжения и тока. Серия Компоненты серии образуют серию
Размер файла: 1 МБ
Количество страниц: 33
Веб-сайт: Oakton.edu
Категория : Используйте слова
в предложении Требуется
CV Physiology Series и параллельные сосудистые сети
2 часа назад Кроме того, каждый сосудистый сегмент будет иметь сегментарное сопротивление (R x), которое определяется длиной и радиусом каждого из сосудов, составляющих сегмент. из параллельных сосудов (см. расчет параллельного сопротивления ).Для цепи сопротивления серии общее сопротивление (RT) равно сумме отдельных сопротивлений
Веб-сайт: Cvphysiology.com
Категория : Использование и в предложении
Сопротивление , Радиус, сопротивления
Последовательные и параллельные комбинации
3 часа назад EE 201 серии / параллельные комбинаций — 12 Разрыв сетей с использованием серий и параллельных R 3 R 4 R 5 R eq R 2 Но не все схемы представляют собой простые комбинации R 1 из серии или параллельных резисторов .В исходном примере схемы явно есть некоторые элементы серии …
Размер файла: 2 МБ
Количество страниц: 13
Веб-сайт: Tuttle.merc.iastate.edu
Категория : Используйте и в предложении
Резисторы
Раздел 6 Параллельный ток, напряжение и сопротивление и
3 часа назад • Соберите переключатель в цепи с параллельными компонентами для управления конкретным напольная лампа.• Используйте сохранение энергии, чтобы определить, как токи и напряжения распределяются в параллельных цепях серии и . • Используйте закон Ома, чтобы получить уравнения для общего сопротивления нескольких резисторов в серии и параллельных цепей .
Размер файла: 755 КБ
Количество страниц: 19
Веб-сайт: Aurorak12.org
Категория : Использование и в предложении
Resistance, Lawistors
III Последовательные и параллельные резисторы
5 часов назад Закон Ома III — Резисторы серии и , параллельные Однако все провода, которые выполняют соединения, и сами соединения квалифицируются как последовательное сопротивление .Провода имеют сопротивление , которое зависит от размера, длины и типа материала. Провода добавляют последовательное сопротивление к цепям , так же как…
Размер файла: 578 КБ
Количество страниц: 18
Веб-сайт: Phys.utk.edu
Категория Используйте в предложенииРезисторы, сопротивление
Что такое последовательная параллельная цепь? Последовательно параллельный
8 часов назад Поскольку схема представляет собой комбинацию серии и параллельной , мы не можем применить правила для напряжения, тока и сопротивления «поперек стола», чтобы начать анализ, как мы могли бы, когда контуров были так или иначе.Например, если вышеупомянутая схема была простой серии , мы могли бы просто сложить R 1 — R 4, чтобы получить в целом
Веб-сайт: Allaboutcircuits.com
Категория : Используйте в предложении
Правила, сопротивление
Эксперимент № 6, Последовательные и параллельные схемы, законы Кирхгофа
3 часа назад Прямое сопротивление Измерения с помощью цифрового омметра. 3.2.1 Сопротивление в параллельном и Серии .Измерения попадают в раздел данных отчета. 1. Измерьте и запишите в разделе данных лабораторного отчета сопротивление угольных резисторов R1, R2, R3 непосредственно с помощью цифрового вольтметра (Agilent 34405A), настроенного для измерения сопротивления в омах (функциональный переключатель Ом
Веб-сайт: Umb.edu
Категория : Использование и в предложении
Сопротивление, отчет, запись, резисторы
Последовательное и параллельное сопротивление Калькулятор Высокое
7 часов назад рассчитать Сопротивление в цепи [8] 2017/04/07 01:03 Уровень 60 лет и старше / Офисный работник / Государственный служащий / Очень / Чтобы улучшить этот «Калькулятор сопротивления в серии , и , параллельный », пожалуйста, заполните анкету.Возраст До 20 лет Возраст 20 лет
Веб-сайт: Keisan.casio.com
Категория : Используйте в предложении
Сопротивление
Калькулятор параллельного и последовательного сопротивленияApogeeweb
6 часов назад Таким образом, общее сопротивление будет выше. В параллельной схеме , величина, обратная действующему сопротивлению , равна сумме обратных величин отдельных сопротивлений. Так что эффективное сопротивление меньше.6. Какое сопротивление эквивалентно в серии ? В схеме
серии эквивалентное сопротивление является алгебраической суммой сопротивлений.Веб-сайт: Apogeeweb.net
Категория : Использование и в предложении
Сопротивление, Взаимное, Взаимное, Сопротивление, Сопротивления
Параллельные цепи серииКак решить
для общего сопротивления
часов назад Спасибо за просмотр, если это вам помогло, подумайте о том, чтобы сделать пожертвование.В этом видео показано, как найти общее сопротивление цепи , чтоВеб-сайт: Youtube.com
Категория : использовать в предложении
Сопротивление
Последовательный Параллельный постоянный ток Рабочий лист электрических цепей постоянного тока
2 часа назад В этой серии — параллельной цепи резисторы R1 и R2 находятся в серии друг с другом, но резистор R3 не входит ни в серию , ни в параллельную цепь с любым из них. R1 или R2: Обычно первым шагом в математическом анализе цепи , такой как эта, является определение общего сопротивления цепи .
Веб-сайт: Allaboutcircuits.com
Категория : Используйте слова в предложении
Резисторы, резистор, сопротивление
Каково общее сопротивление цепи
6 часов назад Параллельная цепь имеет два или более путей для прохождения тока. Вы можете найти общее сопротивление в параллельной цепи по следующей формуле: 1 / Rt = 1 / R1 + 1 / R2 + 1 / R3 +…. Rt = R (t) итал.Если один из параллельных путей разорван, ток будет продолжать течь по всем другим путям.
Веб-сайт: Bridgitmendlermusic.com
Категория : Использование в предложении
Resistance, Rt
Series and Parallel Circuits Boston University
7 часов назад Series и . 7-10-00 Раздел 19.1 Последовательные цепи . Цепь серии — это цепь , в которой резисторы расположены в цепочке, поэтому ток имеет только один путь.Ток через каждый резистор одинаков. Общее сопротивление цепи находится простым сложением сопротивлений отдельных резисторов:
Веб-сайт: Physics.bu.edu
Категория : Использование и в предложение
Резисторы, резистор, сопротивление
Навыки параллельных цепей 6 серий Общие
6 часов назад последовательная цепь , I R1 должен равняться I Req1.Дано: Решение: Медиа-ресурсы Wisc-Online.com • Серия — Параллельная Цепи постоянного тока Анализ • Расчет мощности в параллельной цепи серии / • Влияние реостата в параллельной цепи серии — Проверка знаний схемы 1. См. Рисунок 5 (A). Если следующие резисторы были заменены на указанные значения: R 1
Веб-сайт: Skillscommons.org
Категория : Используйте слова в предложении
Ресурсы, реостат, ссылка, резисторы, замена
Что такое сопротивление? Глобус последовательной и параллельной цепи
Just Now Серия и Сопротивление параллельной цепи в цепи .Цепь сопротивления серии . Если различные сопротивления предполагают, что R 1, R 2, R 3 соединены вместе в , серия , как показано на рисунке ниже, называется цепью последовательного сопротивления . Эквивалентное или общее сопротивление задается уравнением.
Расчетное время чтения: 3 минуты
Веб-сайт: Circuitglobe.com
Категория : Используйте a в предложении
Сопротивление, сопротивления
Эксперимент 4 ~ резисторы 9000 последовательно
9 часов назад Эксперимент 4 ~ Резисторы серии и Параллельно Цель: В этом эксперименте вы настроите три схемы : одну с резисторами серии , одну с резисторами в схема с помощью омметра.Это сопротивление между точками P и Q на рисунке 4a. Запишите значение в верхней части таблицы данных 2.
Размер файла: 219 КБ
Количество страниц: 6
Веб-сайт: Umsl.edu
Категория : Использование в предложении
Резисторы, сопротивление, запись
Как решить любую проблему последовательной и параллельной цепи YouTube
3 часа назад Как вы проанализируете схему с резисторами в серии и параллельных конфигурациях ? С помощью метода «Разбей — построи!» http: // www.jesseleemason.com Mu
Веб-сайт: Youtube.com
Категория : использовать в предложении
Резисторы
Последовательные и параллельные комбинации резисторов
1 час назад Тогда общее сопротивление из параллельной секции добавляется к любому последовательному сопротивлению , чтобы найти общее сопротивление из серии — параллельная комбинация цепь .Рисунок 12 Серия — параллельное соединение резисторов. ПРИМЕР 8. Проблема: 9-омный резистор, R 1, и 60-омный резистор, R 2, соединены по параллельно друг с другом и в серии с 40-омным
Расчетное время считывания: 8 минут
Веб-сайт: Electricalacademia.com
Категория : использование в предложении
Сопротивление, резисторы, резисторы серии
и параллельные резистивные цепи
2 часа назад Объедините серию
2 часа назад
резисторов, а затем параллельных резисторов на правой ветви.= 2 Новая схема — это B A C Рисунок 7: Эквивалентная схема — объединение параллельных цепей серий и Помеченные узлы показаны на предыдущей диаграмме. Набор из двух резисторов по 2 Ом в сумме дает 4 Ом, потому что они входят в серию . Примените KCL на узле A.Размер файла: 386KB
Количество страниц: 18
Веб-сайт: Maplesoft.com
Категория : Использование и в предложении
Резисторы, Right
Читатели спрашивают: как резисторы добавляются последовательно и параллельно?
6 часов назад Итак, эквивалентное сопротивление меньше, когда резисторы соединены параллельно .Как добавить сопротивление в цепь серии ? В цепи серии вам нужно будет вычислить общее сопротивление цепи , чтобы вычислить силу тока. Это делается путем сложения индивидуальных значений каждого компонента в серии .
Веб-сайт: Lastfiascorun.com
Категория : Используйте слова в предложении
Сопротивление, резисторы
В чем разница между последовательными и параллельными схемами
3 часа назад проводных схем серии наиболее просты для понимания, поскольку ток течет в одном непрерывном и плавном направлении.И чем больше работы у вас будет выполнять цепь серии , тем больше будет уменьшаться ваш ток. Параллельные схемы немного сложнее, позволяя подключать несколько схем …
Веб-сайт: Autodesk.com
Категория : использование между в предложении
Серияи параллельные схемы: полное Поломка
5 часов назад Компоненты схемы серии соединены между собой.Если один сломается или выйдет из строя, остальные не включатся. Классический пример — рождественские огни. Чем больше компонентов будет в цепи серии , тем больше будет сопротивление . Параллельная цепь В параллельной цепи ток должен проходить как минимум через две разные ветви.
Веб-сайт: Edrawsoft.com
Категория : Используйте слова в предложении
Сопротивление
Последовательные и параллельные цепи Википедия
8 часов назад Схема состоит исключительно из компонентов, соединенных в серия известна как цепь серии ; аналогично, одна, полностью подключенная в параллельную цепь , известна как параллельная цепь .Многие схемы могут быть проанализированы как комбинация параллельных цепей серии и вместе с другими конфигурациями. В цепи серии , ток, протекающий через каждую из
Веб-сайт: En.wikipedia.org
Категория : использование и в предложении
2.2.3 Цепи с обоими сериями и Параллельные элементы
7 часов назад 2.2.3 Цепи с обоими элементами серии и , параллельными .Большинство систем питания фактически настроено как « контуров » или контуров, и нам может потребоваться найти эквивалентное параллельное сопротивление серии – от начала контура до конца. На рисунке ниже показан особенно неприятный пример, но мы можем разбить его на несколько простых шагов.
Веб-сайт: E-education.psu.edu
Категория : Использование и в предложении
Сопротивление
Последовательные и параллельные резисторы Практические проблемы онлайн
7 часов назад Серии и параллельные резисторы на Brilliant, крупнейшем сообществе специалистов по решению математических и научных задач.Блестяще. Цепи RC (постоянный ток) R 2 = 1 0 Ом, каков общий эквивалент сопротивления ? 15
Веб-сайт: Brilliant.org
Категория : Использование и в предложении
Резисторы, Rc, сопротивление
Сопротивление в последовательной, параллельной или последовательно-параллельной цепях
9 часов назад Расчет сопротивление в цепях , параллельных или параллельных цепях . Параллельный Чтобы найти общее сопротивление параллельной цепи , вы должны разделить по одному на каждый из резисторов. Затем сложить их и еще раз разделить единицу на ваш окончательный ответ. Например, если у вас 25 Ом, 30 Ом , и набором резисторов 18 Ом, сделайте следующее.
Веб-сайт: Compworks.faithweb.com
Категория : Использование в предложении
Сопротивление, резисторы
Как рассчитать эквивалентное сопротивление (последовательное и параллельное
1 час назад Что эквивалентно Сопротивление ? Эквивалентное сопротивление определяется как точка, в которой общее сопротивление измеряется в параллельной или последовательной цепи (либо во всей цепи , либо в части цепи ) .Эквивалентное сопротивление определяется между двумя терминалами или узлами сети. Эквивалент сопротивления может показаться сложным, но это просто технический способ сказать «общее сопротивление ».
Расчетное время чтения: 8 минут
Веб-сайт: Electrical4u.com
Категория : использовать в предложении
Сопротивление
Последовательные и параллельные резисторы Цель отчета
часов назад Определите эквивалент сопротивления нескольких резисторов в комбинации серии — параллельно .Знайте, как правильно разместить амперметры и вольтметры в цепи . Знайте, что падение напряжения IR в цепи измеряет падение напряжения в этой части цепи Теория: Последовательная цепь состоит из устройств, соединенных одним замкнутым контуром.
Веб-сайт: Devinbristow.com
Категория : Использование в предложении
Сопротивление, резисторы
6.2 Последовательные и параллельные резисторы — Введение в
3 часа назад Эта комбинация параллельно находится в серии с двумя другими резисторами, поэтому эквивалентное сопротивление цепи равно.Таким образом, напряжение, подаваемое батареей, составляет. Один из способов проверить соответствие ваших результатов — это рассчитать мощность, потребляемую батареей, и мощность, рассеиваемую резисторами.
Веб-сайт: Openpress.usask.ca
Категория : Использование в предложении
Резисторы, сопротивление, результаты
Эксперимент 16: Последовательные и параллельные схемы
8 часов назад 86 Prelab 16 : Параллельные схемы серий и Имя: 1.Что такое схема серии ? (10 баллов) 2. Что такое параллельная цепь ? (10 баллов) 3. Является ли эквивалентное сопротивление , R eq, цепи серии больше или меньше, чем любой отдельный резистор? (10 баллов) 4. Является ли эквивалентное сопротивление , R
Веб-сайт: Phy.olemiss.edu
Категория : Использование и в предложении
Сопротивление, резистор
Разница между последовательными и параллельными цепями с
4 часа назад 2) Офисы используют параллельных цепей для питания устройства, но цепи серии управляют питанием.3) Предохранители и цепи . Прерыватели являются примером цепей серии , управляющих работой параллельных цепей . 4) Наши компьютеры содержат миллионы крошечных параллельных цепей серий и , работающих вместе, чтобы поддерживать его…
Расчетное время чтения: 3 минуты
Веб-сайт: Byjus.com
Категория : Используйте и в предложении
Электрические / электронные последовательные цепи
Прямо сейчас Параллельная схема имеет совсем другие характеристики, чем последовательная схема .Во-первых, общее сопротивление параллельной цепи НЕ равно сумме резисторов (как в последовательной цепи ). Общее сопротивление в параллельной цепи всегда меньше любого из сопротивлений ответвления.
Веб-сайт: Swtc.edu
Категория : Используйте слова в предложении
Сопротивление, резисторы, сопротивления
Резисторы в последовательной и параллельной цепях
2 часа назад Резисторы в цепях Чтобы определить ток или напряжение в a Чтобы определить ток или напряжение в цепи , содержащей несколько резисторов, цепи , содержащей несколько резисторов, сначала необходимо рассчитать общее сопротивление и общее сопротивление .рассчитано. Резисторы можно комбинировать в серии или резисторы
Веб-сайт: Slideshare.net
Категория : использовать в предложении
Резисторы, сопротивление
Ток, напряжение и сопротивление последовательно и параллельно
5 часов назад Ток, напряжение и сопротивление в параллельных цепях серии и Этот эксперимент разработан для исследования взаимосвязи между током и разностью потенциалов в простых цепях и параллельных резисторов серии с использованием идей сохранение энергии и сохранение заряда.
Веб-сайт: Minerva.union.edu
Категория : Использование и в предложении
Сопротивление, взаимосвязь, резистор
Серияи параллельные схемы learn.sparkfun.com
9 часов назад Уведомление что в некоторых узлах (например, между R 1 и R 2) ток на входе такой же, как и на выходе. В других узлах (в частности, в трехстороннем соединении между R 2, R 3 и R 4) основной ( синий) ток разделяется на два разных.Это ключевое различие между series и parallel !. Цепи серии Определение . Два компонента относятся к серии , если они имеют общий узел и если один и тот же
Веб-сайт: Learn.sparkfun.com
Категория : Используйте и в предложении
Как рассчитать сопротивление для 4 параллельных резистора. Параллельное соединение разных сопротивлений
Определение параллельного соединения
Параллельное соединение электрических элементов (проводников, сопротивлений, конденсаторов, индуктивностей) — это такое соединение, при котором соединенные элементы цепи имеют два общих узла соединения.
Другое определение: сопротивления подключаются параллельно, если они подключены к одной и той же паре узлов.
Графическое обозначение схемы параллельного включения
На рисунке ниже представлена схема параллельного включения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (точки подключения).
В электротехнике принято, но не обязательно, протягивать провода горизонтально и вертикально.Поэтому можно изобразить ту же схему, что и на рисунке ниже. Это слишком параллельное соединение одинаковых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном подключении величина, обратная эквивалентному сопротивлению, равна сумме обратных величин всех параллельно соединенных сопротивлений. Эквивалентная проводимость равна сумме всех одновременно подключенных проводимостей. электрическая цепь.
Для вышеприведенной схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае, когда два резистора соединены параллельно:
Сопротивление эквивалентной цепи определяется по формуле:
В случае подключения «n» того же сопротивления, эквивалентное сопротивление можно рассчитать по специальной формуле:
Формулы для частного расчета выводятся из основной формулы.
Формула для расчета параллельного включения конденсаторов (конденсаторов)
При параллельном соединении конденсаторов (конденсаторов) эквивалентная емкость равна сумме параллельно соединенных конденсаторов:
Формула для расчета индуктивности параллельного включения
При параллельном соединении индуктивностей эквивалентная индуктивность рассчитывается так же, как эквивалентное сопротивление при параллельном соединении:
Следует обратить внимание, что взаимные индуктивности в формуле не учитываются.
Пример коагуляции параллельного сопротивления
Для электрической схемы участка необходимо найти параллельное соединение сопротивлений, чтобы преобразовать их в единицу.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллелен, потому что на одном конце он подключен к E1. R1 — один конец подключен к R5, а не к узлу. R5 — одним концом подключен к R1, а не к узлу. Также можно сказать, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Параллельный ток
При параллельном соединении сопротивлений ток через каждое сопротивление обычно разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном подключении
При параллельном включении разность потенциалов между узлами, соединяющими элементы схемы, одинакова для всех элементов.
Приложение для параллельного подключения
1. В промышленности изготавливаются сопротивления определенных количеств.Иногда необходимо получить значение сопротивления вне этой серии. Для этого можно параллельно подключить несколько сопротивлений. Эквивалентное сопротивление всегда будет меньше наибольшего значения сопротивления.
2. Делитель тока.
В каждой цепи есть резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: фиксированные и переменные. При разработке любой электрической схемы и ремонте электронных изделий часто бывает необходимо использовать резистор, имеющий необходимый номинал.
Несмотря на то, что для резисторов существуют различные значения , может случиться так, что не удастся найти нужный или даже один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может стать использование последовательного и параллельного подключения. Прочитав эту статью, вы узнаете об особенностях расчета и выбора различных значений сопротивления.
Часто при изготовлении любого устройства используют резисторы, которые подключаются по последовательной схеме.Эффект от использования такого варианта сборки сводится к увеличению общего сопротивления цепи. Для этого варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если сборка деталей выполняется по параллельной схеме, здесь нужно рассчитать сопротивление по формулам ниже.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача уменьшить общее сопротивление, и, кроме того, увеличить мощность для группы элементов, соединенных параллельно, которая должна быть больше, чем при их раздельном соединении.
Расчет сопротивления
В случае соединения частей между собой по параллельной схеме для расчета общего сопротивления будет использоваться следующая формула:
R (всего) = 1 / (1 / R1 + 1 / R2 + 1 / R3 + 1 / Rn).
- R1- R3 и Rn — резисторы, включенные параллельно.
Причем, если схема создана на основе всего двух элементов, то для определения общего номинального сопротивления используйте следующую формулу:
R (всего) = R1 * R2 / R1 + R2.
- R (total) — полное сопротивление;
- R1 и R2 — резисторы, включенные параллельно.
Универсальная схема расчета
Применительно к радиотехнике следует обратить внимание на одно важное правило: если элементы соединены между собой по параллельной схеме имеют одинаковый показатель , то для расчета общего номинала необходимо общее значение разделить на количество подключаемых узлов:
- R (total) — суммарное значение сопротивления;
- R — номинал резистора, включенного параллельно;
- n — количество подключенных узлов.
Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования схемы параллельного подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключенного к цепи.
Пример расчета
Для большей наглядности мы можем рассмотреть следующий пример: предположим, что у нас есть три резистора, номиналы которых составляют соответственно 100, 150 и 30 Ом. Если мы используем первую формулу для определения общей стоимости, мы получим следующее:
R (всего) = 1 / (1/100 + 1/150 + 1/30) = 1 / (0.01 + 0,007 + 0,03) = 1 / 0,047 = 21,28 Ом.
Если произвести несложные вычисления, можно получить следующее: для схемы, состоящей из трех частей, где наименьшее значение сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального номинала в цепочке почти на 30%.
Важные нюансы
Обычно для резисторов используется параллельное включение, когда стоит задача создать сопротивление большей мощности.Для ее решения потребуются резисторы, которые должны иметь одинаковое сопротивление и мощность. С помощью этой опции вы можете определить общую мощность как : мощность одного элемента должна быть умножена на общее количество всех резисторов, составляющих цепь, соединенных друг с другом в соответствии с параллельной цепью.
Допустим, если мы используем пять резисторов номиналом 100 Ом и мощностью каждого 1 Вт, которые соединены между собой по параллельной схеме, то общее сопротивление будет равно 20 Ом, а мощность будет 5 Вт.
Если взять те же резисторы, но подключить их по последовательной схеме, то конечная мощность будет 5 Вт, а общий номинал будет равен 500 Ом.
Заключение
Параллельная разводка резисторов очень востребована по той причине, что часто возникает задача создания такого номинала, которого нельзя достичь простым параллельным подключением. При этом процедура вычисления этого параметра довольно сложная, , где необходимо учитывать разные параметры.
Здесь важную роль играет не только количество подключаемых элементов, но и рабочие параметры резисторов — в первую очередь сопротивление и мощность. Если один из подключаемых элементов будет иметь несоответствующий индикатор, то это не решит эффективно проблему создания необходимого номинала в цепи.
Параллельное соединение резисторов — один из двух типов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.Часто или параллельно с целью создания более сложных электронных схем.
Схема параллельного подключения показана на рисунке ниже. При параллельном соединении резисторов напряжение на всех резисторах будет одинаковым, а ток, протекающий через них, будет пропорционален их сопротивлению:
Формула для параллельного включения резисторов
Суммарное сопротивление нескольких параллельно включенных резисторов определяется по следующей формуле:
Ток, протекающий через одиночный резистор, согласно, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства возникла необходимость в установке резистора сопротивлением 8 Ом.Если просмотреть весь номинальный ряд стандартных номиналов резисторов, то мы увидим, что в нем нет резистора с сопротивлением 8 Ом.
Выход из этой ситуации — использование двух параллельно включенных резисторов. Эквивалентное значение сопротивления для двух параллельно включенных резисторов рассчитывается следующим образом:
Это уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. Следовательно, когда R = 8 Ом, R1 и R2 должны иметь значение 2 × 8 = 16 Ом.
Теперь проверим, рассчитав суммарное сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, подключив параллельно два резистора по 16 Ом.
Пример расчета № 2
Найдите полное сопротивление R трех параллельно соединенных резисторов:
Суммарное сопротивление R рассчитывается по формуле:
Этот метод расчета можно использовать для расчета любого количества отдельных сопротивлений, подключенных параллельно.
Один важный момент, который необходимо помнить при расчете параллельно соединенных резисторов, заключается в том, что полное сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать схемы подключения комплексных резисторов
Более сложные соединения резисторов можно рассчитать путем систематической группировки резисторов. На рисунке ниже нужно рассчитать полное сопротивление цепи, состоящей из трех резисторов:
Для упрощения расчетов сначала сгруппируем резисторы по параллельному и последовательному включению.
Резисторы R2 и R3 включены последовательно (группа 2). Они, в свою очередь, подключены параллельно резистору R1 (группа 1).
Последовательное соединение резисторов группы 2 рассчитывается как сумма сопротивлений R2 и R3:
В результате упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей цепи можно рассчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить по законам Кирхгофа.
Ток, протекающий в цепи параллельно включенных резисторов
Полный ток I, протекающий в цепи параллельных резисторов, равен сумме отдельных токов, протекающих во всех параллельных ветвях, и ток в одной ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, на каждый резистор подается одинаковое напряжение. А поскольку значение сопротивления в параллельной цепи может быть разным, то величина тока, протекающего через каждый резистор, также будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, протекающий через каждый из резисторов (I1 и I2), будет отличаться друг от друга, поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который входит в цепь в точке «A», должен выходить из цепи в точке «B».
Первое правило Кирхгофа гласит: «Полный ток, исходящий из цепи, равен току, входящему в цепь.«
Таким образом, протекающий полный ток в цепи можно определить как:
Затем, используя закон Ома, мы можем вычислить ток, протекающий через каждый резистор:
Ток протекающий через R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток протекающий через R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить с помощью закона Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0.8 мА (то же)
, где 15 кОм — общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в заключение следует отметить, что большинство современных резисторов маркированы цветными полосами и их назначение можно встретить.
Параллельное соединение резисторов — онлайн калькулятор
Для быстрого расчета общего сопротивления двух или более резисторов, соединенных параллельно, вы можете использовать следующий онлайн-калькулятор:
Подвести итог
Когда два или более резистора соединены так, что оба вывода одного резистора подключены к соответствующим выводам другого резистора или резисторов, они считаются подключенными параллельно друг другу.Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга в зависимости от сопротивления каждого резистора.
Эквивалент или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, включенного в параллельное соединение.
На практике часто встречается задача определения сопротивления проводников и резисторов при разных способах подключения.В статье обсуждается, как рассчитывается сопротивление, и некоторые другие технические вопросы.
Сопротивление проводника
Все проводники имеют тенденцию препятствовать прохождению электрического тока, это называется электрическим сопротивлением R, оно измеряется в омах. Это главное свойство проводниковых материалов.
Для проведения электрических расчетов применяется удельное сопротивление — ρ Ом · м / мм2. Все металлы являются хорошими проводниками, медь и алюминий используются чаще всего, а железо — гораздо реже.Лучший проводник — серебро, его используют в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.
При расчете сопротивления используется известная из школьного курса физики формула:
R = ρ · l / S, S — площадь сечения; l — длина.
Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.
и нагревательный провод
Для практических расчетов режимов работы проводников используется понятие плотности тока — δ А / мм 2, она рассчитывается по формуле:
δ = I / S, I — ток , S — поперечное сечение.
Ток, проходящий через проводник, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приведены в. Для жил нагревательных приборов существуют свои нормативы плотности тока.
Если плотность δ выше допустимой, проводник может разрушиться, например, если кабель перегреется, его изоляция разрушится.
Правила регулируют расчет кондукторов для отопления.
Способы подключения проводов
Любой проводник гораздо удобнее изобразить на схемах как электрическое сопротивление R, тогда их будет легче читать и анализировать. Подключить сопротивления можно всего тремя способами. Первый способ самый простой — последовательное подключение.
На фото видно, что импеданс равен: R = R 1 + R 2 + R 3.
Второй способ посложнее — параллельное подключение. Расчет сопротивления при параллельном включении выполняется поэтапно.Рассчитайте общую проводимость G = 1 / R, а затем импеданс R = 1 / G.
Вы можете сделать иначе, сначала рассчитать общее сопротивление на R1 и R2, затем повторить операцию и найти R.
Третий способ подключения самый сложный — смешанное подключение, то есть присутствуют все рассмотренные варианты. Схема представлена на фото.
Для расчета этой схемы ее следует упростить; для этого резисторы R2 и R3 заменяются одним R2.3. Получается простая схема.
R2,3,4 = R2,3 · R4 / (R2,3 + R4).
Схема становится еще проще, остаются резисторы с последовательным включением. В более сложных ситуациях используется тот же метод преобразования.
Типы проводов
В электронной технике на производстве проводники представляют собой тонкие полоски медной фольги. Из-за небольшой длины сопротивления у них мало, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном подключении уменьшается из-за увеличения поперечного сечения.
Большое сечение жил — это обмоточные провода. Доступны они разного диаметра — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей изготавливаются медные стержни прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельных меньшего размера.
К особому сечению проводников относятся провода и кабели, промышленность предоставляет самый широкий выбор марок для самых разных нужд.Часто приходится заменять один кабель несколькими меньшими отрезками. Причины тому самые разные, например, кабель сечением 240 мм 2 очень сложно прокладывать на трассе с крутыми изгибами. Его заменяют на 2 × 120 мм 2, и проблема решается.
Расчет проводов на обогрев
Проводник нагревается протекающим током, если его температура превышает допустимую, происходит разрушение изоляции. ПУЭ предусматривает расчет токопроводов на обогрев, исходными данными для него являются сила тока и условия окружающей среды, в которых проводник проложен.Согласно этим данным, рекомендуемый проводник или кабель выбирается из таблиц в OLC).
На практике бывают ситуации, когда нагрузка на существующий кабель сильно увеличивается. Выхода два — заменить кабель на другой, может быть дорого, или проложить еще один параллельно ему, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном включении уменьшается, следовательно, уменьшается тепловыделение.
Чтобы правильно подобрать сечение второго кабеля, воспользуйтесь таблицами PES, важно не ошибиться с определением его рабочего тока.В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитывать сопротивление при параллельном подключении двух кабелей, чтобы более точно определить их теплоотдачу.
Расчет проводов на потерю напряжения
При расположении потребителя R n на большом расстоянии L от источника энергии U 1 на проводах линии остается довольно большое количество. К потребителю R n поступает напряжение U 2 значительно ниже начального U 1.Практически в качестве нагрузки выступает различное электрооборудование, подключенное к линии параллельно.
Чтобы решить эту проблему, рассчитайте сопротивление, когда все оборудование подключено параллельно, и сопротивление нагрузки R n. Далее определяем сопротивление проводов линии.
R l = ρ · 2L / S,
Здесь S — сечение провода, мм 2.
В этой теме можно привести множество примеров из нашей повседневной жизни, касающихся параллельного соединения сопротивлений.Параллельное соединение одинаковых сопротивлений — яркий пример подключения люстры с n-м числом ламп и с одинаковым сопротивлением для каждой лампы \ Рис.1 \.
Если предположить, что в люстре, состоящей из нескольких ламп \ с одинаковым сопротивлением \ одна лампа перегорела, а другую мощность заменили лампой другой мощности — в этом случае подключение люстры будет иметь вид параллельное соединение с разным сопротивлением.
Какие еще примеры можно привести из практики — с параллельным соединением сопротивлений? Допустим, вы подключили в своей квартире три бытовых электроприбора через удлинитель:
- плита электрическая;
- стиральная машина;
- телевидение.
Природа этого соединения будет сопротивления параллельного соединения разного размера. То есть для каждого прибора сопротивление имеет свое значение.
Расчет сопротивления при параллельном подключении
Как уже было сказано, при параллельном включении проводятся расчеты сопротивлений:
- с таким же сопротивлением;
- с разным сопротивлением
, а также выполнены расчеты сопротивлений для смешанного включения резисторов, при последовательном и параллельном включении \\ для одной цепи \\.Расчет сопротивления для смешанных подключений резисторов, больше подходит для различных блок-схем:
- аудиоаппаратура;
- видеооборудование.
К этой теме расчеты для смешанных соединений отношения не имеют.
Параллельное соединение одинаковых сопротивлений
Представьте себе параллельное соединение, например, трех равных по величине сопротивлений \\ рис.2 \\, где R1 = R2 = R3 = 36 Ом \ сопротивление лампы накаливания мощностью 95 Вт. Напряжение 220 В подключается к двум узловым точкам \ A, B \.Необходимо рассчитать суммарное сопротивление всех трех ламп.
Для расчета общего сопротивления \ R total \ нам нужно 36 Ом разделить на количество сопротивлений. Решение простое, Rtotal = 12 Ом. То есть формула для расчета таких вычислений выглядит так:
R итого = R / n
Параллельное соединение разных сопротивлений
Допустим, мы берем выборочно три резистора, сопротивление:
- R1 = 20 Ом;
- R2 = 40 Ом;
- R3 = 10 Ом.
Необходимо определить полное сопротивление резисторов при параллельном включении. Для этого расчета мы используем формулу:
1 / R всего = 1 / R1 + 1 / R2 + 1 / R3.
Подставьте значения в формулу:
1 / R всего = 1/20 + 1/40 + 1/10 = 7/40 = 0,18
получаем: Rtotal = 1 / 0,18 = 5,5 Ом.
резисторов последовательно и параллельно
резисторов последовательно и параллельноДалее: Правила Кирхгофа Up: Электрический ток Предыдущее: ЭДС и внутреннее сопротивление Резисторы, вероятно, встречаются чаще всего. компоненты в электронных схемах.Практические схемы часто содержат очень сложные комбинации резисторов. Поэтому полезно иметь набор правил для поиска эквивалентных сопротивление некоторого общего расположения резисторов. Оказывается, мы можем всегда находите эквивалентное сопротивление повторным применением два простых правил. Эти правила относятся к резисторам, включенным последовательно, и в параллели.
Рассмотрим два резистора, включенных в серию , как показано на рис.18.
Понятно, что через оба резистора протекает одинаковый ток.
Ибо, если бы это было не так, заряд накапливался бы в одном или другом
резисторов, которые не соответствовали бы
установившаяся ситуация (таким образом нарушая
основное предположение этого раздела). Предположим, что падение потенциала
от точки к точке есть. Это падение представляет собой сумму потенциальных
падает и на двух резисторах и соответственно.
Таким образом,
| (135) |
Согласно закону Ома, эквивалентное сопротивление между и — отношение падения потенциала в этих точках и ток, протекающий между ними.Таким образом,
| (136) |
давая
| (137) |
Здесь мы использовали тот факт, что ток является общим для все три резистора. Следовательно, правило
Эквивалентное сопротивление двух последовательно соединенных резисторов равно сумма отдельных сопротивлений.Для резисторов, соединенных последовательно, уравнение.(137) обобщает к .
Рассмотрим два резистора, соединенных параллельно , как показано на рис. 19. Это
Из рисунка видно, что падение потенциала на двух резисторах равно
тем же. В общем, однако, токи и которые протекают
через резисторы и соответственно разные.
По закону Ома эквивалентное сопротивление
между и — отношение падения потенциала
через эти точки и текущий
которая течет между ними.Этот ток должен равняться сумме
токи и протекающие через два резистора, в противном случае
заряд будет накапливаться на одном или обоих переходах в цепи.
Таким образом,
| (138) |
Следует, что
| (139) |
давая
| (140) |
Здесь мы использовали тот факт, что падение потенциала является общим для всех трех резисторов.Ясно, что правило
Обратное эквивалентное сопротивление двух сопротивлений. подключенных параллельно — это сумма обратных величин индивидуальные сопротивления.Для резисторов, соединенных параллельно, уравнение. (140) обобщает на .
Далее: Правила Кирхгофа Up: Электрический ток Предыдущее: ЭДС и внутреннее сопротивление Ричард Фицпатрик 2007-07-14
Последовательные и параллельные резисторы
При изучении электрического тока мы обычно описываем сопротивление как препятствие на пути тока.Резисторы — это устройства, обеспечивающие сопротивление току. В нашей повседневной жизни наши устройства имеют более одного сопротивления в цепях. Становится важным изучить влияние различных схем сопротивления и их влияние на схему. Часто в реальных ситуациях требуется рассчитать необходимое сопротивление для всей цепи, а иногда и для ее части. В таких случаях может оказаться полезным знание расчета эквивалентных сопротивлений, давайте подробно рассмотрим эти концепции.
Резисторы и сопротивление
Резисторы — это электрические устройства, ограничивающие прохождение тока в цепи. Это омическое устройство, что означает, что оно подчиняется закону Ома V = IR. В большинстве схем имеется только один резистор, но иногда в схеме может присутствовать более одного резистора. В этом случае ток, протекающий по цепи, зависит от эквивалентного сопротивления комбинации. Эти комбинации могут быть сколь угодно сложными, но их можно разделить на два основных типа:
Внимание, читатель! Все, кто говорит, что программирование не для детей, просто еще не встретили подходящих наставников.Присоединяйтесь к демонстрационному классу для первого шага к курсу кодирования, специально разработан для учащихся 8-12 классов.
Студенты узнают больше о мире программирования в этих бесплатных классах , которые определенно помогут сделать правильный выбор карьеры в будущем.
- Комбинация серий
- Параллельная комбинация
Комбинация серий
На приведенном ниже рисунке три резистора соединены последовательно с батареей с напряжением V.В такой комбинации резисторы обычно подключаются последовательно друг за другом. Ток через каждый резистор одинаков. На рисунке справа показано эквивалентное сопротивление трех сопротивлений. В случае последовательной комбинации сопротивлений эквивалентное сопротивление определяется алгебраической суммой отдельных сопротивлений.
Пусть V 1 , V 2 и V 3 будут напряжениями на всех трех сопротивлениях.Известно, что ток, протекающий по ним, одинаков.
V = V 1 + V 2 + V 3
Расширяя уравнение,
IR = IR 1 + IR 2 + IR 3
R = R 1 + R 2 + R 3
Параллельная комбинация
На приведенном ниже рисунке показаны три резистора, подключенных параллельно батарее с напряжением V.В этом типе соединения резисторы обычно подключаются параллельными проводами, отходящими от общей точки. В этом случае напряжение на каждом резисторе одинаковое. На рисунке справа показано эквивалентное сопротивление трех сопротивлений.
Соотношение между напряжением и током определяется как,
V = IR
Его можно переписать как,
I = V / R
Напряжения на отдельных резисторах будут,
I 1 = V / R 1 , I 2 = V / R 2 , I 3 = V / R 3
Суммарный ток на всех сопротивлениях будет,
I = I 1 + I 2 + I 3
Подставив выражения для отдельных напряжений,
I = V / R 1 + V / R 2 + V / R 3
Пусть эквивалентная емкость R,
V / R = V / R 1 + V / R 2 + V / R 3
После упрощения приведенного выше уравнения соотношение становится,
В целом для конденсаторов R 1 , R 2 , R 3 ,….
Примеры проблем
Вопрос 1: Три сопротивления 3, 5 , и 10 Ом соединены последовательно. Найдите эквивалентное сопротивление для системы.
Ответ:
Формула для последовательного сопротивления определяется как,
R = 1 + R 2 + R 3
Дано: 1 = 3 , R 2 = 5 и R 3 = 10
Подставив эти значения в уравнение,
R = 1 + R 2 + R 3
⇒ R = 3 + 5 + 10
⇒ R = 18 Ом
Вопрос 2: Три сопротивления 2, 2 , и 4 Ом подключены параллельно.Найдите эквивалентное сопротивление для системы.
Ответ:
Формула для параллельного сопротивления определяется как,
Дано: 1 = 2, 2 = 2 и 3 = 4
Подставляя эти значения в уравнении:
⇒
⇒
⇒ Ω
Вопрос 3: Найдите эквивалентное сопротивление для системы, показанной на рисунке ниже.
Ответ:
Формула для параллельного сопротивления определяется как,
А формула для последовательного сопротивления определяется как,
R = 1 + R 2 + R 3 +….
Это комбинация параллельных и последовательных сопротивлений.
Подставляя эти значения в уравнение,
R 1 = 10 Ом, R2 = 2,5 Ом
R = 1 + R 2
⇒ R = 10 + 2.5
⇒ R = 12,5
⇒
⇒
⇒ Ω
Вопрос 4: Найдите эквивалентное сопротивление для системы, показанной на рисунке ниже.
Ответ:
Формула для параллельного сопротивления определяется как,
А формула для последовательного сопротивления имеет вид,
R = 1 + R 2 + R 3 +….
Это комбинация параллельных и последовательных сопротивлений.
Подставляя эти значения в уравнение,
R 1 = 100 Ом, R2 = 25 Ом
R = 1 + R 2
⇒ R = 100 + 25
⇒ R = 125
⇒
⇒
⇒ Ω
Вопрос 5: Найдите эквивалентное сопротивление для системы, показанной на рисунке ниже.
Ответ:
Формула для параллельного сопротивления определяется как,
А формула для последовательного сопротивления имеет вид,
R = 1 + R 2 + R 3 +…
Это комбинация параллельных и последовательных сопротивлений.
Подставляя эти значения в уравнение,
R 1 = 10 Ом, R2 = 0,3 Ом
⇒
⇒
⇒
⇒ R = 0,29
R = 1 R = 1 R 2
⇒ R = 0,29 + 25
⇒ R = 25,29 Ом
Калькулятор последовательной и параллельной цепей
Вычислитель эквивалентной последовательной и параллельной цепей
Здесь мы изучаем расчет эквивалентной или полной последовательной цепи и параллельной цепи.
Во-первых, вы должны знать об основных понятиях, таких как последовательное и параллельное соединение цепей с соединенными различными элементами.
В предыдущем учебном пособии я объяснил последовательную цепь и параллельную цепь на примере.
1. Калькулятор последовательной цепи —
При последовательном подключении электрические элементы или компоненты соединяются последовательно или последовательно.
Например, данная схема называется последовательной схемой, когда компоненты электроники (такие как сопротивление R1, R2 и R3) соединены одним путем с подключенным источником напряжения (Vs).
Когда в цепь подается напряжение, течет такой же ток (I). Но другое (или падение) напряжения (V1, V2 и V3) произошло на всем последовательно подключенном сопротивлении.
Сумма падений напряжения на отдельных последовательно соединенных сопротивлениях равна приложенному напряжению (т.е. V = V1 + V2 + V3).
Давайте проверим, вот несколько важных формул для различных компонентов, соединенных последовательно.
Для расчета тока в серии:
Общий ток, (Ieq) = (I1 = I2 = I3 = I4 = 15 =...... = In) (Единица - Ампер)
Примечание: Один и тот же ток течет или возникает на разных подключенных компонентах в последовательной цепи.
Для расчета напряжения в серии:
Общий ток, (Veq) = (V1 + V2 + V3 + V4 = V5 = ...... = Vn) (Единица-вольт)
Для расчета сопротивления в серии:
Общее сопротивление, (Треб.) = (R1 + R2 + R3 + R4 + R5 + ...... + Rn) (Единицы - Ом)
Для расчета проводимости серий:
Общая проводимость, (Geq) = [1 / ((1 / G1) + (1 / G2) + (1 / G3) + (1 / G4) + (1 / G5) +...... + (1 / Gn))] (Единица - Сименс)
Для расчета емкости в серии:
Общая емкость, (Ceq) = [1 / ((1 / C1) + (1 / C2) + (1 / C3) + (1 / C4) + (1 / C5) + ...... + ( 1 / Cn))] (Единица - Фарад)
Для расчета индуктивности в серии:
Общая индуктивность, (Leq) = (L1 + L2 + L3 + L4 + L5 ...... + Ln) (Единица измерения - Генри)
Это простое описание последовательной цепи с различными формулами.
2. Вычислитель параллельной цепи:
При параллельном подключении несколько электрических элементов или компонентов соединяются параллельно.
Например, когда электронные компоненты (такие как сопротивление R1, R2 и R3) подключены в параллельную ветвь с подключенным источником напряжения (Vs).
Когда в цепь подается напряжение, течет такой же ток (I). Но различное (или падение) напряжение (V1, V2 и V3) возникло на всем параллельно подключенном сопротивлении.
Сумма падений напряжения на отдельных параллельно соединенных сопротивлениях равна приложенному напряжению (т.е. V = V1 + V2 + V3).
Давайте проверим, вот несколько важных формул для различных подключенных компонентов в параллельной цепи.
Для расчета параллельного тока:
Общий ток, (Ieq) = (I1 + I2 + I3 + I4 + 15 + ...... + In) (Единица - Ампер)
Для расчета параллельного напряжения:
Общее напряжение, (Veq) = (V1 = V2 = V3 = V4 = V5 =...... + Vn) (Единица- Вольт)
Примечание: одинаковое напряжение или разность потенциалов возникают на разных подключенных компонентах.
Для расчета сопротивления параллельно:
Общее сопротивление, (Треб.) = [1 / ((1 / R1) + (1 / R2) + (1 / R3) + (1 / R4) + (1 / R5) + ...... + ( 1 / Rn))] (Единица- Ом)
Для расчета проводимости серий:
Общая проводимость, (Geq) = (G1 + G2 + G3 + G4 + G5 +...... + Gn) (Единица- Сименс)
Для расчета емкости в серии:
Общая емкость, (Ceq) = (C1 + C2 + C3 + C4 + C5 + ...... + Cn) (единицы - Фарады)
Для расчета индуктивности в серии:
Общая индуктивность, (Leq) = [1 / ((1 / L1) + (1 / L2) + (1 / L3) + (1 / L4) + (1 / L5) + ...... + ( 1 / Ln))] (Блок - Генри)
Это простое описание параллельной цепи с различными формулами.
python — Расчет параллельно подключенного сопротивления
Ниже две алгебраически эквивалентные формулы для параллельных резисторов:
par1 (r1, r2) = (r1 * r2) / (r1 + r2), или
пар2 (r1, r2) = 1 / (1 / r1 + 1 / r2)
Следующие две функции Python, каждая из которых вычисляет формулу parallel_resistors:
def par1 (r1, r2):
вернуть div_interval (mul_interval (r1, r2), add_interval (r1, r2))
def par2 (r1, r2):
один = интервал (1, 1)
rep_r1 = div_interval (один, r1)
rep_r2 = div_interval (один, r2)
вернуть div_interval (один, add_interval (rep_r1, rep_r2))
Ниже представлена абстракция интервальной арифметики, которая используется вышеупомянутыми функциями par1 и par2 .
интервал определения (a, b):
"" "Построить интервал от a до b." ""
возврат (а, б)
def lower_bound (x):
"" "Вернуть нижнюю границу интервала x." ""
вернуть x [0]
def upper_bound (x):
"" "Вернуть верхнюю границу интервала x." ""
вернуть x [1]
def div_interval (x, y):
"" "Возвращает интервал, содержащий частное любого значения в x, разделенное
на любое значение по y.
Деление реализовано как умножение x на величину, обратную y.
>>> str_interval (div_interval (интервал (-1, 2), интервал (4, 8)))
'-0.От 25 до 0,5 '
"" "
assert (lower_bound (y)> 0 или upper_bound (y) <0), «что означает деление на интервал, охватывающий ноль»
обратный_у = интервал (1 / верхняя_ граница (у), 1 / нижняя_ граница (у))
вернуть mul_interval (x, reciprocal_y)
def str_interval (x):
"" "Вернуть строковое представление интервала x.
>>> str_interval (интервал (-1, 2))
'От -1 до 2'
"" "
вернуть '{0} в {1}'. формат (нижняя_ граница (x), верхняя_ граница (x))
def add_interval (x, y):
"" "Возвращает интервал, содержащий сумму любых значений в интервале x и
любое значение в интервале y.>>> str_interval (add_interval (интервал (-1, 2), интервал (4, 8)))
«От 3 до 10»
"" "
lower = lower_bound (x) + lower_bound (y)
верхняя = верхняя_ граница (x) + верхняя_ граница (y)
интервал возврата (нижний, верхний)
def mul_interval (x, y):
"" "Возвращает интервал, содержащий произведение любого значения в x и любого
значение в y.
>>> str_interval (mul_interval (интервал (-1, 2), интервал (4, 8)))
'От -8 до 16'
"" "
p1 = нижняя_ граница (x) * нижняя_ граница (y)
p2 = нижняя_ граница (x) * верхняя_ граница (y)
p3 = верхняя_ граница (x) * нижняя_ граница (y)
p4 = верхняя_ граница (x) * верхняя_ граница (y)
интервал возврата (min (p1, p2, p3, p4), max (p1, p2, p3, p4))
Результат теста:
>>> r1 = интервал (1, 2)
>>> r2 = интервал (3, 4)
>>> par1 (r1, r2)
(0.5, 2.0)
>>> par2 (r1, r2)
(0,75, 1,3333333333333333)
Мы замечаем разный результат для par1 и par2 , которые вычисляют с помощью разных, но алгебраически эквивалентных выражений.
Для указанных выше входных данных r1 и r2 ниже приведены вычисления.
par1 -> return mul_interval ((3, 8), (1/6, 1/4)) = (1/2, 2)
=======
rep_r1 = div_interval ((1, 1), (1, 2)) = (1/2, 1)
rep_r2 = div_interval ((1, 1), (3, 4)) = (1/4, 1/3)
par2 -> return div_interval ((1, 1), (3/4, 4/3)) = (3/4, 4/3)
Причина различного интервала связана с форматом с плавающей запятой IEEE, где каждые div_interval теряют точность.
Я правильно понимаю?
резисторов, включенных параллельно | Формула параллельной цепи — Earth Bondhon
Параллельная цепь резистора
Параллельные резисторы
Шунтирующая цепь — это цепь, у которой есть 2 или несколько путей для прохождения электричества, при этом единицы площади массы параллельны каждой альтернативе.Если массы в этой цепи были легкими лампочками и одна перегорела, ток все еще течет к другим, потому что они все еще находятся в чрезмерно сильном.
Компоненты:
01. Фиксированный резистор: [См. «Купить», «Banggood» | Амазонка]
02. Резистор потенциометра: [См. Купить Нажмите на Banggood | Амазонка]
Определение параллельных цепей
Если элементы имеют 2 общих узла, они работают параллельно.Вот пример схемы из 3 резисторов, подключенных параллельно к электрической батарее.
Цепь положительного полюса аккумуляторной батареи, ток течет к 1 … и 2 и 3 рандов. Узел, подключающий аккумулятор к R 1 , дополнительно подключается к противоположным резисторам. противоположные концы этих резисторов одинаково связаны, так что обратно к отрицательной клемме батареи. Существует 3 различных способа прохождения тока перед возвратом в батарею, а также соответствующие резисторы, которые, как уже упоминалось, должны быть включены параллельно.
Если все последовательные части имеют одинаковые токи, протекающие через них, все параллельные части имеют эквивалентное падение — последовательно: ток; параллельно: напряжение.
РАСЧЕТ ПАРАЛЛЕЛЬНЫХ ЦЕПЕЙ
Замкнутая цепь — это цепь, по которой электричество может перемещаться по множеству совершенно разных путей. Это своего рода водоток, который был разделен на более мелкие потоки, однако все потоки служат одной и той же цели, чтобы снова создать водоток.
Замкнутая цепь имеет совершенно другие характеристики, чем электрическая цепь. Во-первых, полного сопротивления замкнутой цепи недостаточно для добавления резисторов (как в чрезмерно последовательной цепи). полное сопротивление в чрезвычайно замкнутой цепи обычно равно любому сопротивлению ответвления. Добавление большого количества параллельных сопротивлений к путям приводит к уменьшению полного сопротивления в цепи. Когда вы добавляете много и много ответвлений в схему, полный ток может увеличиваться в результате того, что закон гласит, что чем ниже сопротивление, тем выше настоящее.
Уравнение параллельного резистора
Цепь положительного полюса аккумуляторной батареи, ток течет к 1 … и 2 и 3 рандов. Узел, подключающий аккумулятор к R 1 , дополнительно подключается к противоположным резисторам. противоположные концы этих резисторов одинаково связаны, так что обратно к отрицательной клемме батареи. Существует 3 различных способа прохождения тока перед возвратом в батарею, а также соответствующие резисторы, которые, как уже упоминалось, должны быть включены параллельно.
Если все последовательные части имеют одинаковые токи, протекающие через них, все параллельные части имеют эквивалентное падение — последовательно: ток; параллельно: напряжение.
Уравнение параллельного резистора
Если 2 сопротивления или импеданса, соединенные параллельно квадрату, равны и имеют одинаковую цену, то полное или эквивалентное сопротивление RT может составлять 0,5, равное 1 сопротивлению. с возможностью R / 2 и для 3 одинаковых резисторов, включенных параллельно, R / 3 и т. д.
Обратите внимание, что эквивалентное сопротивление часто является наименьшим сопротивлением в параллельной сети, поэтому общее сопротивление RT может постоянно уменьшаться по мере увеличения площади параллельных резисторов.
Параллельные резисторы Пример
Рассчитайте индивидуальные токи ответвления и общий ток, потребляемый от оборудования, для последующего набора резисторов, соединенных параллельно в очень параллельной комбинации.
Поскольку предлагаемое напряжение является общим для всех или любых резисторов в одном контуре, мы можем использовать закон Ома для расчета тока отдельной ветви следующим образом.
Тогда общий ток цепи I T , протекающий в параллельную комбинацию резисторов, будет:
Этот общий ток цепи в пять ампер можно даже найти и проверить, найдя эквивалентное сопротивление цепи RT параллельной ветви и разделив его на доступное напряжение VS следующим образом.
Сопротивление эквивалентной цепи:
Тогда ток в цепи будет:
Параллельные резисторы Пример 2
01. Параллельная цепь имеет два или более путей для прохождения тока через
Просто помните, что ПАРАЛЛЕЛЬНЫЙ означает, что два пути идут к тысячам путей.Поток электричества делится посередине каждого в соответствии с сопротивлением на каждом маршруте.
02. Сумма токов, протекающих по каждому пути, равна общему току, протекающему от источника.
Если один переулок потребляет 1 ампер, а придаток потребляет 1 ампер позже, разгибание составляет 2 ампера у источника. Если в одной и той же схеме на 2 А есть 4 ответвления, в дополнение к одной полосе может возникнуть эффект наложения 1 / 4А (.25A), соседняя 1 / 4A (0,25), соседняя 1 / 2A (0,5A) и последняя 1A.
Не причиняй боли, если ты будешь принимать во внимание телесное восприятие, тебе будет сложно понять это.

