Сопротивление проводника формула через длину. Формула сопротивления проводника через длину: зависимость, расчет, факторы влияния

Как рассчитать сопротивление проводника по его длине. От чего зависит сопротивление проводника. Какие факторы влияют на сопротивление проводника. Как связаны удельное сопротивление и длина проводника.

Что такое электрическое сопротивление проводника

Электрическое сопротивление — это свойство проводника препятствовать прохождению электрического тока. Чем выше сопротивление, тем труднее току протекать через проводник.

Сопротивление проводника зависит от нескольких факторов:

• Длины проводника
• Площади поперечного сечения
• Материала проводника
• Температуры

Единица измерения сопротивления — Ом. Обозначается буквой R.

Формула расчета сопротивления проводника через длину

Основная формула для расчета сопротивления проводника имеет вид:

R = ρ * L / S

где:

• R — сопротивление проводника (Ом)
• ρ (ро) — удельное сопротивление материала проводника (Ом·м)
• L — длина проводника (м)
• S — площадь поперечного сечения проводника (м²)

Из этой формулы видно, что сопротивление проводника прямо пропорционально его длине. То есть чем длиннее проводник, тем больше его сопротивление.

Зависимость сопротивления от длины проводника

Рассмотрим более подробно, как связаны сопротивление и длина проводника:

1. При увеличении длины проводника в 2 раза, его сопротивление также увеличивается в 2 раза.
2. При уменьшении длины проводника в 3 раза, его сопротивление уменьшается в 3 раза.
3. Сопротивление прямо пропорционально длине: R ~ L

Такая зависимость объясняется тем, что в более длинном проводнике электронам приходится преодолевать большее расстояние, сталкиваясь с большим количеством атомов кристаллической решетки.

Удельное сопротивление проводника

Удельное сопротивление — это характеристика материала проводника, показывающая его способность проводить электрический ток. Обозначается греческой буквой ρ (ро).

Физический смысл удельного сопротивления — это сопротивление проводника длиной 1 м и площадью поперечного сечения 1 м².

Единица измерения удельного сопротивления — Ом·м.

Значения удельного сопротивления для некоторых материалов при 20°C:

• Серебро — 1,6 * 10^-8 Ом·м
• Медь — 1,7 * 10^-8 Ом·м
• Алюминий — 2,8 * 10^-8 Ом·м
• Железо — 9,8 * 10^-8 Ом·м

Как площадь сечения влияет на сопротивление проводника

Площадь поперечного сечения проводника также влияет на его сопротивление. Чем больше площадь сечения, тем меньше сопротивление проводника.

Зависимость сопротивления от площади сечения обратно пропорциональная:

R ~ 1/S

То есть:

• При увеличении площади сечения в 2 раза, сопротивление уменьшается в 2 раза
• При уменьшении площади сечения в 3 раза, сопротивление увеличивается в 3 раза

Это объясняется тем, что в проводнике с большим сечением электроны имеют больше пространства для движения, меньше сталкиваются друг с другом.

Влияние температуры на сопротивление проводника

Температура также влияет на сопротивление проводников. Для большинства металлов зависимость следующая:

• При повышении температуры сопротивление увеличивается
• При понижении температуры сопротивление уменьшается

Это связано с тем, что при нагревании усиливаются колебания атомов кристаллической решетки, что создает дополнительные препятствия для движения электронов.

Зависимость сопротивления от температуры для металлов можно выразить формулой:

R = R0(1 + αΔt)

где:

• R — сопротивление при данной температуре
• R0 — сопротивление при 0°C
• α — температурный коэффициент сопротивления
• Δt — изменение температуры

Примеры расчета сопротивления проводника

Рассмотрим несколько примеров расчета сопротивления проводника:

Пример 1

Медный провод имеет длину 100 м и площадь поперечного сечения 2 мм². Рассчитайте его сопротивление.

Дано:

• L = 100 м
• S = 2 мм² = 2 * 10^-6 м²
• ρ (медь) = 1,7 * 10^-8 Ом·м

Решение:

R = ρ * L / S = (1,7 * 10^-8) * 100 / (2 * 10^-6) = 0,85 Ом

Ответ: сопротивление медного провода равно 0,85 Ом.

Пример 2

Как изменится сопротивление алюминиевого провода, если его длину увеличить в 3 раза, а площадь сечения уменьшить в 2 раза?

Решение:

R ~ L/S

Изменение сопротивления: R2/R1 = (3L/0.5S) / (L/S) = 6

Ответ: сопротивление провода увеличится в 6 раз.

Применение формулы сопротивления в электротехнике

Формула расчета сопротивления проводника через его длину широко применяется в электротехнике и электронике для решения различных задач:

• Расчет параметров электрических цепей
• Проектирование кабельных линий
• Выбор проводов и кабелей нужного сечения
• Определение потерь электроэнергии в проводах
• Расчет нагревательных элементов

Зная формулу и зависимости, инженеры могут подбирать оптимальные параметры проводников для различных применений.

Удельное сопротивление проводника – формула, определение, таблица для расчета

4.7

Средняя оценка: 4.7

Всего получено оценок: 99.

4.7

Средняя оценка: 4.7

Всего получено оценок: 99.

Проводниками в физике называют материалы, общим свойством которых является способность хорошо проводить электрический ток. Большое количество свободных носителей электрического заряда (электронов и ионов), имеющееся в проводниках, при воздействии на них электрического поля, создает направленное, упорядоченное перемещение, то есть электрический ток. Величины токов для разных проводников с одинаковыми геометрическими размерами и одинаковой напряженностью электрического поля могут существенно отличаться. Физическая величина, характеризующая способность различных материалов по разному проводить электрический ток, называется удельным электрическим сопротивлением.

Вспомним закон Ома

Основным законом, устанавливающим связь между электрическим напряжением U, током I и сопротивлением R, является закон Ома:

$ I = {U \over R} $ (1).

Закон был открыт немецким ученым Георгом Омом в 1826 г. экспериментальным путем. Ученый измерял величину тока при различных напряжениях, которое он варьировал с помощью гальванических батарей, меняя их количество.

От чего зависит величина сопротивления

R ?

Дальнейшие эксперименты показали, что:

• Величина R прямо пропорциональна длине проводника, то есть чем больше длина проводник L, тем больше тем больше его сопротивление, причем зависимость линейная, то есть R∼ L;
• Величина R , обратно пропорциональна поперечной площади проводника S, то есть $ R ∼ {1\over S } $;
• Поскольку у проводников из разных материалов с одинаковыми размерами S и L сопротивления отличались, то была введена физическая величина, названная удельным сопротивлением ρ.

Рис. 1. Проводник длиной L, поперечным сечением S и током I

Тогда выражение для величины сопротивления приобрело следующий вид:

$ R = ρ * {L\over S} $ (2). 2]}\over [м]} $ (5).

Тогда числовые значения ρ, становятся более удобными для восприятия. Например, удельное сопротивление железа ρ_ж = 130000 (Ом*м) = 0,13 (Ом*мм²)/м. В справочниках данные приводятся в этом в последнем, более компактном представлении.

Температурная зависимость

ρ(Т)

Для большинства материалов проведены многочисленные эксперименты по измерению значений удельных сопротивлений. Данные по большинству проводников можно найти в справочных таблицах.

Удельное сопротивление металлов и сплавов, Ом*мм²/м

(при Т = 20⁰С)

Серебро	0,016	Бронза (сплав)	0,1
Медь	0,017	Олово	0,12
Золото	0,024	Сталь (сплав)	0,12
Алюминий	0,028	Свинец	0,21
Иридий	0,047	Никелин (сплав)	0,42
Молибден	0,054	Манганин (сплав)	0,45
Вольфрам	0,055	Константан (сплав)	0,48
Цинк	0,06	Титан	0,58
Латунь (сплав)	0,071	Ртуть	0,958
Никель	0,087	Нихром (сплав)	1,1
Платина	0,1	Висмут	1,2

Чаще всего приводятся значения ρ при нормальной, то есть комнатной температуре 20⁰С. Но оказалось, что при повышении температуры удельное сопротивление возрастает по линейному закону в соответствии с формулой:

$ ρ(Т) = ρ0 * (1 + α*T)$ (6),

где: ρ₀ — удельное сопротивление проводника при температуре 0⁰С, α — температурный коэффициент удельного сопротивления, который тоже имеет для каждого вещества свое, индивидуальное, значение. Из формулы (6) следует, что коэффициент α имеет размерность [ ⁰C^-1 ] или [ 1\⁰C ].

Рис. 2. Температурная зависимость удельного сопротивления проводника

В соответствии с законом Джоуля-Ленца при протекании электрического тока т выделяется тепло, а значит происходит рост температуры проводника. Кроме этого, в зависимости от области применения, электрические приборы могут работать как при пониженных (минусовых), так и при высоких температурах. Для точных расчетов электрических цепей необходимо учитывать зависимость

ρ(Т). Величину α для конкретного материала можно узнать из справочной литературы.

Рис. 3. Справочные значения температурного коэффициента удельного сопротивления проводников

Что мы узнали?

Итак, мы узнали, что величина, характеризующая способность различных материалов по разному проводить электрический ток, называется удельным электрическим сопротивлением. Приведена формула (3) для определения удельного сопротивления проводника ρ. Линейная температурная зависимость удельного сопротивления ρ(Т) описывается формулой (6).

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Максим Разуваев

  3/10

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 99.

---

А какая ваша оценка?

От чего зависит сопротивление

☰

Сила тока в проводнике прямо пропорциональна напряжению на нем. Это значит, что с увеличением напряжения увеличивается и сила тока. Однако при одинаковом напряжении, но использовании разных проводников сила тока различна. Можно сказать по-другому. Если увеличивать напряжение, то хотя сила тока и будет увеличиваться, но везде по-разному, в зависимости от свойств проводника.

Зависимость силы тока от напряжения для данного конкретного проводника представляет собой сопротивление этого проводника. Оно обозначается R и находится по формуле R = U/I. То есть сопротивление определяется как отношение напряжения к силе тока. Чем больше сила тока в проводнике при данном напряжении, тем меньше его сопротивление. Чем больше напряжение при данной силе тока, тем больше сопротивление проводника.

Формулу можно переписать по отношению к силе тока: I = U/R (закон Ома). В таком случае нагляднее, что чем больше сопротивление, тем меньше сила тока.

Можно сказать, что сопротивление как бы мешает напряжению создавать большую силу тока.

Само сопротивление является характеристикой проводника. Оно не зависит от поданного на него напряжения. Если будет подано большое напряжение, то изменится сила тока, но не изменится отношение U/I, т. е. не изменится сопротивление.

От чего же зависит сопротивление проводника? Оно зависти от

• длины проводника,
• площади его поперечного сечения,
• вещества, из которого изготовлен проводник,
• температуры.

Чтобы связать вещество и его сопротивление, вводится такое понятие как удельное сопротивление вещества. Оно показывает, какое будет сопротивление в данном веществе, если проводник из него будет иметь длину 1 м и площадь поперечного сечения 1 м². Проводники такой длины и толщины, изготовленные из разных веществ, будут иметь разные сопротивления. Это связано с тем, что у каждого металла (чаще всего именно они являются проводниками) своя кристаллическая решетка, свое количество свободных электронов.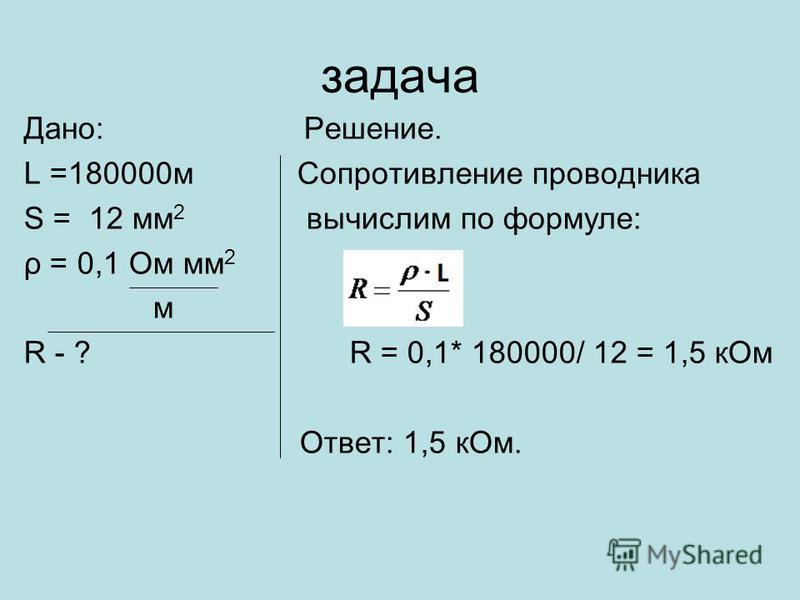

Чем меньше удельное сопротивление вещества, тем лучшим проводником электрического тока оно является. Маленьким удельным сопротивлением обладают, например, серебро, медь, алюминий; куда большее у железа, вольфрама; очень большое у различных сплавов.

Чем длиннее проводник, тем большее сопротивление он имеет. Это становится понятно, если принять во внимание, что движению электронов в металлах мешают ионы, составляющие кристаллическую решетку. Чем их больше, т. е. чем длиннее проводник, тем больше у электрона шанс замедлить свой путь.

Однако увеличение площади поперечного сечения делает как бы дорогу шире. Электронам легче течь и не сталкиваться с узлами кристаллической решетки. Поэтому чем толще проводник, тем его сопротивление меньше.

Таким образом, сопротивление прямо пропорционально зависит от удельного сопротивления (ρ) и длины (l) проводника и обратно пропорционально зависит от площади (S) его поперечного сечения. Получаем формулу сопротивления:

R = ρl/S

В этой формуле на первый взгляд не отражается зависимость сопротивления проводника от его температуры.

Однако удельное сопротивление вещества меряется при определенной температуре (обычно 20 °C). Поэтому температура учитывается. Для вычислений удельные сопротивления берут из специальных таблиц.

Для металлических проводников чем больше температура, тем сопротивление больше. Это связано с тем, что при повышении температуры ионы решетки начинают сильнее колебаться и больше мешать движению электронов. Однако в электролитах (растворах, где заряд несут ионы, а не электроны) с повышением температуры сопротивление уменьшается. Здесь это связано с тем, что чем выше температура, тем больше происходит диссоциация на ионы, и они быстрее двигаются в растворе.

Знать связь между сопротивлением и длиной

Мы знаем, что сопротивление — это противодействие току, протекающему по цепи. Сопротивление — это предотвращение крупных бедствий, таких как короткий путь или большой ущерб имуществу.

Однако сопротивление хорошо связано с длиной.

Предположим, что сопротивление — это прерыватель скорости, а скорость вашего автомобиля — это ток.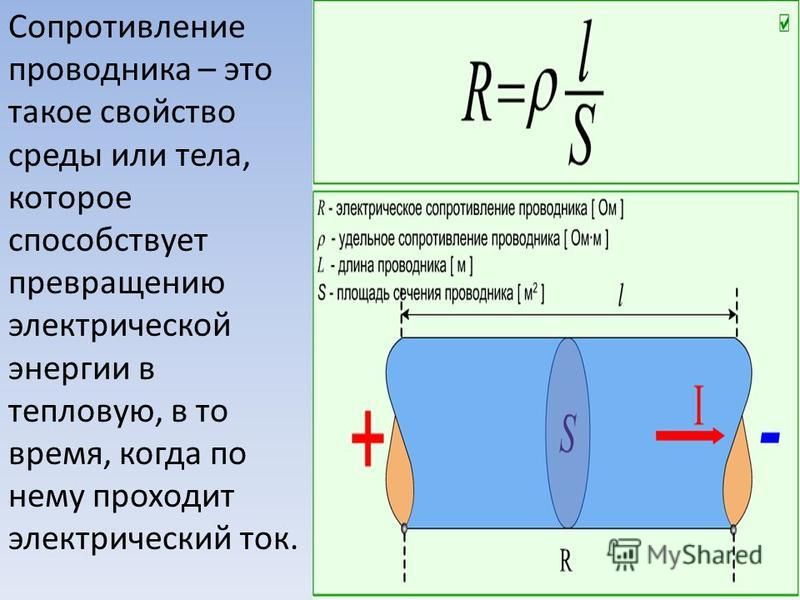 Теперь, когда прерыватель скорости находится посередине дороги, а не на ее концах. Вы попытаетесь вывести свой скоростной автомобиль с обочины, сбить его и попасть в аварию.

Что такое сопротивление?

Электрон, путешествуя по проводам, сталкивается с сопротивлением, которое в основном является препятствием для потока заряда. Для движущегося электрона путешествие от одного конца к другому — не прямой путь, а зигзагообразный путь, потому что они сталкиваются с ионами в проводящем материале. Таким образом, электроны сталкиваются с препятствием для своего движения, что затрудняет протекание тока. Это вызывает сопротивление.

В то время как разница электрических потенциалов между двумя клеммами способствует движению заряда, сопротивление препятствует этому. Таким образом, скорость, с которой заряд перетекает от одной клеммы к другой, является результатом совместного действия этих двух факторов.

Связь между длиной и сопротивлением

В приведенном выше примере мы обсудили, как длина и сопротивление связаны друг с другом. Теперь давайте поговорим об этом подробно.

Теперь вы сталкиваетесь с дорогой, на которой тормоза скорости вдвое больше, чем раньше. Теперь вам нужно быть очень уверенным, прежде чем вы достигнете края прерывателя скорости, потому что в это время ваше очень быстрое транспортное средство будет проходить через множество резисторов (прерывателей скорости), и ваше транспортное средство в конечном итоге замедлится.

Таким образом, математически уравнение может быть выражено следующим образом:

R ∝ L ……(1)

Вы едете на своем автомобиле по дороге и обязательно пересекаете тормоза, потому что перед вами есть большая пробка на дороге. Теперь, если длина меньше, и вместо того, чтобы разносить эти прерыватели на расстояние, они соединяются встык, так что вы заметили здесь, что площадь уменьшается вдвое, но если вы будете ехать быстро, ваш автомобиль снова подпрыгнет. есть риск.

Итак, здесь даже если длина меньше; правда, площадь уменьшилась вдвое, все равно надо быть медленным. Это означает, что сопротивление прямо пропорционально, даже если площадь уменьшена вдвое.

Итак, математически мы можем записать уравнение как:

R ∝ 1/A ……(2)

Теперь давайте разберемся с сопротивлением длины провода с точки зрения физики.

Зависимость между сопротивлением и длиной провода

Предположим, что имеются два проводника в виде прямоугольных пластин (одинаковых по форме и размеру), соединенных встык. Каждый из них имеет длину как «L» и площадь поперечного сечения как «А».

(Изображение скоро будет загружено)

Когда разность потенциалов «V» приложена к любой пластине, начинает течь ток «I». Итак, по закону Ома имеем соотношение:

ROLD = V/I….(3)

Где R — сопротивление между проводниками, одинаковое в каждом и измеряемое в Омах. Поскольку эти два проводника расположены бок о бок, общая длина становится «2L», а ток в них становится «I/2», потому что, если «I» — это общий ток, протекающий через оба проводника, а «V» — это одинаковая разность потенциалов на проводниках, поэтому каждый из этих проводников получает ток «1/2».

Таким образом, новое сопротивление комбинации равно Rc, и математически мы получаем наше выражение следующим образом:

      \[R_{c} = \frac{V}{I/2} = \frac{2V} {I}\]

          

Глядя на уравнение (3), мы находим уникальное соотношение между старым сопротивлением и сопротивлением комбинации, которое выглядит следующим образом:

Rc =  2 ROLD …..(4)

Уравнение (4) подразумевает, что при удвоении длины сопротивление комбинированных плит, т. е. Rc, становится удвоенным по сравнению со старым сопротивлением «R».

Сопротивление и длина провода

Теперь снова рассмотрим те же две пластины. Здесь вместо того, чтобы размещать их бок о бок, мы размещаем их друг над другом. Мы можем видеть это расположение ниже:

(Изображение будет загружено в ближайшее время)

Здесь мы можем заметить одну вещь: длина каждого проводника остается «L», однако площадь поперечного сечения, т. е. «A/2», вместо «A», потому что площадь каждого проводника прибавляется, чтобы стать «A». Здесь общим является то, что общий ток равен «I» по обоим проводникам, поэтому по каждому проводнику ток снова будет «I/2».

Снова используя закон Ома, мы получаем следующее уравнение: frac{V}{I/2} = \frac{2V}{I}\] ……(6)

Из уравнений (5) и (6) получаем новое соотношение:

RP = 2 ROLD1 …..(7)

Из уравнения (7) мы можем заметить, что при уменьшении площади вдвое сопротивление удваивается.

Мы пришли к выводу, что при удвоении длины и уменьшении вдвое площади поперечного сечения сопротивление в каждом случае удваивается, а значит, мы доказали соотношения в уравнениях (1) и (2). Теперь мы найдем новые отношения, так что давайте начнем.

Связь между сопротивлением и длиной

Здесь объединим уравнения (1) и (3):

R ∝ L/A

Теперь, убрав знак пропорциональности, получим следующую формулу сопротивления на единицу длины:

R = ⍴ L/A …. .(8)

Или,

⍴ = RA/L

Здесь ⍴ называется константой пропорциональности, или удельным сопротивлением, или удельным сопротивлением материального проводника. Измеряется в Ом-м.

Итак, сопротивление на единицу длины называют еще удельным сопротивлением материала (проводника).

⍴ = R/L (где A — постоянное значение).

Другие факторы, влияющие на сопротивление

Сопротивление зависит от двух других факторов помимо длины.

Площадь поперечного сечения и сопротивление: Площадь поперечного сечения проводов напрямую влияет на величину сопротивления. Более широкие провода имеют большую площадь поперечного сечения, и чем шире провод, тем меньше сопротивление потоку электрического заряда. Когда все остальные переменные остаются неизменными, заряд будет течь с большей скоростью по более широким проводам, чем по более тонким проводам. Сопротивление более тонкого провода меньше, чем сопротивление толстого провода, так как в тонком проводе меньше электронов для передачи тока. Таким образом, зависимость между сопротивлением и площадью поперечного сечения провода обратно пропорциональна.

Материал и сопротивление: Не все материалы одинаковы с точки зрения их способности проводить. Некоторые материалы оказывают меньшее сопротивление протекающему заряду, чем другие, и поэтому они являются лучшими проводниками. Итак, проводящая способность материала зависит от его удельного сопротивления. Удельное сопротивление зависит от электронной структуры материала и температуры. Удельное сопротивление увеличивается с повышением температуры для большинства материалов.

Серебро не используется в проводах, даже если оно является лучшим проводником из-за его высокой стоимости. Медь и алюминий обладают высокой электропроводностью, а также являются одними из самых дешевых материалов.

Резюме

Короче говоря, сопротивление провода увеличивается по мере увеличения длины провода. Длинный провод имеет большее сопротивление, чем короткий провод.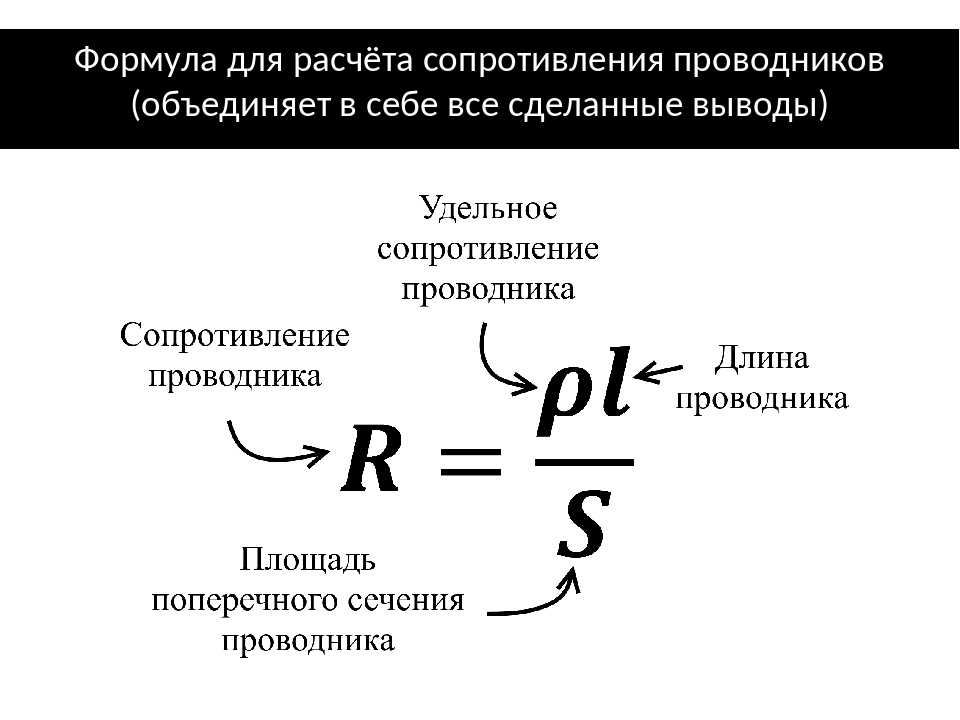 Это связано с тем, что в длинном проводе электроны сталкиваются с большим количеством ионов, проходя через них. Таким образом, зависимость между сопротивлением и длиной провода пропорциональна.

Объяснение урока: Сопротивление и удельное сопротивление проводников

В этом объяснении мы узнаем, как связать размеры и движение свободных электронов через объект с его сопротивление.

Электрическое сопротивление объекта определяется по следующей формуле.

Формула: электрическое сопротивление

Для объекта, который имеет разность потенциалов 𝑉 и ток 𝐼, через него сопротивление 𝑅 объекта определяется выражением 𝑅=𝑉𝐼.

Сопротивление — это свойство объекта. Сопротивление объекта зависит от двух факторов:

• размеров объекта,
• свойства вещества, из которого состоит объект, называемого удельным сопротивлением вещества.

Сначала рассмотрим, как размеры объекта влияют на сопротивление объекта.

На следующем рисунке показаны три резистора. Площадь стороны резисторов в 𝑥𝑦-плоскости площадь поперечного сечения каждого резистора.

Резистор A и резистор B имеют одинаковую площадь поперечного сечения. Это больше, чем площадь поперечного сечения резистора C.

Резистор A и резистор C имеют одинаковую длину в 𝑧-направлении. Это больше, чем длина резистора B.

Длина и площадь поперечного сечения резистора влияют на то, как свободные электроны проходят через резистор. Чтобы понять это, полезно рассмотреть модель внутренней структуры резистора.

Резистор, изготовленный из электропроводящего металла, состоит из решетки атомов, имеющих один или несколько электронов в их внешние орбиты очень слабо связаны с ядром атома и могут быть переброшены от одного такого атома к другому с помощью небольшая электрическая сила.

Резистор можно смоделировать как состоящий из положительно заряженных ионов и свободных электронов, которые проходят между ионами. Свобода электроны можно смоделировать как движущиеся подобно движению частиц газа.

На следующем рисунке показана поверхность поперечного сечения резистора, к которому приложена разность потенциалов. перпендикулярно площади поперечного сечения.

Величина тока из-за приложенной разности потенциалов определяется по следующей формуле.

Формула: Электрический ток

Для объекта, в котором заряд 𝑄 проходит точку на объекте во времени 𝑡, ток, 𝐼, в объекте задается 𝐼=𝑄𝑡.

Заряды, проходящие через резистор, представляют собой свободные электроны.

Рисунок, представляющий структуру резистора, показывает нам, что чем больше площадь поперечного сечения резистора, тем больше количество свободных электронов, которые могут занять эту область.

Таким образом, мы можем изменить формулу для электрического тока в виде 𝐼∝𝐴×1𝑡, где 𝐴 — площадь поперечного сечения резистора.

Время, необходимое свободному электрону, чтобы пройти длину резистора, 𝑡, определяется выражением 𝑡=𝑙𝑣, где 𝑣 — средняя скорость свободных электронов, а 𝑙 — длина резистора.

Таким образом, мы можем изменить формулу для электрического тока в виде 𝐼∝𝐴×𝑣𝑙𝐼∝𝐴𝑣𝑙.

Мы видели, что 𝑅=𝑉𝐼.

Для постоянной разности потенциалов это можно выразить как 𝑅∝1𝐼.

Мы можем подставить выражение для 𝐼 в это выражение для 𝑅. Это дает нам 𝑅∝𝑙𝐴𝑣.

Это можно выразить в форме, которая выделяет величины, соответствующие размерам резистора, следующим образом: 𝑅∝1𝑣×𝑙𝐴.

Итак, мы видим, что влияние размеров резистора влияет на сопротивление резистора следующим образом:

• сопротивление резистора прямо пропорционально длине резистора,
• сопротивление резистора обратно пропорциональна площади поперечного сечения резистора.

Как упоминалось ранее, фактор, влияющий на сопротивление резистора, обусловленный материалом резистора. а не его размеры называют удельным сопротивлением вещества. Символ 𝜌 используется для удельного сопротивления.

Как мы уже видели, 𝑅∝1𝑣×𝑙𝐴, мы видим, что 𝜌∝1𝑣.

Чем больше удельное сопротивление вещества, тем медленнее в нем движутся свободные электроны.

Сопротивление резистора можно точно выразить с помощью удельного сопротивления следующим образом: 𝑅=𝜌𝑙𝐴.

Удельное сопротивление вещества зависит от двух величин:

• скорости, с которой свободные электроны могут двигаться через вещество,
• плотности свободных электронов в веществе.

Отсюда видно, что скорость, с которой свободные электроны могут двигаться через вещество, и плотность свободных электронов в веществе зависят друг от друга.

Формула, связывающая сопротивление и удельное сопротивление, может быть изменена таким образом, чтобы удельное сопротивление рассматривалось следующим образом: 𝑅×𝐴𝑙=𝜌𝑙𝐴×𝐴𝑙=𝜌.

Отсюда мы можем определить удельное сопротивление.

Определение: Удельное сопротивление

Для объекта с сопротивлением 𝑅, площадью поперечного сечения 𝐴 и длиной 𝑙, удельное сопротивление 𝜌 определяется выражением 𝜌=𝑅𝐴𝑙.

Единица СИ количества, заданного 𝐴𝑙 дан кем-то ммм=; следовательно, единица удельного сопротивления в СИ определяется выражением Ом⋅.

Прописью это записывается как ом-метр .

Удельное сопротивление вещества зависит от температуры. Для объектов из большинства веществ удельное сопротивление увеличивается с ростом температура объекта повышается. Скорость столкновений между ионами и свободными электронами увеличивается по мере того, как температура увеличивается, что уменьшает чистое движение свободных электронов через проводник. Механизм для этого описано в конце объяснения.

Рассмотрим пример, в котором определяется удельное сопротивление вещества.

Пример 1: Определение удельного сопротивления вещества

Провод из неизвестного вещества имеет сопротивление 125 мОм. Провод имеет длину 1,8 м и сечение 2,35×10 м ² . Чему равно сопротивление вещества из чего сделана проволока? Дайте ответ в экспоненциальном представлении с точностью до одного десятичного знака.

Ответ

Удельное сопротивление 𝜌 вещества определяется по формуле 𝜌=𝑅𝐴𝑙, где 𝑅 — сопротивление провода, 𝐴 — площадь поперечного сечения провода, 𝑙 — длина провода.

Подставляя значения, указанные в вопросе, находим, что 𝜌=125×10×2,35×101,8.Ωмм

Это можно записать как 𝜌=0,125×2,35×101,8 Оммм

Тогда это можно записать как 𝜌=0,125×2,35×101,8=2,9375×10⋅1,8.ОмммОммм

До одного десятичного знака это 1,6×10⋅. Ом·м

Рассмотрим пример, в котором определяются размеры резистора, изготовленного из вещества с известным удельным сопротивлением.

Пример 2: Определение размеров резистора известного удельного сопротивления

Медный провод сопротивлением 12,8 мОм имеет поперечное сечение площадь 1,15×10 м ² . Найдите длину провод. Используйте 1,7×10 Ом⋅м для удельное сопротивление меди. Дайте ответ с точностью до одного десятичного знака.

Ответ

Удельное сопротивление 𝜌 вещества определяется по формуле 𝜌=𝑅𝐴𝑙, где 𝑅 — сопротивление провода, 𝐴 — площадь поперечного сечения провода, а 𝑙 — длина провода.

Эту формулу можно изменить так, чтобы 𝑙 стало предметом следующим образом: 𝜌×𝑙=𝑅𝐴𝑙×𝑙=𝑅𝐴𝜌𝑙=𝑅𝐴𝜌𝑙𝜌=𝑅𝐴𝜌=𝑙𝑙=𝑅𝐴𝜌.

Подставляя значения, указанные в вопросе, находим, что 𝑙=12,8×10×1,15×101,7×10⋅𝑙=1,28×10×1,15×101,7×10⋅𝑙=1,472×10⋅1,7×10⋅𝑙=1,472×101,7×10. ΩмΩмΩмΩмΩмΩмΩмм

С точностью до одной десятой это 8,7 м.

Рассмотрим еще один пример, в котором определяются размеры резистора, изготовленного из вещества с известным удельным сопротивлением.

Пример 3: Определение размеров резистора известного удельного сопротивления

Медный провод с сопротивлением 22 мОм имеет длину 6,2 м. Найдите площадь поперечного сечения. Использовать 1,7×10 Ом⋅м для удельного сопротивления меди. Дайте ответ в экспоненциальном представлении с точностью до одного десятичного знака.

Ответ

Удельное сопротивление 𝜌 вещества определяется по формуле 𝜌=𝑅𝐴𝑙, где 𝑅 — сопротивление провода, 𝐴 — площадь поперечного сечения провода, 𝑙 — длина провода.

Эту формулу можно изменить, чтобы сделать 𝐴 предметом следующим образом: 𝜌×𝑙=𝑅𝐴𝑙×𝑙=𝑅𝐴𝜌𝑙=𝑅𝐴𝜌𝑙𝑅=𝑅𝐴𝑅=𝐴𝐴=𝜌𝑙𝑅.

Подставляя значения, указанные в вопросе, находим, что 𝐴=1,7×10⋅×6,222×10𝐴=1,7×10⋅×6,22,2×10𝐴=1,054×10⋅2,2×10.0003

До одного десятичного знака это 4,8×10,m

Мы видели, что заряд, проходящий через точку на резисторе за время, определяется выражением 𝑄=𝐼𝑡.

Заряд, проходящий через точку на резисторе за время, определяется выражением 𝑄=𝑒×𝑁, где 𝑒 — заряд электрона, а 𝑁 — количество электронов, прошедших мимо точки.

Значение 𝑁 зависит от плотности свободных электронов в веществе 𝑛 и объема резистор из этого вещества. Для однородного резистора объем резистора равен произведению его длины на поперечное сечение. область. Мы видим тогда, что 𝑁=𝑛×𝐴×𝑙.

Заряд, проходящий через точку на резисторе за время, теперь может быть записан как 𝑄=𝑛𝑒𝐴𝑙.

Разделив обе части уравнения на время, за которое движется заряд, получим 𝑄𝑡=𝑛𝑒𝐴𝑙𝑡.

Мы видим, что 𝑙𝑡=𝑣, где 𝑣 — средняя скорость, с которой электроны проходят через резистор. Термин, используемый для 𝑣 есть дрейфовая скорость свободных электронов .

Мы знаем, что 𝑄𝑡=𝐼; следовательно, мы получаем формулу, связывающую ток в резисторе со средней скоростью, с которой электроны проходят через резистор.

Формула: Ток в зависимости от скорости дрейфа свободных электронов

Для резистора из вещества с плотностью свободных электронов 𝑛, имеющего площадь поперечного сечения 𝐴 и несет ток 𝐼, 𝐼=𝑛𝑒𝐴𝑣, где 𝑒 — заряд электрона, а 𝑣 — дрейфовая скорость свободных электронов в резистор.

Теперь рассмотрим пример, в котором определяется скорость дрейфа.

Пример 4. Определение дрейфовой скорости свободных электронов

Ток силой 1,4 А по медному проводу переносится свободными электронами. Площадь поперечного сечения провода составляет 2,5×10 м ² . Найдите среднюю скорость на какие свободные электроны проходят через провод. Используйте значение 1,6×10 Кл для заряда электрона и значение 8,46×10 м ⁻³ для плотности свободных электронов в меди. Дайте ответ в экспоненциальном представлении с точностью до одного десятичного знака.

Ответ

Ток в проводе связан со средней скоростью свободных электронов соотношением 𝐼=𝑛𝑒𝐴𝑣, где 𝑛 — плотность свободных электронов меди, 𝑒 — заряд электрона, 𝐴 — площадь поперечного сечения проволоки, а 𝑣 — скорость дрейфа свободной электроны в проводе.

Скорость дрейфа можно сделать предметом уравнения следующим образом: 𝐼𝑛𝑒𝐴=𝑛𝑒𝐴𝑣𝑛𝑒𝐴=𝑣.

Подставляя значения, указанные в вопросе, находим, что 𝑣=1.48.46×10×1.6×10×2.5×10𝑣=1.433840𝑣=1.433840.AmCmmsCsCm

До одного десятичного знака это 4,1×10/. мс

Скорость дрейфа свободных электронов удивительно мала.

Когда электрическая цепь замкнута, ток в цепи присутствует почти сразу во всей цепи. Задержка не воспринимаемые органами чувств человека. Это может заставить кого-то предположить, что отдельные свободные электроны должны двигаться по всей длине цепь за незначительное время.

На следующем рисунке представлено неверное понимание движения свободных электронов по цепи.

Важно отметить, что в этой неверной модели свободные электроны присутствуют только в начальной и конечной точках цепь. На самом деле свободные электроны присутствуют по всей цепи. Это показано на следующем рисунке.

На рисунке видно, что выделенные свободные электроны движутся намного медленнее, чем в неправильной модели, но свободных электронов намного больше. движутся электроны.

Свободные электроны в проводнике на самом деле не движутся равномерно, как показано на предыдущих диаграммах. Движение на этих диаграммах показано суммарное движение электронов, а не движение отдельных электронов.

На следующем рисунке лучше представлены движения отдельных электронов. Только движение четырех отдельных электронов, выбирается случайным образом.

Мы видим, что хотя только часть электронов имеет скорость с положительной составляющей в направлении тока, результирующая скорость этих электронов (показана серым штриховым вектором) имеет такую ​​составляющую.

Понимание того, что движения отдельных электронов значительно отличаются от направления чистого движения электронов помогает объяснить, почему удельное сопротивление имеет тенденцию увеличиваться с температурой.

На следующем рисунке показан один и тот же проводник при двух разных температурах.

При более высокой температуре ион в проводнике будет иметь тенденцию претерпевать большие изменения смещения вокруг своего среднего положении, чем при более низкой температуре. Таким образом, диапазон возможных положений ионов увеличивается, как показано на рисунке.

Это означает, что столкновения между ионами и электронами становятся более вероятными. Чем больше столкновений происходит между ионами и электронов, тем больше уменьшается ток в проводнике и, следовательно, тем больше увеличивается удельное сопротивление проводника.

Давайте теперь обобщим то, что было изучено в этом объяснителе.

Ключевые моменты

• Сопротивление объекта зависит от размеров объекта и свойства вещества, из которого состоит объект называют удельным сопротивлением вещества.
• Для объекта с сопротивлением 𝑅, площадью поперечного сечения 𝐴 и длиной 𝑙, удельное сопротивление 𝜌 определяется выражением 𝜌=𝑅𝐴𝑙.
• Удельное сопротивление измеряется в ом-метрах. (Ом⋅м).
• Чем больше удельное сопротивление вещества, тем больше энергии требуется для создания тока в объекте, сделанном из вещество.