Сопротивление соединения проводников. Параллельное и последовательное соединение проводников: основные характеристики и применение

Как рассчитать сопротивление при параллельном соединении проводников. Каковы основные закономерности для силы тока и напряжения в параллельной цепи. Почему параллельное соединение используется в бытовой электропроводке. Как решать задачи на смешанное соединение проводников.

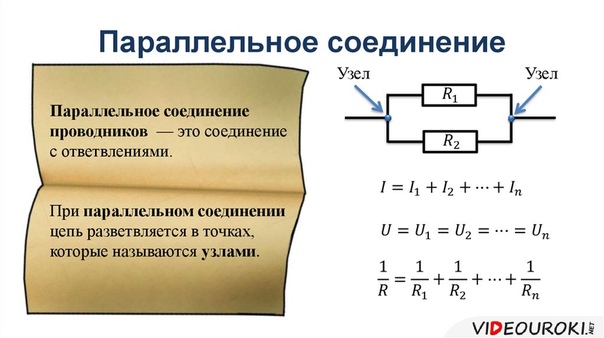
Параллельное соединение проводников: основные характеристики

Параллельное соединение проводников широко применяется в электротехнике и бытовой электропроводке. При таком соединении все проводники подключаются к одним и тем же точкам цепи. Рассмотрим основные характеристики параллельного соединения:

Напряжение при параллельном соединении

Напряжение на всех параллельно соединенных участках цепи одинаково и равно напряжению на входе разветвления:

U = U1 = U2 = … = Un

Это свойство позволяет подключать к одной сети приборы с одинаковым номинальным напряжением.

Сила тока при параллельном соединении

Общий ток в неразветвленной части цепи равен сумме токов в отдельных ветвях:

I = I1 + I2 + … + In

Это позволяет подключать несколько потребителей, не превышая допустимый ток в подводящих проводах.

Сопротивление при параллельном соединении

Общее сопротивление параллельно соединенных проводников определяется по формуле:

1/R = 1/R1 + 1/R2 + … + 1/Rn

Важно отметить, что общее сопротивление всегда меньше сопротивления любого из параллельно соединенных проводников.

Применение параллельного соединения в бытовой электропроводке

Параллельное соединение широко используется в бытовой электропроводке по следующим причинам:

• Все электроприборы рассчитаны на одинаковое напряжение сети (220 В в России)
• При параллельном подключении напряжение на всех приборах одинаково
• Можно включать и выключать приборы независимо друг от друга
• При выходе из строя одного прибора остальные продолжают работать

Таким образом, параллельное соединение обеспечивает удобство и безопасность использования бытовых электроприборов.

Сравнение параллельного и последовательного соединения проводников

Рассмотрим основные отличия параллельного и последовательного соединения проводников:

Характеристика	Параллельное соединение	Последовательное соединение
Напряжение	Одинаково на всех участках	Сумма напряжений на участках
Сила тока	Сумма токов в ветвях	Одинакова на всех участках
Сопротивление	Меньше наименьшего из сопротивлений	Сумма сопротивлений участков

Как мы видим, характеристики параллельного и последовательного соединения противоположны. Это определяет области их применения в различных электрических схемах.

Решение задач на параллельное соединение проводников

При решении задач на параллельное соединение проводников следует придерживаться следующего алгоритма:

1. Определить, какие величины даны в условии задачи
2. Записать формулы для параллельного соединения:
   • U = U1 = U2 = … = Un
   • I = I1 + I2 + … + In
   • 1/R = 1/R1 + 1/R2 + … + 1/Rn
3. Применить закон Ома для участка цепи: I = U/R
4. Составить систему уравнений и решить ее относительно искомых величин

Рассмотрим пример решения задачи на параллельное соединение проводников.

Пример задачи

Два резистора сопротивлением 10 Ом и 15 Ом соединены параллельно. Напряжение на концах соединения 12 В. Определите:

1. Общее сопротивление цепи
2. Силу тока в каждом резисторе
3. Общую силу тока в цепи

Решение

1. Общее сопротивление:

   1/R = 1/R1 + 1/R2 = 1/10 + 1/15 = 0.1 + 0.067 = 0.167

   R = 1/0.167 = 6 Ом

2. Сила тока в резисторах:

   I1 = U/R1 = 12/10 = 1.2 А

   I2 = U/R2 = 12/15 = 0.8 А

3. Общая сила тока:

   I = I1 + I2 = 1.2 + 0.8 = 2 А

Проверим результат по закону Ома:

I = U/R = 12/6 = 2 А

Полученное значение совпадает с рассчитанным ранее, что подтверждает правильность решения.

Смешанное соединение проводников

В реальных электрических схемах часто встречается смешанное соединение, сочетающее параллельные и последовательные участки. При решении задач на смешанное соединение следует:

1. Разбить схему на участки с однотипным соединением
2. Рассчитать эквивалентное сопротивление для каждого участка
3. Заменить участки эквивалентными сопротивлениями
4. Повторять процесс, пока вся схема не сведется к одному эквивалентному сопротивлению

Такой подход позволяет решать даже сложные задачи со смешанным соединением проводников.

Практическое применение знаний о параллельном соединении

Понимание принципов параллельного соединения проводников важно не только для решения учебных задач, но и для практического применения:

• Проектирование электрических сетей в зданиях
• Расчет нагрузки на электрическую сеть при подключении бытовых приборов
• Разработка электронных устройств
• Диагностика неисправностей в электрических цепях

Эти знания помогают создавать безопасные и эффективные электрические системы в различных областях техники.

Заключение

Параллельное соединение проводников — важная тема в изучении электричества. Понимание его особенностей позволяет:

• Рассчитывать характеристики электрических цепей
• Проектировать бытовые и промышленные электросети
• Обеспечивать безопасность при работе с электрооборудованием

Применение полученных знаний на практике поможет в решении различных технических задач, связанных с электричеством.

Параллельное соединение проводников – законы, формулы и схема сопротивления цепи

4

Средняя оценка: 4

Всего получено оценок: 124.

4

Средняя оценка: 4

Всего получено оценок: 124.

Электрические цепи представляют собой набор электронных компонент (сопротивлений, конденсаторов и т.д.), соединенных в различном порядке. От источника электрического тока (аккумулятора) энергия подается по подводящим цепям к различным элементам цепи. Самыми распространенными способами соединений являются параллельное и последовательное соединения. Рассмотрим далее параллельное соединение проводников.

Что такое резистор

Резистор (от английского слова resistor — сопротивление) — это простейший пассивный элемент, применяемый для регулирования силы тока или ограничения электрической мощности. На электрических схемах изображается в виде прямоугольника. Геометрические размеры реальных резисторов зависят от величины их сопротивления, которое измеряется в единицах, названых в честь немецкого физика Георга Ома.

Рис. 1. Резистор R – обозначение на схеме и настоящие резисторы.

Напомним, что закон Ома для электрических цепей описывается формулой:

$$R={U \over I}$$

где:

R — сопротивление, Ом;

U — напряжение, В;

I — сила тока в амперах, А.

Напряжение и ток измеряются приборами — вольтметром и амперметром.

Параллельное соединение

Если взять два резистора R₁ и R₂ и соединить их так, что начала (левые концы) соединятся в одной точке, а правые концы соединятся в другой точке, то это и будет параллельное соединение.

Рис. 2. Схема параллельного соединения двух резисторов

Элементы цепи (резисторы) соединяются между собой проводниками, сопротивление которых обычно мало, и им можно пренебречь. Когда требуются более точные расчеты для больших и сложных схем, то учет этих сопротивлений необходим.

После подключения к левому и правому концу источника напряжения

U, в цепи потечет ток. Поскольку R₁ и R₂ могут отличаться друг от друга, то и значения токов I₁ и I₂ через них тоже будут разные.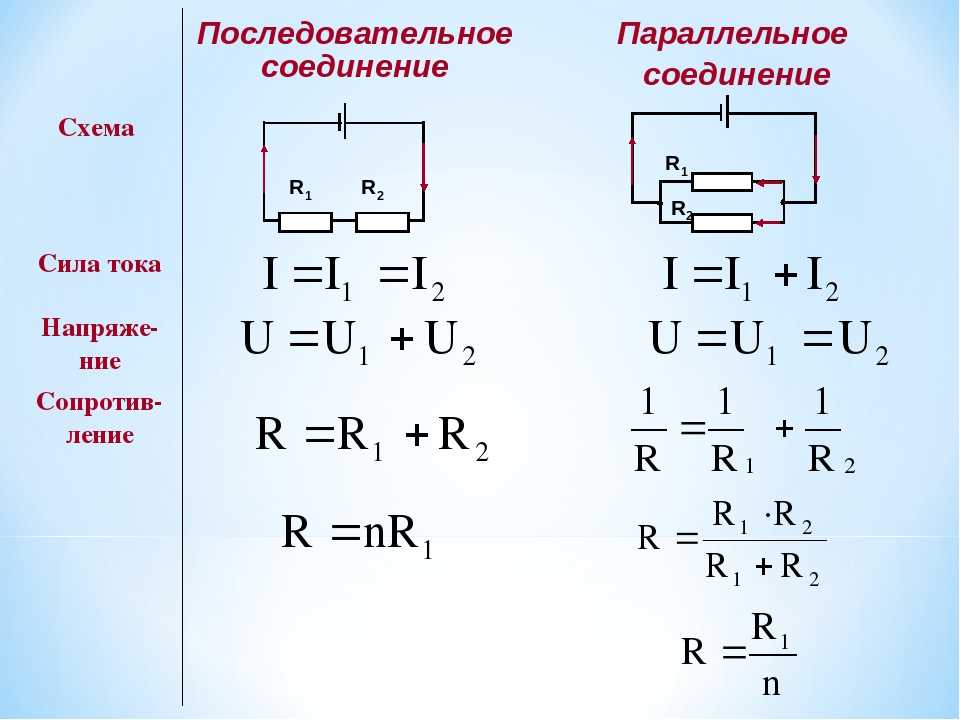 Зная напряжение U, которое подано на оба резистора, и используя формулу закона Ома, можно рассчитать токи I₁ и I₂ :

$$ I1={U \over R1}$$

$$ I2={U \over R2}$$

Общий ток I в цепи является суммой токов I1 и I2:

$$ I= I1+I2 $$

Тогда, используя выражения для токов I1 и I2, получим следующую формулу:

$$ {U \over R}={ U \over R1}+ {U \over R2}$$

Сокращая обе части последнего уравнения на U, получим следующее выражение для обратной величины общего сопротивления R:

$$ {1\over R}={ 1 \over R1}+ {1 \over R2}$$

Используя последнюю формулу и правило сложения дробей, получим выражение для расчета сопротивления цепи, состоящей из двух резисторов:

$$ R={R1* R2 \over R1+R2}$$

Если параллельно соединить два одинаковых резистора (R₁=R₂) то пользуясь последней формулой получим, что общее сопротивление цепи будет вдвое меньше величины отдельного сопротивления.

Параллельное соединение большого числа резисторов

Если параллельно соединить N резисторов — R_1,R_2… R_N, то, пользуясь вышеприведенными формулами и соображениями, можно получить выражение для обратной величины общего сопротивления такой цепи:

$$ {1\over R}={ 1 \over R1}+ {1 \over R2}+…+{1 \over RN}$$.

Рис. 3. Схема параллельного соединения нескольких резисторов R_1,R_2… R_n:.

Рассмотрим частный случай, когда все N резисторов одинаковы и равны R

₀. Тогда общее сопротивление цепи равно:

$$ R={R0 \over N}$$

Таким образом, можно сформулировать общее правило: при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлений параллельно включенных проводников.

Что мы узнали?

Итак, мы узнали законы параллельного соединения проводников (сопротивлений) в электрических цепях. Нами был получены формулы для расчетов сопротивления цепи, состоящей из двух и более резисторов.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4

Средняя оценка: 4

Всего получено оценок: 124.

---

А какая ваша оценка?

Параллельное соединение проводников • 8 класс • Физика

Содержание

На прошлом уроке мы рассмотрели последовательное соединение проводников. При нем сила тока на всех участках цепи одинакова ($I = I_1 = I_2 = … = I_n$), а сопротивление всей цепи складывается из сопротивлений всех проводников, составляющих ее ($R = R_1 + R_2 + … + R_n$). Напряжение (подобно сопротивлению) всей цепи рассчитывается сложением напряжений на концах всех элементов, составляющих такую электрическую цепь ($U = U_1 + U_2 + … + U_n$).

На данном уроке мы рассмотрим другой вид соединения проводников — параллельный. Так мы подсоединяли вольтметр, когда измеряли напряжение на каком-либо участке цепи. Сейчас же мы рассмотрим закономерности для силы тока, сопротивления и напряжения в цепи для такого типа соединения.

Параллельное включение элементов в электрическую цепь

Какое соединение проводников называют параллельным?

Соберем электрическую цепь с таким соединением. Цепь будет состоять из источника тока, ключа и двух электроламп. Электролампы включены в цепь параллельно (рисунок 1).

Рисунок 1. Электрическая цепь с параллельным подключением электроламп

Схема этой электрической цепи изображена на рисунке 2.

Рисунок 2. Схема электрической цепи с параллельным подключением электроламп

На схеме обозначены две точки A и B. Важный момент:

При параллельном соединении все входящие в него проводники одним своим концом присоединяются к точке A, а вторым концом — к другой точке B.

Так мы можем подключить еще несколько ламп или некоторое количество других потребителей электроэнергии. Поэтому все закономерности, которые мы рассмотрим далее, будут справедливы для любого количества параллельно подключенных в цепь проводников между точками A и B.

{"questions":[{"content":"Если вы хотите включить в электрическую цепь параллельно три электролампы, то необходимо, чтобы [[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["провода, идущие от электроламп, одним своим концом были присоединены к одной определенной точке, а вторым проводом — к другой определенной точке цепи","провода, идущие от электроламп, были соединены сначала друг с другом, а далее — с остальными элементами цепи","хотя бы одна электролампа была подключена в цепь последовательно"],"answer":[0]}}}]}

Напряжение в цепи при параллельном соединении проводников

Вольтметр подсоединяется в цепь параллельно. Взгляните на рисунок 3.

Рисунок 3. Схема цепи для измерения вольтметром напряжения при параллельном соединении проводников

Можно ли сказать, что мы измеряем напряжение только на одной из ламп? Нет. Получается, что одновременно мы измеряем напряжения и на одной, и на другой лампе. Мы приходим к следующему заключению.

Напряжение на участке цепи AB и на концах всех параллельно соединенных проводников одно и то же:
$U = U_1 = U_2 = … = U_n$.

Значит, напряжение — это электрическая величина, которая одинакова для всех проводников, соединенных параллельно.

По этой причине в быту и технике очень удобно применять параллельный тип соединения проводников. Почему?

Во-первых, в таком случае все потребители электроэнергии изготавливаются в расчете на одну и ту же величину напряжения. Во-вторых, если исключить из цепи один потребитель, то другие продолжат работать. Цепь останется замкнутой.

{"questions":[{"content":"Какая величина одинакова для всех проводников, соединенных параллельно?[[choice-7]]","widgets":{"choice-7":{"type":"choice","options":["напряжение","сила тока","сопротивление"],"explanations":["","Сила тока одинакова для всех проводников, если они соединены последовательно.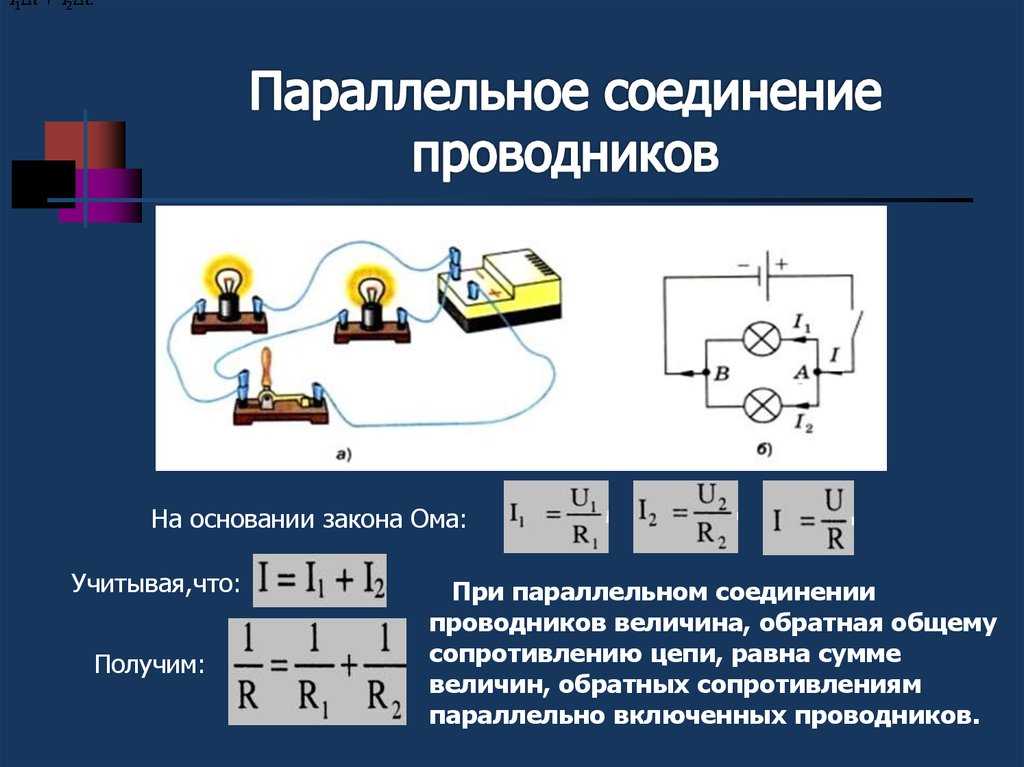 ","Сопротивление — определенная величина для каждого проводника."],"answer":[0]}}}]}

Сила тока в цепи при параллельном соединении проводников

Теперь рассмотрим, что происходит с силой тока при параллельном подключении.

Взгляните на рисунок 4, а. В точке B ток разветвляется на два тока: $I_1$ и $I_2$.

Рисунок 4. Разветвление тока при параллельном подключении проводников

Эти два тока сходятся снова в точке A. По смыслу этот момент очень похож на разветвление реки (рисунок 4, б) на два потока воды, которые через какое-то расстояние вновь сходятся в одно русло.

Как выражается сила тока в цепи до ее разветвления через силы токов в отдельных ветвях разветвления?

Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединенных проводниках:
$I = I_1 + I_2 + … + I_n$.

{"questions":[{"content":"Сила тока на участке цепи после разветвления (на участке с параллельно включенным в цепь проводником) будет[[choice-12]]","widgets":{"choice-12":{"type":"choice","options":["меньше силы тока до разветвления цепи","больше силы тока до разветвления цепи","будет равна силе тока до разветвления цепи"],"explanations":["Так как после разветвления ток разделяется на несколько токов, то сила тока на каждом параллельно соединенном проводнике будет меньше, чем до разветвления. ","",""],"answer":[0]}}}]}

Сопротивление в цепи при параллельном соединении проводников

Перейдем к сопротивлению. При параллельном соединении можно представить все проводники как один. Этот один проводник будет явно больше в диаметре, чем каждый из них по отдельности. Получается, что площадь поперечного сечения проводника как бы увеличивается при таком соединении.

Сопротивление рассчитывается по формуле $R = \frac{\rho l}{S}$. Чем больше поперечное сечение, тем меньше сопротивление.

Значит, общее сопротивление цепи уменьшается. Оно становится меньше сопротивления каждого из проводников, которые входят в такую электрическую цепь.

В цепи на рисунке 1 у нас две одинаковые лампы с сопротивлениями $R_1$. Общее сопротивление цепи $R$  будет в два раза меньше сопротивления каждой лампы: $R = \frac{R_1}{2}$.

Общее сопротивление цепи при параллельном соединении проводников рассчитывается по формуле:
$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + … + \frac{1}{R_n}$.

Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?

Очевидно, что чем больше проводников будет в разветвлении, тем меньше будет общее сопротивление цепи.

{"questions":[{"content":"При параллельном включении в цепь дополнительного проводника общее сопротивление цепи [[choice-18]]","widgets":{"choice-18":{"type":"choice","options":["уменьшится","увеличится","не изменится"],"answer":[0]}}}]}

Пример параллельного соединения проводников

Взгляните на рисунок 5. Здесь изображена часть схемы электрической цепи. Здесь параллельно включены электрические лампы, нагревательные приборы и электродвигатель.

Рисунок 5. Параллельное включение в цепь различных потребителей электроэнергии

Где может использоваться такая схема соединения?
Например, в жилых помещениях. В точках A и B провода вводятся в квартиру.

Также в наших квартирах все стандартные розетки находятся под одинаковым напряжением в $220 \space В$. Большинство производителей техники изготавливают приборы как раз под это напряжение.

Использовать параллельное подключение к одной и той же цепи очень удобно, поскольку в нее могут быть включены самые разные потребители энергии (рисунок 6).

Рисунок 6. Подключение к сети различных бытовых приборов

Благодаря такому способу подключения, выключая свет в своей квартире, мы не выключаем его и у наших соседей. Любые электроприборы могут работать независимо от подключения или отключения в сеть других.

На практике также часто можно увидеть смешанное соединение проводников. В таких цепях присутствует и последовательный тип соединении, и параллельный.

{"questions":[{"content":"На какое напряжение рассчитано большинство бытовых электроприборов?[[choice-21]]","widgets":{"choice-21":{"type":"choice","options":["$220 \\space В$","$200 \\space В$","$100 \\space В$","На произвольное значение"],"answer":[0]}}}]}

Пример задачи

В осветительную сеть комнаты включены две электрические лампы, сопротивления которых равны $200 \space Ом$ и $300 \space Ом$. Напряжение в сети составляет $120 \space В$. Определите силу тока в каждой лампе, силу тока в проводящих проводах (то есть силу тока до разветвления), общее сопротивление участка, состоящего из двух ламп.

Подразумевается, что лампы подключены в сеть параллельно. Запишем условие задачи и решим ее.

Дано:
$R_1 = 200 \space Ом$
$R_2 = 300 \space Ом$
$U = 120 \space В$

$I_1 — ?$
$I_2 — ?$
$I — ?$
$R — ?$

Решение:

Запишем закон Ома для участка цепи с первой лампой:
$I_1 = \frac{U_1}{R_1}$.

Значение сопротивления нам известно. Что с напряжением на этом участке?
Так как лампы подсоединены параллельно, то напряжение на каждой будет равно напряжению во всей цепи:
$U_1 = U_2 = U = 120 \space В$
Тогда мы можем рассчитать силу тока в каждой лампе.

Сила тока в первой лампе:
$I_1 = \frac{U}{R_1}$,
$I_1 = \frac{120 \space В}{200 \space Ом} = 0.6 \space А$.

Сила тока во второй лампе:
$I_2 = \frac{U}{R_2}$,
$I_2 = \frac{120 \space В}{300 \space Ом} = 0. 4 \space А$.

Сила тока до разветвления будет равна сумме сил этих двух токов в лампах:
$I = I_1 + I_2$,
$I = 0.6 \space А + 0.4 \space А = 1 \space А$.

Общее сопротивление цепи мы можем определить двумя способами.

Способ №1
Используя закон Ома для участка цепи, состоящего из двух параллельно соединенных ламп:
$I = \frac{U}{R}$,
$R = \frac{U}{I}$,
$R = \frac{120 \space В}{1 \space А} = 120 \space Ом$.

Способ №2
Используя формулу для расчета сопротивления при параллельном соединении проводников:
$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}$,
$\frac{1}{R} = \frac{1}{200 \space Ом} + \frac{1}{300 \space Ом} = \frac{5}{600 \space Ом} = \frac{1}{120 \space Ом}$.

Отсюда, $R = \frac{1}{\frac{1}{120 \space Ом}} = 120 \space Ом$.

При решении этой задачи мы убедились, что общее сопротивление цепи меньше сопротивления каждого из параллельно подключенных проводников: $R < R_1 < R_2$.

Ответ: $I_1 = 0. 6 \space А$, $I_2 = 0.4 \space А$, $I = 1 \space А$, $R = 120 \space Ом$.

Упражнения

Упражнение №1

Два проводника сопротивлением $10 \space Ом$ и $15 \space Ом$ соединены параллельно и подключены к напряжению в $12 \space В$. Определите силу тока в каждом проводнике и силу тока до разветвления.

Дано:
$R_1 = 10 \space Ом$
$R_2 = 15 \space Ом$
$U = 12 \space В$

$I_1 — ?$
$I_2 — ?$
$I — ?$

Показать решение и ответ

Скрыть

Решение:

Напряжение будет одинаковое как во всей цепи, так и на концах каждого из двух проводников.

Запишем закон Ома для первого проводника и рассчитаем силу тока в нем:
$I_1 = \frac{U}{R_1}$,
$I_1 = \frac{12 \space В}{10 \space Ом} = 1.2 \space А$.

То же самое сделаем для второго проводника:
$I_2 = \frac{U}{R_2}$,
$I_2 = \frac{12 \space В}{15 \space Ом} = 0.8 \space А$.

Сила тока до разветвления в цепи будет равна сумме сил тока в каждом проводнике:
$I = I_1 + I_2$,
$I = 1. 2 \space А + 0.8 \space А = 2 \space А$.

Ответ: $I_1 = 1.2 \space А$, $I_2 = 0.8 \space А$, $I = 2 \space А$.

Упражнение №2

Почему бытовые приборы в помещении необходимо соединять параллельно?

Потому что бытовые приборы рассчитаны на то же напряжение, которое подается от городской сети — $220 \space В$. При параллельном соединении это напряжение будет одинаковым на всех участках цепи.

Также параллельное соединение позволяет включать и выключать приборы независимо друг от друга, что невозможно при последовательном соединении.

Упражнение №3

Три потребителя с сопротивлениями $20 \space Ом$, $40 \space Ом$ и $24 \space Ом$ соединены параллельно. Напряжение на концах этого участка цепи равно $24 \space В$. Определите силу тока в каждом потребителе, общую силу тока в участке цепи и сопротивление участка цепи.

Дано:
$R_1 = 20 \space Ом$
$R_2 = 40 \space Ом$
$R_3 = 24 \space Ом$
$U = 24 \space В$

$I_1 — ?$
$I_2 — ?$
$I_3 — ?$
$I — ?$
$R — ?$

Показать решение и ответ

Скрыть

Решение:

Напряжение на концах этого участка цепи будет равно напряжению на концах каждого потребителя, так как они соединены параллельно: $U_1 = U2 = U_3 = U = 24 \space В$.

Используя закон Ома для участка цепи, рассчитаем силу тока на каждом потребителе электроэнергии.

Для первого потребителя:
$I_1 = \frac{U}{R_1}$,
$I_1 = \frac{24 \space В}{20 \space Ом} = 1.2 \space А$.

Для второго потребителя:
$I_2 = \frac{U}{R_2}$,
$I_2 = \frac{24 \space В}{40 \space Ом} = 0.6 \space А$.

Для третьего потребителя:
$I_3 = \frac{U}{R_3}$,
$I_3 = \frac{24 \space В}{24 \space Ом} = 1 \space А$.

Сила тока до разветвления в цепи будет равна сумме сил тока в каждом потребителе электроэнергии:
$I = I_1 + I_2 + I_3$,
$I = 1.2 \space А + 0.6 \space А + 1 \space А = 2.8 \space А$.

Теперь используем закон Ома, представляя участок цепи с тремя потребителями как единый участок цепи:
$I = \frac{U}{R}$,
$R = \frac{U}{I}$,
$R = \frac{24 \space В}{2.8 \space А} \approx 8.6 \space Ом$. 

Ответ: $I_1 = 1.2 \space А$, $I_2 = 0.6 \space А$, $I_3 = 1 \space А$, $I = 2.8 \space А$, $R \approx 8. 6 \space Ом$.

Упражнение №4

Два проводника имеют сопротивления, равные $5 \space Ом$ и $500 \space Ом$. Почему при последовательном соединении этих проводников их общее сопротивление будет больше $500 \space Ом$, а при параллельном соединении меньше $5 \space Ом$?

При последовательном соединении проводников общее сопротивление цепи будет равно сумме сопротивлений составляющих ее проводников.
Общее сопротивление при последовательном соединении:
$R = R_1 + R_2 = 5 \space Ом + 500 \space Ом = 505 \space Ом$.

Это значение действительно больше, чем $500 \space Ом$.

При параллельном соединении общее сопротивление мы рассчитываем следующим образом:
$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}$,
$\frac{1}{R} = \frac{1}{5 \space Ом} + \frac{1}{500 \space Ом} = \frac{101}{500 \space Ом}$,
$R = \frac{1}{\frac{101}{500 \space Ом}} = \frac{500 \space Ом}{101} \approx 5 \space Ом$.

Согласитесь, что $5 \space Ом$ намного меньше, чем $500 \space Ом$.

Можно посмотреть на этот вопрос и с другой стороны. Сопротивление рассчитывается по формуле $R = \frac{\rho l}{S}$. Оно прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения.

При последовательном соединении проводников мы можем сказать, что длина проводника увеличивается. Значит, увеличивается и сопротивление. Общее сопротивление будет больше, чем сопротивление каждого отдельного проводника.

А при параллельном соединении увеличивается площадь поперечного сечения. Значит,  сопротивление будет уменьшаться. Получается, что общее сопротивление такой цепи будет меньше сопротивления каждого из проводников.

Упражнение №5

На рисунке 7 изображена схема смешанного соединения проводников, сопротивления которых: $R_1 = 4 \space Ом$, $R_2 = 6 \space Ом$, $R_3 = 12 \space Ом$, $R_4 = 2 \space Ом$. Амперметр показывает силу тока $1 \space А$. Определите напряжение между точками В и С и силу тока в каждом проводнике.

Рисунок 7. Схема электрической цепи со смешанным соединением проводников к упражнению №5

Дано:
$R_1 = 4 \space Ом$
$R_2 = 6 \space Ом$
$R_3 = 12 \space Ом$
$R_4 = 2 \space Ом$
$I_3 = 1 \space А$

$U — ?$
$I_1 — ?$
$I_2 — ?$
$I_4 — ?$

Показать решение и ответ

Скрыть

Решение:

Амперметр подсоединен последовательно с проводником $R_3$. Он показывает силу тока $I_3 = 1 \space А$. Это сила тока после разветвления.

Используя закон Ома для этого проводника, рассчитаем напряжение на его концах:
$I_3 = \frac{U_3}{R_3}$,
$U_3 = I_3R_3$,
$U_3 = 1 \space А \cdot 12 \space Ом = 12 \space В$.

Так как проводники $R_3$ и $R_2$ подключены в цепь параллельно, то напряжение на каждом из этих проводников будет равно напряжению на участке цепи, который их включает. Это и есть напряжение между точками B и C:
$U = U_3 = 12 \space В$.

По закону Ома рассчитаем силу тока на проводнике $R_2$:
$I_2 = \frac{U}{R_2}$,
$I_2 = \frac{12 \space В}{6 \space Ом} = 2 \space А$.

Теперь мы можем рассчитать силу тока до его разветвления — на проводниках $R_1$ и $R_4$. При этом $I_1 = I_4 = I$, потому что эти проводники включены в цепь последовательно. Это значит, что сила тока в любом участке такой цепи будет одинаковой. В нашем случае на проводнике $R_1$ и $R_4$.

Рассчитаем эту силу тока, используя величины, полученные с параллельно соединенных проводников. Сила тока до разветвления будет равна сумме сил тока в каждом проводнике после разветвления:
$I = I_2 + I_3$,
$I = 1 \space А + 2 \space А = 3 \space А$.

Ответ: $U = 12 \space В$, $I_1 = I_4 = I = 3 \space А$, $I_2 =  2 \space А$, $I_3 = 1 \space А$. 

Сопротивление контакта разъема | Технология АТЛ

Опубликовано 8 июля 2020 г. (28 декабря 2020 г. ) Майк Андерсон

Содержание

• Что такое контактное сопротивление?
• Удельное сопротивление
• Контактное сопротивление
• В чем причина сопротивления контактов?
• Сужение
• Сопротивление пленки
• Релаксация стресса
• Как снизить риск непреднамеренного сопротивления контактов разъема?
• Дополнительные ресурсы.

Выход из строя одного электрического соединения в операционной может привести к летальному исходу.

К сожалению, существует много различных причин отказа электрического соединения.

Понимание того, где может произойти сбой и что может потенциально его вызвать, может помочь вам в разработке более эффективных медицинских устройств, работающих на энергии.

Одной из потенциальных причин отказа электрического соединения является нежелательный/неизвестный уровень контактного сопротивления.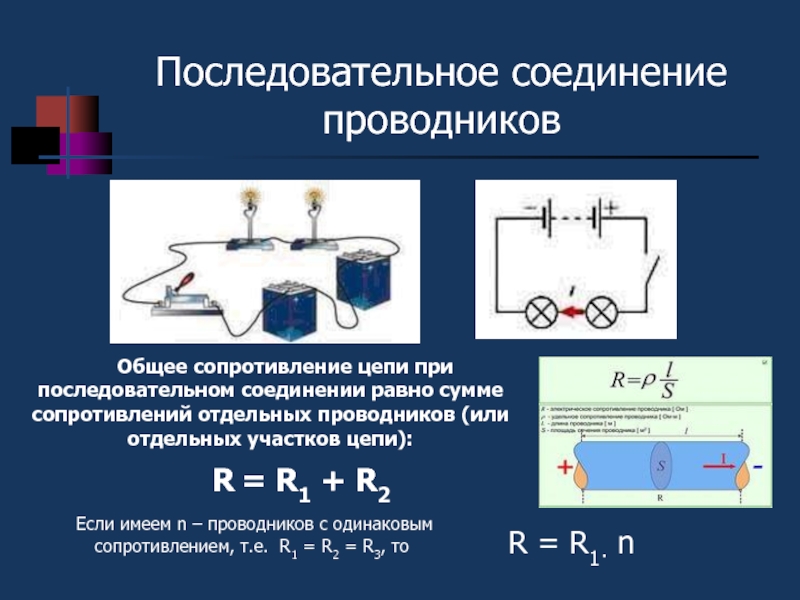

В этом сообщении блога мы обсудим контактное сопротивление, его причины, как его обнаружить и некоторые способы его предотвращения.

Рекомендуется: Решения для межсоединений для медицинских устройств [Полное руководство]

---

Что такое контактное сопротивление?

Прежде чем углубляться в контактное сопротивление, важно понять, что такое «сопротивление».

Говоря об электрических компонентах и ​​цепях, сопротивление относится к противодействию протеканию электрического тока.

Другими словами, сопротивление описывает способность материала предотвращать/замедлять поток электричества.

При этом элементы, которые являются хорошими проводниками (например, серебро, медь и т. д.), имеют низкое сопротивление, в то время как элементы, которые являются хорошими изоляторами (например, резина, стекло и т. д.), как правило, имеют высокое сопротивление.

Говоря о решениях для межсоединений, обычно выделяют две широкие категории сопротивления: удельное сопротивление и контактное сопротивление .

Удельное сопротивление

Удельное сопротивление (иногда называемое «внутренним сопротивлением» или «сопротивлением материала») описывает сопротивление самого материала (при заданном размере и площади).

Когда кто-то говорит, что медь имеет низкое сопротивление, они имеют в виду удельное сопротивление меди.

Контактное сопротивление

Контактное сопротивление , с другой стороны, описывает сопротивление, возникающее при соприкосновении двух проводников друг с другом.

Когда два кабеля соединены и напряжение кабелей изменяется (в основном) непреднамеренно в результате этого соединения, это обычно вызвано контактным сопротивлением.

Сравнение удельного сопротивления и контактного сопротивления.

---

В чем причина сопротивления контактов?

Чтобы было ясно, существование сопротивления не является чем-то плохим.

На самом деле, многие энергетические продукты (включая медицинские устройства) используют механизмы для контроля или создания сопротивления.

Резисторы, которые Merriam Webster определяет как «устройство, имеющее электрическое сопротивление и используемое в электрической цепи для защиты, работы или управления током», являются прекрасным примером этой концепции.

Контактное сопротивление, однако, это совсем другая история.

Как правило, контактное сопротивление не заложено в устройстве, разъеме или цепи.

Вместо этого устройства, соединители и схемы спроектированы с учетом наличия контактного сопротивления и — в большинстве случаев — предназначены для предотвращения или смягчения его возможного воздействия.

При этом контактное сопротивление обычно вызывается тремя причинами: сужением , сопротивлением пленки и расслаблением напряжения .

Сужение

Сужение описывает сужение истинной контактной поверхности при контакте двух материалов.

Когда два материала вступают в контакт, часто предполагается, что электроны текут по всей площади поверхности материалов.

На самом деле, из-за поведения электронов, выходящего за рамки этого сообщения в блоге, даже когда два плоских материала идеально прижаты друг к другу, настоящий контакт будет установлен только в определенных точках.

Пример сужения, вызывающего контактное сопротивление.

Сопротивление пленки

Сопротивление пленки описывает сопротивление, создаваемое появлением нежелательного резистивного материала на поверхности («пленке») контакта.

Сопротивление пленки имеет два источника: окисление и загрязнение .

Вообще говоря, окисление описывает потерю электронов.

К сожалению, большинство металлов обычно классифицируются как «легкоокисляемые».

Когда дело доходит до электрических разъемов, окисление происходит, когда слой оксидов на контакте поглощает влагу.

Окисление вызывает коррозию контактов разъема, увеличивая контактное сопротивление и отрицательно влияя на напряжение, проходящее через соединение.

Загрязнение происходит при попадании постороннего мусора на контакт разъема.

Если контакты покрыты связующим веществом, грязью или чем-либо еще, что может нарушить соединение, контактное сопротивление увеличивается.

Пример загрязнения, вызывающего контактное сопротивление.

Релаксация стресса

Со временем и/или при чрезмерном использовании материал может деформироваться, и форма вашего контакта может отличаться от первоначальной.

Эту деформацию и изменение часто называют «релаксацией напряжения».

Релаксация напряжения потенциально может увеличить сопротивление, поскольку может снизить контактную силу и способность контакта «стираться» (оба понятия обсуждаются в следующем разделе).

Для высокотемпературных сред с высокой частотой циклов релаксация напряжения может быть основной причиной контактного сопротивления.

Пример релаксации напряжений, вызывающей контактное сопротивление.

---

Как снизить риск непреднамеренного сопротивления контактов разъема?

Хотя невозможно полностью исключить вероятность непреднамеренного появления сопротивления контактов, есть несколько мер предосторожности, которые инженеры могут принять во время разработки устройства, чтобы снизить риски, связанные с сопротивлением контактов.

Сначала выберите правильный материал для контактов.

Глубокое понимание того, как будут изготавливаться контакты (например, потребуется ли для них процесс, который потенциально может привести к загрязнению?) и условия применения (например, будет ли разъем вступать в контакт с такими жидкостями, как кровь или физиологический раствор? ) может помочь вам выбрать экономичный материал, обладающий необходимыми профилактическими характеристиками.

Во-вторых, убедитесь, что у вас достаточное усилие прижима.

Ток может проходить от одного проводника к другому, только если они соприкасаются.

Если точки контакта слабо соприкасаются, то есть если контакты не сжимаются вместе, разъем будет испытывать контактное сопротивление.

Обеспечение достаточного контактного усилия для создания надежного соединения между точками имеет большое значение для снижения потенциального контактного сопротивления.

В-третьих, спроектируйте «очистку» контактной системы.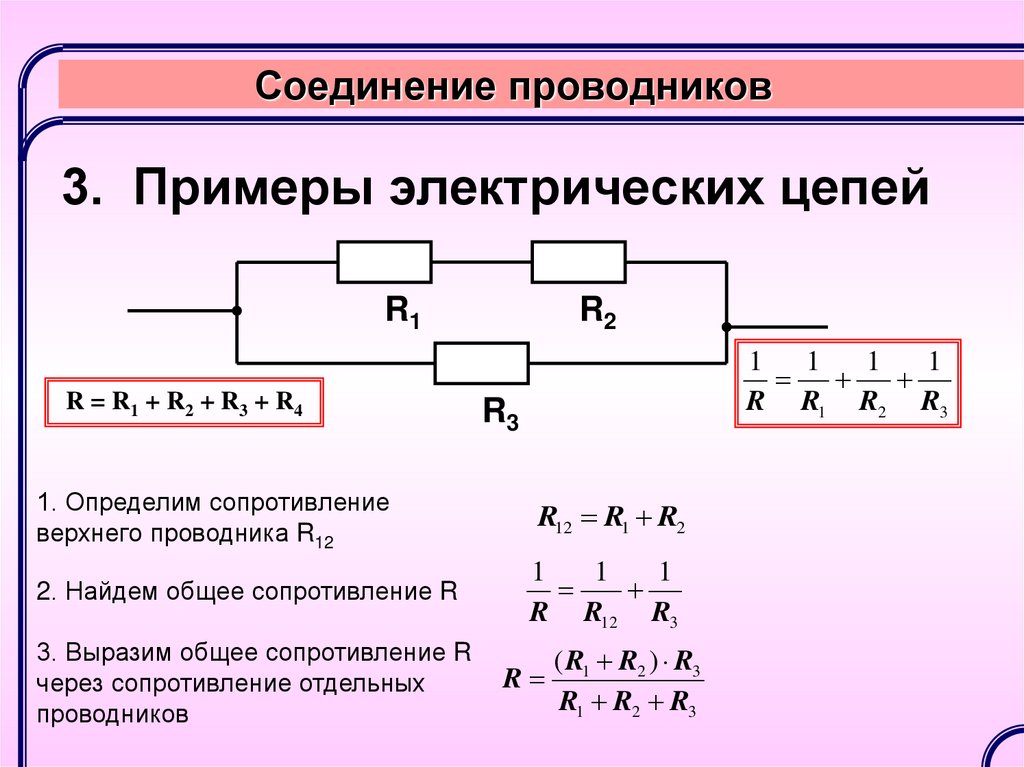

Большинство современных контактов спроектированы таким образом, чтобы «вытирать» загрязнения при подключении.

При достаточном контактном усилии и прочном крае контакт может отталкивать загрязнения от себя и своего ответного элемента при соединении.

Наконец, перед использованием убедитесь, что контакты разъема чистые.

Для одноразовых устройств ключевым моментом является обеспечение отсутствия мусора, загрязнения или окисления на контактах до того, как они покинут производственное предприятие.

Для многоразовых устройств, которые должны выдерживать автоклавирование, следует учитывать не только производственный процесс, но и процесс после стерилизации.

Будут ли ваши контактные поверхности окисляться или подвергаться коррозии после цикла автоклавирования?

Есть ли потенциальное место во время/после цикла автоклавирования, где мусор может попасть на контакт?

Эти четыре соображения ни в коем случае не являются исчерпывающим списком способов снижения риска непреднамеренного контактного сопротивления, но они представляют собой полезную отправную точку.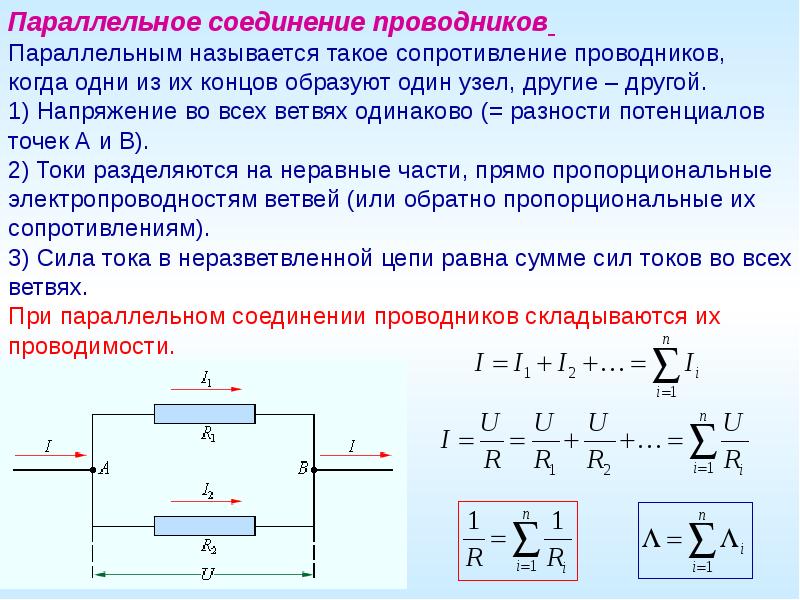

Чтобы получить помощь в выборе подходящего материала, разработке соединения с нужной контактной силой или разработке многоразового соединителя, мы рекомендуем обратиться к специалисту.

---

Дополнительные ресурсы.

Сопротивление контакта — это только один аспект проекта межсоединений.

Чтобы узнать больше о решениях для межсоединений, загрузите наше исчерпывающее руководство.

Основы сопротивления проводников на высоких частотах

С появлением систем на частотах выше 60 Гц мы наблюдаем повышенный интерес к рейтингу кабелей в этих приложениях. Конечно, здесь на ум приходят компьютерные системы мэйнфреймов, работающие на частоте 400 Гц.

Есть несколько факторов, которые существенно влияют на сопротивление проводника при увеличении частоты. Поговорим о каждом подробно и предложим предлагаемый метод определения силы тока проводника на частоте 400 Гц по сравнению с таковой на частоте 60 Гц.

Ключевые факторы

В общем, вы должны проектировать 3-фазные энергосистемы с частотой 400 Гц так же, как и системы с частотой 60 Гц, но вы должны понимать, что более высокая частота будет увеличивать скин-эффект и эффекты близости в проводнике. Это, в свою очередь, увеличит эффективное сопротивление проводника. Повышенная частота также увеличит реактивное сопротивление цепи, что в сочетании с сопротивлением увеличит падение напряжения.

Более высокая частота также увеличивает влияние магнитных материалов на реактивное сопротивление и нагрев кабеля. Именно по этой причине не следует прокладывать проводники частотой 400 Гц в магнитопроводе или слишком близко к магнитным конструкциям в здании.

Потери из-за частоты пропорциональны квадрату линейного тока. Так что для очень малых токов этими потерями можно пренебречь. Однако для больших токов они могут быть значительными.

Кабели в воздушной и немагнитной трубе

Мы ограничим наше обсуждение здесь одножильным 600-вольтовым кабелем. Для частот примерно до 1000 Гц можно предположить, что реактивное сопротивление прямо пропорционально частоте. Уменьшением индуктивности из-за частот до этой величины можно пренебречь, потому что оно минимально — и намеренно вносимая погрешность ничтожна. Однако для частот выше 1000 Гц следует включить поправку на индуктивность. В этих случаях индуктивность определяется следующим уравнением:

L = ([0,1404 × log ₁₀ 2S/D _C ] + [0,0153 × L/L _O ]) × 10 ^-3 Генри на 1000 футов

Где,

L = индуктивность относительно нейтрали

L/L _O = поправочный коэффициент из таблицы 1 (нажмите здесь, чтобы увидеть таблицу 1 )

S = осевое расстояние между проводниками (дюймы)

D _C = Диаметр проводника (дюймы)

Расчет коэффициентов сопротивления

Из оригинальной статьи Неера Макграта под названием «Расчет повышения температуры и нагрузочной способности кабельных систем» мы знаем, что для любой кабельной системы отношение сопротивления проводника переменному/постоянному току (R _AC /R _DC ) равно выражается следующим уравнением:

R _AC /R _DC = 1 + Y _C + Y _S + Y _P (уравнение 1)

Где Y _C , Y _S и Y _P — это эффекты проводника, оболочки и кабелепровода соответственно. Поскольку мы рассматриваем только неметаллические оболочки в воздухе или в неметаллическом трубопроводе, нас должно интересовать только Y _C в нашем обсуждении.

В статье Неера Макграта также показано, что вы можете выразить Y _C следующим образом:

Y _C = Y _CS + Y _CP

Где Y _CS — компонент проводника из-за скин-эффекта , а Y _CP — компонент проводника из-за эффекта близости .

Таким образом, принимая во внимание приведенные выше комментарии, уравнение 1 принимает вид:

.

R _AC /R _DC = 1 + Y _CS + Y _CP (уравнение 2)

Скин-эффект и эффект близости являются функцией F _(x) , которая для сплошных и концентрических круглых проводников приведена в таблице 1. Таким образом, для Y _CS и Y _CP мы имеем следующие уравнения:

Y _CS = F _(x) (уравнение 3)

Y _CP = F _(x) K ² × [ (1,18/F _(X) + 0,27) + 0,312K ² ] (уравнение 4)

Где,

К = Д _С /С,

x = 0,0276 × √f/R _DC

f = частота в Гц

R _DC = сопротивление проводника постоянному току при рабочей температуре (Ом на 1000 футов)

D _C = диаметр проводника (дюймы)

S = осевое расстояние между проводниками (дюймы)

F _(х) = функция x из таблицы 1

Таблица 2 (нажмите здесь, чтобы увидеть Таблица 2 ) перечислены отношения сопротивления переменному/постоянному току, рассчитанные по уравнениям 3 и 4.