Как рассчитать общее сопротивление электрической цепи при последовательном и параллельном соединении резисторов. Какие формулы используются для определения эквивалентного сопротивления при смешанном соединении. Как применяется метод свертывания схемы для нахождения общего сопротивления сложной цепи.
Основные способы соединения резисторов в электрической цепи
В электрических схемах резисторы могут соединяться тремя основными способами:
- Последовательное соединение
- Параллельное соединение
- Смешанное соединение
Каждый из этих способов имеет свои особенности и формулы для расчета общего эквивалентного сопротивления цепи. Рассмотрим их подробнее.
Расчет общего сопротивления при последовательном соединении
При последовательном соединении резисторов общее сопротивление цепи равно сумме сопротивлений всех резисторов:
Rобщ = R1 + R2 + R3 + … + Rn
Где Rобщ — общее сопротивление цепи, а R1, R2, R
Особенности последовательного соединения:
- Сила тока одинакова на всех участках цепи
- Напряжение на концах цепи равно сумме напряжений на отдельных резисторах
- Общее сопротивление всегда больше сопротивления любого отдельного резистора
Формула расчета общего сопротивления при параллельном соединении
При параллельном соединении резисторов для расчета общего сопротивления используется следующая формула:
1/Rобщ = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Где Rобщ — общее сопротивление цепи, а R1, R2, R3 и т.д. — сопротивления отдельных параллельно соединенных резисторов.
Ключевые свойства параллельного соединения:
- Напряжение одинаково на всех параллельных ветвях
- Общий ток равен сумме токов в отдельных ветвях
- Общее сопротивление всегда меньше сопротивления любого отдельного резистора
Определение эквивалентного сопротивления при смешанном соединении
При смешанном соединении в цепи присутствуют как последовательно, так и параллельно соединенные участки. В этом случае для нахождения общего сопротивления применяется метод поэтапного свертывания схемы:
- Выделяются группы последовательно или параллельно соединенных резисторов
- Для каждой группы рассчитывается эквивалентное сопротивление
- Полученные эквивалентные сопротивления объединяются дальше, пока не останется одно общее
Метод свертывания для расчета сложных электрических цепей
Метод свертывания позволяет рассчитать эквивалентное сопротивление сложной разветвленной цепи. Основные этапы метода:
- Схема разбивается на простые участки с последовательным или параллельным соединением
- Для каждого участка вычисляется эквивалентное сопротивление
- Полученные участки объединяются в более крупные блоки
- Процесс повторяется, пока вся схема не будет свернута к одному эквивалентному сопротивлению
Особенности расчета цепей со смешанным соединением резисторов
При расчете цепей со смешанным соединением важно учитывать следующие моменты:
- Последовательность выполнения расчетов — от внутренних участков к внешним
- Правильное определение типа соединения на каждом этапе
- Аккуратное применение формул для последовательного и параллельного соединения
- Проверка полученных промежуточных результатов
Примеры расчета общего сопротивления для разных типов соединений
Рассмотрим несколько примеров расчета общего сопротивления для различных схем соединения резисторов:
Пример 1: Последовательное соединение
Дано: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом
Rобщ = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом
Пример 2: Параллельное соединение
Дано: R1 = 6 Ом, R2 = 3 Ом
1/Rобщ = 1/R1 + 1/R2 = 1/6 + 1/3 = 1/2
Rобщ = 2 Ом
Пример 3: Смешанное соединение
Рассмотрим схему, где R1 и R2 соединены параллельно, а их общее сопротивление последовательно с R3:
Дано: R1 = 4 Ом, R2 = 4 Ом, R3 = 2 Ом
- Находим эквивалентное сопротивление параллельного участка: 1/Rэкв = 1/R1 + 1/R2 = 1/4 + 1/4 = 1/2 Rэкв = 2 Ом
- Рассчитываем общее сопротивление: Rобщ = Rэкв + R3 = 2 + 2 = 4 Ом
Применение законов Кирхгофа для анализа сложных электрических цепей
В случаях, когда метод свертывания не позволяет полностью решить задачу, применяются законы Кирхгофа:
- Первый закон Кирхгофа: сумма токов, входящих в узел, равна сумме токов, выходящих из узла
- Второй закон Кирхгофа: алгебраическая сумма напряжений в любом замкнутом контуре равна нулю
Эти законы позволяют составить систему уравнений для нахождения токов и напряжений в сложных разветвленных цепях.
Влияние температуры на сопротивление электрической цепи
При расчете общего сопротивления важно учитывать, что сопротивление проводников зависит от температуры:
R = R0(1 + αΔt)
Где R — сопротивление при текущей температуре, R0 — сопротивление при начальной температуре, α — температурный коэффициент сопротивления, Δt — изменение температуры.
Электрическая цепь и электрическое сопротивление
Электрической цепью называется путь, по которому проходит электрический ток. Чтобы по электрической цепи проходил ток, она должна быть замкнутой. Простейшая электрическая цепь состоит из трех основных частей: источника электрического тока, приемника (потребителя) электрического тока и системы соединительных проводов с вспомогательными приборами (включатели и переключатели тока, измерительные приборы и т. п.).
В качестве источников электрического тока могут служить: механические — электрические генераторы, в которых механическая энергия преобразуется в электрическую; химические— гальванические элементы и аккумуляторы, в которых химическая энергия преобразуется в электрическую; тепловые — термоэлементы, преобразующие тепловую энергию в электрическую; лучевые — фотоэлементы, преобразующие световую энергию в электрическую.
Приемниками электрического тока могут служить электродвигатели, электролампы, электронагревательные приборы и т.
п.
Часть электрической цепи, состоящая из приемников электрической энергии и соединительных проводов, называется внешней цепью. Токопроводящие пути самого источника электрической энергии называются внутренней цепью.
Если оборвать электрическую цепь на каком-либо участке, то ток по всей цепи прекращается. Замыкание и размыкание цепи осуществляется выключателем или рубильником.
Для измерения величин, характеризующих электрический ток, в цепь могут быть включены измерительные приборы.
Все вещества обладают различной способностью оказывать сопротивление прохождению электрического тока. Эта способность веществ оказывать сопротивление прохождению электрического тока называется электрическим сопротивлением.
Величина сопротивления измеряется в омах и обозначается буквой R или r. За 1 ом принято сопротивление ртутного столба длиной 106,3 см и поперечным сечением 1 мм2 при 0°С.
В практике применяются также единицы электрического сопротивления килоом (1 ком=1000 ом) и мегом (1 Мом=1 000 000 ом).
Величина сопротивления зависит от длины, поперечного сечения и материала, из которого изготовлен проводник. Эта зависимость выражается следующей формулой:
где R — сопротивление проводника, ом;
р — удельное сопротивление материала проводника, ом мм 2/м;
I — длина проводника, м;
S — поперечное сечение проводника, мм2.
Как видно из формулы, чем длиннее проводник и меньше его поперечное сечение, тем больше его сопротивление.
Удельным сопротивлением материала называется сопротивление проводника из данного материала длиной в 1 м и поперечным сечением 1 мм2 при 0°С. Обычно различные проводники сравниваются по этому показателю. Например, серебро, медь, алюминий обладают небольшим сопротивлением, а такие сплавы, как константан (сплав меди, никеля и марганца), нихром (сплав никеля, хрома, железа, марганца), никелин и другие обладают сопротивлением значительно большим.
Помимо размеров и материала, на сопротивление проводника влияет его температура. Так, почти у всех металлических проводников при повышении температуры сопротивление увеличивается. И только вышеперечисленные сплавы: константан, нихром, никелин и другие практически почти не изменяют своего сопротивления при нагревании и способны выдерживать высокие температуры, благодаря чему эти сплавы и получили широкое применение в электротехнике.
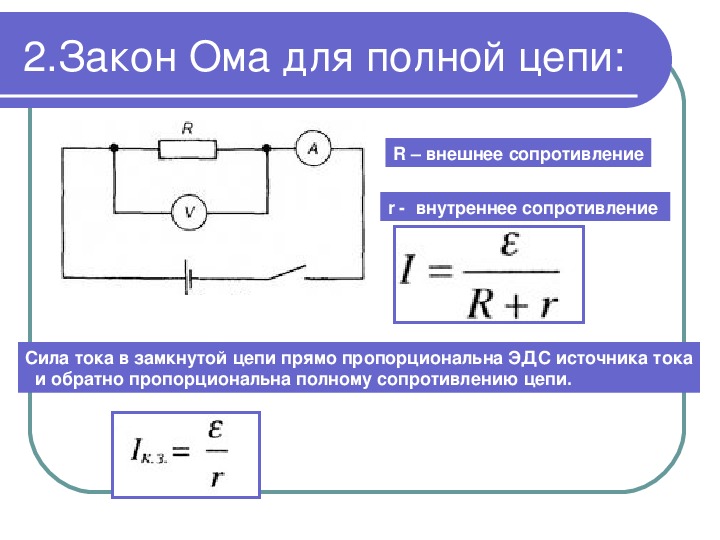
Зависимость между величинами, характеризующими электрическую цепь, т.е. силой тока, э. д. с. и сопротивлением, устанавливается законом Ома, который формулируется следующим образом:
сила тока в замкнутой неразветвленной цепи прямо пропорциональна электродвижущей силе и обратно пропорциональна сопротивлению цепи.
Закон Ома выражается формулой:
где I — сила тока, а;
Е — э. д. с. источника электрической энергии, в;
R — сопротивление внешнего участка цепи, ом;
r— сопротивление внутреннего участка цепи, ом.
Эта формула может быть записана и в таком виде:
т. е. электродвижущая сила, создаваемая источником электрической энергии, равна величине тока, умноженной на общее сопротивление цепи, и складывается из двух слагаемых, из которых первое (IR) представляет собой разность потенциалов на зажимах внешнего сопротивления, называется напряжением на зажимах внешней цепи и обозначается через U, а второе слагаемое (Ir) носит название падения напряжения на внутреннем участке цепи.
Для внешней цепи и для отдельных ее участков закон Ома обычно записывается в следующем виде:
т. е. сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению данного участка цепи.
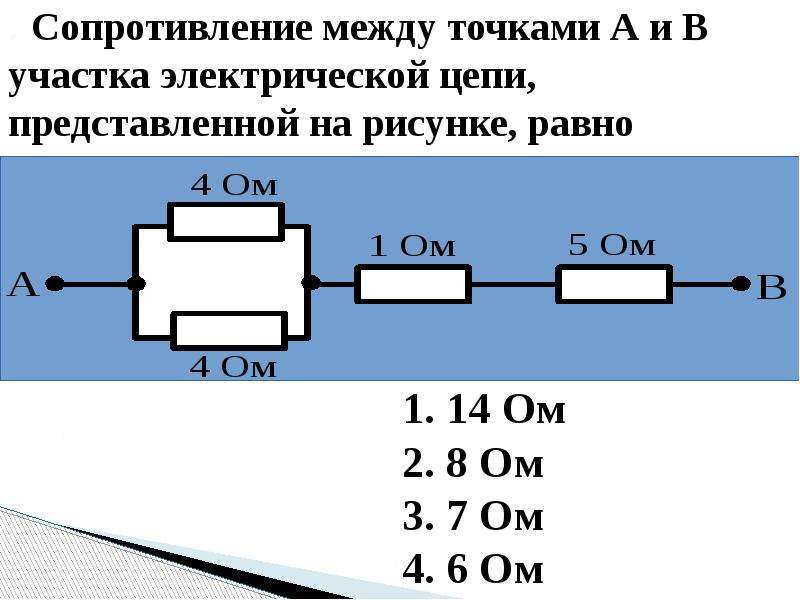
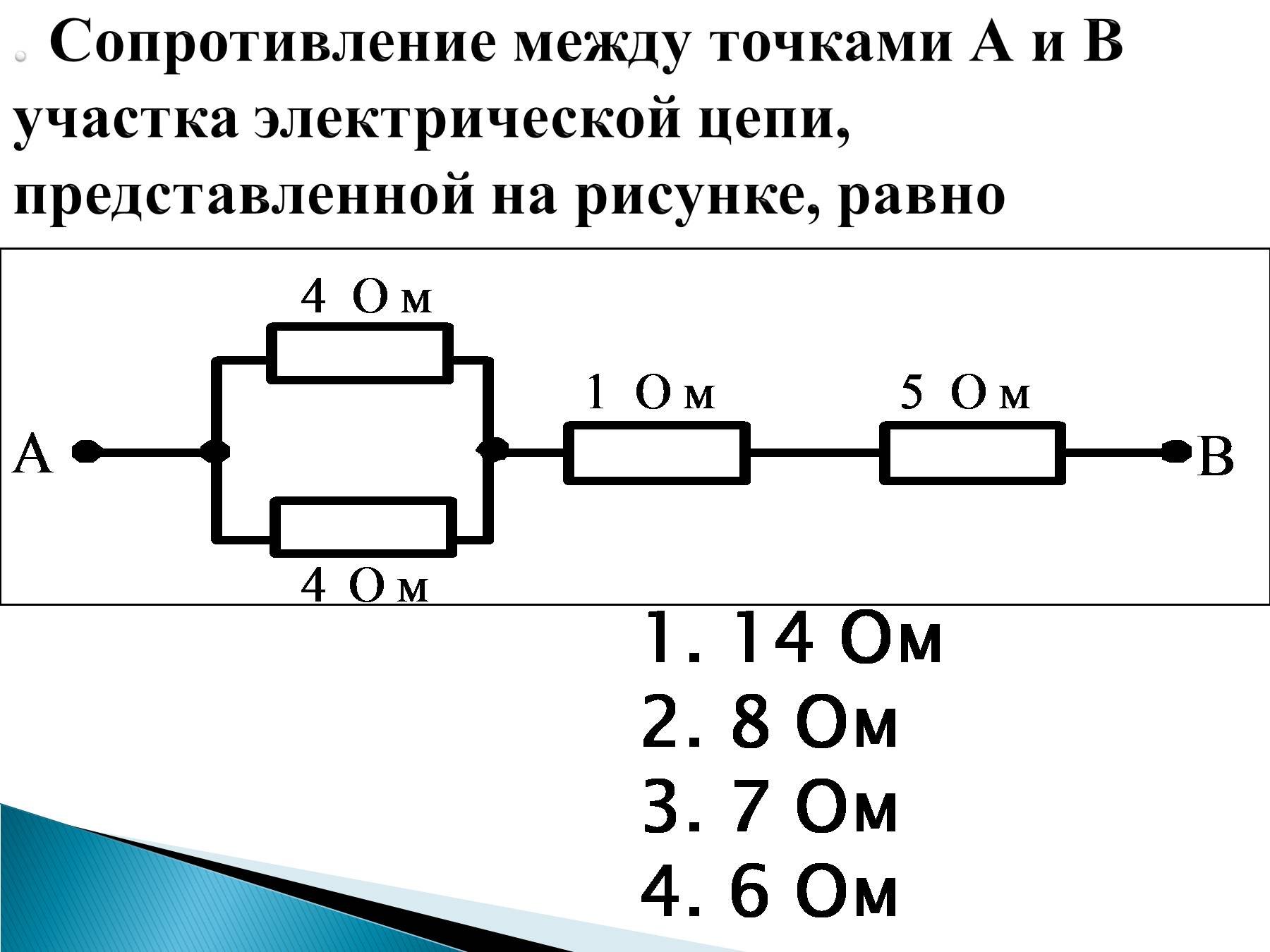
Различные сопротивления в электрическую цепь можно включить последовательно, параллельно и смешанным способом (рис. 159).
Последовательным соединением сопротивлений называют такое соединение, когда конец одного сопротивления соединяют с началом второго, конец второго с началом третьего и т.
д., а конец последнего и начало первого сопротивлений подключаются к зажимам источника тока (см. 159, а). Основным свойством последовательного соединения является то, что при таком соединении сила тока во всех сопротивлениях внешней и внутренней цепи одинакова и согласно закону Ома
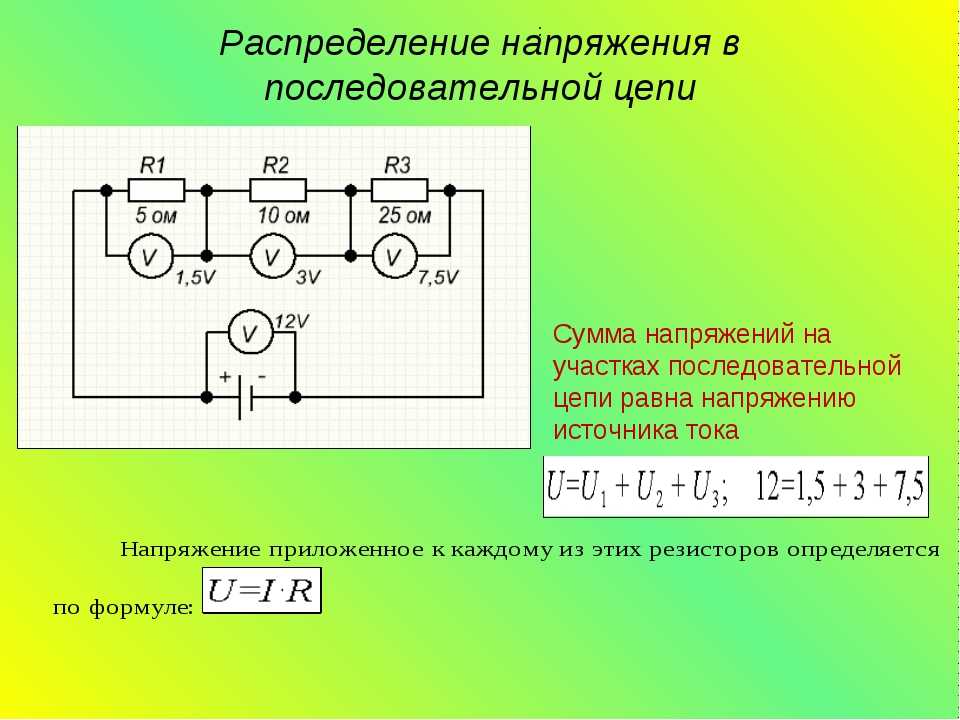
Общее сопротивление последовательной цепи равно сумме всех соединенных сопротивлений, т. е.
Напряжение на зажимах источника тока при последовательно соединенных сопротивлениях равно произведению величины тока на сопротивление внешнего участка цепи. Обозначив через U1, U2, U3, U4, напряжения на концах каждого сопротивления, получим:
а следовательно,
Напряжение на полюсах источника тока при последовательном соединении сопротивлений равно сумме напряжений на отдельных участках цепи.
Параллельным, соединением сопротивлений называется такое соединение, при котором начала всех сопротивлений соединяются в один общий узел, а концы — в другой.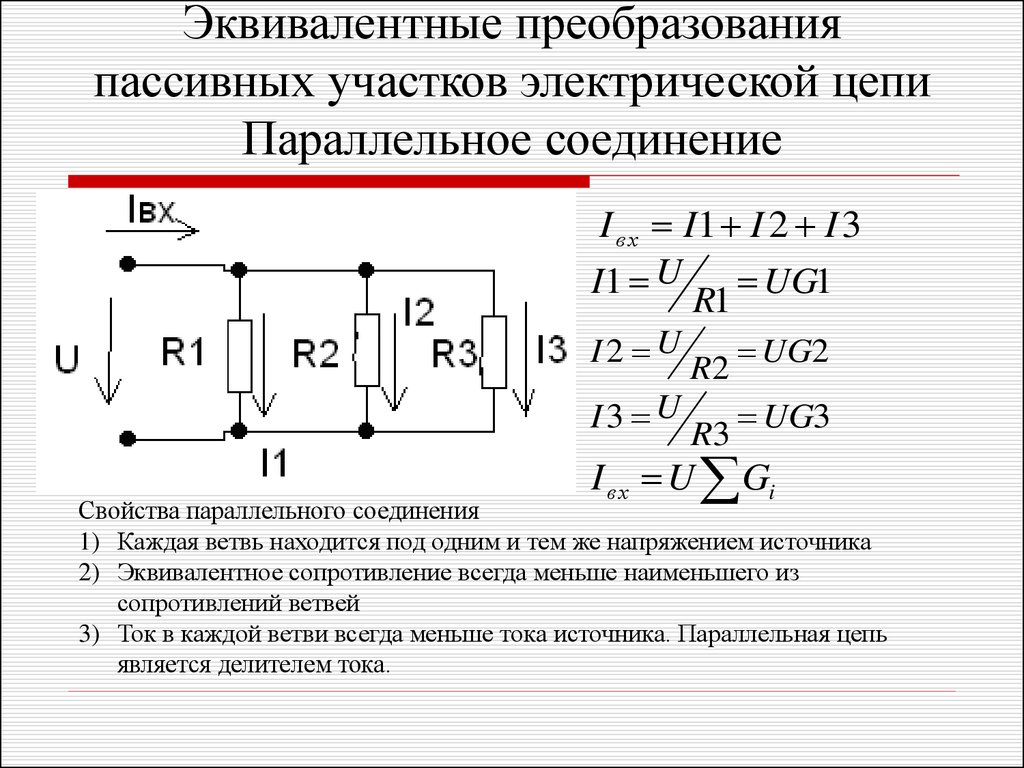
При этом зажимы источника тока включаются к узлам цепи А и В (рис. 159, б).
Если напряжение между точками А и В равно U, то такое же напряжение будет между началом и концом каждого сопротивления. Тогда для каждого участка цепи по закону Ома можно написать:
т. е. при параллельно соединенных сопротивлениях ток будет больше там, где меньше сопротивление.
Основным свойством параллельного соединения является то, что в каждом разветвлении цепи устанавливается своя сила тока, обратно пропорциональная сопротивлению данного участка цепи.
В точке В ток разветвляется в нескольких направлениях (на несколько ветвей), а в сумме он равен I. Поэтому при параллельном соединении нескольких сопротивлений ток, подведенный к этим сопротивлениям, равен сумме токов во всех сопротивлениях:
Для определения общего сопротивления параллельной цепи пользуются следующим соотношением: общая проводимость (обратная величина сопротивлению) параллельной цепи равна сумме проводимостей отдельных разветвлений цепи, т.
е.
Если в электрической цепи часть сопротивлений включена последовательно, а часть параллельно, то такое соединение называется смешанным. На рис. 159, в сопротивления R 1и R2 соединены последовательно, a R3 и R4 — параллельно.
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
-
2.
5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
5 Механические колебания и волны
СТО
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
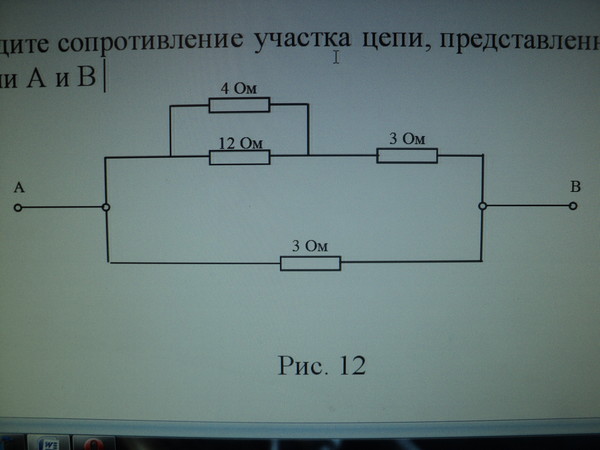
Как найти эквивалентное сопротивление цепи формула
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник».
Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.
Электрическая цепь с последовательным соединением элементов
Рис. 1.4
Рис. 1.5
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5).
После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
,
и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
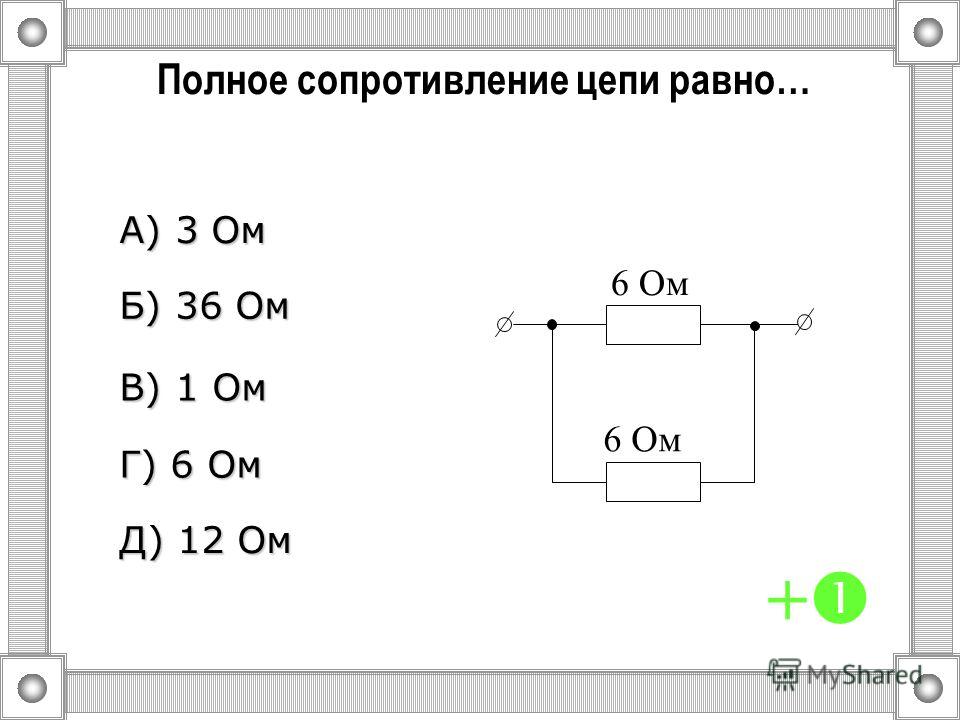
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I1 + I2 + I3, т.е. ,
откуда следует, что
.
В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
Отсюда следует, что
,
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):
На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.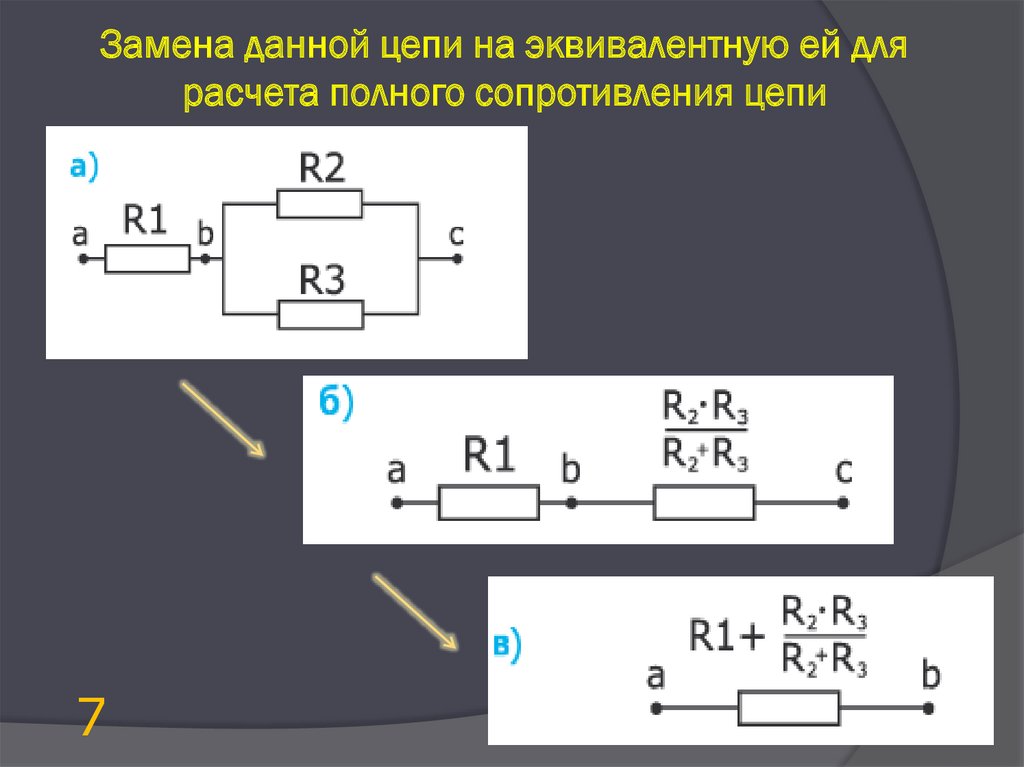
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
.
Рис. 1.10
Рис. 1.11
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
Рис. 1.12
Рис. 1.13
В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис.
1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:
; ; .
Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:
; ; .
После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)
.
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.
Электрическая цепь с последовательным соединением элементов
Рис. 1.4
Рис.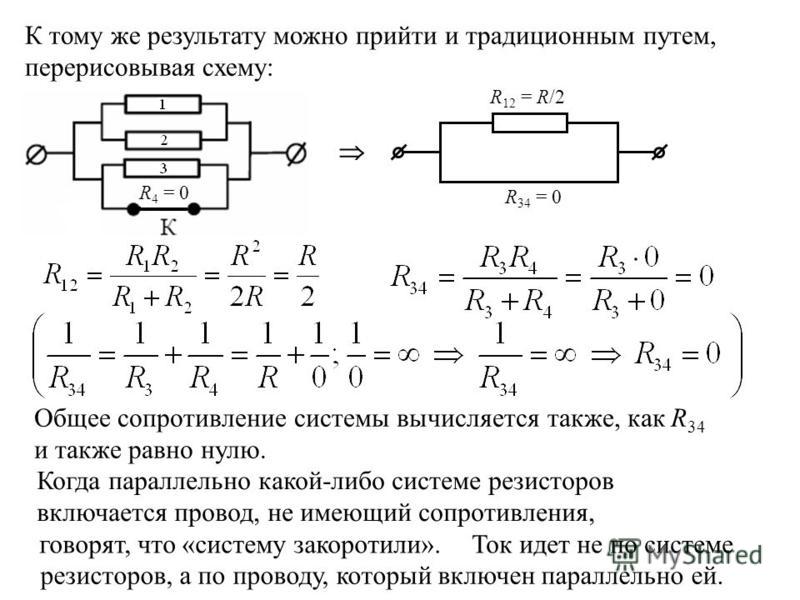
1.5
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
,
и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I1 + I2 + I3, т.е. ,
откуда следует, что
.
В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис.
1.6)
Отсюда следует, что
,
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):
На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
.
Рис. 1.10
Рис. 1.11
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис.
1.12). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
Рис. 1.12
Рис. 1.13
В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:
; ; .
Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:
; ; .
После проведенных преобразований (рис.
1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)
.
Расчёт электрических схем, содержащих несколько сопротивлений (резисторов), при нахождении силы тока в цепи, напряжения или мощности, производится с использованием метода свёртывания. Метод заключается в том, чтобы найти эквивалентное сопротивление выделенных участков цепи. Основная задача – замена резисторов, имеющих различное подключение относительно друг друга, на эквивалент (Rэкв.).
Определение эквивалентного сопротивления
При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное.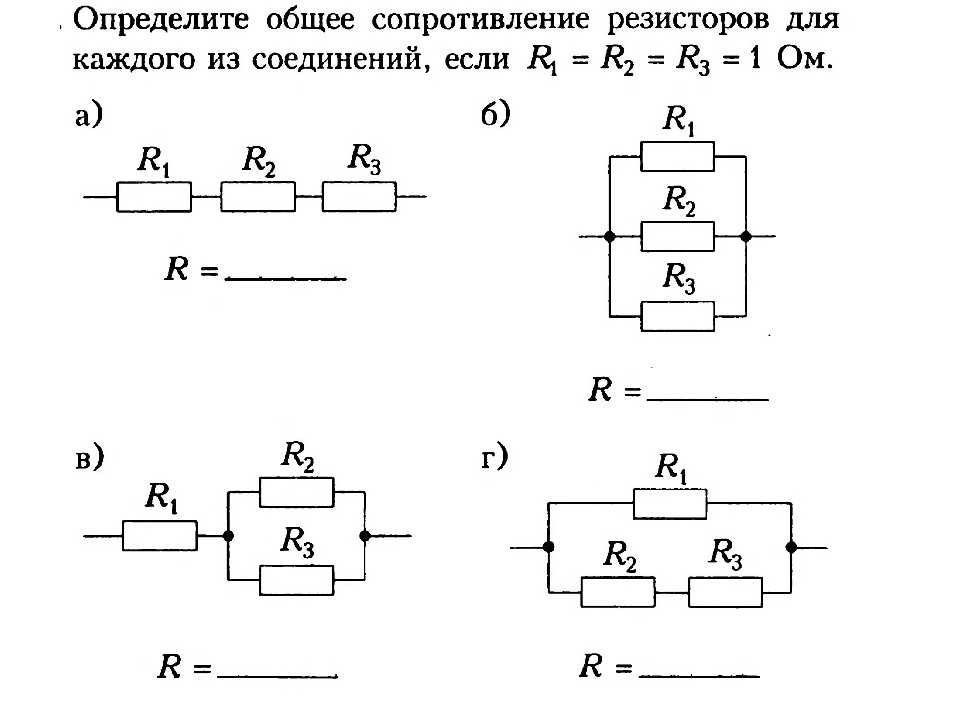
Остальные конфигурации – это лишь их вариации.
Последовательное соединение элементов
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.
В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
Следовательно, рассчитать можно общее:
Rэкв.
= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Параллельное соединение
Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.
Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:
- общий ток: I = I1 + I2 + … + In;
- общее напряжение: U = U1 = U2 = … = Un;
- Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.
= Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.
Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.
Расчёт при смешанном соединении устройств
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент.
Вновь начинают искать подобные простые соединения.
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.
Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.
Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
= (R1*R2)/R1+R2;У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
Требуется рассчитать токи на всех резистивных элементах.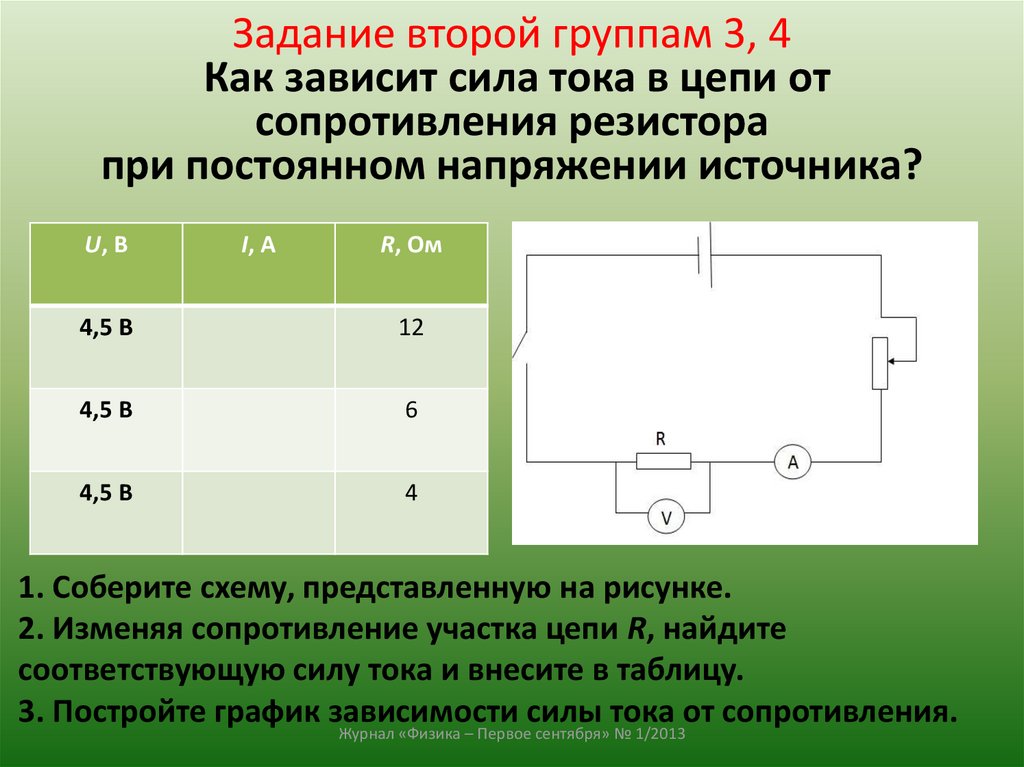
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.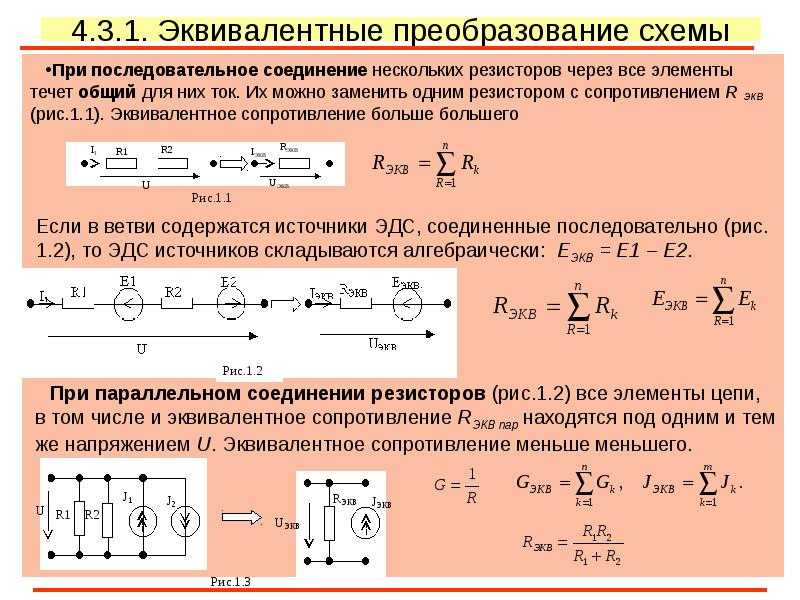
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD:
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Стоит заметить! Ток, протекающий через R4 и R5, по своему значению равен току на отрезке, не имеющем разветвления.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.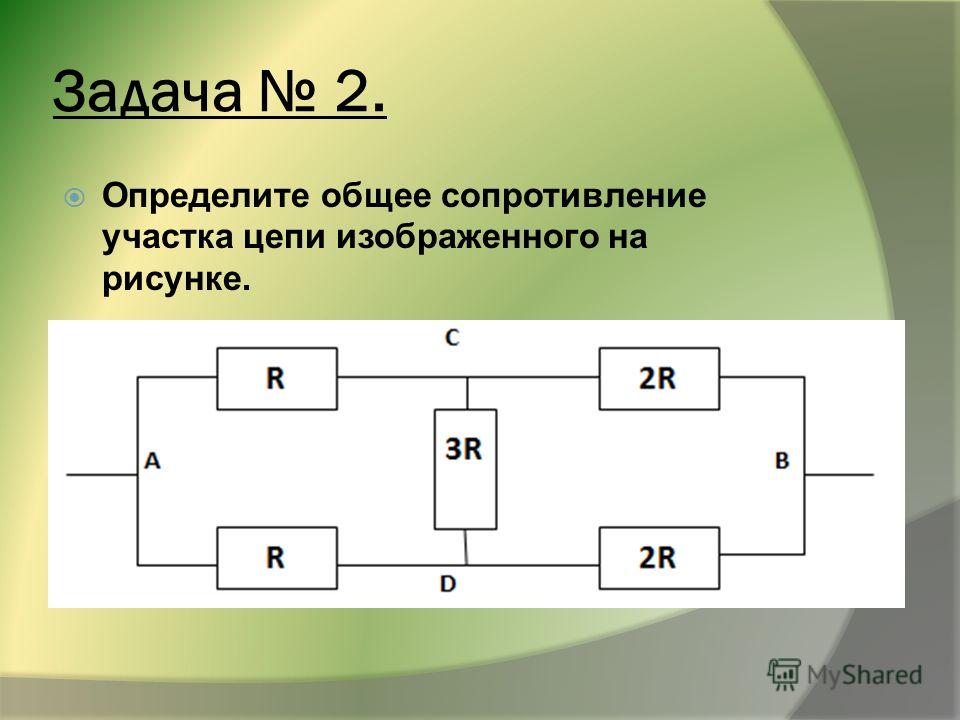
Видео
Что такое сопротивление — основные понятия » Electronics Notes
Электрическое сопротивление — один из ключевых атрибутов электрической цепи — оно определяет ток, протекающий при заданном напряжении.
Учебное пособие по сопротивлению Включает:
Что такое сопротивление
Закон Ома
Омические и неомические проводники
Сопротивление лампы накаливания
Удельное сопротивление
Таблица удельных сопротивлений для обычных материалов
Температурный коэффициент сопротивления
Коэффициент сопротивления по напряжению, VCR
Электрическая проводимость
Последовательные и параллельные резисторы
Таблица параллельных резисторов
В электрической цепи можно выполнить три основных измерения. Напряжение и ток — это первые два, а третье — сопротивление.
Поскольку электрическое сопротивление является основным понятием в электрических и электронных схемах, необходимо ответить на некоторые вопросы: что такое сопротивление, что такое резисторы и как сопротивление влияет на цепи.
Что такое сопротивление?
Прежде чем смотреть, что такое сопротивление, необходимо немного разобраться с током и что это такое. По существу поток тока в материале состоит из движения электронов в одном направлении. Во многих материалах внутри структуры беспорядочно движутся свободные электроны. Пока они движутся случайным образом, текущего потока нет, потому что число, движущееся в одном направлении, будет равно числу, движущемуся в другом. Только когда потенциал вызывает дрейф в определенном направлении, можно сказать, что ток течет.
Что такое сопротивление
Сопротивление — это препятствие потоку электронов в материале. В то время как разность потенциалов на проводнике способствует потоку электронов, сопротивление препятствует этому. Скорость, с которой заряд течет между двумя терминалами, является комбинацией этих двух факторов.
Если в цепь поместить два разных проводника, то количество тока, протекающего по каждому из них, может быть неодинаковым.
На это есть ряд причин:
- Во-первых, это легкость, с которой электроны могут двигаться внутри структуры материала. Если электроны прочно связаны с кристаллической решеткой, то будет непросто вырвать их на свободу, чтобы мог произойти дрейф электронов в том или ином направлении. В других материалах очень много свободных электронов беспорядочно дрейфуют по решетке. Именно эти материалы позволяют току течь легче.
- Еще одним фактором, влияющим на электрическое сопротивление предмета, является его длина. Чем короче длина материала, тем меньше его общее сопротивление.
- Третий — площадь поперечного сечения. Чем шире площадь поперечного сечения, тем меньше сопротивление, поскольку больше площадь, через которую может протекать ток.
В большинстве случаев требуется, чтобы проводники пропускали ток с как можно меньшим сопротивлением. В результате широко используется медь, поскольку ток легко течет по ее структуре. Кроме того, его площадь поперечного сечения сделана достаточно широкой, чтобы пропускать ток без какого-либо чрезмерного сопротивления.
В некоторых случаях необходимо иметь элементы, сопротивляющиеся протеканию тока. Эти элементы называются резисторами, и они сделаны из материалов, которые не проводят электричество, а также из таких материалов, как медь или другие металлы.
Аналогия сопротивления
Понятие сопротивления не всегда легко понять, потому что невозможно визуально увидеть задействованные величины: напряжение, ток и сопротивление сами по себе являются довольно невидимыми невооруженным глазом величинами, хотя их можно обнаружить и измерить в различных способы.
Одной из аналогий, которая помогает ввести понятие сопротивления, является резервуар для воды с трубой, выходящей из него. Хотя мы не хотим заходить слишком далеко в аналогии, она помогает объяснить основную концепцию.
Аналогия резервуара для воды и трубы для иллюстрации концепции сопротивления В этой аналогии давление воды, вызванное высотой воды, аналогично напряжению, поток воды аналогичен току, а ограничение воды поток, вызванный трубой, аналогичен сопротивлению.
. Можно видеть, что если бы труба была сужена или добавлен кран, поток воды был бы еще больше ограничен, и воды вытекало бы меньше. Это было бы аналогично увеличению сопротивления в электрической цепи, и это уменьшило бы ток.
Простая схема, показывающая напряжение и сопротивлениеВ простой цепи, состоящей из батареи или источника напряжения и резистора, если предположить, что соединительные провода не имеют сопротивления, то чем выше сопротивление, тем меньше будет протекать ток.
Кран в аналогии с водопроводной системой соответствует изменению сопротивления резистора. Когда кран закрыт, это эквивалентно выключателю, останавливающему подачу тока в электрическую цепь.
Связь между сопротивлением, напряжением и током
По аналогии с системой резервуаров для воды можно представить, что увеличение напряжения в электрической цепи повысит уровень протекающего тока.
Аналогичным образом, уменьшение сопротивления также увеличивает уровень тока.
На самом деле существует зависимость между напряжением, сопротивлением и током. Зная две переменные, можно вычислить третью.
Соотношение между сопротивлением, напряжением и током известно как закон Ома и является одним из фундаментальных соотношений в электротехнике и электронике.
Подробнее о . . . . Закон Ома.
Обозначение сопротивления
Как уже упоминалось, основной единицей электрического сопротивления является Ом. Это часто обозначается греческим символом Ω.
В дополнение к этому перед базовой единицей могут стоять множители. Это связано с тем, что диапазон значений электрического сопротивления может охватывать многие десятилетия, и необходимо иметь простое обозначение, которое не основано на подсчете количества нулей в числе, поскольку это может легко привести к ошибкам.
| Множитель | Значение | Имя |
|---|---|---|
| Р | шт. | Ом, Ом |
| к | тысяч | кОм, кОм |
| М | миллионов | МОм, МОм |
Иногда встречаются сопротивления менее одного ома, они измеряются в миллиомах (м) тысячных долях ома.
Обычно, когда сопротивление указано на электронной схеме, оно обозначается как 10R для резистора на десять Ом, 10k для резистора на десять тысяч Ом и 10M для резистора на десять МОм. Причина этого в том, что греческую букву омега использовать не так просто, как префиксы R, k и M.
Что такое резисторы?
Чтобы можно было ограничить ток в конкретной цепи, можно использовать компонент, известный как резистор. Резисторы бывают самых разных форм: от больших проводных компонентов или даже некоторых с клеммами до очень маленьких компонентов для поверхностного монтажа, используемых сегодня во многих электронных схемах.
Резисторы могут быть изготовлены из различных материалов, углерода, оксида металла, металлической пленки, резистивной проволоки и т.
п. Резисторы могут быть разных форматов — разные типы резисторов имеют немного разные характеристики, а это означает, что они могут использоваться в разных схемах.
Правильный выбор резистора может помочь схеме работать должным образом. Хотя резистор с сопротивлением 10 кОм будет иметь одинаковое сопротивление, независимо от того, из чего он сделан, такие характеристики, как температурная стабильность, шум, долговременная стабильность, паразитная индуктивность и т. п., могут быть разными для разных типов, и это может повлиять на производительность в некоторых схемах. .
Примечание по резисторам и типам резисторов:
Резисторы используются в электрических и электронных схемах для различных целей, но в каждом случае они сопротивляются протеканию тока. Существует множество различных типов резисторов — их параметры означают, что одни типы больше подходят для конкретных приложений, чем другие.
Подробнее о Резисторы и типы резисторов
Сводка сопротивления
При работе с любыми электрическими и электронными цепями необходимо знать, что такое сопротивление и как сопротивление влияет на цепь.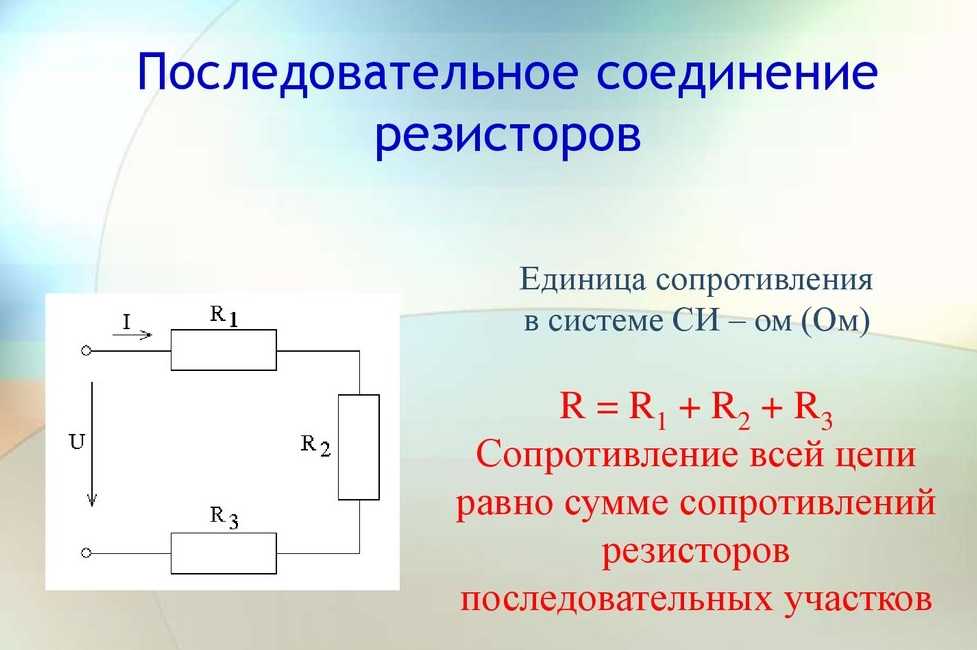
Ввиду важности сопротивления в цепях широко используются резисторы, возможно, наиболее часто используемые компоненты в электронных схемах. Эти компоненты очень просты в использовании, и расчеты, связанные с ними, обычно просты.
Дополнительные основные понятия и руководства по электронике:
Напряжение
Текущий
Сила
Сопротивление
Емкость
Индуктивность
Трансформеры
Децибел, дБ
Законы Кирхгофа
Q, добротность
РЧ-шум
Сигналы
Вернуться в меню основных понятий электроники . . .
Объяснение урока: Анализ комбинированных цепей
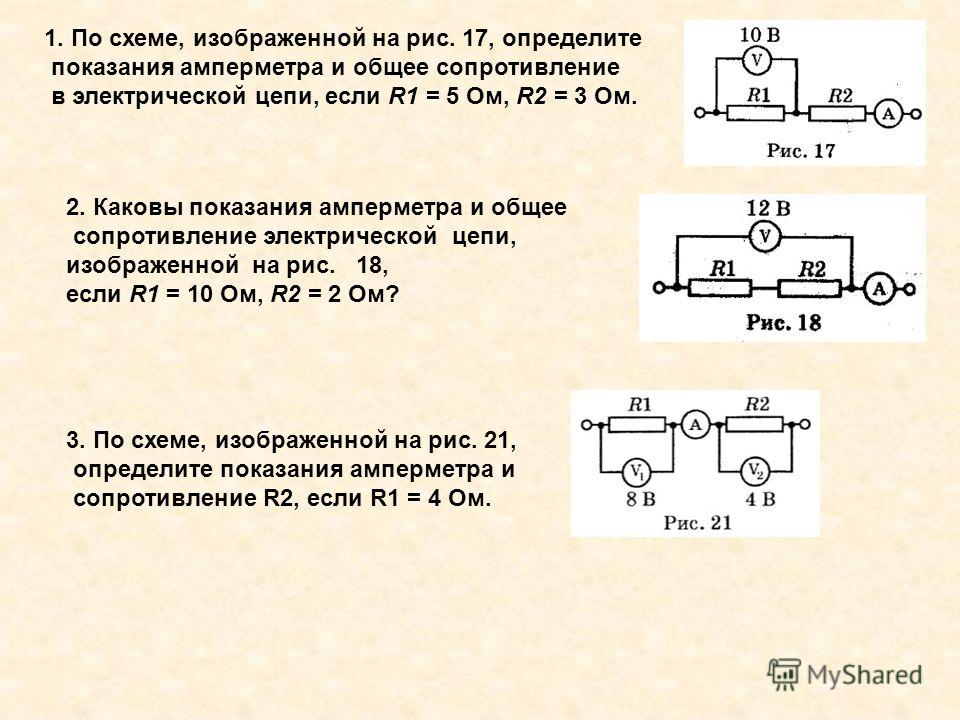
В этом объяснении мы научимся определять токи через и напряжения на участках цепей, содержащих резисторы как последовательно, так и параллельно.
Напомним, что последовательно соединенные резисторы соединяются в один проводящий путь. На приведенной ниже схеме показаны три последовательно соединенных резистора.
В показанном выше примере полное сопротивление цепи,
𝑅, это
𝑅=𝑅+𝑅+𝑅.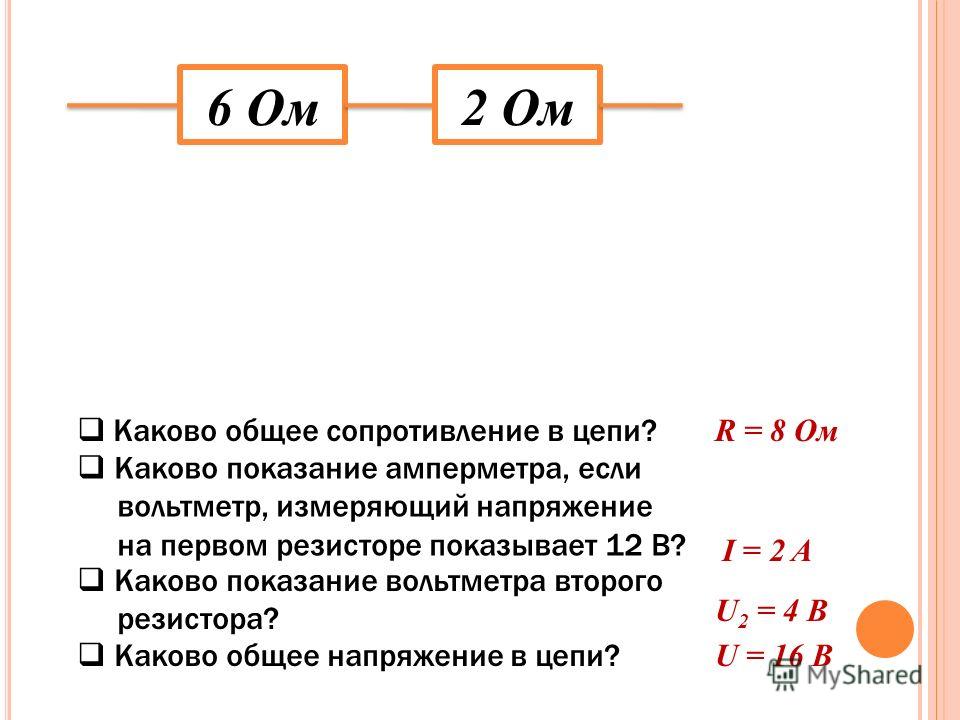
Это распространяется на любое количество последовательно соединенных резисторов: 𝑅=𝑅+𝑅+⋯+𝑅.
С другой стороны, резисторы соединены параллельно по нескольким токопроводящие пути. На приведенной ниже схеме показаны три резистора, соединенные последовательно. параллельно.
В показанном выше примере полное сопротивление цепи, 𝑅, это 𝑅=1𝑅+1𝑅+1𝑅.
Это распространяется на любое количество резисторов, включенных параллельно: 𝑅=1𝑅+1𝑅+⋯+1𝑅.
Комбинированная схема содержит секции резисторов, соединенных последовательно и параллельно. На приведенной ниже схеме показаны два резистора, соединенные последовательно с двумя резисторы параллельно.
В приведенном выше примере участок цепи, содержащий 𝑅 и 𝑅 последовательно, а участок цепи, содержащий 𝑅 и 𝑅 параллельны.
Чтобы проанализировать эту схему, каждый набор резисторов можно преобразовать в их
эквивалентный резистор. На приведенной ниже диаграмме показано, как последовательно подключить два резистора.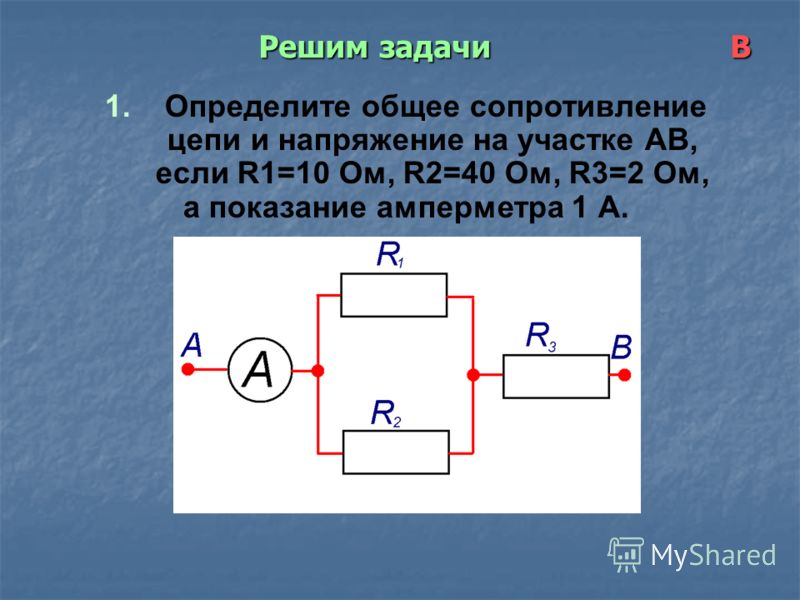
и два резистора параллельно могут быть преобразованы в один эквивалентный
резисторы, которые затем могут быть преобразованы в окончательный эквивалентный резистор для
вся схема.
Раздел серии, содержащий 𝑅 и 𝑅 можно преобразовать в его эквивалентный резистор, 𝑅: 𝑅=𝑅+𝑅.
Параллельная секция, содержащая 𝑅 и 𝑅 можно преобразовать в эквивалентный ему резистор, 𝑅: 𝑅=1𝑅+1𝑅.
Затем, наконец, эквивалентное сопротивление всей цепи, 𝑅, это 𝑅=𝑅+𝑅.
Давайте рассмотрим пример этого вопроса.
Пример 1: Определение эквивалентного сопротивления комбинированной цепи
Показанная схема содержит как последовательные, так и параллельные комбинации резисторов.
- Какова общая сила тока в показанной цепи? Дайте свой ответ на один десятичный знак.
- Какова общая мощность, рассеиваемая цепью? Дай свой ответ
до одного десятичного знака.
Ответ
Часть 1
В первой части этого вопроса мы должны рассчитать общий ток в схема. Для этого необходимо найти эквивалентное сопротивление схема.
Мы начнем с маркировки компонентов на принципиальной схеме.
Первый шаг расчета эквивалентного сопротивления цепи: найти эквивалентное сопротивление параллельного участка, состоящего из 𝑅 и 𝑅. Обозначим эквивалентное сопротивление этого параллельного участка на 𝑅: 𝑅=1𝑅+1𝑅.
Подстановка известных значений для 𝑅=2,5Ом и 𝑅=3,2Ω дает нам 𝑅=12,5+13,2𝑅=1,40.ΩΩΩΩ
Теперь мы можем рассчитать эквивалентное сопротивление всей цепи, 𝑅: 𝑅=𝑅+𝑅+𝑅.
Подставляя известные значения для 𝑅=1,6Ω и 𝑅=1,5Ом и значение 𝑅, которое мы рассчитали как 1,40 Ом дает нам 𝑅=1,6+1,5+1,4𝑅=4,5.ΩΩΩΩΩ
Тогда мы можем использовать закон Ома для расчета полного тока в цепи,
при 𝑉=5,5 В:
𝐼=𝑉𝑅𝐼=5,54,5.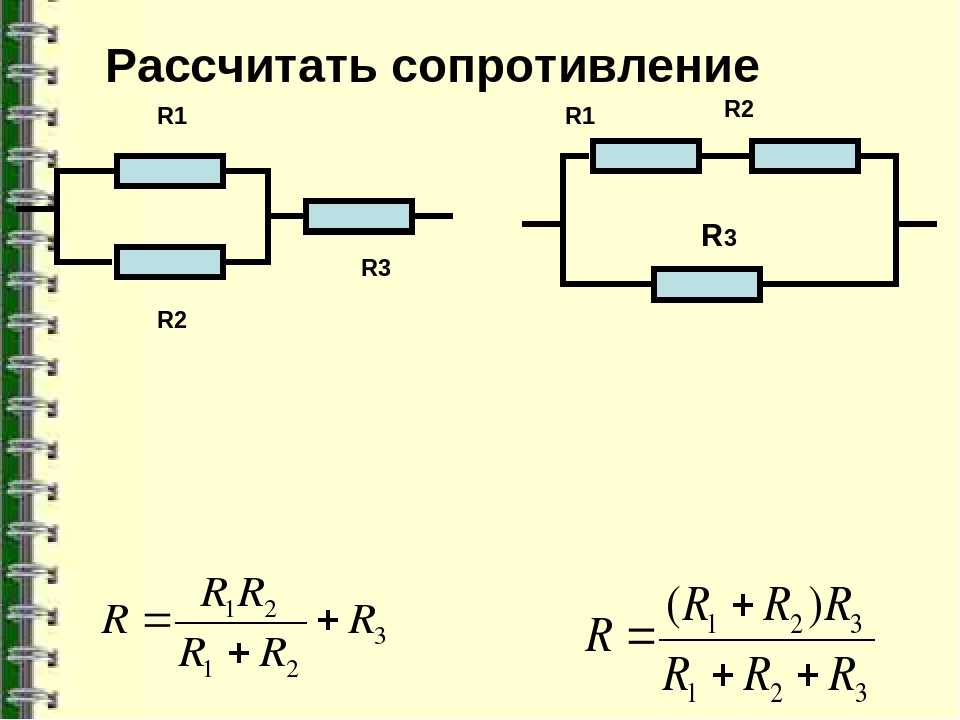
ВОм
Суммарный ток в цепи с точностью до одного десятичного знака составляет 𝐼=1.2.A
Часть 2
Полная мощность, рассеиваемая в цепи, может быть рассчитана путем умножения ток в цепи на полное падение потенциала на схема: 𝑃=𝐼𝑉𝑃=1,2×5,5.AV
Полная мощность, рассеиваемая в цепи, с точностью до одного десятичного знака равна 𝑃=6.7.W
Эти методы анализа комбинированных цепей также можно использовать для анализировать схемы, содержащие компоненты, отличные от резисторов. Мы сейчас проработайте пример вопроса об этом.
Пример 2. Анализ цепей, содержащих компоненты, отличные от Резисторы
Ток измеряется амперметром в цепи, показанной на схеме. Амперметр имеет сопротивление 2,5 мкОм.
- Какие показания будут на амперметре? Дай свой ответ до одного десятичного знака.
- Какими были бы показания амперметра, если бы он был подключен к
параллельно
Резистор 3,5 Ом? Отдай свое
ответ до одного десятичного знака.
Ответ
Часть 1
В первой части вопроса нам предлагается рассчитать сумму текущего через цепь. Для этой цели мы можем заменить амперметр на резистор эквивалентного сопротивления.
Мы можем обобщить это на диаграмме, где каждый резистор помечен. 𝑅 — эквивалентное сопротивление для амперметра.
Общее сопротивление цепи равно 𝑅=𝑅+𝑅+𝑅𝑅=2,5+3,5+2,5×10𝑅=6,0000025.ΩΩΩΩΩ
Ток в цепи можно рассчитать по закону Ома: 𝐼=126,0000025𝐼=1,9999991.VΩA
Амперметр будет показывать до одного десятичного знака 2,0 А. Давайте сравните это с идеальным амперметром, который имеет нулевое внутреннее сопротивление.
Общее сопротивление цепи будет точно равно сумме из двух резисторов: 𝑅=2,5+3,5𝑅=6,0.ΩΩΩΩ
Это означает, что ток в цепи равен 𝐼=126.0𝐼=2.0.VΩA
Таким образом, амперметр покажет точно
2,0 А.
Это
подчеркивает, насколько важно иметь амперметр с очень низким
внутреннее сопротивление. Если внутреннее сопротивление достаточно низкое, т.
в данном примере, им можно пренебречь при расчетах.
Часть 2
Во второй части вопроса нам предлагается рассмотреть, что произойдет, если амперметр будет подключен параллельно Резистор 3,5 Ом.
Заменив амперметр его эквивалентным резистором, мы можем нарисуй на схеме.
Теперь мы должны рассчитать эквивалентное сопротивление, 𝑅, параллельного участка цепи: 𝑅=13,5+12,5×10𝑅=(0,28+400000)𝑅=400000,28𝑅=2,499998×10,ΩΩΩ
9 амперметр такой низкий по сравнению до 3,5 Ом резистора, что он полностью доминирует над эквивалентным сопротивлением два.
Тогда общее сопротивление цепи равно 𝑅=2,5+2,499998×10 𝑅=2,5000025, Ом
Затем ток в цепи можно рассчитать по закону Ома:
𝐼=122,5000025𝐼=4,799995.
VΩA
Итак, с точностью до одного десятичного знака амперметр показывает 4,8 А.
Рассчитаем показание тока, если эквивалентное сопротивление параллельным сечением в расчете пренебрегают: 𝐼=122,5𝐼=4,8.VΩA
Как видно, внутреннее сопротивление амперметра настолько мало, что эквивалентным сопротивлением параллельного участка можно пренебречь.
В то время как эквивалентное сопротивление позволяет нам анализировать многие комбинированные схемы, есть некоторые, которые нельзя решить, используя только эквивалентное сопротивление.
Цепь, показанная на следующей принципиальной схеме, не может быть проанализирована с помощью только эквивалентное сопротивление.
Поскольку есть две батареи, мы не можем рассчитать эквивалентное сопротивление из 𝑅 и 𝑅.
Для анализа таких цепей мы можем использовать законы Кирхгофа.
Первый закон Кирхгофа гласит, что ток в переходе или узле в
цепь должна быть такой же, как и ток, выходящий из перехода или узла.
Определение: Первый закон Кирхгофа
Первый закон Кирхгофа утверждает, что сумма токов в соединение/узел в цепи, 𝐼+𝐼+⋯()()inin, должно быть таким же, как сумма токов из узла/узла, 𝐼+𝐼+⋯()()outout: 𝐼+𝐼+⋯=𝐼+𝐼+⋯.()()()()ininoutout
Например, предположим, что в следующем соединении цепи есть токи 𝐼 и 𝐼 на перекрестке и 𝐼 с перекрестка.
Первый закон Кирхгофа гласит, что сумма токов в переходе, 𝐼+𝐼, должны равняться сумме токов из перекресток, 𝐼: 𝐼+𝐼=𝐼.
Второй закон Кирхгофа позволяет нам анализировать разность потенциалов на различных точках комбинационной цепи.
Второй закон Кирхгофа гласит, что сумма всех разностей потенциалов между компонентами в цикле должны быть равны нулю.
На следующей принципиальной схеме показано последовательное подключение трех резисторов к батарее.
Определение: второй закон Кирхгофа
Сумма разности потенциалов на каждом компоненте контура равна нуль: 𝑉+𝑉+⋯+𝑉=0,
В схеме примера разность потенциалов на ячейке равна
𝑉, а на трех резисторах разность потенциалов равна
𝑉, 𝑉 и 𝑉 соответственно.
Закон Кирхгофа гласит, что сумма разностей потенциалов по всем компоненты в цикле равны нулю. То есть, 𝑉+𝑉+𝑉+𝑉=0,
В этом случае разность потенциалов на ячейке положительна и равна по модулю равна полной разности потенциалов на трех резисторы.
Законы Кирхгофа можно использовать для сравнения цепей. Мы будем работать через пример вопрос об этом сейчас.
Пример 3. Анализ нескольких похожих цепей
Схемы (a) и (b) очень похожи, но немного отличаются друг от друга. Другой. Какова разница в полном токе между цепью, показанной на рис. схеме (а) и цепи, показанной на схеме (б)? Дайте ответ с точностью до одного десятичного знака.
Ответ
Начнем с анализа схемы (b).
Мы можем использовать второй закон Кирхгофа для петли, образованной цепью. Отзывать
что второй закон Кирхгофа гласит, что сумма разностей потенциалов
по каждому компоненту в цикле должен равняться нулю.
Обозначим разность потенциалов на 800 мОм резистор как 𝑉 и разность потенциалов на Резистор 960 мОм как 𝑉.
Два резистора можно преобразовать в один эквивалентный резистор, который мы будет коллировать 𝑅 со следующим сопротивлением: 𝑅=880+960𝑅=1840.мОммОммОм
Разность потенциалов на этом эквивалентном резисторе равна 𝑉 и равно 𝑉=𝑉+𝑉.
Сумма разности потенциалов на каждом компоненте в цепи (b) можно записать как 2,5+1,4−𝑉−𝑉=0,ВВВ или, учитывая эквивалентный резистор, 𝑅, это можно записать как 2,5+1,4−𝑉=0𝑉=3,9.VVVV
Итак, разность потенциалов на этом эквивалентном резисторе равна 3,9 В.
Ток в цепи (b), 𝐼, можно рассчитать, используя Закон Ома, сначала преобразуя сопротивление из миллиомы в Ом: 𝐼=𝑉𝑅𝐼=3,91,84𝐼=2,12.VΩA
Теперь проанализируем схему (а).
Схема (а) почти идентична схеме (б), за исключением того, что Батарея 1,4 В есть перевернулся. Когда мы на этот раз применим второй закон Кирхгофа, эта батарея вносит в уравнение отрицательную разность потенциалов.
Объединение резисторов в эквивалентный резистор, как мы это делали ранее, мы можем написать 2.5−1.4−𝑉=0𝑉=1.1.VVVV
Таким образом, разность потенциалов на этом эквивалентном резисторе равна 1,1 В.
Ток в цепи (a), 𝐼, можно рассчитать, используя Закон Ома, сначала преобразуя сопротивление из миллиомы в Ом: 𝐼=𝑉𝑅𝐼=1,11,84𝐼=0,60.VΩA
Тогда разница токов между двумя цепями равна 𝐼−𝐼=2,12−0,06𝐼−𝐼=1,52.AAA
Разница в общем токе между цепью, показанной на схеме (а) и схема, показанная на диаграмме (б), поэтому 1,5 А до одного десятичного знака.
Законы Кирхгофа также можно использовать для анализа комбинационных цепей.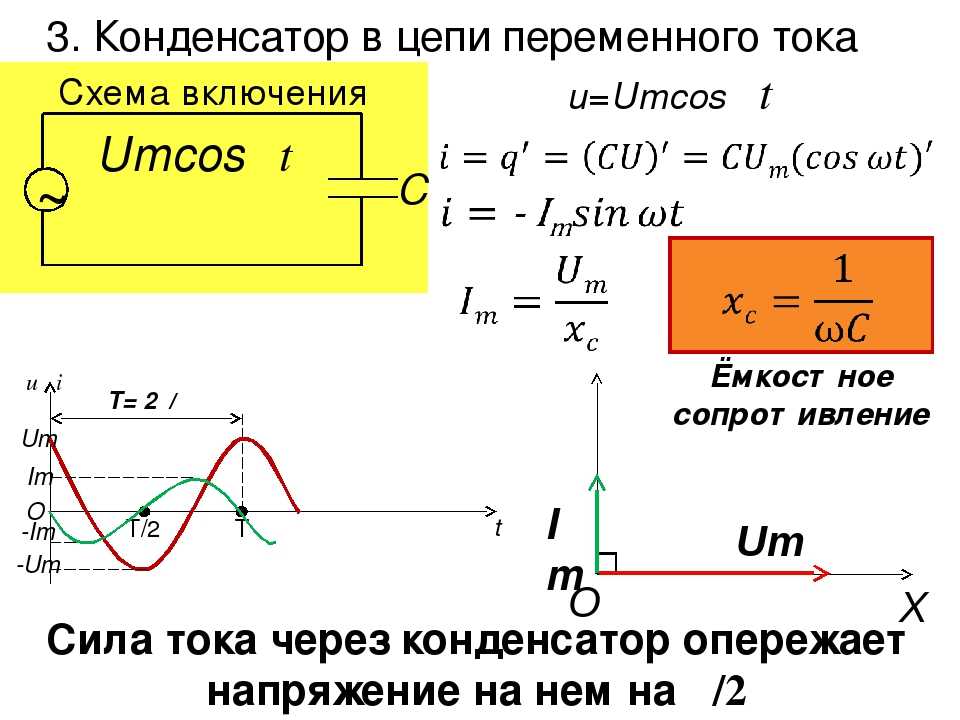
Когда мы
учитывая комбинированную схему, мы должны идентифицировать петли и соединения/узлы.
Например, следующая принципиальная схема содержит несколько резисторов и аккумуляторы в разных цепях цепи.
Мы можем идентифицировать два узла в этой цепи и три петли. Это проиллюстрировано на следующей диаграмме.
Теперь мы поработаем над примером вопроса, где мы должны использовать Кирхгофа. законы для анализа комбинационной цепи.
Пример 4. Использование законов Кирхгофа для анализа комбинационных цепей
На схеме показана схема, содержащая несколько ячеек.
- Какой ток через Резистор 20 Ом?
- Какой ток на минусовой клемме Батарея 5,0 В?
- Какой ток на отрицательной клемме Аккумулятор 10,0 В?
Ответ
Часть 1
Начнем с обозначения принципиальной схемы.
Токи в каждой ветви цепи маркируются в соответствии с
узел в нижней части схемы.
Ток от
Ячейка 10,0 В к узлу
помечен 𝐼 и считается током в
узел. Ток от узла к
20 Ом помечено
𝐼 и считается вне узла. Электрический ток
от узла к
Ячейка 5,0 В помечена
𝐼 и считается вне узла.
Мы можем применить второй закон Кирхгофа к каждому контуру цепи, чтобы найти разность потенциалов на каждом резисторе.
Начиная с цикла, содержащего 𝑉 и 𝑅, имеем 𝑉−𝑉=0,В поэтому разность потенциалов на 𝑅 равна 𝑉=10.0.V
Используя закон Ома, мы можем рассчитать ток через 𝑅: 𝐼=𝑉𝑅𝐼=10,020𝐼=0,5.VΩA
Это равно 𝐼. Ток через Резистор 20 Ом 𝐼 и, следовательно, равно 0,5 А.
Часть 2
Далее мы можем посмотреть на цикл, содержащий 𝑉, 𝑉 и 𝑅: 𝑉+𝑉−𝑉=05,0+10,0−𝑉=0,VVVV
Итак, разность потенциалов на 𝑅 равна 𝑉=15,0.V
Из закона Ома мы можем рассчитать ток через 𝑅:
𝐼=𝑉𝑅𝐼=15,015𝐼=1,0.
VΩA
Это равно 𝐼. Ток на минусе терминал 5,0 А аккумулятор 𝐼 и, следовательно, равно 1,0 А.
Часть 3
Используя первый закон Кирхгофа, мы можем вычислить 𝐼 из узел в нижней части схемы: 𝐼=𝐼+𝐼𝐼=1.0+0.5=1.5.A
Ток на отрицательной клемме Батарея 10,0 В есть 𝐼 и поэтому равно 1,5 А.
Пример 5. Использование законов Кирхгофа для анализа комбинационных цепей с Unknown Components
В показанной цепи сопротивление одного из резисторов неизвестно. Общая ток в цепи есть 0,25 А.
- Найдите текущий 𝐼. Отдай свое ответ до двух знаков после запятой.
- Найти текущий 𝐼. Дайте ответ на два десятичные знаки.
- Найдите разность потенциалов на неизвестном резисторе. Дайте свой ответ на Ближайшая вольт.
Ответ
Часть 1
Начнем с маркировки компонентов схемы.
В первой части вопроса нам предлагается найти 𝐼, ток через 𝑅. Для этого нам нужно найти разность потенциалов на параллельном участке цепи.
Мы можем преобразовать параллельный участок цепи в эквивалентный резистора по следующей формуле: 𝑅=1𝑅+1𝑅.
Вставка значений 𝑅=2,5Ом и 𝑅=3,2Ω дает нам 𝑅=12,5+13,2𝑅=1,40,ΩΩΩ
Зная, что ток в цепи 0,25 А, потенциал разницу между эквивалентным резистором можно рассчитать, используя сопротивление Ом. закон: 𝑉=𝐼𝑅𝑉=0,25×1,40𝑉=0,35.AΩV
Эта разность потенциалов одинакова на обеих ветвях параллельного участок цепи. Тогда ток 𝐼 может быть рассчитывается по закону Ома: 𝐼=𝑉𝑅𝐼=0,352,5𝐼=0,14.VΩA
Часть 2
Во второй части вопроса нам предлагается рассчитать текущий 𝐼.
Мы уже рассчитали разность потенциалов на параллели
участок цепи, поэтому мы можем применить закон Ома к
𝑅:
𝐼=𝑉𝑅𝐼=0,353,2𝐼=0,11.
VΩA
Часть 3
В третьей части этого вопроса нам предлагается рассчитать потенциал разница на неизвестном резисторе.
Мы можем использовать второй закон Кирхгофа, чтобы решить эту задачу. Кирхгофа Второй закон гласит, что сумма разностей потенциалов на каждом отдельная компонента в цикле равна нулю. Для этой схемы мы запишет разность потенциалов через 𝑅 как 𝑉, по параллельному сечению как 𝑉, а поперек 𝑅 как 𝑉: 12−𝑉−𝑉−𝑉=0,V
Мы уже рассчитали 𝑉=0,35В. 𝑉 можно рассчитать по закону Ома: 𝑉=𝐼𝑅𝑉=0,25×2,2𝑉=0,55.AΩV
Мы можем подставить их в уравнение для второго закона Кирхгофа, помня, что это уменьшение потенциала, поэтому они отрицательны: 12−𝑉−0,55−0,35=0,VVV
Затем мы можем изменить это, чтобы получить значение разности потенциалов через 𝑅 неизвестный резистор: 𝑉=11,1.V
Итак, разность потенциалов на неизвестном резисторе с точностью до
вольт,
11 В.
Давайте обобщим то, что мы узнали из этого объяснения, в следующем ключевые моменты.
Ключевые точки
- В комбинированных цепях мы можем идентифицировать части цепей, соединенные параллельно и цепи последовательно. Мы можем рассчитать эквивалентное сопротивление этих разделы для анализа комбинированной схемы.
- Первый закон Кирхгофа гласит, что сумма токов в соединение/узел в цепи, 𝐼+𝐼+⋯()()inin, должно совпадать с сумма токов из узла/узла, 𝐼+𝐼+⋯()()outout: 𝐼+𝐼+⋯=𝐼+𝐼+⋯.()()()()ininoutout
- Второй закон Кирхгофа гласит, что сумма разности потенциалов по каждому компоненту, 𝑉,𝑉,…𝑉, в цикле равно нулю: 𝑉+𝑉+⋯+𝑉=0.
- В комбинированных схемах мы можем идентифицировать петли и узлы, которые позволяют нам применять законы Кирхгофа для анализа цепи.
gif»> 
gif»>
Некоторые вещества сопротивляются току больше, чем другие. Если вещество оказывает очень большое сопротивление току, оно называется изолятором. Если его сопротивление току очень мало, его называют проводником. Удельное сопротивление относится к способности веществ сопротивляться току. Хорошие проводники имеют низкое удельное сопротивление, а изоляторы — высокое удельное сопротивление.
gif»>
Номинал переменного резистора — это его сопротивление при максимальном значении.
Цветовой код состоит из различных цветовых полос, которые указывают значения сопротивления резисторов в омах, а также класс допуска. Приведенная ниже таблица цветовых кодов номинального сопротивления резистора используется для определения номинального сопротивления резисторов.
gif»>
Первая полоса всегда является полосой, ближайшей к концу резистора. Из таблицы видно, что числовое значение коричневого цвета в 1-м столбце диапазона равно 1.
gif»>
Схема на рис. 4 имеет три параллельных резистора.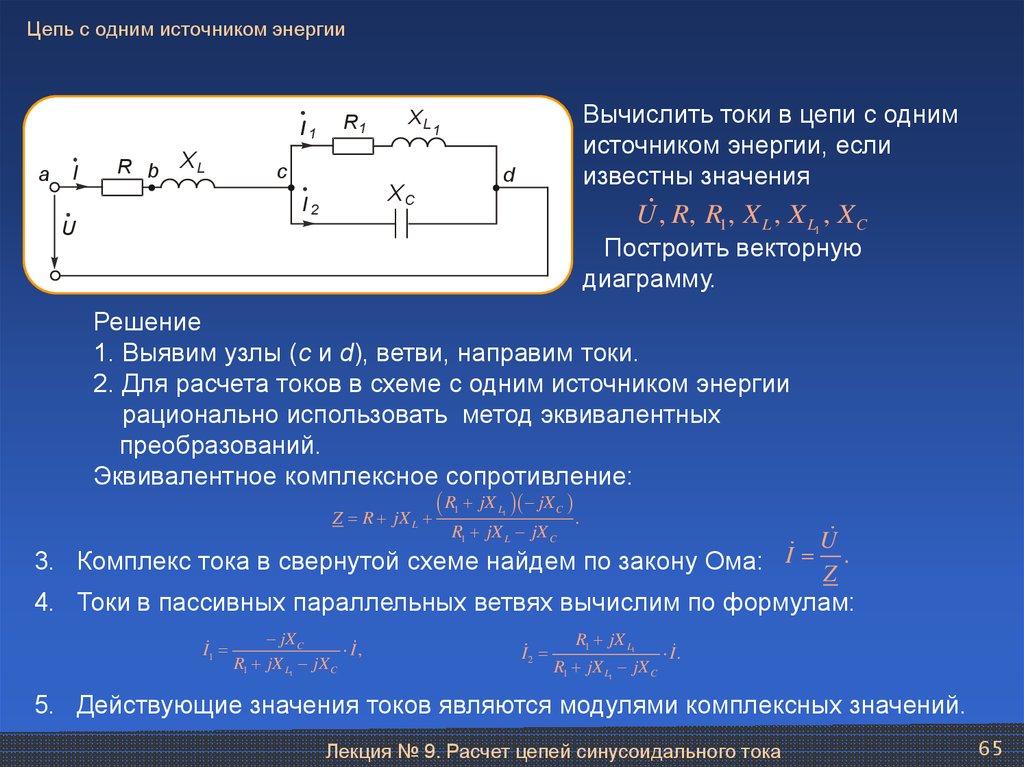
Эти цепи называются составными цепями. Схема на рисунке 5 ниже является составной схемой.
Следовательно, общее сопротивление составной цепи можно рассчитать следующим образом:
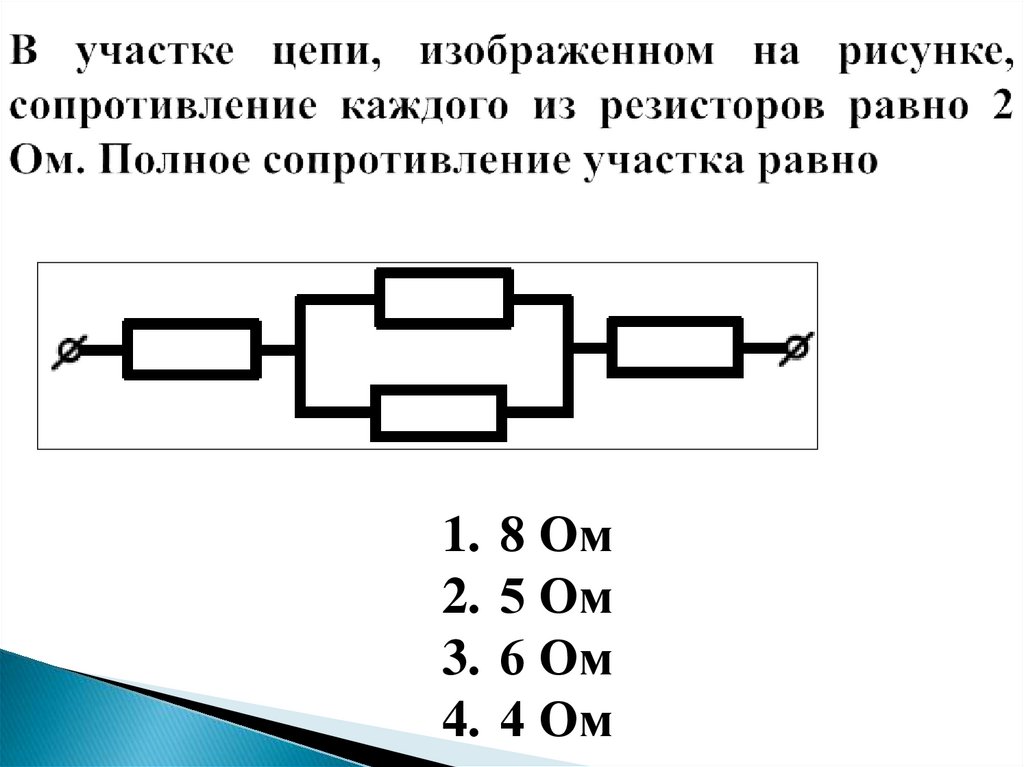Технология магнитно-резонансной томографии (МРТ), использующая сверхпроводники, произвела революцию в материаловедении и медицине. Сверхпроводимость была бы особенно полезна для передачи электроэнергии. В настоящее время около 15 процентов электроэнергии, проходящей по медным линиям электропередачи, теряется из-за сопротивления.
Компьютеры можно было сделать еще меньше и быстрее. Другие удивительные приложения, такие как поезда на магнитной подушке и запуск космических кораблей, станут гораздо более осуществимыми.
