Сопротивление в цепи переменного тока: объяснение основных понятий и формул

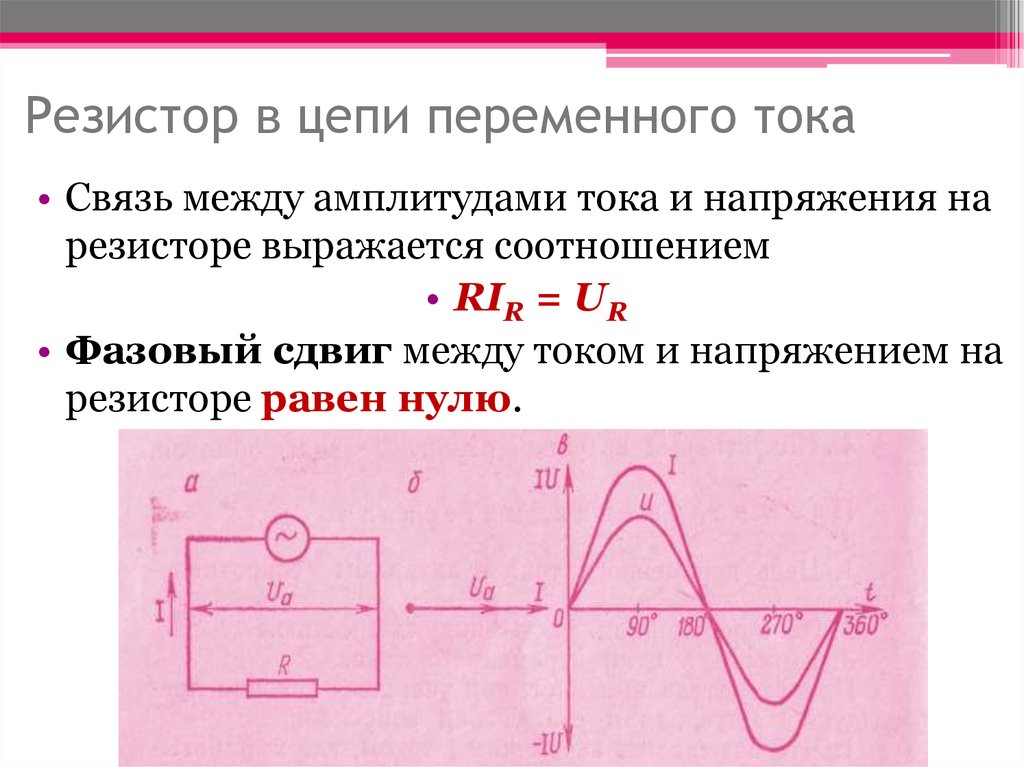
Что такое активное, индуктивное и емкостное сопротивление в цепи переменного тока. Как рассчитать полное сопротивление цепи. Какие факторы влияют на сопротивление в цепи переменного тока. Как сопротивление в цепи переменного тока отличается от сопротивления в цепи постоянного тока.

Что такое сопротивление в цепи переменного тока

Сопротивление в цепи переменного тока — это комплексная величина, которая характеризует противодействие элементов цепи протеканию переменного электрического тока. В отличие от цепей постоянного тока, где есть только активное сопротивление, в цепях переменного тока выделяют три вида сопротивлений:

• Активное сопротивление (R) — обусловлено преобразованием электрической энергии в тепловую
• Индуктивное сопротивление (XL) — создается катушками индуктивности
• Емкостное сопротивление (XC) — создается конденсаторами

Полное сопротивление цепи переменного тока называется импедансом (Z) и включает в себя все три вида сопротивлений.

Активное сопротивление в цепи переменного тока

Активное сопротивление в цепи переменного тока аналогично сопротивлению в цепи постоянного тока. Оно обусловлено преобразованием электрической энергии в тепловую при протекании тока по проводнику. Активное сопротивление не зависит от частоты переменного тока и рассчитывается по формуле:

R = ρ * l / S

где:

• R — активное сопротивление, Ом
• ρ — удельное сопротивление материала проводника, Ом*м
• l — длина проводника, м
• S — площадь поперечного сечения проводника, м²

Индуктивное сопротивление в цепи переменного тока

Индуктивное сопротивление создается катушками индуктивности в цепи переменного тока. Оно обусловлено явлением самоиндукции — возникновением ЭДС самоиндукции при изменении тока в катушке. Индуктивное сопротивление зависит от частоты переменного тока и рассчитывается по формуле:

XL = ωL = 2πfL

где:

• XL — индуктивное сопротивление, Ом
• ω — угловая частота, рад/с
• f — частота переменного тока, Гц
• L — индуктивность катушки, Гн

Емкостное сопротивление в цепи переменного тока

Емкостное сопротивление создается конденсаторами в цепи переменного тока. Оно обусловлено периодической зарядкой и разрядкой конденсатора при протекании переменного тока. Емкостное сопротивление также зависит от частоты переменного тока и рассчитывается по формуле:

XC = 1 / (ωC) = 1 / (2πfC)

где:

• XC — емкостное сопротивление, Ом
• ω — угловая частота, рад/с
• f — частота переменного тока, Гц
• C — емкость конденсатора, Ф

Полное сопротивление (импеданс) цепи переменного тока

Полное сопротивление цепи переменного тока, или импеданс, включает в себя все виды сопротивлений — активное, индуктивное и емкостное. Импеданс рассчитывается по формуле:

Z = √(R² + (XL — XC)²)

где:

• Z — полное сопротивление (импеданс), Ом
• R — активное сопротивление, Ом
• XL — индуктивное сопротивление, Ом
• XC — емкостное сопротивление, Ом

Факторы, влияющие на сопротивление в цепи переменного тока

На сопротивление в цепи переменного тока влияют следующие основные факторы:

• Частота переменного тока — с увеличением частоты возрастает индуктивное сопротивление и уменьшается емкостное
• Параметры элементов цепи — индуктивность катушек, емкость конденсаторов, активное сопротивление проводников
• Схема соединения элементов — последовательное или параллельное
• Наличие нелинейных элементов в цепи
• Температура — влияет на активное сопротивление проводников

Отличия сопротивления в цепях переменного и постоянного тока

Основные отличия сопротивления в цепях переменного и постоянного тока заключаются в следующем:

1. В цепи постоянного тока присутствует только активное сопротивление, а в цепи переменного тока — активное, индуктивное и емкостное.
2. Сопротивление в цепи постоянного тока не зависит от частоты, а в цепи переменного тока индуктивное и емкостное сопротивления зависят от частоты.
3. В цепи постоянного тока катушки индуктивности и конденсаторы не оказывают сопротивления току, а в цепи переменного тока они создают индуктивное и емкостное сопротивления.
4. Закон Ома для цепи постоянного тока имеет вид I = U / R, а для цепи переменного тока — I = U / Z, где Z — полное сопротивление (импеданс).
5. В цепи переменного тока возникает сдвиг фаз между током и напряжением, чего не происходит в цепи постоянного тока.

Практическое применение знаний о сопротивлении в цепях переменного тока

Понимание особенностей сопротивления в цепях переменного тока имеет важное практическое значение в различных областях электротехники и электроники:

• Проектирование электрических сетей и систем электроснабжения
• Разработка и настройка радиотехнических устройств
• Создание фильтров и частотных разделителей в аудиотехнике
• Оптимизация работы электродвигателей переменного тока
• Расчет и проектирование систем электрической защиты

Правильный учет всех видов сопротивлений в цепях переменного тока позволяет обеспечить эффективную и безопасную работу электрических и электронных устройств.

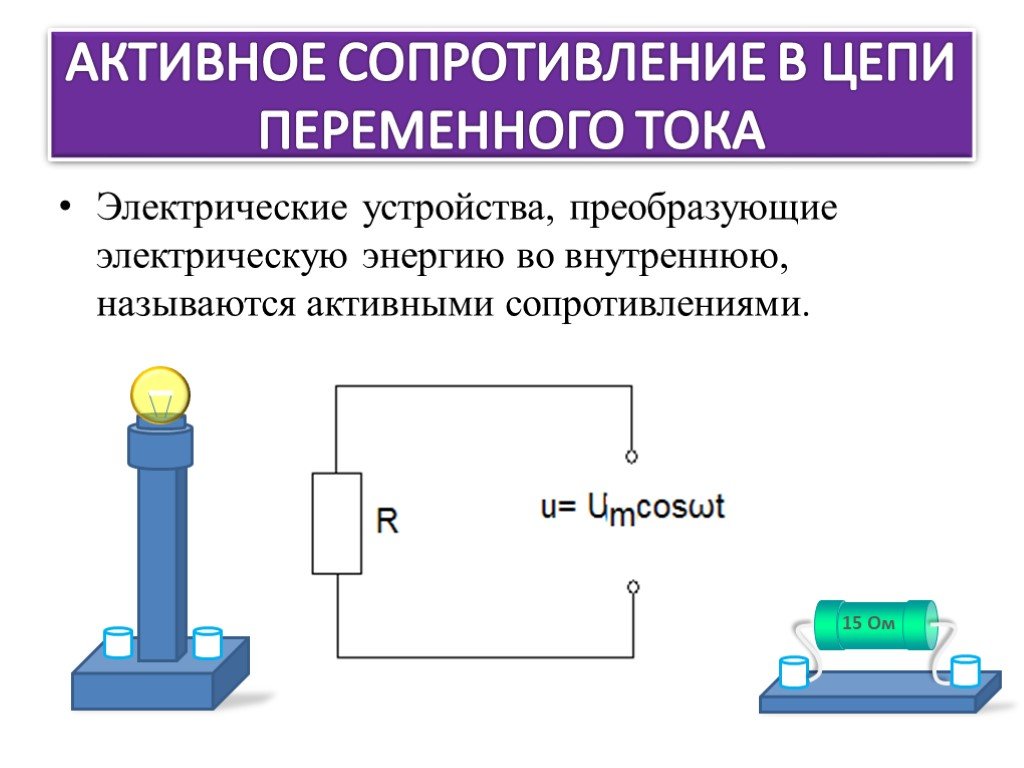
основные понятия, формула для расчёта

Конденсатор оказывает определённое сопротивление переменному току и совершенно не проводит постоянный. Это свойство находит применение в различных областях радиоэлектроники и электротехники. Ёмкостное сопротивление в цепи переменного тока зависит от частоты последнего и ёмкости конденсатора.

• Основные понятия
• Формула сопротивления
• Применение на практике

Основные понятия

Ёмкостное сопротивление — это величина, которая создаётся конденсатором, включённым в цепь. Сопротивление подводящих проводов должно быть непренебрежимо большим. При подаче переменного тока возникают процессы, обусловленные периодическим зарядом и разрядом конденсатора.

Период разбивается на четыре четверти. В течение первой четверти напряжение растёт. В этот момент по цепи проходит зарядный ток, сила которого будет уменьшаться, достигнув нуля, когда электродвижущая сила достигнет положительного максимума. Конденсатор полностью заряжен. После этого начнётся спад напряжения. Конденсатор будет разряжаться через подключённую к нему нагрузку. По цепи потечёт ток.

К концу полупериода величина напряжения будет равна нулю, а сила тока будет наибольшей. Разрядка завершена. В начале третьей четверти электродвижущая сила будет возрастать, изменив своё направление. Вновь начнётся процесс заряда. Направление зарядного тока в третью четверть будет таким же, как и в предыдущую. По мере зарядки конденсатора эта величина будет убывать. К концу третьей четверти процесс зарядки будет завершён.

Электродвижущая сила достигнет своего наибольшего отрицательного значения. А на той обкладке, на которой в течение первого полупериода был положительный заряд, теперь будет отрицательный. Во время четвёртой четверти значение электродвижущей силы снова будет стремиться к нулю. Конденсатор будет разряжаться. Соответственно, в цепи появится постепенно нарастающий ток. Процесс повторяется. Таким образом, фаза переменного тока в конденсаторной цепи опережает фазу напряжения на 90 градусов.

Формула сопротивления

Формула ёмкостного сопротивления выводится следующим образом:

• Вначале следует вычислить угловую частоту. Для этого частоту протекающего по цепи тока (в герцах) необходимо умножить на удвоенное число «пи».
• Затем полученное число следует перемножить на ёмкость конденсатора в фарадах.

Чтобы получить значение ёмкостного сопротивления в омах, следует разделить единицу на число, полученное после умножения угловой частоты на ёмкость. Из этой формулы вытекает, что чем больше ёмкость конденсатора или частота переменного тока, тем меньше его сопротивление.

Когда частота будет равна нулю (постоянный ток), ёмкостное сопротивление станет бесконечно большим. Конденсатор очень большой ёмкости будет проводить ток в широком диапазоне частот.

Применение на практике

Свойства конденсатора используются при конструировании различных фильтров.

Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:

• Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
• Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.

Ещё одна область применения — отделение переменной составляющей от постоянной. Например, в оконечных каскадах усилителей звуковой частоты. Чем выше ёмкость, тем более низкую частоту способен воспроизвести подключённый громкоговоритель.

В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда.

В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.

Благодаря своим свойствам конденсаторы используются в тех случаях, когда необходимо передать и постоянный, и переменный ток по одним и тем же проводам. Источник постоянного напряжения подключается к общему проводу и второму выводу ёмкости, через которую присоединяется источник переменного напряжения. На другой стороне происходит разделение: потребитель переменного подключается через конденсатор той же ёмкости, а потребитель постоянного — напрямую, до выводов детали.

Распространённый пример подобного использования — это телевизионная наружная антенна с усилителем. Сам телевизор или подключаемое к кабелю устройство, называемое «инжектором», подаёт напряжение питания. В антенном усилителе происходит разделение и фильтрация сигналов. Таким образом, ёмкостное сопротивление конденсатора находит широкое применение. Фильтры обеспечивают задержку одних сигналов и прохождение — других.

Благодаря этому свойству, можно передавать сразу и переменное, и постоянное напряжение, что имеет немаловажное значение при построении некоторых линий связи.

Физика Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока

Материалы к уроку

• Конденсатор и катушка индуктивности в цепи переменного тока.doc»>12. Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока.doc

  55 KBСкачать

• 12. Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока.ppt

  2.78 MBСкачать

Конспект урока

Огромное практическое значение имеют незатухающие вынужденные колебания. Свободные электромагнитные колебания в контуре быстро затухают и поэтому практически не используются. Переменный ток, используемый потребителями, представляет собой не что иное, как вынужденные электромагнитные колебания.  Частота переменного тока показывает число колебаний за 1 секунду. Стандартная частота промышленного тока равна 50 Герц. Значит, на протяжении 1 с ток 50 раз течет в одну сторону и 50 раз в другую. Частота 50 Герц принята для промышленного тока во многих странах мира.

Сила тока и напряжение меняются со временем по гармоническому закону. Это вытекает из следующих рассуждений. Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводников будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц и, следовательно, гармонические колебания силы тока. При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Если время распространения изменений поля в цепи гораздо меньше периода колебаний напряжения, то можно считать, что электрическое поле во всей цепи меняется почти мгновенно при изменении напряжения на концах цепи.  Переменное напряжение, использующее потребителями в осветительной сети, создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генераторов переменного тока.  Поток магнитной индукции, который пронизывает проволочную рамку, пропорционален косинусу угла альфа между нормалью к рамке и вектором магнитной индукции. При равномерном вращении рамки угол альфа увеличивается прямо пропорционально времени. Поэтому поток магнитной индукции меняется гармонически. Согласно закону электромагнитной индукции, ЭДС индукции в рамке равна взятой со знаком минус скорости изменения потока магнитной индукции по времени. Иначе ЭДС электромагнитной индукции равна производной потока магнитной индукции по времени. При изменении напряжения по гармоническому закону напряженность электрического поля в проводнике изменяется по такому же закону. Под действием переменного электрического поля в проводнике возникает переменный электрический ток, частота и фаза колебаний которого совпадает с частотой и фазой колебаний напряжения. Цепи с резистором. Цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением, называемым активным сопротивлением. 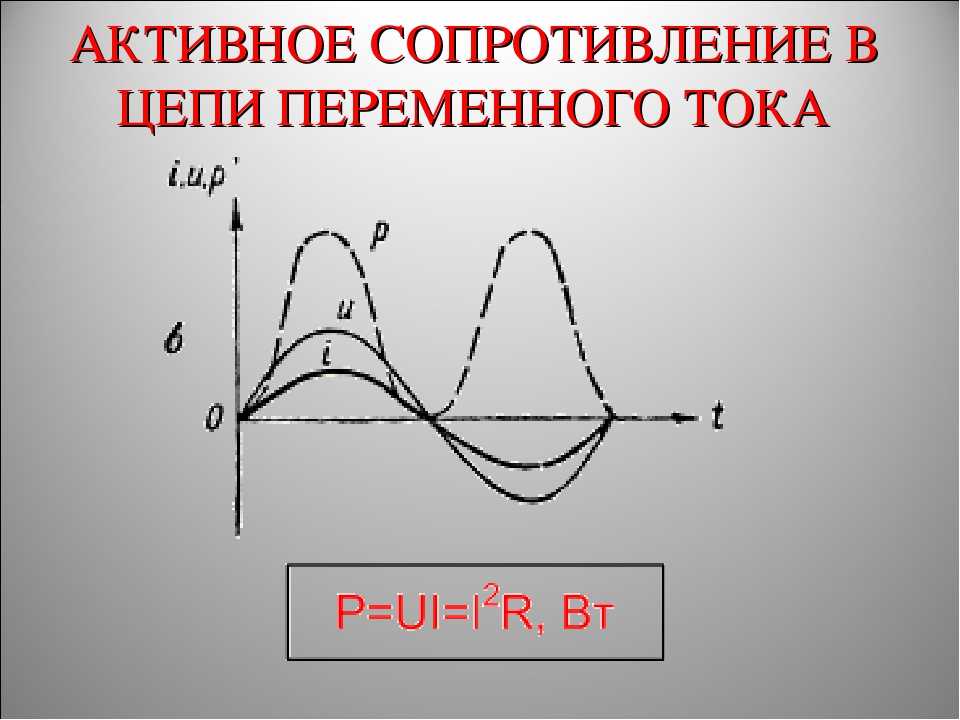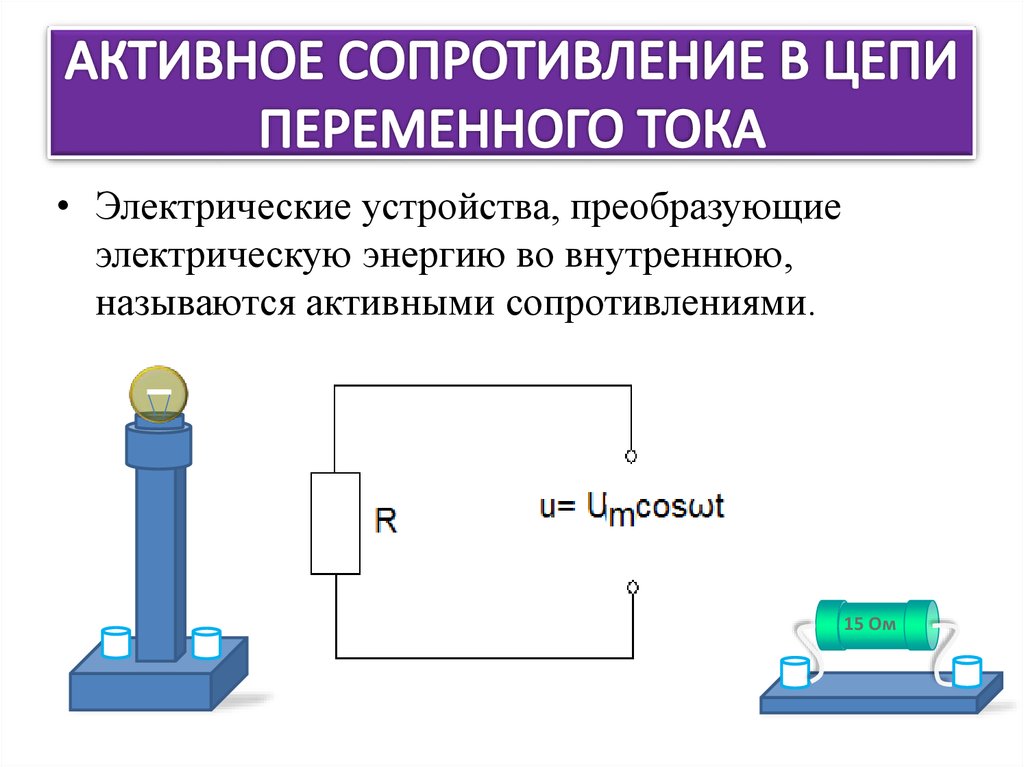При наличии нагрузки, обладающей активным сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются. В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения. В цепи переменного тока промышленной частоты, равной 50 Герц, сила тока и напряжение изменяются сравнительно быстро. Мощность в цепи постоянного тока на участке с сопротивлением равна по определению произведению квадрата силы тока на сопротивление. На протяжении очень малого интервала времени переменный ток можно считать неизменным. Поэтому мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление, определяется произведением квадрата мгновенного значения силы тока на сопротивление. Под средней за период мощностью переменного тока понимают отношение суммарной энергии, поступающей в цепь за период, к периоду. Человеку необходимо знать среднюю мощность тока на участке цепи за большой промежуток времени, включающий много периодов.  
Здесь изображен график зависимости мгновенной мощности от времени. На протяжении одной четверти периода мощность больше половины амплитудного значения. Но на протяжении следующей четверти периода мощность меньше этой величины. На протяжении одной четверти периода эта функция пробегает ряд положительных значений.  Половина квадрата амплитуды силы тока в колебательном электромагнитном контуре   есть среднее за период значение квадрата силы тока. Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока. Всегда можно подобрать такое значение силы постоянного тока, чтобы энергия, выделяемая за некоторое время этим током, равнялась энергии, выделяемой за то же время переменным током. Действующее значение силы переменного тока равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время. Нам важны общие характеристики колебаний, такие как амплитуда, период, частота, действующие значения силы тока и напряжения и средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.  Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения. Мощность в цепи переменного тока определяется действующими значениями силы тока и напряжения. Мощность равна произведению силы тока и напряжения.  Фактически цепь, содержащая конденсатор, оказывается разомкнутой, так как обкладки конденсатора разделены диэлектриком. Поэтому постоянный ток не может существовать в цепи, содержащей конденсатор. Переменный ток способен течь в цепи, содержащей конденсатор. Проведем опыт. Составим последовательную цепь из конденсатора и лампы накаливания.  Постоянное напряжение на зажимах источника равно действующему значению переменного напряжения. При включении постоянного напряжения лампа не светится. Но при включении переменного напряжения лампа загорается. При этом емкость конденсатора достаточно велика. Происходит периодическая зарядка и разрядка конденсатора под действием переменного напряжения. Ток, текущий в цепи при перезарядке конденсатора, нагревает нить лампы. Рассмотрим цепь, содержащую только конденсатор, где сопротивлением проводов и обкладок конденсатора можно пренебречь. Напряжение на конденсаторе совпадает по значению с напряжением на концах цепи. Следовательно, заряд конденсатора меняется по гармоническому закону. Сила тока представляет собой производную заряда по времени. Приведем графики зависимости силы тока и напряжения от времени. Видно, что колебания силы тока опережают колебания напряжения на конденсаторе на пи вторых.  Амплитуда силы тока равна произведению максимального напряжения емкости конденсатора и циклической частоты колебаний. Величину икс-цэ, равную обратному произведению циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления в законе Ома.  Это и позволяет рассматривать емкостное сопротивление как сопротивление конденсатора переменному току. Чем больше емкость конденсатора, тем больше ток перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. С увеличением емкости конденсатора емкостное сопротивление уменьшается. Уменьшается оно и с увеличением частоты.
Индуктивность в цепи влияет на силу переменного тока. Это можно доказать с помощью простого опыта. Составим цепь из катушки большой индуктивности и электрической лампы накаливания. С помощью переключателя можно подключить эту цепь или к источнику постоянного напряжения, или к источнику переменного напряжения с равными значениями. Лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы переменного тока в рассматриваемой цепи меньше силы постоянного тока. Здесь проявляется самоиндукция.  При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь со временем сила тока достигает наибольшего установившегося значения, соответствующего данному постоянному напряжению. 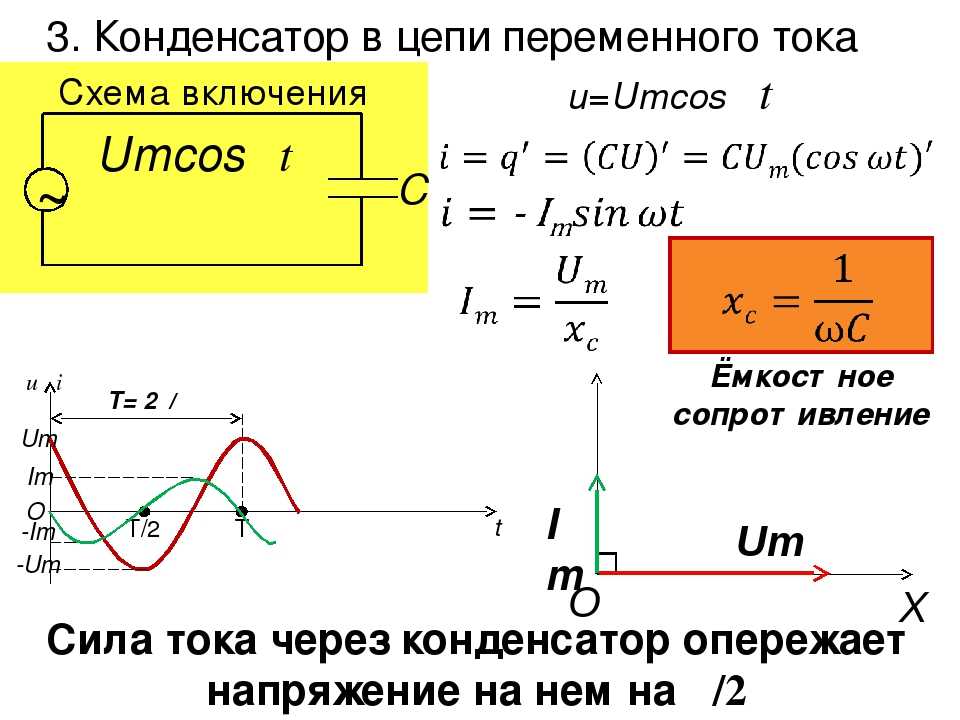Если напряжение быстро меняется, то сила тока не будет достигать тех значений, которые оно бы приобрело с течением времени при постоянном напряжении. Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения. При изменении силы тока по гармоническому закону ЭДС самоиндукции будет равна противоположному значению производной индуктивности.  Так как удельная работа кулоновского поля равна напряжению на концах катушки, то напряжение на концах катушки оказывается гармонически связанным с амплитудным значением напряжения контура. Следовательно, колебания напряжения на катушке опережают колебания силы тока на пи-пополам. В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю. В момент, когда напряжение становится равным нулю, сила тока будет максимальной. Величину икс-эл, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением. Амплитуда силы тока в катушке можно найти отношением амплитуды напряжения на индуктивное сопротивление. Так выглядит закон Ома для цепи постоянного тока с катушкой. Индуктивное сопротивление увеличивается с ростом частоты, значит, катушка хорошо проводит низкочастотные колебания и плохо – высокочастотные, а для постоянного тока оно равно нулю. Рассмотрим использование частотных свойств конденсатора и катушки индуктивности. Реальные электрические цепи содержат все виды сопротивлений: активное, индуктивное, емкостное, поэтому ток в реальной цепи зависит от ее полного эквивалентного сопротивления.
Конденсатор хорошо проводит высокочастотные колебания и плохо – низкочастотные колебания. Катушка наоборот: хорошо проводит низкочастотные колебания и плохо – высокочастотные колебания. Эти свойства позволяют создать различные частотные фильтры – схемы, позволяющие выделить из всего сигнала низкочастотные и высокочастотные составляющие.
Колебательный контур обладает замечательным свойством – пропускать колебания только определенной частоты, зависящей от емкости конденсатора и индуктивности катушки, под действием резонанса. 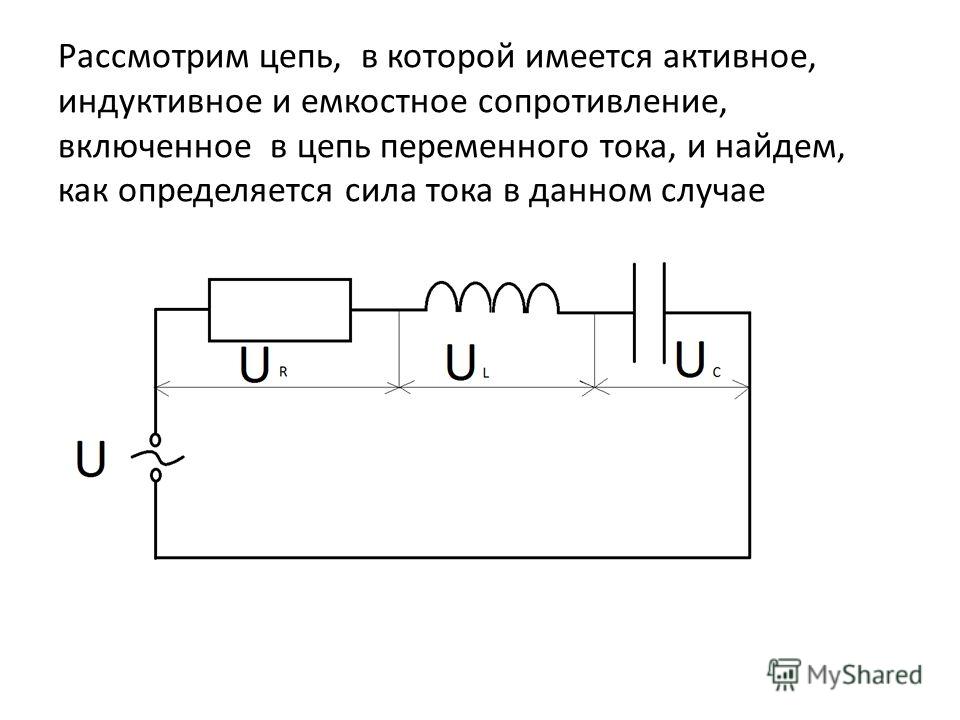Эти свойства контура широко применяются в радио- и телеприёмной и передающей аппаратуре для селекции сигналов.
Задача 
Конденсатор включен в цепь переменного тока с частотой 200 Герц. Напряжение в цепи 40 Вольт, сила тока 0,64 Ампера. Какова емкость конденсатора?
Вспомнив закон Ома для цепи с колебательным контуром, выразим емкость конденсатора как отношение силы тока к напряжению и циклической частоте. Чтобы определить циклическую частоту, необходимо частоту переменного тока разделить на два-пи. Получаем результат 0,5 микрофарад есть емкость конденсатора.
 

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитора

46. Полное сопротивление в цепи переменного тока.

Обычно цепь переменного тока включает в себя и активное сопротивление, и емкость, и индуктивность. Полное сопротивление (Z) — это векторная сумма всех сопротивлений: активного, емкостного и индуктивного. — полное сопротивление цепи.

— активное сопротивление. — индуктивное сопротивление. — полное сопротивление определяет силу тока в цепи по закону Ома. — емкостное сопротивление.

I — действующее значение силы тока (един.измер. А)

U— действующее значение напряжения(един.измер. В)

X_L — индуктивное сопротивление(един.измер. Ом)

ω — циклическая частота переменного тока(един.измер. рад/с)

L – индуктивность(ед.из. Гн)

C – емкость (ед.из. Ф)

X_C — индуктивное сопротивление (ед.из. Ом)

Z — полное сопротивление (Ом)

R — активное сопротивление (Ом)

ρ — удельное сопротивление проводника (Ом/м)

l — длина проводника (м)

S — площадь сечения проводника (м²

Импеданс – основные понятия.

При прохождении через ткани переменного тока, изменяющегося по гармоническому закону

I(t) =I₀ cos ωt,

падение напряжения на биологической ткани изменяется по закону

U (t)=U_o⋅cos (ωt+ϕ).

Величиной, определяющей соотношение между напряжением и силой переменного тока, является импеданс — полное электрическое сопротивление цепи переменному току.

На опыте напряжение отстает по фазе от тока (ϕ<0), что характерно для электрических цепей, состоящих из резисторов и конденсаторов.

Для биологического объекта импеданс носит составной (комплексный) характер Z=(R,X). Его активная составляющая R связана, в первую очередь, с проводимостью внутренних жидких сред, являющихся электролитами. Различные процессы в тканях, сопровождающиеся необратимыми потерями энергии, также дают вклад в величину активной составляющей импеданса. Реактивная компонента X определяется емкостными свойствами исследуемой ткани, в частности, емкостью биологических мембран. Кроме того, в емкостную составляющую импеданса дает вклад и область контакта стимулирующих электродов с биологическими тканями.

Абсолютная величина (модуль) электрического импеданса определяется выражением .22XRZ+=

На опыте величина импеданса может быть определена по измерениям амплитудных (или эффективных) значений напряжения U_o и силы тока I_o

⏐Z⏐ = U_o/I_o (или ⏐Z⏐ = U_эфф/I_эфф)_.

Фазовый сдвиг ϕ определяет отношение реактивной и активной составляющих импеданса

tg ϕ = X/R.

Значения угла сдвига фаз, полученные при частоте 1 кГц для различных биологических объектов, приведены в таблице 1.

Таблица 1. Угол сдвига фаз (в градусах) для различных видов тканей.

Объект	ϕ , град.
Кожа человека, лягушки Нерв лягушки Мышцы кролика	-55 -64 -65

Составную (комплексную) величину Z принято изображать в виде векторной диаграммы, на которой ось абсцисс — величина активного сопротивления, ось ординат — величина реактивного сопротивления.

Абсолютная величина импеданса ⏐Z⏐ и фазовый сдвиг ϕ являются функциями частоты переменного тока. Зависимость электрического импеданса от частоты носит название дисперсии импеданса.

Физические основы реологии.

Величина импеданса тканей зависит от их физиологического состояния, в частности от их кровоснабжения. При кровенаполнении сосудов происходит изменение величины импеданса в такт с работой сердца. По величине изменений импеданса можно судить о состоянии сердечно-сосудистой системы.

Реология — диагностический метод, основанный на регистрации изменения величины импеданса тканей в процессе сердечной деятельности.

Величина импеданса тканей |Z| состоит из двух составляющих |Z| = |Z_o| + |z(t)|: постоянной — |Z_o| и изменяющейся во времени в соответствии с работой сердца – |z(t)|.

На практике, на исследуемый участок тела накладывают электроды площадью несколько см² и пропускают переменный ток частотой ≈ 30 − 40 кГц. Выбор частоты определяется несколькими факторами: электробезопасностью, исключением влияния электродов и емкости их контакта с кожей, уменьшением зависимости величины импеданса от механических воздействий на исследуемую ткань. Наполнение сосудов кровью изменяет расстояния между отдельными участками ткани, что должно приводить к изменению ёмкостного сопротивления. Но вклад макроскопических объемов тканей в реактивную составляющую импеданса существенен только в области α- дисперсии. Следовательно, изменения импеданса во времени обусловлены влиянием притока и оттока крови на активную составляющую полного сопротивления.

При прохождении через ткани электрического тока I = I_o⋅cos ωt величина напряжения будет изменяться по закону

U = U_ο cos (ωt + ϕ) = I_o⋅( ⏐Z_o⏐ + ⏐z(t)⏐ )⋅cos (ωt +ϕ ).

Электрическими методами выделяют из регистрируемого сигнала составляющую, пропорциональную |z(t)|, содержащую информацию о состоянии кровоснабжения изучаемого участка тканей − реограмму.

Для парных анатомических образований проводят запись реограммы на правой и левой стороне тела.

Разница между сопротивлением постоянному и переменному току

Сопротивление

Свойство вещества или материала, препятствующее прохождению через него электричества, называется сопротивлением. протекание тока через него.

Примерами резисторов с высоким сопротивлением являются дерево, воздух, слюда, стекло, резина, вольфрам и т. д.

Единица сопротивления: « Ом », обозначается как Ом и представляется как « R ».

• Связанная запись: AC или DC – что более опасно и почему?

 

Сопротивление переменному току

Проще говоря, сопротивление в цепях переменного тока называется импедансом. Или

Общее сопротивление (сопротивление, индуктивное сопротивление и емкостное сопротивление) в цепях переменного тока называется импедансом (Z).

Объяснение:

Когда переменный ток проходит через провод (резистор, катушку индуктивности, конденсатор), то ток создает магнитное поле на этом проводе, которое противодействует потоку переменного тока в нем вместе с сопротивлением этого провода. Эта противоположная причина называется индуктивностью, или индуктивность является свойством катушки (или провода), из-за которого противодействует любому увеличению или уменьшению тока или потока через нее. Кроме того, мы знаем, что индуктивность существует только в переменном токе, потому что величина тока постоянно меняется

Индуктивное реактивное сопротивление X _L , свойство катушки или провода в цепи переменного тока, которое препятствует изменению тока. Единица измерения индуктивного сопротивления такая же, как сопротивление, емкостное сопротивление, т.е. Ом (Ом), но репрезентативным символом емкостного сопротивления является X _L .

Аналогично,

Емкостное реактивное сопротивление в емкостной цепи является сопротивлением току, протекающему только в цепях переменного тока. Единица емкостного реактивного сопротивления такая же, как сопротивление, индуктивное реактивное сопротивление, т.е. Ом (Ом), но репрезентативным символом емкостного реактивного сопротивления является X _С .

• Запись по теме: Что происходит, когда линия переменного тока касается линии постоянного тока?

Измерение сопротивления переменному току

Формулы электрического сопротивления и импеданса в цепях переменного тока

В цепях переменного тока (емкостная или индуктивная нагрузка), сопротивление = полное сопротивление, т. е. R = Z

Z = √ (R ^{2 X} 5 + 1 L ² )… В случае индуктивной нагрузки

Z = √ (R ² + X _C ² )… В случае емкостной нагрузки

Z = √ (R ² + (X _L – X _C ) ² …Для индуктивных и емкостных нагрузок

Полезно знать: 9 0

X

Где; = Inductive reactance

X _L = 2π f L…Where L = Inductance in Henry

And;

X _C = Capacitive reactance

X _C = 1/2π f C … Где C = емкость в фарадах.0028

Сопротивление постоянному току

Мы знаем, что в цепях постоянного тока не существует концепции индуктивных и емкостных сопротивлений. т. е. емкостное и индуктивное сопротивления в цепях постоянного тока равны нулю, поскольку в цепях постоянного тока нет частоты, т. е. величина постоянного тока постоянна. Поэтому в игру вступает только исходное сопротивление провода.

Полезно знать:

Вот почему сопротивление, предлагаемое проводом, ниже для постоянного тока, чем для переменного тока, поскольку линии переменного тока нуждаются в большей изоляции, чем линии постоянного тока.

Измерение сопротивления постоянному току

Формулы электрического сопротивления

В цепях постоянного тока сопротивление рассчитывается по закону Ома.

Р = В/И.

Полезно знать:

При решении электрических цепей для нахождения сопротивления и вы не уверены, какую из них следует учитывать, сопротивления переменному или постоянному прошел постоянный ток, возьмите сопротивление постоянному току.

• Запись по теме: Почему в электронных схемах используется постоянный ток вместо переменного?

Что больше — сопротивление переменному или постоянному току?

Поскольку мы знаем, что частота в источнике постоянного тока равна нулю, поэтому нет скин-эффекта (поведение переменного тока, протекающего через поверхность, т. е. внешний слой проводника, а не через сердцевину провода). в цепях постоянного тока. Из-за скин-эффекта сопротивление переменному току в цепях переменного тока больше, чем подача постоянного тока в цепях постоянного тока .

Формула эффекта кожи

δ = √(2ρ/ωµ)

Где;

• δ = глубина скин-эффекта
• ρ = Удельное сопротивление
• ω = 2π f  = Угловая частота
• µ = проницаемость проводника

Короче говоря, частота прямо пропорциональна скин-эффекту, т. е. при увеличении частоты скин-эффект также увеличивается там, где нет частоты и скин-эффекта на постоянном токе.

Как правило;

Сопротивление переменному току = 1,6 x сопротивление постоянному току

Похожие посты:

• Разница между батареей и конденсатором
• Разница между током и напряжением
• Почему переменный ток требует большей изоляции, чем постоянный ток при том же уровне напряжения?
• Почему мы не можем хранить переменный ток в батареях вместо постоянного тока?
• Почему используется резистор с нулевым сопротивлением? Применение резисторов 0 Ом
• Калькулятор цветового кода резистора — расчет 3-, 4-, 5- и 6-полосных резисторов

Показать полную статью

Связанные статьи

Кнопка «Вернуться к началу»

Что такое сопротивление постоянному и переменному току?

Когда электростанции снабжают электроэнергией здания и домохозяйства, они передают ее на большие расстояния в виде постоянного тока (DC). Но бытовая техника и электроника обычно используют переменный ток (AC).

Преобразование между двумя формами может показать вам, чем сопротивления для форм электричества отличаются друг от друга и как они используются в практических приложениях. Вы можете придумать уравнения постоянного и переменного тока, чтобы описать различия в сопротивлении постоянному и переменному току.

В то время как мощность постоянного тока течет в одном направлении в электрической цепи, ток от источников питания переменного тока чередуется между прямым и обратным направлениями через равные промежутки времени. Эта модуляция описывает, как изменяется переменный ток и принимает форму синусоиды.

Это различие также означает, что вы можете описать мощность переменного тока с помощью измерения времени, которое вы можете преобразовать в пространственное измерение, чтобы показать вам, как напряжение изменяется в различных областях самой цепи. Используя основные элементы схемы с источником питания переменного тока, можно описать сопротивление математически.

Сопротивление постоянному току и переменному току

Для цепей переменного тока обработайте источник питания с помощью синусоиды наряду с ​ Закон Ома ​,

V=IR ​ и сопротивление ​ R ​, но используйте ​ импеданс Z ​ ​ вместо ​ R. ​

Сопротивление цепи переменного тока можно определить так же, как и для цепи постоянного тока: путем деления напряжения на ток. В случае цепи переменного тока сопротивление называется импедансом и может принимать другие формы для различных элементов цепи, таких как индуктивное сопротивление и емкостное сопротивление, измерение сопротивления катушек индуктивности и конденсаторов соответственно. Катушки индуктивности создают магнитные поля для хранения энергии в ответ на ток, в то время как конденсаторы накапливают заряд в цепях.

Вы можете представить электрический ток через сопротивление переменного тока

I=I_m\sin{(\omega t + \theta)}

для максимального значения тока ​ Im ​, как разность фаз ​ θ ​, угловая частота контура ω ​ и время ​ t ​. Разность фаз — это измерение угла самой синусоиды, показывающее, насколько ток не совпадает по фазе с напряжением. Если ток и напряжение находятся в фазе друг с другом, то фазовый угол будет равен 0°.

​ Частота ​ является функцией того, сколько синусоидальных волн прошло через одну точку за одну секунду. Угловая частота – это частота, умноженная на 2π для учета радиального характера источника питания. Умножьте это уравнение для тока на сопротивление, чтобы получить напряжение. Напряжение принимает аналогичную форму

V=V_m\sin{(\omega t)}

для максимального напряжения V. Это означает, что вы можете рассчитать импеданс переменного тока как результат деления напряжения на ток, который должен быть равен 92}

для индуктивного сопротивления X _L , емкостного сопротивления X _C для определения импеданса переменного тока Z. Это позволяет измерить импеданс по переменному току индукторов и конденсаторов схемы. Вы также можете использовать уравнения X _L = 2πfL и X _C = 1/2πfC , чтобы сравнить эти значения сопротивления с индуктивностью L и емкостью 9 C . индуктивность в генри и емкость в фарадах.

Уравнения для цепей постоянного и переменного тока

Хотя уравнения для цепей переменного и постоянного тока принимают разные формы, они оба основаны на одних и тех же принципах. Учебное пособие по цепям постоянного и переменного тока может продемонстрировать это. Цепи постоянного тока имеют нулевую частоту, потому что, если бы вы наблюдали за источником питания для цепи постоянного тока, вы не увидели бы какой-либо формы волны или угла, под которым вы могли бы измерить, сколько волн пройдет через данную точку. Цепи переменного тока показывают эти волны с гребнями, впадинами и амплитудами, которые позволяют вам использовать частоту для их описания.

Сравнение уравнений постоянного тока и цепи может показать разные выражения для напряжения, тока и сопротивления, но основные теории, лежащие в основе этих уравнений, одинаковы. Различия в уравнениях цепей постоянного и переменного тока обусловлены природой самих элементов схемы.

Вы используете закон Ома ​ V = IR ​ в обоих случаях, и вы суммируете ток, напряжение и сопротивление в различных типах цепей одинаково для цепей постоянного и переменного тока. Это означает суммирование падений напряжения на замкнутом контуре как равное нулю и вычисление тока, который входит в каждый узел или точку электрической цепи, как равного выходному току, но для цепей переменного тока вы используете векторы.

Учебное пособие по цепям постоянного и переменного тока

Если у вас есть параллельная цепь RLC, то есть цепь переменного тока с резистором, катушкой индуктивности (L) и конденсатором, расположенными параллельно друг другу и параллельно источнику питания, вы должны рассчитать ток, напряжение и сопротивление (или, в данном случае, импеданс) так же, как и для цепи постоянного тока.

Общий ток от источника питания должен быть равен вектору ​ суммы токов, протекающих по каждой из трех ветвей. Векторная сумма означает возведение в квадрат значения каждого тока и их суммирование, чтобы получить 92

для тока подачи I _S , CERCESTOR CURCE I _R , ток индуктора I _L и ток конденсатора I _C . Это контрастирует с вариантом схемы постоянного тока, который был бы

I_S=I_R+I_L+I_C

Поскольку падение напряжения на ветвях остается постоянным в параллельных цепях, мы можем рассчитать напряжения на каждой ветви в параллельной цепи RLC как 2}

Это значение ​ 1/Z ​ также называется полной проводимостью цепи переменного тока. Напротив, падение напряжения на ветвях для соответствующей цепи с источником постоянного тока будет равно напряжению источника питания В .

Для последовательной цепи RLC, цепи переменного тока с резистором, катушкой индуктивности и конденсатором, расположенными последовательно, можно использовать те же методы. Вы можете рассчитать напряжение, ток и сопротивление, используя те же принципы установки тока, входящего и выходящего из узлов и точек, как равные друг другу, при суммировании падений напряжения на замкнутых контурах как равных нулю.

Ток в цепи будет одинаковым для всех элементов и определяется током источника переменного тока ​ I= I _m x sin(ωt) ​. Напряжение, с другой стороны, может быть суммировано по контуру как напряжение питания В _S , напряжение резистора В _R , напряжение дросселя В _L ​ и напряжение конденсатора ​ В _C ​.

Для соответствующей цепи постоянного тока ток будет просто ​ В/об ​ согласно закону Ома, а напряжение также будет ​ В _s — В _R — В _L — В _C ​ = 0 для каждого последовательно включенного компонента. Разница между сценариями постоянного и переменного тока заключается в том, что для постоянного тока вы можете измерить напряжение резистора как IR , напряжение катушки индуктивности как LdI/dt и напряжение конденсатора как QC ​ (для заряда C ​ и емкости Q) ​, напряжения для цепи переменного тока будут ​ V _R = IR, VL = IX _L ​( sin( ωt + 90 ​°​ ) ​ и ​ VC = ​ ​ IX _C sin(ωt — 90 ​°​ ). Это показывает, как в цепях RLC переменного тока индуктор находится впереди источника напряжения на 90°, а конденсатор позади на 90°.

Сопротивление переменному току и импеданс — Electronics-Lab.com

Введение

Электрическое сопротивление — это свойство, которое характеризует, как конкретный компонент создает сопротивление протеканию тока, когда на его клеммы подается разность потенциалов. В этом уроке мы сосредоточимся на сопротивлении, которое создает резистор, когда на него подается переменное напряжение.

В самом первом разделе, чтобы не ограничиваться законом Ома, в простой презентации даются некоторые подробности о концепции сопротивления и компонентах резистора. Во втором разделе мы увидим сходство поведения сопротивления в режиме переменного и постоянного тока.

В следующих разделах будут освещены два явления, которые вызывают различия между сопротивлением резисторов переменному и постоянному току, особенно при увеличении частоты.

Представление: удельное сопротивление

В этом разделе мы более четко определим, что такое сопротивление и от чего оно зависит. Как следует из названия, первичное понятие называется , а удельное сопротивление . Рассмотрим материал в виде параллелепипеда с сечением А и длиной L с двумя клеммами, как показано на рис. 1:

рис. 1: резистор с электрическими контактами

Удельное сопротивление ρ выражается в Ом·м и является внутренним свойством материала. Это означает, что удельное сопротивление не зависит от геометрии. Значение удельного сопротивления любого материала можно просто найти в онлайн-таблицах или в книгах.

Кроме того, удельное сопротивление является одной из редких физических величин, которая варьируется в стольких порядках. Например, медь является одним из наименее резистивных материалов, ее удельное сопротивление равно ρ _медь =1,7×10 ^-8 Ом. м . С другой стороны, тефлон является одним из самых резистивных материалов с удельным сопротивлением ρ _Тефлон >10 ²³ Ом·м.

Для определенной геометрии, такой как Рис. сопротивление, если оно зависит от геометрии и собственного удельного сопротивления материала:

• Если длина увеличивается, электронам приходится проходить через материал с большим сопротивлением, поэтому сопротивление увеличивается.
• Если поперечное сечение уменьшается, для электронов остается меньше возможных путей (например, для простой дороги или четырехполосного шоссе), поэтому сопротивление увеличивается.
• Если удельное сопротивление увеличивается, материал по своей природе более удельное сопротивление, поэтому сопротивление снова увеличивается.

Резисторы обычно изготавливаются из керамического или угольного порошка, удельное сопротивление ρ _{углерод} ≅ 10 ^-3 Ом. м . Например, если мы выберем соотношение L/A=1000·, мы получим сопротивление в несколько Ом.

Сходства в режиме переменного тока

В режиме постоянного тока сопротивление, создаваемое резистором, чрезвычайно просто описать, оно описывается законом Ома . Это линейная зависимость между напряжением В и током I , где эти две величины связаны коэффициентом R, называемым сопротивлением , например U=R×I .

рис. 2: Иллюстрация постоянного напряжения, приложенного к резистору

Итак, что произойдет, если мы заменим источник постоянного тока источником переменного тока в Рисунок 2 ? Можно ли еще применить закон Ома?

Ответ прост, при нормальных условиях частоты и амплитуды (не слишком высокой) резистор ведет себя строго так же, как и в режиме постоянного тока. Таким образом, комплексный импеданс сопротивления представляет собой действительное число Z=R+j×0=U/I .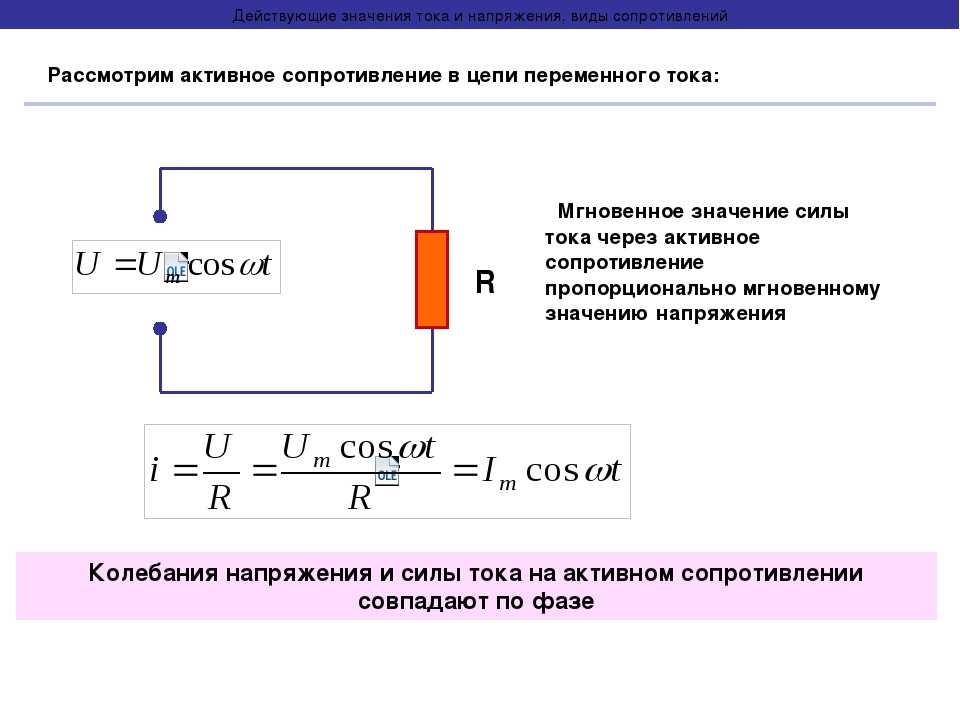

В режиме постоянного тока мощность, генерируемая при нагреве, определяется как произведение напряжения и тока: P=U×I . Это верно и в режиме переменного тока для мгновенной мощности: P(t)=U(t)×I(t) . Однако интереснее сосредоточиться на средней мощности P _avg , рассеиваемой джоулевым нагревом. Формула для P _avg приведена ниже в Уравнении 2 , где Φ указывает фазовый сдвиг между напряжением и током:

eq 2 : Выражение средней мощности

к учебнику по комплексным числам, чтобы понять, что фазовый сдвиг Φ равен нулю. Нижние индексы «RMS» означают среднеквадратичное значение, его определение полностью объяснено в руководстве по форме сигнала переменного тока.

Для частного случая чисто резистивной цепи выражение средней мощности сокращается, таким образом, до P _avg =U _RMS ×I _RMS .

Несоответствия в режиме переменного тока

В этом последнем разделе мы выделяем два эффекта, которые изменяют сопротивление переменному току по сравнению с сопротивлением постоянному току, когда частота источника переменного тока сильно увеличивается. Раздел разделен на два подраздела для независимого рассмотрения этих явлений.

Скин-эффект

Прежде чем говорить об этом явлении, нужно понять его происхождение. Этот первый эффект связан с законом электромагнитной индукции , который мы упоминали в учебнике по форме волны переменного тока.

Закон индукции или Закон Ленца гласит, что при рассмотрении замкнутой электрической цепи C, в которую проникает переменное магнитное поле B ₁ (t), генерируется ток I для создания противоположного магнитного поля B ₂ (t) для смягчения вариации B ₁ (т).

рис. 3 : Иллюстрация явления индукции

Этот электромагнитный эффект широко присутствует во многих технологиях и может использоваться по-разному, например, как работают индукторы, турбины, трансформаторы или индукционные плиты.

Теперь вернемся к резистивному материалу, который уже представлен в Рисунок 1 . Точно так же, как переменное магнитное поле создает токовые петли, переменный ток I(t) также генерирует магнитные петли B(t). Поскольку внутри резистивного материала образуются магнитные петли, они создают такие, как показано на рис. 9.0003 Рисунок 3 токовые петли. Эти токовые петли имеют особое название: они называются Вихревые токи или Токи Фуко .

рис. 4 : Иллюстрация скин-эффекта

Такие токи концентрируются на границе резистивного материала, как показано на рис. 4 выше. Это явление, называемое скин-эффектом , имеет тенденцию становиться более важным, когда частота переменного тока I(t) увеличивается.

Самый важный параметр, описывающий скин-эффект, называется глубина кожи и отмечено δ . Он обозначает толщину от границы резистивного материала, где сосредоточена большая часть вихревых токов.

Это значение пропорционально 1/√f , где f — частота. Следовательно, увеличение частоты приводит к уменьшению глубины скин-слоя. Когда частота переменного тока становится очень высокой, большая часть тока сосредоточена в небольшой области вблизи границы резистивного материала, как показано на рис. 5 9 .0004 :

рис. 5 : Описание глубины скин-слоя и профиля распределения тока

Эффективное поперечное сечение A материала становится тогда меньше и, следовательно, в соответствии с уравнением 1 , сопротивление увеличивается.

При определенном значении частоты, которое зависит от материала, скин-эффект имеет тенденцию увеличивать сопротивление переменному току по сравнению с сопротивлением постоянному току: R _AC >R _DC .

Эффект близости

Электромагнитная индукция также является причиной другого эффекта, известного как эффект близости , который может сильно повлиять на сопротивление цепи переменному току. Эффект близости наблюдается, когда по двум или более близлежащим проводникам течет ток.

Рассмотрим для простоты примера два параллельных провода W ₁ и W ₂ , по которым проходит одинаковый переменный ток I(t). Если частота тока достаточно высока, магнитная петля B(t) будет генерироваться W ₁ (также W ₂ , но не представленной в ).0004 ) вокруг себя. Если провода расположены достаточно близко, магнитная петля пересекает второй провод и генерирует, как объяснялось ранее, вихревые токи в Вт ₂ :

рис. 6: Иллюстрация эффекта близости

Поскольку эффект симметричен, Вт ₂ также индуцирует вихревые токи в W ₁ . Текущий профиль концентрации для этого примера будет выглядеть так, как показано на Рис. 7 ниже:

Рис. 7: Распределение тока из-за эффекта близости

Подобно скин-эффекту, эффект близости является результатом изменения распределения тока в резистивных материалах, что приводит к увеличению сопротивления за счет уменьшения эффективного поперечного сечения. Этот эффект также усиливается при увеличении частоты и может привести к разнице между сопротивлениями переменного и постоянного тока на один или несколько порядков.

Заключение

В этом руководстве основное внимание уделяется сходствам и различиям между значением сопротивления резистивного материала в режиме постоянного и переменного тока.

Прежде всего, мы представили, из чего именно состоит сопротивление, представив понятие удельного сопротивления. Мы видели, что сопротивление зависит от этого внутреннего свойства и от геометрии рассматриваемого материала.

Во втором разделе мы исследуем сопротивление переменному току в нормальных рабочих условиях (не слишком высокая частота). Закон Ома может применяться как в режиме переменного тока, так и в режиме постоянного тока. Более того, поскольку сдвиг фаз не наблюдается, выражение мощности аналогично тому, как в режиме постоянного тока, с использованием среднеквадратичных значений для величин напряжения и тока.

В последнем разделе два явления указывают на тот факт, что при увеличении частоты сопротивление переменному току может стать намного выше, чем сопротивление постоянному току.

Первый эффект называется скин-эффектом и обусловлен перераспределением тока вблизи границы проводника. Это уменьшает эффективное поперечное сечение, по которому проходит ток, что увеличивает сопротивление.

Второй эффект — это эффект близости и возникает, когда по двум близлежащим проводникам одновременно протекает переменный ток достаточно высокой частоты. Это также приводит к перераспределению тока внутри обоих проводников вблизи одной из их границ, что, подобно скин-эффекту, увеличивает сопротивление проводов.

Однако эти эффекты начинают сильно влиять на схему только при очень высокой частоте. Например, при частоте 50 Гц медные провода не обязательно должны быть шире 8 мм в радиусе, поскольку толщина скин-слоя на этой частоте составляет около 9 мм.