Средневыпрямленное напряжение: формулы, расчет и измерение — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое средневыпрямленное напряжение и как его рассчитать. Как измерить средневыпрямленное напряжение мультиметром. Чем отличается средневыпрямленное напряжение от действующего и амплитудного. Какие формулы используются для расчета средневыпрямленного напряжения.

Содержание

Что такое средневыпрямленное напряжение

Средневыпрямленное напряжение — это один из важных параметров переменного напряжения, наряду с действующим и амплитудным значениями. Давайте разберемся, что оно собой представляет и чем отличается от других характеристик переменного напряжения.

Средневыпрямленное напряжение (Uср.выпр) — это среднее значение модуля мгновенных значений переменного напряжения за период. То есть это усредненное значение напряжения без учета его знака.

Для синусоидального сигнала средневыпрямленное напряжение связано с амплитудным значением следующим соотношением:

Uср.выпр = 0.637 * Umax

где Umax — амплитудное (максимальное) значение напряжения.

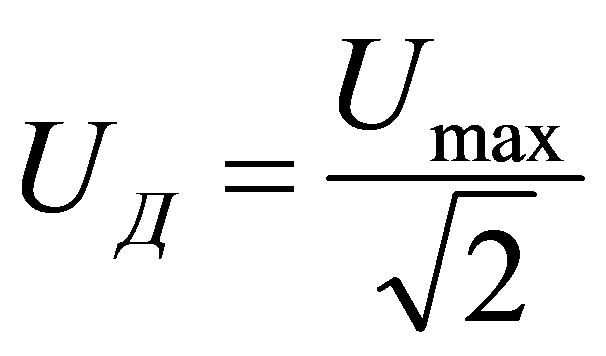
Формулы для расчета средневыпрямленного напряжения

Для расчета средневыпрямленного напряжения используются следующие основные формулы:

Для синусоидального сигнала: Uср.выпр = 0.637 * Umax = 0.9 * Uд
Для прямоугольного сигнала: Uср.выпр = Umax
Для треугольного сигнала: Uср.выпр = 0.5 * Umax

где Umax — амплитудное значение, Uд — действующее значение напряжения.

Как измерить средневыпрямленное напряжение

Для измерения средневыпрямленного напряжения используются специальные вольтметры средневыпрямленного значения. Принцип их работы основан на выпрямлении переменного сигнала и измерении его среднего значения.

Основные способы измерения средневыпрямленного напряжения:

С помощью аналогового вольтметра с выпрямителем
Цифровым мультиметром в режиме измерения средневыпрямленного напряжения
Осциллографом с функцией измерения средних значений

При измерении важно учитывать, что большинство мультиметров по умолчанию измеряют действующее значение напряжения. Для корректного измерения средневыпрямленного значения нужно использовать специальный режим или вносить поправочный коэффициент.

Отличия от действующего и амплитудного значений

Средневыпрямленное напряжение следует отличать от других параметров переменного напряжения:

Действующее напряжение (Uд) — эквивалентно постоянному напряжению по выделяемой мощности
Амплитудное напряжение (Umax) — максимальное мгновенное значение
Средневыпрямленное напряжение (Uср.выпр) — среднее значение модуля напряжения

Для синусоидального сигнала соотношение между этими величинами следующее:

Uср.выпр = 0.9 * Uд = 0.637 * Umax

То есть средневыпрямленное значение всегда меньше действующего и тем более амплитудного.

Применение средневыпрямленного напряжения

Знание средневыпрямленного значения напряжения необходимо в следующих случаях:

Расчет выпрямителей переменного тока
Анализ работы импульсных источников питания
Оценка формы сигнала в электронных схемах
Калибровка измерительных приборов

Средневыпрямленное напряжение позволяет оценить энергетические характеристики сигнала независимо от его формы. Это делает данный параметр полезным при анализе несинусоидальных сигналов.

Погрешности при измерении средневыпрямленного напряжения

При практических измерениях средневыпрямленного напряжения возникают следующие основные погрешности:

Погрешность из-за нелинейности выпрямителя
Температурная погрешность
Частотная погрешность на высоких частотах
Погрешность из-за отклонения формы сигнала от идеальной

Для повышения точности измерений рекомендуется:

Использовать прецизионные выпрямительные диоды
Применять температурную компенсацию
Учитывать частотную зависимость при высокочастотных измерениях
Калибровать прибор на реальной форме измеряемого сигнала

При правильном подходе погрешность измерения средневыпрямленного напряжения может быть снижена до 0.1-0.5%.

Расчет средневыпрямленного напряжения для различных сигналов

Рассмотрим примеры расчета средневыпрямленного напряжения для разных форм сигнала:

Синусоидальный сигнал

Для синусоидального напряжения с амплитудой 100 В:

Uср.выпр = 0.637 * Umax = 0.637 * 100 = 63.7 В

Прямоугольный сигнал

Для прямоугольного сигнала с амплитудой 50 В:

Uср.выпр = Umax = 50 В

Треугольный сигнал

Для треугольного сигнала с амплитудой 200 В:

Uср.выпр = 0.5 * Umax = 0.5 * 200 = 100 В

Как видим, значение средневыпрямленного напряжения существенно зависит от формы сигнала.

Преимущества и недостатки измерения средневыпрямленного напряжения

Измерение средневыпрямленного напряжения имеет ряд особенностей:

Преимущества:

Простота реализации измерительной схемы
Низкая стоимость измерительных приборов
Высокая чувствительность на низких частотах

Недостатки:

Зависимость показаний от формы сигнала
Невысокая точность на высоких частотах
Чувствительность к помехам и искажениям сигнала

В целом, измерение средневыпрямленного напряжения оптимально для оценки энергетических параметров сигнала в низкочастотных цепях.

Параметры переменного напряжения — Практическая электроника

Как вы помните из предыдущей статьи, переменное напряжение — это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.

Среднее значение напряжения

Среднее значение переменного напряжения Uср

— это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.

среднее значение напряжения за период

Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком «минус». А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.

То же самое касается и других сигналов, например, двухполярного меандра. Меандр — это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.

меандр

Средневыпрямленное значение напряжения

Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая «пробивает пол» берут не с отрицательным знаком, а с положительным.

средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.

На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:

выпрямленное переменное напряжение после диодного моста

Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:

Среднеквадратичное значение напряжения

— это значение постоянного напряжения, который, проходя через нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение обозначается так: RMS (rms) — root mean square.

Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды K_a:

Вот некоторые значения коэффициента амплитуды K_aдля некоторых сигналов переменного напряжения:

Более точные значения 1,41 и 1,73 — это √2 и √3 соответственно.

Как измерить среднеквадратичное значение напряжения

Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS — как вы уже знаете — это среднеквадратическое значение. А что за буква «T» впереди? Думаю, вы помните, как раньше была мода на одно словечко: «тру». «Она вся такая тру…», «Ты тру или не тру?» и тд. Тру (true) —

с англ. правильный, верный.

[quads id=1]

Так вот, T-RMS расшифровывается как True RMS — «правильное среднеквадратическое значение». Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип «T-RMS».

мультиметр с True RMS

Проведем небольшой опыт. Давайте соберем вот такую схемку:

Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц

генератор частоты

А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

треугольный сигнал

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?

Так как один квадратик у нас равняется 1 Вольт (мы это видим внизу осциллограммы в красной рамке), то получается, что амплитуда Umax этого треугольного сигнала равняется 4 Вольта. Для того, чтобы рассчитать среднеквадратическое напряжение, мы воспользуемся формулой:

Итак, смотрим нашу табличку и находим интересующий нас сигнал:

Для нас не важно, пробивает ли сигнал «пол» или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды K_a= 1,73.

Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала

Проверяем нашим прибором, так ли оно на самом деле?

Супер! И в правду Тrue RMS.

Замеряем это же самое напряжение с помощью моего китайского мультиметра

Он меня обманул :-(. Он умеет измерять только среднеквадратическое значение синусоидального сигнала, а у нас сигнал треугольный.

Самый интересный сигнал в плане расчетов — это двуполярный меандр, ну тот есть тот, который «пробивает пол».

Его амплитудное

Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.

Вот вам небольшая картинка, чтобы не путаться

среднее, среднеквадратичное и пиковое значения напряжения

Сред. — средневыпрямленное значение сигнала. Это и есть площадь под кривой
СКЗ — среднеквадратичное напряжение. Как мы видим, для синусоидальных сигналов, оно будет больше, чем средневыпрямленное.
Пик. — амплитудное значение сигнала
Пик-пик. — размах или двойная амплитаду. Или иначе, амплитуда от пика до пика.

Так что же все-таки показывает мультиметр при измерении переменного напряжения? Показывает он НЕ амплитудное, НЕ среднее и НЕ среднее выпрямленное напряжение, а среднее квадратическое, то есть действующее напряжение! Об этом всегда помним.

%d1%81%d1%80%d0%b5%d0%b4%d0%bd%d0%b5%d0%b2%d1%8b%d0%bf%d1%80%d1%8f%d0%bc%d0%bb%d0%b5%d0%bd%d0%bd%d0%be%d0%b5%20%d0%bd%d0%b0%d0%bf%d1%80%d1%8f%d0%b6%d0%b5%d0%bd%d0%b8%d0%b5 — со всех языков на все языки

Все языкиАбхазскийАдыгейскийАфрикаансАйнский языкАканАлтайскийАрагонскийАрабскийАстурийскийАймараАзербайджанскийБашкирскийБагобоБелорусскийБолгарскийТибетскийБурятскийКаталанскийЧеченскийШорскийЧерокиШайенскогоКриЧешскийКрымскотатарскийЦерковнославянский (Старославянский)ЧувашскийВаллийскийДатскийНемецкийДолганскийГреческийАнглийскийЭсперантоИспанскийЭстонскийБаскскийЭвенкийскийПерсидскийФинскийФарерскийФранцузскийИрландскийГэльскийГуараниКлингонскийЭльзасскийИвритХиндиХорватскийВерхнелужицкийГаитянскийВенгерскийАрмянскийИндонезийскийИнупиакИнгушскийИсландскийИтальянскийЯпонскийГрузинскийКарачаевскийЧеркесскийКазахскийКхмерскийКорейскийКумыкскийКурдскийКомиКиргизскийЛатинскийЛюксембургскийСефардскийЛингалаЛитовскийЛатышскийМаньчжурскийМикенскийМокшанскийМаориМарийскийМакедонскийКомиМонгольскийМалайскийМайяЭрзянскийНидерландскийНорвежскийНауатльОрокскийНогайскийОсетинскийОсманскийПенджабскийПалиПольскийПапьяментоДревнерусский языкПортугальскийКечуаКвеньяРумынский, МолдавскийАрумынскийРусскийСанскритСеверносаамскийЯкутскийСловацкийСловенскийАлбанскийСербскийШведскийСуахилиШумерскийСилезскийТофаларскийТаджикскийТайскийТуркменскийТагальскийТурецкийТатарскийТувинскийТвиУдмурдскийУйгурскийУкраинскийУрдуУрумскийУзбекскийВьетнамскийВепсскийВарайскийЮпийскийИдишЙорубаКитайский

Все языкиАбхазскийАдыгейскийАфрикаансАйнский языкАлтайскийАрабскийАварскийАймараАзербайджанскийБашкирскийБелорусскийБолгарскийКаталанскийЧеченскийЧаморроШорскийЧерокиЧешскийКрымскотатарскийЦерковнославянский (Старославянский)ЧувашскийДатскийНемецкийГреческийАнглийскийЭсперантоИспанскийЭстонскийБаскскийЭвенкийскийПерсидскийФинскийФарерскийФранцузскийИрландскийГалисийскийКлингонскийЭльзасскийИвритХиндиХорватскийГаитянскийВенгерскийАрмянскийИндонезийскийИнгушскийИсландскийИтальянскийИжорскийЯпонскийЛожбанГрузинскийКарачаевскийКазахскийКхмерскийКорейскийКумыкскийКурдскийЛатинскийЛингалаЛитовскийЛатышскийМокшанскийМаориМарийскийМакедонскийМонгольскийМалайскийМальтийскийМайяЭрзянскийНидерландскийНорвежскийОсетинскийПенджабскийПалиПольскийПапьяментоДревнерусский языкПуштуПортугальскийКечуаКвеньяРумынский, МолдавскийРусскийЯкутскийСловацкийСловенскийАлбанскийСербскийШведскийСуахилиТамильскийТаджикскийТайскийТуркменскийТагальскийТурецкийТатарскийУдмурдскийУйгурскийУкраинскийУрдуУрумскийУзбекскийВодскийВьетнамскийВепсскийИдишЙорубаКитайский

220 Вольт действующее или амплитудное

Как вы помните из предыдущей статьи, переменное напряжение – это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.

Среднее значение напряжения

Среднее значение переменного напряжения Uср – это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.

среднее значение напряжения за период

Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком “минус”. А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.

То же самое касается и других сигналов, например, двухполярного меандра. Меандр – это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.

меандр

Средневыпрямленное значение напряжения

Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая “пробивает пол” берут не с отрицательным знаком, а с положительным.

выпрямленное переменное напряжение после диодного моста

Среднеквадратичное значение напряжения

Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже простым графиком не отделаешься. Среднеквадратичное значение – это значение постоянного напряжения, который, проходя через нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение обозначается так: RMS (rms) – root mean square.

Вот некоторые значения коэффициента амплитуды K_aдля некоторых сигналов переменного напряжения:

Более точные значения 1,41 и 1,73 – это √2 и √3 соответственно.

Как измерить среднеквадратичное значение напряжения

Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS – как вы уже знаете – это среднеквадратическое значение. А что за буква “T” впереди? Думаю, вы помните, как раньше была мода на одно словечко: “тру”. “Она вся такая тру…”, “Ты тру или не тру?” и тд. Тру (true) – с англ. правильный, верный.

Так вот, T-RMS расшифровывается как True RMS – “правильное среднеквадратическое значение”. Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип “T-RMS”.

мультиметр с True RMS

Проведем небольшой опыт. Давайте соберем вот такую схемку:

Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц

А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?

Итак, смотрим нашу табличку и находим интересующий нас сигнал:

Для нас не важно, пробивает ли сигнал “пол” или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды K_a= 1,73.

Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала

Проверяем нашим прибором, так ли оно на самом деле?

Супер! И в правду Тrue RMS.

Замеряем это же самое напряжение с помощью моего китайского мультиметра

Самый интересный сигнал в плане расчетов – это двуполярный меандр, ну тот есть тот, который “пробивает пол”.

Его амплитудное Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.

Вот вам небольшая картинка, чтобы не путаться

среднее, среднеквадратичное и пиковое значения напряжения

Сред. – средневыпрямленное значение сигнала. Это и есть площадь под кривой
СКЗ – среднеквадратичное напряжение. Как мы видим, для синусоидальных сигналов, оно будет больше, чем средневыпрямленное.
Пик. – амплитудное значение сигнала
Пик-пик. – размах или двойная амплитаду. Или иначе, амплитуда от пика до пика.

♦Переменный электрический ток в нашей бытовой электросети представляет собой синусоиду, как на рисунке 1.

Напряжение меняет свою величину от 0 до + Umax и от 0 до — Umax . Полный цикл этих изменений называется периодом.
Период измеряется в секундах и обозначается буквой Т .
Количество периодов переменного тока за 1 секунду, есть частота f .
Частота переменного тока f измеряется в герцах .

f = 1 / T.

Например.
Частота в нашей электрической сети 50 Гц . Период этих колебаний будет равен:

T = 1 / f = 1 / 50 = 0,02 сек.

Наибольшее значение изменяющегося переменного напряжения – тока называется амплитудным значением или амплитудой.

Umax = Ua и Imax = Ia

За один период напряжение принимает эти значения два раза: + Ua и — Ua .

♦ Если подключить в цепь переменного напряжения какую-нибудь активную нагрузку, например паяльник, в цепи потечет переменный электрический ток, так же принимающий значения +Ia и — Ia , и повторяющий форму синусоиды.
На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный. Выделение тепла не зависит от направления тока в цепи.
Выделенное тепло будет равно той энергии, которую затрачивает электрический ток при прохождении по сопротивлению нагрузки.
Введено понятие действующего значения переменного напряжения Uд и тока Iд.

Действующее значение переменного тока — это такое значение величины постоянного тока, который проходя по сопротивлению нагрузки за тот же промежуток времени, выделит такое же количество тепла, что и переменный ток.

♦ Переменный ток оказывает такое же тепловое действие, как и постоянный ток, если амплитуда синусоидального переменного тока превышает величину постоянного тока в 1,41 раз .
Следовательно действующее (или эффективное) значение переменного тока будет равно:

Iд = Ia / 1,41 = 0,707 Ia. – действующее значение переменного тока

Uд = Ua / 1,41 = 0,707 Ua — действующее значение переменного напряжения

На все эти теоретические размышления можно посмотреть иначе!

♦Имеем синусоиду переменного напряжения длительностью в 1 период как на рисунке 1 .
После выпрямительных диодов оно принимает вид как на рисунке 2.

Нижняя половинка синусоиды перевернута вверх, чтобы удобнее было представить процесс преобразования.

♦На рисунке приняты обозначения:

Um = Ua = 1 — амплитудное значение величины переменного напряжения. Значение Ua примем за единицу.

Из формулы приведенной выше Uд = 1 / 1,41 = 0,707 — действующее напряжение равно 0,707 от амплитудного значения Ua = 1.
Заштрихованная часть синусоиды обозначает затраченную на нагревание паяльника электрическую энергию. В промежутках между половинками синусоид ток по цепи не протекает, а следовательно и не выделяется электрическая мощность.
♦Проведем линию, обозначающую Uд = 0,707.
Она отсекает верхнюю часть половинок синусоид.
Если эти отсеченные вершинки синусоиды уложить в провалы между полупериодами, получится полностью заполненная площадь соответствующая значениям постоянного напряжения U и тока I.
Получается, что мощность синусоидального переменного тока с амплитудными значениями Ua и Ia равна мощности действующего значения Uд и Iд переменного тока и равна мощности постоянного тока со значениями U и I .
Одна и та же электрическая мощность, выраженная в трех видах.

P = Ua х Ia = Uд х Iд = U х I

♦ Электрические приборы для измерения переменного напряжения и тока отградуированы на отображение действующих значений Uд и Iд .
В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно 220 вольт .
Максимальное, амплитудное значение напряжения в сети равно:
Um = Ua = Uд х 1,41 = 220 х 1,41 = 310,2 вольт.

Процесс поэтапного преобразования переменного напряжения в пульсирующее напряжение, а затем в постоянное напряжение, наблюдается в схемах выпрямителей.

Амплитудное значение

Автор Yes.I.Am задал вопрос в разделе Техника

что такое амплитудное значение напряжения? какое амплитудное значение напряжение в сети 220в? и получил лучший ответ

Ответ от White Rabbit[гуру]
Амплитудное значение — это МАКСИМАЛЬНОЕ мгновенное напряжение переменного тока. В то время как те 220 вольт — это ДЕЙСТВУЮЩЕЕ значение, то есть напряжение ПОСТОЯННОГО тока, такого, который греет проводник так же, как наш переменный (это — официальное ОПРЕДЕЛЕНИЕ 🙂 Для синусоидального тока действующее и амплитудное значение (как легко показать интегрированием) связано через Корень из 2. Для сети 220 амплитуное значение = 220*корень (2)=311 вольт

Измерение средневыпрямленного значения переменного напряжения при значительном искажении синусоидальности сигнала — Измерения

В 7.2.2017 в 11:33, Дмитрий Борисович сказал:
Наверное только у Вас какие то «непонятки».

Вы дали пояснение, из которого я понял только то, что мне следует разъяснить «свои непонятки».

Допустим, мне принесли прибор и говорят

— этот вольтметр измеряет средневыпрямленное значение переменного напряжения.

При условиях: частота напряжения 45-55 Гц, искажение синусоидальности — до 10% погрешность средневыпрямленного значения не выше 0,5% от верхнего значения диапазона измерений. Сертификат калибровки прилагается.

Ок. купил.

Далее, инспектор от заказчика мне говорит: посмотрим, как откалиброван ваш прибор. От какого эталона прослеживается передача единицы величины и по какой методике?

Варианты

ГЭТ 89-2008 ГПСЭ единицы электрического напряжения (вольта) в диапазоне частот 10 — 3·107 Гц (ГОСТ Р 8.648-2015)

ГЭТ 182-2010 ГПСЭ единицы импульсного электрического напряжения с длительностью импульса от 4·10-11 до 1·10-5 с (ГОСТ Р 8.761-2011)

Вариант 1 подходит для вольтметров СКЗ, но для неидеальной синусоиды про вольтметр, измеряющий средневыпрямленное значение ничего сказать нельзя. В то числе то, что было заявлено выше.

Вариант 2 подходит для осциллографов и генераторов сигналов. Про «вольтметры средних значений» там ни слова, да и не должно быть. Средневыпрямленное значение напряжения, имея осциллограмму, можно рассчитать математически, справка выше была приложена. Можно даже вывести формулу погрешности (или неопределенности) и это значение также можно рассчитать. «На пальцах» все это рассчитать не получится, поэтому потребуется программное обеспечение. Далее требуется гарантия, что это программное обеспечение все считает правильно — то есть ПО должно пройти экспертизу.

Далее возникает вопрос: хорошо, с этим сигналом вольтметр справился хорошо, а с этим как будет? (вариантов сигналов с искажением даже до 10% — бесконечность). Соответственно требуется опять-таки экспертиза, что результат такого измерения (серии измерений) можно распространить на все случаи жизни. Предположим, метрологическому НИИ вполне это по силам.

Итого можем получить методику калибровки. И даже поверки, если все это утвердить в Росстандарте, в том числе поверочную схему. Это в теории. На практике — эталон мгновенных значений штука не такая уж точная — 0,1%. Получится ли из этого сделать поверку прибора класса 0,5? Скорее, да чем нет.

В общем, пока писал, разобрался, что белых пятен, можно сказать, нет, если не брать СГРОЕИ. А если потребовать поверку — ясно что делать. Но все это не так дешево как хотелось бы. Хотелось бы купить прибор в пределах 40 т.р. и больше ни о чем, кроме работы с ним, не думать.

Изменено 8 Февраля 2017 пользователем vvsalii

Средневыпрямленное значение — Большая Энциклопедия Нефти и Газа, статья, страница 4

Средневыпрямленное значение

Cтраница 4

Электронные вольтметры переменного напряжения разделяются на линейные, у которых отклонение указателя пропорционально средневыпрямленному значению напряжения, квадратичные — отклонение пропорционально ереднеквадратическому ( действующему) значению и амплитудные — отклонение пропорционально амплитудному значению. Однако нужно иметь в виду, что шкалу любого вольтметра градуируют в среднеквадратических значениях напряжения синусоидальной формы. Исключение составляют вольтметры, предназначенные для измерения импульсных напряжений, шкала которых градуируется в амплитудных значениях. [46]

Однако эти соотношения могут быть использованы и для вольтметров типа ВЗ-38, измеряющих средневыпрямленное значение напряжения. [47]

Синусоидальное напряжение, В, и — 14 bin at подается на вольтметры средневыпрямленного значения с одно — и дв хполупериодным выпрямителем, амплитудный, среднеквадратический. [48]

В приборе, построенном по схеме на рис. 9.2, б, преобразователь средневыпрямленного значения выполнен по мостовой схеме. Как положительный, так и отрицательный полупериоды тока протекают через магнитоэлектрический прибор в одном направлении, поэтому его показание равно средневыпрямленному значению измеряемого тока. [49]

Простейший преобразователь средневыпрямленного значения выполняют на основе двухполупериодных выпрямителей, применяемых для измерения средневыпрямленного значения тока. [50]

Детектор средневыпрямленного значения — это преобразователь переменного напряжения в постоянный ток, пропорциональный средневыпрямленному значению измеряемого напряжения. [51]

Преобразователь средневыпрямленного значения — устройство, преобразующее переменное напряжение в постоянный ток, пропорциональный средневыпрямленному значению напряжения. [52]

Двухполупериодная схема выпрямления ( рис. 1.3 s, г) вдвое чувствительнее однополупериодной, так как средневыпрямленное значение тока согласно (1.2) / ср. [54]

Фактически измеряемый прибором параметр напряжения определяется типом преобразователя: каков преобразователь — пиковый, квадратичный или средневыпрямленного значения, таков и фактически измеряемый параметр. Данный вольтметр измеряет только параметр, соответствующий типу преобразователя. [55]

Фактически измеряемый прибором параметр напряжения определяется типом детектора: каков детектор — пиковый, квадратичный или средневыпрямленного значения, — таков и фактически измеряемый параметр. Если в градуировочной ф-ле ( 5 — 84) коэффициент е1, то показание прибора дает непосредственно измеряемый параметр. [56]

Скорость убывания абсолютной погрешности измерений при итерациях по алгоритму (2.32) определяется выражением (2.28), полученным для преобразователя средневыпрямленных значений. Как следует из (2.33), статические погрешности измерительного тракта преобразователя корректируются. При этом идентичности характеристик АД и АДг ( рис. 2.13, а) уже не требуется, так как используется только один амплитудный детектор. [57]

В соответствии с проведенной выше классификацией вольтметры переменного напряжения разделяют на пиковые ( амплитудные), вольтметры среднеквадратических и средневыпрямленных значений. [58]

Простейшими вольтметрами средних значений являются выпрямительные вольтметры на основе пассивных ( без применения усилительных схемных элементов) преобразователей средневыпрямленных значений. [60]

Страницы: 1 2 3 4

амплитудное, среднее, среднеквадратическое и средневыпрямленное значение.

Уровень переменного напряжения можно определить по амплитудному, среднеквадратическому, среднему или средневыпрямленному значениям. Амплитуда(пиковое значение) Um-наибольшее мгновенное значение напряжения за интервал наблюдения или за период. Измеряемые на практике напряжения могут иметь различный вид, например, форму импульсов, синусоидального или несинусоидального колебаний- суммы синусоиды с постоянной составляющей и т.д. При разнополярных несимметричных кривых формы напряжения различают два амплитудных значения: положительное Um и отрицательное Um.

Среднее квадратическое значение напряжения есть корень квадратный из среднего квадрата его мгновенного значения за время измерения(за период):

Если периодический сигнал несинусоидален, то квадрат среднего квадратического значения равен сумме квадратов постоянной составляющей и средних квадратических значений гармоник :

= +++ …

Среднее значение(постоянная составляющая) напряжения равно среднему арифметическому всех мгновенных значений за период :

Средневыпрямленное напряжение определяется как среднее арифметическое абсолютных мгновенных значений за период :

Для напряжения одной полярности среднее и средневыпрямленное значения равны. Для разнополярных напряжений эти значения могут существенно отличаться. Так, для гармонического напряжения .

Чаще измеряют среднее квадратическое изменение напряжения, так как этот параметр связан с мощностью, нагревом, потерями. Однако проще измерить амплитудное или средневыпрямленное значение и произвести пересчёт с применением коэф. Амплитуды Ка и формы Кф : Ка = , Ка =.

В частности, для синусоидальной (гармонической) формы переменного напряжения : Ка = 1,41; Кф = 1,11.

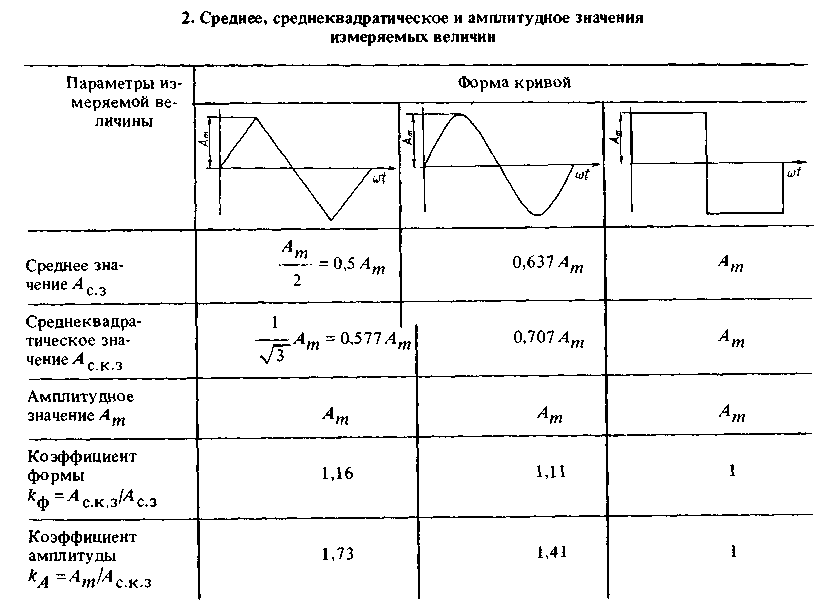
Значения этих коэффициентов для наиболее употребляемых видов сигналов и соотношения между ними даны в табл., где все напряжения для упрощения обозначены буквой .

2 Преобразователи пикового значения: с открытым и закрытым входами: схемы, принцип действия.

Преобразователи пикового значения. Особенность преобразователя этого вида заключается в том, что напряжение на его выходе непосредственно соответствует пиковому (амплитудному) значению напряжения, поданного на вход преобразователя. Он должен содержать элемент, запоминающий пиковое значение напряжения. Обычно это конденсатор, заряжаемый через диод до пикового значения.

Необходимо подчеркнуть, что преобразователи пикового значения, которые в дальнейшем для кратности будем называть пиковыми, — самые широкополосные преобразователи напряжения переменного тока в напряжение постоянного тока.

Пиковый (амплитудный) детектор — это детектор, напряжение на выходе которого непосредственно соответствует измеряемому пиковому (амплитудному) значению напряжения. Пиковый детектор должен содержать элемент, запоминающий пиковое значение напряжения. Таким элементом обычно служит конденсатор, заряжаемый через диод до пикового значения.

Пиковые детекторы

При измерении напряжений, не содержащих постоянной составляющей, детекторы с открытым и закрытым входом дают одинаковые результаты: напряжения на конденсаторах С в обоих случаях весьма близки к U_м и показания обоих вольтметров пропорциональны амплитуде измеряемого напряжения.

Если ко входу (рис. а), подводится напряжение u_х = U_о + U^′_мsinωt, в котором содержатся и постоянная и переменная составляющие, то прибор будет измерять пиковое значение U_м =U_о + U^′_м. В случае подачи пульсирующего напряжения на вход детектора с закрытым входом вольтметр измеряет пиковое значение U^′_м напряжения без постоянной составляющей.

Значения переменного напряжения (тока) — Студопедия

Далее для определенности будем говорить о параметрах напряжения, хотя они справедливы и для токов.

Мгновенное значение — значение сигнала в определённый момент времени, функцией которого является ( ).

Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой осциллограф.

Пиковое (амплитудное) значение — наибольшее мгновенное значение напряжения или силы тока за период

Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.

Среднеквадратичное значение (устар. действующее, эффективное) — корень квадратный из среднего значения квадрата сигнала.

Среднеквадратичные значения являются самыми распространёнными, т. к. они наиболее удобны для практических расчётов, когда говорят просто о напряжении или силе тока, то по умолчанию имеются в виду именно их среднеквадратичные значения. В среднеквадратичных значениях проградуированы показывающие устройства всех вольтметров и амперметров переменного тока, однако, большинство приборов дают правильные показания для этих значений только при форме тока близкой к синусоидальной, некритичны к форме сигнала только приборы с термопреобразователем, специальным квадратичным детектором или квадратичным АЦП. Квадрат среднеквадратичного значения напряжения численно равен средней мощности, рассеиваемой на сопротивлении 1Ом.

Среднее значение — постоянная составляющая напряжения или силы тока

На практике используется редко Геометрически это разность площадей под и над осью времени.

Средневыпрямленное значение — среднее значение модуля сигнала

На практике используется редко, однако большинство измерительных приборов переменного тока (те, в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям. Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.

диодов — Как найти среднее значение полупрямого выпрямленного синусоидального сигнала

Аналитическое выражение среднего значения не так уж сложно, и его трудно получить, поэтому я не уверен, почему в учебнике было приведено приближенное выражение.

Я получу точное выражение, используя кусочно-линейную модель диода, которая является более общей, чем упрощенная модель и идеальная модель. Вы можете прочитать об этих моделях / приближениях, а также об экспоненциальной модели Шокли здесь .В этой модели область блокировки / выключения / обратного смещения предназначена для \ $ v \ lt V_ \ gamma \ $, в то время как область проводимости / включения / прямого смещения предназначена для \ $ i \ gt 0 \ $; Диод математически моделируется следующими одновременными уравнениями:

\ $ v_ \ text {D} (t) = V_ \ gamma + R_ \ text {D} \, i_ \ text {D} (t) \ iff i_ \ text {D} (t) \ ge 0 \ tag * {} \

\ $ v_ \ text {D} (t) \ le V_ \ gamma \ iff i_ \ text {D} (t) = 0 \ tag * {} \ $

Для данного диода \ $ V_ \ gamma> 0 \ $ и \ $ R_ \ text {D}> 0 \ $ являются известными константами.Если реальный диод, который вы моделируете, представляет собой кремниевый диод, тогда \ $ V_ \ gamma = 0.7 \ text {V} \ $, а если это германиевый диод, то \ $ V_ \ gamma = 0.3 \ text {V} \ $.

Принципиальная схема выпрямителя:

Рисунок 1. Принципиальная схема однофазного неуправляемого выпрямителя с чисто резистивной нагрузкой и синусоидальным мгновенным входным напряжением. Источник изображения: собственный.

Выходное мгновенное напряжение:

\ $ v_ \ text {out} (t) = \ begin {cases} 0 \ text {V} & \ text {, если $ k T + \ le t \ le k T + t_1 $} \\ \ dfrac { R} {R + R_ \ text {D}} (v_ \ text {in} (t) — V_ \ gamma) & \ text {, если $ k T + t_1 \ le t \ le k T + t_2 $} \ \ 0 \ text {V} & \ text {, если $ k T + t_2 \ le t \ le k T + T $} \ end {cases} \ tag 1 \ $

, где \ $ k \ $ — любое целое число, и:

\ $ v_ \ text {in} (t) = V_ \ text {m} \ sin {(\ omega t)}, \ tag 2 \ $

\ $ t_1 = \ dfrac {\ sin ^ {- 1} {(V_ \ gamma / V_ \ text {m})}} {\ omega}, \ tag 3 \ $

\ $ t_2 = \ dfrac {\ pi — \ sin ^ {- 1} {(V_ \ gamma / V_ \ text {m})}} {\ omega}, \ tag 4 \ $

\ $ T = \ dfrac {2 \ pi} {\ omega}, \ tag 5 \ $

с известными константами \ $ \ omega \ $ и \ $ V_ \ text {m}> V_ \ gamma \ $. 2} — V_ \ gamma \ dfrac { \ pi} {2} \ right) \\ & = \ dfrac {1} {\ pi} V_ \ text {m} — \ dfrac {\ pi} {2} \ dfrac {1} {\ pi} V_ \ gamma \ tag * {} \ end {align} \

долл. США

\ $ \ implies \ boxed {V_ \ text {out, avg} \ приблизительно \ dfrac {V_ \ text {m}} {\ pi} — \ dfrac {V_ \ gamma} {2} \ quad \ text {, упрощенный модель с $ V_ \ gamma \ ll V_ \ text {m} $}} \ tag {13} \ $

, формула, которую показывает ваш учебник .

Если вместо этого мы используем идеальную модель (, т.е. , мы устанавливаем \ $ R_ \ text {D} = 0 \ text {} \ Omega \ $ и \ $ V_ \ gamma = 0 \ text {V} \ $), тогда уравнения (1), (3), (4) и (10) упрощаются до:

\ $ v_ \ text {out} (t) = \ begin {cases} 0 \ text {V} & \ text {, если $ k T + \ le t \ le k T + t_1 $} \\ v_ \ text {in} (t) & \ text {, если $ k T + t_1 \ le t \ le k T + t_2 $} \\ 0 \ text {V} & \ text {, если $ k T + t_2 \ le t \ le k T + T $} \ end {ases} \ tag {14} \ $

\ $ t_1 = 0 \ text {s} \ tag {15} \ $

\ $ t_2 = \ dfrac {\ pi} {\ omega} = \ dfrac {T} {2} \ tag {16} \ $

\ $ \ boxed {V_ \ text {out, avg} = \ dfrac {V_ \ text {m}} {\ pi} \ quad \ text {, идеальная модель}} \ tag {17} \ $

В качестве числового примера ниже показан график в Wolfram Mathematica с использованием кусочно-линейной модели входного мгновенного напряжения (ур.(2)), мгновенное выходное напряжение (уравнение (1)), среднее выходное напряжение (уравнение (12)) и среднеквадратичное выходное напряжение (полученное , здесь ), из \ $ t = 0 \ text {s} \ $ в \ $ t = 2T \ $, где \ $ V_ \ text {m} = 4 \ text {V} \ $, \ $ \ omega = 2 \ pi \ text {rad / s} \ $, \ $ R = 10 \ text {} \ Omega \ $, \ $ V_ \ gamma = 0.7 \ text {V} \ $ и \ $ R_ \ text {D} = 0.1 \ text {} \ Omega \ $.

Рис. 2. Осциллограммы мгновенного входного напряжения, мгновенного выходного напряжения, среднего выходного напряжения и среднеквадратичного выходного напряжения однофазного неуправляемого выпрямителя с синусоидальным входным мгновенным напряжением и чисто резистивной нагрузкой.Источник изображения: собственный.

Ниже мы сравниваем ур. (12) (упрощенная модель) и ур. (13) (упрощенная модель с \ $ V_ \ gamma \ ll V_ \ text {m} \ $), от \ $ V_ \ text {m} = V_ \ gamma \ $ до \ $ V_ \ text {m} = 480 \ sqrt {2} \ text {V} \ $, где \ $ V_ \ gamma = 0.7 \ text {V} \ $; Соблюдайте погрешность крайне мала:

Рис. 3. Осциллограммы среднего выходного напряжения с использованием упрощенной модели и среднего выходного напряжения с использованием упрощенной модели с \ $ V_ \ gamma \ ll V_ \ text {m} \ $. Источник изображения: собственный.

Пиковое значение, среднее значение и среднеквадратичное значение напряжения

Термин «среднеквадратичное значение» означает «среднеквадратическое значение», также называемое эквивалентом переменного тока и постоянного напряжения.

Термин «среднеквадратичное значение» означает «среднеквадратическое значение», также называемое эффективным или тепловым значением переменного тока, эквивалентно напряжению постоянного тока, которое будет обеспечивать такое же количество тепловыделения в резисторе, как и напряжение переменного тока. если применяется к тому же резистору.

RMS не является «средним» напряжением, и его математическое отношение к пиковому напряжению зависит от типа формы сигнала. Среднеквадратичное значение — это квадратный корень из среднего (среднего) значения функции квадрата мгновенных значений.

Поскольку напряжение переменного тока повышается и понижается со временем, для получения заданного среднеквадратичного напряжения требуется большее напряжение переменного тока, чем для постоянного тока. Например, для достижения среднеквадратичного значения 120 вольт (0,707 x169) потребуется пиковое значение переменного тока 169 вольт.

В этом примере величина нагрева напряжения 169 переменного тока эквивалентна значению нагрева источника постоянного тока на 120 вольт.Большинство мультиметров, будь то вольтметры или амперметры, измеряют среднеквадратичное значение, принимая чисто синусоидальную форму волны.

Важные термины, которые следует запомнить

Пиковое напряжение (Vp)

Максимальное мгновенное значение функции, измеренное от нулевого напряжения. Для формы волны, показанной выше, пиковая амплитуда и пиковое значение одинаковы, поскольку среднее значение функции равно нулю вольт.

Пиковое напряжение (В пик-пик)

Полное напряжение между положительным и отрицательным пиками формы волны; то есть сумма величин положительного и отрицательного пиков.

RMS напряжение (Vrms)

Среднеквадратичное или эффективное значение сигнала.

Среднее напряжение (Vavg)

Уровень формы волны, определяемый условием, что площадь, ограниченная кривой выше этого уровня, в точности равна площади, ограниченной кривой ниже этого уровня.

Важные уравнения, которые следует запомнить

Vp x 0,707 = Vrms
Vrms = 1,11 x Vavg
1.414 x Vrms = Vp
Vavg = 0,637 x Vp

Дополнительная литература / Источники

NTE Electronics NTE5301 Кремниевый мостовой выпрямитель, двухполупериодный, однофазный, средний выпрямленный выходной ток 8 ампер, пиковое повторяющееся обратное напряжение 600 В: автомобильные генераторы-выпрямители: Amazon.com: Industrial & Scientific

Депозит без импортных сборов и 15 долларов США.10 Доставка в РФ Подробности Доступно по более низкой цене у других продавцов, которые могут не предлагать бесплатную доставку Prime.
Убедитесь, что это подходит введя номер вашей модели.
Низкое прямое падение напряжения
Возможность высокого тока
Высокая надежность
Устойчивость к высоким импульсным токам
Идеально подходит для печатных плат
]]>
Характеристики
Фирменное наименование NTE Electronics
Цвет Один цвет
Ean 0768249549918
Глобальный торговый идентификационный номер 00768249549918
Вес изделия 4.5 унций
Номер модели NTE5301
Номинальный ток 8 ампер
Количество позиций 1
Номер детали NTE5301
Размер Один размер
Диапазон температур -55-150 градусов Цельсия
Код UNSPSC 32120000
UPC 768249549918
Напряжение 600 вольт
Среднеквадратичное значение, среднее значение, пиковое значение, пик-фактор, форм-фактор в AC
Что такое среднеквадратичное значение, пиковое значение, среднее значение, значение экземпляра, форм-фактор, пик-фактор и другие термины, относящиеся к цепям переменного тока и синусоиде?
Токи постоянного и переменного тока
Известно, что полярность постоянного напряжения и направление постоянного тока всегда одинаковы i.е. это однонаправленное значение, которое не меняет полярность, а также направление, как показано на рис. 1.
С другой стороны, (AC) переменный ток или напряжение — это тот, который регулярно меняет свое направление, а также свое значение. Другими словами, переменный ток (AC) — это тип тока, который течет сначала в одном направлении, а во-вторых, он течет в противоположном направлении. В каждом цикле он меняет значение от нуля до максимального и снова достигает нулевого значения.
Значение переменного тока или напряжения может быть выражено в переменном токе (синусоидальном) Синусоидальная волна, как показано на рис. (1) ниже.
Рис. 1 Разница между переменным током и постоянным током
В переменном токе невозможно представить величины, поскольку его амплитуда синусоидальной волны переменного тока непрерывно изменяется со временем.
Таким образом, у нас есть несколько вариантов выражения амплитуды и различных значений, связанных с синусоидальной волной переменного тока, например:
RMS Value
Average Value
Мгновенное значение
Maximum or Peak Value
Peak to Peak Value
Пик-фактор
Форм-фактор
Прочие связанные термины
Мы подробно обсудим их все ниже.
Что такое среднеквадратичное значение?
Значение RMS ( среднеквадратическое значение ) (также известное как эффективное значение или виртуальное значение ) переменного тока (AC) — это значение постоянного тока (DC) при протекании через цепь или резистор в течение определенного периода времени и производит такое же количество тепла, которое вырабатывается переменным током (AC) при протекании через ту же цепь или резистор в течение определенного времени.
Значение переменного тока, которое при прохождении через нагревательный элемент (например, резистор) будет выделять такое же количество тепла, как и постоянный ток через элемент, называется значением R.M.S.
Короче говоря,
Среднеквадратичное значение переменного тока состоит в том, что по сравнению с постоянным током и переменный, и постоянный ток выделяют одинаковое количество тепла при прохождении через одну и ту же цепь в течение определенного периода времени.
Для синусоидальной волны
или
I _RMS = 0.707 x I _M, E _RMS = 0,707 E _M
Фактически, RMS-значение синусоидальной волны является мерой теплового эффекта синусоидальной волны. Например, когда резистор подключен к источнику переменного напряжения, он выделяет определенное количество тепла (рис. 2-а). Когда тот же резистор подключен к источнику постоянного напряжения, как показано на (рис. 2 — b). Регулируя значение постоянного напряжения, чтобы получить такое же количество тепла, которое ранее выделялось в источнике переменного напряжения на рис.Это означает, что среднеквадратичное значение синусоидальной волны равно источнику постоянного напряжения, производящему такое же количество тепла, выделяемого источником переменного напряжения.
Рис. 2 — Среднеквадратичные значения тока и напряжения
Проще говоря, уровень внутреннего напряжения в США составляет 110 В, а в Великобритании — 220 В переменного тока. Этот уровень напряжения показывает эффективное значение (110 В или 220 В R.M.S) и показывает, что домашняя розетка способна обеспечить такое же количество средней положительной мощности, что и напряжение 110 В или 220 В постоянного тока.
Имейте в виду, что амперметры и вольтметры, подключенные к цепям переменного тока, всегда показывают среднеквадратичные значения (тока и напряжения).
Для синусоидального сигнала переменного тока среднеквадратичные значения тока и напряжения:
I _RMS = 0,707 x I _M, В _RMS = 0,707 В _M
Чтобы найти среднеквадратичное значение синусоидальной волны, мы можем использовать следующие два метода.
Метод средней ординаты
Метод интегрирования.
Давайте посмотрим, как найти значения R.M.S синусоидальной волны.
Методы определения среднеквадратичного значения синусоидальной волны.
Аналитический метод
Метод 1
Мы знаем, что значение синусоидального переменного тока (AC) =
I _m Sin ω θ = I _m Sin θ
Среднее квадратическое значение мгновенных значений тока за половину или полный цикл составляет:
Квадратный корень из этого значения:
Следовательно, среднеквадратичное значение тока равно (если положить I = I _м Sin θ):
Теперь,
Следовательно, мы можем обнаружить, что для симметричного синусоидального тока:
I _RMS = максимальное значение тока x 0.707
Метод 2.
Пусть i = Sin ω θ = I _м Sin θ
Среднее значение i ₂
Метод 3 Sin
Пусть i = θ = I _м Sin θ
Графический или среднеординатный метод
Этот метод известен как средний ординатный или графический метод определения значения среднеквадратичного напряжения по средним ординатам или нахождения мгновенного значения Форма волны переменного тока.Для ясного понимания ниже пояснения приведен решенный пример.
В синусоидальной волне переменного тока существует множество мгновенных напряжений, и это зависит от временного интервала. Как показано на рисунке 3 ниже, где число средних ординат равно 12 (чем больше средних ординат, тем точнее будет результат). Он показывает при t = 1, t = 2, t = 3…. tn, мгновенные уровни напряжения равны V ₁, V ₂, V ₃…. V _n соответственно.
Рис. 3 — Среднеординатный или графический метод для RMS
Во-первых, мы найдем мгновенные значения напряжений для каждого периода времени, например t = 1, t = 2… t = n и т. Д.Чтобы найти значение RMS, нам нужно будет найти квадратные значения каждого уровня напряжения в форме волны переменного тока, которая показывает квадратную часть значения RMS.
V ₁ ² + V ₂ ² + V ₃ ² +… .. V _n ²
Теперь квадратные значения напряжений делятся на количество средних ординат, которое показывает среднее значение среднеквадратичного напряжения.
Например,
Число ординат, использованных на рис. 3 выше, = 12
Предположим, что пиковое значение напряжения (Max Voltage i.е. амплитуда = V _PK или V _Max) составляет 12 В для переменного сигнала. Форма волны разделена на 12 средних ординат, как показано ниже:
, рассчитанное как напряжение 9286000 :
Таким образом, значение RMS напряжения равно 6.97 В, используя графический метод или метод средней оси ординат, чтобы найти среднеквадратичное значение напряжения.
Уравнения среднеквадратичного напряжения и тока
Среднеквадратичные значения тока и напряжения, связанные с пиковым значением или максимальным значением (оба одинаковы).
V _RMS = 0,707 x V _PK, I _RMS = 0,707 x I _PK
V _RMS = 0,707 x V _{M _RMS = 0,707 x V _{M = 0.707 x I _M}}
Действующие значения тока и напряжения, относящиеся к размаху .
В _RMS = 0,3536 x V _P-P, I _RMS = 0,3536 x I _P-P
Действующие значения тока и напряжения относительно среднего значения.
V _RMS = 1,11 x V _AV, I _RMS = 1,11 x I _AV
Здесь все на одном изображении.
Формулы среднеквадратичного значения напряжения для различных форм волны
В приведенной ниже таблице формулы среднеквадратичного значения напряжения показаны для различных типов синусоидальных форм волны.
Напряжение 2 В 4 В 6 В 8 В 10 В 12 В 10 В 9020 5 9020 6 9020 6 9020 6 9020 6 4V 2V 0V
Угол 15 ^o 30 ^o 45 ^o 60 ^o 9049 9049 9049 9020 105 ^o 120 ^o 135 ^o 150 ^o 165 ^o 180 ^o
выпрямленная полуволна _PK / √2 3
Тип сигнала Формула для среднеквадратичного значения (В _RMS)
Синусоидальная волна В _PK / √2
Двухполупериодная выпрямленная синусоидальная волна В _PK / √2
Прямоугольная волна В _PK
PK Треугольная форма волны 9035 √
Пилообразная форма волны В _PK / √3
Калькулятор среднеквадратичного напряжения
В калькуляторе среднеквадратичного значения напряжения вы можете рассчитать значение среднеквадратичного напряжения из различных связанных значений, таких как Среднее значение, Пик Значение и максимальное значение.
Что такое среднее значение
Если мы преобразуем синусоидальную волну переменного тока в синусоидальную волну постоянного тока (DC) через выпрямители, то преобразованное значение в постоянный ток будет известно как среднее значение этой синусоиды переменного тока. волна.
Рис. 4 — Среднее значение напряжения
Если максимальное значение переменного тока равно «I _MAX», то значение преобразованного постоянного тока через выпрямитель будет «0,637 I _M», которое известно как среднее значение Синусоидальная волна переменного тока (I _AV).
Среднее значение тока = I _AV = 0,637 I _M
Среднее значение напряжения = E _AV = 0,637 E _M
Среднее значение (также известное как Среднее значение) переменного тока (AC) выражается тем постоянным током (DC), который передает по любой цепи такое же количество заряда, какое передается этим переменным током (AC) в течение того же времени.
Имейте в виду, что среднее или среднее значение полной синусоидальной волны равно «нулю», значение тока в первой половине (положительное) равно следующему полупериоду (отрицательное) в противоположном направлении.Другими словами, в положительном и отрицательном полупериоде присутствует одинаковое количество тока, который течет в противоположном направлении, поэтому среднее значение для полной синусоидальной волны будет «0». По этой причине мы не используем среднее значение для покрытия и зарядки аккумулятора. Если волна переменного тока преобразуется в постоянный ток через выпрямитель, ее можно использовать для электрохимических работ.
Рис. 5 — Среднее значение тока
Короче говоря, среднее значение синусоидальной волны, взятой за полный цикл, всегда равно нулю, потому что положительные значения (выше точки пересечения нуля) смещают или нейтрализуют отрицательные значения (ниже точки пересечения нуля.)
Связанный пост: Соединение звездой (Y): трехфазная мощность, значения напряжения и тока
Методы определения среднего значения синусоидальной волны.
Среднеординатный или графический метод
В этом методе полупериод синусоидальной волны делится на равное количество периодов времени, причем продолжительность каждого периода времени равна «t / n».
Предположим, что средние значения мгновенных токов в каждом временном интервале равны I ₂, 1 ₂, I ₃… I _n.Чтобы найти среднее значение для каждого временного интервала, левая и правая вертикальные линии складываются и делятся на два. То же самое применимо ко всем временным интервалам, чтобы найти среднее значение для каждого экземпляра.
Теперь все средние значения складываются и делятся на числовые средние ординаты (то есть периоды времени), которые показывают общее среднее значение полупериода синусоидальной волны. формула для среднего значения показана ниже:
Пример:
Рис. Текущий i.е. амплитуда = I _PK или I _Max) составляет 12 А для переменного сигнала. Форма волны разделена на 12 средних ординат, как показано ниже:
9020 6A 4A
Ток 2A 4A 6A 8A 10A 12A 2A 0A
Угол 15 ^o 30 ^o 45 ^o 60 ^o 9049 9049 9049 9020 105 ^o 120 ^o 135 ^o 150 ^o 165 ^o 180 ^o
Текущее значение 6A, используя графический метод или метод средней ординаты, чтобы найти среднее значение тока.
Аналитический метод
Мы знаем, что стандартное уравнение переменного тока:
i = Sin ω θ = I _м Sin θ
Максимальное значение тока на синусоиде = I _м
Среднее значение тока на синусоиде = I _AV
Мгновенное значение тока на синусоиде = i
Угол, указанный для « i » после нулевого положения тока = θ
Угол полупериода = Π радиан
Угол полного круга = 2π радиан
(a) Среднее значение полного цикла:
Пусть i = Sin ω θ = I _м Sin θ
Таким образом, среднее значение синусоидальной волны за полный цикл равна нулю.
(b) Среднее значение тока за полупериод
Среднее значение тока (полупериод)
I _AV = 0,637 В _M
Аналогично среднее значение напряжения за полупериод
В _AV = 0,637 В _M
Уравнения среднего напряжения и тока
Его среднее значение среднего напряжения или тока равно умножению максимального или пикового значения напряжения и ток соответственно с постоянной 0.637.
Например, если максимальное значение или пиковое значение синусоидальной волны составляет 360 В _PK или 360 В _Макс, используя приведенное выше уравнение, среднее значение напряжения будет:
0,637 x 360 В _PK = 229,32 Av .
Формулы среднего значения и среднеквадратичного значения для различных форм волны
В приведенной ниже таблице формулы среднего значения и среднеквадратичного значения напряжения показаны для различных типов синусоидальных форм волны.
Тип сигнала Формула для среднеквадратичного напряжения Формула для среднего напряжения
Синусоидальная волна В _RMS = V = V
05 PK = 0
Полное выпрямленное напряжение В _СКЗ = В _PK / √2 В _AV = 0.637 В _PK
Половина выпрямленного сигнала В _RMS = В _PK/2 В _AV = 0,318 В _PK
Синусоидальная волна со смещением постоянного тока RMS = √ (VDC ² + V _PK ²/2) V _AV = Vdc
Половина синусоиды с длительностью T и частотой f V PK _RMS = V _{V x √ (fx T / 2)} V _AV = 2f x T x V _PK / π
Положительный прямоугольный сигнал с длительностью T и частотой f V _RMS = V _PK x √ (fx T) V _AV = fx T x V _PK
Волна зубьев пилы с длительностью T и частотой f V _RMS = V _PK x √ (fx T / 3) V _AV = fx T x V _PK/2
Трапециевидная волна e с частотой f, верхним сегментом T и базовым сегментом B. V _RMS = V _PK x √ (fx ((BT) + 3xT) / 3) V _AV = fx V _PK x ((T + B) / 2)
Что такое мгновенное значение
Значение, достигаемое переменной величиной в любой момент времени, называется мгновенным значением. Обозначается буквами «i» и e.
другими словами, значение переменного тока или напряжения в любой конкретный момент мы называем мгновенным значением.
На рис. 7 ниже показаны различные мгновенные значения напряжений или токов в определенный момент и период времени.Значения мгновенного тока или напряжения равны «+» в положительном цикле и «-» в отрицательном цикле в синусоидальной волне. Кривые показывают значения различных мгновенных напряжений, в то время как такая же кривая может быть построена и для тока. На рис. 7 значения мгновенных напряжений составляют 2,5 В при 1 мкс, 5,1 В при 2 мкс, 8,9 В при 3 мкс. В то время как это -2,3 В при 4 мкс, -6,1 В при 5 мкс и -9,2 В при 6 мкс.
Рис. 7 — Мгновенное значение напряжения
Что такое пиковое напряжение или максимальное значение напряжения?
Пиковое значение также известно как Максимальное значение , Пиковое значение или Амплитуда .Это максимальное значение переменного тока или напряжения из положения «0» независимо от положительного или отрицательного полупериода в синусоидальной волне, как показано на рис. 8. Оно выражается как I _M и E _M или В _P и I _M.
Уравнения для значения пикового напряжения :
В _P = √2 x V _RMS = 1,414 В _RMS
V _P = V _PP/2 = 0.5 В _PP
В _P = π / 2 x V _AV = 1,571 x V _AV
Другими словами, это значение напряжения или тока на положительном или отрицательном полюсе. максимум (пики) относительно нуля. Проще говоря, это мгновенное значение с максимальной интенсивностью.
Рис. 8 — Пиковые или максимальные значения напряжений
Пик до пика Значение
Сумма положительных и отрицательных пиковых значений называется размахом до пика.Выражается как I _PP или V _PP.
Уравнения и формулы для Пиковое напряжение следующие:
В _PP = 2√2 x В _RMS = 2,828 x V _RMS RMS V _PP = 2 x V _P
V _PP = π x V _AV = 3,141 x V _AV
Другими словами, от пика до пика значение синусоидальной волны — это напряжение или ток от положительного пика до отрицательного пика, и его значение в два раза больше по сравнению с пиковым значением или максимальным значением, как показано на рис. 8 выше.
Что такое пик-фактор
Пик-фактор также известен как пик-фактор или коэффициент амплитуды.
Это соотношение между максимальным значением и среднеквадратичным значением переменной волны.
Для синусоидального переменного напряжения:
Для синусоидального переменного тока:
Что такое форм-фактор
Отношение между среднеквадратичным значением и средним значением переменной величины (тока или напряжения) равно известный как форм-фактор.
В приведенной ниже таблице формулы и значения форм-фактора показаны для различных типов синусоидальных форм волны.
Другие термины, относящиеся к цепям переменного тока
Форма волны
Путь, отслеживаемый величиной (например, напряжением или током), нанесенной на график как функция некоторой переменной (такой как время, градус, радианы, температура и т. Д.)) называется формой волны.
Цикл
Один полный набор положительных и отрицательных значений переменного качества (таких как напряжение и ток) известен как цикл.
Часть сигнала, содержащаяся в одном периоде времени, называется циклом.
Расстояние между двумя одинаковыми точками, связанное со значением и направлением, называется циклом.
Цикл — это полное чередование.
Период
Время, необходимое переменной величине (например, току или напряжению) для завершения одного цикла, называется ее периодом времени «T».
Он обратно пропорционален частоте « f » и обозначается буквой «T», где единицей периода времени является секунда.
Математически;
T = 1/ f
Частота
Частота — это число, если количество циклов проходит за секунду. Он обозначается буквой «f» и имеет единицу цикла в секунду, то есть Гц (Герты).
Число завершенных циклов за 1 секунду называется частотой.
Это количество циклов переменного количества в секунду в герцах.
Частота — это количество циклов, которые синусоидальная волна завершается за одну секунду, или количество циклов, которые происходят за одну секунду.
f = 1 / T
Амплитуда
Максимальное положительное или отрицательное значение переменной величины, такой как напряжение или ток, называется ее амплитудой. Обозначается V _P, I _P или E _MAX и I _MAX.
Чередование
Один полупериод синусоидального сигнала (отрицательного или положительного) известен как чередование, диапазон которого составляет 180 °.
Рис. 9 — Различные термины, используемые в цепях переменного тока и синусоиде
Связанные сообщения:
Среднее выпрямленное значение
Среднее арифметическое изменение размера равно нулю и поэтому не подходит для характеристики переменной величины. Самый простой с метрологической точки зрения способ получить количественное заключение об изменении, величина которого является исправленным значением. Этот термин, используемый в электротехнике, является средним величиной этого размера (англ. Average rectified value (ARV)).
Предпочтительно применяется выпрямленное значение переменного тока или переменного напряжения.
4,1 Для размера пазухи
4,2 Для отвода синусоидального напряжения
4,3 Для импульсного напряжения
4.4 Для переменной составляющей импульсного напряжения
Вступление
Выпрямленное значение переменного тока указывает на то, что такое же количество заряда постоянного тока, переносимое как усредненное по времени, является выпрямленным переменным током.
Математическое определение:
Форма сигнала не может быть легко описана математически, можно применить следующее для расчета метода аппроксимации стандартного значения
При этом выборочные и мгновенные значения, которые считываются с более равным интервалом в течение периода сигнала. это
Порядок — только сумма и форма — не подлежат обмену местами. Следовательно, они должны быть подключены к обозначениям (см. Выше), чтобы быть узнаваемыми.Следует избегать написания (неправильный порядок) и | | (порядок неясен).
Для наиболее распространенного случая синусоидального переменного количества выпрямленное значение составляет (2 / π), умноженное на максимальное значение (пиковое значение).
Применение в метрологии
Индикация того, что измерительные приборы работают так медленно, что вы можете прочитать измеренные значения. С быстрыми изменениями, которые не могут быть обнаружены человеческим глазом, они показывают средний размер, например, электромеханически усредненный с движением движущейся катушки, усредненный электронным способом с помощью метода двойного наклона, см. Также Цифровые технологии измерения.Среднее значение переменной величины равно нулю, но (согласно определению обменной величины см.). Самый простой способ измерить размер — измерить их прямую ориентировочную ценность. Более сложный способ — измерить его эффективное значение. Физически это эквивалент постоянного тока с учетом активной мощности типоразмера. В искусстве эффективная ценность намного важнее; Измерительные приборы изменения размеров предназначены для обеспечения отображения этого значения.
Тем не менее, исправленные значения визуальных инструментов широко используются.Но показать не выпрямленное значение, а его 1,11-кратное. Это синусоидальная кривая, среднеквадратичное значение, см. Ниже в разделе «Сравнение». Это позволяет устройствам отображать среднеквадратичное значение — благодаря обнаружению значения прямого наведения. Разумно и правильно — это единственная синусоидальная форма для хода, которая возникает, однако, во многих размерах меняет измерительные задачи. Однако для любой другой формы сигнала использование таких устройств сомнительно или бессмысленно, см. Ниже в разделе «Последствия».
Также сомнительно бессмысленно измерение сигнала переменного тока, сигнал накладывается на сигнал постоянного тока, см. Ниже в разделе «смешанное напряжение».Следовательно, его обнаруживает часть измерительных приборов, только переменная составляющая.
Вывод
Среднее значение находится на временной диаграмме сигнала, определяемой из области, которая простирается по высоте между сигнальной линией и нейтральной линией, а по ширине составляет примерно длину полного периода. Прямоугольник, имеющий такую же площадь и одинаковую ширину, среднюю высоту поверхности; эта высота средняя. Площадь определяется интегрированием, прямоугольник — умножением.
Соответственно, выпрямленное значение получается из области выпрямленного сигнала; это означает
Отсюда формула
Результат для размера синуса
Синусоидальная переменная величина, короткий размер синуса, удовлетворяет уравнению
Поскольку поверхность должна формироваться в течение всего периода функции, это не зависит от начальной точки во времени поверхности. Нулевой фазовый угол не нужно учитывать; Его планируется упростить до 0.
Как показано на рисунке, выпрямленный сигнал периодически появляется, так что вместо него можно выполнить счет.
In, чтобы можно было опустить знак суммы.
С
Упростив до
Результат для стравливающего синусоидального напряжения
Часто возникающее из-за угла сдвига фаз, показанное на рисунке слева, по существу является синусоидальным напряжением, но после каждого перехода через ноль остается равным нулю, и только один раз, а затем синусоидальная волна включается снова.Для этого напряжения результаты
При 0 ≤ a
Результат для импульсного напряжения
Напряжение, показанное на рисунке выше u, представляет собой смешанное напряжение; он возникает из-за периодически в течение продолжительности aT выключения и выключения в течение оставшегося периода положительного напряжения постоянного тока U. Поскольку здесь нет отрицательных мгновенных значений, средние выпрямленные значения и имеют одинаковую величину;
0 ≤ a ≤ 1, граничные случаи a = 0 и a = 1, питание никогда не включается и постоянное напряжение.
Постоянная составляющая смешанного напряжения, которая накладывается на переменную составляющую.
Результат для переменного компонента
Переменная составляющая импульсного напряжения показана на рисунке внизу слева. Здесь снова среднее значение = 0
Выпрямление получается по кривой, показанной ниже; выпрямленное значение получается из среднего значения. Поверхность на протяжении одного периода состоит из двух прямоугольников, каждый из которых имеет размер.Это
Результат для смешанного напряжения
Для смешанного напряжения следует различать два случая.
1 На сопроводительном рисунке слева постоянная составляющая (по абсолютной величине) больше пикового значения переменного тока. Кривая не пересекает нулевую линию. В этом случае выпрямленное значение равно величине постоянной составляющей. В обсуждение альтернативный компонент не входит.
2 На рисунке справа составляющая постоянного тока (по абсолютной величине) меньше пикового значения составляющей переменного тока.Кривая пересекает нулевую линию. В этом случае определение прямого ориентировочного значения не имеет смысла; он не содержит указаний на компоненты постоянного тока и переменного тока, а также на их соотношение.
Сравнение со среднеквадратичным выпрямленным значением
Отношение среднеквадратичного значения к выпрямленному значению называется форм-фактором.
Это позволяет судить по форме волны переменного или смешанного размера. Он ≥ 1 и больше, конечно «странный».
Для размера синуса
Для стравливающего синусоидального напряжения
Для импульсного напряжения
Предельный случай a = 0 дает V = 0 и исключается из сравнения.
Для переменной составляющей импульсного напряжения
Предельные случаи a = 0 и a = 1 не содержат знакопеременной составляющей и исключаются.
Метрологические последствия
Прибор для формирования выпрямленных значений может привести к значительной погрешности измерения, поскольку он масштабируется и регулируется так, чтобы отображаемое значение было действующим значением.
При использовании этих устройств рекомендуется соблюдать осторожность. Относительная погрешность формы сигнала может легко превышать диапазон «несколько процентов». Синусоидальная форма все еще чаще всего встречается в напряжении в электросети; есть область действия этих устройств. Но даже сетевое напряжение искажается множеством электронных нелинейных нагрузок. Тем более, потребление мощности от сети часто искажается настолько, что при измерении прямого ориентировочного значения невозможно сделать разумный вывод о силе тока.
Документы
Электрические измерения
Электромагнитная теория
Цепи пиковых значений, среднеквадратичных значений и усреднения
AN012 — Цепи пиковых значений, среднеквадратичных значений и усреднения
Тип сигнала Формула для форм-фактора Значение
Синусоидальная волна π / 2√2 полуволна, выпрямленная 90π / 2 1,5707963
Двухполупериодная выпрямленная синусоида π / 2√2 1.11072073
Прямоугольная волна 1 1
Треугольная форма волны 2 / √3 1,15470054

Elliott Sound Products АН-012
Род Эллиотт (ESP)
Основной индекс Прил. Примечания Индекс
Измерение напряжения переменного тока
Существует бесчисленное множество причин для измерения напряжения переменного тока, и во многих случаях тип используемого измерения может иметь решающее значение.За некоторыми исключениями, постоянный ток из переменного тока формы сигнала удаляется с помощью конденсатора, а затем напряжение выпрямляется. Для большинства измерительных систем это будет выполняться с использованием одной из схем полноволнового прецизионного выпрямителя, описанных в AN-001. Эта часть процесса имеет решающее значение, и тип используемой схемы определяется требуемой точностью, частотой сигнала и уровнем.
Даже самый лучший прецизионный выпрямитель даст плохие результаты, если уровень сигнала слишком низкий, поэтому часто требуется предусилитель.Высокие частоты (выше 1 МГц) создают дополнительные проблемы, которые здесь не рассматриваются. Я сконцентрируюсь на системах, которые работают на обычных звуковых частотах, включая частоты сети (50 и 60 Гц). Охватываемый диапазон часто может быть очень ограничен, особенно когда система разработана специально для работы в сети и других частотах ниже 1 кГц или около того.
Когда сигнал должен быть оцифрован, есть два варианта. Сигнал можно подавать непосредственно на АЦП (аналого-цифровой преобразователь) без выпрямления, а все вычисления выполняются в цифровом виде.Входящий сигнал должен быть сдвинут по уровню (обычно так, чтобы ноль был представлен 2,50 В постоянного тока), а частота цифровой дискретизации должна быть абсолютным минимумом или удвоенной максимальной частотой, представляющей интерес. Например, для частот до 20 кГц требуется минимальная частота дискретизации 40 кГц, и, как мы знаем, общий стандарт — 44,1 кГц, используемый для звука качества компакт-диска.
Второй вариант — оставаться в аналоговой области, и сигнал может быть отображен движением измерителя с подвижной катушкой или оцифрован с использованием низкочастотного АЦП, который используется в большинстве мультиметров.В некоторых случаях выпрямленный переменный ток не используется для управления какой-либо формой измерения, но может использоваться для обеспечения автоматической регулировки усиления (AGC), сжатия, ограничения или других функций в системе обработки звука.
Схемы, описанные ниже, предполагают второй вариант. У входящего переменного тока будет удалена любая составляющая постоянного тока с помощью разделительного конденсатора, и он будет выпрямляться с помощью прецизионного выпрямителя. Затем импульсный выходной сигнал постоянного тока выпрямителя обрабатывается для получения требуемого типа измерения — пикового, среднеквадратичного или среднего.Результат может сильно различаться в зависимости от используемого метода, и некоторые результаты могут быть неожиданными.

Рисунок 1 — Прецизионный полноволновой выпрямитель
Для единообразия я возьму выпрямитель, показанный выше. Это взято из AN-001, рис. 6, и было выбрано, потому что это простая схема, которая хорошо работает. Можно использовать любые другие схемы, но для обнаружения пиков всем им требуется полуволновой выпрямитель после основного выпрямителя, потому что конденсатор должен заряжаться через схему, которая не разряжает его снова.
В некоторых случаях можно обойтись очень упрощенными схемами, но все зависит от приложения и ожидаемой степени точности. В некоторых случаях (например, при обработке звука) точность не требуется, и нелинейное поведение может быть преимуществом, а не ограничением.
Важно понимать, что все методы измерения могут приводить к ошибкам, и что не существует единого метода обнаружения, подходящего для всех форм сигналов. Более подробно ошибки и ограничения обсуждаются в выводах в конце этой статьи.
Пиковое значение
Получить пиковое значение формы волны довольно просто, если не требуется особая точность, и это одно из самых распространенных значений, особенно для схем обработки звука. Например, ограничитель звуковых пиков по определению должен применять ограничение на основе пикового значения формы волны. Большинство компрессоров / лимитеров работают на этой основе, но некоторые могут также использовать среднее значение, а небольшое количество использует преобразователи RMS для получения управляющего напряжения.
Эта статья не посвящена аудиокомпрессорам или лимитерам, поэтому, если вы хотите получить больше информации по этой теме, вам придется просмотреть различные проекты ESP (см. Список проектов ESP и выполните поиск по запросу «limiter»).Конечно, в сети есть много других схем, и вы увидите множество вариаций.
Во многих случаях при выпрямлении переменного напряжения может использоваться пиковое напряжение, поскольку это самый быстрый метод измерения. Если входной сигнал является синусоидальным, при желании измеритель может быть откалиброван по среднеквадратичному значению. В этих условиях измеритель просто откалиброван так, что при входном напряжении 1 В постоянного тока измеритель будет отображать ровно 707 мВ. Это основано на квадратном корне из 2 (√2), который равен 1.414 (и 0,707 — его аналог). Большинство читателей знают, что пиковое значение синусоиды 1 В составляет 1,414 В, но могут не знать об ограничениях этого метода измерения.
Все, что требуется в некоторых случаях, — это конденсатор, но это зависит от используемой схемы прецизионного выпрямителя. Большинству двухполупериодных выпрямителей требуется выходной диод (нормально, если точность не требуется) или прецизионный полуволновой выпрямитель, как показано ниже. Дополнительный диод / полуволновой выпрямитель необходим, чтобы конденсатор не разряжался обратно через выходной операционный усилитель выпрямителя.Очень упрощенная версия показана на рисунке 2, и ее можно использовать, например, для схемы ограничителя пиков. Однако это не полезно для точных измерений. Если R4 не включен, необходимы некоторые средства для разряда C1, иначе он будет сохранять напряжение неопределенно долго, но с учетом дрейфа из-за утечки диодов и конденсаторов.

Рисунок 2 — Упрощенный детектор пиковых показаний
Самый простой полуволновой пиковый детектор использует не что иное, как диод, пару резисторов и конденсатор.Двухполупериодный вариант этого показан выше, но поскольку диоды не входят в контур обратной связи, он страдает высокой нелинейностью из-за прямого напряжения диодов. Такое расположение подходит, если вам не нужна абсолютная точность или если диапазон измеряемых напряжений ограничен. Например, если вам нужно только обнаружить напряжение от 5 В до 10 В (пиковое), ошибка, вносимая диодом, минимальна и легко компенсируется, но для прецизионной схемы этого недостаточно.Схема является двухполупериодной, потому что есть прямой и инвертированный драйвер для диодов.
Два резистора (R4 и R5) определяют, насколько быстро конденсатор заряжается (R5) и разряжается (R4). Они подключены, как показано на рисунке, поэтому они не создают делитель напряжения, как в случае, если бы R4 был напрямую подключен к накопительной / сглаживающей крышке (C1). Время заряда (атаки) определяется соотношением значений R5 и C1. Если R5 составляет 1 кОм, а C1 — 1 мкФ, время заряда (с постоянным током и до 63.2% от максимума, или постоянная времени) составляет 1 мс, а полное напряжение (в пределах 1%) будет доступно примерно через 5 мс. Время затухания определяется соотношением последовательно соединенных C1 и R4 плюс R5. Для показанных значений достаточно близко к 1 секунде. Для входа переменного тока это зависит от частоты.

Рисунок 3 — Прецизионный детектор пиковых показаний
Когда используется настоящий прецизионный пиковый детектор, конденсатор всегда заряжается почти мгновенно, потому что он находится в контуре обратной связи операционного усилителя.Это не всегда удобно, особенно для обработки звука, когда необходимо программировать время атаки и спада. Для измерений он обеспечивает максимально быстрое считывание со стабильным напряжением, доступным всего за один цикл, но, как правило, в пределах пары циклов входной формы волны.
По ряду причин (основанных на простой реальности и физике) напряжение на C1 может быть немного ниже ожидаемого. Обычно он составляет около 0,4% при входном сигнале 100 мВ, но погрешность увеличивается с уменьшением уровня, и наоборот.Если есть какое-либо перерегулирование входного сигнала, напряжение на C1 будет на выше, чем ожидалось, на . Тщательная компоновка важна, если вам нужна точная схема.
Пиковые показания не распространены в измерительных схемах, кроме программных измерителей пиковых значений (PPM), где их использование необходимо (по определению). Обнаружение пиков — обычно неточное — гораздо более распространено в системах обработки звука. Если вы используете определение пика, как описано здесь, для обычного измерения (с калибровкой RMS), показание «RMS» будет точным только тогда, когда на входе будет синусоида.Для других сигналов будут очевидны серьезные ошибки.
Когда вам нужно контролировать амплитуду самых высоких пиков сигнала (обычно аудио, но не всегда), вам также необходимо определить время затухания. Если он слишком короткий, у вас не будет времени увидеть пики (а указатель аналогового движения не может двигаться достаточно быстро). Если время затухания слишком велико, вы не сможете увидеть другие (меньшие) пики, пока указатель не опустится до уровня новых пиков. Баллистика профессиональных ППМ зависит от используемых стандартов — существует несколько различных версий.
Среднее значение
В большинстве систем измерения чаще используется среднее значение, чем пиковое. Это происходит «автоматически», если движение счетчика с подвижной катушкой используется после прецизионного выпрямителя, потому что отклонение стрелки зависит от среднего тока. Как и в случае пикового измерения, среднеквадратичное значение для синусоиды получается просто путем масштабирования выпрямленного напряжения, и в этом случае измеритель будет настроен на показание 707 мВ при входном 637 мВ.Среднее значение синусоиды определяется …
2 × V _(пик) / π = 0,6366 (0,637) для пикового синусоидального сигнала 1 В (707 мВ RMS)
Важно понимать, что среднее значение синусоиды (как описано выше) можно использовать только после исправления. Если сигнал не исправлен, среднее значение равно нулю! Это потому, что положительное и отрицательное напряжения точно равны, поэтому они компенсируются. Для речевых или музыкальных сигналов могут быть большие расхождения между среднеквадратичным и средним значениями после исправления, но большинство аналоговых измерителей используют усреднение, потому что до сравнительно недавнего времени было трудно достичь истинного измерения среднеквадратичного значения.

Рисунок 4 — Прецизионный детектор среднего показания
Хотя на рис. 4 показаны как входные, так и выходные буферы, они могут не понадобиться в зависимости от приложения. Постоянная времени R2 и C1 должна быть выбрана для получения разумного времени усреднения в зависимости от входной частоты. Если не требуется измерять очень низкие частоты, показанные значения обычно работают хорошо. Постоянная времени составляет 1 секунду, поэтому точное напряжение невозможно получить в течение примерно 5 секунд.
Выходные данные, показанные на Рисунке 4, можно использовать для управления измерителем с подвижной катушкой (даже если движение измерителя само по себе привело бы к усреднению) или можно оцифровать для отображения на ЖК-экране или светодиодном экране. В большинстве дешевых цифровых мультиметров для получения показаний сигналов переменного тока используются схемы этого типа, а измеритель откалиброван по среднеквадратичному значению. Все, что нужно, — это обеспечить небольшое усиление, поэтому измеритель показывает 707 мВ, когда выход постоянного тока из усредняющего фильтра составляет 637 мВ (или любое кратное или кратное этим напряжениям).
Показание «RMS» является точным только тогда, когда на входе синусоида. Ошибка может быть значительной, как описано в следующем разделе.
Однако подавляющее большинство мультиметров (аналоговых и цифровых) используют метод калибровки среднеквадратичного значения среднего показания. Чтобы избежать неизбежных ошибок с несинусоидальными сигналами, вы должны использовать измеритель «истинного среднеквадратичного значения». Если вы измеряете только синусоиды (или их разумные копии), ошибки не будут значительными, и средний измеритель показаний будет идеально подходить для ваших нужд.
RMS чтение
Ранние измерители «истинного среднеквадратичного значения» были чрезвычайно дорогими, и они использовали различные средства для получения значения среднеквадратичного значения входного сигнала. В одном популярном методе использовалась термопара, измеряющая температуру чувствительного элемента, который, в свою очередь, управлялся подходящим усилителем. Среднеквадратичное значение формы волны определяется как напряжение переменного тока (любой формы волны), обеспечивающее точно такую же мощность (эффект нагрева), что и такое же напряжение постоянного тока. Итак, если вы измеряете превышение температуры резистора, питаемого от 10 В постоянного тока и 10 В среднеквадратичного переменного тока, оно будет одинаковым для обоих.Не имеет значения, был ли переменный ток синусоидальной, прямоугольной или сложной формой волны, такой как аудиосигнал, при условии, что сигнал был устойчивым во время измерения.
До появления первых микросхем, которые могли выполнять преобразование, очень немногие мастерские имели доступ к истинному вольтметру среднеквадратичного значения из-за его стоимости, и даже ранние версии на основе микросхем были намного дороже, чем среднеквадратичные калиброванные среднеквадратичные значения. версии. Они по-прежнему наиболее распространены, и следует предполагать, что все счетчики используют средние показания, если только они не , конкретно заявлено как истинное среднеквадратичное значение.
Прежде чем мы продолжим, важно понять, что именно означает «RMS». Это сокращение от «среднеквадратичного значения», где мы берем отсчеты напряжения, возводим их в квадрат, получаем среднее (среднее) значение квадратов (сумму значений, деленную на количество отсчетов) и, наконец, извлекаем квадратный корень из означает, что дает нам значение RMS. Давайте посмотрим на цикл синусоиды, чтобы увидеть, как это работает …

Рисунок 5 — Синусоида, измеренная с интервалом 30 °
Синусоидальную волну можно измерить в любом количестве точек, при этом четыре точки являются минимумом (0, 90, 180, 270 градусов), но в этом примере использовались интервалы 30 °, поскольку это упрощает понимание процесса.Для других форм волны вам нужно достаточно точек данных, чтобы получить точное представление о мгновенных напряжениях в каждой точке формы волны. Из этих измеренных напряжений (которые можно легко рассчитать для синусоидальной, треугольной или прямоугольной («квадратной») формы волны) вы можете затем вычислить истинное среднеквадратичное значение напряжения для синусоиды.
Математически напряжение — это просто синус фазового угла, умноженный на пиковое напряжение. Sin (30) равен 0,5, sin (60) равен 0,866 и т. Д. Обратите внимание, что 360 ° не включается в расчет, потому что это означает начало следующего цикла переменного тока, а не конец текущего цикла.В приведенной ниже таблице используется пиковое напряжение 1 В (0,707 В RMS).
Обычно невозможно рассчитать напряжения в соответствующих точках сложной формы волны, поэтому ее можно распечатать на миллиметровой бумаге и измерить, или сделать цифровую выборку и произвести вычисления на основе значения каждой выборки. Это метод, используемый для полностью цифровых измерительных систем. Я сомневаюсь, что в наши дни многие люди захотят использовать миллиметровую бумагу, но она определенно сработает, если у вас хватит терпения.
Измерение # Градусы Напряжение Квадрат
1 0 0 0
2 30 0.5 0,25
3 60 0,866 0,75
4 90 1 1
5 120 0,866 0,75
6 150 0,5 0,25
7 180 0 0
8 210 0,5 0.25
9 240 0,866 0,75
10 270 1 1
11 300 0,866 0,75
12 330 0,5 0,25
Сумма 6,0
Среднее, иначе Среднее (сумма / 12) 0.50
Квадратный корень среднего 0,707
Таблица 1 — Выведение среднего квадрата
Теперь, когда вы знаете точный способ вычисления RMS-значения, очевидно, что версия IC должна выполнять аналогичные функции. Следующий вопрос может быть «почему?». Люди использовали измерители средних значений, откалиброванные для отображения «RMS» в течение многих лет, так зачем возиться с настоящими преобразователями RMS. Все дело в точности и ошибках, вносимых процессом усреднения.В следующей таблице перечислены ошибки с разными формами сигналов — как вы можете видеть, в некоторых случаях они могут быть очень серьезными.
Форма волны — пик 1 В Коэффициент амплитуды
В _ПИК / В _RMS Истинное среднеквадратичное значение Измеритель среднего / среднеквадратичного значения¹ Ошибка (%)
Неискаженная синусоида 1,414 0,707 0,707 0
Симметричная прямоугольная волна 1.00 1,00 1,11 +11,0
Неискаженная треугольная волна 1,73 0,577 0,555 -3,8
Гауссов шум — 98% пиков <1 В 3 0,333 0,295 -11,4
Прямоугольный 2 0,5 0,278 -44
Последовательность импульсов 10 0.1 0,011 -89
Форма волны SCR — рабочий цикл 50% 2 0,495 0,354 -28
Форма волны SCR — рабочий цикл 25% 4,7 0,212 0,150 -30
Таблица 2 — Средняя ошибка чтения с разными формами сигналов
Считывание средней отвечающей цепи, откалиброванной по среднеквадратичному значению синусоидальной волны (В)
При измерении напряжения и тока переменного тока мы склонны предполагать, что они являются среднеквадратичными, и соответственно производить расчеты мощности.Средняя мощность (обычно — и неправильно — называемая «среднеквадратичная мощность») — это просто произведение среднеквадратичного напряжения и среднеквадратичного тока, но если форма сигнала не является синусоидальной, ошибка может означать, что полученный нами ответ может быть далеким от истины. . Измерение уровня сигнала музыки или речи ничем не отличается — высокий коэффициент амплитуды (V пик / V RMS ) всегда даст ответ, который намного ниже реального. Проблемы возникают не только из-за синусоидального сигнала, но и из-за его пик-фактора, а очень высокий пик-фактор даже может вызвать проблемы со многими ИС преобразователя среднеквадратичного значения.Пик-факторы до 5 обычно подходят для обычных ИС преобразователей среднеквадратичного значения, но превышение этого значения может вызвать внутреннюю перегрузку, и измерение все равно может иметь значительную ошибку.
AD737 — это в значительной степени законченная система на кристалле. Единственное, что вам нужно добавить, это резистор и несколько конденсаторов, а в таблице данных есть много примеров и другой информации, которые помогут вам создать работающий преобразователь среднеквадратичного значения в постоянный ток. C2 (усредняющий конденсатор, C avg ) и C3 (выходной фильтрующий колпачок) должны быть типами с малой утечкой.

Рисунок 6 — Преобразователь истинного среднеквадратичного значения в постоянный ток
Рисунок выше упрощен и показывает только основы. Обратите внимание, что выходной сигнал инвертирован, поэтому при пиковом значении 1 В (707 мВ RMS) на выходе будет -707 мВ. Выход также имеет высокий импеданс и не должен быть нагружен внешней схемой, поэтому в идеале выход должен быть подключен к выходному буферу, как показано в проекте 140. Схема проекта также включает положение для регулировки усиления и регулировки смещения постоянного тока, как из которых потребуется, если вам нужно измерить низкие напряжения (менее 10 мВ RMS).Хотя на рис. 6 показано входное пиковое значение 1 В, вход AD737 в идеале должен быть ограничен примерно 200 мВ RMS, в противном случае возможна внутренняя перегрузка с некоторыми формами сигналов.
Значения C2 и C3 являются компромиссом, и C2 (C avg ), в частности, определяет время установления. При низком входном напряжении (скажем) 1 мВ) цепи потребуется примерно 30 секунд для стабилизации, а при входном 200 мВ она упадет примерно до 150 мс. Если для C avg используется меньшее значение, время установления уменьшается, но ошибка низкой частоты увеличивается с увеличением коэффициента амплитуды.Показанные значения (100 мкФ для каждого) были определены после долгих экспериментов с IC и в целом дают хорошие результаты.
Заключение
Здесь показаны три основных метода измерения, и какой из них лучше всего подходит для данной задачи, зависит от вашего приложения. Для точных измерений мощности почти всегда предпочтительным является истинное среднеквадратичное значение, но если вы работаете только с синусоидальными волнами, то вам подойдет измеритель среднего показания (с калибровкой среднеквадратичного значения). Для измерения сложных сигналов, таких как речь, музыка, полное гармоническое искажение (THD) и т.п., вам действительно нужно истинное среднеквадратичное значение (хотя, к сожалению, большинство измерителей искажений имеют средний отклик).
Для обработки звука (компрессоры, лимитеры и т. Д.) Обнаружение пиков является наиболее распространенным, хотя некоторые компрессоры также включают в себя схему среднего отклика. Иногда можно утверждать, что это «RMS», но на практике так бывает редко. Также маловероятно, что будет какая-либо слышимая разница, поэтому дополнительная стоимость преобразователя RMS обычно не гарантируется. Это особенно верно, поскольку компрессия и ограничение так часто используются, чтобы сделать все на одном уровне, так что это звучит плоско и безжизненно.
Измерители пиковых значений
не редкость в студиях звукозаписи и вещания, и многие люди знают о так называемом PPM (Peak Program Meter), который используется для индикации абсолютных пиковых значений речевого / музыкального сигнала. Это особенно важно для цифровых записей, потому что они имеют «жесткий» предел — обычно называемый 0dBfs (полная шкала) — абсолютный максимальный уровень входного сигнала аналого-цифрового преобразователя (АЦП) до его отсечения. В отличие от аналоговой ленты (например), здесь нет поведения «мягкого клипа», поэтому PPM используется для обозначения пиков формы сигнала.PPM также распространен в вещательных студиях, потому что максимальная разрешенная глубина модуляции (AM) или отклонение (FM) никогда не должна превышаться. Полное обсуждение PP Metering выходит за рамки этой статьи, но в сети есть много информации для тех, кто хочет знать больше.
В полностью цифровых системах, таких как комплекты для проверки звука и другие измерительные системы (в частности, осциллографы), пиковые, средние и среднеквадратичные значения обычно вычисляются на основе вычислений для каждой выборки и обеспечивают точный результат даже для очень сложных сигналов.Можно положиться на мой цифровой осциллограф, чтобы дать точное среднеквадратичное значение с очень высокими коэффициентами амплитуды (в некоторых случаях более 20), где истинный измеритель среднеквадратичных значений с использованием аналоговой обработки (возможно, AD737) даст неправильный ответ, поскольку коэффициент амплитуды превышает 5 может вызвать внутреннюю перегрузку.
Цель этой инструкции по применению — продемонстрировать различные типы измерений, чтобы вы могли выбрать тот, который, скорее всего, удовлетворит ваши потребности. Хотя истинное среднеквадратичное значение для всего может поначалу показаться хорошей идеей, это не всегда лучший выбор.Стоимость — одна из потенциальных проблем, но время установления (особенно для сигналов низкого уровня) может означать, что единственный разумный выбор — использовать усреднение. Тогда бывают моменты, когда вы должны знать пиковое значение, и пиковый детектор — единственное, что будет отображать пики напряжения.
Ссылки
AD737 — Технические данные преобразователя True RMS в DC
Project 140 — Преобразователь True RMS с использованием AD737
Основной индекс Прил.Указатель примечаний
Уведомление об авторских правах. Эта статья, включая, но не ограничиваясь, весь текст и диаграммы, является интеллектуальной собственностью Рода Эллиотта и © 2016. Воспроизведение или повторная публикация любыми средствами, электронными, механическими или электромеханическими, строго запрещены в соответствии с Международные законы об авторском праве. Автор (Род Эллиотт) предоставляет читателю право использовать эту информацию только для личного использования, а также разрешает сделать одну (1) копию для справки.Коммерческое использование запрещено без письменного разрешения Рода Эллиотта.
Журнал изменений: страница создана и авторские права © Род Эллиотт, июль 2016 г.

Среднеквадратичное значение формы сигнала и средние значения
Синусоида
Полноволновое выпрямление
Полуволновое выпрямление
Переменный ток, наложенный на постоянный ток
Периодические полусинусоиды
Прямоугольная волна
Пилообразная волна
Трапецеидальная волна
Стандартная формула для расчета среднеквадратичных значений (среднеквадратичных) значений сигнала I (t):
Уравнение для определения среднеквадратичного значения сигнала
В таблицах ниже показаны уравнения для расчета среднеквадратичных и средних значений типичной формы сигнала.
Форма волны тока
Конфигурация
I _RMS
I _{СРЕДНЕЕ}
Диаграмма для расчета среднеквадратичного значения синусоидальной волны
Синусоидальная волна
0
Форма волны тока
Конфигурация
I _RMS
I _{СРЕДНЕЕ}
Диаграмма для расчета среднеквадратичного значения выпрямленной синусоидальной волны (полная волна)
Полноволновая выпрямленная синусоида
0.637I _уп.
Форма волны тока
Конфигурация
I _RMS
I _{СРЕДНЕЕ}
Диаграмма для расчета среднеквадратичного значения полуволнового выпрямленного синусоидального сигнала
Синусоидальная полуволновая выпрямленная волна
0.318I _уп.
Форма волны тока
Конфигурация
I _RMS
I _{СРЕДНЕЕ}
Диаграмма для синусоидальной волны с расчетом среднеквадратичного смещения постоянного тока
Постоянный ток с наложенной синусоидой
I _{постоянного тока}
Форма волны тока
Конфигурация
I _RMS
I _{СРЕДНЕЕ}
Диаграмма для расчета среднеквадратичного значения повторяющейся полусинусоидальной волны
Полусинусоиды длительности T и частоты f
(2fI _pk T) /
п.
Форма волны тока
Конфигурация
I _RMS
I _{СРЕДНЕЕ}
Диаграмма для вычисления среднеквадратичного значения повторяющейся прямоугольной волны
Квадратные волны длительностью T и частотой f
ФИ _ПК Т
Форма волны тока
Конфигурация
I _RMS
I _{СРЕДНЕЕ}
Диаграмма для расчета среднеквадратичного значения повторяющейся пилообразной волны
Пилообразная форма волны длительности T и частоты f
0.
Навигация по записям
Сч я: СЧЯ — это… Что такое СЧЯ?
Радиотехника с90в: Ошибка 404. Страница не найдена
Похожие записи

21.11.2024 0
Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании

19.11.2024 0
Новорожденный какает слизью: причины появления слизи в кале грудничка

19.11.2024 0
Гемангиома у новорожденных: причины, виды, лечение и профилактика
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Рубрики
Автолюбителям
Датчик
Лайфхаки
Преобразователь
Своими руками
Схемы
Усилитель
Разное
Карта сайта
© M-Gen

Что такое средневыпрямленное напряжение

Формулы для расчета средневыпрямленного напряжения

Как измерить средневыпрямленное напряжение

Отличия от действующего и амплитудного значений

Применение средневыпрямленного напряжения

Погрешности при измерении средневыпрямленного напряжения

Расчет средневыпрямленного напряжения для различных сигналов

Синусоидальный сигнал

Прямоугольный сигнал

Треугольный сигнал

Преимущества и недостатки измерения средневыпрямленного напряжения

Преимущества:

Недостатки:

Параметры переменного напряжения — Практическая электроника

Среднее значение напряжения

Средневыпрямленное значение напряжения

Среднеквадратичное значение напряжения

Как измерить среднеквадратичное значение напряжения

%d1%81%d1%80%d0%b5%d0%b4%d0%bd%d0%b5%d0%b2%d1%8b%d0%bf%d1%80%d1%8f%d0%bc%d0%bb%d0%b5%d0%bd%d0%bd%d0%be%d0%b5%20%d0%bd%d0%b0%d0%bf%d1%80%d1%8f%d0%b6%d0%b5%d0%bd%d0%b8%d0%b5 — со всех языков на все языки

220 Вольт действующее или амплитудное

Среднее значение напряжения

Средневыпрямленное значение напряжения

Среднеквадратичное значение напряжения

Как измерить среднеквадратичное значение напряжения

Амплитудное значение

Измерение средневыпрямленного значения переменного напряжения при значительном искажении синусоидальности сигнала — Измерения

Средневыпрямленное значение — Большая Энциклопедия Нефти и Газа, статья, страница 4

Средневыпрямленное значение

амплитудное, среднее, среднеквадратическое и средневыпрямленное значение.

2 Преобразователи пикового значения: с открытым и закрытым входами: схемы, принцип действия.

Значения переменного напряжения (тока) — Студопедия

диодов — Как найти среднее значение полупрямого выпрямленного синусоидального сигнала

Пиковое значение, среднее значение и среднеквадратичное значение напряжения

Термин «среднеквадратичное значение» означает «среднеквадратическое значение», также называемое эквивалентом переменного тока и постоянного напряжения.

Важные термины, которые следует запомнить

Важные уравнения, которые следует запомнить

Дополнительная литература / Источники

Комментарии

Характеристики

Среднеквадратичное значение, среднее значение, пиковое значение, пик-фактор, форм-фактор в AC

Формулы среднеквадратичного значения напряжения для различных форм волны

Калькулятор среднеквадратичного напряжения

Формулы среднего значения и среднеквадратичного значения для различных форм волны

Амплитуда

Чередование

Среднее выпрямленное значение

Вступление

Применение в метрологии

Вывод

Результат для размера синуса

Результат для стравливающего синусоидального напряжения

Результат для импульсного напряжения

Результат для переменного компонента

Результат для смешанного напряжения

Сравнение со среднеквадратичным выпрямленным значением

Для размера синуса

Для стравливающего синусоидального напряжения

Для импульсного напряжения

Для переменной составляющей импульсного напряжения

Метрологические последствия

Документы

Цепи пиковых значений, среднеквадратичных значений и усреднения

Среднеквадратичное значение формы сигнала и средние значения

Похожие записи

Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании

Новорожденный какает слизью: причины появления слизи в кале грудничка

Гемангиома у новорожденных: причины, виды, лечение и профилактика

Добавить комментарий Отменить ответ