Как рассчитать параллельное и последовательное соединение резисторов. Какие формулы использовать для вычисления общего сопротивления. Как работает онлайн-калькулятор для расчета параллельного соединения резисторов. Какие факторы влияют на сопротивление проводников.
Основные виды соединения резисторов
Существует три основных способа соединения резисторов в электрической цепи:
- Параллельное соединение
- Последовательное соединение
- Смешанное соединение
Каждый из этих способов имеет свои особенности и применяется для решения различных задач в электротехнике. Рассмотрим подробнее параллельное и последовательное соединение.
Параллельное соединение резисторов
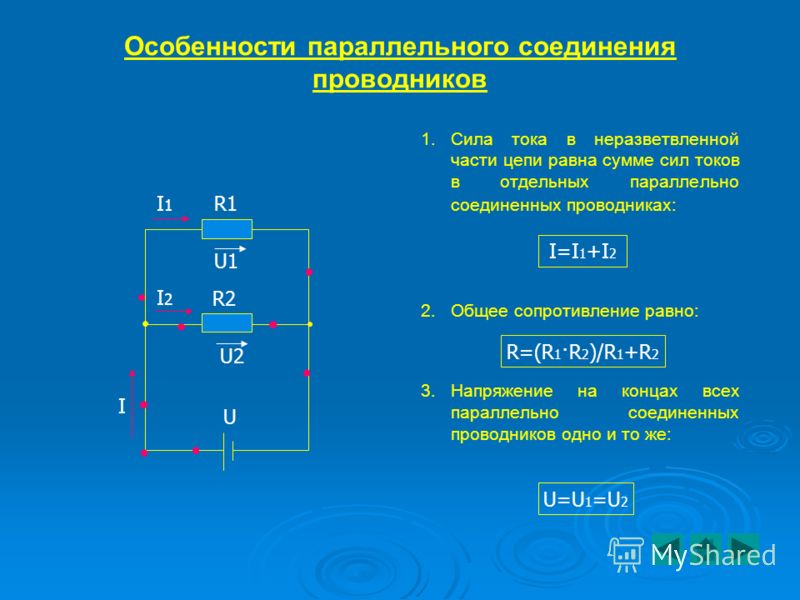
При параллельном соединении все выводы резисторов соединяются в двух общих точках. Основные характеристики параллельного соединения:
- Напряжение на всех резисторах одинаковое
- Общий ток равен сумме токов через каждый резистор
- Общее сопротивление всегда меньше сопротивления наименьшего из резисторов
Формула для расчета параллельного соединения
Общее сопротивление при параллельном соединении рассчитывается по формуле:
1/R = 1/R1 + 1/R2 + … + 1/Rn
Где R — общее сопротивление, R1, R2, …, Rn — сопротивления отдельных резисторов.
Пример расчета параллельного соединения
Рассчитаем общее сопротивление трех параллельно соединенных резисторов: 10 Ом, 20 Ом и 30 Ом.
1/R = 1/10 + 1/20 + 1/30 = 0.1 + 0.05 + 0.033 = 0.183
R = 1/0.183 = 5.46 Ом
Таким образом, общее сопротивление составит 5.46 Ом.
Последовательное соединение резисторов
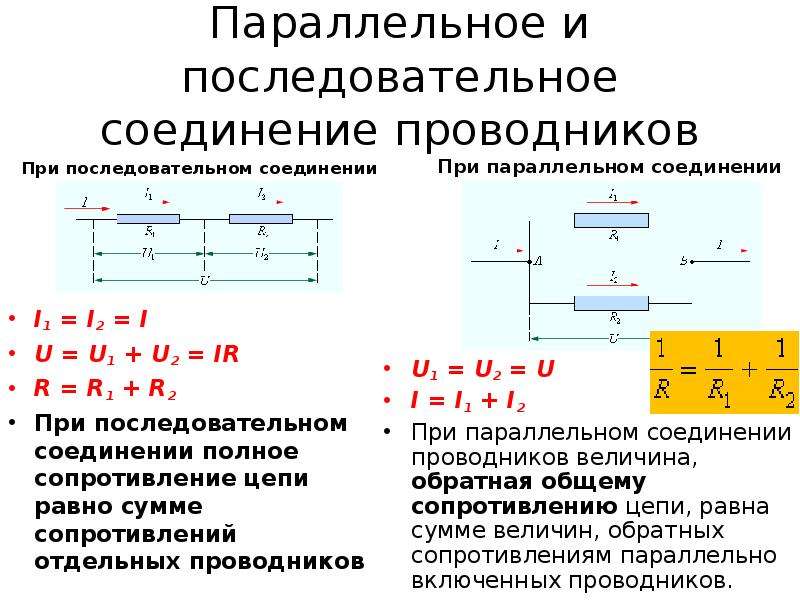
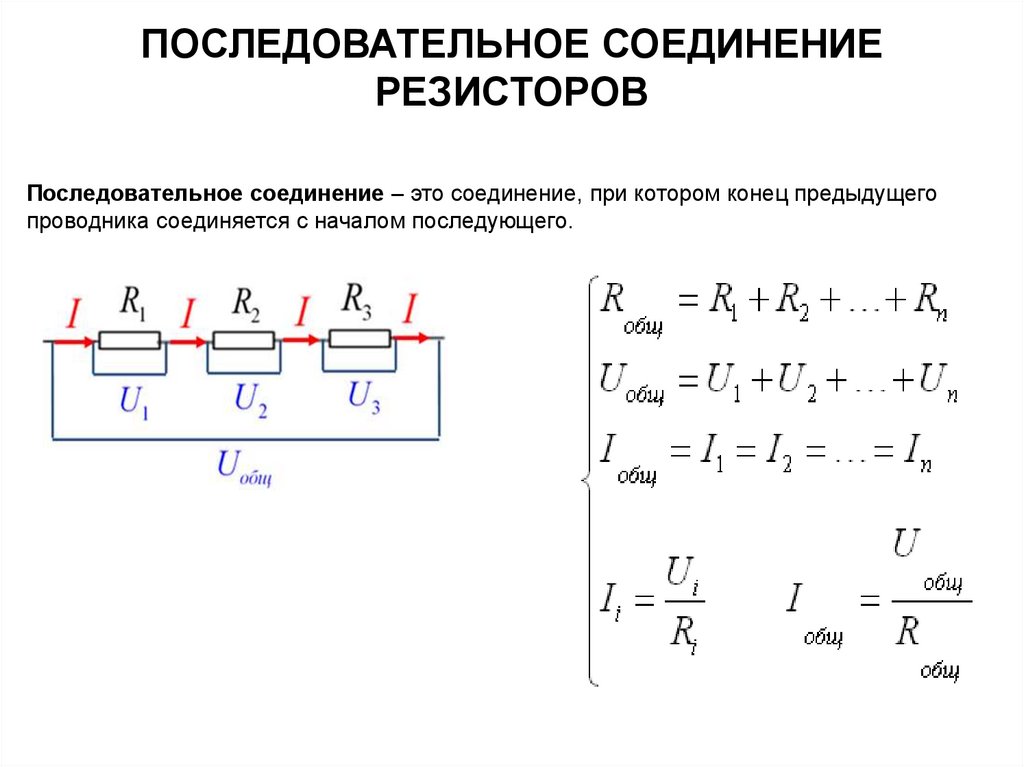
При последовательном соединении резисторы соединяются друг за другом. Основные характеристики:
- Ток через все резисторы одинаковый
- Общее напряжение равно сумме напряжений на каждом резисторе
- Общее сопротивление равно сумме сопротивлений всех резисторов
Формула для расчета последовательного соединения
Общее сопротивление при последовательном соединении рассчитывается по формуле:R = R1 + R2 + … + Rn
Где R — общее сопротивление, R1, R2, …, Rn — сопротивления отдельных резисторов.
Пример расчета последовательного соединения
Рассчитаем общее сопротивление трех последовательно соединенных резисторов: 10 Ом, 20 Ом и 30 Ом.
R = 10 + 20 + 30 = 60 Ом
Общее сопротивление составит 60 Ом.
Онлайн-калькулятор для расчета параллельного соединения резисторов
Для быстрого расчета общего сопротивления при параллельном соединении можно воспользоваться онлайн-калькулятором. Принцип работы калькулятора:
- Введите количество параллельно соединенных резисторов
- Укажите сопротивление каждого резистора в Омах
- Нажмите кнопку «Рассчитать»
- Калькулятор выведет результат — общее эквивалентное сопротивление
Такой калькулятор значительно упрощает и ускоряет расчеты, особенно при большом количестве резисторов.
Факторы, влияющие на сопротивление проводников
На величину электрического сопротивления проводников оказывают влияние следующие основные факторы:
Материал проводника
Удельное сопротивление материала определяет его способность проводить электрический ток. Металлы имеют низкое удельное сопротивление, диэлектрики — очень высокое.
Геометрические размеры
Сопротивление проводника прямо пропорционально его длине и обратно пропорционально площади поперечного сечения. Чем длиннее проводник, тем выше сопротивление. Чем толще проводник, тем ниже сопротивление.

Температура
С повышением температуры сопротивление металлов увеличивается, а полупроводников — уменьшается. Это связано с изменением подвижности носителей заряда.
Механические напряжения
Деформация проводника (растяжение, сжатие, изгиб) приводит к изменению его сопротивления за счет изменения межатомных расстояний в кристаллической решетке.
Применение различных соединений резисторов
Параллельное и последовательное соединение резисторов широко применяется в электронике и электротехнике для решения различных задач:
Параллельное соединение
- Увеличение общей мощности резистивной нагрузки
- Создание делителей тока
- Получение дробных номиналов сопротивлений
Последовательное соединение
- Увеличение общего сопротивления цепи
- Создание делителей напряжения
- Ограничение тока в цепи
Правильный выбор способа соединения резисторов позволяет оптимизировать работу электрических схем и добиться требуемых характеристик.
Расчет сложных схем соединения резисторов
Для расчета сложных схем, содержащих как параллельные, так и последовательные участки, применяется метод поэтапного преобразования:
- Схема разбивается на простые участки с параллельным или последовательным соединением
- Рассчитывается эквивалентное сопротивление каждого участка
- Полученные эквивалентные сопротивления объединяются в новую упрощенную схему
- Процесс повторяется, пока не будет получено общее сопротивление всей цепи
Для особо сложных схем применяются специальные методы расчета, такие как метод контурных токов или метод узловых потенциалов.
Заключение
Понимание принципов параллельного и последовательного соединения резисторов является фундаментальным для работы с электрическими цепями. Правильное применение формул расчета и использование онлайн-калькуляторов позволяет быстро и точно определять параметры резистивных цепей. При проектировании электронных устройств важно учитывать факторы, влияющие на сопротивление, чтобы обеспечить стабильную и эффективную работу схем.
Параллельное и последовательное соединение резисторов (сопротивлений)
Содержание
- Отличия от последовательного и смешанного подключений
- Объединение резистивных радиокомпонентов
- Параллельное соединение резисторов онлайн калькулятор
- Как правильно рассчитать сопротивление
- Как рассчитать сложные схемы соединения резисторов
- Формула параллельного соединения резисторов
- Типы проводников
- Зависимость сопротивления
- Последовательное соединение резисторов.
Отличия от последовательного и смешанного подключений
Иные способы соединения понятны из показанных на картинке примеров. Без специальных вычислений понятно, что параллельное включение резисторов создает несколько путей прохождения тока. Следовательно, в отдельных цепях его сила будет меньше, по сравнению с контрольными точками на входе и выходе. Вместе с тем напряжение в отмеченных местах остается неизменным.
Последовательное соединение резисторов увеличивает общее электрическое сопротивление. Ток в этой цепи (по базовым принципам) не будет изменяться. Однако на каждом пассивном элементе можно будет обнаружить измерительным прибором соответствующее падение напряжения.
Ток в этой цепи (по базовым принципам) не будет изменяться. Однако на каждом пассивном элементе можно будет обнаружить измерительным прибором соответствующее падение напряжения.
Смешанный вариант – это объединение представленных выше соединений. Различные комбинации используют для деления напряжения, решения других задач. Для упрощения расчетов суммируют последовательность соединенных сопротивлений в отдельных цепях:
Rобщ = R1 + R2 + … + Rn.
Вне зависимости от сложности схемы, на входе и выходе по первому закону Кирхгофа токи будут одинаковыми.
Объединение резистивных радиокомпонентов
Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
https://youtube.com/watch?v=jJX6IsRhnhs
Параллельное соединение
При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.
Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).
При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:
- Номинал резистора в 16 Ом подойдет.
- Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).
В некоторых случаях следует потратить больше времени на подбор необходимых номиналов.
- Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
- Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.
Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
Последовательное подключение
Последовательное включение резисторов также применяется в радиотехнике.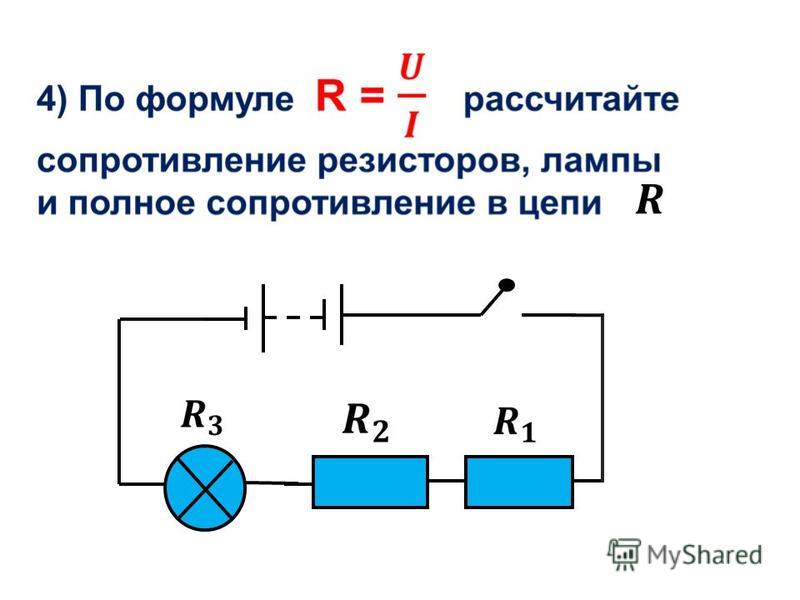
- Ток не изменяется на участке цепи.
- Общее напряжение равно сумме падений напряжений на каждом резисторе.
- Rобщ = R1 + R2 + … + Rn.
Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:
- I = I1 = I2 = 0,5 (А).
- Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
- Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).
Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам.
Параллельное соединение резисторов онлайн калькулятор
Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться
Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:
Данный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.
Для этого вам необходимо:
- Указать в графе “количество резисторов” их число, в нашем примере их три;
- После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;
- Далее нажмите кнопку “рассчитать” и в окошке “параллельное сопротивление в цепи” вы получите значение сопротивления в 10 Ом.
Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку “сбросить”, чтобы обнулить значение параллельно включенных элементов калькулятора.
Подключение магнитного пускателя через кнопочный пост видео
Для расчета суммарного сопротивления калькулятором используется такое соотношение:
- Rсум – суммарное сопротивление параллельно соединенных элементов
- R1 – сопротивление первого резистора;
- R2 – сопротивление второго резистора;
- R3 – сопротивление третьего резистора;
- Rn – сопротивление n-ого элемента.
Таким образом, в рассматриваемом примере параллельно включены три резистора, поэтому формула для определения суммарного сопротивления будет иметь такой вид:
Чтобы выразить величину суммарного сопротивления необходимо умножить обе половины уравнения на произведение сопротивлений всех трех резисторов. После этого перенести составляющие элементы по правилу пропорции и получить значение сопротивления:
Как видите, расчет параллельного сопротивления резисторов вручную требует немалых усилий, поэтому куда проще его сделать на нашем онлайн калькуляторе.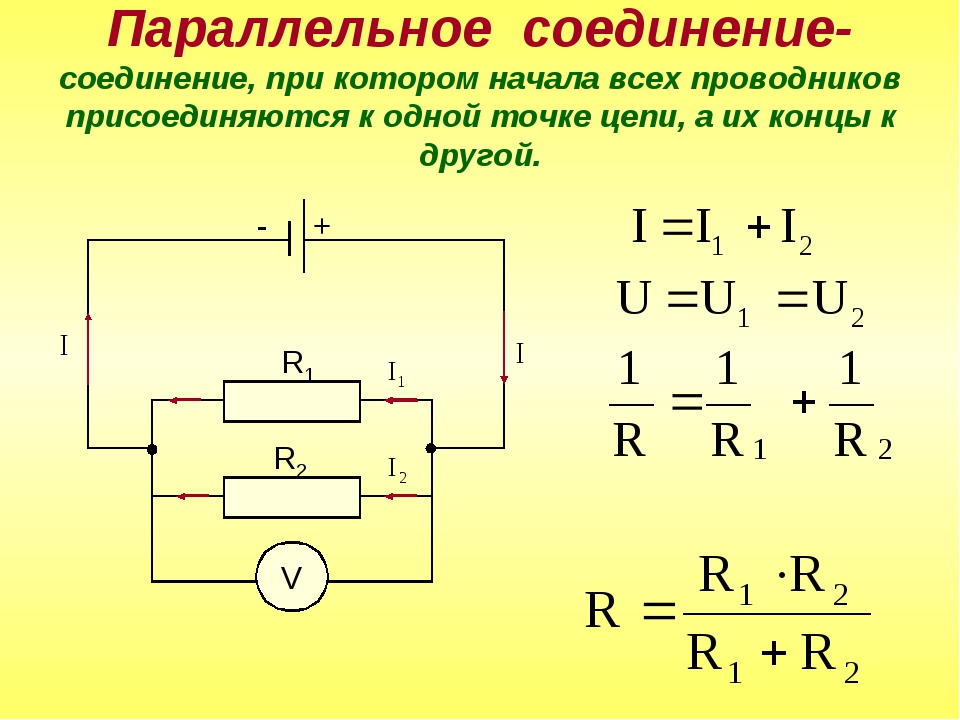
Обратите внимание, при наличии элементов с сопротивлением в разной размерности Ом, кОм, МОм, их необходимо привести к одной величине, прежде чем производить расчет. К примеру, в Ом и указывать в поле калькулятора для расчета параллельного соединения резисторов значение непосредственно в Омах
Онлайн калькулятор для расчета параллельного сопротивления позволит установить общее эквивалентное сопротивление в цепи R1 + R2 +Rn. Данный калькулятор можно смело назвать одним из самых простых и эффективных.
Литейная машина под давлением
Для получения результатов вам необходимо ввести:
- Количество резисторов.
- Указать мощность каждого резистора (Ом).
- Нажать кнопку «Расчитать».
В результате вы сможете получить точно сопротивление резисторов в сети
Калькулятор для расчета параллельного сопротивления позволит безошибочно все определить, а это очень важно, так как ручной расчет считается достаточно сложным и трудоемким процессом.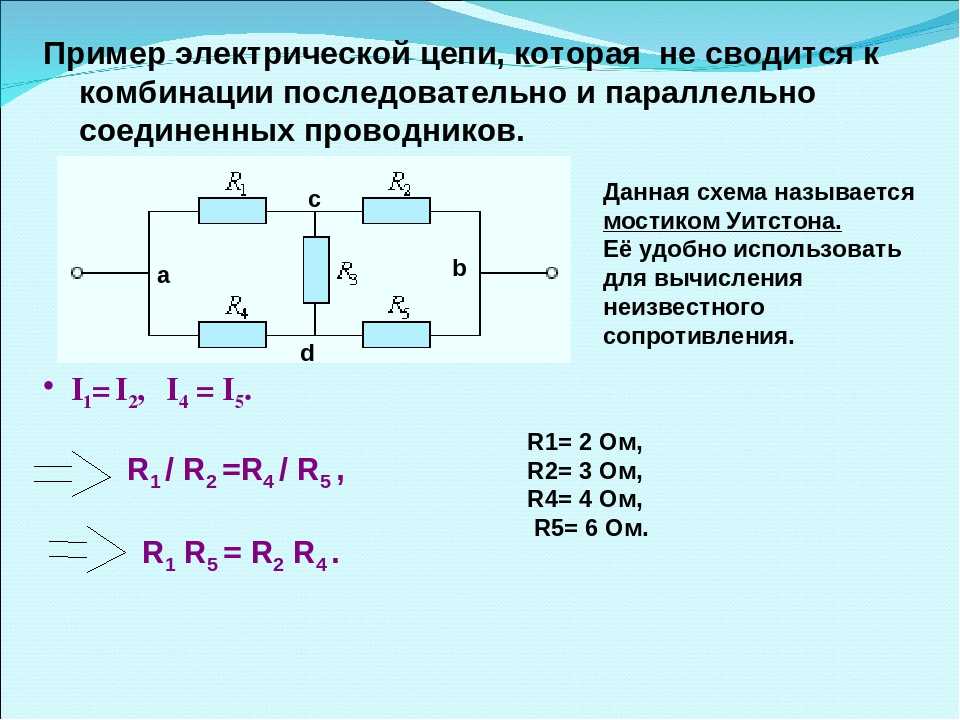 Наш калькулятор с легкостью поможет вам справиться со всем
Наш калькулятор с легкостью поможет вам справиться со всем
Для того чтобы определить общее эквивалентное сопротивление, можно воспользоваться точным и удобным калькулятором. Где, внеся данные по количеству резисторов, калькулятор произведет расчет в автоматическом режиме.
Данное соединение является одним из 2-ух видов, в данном случае оба вывода 1-го из резисторов соединяются с выводами 2-го резистора. В иных случаях их принято соединять параллельно или последовательно, чтобы можно было создать схемы сложного типа.
Многофункциональный станок своими руками чертежи
Для того чтобы найти ток, который протекает через определенный резистор, следует использовать формулу: Произведем расчеты согласно примеру Разрабатывается устройство, в котором есть необходимость использовать резистор, которое имеет сопротивление 8Ом. Исходя из того, что номинальный ряд согласно стандартным значениям таких резисторов не имеет, выходом будет использование 2-ух резисторов соединенных параллельно.
Для такого способа производятся следующие расчеты: Данная формула показывает, что в случае когда R1 = R2, R будет составлять ровно половину сопротивления 1-го из 2-ух резисторов. И если R=8Ом, то соответственно R1 и R2 = 2*8=16Ом.
Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.
Как правильно рассчитать сопротивление
Для выбора и установки элементов в цепь нужно заранее просчитать номинал и мощность составных частей.
Применяют для этого правило Ома для участка цепи, чтобы рассчитать сопротивление, выражение выглядит так:
R = U/I.
U — будет напряжением на выводах компонента.
I — показатель тока на участке цепи.
Это выражение используется для токов постоянного направления.
Если трудно самостоятельно рассчитать этот показатель, то существуют специальные онлайн-калькуляторы. Туда необходимо вставить имеющиеся значения и можно получить результат за секунды. Но поскольку закон Ома изучается еще в школе, то не составит проблем провести вычисления самостоятельно.
Туда необходимо вставить имеющиеся значения и можно получить результат за секунды. Но поскольку закон Ома изучается еще в школе, то не составит проблем провести вычисления самостоятельно.
Внимание! Если нет опыта в работе с электрикой, желательно не выполнять ремонт проводки самостоятельно, потому что при неправильной работе может случиться короткое замыкание, что чревато возникновением пожара. Также необходимо помнить, что при работе с проводкой нужно полностью обесточить сеть
Подключение для светодиодов
В заключении необходимо отметить, что подключать резисторы можно тремя способами: параллельно, последовательно и смешанно. Для тех, кто не имеет особых навыков работы с электрикой, рекомендуется выбирать последовательный метод соединения.
Как рассчитать сложные схемы соединения резисторов
Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.
Перед нами сложная схема – задача рассчитать общее сопротивление:
- R2, R3, R4 объединим в последовательную группу – применим формулу R2,3,4 = R2+R3+R4.
- R5 и R2,3,4 – параллельно соединенные резисторы, рассчитаем R5,2,3,4 = 1/ (1/R5+1/R2,3,4).
- R5,2,3,4, R1, R6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R5,2,3,4+R1+R6.
Для больших схем существуют специальные методы, облегчающие расчет. Один из таких методов – эквивалентное преобразование «треугольника» в «звезду». Такая система расчета применяется в том случае, когда невозможно по схеме определить последовательное или параллельное подключение резисторов.
Преобразование «звезда-треугольник»
Для соединения резистивных элементов, кроме вышеописанных способов, существует несколько других видов соединения:
- «звезда» – соединение трех ветвей с одним общим узлом;
- «треугольник» – соединение ветвей схемы в виде треугольника, сторонами которого служат ветви, вершины представляют узлы.

Эквивалентность замены предполагает стабильность токов, входящих в каждый узел, при одинаковых напряжения между одноименными узлами «треугольника» и «звезды».
Сопротивление резистора луча «звезды» равно произведению сопротивлений резисторов прилегающих сторон «треугольника», деленному на сумму сопротивлений резисторов трех сторон «треугольника».
RA = RAB RAC/(RAB+RAC+RDC).
Сопротивление резисторов сторон «треугольника» равно сумме произведения сопротивлений резисторов двух прилегающих лучей «звезды», деленного на сопротивление третьего луча.
RAB=(RARB+RARC+RBRС)/RC
О разнице подключения звезда и треугольник читайте здесь.
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом.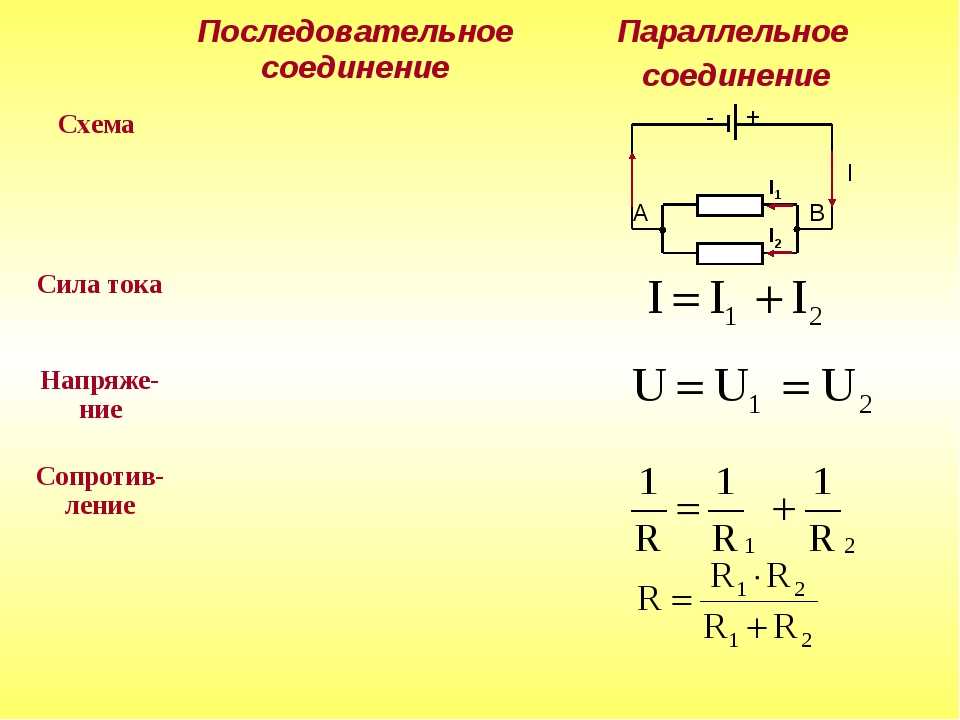 Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
- Таким образом, протекающий общий ток в цепи можно определить как:
- I = I1 + I2
- Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
- Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
- Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
- Таким образом, общий ток будет равен:
- I = 0,545 мА + 0,255 мА = 0,8 мА
- Это также можно проверить, используя закон Ома:
- I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
- где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
- И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
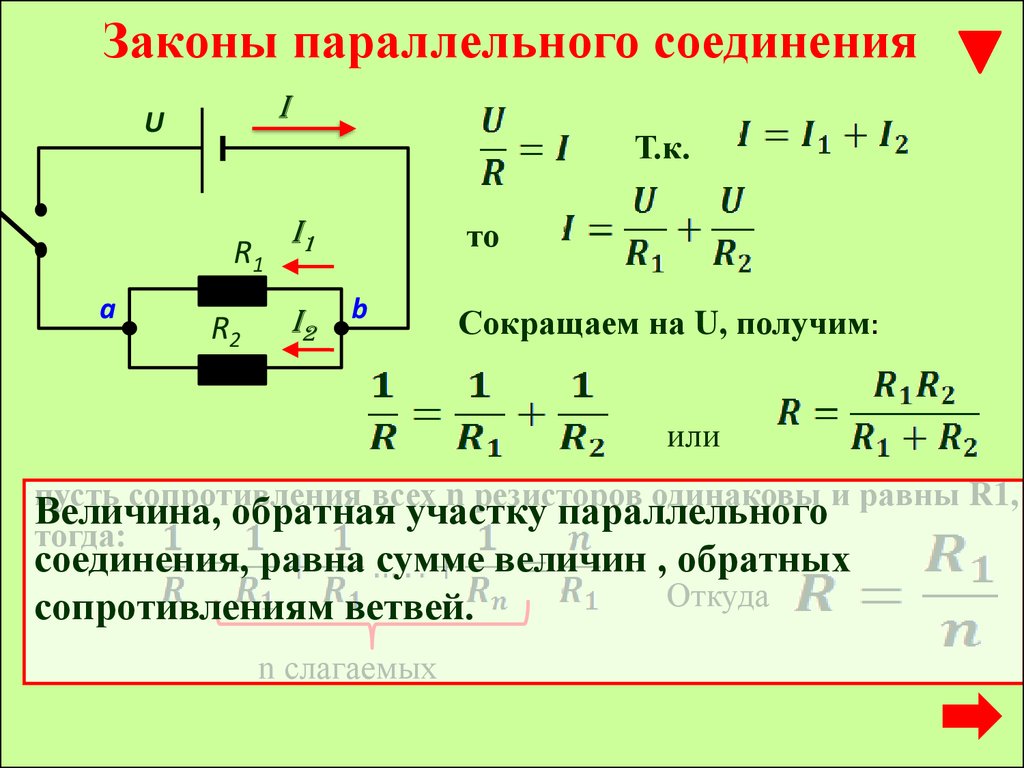
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации.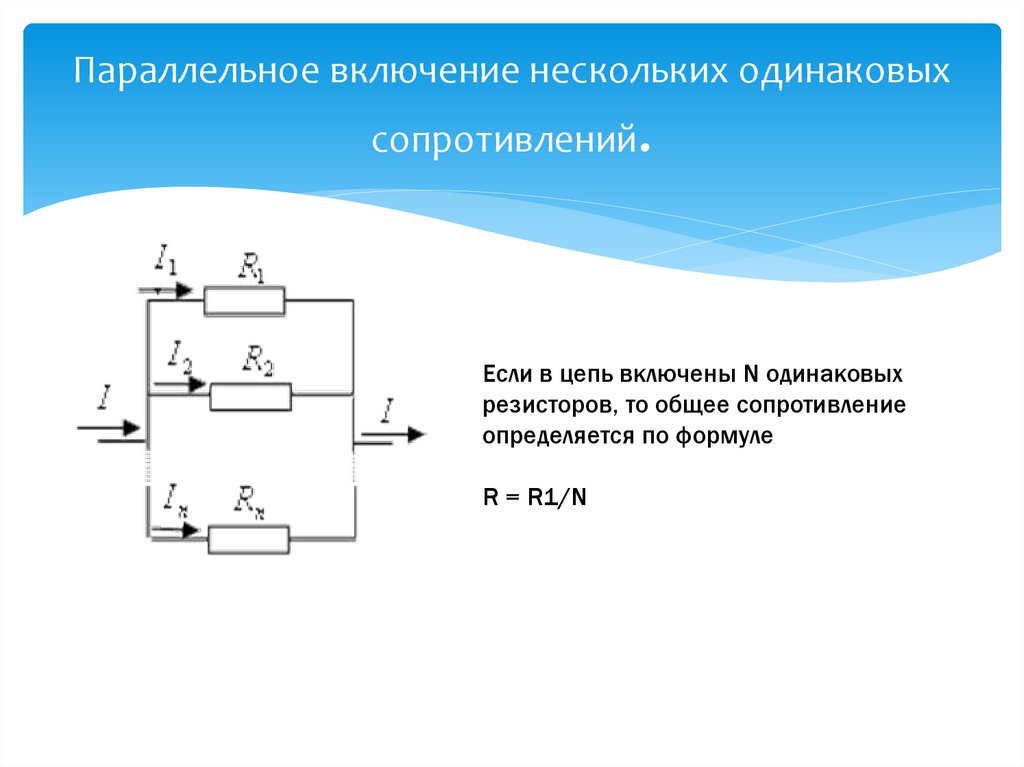 Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала.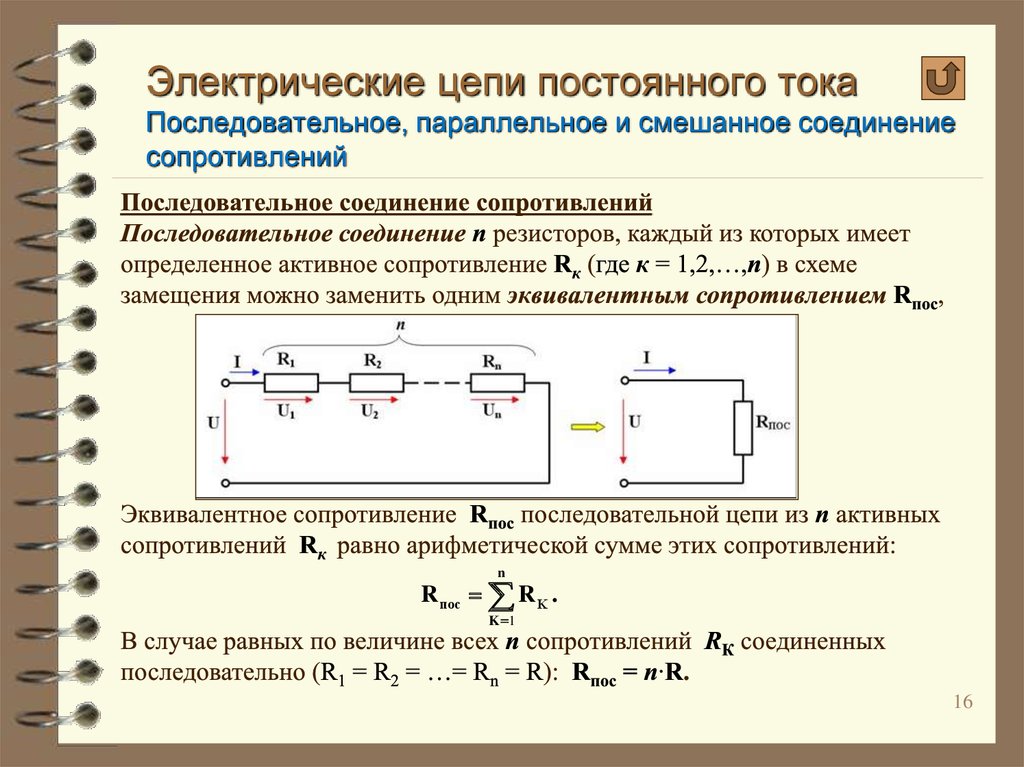 Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.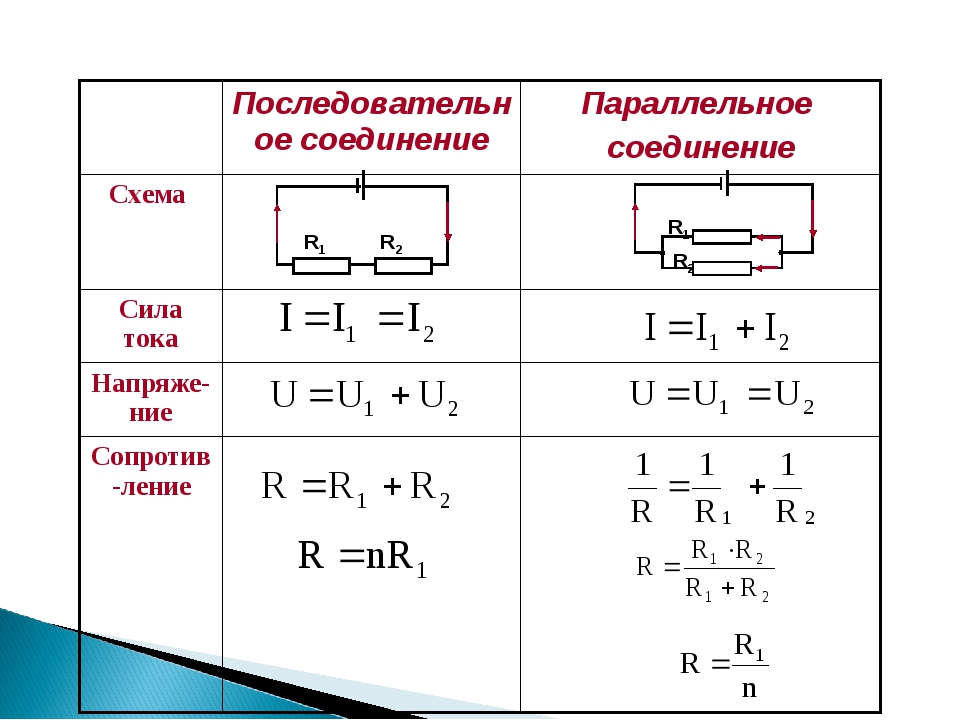
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * . Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.
Последовательное соединение резисторов.
Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.
В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них.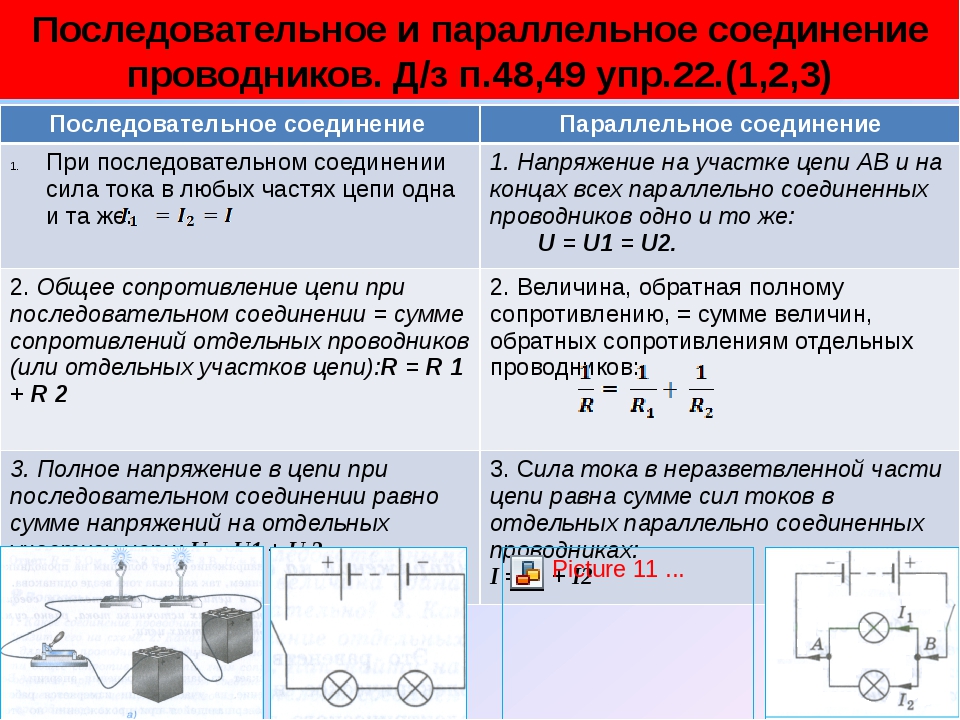 При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:
При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:
Например.При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.
При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.
Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.
Tags: автомат, ампер, бра, бросить, вид, выбор, дом, е, звезда, как, кт, магнит, мощность, напряжение, номинал, подключение, полоска, потенциал, правило, принцип, провод, проект, пуск, р, размер, расчет, резистор, ремонт, ряд, сад, свет, светодиод, сеть, система, соединение, соединение резистор, сопротивление, схема, тен, тип, ток, треугольник, ук, электричество, эффект
Параллельные резисторы онлайн.
 Соединение резисторов
Соединение резисторовОпределение параллельного соединения
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Формулы для частного рассчета вытекают из основной формулы.
Формула для расчета параллельного соединения емкостей (конденсаторов)
При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:
Формула для расчета параллельного соединения индуктивностей
При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:
Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Ток при параллельном соединении
При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.
Применение параллельного соединения
1. В промышленности изготавливаются сопротивления определенных величин.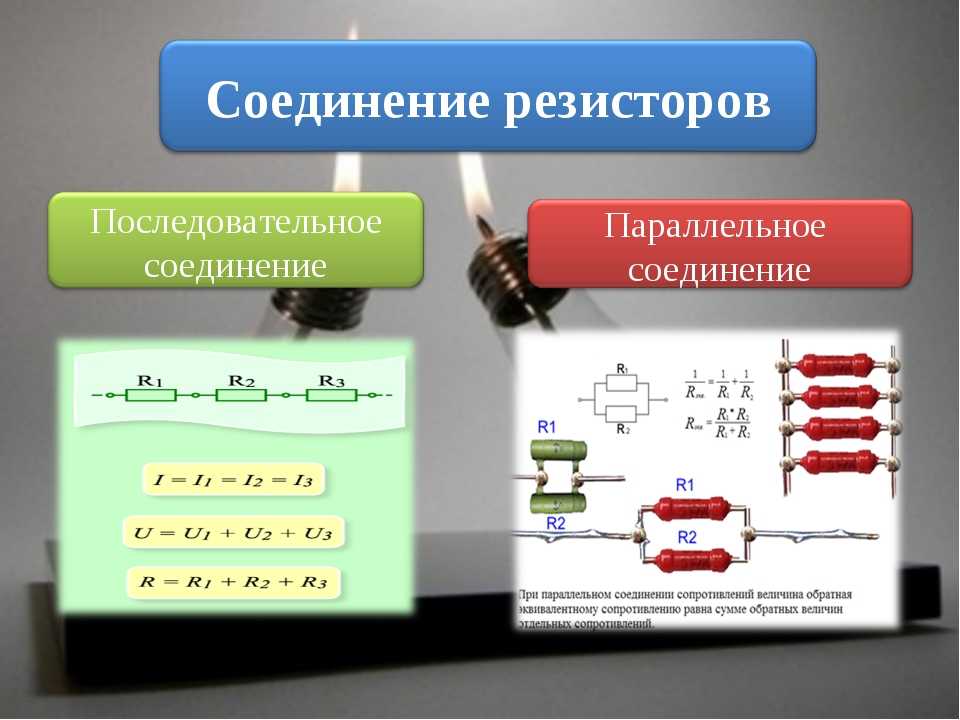 Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
2. Делитель токов.
В этой теме можно привести множество примеров из нашей повседневной жизни, касающихся параллельного подключения сопротивлений. Параллельное соединение одинаковых сопротивлений — это наглядный пример подключения люстры с n-ым количеством ламп и с одинаковым сопротивлением для каждой лампы \рис.1\.
Если допустим в люстре состоящей из нескольких ламп \с одинаковым сопротивлением\ перегорела одна лампа и была произведена замена на лампочку другой мощности, — в этом случае, подключение люстры будет выглядеть как параллельное подключение с разным сопротивлением.
Какие еще можно привести примеры из практики — при параллельном подключении сопротивлений? Допустим, Вы подключили в своей квартире через удлинитель три бытовых электроприбора:
- электроплиту;
- стиральную машину;
- телевизор.
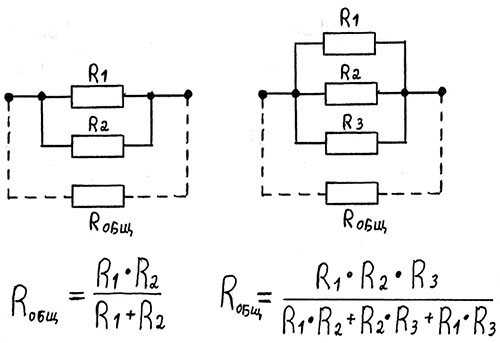
Характер такого подключения примет значение как для параллельного подключения сопротивлений , разных по величине. То-есть, для каждого электроприбора, сопротивление имеет свое значение.
Расчет сопротивления при параллельном соединении
Как уже упоминалось, расчеты сопротивлений при параллельном соединении проводятся:
- с одинаковым сопротивлением;
- с разным сопротивлением,
а также, проводятся расчеты сопротивлений для смешанных соединений резисторов, при последовательном и параллельном соединениях \для одной цепи\. Расчет сопротивления для смешанных соединений резисторов, больше подходит к различным блок-схемам:
- аудиотехники;
- видеотехники.
К этой теме, расчеты для смешанных соединений, отношения не имеют.
Параллельное соединение одинаковых сопротивлений
Представим параллельное подключение, к примеру, трех сопротивлений \рис.2\ равных по величине, где R1=R2=R3=36 Ом \сопротивление лампы накаливания мощностью на 95 Вт\.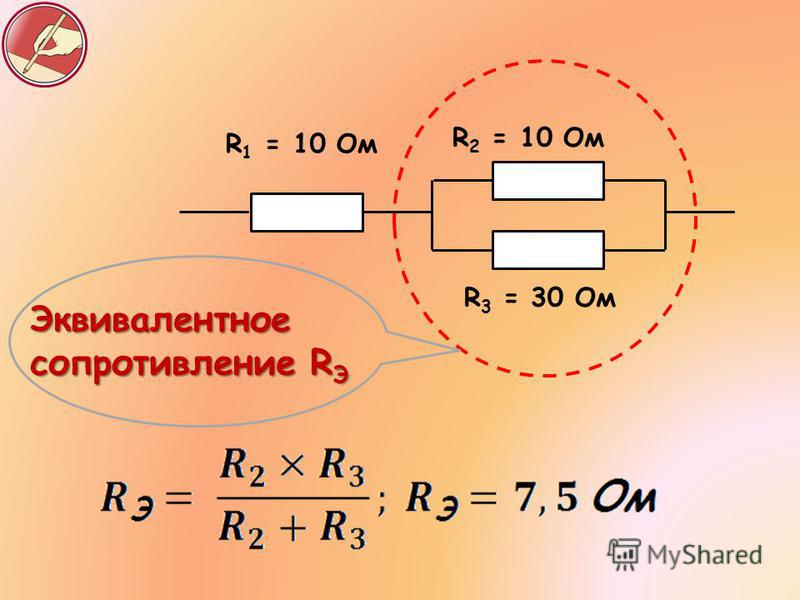 К двум узловым точкам \А, В\ подключено напряжение 220 В. Нужно вычислить общее сопротивление всех трех ламп.
К двум узловым точкам \А, В\ подключено напряжение 220 В. Нужно вычислить общее сопротивление всех трех ламп.
Для расчета общего сопротивления \Rобщ.\, нам необходимо 36 Ом разделить на количество сопротивлений. Решение простое, Rобщ.=12 Ом. То-есть, формула для расчета подобных вычислений выглядит как:
Rобщ. = R /n
Параллельное соединение разных сопротивлений
Допустим, возьмем выборочно три резистора, сопротивлением:
- R1=20 Ом;
- R2=40 Ом;
- R3=10 Ом.
Нужно определить общее сопротивление резисторов при параллельном соединении. Для данного расчета воспользуемся формулой:
1/Rобщ.=1/R1+1/R2+1/R3.
Подставляем значения в формулу:
1/Rобщ. = 1/20+1/40+1/10=7/40=0,18
получаем: Rобщ.=1/0,18=5,5 Ом.
Параллельное соединение резисторов
— одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.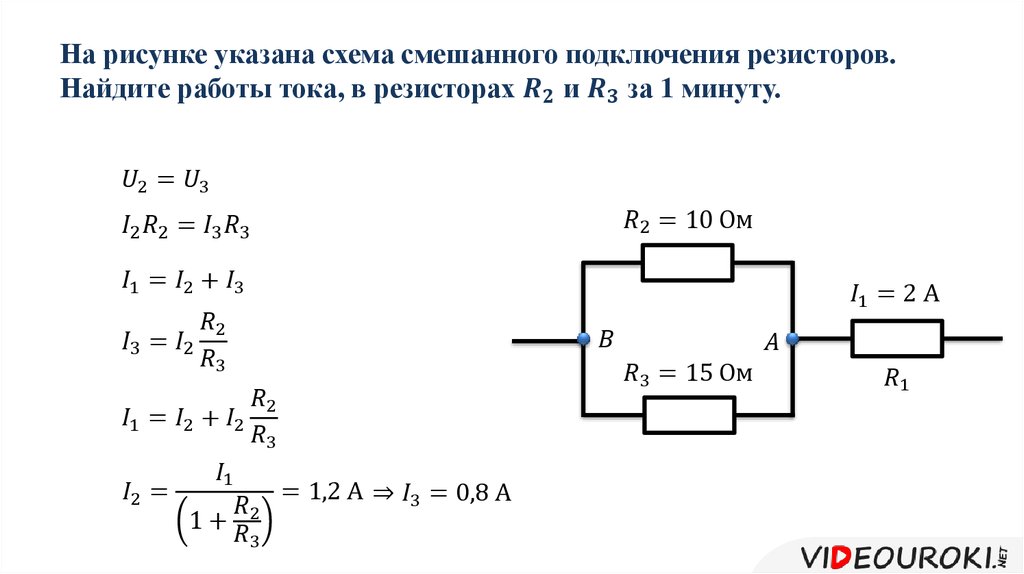 Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов.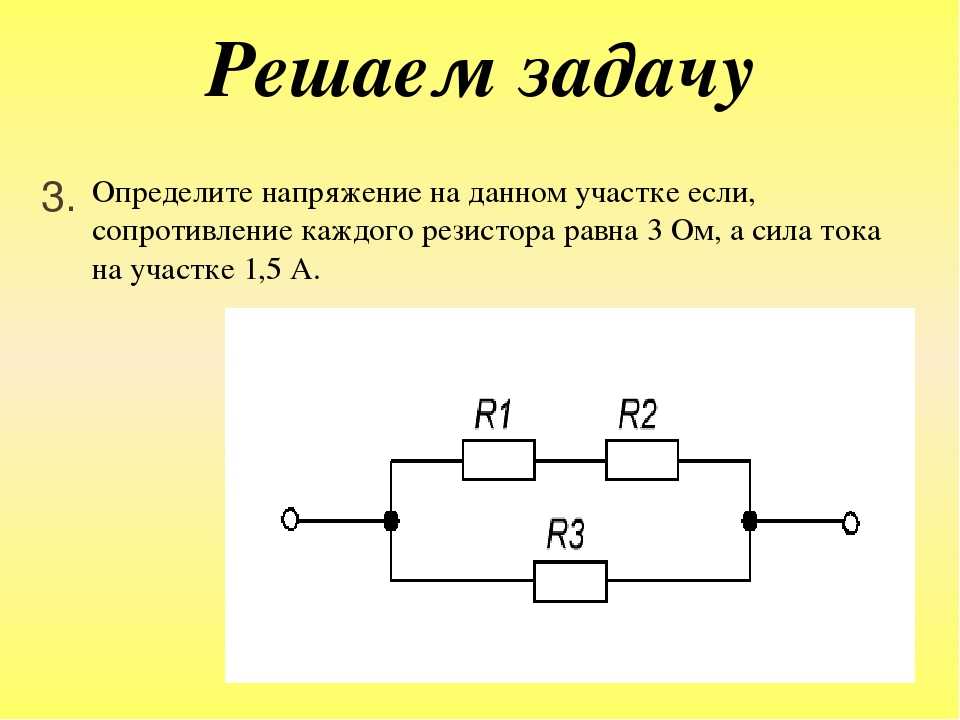 При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.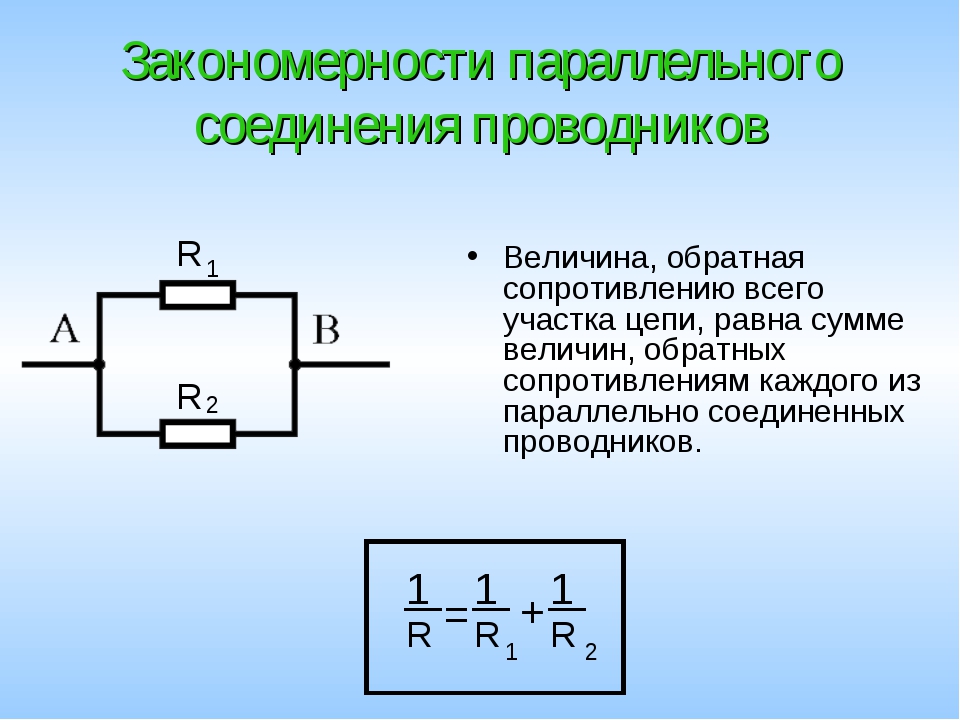
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.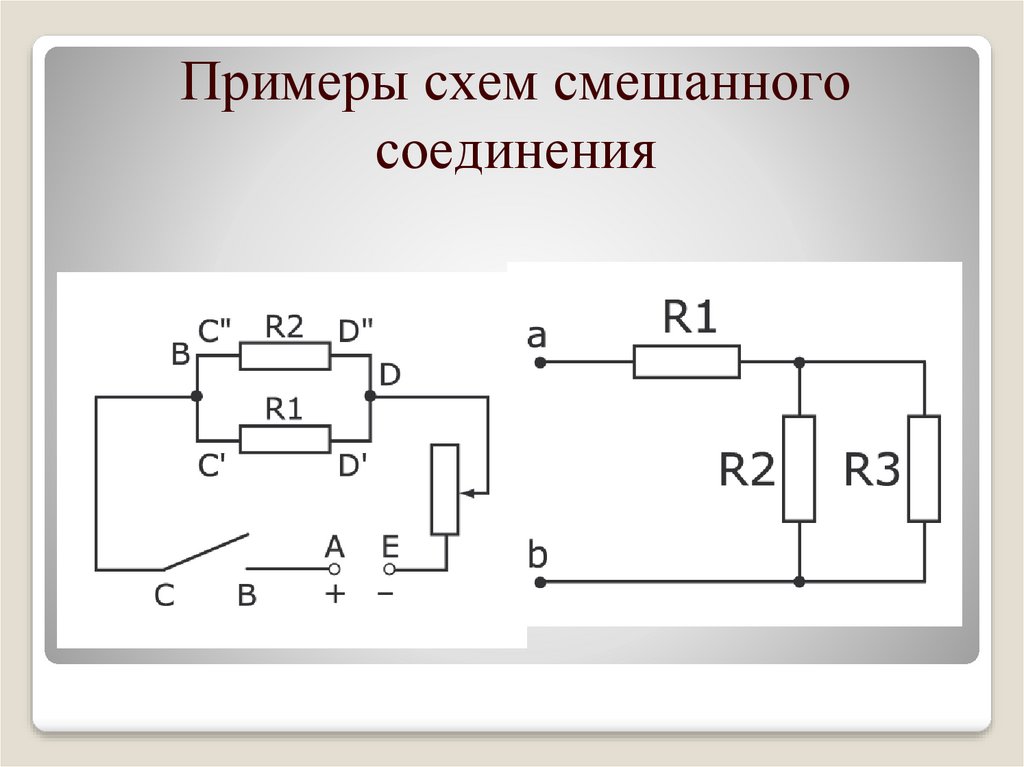
Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление , используя нижеописанные формулы.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.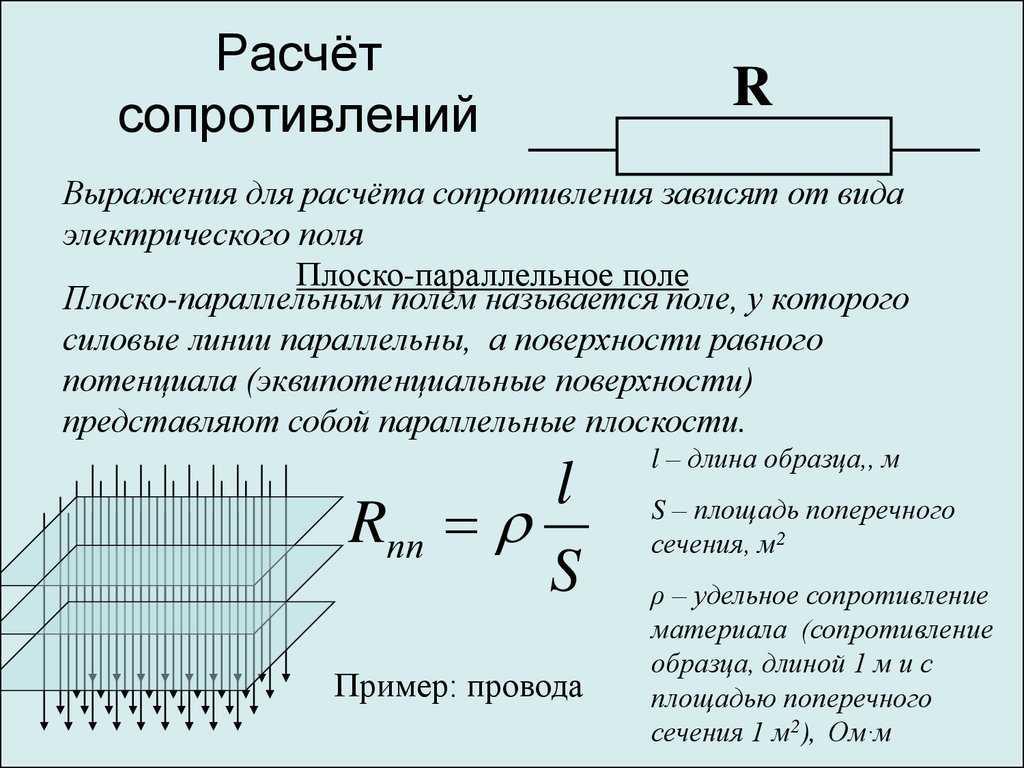
Расчет сопротивления
В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:
R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).
- R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.
Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:
R(общ)=R1*R2/R1+R2.
- R(общ) – суммарное сопротивление;
- R1 и R2 – резисторы, подсоединенные по параллельной схеме.
Универсальная схема расчета
Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель , то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
- R(общ) – суммарное значение сопротивления;
- R – номинал резистора, подсоединенного по параллельной схеме;
- n – число подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.
Пример расчета
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Важные нюансы
Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом
: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом
: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Заключение
Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения.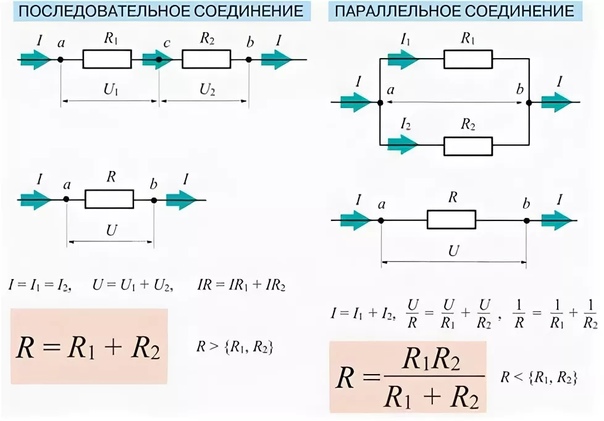 При этом процедура расчета этого параметра отличается достаточной сложностью
, где необходимо учитывать разные параметры.
При этом процедура расчета этого параметра отличается достаточной сложностью
, где необходимо учитывать разные параметры.
Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку.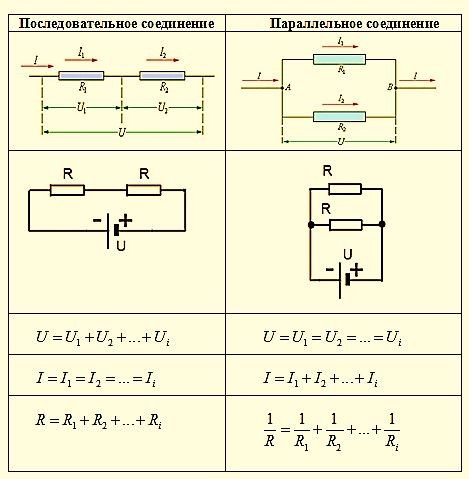 Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Мощность параллельно соединенных резисторов
Вычисление сопротивления и мощности при параллельном и последовательном соединении резисторов. Оглавление :: Поиск Техника безопасности :: Помощь. Параллельное или последовательное соединение включение применяется обычно в нескольких случаях. Во-первых , если нет резистора номинала.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Параллельное соединение резисторов: расчет сопротивления
- Параллельное соединение
- Работа и мощность тока
- Соединение резисторов
- Калькулятор онлайн для параллельного соединения резисторов: общие сведения, формулы расчета
- Последовательное и параллельное соединение резисторов
- Параллельное соединение сопротивлений
- Последовательное и параллельное соединение резисторов
- Соединение резисторов
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Урок 11. ВСЕ Способы соединения резисторов
ВСЕ Способы соединения резисторов
Параллельное соединение резисторов: расчет сопротивления
Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:.
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:. При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет. Выходом из данной ситуации будет использование двух параллельно соединенных резисторов.
Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:. Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов.
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:. Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом. Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:. Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно группа 2. Они в свою очередь соединены параллельно с резистором R1 группа 1. В результате мы упрощаем схему в виде двух параллельных резисторов.
Теперь общее сопротивление всей схемы можно посчитать следующим образом:. Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях. Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться по определению закона Ома.
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях. Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться по определению закона Ома.
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов I1 и I2 будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны. И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь. Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:.
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно.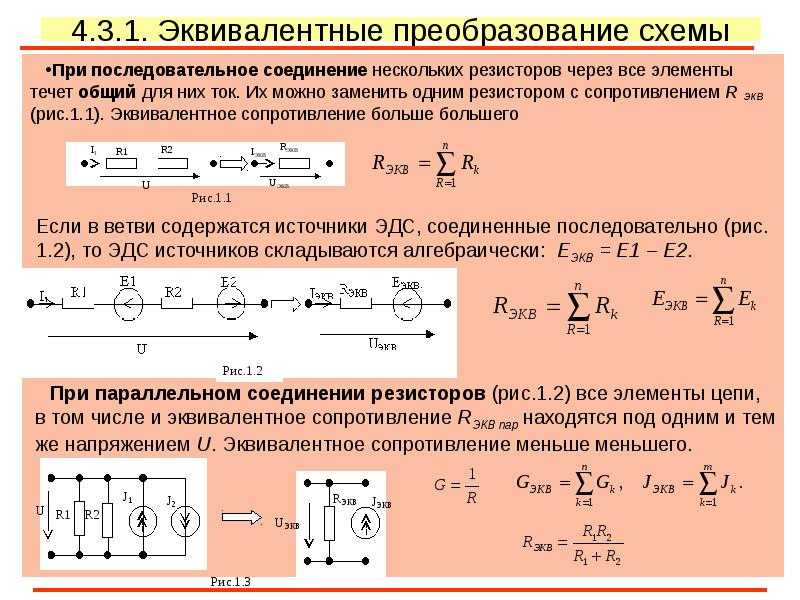 Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение. Делитель напряжения используется в электрических цепях, если необходимо понизить напряжение и получить несколько его фиксированных значений.
Состоит он из двух и более элементов резисторов, реактивных сопротивлений. Элементарный делитель можно представить как два участка цепи, называемые плечами. Участок между положительным напряжением и нулевой точкой — верхнее плечо, между нулевой и минусом — нижнее плечо. Делитель напряжения на резисторах может применятmся как для постоянного, так и для переменного напряжений.
Применяется для низкого напряжения и не предназначен для питания мощных машин. Простейший делитель состоит из двух последовательно соединенных резисторов:.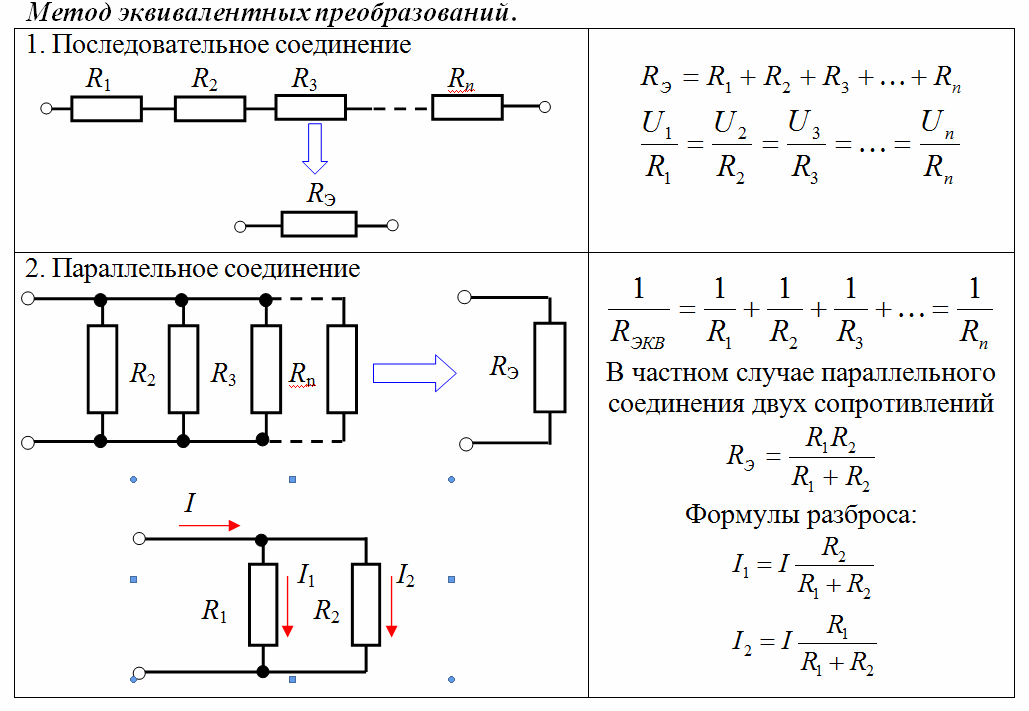 На резистивный делитель напряжения подается напряжение питающей сети U, на каждом из сопротивлений R1 и R2 происходит падение напряжения. Сумма U1 и U2 и будет равна значению U. Падение напряжения будет прямо пропорционально значению сопротивления и величине тока. Согласно первому закону Кирхгофа, величина тока, протекающего через сопротивления одинакова.
На резистивный делитель напряжения подается напряжение питающей сети U, на каждом из сопротивлений R1 и R2 происходит падение напряжения. Сумма U1 и U2 и будет равна значению U. Падение напряжения будет прямо пропорционально значению сопротивления и величине тока. Согласно первому закону Кирхгофа, величина тока, протекающего через сопротивления одинакова.
С чего следует, что падение напряжения на каждом резисторе 2,3 :. Если подставить данное выражение в 2 и 3 , то получим формулы расчета падения напряжения для делителя напряжения на резисторах 6, 7 :. Необходимо упомянуть, что значения сопротивлений делителя должны быть на порядок или два все зависит от требуемой точности питания меньше, чем сопротивление нагрузки.
Если же это условие не выполняется, то при приведенном расчете подаваемое напряжение будет посчитано очень грубо. Для повышения точности необходимо сопротивление нагрузки принять как параллельно подсоединенный резистор к делителю. А также использовать прецизионные высокоточные сопротивления.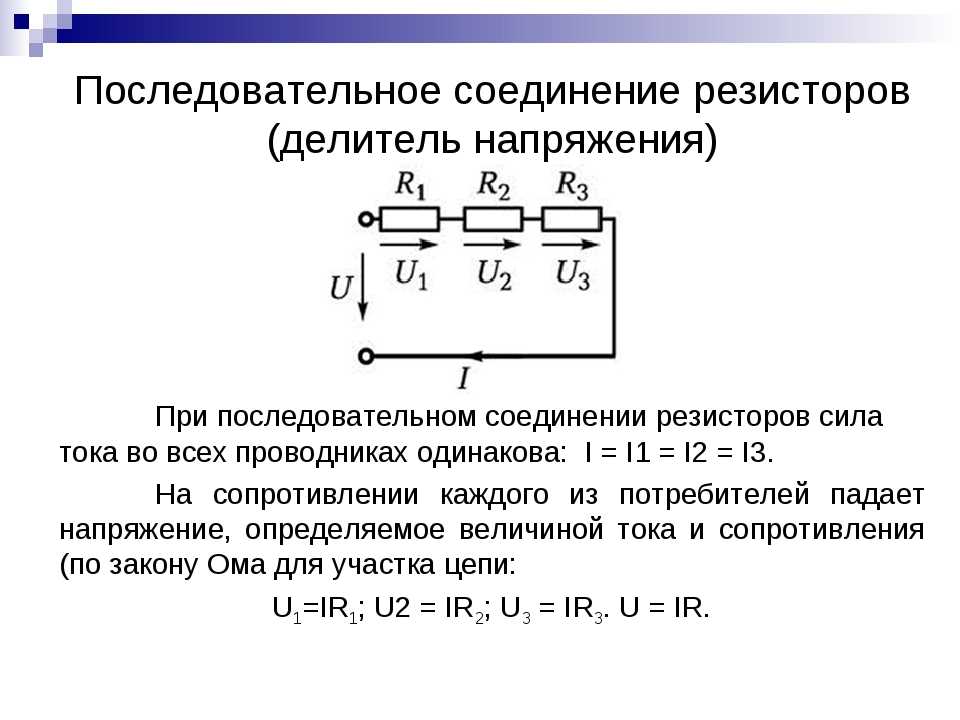 Пусть источник питания выдает 24 В постоянного напряжения, примем, что величина сопротивления нагрузки переменная, но минимальное значение равно 15 кОм.
Пусть источник питания выдает 24 В постоянного напряжения, примем, что величина сопротивления нагрузки переменная, но минимальное значение равно 15 кОм.
Необходимо рассчитать параметры резисторов для делителя, выходное напряжение которого равно 6 В. Использование делителя напряжения очень неэкономичный, затратный способ понижения величины напряжения, так как неиспользуемая энергия рассеивается на сопротивлении превращается в тепловую энергию.
КПД очень низкий, а потери мощности на резисторах вычисляются формулами 8,9 :. Делитель напряжения на конденсаторах применяется в схемах высокого переменного напряжения, в данном случае имеет место реактивное сопротивление.
Исходя из формулы 10 , видно, что сопротивление конденсатора зависит от двух параметров: С и f. Чем больше ёмкость конденсатора, тем сопротивление его ниже обратная пропорциональность. Для ёмкостного делителя расчет имеет такой вид 11, 12 :. Еще один делитель напряжения на реактивных элементах — индуктивный, который нашел применение в измерительной технике.
Сопротивление индуктивного элемента при переменном напряжении прямо пропорционально величине индуктивности 13 :. Светодиод имеет очень небольшое внутреннее сопротивление, если его подключить напрямую к блоку питания, то сила тока будет достаточной высокой, чтобы он сгорел.
Медные или золотые нити, которыми кристалл подключается к внешним выводам, могут выдерживать небольшие скачки, но при сильном превышении перегорают и питание прекращает поступать на кристалл. Онлайн расчёт резистора для светодиода производится на основе его номинальной рабочей силы тока.
Как правило окажется, что резисторы с таким номиналом не выпускаются, и вам будет показан ближайший стандартный номинал. Если не удаётся сделать точный подбор сопротивления, то используйте больший номинал. Подходящий номинал можно сделать подключая сопротивление параллельно или последовательно. Расчет сопротивления для светодиода можно не делать, если использовать мощный переменный или подстроечный резистор.
Наиболее распространены типа на 0,5W. То есть их сопротивление может погрешность в этих пределах в положительную или отрицательную сторону. Чтобы определить полярность можно подать небольшое напряжение или использовать функцию проверки диодов на мультиметре. Отличается от режима измерения сопротивления, обычно подаётся от 2В до 3В. Так же при расчёте светодиодов следует учитывать разброс параметров, для дешевых они будут максимальны, для дорогих они будут более одинаковыми.
То есть их сопротивление может погрешность в этих пределах в положительную или отрицательную сторону. Чтобы определить полярность можно подать небольшое напряжение или использовать функцию проверки диодов на мультиметре. Отличается от режима измерения сопротивления, обычно подаётся от 2В до 3В. Так же при расчёте светодиодов следует учитывать разброс параметров, для дешевых они будут максимальны, для дорогих они будут более одинаковыми.
Чтобы проверить этот параметр, необходимо включить их в равных условиях, то есть последовательно. Уменьшая тока или напряжение снизить яркость до слегка светящихся точек. Визуально вы сможете оценить, некоторые будут светится ярче, другие тускло.
Чем равномернее они горят, тем меньше разброс. Калькулятор расчёта резистора для светодиода подразумевает, что характеристики светодиодных чипов идеальные, то есть отличие равно нулю. Напряжение падения для распространенных моделей маломощных до 10W может быть от 2В до 12В.
Кристаллы включаются цепочками последовательно, затем они объединяются в параллельные цепи. Прежде чем подобрать резистор для светодиода на онлайн калькуляторе, следует убедится в параметрах диодов. Китайцы на Aliexpress продают множество led, выдавая их за фирменные.
Прежде чем подобрать резистор для светодиода на онлайн калькуляторе, следует убедится в параметрах диодов. Китайцы на Aliexpress продают множество led, выдавая их за фирменные.
Всё самое плохое обычно делается под брендом Epistar. Цифры в маркировке обозначают лишь размер корпуса 5,6мм на 3,0мм.
В фирменных такой большой корпус используется для установки мощных кристаллов на 0,5W , поэтому у покупателей диодов СМД напрямую ассоциируется с мощностью 0,5W. Хитрый китаец этим пользуется, и в корпус устанавливает дешевый и слабенький кристалл в среднем на 0,1W , при этом указывая потребление энергии 0,5W. Наглядным примером будут автомобильные лампы и светодиодные кукурузы, в которых поставлено большое количество слабеньких и некачественных ЛЕД чипов.
Обычный покупатель считает, чем больше светодиодов чем лучше светит и выше мощность. Ищут хорошего продавца, который обещает определённые параметры, заказывают , ждут доставку месяц. После тестов оказывается, что китайский продавец обманул, продал барахло. Повезёт, если на седьмой раз придут приличные диоды, а не барахло. Обычно сделают 5 заказов, и не добившись результата и идут делать заказ в отечественный магазин, который может сделать обмен. Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов — параллельное подключение и последовательное.
Повезёт, если на седьмой раз придут приличные диоды, а не барахло. Обычно сделают 5 заказов, и не добившись результата и идут делать заказ в отечественный магазин, который может сделать обмен. Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов — параллельное подключение и последовательное.
Также возможно и смешанное, то есть последовательно параллельное соединение. Все зависит от назначения компонента и выполняемой им функции. А значит, и резисторы не избежали этих правил. Последовательное и параллельное сопротивление резисторов это по сути то же самое, что и параллельное и последовательное подключение источников света.
В параллельной цепи схема подключения подразумевает вход на все резисторы из одной точки, а выход из другой. Попробуем разобраться, каким образом выполняется последовательное соединение, а каким — параллельное.
И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение.
Начать следует с определений и правил. Виды соединения потребителей или элементов играют очень важную роль, ведь именно от этого зависят характеристики всей схемы, параметры отдельных цепей и тому подобное. Для начала попробуем разобраться с последовательным подключением элементов к схеме.
То есть общие значения равны сумме всех сопротивлений. При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно.
Параллельное соединение
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при параллельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов. Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию.
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию.
Существует два основных способа соединения резисторов: расчета сопротивления цепи параллельно соединенных резисторов. так и при параллельном их соединении итоговая мощность будет равна сумме мощностей.
Работа и мощность тока
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов. Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока.
Таким образом, с уменьшением сопротивления происходит заметное возрастание тока.
Соединение резисторов
Регистрация Вход. Ответы Mail. Вопросы — лидеры Не взлетает квадрокоптер 1 ставка. Правильна ли Специальная теория относительности?
Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике. Здесь мы будем рассматривать только участок цепи , включающий в себя соединение резисторов.
Калькулятор онлайн для параллельного соединения резисторов: общие сведения, формулы расчета
Теория и практика. Кейсы, схемы, примеры и технические решения, обзоры интересных электротехнических новинок. Уроки, книги, видео. Профессиональное обучение и развитие. Сайт для электриков и домашних мастеров, а также для всех, кто интересуется электротехникой, электроникой и автоматикой. Мощность резистора: обозначение на схеме, как увеличить, что делать, если нет подходящего.
Последовательное и параллельное соединение резисторов
При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла.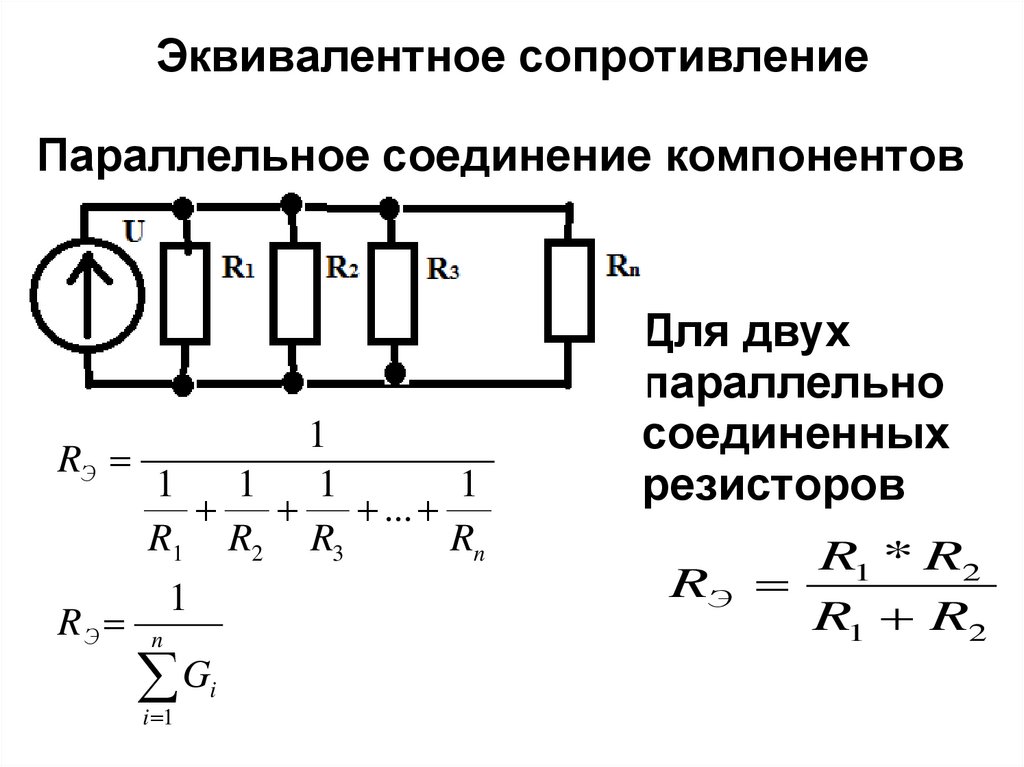 При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию. При последовательном соединении проводников сила тока во всех проводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников. При параллельном соединении падение напряжения между двумя узлами , объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи , равна сумме величин, обратных сопротивлениям параллельно включённых проводников.
При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию. При последовательном соединении проводников сила тока во всех проводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников. При параллельном соединении падение напряжения между двумя узлами , объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи , равна сумме величин, обратных сопротивлениям параллельно включённых проводников.
параллельное соединение резисторов. такую вот цепочку параллельно соединенных резисторов можно заменить Как мы помним из статьи про мощность произведение тока на напряжение есть мощность.
Параллельное соединение сопротивлений
Сопротивление трёх одинаковых резисторов, соединённых параллельно, в три раза меньше, чем сопротивление одного резистора. Сопротивление двух одинаковых резисторов, соединённых параллельно, в два раза меньше, чем сопротивление одного резистора.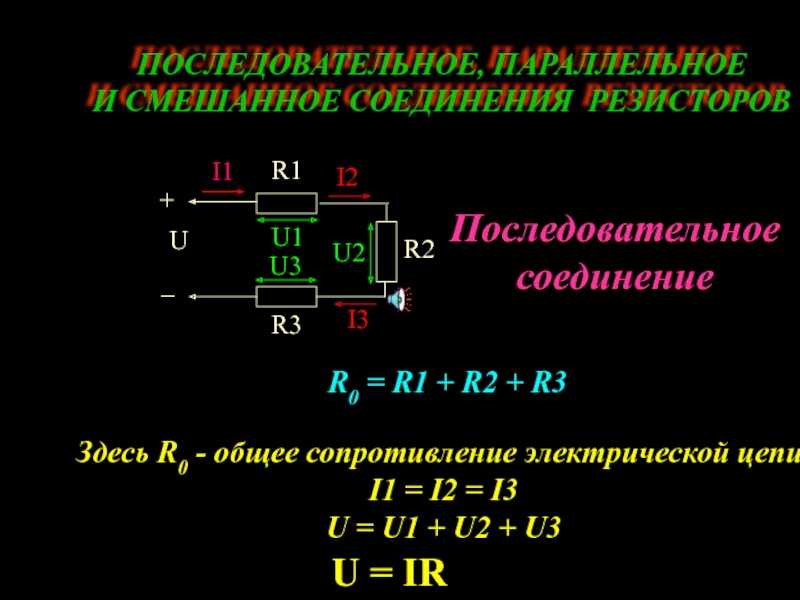 Параллельным соединением сопротивлений называется такое соединение, когда начала сопротивлений соединены в одну общую точку, а концы — в другую.
Параллельным соединением сопротивлений называется такое соединение, когда начала сопротивлений соединены в одну общую точку, а концы — в другую.
Последовательное и параллельное соединение резисторов
ВИДЕО ПО ТЕМЕ: Расчет общего сопротивления последовательно и параллельно соединенных резистов
Работу электрического поля по перемещению свободных зарядов в проводнике называют работой тока. Рассмотрим практически важный случай, когда основным действием тока является тепловое действие. Докажите, что количество теплоты Q, выделившееся в проводнике с током, выражается также формулами. Джоуль за несколько лет до открытия закона сохранения энергии. Закон Джоуля — Ленца: количество теплоты, выделившееся за время t в проводнике сопротивлением R, сила тока в котором равна I, выражается формулой.
О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта.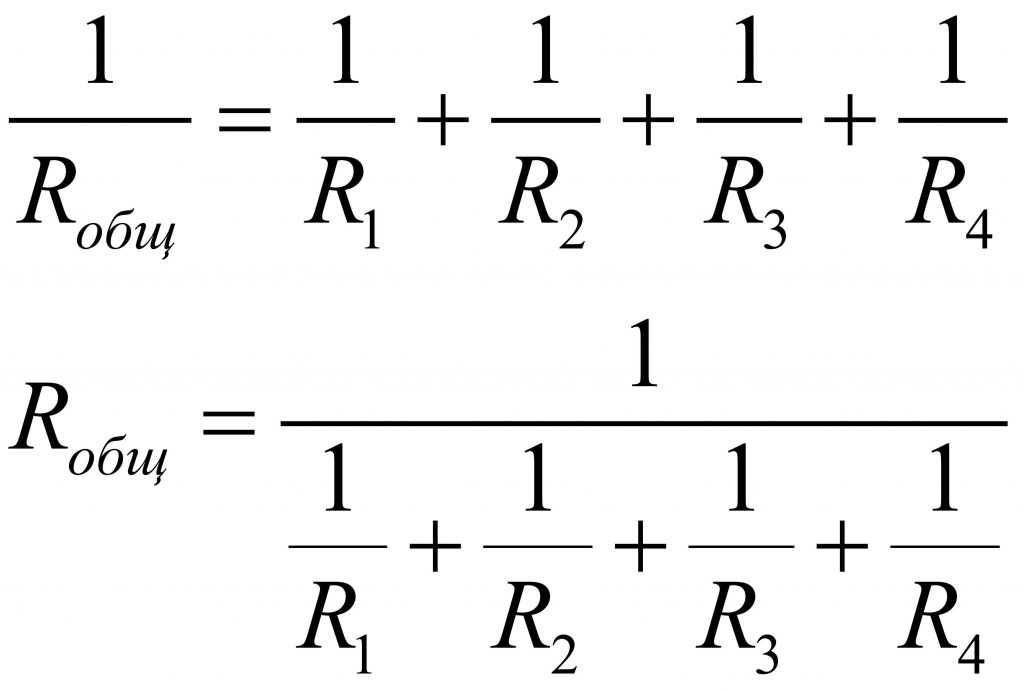
Соединение резисторов
Это такой тип подключения, в котором конец одного сопротивления соединен с началом второго, а конец второго сопротивления с началом третьего и так далее по цепочке:. То есть при последовательном соединении сопротивления подключатся друг за другом в одну цепочку. При таком подключении через них будет протекать один общий ток. Поэтому, для последовательного соединения резисторов можно сказать, что между точками А и Б смотри рисунок существует только один путь протекания тока. Таким образом, чем выше количество последовательно соединенных сопротивлений, тем более высокое сопротивление они оказывают протеканию тока, то есть общее сопротивление увеличивается. Рассчитывается последовательное соединение по следующей простейшей формуле из курса электротехники:.
Последовательное соединение сопротивлений. Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока рис. Такое соединение сопротивлений называется последовательным.
Такое соединение сопротивлений называется последовательным.
в последовательном и параллельном построении формулы » Electronics Notes
Вывод формул для расчета полного сопротивления резисторов, соединенных последовательно и параллельно.
Учебное пособие по сопротивлению Включает:
Что такое сопротивление
Закон Ома
Омические и неомические проводники
Сопротивление лампы накаливания
Удельное сопротивление
Таблица удельных сопротивлений для обычных материалов
Температурный коэффициент сопротивления
Коэффициент сопротивления по напряжению, VCR
Электрическая проводимость
Последовательные и параллельные резисторы
Таблица параллельных резисторов
Формулы для расчета полного сопротивления для ряда резисторов, включенных последовательно, а также для резисторов, включенных параллельно, хорошо известны.
Что может быть менее известно, так это рассуждение и вывод формул.
В некоторых случаях может потребоваться понимание того, как вывести формулы для набора резисторов, соединенных последовательно или параллельно, а также это помогает понять общую теорию цепей.
Основой для вывода уравнений как для последовательных, так и для параллельных формул резисторов является использование законов Кирхгофа. Используя их, выводы уравнений относительно просты.
Расчет общего сопротивления резисторов в серии
Уравнение для полного сопротивления ряда резисторов, включенных параллельно, представляет собой сумму всех резисторов, приведенных ниже.
Резисторы серииRобщ=R1+R2+R3+ ….
Первый этап доказательства формулы заключается в рассмотрении случая двух последовательно соединенных резисторов, чтобы увидеть, как ведет себя схема.
Резисторы, включенные последовательно — отдельные резисторы, токи и напряженияЗдесь показаны два резистора, но тот же вывод можно легко расширить до любого количества резисторов.

Есть два факта, которые необходимо учитывать при выводе формулы для полного сопротивления набора резисторов, соединенных последовательно. Во-первых, по цепи течет один и тот же ток. Один и тот же ток протекает через источник напряжения и резисторы.
Во-вторых, законы Кирхгофа гласят, что сумма напряжений в цепи равна нулю. Таким образом, сумма падений напряжения на резисторах равна напряжению, выдаваемому источником в показанной цепи.
Из закона Ома:
V1=IR1 & V2=IR2
Затем из закона Кирхгофа:
V-V1-V2=0 или V=V1+V2
Затем подставляя вместо V 20 4 и V
V=IR1+IR2=I(R1+R2)
Это упрощает до:
VI=R1+R2
Но V/I = R total , поэтому
Rtotal=R1+R2
59 Используя по той же логике можно расширить это до общего случая нескольких резисторов:
Rtotal=R1+R2+R3+ . …
…
Расчет общего сопротивления резисторов, включенных параллельно
Часто бывает так, что несколько резисторов располагаются параллельно. Во многих случаях это происходит при разработке электронных схем и т. д.
Ниже приведена стандартная формула для расчета общего сопротивления нескольких резисторов или резисторов, включенных параллельно.
1Rобщ=1R1+1R2+1R3+……
Вывод общего уравнения для набора нескольких параллельных резисторов довольно прост. Принимая во внимание основные аспекты схемы, можно легко вывести общее уравнение для набора резисторов, включенных параллельно.
Параллельные резисторы — отдельные резисторы, токи и напряженияПри выводе формулы для полного сопротивления набора параллельно соединенных резисторов необходимо учитывать ток, протекающий через каждый резистор по очереди, и понимать, что каждый резистор имеет одинаковая разность потенциалов или напряжение на нем.
Первое, что нужно понять, это то, что сумма токов, протекающих через отдельные резисторы, равна общему току, обеспечиваемому источником напряжения, как показано на диаграмме:
I=I1+I2+I3+ . ..In
..In
Зная, что I=V/R по закону Ома, можно соотнести уровни протекающих токов с точки зрения напряжения (которое одинаково для всех, поскольку они параллельны) и сопротивления.
I=VR1+VR2+VR3+ …VRn
Тогда, разделив обе части на V, мы получим:
IV=1R1+1R2+1R3+ …1Rn
Но поскольку I/V равно 1/ Всего R , это можно заменить в уравнении, чтобы получить:
1Rtotal=1R1+1R2+1R3+ …1Rn
Можно видеть, что вычислить общее сопротивление ряда параллельно соединенных резисторов очень просто.
Вывод формулы для двух резисторов, включенных параллельно
В различных электрических и электронных конструкциях или установках часто бывает необходимо рассчитать общее сопротивление двух резисторов, включенных параллельно.
В этом случае уравнение можно значительно упростить, что значительно упрощает вычисление полного сопротивления.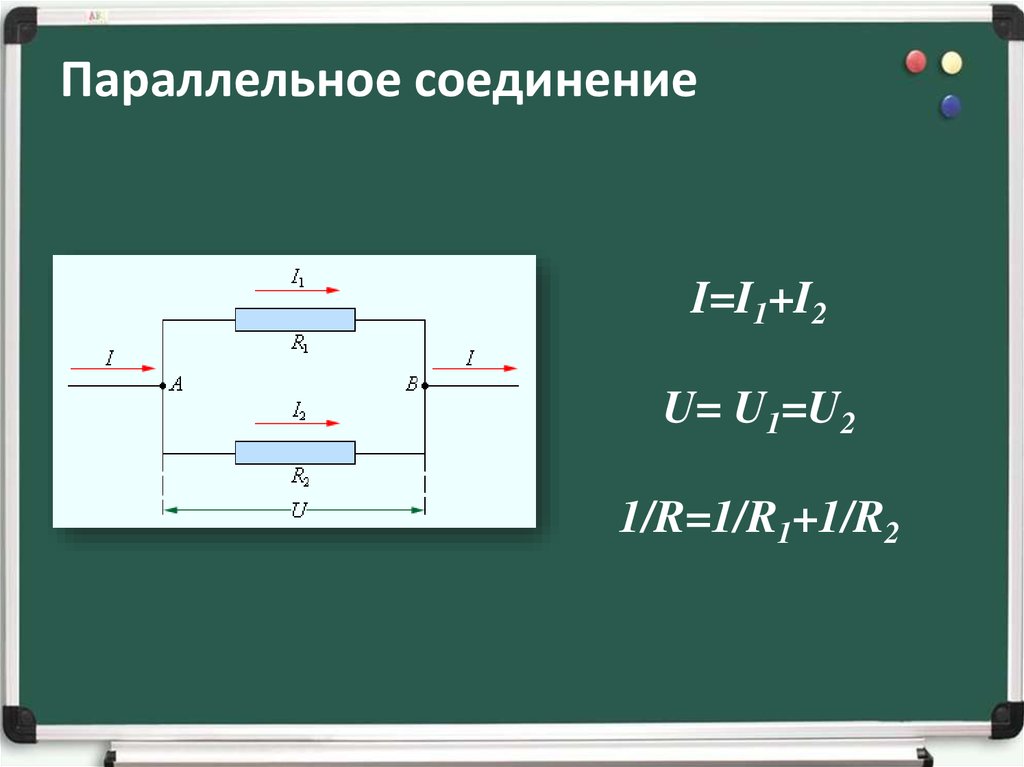
Rобщ=R1R2R1+R2
Получение этого уравнения относительно простое, требующее некоторых простых манипуляций с общим уравнением для параллельных резисторов, но упрощенное до включения только двух электронных компонентов.
1Rtotal=1R1+1R2
Multiplying through by R total gives:
1=RtotalR1+RtR2
Then multiple by R 1 and R 2
R1R2=RtotalR2+RtotalR1
Isolate R всего R1R2=Rtotal(R2+R1)
Затем разделите на (R 1 + R 2 )
Rtotal =R1R2R2+R1
Используя эту формулу, очень легко вычислить общее сопротивление двух резисторов, включенных параллельно
Уравнения для определения полного сопротивления наборов резисторов, соединенных последовательно и параллельно, широко используются во многих областях, от электрических работ до проектирования электронных схем, а также во множестве других областей. Хотя нет необходимости все время выводить уравнения из первых принципов, полезно понять, как это можно сделать, поскольку это дает гораздо лучшее понимание того, что происходит.
Хотя нет необходимости все время выводить уравнения из первых принципов, полезно понять, как это можно сделать, поскольку это дает гораздо лучшее понимание того, что происходит.
Дополнительные основные понятия и руководства по электронике:
Напряжение
Текущий
Сила
Сопротивление
Емкость
Индуктивность
Трансформеры
Децибел, дБ
Законы Кирхгофа
Q, добротность
РЧ-шум
Сигналы
Возврат в меню основных понятий электроники. . .
Объяснение урока: Параллельные схемы | Nagwa
В этом объяснителе мы научимся рассчитывать разность потенциалов, ток и сопротивление в разных точках простых параллельных цепей.
На приведенной ниже схеме показана схема, состоящая из ячейки и резистора. Разность потенциалов, обеспечиваемая ячейкой, равна 𝑉, ток в цепи равно 𝐼, а сопротивление резистора равно 𝑅.
В приведенной выше схеме есть только один путь, по которому могут течь электроны, чтобы двигаться от одного конца ячейки к другому. Однако в приведенной ниже схеме
есть два пути, по которым электроны могут течь, чтобы двигаться от одного конца ячейки к другому.
Однако в приведенной ниже схеме
есть два пути, по которым электроны могут течь, чтобы двигаться от одного конца ячейки к другому.
Путь между двумя терминалами ячейки разветвляется на две ветви в точке A. Пути снова соединяются в точке B. На каждом пути есть резистор.
Когда существует несколько различных путей, по которым электроны могут пройти между выводами ячейки, как этот, мы говорим, что эта часть цепи параллельно . Если в цепи есть элементы, включенные последовательно и параллельно, то она называется комбинированной схемой. Когда все компоненты цепи соединены только параллельными соединениями, это называется параллельной цепью.
Давайте рассмотрим пример.
Пример 1: Идентификация компонентов, соединенных параллельно
На схеме показаны четыре цепи. Какая цепь содержит два резистора, включенных параллельно?
Ответ
Компоненты подключены параллельно , если они находятся на разных путях цепи.
В цепи а есть два резистора, но они находятся на одном пути, а не на разных. Электроны, идущие от одного конца клетки к другому, должны пройти через оба резистора. Следовательно, они последовательно, а не параллельно.
Схема b очень похожа на схему; единственное отличие состоит в том, что компоненты размещены на разных сторонах диаграммы. Это не влияет независимо от того, соединены ли компоненты последовательно или параллельно, эти компоненты также соединены последовательно.
В схеме d есть два возможных пути движения электронов между клеммами ячейки, но один путь проходит через лампочку, а другой — через два резистора последовательно. Резисторы параллельны лампочке, но не друг другу.
В схеме c также есть два возможных пути движения электронов, каждый из которых содержит резистор. Эти резисторы включены параллельно.
Правильный ответ: схема c.
Определить, где именно начинается и где заканчивается параллельная цепь, может быть непросто. Рассмотрим следующие параллельные схемы.
Рассмотрим следующие параллельные схемы.
Несмотря на то, что кажется, что они начинаются и заканчиваются в разных местах, эти цепи эквивалентны. Обведенная площадь обоих точно такая же: раскол, с 𝑅 на одном пути и 𝑅 на другом, то оба пути в конце сходятся.
Пока пути, по которым проходят токи, одинаковы, цепи эквивалентны. На схеме ниже есть еще две схемы, которые эквивалентны.
Ориентация компонентов не имеет значения, если схема может быть описана одинаково — в данном случае это разделение на два пути, один содержит 𝑅, а другой 𝑅, которые затем снова собираются вместе.
На приведенной ниже схеме показаны четыре полностью эквивалентные схемы с двумя резисторами и лампочкой.
Эти схемы эквивалентны, поскольку компоненты соединены параллельно. Все они могут быть описаны как раздвоение пути, одно из которых содержит
два резистора, а другой содержит лампочку, а затем пути снова собираются вместе. На рисунке ниже это описание показано визуально с использованием двух схем.
Давайте рассмотрим пример.
Пример 2. Определение эквивалентных схем цепей
На схеме показаны четыре цепи с компонентами, соединенными параллельно. Какие две схемы эквивалентны?
Ответ
Рассмотрим пути в этих цепях. Цепь а имеет разделение с резистором 10 Ом. на одном пути и лампочка и резистор 20 Ом на другом.
Цепь b имеет разделение с резистором 20 Ом на одном пути и лампочкой и Резистор 10 Ом с другой стороны.
Цепь c сначала имеет резистор 20 Ом, а затем разделяется на две цепи с лампочкой на одной и другой. резистор 10 Ом с другой стороны. Примечательно, что это не настоящая параллельная схема, а скорее комбинированная схема, так как он имеет компоненты как последовательно, так и параллельно.
Цепь d разделена, с резистором 10 Ом на одном пути и лампочкой и резистор 20 Ом с другой стороны.
Если ток проходит по одному и тому же пути через одни и те же компоненты, цепи эквивалентны. Два, которые описываются одинаково, это a и d.
Два, которые описываются одинаково, это a и d.
В параллельной цепи разность потенциалов на каждой параллельной ветви будет одинаковой. Независимо от значений сопротивления компонентов на этих путях, разность потенциалов на каждом из них будет одинаковой. На приведенной ниже диаграмме показаны два вольтметра, измеряющие разность потенциалов на двух резисторах.
Если 𝑅 равно 1 Ом и 𝑅 равно 1 000 Ом, не имеет значения. Разность потенциалов между ними составляет 20 В.
Правило: Разность потенциалов между компонентами, включенными параллельно
Разность потенциалов на каждой ветви параллельной цепи одинакова: 𝑉=𝑉=𝑉=….
Давайте рассмотрим пример.
Пример 3: поиск потенциальных различий между компонентами, включенными параллельно
На схеме показаны два резистора, подключенных параллельно к ячейке. Если разность потенциалов на 3 Ом резистор 18 В, какова разность потенциалов на резистор 6 Ом?
Ответ
Разность потенциалов между параллельными компонентами определяется правилом
𝑉=𝑉=𝑉=….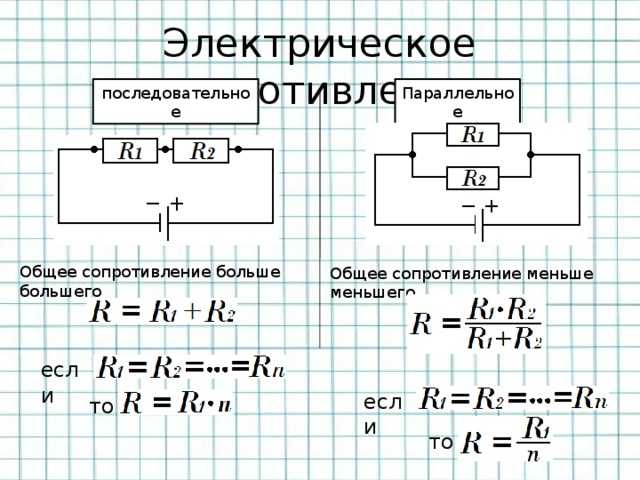
Для этой схемы с двумя компонентами правило выглядит так 𝑉=𝑉.
Нам дано значение разности потенциалов на резисторе 3 Ом, 𝑉, быть 18 В. Разность потенциалов на резисторе 6 Ом тогда должно быть одинаково: 18 В.
В отличие от разности потенциалов на разных ветвях, которая одинакова для каждой ветви, ток в каждой ветви может быть разным.
Напомним, что сопротивление — это противодействие потоку электрического заряда. Если одна ветвь имеет большее сопротивление, чем другая, заряду будет труднее течь по ней. и поэтому ток в нем будет слабее, а ток в другом ответвлении сильнее.
Однако все электроны из ячейки должны пройти по одной из ветвей. Следовательно, суммарный ток по всем ветвям будет равен к току до того, как путь цепи разделился.
На приведенной ниже диаграмме общий ток 𝐼total равен сумме токов в отдельных ветвях, 𝐼 и 𝐼.
Правило: Суммарный ток в параллельных цепях цепи
Суммарный ток параллельных компонентов, 𝐼total, равен сумме токов в каждой цепи:
𝐼=𝐼+𝐼+𝐼+…, всего
где 𝐼, 𝐼, 𝐼 и т.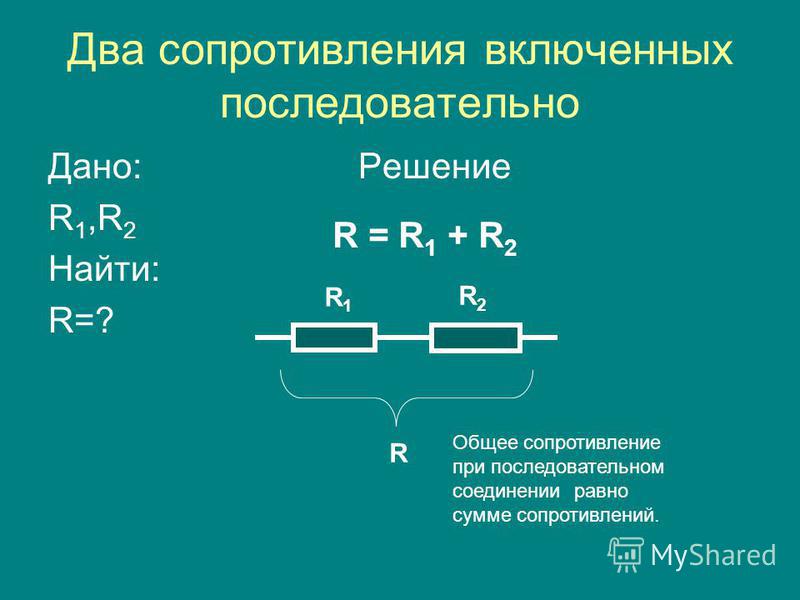 д. — токи на определенном пути.
д. — токи на определенном пути.
Точный способ разделения тока зависит от сопротивления каждого пути. На приведенной ниже диаграмме показана цепь, которая разделена на три пути с током в каждом.
Нам дан общий ток 𝐼общий и ток в двух путях вдоль резисторов 𝑅 и 𝑅. Мы можем использовать их, чтобы найти ток через крайний левый путь, 𝐼.
Суммарный ток в цепи равен 9 А. Средний путь можно назвать 𝐼, а крайний правый путь 𝐼, равный 5 A и 1 A соответственно. Мы можем использовать правило для полного тока вдоль параллельных путей, чтобы представить это как уравнение: 𝐼=𝐼+𝐼+𝐼.Всего
Подставляя наши известные значения тока, уравнение принимает вид (9)=𝐼+(5)+(1)9=𝐼+6.AAAAAA
Чтобы найти 𝐼, нам нужно вычесть 6 А с обеих сторон: 9−6=𝐼+6−63=𝐼.AAAAA
Итак, ток по крайнему левому пути, 𝐼, равен 3 А.
Предположим теперь, что нам не задан ток по пути, как в диаграмма ниже.
Мы можем определить, сколько тока проходит по каждому пути, сравнив значения сопротивления.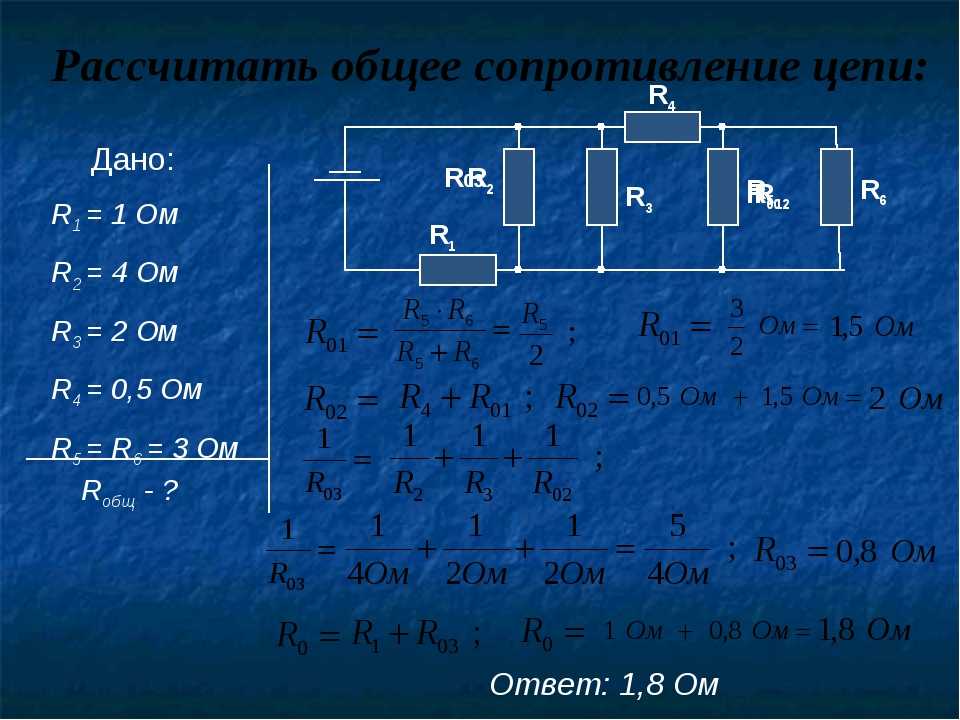 На приведенной выше схеме резисторы имеют одинаковое значение
сопротивления 𝑅. Это означает, что ток будет равномерно разделен между двумя путями:
𝐼=𝐼.
На приведенной выше схеме резисторы имеют одинаковое значение
сопротивления 𝑅. Это означает, что ток будет равномерно разделен между двумя путями:
𝐼=𝐼.
Итак, глядя на общий ток, 𝐼=𝐼+𝐼.total
Подстановка всех токов на 𝐼, поскольку они одинаковы, дает нам 𝐼=𝐼+(𝐼)𝐼=2𝐼.totaltotal
Чтобы найти 𝐼, мы просто делим обе части на 2: 𝐼2=2𝐼2𝐼2=𝐼.totaltotal
Таким образом, отдельные пути имеют половину общего тока. Суммарный ток равен 8 А, поэтому 𝐼2=4.totalA
Поскольку 𝐼 и 𝐼 равны друг другу, они оба равны 4 А.
Давайте рассмотрим несколько примеров вопросов.
Пример 4: Определение токов через компоненты, соединенные параллельно
Цепь, показанная на схеме, состоит из двух резисторов, подключенных параллельно к ячейке. Значение 𝐼total равно до 30 А. Каково значение 𝐼?
Ответ
Суммарный ток в цепи с параллельными элементами определяется по правилу
𝐼=𝐼+𝐼+𝐼+…. total
total
Всего для двух компонентов на разных путях это правило становится 𝐼=𝐼+𝐼.Всего
Два резистора на дорожках в этой цепи одинаковы, поэтому ток распределяется между ними поровну. Это означает, что текущий 𝐼 то же, что и 𝐼: 𝐼=𝐼.
Подстановка этого соотношения в правило для полного тока дает 𝐼=(𝐼)+𝐼𝐼=2𝐼.totaltotal
Теперь, чтобы найти 𝐼, разделим обе части на 2: 𝐼2=2𝐼2.total
Это приводит к тому, что 2 в правой части уравнения отменяется, оставляя 𝐼2=𝐼.всего
Суммарный ток равен 30 А. Подстановка этого значения дает значение 𝐼: (30)2=15.AA
Итак, значение 𝐼 равно 15 А.
Чтобы проследить, как ток изменяется в зависимости от сопротивления пути, мы должны сначала посмотреть, как найти общее сопротивление компонентов, включенных параллельно. .
Правило: общее сопротивление компонентов, расположенных параллельно
Для ряда компонентов, расположенных параллельно, общее сопротивление 𝑅total равно
1𝑅=1𝑅+1𝑅+1𝑅+…, всего
где 𝑅 — сопротивление первой составляющей, 𝑅 — второй и т. д.
д.
Давайте используем это уравнение только с двумя резисторами, 𝑅 и 𝑅, чтобы продемонстрировать, как найти 𝑅общий сам по себе. Это делает уравнение 1𝑅=1𝑅+1𝑅.total
Мы можем взять обратное значение обеих частей, чтобы получить 𝑅total слева: 1=1+.total
Деление на дробь равносильно умножению на знаменатель, поэтому левая часть становится 1=1×𝑅1=𝑅.totaltotaltotal
Это делает уравнение 𝑅=1+.total
Теперь умножим обе части на 𝑅𝑅; поскольку это всего лишь один, он сохранит 𝑅полный член в левой части: 𝑅×𝑅𝑅=1+×𝑅𝑅.Всего
Дробь означает, что верх и низ будут распределяться поперек для дроби с правой стороны: 𝑅×1=1×𝑅𝑅+𝑅=𝑅+.totaltotal
𝑅 больше 𝑅, так что уравнение теперь равно единице 𝑅=𝑅1+.total
Теперь умножим обе части на 𝑅𝑅: 𝑅×𝑅𝑅=𝑅1+×𝑅𝑅.total
Умножая 𝑅 сверху и снизу для правой части, получаем
𝑅×1=𝑅×𝑅𝑅1+. total
total
𝑅 распределяется по знаменателю: 𝑅=𝑅𝑅𝑅+.total
𝑅𝑅 в знаменателе равно 1, что дает 𝑅=𝑅𝑅(𝑅+𝑅).total
Таким образом, при наличии двух резисторов это уравнение можно использовать для определения общего сопротивления цепи.
Правило: полное сопротивление двухкомпонентной параллельной цепи
Когда два компонента проходят параллельные пути, общее сопротивление 𝑅total равно 𝑅=𝑅𝑅(𝑅+𝑅), всего где 𝑅 — сопротивление первого компонента, а 𝑅 — сопротивление второго компонента.
В приведенной ниже схеме мы можем вычислить 𝑅total, используя это правило.
Примем 𝑅 за 5 Ом и 𝑅 за 20 Ом. Ввод этих значений в уравнение для полного сопротивления дает 𝑅=(5)(20)(5)+(20)=100(25).totalΩΩΩΩΩΩ
Деление на омы отменяет квадрат в омах член в числителе, дающий общее сопротивление как 100(25)=4.ΩΩΩ
Давайте рассмотрим пример.
Пример 5. Определение того, как изменяется ток в зависимости от количества параллельных путей в цепи
Учащийся устанавливает цепь, показанную на схеме.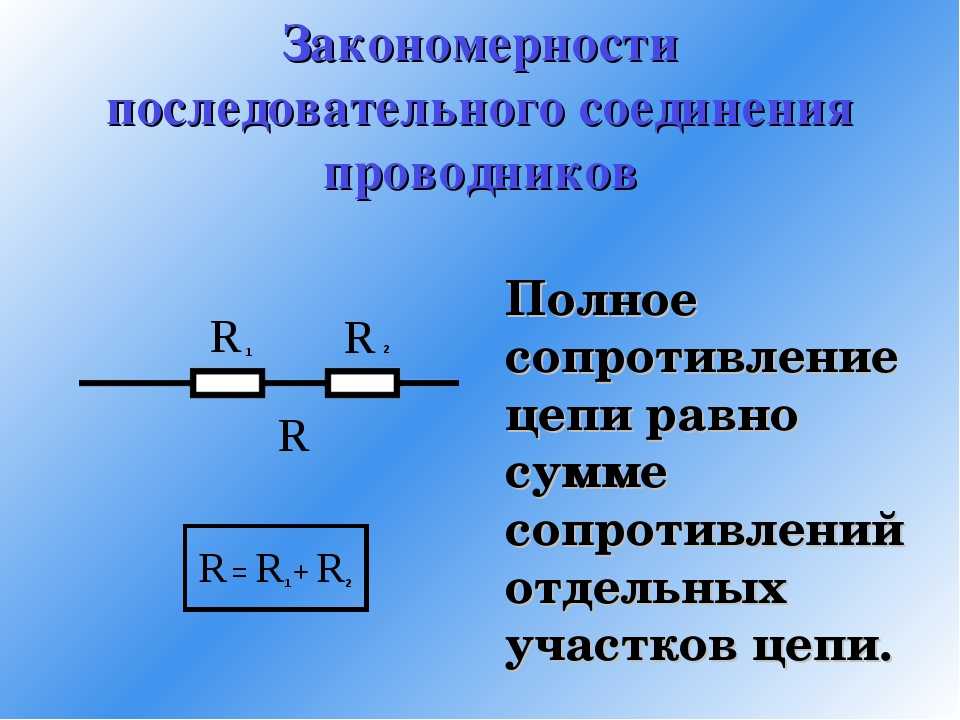 Изначально переключатель разомкнут. Когда ученик замкнет переключатель, будет ли ток течь через
схема увеличения или уменьшения?
Изначально переключатель разомкнут. Когда ученик замкнет переключатель, будет ли ток течь через
схема увеличения или уменьшения?
Ответ
Чтобы определить полный ток в цепи, закон Ома можно выразить через ток: 𝐼=𝑉𝑅.
Разность потенциалов в этой цепи фиксируется ячейкой, но сопротивление может изменяться, когда путь снизу закрыт. Назовем резисторы как 𝑅 и 𝑅 нравится так.
Первоначально, когда переключатель разомкнут, в нижней ветви этой цепи отсутствует ток. Все электроны из клетки будут проходить только через 𝑅. Таким образом, полное сопротивление можно описать как 𝑅=𝑅.total
Когда ключ замкнут, в ветвях, содержащих как 𝑅, так и 𝑅, будет ток. Напомним, что общая сопротивление в цепи с двумя параллельными резисторами определяется по уравнению 𝑅=𝑅𝑅(𝑅+𝑅).всего
Теперь, независимо от значения 𝑅, общее сопротивление будет уменьшаться. Это потому, что умножение 𝑅
на 𝑅, то деление на сумму всегда будет меньше, чем 𝑅 само по себе:
𝑅>𝑅𝑅(𝑅+𝑅).
Чтобы убедиться в этом, предположим, что 𝑅 равно 1 Ом, и проверим 𝑅 как 0,1 Ом и 1 000 Ом: 𝑅=1.Ω
Заменив 0,1 Ω на 𝑅, общее сопротивление 𝑅total станет 𝑅𝑅(𝑅+𝑅)(1)(0,1)((0,1)+(1))=0,099.ΩΩΩΩΩΩΩ
Теперь давайте попробуем заменить 1 000 Ом на 𝑅: (1)(1000)((1000)+(1))=0,999.ΩΩΩΩΩΩ
Мы видим, что в обоих этих случаях окончательный результат меньше, чем просто 𝑅.
Значит, если общее сопротивление уменьшается, то по закону Ома общий ток в цепи должен увеличиваться, так как ток обратно пропорционален к сопротивлению: 𝐼=𝑉𝑅.
Правильный ответ: ток увеличивается при замыкании ключа.
Теперь, когда мы видим, как работают ток, сопротивление и разность потенциалов в параллельных цепях, мы можем использовать эти правила, чтобы найти нужные значения в цепи.
Давайте рассмотрим пример.
Пример 6: Определение значений разности потенциалов и тока для компонентов, соединенных параллельно
Схема, показанная на схеме, состоит из двух резисторов, подключенных параллельно к ячейке. Значение тока, даваемое вторым амперметром,
𝐼 равно 3 А. Каково значение 𝐼total?
Значение тока, даваемое вторым амперметром,
𝐼 равно 3 А. Каково значение 𝐼total?
Ответ
Мы знаем, что в параллельной цепи полный ток равен сумме всех токов в параллельных цепях. Таким образом, для этой цепи полный ток равен 𝐼=𝐼+𝐼.total
Это означает, что мы должны найти ток второго пути, 𝐼, поэтому мы можем добавить его к 𝐼 и найти общий ток. Мы можем сделать это, рассмотрев потенциальные различия на каждом пути.
Нам не известна разность потенциалов клетки, но мы знаем, что разность потенциалов одинакова на обоих путях: 𝑉=𝑉.
Это дает возможность использовать закон Ома, чтобы связать два пути вместе. Однако прежде чем мы это сделаем, предположим, что резистор вдоль путь 𝐼 — это 𝑅, а путь 𝐼 — это 𝑅.
Разность потенциалов по первому пути, используя закон Ома, можно записать как
𝑉=𝐼𝑅
и второй путь как
𝑉=𝐼𝑅,
но поскольку 𝑉=𝑉, мы можем связать эти уравнения как
𝐼𝑅=𝐼𝑅.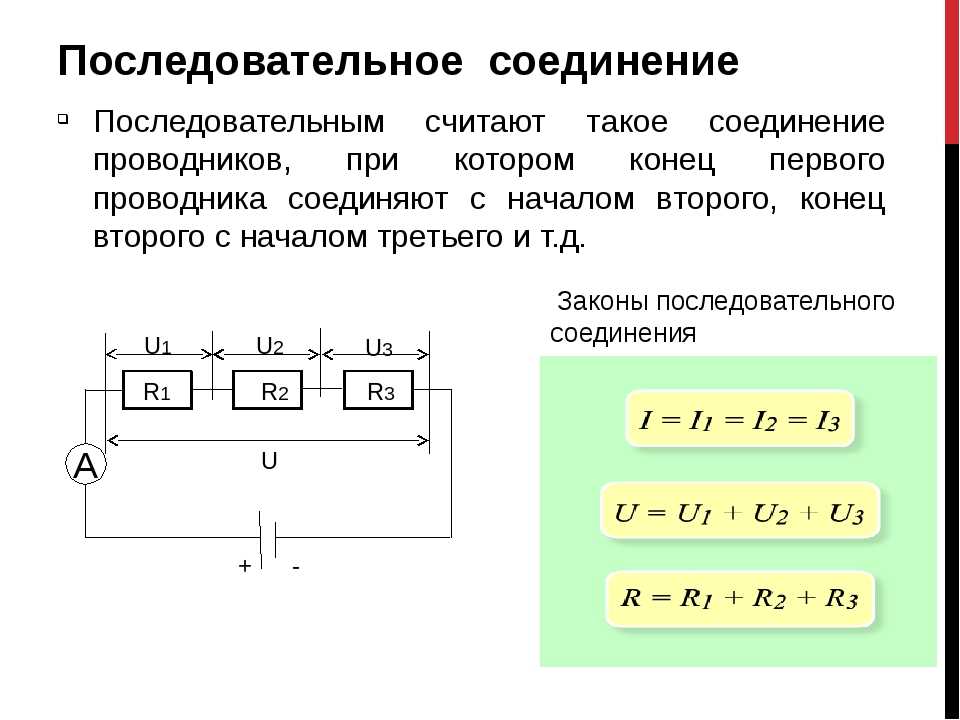
Теперь мы можем найти желаемое значение 𝐼, разделив обе части на 𝑅: 𝐼𝑅𝑅=𝐼𝑅𝑅.
Отмена с левой стороны дает 𝐼=𝐼𝑅𝑅.
𝐼 равно 3 А, 𝑅 равно 4 Ом, и 𝑅 равно 12 Ом. Подставляя эти значения в уравнение, получаем 𝐼=(3)(12)(4).AΩΩ
Теперь мы разделим единицы измерения омов, сократив их как в числителе, так и в знаменателе, что даст 𝐼=(3)(3)𝐼=9.AA
Теперь, когда у нас есть 𝐼, мы просто добавляем его вместе с 𝐼, чтобы получить общий ток: 𝐼=9+3𝐼=12.totaltotalAAA
Итак, общий ток 12 ампер.
Давайте подытожим то, что мы узнали из этого объяснения.
Ключевые точки
- Компоненты параллельны, если существует более одного пути прохождения тока.
- Параллельные цепи — это цепи, в которых все компоненты включены параллельно.
- Для ряда компонентов, расположенных на параллельных путях, общее сопротивление 𝑅total равно
1𝑅=1𝑅+1𝑅+1𝑅+…, всего
где 𝑅 — сопротивление первой составляющей, 𝑅 — второй и т.
 д.
д. - Для 2 резисторов, включенных параллельно, 𝑅=𝑅𝑅(𝑅+𝑅).total
- Полный ток 𝐼total в параллельной цепи делится между различными ветвями цепи так, что 𝐼=𝐼+𝐼+𝐼+….total
- Разность потенциалов на каждой параллельной ветви цепи одинакова: 𝑉=𝑉=𝑉=….
Базовая электрическая теория в двух словах
теория|
Правило №1: |
Один и тот же ток протекает через каждую часть серии схема. |
|
Правило №2: |
Общее сопротивление последовательной цепи равно сумма индивидуальных сопротивлений. |
|
Правило №3: |
Суммарное напряжение в последовательной цепи равно
к сумме отдельных падений напряжения.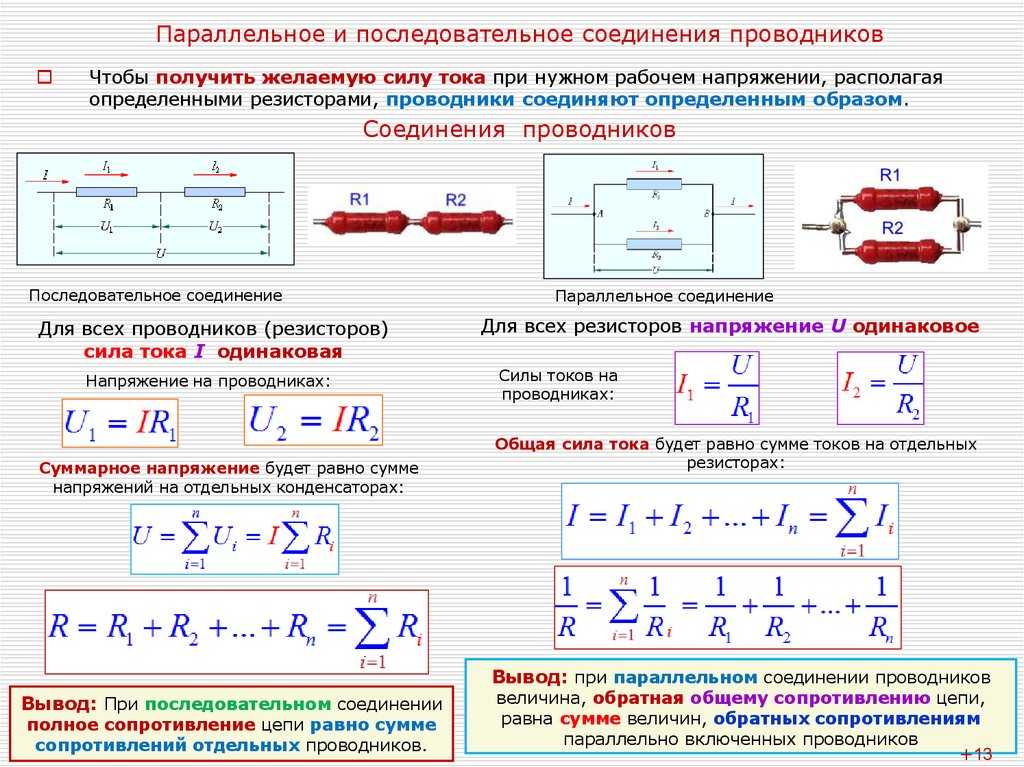 |
|
Правило 4: |
Падение напряжения на резисторе в последовательной цепи пропорциональна размеру резистора. |
|
Правило №5: |
Суммарная мощность, рассеиваемая в последовательной цепи, равна равна сумме индивидуальных потерь энергии. |
|
АМПЕР = |
ВОЛЬТ
СОПРОТИВЛЕНИЕ |
|
СОПРОТИВЛЕНИЕ = |
ВОЛЬТ
АМПЕР |
|
ВОЛЬТ = |
АМПЕРЫ x СОПРОТИВЛЕНИЕ |
|
Правило №1: |
На каждой ветви
параллельной цепи и равно напряжению источника. |
|
Правило № 2: |
Ток через ветку параллельной сети обратно пропорциональна величине сопротивления ветви. |
|
Правило №3: |
Суммарный ток параллельной цепи равен сумма токов отдельных ветвей цепи. |
|
Правило №4: |
Общее сопротивление параллельной цепи равно обратной величине суммы обратных величин отдельных сопротивлений цепи. |
|
Правило № 5: |
Суммарная мощность, рассеиваемая в параллельной цепи, равна равна сумме индивидуальных потерь энергии. |
|
ОБЩЕЕ НАПРЯЖЕНИЕ = |
E(1) = E(2) = E(3) .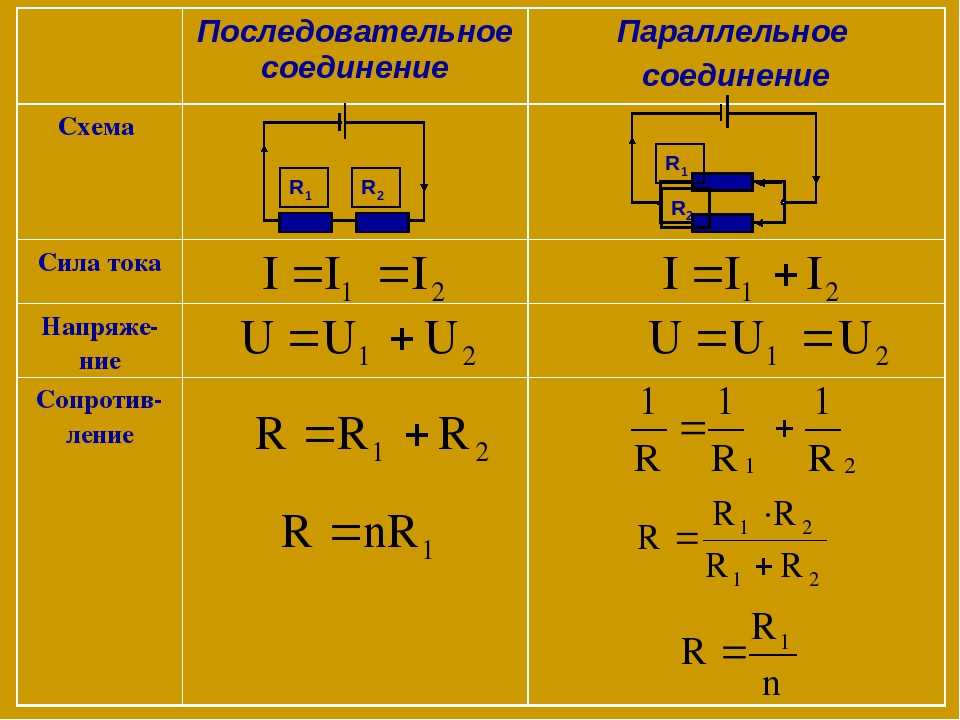 .. и т. д. .. и т. д. |
|
ВСЕГО СОПРОТИВЛЕНИЕ = |
ВОЛЬТ
АМПЕР |
|
ВОЛЬТ = |
ОБЩЕЕ НАПРЯЖЕНИЕ
ВСЕГО АМП |
ТО ОПРЕДЕЛИТЕ ОБЩЕЕ СОПРОТИВЛЕНИЕ В ПАРАЛЛЕЛЬНОЙ ЦЕПИ, КОГДА СУММАРНЫЙ ТОК И ОБЩЕЕ НАПРЯЖЕНИЕ НЕИЗВЕСТНО, ИСПОЛЬЗУЙТЕ ЛЮБУЮ ИЗ СЛЕДУЮЩИХ ФОРМУЛ:
|
РТ = |
1
___________________ 1 + 1 + 1 + ……и т. д. R1 R2 R3 |
|
| ДЛЯ ДВУХ РЕЗИСТОРОВ, ПОДКЛЮЧЕННЫХ ПАРАЛЛЕЛЬНО, ИСПОЛЬЗУЙТЕ ЭТО ФОРМУЛА НАЗЫВАЕТСЯ «ПРОИЗВЕДЕНИЕ НА СУММУ» | ||
|
RT = |
Р(1)
* Р(2)
Р(1) + Р(2) |
|
МОЩНОСТЬ В ОДНОЙ ФАЗЕ
РЕЗИСТИВНЫЕ ЦЕПИ
ГДЕ КОЭФФИЦИЕНТ МОЩНОСТИ
100 ПРОЦЕНТОВ
(ЭТИ
ФОРМУЛЫ ОБЫЧНО ИСПОЛЬЗУЮТСЯ ДЛЯ РЕШЕНИЯ БОЛЬШИНСТВА ПРОБЛЕМ С МОЩНОСТЬЮ ЦЕПИ НА ИСПЫТАНИЯХ)
ТО
ОПРЕДЕЛИТЬ МОЩНОСТЬ, ПОТРЕБЛЯЕМУЮ ОТДЕЛЬНЫМ СОПРОТИВЛЕНИЕМ В ПОСЛЕДОВАТЕЛЬНОЙ ЦЕПИ
ИСПОЛЬЗУЙТЕ ЭТУ ФОРМУЛУ:
|
МОЩНОСТЬ = |
I 2 x R |
ТО
ОПРЕДЕЛИТЬ МОЩНОСТЬ, ПОТРЕБЛЯЕМУЮ ОТДЕЛЬНЫМ РЕЗИСТОРОМ В ПАРАЛЛЕЛЬНОЙ ЦЕПИ
ИСПОЛЬЗУЙТЕ ЭТУ ФОРМУЛУ:
|
МОЩНОСТЬ = |
Е 2
Р |
ТО ОПРЕДЕЛИТЕ ОБЩУЮ МОЩНОСТЬ, ПОТРЕБЛЯЕМУЮ ОТДЕЛЬНОЙ ЦЕПЬЮ, ИСПОЛЬЗУЙТЕ ЭТУ ФОРМУЛУ:
МОЩНОСТЬ = Е
(ОБЩЕЕ НАПРЯЖЕНИЕ) x I (ОБЩИЙ ТОК)
ПРАВИЛА БОЛЬШОГО ПАЛЬЦА:
-
ТЕ
СУММАРНОЕ СОПРОТИВЛЕНИЕ СОЕДИНЕННЫХ РЕЗИСТОРОВ ВСЕГДА МЕНЬШЕ ЗНАЧЕНИЯ
ЛЮБОГО ОДНОГО РЕЗИСТОРА.

- ТЕ ОБЩЕЕ СОПРОТИВЛЕНИЕ ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРОВ, КОТОРЫЕ ВСЕ ОДИНАКОВЫ ЗНАЧЕНИЕ, ДЕЛЕННОЕ НА КОЛИЧЕСТВО РЕЗИСТОРОВ.
- ВСЕГДА ИСПОЛЬЗУЙТЕ ПРАВИЛО ПРОИЗВЕДЕНИЯ НА СУММУ, ЧТОБЫ РАЗБИТЬ ДВА ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРА НА ОДИН РЕЗИСТОР. ЭТО ГОРАЗДО ПРОЩЕ, ЧЕМ ПЫТАТЬСЯ РЕШАТЬ БОЛЬШИЕ АЛГЕБРАИЧЕСКИЕ ЗАДАЧИ. ВЫРАЖЕНИЯ.
- 746 ВАТТ РАВНЫ ОДНОЙ ЛОШАДЕЙНОЙ СИЛЕ
- ЭФФЕКТИВНОСТЬ РАВНО ВЫХОДУ, ДЕЛЕННОМУ НА ВХОД
- В ИНДУКТИВНЫЕ ЦЕПИ ТОК ОТСТАЕТ НАПРЯЖЕНИЕ.
- В НАПРЯЖЕНИЕ ТОКОВОДОВ ЕМКОСТНЫХ ЦЕПЕЙ.
- МОЩНОСТЬ КОЭФФИЦИЕНТ ЯВЛЯЕТСЯ ПОКАЗАТЕЛЕМ НАСКОЛЬКО ТОК ОПЕРЕЖАЕТ ИЛИ ОТСТАЕТ НАПРЯЖЕНИЕ.
МОЩНОСТЬ ПЕРЕМЕННАЯ ТОКОВЫЕ ЦЕПИ, ГДЕ КОЭФФИЦИЕНТ МОЩНОСТИ НЕ 100 ПРОЦЕНТОВ
(Истинная СИЛА) = E x I x КОЭФФИЦИЕНТ МОЩНОСТИ (ДЛЯ ОДНА ФАЗ)
(Истинная СИЛА) = E x I x 1,732 X КОЭФФИЦИЕНТ МОЩНОСТИ (ДЛЯ ТРЕХФАЗНЫЙ)
ЭТО
МОЩНОСТЬ ТАКЖЕ НАЗЫВАЕТСЯ ИСТИННОЙ МОЩНОСТЬЮ ИЛИ РЕАЛЬНОЙ МОЩНОСТЬЮ В ПРОТИВОПОЛОЖНОСТИ КАЖУЩЕЙСЯ МОЩНОСТИ
НАХОДИМСЯ ПОДСЧЁТОМ ВОЛЬТ-АМПЕР.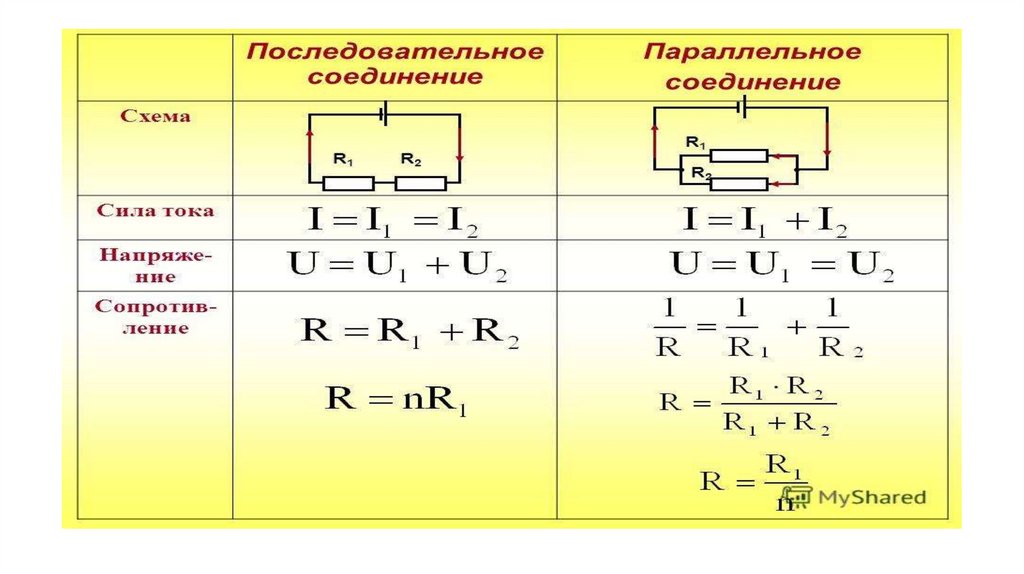
Ваттметр показывает истинную мощность.
Полная мощность = ВОЛЬТ-АМПЕР = Е х I (ДЛЯ ОДНОФАЗНЫЙ)
Полная мощность = ВОЛЬТ-АМПЕР = E x I x 1,732 (ДЛЯ ТРИ ФАЗЫ)
ИТ МОЖЕТ ЛЕГКО ОПРЕДЕЛИТЬСЯ АЛГЕБОЙ, ЧТО
|
КОЭФФИЦИЕНТ МОЩНОСТИ = |
ИСТИННАЯ СИЛА
ПОЛНАЯ МОЩНОСТЬ |
МОТОР ФОРМУЛЫ ПРИМЕНЕНИЯ
|
ЛОШАДИНАЯ МОЩНОСТЬ
=
|
1,732 x ВОЛЬТ x АМПЕР x КПД x коэффициент мощности
746 |
|
ТРЕХФАЗНЫЕ АМПЕРЫ =
|
746 х ЛОШАДЕЙНЫХ МОЩНОСТЕЙ
1,732 x ВОЛЬТ x КПД x КОЭФФИЦИЕНТ МОЩНОСТИ |
|
СИНХРОННЫЙ Об/мин = |
ГЕРЦ x 120
КОЛИЧЕСТВО ПОЛЮСОВ |
МОТОР
МАРКИРОВКА И СОЕДИНЕНИЯ
СОЕДИНЕНИЯ
ДЛЯ ДЕВЯТИ ВЫВОДОВ
ТРИ
ФАЗНЫЕ ДВИГАТЕЛИ
ТРИ ФАЗНАЯ ЗВЕЗДА ИЛИ Y
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ТРИ
ФАЗ ДЕЛЬТА
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ДЕЛЬТА СОЕДИНЕНИЕ ЗВЕЗДОЙ ДЛЯ ТРАНСФОРМАТОРА
МОТОР
КОНТРОЛЛЕР С ТРИ
СТАРТ
СТОП
(УДЕРЖАНИЕ
КОНТАКТЫ НЕ ПОКАЗАНЫ)
ТРАНСФОРМАТОР КОЭФФИЦИЕНТ ОБОРОТОВ
Эп = Тп
Es Ts
Где
Ep — первичное напряжение
Es — вторичное напряжение
Tp — количество витков в первичной обмотке.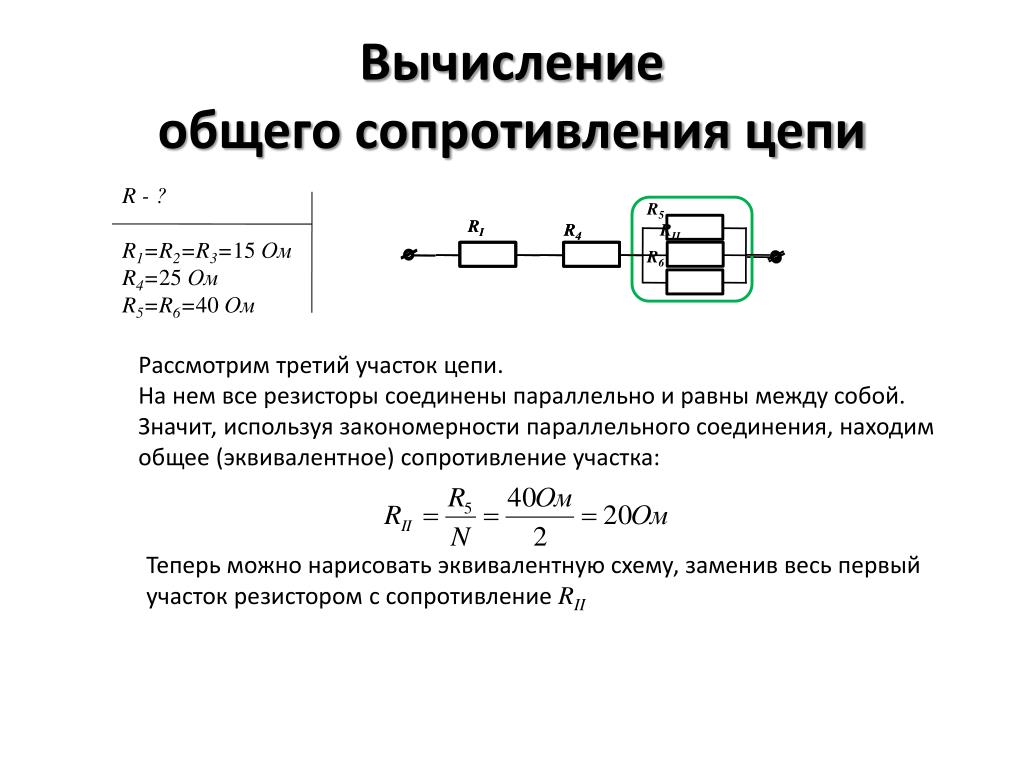
Ts — количество витков во вторичной обмотке.
Подключение переключателя
4-ходовой
D-S, E-R, F-T, G-W
3-ходовой
от А до Я, от В до Y, от С до Х
Пример заполнения кабельного лотка
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
РЕЙТИНГ NEMA ДЛЯ КОРПУСА
NEMA и другие организации установили стандарты конструкции корпуса для аппаратуры управления. В целом, оборудование будет закрыто по одной или нескольким из следующих причин:
- Предотвращайте случайный контакт с токоведущими частями.
- Защитите управление от вредного воздействия окружающей среды условия.
- Предотвратите взрыв или пожар, которые могут в результате электрической дуги, вызванной системой управления.
NEMA I — ОБЩЕЕ НАЗНАЧЕНИЕ
Корпус общего назначения предназначен
в первую очередь для предотвращения случайного контакта с закрытым устройством. Это
подходит для общего применения внутри помещений, где он не подвергается воздействию
к необычным условиям эксплуатации. Корпус NEMA I служит защитой
от пыли и легких непрямых брызг, но не является пыленепроницаемым.
Это
подходит для общего применения внутри помещений, где он не подвергается воздействию
к необычным условиям эксплуатации. Корпус NEMA I служит защитой
от пыли и легких непрямых брызг, но не является пыленепроницаемым.
NEMA 3 — ПЫЛЕЗАЩИТНЫЙ, ВОДОНЕПРОНИЦАЕМЫЙ
Этот корпус предназначен для обеспечения надлежащая защита от определенных погодных опасностей. Корпус NEMA 3 подходит для применения на открытом воздухе, в доках кораблей, на каналах и в строительстве работы, так и для применения в метро и туннелях. Он также устойчив к мокрому снегу.
NEMA 3R — ДОЖДЕВОЙ, УСТОЙЧИВЫЙ К МОЛОДУ
Этот корпус защищает от помех в эксплуатации содержащегося оборудования из-за дождя и сопротивляется повреждениям от воздействия мокрого снега. Он разработан с концентраторами кабелепровода и внешним креплением, а также условия дренажа.
NEMA 4 — ВОДОНЕПРОНИЦАЕМОСТЬ
Водонепроницаемая оболочка предназначена
пройти испытание шланга, описанное в следующем примечании: «Корпуса должны
быть проверены путем воздействия струи воды. Шланг с насадкой один дюйм
должны использоваться и должны подавать не менее 65 галлонов в минуту. Вода
должны быть направлены на ограждение с расстояния не менее 10
футов и в течение пяти минут. В этот период он может быть направлен
в любом одном или нескольких направлениях по желанию. Не должно быть утечки
воды в корпус в этих условиях».
Шланг с насадкой один дюйм
должны использоваться и должны подавать не менее 65 галлонов в минуту. Вода
должны быть направлены на ограждение с расстояния не менее 10
футов и в течение пяти минут. В этот период он может быть направлен
в любом одном или нескольких направлениях по желанию. Не должно быть утечки
воды в корпус в этих условиях».
Корпус NEMA 4 подходит для применение на открытом воздухе в доках кораблей и на молочных заводах, пивоваренных заводах и т. д.
NEMA 4X — ВОДОНЕПРОНИЦАЕМЫЙ, СТОЙКИЙ К КОРРОЗИИ
Эти корпуса обычно изготавливаются по линиям корпусов NEMA 4, за исключением того, что они сделаны из материала что обладает высокой устойчивостью к коррозии. По этой причине они идеально в таких приложениях, как бумажные фабрики, упаковка мяса, удобрения и химикаты заводы, где загрязняющие вещества обычно разрушают стальную оболочку над Период времени.
NEMA 7 – ОПАСНЫЕ ЗОНЫ – КЛАСС я
Эти корпуса предназначены для
требования к применению Национального электротехнического кодекса для класса
I опасные места. В этом типе оборудования прерывание цепи
происходит в воздухе.
В этом типе оборудования прерывание цепи
происходит в воздухе.
«Помещения класса I — это места, в которых легковоспламеняющиеся газы или пары присутствуют или могут присутствовать в воздухе в количествах, достаточно для образования взрывоопасных или воспламеняющихся смесей».
NEMA 9 ОПАСНЫЕ ЗОНЫ — КЛАСС II
Эти корпуса предназначены для требования к применению Национального электротехнического кодекса для класса II опасные места.
«Помещения класса II — это помещения, опасны из-за наличия горючей пыли».
Буква или буквы, следующие за номер типа указывает на конкретную группу или группы опасных зон (как определено в Национальном электротехническом кодексе), для которых корпус разработан. Обозначение является неполным без суффиксной буквы или букв.
NEMA 12 — ПРОМЫШЛЕННОЕ ИСПОЛЬЗОВАНИЕ
Корпус NEMA 12 предназначен для
использование в тех отраслях промышленности, где желательно исключить такие материалы, как
пыль, ворсинки, волокна и летучие частицы, масло см.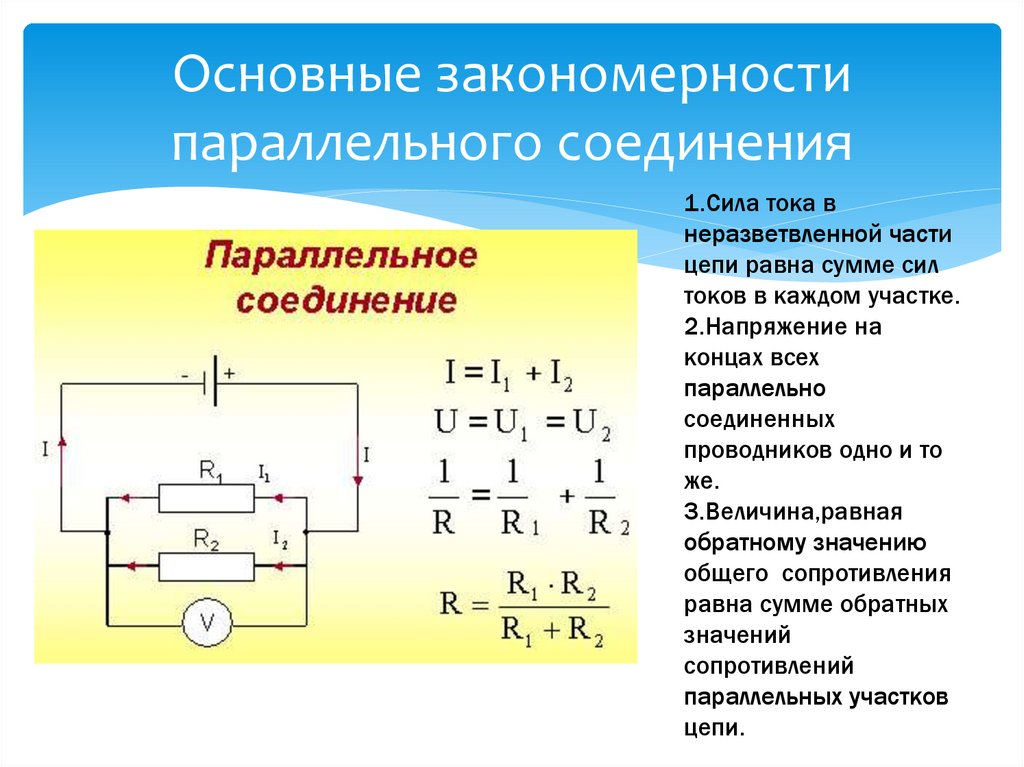

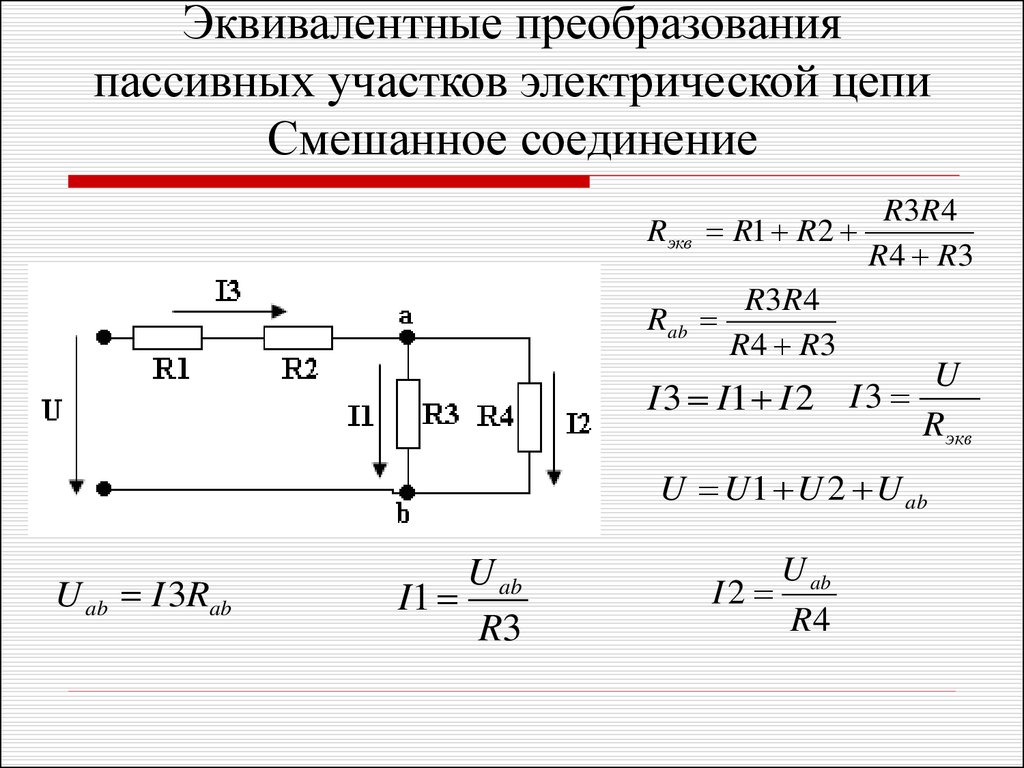 22(A).
22(A).
 10
10 