Что такое логическая операция XOR. Как работает вентиль исключающего ИЛИ. Какая таблица истинности у XOR. Где применяется операция исключающего ИЛИ. Как реализовать XOR с помощью базовых логических элементов.
Что такое операция исключающего ИЛИ (XOR)
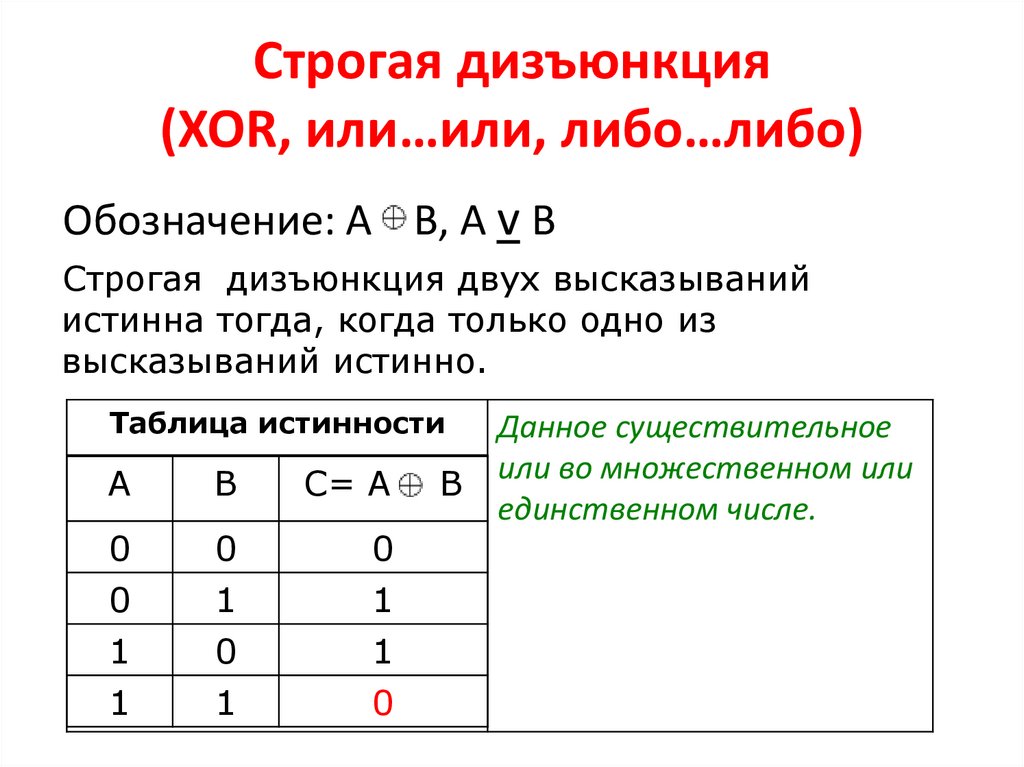
Исключающее ИЛИ (XOR) — это логическая операция, которая возвращает истинное значение тогда и только тогда, когда входные значения различны. Другими словами, XOR дает результат «истина», если ровно один из входов истинен, но не оба.
Операция XOR обозначается символом ⊕. Ее можно определить через базовые логические операции следующим образом:
A ⊕ B = (A ∨ B) ∧ ¬(A ∧ B)
То есть XOR эквивалентно комбинации операций ИЛИ, И и НЕ.
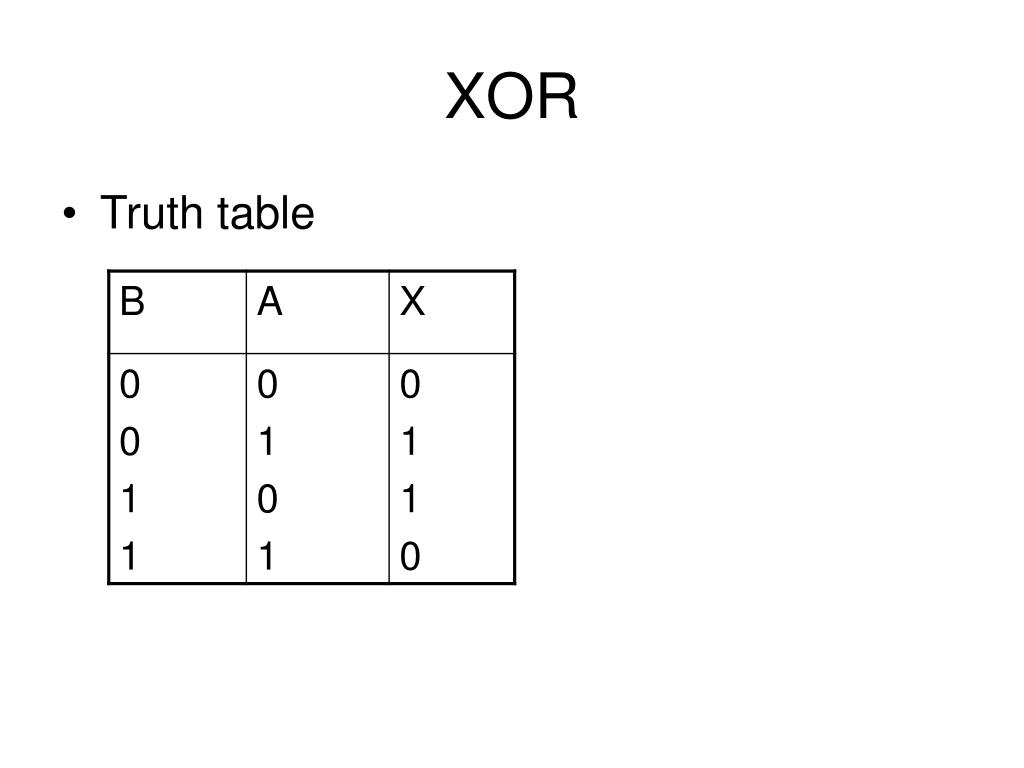
Таблица истинности XOR
Таблица истинности для операции исключающего ИЛИ выглядит следующим образом:
| A | B | A ⊕ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Как видно из таблицы, результат XOR равен 1 только когда входы различны (0 и 1 или 1 и 0). Во всех остальных случаях результат равен 0.
Принцип работы вентиля XOR
Логический элемент XOR реализует операцию исключающего ИЛИ на аппаратном уровне. Он имеет два входа и один выход. Выход элемента XOR принимает значение 1 (высокий уровень), только если значения на его входах различны. Если оба входа имеют одинаковое значение (оба 0 или оба 1), выход равен 0 (низкий уровень).
Работу вентиля XOR можно описать следующей логической функцией:
Y = A’B + AB’
Где A и B — входы, Y — выход, а штрих обозначает инверсию.
Реализация XOR через базовые логические элементы
Хотя XOR является самостоятельной логической операцией, ее можно реализовать с помощью комбинации базовых логических элементов. Рассмотрим несколько вариантов такой реализации:
С помощью элементов И, ИЛИ и НЕ
XOR можно собрать из следующих элементов:
- 2 инвертора (НЕ)
- 2 элемента И
- 1 элемент ИЛИ
Схема будет выглядеть так:
- Инвертируем входы A и B
- Подаем A и инвертированный B на первый элемент И
- Подаем инвертированный A и B на второй элемент И
- Выходы элементов И подаем на элемент ИЛИ
Через элементы И-НЕ (NAND)
XOR также можно реализовать с помощью 4 элементов И-НЕ:
- Подаем A и B на первый элемент И-НЕ
- Подаем A и выход первого И-НЕ на второй И-НЕ
- Подаем B и выход первого И-НЕ на третий И-НЕ
- Выходы второго и третьего И-НЕ подаем на четвертый И-НЕ
Применение операции XOR
Исключающее ИЛИ находит широкое применение в цифровой технике и криптографии. Рассмотрим основные области использования XOR:
Арифметические схемы
XOR используется в схемах сложения двоичных чисел. Например, однобитный полусумматор реализуется с помощью одного элемента XOR (для вычисления суммы) и одного элемента И (для вычисления переноса).
Обнаружение ошибок
XOR применяется в алгоритмах обнаружения и исправления ошибок при передаче данных. Например, в схемах контроля четности XOR используется для подсчета количества единичных битов.
Криптография
Операция XOR часто используется в криптографических алгоритмах. Ее свойства позволяют легко шифровать и дешифровать данные при наличии ключа. XOR обладает следующим важным свойством:
(A ⊕ B) ⊕ B = A
То есть, если зашифровать данные A ключом B с помощью XOR, а затем выполнить XOR результата с тем же ключом B, получим исходные данные A.
Генерация псевдослучайных чисел
XOR используется в линейных регистрах сдвига с обратной связью для генерации псевдослучайных последовательностей битов.
Свойства операции XOR
Исключающее ИЛИ обладает рядом важных свойств:
- Коммутативность: A ⊕ B = B ⊕ A
- Ассоциативность: (A ⊕ B) ⊕ C = A ⊕ (B ⊕ C)
- Самообратимость: A ⊕ A = 0
- Нейтральный элемент 0: A ⊕ 0 = A
- XOR с 1 эквивалентно отрицанию: A ⊕ 1 = ¬A
Эти свойства делают XOR очень удобной операцией для многих алгоритмов и схем.
Реализация XOR в интегральных микросхемах
Существует ряд стандартных интегральных микросхем, реализующих функцию XOR:
- 74LS86 — четырехканальный двухвходовой элемент XOR (TTL логика)
- 4030 — четырехканальный двухвходовой элемент XOR (CMOS логика)
- 74136 — четырехканальный двухвходовой элемент XOR с открытым коллектором
Эти микросхемы позволяют легко использовать функцию XOR в цифровых схемах без необходимости собирать ее из базовых логических элементов.
XOR с тремя и более входами
Хотя классический XOR имеет два входа, можно расширить эту операцию на большее количество входов. Многовходовый XOR дает результат 1, если число единиц на входе нечетное.
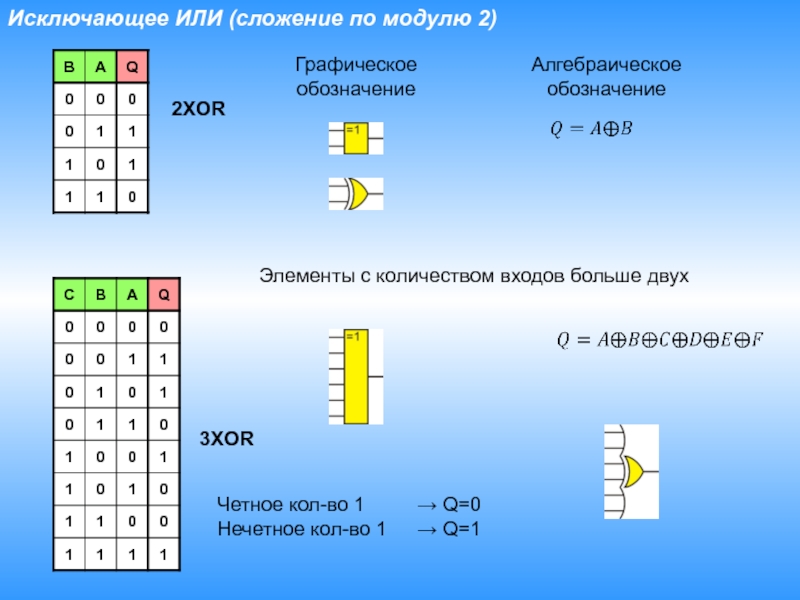
Таблица истинности для трехвходового XOR:
| A | B | C | A ⊕ B ⊕ C |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Многовходовый XOR можно реализовать каскадным соединением двухвходовых элементов XOR.
Заключение
Операция исключающего ИЛИ (XOR) — важный инструмент в цифровой логике и обработке данных. Ее уникальные свойства делают ее незаменимой во многих областях, от простых арифметических схем до сложных криптографических алгоритмов. Понимание принципов работы и свойств XOR необходимо для эффективного проектирования цифровых систем и разработки алгоритмов обработки данных.
Операция «исключающее или»
Операция исключающее ИЛИ (неравнозначность, сложение по модулю два) обозначается символом и отличается от логического ИЛИ только приA=1 и B=1.
Таким образом, неравнозначность двух высказываний Х1 и Х2 называют такое высказывание Y, которое истинно тогда и только тогда, когда одно из этих высказываний истинно, а другое ложно.
Определение данной операции может быть записано в виде таблицы истинности (таблица 6):
Таблица 6 – Таблица истинности операции «ИСКЛЮЧАЮЩЕЕ ИЛИ»
Х1
Х2
Y
1
1
0
1
0
1
0
1
1
0
0
0
Как
видно из таблицы 6, логика работы элемента
соответствует его названию.
Это тот же элемент «ИЛИ» с одним небольшим отличием. Если значение на обоих входах равно логической единице, то на выходе элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ», в отличие от элемента «ИЛИ», не единица, а ноль.
Операция «ИСКЛЮЧАЮЩЕЕ ИЛИ» фактически сравнивает на совпадение два двоичных разряда.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет своё название и обозначение (таблица 7).
Таблица 7 – Основные логические операции
Обозначение операции | Читается | Название операции | Альтернативные обозначения |
¬ | НЕ | Отрицание (инверсия) | Черта сверху |
^ | И | Конъюнкция (логическое умножение) | & |
v | ИЛИ | Дизъюнкция (логическое сложение) | + |
→ | Если … то | Импликация | |
↔ | Тогда и только тогда | Эквиваленция | ~ |
XOR | Либо … либо | ИСКЛЮЧАЮЩЕЕ ИЛИ (сложение по модулю 2) |
Порядок выполнения логических операций в сложном логическом выражении
Система
логических операций инверсии, конъюнкции,
дизъюнкции позволяет построить сколь
угодно сложное логическое выражение.
При вычислении значения логического выражения принят определённый порядок выполнения логических операций.
1. Инверсия.
2. Конъюнкция.
3. Дизъюнкция.
4. Импликация.
5. Эквивалентность.
Для изменения указанного порядка выполнения операций используются скобки.
Логические выражения и таблицы истинности
Логические выражения
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Запишем в форме логического выражения составное высказывание «(2·2=5 или 2∙2=4) и (2∙2≠5 или 2∙2≠4)».
Проанализируем
составное высказывание.
Оно содержит
два простых высказывания:
А = «2•2=5»—ложно (0),
В = «2•2=4»—истинно (1).
Тогда составное высказывание можно записать в следующей форме:
«(А или В) и (Ā или В)».
Теперь необходимо записать высказывание в форме логического выражения с учётом последовательности выполнения логических операций. При выполнении логических операций определён следующий порядок их выполнения:
инверсия, конъюнкция, дизъюнкция.
Для изменения указанного порядка могут использоваться скобки:
F = (A v В) & (Ā v В).
Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.
Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:
F =
(A
v
В)
&
(Ā v
В)
= (0
v
1)
&
(1
v
0)
= 1 & 1 = 1.
Таблицы истинности
Таблицы, в которых логические операции отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний, называются таблицами истинности.
Простые высказывания обозначаются переменными (например, A и B).
При построении таблиц истинности целесообразно руководствоваться определённой последовательностью действий:
необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
количество строк = 2n.
В нашем случае логическая функция
имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4;
необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.
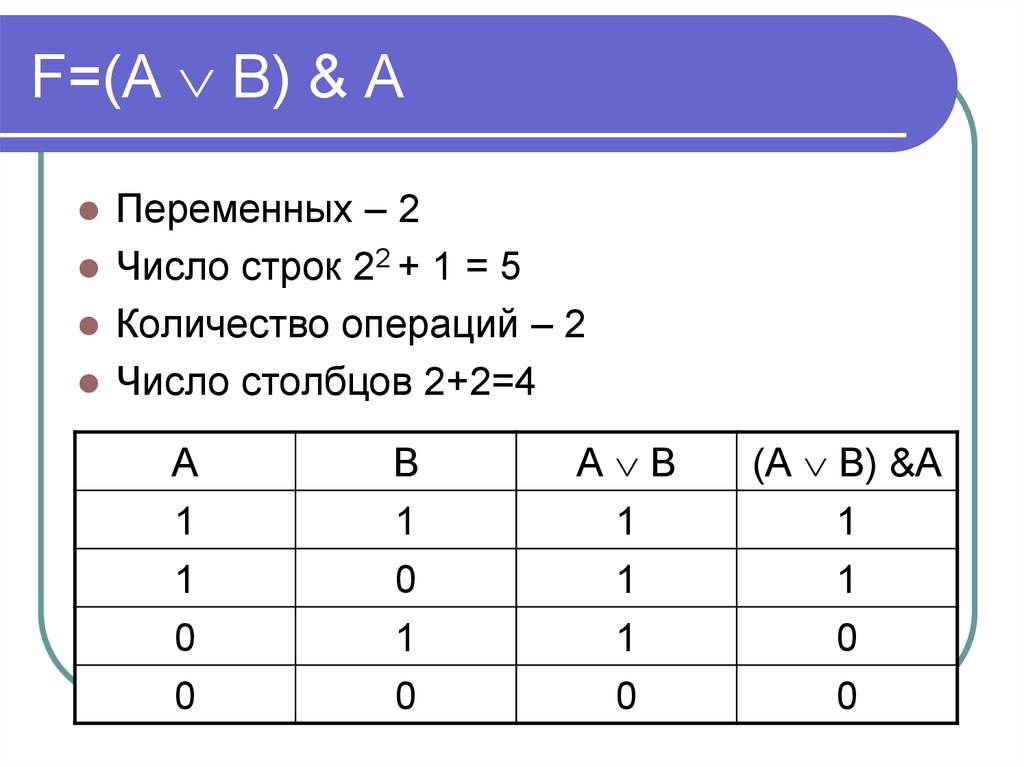
В нашем случае количество переменных равно двум: А и В, а количество логических операций — пяти (таблица 8), то есть количество столбцов таблицы истинности равно семи;
необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных;
необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
Таблица 8 – Таблица истинности логической функции
(курс 68 ч.) §10. Другие логические операции
Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, углубленный уровень)
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 9 классы | Планирование уроков на учебный год (по учебнику К.
Ю. Полякова, Е.А. Еремина, углубленный уровень) | §10. Другие логические операции
Содержание урока
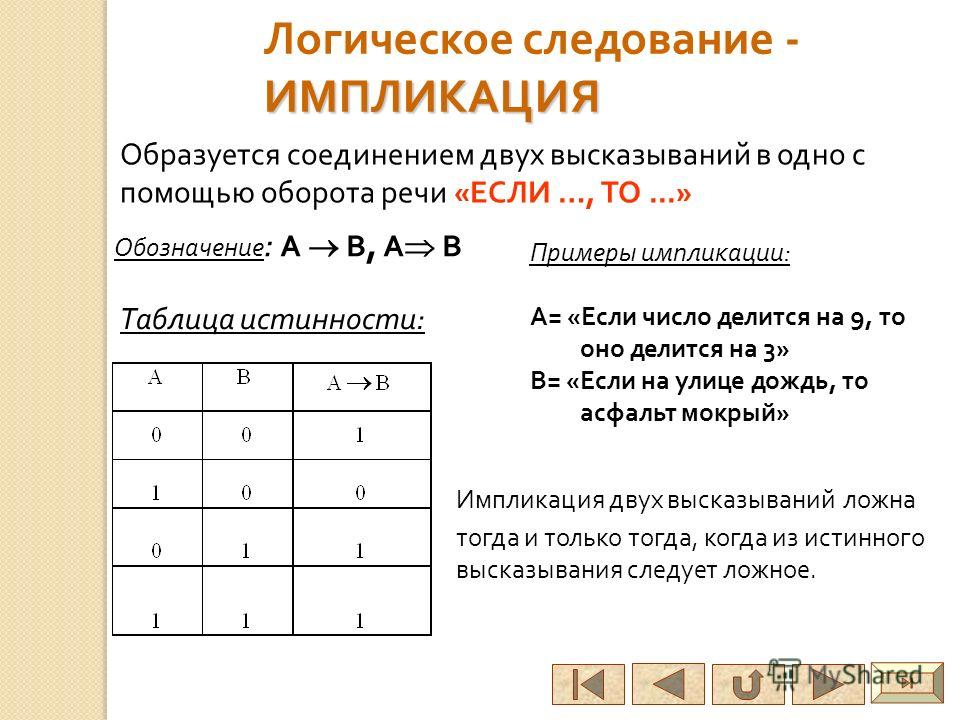
Импликация
Эквиваленция
Исключающее ИЛИ
Шифрование
Выводы
Вопросы и задания
Практическая работа № 8 «Шифрование»
Функция, которую вы исследовали в последнем задании, называется исключающее ИЛИ. Её результат равен 1, если значения входных сигналов не равны (рис. 2.15).
Рис. 2.15
Исключающее ИЛИ обозначается знаком ⊕. Смысл этой операции хорошо передаёт поговорка «либо пан, либо пропал»: возможен только один вариант из двух, но не оба одновременно.
Сравните таблицы истинности обычной операции «ИЛИ» и «исключающего ИЛИ».
Сравните таблицы истинности логических функций А ⊕ В и А ↔ В. Какая формула связывает две эти операции?
Операция исключающее ИЛИ иначе называется разделительной дизъюнкцией (это значит «один или другой, но не оба вместе») или сложением по модулю два.
Второе название связано с тем, что её результат равен остатку от деления арифметической суммы А + В на 2:
А ⊕ В = (А + В) mod 2.
Здесь mod обозначает операцию взятия остатка от деления.
Составьте таблицы истинности логических функций А ⊕ 0, А ⊕ 1 и А ⊕ А. Сравните значения каждой функции со столбцом А. Как можно упростить эти формулы?
Сравните таблицу истинности логической функции А • B + А • В (см. задание выше) с таблицей истинности операции исключающее ИЛИ. Какую формулу вы только что доказали?
Постройте таблицу истинности логической функции (А + В) • (А + B). Сравните её с таблицами истинности известных вам функций с двумя переменными. Какую формулу вы только что доказали?
Составьте таблицу истинности логической функции (А ⊕ В) ⊕ В. Сравните столбец значений функции со столбцом А. Какую формулу можно записать в результате сравнения?
Из результатов выполнения последнего задания следует важный вывод: если два раза применить к значению А операцию исключающее ИЛИ с одним и тем же значением В, то мы восстановим исходное значение А.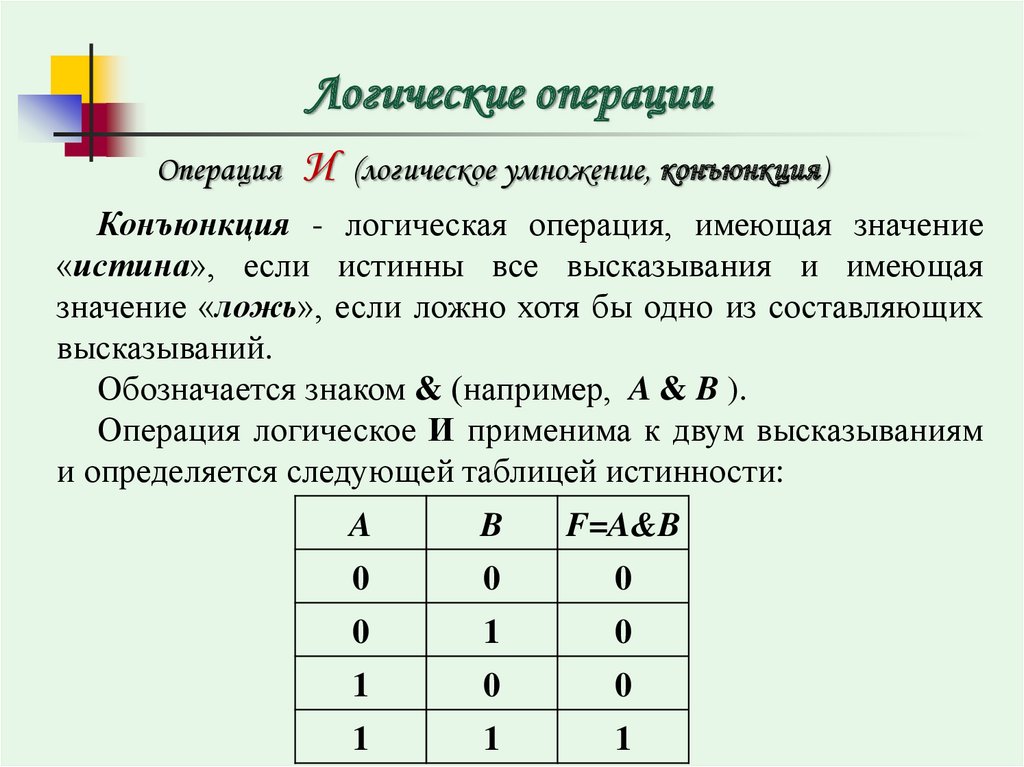
В этом смысле исключающее ИЛИ — обратимая операция.
Какие ещё обратимые логические операции вы знаете?
Используя дополнительные источники, выясните, в каких языках программирования есть логическая операция «исключающее ИЛИ» и как она обозначается.
Запишите в тетради формулы, с помощью которых можно представить операции импликацию, эквиваленцию и исключающее ИЛИ через базовые логические операции: НЕ, И и ИЛИ.
Используйте результаты выполнения заданий в рабочей тетради.
Следующая страница Шифрование
Cкачать материалы урока
XOR Gate — таблица истинности, символ, диаграмма, применение, свойства
Test Series
Прияншу Вайш комбинируя стандартные логические вентили. Вентиль XOR широко используется в схемах обнаружения ошибок, арифметико-логических схемах и компараторах вычислительной логики.
Логический элемент Исключающее ИЛИ выдает результат, только если два его входа не одинаковы, а именно, если один из них равен единице (высокий уровень), а другой равен нулю (низкий уровень).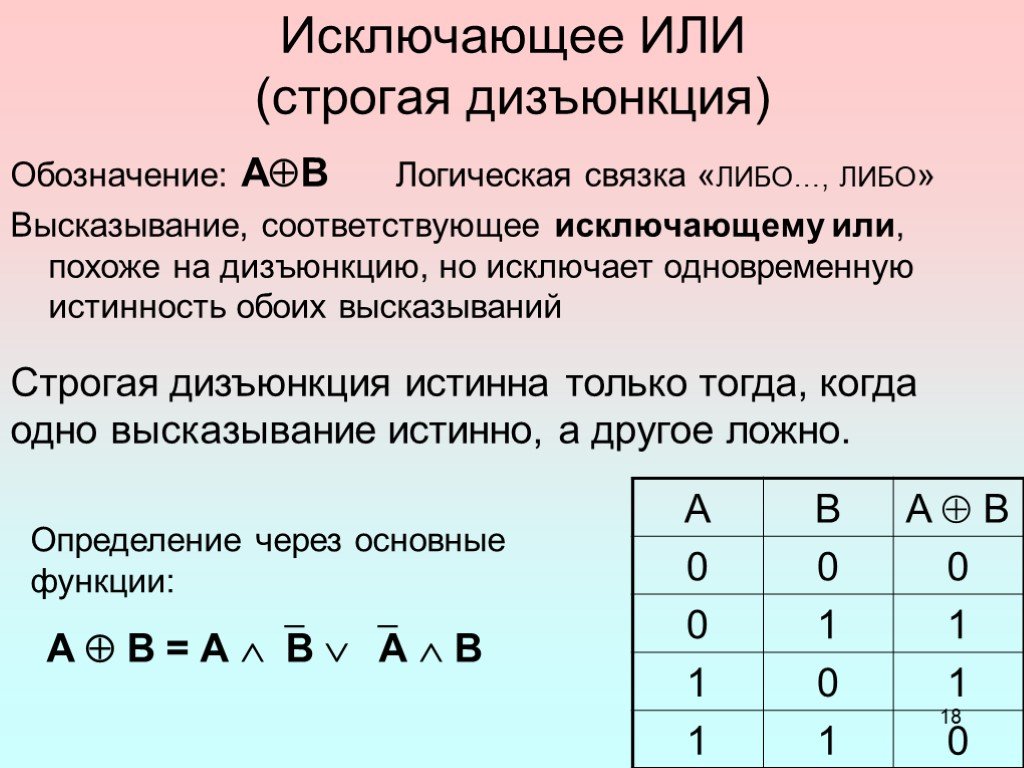
В этой статье мы узнаем о вентиле исключающее ИЛИ (XOR), его логическом символе, таблице истинности, принципиальной схеме, приложениях и различных свойствах.
Загрузить Формулы для GATE Информатика. Программирование и структуры данных
Содержание
- 1. Что такое XOR Gate?
- 2. Что такое таблица истинности XOR Gate?
- 3. Применение шлюза XOR
- 4. Включение и отключение входов
- 5. Свойства шлюза XOR
Прочитать статью полностью
Что такое шлюз XOR?
Элемент исключающее ИЛИ представляет собой логический элемент с двумя входами и одним выходом, выход которого считается ВЫСОКИМ (один) только тогда, когда один из его входов имеет ВЫСОКИЙ уровень (один).
Символ вентиля XOR
Логический символ вентиля XOR с двумя входами показан ниже:
Выражение вентиля XOR
Если входные переменные представлены A и B, то логическое выражение для вывода будет
_ _
Y = AB + AB = A ⊕ B
Загрузить формулы для GATE Компьютерные науки.
Дискретная математика
Что такое таблица истинности XOR Gate?
Практически не существует логического элемента XOR с тремя или более входами. Но когда более чем две переменные являются XOR, два входных вентиля XOR каскадируются, где предполагается, что выход равен «1», когда нечетное количество входных переменных равно «1».
Логический элемент XOR также известен как детектор нечетного числа единиц во входных данных.
Рисунок: Таблица истинности вентиля XOR
Загрузить формулы для GATE Computer Science Engineering — Algorithms
Применение вентиля XOR
Наиболее важным применением вентиля XOR является «генерация и обнаружение четности». Следовательно, он также известен как «лестничный переключатель». Показана схема переключения вентиля XOR.
Логический элемент Исключающее ИЛИ подчиняется как коммутативному, так и ассоциативному закону.
Включение и отключение входов
Для вентиля XOR
Для управления = 0;
A | Control | Y |
0 | 0 | 0 |
1 | 0 | 1 |
Таким образом, логический элемент EX-OR действует как буфер для контролируемого ввода логического «0».
Для управления = 1;
A | Control | Y |
0 | 1 | 1 |
1 | 1 | 0 |
Таким образом, логический элемент XOR действует как инвертор для управляющего входа логической «1».
Свойства XOR Gate
A ⊕ A = 0
A ⊕ 0 = A
A ⊕ A̅ = 1
A ⊕ 1 = A̅
A ⊕ A ⊕ A = A
следует:
Часто задаваемые вопросы о XOR Gate Таблица истинности
Что такое XOR gate?
Вентиль XOR широко используется в схемах цифровой обработки данных и известен как вентиль Исключающее ИЛИ. Вентиль XOR имеет высокий выход только тогда, когда нечетное количество входов имеет высокий уровень. Например, для двух входных логических элементов XOR выход будет высоким, когда набор входных данных равен 01 или 10.
Является ли EXOR или XOR базовыми воротами?
Способность логического элемента XOR сравнивать два логических уровня и выдавать результат, зависящий от входного состояния, полезна во многих вычислительных схемах. Хотя это не базовый логический вентиль, его универсальность и полезность превратили его в стандартный логический вентиль.
Как работает вентиль XOR?
Вентиль XOR (иногда называемый EOR, EXOR и произносится как Исключающее ИЛИ) — это цифровой логический вентиль, который дает истинный (либо 1, либо ВЫСОКИЙ) выходной сигнал, когда количество истинных входных сигналов является нечетным. Вентилятор XOR реализует исключающее ИЛИ, которое является истинным выходным результатом, если один из входов входов вентиля истинен.
Что такое таблица истинности вентиля XOR?
Логический элемент исключающее ИЛИ с двумя входами также распознается как логический элемент включающее ИЛИ, потому что, когда оба входа, скажем, A и B, установлены в логическую единицу (высокий уровень), выход отображается как «0» или низкий уровень, то есть в XOR, логический выход «1» достигается только тогда, когда либо A = «1», либо B = «1», но не оба вместе в одной и той же точке.
Что такое эксклюзивные ворота?
Вентиль исключающее ИЛИ (вентиль XOR) — это цифровой логический вентиль, реализованный с использованием транзисторов, которые действуют как электронный переключатель, используемый при реализации логических функций. Он построен путем объединения стандартных логических вентилей, таких как общие вентили И-НЕ и ИЛИ-НЕ, для выполнения более сложной функции этого вентиля.
Gate & PSU CS
Commortch ScienceGategate CSENIELITOTHETHETHETHETHETHETHETHETHETHER EXAMPLECTOTHER TEMPSMOCK
Избранные статьи
Следуют США.
GradeStack Learning Pvt. Ltd.Windsor IT Park, Tower — A, 2-й этаж,
Sector 125, Noida,
Uttar Pradesh 201303
Exclusive OR Gate (XOR Gate)
В этом уроке мы узнаем о Ex OR Gate.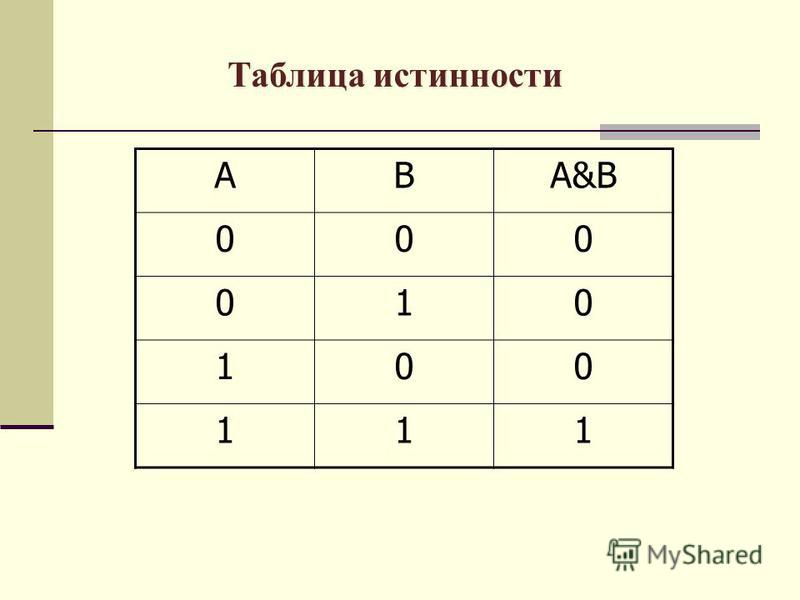
Ворота Ex ИЛИ — это ворота исключающего ИЛИ. Это не часто используется как инклюзивный вентиль ИЛИ, который представляет собой не что иное, как обычный вентиль ИЛИ. Ворота XOR имеют свое значение. Мы изучим символ, таблицу истинности XOR Gate, реализацию с использованием других вентилей (AND, OR, NAND, NOR), популярные микросхемы XOR и некоторые важные приложения Exclusive OR Gate (XOR Gate).
[адсенс1]
Схема
Введение в вентиль XOR
Вентиль исключающего ИЛИ, также известный как вентиль EX OR или вентиль XOR, является важным цифровым логическим вентилем, который реализует исключающую или логическую схему, т. е. выход имеет ВЫСОКИЙ уровень, если и только если один из входов ВЫСОКИЙ. Если оба входа НИЗКИЙ или ВЫСОКИЙ, то выход НИЗКИЙ.
Символ XOR
Существует несколько стандартов для определения электронных компонентов. Как правило, мы следуем стандартам IEEE (Институт инженеров по электротехнике и электронике) и IEC (Международная электротехническая комиссия).
Логический символ XOR в стандартах IEEE и IEC показан ниже.
Логическое выражение для вентиля XOR не может быть определено напрямую, как вентили AND, OR. Поскольку это гибридный вентиль, логическое выражение вывода вентиля XOR задается комбинацией умножения, сложения и инвертирования входных данных. Мы должны использовать карты Карно или K-карты вместе с таблицей истинности, чтобы получить логическое выражение вентиля XOR.
Таблица истинности XOR
Таблица истинности вентиля XOR показана в таблице ниже. Отсюда ясно, что вентиль XOR выдает логический НИЗКИЙ уровень, т. е. логический «0» на своем выходе, когда оба входа одинаковы (оба могут быть НИЗКИМИ или оба могут быть ВЫСОКИМ).
низкий логический уровень, т. е. логический «0», на его выходе, когда Когда два входа различны, он выдает на своем выходе логическое высокое значение, т. е. логическую «1».
| Входы | Выход | |
| А | Б | В |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Представление K-карты приведенной выше таблицы истинности XOR Gate показано ниже.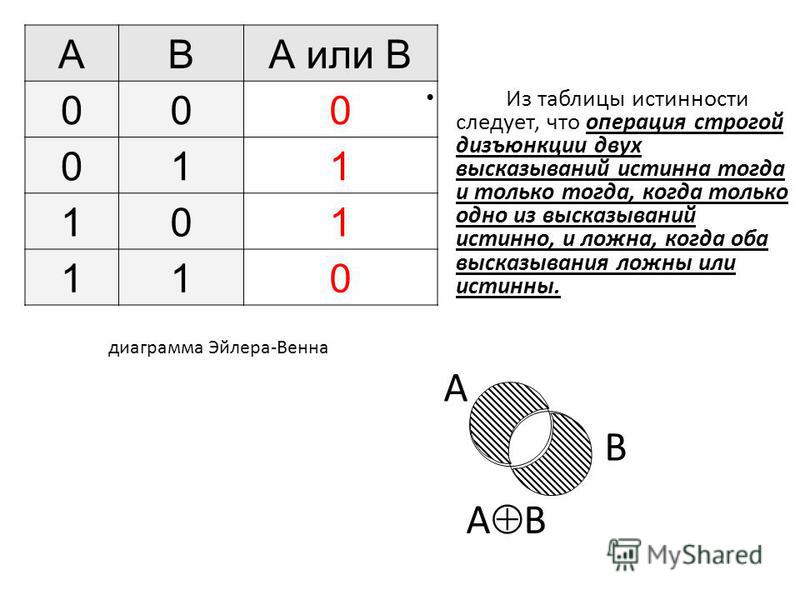
Логическое выражение XOR
Используя приведенную выше таблицу истинности и соответствующую K-карту, теперь мы можем получить логическое выражение для XOR Gate. Если A и B являются входами вентиля XOR, его выход задается как:
A B + A B
Выход XOR представлен как:
A ⊕ B
Можно также записать как:
(A + B) (A + B)
Применяя закон Де Моргана, приведенное выше логическое выражение можно также записать как:
(A + B) (A B)
Эквивалентная схема вентиля XOR
Вентиль EX-OR определяется как гибридный логический вентиль с 2 входами для выполнения операции исключающего дизъюнкции. Из приведенных выше расчетов основное логическое выражение вентиля XOR:
А Б + А Б
Итак, схема исключающего ИЛИ с двумя входами разработана с использованием вентилей И, ИЛИ и НЕ, как показано ниже.
Выход двухвходового вентиля XOR имеет ВЫСОКИЙ уровень только тогда, когда один из его входов имеет ВЫСОКИЙ уровень.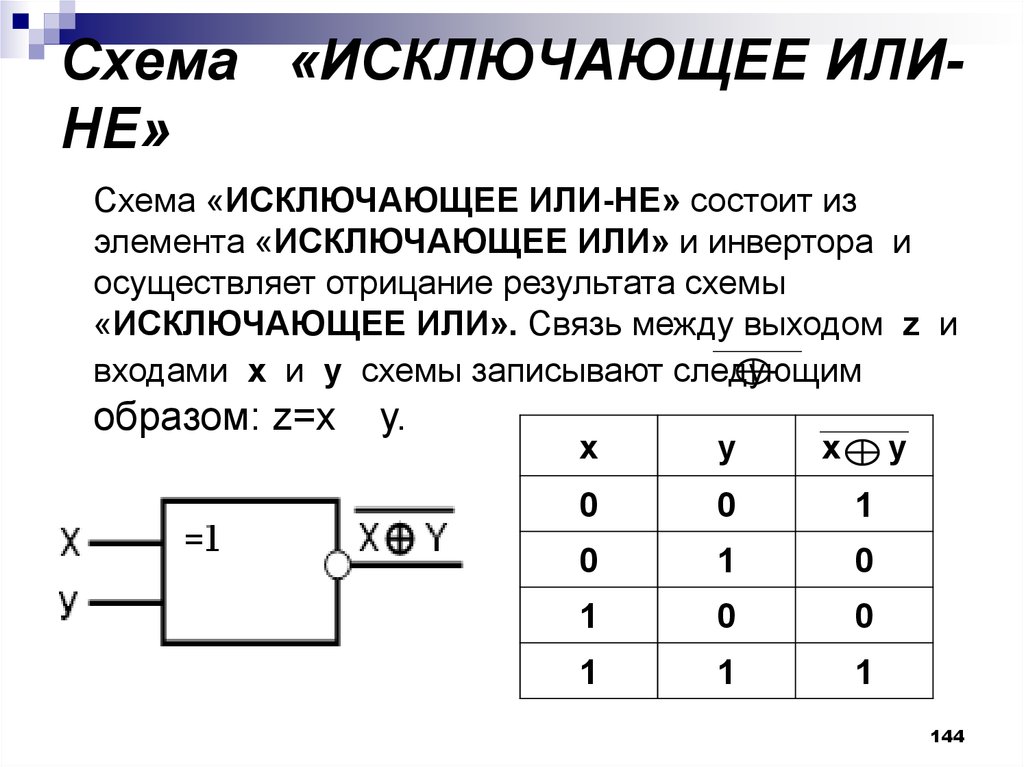
Если оба входа одинаковы, то выход НИЗКИЙ.
Шлюз XOR с использованием базовых логических вентилей
Если конкретный вентиль недоступен напрямую, мы можем спроектировать вентиль XOR с использованием нескольких вентилей. Ворота EX-OR могут быть разработаны с использованием базовых логических вентилей, таких как вентиль НЕ-И и вентиль ИЛИ-НЕ, поскольку они являются универсальными вентилями.
[адсенс2]
С вентилями NOR
Давайте теперь посмотрим, как мы можем реализовать вентиль XOR с помощью вентилей NOR. Для этого нам нужно переписать приведенное выше логическое уравнение XOR.
Q = А Б + А Б
Q = А В + А В + А А + В В
Q = (А + В) (А + В)
Q = (A + B) (A + B) = (A’ + B’) (A + B)
Взяв дополнение с обеих сторон, получим:
Q = ((A’ + B’) (A + B))
Используя закон де Моргана, получаем:
Q = (A’ + B’) + (A + B) = (A’ + B’)’ + (A + B)’
Еще раз взяв дополнение с обеих сторон, мы получим:
Q = ((A’ + B’)’ + (A + B)’) = ((A’ + B’)’ + (A + B) ‘)’
Похоже, что это уравнение может быть реализовано с помощью NOR Gates.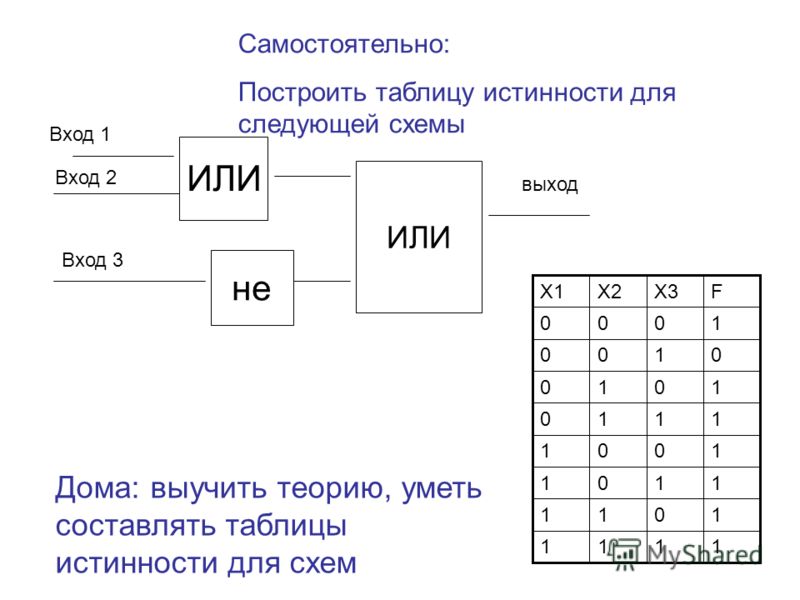
Всего нам нужно пять вентилей ИЛИ-НЕ (два для инвертирования А и В, один для инвертирования ИЛИ-НЕ для А и В, один для ИЛИ-НЕ для А’ и В’ и последний для получения приведенного выше уравнения). На следующем изображении показан шлюз XOR, реализованный с использованием шлюзов NOR.
С вентилями NAND
Давайте теперь посмотрим, как мы можем реализовать вентиль XOR с помощью вентилей NAND. Для этого нам нужно переписать приведенное выше логическое уравнение XOR.
Q = А Б + А Б
Q = А В + А В + А А + В В
Q = (А + В) (А + В)
Q = (A + B) (A + B) = (A + B) (A’ + B’)
Применяя закон де Моргана ко второму члену в приведенном выше уравнении, мы получаем:
Q = (A + B) ( AB )
Теперь нам нужно реализовать эту схему с использованием вентилей И-НЕ.
Q = A (AB) + B (AB) = A (AB)’ + B (AB)’
Взяв дополнение с обеих сторон, мы получим:
Q = (A ( AB ) + B ( AB ))’ = (A (AB)’ + B (AB)’)
Q = (A ( A B ))’ (B ( A B ))’ = (A (AB)’) (B (AB)’)
Наконец, еще раз нанесите дополнение с обеих сторон.
Q = (A ( A B )’)’ (B (A B)’)’ = ((A (AB)’)’ (B (AB)’)’)’
Похоже, что это уравнение может быть реализовано с помощью NAND Gates. Нам нужны полностью наши вентили NAND. На следующем изображении показан вентиль XOR, реализованный с использованием вентилей NAND.
Использование вентилей И, ИЛИ и И-НЕ
Давайте теперь посмотрим, как мы можем реализовать вентиль исключающее ИЛИ, используя вентили И, И и ИЛИ. Для этого нам нужно переписать приведенное выше логическое уравнение XOR.
Q = А Б + А Б
Q = А В + А В + А А + В В
Q = (А + В) (А + В)
Q = (A + B) (A + B) = (A + B) (A’ + B’)
Применяя закон де Моргана ко второму члену в приведенном выше уравнении, мы получаем:
Q = (A + B) ( AB )
Для первого члена в приведенном выше уравнении требуется вентиль ИЛИ, для второго члена нужен вентиль НЕ-И, а окончательное уравнение можно получить с помощью вентиля И.
Импульсная работа логического элемента XOR
Импульсная работа логического элемента XOR с 2 входами показана ниже.
3-входовые вентили Ex-OR
В некоторых случаях нам необходимо иметь вентили XOR с более чем 2 входами. Функция XOR с более чем двумя входами называется «Нечетная функция» или «Сумма по модулю-2». Булева функция для логического элемента XOR с 3 входами:
Q = A ⊕ B ⊕ C = A B C + A B C + A B C + A B C
Таблица истинности и логический символ для 3-входового вентиля исключающее ИЛИ приведены ниже.
Логический символ вентиля Ex-OR с 3 входами
Таблица истинности вентиля XOR с 3 входами
Для вентилей XOR с 3 входами мы можем иметь ВЫСОКИЙ вход, когда нечетное количество входов находится на ВЫСКОМ уровне. Таким образом, вентиль ИЛИ с тремя входами называется «вентиль ИЛИ с нечетным функционированием».
| Входы | Выход | ||
| А | Б | С | В |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Общедоступные TTL и CMOS логические микросхемы Ex-OR
Ниже приведен список некоторых общедоступных микросхем исключающего ИЛИ.
| Номер ИС | Описание |
| 4030 | Счетверенные вентили исключающего ИЛИ с 2 входами |
| 4070 | Счетверенные вентили исключающего ИЛИ с 2 входами |
| 7486 | Счетверенные вентили исключающего ИЛИ с 2 входами |
| 74LS86 | Счетверенные вентили исключающего ИЛИ с 2 входами |
| 741G86 | Одиночный вентиль Ex-OR с 2 входами |
| 74136 | Счетверенные вентили XOR с 2 входами и выходами с открытым коллектором |
| 74386 | Счетверенные вентили исключающего ИЛИ с 2 входами |
Из них самой популярной микросхемой EX-OR Gate на основе TTL Logic является 74LS86, представляющая собой Quad XOR IC с двумя входами. Что касается микросхемы XOR Gate на основе CMOS Logic, CD4030 Quad XOR IC с 2 входами является популярным выбором.
7486 Четырехканальная микросхема исключающего ИЛИ с двумя входами
IC 7486 представляет собой четырехканальную схему XOR с двумя входами, т. е. содержит четыре вентиля XOR с двумя входами в одном корпусе. Схема выводов и описание выводов микросхемы показаны ниже.
| Номер контакта | Описание |
| 1 | Строб 1 Вход A |
| 2 | Строб 1 Вход B |
| 3 | Строб 1 Выход Y |
| 4 | Строб 2 Вход A |
| 5 | Строб 2, вход B |
| 6 | Строб 2 Выход Y |
| 7 | Земля |
| 8 | Строб 3 Выход Y |
| 9 | Строб 3, вход А |
| 10 | Строб 3 Вход B |
| 11 | Строб 4 Выход Y |
| 12 | Строб 4, вход A |
| 13 | Строб 4 Вход B |
| 14 | Положительное питание |
Применение Ex-OR Gate
XOR Logic Gate используется во многих приложениях.
Некоторые из них объясняются ниже.
Используется в сумматоре (сложение)
Мы можем разработать однобитовый сумматор (также известный как полусумматор), который будет добавлять два бита и давать на выходе один бит. Одноразрядный сумматор, разработанный с использованием вентиля XOR, показан ниже.
Например, если мы добавим два бита «1» и «1» в двоичном сложении, мы получим ответ «10», а в методе десятичного сложения мы получим 2. Основной принцип полусумматоров заключается в том, что конечная сумма достигается выходом вентиля XOR, а бит переноса вычисляется вентилем AND.
Мы можем каскадировать множество однобитовых сумматоров, чтобы сформировать n-битный сумматор, чтобы вычислить сумму более длинных двоичных чисел.
Генерация псевдослучайных чисел
Линейные регистры сдвига также называются генераторами псевдослучайных чисел (PNR). Чтобы генерировать случайные числа, мы располагаем логический вентиль XOR в определенном порядке, формируя регистр сдвига с линейной обратной связью.
Корреляция и обнаружение последовательности
Логический элемент XOR способен выдавать входной сигнал низкого уровня, т. е. 0, когда все его входы имеют ВЫСОКИЙ или НИЗКИЙ уровень. Когда мы ищем определенную последовательность битов в длинной последовательности данных, мы используем вентили XOR, чтобы найти требуемую последовательность битов данных.
Точность нахождения необходимой строки битов данных в целевой последовательности определяется путем подсчета количества полученных нулей. Во многих устройствах связи, таких как декодеры и приемники CDMA, мы используем корреляторы, которые используются для извлечения четности конкретной последовательности псевдослучайных чисел в группе последовательностей PRN.
Заключение
Полное руководство по Exclusive OR Gate (XOR Gate). Вы изучили символ, таблицу истинности и логическое выражение вентиля XOR, реализацию вентиля XOR с использованием вентилей NOR и NAND, вентиль XOR с 3 входами, его символ, таблицу истинности и логическое выражение, некоторые распространенные и популярные микросхемы XOR, а также некоторые важные приложения XOR Gate.
