Что такое тензорезистор. Как работает тензорезистор. Какие основные характеристики тензорезисторов. Где применяются тензорезисторы. Как устроен тензорезистор. Какие бывают виды тензорезисторов.
Что такое тензорезистор и принцип его работы
Тензорезистор — это специальный резистор, электрическое сопротивление которого изменяется при механической деформации. Принцип работы тензорезистора основан на тензорезистивном эффекте — изменении удельного сопротивления проводника при его деформации.
При растяжении проводника его длина увеличивается, а поперечное сечение уменьшается, что приводит к увеличению сопротивления. При сжатии наблюдается обратный эффект — сопротивление уменьшается. Эта зависимость сопротивления от деформации и лежит в основе работы тензорезисторов.
Основные характеристики тензорезисторов
Ключевыми характеристиками тензорезисторов являются:
- Коэффициент тензочувствительности — показывает относительное изменение сопротивления при деформации
- Базовое сопротивление — номинальное сопротивление недеформированного тензорезистора
- Рабочий диапазон деформаций — максимально допустимая деформация
- Температурный коэффициент сопротивления — изменение сопротивления при изменении температуры
- Нелинейность — отклонение характеристики от линейной зависимости
Конструкция и виды тензорезисторов
По конструкции тензорезисторы делятся на:

- Проволочные — чувствительный элемент выполнен из тонкой проволоки
- Фольговые — используется тонкая металлическая фольга
- Пленочные — тензочувствительный слой напыляется на подложку
- Полупроводниковые — на основе полупроводниковых материалов
Чувствительный элемент обычно имеет форму решетки или меандра для увеличения длины проводника. Он закрепляется на гибкой подложке, которая наклеивается на исследуемый объект.
Области применения тензорезисторов
Основные сферы использования тензорезисторов:- Измерение деформаций, механических напряжений и вибраций в деталях и конструкциях
- Создание датчиков силы, давления, веса, крутящего момента
- Тензометрические весы и силоизмерительные устройства
- Системы контроля нагрузок в различных отраслях промышленности
- Медицинская техника (измерение давления, пульса и др.)
Преимущества и недостатки тензорезисторов
Преимущества тензорезисторов:
- Высокая чувствительность и точность измерений
- Малые габариты и вес
- Простота конструкции
- Возможность дистанционных измерений
- Широкий диапазон измеряемых величин
Недостатки:

- Нелинейность характеристики
- Влияние температуры на показания
- Ползучесть (изменение показаний со временем)
- Гистерезис
Схемы включения тензорезисторов
Наиболее распространенной схемой включения тензорезисторов является мостовая схема Уитстона. Она позволяет компенсировать температурную погрешность и повысить чувствительность.
В простейшем случае тензорезистор включается в одно плечо моста. Для повышения точности применяют дифференциальные схемы с двумя или четырьмя активными плечами.
Выбор и монтаж тензорезисторов
При выборе тензорезисторов учитывают:
- Диапазон и характер измеряемых деформаций
- Условия эксплуатации (температура, влажность и т.д.)
- Материал исследуемого объекта
- Требуемую точность измерений
Монтаж тензорезисторов — ответственная операция, от которой зависит точность измерений. Основные этапы:
- Подготовка поверхности (очистка, обезжиривание)
- Нанесение клея
- Наклейка тензорезистора
- Прижим и полимеризация клея
- Проверка сопротивления изоляции
- Подключение проводов
- Нанесение защитного покрытия
Калибровка тензометрических систем
Для получения точных результатов измерения тензометрические системы необходимо калибровать. Основные методы калибровки:

- Механическая калибровка — с помощью нагружения эталонными грузами
- Электрическая калибровка — подключение калиброванных сопротивлений
- Имитация деформации с помощью специальных приспособлений
При калибровке определяют: — Коэффициент преобразования деформации в электрический сигнал — Линейность характеристики — Гистерезис — Повторяемость результатов
Обработка сигналов тензорезисторов
Сигнал с тензорезисторного моста обычно составляет единицы милливольт. Для его обработки применяют:
- Усилители с низким уровнем шумов
- Аналого-цифровые преобразователи
- Фильтры для подавления помех
- Схемы температурной компенсации
- Микроконтроллеры для цифровой обработки
Современные тензометрические системы позволяют проводить измерения с высокой точностью и в реальном времени передавать данные для анализа и визуализации.
Тензорезисторы определение и принципы работы
Что такое деформация?
Внешнее усилие, прикладываемое к упругому материалу, создает механическое напряжение, которое, в свою очередь, вызывает деформацию материала. В случае, если приложено усилие растяжения, длина материала L увеличивается и становится равной L + ΔL. Отношение ΔL к L, т.е. ΔL/L, называется деформацией. С другой стороны, если приложено усилие сжатия, длина L уменьшается до значения L-ΔL. В этом случае деформация равна (-ΔL/L).

Что такое тензорезистор?
Электрическое сопротивление металла изменяется пропорционально механической деформации, вызванной приложенным к металлу внешним усилием. При креплении тонкого слоя металла к объекту измерения поверх тонкого слоя диэлектрика, металл деформируется в зависимости от деформации объекта измерения и изменения его электрического сопротивления. Таким образом, тензорезистор — это чувствительный элемент, преобразующий собственную деформацию в изменение электрического сопротивления.
Конструкция тензорезистора
Тензорезистор состоит из решетки, выполненной из тонкой проволоки или металлической фольги, уложенной на изоляционную подложку, и подсоединенных выводов тензорезистора.

Принцип работы тензорезистора
При деформации объекта измерения эта деформация передается резистивной проволоке или резистивной фольге тензорезистора через его основание (подложку). В результате сопротивление проволоки или фольги изменяется. Это изменение точно пропорционально деформации,что отражает следующее уравнение:

Если R=R1=R2=R3=R4, сопротивление тензорезистора, из-за деформации, меняется и становится равным R+ΔR. Таким образом, изменение выходного напряжения Δe из-за деформации задается следующим выражением:
.jpg)
При измерении деформации с помощью тензорезистора, он подключается к измерительному прибору, называемому тензометром. Тензометр содержит мост Уитстона и подает напряжение возбуждения. Измеренное значение деформации отображается на цифровом дисплее и/или выводится в виде аналоговых сигналов.
На нашем сайте Вы можете купить (заказать) качественные японские тензорезисторы от производителя, аксессуары и химию (клеи и защитные покрытия) для тензорезисторов с отличным соотношением цена-качество. Для этого отставьте заявку на обратный звонок и наши специалисты свяжутся с вами в ближайшее время или напишите нам сообщение. В комментарии можно указать, какие модели тензорезисторов вы бы хотели заказать.
КРАТКО О ТЕНЗОРЕЗИСТОРАХ
ОБЩИЕ СВЕДЕНИЯ О ТЕНЗОРЕЗИСТОРАХ
Тензодатчики и тензорезисторы. Давайте посмотрим, что связывает тензодатчик и тензорезистор.
Тензорезистор (от лат. tensus — напряжённый и лат. resisto — сопротивляюсь) — резистор, сопротивление которого изменяется в зависимости от его деформации. Тензорезисторы используются в тензометрии. С помощью тензорезисторов можно измерять деформации механически связанных с ними элементов. Тензорезистор является основной составной частью тензодатчиков.
Принцип действия
При растяжении проводящих элементов тензорезистора увеличивается их длина и уменьшается поперечное сечение, что увеличивает сопротивление тензорезистора, при сжатии — уменьшается.

Принцип действия проиллюстрирован на анимированном изображении. Для наглядности на изображении величина деформации тензорезистора утрированно увеличена, как и изменение сопротивления. В реальности относительные изменения сопротивления весьма малы (менее ~10−3) и для их измерений требуются чувствительные вольтметры или преобразователи (АЦП, весоизмерительные преобразователи (терминалы)), прецизионные усилители. Таким образом, деформации преобразуются в изменение электрического сопротивления проводников или полупроводников и далее — в электрический сигнал, обычно сигнал напряжения.
Мы не будем останавливаться подробно на электромеханических параметрах тензорезисторов. Отметим только, что чувствительность характеризуется коэффициентом чувствительности и зависит от применяемых материалов. А температурный коэффициент является вредным побочным эффектом, влияющий на показания.
Тензорезисторы широко используются в качестве чувствительного элемента, датчиков для измерения сил, давления. Собственно тензометрические датчики или сокращенно тензодатчики получили свое название от тензорезисторов.
Электрическая схема подключения тензорезистора
Обычно тензорезисторы включают в одно или два плеча сбалансированного моста Уитстона, питаемого от источника постоянного тока (диагональ моста A—D). С помощью переменного резистора производится балансировка моста, так, чтобы в отсутствие приложенной силы напряжение диагонали сделать равным нулю. С диагонали моста B—C снимается сигнал, далее подаваемый на измерительный прибор, дифференциальный усилитель или АЦП.
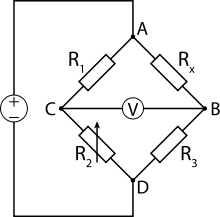
Измерительный мост с вольтметром в диагонали. Тензорезистор обозначен Rx
При выполнении соотношения R1/R2=R2/R3 напряжение диагонали моста равно нулю. При деформации изменяется сопротивление Rx (например, увеличивается при растяжении), это вызывает снижение потенциала точки соединения резисторов Rx и R3(точки B) и изменение напряжения диагонали B—C моста — полезный сигнал.
Изменение сопротивления Rx может происходить не только от деформации, но и от влияния других факторов, главный из них — изменение температуры, что вносит погрешность в результат измерения деформации. Для снижения влияния температуры применяют сплавы с низким ТКС, термостатируют объект, вносят поправки на изменение температуры и/или применяют дифференциальные схемы включения тензорезисторов в мост.
Например, в схеме на рисунке вместо постоянного резистора R3 включают такой же тензорезистор, как и Rx, но при деформации детали этот резистор изменяет своё сопротивление с обратным знаком. Это достигается наклейкой тензорезисторов на поверхности по-разному деформируемых зон детали, например, с разных сторон изгибаемой балки или с одной стороны, но со взаимно перпендикулярной ориентацией. При изменении температуры, если температура обоих резисторов равна, знак и величина изменения сопротивления, вызванного изменением температуры, равны, и температурный уход при этом компенсируется.
Также промышленностью выпускаются специализированные микросхемы для работы совместно с тензорезисторами, в которых помимо усилителей сигнала часто предусмотрены источники питания моста, схемы термокомпенсации, АЦП, цифровые интерфейсы для связи с внешними цифровыми системами обработки сигналов и другие полезные сервисные функции.
Конструкция
Обычно современные тензорезисторы представляют собой чувствительный элемент в виде зигзагообразного проводника, нанесенного на гибкую подложку. Тензорезистор приклеивается подложкой на поверхность исследуемого на деформации объекта. Проводники тензорезисторов обычно изготавливаются из тонкой металлической проволоки, фольги, или напыляются в вакууме для получения плёнки полупроводника или металла. В качестве подложки обычно используют ткань, бумагу, полимерную плёнку, слюду и др. Для присоединения чувствительного элемента в электрическую цепь тензорезистор имеет выводные проволочные концы или контактные площадки.
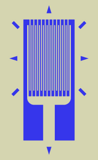
Плёночный тензорезистор. На подложку через фигурную маску в вакууме напылена или сформирована методами фотолитографии плёнка металла. Для подключения электродов выполнены контактные площадки (снизу). Метки облегчают ориентацию при монтаже.
Плёночные металлические тензорезисторы имеют площадь около 2‑10 мм2.
Конфигурация
Тензодатчики, как правило, приклеиваемые, состоят из:
- элемента чувствительного к деформации;
- тонкой плёнки, которая является изолятором и несущей основой для чувствительного элемента;
- контактных площадок для присоединения выводных проводов.
Элемент, чувствительный к деформации, представляет собой решётку, которая вытравлена способом фотолитографии или отштампована из очень тонкого листа металлической фольги толщиной 2,5 мкм. Конфигурация выбирается таким образом, чтобы обеспечить сопротивление равное 100 Ом при достаточно малой длине и ширине. Выпускаются датчики, длина которых меняется в диапазоне от 2 до 150 мкм. Выпускаются датчики специального назначения (мембранные датчики давления, напряжения, датчики деформации сдвига).
Несущая основа
Применяются материалы такие, как:
- акриловые;
- полиамидные;
- фенольные;
- эпоксидно-стеклянные;
- бумага;
- эпоксидные;
- эпоксидно-полиамидные;
- эпоксидно-фенольные;
- фенольно-стеклянные.
В большинстве случаев применяются полиамидная плёнка, отличающаяся прочностью, гибкостью и совместимостью с большинством связующих. Применяется плёнка с эпоксидной смолы. Её особенности:
- линейно-упругое поведение материала;
- отсутствие гистерезиса.
Полимеры, армированные стекловолокном, применяются в датчиках для работ в циклических деформациях. В датчиках, работающих при повышенных температурах, используются основы из эпоксидных и фенольных смол, армированных стекловолокном.
Клеи, с помощью которых приклеивают тензодатчики
Клей, с помощью которого приклеивают тензодатчик на образец, должен обладать прочностью, линейной упругостью и стабильностью в течение длительного периода времени.
Комбинация датчика: его несущая основа и клеи требуют самого серьезного внимания. Необходимо применять апробируемые клеи и соблюдать процедуры нанесения и сушки.
В качестве клея наиболее широко используется метил-2-цианоакриад, эпоксидная смола, полимид и некоторые виды керамики.
Цианоакриад не требует ни нагрева, ни отвердителей для инициирования полимеризации. Для ускорения полимеризации на одну из поверхностей может быть нанесён катализатор. Благодаря очень быстрой полимеризации этот клей является идеальным компонентом для тензодатчиков общего назначения. Минутного нажатия большим пальцем и двух минутной паузы оказывается достаточно. Он может использоваться в диапазоне температур от -32 до +65°С. Он обеспечивает правильное измерение деформации не выше 6%. Прочность клея снижается со временем из-за поглощения влаги, поэтому его необходимо защищать при длительной эксплуатации.
Эпоксидный состоит из смолы и отвердителя, который вступает в реакцию со смолой, обеспечивая полимеризацию. В некоторых случаях для вязкости смолы в нее добавляют растворитель. Разбавленные смолы (эпоксидно-фенольные) более предпочтительны, так как образуют очень тонкие высокопрочные, однородные плёнки со слабо выраженной ползучестью и гистерезисом. Для обеспечения тонкого однородного слоя к датчику должно быть приложено давление от 70 до 210 кПа. чтобы гарантировать полную полимеризацию эпоксидные клеи подвергают повышенной температуре в течение нескольких часов. По-видимому, наилучшими являются эпоксидно-фенольные клеи с рабочим диапазоном температур от -269 до +260°С. Допустимое относительное удельное изменение находится в пределах 3-10%.
Полиамидные представляют собой однокомпонентный полимер, который может применяться в диапазоне температур от -260 до +399°С. Полиамид утверждается при давлении 275кПа при температуре 260°С.
Итак, для отверждения нужны сравнительно высокие давления и температуры (например, 8 — 10 кгс/мм2, 170° С). Поверхность упругого элемента перед приклеиванием тщательно очищается механическими и химическими средствами, а затем к ней приклеивают тензорезисторы на слои соответствующих клеящих и изолирующих веществ. Процесс отверждения ведут по специальной температурно-временной программе. После окончания процессов «послеотверждения», если таковые имеют место, приклеенные тензорезисторы защищаются от действия окружающей среды.
После отвердения клеев тензодатчики должны быть покрыты герметиком (парафин, каучук, полимеритан).
Конструкция закрепления также имеет большое значение для работы датчика (рис. 1). В классической конструкции (а) применяется «утопленный» тензорезистор (например, в основе из фенольного клея), который наклеивается на упругий элемент с помощью клея (например, фенольного). В конструкции (б) голый тензорезистор (например, полупроводниковый) приклеивают через подложку (например, из специальной бумаги), пропитанную клеем. В обоих случаях возникает относительно толстая прослойка толщиной d2, (» 20 — 50 мкм), которая образуется по существу вязкой средой и служит причиной явлений ослабления напряжений. Поскольку прослойка выполняет одновременно функцию изоляции, она не может делаться сколь угодно тонкой. Поэтому в более новой конструкции задачи изоляции и крепления разделены. Здесь сначала наносится изоляционный слой, (расплавленная эмаль или керамика), который обладает существенно лучшими механическими свойствами, чем клей. Теперь собственно клеевой слой может выполняться очень тонким (< 1 мкм) и должен только заполнить неровности поверхностей. В этой конструкции практически полностью пренебрежимо ослабление напряжений, вызванное клеем.
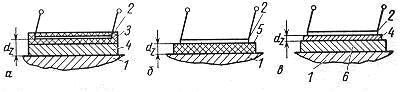
Рисунок 1 — Конструкции тензорезисторных чувствительных элементов датчиков
а и б — обычные конструкции с толстыми клеевыми слоями dz;
в — современная конструкция с тонким клеевым слоем dz.
1 — упругий элемент; 2 — тензорезистор; 3 — основа тензорезистора; 4 — клеевой слой; 5 -подложка, пропитанная клеем; 6 — изолирующий слой с хорошими механическими свойствами
Явления ослабления напряжения рассматривались до сих пор всегда в связи с процессами в клее и конструкцией крепления тензорезисторов. Это понятно, так как в период становления техники измерений, основанной на тензорезисторах, на исследование и уменьшение ползучести клеев было направлено основное внимание. Однако в настоящее время можно уменьшить эти эффекты, по крайней мере до порядка значений ослабления напряжений, вызванных другими причинами (например, самим упругим элементом). Поэтому ослабление клея следует рассматривать только вместе с другими явлениями, если ими вообще нельзя пренебречь. Различные причины погрешностей тензорезисторных датчиков сопоставлены ниже:
Ослабления в упругом элементе
Вязкое ослабление из-за клеевых слоев благодаря современным способам приклеивания становится часто пренебрежимо малым.
Температурный уход нуля возникает из-за тепловых волн, распространяющихся по упругому элементу, при выравнивании теплового состояния, если тензорезисторы имеют большие температурные коэффициенты сопротивления (полупроводниковые тензорезисторы).
Термоэлектрические эффекты возникают из-за процессов перераспределения потерь мощности в мосте; также заметны только у полупроводниковых тензорезисторов.
Ослабление клея — единственный эффект, который по своей природе противоположен действию силы. Поэтому он может в принципе компенсировать эффекты ослабления, совпадающие по своему характеру с силой, однако из-за различных постоянных времени этих эффектов лишь не полностью и с большой зависимостью от температуры.
Защита от воздействия окружающей среды. Чувствительные элементы после их приклеивания должны защищаться от воздействий окружающей среды, чтобы препятствовать прежде всего действию влажности. Для этого после отверждения, по возможности еще в теплом состоянии, они покрываются защитными лаками. Чтобы воспрепятствовать образованию сквозных пор, такую операцию повторяют, как правило, несколько раз.
Полученные таким образом тонкие слои не могут полностью и на длительное время исключить диффузию паров воды. Это достигается только благодаря герметически плотным металлическим корпусам, которые часто заполняются еще достаточно большим запасом гигроскопичного вещества или сухим инертным газом. Однако влага, внедрившаяся в чувствительные элементы, несмотря на все эти меры, вызывает два эффекта:
1. Уменьшение сопротивления изоляции между тензорезистором и упругим элементом. В идеальном случае это сопротивление бесконечно велико. При конечном сопротивлении изоляции Ris получаются условия, отраженные на рис. 2. Благоприятнейший случай изображен на рис. 2,а, где Ris, равномерно распределено на четыре части моста; разбаланса моста нет. Для неблагоприятнейшего случая расчет дает погрешность нуля:
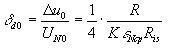
где eNcp — средняя номинальная деформация и R0 — основное сопротивление тензорезисторов. Эти соотношения для тензорезисторов с большим коэффициентом тензочувствительности (для полупроводниковых) не имеют такого значения.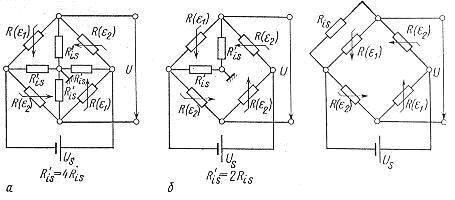
Рисунок 2 — Влияние уменьшения сопротивления изоляции
Ris — дискретная эквивалентная схема. a — благоприятный случай: уменьшение Ris распределено равномерно; б — неблагоприятный случай: уменьшение Ris действует на один тензорезистор.
Разбухание клеевого слоя вызывает кажущуюся деформацию, а этим самым — дополнительную погрешность нуля. Можно с уверенностью считать, что этот эффект значительно сильнее, чем эффект от сопротивления изоляции. Но уменьшение Ris может служить в качестве меры внедрившейся влаги и поэтому — общей ожидаемой погрешности нуля. Можно принять, что разбухание также достаточно мало, если сопротивление изоляции более 109 Ом.
Тензорезистор — Википедия

Тензорези́стор (от лат. tensus — напряжённый и лат. resisto — сопротивляюсь) — резистор, сопротивление которого изменяется в зависимости от его деформации[1]. Тензорезисторы используются в тензометрии. С помощью тензорезисторов можно измерять деформации механически связанных с ними элементов[2]. Тензорезистор является основной составной частью тензодатчиков, применяющихся для косвенного измерения силы, давления, веса, механических напряжений, крутящих моментов и пр.
Принцип действия
При растяжении проводящих элементов тензорезистора увеличивается их длина и уменьшается поперечное сечение, что увеличивает сопротивление тензорезистора, при сжатии — уменьшает.
Принцип действия проиллюстрирован на анимированном изображении. Для наглядности на изображении величина деформации тензорезистора утрированно увеличена, как и изменение сопротивления. В реальности относительные изменения сопротивления весьма малы (менее ~10−3) и для их измерений требуются чувствительные вольтметры или прецизионные усилители или прецизионные усилители + АЦП. Таким образом, деформации преобразуются в изменение электрического сопротивления проводников или полупроводников и далее — в электрический сигнал, обычно сигнал напряжения.
Полупроводниковый тензорезистор обладает гораздо большей чувствительностью из-за изменения свойств полупроводникового материала при деформации.[3]
Электромеханические параметры
Чувствительность
Чувствительность тензорезистора характеризуется безразмерным параметром — коэффициентом тензочувствительности K f , {\displaystyle K_{f},} который определяется как:
- K f = Δ R / R 0 ϵ , {\displaystyle K_{f}={\frac {\Delta R/R_{0}}{\epsilon }},}
где:
- Δ R {\displaystyle \Delta R} — абсолютное изменение сопротивления, вызванное деформацией, Ом;
- R 0 {\displaystyle R_{0}} — начальное сопротивление недеформированного тензорезистора, Ом;
- ϵ {\displaystyle \epsilon } — относительная деформация.
Относительная деформация определяется как:
- ϵ = Δ L / L 0 , {\displaystyle \epsilon =\Delta L/L_{0},}
где
- Δ L {\displaystyle \Delta L} — абсолютное изменение длины, м;
- L 0 {\displaystyle L_{0}} — длина недеформированного тензорезистора, м.
Для плёночных металлических тензорезисторов параметр K f {\displaystyle K_{f}} слабо зависит от деформации и немного превышает 2[4].
При включении тензорезистора в мост Уитстона, в котором остальные 3 резистора постоянны (не имеют возможности регулирования сопротивления), выходное напряжение диагонали этого моста выражается формулой:
- v = V b ⋅ K f ⋅ ϵ 4 , {\displaystyle v={\frac {V_{b}\cdot K_{f}\cdot \epsilon }{4}},}
где:
- V b {\displaystyle V_{b}} — напряжение питания моста, В.
Типичные значения коэффициента тензочувствительности для разных материалов приведены в таблице.
| Материал | Коэффициент тензочувствительности |
|---|---|
| Металлическая фольга | 2-5 |
| Тонкая металлическая плёнка (например, константановая) | 2 |
| Монокристаллический кремний | От −125 до +200 |
| Поликристаллический кремний | ±30 |
| Тонкоплёночные резистивные материалы | 100 |
Температурный коэффициент
При изменении температуры изменяется сопротивление тензорезистора, не связанное с деформацией. Это является вредным побочным эффектом. Через коэффициент тензочувствительности относительное изменение сопротивления выражается формулой:
- Δ R R = K f ⋅ ε + α ⋅ θ , {\displaystyle {\frac {\Delta R}{R}}=K_{f}\cdot \varepsilon +\alpha \cdot \theta ,}
где:
Электрическая схема подключения тензорезистора
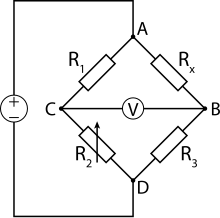
Обычно тензорезисторы включают в одно или два плеча сбалансированного моста Уитстона, питаемого от источника постоянного тока (диагональ моста A—D). С помощью переменного резистора R 2 {\displaystyle R_{2}} производится балансировка моста, так, чтобы в отсутствие приложенной силы напряжение диагонали сделать равным нулю. С диагонали моста B—C снимается сигнал, далее подаваемый на измерительный прибор, дифференциальный усилитель или АЦП.
При выполнении соотношения R 1 R 2 = R x R 3 {\displaystyle {\frac {R_{1}}{R_{2}}}={\frac {R_{x}}{R_{3}}}} напряжение диагонали моста равно нулю. При деформации изменяется сопротивление R x {\displaystyle R_{x}} (например, увеличивается при растяжении), это вызывает снижение потенциала точки соединения резисторов R x {\displaystyle R_{x}} и R 3 {\displaystyle R_{3}} (точки B) и изменение напряжения диагонали B—C моста — полезный сигнал.
Изменение сопротивления R x {\displaystyle R_{x}} может происходить не только от деформации, но и от влияния других факторов, главный из них — изменение температуры, что вносит погрешность в результат измерения деформации. Для снижения влияния температуры применяют сплавы с низким ТКС, термостатируют объект, вносят поправки на изменение температуры и/или применяют дифференциальные схемы включения тензорезисторов в мост.
Например, в схеме на рисунке вместо постоянного резистора R 3 {\displaystyle R_{3}} включают такой же тензорезистор, как и R x {\displaystyle R_{x}} , но при деформации детали этот резистор изменяет своё сопротивление с обратным знаком. Это достигается наклейкой тензорезисторов на поверхности по-разному деформируемых зон детали, например, с разных сторон изгибаемой балки или с одной стороны, но со взаимно перпендикулярной ориентацией. При изменении температуры, если температура обоих резисторов равна, знак и величина изменения сопротивления, вызванного изменением температуры, равны, и температурный уход при этом компенсируется.
Также промышленностью выпускаются специализированные микросхемы для работы совместно с тензорезисторами, в которых помимо усилителей сигнала часто предусмотрены источники питания моста, схемы термокомпенсации, АЦП, цифровые интерфейсы для связи с внешними цифровыми системами обработки сигналов и другие полезные сервисные функции.
Конструкция
 Плёночный тензорезистор. На подложку через фигурную маску в вакууме напылена или сформирована методами фотолитографии плёнка металла. Для подключения электродов выполнены контактные площадки (снизу). Метки облегчают ориентацию при монтаже.
Плёночный тензорезистор. На подложку через фигурную маску в вакууме напылена или сформирована методами фотолитографии плёнка металла. Для подключения электродов выполнены контактные площадки (снизу). Метки облегчают ориентацию при монтаже.Обычно современные тензорезисторы представляют собой чувствительный элемент в виде зигзагообразного проводника, нанесенного на гибкую подложку. Тензорезистор приклеивается подложкой на поверхность исследуемого на деформации объекта. Проводники тензорезисторов обычно изготавливаются из тонкой металлической проволоки, фольги, или напыляются в вакууме для получения плёнки полупроводника или металла. В качестве подложки обычно используют ткань, бумагу, полимерную плёнку, слюду и др. Для присоединения чувствительного элемента в электрическую цепь тензорезистор имеет выводные проволочные концы или контактные площадки.
Плёночные металлические тензорезисторы имеют площадь около 2‑10 мм2.
Применение
Тензорезисторы используются в качестве первичных преобразователей в тензометрах и тензостанциях при измерениях механических величин (деформации, силы, крутящего момента, перемещения, также, для измерения давления в манометрах и пр.)
См. также
Примечания
Ссылки


Тензорези́стор (от лат. tensus — напряжённый и лат. resisto — сопротивляюсь) — резистор, сопротивление которого изменяется в зависимости от его деформации[1]. Тензорезисторы используются в тензометрии. С помощью тензорезисторов можно измерять деформации механически связанных с ними элементов[2]. Тензорезистор является основной составной частью тензодатчиков, применяющихся для косвенного измерения силы, давления, веса, механических напряжений, крутящих моментов и пр.
Принцип действия
При растяжении проводящих элементов тензорезистора увеличивается их длина и уменьшается поперечное сечение, что увеличивает сопротивление тензорезистора, при сжатии — уменьшает.
Принцип действия проиллюстрирован на анимированном изображении. Для наглядности на изображении величина деформации тензорезистора утрированно увеличена, как и изменение сопротивления. В реальности относительные изменения сопротивления весьма малы (менее ~10−3) и для их измерений требуются чувствительные вольтметры или прецизионные усилители или прецизионные усилители + АЦП. Таким образом, деформации преобразуются в изменение электрического сопротивления проводников или полупроводников и далее — в электрический сигнал, обычно сигнал напряжения.
Полупроводниковый тензорезистор обладает гораздо большей чувствительностью из-за изменения свойств полупроводникового материала при деформации.[3]
Электромеханические параметры
Чувствительность
Чувствительность тензорезистора характеризуется безразмерным параметром — коэффициентом тензочувствительности K f , {\displaystyle K_{f},} который определяется как:
- K f = Δ R / R 0 ϵ , {\displaystyle K_{f}={\frac {\Delta R/R_{0}}{\epsilon }},}
где:
- Δ R {\displaystyle \Delta R} — абсолютное изменение сопротивления, вызванное деформацией, Ом;
- R 0 {\displaystyle R_{0}} — начальное сопротивление недеформированного тензорезистора, Ом;
- ϵ {\displaystyle \epsilon } — относительная деформация.
Относительная деформация определяется как:
- ϵ = Δ L / L 0 , {\displaystyle \epsilon =\Delta L/L_{0},}
где
- Δ L {\displaystyle \Delta L} — абсолютное изменение длины, м;
- L 0 {\displaystyle L_{0}} — длина недеформированного тензорезистора, м.
Для плёночных металлических тензорезисторов параметр K f {\displaystyle K_{f}} слабо зависит от деформации и немного превышает 2[4].
При включении тензорезистора в мост Уитстона, в котором остальные 3 резистора постоянны (не имеют возможности регулирования сопротивления), выходное напряжение диагонали этого моста выражается формулой:
- v = V b ⋅ K f ⋅ ϵ 4 , {\displaystyle v={\frac {V_{b}\cdot K_{f}\cdot \epsilon }{4}},}
где:
- V b {\displaystyle V_{b}} — напряжение питания моста, В.
Типичные значения коэффициента тензочувствительности для разных материалов приведены в таблице.
| Материал | Коэффициент тензочувствительности |
|---|---|
| Металлическая фольга | 2-5 |
| Тонкая металлическая плёнка (например, константановая) | 2 |
| Монокристаллический кремний | От −125 до +200 |
| Поликристаллический кремний | ±30 |
| Тонкоплёночные резистивные материалы | 100 |
Температурный коэффициент
При изменении температуры изменяется сопротивление тензорезистора, не связанное с деформацией. Это является вредным побочным эффектом. Через коэффициент тензочувствительности относительное изменение сопротивления выражается формулой:
- Δ R R = K f ⋅ ε + α ⋅ θ , {\displaystyle {\frac {\Delta R}{R}}=K_{f}\cdot \varepsilon +\alpha \cdot \theta ,}
где:
Электрическая схема подключения тензорезистора

Обычно тензорезисторы включают в одно или два плеча сбалансированного моста Уитстона, питаемого от источника постоянного тока (диагональ моста A—D). С помощью переменного резистора R 2 {\displaystyle R_{2}} производится балансировка моста, так, чтобы в отсутствие приложенной силы напряжение диагонали сделать равным нулю. С диагонали моста B—C снимается сигнал, далее подаваемый на измерительный прибор, дифференциальный усилитель или АЦП.
При выполнении соотношения R 1 R 2 = R x R 3 {\displaystyle {\frac {R_{1}}{R_{2}}}={\frac {R_{x}}{R_{3}}}} напряжение диагонали моста равно нулю. При деформации изменяется сопротивление R x {\displaystyle R_{x}} (например, увеличивается при растяжении), это вызывает снижение потенциала точки соединения резисторов R x {\displaystyle R_{x}} и R 3 {\displaystyle R_{3}} (точки B) и изменение напряжения диагонали B—C моста — полезный сигнал.
Изменение сопротивления R x {\displaystyle R_{x}} может происходить не только от деформации, но и от влияния других факторов, главный из них — изменение температуры, что вносит погрешность в результат измерения деформации. Для снижения влияния температуры применяют сплавы с низким ТКС, термостатируют объект, вносят поправки на изменение температуры и/или применяют дифференциальные схемы включения тензорезисторов в мост.
Например, в схеме на рисунке вместо постоянного резистора R 3 {\displaystyle R_{3}} включают такой же тензорезистор, как и R x {\displaystyle R_{x}} , но при деформации детали этот резистор изменяет своё сопротивление с обратным знаком. Это достигается наклейкой тензорезисторов на поверхности по-разному деформируемых зон детали, например, с разных сторон изгибаемой балки или с одной стороны, но со взаимно перпендикулярной ориентацией. При изменении температуры, если температура обоих резисторов равна, знак и величина изменения сопротивления, вызванного изменением температуры, равны, и температурный уход при этом компенсируется.
Также промышленностью выпускаются специализированные микросхемы для работы совместно с тензорезисторами, в которых помимо усилителей сигнала часто предусмотрены источники питания моста, схемы термокомпенсации, АЦП, цифровые интерфейсы для связи с внешними цифровыми системами обработки сигналов и другие полезные сервисные функции.
Конструкция
 Плёночный тензорезистор. На подложку через фигурную маску в вакууме напылена или сформирована методами фотолитографии плёнка металла. Для подключения электродов выполнены контактные площадки (снизу). Метки облегчают ориентацию при монтаже.
Плёночный тензорезистор. На подложку через фигурную маску в вакууме напылена или сформирована методами фотолитографии плёнка металла. Для подключения электродов выполнены контактные площадки (снизу). Метки облегчают ориентацию при монтаже.Обычно современные тензорезисторы представляют собой чувствительный элемент в виде зигзагообразного проводника, нанесенного на гибкую подложку. Тензорезистор приклеивается подложкой на поверхность исследуемого на деформации объекта. Проводники тензорезисторов обычно изготавливаются из тонкой металлической проволоки, фольги, или напыляются в вакууме для получения плёнки полупроводника или металла. В качестве подложки обычно используют ткань, бумагу, полимерную плёнку, слюду и др. Для присоединения чувствительного элемента в электрическую цепь тензорезистор имеет выводные проволочные концы или контактные площадки.
Плёночные металлические тензорезисторы имеют площадь около 2‑10 мм2.
Применение
Тензорезисторы используются в качестве первичных преобразователей в тензометрах и тензостанциях при измерениях механических величин (деформации, силы, крутящего момента, перемещения, также, для измерения давления в манометрах и пр.)
См. также
Примечания
Ссылки
Тензорезистор — Википедия


Тензорези́стор (от лат. tensus — напряжённый и лат. resisto — сопротивляюсь) — резистор, сопротивление которого изменяется в зависимости от его деформации[1]. Тензорезисторы используются в тензометрии. С помощью тензорезисторов можно измерять деформации механически связанных с ними элементов[2]. Тензорезистор является основной составной частью тензодатчиков, применяющихся для косвенного измерения силы, давления, веса, механических напряжений, крутящих моментов и пр.
Принцип действия
При растяжении проводящих элементов тензорезистора увеличивается их длина и уменьшается поперечное сечение, что увеличивает сопротивление тензорезистора, при сжатии — уменьшает.
Принцип действия проиллюстрирован на анимированном изображении. Для наглядности на изображении величина деформации тензорезистора утрированно увеличена, как и изменение сопротивления. В реальности относительные изменения сопротивления весьма малы (менее ~10−3) и для их измерений требуются чувствительные вольтметры или прецизионные усилители или прецизионные усилители + АЦП. Таким образом, деформации преобразуются в изменение электрического сопротивления проводников или полупроводников и далее — в электрический сигнал, обычно сигнал напряжения.
Полупроводниковый тензорезистор обладает гораздо большей чувствительностью из-за изменения свойств полупроводникового материала при деформации.[3]
Электромеханические параметры
Чувствительность
Чувствительность тензорезистора характеризуется безразмерным параметром — коэффициентом тензочувствительности K f , {\displaystyle K_{f},} который определяется как:
- K f = Δ R / R 0 ϵ , {\displaystyle K_{f}={\frac {\Delta R/R_{0}}{\epsilon }},}
где:
- Δ R {\displaystyle \Delta R} — абсолютное изменение сопротивления, вызванное деформацией, Ом;
- R 0 {\displaystyle R_{0}} — начальное сопротивление недеформированного тензорезистора, Ом;
- ϵ {\displaystyle \epsilon } — относительная деформация.
Относительная деформация определяется как:
- ϵ = Δ L / L 0 , {\displaystyle \epsilon =\Delta L/L_{0},}
где
- Δ L {\displaystyle \Delta L} — абсолютное изменение длины, м;
- L 0 {\displaystyle L_{0}} — длина недеформированного тензорезистора, м.
Для плёночных металлических тензорезисторов параметр K f {\displaystyle K_{f}} слабо зависит от деформации и немного превышает 2[4].
При включении тензорезистора в мост Уитстона, в котором остальные 3 резистора постоянны (не имеют возможности регулирования сопротивления), выходное напряжение диагонали этого моста выражается формулой:
- v = V b ⋅ K f ⋅ ϵ 4 , {\displaystyle v={\frac {V_{b}\cdot K_{f}\cdot \epsilon }{4}},}
где:
- V b {\displaystyle V_{b}} — напряжение питания моста, В.
Типичные значения коэффициента тензочувствительности для разных материалов приведены в таблице.
| Материал | Коэффициент тензочувствительности |
|---|---|
| Металлическая фольга | 2-5 |
| Тонкая металлическая плёнка (например, константановая) | 2 |
| Монокристаллический кремний | От −125 до +200 |
| Поликристаллический кремний | ±30 |
| Тонкоплёночные резистивные материалы | 100 |
Температурный коэффициент
При изменении температуры изменяется сопротивление тензорезистора, не связанное с деформацией. Это является вредным побочным эффектом. Через коэффициент тензочувствительности относительное изменение сопротивления выражается формулой:
- Δ R R = K f ⋅ ε + α ⋅ θ , {\displaystyle {\frac {\Delta R}{R}}=K_{f}\cdot \varepsilon +\alpha \cdot \theta ,}
где:
Электрическая схема подключения тензорезистора

Обычно тензорезисторы включают в одно или два плеча сбалансированного моста Уитстона, питаемого от источника постоянного тока (диагональ моста A—D). С помощью переменного резистора R 2 {\displaystyle R_{2}} производится балансировка моста, так, чтобы в отсутствие приложенной силы напряжение диагонали сделать равным нулю. С диагонали моста B—C снимается сигнал, далее подаваемый на измерительный прибор, дифференциальный усилитель или АЦП.
При выполнении соотношения R 1 R 2 = R x R 3 {\displaystyle {\frac {R_{1}}{R_{2}}}={\frac {R_{x}}{R_{3}}}} напряжение диагонали моста равно нулю. При деформации изменяется сопротивление R x {\displaystyle R_{x}} (например, увеличивается при растяжении), это вызывает снижение потенциала точки соединения резисторов R x {\displaystyle R_{x}} и R 3 {\displaystyle R_{3}} (точки B) и изменение напряжения диагонали B—C моста — полезный сигнал.
Изменение сопротивления R x {\displaystyle R_{x}} может происходить не только от деформации, но и от влияния других факторов, главный из них — изменение температуры, что вносит погрешность в результат измерения деформации. Для снижения влияния температуры применяют сплавы с низким ТКС, термостатируют объект, вносят поправки на изменение температуры и/или применяют дифференциальные схемы включения тензорезисторов в мост.
Например, в схеме на рисунке вместо постоянного резистора R 3 {\displaystyle R_{3}} включают такой же тензорезистор, как и R x {\displaystyle R_{x}} , но при деформации детали этот резистор изменяет своё сопротивление с обратным знаком. Это достигается наклейкой тензорезисторов на поверхности по-разному деформируемых зон детали, например, с разных сторон изгибаемой балки или с одной стороны, но со взаимно перпендикулярной ориентацией. При изменении температуры, если температура обоих резисторов равна, знак и величина изменения сопротивления, вызванного изменением температуры, равны, и температурный уход при этом компенсируется.
Также промышленностью выпускаются специализированные микросхемы для работы совместно с тензорезисторами, в которых помимо усилителей сигнала часто предусмотрены источники питания моста, схемы термокомпенсации, АЦП, цифровые интерфейсы для связи с внешними цифровыми системами обработки сигналов и другие полезные сервисные функции.
Конструкция
 Плёночный тензорезистор. На подложку через фигурную маску в вакууме напылена или сформирована методами фотолитографии плёнка металла. Для подключения электродов выполнены контактные площадки (снизу). Метки облегчают ориентацию при монтаже.
Плёночный тензорезистор. На подложку через фигурную маску в вакууме напылена или сформирована методами фотолитографии плёнка металла. Для подключения электродов выполнены контактные площадки (снизу). Метки облегчают ориентацию при монтаже.Обычно современные тензорезисторы представляют собой чувствительный элемент в виде зигзагообразного проводника, нанесенного на гибкую подложку. Тензорезистор приклеивается подложкой на поверхность исследуемого на деформации объекта. Проводники тензорезисторов обычно изготавливаются из тонкой металлической проволоки, фольги, или напыляются в вакууме для получения плёнки полупроводника или металла. В качестве подложки обычно используют ткань, бумагу, полимерную плёнку, слюду и др. Для присоединения чувствительного элемента в электрическую цепь тензорезистор имеет выводные проволочные концы или контактные площадки.
Плёночные металлические тензорезисторы имеют площадь около 2‑10 мм2.
Применение
Тензорезисторы используются в качестве первичных преобразователей в тензометрах и тензостанциях при измерениях механических величин (деформации, силы, крутящего момента, перемещения, также, для измерения давления в манометрах и пр.)
См. также
Примечания
Ссылки
Термин | Определение |
ОБЩИЕ ПОНЯТИЯ | |
1. Тензорезистивный эффект Тензоэффект D. Tensowiderstandseffekt Е. Tensity resistive effect F. Effet de tension en | Свойство проводников и полупроводников изменять электрическое сопротивление при объемном или линейном деформировании |
2. Тензорезистор D. .
F. Jauge . Jauge fil (Измененная редакция, Изм. N 3). | Измерительный преобразователь линейной деформации в изменение активного сопротивления, принцип действия которого основан на тензорезистивном эффекте |
2а. Приклеиваемый тензорезистор Е. Banded strain gauge | Тензорезистор, закрепляемый на поверхности объекта с помощью связующего |
2б. Привариваемый тензорезистор Е. Weldable strain gauge | Тензорезистор с металлической подложкой, закрепляемый на поверхности объекта с помощью точечной или иной сварки |
3, 4. (Исключены, Изм. N 2). | |
5. Термокомпенсированный тензорезистор D. Temperaturkompensierter Е. Temperature compensated strain gauge F. Jauge compensation thermique | Тензорезистор, у которого интервал термокомпенсации (22) совпадает с рабочей областью температур |
6. Тензотерморезистор | Измерительный преобразователь, содержащий тензорезистор и терморезистор, чувствительные элементы которых закреплены на общей подложке |
7. Тензорезисторная розетка D. DMS-Rosette Е. Strain gauge rosette F. Rosette | Измерительный преобразователь, содержащий на общей подложке чувствительные элементы тензорезистора, главные оси которых ориентированы под определенными углами друг к другу. Примечание. В зависимости от числа и формы чувствительных элементов различают двух-, трех- и четырехэлементные тензорезисторные розетки и мембранные тензорезисторные розетки |
7a. Тензорезисторная цепочка D. DMS-Kette Е. Strain gauge chain | Совокупность чувствительных элементов тензорезистора или тензорезисторных розеток, расположенных на общей подложке в определенной последовательности |
КОНСТРУКТИВНЫЕ ЭЛЕМЕНТЫ ТЕНЗОРЕЗИСТОРОВ | |
8. Чувствительный элемент тензорезистора Чувствительный элемент D. Empfindlicher Element. Е. Sensing element. Grid F. sensible. Grille | Элемент конструкции тензорезистора, преобразующий линейную деформацию в изменение активного сопротивления |
9. Вывод тензорезистора Вывод D. Е. Lead F. Fil sorti | Элемент конструкции тензорезистора, предназначенный для электрического соединения чувствительного элемента с внешней измерительной цепью |
10. Подложка тензорезистора Подложка D. Е. Backing. Carrier. Matrix F. Support | Несущий элемент конструкции тензорезистора, на котором закреплены чувствительный элемент и выводы тензорезистора |
11. Связующее тензорезистора Связующее D. Klebstoff Е. Adhesive F. | Материал, используемый для закрепления чувствительного элемента и выводов тензорезистора на подложке или тензорезистора на объекте |
12. Защитный элемент тензорезистора Защитный элемент D. Abdeckung Е. Protective element F. protecteur | Элемент конструкции тензорезистора, закрепленный на подложке поверх чувствительного элемента и предназначенный для его защиты от повреждений |
13. Главная ось тензорезистора Главная ось D. Messrichtung des DMS Е. Measurement axis
| Ось чувствительного элемента тензорезистора, направление которой совпадает с направлением его максимальной чувствительности |
13а. Поперечная ось тензорезистора Поперечная ось Е. Transverse axis | Ось чувствительного элемента тензорезистора, расположенная под углом 90° к главной оси |
14. База тензорезистора База D. Aktive Е. Active gauge length. Gauge length
Longueur de la grille (Измененная редакция, Изм. N 3). | Длина активной части чувствительного элемента, определяемая как размер между внутренними краями поперечных участков чувствительного элемента в направлении главной оси. Примечание. Для тензорезисторов с чувствительным элементом круговой формы (кольцевой, спиральной) данный термин не применяется |
ОСНОВНЫЕ ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ ТЕНЗОРЕЗИСТОРОВ | |
15. Начальное сопротивление тензорезистора Начальное сопротивление D. Bezugswiderstand Е. Initial gauge resistance F. initiale | Сопротивление установленного тензорезистора при начальных значениях влияющих величин* и деформации |
_______________ | |
16. Выходной сигнал тензорезистора Выходной сигнал D. Ausgangssignal Е. Output signal F. Signal de sortie | Отношение приращения сопротивления тензорезистора, вызванного воздействием деформации или влияющей величины, к его начальному сопротивлению |
17. Функция преобразования тензорезистора Функция преобразования (Измененная редакция, Изм. N 3). | Зависимость выходного сигнала тензорезистора от деформации при фиксированных значениях влияющих величин |
18. Чувствительность тензорезистора Чувствительность D. K-Faktor. Empfindlichkeit Е. Gauge factor. Sensitivity
| Отношение изменения выходного сигнала тензорезистора к вызвавшему его изменению деформации, направленной вдоль главной оси тензорезистора, при фиксированных значениях влияющих величин |
19. (Исключен, Изм. N 3). | |
20. Поперечная чувствительность тензорезистоpa Поперечная чувствительность D. Querempfindlichkeit Е. Transverse sensitivity F. Sensibilite transversal | Отношение изменения выходного сигнала тензорезистора, установленного перпендикулярно к одноосной деформации, к изменению выходного сигнала такого же тензорезистора, установленного параллельно этой деформации, выраженное в процентах |
21. Температурная характеристика сопротивления тензорезистора Температурная характеристика сопротивления D. Temperaturgang von Е. Resistance temperature characteristic | Зависимость выходного сигнала тензорезистора, установленного на свободно расширяющийся образец с заданным коэффициентом линейного расширения, от температуры |
22. Интервал термокомпенсации тензорезистора D. Temperaturkompensationsbereich Е. Temperature compensation range F. compensation thermique | Интервал в рабочей области температур, в пределах которого значения температурной характеристики сопротивления тензорезистора не выходят за нормированные пределы |
23. Дрейф выходного сигнала тензорезистора Дрейф выходного сигнала D. Drift Е. Drift F. (Измененная редакция, Изм. N 3). | Изменение выходного сигнала тензорезистора во времени при фиксированных значениях влияющих величин и отсутствии деформации тензорезистора |
24. Ползучесть тензорезистора Ползучесть D. Kriechen Е. Creep F. Fluage | Изменение выходного сигнала тензорезистора во времени при фиксированном значении деформации, вызвавшей этот сигнал, и при фиксированных значениях влияющих величин с учетом поправки на дрейф |
25. Усталостная характеристика тензорезистора Усталостная характеристика D. Dauerschwingcharakteristik Е. Fatigue characteristic F. Tenue la fatigue | Зависимость числа симметричных циклов деформирования, при котором происходит отказ установленного тензорезистора от амплитуды деформаций |
26. Механический гистерезис тензорезистора Механический гистерезис D. Mechanische Hysterese Е. Mechanical hysteresis | Различие между значениями выходного сигнала тензорезистора при возрастании и уменьшении деформации |
База | 14 |
База тензорезистора | 14 |
Вывод | 9 |
Вывод тензорезистора | 9 |
Гистерезис механический | 26 |
Гистерезис тензорезистора механический | 26 |
Дрейф выходного сигнала | 23 |
Дрейф выходного сигнала тензорезистора | 23 |
Интервал термокомпенсации тензорезистора | 22 |
Ось главная | 13 |
Ось поперечная | 13а |
Ось тензорезистора главная | 13 |
Ось тензорезистора поперечная | 13а |
Подложка | 10 |
Подложка тензорезистора | 10 |
Ползучесть | 24 |
Ползучесть тензорезистора | 24 |
Розетка тензорезистора | 7 |
Связующее | 11 |
Связующее тензорезистора | 11 |
Сигнал выходной | 16 |
Сигнал тензорезистора выходной | 16 |
Сопротивление начальное | 15 |
Сопротивление тензорезистора начальное | 15 |
Тензорезистор | 2 |
Тензорезистор привариваемый | 2б |
Тензорезистор приклеиваемый | 2а |
Тензорезистор термокомпенсированный | 5 |
Тензотерморезистор | 6 |
Тензоэффект | 1 |
Функция преобразования | 17 |
Функция преобразования тензорезистора | 17 |
Характеристика сопротивления температурная | 21 |
Характеристика сопротивления тензорезистора температурная | 21 |
Характеристика тензорезистора усталостная | 25 |
Характеристика усталостная | 25 |
Цепочка тензорезисторная | 7а |
Чувствительность | 18 |
Чувствительность поперечная | 20 |
Чувствительность тензорезистора | 18 |
Чувствительность тензорезистора поперечная | 20 |
Элемент защитный | 12 |
Элемент тензорезистора защитный | 12 |
Элемент тензорезистора чувствительный | 8 |
Элемент чувствительный | 8 |
Эффект тензорезистивный | 1 |
Abdeckung | 12 |
9 | |
Ausgangssignal | 16 |
Bezugswiderstand | 15 |
Dauerschwingcharakteristik | 25 |
2 | |
DMS | 2 |
DMS, temperaturkompensierter | 5 |
Drift | 23 |
Element, empfindlicher | 8 |
Empfindlichkeit | 18 |
Hysterese, mechanische | 26 |
Kette-DMS | 7а |
K-Faktor | 18 |
Klebstoff | 11 |
Kriechen | 24 |
Messgitter | 8 |
, aktive | 14 |
Messrichtung des DMS | 13 |
Querempfindlichkeit | 20 |
Rosette-DMS | 7 |
Temperaturgang von DMS | 21 |
Temperaturkompensationsbereich | 22 |
Tensowiderstandseffekt | 1 |
| 10 |
Widerstandstemperaturcharakteristik | 21 |
Adhesive | 11 |
Backing | 10 |
Carrier | 10 |
Chain, strain gauge | 7а |
Characteristic, fatigue | 25 |
Characteristic, temperature, resistance | 21 |
Creep | 24 |
Drift | 23 |
Effect, resistive, tensity | 1 |
Element, protective | 12 |
Element sensing | 8 |
Hysteresis, mechanical | 26 |
Grid | 8 |
Gauge factor. Sensitivity | 18 |
Gauge length | 14 |
Lead | 9 |
Length, gauge, active | 14 |
Matrix | 10 |
Measurement axis | 13 |
Range, compensation, temperature | 22 |
Resistance, gauge, initial | 15 |
Rosette, strain gauge | 7 |
Sensitivity | 18 |
Signal, output | 16 |
Strain gauge | 2 |
Strain gauge, bonded | 2а |
Strain gauge, resistance | 2 |
Strain gauge, resistive | 2 |
Strain gauge, temperature compensated | 5 |
Strain gauge, weldable | 2б |
Transverse axis | 13a |
Transverse sensitivity | 20 |
11 | |
Axe de mesure de jauge | 13 |
23 | |
Effet de tension en | 1 |
Element protecteur | 12 |
Element sensible | 8 |
Facteur de jauge | 18 |
Fil sorti | 9 |
Fluage | 24 |
Grille | 8 |
Jauge compensation thermique | 5 |
Jauge fil | 2 |
Jauge | 2 |
Longueur active de la jauge | 14 |
Longueur de la grille | 14 |
compensation thermique | 22 |
initiale | 15 |
Rosette | 7 |
18 | |
transversal | 20 |
Signal de sortie | 16 |
Support | 10 |
Tenue la fatigue | 25 |
Термин | Определение |
1. Тип тензорезистора Тип D. DMS-Typ | Тензорезисторы, обладающие номинально одинаковым комплексом конструкционно-технологических и метрологических свойств и характеристик |
2. Типоразмер тензорезистора Типоразмер | Тензорезисторы одного типа, имеющие одинаковую номинальную базу и одинаковое номинальное сопротивление |
3. Партия тензорезисторов Партия D. DMS-Los Е. Bath | Совокупность тензорезисторов одного типоразмера, изготовленных одним непрерывным технологическим запуском из тензорезисторного материала одной плавки, подвергнутого одинаковой механической и термической обработке |
4. Группа тензорезисторов Группа Е. Group | Совокупность тензорезисторов одной партии, разность между индивидуальными значениями одной или нескольких заданных характеристик которых не превышает нормированной величины |
5. Тензорезистивный материал Е. Strain-sensing material | Материал, обладающий комплексом свойств, необходимых для изготовления чувствительного элемента тензорезистора, например, тензорезистивная проволока, тензорезистивная фольга и др. |
6. (Исключен, Изм. N 1). | |
7. Предельная деформация тензорезистора Предельная деформация D. Maximale Dehnbarkeit | Наибольшая деформация, при воздействии которой значения функции преобразования тензорезистора находятся в нормированных пределах |
принцип действия, описание, виды, схемы
Измерение напряжений и усилий в действующих узлах и конструкциях оборудования считается одной из наиболее сложных задач. Между тем в процессе эксплуатации техника подвергается разным видам нагрузок, которые определяют долговечность и надежность оборудования. Решение поставленных задач возможно с помощью тензометрических датчиков. Установка подобных устройств целесообразна тогда, когда в дополнение к производственным факторам добавляются остаточные напряжения, постепенно накапливаемые в ходе работы.
Описание и назначение
При измерении деформаций, напряжений и усилий при помощи тензометрических датчиков используют изменение значений омического сопротивления материала, которое вызывается упругими деформациями металлической проволоки или полупроводников стержневого исполнения. Изменение сопротивления датчика передаётся при помощи кабеля или бесконтактным путем на измерительный мост. Там оно преобразуется в усиленные электрические сигналы, которые и фиксируются прибором.


Все типы тензометрических датчиков (или, иначе – тензорезисторов) используют зависимость между напряжениями и деформациями – закон Гука – который справедлив в области упругих деформаций. Согласно закону Гука изменение электросопротивления, отнесённое к исходному значению данного параметра до деформации, пропорционально изменению удлинения, отнесённому к первоначальной длине измерительного элемента. Применяя коэффициент пропорциональности, который зависит от диапазона измеряемых параметров и материала устройства, устанавливают зависимость между нагрузкой на датчик и его удлинением:
ΔR/R = k×Δl/l,
где:
R – исходное значение электрического сопротивления;
ΔR – изменение значения электрического сопротивления в процессе деформации;
k – коэффициент пропорциональности;
Δl – изменение длины при деформировании;
l – исходная длина измерительного элемента до приложения к нему эксплуатационной нагрузки.
Указанный тип устройств используется в весоизмерительной технике, поскольку относится к тензорным, определяющим усилия и внешние нагрузки.


Виды
Применяемость рассматриваемых измерительных элементов определяется материалом, из которого выполнен датчик. Чаще всего исходным материалом служит сплав константан, состоящий из 40% никеля и 60% меди. Для константана k ≈ 2; таким же порядком значений (1.5…3,5) обладают и другие сплавы постоянного электросопротивления.
Датчики полупроводникового типа имеют более высокие значения коэффициента пропорциональности. В зависимости от материала полупроводника (кремний или германий), а также состава легирующих добавок значения коэффициента достигают 50…70. В связи с этим полупроводниковые тензометрические датчики более чувствительны, и их применяют для оценки малых удлинений. Вместе с тем полупроводниковые датчики характеризуются повышенными отклонениями своего удлинения в диапазонах 1,5…9 % относительного удлинения. Для проволочных датчиков этот показатель не превышает 0,5%.


Конструкции тензометрических датчиков проволочного типа разрабатываются с учетом следующих ограничений:
- С целью получения достаточной точности измерений величина сопротивления проволочного элемента должна находиться в пределах 100…1000 Ом;
- Диаметр проволоки целесообразно иметь в диапазоне 0,01…0,03 мм;
- Длина проволочного элемента не должна превышать 250…300 мм.
В некоторых случаях приведенные ограничения не позволяют устанавливать тензометрические датчики в виде проволок, поэтому измерительные устройства изготавливают из фольги или плоских измерительных решеток. Для предохранения от повреждений, которые могут возникнуть при транспортировке или сборке таких датчиков, для их крепления в напольном исполнении применяют подложку из бумаги или тонкого пластика.
Чтобы обеспечить электрический контакт с измерительной решеткой, на подложке размещают проволочные выводы, которые затем присоединяются к датчику при помощи пайки.


Виды тензодатчиков, включающих в себя активный измерительный элемент, контактные выводы и подложку:
- Плоский проволочный.
- Фольговый.
- Полупроводниковый, с одним или двумя стержнями.
- Трубчатый.
Краткая характеристика наиболее распространённых исполнений тензодатчиков приводится далее.
- Консольные. Предназначены для измерения крутящих и изгибающих моментов, устанавливаются в метах наибольшего прогиба конструкций.
- Цилиндрические. Наименее компактны, зато позволяют определять значительные напряжения, приближающиеся по своим значениям к пределу текучести лимитирующего материала.
- S-образные. Дают возможность оценивать трехмерные деформации при объемном напряженно-деформированном состоянии. Чаще других нуждаются в поверке.


Устройство и принцип работы
По типу воздействия на исполнительные элементы конструкции различают тактильные, резистивные, пьезорезонансные, пьезоэлектрические, магнитные и емкостные датчики.
Тактильные
Срабатывают в результате механического действия на чувствительную поверхность. Позволяют устанавливать минимальные деформации, но при неточных настойках могут подавать и ложный сигнал.
Резистивные
Наиболее распространенный тип датчиков. Требуют подключения к слаботочной управляющей цепи, поскольку включают в себя тензорезисторный контур. Надежны при любом состоянии окружающей среды.
Пьезорезонансные
Относятся к устройствам полупроводникового типа, нуждаются в надежном обслуживании и тонкой настройке. Работают по принципу сравнения эталонного сигнала с фактическим.
Пьезоэлектрические
По своему действию подобны измерителям предыдущего типа, но подают сигнал при изменении значений контактных деформаций, прикладываемых к чувствительному элементу.
Магнитные
Изготавливаются из сплавов с переменным значением коэрцитивной силы, используются при измерении усилий в узлах оборудования, работающих в сильных электромагнитных полях.
Емкостные
Предназначены для измерения малых механических напряжений в деталях со сложной конфигурацией, когда изменение длины токопроводящей проволоки изменяет ее электрическую емкость.
Характеристика
Для изготовления тензометрических датчиков необходимо использовать материалы проволок, относительное изменение сопротивления которых пропорционально удлинению в максимальном диапазоне деформаций. При этом коэффициент пропорциональности k должен иметь большие значения. Для компактных устройств со значительной чувствительностью приходится применять материалы, обладающие высоким удельным сопротивлением. При этом температурная зависимость удельного сопротивления при изменении внешних условий должна быть незначительной, а лучше и вовсе отсутствовать.


Условия оптимального использования тензорезисторов:
- Малое различие между коэффициентами теплового расширения материала конструкции (или узла) и измерительной проволоки устройства.
- Нечувствительность к термическим напряжениям, которые возникают при соединении измерительного элемента с контролируемой частью оборудования или конструкции (для такого присоединения чаще всего используют пайку).
- Хорошая обрабатываемость паяных соединений, которая не изменяет эксплуатационные параметры оборудования.
- Надежность соединения, учитывающая возможные динамические удары и перемещения.
На параметр пропорциональности k влияют коэффициент Пуассона ε (представляющий собой условную меру изменения поперечного сечения детали при приложении к ней растягивающих напряжений) и теплофизические параметры материала, из которого изготовлен тензометрический прибор.


Схемы подключения
Конструкции тензометрических датчиков, в частности, их малая жесткость, вынуждают применять особые способы подключения рассматриваемых элементов. Например, участки проволочной решетки в местах возможного изгиба при деформации часто располагаются поперечно к направлению измерений. Они воспринимают составляющие удлинения, действующие именно в этом направлении, и поэтому недостаточно точно реагируют на силы и деформации продольного направления. Отношение чувствительности измерения удлинений в продольном и поперечном направлениях для датчиков проволочного исполнения находятся в пределах от -0,01 до +0,04.
Влияние описанного фактора уменьшается, если для измерения напряжений, крутящих моментов или усилий использовать фольговые силоизмерительные датчики. По аналогии с печатными схемами, измерительная фольговая решетка, которая расположена на пластмассовой подложке, может быть получена в результате травления тонкой металлической фольги. Кроме того, токовая нагрузка на тензометрические датчики фольгового типа больше, чем на проволочные, вследствие чего тепло от фольговых тензометров отводится лучше.


Тензорезисторы часто приклеиваются к исследуемому конструктивному элементу. Клеевое соединение обеспечивает постоянную передачу деформации через подложку на измерительную решетку. Поэтому к клеям предъявляется также и ряд особых требований:
- Высокое сопротивление ползучести.
- Отсутствие гистерезиса.
- Влагостойкость.
- Адгезионная способность.
- Температуростойкость.
Наибольшую эксплуатационную надежность проявляют эпоксидные смолы холодного твердения. Для экспериментального определения многосторонней деформации используют розеточную систему данных устройств, которые образуют измерительный мост. При этом образованная схема состоит из не менее, чем четырех закрепленных на подложке датчиков, которые размещаются крестообразно, треугольником, т-образно, в виде звезды. Благодаря многолучевому размещению тензорезисторов их удлинения измеряются в двух, трех или четырех направлениях.


Сферы применения
Кроме определения удлинений, которые вызываются действием внешних нагрузок на конструктивные части оборудования, тензометрические датчики могут применяться для измерения собственных (остаточных) напряжений в момент их релаксации, это явление происходит при высверливании или разрезке некоторых конструктивных деталей и узлов.
Тонкопленочные датчики давления, которые изготавливаются путем осаждения из паровой фазы или распыления, используются для определения усилий, напряжений, крутящих моментов и деформаций в изоляционных элементах, которые размещаются непосредственно на полированных мембранах. Для калибровки резистивных элементов используется лазерная подгонка, повышающая точность замеров. Диффузионные полупроводниковые датчики давления могут проникать в кремниевую чувствительную к давлению диафрагму, и не связаны со свойствами поверхности. Это позволяет использовать их в технологиях миниатюрного тензометрирования.
Основным преимуществом тонкопленочных преобразователей является устранение нестабильности, вызванной клеем.
Технология тонких пленок считается более современной и обеспечивает превосходную стабильность при нулевом температурном режиме и полной чувствительности, а также высокую долговечность.
Часто применяемые условия для использования тензодатчиков перечислены далее.
Измерение веса
Необходимо в системах напольного типа, при помощи которых определяют массу груза. Характеризуются минимальными требованиями к точности монтажа и наладки.
Измерение давления
Используется в технологических линиях обработки металлов давлением. Одновременно производится также измерение рабочих сил и упругих деформаций. Датчики снабжаются силоизмерительным устройством с цифровой индикацией.
Измерение крутящего момента
Применяется для испытательного оборудования станций технического обслуживания автомобильного транспорта.
Определение ускорения
Иногда используется в экспериментальных лабораториях, где занимаются проектированием и испытаниями высокоскоростной рельсовой и безрельсовой техники.
Контроль перемещения
Самые распространенные отрасли применения – сейсмологические станции и фундаменты высокоточного массивного оборудования, преимущественно энергетического.
Плюсы и минусы
Тензорные датчики компактны, удобны при установке, практически не ограничивают работоспособность конструкции, где они установлены. Вместе с тем они часто подвержены эффекту старения, чувствительны к температурным напряжениям и иногда характеризуются повышенным разбросом получаемых данных. Тонкоплёночные тензорезисторы, кроме того, характеризуются низким уровнем выходного сигнала, ограниченными частотными характеристиками и влиянием высокого напряжения на точность получаемых результатов. Чаще других типов применяются в качестве весовых, а также для определения комплекса силовых факторов, постоянно изменяющихся в процессе работы оборудования или конструкции.
Преимущества тензометрических технологий:
- Быстрое время отклика;
- Простота компенсации температурных эффектов;
- Малая чувствительность к динамическим воздействиям.
Недостатки:
- Невозможность обеспечить более низкие диапазоны измерений;
- Снижение точности показаний при вибрациях;
- Необходимость точного совмещения с окружающей средой;
- Сложность первоначальной настройки.
Выпуск современных тензометрических датчиков регламентируется требованиями ГОСТ 21616-91.
90000 types, principle of operation and device 90001 90002 In various modern spheres of human activity there is a need of different control structures by measuring parameters and the current state of the given element. Indispensable helpers in this case are strain gauge sensors. 90003 90002 Leading technology are increasingly using electronic load cells, which are the most widespread strain of the model. Strain gage elements to measure weight, force, pressure, movement, etc. 90003 90002 Widely used load cells for scales, industrial machines, different engines, are used in the construction field and many other areas.90003 90008 Facebook 90009 90002 In various industrial sectors applies a huge variety of strain gauge transducers. The following types of devices: 90003 90012 90013 Tools measure the force — sensors scan parameters change effort and the load; 90014 90013 Devices for measuring the projection of the acceleration — accelerometers; 90014 90013 Measuring tools moving of test materials; 90014 90013 Strain gauge devices pressure — characterized by the control of parameters of pressure of the different elements in different environments; 90014 90013 Strain gauge torque converters.90022 90014 90024 90002 For scales strain gauges are the most typical the feature. Depending on the application structure of the cargo receiving surface sensors are used the following types: 90003 90012 90013 Appliances cantilever type; 90014 90013 Measuring device in the form of the Latin letter S; 90014 90013 Strain gauges in the form of puck; 90014 90013 Measuring devices resembling the shape of a barrel. 90014 90024 90002 There is a classification of measuring load cells, depending on the design features — element sensitivity.Source material is defined these models: 90003 90012 90013 Wire — are in the form of wire, two-component material is nichrome, elemental connection resistant, thermostable alloy Constantan; 90014 90013 Strain gauges, foil — uses thin strips of foil; 90014 90013 Solid-state sensors — are made of chemical elements like silicon, Galiy, germanium. 90014 90024 90008 Principle of operation 90009 90002 The principle of the device used centerfest. Its essence is to change the working counter and semi — conductor elements during expansion or contraction — mechanical deformation.90003 90002 Recommended 90003 90053 90002 IPTV settings «Rostelecom». IPTV channels 90003 90002 Analog TV is gradually disappearing into the background. His place faster pace is a free IPTV Rostelecom. And it’s really convenient, because digital channels to look better because of better picture, sound. But first you need to clarify some points …. 90003 90058 90002 IMEI: how to change the phone yourself 90003 90002 If you need to change the IMEI on your phone, this article will provide complete and correct information about what is IMEI code, what is it for, and how to change it.What is IMEI you May have already encountered this concept, then you know that the … 90003 90063 90002 Washing machine Bosch MAXX 4: operating instructions 90003 90002 All well-known manufacturer of Bosh, before you present to the world another new, not only conducts many tests, but uses all available methods to ensure maximum safety. To washing machine MAXX 4 pleased his master as long as possible, the set to her … 90003 90068 90002 Load cells represent a constructive set of lode cell, which has a communication point on the panel.The latter is connected with the material to be measured. Functional diagram of the actuation strain gauge is that there is an influence on the element sensitivity. The connection of the power source is carried out using elektroauto who have contact with the sensitive plate. 90003 90002 Contact locations characterized by the presence of DC voltage. The load cell takes the item through special underlay. The mass of the material interrupts the circuit due to the deformation of the distortion. The resulting process transformered into electric current signal.90003 90002 Strain-gauge pressure sensor is often used with tensorielle AC. This system is made of amplitude modulation of the voltage which is supplied directly to the transducer sensors. 90003 90008 Device sensors 90009 90002 Strain gauge measurement tool consists of: 90003 90012 90013 Elastic element; 90014 90013 Lode cell; 90014 90013 Housing; 90014 90013 Sealed connector. 90014 90024 90002 Under the elastic element refers to the body that receives the load. Mostly made from special steel, which have already undergone heat treatment.This has an impact on obtaining stable readings. Form fabrication is presented in the form of a rod, ring or the console. The core design is more popular and widespread. 90003 90002 The lode cell — chicken wire or metal foil resistor node, which is attached to the rod. This detail of the strain gauge changes its resistance to deformation rod, deformation and distortion, in turn, proportional to the load. 90003 90002 The body of the measuring device prevents the internal structure from all kinds of mechanical damage, including from the negative influences of the environment.The housing complies with the international standard and has various forms. 90003 90002 A Sealed connector is needed for communication with additional sensor equipment (scales, amplifiers, etc.) via cable. There are a variety of circuit connections. Features of some load cells provide a replacement cable. 90003 90097 90008 Sensors measure the force 90009 90002 Strain gauge force sensors have a different common name — dynamometers. These measuring instruments are an integral part of the weighing equipment.Their necessity can hardly be overestimated, as they operate in all technological automated systems of any production. They have found application in agriculture, medicine, metallurgy, automotive industry, etc. 90003 90002 In this method of measurement takes a lot of manipulation, and in line with this, there are several types of strain gauges: 90003 90012 90013 Tactile — are divided into converters, effort, slippage and touch; 90014 90013 Resistive — used by the lode cell and have a linear signal output; 90014 90013 Piezoresonance — characterized by direct and reverse effect which provides a sensor-resonator; 90014 90013 Piezoelectric — resistant to ambient temperatures, high strength, used direct piezoelectric effect; 90014 90013 Magnetic — operate on the phenomenon of magnetostriction, changing the geometry of the dimensions in a magnetic field; 90014 90013 Capacitive-measurement means of the parametric type is the condenser.90116 90014 90024 90008 Sensors measuring weight 90009 90002 Strain gauge load cells consist of three elements: 90003 90123 90013 Lode cell. 90014 90013 Beam bending. 90014 90013 Cable. 90014 90130 90002 Sensors are used in weighing equipment for industrial use and personal use. The more popular the data measurement means in the area of manufacturing and are of such types: 90003 90012 90013 Console device-aluminum or steel billet. Steel can be made in the form of barrels or washers possess high integrity; 90014 90013 Beam device — measure the load on the platform and bridge structures.90137 90014 90024 90008 The Advantages of load cells 90009 90002 They are as follows: 90003 90012 90013 Precision measurements of parameters. 90014 90013 Do Not allow the distortion of information. 90014 90013 Compatible with measured stress. 90014 90013 Compact size. 90014 90024 90002 The only Disadvantage is the loss of sensitivity of the operating elements at the critical temperature. 90003 ….90000 THE STRAIN GAGE PRESSURE TRANSDUCER 90001 90002 Weight Measurement Technology 90003 90004 90005 Kistler-Morse (KM) introduced bolt-on weight measuring systems three decades ago.These devices featured Walter Kistler s invention, the Microcell. Over the years, many improvements were made to the Microcell 90006 More information 90007 90002 Subminiature Load Cell Model 8417 90003 90004 90011 w Technical Product Information Subminiature Load Cell 1. Introduction … 2 2. Preparing for use … 2 2.1 Unpacking … 2 2.2 Using the instrument for the first time … 2 2.3 Grounding and potential connection … 90006 More information 90007 90002 15.MODULUS OF ELASTICITY 90003 90004 90017 Chapter 5 Modulus of Elasticity 5. MODULUS OF ELASTICITY The modulus of elasticity (= Young s modulus) E is a material property, that describes its stiffness and is therefore one of the most important 90006 More information 90007 90002 Typical Aluminum GFM Mass Flow Meter 90003 90004 90023 MASS FLOW METERS Design Features n Rigid metallic construction. n Maximum pressure of 1000 psig (70 bars).n Leak integrity 1 x 10-9 of helium. n NIST traceable certification. n Built-in tiltable LCD readout. 90006 More information 90007 90002 SEMICONDUCTOR TECHNICAL DATA 90003 90004 90029 SEMICONDUCTOR TECHNICAL DATA Order this document by MPX5050 / D The MPX5050 series piezoresistive transducer is a state of the art monolithic silicon pressure sensor designed for a wide range of applications, 90006 More information 90007 90002 Bourns Resistive Products 90003 90004 90035 Bourns Resistive Products Diverse Requirements Drive Innovations to Pulse Resistors Introduction Countless circuits depend on the protection provided by one of the most fundamental types of passive components: 90006 More information 90007 90002 DIRECT CURRENT GENERATORS 90003 90004 90041 DIRECT CURRENT GENERATORS Revision 12:50 14 Nov 05 INTRODUCTION A generator is a machine that converts mechanical energy into electrical energy by using the principle of magnetic induction.This principle 90006 More information 90007 90002 Stress Strain Relationships 90003 90004 90047 Stress Strain Relationships Tensile Testing One basic ingredient in the study of the mechanics of deformable bodies is the resistive properties of materials. These properties relate the stresses to the 90006 More information 90007 90002 Resistor Theory and Technology 90003 90004 90053 Resistor Theory and Technology Felix Zandman Chairman, Scientific Director, and CEO, Vishay Intertechnology, Inc.Paul-Rene Simon Consultant Joseph Szwarc Chief Engineer, Vishay Israel Ltd SciTECH PUBLISHING; 90006 More information 90007 90002 Fundamentals of Mass Flow Control 90003 90004 90059 Fundamentals of Mass Flow Control Critical Terminology and Operation Principles for Gas and Liquid MFCs A mass flow controller (MFC) is a closed-loop device that sets, measures, and controls the flow of 90006 More information 90007 90002 MATERIALS AND MECHANICS OF BENDING 90003 90004 90065 HAPTER Reinforced oncrete Design Fifth Edition MATERIALS AND MEHANIS OF BENDING A.J. lark School of Engineering Department of ivil and Environmental Engineering Part I oncrete Design and Analysis b FALL 90006 More information 90007 90002 PRODUCT PROFILE FEATURES 90003 90004 90071 PRODUCT PROFILE Pressure Transmitters & Pneumatic Transducer Airflow Transmitter, Differential Air Pressure Transmitter and Differential & Gauge Liquid / Gas Pressure Transmitter FEATURES AIRFLOW TRANSMITTER 90006 More information 90007 90002 AAV003-10E Current Sensor 90003 90004 90077 Datasheet AAV003-10E Current Sensor Key Features For Low Current Detection On-Chip Current Strap for Precise Operation 80 ma to +80 ma Linear Range Sensitivity up to 2 mv / ma AC or DC Measurement Ultraminiature 90006 More information 90007 90002 Load Cell Troubleshooting 90003 90004 90083 VPG TRANSDUCERS Load Cells and Weigh Modules Technical Note VPGT-08 Scope Load cells are designed to sense force or weight under a wide range of adverse conditions; they are not only the most essential 90006 More information 90007 90002 AA and AB-Series Analog Sensors 90003 90004 90089 AA and AB-Series Analog Sensors AA and AB-Series Analog Sensors NVE s AA and AB-Series analog GMR sensors offer unique and unparalleled magnetic sensing capabilities.These sensors are characterized by 90006 More information 90007 90002 Air Data Computers. The Beginning 90003 90004 90095 Air Data Computers Air Data Computers have been with us for many years now and have become increasingly more important, never more so then now as the RVSM mandate deadline approaches. The conventional 90006 More information 90007 90002 APPLICATION NOTES OF SIGNAL ISOLATORS 90003 90004 90101 APPLICATION NOTES OF SIGNAL ISOLATORS Summary of Topics Page 一 General Characteristics of Signal Isolator 二 The reasons and solutions about interfere 三 Comparison of supplied by loop circuit, extra power, 90006 More information 90007 90002 Soil Suction.Total Suction 90003 90004 90107 Soil Suction Total Suction Total soil suction is defined in terms of the free energy or the relative vapor pressure (relative humidity) of the soil moisture. Ψ = v RT ln v w 0ω v u v 0 (u) u = partial 90006 More information 90007 90002 Measurement of Capacitance 90003 90004 90113 Measurement of Capacitance Pre-Lab Questions Page Name: Class: Roster Number: Instructor :.A capacitor is used to store. 2. What is the SI unit for capacitance? 3. A capacitor basically consists of two 90006 More information 90007 90002 APPLICATION NOTE AP050830 90003 90004 90119 APPLICATION NOTE AP050830 Selection and use of Ultrasonic Ceramic Transducers Pro-Wave Electronics Corp. E-mail: [email protected] URL: http://www.prowave.com.tw The purpose of this application note 90006 More information 90007 .90000 Principles and Characteristics of Distance Protection 90001 90002 Introduction to Distance Protection 90003 90004 Distance relays are one of the most important protection elements in a transmission line. 90005 90006 90006 Principles and Characteristics of Distance Protection 90004 These relays may sometimes be set based in percentages of the line impedances, for example a typical setting for 90009 zone 1 90010 is 90009 80% 90010 of the impedance of the line in order to not reach the remote end, the 90009 zone 2 90010 can be set at 90009 120% 90010 of the impedance of the line in order to dependably overreach the line, 90009 Zone 3 90010 sometimes are disabled or set to cover an adjacent line.90005 90004 Distance relays characteristics may be 90009 Mho 90010, 90009 Quadrilateral 90010, 90009 Offset Mho 90010, etc. In the case of the quadrilateral characteristic or long reaching mho characteristics, additional care may be required to remain secure during heavy load. 90005 90004 In the case of parallel lines, the mutual coupling of these lines can cause distance relays to under reach and over reach. For this reason the relay setting must consider this effect, some relays have algorithms to compensate, but it is necessary to use the current of the parallel line which adds complexity to the installation.90005 90004 In some countries there criteria that a distance protection can not reach fault in other voltage levels, because fault clearing times in sub transmission levels may be slower than fault clearing times at the transmission level. 90005 90004 The problem of combining 90009 fast fault clearance 90010 with 90009 selective tripping 90010 of plant is a key aim for the protection of power systems. 90005 90004 To meet these requirements, high-speed protection systems for transmission and primary distribution circuits that are suitable for use with the 90009 automatic reclosure of circuit breakers 90010 are under continuous development and are very widely applied.90005 90004 Distance protection, in its basic form, is a non-unit system of protection offering considerable economic and technical advantages. 90005 90004 Unlike phase and neutral overcurrent protection, the key advantage of distance protection is that its fault coverage of the protected circuit is virtually independent of source impedance variations. 90005 90046 90046 Figure 1 — Advantages of distance over overcurrent protection 90004 Distance protection is comparatively simple to apply and it can be fast in operation for faults located along most of a protected circuit.It can also provide both primary and remote back-up functions in a single scheme. It can easily be adapted to create a unit protection scheme when applied with a signalling channel. 90005 90004 In this form it is eminently suitable for application with high-speed auto- reclosing, for the protection of critical transmission lines. 90005 90052 90053 Principles of Distance Relays 90054 90004 Since the impedance of a transmission line is proportional to its length, for distance measurement it is appropriate to use a relay capable of measuring the impedance of a line up to a predetermined point (90009 the reach point 90010).90005 Such a relay is described as a 90009 distance relay 90010 and is designed to operate only for faults occurring between the relay location and the selected reach point, thus giving discrimination for faults that may occur in different line sections. 90004 The basic principle of distance protection involves the division of the voltage at the relaying point by the measured current. The apparent impedance so calculated is compared with the reach point impedance. If the measured impedance is less than the reach point impedance, it is assumed that a fault exists on the line between the relay and the reach point.90005 90004 The reach point of a relay is the point along the line impedance locus that is intersected by the boundary characteristic of the relay. 90005 90004 Since this is dependent on the ratio of voltage and current and the phase angle between them, it may be plotted on an R / X diagram. The loci of power system impedances as seen by the relay during faults, power swings and load variations may be plotted on the same diagram and in this manner the performance of the relay in the presence of system faults and disturbances may be studied.90005 90052 90053 Relay performance 90054 90004 Distance relay performance is defined in terms of 90009 reach accuracy 90010 and 90009 operating time 90010. Reach accuracy is a comparison of the actual ohmic reach of the relay under practical conditions with the relay setting value in ohms. 90005 90004 Reach accuracy particularly depends on the 90009 level of voltage presented to the relay under fault conditions 90010. 90005 90004 The impedance measuring techniques employed in particular relay designs also have an impact.Operating times can vary with fault current, with fault position relative to the relay setting, and with the point on the voltage wave at which the fault occurs. 90005 90004 Depending on the measuring techniques employed in a particular relay design, measuring signal transient errors, such as those produced by Capacitor Voltage Transformers or saturating CT’s, can also adversely delay relay operation for faults close to the reach point. It is usual for electromechanical and static distance relays to claim both maximum and minimum operating times.90005 90004 However, for modern digital or numerical distance relays, the variation between these is small over a wide range of system operating conditions and fault positions. 90005 90052 90053 Distance Relay Characteristics 90054 90004 Some numerical relays measure the absolute fault impedance and then determine whether operation is required according to impedance boundaries defined on the 90009 R / X diagram 90010. 90005 90004 Traditional distance relays and numerical relays that emulate the impedance elements of traditional relays do not measure absolute impedance.They compare the measured fault voltage with a replica voltage derived from the fault current and the zone impedance setting to determine whether the fault is within zone or out-of-zone. Distance relay impedance comparators or algorithms which emulate traditional comparators are classified according to their polar characteristics, the number of signal inputs they have, and the method by which signal comparisons are made. 90005 90004 The common types compare either the relative amplitude or phase of two input quantities to obtain operating characteristics that are either straight lines or circles when plotted on an R / X diagram.At each stage of distance relay design evolution, the development of impedance operating characteristic shapes and sophistication has been governed by the technology available and the acceptable cost. 90005 90004 Since many traditional relays are still in service and since some numerical relays emulate the techniques of the traditional relays, a brief review of impedance comparators is justified. 90005 90052 90053 Example of Modern Distance Protection Relay 90054 90102 90102 SIPROTEC 7SA522 protection relay — Single line diagram (provides full-scheme distance protection and incorporates all functions usually required for the protection of a power line) 90004 90009 This particulary relay has following ANSI protection functions: 90010 90005 90108 90109 90110 90111 90009 ANSI 90010 90114 90111 90009 Description 90010 90114 90111 90009 ANSI 90010 90114 90111 90009 Description 90010 90114 90127 90110 90111 21 / 21N 90114 90111 Distance protection 90114 90111 50HS 90114 90111 Switch-onto-fault protection 90114 90127 90110 90111 FL 90114 90111 Fault locator 90114 90111 50BF 90114 90111 Breaker failure protection 90114 90127 90110 90111 50N / 51N; 67N 90 114 90111 Directional ground-fault protection 90114 90111 59/27 90114 90111 Overvoltage / undervoltage protection 90114 90127 90110 90111 50/51/67 90114 90111 Backup overcurrent protection 90114 90111 81O / U 90114 90111 Over / underfrequency protection 90114 90127 90110 90111 50 STUB 90114 90111 STUB-bus overcurrent stage 90114 90111 25 90 114 90111 Synchro-check 90114 90127 90110 90111 68 / 68T 90114 90111 Power swing detection / tripping 90114 90111 79 90 114 90111 Auto-reclosure 90114 90127 90110 90111 85/21 90114 90111 Teleprotection for distance protection 90114 90111 74TC 90114 90111 Trip circuit supervision 90114 90127 90110 90111 27WI 90114 90111 Weak-infeed protection 90114 90111 86 90 114 90111 Lockout (CLOSE command — interlocking) 90114 90127 90110 90111 85 / 67N 90114 90111 Teleprotection for ground-fault protection 90114 90213 90213 90127 90216 90217 90052 90053 Distance Protection Theory (VIDEO) 90054 90004 90222 90223 90005 90004 90009 Resource: 90010 Network protection and automation guide — Areva; SIPROTEC47SA522 — Distance Protection Relay for Transmission Lines; An Example Distance Protection Application with Complicating Factors by Yofre Jacome and Charles F Henville 90005 .90000 Strain Gage Rosettes: Selection, Application and Data Reduction 90001 90002 90003 Transcription 90004 90005 1 VISH AY micro — measurements Strain Gages and Instruments Tech Note TN-515 Strain Gage Rosettes: Selection, Application and Data Reduction 1.0 Introduction A strain gage rosette is, by definition, an arrangement of two or more closely positioned gage grids, separately oriented to measure the normal strains along different directions in the underlying surface of the test part.Rosettes are designed to perform a very practical and important function in experimental stress analysis. It can be shown that for the not-uncommon case of the general biaxial stress state, with the principal directions unknown, three independent strain measurements (in different directions) are required to determine the principal strains and stresses. And even when the principal directions are known in advance, two independent strain measurements are needed to obtain the principal strains and stresses.To meet the foregoing requirements, the Vishay Micro- Measurements Division manufactures three basic types of strain gage rosettes (each in a variety of forms): Tee: two mutually perpendicular grids. 45 -Rectangular: three grids, with the second and third grids angularly displaced from the first grid by 45 and 90, respectively. 60 -Delta: three grids, with the second and third grids 60 and 10 away, respectively, from the first grid. Representative gage patterns for the three rosette types are reproduced in Figure 1.In common with single-element strain gages, rosettes are manufactured from different combinations of grid alloy and backing material to meet varying application requirements. They are also offered in a number of gage lengths, noting that the gage length specified for a rosette refers to the active length of each individual grid within the rosette. As illustrated in Figure, rectangular and delta rosettes may appear in any of several geometrically different, but functionally equivalent, forms. Guidance in choosing the most suitable rosette for a particular application is provided in Section.0, where selection considerations are reviewed. Rectangular Delta Figure Geometrically different, but functionally equivalent configurations of rectangular and delta rosettes. 5X (a) Revision 5-Mar-08 5X (b) Figure 1 Basic rosette types, classified by grid orientation: (a) tee; (B) 45º-rectangular; (C) 60º delta. 5X (c) 151 90006 90005 2 Tech Note TN-515 Since biaxial stress states occur very commonly in machine parts and structural members, it might be presumed that half or so of the strain gages used in experimental stress analysis would be rosettes.This does not seem to be the case, however, and ten percent (or less) rosette usage may be more nearly representative. To what degree this pattern of usage reflects an inclination for on-site makeup of rosettes from single-element gages, or simply an undue tendency to assume uniaxiality of the stress state, is an open question. At any rate, neither practice can generally be recommended for the accurate determination of principal strains. It must be appreciated that while the use of a strain gage rosette is, in many cases, a necessary condition for obtaining the principal strains, it is not a sufficient condition for doing so accurately.Knowledgeability in the selection and application of rosettes is critical to their successful use in experimental stress analysis; and the information contained in this Tech Note is intended to help the user obtain reliably accurate principal strain data..0 Rosette Selection Considerations A comprehensive guide for use in selecting Vishay Micro- Measurements strain gages is provided in Reference 1. This publication should first be consulted for recommendations on the strain-sensitive alloy, backing material, selftemperature-compensation number, gage length, and other strain gage characteristics suitable to the expected application.In addition to basic parameters such as the foregoing, which must be considered in the selection of any strain gage, two other parameters are important in rosette selection. These are: (1) the rosette type tee, rectangular, or delta; and () the rosette construction planar (singleplane) or stacked (layered). The tee rosette should be used only when the principal strain directions are known in advance from other considerations. Cylindrical pressure vessels and shafts in torsion are two classical examples of the latter condition.However, care must be exercised in all such cases that extraneous stresses (bending, axial stress, etc.) are not present, since these will affect the directions of the principal axes. Attention must also be given to nearby geometric irregularities, such as holes, ribs, or shoulders, which can locally alter the principal directions. The error magnitudes due to misalignment of a tee rosette from the principal axes are given in Reference. As a rule, if there is uncertainty about the principal directions, a three-element rectangular or delta rosette is preferable.When necessary (and, using the proper data-reduction relationships), the tee rosette can be installed with its axes at any precisely known angle from the principal axes; but greatest accuracy will be achieved by alignment along the principal directions. In the latter case, except for the readily corrected error due to transverse sensitivity, the two gage elements in the rosette indicate the corresponding principal strains directly. 15 Where the directions of the principal strains are unknown, a three-element rectangular or delta rosette is always required; and the rosette can be installed without regard to orientation.The data-reduction relationships given in Section 4.0 yield not only the principal strains, but also the directions for the principal axes relative to the reference grid (Grid 1) of the rosette. Functionally, there is little choice between the rectangular and delta rosettes. Because the gage axes in the delta rosette have the maximum possible uniform angular separation (effectively 10), this rosette is presumed to produce the optimum sampling of the underlying strain distribution. Rectangular rosettes have historically been the more popular of the two, primarily because the data-reduction relationships are somewhat simpler.Currently, however, with the widespread access to computers and programmable calculators, the computational advantage of the rectangular rosette is of little consequence. As a result of the foregoing, the choice between rectangular and delta rosettes is more apt to be based on practical application considerations such as availability from stock, compatibility with the space available for installation, convenience of solder tab arrangement, etc. All three types of rosettes (tee, rectangular, and delta) are manufactured in both planar and stacked versions.As indicated (for the rectangular rosette) in Figure 3, the Planar Stacked Figure 3 Rectangular rosettes (of the same gage length) in planar and stacked construction. Revision 5-Mar-08 90006 90005 3 planar rosette is etched from the strain-sensitive foil as an entity, with all gage elements lying in a single plane. The stacked rosette is manufactured by assembling and laminating two or three properly oriented single-element gages. When strain gradients in the plane of the test part surface are not too severe, the normal selection is the planar rosette.This form of rosette offers the following advantages in such cases: Thin and flexible, with greater conformability to curved surfaces; Minimal reinforcing effect; Superior heat dissipation to the test part; Available in all standard forms of gage construction, and generally accepts all standard optional features; Optimal stability; Maximum freedom in leadwire routing and attachment. The principal disadvantages of the planar rosette arise from the larger surface area covered by the sensitive portion of the gage.When the space available for gage installation is small, a stacked rosette may fit, although a planar one will not. More importantly, where a steep strain gradient exists in the surface plane of the test part, the individual gage elements in a planar rosette may sense different strain fields and magnitudes. For a given active gage length, the stacked rosette occupies the least possible area, and has the centroids (geometric centers) of all grids lying over the same point on the test part surface.Thus, the stacked rosette more nearly approaches measurement of the strains at a point. Although normally a trivial consideration, it can also be noted that all gages in a stacked rosette have the same gage factor and transverse sensitivity, while the grids in a planar rosette will differ slightly in these properties, due to their different orientations relative to the rolling direction of the strain-sensitive foil. The technical data sheet accompanying the rosettes fully documents the separate properties of the individual grids.It should be realized, however, that the stacked rosette is noticeably stiffer and less conformable than its planar counterpart. Also, because the heat conduction paths for the upper grids in a stacked rosette are much longer, the heat dissipation problem may be more critical when the rosette is installed on a material with low thermal conductivity. Taking into account their poorer heat dissipation and their greater reinforcement effects, stacked rosettes may not be the best choice for use on plastics and other nonmetallic materials.A stacked rosette can also give erroneous strain indications when applied to thin specimen in bending, since the grid plane of the uppermost gage in a three-gage stack may be as much as in [0.11 mm] above the specimen surface. In short, the stacked rosette should ordinarily be reserved for applications in which the requirement for minimum surface area dictates its selection. Revision 5-Mar Gage Element Numbering Numbering, as used here, refers to the numeric (or alphabetic) sequence in which the gage elements in a rosette are identified during strain measurement, and for substitution of measured strains into data-reduction relationships such as those given in Section 4.0. Contrary to a widely held impression, the subject of gage numbering is not necessarily a trivial matter. It is, in fact, basic to the proper, and complete, interpretation of rosette measurement. 3 With any three-element rosette, misinterpretation of the rotational sequence (CW or CCW), for instance, can lead to incorrect principal strain directions. In the case of the rectangular rosette, an improper numbering order will produce completely erroneous principal strain magnitudes, as well as directions.These errors occur when the gage user s numbering sequence differs from that employed in the derivation of the data-reduction relationships. To obtain correct results using the data-reduction relationships provided in Section 4.0 (and in the Appendix), the grids in three-element rosettes must be numbered in a particular way. It is always necessary in a rectangular rosette, for instance, that grid numbers 1 and 3 be assigned to two mutually perpendicular grids. Any other arrangement will produce incorrect principal strains.Following are the general rules for proper rosette numbering. With a rectangular rosette, the axis of Grid must be 45 away from that of Grid 1; and Grid 3 must be 90 deg away, in the same rotational direction. Similarly, with a delta rosette, the axes of Grids and 3 must be 60 and 10 away, respectively, in the same direction from Grid 1. In principle, the preceding rules could be implemented by numbering the grids in either the clockwise or counterclockwise direction , as long as the sequence is correct.Counterclockwise numbering is preferable, however, because it is consistent with the usual engineering practice of denoting counterclockwise angular measurement as positive in sign. The gage grids in all Vishay Micro- Measurements general-purpose, three-element planar rosettes (rectangular and delta) are numerically identified, and numbered in the counterclockwise direction. * Examples of the grid numbering for several representative rosette types are illustrated in Figure 4 . At first glimpse, it might appear that gage patterns (b) and (c) are numbered clockwise instead of counterclockwise.But when these patterns are examined more closely, and when the axis of Grid is transposed across the grid-circle diameter to satisfy the foregoing numbering rules, it can be seen that the rosette numbering is counterclockwise in every case. * Also supplies special-purpose planar rectangular rosettes designed exclusively for use with the hole-drilling method of residual stress analysis. Since these rosettes require different data-reduction relationships, procedures, and interpretation, they are numbered clockwise to distinguish them from general-purpose rosettes.153 90006 90005 4 Figure 4 Counterclockwise numbering of grids in general-purpose strain gage rosettes (see text). (A) stacked rosettes are not numbered, as a matter of manufacturing economics. The user should number the gages in stacked rosettes according to the rules given here and illustrated in Figures and Principal Strains and Directions from Rosette Measurements The equations for calculating principal strains from three rosette strain measurements are derived from what is known as a strain-transformation relationship .As employed here in its simplest form, such a relationship expresses the normal strain in any direction on a test surface in terms of the two principal strains and the angle from the principal axis to the direction of the specified strain. This situation can be envisioned most readily with the aid of the well-known Mohr s circle for strain, as shown in Figure 5 **. It can be seen from Figure 5a (noting that the angles in Mohr s circle are double the physical angles on the test surface) that the normal strain at any angle θ from the major principal axis is simply expressed by: (b) ε θ = 154 ε + ε ε ε + PP cos θ (1) ** The Mohr s circle in Figure 5 is constructed with positive shear strain plotted downward.This is done so that the positive rotational direction in Mohr s circle is the same (CCW) as for the rosette, while maintaining the usual sign convention for shear (ie, positive shear corresonds to a reduction in the initial right angle at the origin of the XY axes as labeled in Figure 5b). (C) Figure 5 Strain transformation from the principal strains to the strain in any direction: (a) ε θ in terms of principal strains ε P, and ε, as shown by Mohr s circle for strain; (B) rectangular rosette installed on a test surface, with Grid 1 at the arbitrary angle θ from the major principal axis; (C) axes of the rectangular rosette superimposed on Mohr s circle for strain.Revision 5-Mar-08 90006 90005 5 Figure 5b represents a small area of the test surface, with a rectangular rosette installed, and with the reference grid (# 1) oriented at θ degrees from ε p. Mohr s circle, with the axes of the rosette superimposed, is shown in Figure 5c. By successively substituting into Equation (1) the angles for the three grid directions, the strain sensed by each grid can be expressed as follows: ε + ε ε ε ε1 = + ε PP cos θ o εp + ε εp ε = + cos θ + 45 (a) (b) φ 1 ε ε ε = θ = tan ε ε (5) 1 3 The physical direction of the acute angle given by either Equation (4) or Equation (5) is always counterclockwise if positive, and clockwise if negative.The only difference is that θ is measured from the principal axis to Grid 1, while φ is measured from Grid 1 to the principal axis. Unfortunately, since tan φ tan (φ + 90), the calculated angle can refer to either principal axis; and hence the identification in Equation (5) as φ. This ambiguity can readily be resolved (for the rectangular rosette) by application of the following simple rules: εp + ε εp ε ε3 = + cos θ + 90 Revision 5-Mar-08 o (c) When the rosette is installed on a test part subjected to an arbitrary strain state, the variables on the right-hand side of Equations () are unknown.But the strains ε 1, ε and ε 3 can be measured. Thus, by solving Equations () simultaneously for the unknown quantities ε P, ε, and θ, the principal strains and angle can be expressed in terms of the three measured strains. Following is the result of this procedure: ε1 + ε3 1 ε = ε1 ε ε ε3 ± + 1 ε1 ε θ = + ε 3 tan 1 ε ε 1 3 If the rosette is properly numbered, the principal strains can be calculated from Equation ( 3) by substituting the measured strains for ε 1, ε and ε 3. The plus and minus alternatives in Equation (3) yield the algebraically maximum and minimum principal strains, respectively.Unambiguous determination of the principal angle from Equation (4) requires, however, some interpretation, as described in the following. To begin with, the angle θ represents the acute angle from the principal axis to the reference grid of the rosette, as indicated in Figure 5. In the practice of experimental stress analysis, it is somewhat more convenient, and easier to visualize, if this is reexpressed as the angle from Grid 1 to the principal axis. To change the sense of the angle requires only reversing the sign of Equation (4).Thus: (3) (4) (a) if ε 1> ε 3, then φ = φ P (b) if ε 1 <ε 3, then φ = φ (c) if ε 1 = ε 3 and ε <ε 1, then φ = φ P = 45º (d) if ε 1 = ε 3 and ε> ε 1, then φ = φ P = + 45º (e) if ε 1 = ε = ε 3, then φ is indeterminate (equal biaxial strain). The reasoning which underlies the preceding rules becomes obvious when a sketch is made of the corresponding Mohr s circle for strain, and the rosette axes are superimposed as in Figure 5c. A similar technique for assuring correct interpretation of the angle is given in the form of a step-bystep algorithm in Reference 3.The preceding development has been applied to the rectangular rosette, but the same procedure can be used to derive corresponding data-reduction equations for the delta rosette shown in Figure 6. When grid angles θ, θ + 60, and θ + 10 are successively substituted into Equation (1), the resulting three equations can again be solved simultaneously for the principal strains and angle. Thus, for the delta rosette: ε1 + ε + ε3 ε = ε1 ε ε ε3 ε3 ε1 3 3 ± ε3 ε θ = tan 1 ε ε ε 1 3 As in the case of Equation (4), the angle θ calculated from Equation (7) refers to the angular displacement of Grid 1 from the principal axis.The sense of the angle can again be changed by reversing its sign to give the angle from Grid 1 to a principal axis: φ (6) (7) 1 3 ε ε3 = θ = tan 1 ε ε ε (8) 90006 90005 6 ε + ε3 (a) if ε1>, then φ, ε + ε3 (b) if ε1 <, then φ P = φ P = φ ε + ε3 (c) if ε1 =, and ε <ε1, then φ = φp = 45 o ε + ε3 (d) if ε1 =, and ε> ε1, then φ = φp = + 45 o (a) (3) if ε1 = ε = ε3 then φ, (equal biaxial strain) P is indeterminate When the principal angle is calculated automatically by computer from Equation (5) or Equation (8), it is always necessary of course, to avoid the condition of division by zero if ε 1 = ε 3 with a rectangular rosette, or ε 1 = ( ε + ε 3) / with a delta rosette.For this reason, the computer should be programmed to perform the foregoing (c) and (d) tests, in each case, prior to calculating the arc-tangent. Once the principal strains have been determined from Equation (3) or Equation (6), the strain state in the surface of the test part is completely defined. If desired, the maximum shear strain can be obtained directly from: γ MAX = ε P ε (9) In every case [Equations (4), (5), (7), and (8)], the angles are to be interpreted as counterclockwise if positive, and clockwise if negative.Equation (8) embodies the same ambiguity with respect to the tan φ and tan (φ + 90) as Equation (5). As before, the ambiguity can easily be resolved (for the delta rosette) by considering the relative magnitudes (algebraically) among the individual strain measurements; namely: 156 (b) Figure 6 Delta rosette: (a) installed on a test surface, with Grid 1 at the angle of θ from the major principal strain direction; (B) rosette grid axes superimposed on Mohr s circle for strain. Note that Grid is to be viewed as + 60º (CCW) from Grid 1 in the rosette, and + 10º in Mohr s circle.Intuitive understanding of the strain state can also be enhanced by sketching the corresponding Mohr s circle, approximately to scale. In Equations (3) and (6), the first term represents, in each case, the distance from the origin to the center of the circle, and the second term represents the radius, or γ MAX /. With the angle φ calculated, further insight can be gained by superimposing the rosette grid axes on the Mohr s circle, as in Figures 5c and 6b. 5.0 Principal Stresses from Principal Strains As previously noted, a three-element strain gage rosette must be employed to determine the principal strains in a general biaxial stress state when the directions of the principal axes are unknown.The usual goal of experimental stress analysis, however, is to arrive at the principal stresses, for comparison with some criterion of failure. With the strain state fully established as described in Section 4.0, the complete state of stress (in the surface of the test part) can also be obtained quite easily when the test material meets certain requirements on its mechanical properties. Since some types of strain gage instrumentation, such as Revision 5-Mar-08 90006 90005 7 our System 6000, calculate both the principal strains and the principal stresses, the following material is provided as background information.If the test material is homogeneous in composition, and is isotropic in its mechanical properties (ie, the properties are the same in every direction), and if the stress / strain relationship is linear, with stress proportional to strain, then the biaxial form of Hooke s law can be used to convert the principal strains into principal stresses. This procedure requires, of course, that the elastic modulus (E) and Poisson s ratio (ν) of the material be known. Hooke s law for the biaxial stress state can be expressed as follows: σ σ E = ε + νε 1 ν PPE = ε + νε 1 ν P Revision 5-Mar-08 (10a) (10b) The numerical values of the principal strains calculated form Equation (3) or Equation (6) can be substituted into equations (10), along with the elastic properties, to obtain the principal stresses.As an alternative, Equation (3) or Equation (6) depending on the rosette type) can be substituted algebraically into Equations (10) to express the principal stresses directly in terms of the three measured strains and the material properties. The results are as follows: Rectangular: σ Delta: σ E ε1 + ε3 = ± (ε1 ε) + ε ε ν + (3) 1 1 ν ε1 + ε + ε3 E ± 1 ν = 3 (ε1 ε) + ( ε ε3) + ε3 1+ ν ε (1) (11) (1) When the test material is isotropic and linear-elastic in its mechanical properties (as required for the validity of the preceding strain-to-stress conversion), the principal stress axes coincide in direction with the principal strains.Because of this, the angle from Grid 1 of the rosette to Tech Note TN-515 the principal stress direction is given by Equation (5) for rectangular rosettes, and by Equation (8) for delta rosettes. 6.0 Errors, Corrections, and Limitations The obvious aim of experimental stress analysis is to determine the significant stresses in a test object as accurately as necessary to assure product reliability under expected service conditions. As demonstrated in the preceding sections of this Tech Note, the process of obtaining the principal stresses involves three basic, and sequential, steps: (1) measurement of surface strains with a strain gage rosette; () Transformation of measured strains to principal strains; and (3) conversion of principal strains to principal stresses.Each step in this procedure has its own characteristic error sources and limits of applicability; and the stress analyst must carefully consider these to avoid potentially serious errors in the resulting principal stresses. Of first importance is that the measured strains be as free as possible of error. Strain measurements with rosettes are subject, of course, to the same errors (thermal output, transverse sensitivity, leadwire resistance effects, etc.) as those with single-element strain gages.Thus, the same controlling and / or corrective measures are required to obtain accurate data. For instance, signal attenuation due to leadwire resistance should be eliminated by shunt calibration 4, or by numerically correcting the strain data for the calculated attenuation, based on the known resistances of the leadwires and strain gages. Because at least one of the gage grids in any rosette will in every case be subjected to a transverse strain which is equal to or greater than the strain along the grid axis, consideration should always be given to the transverse-sensitivity error when performing rosette data reduction.The magnitude of the error in any particular case depends on the transversesensitivity coefficient (K t) of the gage grid, and on the ratio of the principal strains (ε P / ε). In general, when K t 1%, the transverse-sensitivity error is small enough to be ignored. However, at larger values of K t, depending on the required measurement accuracy, correction for transverse sensitivity may be necessary. Detailed procedures, as well as correction equations for all cases and all rosette types, are given in Reference 5.When strain measurements must be made in a variable thermal environment, the thermal output of the strain gage can produce rather large errors, unless the instrumentation can be zero-balanced at the testing temperature, under strain-free conditions. In addition, the gage factor of the strain gage changes slightly with temperature. Reference 6 provides a thorough treatment of errors due to thermal effects in strain gages, including specific compensation and correction techniques for minimizing these errors.After making certain that strain measurement errors such 157 90006 90005 8 Tech Note TN-515 as the foregoing have been eliminated or controlled to the degree feasible, attention can next be given to possible errors in the strain-transformation procedure for obtaining the principal strains. A potentially serious source of error can be created when the user attempts to make up a rosette on the specimen from three conventional single-element gages. The error is caused by misalignment of the individual gages within the rosette.If, for example, the second and third gages in a rectangular rosette configuration are not accurately oriented at 45 and 90, respectively, from the first gage, the calculated principal strains will be in error. The magnitude of the error depends, of course, on the magnitude (and direction) of the misalignment; but it also depends on the principal strain ratio, ε P / ε, and on the overall orientation of the rosette with respect to the principal axes. For certain combinations of principal strain ratio and rosette orientation, 5-degree alignment errors in gages and 3 relative to Gage 1 can produce an error of 0 percent or more in one of the principal strains.Since it is very difficult for most persons to install a small strain gage with the required precision in alignment, the user is well-advised to employ commercially available rosettes. The manufacturing procedures for Vishay Micro- Measurements strain gage rosettes are such that errors due to grid alignment within the rosette need never be considered. For those cases in which it is necessary, for whatever reason, to assemble a rosette from single-element gages, extreme care should be exercised to obtain accurate gage alignment.And when the principal strain directions can be predicted in advance, even approximately, alignment of Gage 1 or 3 in a rectangular rosette, or alignment of any gage in a delta rosette, with a principal axis, will minimize the error in that principal strain caused by inter-gage misalignment. The strain-transformation relationships and data-reduction equations given in Section 4.0 assume a uniform state of strain at the site of the rosette installation. Since the rosette necessarily covers a finite area of the test surface, severe variations in the strain field over this area can produce significant errors in the principal strains particularly with planar rosettes.7 For this type of application, the stacked rosette is distinctly superior; both because it covers a much smaller area (for the same gage length), and because the centroids of all three grids lie over the same point on the test surface. The requirements for a homogeneous material and uniform strain state can be (and are) relaxed under certain circumstances. A case in point is the use of strain gage rosettes on fiber-reinforced composite materials. If the distance between inhomogeneities in the material (i.e., fiber-to-fiber spacing) is small compared to the gage length of the rosette, each grid will indicate the macroscopic or average strain in the direction of its axis. These measured strains (after the usual error corrections) can be substituted 158 into Equation (3) or Equation (6) to obtain the macroscopic principal strains for use in the stress analysis of test objects made from composite materials. 8 As noted later in this section, however, Equations (10) — (1) can not be used for this purpose.There is an additional limitation to the strain-transformation relationship in Equation (1) which, although not frequently encountered in routine experimental stress analysis, should be noted. The subject of the strain distribution about a point, as universally treated in handbooks and in mechanics of materials textbooks, is developed from what is known as infinitesimal-strain theory. That is, in the process of deriving relatively simple relationships such as Equation (1), the strain magnitudes are assumed to be small enough so that normal- and shear-strain approximations of the following types can be employed without introducing excessive error: ε + ε ε (13) sin γ tanγ γ (14) Although often unrecognized, these approximations are embodied in the equations used throughout the contemporary practice of theoretical and experimental stress analysis (where strain transformation is involved).This includes the concept of Mohr s circle for strain, and thus all of the equations in Section 4.0, which are consistent with the strain circle. Infinitesimal-strain theory has proven highly satisfactory for most stress analysis applications with conventional structural materials, since the strains, if not truly infinitesimal, are normally very small compared to unity. Thus, for a not-untypical working strain level of 0.00 (000με), the error in ignoring ε compared to ε is only about 0. percent.However, strain gage rosettes are sometimes used in the measurement of much larger strains, as in applications on plastics and elastomers, and in post-yield studies of metal behavior. Strain magnitudes greater than about 0.01 (10 000με) are commonly referred to as large or finite, and, for these, the strain-transformation relationship in Equation (1) may not adequately represent the actual variation in strain about a point. Depending on the strain magnitudes involved in a particular application, and on the required accuracy for the principal strains, it may be necessary to employ large-strain analysis methods for rosette data reduction.9 The final step in obtaining the principal stresses is the introduction of Hooke s law [Equations (10)] for the biaxial stress state. To convert principal strains to principal stresses with Hooke s law requires, of course, that the elastic modulus and Poisson s ratio of the test material be known. Since the calculated stress is proportion to E, any error in the elastic modulus (for which a 3 to 5 percent Revision 5-Mar-08 90006 90005 9 uncertainty is common) is carried directly through to the principal stress.An error in Poisson s ratio has a much smaller effect because of the subordinate role of ν in the relationship. It is also necessary for the proper application of Hooke s law that the test material exhibit a linear relationship between stress and strain (constant E) over the range of working stresses. There is normally no problem in satisfying this requirement when dealing with common structural materials such as the conventional steel and aluminum alloys. Other materials (e.g., some plastics, cast iron and magnesium alloys, etc.) May, however, be distinctly nonlinear in their stress / strain characteristics. Since the process of transformation from measured strains to principal strains is independent of material properties, the correct principal strains in such materials can be determined from rosette measurements as described in this Tech Note. However, the principal strains can not be converted accurately to principal stresses with the biaxial Hooke s law if the stress / strain relationship is perceptibly nonlinear. A further requirement for the valid application of Hooke s law is that the test material be isotropic in its mechanical properties (i.e., that the elastic modulus and Poisson s ratio be the same in every direction). Although severely cold-worked metals may not be perfectly isotropic, this deviation from the ideal is commonly ignored in routine experimental stress analysis. In contrast, high-performance composite materials are usually fabricated with directional fiber reinforcement, and are thus strongly directional (orthotropic or otherwise anisotropic) in their mechanical properties. Hooke s law as expressed in Equations (10) is not applicable to these materials; and special constitutive relationships are required to determine principal stresses from rosette strain measurements.8 References 1. Tech Note TN-505, Strain Gage Selection Criteria, Procedures, Recommendations .. Tech Note TN-511, Errors Due to Misalignment of Strain Gages. 3. Perry, C.C., Data-Reduction Algorithms for Strain Gage Rosette Measurements, Experimental Techniques. May, 1989, pp Tech Note TN-514, Shunt Calibration of Strain Gage Instrumentation. 5. Tech Note TN-509, Errors Due to Transverse Sensitivity in Strain Gages. 6. Tech Note TN-504, Strain Gage Thermal Output and Gage Factor Variation with Temperature.7. Troke, .W., Flat versus Stacked Rosettes, Experimental Mechanics, May, 1967, pp. 4A-8A. 8. Tsai, S.W. and H.T. Hahn, Introduction to Composite Materials, Technomic Publishing Company, Meyer, M.L., Interpretation of Surface-Strain Measurements in terms of Finite Homogeneous Strains. Experimental Mechanics, December, 1963, pp Revision 5-Mar 90006 90005 10 Appendix Derivation of Strain-Transformation Relationship [Equation (1) in text] from Deformation Geometry Consider a small area of a test surface, as sketched in Figure A-1.The line O- of length L O, and at the angle θ from the X axis, is scribed on the surface in the unstrained state. When uniform principal strains ε P and ε are applied in the directions of the X and Y axes, respectively, the point P moves to P as a result of the displacements ΔX and ΔY (greatly exaggerated in the sketch). It is evident from the figure that: But, cos 1 θ = (cos 1 + θ) 1 sin θ = (cos 1 θ) After substituting the above identities, ε ε ε ε εθ = + + PP cos θ (A-6 ) ΔX = ε P (LO cos θ) ΔY = ε (LO sin θ) (A-1) (A-) It can also be seen (Figure A-), by enlarging the detail in the vicinity of points P and P , that for small strains: ΔL ΔX cos θ + ΔY sin θ Substituting from Equations (A-1) and (A-), Or, ΔL LO (ε P cos θ + ε sin θ) εθ = L = εp cos θ + ε sin θ Lo (A-3) (A-3) (A-5) Alternate Data Reduction Equations In the extensive technical literature dealing with strain gage rosettes, the user will often encounter data-reduction relationships which are noticeably different from one another , and from those in the body of this Tech Note.As a rule, these published equations yield the same results, and differ only in algebraic format although proving so in any given case may be rather time consuming. Since certain forms of the equations may be preferred for mnemonic reasons, or for computational convenience, several alternative expressions are given here. All of the following are equally correct when the gage elements in the rosette are numbered as described in this Tech Note. 160 Figure A-1 Figure A- Revision 5-Mar-08 90006 90005 11 Rectangular Rosette: ε ε ε1 + ε3 = ε1 + ε3 = 1 ε = C ± C ε1 ± + (+) ε1 ε3 ε ε1 ε3 ± (ε ε) + (ε ε) 3/1 + (C ε) (A-7) (A-8) (A-9) where: ε + ε C = 1 3 (A-9) Delta Rosette: ε ε + ε + ε 1 3 ε1 ε + ε3 = ± (ε ε3 3 ε1 + ε + ε3 ε = ± (ε1 ε) + (ε ε3) + (ε3 ε1) / 9 3 ε C ε C 1 C ε C ε3 / 3 = ± () + () + ()) (A-10) (A-11) (A-1) where: C = ε ε ε 3 Cartesian Strain Components from Rosette Measurements It is sometimes desired to obtain the Cartesian components of strain (ε X, ε Y, and γ XY) relative to a specified set of XY coordinate axes.This need can arise, for example, when making strain measurements on orthotropic composite materials. The Cartesian strain components are also useful when calculating principal strains from rosette data using matrix transformation methods. * When the X axis of the coordinate system coincides with the axis of the reference grid (Grid 1) of the rosette, the Cartesian components of strain are as follows: Rectangular Rosette: Y ε X = ε 1 ε Y = ε 3 γ XY = ε X (ε 1 + ε 3) * Milner, RR, A Modern Approach to Principal Stresses and Strains, Strain, November, 1989, pp Revision 5-Mar X 161 90006 90005 12 Delta Rosette: ε X = ε 1 Y εy = ε + ε3 ε1 / 3 3 γ = ε ε / 3 XY 3 1 X The foregoing assumes in each case that the gage elements in the rosette are numbered counterclockwise as indicated.When the calculated γ XY is positive in sign, the initial right angle at the origin of the XY coordinate system is decreased by the amount of the shear strain. 16 Revision 5-Mar-08 90006.
