Ток при последовательном соединении резисторов. Последовательное и параллельное соединение проводников: основные свойства и формулы расчета

Какие основные свойства последовательного и параллельного соединения проводников. Как рассчитать общее сопротивление при разных типах соединений. Какие формулы используются для расчета тока и напряжения в цепях с последовательным и параллельным соединением.

Основные свойства последовательного соединения проводников

При последовательном соединении проводников наблюдаются следующие ключевые свойства:

• Сила тока одинакова во всех элементах цепи
• Общее напряжение равно сумме напряжений на отдельных элементах
• Общее сопротивление равно сумме сопротивлений всех элементов

Таким образом, для последовательного соединения справедливы формулы:

I = I1 = I2 = … = In

U = U1 + U2 + … + Un

R = R1 + R2 + … + Rn

Где I — сила тока, U — напряжение, R — сопротивление.

Расчет параметров при последовательном соединении

Как рассчитать общее сопротивление при последовательном соединении нескольких резисторов? Используется простая формула суммирования:

R = R1 + R2 + R3 + … + Rn

Например, если соединить последовательно резисторы 10 Ом, 20 Ом и 30 Ом, общее сопротивление составит:

R = 10 + 20 + 30 = 60 Ом

Напряжение на каждом элементе можно рассчитать по закону Ома:

U1 = I * R1

U2 = I * R2

и т.д.

Основные свойства параллельного соединения проводников

При параллельном соединении проводников наблюдаются следующие ключевые свойства:

• Напряжение одинаково на всех элементах цепи
• Общий ток равен сумме токов через отдельные элементы
• Величина, обратная общему сопротивлению, равна сумме величин, обратных сопротивлениям элементов

Для параллельного соединения справедливы формулы:

U = U1 = U2 = … = Un

I = I1 + I2 + … + In

1/R = 1/R1 + 1/R2 + … + 1/Rn

Расчет параметров при параллельном соединении

Как рассчитать общее сопротивление при параллельном соединении резисторов? Используется формула:

1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

Для двух резисторов формула упрощается:

R = (R1 * R2) / (R1 + R2)

Например, при параллельном соединении резисторов 10 Ом и 20 Ом общее сопротивление составит:

R = (10 * 20) / (10 + 20) = 200 / 30 ≈ 6.67 Ом

Ток через каждый элемент рассчитывается по закону Ома:

I1 = U / R1

I2 = U / R2

и т.д.

Смешанное соединение проводников

На практике часто встречаются схемы со смешанным (последовательно-параллельным) соединением элементов. В этом случае расчет ведется поэтапно:

1. Находят эквивалентные сопротивления для параллельных участков
2. Рассчитывают общее сопротивление, учитывая последовательные и эквивалентные параллельные участки
3. Определяют общий ток и напряжения на участках
4. Рассчитывают токи в параллельных ветвях

Такой алгоритм позволяет проанализировать работу сложных электрических схем.

Применение различных типов соединений

Где на практике применяются последовательное и параллельное соединения проводников?

• Последовательное соединение используется в электрических гирляндах, при подключении измерительных приборов, для создания делителей напряжения
• Параллельное соединение применяется для подключения бытовых электроприборов к сети, в автомобильной электрике, для создания токовых шунтов
• Смешанное соединение встречается в сложных электронных схемах, системах электроснабжения

Правильный выбор типа соединения позволяет оптимизировать работу электрических цепей и добиться нужных характеристик.

Преимущества и недостатки разных типов соединений

Какие преимущества и недостатки имеют последовательное и параллельное соединения проводников?

Последовательное соединение:

Преимущества:

• Простота конструкции
• Возможность получить большое общее сопротивление
• Удобно для измерения тока

Недостатки:

• При выходе из строя одного элемента перестает работать вся цепь
• Сложно обеспечить одинаковое напряжение на элементах

Параллельное соединение:

Преимущества:

• Одинаковое напряжение на всех элементах
• При выходе из строя одного элемента остальные продолжают работать
• Возможность получить малое общее сопротивление

Недостатки:

• Сложность конструкции при большом количестве элементов
• Необходимость обеспечивать большой общий ток

Понимание этих особенностей позволяет грамотно проектировать электрические схемы для различных применений.

Решение задач на последовательное и параллельное соединение

Рассмотрим примеры решения типовых задач на расчет цепей с последовательным и параллельным соединением проводников.

Задача 1. Последовательное соединение

К источнику напряжения 12 В подключены последовательно три резистора с сопротивлениями 2 Ом, 3 Ом и 7 Ом. Определить силу тока в цепи и напряжение на каждом резисторе.

Решение:

1. Находим общее сопротивление: R = 2 + 3 + 7 = 12 Ом
2. Рассчитываем силу тока: I = U / R = 12 В / 12 Ом = 1 А
3. Определяем напряжение на резисторах:
   • U1 = I * R1 = 1 А * 2 Ом = 2 В
   • U2 = I * R2 = 1 А * 3 Ом = 3 В
   • U3 = I * R3 = 1 А * 7 Ом = 7 В

Задача 2. Параллельное соединение

К источнику напряжения 6 В подключены параллельно два резистора с сопротивлениями 4 Ом и 6 Ом. Определить общее сопротивление цепи, общий ток и токи через резисторы.

Решение:

1. Находим общее сопротивление: 1/R = 1/4 + 1/6; R = 24/10 = 2.4 Ом
2. Рассчитываем общий ток: I = U / R = 6 В / 2.4 Ом = 2.5 А
3. Определяем токи через резисторы:
   • I1 = U / R1 = 6 В / 4 Ом = 1.5 А
   • I2 = U / R2 = 6 В / 6 Ом = 1 А

Решение подобных задач позволяет лучше понять принципы работы электрических цепей с различными типами соединений проводников.

Параллельное включение резисторов. Параллельное соединение резисторов, а также последовательное

Автор Vic На чтение 18 мин Просмотров 7.2к. Опубликовано 25.04.2021

Содержание

1. Что такое резистор и для чего он нужен
2. Понятие параллельного подключения резисторов
3. Типы проводников
4. Последовательное подключение
5. Теоретическая часть
6. Примеры расчета
7. Общее сопротивление Rобщ
8. Смешанное подключение
9. Что ещё нужно учитывать при подключении резисторов
10. Общее сопротивление Rобщ
11. Схема параллельного соединения
12. Как высчитывать сопротивление составных резисторов
13. Какая мощность тока при последовательном и параллельном соединении
14. Мощность при параллельном соединении
15. Мощность при последовательном соединении
16. Параллельное соединение проводников
17. Сопротивление при параллельном соединении проводников
18. Напряжение при параллельном соединении проводников
19. Сила тока при параллельном соединении проводников
20. Зависимость сопротивления
21. Электрические величины
22. Тип и геометрические параметры
23. Температурные показатели
24. Свойства резисторов при параллельном подключении
25. Формула для вычисления напряжения
26. Отличия между двумя видами подключений
27. Как рассчитать сложные схемы соединения резисторов

Что такое резистор и для чего он нужен

Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.

Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.

Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.

Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).

Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.

Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:

1. С правого края – правый.
2. С левого края – левый.

Понятие параллельного подключения резисторов

При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.

При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.

Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Последовательное подключение

При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.

При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.

Теоретическая часть

Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2). Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают. R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых. Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.

Последовательное подключение.

Примеры расчета

Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:

• U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
• U2 = R2 * I = 800 Ом * 2А = 1600 В.

Будет интересно➡  SMD резисторы: что это такое и для чего используются?

Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток.   R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.

Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2  А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.

А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором  — 1600 В.  При этом напряжение источника питания — 4000 В. Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление Rобщ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Смешанное подключение

При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.

Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.

Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.

Что ещё нужно учитывать при подключении резисторов

Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.

При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.

Общее сопротивление Rобщ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.

То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.

Предлагаем также почитать интересный материал про малоизвестные факты о двигателях постоянного тока в другой нашей статье.

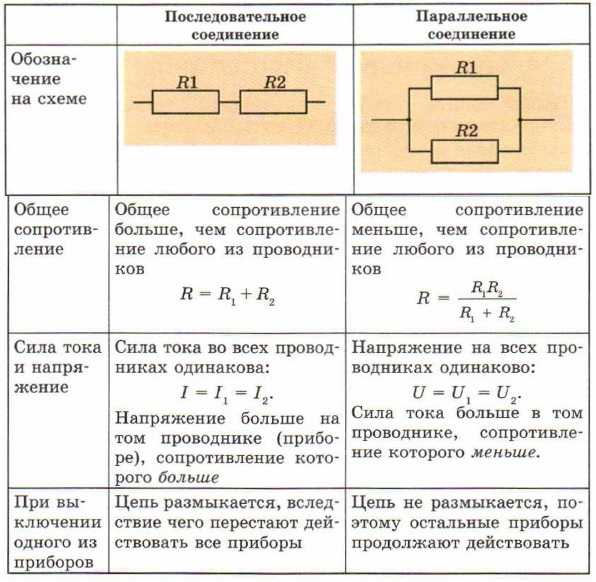
Схема параллельного соединения

Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.

Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.

Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом. Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.

Как высчитывать сопротивление составных резисторов

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.

Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом.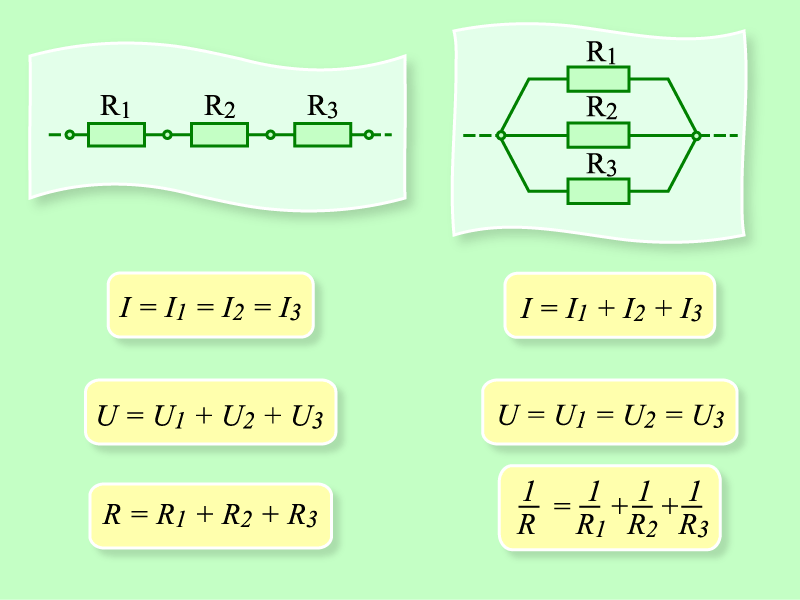 Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.

Какая мощность тока при последовательном и параллельном соединении

Определение мощности отдельного резистивного элемента производится по формуле

P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.

Мощность при параллельном соединении

Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где

• R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
• I – сила тока в цепи.

При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.

Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.

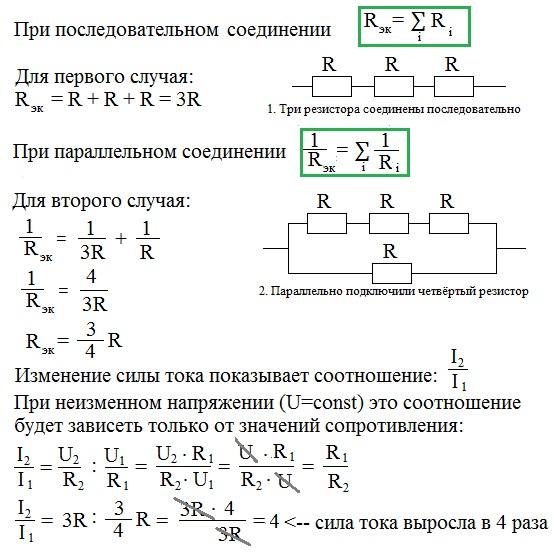
Мощность при последовательном соединении

Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где

• R – рассчитанное нами сопротивление для определенной схемы;
• U – падение напряжения на данном резистивном элементе.

Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.

Параллельное соединение проводников

Параллельное соединение проводников выглядит вот так.

параллельное соединение резисторов

Ну что, думаю, начнем с сопротивления.

Сопротивление при параллельном соединении проводников

Давайте пометим клеммы как А и В

В этом случае общее сопротивление RAB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников

Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.

Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников

Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.

Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что

I1 = U/R1

I2 = U/R2

I3 = U/R3

Если бы у нас еще были резисторы, соединенные параллельно, то для них

In = U/Rn

В этом случае, сила тока в цепи будет равна:

Задача

Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Решение

Воспользуемся формулами, которые приводили выше.

I1 = U/R1

I2 = U/R2

I3 = U/R3

Если бы у нас еще были резисторы, соединенные параллельно, то для них

In = U/Rn

Следовательно,

I1 = U/R1 = 10/2=5 Ампер

I2 = U/R2 = 10/5=2 Ампера

I3 = U/R3 = 10/10=1 Ампер

Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи

I=I1 + I2 + I3 = 5+2+1=8 Ампер

2-ой способ найти I

I=U/Rобщее

Чтобы найти Rобщее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.

I=U/Rобщее = 10/1,25=8 Ампер.

Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.

Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

1. Температура окружающей среды и материала.
2. Электрические величины.
3. Геометрические свойства вещества.
4. Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

1. Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
2. Визуально определить форму материала.
3. Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * [1 + a * (t — 20)] * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.

Свойства резисторов при параллельном подключении

При данном виде соединении скачки напряжения будут одинаковы на всех участках цепи. При этом показатель, обратный суммарному сопротивлению цепи, равен общей величине резисторов.

Обратите внимание! F тока в неразветвленной точке цепи равняется суммарной силе тока на отдельных участках проводника.

Стандартная формула напряжения

Формула для вычисления напряжения

При данном виде соединения все линии будут находиться в двух точках. Потому напряжение для всех резисторов будет равным.

При подсоединении двух и более приборов друг с другом, напряжение на выводах такой схемы — это показатель на каждом резисторе.

Напряжения условно обозначаются как U. По закону Ома, зная, что I = U/R, можно рассчитать по формуле:

U = U1 = U2 = … = Uобщ.

Обратите внимание! Помимо вычисления напряжения, рекомендуется знать мощность проводников. Они не должны сильно отличаться друг от друга. Параллельное соединение также можно встретить в лампочках, кабелях сигнализации автомобиля, фарах и прочем.

Также иногда можно встретить смешанный вид подключения. Это когда в цепи применяется два типа подключения, и параллельное, и последовательное. Оно чаще всего используется в контурных обогревателях.

Желательно изучить каждый вид подключения и схемы к ним. Профессиональные электрики рекомендует не выполнять подключений самостоятельно, если у человека совсем нет опыта в этой сфере. Так как в цепи может случиться короткое замыкание или возгорание, в лучшем случае выход из строя прибора.

Определение мощности на примере ламп

В заключении необходимо отметить, каждому человеку желательно знать свойства последовательного и параллельного соединения проводников. Чтобы в будущем не путаться при выполнении простых работ в электрике своего дома.

Отличия между двумя видами подключений

Схема последовательного подключения говорит о том, что проводники установлены в особом расположении друг за другом. Поэтому сила тока у них одинаковая. Эти элементы создают в цепи Uобщее.

Пример подключения с предохранителем

Заряды не собираются в узлах электрической цепи, иначе было бы видно, как напряжение меняется. Минусом этой схемы будет то, что если любой элемент сломается, то вся цепь разорвется и перестанет работать. Например, если взять новогоднюю гирлянду. Если одна лампочка перестала работать, то другие тоже не загораются. Это и будет главным различием между последовательным и параллельным соединением. Ниже описана характеристика резисторов при параллельном объединении.

Как рассчитать сложные схемы соединения резисторов

Если соединять большее количество элементов, надо в рассмотренные формулы добавить необходимое количество слагаемых.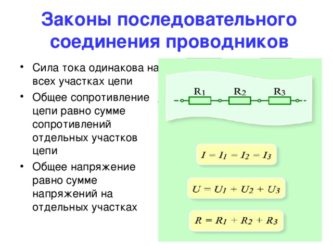

Исходные данные:

• источник постоянного тока 12V;
• сопротивление параллельных резисторов, Ом: 10, 40, 60, 80.

Расчет:

• основная формула: 1/Rэкв = 1/R1 + 1/R2 + 1/R3 + 1/R4;
• подставив исходные данные, вычисляют проводимость: G = 1/Rэкв =1/10 + 1/40 + 1/60 +1/80 = 0,1 + 0,025 + 0,0166 +0,0125 = 0,1541;
• эквивалентное сопротивление: Rэкв = 1/0,1541 ≈ 6,5 Ом;
• ток в цепи: Iобщ = Uип/ Rэкв = 12/ 6,5 ≈ 1,85 А.

Сложные схемы

По аналогичной технологии делают расчеты более сложных цепей. На рисунке обозначены номиналы сопротивлений. В обоих случаях применяется одинаковый источник питания с Uип = 12V.

Расчет 1 (последовательное и параллельное соединение):

• для каждого параллельного участка можно использовать формулу: Rобщ = 1/ (1/R1 + 1/R2) = R1*R2/R1 + R2;
• эквивалентное сопротивление первой части: Rэкв1 = (2*4)/ (2+4) = 1,3 Ом;
• второй: Rэкв2 = (15*5)/ (15+5) = 3,75 Ом;
• общее: Rэкв = 1,3 + 10 + 3,75 = 15,05 Ом;
• Iобщ = Uип/ Rэкв = 12/ 15,05 ≈ 0,8 А.

Расчет 2 (сложное параллельное соединение):

• в этом варианте сначала вычисляют проводимость части (R3, R4, R5) по формуле: G345 = 1/5 + 1/10 + 1/ 20 =7/20 = 0,35 сим;
• Rэкв (345) = 1/0,35 ≈ 2,857 Ом;
• суммарное значение для цепи: R1 + R2 = 20 Ом;
• по аналогии с предыдущим способом определяют: G12345 = 0,4 сим и Rэкв(12345) = (20*2,857)/ 20 + 2,857) ≈ 2,5 Ом;
• после добавления последнего элемента (R6=7,5 Ом) получают итоговый результат: Rэкв = 2,5 + 7,5 = 10 Ом;
• делением определяют силу тока в нагрузке, подключенной к источнику тока 12 V: I = 12/10 = 1,2 А.

В последнем примере применен дополнительный компонент цепи (R6). Соответственно, для этой схемы не будет выполняться рассмотренная выше пропорция равенства напряжений (источника и на подключенной нагрузке).

В этом случае разница потенциалов на шестом резисторе составит:

U6 = I *R6 = 1,2 * 7,5 = 9 В.

Соответственно, изменится напряжение между контрольными точками:

Uав = I * Rэкв(12345) = 1,2*2,5 = 12-9 =3V.

Вторая часть формулы демонстрирует проверку вычитанием напряжений (Uип — U6).

Источники

• https://onlineelektrik.ru/eoborudovanie/kondensatori/parallelnoe-soedinenie-rezistorov-a-takzhe-posledovatelnoe.html
• https://rusenergetics.ru/praktika/raschet-soprotivleniya-rezistorov
• https://ElectroInfo.net/radiodetali/rezistory/kak-otlichaetsja-parallelnoe-i-posledovatelnoe-soedinenie-rezistorov.html
• https://www.RusElectronic.com/serial-and-parallel/
• https://rusenergetics.ru/polezno-znat/parallelnoe-soedinenie
• https://amperof.ru/teoriya/parallelnoe-soedinenie-rezistorov.html

Последовательное соединение резисторов

При последовательном соединении резисторов, на этом участке цепи ток будет все время одинаковым.

Формула расчета простая — Суммарное сопротивление на участке цепи будет равна сумме значений сопротивлений всех резисторов, включенных в цепь. Вид формулы следующий

Rсум=∑R, где R – значение каждого из резисторов в цепи

т.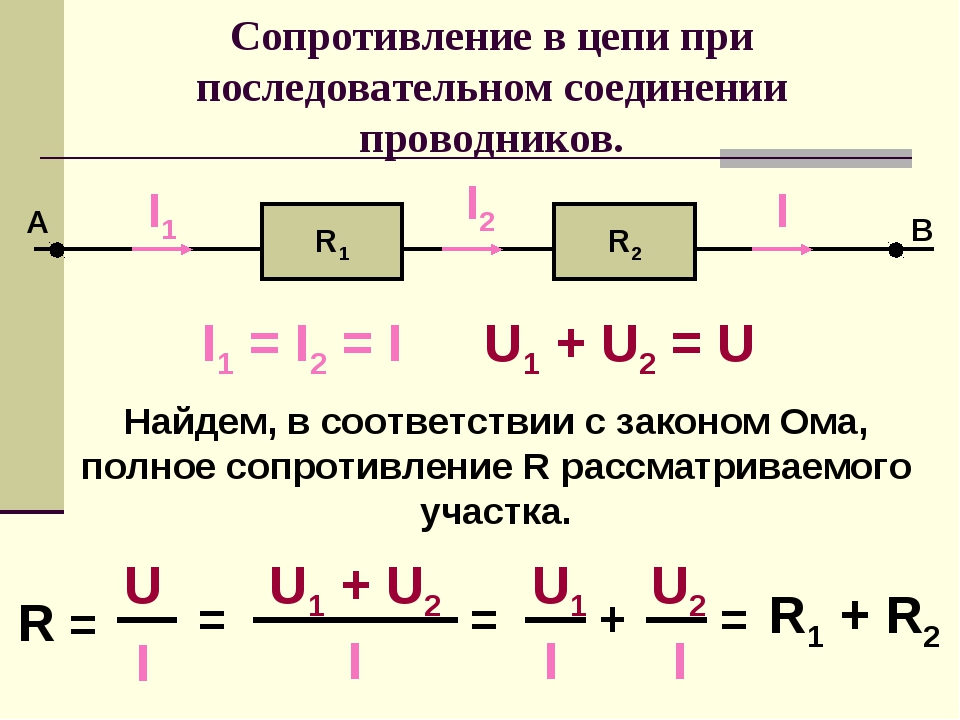  е. Вам надо сложить сопротивление всех резисторов в цепи и их сумма покажет общее сопротивление.

Давайте сделаем шаг в сторону, чтобы проще было понять смысл суммарного сопротивления.

Ток течет по цепи, и визуально его можно представит, как поток воды, который течет сквозь трубу.

Трубы меньшего диаметра — по сути, являются резисторами, которые затрудняют проток и делают его меньше. Например, вы когда-нибудь пробовали потянуть напиток из кружки через очень очень узкую трубочку? Усилий можно делать много, но поток в рот будет все равно слишком маленьким. И чем больше таких разных сужений будет, тем сложнее вам будет тянуть напиток через трубочку. По такому же принципу работают резисторы, уменьшая ток.

Закон Ома гласит, что ток равен напряжению, деленному на сопротивление.

I=U/R

Давайте рассмотрим примеры использования формулы, а заодно изучим понятие падения напряжения.

Пример №1

Дана схема цепи с последовательным сопротивлением трех резисторов.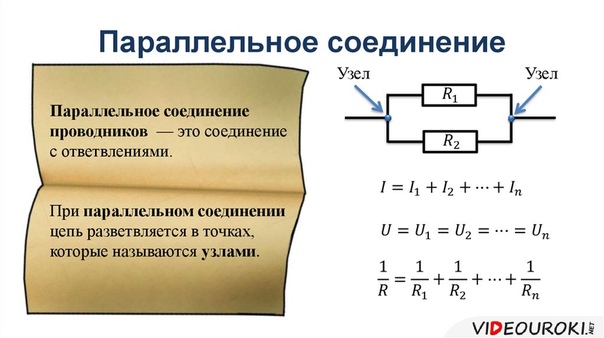

Источник постоянного тока с напряжением на входе 24 V

Три резистора, соединенных последовательно, с сопротивлениями, 6,3 и 3 Ом соответственно. Т.е. R1=6 Ом, R2=3 Ом, R3=3 Ом

Cхема простейшей цепи постоянного тока с последовательным соединением Резисторов

Определим суммарное сопротивление этой простой цепи:

Согласно нашей формуле, суммарное сопротивление последовательно соединенных транзисторов будет равно сумме всех сопротивлений:

Rсум=6Ом+3Ом+3Ом=12 Ом

Давайте определим ток на участке по формуле выше:

I=Uвх/Rсум

I=24В/12Ом=2А

Таким образом, мы определили, что ток на всем участке будет равен 2 амперам.

Давайте определим падение напряжения на каждом элементе нашей цепи.

Еще небольшое отступление. Каждый резистор будет как бы забирать часть напряжения на себя, и чем выше его сопротивление, тем больше напряжения будет на нем «падать».

В любом замкнутом контуре, сумма напряжений равна нулю. Таким образом, в нашем случае справедлива формула Uвх=Ur1+ Ur2+ Ur3

А как определить эти значения? Очень просто. Мы знаем, что ток везде одинаковый, и знаем значения каждого отдельного сопротивления R1,R2,R3.

Тогда Ur1= R1*I=6Ом*2А=12В

Ur2= R2*I=3Ом*2А=6В

Ur3= R3*I=3Ом*2А=6В

Пример №2

Схема цепи с последовательным сопротивлением двух резисторов.

Схема с двумя резисторами, подключенными последовательно

Источник постоянного тока с напряжением на входе 12 V

Два резистора, соединенных последовательно, с сопротивлениями, 2,1 Ом соответственно. Т.е. R1=2 Ом, R2=1 Ом

Далее все расчеты аналогичны.

Шаг первый — определяем суммарное значение сопротивления: Rсум=2Ом+1Ом=3Ом

Шаг второй — определяем ток в этом участке цепи: I=12В/3Ом=4А

Шаг третий — считаем падения напряжения на каждом элементе цепи с последовательным сопротивлением двух резисторов:

Ur1= R1*I=2Ом*4А=8В

Ur2= R2*I=1Ом*4А=4В

Как и в прошлом расчете, сумма падений напряжений (8+4) будет равна входному напряжению.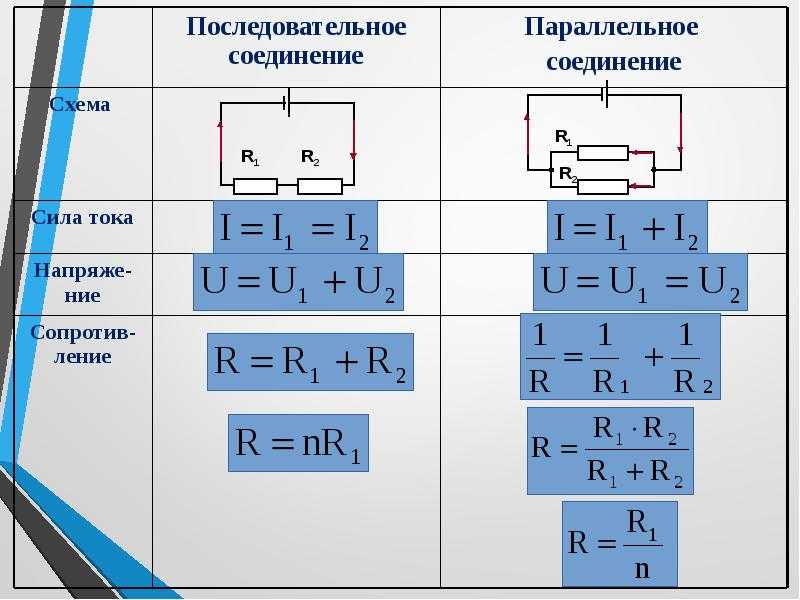

Обратите внимание, что в случае последовательного соединения резисторов, суммарное сопротивление всегда будет больше любого отдельно взятого резистора в этой цепи.

Надеюсь, что это поможет вам в понимании. Если есть какие-то вопросы по написанному материалу, то пишите в комментах.

Цепи постоянного тока серии

— Цепи постоянного тока

Цепи постоянного тока

Цепь серии определяется как цепь, содержащая только один путь для текущего потока. Чтобы сравнить базовую схему и более сложная последовательная цепь, на рисунке ниже показаны две цепи. Основная схема имеет только одна лампа, а в последовательной цепи три лампы соединены последовательно.

Сравнение основных и последовательных схем.

Сопротивление в последовательной цепи

Ссылаясь на рисунок выше, ток в последовательной цепи должен протекать через каждая лампа для завершения электрического пути в цепи. Каждая дополнительная лампа оказывает дополнительное сопротивление. В последовательной цепи полное сопротивление цепи R _t равно сумме индивидуальные сопротивления .

В виде уравнения:

Примечание. Нижний индекс n обозначает любое количество дополнительных сопротивлений, которые может быть в уравнении.

Пример: На рисунке ниже последовательная цепь, состоящая из трех резисторов: показаны один из 10 Ом, один из 15 Ом и один из 30 Ом. Источник напряжения дает 110 В. Чему равно полное сопротивление?

Расчет полного сопротивления в последовательной цепи.

Дано:
R ₁ = 10 Ом, R ₂ = 15 Ом, R ₃ = 30 Ом

Решение:

В некоторых схемах общее сопротивление известно, а значение необходимо определить один из резисторов цепи. Уравнение R _t = R ₁ + R ₂ + R ₃ можно транспонировать, чтобы найти значение неизвестного сопротивления.

Пример:
На рисунке ниже полное сопротивление цепи с тремя резисторами составляет 40 Ом. Два резистора цепи 10 Ом каждый. Рассчитайте значение третьего резистора ( R ₃ ).

Расчет значения одного сопротивления в последовательной цепи.

Дано:
R _t = 40 Ом, R ₁ = 10 Ом, R ₂ = 10 Ом, Ч ₃ = ?

Решение:

Вычитание ( R ₁ + R ₂ ) с обеих сторон уравнение

Ток в последовательной цепи

Так как в последовательной цепи ток проходит только один путь, то один и тот же ток должен протекать через каждый компонент цепи. Чтобы определить ток в последовательной цепи, только ток через один из компоненты должны быть известны.

Тот факт, что один и тот же ток протекает через каждый компонент серии цепь можно проверить, вставив счетчики в цепь в различных точках, как показано на рисунке ниже. Если бы это было сделано, каждый метр окажется, что они указывают на одно и то же значение тока.

Ток в последовательной цепи.

Напряжение в последовательной цепи

Падение напряжения на резисторе в цепи, состоящей из одного резистор и источник напряжения — это общее напряжение в цепи, равное равно приложенному напряжению. Полное напряжение в последовательной цепи, которое состоит из более чем одного резистора и равно приложенному напряжению, но состоит из суммы падений напряжения на отдельных резисторах. В любой серии цепи сумма падений напряжения на резисторе должна равняться напряжению источника. Это утверждение может быть подтверждено исследованием схемы, показанной на рис. рисунок ниже.

Расчет отдельных падений напряжения в последовательной цепи.

В этой цепи сброшен потенциал источника ( В _t ) 20 В. через последовательную цепь, состоящую из двух резисторов по 5 Ом. Общая сопротивление цепи ( R _t ) равно сумме два отдельных сопротивления или 10 Ом. По закону Ома схема ток можно рассчитать следующим образом:

Дано: В _t = 20 В, R _t = 10 Ом
Решение:

Поскольку известно, что номинал резисторов равен 5 Ом каждый, а ток через резисторы равен 2 А, напряжение на них падает резисторы можно рассчитать. Напряжение ( В ₁ ) через R ₁ поэтому:

Дано: I ₁ = 2 А, R ₁ = 5 Ом
Решение:

Осмотрев схему, можно увидеть, что R ₂ то же омическое значение как R ₁ и проводит такой же ток. Напряжение падение на R ₂ поэтому также равно 10 В. Сложение этих двух 10-вольтовых падений вместе дает общее падение 20 В, точно равно приложенному напряжению. Тогда для последовательной цепи:

Пример: Последовательная цепь состоит из трех резисторов со значениями 20 Ом, 30 Ом и 50 Ом соответственно. Найдите прикладной напряжение, если ток через резистор 30 Ом равен 2 А.

Для решения задачи сначала рисуется и маркируется принципиальная схема (рисунок ниже).

Расчет приложенного напряжения в последовательной цепи.

Дано: R ₁ = 20 Ом, R ₂ = 30 Ом, R ₃ = 50 Ом, I = 2 А

Решение: поскольку задействованная цепь представляет собой последовательную цепь, те же 2 А ток течет через каждый резистор. По закону Ома напряжение падает на каждый из трех резисторов может быть рассчитан и составляет:

Когда известны отдельные капли, их можно сложить, чтобы найти общее количество. или приложенное напряжение:

Примечание. Когда вы используете закон Ома, величины для уравнения должны быть равны . взято из той же части схемы. В приведенном выше примере напряжение на R ₂ было рассчитано с использованием тока через R ₂ и сопротивление R ₂ .

Величина падения напряжения на резисторе определяется приложенным напряжения и пропорциональна сопротивлениям цепи. Напряжение падает которые возникают в последовательной цепи, прямо пропорциональны сопротивлениям. Это результат того, что через каждый резистор протекает одинаковый ток. чем больше омическое сопротивление резистора, тем больше падение напряжения на нем.

Серия

и параллельные резисторные цепи

Электронные компоненты соединяются разными способами. Две простейшие формы соединений — последовательное и параллельное. связи.

Если компоненты соединены в цепи последовательно, то цепь называется последовательной. Если резисторы соединены последовательно в цепи, то цепь называется цепью последовательного резистора.

Если компоненты соединены в цепи параллельно, то цепь называется параллельной. Если резисторы соединены в цепи параллельно, то цепь называется параллельной цепью резисторов.

Серийный резистор цепь

А Цепь последовательного резистора представляет собой электронную схему, в которой все резисторы соединены один за другим по одному и тому же пути чтобы через каждый и каждый резистор.

полное сопротивление такой цепи получается просто суммирование значений сопротивления отдельных резисторов.

Р _Т = Р ₁ + Р ₂ + Р ₃ + Р ₄ ……..и т. д.

Для Например, если пять резисторов соединены последовательно. Тогда полное сопротивление цепи равно:

Р _Т = Р ₁ + Р ₂ + Р ₃ + Р ₄ + R ₅

Все ток, протекающий через первый резистор, не имеет другого путь идти. Следовательно, он также должен пройти через второй резистор, третий резистор, четвертый резистор и так далее.

Пример:

А Схема последовательного резистора показана на рисунке ниже. Этот схема состоит из пяти резисторов, соединенных последовательно и источник постоянного напряжения.

Если значения пяти резисторов: R ₁ = 4 Ом, R ₂ = 4 Ом, R ₃ = 2 Ом, R ₄ = 2 Ом, R ₅ = 3 Ом и батарея постоянного тока = 15 В, тогда

Общее сопротивление это Р _Т = Р ₁ + Р ₂ + Р ₃ + Р ₄ + R ₅ = 4 + 4 + 2 + 2 + 3 = 15 Ом.

Вспомните формулу закона Ома, V = I R

Зная любые две переменные в приведенное выше уравнение, мы можем легко найти оставшееся неизвестное переменная.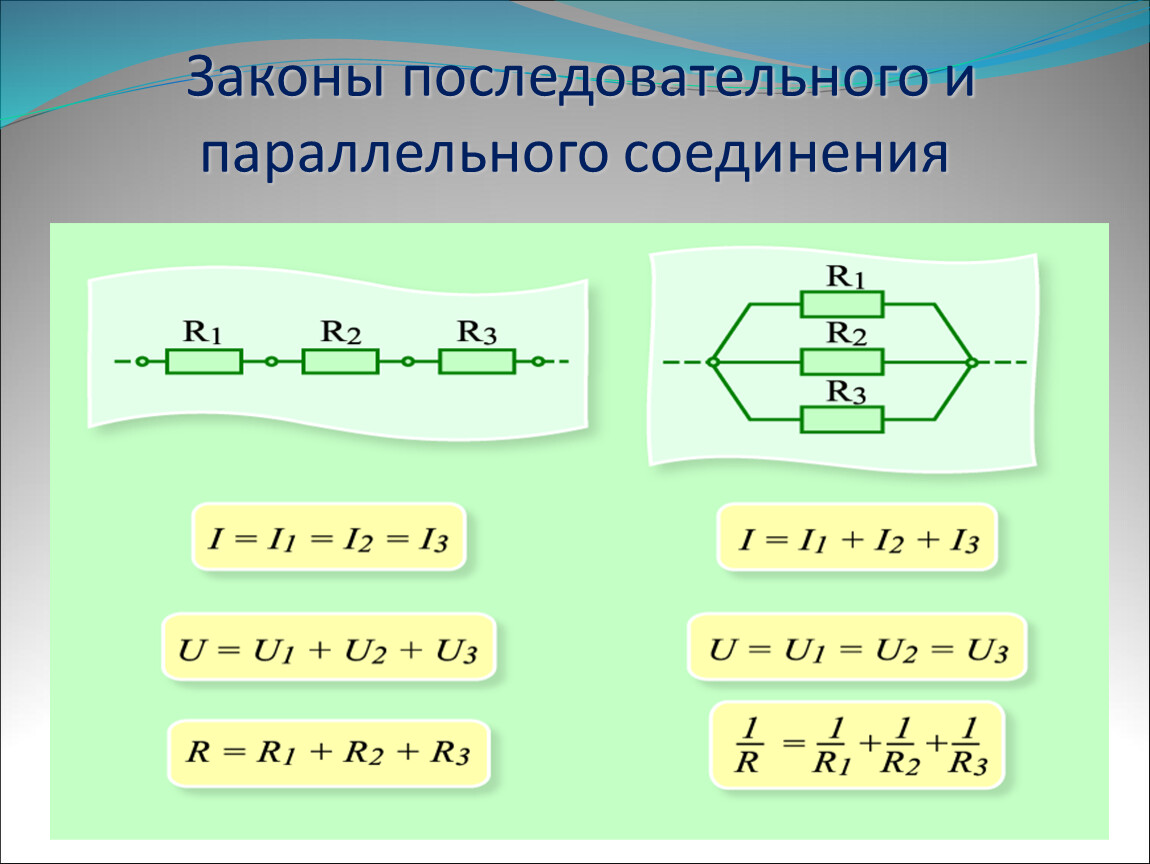

Нам известно значение полного сопротивления Т.е. R _T = 15 Ом и значение напряжения I.e. V = 15 В

Теперь нам нужно найти оставшееся неизвестное значение тока I.

Текущий ток через каждый резистор будет 1 А.

Напряжение на каждый резистор в последовательной цепи отличается. Если все резисторы в последовательной цепи имеют одинаковое значение сопротивления тогда напряжение через каждый резистор одинаковый. С другой стороны, если каждый резистор имеет другое значение сопротивления, то напряжение на каждом резисторе разный.

Напряжение на резистор (R ₁ ) есть V ₁ = I × R ₁ = 1 × 4 = 4 В

Напряжение на резистор (R ₂ ) равен В ₂ = I × R ₂ = 1 × 4 = 4 В

Напряжение на резистор (R ₃ ) равен В ₃ = I × R ₃ = 1 × 2 = 2 В

Напряжение на резистор (R ₄ ) составляет В ₄ = I × R ₄ = 1 × 2 = 2 В

Напряжение на резистор (R ₅ ) равен В ₅ = I × R ₅ = 1 × 3 = 3 В

Общее напряжение в последовательная цепь равна сумме всех отдельных суммарные напряжения

Т. е. В _Т = В ₁ + В ₂ + В ₃ + V ₄ + ……….+V _N

В нашей схеме общее напряжение равно сумме разностей потенциалов через Р _1, , _{Р 2 , Р 3 , R 4 и R 5 .}

Т.е. В _Т = В ₁ + В ₂ + В ₃ + В ₄ + В ₅ = 4 + 4 + 2 + 2 + 3 = 15 В.

Параллельно Цепь резистора

А Цепь параллельных резисторов представляет собой электронную схему, в которой все резисторы соединены рядом в разные пути, чтобы один и тот же ток не протекал через каждый резистор. Параллельная схема показывает несколько путей к протекать электрический ток.

ток в параллельной цепи распадается, при этом некоторый ток протекающие по каждой параллельной ветви и воссоединяющиеся, когда ветви встречаются снова. Следовательно, электрический ток через каждый резистор будет другим. Однако напряжение на каждый резистор одинаковый.

полное сопротивление параллельной цепи резистора получается по формуле суммируя обратные величины (1/R) значений сопротивления отдельные резисторы, а затем взяв обратную величину общий.

Для Например, если три резистора соединены параллельно. Затем общее сопротивление цепи

Пример:

А Схема параллельного резистора показана на рисунке ниже. Этот схема состоит из трех резисторов, соединенных параллельно и источник постоянного напряжения.

Если значения трех резисторов: R ₁ = 8 Ом, R ₂ = 8 Ом, R ₃ = 4 Ом и батарея постоянного тока = 14 В, затем

общее сопротивление

Суммарный ток течет по цепи

Как напряжение на каждом резисторе параллельно схема, мы можем использовать омы закон найти ток отдельной ветви следующим образом.