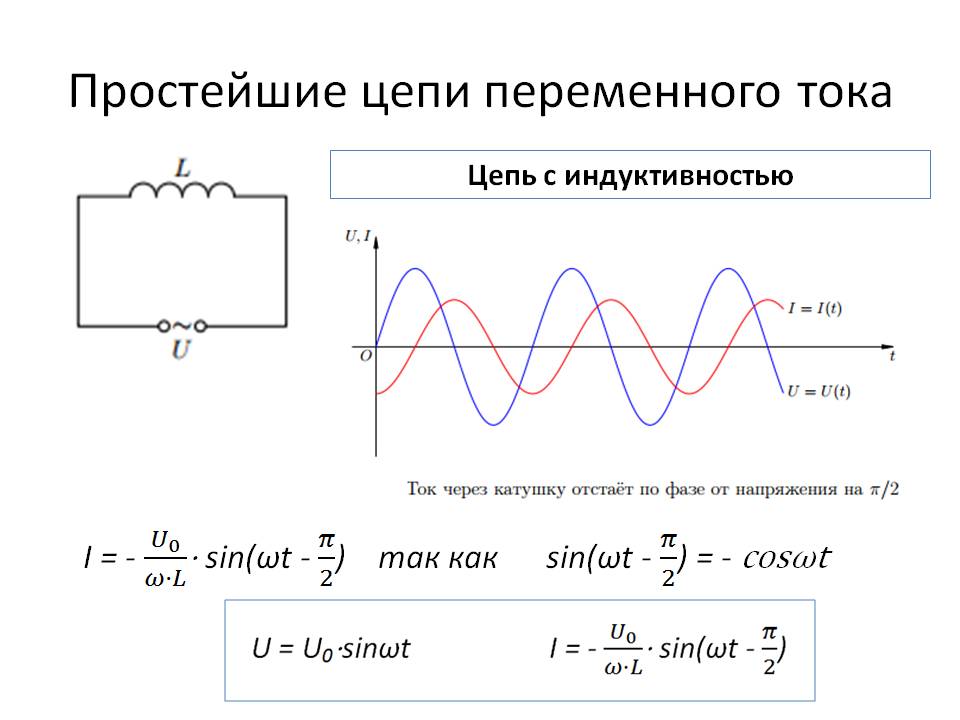
Как работает катушка индуктивности в цепи переменного тока. Какие формулы описывают ее поведение. Почему возникает индуктивное сопротивление. Как применяются катушки в электротехнике и электронике.
Принцип работы катушки индуктивности в цепи переменного тока
Катушка индуктивности является одним из ключевых элементов электрических цепей. В цепях постоянного тока она ведет себя как обычный проводник, но в цепях переменного тока ее поведение кардинально меняется. Это связано с явлением самоиндукции, которое возникает в катушке при изменении протекающего через нее тока.
При протекании переменного тока через катушку в ней возникает переменное магнитное поле. Изменение этого поля индуцирует в витках катушки ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока. В результате ток в катушке отстает по фазе от приложенного напряжения на 90°.
Индуктивное сопротивление катушки
Сопротивление, которое катушка оказывает переменному току, называется индуктивным сопротивлением. Оно зависит от индуктивности катушки и частоты тока:
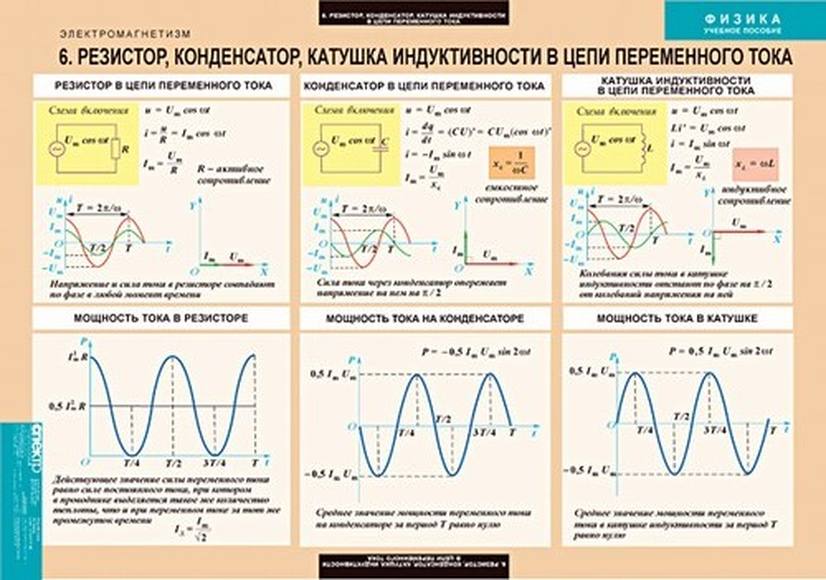
XL = ωL = 2πfL
где XL — индуктивное сопротивление (Ом), ω — угловая частота (рад/с), f — частота (Гц), L — индуктивность катушки (Гн).
Как видно из формулы, индуктивное сопротивление прямо пропорционально частоте тока. При постоянном токе (f = 0) оно равно нулю.
Закон Ома для цепи с катушкой индуктивности
Для цепи переменного тока, содержащей только идеальную катушку индуктивности, закон Ома записывается в виде:
I = U / XL
где I — действующее значение силы тока, U — действующее значение напряжения.
При этом важно помнить, что ток отстает по фазе от напряжения на 90°.
Мощность в цепи с катушкой индуктивности
Мгновенная мощность в цепи с идеальной катушкой индуктивности изменяется по закону:
p(t) = u(t) * i(t) = UmImsin(ωt)cos(ωt) = (UmIm/2)sin(2ωt)Средняя мощность за период равна нулю. Это означает, что идеальная катушка не потребляет энергию, а лишь обменивается ею с источником.
Реальная катушка в цепи переменного тока
Реальная катушка обладает не только индуктивностью, но и активным сопротивлением. Поэтому ее можно представить как последовательное соединение идеальной катушки и резистора. В этом случае полное сопротивление катушки (импеданс) определяется формулой:
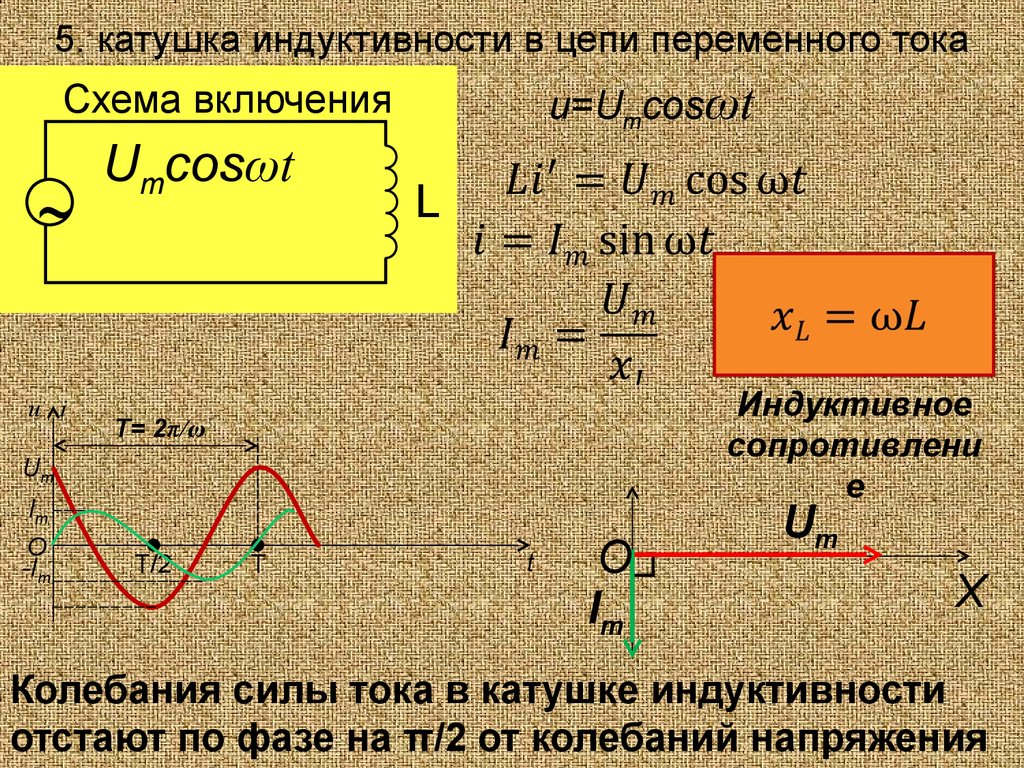
Z = √(R2 + XL2)
где R — активное сопротивление катушки.
Ток в цепи с реальной катушкой отстает от напряжения на угол φ, который определяется соотношением:
tg φ = XL / R
Применение катушек индуктивности в электротехнике и электронике
Катушки индуктивности широко применяются в различных областях электротехники и электроники благодаря их способности накапливать энергию в магнитном поле и оказывать сопротивление переменному току. Вот некоторые примеры их использования:
- Фильтры в электрических цепях
- Элементы колебательных контуров
- Дроссели в импульсных источниках питания
- Элементы систем зажигания в автомобилях
- Компоненты антенн и систем беспроводной связи
Особенности поведения катушки при высоких частотах
При работе на высоких частотах в катушках индуктивности проявляются дополнительные эффекты, которые необходимо учитывать:
- Увеличение активных потерь из-за скин-эффекта и эффекта близости
- Появление паразитной межвитковой емкости
- Возможность возникновения резонансных явлений
Эти эффекты могут существенно изменить характеристики катушки на высоких частотах и ограничить диапазон ее применения.
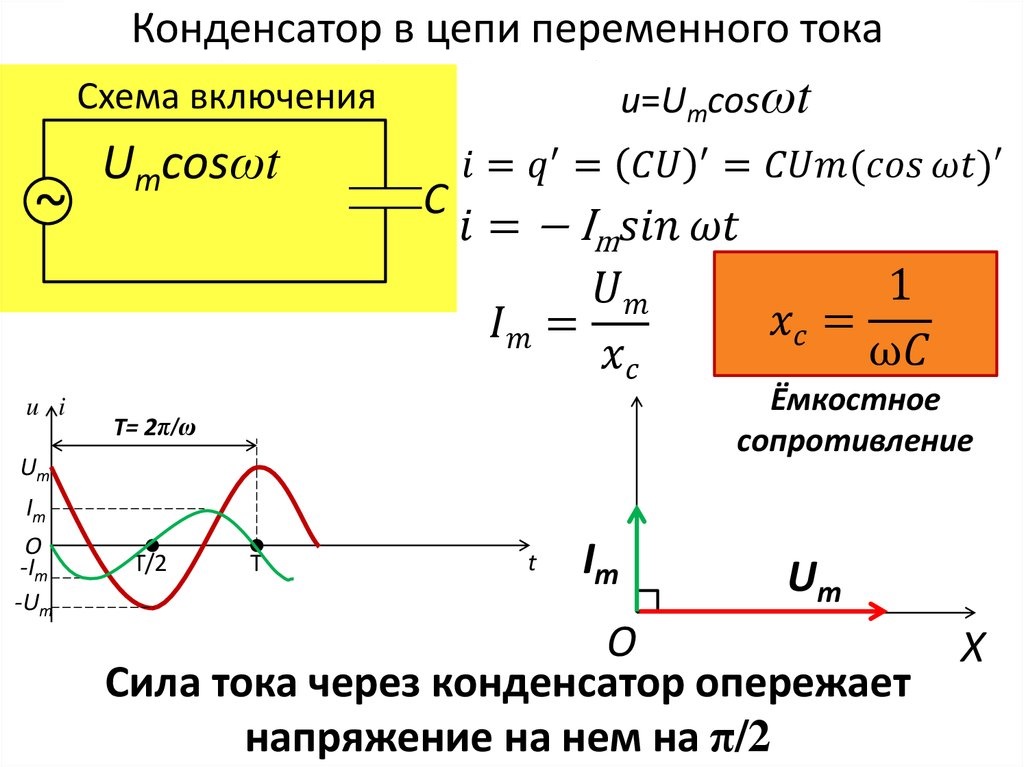
Сравнение катушки индуктивности и конденсатора в цепи переменного тока
Катушка индуктивности и конденсатор в цепи переменного тока проявляют в некотором смысле противоположные свойства:- В катушке ток отстает от напряжения на 90°, а в конденсаторе — опережает на 90°
- Индуктивное сопротивление растет с увеличением частоты, а емкостное — уменьшается
- Катушка накапливает энергию в магнитном поле, а конденсатор — в электрическом
Эти различия позволяют использовать комбинации катушек и конденсаторов для создания различных фильтров и резонансных цепей.
Влияние магнитопровода на свойства катушки индуктивности
Использование магнитопровода (сердечника) позволяет значительно увеличить индуктивность катушки при тех же габаритах. Однако это также вносит дополнительные особенности в ее работу:
- Появление нелинейности из-за насыщения магнитопровода
- Увеличение потерь на перемагничивание и вихревые токи
- Зависимость индуктивности от температуры
Выбор материала и конструкции магнитопровода зависит от конкретного применения катушки и требуемых характеристик.
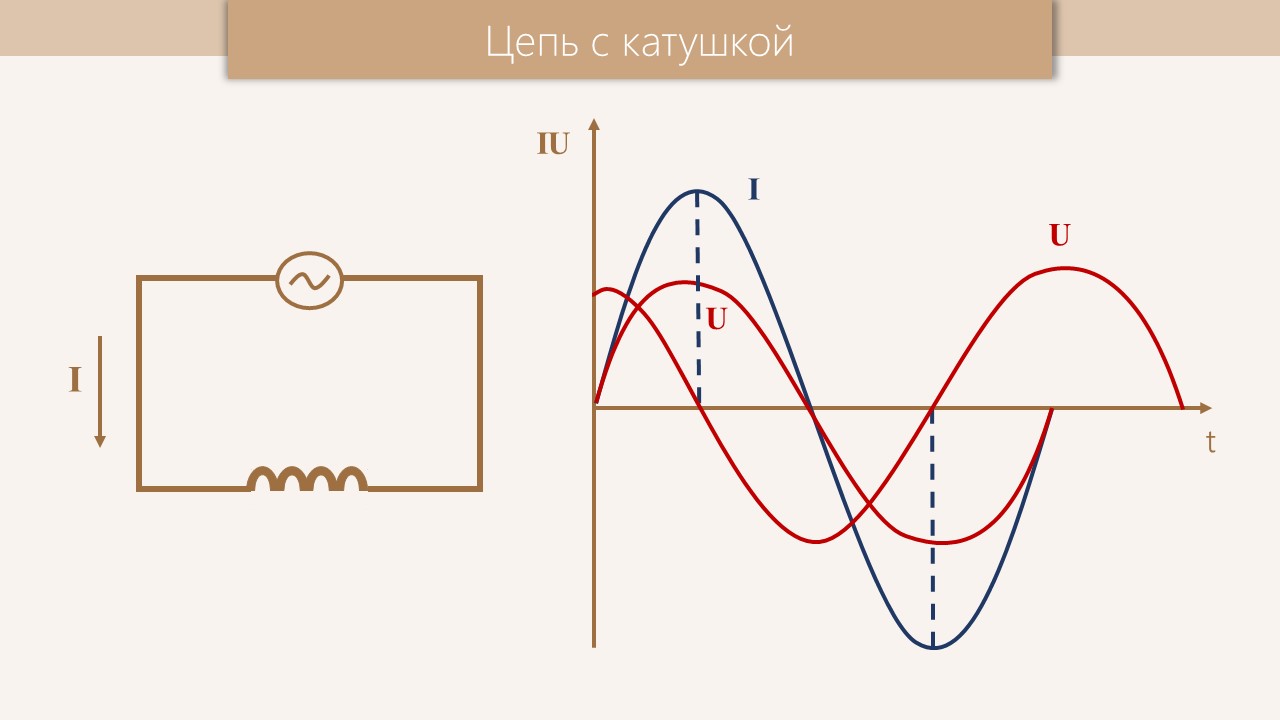
Катушка индуктивности в цепях переменного тока
Переменный электрический ток:
До сих пор рассматривались электрические цепи, содержащие в различных сочетаниях резисторы, конденсаторы и катушки, с источником постоянного тока либо без него. Теперь рассмотрим подключение таких цепей к источнику переменного тока.
Пусть источник тока создает переменное гармоническое напряжение (рис. 194)
Согласно закону Ома сила тока на участке цепи, содержащем только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
где — амплитудное значение силы тока в цепи.
Как видно, сила тока в такой цепи также меняется с течением времени по синусоидальному закону.
Величины называются амплитудными значениями
напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.Зная мгновенные значения U(t) и I(t), можно вычислить мгновенную мощность которая, в отличие от цепей постоянного тока, изменяется с течением времени.
С учетом зависимости силы тока от времени в цепи перепишем выражение для мгновенной тепловой мощности на резисторе в виде
Поскольку мгновенная мощность меняется со временем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно.
Перепишем формулу для мощности по-другому:
Первое слагаемое не зависит от времени. Второе слагаемое — переменная составляющая — функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю (см. рис. 194).
Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле
Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.
Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Поскольку для постоянного тока то с учетом ранее полученного выражения для среднего значения мощности переменного тока действующее значение силы тока
Аналогично можно ввести действующее значение и для напряжения
Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе (см. рис. 194).
Таким образом, резисторы оказывают сопротивление как постоянному, так и переменному току, при этом в обоих случаях в них происходит превращение электрической энергии во внутреннюю. Вследствие этого сопротивление резисторов R получило название активного или омического сопротивления.
Реальный соленоид (катушка индуктивности) обладает активным сопротивлением R и индуктивностью L. В цепях постоянного тока главную роль играет его сопротивление R, тогда как в цепях переменного тока — его индуктивность L.
Рассмотрим физические процессы, происходящие в идеальной катушке, у которой отсутствует активное сопротивление (R=0), при включении ее в цепь переменного тока.
В катушке индуктивностью L переменный ток вызывает появление ЭДС самоиндукции:
где — амплитудное значение ЭДС самоиндукции (рис. 195).
При возрастании силы тока ЭДС самоиндукции согласно правилу Ленца будет препятствовать его увеличению. Для идеальной катушки, активное сопротивление которой равно нулю (R=0), согласно закону Ома для полной цепи где U(t) напряжение на концах катушки.
Следовательно, в любой момент времени внешнее напряжение на концах катушки равно по модулю и противоположно по знаку ЭДС самоиндукции в катушке:
Сравнивая выражения для мгновенных значений силы тока I(t) и напряжения U(t), видим, что для их амплитудных значений можно записать закон Ома в виде
Величину называют индуктивным сопротивлением катушки.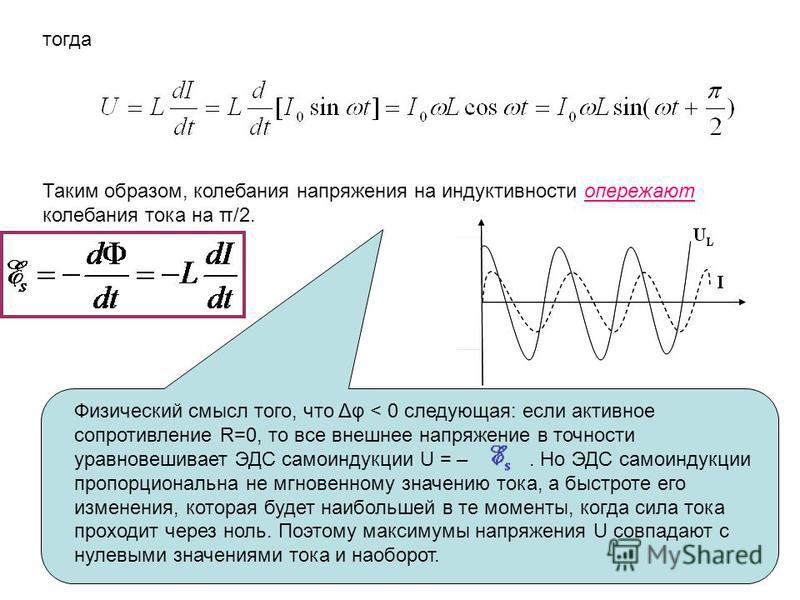
Обратите внимание на то, что фазы колебаний силы тока и напряжения не совпадают. Наличие сдвига фаз означает, что мгновенное значение напряжения U на катушке индуктивности опережает мгновенное значение силы I переменного тока по фазе на Такой сдвиг фаз между колебаниями силы тока и напряжения характерен в целом для цепей переменного тока, содержащих элементы, обладающие индуктивностью.
Закон Ома для цепи переменного тока, содержащей только катушку индуктивности, выполняется и для действующих значении силы тока и напряжения так как тогда
Таким образом, если в цепь переменного тока включена катушка индуктивности, то закон Ома выполняется для амплитудных и действующих значений силы тока и напряжения, но не выполняется для их мгновенных значений, так как мгновенные значения силы тока и напряжения не совпадают по фазе (см. рис. 195).
Мгновенная мощность, потребляемая катушкой индуктивности от источника переменного тока, определяется по формуле
Поскольку среднее за период значение функции равно нулю, то и средняя мощность за период также равна нулю:
Как видно из рисунка 195, цепь с идеальной катушкой индуктивности в течение первой и третьей четвертей периода работает в режиме потребителя, запасая энергию магнитного поля в катушке, а в течение второй и четвертой — в режиме генератора, возвращая источнику запасенную энергию.
Поскольку потерь энергии в этом случае не происходит, то индуктивное сопротивление называют реактивным.
Катушка индуктивности в цепи переменного тока кратко – формулы и опредделение (11 класс)
4.2
Средняя оценка: 4.2
Всего получено оценок: 74.
Обновлено 10 Января, 2021
4.2
Средняя оценка: 4.2
Всего получено оценок: 74.
Обновлено 10 Января, 2021
В цепи постоянного тока катушка индуктивности ведет себя так же, как обычный длинный провод. Однако для переменного тока ситуация существенно иная. Поговорим кратко о катушке индуктивности в цепи переменного тока.
Сущность индуктивного сопротивления
Из курса физики в 11 классе известно, что катушке индуктивности присуще явление самоиндукции. Оно состоит в том, что при изменении величины тока, протекающего по катушке, магнитное поле, порожденное этим током, также меняется. Это приводит к изменению магнитного потока через катушку.
А по закону электромагнитной индукции изменение магнитного потока вызывает появление в контуре ЭДС. Эта ЭДС по правилу Ленца направлена так, чтобы препятствовать причине, ее порождающей. Иными словами, при изменении тока в катушке индуктивности в ней возникает некоторая ЭДС, которая препятствует изменению этого тока.
Получается, что катушка «сопротивляется» любым изменениям тока в ней. Если ток возрастает, она не дает ему возрастать. Если ток убывает, она не дает ему убывать. Для переменного тока, который постоянно изменяет свое значение по гармоническому закону, катушка постоянно «сопротивляется». Таким образом, для переменного тока можно говорить об особом, индуктивном, сопротивлении катушки (на постоянном токе это сопротивление равно нулю).
Это сопротивление существенно отличается от сопротивления активного. Если на активном сопротивлении работа тока преобразуется в тепло, то на сопротивлении катушки во время возрастания тока его работа преобразуется в энергию магнитного поля в катушке, а во время убывания она возвращается из магнитного поля в энергию тока.
Катушка как бы «имеет реакцию» на изменение тока через нее за счет индуктивности. Поэтому такое сопротивление называется реактивным.
Реактивное сопротивление катушки индуктивности
Поскольку в первую половину периода энергия электрического тока запасается в магнитном поле катушки, а во вторую — возвращается в цепь, то в среднем работа электрического тока равна по модулю работе ЭДС самоиндукции, но имеет противоположный знак:
$$e_i =-u$$
Однако амплитудные значения напряжения и тока на катушке индуктивности достигаются неодновременно.
Мгновенное значение тока:
$$i =I_msin \omega t$$
Мгновенное значение напряжения:
$$u =L\omega I_m cos \omega t$$
Учитывая, что максимальная амплитуда напряжения $U_m$ равна $ L\omega I_m $, и приводя к синусу, получаем:
$$u =U_m sin(\omega t+{\pi \over 2})$$
Таким образом, колебания силы тока в катушке индуктивности отстают от колебаний напряжения на четверть периода. В этом важное отличие реактивного сопротивления от активного, где отставания между током и напряжения нет.
Амплитуда силы тока в катушке равна:
$$I_m={U_m\over \omega L}$$
Сравним эту формулу с законом Ома, который используется для определения силы тока в цепи:
$$I={U\over R}$$
Можно видеть, что эти формулы аналогичны, и величина $ \omega L$ играет роль сопротивления. То есть реактивное сопротивление катушки индуктивности (индуктивное сопротивление) равно:
$$X_L= \omega L$$
Отметим, что реактивное сопротивление катушки прямо пропорционально циклической частоте переменного тока. Чем она больше, тем больше сопротивление.
Поскольку любой проводник обладает некоторой индуктивностью, то на очень высоких частотах даже эта малая индуктивность обычных проводников достаточно сильно влияет на сигнал. Поэтому приходится применять специальные меры для ее компенсации. Например, применять вместо проводов волноводы — пустотелые металлические конструкции:
Рис. 3. Волноводы.Что мы узнали?
Катушка индуктивности в цепи переменного тока обладает реактивным сопротивлением, пропорциональным частоте.
Первую половину периода она запасает энергию электрического тока в виде магнитного поля, а вторую половину периода возвращает эту энергию электрическому току. При этом колебания силы тока в катушке индуктивности отстают от колебаний напряжения на четверть периода.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 74.
А какая ваша оценка?
Inductors—Часть 2. Основы индукторов ②｜Electronics ABC｜TDK Techno Magazine
Inductors―Part 2 Основы индукторов ②
- фейсбук
- твиттер
- Линкедин
Эта статья переиздана. Прошлые статьи были реорганизованы и переписаны. Он включает информацию о прошлых технологиях и продуктах, которая в настоящее время не обрабатывается TDK.
Поведение катушки индуктивности при постоянном токе
Переходная характеристика катушки
Благодаря эффекту самоиндукции катушки (индукторы) создают электродвижущую силу (индуктивная электродвижущая сила), которая направлена таким образом, чтобы противодействовать изменению тока. Следовательно, при подаче напряжения на катушку ток не сразу начинает течь, а при снятии напряжения ток не сразу прекращается. Неравномерное изменение тока или напряжения, которое происходит, например, в точке включения или выключения, называется переходной характеристикой (переходным явлением) катушки. Например, в схеме, показанной ниже, где катушка и неоновая лампа (напряжение начала разряда не менее нескольких десятков вольт) соединены параллельно, простое замыкание выключателя батареи (напряжение всего несколько вольт) не даст результата.
вызвать загорание неоновой лампы. Но если переключатель разомкнуть, когда через катушку течет ток, неоновая лампа загорится. Электродвижущая сила (V), создаваемая катушкой из-за эффекта самоиндукции, пропорциональна коэффициенту изменения тока (ΔI/Δt). Когда переключатель установлен в положение ON, ток постепенно увеличивается, поэтому электродвижущая сила не превышает напряжения источника питания. Но когда переключатель установлен в положение OFF, протекающий ток мгновенно отключается, что означает, что коэффициент изменения тока велик, вызывая создание большой электродвижущей силы, достаточной для зажигания неоновой лампы.
Энергия, накопленная катушкой
В приведенной выше схеме неоновая лампа может загореться, потому что катушка накапливает энергию. Эта энергия пропорциональна индуктивности катушки и квадрату тока.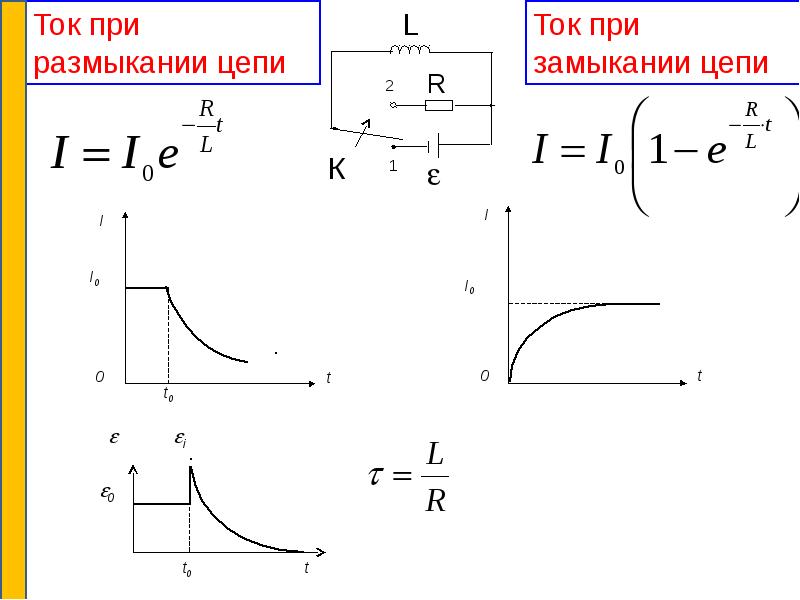
Когда переключатель установлен в положение OFF, накопленная энергия мгновенно высвобождается, создавая высокую электродвижущую силу.
Поведение катушки с переменным током
Индуктивное реактивное сопротивление (XL)
Катушка (индуктор) плавно пропускает постоянный ток, но оказывает сопротивление переменному току. Сопротивление увеличивается в сторону более высоких частот. Этот эффект называется индуктивным сопротивлением (XL) катушки. Между частотой переменного тока (f) и индуктивностью (L) существует следующая зависимость.
Осциллограмма напряжения и осциллограмма тока цепи переменного тока с катушкой
Переменный ток от промышленной розетки переменного тока имеет синусоидальную форму.
Когда катушка подключена к источнику переменного тока, эффект самоиндукции будет создавать электродвижущую силу, направленную таким образом, чтобы противодействовать изменению тока. Таким образом, изменение тока задерживается на 90 градусов (1/4 цикла) по отношению к изменению напряжения.
Намагниченность сердечника и магнитная проницаемость
Кривая намагничивания и магнитное насыщение
Магнитный поток (Φ), создаваемый в катушке, пропорционален индуктивности (L) и протекающему току (I). Поскольку индуктивность пропорциональна магнитной проницаемости, использование магнитного материала с высокой магнитной проницаемостью и применение большого тока приведет к созданию более сильного магнитного потока.
Однако существуют пределы способности магнитного материала собирать магнитный поток, и когда ток увеличивается до определенной точки, сердечник достигает магнитного насыщения. Плотность магнитного потока (B) в этой точке называется максимальной плотностью магнитного потока (Bm).
Процесс намагничивания сердечника и изменение магнитной проницаемости
По мере намагничивания сердечника магнитная проницаемость сердечника изменяется. Как показано на графике ниже, магнитная проницаемость (μ) выражается градиентом кривой намагничивания сердечника (θ). Начальный градиент вблизи начала кривой представляет собой начальную магнитную проницаемость (µ0). Эта начальная магнитная проницаемость обычно называется магнитной проницаемостью, и это также значение, указанное в каталогах ферритовых материалов. Увеличение тока в катушке и, следовательно, увеличение намагниченности в конечном итоге приведет к тому, что магнитная проницаемость достигнет максимально возможного значения.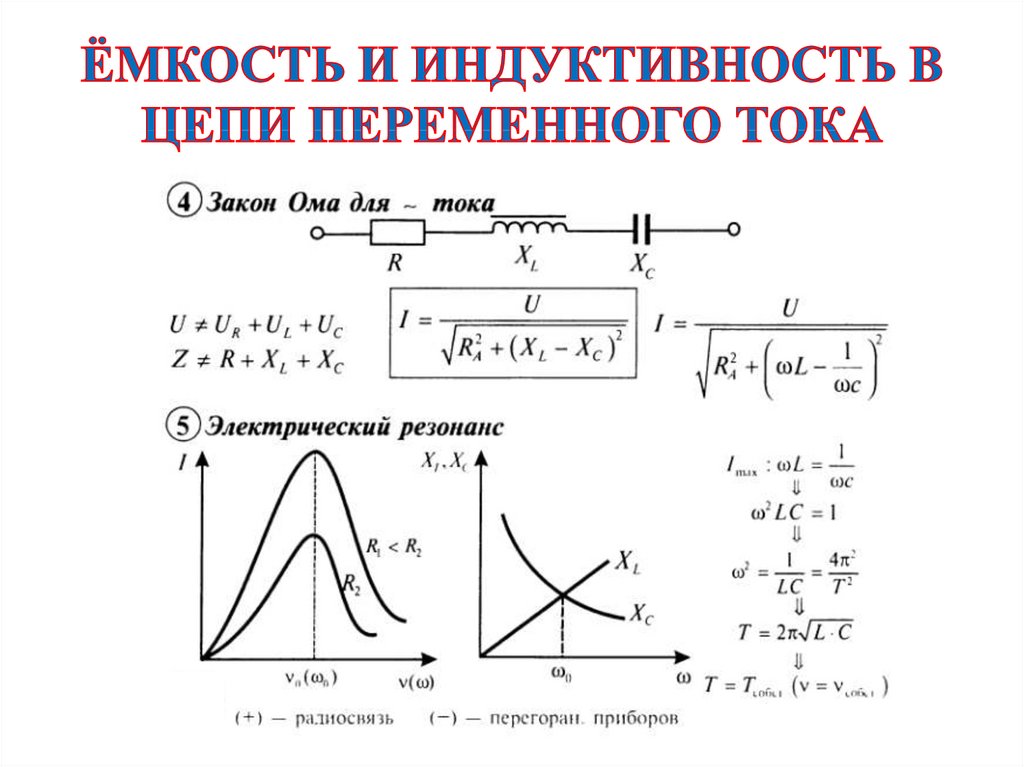
Это называется максимальной магнитной проницаемостью (мкм), за пределами которой значение снова падает.
Потери на вихревые токи в сердечнике
При подаче переменного тока на катушку создается электродвижущая сила, противодействующая изменению магнитного потока, и в сердечнике течет концентрический ток. Это называется вихревым током, и он лишает систему мощности RI2 (R: сопротивление, I: ток), которая выделяется в виде джоулева тепла. Это называется потерями на вихревые токи. В металлических сердечниках с низким электрическим сопротивлением потери на вихревые токи более выражены. Многослойные сердечники, используемые для силовых трансформаторов, представляют собой попытку уменьшить потери на вихревые токи. Однако потери будут увеличиваться в направлении более высоких частот, вызывая выделение большего количества тепла.
Поскольку феррит имеет высокое удельное сопротивление, потери на вихревые токи малы, что делает этот материал подходящим для многих применений, таких как высокочастотные катушки и высокочастотные трансформаторы.
. Почему ток в данной катушке индуктивности не может измениться мгновенно?
Еще одно упрощенное объяснение, но основанное на энергии…
С конденсаторами и катушками, чтобы внести изменения, мы должны убрать часть ЭМ энергии из каждого компонента или добавить немного ЭМ энергии в каждый компонент.
Какова скорость передачи электрической энергии в проводах? Это ватты, скорость потока энергии в джоулях в секунду, пропорциональная V * I.
Если бы мы хотели мгновенно изменить конденсатор или катушку, нам пришлось бы передать часть энергии их поля МГНОВЕННО , то есть нам нужно передать несколько джоулей за НОЛЬ секунд, что означает бесконечную скорость джоулей в секунду или бесконечную мощность.
Другими словами, в катушках/конденсаторах скорость любого изменения примерно пропорциональна ваттам, скорости перемещения энергии поля в джоулях/сек. Более высокие ватты дают более быстрые изменения их внутренних полей. Бесконечные ватты могут дать мгновенные изменения. Чтобы создать почти мгновенную передачу энергии, нам потребуются либо огромные вольты, либо огромные амперы, либо и то, и другое.
Зная это, мы можем вернуться назад и рассмотреть фактические значения вольт и ампер.
В случае конденсатора напряжение (в некоторой степени) постоянно, а скорость передачи энергии в любой момент времени пропорциональна току (в ваттах = Vconst * I = скорость передачи энергии в джоулях/сек.) In конденсаторы, так как напряжение частично фиксировано, ток начинает действовать как скорость потока энергии (хотя это и не так). Итак, как отмечают здесь другие, нам нужен бесконечный ток, если мы хотим создать бесконечные ватты, чтобы перемещать часть энергии конденсатора мгновенно, что затем мгновенно увеличивает напряжение конденсатора до нового значения.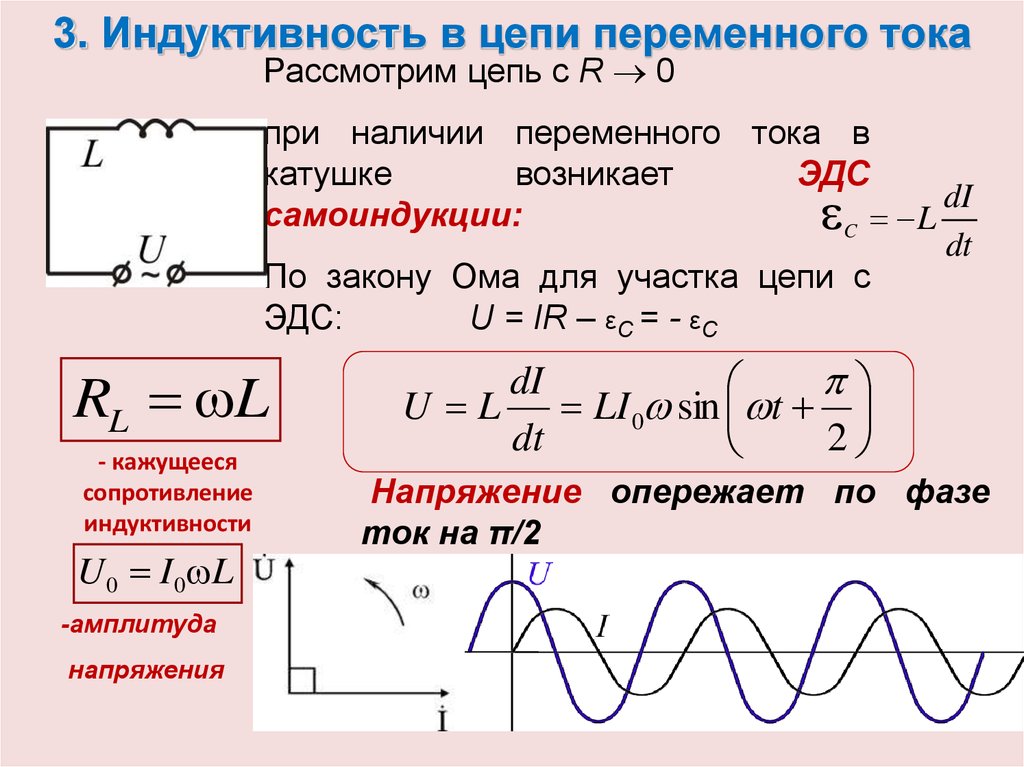
В катушках ток (в некоторой степени) постоянен, а скорость передачи энергии пропорциональна напряжению. В катушках, поскольку ток частично фиксирован, напряжение начинает действовать как скорость потока энергии (хотя это и не так). Для мгновенной передачи энергии нам потребовались бы бесконечные ватты = V * Iconst, что требует бесконечного напряжения, если мы хотел мгновенно переместить часть энергии катушек, что затем мгновенно заставляет ампер перейти к новому значению.
Заблуждения: разве ток не похож на поток энергии? Неа. Путь тока представляет собой замкнутые петли, полные круги. Заряд не переходит от одного компонента к другому, вместо этого он вращается, как вращающийся маховик, или как приводной ремень с замкнутым контуром. Заряд есть везде в проводниках, и во время тока он вращается. Очевидно, что ток не является потоком энергии. (Напряжение также не является потоком энергии, напряжение является мерой электростатических полей, распространяющихся между парами проводников.
