Ток в параллельной цепи. Параллельные электрические цепи: принципы работы, расчет параметров и применение

Что такое параллельная электрическая цепь. Как рассчитать токи в ветвях параллельной цепи. Как найти общее сопротивление параллельно соединенных резисторов. Какие особенности имеет напряжение в параллельной цепи. Где применяются параллельные соединения в электротехнике.

Что представляет собой параллельная электрическая цепь

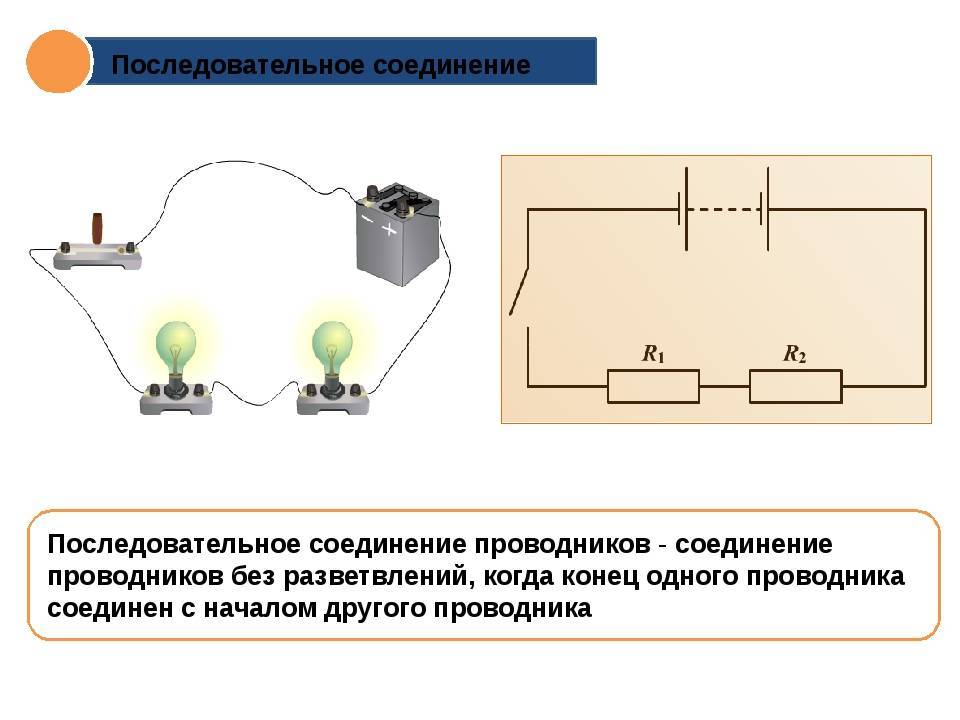
Параллельная электрическая цепь — это схема, в которой элементы (резисторы, конденсаторы, катушки индуктивности и др.) соединены таким образом, что ток имеет несколько путей протекания. Основные особенности параллельного соединения:

• Ток от источника разветвляется на несколько ветвей
• Напряжение на всех параллельных ветвях одинаково
• Общий ток равен сумме токов в отдельных ветвях
• Общее сопротивление меньше сопротивления любого из параллельных элементов

Параллельное соединение позволяет подключать несколько потребителей к одному источнику питания. При этом выход из строя одного элемента не нарушает работу остальных.

Как рассчитать токи в ветвях параллельной цепи

Для расчета токов в параллельной цепи используется закон Ома и первое правило Кирхгофа. Алгоритм расчета:

1. Определить общее напряжение на параллельном участке
2. Рассчитать ток в каждой ветви по закону Ома: I = U / R
3. Проверить, что сумма токов в ветвях равна общему току

Пример расчета для двух параллельных резисторов:

• R1 = 100 Ом, R2 = 200 Ом
• Напряжение U = 12 В
• I1 = U / R1 = 12 В / 100 Ом = 0.12 А
• I2 = U / R2 = 12 В / 200 Ом = 0.06 А
• Общий ток I = I1 + I2 = 0.12 А + 0.06 А = 0.18 А

Таким образом, ток распределяется обратно пропорционально сопротивлениям ветвей.

Расчет общего сопротивления параллельно соединенных резисторов

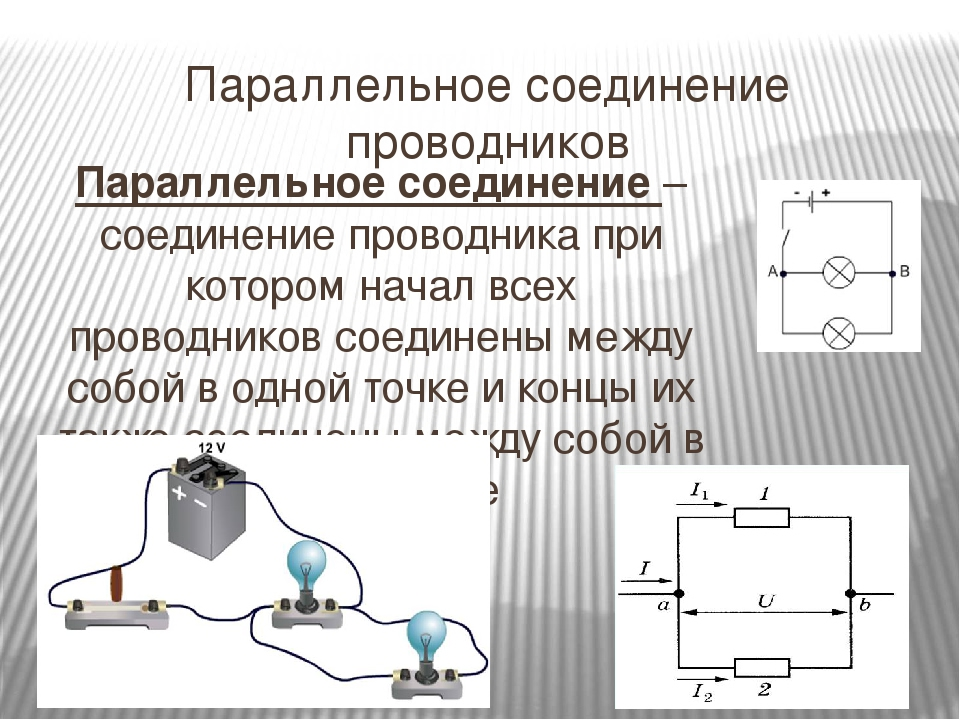
Общее сопротивление параллельно соединенных резисторов всегда меньше сопротивления любого из них. Для расчета используется формула:

1/R = 1/R1 + 1/R2 + 1/R3 + …

Где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.

Для двух параллельных резисторов формула упрощается:

R = (R1 * R2) / (R1 + R2)

Пример расчета для трех параллельных резисторов 100 Ом, 200 Ом и 300 Ом:

1/R = 1/100 + 1/200 + 1/300 = 0.01 + 0.005 + 0.0033 = 0.0183

R = 1 / 0.0183 = 54.6 Ом

Как видим, общее сопротивление (54.6 Ом) меньше любого из параллельных резисторов.

Особенности напряжения в параллельной цепи

Одним из ключевых свойств параллельного соединения является равенство напряжений на всех элементах. Это объясняется тем, что:

• Все элементы подключены к одним и тем же точкам цепи
• Разность потенциалов между этими точками одинакова для всех ветвей
• Падение напряжения на любом элементе равно приложенному напряжению

Данное свойство позволяет подключать параллельно устройства с одинаковым номинальным напряжением. Например, лампы освещения в квартире включены параллельно и работают от одного напряжения 220 В.

Где применяются параллельные соединения в электротехнике

Параллельные цепи широко используются в электротехнике и электронике:

• Подключение бытовых электроприборов к сети — все розетки соединены параллельно
• Системы освещения — лампы и светильники включаются параллельно
• Электропитание автомобиля — фары, стеклоподъемники и другие потребители подключены к аккумулятору параллельно
• Блоки питания электронных устройств — для получения разных напряжений
• Параллельное включение аккумуляторов для увеличения емкости
• Шунтирование измерительных приборов

Параллельное соединение обеспечивает надежность — при выходе из строя одного элемента остальные продолжают работать. Это важно для ответственных систем.

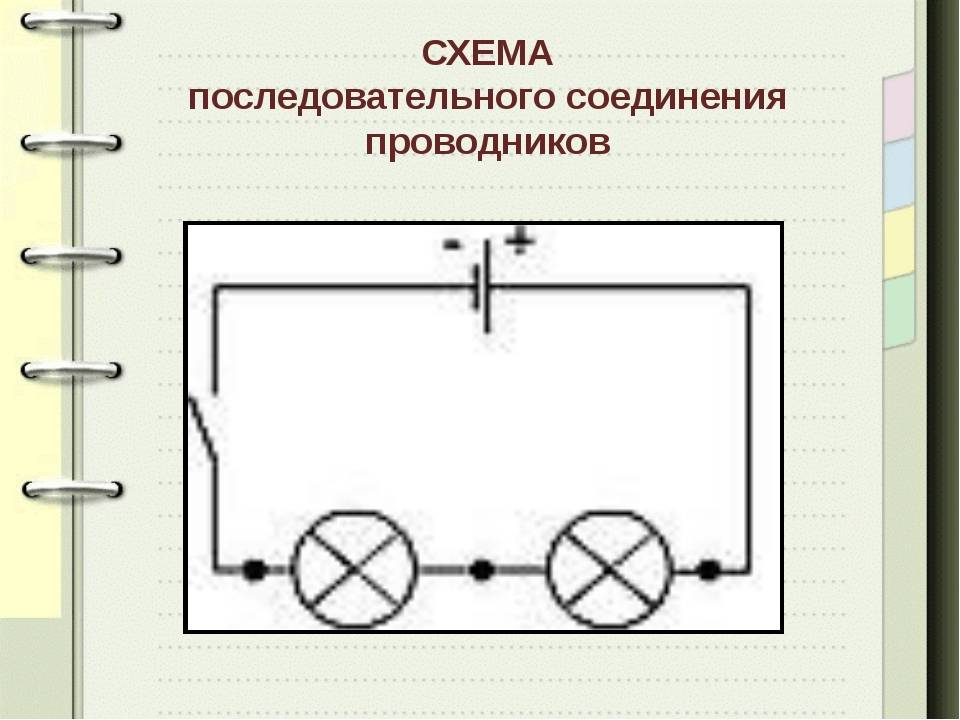
Сравнение параллельного и последовательного соединения

Параллельное и последовательное соединения имеют противоположные свойства:

Параметр	Параллельное соединение	Последовательное соединение
Напряжение	Одинаково на всех элементах	Сумма напряжений на элементах
Ток	Сумма токов в ветвях	Одинаков во всех элементах
Сопротивление	Меньше любого из элементов	Сумма сопротивлений элементов

Выбор типа соединения зависит от решаемой задачи. Часто в сложных схемах комбинируют оба вида соединений.

Методы расчета сложных параллельных цепей

Для анализа разветвленных параллельных цепей используются различные методы:

• Метод преобразования схемы — упрощение путем замены параллельных участков эквивалентными сопротивлениями
• Метод узловых потенциалов — составление уравнений для токов в узлах схемы
• Метод контурных токов — составление уравнений для замкнутых контуров
• Метод наложения — расчет токов от каждого источника отдельно
• Метод эквивалентного генератора — замена части схемы эквивалентным источником

Выбор метода зависит от сложности схемы и поставленной задачи. Для простых цепей достаточно применения законов Ома и Кирхгофа.

Параллельное соединение источников тока

Параллельное подключение нескольких источников тока позволяет увеличить силу тока в нагрузке. При этом:

• Напряжение на нагрузке равно ЭДС источников (при их равенстве)
• Общий ток равен сумме токов отдельных источников
• Внутреннее сопротивление уменьшается

Пример: два аккумулятора по 12 В и 60 Ач, соединенные параллельно, дадут напряжение 12 В и емкость 120 Ач.

Важно соблюдать полярность при параллельном подключении источников. Разнополярное включение может привести к короткому замыканию.

примеры задач и подробные факты —

By Кошики Банерджи

В этой статье мы обсудим различные методы расчета напряжения в параллельных цепях. При параллельном соединении цепь делится на ветви, чтобы ток равномерно протекал через все из них.

Параллельные схемы подчиняются закону сохранения энергии. Напряжение можно сказать как электрическая работа, выполненная на единицу заряда. Электрические поля консервативны, что означает, что электромонтажные работы зависят только от начальной и конечной точек. Все ветви имеют общий начальный и конечный узел при параллельном подключении. Следовательно, напряжение равно.

Подробнее… ..Функция параллельной цепи: полная информация и ответы на часто задаваемые вопросы

Как рассчитать напряжение в параллельной цепи — численные примерыПараллельная цепь RLC; «Файл: Example9d.png» by 1sfoerster под лицензией CC BY-SA 3.0

Q1. Как показано на схеме, два резистора одинакового номинала подключены к источнику напряжения параллельно. Приведены некоторые значения: i₁= 3 А, эквивалентное сопротивление R_eq= 15 Ом. Найдите напряжение источника V_s. 

Предположим, что R₁ = R₂ = R ом. Следовательно, эквивалентное сопротивление,

R_eq = (1/R + 1/R)^-1 = R/2 Ом

Учитывая R / 2 = 15, Таким образом, значение каждого резистора = 15 × 2 = 30 Ом. Значение тока я₁ дается как 3 А.

Поскольку это параллельная цепь, напряжение на одной ветви будет таким же, как и на любой другой ветви, и это также будет напряжение питания. Следовательно, напряжение источника,

V_s = ток в ответвлении x соответствующее значение сопротивления = i₁ х R = 3 х 30 = 90 В 

Q2. Параллельная сеть состоит из пяти резисторов: R, 2R, 4R, 8R и 16R. Чистый ток в сети равен I. Найдите напряжение в ветви, содержащей резистор 4R.

Сначала найдем эквивалентное сопротивление сети для расчет напряжения в любой точке сети. Эквивалент сопротивление в параллели схема есть,

R_eq = (1/р₁ + 1 / R₂ + 1 / R₃ … + 1/Р_n)^-1

Здесь, R_eq = ((1/R + (1/2R + (1/4R + (1/8R + (1/16R))^-1 = (16R/31)Ом

Полный ток в цепи определяется как I Amp.

Следовательно, напряжение источника V_s = I x 16R/31 = 16IR/31 В

Мы знаем, что напряжение источника параллельной схемы такое же, как напряжение в любой ветви схемы. Итак, напряжение в ветви, содержащей резистор 4R, составляет 16IR / 31 В.

Как рассчитать напряжение в параллельной цепи — часто задаваемые вопросы

Как найти полное напряжение в параллельной цепи?

В параллельной цепи полное напряжение совпадает с напряжениями ветви. Другими словами, напряжение остается неизменным на всех ветвях, соединенных параллельно. Ветви — это просто разные пути для тока.

Шаги для расчета напряжение в параллельной цепи с сопротивлением и общий ток:

• Найдите эквивалентное сопротивление по формуле: R_eq = (1/р₁ + 1 / R₂ + 1 / R₃ … + 1/Р_n)^-1
• Умножьте Req на общий ток.

Если даны только одно сопротивление и соответствующее значение тока, умножьте их, чтобы получить напряжение.

Подробнее ……Примеры параллельных цепей: полная информация и часто задаваемые вопросы

Как найти недостающее напряжение в параллельной цепи?

Под «отсутствующим напряжением» в параллельной цепи мы подразумеваем подаваемое напряжение, так как оно одинаково для всех ветвей. Итак, если у нас есть какое-либо значение тока и сопротивления, мы можем узнать напряжение в параллельной цепи.

Разберемся в этом на примере. Предположим, есть два резистора по 2 Ом и 4 Ом, соединенные параллельно. Ток, проходящий через резистор сопротивлением 2 Ом, равен 1.5 А. Нам известно напряжение питания V_s= напряжение ветви В₁ = напряжение ветви В₂. Следовательно, недостающее напряжение V = iR = 2 x 1.5 = 3 x V.

Как найти напряжение источника в последовательно-параллельной цепи?

По принципу параллельной схемы напряжение в каждой ветви одинаково и равно напряжению источника.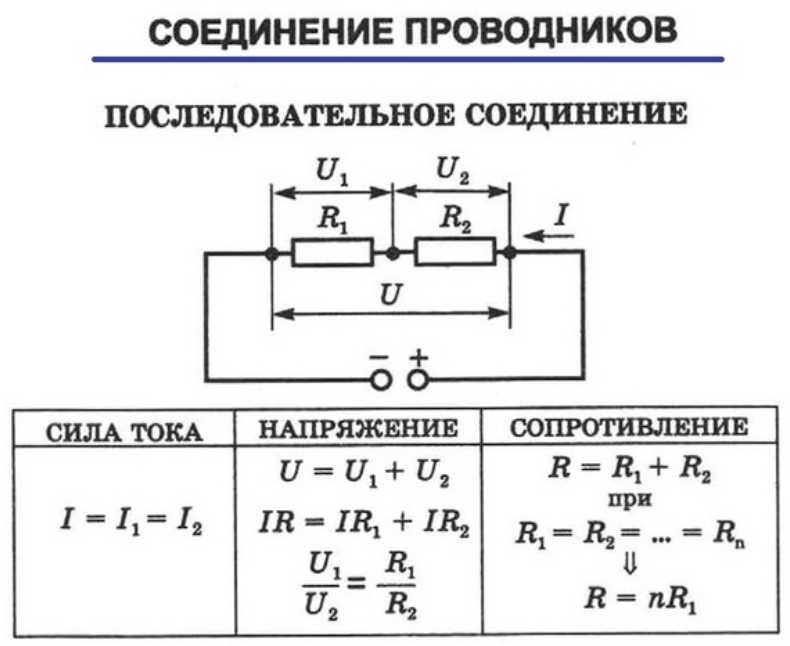 Если напряжение источника составляет Vs, а напряжения ответвлений равны V₁, V₂,… .V_n затем V_s V =₁ V =₂ =…. = V_n.

Если напряжение источника задано, у нас уже есть напряжения ответвлений. Если напряжение источника неизвестно, а значения тока указаны, мы можем узнать напряжение с помощью закона Ома. Например, если ток через ветвь равен 5 А, а значение сопротивления равно 2 Ом, напряжение будет просто 5 × 2 = 10 В.

Подробнее ……В настоящее время одинаково параллельно: полная информация и часто задаваемые вопросы

Как найти приложенное напряжение в параллельной цепи?

Приложенное напряжение в параллельной цепи относится к напряжению источника или напряжению батареи. Оно задано, или мы можем вычислить его с помощью другой предоставленной информации, такой как значения тока и сопротивления.

Приложенные напряжения означают напряжение, подаваемое на элемент. В параллельной цепи приложенное напряжение равно общему напряжению. Это также то же самое, что и падение напряжения в отдельных ветвях цепи. Но если параллельная цепь — не единственная часть сети, приложенное напряжение и напряжения ответвлений не будут равны.

Факультативный курс физики, 10 кл.

Факультативный курс физики, 10 кл.

Кабардин О. Ф. и др. Факультативный курс физики: 10 кл.: Учеб. пособие для учащихся / О. Ф. Кабардин, В. А. Орлов, Н. И. Шефер.— 3-е изд., перераб. — М.: Просвещение, 1987. — 208 с. Пособие содержит необходимый теоретический материал, примеры решения задач, заданий для самопроверки и экспериментальные задания в соответствии с программой факультативного курса X класса. Оглавление ПРЕДИСЛОВИЕ Глава I. КОЛЕБАНИЯ § 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И СПОСОБЫ ИХ ОПИСАНИЯ § 2. ПОНЯТИЕ О ГАРМОНИЧЕСКОМ АНАЛИЗЕ ПЕРИОДИЧЕСКИХ ПРОЦЕССОВ Гармонический анализ. Анализ звука. § 3. ИНДУКТИВНОЕ И ЕМКОСТНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА Индуктивное сопротивление. Активное сопротивление. § 4. ЗАКОН ОМА ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА Мощность в цепи переменного тока. § 5. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ Резонанс при параллельном соединении элементов цепи переменного тока. § 6. ТРЕХФАЗНЫЙ ТОК Трехфазный генератор. Соединение фаз генератора звездой. Соединение нагрузки звездой. Соединение фазных обмоток генератора треугольником. Соединение нагрузки треугольником. Асинхронный трехфазный двигатель. § 7. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ § 8. ПРАКТИЧЕСКИЕ ЗАДАНИЯ 2. Измерение сопротивления конденсатора в цепи переменного тока 3. Измерение индуктивности катушки в цепи переменного тока 4. Исследование электрических схем с R-, L- и С-элементами и определение параметров этих элементов Глава II. ВОЛНЫ § 9. МЕХАНИЧЕСКИЕ ВОЛНЫ Зависимость скорости звука от свойств среды. Характеристики звука и слух человека. § 10. ЗАПИСЬ И ВОСПРОИЗВЕДЕНИЕ ЗВУКА Изготовление граммофонных пластинок. Стереофоническая звукозапись. Магнитная запись звука. § 11. ЭФФЕКТ ДОПЛЕРА § 12. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ Излучение электромагнитных волн электрическим зарядом, совершающим гармонические колебания. § 13. ЗОНЫ ФРЕНЕЛЯ Зоны Френеля. Объяснение свойства прямолинейности распространения света. Пластинка зон. Дифракция от круглого экрана. § 14. ГЕОМЕТРИЧЕСКАЯ ОПТИКА Принцип Ферма. Закон отражения света. Закон преломления. Линзы. Аберрация линз. Оптические приборы. Зрительная труба и телескоп. § 15. ДИФРАКЦИЯ СВЕТА Дифракция от круглого отверстия. Дифракция и разрешающая способность оптических приборов. Дифракция от одной щели. Дифракция от двух щелей. Дифракционная решетка. Применение и изготовление дифракционных решеток. § 16. ГОЛОГРАФИЯ Фотография. Голография. Голография с записью в трехмерной среде. Свойства и особенности голограмм. Применения голографии. § 17. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ § 18. ПРАКТИЧЕСКИЕ ЗАДАНИЯ Глава III. КВАНТЫ И ЧАСТИЦЫ § 19. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА Гипотеза Планка. § 20. ФОТОН Затруднения волновой теории в объяснении фотоэффекта. Фотоны. Эффект Комптона. Опыт Боте. Дуализм свойств света. § 21. КВАНТЫ И АТОМЫ Квантовые постулаты Бора. Спектр атома водорода. Квантование момента импульса. Схема энергетических уровней. Опыт Франка и Герца. § 22. ОПТИЧЕСКИЕ КВАНТОВЫЕ ГЕНЕРАТОРЫ Инверсная населенность уровней. Условия, необходимые для создания в веществе инверсной населенности энергетических уровней. Устройство рубинового лазера. Устройство газовых лазеров. Применения лазеров. § 23. НЕЛИНЕЙНАЯ ОПТИКА Явление просветления среды. Самофокусировка лазерного луча. Нарушение принципа суперпозиции световых пучков и преобразование частоты света. Многофотонные процессы. Механизм влияния света на оптические свойства среды. § 24. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ Сплошной спектр излучения вещества в газообразном состоянии. Рентгеновские спектры. Молекулярные спектры. Радиоспектроскопия. Радиоволны космического происхождения. § 25. ЯДЕРНЫЕ СПЕКТРЫ Эффект Мессбауэра. § 26. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ Нуклоны. Спектры элементарных частиц. Кварки. § 27. ЧАСТИЦЫ И ВОЛНЫ Волновые свойства электрона. Гипотеза де Бройля и атом Бора. Интерференция волн де Бройля. Соотношение неопределенностей. Взаимные превращения света и вещества. § 28. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ ОТВЕТЫ

Урок Видео: Параллельные цепи | Nagwa

Стенограмма видео

В этом видео мы изучаем параллельные схемы. Цепи параллельны, в отличие от последовательной цепи, другого основного типа электрической цепи. Есть много замечательных вещей, которые можно узнать о параллельных цепях. И по ходу дела мы обнаружим полезную аналогию между параллельными электрическими цепями и параллельным течением воды. Итак, давайте приступим к делу. И для начала определим, что такое параллельная схема.

Возможно, лучший способ понять параллельную цепь — это знать, что в такой цепи ток протекает более чем по одному пути. Другой способ сказать это — сказать, что ток разделяется или разделяется в какой-то точке параллельной цепи. Например, рассмотрим эту схему. Если мы проследим путь обычного тока, мы увидим, что этот ток будет двигаться по часовой стрелке. Он будет закручиваться вокруг этого изгиба, проходить через этот первый резистор. И тогда он попадет в эту точку ветвления.

В этот момент с током происходит кое-что интересное. Как мы видим, есть два пути, чтобы добраться до этой части схемы, мимо параллельной ветки. Один путь должен пройти через эту верхнюю ветвь с резистором 𝑅 два. И один путь — пройти через нижнюю ветвь. Как вы думаете, куда пойдет ток? Получается, что, исходя из соотношения 𝑅 два к 𝑅 трем, часть тока идет по верхней ветви. А остальная часть начального тока идет по нижней ветви.

Это действительно очень интересно, потому что мы можем подумать, что весь ток пойдет на ту из этих двух ветвей, которая имеет наименьшее сопротивление. И ни один из текущих не пойдет к другому. Но это не то, что происходит на самом деле. Даже когда одно из этих значений сопротивления больше другого, по той ветви с большим общим сопротивлением протекает некоторый ток. Итак, у нас есть ток, проходящий через верхнюю ветвь. И у нас также есть некоторый ток, проходящий через нижнюю ветвь. Когда эти ветви снова соединяются, так что остается только один путь для протекания тока, ток воссоединяется и продолжается по цепи.

Есть несколько вещей, которые мы можем заметить о том, как этот ток проходит через разветвленную часть этой параллельной цепи. Во-первых, давайте применим несколько меток. Предположим, что общий ток в нашей цепи равен 𝐼. И затем, мы скажем, как только ток разветвится, ток, проходящий через верхнюю ветвь, мы назовем 𝐼 sub 𝑢, а ток, проходящий через нижнюю ветвь, мы назовем 𝐼 sub 𝑙. Эти три потока можно связать математически. Можно сказать, что полный ток 𝐼 равен сумме токов через верхнюю и нижнюю ветви. Это имеет смысл, если мы вспомним нашу аналогию проточной воды с параллельными цепями.

Если бы у нас был ручей, текущий и достигший точки разветвления, то мы знаем, что общая вода, которая была в ветвях, должна была бы в сумме равняться общей воде, которая была в ручье с самого начала. То есть вода в ветках должна откуда-то браться. А откуда оно исходит, так это выше по течению. Точно так же токи, протекающие по различным ветвям нашей параллельной цепи, должны в сумме равняться общему току, питающему эти ветви. И, кстати, это верно независимо от того, есть ли у нас две ветви, или три ветви, или четыре, или любое количество ветвей в нашей параллельной цепи.

Еще одна вещь, на которую следует обратить внимание в отношении тока в параллельной цепи, заключается в том, что когда этот ток делится на ветви цепи, как мы уже упоминали, эти значения тока могут не совпадать.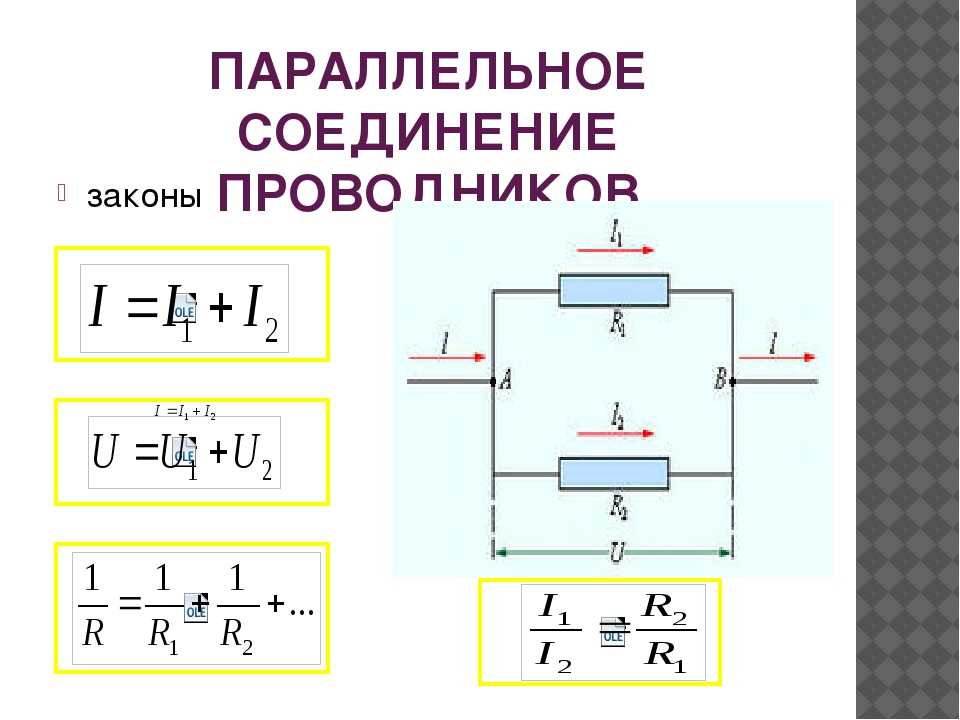 Другими словами, в нашем случае 𝐼 sub 𝑢 может не равняться 𝐼 sub 𝑙. Относительное значение этих токов зависит от отношения сопротивления ветви, через которую проходит каждый из них.

Здесь может помочь наша аналогия с текущей водой. Что касается ветвей этого текущего потока, скажите, что на одной из ветвей много препятствий, много палок, камней и листьев на пути. Но, с другой стороны, скажем, что на другой ветви очень мало препятствий. Более или менее вода может течь беспрепятственно.

Как вы думаете, через какую из этих двух ветвей будет протекать больше тока, через ту, где много препятствий, или ту, где мало? Мы обнаружим, что ветвь с меньшим количеством препятствий способна обрабатывать и обрабатывает больший ток. Эта нижняя ветвь, по которой вода может течь, не сталкиваясь со многими препятствиями, может быть большей частью воды в ручье, тогда как верхняя ветвь может просто проходить струйку.

То же самое происходит и в электрических цепях. Если одна из наших параллельных ветвей имеет гораздо большее общее сопротивление, чем другая, то это будет означать, что через эту ветвь проходит сравнительно меньший ток по сравнению с другими ветвями. Есть еще те, которые текут, но не так много, как ответвления с гораздо меньшим сопротивлением.

И, кстати, мы только что произвольно подчеркивали верхнюю ветвь, чтобы показать, что она имеет большее сопротивление. На самом деле мы еще не видели, чтобы это было правдой. А пока мы собираемся оставить эти отношения общими. 𝑅 sub two может быть больше или меньше 𝑅 sub three для наших целей. Но в любом случае, если бы одна из этих ветвей электрической цепи имела большее сопротивление, чем другая, то по ней протекал бы меньший ток, чем по ветви с наименьшим сопротивлением.

Очень кратко, если бы все-таки случилось так, что 𝑅 саб два было равно 𝑅 саб три, то есть сопротивления наших параллельных ветвей были одинаковыми, то это означало бы, что ток будет делиться по этим ветвям поровну. Другими словами, 𝐼 sub 𝑢 будет равно 𝐼 sub 𝑙. Итак, немного о токе в параллельных цепях. Теперь перейдем к разговору о сопротивлении в этих цепях.

Мы уже немного коснулись этого в нашей аналогии с текущей водой.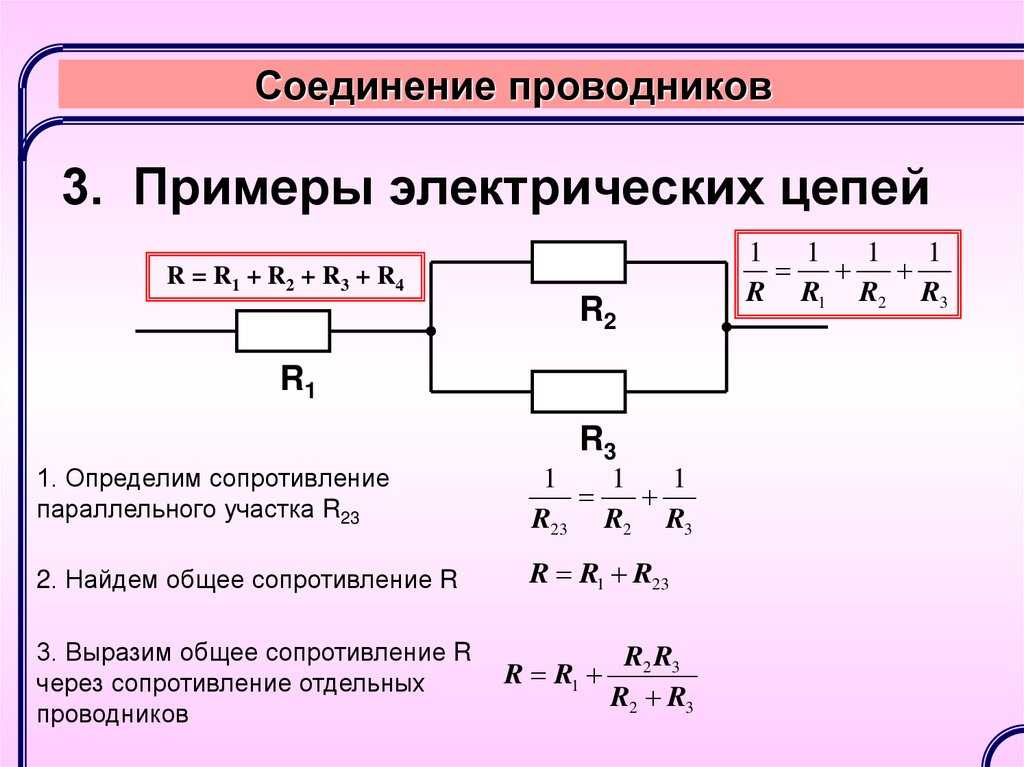 Но на самом деле, когда дело доходит до параллельных цепей, животрепещущий вопрос о сопротивлении заключается в том, каково сопротивление параллельных ветвей в цепи. То есть, если бы мы рассматривали этот участок цепи в целом, то каково было бы эквивалентное или эффективное сопротивление этой части. В ответ на этот вопрос есть правило сложения для параллельно расположенных резисторов, которое мы можем изучить.

Когда дело доходит до этого конкретного примера схемы, которую мы имеем для параллельной цепи, мы видим, что у нас просто два резистора, расположенных параллельно. Но, вообще, у нас может быть любое количество параллельных резисторов. Мы могли бы иметь резисторы 𝑛 параллельно. Сохраняя это число в совершенно общем виде, мы можем сказать, что единица на полное сопротивление набора параллельно расположенных ветвей равна единице на сопротивление первой ветви плюс единица на сопротивление второй ветви плюс точка точка точка, вплоть до один над сопротивлением 𝑛-й ветви.

Обратите внимание, что это уравнение для четырех резисторов, соединенных параллельно, имеет совсем другую форму, чем уравнение для резисторов, соединенных последовательно. Мы не можем использовать одно и то же уравнение для обоих. Как мы уже говорили, это уравнение для сопротивления параллельных резисторов предполагает общее количество резисторов, 𝑛 может быть любым целым числом. Однако бывает так, что часто мы сталкиваемся с цепью, имеющей две параллельные ветви, ни больше, ни меньше. Эта ситуация с двумя параллельно расположенными резисторами достаточно распространена, поэтому стоит упростить это общее уравнение для случая, когда 𝑛 равно двум.

Когда 𝑛 равно двум, у нас есть две параллельные ветви. И единица сверх общего сопротивления этих ветвей равна единице сверхсопротивления первой ветви плюс единица сверхсопротивления второй. И допустим, в качестве следующего шага мы умножаем обе части этого уравнения на 𝑅 sub 𝑡 раз 𝑅 sub один раз 𝑅 sub два, другими словами, все три сопротивления, упомянутые в уравнении. Если мы сделаем это, то после исключения общих множителей, которые появляются в числителе и знаменателе, мы получим, что 𝑅 sub один раз 𝑅 sub два, сопротивления двух параллельных ветвей равны 𝑅 sub 𝑡 умножить на 𝑅 sub два плюс 𝑅 sub 𝑡 раз 𝑅 под один.

Мы видим, что в правой части мы можем выделить 𝑅 подчлен 𝑡. Если мы сделаем это, а затем разделим обе части уравнения на 𝑅 минус один плюс 𝑅 минус два, то член в правой части сократится. И тогда, если мы выпишем полученное уравнение, мы найдем, что 𝑅 sub 𝑡, которое в данном случае является полным эквивалентным сопротивлением двух параллельных ветвей, равно сопротивлению первой ветви, умноженному на сопротивление второй ветви, разделить на сумму их сопротивлений. Поскольку схемы, имеющие ровно две параллельные ветви, довольно распространены, это соотношение стоит иметь в виду, хотя, как мы знаем, мы всегда можем вывести его из общего уравнения для 𝑛 резисторов.

Глядя на это уравнение, мы можем увидеть интересное сравнение между общим сопротивлением и отдельными резисторами 𝑅 sub one и 𝑅 sub two. Чтобы увидеть это более ясно, давайте вернемся к нашей примерной схеме. И мы применим фактические значения сопротивления к нашим сопротивлениям 𝑅 меньше трех и 𝑅 меньше двух. Предположим, что 𝑅 sub two, сопротивление верхней ветви, равно двум омам, а 𝑅 sub three, сопротивление нижней ветви, равно четырем омам. А теперь вопрос. Каково будет общее сопротивление этих двух параллельно соединенных резисторов? Другими словами, что такое 𝑅 sub 𝑡, эквивалентное сопротивление.

Согласно нашему уравнению для двух резисторов, полное сопротивление здесь равно их произведению, два ома на четыре ома, деленному на их сумму, два ома плюс четыре ома. Мы получаем восемь омов в квадрате на шесть омов. И коэффициент Ом компенсируется. И в простейшем случае общее эквивалентное сопротивление этих двух резисторов, включенных параллельно, составляет четыре трети ома.

Обратите внимание на кое-что интересное. Это общее значение меньше любого из отдельных значений резисторов, 𝑅 два или 𝑅 три. Таким образом, расположив эти резисторы параллельно, мы эффективно уменьшили их общее сопротивление. И на самом деле, это всегда верно для резисторов, включенных параллельно. Общее, или эффективное, или эквивалентное сопротивление набора параллельных ветвей всегда меньше, чем сопротивление любой из ветвей. Это действительно интересно, потому что это означает, что мы можем уменьшить общее сопротивление, добавив больше резисторов. Они просто должны иметь все меньшие и меньшие значения. Хорошо.

До сих пор мы говорили о токе и сопротивлении в параллельных цепях. Теперь поговорим о разности потенциалов. И здесь кульминация в том, что разность потенциалов на параллельных ветвях цепи одинакова. Это означает, что в случае с этой схемой, если бы мы измерили разность потенциалов на верхней ветви, она была бы такой же, как разность потенциалов на нижней ветви. Есть веская причина, почему это так. Вместо того, чтобы думать об этом с точки зрения электрического потенциала, давайте на мгновение подумаем с точки зрения гравитационного потенциала. Скажем, у нас есть две высоты, одна выше другой. Мы назовем их ℎ один и ℎ два.

Далее представим, что у нас есть объект, который начинается с ℎ единицы. А затем он следует по определенному пути, чтобы добраться до ℎ два. Но затем есть еще один объект, который начинается с ℎ один и идет другим путем, чтобы добраться до ℎ два, и заканчивается в той же точке. И скажем, есть еще третий объект, начинающийся с ℎ единицы. Этот идет очень необычным путем, но в конечном итоге заканчивается на ℎ два. Как мы видим, все три объекта прошли одинаковую разницу высот и, следовательно, испытали одинаковое изменение гравитационного потенциала.

Мы могли бы думать об этих разных путях, которые мы нарисовали, как о разных параллельных ветвях электрической цепи. Несмотря на то, что пути различны, поскольку разница в их начальной и конечной точках одинакова, это означает, что их общая разница гравитационного потенциала одинакова. И то же самое с электрическим потенциалом в нашей параллельной цепи.

Допустим, нам нужно измерить разность электрических потенциалов между здесь и здесь в нашей цепи, другими словами, на параллельной части цепи. Какими бы путями ни шел электрический ток от начальной точки к конечной, мы знаем, что разность потенциалов на этих путях должна быть одинаковой. И этот факт очень помогает нам, когда мы пытаемся вычислить разные величины в параллельных электрических цепях.

Вот пример. Допустим, наша ячейка в этом случае обеспечивает общую разность потенциалов 10 вольт. И еще допустим, что наш резистор 𝑅 sub one равен пяти Ом. Зная все это, мы удивляемся, что ток проходит через нижнюю ветвь нашей параллельной секции, 𝐼 sub 𝑙. Давайте теперь найдем этот ток, используя то, что мы уже узнали о параллельных цепях.

В качестве общей стратегии решения, вот что мы сделаем. Во-первых, мы будем работать, чтобы найти общий ток в заглавной цепи 𝐼. Мы сделаем это, применив к этой схеме закон Ома. Затем, используя этот закон, мы рассчитаем, сколько напряжения падает на резисторе 𝑅 единица. Как только мы это узнаем, мы сможем решить, какое напряжение должно упасть на оставшейся части цепи. И как только это будет решено, мы сможем снова использовать закон Ома, чтобы найти 𝐼 sub 𝑙, ток через нижнюю ветвь.

Итак, приступим. И, как мы уже упоминали, мы начнем с использования закона Ома для определения общего тока в цепи. Чтобы определить этот ток, нам нужно знать общую разность потенциалов, а также общее сопротивление. Мы знаем общую разность потенциалов 10 вольт. Но мы еще не знаем общего сопротивления. Чтобы решить эту проблему, нам нужно добавить эти два резистора, которые включены параллельно, резисторы на два Ома и резисторы на четыре Ома, а затем добавить это эквивалентное сопротивление к 𝑅 меньшему.

Чтобы сложить эти два параллельных резистора, четырехомный и двухомный, мы можем вспомнить наше правило для двух параллельно расположенных резисторов, что их эквивалентное сопротивление равно их произведению, деленному на их сумму. И вспомните, что в нашем случае мы уже нашли это эквивалентное сопротивление. Это четыре трети ома. Чтобы получить общее сопротивление цепи, мы добавим это значение, четыре трети ома, к пяти омам, резистор 𝑅 один, который расположен последовательно с параллельной частью цепи.

Когда мы суммируем эти сопротивления в соответствии с правилом последовательного сложения, мы находим, что оно равно девятнадцати третям ома. Это общее эквивалентное сопротивление всех трех резисторов в нашей схеме. Теперь, чтобы найти общий ток в нашей цепи, мы разделим общее напряжение на общее сопротивление, 10 вольт разделить на девятнадцать третей ома. Получается тридцать девятнадцатых ампера.

Теперь мы знаем общий ток в цепи. Давайте выясним разность потенциалов на нашем резисторе 𝑅 sub one. Согласно закону Ома, это будет равно току, протекающему через этот резистор, тридцати девятнадцатым ампера, умноженному на его сопротивление, равное пяти омам. Если записать в виде дроби, получится 150 на 19.вольт. Заметьте, кстати, что в десятичном виде это примерно равно семи с половиной вольтам. Другими словами, это большая часть нашей общей разности потенциалов, 10 вольт.

Наш следующий шаг — найти разность потенциалов на параллельном участке нашей цепи. И сделаем это, вычтя это значение, сто пятьдесят девятнадцатых вольта, из нашей общей разности потенциалов в 10 вольт. Мы назовем эту разность потенциалов 𝑉 sub 𝑝. И это равно 190 больше 19 вольт, это 10 вольт, минус 150 больше 19 вольт. И это выходит к 40 над 19 вольтами.

Это означает, что каждая из двух ветвей нашей параллельной цепи испытывает разность потенциалов в сорок девятнадцатых вольта. Используя еще раз закон Ома, мы можем сказать, что ток в нижней ветви равен разности потенциалов на этой ветви, деленной на ее сопротивление. Когда мы вычисляем эту долю, мы получаем результат десять девятнадцатых ампера. Именно столько тока протекает по нижней ветви нашей параллельной цепи.

Давайте теперь обобщим то, что мы уже узнали о параллельных цепях. Для начала в этом уроке мы увидели, что параллельные цепи имеют более одного пути прохождения тока. Мы также видели, что поток разделяется по различным предлагаемым ему путям. Мы также видели, что для 𝑛 резисторов, расположенных параллельно, единица сверх их полного эквивалентного сопротивления равна единице сверхсопротивления первого резистора плюс единица сверхсопротивления второго резистора плюс вплоть до единицы сверхсопротивления второго резистора. 𝑛й резистор. Мы также видели, что когда у нас есть ровно два резистора параллельно, их общее сопротивление равно их произведению, деленному на их сумму. И, наконец, мы увидели, что разность потенциалов на параллельных ветвях цепи одинакова.

Что?, последовательное или параллельное, измерение, ток и напряжение

29 ноября 2022 г. 17 августа 2022 г.

В этом посте

Мы собираемся перейти к схемам и их компонентам. Следующие символы используются для обозначения компонентов схемы, которые обычно используются в физике.

Вы должны быть знакомы с этими символами, как вы увидите, и, возможно, вам придется использовать эти символы или их небольшие вариации в экзаменационных вопросах по электричеству и цепям.

Электрические цепи всегда включают в себя источник электроэнергии для обеспечения напряжения, провода, обеспечивающие путь прохождения тока, и компонент, который можно использовать для демонстрации того, что ток распространяется по цепи. Лампы и светоизлучающие диоды ( Светодиоды ) являются примерами компонентов, которые можно использовать для индикации наличия тока в цепи.

Оба эти компонента загораются или светятся только тогда, когда через них проходит ток. Если компоненты подключены к цепи, но не светятся, это указывает на то, что ток не течет и должен быть либо обрыв в проводе, либо отсутствие напряжения, толкающего электроны по цепи.

Последовательные и параллельные цепи и их применение

Электрические цепи могут быть соединены последовательно или параллельно . Эти различные типы схем имеют ключевые сходства и различия, которые делают их подходящими для различных целей. Вы должны быть в состоянии объяснить, почему последовательная или параллельная схема более подходит для конкретных приложений.

Последовательные цепи

В последовательной цепи компоненты соединяются один за другим в линию. Ток, протекающий через каждый компонент, всегда одинаков, независимо от их положения в цепи.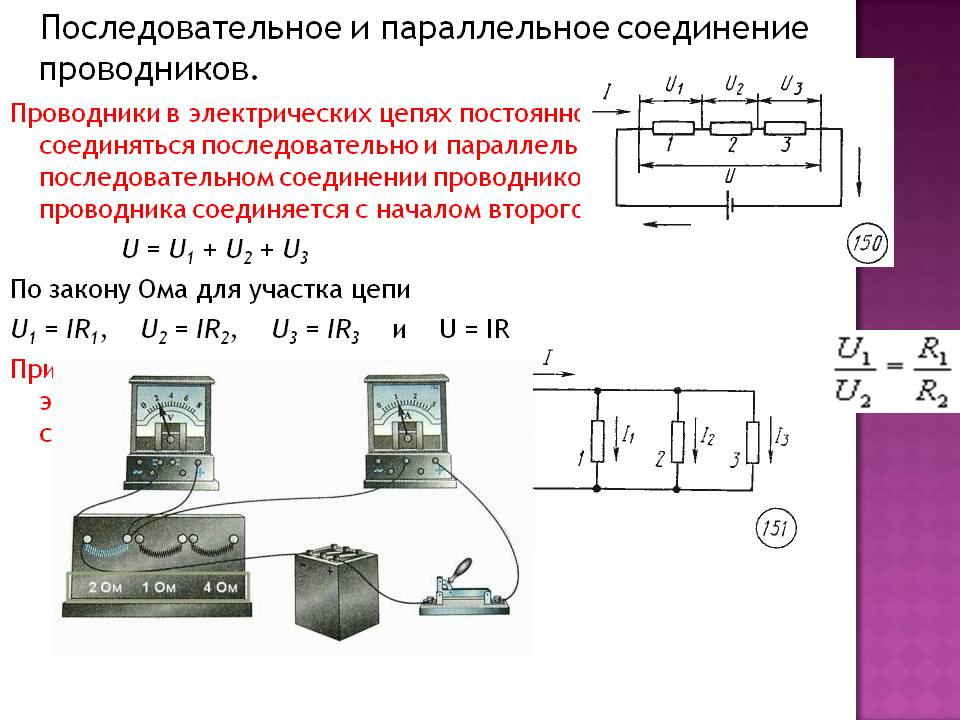 На приведенной ниже схеме показан пример последовательной цепи:

Электричество проходит по всем проводам цепи. Это означает, что электричество должно пройти через каждый компонент цепи и вернуться к исходной точке. Если один компонент в последовательной цепи будет удален или отключен, цепь будет разорвана, и электричество больше не сможет течь.

Например, рассмотрим набор елочных огней, соединенных последовательно. Если одна из лампочек сломалась, электричество не может пройти к следующей лампочке. Цепь будет разорвана, и ни один из огней не загорится. Поэтому было бы очень трудно определить, какая лампочка неисправна. Понятно, почему последовательная схема была бы плохим выбором для домашнего освещения!

P параллельные цепи

В параллельной цепи каждый компонент может быть помещен на отдельные петли, параллельные друг другу. Напряжение на всех компонентах в параллельной цепи одинаково, а ток — нет. Ток распределяется поровну между всеми отдельными ветвями цепи. Сумма токов, измеренных на каждой ветви цепи, должна быть равна общему току, протекающему по цепи. Это означает, что общий ток, протекающий по цепи, распределяется между каждой параллельной ветвью компонента. На приведенной ниже схеме показан пример параллельной цепи:

Поскольку каждый компонент в параллельной цепи находится в отдельном контуре цепи, при обрыве одного компонента ток все еще может проходить по другим неразрывным ветвям. Таким образом, компоненты в других ветвях по-прежнему смогут работать. Вернемся к нашему предыдущему примеру с елочными огнями. Если бы лампы были соединены в параллельную цепь и одна из лампочек вышла из строя, остальные лампы продолжали бы гореть. Тогда было бы очень легко определить и заменить сломанную лампочку. Параллельные цепи используются в бытовом освещении по той же причине. Например, если на кухне перегорела лампочка, остальные лампы в доме останутся гореть. Последовательные и параллельные схемы имеют разные характеристики, что делает их подходящими для разных приложений.

В последовательной цепи:

• Один переключатель может одновременно включать и выключать все компоненты.
• Если одна лампочка или устройство сломается, все остальные лампочки или устройства перестанут работать.
• Напряжение, обеспечиваемое ячейкой или источником питания, распределяется между всеми компонентами. Чем больше лампочек добавлено в последовательную цепь, тем тусклее они будут.
• Чем больше сопротивление любого компонента, тем больше доля напряжения в цепи.

В параллельной цепи:

• Выключатели могут быть размещены в разных частях цепи для индивидуального включения и выключения каждой лампочки.
• Если одна лампочка или устройство сломается, пострадают только лампочки на той же ветке.
• Каждая ветвь цепи получает одинаковое напряжение, поэтому, если в цепь параллельно добавить дополнительные лампочки, их яркость не изменится.

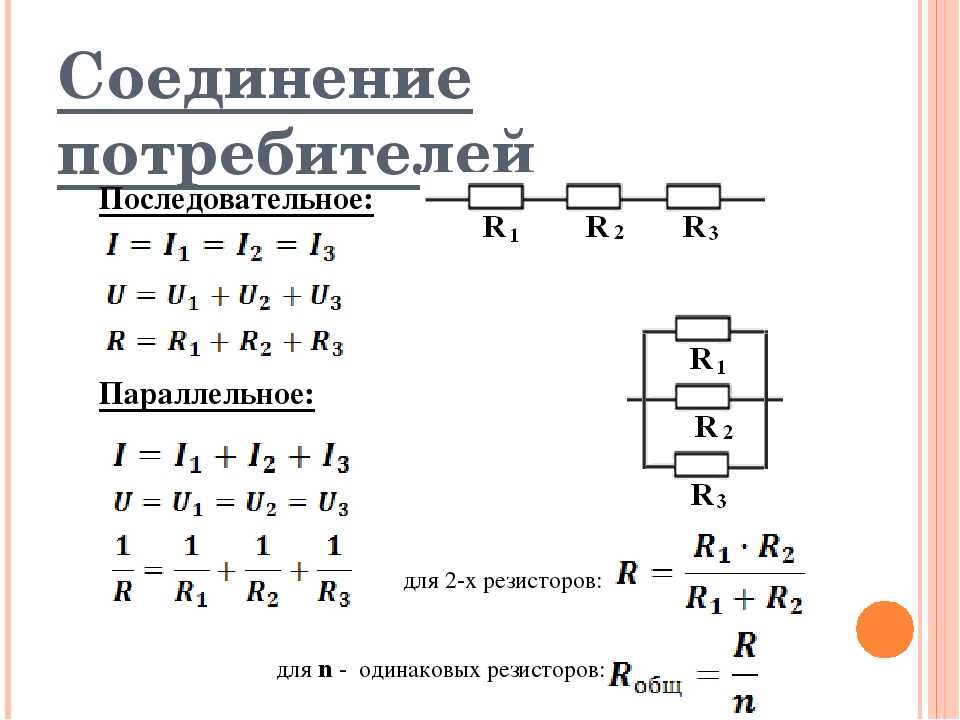
Декоративные гирлянды обычно соединяются последовательно. Это потому, что каждой лампочке нужно только низкое напряжение. Если напряжение от сети распределяется между каждой лампочкой, они все равно получают достаточно энергии для производства света. Если одна из лампочек неправильно установлена ​​в патроне или сломается, цепь больше не будет замкнутой, и ни одна из лампочек не загорится.

Свет в ваших домах подключен параллельно. Каждая лампочка может включаться и выключаться отдельно, и яркость лампочек не меняется, когда другие лампочки включены или выключены. Если одна лампочка сломается или будет удалена, вы все равно сможете использовать другие лампочки в доме.

Ток и напряжение в последовательных и параллельных цепях

Ток в цепи обычно измеряют с помощью устройства, называемого амперметром. Амперметр помещают последовательно с компонентом, через который проходит ток, и поэтому он становится частью цепи. Он способен измерять величину тока, протекающего через него.

Амперметр должен иметь низкое сопротивление, так как в противном случае ток уменьшится, и измеренное значение будет неточным. На диаграмме напротив показано типичное положение амперметра по отношению к цепи.

Для измерения разности потенциалов или напряжения на компонентах цепи, таких как элементы или лампы, мы используем устройство, известное как вольтметр. Вольтметры должны быть подключены параллельно или параллельно компоненту, на котором мы измеряем разность потенциалов.

Вольтметр, подключенный параллельно компоненту, измеряет количество энергии, передаваемой каждому кулону заряда, прошедшего через него. На диаграмме напротив показано типичное положение вольтметра в цепи, где он расположен параллельно компоненту, на котором он измеряет разность потенциалов.

Ток и напряжение в последовательной цепи

В последовательной цепи ток, протекающий через все компоненты, одинаков. Поэтому, если ток измерялся в какой-либо точке цепи, он всегда должен быть равен. Например, если в начале цепи был измерен ток 0,4 А, то ток, измеренный в любой другой точке цепи, также должен быть равен 0,4 А.

Величина тока зависит от общего напряжения, выдаваемого элементами или батареями, а также от количества и характера компонентов, включенных в цепь. Если добавить больше компонентов, ток уменьшится, поскольку каждый из них оказывает сопротивление потоку электричества.

Напряжение в последовательной цепи не одинаково для всех компонентов. Напряжение распределяется поровну между компонентами цепи, если их сопротивления равны. Например, если батарея в последовательной цепи производит 6 В, и у нас есть три компонента в цепи, напряжение, измеренное на каждом компоненте, будет 2 В. Если сопротивления компонентов неодинаковы, напряжение, измеренное на компонентах, будет различным.

Посмотрите на изображения двух последовательных цепей выше. Тот, что слева, показывает результаты размещения вольтметра в цепи в разных точках, и мы видим, что 6 вольт — это мощность от батареи.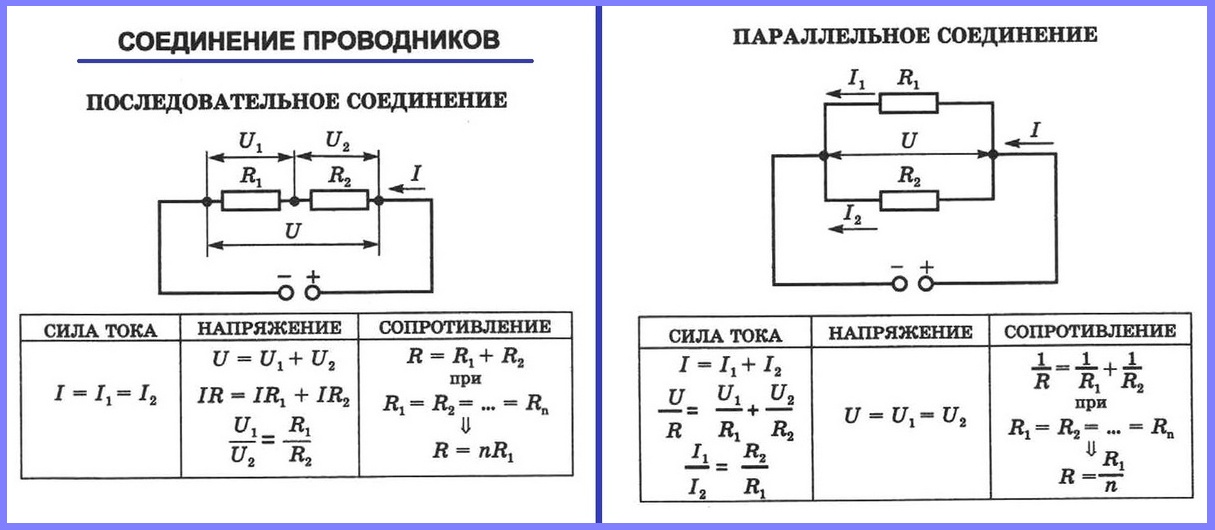 Затем он разделяется между компонентами, так что каждый из них имеет измерение 3 В. На изображении справа показана та же схема, но на этот раз с показаниями амперметра. Мы видим, что ток (измеряемый в амперах) одинаков по всей цепи.

Ток и напряжение в параллельной цепи

В параллельной цепи ток делится по разным ветвям, а затем снова объединяется при возвращении в батарею. Ток, измеренный до и после ветвей, должен быть одинаковым. Каждая ветвь цепи будет измеряться в процентах от начального тока. Сумма токов, измеренных на всех ветвях, должна быть равна общему току, измеренному в начале и конце цепи.

Например, рассмотрим параллельную цепь с двумя ответвлениями, где начальный измеренный ток равен 0,4 А. Каждая из двух ветвей имеет только одну луковицу. Ток будет проходить через обе ветви и обе лампы одинаково, поэтому ток, измеренный на обеих ветвях, будет 0,2 А, как показано на диаграмме выше.

Напряжение или разность потенциалов (p.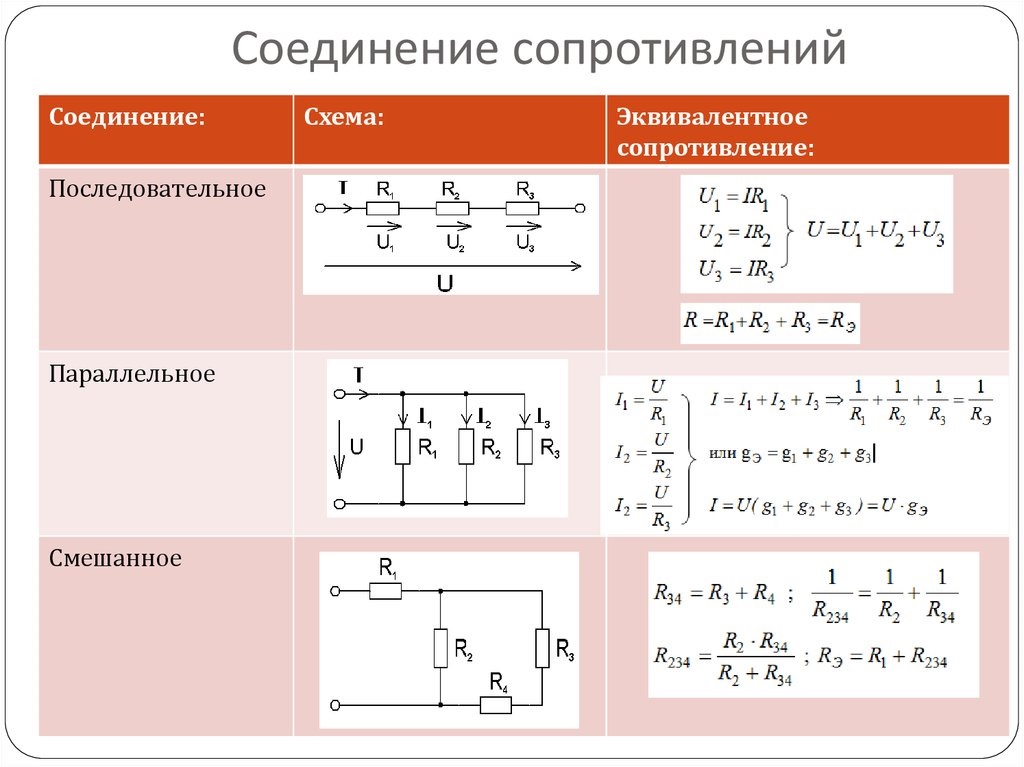 d.) между компонентами, соединенными в параллельную цепь, всегда равны. Каждая ветвь будет иметь точно такой же p.d. и это значение не меняется, в отличие от последовательной цепи. Например, на приведенной выше схеме показана параллельная цепь с двумя ответвлениями. Аккумулятор имеет р.д. 6 В, и каждая ветвь также имеет p.d. 6V

Как измерить ток

Для измерения тока, протекающего по цепи, мы используем амперметр. Амперметр подключается последовательно с компонентами и измеряет скорость, с которой заряд течет по цепи.

Как мы уже говорили, электрический заряд измеряется в кулонах (Кл). Один кулон эквивалентен примерно шести миллионам, миллионам, миллионам электронов. Это должно дать вам представление о том, насколько крошечными на самом деле являются электроны! Один кулон заряда, проходящий через объект каждую секунду, равен одному амперу.

Для расчета заряда, проходящего через провод, мы используем уравнение:

Q=I×t
где Q= заряд (в кулонах), I= ток (в амперах) и t= время (в секундах)

Вы должны быть в состоянии изменить это уравнение, чтобы найти ток, заряд или время в зависимости от значений, указанных в экзаменационном вопросе.

Чтобы найти ток, заряд и время, мы можем использовать формулу треугольника, как показано на диаграмме ниже. Значение, которое вы хотите рассчитать, закрыто, и вы смотрите на два оставшихся значения. Если они показаны один поверх другого, то вам нужно разделить верхнее число на нижнее число. Если они отображаются рядом, то вы должны умножить два значения.

Пример

Если по проводу протекает ток 12 А в течение 8 секунд, рассчитайте заряд.

Здесь мы используем наше уравнение Q=I×t и подставляем ток и время:

Q=I×t
Q=12A×8s
Q=96 кулонов

Пример

Если заряд 120C и затраченное время составило 12 секунд, рассчитайте необходимый ток. Здесь мы перестраиваем уравнение, чтобы получить I = Q  t, и подставляем значения:

Передача энергии

Как обсуждалось ранее, энергия, переданная компонентам (в джоулях), может быть рассчитана с использованием следующего уравнения: также можно рассчитать с помощью уравнения:

Пример

Рассчитайте энергию, переданную за период 45 секунд, если ток равен 30 А, а напряжение равно 5 В.

Передаваемая энергия = 30 А x 5 В x 45 с

Передаваемая энергия = 6750 Дж

Исследование взаимосвязи между током и напряжением

Зависимость между напряжением и током можно исследовать экспериментально для различных компонентов. Метод такого эксперимента описан следующим образом:

1. Соберите последовательную цепь, содержащую батарею, амперметр, тестируемый компонент, вольтметр, помещенный на компонент, и переменный резистор.
2. Запишите начальный ток и напряжение, показанные на амперметре и вольтметре.
3. Измените настройку переменного резистора, чтобы изменить ток, протекающий по цепи, и напряжение на компоненте.
4. Сделайте еще одно показание измененного тока и напряжения.
5. Повторите шаги 3 и 4 не менее пяти раз, чтобы выполнить несколько измерений тока и напряжения.
6. Дважды повторите шаги 2–5 и рассчитайте среднее напряжение для каждого тока.
7. Поменяйте местами провода так, чтобы клеммы ячейки поменялись местами, и повторите шаги 2–6.