Что означают основные условные знаки на топографических картах. Какие виды условных обозначений существуют. Как правильно читать и использовать топографические символы на картах.
Что такое условные знаки на топографических картах
Условные знаки на топографических картах — это графические символы, используемые для обозначения различных объектов местности и ее характеристик. Они являются своеобразной «азбукой» карты, позволяющей передать большой объем информации в компактном виде.
Основные функции условных знаков на топографических картах:
- Отображение расположения и характера природных и искусственных объектов
- Передача качественных и количественных характеристик местности
- Обеспечение возможности измерения по карте
- Облегчение чтения и использования карты
Без знания условных обозначений невозможно правильно «прочитать» топографическую карту и получить необходимую информацию о местности. Поэтому умение расшифровывать топографические символы является важным навыком для всех, кто использует карты.

Основные виды условных знаков
Выделяют следующие основные виды условных знаков на топографических картах:
1. Площадные знаки
Используются для обозначения объектов, занимающих на карте некоторую площадь — лесов, полей, населенных пунктов и т.д. Выражаются в виде заштрихованных или закрашенных областей.
2. Линейные знаки
Применяются для изображения объектов линейного характера — дорог, рек, границ и т.п. Отображаются в виде различных линий.
3. Внемасштабные знаки
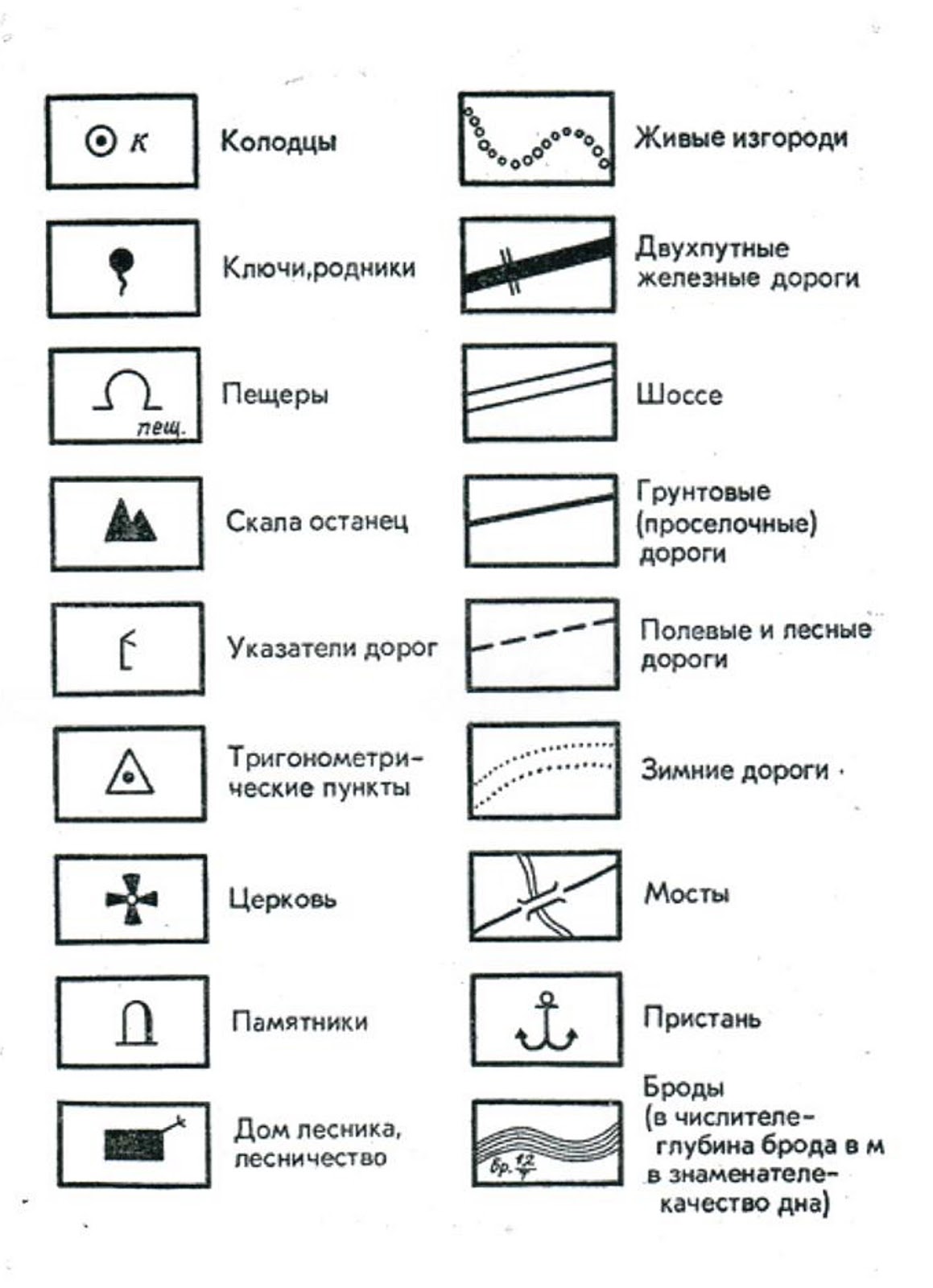
Обозначают объекты, размеры которых не выражаются в масштабе карты — отдельные здания, мосты, колодцы и др. Изображаются условными геометрическими фигурами или пиктограммами.
4. Пояснительные знаки
Дополняют другие знаки характеристиками объектов — направление течения рек, материал мостов, породы деревьев в лесу и т.д.
Как правильно читать условные знаки на картах
Для правильного чтения топографических карт необходимо:
- Изучить легенду карты с расшифровкой всех используемых условных обозначений
- Обращать внимание на цвет знаков — он несет дополнительную смысловую нагрузку
- Учитывать размер и форму знаков — они передают характеристики объектов
- Анализировать взаимное расположение знаков для понимания взаимосвязей объектов
- Использовать пояснительные подписи для уточнения информации
При правильном подходе условные обозначения позволяют получить с топографической карты максимум полезной информации о местности.
Цветовая гамма условных знаков
Цвет условных знаков на топографических картах не случаен и несет определенную смысловую нагрузку:
- Синий — водные объекты (реки, озера, моря)
- Зеленый — растительность (леса, луга, сады)
- Коричневый — рельеф местности (горизонтали, обрывы)
- Черный — большинство искусственных объектов
- Оранжевый — автомобильные дороги
- Красный — выделение важных объектов
Знание цветовой гаммы помогает быстрее ориентироваться в карте и находить нужные объекты.
Масштабные и внемасштабные условные знаки
На топографических картах используются два основных типа условных знаков:
Масштабные знаки
Отображают объекты, размеры которых могут быть выражены в масштабе карты. По таким знакам можно определить реальные размеры объектов. К ним относятся:
- Контуры лесов, полей, населенных пунктов
- Очертания крупных водоемов
- Линии дорог, каналов и т.п.
Внемасштабные знаки
Используются для объектов, размеры которых не могут быть отображены в масштабе карты. Их размер на карте не соответствует реальному. К ним относятся:

- Значки отдельных зданий
- Мосты, переправы
- Источники, колодцы
- Геодезические пункты
Важно понимать разницу между этими типами знаков при чтении карты.
Особенности изображения рельефа на топографических картах
Рельеф местности — один из важнейших элементов топографических карт. Для его изображения используются следующие способы:
Горизонтали
Основной способ изображения рельефа. Горизонтали — это линии, соединяющие точки с одинаковой высотой над уровнем моря. По расположению горизонталей можно определить характер и крутизну склонов.
Отметки высот
Абсолютные высоты характерных точек рельефа (вершин, низин, перевалов) указываются числами в метрах.
Специальные знаки
Для обозначения особых форм рельефа используются дополнительные знаки:
- Обрывы
- Овраги
- Скалы
- Ямы
Условные знаки гидрографии
Для изображения водных объектов на топографических картах применяется целый комплекс условных знаков:
Реки и ручьи
Отображаются синими линиями различной толщины в зависимости от ширины. Стрелками показывается направление течения.
Озера и водохранилища
Изображаются синей заливкой контура. Подписываются названия и глубины.
Болота
Обозначаются специальной штриховкой голубого цвета. Указывается тип болота и его проходимость.
Источники и колодцы
Отмечаются точечными знаками с указанием типа (родник, колодец и т.д.).
Знание этих обозначений критически важно при планировании маршрутов и ориентировании на местности.
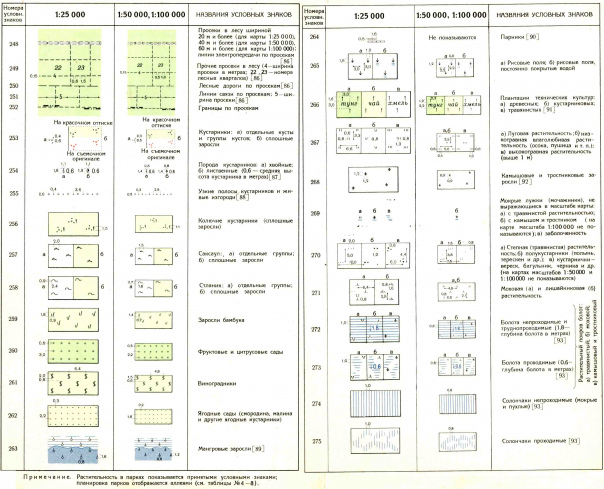
Условные знаки растительности и грунтов
Растительный покров и характер поверхности также отображаются на топографических картах с помощью условных знаков:
Леса
Обозначаются зеленой заливкой. Указывается преобладающая порода деревьев, высота и толщина стволов.
Кустарники
Отображаются мелкой зеленой штриховкой или значками.
Луга и пастбища
Обозначаются белым фоном с зелеными значками травы.
Пески и каменистые поверхности
Изображаются точечной штриховкой соответствующего цвета.
Эти обозначения позволяют оценить проходимость местности и спланировать оптимальный маршрут.
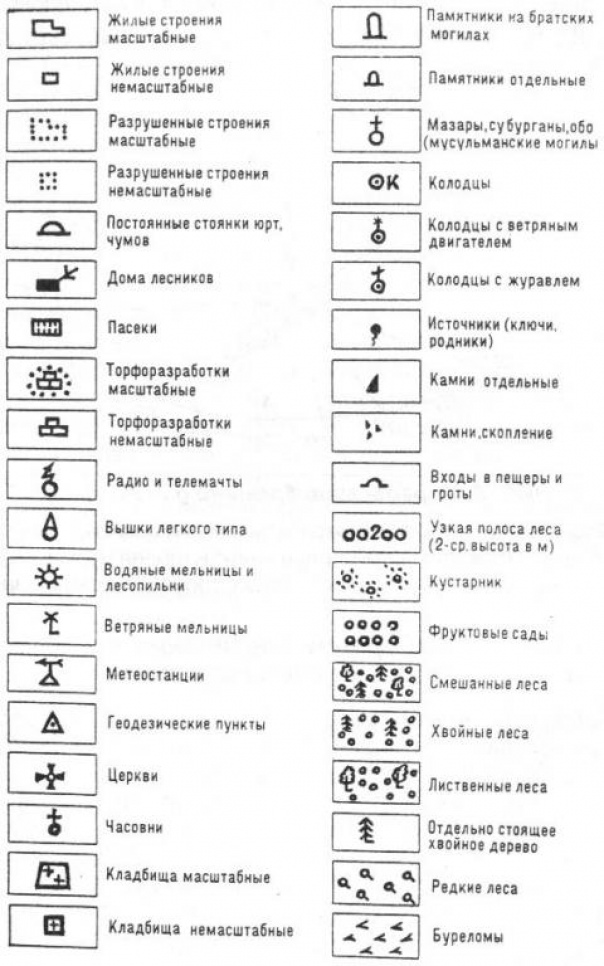
Условные знаки населенных пунктов и отдельных строений
Населенные пункты и различные постройки на топографических картах обозначаются следующим образом:
Города
Изображаются оранжевой или розовой заливкой с четкой границей. Подписывается название и число жителей.
Сельские населенные пункты
Обозначаются желтой заливкой. Указывается тип (село, деревня и т.д.) и название.
Отдельные строения
Отмечаются внемасштабными значками черного цвета. Форма значка указывает на тип здания (жилой дом, промышленный объект и т.п.).
Культовые сооружения
Обозначаются специальными значками (крест для церкви, полумесяц для мечети и т.д.).
Знание этих обозначений помогает быстро находить на карте населенные пункты и важные объекты.
| 0-9 | |
| 1-й, 1-я, 1-е | Первый,-ая, -ое, -ые (часть собственного названия) |
| 2-й, 2-я, 2-е | Второй, -ая, -ое, -ые (часть собственного названия) |
| 3-й, 3-я, 3-е, 3-й | Третий, -ья, -ье, ьи (часть собственного названия) |
| А | |
| А | Асфальт, асфальтобетон (материал покрытия дорог) |
| абразив. | Абразивный завод |
| авт. | Автомобильный завод |
авторем. |
Авторемонтный завод, авторемонтные мастерские |
| алб. | Алебастровый завод |
| алмаз. | Алмазное месторождение, алмазный прииск |
| анг. | Ангар |
| анил. | Анилино-красочный завод |
| АО | Автономная область (при собственном названии) |
| апат. | Апатитовые разработки |
| ар. | Арык (при собственном названии) |
| арт. к. | Артезианский колодец |
| арх. | Архипелаг (при собственном названии) |
асб. |
Асбестовый завод, карьер, рудник, асбестообогатительная фабрика |
| АССР | Автономная Советская Социалистическая Республика (при собственном названии) |
| астр. | Астрономический пункт |
| асф. | Асфальтовый завод |
| аэрд. | Аэродром |
| аэрп. | Аэропорт |
| Б | |
| Б | Булыжник (материал покрытия дорог) |
| б. бак. | Будка бакенщика |
б. тр. тр. |
Будка трансформаторная |
| б., бал. | Балка (при собственном названии) |
| Б., Бол. | Большой, -ая, -ое, -ие (часть собственного названия) |
| Барак | |
| бас. | Бассейн |
| бер. | Береза (порода леса) |
| Бет. | Бетонный (материал плотины) |
| биол. ст. | Биологическая станция |
| б-ка | Банка |
| бл.-п. | Блокпост (железнодорожный) |
Ближн. |
Ближний, -яя, -ее, -не (часть собственного названия) |
| бол. | Болото (при собственном названии) |
| больн. | Больница |
| Бр | Брусчатка (материал покрытия дорог) |
| бр. | Брод |
| бр. мог. | Братская могила |
| буг. | Бугор (при собственном названии) |
| булг. | Булгуннях |
| бум. | Бумажной промышленности (комбинат, фабрика) |
| бур. | Буровая вышка, скважина |
бух. |
Бухта (при собственном названии) |
| В | |
| В | Вязкий (грунт дна реки) |
| ваг. | Вагоноремонтный, вагоностроительный завод |
| вдкч. | Водокачка |
| вдп. | Водопад |
| вдпр. ст. | Водопроводная станция |
| вдхр. | Водохранилище |
| Вел.,/td> | Великий, -ая, ое, ие (часть собственного названия). |
| Верх. | Верхний, -яя, -ее, -ие (часть собственного яазвания) |
вет.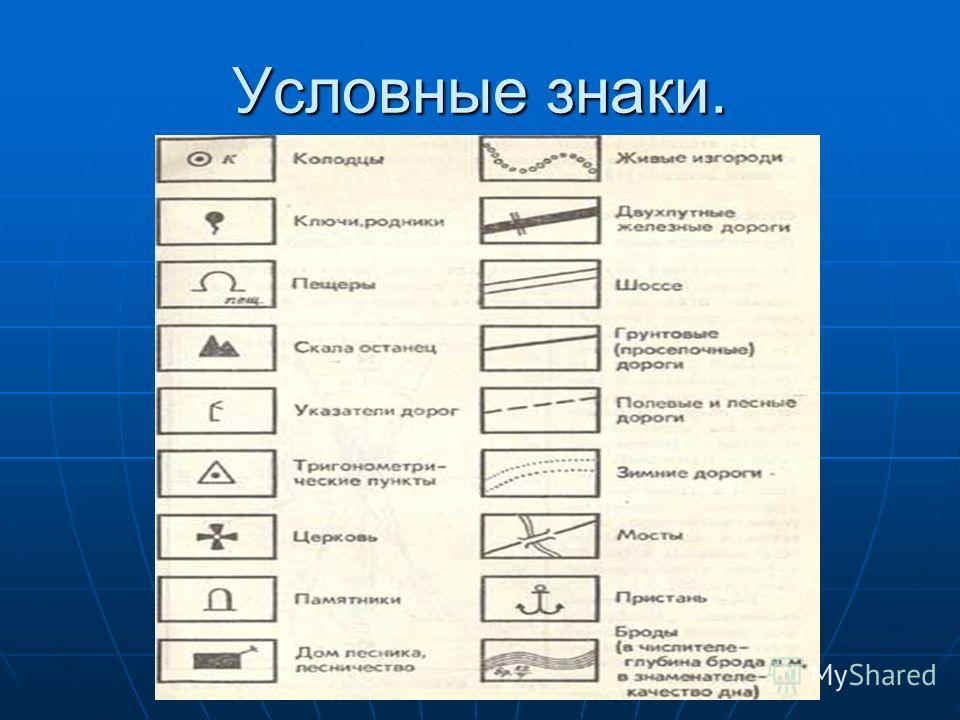 |
Ветеринарный пункт |
| вечнозел. | Вечнозеленые лиственные породы леса |
| вин. | Винодельческий, винокуренный завод |
| вкз. | Вокзал |
| влк. | Вулкан (при собственном названии) |
| вод. | Водонапорная башня |
| вод. п. | Водомерный пост |
| вод. ст. | Водная станция |
| возвыш. | Возвышенность (при собственном названии) |
| Вост. | Восточный, -ая, -ое, -ые (часть собственного названия). |
| впад. | Впадина (при собственном названии) |
| Выс. | Выселки (часть собственного названия) |
| Г | |
| Г | Гравий (материал покрытия дорог) |
| г. | Гора (при собственном названии) |
| г. дв. | Господский двор (на иностранной территории) |
| г. прох. | Горный проход (при собственном названии) |
| г.-сол. | Горько-соленая (вода в озерах, источниках, колодцах) |
гав. |
Гавань (при собственном названии) |
| газ. | Газовый завод, газовая вышка, скважина |
| газг. | Газгольдер |
| гал. | Галантерейной промышленности (завод, фабрика) |
| галеч. | Галечник (продукт добычи) |
| гар. | Гараж |
| гвозд. | Гвоздильный завод |
| гидр. скв. | Гидрологическая скважина |
| гидрол. ст. | Гидрологическая станция |
| гидромет. ст. | Гидрометеорологическая станция |
гипс.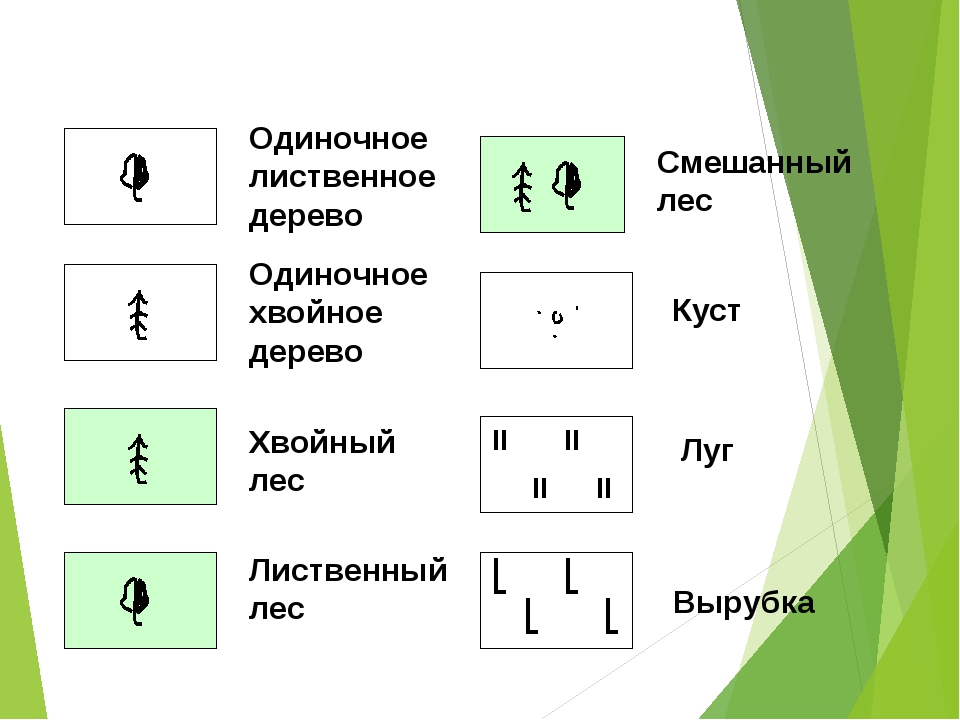 |
Гипсовый завод, карьер, рудник |
| Гл. | Главный (часть собственного названия) |
| гл. | Глубина |
| глин. | Глина (продукт добычи) |
| глиноз. | Глиноземный завод |
| гонч. | Гончарный завод |
| гор. | Горячий источник |
| гост. | Гостиница |
| гряз. | Грязевой вулкан |
| ГСМ | Горюче-смазочных материалов (склад) |
| гсп. | Госпиталь |
| ГЭС | Гидроэлектростанция |
| Д | |
| Д | Деревообрабатывающей промышленности (завод, фабрика) древ. Деревянный (материал моста, плотины) Деревянный (материал моста, плотины) |
| Д. О. | Дом отдыха |
| дв. | Дальний, -яя, -ее, -ие (часть собственного названия) . Дальн. Двор |
| дет. д. | Детский дом |
| джут. | Джутовый завод |
| дол. | Долина (при собственном названии) |
| домостр. | Домостроительный завод, комбинат |
| древ. уг. | Древесный уголь (продукт обжига) |
| дров. | Дровяной склад |
| дрож. | Дрожжевой завод |
| Е | |
ер. |
Ерик (при собственном названии) |
| Ж | |
| ЖБ | Железобетонный (материал моста, плотины) |
| жел. | Железистый источник, железообогатительная фабрика, место добычи железной руды |
| жел.-кисл. | Железнокислый источник |
| животн. | Животноводческий совхоз, животноводческая ферма |
| З | |
| заим. | Заимка (при собственном названии) |
зал.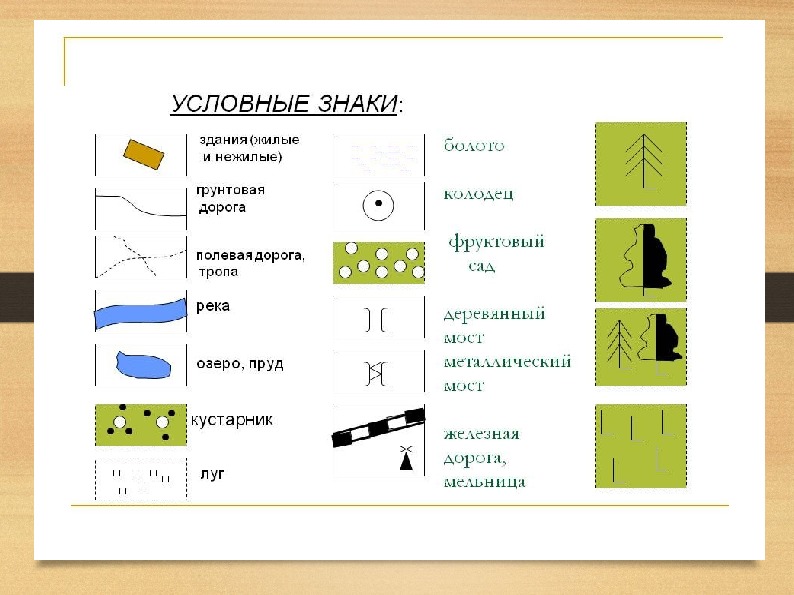 |
Залив (при собственном названии) |
| зап. | Запань |
| Зап. | Западный, -ая, -ое, -ые (часть собственного названия) |
| запов. | Заповедник (при собственном названии) |
| засып. | Засыпанный колодец |
| зат. | Затон (при собственном названии) |
| звер. | Звероводческий совхоз, питомник |
| Зем. | Земляной (материал плотины) |
| земл. | Землянка |
| зерк. | Зеркальный завод |
зерн. |
Зерноводческий совхоз |
| зим. | Зимовка, зимовье |
| зол. | Золотой (прииск, месторождение) |
| зол.-плат. | Золото-платиновые разработки |
| И | |
| игр. | Игрушечная фабрика |
| изв. | Известковый карьер, известь (продукт обжига) |
| изумр. | Изумрудные копи |
| им. | Имени (часть собственного названия) |
| инст. | Институт |
иск. волок. волок. |
Искусственного волокна (фабрика) |
| ист. | Источник |
| К | |
| К | Каменистый (грунт дна реки) |
| К | Каменный (материал моста, плотины) |
| К | Камень колотый (материал покрытия дорог) |
| К. | Колодец (при отсутствии собственного названия) |
| к. | Колодец (при собственном названии) |
| каз. | Казарма |
| кам. | Каменоломня, камень |
кам.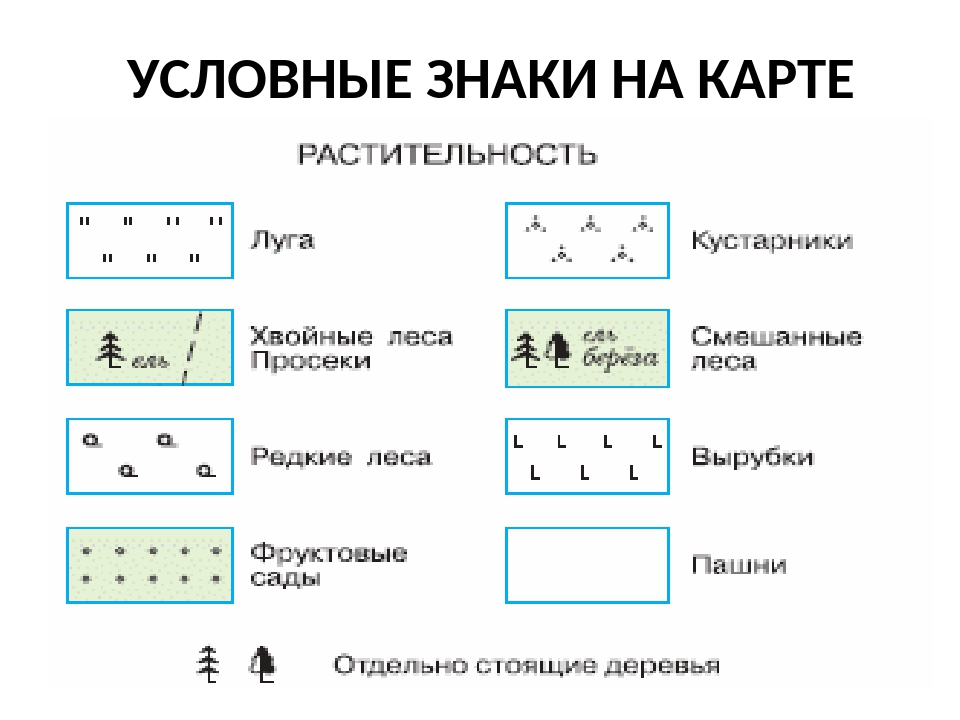 стб. стб. |
Каменный столб |
| кам.-дроб. | Камнедробильный завод |
| камв. | Камвольный комбинат, камвольная фабрика |
| кан. | Канал |
| канат. | Канатный завод |
| каол. | Каолин (продукт добычи), каолиновый обогатительный завод |
| каракул. | Каракулеводческий совхоз |
| карант. | Карантин |
| кауч. | Каучуковый завод, плантация каучуконосов |
| керам. | Керамический завод |
кин. |
Кинематографической промышленности (завод, фабрика) |
| кирп. | Кирпичный завод |
| Кл. | Клинкер (материал покрытия дорог) |
| кладб. | Кладбище |
| клх. | Колхоз |
| клх. дв. | Колхозный двор |
| кож. | Кожевенный завод |
| кокс. | Коксохимический завод |
| кол. | Колония (при собственном названии) |
| комбик. | Комбикормовый завод |
компрес. ст. ст. |
Компрессорная станция |
| кон. | Коневодческий совхоз, конный завод |
| конд. | Кондитерская фабрика |
| конопл. | Коноплеводческий совхоз |
| конс. | Консервный завод |
| котл. | Котловина (при собственном названии) |
| коч. | Кочевье |
| кош. | Кошара |
| кр. | Край (при собственном названии) |
| Кр., Красн. | Красный, -ая, -ое, -ые (часть собственного названия) |
крахм. |
Крахмало-паточный, крахмальный завод |
| креп. | Крепость |
| круп. | Крупяной завод, крупорушка |
| кум. | Кумирня |
| кур. | Курорт |
| кург. | Курган, курганы (при собственном названии) |
| Л | |
| лаг. | Лагуна |
| лакокр. | Лакокрасочный завод |
| Лев. | Левый, -ая, -ое, -ые (часть собственного названия) |
ледн. |
Ледник, ледники (при собственном названии) |
| лесн. | Лесника дом |
| леснич. | Лесничество |
| лесоуч. | Лесоучасток |
| лесп. | Лесопильный завод |
| лесхоз. | Леспромхоз |
| лет. | Летник, летовка |
| леч. | Лечебница |
| ЛЗС | Лесозащитная станция |
| лим. | Лиман (при собственном названии) |
| листв. | Лиственница (порода леса) |
льновод. |
Льноводческий совхоз |
| льнообр. | Льнообрабатывающий завод |
| М | |
| М | Металлический (материал моста) |
| м. | Мыс (при собственном названии) |
| М., Мал. | Малый, -ая, -ое, -ые (часть собственного названия) |
| мак. | Макаронная фабрика |
| марганц. | Марганцевая руда (продукт добычи) |
| маргар. | Маргариновый завод |
маслоб. |
Маслобойный завод |
| маслод. | Маслодельный завод |
| маш. | Машиностроительный завод |
| меб. | Мебельная фабрика |
| медепл. | Медеплавильный завод, комбинат |
| медн. | Медные разработки |
| мет. | Металлургический завод, завод металлоизделий |
| мет. ст. | Метеорологическая станция |
| мет.-обр. | Металлообрабатывающий завод |
| мех. | Меховая фабрика |
| МЖС | Машинно-животноводческая станция |
мин. |
Минеральный источник |
| ММС | Машинно-мелиоративная станция |
| мог. | Могила, могилы |
| мол. | Молочный завод |
| мол.-мясн. | Молочно-мясной совхоз |
| мон. | Монастырь |
| мрам. | Мрамор (продукт добычи) |
| МТМ | Машинно-тракторная мастерская |
| МТФ | Молочнотоварная ферма |
| муз. инстр. | Музыкальных инструментов (фабрика) |
мук. |
Мельница (мукомольная) |
| мыл. | Мыловаренный завод |
| мясн. | Мясной промышленности (завод, комбинат) |
| Н | |
| набл. | Наблюдательная вышка |
| наполн. | Наполняемость колодца |
| нац. окр. | Национальный округ (при собственном названии) |
| недейств. | Недействующая (железная дорога) |
| нефт. | Нефтедобыча, нефтеперегонный завод, нефтехранилище, нефтяная вышка, скважина |
Ниж. |
Нижний, -яя, -ее, -ие (часть собственного названия) |
| низм. | Низменность (при собственном названии) |
| ник. | Никелевый рудник |
| Нов. | Новый, -ая, -ое, -ые (часть собственного названия) |
Условные обозначения для векторных слоев—ArcGIS Pro
Если данные находятся в векторном слое, можно изменить способ отображения данных, отобразив с помощью символов векторный слой. ArcGIS Pro предоставляет множество методов символизации, известных как символы, для векторных слоев:
- Единый символ – отрисовывает все пространственные объекты слоя одним и тем же условным знаком.
- Уникальные значения – применяют разные условные знаки к разным группам пространственных объектов на основании одного или нескольких полей.
- Градуированные цвета – показывают количественные различия объектов благодаря спектру цветов.
- Градуированные символы – показывают количественные различия между картографируемыми объектами символами разных размеров.
- Двумерные цвета – используют градуированные цвета для отображения количественных различий в значениях объектов между двумя полями.
- Неклассифицированные цвета – показывают качественные отличия в значениях объектов с помощью цветового спектра, который не разбит на дискретные классы.
- Пропорциональные символы – представляют количественные значения в виде серии неклассифицированных пропорционально масштабированных символов.
- Плотность точек – отображение количеств как точечных символов, распределенных внутри полигонов. Этот метод доступен только для полигональных объектов.
- Диаграммы — отображает количественные значения в нескольких полях с помощью диаграмм.

- Карта интенсивности – отображает плотность точек при помощи непрерывного градиента цвета.
- Словарь – применяет символы к данным с использованием нескольких атрибутов.
Большинством векторных слоев используется один из этих типов символов. В зависимости от типа данных, вы можете выбрать из нескольких или всех типов символов. После применения эти варианты условных обозначений отобразят пространственные объекты слоя символами по умолчанию.
Также можно вернуться из режима форматирования символов на панели Символы, если щелкнуть символ на вкладке Основные символы. В режиме Форматировать символ есть две вкладки:
Если вы работаете одновременно лишь с одним символом, можете изменить любое из его свойств и даже структуру, добавив или удалив компоненты. При выборе нескольких символов можно изменять только основные свойства символов в зависимости от их типа, как показано в следующей таблице:
| Тип символа | Основные свойства |
|---|---|
Полигон |
|
Линия |
|
Точка |
|
Сетка |
Применение символов к векторным слоям
- Выберите векторный слой на панели Содержание, щелкнув его название.
На ленте появится контекстная вкладка Векторный слой.
- Для Векторный слой вкладки Отображение в группе Оформление щелкните стрелку под Символы , чтобы выбрать, как отображать слой:
Появится панель Символы, позволяющая дополнительно настроить способ классификации и обозначения слоя.

- Щелкните символ на панели Символы, чтобы открыть панель Символы в режиме Формат символа и внести изменения.
Чтобы изменить основные свойства более чем одного символа за раз, нажмите Shift+щелчок или Ctrl+щелчок, чтобы выбрать символы, затем щелкните правой кнопкой мыши и выберите Формат символов. Чтобы изменить все символы, щелкните Больше > Форматировать все символы.
- В режиме форматирования символов на панели Символы либо выберите новый стиль на палитре символов, либо измените имеющиеся символы:
Если щелкнуть символ в Галерее, он сразу же применится к выбранному классу или классам слоя.
- Вы можете изменить текущий символ или символы на вкладке Символ в Свойствах.
- Предварительный просмотр выбранных символов доступен в нижней части панели Символы в режиме форматирования символов. С помощью стрелок сбоку от предварительного просмотра можно просмотреть ряд символов одновременно, если выбрано несколько символов.
 Чтобы узнать, как предварительно просмотреть символы, см. Просмотр текущего символа.
Чтобы узнать, как предварительно просмотреть символы, см. Просмотр текущего символа. - Щелкните Применить, чтобы подтвердить изменения условных обозначений и перерисовать карту.
- Предварительный просмотр выбранных символов доступен в нижней части панели Символы в режиме форматирования символов. С помощью стрелок сбоку от предварительного просмотра можно просмотреть ряд символов одновременно, если выбрано несколько символов.
- Нажмите кнопку Назад , чтобы вернуться к панели Символы.
Подсказка:
Также можно вернуться в режим форматирования символов на панели Символы, если щелкнуть символ на панели Содержание.
Применение условного символа легенды
Для одного символа, уникальных значений, градуированных цветов и градуированных символов можно дополнительно обозначить данные векторного слоя, изменив участок легенды любого линейного или полигонального векторного слоя. Образцы символов легенды изменяют форму предварительного просмотра символа, отображаемую на панелях Символы и Содержание, а также в легендах компоновки.
Чтобы изменить форму образца легенды слоя, выполните следующие действия:
- Выберите векторный слой на панели Содержание, щелкнув его название.

На ленте появится контекстная вкладка Векторный слой.
- В группе вкладок Векторный слой на вкладке Оформление в группе Отображение щелкните кнопку Символы .
- На панели Символы на вкладке Основные символы щелкните стрелку ниспадающего списка Обновить форму условного символа легенды рядом с символом.
- Выберите форму условного символа легенды из меню.
Линия
- Горизонтальный
- Зигзаг
- Под углом
- Дуга
- Кривая
- Тропа
- Река
Полигон
- Прямоугольник
- Скругленный прямоугольник
- Окружность
- Эллипс
- Здание
- Граница
- Водоемы
- Природная область
- Квадратная область
- Шестиугольная область (плоская вершина)
- Шестиугольная область (заостренная вершина)
Связанные разделы
Отзыв по этому разделу?
Заменить символы и условные обозначения
Символ служит для графического представления определенной , он не содержит логики. За условным обозначением стоит символ, размещенный в схеме соединений, для которого назначена функция (а также логика). По этой причине при замене возникает следующая разница: при замене символа логика (т. е. функция) сохраняется. Меняется только графическое представление. если меняется напротив Условное обозначение, то функция также заменяется. В обоих случаях новый символ выбирается через выбор символов.
За условным обозначением стоит символ, размещенный в схеме соединений, для которого назначена функция (а также логика). По этой причине при замене возникает следующая разница: при замене символа логика (т. е. функция) сохраняется. Меняется только графическое представление. если меняется напротив Условное обозначение, то функция также заменяется. В обоих случаях новый символ выбирается через выбор символов.
Можно поменять только в случае, когда они подходят к функции условного . При этом EPLAN проверяет количество точек выводов меняемого символа. В выборе символа на выбор предлагаются только символы, которые имеют равное или меньшее количество выводов устройства чем заменяемый символ. Нельзя выбрать символы, которые имеют больше выводов устройства, чем есть в схеме соединений. При определении функции с переменным числом выводов устройства предлагаются все символы. При замене символа определение функции сохраняется.
Условия:
- Вы открыли проект и как минимум одну библиотеку символов.

- В Графическом редакторе открыта страница проекта.
- Выделите заменяемый символ.
- Выберите пункт всплывающего меню Свойства.
- Выберите в диалоговом окне Свойства <…> вкладку Данные символа / функции.
- Щелкните в поле Номер / Имя по […].
Откроется диалоговое окно Выбор символа. Символ выделяется в дереве или в списке и отображается в окне предварительного просмотра.
- если должны отображаться только символы одинаковой категории функции, активируйте флаг Отобразить только символы с одинаковой категорией функции.
- если вы хотите поменять только символ и определение функции должно остаться сохраненным, активируйте флаг Заменить только символ. (В этом случае будут предложены символы, которые имеют не больше выводов устройства, чем текущее определение функции.
 )
) - Выберите нужный новый символ.
- Подтвердите ввод.
Символ меняется в схеме соединений.
См. также
Диалоговое окно Выбор символа
Вкладка Данные символа / функции
Условные знаки на топографической карте местности: основные виды
uslovnye znaki kartyУсловные обозначения карте или плане являются своего рода их азбукой, по которой их можно прочесть, узнать характер местности, наличие определенных объектов, оценить ландшафт. Как правило, условные знаки на карте передают общие черты с существующими в реальности географическими объектами. Умение расшифровывать картографические обозначения незаменимо при совершении туристических походов, особенно в далекую и незнакомую местность.
Условные обозначения на картах и планах
Все обозначенные на плане объекты можно измерить в масштабах карты, чтобы представлять их реальные размеры. Таким образом, условные знаки на топографической карте – это ее «легенда», их расшифровка с целью дальнейшего ориентирования на местности.Однородные предметы обозначаются одинаковым цветом или штрихом.
Таким образом, условные знаки на топографической карте – это ее «легенда», их расшифровка с целью дальнейшего ориентирования на местности.Однородные предметы обозначаются одинаковым цветом или штрихом.
Все очертания объектов, расположенных на карте, по способу графического изображения, делятся на несколько видов:
- Площадные
- Линейные
- Точечные
Первый вид составляют объекты, занимающие большую площадь на топографической карте, которые выражены областями, заключенными в границы в соответствии с масштабами карты. Это такие объекты, как озера, леса, болота, поля.
Линейные обозначения – это очертания в виде линий, их можно заметить в масштабах карты по длине объекта. Это реки, железные или автомобильные дороги, линии электропередач, просеки, ручьи и т.п.
Точечные очертания (внемасшатабные) обозначают предметы маленьких размеров, не способные выражаться в масштабах карты. Это могут быть как отдельные города так и деревья, колодцы, трубы и прочие мелкие единичные объекты.
Условные обозначения наносятся для того, чтобы иметь как можно более полное представление об указанной местности, но это не говорит о том, что идентифицированы абсолютно все малейшие детали реального отдельно взятого района или города. План указывает лишь те объекты, которые имеют большое значение для народного хозяйства, службы МЧС, а также военнослужащих.
Виды условных знаков на картах
Условные обозначения, используемые на картах военныхЧтобы опознавать знаки карты, нужно уметь их расшифровывать. Условные символы делятся на масштабные, внемасштабные и пояснительные.
- Масштабные символы указывают на местные объекты, способные своими размерами выражаться в масштабах топографической карты. Их графическое обозначение проявляется в виде мелкого пунктира или тонкой линии. Область внутри границы заполняется условными значками, которые соответствуют наличию реальных объектов на этой местности. По масштабным знакам на карте или плане можно измерять площадь и размеры реального топографического объекта, а также его очертания.
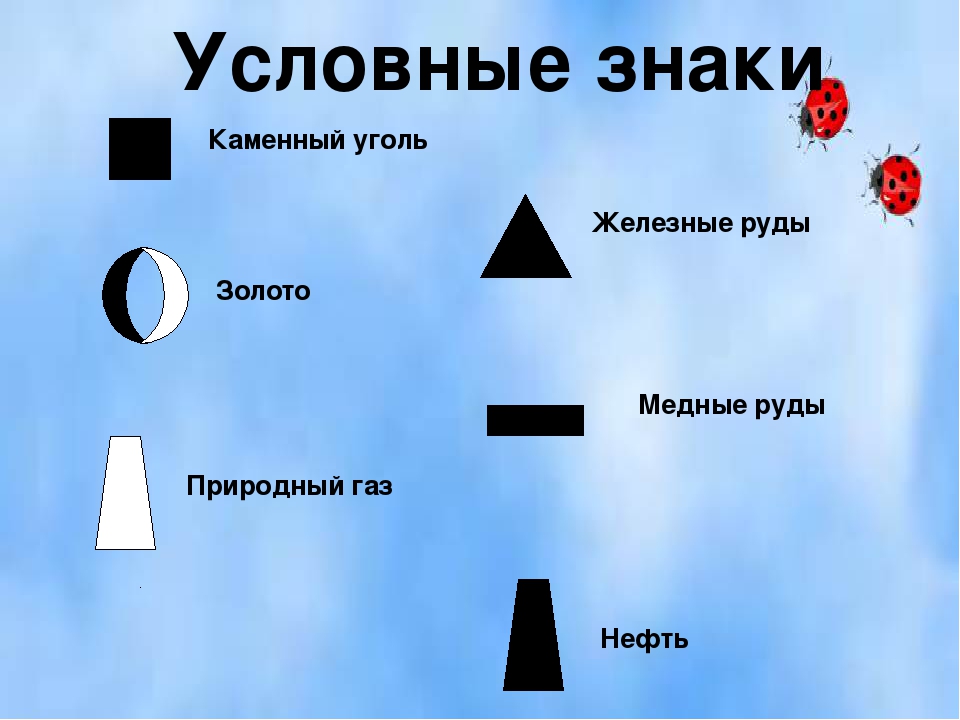
- Внемасштабные условные обозначения указывают на предметы, которые не могут быть отображены в масштабах плана, о размерах которых нельзя судить. Это какие-то отдельные строения, колодца, вышки, трубы, километровые столбы и прочее. Внемасштабные обозначения не указывают размеры объекта, расположенного на плане, поэтому сложно определить реальную ширину, длину трубы, элеватора или отдельно стоящего дерева. Целью внемасштабных обозначений является точное указание конкретного объекта, что всегда важно при ориентировании во время путешествия в незнакомой местности. Точное указание местоположения указанных объектов осуществляется главной точкой условного знака: это может быть центр или нижняя средняя точка фигуры, вершина прямого угла, нижний центр фигуры, ось условного обозначения.
- Пояснительные знаки служат для раскрытия информации масштабных и внемасштабных обозначений. Они дают дополнительную характеристику объектам, расположенным на плане или карте, например, указание стрелками направления течения реки, обозначения породы леса специальными знаками, грузоподъемности моста, характер покрытия дорог, толщина и высота деревьев в лесу.

Кроме этого, топографические планы помещают на себе другие обозначения, служащие дополнительной характеристикой для некоторых указанных объектов:
Некоторые подписи используются полностью, некоторые – в сокращенном виде. Полностью расшифровываются наименования населенных пунктов, названия рек, озер. Сокращенные подписи используются для указания более подробных характеристик некоторых объектов.
- Цифровые условные обозначения
Применяются для обозначения ширины и длины рек, автомобильных и железных дорог, линий передач, высоты точек над уровнем моря, глубины бродов и т.д. Стандартное обозначение масштаба карты всегда одинаковое и зависит лишь от размера этого масштаба (например, 1:1000, 1:100, 1:25000 и т.д.).
Для того чтобы как можно проще ориентироваться по карте или плану, условные знаки обозначаются различными цветами. Чтобы отличать даже малейшие объекты, используется более двадцати различных оттенков, от интенсивно окрашенных областей до менее ярких.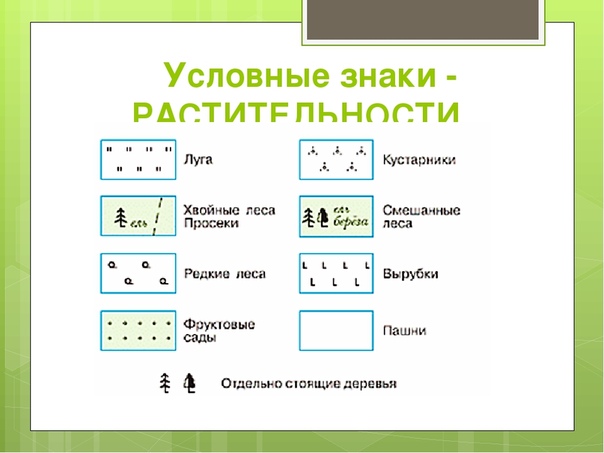 Чтобы карта легко читалась, внизу нее приводится таблица с расшифровкой цветовых обозначений. Так, обычно водные объекты обозначаются синим, голубым, бирюзовым цветом; лесные объекты зеленым; рельеф местности – коричневым; городские кварталы и малые населенные пункты – серо-оливковым; шоссе и автодороги – оранжевым; государственные границы – фиолетовым, нейтральная область – черным. Причем, кварталы с огнестойкими строениями и сооружениями обозначаются оранжевым цветом, а кварталы с неогнестойкими сооружениями и улучшенными грунтовыми дорогами – желтым цветом.
Чтобы карта легко читалась, внизу нее приводится таблица с расшифровкой цветовых обозначений. Так, обычно водные объекты обозначаются синим, голубым, бирюзовым цветом; лесные объекты зеленым; рельеф местности – коричневым; городские кварталы и малые населенные пункты – серо-оливковым; шоссе и автодороги – оранжевым; государственные границы – фиолетовым, нейтральная область – черным. Причем, кварталы с огнестойкими строениями и сооружениями обозначаются оранжевым цветом, а кварталы с неогнестойкими сооружениями и улучшенными грунтовыми дорогами – желтым цветом.
Единая система условных обозначений карт и планов местности имеет в своей основе следующие положения:
- Каждый графический знак всегда соответствует какому-либо определенному типу или явлению.
- У каждого знака существует свой четкий рисунок.
- Если карта и план отличаются масштабом, объекты не будут различаться своим обозначением. Разница будет только в их размерах.
- Рисунки реальных объектов местности обычно указывают на ассоциативную связь с ним, поэтому воспроизводят профиля или внешний вид этих объектов.
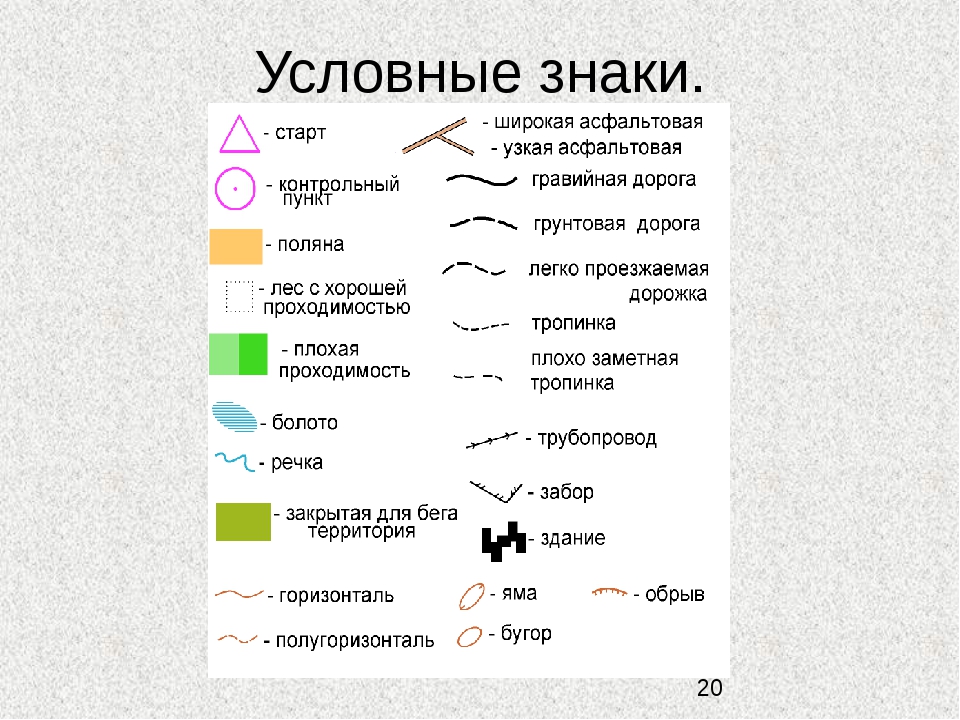
Для установления ассоциативной связи знака и объекта существует 10 типов формирования композиций:
- Знаковый способ. Геометрические, буквенные, графические значки для обозначения положения объектов.
- Линейные знаки.
- Изолинии. Этот способ указывает на явления сплошного характера, обозначаемые числами – температуры, давления, выпавших осадков, земного рельефа. Это кривые линии, соединяющие несколько точек с одинаковым числовым значением. Они делятся на изотермы, изобары, изогипсы, изогисты, изотахи.
- Способ качественного фона. С помощью этого способа выделяются качественно однородные участки по природным, политическим, социально-экономическим показателям. Таким образом, можно увидеть типы почвы, виды растительности, районы на административной карте.
Способ качественного фона в картографии
- Метод диаграммы. Отображает определенные количественные явления в конкретном месте, например, годовое изменение температуры, количество выпавших осадков и тп.
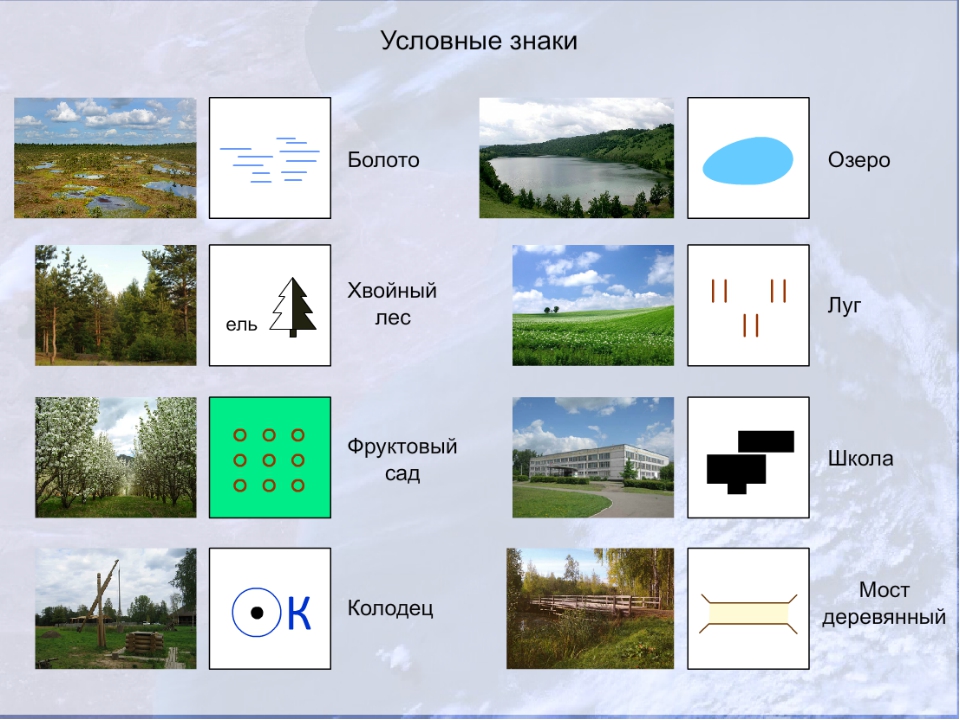
- Точечный метод. Отображает массовые явления, которые трудно отобразить по отдельности – расселение народа, размещение поголовья скота и т.д.
- Ареальный способ. Метод картографического отображения границ размещения какого-либо явления.
- Метод знаков передвижения. Показывает пространственные перемещения.
- Картодиаграммы.
- Способ картограммы.
расшифровка обозначений для стирки на ярлыках одежды
Когда мы покупаем одежду из текстиля, то непременно
рассматриваем её изнанку, чтобы убедиться в качестве обработки швов и крепления
фурнитуры. Мы обязательно увидим вшитую в один из швов этикетку со значками. Символы
на ней означают допустимые виды ухода за вещью с учётом свойств ткани, из
которой она сшита.
Мы обязательно увидим вшитую в один из швов этикетку со значками. Символы
на ней означают допустимые виды ухода за вещью с учётом свойств ткани, из
которой она сшита.
Что значат символы
Основная символика для информирования потребителей о правилах ухода за конкретным изделием разработана международными организациями и зафиксирована в стандартах международной системы ISO. Обозначения в виде пиктограмм наносятся на ярлыки, которые надёжно крепятся к одежде.
На ярлыке в форме пиктограмм размещена сложная инструкция по уходу за одеждой. Понимая значения символов, вы всё сделаете правильно.
Символы размещаются в строго установленном порядке, при этом
возможно применение более одного знака для процесса, если нужно уточнить
условия ухода за изделием. Кроме символов могут быть и надписи, поясняющие и
уточняющие тонкости чистки.
Есть пять основных обозначений для основных способов по уходу за предметами из вашего гардероба:
– эта картинка используется, чтобы информировать владельца о допустимых параметрах стирки изделия. Если внутри этого знака проставлено число – это температура воды, при которой следует стирать вещь.
– этот знак обозначает процесс сушки (и отжима). В этом квадрате дополнительные символические обозначения устанавливают, как можно отжимать и просушивать изделие.
– о смысле этого символа легко догадаться. Дополнительные точки и штрихи на этом «утюжке» задают температурный режим глажки.
–
этот значок информирует потребителей
о том, допустимо ли применять отбеливание, а дополнения к нему конкретизируют
условия процедуры.
– здесь показывается, разрешена ли профессиональная химчистка. А буквы и дополнительные штрихи на картинке адресованы её работникам. Они указывают, рекомендована сухая или влажная чистка и какие химические вещества допустимо применять.
В системе основных условных обозначений применяются также значки:
- горизонтальное подчёркивание символа говорит о том, что рекомендуется смягчить режим обработки;
- двойное подчёркивание – обработка должна быть деликатной, щадящей;
- символ, перечёркнутый крест-накрест, означает запрет такого ухода за изделием.
Все дополнения к приведённым выше картинкам показаны в таблице с вариантами значений символов и их расшифровкой.
Производители одежды из разных государств дополняют их
своими пиктограммами. Делается это в интересах заботливых хозяек, желающих в
точности соблюсти рекомендации по уходу за одеждой.
Делается это в интересах заботливых хозяек, желающих в
точности соблюсти рекомендации по уходу за одеждой.
Расшифровка обозначений на ярлыках одежды
Чтобы удобнее было пользоваться информацией, приведённой ниже, использовано общепринятое обозначение температуры (t°), температура везде указана по Цельсию. Некоторые значки применяются в национальных системах маркировки (США, Китай).
Стирка
Некоторые характеристики разных режимов стирки.
Обычный режим зависит от нагрева воды.
Цель мягкого режим (или щадящего) в том, чтобы снизить вероятность повреждения вещей, осторожно прополоскать и отжать их в машине с центрифугой.
При очень мягком режиме используется много воды, вещи обрабатываются бережно. Отжим ещё слабее, чем при мягкой обработке, или вещи не отжимают вовсе. Выжимать руками нельзя.
Разрешена ручная и машинная стирка (все этапы, в том числе и замачивание).
Стирка в щадящем (мягком) режиме.
Деликатная стирка (очень мягкий режим).
Стирка запрещена.
Разрешается машинная стирка. Внутри значка должны быть указаны градусы – они задают режим.
Max t°= 95°, обычный режим. Допускается кипячение. (Хлопок, лён, белые или цветные вещи, стойкие к кипячению.)
Max t°= 95°, мягкий режим.
Max, t°= 70°, обычный режим. (Хлопок, лён, белые или не линяющие цветные вещи.)
Max t°= 60°, обычная обработка. (Хлопок, полиэстер – тонкое бельё, например.)
Max t°= 60°, мягкий режим.
Max t°= 50°, обычная обработка.
Max t°= 50°, мягкий режим.
Max t°= 40°, обычная обработка, нейтральные моющие средства, тёплая вода. (Цветные, пёстрые вещи из хлопка, вискозы, синтетиков.)
Max t°= 40°, мягкий режим.
Max t°= 40°,очень мягкий режим.
Max t°= 30°, обычная обработка, деликатный стиральный порошок, прохладная вода. (Шерсть, шёлк.)
Max t°= 30°, мягкий режим.
Max t°= 30°,очень мягкий режим.
Стирать исключительно руками, в чуть тёплой воде, тереть вещи и отжимать их с силой нельзя. Max t°= 30°—40°.
Отбеливание
– любым окисляющим реагентом.
– только кислородосодержащими/нехлорными реагентами.
Отбеливание запрещено.
Сушка (отжим)
Можно сушить, отжимать.
Рекомендовано сушить (отжимать) в электросушильной и стиральной машинах.
Сушить (отжимать) запрещено. (Значок применяется только вместе со значком «стирка запрещена».)
– сушка барабанная
Рекомендовано – в центрифуге при высокой температуре.
Рекомендуется режим с max t°= 80° на выходе.
Мягкий режим сушки, t° средняя.
Max t°= 60° на выходе.
Max t° на выходе – 60°. Мягкий режим.
Max t° на выходе – 60°. Очень мягкий режим.
Сушка и отжим при нормальной t°.
Нельзя использовать барабанную сушку.
– сушка естественная
Выстиранные и отжатые вещи – на веревке или плечиках.
Выстиранные НЕ отжатые вещи – на веревке или плечиках.
Выстиранные и отжатые вещи – на плоскости.
– сушка естественная в тени
Выстиранные и отжатые вещи – в тени, на веревке или плечиках.
Выстиранные НЕ отжатые вещи – в тени, на веревке или плечиках.
Выстиранные и отжатые вещи сушить в тени, разложив на плоскости.
– перекручивание
Изделие можно выжимать вручную.
Не перекручивать: ручной отжим (выкручивание) запрещён.
Глажение и прессование
Max t° подошвы утюга = 200° (метка, как у терморегулятора утюга). Можно отпаривать.
Max t° подошвы утюга = 150°.
Max t° подошвы утюга = 110°, без пара. Отпаривание может безнадёжно испортить вещь.
Не гладить.
Не отпаривать.
Профессиональный уход/чистка
– сухая чистка
Сухая чистка (химчистка).
Химчистка запрещена
Химчистка с органическими растворителями.
Чистка в тетрахлорэтилене и любых растворителях, разрешённых для F. Обычный режим.
Чистка в тетрахлорэтилене и любых растворителях, разрешённых для F. Мягкий режим.
Чистка в углеводородах (t° дистилляции в пределах 150°÷210°, t° возгорания – в пределах 38°÷70°). Обычный режим.
Чистка в углеводородах (t° дистилляции в пределах 150°÷210°, t° возгорания – в пределах 38°÷70°). Мягкий режим.
– сокращённый цикл (значок можно размещать со значком-буквой).
– сниженная влажность (значок можно размещать со значком-буквой).
– низкая температура (значок можно размещать со значком-буквой)
– без финишной обработки паром (значок можно размещать со значком-буквой).
– аквачистка
Нормальный режим
Мягкий режим.
Очень мягкий режим (деликатная чистка).
Аквачистка запрещена.
Дополнительные символы:
Влажность повышена, дождь
Фронтальная загрузка в стиральную машину
Вертикальная загрузка в стиральную машину
Сушилка
Средство для стирки / чистки
Бельевой контейнер
Нагруженный бельевой контейнер
Утюг
Брюки
Футболка
| Стирка разрешена | |
| Стирка запрещена | |
| Только ручная стирка при температуре максимум 30, не тереть, не отжимать | |
| Ручная или машинная стирка при температуре не выше указанной | |
| Если корытце подчёркнуто одной или двумя чертами, это обозначает, что нужно соблюдать особые меры предосторожности. Ручная или машинная стирка. Внимательно придерживаться указанной температуры, не подвергать сильной механической обработке, полоскать, переходя постепенно к холодной воде, при отжиме в стиральной машине ставить медленный режим вращения центрифуги | |
| Очень деликатная обработка в большом количестве воды, минимальная механическая обработка, быстрое полоскание при низких оборотах | |
| Стирка с кипячением | |
| Можно отбеливать | |
| Не отбеливать, нельзя использовать хлоросодержащие моющие средства и стиральные порошки с отбеливателями | |
| Разрешена стирка с отбеливателями, содержащими хлор; использовать только холодную воду, следить за полным растворением порошка | |
| При стирке не использовать средства, содержащие отбеливатели (хлор) | |
| Разрешено гладить | |
| Гладить запрещено | |
| Разрешено гладить при максимальной температуре 100; допустимо для шерсти и смешанных волокон с полиэстером и вискозой, использовать влажную ткань | |
| Разрешено гладить при ;максимальной температуре 150; допустимо для шерсти и смешанных волокон с полиэстером и вискозой, использовать влажную ткань | |
| Разрешено гладить при максимальной температуре 200; допустимо для льна и хлопка, можно слегка увлажнять изделие | |
| Только сухая чистка | |
| Не подвергать химчистке | |
| Сухая чистка с любым растворителем | |
| Специальное обозначение для химической чистки: чистка только с углеводородом, хлорным этиленом и монофтортрихлорметаном | |
| Специальное обозначение для химической чистки: чистка с использованием только углеводорода и трифтортрихлорметана | |
|
Специальное обозначение для химической чистки: чистка только с углеводородом, хлорным этиленом и монофтортрихлорметаном при ограниченном добавлении воды, контроле над механическим воздействием и температуры сушки |
|
| Специальное обозначение для химической чистки: чистка только с углеводородом и трифтортрихлорметаном при ограниченном добавлении воды, контроле над механическим воздействием и температуры сушки | |
| Разрешено отжимать в стиральной машине и высушивать электросушилкой | |
|
Не разрешено отжимать в стиральной машине и высушивать в электросушилке |
|
| Высушивать при теплой температуре | |
| Высушивать при горячей температуре | |
| После отжима разрешена вертикальная сушка | |
| Сушить без отжима | |
| Сушить на вешалке | |
| Сушить на горизонтальной поверхности |
Библиотека условных обозначений для QGIS
Описание библиотеки условных обозначений для QGIS, установка, получение и примеры
Редактор стилей QGIS позволяет создавать красивые и сложные условные обозначения для ваших проектов. Но этот процесс может оказаться трудоёмок для сложных условных обозначений, поэтому мы решили помочь всем пользователям QGIS и создали набор условных знаков, на основе общепринятых в России условных обозначениях для топографических карт.
[править] Общее описание
Библиотека символов распространяется под лицензией CC-BY (более подробная информация в license.txt), что делает его пригодным для коммерческого использования и создания производных произведений.
Набор условных знаков представлен в двух вариантах:
- все условные знаки представлены одним файлом (all.xml)
- условные знаки разбиты на несколько тематических категорий, каждой из которых соответствует свой .xml файл (в директории by-type/):
- границы (boundary.xml)
- грунты (ground.xml)
- водные объекты (hydro.xml)
- промышленные, сельскохозяйственные и социально-культурные объекты (industrial.xml)
- железные дороги (railroad.xml)
- рельеф (relief.xml)
- дороги (road.xml)
- растительность (vegetation.xml)
Название каждого условного знака оканчивается одним или двумя числами и буквой «к», которые обозначают масштаб карты для которой данный условных знак подходит больше всего. Например, знак «виноградники_25к-50к» подойдёт для карт масштабов 1:25 000 — 1:50 000. Если название условного знака заканчивается на «_эк», значит он предназначен для более наглядного отображения на экране монитора.
[править] Инструкция по установке
Используйте QGIS 1.7 или более позднюю версию.
- Скачайте архив с условными знаками.
- Скопируйте содержимое директории svg/ в директорию со значками qgis (Linux: /usr/share/qgis/svg; Windows: OSGeo4W\apps\qgis\svg), или добавьте путь к ней в настройках (Установки->Параметры, вкладка Отрисовка -> «Значки в формате SVG»)
- Вызовите менеджер стилей: Настройки->Менеджер стилей.
- Нажмите кнопку «Импорт».
- Укажите путь к файлу «all.xml» из данного архива либо нужный из директории by-type/
- Выберете нужные символы или выделите все и нажмите кнопку «Импорт».
Обратите внимание, что в импортированных символах не должно быть красных кружков.
Если вы видите красные кружки в символах (или не видите некоторых символов, хотя их имена присутствуют в менеджере стилей), это означает что пути к SVG иконкам, использованным в данных символах импортированы неправильно. Это можно исправить, отредактировав файл «symbology-ng-style.xml», НАХОДЯЩИЙСЯ В ПАПКЕ QGIS ВАШЕГО ПОЛЬЗОВАТЕЛЯ (Linux: ~/.qgis; Windows: users\имя пользователя\.qgis): скопируйте нужные пути из файла «all.xml» ИЗ ДАННОГО АРХИВА. Например, если нужно исправить условный знак «Виноградники (точечный)_100к», находим соответствующее описание в файле all.xml. Оно будет начинаться с:
<symbol outputUnit="MM" alpha="1" type="marker" name="Виноградники (точечный)_100к">
Чуть ниже вы увидите строчку:
<prop k="name" v="/vegetation_grounds/vinary_25k.svg"/>
Скопируйте её и замените соответствующую строчку в файле «symbology-ng-style.xml»
[править] Галерея условных знаков
Линейные условные знаки Заливки Точечные условные знаки Пример карты, оформленной условными знаками из набора[править] Ссылки по теме
Создание комплексных условных знаков в QGIS: «шлюз»
Полный список логических символов
В философии и математике логика играет ключевую роль в формализации правильных дедуктивных выводов и других форм рассуждений. Ниже приводится исчерпывающий список наиболее известных символов в логике, включающий символы из логики высказываний, логики предикатов, булевой логики и модальной логики.
Для удобства чтения эти символы разбиты на таблиц по их функциям. Другие исчерпывающие списки символов, сгруппированные по теме и типу, также можно найти на соответствующих страницах ниже (или на панели навигации).
Предпочитаете версию в формате PDF?
Получите общее резюме математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX.
Константы
В логике константы часто используются для обозначения определенных объектов в логической системе. В следующей таблице представлены наиболее известные из них, а также их соответствующие примеры и значения.
Переменные
Подобно другим областям математики, переменных используются в качестве символов-заполнителей для различных логических объектов.В следующей таблице приведены наиболее известные из них, а также их соответствующие примеры и значения.
| Название символа | Пояснение | Пример |
|---|---|---|
| $ x, y, w, z $ | Переменные количественного определения | $ x_1 + x_2 = y $ |
| $ \ mathbf {x}, \ mathbf {y}, \ mathbf {w}, \ mathbf {z} $ | Метапеременные для переменных количественного определения | Для всех переменных $ \ mathbf {x} _1 $ и $ \ mathbf {x} _2 $, ‘$ \ mathbf {x} _1 = \ mathbf {x} _2 $’ — формула. |
| $ f, g, h $ | Функциональные символы | $ h \ left (f_1 (x), g (x, y) \ right) $ |
| $ \ mathbf {s}, \ mathbf {t} $ | Метапеременные для терминов | Для всех терминов $ \ mathbf {t} _1 $ и $ \ mathbf {t} _2 $, ‘$ f (\ mathbf {t} _1, \ mathbf { t} _2) $ ‘- это термин. |
| $ P, Q, R $ | Пропозициональные / Предикатные символы | $ P (x, a) \ land Q_1 (z) $ |
| $ \ alpha, \ beta, \ gamma , \ phi, \ psi $ | Метапеременные для формул | Для всех формул $ \ alpha $ и $ \ beta $, $ \ alpha \ land \ beta \ Equiv \ beta \ land \ alpha $. |
| $ \ Sigma, \ Phi, \ Psi $ | Метапеременные для набора из предложений | Если $ \ Sigma $ несовместим, то $ \ Sigma \ cup \ Phi $ тоже. |
| $ \ mathcal {L} $ | Метапеременная для формальных языков | Если $ \ mathcal {L} $ — язык с равенством и константой $ a $, то ‘$ a = a $’ будет формула в $ \ mathcal {L} $. |
Операторы
Операторы — это символы, используемые для обозначения математических операций, которые служат для преобразования одного или нескольких входов в аналогичный выход.В логике эти операторы включают логические связки из пропозициональной / модальной логики, кванторы из логики предикатов, а также другие операторы, связанные с синтаксической заменой и семантической оценкой.
Унарные логические связки
| Имя символа | Пояснение | Пример |
|---|---|---|
| $ \ lnot P $, $ \ sim \! \! P $, $ \ overline {P} $ | Отрицание $ P $ (не $ P $) | $ \ lnot \ lnot P \ Equiv P $ |
| $ \ Diamond P $ | Возможно $ P $ | Если $ \ Diamond P $ , то $ \ Diamond \ Diamond P $. |
| $ \ Box P $ | Обязательно $ P $ | Если $ \ Box P $, то $ \ neg \ Diamond \ neg P $. |
Двоичные логические связки
| Имя символа | Пояснение | Пример |
|---|---|---|
| $ P \ land Q $ | Соединение (P $ и Q $) | $ P \ land P \ эквив P $ |
| $ P \ lor Q $ | Дизъюнкция ($ P $ или $ Q $) | $ \ neg (P \ lor Q) \ эквив $ $ \ neg P \ land \ neg Q $ |
| $ P \ veebar Q $, $ P \ oplus Q $ | Исключительная дизъюнкция ($ P $ xor $ Q $) | $ P \ oplus Q \ Equiv $ $ (P \ lor Q) \ land \ neg (P \ land Q) $ |
| $ P \ uparrow Q $ | Отрицание конъюнкции ($ P $ nand $ Q $) | $ P \ uparrow Q \ Equiv \ neg (P \ land Q) $ |
| $ P \ downarrow Q $ | Отрицание дизъюнкции ($ P $ или $ Q $) | $ P \ downarrow Q \ Equiv \\ (\ neg P \ land \ neg Q ) $ |
| $ P \ to Q $ | Условное (Если $ P $, то $ Q $) | Для всех $ P $, $ P \ to P $ является тавтологией. |
| $ P \ not \ to Q $ | Безусловный (Not ‘if $ P $, then $ Q $’) | $ P \ not \ to Q \ Equiv P \ land \ neg Q $ |
| $ P \ leftarrow Q $ | Условное преобразование (Если $ Q $, то $ P $) | $ Q \ leftarrow (P \ land Q) $ |
| $ P \ not \ leftarrow Q $ | Converse безусловный (Not ‘if $ Q $, then $ P $’) | $ (P \ to Q) \ land \\ (P \ not \ leftarrow Q) $ |
| $ P \ leftrightarrow Q $ | Biconditional ($ P $ тогда и только тогда, когда $ Q $) | $ P \ leftrightarrow Q \ Equiv $ $ (P \ to Q) \ land (P \ leftarrow Q) $ |
| $ P \ not \ leftrightarrow Q $ | Без условных обозначений (Не ‘$ P $ тогда и только тогда, когда $ Q $’) | Если $ P \ not \ to Q $, то $ P \ not \ leftrightarrow Q $.2) | $
| $ \ существует! \ mathbf {x} $ | Количественная оценка уникальности (Существует уникальный $ \ mathbf {x} $) | $ \ exists! \, q, r \ in \ mathbb {Z} \, $ $ ( n = dq + r \, \ land $ $ 0 \ le | r | |
| $ \ mathrm {N} \ mathbf {x} $, $ \ nexists \ mathbf {x} $ | Количественная оценка отсутствия ($ \ mathbf {x} $ не существует) | $ \ mathrm {N} x P (x) \ Equiv \\ \ forall x \, \ neg P (x) $ |
| $ \ exists_n \ mathbf {x} $ | Числовое определение (Есть ровно $ n $ $ \ mathbf {x} $) | $ \ exists_3 x \ in \ mathbb {Z} \, (5 < x <9) $ |
| $ \ exists _ {\ ge n} \ mathbf {x} $ | Числовое определение (Есть не менее $ n $ $ \ mathbf {x} $) | $ \ существует _ {\ ge 2} x \, Q (x) \ эквив $ $ \ существует x \ существует y \, (Q (x) \ land $ $ Q (y) \ land x \ ne y) $ |
| $ \ exists _ {\ le n} \ mathbf {x} $ | Численное определение 9 0004 (Максимум $ n $ $ \ mathbf {x} $) | $ \ exists _ {\ le 10} x \, (x ^ 2 \ le 100) \ Equiv $ $ \ neg \ left (\ существует _ {\ ge 11} x \, (x ^ 2 \ le 100) \ right) $ |
Операторы на основе подстановки
| Имя символа | Пояснение | Пример |
|---|---|---|
| $ \ mathbf {t} [\ mathbf {x} / \ mathbf {t} _0] $ | Замещенный термин (термин $ \ mathbf {t} $ с вхождениями $ \ mathbf {x} $ заменен на $ \ mathbf {t} _0 $) | $ (x ^ 2 + y) [x / 1] [y / 5] = $ 1 ^ 2 + 5 $ |
| $ \ mathbf {\ alpha} [\ mathbf {x} / \ mathbf {t_0}] $ | Замещенная формула (формула $ \ mathbf {\ alpha} $ с свободными вхождениями $ \ mathbf {x} $ заменена термином $ \ mathbf {t_0} $) | $ (\ forall x (x = y)) [x / a] = $ $ \ forall x (x = y) $ |
Операторы на основе оценки
| Название символа | Пояснение ation | Пример |
|---|---|---|
| $ \ mathbf {t} ^ {\ sigma} $ | Референт термина $ \ mathbf {t} $ при оценке $ \ sigma $ | $ \ left (f ( a, b) \ right) ^ {\ sigma} = $ $ \ mathrm {отец} (\ mathrm {Al}, \ mathrm {Bob}) $ |
| $ \ alpha ^ {\ sigma} $ | Истинное значение формулы $ \ alpha $ при оценке $ \ sigma $ | Если $ P ^ {\ sigma} $ — симметричное отношение, то $ \ left (P (x, y) \ right) ^ {\ sigma } = \\ \ left (P (y, x) \ right) ^ {\ sigma} $ |
| $ \ sigma (\ mathbf {x} / u) $ | Переоценка $ \ sigma $, где переменная $ \ mathbf {x} $ переоценивается как $ u $ | $ (\ forall x \, \ alpha) ^ {\ sigma} = \ top $ тогда и только тогда, когда для всех $ u $ во вселенной дискурса $ U $, $ \ alpha ^ {\ sigma (x / u)} = \ top $. |
Реляционные символы
В логике реляционных символа играют ключевую роль в превращении одной или нескольких математических сущностей в формулы и предложения и могут встречаться как внутри логической системы, так и вне ее (как металогические символы). В следующей таблице приведены наиболее известные из этих символов, а также их соответствующие значения и примеры.
| Имя символа | Пояснение | Пример |
|---|---|---|
| $ \ mathbf {t} _1 = \ mathbf {t} _2 $ | Идентификационный символ в логической системе с равенством | ‘$ \ neg \ left (1 = s (1) \ right) $ ‘- формула на языке арифметики первого порядка. |
| $ \ alpha \! \ подразумевает \! \ beta $ | Предложение $ \ alpha $ подразумевает предложения $ \ beta $ | $ \ forall x \, (x \ ge 1) \! \ подразумевает 1 \ ge 1 $ |
| $ \ alpha \! \ impliedby \! \ beta $ | Предложение $ \ alpha $ — , подразумеваемое предложением $ \ beta $ | $ 5 \ mid x \! \ impliedby \! 5 \ mid 7x $ |
| $ \ alpha \ Equiv \ beta $, $ \ alpha \ Leftrightarrow \ beta $, $ \ alpha \! \ iff \! \ beta $ | Предложение $ \ alpha $ и $ \ beta $ логически эквивалентно | $ \ neg (P \ to Q) \ Equiv \\ P \ land \ neg Q $ |
| $ \ sigma \ models \ alpha $ | Оценка $ \ sigma $ удовлетворяет формуле $ \ alpha $ | Если $ \ phi ^ {\ sigma} = \ top $, то $ \ sigma \ models \ phi $. |
| $ \ Phi \ models \ phi $ | Набор предложений $ \ Phi $ влечет за собой предложения $ \ phi $ ($ \ phi $ является логическим следствием $ \ Phi $) | Если $ \ Phi \ models \ phi $, затем $ \ Phi \ cup \ Psi \ models \ phi $. |
| $ \ Phi \ nvDash \ phi $ | Набор предложений $ \ Phi $ не влечет за собой предложений $ \ phi $ | $ \ {P \ to Q, Q \ to R \} \ nvDash R $ |
| $ \ models \ phi $ | Предложение $ \ phi $ — тавтология | $ \ models \ forall x \, (x = x) $ |
| $ \ Phi \ vdash \ phi $ | Набор предложений $ \ Phi $ доказывает предложения $ \ phi $ | $ \ forall x \, P (x, a) \ vdash \\ P (a, a) $ |
| $ \ Phi \ nvdash \ phi $ | Набор предложений $ \ Phi $ не доказывает предложение $ \ phi $ | $ \ exists x \, R (x) \ nvdash R (a) $ |
| $ \ vdash \ phi $ | Предложение $ \ phi $ является теоремой | $ \ vdash \ forall x \ forall y \, (x = y \ to $ $ y = x) $ |
| $ \ phi \ потому что \ Phi $ | $ \ phi $, потому что $ \ Phi $ | $ A = 95 ^ {\ circ} \ потому что $ $ A + B = 180 ^ {\ circ}, $ $ B = 85 ^ {\ circ} $ |
| $ \ Phi \ следовательно \ phi $ | $ \ Phi $, следовательно $ \ phi $ | $ P \ lor Q, \ neg P \\ \ поэтому Q $ |
Для основного списка символов см. математические символы.Список символов, разделенных на категории тип и предмет , см. На соответствующих страницах ниже.
Предпочитаете версию в формате PDF?
Получите общее резюме математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX.
Дополнительные ресурсы
Символы условного форматирования — Xelplus
Как использовать собственные символы в Excel и их условное форматирование
Вы хотите использовать символы в отчетах, чтобы привлечь внимание к определенным задачам или результатам? Вы считаете, что значки, доступные в условном форматировании Excel, ограничены? Хотите что-то другое, чтобы ваш отчет выделялся среди других?
Вы можете использовать свои собственные символы в Excel и условно их форматировать. Вам не нужно выбирать между наборами значков, доступными в рамках условного форматирования, вместо этого выберите практически любой символ, который вам нравится, и условно отформатируйте его.
Планирование проекта — внимание к просроченным задачам
В этом примере я покажу вам, как можно использовать символы и цветовое кодирование типа светофора, чтобы привлечь внимание к задачам, срок выполнения которых истек. Таким образом вы можете визуально указать, какие задачи выполнены, а какие еще не решены.Я использую комбинацию символов и функцию условного форматирования Excel для достижения следующего:
Настройка данных
В примере показан временной план проекта с задачами, датой начала и датой окончания. Дата окончания рассчитывается функцией РАБДЕНЬ () в соответствии с указанным количеством рабочих дней. (Ссылка на использование функции РАБДЕНЬ () находится здесь).
Вместо того, чтобы просто видеть дату окончания каждой задачи, использование символов может помочь вам визуально увидеть их индивидуальный статус.Так как сегодняшняя дата будет использоваться в качестве справочной для просроченных задач, используйте функцию СЕГОДНЯ () , чтобы автоматически вставлять сегодняшнюю дату каждый раз при открытии книги.
Ячейка A1 = Сегодня ()
Добавьте столбец, который будет служить индикатором того, что вы выполнили задачу. Обозначьте это как «Готово» (Y), где вы можете ввести «Y», если задача была завершена.
Как использовать символы в Excel
Хотя вы можете использовать символы, доступные в наборах значков условного форматирования, вы также можете использовать свои собственные персонализированные значки.
Чтобы вставить символ по вашему выбору:
- На вкладке Insert перейдите к Symbols .
- Выберите шрифт. Для Arial доступно множество символов, но в этом примере возьмем символы из Wingdings 2 .
- Щелкните символ, который хотите использовать, затем щелкните Вставить . Обратите внимание, что он вставляет этот значок в выбранную ячейку вашей электронной таблицы.
- Закройте окно «Символ».
Когда вы щелкаете по ячейке, содержащей вставленный символ, например, галочку, вы увидите в строке формул, что она фактически помещает букву «P», отформатированную шрифтом Wingdings 2, чтобы она выглядела как галочка.Если вы измените шрифт этой ячейки обратно на стандартный, отобразится буква P. Если вы используете символы из нестандартного шрифта, такого как Wingdings 2, вы должны убедиться, что ячейки отформатированы с именно этот шрифт.
Выберите два других символа для отложенных задач (часы) и отложенных задач (телефон).
Чтобы убедиться, что символы отображаются соответствующим образом, используйте коды символов символов. Перейдите в окно Insert Symbol , чтобы найти символьный код каждого символа.После нажатия на символ вы можете увидеть соответствующий ему код символа внизу, который равен 80 для галочки. Соответствующие коды символов для символов показаны ниже:
Запишите эти коды символов, поскольку они будут использоваться в условных формулах позже. Формула для правильной вставки символов:
= СИМВОЛ (код символа)
Использование вложенной функции IF ()
Мы хотим, чтобы Excel показывал нам эти три разных символа в зависимости от их статуса.Поскольку у нас есть три условия, мы можем использовать вложенную формулу IF (). В качестве первого логического теста завершенная задача (обозначенная буквой Y в столбце «Готово») должна иметь галочку. После синтаксиса IF () формула записывается как
Ячейка F1 = ЕСЛИ (E3 = "Y", СИМВОЛ (80) ..
Второе условие: если дата окончания меньше сегодняшней даты, мы хотим получить символ телефона, который символизирует отложенную задачу. Для этого мы можем добавить второй IF:
= ЕСЛИ (D3 <$ A $ 1, CHAR (39)…
Где A1 = сегодняшняя дата
(ссылка на эту ячейку должна быть исправлена.
Быстрый способ сделать это - нажать кнопку F4)
Наконец, если он не удовлетворяет всем этим условиям, потому что крайний срок для задачи в будущем, он должен отображать символ часов. Окончательная формула выглядит так:
Ячейка F1 = ЕСЛИ (E4 = "Y", СИМВОЛ (80), ЕСЛИ (D4 <$ A $ 1, СИМВОЛ (39), СИМВОЛ (137)))
Если столбец по-прежнему отформатирован стандартным шрифтом Arial, вместо символов будут отображаться другие символы. Чтобы исправить это, выделите столбец, содержащий символы, и измените шрифт на правильный, то есть Wingdings 2.
Форматирование символов
Вы можете дополнительно обозначить цветом столбец, содержащий символы, для лучшей визуализации;
Кажется, для этого требуется 3 правила условного форматирования, но вы можете сэкономить на форматировании 1, предварительно отформатировав ячейки для одного из условий. Например, по умолчанию отформатируйте их в серый цвет, поскольку именно так мы хотим, чтобы ячейки, содержащие последнее условие (часы), выглядели так, а осталось создать правила для двух других условий.
Выделите столбец, содержащий символы. Перейдите на главную страницу > Условное форматирование > Новое правило . Используйте этот параметр для форматирования только ячеек, которые содержат значение ячейки, равное значку галочки. Для этого введите out = CHAR (80), чтобы обратиться к соответствующему символу.
Щелкните Формат . Укажите форматирование стиля цвета и шрифта. Для галочки отформатируйте цвет на зеленый и измените стиль шрифта на полужирный.Щелкните ОК .
Добавьте еще одно правило для форматирования ячеек, содержащих символ телефона, в красный цвет с полужирным шрифтом.
Если вы хотите улучшить общий вид таблицы, объедините заголовок столбца Готово (Y) в E2 и F2 и соответственно измените ширину столбца. Добавьте к нему нижнюю границу, и все готово.
Посмотрите шаги в этом видео:
2. «Если… то…». и «Дело не в том, что…» - Краткое введение в логику
2.1 Условный
Как мы отметили в главе 1, есть предложения естественного языка, такого как английский, которые не являются атомарными предложениями. Наши примеры включают
Если Линкольн победит на выборах, то Линкольн станет президентом.
Земля не является центром Вселенной.
Мы можем рассматривать их как атомарные предложения, но тогда мы потеряем много важной информации. Например, первое предложение говорит нам кое-что о взаимосвязи между элементарными предложениями «Линкольн побеждает на выборах» и «Линкольн будет президентом».И второе предложение выше, как можно предположить, будет иметь интересную связь с предложением «Земля - центр Вселенной». Чтобы сделать эти отношения явными, нам нужно будет понять, что означают «если… то…» и «нет». Таким образом, было бы полезно, если бы наш логический язык мог выражать такие предложения таким образом, чтобы эти элементы были явными. Начнем с первого.
Предложение «Если Линкольн победит на выборах, то Линкольн будет президентом» содержит два элементарных предложения: «Линкольн победит на выборах» и «Линкольн станет президентом».Таким образом, мы могли бы представить это предложение, позволив
Линкольн побеждает на выборах
будет представлено на нашем логическом языке как
-П
А давая
Линкольн станет президентом
будет представлено
квартал
Тогда все выражение можно представить в виде
Если P, то Q
Однако было бы полезно заменить английскую фразу «if… then…» одним символом на нашем языке. Наиболее часто используемый такой символ - «→».Таким образом, мы бы написали
P → Q
Однако следует отметить еще одну вещь. Возможно, мы захотим объединить это сложное предложение с другими предложениями. В этом случае нам нужен способ определить, что это одно предложение, когда оно сочетается с другими предложениями. Есть несколько способов сделать это, но наиболее знакомый (хотя и не самый элегантный) - использовать круглые скобки. Таким образом, запишем наше выражение
(P → Q)
Этот вид приговора называется «условным».Его также иногда называют «материальным условием». Первое составное предложение (предложение перед стрелкой, которое в этом примере - «P») называется «антецедентом». Второе предложение (то, которое стоит после стрелки, в данном примере - «Q»), называется «консеквент».
Мы умеем писать условные выражения, но что они означают? Как и раньше, мы примем значение, которое придают условия истинности, то есть описание того, когда предложение является истинным или ложным. Мы делаем это с помощью таблицы истинности.Но теперь наше предложение состоит из двух частей, которые являются атомарными предложениями, P и Q. Обратите внимание, что любое атомарное предложение может быть истинным или ложным. Это означает, что мы должны рассмотреть четыре возможных типа ситуаций. Мы должны учитывать, когда P истинно, а когда ложно, но тогда нам нужно рассмотреть эти два типа ситуаций дважды: один раз, когда Q истинно, и один раз, когда Q ложно. Таким образом, левая часть нашей таблицы истинности будет выглядеть так:
Мы должны рассмотреть четыре возможных варианта развития мира.
Обратите внимание, что, поскольку существует два возможных значения истинности (истина и ложь), всякий раз, когда мы рассматриваем другое атомарное предложение, существует вдвое больше способов, которыми может быть мир, которые мы должны рассмотреть. Таким образом, для n атомарных предложений наша таблица истинности должна иметь 2n строк. В случае условного выражения, сформированного из двух элементарных предложений, как в нашем примере (P → Q), наша таблица истинности будет иметь 22 строки, что составляет 4 строки. Мы видим, что это именно так.
Теперь мы должны решить, что означает условие.В какой-то степени это зависит от нас. Важно то, что, как только мы определим семантику условного оператора, мы будем придерживаться нашего определения. Но мы хотим уловить как можно больше смысла английского «if… then…», оставаясь при этом абсолютно точными в нашем языке.
Давайте рассмотрим все, чем может быть мир. Для первой строки таблицы истинности у нас есть, что P истинно, а Q истинно. Предположим, мир таков, что Линкольн побеждает на выборах, и Линкольн также будет президентом.Тогда, сказал бы я правду, если бы сказал: «Если Линкольн победит на выборах, то Линкольн станет президентом»? Большинство людей согласны с этим. Точно так же предположим, что Линкольн победит на выборах, но Линкольн не будет президентом. Будет ли верным предложение «Если Линкольн победит на выборах, то Линкольн станет президентом»? Большинство согласны с тем, что сейчас это было бы ложью. Итак, первые строки нашей таблицы истинности бесспорны.
| п. | Q | (P → Q) |
|---|---|---|
| т | т | Т |
| т | F | F |
| ф | т | |
| Ф | F |
Однако некоторым студентам трудно определить, какие значения истинности должны быть в следующих двух строках.Обратите внимание, что наш принцип двухвалентности требует, чтобы мы заполняли эти строки. Мы не можем оставить их пустыми. Если бы мы это сделали, мы бы сказали, что иногда условное выражение не может иметь истинного значения; то есть мы могли бы сказать, что иногда некоторые предложения не имеют значения истинности. Но наш принцип двухвалентности требует, чтобы во всех ситуациях каждое предложение было либо истинным, либо ложным, но никогда и тем и другим, никогда ни тем и другим. Итак, если мы собираемся соблюдать принцип двухвалентности, тогда мы должны указать либо T, либо F для каждой из последних двух строк.
Здесь полезно изменить наш пример. Давайте рассмотрим два разных примера, чтобы проиллюстрировать, как лучше всего заполнить оставшуюся часть таблицы истинности для условного выражения.
Сначала предположим, что я говорю вам следующее: «Если вы дадите мне 50 долларов, я куплю вам билет на концерт сегодня вечером». Пусть
Ты дашь мне 50 долларов
будет представлено в нашей логике
R
и пусть
Я куплю тебе билет на концерт сегодня вечером.
будет представлено
S
Тогда наше предложение -
(R → S)
И его таблица истинности - насколько мы сейчас понимаем - это:
| R | S | (R → S) |
|---|---|---|
| т | т | Т |
| т | F | F |
| Ф | т | |
| Ф | F |
То есть, если вы дадите мне деньги, и я куплю вам билет, мое утверждение, что «Если вы дадите мне 50 долларов, я куплю вам билет на концерт сегодня вечером», верно.И, если вы дадите мне деньги, а я не куплю вам билет, я солгал, и мое заявление не соответствует действительности. А теперь предположим, что вы не дадите мне 50 долларов, а я куплю вам билет на концерт в подарок. Было ли мое заявление ложным? Нет. Я просто купил тебе билет в подарок, но, по-видимому, купил бы его, если бы ты дал мне деньги. Точно так же, если вы не дадите мне денег, и я не куплю вам билет, это полностью согласуется с моим утверждением.
Итак, лучший способ заполнить таблицу истинности следующий.
| R | S | (R → S) |
|---|---|---|
| т | т | Т |
| т | F | F |
| Ф | т | Т |
| ф | F | Т |
Во-вторых, рассмотрим другое предложение, которое имеет то преимущество, что оно очень четкое по отношению к этим последним двум строкам.Предположим, что a - конкретное натуральное число, только мы с вами не знаем, что это за число (натуральные числа - это целые положительные числа: 1, 2, 3, 4…). Рассмотрим теперь следующее предложение.
Если a делится без остатка на 4, то a без остатка делится на 2.
(Под «делимым без остатка» я имею в виду делимый без остатка). Первое, что нужно спросить себя: верно ли это предложение? Я надеюсь, что мы все согласимся, что это так, даже если мы не знаем, что такое a. Пусть
a делится на 4 без остатка
будет представлено в нашей логике
U
и пусть
a делится на 2 без остатка
будет представлено
В
Тогда наше предложение -
(U → V)
И его таблица истинности - насколько мы сейчас понимаем - это:
| U | В | (U → V) |
|---|---|---|
| т | т | Т |
| т | F | F |
| Ф | т | |
| ф | F |
Теперь рассмотрим случай, когда а равно 6.Это похоже на третью строку таблицы истинности. Это не тот случай, когда 6 без остатка делится на 4, но это случай, когда 6 без остатка делится на 2. И рассмотрим случай, когда a равно 7. Это похоже на четвертую строку таблицы истинности; 7 не делится без остатка ни на 4, ни на 2. Но мы согласились, что условие истинно - независимо от значения a! Итак, таблица истинности должна быть: [3]
| U | В | (U → V) |
|---|---|---|
| т | т | Т |
| т | F | F |
| Ф | т | Т |
| ф | F | Т |
Следуя этой схеме, мы также должны заполнить нашу таблицу о выборах:
| п. |
Q | (P → Q) |
|---|---|---|
| т | т | Т |
| т | F | F |
| Ф | т | Т |
| Ф | F | Т |
Если вас это не устраивает, может быть полезно подумать об этих последних двух строках как о пустых случаях.Условное выражение говорит нам о том, что происходит, если антецедент верен. Но когда антецедент ложен, мы просто по умолчанию принимаем истинное значение.
Теперь мы готовы предложить более формальным образом синтаксис и семантику условного оператора.
Синтаксис условного оператора: если Φ и Ψ - предложения, то
(Φ → Ψ)
- это приговор.
Семантика условного оператора задается таблицей истинности. Для любых предложений Φ и Ψ:
| Φ | Ψ | (Φ → Ψ) |
|---|---|---|
| т | т | Т |
| т | F | F |
| Ф | т | Т |
| Ф | F | Т |
Помните, что эта таблица истинности теперь является определением.Он определяет значение «→». Мы соглашаемся использовать символ «→» для обозначения этого и впредь.
Элементы логики высказываний, такие как «→», которые мы добавляем в наш язык, чтобы сформировать более сложные предложения, называются «функциональными связками истинности». Надеюсь, понятно почему: значение этого символа дано в функции истинности. (Если вы не знакомы или не уверены в идее функции, подумайте о функции как о машине, которая принимает один или несколько входных данных, а затем всегда выдает ровно один выход.Для условного выражения входными данными являются два значения истинности; и на выходе получается одно значение истинности. Например, поместите T F в функцию истинности под названием «→», и вы получите F.)
2.2 Альтернативные фразы на английском языке для условного. Только если.
English включает множество альтернативных фраз, которые кажутся эквивалентными условному. Кроме того, в английском и других естественных языках порядок условных обозначений иногда меняется на обратный. Мы можем уловить общий смысл этих случаев, осознав, что каждая из следующих фраз будет переведена как (P → Q).(В этих примерах мы смешиваем английский язык и нашу логику высказываний, чтобы лаконично проиллюстрировать вариации.)
Если P, то Q.
Q, если П.
При условии, что P, Q.
Q, при условии, что P.
Учитывая, что P, Q.
Q, учитывая, что P.
При условии, что P, Q.
Q, при условии, что P.
Когда P, то Q.
Q, когда P.
P означает
Q.Q подразумевается P.
P достаточно для Q.
Q необходимо для P.
Странность английского языка заключается в том, что слово «only» меняет значение «if». Вы можете убедиться в этом, если рассмотрите следующие два предложения.
Фифи - это кошка, если Фифи - млекопитающее.
Фифи - кошка, только если Фифи - млекопитающее.
Предположим, мы знаем, что Фифи - это организм, но мы не знаем, что это за организм. Фифи могла быть собакой, кошкой, серым китом, божьей коровкой, губкой. Кажется очевидным, что первое предложение не обязательно верно.Если, например, Фифи - серый кит, то верно, что Фифи - млекопитающее, но неверно, что Фифи - кошка; Итак, первое предложение было бы ложным. Но второе предложение выглядит так, как будто оно должно быть правдой (учитывая то, что мы с вами знаем о кошках и млекопитающих).
Таким образом, мы должны осознавать, что «только если» не означает то же самое, что и «если». (Если бы это было так, эти два предложения имели бы одинаковое значение истинности во всех ситуациях.) На самом деле кажется, что «только если» лучше всего можно выразить условным выражением, где «только если» появляется перед следствием (помните, консеквент - это вторая часть условного выражения, на которую указывают стрелки).Таким образом, предложений такой формы:
P только если Q.
Только если Q, P.
лучше всего выражается формулой
(P → Q)
2.3 Проверьте свое понимание условного
Иногда условные выражения сбивают с толку. Отчасти это происходит потому, что некоторые люди путают их с другим типом связки, определяющей функцию истины, о которой мы узнаем позже, которая называется «бикондиционной». Кроме того, иногда «if… then…» используется в английском языке по-другому (см. Раздел 17.7, если вам интересно узнать об альтернативных возможных значениях). Но с этого момента мы будем понимать условность, как описано выше. Чтобы проверить, правильно ли вы усвоили условное выражение, рассмотрите следующую загадку. [4]
У нас есть набор из четырех карт на рисунке 2.1. Каждая карта обладает следующим свойством: с одной стороны у нее есть форма, а с другой - буква. Мы перемешиваем и перемешиваем карты, переворачивая некоторые во время перемешивания. Затем выкладываем четыре карты:
Фигура 2.1Учитывая наше ограничение, заключающееся в том, что каждая карта имеет букву на одной стороне и форму на другой, мы знаем, что карта 1 имеет форму на невидимой стороне; карта 2 имеет букву на невидимой стороне; и так далее.
Рассмотрим теперь следующую претензию:
Для каждой из этих четырех карт, если карта имеет Q на лицевой стороне карты, то у нее есть квадрат на стороне формы карты.
Вот наша загадка: какое минимальное количество карт мы должны перевернуть, чтобы проверить, верно ли это утверждение для всех четырех карт; и какие это карты, которые мы должны перевернуть? Конечно, мы могли бы перевернуть их все, но головоломка просит вас идентифицировать все и только карты, которые будут проверять претензию.
Прекратите читать сейчас и посмотрите, сможете ли вы определиться с ответом. Имейте в виду, что люди обычно плохо справляются с этой головоломкой. Подумайте об этом немного. Ответ дан ниже в задаче 1.
2.4 Альтернативные символы условного
Некоторые книги по логике и некоторые логики используют альтернативные символы для различных функциональных связок истинности. Значения (то есть таблицы истинности) всегда одинаковы, но используемые символы могут быть разными. По этой причине мы найдем время в этом тексте, чтобы кратко рассмотреть альтернативные символы.
Условное условие иногда обозначается следующим символом: «⊃». Таким образом, в таком случае (P → Q) будет записано
(P⊃Q)
2,5 Отрицание
В главе 1 мы рассматривали в качестве примера предложение
Земля не является центром Вселенной.
На первый взгляд такое предложение может показаться принципиально непохожим на условное. В нем не два предложения, а только одно. В предложении есть «не», но оно не связывает два предложения.Однако мы все еще можем думать об этом предложении как о построении функциональной связки истины, если мы готовы признать, что это предложение эквивалентно следующему предложению.
Это не тот случай, когда Земля является центром Вселенной.
Если это предложение эквивалентно предыдущему, то мы можем трактовать «Это не так» как функциональную связку истинности. Традиционно заменять эту громоздкую английскую фразу одним символом «¬». Тогда, смешав нашу логику высказываний с английской, мы получим
¬Земля - центр Вселенной.
И если мы позволим W быть предложением на нашем языке, имеющим значение Земля - центр Вселенной , мы напишем
¬W
Эта связка называется «отрицание». Его синтаксис: если Φ - предложение, то
¬Φ
- это приговор. Мы называем такое предложение «приговором отрицания».
Семантика отрицательного предложения также очевидна и дается следующей таблицей истинности.
Отрицать истинный приговор - значит говорить неправду.Отрицать ложное предложение - значит сказать правду.
Наш синтаксис всегда рекурсивен. Это означает, что синтаксические правила можно многократно применять к продукту правила. Другими словами, наш синтаксис говорит нам, что если P - предложение, то ¬P - это предложение. Но теперь обратите внимание, что снова применяется то же правило: если ¬P - это предложение, то ¬¬P - это предложение. И так далее. Точно так же, если P и Q - предложения, синтаксис условного выражения говорит нам, что (P → Q) - это предложение. Но тогда так же ¬ (P → Q), как и (¬ (P → Q) → (P → Q)).И так далее. Если у нас есть только одно атомарное предложение, наш рекурсивный синтаксис позволит нам формировать бесконечно много разных предложений с отрицанием и условным выражением.
2.6 Альтернативные символы для отрицания
В некоторых текстах может использоваться символ «~» для отрицания. Таким образом, ¬P будет выражено с помощью
.~
п.2.7 Проблемы
- Ответ на нашу карточную игру был таков: вам нужно перевернуть только карты 3 и 4. Поначалу это может показаться многим запутанным.Но помните значение условия: оно может быть ложным только в том случае, если первая часть истинна, а вторая ложна. Предложение, которое мы хотим проверить, звучит так: «Для каждой из этих четырех карт, если карта имеет Q на стороне буквы карты, то у нее есть квадрат на стороне формы карты». Пусть Q означает «у карты есть Q на лицевой стороне карты». Пусть S означает «карта имеет квадрат на стороне формы карты». Затем мы могли бы составить таблицу истинности, чтобы выразить смысл проверяемого утверждения:
| Q | S | (Q → S) |
| т | т | Т |
| т | F | F |
| Ф | т | Т |
| Ф | F | Т |
Посмотрите на карты.Первая карта имеет букву R. Итак, предложение Q ложно. Но тогда мы оказываемся в ситуации, подобной двум последним строкам таблицы истинности, и условное выражение не может быть ложным. Нам не нужно проверять эту карту. На второй карте есть квадрат. Это означает, что S верно для этой карты. Но тогда мы оказываемся в ситуации, представленной либо первой, либо третьей строкой таблицы истинности. Опять же, утверждение, что (Q → S) не может быть ложным ни в одном случае по отношению к этой карте, поэтому нет смысла проверять эту карту.Третья карта показывает Q. Это соответствует ситуации, которая похожа на первую или вторую строку таблицы истинности. Тогда мы не можем сказать, истинно или ложно (Q → S) для этой карты, не перевернув карту. Точно так же последняя карта показывает ситуацию, когда S ложно, поэтому мы находимся в ситуации, представленной либо второй, либо последней строкой таблицы истинности. Мы должны перевернуть карту, чтобы определить, является ли (Q → S) истинным или ложным для этой карты.
Попробуйте решить эту головоломку еще раз. Рассмотрим следующее утверждение о тех же четырех картах: если на лицевой стороне карты есть звезда, значит, на буквенной стороне карты есть буква R.Какое минимальное количество карт вы должны перевернуть, чтобы проверить это заявление? Какие это карты?
- Рассмотрим следующие четыре карты на рисунке 2.2. Каждая карта имеет букву на одной стороне и фигуру на другой стороне.
Для каждого из следующих утверждений, чтобы определить, верно ли утверждение для всех четырех карт, опишите (1) минимальное количество карт, которое вы должны перевернуть, чтобы проверить претензию, и (2) какие эти карты находятся.
- На лицевой стороне карты нет буквы Q.
- На лицевой стороне карты нет восьмиугольника.
- Если на стороне формы карты есть треугольник, то на стороне буквы карты есть буква P.
- Буква R отображается на лицевой стороне карты только в том случае, если на лицевой стороне карты есть ромб.
- На лицевой стороне карты изображен шестиугольник, при условии, что на лицевой стороне карты есть буква P.
- Ромб появляется на лицевой стороне карты только в том случае, если на лицевой стороне карты есть буква P.
3. Что из следующего имеет правильный синтаксис? Какие из них имеют неправильный синтаксис?
- P → Q
- ¬ (P → Q)
- (¬P → Q)
- (P¬ → Q)
- (P → ¬Q)
4. Используйте следующий ключ перевода, чтобы перевести следующие предложения в логику высказываний.
| Ключ перевода | |
|---|---|
| Логика | Английский |
| пол. | Абэ умеет. |
| Q | Абэ честный. |
- Если Эйб честен, Эйб может.
- Абэ не умеет.
- Абэ не может только в том случае, если Абэ нечестен.
- Абэ может, при условии, что Абэ нечестен.
- Если Эйб не может, значит, Абэ нечестен.
5. Составьте свой собственный ключ перевода, чтобы перевести следующие предложения в логику высказываний. Затем используйте свой ключ, чтобы перевести предложения в логику высказываний.Ваш ключ перевода должен содержать только атомарные предложения. Это должны быть все и только элементарные предложения, необходимые для перевода следующих английских предложений. Пусть вас не беспокоит, что некоторые предложения неверны.
- Джози кошка.
- Джози - млекопитающее.
- Джози не млекопитающее.
- Если Джози не кошка, значит, Джози не млекопитающее.
- Джози - рыба.
- Если Джози - млекопитающее, Джози не рыба.
- Джози - кошка, только если Джози - млекопитающее.
- Джози - рыба, только если Джози не млекопитающее.
- Дело не в том, что Джози не млекопитающее.
- Джози не кошка, если Джози рыба.
6. В этой задаче будет использоваться принцип рекурсивности нашего синтаксиса. Перевод этих предложений сложнее. Составьте свой собственный ключ перевода, чтобы перевести следующие предложения в логику высказываний. Ваш ключ перевода должен содержать только атомарные предложения; это должны быть все и только элементарные предложения, необходимые для перевода следующих английских предложений.
- Том не может не сдать экзамен.
- Если Том учится, Том сдаст экзамен.
- Дело не в том, что если Том учится, то Том сдает экзамен.
- Если Том не учится, то Том не сдаст экзамен.
- Если Том учится, Том сдаст экзамен - при условии, что он вовремя проснется.
- Если Том сдает экзамен, то если Стив учится, Стив сдает экзамен.
- Дело не в том, что если Том сдает экзамен, то, если Стив учится, Стив сдает экзамен.
- Если Том не сдает экзамен, то если Стив учится, Стив сдает экзамен.
- Если Том не сдает экзамен, это не тот случай, когда Стив будет учиться, Стив будет сдавать экзамен.
- Если Том не сдает экзамен, то если Стив не учится, Стив не сдает экзамен.
7. Составьте свой собственный ключ перевода, чтобы переводить следующие предложения на английский язык. Выпишите английские эквиваленты в английских предложениях, которые кажутся (насколько это возможно) естественными.
- (R → S)
- ¬¬R
- (S → R)
- (¬S → ¬R)
- ¬ (R → S)
[3] Во втором примере с неизвестным номером a одна вещь немного забавна. Мы не сможем найти число, которое делится без остатка на 4 и не делится без остатка на 2, поэтому мир никогда не будет похож на второй ряд этой таблицы истинности. Об этом нужно сказать две вещи. Во-первых, эта странность возникает из-за математических фактов, а не фактов нашей логики высказываний, то есть нам нужно знать, что означает «делимый», что означают «4» и «2» и так далее, чтобы понять предложение. .Итак, когда мы видим, что вторая строка невозможна, мы основываем это на нашем знании математики, а не на знании логики высказываний. Во-вторых, некоторые условные выражения могут быть ложными. При определении условного выражения нам необходимо учитывать все возможные условные выражения; Итак, мы должны определить условное выражение для любого случая, когда антецедент истинен, а следствие ложно, даже если этого не может произойти в данном конкретном примере.
Краткое содержание главы
Глава 7
Логика высказываний - это изучение того, как простые высказывания (базовые компоненты в логике высказываний) изменяются, чтобы сформировать составные высказывания, и того, как истина является функцией простых высказываний и составных элементов.Простой оператор - это оператор, не имеющий в качестве компонента какого-либо другого оператора. Составной оператор - это оператор, в состав которого входит хотя бы один простой оператор.
Чтобы облегчить изучение логики высказываний, утверждения обычного языка переводятся в нотацию логики высказываний. Логическая запись включает заглавные буквы, A – Z для обозначения простых утверждений и логические операторы для обозначения составных элементов. Имеется пять символов логического оператора: тильда , точка , клин , подкова и тройная черта.
Тильда - символ отрицания. Слово «не» и фраза «это не тот случай» используются для отрицания следующего за ними утверждения (мы называем их использование «отрицанием»). Точка - это символ конъюнкции, который соединяет два различных утверждения (называемых «конъюнктами»). Дизъюнкция - это составное утверждение, которое имеет два различных утверждения (называемых «дизъюнкциями»), соединенных символом клина. В обычном языке слово «если» обычно предшествует условному выражению: «только если» обычно предшествует условному выражению.Символ подковы используется для перевода условного оператора. Двухусловное выражение - это составное выражение, состоящее из двух условных выражений: одно обозначается словом «если», а другое - фразой «только если».
Когда мы конструируем составные утверждения, мы стремимся создавать правильно сформированные формулы, которые являются грамматически правильными формами составных утверждений. У каждого составного оператора, содержащего два или более операторов, есть главный оператор. Это логический оператор, в диапазоне которого находится самый большой компонент или компоненты в составном операторе.
Каждое утверждение имеет значение истинности, то есть каждое утверждение истинно или ложно. Значение истинности сложного предложения с функцией истинности определяется значениями истинности его компонентов и определениями задействованных логических операторов. Любое сложное предложение с функциональной истинностью, которое может быть определено таким образом, называется «функцией истинности».
Определения истинности для логических операторов отображаются как формы утверждений в таблице истинности. Форма оператора - это набор переменных оператора и логических операторов.Таблица истинности - это набор значений истинности для сложного предложения с функциональной истинностью, который показывает для каждого возможного случая, как значение истинности предложения определяется значениями истинности его простых компонентов.
Важно знать следующие концепции, связанные с использованием и результатами таблиц истинности:
-
Инклюзивная дизъюнкция: обе дизъюнкции могут быть истинными одновременно.
-
Исключительная дизъюнкция: когда обе дизъюнкции не могут быть истинными одновременно.
-
Порядок операций: порядок обработки логических операторов в предложении с функцией истинности; это пошаговый метод создания полной таблицы истинности.
-
Условные утверждения: утверждения, которые не обязательно истинны или ложны (иногда они верны, иногда ложны).
-
Неконфликтные утверждения: утверждения, при которых значения истинности в главном столбце оператора не зависят от значений истинности составных частей.
-
Тавтология: утверждение, которое обязательно верно.
-
Внутреннее противоречие: утверждение, которое обязательно ложно.
-
Логически эквивалентно: Когда два функциональных утверждения истинности кажутся разными, но имеют идентичные таблицы истинности.
-
Противоречивые утверждения: два утверждения, которые имеют противоположные значения истинности в каждой строке соответствующих таблиц истинности.
-
Согласованные утверждения: два (или более) утверждения, в соответствующих таблицах истинности которых есть хотя бы одна строка, где истинны основные операторы.
-
Несогласованные утверждения: два (или более) утверждения, в соответствующих таблицах истинности которых нет ни одной строки, где истинны основные операторы.
-
Форма аргумента: набор логических операторов и переменных оператора, в котором последовательная замена переменных оператора операторами приводит к получению аргумента.
-
Modus ponens : Действительная форма аргумента (также называемая , подтверждающая антецедент ).
-
Ошибка подтверждения консеквента: неверная форма аргумента; это формальная ошибка.
-
Modus tollens : Действительная форма аргумента (также обозначается как , отрицающая консеквент ).
-
Ошибка отрицания антецедента: неверная форма аргумента; это формальная ошибка.
Как создавать значки с условным форматированием в Excel
Итог: Изучите технику применения условного форматирования к новым значкам в Excel.
Уровень квалификации: Средний
Скачать файл Excel
Файл, с которым я работаю в видео, можно найти ниже. Вы также можете загрузить версию «Follow Along», если хотите попрактиковаться в построении отчета.
Отчет о посещаемости Dunder Mifflin - Follow Along.xlsx (24,4 КБ)
Отчет о посещаемостиDunder Mifflin - Final.xlsx (166,6 КБ)
Совместимость: В этом файле используются новые функции динамического массива, которые доступны только в последней версии Office 365.Сюда входят версии Excel для настольных компьютеров и веб-приложений.
Я также опубликовал бонусный эпизод из этой серии, в котором рассказывается, как сделать панель мониторинга в более старых версиях Excel, используя вместо этого сводные таблицы.
Создание панели мониторинга посещаемости
Этот пост является заключительной частью из серии из шести статей, в которой объясняется, как создать интерактивную информационную панель для посещаемости . Этот отчет о посещаемости был записан на конкурс Excel Hash.Я рекомендую вам ознакомиться с первыми пятью сообщениями здесь:
- Как использовать функцию XOR
- Как использовать XLOOKUP для поиска в обратном порядке
- Возвращает несколько значений для формулы поиска в Excel с ФИЛЬТРОМ и УНИКАЛЬНЫМ
- Как сортировать по формуле в Excel с помощью функций SORT и SORTBY
- Как создать динамический раскрывающийся список, который автоматически расширяется
Иконки в специальном формате
Для нашей последней задачи по созданию панели мониторинга посещаемости мы хотим создать значков, которые изменяют в зависимости от производительности отдела.В частности, когда отдел превышает целевое значение посещаемости, значок фейерверка будет окрашен в цвет , а значок грозового облака станет серым.
И наоборот, когда отдел не достигает своей цели, грозовое облако окрашивается в цвет , а фейерверк - в серый цвет.
Выбор значков
Чтобы найти нужные значки, вы можете использовать новое окно Значки , в котором есть функция поиска . Чтобы открыть это окно, перейдите на вкладку Вставить на ленте.Выберите Иллюстрации , а затем Иконки .
Выберите значки, которые нужно вставить. (Вы можете вставить несколько штук за раз.)
Форматирование изображений
Мы собираемся изменить наши значки на картинку, внося в нее некоторые изменения. Начните с изменения цвета значков на светло-серый. Это можно сделать, выбрав Graphics Fill на вкладке Graphics Format на ленте.
Затем вставьте белый квадрат, который будет фоном для вашего значка.Вы можете вставить этот квадрат, перейдя на вкладку Вставить на ленте, нажав кнопку Иллюстрации и выбрав Фигуры . Вы получите меню форм на выбор, и вы можете выбрать прямоугольную форму.
Нарисуйте квадрат вокруг значка и измените цвет Shape Fill на белый. Измените настройку Shape Outline на No Outline . Затем щелкните фигуру правой кнопкой мыши и выберите На задний план в появившемся меню.Это поместит белый фон позади вашего значка.
Выделив фоновую форму, удерживайте кнопку Ctrl на клавиатуре и также выберите значок. Затем щелкните правой кнопкой мыши и выберите Group , чтобы сгруппировать две фигуры вместе.
Скопируйте эту новую группу, а затем вставьте ее в другое место на листе. Но не делайте обычную пасту. Щелкните правой кнопкой мыши и выберите Параметры вставки , затем Изображение . При этом группа из двух фигур превращается в одно изображение.
Выбрав новое изображение, перейдите на вкладку Формат изображения на ленте и выберите параметр Цвет . Внизу этого меню находится Установить прозрачный цвет .
При этом курсор мыши изменяется так, что все, что вы нажимаете далее, будет иметь прозрачную заливку . Другими словами, он будет прозрачным, а не цветным.
Вы захотите повторить все это форматирование и для вашего второго значка.
Условное форматирование
Теперь, когда у нас есть значки, которые вы можете видеть, мы собираемся установить их в на определенные ячейки , на которые мы можем ссылаться в нашем условном форматировании .
На вкладке Home вы можете выбрать Conditional Formatting и Manage Rules . Это вызывает Диспетчер правил условного форматирования . Я установил правила для обеих ячеек, в которых есть значки.
Одно из правил заполняет грозовое облако синим градиентом , если фактическое число посещаемости на меньше , чем целевое число. Другое правило заполняет фейерверк градиентом оранжевого цвета , если фактическое значение на выше , чем цель.Если не соблюдаются условия для их форматирования таким образом, цвет значка будет просто светло-серым .
Теперь, когда мы создали наши правила условного форматирования для этих двух ячеек, мы можем скопировать и вставить их на лист Dashboard . При вставке мы хотим Специальная вставка как Связанное изображение .
Добавление текстовых полей
Наконец, мы собираемся добавить текстовых полей под каждым значком, которые также являются условными.В этих текстовых полях отображается число или остается пустым , в зависимости от того, выше или ниже среднее значение по отделу общей цели. Это связано с тем, что эти текстовые поля связаны с ячейкой на листе Calc , которая имеет формулу IF , которая описывает эти условия.
Добавление текстовых полей выполняется легко. Просто перейдите на вкладку Insert на ленте, нажмите кнопку Text и выберите Text Box .Затем вы можете нарисовать текстовое поле на листе с помощью мыши.
Чтобы связать текстовое поле, просто щелкните по нему, введите знак равно (=) в строке формул и выберите ячейку на листе Calc , с которой вы хотите связать ее. Вы можете отформатировать текстовое поле, как хотите.
Похожие сообщения
У меня есть еще два сообщения об условном форматировании, которые я предлагаю вам проверить:
Заключение
Мы сделали это! Мы воссоздали интерактивный отчет о посещаемости , который хотел видеть Майкл Скотт из The Office , с грозовыми облаками и фейерверками.
Я надеюсь, что этот пост и вся серия оказались полезными для вас, и что вы получите около новых навыков и методов , которые вы можете реализовать в своем офисе .
Если у вас есть вопросы по поводу каких-либо шагов, которые мы предприняли для создания этих условно отформатированных значков, дайте мне знать в комментариях. Спасибо, что подписались!
Раздел 1.6 Обзор
Раздел 1.6 ОбзорПредикаты и квантификаторы
Предикаты | Правда Набор | Квантификаторы | Отрицание Количественные отчеты | Определения Универсальные условные операторы | Отрицание универсальных условных операторовПредикаты
Предикат - это та часть утверждения, которая дает информацию о предмет.В логике предикат может быть представлен с помощью предиката . символы и переменные предиката. Рассмотрим следующее:
Пусть P будет предикатным символом для учится на бакалавриат степень в GSU, и пусть x будет предикатной переменной, которая берет свое значение из набора всех студентов. Тогда приведенное выше предложение символически представленный как x учится на степень бакалавра в GSU или P ( x ) .
Приведенное выше утверждение может быть уточнено. Пусть у тоже быть переменной-предикатом, принимающей значение из набора всех колледжей, и пусть R обозначает , учится на степень бакалавра в. Вышеупомянутое предложение теперь может быть представлено как x учится на степень бакалавра y , или R ( x, y ) .
Предикат - это предложение, содержащее определенное количество переменных, и становится утверждением, когда конкретные значения подставляются вместо переменные предиката.Значения взяты из домена из переменные предиката: область x - это набор всех студентов, а домен y - это набор всех колледжей. Значения в этих наборах могут быть представлены словами или символами.
Набор можно определить, просто заключив элементы набора в скобки. Для например, {2, 3, 5, 7} - это набор простых чисел меньше 10. При использовании символов наборы обычно представлены заглавными буквами, а элементы набора - строчными дело.Пусть T будет набором простых чисел меньше 10, а x быть элементом Т ; это отношение может быть представлено обозначением x T . Аналогично обозначение x T означает, что x не является элементом (или x не входит) Т .
Наборы правды
Когда элементы заменяются переменными в предикате, результат либо правда или ложь.Пусть P будет набором всех простых чисел, пусть x быть элементом P , и пусть R означает " x - простое число меньше 10 ". Символически предикат представлен как R ( x ) , где x P . Для x = 5, R ( x ) верно, но если x = 13, тогда R ( x ) ложно.Набор истинности предиката R ( x ) - это набор всех элементов, которые делают R ( x ) истинным. Это символически обозначается как:
{ x P | R ( x ) }
, который читается как "набор всех x в P , таких как что R ( x ) "или" x является элементом P , так что R ( x ) является истинным ".(Вертикальная полоса '|' переводится как "такой, что".)
Использование и
Данные предикаты P ( x ) и Q ( x ) , где x имеет домен D :
P ( x ) Q ( x ) означает, что каждый элемент в наборе истинности P ( x ) также находится в Q ( x ).
P ( x ) Q ( x ) означает, что P ( x ) и Q ( x ) имеют одинаковую истину наборы .
Квантификаторы: и
Квантификаторы относятся к заданным количествам, таким как «некоторые» или «все», указание количества элементов, для которых предикат истинен.Символ переводится как "для все "," дано любому "," для каждого "или" для каждого ", и известен как универсальный квантор . Символ квантор существования и означает по-разному "для некоторых", "существует", "есть" или "по крайней мере один ".
Универсальный оператор - это утверждение, что истинно тогда и только тогда, когда оно истинно для каждой переменной предиката в данном домен. Рассмотрим следующий пример:
Пусть B будет набором всех видов не исчезнувших птиц, а b быть переменной-предикатом, такой что b B .Пусть Q будет заявлением « b может летать», а R быть заявлением « b либо плотояден, либо нет». Универсальные утверждения для этих двух предикатов могут быть представлены как « b B, Q ( b ) " («для всех птиц b , входящих в набор не исчезнувших видов. птиц, b может летать ") и" b B, R ( b ) "(попробуйте сами разгадать здесь формулировку!).С участием немного подумав, очевидно, что Q ( b ) ложно, так как существуют нелетающие птицы, такие как страусы и пингвины. R ( b ) , г. однако это очевидно верно, поскольку о любом виде птиц можно сказать, что они либо едят мясо, либо нет.
Экзистенциальное утверждение - утверждение это верно, если есть хотя бы одна переменная в домене переменной для которых утверждение верно.
Опять же, используя определенный выше набор птиц и предикат R ( b ) , экзистенциальное утверждение записывается как « b Б, R ( b ) "(" Для некоторых птиц b , которые находятся в множество не исчезнувших видов птиц, b умеет летать »). Теперь рассмотрим новый предикат W ( b ) , где W означает «больше» чем слон ».Экзистенциальное утверждение " b B, W ( b ) " можно перевести как «Существует птица, которая больше слона». Это утверждение неверно, поскольку ни один член набора B не больше слона.
| Практические упражнения |
Отрицание количественно Выписки
Если универсальная выписка - выписка это верно тогда и только тогда, когда это верно для каждой переменной предиката в пределах данный домен (как указано выше), то логически неверно, если существует даже один случай, который делает его ложным.Как обсуждалось ранее, заявление « Все птицы летают . "ложно. Но его отрицание не" Нет птиц летают ". (также заведомо ложное). Вместо этого правильным отрицанием будет " Некоторые птицы не летайте ». Условно:
Отрицание универсального утверждения («все есть») логически эквивалент экзистенциального утверждения («Некоторые не являются»).
Точно так же экзистенциальное утверждение является false, только если все элементы в его домене ложны.Отрицание из «Некоторые птицы крупнее слонов» - «Птиц нет. больше слонов. "
Отрицание экзистенциального утверждения («некоторые есть») логически эквивалент универсального утверждения («не все»).
| D Э Ф И Н И Т И Я С | |
| Предикат | предложение, содержащее определенное количество переменных, который становится утверждением, когда конкретные значения подставляются вместо переменных предиката. |
| Набор истины | для предиката P ( x ) где D - это область x , набор всех переменных в D , что делает P ( x ) истинным. Символически { x D | P ( x )} . |
| | | символ для "такого, что". |
| Универсальный квантор, означающий «для всех», «за каждого», «за каждого» и т. д. | |
| Квантор существования, что означает «для некоторых», «есть», «есть» и т. д. | |
| Универсальный условный Заявление | .
Выписка формы: x , если P ( x ) , то Q ( x ) . |
| Экзистенциальное условное Заявление | .
Выписка формы: x так что, если P ( x ) , то Q ( x ) . |
| Практические упражнения |
Универсальные условные операторы
Помните условные операторы? Универсальный условный оператор - это просто универсальный оператор с состояние и символически представлено как:
x ,
если P ( x ) , то Q ( x )
или
x ,
P ( x ) Q ( x )
Понимание универсальных условных операторов расширит ваше понимание из if-then (условных) утверждений, в частности, почему истина таблица оператора if-then строится как есть.Напомним, что условное утверждение ложно, только если его гипотеза верна и результат ложно, и примените это к более раннему примеру условного оператора:
Если меня кто-нибудь ударит ногой, я закричу "ай!"
Очевидно, если кто-то пинает вас и вы кричите «ай!», То Вышеуказанное условное утверждение верно. Но предположим, что вы уронили молоток на свой ноги и орать ай? Или с вами ничего не происходит, и вы поэтому ничего не говорите? Ни одна из этих ситуаций не делает приведенное выше утверждение ложным, поэтому оно становится по умолчанию true.Единственное, что делает это утверждение ложным, - это если кто-то пинает вас, а вы не кричите «ай!».
Представление этого утверждения в форме универсального условного оператора дает следующие:
За все, что может случиться со мной, если кто-то пинает меня, тогда я кричу "ай!"
Если вы считаете, что единственный экземпляр, который делает это ложным, является истинным гипотеза (кто-то вас пинает) и ложный вывод (вы не кричите ай), должно стать очевидным, что это утверждение верно для всего еще.В частности, это всегда верно, когда гипотеза ложна.
| Практические упражнения |
Отрицательный универсальный Условные отчеты
Чтобы понять отрицание универсального условного оператора, сначала обзор if-then (условных) отрицаний и отрицаний универсального («для всех») выписки:
Отрицание условного оператора (если-то) логически эквивалентно на заявления и .
Отрицание универсального утверждения логически эквивалентен экзистенциальному утверждению.
Подстановка условного оператора в универсальный оператор дает следующий результат:
| Практические упражнения |
Используйте функцию условного форматирования Excel для отображения простых значков
Понимание ваших данных и того, как работает условное форматирование Excel, является ключом к точному использованию значков для представления данных.
Я быстрее реагирую на символы, чем на слова и значения, но Excel отображает текстовые и числовые значения, а не символы. Верно? Уже нет. Используя условное форматирование (в 2007 и 2010 годах), вы можете быстро отображать значки, которые могут значить для ваших пользователей больше, чем значения, которые они представляют.
Чтобы продемонстрировать эту функцию, я буду работать с данными, импортированными из таблицы Products в базе данных Northwind, которая поставляется с Access.Вы можете работать с любыми данными, которые вам нравятся, но данные о продуктах создают некоторые интересные проблемы. Данные содержат столбец текстовых значений, которые показывают, продает ли компания продукт по-прежнему. Это значение «прекращено» - ЛОЖЬ, если продукт не был снят с производства, что означает, что он доступен. Когда продукт снят с производства, значение - ИСТИНА. Это немного противоречит интуиции, но это одна из проблем.
Простой способ не всегда сработает
Во-первых, давайте попробуем самое простое решение Excel для отображения значков:
- Выберите данные.В этом примере это L2: L46 (значения ИСТИНА и ЛОЖЬ).
- Щелкните вкладку "Главная".
- Выберите «Наборы значков» и выберите набор значков.
Не удивляйтесь, когда кажется, что ничего не происходит. Это потому, что значения ИСТИНА и ЛОЖЬ являются текстовыми. В этом случае очистите формат набора значков, потому что он появится позже, когда вы будете ссылаться на форматированные значения. Чтобы очистить правило, повторите шаги с 1 по 2 выше. Выберите «Очистить правила», а затем выберите «Очистить правила из выбранных ячеек».
Поскольку текстовые значения не работают, давайте попробуем промежуточное значение. Вставьте два столбца справа от L: Доступно и ABS (). Затем заполните оба столбца функцией ABS (), чтобы оценить значения ИСТИНА и ЛОЖЬ в столбце L. Не позволяйте включению столбца N сбивать вас с толку. Техника в этом не нуждается, но я подумал, что будет полезно показать абсолютные значения в стороне от значков (позже).
Теперь выберите M2: M46 и повторите предыдущий процесс. На этот раз Excel отображает значки, но не значки, которые вы могли ожидать.Визуально красные значки x сообщают пользователю, что элемент недоступен. К сожалению, они не представляют данные точно. В этом случае значение FALSE в столбце L означает, что данные , а не были прекращены, поэтому доступно.
Знание ваших данных ничем не заменит. Excel отображает соответствующие значки, но вы можете полностью упустить то, что эти значки не отражают назначение данных.
Использовать условное форматирование
Есть фикс.Наборы значков основаны на условном форматировании - просто измените правило по умолчанию следующим образом:
- Выберите диапазон (M2: M46).
- Щелкните вкладку "Главная".
- Щелкните раскрывающееся меню «Условное форматирование» в группе «Стили».
- Выберите «Управление правилами».
- Выберите правило в списке и нажмите «Изменить правило». Условные значения по умолчанию - 67 и 33. Нам нужно их изменить.
- Щелкните Обратный порядок значков. Не пропускайте этот шаг, иначе методика не сработает.
- Измените значение красного значка x с 67 на 1.
- Измените значение желтого восклицательного значка с 33 на 1.
- Не беспокойтесь о значении зеленой галочки - Excel обновит его автоматически в соответствии с новыми настройками.
- Установите флажок «Показать только значок».
- Дважды щелкните OK. Оно работает!
Рассмотрим условные правила:
- Если значение больше или равно 1, Excel отображает красный крестик.(Этот значок соответствует ИСТИННЫМ значениям в столбце L; данный элемент больше не выпускается.)
- Если значение меньше единицы и больше или равно 1, Excel отображает желтый восклицательный знак. Фактически, мы прекратили работу этой модели - она никогда не сможет удовлетворить обоим условиям.
- Если значение меньше 1, Excel отображает зеленую галочку. (Этот значок означает ЛОЖЬ в столбце L; выпуск данного элемента не прекращен.)
При изменении настроек последний в работе не видел - просто пришлось мне поверить.Если вы снова откроете это диалоговое окно, вы увидите, что Excel автоматически обновил третье и последнее условие. Этот метод основан на большом количестве внутренних преобразований. Это может отлично сработать или создать полный беспорядок.
Как вы можете видеть ниже, наборы значков работают не только с любыми значениями. Функция ABS () работает, потому что она преобразует текстовые значения ЛОЖЬ И ИСТИНА, но не может преобразовать только любое текстовое значение. Кроме того, если вы введете числовое значение, отличное от 1 или 0, вы получите неожиданные результаты.Правило набора значков работает, вы только что ввели недопустимые данные.

 Также доступны вложенные свойства для этого слоя:
Также доступны вложенные свойства для этого слоя: 