Что такое индуктивное сопротивление. Как рассчитать индуктивное сопротивление катушки. От чего зависит величина индуктивного сопротивления. В каких единицах измеряется индуктивное сопротивление.
Что такое индуктивное сопротивление
Индуктивное сопротивление — это сопротивление, которое оказывает катушка индуктивности переменному току. В отличие от активного сопротивления, индуктивное сопротивление не приводит к потерям энергии в виде тепла. Вместо этого энергия периодически запасается в магнитном поле катушки и возвращается обратно в цепь.
Величина индуктивного сопротивления зависит от двух факторов:
- Индуктивности катушки L (в генри)
- Частоты переменного тока f (в герцах)
Чем больше индуктивность катушки и выше частота тока, тем больше индуктивное сопротивление.
Формула для расчета индуктивного сопротивления
Индуктивное сопротивление XL рассчитывается по формуле:
XL = 2πfL
где:
- XL — индуктивное сопротивление (Ом)
- f — частота переменного тока (Гц)
- L — индуктивность катушки (Гн)
- π ≈ 3,14
Из формулы видно, что индуктивное сопротивление прямо пропорционально частоте и индуктивности.

Единицы измерения индуктивного сопротивления
Индуктивное сопротивление измеряется в омах (Ом), как и обычное активное сопротивление. Однако для обозначения индуктивного сопротивления используется символ XL, чтобы отличать его от активного сопротивления R.
Зависимость индуктивного сопротивления от частоты
При увеличении частоты переменного тока индуктивное сопротивление возрастает. Это происходит из-за того, что при более высокой частоте магнитное поле катушки изменяется быстрее, вызывая большую ЭДС самоиндукции.
Зависимость индуктивного сопротивления от частоты можно представить графически:
«` «`Как видно из графика, при нулевой частоте (постоянный ток) индуктивное сопротивление равно нулю. При увеличении частоты оно возрастает по экспоненте.
Индуктивное сопротивление на постоянном токе
Для постоянного тока индуктивное сопротивление катушки равно нулю. Это объясняется тем, что при постоянном токе магнитное поле катушки не изменяется, следовательно, не возникает ЭДС самоиндукции, препятствующая току.

На практике это означает, что катушка индуктивности на постоянном токе ведет себя как короткое замыкание (если пренебречь активным сопротивлением обмотки).
Сравнение индуктивного и активного сопротивления
Хотя индуктивное и активное сопротивление измеряются в одних единицах (омах), между ними есть важные различия:
- Активное сопротивление не зависит от частоты, а индуктивное — зависит
- На активном сопротивлении происходит необратимое преобразование электрической энергии в тепловую, а на индуктивном — обратимое преобразование в энергию магнитного поля
- Ток через активное сопротивление совпадает по фазе с напряжением, а через индуктивное — отстает на 90°
Применение понятия индуктивного сопротивления
Понятие индуктивного сопротивления широко используется в электротехнике и радиотехнике для анализа цепей переменного тока. Вот некоторые примеры применения:
- Расчет импеданса (полного сопротивления) цепей переменного тока
- Проектирование фильтров и резонансных контуров
- Анализ работы трансформаторов и электрических машин
- Согласование импедансов в линиях связи
Как измерить индуктивное сопротивление
Измерить индуктивное сопротивление можно следующими способами:
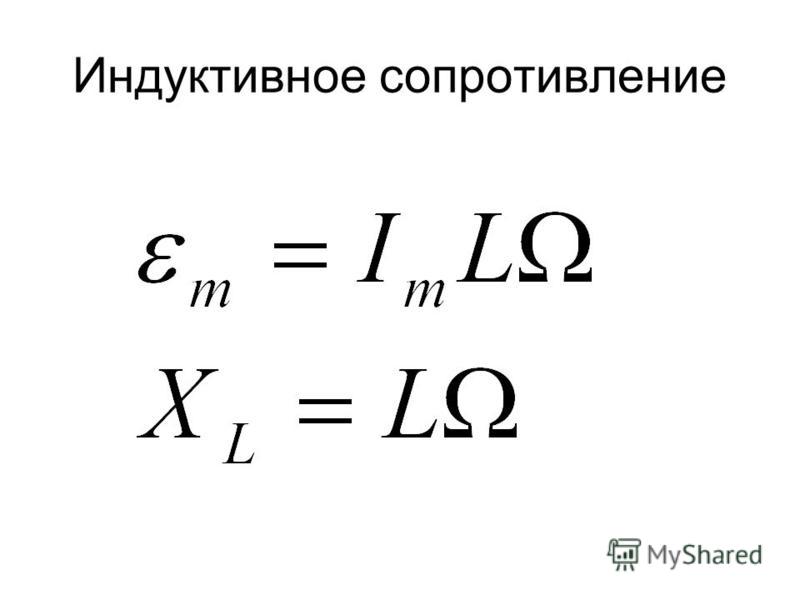
- Расчетным методом, зная индуктивность катушки и частоту тока
- С помощью RLC-метра, который напрямую измеряет импеданс
- Методом вольтметра-амперметра на переменном токе
Рассмотрим последний метод подробнее. Для измерения индуктивного сопротивления катушки нужно:
- Подключить катушку к источнику переменного напряжения известной частоты
- Измерить напряжение на катушке (U) и ток через нее (I)
- Рассчитать индуктивное сопротивление по формуле: XL = U / I
Важно учесть, что этот метод дает точные результаты только для идеальной катушки без активного сопротивления. На практике нужно учитывать и активную составляющую.
Индуктивное сопротивление в цепях переменного тока
В цепях переменного тока индуктивное сопротивление играет важную роль. Оно влияет на:
- Величину тока в цепи
- Сдвиг фаз между током и напряжением
- Распределение напряжений на элементах цепи
- Резонансные явления
Рассмотрим простейшую цепь, состоящую из источника переменного напряжения и катушки индуктивности:
«` «`В такой цепи ток будет определяться по закону Ома для цепи переменного тока:

I = U / XL
где U — действующее значение напряжения источника, а XL — индуктивное сопротивление катушки на частоте источника.
Влияние индуктивного сопротивления на фазу тока
Одно из важных свойств индуктивного сопротивления — это создание сдвига фаз между током и напряжением. В цепи с чисто индуктивным сопротивлением ток отстает от напряжения на 90° (или π/2 радиан).
Это можно проиллюстрировать с помощью векторной диаграммы:
«` «`- Синий вектор представляет напряжение
- Красный вектор представляет ток
- Угол между векторами составляет 90°
Этот сдвиг фаз объясняется тем, что в индуктивности энергия периодически запасается в магнитном поле и возвращается обратно в цепь, что приводит к задержке тока относительно напряжения.
Заключение
Индуктивное сопротивление — важное понятие в теории цепей переменного тока. Оно характеризует противодействие катушки индуктивности переменному току и зависит от частоты этого тока. Понимание природы и свойств индуктивного сопротивления необходимо для анализа и проектирования различных электрических и электронных устройств.

Реактивное сопротивление — Википедия
В электрических и электронных системах реактивное сопротивление (также реактанс) — это сопротивление элемента схемы вызванное изменением тока или напряжения из-за индуктивности или ёмкости этого элемента. Понятие реактивного сопротивления аналогично электрическому сопротивлению, но оно несколько отличается в деталях.
В векторном анализе реактивное сопротивление используется для вычисления амплитудных и фазовых изменений синусоидального переменного тока, проходящего через элемент цепи. Обозначается символом X{\displaystyle \scriptstyle {X}}. Идеальный резистор имеет нулевое реактивное сопротивление, тогда как идеальные индуктивности и конденсаторы имеют нулевое сопротивление — то есть, реагируют на ток только по наличию реактивного сопротивления. Величина реактивного сопротивления индуктора увеличивается пропорционально увеличению частоты, в то время как величина реактивного сопротивления конденсатора уменьшается пропорционально увеличению частоты.
Конденсатор состоит из двух проводников, разделённых изолятором, также известным как диэлектрик.
Ёмкостное сопротивление
В литературе существует два варианта определения реактивного сопротивления для конденсатора. Одним из них является использование единого понятия реактивного сопротивления в качестве мнимой части полного сопротивления, и, в этом случае, реактивное сопротивление конденсатора является отрицательным числом[1][2][3]:
- XC=−1ωC=−12πfC{\displaystyle X_{C}=-{\frac {1}{\omega C}}=-{\frac {1}{2\pi fC}}}.
Другой выбор состоит в том, чтобы определить ёмкостное сопротивление как положительное число[4][5][6],
- XC=1ωC=12πfC{\displaystyle X_{C}={\frac {1}{\omega C}}={\frac {1}{2\pi fC}}}.
В этом случае нужно помнить о добавлении отрицательного знака к импедансу то есть Zc=−jXc{\displaystyle Z_{c}=-jX_{c}}.
На низких частотах конденсатор эквивалентен разомкнутой цепи, если в диэлектрике ток не течёт.
Постоянное напряжение, приложенное к конденсатору, вызывает накопление положительного заряда на одной обкладке и накопление отрицательного заряда на другой обкладке; электрическое поле за счёт накопленного заряда является источником который противодействует току. Когда потенциал, связанный с зарядом, точно уравновешивает приложенное напряжение, ток падает до нуля.
Приводимый в действие источником переменного тока (идеальный источник переменного тока), конденсатор будет накапливать только ограниченное количество заряда, прежде чем разность потенциалов изменит полярность и заряд вернётся к источнику. Чем выше частота, тем меньше накапливается заряд и тем меньше противодействие току.
Индуктивное реактивное сопротивление — это свойство, проявляемое индуктивностью, и индуктивное реактивное сопротивление существует благодаря тому, что электрический ток создаёт вокруг него магнитное поле. В контексте цепи переменного тока (хотя эта концепция применяется при любом изменении тока), это магнитное поле постоянно изменяется в результате изменения тока, который меняется во времени. Именно это изменение магнитного поля создаёт другой электрический ток в том же проводе (противо-ЭДС), в направлении, противоположном потоку тока, изначально ответственного за создание магнитного поля. Это явление известно как закон Ленца. Следовательно,
Для идеальной катушки индуктивности в цепи переменного тока сдерживающее влияние на изменение протекания тока приводит к задержке или сдвигу фаз переменного тока относительно переменного напряжения. В частности, идеальная индуктивность (без сопротивления) вызовет отставание тока от напряжения на четверть цикла или на 90°.
В электроэнергетических системах индуктивное реактивное сопротивление (и ёмкостное реактивное сопротивление, однако индуктивное реактивное сопротивление более распространено) может ограничивать пропускную способность линии электропередач переменного тока, поскольку мощность не передаётся полностью, когда напряжение и ток находятся в противофазе (подробно описано выше). То есть ток будет течь для противофазной системы, однако реальная мощность в определённые моменты времени не будет передаваться, потому что будут моменты, в течение которых мгновенный ток будет положительным, а мгновенное напряжение отрицательным, или наоборот, подразумевая отрицательную мощность передачи. Следовательно, реальная работа не выполняется, когда передача энергии является «отрицательной». Однако ток всё ещё течёт, даже когда система находится в противофазе, что приводит к нагреву линий электропередачи из-за протекания тока. Следовательно, линии электропередачи могут только сильно нагреваться (иначе они физически сильно прогибаются из-за тепла, расширяющего металлические линии электропередачи), поэтому операторы линий электропередачи имеют «потолок» в отношении величины тока, который может протекать через данную линию, и чрезмерное индуктивное сопротивление ограничивает мощность линии. Поставщики электроэнергии используют конденсаторы для сдвига фазы и минимизации потерь в зависимости от схемы использования.
Индуктивное реактивное сопротивление XL{\displaystyle \scriptstyle {X_{L}}} пропорционально частоте синусоидального сигнала f{\displaystyle \scriptstyle {f}} и индуктивности L{\displaystyle \scriptstyle {L}}, которая зависит от геометрических размеров и формы индуктивности.
- XL=ωL=2πfL{\displaystyle X_{L}=\omega L=2\pi fL}
Средний ток, протекающий через индуктивность L{\displaystyle \scriptstyle {L}} последовательно с синусоидальным источником переменного напряжения среднеквадратичной амплитуды A{\displaystyle \scriptstyle {A}} и частоты f{\displaystyle \scriptstyle {f}} равен:
- IL=AωL=A2πfL{\displaystyle I_{L}={A \over \omega L}={A \over 2\pi fL}}.
Поскольку прямоугольная волна (источник прямоугольного сигнала) имеет несколько амплитуд на синусоидальных гармониках (согласно теореме Фурье), средний ток, протекающий через индуктивность L{\displaystyle \scriptstyle {L}} последовательно с прямоугольным источником переменного напряжения среднеквадратичной амплитуды A{\displaystyle \scriptstyle {A}} и частота f{\displaystyle \scriptstyle {f}} равно:
- IL=Aπ28ωL=Aπ16fL{\displaystyle I_{L}={A\pi ^{2} \over 8\omega L}={A\pi \over 16fL}}
создавая иллюзию как если бы реактивное сопростивление прямоугольной волны на 19 % меньше XL=16πfL{\displaystyle X_{L}={16 \over \pi }fL} , чем реактивное сопротивление синусоидального сигнала с той же частотой:
Любой проводник конечных размеров имеет индуктивность; индуктивность обычно делается из электромагнитных катушек, состоящих из множества витков провода. Согласно закону электромагнитной индукции Фарадея возникает противоэдс E{\displaystyle \scriptstyle {\mathcal {E}}} (ток, противоположный напряжению) в проводнике из-за скорости изменения плотности магнитного потока B{\displaystyle \scriptstyle {B}} через токовую петлю.
- E=−dΦBdt{\displaystyle {\mathcal {E}}=-{{d\Phi _{B}} \over dt}}
А для индуктивности состоящей из N{\displaystyle \scriptstyle N} витков соответственно
- E=−NdΦBdt{\displaystyle {\mathcal {E}}=-N{d\Phi _{B} \over dt}}
Противо-ЭДС — это источник противодействия току. Постоянный ток имеет нулевую скорость изменения и рассматривает катушку индуктивности как обычный проводник (так как она сделано из материала с низким удельным сопротивлением). Переменный ток имеет усреднённую по времени скорость изменения, которая пропорциональна частоте, что вызывает увеличение индуктивного сопротивления с частотой.
Как реактивное сопротивление X{\displaystyle \scriptstyle {X}} так и обычное сопротивление R{\displaystyle \scriptstyle {R}} компоненты импеданса Z{\displaystyle \scriptstyle {Z}}.
- Z=R+jX{\displaystyle Z=R+jX}
где:
Когда и конденсатор и индуктор соединены последовательно в цепь, их вклады к полному импедансу цепи противоположны. Ёмкостное сопротивление XC{\displaystyle \scriptstyle {X_{C}}}, и индуктивное сопротивление XL{\displaystyle \scriptstyle {X_{L}}},
вносят свой вклад в общее реактивное сопротивление X{\displaystyle \scriptstyle {X}} в виде суммы
- X=XL+XC=ωL−1ωC{\displaystyle {X=X_{L}+X_{C}=\omega L-{\frac {1}{\omega C}}}}
где:
- XL{\displaystyle \scriptstyle {X_{L}}} — индуктивное сопротивление, измеряемое в омах;
- XC{\displaystyle \scriptstyle {X_{C}}} — ёмкостное сопротивление, измеряемое в омах;
- ω{\displaystyle \omega } — угловая частота, 2π{\displaystyle 2\pi } умноженная на частоту в Гц.
Отсюда:[3]
- if X>0{\displaystyle \scriptstyle X>0}, то реактанс имеет вид индуктивности;
- if X=0{\displaystyle \scriptstyle X=0}, импеданс чисто реальный;
- if X<0{\displaystyle \scriptstyle X<0}, то реактанс имеет вид ёмкости.
Замечание, в случае определения XL{\displaystyle \scriptstyle {X_{L}}} и XC{\displaystyle \scriptstyle {X_{C}}} как положительный величин, то формула меняет знак на отрицательный:[5]
- X=XL−XC=ωL−1ωC{\displaystyle {X=X_{L}-X_{C}=\omega L-{\frac {1}{\omega C}}}},
но конечное значение одинаково.
Фазовые отношения[править | править код]
Фаза напряжения на чисто реактивном устройстве (конденсатор с бесконечным сопротивлением или индуктивности с нулевым сопротивлением) отстаёт от тока на π/2{\displaystyle \scriptstyle {\pi /2}} радиан для ёмкостного сопротивления и опережает ток на π/2{\displaystyle \scriptstyle {\pi /2}} радиан для индуктивного сопротивления. Без знания сопротивления и реактивного сопротивления невозможно определить соотношение между напряжением и током.
- Z~C=1ωCej(−π2)=j(−1ωC)=jXCZ~L=ωLejπ2=jωL=jXL{\displaystyle {\begin{aligned}{\tilde {Z}}_{C}&={1 \over \omega C}e^{j(-{\pi \over 2})}=j\left({-{\frac {1}{\omega C}}}\right)=jX_{C}\\{\tilde {Z}}_{L}&=\omega Le^{j{\pi \over 2}}=j\omega L=jX_{L}\quad \end{aligned}}}
Для реактивной компоненты синусоидальное напряжение на компоненте находится в квадратуре (разность фаз π/2{\displaystyle \scriptstyle {\pi /2}}) с синусоидальным током через компонент. Компонент попеременно поглощает энергию из контура и затем возвращает энергию в контур, таким образом, чистое реактивное сопротивление не рассеивает мощность.
- Shamieh C. и McComb G., Electronics for Dummies, John Wiley & Sons, 2011.
- Мид Р., Основы электроники, Cengage Learning, 2002.
- Young, Hugh D.; Roger A. Freedman; A. Lewis Ford (2004) [1949]. Сирс и Земанский университет физики (11-е изд.). Сан-Франциско : Эддисон Уэсли . ISBN Young, Hugh D.; Roger A. Freedman; A. Lewis Ford (2004) [1949]. Young, Hugh D.; Roger A. Freedman; A. Lewis Ford (2004) [1949].
- ↑ 1 2 Irwin, D. (2002). Basic Engineering Circuit Analysis, page 274. New York: John Wiley & Sons, Inc.
- ↑ Hayt, W.H., Kimmerly J.E. (2007). Engineering Circuit Analysis, 7th ed., McGraw-Hill, p. 388
- ↑ 1 2 Glisson, T.H. (2011). Introduction to Circuit Analysis and Design, Springer, p. 408
- ↑ Horowitz P., Hill W. (2015). The Art of Electronics, 3rd ed., p. 42
- ↑ 1 2 Hughes E., Hiley J., Brown K., Smith I.McK., (2012). Hughes Electrical and Electronic Technology, 11th edition, Pearson, pp. 237—241
- ↑ Robbins, A.H., Miller W. (2012). Circuit Analysis: Theory and Practice, 5th ed., Cengage Learning, pp. 554—558
ru.wikipedia.org
Индуктивное сопротивление | Формулы и расчеты онлайн
Индуктивность L в электрической цепи вызывает запаздывание тока (см Самоиндукция). Вследствие этого ток достигает максимального значения Im позже напряжения. Если R = 0, приложенное напряжение противоположно индуцированному напряжению:
\[ u = L \frac{di}{dt} = \frac{d}{dt}(LI_{m} \sin(ωt)) \]
отсюда
\[ u = ωLI_{m} \cos(ωt) \]
или
\[ u = ωLI_{m} \sin(ωt + \frac{π}{2}) \]

Индуктивное сопротивление — графики тока и напряжения
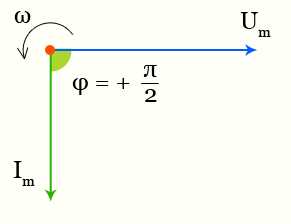
Между напряжением и током возникает разность фаз (сдвиг фаз) равная +π/2.
B цепи переменного тока, содержащей только индуктивность, напряжение опережает ток на π/2 (или Т/4).
Из написанного выше равенства следует, что амплитуда напряжения Um = ωLIm. Сопоставляя это выражение с законом Ома Um = RIm, мы видим, что величина ωL играет роль сопротивления.
Цепь переменного тока, содержащая индуктивность L, обладает сопротивлением переменному току; оно называется индуктивным сопротивлением XL.
Единица СИ индуктивного сопротивления: [XL] = Ом.
Если
| XL | индуктивное сопротивление цепи переменного тока, | Ом |
|---|---|---|
| L | индуктивность цепи, | Генри |
| ω = 2πf | круговая частота переменного тока, | Радиан/Секунда |
то имеем
\[ X_{L} = ωL \]
При наличии в цепи только индуктивного сопротивления сила тока определяется выражением
\[ I = \frac{U}{ωL} \]
Вычислить, найти индуктивное сопротивление
В помощь студенту
Индуктивное сопротивление |
стр. 686 |
|---|
www.fxyz.ru
Индуктивное сопротивление катушки — Основы электроники
Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением.
Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.
Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.
При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь. Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).
Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.
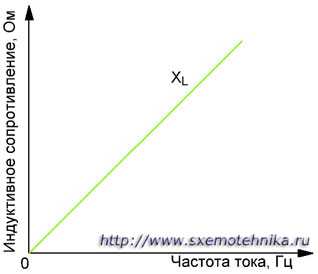
Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.
Индуктивное сопротивление обозначается буквой XL и измеряется в омах.
Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле
XL=2π• f •L
где XL — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн
Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так:
XL=ω•L
Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.
Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
www.sxemotehnika.ru
Индуктивное реактивное сопротивление: формулы, схемы
В данной статье мы подробно поговорим про индуктивное сопротивление, реактивное сопротивление и треугольники напряжения, сопротивления и силы.
Введение
Итак, мы рассмотрели поведение индукторов, подключенных к источникам постоянного тока, и, надеюсь, теперь мы знаем, что когда на индуктор подается постоянное напряжение, рост тока через него происходит не мгновенно, а определяется индуктором, индуцированным самим индуктором или обратным значением ЭДС.
Также мы видели, что ток индукторов продолжает расти, пока не достигнет своего максимального установившегося состояния после пяти постоянных времени. Максимальный ток, текущий через индукционную катушку ограничиваются только резистивной частью катушек обмотки в омах, и как мы знаем из закона Ома, это определяется отношением напряжения к току V / R .
Когда переменное напряжение подается на катушку индуктивности, поток тока через него ведет себя совершенно иначе, чем при приложении постоянного напряжения. Эффект синусоидального питания приводит к разности фаз между напряжением и формами тока. Теперь в цепи переменного тока противодействие току, протекающему через обмотки катушек, зависит не только от индуктивности катушки, но и от частоты сигнала переменного тока.
Сопротивление току, протекающему через катушку в цепи переменного тока, определяется сопротивлением переменного тока, более известным как полное сопротивление (Z) цепи. Но сопротивление всегда связано с цепями постоянного тока, поэтому, чтобы отличить сопротивление постоянного тока от сопротивления переменного тока, обычно используется термин «реактивное сопротивление» .
Как и сопротивление, значение реактивного сопротивления также измеряется в омах, но ему присваивается символ X (заглавная буква «X»), чтобы отличить его от чисто резистивного значения.
Поскольку интересующий нас компонент является индуктором, реактивное сопротивление индуктора поэтому называется «Индуктивное реактивное сопротивление». Другими словами, электрическое сопротивление индуктивности при использовании в цепи переменного тока называется индуктивным сопротивлением .
Индуктивное сопротивление, которому дается символ X L , является свойством в цепи переменного тока, которое противодействует изменению тока. В наших уроках о конденсаторах в цепях переменного тока мы видели, что в чисто емкостной цепи ток I C «опережает» напряжение на 90 o . В чисто индуктивной цепи переменного тока верно обратное: ток I L отстает от напряжения на 90 o или (π / 2 рад).
Схема индуктивности переменного тока

В приведенной выше чисто индуктивной цепи индуктор подключен непосредственно через напряжение питания переменного тока. Когда напряжение питания увеличивается и уменьшается с частотой, самоиндуцированная обратная ЭДС также увеличивается и уменьшается в катушке по отношению к этому изменению.
Мы знаем, что эта самоиндуцированная ЭДС прямо пропорциональна скорости изменения тока через катушку и имеет наибольшее значение при переходе напряжения питания от положительного полупериода к отрицательному полупериоду или наоборот в точках 0о и 180о вдоль синусоиды.
Следовательно, минимальная скорость изменения напряжения возникает, когда синусоида переменного тока пересекается при своем максимальном или минимальном пиковом уровне напряжения. В этих положениях в цикле максимальный или минимальный токи протекают через цепь индуктора, и это показано ниже.
Векторная диаграмма индуктора переменного тока
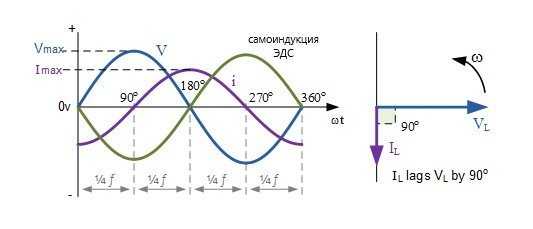
Эти формы напряжения и тока показывают, что для чисто индуктивной цепи ток отстает от напряжения на 90 o . Также можно сказать, что напряжение опережает ток на 90 o . В любом случае общее выражение заключается в том, что ток отстает, как показано на векторной диаграмме. Здесь вектор тока и вектор напряжения показаны смещенными на 90 o . Ток отстает от напряжения .
Мы можем также написать это заявление как, V L = 0 ö и I L = -90 о по отношению к напряжению, V L . Если форма волны напряжения классифицируется как синусоида, то ток I L можно классифицировать как отрицательный косинус, и мы можем определить значение тока в любой момент времени как:
Где:
ω в радианах в секунду, а
t в секундах.
Поскольку ток всегда отстает от напряжения на 90 o в чисто индуктивной цепи, мы можем найти фазу тока, зная фазу напряжения или наоборот. Так что если мы знаем значение V L , то I L должно отставать на 90 o . Аналогичным образом, если мы знаем значение I L, то V L, следовательно, должно опережать на 90 o . Затем это отношение напряжения к току в индуктивном контуре будет производить уравнение, определяющее индуктивное сопротивление Х L катушки.
Мы можем переписать уравнение для индуктивного сопротивления в более привычную форму, которая использует обычную частоту питания вместо угловой частоты в радианах ω и это будет выглядеть так:
Где:
ƒ — частота,
L — индуктивность катушки и
2πƒ = ω .
Из приведенного выше уравнения для индуктивного реактивного сопротивления можно видеть, что, если увеличить частоту, либо индуктивность, общее значение индуктивного реактивного сопротивления также увеличится. Когда частота приближается к бесконечности, реактивное сопротивление индукторов также увеличивается до бесконечности, действуя как разомкнутая цепь.
Однако, когда частота приближается к нулю или постоянному току, реактивное сопротивление индукторов будет уменьшаться до нуля, действуя как короткое замыкание. Это означает, что индуктивное сопротивление «пропорционально» частоте.
Другими словами, индуктивное реактивное сопротивление увеличивается с частотой, в результате чего X L будет небольшим на низких частотах, а X L будет высоким на высоких частотах, что продемонстрировано на графике ниже.
Индуктивное сопротивление от частоты

Затем мы видим, что при постоянном токе индуктор имеет нулевое реактивное сопротивление (короткое замыкание), на высоких частотах индуктор имеет бесконечное реактивное сопротивление (разомкнутая цепь).
Питание от сети переменного тока серии LR
До сих пор мы рассматривали чисто индуктивную катушку, но невозможно иметь чистую индуктивность, поскольку все катушки, реле или соленоиды будут иметь определенное сопротивление, независимо от того, насколько мало связано с витками используемого провода. Тогда мы можем рассматривать нашу простую катушку как последовательное сопротивление с индуктивностью (LR).
В цепи переменного тока, которая содержит как индуктивность L и сопротивление R, напряжение V будет векторная сумма двух компонентов напряжения, V R и V L . Это означает, что ток, протекающий через катушку еще будет отставать от напряжения, но на величину меньше чем 90 ö в зависимости от значений V R и V L .
Новый фазовый угол между напряжением и током известен как фазовый угол цепи и обозначается греческим символом фи, Φ .
Чтобы получить векторную диаграмму зависимости между напряжением и током, необходимо найти эталонный или общий компонент. В последовательно соединенной цепи RL ток является общим, так как один и тот же ток течет через каждый компонент. Вектор этой эталонной величины обычно рисуется горизонтально слева направо.
Из наших руководств о резисторах и конденсаторах, мы знаем, что ток и напряжение в цепи переменного резистивного тока, оба «в фазе» и, следовательно, вектор V R рисуется с наложением на текущую или контрольную линию.
Из вышесказанного также известно, что ток «отстает» от напряжения в чисто индуктивной цепи и, следовательно, вектор V L отображается на 90 o перед опорным током и в том же масштабе, что и V R, это показано ниже.
Цепь переменного тока серии LR
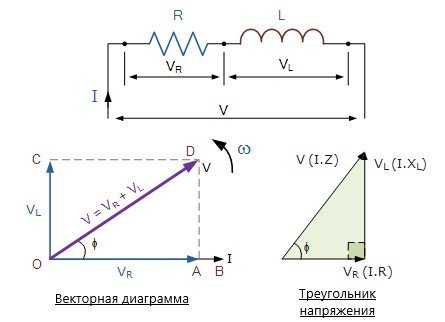
На приведенной выше векторной диаграмме видно, что луч OB представляет текущую опорную линию, луч OA — это напряжение резистивного компонента, которое в фазе с током, луч OC показывает индуктивное напряжение, которое составляет 90 o перед током, поэтому видно, что ток отстает от напряжения на 90 o , луч OD дает нам результирующее или питающее напряжение в цепи. Треугольник напряжения выводится из теоремы Пифагора и имеет вид:
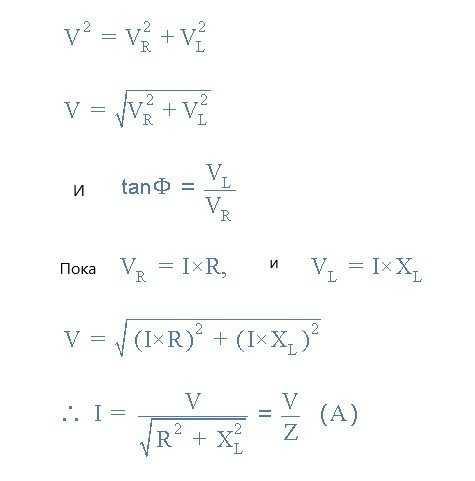
Треугольник сопротивления
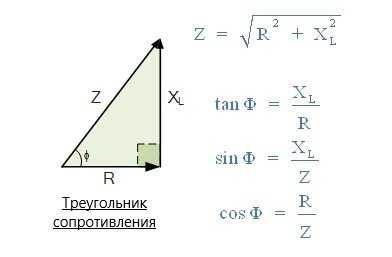
В цепи постоянного тока отношение напряжения к току называется сопротивлением. Однако в цепи переменного тока это отношение известно как полное сопротивление Z с единицами измерения в омах. Полное сопротивление — это полное сопротивление току в «цепи переменного тока», содержащее как сопротивление, так и индуктивное сопротивление.
Если мы разделим стороны треугольника напряжения выше на ток, получим еще один треугольник, стороны которого представляют сопротивление, реактивное сопротивление и полное сопротивление катушки. Этот новый треугольник называется «Треугольник сопротивления».
Силовой треугольник индуктора переменного тока
Существует еще один тип конфигурации треугольника, который мы можем использовать для индуктивной цепи, и это «силовой треугольник». Мощность в индуктивной цепи называется реактивной мощностью или вольт-амперной реактивной, символ Var, который измеряется в вольт-амперах. В цепи переменного тока серии RL ток отстает от напряжения питания на угол Φ o .
В чисто индуктивной цепи переменного тока ток будет сдвинут по фазе на 90 o к напряжению питания. Таким образом, общая реактивная мощность, потребляемая катушкой, будет равна нулю, так как любая потребляемая мощность компенсируется генерируемой самоиндуцированной ЭДС-мощностью. Другими словами, полезная мощность в ваттах, потребляемая чистым индуктором в конце одного полного цикла, равна нулю, так как энергия берется из источника и возвращается к нему.
Реактивная мощность ( Q ) катушки может быть задана как: I 2 x X L (аналогично I 2 R в цепи постоянного тока). Затем три стороны силового треугольника в цепи переменного тока представлены кажущейся мощностью ( S ), реальной мощностью ( P ) и реактивной мощностью ( Q ), как показано.
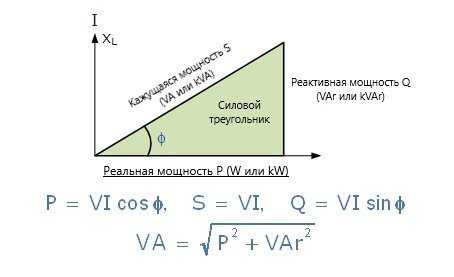
Обратите внимание, что данный индуктор или катушка будет потреблять мощность в ваттах из — за сопротивления обмоток, создающих сопротивление Z.
meanders.ru
Сопротивление индуктивное Википедия
В электрических и электронных системах реактивное сопротивление (также реактанс) — это сопротивление элемента схемы вызванное изменением тока или напряжения из-за индуктивности или ёмкости этого элемента. Понятие реактивного сопротивления аналогично электрическому сопротивлению, но оно несколько отличается в деталях.
В векторном анализе реактивное сопротивление используется для вычисления амплитудных и фазовых изменений синусоидального переменного тока, проходящего через элемент цепи. Обозначается символом X{\displaystyle \scriptstyle {X}}. Идеальный резистор имеет нулевое реактивное сопротивление, тогда как идеальные индуктивности и конденсаторы имеют нулевое сопротивление — то есть, реагируют на ток только по наличию реактивного сопротивления. Величина реактивного сопротивления индуктора увеличивается пропорционально увеличению частоты, в то время как величина реактивного сопротивления конденсатора уменьшается пропорционально увеличению частоты.
Ёмкостное сопротивление
Конденсатор состоит из двух проводников, разделённых изолятором, также известным как диэлектрик.
Ёмкостное сопротивление — это сопротивление изменению напряжения на элементе. Ёмкостное сопротивление XC{\displaystyle \scriptstyle {X_{C}}} обратно пропорционально частоте сигнала f{\displaystyle \scriptstyle {f}} (или угловой частоты ω) и ёмкости C{\displaystyle \scriptstyle {C}}[1].
В литературе существует два варианта определения реактивного сопротивления для конденсатора. Одним из них является использование единого понятия реактивного сопротивления в качестве мнимой части полного сопротивления, и, в этом случае, реактивное сопротивление конденсатора является отрицательным числом[1][2][3]:
- XC=−1ωC=−12πfC{\displaystyle X_{C}=-{\frac {1}{\omega C}}=-{\frac {1}{2\pi fC}}}.
Другой выбор состоит в том, чтобы определить ёмкостное сопротивление как положительное число[4][5][6],
- XC=1ωC=12πfC{\displaystyle X_{C}={\frac {1}{\omega C}}={\frac {1}{2\pi fC}}}.
В этом случае нужно помнить о добавлении отрицательного знака к импедансу то есть Zc=−jXc{\displaystyle Z_{c}=-jX_{c}}.
На низких частотах конденсатор эквивалентен разомкнутой цепи, если в диэлектрике ток не течёт.
Постоянное напряжение, приложенное к конденсатору, вызывает накопление положительного заряда на одной обкладке и накопление отрицательного заряда на другой обкладке; электрическое поле за счёт накопленного заряда является источником который противодействует току. Когда потенциал, связанный с зарядом, точно уравновешивает приложенное напряжение, ток падает до нуля.
Приводимый в действие источником переменного тока (идеальный источник переменного тока), конденсатор будет накапливать только ограниченное количество заряда, прежде чем разность потенциалов изменит полярность и заряд вернётся к источнику. Чем выше частота, тем меньше накапливается заряд и тем меньше противодействие току.
Индуктивное сопротивление
Индуктивное реактивное сопротивление — это свойство, проявляемое индуктивностью, и индуктивное реактивное сопротивление существует благодаря тому, что электрический ток создаёт вокруг него магнитное поле. В контексте цепи переменного тока (хотя эта концепция применяется при любом изменении тока), это магнитное поле постоянно изменяется в результате изменения тока, который меняется во времени. Именно это изменение магнитного поля создаёт другой электрический ток в том же проводе (противо-ЭДС), в направлении, противоположном потоку тока, изначально ответственного за создание магнитного поля. Это явление известно как закон Ленца. Следовательно, индуктивное сопротивление — это противодействие изменению тока через элемент.
Для идеальной катушки индуктивности в цепи переменного тока сдерживающее влияние на изменение протекания тока приводит к задержке или сдвигу фаз переменного тока относительно переменного напряжения. В частности, идеальная индуктивность (без сопротивления) вызовет отставание тока от напряжения на четверть цикла или на 90°.
В электроэнергетических системах индуктивное реактивное сопротивление (и ёмкостное реактивное сопротивление, однако индуктивное реактивное сопротивление более распространено) может ограничивать пропускную способность линии электропередач переменного тока, поскольку мощность не передаётся полностью, когда напряжение и ток находятся в противофазе (подробно описано выше). То есть ток будет течь для противофазной системы, однако реальная мощность в определённые моменты времени не будет передаваться, потому что будут моменты, в течение которых мгновенный ток будет положительным, а мгновенное напряжение отрицательным, или наоборот, подразумевая отрицательную мощность передачи. Следовательно, реальная работа не выполняется, когда передача энергии является «отрицательной». Однако ток всё ещё течёт, даже когда система находится в противофазе, что приводит к нагреву линий электропередачи из-за протекания тока. Следовательно, линии электропередачи могут только сильно нагреваться (иначе они физически сильно прогибаются из-за тепла, расширяющего металлические линии электропередачи), поэтому операторы линий электропередачи имеют «потолок» в отношении величины тока, который может протекать через данную линию, и чрезмерное индуктивное сопротивление ограничивает мощность линии. Поставщики электроэнергии используют конденсаторы для сдвига фазы и минимизации потерь в зависимости от схемы использования.
Индуктивное реактивное сопротивление XL{\displaystyle \scriptstyle {X_{L}}} пропорционально частоте синусоидального сигнала f{\displaystyle \scriptstyle {f}} и индуктивности L{\displaystyle \scriptstyle {L}}, которая зависит от геометрических размеров и формы индуктивности.
- XL=ωL=2πfL{\displaystyle X_{L}=\omega L=2\pi fL}
Средний ток, протекающий через индуктивность L{\displaystyle \scriptstyle {L}} последовательно с синусоидальным источником переменного напряжения среднеквадратичной амплитуды A{\displaystyle \scriptstyle {A}} и частоты f{\displaystyle \scriptstyle {f}} равен:
- IL=AωL=A2πfL{\displaystyle I_{L}={A \over \omega L}={A \over 2\pi fL}}.
Поскольку прямоугольная волна (источник прямоугольного сигнала) имеет несколько амплитуд на синусоидальных гармониках (согласно теореме Фурье), средний ток, протекающий через индуктивность L{\displaystyle \scriptstyle {L}} последовательно с прямоугольным источником переменного напряжения среднеквадратичной амплитуды A{\displaystyle \scriptstyle {A}} и частота f{\displaystyle \scriptstyle {f}} равно:
- IL=Aπ28ωL=Aπ16fL{\displaystyle I_{L}={A\pi ^{2} \over 8\omega L}={A\pi \over 16fL}}
создавая иллюзию как если бы реактивное сопростивление прямоугольной волны на 19 % меньше XL=16πfL{\displaystyle X_{L}={16 \over \pi }fL} , чем реактивное сопротивление синусоидального сигнала с той же частотой:
Любой проводник конечных размеров имеет индуктивность; индуктивность обычно делается из электромагнитных катушек, состоящих из множества витков провода. Согласно закону электромагнитной индукции Фарадея возникает противоэдс E{\displaystyle \scriptstyle {\mathcal {E}}} (ток, противоположный напряжению) в проводнике из-за скорости изменения плотности магнитного потока B{\displaystyle \scriptstyle {B}} через токовую петлю.
- E=−dΦBdt{\displaystyle {\mathcal {E}}=-{{d\Phi _{B}} \over dt}}
А для индуктивности состоящей из N{\displaystyle \scriptstyle N} витков соответственно
- E=−NdΦBdt{\displaystyle {\mathcal {E}}=-N{d\Phi _{B} \over dt}}
Противо-ЭДС — это источник противодействия току. Постоянный ток имеет нулевую скорость изменения и рассматривает катушку индуктивности как обычный проводник (так как она сделано из материала с низким удельным сопротивлением). Переменный ток имеет усреднённую по времени скорость изменения, которая пропорциональна частоте, что вызывает увеличение индуктивного сопротивления с частотой.
Полное сопротивление
Как реактивное сопротивление X{\displaystyle \scriptstyle {X}} так и обычное сопротивление R{\displaystyle \scriptstyle {R}} компоненты импеданса Z{\displaystyle \scriptstyle {Z}}.
- Z=R+jX{\displaystyle Z=R+jX}
где:
Когда и конденсатор и индуктор соединены последовательно в цепь, их вклады к полному импедансу цепи противоположны. Ёмкостное сопротивление XC{\displaystyle \scriptstyle {X_{C}}}, и индуктивное сопротивление XL{\displaystyle \scriptstyle {X_{L}}},
вносят свой вклад в общее реактивное сопротивление X{\displaystyle \scriptstyle {X}} в виде суммы
- X=XL+XC=ωL−1ωC{\displaystyle {X=X_{L}+X_{C}=\omega L-{\frac {1}{\omega C}}}}
где:
- XL{\displaystyle \scriptstyle {X_{L}}} — индуктивное сопротивление, измеряемое в омах;
- XC{\displaystyle \scriptstyle {X_{C}}} — ёмкостное сопротивление, измеряемое в омах;
- ω{\displaystyle \omega } — угловая частота, 2π{\displaystyle 2\pi } умноженная на частоту в Гц.
Отсюда:[3]
- if X>0{\displaystyle \scriptstyle X>0}, то реактанс имеет вид индуктивности;
- if X=0{\displaystyle \scriptstyle X=0}, импеданс чисто реальный;
- if X<0{\displaystyle \scriptstyle X<0}, то реактанс имеет вид ёмкости.
Замечание, в случае определения XL{\displaystyle \scriptstyle {X_{L}}} и XC{\displaystyle \scriptstyle {X_{C}}} как положительный величин, то формула меняет знак на отрицательный:[5]
- X=XL−XC=ωL−1ωC{\displaystyle {X=X_{L}-X_{C}=\omega L-{\frac {1}{\omega C}}}},
но конечное значение одинаково.
Фазовые отношения
Фаза напряжения на чисто реактивном устройстве (конденсатор с бесконечным сопротивлением или индуктивности с нулевым сопротивлением) отстаёт от тока на π/2{\displaystyle \scriptstyle {\pi /2}} радиан для ёмкостного сопротивления и опережает ток на π/2{\displaystyle \scriptstyle {\pi /2}} радиан для индуктивного сопротивления. Без знания сопротивления и реактивного сопротивления невозможно определить соотношение между напряжением и током.
- Z~C=1ωCej(−π2)=j(−1ωC)=jXCZ~L=ωLejπ2=jωL=jXL{\displaystyle {\begin{aligned}{\tilde {Z}}_{C}&={1 \over \omega C}e^{j(-{\pi \over 2})}=j\left({-{\frac {1}{\omega C}}}\right)=jX_{C}\\{\tilde {Z}}_{L}&=\omega Le^{j{\pi \over 2}}=j\omega L=jX_{L}\quad \end{aligned}}}
Для реактивной компоненты синусоидальное напряжение на компоненте находится в квадратуре (разность фаз π/2{\displaystyle \scriptstyle {\pi /2}}) с синусоидальным током через компонент. Компонент попеременно поглощает энергию из контура и затем возвращает энергию в контур, таким образом, чистое реактивное сопротивление не рассеивает мощность.
Примечания
- Shamieh C. и McComb G., Electronics for Dummies, John Wiley & Sons, 2011.
- Мид Р., Основы электроники, Cengage Learning, 2002.
- Young, Hugh D.; Roger A. Freedman; A. Lewis Ford (2004) [1949]. Сирс и Земанский университет физики (11-е изд.). Сан-Франциско : Эддисон Уэсли . ISBN Young, Hugh D.; Roger A. Freedman; A. Lewis Ford (2004) [1949]. Young, Hugh D.; Roger A. Freedman; A. Lewis Ford (2004) [1949].
- ↑ 1 2 Irwin, D. (2002). Basic Engineering Circuit Analysis, page 274. New York: John Wiley & Sons, Inc.
- ↑ Hayt, W.H., Kimmerly J.E. (2007). Engineering Circuit Analysis, 7th ed., McGraw-Hill, p. 388
- ↑ 1 2 Glisson, T.H. (2011). Introduction to Circuit Analysis and Design, Springer, p. 408
- ↑ Horowitz P., Hill W. (2015). The Art of Electronics, 3rd ed., p. 42
- ↑ 1 2 Hughes E., Hiley J., Brown K., Smith I.McK., (2012). Hughes Electrical and Electronic Technology, 11th edition, Pearson, pp. 237—241
- ↑ Robbins, A.H., Miller W. (2012). Circuit Analysis: Theory and Practice, 5th ed., Cengage Learning, pp. 554—558
wikiredia.ru
что это такое и от чего зависит
В радиотехнике часто приходится сталкиваться с индуктивным сопротивлением. Его источником являются катушки. Они представляют собой двухполюсник, намотанный медным эмалированным проводом (обычно это ПЭТВ) на ферритовый или железный сердечник. Подобные детали встречаются в широком перечне оборудования: от древних советских радиоприёмников до материнских плат ПК последних моделей.
Катушки индуктивности
Формулы, зависимости и виды индуктивности
Электрическая индуктивность L – это величина, равная коэффициенту пропорциональности между током I, протекающим в замкнутом контуре, и создаваемым им магнитным потоком, иначе называемым потокосцеплением Y:
Y = LI.
Если к выводам катушки на некоторое время приложить напряжение, то в ней начнёт протекать ток I и формироваться магнитное поле. Чем меньше индуктивность L, тем быстрее протекает данный процесс. В итоге рассматриваемый двухполюсник накопит некоторое количество потенциальной энергии. При отключении питания он будет стремиться её вернуть. В результате на выводах катушки образуется ЭДС самоиндукции E, которая многократно превышает изначально приложенное напряжение. Подобная технология ранее использовалась в магнето систем зажигания ДВС, а сейчас широко встречается в повышающих DC-DC преобразователях.
Формула ЭДС самоиндукции, здесь t – это время, в течение которого ток I уменьшится до нуля
Простой DC-DC повышающий преобразователь
Катушка (она же – дроссель) – это радиодеталь с ярко выраженной индуктивностью, ведь именно для этого её и создавали. Однако подобным свойством обладают в принципе все элементы. Например, конденсатор, резистор, кабель, просто кусок провода и даже тело человек также имеют некоторую индуктивность. В расчетах ВЧ схем это обязательно принимается во внимание.
Важно! Проводя измерение индуктивности специализированным прибором, стоит помнить, что нельзя держаться руками за оба его вывода. В противном случае показания могут измениться и будут неверными. Вызвано это включением в измеряемую цепь тела человека с его собственной индуктивностью.
Сопротивление катушки переменному току
Гораздо интереснее дела обстоят с индуктивностью в контуре переменного тока. Любая катушка содержит в себе две составляющие сопротивления:
- Активную;
- Индуктивную.
При постоянном токе учитывается только первый фактор, а при переменном – оба. Формула индуктивного сопротивления XL катушки имеет следующий вид:
XL = 2pfL,
где:
- p = 3.14;
- f – частота переменного тока, Гц;
- L – индуктивность катушки, Гн.
Полное сопротивление катушки Z, называемое импедансом, определяется, исходя из активной R и индуктивной XL составляющих.
Импеданс катушки
Важно! Если катушка установлена в печатную плату, то для проверки её следует отпаять. В таком случае индуктивность будет измеряться независимо от других компонентов, что существенно повысит точность показаний прибора.
Расчёт индуктивного сопротивления катушки
Любая индуктивность, в т.ч. катушка, оказывает переменному току некоторое сопротивление. Как его рассчитать, было описано выше. Из формулы XL=2pfL видно, что сопротивление дросселя в первую очередь зависит от частоты протекающего по нему тока и его индуктивности. При этом с обоими параметрами связь прямо пропорциональная.
Частота – это характеристика внешней среды, индуктивность катушки зависит от ряда её геометрических свойств:
L=u0urN2S/l,
где:
- u0 – магнитная проницаемость вакуума – 4p*10-7 Гн/м;
- ur – относительная проницаемость сердечника;
- N – количество витков дросселя;
- S – его поперечное сечение в м2;
- l – длина катушки в метрах.
Располагая вышеописанными формулами и информацией о материале и размерах катушки, можно достаточно точно прикинуть её индуктивное сопротивление без каких-либо измерительных приборов.
Дополнительная информация. Некоторые цифровые мультиметры имеют режим замера индуктивности. Подобная функция встречается редко, однако иногда оказывается очень полезной. Поэтому при выборе прибора стоит обратить внимание на то, способен ли он измерять индуктивность.
Где применяется катушка (дроссель, индуктивность)
Дроссели имеют примитивную конструкцию: просто намотанный витками на каком-либо сердечнике проводник. В то же время в таком приборе нечему ломаться. Также у дросселей широчайший функционал и десятки применений. Из всего этого следует, что в какой бы точке города ни находился человек, в радиусе 1 км от него всегда будут тысячи катушек индуктивности, настолько они распространены.
Катушка как электромагнит
Самое простое применение катушки – это электромагнит. С подобным применением каждый сталкивается, заходя в подъезд. Сила, удерживающая дверь на месте и препятствующая несанкционированному доступу чужака, берётся из электромагнита. Он находится сверху.
Электрический ток, проходя по виткам катушки, создаёт вокруг неё переменное электромагнитное поле. Оно возбуждает в металлическом «бруске», расположенном на двери, вихревые токи, которые так же создают магнитное поле. В результате получаются два управляемых магнита. Они притягиваются друг к другу. Тем самым дверь надёжно удерживается на месте.
Другое применение электромагнитов в быту – индукционные плиты. Катушка наводит в металлической посуде переменный высокочастотный ток. Он, в свою очередь, своим тепловым действием разогревает кастрюлю. В промышленности нечто подобное используется для разогрева и плавки металлов. Только в таком случае применяются на порядки более высокие мощности и другие частоты тока.
Индукционный нагрев металла
Индуктивность как фильтр
Импульсные блоки питания, электрические двигатели и диммеры для регулировки яркости ламп накаливания выбрасывают в сеть большое количество искажений и помех. Вызвано это неравномерностью потребляемого тока. Для борьбы с подобными сетевыми шумами применяются специальные фильтры на основе конденсаторов и дросселей.
Данный узел представляет собой небольшую катушку из медного эмалированного провода диаметром 0,2-2 мм. Обмотка наматывается на ферритовый сердечник. Чаще всего он изготовлен в форме кольца, немного реже встречаются так называемые «гантельки».
Подобные фильтры имеются в компьютерных блоках питания, компактных люминесцентных лампах (иногда не ставят, экономят), на выходах сварочных инверторов.
Также фильтр может быть звуковым. Его задача – срезать определённый диапазон частот. Индуктивные свойства этого прибора таковы, что он хорошо проводит низкие частоты, а высокие – приглушает. Поэтому дроссели используют для того, чтобы до динамиков дошёл только бас. По факту ослаблено будут слышны и другие частоты. Для более эффективной работы фильтра нужны дополнительные детали: конденсаторы и операционные усилители.
Самодельный звуковой фильтр
Катушка как источник ЭДС
Китайская промышленность удивила школьников 2000-х новой игрушкой – вечным фонариком. Его не нужно было заряжать. Фонарик работал от катушки индуктивности, около которой под действием движения рук перемещался магнит. Он наводил в обмотке переменную ЭДС, которая питала осветительный прибор.
Подобное явление объясняется законом электромагнитной индукции. Если проводник (рамка) находится в переменном электромагнитном поле, то в нём начинает наводиться электродвижущая сила. Иными словами, появляется напряжение.
Закон этот совсем неигрушечный, ведь он используется в работе генераторов на подавляющем большинстве электростанций, в том числе любые ТЭЦ, ГЭС, АЭС и ветряки. По подобному принципу работают динамомашины, питающие фары велотранспорта.
Принцип работы генератора
Две катушки – трансформатор
Ещё одно распространённое применение – это электрический трансформатор. Конструктивно он состоит из двух и более катушек, расположенных на одном железном или ферритовом сердечнике. Подобный агрегат работает только с переменным напряжением. Если на первичную обмотку подать ток, то он создаст в сердечнике магнитный поток. Он, в свою очередь, наведёт ЭДС во вторичной обмотке. Напряжения во входной и выходной катушках прямо зависят от количества их витков.
Таким образом, можно трансформировать 220 В из розетки в 12 В, необходимых для питания небольшой стереосистемы, или преобразовать 10 000 вольт в 220 для передачи от подстанции к жилым домам. Подобным методом можно добиться и повышения напряжения, т.е. превратить 12 В обратно в 220.
Устройство трансформатора
Катушка индуктивности — элемент колебательного контура
Сейчас это уже редкость, но раньше для подстройки нужной радиостанции использовали колебательный контур. Он состоит из двух элементов, включенных параллельно: катушки индуктивности и переменного конденсатора. Работая в паре, они способны выделить из множества окружающих сигналов именно тот, который требуется. При попадании на антенну приёмника нужной частоты электромагнитных волн колебательный контур входит в резонанс. Процесс сопровождается лавинообразным увеличением ЭДС. Частота, на которой это происходит, зависит от индуктивности катушки и ёмкости конденсатора.
Катушка индуктивности – дроссель ДРЛ ламп
Несмотря на то, что освещение улиц и промышленных предприятий стремительно переходит на LED светильники, по СНГ всё ещё осталось огромное количество мест, где используются устаревшие дуговые ртутные люминесцентные лампы типа ДРЛ. Более всего они распространены в мелких городах и на второстепенных улицах. Их можно узнать по характерному холодно-белому свету и долгому розжигу.
ДРЛ лампы не способны работать без пускорегулирующего дросселя. Он обладает высоким индуктивным сопротивлением и призван ограничить пусковой ток осветительного прибора. Дроссели для ламп подбираются, исходя из их мощности. Наиболее распространённые номиналы – 250, 400 и 1000 Вт. Информация о мощности указывается на самом дросселе. Там же можно найти схемы включения.
Из вышесказанного можно подчеркнуть, что катушка индуктивности является консервативным и давно освоенным на практике электронным компонентом. Однако спрос на его применение по-прежнему не спадает. Поэтому знания, необходимые для расчета катушек и их правильного включения, необходимы каждому специалисту, имеющему дело с электроникой.
Видео
amperof.ru
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ — это… Что такое ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ?
- ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ
- ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ
-
сопротивление переменному току, создаваемое в проводах, электр. машинах и трансформаторах самоиндукцией. Величина И. с. пропорциональна частоте переменного тока индуктивности цепи.
Технический железнодорожный словарь. — М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров. 1941.
.
- ИНДИКАТОРНЫЙ КОЭФФИЦИЕНТ
- ИНДУКТИВНОСТЬ
Смотреть что такое «ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ» в других словарях:
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ — в аэродинамике, часть аэродинамического сопротивления крыла, обусловленная вихрями, оси к рых берут начало на крыле и направлены вниз по потоку. Эти, т. н. свободные, вихри происходят от перетекания воздуха у торцов крыла (рис. 1) из области под… … Физическая энциклопедия
Индуктивное сопротивление — часть сопротивления аэродинамического (сопротивления давления) крыла конечного размаха, связанная с образованием (индуцированием отсюда название) вихревой пелены за крылом и определяемая затратами энергии на поддержание крупномасштабного течения … Энциклопедия техники
индуктивное сопротивление — Реактивное сопротивление, обусловленное собственной индуктивностью элемента электрической цепи и равное произведению значений индуктивности и угловой частоты. [ГОСТ Р 52002 2003] EN inductive reactance reactance having a positive value [IEV ref… … Справочник технического переводчика
Индуктивное сопротивление — может означать: Составляющую лобового сопротивления в аэродинамике; Составляющую полного электрического сопротивления в электротехнике … Википедия
индуктивное сопротивление — величина, характеризующая сопротивление, оказываемое переменному току индуктивностью цепи (или её участка). Индуктивное сопротивление синусоидальному току xL = ωL, где ω угловая частота, L индуктивность. * * * ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ… … Энциклопедический словарь
индуктивное сопротивление — 148 индуктивное сопротивление Реактивное сопротивление, обусловленное собственной индуктивностью элемента электрической цепи и равное произведению значений индуктивности и угловой частоты Источник: ГОСТ Р 52002 2003: Электротехника. Термины и… … Словарь-справочник терминов нормативно-технической документации
индуктивное сопротивление — induktyvioji varža statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. inductive reactance vok. induktiver Widerstand, m rus. индуктивное сопротивление, n pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
индуктивное сопротивление — induktyvioji varža statusas T sritis fizika atitikmenys: angl. inductive reactance vok. Induktanz, f; induktive Reaktanz, f; induktiver Blindwiderstand, m rus. индуктивное сопротивление, n pranc. réactance inductive, f … Fizikos terminų žodynas
Индуктивное сопротивление — I Индуктивное сопротивление в электротехнике, см. Сопротивление индуктивное. II Индуктивное сопротивление в аэродинамике, часть аэродинамического сопротивления (См. Аэродинамическое сопротивление) крыла, обусловленная вихрями, оси … Большая советская энциклопедия
индуктивное сопротивление — [inductive impedance (полн.) inductive reactance (реакт.)] величина, характеризующая сопротивление переменному току индуктивностью цепи (ее участка), единица измерения 1 Ом; Смотри также: Сопротивление электрическое сопротивление … Энциклопедический словарь по металлургии
dic.academic.ru

