Что такое математическое ожидание случайной величины. Как вычислить дисперсию дискретной и непрерывной случайной величины. Какие формулы используются для нахождения плотности вероятности. Как связаны функция распределения и плотность вероятности.
Математическое ожидание случайной величины
Математическое ожидание — одна из важнейших числовых характеристик случайной величины. Оно характеризует среднее значение случайной величины.
Для дискретной случайной величины X математическое ожидание вычисляется по формуле:
M(X) = x1p1 + x2p2 + … + xnpn
где xi — возможные значения случайной величины, pi — соответствующие им вероятности.
Для непрерывной случайной величины X математическое ожидание определяется интегралом:
M(X) = ∫xf(x)dx
где f(x) — плотность вероятности случайной величины X.
Свойства математического ожидания
- M(C) = C, где C — константа
- M(CX) = CM(X)
- M(X + Y) = M(X) + M(Y)
- M(XY) = M(X)M(Y), если X и Y независимы
Дисперсия случайной величины
Дисперсия характеризует рассеяние случайной величины вокруг ее математического ожидания. Она определяется как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D(X) = M[(X — M(X))²]
Для дискретной случайной величины дисперсия вычисляется по формуле:
D(X) = (x1 — M(X))²p1 + (x2 — M(X))²p2 + … + (xn — M(X))²pn
Для непрерывной случайной величины:
D(X) = ∫(x — M(X))²f(x)dx
Свойства дисперсии
- D(C) = 0, где C — константа
- D(CX) = C²D(X)
- D(X + Y) = D(X) + D(Y), если X и Y независимы
Плотность вероятности непрерывной случайной величины
Плотность вероятности f(x) — это производная от функции распределения F(x):
f(x) = F'(x)
Основные свойства плотности вероятности:
- f(x) ≥ 0 для всех x
- ∫f(x)dx = 1 (интеграл по всей области определения)
- P(a ≤ X ≤ b) = ∫abf(x)dx
Функция распределения случайной величины
Функция распределения F(x) определяет вероятность того, что случайная величина X примет значение меньше x:
F(x) = P(X < x)
Для непрерывной случайной величины функция распределения связана с плотностью вероятности соотношением:
F(x) = ∫-∞xf(t)dt
Свойства функции распределения
- 0 ≤ F(x) ≤ 1
- F(x) — неубывающая функция
- limx→-∞F(x) = 0, limx→+∞F(x) = 1
- P(a < X ≤ b) = F(b) - F(a)
Числовые характеристики биномиального распределения
Биномиальное распределение описывает число успехов в серии из n независимых испытаний, каждое из которых имеет вероятность успеха p.

Основные характеристики:
- Математическое ожидание: M(X) = np
- Дисперсия: D(X) = np(1-p)
- Вероятность получения k успехов: P(X = k) = Cnkpk(1-p)n-k
Числовые характеристики распределения Пуассона
Распределение Пуассона описывает число событий, происходящих за фиксированный интервал времени или в фиксированной области пространства.
Основные характеристики:
- Математическое ожидание: M(X) = λ
- Дисперсия: D(X) = λ
- Вероятность наступления k событий: P(X = k) = (λke-λ) / k!
Числовые характеристики равномерного распределения
Равномерное распределение описывает случайную величину, которая с равной вероятностью принимает любое значение на заданном интервале [a, b].
Основные характеристики:
- Математическое ожидание: M(X) = (a + b) / 2
- Дисперсия: D(X) = (b — a)² / 12
- Плотность вероятности: f(x) = 1 / (b — a) для x ∈ [a, b], f(x) = 0 для x ∉ [a, b]
Числовые характеристики нормального распределения
Нормальное (гауссово) распределение — одно из важнейших в теории вероятностей, описывающее многие природные явления.

Основные характеристики:
- Математическое ожидание: M(X) = μ
- Дисперсия: D(X) = σ²
- Плотность вероятности: f(x) = (1 / (σ√(2π))) * e-((x-μ)² / (2σ²))
Практические примеры использования числовых характеристик
Рассмотрим несколько примеров применения числовых характеристик случайных величин в реальных задачах:
Пример 1: Анализ продаж в магазине
Предположим, что ежедневные продажи в магазине подчиняются нормальному распределению со средним значением 1000 долларов и стандартным отклонением 200 долларов. Какова вероятность, что в случайно выбранный день продажи превысят 1500 долларов?
Решение:
- Нормализуем значение: z = (1500 — 1000) / 200 = 2.5
- Используя таблицу стандартного нормального распределения, находим P(Z > 2.5) ≈ 0.0062
Таким образом, вероятность того, что продажи превысят 1500 долларов, составляет примерно 0.62%.
Пример 2: Контроль качества на производстве
На производстве выпускаются детали, длина которых должна быть 50 мм. Известно, что длина деталей распределена нормально со средним 50 мм и стандартным отклонением 0.1 мм. Какой процент деталей имеет длину от 49.8 до 50.2 мм?

Решение:
- Нормализуем границы: z1 = (49.8 — 50) / 0.1 = -2, z2 = (50.2 — 50) / 0.1 = 2
- Используя таблицу стандартного нормального распределения, находим P(-2 < Z < 2) ≈ 0.9545
Таким образом, около 95.45% деталей имеют длину в пределах от 49.8 до 50.2 мм.
Методы оценки числовых характеристик по выборочным данным
При работе с реальными данными мы часто имеем дело с выборкой, а не с генеральной совокупностью. В этом случае используются выборочные оценки числовых характеристик.
Выборочное среднее
Выборочное среднее является оценкой математического ожидания:x̄ = (x1 + x2 + … + xn) / n
Выборочная дисперсия
Выборочная дисперсия является оценкой дисперсии генеральной совокупности:
s² = Σ(xi — x̄)² / (n — 1)
Обратите внимание на деление на (n — 1), а не на n. Это делает оценку несмещенной.
Выборочное стандартное отклонение
Выборочное стандартное отклонение — это квадратный корень из выборочной дисперсии:
s = √(s²)
Заключение
Числовые характеристики случайных величин играют ключевую роль в теории вероятностей и математической статистике. Они позволяют описывать и анализировать случайные явления, прогнозировать их поведение и принимать обоснованные решения в условиях неопределенности.

Понимание математического ожидания, дисперсии, плотности вероятности и функции распределения необходимо для эффективного применения вероятностных методов в различных областях науки и практики — от физики и инженерии до экономики и социологии.
Теория вероятностей
Теория вероятностей
Тема: Числовые характеристики случайных величин
1)Непрерывная случайная величина задана плотностью распределения вероятностей: Тогда ее математическое ожидание равно …
|
|
2) Непрерывная случайная величина задана плотностью распределения вероятностей Тогда математическое ожидание a и среднее квадратическое отклонение этой случайной величины равны …
|
|
3) Дискретная случайная величина X задана законом распределения вероятностей: Тогда ее математическое ожидание равно …
|
2,1 |
4) Дискретная случайная величина X задана законом распределения вероятностей: Тогда ее дисперсия равна …
|
0,96 |
5) Непрерывная случайная величина задана плотностью распределения вероятностей Тогда математическое ожидание a и среднее квадратическое отклонение этой случайной величины равны …
|
|
Тема: Теоремы сложения и умножения вероятностей
1)В
электрическую цепь параллельно включены
два элемента, работающие независимо
друг от друга. Вероятности отказов
элементов равны соответственно 0,05 и
0,20. Тогда вероятность того, что тока в
цепи не будет, равна …
Вероятности отказов
элементов равны соответственно 0,05 и
0,20. Тогда вероятность того, что тока в
цепи не будет, равна …
|
|
Введем обозначения событий: (откажет – ый элемент), (тока в цепи не будет). Тогда и
2) Из урны, в которой лежат 7 белых и 3 черных шара, наудачу по одному извлекают два шара без возвращения. Тогда вероятность того, что хотя бы один шар будет белым, равна …
|
|
3) Из урны, в которой лежат 4 белых и 6 черных шаров, наудачу по одному извлекают два шара без возвращения. Тогда вероятность того, что оба шара будут черными, равна …
|
|
4)
В
электрическую цепь последовательно
включены два элемента, работающие
независимо друг от друга. Вероятности
отказов элементов равны соответственно
0,2 и 0,15. Тогда вероятность того, что ток
в цепи будет, равна …
Вероятности
отказов элементов равны соответственно
0,2 и 0,15. Тогда вероятность того, что ток
в цепи будет, равна …
|
0,68 |
5) В электрическую цепь параллельно включены два элемента, работающие независимо друг от друга. Вероятности отказов элементов равны соответственно 0,05 и 0,20. Тогда вероятность того, что тока в цепи не будет, равна …
|
|
6) Из урны, в которой лежат 7 белых и 3 черных шара, наудачу по одному извлекают два шара без возвращения. Тогда вероятность того, что хотя бы один шар будет белым, равна …
Тема: Законы распределения вероятностей непрерывных случайных величин
1)Непрерывная случайная величина задана плотностью распределения вероятностей: Тогда вероятность равна …
|
|
2) Непрерывная случайная величина задана плотностью распределения вероятностей: Тогда значение параметра равно …
|
|
3) Непрерывная случайная величина задана функцией распределения вероятностей: Тогда ее плотность распределения вероятностей имеет вид …
|
|
4) Непрерывная случайная величина задана функцией распределения вероятностей: Тогда ее плотность распределения вероятностей имеет вид …
5) Дан график плотности распределения вероятностей непрерывной случайной величины : Тогда график ее функции распределения вероятностей имеет вид …
Тема: Определение вероятности
1)Игральная
кость бросается один раз. Тогда вероятность
того, что на верхней грани выпадет
нечетное число очков, равна …
Тогда вероятность
того, что на верхней грани выпадет
нечетное число очков, равна …
|
|
2) Из урны, в которой находятся 6 черных, 4 белых и 10 зеленых шаров, вынимают случайным образом один шар. Тогда вероятность того, этот шар будет белым, равна …
|
0,2 |
3) После бури на участке между 50-ым и 70-ым километрами высоковольтной линии электропередач произошел обрыв проводов. Тогда вероятность того, что авария произошла между 60-ым и 63-им километрами, равна …
|
|
4)
В
партии из 10 деталей имеется 3 бракованные. Наудачу отобраны три детали. Тогда
вероятность того, что все отобранные
детали будут бракованными, равна …
Наудачу отобраны три детали. Тогда
вероятность того, что все отобранные
детали будут бракованными, равна …
|
|
5) Из урны, в которой находятся 6 черных, 4 белых и 10 зеленых шаров, вынимают случайным образом один шар. Тогда вероятность того, этот шар будет белым, равна …
|
0,2 |
Следовательно, .
6) В партии из 10 деталей имеется 3 бракованные. Наудачу отобраны три детали. Тогда вероятность того, что все отобранные детали будут бракованными, равна …
Тема:
Полная вероятность. Формулы Байеса
Формулы Байеса
1)Собирается партия исправных изделий с двух предприятий. Первое предприятие поставляет 30% всех изделий, а второе – 70%. Вероятность исправной работы изделия первого предприятия равна 0,8, второго – 0,7. Тогда вероятность того, что случайно взятое изделие будет неисправным, равна …
|
|
2) В первой урне 2 белых и 8 черных шаров. Во второй урне 3 черных и 7 белых шаров. Из наудачу взятой урны вытаскивается один шар. Тогда вероятность того, что этот шар черный, равна …
|
|
3)
Собирается партия исправных изделий с
двух предприятий. Первое предприятие
поставляет 60% всех изделий, а второе –
40%. Вероятность исправной работы изделия
первого предприятия равна 0,9, второго
– 0,8. Тогда вероятность того, что случайно
взятое изделие будет работать исправно,
равна …
Тогда вероятность того, что случайно
взятое изделие будет работать исправно,
равна …
|
|
4) В первой урне 7 черных и 3 белых шара. Во второй урне 4 черных и 6 белых шаров. Из наудачу взятой урны вытаскивается один шар, который оказался белым. Тогда вероятность того, что этот шар был вынут из первой урны, равна …
Тема: Законы распределения вероятностей дискретных случайных величин
1)Дискретная случайная величина задана законом распределения вероятностей: Тогда ее функция распределения вероятностей имеет вид …
|
|
2) Дискретная случайная величина задана законом распределения вероятностей: Тогда значение a равно …
|
|
3)
Вероятность появления события
в
каждом из 10 независимых испытаний равна
. Тогда вероятность того, что в этих
испытаниях событие
наступит
6 раз можно вычислить как …
Тогда вероятность того, что в этих
испытаниях событие
наступит
6 раз можно вычислить как …
|
|
4) Дискретная случайная величина задана законом распределения вероятностей: Тогда вероятность равна …
|
|
5) Непрерывная случайная величина задана функцией распределения вероятностей:
Тогда ее плотность распределения вероятностей имеет вид …
Математика — ответы часть 1
Главная / Ответы на новые тесты / Математика / Страница 1 Упражнение 10674:Номер
Flash-графикa используется для создания ...
Ответ:
 изображения для веб-страниц 
 объемных изображений 
 изображения природных ландшафтов 
 инженерных чертежей 
Упражнение 10675:
Номер
А23 = 12
Ответ:
 А23 = -34 
 А23 = 34 
 А23 = -12 
Упражнение 10676:
Номер
Академик Сергей Алексеевич Лебедев знаменит тем, что ...
Ответ:
 является создателем первой отечественной вычислительной машины 
 разработал первую российскую операционную систему 
 написал первый ученик по информатике 
 возглавлял комитет Государственной Думы по информатике и компьютеризации 
Упражнение 10677:
Номер
Аппаратно-независимым форматом, одинаково точно воспроизводящим как текст, так и графику, является формат ...
Ответ:
 PDF 
 GIF 
 JPEG 
 BMP 
Упражнение 10678:
Номер
Банк выдал пять кредитов.Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна ...
Ответ:
 0,0081 
 0,081 
 0,06 
 0,0729 
Упражнение 10679:
Номер
Большая часть рисунков, входящих в коллекцию клипов MS Clipart, являются файлами формата ...
Ответ:
 wmf 
 jpeg 
 mpeg 
 avi 
Упражнение 10680:
Номер
Бумажные носители информации – перфокарты и перфоленты, начали широко использоваться при работе с ЭВМ \_\_\_\_\_\_\_\_\_ поколения.
Ответ:
 второго 
 первого 
 четвертого 
 третьего 
Упражнение 10681:
Номер
В Microsoft Excel в объемных модификациях диаграмм различных типов третью ось называют осью ...
Ответ:
 рядов 
 значений 
 категорий 
 аппликат 
Упражнение 10682:
Номер
В Microsoft Excel диаграмма, имеющая три оси, относится к типу ...
Ответ:
 «Объемная» 
 «Кольцевая» 
 «Точечная» 
 «Биржевая» 
Упражнение 10683:
Номер
В Microsoft Excel легендой диаграммы называется ...
Ответ:
 список условных обозначений 
 заголовок диаграммы 
 разметка и название осей 
 описание маркеров 
Упражнение 10684:
Номер
В Microsoft Excel основными элементами, из которых строятся ряды диаграмм, являются ...
Ответ:
 маркеры 
 легенды 
 линии сетки 
 оси 
Упражнение 10685:
Номер
В двух одинаковых коробках упакованы баночки с йогуртом. Вероятность того, что в первой коробке окажутся баночки с истекшим сроком хранения, равна p, а вероятность наличия такой продукции для второй коробки равна 0,25. Установите соответствие между значениями p и вероятностью того, что выбранная случайным образом баночка из наугад выбранной коробки оказалась с истекшим сроком хранения:1) p = 0,152) p = 0,65
Ответ:
 0,2 
 0,45 
 0,5 
Упражнение 10686:
Номер
В пакете находится 32 шоколадные конфеты с различной начинкой.Известно, что конфет с каждой начинкой в пакете поровну. Хрюша съел одну конфетку. Она оказалась с ореховой начинкой. При этом Хрюша получил информацию количеством 2 бита. Тогда конфет с ореховой начинкой в пакете осталось ...
Ответ:
 7 
 6 
 4 
 8 
Упражнение 10687:
Номер
В поисковом запросе используется ключевое слово вида «автомати*». Тогда в документах, отобранных по этому запросу, могут встретиться слова ...
Ответ:
 «автоматический», «автоматизация» 
 «автоматный», «автоматрица» 
 «полуавтоматический», «экспресс-автоматизация» 
 «завод-автомат», полуавтомат 
Упражнение 10688:
Номер
В поисковом запросе символ «*» в ключевом слове означает ...
Ответ:
 любую последовательность символов 
 любой один символ 
 поиск страниц, на которых нет ключевого слова 
 поиск ключевого слова во всех формах и падежах 
Упражнение 10689:
Номер
В поисковом запросе символ «?» в ключевом слове означает ...
Ответ:
 любой один символ 
 любая последовательность символов 
 поиск страниц, на которых нет ключевого слова 
 поиск ключевого слова во всех формах и падежах 
Упражнение 10690:
Номер
В поисковом запросе указали ключевое слово вида «пере???ка».Тогда в отобранных документах могут содержаться слова ...
Ответ:
 «пересылка», «переноска», «перекачка» 
 «перестройка», «перегрузка», «перегородка» 
 «переучет», «перезачет», «перевычет» 
 «прополка», «пробежка», «протяжка» 
Упражнение 10691:
Номер
В поисковых запросах кавычки вида « » или “ ” применяются для поиска документов, в которых содержатся ...
Ответ:
 слова точно в том виде и порядке, в котором они были заданы в запросе 
 любые слова, кроме заключенных в кавычки 
 какие-либо из слов, заключенных в кавычки 
 слова, являющиеся заголовками этих документов 
Упражнение 10692:
Номер
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24.Тогда выборочная дисперсия равна ...
Ответ:
 11,25 
 19,5 
 15 
 21,25 
Упражнение 10693:
Номер
В системах счисления цифрой называется ...
Ответ:
 символ для записи чисел 
 основание системы счисления 
 одноразрядное число 
 название числа 
Упражнение 10694:
Номер
В современных мобильных устройствах – смартфонах, коммуникаторах, навигаторах, планшетных компьютерах, а также в различных платежных и справочных терминалах, для ввода данных широко используются ...
Ответ:
 сенсорные экраны 
 веб-камеры 
 джойстики 
 трекболы 
Упражнение 10695:
Номер
В современных портативных компьютерах для замены манипулятора типа мышь используется ...
Ответ:
 сенсорная панель 
 специальные кнопки на клавиатуре 
 джойстик 
 трекбол 
Упражнение 10696:
Номер
В электрическую цепь параллельно включены три элемента, работающие независимо друг от друга.Вероятности отказов элементов равны соответственно 0,05, 0,1 и 0,20. Тогда вероятность того, что тока в цепи не будет, равна ...
Ответ:
 0,001 
 0,35 
 0,999 
 0,01 
Упражнение 10697:
Номер
В электрическую цепь последовательно включены два элемента, работающие независимо друг от друга. Вероятности отказов элементов равны соответственно 0,1 и 0,15. Тогда вероятность того, что тока в цепи не будет, равна ...
Ответ:
 0,235 
 0,765 
 0,22 
 0,015 
Упражнение 10698:
Номер
В электрическую цепь последовательно включены три элемента, работающие независимо друг от друга.Вероятности отказов элементов равны соответственно 0,1, 0,2 и 0,15. Тогда вероятность того, что тока в цепи не будет, равна ...
Ответ:
 0,388 
 0,612 
 0,45 
 0,003 
Упражнение 10699:
Номер
Ваня на скорости 2 Мегабита в секунду закачал на свою страничку в «Facebook» собственную фотографию на байке «Harley-Davidson». Закачанный файл имеет объем 3 Мегабайта, время закачки составило \_\_\_\_\_ сек.
Ответ:
 12 
 24 
 8 
 1 
Упражнение 10700:
Номер
Варианты с частотой 3 содержат выборки ...
Ответ:
 1, 1, 2, 2, 3, 3, 4, 4, 4, 6 
 5, 5, 5, 6, 7, 7, 8 
 1, 2, 2, 3, 3, 3, 3, 4, 6 
 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7 
Упражнение 10701:
Номер
Васе на день рождения подарили 3G-модем. Первым делом Вася за 8 секунд на скорости 2 Мегабита в секунду скачал файл «Хара-мамбуру.mp3». Записанный на диск файл «Хара-мамбуру.mp3» будет иметь объем ...
Ответ:
 2 Мегабайта 
 16 Мегабайт 
 8 Мегабайт 
 4 Мегабайта 
Упражнение 10702:
Номер
Веб-сервер, предоставляющий прямой доступ к множеству других серверов, и некоторый набор веб-сервисов, называется ...
Ответ:
 порталом 
 провайдером 
 поисковым каталогом 
 медиа-сервером 
Упражнение 10703:
Номер
Веб-серфингом называется ...
Ответ:
 свободный поиск данных в Интернете с переходом по гиперссылкам на различные веб-страницы 
 услуга по проектированию, дизайну и разработке интерактивных динамических веб-сайтов 
 услуга предоставления вычислительных мощностей для физического размещения веб-сайтов 
 рассылка электронных сообщений через интернет-почту 
Упражнение 10704:
Номер
Веб-хостингом называется ...
Ответ:
 услуга предоставления вычислительных мощностей для физического размещения веб-сайтов 
 услуга по проектированию, дизайну и разработке интерактивных динамических веб-сайтов 
 свободный поиск произвольных данных в Интернете с занесением результатов в базу данных 
 защита данных, составляющих содержание веб-сайта, от различного вредоносного программного обеспечения 
Упражнение 10705:
Номер
Векторные изображения операционной системы Windows хранятся в формате ...
Ответ:
 WMF 
 PSD 
 BMP 
 GIF 
Упражнение 10706:
Номер
Вероятность ошибки второго рода при проверке статистической гипотезы равна 0,1. Тогда вероятность принятия ложной нулевой гипотезы равна ...
Ответ:
 0,1 
 0,9 
 0,05 
 0,99 
Упражнение 10707:
Номер
Вероятность поражения цели первым стрелком равна 0,9, а вторым – 0,85.Оба стрелка стреляют одновременно. Тогда вероятность поражения цели, равна ...
Ответ:
 0,985 
 0,775 
 0,875 
 1,75 
Упражнение 10708:
Номер
Вероятность поражения цели первым стрелком равна 0,95, а вторым – 0,80. Оба стрелка стреляют одновременно. Тогда вероятность того, что цель будет поражена только одним стрелком, равна ...
Ответ:
 0,23 
 0,95 
 0,875 
 0,17 
Упражнение 10709:
Номер
Взаимное расположение прямых 4x — 2y — 6 = 0 и 8x — 4y — 2 = 0 на плоскости – прямые ...
Ответ:
 параллельны 
 пересекаются 
 перпендикулярны 
 совпадают 
Упражнение 10710:
Номер
Выборочная дисперсия выборки, заданной вариационным рядом 1, 1, 1, 2, 3, 3, 4, 4, 4, 7, равна ...
Ответ:
 3,2 
 3,4 
 0,6 
 3 
Упражнение 10711:
Номер
Гипотезой о виде распределения случайной величины является ...
Ответ:
 «Сумма дневных продаж магазина – нормально распределенная случайная величина» 
 «Средние значения случайных величин (суммы дневных продаж двух магазинов), распределенных по нормальному закону, равны между собой» 
 «Среднее время излечения головной боли данным медицинским препаратом составляет 30 минут» 
 «Отклонение массы пакетов с мукой от стандарта – случайная величина» 
Упражнение 10712:
Номер
Гипотезой о значении параметра известного распределения является ...
Ответ:
 «Средний вес учащихся первого класса школ Москвы (вес – нормально распределенная случайная величина) составляет 35 кг» 
 «Наиболее часто встречающийся вес у учащихся первого класса школ Москвы составляет 35 кг» 
 «Средний вес учащихся первого класса школ Москвы – случайная величина, распределенная по нормальному закону» 
 «Средний вес учащихся первого класса школ Москвы – равномерно распределенная случайная величина» 
Упражнение 10713:
Номер
Графическая подсистема текстового редактора MS Word использует \_\_\_\_\_\_\_\_\_\_ графику.
Ответ:
 векторную 
 растровую 
 фрактальную 
 flash 
Упражнение 10714:
Номер
Графическим форматом, используемым в Интернете и поддерживающим только 256 цветов, является формат ...
Ответ:
 GIF 
 TIFF 
 PSD 
 JPEG 
Упражнение 10715:
Номер
Дан вариационный ряд 1, 2, 6, 6, 7, 9, 12, 13, 13, 13.Сумма моды и медианы данного ряда равна ...
Ответ:
 21 
 22 
 20 
 14 
Упражнение 10716:
Номер
Дан вариационный ряд 15, 15, 15, 15, 18, 20, 22, 24, 24. Его мода имеет частоту, равную ...
Ответ:
 4 
 15 
 2 
 18 
Упражнение 10717:
Номер
Дан доверительный интервал (–0,28; 1,42) для оценки математического ожидания нормально распределенного количественного признака.Тогда при уменьшении надежности (доверительной вероятности) оценки доверительный интервал может принять вид ...
Ответ:
 (–0,14; 1,28) 
 (–0,37; 1,51) 
 (–0,14; 1,42) 
 (0; 1,42) 
Упражнение 10718:
Номер
Дан доверительный интервал (4,26;9,49) для оценки среднего квадратического отклонения нормально распределенного количественного признака. Тогда при увеличении надежности (доверительной вероятности) оценки доверительный интервал может принять вид ...
Ответ:
 (4,14; 9,61) 
 (4,26; 9,61) 
 (4,14; 9,49) 
 (4,06; 9,59) 
Упражнение 10719:
Номер
Дан доверительный интервал (12,02; 16,28) для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид ...
Ответ:
 (11,71; 16,59) 
 (12,52; 15,78) 
 (12,02; 16,92) 
 (9,89; 16,28) 
Упражнение 10720:
Номер
Дан доверительный интервал (16,64; 18,92) для оценки математического ожидания нормально распределенного количественного признака.Тогда при увеличении объема выборки этот доверительный интервал может принять вид ...
Ответ:
 (17,18; 18,38) 
 (16,15; 19,41) 
 (17,18; 18,92) 
 (16,15; 18,38) 
Упражнение 10721:
Номер
Дан доверительный интервал (20,2; 25,4) для оценки математического ожидания нормально распределенного количественного признака при известном среднем квадратическом отклонении генеральной совокупности. Тогда при увеличении объема выборки в четыре раза этот доверительный интервал примет вид ...
Ответ:
 (21,5; 24,1) 
 (17,6; 28,0) 
 (21,45; 24,15) 
 (12,0; 33,6) 
Упражнение 10722:
Номер
Дан доверительный интервал (24,6;26,8) для оценки математического ожидания нормально распределенного количественного признака при известном среднем квадратическом отклонении генеральной совокупности. Тогда при уменьшении объема выборки в четыре раза этот доверительный интервал примет вид ...
Ответ:
 (23,5;27,9) 
 (21,3; 30,1) 
 (25,15; 26,25) 
 (23,3;28,1) 
Упражнение 10723:
Номер
Дан доверительный интервал (25,44; 26,98) для оценки математического ожидания нормально распределенного количественного признака.Тогда при увеличении надежности (доверительной вероятности) оценки доверительный интервал может принять вид ...
Ответ:
 (24,04; 28,38) 
 (25,74; 26,68) 
 (24,04; 26,98) 
 (24,14; 28,38) 
Последовательное и параллельное соединения источников тока
Решение:
Внутреннее сопротивление элементов
Сопротивление параллельно включенных резисторов
Общая э. д. с. элементов e0=2e Согласно закону Ома для полной цепи
15 Сопротивления резисторов R1 и R2 и э. д. с. ε1 и ε2 источников тока в схеме, изображенной на рис. 127, известны. При какой э.д.с. ε3 третьего источника ток через резистор R3 не течет?
д. с. ε1 и ε2 источников тока в схеме, изображенной на рис. 127, известны. При какой э.д.с. ε3 третьего источника ток через резистор R3 не течет?
Решение:
Выберем направления токов I1, I2 и I3 через резисторы R1, R2 и R3, указанные на рис. 363. Тогда I3=I1+I2. Разность потенциалов между точками а и b будет равна
Если
Исключая I1 находим
16 Цепь из трех одинаковых последовательно соединенных элементов с э.д.с. ε и внутренним сопротивлением r замкнута накоротко (рис. 128). Какое напряжение покажет вольтметр, подключенный к зажимам одного из элементов?
Решение:
Рассмотрим ту же схему без вольтметра (рис. 364). Из закона Ома для полной цепи находим
Из закона Ома для участка цепи между точками а и b получим
Подключение вольтметра к точкам, разность потенциалов между которыми равна нулю, ничего не может изменить в цепи. Поэтому вольтметр будет показывать напряжение, равное нулю.
Поэтому вольтметр будет показывать напряжение, равное нулю.
17 Источник тока с э.д.с. ε0 включен в схему, параметры которой даны на рис. 129. Найти э.д.с. ε источника тока и направление его подключения к выводам а и b, при которых ток через резистор с сопротивлением R2 не идет.
Решение:
Подключим источник тока к выводам а и b и выберем направления токов, указанные на рис. 365. Для узла е имеем I=I0+I2. При обходе контуров aefb и ecdf по часовой стрелке получим
Используя условие I2 = 0, находим
Знак минус показывает, что полюсы источника тока на рис. 365 нужно поменять местами.
18 Два элемента с одинаковыми э.д.с. ε включены в цепь последовательно. Внешнее сопротивление цепи R = 5 Ом. Отношение напряжения на зажимах первого элемента к напряжению на зажимах второго элемента равно 2/3. Найти внутренние сопротивления элементов r1 и r2, если r1=2r2.
Решение:
19 Два одинаковых элемента с э.д.с. ε=1,5 В и внутренним сопротивлением r = 0,2 Ом замкнуты на резистор, сопротивление которого составляет в одном случае R1=0,2 Oм, В другом — R2 = 20 Ом. Как нужно соединить элементы (последовательно или параллельно) в первом и во втором случаях, чтобы получить наибольший ток в цепи?
Решение:
При параллельном соединении двух элементов внутреннее сопротивление и э.д.с. равны r/2 и ε при последовательном соединении они равны 2r и 2ε. Через резистор R при этом текут токи
Отсюда видно, что I2>I1, если R/2+r<R+r/2, т. е. если r1=r; следовательно, токи при параллельном и последовательном соединениях одинаковы. Во втором случае R2>r.Поэтому ток больше при последовательном соединении.
20 Два элемента с э.д.с. ε1=4В и ε2 = 2В и внутренними сопротивлениями r1 = 0,25 Ом и r2 = 0,75 Ом включены в схему, изображенную на рис. 130. Сопротивления резисторов R1 = 1 Ом и R2 = 3 Ом, емкость конденсатора С=2 мкФ. Найти заряд на конденсаторе.
130. Сопротивления резисторов R1 = 1 Ом и R2 = 3 Ом, емкость конденсатора С=2 мкФ. Найти заряд на конденсаторе.
Решение:
21 К батарее из двух параллельно включенных элементов с э.д.с. ε1 и ε2 и внутренними сопротивлениями r1 и r2 подключен резистор с сопротивлением R. Найти ток I, текущий через резистор R, и токи I1 и I2 в первом и втором элементах. При каких условиях токи в отдельных цепях могут быть равными нулю или изменять свое направление на обратное?
Решение:
Выберем направления токов, указанные на рис. 366. Для узла b имеем I-I1-I2=0. При обходе контуров abef и bcde по часовой стрелке получим
Из этих уравнений находим
Ток I=0 тогда, когда изменена полярность включения одного из элементов и, кроме того, выполнено условие
Ток I1=0 при
а ток I2 = 0 при
Токи I1 и I2 имеют направления, указанные на рис. 366, если
366, если
Они меняют свое направление при
22 Батарея из n одинаковых аккумуляторов, соединенных в одном случае последовательно, в другом— параллельно, замыкается на резистор с сопротивлением R. При каких условиях ток, текущий через резистор, в обоих случаях будет один и тот же?
Решение:
При n(R-r) = R-r. Если R=r, то число элементов произвольно; если R№r, задача не имеет решения (n=1).
23 Батарея из n = 4 одинаковых элементов с внутренним сопротивлением r=2 Ом, соединенных в одном случае последовательно, в другом — параллельно, замыкается на резистор с сопротивлением R=10Ом. Во сколько раз показание вольтметра н одном случае отличается от показания вольтметра в другом случае? Сопротивление вольтметра велико по сравнению с R и r.
Решение:
где V1 — показание вольтметра при последовательном соединении элементов, V2-при параллельном.
24 Как изменится ток, текущий через резистор с сопротивлением R = 2 Ом, если n =10 одинаковых элементов, соединенных последовательно с этим резистором, включить параллельно ему? Э. д.с. элемента ε = 2 В, его внутреннее сопротивление r = 0,2 Ом.
д.с. элемента ε = 2 В, его внутреннее сопротивление r = 0,2 Ом.
Решение:
25 Батарея составлена из N=600 одинаковых элементов так, что n групп соединены последовательно и в каждой из них содержится т элементов, соединенных параллельно. Э.д.с. каждого элемента ε = 2 В, его внутреннее сопротивление r = 0,4 Ом. При каких значениях n и m батарея, будучи замкнута на внешнее сопротивление R = 0,6 Ом, отдаст во внешнюю цепь максимальную мощность? Найти при этом ток, текущий через сопротивление R.
Решение:
Общее число элементов N=nm (рис. 367). Ток во внешней цепи
где r/m— внутреннее сопротивление группы из т параллельно соединенных элементов, а nr/m — внутреннее сопротивление n групп, соединенных последовательно. Максимальная мощность отдается во внешнюю цепь при равенстве сопротивления R внутреннему сопротивлению батареи элементов nr/m, т. е.
При этом через сопротивление R течет точек I=46 А.
26 Емкость аккумулятора Qo=80А⋅ч. Найти емкость батареи из n = 3 таких аккумуляторов, включенных последовательно и параллельно.
Решение:
При последовательном соединении через все аккумуляторы батареи течет один и тот же ток, поэтому все они разрядятся в течение одного и того же времени. Следовательно, емкость батареи будет равна емкости каждого аккумулятора:
При параллельном соединении n аккумуляторов через каждый из них течет 1/n часть общего тока; поэтому при том же разрядном токе в общей цепи батареи будет разряжаться в n раз дольше, чем один аккумулятор, т. е. емкость батареи в п раз больше емкости отдельного аккумулятора:
Заметим, однако, что энергия
отдаваемая батареей в цепь, и при последовательном и при параллельном соединении n аккумуляторов в n раз больше энергии, отдаваемой одним аккумулятором. Это происходит потому, что при последовательном соединении э. д. с. батареи в n раз больше э. д. с. одного аккумулятора, а при параллельном соединении э. д.с. батареи остается той же, что и для каждого аккумулятора, но Q увеличивается в n раз.
д.с. батареи остается той же, что и для каждого аккумулятора, но Q увеличивается в n раз.
27 Найти емкость батареи аккумуляторов, включенных по схеме, изображенной на рис.131. Емкость каждого аккумулятора Q0=64 А⋅ч.
Решение:
Каждая группа из пяти аккумуляторов, включенных последовательно, имеет емкость
Три параллельно включенные группы дают общую емкость батареи
28 Мост для измерения сопротивлений сбалансирован так, что ток через гальванометр не идет (рис. 132). Ток в правой ветви I=0,2 А. Найти напряжение V на зажимах источника тока. Сопротивления резисторов R1 = 2 Ом, R2 = 4 Ом, R3 = 1 Ом.
Решение:
29 Найти токи, протекающие в каждой ветви цепи, изображенной на рис. 133. Э.д.с. источников тока ε1 = 6,5 В и ε2 = 3,9 В. Сопротивления резисторов R1=R2=R3=R4=R5=R6=R=10 Ом.
Решение:
Составляем уравнения Кирхгофа в соответствии с направлениями токов, указанными на рис. 133: I1 + I2 — I3 = 0 для узла b;
I3 — I4 — I5 =0 для узла h; I5 — I1 — I6 = 0 для узла f: при этом
Для контура abfg (обход по часовой стрелке),
Для контура bcdh (обход против часовой стрелки) и
для контура hdef (обход по часовой стрелке). Решая эту систему уравнений с учетом, что все сопротивления одинаковы и равны R=10 Ом, получим
Отрицательные значения токов I2, I4 и I6 показывают, что при данных э.д.с. источников и сопротивлениях резисторов эти токи текут в стороны, противоположные указанным на рис. 133.
Задачи по теории вероятностей. Вероятность появления хотя бы одного события
Задачи по теории вероятностей
Вероятность появления хотя бы одного события
Содержание
- В электрическую цепь последовательно включены три элемента, работающие независимо один от другого.
 Вероятности отказов первого, второго и третьего элементов соответственно равны: р1 = 0,1; р2 = 0,15; р3 = 0,2. Найти вероятность того, что тока в цепи не будет.
Вероятности отказов первого, второго и третьего элементов соответственно равны: р1 = 0,1; р2 = 0,15; р3 = 0,2. Найти вероятность того, что тока в цепи не будет. - Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
- Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4: 0,6; 0,7.
- Три исследователя, независимо один от другого, производят измерения некоторой физической величины. Вероятность того, что первый исследователь допустит ошибку при считывании показаний прибора, равна 0,1. Для второго и третьего исследователей эта вероятность соответственно равна 0,15 и 0,2. Найти вероятность того, что при однократном измерении хотя бы один из исследователей допустит ошибку
- Вероятность успешного выполнения упражнения для каждого из двух спортсменов равна 0,5.
 Спортсмены выполняют упражнение по очереди, причем каждый делает по две попытки. Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами.
Спортсмены выполняют упражнение по очереди, причем каждый делает по две попытки. Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами. - Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.
- Вероятность хотя бы одного попадания стрелком в мишень при трех выстрелах равна 0,875. Найти вероятность попадания при одном выстреле.
- Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.
- Многократно измеряют некоторую физическую величину. Вероятность того, что при считывании показаний прибора допущена ошибка, равна р. Найти наименьшее число измерений, которое необходимо произвести, чтобы с вероятностью Р > можно было ожидать, что хотя бы один результат измерений окажется неверным.

Содержание
Метки задачи, теория вероятностей. Смотреть запись.
Теоремы сложения и умножения вероятностей.
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В урну, в которой лежат 6 белых и 5 черных шаров добавляют два черных шара. После этого наудачу по одному извлекают три шара без возвращения. Тогда вероятность того, что хотя бы один шар будет белым, равна …
Решение:
Введем обозначения событий: Ak – k – ый вынутый шар будет белым, A – хотя бы один шар будет белым. Тогда где – k – ый вынутый шар не будет белым. Так как по условию задачи события и зависимы, то
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В урну, в которой лежат 6 белых и 5 черных шаров добавляют два белых шара. После этого наудачу по одному извлекают три шара без возвращения. Тогда вероятность того, что все три шара будут белыми, равна …
После этого наудачу по одному извлекают три шара без возвращения. Тогда вероятность того, что все три шара будут белыми, равна …
Решение:
Введем обозначения событий: Ak – k – ый вынутый шар будет белым, A – все три шара будут белыми. Тогда и так как по условию задачи события и зависимы, то
ЗАДАНИЕ N 38 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Из урны, в которой лежат 3 белых и 7 черных шара, наудачу по одному извлекают два шара без возвращения. Тогда вероятность того, что только один из извлеченных шаров будет белым, равна …
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В электрическую цепь последовательно включены два элемента, работающие независимо друг от друга. Вероятности отказов элементов равны соответственно 0,1 и 0,15. Тогда вероятность того, что тока в цепи не будет, равна …
Тогда вероятность того, что тока в цепи не будет, равна …
| 0,235 | |||
| 0,765 | |||
| 0,22 | |||
| 0,015 |
Решение:
Введем обозначения событий: Ak (откажет k – ый элемент), A (тока в цепи не будет).
Тогда
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказов элементов равны соответственно 0,1, 0,2 и 0,15. Тогда вероятность того, что тока в цепи не будет, равна …
| 0,388 | |||
| 0,612 | |||
| 0,45 | |||
| 0,003 |
Решение:
Введем обозначения событий: Ak (откажет k – ый элемент), A (тока в цепи не будет, то есть откажет хотя бы один элемент).
Тогда
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В электрическую цепь параллельно включены три элемента, работающие независимо друг от друга. Вероятности отказов элементов равны соответственно 0,05, 0,1 и 0,20. Тогда вероятность того, что тока в цепи не будет, равна …
| 0,001 | |||
| 0,35 | |||
| 0,999 | |||
| 0,01 |
Решение:
Введем обозначения событий: Ak (откажет k – ый элемент), A (тока в цепи не будет).
Тогда
ЗАДАНИЕ N 38 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Наладчик обслуживает три станка. Вероятность того, что в течение часа потребует его вмешательства первый станок, равна ; второй – ; третий – . Тогда вероятность того, что в течение часа потребует вмешательства наладчика только один станок, равна …
Вероятность того, что в течение часа потребует его вмешательства первый станок, равна ; второй – ; третий – . Тогда вероятность того, что в течение часа потребует вмешательства наладчика только один станок, равна …
| 0,329 | |||
| 0,1 | |||
| 0,45 | |||
| 0,003 |
Решение:
Введем обозначения событий: Ak (вмешательства наладчика потребует k – ый станок), A (вмешательства наладчика потребует только один станок).
Тогда
Учитывая, что получаем
ЗАДАНИЕ N 35 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Студент знает ответы на 15 из 20 вопросов программы. Тогда вероятность того, что студент ответит на один из двух предложенных ему вопросов, равна …
Тогда вероятность того, что студент ответит на один из двух предложенных ему вопросов, равна …
Решение:
Введем обозначения событий: Ak (студент знает ответ на k – ый предложенный ему вопрос), A (студент знает ответы на один из двух предложенных ему вопросов).
Тогда А так как по условию задачи события и зависимы, то
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Студент знает ответы на 15 из 20 вопросов программы. Тогда вероятность того, что студент ответит на все три предложенных ему вопроса, равна …
Решение:
Введем обозначения событий: Ak (студент знает ответ на k – ый предложенный ему вопрос), A (студент знает ответы на все три предложенных ему вопроса).
Тогда А так как по условию задачи события и зависимы, то
ЗАДАНИЕ N 37 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый вопрос, равна 0,8, на второй – 0,9, на третий – 0,7. Тогда вероятность того, что студент ответит на все три вопроса, равна …
Вероятность того, что студент ответит на первый вопрос, равна 0,8, на второй – 0,9, на третий – 0,7. Тогда вероятность того, что студент ответит на все три вопроса, равна …
| 0,504 | |||
| 0,8 | |||
| 0,576 | |||
| 0,496 |
Решение:
Введем обозначения событий: Ak (студент знает ответ на k – ый вопрос), A (студент ответит на все три вопроса).
Тогда
и
Задача об определении надежности электрической цепи.
Здесь мы рассмотрим пример вероятностной модели (основные понятия теории вероятностей находятся в теоретическом разделе 5 темы).
Предположим, что в электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказов 1-го, 2-го и 3-го элементов соответственно равны Р1 = 0,1, Р2 = 0,15, Р3 = 0,2. Будем считать цепь надежной, если вероятность того, что в цепи не будет тока, не более 0,4. Требуется определить, является ли цепь надежной.
Вероятности отказов 1-го, 2-го и 3-го элементов соответственно равны Р1 = 0,1, Р2 = 0,15, Р3 = 0,2. Будем считать цепь надежной, если вероятность того, что в цепи не будет тока, не более 0,4. Требуется определить, является ли цепь надежной.
1. Построение модели. Так как элементы включены последовательно, то тока в цепи не будет, если откажет хотя бы один из элементов.
Пусть А – событие, состоящее в том, что тока в цепи не будет; событие Аi (i = 1, 2, 3) заключается в том, что i-тый элемент работает. Тогда Р(А1) = 1 – 0,1 = 0,9, Р(А2) = 1- 0,15 = 0,85, Р(А3) = 1 – 0,2 = 0,8. Очевидно, что событие, состоящее в том, что по цепи проходит ток, равно событию, заключающемуся в том, что все три элемента работают, т.е. равно произведению трех независимых событий А1, А2и А3(наступление каждого из этих событий не зависит от наступления двух других).
2. Решение математической задачи, к которой приводит модель. По теореме о вероятности произведения независимых событий Р(А1А2А3) = Р(А1)Р(А2)Р(А3) = 0,9·0,85 ·0,8 = 0,612. Тогда Р(А) + Р(А1А2А3) = 1. Поэтому Р(А) = 1 – 0,612 = 0,388 < 0,4.
3. Интерпретация полученных следствий из математической модели. Р(А) = 0,388 < 0,4. Следовательно, цепь является надежной.
Задача о диете.
Дама просто приятная решила похудеть и, как это нередко случается, обратилась за советом к подруге. Подруга – дама приятная во всех отношениях, посоветовала ей перейти на рациональное питание, состоящее из двух новомодных продуктов Р и Q.
Дневное питание этими новинками должно давать не более 14 единиц жира (чтобы похудеть), но и не менее 300 калорий (чтобы не сойти с дистанции раньше). На банке с продуктом Р написано, что в одном килограмме этого продукта содержится 15 единиц жира и 150 калорий, а на банке с продуктом Q – 4 единицы жира и 200 калорий соответственно. При этом цена 1 кг продукта Р равна 15 у.е., а 1 кг продукта Q – 25 у.е.
На банке с продуктом Р написано, что в одном килограмме этого продукта содержится 15 единиц жира и 150 калорий, а на банке с продуктом Q – 4 единицы жира и 200 калорий соответственно. При этом цена 1 кг продукта Р равна 15 у.е., а 1 кг продукта Q – 25 у.е.
Так как дама просто приятная в это время была несколько стеснена в средствах, то ее интересовал ответ на следующий вопрос: в какой пропорции нужно брать эти удивительные продукты Р и Q для того, чтобы выдержать условия диеты и истратить как можно меньше денег?
1. Построение модели. Обозначим через х количество продукта Р, а через у – количество продукта Q, требуемые для выполнения условий диеты.
Количество единиц жира, содержащегося в х кг продукта Р и в у кг продукта Q, равно 15х + 4у и по условию диеты не должно превосходить 14. Поэтому .
В свою очередь, количество калорий, содержащихся в х кг продукта Р и в у кг продукта Q, равно 150х + 200у и должно быть не меньше 300. Значит, .
Значит, .
Теперь о стоимости продуктов. Она равна z(х; у) = 15x + 25y и в соответствии с высказанными пожеланиями должна быть минимальной. Последнее записывается так: z(х; у) = 15x + 25y → min.
Итак, мы получили систему неравенств
которая является математической моделью задачи.
Полученная система неравенств называется системой ограничений задачи, а функция z(х; у) называется целевой функцией задачи.
2. Решение математической задачи, к которой приводит модель. Для решения применим координатно-графический метод.
Решением системы ограничений является многоугольник, полученный путем пересечения областей решений всех неравенств системы. Решением линейного неравенства является одна из полуплоскостей, на которые прямая, соответствующая данному неравенству, делит координатную плоскость. Для определения искомой полуплоскости берется точка, не лежащая на прямой, ее координаты подставляются в неравенство. Если в результате получается верное числовое неравенство, то решением является полуплоскость, содержащая выбранную точку. В противном случае, решением является другая полуплоскость.
Если в результате получается верное числовое неравенство, то решением является полуплоскость, содержащая выбранную точку. В противном случае, решением является другая полуплоскость.
Введем на плоскости прямоугольную систему координат хОу и построим многоугольник решений системы ограничений нашей задачи.
Из условий х ≥ 0 и у ≥ 0 вытекает, что все точки, которые удовлетворяют системе ограничений, лежат в первой координатной четверти.
Теперь решим неравенство . Ему соответствует прямая, заданная уравнением , которая проходит через точки и . Для проверки возьмем точку О(0; 0): 15 · 0 + 4 · 0 = 0 ≤ 14. Так как 0 ≤ 14 – верное неравенство, то решением неравенства является полуплоскость, содержащая точку О.
Обращаясь подобным же образом с неравенством , находим точки пересечения прямой с осями координат – точки С(2; 0) и D(0; 1,5). Для проверки также возьмем точку О(0; 0): 150 · 0 + 200 · 0 = 0 ≥ 300. Так как 0 ≥ 300 – неверное числовое неравенство, то решением неравенства является полуплоскость, не содержащая точку О.
Так как 0 ≥ 300 – неверное числовое неравенство, то решением неравенства является полуплоскость, не содержащая точку О.
Рисунок 7.4
Пересечением всех полуплоскостей является треугольник BDK (рис. 7.4). Точка К является точкой пересечения прямых АВ и CD и имеет координаты .
Теперь среди всех точек треугольника найдем ту, координаты которой удовлетворяют условию минимальности целевой функции z.
Для этого построим так называемую линию нулевого уровня функции z, которая задается уравнением z(x; y) = 0. Будем двигать эту прямую в направлении вектора , координатами которого являются соответствующие коэффициенты целевой функции, до места первой встречи этой прямой с треугольником BDK. Искомой точкой будет точка К . То есть искомые значения х = , у = 1.
3. Интерпретация полученных следствий из математической модели. Таким образом, чтобы выполнить условия диеты и истратить при этом как можно меньше средств, продукты Р и Q нужно брать в отношении х : у = : 1 = 2 : 3. То есть на 2 части продукта Р брать 3 части продукта Q.
То есть на 2 части продукта Р брать 3 части продукта Q.
Выводы
Модель – это условный образ объекта, построенный для упрощения его исследования.
Конечно, при попытке упрощенного описания ситуации некоторыми обстоятельствами приходится пренебрегать, считая их несущественными. Однако единого взгляда на то, что именно существенно, а что не очень, по-видимому, нет. Можно, например, не обращать внимания на то, что начался дождик. Но одно дело пробежать под накрапывающим дождем сотню метров, и совсем другое – часовая прогулка под таким дождем без зонта.
Предлагая построенную или выбранную нами модель, мы непременно должны указывать пределы, в которых ею можно пользоваться, и предупреждать о том, что нарушение этих ограничений приводит (и, скорее всего, приведет) к серьезным ошибкам. Коротко говоря, у каждой модели есть свой ресурс.
Покупая блузку или рубашку, мы привыкли к наличию меток, на которых указаны максимально допустимая температура глажения, дозволенные виды стирки и т. п. Это, конечно, ни в коей мере не означает, что нам запрещается, взяв докрасна раскаленный утюг, пройтись им по ткани раз-другой. Такое мы сделать можем. Но вот захотим ли мы носить блузку или рубашку после такого глажения?
п. Это, конечно, ни в коей мере не означает, что нам запрещается, взяв докрасна раскаленный утюг, пройтись им по ткани раз-другой. Такое мы сделать можем. Но вот захотим ли мы носить блузку или рубашку после такого глажения?
Таким образом, построение модели опирается на значительное упрощение изучаемой ситуации и, следовательно, к получаемым на ее основе выводам нужно относиться достаточно осторожно – модель может не все.
Вместе с тем, даже весьма грубая на вид идеализация нередко позволяет глубже вникнуть в суть проблемы. Пробуя как-то влиять на параметры модели (выбирать их, управлять ими), мы получаем возможность подвергнуть исследуемое явление качественному анализу и сделать выводы общего характера.
Контрольные вопросы
1 Что такое модель, моделирование?
2 Какие два подхода различают в моделировании? В чем их особенность?
3 Перечислите типы моделей. Дайте им краткую характеристику.
4 В чем важность математического моделирования?
5 Перечислите этапы математического моделирования. Охарактеризуйте каждый этап.
Охарактеризуйте каждый этап.
6 Как можно классифицировать математические модели?
7 Приведите пример задачи математического моделирования.
8 Почему нужно с осторожностью относиться к выводам, полученным на основе модели?
Вероятность появления хотя бы одного события
Пусть события независимы всовокупности, причем , ;пусть в результате испытания могут наступить все события, либо часть из них, либо ни одно из них.
Вероятность наступления события А, состоящего в появлении хотя бы одного из событий , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий Ā1, Ā2 , ……, Ān:
В частности, если все п событий имеют одинаковую вероятность, равную p , то вероятность появления хотя бы одного из этих событий
,
42. В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего элементов соответственно равны: р1—0,1;
Вероятности отказов первого, второго и третьего элементов соответственно равны: р1—0,1;
р2, = 0,15; р3, = 0,2. Найти вероятность того, что тока в цепи не будет.
Решение. Элементы включены последовательно, поэтому тока в цепи не будет (событие A), если откажет хотя бы один из элементов.
Искомая вероятность
43.Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
44. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,6; 0,7.
45. Три исследователя, независимо один от другого, производят измерения некоторой физической величины.
Вероятность того, что первый исследователь допустит ошибку при считывании показаний прибора, равна 0,1. Для второго и третьего исследователей эта вероятность соответственно равна 0,15 и 0,2. Найти вероятность того, что при однократном измерении хотя бы один из исследователей допустит ошибку.
46. Вероятность успешного выполнения упражнения для каждого из двух спортсменов равна 0,5. Спортсмены выполняют упражнение по очереди, причем каждый делает по две попытки. Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами.
Решение. Для вручения приза достаточно, чтобы хотя бы одна из четырех попыток была успешной. Вероятность успешной попытки р=0,5, а неуспешной q=1—0,5 = 0,5. Искомая вероятность
47. Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.
Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.
48. Вероятность хотя бы одного попадания стрелком в мишень при трех выстрелах равна 0,875. Найти вероятность попадания при одном выстреле.
Решение. Вероятность попадания в мишень хотя бы при одном из трех выстрелов (событие А) равна
,
где q—вероятность промаха.
По условию, Р(А) = 0,875. Следовательно,
, или .
Отсюда .
Искомая вероятность
p=1-q=1-0,5=0,5
49. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.
50. Многократно измеряют некоторую физическую величину. Вероятность того, что при считывании показаний прибора допущена ошибка, равна р. Найти наименьшее число измерений, которое необходимо произвести, чтобы с вероятностью Р > α можно было ожидать, что хотя бы один результат измерений окажется неверным.
Формула Байеса
Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) , ,… , которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формулам Байеса
(į = 1,2,…..,n),
где
51. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй — 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.
Решение. Обозначим через А событие — деталь отличного качества. Можно сделать два предположения (гипотезы): B1—деталь произведена первым автоматом, причем (поскольку первый автомат производит вдвое больше деталей, чем второй) Р(В1) = 2/3; В2— деталь произведена вторым автоматом, причем Р (В2)=1/3.
Условная вероятность того, что деталь будет отличного качества, если она произведена первым автоматом, .
Условная вероятность того, что деталь будет отличного качества, если она произведена вторым автоматом, .
Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности равна
Искомая вероятность того, что взятая отличная деталь произведена первым автоматом, по формуле Байеса равна
52. В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?
53. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.
Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.
Узнать еще:
Учебное пособие по физике: схемы серии
Как упоминалось в предыдущем разделе Урока 4, два или более электрических устройства в цепи могут быть соединены последовательным или параллельным соединением. Когда все устройства соединены последовательным соединением, схема называется последовательной схемой . В последовательной цепи каждое устройство подключается таким образом, что существует только один путь, по которому заряд может проходить через внешнюю цепь. Каждый заряд, проходящий через контур внешней цепи, будет последовательно проходить через каждый резистор.
Краткое сравнение и контраст между последовательными и параллельными цепями было сделано в предыдущем разделе Урока 4. В этом разделе было подчеркнуто, что добавление большего количества резисторов к последовательной цепи приводит к довольно ожидаемому результату — увеличению общего сопротивления. . Поскольку в цепи есть только один путь, каждый заряд встречает сопротивление каждого устройства; поэтому добавление большего количества устройств приводит к увеличению общего сопротивления. Это увеличенное сопротивление служит для уменьшения скорости протекания заряда (также известной как ток).
В этом разделе было подчеркнуто, что добавление большего количества резисторов к последовательной цепи приводит к довольно ожидаемому результату — увеличению общего сопротивления. . Поскольку в цепи есть только один путь, каждый заряд встречает сопротивление каждого устройства; поэтому добавление большего количества устройств приводит к увеличению общего сопротивления. Это увеличенное сопротивление служит для уменьшения скорости протекания заряда (также известной как ток).
Эквивалентное сопротивление и ток
Заряды проходят через внешнюю цепь со скоростью, которая везде одинакова. В одном месте ток не больше, чем в другом. Фактическое количество тока обратно пропорционально общему сопротивлению. Существует четкая взаимосвязь между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов.Что касается батареи, которая нагнетает заряд, наличие двух последовательно соединенных резисторов сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 12 Ом. Наличие трех последовательно соединенных резисторов сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 18 Ом. И наличие четырех последовательно соединенных резисторов 6 Ом было бы эквивалентно наличию в цепи одного резистора 24 Ом.
Наличие трех последовательно соединенных резисторов сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 18 Ом. И наличие четырех последовательно соединенных резисторов 6 Ом было бы эквивалентно наличию в цепи одного резистора 24 Ом.
Это концепция эквивалентного сопротивления. Эквивалентное сопротивление схемы — это величина сопротивления, которая потребуется одному резистору, чтобы сравняться с общим эффектом от набора резисторов, присутствующих в схеме.Для последовательных цепей математическая формула для вычисления эквивалентного сопротивления (R eq ) составляет
. рэндов экв. = 1 рэндов + 2 рэндов + 3 рэндов + …, где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, соединенных последовательно.
Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже. Создайте себе проблему с любым количеством резисторов и любыми номиналами. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.
Создайте себе проблему с любым количеством резисторов и любыми номиналами. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.
Ток в последовательной цепи везде одинаковый. Заряд НЕ накапливается и не начинает накапливаться в любом заданном месте, так что ток в одном месте больше, чем в других местах. Заряд НЕ расходуется резисторами, поэтому в одном месте его меньше по сравнению с другим. Можно представить, что заряды движутся вместе по проводам электрической цепи и везде движутся с одинаковой скоростью.Ток — скорость, с которой течет заряд — везде одинаков. То же самое на первом резисторе, как на последнем резисторе, как в батарее. Математически можно написать
I аккумулятор = I 1 = I 2 = I 3 = …
, где I 1 , I 2 и I 3 — значения тока в отдельных местах расположения резисторов.
Эти значения тока легко вычислить, если известно напряжение батареи и известны отдельные значения сопротивления. Используя значения отдельных резисторов и приведенное выше уравнение, можно рассчитать эквивалентное сопротивление. А используя закон Ома (ΔV = I • R), можно определить ток в батарее и, следовательно, через каждый резистор, найдя соотношение напряжения батареи и эквивалентного сопротивления.
Используя значения отдельных резисторов и приведенное выше уравнение, можно рассчитать эквивалентное сопротивление. А используя закон Ома (ΔV = I • R), можно определить ток в батарее и, следовательно, через каждый резистор, найдя соотношение напряжения батареи и эквивалентного сопротивления.
I аккумулятор = I 1 = I 2 = I 3 = ΔV аккумулятор / R экв
Разность электрических потенциалов и падения напряжения
Как обсуждалось в Уроке 1, электрохимический элемент схемы подает энергию на заряд, чтобы перемещать его через элемент и устанавливать разность электрических потенциалов на двух концах внешней цепи.Элемент с напряжением 1,5 В создает разность электрических потенциалов во внешней цепи 1,5 В. Это означает, что электрический потенциал на положительной клемме на 1,5 В больше, чем на отрицательной клемме. Когда заряд движется по внешней цепи, он теряет 1,5 вольт электрического потенциала. Эта потеря электрического потенциала обозначается как падение напряжения . Это происходит, когда электрическая энергия заряда преобразуется в другие формы энергии (тепловую, световую, механическую и т. Д.).) внутри резисторов или нагрузок. Если электрическая цепь, питаемая от элемента на 1,5 В, оснащена более чем одним резистором, то совокупная потеря электрического потенциала составляет 1,5 В. Для каждого резистора существует падение напряжения, но сумма этих падений составляет 1,5 В — то же самое, что и номинальное напряжение источника питания. Это понятие может быть выражено математически следующим уравнением:
Когда заряд движется по внешней цепи, он теряет 1,5 вольт электрического потенциала. Эта потеря электрического потенциала обозначается как падение напряжения . Это происходит, когда электрическая энергия заряда преобразуется в другие формы энергии (тепловую, световую, механическую и т. Д.).) внутри резисторов или нагрузок. Если электрическая цепь, питаемая от элемента на 1,5 В, оснащена более чем одним резистором, то совокупная потеря электрического потенциала составляет 1,5 В. Для каждого резистора существует падение напряжения, но сумма этих падений составляет 1,5 В — то же самое, что и номинальное напряжение источника питания. Это понятие может быть выражено математически следующим уравнением:
Чтобы проиллюстрировать этот математический принцип в действии, рассмотрим две схемы, показанные ниже на диаграммах A и B. Предположим, вас попросили определить два неизвестных значения разности электрических потенциалов между лампочками в каждой цепи.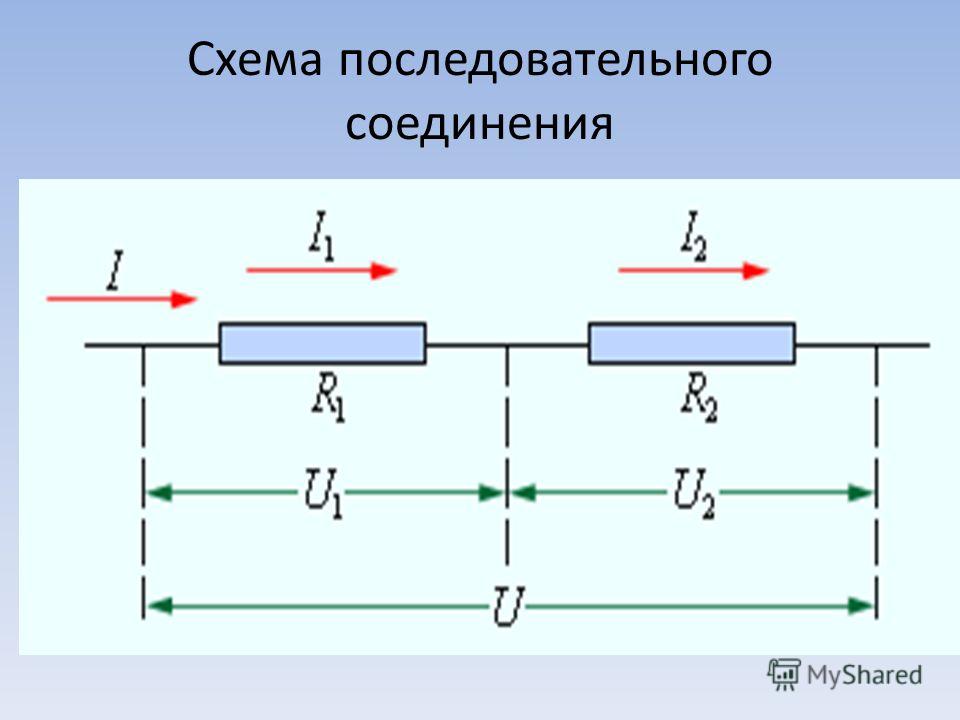 Чтобы определить их значения, вам нужно будет использовать приведенное выше уравнение. Батарея обозначается обычным схематическим символом, а рядом с ней указывается ее напряжение. Определите падение напряжения для двух лампочек и затем нажмите кнопку «Проверить ответы», чтобы убедиться, что вы правы.
Чтобы определить их значения, вам нужно будет использовать приведенное выше уравнение. Батарея обозначается обычным схематическим символом, а рядом с ней указывается ее напряжение. Определите падение напряжения для двух лампочек и затем нажмите кнопку «Проверить ответы», чтобы убедиться, что вы правы.
Ранее в Уроке 1 обсуждалось использование диаграммы электрических потенциалов. Диаграмма электрических потенциалов — это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим приведенную ниже принципиальную схему и соответствующую диаграмму электрических потенциалов.
Схема, показанная на схеме выше, питается от источника энергии 12 В.В цепи последовательно соединены три резистора, каждый из которых имеет собственное падение напряжения. Отрицательный знак разности электрических потенциалов просто означает потерю электрического потенциала при прохождении через резистор.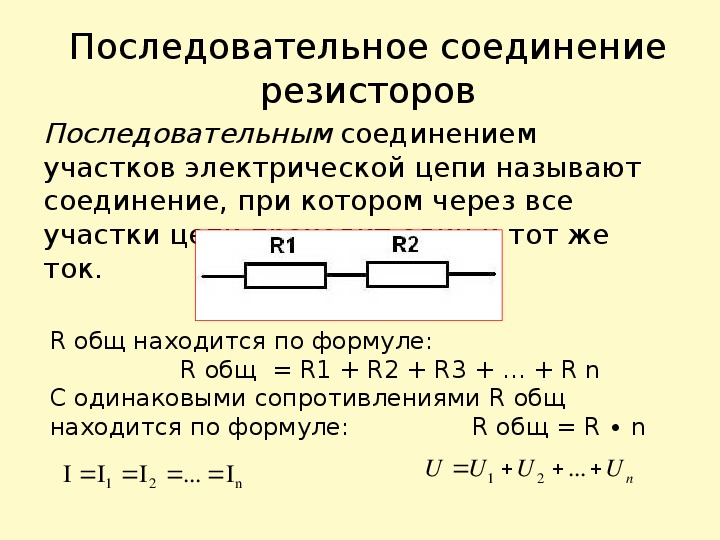 Обычный ток направляется по внешней цепи от положительной клеммы к отрицательной. Поскольку схематический символ источника напряжения использует длинную полосу для обозначения положительной клеммы, точка A на схеме находится на положительной клемме или клемме с высоким потенциалом.В точке A электрический потенциал 12 вольт, а в точке H (отрицательный вывод) — 0 вольт. Проходя через батарею, заряд приобретает электрический потенциал 12 вольт. А при прохождении через внешнюю цепь заряд теряет 12 вольт электрического потенциала, как показано на диаграмме электрических потенциалов, показанной справа от принципиальной схемы. Эти 12 вольт электрического потенциала теряются в три этапа, каждый из которых соответствует прохождению через резистор. При прохождении через соединительные провода между резисторами происходит небольшая потеря электрического потенциала из-за того, что провод оказывает относительно небольшое сопротивление потоку заряда.Поскольку точки A и B разделены проводом, они имеют практически одинаковый электрический потенциал 12 В.
Обычный ток направляется по внешней цепи от положительной клеммы к отрицательной. Поскольку схематический символ источника напряжения использует длинную полосу для обозначения положительной клеммы, точка A на схеме находится на положительной клемме или клемме с высоким потенциалом.В точке A электрический потенциал 12 вольт, а в точке H (отрицательный вывод) — 0 вольт. Проходя через батарею, заряд приобретает электрический потенциал 12 вольт. А при прохождении через внешнюю цепь заряд теряет 12 вольт электрического потенциала, как показано на диаграмме электрических потенциалов, показанной справа от принципиальной схемы. Эти 12 вольт электрического потенциала теряются в три этапа, каждый из которых соответствует прохождению через резистор. При прохождении через соединительные провода между резисторами происходит небольшая потеря электрического потенциала из-за того, что провод оказывает относительно небольшое сопротивление потоку заряда.Поскольку точки A и B разделены проводом, они имеют практически одинаковый электрический потенциал 12 В. Когда заряд проходит через свой первый резистор, он теряет 3 В электрического потенциала и падает до 9 В в точке C. точка D отделена от точки C простым проводом, она имеет практически тот же электрический потенциал 9 В, что и C. Когда заряд проходит через второй резистор, он теряет 7 В электрического потенциала и падает до 2 В в точке E. Поскольку точка F отделена от точки E простым проводом, она имеет практически тот же электрический потенциал 2 В, что и E.Наконец, когда заряд проходит через свой последний резистор, он теряет 2 В электрического потенциала и падает до 0 В в точке G. В точках G и H в заряде заканчивается энергия, и ему требуется повышение энергии, чтобы пройти через внешний резистор. схема снова. Прирост энергии обеспечивается аккумулятором при перемещении заряда с H на A.
Когда заряд проходит через свой первый резистор, он теряет 3 В электрического потенциала и падает до 9 В в точке C. точка D отделена от точки C простым проводом, она имеет практически тот же электрический потенциал 9 В, что и C. Когда заряд проходит через второй резистор, он теряет 7 В электрического потенциала и падает до 2 В в точке E. Поскольку точка F отделена от точки E простым проводом, она имеет практически тот же электрический потенциал 2 В, что и E.Наконец, когда заряд проходит через свой последний резистор, он теряет 2 В электрического потенциала и падает до 0 В в точке G. В точках G и H в заряде заканчивается энергия, и ему требуется повышение энергии, чтобы пройти через внешний резистор. схема снова. Прирост энергии обеспечивается аккумулятором при перемещении заряда с H на A.
В Уроке 3 закон Ома (ΔV = I • R) был введен как уравнение, которое связывает падение напряжения на резисторе с сопротивлением резистора и током на резисторе.Уравнение закона Ома можно использовать для любого отдельного резистора в последовательной цепи. При объединении закона Ома с некоторыми принципами, уже обсужденными на этой странице, возникает большая идея.
При объединении закона Ома с некоторыми принципами, уже обсужденными на этой странице, возникает большая идея.
В последовательных цепях резистор с наибольшим сопротивлением имеет наибольшее падение напряжения.
Поскольку в последовательной цепи ток везде одинаковый, значение I ΔV = I • R одинаково на каждом из резисторов последовательной цепи. Таким образом, падение напряжения (ΔV) будет изменяться с изменением сопротивления.Где бы сопротивление ни было наибольшим, падение напряжения будет наибольшим у этого резистора. Уравнение закона Ома можно использовать не только для прогнозирования того, что резистор в последовательной цепи будет иметь наибольшее падение напряжения, но и для расчета фактических значений падения напряжения.
| Δ В 1 = I • R 1 | Δ В 2 = I • R 2 | Δ В 3 = I • R 3 |
Математический анализ последовательных цепей
Приведенные выше принципы и формулы могут быть использованы для анализа последовательной цепи и определения значений тока и разности электрических потенциалов на каждом из резисторов в последовательной цепи. Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока в батарее (I до ), а также падений напряжения и тока для каждого из трех резисторов.
Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока в батарее (I до ), а также падений напряжения и тока для каждого из трех резисторов.
Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.
R экв = R 1 + R 2 + R 3 = 17 Ом + 12 Ом + 11 Ом = 40 ОмТеперь, когда известно эквивалентное сопротивление, ток в батарее можно определить с помощью уравнения закона Ома.При использовании уравнения закона Ома (ΔV = I • R) для определения тока в цепи важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R. Расчет показан здесь:
I до = ΔV аккумулятор / R eq = (60 В) / (40 Ом) = 1,5 А Значение тока 1,5 А — это ток в месте расположения батареи. Для последовательной цепи без точек разветвления ток везде одинаковый.Ток в месте расположения батареи такой же, как ток в каждом месте расположения резистора. Впоследствии 1,5 ампер — это значение I 1 , I 2 и I 3 .
Для последовательной цепи без точек разветвления ток везде одинаковый.Ток в месте расположения батареи такой же, как ток в каждом месте расположения резистора. Впоследствии 1,5 ампер — это значение I 1 , I 2 и I 3 .
Осталось определить три значения — падение напряжения на каждом отдельном резисторе. Закон Ома снова используется для определения падений напряжения для каждого резистора — это просто произведение тока на каждом резисторе (вычисленное выше как 1.5 ампер) и сопротивление каждого резистора (указано в постановке задачи). Расчеты показаны ниже.
|
ΔV 1 = I 1 • R 1 ΔV 1 = (1,5 A) • (17 Ом) ΔV 1 = 25,5 В |
ΔV 2 = I 2 • R 2 ΔV 2 = (1,5 A) • (12 Ом) ΔV 2 = 18 В |
ΔV 3 = I 3 • R 3 ΔV 3 = (1. ΔV 3 = 16,5 В |
В качестве проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли вычисленные значения принципу, согласно которому сумма падений напряжения для каждого отдельного резистора равна номинальному напряжению батареи. Другими словами, ΔV батареи = ΔV 1 + ΔV 2 + ΔV 3 ?
ΔV аккумулятор = ΔV 1 + ΔV 2 + ΔV 3 ?Это 60 В = 25.5 В + 18 В + 16,5 В?
60 В = 60 В?
Да !!
Математический анализ этой последовательной схемы включал смесь концепций и уравнений. Как это часто бывает в физике, отделение понятий от уравнений при принятии решения физической проблемы является опасным актом. Здесь необходимо учитывать концепции, согласно которым ток везде одинаков и что напряжение батареи эквивалентно сумме падений напряжения на каждом резисторе, чтобы завершить математический анализ. В следующей части Урока 4 параллельные цепи будут проанализированы с использованием закона Ома и концепций параллельных цепей. Мы увидим, что подход сочетания концепций с уравнениями будет не менее важен для этого анализа.
В следующей части Урока 4 параллельные цепи будут проанализированы с использованием закона Ома и концепций параллельных цепей. Мы увидим, что подход сочетания концепций с уравнениями будет не менее важен для этого анализа.
Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействовать — это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom.Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключить их так, как хотите. Вольтметры и амперметры позволяют измерять ток и падение напряжения.
 Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение.Это просто. Это весело. И это безопасно (если вы не используете его в ванне).
Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение.Это просто. Это весело. И это безопасно (если вы не используете его в ванне).
Проверьте свое понимание
1. Используйте свое понимание эквивалентного сопротивления, чтобы заполнить следующие утверждения:
а. Два резистора сопротивлением 3 Ом, включенные последовательно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.
г. Три резистора сопротивлением 3 Ом, включенные последовательно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.
г. Три резистора сопротивлением 5 Ом, включенные последовательно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
г. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом включены последовательно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
e. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом включены последовательно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
ф. Три резистора с сопротивлением 12 Ом, 3 Ом и 21 Ом включены последовательно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
2. По мере увеличения количества резисторов в последовательной цепи общее сопротивление __________ (увеличивается, уменьшается, остается прежним) и ток в цепи __________ (увеличивается, уменьшается, остается прежним).
3. Рассмотрим следующие две схемы последовательных цепей. На каждой диаграмме используйте стрелки, чтобы указать направление обычного тока. Затем сравните напряжение и ток в обозначенных точках для каждой диаграммы.
4. Три одинаковые лампочки подключены к D-ячейке, как показано справа.Какое из следующих утверждений верно?
а.Все три лампочки будут иметь одинаковую яркость.
г. Лампа между X и Y будет самой яркой.
г. Лампа между Y и Z будет самой яркой.
г. Лампочка между Z и батареей будет самой яркой.
5. Три одинаковые лампочки подключены к батарее, как показано справа.Какие настройки можно было бы внести в схему, чтобы увеличить ток, измеряемый в точке X? Перечислите все подходящие варианты.
а. Увеличьте сопротивление одной из лампочек.г. Увеличьте сопротивление двух лампочек.
г. Уменьшите сопротивление двух лампочек.
г. Увеличьте напряжение аккумулятора.
e. Уменьшите напряжение аккумулятора.
ф. Удалите одну из луковиц.
6. Три одинаковые лампочки подключены к батарее, как показано справа. W, X, Y и Z обозначают места на трассе. Какое из следующих утверждений верно?
а.Разница потенциалов между X и Y больше, чем между Y и Z.
г. Разница потенциалов между X и Y больше, чем между Y и W.
г. Разность потенциалов между Y и Z больше, чем между Y и W.
г. Разность потенциалов между X и Z больше, чем между Z и W.
e. Разность потенциалов между X и W больше, чем на батарее.
ф. Разница потенциалов между X и Y больше, чем между Z и W.
7.Сравните схему X и Y ниже. Каждый питается от 12-вольтовой батареи. Падение напряжения на резисторе 12 Ом в цепи Y равно ____ падению напряжения на единственном резисторе в цепи X.
а. меньше чемг. больше
г. то же, что
8. Аккумулятор на 12 В, резистор на 12 Ом и лампочка подключаются, как показано на схеме X ниже.Резистор на 6 Ом добавлен к резистору на 12 Ом и лампочке, чтобы создать цепь Y, как показано. Лампочка появится ____.
Лампочка появится ____.
а. диммер в контуре Xг. диммер в контуре Y
г. одинаковая яркость в обеих цепях
9. Три резистора включены последовательно. При размещении в цепи с источником питания 12 В.Определите эквивалентное сопротивление, полный ток цепи, падение напряжения и ток на каждом резисторе.
Выяснение того, подключены ли электрические компоненты последовательно или параллельно (просто взглянув на принципиальную схему)
Выявление, если электрические компоненты соединены последовательно или параллельно (просто взглянув на принципиальную схему) — Physics Stack ExchangeСеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.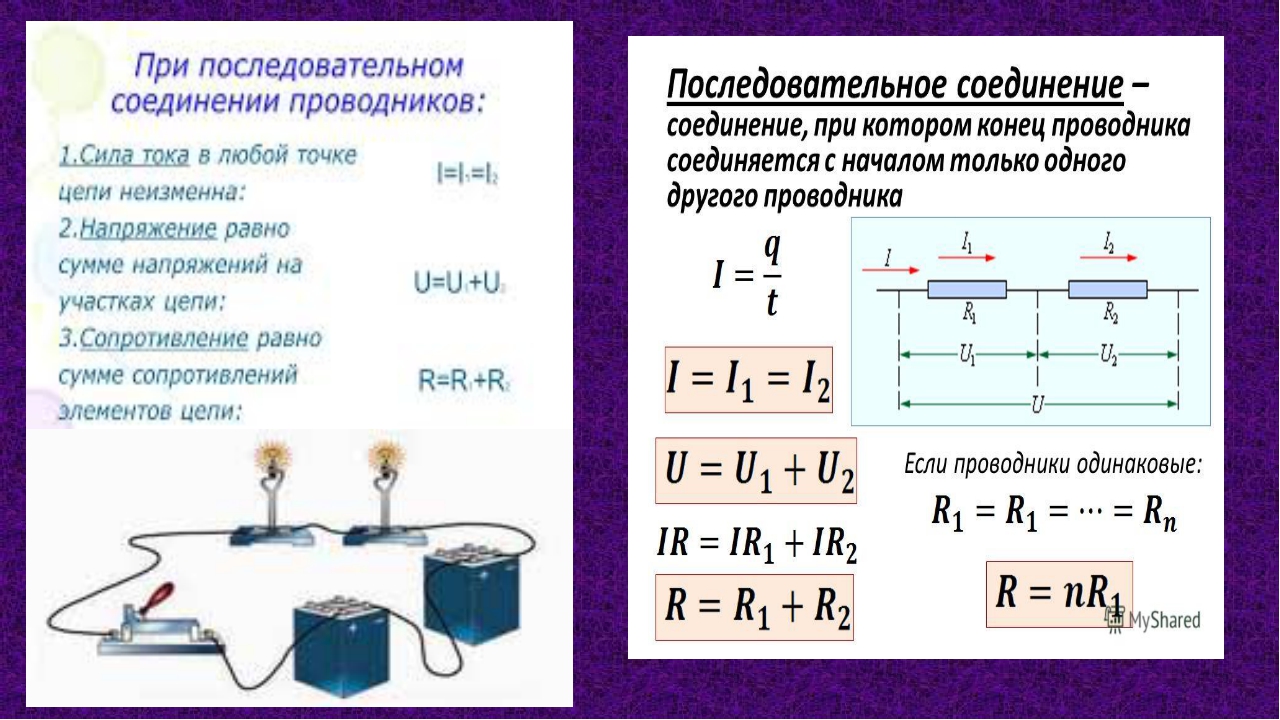
- 0
- +0
- Авторизоваться Зарегистрироваться
Physics Stack Exchange — это сайт вопросов и ответов для активных исследователей, ученых и студентов-физиков.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 59 раз
$ \ begingroup $ Закрыто.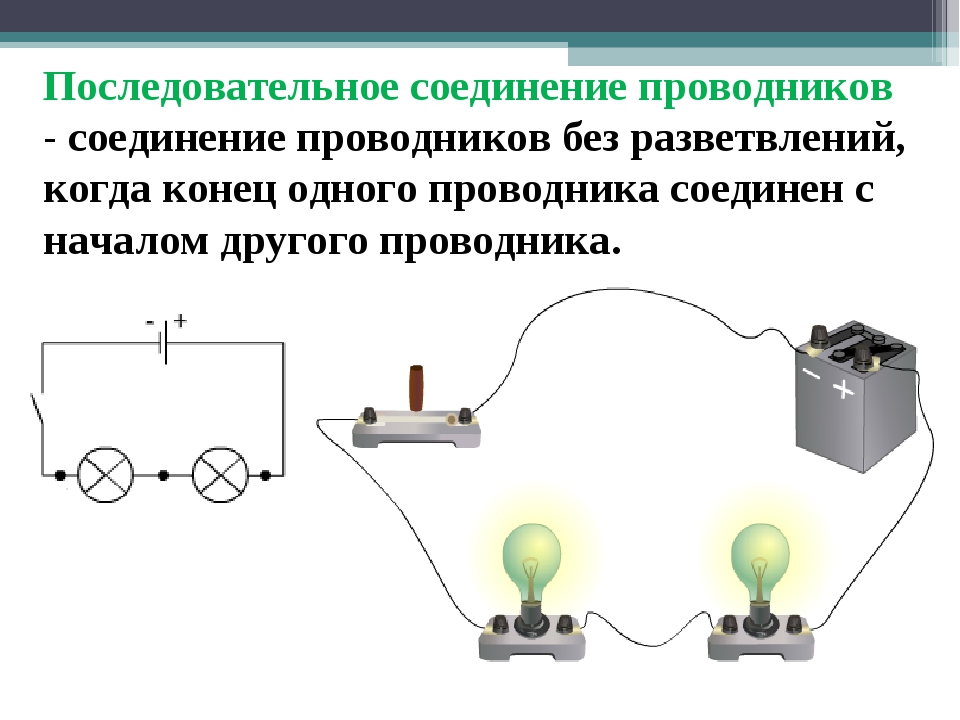 Этот вопрос не по теме. В настоящее время он не принимает ответы.
Этот вопрос не по теме. В настоящее время он не принимает ответы.
Хотите улучшить этот вопрос? Обновите вопрос, чтобы он соответствовал теме Physics Stack Exchange.
Закрыт 11 месяцев назад.
Есть ли способ узнать, находятся ли электрические компоненты в данной цепи параллельно / последовательно, просто взглянув на принципиальную схему.Если да, может кто-нибудь дать правила для этого?
Создан 01 июн.
$ \ endgroup $ $ \ begingroup $Если два элемента в цепи соединены «встык», так что весь ток, проходящий через один, должен проходить через другой, то они включены последовательно.Если они соединены «бок о бок» так, чтобы между ними делился ток, они будут параллельны. Джокер — это «мост»: два последовательно, рядом еще два последовательно, и пятый элемент, соединяющий средние точки.
Создан 01 июн.
Р.В. Берд Птица6,37922 золотых знака33 серебряных знака1212 бронзовых знаков
$ \ endgroup $ $ \ begingroup $Если все элементы между двумя выводами имеют одинаковый ток, проходящий через них, они соединены последовательно.$ V = \ sum I_i R_i $ и все $ I_i $ одинаковы, поэтому $ V = I \ sum R_i $.
Если все они имеют одинаковое напряжение, они подключены параллельно. $ I = \ sum {V_i \ over R_1} $ и все $ V_i $ одинаковы, поэтому $ I = V \ sum {1 \ over R_i} $
Если ни одно из вышеперечисленных утверждений не соответствует действительности, просто вернитесь к законам Кирхгофа.
Создан 01 июн.
Роджер Дж. Барлоу8,45911 золотых знаков1414 серебряных знаков3838 бронзовых знаков
$ \ endgroup $ Physics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Элемент схемы — обзор
6.2.1.1 Толстопленочные процессы
Между первоначальным чертежом заказчика и окончательной схемой существует много этапов.
Элементы схемы размечаются с использованием системы автоматизированного проектирования (САПР), из которой с помощью фотоплоттера изготавливаются фотопозитивы для каждой отдельной краски, предназначенной для печати на подложке. САПР также подготовит все необходимые чертежи и инструкции для производственного персонала. Типичная ширина проводящей линии составляет 0,25–0,75 мм (0,010–0,030 дюйма), а резисторы обычно имеют квадрат не менее 1,25 мм (0,050 дюйма).
Фотопозитив экспонируется и проявляется на экране, покрытом U.В. чувствительная эмульсия. Сито из нержавеющей стали или синтетической ткани с размером ячеек от 2,4 до 16 ячеек / мм (60-400 ячеек / дюйм). Толстопленочная паста, нанесенная на трафарет, печатается на подложке с помощью подвижного гибкого ракеля.
Печатные машины могут быть загружены вручную или оснащены механическими системами подачи, которые принимают материалы из магазинов и переносят отпечатанные материалы на ленточные сушилки. Высушенные пасты обжигаются в многозонных ленточных печах с контролируемым температурно-временным профилем.Типичный профиль для проводников / резисторов составляет 60 минут, из них 10 минут при максимальной температуре 850 ° C.
Подстройка резисторов осуществляется с помощью энергии лазера, что дает такие преимущества, как скорость, точность и чистота. На подложках, напечатанных с использованием нескольких схем, разметка выполняется с помощью более мощного лазера, поэтому отдельные схемы можно вырезать.
Компоненты, соединенные пайкой, размещаются на контактных площадках с нанесенным припоем. Для достижения необходимого объема работы это обычно выполняется с помощью машин для захвата и размещения с компьютерным управлением, которые берут каждый компонент с отдельной катушки и размещают их в правильном положении.Есть несколько методов, используемых для оплавления паяльной пасты, например, с использованием нагретых лент, туннельных печей в атмосфере азота и инфракрасных ламп.
После процессов пайки с использованием флюса блоки можно очистить, но многие системы пайки теперь являются «нечистыми», поскольку флюс не представляет опасности для работы схемы.
Планируется прекратить использование припоев, содержащих свинец, в электронике по экологическим причинам. Есть несколько систем, которые можно использовать в качестве альтернативы, используя олово, легированное множеством других металлов.Наибольшее изменение, влияющее на их использование в гибридах, заключается в том, что температура плавления обычно на 30-40 ° C выше, чем у эвтектики олово / свинец, и компоненты должны выдерживать нагрев до более высокой температуры во время сборки.
Полупроводниковые чипы обычно приклеиваются эпоксидной смолой. Его можно сделать проводящим с помощью серебряного или золотого порошка. Проводящая эпоксидная смола также используется для крепления конденсаторов к золотым проводникам, потому что припой очень быстро растворяет золото. Голые микросхемы скреплены алюминиевыми или золотыми проволоками примерно 0 °.Диаметр 025 мм (0,001 дюйма). Алюминиевая проволока не используется с проводниками из чистого золота, потому что прочность связи быстро ухудшается.
Гибриды могут быть установлены на их собственных выводах или внутри металлического или керамического корпуса, который имеет свои собственные выводы. Терминалы поставляются в барабанах, по 50 000 штук на непрерывной полосе. Машины для вставки обрезают ненужные клеммы и вставляют подложки в полосу, после чего наматывают полосу. Затем полоса пропускается через машину для пайки волной припоя, затем припаянная полоса может быть обработана на финишной машине, которая вырезает каждую единицу из полосы, проверяет ее и упаковывает.
Металлические упаковки закрываются пайкой или привариванием крышки или крышки к коллектору, на котором установлена подложка. Внутри корпуса поддерживается атмосфера сухого азота, чтобы предохранить контур от коррозии. Сами пакеты защищены пленками из олова, припоя, никеля или золота.
Основные электрические схемы-компоненты, типы
Что такое электрическая цепь?
Электрическая цепь — это замкнутый путь для передачи электрического тока через среду электрических и магнитных полей.Поток электронов через петлю составляет электрический ток. Электроны входят в цепь через «Источник», которым может быть батарея или генератор. Источник обеспечивает электроны энергией, создавая электрическое поле, которое обеспечивает электродвижущую силу.
Электроны покидают цепь через нагрузку на землю, замыкая тем самым замкнутый путь. Нагрузкой или выходом может быть любое простое бытовое устройство, такое как телевизор, лампа, холодильник, или сложная нагрузка, например, на гидроэлектростанции.
Простая электрическая цепь состоит из источника (например, батареи), проводов в качестве проводящей среды и нагрузки (например, лампочки). Батарея обеспечивает необходимую энергию для потока электронов к лампочке.
Основные элементы схемы
Как упоминалось выше во введении, схема представляет собой соединение элементов между собой. Эти элементы подразделяются на активные и пассивные в зависимости от их способности генерировать энергию.
Активные элементы схемы
Активные элементы — это элементы, которые могут генерировать энергию.Примеры включают батареи, генераторы, операционные усилители и диоды. Обратите внимание, что в электрической цепи элементы источника являются наиболее важными активными элементами.
Источники энергии, будь то источник напряжения или тока, бывает двух типов — независимые и зависимые источники. Примером независимого источника является батарея, которая обеспечивает постоянное напряжение в цепи, независимо от тока, протекающего через клеммы.
Примером зависимого источника является транзистор, который обеспечивает ток в цепи в зависимости от приложенного к нему напряжения.Другой пример — операционный усилитель, который выдает напряжение в зависимости от дифференциального входного напряжения, приложенного к его клеммам.
Пассивные элементы схемы
Пассивные элементы можно определить как элементы, которые могут управлять потоком электронов через них. Они либо увеличивают, либо уменьшают напряжение. Вот несколько примеров пассивных элементов.
Резистор : резистор препятствует прохождению тока через него. Для линейной цепи применим закон Ома, который гласит, что напряжение на резисторе прямо пропорционально току, протекающему через него, а пропорциональная константа — это сопротивление.
Индуктор : Индуктор накапливает энергию в форме электромагнитного поля. Напряжение на катушке индуктивности пропорционально скорости изменения тока, протекающего через нее.
Конденсатор : Конденсатор накапливает энергию в виде электростатического поля. Напряжение на конденсаторе пропорционально заряду.
Типы электрических цепей
Цепи постоянного тока
В цепях постоянного тока применяемое возбуждение является постоянным источником.В зависимости от типа соединения активных и пассивных компонентов с источником цепь можно разделить на последовательные и параллельные.
Последовательные цепи
Когда несколько пассивных элементов соединены последовательно с источником энергии, такая схема называется последовательной схемой. В последовательной цепи через каждый элемент протекает одинаковое количество тока, и напряжение делится. В последовательной цепи, поскольку элементы соединены в линию, если среди них есть неисправный элемент, полная цепь действует как разомкнутая цепь.
- Для резистора, подключенного в цепи постоянного тока, напряжение на его выводах прямо пропорционально току, проходящему через него, таким образом, сохраняется линейная зависимость между напряжением и током. Для резисторов, соединенных последовательно, общее сопротивление равно сумме всех значений сопротивлений.
- Для конденсаторов, соединенных последовательно, общая емкость равна сумме обратных величин всех значений емкости.
- Для катушек индуктивности, соединенных последовательно, общая индуктивность равна сумме всех значений индуктивности.
Параллельные схемы
В параллельной схеме один вывод всех элементов подключен к одному выводу источника, а другой вывод всех элементов подключен к другому выводу источника.
В параллельных цепях напряжение в параллельных элементах остается неизменным, а ток изменяется. Если среди параллельных элементов есть неисправный элемент, это не повлияет на схему.
- Для резисторов, соединенных параллельно, полное сопротивление равно сумме обратных величин всех значений сопротивления.
- Для конденсаторов, соединенных последовательно, общая емкость равна сумме всех значений емкости.
- Для катушек индуктивности, соединенных последовательно, общая индуктивность равна сумме всех обратных значений индуктивности.
Цепи переменного тока
Цепи переменного тока — это те цепи, чьим элементом возбуждения является источник переменного тока. В отличие от источника постоянного тока, который является постоянным источником переменного тока, он имеет переменные ток и напряжение через равные промежутки времени. Как правило, для приложений с большой мощностью используются цепи переменного тока.
Простая схема переменного тока с использованием сопротивления
Для переменного тока, проходящего через резистор, соотношение тока и напряжения зависит от фазы и частоты источника питания. Приложенное напряжение будет постоянно меняться со временем, и закон Ома можно использовать для расчета тока, проходящего через резистор в любой момент времени.
Другими словами, если в момент времени t секунд значение напряжения равно v вольт, ток будет:
i = v / R
, где значение R всегда постоянно.
Приведенное выше уравнение показывает, что полярность тока зависит от полярности напряжения. Кроме того, как ток, так и напряжение достигают своей максимальной и нулевой точек одновременно. Таким образом, для резистора напряжение совпадает по фазе с приложенным током.
Рассмотрим приведенную ниже принципиальную схему
Когда переключатель замкнут, ток проходит через резистор и определяется уравнением ниже
i = Im cos (ωt + Φ)
Напряжение, V = IR = RIm cos (ωt + Φ)
Для резистора значения напряжения и тока будут расти и падать одновременно.Следовательно, разность фаз между напряжением и током равна нулю.
Цепь переменного тока с использованием чистой индуктивности
Катушка из тонкой проволоки, намотанная на цилиндрический сердечник, известна как индуктор. Сердечник может быть воздушным сердечником (многослойным полым) или железным сердечником. Когда через индуктор протекает переменный ток, магнитное поле также изменяется. Это изменение магнитного поля приводит к индуцированному напряжению на катушке индуктивности. Согласно закону Ленца, индуцированное напряжение таково, что оно противодействует протеканию через него тока.
Во время первого полупериода напряжения источника индуктор накапливает энергию в виде магнитного поля, а в следующей половине он выделяет энергию.
Индуцированная ЭДС определяется следующим образом:
e = Ldi / dt
Здесь L — самоиндукция.
Теперь, приложенное входное напряжение переменного тока определяется как v (t) = Vm Sinωt
Ток через катушку индуктивности равен: I (t) = Im Sinωt
Таким образом, напряжение на катушке индуктивности будет
e = L di / dt = wLI_m coswt = wLI_m sin (wt + 90)
Таким образом, для катушки индуктивности напряжение опережает ток на 90 градусов.
Теперь сопротивление катушки индуктивности называется реактивным сопротивлением и выражается как
Таким образом, импеданс или сопротивление пропорционально скорости изменения тока катушки индуктивности.
Схема переменного тока с конденсатором
При постоянном питании постоянного тока пластины конденсатора заряжаются до приложенного напряжения, временно накапливают этот заряд и затем начинают разряжаться. Когда конденсатор полностью заряжен, он блокирует ток, поскольку пластины насыщаются.
Когда на конденсатор подается напряжение переменного тока, скорость заряда и разряда зависит от частоты источника питания.Напряжение на конденсаторе отстает от протекающего через него тока на 90 градусов.
Ток через конденсатор определяется как
e = Ldi / dt
Емкостное реактивное сопротивление определяется как:
e = Ld / idt
Таким образом, полное сопротивление или реактивное сопротивление источника переменного тока обратно пропорционально частоте источника питания. .
Что такое короткое замыкание и обрыв?
Короткое замыкание
Соединение с низким или незначительным сопротивлением между двумя проводниками в электрической цепи называется коротким замыканием.Короткое замыкание приведет к выделению большего количества тепла и, в конечном итоге, к искрам, пламени или дыму.
Короткое замыкание может быть вызвано неплотными контактами, неисправной изоляцией, резким пережевыванием проводов вредителями или старыми приборами. Один из лучших и часто используемых методов предотвращения повреждений в результате короткого замыкания — это использование предохранителя или автоматического выключателя.
Обрыв цепи
Обрыв цепи вызван обрывом в электрической цепи. Когда какой-либо элемент в цепи остается неподключенным, создается разомкнутая цепь.В то время как напряжение на разомкнутой цепи имеет некоторое конечное значение, ток равен нулю.
Защита цепи
Преднамеренная установка слабого звена в электрической цепи называется защитой цепи. Целью этой установки является предотвращение повреждений из-за короткого замыкания, превышения температуры и других повреждений.
Устройство защиты цепи может быть предохранителем, автоматическим выключателем, тиристором или переключателем. Схема серии
— Энергетическое образование
Рисунок 1.Пример последовательной схемы, генерируемой через PHET [1] .Многие электрические компоненты в электрической цепи имеют два вывода (конца). В результате их можно соединить одним из двух способов; последовательно (один электрический вывод касается другого) или параллельно (оба провода соприкасаются).
Цепь серии обеспечивает ровно один путь между любыми двумя точками для электрического тока. Эти схемы имеют то преимущество, что каждый компонент очень зависит от других компонентов.Это означает, что при удалении одного компонента все компоненты отключаются. Хотя, как правило, это плохая идея (было бы неприятно, если бы лампочка выключилась только потому, что выключили телевизор), есть ряд приложений, где это работает лучше. Рождественские огни в старинном стиле были такими, поэтому, если одна лампочка перегорела, загорелись все. Новые гирлянды рождественских гирлянд немного сложнее, а это означает, что гаснет только одна лампочка, а не вся гирлянда.
Электрические выключатели включены последовательно с различными электрическими устройствами (в случае удлинителя один выключатель может быть включен последовательно с несколькими электрическими приборами, включенными параллельно) по всему дому.Выключатель света, включенный последовательно с электрическим светом, выключит свет при открытии. Это произойдет так быстро, что люди не смогут даже обнаружить временную задержку между включением переключателя и выключением света.
Защитные устройства, такие как автоматические выключатели и предохранители, включены последовательно с электрическими розетками в доме. Весь ток, который будет проходить через электрическое устройство, должен сначала пройти через автоматический выключатель (или предохранитель). Если будет протекать слишком большой ток (что может привести к пожару), сначала сработает автоматический выключатель (или сгорит предохранитель).Поскольку каждая цепь параллельна, даже если одна цепь будет перегружена (отключение автоматического выключателя или перегорание предохранителя), это не повлияет на другие цепи. Точно так же разные дома в районе расположены параллельно. Сосед, готовящий ужин, не влияет на кого-то, гладильного в другом доме на другом участке.
Различные части электрической сети обычно соединяются последовательно. Трансформатор включен последовательно с распределительной сетью и системой передачи. Это означает, что если какая-либо часть электрической сети выйдет из строя, люди испытают отключение электричества.Это привело к тому, что большинство электроэнергетических компаний (люди, обеспечивающие электроэнергию потребителя) предоставили параллельные резервные пути, по которым электричество доставляется к потребителю.
Для дальнейшего чтения
Для получения дополнительной информации см. Соответствующие страницы ниже:
Список литературы
электросчетчиков
Вольтметры
Вольтметры — это инструменты, используемые для измерения разности потенциалов между двумя точками в цепи.Вольтметр подключается параллельно измеряемому элементу, что означает создание пути переменного тока вокруг измеряемого элемента и через вольтметр. Вы правильно подключили вольтметр, если вы можете удалить вольтметр из цепи, не разрывая цепь. На схеме справа вольтметр подключен для правильного измерения разности потенциалов на лампе. Вольтметры имеют очень высокое сопротивление, чтобы минимизировать ток, протекающий через вольтметр, и влияние вольтметра на цепь.
Амперметры
Амперметры — это инструменты, используемые для измерения тока в цепи. Амперметр включен последовательно со схемой, так что измеряемый ток протекает непосредственно через амперметр. Чтобы правильно вставить амперметр, цепь должна быть разорвана. Амперметры имеют очень низкое сопротивление, чтобы минимизировать падение потенциала через амперметр и воздействие амперметра на цепь, поэтому включение амперметра в цепь параллельно может привести к очень высоким токам и может вывести из строя амперметр.На схеме справа амперметр подключен правильно для измерения тока, протекающего по цепи.
Вопрос: На электрической схеме справа возможно расположение амперметра и вольтметра обозначены кружками 1, 2, 3 и 4. Где должен быть расположен амперметр, чтобы правильно измерить полный ток и где должен ли вольтметр быть правильно расположен измерить общее напряжение?
Ответ: Для измерения полного тока амперметр должен быть помещен в положение 1, так как весь ток в цепи должен проходить через этот провод, а амперметры всегда подключаются последовательно.
Для измерения общего напряжения в цепи вольтметр может быть размещен либо в позиции 3, либо в позиции 4. Вольтметры всегда размещаются параллельно с анализируемым элементом цепи, а позиции 3 и 4 эквивалентны, потому что они соединены проводами ( и потенциал всегда одинаков в любом месте идеального провода).
Вопрос: На какой схеме ниже правильно показано соединение амперметра A и вольтметра V для измерения сквозного тока и разности потенциалов на резисторе R?
Ответ: (4) показывает амперметр, включенный последовательно, и вольтметр, подключенный параллельно резистору.
Вопрос: По сравнению с сопротивлением измеряемой цепи внутреннее сопротивление вольтметра спроектировано так, чтобы оно было очень высоким, поэтому счетчик не будет потреблять ток из цепи
- мало тока из цепи
- большая часть тока из цепи
- весь ток из схемы
Ответ: (2) вольтметр должен потреблять как можно меньше тока из схемы, чтобы минимизировать его влияние на схему, но для работы требуется небольшое количество тока.
2.2.3 Цепи с последовательными и параллельными элементами
Большинство энергосистем фактически настроено как «цепи» или контуры, и нам может потребоваться найти эквивалентное последовательно-параллельное сопротивление от начала контура до конца. На рисунке ниже показан особенно неприятный пример, но мы можем разбить его на несколько простых шагов.
Рисунок 2.7: Сложная последовательно-параллельная схемаЩелкните здесь, чтобы увидеть текстовое описание рисунка 2.7
Схема представлена прямоугольником, который разделен по вертикали на большую и меньшую секции. Слева находится закрашенный кружок со знаком плюс и минус, обозначенный как 120V. В схеме 4 резистора. Первый находится в верхней части большой части прямоугольника и обозначен как 4 Ом. Следующий находится в верхней части маленькой стороны схемы и обозначен как 3 Ом. В правой части прямоугольника есть резистор, обозначенный как 6 Ом.Последний резистор находится на делении и имеет маркировку 18 Ом. Под резистором 4 Ом находится стрелка, указывающая вправо, с надписью i s . Резистор на 18 Ом имеет направленную вниз стрелку, обозначенную i 1 , а резистор на 6 Ом имеет направленную вниз стрелку, обозначенную i 2 .
Источник: Сет Блумсак
На этом рисунке у нас есть источник 120 В (например, небольшая батарея), который передает ток через показанную сеть резисторов. Какое эквивалентное сопротивление во всей цепи, от положительной до отрицательной клеммы аккумулятора?
Шаг 1. Возьмем резистор 3 Ом и резистор 6 Ом и вычислим эквивалентное последовательное сопротивление следующим образом: 3 Ом + 6 Ом = 9 Ом.Это дает новое представление схемы ниже.
Рисунок 2.8: Первый шаг упрощения сложной схемыЩелкните здесь, чтобы увидеть текстовое описание рисунка 2.8
Схема представлена прямоугольником, который разделен по вертикали на большую и меньшую части. Слева находится закрашенный кружок со знаком плюс и минус, обозначенный как 120V. В цепи 3 резистора. Первый находится в верхней части большой части прямоугольника и обозначен как 4 Ом.В правой части прямоугольника есть резистор, обозначенный как 9 Ом. Последний резистор находится на делении и имеет маркировку 18 Ом.Источник: Сет Блумсак
На шаге 2 мы вычислим эквивалентное параллельное сопротивление элементов 9 Ом и 18 Ом. Мы рассчитываем это как:
1 (19 + 118) = 1 (218 + 118) = 1 (16) = 6 Ом
Рисунок 2.9: Второй шаг упрощения сложной схемыЩелкните здесь, чтобы увидеть текстовое описание рисунка 2.9
На схеме показана более простая схема, представленная прямоугольником со встроенным кружком с левой стороны.Внутри круга есть символы плюса и минуса, обозначенные как 120 В. В верхней части схемы находится резистор с маркировкой 4 Ом, а с правой стороны схемы — резистор с маркировкой 6 Ом
.Источник: Сет Блумсак
На последнем этапе мы возьмем последовательное сопротивление элементов 4 Ом и 6 Ом: 4 Ом + 6 Ом = 10 Ом.
В этих нескольких шагах мы показали, что две цепи на рисунке ниже имеют точно такое же эквивалентное сопротивление.
Фигура 2.10: Сложная последовательно-параллельная схема (слева) и ее эквивалентная простая схема (справа)Щелкните здесь, чтобы увидеть текстовое описание рисунка 2.10
Схема с рисунка 2.8 рядом с простой схемой. Простая схема представлена прямоугольником со встроенным кружком с левой стороны с символом плюс и минус внутри, обозначенным 120 В.

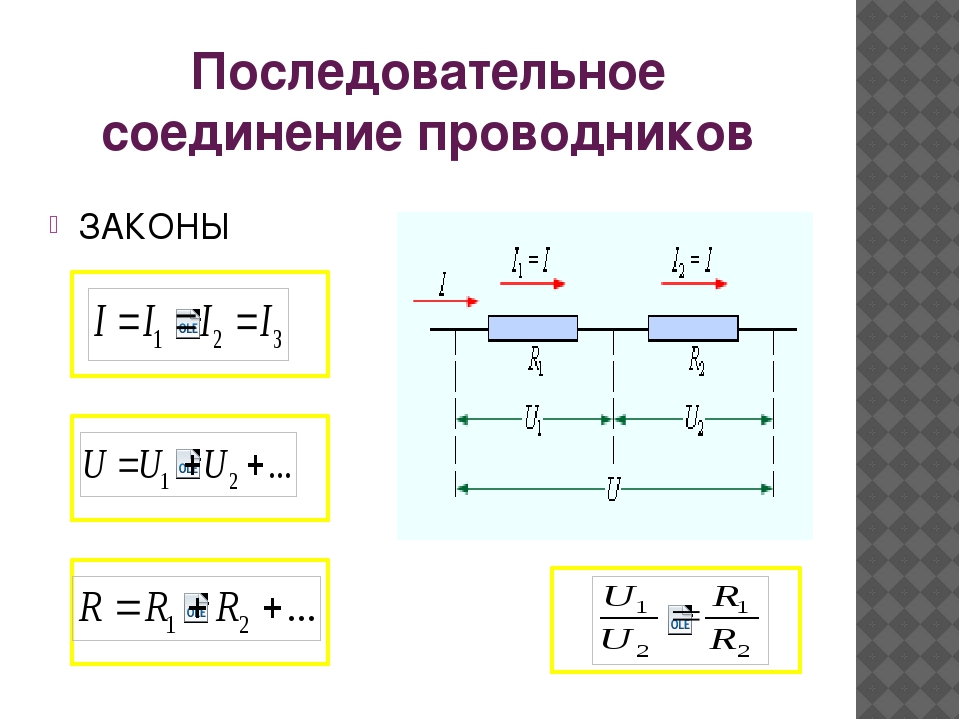 5 А) • (11 Ом)
5 А) • (11 Ом) 