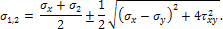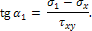Что такое механическое напряжение в материалах. Какие бывают виды напряжений. Как рассчитать напряжения в элементах конструкций. Какие факторы влияют на возникновение внутренних напряжений в материалах.
Основные виды напряжений в материалах
Механическое напряжение — это мера интенсивности внутренних сил, возникающих в материале под действием внешних нагрузок. Различают следующие основные виды напряжений:
- Нормальные напряжения (растяжение-сжатие)
- Касательные напряжения (сдвиг)
- Изгибные напряжения
- Крутящие напряжения
Рассмотрим подробнее каждый вид напряжений и методы их расчета.
Нормальные напряжения при растяжении-сжатии
Нормальные напряжения возникают при действии сил вдоль оси стержня и направлены перпендикулярно поперечному сечению. Они рассчитываются по формуле:
σ = F / A
где:
- σ — нормальное напряжение
- F — приложенная сила
- A — площадь поперечного сечения
При растяжении нормальные напряжения считаются положительными, при сжатии — отрицательными.
Касательные напряжения при сдвиге
Касательные напряжения возникают при действии сил, стремящихся сдвинуть одну часть тела относительно другой. Они направлены параллельно плоскости сдвига и рассчитываются по формуле:
τ = F / A
где:
- τ — касательное напряжение
- F — сдвигающая сила
- A — площадь сдвига
Изгибные напряжения
Изгибные напряжения возникают в поперечных сечениях балок при действии изгибающего момента. Максимальные нормальные напряжения при изгибе рассчитываются по формуле:
σmax = M / W
где:
- σmax — максимальное нормальное напряжение
- M — изгибающий момент
- W — момент сопротивления сечения
Крутящие напряжения
Крутящие напряжения возникают в поперечных сечениях валов при действии крутящего момента. Максимальные касательные напряжения при кручении определяются по формуле:
τmax = T / Wp
где:
- τmax — максимальное касательное напряжение
- T — крутящий момент
- Wp — полярный момент сопротивления сечения
Факторы, влияющие на возникновение внутренних напряжений
На образование внутренних напряжений в материалах влияют следующие основные факторы:

- Неоднородное распределение деформаций по объему тела
- Наличие концентраторов напряжений (отверстия, надрезы, трещины)
- Неравномерный нагрев или охлаждение
- Фазовые и структурные превращения в металлах
- Технологические процессы обработки
Учет данных факторов позволяет прогнозировать и минимизировать возникновение нежелательных внутренних напряжений в элементах конструкций.
Классификация внутренних напряжений по масштабу
Различают следующие виды внутренних напряжений в зависимости от масштаба их проявления:
- Напряжения 1-го рода (макронапряжения) — уравновешиваются в объеме всего тела
- Напряжения 2-го рода (микронапряжения) — уравновешиваются в объеме отдельных зерен или кристаллитов
- Напряжения 3-го рода — локализуются в объеме кристаллической решетки
Такая классификация позволяет оценить влияние внутренних напряжений на свойства материалов на разных структурных уровнях.
Методы расчета напряжений в элементах конструкций
Для расчета напряжений в элементах конструкций применяются следующие основные методы:
- Аналитические методы сопротивления материалов
- Численные методы (метод конечных элементов)
- Экспериментальные методы (тензометрия, фотоупругость)
- Комбинированные расчетно-экспериментальные методы
Выбор метода зависит от сложности геометрии, условий нагружения и требуемой точности расчета напряженного состояния конструкции.
Допускаемые напряжения и коэффициент запаса прочности
При проектировании элементов конструкций важно обеспечить, чтобы действующие напряжения не превышали допускаемых значений. Допускаемое напряжение [σ] определяется как:
[σ] = σпр / n
где:
- σпр — предельное напряжение материала
- n — коэффициент запаса прочности
Коэффициент запаса прочности выбирается с учетом ответственности конструкции, точности расчета, условий эксплуатации и обычно составляет 1.5-3.
Примеры расчета напряжений в типовых элементах конструкций
Рассмотрим несколько примеров расчета напряжений для наиболее распространенных случаев нагружения элементов конструкций.
Пример 1. Расчет нормальных напряжений в растянутом стержне
Дано: стальной стержень диаметром d = 20 мм растягивается силой F = 50 кН.
Решение:
- Площадь поперечного сечения: A = πd2/4 = 3.14*202/4 = 314 мм2
- Нормальное напряжение: σ = F/A = 50000/314 = 159 МПа
Пример 2. Расчет касательных напряжений в болтовом соединении
Дано: болт диаметром d = 16 мм нагружен срезающей силой F = 30 кН.
Решение:
- Площадь среза: A = πd2/4 = 3.14*162/4 = 201 мм2
- Касательное напряжение: τ = F/A = 30000/201 = 149 МПа
Пример 3. Расчет изгибных напряжений в балке
Дано: стальная балка прямоугольного сечения 100×200 мм нагружена изгибающим моментом M = 50 кНм.
Решение:
- Момент сопротивления: W = bh2/6 = 100*2002/6 = 666667 мм3
- Максимальное нормальное напряжение: σmax = M/W = 50*106/666667 = 75 МПа
Подобные расчеты позволяют оценить уровень напряжений и подобрать оптимальные размеры элементов конструкций.
Заключение
Понимание видов напряжений и методов их расчета является основой для проектирования надежных и эффективных конструкций. Правильная оценка напряженного состояния позволяет:
- Обеспечить прочность и долговечность элементов конструкций
- Оптимизировать размеры и массу изделий
- Предотвратить разрушение от перегрузок
- Повысить эксплуатационную надежность техники
Поэтому расчет и анализ напряжений — важнейший этап проектирования в машиностроении, строительстве и других отраслях.

Виды напряжения | Теория
Электрическое напряжение — это величина, численно равная работе по перемещению единицы электрического заряда между двумя произвольными точками электрической цепи.
Движение электронов может меняться в зависимости от полярности напряжения. Поэтому различают разные виды напряжения.
Постоянное напряжение
Электроны всегда движутся силой и в одном направлении.
Обозначение:
— или DC (Direct Current)

Переменное напряжение
Электроны многократно меняют свое направление за рассматриваемую единицу времени.
Обозначение:
_ или AC (Alternating Current)
Параметры синусоидального переменного напряжения:
- Us пиковое напряжение
- Uss размах пульсации напряжения
- Ueff эффективное значение напряжения
- Uss = 2 * Us
- Ueff = 0,707 * Us
Смешанное напряжение
В результате наложения (смешения) постоянного и переменного напряжения могут создаваться смешанные напряжения, при которых меняется только величина напряжения, но не направление.
Обозначение:
DC (Direct Current)

Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела.
Деформацией называется изменение размеров и формы тела под действием приложенных сил.
Напряжением называется отношение действующего усилия к площади поперечного сечения тела или образца σ = P/F. В зависимости от направления действия силы нормальные напряжения подразделяют на растягивающие и сжимающие. Различают временные и остаточные напряжения. Временные напряжения возникают под действием внешней нагрузки и исчезают после ее снятия, остаточные — остаются в теле после прекращения действия нагрузки.
Если после прекращения действия внешних сил изменения формы, структуры и свойств тела полностью устраняются, то такая деформация называется
При возрастании напряжений выше предела упругости деформация становится необратимой. При снятии нагрузки устраняется лишь упругая составляющая деформации, оставшаяся часть называется пластической деформацией.
Норм напряжение:
Составляющая напряжений, направленных по нормали к площадке ее действия.
Касат напряжение:
Составляющая напряжений, лежащих в плоскости сечения.
Правила знаков:
Нормальные напряжения σ принимаются положительными (т.е. σ>0), если они растягивают выделенный элемент бруса.
Касательные напряжения τ принимаются положительными (т.е. τ>0), если они стремятся повернуть рассматриваемый элемент бруса по ходу часовой стрелки.
При растяжении-сжатии
Внутренняя продольная сила N, которая стремится растянуть рассматриваемую частьбруса, считается положительной. Сжимающая продольная сила имеет отрицательный знак.
При кручении
Внутренний скручивающий момент T считается положительным, если он стремится повернуть рассматриваемую часть бруса против хода часовой стрелки, при взгляде на него со стороны внешней нормали.
При изгибе
Внутренняя поперечная сила Q считается положительной, в случае, когда она стремится повернуть рассматриваемую часть бруса по ходу часовой стрелки.
Внутренний изгибающий момент M положителен, когда он стремится сжать верхние волокна бруса.
Деформация при растяжении-сжатии Δl считается положительной, если длина стержняпри этом увеличивается.
При плоском поперечном изгибе
Вертикальное перемещение сечения бруса принимается положительным, если оно направлено вверх от начального положения.
Правило знаков при составлении уравнений статики
— для проекций сил на оси системы координат
Проекции внешних сил на оси системы координат принимаются положительными, если их направление совпадает с положительным направлением соответствующей оси.
— для моментов
Сосредоточенные моменты и моменты сил в уравнениях статики записываются с положительным знаком, если они стремятся повернуть рассматриваемую систему против хода часовой стрелки.
Правило знаков при составлении уравнений статики для неподвижных систем
При составлении уравнений равновесия статичных (неподвижных) систем (например, приопределении опорных реакций), последние два правила упрощаются до вида:
Проекции сил и моменты, имеющие одинаковое направление принимаются положительными, а соответственно проекции сил и моменты обратного направления – отрицательными.
ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Если все векторы напряжений параллельны одной и той же плоскости, напряженное состояние называется плоским (рис. 1). Иначе: напряженное состояние является плоским, если одно из трех главных напряжений равно нулю.
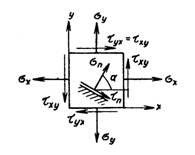
Рисунок 1.
Плоское напряженное состояние реализуется в пластине, нагруженной по ее контуру силами, равнодействующие которых расположены в ее срединной плоскости (срединная плоскость — плоскость, делящая пополам толщину пластины).
Направления напряжений на рис. 1 приняты за положительные. Угол α положителен, если он откладывается от оси х к оси у. На площадке с нормалью n:
|
| (1) |
при 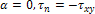 .
.
Нормальное
напряжение σn положительно,
если оно растягивающее. Положительное
напряжение  показано
на рис. 1. Правило знаков для
показано
на рис. 1. Правило знаков для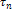 по
формуле (1) то же самое, что для
напряжений
по
формуле (1) то же самое, что для
напряжений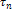 по
формуле (1).
по
формуле (1).
Данное здесь правило знаков относится к наклонным площадкам. В статье «Объёмное напряженное состояние» сформулировано правило знаков для компонентов напряжений в точке, т. е. для напряжений на площадках, перпендикулярных осям координат. Это правило знаков принято в теории упругости.
Главные напряжения на площадках, перпендикулярных плоскости напряжений:
| (2) |
(Поскольку здесь рассматриваются только два главных напряжения, они обозначены через σ1 и σ2, хотя может оказаться, что σ2<0, т. е. σ2 не будет средним из трех главных напряжений). Угол α1 составляемый нормалью к первой главной площадке с осью х, находится из равенства:
| (3) |
Наибольшее и наименьшее касательные напряжения
| (4) |
Эти напряжения действуют на площадках, расположенных под углом 45° к первой и второй главным площадкам.
Если главные напряжения σ1 и σ2 имеют одинаковый знак, то наибольшее касательное напряжение действует на площадке, расположенной под углом 45° к плоскости напряжений (плоскости ху). В этом случае:
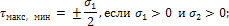
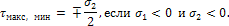
В стенке балки (здесь имеется в виду обычная балка, а не балка-стенка) при ее изгибе силами реализуется частный случай плоского напряженного состояния. В стенках балки одно из нормальных напряжений σy равно нулю. В этом случае напряжения получатся по формулам (1), (2) и (4), если в этих формулах положить σy=0. Положение первой главной площадки определяется формулой (3).
РАСТЯЖЕНИЕ ПО ДВУМ НАПРАВЛЕНИЯМ (рис 2):
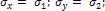

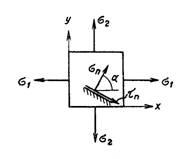
Рисунок 2.
При
σ1>0
и σ2<0 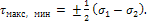
При
σ1>0
и σ2>0 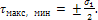
При
σ1<0
и σ2<0 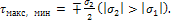
ЧИСТЫЙ СДВИГ (рис. 3)


Мерой интенсивности распределения внутренних сил R в окрестности точки в пределах данного сечения площадью A являются напряжения p, измеряемые в единицах силы, отнесенной к единице площади dA
Полные напряжения в точке
Единица измерения напряжений — Паскаль (Н/м2=Па).
Рассмотрим подробнее:
Система приложенных к телу внешних нагрузок, приводит к возникновению в его сечениях внутренней силы R и момента M
Внутренние сила и момент в сечении брусаПри этом надо понимать что внутренняя сила и внутренний момент воздействуют на всё сечение бруса в целом.
Выделим в рассматриваемом сечении элементарную площадку dA бесконечно малой площади.
Элементарная площадка в сечении брусаПолное напряжение – часть внутренних усилий, приходящаяся на конкретную точку сечения.
Вектор полного напряжения в точкеОбозначение полного напряжения в точке – p.
Единица измерения – Паскаль [Па] (Н/м2).
Ввиду того, что большинство конструкционных материалов обладает высокой прочностью часто напряжения, возникающие в них, измеряются в кратных величинах, например мегапаскаль [МПа].
В общем случае вектор полного напряжения в точке может располагаться под любым углом к сечению. В таких случаях для существенного упрощения расчетов его удобно раскладывать на составляющие (проекции):
Нормальное и касательное напряженияПроекция вектора полного напряжения p на нормаль к сечению называется нормальным напряжением и обозначается через σ, а проекция вектора полного напряжения на плоскость сечения называется касательным напряжением и обозначается через τ.
Разложение вектора полного напряжения на две указанные составляющие имеет конкретный физический смысл – с нормальным напряжением связано разрушение путем отрыва, а с касательным – разрушение путем сдвига или среза.
В частных случаях (например при растяжении-сжатии и кручении) в поперечных сечениях бруса имеют место только нормальные и только касательные напряжения соответственно.
При решении таких задач, величина нормальных и касательных напряжений сравнивается с соответствующими допустимыми значениями напряжений.
Примеры расчета напряжений >>
Виды напряжений — Студопедия
В случае одноосного растяжения возникающие в теле напряжения равны. Сила Р, (рис. 7) приложенная к некоторой площадке F, обычно направлена к ней под некоторым углом. Поэтому в теле возникают нормальные и касательные напряжения.
Образование внутренних напряжений связано в основном с неоднородным распределением деформаций (в том числе и микродеформаций) по объему тела.
Наличие в испытуемом образце механических надрезов, трещин внутренних дефектов металла приводит к неравномерному распределению напряжений, создавая у основания надреза пиковую концентрацию нормальных напряжений (нормальные напряжения бывают растягивающими и сжимающими) (см. рис. 7). Действие надрезов, сделанных в образце, аналогично конфигурации изделий, имеющих сквозные отверстия, резьбу и т.п., или влиянию внутренних дефектов металла (неметаллических включений, графитных выделений в чугуне, трещин и др.), нарушающих его цельность. Поэтому всевозможные надрезы, отверстия, галтели и другие источники концентрации напряжений называют концентраторами напряжений.
Напряжения вызываются различными причинами.Различают временные,обусловленные действием внешней нагрузки и исчезающие после ее снятия, и внутренние остаточные напряжения, возникающие и уравновешивающиеся в пределах тела без действия внешней нагрузки.
Внутренние напряжения наиболее часто возникают в процессе быстрого нагрева или охлаждения металла вследствие неодинакового расширения (сжатия) поверхностных и внутренних слоев. Эти напряжения называют тепловыми.
Кроме того, напряжения возникают в процессе кристаллизации, при неравномерной деформации, при термической обработке вследствие структурных превращений по объему и т.д., эти напряжения называют фазовыми или структурными.
Внутренние напряжения классифицируют на:
Напряжения 1 рода (или зональные), называемые также макронапряжениями, они уравновешиваются в объеме всего тела, возникают главным образом в результате технологических процессов, которым подвергают деталь в процессе ее изготовления.
Напряжения 2 рода уравновешиваются в объеме зерна (кристаллита) или нескольких блоков (субзерен), их называют иначе микронапряжениями. Чаще всего они возникают в процессе фазовых превращений и деформации металла, когда разные кристаллиты и блоки внутри них оказываются в различном упругонапряженном состоянии.
Напряжения 3 рода, локализующиеся в объемах кристаллической ячейки, представляют собой статические искажения решетки, т. е. смещения атомов на доли ангстрема из узлов кристаллической решетки.
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ, раздел механики твердого тела, изучающий напряжения и деформации, которые обусловлены силами, действующими на твердые тела – элементы конструкции. Эту дисциплину можно характеризовать и как науку о методах расчета элементов конструкции на прочность, жесткость и устойчивость.
Напряжение, создаваемое в твердом теле внешними нагрузками, есть мера (с размерностью силы на единицу площади) интенсивности внутренних сил, действующих со стороны одной, мысленно отсекаемой, части тела на другую, оставшуюся (метод сечений). Внешние нагрузки вызывают деформацию тела, т.е. изменение его размеров и формы. В сопротивлении материалов исследуются соотношения между нагрузками, напряжениями и деформациями, причем исследования ведутся, с одной стороны, путем математического вывода формул, связывающих нагрузки с вызываемыми ими напряжениями и деформациями, а с другой – путем экспериментального определения характеристик материалов, применяемых в строениях и машинах. См. также МЕТАЛЛОВ МЕХАНИЧЕСКИЕ СВОЙСТВА; МЕТАЛЛОВ ИСПЫТАНИЯ. По найденным формулам с учетом результатов испытания материалов рассчитываются размеры элементов строений и машин, обеспечивающие сопротивление заданным нагрузкам. Сопротивление материалов не относится к точным наукам, так как многие его формулы выводятся на основе предположений о поведении материалов, которые не всегда точно выполняются. Тем не менее, пользуясь ими, грамотный инженер может создавать надежные и экономичные конструкции.
С сопротивлением материалов тесно связана математическая теория упругости, в которой тоже рассматриваются напряжения и деформации. Она позволяет решать те задачи, которые с трудом поддаются решению обычными методами сопротивления материалов. Однако между сопротивлением материалов и теорией упругости нет четкой границы. Хотя почти все задачи о распределении напряжений решены методами математического анализа, при сложных условиях эти решения требуют трудоемких выкладок. И тогда на помощь приходят экспериментальные методы анализа напряжений.
НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ
Виды напряжений.
Самое важное понятие в сопротивлении материалов – это понятие напряжения как силы, действующей на малую площадку и отнесенной к площади этой площадки. Напряжения бывают трех видов: растяжения, сжатия и сдвига.
Если на металлическом стержне подвешен груз, как показано на рис. 1,а, то такой стержень называется растянутым или работающим на растяжение. Напряжение S, создаваемое силой P в растянутом стержне с площадью поперечного сечения, равной A, дается выражением S = P/A. Если вес груза равен 50 000 Н, то растягивающая сила тоже равна 50 000 Н. Далее, если ширина стержня равна 0,05 м, а толщина – 0,02 м, так что площадь поперечного сечения составляет 0,001 м2, то растягивающее напряжение равно 50 000/0,001 = 50 000 000 Н/м2 = 50 МПа. Растянутый стержень длиннее, чем до приложения растягивающих сил.
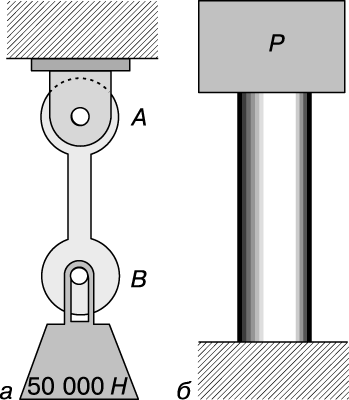
Рассмотрим короткий цилиндр (рис. 1,б), на верхний торец которого положен груз. При этом во всех поперечных сечениях цилиндра действуют напряжения сжатия. Если напряжение равномерно распределено по всему сечению, то справедлива формула S = P/A. Сжатый цилиндр короче, чем в отсутствие деформаций.
Напряжение сдвига возникает, например, в болте (рис. 2,а), на котором верхним концом держится растянутый стержень AB с грузом 50 000 Н (рис. 1,а). Болт удерживает стержень, действуя с силой 50 000 Н, направленной вверх, на ту часть стержня, которая расположена непосредственно над отверстием в стержне, а стержень в свою очередь давит на среднюю часть болта с силой 50 000 Н. Силы, действующие на болт, приложены так, как показано на рис. 2,б. Если бы болт был сделан из материала с низким пределом прочности на сдвиг, например из свинца, то он был бы срезан по двум вертикальным плоскостям (рис. 2,в). Если же болт стальной и достаточно большого диаметра, то он не срежется, но в двух его вертикальных поперечных сечениях будут существовать напряжения сдвига. Если напряжения сдвига равномерно распределены, то они даются формулой S = P/A. Полная сила сдвига, действующая в каждом из поперечных сечений, равна 25 000 Н, и если диаметр болта равен 0,02 м (площадь поперечного сечения равна приблизительно 0,0003 м2), то напряжение сдвига Ss будет составлять 25 000 Н/0,0003 м2, т.е. немногим более 80 МПа.
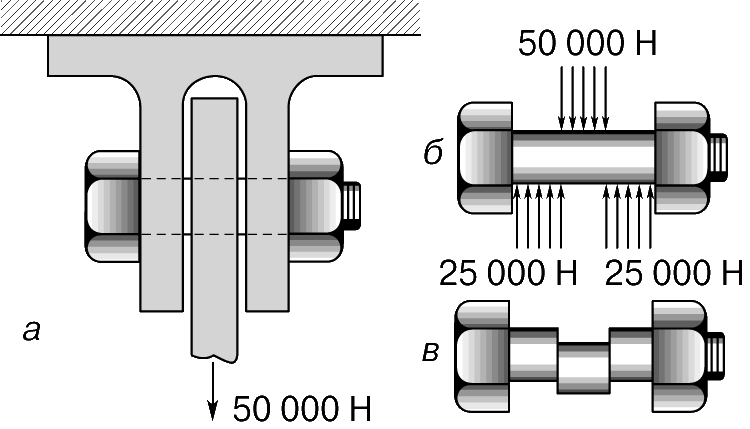
Напряжения растяжения и сжатия направлены по нормали (т.е. вдоль перпендикуляра) к площадке, в которой они действуют, а напряжение сдвига – параллельно площадке. Поэтому напряжения растяжения и сжатия называются нормальными, а напряжения сдвига – касательными.
Деформация.
Деформацией называется изменение размера тела под действием приложенных к нему нагрузок. Деформация, отнесенная к полному размеру, называется относительной. Если изменение каждого малого элемента длины тела одинаково, то относительная деформация называется равномерной. Относительную деформацию часто обозначают символом d, а полную – символом D. Если относительная деформация постоянна по всей длине L, то d = D/L. Например, если длина стального стержня до приложения растягивающей нагрузки равна 2,00 м, а после нагружения – 2,0015 м, то полная деформация D равна 0,0015 м, а относительная – d = 0,0015/2,00 = 0,00075 (м/м).
Почти для всех материалов, применяемых в строениях и машинах, относительная деформация пропорциональна напряжению, пока оно не превысит т.н. предела пропорциональности. Это очень важное соотношение называется законом Гука. Оно было экспериментально установлено и сформулировано в 1678 английским изобретателем и часовых дел мастером Р.Гуком. Данное соотношение между напряжением и деформацией для любого материала выражается формулой S = Ed, где E – постоянный множитель, характеризующий материал. Этот множитель называют модулем Юнга по имени Т.Юнга, который ввел его в 1802, или же модулем упругости. Из обычных конструкционных материалов наибольший модуль упругости у стали; он равен примерно 200 000 МПа. В стальном стержне относительная деформация, равная 0,00075, из приводившегося ранее примера вызывается напряжением S = Ed = 200 000 ґ 0,00075 = 150 МПа, что меньше предела пропорциональности конструкционной стали. Если бы стержень был из алюминия с модулем упругости около 70 000 МПа, то, чтобы вызвать ту же самую деформацию 0,00075, достаточно было бы напряжения немногим более 50 МПа. Из сказанного ясно, что упругие деформации в строениях и машинах очень малы. Даже при сравнительно большом напряжении 150 МПа из приведенного выше примера относительная деформация стального стержня не превышает одной тысячной. Столь большая жесткость стали – ее ценное качество.
Чтобы наглядно представить деформацию сдвига, рассмотрим, например, прямоугольную призму ABCD (рис. 3). Ее нижний конец жестко заделан в твердое основание. Если на верхнюю часть призмы действует горизонтальная внешняя сила F, она вызывает деформацию сдвига, показанную штриховыми линиями. Смещение D есть полная деформация на длине (высоте) L. Относительная деформация сдвига d равна D/L. Для деформации сдвига тоже выполняется закон Гука при условии, что напряжение не превышает предела пропорциональности для сдвига. Следовательно, Ss = Esd, где Es – модуль сдвига. Для любого материала величина Es меньше E. Для стали она составляет около 2/5 E, т.е. приблизительно 80 000 МПа. Важный случай деформации сдвига – деформация в валах, на которые действуют внешние скручивающие моменты.
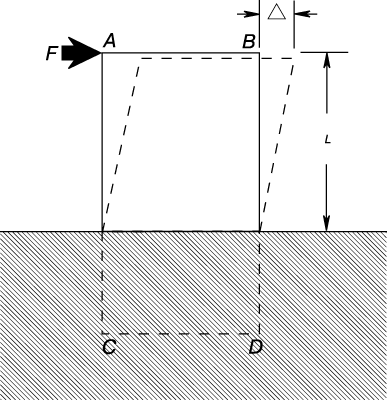
Выше речь шла об упругих деформациях, которые вызываются напряжениями, не превышающими предела пропорциональности. Если же напряжение выходит за предел пропорциональности, то деформация начинает расти быстрее, чем напряжение. Закон Гука перестает быть справедливым. В случае конструкционной стали в области, лежащей чуть выше предела пропорциональности, небольшое увеличение напряжения приводит к увеличению деформации во много раз по сравнению с деформацией, соответствующей пределу пропорциональности. Напряжение, при котором начинается столь быстрый рост деформации, называется пределом текучести. Материал, в котором разрушению предшествует большая неупругая деформация, называется пластичным.
ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ
Допускаемое (допустимое) напряжение – это значение напряжения, которое считается предельно приемлемым при вычислении размеров поперечного сечения элемента, рассчитываемого на заданную нагрузку. Можно говорить о допускаемых напряжениях растяжения, сжатия и сдвига. Допускаемые напряжения либо предписываются компетентной инстанцией (скажем, отделом мостов управления железной дороги), либо выбираются конструктором, хорошо знающим свойства материала и условия его применения. Допускаемым напряжением ограничивается максимальное рабочее напряжение конструкции.
При проектировании конструкций ставится цель создать конструкцию, которая, будучи надежной, в то же время была бы предельно легкой и экономной. Надежность обеспечивается тем, что каждому элементу придают такие размеры, при которых максимальное рабочее напряжение в нем будет в определенной степени меньше напряжения, вызывающего потерю прочности этим элементом. Потеря прочности не обязательно означает разрушение. Машина или строительная конструкция считается отказавшей, когда она не может удовлетворительно выполнять свою функцию. Деталь из пластичного материала, как правило, теряет прочность, когда напряжение в ней достигает предела текучести, так как при этом из-за слишком большой деформации детали машина или конструкция перестает соответствовать своему назначению. Если же деталь выполнена из хрупкого материала, то она почти не деформируется, и потеря ею прочности совпадает с ее разрушением.
Запас прочности.
Разность напряжения, при котором материал теряет прочность, и допускаемого напряжения есть тот «запас прочности», который необходимо предусматривать, учитывая возможность случайной перегрузки, неточностей расчета, связанных с упрощающими предположениями и неопределенными условиями, наличия не обнаруженных (или не обнаружимых) дефектов материала и последующего снижения прочности из-за коррозии металла, гниения дерева и пр.
Коэффициент запаса.
Коэффициент запаса прочности какого-либо элемента конструкции равен отношению предельной нагрузки, вызывающей потерю прочности элемента, к нагрузке, создающей допускаемое напряжение. При этом под потерей прочности понимается не только разрушение элемента, но и появление в нем остаточных деформаций. Поэтому для элемента конструкции, выполненного из пластичного материала, предельным напряжением является предел текучести. В большинстве случаев рабочие напряжения в элементах конструкции пропорциональны нагрузкам, а поэтому коэффициент запаса определяется как отношение предела прочности к допускаемому напряжению (коэффициент запаса по пределу прочности). Так, если предел прочности конструкционной стали равен 540 МПа, а допускаемое напряжение – 180 МПа, то коэффициент запаса равен 3.
РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ
В сопротивлении материалов большое внимание уделяется выводу соотношений между заданными нагрузками, размерами и формой элемента конструкции, несущего эти нагрузки или сопротивляющегося им, и напряжениями, возникающими в определенных сечениях элемента конструкции. Как правило, цель расчетов состоит в том, чтобы найти необходимые размеры элемента, при которых максимальное рабочее напряжение в нем не будет превышать допускаемого.
В элементарном курсе сопротивления материалов рассматривается ряд типичных случаев равномерного распределения напряжений: растянутые стержни, короткие сжатые стержни, тонкостенные цилиндры, работающие под давлением внутренней среды (котлы и резервуары), заклепочные и сварные соединения, температурные напряжения и такие статически неопределимые системы, как растянутые стержни из нескольких разных материалов.
Если напряжение одинаково во всех точках поперечного сечения, то S = P/A. Конструктор находит необходимую площадь поперечного сечения, поделив заданную нагрузку на допускаемое напряжение. Но нужно уметь отличать случаи, в которых напряжение действительно распределено равномерно, от других, сходных случаев, в которых этого нет. Необходимо также (как в задаче о заклепочных соединениях, в которых существуют напряжения и растяжения, и сжатия, и сдвига) находить плоскости, в которых действуют напряжения разного вида, и определять максимальные местные напряжения.
Тонкостенный цилиндр.
Такой резервуар выходит из строя (разрывается), когда напряжение растяжения в его оболочке становится равным пределу прочности материала. Формулу, связывающую толщину стенки t, внутренний диаметр резервуара D, напряжение S и внутреннее давление R, можно вывести, рассмотрев условия равновесия кольца, вырезанного из его оболочки двумя поперечными плоскостями, разделенными расстоянием L (рис. 4,а). Внутреннее давление действует на внутреннюю поверхность полукольца с направленной вверх силой, равной произведению RDL, а напряжения в двух горизонтальных концевых сечениях полукольца создают две направленные вниз силы, каждая из которых равна tLS. Приравнивая, получаем
RDL = 2tLS, откуда S = RD/2t.
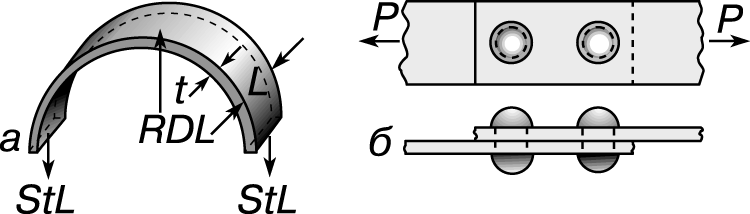
Заклепочное соединение.
На рис. 4,б представлено двухзаклепочное соединение двух полос внахлестку. Такое соединение может выйти из строя из-за перерезывания обеих заклепок, разрыва одной из полос в том месте, где она ослаблена отверстием под заклепку, или из-за слишком больших напряжений смятия по площади соприкосновения заклепки с полосой. Напряжение смятия в заклепочном соединении вычисляется как нагрузка на одну заклепку, деленная на диаметр заклепки и на толщину полосы. Допускаемой для такого соединения принимается наименьшая из нагрузок, соответствующих допускаемым напряжениям трех указанных видов.
Вообще говоря, напряжение, действующее в поперечном сечении растянутого или короткого сжатого стержня, можно с полным основанием считать равномерно распределенным, если равные и противоположно направленные нагрузки приложены так, что равнодействующая каждой из них проходит через центр тяжести рассматриваемого поперечного сечения. Но нужно иметь в виду, что ряд задач (и к ним относится задача о напряжениях смятия в заклепочном соединении) решается в предположении о равномерном распределении напряжения, хотя это заведомо не соответствует действительности. Допустимость такого подхода проверяется опытным путем.
НЕРАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ
Многие элементы строений и детали машин нагружаются так, что напряжения во всех их поперечных сечениях распределены неравномерно. Чтобы вывести формулы для расчета напряжений в таких условиях, мысленно разрезают элемент плоскостью, которая дает нужное поперечное сечение, на две части и рассматривают условия равновесия одной из них. На эту часть действуют одна или несколько заданных внешних сил, а также силы, эквивалентные напряжениям в данном поперечном сечении. Действующие напряжения должны удовлетворять условиям равновесия и соответствовать деформациям. Эти два требования составляют основу для решения задачи. Второе из них подразумевает справедливость закона Гука. Типичными элементами с неравномерным распределением напряжений являются нагруженные балки, валы под действием скручивающих сил, растянутые или сжатые стержни с дополнительным изгибом и колонны.
БАЛКИ.
Балка – это длинный стержень с опорами и нагрузками, работающий в основном на изгиб. Поперечное сечение балки обычно одинаково по всей ее длине. Силы, с которыми опоры действуют на балку, называются реакциями опор. Наиболее распространены два вида балок: консольная (рис. 5,а) и балка с двумя опорами, называемая простой (рис. 5,б). Под действием нагрузок балка прогибается. При этом «волокна» на ее верхней стороне сокращаются, а на нижней – удлиняются. Очевидно, что где-то между верхней и нижней сторонами балки имеется тонкий слой, длина которого не изменяется. Он называется нейтральным слоем. Изменение длины волокна, расположенного между верхней (или нижней) стороной балки и ее нейтральным слоем, пропорционально расстоянию до нейтрального слоя. Если справедлив закон Гука, то напряжения тоже пропорциональны этому расстоянию.
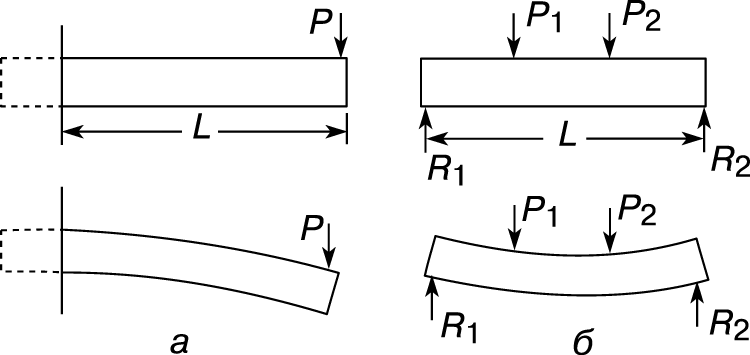
Формула изгиба.
На основе указанного распределения напряжений, дополненного условиями статики, выведена т.н. формула изгиба, в которой напряжение выражается через нагрузки и размеры балки. Она обычно представляется в виде S = Mc/I, где S – максимальное напряжение в рассматриваемом поперечном сечении, c – расстояние от нейтрального слоя до наиболее напряженного волокна, M – изгибающий момент, равный сумме моментов всех сил, действующих по одну сторону от этого сечения, а I – момент инерции поперечного сечения (определенная функция формы и размеров последнего). Характер изменения нормальных напряжений в поперечном сечении балки показан на рис. 6.
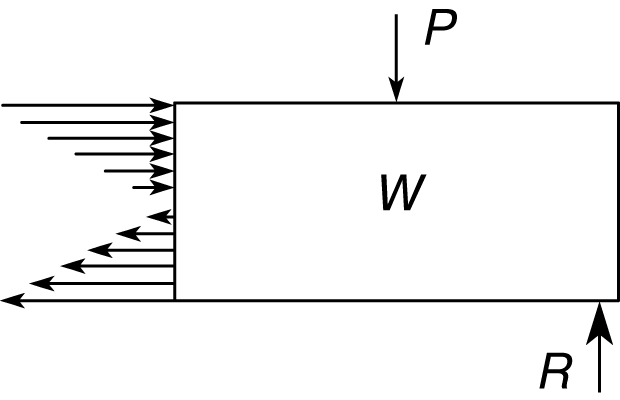
В поперечных сечениях балок действуют также касательные напряжения. Их вызывает равнодействующая всех вертикальных сил, приложенных по одну сторону поперечного сечения горизонтальной балки. Сумма всех внешних сил и реакций, действующих на одну из двух частей балки, называется сдвигом в сечении балки и обычно обозначается через V. Касательные напряжения неравномерно распределены по сечению: они равны нулю на верхнем и нижнем краях сечения и почти всегда максимальны в нейтральном слое.
Прогиб балки.
Часто требуется рассчитать прогиб балки, вызванный действием нагрузки, т.е. вертикальное смещение точки, лежащей в нейтральном слое. Это очень важная задача, поскольку прогиб и кривизну балки нужно знать при решении задач, относящихся к широкому кругу т.н. статически неопределимых систем.
Еще в 1757 Л.Эйлер вывел формулу для кривизны изогнутой балки. В этой формуле кривизна балки выражается через переменный изгибающий момент. Чтобы найти ординату упругой кривой (прогиб), необходимо брать двойной интеграл. В 1868 О.Мор (Германия) предложил метод, основанный на эпюрах изгибающих моментов. Этот графоаналитический метод имеет огромное преимущество перед прежними методами, так как позволяет свести все математические вычисления к сравнительно простым арифметическим выкладкам. Он дает возможность вычислять прогиб и наклон в любой точке балки при любой нагрузке.
Статически неопределимые балки.
Многие балки, используемые в строениях и машинах, имеют более двух опор или только две опоры, но с заделкой одного из концов, исключающей возможность поворота. Такие балки называются статически неопределимыми, поскольку уравнений статики недостаточно для определения реакций в опорах и моментов в заделке. Чаще всего рассматриваются подобные балки трех типов: с одним заделанным (защемленным) концом и одной опорой, с заделанными обоими концами и неразрезные балки, имеющие более двух опор (рис. 7).
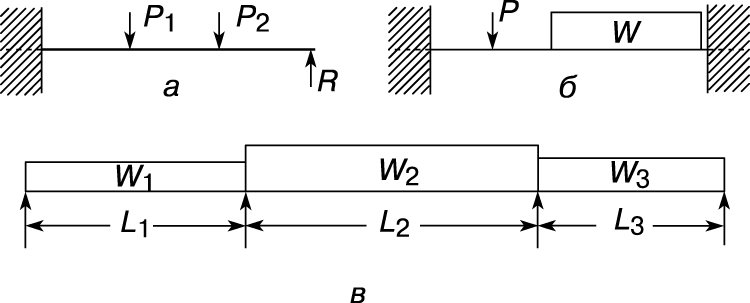
Первое решение задачи о неразрезных балках было опубликовано французским инженером Б.Клапейроном в 1857. Он доказал т.н. теорему о трех моментах. Уравнение трех моментов представляет собой соотношение между изгибающими моментами в трех последовательных опорах одной неразрезной балки. Например, в случае неразрезной балки с равномерной нагрузкой на каждом пролете это уравнение имеет вид
MAL1 + 2MB (L1 + L2) + MCL2 = – (W1L13)/4 – (W2L23)/4.
Здесь MA, MB и MC – изгибающие моменты в трех опорах, L1 и L2 – длины левого и правого пролетов, W1 – нагрузка на левый пролет, а W2 – нагрузка на правый пролет. Нужно написать такое уравнение для каждой пары смежных пролетов, а затем решить полученную систему уравнений. Если число пролетов равно n, то число уравнений будет равно n – 1.
В 1930 Х.Кросс опубликовал свой метод расчета широкого круга статически неопределимых рам и неразрезных балок. Его «метод распределения моментов» позволяет обходиться без решения систем уравнений, сводя все вычисления к сложению и вычитанию чисел.
НАПРЯЖЕНИЕ ПРИ КРУЧЕНИИ.
Если к концам вала приложены равные, но противоположно направленные внешние скручивающие моменты, то во всех его поперечных сечениях существуют только касательные напряжения, т.е. напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг. В круговом поперечном сечении вала деформации сдвига и касательные напряжения равны нулю в центре и максимальны на краю; в промежуточных точках они пропорциональны расстоянию от центра тяжести сечения. Обычная формула для максимального касательного напряжения при кручении такова: S = Tc/J, где T – скручивающий момент на одном конце, c – радиус вала и J – полярный момент сечения. Для круга J = pr4/2. Эта формула применима только в случае кругового поперечного сечения. Формулы для валов с поперечным сечением другой формы выводятся путем решения соответствующих задач методами математической теории упругости с привлечением в некоторых случаях методов экспериментального анализа.
СЛОЖНОЕ СОПРОТИВЛЕНИЕ.
Нередко приходится рассчитывать балки, на которые в дополнение к поперечным нагрузкам действуют продольные силы растяжения или сжатия, приложенные к концам. В таких случаях напряжение в любой точке поперечного сечения равно алгебраической сумме нормального напряжения, создаваемого продольной нагрузкой, и изгибного напряжения, создаваемого поперечными нагрузками. Общая формула для напряжения в случае совместного действия изгиба и растяжения-сжатия такова: S = ± (P/A) ± (Mc/I), где знак «плюс» относится к растягивающему напряжению.
КОЛОННЫ.
Каркасы зданий и фермы мостов состоят в основном из растянутых стержней, балок и колонн. Колонны – это длинные сжатые стержни, примером которых в каркасах зданий могут служить вертикальные стержни, несущие межэтажные перекрытия.
Если длина сжатого стержня более чем в 10–15 раз превышает его толщину, то под действием критических нагрузок, приложенных к его концам, он, потеряв устойчивость, изогнется, даже если нагрузки номинально приложены по его оси (продольный изгиб). Вследствие такого изгиба нагрузка оказывается внецентренной. Если эксцентриситет в среднем поперечном сечении колонны равен D, то максимальное сжимающее напряжение в колонне будет равно (P/A) + (PDc/I). Отсюда видно, что допускаемая нагрузка для колонны должна быть меньше, чем для короткого сжатого стержня.
Формулу для устойчивости гибких колонн вывел в 1757 Л.Эйлер. Максимальная нагрузка P, которую может нести гибкая колонна высотой L, равна mEA /(L/r)2, где m – постоянный множитель, зависящий от конструкции основания, A – площадь поперечного сечения колонны, а r – наименьший радиус инерции поперечного сечения. Отношение L/r называется гибкостью (при продольном изгибе). Как нетрудно видеть, допускаемая нагрузка быстро убывает с увеличением гибкости колонны. В случае колонн с малой гибкостью формула Эйлера непригодна, и конструкторы вынуждены пользоваться эмпирическими формулами.
В строениях часто встречаются внецентренно нагруженные колонны. В результате точного теоретического анализа таких колонн были получены «формулы секанса». Но расчеты по этим формулам весьма трудоемки, а потому часто приходится прибегать к эмпирическим методам, дающим хорошие результаты.
СЛОЖНЫЕ НАПРЯЖЕННЫЕ СОСТОЯНИЯ
Напряжение в какой-либо точке той или иной плоскости нагруженного тела, вычисленное по обычным формулам, не обязательно будет наибольшим в этой точке. Поэтому важное значение имеет вопрос о соотношениях между напряжениями в разных плоскостях, проходящих через одну точку. Такие соотношения являются предметом раздела механики, посвященного сложным напряженным состояниям.
Соотношения между напряжениями.
Напряженное состояние в некоторой точке любого нагруженного тела можно полностью охарактеризовать, представив напряжения, действующие на грани элементарного куба в этой точке. Часто встречаются случаи, к которым относятся и рассмотренные выше, двухосного (плоского) напряженного состояния с напряжениями, равными нулю, на двух противоположных гранях куба. Напряжения, существующие в точке тела, неодинаковы в плоскостях с разным наклоном. Исходя из основных положений статики, можно сделать ряд важных выводов о соотношении между напряжениями в разных плоскостях. Приведем три из них:
1. Если в некоторой точке заданной плоскости имеется касательное напряжение, то точно такое же напряжение имеется в проходящей через эту точку плоскости, перпендикулярной заданной.
2. Существует плоскость, в которой нормальное напряжение больше, чем в любой другой.
3. В плоскости, перпендикулярной этой плоскости, нормальное напряжение меньше, чем в какой-либо другой.
Максимальное и минимальное нормальные напряжения, о которых говорится в п. 2 и 3, называются главными напряжениями, а соответствующие плоскости – главными плоскостями.
Необходимость в анализе главных напряжений на основе указанных соотношений не всегда возникает, так как простые формулы, которыми обычно пользуются инженеры, в большинстве случаев дают именно максимальные напряжения. Но в некоторых случаях, например при расчете вала, сопротивляющегося одновременно скручивающему и изгибающему моментам, нельзя обойтись без соотношений для сложного напряженного состояния.
БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ
В задачах, о которых говорилось выше, рассматривались напряжения либо равномерно распределенные, либо линейно меняющиеся с удалением от нейтральной оси, где напряжение равно нулю. Однако во многих случаях закон изменения напряжения более сложен.
В качестве примера задач с нелинейным распределением напряжений можно привести искривленные балки, толстостенные сосуды, работающие под высоким внутренним или наружным давлением, валы некругового поперечного сечения и нагруженные тела с резкими изменениями поперечного сечения (канавками, буртиками и т.д.). Для таких задач рассчитываются коэффициенты концентрации напряжений.
Кроме того, выше речь шла только о статических нагрузках, постепенно прилагаемых и снимаемых. Переменные же и периодически меняющиеся нагрузки, многократно повторенные, могут приводить к потере прочности, даже если они не превышают статического предела прочности рассматриваемого материала. Такие отказы называются усталостными, а проблема их предотвращения приобрела важное значение в наш век машин и механизмов, работающих на необычайно высоких скоростях. См. также СТАТИКА; ПРОЧНОСТНОЙ РАСЧЕТ КОНСТРУКЦИЙ; КОНСТРУКЦИОННЫЕ И СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ.
Напряженное состояние и гипотезы прочности
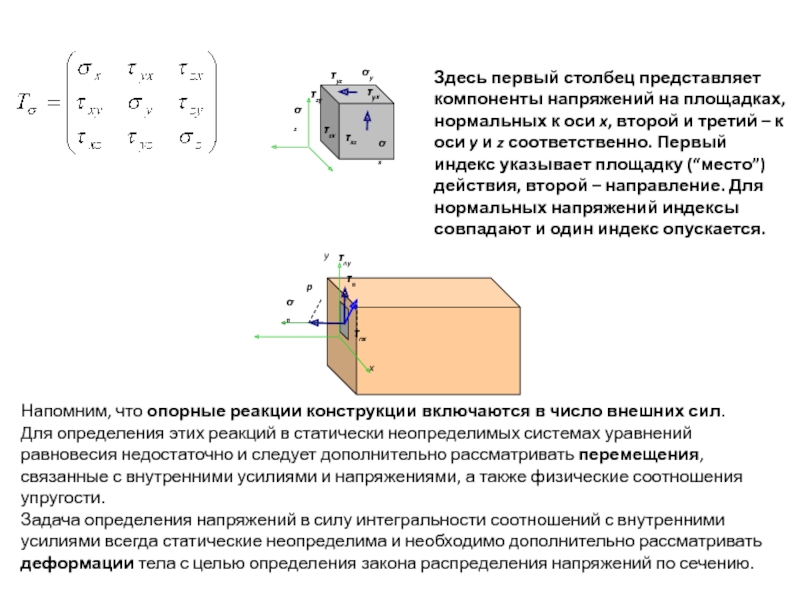
Понятие о напряжениях в точке
На основании допущения о сплошности тела можно считать, что внутренние силы непрерывно распределены по всему сечению.
Выделим в произвольной точке малую площадку ΔA, а равнодействующую внутренних сил на этой площадке обозначим ΔR. Отношение
представляет собой среднее напряжение на данной площадке.
Если площадку ΔA уменьшить, то в пределе получим полное напряжение в точке
Полное напряжение р может быть разложено на три составляющие: по нормали к плоскости сечения и по двум осям в плоскости сечения. Проекция вектора полного напряжения р на нормаль обозначается через σ и называется нормальным напряжением.
Составляющие в плоскости сечения называются касательными напряжениями и обозначаются τ. В зависимости от расположения и наименования осей обозначения σ и τ снабжаются системой индексов.
Связь между напряжениями и внутренними силами
Установим связь между напряжениями и внутренними силами, возникающими в поперечном сечении стержня. Для этой цели выделим на сечении бесконечно малую площадку dA и приложим к ней элементарные силы σ dA, τx dA, τy dA.
Суммируя проекции этих элементарных сил, а также их моменты относительно осей Ox, Oy, Oz, найдём;
Знак «А» у интеграла показывает, что интегрирование проводится по всей площади поперечного сечения. Приведённые формулы позволяют определить равнодействующие внутренних сил через напряжения, если известен закон распределения последних по сечению.
Обратную задачу с помощью только одних этих уравнений решить нельзя, так как одной и той же величине внутреннего усилия, например N, могут соответствовать различные законы распределения нормальных напряжений по сечению.
Одной из основных задач сопротивления материалов является задача об определении напряжений через равнодействующие внутренних сил. При этом оказывается, что решить эту задачу можно только, рассматривая параллельно с условиями равновесия и условия деформации бруса.
Объемное напряженное состояние
Совокупность напряжений, действующих по площадкам, проведенным через исследуемую точку, составляет напряженное состояние в рассматриваемой точке. На площадках общего положения действуют нормальные и касательные напряжения (рис. 3.1).
Рис. 3.1
Значения касательных напряжений на взаимно перпендикулярных площадках подчиняются закону парности касательных напряжений:
Относительные деформации и напряжения связаны обобщенным законом Гука.
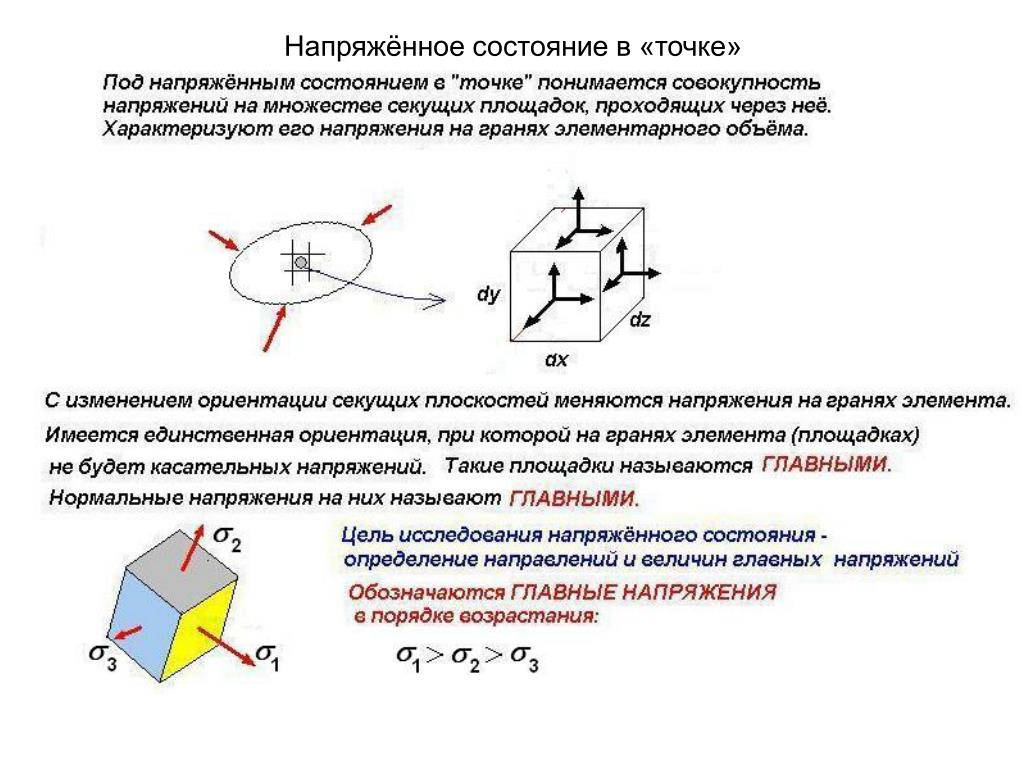
Площадки, на которых отсутствуют касательные напряжения, называются главными, а нормальные напряжения, действующие по этим площадкам, называются главными напряжениями (рис. 3.2).
Обозначение главных напряжений:
Напряженное состояние называется объемным или трехосным, если
Рис. 3.2
Относительное изменение объема:
где К – модуль объемной упругости,
Удельная потенциальная энергия упругой деформации:
— полная
— изменение объема
— изменение формы
Плоское напряженное состояние
Напряженное состояние называется плоским или двухосным, если одно из главных напряжений равно нулю (рис. 3.3).
Рис.3.3
Напряжения на наклонной площадке (рис. 3.4,а)
Величина и направление главных напряжений (рис. 3.4,б)
Чистый сдвиг σx = σy = 0 (рис. 3.4,в)
Рис. 3.4
Линейное напряженное состояние
Напряженное состояние называется линейным или одноосным, если два главных напряжения равны нулю.
Проверка прочности при линейном напряженном состоянии проводится по условию прочности:
В сложном напряженном состоянии проверку прочности проводят по гипотезам прочности по эквивалентному напряжению:
Величина σэкв определяется, исходя из принятого критерия эквивалентности, лежащего в основе одной из гипотез разрушения или гипотез прочности, при котором сложное напряженное состояние заменяется эквивалентным ему растяжением или сжатием.
Гипотезы прочности
Примеры расчета напряжений >
Осевое растяжение-сжатие >
Виды напряжений
В случае одноосного растяжения возникающие в теле напряжения равны. Сила Р, (рис. 7) приложенная к некоторой площадке F, обычно направлена к ней под некоторым углом. Поэтому в теле возникают нормальные и касательные напряжения.
Образование внутренних напряжений связано в основном с неоднородным распределением деформаций (в том числе и микродеформаций) по объему тела.
Наличие в испытуемом образце механических надрезов, трещин внутренних дефектов металла приводит к неравномерному распределению напряжений, создавая у основания надреза пиковую концентрацию нормальных напряжений (нормальные напряжения бывают растягивающими и сжимающими) (см. рис. 7). Действие надрезов, сделанных в образце, аналогично конфигурации изделий, имеющих сквозные отверстия, резьбу и т.п., или влиянию внутренних дефектов металла (неметаллических включений, графитных выделений в чугуне, трещин и др.), нарушающих его цельность. Поэтому всевозможные надрезы, отверстия, галтели и другие источники концентрации напряжений называют концентраторами напряжений.
Напряжения вызываются различными причинами. Различают временные, обусловленные действием внешней нагрузки и исчезающие после ее снятия, и внутренние остаточные напряжения, возникающие и уравновешивающиеся в пределах тела без действия внешней нагрузки.
Внутренние напряжения наиболее часто возникают в процессе быстрого нагрева или охлаждения металла вследствие неодинакового расширения (сжатия) поверхностных и внутренних слоев. Эти напряжения называют тепловыми.
Кроме того, напряжения возникают в процессе кристаллизации, при неравномерной деформации, при термической обработке вследствие структурных превращений по объему и т.д., эти напряжения называют фазовыми или структурными.
Внутренние напряжения классифицируют на:
Напряжения 1 рода (или зональные), называемые также макронапряжениями, они уравновешиваются в объеме всего тела, возникают главным образом в результате технологических процессов, которым подвергают деталь в процессе ее изготовления.
Напряжения 2 рода уравновешиваются в объеме зерна (кристаллита) или нескольких блоков (субзерен), их называют иначе микронапряжениями. Чаще всего они возникают в процессе фазовых превращений и деформации металла, когда разные кристаллиты и блоки внутри них оказываются в различном упругонапряженном состоянии.
Напряжения 3 рода, локализующиеся в объемах кристаллической ячейки, представляют собой статические искажения решетки, т. е. смещения атомов на доли ангстрема из узлов кристаллической решетки.
Упругая и пластическая деформация
Упругой называют деформацию, влияние которой на форму, структуру и свойства тела полностью устраняется после прекращения действия внешних сил. Упругая деформация не вызывает заметных остаточных изменений в структуре и свойствах металла; под действием приложенной нагрузки происходит незначительное, полностью обратимое смещение атомов, или поворот блоков кристалла. После снятия нагрузки смещенные атомы вследствие действия сил притяжения или отталкивания возвращаются в исходное равновесное состояние, и кристаллы приобретают первоначальную форму и размеры.
При достижении касательными напряжениями предела или порога упругости деформация становится необратимой. При снятии нагрузки устраняется лишь упругая составляющая деформации. Часть же деформации, которую называют пластической, остается.
Пластическая деформация в кристаллах может осуществляется скольжением и двойникованием. Скольжение — смещение отдельных частей кристалла — одной части относительно другой происходит под действием касательных напряжений, когда эти напряжения в плоскости и в направлении скольжения достигают определенной критической величины.
Схема упругой и пластической деформаций металла с кубической структурой, подвергнутого действию напряжений сдвига, показана на рис.9..
Скольжение в кристаллической решетки протекает по плоскостям и направлениям с наиболее плотной упаковкой атомов, где сопротивление сдвигу (τ ) наименьшее. Это объясняется тем, что расстояние между соседними атомными плоскостями наибольшее, т.е. связь между ними наименьшая.
Чем больше в металле возможных плоскостей и направлений скольжения, тем выше его способность к пластической деформации.
Пластическая деформация металлов с плотноупакованными решетками К12 и Г12, кроме скольжения, может осуществляться двойникованием, которое сводится к переориентировке части кристалла в положение, симметричное по отношению к первой части относительно плоскости, называемой плоскостью двойникования (рис. 8). Двойникование, подобно скольжению, сопровождается прохождением дислокации сквозь кристалл.
Регулятор напряжения используется для регулирования уровней напряжения. Когда требуется стабильное, надежное напряжение, то регулятор напряжения является предпочтительным устройством. Он генерирует фиксированное выходное напряжение, которое остается постоянным при любых изменениях входного напряжения или условий нагрузки. Он действует как буфер для защиты компонентов от повреждений. Регулятор напряжения — это устройство с простой конструкцией прямой связи, в которой используются контуры управления с отрицательной обратной связью.Существует в основном два типа регуляторов напряжения: линейные регуляторы напряжения и импульсные регуляторы напряжения; они используются в более широких приложениях. Линейный регулятор напряжения является самым простым типом регулятора напряжения. Это доступно в двух типах, которые являются компактными и используются в системах низкого напряжения и низкого напряжения. Давайте обсудим различные типы регуляторов напряжения.

 Регулятор напряжения
Регулятор напряженияТипы регуляторов напряжения и принцип их работы
По существу, существует два типа регуляторов напряжения: линейный регулятор напряжения и импульсный регулятор напряжения.
- Существует два типа линейных регуляторов напряжения: серия и шунт.
- Существует три типа переключающих регуляторов напряжения: повышающие, понижающие и инверторные.
Линейный регулятор
Линейный регулятор действует как делитель напряжения. В омическом регионе он использует FET. Сопротивление регулятора напряжения зависит от нагрузки, что приводит к постоянному выходному напряжению.
Преимущества линейного стабилизатора напряжения
- Дает низкое пульсирующее напряжение на выходе
- Быстрое время отклика на нагрузку или изменения линии
- Низкие электромагнитные помехи и меньше шума
Недостатки линейного стабилизатора напряжения
- КПД очень низкий
- Требуется большое пространство — необходим радиатор
- Напряжение выше входа не может быть увеличено
В последовательном регуляторе напряжения используется переменный элемент, размещенный последовательно с нагрузкой.Изменяя сопротивление этого последовательного элемента, напряжение, падающее на него, может быть изменено. И напряжение на нагрузке остается постоянным.


 Регулятор напряжения серии
Регулятор напряжения серии 
Величина потребляемого тока эффективно используется нагрузкой; это главное преимущество серийного стабилизатора напряжения. Даже когда нагрузка не требует тока, последовательный регулятор не потребляет полный ток. Следовательно, последовательный регулятор значительно эффективнее, чем шунтирующий регулятор напряжения.
 Серия
Серия  Схема стабилизатора напряжения Схема стабилизатора напряжения
Схема стабилизатора напряжения Схема стабилизатора напряженияРегулятор напряжения шунта
Регулятор напряжения шунта работает, обеспечивая путь от напряжения питания к земле через переменное сопротивление. Ток, проходящий через шунтирующий регулятор, отклоняется от нагрузки и бесполезно течет на землю, что делает эту форму обычно менее эффективной, чем последовательный регулятор. Это, однако, более простое, иногда состоящее только из напряжения опорного диода, и используется в очень маломощных схемах, в котором впустую ток слишком мал, чтобы быть озабоченность.Эта форма очень распространена для опорных цепей напряжения. Шунтирующий регулятор обычно может только поглощать (поглощать) ток.

 Шунтирующий регулятор напряжения
Шунтирующий регулятор напряженияПрименения шунтирующих регуляторов
Шунтирующие регуляторы используются в:
- Импульсные источники питания с низким выходным напряжением
- Цепи источника тока и приемника
- Усилители ошибок
- Регулируемое напряжение или ток Линейные и переключающие Источники питания
- Контроль напряжения
- Аналоговые и цифровые схемы, для которых требуются прецизионные задания
- Прецизионные ограничители тока
Импульсный регулятор напряжения
Импульсный регулятор быстро включает и выключает последовательное устройство.Рабочий цикл коммутатора устанавливает количество заряда, передаваемого нагрузке. Это контролируется механизмом обратной связи, аналогичным механизму линейного регулятора. Импульсные регуляторы эффективны, потому что последовательный элемент либо полностью проводящий, либо отключен, потому что он практически не рассеивает мощность. Импульсные регуляторы способны генерировать выходные напряжения, которые выше входного напряжения или противоположной полярности, в отличие от линейных регуляторов.

 Импульсный регулятор напряжения
Импульсный регулятор напряженияИмпульсный регулятор напряжения быстро включается и выключается для изменения выхода.Требуется управляющий генератор, а также компоненты для хранения зарядов.
В импульсном регуляторе с импульсной модуляцией изменяется частота, постоянный коэффициент заполнения и спектр шума, налагаемый PRM; отфильтровать этот шум сложнее.
Импульсный регулятор с широтно-импульсной модуляцией, постоянной частотой, изменяющимся рабочим циклом, эффективен и прост в фильтрации шума.
В импульсном стабилизаторе ток непрерывного режима через индуктор никогда не падает до нуля.Это позволяет максимальную выходную мощность. Это дает лучшую производительность.
В импульсном регуляторе ток прерывистого режима через индуктор падает до нуля. Это дает лучшую производительность, когда выходной ток низкий.
Коммутационные топологии
Имеет два типа топологий: диэлектрическая изоляция и неизолированная.
Неизоляция: Основана на небольших изменениях Vout / Vin. Примерами являются повышающий регулятор напряжения (Boost) — повышает входное напряжение; Step Down (Buck) — понижает входное напряжение; Step up / Step Down (boost / buck) Регулятор напряжения — понижает или повышает или инвертирует входное напряжение в зависимости от контроллера; Зарядный насос — обеспечивает несколько входов без использования индуктора.
Диэлектрик — Изоляция: Он основан на радиации и интенсивной среде.
Преимущества коммутационных топологий
Основными преимуществами импульсного источника питания являются экономичность, размер и вес. Это также более сложная конструкция, способная работать с более высокой энергоэффективностью. Импульсный регулятор напряжения может обеспечивать выходной сигнал, который больше или меньше или инвертирует входное напряжение.
Недостатки коммутационных топологий
- Более высокое выходное пульсирующее напряжение
- Более медленное переходное время восстановления
- EMI производит очень шумную выходную мощность
- Очень дорого
Регулятор повышающего напряжения
Также повышающие переключающие преобразователи называемые повышающими импульсными регуляторами, обеспечивают более высокое выходное напряжение за счет повышения входного напряжения.Выходное напряжение регулируется, пока потребляемая мощность находится в пределах спецификации выходной мощности схемы. Для управления цепочками светодиодов используется повышающий импульсный регулятор напряжения.
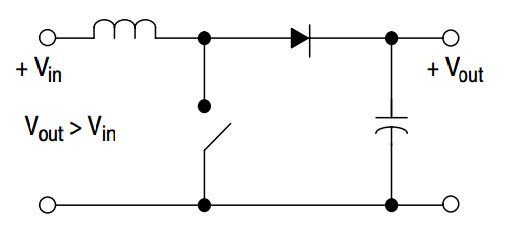

Повышающий регулятор напряжения
Предположим, что схема без потерь Pin = Pout (входные и выходные мощности одинаковы)
Затем V в I в = V из I из ,
I из / I в = (1-D)
Из этого следует, что в этой схеме
- мощности остаются неизменными
- Увеличивается напряжение
- Ток уменьшается
- Эквивалентно преобразователю постоянного тока
Step Down ( Бак) Регулятор напряжения
Понижает входное напряжение.
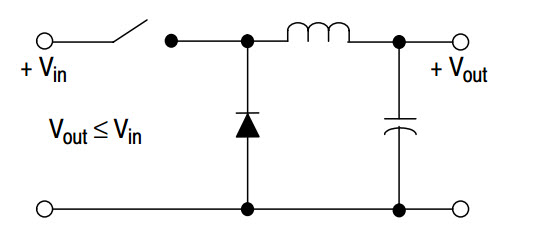
 Регулятор понижающего напряжения
Регулятор понижающего напряженияЕсли входная мощность равна выходной мощности, то
P в = P из ; V в I в = V из I из ,
I из / I из = V в / V из = 1 / D
Преобразователь с понижением частоты эквивалентен к трансформатору постоянного тока, в котором отношение витков находится в диапазоне 0-1.
Step Up / Step Down (Boost / Buck)
Он также называется инвертором напряжения.Используя эту конфигурацию, можно повышать, понижать или инвертировать напряжение в соответствии с требованиями.
- Выходное напряжение противоположной полярности входа.
- Это достигается за счет VL-диода с обратным смещением в прямом направлении во время выключения, выработки тока и зарядки конденсатора для выработки напряжения во время выключения
- Используя этот тип импульсного регулятора, можно достичь КПД 90%.
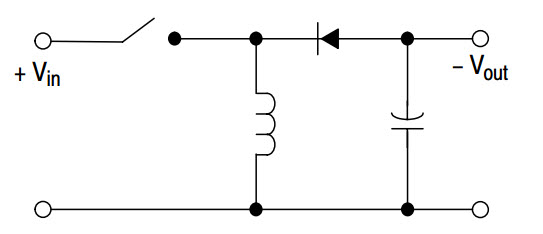
 Повышающий / понижающий регулятор напряжения
Повышающий / понижающий регулятор напряженияРегулятор напряжения генератора
Генераторы вырабатывают ток, необходимый для удовлетворения электрических требований автомобиля при работе двигателя.Он также пополняет энергию, которая используется для запуска автомобиля. Генератор переменного тока способен генерировать больший ток на более низких скоростях, чем генераторы постоянного тока, которые когда-то использовались большинством транспортных средств. Генератор переменного тока состоит из двух частей:

 Регулятор напряжения генератора
Регулятор напряжения генератора Статор — это стационарный компонент, который не перемещается. Он содержит набор электрических проводников, намотанных на катушки поверх железного сердечника.
Ротор / арматура — это движущийся компонент, который создает вращающееся магнитное поле любым из следующих трех способов: (i) индукция (ii) постоянные магниты (iii) с использованием возбудителя.
Электронный регулятор напряжения
Простой регулятор напряжения может быть изготовлен из резистора, включенного последовательно с диодом (или рядом диодов). Из-за логарифмической формы V-I кривых диода напряжение на диоде изменяется незначительно из-за изменений потребляемого тока или изменений на входе. Когда точный контроль напряжения и эффективность не важны, эта конструкция может работать нормально.

 Электронный регулятор напряжения
Электронный регулятор напряженияТранзисторный регулятор напряжения
Электронные регуляторы напряжения имеют нестабильный источник опорного напряжения, который обеспечивается диодом Зенера, который также известен как обратный пробой рабочего напряжения диода.Он поддерживает постоянное выходное напряжение постоянного тока. Пульсирующее напряжение переменного тока блокируется, но фильтр не может быть заблокирован. Регулятор напряжения также имеет дополнительную цепь для защиты от короткого замыкания, а также схему ограничения тока, защиту от перенапряжения и теплового отключения.

 Транзисторный регулятор напряжения
Транзисторный регулятор напряженияЭто все о различных типах регуляторов напряжения и принципах их работы. Мы считаем, что информация, представленная в этой статье, поможет вам лучше понять эту концепцию.Кроме того, по любым вопросам, касающимся этой статьи или любой помощи в реализации электрических и электронных проектов, вы можете обратиться к нам, оставив комментарий в разделе комментариев ниже. Вот вам вопрос — где мы будем использовать регулятор напряжения генератора?
Фото Кредиты:
.Разница между напряжением и током
Напряжение и ток — это два основных аспекта электричества. Напряжение — это тип электромагнитной силы, воздействие которой вызывает протекание электрического тока в цепи. Величина напряжения и тока зависят друг от друга, но эти два термина в некоторой степени отличаются друг от друга.
Одно из основных различий между напряжением и током заключается в том, что напряжение — это разница между двумя точками, а ток — это поток электрических зарядов между этими двумя точками электрического поля.Некоторые другие различия между ними описаны ниже в сравнительной таблице.
Содержимое: напряжение против тока
- Сравнительная таблица
- Определение
- Ключевые различия
- Заключение
Сравнительная таблица
| Основа для сравнения | Напряжение | Ток |
|---|---|---|
| Определение | Разница между двумя точками электрического поля | Поток зарядов между двумя точками |
| Единица | Вольт | Ампер |
| Symbol | V | I |
| Формула | 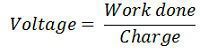 | 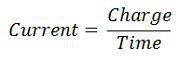 |
| Создано поле | Магнитное поле | Электростатическое поле |
| Типы | Переменное напряжение и постоянное напряжение | Переменный ток и постоянный ток |
| Полярность | Переменное напряжение меняется, но постоянное напряжение не может изменить его полярность. | Переменный ток меняет свою полярность, но полярность постоянного тока остается постоянной. |
| Производит | Генератор | Напряжение |
| Измеритель | Вольтметр | Амперметр |
| Заряд | 1 Вольт = 1 Дж / кулон | 1 Ампер = 1 Кулон / секунда |
| Неравный во всех компонентах | В равной степени распределен во всех компонентах | |
| Параллельное соединение | Величина напряжения остается одинаковой во всех компонентах | Величина тока варьируется во всех компонентах. |
| Потери | Из-за полного сопротивления | Из-за пассивных элементов |
| Отношение | Это причина тока | Это влияние напряжения |
Определение напряжения
Напряжение является типом электромагнитной силы. Когда величина напряжения высокая, через цепь протекает большой ток, а когда величина его мала, через него протекает меньше тока.Напряжение представлено символом V, а их единица СИ — вольт.
Напряжение в основном классифицируется на два типа, то есть переменное напряжение и постоянное напряжение. Переменное напряжение меняет полярность, а постоянное напряжение не меняет полярность. Постоянное напряжение создается разностью потенциалов между клеммами электрохимической ячейки, а переменное напряжение вызывается генератором переменного тока.
 Иногда в линии передачи напряжение на передающем конце меньше, чем напряжение на принимающем конце.Напряжение рассеивается в виде тепла, и, следовательно, эта потеря напряжения называется падением напряжения. Падение напряжения происходит из-за большой нагрузки. Когда тяжелая нагрузка подключена через линию, она потребляет сильный ток, из-за которого происходит потеря напряжения.
Иногда в линии передачи напряжение на передающем конце меньше, чем напряжение на принимающем конце.Напряжение рассеивается в виде тепла, и, следовательно, эта потеря напряжения называется падением напряжения. Падение напряжения происходит из-за большой нагрузки. Когда тяжелая нагрузка подключена через линию, она потребляет сильный ток, из-за которого происходит потеря напряжения.
Когда напряжение на приемном конце превышает напряжение на передающем конце, в линии происходит повышение напряжения. Повышение напряжения называется эффектом Ферранти, и это происходит главным образом из-за тока зарядки линии электропередачи.
Определение тока
Ток — это влияние напряжения. Когда разность потенциалов приложена к проводящему материалу, носитель электрического заряда начинает перемещаться от одного атома к другому. Ток представлен символом I, а его единица СИ — ампера. Один ампер тока представляет собой носитель заряда 6,24 × 10 18 . Большинство носителей заряда являются отрицательными носителями заряда, и направление потока тока от отрицательной точки к относительно положительной точке.
 Электрический ток в основном делится на два типа, то есть переменный ток и постоянный ток. В постоянном токе электроны текут только в направлении, а в переменном токе направление электронов меняется на каждую миллисекунду.
Электрический ток в основном делится на два типа, то есть переменный ток и постоянный ток. В постоянном токе электроны текут только в направлении, а в переменном токе направление электронов меняется на каждую миллисекунду.
Ключевые различия между напряжением и током
- Напряжение представляет собой разность электрических зарядов между двумя точками электрического поля, тогда как ток представляет собой поток электрических зарядов между точками электрического поля.
- Единица измерения напряжения в СИ (Международная единица измерения стандарта) — вольт, а единица измерения тока в СИ — в амперах.
- Напряжение представлено символом V , в то время как ток представлен символом I .
- Напряжение определяется как отношение выполненной работы к заряду, а ток — как отношение заряда ко времени .
- Напряжение генерирует магнитное поле вокруг него, в то время как ток создает электростатическое поле вокруг него.
- Полярность переменного напряжения остается неизменной, и из-за этого переменного напряжения индуцируется переменный ток. Но полярность постоянного напряжения остается постоянной, и их влияние вызывает постоянный ток.
- Напряжение — это разница между точкой в электрическом поле, тогда как ток вызван потоком электрона в электрическом поле.
- Напряжение измеряется прибором, называемым вольтметром, тогда как ток измеряется амперметром.
- Один вольт равен 1 Дж / кулон, тогда как один Ампер равен одному столбцу / секунда.
- В последовательной цепи величина напряжения остается разной во всех компонентах схемы, тогда как величина тока остается одинаковой.
- В параллельной цепи напряжение на всех ветвях цепи остается одинаковым, тогда как ток неравномерно распределен в компоненте схемы.
- Падение напряжения происходит в основном из-за полного сопротивления цепи, тогда как падение тока происходит из-за пассивного элемента (например, резистора) цепи.
- Полное сопротивление — это препятствие, индуцируемое электрической цепью для протекания электрического тока, когда на них подается разность потенциалов.
- Напряжение является причиной тока, тогда как ток — это влияние напряжения.
Заключение
Согласно закону Ома, напряжение прямо пропорционально току. Количественное напряжение генерируется, когда поток прерывается проводником, который находится между вращающимся магнитным полем.Это напряжение индуцирует ток в цепи. Таким образом, мы можем сказать, что напряжение может существовать без тока, но ток не может существовать без напряжения. Другими словами, ток — это влияние напряжения, а напряжение — причина тока.
,Определение: Регулятор, у которого нет вращающихся частей, такой тип регулятора называется регулятор статического напряжения. Их схема состоит из таких устройств, как трансформаторы, конденсаторы, резисторы, транзисторы, магнитные усилители и т. Д. Регуляторы такого типа не имеют потерь на трение и износ (потому что у них нет вращающихся частей). Это не требует постоянного внимания, таким образом, снижается стоимость системы
Типы статического регулятора напряжения
Регулятор статического напряжения превосходит электромеханические регуляторы в отношении точности управления, реакции, надежности и обслуживания.Регулятор статического напряжения в основном подразделяется на два типа. Они есть;
- Регулятор Напряжения Типа Сервопривода
- Магнитный усилитель-регулятор
Типы статического стабилизатора напряжения подробно описаны ниже;
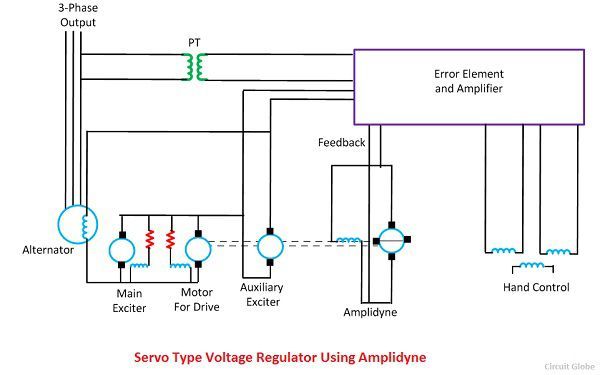
1. Регулятор напряжения сервомотора
Главной особенностью серворегулятора напряжения является использование ампидина. Амплидин представляет собой тип электромеханического усилителя, который усиливает сигнал. Система содержит основной возбудитель, приводимый в действие от вала генератора переменного тока, и вспомогательный возбудитель, обмотка возбуждения которого контролируется амплидином.
Вспомогательный возбудитель и амплидин приводятся в действие двигателем постоянного тока, соединенным с обеими машинами. Основной возбудитель имеет насыщенную магнитную цепь и, следовательно, имеет грубое выходное напряжение. Якорь главного и вспомогательного возбудителя соединены последовательно, и эта последовательная комбинация возбуждает обмотку возбуждения генератора.
Работа серворегулятора напряжения
Трансформатор потенциала обеспечивает сигнал, который пропорционален выходному сигналу генератора переменного тока.Выходные клеммы генератора подключены к электронному усилителю. Когда происходит отклонение в выходном напряжении генератора переменного тока, то электронный усилитель посылает напряжение на амплид. Выход амплидина подает напряжение в поле управления амплидином и, следовательно, изменяет поле вспомогательного возбудителя. Таким образом, вспомогательный и основной возбудители последовательно регулируют ток возбуждения генератора переменного тока.
 2. Магнитный усилитель-регулятор
2. Магнитный усилитель-регулятор
Основным компонентом магнитных усилителей является стальной сердечник с дополнительной обмоткой, питаемой постоянным током.Дополнительная обмотка используется для управления переменным током относительно большой мощности с использованием постоянного тока малой мощности. Стальной сердечник регулятора состоит из двух одинаковых обмоток переменного тока, также называемых нагрузочной обмоткой. Обмотка переменного тока подключается либо последовательно, либо параллельно, а последовательно с ними возникает нагрузка.
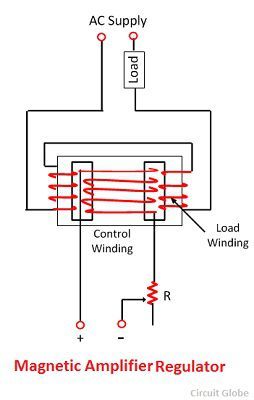 Последовательная обмотка используется, когда требуются кратковременные отклики и высокое напряжение, тогда как параллельная обмотка используется для медленного отклика. На обмотку управления подается постоянное напряжение.Когда в обмотке нагрузки нет тока, обмотка переменного тока предлагает самый высокий потенциал и индуктивность по отношению к потенциалу переменного тока. Вследствие этого переменный ток на нагрузку ограничивается низким значением индуктивного сопротивления, а напряжение нагрузки мало.
Последовательная обмотка используется, когда требуются кратковременные отклики и высокое напряжение, тогда как параллельная обмотка используется для медленного отклика. На обмотку управления подается постоянное напряжение.Когда в обмотке нагрузки нет тока, обмотка переменного тока предлагает самый высокий потенциал и индуктивность по отношению к потенциалу переменного тока. Вследствие этого переменный ток на нагрузку ограничивается низким значением индуктивного сопротивления, а напряжение нагрузки мало.
Когда подается постоянное напряжение, магнитный поток постоянного тока проходит через сердечник, и сердечник приближается к магнитному насыщению. Это уменьшает индуктивность и полное сопротивление обмоток переменного тока. Поток переменного тока через обмотку возбуждения увеличивается с увеличением потока постоянного тока через обмотку управления.Таким образом, изменение величины тока нагрузки в небольшом диапазоне вызывает изменение напряжения нагрузки в широком диапазоне.
,Основы, дизайн, принцип работы и типы
Большинство бытовых электронных устройств, таких как мобильные телефоны, ТВ, радио, MP3-плееры и т. Д., Представляют собой комбинацию цифровой и аналоговой электроники. Везде, где есть беспроводная передача / прием или аудиосигналы, участвующие в электронном проектировании, нам понадобятся периодические колебательные электронные сигналы, которые называются Осциллирующими сигналами и очень полезны для беспроводной передачи или для выполнения операций, связанных с синхронизацией.
Генератор в электронике обычно относится к схеме, которая способна генерировать сигналы. Эта форма волны может быть синусоидальной, треугольной или даже типа зубьев пилы. Некоторые из наиболее распространенных схем генератора — это схема LC, схема бака и т. Д. Генератор , управляемый напряжением, представляет собой генератор, который генерирует колебательные сигналы (сигналы) с переменной частотой. Частота этого сигнала варьируется в зависимости от величины входного напряжения.Сейчас вы можете представить себе генератор напряжения, управляемый напряжением (VCO), который представляет собой черный ящик, который принимает напряжение переменной величины и выдает выходной сигнал переменной частоты, а частота выходного сигнала прямо пропорциональна величине входного напряжения. , Мы узнаем больше об этом черном ящике и как использовать его в наших проектах в этом уроке.

Принцип работы VCO
Существует много типов схем ГУН ; очень простой можно построить, просто используя конденсатор, индуктор и резистор для создания цепи в баке.Также операционные усилители, мультивибраторы, транзисторы, 555 таймеров также могут быть использованы для построения колебательных контуров . Кроме того, существуют специальные IC-пакеты, такие как LM566, LM567 и т. Д., Которые могут выступать в качестве VCO. Чтобы понять основную идею VCO, давайте рассмотрим генератор RC.
В генераторе RC частота выходной волны зависит от значения конденсатора, используемого в цепи, так как частота задается формулами
Частота (f) = 1/ 2 πRC
Следовательно, в этом случае частота колебаний обратно пропорциональна величине емкости, используемой в цепи.Поэтому теперь, чтобы контролировать выходную частоту и заставить ее работать в качестве VCO, мы должны изменить емкость конденсатора в зависимости от значения входного напряжения. Этого можно добиться с помощью варакторных диодов. Эти диоды изменяют значение емкости на них в зависимости от приложенного напряжения. Пример выходного графика VCO показан ниже.
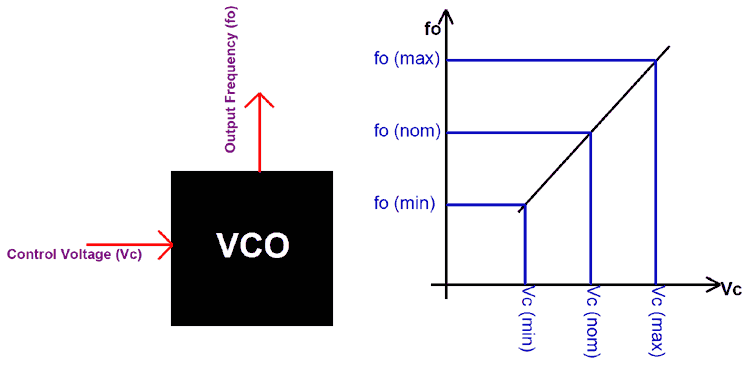
Предположим, что управляющее напряжение равно Vc, а выходная частота равна fo. Затем при нормальных условиях работы VCO подается номинальное напряжение, для которого VCO генерирует номинальную частоту.Когда входное напряжение (управляющее напряжение) увеличивается, выходная частота увеличивается, и наоборот, это также возможно.
Типы управляемых напряжением генераторов
Существует много типов цепей ГУН, используемых в различных приложениях, но их можно в целом классифицировать на два типа в зависимости от их выходного напряжения.
Гармонические осцилляторы: Если форма сигнала на выходе генератора синусоидальна, то она называется гармоническими осцилляторами.К этой категории относятся цепи RC, LC и Tank. Эти типы генераторов сложнее реализовать, но они лучше устойчивы, чем генератор релаксации. Гармонические осцилляторы также называют линейным генератором, управляемым напряжением.
Осциллятор релаксации: Если выходной сигнал генератора имеет пилообразную или треугольную форму, то генератор называется Осциллятором релаксации. Они сравнительно просты в реализации и, следовательно, наиболее широко используются.Осциллятор релаксации может быть далее классифицирован как
- Генератор с управлением по напряжению
- Заземленный конденсатор Управляемый напряжением генератор
- Кольцо с управляемым напряжением, управляемое напряжением, генератор
Генератор с управлением напряжением — Практическое применение
Как упоминалось ранее, VCO может быть просто сконструирован с использованием пары RC или LC, но в реальных приложениях никто этого не делает.Существует специальная микросхема, которая может генерировать колебания на основе входного напряжения. Одной из таких широко используемых микросхем является LM566 от National Semiconductor.
Эта микросхема способна генерировать как треугольную, так и прямоугольную волну , и номинальную частоту этой волны можно установить с помощью внешнего конденсатора и резистора. Позже эта частота также может изменяться в режиме реального времени в зависимости от входного напряжения, подаваемого на нее.
Схема контактов микросхемы LM566 показана ниже
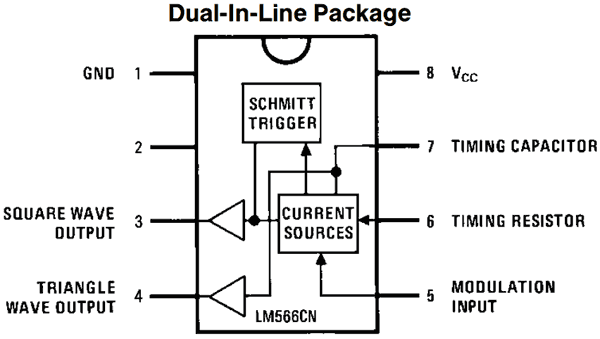
Микросхема может работать от одного источника питания или от двойной шины питания с рабочим напряжением до 24 В.Контакты 3 и 4 являются выходными контактами, которые дают нам прямоугольную волну и треугольную волну соответственно. Номинальную частоту можно установить, подключив правильное значение конденсатора и резистора к контактам 7 и 6.
Формулы для расчета значений R и C на основе выходной частоты (Fo) задаются формулами
Fo = 2,4 (Vss - Vc) / Ro + Co + Vss
Где,
Vss — это напряжение питания (здесь 12 В), а Vc — управляющее напряжение, подаваемое на вывод 5, в зависимости от величины которого регулируется выходная частота.(Здесь мы сформировали делитель потенциала, используя резистор 1,5 кОм и резистор 10 кОм для подачи постоянного напряжения на вывод 5). Примерная принципиальная схема для LM566 показана ниже
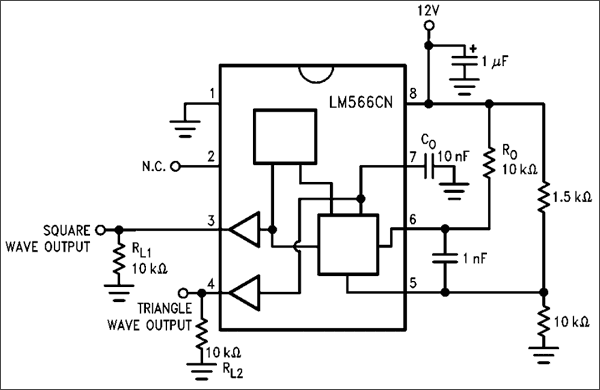
В практических приложениях резисторы 1,5 кОм и 10 кОм можно игнорировать, а управляющее напряжение можно напрямую подавать на вывод 5. Вы также можете изменить значение Ro и Co в зависимости от требуемого диапазона выходной частоты. Также см. Таблицу данных, чтобы проверить, насколько линейно изменяется выходная частота относительно входного управляющего напряжения.Значение выходной частоты регулируется с помощью управляющего напряжения (на выводе 5) в соотношении 10: 1, что помогает нам обеспечивать широкий диапазон управления.
Приложения VCO
- Переключение частоты
- Частотные идентификаторы
- Клавиатура Тоновые распознаватели
- Генераторы часов / сигналов / функций
- Используется для построения фазовых петель.
Генератор, управляемый напряжением, является основным функциональным блоком в системе фазовой автоподстройки частоты.Итак, давайте также разберемся с фазовой автоподстройкой частоты , почему это важно и что VCO делает внутри фазовой автоподстройки частоты.
Что такое фазовая автоподстройка частоты (ФАПЧ)?
Phase Locked Loop, также называемый PPL, представляет собой систему управления, в основном состоящую из трех важных блоков. Это фазовый детектор, фильтр нижних частот и генератор, управляемый напряжением. Вместе эти три формируют систему управления, которая постоянно регулирует частоту выходного сигнала в зависимости от частоты входного сигнала.Блок-схема ФАПЧ показана ниже
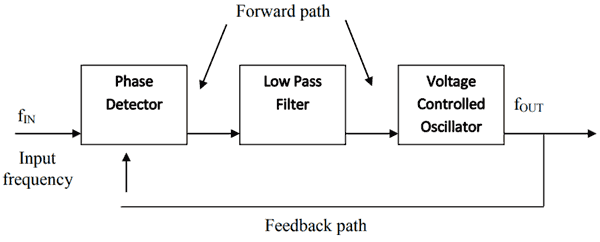
Система PLL используется в приложениях, где высокая стабильная частота (f OUT ) должна быть получена из нестабильного частотного сигнала (f IN ). Основная функция схемы ФАПЧ — производить выходной сигнал с той же частотой, что и входной сигнал. Это очень важно в беспроводных приложениях, таких как маршрутизаторы, радиочастотные системы передачи, мобильные сети и т. Д.
Фазовый детектор сравнивает входную частоту (f IN ) с выходной частотой (f OUT ), используя предоставленный путь обратной связи.Разница в этих двух сигналах сравнивается и дается в терминах значения напряжения и называется сигналом напряжения ошибки. Этот сигнал напряжения также будет иметь некоторый высокочастотный шум, связанный с ним, который может быть отфильтрован с помощью фильтра низких частот. Затем этот сигнал напряжения подается на ГУН, который, как мы уже знаем, изменяет выходную частоту на основе предоставленного сигнала напряжения (управляющего напряжения).
PLL — Практическое применение
Одной из наиболее часто используемых интегральных схем PLL является LM567 .Это интегральная схема тонального декодера, то есть она слушает тональный сигнал определенного пользователем типа на контакте 3, и если этот тон получен, он соединяет выход (контакт 8) с землей. Таким образом, в основном, для прослушивания всего имеющегося на частоте звука и продолжает сравнивать частоту этих звуковых сигналов с заданной частотой, используя технику PLL. Когда частоты совпадают с выходным контактом, он становится низким. Ниже показан вывод микросхемы LM567, схема очень чувствительна к шуму, поэтому не удивляйтесь, если вы не сможете заставить эту микросхему работать на макете.
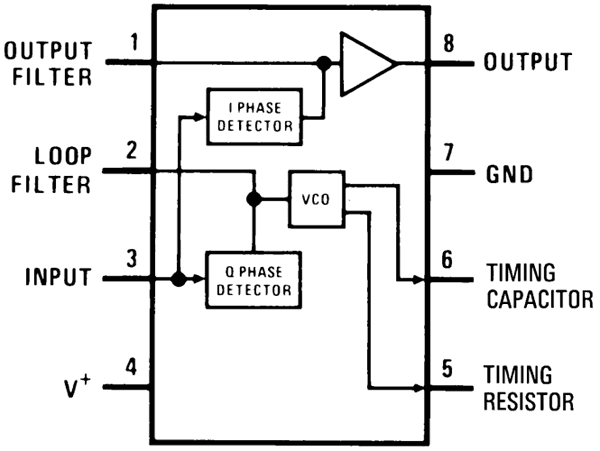
Как показано на выводе, ИС состоит из цепи детектора фазы I и Q внутри нее. Эти фазовые детекторы проверяют разницу между установленной частотой и частотой входящего сигнала. Внешние компоненты используются для установки значения этой установленной частоты. Микросхема также состоит из схемы фильтра, которая будет фильтровать шум случайного переключения, но для этого требуется внешний конденсатор, подключенный к контакту 1. Контакт 2 и используется для установки полосы пропускания микросхемы. Чем выше емкость, тем меньше будет емкость. пропускная способность.Контакты 5 и 6 используются для установки значения установленной частоты. Это значение частоты можно рассчитать с помощью приведенных ниже формул
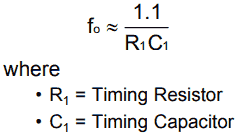
Основная схема для микросхемы LM567 показана ниже.
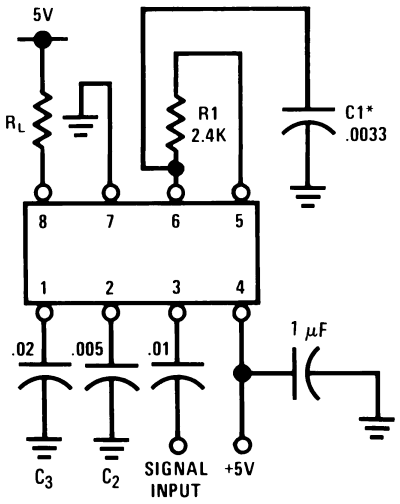
Входной сигнал, частоту которого необходимо сравнить, подается на вывод 3 через фильтрующий конденсатор со значением 0,01 мкФ. Эта частота сравнивается с установленной частотой. Частота устанавливается с помощью резистора 2,4 кОм (R1) и 0.0033 Конденсатор (C1), эти значения могут быть рассчитаны в соответствии с установленной вами частотой с использованием приведенных выше формул.
Когда входная частота соответствует установленной частоте, выходной контакт (контакт 8) будет заземлен. В противном случае этот штифт останется высоким. Здесь мы использовали резистор (R L ) в качестве нагрузки, но обычно это будет светодиод или зуммер, как того требует конструкция. Таким образом, LM567 использует способность VCO сравнивать частоты , что очень полезно в приложениях, связанных со звуком / беспроводным соединением.
Надеюсь, у вас есть хорошее представление о VCO, если у вас есть какие-либо сомнения, разместите их в разделе комментариев или используйте форумы.
Также проверьте:
,