Восьмиразрядный двоичный код: Виды двоичных кодов

Виды двоичных кодов

В микропроцессорах двоичные коды используются для представления любой обрабатываемой информации. При этом разрядность обрабатываемых чисел может превышать разрядность самого процессора и используемой в нЈм памяти. В этом случае длинное число может занимать несколько ячеек памяти и обрабатываться несколькими командами процессора. При обработке все ячейки памяти, выделенные под многобайтное число, рассматриваются как одно число.

Для представления числовой информации могут использоваться знаковые и беззнаковые коды. Для определЈнности примем длину слова процессора равной восьми битам.

Беззнаковые двоичные коды.

Первый вид двоичных кодов, который мы рассмотрим — это целые беззнаковые коды. В этих кодах каждый двоичный разряд представляет собой степень цифры 2:

При этом минимально возможное число, которое можно записать таким двоичным кодом, равно 0. Максимально возможное число, которое можно записать таким двоичным кодом, можно определить как:

Этими двумя числами полностью можно определить диапазон, чисел которые можно представить таким двоичным кодом. В случае двоичного восьмиразрядного беззнакового целого числа диапазон будет: диапазон чисел, которые можно записать таким кодом: 0 .. 255. Для шестнадцатиразрядного кода этот 0 .. 65535. В восьмиразрядном процессоре для хранения такого числа используется две ячейки памяти, расположенные в соседних адресах. Для работы с такими числами используются специальные команды.

Второй вид двоичных кодов, который мы рассмотрим — это прямые целые знаковые коды. В этих кодах старший разряд в слове используется для представления знака числа. В прямом знаковом коде нулем обозначается знак ‘+’, а единицей — знак ‘-‘. В результате введения знакового разряда диапазон чисел смещается в сторону отрицательных чисел:

В случае двоичного восьмиразрядного знакового целого числа диапазон чисел, которые можно записать таким кодом: -127 .. +127. Для шестнадцатиразрядного кода этот диапазон будет: -32767 .. +32767. В восьмиразрядном процессоре для хранения такого числа тоже используется две ячейки памяти, расположенные в соседних адресах.

Недостатком такого кода является то, что знаковый разряд и цифровые разряды приходится обрабатывать раздельно. Алгоритм программ, работающий с такими кодами получается сложный. Для выделения и изменения знакового разряда приходится применять механизм маскирования разрядов, что резко увеличивает размер программы и уменьшает ее быстродействие. Для того, чтобы алгоритм обработки знакового и цифровых разрядов не различался, были введены обратные двоичные коды.

Знаковые обратные двоичные коды. 

Обратные двоичные коды отличаются от прямых только тем, что отрицательные числа в них получаются инвертированием всех разрядов числа. При этом знаковый и цифровые разряды не различаются. Алгоритм работы с такими кодами резко упрощается.

Тем не менее при работе с обратными кодами требуется специальный алгоритм распознавания знака, вычисления абсолютного значения числа, восстановления знака результата числа. Кроме того, в прямом и обратном коде числа для запоминания числа 0 используется два кода, тогда как известно, что число 0 положительное и отрицательным не может быть никогда.

Знаковые дополнительные двоичные коды.

От перечисленных недостатков свободны дополнительные коды. Эти коды позволяют непосредственно суммировать положительные и отрицательные числа не анализируя знаковый разряд и при этом получать правильный результат. Все это становится возможным благодаря тому, что дополнительные числа являются естественным кольцом чисел, а не исскуственным образованием как прямые и обратные коды. Кроме того немаловажным является то, что вычислять дополнение в двоичном коде чрезвычайно легко. Для этого достаточно к обратному коду добавить 1:

Диапазон чисел, которые можно записать таким кодом: -128 .. +127. Для шестнадцатиразрядного кода этот диапазон будет: -32768 .. +32767. В восьмиразрядном процессоре для хранения такого числа используется две ячейки памяти, расположенные в соседних адресах.

В обратных и дополнительных кодах наблюдается интересный эффект, который называется эффект распространения знака. Он заключается в том, что при преобразовании однобайтного числа в двухбайтное достаточно всем битам старшего байта присвоить значение знакового бита младшего байта.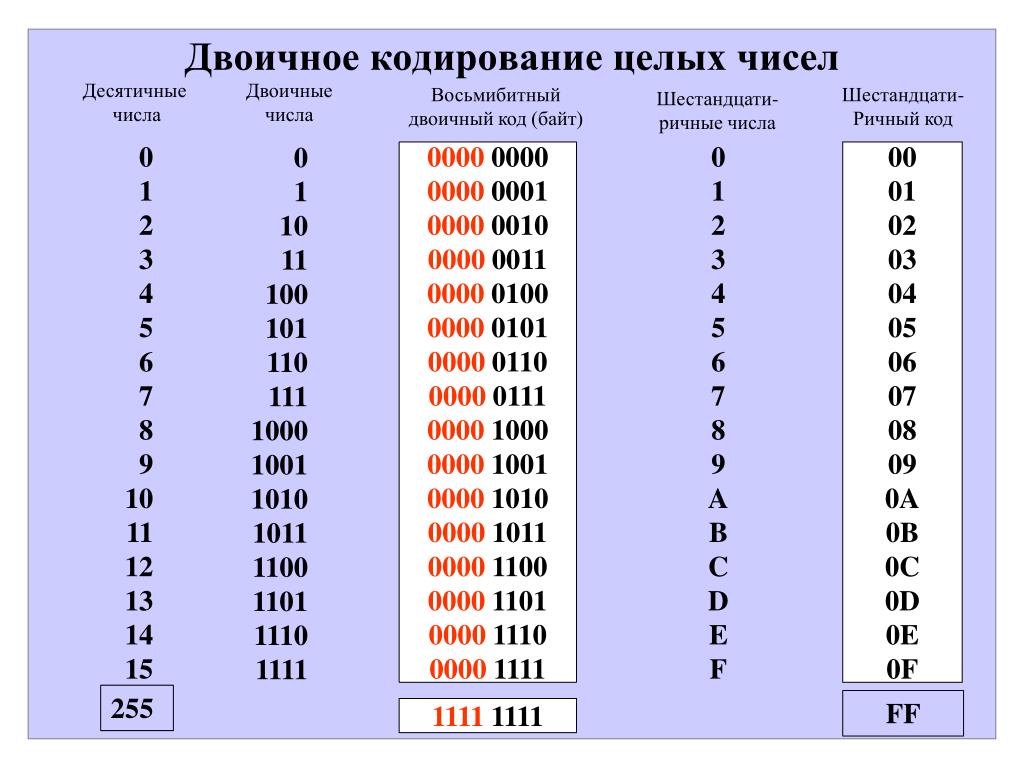 То есть для хранения знака числа можно использовать сколько угодно старших бит. При этом значение кода совершенно не изменяется.

Использование для представления знака числа двух бит предоставляет интересную возможность контролировать переполнения при выполнении арифметических операций. Рассмотрим несколько примеров.

1) Просуммируем числа 12 и 5

В этом примере видно, что в результате суммирования получается правильный результат. Это можно проконтролировать по флагу переноса C, который совпадает со знаком результата (действует эффект распространения знака).

2) Просуммируем два отрицательных числа -12 и -5

В этом примере флаг переноса C тоже совпадает со знаком результата, то есть переполнения не произошло и в этом случае

3) Просуммируем положительное и отрицательное число -12 и +5

В этом примере при суммировании положительного и отрицательного числа автоматически получается правильный знак результата. В данном случае знак результата отрицательный.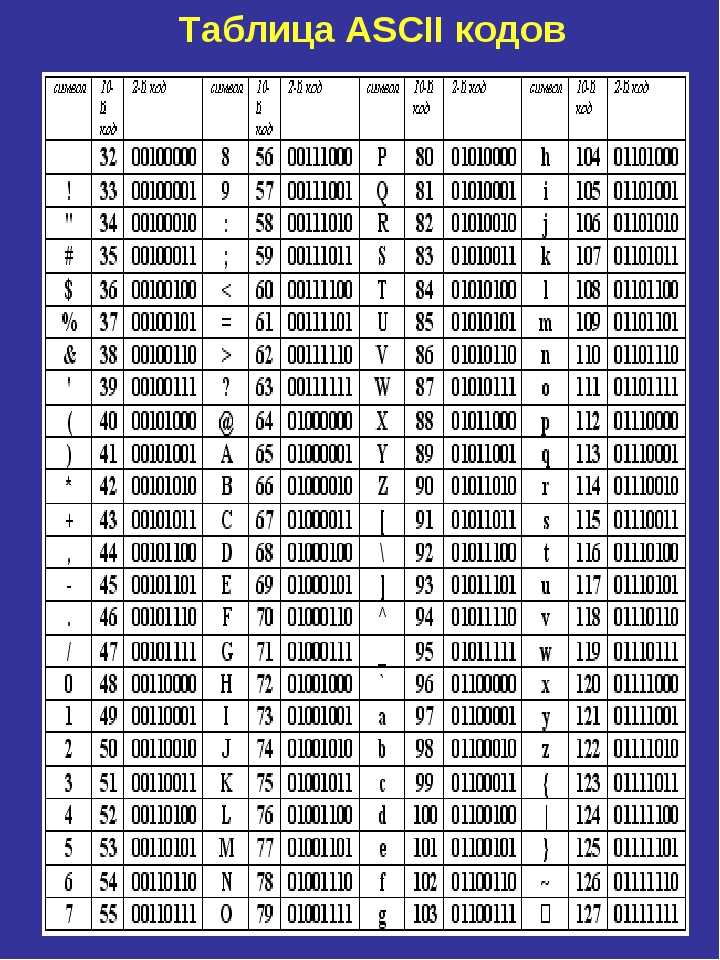 Флаг переноса совпадает со знаком результата, поэтому переполнения не было (мы можем убедиться в этом непосредственными вычислениями на бумаге или на калькуляторе).

4) Просуммируем положительное и отрицательное число +12 и -5

В данном примере знак результата положительный. Флаг переноса совпадает со знаком результата, поэтому переполнения не было и в этом случае.

5)Просуммируем числа 100 и 31

В этом примере видно, что в результате суммирования произошло переполнение восьмибитовой переменной, т.к. в результате операции над положительными числами получился отрицательный результат. Однако если рассмотреть флаг переноса, то он не совпадает со знаком результата. Эта ситуации является признаком переполнения результата и легко обнаруживается при помощи операции «исключающее ИЛИ» над старшим битом результата и флагом переноса C. Большинство процессоров осуществляют эту операцию аппаратно и помещают результат во флаг переполнения OV.

В этом примере результате операции над отрицательными числами в результате суммирования произошло переполнение восьмибитовой переменной, т.

к. получился положительный результат. И в этом случае если рассмотреть флаг переноса C, то он не совпадает со знаком результата. Отличие от предыдущего случая только в комбинации этих бит. В примере 5 говорят о переполнении результата (комбинация 01), а в примере 6 об антипереполнении результата (комбинация 10).

Представление дробных чисел в двоичном коде с фиксированной запятой.

Кроме целых чисел часто требуется работать с дробными числами. Следующий вид двоичных кодов, который мы рассмотрим — это дробные коды. Как и в случае целых чисел, дробные числа могут быть беззнаковые и знаковые. Для записи знаковых чисел могут быть использованы прямые, обратные и дополнительные коды. Принцип их построения точно такой же, как и в случае целых чисел.

Рассмотрим, как можно записать дробное число. До сих пор мы предполагали, что двоичная запятая находится правее самого младшего разряда. Но кто сказал, что она должна всегда находиться в этом месте? Мы можем договориться, что запятая находится слева от самого старшего разряда, и тогда в такой переменной можно будет записывать только дробные числа:

Или договоримся, что она находится точно посередине переменной, и тогда мы сможем записывать смешанные числа:

Остальные случаи рассматривать не будем.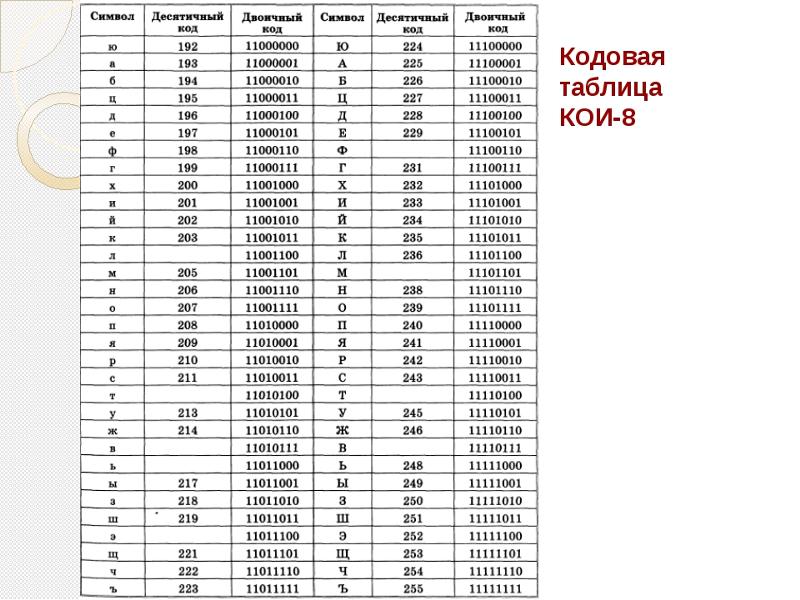 Они строятся точно так же как и для целых чисел.

Представление чисел в двоичном коде с плавающей запятой.

Часто приходится обрабатывать очень большие числа (например, расстояние между звЈздами) или наоборот очень маленькие числа (например, размеры атомов или электронов). При таких вычислениях пришлось бы использовать числа с очень большой разрядностью. В то же время нам не нужно знать расстояние между звЈздами с точностью до миллиметра. Для вычислений с такими величинами числа с фиксированной запятой неэффективны.

В десятичной арифметике для записи таких чисел используется алгебраическая форма. При этом число записывается в виде мантиссы, умноженной на 10 в степени, отображающей порядок числа, Например:

0,2*105; 0,16*10-38

Для записи двоичных чисел тоже используется такая форма записи. Эта форма записи называется запись числа с плавающей точкой. Напомним, что мантисса не может быть больше единицы и после запятой в мантиссе не может записываться ноль.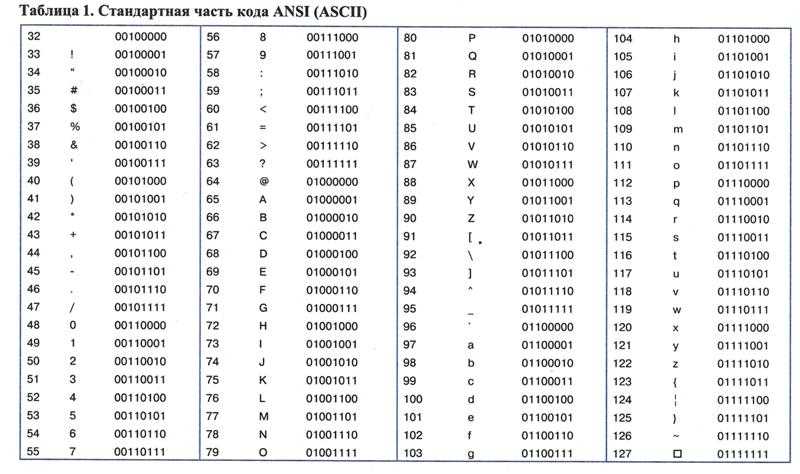

А теперь рассмотрим промышленные стандарты, используемые для представления чисел в компьютерах. Существует стандарт IEEE 754 для представления чисел с одинарной точностью (float) и с двойной точностью (double). Для записи числа в формате с плавающей запятой одинарной точности требуется тридцатидвухбитовое слово. Для записи чисел с двойной точностью требуется шестидесятичетырЈхбитовое слово. Чаще всего числа хранятся в нескольких соседних ячейках памяти процессора. Форматы числа в формате с плавающей запятой одинарной точности и числа в формате с плавающей запятой удвоенной точности приведены на рисунке

На рисунке буквой S обозначен знак числа, 0 — это положительное число, 1 — отрицательное число. e обозначает смещЈнный порядок числа. Смещение требуется, чтобы не вводить в число еще один знак. СмещЈнный порядок всегда положительное число. Для одинарной точности для порядка выделено восемь бит. Для смещЈнного порядка двойной точности отводится 11 бит. Для одинарной точности смещение принято 127, а для двойной точности — 1023. В десятичной мантиссе после запятой могут присутствовать цифры 1:9, а в двоичной — только 1. Поэтому для хранения единицы после двоичной запятой не выделяется отдельный бит в числе с плавающей запятой. Единица подразумевается, как и двоичная запятая. Кроме того, в формате чисел с плавающей запятой принято, что мантисса всегда больше 1. То есть диапазон значений мантиссы лежит в диапазоне от 1 до 2.

Рассмотрим несколько примеров:

1) Определить число с плавающей запятой, лежащее в четырЈх соседних байтах:

11000001 01001000 00000000 00000000

— Знаковый бит, равный 1 показывает, что число отрицательное.

— Экспонента 10000010 в десятичном виде соответствует числу 130. Вычтя число 127 из 130, получим число 3.

— Теперь запишем мантиссу: 1,100 1000 0000 0000 0000 0000

— И, наконец, определим десятичное число: 1100,1b = 12,5d

2) Определить число с плавающей запятой, лежащее в четырЈх соседних байтах:

11000011 00110100 00000000 00000000

— Знаковый бит, равный 1 показывает, что число отрицательное.

— Экспонента 10000110 в десятичном виде соответствует числу 134. Вычтя число 127 из 134, получим число 7.

— Теперь запишем мантиссу: 1,011 0100 0000 0000 0000 0000

— И, наконец, определим десятичное число: 10110100b=180d

Для того чтобы записать ноль, достаточно записать в смещенный порядок число 00000000b. Значение мантиссы при этом не имеет значения. Число, в котором все байты равны 0, тоже попадает в этот диапазон значений.

Бесконечность соответствует смещенному порядку 11111111b и мантиссе, равной 1,0. При этом существует минус бесконечность и плюс бесконечность (переполнение и антипереполнение), которые часто отображаются на экран монитора как +INF и -INF.

Все остальные комбинации битов (в том числе и все единицы) воспринимаются как не числа и отображаются на экран: NaN.

Запись десятичных чисел.

Иногда бывает удобно хранить числа в памяти процессора в десятичном виде (Например, для вывода на экран дисплея). Для записи таких чисел используются двоично-десятичные коды.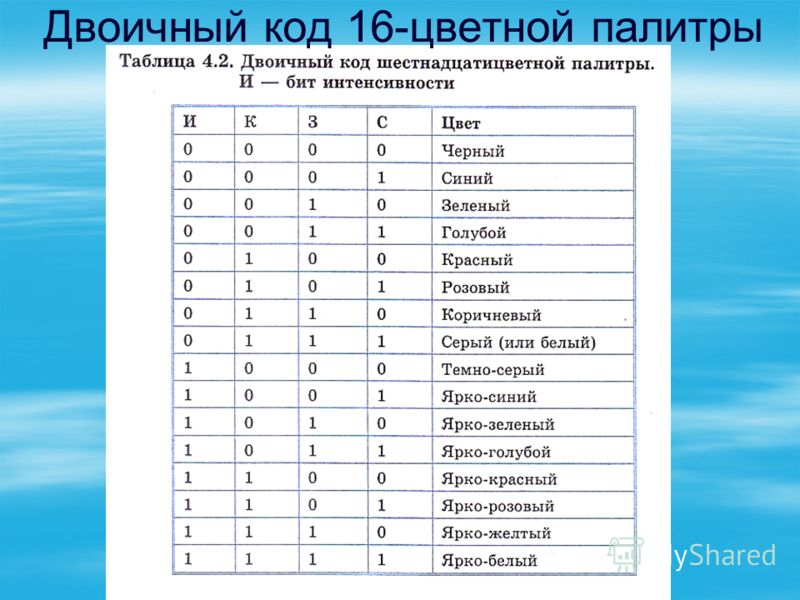 Для записи одного десятичного разряда используется четыре двоичных бита. Эти четыре бита называются тетрадой. Иногда встречается название, пришедшее из англоязычной литературы: нибл. При помощи четырех бит можно закодировать шестнадцать цифр. Лишние комбинации в двоично-десятичном коде являются запрещенными. Таблица соответствия двоично-десятичного кода и десятичных цифр приведена ниже:

Остальные комбинации двоичного кода в тетраде являются запрещенными. Запишем пример двоично-десятичного кода:

1258 = 0001 0010 0101 1000

589 = 0000 0101 1000 1001

Достаточно часто в памяти процессора для хранения одной десятичной цифры выделяется одна ячейка памяти (восьми, шестнадцати или тридцатидвухразрядная). Это делается для повышения скорости работы программы. Для того, чтобы отличить такой способ записи двоично-десятичного числа от стандартного, способ записи десятичного числа, как это показано в примере, называется упакованной формой двоично-десятичного числа.

Суммирование двоично-десятичных чисел.

Суммирование двоично-десяичных чисел можно производить по правилам обычной двоичной арифметики, а затем производить двоично-десятичную коррекцию. Двоично-десятичная коррекция заключается в проверке каждой тетрады на допустимые коды. Если в какой либо тетраде обнаруживается запрещенная комбинация , то это говорит о переполнении. В этом случае необходимо произвести двоично-десятичную коррекцию. Двоично-десятичная коррекция заключается в дополнительном суммировании числа шесть (число запрещенных комбинаций) с тетрадой, в которой произошло переполнение или произошЈл перенос в старшую тетраду. ПриведЈм два примера:

Запись текстов в памяти процессора.

Все символы и буквы могут быть закодированы при помощи восьми двоичных символов. Наиболее распространенными таблицами являются таблицы ASCII с национальными расширениями, применяющиеся в DOS (и которые можно использовать для записи текстов в микропроцессорах), и таблицы ANSI, применяющиеся в WINDOWS. В таблицах ASCII и ANSI первые 128 символов совпадают. В этой части таблицы содержатся символы цифр, знаков препинания, латинские буквы верхнего и нижнего регистров и управляющие символы. Национальные расширения символьных таблиц и символы псевдографики содержатся в последних 128 кодах этих таблиц, поэтому русские тексты в операционных системах DOS и WINDOWS не совпадают.

---

[Назад] [Содержание] [Вперёд]

Двоичное кодирование (8 класс) Информатика и ИКТ

В общем случае, чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.

Алфавит — набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита — это количество входящих в него символов (знаков).

Алфавит, содержащий два символа, называется двоичным алфавитом (см. рис. ниже). Представление информации с помощью двоичного алфавита называют двоичным кодированием. Закодировав таким способом информацию, мы получим её двоичный код.

Рассмотрим в качестве символов двоичного алфавита цифры 0 и 1.

Покажем, что любой алфавит можно заменить двоичным алфавитом. Прежде всего, присвоим каждому символу рассматриваемого алфавита порядковый номер. Номер представим с помощью двоичного алфавита. Полученный двоичный код будем считать кодом исходного символа.

Если мощность исходного алфавита больше двух, то для кодирования символа этого алфавита потребуется не один, а несколько двоичных символов. Другими словами, порядковому номеру каждого символа исходного алфавита будет поставлена в соответствие цепочка (последовательность) из нескольких двоичных символов.

Правило двоичного кодирования символов алфавита мощности больше двух представим схемой на рисунке ниже.

Двоичные символы (0, 1) здесь берутся в заданном алфавитном порядке и размещаются слева направо. Двоичные коды (цепочки символов) читаются сверху вниз. Все цепочки из двух двоичных символов (кодовые комбинации) позволяют представить четыре различных символа произвольного алфавита:

Цепочки из трёх двоичных символов получаются дополнением двузначных двоичных кодов справа символом 0 или 1.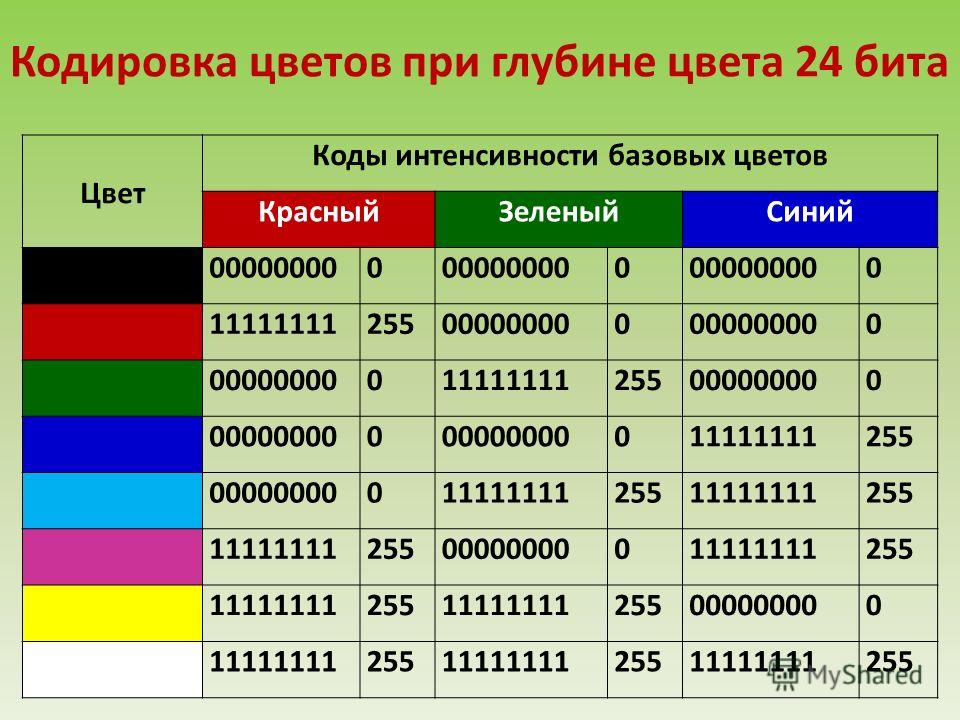 В итоге трёхзначных двоичных кодовых комбинаций получается 8 – вдвое больше, чем двузначных:

Соответственно, четырёхзначный двоичный код позволяет получить 16 кодовых комбинаций, пятизначный — 32, шестизначный — 64 и т. д.

Длину двоичной цепочки — количество символов в двоичном коде – называют разрядностью двоичного кода.

Обратите внимание, что 2= 2¹, 4 = 2², 8 = 2³, 16 = 2⁴, 32 = 2⁵ и т. д.

Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода — буквой i, то выявленная закономерность в общем виде будет записана так: N=2ⁱ.

Задача. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. Какой разрядности потребуется двоичный код, если алфавит, используемый племенем Мульти, содержит 16 символов? Выпишите все кодовые комбинации.

Решение. Так как алфавит племени Мульти состоит из 16 символов, то и кодовых комбинаций им нужно 16.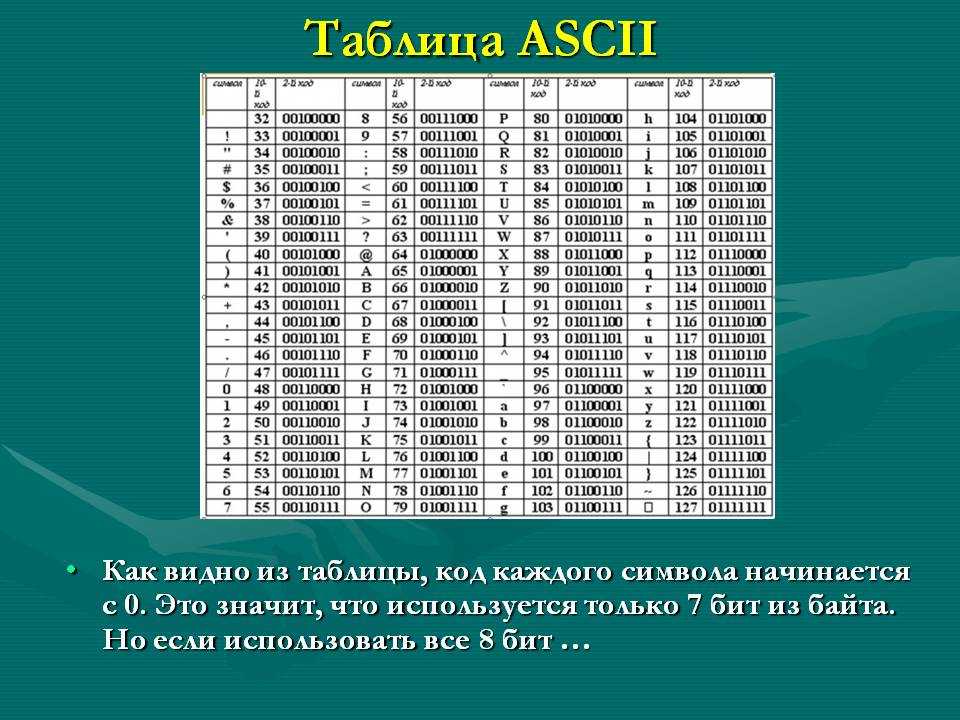 В этом случае длина (разрядность) двоичного кода определяется из соотношения: 16 = 2ⁱ. Отсюда i=4.

Чтобы выписать все кодовые комбинации из четырёх 0 и 1, воспользуемся схемой на рисунке выше: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.

Самое главное:

• Чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка.
• Алфавит языка — набор отличных друг от друга символов, используемых для представления информации. Мощность алфавита — это количество входящих в него символов.
• Алфавит, содержащий два символа, называется двоичным алфавитом. Представление информации с помощью двоичного алфавита называют двоичным кодированием.

Вопросы и задания:

1. Что такое алфавит языка?
2. Что такое мощность алфавита? Может ли алфавит состоять из одного символа?
3. Какие символы могут входить в двоичный алфавит?
4. Сколько существует различных последовательностей из символов «плюс» и «минус» длиной ровно пять символов?
5. Как связаны мощность алфавита и разрядность двоичного кода, достаточного для кодирования всех символов этого алфавита?
6. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. 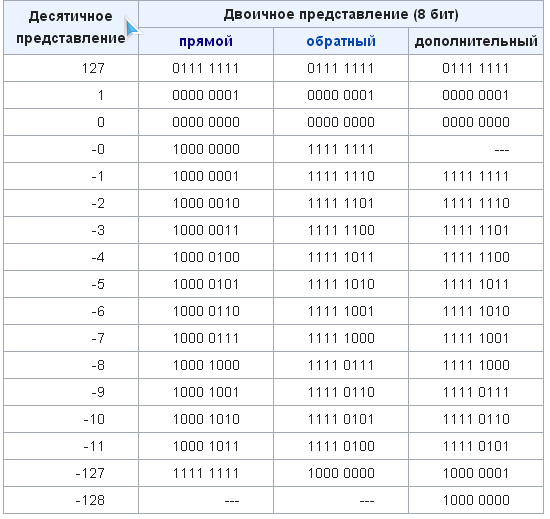Достаточно ли пятиразрядного двоичного кода, если алфавит, используемый племенем Мульти, содержит 26 символов?
   (Решение:
   С помощью пятиразрядного двоичного кода можно закодировать 2⁵ = 32 различных символов алфавита. Поэтому для кодирования 26 символов алфавита достаточно пятиразрядного кода.)
7. От разведчика была получена следующая шифрованная радиограмма, переданная с использованием азбуки Морзе: — • • — • • — — • • — — — — •
   При передаче радиограммы было потеряно разбиение на буквы, но известно, что в радиограмме использовались только следующие буквы:
   Определите текст радиограммы.
   (Решение:
   НАИГАЧ)

Содержание

Понравилось?

Нравится

Твитнуть



Диапазон двоичных чисел

Узнайте, как диапазон значений, которые может представлять двоичное число, зависит от количества доступных битов.

На этом шаге вы узнаете, как диапазон значений, которые может представлять двоичное число, зависит от количества доступных битов.

При использовании десятеричных чисел каждый раз, когда мы увеличиваем количество доступных цифр, диапазон значений умножается на 10, потому что десятеричные числа имеют основание 10. Например, когда в десятеричных числах доступна одна цифра, диапазон значений равен 0— 9, поэтому имеется 10 различных значений.

При увеличении количества цифр на единицу диапазон теперь умножается на 10 от 0–9 (10 значений) до 0–99 (100 значений). Добавление третьей цифры снова умножает диапазон на 10 до 0–999 (1000 значений).

Увеличение диапазона двоичных чисел

Поскольку двоичное число находится в системе счисления 2, каждая дополнительная двоичная цифра (бит) будет умножать диапазон чисел на 2.

Например, диапазон значений 5-битного двоичного числа — от 0 до 31, то есть 32 различных значения. Наименьшее значение представлено пятью нулями:

16	8	4	2	1
0	0	0	0	0

, а наибольшее число представлено пятью единицами:

16	8	4	2	1
1	1	1	1	1

что в денарах равно 16 + 8 + 4 + 2 + 1 = 31

Если число битов увеличивается на 1, с пяти до шести, диапазон удваивается с 0–31 (32 значения) до 0–63 (64 значения):

32	16	8	4	2	1
1	1	1	1	1	1

что в денарах равно 32 + 16 + 8 + 4 + 2 + 1 = 63

Как вы думаете, каким будет диапазон для 8-битного числа?

128	64	32	16	8	4	2	1

Максимальное значение, которое может быть представлено 8-битным числом, равно 255, поэтому диапазон будет от 0 до 255 (256 значений).

128	64	32	16	8	4	2	1
1	1	1	1	1	1	1	1

Количество значений можно быстро вычислить, вычислив 2 ⁿ , где n — количество доступных битов, например 2 ⁸ = 256 значений. Диапазон значений от 0 до 2 ⁿ – 1, например от 0 до 2 ⁸ – 1 = 0–255.

Почему важен диапазон?

Существуют определенные правила, которым следуют компьютеры, основанные на количестве битов, доступных для двоичного числа. Это ключ к тому, как компьютеры взаимодействуют и интерпретируют двоичные числа для представления вещей в цифровом виде; от текста к изображениям к звуку.

Наборы символов

Американский стандартный код для обмена информацией (ASCII) был разработан для создания международного стандарта кодирования латинского алфавита и был принят в 1963, чтобы информация могла интерпретироваться между компьютерами.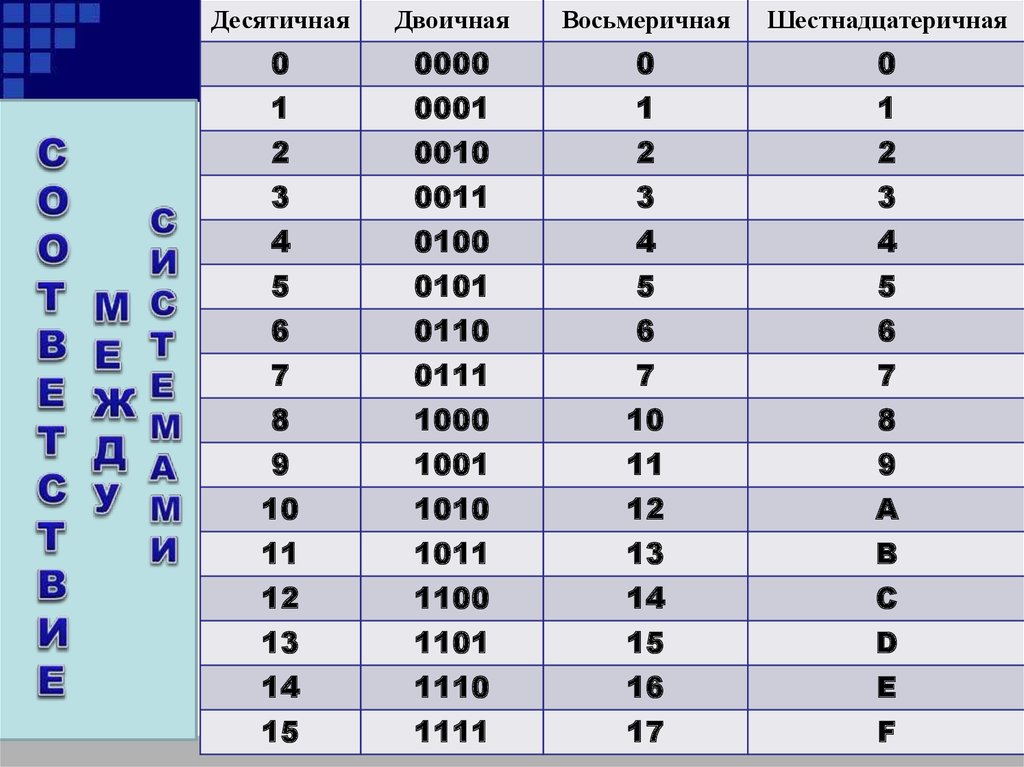

Набор символов ASCII использует 7 бит, что позволяет использовать 128 различных символов. Они использовались для представления строчных и прописных букв английского алфавита, цифр, символов и некоторых команд.

Переход на 8-битную вычислительную технологию означал, что нужно было использовать один дополнительный бит. С этой дополнительной цифрой Extended ASCII кодирует до 256 символов, что полезно для большинства европейских языков.

Unicode был разработан для решения проблемы представления символов из языков по всему миру. Метод кодирования Unicode UTF-8 использует от 8 до 32 бит на символ. Это позволяет представить более 1 миллиона символов, охватывающих символы, которые вы найдете во многих языках.

Цвета RGB

Другим примером является система RGB (красный, синий, зеленый), которая часто используется для компьютерных экранов и цветного освещения. Каждый отдельный цвет представлен 8 битами и измеряется по шкале от 0 («ни одного из этих цветов») до 255 («наиболее интенсивный возможный цвет»). Это означает, что существует 256 оттенков каждого цвета света (256 красных, 256 синих и 256 зеленых).

Таким образом можно представить очень большое разнообразие цветов. Поскольку красный, зеленый и синий могут отображаться с разной интенсивностью, эти цвета при смешивании могут создавать более 16 миллионов уникальных оттенков:

256 красных × 256 зеленых × 256 синих = 16777216 оттенков цвета

Количество цветов напрямую связано с количеством доступных битов.

Какой диапазон?

Попробуйте определить диапазон значений для следующего количества битов и напишите свои ответы в комментариях:

• 10
• 32
• 64

На следующем шаге вы рассмотрите двоичные сдвиги и то, как сдвиг двоичного числа влево или вправо влияет на значение.

Как читать и записывать двоичный код

Перейти к содержимому

Статья

Обновлено 13 декабря 2022 г. | Время чтения ~ 3 минуты

Если вы еще не владеете двоичным кодом, вы попали на нужную статью. Не волнуйся; это проще, чем вы думаете. Двоичный код настолько прост, насколько это возможно. Он либо включен, либо выключен. 1с и 0с. IP-адреса и подсети состоят из 32 бит каждый, разделенных на четыре 8-битных «октета».

Что такое двоичный код?

Двоичный код — это тип кода, используемый компьютерами, в котором два числа, 0 и 1, представляют два возможных состояния: включено и выключено. Давайте разберем, что это на самом деле означает, на примере. Наименьшая единица кода, которую может обработать компьютер, называется «бит». Вот образец из 4 фрагментов двоичного кода, по 8 бит в каждом фрагменте, которые мы называем «октетами». Хотя вы еще этого не знаете, это отправная точка для двоичного кода, который мы можем видеть за IP-адресом: 

Используя 8 битов в каждом октете, мы можем создать любое число от 0 до 255 (256 значений). Теперь давайте посмотрим на ту же последовательность, но с большими значениями. Если мы внимательнее посмотрим на один октет, то увидим, как каждый бит представляет степени числа 2, например:

Здесь двоичный код немного сбивает с толку большинство людей, прежде всего потому, что двоичный код для нас — это представление числовых значений — и нам, людям, может быть трудно это понять… но не компьютеру. 1. 92, что дает нам 4 действительных состояния.

Как написать что-то в двоичном коде?

Этот мыслительный процесс легче осмыслить, если мы включаем биты справа налево в последовательном порядке. Маски подсети в полной мере используют эту методологию и являются их целью. Чтобы сгенерировать числовые значения для этого октета, нам не нужно беспокоиться ни о чем, кроме простого сложения. Мы знаем, что с помощью 8 бит мы можем генерировать числа от 0 до 255.

Как вы можете видеть на графиках выше и ниже, каждый бит представлен числовым значением: 128, 64, 32 и так далее. Если мы сложим их все вместе, перевернув все биты в 1, мы получим значение 255 с общим количеством 256 значений, если мы включим 0 (что мы и делаем). Чтобы получить любое значение в диапазоне от 0 до 255, мы просто «включаем» любые биты, которые в сумме дают то, что нам нужно. Посмотрим, как выглядит число 192:

128 + 64 = 192. Просто. Глядя на IP-адрес 192.168.44.13 в двоичном виде, теперь он выглядит так:

128 + 64 = 192

128 + 32 + 8 = 168

32 + 8 + 4 = 44

8 + 4 + 1 = 13

Попробуйте .